ЛЕКЦИЯ 1

Понятие величины – основное понятие, с которым встречаются в естественнонаучной и технической областях.

Под величиной понимают всё то, что может быть измерено и выражено числом.

Среди величин различают постоянные и переменные.

Действительные числа, числовая ось.

Целые положительные числа 1,2,3… называются натуральными. Множество натуральных чисел обозначают  N.

Рациональные числа – все целые, нуль и дробные числа.

Каждое рациональное число можно представить в виде , где p – целое число, q – натуральное число.

Рациональное число можно представить также в виде периодической десятичной дроби. Иррациональные числа – бесконечная непериодическая дробь.

Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают R.

Каждое действительное число изображается точкой числовой оси и, обратно, каждой точке числовой оси соответствует единственное действительное число.

1. Интервалом называется множество действительных чисел х, удовлетворяющих неравенству a < x < b, где a, b – действительные числа. Обозначается (a, b).

2. Отрезком (сегментом) называется множество действительных чисел, удовлетворяющих неравенству a ≤ x ≤ b. Обозначается [a, b].

3. Интервал длины 2ε, с центром в точке х₀ называют окрестностью точки х₀ х₀ – ε < х < х₀ + ε .

4. Интервалы могут быть бесконечные: (а, + ∞), (- ∞, а), (-∞, +∞), [a, + ∞),

(- ∞, a].

Абсолютная величина (модуль) действительного числа.

Определение. Абсолютной величиной (или модулем) действительного числа а называется неотрицательное действительное число, удовлетворяющее условиям:

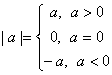
Из определения следует, что а ≤ │а│ для любого а.

Свойства абсолютных величин.

1. Абсолютная величина алгебраической суммы нескольких действительных чисел не больше суммы абсолютных величин слагаемых

.

2. Абсолютная величина разности не меньше абсолютных величин уменьшаемого и вычитаемого

>.

3. Абсолютная величина произведения равна произведению абсолютных величин

.

4. Абсолютная величина частного равна частному абсолютных величин  делимого и делителя

.

ФУНКЦИИ

Определение: Переменная у называется функцией переменной  х, если:

1)   задано множество D значений х;

2) задан закон, по которому любому значению хD соответствует одно или несколько значений у, где х – независимая переменная (аргумент),                у – зависимая переменная (функция).

Множество всех значений, которые может принимать х, называется областью определения этой функции.

Некоторые характеристики функций.

Частное значение функции – это значение при конкретном значении аргумента, пусть у=f(x), при х = х₀ получаем частное значение у₀ = f(x₀).

Определение 1. Значение переменной х, при котором функция обращается в нуль, то есть f(x) = 0 называется нулём (или корнем) функции.

Определение 2. Функция у=f(x) называется чётной, если при изменении знака у аргумента значение функции не меняется: f(-x)=f(x). График чётной функции симметричен относительно оси ОY.

Определение 3. Функция у=f(x) называется нечётной, если при изменении знака у аргумента изменяется только знак значения функции: f(-x) = - f(x). График нечётной функции симметричен относительно начала координат.

Определение 4. Функция у=f(x) называется периодической, если существует такое постоянное число Т ≠ 0, что f(x+Т) = f(x). Наименьшее положительное число Т называют периодом.

Определение 5. Элементарной функцией называется функция, которую можно задать одной формулой, составленной из простейших функций и постоянных с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции. Функции, заданные различными аналитическими выражениями, называются неэлементарными.

Определение 6. Графиком функции у=f(x) называется геометрическое место точек плоскости ОХY, для каждой из которых аргумент х является абсциссой, а соответствующее значение функции у – ординатой.

Преобразование графиков.

Пусть известен график функции у=f(x). Зная правила преобразования графиков, можно построить графики функции у=f(x-a), y=f(x)+b, y=f(Ax), y=Bf(x),  y=-f(x), y=f(-x).

1. График функции у=f(x-a) получается из исходного графика путем параллельного переноса вдоль оси ОХ на а единиц вправо, если а>0 или влево, если а<0.

2. График функции  y=f(x)+b получается из исходного графика путем параллельного переноса вдоль оси ОУ на b единиц вверх, если b>0 или вниз, если b<0.

3. График функции y=f(Ax) А>0, А≠1 получается из исходного графика путем сжатия в А раз вдоль оси ОХ, если А>1, или растяжения в  раз вдоль оси ОХ, если 0<А<1.

Сжатие вдоль оси ОХ – это уменьшение абсцисс точек исходного графика без изменения ординат. Растяжение вдоль оси ОХ – это увеличение абсцисс точек исходного графика без изменения ординат.

4. График функции y=Bf(x), В>0, В≠1 получается из исходного графика путем сжатия в  раз вдоль оси ОУ, если 0<В<1, или растяжения в В раз по оси ОY, если В>1.

Сжатие вдоль оси ОY – это уменьшение ординат точек исходного графика без изменения абсцисс. Растяжение вдоль оси ОY– это увеличение ординат точек исходного графика без изменения абсцисс.

5. График функции у=f(-x) получается из исходного графика путем симметричного отображения относительно оси ОY

6. График функции у=-f(x) получается из исходного графика путем симметричного отображения относительно оси ОХ.

ЛЕКЦИЯ 2

Основные элементарные функции.

Рассмотрим свойства и графики основных простейших функций.

1. Линейная функция. Линейной функцией называется такая функция, которая задаётся формулой , где k и b– действительные числа. Если, в частности, k=0, то получаем постоянную функцию ; если b=0, то получаем прямую пропорциональность .

Свойства линейной функции  при k≠0, b≠0:

1) Область определения функции – множество всех действительных чисел.

2) Функция ни четна, ни нечетна.

3) При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой.

Теорема. Графиком линейной функции является прямая.

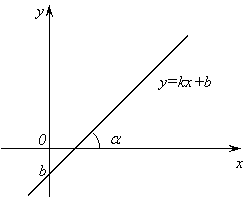
Рис. 1.

Число k называется угловым коэффициентом прямой, оно равно тангенсу угла  между прямой и положительным лучом оси х, то есть .

2. Обратная пропорциональность. Обратной пропорциональностью называют функцию, заданную формулой , где k≠0. Число k называют коэффициентом обратной пропорциональности.

1) Область определения – множество всех действительных чисел, кроме нуля.

2)  - нечётная функция (поскольку .

3) Если k>0, то функция  убывает на промежутке (0;+∞) и на промежутке (-∞;0). Если k<0, то функция  возрастает на промежутке (-∞;0) и на промежутке (0;+∞).

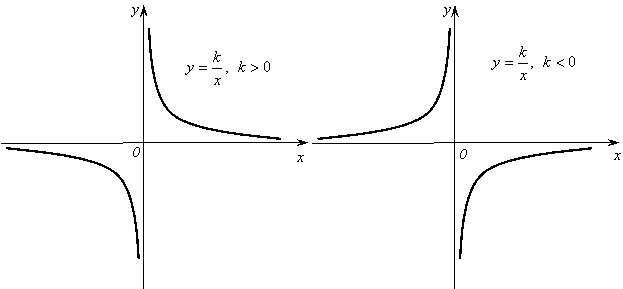
Рис. 2.

  График обратной пропорциональности  называют гиперболой.

3. Функция .

1) Область определения – вся числовая прямая.

2) - чётная функция .

3) На промежутке [0;+∞) функция возрастает.

4) На промежутке (-∞;0] функция убывает.

Графиком функции  является парабола. Этот график изображен на рисунке 3.

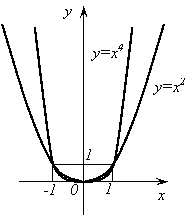
Рис. 3.

4. Функция .

1) Область определения функции – вся числовая прямая.

2)  - нечётная функция .

3) Функция  возрастает на всей числовой прямой.

График функции изображен на рисунке 4. Он называется кубической параболой.

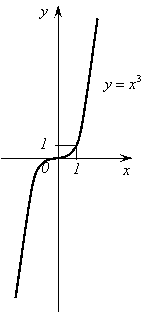
Рис. 4.

5. Функция  .

1) Область определения – луч [0;+∞). Это следует из того, что выражение определено лишь при х≥0.

2) Область значений - [0;+∞).

3) Функция ни четна, ни нечётна.

4) Функция возрастает на луче [0;+∞).

График функции изображен на рисунке 5.

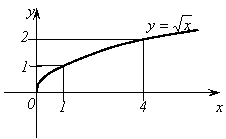
Рис. 5.

6. Функция - целая часть числа. Если <1, то ; если < 2, то ; если < 0, то  и т.д. График функции  изображен на рисунке 6.

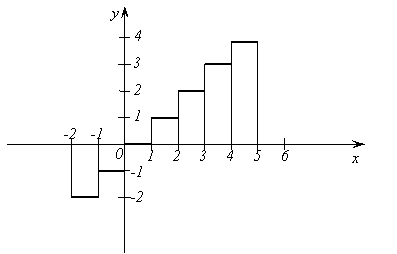
Рис. 6.

7. Функция  - дробная часть числа. Построим график функции . Заметим, что , поэтому достаточно сначала построить ветвь графика на любом промежутке длиной 1, например на . Если <1, то , а потому.

На рисунке 7 изображен график функции  на промежутке , а на рисунке 8 изображен график функции  на всей числовой оси.

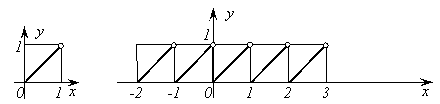                   Рис. 7.                           Рис. 8.

8. Показательная функция. Показательная функция задается формулой , где >0 и .

1) Область определения функции – вся числовая прямая.

2) Область значений функции – промежуток .

3) Функция не является ни четной, ни нечетной. Это следует из того, что  и  .

4) Функция возрастает на всей числовой прямой.

График показательной функции изображен на рисунке 9.

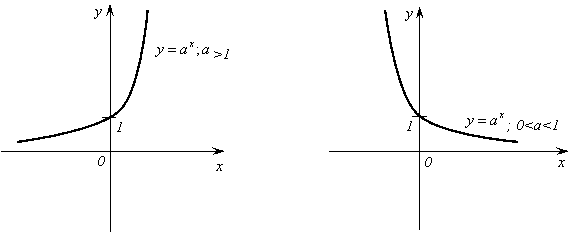
Рис. 9.

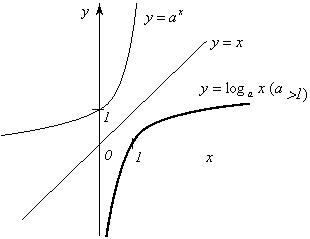
9. Логарифмическая функция. Логарифмическая функция  является обратной к показательной функции  и обладает следующими свойствами:

1) Область определения – .

2) Область значений – .

3) Функция ни четная, ни нечетная.

4) Функция возрастает на промежутке  при >1, убывает на  при < <1.

График функции   изображен на рисунке 10.

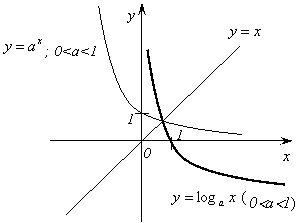Рис. 10.

10. Функция .

1) Область определения – множество всех действительных чисел.

2) Область значений – отрезок .

3) Функция периодическая; основной период равен .

4) Функция нечетная.

Функция возрастает на промежутках  и убывает на промежутках , .

График функции изображен на рисунке  11.

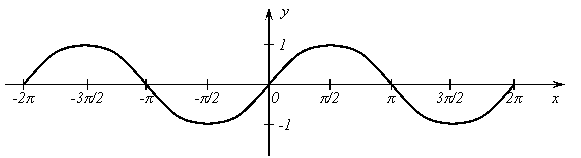Рис. 11.

11. Функция .

1) Область определения – множество всех действительных чисел.

2) Область значений – отрезок .

3) Функция периодическая; основной период равен .

4) Функция четная.

5) Функция убывает на промежутках  и возрастает на промежутках , .

График функции изображен на рисунке 12.

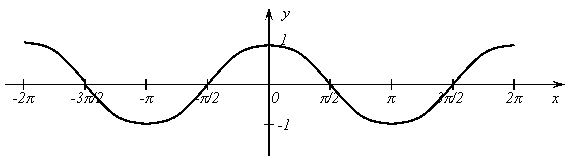Рис. 12.

12. Функция .

1) Область определения: .

2) Область значений – вся числовая прямая.

3) - основной период функции.

4) Функция нечетная.

5) Функция возрастает на промежутках , .

График функции изображен на рисунке 13.

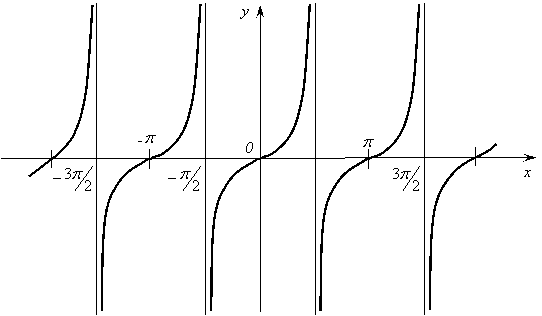
Рис. 13.

13. Функция .

1) Область определения: .

2) Область значений – вся числовая прямая.

3) Функция периодическая с основным периодом .

4) Функция  нечетная.

5) Функция убывает на промежутках , .

График функции изображен на рисунке 14.

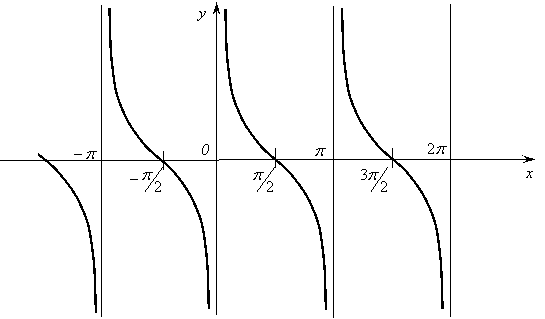
Рис. 14.

14. Функция является обратной к функции .

1) Область определения – отрезок .

2) Область значений – отрезок .

3) Функция нечетная: .

4) Функция возрастающая.

Из сказанного выше следует, что записи и , , эквивалентны. Подставив в равенство  вместо  его выражение, то есть , получим . Следовательно, для любого  из  имеем:

,  .

Последние два соотношения позволяют истолковать, где , так: - это число, взятое в пределах от  до  и такое, что его синус равен .

График функции изображен на рисунке 15.

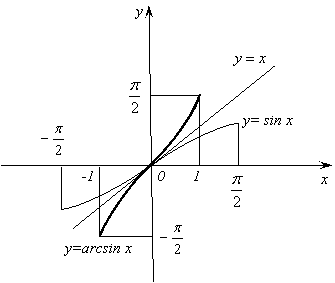
Рис. 15.

15. Функция является обратной к функции .

1) Область определения – отрезок .

2) Область значений – отрезок .

3) Функция не является ни четной, ни нечетной.

4) Функция убывающая.

Из сказанного выше следует, что записи и , , эквивалентны. Подставив в равенство  вместо  выражение , получим . Следовательно, для любого  из  имеем:

,  .

Последние два соотношения позволяют истолковать , где , так: - это число, взятое в пределах от  до  и такое, что его косинус равен .

Отметим, что имеет место следующее тождество:

.

В его справедливости можно убедиться с помощью графика функции , изображенного на рисунке 16.

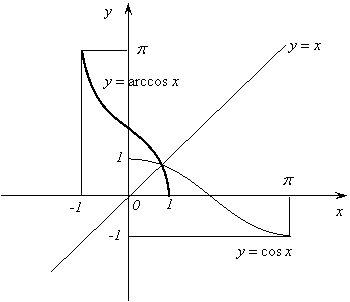
Рис. 16.

16. Функция является обратной к функции .

1) Область определения – множество всех действительных чисел.

2) Область значений функции – интервал .

3) Функция нечетная: .

4) Функция возрастающая.

Из сказанного выше следует, что записи и , < < , эквивалентны. Для любого  имеем:

,  < < .

Последние соотношения позволяют истолковать так: - это число, взятое в пределах от  до  (исключая сами значения  и ) и такое, что его тангенс равен .

График функции изображен на рисунке  17.

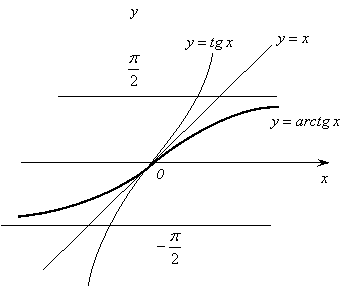
Рис. 17.

17. Функция является обратной к функции .

1) Область определения – множество всех действительных чисел.

2) Область значений функции – интервал .

3) Функция не является ни четной, ни нечетной.

4) Функция убывающая.

Из сказанного выше следует, что записи и , < < , эквивалентны. Для любого  имеем:

,  < < .

Последние соотношения позволяют истолковать так: - это число, взятое в пределах от  до (исключая сами значения  и) и такое, что его котангенс равен .

Имеет место тождество

.

График функции изображен на рисунке 18.

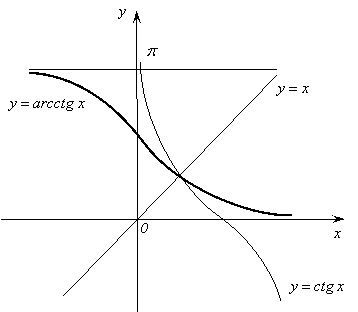
Рис. 18.

Дробно-линейная функция.

Определение: Дробно-линейной функцией называется функция вида:

,

где a, b, c, d – const, c ≠ 0. Эта функция определена всюду, кроме .

Выясним, как выглядит график этой функции. Приведем функцию к виду:

.

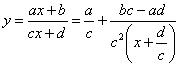Обозначим  .

Тогда получим                                                                                       (1)

Согласно правилам преобразования графиков, график функции (1) может быть построен с помощью следующих действий:

1. построим график функции ;

2.    - сделаем параллельный перенос предыдущего графика вдоль оси ОХ на а₁ единиц влево или вправо;

3.  - сделаем параллельный перенос предыдущего графика вдоль оси ОУ на b₁ единиц вверх или вниз.

Таким образом, графиком дробно-линейной функции является гипербола, центр которой находится в точке О₁ (а₁, b₁).

ЛЕКЦИЯ 3

ТЕОРИЯ     ПРЕДЕЛОВ

Числовые последовательности.

Зададим правило, по которому каждому натуральному числу n будет соответствовать действительное число х_n , то есть мы получим бесконечный ряд чисел х₁, х₂, …, х_n, который называется числовой последовательностью. Числа х₁, х₂,…, х_n,… называют членами последовательности, х_n – общий член последовательности. Например: х_n=2ⁿ.

Предел последовательности.

Определение. Число А называется пределом последовательности

                                              х₁, х₂,.., х_n, .…. ,                                                  (2)

если любая ε – окрестность числа А содержит все члены этой    последовательности, начиная с некоторого номера.

Записывается это так: .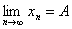

Тот факт, что все члены последовательности (2) с некоторого номера попадают в ε – окрестность числа А, означает, что члены последовательности удовлетворяют неравенству: a-ε<x_n<a+ε или -ε<x_n-a<ε или │x_n-a│< ε. Тогда определение предела последовательности можно сформулировать так.

Определение. Число А называется пределом последовательности (2), если для всякого ε>0 все члены последовательности, начиная с некоторого номера удовлетворяют неравенству:

│x_n-a│< ε                                                              (3)

Геометрически неравенство (3) означает, что расстояние точки x_n до точки А должно быть меньше ε. Предел последовательности может быть конечным, если А – конечное число, или бесконечным, если значения последовательности неограниченно увеличиваются, в этом случае записывают .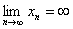

Этот факт на языке ε можно сформулировать так: последовательность x_n имеет своим пределом ∞, если существует такое М, что, начиная с некоторого номера, члены последовательности удовлетворяют неравенству │x_n│> M.

Ограниченные и монотонные последовательности.

Определение 1. Последовательность {x_n} называется ограниченной, если существует такое положительное число М, что для любого nN выполняется неравенство │x_n│≤ М. В противном случае, последовательность называется неограниченной.

Определение 2. Последовательность {x_n} называется возрастающей, если для любого n выполняется неравенство: x_n+1≥x_n. Если же x_n+1>x_n, то последовательность называется строго возрастающей.

Определение 3. Последовательность {x_n} называется убывающей, если для любого n выполняется неравенство: x_n+1≤x_n. Если же x_n+1<x_n, то последовательность называется строго убывающей.

Все эти последовательности называются монотонными последовательностями.

Справедлива теорема Вейерштрасса.

Теорема. Всякая монотонная ограниченная последовательность имеет конечный предел.

ЛЕКЦИЯ 4

Предел функции.

Определение. Число А называется пределом функции у=f(x) при х→х₀, если для каждого положительного числа ε, можно указать такое положительное число δ, что для всех х отличных от х₀, и удовлетворяющих неравенству

│х – х₀│< δ  имеет место неравенство │f(x) - A│< ε.

Рассмотрим два частных случая.

1. Пусть х→ ∞.

Определение. Число А называется пределом функции у=f(x) при х→∞, если каково бы ни было ε>0, можно найти такое число N>0, что для всех х>N, выполняется неравенство │f(x) - A│< ε.

Записывают

2. Пусть х→ - ∞.

Определение. Число А называется пределом функции у=f(x) при х→ -∞, если каково бы ни было ε>0, можно найти такое число М>0, что для всех х<М, выполняется неравенство │f(x) - A│< ε.

Записывают.

Замечания:

1. Следует заметить, что при рассмотрении предела функции у=f(x) при х→х₀, в самой точке х₀ функция может быть не определена.

2. Если функция имеет предел, то этот предел единственный.

Бесконечно большие и бесконечно малые величины.

Определение 1.  Функцию у=f(x) называют бесконечно большой при х→х₀, если .

Нельзя смешивать постоянное очень большое число с бесконечно большой величиной.

Определение 2. Функция, стремящаяся к нулю при х→х₀, называется бесконечно малой при х→х₀, если  .

Определение 3. Функция f(x) называется бесконечно малой при х→х₀, если для любого положительного ε можно найти положительное δ, что для всех х, удовлетворяющих неравенству │х – х₀│< δ, имеет место │f(x)│< ε.

Замечания:

Нельзя смешивать постоянное очень малое число с бесконечно малой величиной.

Между бесконечно малыми и бесконечно большими величинами существует связь, определяемая следующей теоремой.

Теорема. Если f(x) – бесконечно большая величина при х→х₀ , то – бесконечно малая при х→х₀. Если φ(х) – бесконечно малая величина при х→х₀, то  – бесконечно большая при х→х₀.

Ограниченные функции.

Определение. Функция у=f(x) называется ограниченной на данном интервале, если существует такое положительной число М, что для всех х, принадлежащих этому интервалу, выполняется неравенство │f(x)│≤М. В противном случае, функция называется неограниченной.

Определение. Функция называется ограниченной при х→х₀, если в некоторой окрестности точки х₀ эта функция ограниченна.

Замечания:

1. Всякая константа – ограниченная функция.

2. Если функция имеет конечный предел при х→х₀, то она ограниченна.

3. Бесконечно большая величина при х→х₀ – неограниченная функция.

4. Бесконечно малая величина – есть функция ограниченная.

Теоремы о связи функции с ее пределом.

Для дальнейшего изучения теории пределов очень важными являются следующие теоремы.

Теорема (прямая). Если функция у=f(x) при х→х₀  имеет предел равный А, то есть , то f(x) можно представить в виде f(x)=А+α(х), где α(х)→0 при х→х₀.

Теорема (обратная). Если функцию у=f(x) можно представить в виде f(x)=А+α(х), где α(х)→0 при х→х₀, то .

Свойства бесконечно малых и бесконечно больших величин.

1. Алгебраическая сумма двух бесконечно малых функций есть функция бесконечно малая.

Это свойство можно обобщить на случай любого конечного числа слагаемых.

2. Произведение бесконечно малой функции на функцию ограниченную при х→х₀ , есть функция бесконечно малая.

3. Произведение конечного числа бесконечно малых функций есть функция бесконечно малая.

4. Произведение константы на бесконечно малую функцию есть функция бесконечно малая.

5. Частное от деления бесконечно малой функции α(х) на функцию z(x), имеющую предел не равный нулю, есть функция бесконечно малая.

Аналогичными свойствами обладают бесконечно большие величины:

1. Сумма конечного числа бесконечно больших функций есть функция бесконечно большая.

2. Произведение конечного числа бесконечно больших функций есть функция бесконечно большая.

3. Произведение бесконечно большой функции на ограниченную функцию есть функция бесконечно большая.

4. Произведение бесконечно большой функции на константу есть функция бесконечно большая.

5. Частное от деления бесконечно большой функции на функцию z(x), имеющую предел не равный нулю, есть функция бесконечно большая.

Замечание: Разность бесконечно больших величин дает  неопределенность (∞ - ∞).

ЛЕКЦИЯ 5

Основные теоремы о пределах.

Теорема 1. Предел алгебраической суммы конечного числа слагаемых равен алгебраической сумме пределов этих слагаемых, если последние существуют:

.

Доказательство для n=2. Пусть ; , тогда u₁=а₁+α₁, u₂=а₂+α₂,  где α₁→0, α₂→0 при х→х₀, и u₁+u₂=(а₁+а₂)+(α₁+α₂), где а₁+а₂=const, α₁+α₂→0 при х→х₀. По теореме о связи функции с ее пределом будем иметь, что . Теорема доказана.

Теорема 2. Предел произведения конечного числа сомножителей равен произведению пределов этих сомножителей, если последние существуют:

.

Доказательство для n=2. Пусть ; , тогда u₁=а₁+a₁, u₂=а₂+α₂, где α₁→0, α₂→0 при х→х₀, и u₁·u₂=(а₁+а₂)·(α₁+α₂)= а₁а₂+α₁а₂+α₂а₁+α₂α₁, где       а₁а₂=const, α₁а₂→0, α₂а₁→0, α₂α₁→0 при х→х₀. По теореме о связи функции с ее пределом будем иметь, что . Теорема доказана.

Следствие. Постоянный множитель можно выносить за знак предела:

.

Теорема 3. Предел частного двух функций равен частному пределов этих функций при условии, что предел знаменателя не равен нулю:

.

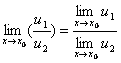Доказательство аналогично доказательству теорем 1 и 2.

Теоремы о пределах функций, связанные с неравенствами.

Теорема 4. Если между соответствующими значениями функций u(x), v(x), ω(x) выполняются неравенства u(x)≤v(x)≤ω(x), при этом u(x), ω(x) при х→х₀ стремятся к одному и тому же пределу а, то функция v(x) при х→х₀ стремится к этому же пределу.

Теорема 5. Если функция у=f(x) принимает неотрицательные значения, то есть f(x)≥0, и имеет предел равный а, то этот предел тоже неотрицателен, то есть а ≥ 0.

Теорема 6. Если между соответствующими значениями функций u(x), v(x), имеющих предел при х→х₀, выполняется неравенство u(x)≤v(x), то .

Эти теоремы облегчают вычисление пределов.

Первый замечательный предел.

Рассмотрим функцию . Эта функция при х=0 неопределенна. Рассмотрим  и докажем, что он равен 1. Заметим, что и . При вычислении  теорему о пределе дроби применять нельзя, так как предел знаменателя равен 0.

Рассмотрим окружность радиуса 1. АОС – центральный угол, обозначим его через х, причем 0<х<.

x

0

A

B

Д

С

Рис. 19.

Рассмотрим площади треугольников АОС и ВОС, и площадь сектора АОС. Из рисунка 19 видно

S_ΔАОС<S_{сектора АОС} <S_ΔВОС                                           (4)

S_ΔАОС=0,5·ОС·АD=0,5·sin x; S_{сектора АОС} =0,5·ОС²·АС=0,5·1·х=0,5х;

S_ΔВОС=0,5·ОС·ВС=0,5·1·tg x=0,5·tg x. Тогда неравенство (4) принимает вид:

0,5·sin x < 0,5·x < 0,5·tg x

Разделим обе части на 0,5·sin x, получим

<  <

или

<  < .                                              (5)

Неравенство (5) получено в предположении, что х>0. Оно верно и при х<0, так как при х<0 имеем  =  и cos (-x) = cos x.

Перейдем к пределу в двойном неравенстве (5) при х→0 .

Так как  и , то по теореме 4 имеем, что

.                                                 (6)

Этот предел называется первым замечательным пределом.

График функции  имеет вид:

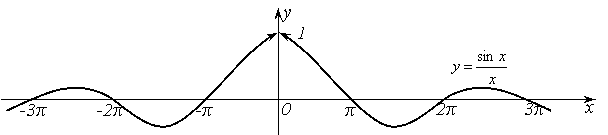
Рис. 20.

Примеры.

1. .

2. (k=const).

3. .

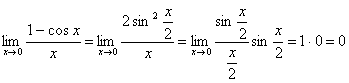4.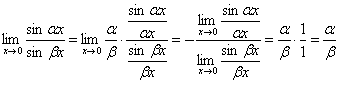 (α = const, β = const).

Второй замечательный предел.

Рассмотрим переменную величину , где n =1,2,3… . Можно доказать, что возрастает и <<, то есть эта последовательность имеет конечный предел. Этот предел обозначается ‘e’.

Определение. Предел переменной величины при n→∞ называется числом е

.                                                   (7)

Это число е = 2,7182818284…

Мы рассмотрели последовательность  , n=1,2,3… При непрерывном изменении переменной х и если х→∞, то  и . То есть получаем, что

.                                                 (8)

Этот предел называется вторым замечательным пределом.

Второй замечательный предел можно записать в виде

.                                                 (9)

Число е – иррациональное число, оно играет очень важную роль в математическом анализе.

Мы рассматривали логарифмическую функцию у=log_ax, а ≠ 1, а > 0, а – основание логарифма. Если основанием логарифма является е, то log_ex = ln x и называется натуральным логарифмом. Функция у = е^х называется экспонентой.

Примеры:

1.

 2.

 3.

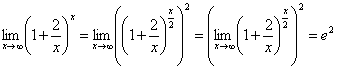
 4.

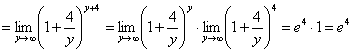
ЛЕКЦИЯ 6

Гиперболические функции.

Во многих приложениях математического анализа встречаются комбинации показательных функций вида  и . Эти комбинации рассматривают как новые функции и обозначают так:

                                         (10)

Первую из функций (10) называют гиперболическим синусом, вторую – гиперболическим косинусом. С помощью этих функций можно определить еще две функции  и :

 - гиперболический тангенс

                                              (11)

 - гиперболический котангенс.      

Функции shx, chx, thx определены, очевидно, для всех значений х. Функция же cthx определена всюду, за исключением точки х=0. Графики гиперболических функций представлены на рисунке 21.

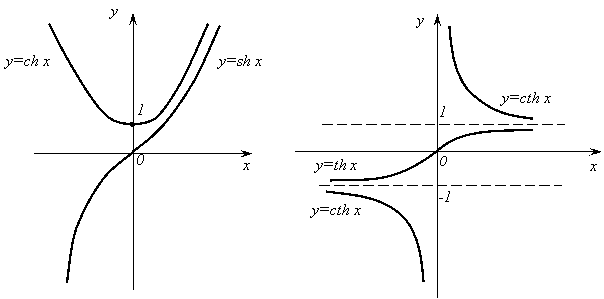
Рис. 21.

Сравнение бесконечно малых функций.

Для того чтобы сравнить между собой две бесконечно малые функции, надо вычислить предел их отношения. Пусть a(х) и b(х) – бесконечно малые функции при х®х₀.

1. Если , тогда a(х) называется бесконечно малой функцией более высокого порядка, чем b(х).

2. Если , тогда a(х) и b(х) называются бесконечно малыми функциями одного порядка.

3. Если , тогда a(х) называется бесконечно малой функцией более низкого порядка, чем b(х).

4. Если , тогда a(х) и b(х) называются эквивалентными.

Справедливо утверждение: предел отношения бесконечно малых функций не изменится, если заменить их эквивалентными бесконечно малыми функциями.

Примеры:

1. sinx~x при х®0, так как .

2. arcsinx~x при х®0, так как .

3. arctgx~x при х®0, так как .

Односторонние пределы.

Если при нахождении предела рассматривать значения х только слева от, то такой предел называется левосторонним пределом и обозначается

.

Если рассматривать значения х только справа от , то такой предел называется правосторонним пределом и обозначается

.

Левый и правый пределы называют односторонними. Справедливо утверждение:

Если , то существует f(x₀+0) и f(x₀-0) причём f(x₀+0)=f(x₀-0)=A. Верно и обратное утверждение.

ЛЕКЦИЯ 7

Непрерывность функции.

Определение 1. Функция называется непрерывной в точке , если:

1. функция определена в точке x₀ и некоторой её окрестности;

2. функция имеет предел при x®x₀;

3. предел функции при x®x₀ совпадает со значениями функции в этой точке,

.

При рассмотрении графика непрерывной функции можно заметить, что если аргумент стремится к x₀, то значение функции стремится к  f(x₀). Точка x₀ называется точкой непрерывности функции .

 Если в точке x=x₀ нарушается какое-либо из трёх условий непрерывности, то  называется точкой разрыва функции . В этом случае функция называется разрывной в этой точке.

Можно дать иную формулировку непрерывности функции, опираясь на понятия приращения аргумента и приращения функции. Пусть функция f(x) определена на (а,b). Разность x-x₀, где хÎ(а,b) и хÎ(а,b) называется приращением аргумента и обозначается Dх, а разность f(x)-f(x₀) называется приращением функции, соответствующим данному приращению аргумента Dх, и обозначается Df, то есть , . В этих обозначениях определение непрерывности функции в точке принимает следующий вид.

Определение 2. Функция f(x), хÎ(а,b) называется непрерывной в точке х₀Î(а,b), если . Отсюда следует, что приращение непрерывной в точке x₀, функции есть функция бесконечно малая при Dх®0.

Определение 3. Функция называется непрерывной при , если для любого e>0, существует такое d=d(e)>0, что для всех x, удовлетворяющих неравенству 0£½х-х₀½<d, выполняется ½f(x)-f(x₀)½<e.

Определение непрерывности функции можно сформулировать с помощью односторонних пределов.

Определение 4. Функция f(x) называется непрерывной в точке х₀, если её односторонние пределы при x®x₀ равны между собой и совпадают со значением функции в этой точке.

Классификация точек разрыва.

1. Если f(x₀-0)=f(x₀+0)=f(x₀), то в точке  функция непрерывна.

2. Если f(x₀-0)=f(x₀+0)¹f(x₀), или в точке x₀ функция вообще не определена, то при  функция имеет устранимый разрыв.

3. Если f(x₀-0) и f(x₀+0) принимает конечные значения и f(x₀+0)¹f(x₀ - 0), то в точке  функция имеет разрыв первого рода (скачок).

4. Если хотя бы один из односторонних пределов f(x₀ -0) или f(x₀+0) равен ±¥, то в точке функция имеет разрыв второго рода (бесконечный разрыв).

Действия над непрерывными функциями.

Если над непрерывными функциями производить операции сложения, умножения и деления, а так же взятия функции от функции, то в результате будем получать непрерывные функции. Имеют место теоремы.

Теорема 1. Если функции f(x) и j(х) непрерывны в точке х₀, то их сумма, разность и произведение также непрерывны в этой точке, если кроме того j(х₀)¹0, то функция непрерывна в точке х₀.

Теорема 2. Если функции u=j(х) непрерывны в точке х₀, а функция непрерывна в точке u₀=j(x₀), то сложная функция f(j(х)) непрерывна в точке х₀.

Теорема 3. Всякая элементарная функция непрерывна в каждой точке, где она определена.

Свойства функций непрерывных на отрезке.

Определение 5. Функция f(x) называется непрерывной в интервале (на отрезке), если она непрерывна во всех точках этого интервала (отрезка).   

Теорема 4. Если функция непрерывна на замкнутом отрезке [a, b], то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Эта теорема делается неверной, если функция непрерывна на (а,b).

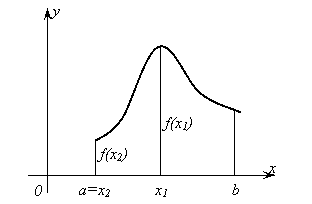
Рис. 22.

Теорема 5. Если функция непрерывна при хÎ[a, b] и на его концах принимает значения разных знаков, то внутри этого отрезка найдется, по крайней мере, одна точка , в которой  f(c)=0.

Геометрический смысл этой теоремы заключается в том, что если точки графика  лежат по разные стороны относительно оси ОХ, то график функции пересечёт ось ОХ хотя бы в одной точке.

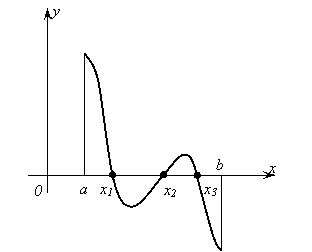
Рис. 23.

Теорема 6. Если функция непрерывна при хÎ[a, b], и f(a)=A,  f(b)=B, то для любого числа С, заключенного между А и В, найдется внутри сегмента

[a, b] такая точка , что f(c)=С.

Геометрический смысл этой теоремы очевиден. Рассмотрим график функции . Пусть f(a)=A, f(b)=B тогда прямая y=С, где С – любое число, заключённое между А и В, пересечёт график функции , по крайней мере, в одной точке. 

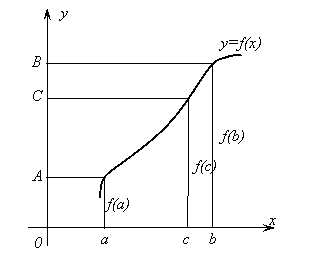
Рис. 24.

ЛЕКЦИЯ 8

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

 ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Приращение аргумента и приращение функции.

Пусть дана функция.  Рассмотрим два значения её аргумента: исходное х₀ и новое х. Разность значений аргумента х-х₀ называется приращением аргумента и обозначается Dх:

, тогда .                                       (12)

В точке х₀ значение функции f(х₀) – исходное, в точке х – значение f(x) новое. Аналогично разность f(х)-f(x₀) называется приращением функции и обозначается Dy:

Dy=f(x)-f(x₀), тогда f(x)=f(x₀)+ Dy.                                 (13)

Определение. Производной функции в точке х₀ называется предел отношения приращения функции Dy к приращению аргумента Dх, при произвольном стремлении Dх к нулю, если этот предел существует и конечен, то есть

.                                                   (14)

Производная обозначается .

Операция нахождения производной функции называется дифференцированием.

Геометрический смысл производной.

Пусть на плоской кривой L задана точка М₀. Рассмотрим точку М тоже лежащую на этой кривой. Если точка М перемещается по кривой L, а точка М₀ остаётся неподвижной, то секущая М₀М будет менять своё положение. Допустим, что существует прямая C, проходящая через точку М₀, которая обладает следующими свойствами: если точка М при перемещении её по кривой L неограниченно приближается к точке М₀, то угол между прямой C и секущей М₀М стремится к нулю. Тогда эта прямая С называется касательной к кривой L в точке М₀ , рисунок 25.

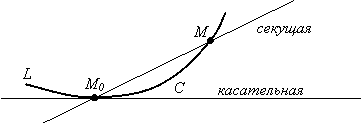
Рис. 25.

Определение. Касательная есть прямая, занимающая предельное положение секущей.

Рассмотрим теперь график функции  на рисунке 26. Этот график имеет в точке М₀ с абсциссой х₀ невертикальную касательную. Найдем угловой коэффициент касательной k=tga, a - угол, образованный касательной и осью ОХ. Через точки М₀ и М₁ проведем секущую М₀М₁. Точка М₁ имеет абсциссу х₀+Dх. Угловой коэффициент секущей . Если Dх®0, то в силу непрерывности функции Dy®0 и, следовательно, точка М₁ перемещаясь по графику, приближается к точке М₀, при этом секущая стремится к положению касательной, а это означает, что , следовательно, . Таким образом, мы получили, что .

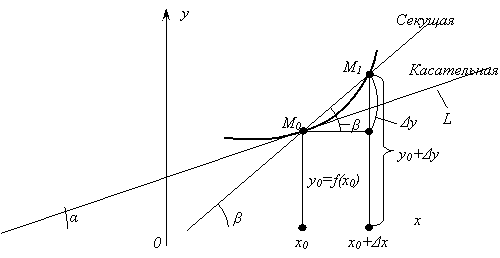Рис. 26.

Отсюда следует геометрический смысл производной: угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен значению производной этой функции в точке х₀, то есть .

Уравнение касательной, проведенной к кривой  в (х₀;y₀) точке будет иметь вид

                                              (15)

Механический смысл производной.

Пусть материальная точка движется по прямой в одном направлении по закону : где t – время, – путь, проходимый точкой за время t. Отметим некоторый момент времени t₀. К этому моменту точка прошла путь . Поставим задачу об определении скорости v₀ в момент t₀. Рассмотрим другой момент времени t₀+Dt. Ему соответствует пройденный путь s=s(t₀+Dt). Тогда за время Dt точка пройдет путь Ds=s-s₀=s(t₀+Dt)-s(t₀). Средняя скорость за время Dt определяется по формуле:

,

(16)

v_ср – есть переменная величина, зависящая от Dt. Скоростью v₀ в момент t₀ называется предел средней скорости v_ср при Dt®0, то есть  или

,

(17)

В числителе стоит приращение функции s=s(t), а в знаменателе – приращение аргумента t. Механический смысл производной заключается в следующем: скорость v прямолинейного движения материальной точки в момент времени t есть производная от пути s по времени t.

Дифференцируемость функции.

Определение 1. Функция, имеющая производную в точке , называется дифференцируемой в этой точке.

Определение 2. Функция называется дифференцируемой на интервале (на отрезке), если она дифференцируема в каждой точке данного интервала (отрезка).

Справедлива теорема.

Теорема. Если функция дифференцируема в точке х₀, то она в этой точке непрерывна.

Доказательство.

На основании определения 2 непрерывности функции, для доказательства теоремы надо доказать, что если функция дифференцируема в точке х₀, то её приращение в этой точке стремится к нулю.

Пусть х получит приращение Dх, тогда функция получит приращение Dy.

Рассмотрим тождество .

 Тогда , то есть . Обратное утверждение неверно, то есть не всякая непрерывная функция является дифференцируемой. Рассмотрим пример функции, которая непрерывна в точке , но не дифференцируема в этой точке.

Пример. f(x)=|x| - эта функция непрерывна при x=0, так как . Докажем, что в точке x=0 эта функция не имеет производной. В точке x=0 имеем: Dх=x-0=x, .

Тогда , а .То есть односторонние пределы не равны, следовательно,  не существует, а это означает, что не существует производная функции f (x)=|x| в точке x=0.

ЛЕКЦИЯ 9

Основные правила нахождения производных.

Теорема 1. Если функции u=u(x), v=v(x) дифференцируемы в точке x₀,  то в этой точке дифференцируема их сумма, причем производная суммы равна сумме производных слагаемых .

Доказательство.

Рассмотрим функцию y=f(x)=u(x)+v(x). Так как u=u(x) и v=v(x) дифференцируемы, то

; .

Так как Du=u(x+Dx)-u(x) и Dv=v(x+Dx)-v(x), то Dy=f(x+Dx)-f(x)=(u(x+Dx)+v(x+Dx))-

- (u(x)+v(x))= (u(x+Dx)-u(x))+(v(x+Dx)-v(x))=Du+Dv.

Тогда

 То есть .

Формула обобщается на случай конечного числа слагаемых.

Теорема 2. Если функции u=u(x), v=v(x)  дифференцируемы в точке х₀, то в этой точке дифференцируемо их произведение, причём

.

Следствие 1. Постоянный множитель можно вынести за знак производной

.

Следствие 2. Производная разности равна разности производных

.

Теорема 3. Если функции u=u(x), v=v(x)  дифференцируемы в точке х₀ и v(x₀)¹0, то в этой точке дифференцируемо их частное, причём .

Теоремы 2 и 3 доказываются аналогично.

Производная обратной функции.

Пусть дана функция , где х – независимая переменная, y – функция. В этой функциональной зависимости мы можем произвольно менять  и получать соответствующие значения х, решая уравнение  относительно х, то есть получим x=j(y). Такие две функции называются взаимообратными.

Замечание 1. Область изменения функции  является областью определения обратной функции x=j(y).

Замечание 2. Если аргумент обратной функции обозначить х, а функцию y, то графики взаимообратных функций симметричны относительно биссектрисы 1 и 3 координатных углов.

Замечание 3. Функция может иметь одну или несколько обратных функций.

Теорема. Пусть функция х=f(y) – монотонна и дифференцируема на некотором интервале, и имеет производную в точке “y” этого интервала не равную нулю. Тогда будет существовать обратная функция  и её производная в соответствующей точке “x”вычисляется по формуле

.

Таблица производных простейших функций.

Используя определение производной и свойства пределов функций можно вычислить производные всех простейших функций.

Производная сложной функции.

Пусть y=f(u) и u=u(x). Тогда функция y=f(u(x)) называется сложной функцией от х.

Теорема. Если функция u=u(x) имеет производную  в точке х, а функция y=f(u) имеет производную  в соответствующей точке u, то сложная функция y=f(u(x)) в данной точке х имеет производную

.

Доказательство:

Придадим х приращение Dх. Тогда u=u(x) и y=f(u) получают соответственно приращения Du и Dy. Рассмотрим , и представим в виде . Переходя к пределу при Dx®0, получим . Так как Du®0 при Dx®0, то , а , то тогда .

Теорема доказана.

Используя доказанную теорему и таблицу производных простейших функций, запишем таблицу производных сложных функций.

ЛЕКЦИЯ 10

Дифференциал функции и его геометрический смысл.

Пусть функция  имеет производную при данном значении х, тогда

.

(18)

По свойству предела функции имеем:

.

(19)

где a - бесконечно малая величина при Dx®0.

Отсюда получаем

.

(20)

То есть приращение функции Dy состоит из двух слагаемых:  и aDx. Так как величина aDx®0 быстрее, чем Dx, то слагаемое  играет главную роль в (20). Это слагаемое называется главной частью приращения функции и оно линейно относительно Dx.

Определение. Главная часть приращения функции называется дифференциалом функции y=f(x).

Таким образом, дифференциал функции равен произведению производной этой функции на произвольное приращение Dx аргумента. Дифференциал функции обозначается dy. Таким образом, по определению имеем

.

(21)

Дифференциалом независимой переменной называется её приращение Dx и обозначается dх. Тогда (21) примет вид

.

(22)

Свойства дифференциалов.

Дифференциал обладает следующими свойствами:

1.

2.

3. , при условии .

Выясним геометрический смысл дифференциала. Для этого проведем к графику функции y=f(x) в точке М(х;y) касательную и обозначим через a её угол с осью Ох (см. рис.27). Рассмотрим ординату этой касательной для точки x+Dx. Отрезок NP, равный разности между этой ординатой и ординатой касательной для точки х, назовем приращением ординаты касательной. Покажем, что этот отрезок равен дифференциалу dy. Из прямоугольного треугольника MNP имеем:

, или .

Но, согласно геометрическому смыслу производной, . Поэтому

.

Итак, мы выяснили геометрический смысл дифференциала: дифференциал функции y=f(x) в точке х равен приращению ординаты касательной, проведенной к кривой в данной точке.   

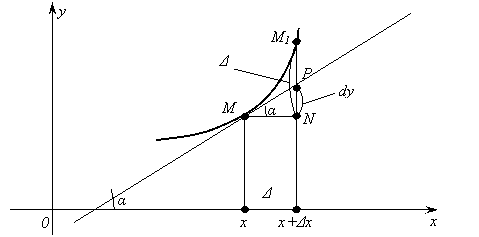
Рис. 27.

Дифференциал сложной функции.

Если х является независимой переменной, то дифференциал функции y=f(x) вычисляется по формуле:

.

(23)

Покажем, что эта форма сохраняется и в том случае, когда «х» не является независимой переменной, а является функцией от t. Действительно, пусть y=f(x) и х=j(t), то есть является сложной функцией от t.

Тогда . По правилу дифференцирования сложной функции имеем . Отсюда , так как .

Мы доказали следующую теорему.

Дифференциал сложной функции y=f(x), для которой х=j(t), имеет такой же вид , как если бы аргумент х был независимой переменной.

Свойство дифференциала сложной функции, выражаемое этой теоремой, называется инвариантностью формы первого дифференциала.

Из формулы (23) следует, что выражение для производной  сохраняет свой вид и для случая, когда аргумент х не является независимой переменной.

Производные высших порядков.

Пусть функция y=f(x) дифференцируема на некотором интервале, тогда её производная  является функцией от х. Пусть   тоже имеет производную, которая называется второй производной: . Производная второй производной называется третьей производной. Обозначается: и так далее.

Определение. Производной n-го порядка функции y=f(x) называется первая производная от производной (n-1)-го порядка

.

Производные второго,  третьего и так далее обозначаются ещё 

.

ЛЕКЦИЯ 11

Дифференциалы высших порядков.

Пусть дана функция y=f(x). Её дифференциал  можно рассматривать, как функцию от х, и тогда можно найти дифференциал от первого дифференциала, который называется дифференциалом второго порядка и обозначается d²y, т.е. по определению имеем . Аналогично определяются и вычисляются дифференциалы третьего порядка, четвертого и так далее порядков: .

Дифференцирование функции заданной параметрически.

Пусть даны две функции переменной t

(24)

которые рассматриваются для одних и тех же значений t, тогда каждому из этих значений при t=t₀ соответствует определенное значение х₀ и определенное значение y₀, то есть определенная точка М(x₀;y₀) графика. Когда t пробегает все значения из области определения функций (1), точка М(x;y) описывает некоторую линию С в плоскости ХОY. Уравнения (1) называются параметрическими уравнениями этой линии, а переменная t-параметром.

Рассмотрим функцию y=f(x), заданную параметрическими уравнениями (24), причём функции x(t) и y(t) дифференцируемы и .

Найдем производную . Известно, . Так как  и , то .

Обозначим , , тогда

(25)

Используя формулу (25), можно вычислить производную второго порядка

.

Таким образом,

.

(26)

Используя формулы (25) и (26), можно вычислять производные любого порядка.

Теоремы о дифференцируемых функциях.

Теорема Ролля (о корнях производной).

Если функция y=f(x) непрерывна на отрезке [a,b], дифференцируема во всех его внутренних точках и на концах отрезка равна нулю, то существует, по крайней мере, одна точка x=c, а<c<b, в которой .

Доказательство.

Так как функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своего наибольшего значения М и наименьшего значения m.

Если М=m, то функция y=f(x) постоянна, то есть при всех значениях х значения f(x)=c и, следовательно, , при любом значении х из отрезка [a,b]. Предположим, M¹m. Пусть M>0, и при x=c, f(c)=M. Точка x=c - должна быть внутренней точкой отрезка [а,b], так как по условию теоремы f(а)=f(b)=0.  

Так как f(c) – наибольшее значение на отрезке [a,b], то f(c+Dx)-f(c)£0 при Dx>0 и Dx<0.

Тогда

, если >0 и , если <0

(27)

В неравенствах (27) перейдём к пределу при → 0 , получим

, >0

, <0

Но полученные соотношения могут выполняться лишь, если .Что и требовалось доказать.

Геометрически теорему Ролля можно объяснить следующим образом: если график непрерывной на [a,b] и дифференцируемой внутри него функции пересекает ось ОХ в двух точках x=а, x=b, то между этими точками найдется хотя бы одна точка с, а<c<b, для которой касательная к графику параллельна  оси ОХ.

Замечание 1. Доказанная теорема остается справедливой и для такой дифференцируемой функции, которая на концах отрезка [a,b] принимает равные значения, то есть  f(а)=f(b).

Замечание 2. Если функция f(x) такова, что её производная существует не во всех точках внутри отрезка [a,b], то утверждение теоремы может оказаться неверным. Например, функция непрерывна на концах сегмента

[-1;1] и обращается в нуль на концах отрезка: f(-1)=f(1)=0, однако производная  внутри данного сегмента в нуль не обращается. Происходит это потому, что при х=0 производная не существует. Из рисунка 28 видно, что в этом случае на сегменте [-1;1] не существует касательной, параллельной оси ОХ.

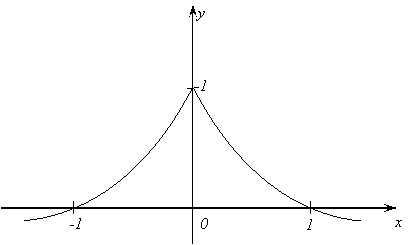
Рис. 28.

Теорема Лагранжа (о конечных приращениях).

Если функция y=f(x) непрерывна на отрезке [a,b], дифференцируема во всех его внутренних точках, то внутри отрезка [a,b] найдется, по крайней мере, одна точка x=c, а<c<b, что f(b)-f(a)=f ^/(c)(а-b) или

.

(28)

Геометрический смысл теоремы Лагранжа.

Из рисунка 29 видно, что выражение  есть угловой коэффициент хорды АВ, соединяющей концы дуги АВ. Из геометрического смысла производной имеем:  - есть угловой коэффициент касательной, проведенной к кривой в точке x=c. Таким образом, теорема Лагранжа утверждает, что на графике функции y=f(x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги АВ. 

Рис. 29.

Формулу (28) часто называют формулой конечных приращений.

Теорема Коши (об отношении приращений двух функций).

Если f(x) и j(x) – две функции непрерывные на отрезке [a,b] и дифференцируемые внутри него, причем  нигде внутри отрезка не обращается в нуль. Тогда внутри отрезка [a,b] найдется такая точка x=c, a<c<b, что

.

(29)

Теоремы Лагранжа и Коши доказываются с помощью теоремы Ролля.

Замечание 1. Теорема Лагранжа есть частный случай теоремы Коши, если j(x) = x.

Замечание 2. Из условия теоремы Коши следует, что j(b)¹j(а), так как в противном случае по теореме Ролля в некоторой точке cÎ(а,b), j¢(c)=0, что противоречит условию теоремы Коши: j¢(x)¹0 при всех xÎ(а,b).

Правила Лопиталя.

Правила Лопиталя дают возможность раскрывать неопределенности  и  с помощью производных.

Правило 1. (раскрытие неопределенности типа ).

Пусть f(x) и j(x) функции, которые на некотором отрезке [a,b] удовлетворяют условиям теоремы Коши и обращаются в ноль в точке x=x₀ из этого отрезка, причем j¢(x₀)¹0. Тогда, если при  существует предел отношения , то существует и предел отношения  при x®x₀, причем .

Доказательство.

Возьмем на отрезке [a,b] какую-нибудь точку x ¹ x₀, тогда по теореме Коши будем иметь

,

(30)

где х₀<x<х. Но f(x₀)=j(x₀)=0 тогда равенство (1) перепишется в виде:

,

(31)

Если x®x₀, то и x®х₀, так как х₀<x<х.

Если , то и, следовательно,

.

То есть .

Теорема доказана.

Замечание 1. Если  и их производные  и j^|(x) удовлетворяют условиям теоремы Коши, то правила Лопиталя можно применять к отношению , то есть .

Правило 2. (раскрытие неопределенности типа ).

Пусть функции f(x) и j(x) непрерывны и дифференцируемы в окрестности точки x₀, причем производная j^|(x₀)¹0. Пусть  и , тогда, если существует предел отношения  при x®x₀, то существует и предел отношения  при x®x₀, причем  .

Примеры.

1. .

2.

ЛЕКЦИЯ 12

ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ

ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ

Монотонность функции.

Определение. Функция называется возрастающей в интервале, если большему значению аргумента соответствует большее значение функции.

Функция называется убывающей в интервале, если большему значению аргумента соответствует меньшее значение функции.

Интервал, где функция возрастает, называется интервалом возрастания функции.

Интервал, где функция убывает, называется интервалом убывания функции. Эти интервалы называются интервалами монотонности функции.

Применим понятие производной к исследованию функции на монотонность. Необходимые и достаточные условия монотонности функции устанавливают теоремы:

Теорема 1. (необходимый признак монотонности)

1) Если функция  в интервале возрастает, то её производная  для х, принадлежащих этому интервалу.

2) Если функция  в интервале убывает, то её производная  для х, принадлежащих этому интервалу.

3) Если функция  в интервале не изменяется, то её производная  для х, принадлежащих этому интервалу.

Теорема 2. (достаточный признак монотонности)

1) Если для функции f(x) её производная >0 в некотором интервале, то f(x) в этом интервале возрастает.

2) Если для функции f(x) её производная <0 в некотором интервале, то f(x) в этом интервале убывает.

3) Если для функции f(x) её производная  в некотором интервале, то f(x) в этом интервале не изменяется.

Эти две теоремы выражают следующий геометрический факт: если на [a,b] функция возрастает, то касательная к кривой в каждой точке этого отрезка образует с осью ОХ острый угол j или в отдельных точках – горизонтальна, tgj³0.

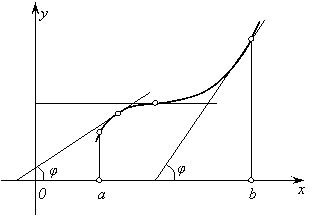
Рис. 30.

Если на [a,b] функция f(x) убывает, то касательная к кривой в каждой точке этого отрезка образует с осью ОХ тупой угол j или в отдельных точках горизонтальна, tgj≤0.

Рис. 31.

Экстремум функции.

Определение 1. Функция  в точке х₀ имеет максимум, если существует такая окрестность точки x = x₀, что для всех x ¹ x₀ принадлежащих этой окрестности выполняется неравенство: f(x)< f(x₀).

Определение 2. Функция  в точке х₀ имеет минимум, если существует такая окрестность точки x = x₀, что для всех x ¹ x₀ принадлежащих этой окрестности выполняется неравенство: f(x)> f(x₀).

Максимум и минимум объединяются одним общим названием экстремум. Однако следует иметь в виду, что если в некоторой точке функция имеет максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. Из определения максимума следует, что максимум – наибольшее значение функции в некоторой окрестности рассматриваемой точки. Аналогичное замечание можно сделать относительно минимума. В частности может оказаться, что значение функции в точке минимума будут больше, чем значение функции в точке максимума.

Теорема 1. (необходимое условие существования экстремума)

Если дифференцируемая в точке x = x₀ функция  имеет в этой точке экстремум, то её производная при x = x₀ обращается в ноль: .

Доказательство.

Пусть  имеет в точке x = x₀ максимум. Тогда при достаточно малых по абсолютному значению приращения Dх, Dх¹0 имеет место: <, то есть < 0.

 Тогда знак отношения   будет определяться знаком Dх:

> 0, при Dх<0

< 0, при Dх>0

Согласно определению производной , причем этот предел не зависит от того, как Δх→0, следовательно, если Δх→0 оставаясь отрицательным, то , а если Δх→0, оставаясь положительным, то . Но это возможно лишь, если . Аналогично доказывается для случая минимума функции. Эта теорема имеет следующее геометрическое истолкование: если в точке экстремума функция имеет производную, то касательная к кривой  в этой точке параллельна оси ОХ, то есть              k = tgφ = 0. Из этой теоремы следует, что равенство нулю первой производной есть только необходимое условие, и не является достаточным условием существования экстремума. До сих пор рассматривался только случай, когда функция  имела производную в точке экстремума. Могут, однако, встретиться случаи, когда в точках экстремума функция не имеет производной. Рассмотрим следующий пример. 

Пример.  f(x)= |x|. График этой функции изображен на рисунке.

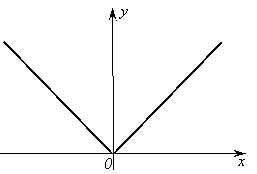
Рис. 32.

 При х=0 эта функция не имеет производной. Но очевидно, что в точке х=0 функция имеет минимум.   

Рассмотренный пример позволяет дополнить сформулированный необходимый признак существования экстремума следующим образом.

Если непрерывная функция  имеет в точке  экстремум, то производная функции обращается в этой точке в нуль или не существует.

Точка х = х₀ из области определения функции , в которой первая производная обращается в нуль или не существует, называется критической точкой этой функции. Из сказанного следует, что экстремум функция может иметь только в критических точках, однако не во всякой критической точке функция имеет экстремум. Чтобы определить будет ли в критической точке экстремум, надо исследовать эту точку с помощью теоремы 2.

Теорема   2. (достаточные условия существования экстремума).

Если непрерывная функция  имеет производную во всех точках некоторого интервала, содержащего критическую точку x = x₀ и, если при переходе аргумента слева направо через критическую точку x = x₀ меняет знак с плюса на минус, то функция в этой точке имеет максимум. Если же производная меняет знак с минуса на плюс, то в этой точке x = x₀ функция имеет минимум.

Замечание 1. Если  ни при каком значении хÎ[a,b], то функция не имеет экстремума на этом отрезке.

Замечание 2. Если  не меняет знак при переходе через критическую точку, то функция в этой точке не имеет экстремума.

Пример.

Найти интервалы монотонности и экстремумы функции .

Решение. Найдем , и решим уравнением . Так как функция определена всюду, то  и  являются критическими точками. Исследуем знак первой производной в окрестности каждой критической точки.

При хÎ(-¥;-2) > 0, при хÎ(-2;2) < 0, а при хÎ(2;+¥) > 0. Следовательно, в интервалах (-¥;-2) и (2;+¥) функция возрастает, а в интервале (-2;2) функция убывает.

Точка  – точка максимума, , а – точка минимума, .

Наибольшее и наименьшее значение функции на отрезке.

Рассмотрим функцию , непрерывную на отрезке [a,b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений либо на границе сегмента, либо внутри него. Если наибольшее (или наименьшее) значение функции достигается во внутренней точке с сегмента, то это значение является максимумом (или минимумом) функции, так как неравенство (или ), имеющее место для всех точек х сегмента [a,b], выполняется и для любой окрестности точки, лежащей внутри сегмента [a,b].

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на сегменте [a,b].

1. Находим все критические точки функции в интервале (a,b) и вычисляем в них значения функции.

2. Вычисляем значения функции на концах сегмента – в точках и .

3. Из всех этих значений выбираем наибольшее и наименьшее.

Замечание. Очевидно, что непрерывная на сегменте функция имеет во внутренней точке этого сегмента только один экстремум, то в этой точке она имеет наибольшее значение в случае максимума и наименьшее – в случае минимума.

Пример. Найти наибольшее и наименьшее значения функции  на сегменте .

Решение.

a) Находим все критические точки функции на интервале :

.

Решим уравнение .

.

Отсюда .

Вычисляем значения функции на концах сегмента:

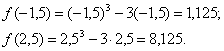
Таким образом, наибольшее значение функции  достигается на правом конце сегмента в точке . Наименьшее значение функции  и достигается в точке .  

Замечание.

В некоторых случаях при исследовании функции на экстремум оказывается удобным следующий признак существования экстремума, основанный на знаке второй производной.

Теорема 3. Пусть в точке  первая производная функции  равна нулю: , а вторая производная существует и отлична от нуля: . В этом случае если < 0, то в точке  функция имеет максимум, если же > 0, то в точке  функция имеет минимум.

Пример. Найти экстремум функции на сегменте .

Решение.

1. Находим производную  .

2. Приравниваем производную к нулю и находим корни производной, принадлежащие :

, , , .

3. Находим вторую производную  и определяем её знак в точках  и . В точке  имеем:  > 0. В точке  имеем < 0.

         Следовательно, в точке  функция имеет минимум:

.

А в точке  функция имеет максимум:

.

В тех случаях, когда в критической точке вторая производная обращается в нуль или не существует, второй достаточный признак существования экстремума не применим. В этих случаях приходится пользоваться достаточным признаком, основанным на перемене знака первой производной.

ЛЕКЦИЯ 13

Выпуклость и вогнутость графика функции.

Определение 1. График функции y=f(x)   называется выпуклым в интервале, если он расположен ниже любой своей касательной на этом интервале.

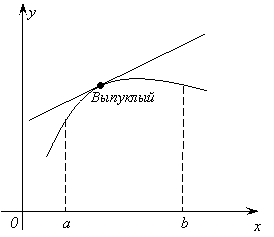
Рис. 33.

Определение 2. График функции y=f(x)   называется вогнутым в интервале, если он расположен выше любой своей касательной на этом интервале.

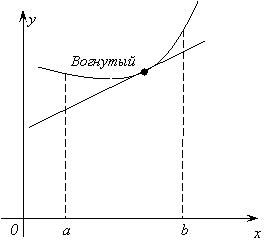
Рис. 34.

Определение 3. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой части, называется точкой перегиба.

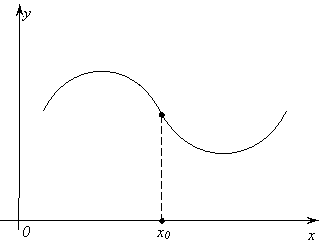
Рис. 35.

При исследовании функции и построении графика бывает необходимо находить интервалы выпуклости, вогнутости и точки перегиба. Эти вопросы решаются с помощью второй производной.

Теорема 4. Пусть функция y=f(x) имеет вторую производную во всех точках интервала (α,b). Если во всех точках этого интервала < 0, то график функции на этом интервале – выпуклый. Если >0, то график функции на этом интервале – вогнутый. Чтобы найти точки перегиба, нужно найти точки, где вторая производная меняет знак. Исследование на перегиб проводится с помощью двух теорем.

Теорема 5. (необходимое условие существование перегиба).

Пусть функция y=f(x) непрерывна во всех точках интервала (α;b). Тогда, если точка с абсциссой х₀Î(α,b), является точкой перегиба графика функции y=f(x), то или не существует. 

Точка х=х₀ из области определения функции y=f(x), в которой вторая производная обращается в ноль или не существует, называется критической точкой или точкой подозрительной на перегиб. Значит, перегиб следует искать среди критических точек. Чтобы выяснить является ли полученная критическая точка точкой перегиба, применяют следующую теорему.

Теорема 6. (достаточные условия существования перегиба).

Если вторая производная непрерывной функции меняет знак при переходе через критическую точку х=х₀, то эта точка будет точкой перегиба графика функции.

Замечание 1. Если вторая производная не обращается в ноль ни в одной точке некоторого интервала, то график функции на этом интервале перегиба не имеет.

Замечание 2. Если при переходе через критическую точку вторая производная не меняет знак, то в критической точке график функции перегиба не имеет.

Пример.

Найти интервалы выпуклости, вогнутости и точки перегиба графика функции

.

Решение. Найдем  и . Вторая производная не обращается в нуль ни в одной точке из области определения, при  она не существует. Так как функция всюду определена, то – критическая точка. При > 0; при < 0. Следовательно, в интервале –график функции вогнутый, в интервале – выпуклый. Точка  – точка перегиба. Значение функции в точке перегиба .

Асимптоты графика функции.

При построении графика важно определить, как ведет себя график функции, когда х  удаляется от начала координат в бесконечность.

Определение. Асимптотой графика функции f(x) называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

Асимптоты могут быть вертикальными, горизонтальными или наклонными.

1. Вертикальные асимптоты.

Вертикальные асимптоты – это прямые, параллельные оси ОY. Пусть при х®х₀-0 или при х®х₀+0 функция неограниченно возрастает по абсолютной величине, то есть  или . Тогда прямая х=х₀ является вертикальной асимптотой.

Очевидно и обратное, если х=х₀ – вертикальная асимптота, то хотя бы один из односторонних пределов  или  бесконечен. Таким образом, для отыскания вертикальных асимптот графика функции y=f(x) надо найти те значения х=х₀, при которых функция не существует. Из определения следует, что если график функции имеет вертикальную асимптоту, то её уравнение: х=х₀.

Если функция y=f(x) всюду определена, то, очевидно, её график не имеет вертикальных асимптот.

2. Наклонные асимптоты.

  Пусть график функции y=f(x) имеет наклонную асимптоту, уравнение которой имеет вид: y=kx+b. Необходимо определить k и b. Поступим следующим образом. Из точки М отпустим перпендикуляр на асимптоту. Из определения асимптоты следует, что при х®¥, MN®0

.

(32)

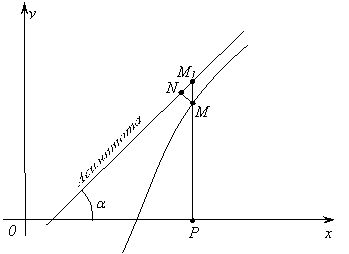
Рис. 36.

Рассмотрим DM₁MN: M₁M=MN/cosa, где a - угол наклона асимптоты к оси ОХ, a - величина постоянная, тогда M₁M®0 одновременно с MN, то есть .

Так как  M₁M=PM₁-PM=y_ас. – y_граф.=(kx+b)-f(x), то,

.

(33)

Тогда из (33) получаем, что величина

.

(34)

есть бесконечно малая при х®+¥. Разделим обе части равенства (34) на х

.

(35)

Перейдем к пределу в (35) при х®+¥, получим

.

(36)

Так как , то

и  .

(37)

Из (35), (36), (37) получаем

.

(38)

Определим параметр b. Так как  f(x)-(kx+b)=β(x), то

b=f(x)-kx-β(x).                                                           (39)

Перейдем в (39) к пределу при х→+∞:

,

(40)

где k вычисляется по формуле (38). Таким образом, для нахождения наклонной асимптоты надо найти пределы (38) и (40). Если хотя бы один из этих пределов равен бесконечности или не существует, то график функции наклонной асимптоты не имеет.

3. Горизонтальные асимптоты.

Если , а  существует и конечен, то график имеет горизонтальную асимптоту  y=b.

Замечание 1. Аналогично находятся горизонтальные и вертикальные асимптоты при х→ - ∞.

Замечание 2. Пределы (38) и (40) могут быть разными при х→+∞ и при   х→ - ∞.

Пример.

Найти асимптоты графика функции .

Решение. Данная функция определена и непрерывна на всей числовой оси. Следовательно, асимптот, параллельных оси Оу, график не имеет.

Находим асимптоты, не параллельные оси Оу.

1) ; ,

.

Итак, уравнение асимптоты при : .

2) ; ,

.

Уравнение асимптоты при : .

Таким образом, график функции  имеет две различные асимптоты, не параллельные оси Оу:

при ,

при .

Общая схема исследования функции y=f(x) и построения её графика.

Исследование функции и построение её графика проводят по следующей схеме:

1. Находят область определения функции y=f(x).

2. Исследуют функцию на четность (нечетность).

3. Исследуют функцию на периодичность.

4. Находят точки пересечения графика с осями координат.

5. Находят вертикальные, горизонтальные, наклонные асимптоты.

6. Находят интервалы монотонности и экстремумы функции.

7. Находят интервалы выпуклости, вогнутости и точки перегиба графика.

8. По проведенному исследованию строят график функции.

ЛЕКЦИЯ 14

ИНТЕГРИРОВАНИЕ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО

Неопределенный интервал.

Первообразная.

В дифференциальном исчислении мы решали такую задачу: по данной функции найти её производную. Однако многочисленные задачи техники проводят к постановке обратной задачи: для данной функции f(x) найти такую функцию F(x), производная которой равнялась бы заданной функции f(x), то есть

.

(41)

Поставленную задачу можно сформулировать в следующей равносильной форме: для данной функции f(x) найти такую функцию F(x), производная которой равнялась бы  f(x).

Определение. Первообразной функцией для данной функции f(x) называется функция F(x), производная которой равняется функции f(x), то есть выполняется равенство (41).

 Например: , первообразной для неё является функция

 или .

Возникает вопрос: для всякой ли функции существует первообразная?

Ответ на этот вопрос даёт следующая теорема.

Теорема. Любая функция, непрерывная на отрезке, имеет на этом отрезке первообразную.

Задача отыскания по данной функции её первообразной решается не однозначно. Действительно, первообразной для f(x)=sin x является F(x)=-cos x, так как , однако  тоже является первообразной для , так как , и , тоже является первообразной для sin x, так как .

Таким образом, справедлива следующая теорема.

Теорема. Если функция есть первообразная для функции f(x) на отрезке [a,b], то всякая другая первообразная для f(x) отличается от F(x) на константу, то есть может быть представлена в виде: , где C – произвольная постоянная.

Доказательство: Пусть Ф(х) – любая другая первообразная функции f(x), тогда , то есть Ф(х) и F(x) имеют равные производные, следовательно, эти функции отличаются друг от друга на константу, то есть , следовательно, .

Отсюда следует, что выражение  охватывает совокупность всех первообразных для данной функции  f(x).

Определение: Если F(x) – одна из первообразных для функции f(x), то выражение , где C – произвольная постоянная, называется неопределённым интегралом для  f(x). Обозначается .

Таким образом,

,

(42)

где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.

Действие отыскания неопределенного интеграла для данной функции называется интегрированием этой функции.

Геометрический смысл неопределенного интеграла.

Если , то очевидно, что F(x) есть первообразная для f(x) и геометрически представляет кривую, а функция  есть семейство кривых, каждая из которых может быть получена из кривой  параллельным переносом вдоль оси ОY.

График первообразной  называется интегральной кривой. Таким образом, геометрический смысл неопределенного интеграла состоит в следующем: неопределенный интеграл геометрически представляется семейством всех интегральных кривых.

Таблица неопределенных интегралов

1.	, (n≠ -1)
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.

Замечание 1. Не существует первообразной для корня, дроби и произведения. Чтобы найти первообразную для корня, его надо представить в виде степени с дробным показателем. Чтобы найти первообразную дроби и произведения, их надо преобразовать в сумму.

Замечание 2. Неопределенный интеграл инвариантен относительно переменной. Все формулы в таблице неопределенных интегралов доказываются по определению.

Основные свойства неопределенного интеграла.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

2. Неопределенный интеграл от алгебраической суммы конечного числа слагаемых функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, то есть:

.

3. Постоянный множитель можно выносить за знак неопределенного интеграла, то есть:

,  A≠0

4. Неопределенный интеграл от дифференциала функции f(x) равен самой функции f(x):

.

ЛЕКЦИЯ 15

Основные методы интегрирования.

1. Интегрирование методом разложения подынтегральной функции.

Рассмотрим на примерах.

1. .

2..

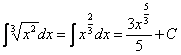2. Метод подведения под знак дифференциала.

Чтобы применять этот метод необходимо знать таблицу дифференциалов.

Примеры:

1.

2.

Используя этот метод, можно получить часто встречающиеся формулы:

1		4
2		5
3

Докажем первую из них:

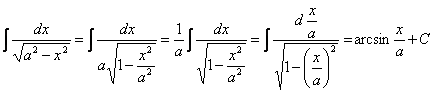
Интегрирование методом замены переменной.

Очень часто, введением новой переменной удаётся заданный интеграл  свести к новому интегралу, который вычисляется легче, чем заданный. Этот метод называется методом замены переменной или методом подстановки. Введем вместо х новую переменную t, связанную с х соотношением , где - непрерывная монотонная функция, имеющая непрерывную производную . Тогда имеет место равенство:

,

она называется формулой замены переменной в неопределенном интеграле.

Пример:

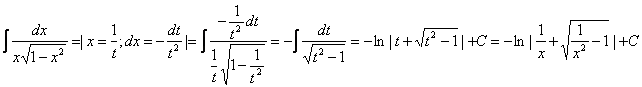
Метод интегрирования по частям.

Пусть функции u(x) и υ(x) – две дифференцируемые функции от х. Тогда дифференциал произведения вычисляется по формуле

.

Отсюда . Интегрируя обе части последнего равенства, получим

.

(43)

Формула (43) называется формулой интегрирования по частям в неопределенном интеграле.

Основные типы интегралов, которые нужно вычислять методом интегрирования по частям:

1.

2.

3.

4.  а)

б)

    в)

     г)

           При вычислении каждого из этих интегралов , а обратная тригонометрическая функция обозначается за u.

5.

6. а)

    б)

Эти интегралы вычисляются двукратным интегрированием по частям, а затем решается уравнение относительно заданного интеграла.

ЛЕКЦИЯ 16

Интегрирование рациональных функций.

Рациональной дробью называется функция вида

.

(44)

где P_m(x) и Q_n(x) – многочлены степени m и n соответственно.

Рациональная дробь называется правильной, если степень числителя строго меньше степени знаменателя. В противном случае, дробь называется неправильной.

Теорема 1. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной  рациональной дроби.

То есть, если m≥ n, то 

,

(45)

где L(x) – многочлен, а  - правильная рациональная дробь.

Такое представление можно получить путем деления многочлена на многочлен.

Рассмотрим , где m≥ n. Пусть дробь – разложена по формуле (45), проинтегрируем обе части (45),  получим

.

Таким образом, интегрирование неправильной рациональной дроби , где m≥ n, сводится к интегрированию многочлена L(x) и правильной рациональной дроби .

Интегрирование функций, содержащих квадратный трёхчлен.

Рассмотрим интегралы:

.

.

Выделим полный квадрат из квадратного трёхчлена:

Обозначим , тогда ; тогда, и получаем

.

Получившийся интеграл вычисляем по таблице.

Аналогично вычисляется

.

Примеры:

Простейшие дроби и их интегрирование.

Простейшими дробями называются дроби вида:

I.  - дробь первого типа.

II. - дробь второго типа.

III.  - дробь третьего типа, (D<0).

IV.  - дробь четвёртого типа, (D<0).

Проинтегрируем каждую из этих типов дробей.

I. .

II. .

Дроби третьего и четвёртого типа интегрируются как функции, содержащие квадратный трёхчлен.

ЛЕКЦИЯ 17

Разложение правильной рациональной дроби на сумму простейших.

Некоторые сведения о многочленах.

Определение: Корнем многочлена Q_n(x) называется всякое число x₀ (действительное или комплексное), при котором многочлен Q_n(x) обращается в ноль, то есть Q_n(x₀)=0.

Теорема 1. Всякий многочлен степени n может быть представлен в виде произведения линейных множителей вида (х-х₀) и постоянного числа a_n, где a_n – коэффициент при старшей степени многочлена Q_n(x):

.

(46)

Среди этих корней могут быть как действительные, так и комплексные.

Теорема 2.

Если многочлен Q_n(x) имеет корень x₀+iy₀, то сопряженное число x₀-iy₀ тоже является корнем многочлена Q_n(x) той же кратности.

Отсюда следует, что если в разложении (46) имеется множитель , соответствующий комплексному корню , то в этом разложении имеется и множитель , соответствующий сопряженному корню . Рассмотрим

, где , .

Из этого следует, что произведение линейных множителей, соответствующих комплексно сопряженным корням, можно заменить квадратным трёхчленом с действительными коэффициентами.

Тогда можно сделать вывод, что всякий многочлен с действительными коэффициентами можно представить в виде:

.      (47)

В этом разложении линейные множители соответствует действительным корням, а квадратные трехчлены - комплексным корням, где k₁, k₂, …,α₁, α₂,…,α_i - кратности этих корней, а а₀, p₁, p₂…q₁, q₂,…- действительные числа.

Пусть дана правильная рациональная дробь , m<n причём многочлен можно разложить на множители:

,        (48)

где квадратные трёхчлены не имеют действительных корней.

Имеет место следующая теорема.

Теорема. Правильную рациональную дробь , где Q_n(x) имеет разложение (48), можно единственным образом разложить на сумму простейших дробей, то есть представить в виде

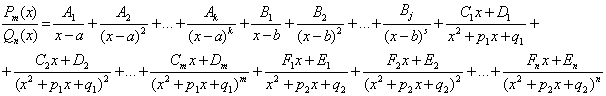 (49)

где A_k, B_j, C_m, D_m, F_n, E_n - коэффициенты (действительные числа).

Из формулы (49) следует, что линейным множителям соответствуют дроби I, II типов; квадратным множителям соответствуют дроби III и IV типов.

Метод неопределенных коэффициентов.

Одним из наиболее простых методов вычисления коэффициентов в разложении (49) является метод неопределенных коэффициентов.

Он основан на свойствах дробей и свойствах многочленов.

Рассмотрим на примере.

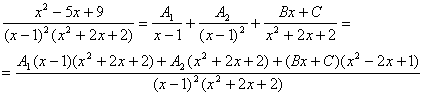
Дроби равны, следовательно, равны их числители,

;

.

Два многочлена тогда и только тогда тождественно равны друг другу, когда коэффициенты при одинаковых степенях х равны, то есть получаем систему уравнений для нахождения коэффициентов.

х³      А₁+В=0

х²    А₁+А₂-2В+С=1

х     2А₂+В+2С=-5

х⁰   -2А₁+2А₂+С=9

Решая полученную систему линейных уравнений, получим

, , , .

В результате заданную дробь разложим на сумму простейших дробей:

.

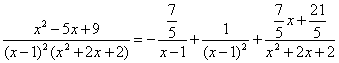Сформулируем основные правила интегрирования рациональной дроби.

1. Если рациональная дробь неправильная, то её представляют в виде суммы многочлена и правильной рациональной дроби (делением многочлена в числителе на многочлен в знаменателе).

2. Разлагают знаменатель правильной дроби на множители.

3. Правильную рациональную дробь разлагает на сумму простейших методом неопределенных коэффициентов.

4. Интегрируют многочлен и полученные простейшие дроби.

ЛЕКЦИЯ 18

Интегрирование тригонометрических функций.

Рассмотрим некоторые частные случаи интегралов от тригонометрических функций.

I. , n≥m, m≥0, n - чётное,  m - нечётное или n - нечётное, m - чётное.

а) .

 б) .

II. , n≥0, m≥0,  n - чётное,  m - чётное.

Применяются формулы: , .

а)

.

III. Интегралы вида

а)

b)

c)

вычисляются путем применения формул соответственно

.

.

.

IV. Интегралы вида , где R(tgx) - некоторая рациональная функция, вычисляются следующим образом:

.

Пример:

.

Интегралы вида  вычисляются с помощью подстановки, которая называется универсальной тригонометрической подстановкой.

Пример

.

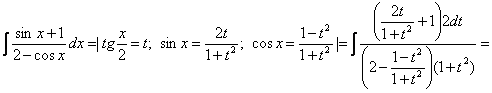
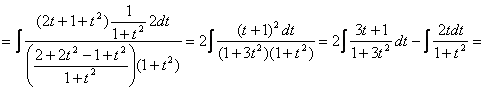
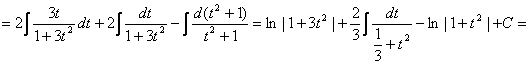
Интегрирование некоторых иррациональных функций.

I. а)Интеграл вида  вычисляется подстановкой .

b)Интеграл вида вычисляется подстановкой , где α=НОК  (m,n,k),   .

Примеры:

1.

.

2.

.

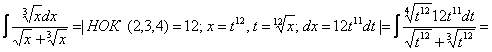
II. Тригонометрические подстановки:

а)  вычисляется с помощью подстановки .

b)  вычисляется с помощью подстановки .

c)  вычисляется с помощью подстановки .

Пример

ЛЕКЦИЯ 19

Определённый интеграл.

Задачи, приводящие к понятию определенного интеграла

1) Задача о вычислении площади криволинейной трапеции.

Рассмотрим фигуру ограниченную сверху непрерывной кривой y=f(x), f(x)≥0, xÎ[a,b], снизу осью ОХ, с боков прямыми х=а, х=b. Такая фигура называется криволинейной трапецией.

Рис. 37.

Поставим задачу о вычислении площади этой криволинейной трапеции. Разобьем отрезок [a,b] на n частей с помощью (n-1) точек деления с абсциссами х₁<х₂<…<х_n-1, полагая х₀=а и х_n=b.

Рис. 38.

Тогда отрезок [a,b] разобьётся на n отрезков [x₀, x₁]; [x₁, x₂];…[x_n-1, x_n]. Через точки деления  проведем прямые параллельные оси OY, тем самым всю криволинейную трапецию разобьём на n малых криволинейных трапеций.

Очевидно, что площадь всей криволинейной трапеции равна сумме площадей всех n малых криволинейных трапеций.

То есть

 ,                                           (50)

где - площадь i-той криволинейной трапеции.

Можно равенство (50) записать в виде

                                                       (51)

Для вычисления площади  поступим следующим образом: в каждом из отрезков [x_i-1, x_i] выберем произвольную точку <<и построим в этой точке ординату f(x_i).

Обозначим основание каждой малой криволинейной трапеции , тогда . Построим на каждом отрезке [x_i-1, x_i] прямоугольник с высотой f(x_i), и площадь малой криволинейной трапеции заменим площадью этого прямоугольника равной  f(x_i)Dх_i. Таким образом, .

Заменив площадь каждой малой трапеции площадью прямоугольника, получим ступенчатую фигуру, площадь которой равна сумме площадей прямоугольников. Площадь этой ступенчатой фигуры даёт приближенное значение площади криволинейной трапеции, таким образом, для площади S криволинейной трапеции получаем приближенное равенство

                        или

                                                     (52)

Обозначим через l наибольшую из длин

.

С уменьшением l точность приближённой формулы (52) увеличивается. Поэтому вполне естественно за точное значение площади S криволинейной трапеции принять предел площади ступенчатой фигуры при условии, что l®0:

.                                            (53)

Таким образом, вычисление площади криволинейной трапеции привело нас к нахождению предела (53).  

2) Задача о работе переменной силы.

Если материальная точка под действием силы , не меняющейся ни по величине, ни по направлению, переместилась на расстояние l в направлении действия силы, то работа силы равна

,                                                     (54)

где F - величина действующей силы.

Рассмотрим теперь случай, когда сила  меняется по величине и сохраняет постоянное направление. Пусть под действием этой силы материальная точка перемещается по прямой, направленной вдоль линии действия силы. Поставим задачу о вычислении работы этой силы .

Примем прямую, вдоль которой перемещается материальная точка за ось ОХ. Далее, пусть начальная и конечная точки пути имеют соответственно абсциссы а и b (a<b). В каждой точке отрезка [a,b] величина силы имеет определенное значение, то есть является некоторой функцией абсциссы: . Эту функцию будем считать непрерывной. Разобьем отрезок  [a,b] на n малых отрезков [x₀, x₁]; [x₁, x₂];…[x_n-1, x_n]. Длины этих отрезков равны Dx_i = x₁-x₀, Dx₂=x₂-x₁, _….. ,Dx_n= x_n- x_n-1.

Работа силы на всём пути [a,b] будет равна сумме работ на каждом малом участке Dx_i:

                                                    (55)

где А - работа на участке [a,b], и DА_i - работа на малом участке.

Выберем в каждом Dx_i точку <<.

Рис. 39.

Будем отрезки Dx_i брать достаточно мелкими, и тогда можем считать, что на каждом таком малом отрезке Dx_i величина силы имеет постоянное значение равное её значению в точке x_i: . В этом предположении работа силы на пути  будет равна согласно формуле (54)

                                                (56)

Но на самом деле сила на отрезке Dx_i не постоянна, поэтому формула (56) даёт лишь приближённое значение работы на малом участке. Таким образом, , а вся работа на отрезке [a,b]

                                                (57)

Это приближенное равенство тем точнее, чем меньше Dx_i. Обозначим . За точное значение работы на всем пути [a,b] примем предел суммы (57) при условии, что l®0:

.                                         (58)

Определенный интеграл.

В каждой из разобранных задач при их решении использовался один и тот же приём: нахождения предела определенного вида сумм. Решение каждой задачи было связано с некоторым действием, производимым над функцией, которая была непрерывна на рассматриваемом отрезке.

Отвлекаясь от конкретной задачи, рассмотрим функцию f(x), непрерывную на отрезке [а,b].

1. Разобьём отрезок [а,b] на n частей точками a=x₀, x₁,…, x_n-1, x_n=b.

2. В каждом из малых отрезков [x_i-1,x_i] выберем точки .

3. Обозначим  и вычислим все произведения  и составим сумму этих произведений. Вычислим

  или  .          (59)

Сумма вида (59) называется интегральной суммой.

1) Обозначим , l называется шагом разбиения.

Пусть число n отрезков разбиения неограниченно растёт и l®0. Если при этом интегральная сумма S_n имеет предел S, который не зависит ни от способа разбиения отрезка [a,b], ни от выбора точек x_i в каждом из малых отрезков, то это число S называется определенным интегралом от функции f(x) на [a,b] и обозначается .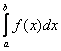

Таким образом, 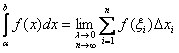.                                                     (60)                                              

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а [a,b]- отрезком интегрирования.

Определение. Определенный интеграл есть число равное пределу вида (60), к которому стремится последовательность интегральных сумм (59), когда шаг разбиения стремится к нулю и число разбиений неограниченно увеличивается.

Возвращаясь теперь к рассмотренным ранее задачам, видим, что:

1) Площадь криволинейной трапеции, ограниченной кривой y=f(x), где f(x)³0, для всех xÎ[a,b] численно равна определенному интегралу от функции y=f(x). В этом и состоит геометрический смысл определенного интеграла;

2) Работа А переменной силы, величина которой F=f(x) равна определенному интегралу от силы. В этом состоит механический смысл определенного интеграла.

Возникает вопрос, при каких условиях существуют определенный интеграл? Ответ даёт теорема существования определенного интеграла.

Теорема. Если функция y=f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке (без доказательства).

Замечания.

1. Для заданной функции y=f(x) и заданного отрезка [a,b] существует бесконечно много интегральных сумм, значения которых зависят от выбора точек деления и от выбора точек x_i.

2. Интегральная сумма (59) не зависит от того, какой буквой обозначен аргумент заданной функции, а, следовательно, и её предел, то есть определенный интеграл не зависит от обозначения переменной: .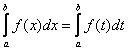

3. Определенный интеграл может существовать для некоторых разрывных функций, ограниченных на отрезке [a,b], имеющих конечное число точек разрыва на этом отрезке.

ЛЕКЦИЯ 20

Свойства определенного интеграла.

1. Постоянный множитель можно вынести за знак определенного интеграла.

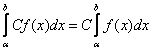, где .

Доказательство

.

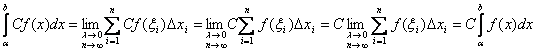2. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых.

.

Доказательство провести самостоятельно.

3. .

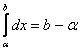Доказательство f(x)=1. Следовательно, .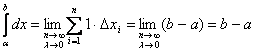

4. Если отрезок интегрирования [a,b] разбить на две части [a,c] и [c,b], то

.

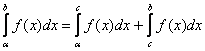Геометрически свойство 4 выражает тот факт, что площадь криволинейной трапеции с основанием [a,b] равна сумме площадей криволинейных трапеций с основаниями [a,c] и [c,b].

5. При перестановке границ интегрирования определённый интеграл меняет знак на противоположный.

.

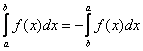6. Определенный интеграл с равными нижним и верхним пределами  равен 0.

.

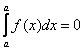7. Если на отрезке [a,b],  f(x)³0, то .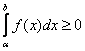

Доказательство. Так как f(x_i)³0  и Dx_i>0, то интегральная сумма .

Следовательно, и предел этой интегральной суммы, при l®0 тоже неотрицателен, то есть

.

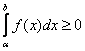8. Если на отрезке [a,b] функции f(x) и j(x) удовлетворяют неравенству , то .

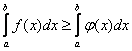Доказательство. Так как , то . Тогда по свойству 7 имеем:

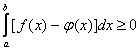,                                         (61)

а по свойству 2 .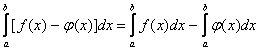

Из неравенства (61) имеем:

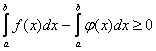, откуда   .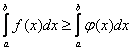

Это свойство имеет простой геометрический смысл: пусть f(x)³j(x)³0 при xÎ[a,b]. Тогда криволинейная трапеция, ограниченная кривой y=f(x), содержит криволинейную трапецию, ограниченную кривой y=j(x), поэтому площадь первой фигуры не меньше площади второй фигуры.

9. Теорема о среднем.

Если функция f(x) - непрерывна на отрезке [a,b], то существует такая точка xÎ(a,b), что

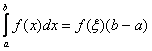.                                      (62)

Доказательство.

Так как f(x) - непрерывна на [a,b], то она достигает на этом отрезке своего наибольшего и наименьшего значения. Обозначим их соответственно через M и m. Тогда для любого xÎ[a,b] выполняется неравенство:

                                            (63)

На основании свойства 7 и 1 получим:

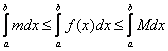  или  .

Но 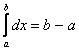, следовательно,

.                               (64)

Разделив обе части (64) на >0, получим

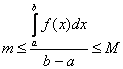                                                (65)

Обозначим

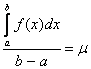,                                                    (66)

где m - некоторое число. Из (65) следует, что m - является промежуточным значением функции между m и M: то есть m£m£M.

Так как непрерывная на отрезке [a,b] функция f(x) принимает все промежуточные значения, то на отрезке [a,b] найдётся токае значение xÎ(a,b), a<x<b для которого  f(x)=m.

Если в (66) вместо m подставить  f(x), то получим

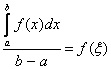                                                (67)

или        

.   

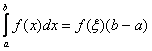Теорема доказана.

Таким образом, определенный интеграл непрерывной функции равен значению подынтегральной функции в некоторой промежуточной точке, умноженной на длину отрезка интегрирования. Эта теорема имеет простое геометрическое истолкование.

Пусть f(x) при xÎ[a,b]. Определенный интеграл 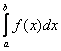 численно равен площади криволинейной трапеции аАСb (рис.). Построим прямоугольник аА₁В₁b с тем же основанием (b-a), что и у криволинейной трапеции и с высотой, равной f(x).

Рис. 40.

Произведение f(x)(b-a) численно равно площади этого прямоугольника. Формула (62) утверждает, что криволинейная трапеция равновелика прямоугольнику с тем же основанием и с высотой, равной ординате кривой в некоторой промежуточной точке x основания.

Значение функции в точке, определенное из формулы (62), называется средним значением функции на отрезке [a,b], то есть .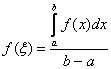

ЛЕКЦИЯ 21

Формула Ньютона-Лейбница.

Пусть f(x) непрерывна на [a,b], тогда она интегрируема на любом отрезке [a,х], где . Рассмотрим функцию

                                                   (68)

Эта функция называется интегралом с переменным верхним пределом. В формуле (68) переменную интегрирования обозначили через t, чтобы не смешивать её с верхней границей х. Значение интеграла от этого не изменится.

Эта функция Ф(х) обладает свойством, выраженным в следующей теореме.

Теорема Барроу. Пусть f(x) - непрерывная функция на отрезке [a,b] и .  Тогда, функция Ф(х) имеет производную на отрезке [a,b] и , то есть .

Доказательство.

Придадим х приращение Dх. Тогда .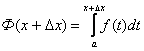

Рассмотрим 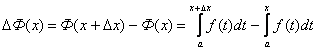                               (69)

Так как 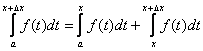 , (по свойству 3).

Тогда равенство (69) примет вид:

К последнему интегралу 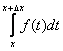  применим теорему о среднем:

< <.

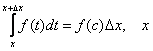Тогда .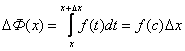

По определению производной .

Так как  f(x) - непрерывна на [a,b], то при Dх®0, х+Dх®х и х<с<х+Dх, то при Dх®0 точка с®х, таким образом, будем иметь .

Теорема доказана.

Эта теорема определяет связь между операциями определенного интегрирования и дифференцирования и показывает, что 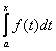есть первообразная для f(x).

Замечание. Из доказанной теоремы следует, что всякая непрерывная функция имеет первообразные, одной из которой является функция .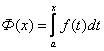

Мы установили, что функция 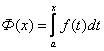 является первообразной для непрерывной подынтегральной функции f(x). Всякая другая первообразная для функции  f(x) отличается от Ф(х) на константу, то есть Ф(х)=F(x)+С, или

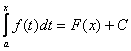                                               (70)

Константу С легко найти, если заметить, что .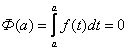

Следовательно, если в (70) подставить х=а, получим 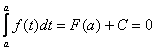. Отсюда С=-F(a). Следовательно,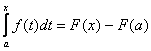

При x=b получаем

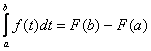                                            (71)

Формула (71) называется формулой Ньютона-Лейбница. Мы видим из (71), что определенный интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.

Замечание: для разрывных функций формула (71) может не иметь места.

ЛЕКЦИЯ  22

Замена переменной в определенном интеграле.

Теорема. Пусть дан 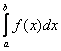, где f(x) - непрерывная на отрезке [a,b]  функция. Перейдем от переменной х к t, полагая x=j(t). Пусть j(a)=a и j(b)=b.

Предположим ещё:

1. Функция j(t) и её производная непрерывны при a£ t£b.

2. При изменении t от a к b значения j(t) не выходят за пределы отрезка [a,b].

Тогда имеет место формула, которая называется формулой замены переменной в определенном интеграле:

.                                      (72)

Пример. Найти .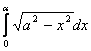

Решение. Полагая , получим . При ; при . Итак, .

Следовательно, применяя формулу замены переменной, найдем

.

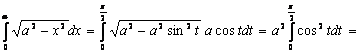
Заметим, что часто вместо замены переменной употребляют обратную замену ; однако при этом необходимо, чтобы функция, обратная функции  существовала, и чтобы для этой обратной функции выполнялись условия, при которых справедлива формула замены переменной (72).

Замечание: при вычислении определенного интеграла по формуле (72) к прежней переменной не возвращаются.

Интегрирование по частям в определенном интеграле.

Пусть u(x) и (x) - непрерывные функции при , и имеют на этом отрезке непрерывные производные.

Тогда .

Проинтегрируем это равенство в пределах от а до b:

.                    (73)

По формуле Ньютона-Лейбница

,

тогда равенство (73) примет вид:

,

откуда получаем формулу

                                        (74)

Эта формула (74) называется формулой интегрирования по частям в определенном интеграле. Следует иметь в виду, что пределы интегрирования относятся к независимой переменной.

Пример.

ЛЕКЦИЯ  23

Геометрические приложения определенного интеграла.

1. Вычисление площади криволинейной трапеции.

Пусть дана криволинейная трапеция, ограниченная графиком , тогда площадь этой криволинейной трапеции вычисляется по формуле 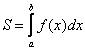, где f(x) непрерывная на отрезке [a,b]. Если f(x)<0, то .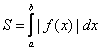

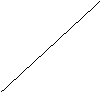
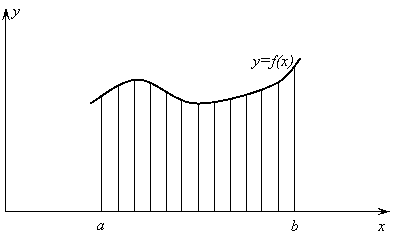
Рис. 41.

2. Вычисление площади плоской фигуры.

Пусть плоская фигура ограничена кривыми  и , причём при , тогда .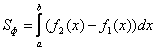

Рис. 42.

3. Вычисление площади криволинейного сектора в полярных координатах.

Пусть дан криволинейный сектор ОАВ, ограниченный радиус-векторами  и  и кривой, уравнение которой задано в полярных координатах: . При этом предположим, что  - непрерывная функция для всех , удовлетворяющих условию: . Тогда

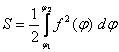,                                            (75)

φ=φ₁

φ=φ₂

r=f(φ)

Рис. 43.

Таким образом, площадь криволинейного сектора, ограниченного кривой , лучами  и вычислим по формуле (75).

4. Вычисление длины дуги плоской кривой.

Пусть кривая задана уравнением , где  - непрерывная функция, имеющая непрерывную производную при всех . Тогда дуга АВ этой кривой имеет длину, которая вычисляется по формуле:

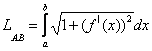                                             (76)

Рис. 44.

Если кривая задана параметрическими уравнениями ,

то длина дуги вычисляется по формуле

                                          (77)

Длина дуги АВ кривой, заданной уравнением в полярных координатах ,  (функция  и  непрерывны при ), вычисляется по формуле

                                    (78)

5. Объём тела вращения.

Рассмотрим криволинейную трапецию с основанием [a,b], ограниченную непрерывной функцией . Будем вращать эту трапецию вокруг оси ОХ. Тогда объём полученного тела вращения вычисляется по формуле

                                           (79)

Рис. 45.

ЛЕКЦИЯ  24

Несобственные интегралы с бесконечными пределами (I рода)

При определении определенного интеграла мы предполагаем, что областью интегрирования является конечный отрезок [a,b]. Если мы теперь рассмотрим функцию , определенную на интервале [a;+¥], то даже, если f(x) непрерывна, то обычное определение интеграла становится неприемлемым, так как  в этом случае нельзя говорить об интегральных суммах, потому что при любом разбиении интервала [a;+¥] на конечное число частей, одна из этих частей будет бесконечно большой. Обобщим понятие определенного интеграла на случай, когда область интегрирования - бесконечная.

Рассмотрим , функция  непрерывная на отрезке >1 и .

При , т.е. .

Этот предел будем называть несобственным интегралом.

Рассмотрим общий случай. Пусть функция  непрерывна при . Тогда на любом конечном отрезке [a,b], > 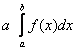существует и его можно вычислить по формуле Ньютона-Лейбница.

Определение. Если существует конечный предел 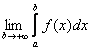, то этот предел называют несобственным интегралом от функции f(x) на интервале [a;+¥]  и обозначают 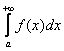, то есть

                                       (80)

В этом случае говорят, что несобственный интеграл 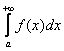 существует или сходится. Если предел (80) не существует, или равен бесконечности, то говорят, что несобственный интеграл расходится. Аналогично определяется

.                                       (81)

 Несобственный интеграл с двумя бесконечными пределами определяется формулой

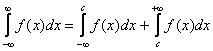,                             (82)

где <<.

Интеграл (82) существует только тогда, когда существует каждый из интегралов  и .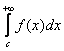

Если y=f(x) непрерывна и положительна на бесконечном интервале, и если 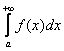существует, то геометрический смысл его состоит в том, что 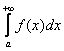 выражает площадь бесконечной криволинейной трапеции, ограниченной кривой y=f(x), бесконечным интервалом [a;+¥] и прямой х=a.

y

x

a

y=f(x)

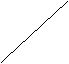
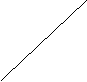
Рис. 46.

Пример. Установить, при каких значениях α интеграл   сходится и при каких расходится.

Решение. Так как (при α≠1)

, то .

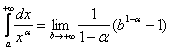Следовательно, относительно рассматриваемого интеграла можно сделать следующие выводы:

если α>1, то 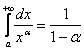 ,  интеграл сходится;

если α<1, то 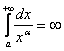 ,  интеграл расходится;

при α=1 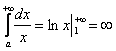интеграл расходится.

В общем случае  при α≤1 расходится; при α>1 сходится.

Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение. Для этого могут быть полезными следующие теоремы.

Теорема 1. Если для всех х (х≥а) выполняется неравенство и если 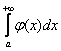 сходится, то  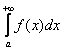также сходится, при этом

 ≤ .

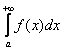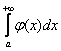Теорема 2. Если для всех х (х≥а) выполняется неравенство , причём 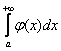 расходится, то расходится и интеграл .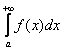

Теорема 3. Если интеграл  сходится, то сходится и интеграл .

Аналогичные признаки справедливы и для .

Несобственные интегралы от разрывных функций (II рода).

Пусть функция y=f(x) определена и непрерывна при , а при терпит разрыв. В этом случае определение интеграла от функции f(x) на отрезке [a,b] как предела интегральной суммы неприменимо, так как предел может и не существовать.

Рассмотрим пример

,

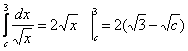при с®0 имеем .

Этот предел называется несобственным интегралом на  от функции , его обозначают .

Таким образом, .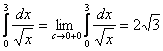

Обобщим это понятие.

Пусть y=f(x) разрывна при  и непрерывна на . Если при определенный интеграл 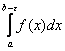 имеет конечный предел, то этот предел называют несобственным интегралом от разрывной функции и обозначается 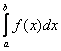, то есть

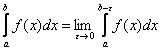                                        (83)

В этом случае говорят, что несобственный интеграл 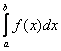 существует или сходится. Если предел в (83) не существует или равен бесконечности, то несобственный интеграл расходится. Если  f(x) разрывна при , то

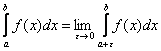.                                       (84) 

Если f(x) разрывна при , где <<, то отрезок [a,b] разобьём на два отрезка [a,c] и [c,b], и тогда

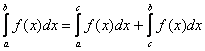.                             (85)

Если оба несобственных интеграла в (85) сходятся, то и 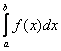- тоже сходится.

Пусть f(x) разрывна и при x=a и при x=b, тогда выберем внутри отрезка [a,b] произвольную точку с, , тогда

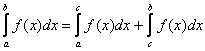.                                  (86)

И аналогично, если оба интеграла в правой части (86) сходятся, то и 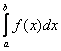- тоже будет сходится.

Для определения сходимости несобственных интегралов от разрывных функций и оценки их значений часто могут быть применены теоремы аналогичные теоремам для оценки интегралов с бесконечными пределами.

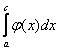Теорема 1. Если на отрезке [a,c] функции  и  разрывны в точке с, причём во всех точках этого отрезка выполнены неравенства , и  сходится, то и 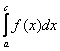 также сходится.

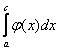Теорема 2. Если на отрезке [a,c] функции  и  разрывны в точке с, причём во всех точках этого отрезка выполнены неравенства , и  расходится, то и 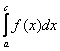 также расходится.

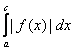 Теорема 3. Если функция  - функция знакопеременная на отрезке [a,c], разрывная только в точке с, и несобственный интеграл  от абсолютной величины этой функции сходится, то сходится также интеграл 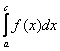 от самой функции.

В качестве функций, с которыми удобно сравнивать функции, стоящие под знаком несобственного интеграла, часто берут . Легко проверить, что 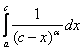 сходится при α<1, расходится при α≥1.

Это же относится и к интегралам 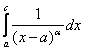.
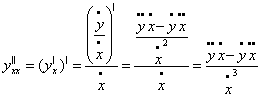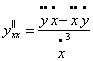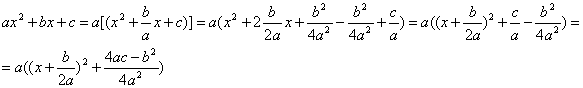
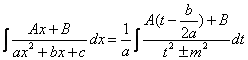