УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Кафедра высшей математики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для выполнения самостоятельных работ по дисциплине
«Высшая математика» (часть II)
для студентов дневного отделения.
Ташкент 2005
Предисловие
Важным фактором усвоения высшей математики и овладение её методами является самостоятельная работа студентов. Система специально подобранных задач активизирует самостоятельную работу студентов и спосоствует более глубокому изучению курса высшей математики.
Методические указания содержат теоретические сведения, систематизированый набор задач. Приведены подробные решения типовых примеров; программа курса по темам: «Неопределённый и определённый интегралы. Приложения определённого интеграла. Несобственный интеграл»
«Функции нескольких переменных», «Дифференциальные уравнения», «Операционное исчесление». Приводится список литературы, изучение которой способствует успешной самостоятельной работе.
Методические указания могут быть полезны студентам как дневного, так и заочного отделений.
Программа курса «Высшая математика» и вопросы итогового контроля для студентов з/о (телекоммуникация, информатика). Часть II.
- Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов.
- Замена переменных и формула интегрирования по частям в неопределенном интеграле.
- Методы интегрирования: дробно-рациональной функции, тригонометрических выражений, иррациональностей.
II. Определенный интеграл и приложения. Несобственные интегралы.
1. Определение и свойства определенного интеграла. Теорема о среднем. Теорема существования определенного интеграла.
- Интеграл с переменным верхним пределом. Теорема о производной от интеграла с переменным верхним пределом по этому пределу. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
- Вычисление площади плоской фигуры, объемов тел и длина дуги плоской кривой с помощью определенного интеграла.
- Несобственные интегралы I и II рода. Признаки сходимости несобственных интегралов.
III. Функции нескольких переменных.
1. Определение функции нескольких переменных. Область определения. Предел. Непрерывность.
2. Частные производные I порядка. Частные и полный дифференциал. Частные производные и дифференциалы высших порядков. Теорема о смешанных производных.
3. Производная сложной функции. Полная производная. Дифференцирование функции, заданной неявно.
4. Экстремум функции двух переменных. Нахождение наибольшего и наименьшего значений функции в замкнутой области.
IV. Дифференциальные уравнения.
1. Дифференциальные уравнения, основные понятия и определения. Задачи Коши для дифференциального уравнения I порядка.
2. Дифференциальные уравнения I порядка: с разделяющимися переменными, однородные, линейные, Бернулли.
3. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
4. Линейные дифференциальные уравнения высших порядков. Теорема о структуре общего решения линейного дифференциального уравнения. Определитель Вронского.
5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод вариации произвольных постоянных. Нахождение частного решения линейного уравнения с постоянными коэффициентами по правой части специального вида.
6. Системы обыкновенных дифференциальных уравнений.
V. Операционное исчисление.
1. Преобразование Лапласа. Свойства. Теоремы: линейности, подобия, смещения, запаздывания, дифференцирования и интегрирования оригиналов и изображений. Свертка оригиналов. Интеграл Дюамеля.
2. Операционный метод решения линейных дифференциальных уравнений и систем линейных дифференциальных уравнений с постоянными коэффициентами.
F¢(x)= f(x)
или ![]() f (x) dx = F(x) + C
f (x) dx = F(x) + C
F(x) – первообразная для f (x), C – постоянная
Свойства неопределенного интеграла
10.
![]() f (x)
f (x)
20. d ![]() f (x) dx
f (x) dx
30. ![]() dF(x)= F(x) + C
dF(x)= F(x) + C
40.
![]() K f (x)
dx = K
K f (x)
dx = K![]() f (x)
dx, K
–постоянная
f (x)
dx, K
–постоянная
50. ![]()
![]() dx =
dx = ![]() f (x) dx ±
f (x) dx ± ![]() g(x) dx ±
g(x) dx ± ![]() h(x) dx
h(x) dx
60. ![]() f (x) dx = F(x) + C и u= j(x), то
f (x) dx = F(x) + C и u= j(x), то ![]() f(u)du = F(u) + C
f(u)du = F(u) + C
Таблица основных интегралов
1.
![]() dx = x
+C
dx = x
+C
2.
![]() xn dx=
xn dx= ![]() , n ¹ -1, n
– постоянная
, n ¹ -1, n
– постоянная
3.
![]()
4.
![]()
![]() =
= ![]()
5.
![]()
6.
![]() , k – постоянная
, k – постоянная
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
1.1. Непосредственное интегрирование и замена переменной в неопределенном интеграле.
1.
![]()
2.
![]()
1.2. Интегрирование по частям.
![]()


1.3. Интегрирование рациональных дробей.
Выделение полного квадрата из квадратного трёхчлена.
ax2 + bx + c = a
(x+![]()
![]()
![]()
![]()
![]()
Интегралы
![]() называются
интегралами от простейших дробей. Интегрирование дробно – рациональных функций
называются
интегралами от простейших дробей. Интегрирование дробно – рациональных функций ![]()
а) Если n ³ m , тогда
![]() где
где
![]() -
неправильная дробь.
-
неправильная дробь.
L n –m
– целая часть под интегральной
дроби, она выделяется делением числителя на знаменатель по правилу деления
многочлена на многочлен, а ![]() - правильная рациональная дробь.
- правильная рациональная дробь.
б)
Если n < m, тогда ![]() -
правильная рациональную дробь. Любая правильную рациональную дробь
-
правильная рациональную дробь. Любая правильную рациональную дробь ![]() ,
знаменатель которой разложен на линейные и квадратичные множителем вида:
,
знаменатель которой разложен на линейные и квадратичные множителем вида:
![]() где трехчлены
где трехчлены ![]() имеют
комплексные сопряжённые корни, можно представить в виде суммы простейших дробей
следующим образом:
имеют
комплексные сопряжённые корни, можно представить в виде суммы простейших дробей
следующим образом:
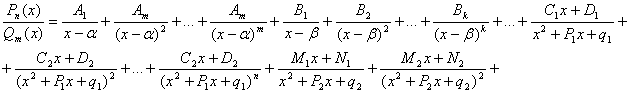
![]() (1)
(1)
где Ai, Bi, Mi, Ci, Di, … - некоторые числа. В этом разложении для каждого множителя в разложении знаменателя Qm(x) записывается столько простейших слагаемых дробей, каково его кратность (m, k, n, s, …). Неопределенные коэффициенты Ai, Bi, Mi, Ci, Di, … находится методом сравнения, либо методом подстановки.
После разложения на элементарные дроби по формуле (1) интегрирование всякой правильной рациональной дроби сводится к нахождению интегралов вида:
1) 
2) ![]() (m
¹1),
(m
¹1),
3) ![]() (р2 – 4q < 0),
(р2 – 4q < 0),
4) ![]() (р2 – 4q < 0) - этот
интеграл берется проще с помощью тригонометрических подстановках.
(р2 – 4q < 0) - этот
интеграл берется проще с помощью тригонометрических подстановках.
1.5. Интегрирование тригонометрических функций.
1)
Интегралы вида ![]() :
:
а) если показатель степени n – нечет положительный, m – любые число, то применяется подстановка sinx = t;
б) если показатель степени m – нечетный положительный, n – любые число, то применяется подстановка cosx = t;
в) если оба показатель степени m и n – четные положительные числа, то следует применять формулы понижения степени:
sin2x = ![]() cos2x=
cos2x=![]()
![]()
г) если сумма показателей (n+m) –
нечетная, m![]() , n
, n![]() , то
применяется подстановка tgx = t (или ctgx = t),
x = arctg t,
, то
применяется подстановка tgx = t (или ctgx = t),
x = arctg t,
sinx = 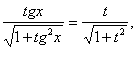
cosx = ![]() dx =
dx = ![]()
2)
Интегралы вида ![]() где m > 0, целая,
берутся подстановкой
где m > 0, целая,
берутся подстановкой
tgx = t, x
= arctgt; dx = ![]()
3)
Интегралы вида ![]() где R – рациональная функция, приводится к интегралам от
рациональных функций с помощью универсальной подстановки tg
где R – рациональная функция, приводится к интегралам от
рациональных функций с помощью универсальной подстановки tg![]() В результате этой подстановки имени
В результате этой подстановки имени
sinx =  cosx =
cosx = 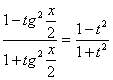 ,
,
![]() dx=
dx=![]() .
.
Таким образом
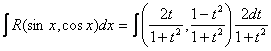
4)
Интегралы ![]() и
и ![]() берутся с помощью тригонометрических
формул:
берутся с помощью тригонометрических
формул:
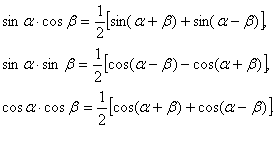
![]() 1.6. Интегрирование некоторых иррациональных функций.
1.6. Интегрирование некоторых иррациональных функций.
![]()
1.
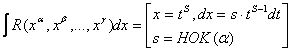
где НОК – наименьшее общее кратное.
2.
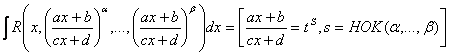
3. Тригонометрические подстановки.
![]() а)
а) 
![]() б)
б) 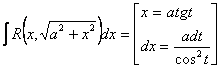
![]()
![]() в)
в) ![]()
![]()
г) ![]()
II. Несобственные интегралы.
I - род, это интегралы с бесконечными пределами.
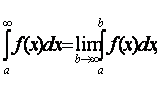


II – род, подынтегральная функция имеет бесконечный разрыв.
![]()
![]()
III. Приложения определенного интеграла.
а) Вычисление площадей плоских фигур.
|
|
![]()
![]() а)
а) ![]()

 б)
б) ![]()
б) Вычисление объём тема вращения.
|
|
|
|
|
|
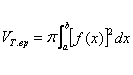 вокруг оси ОХ
вокруг оси ОХ![]()
![]() вокруг оси ОУ
вокруг оси ОУ
в) Вычисление длины дуги плоской кривой.
Если ![]()
Если 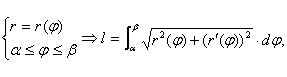
Если 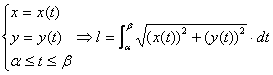
1.21. Вычислить неопределенные интегралы.
а)
![]()
К подынтегральной функции применим формулу ![]() .
.
Следовательно, имеем
![]() .
.
Чтобы
вычислить интеграл ![]() , применим формулу интегрирования по
частям. Положим u=x, dv=cosxdx, тогда du=dx
, применим формулу интегрирования по
частям. Положим u=x, dv=cosxdx, тогда du=dx ![]() .
Отсюда
.
Отсюда
![]()
Таким образом ,
![]() .
.
б)
![]()
Выделяем полный квадрат из квадратного трёхчлена 9+6x-3x2 =-3(x2 –2x-3)=
![]() и вводим новую перемен t = x-1, тогда получим: dx = dt и
и вводим новую перемен t = x-1, тогда получим: dx = dt и
![]() .
.
Первый интеграл преобразуем к табличному, умножая и деля на –2 и заменяя –2 tdt через d(u – t2), а второй табличный, следовательно:
 Возвращаясь
к переменной х, имеем
Возвращаясь
к переменной х, имеем
![]()
в)
![]()
Выделим из подынтегральной неправильной дроби целую часть, деля числитель на знаменатель:
 2x5+6x3+1 x4+3x2
2x5+6x3+1 x4+3x2
2x5+6x3 2x
1
![]()
В
интеграле ![]() подынтегральную функцию
представляем в виде суммы элементарных дробей следующим образом:
подынтегральную функцию
представляем в виде суммы элементарных дробей следующим образом:
![]()
Для определения коэффициентов А, В, С, Д применим метод сравнения коэффициентов при одинаковых степенях «х».
1= Aх(x2+3)+B(x2+3)+(CX+D)x2 =
(A+C)x3+(B+D)x2+3Aх+3B.
![]() x5 A+C
=0,
C =0,
x5 A+C
=0,
C =0,
x4 B+D =0,![]() D = -
D = - ![]() ,
,
x1 3A
=0,
A =0,
x0 3B
=1
B =![]() .
.
Следовательно:
![]()
Подставляя под интеграл и интегрируя элементарных дроби, получим:
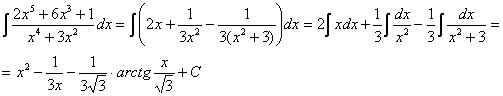
г)
![]()
Подынтегральная функция зависит от sinx и cosx, применим подстановку
tg![]()
![]() тогда
тогда
![]()
![]()
![]() и
и
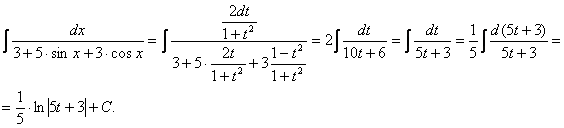
Возвращаясь к старой переменной, получим
![]() .
.
д)
![]()
Чтобы вычислить данный интеграл, найдём S= HOK (2;3) =6, значить
1+x =t6, тогда dx = 6t5 dt и
![]()
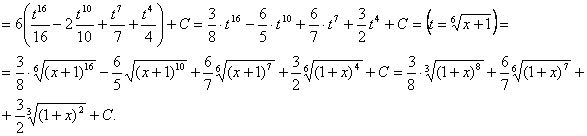
Вычислить несобственные интегралы.
а)
![]()
Найдем
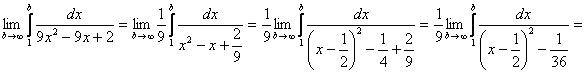
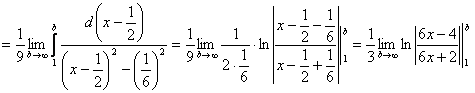 =
=
=![]() т.е.
т.е.
несобственный интеграл сходится.
б)
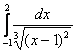
Здесь подынтегральная функция имеет бесконечный разрыв точке x=1, лежащей внутри интегрирования [-1;2]. Поэтому, согласно определения
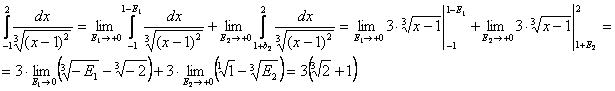 Несобственный интеграл сходится.
Несобственный интеграл сходится.
3.21. Вычислить площадь фигуры ограниченной кривой.
![]() и прямыми y=0, x=0,
и прямыми y=0, x=0, ![]()
Площадь фигуры будем вычислять по формуле:
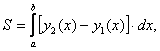 где
где
![]() y1=0
.Имеем
y1=0
.Имеем


кв.ед.
4.21. Вычислить объём фигуры, образованной вращением вокруг оси ОХ фигуры, ограниченной кривой y2=(x-1)3 и прямой x=2.
|
|
|
|
|
|
Объём фигуры найдем по формуле
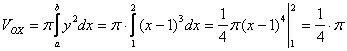 (куб.ед.)
(куб.ед.)
5.21. Вычислить длину дуги кривой.
![]()
![]()
Так как уравнение кривой задано в параметрическом виде, длину её дуги будем искать по формуле
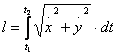
Найдем производные по параметру t:
![]()

Следовательно

III. Функции нескольких переменных. Область определения.
Предел. Непрерывность.
Функцией двух перемен называется правило, по которому каждой паре
действительных чисел (х,у)![]() Д, соответствует одно
определенное действительное значение переменной
Д, соответствует одно
определенное действительное значение переменной ![]() .
.
При этом х и у называются независимыми переменными (или аргументами), z – зависимой переменной (или функций), а множество Д – область определения, а Е – множество значений функции. Записываются: z= =f(x; y).
Графиком функции двух переменных z=f(x; y) в прямоугольной системе координат в пространстве является некоторая поверхность.
Аналогично определяется функция любого числа переменных x= f(x, y, z,.. ,t ).
Окрестностью точки P0(x0;y0) Расм
 называется внутренность круга с
называется внутренность круга с
центром в этой точке. Если радиус
круга
равен ![]() , то говорят
, то говорят
![]() - окрестность точки. Очевидно,
- окрестность точки. Очевидно,
что любая точка P(x;y), принадлежащая
![]() - окрестность точки P0(x0;y0), находится
- окрестность точки P0(x0;y0), находится
от
этой точке на расстоянии меньшим ![]() .
.
Определение. Число А называется пределом функции двух переменных z=f(x;y)= f(P) при Р®Р0
, если для любого числа Е>0 найдется такая ![]() - окрестность
точки P0(x0;y0), что для
любой точки P(x;y) этой окрестности (за исключением, быть может, точки P0)
имеет место неравенство
- окрестность
точки P0(x0;y0), что для
любой точки P(x;y) этой окрестности (за исключением, быть может, точки P0)
имеет место неравенство
![]() <Е или
<Е или
![]() <Е,
<Е,
Записывают ![]() или
или ![]()
Функция двух переменных называется бесконечно малой при Р®Р0 ,если ее предел равен нулю,
то есть ![]() .
.
Определение. Функция двух переменных z=f(x;y)= f(P) называется непрерывной в точке Р0 , если она определена в этой точки и ее окрестность и
![]() или
или ![]() .
.
Точка Р0 называется точкой непрерывности этой функции.
Если в точке Р0 функция неопределена, или ![]() то Р0
называется точкой разрыва.
то Р0
называется точкой разрыва.
Производные и дифференциалы функции нескольких переменных.
Для функции двух переменных z=f(x,y) зафиксируем у , положив у=у0.
разность ![]() называется частным по х
функции z=f(x,y) в точке P0(x0,,y0),а если зафиксировать х положив х=х0,
то разность
называется частным по х
функции z=f(x,y) в точке P0(x0,,y0),а если зафиксировать х положив х=х0,
то разность ![]() называется частным приращением по
у для этой функции в точке P0(x0,,y0).
называется частным приращением по
у для этой функции в точке P0(x0,,y0).
Определение. Частной производной от функции z=f(x,y) по независимой переменной х называется производная
![]()
Частной производной по у называется производная
![]() ;
;
При вычисления частных производных применяются правило и формулы дифференцирования, справедливые для дифференцирования функции одного переменного. Во всех этих правилах и формулах при нахождении частной производной по какому-либо аргументу все остальные аргументы считаются постоянными.
Пример. Найти частных производные функции z=f(x,y)= х2+у3-3ху+5
Решение .

Полным приращением функции z=f(x,y) в точке P0(x0;y0) называется разность ![]() где Δх
и Δу
приращения аргументов функции.
где Δх
и Δу
приращения аргументов функции.
Функции z=f(x,y) называется дифференцируемой в точке P(x;y), если в этой точке полное приращение, представило в виде
![]() (1)
(1)
где
Δх и Δу приращение аргументов х и у в
некоторой точке P(x;y), А и В постоянные, независящие от Δх и
Δу, ![]() - бесконечно малая более высокого
порядка, чем расстояния
- бесконечно малая более высокого
порядка, чем расстояния ![]()
![]() между точками P(x;y) и
между точками P(x;y) и ![]() то
есть
то
есть
![]()
Определение. Главная часть приращения функции t=f(x,y) линейно относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается dz.
Из определения имеем
![]() (2)
Величины А и В не зависят от Δх и Δу,но зависят от
точки P(x;y), в которой этот дифференциал рассматривается,
то есть является функцией от
(2)
Величины А и В не зависят от Δх и Δу,но зависят от
точки P(x;y), в которой этот дифференциал рассматривается,
то есть является функцией от
х и у.
Теорема. Если функция z=f(x,y) в точке P(x ,y) дифференцируемо,
то она имеет в точке первые частые производные ![]() и
и ![]() причем,
причем,
![]()
![]()
Дифференциалы независимых переменных совпадают с их приращением, то есть ![]() .
(3)
.
(3)
На основании теоремы (2) и (3), получаем формулу для вычисления полного дифференциала:
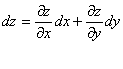
Аналогично определяется частные производные первого порядка и полный дифференциал функции трех переменных.
Частные производные функции нескольких переменных являются функциями тех же переменных. Эти функции могут иметь частные производные, которые называются частными производными второго порядка.
Функции двух переменных z=f(x,y) имеет четыре частных производных второго порядка
![]()
![]()
![]()
![]()
![]()
Аналогично определяются и обозначаются частные производные третьего и более высокого порядка.
Частная производная второго порядка и более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной:
![]() и т.д.
и т.д.
Теорема. Две смешанные частные производные одной и той же функции, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны.
Таким образом: ![]()
![]() и
т.д.
и
т.д.
Дифференциалом второго порядка от функции z=f(x,y) называется дифференциал от ее полного дифференциала, то есть: d2z = d(dz).
В общем случае: dnz = d(dn-1z).
Полный дифференциал второго порядка вычисляется по формуле:
![]()
вообще имеет место символическая формула:
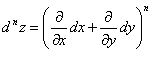
Пример. Найти частные производные второго порядка функции z=3cos(x2+y2).
Решение. Для функции двух переменных z=f(x,y) могут быть указаны четыре частные производные второго порядка, а именно:
![]()
![]()
![]()
![]()
Находим эти частные производные:
![]()
![]()
![]()
![]()
![]()
![]()
Экстремум функции двух переменных.
Пусть функция двух переменных z=f(x,y) задано в некоторой области D.
Определение. Функция двух переменных z=f(x,y)=f(Р0) имеет в точке P0(x0;y0) из области D максимум (минимум), если существует токая окрестность этой точки, что для всех точки P(x ,y) из этой окрестности, отличных от точки P0 выполняется неравенство.
f(P0) > f(P) (f(P0)< f(P)).
Точка P0 , в которой z=f(Р) имеет максимум (или минимум) называется точкой максимума (или минимума). Общее название для максимума и минимума – экстремум.
Теорема 1(необходимый признак существования экстремума). Если P0(x0;y0) есть точка экстремума функции z=f(x,y),
то
 в предложением, что
указанные производные существуют в этой точке P0(x0;y0).
в предложением, что
указанные производные существуют в этой точке P0(x0;y0).
Точки из области определения функции двух переменных, в которых первые частные производные равны нулю, или не существуют, называется критическими точками этой функции.
Из теоремы 1 следует, что точки экстремума функции искать среди ее критических точек. Однако не всякая критическая точка будет являться точкой экстремума, т.е. теорема 1 не является достаточным признаком.
Теорема.
Пусть ![]()
![]()
![]()
![]() и
и
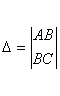
тогда, если:
1) D > 0, то f(x0,y0)=zmax при А< 0,
f(x0,y0)=zmin при А> 0.
2) D < 0, то экстремума нет в критической точке P0(x0;y0)
3) D = 0, то экстремума может быть, а может и не быть (сомнительной случай).
Пример. Найти экстремумы функции z = 2x3-xy2+5x2+y2.
Решение.
Находим первые частные производные z![]() = 6x2-y2+10x,
= 6x2-y2+10x,
z![]() =-2xy+zy. Приравнивая эти производные нулю, после элементарных
преобразования приходим к системе уравнений:
=-2xy+zy. Приравнивая эти производные нулю, после элементарных
преобразования приходим к системе уравнений:
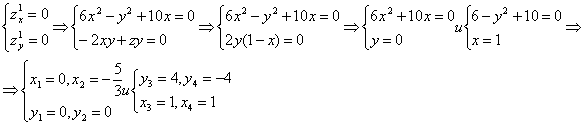
Р1 (0;0), Р2 (![]() ),
Р3 (1;4) и Р (1;-4).
),
Р3 (1;4) и Р (1;-4).
Теперь найдем второе частные производные.
![]()
![]()
![]()
1) Р1 (0; 0).
А = 10, В = 0, С = 2.
D = АС – В2 = 20 > 0,А = 10 > 0. Р0 (0; 0) – точка минимума, а zmin = 0.
2)
Р2 (![]() )
)
А = 12![]() В=0
В=0
С = -2 ![]()
![]() < 0, в точке Р2
экстремум нет.
< 0, в точке Р2
экстремум нет.
3) Р3 (1;4)
А = 12 + 10 = 22, В = - 8, С = -2. 1 + 2 = 0
D = АС – В2 = 22 . 0 – (- 8)2 = - 64 < 0, в точке Р3 экстремум нет.
4) Р4 (1;-4)
А = 12 +10 = 22, В = 8, С = - 2 + 2 = 0
D = АС – В2 = -64 < 0, в точке Р4 экстремум нет.
Итак, данная функция имеет экстремум в точке P1(0; 0) – минимум
f (P1) = 0.
IV. Дифференциальные уравнения.
Уравнения с разделяющие переменным.
Дифференциальное уравнение первого порядка P (x; y)dx + Q (x; y)dy = 0 называется уравнением с разделяющимися переменными, если функции
P (x; y) и Q (x; y) разлагаются на множители, зависящие каждый только от одной переменной, то есть имеет вид
![]() (1)
(1)
Разделив переменные уравнение (1) можно привести к виду
![]()
Почленном интегрируя получим общий интеграл
![]()
Примеры. Найти общие интегралы дифференциальных уравнений
1. (x+1)3dy - (y-2)2dx = 0
Разделим переменные в уравнении разделив на (x+1)3(y-2)2.
![]()
Почленном интегрируя, получим:

или ![]()
![]()
2.
![]() .
.
Разрешим уравнение относительно у1, получим
![]() .
.
Выразим призводную через дифференциалы переменных
![]()
Разделим переменные
![]()
Интегрируя находим общий интеграл

![]()
Однородные уравнения первого порядка.
Функция f(х;у) называется однородной порядка n, если
f(tx; ty) = tn
f(x; y).
Дифференциальное уравнение у1 = f(х;у) называется однородным, если функция f(х;у) является однородной функцией порядка n = 0, т.е.
f(tx; ty) = f(x; y). (2).
Однородное уравнение приводится к уравнению с разделяющимися переменными
посредством замены ![]() где u = u(x).
где u = u(x).
Примеры. Проинтегрировать уравнения.
1.
![]() .
.
Разрешим уравнение относительно производной

Проверим выполнение условия (2).
![]()
Вводим функцию u(x), пологая ![]()
![]() тогда
тогда
![]() и
подставим в уравнение.
и
подставим в уравнение.

![]() или
или ![]()
Разделим переменные, получим
![]()
Интегрируя, найдем:
![]()

Исключая
вспомогательную функцию u (u = ![]() ),получим
),получим
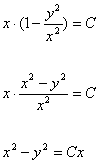
![]() - общий интеграл заданного дифференциального
уравнения.
- общий интеграл заданного дифференциального
уравнения.
2.
![]()
Установим, что данное уравнение - однородное:
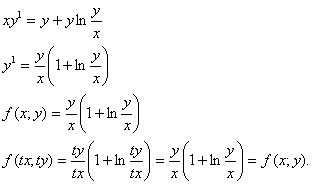
Положим
![]()
![]() и подставим в уравнение
и подставим в уравнение

Разделим переменные

и интегрируем
![]()
![]()
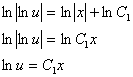
![]() или
или ![]()
Отсюда
![]()
Линейные уравнения первого порядка и уравнения Бернулли.
Уравнение вида
![]() (3)
(3)
где P(x) и Q(x) известные функции от х называются линейными.
Путем замены ![]() где
где
![]() и
и
![]() вспомогательные
функции уравнение (3) сводится к двум уравнениями с разделяющимися переменными
относительно каждой из вспомогательных функций.
вспомогательные
функции уравнение (3) сводится к двум уравнениями с разделяющимися переменными
относительно каждой из вспомогательных функций.
Уравнение вида
![]() (4)
(4)
называется уравнением Бернулли. Разделим обе части (4) на уn, получим
![]()
Обозначим
![]() где
где
![]()
тогда
![]()
И уравнение примет
![]() (5).
(5).
Уравнение (5) это линейное уравнение.
Примеры. Решить дифференциальные уравнения.
1.
![]()
Это линейное уравнение. Полагаем ![]() тогда
тогда ![]() и уравнение преобразуется к виду
и уравнение преобразуется к виду
![]() или
или
![]()
Так как одну из вспомогательных функций u или
v можно
взять произвольно, то выберем в качестве v такой частный интеграл уравнения ![]()
Тогда для отыскания функции u решим
уравнение ![]()
Решим
первое из этих уравнений ![]() Разделим переменные
Разделим переменные

При
интегрируем обе части, получим ![]()
![]() отсюда
получим простейший частный интеграл при С=1:
отсюда
получим простейший частный интеграл при С=1:
![]()
подставим
полученное v во второе уравнение, получим
![]() или
или ![]() Интегрируя,
получим
Интегрируя,
получим ![]() Тогда
Тогда ![]() или
или ![]()
2. х2у2у1+ху3 = 1.
Разделим
обе части на х2у2, получим ![]() Это
уравнение Бернулли. Разделим обе части на у-2.
Это
уравнение Бернулли. Разделим обе части на у-2. ![]() и
обозначим у3 = z.
Тогда 3у2у1 = z1 и
и
обозначим у3 = z.
Тогда 3у2у1 = z1 и ![]() .
После замены получим уравнение
.
После замены получим уравнение ![]() , которое является линейным
относительно функции z. Положим
, которое является линейным
относительно функции z. Положим ![]()
![]() получим
получим
![]() перепишем его в виде
перепишем его в виде ![]() .(*)
.(*)
Решим дифференциальное уравнение
![]()
![]()
![]()
Интегрируя, найдем ![]() При с = 1, простейший
частных интеграл будет
При с = 1, простейший
частных интеграл будет ![]() После подстановки в
уравнение (*) , получим
После подстановки в
уравнение (*) , получим ![]() откуда
откуда ![]() а
а
![]() .
В результате получим решение уравнения (*)
.
В результате получим решение уравнения (*)
![]() или
или
![]()
Возвращаясь
к функции у, получим ![]() .
.
Уравнения высших порядков, допускающие понижения порядка.
1.
Уравнение n–го порядка ![]() решается
последовательным интегрированием. После n кратного интегрирования, получаем общие решение это
уравнения в виде
решается
последовательным интегрированием. После n кратного интегрирования, получаем общие решение это
уравнения в виде
![]()
2.
Уравнение 2-го порядка ![]() решается подстановкой
решается подстановкой ![]()
![]()
3.
Уравнение 2-го порядка ![]() решается подстановкой
решается подстановкой ![]()
![]()
Примеры. Решить уравнения.
1.
![]()
Умножим
обе части этого уравнения на ![]() и интегрируя получим
и интегрируя получим
![]() или
или
![]()
Умножая
последнее уравнение на ![]() и интегрируя, получим
и интегрируя, получим
![]() или
или
![]()
Умножая
последнее уравнение на ![]() и интегрируя, получим решения
заданного уравнения.
и интегрируя, получим решения
заданного уравнения.
![]() или
или
![]()
2.
![]()
Положим
![]()
![]() получим
получим
![]() Разделим переменные и
проинтегрируем
Разделим переменные и
проинтегрируем ![]()
![]() .
.
Откуда
![]() или
или ![]() . Заметив р через
. Заметив р через ![]() ,
получим уравнение
,
получим уравнение
![]() или
или
![]()
Интегрируя, найдем общее решение заданного уравнения
![]() .
.
3.
![]() если
если ![]()
![]()
Положим
![]()
![]() получим
получим
![]() или
или
![]()
Это
уравнение Бернулли. Разделим на ![]() , получим
, получим
![]() и положим
и положим ![]() , тогда
, тогда
![]() и
и
![]() .
.
Уравнение примет вид
![]() или
или
![]() .
.
Получим линейное уравнение 1-го порядка, для решения которого положим ![]() где
где
![]()
![]() -
вспомогательные функции. Тогда
-
вспомогательные функции. Тогда ![]() и после подстановки, получим
уравнение
и после подстановки, получим
уравнение
![]() или
или

Решим
дифференциальное уравнение ![]() Разделив переменные и интегрируя,
получим
Разделив переменные и интегрируя,
получим
![]()
откуда
![]()
![]()
Для нахождения функции u, решим уравнение.
![]() откуда
откуда ![]() , то есть
, то есть ![]()
Зная u и v, найдем z:
![]() а затем р из замены
а затем р из замены ![]() отсюда
отсюда
![]() заменяя р на
заменяя р на ![]() ,
получим
,
получим ![]()
![]() Используя начальные условия
Используя начальные условия ![]() и
и
![]() ,
найдем С.
,
найдем С. ![]() отсюда С = 1. Тогда
отсюда С = 1. Тогда ![]() Разделяя
переменные, получим
Разделяя
переменные, получим ![]()
После интегрирования получим:
![]()
Вычислим интеграл в левой части.

![]()
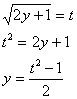
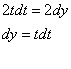 =
= 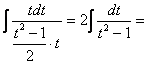
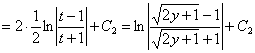 .
.
Таким образом, получим общий интеграл
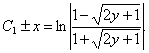
Используя,
что ![]() , найдем С1.
, найдем С1.

Тогда частный интеграл заданного уравнения
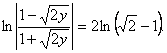
![]()
Линейные однородные уравнения второго порядка с постоянным коэффициентами.
Уравнение вида ![]() называется линейным однородным
дифференциальным уравнением. Обозначим
называется линейным однородным
дифференциальным уравнением. Обозначим ![]() - общее решение
этого уравнения.
- общее решение
этого уравнения.
Общее решение ![]() где у1, у2
– линейно - независимые частные решения линейного однородного уравнения.
где у1, у2
– линейно - независимые частные решения линейного однородного уравнения.
Общее решение ![]() находится с помощью
характеристического уравнения
находится с помощью
характеристического уравнения ![]() которое
получается из данного дифференциального уравнения, сохраняя
коэффициенты p
и q, а у, у1,
у11 , заменив соответственно 1, к, к2.
Рассмотрим три случая решения характеристического уравнения.
которое
получается из данного дифференциального уравнения, сохраняя
коэффициенты p
и q, а у, у1,
у11 , заменив соответственно 1, к, к2.
Рассмотрим три случая решения характеристического уравнения.
1.
Корни к1, к2
– действительны и различны. Тогда ![]()
![]() а
а ![]()
2.
Корни к1, к2
действительны и равные. к1 = к2 = к. Тогда ![]()
![]() а
а
![]()
3.
Корни к1, к2 - комплексно
– сопряженные, ![]()
![]() Тогда
Тогда ![]()
![]() а
а
![]()
Примеры. Решить уравнения.
1.
![]()
Составим характеристическое уравнение ![]() корни: к1
= -1, к2 =6. Тогда
корни: к1
= -1, к2 =6. Тогда ![]()
2.
![]()
Характеристическое
уравнение имеет вид ![]()
![]() . Тогда
. Тогда ![]()
3.
![]()
![]() Характеристическое уравнение имеет вид
Характеристическое уравнение имеет вид ![]()
![]() .
Тогда
.
Тогда ![]() и используя начальные условия,
получим
и используя начальные условия,
получим
![]() 1 = С1
отсюда найдем
1 = С1
отсюда найдем
![]() 2 = 3С1 + С2
С1 = 1, С2 = -1
2 = 3С1 + С2
С1 = 1, С2 = -1
Тогда
получим ![]() - частное решение заданного
уравнения.
- частное решение заданного
уравнения.
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
Уравнение вида ![]() называется линейным неоднородным
уравнением второго порядка.
называется линейным неоднородным
уравнением второго порядка.
Обозначим ![]() - общее решение соответствующий
однородного уравнения,
- общее решение соответствующий
однородного уравнения, ![]() - частное решение неоднородного
уравнения, соответствующее правой части и
- частное решение неоднородного
уравнения, соответствующее правой части и ![]() - общее решение
данного неоднородного уравнения. Тогда
- общее решение
данного неоднородного уравнения. Тогда
![]()
Для
некоторых специальных видов f(x) частное
решение ![]() можно найти методом
неопределенных коэффициентов. По виду правой части f(x) можно указа я вид
можно найти методом
неопределенных коэффициентов. По виду правой части f(x) можно указа я вид ![]() в следующих
случаях.
в следующих
случаях.
1. Если ![]() и a совпадает с
одним корнем характеристического уравнения, то
и a совпадает с
одним корнем характеристического уравнения, то
![]()
2. Если ![]() и a совпадает с
одним корнем характеристического уравнения, то
и a совпадает с
одним корнем характеристического уравнения, то
![]()
3. Если ![]() и a совпадает с
двумя корнем характеристического уравнения, то
и a совпадает с
двумя корнем характеристического уравнения, то
![]()
4. Если ![]() и числа
и числа ![]() не
совпадает с корнями характеристического уравнения, то
не
совпадает с корнями характеристического уравнения, то
![]() где
где
![]() -
степень многочленов.
-
степень многочленов.
5. Если ![]() и числа
и числа ![]() совпадает
с корнями характеристического уравнения, то
совпадает
с корнями характеристического уравнения, то
![]()
Если ![]() то
то ![]() где
где
![]() -
частное решение, соответствующее правой части
-
частное решение, соответствующее правой части ![]() а
а
![]() -
частное решение, соответствующее правой части
-
частное решение, соответствующее правой части ![]()
Примеры. Найти частное решение дифференциального уравнения, соответствующее заданным начальным условиям.
1. ![]()
![]()
![]()
Характеристическое
уравнение имеет вид ![]() его корни
его корни ![]()
![]()
Общее решение однородного уравнения
![]()
Правая
часть ![]() и, следовательно,
и, следовательно, ![]() ,
не совпадает с корнями характеристического уравнения. Тогда согласно пункту
1,
,
не совпадает с корнями характеристического уравнения. Тогда согласно пункту
1, ![]() Чтобы найти
коэффициенты А, В, С, найдем
Чтобы найти
коэффициенты А, В, С, найдем ![]() и
и ![]() и
подставим в заданное уравнение. После сокращения на
и
подставим в заданное уравнение. После сокращения на ![]() и
приведения подобных членов, получим
и
приведения подобных членов, получим
2АХ2 + (6А + 2В)х + (2А + 3В +2С) = х2 + х.
Сравнивая коэффициенты при одинаковых степенях, получаем систему уравнений.
![]() 2А = 1
2А = 1
6А + 2В = 1
2А + 3В + 2С = 0
Решив
эту систему, получим ![]()
![]()
![]() Таким
образом
Таким
образом
![]() а
а
![]()
Для
нахождения С1 и С2 используем начальные
условия. Найдем ![]() Тогда
Тогда
![]()
![]()
Решим систему С1 + С2 = 1, получи
С1 +2 С2 =- 1,
С1 = 3; С2 = - 2.
Подставим
в ![]() полученные значения С1 и
С2
полученные значения С1 и
С2
![]()
Решая
характеристическое уравнение К2 + 9 = 0, находим корни: ![]()
Следовательно,
![]()
Правая часть ![]() и числа
и числа ![]() совпадают с
корнями характеристического уравнения. Поэтому, согласно пункту 5,
совпадают с
корнями характеристического уравнения. Поэтому, согласно пункту 5,
![]()
![]()
![]()
Подставляя в заданное уравнение, получим
![]()
Сравнивая
коэффициенты при ![]() и
и ![]() ,
,
![]() найдем 6А = 6,
откуда А = 1, В = 0
найдем 6А = 6,
откуда А = 1, В = 0
6В = 0
Тогда
![]() а
а
![]()
Найдем
![]() и используя начальные
условия, найдем С1 и С2.
и используя начальные
условия, найдем С1 и С2.
![]()
Таким
образом и С1 = 1, С2 = 1 и ![]()
Метод вариации произвольных постоянных.
Пусть дано дифференциальное уравнение
![]() ,
,
где
![]() не
является функций специального вида и подобрать вид частного решения по виду
правой части и корнями характеристического уравнения нельзя. В этом случае
можно применить метод вариации произвольных постоянных. Этот метод является
более общим и применим к уравнениям с любой непрерывной частью
не
является функций специального вида и подобрать вид частного решения по виду
правой части и корнями характеристического уравнения нельзя. В этом случае
можно применить метод вариации произвольных постоянных. Этот метод является
более общим и применим к уравнениям с любой непрерывной частью ![]() .
.
Согласно методу вариации произвольных постоянных, составляем однородное уравнение, соответствующее заданному неоднородному уравнению
![]() и
и
находим
его общее решение. ![]() Общее решение заданного
неоднородного уравнение будем искать в таком же виде, где будем считать С1
и С2 не постоянными, а некоторыми функциями о х, то
есть
Общее решение заданного
неоднородного уравнение будем искать в таком же виде, где будем считать С1
и С2 не постоянными, а некоторыми функциями о х, то
есть
![]()
Производные этих
функций ![]() и
и ![]() определяются из системы
уравнений:
определяются из системы
уравнений:
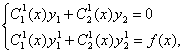
где у1 и у2 – частные решения однородного уравнения.
Примеры. Решить уравнения
1.
![]()
Решим
соответствующее однородное уравнение ![]() его корни
его корни ![]() Тогда
Тогда
![]()
![]() Общее
решение однородного уравнения
Общее
решение однородного уравнения
![]()
Согласно методу вариации произвольных постоянных, общее решение заданного
уравнения ![]() продифференцирововав у1
и у2 , составим систему уравнений для нахождения
продифференцирововав у1
и у2 , составим систему уравнений для нахождения ![]() и
и
![]() :
:

После упрощения, получим

Решая эту систему, найдем
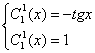
Отсюда
![]()
![]()
Тогда
![]()
или
![]()
2.
![]()
Решим
характеристическое уравнение ![]() корни его
корни его ![]()
![]() Частные
решения
Частные
решения ![]()
![]()
Тогда
![]() положим
положим ![]() и
и ![]() и
и
![]()
Для
определения ![]() и
и ![]() составим
систему уравнений
составим
систему уравнений

Решая систему , получим
![]()
![]()
Интегрируя, получим
![]()
![]()
Таким образом:
![]()
![]()
Следовательно общее решение запишется в виде
![]()
или
![]()
V. Операционное исчисление
Функция f(t) называется оригиналом, если она удовлетворяет условиям:
1) f(t) непрерывна или кусочно непрерывна в (0;+¥);
2) для всех t<0: f(t)=0;
3) f(t) функция
ограниченного роста, возрастает не быстрее показательной функции, то есть
существуют такие постоянные M>0 и S0³0, что для всех t: ![]() <
< ![]()
Изображением
f(t) по Лапласу называется функция f(p) комплексного переменного ![]() ,
определяемая равенством:
,
определяемая равенством: 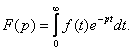
Обозначает:
![]()
Читается:
![]() является
изображением f(t) Свойства и
основные теоремы Лапласа.
является
изображением f(t) Свойства и
основные теоремы Лапласа.
1. Теорема линейности.
Если
![]() ,
то
,
то ![]() а С1 и С2-
постоянные, то
а С1 и С2-
постоянные, то ![]()
С1 F(p) + C2Ф(p).
2. Теорема подобия.
Если
![]() ,
то
,
то ![]() а постоянная.
а постоянная.
3. Теорема смещения.
Если
![]() ,
то
,
то ![]()
4. Теорема запаздывания.
Если
![]() ,
то
,
то ![]()
![]()
5. Теорема дифференцирования оригинала .
Если
![]() ,
то
,
то ![]() ;
;
![]() и
т.д.
и
т.д.
![]()
6. Теорема интегрирования оригинала.
Если
![]() ,
то
,
то ![]()
7. Теорема дифференцирования изображения.
Если
![]() ,
то
,
то ![]()
![]()
![]()
8. Теорема интегрирования изображения.
Если
![]() и
и
 существует,
то
существует,
то 
9. Теорема о свертке.
Сверткой двух оригиналов называется:

Если
![]() и
и
![]() то
то
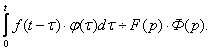
10. Интеграл Дюамеля.
Если
![]() и
и
![]() то
то
 или,
или, ![]()
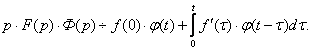
Таблица изображений по Лапласу.
1)
![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5)
![]() 6)
6) ![]() 7)
7) ![]() 8)
8) ![]()
9)
![]() 10)
10) ![]()
11)
![]() 12)
12) ![]()
13)
![]() 14)
14) ![]() 15)
15) ![]()
Примеры нахождения изображений.
1.
Найти изображений ![]()
Преобразуем
![]()
 По
таблице:
По
таблице: ![]()
![]()
По
теореме линейности: ![]()
2.
Найти изображение ![]() .
.
По
таблице ![]()
Воспользуемся теоремой дифференцирования.
Изображения:
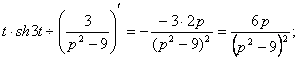

Примеры
нахождения оригинала по изображению ![]() - правильная
рациональная дробь. Эту разлагаем на сумму элементарных (простейших) дробей, а
затем по таблице находим по изображению оригинала.
- правильная
рациональная дробь. Эту разлагаем на сумму элементарных (простейших) дробей, а
затем по таблице находим по изображению оригинала.
1)
![]() Найти
Найти ![]() .
.
Находим А, В, С, Д.
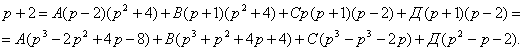
Сравниваем коэффициенты при соответствующих степенях х:
![]()
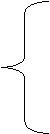
![]() р3
А + В + С =
0,
А = -
р3
А + В + С =
0,
А = -![]()
р2
-2А + В – С + Д =
0,
В = ![]()
р 4А + 4В - 2С – Д =
1,
С = ![]()
р0
-8А + 4В - 2Д =
2
Д = - ![]()
![]()
![]()
Если
![]() - правильная рациональная простые
корни р1, р2, …, рn , то можно применить формулу Хевисайда:
- правильная рациональная простые
корни р1, р2, …, рn , то можно применить формулу Хевисайда:
![]()
2)
![]() Найти
Найти ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами операционным методам.
Рассмотрим линейное дифференциальное уравнение с постоянными коэффициентами:
![]() (1)
(1)
Надо найти решение уравнения (1), удовлетворяющее начальным условиям:
![]()
![]() (2)
(2)
Пусть ![]() и
и ![]() .
.
Применим к обеим части (1) преобразование Лапласа и используя теорему о дифференцирование оригинала и линейности, перейдем от дифференциального уравнения (1) с начальными условиями (2) к операторному уравнению (3)
![]() (3)
(3)
Находим решение операторного уравнения:
![]() (4)
(4)
По ![]() находим оригинал – функцию
находим оригинал – функцию ![]() ,
которая является решением задача (1) – (2).
,
которая является решением задача (1) – (2).
Пример.
1. Найти частное решение дифференциального уравнения ![]() ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям: ![]()
![]()
Пусть ![]() , тогда
, тогда ![]() ,
,
![]()
![]() .
.
Получаем операторного уравнение
![]()
![]() отсюда
отсюда
![]()
По изображению ![]() находим
находим ![]() . Для этого разложим
дробь на сумму простейших.
. Для этого разложим
дробь на сумму простейших.
![]()
![]()
При
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда
![]() и
и
![]() .
.
2. Найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям:
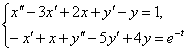
![]()
![]()
![]()
![]()
![]()
Пусть
![]() ,
тогда
,
тогда ![]() ,
,
![]()
Пусть
![]() ,
тогда
,
тогда ![]() ,
,
![]()
![]()
![]()
Получим соответствующую систему операторных уравнений:

Находим решение этой системы. Для этого воспользуемся методам Крамера.


![]()

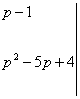
![]()
![]()

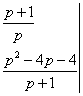
![]()
![]()
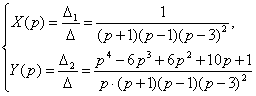
По
изображению ![]() , находим
, находим ![]() и по
и по ![]() ,
находим
,
находим ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() тогда
тогда
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() тогда
тогда
![]() .
.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.
1.1. – 1.20. Вычислите неопределенные интегралы.
Решать неопределенных интегралов.
1.1.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]() д)
д)
![]()
1.2.
а) ![]() б)
б) ![]() в)
в)
![]()
г) ![]() д)
д) ![]()
1.3.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.4.
а) ![]() б)
б) ![]() в)
в)
![]() г)
г)
![]()
д) ![]()
1.5.
а) ![]() б)
б) ![]() в)
в)
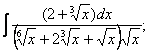
г) ![]() д)
д) ![]()
1.6.
а) ![]() б)
б) ![]() в)
в)
![]() г)
г) ![]()
д) ![]()
1.7.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.8.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.9.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.10.
а) ![]() б)
б) ![]() в)
в)  г)
г)
![]()
д) ![]()
1.11.
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]()
1.12.
а) ![]() б)
б) ![]() в)
в)  г)
г)
![]()
д) ![]()
1.13.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.14.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.15.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.16.
а) ![]() б)
б) ![]() в)
в)
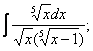 г)
г)
![]()
д) ![]()
1.17.
а) ![]() б)
б) ![]() в)
в)
![]() г)
г) ![]()
д) ![]()
1.18.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)
![]()
д) ![]()
1.19.
а) ![]() б)
б) ![]() в)
в)  г)
г)
![]()
д) ![]()
1.20.
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]()
2.1. – 2.20. Вычислить несобственный интеграл.
2.1.
а)  б)
б) 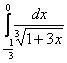
2.2.
а) 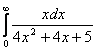 б)
б) 
2.3.
а) 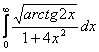 б)
б) 
2.4.
а) ![]() б)
б) 
2.5.
а) 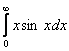 б)
б) 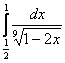
2.6.
а) ![]() б)
б) 
2.7.
а) 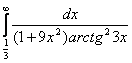 б)
б) 
2.8.
а)  б)
б) 
2.9.
а) ![]() б)
б) 
2.10.
а) ![]() б)
б) 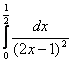
2.11.
а)  б)
б) 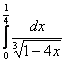
2.12.
а) ![]() б)
б) 
2.13.
а) ![]() б)
б) 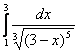
2.14.
а) 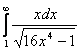 б)
б) 
2.15.
а) 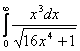 б)
б) 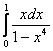
2.16.
а) 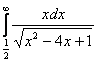 б)
б) 
2.17.
а) ![]() б)
б) 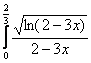
2.18.
а) 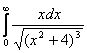 б)
б) 
2.19.
а) 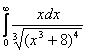 б)
б) 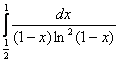
2.20.
а)  б)
б) 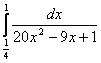
3.1. – 3.20. Вычислить площадь, ограниченную линями:
3.1.
![]()
![]()
3.2.
![]()
![]()
![]()
3.3.
![]()
![]()
3.4.
![]()
![]()
![]()
![]()
3.5.
![]()
![]()
![]()
3.6.
![]()
![]()
3.7.
![]()
![]()
![]()
3.8.
![]()
3.9.
![]()
![]()
3.10.
![]()
![]()
![]()
3.11.
![]()
![]()
3.12.
![]()
![]()
![]()
3.13.
![]()
![]()
![]()
3.14.
![]()
![]()
![]()
3.15.
![]()
![]()
![]()
3.16.
![]()
![]()
![]()
3.17.
![]()
![]()
![]()
3.18.
![]()
![]()
![]()
3.19.
![]()
![]()
![]()
3.20.
![]()
![]()
![]()
![]()
4.1. – 4.20. Определить длину дуги кривой:
4.1.
![]() ,
, ![]()
4.2.
![]()
![]()
4.3.
![]()
![]()
4.4.
![]()
![]()
![]()
4.5.
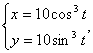
![]()
4.6.

![]()
4.7.
![]()
![]()
4.8.
![]()
![]()
4.9.
![]()
![]()
4.10.
![]()
![]()
4.11.
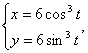
![]()
4.12.
![]()
![]()
4.13.
![]()
![]()
4.14.
![]()
![]()
4.15.
![]()
![]()
4.16.
![]()
4.17.
![]()
![]()
4.18.

![]()
4.19.
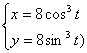
![]()
4.20.
![]() ;
; ![]()
5.1. – 5.20. Определить объем тела, образованного вращения фигуры, ограниченном линиями.
5.1.
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.2.
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.3.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.4.
![]()
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.5.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.6.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.7.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.8.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.9.
![]()
![]() вокруг оси Оу
вокруг оси Оу
5.10.
![]()
![]() вокруг оси Оу
вокруг оси Оу
5.11.
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.12.
![]() вокруг оси Ох
вокруг оси Ох
5.13.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.14.
![]()
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.15.
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.16.
![]()
![]() вокруг оси Ох
вокруг оси Ох
5.17.
![]()
![]()
![]()
![]() вокруг оси Оу
вокруг оси Оу
5.18.
![]()
![]()
![]()
![]() вокруг оси Оу
вокруг оси Оу
5.19.
![]()
![]()
![]() вокруг оси Оу
вокруг оси Оу
5.20.
![]()
![]()
![]() вокруг оси Оу
вокруг оси Оу
6.1. – 6.20. Найти частные производные второго порядка функции
z = f ( x; y ).
6.1.
![]()
6.2.
![]()
6.3.
![]()
6.4.
![]()
6.5.
![]()
6.6.
![]()
6.7.
![]()
6.8.
![]()
6.9.
![]()
6.10.
![]()
6.11.
![]()
6.12.
![]()
6.13.
![]()
6.14.
![]()
6.15.
![]()
6.16.
![]()
6.17.
![]()
6.18.
![]()
6.19.
![]()
6.20.
![]()
7.1. – 7.20. Найти экстремум функции z = f ( x; y ).
7.1.
![]()
7.2.
![]()
7.3.
![]()
7.4.
![]()
7.5.
![]()
7.6.
![]()
7.7.
![]()
7.8.
![]()
7.9.
![]()
7.10.
![]()
7.11.
![]()
7.12.
![]()
7.13.
![]()
7.14.
![]()
7.15.
![]()
7.16.
![]()
7.17.
![]()
7.18.
![]()
7.19.
![]()
7.20.
![]()
8.1. – 8.20. Найти общий интеграл или общее решение дифференциальных уравнений первого порядка.
8.1.
а) ![]()
б) ![]()
в) ![]()
8.2.
а) ![]()
б) ![]()
в) ![]()
8.3.
а) ![]()
б) ![]()
в) ![]()
8.4.
а) ![]()
б) ![]()
в) ![]()
8.5.
а) ![]()
б) ![]()
в) ![]()
8.6.
а) ![]()
б) ![]()
в) ![]()
8.7.
а) ![]()
б) ![]()
в) ![]()
8.8.
а) ![]()
б) ![]()
в) ![]()
8.9.
а) ![]()
б) ![]()
в) ![]()
8.10.
а) ![]()
б) ![]()
в) ![]()
8.11.
а) ![]()
б) ![]()
в) ![]()
8.12.
а) ![]()
б) ![]()
в) ![]()
8.13.
а) ![]()
б) ![]()
в) ![]()
8.14.
а) ![]()
б) ![]()
в) ![]()
8.15.
а) ![]()
б) ![]()
в) ![]()
8.16.
а) ![]()
б) ![]()
в) ![]()
8.17.
а) ![]()
б) ![]()
в) ![]()
8.18.
а) ![]()
б) ![]()
в) ![]()
8.19.
а) ![]()
б) ![]()
в) ![]()
8.20.
а) ![]()
б) ![]()
в) ![]()
9.1. – 9.20. Найти общее решение или общий интеграл дифференциальных уравнений второго порядка.
9.1.
а) ![]()
б) ![]()
9.2.
а) ![]()
б) ![]()
9.3.
а) ![]()
б) ![]()
9.4.
а) ![]()
б) ![]()
9.5.
а) ![]()
б) ![]()
9.6.
а) ![]()
б) ![]()
9.7.
а) ![]()
б) ![]()
9.8.
а) ![]()
б) ![]()
9.10.
а) ![]()
б) ![]()
9.11.
а) ![]()
б) ![]()
9.12.
а) ![]()
б) ![]()
9.13.
а) ![]()
б) ![]()
9.14.
а) ![]()
б) ![]()
9.15.
а) ![]()
б) ![]()
9.16.
а) ![]()
б) ![]()
9.17.
а) ![]()
б) ![]()
9.18.
а) ![]()
б) ![]()
9.19.
а) ![]()
б) 
9.20.
а) ![]()
б)![]()
10.1. – 10.20. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
10.1.
![]()
![]()
![]()
10.2.
![]()
![]()
![]()
10.3.
![]()
![]()
![]()
10.4.
![]()
![]()
![]()
10.5.
![]()
![]()
![]()
10.6.
![]()
![]()
![]()
10.7.
![]()
![]()
![]()
10.8.
![]()
![]()
![]()
10.9.
![]()
![]()
![]()
10.10.
![]()
![]()
![]()
10.11.
![]()
![]()
![]()
10.12.
![]()
![]()
![]()
10.13.
![]()
![]()
![]()
10.14.
![]()
![]()
![]()
10.15.
![]()
![]()
![]()
10.16.
![]()
![]()
![]()
10.17.
![]()
![]()
![]()
10.18.
![]()
![]()
![]()
10.19.
![]()
![]()
![]()
10.20.
![]()
![]()
![]()
11.1. – 11.20. Найти изображения функций.
11.1.
![]()
11.2.
![]()
11.3.
![]()
11.4.
![]()
11.5.
![]()
11.6.
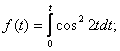
11.7.
![]()
11.8.
![]()
11.9.
![]()
11.10.
![]()
11.11.
![]()
11.12.
![]()
11.13.
![]()
11.14.
![]()
11.15.
![]()
11.16.
![]()
11.17.
![]()
11.18.
![]()
11.19.
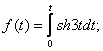
11.20.
![]()
12.1. – 12.20. Решить дифференциальное уравнение операционным методом.
12.1.
![]()
![]()
![]()
12.2.
![]()
![]()
![]()
12.3.
![]()
![]()
![]()
12.4.
![]()
![]()
![]()
12.5.
![]()
![]()
![]()
12.6.
![]()
![]()
![]()
12.7.
![]()
![]()
![]()
12.8.
![]()
![]()
![]()
![]()
12.9.
![]()
![]()
![]()
12.10.
![]()
![]()
![]()
12.11.
![]()
![]()
![]()
![]()
12.12.
![]()
![]()
![]()
12.13.
![]()
![]()
![]()
12.14.
![]()
![]()
![]()
12.15.
![]()
![]()
![]()
12.16.
![]()
![]()
![]()
12.17.
![]()
![]()
![]()
![]()
12.18.
![]()
![]()
![]()
12.19.
![]()
![]()
![]()
12.20.
![]()
![]()
![]()
![]()
13.1. – 13. 20. Решить систему дифференциальных уравнений операционных методам.
13.1.
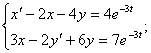
![]()
![]()
13.2.
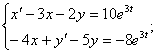
![]()
![]()
13.3.

![]()
13.4.

![]()
![]()
13.5.

![]()
![]()
13.6.
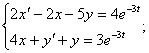
![]()
![]()
13.7.

![]()
![]()
13.8.
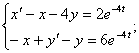
![]()
![]()
13.9.
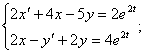
![]()
![]()
13.10.
![]()
![]()
![]()
13.11.
![]()
![]()
![]()
13.12.
![]()
![]()
![]()
13.13.
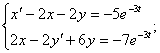
![]()
![]()
13.14.

![]()
![]()
13.15.

![]()
![]()
13.16.
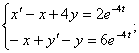
![]()
![]()
13.17.
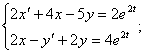
![]()
![]()
13.18.

![]()
13.19.
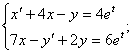
![]()
![]()
13.20.
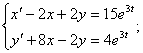
![]()
![]()
ЛИТЕРАТУРА
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 1970 – 1985, т.1,2.
2. Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости (задачи и упражнения). – М.: Наука, 1971.
3. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1977, 1980 года.
4. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1978 год.
5. Соатов Ё.У. «Олий математика» Тошкент. Укитувчи. 1994 й. I ва II том.
Методическое указания
для выполнению самостоятельных работ
по дисциплин «Высшая математика»
(часть II) для студентов дневного отделение
Олий математика кафедраси мажлисида
курилди ва босмадан чикаришга тавсия
этилди ( 2005, - баённома)
Тузувчилар: доцент Маматов А.Э.,
доцент Рахматов Р.Р.,
Катта укитувчилар:
Шопен И.Л.,
Ходжабагян А.Г.,
Мирахмедова М.И.
Маъсул мухаррир академик Абуталиев Ф.Б.
Мухаррир Парпиева К.
Корректор Павлова С.И.