ТОШКЕНТ ЭЛЕКТРОТЕХНИКА АЛОКА ИНСТИТУТИ
ОЛИЙ МАТЕМАТИКА
кафедраси
ОЛИЙ МАТЕМАТИКА
махсус факультет талабалари учун
ўқув-услубий қўлланма
Тошкент 2002
Суз боши
Талабалар математика фанини узлаштиришида ва унинг методларини эгаллашида уларнинг мустакил ишлаши асосий омиллардан биридир. Бажарилиши ишчи дастурида кузда тутилган вазифаларни іисоблаш тизимидан иборат булган семестрга мулжалланган уй вазифалари математика курсини урганишда мустакил ишлаш куникмаларини ривожлантиришга іизмат килади.
Семестр давомида уй вазифалари бажарилиши укитувчи томонидан назорат килиб борилади. Вазифалар талабалар томонидан уз вактида ёзма равишда бажарилиб, текшириш учун укитувчига топширилиши зарур. Бажарилган иш іимоя килиш билан якунланади. Іимоя пайтида талаба назарий саволларга тугри жавоб бера билиши, вазифаларнинг ечимини тушунтира билиши, шунга ухшаш мисол ва масалаларни еча билиши керак.
Курс дастури ва масалаларнинг шартлари узбек ва рус тилларида берилган, зарурий адабиётлар руйхати курсатилган.
Предисловие
Важным фактором усвоения математики и овладения её методами является самостоятельная работа студентов. Развитию навыков в самостоятельной работе по изучению курса математики способствует система расчетных заданий – семестровое домашнее задание, выполнение которых предусмотрено рабочей программой курса. Выполнение студентами семестровых домашних заданий контролируется преподавателем. Студенту необходимо выполнить задание в письменной форме и вовремя сдать преподавателю на проверку. Завершающим этапом является защита задания. Во время защиты студент должен уметь правильно отвечать на теоретические вопросы, пояснить решения заданий, решать задания аналогичного типа.
Программа курса и условия заданий приведены на узбекском и русском языках, указана необходимая литература.
Биринчи кисм
Саволлар.
I. Детерминантлар ва чизикли тенгламалар системаси.
1. 2-, 3-ва n - тартибли детерминантлар . Уларнинг хоссалари ва іисоблаш усуллари.
2. Чизикли тенгламалар системаси. Крамер коидаси.
II. Векторлар
3.Текисликда ва фазода векторлар. Векторлар устида чизикли амаллар
4.Чизикли эркли ва чизикли эрксиз векторлар. Текисликда ва фазода базиснинг таърифи. Векторни базис векторлар буйича ёйилмаси.
5.Ту¼рибурчакли координаталар системаси. Координаталари оркали берилган векторлар устида амаллар.
6.Векторларнинг скаляр, вектор ва аралаш купайтмаси. Уларнинг асосий хоссалари ва купайтмаларнинг купайтувчи векторлар координаталари оркали ифодаси.
III Аналитик геометрия
7. Текислик тенгламаси. Текислик тенгламасининг асосий куринишлари.
8. Текисликда ва фазода ту¼ри чизик, асосий масалалар.
9. Иккинчи тартибли чизиклар. Айлана, эллипс, гипербола ва парабола. Уларнинг каноник тенгламалари ва асосий хоссалари.
10. Иккинчи тартибли сиртлар.
IV Матрицалар.
11. Матрицалар ва улар устида амаллар.
12. Тескари матрица. Матрицанинг ранги.
13. Чизикли тенгламалар системасининг матрицали куриниши. Кронекер – Капелли теоремаси. Чизикли тенгламалар системасини текширинг.
14. Бир жинсли чизикли тенгламалар системаси. Фундаментал ечимлар туплами.
V Комплекс сонлар.
15. Комплекс соннинг алгебраик, тригонометрик ва курсаткичли куринишлари.
16. Комплекс сонлар устида амаллар. Муавр формулалари.
17. Эйлер формулалари.
18. Купхадни купайтувчиларга ажратиш.
Иккинчи кисм
Бир узгарувчили функциянинг дифференциал ва интеграл іисоби.
1. Функция. Унинг хоссалари, графиклари ва графикларни узгартириш. Элементар функциялар ва уларнинг графиклари.
2. Кутб координат системаси. Шу системада функциялар графикларини ясаш.
3. Кетма- кетликнинг лимити. Функция лимити. Чексиз кичик ва чексиз катта микдорлар,уларнинг хоссалари.
4. Функция узлуксизлиги. Функциянинг узилиш нукталари.
5. Функция іосиласи. Іосила іисоблаш коидалари. Іосилалар жадвали.
6. Функция дифференциали. Такрибий іисоблашда дифференциалнинг кулланиши.
7. Юкори тартибли іосилалар ва дифференциаллар.
8. Лопитал коидаси.
9. Дифференциал іисоб ёрдамида функцияни тула текшириш.
10. Аникмас интеграл ва хоссалари.
11. Аникмас интеграллар жадвали.
12. Аникмас интегралларни іисоблаш усуллари.
13. Аник интеграл. Ньютон-Лейбниц формуласи.
14. Аник интегралнинг кулланилиши.
15. Хосмас интеграллар.
Первая часть
Вопросы.
I. Определители и системы линейных уравнений.
1. Определители 2-го, 3-го и n-го порядков, способы вычисления и их свойства.
2. Системы линейных уравнений, правило Крамера.
II. Векторы.
3. Векторы на плоскости и в пространстве, линейные операции над векторами.
4. Линейная зависимость и линейная независимость векторов. Базис на плоскости и в пространстве, разложение вектора по базисным векторам.
5. Прямоугольная система координат, действия над векторами, заданными своими координатами.
6. Скалярное, векторное и смешанное произведение векторов. Основные свойства этих действий и выражение через координаты сомножителей.
III. Аналитическая геометрия.
7. Уравнение плоскости, основные виды уравнений плоскости.
8. Прямая на плоскости и в пространстве, основные задачи.
9. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Канонические уравнения линий второго порядка и их свойства.
10. Поверхности второго порядка.
IV. Матрицы.
11. Матрицы и действия над ними.
12. Обратная матрица. Ранг матрицы.
13. Матричная запись систем линейных уравнений. Теорема Кронекера – Капелли. Исследование систем линейных уравнений.
14. Однородные системы линейных уравнений, фундаментальная совокупность решений.
V. Комплексные числа.
15. Алгебраическая, тригонометрическая и показательная формы комплексного числа.
16. Действия над комплексными числами. Формула Муавра.
17. Формулы Эйлера.
18. Разложение многочленов на множители.
Вторая часть
Дифференциальное и интегральное исчисление функции одной переменной.
Вопросы.
1. Функция. Простейшие свойства. Графики, их преобразования. Элементарные функции, их графики.
2. Полярная система координат. Построение графиков функций в полярной системе координат.
3. Предел последовательности. Предел функции. Бесконечно малые и бесконечно большие, их свойства.
4. Непрерывность функции. Точки разрыва функции.
5. Производная функции. Правила нахождения производных. Таблица производных.
6. Дифференциал функции. Применение дифференциала к приближенным вычислениям.
7. Производные и дифференциалы высших порядков.
8. Правила Лопиталя.
9. Исследование функции с помощью дифференциального исчисления.
10. Неопределенный интеграл, простейшие свойства.
11. Таблица неопределенных интегралов.
12. Методы вычисления неопределенных интегралов.
13. Определенный интеграл. Формула Ньютона – Лейбница.
14. Приложения определенного интеграла.
15. Несобственные интегралы.
АДАБИЕТЛАР
ЛИТЕРАТУРА
1. Пискунов Н. С. Дифференциальное и интегральное исчисление.
Т. 1, 2.М: Наука, 1970, 1972, 1976.
2. Шнейдер В. Е., Слуцкий А. И., Шумов А. С. Краткий курс по высшей математике. Т. 1, 2. М: Высшая школа, 1978.
3. Берман Г. Н. Сборник задач по курсу математического анализа.
М: Наука, 1975.
4. Минорский В. П. Сборник задач по высшей математике.
М: Наука, 1978 .
5. Кузнецов Л. А. Сборник задач по высшей математике (типовые расчеты).
М: Высшая школа, 1983.
6. Соатов Е. У. Олий математика. 1, 2, 3 том. Т: Укитувчи, 1994.
7. Абдуалимов Б. А. Олий математика. Т: Ыкитувчи, 1994 .
8. Бакельман И. Я. Аналитик геометрия ва чизикли алгебра.
Т: Укитувчи, 1978 .
1.01-1.20 – вазифалар задания -1.01-1.20.
Вектор алгебра ва аналитик геометрия элементлари.
А1А2А3А4- пирамида учларининг координаталари берилган.
Топиш керак:
1) А1А2 киррасининг узунлигини;
2) А1А2 ва А1А4 кирралар орасидаги бурчакни;
3) А1А4 кирра билан А1А2А3 ё¼и орасидаги бурчакни;
4) А1А2А3 ё¼ининг юзасини;
5) Пирамиданинг іажмини;
6) А1А2 ту¼ри чизик тенгламасини;
7) А1А2А3текислик тенгламасини;
8) А4 учидан А1А2А3 ё¼ига туширилган баландлик тенгламасини. Чизмани ясанг
Элементы векторной алгебры и аналитической геометрии.
Даны координаты вершин пирамиды А1А2А3А4 .
Найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребрами А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объем пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
Сделать чертеж.
1.01. А1(0;0;1), А2(0;1;0), А3(1;0;0),А4(0;0;0)
1.02. А1(1;1;2), А2(1;2;1), А3(2;1;1),А4(1;4;3)
1.03. А1(2;2;4), А2(2;4;2), А3(4;2;2),А4(5;1;0)
1.04. А1(3;3;6), А2(3;6;3), А3(6;3;3),А4(6;5;3)
1.05. А1(3;4;7), А2(3;7;4), А3(6;4;4),А4(1;1;1)
1.06. А1(1;3;5), А2(0;2;0), А3(2;3;4),А4(1;4;4)
1.07. А1(1;3;5), А2(0;2;0), А3(2;3;4),А4(1;4;4)
1.08. А1(10;2;4), А2(10;3;3), А3(11;2;3),А4(10;2;3)
1.09. А1(1;2;1), А2(1;3;0), А3(2;2;0),А4(1;2;0)
1.10. А1(-2;-1;1), А2(-2;0;0), А3(-1;-1;0),А4(-2;-1;0)
1.11. А1(5;5;8), А2(3;6;7), А3(4;5;7),А4(3;5;7)
1.12. А1(1;2;3), А2(1;3;2), А3(2;2;2),А4(1;2;2)
1.13. А1(1;2;0), А2(4;3;-1), А3(6;4;1),А4(4;2;-1)
1.14. А1(6;7;1), А2(6;8;0), А3(7;7;0),А4(6;7;0)
1.15. А1(4;2;5), А2(0;7;2), А3(0;2;7),А4(1;5;0)
1.16. А1(4;4;10), А2(4;10;2), А3(2;8;4),А4(9;6;4)
1.17. А1(4;6;5), А2(6;9;4), А3(2;10;10),А4(7;5;9)
1.18. А1(3;5;4), А2(8;7;4), А3(5;10;4),А4(4;7;8)
1.19. А1(10;6;6), А2(-2;8;2), А3(6;8;9),А4(7;10;3)
1.20. А1(1;8;2), А2(5;2;6), А3(5;7;4),А4(4;10;9)
2.01– 2.20 – вазифалар задания – 1.01-1.20
2.01. Агар параллелограмнинг диагоналлари Р(-1;0) нуктада кесишиши маълум булса, унинг х + у = 1 ва у + 1 = 0 томонлари кесишган нуктасидан утмайдиган диагоналининг тенгламаси топилсин.
2.02. А(-1;2)
нуктадан утувчи шундай ту¼ри чизик тенгламасини тузингки, бу ту¼ри
чизикнинг узаро параллел булган 
ва 
ту¼ри
чизиклар орасидаги кесманинг урта нуктаси х-у-6=0 ту¼ри чизикда ётсин.
2.03. Агар А(-5;5) ва В(3;1) учбурчакнинг учлари, Д(2;5) эса баландликлари кесишган нукта булса, учбурчак томонларининг тенгламасини тузинг.
2.04. Квадрат
томонларидан бирининг тенгламаси 
ва диагоналлари кесишган
нукта Р(0;-1) берилган.
Квадратнинг колган учта томонининг тенгламалари топилсин.
2.05. Параллелограмм икки томонининг тенгламалари 
ва 
іамда
диагоналларидан бирининг тенгламаси х – 2 = 0 берилган. Параллелограмм
учларининг координаталари топилсин.
2.06. Учбурчакнинг икки А(-3;3) ,В(5;-1) ва баландликлари кесишган Д(1;3) нукта берилган. Учбурчак томонларининг тенгламаларини тузинг.
2.07. Учбурчак
икки томонининг тенгламалари 
ва 
берилган.
Унинг медианалари Р(0;2) нуктада кесишади. Учбурчак учинчи томониннинг
тенгламасини тузинг.
2.08. Учбурчак икки учи А(2;-2), В(3;-1) ва медианалари кесишган нукта Р(1;0) берилган. Шу учбурчак баландликлари кесишган нуктани топинг.
2.09. Учбурчак икки баландлигининг тенгламалари х + у = 4 ва у = 2х іамда учларидан бири А(0;2) берилган. Учбурчак томонларининг тенгламаси топилсин.
2.10. Учбурчак икки медианасининг тенгламаси х – 2у + 1 = 0, у – 1= 0 ва учларидан бири А(1;3) берилган. Учбурчак томонларининг тенгламаси топилсин.
2.11. Учбурчак икки томонининг тенгламаси 5х –2у – 8 = 0 ва 3х –2у- 8=0 берилган, учинчи томонининг уртаси эса координаталар боши билан устма-уст тушади. Учинчи томони тенгламасини тузинг.
2.12. АВСД трапециянинг кетма-кет учлари А(-3;2), В(4;-1), С(1;3) (АД║ВС) берилган. Диагоналлари узаро перпендикуляр. Трапециянинг туртинчи учи Д нинг координаталарини топинг.
2.13. Учбурчак икки томонининг тенгламалари 4х - 5у + 9 = 0 ва х + 4у – 3 = 0 берилган. Агар шу учбурчак медианалари Р(3;1) нуктада кесишгани маълум булса, учбурчак учинчи томонининг тенгламаси топилсин.
2.14. Ромб томонларидан бирининг тенгламаси 5х + 2у – 9 = 0. Агар ромб диагоналлари 0(0;0) нуктада кесишган булиб, улардан бирининг тенгламаси у = 2х булса, ромбнинг колган учта томони тенгламасини тузинг.
2.15. Учбурчак томонларининг урталари берилган: Р(1;2) –АВ томонининг уртаси, R(-4;3) – ВС томонининг уртаси, Q(5;-1) – АС томонининг уртаси. СF баландлик ва АR медиана кесишган нукта топилсин.
2.16. Ромб томонларидан бирининг тенгламаси х – 3у + 10 = 0 ва диагоналларидан бири х + 4у – 4 = 0. Ромб диагоналлари Р(0;1) нуктада кесишади. Ромбнинг колган томонларининг тенгламаси топилсин.
2.17. Агар ромб икки томонининг тенгламалари 2х – у + 4 = 0 ва 2х – у + 10 = 0 іамда диагоналларидан бирининг тенгламаси х + у + 2 =0 булса, ромб учларининг координаталари топилсин.
2.18. Агар квадрат томонларидан бири 4х + 3у - 12 = 0 ту¼ри охири координата укларида ётувчи кесмадан иборат булса, колган учта томонининг тенгламаси топилсин.
2.19. Агар ту¼ри чизик бурчакли тенгёнли учбурчакнинг ту¼ри бурчагининг учи С(3;-1) ва гипотенузасининг тенгламаси 3х – 2у + 2 = 0 булса, А ва В учларини топинг.
2.20. Тенгёнли учбурчак ён томонларининг тенгламаси 3х + у = 0 ва х –3у = 0 ва М(5;0) нукта унинг асосида ётувчи нукта. Учинчи томонининг тенгламасини топинг.
2.01. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон х + у = 1 и у + 1 = 0, если известно, что диагонали пересекаются в точке Р(-1;0).
2.02. Составить
уравнение прямой, проходящей через точку А(-1;2) так, что середина отрезка,
заключенного между параллельными прямыми 
и лежит на
прямой 
.
2.03. Составить уравнения сторон треугольника, если А(-5;5) и В(3;1) – вершины, а Д(2;5) точка пересечения его высот.
2.04. Дано
уравнение одной из сторон квадрата и точка пересечения его
диагоналей 
. Написать
уравнения трех остальных сторон квадрата.
2.05. Уравнения
двух сторон параллелограмма и , а уравнение
одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
2.06. Даны две вершины А(-3;3) и В(5;-1) треугольника и Д(1;3) – точка пересечения высот. Составить уравнение сторон треугольника.
2.07. Даны
уравнения двух сторон треугольника и . Его медианы
пересекаются в точке Р(0;2). Составить уравнение третьей стороны треугольника.
2.08. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Найти точку пересечения высот этого треугольника.
2.09. Даны
уравнения высот треугольника 
и 
, и одна из
его вершин А(0;2). Составить уравнения сторон треугольника.
2.10. Даны
уравнения двух медиан треугольника 
и 
и одна из его
вершин А(1;3). Составить уравнения сторон треугольника.
2.11. Две
стороны треугольника заданы уравнениями 
и 
, а середина
третьей стороны совпадает с началом координат. Составить уравнение третьей
стороны.
2.12. Даны последовательные вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСД (АД║ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты четвертой вершины Д.
2.13. Даны
уравнения двух сторон треугольника 
и 
. Найти
уравнение третьей стороны, если известно, что медианы этого треугольника
пересекаются в точке Р(3;1).
2.14. Уравнение
одной из сторон ромба 
. Найти уравнения
остальных трех сторон ромба, если О(0;0) – точка пересечения его диагоналей,
одна из которых имеет уравнение .
2.15. Даны середины сторон треугольника АВС: Р(1;2) – середина АВ, Q(5-;1) – середина АС, R(-4;3) – середина ВС. Найти точку пересечения высоты СF и медианы AR.
2.16. Даны
уравнения одной стороны ромба 
и одной диагонали 
.
Диагонали ромба пересекаются в точке Р(0;1). Найти уравнения остальных сторон
ромба.
2.17. Найти
координаты вершин ромба, если известны уравнения двух его сторон 
и 
и
уравнение одной из его диагоналей 
.
2.18. Составить
уравнения трех сторон квадрата, если известно, что четвертой стороной является
отрезок прямой 
, концы которого лежат
на осях координат.
2.19. Найти
вершины прямоугольного равнобедренного треугольника, если дана вершина прямого
угла С(3; 1) и уравнение гипотенузы 
.
2.20. Даны
уравнения боковых сторон равнобедренного треугольника 
и 
и
точка М(5;0) на его основании. Найти периметр и площадь треугольника.
3.01– 3.20 - вазифалар задания – 3.01-3.20
ту¼ри чизик. (Р)
текислик тенгламалари ва А(х0,у0,z0)
нуктанинг координаталари берилган. Топиш керак:
1)
ту¼ри чизикнинг
каноник тенгламасини;
2)
ту¼ри чизик билан
(Р) текисликнинг кесишган нуктасини;
3) А нуктадан (Р) текисликкача булган масофани;
4) А нуктадан утиб, (Р) текисликка перпендикуляр булган ты\ри чизи= тенгламасини.
Даны уравнения прямой (), плоскости (P) и координаты точки А(x0,
y0, z0).
Найти:
1. каноническое
уравнение прямой ();
2. точку
пересечения прямой () и плоскости (Р)
3.01. 
(Р) х+2у-z-6=0; А(4;4;-6).
3.02. 
(Р)
х-2у+3z-5=0; А(2;-4;3).
3.03.
(Р) 2х+у-z-4=0; А(3;2;-2).
3.04. 
(Р)
3х+4у+3z-14=0; А(-5;-6;-5).
3.05. 
(Р)
3х-4у+5z+1=0; А(3;5;-2).
3.06. 
(Р)
5х-4у+6z-1=0; А(1;5;3).
3.07. 
(Р)
3х+2у-z-2=0; А(6;5;-2).
3.08. 
(Р)
х+2у+3z-1=0; А(2;2;3).
3.09. 
(Р)
2х-4у-3z+1=0; А(3;-4;-2).
3.10. 
(Р)
3х-5у+3z-1=0; А(4;-4;4).
3.11. 
(Р)
2х+у-z-1=0; А(5;2;-1).
3.12. 
(Р)
4х+3у+z+2=0; А(-4;2;-6).
3.13. 
(Р)
3х+2у+4z-2=0; А(-3;-3;-3).
3.14.
(Р) 5х+3у-2z-6=0; А(5;4;1).
3.15. 
(Р)
4х-2у-5z-6=0;
А(2;-4;3).
3.16.
(Р)
3х+2у+3z-15=0; А(-3;0;-3).
3.17.
(Р)
2х+3у-z-4=0; А(-6;3;3).
3.18.
(Р)
х-2у-5z+5=0; А(2;-4;-3).
3.19.
(Р)
2х+3у+z-2=0; А(4;-6;-2).
3.20.
(Р) 2х-у-3z=0; А(-5;1;1).
4.01– 4.20 - вазифалар задания - 4.01-4.20
Координата бошини параллел кучириш билан тенгламаларни каноник куринишга келтиринг. Фокусларнинг координаталарни іисобланг. Чизмасини курсатинг.
Выполнив параллельный перенос осей координат привести уравнение к каноническому виду. Вычислить координаты фокусов. Сделать схематический чертеж.
4.01
а) 
4.02.
а) 
;
б)
;
б)
;
в) 
;
в) 
;
г) 
.
г) 
.
4.03.
а) 
;
4.04. а)
;
б)
;
б) 
;
в) 
;
в) 
;
г) 
.
г) 
.
4.05. а)
; 4.06. а)
;
б) 
; б) 
;
в)
;
в)
;
г) 
. г) 
.
4.07. а)
; 4.08. а) 
;
б) 
; б)
;
в)
;
в) 
;
г)
.
г) 
.
4.09. а)
0
;
4.10. а) 
;
б)
;
б) 
;
в)
;
в) 
;
г) 
. г) 
.
4.11. а)
; 4.12. а) 
;
б) 
; б) 
;
в) 
; в) 
;
г)
.
г) 
.
4.13. а)
4.14.
а) 
б) 
б)
в) 
в)
г)
г)
4.15. а)
; 4.16. а)
;
б)
;
б) 
;
в) 
; в) 
;
г) 
. г) 
.
4.17. а)
; 4.18. а) 
;
б) 
; б) 
;
в) 
; в) 
;
г) 
. г) 
.
4.19. а)
; 4.20. а)
;
б) 
; б) 
;
в) 
; в) 
;
г) 
. г) 
.
5.01– 5.20 - вазифалар задания – 5.01-5.20
Матрицалар—матрицы.
Тенгламадан х, у, z топилсин:
5.01.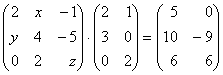 
5.02.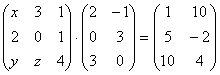 
5.03. 
5.04. 
5.05. 
5.06. 
5.07.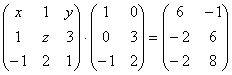 
5.08.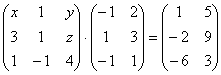 
5.09.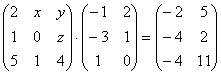 
5.10. 
5.11.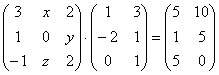 
5.12. 
5.13.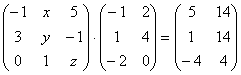 
5.14.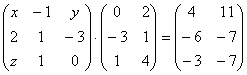 
5.15. 
5.16.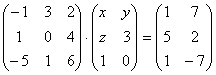 
5.17. 
5.18.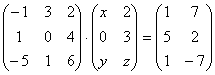 
5.19. 
5.20.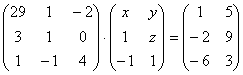 
6.01– 6.20 - вазифалар задания – 6.01-6.20
Матрицали тенгламани ечиб, Х матрицани топинг:
Найти матрицу Х, решив матричное уравнение:
6.01.
6.02.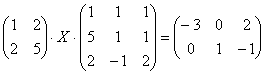 
.
6.03.
.
6.04. 
.
6.05.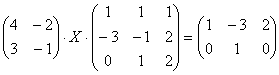
.
6.06. 
.
6.07.
.
6.08.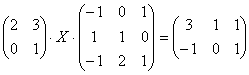 
.
6.09.
.
6.10. 
.
6.11.
.
6.12. 
.
6.13.
.
6.14. 
.
6.15.
. 6.16.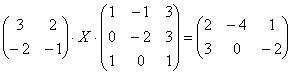
.
6.17.
.
6.18.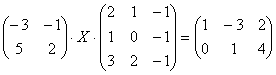 
.
6.19.
. 6.20.
7.01-7.20 - вазифалар задания – 7.01-7.20
Чизикли тенгламалар системаси берилган
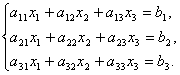
Система биргаликда эканлигини курсатинг ва уни икки усулда ечинг:
1) Гаусс усули;
2) Матрицалар усули.
Данна система линейных уравнений
.
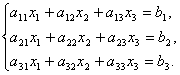Доказать её совместимость и решить двумя способами:
1) методом Гаусса;
2) средствами матричного исчесления.
7.01.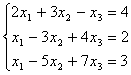 
7.02.
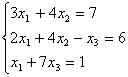
7.03. 
7.04.
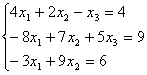
7.05. 
7.06.
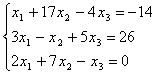
7.07.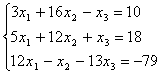 
7.08.
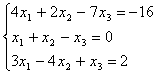
7.09.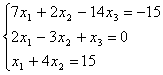 
7.10.
7.11. 
7.12.
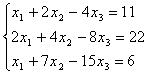
7.13. 
7.14.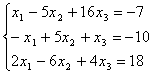 
7.15. 
7.16.
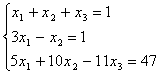
7.17.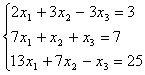 
7.18.
7.19.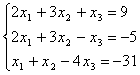 
7.20.
8.01-8.20 - вазифалар задания - 8.01-8.20
Z
комплекс сон берилган. z ва 
сонларни
комплекс текислигида тасвирлаб, 
ва
ларни
іисобланг.
Дано комплексное
число z. На комплексной плоскости изобразить числа z и и вычислить , .
8.01. 
, k=3, m=2,
n=3. 8.02. 
, k=2, m=4, n=4.
8.03. 
, k=4, m=2,
n=5. 8.04. 
, k=5, m=2, n=5.
8.05. 
, k=6, m=4,
n=4. 8.06. 
, k=3, m=5, n=5.
8.07. 
, k=2, m=6,
n=3. 8.08. 
, k=7, m=4, n=6.
8.09. 
, k=5, m=7,
n=4. 8.10. 
, k=4, m=5, n=3.
8.11. 
, k=3, m=4,
n=5. 8.12. 
, k=5, m=3, n=4.
8.13. 
, k=3, m=7,
n=3. 8.14. 
, k=2, m=6, n=6.
8.15. 
, k=3, m=5,
n=4. 8.16. 
, k=4, m=3,
n=5.
8.17. 
, k=6, m=6,
n=3. 8.18. 
, k=2, m=5, n=4.
8.19. 
, k=3, m=7,
n=6. 8.20. 
, k=5, m=6, n=5.
9.01-9.20 – вазифалар задания – 9.01-9.20
Функциянинг аникланиш соіаси топилсин.
Найти область определения функции.
9.01. а) 
; б)
.
9.02. а) 
; б) 
.
9.03. а) 
; б) 
.
9.04. а) 
; б)
.
9.05. а) 
; б) 
.
9.06. а) 
; б) 
.
9.07. а) 
; б) 
.
9.08. а) 
; б)
.
9.09. а) 
; б) 
.
9.10. а) 
; б)
.
9.11. а) 
; б) 
.
9.12. а) 
; б) 
.
9.13. а) 
; б) 
.
9.14. а) 
; б)
.
9.15. а) 
; б)
.
9.16. а) 
; б)
.
9.17. а) 
; б) 
.
9.18. а) 
; б) 
.
9.19. а) 
; б)
.
9.20. а) 
; б) 
.
10.01-10.20 - вазифалар задания - 10.01-10.20
Элементар функциялар графикларини деформациялаш ва силжитиш ёрдамида берилган функциялар графиклари чизилсин.
Построить графики функций с помощью преобразования графика элементарных функций путем деформации и сдвига.
10.01. а) 
; б)
.
10.02. а) 
; б) 
.
10.03. а) 
; б) 
.
10.04. а) 
; б) 
.
10.05. а) 
; б)
.
10.06. а) 
; б) 
.
10.07. а) 
; б) 
.
10.08. а) 
; б) 
.
10.09. а) 
; б) 
.
10.10. а) 
; б) 
.
10.11. а) 
; б) 
.
10.12. а) 
; б) 
.
10.13. а) 
; б)
.
10.14. а) 
; б)
.
10.15. а) 
; б) 
.
10.16. а) 
; б)
.
10.17. а) 
; б)
.
10.18. а) 
; б)
.
10.19. а) 
; б) 
.
10.20. а) 
; б)
.
11.01-11.20 - вазифалар задания – 11.01-11.20
[0,2П] кесмада r = r( 
)
функция берилган. =0 дан бошлаб, 
кадам
билан кутб координаталаридаги нукталар буйича функциянинг шаклини ясанг.
Дана функция r = r( )
на [0,2П]. Построить график функции в полярной системе координат по точкам,
придавая значения через промежуток 
,
начиная от =0.
11.01. 
; 11.02.
;
11.03. 
;
11.04. 
; 11.05. 
; 11.06.
;
11.07. 
; 11.08. 
;
11.09. 
;
11.10. 
;
11.11. 
;
11.12. 
;
11.13. 
; 11.14. 
; 11.15. 
;
11.16. 
;
11.17. 
; 11.18. 
;
11.19. 
; 11.20. 
;
12.01-12.20 – вазифалар задания - 12.01-12.20
Функциянинг курсатилган тартибдаги іосиласи топилсин.
Найти производную функции указанного порядка.
12.01. 
; 
.
12.02. 
; .
12.03. 
; .
12.04. 
; .
12.05. 
; 
.
12.06. 
; .
12.07. 
; .
12.08. 
; .
12.09. 
; .
12.10. 
; .
12.11. 
; .
12.12. 
; .
12.13. 
; .
12.14. 
; 
.
12.15. 
; .
12.16. 
; .
12.17. 
; .
12.18. 
; .
12.19. 
; .
12.20. 
; .
13.01– 13.20 - вазифалар задания - 13.01-13.20
Параметрик куринишда
берилган функциянинг биринчи тартибли 
ва иккинчи тартибли 
іосилаларни
іисобланг.
Найти производные
первого порядка и второго порядка от
функции, заданных параметрически.
13.01. 
; 13.02.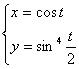 
; 13.03. 
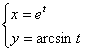; 13.04. 
;
13.05. 
; 13.06. 
; 13.07. 
; 13.08.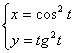 
;
13.09. 
; 13.10. 
; 13.11.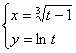 
; 13.12. 
;
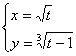13.13. 
; 13.14.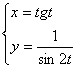 
; 13.15. 
; 13.16.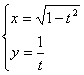 
;
13.17.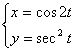 
; 13.18. 
; 13.19. 
; 13.20. 
;
14.01-14.20 - вазифалар задания - 14.01-14.20
Функциянинг дифференциали топилсин.
Найти дифференциал функции.
14.01. 
;
14.02. 
;
14.03. 
; 14.04.
;
14.05. 
; 14.06.
;
14.07. 
; 14.08.
;
14.09. 
; 14.10.
;
14.11. 
;
14.12. 
;
14.13. 
; 14.14.
;
14.15. 
; 14.16.
;
14.17. 
; 14.18.
;
14.19. 
;
14.20. 
.
15.01-15.20 - вазифалар задания – 15.01-15.20
Берилган эгри чизикка х0 нуктада утказилган уринма ва нормал тенгламаси тузилсин.
Составить уравнение касательной и нормали к данной кривой в
точке с абсциссой 
15.01. 
; 
.
15.02. 
; 
.
15.03. 
; .
15.04. 
; 
.
15.05. 
; 
.
15.06. 
; 
.
15.07. 
; .
15.08. 
; .
15.09. 
; 
.
15.10. 
; .
15.11. 
; 
.
15.12. 
; 
.
15.13. 
; .
15.14. 
; .
15.15. 
; 
.
15.16. 
; .
15.17. 
; .
15.18. 
; .
15.19. 
; .
15.20. 
; .
16.01-16.20 - вазифалар задания – 16.01-16.20
Функцияни тула текшириб, унинг графигини ясанг.
Провести полное исследование функции и построить график.
16.01. а) 
; б)
.
16.02. а) 
; б) 
.
16.03. а) 
; б)
.
16.04. а) 
; б)
.
16.05. а) 
; б)
.
16.06. а) 
; б)
.
16.07. а) 
; б)
.
16.08. а) 
; б)
.
16.09. а) 
; б)
.
16.10. а) 
; б)
.
16.11. а) 
; б)
.
16.12. а) 
; б)
.
16.13. а) 
; б) 
.
16.14. а) 
; б)
.
16.15. а) 
; б)
.
16.16. а) 
; б)
.
16.17. а) 
; б)
.
16.18. а) 
; б) 
.
16.19. а) 
; б) 
.
16.20. а) 
; б)
.
17.01-17.20 – вазифалар задания – 17.01-17.20
Аникмас интеграллар іисоблансин.
Найти неопределенные интегралы.
17.01. a) 
; б)
; в) 
;
г) 
; д)
.
17.02. а) 
; б) 
; в)
;
г) 
; д) 
.
17.03. а) 
; б) 
; в)
;
г) 
; д)
.
17.04. а) 
; б) 
; в) 
;
г) 
; д) 
.
17.05. а) 
; б)
; в)
;
г) 
; д) 
.
17.06. а) 
; б) 
; в)
;
г) 
; д) 
.
17.07. а) 
; б)
; в) 
;
г) 
; д) 
.
17.08. а) 
; б)
; в) 
;
г) 
; д)
.
17.09. а) 
; б) 
; в) 
;
г) 
; д) 
.
17.10. а)
; б)
; в) 
;
г) 
; д) 
.
17.11. а) 
; б)
; в) 
;
г) 
; д) 
.
17.12. а)
; б)
; в)
;
г) 
; д) 
.
17.13. а) 
; б) 
; в) 
;
г) 
; д) 
.
17.14. а) 
; б)
; в) 
;
г) 
; д)
.
17.15. а) 
; б)
; в)
;
г) 
; д) 
.
17.16. а) 
; б)
; в) 
;
г) 
; д) 
.
17.17. а) 
; б)
; в) 
;
г) 
; д) .
17.18. а) 
; б) 
; в) 
;
г) 
; д) 
.
17.19. а) 
; б)
; в) 
;
г) 
; д) 
.
17.20. а) 
; б)
; в)
;
г) 
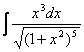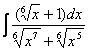; д) 
.
18.01-18.20 - вазифалар задания – 18.01-18.20
Берилган функцияларнинг графиклари билан чегараланган шаклларнинг юзаси іисоблансин.
Вычислить площади фигур, ограниченных графиками функций.
18.01. 
; 
.
18.02. 
; 
.
18.03. 
; 
.
18.04. 
; y=0; 
.
18.05. 
; y=0; 
.
18.06. 
; 
.
18.07. 
; 
.
18.08. 
; 
.
18.09. 
; 
; 
; 
.
18.10. 
; 
; 
; y=0.
18.11. 
; 
.
18.12. 
; 
; x=0.
18.13. 
; y=0; x=0.
18.14. 
; x=0; y=0.
18.15. 
; y=0; 
.
18.16. 
; 
.
18.17. 
; y=0; 
.
18.18. 
; y=0; 
; 
.
18.19. 
; 
.
18.20. 
; y=0; x=1.
19.01-19.20 – вазифалар задания – 19.01-19.20
Эгри чизик ёйининг узунлиги іисоблансин.
Вычислить длины дуг кривых заданных линиями.
19.01. 
; 
.
19.02. 
; 
.
19.03. 
; 
.
19.04. 
; 
.
19.05. 
; 
.
19.06.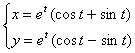 
; 
.
19.07. 
; 
.
19.08. 
; 
.
19.09. 
; 
.
19.10. 
; 
.
19.11. 
; .
19.12. 
; 
.
19.13. 
; 
.
19.14. 
; 
.
19.15. 
; 
.
19.16. 
; 
.
19.17. 
; 
.
19.18. 
; 
.
19.19.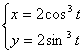 
; 
.
19.20. 
; 
.
20.01-20.20 - вазифалар задания – 20.01-20.20
Берилган функцияларнинг графикларини ук атрофида айлантришдан іосил булган жисмларнинг іажми іисоблансин.
Вычислить объем тел, образованных вращением фигур, ограниченных графиками функций.
20.01. 
; 
; 
. ОХ уки атрофидан
Вокруг оси ОХ.
20.02. 
; 
. ОХ уки атрофидан
Вокруг оси ОХ.
20.03. 
; 
; 
. ОУ уки атрофидан
Вокруг оси ОУ
20.04. 
; ; ; 
. ОУ уки атрофидан
Вокруг оси ОУ
20.05. 
; 
; 
; . ОУ уки атрофидан
Вокруг оси ОУ
20.06. 
; 
; ; 
. ОХ уки атрофидан
Вокруг оси ОХ.
20.07. 
; ; . ОХ уки атрофидан
Вокруг оси ОХ
20.08. 
; 
. ОХ уки атрофидан
Вокруг оси ОХ.
20.09. 
; ; ; . ОХ уки атрофидан
Вокруг оси ОХ.
20.10. ; ; . ОУ уки атрофидан
Вокруг оси ОУ
20.11. 
; ; 
; . ОУ уки атрофидан
Вокруг оси ОУ
20.12. 
; . ОУ уки атрофида
Вокруг оси ОУ
20.13. ; . ОУ уки атрофидан
Вокруг оси ОУ
20.14. 
; ; . ОУ уки атрофидан
Вокруг оси ОУ
20.15. ; . ОУ уки атрофидан
Вокруг оси ОУ
20.16. 
; ; 
; . ОХ уки атрофидан
Вокруг оси ОХ.
20.17. ; y=1; x=2. ОХ уки атрофидан
Вокруг оси ОХ.
20.18. ; 
. ОХ уки атрофидан
Вокруг оси ОХ.
20.19. ; x=0; x=2; y=0.
ОУ уки атрофидан
Вокруг оси ОУ
20.20. ; y=1; x=2. ОХ уки атрофидан
Вокруг оси ОХ.
21.01-21.20 – вазифалар задания – 21.01-21.20
Хосмас интегралларни іисобланг ёки уларнинг узоклашувчи эканини исботланг.
Вычислить несобственный интеграл или доказать его расходимость.
21.01.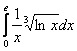 
21.02.
21.03.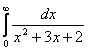 
21.04.
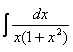
21.05. 
21.06.
21.07. 
21.08.
21.09. 
21.10.
21.11.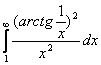 
21.12.
21.13. 
21.14.
21.15.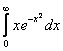 
21.16.
21.17.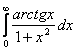 
21.18.
21.19. 
21.20.
Мундарижа.
Сыз боши………………………………………………………………….3
Саволлар……………………………………………………………………4
Адабиётлар…………………………………………………………………7
1-вазифа……………………………………………………………………7
2-вазифа……………………………………………………………………8
3-вазифа……………………………………………………………………12
4-вазифа……………………………………………………………………13
5-вазифа……………………………………………………………………16
6-вазифа……………………………………………………………………17
7-вазифа……………………………………………………………………19
8-вазифа……………………………………………………………………20
9-вазифа……………………………………………………………………21
10-вазифа…………………………………………………………………..22
11-вазифа…………………………………………………………………..23
12-вазифа…………………………………………………………………..24
13-вазифа…………………………………………………………………..25
14-вазифа…………………………………………………………………..25
15-вазифа…………………………………………………………………..26
16-вазифа…………………………………………………………………..27
17-вазифа…………………………………………………………………..28
18-вазифа…………………………………………………………………..31
19-вазифа…………………………………………………………………..31
20-вазифа…………………………………………………………………..33
21-вазифа…………………………………………………………………..34
Олий математикадан махсус факультет талабалари учун erув-услубий reлланма.
Учебно-методическое пособие по высшей математике для студентов специального факультета.
ОЛИЙ МАТЕМАТИКА
Кафедрасининг мажлисида му[окама rилинди ва босмахонада чоп этишга тавсия этилди.
(22.05.02 33 – баённома).
Тузувчилар: к. er. Шопен И. Л.
ассистент Мирахмедова М. И.
Масъул му[аррир: Усмонов Р. Н.
Му[аррир: Парпиева R.
Абдуллаева С. Х.