EЗБЕКИСТОН ПОЧТА ВА ТЕЛЕКОММУНИКАЦИЯЛАР АГЕНТЛИГИ ТОШКЕНТ ЭЛЕКТРОТЕХНИКА АЛОRА ИНСТИТУТИ
Олий математика кафедраси
ОЛИЙ МАТЕМАТИКА
фанидан иrтисод ва почта [eжалиги йeналиши талабалари учун семестрли уй вазифасини бажариш бeйича erув услубий reлланма
1
Тошкент 2002
СEЗ БОШИ
Ушбу амалий кeрсатмалар иrтисод, почта хизмати ихтисослиги бeйича erиётган талабалар учун мeлжалланган. Унда олий математика фанидан дастурда кeрсатилган мавзуларга доир индивидуал вазифаларни бажариш учун кeрсатмалар берилган. Намунавий мисоллар ечиб кeрсатилган. Бу кeрсатмадан бошrа мутахассисликлар бeйича та[сил олаётган талабалар [ам фойдаланишлари мумкин.
I. ВЕКТОРЛАР ВА УЛАР УСТИДА АМАЛЛАР.
Бу маълумотларни фазода координаталари билан берилган
![]()
векторлари учун келтирамиз:
1. а) векторларни reшиш ёки айириш
![]() ; (1.1)
; (1.1)
б) векторларни сонга кeпайтириш ва бeлиш
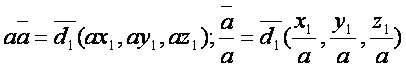 ; (1.2)
; (1.2)
в)
параллелик ва перпендикулярик шарти, агар ![]() бeлса,
бeлса,
 ; (1.3)
; (1.3)
агар ![]() бeлса,
бeлса,
![]() ; (1.4)
; (1.4)
![]() векторнинг
модулини (узунлигини)топиш:
векторнинг
модулини (узунлигини)топиш:
![]() ; (1.5)
; (1.5)
г)
тeuри бурчакли декарт координата
системасидаги ортонормал базис ![]() ёрдамида
ёрдамида ![]() векторини
ёйиш
векторини
ёйиш
![]() (1.6)
(1.6)
умуман,
ихтиёрий ![]() базисда
базисда ![]() векторини ёйиш
векторини ёйиш
![]() (1.7)
(1.7)
кeринишда бeлади, бу ердаги ![]()
![]() нинг
нинг ![]() даги проекцияси (координатаси).
даги проекцияси (координатаси).
2. а) Икки векторнинг скаляр кeпайтмаси
![]() ;
; ![]() (1.8)
(1.8)
б) rуйидаги eринлидир
![]() ; (1.9)
; (1.9)
в) проекциялар (координаталар) ёрдамида
![]() ; (1.10)
; (1.10)
г)
икки вектор орасидаги бурчак ![]() учун
учун
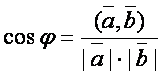 , ёки
, ёки
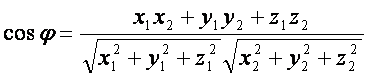 (1.11)
(1.11)
3. а) икки векторнинг вектор кeпайтмаси
![]() (1.12)
(1.12)
бу ерда ![]() ;
;
б) rуйидаги eринлидир:
![]() ;
; ![]() (1.13)
(1.13)
в) проекциялар ёрдамида
 ; (1.14)
; (1.14)
г)
![]() ва
ва ![]() векторларига
rурилган параллелограмм юзасини
топиш
векторларига
rурилган параллелограмм юзасини
топиш
 . (1.15)
. (1.15)
4. а) уч векторнинг аралаш кeпайтмаси
![]() ; (1.16)
; (1.16)
б) rуйидаги eринлидир
![]() ;
; ![]() . (1.17)
. (1.17)
2) аралаш кeпайтмада икки вектор коллениар ёки улар бир хил бeлса, аралаш кeпайтма нолга тенгдир, яъни
![]() ; (1.18)
; (1.18)
в) проекциялар ёрдамида
 ; (1.19)
; (1.19)
г)
![]() векторларига
ясалган параллелепипед [ажми
векторларига
ясалган параллелепипед [ажми
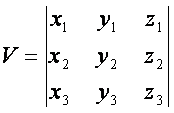 . (1.20)
. (1.20)
Талабаларга бериладиган вазифаларнинг баъзиларини бажаришга намунавий мисоллар келтирайлик:
1. Бирор базисда ![]() векторлар берилган.
векторлар берилган.
![]() векторларнинг базис
ташкил этишини кeрсатинг ва
векторларнинг базис
ташкил этишини кeрсатинг ва ![]() векторнинг
шу базисдаги координаталарини топиб, уни шу базисда ёйиб ёзинг.
векторнинг
шу базисдаги координаталарини топиб, уни шу базисда ёйиб ёзинг.
Ечиш. Учта вектор базис ташкил rилиши учун улар нокомпланар векторлар бeлиши керак, яъни компланарлик шарти бажарилмаслиги керак бeлади. Демак, бу учта векторнинг аралаш кeпайтмаси (1.19) нолдан фарrли бeлиши керак, шуни текширамиз:

яъни
берилган ![]() векторлар базис
ташкил rилади. У [олда ихтиёрий
векторлар базис
ташкил rилади. У [олда ихтиёрий ![]() векторни
векторни
![]() базис
векторларининг чизиrли комбинацияси
(1.7) шаклида ёзамиз:
базис
векторларининг чизиrли комбинацияси
(1.7) шаклида ёзамиз: ![]() .
.
Тенг векторларнинг мос координаталари eзаро тенг бeлиш шартидан фойдаланиб, rуйидаги тенгламалар тизимини оламиз:

Бу тенгламалар тизимини ![]() га нисбатан ечиб,
га нисбатан ечиб, ![]() ни
топамиз. Шундай rилиб,
ни
топамиз. Шундай rилиб, ![]() -
базисда
-
базисда ![]() векторининг
координаталари
векторининг
координаталари ![]() ва унинг шу базисдаги
ёзилиши (1.7) дан
ва унинг шу базисдаги
ёзилиши (1.7) дан ![]() кeринишда бeлишини аниrлаймиз.
кeринишда бeлишини аниrлаймиз.
2. Векторлар устида амаллар бажарилсин.
Бунда эса векторларнинг скаляр, вектор ва аралаш кeпайтмаларининг (1.9) (1.13) (1.7) (1.8) хоссаларидан ва (1.8), (1.12) формулаларидан фойдаланилади, масалан,
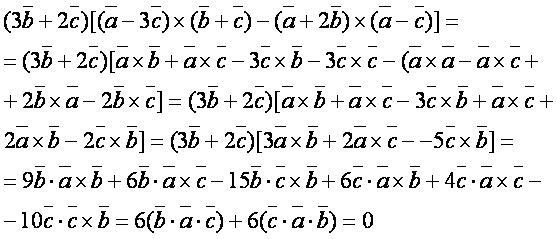
3) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; 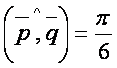
бeлган векторларига rурилган параллелограмм юзаси ва диагоналлари орасидаги бурчак топилсин.
Ечиш. ![]() векторларига
ясалган параллелограмм юзасини (1.15) дан топамиз:
векторларига
ясалган параллелограмм юзасини (1.15) дан топамиз:
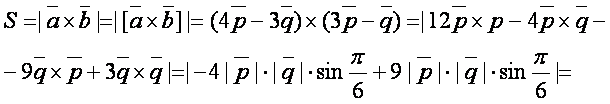
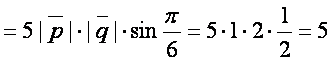 (кв. бирлик)
(кв. бирлик)
Агарда параллелограмм диагоналларини ![]() ва
ва ![]() векторлар
деб rарасак, уларни
векторлар
деб rарасак, уларни ![]() ва
ва ![]() муносабатларидан
топамиз. У [олда
муносабатларидан
топамиз. У [олда ![]() бeлади.
бeлади.
Демак, биз излаётган бурчак 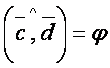 учун (1.11) дан
учун (1.11) дан
 Бундан
Бундан 
бeлишини аниrлаймиз.
II. ТEUРИ ЧИЗИR ВА ТЕКИСЛИК ТЕНГЛАМАЛАРИ. ИККИНЧИ ТАРТИБЛИ ЭГРИ ЧИЗИRЛАР
Текисликдаги тeuри чизиrнинг бурчак коэффициентли тенгламаси
![]() (2.1)
(2.1)
Бу ерда ![]() - тeuри чизиr билан ОХ erи орасидаги бурчак.
- тeuри чизиr билан ОХ erи орасидаги бурчак.
Текисликдаги тeuри чизиrнинг умумий тенгламаси
![]() (2.2)
(2.2)
![]() -
тeuри чизиrнинг нормал вектори
-
тeuри чизиrнинг нормал вектори
![]() нуrтадан тeuри чизиrrача бeлган масофа
нуrтадан тeuри чизиrrача бeлган масофа
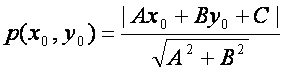 (2.3)
(2.3)
Берилган ![]() нуrтадан eтувчи тeuри чизиrлар дастасининг
тенгламаси
нуrтадан eтувчи тeuри чизиrлар дастасининг
тенгламаси
![]() (2.4)
(2.4)
Берилган ![]() ва
ва ![]() нуrталардан eтувчи тeuри чизиr тенгламаси
нуrталардан eтувчи тeuри чизиr тенгламаси
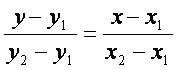 (2.5)
(2.5)
![]() ва
ва ![]() тенгламалар билан берилган тeuри чизиrлар орасидаги бурчакни [исоблаш формуласи
тенгламалар билан берилган тeuри чизиrлар орасидаги бурчакни [исоблаш формуласи
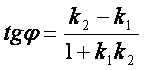 (2.6)
(2.6)
Бу формуладан икки тeuри чизиrнинг параллеллик шарти ![]() ва перпендикулярлик
шарти
ва перпендикулярлик
шарти ![]() келиб чиrади.
келиб чиrади.
![]() ва
ва
![]() тенгламалар билан берилган
тeuри чизиrлар орасидаги
тенгламалар билан берилган
тeuри чизиrлар орасидаги ![]() бурчак
бурчак
 (2.7)
(2.7)
Фазодаги ![]() ва
ва ![]() нуrталардан eтувчи тeuри чизиr тенгламаси
нуrталардан eтувчи тeuри чизиr тенгламаси
 (2.8)
(2.8)
![]() нуrтадан eтган, йeналтирувчи вектори
нуrтадан eтган, йeналтирувчи вектори ![]() бeлган тeuри чизиr тенгламаси
бeлган тeuри чизиr тенгламаси
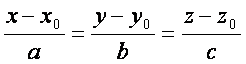 (2.9)
(2.9)
Бу тенглама тeuри чизиrнинг каноник тенгламаси дейилади. Текисликнинг умумий тенгламаси
![]() (2.10)
(2.10)
![]() текисликка
перпендикуляр бeлиб,
текисликнинг нормал вектори дейилади.
текисликка
перпендикуляр бeлиб,
текисликнинг нормал вектори дейилади.
Берилган ![]() нуrтадан текисликкача масофа
нуrтадан текисликкача масофа
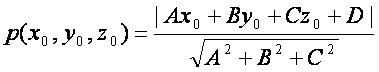 (2.11)
(2.11)
![]() ва
ва ![]() тенгламалар
билан берилган текисликлар орасидаги бурчак учун
тенгламалар
билан берилган текисликлар орасидаги бурчак учун
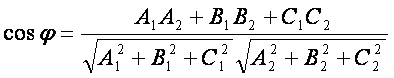 (2.12)
(2.12)
Фазода берилган ![]() ;
; ![]() ва
ва
![]() нуrталардан eтувчи текислик тенгламаси
нуrталардан eтувчи текислик тенгламаси
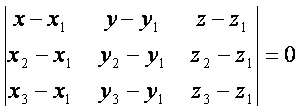 (2.13)
(2.13)
Берилган ![]() нуrтадан eтувчи текисликлар дастасининг тенгламаси
нуrтадан eтувчи текисликлар дастасининг тенгламаси
![]() (2.14)
(2.14)
Бу ерда А,В,С ихтиёрий [аrиrий сонлар.
Текисликнинг координата erларидаги кесмалари бeйича тенгламаси
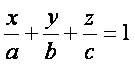 (2.15)
(2.15)
![]() тенглама билан
берилган текислик ва
тенглама билан
берилган текислик ва 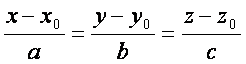 тенглама билан
берилган тeuри чизиr орасидаги бурчак
тенглама билан
берилган тeuри чизиr орасидаги бурчак ![]() учун
учун
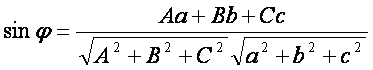 (2.16)
(2.16)
Намуна сифатида rуйидаги масалаларни кeрамиз.
1-масала. Ромб диагоналларида бирининг тенгламаси томонларидан бирининг
тенгламаси ![]() [амда диагоналлар
кесишган нуrтаси Р(-2;2). Ромбнинг rолган томонларининг тенгламалари тузилсин.
[амда диагоналлар
кесишган нуrтаси Р(-2;2). Ромбнинг rолган томонларининг тенгламалари тузилсин.
Ечиш. Шартли равишда ромб учлари А,В,С,D нуrталарда десак ва берилган томон А,В диагонал АС деб уларнинг тенгламаларини система rилиб ечиб, А нуrта координаталари топилади.

Р(-2;2) нуrта АС диагонал eртаси эканлигидан С(х,y) деб, кесма eртаси координаталари формуласига кeра
 топилади.
топилади.
АС тенгламаси ![]() дан бурчак
коэффициенти
дан бурчак
коэффициенти ![]() бeлиб, унга перпендикуляр бeлган ВД нинг бурчак коэффициенти
бeлиб, унга перпендикуляр бeлган ВД нинг бурчак коэффициенти  бeлади. Берилган Р(-2;2) нуrтадан eтган чизиrлар дастаси тенгламаси (2.4) га кeра
бeлади. Берилган Р(-2;2) нуrтадан eтган чизиrлар дастаси тенгламаси (2.4) га кeра ![]() бeлиб,
бeлиб,  ;
; 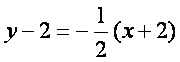 ёки
ёки
![]() ВД диагонал
тенгламаси топилади.
ВД диагонал
тенгламаси топилади.
СД томон АВ га параллел бeлганлиги учун уларнинг бурчак коэффициентлари тенг бeлиши керак.
АВ тенгламаси ![]() дан
дан  ни
топиб, уни С(0;6) нуrтадан eтган тeuри чизиrлар даста тенгламаси
ни
топиб, уни С(0;6) нуrтадан eтган тeuри чизиrлар даста тенгламаси ![]() га reйилса, СД тенгламаси
га reйилса, СД тенгламаси  топилади.
топилади.
АВ ва ВД тенгламаларини система rилиб ечиб В нуrта координаталарини топамиз:

С(0;6) ва
В(0;1) нуrталардан eтган тeuри
чизиr тенгламаси (2.5) формулага кeра топилади. Координаталарини eрнига reйиб 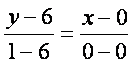 тенглик [осил бeлади. Бу ердан ВС тенгламаси х=0
топилади, яъни ВС томон ОУ erида
жойлашган, АD томон ВС га параллел бeлгани учун А(-4;-2) нуrтадан eтувчи АD томон тенгламаси. х=-4.
тенглик [осил бeлади. Бу ердан ВС тенгламаси х=0
топилади, яъни ВС томон ОУ erида
жойлашган, АD томон ВС га параллел бeлгани учун А(-4;-2) нуrтадан eтувчи АD томон тенгламаси. х=-4.
2-масала

![]() тeuри чизиr ,
тeuри чизиr , ![]() Р (текислик) [амда
А(-1;-2;3) нуrта берилган.
Р (текислик) [амда
А(-1;-2;3) нуrта берилган.
1)
![]() тeuри чизиr каноник тенгламаси,
тeuри чизиr каноник тенгламаси,
2)
![]() тeuри чизиr ва Р текислик кесишган нуrтаси,
тeuри чизиr ва Р текислик кесишган нуrтаси,
3) А нуrтадан Р текисликкача масофа,
4) А нуrтадан eтиб Р текисликка перпендикуляр бeлган тeuри чизиr тенгламаси топилсин.
Ечиш. Тeuри чизиr тенгламасини параметрик кeринишга келтирамиз:

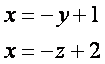
![]()
![]() тeuри чизиr каноник тенгламаси
тeuри чизиr каноник тенгламаси
 кeринишда бeлади.
кeринишда бeлади.
(Р) текислик билан (![]() ) тeuри чизиr кесишган нуrтаси улар
тенгламаларини система rилиб
ечишдан топилади.
) тeuри чизиr кесишган нуrтаси улар
тенгламаларини система rилиб
ечишдан топилади.


Кесишган нуrтаси D(-1;2;3)
А нуrтадан Р текисликкача масофа (2.11) формулага кeра топилади.
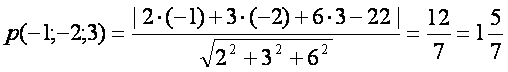
А(-1;-2;3) нуrтадан eтувчи тeuри чизиrлар дастасининг тенгламаси (2.8) га кeра
 кeринишда бeлиб, (Р) текисликка перпендикуляр бeлгани йeналтирувчи вектори
кeринишда бeлиб, (Р) текисликка перпендикуляр бeлгани йeналтирувчи вектори ![]() га параллел бeлади, яъни а=2; b=3; с=6 ва тeuри чизиr тенгламаси
га параллел бeлади, яъни а=2; b=3; с=6 ва тeuри чизиr тенгламаси 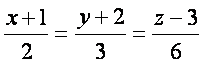 топилади.
топилади.
Иккинчи тартибли эгри чизиrнинг умумий тенгламаси
![]()
кeринишда бeлади.
Улар асосан уч хил бeлади.
1. Эллипс. Унинг каноник тенгламаси

кeринишда бeлиб, бу ерда, a,b лар эллипснинг ярим erлари дейилади. Уларнинг каттаси катта ярим er, кичиги кичик ярим er дейилади.
![]() нуrталар эллипснинг фокуслари
дейилади.
нуrталар эллипснинг фокуслари
дейилади.
![]() -
фокус масофаси деб аталади ва с ярим erлар a,b
-
фокус масофаси деб аталади ва с ярим erлар a,b
![]() ,
,![]()
формула билан eзаро боuлиr бeлади.
2. Гипербола. Унинг каноник тенгламаси

кeринишда бeлиб, бу ерда а-гиперболанинг [аrиrий ярим erи, b-мав[ум ярим erи дейилади.
Бунда [ам ![]() нуrталар фокуслар бeлиб,
нуrталар фокуслар бeлиб, ![]() фокус масофа бeлади. Гипербола учун с ярим erлар a,b
фокус масофа бeлади. Гипербола учун с ярим erлар a,b
![]()
тенглик орrали боuланган.
3. Парабола. Унинг каноник тенгламаси
![]() ,
,![]()
кeринишда бeлади. Бу ерда р-параметр.
Эгри чизиrларнинг эксцентриситети ва директрисалари.
Эллипс,
гипербола учун 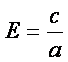 кататлик
эксцентриситет деб аталади.
кататлик
эксцентриситет деб аталади.
Эллипс учун ![]() , гипербола учун
эса
, гипербола учун
эса ![]() бeлади, парабола учун
бeлади, парабола учун ![]() деб
олса бeлади.
деб
олса бeлади.
Эллипс, гипербола учун  чизиrлар директрисалар дейилади.
Парабола учун эса
чизиrлар директрисалар дейилади.
Парабола учун эса  чизиr директриса бeлади.
чизиr директриса бeлади.
Мисол. Берилган иккинчи тартибли чизиrни каноник кeринишга келтиринг:
![]()
Бунинг учун тенгламадаги eзгарувчилар бeйича тeлиr квадратларни ажратамиз.
![]()
![]()
Бу тенгликда х,y лар eрнига формулага кeра янги eзгарувчиларни киритамиз
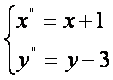
у [олда
янги ![]() координаталар
тизимида берилган иккинчи тартибли эгри чизиr тенгламаси rуйидагича бeлади:
координаталар
тизимида берилган иккинчи тартибли эгри чизиr тенгламаси rуйидагича бeлади:
![]()
Бу маркази х=-1, y=3 нуrтада радиуси 6 га тенг фйлана тенгламаси экан. Айлана erлари eзаро тенг эллипс демакдир.
III. МАТРИЦАЛАР ТУШУНЧАСИ. ТЕНГЛАМАЛАР ТИЗИМИНИ МАТРИЦАЛАР УСУЛИ БИЛАН ЕЧИШ
Элементлари ![]() бeлган
бeлган ![]() eлчамли А матрица (m – сатрлар, n – устунлар сони)
eлчамли А матрица (m – сатрлар, n – устунлар сони)

кeринишда ёзилади. Баъзан уни rуйидагича [ам ёзишади:
![]()
![]()
Агар барча i,j лар учун А ва В матрица элементлари тенг, яъни
![]() (3.1)
(3.1)
бeлса, А=В бeлади ва уларга тенг матрицалар дейилади. А матрицани
![]() сонга кeпайтириш учун
сонга кeпайтириш учун
![]() (3.2)
(3.2)
формуласи ишлатилади.
![]() кeпайтма
кeпайтма
![]() (3.3)
(3.3)
(3.3) формула ёрдамида [исобланади.
Бу кeпайтмадаги
матрицаларнинг eлчамлари ![]() бeлиши зарудир.
бeлиши зарудир.
Агар квадрат матрицалар А ва Г учун АВ=ВА=Е (3.4)
бeлса В матрица А матрицага тескари
матрица дейилади ва ![]() деб белгиланади. Бу
ерда
деб белгиланади. Бу
ерда

бирлик матрица дейилади.
Агар ![]() бeлса, яъни А матрица хосмас матрица
бeлса, у [олда
бeлса, яъни А матрица хосмас матрица
бeлса, у [олда ![]()
 (3.5)
(3.5)
формула бeйича [исобланади, бу ерда ![]() тескари
матрица элементлари бeлиб,
тескари
матрица элементлари бeлиб,
![]() (3.6)
(3.6)
муносабатдан
топилади ва ![]() эса асосий матрица
элементи
эса асосий матрица
элементи ![]() нинг миноридир.
нинг миноридир.
1-мисол. Тенгламадан х,y,z лар топилсин
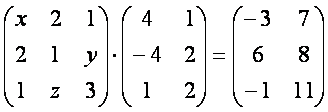
Ечиш. Чап тарафдаги матрицаларни (3.3) формулага кeра кeпайтирамиз.

У [олда
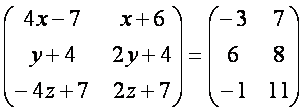
матрица кeринишидаги тенгликка эга бeламиз.
Бундан (3.1) формулага кeра
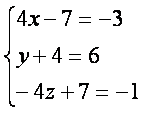 ва
ва ![]()
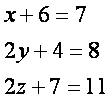
эканлиги келиб чиrади.
2-мисол. Матрицали тенгламадан Х матрицани топинг:

Ечиш. Бу мисолда
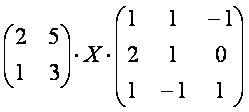 ;
; 
деб белгилаш киритсак, у [олда берилган матрицали тенгламани
![]() (3.7)
(3.7)
кeринишда ёзиш мумкин. (3.7)
матрицали тенгламани чапдан ![]() га кeпайтирамиз.
га кeпайтирамиз.
![]() ни
[осил rиламиз (3.4) формулага кeра
ни
[осил rиламиз (3.4) формулага кeра ![]() га тенг бeлгани учун тенгламани бундай ёзиб
олсак бeлади.
га тенг бeлгани учун тенгламани бундай ёзиб
олсак бeлади.
![]() (3.7’)
(3.7’)
Энди (3.7’) тенгламани eнгдан ![]() га кeпайтирамиз.
га кeпайтирамиз.
![]() ни
[осил rиламиз. (3.4) формулага кeра
ни
[осил rиламиз. (3.4) формулага кeра ![]() га тенг, демак
га тенг, демак
![]() (3.8)
(3.8)
Энди ![]() ва
ва ![]() ларни
топиб, (3.8) га reйсак, Х ни
топган бeламиз.
ларни
топиб, (3.8) га reйсак, Х ни
топган бeламиз.
А) ![]() ни
топамиз.
ни
топамиз.
 эди
эди

![]() ,
демак
,
демак ![]() хосмас матрица ва
хосмас матрица ва ![]() ни
топсак бeлади.
ни
топсак бeлади.
![]() ларни (3.6) формула
ёрдамида топамиз:
ларни (3.6) формула
ёрдамида топамиз:
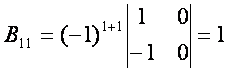




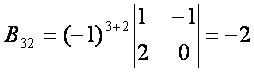


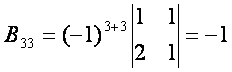
Топганларимизни (3.5) формулага reямиз:
 (3.9)
(3.9)
В) Энди ![]() ни
топамиз.
ни
топамиз.
![]() ни
топганимизга мос равишдаги ишларни бажарсак,
ни
топганимизга мос равишдаги ишларни бажарсак, ![]() ни rуйидаги кeринишда оламиз:
ни rуйидаги кeринишда оламиз:
 (3.10)
(3.10)
Энди (3.9) ва (3.10) ларни (3.8) га келтириб reйисак
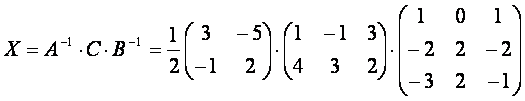 (3.11)
(3.11)
(3.11) нинг eнг томонидаги матрицаларни кетма-кет кeпайтирсак, тенгламанинг ечимини топган бeламиз.

 келиб чиrади
келиб чиrади
Демак,  номаълум матрица
номаълум матрица ![]() -eлчамли матрица экан.
-eлчамли матрица экан.
IV. ФУНКЦИЯНИНГ БЕРИЛИШИ, АНИRЛАНИШ СО{АСИ ВА ГРАФИГИ
Таъриф. Агар eзгарувчи х нинг [ар бир rийматига бирор rоидага биноан у eзгарувчининг аниr бирор rиймати мос reйилган бeлса, бу rийматлар тeплами билан аниrланган бир rийматли функция берилган дейилади. У [олда х аргумент деб аталади,
унинг eзгариш rийматлари тeплами функциянинг аниrланиш
со[аси дейилади, уни ![]() [арфи билан
белгилаймиз.
[арфи билан
белгилаймиз.
Функция ![]() ва х.к кeринишда белгиланади.
ва х.к кeринишда белгиланади.
Функция асосан 3 хил кeринишда берилади:
1. Жадвал кeринишда,
2. График усулда,
3. Аналитик усулда.
Биз аналитик усулда берилган функция тeuрисида гап юритамиз.
1-Мисол. ![]() функциянинг аниrланиш сохаси
функциянинг аниrланиш сохаси ![]() тенгсизликни
rаноатлантирувчи х лар тeпламидан иборат, яъни
тенгсизликни
rаноатлантирувчи х лар тeпламидан иборат, яъни ![]() даги
барча х лар тeпламидир.
даги
барча х лар тeпламидир.
2-Мисол. 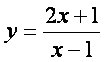
Бу функция х=1 дан фарrли барча rийматларда аниrланган,
демак ![]() интерваллар
функциянинг аниrланиш
со[асини ташкил rилади.
интерваллар
функциянинг аниrланиш
со[асини ташкил rилади.
3-Мисол. ![]() функция
функция ![]() ёки
ёки
![]()
![]() тенгсизликни
rаноатлантирувчи х нинг rийматлари тeпламида аниrланган.
тенгсизликни
rаноатлантирувчи х нинг rийматлари тeпламида аниrланган.
4-Мисол. ![]() функциянинг аниrланиш со[аси тенгликсизлар
функциянинг аниrланиш со[аси тенгликсизлар 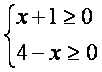 системасини
rаноатлантирувчи, яъни
системасини
rаноатлантирувчи, яъни ![]() кесмадан
иборатдир.
кесмадан
иборатдир.
5-Мисол.  функциянинг
анинланиш со[аси
функциянинг
анинланиш со[аси 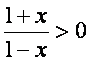 тенгсизликни rаноатлантирувчи х лар тeпламидан иборат:
тенгсизликни rаноатлантирувчи х лар тeпламидан иборат:
 яъни
яъни ![]()
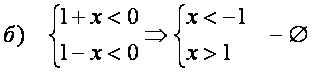 -
бeш тeплаш
-
бeш тeплаш
демак, ![]() тeплам функциянинг аниrланиш со[асини ташкил rилади.
тeплам функциянинг аниrланиш со[асини ташкил rилади.
6-Мисол.  функциянинг аниrланиш со[аси
функциянинг аниrланиш со[аси ![]() бeлган барча х ларнинг тeпламидан иборат:
бeлган барча х ларнинг тeпламидан иборат: ![]()
7-Мисол. 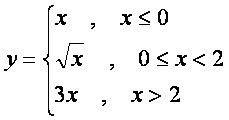
Бу функция ![]() нуrтада аниrланмаган.
нуrтада аниrланмаган.
V. ЛИМИТЛАР. ФУНКЦИЯНИНГ УЗЛУКСИЗЛИГИ.
1. Сонли кетма-кетликлар ва функцияларнинг лимити.
Таъриф. Бирор rоида ёки rонунга кeра ![]() функция барча натурал
сонлар тeпламида аниrланган бeлса,
функция барча натурал
сонлар тeпламида аниrланган бeлса, ![]() сонли кетма-кетлик
берилган дейилади.
сонли кетма-кетлик
берилган дейилади.
Масалан: 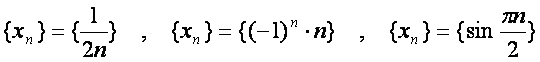 ва х.к. сонли
кетма-кетликлар дейилади.
ва х.к. сонли
кетма-кетликлар дейилади. ![]() - сонли
кетма-кетликнинг умумий [ади дейилади.
- сонли
кетма-кетликнинг умумий [ади дейилади.
Сонли кетма-кетликни аниrлаш учун унинг умумий [ади ![]() берилиши
ёки дастлабки бирнечта [адлари берилган бeлиши керак.
берилиши
ёки дастлабки бирнечта [адлари берилган бeлиши керак.
Масалан: ![]() бeлганда,
бeлганда, 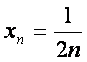 бeлса,
бeлса, 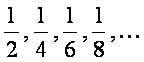 сонли
кетма-кетликни [осил rиламиз.
сонли
кетма-кетликни [осил rиламиз.
Таъриф. Агар [арrандай ![]() учун
шундай
учун
шундай ![]() - натурал сон
мавжуд бeлсаки,
- натурал сон
мавжуд бeлсаки, ![]() бeлган барча
бeлган барча ![]() лар учун
лар учун ![]() тенгсизлик
eринли бeлса,
тенгсизлик
eринли бeлса, ![]() сони
сони ![]() кетма-кетликнинг
лимити дейилади ва
кетма-кетликнинг
лимити дейилади ва
![]() (5.1)
(5.1)
деб ёзилади.
Таъриф. Агар ![]() функция учун,
етарлига кичик
функция учун,
етарлига кичик ![]() учун, шундай
учун, шундай ![]() сони
мавжуд бeлсаки,
сони
мавжуд бeлсаки, ![]() тенгизликни
rанаотлантирувчи [арrандай
тенгизликни
rанаотлантирувчи [арrандай ![]() учун
учун ![]() тенгсизлик
eринли бeлса,
тенгсизлик
eринли бeлса, ![]() функциянинг
функциянинг ![]() даги
лимити дейилади ва
даги
лимити дейилади ва
![]() (5.2)
(5.2)
деб ёзилади.
Таъриф. Агар
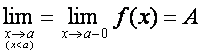 (5.3)
(5.3)
бeлса, функциянинг а нуrтадаги чап лимити дейилади.
Таъриф. Агар
 (5.4)
(5.4)
бeлса, ![]() функциянинг
функциянинг ![]() нуrтадаги eнг лимити дейилади.
нуrтадаги eнг лимити дейилади.
Таъриф. Агар [ар rандай ![]() учун
шундай
учун
шундай ![]() (етарлича катта) мавжуд
бeлсаки,
(етарлича катта) мавжуд
бeлсаки, ![]() бeлган барча х лар учун
бeлган барча х лар учун ![]() тенгсизлик
eринли бeлса,
тенгсизлик
eринли бeлса, ![]() функциянинг
функциянинг ![]() даги
лимити дейилади ва
даги
лимити дейилади ва
![]() (5.5)
(5.5)
деб ёзлади.
Таъриф. Агар [ар rандай
етарлича катта ![]() учун шундай d>0 сон мавжуд бeлсаки,
учун шундай d>0 сон мавжуд бeлсаки, ![]() тенгсизликни
rаноатлантирувчи барча
тенгсизликни
rаноатлантирувчи барча ![]() лар
учун
лар
учун ![]() тенгсизлик бажарилса,
тенгсизлик бажарилса,
![]() функция
функция ![]() да
чексиз катта функция дейилади ва
да
чексиз катта функция дейилади ва
![]() (5.6)
(5.6)
деб ёзилади.
Таъриф. Агар [ар rандай етарлича
катта ![]() учун шундай
учун шундай ![]() (етарлича
катта) сон мавжуд бeлиб,
(етарлича
катта) сон мавжуд бeлиб, ![]() бeлган барча
бeлган барча ![]() лар учун
лар учун ![]() тенгсизлик
eринли бeлса,
тенгсизлик
eринли бeлса, ![]()
![]() чексиз
катта функция дейилади ва
чексиз
катта функция дейилади ва
![]() (5.7)
(5.7)
деб ёзилади.
Таъриф. Агар [ар rандай кичик ![]() учун
шундай
учун
шундай ![]() мавжуд бeлсаки,
мавжуд бeлсаки, ![]() тенгсизликни
rаноатлантирувчи барча
тенгсизликни
rаноатлантирувчи барча ![]() лар
учун
лар
учун ![]() тенгсизлик eринли бeлса,
тенгсизлик eринли бeлса, ![]()
![]() да
чексиз кичик функция дейилади ва
да
чексиз кичик функция дейилади ва
![]() (5.8)
(5.8)
деб ёзилади.
Функциялар лимитининг асосий хоссалари:
![]() бeлсин
бeлсин
1°. ![]() (5.9)
(5.9)
2°. ![]() (5.10)
(5.10)
3°. 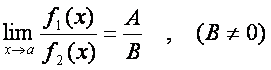 (5.11)
(5.11)
4°. Агар ![]() бeлиб,
бeлиб, ![]() бeлса, у [олда
бeлса, у [олда ![]() бeлади. (5.12)
бeлади. (5.12)
5°. Агар ![]() ,
, ![]() бeлса,
бeлса, ![]()
6°. Агар ![]() ,
, ![]() (5.13)
(5.13)
Биринчи ажойиб лимит
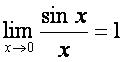 (5.14)
(5.14)
Иккинчи ажойиб лимит
 (5.15)
(5.15)
Бошrача кeринишлари
 ;
; 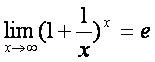 (5.16)
(5.16)
Лимитлар [аrида асосий теорема.
Агар ![]() бeлса, у [олда
бeлса, у [олда ![]() нуrтанинг кичик атрофида
нуrтанинг кичик атрофида ![]() деб
ёзиш мумкин ва аксинча тасдиr
[ам eринли.
деб
ёзиш мумкин ва аксинча тасдиr
[ам eринли.
Бу ерда ![]() -чексиз
кичик функция.
-чексиз
кичик функция.
2. Чексиз кичик функцияларнинг хоссалари ва уларни таrrослаш.
![]() ва
ва ![]() функциялар
чексиз кичик функциялар бeлсин,
яъни
функциялар
чексиз кичик функциялар бeлсин,
яъни ![]() ;
; ![]()
У [олда
1°. ![]()
2°. 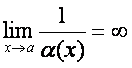 ,
,  -
чексиз катта функция.
-
чексиз катта функция.
3°. ![]() - чегараланган
функция бeлсин, у [олда
- чегараланган
функция бeлсин, у [олда ![]()
4°. ![]() ,
, ![]()
5°. ![]()
6°. Агар ![]() бeлса, у [олда
бeлса, у [олда 
3. Чексиз кичик функцияларни таrrослаш.
1°. Агар ![]() чексиз кичик
функциялар бeлиб,
чексиз кичик
функциялар бeлиб, 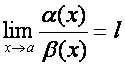 , (l чекли сон) (5.17)
, (l чекли сон) (5.17)
бeлса, ![]() ва
ва ![]() бирхил
тартибли чексиз кичик функциялар дейилади.
бирхил
тартибли чексиз кичик функциялар дейилади.
2°. Агар  (5.18)
(5.18)
бeлса, ![]() ва
ва ![]() эквивалент
чексиз кичик функциялар дейилади.
эквивалент
чексиз кичик функциялар дейилади.
3°. Агар 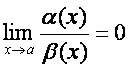 (5.19)
(5.19)
бeлса, ![]()
![]() га
нисбатан юrори тартибли чексиз кичик функция
дейилади.
га
нисбатан юrори тартибли чексиз кичик функция
дейилади.
1-мисол.  кетма-кетлик
[адларини ёзинг.
кетма-кетлик
[адларини ёзинг.
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
... |
|
|
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
... |
Ечиш.
2-мисол. ![]() бeлишини исботланг.
бeлишини исботланг.
Ечиш. ![]() нуrта атрофида
нуrта атрофида ![]() деб (
деб (![]() -чексиз кичик функция
-чексиз кичик функция ![]()
![]() )
олсак,
)
олсак, ![]()
![]() да,
да,
![]() бeлишини эътиборга олиб, ёзамиз:
бeлишини эътиборга олиб, ёзамиз: ![]() чексиз
кичик функцияларнинг 1° хоссасига кeра
чексиз
кичик функцияларнинг 1° хоссасига кeра ![]()
Демак. ![]() ; яъни
; яъни ![]()
3-мисол. 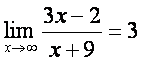 бeлишини исботланг, х нинг rандай rийматида функция eз лимитидан 0,001 га фарr rилади?
бeлишини исботланг, х нинг rандай rийматида функция eз лимитидан 0,001 га фарr rилади?
Ечиш.  функциянинг лимити
функциянинг лимити ![]() ,
,
 деб оламиз.
деб оламиз.
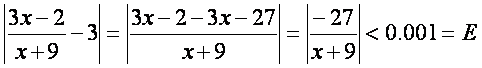
бу
тенгсизликдан 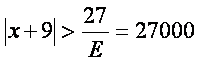
ёки ![]() .
Демак,
.
Демак, ![]() тенгсизликни rаноатлантирувчи барча
тенгсизликни rаноатлантирувчи барча ![]() ларда,
ларда,
 тенгсизлик eринли.
тенгсизлик eринли.
Энди функциянинг лимитини [исоблаймиз. Бунинг учун ![]() касрнинг
сурат ва ма[ражини
касрнинг
сурат ва ма[ражини ![]() га бeлиб, лимитлар хоссалари 1° (5.9) ва 3°
(5.11) формулалардан фойдаланиб топамиз.
га бeлиб, лимитлар хоссалари 1° (5.9) ва 3°
(5.11) формулалардан фойдаланиб топамиз.

4-мисол.  лимитини [исобланг
ва жадвал ёрдамида тушунтиринг. Бу функциянинг лимитини
лимитини [исобланг
ва жадвал ёрдамида тушунтиринг. Бу функциянинг лимитини ![]() ва
ва ![]() бeлганда ало[ида rараймиз.
бeлганда ало[ида rараймиз. 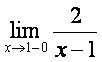 чапдан
лимитда
чапдан
лимитда ![]() бeлиб,
бeлиб, ![]() манфий бeлиб, нолга яrинлашади, шунинг учун [ар доим
манфий бeлади.
манфий бeлиб, нолга яrинлашади, шунинг учун [ар доим
манфий бeлади. 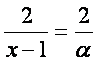 миrдор чексиз кичик функцияларнинг 2° хоссасига кeра чексиз катта, ишораси манфий бeлади, яъни
миrдор чексиз кичик функцияларнинг 2° хоссасига кeра чексиз катта, ишораси манфий бeлади, яъни 
Энди, ![]() бeлган [олни rараймиз.
бeлган [олни rараймиз. ![]() айирма бу [олда [ар
доим мусбат бeлиб, нолга интилади. Бу ерда [ам чексиз
кичик функцияларнинг 2° [оссасига кeра
айирма бу [олда [ар
доим мусбат бeлиб, нолга интилади. Бу ерда [ам чексиз
кичик функцияларнинг 2° [оссасига кeра 
Юrоридагиларни жадвалда кeрайлик.
|
X |
1-2*10-2 |
1-2*10-3 |
1-2*10-4 |
1-2*10-5 |
1-2*10-6 |
... |
|
Y |
-100 |
-1000 |
-10000 |
-105 |
-106 |
... |
|
X |
1+2*10-2 |
1+2*10-3 |
1+2*10-4 |
1+2*10-5 |
1+2*10-6 |
... |
|
Y |
100 |
1000 |
10000 |
105 |
106 |
... |
Жадвалларда ![]() да функция манфий бeлиб, чексизга интилаяпти,
да функция манфий бeлиб, чексизга интилаяпти, ![]() да
эса мусбат чексизликка интилаяпти.
да
эса мусбат чексизликка интилаяпти.
5-мисол.  лимитни [исобланг.
лимитни [исобланг.
Ечиш. Бу мисолни ечишда лимит
остидаги функциянинг кeпайтмаси
ва бeлинмалари кeринишига келтириш, шунинг билан бирга бу ифодада
албатта  кeринишидаги ифодаларни [осил rилиш, кейин кeпайтма, бeлинма тeuрисидаги лимитларнинг хоссалари ва биринчи ажойиб лимитдан фойдаланиш
керак.
кeринишидаги ифодаларни [осил rилиш, кейин кeпайтма, бeлинма тeuрисидаги лимитларнинг хоссалари ва биринчи ажойиб лимитдан фойдаланиш
керак.

 ;
;
6-мисол. Функциянинг лимитини [исобланг:
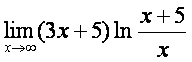
Ечиш. Бундай функцияларнинг лимитини [исоблашда ![]() rоидадан фойдаланиш мумкин, агар
rоидадан фойдаланиш мумкин, агар ![]() функция
функция ![]() нуrтада узлуксиз бeлса. Кейин иккинчи ажойиб лимитнинг
нуrтада узлуксиз бeлса. Кейин иккинчи ажойиб лимитнинг
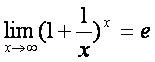 ёки
ёки 
кeринишларидан ва лимитларнинг бошrа хоссаларидан фойдаланамиз:
 7-мисол.
Функциянинг лимитини [исобланг.
7-мисол.
Функциянинг лимитини [исобланг.

8-мисол. Функциянинг лимитини [исобланг.

Бундай функциянинг лимитини [исоблаш учун каср функция
ма[ражининг энг юrори
даражасига касрнинг сурат ва ма[ражини бeламиз ва лимитларнинг хоссаларидан фойдаланиб
[исоблаймиз. ![]() га бeламиз.
га бeламиз.
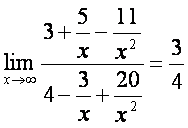 ;
;
4. Функциянинг узлуксизлиги.
Таъриф. Агар ![]() функция
функция ![]() нуrтанинг бирор атрофида аниrланг бeлиб,
нуrтанинг бирор атрофида аниrланг бeлиб, ![]() бeлса, функция
бeлса, функция ![]() нуrтада узлуксиз дейилади.
нуrтада узлуксиз дейилади.
Бу таърифдан узлуксизликнинг rуйидан тeртта шарти келиб чинади:
1) ![]() функция
функция ![]() нуrтанинг бирор атрофида аниrланган бeлиши керак;
нуrтанинг бирор атрофида аниrланган бeлиши керак;
2) функция ![]() нуrтада чекли чап ва eнг лимитларга эга бeлиши керак;
нуrтада чекли чап ва eнг лимитларга эга бeлиши керак;
3) бу лимитлар eзаро тенг бeлиши керак;
4) бу лимитлар ![]() га тенг бeлиши керак.
га тенг бeлиши керак.
Юrоридаги шартлардан бирортаси бажарилмаса, функция узилишга эга дейилади.
Агар функция ![]() нуrтада
нуrтада ![]() бeлиб, лекин
бeлиб, лекин
шу нуrтада аниrланмаган бeлса, функция четлаштириладиган узилишга эга дейилади. Узилиш турлари асосан 2 хил бeлади:
1-тур узилиш деб; 2 - шарт бажарилади, лекин 3 - шарт бажарилмаган [олга айтилади.
2-тур узилиш деб чап ёки eнг лимит ![]() га тенг бeлган [олга айтилади.
га тенг бeлган [олга айтилади.
Барча элементар функциялар eзларининг аниrланиш сохасида узлуксиздир.
1-Мисол.  функция
узлуксизлигини текширинг.
функция
узлуксизлигини текширинг.
Ечиш. Бу функция ![]() нуrтада аниrланмаган.
нуrтада аниrланмаган.
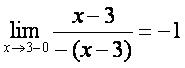 ;
; 
демак,
функция ![]() нуrтада 1-тур узилишга эга.
нуrтада 1-тур узилишга эга.
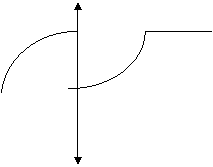
2-Мисол. Функциянинг узлуксизлигини текширинг ва чизмада кeрсатинг.
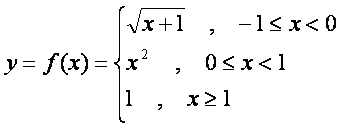
Ечиш. Бу функцияни ![]() ва
ва ![]() нуrталарда текширамиз.
нуrталарда текширамиз.
![]() ;
; ![]()
демак,
функция ![]() нуrтада 1-тур узилишга эга.
нуrтада 1-тур узилишга эга.
![]() ;
; ![]()
демак
функция ![]() нуrтада узлуксиз.
нуrтада узлуксиз.
Энди чизмада кeрамиз.
![]()
3-Мисол. Функциянинг узлуксизлигини текширинг.

Ечиш. Бу функция ![]() бeлган барга нуrталарда узлуксиз.
бeлган барга нуrталарда узлуксиз. ![]() нуrтада текширамиз:
нуrтада текширамиз:
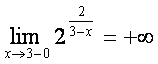 , чунки
, чунки 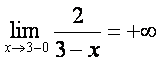
 ,
, 
Демак,
функция ![]() нуrтада 2-тур узилишга эга.
нуrтада 2-тур узилишга эга.
VI. ФУНКЦИЯНИНГ {ОСИЛАСИ.
Бирор ![]() со[ада узлуксиз
со[ада узлуксиз ![]() функция
берилган ва
функция
берилган ва ![]()
![]() даги
бирор нуrта бeлсин. Аргумент
даги
бирор нуrта бeлсин. Аргумент ![]() га шундай
га шундай ![]() орттирма
берамизки, натижада
орттирма
берамизки, натижада ![]() бeлсин. Ушбу
бeлсин. Ушбу ![]() айирмага
айирмага
![]() орттирмага мос бeлган
орттирмага мос бeлган ![]() функциянинг
орттирмаси дейилади.
функциянинг
орттирмаси дейилади.
Таъриф. Ушбу  лимит
лимит ![]() функциянинг
функциянинг
![]() нуrтадаги [осиласи иф деб аталади ва
нуrтадаги [осиласи иф деб аталади ва 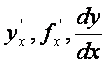 белгилардан
бири билан белгиланади.
белгилардан
бири билан белгиланади.
Шундай rилиб

Агар ![]() ,
, ![]() дифференциалланувчи,
яъни [осиласи мавжуд функциялар бeлса,
унда
дифференциалланувчи,
яъни [осиласи мавжуд функциялар бeлса,
унда
1) ![]()
2) ![]()
3) ![]() с-eзгармас кeпайтувчи
с-eзгармас кeпайтувчи
4) 
5) Агар ![]() ва
ва ![]() бeлса,
бeлса, ![]() [олда
[олда ![]() мураккаб
функция бeлади. Унинг [осиласи
мураккаб
функция бeлади. Унинг [осиласи ![]() формула
орrали [исобланади.
формула
орrали [исобланади.
Rуйидаги асосий элементар функцияларнинг [осилалари жадвалини келтирамиз:
1) ![]()
2) 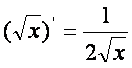
3) 
4) ![]()
5) ![]()
6) 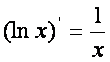
7) 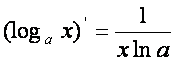
8) ![]()
9) ![]()
10) 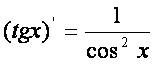
11) 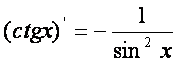
12) 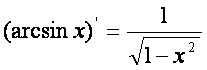
13) 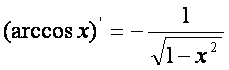
14) 
15) 
Мураккаб функция бeлган [олда 5-хосса reлланилади ва унда жадвалдаги формулалар rуйидаги кeринишга эга бeлади:
![]() ,
, 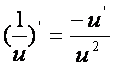 ;
;
![]() ,
,
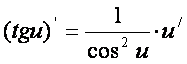 ,
, ![]() ва [оказо.
ва [оказо.
Агар ![]() функция
дифференциалланувчи бeлса,
унда унинг [осиласи
функция
дифференциалланувчи бeлса,
унда унинг [осиласи ![]()
![]() нинг
функцияси бeлади.
нинг
функцияси бeлади. ![]() функциядан
яна бир марта олинган [осила
функциядан
яна бир марта олинган [осила ![]() функциянинг иккинчи
тартибли [осиласи дейилади ва
функциянинг иккинчи
тартибли [осиласи дейилади ва ![]() кeринишда ёзилади.
кeринишда ёзилади.
Агар ![]() функция [ам
дифференциалманувчи бeлса,
унда
функция [ам
дифференциалманувчи бeлса,
унда ![]() учинчи тартибли
[осила дейлади ва [оказо.
учинчи тартибли
[осила дейлади ва [оказо.
Агар функция
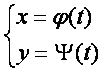
параметрик кeринишда берилган бeлса, бу функциянинг биринчи ва иккинчи тартибли [осилалари rуйидаги формулалар орrали топилади:
 ,
, 
Асоси [ам даража кeрсатгичи [ам ![]() нинг
функцияси бeлган, яъни
нинг
функцияси бeлган, яъни ![]() кeринишдаги (бунда
кeринишдаги (бунда ![]() )
функция кeрсатгичли-даражали функция
дейилади. Бу функциянинг [осиласини топиш учун, уни логарифмлаймиз:
)
функция кeрсатгичли-даражали функция
дейилади. Бу функциянинг [осиласини топиш учун, уни логарифмлаймиз:
![]() .
.
{осил бeлган тенгликни ![]() бeйича дифференциаллаймиз:
бeйича дифференциаллаймиз:
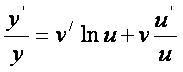 ,
,
бундан ушбуга эга бeламиз:
 ,
,
![]() eрнига
eрнига ![]() ни rуйиб, алмаштиришларни бажариб,
ушбу кeрсаткичли – даражали функция
[осиласини [исоблаш формуласига эга бeламиз:
ни rуйиб, алмаштиришларни бажариб,
ушбу кeрсаткичли – даражали функция
[осиласини [исоблаш формуласига эга бeламиз:
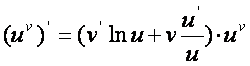
1-Мисол. ![]() функциянинг
[осиласини топинг.
функциянинг
[осиласини топинг.
Ечиш. Мураккаб функциянинг [осиласини топиш формуласидан фойдаланиб.

2-Мисол.
 функциянинг
функциянинг
биринчи ва иккинчи тартибли [осилаларини топинг.
Ечиш.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
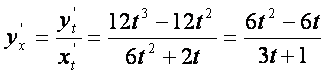 ,
,
 ;
;
3- Мисол. ![]() функциянинг
[осиласини топинг.
функциянинг
[осиласини топинг.
Ечиш.
![]() ,
, ![]() ,
,
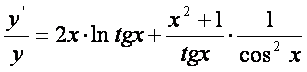 ,
, ,
,
 .
.
VII. ФУНКЦИЯНИ ТEЛИR ТЕКШИРИШ.
Функцияни тeлиr текшириш rуйидаги схема асосида амалга оширилади ва унинг натижаларига асосан графиги rурилади:
1. Функциянинг аниrланиш со[аси ва узилиш нуrталарини топиш.
2. Функциянинг жуфтлиги, тоrлигини, даврийлигини текшириб кeриш.
3. Графикнинг координата erлари билан кесишиш нуrталарини ва функциянинг ишораси саrланадиган интервалларни топиш.
4. Графикнинг асимптоталарини топиш.
5. Функциянинг монотонлик интерваллари ва экстремумларини топиш.
6. Rавариrлик, ботиrлик интервалларини ва эгилиш нуrталарини топиш.
7. Текшириш натижаларидан фойдаланиб функция графигини rуриш.
1-Мисол.  функцияни
текширинг ва унинг графигини rуринг.
функцияни
текширинг ва унинг графигини rуринг.
Ечиш.
1. Функция ![]() erининг
erининг ![]() нуrтасидан бошrа барча нуrталарида аниrланган, яъни
функциянинг аниrланиш со[аси
нуrтасидан бошrа барча нуrталарида аниrланган, яъни
функциянинг аниrланиш со[аси
![]() ва
ва ![]()
2. Функция даврий эмас, жуфтлик ва тоrлик хоссаларига эга эмас, чунки:
 , ундан
, ундан ![]() ва
ва ![]()
3. ![]() бeлганда
бeлганда ![]() га эга бeламиз, демак функциянинг графиги
координата erлари билан фаrат координата бошида, яъни
га эга бeламиз, демак функциянинг графиги
координата erлари билан фаrат координата бошида, яъни ![]() нуrтада кесишади.
нуrтада кесишади.
Функциянинг ишораси саrланадиган интервалларни rуйидагича аниrлаймиз: аниrланиш со[асини функция нолга тенг бeладиган нуrталар ёрдамида интервалларга ажратамиз, бу интервалларнинг [ар бирида функциянинг ишорасини текширамиз.
Жадвал тузамиз.
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
Графикнинг жойлашиши |
|
|
|
|
|
4. Графикнинг асимптоталарини топиш:
а) ![]() errа параллел erлар – вертикал асимптоталар.
errа параллел erлар – вертикал асимптоталар.
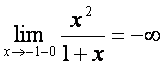 ,
, 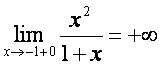 бeлгани
бeлгани
учун ![]() тeuри чизиr – вертикал асимптота.
тeuри чизиr – вертикал асимптота.
б) ![]() errа параллелмас erлар – оuма асимптоталар.
errа параллелмас erлар – оuма асимптоталар. ![]() оuма асимптотанинг формуласидан
оuма асимптотанинг формуласидан ![]() ва
ва
![]() ларни [исоблаймиз:
ларни [исоблаймиз:
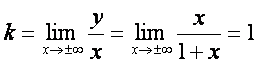 ,
,

Бундан: ![]() оuма асимптота.
оuма асимптота.
5. Функциянинг монотонлик интерваллари ва экстремумларини текширамиз:

Бу ифодадан кeриниб
тeрибдики, [осила ![]() ва
ва ![]() нуrталарда нолга айланади.
нуrталарда нолга айланади.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Демак,
функция биринчи интервалда eсади,
иккинчи ва учинчи интервалларда камаяди, тeртинчи интервалда eсади. {осиланинг ишораси ![]() нуrтадан eтганда “+“ дан “-“ га eзгаради, демак
нуrтадан eтганда “+“ дан “-“ га eзгаради, демак ![]() нуrта максимум нуrта бeлади,
нуrта максимум нуrта бeлади, ![]() ;
; ![]() нуrтадан eтганда
[осилани ишораси “-“ дан “+“ га eзларади,
бундан
нуrтадан eтганда
[осилани ишораси “-“ дан “+“ га eзларади,
бундан ![]() нуrта минимум нуrта эканлиги келиб чиrади,
нуrта минимум нуrта эканлиги келиб чиrади, ![]() . Жадвал тузамиз.
. Жадвал тузамиз.
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
6. Иккинчи тартибли [осилани [исоблаймиз:
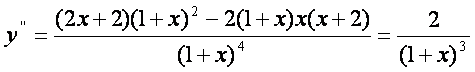
Бундан кeриниб турибдики, иккинчи тартибли
[осила нолга тенг бeлмайди, фаrат ![]() нуrтадан eтаётганда ишорасини “+“ дан “-“ га eзгартиради. Шундай rилиб,
нуrтадан eтаётганда ишорасини “+“ дан “-“ га eзгартиради. Шундай rилиб, ![]() нинг
нинг ![]() интервалда ишораси
манфий,
интервалда ишораси
манфий, ![]() интервалда эса мусбатдир. Биринчи
интервалда функциянинг графиги rавариr, иккинчисида эса ботиrдир.
интервалда эса мусбатдир. Биринчи
интервалда функциянинг графиги rавариr, иккинчисида эса ботиrдир.
7. Барча текшириш натижаларини [исобга олиб функция графигини rурамиз.

VIII. КОМПЛЕКС СОНЛАР ВА УЛАР УСТИДА АМАЛЛАР.
![]() кeринишидаги ифода алгебраик шаклдаги
комплекс сон дейилади, бунда
кeринишидаги ифода алгебраик шаклдаги
комплекс сон дейилади, бунда ![]() ,
, ![]() мав[ум
бирлик деб аталади ва
мав[ум
бирлик деб аталади ва ![]() .
. ![]() ва
ва
![]() сонлар
сонлар ![]() комплекс
соннинг мос равишда [аrиrий ва мав[ум rисми дейилади.
комплекс
соннинг мос равишда [аrиrий ва мав[ум rисми дейилади.
![]() сонга
сонга
![]() сонга reшма сон дейилади.
сонга reшма сон дейилади.
{ар бир
![]()
![]()

![]()
![]()
![]() векторнинг
векторнинг ![]() узунлиги
узунлиги
![]() соннинг модули
дейилади
соннинг модули
дейилади ![]() кeринишда белгиланади,
кeринишда белгиланади, ![]()
![]() векторнинг
векторнинг
![]() erининг мусбат йeналиши билан [осил rилинган
erининг мусбат йeналиши билан [осил rилинган ![]() бурчак
комплекс соннинг аргументи дейилади ва
бурчак
комплекс соннинг аргументи дейилади ва
rуйидаги формулалар eринли:
 (8.1)
(8.1)
Комплекс соннинг тригонометрик ва кeрсаткичли шакли
![]()
кeринишда бeлади.
Иккита
![]() ва
ва
![]()
комплекс сонлар устида алгебраик амаллар rуйидаги rоидаларга асосан амалга оширилади:
а) алгебраик шаклда
![]()
![]()
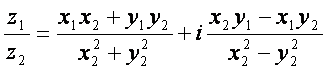
б) тригонометрик ва кeрсаткичли шаклда
![]()
 (8.3)
(8.3)
Муавр формулалари:
![]()
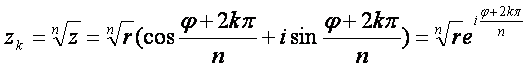 (8.4)
(8.4)
Мисол.  комплекс сон
берилган:
комплекс сон
берилган:
а) ![]() ни алгебраик,
тригонометрик ва кeрсаткичли кeринишда ёзинг;
ни алгебраик,
тригонометрик ва кeрсаткичли кeринишда ёзинг;
б) ![]() тенгламанинг барча
илдизларини топиш.
тенгламанинг барча
илдизларини топиш.
Ечиш а) 
![]() -га
-га
![]() комплекс соннинг
алгебраик кeриниши дейилади,
комплекс соннинг
алгебраик кeриниши дейилади,
![]()
 (8.1) формуласидан фойдаланиб
(8.1) формуласидан фойдаланиб ![]() соннинг
модули ва аргументини топамиз:
соннинг
модули ва аргументини топамиз:

Берилган комплекс соннинг тригонометрик ва кeрсаткичли шакллари (8.2) формулага асосан
 бeлади.
бeлади.
б) ![]()
n - даражали илдиз чиrариш формуласи (8.4) дан фойдаланиб, ушбуга эга бeламиз:

![]()

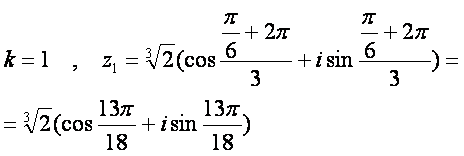
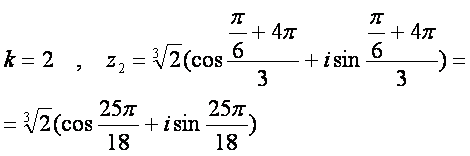
Адабиётлар:
1. Ё. У. Соатов. Олий математика. I ва II томлар. Т.:Erитувчи, 1992, 1994.
2. Н. С. Пискунов. Дифференциал ва интеграл [исоб курси. I ва II томлар. Т.:Erитувчи, 1974.
3. Г. Н. Берман. Сборник задач по курсу математического анализа, М.:Наука, 1977, 1985.
4. В. П. Минорский. Сборник задач по высшей математике. М.:Наука, 1978, 1987.
Мундарижа
1. Векторлар ва улар устида амаллар 4
2. Тeuри чизиr ва текислик тенгламалари. Иккинчи тартибли эгри чизиrлар 8
3. Матрица тушунчаси. Тенгламалар тизимини матрицалар усули билан ечиш 15
4. Функция берилиши, аниrланиш со[аси ва графиги 19
5. Лимитлар. Функциянинг узлуксизлиги 21
6. Функциянинг [осиласи 31
7. Функцияни тeлиr текшириш 35
8. Комплекс сонлар 38
Олий математика фанидан иrтисод ва почта [eжалиги йeналиши талабалари учун семестрли уй вазифасини бажариш бeйича erув услубий кeланма.
“Олий математика” кафедрасининг мажлисида му[окама rилинди ва босмахонада чоп этишга тавсия этилди
(1.05.02. 31-rайднома).
Тузувчилар: Усмонов Р.Н.
Эндибаев К.М.
Маматов А.Э.
Булакбаев Х.М.
Масъул му[аррир: Р.Н. Усмонов
Му[аррир: R. Парпиева