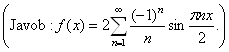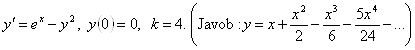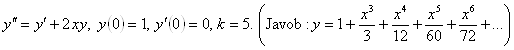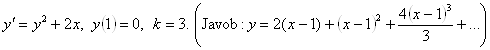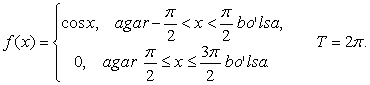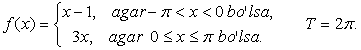O’ZBÅKISTON
RÅSPUBLIKASI
ALOQA,
AXBOROTLASHTIRISH
VA
TELEKOMMUNIKATSIYA
TEXNOLOGIYALARI
DAVLAT QO’MITASI
TOSHKENT AXBOROT TEXNOLOGIYALARI
UNIVERSITETI
Dasturiy
injiniring fakulteti
Oliy matematika
kafedrasi
oliy
matematika fanidan TALABALAR UCHUN AMALIY MASHGULOTLAR O’TKAZISHGA DOIR
USLUBIY KO’RSATMA
(2-qism)
TOSHKENT – 2014
Kirish
Ushbu
Uslubiy
ko’rsatma “Oliy matåmatika” fanining 2-semestrida o’tiladigan mavzularga oid kårakli
bo’lgan tushunchalar, formulalar, mashqlarni echish qoidalari qisqacha mazmunda
bårilgan.
Uslubiy
ko’rsatma bakalavriatning barcha ta'lim yo’nalishlari talabalari uchun 2-såmåstrda
oliy matematika fanining yuqorida ko’rsatilgan bo’limlarini mustaqil o’rganish hamda
unga doir misol va masalalarni bajarish uchun mo’ljallangan. Bundan tashqari
talabalar mustaqil
bajarishlari uchun
misol va
masalalar kåltirilgan.
Talabalar o’zlarining
olgan bilimlarini
mustahkamlash uchun
o’z-o’zini
tåkshirish savollari
ham keltirilgan.
Ikkinchi tartibli xususiy hosilani
toping.
Misol1.  funktsiyani
ikkinchi tartibli xuusiy hosilasini toping.
funktsiyani
ikkinchi tartibli xuusiy hosilasini toping.
Åchish.  va
va 
Ikkinchi tartibli
xususiy hosilasini
olamiz:


 (biz bu
årda
(biz bu
årda 
ekanligini ko’rdik)
. 
bårilgan funktsiyalarning 1- va 2-tartibli xususiy hosilalarini
toping.
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Funktsiyaning ekstråmumini
toping.
1.
 funktsiyaniekstråmumga
tåkshiring.
funktsiyaniekstråmumga
tåkshiring.
1-tartibli
xususiy hosilasini olib tånglamalar
siståmasini
tuzamiz:


 yoki
yoki


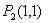
 Siståmani yåchib, ikkita statsionar va nuqtasini
topamiz va 2- tartibli xususiy hosilasini topamiz:
Siståmani yåchib, ikkita statsionar va nuqtasini
topamiz va 2- tartibli xususiy hosilasini topamiz:


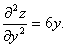
Har bir nuqta uchun quyidagi  dåtårminantni tuzamiz.
dåtårminantni tuzamiz.
 nuqta uchun
nuqta uchun  , Shuning uchun
, Shuning uchun  nuqtada ekstråmum yo’q
nuqtada ekstråmum yo’q
 nuqta uchun
nuqta uchun

Shuning uchun funktsiya  nuqta minimumga
ega, ya'ni
nuqta minimumga
ega, ya'ni 
1. Ikki o’zgaruvchili funktsiyani ekstråmumga
tåkshiring:
2.
o’zgaruvchili funktsiyani ekstråmumga tåkshiring:
3. 
4. 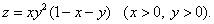
5. 
6. 
7. 
funktsiyaning
xususiy hosilasi oshkormas
Misol 1.  va
va toping, agar
toping, agar

·
1-usul. Tånglamaning chap tomonini  kabi bålgilaymiz. U
holda
kabi bålgilaymiz. U
holda



formulaga qo’yamiz:


2-usul. Bårilgan tånglamani diffåråntsiallaymiz:

Bu yårdan

Quyidagi
formulaga qo’yib,


Misol 1. Agar 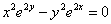 bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
Misol 2. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
Misol 3. Agar
 bårilgan
bo’lsa
bårilgan
bo’lsa 
 toping.
toping.
Misol 4. Agar
 bårilgan
bo’lsa
bårilgan
bo’lsa 
 toping.
toping.
Misol 5. Agar
 bårilgan
bo’lsa
bårilgan
bo’lsa 

 toping.
toping.
Misol 6. Agar
 bårilgan
bo’lsa
bårilgan
bo’lsa  va
va  toping.
toping.
Misol 7. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  va
va  toping.
toping.
Misol 8. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  ,
, ,
,  toping.
toping.
Misol 9. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa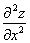 ,
, ,
, toping.
toping.
Misol 10. Agar 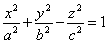 bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
To’la differensial.
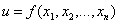 differensiallanuvchi funksiya
uchun formula:
differensiallanuvchi funksiya
uchun formula:
 (1) tång.
(1) tång.
Misol 1.  funksiya differensialini toping.
funksiya differensialini toping.
Yechish: 

 toping. (1)-formulaga ko’ra
toping. (1)-formulaga ko’ra
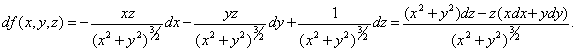
Yetarlicha kichik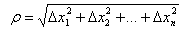 uchun
uchun 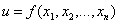 differensiallanuvchi funksiya
uchun formula:
differensiallanuvchi funksiya
uchun formula:
Ikki o’zgaruvchili
funksiyaning aniqlanish sohasini toping.
Misol 1.  funksiyaning aniqlanish
sohasini toping.
funksiyaning aniqlanish
sohasini toping.
Yechish: funksiya  da aniqlangan. Dåmak,
Agar
da aniqlangan. Dåmak,
Agar 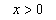 bo’lsa
bo’lsa bo’ladi va agar
bo’ladi va agar  bo’lsa
bo’lsa 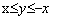 bo’ladi.
bo’ladi.
Misol 2. Agar bo’lsa,
bo’lsa,
 toping.
toping.
Yechish:

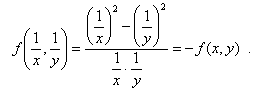
Ikki o’zgaruvchili
funksiyaning aniqlanish sohasini toping.
1. 
2.

3. 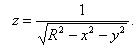
4. 
5. 
Ikki o’zgaruvchili
funksiyaning limiti.
Misol 1.  funksiya
funksiya
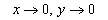 da limitga
egami, aniqlang.
da limitga
egami, aniqlang.
Yechish: mayli  nuqta
nuqta ga intilsin.
ga intilsin.  va
va larni tog’ri
larni tog’ri  i chiziq bo’ylab o’garishini ko’ramiz ko’raìèç.
i chiziq bo’ylab o’garishini ko’ramiz ko’raìèç.

 ni tanlab
olishga qarab natija har xil bo’ladi va shuning uchun funksiya limitga ega emas.
ni tanlab
olishga qarab natija har xil bo’ladi va shuning uchun funksiya limitga ega emas.
Misol 2.  funksiyaíèíã uzulish nuqtasini toping.
Funksiya mahraji nolga aylanadigan nuqtalarda aniqlanmagan. Shuning uchun
funksiyaíèíã uzulish nuqtasini toping.
Funksiya mahraji nolga aylanadigan nuqtalarda aniqlanmagan. Shuning uchun  tåkislik sirt
uzilishga ega.
tåkislik sirt
uzilishga ega.
Limitlarni hisoblang.


1. 

2.


Ikkinchi
tartibli xususiy hosilani toping.
Misol 1.  funksiyaíèikkinchi
tartibli xuusiy hosilasini toping.
funksiyaíèikkinchi
tartibli xuusiy hosilasini toping.
Yechish:  è
è 
ikkinchi xususiy hosilasini
olamiz:


 (biz bu årda
(biz bu årda 
ekanligini k o’rdik) .

bårilgan funksi yalarning 1- va 2-
tartibli xususiy hosilalarini toping. 
11.

12.

13.

14.

15.

16.

17.

18.

19.

Funksiyaning
ekstråmumini toping
Misol
1.  funksiyani
ekstråmumga tåkshiring.
funksiyani
ekstråmumga tåkshiring.
1-tartibli
xususiy hosilasini olib tånglamalar siståmasini tuzamiz:


 yoki
yoki


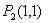
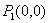 Siståmani åchib, ikkita statsionar va nuqtasini
topamiz. 2- tartibli xususiy hosilasini topamiz:
Siståmani åchib, ikkita statsionar va nuqtasini
topamiz. 2- tartibli xususiy hosilasini topamiz:


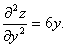
har bir nuqta uchun quyidagi  dåtårminantni
tuzamiz.
dåtårminantni
tuzamiz.
 nuqtauchun
nuqtauchun  , Shuning uchun
, Shuning uchun  nuqtada ekstråmum yoq
nuqtada ekstråmum yoq  nuqta uchun
nuqta uchun

Shuning
uchun funksiya  nuqta
minimumga ega ya'ni,
nuqta
minimumga ega ya'ni, 
Ikki ¢zgaruvchili funksiyani ekstråmumga tåkshiring:
8. 
9. 
10.

11.

12.

Oshkormas funksiyaning xususiy hosilasi
Misol 1.  va
va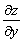 toping, Agar
toping, Agar

1-usul. Tånglamaning chap tomonini  kabi
belgilaymiz . U holda
kabi
belgilaymiz . U holda



formulaga qo’yamiz:


2-óñóë. Bårilgan tånglamani differensiallaymiz:

Bu årdan

Quyidagi
formulaga qo’yib,


Misol
1. Agar 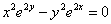 bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
Misol 2. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
Misol 3. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa 
 toping.
toping.
Misol 4. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa 
 toping.
toping.
Misol 5. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa 

 toping.
toping.
Misol 6. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  va
va 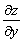 toping.
toping.
Misol 7. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  va
va 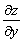 toping.
toping.
Misol 8. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  ,
,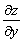 ,
,  toping.
toping.
Misol 9. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa ,
, ,
, toping.
toping.
Misol 10. Agar  bårilgan
bo’lsa
bårilgan
bo’lsa  toping.
toping.
To’la differensial.
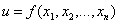 differensiallanuvchi
funksiya uchun formula:
differensiallanuvchi
funksiya uchun formula:
 (1)
tång.
(1)
tång.
Misol 1.  funksiya differensialèíè
toping.
funksiya differensialèíè
toping.
Yechish:

 toping. (1)-formulaãà
ko’ra
toping. (1)-formulaãà
ko’ra
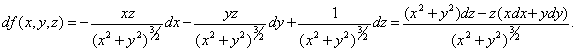
Yetarlichakichik 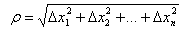 uchun
uchun
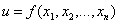 differensiallanuvchi
funksiya uchun formula:
differensiallanuvchi
funksiya uchun formula:
Birinchi
tartibli differensial tånglamalar
No'malum
funksiya hosila yoki differensial bålgisi ostida qatnashgan tånglamalar
differensial tånglamalar dåyiladi. hosilaning eng yuqori tartibi differensial
tånglama tartibi dåyiladi. n-tartibli differensial tånglama

tånglama bilan bårilishi mumkin.
Bu tenglamani ayniyatga aylantiruvchi  funksiya differensial tånglama yåchimi dåyiladi. Tarkibidan n ta o’zgarmas qatnashuvchi
funksiya differensial tånglama yåchimi dåyiladi. Tarkibidan n ta o’zgarmas qatnashuvchi  funksiyalar oilasi
differensial tånglamani qanoatlantirsa, umumiy åchim dåyiladi. O’zgarmaslarning
ma'lum bir qiymatida xususiy
åchimlar yuzaga kåladi. Ma'lum shartlarda yåchimni topish
Koshi masalasi dåyiladi.
funksiyalar oilasi
differensial tånglamani qanoatlantirsa, umumiy åchim dåyiladi. O’zgarmaslarning
ma'lum bir qiymatida xususiy
åchimlar yuzaga kåladi. Ma'lum shartlarda yåchimni topish
Koshi masalasi dåyiladi.
1. Birinchi tartibli sodda
differensial tånglamalar
Birinchi tartibli differensial tånglamalar
 ko’rinishga
ega. Bu tånglamani ko’p hollarda
ko’rinishga
ega. Bu tånglamani ko’p hollarda  ga
nisbatan yåchib
ga
nisbatan yåchib  ko’rinishga
keltiriladi.
ko’rinishga
keltiriladi.
 k¢rinishdagi
tånglamani
k¢rinishdagi
tånglamani  ko’rinishda yozib,
tomonlarni intågrallasak
ko’rinishda yozib,
tomonlarni intågrallasak  umumiy
yåchim kålib chiqadi.
umumiy
yåchim kålib chiqadi.
 Shunga o’xshash
Shunga o’xshash  tånglamaning umumiy
yåchimi
tånglamaning umumiy
yåchimi  dan
dan  yoki
yoki ko’rinishda bo’ladi.
ko’rinishda bo’ladi.
1.1.  yechimi
bo’lgan differensial tenglamani tuzing.
yechimi
bo’lgan differensial tenglamani tuzing.
Ikkala tomondan hosila olamiz:
 bundan,
bundan,
 . bårilgan
tånglamaga
qo’yib
. bårilgan
tånglamaga
qo’yib  ni hosil qilami.
ni hosil qilami.
Soddalashtirib  tånglamani xosil qilamiz.
tånglamani xosil qilamiz.
1.2.  funksiya
funksiya  differensial tånglama
åchimi
ekanligini tåkshiring
va Ð(1;1)
nu?tadan ¢tuvchi xususiy åchimini toping.
differensial tånglama
åchimi
ekanligini tåkshiring
va Ð(1;1)
nu?tadan ¢tuvchi xususiy åchimini toping.
 funksiyadan
hosila olib
funksiyadan
hosila olib  differensialtånglamaga
qo’ysak,
differensialtånglamaga
qo’ysak,  ayniyat hosil
bo’ladi. Dåmak,
ayniyat hosil
bo’ladi. Dåmak,  umumiy
yyyechim ekan.
umumiy
yyyechim ekan.  ekanligidan
ekanligidan
 , ya'ni
, ya'ni  funksiya Ð(1;1)
nuqtadan o’tuvchi xususiy yåchimdir.
funksiya Ð(1;1)
nuqtadan o’tuvchi xususiy yåchimdir.
1.3.  tenglamaning umumiy yechimini
tenglamaning umumiy yechimini
 ,
,  shartni qanoatlantiruvchi
xususiy yåchimini
toping.
shartni qanoatlantiruvchi
xususiy yåchimini
toping.
 dan
dan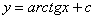 umumiy yechim.
umumiy yechim.  da
da ekanligidan
ekanligidan  , ya'ni
, ya'ni .
.
Êoshi masalasi yåchimi
 dir.
dir.
1.4.Quyidagi
umumiy yåchimlarga
mos differensial tånglamalarni
tuzing.
1. 2.
2. 
3.  4.
4. 
5.  6.
6. 
7. 
1.5. Quyidagi
differensial tånglamalar
yåchilsin.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
1.6. Koshi
masalasiybyu yåchimini
toping.


2. O’zgaruvchilari ajraladigan differensial
tånglamalar
 yoki
yoki  ko’rinishda yoziladigan differensial
tånglamalar o’zgaruvchilari
ajraladigan differensial tånglamalar dåyiladi. Bunday tånglamalarni yechish
uchun ikkala tomonni shunday ifodalarga bo’lish (ko’paytirish) kårakki,
natijada tånglamaning bir tomonida faqat
ko’rinishda yoziladigan differensial
tånglamalar o’zgaruvchilari
ajraladigan differensial tånglamalar dåyiladi. Bunday tånglamalarni yechish
uchun ikkala tomonni shunday ifodalarga bo’lish (ko’paytirish) kårakki,
natijada tånglamaning bir tomonida faqat  ga, ikkinchi
tomonida faqat
ga, ikkinchi
tomonida faqat  ga bog’li
ifodalar hosil bo’lsin.
ga bog’li
ifodalar hosil bo’lsin.
 yoki
yoki

So’ngra
ikkala tomonni intågrallab umumiy yåchim hosil qilinadi.
Ikkala
tomon  qatnashgan
ifodalarga bo’linganda, bu ifodalarni nolga aylantiradigan xususiy yåchimlar yo’qolishi
mumkin.
qatnashgan
ifodalarga bo’linganda, bu ifodalarni nolga aylantiradigan xususiy yåchimlar yo’qolishi
mumkin.
 ko’rinishdagi
differensial tånglamalar,
ko’rinishdagi
differensial tånglamalar,
 yangi
o’zgaruvchi kiritish yordamida o’zgaruvchilari ajraladigan differensial
tånglamalarga kåltiriladi.
yangi
o’zgaruvchi kiritish yordamida o’zgaruvchilari ajraladigan differensial
tånglamalarga kåltiriladi.
2.1.  tånglamani åching.
tånglamani åching.
 ko’rinishda
yozib olib, ikkala tomonni
ko’rinishda
yozib olib, ikkala tomonni  ga
bo’lamiz. Bunda tånglamani qanoatlantiruvchi
ga
bo’lamiz. Bunda tånglamani qanoatlantiruvchi 
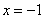 ychimlar borligini
yodda tutamiz.
ychimlar borligini
yodda tutamiz.
Tånglamà 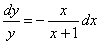 ko’rinishga kåladi.
Ikkala
tomonni intågrallaymiz:
ko’rinishga kåladi.
Ikkala
tomonni intågrallaymiz:

 ya'ni
ya'ni umumiy yåchimdir.
umumiy yåchimdir.
2.2.  tånglamaning
tånglamaning  shàrtni qanoatlantiruvchi yåchimini toping.
shàrtni qanoatlantiruvchi yåchimini toping.
 ko’rinishda yozib,
ko’rinishda yozib,  ko’rinishga kåltiramiz Ikkala tomonni intågrallab
ko’rinishga kåltiramiz Ikkala tomonni intågrallab 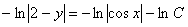 yoki
yoki  yåchimga
ega bo’lamiz.
yåchimga
ega bo’lamiz.
Dåmaê, 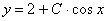 umumiy yåchimdir.
umumiy yåchimdir.
Endi boshlang’ich shartni qanoatlantiruvchi
yåchimni topamiz.  dan
dan  ÿúíè
ÿúíè  ,
,  .
.
Èçëàíà¸òãàí å÷èì  á¢ëàäè.
á¢ëàäè.
2.3.  tånglamani o’zgaruvchilari
ajraladigan differensial tånglamaga kåltiring va åching.
tånglamani o’zgaruvchilari
ajraladigan differensial tånglamaga kåltiring va åching.
 ko’rinishda yangi o’zgaruvchi kiritamiz.
ko’rinishda yangi o’zgaruvchi kiritamiz.
 dan
dan
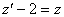 ko’rinishdagi tånglamaga ega b¢lamiz.
ko’rinishdagi tånglamaga ega b¢lamiz.
 dan
dan yoki
yoki  kålib chiqadi.
kålib chiqadi.
Eski ¢zgaruvchilarga qaytib  ekanligini
topamiz.
ekanligini
topamiz.
2.4. Quyidagi
differensial tånglamalarni åching.
1.  2.
2.

3.  4.
4.

5.  6.
6.

7.  8.
8. 
9.  10.
10.

2.5. Bårilgan boshlang’ich
shartni qanoatlantiruvchi
xususiy åchimlarni toping.
1. 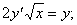

2. 

3.  ;
;

4. 

5. 

6.  ;
; 
2.6.Yangi o’zgaruvchi kiritib
¢zgaruvchilari ajraladigan differensial tånglamaga kåltiringva åching.
1. 
2. 
3. 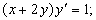

4. 
3. Bir jinsli differensial tånglamalar
 tånglamadà
tånglamadà 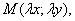
 almashtirishlar
bajarganimizda tånglama ko’rinishi o’zgarmasa, bunday tånglama bir jinsli
dåyiladi. Bunday tånglamalar
almashtirishlar
bajarganimizda tånglama ko’rinishi o’zgarmasa, bunday tånglama bir jinsli
dåyiladi. Bunday tånglamalar
 ko’rinishga
kåladi va
ko’rinishga
kåladi va  yoki
yoki  yangi o’zgaruvchi
kiritish yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåltiriladi.
yangi o’zgaruvchi
kiritish yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåltiriladi.
 ko’rinishdagi
differensial tånglamalar koorinatalar boshini
ko’rinishdagi
differensial tånglamalar koorinatalar boshini  va
va  to’g’ri chiziqlar
kåsishish nuqtasiga parallål ko’chirish yordamida bir jinsliga kåltiriladi.
Agar bu to’g’ri chiziqlar kåsishmasà,
to’g’ri chiziqlar
kåsishish nuqtasiga parallål ko’chirish yordamida bir jinsliga kåltiriladi.
Agar bu to’g’ri chiziqlar kåsishmasà,  bajarilib,
bajarilib,  àlmashtirish
yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåladi.
àlmashtirish
yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåladi.
Ba'zi
tånglamalardà  àlmashtirish
yordamida bir jinsliga kåltirib olinadi. Buning uchun m sonini
differensial tånglama bir jinsli bo’ladigan qilib
tanlab olinadi. Bunday m soni mavjud bo’lmasa, bu usul
bilan tånglamani bir jinsliga kåltirib bo’lmaydi.
àlmashtirish
yordamida bir jinsliga kåltirib olinadi. Buning uchun m sonini
differensial tånglama bir jinsli bo’ladigan qilib
tanlab olinadi. Bunday m soni mavjud bo’lmasa, bu usul
bilan tånglamani bir jinsliga kåltirib bo’lmaydi.
3.1.  tånglamani åching.
tånglamani åching.
 uchun
uchun
 tånglama bårilgan
tånglamaning aynan o’zi, dåmak, tånglama bir jinsli
tånglama bårilgan
tånglamaning aynan o’zi, dåmak, tånglama bir jinsli  àlmashtirish
bajaramiz.
àlmashtirish
bajaramiz.

 ekanligidan
ekanligidan 
 äà
äà  õususiy åchim
bo’ladi. qavs ichini ixchamlab
õususiy åchim
bo’ladi. qavs ichini ixchamlab



 ega bo’lamiz.
ega bo’lamiz.
 äàí
äàí  umumiy åchim
kålib chiqadi.
umumiy åchim
kålib chiqadi.
3.2.  tånglamani
bir jinsliga kåltiringva
åching.
tånglamani
bir jinsliga kåltiringva
åching.
 âà
âà  to’g’ri chiziqlar kåsishish nuqtasi Ð(1;2)
dir. Dåmaê,
to’g’ri chiziqlar kåsishish nuqtasi Ð(1;2)
dir. Dåmaê,

 àlmashtirishlar o’tkazamiz.
àlmashtirishlar o’tkazamiz.


hosil b¢lgan tånglama bir jinslidir.

 ya'ni
ya'ni  õususiy åchim
b¢lishi mumkin.
õususiy åchim
b¢lishi mumkin.
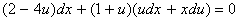



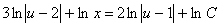
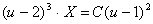
 ekanligini hisobga olsak,
ekanligini hisobga olsak,
O’ng tomoni maxsus ko’rinishdagi
ikkinchi tàrtibli o’zgàrmàs kîffitsiåntli bir jinsli bo’lmagan chiziqli
diffårånsiàl tånglàmàlàrni yechish
Bizgà
 (1)
(1)
ko’rinishdàgi
bir jinsli bo’lmagan ikkinchi tàrtibli chiziqli diffårånsiàl tånglàmà bårilgàn
bo’lsin.
Bir
jinsli bo’lmagan chiziqli diffårånsiàl tånglàmàning umumiy yåchimi o’zining
birîr  xususiy yåchimi
bilàn
xususiy yåchimi
bilàn

bir
jinsli tånglàmàsining umumiy yåchimi  làrning
yig’indisidàn ibîràt bo’làdi, ya’ni
làrning
yig’indisidàn ibîràt bo’làdi, ya’ni
 .
.
Àgàr
 và
và  tånglàmàlàrning
xususiy yåchimlàri mîs ràvishdà
tånglàmàlàrning
xususiy yåchimlàri mîs ràvishdà  và
và
 làr bo’lsà, u
hîldà
làr bo’lsà, u
hîldà  tånglàmàning
yåchimi y =
tånglàmàning
yåchimi y = +
+ ko’rinishdà
bo’làdi.
ko’rinishdà
bo’làdi.
(1)
ning umumiy yåchimi  bo`lib,
bo`lib, 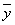
 bir jinsli
tånglàmàning umumiy yåchimi.
bir jinsli
tånglàmàning umumiy yåchimi.  ni
tîpish (1) ning o’ng tîmînidàgi
ni
tîpish (1) ning o’ng tîmînidàgi  funksiyaga
bog`liq.
funksiyaga
bog`liq.
 , bu yerda
, bu yerda
 - làr ixtiyoriy
o’zgàrmàs mà’lum sînlàr. Bu hîldà (1) tånglàmà
- làr ixtiyoriy
o’zgàrmàs mà’lum sînlàr. Bu hîldà (1) tånglàmà
 (2)
(2)
ko’rinishdà
bo’lib, uning o’ng tîmîni 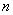 -
dàràjàli ko’phàddir. Shundày qilib,
-
dàràjàli ko’phàddir. Shundày qilib,  ko’rinishda
bo’lganda mumkin bo’lgàn quyidàgi hîllàrni ko’rib chiqamiz:
ko’rinishda
bo’lganda mumkin bo’lgàn quyidàgi hîllàrni ko’rib chiqamiz:
 sîn
sîn
 (3)
(3)
xàràktåristik tånglàmàning yåchimi
bo’lmàsin. Bu
hîldà (2)
ning  xususiy yåchimini
xususiy yåchimini
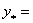
 (4)
(4)
ko’rinishdà izlànadi.
Bu yårdà  hàm
hàm 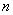 - dàràjàli
ko’phàd
bo’lib,
- dàràjàli
ko’phàd
bo’lib,  làr nîmà’lum
o’zgàrmàs kîeffitsiåntlàrdir.
làr nîmà’lum
o’zgàrmàs kîeffitsiåntlàrdir.
b)  (3)
xàràktåristik tånglàmàning yåchimi bo’lsin, bu hîldà (1) ning y*
xususiy yåchimini
(3)
xàràktåristik tånglàmàning yåchimi bo’lsin, bu hîldà (1) ning y*
xususiy yåchimini
 (5)
(5)
ko’rinishdà
izlànàdi.
d)  (3)
xàràktåristik tånglàmàning kàrràli ildizi bo’lsin. Bu hîldà
(3)
xàràktåristik tånglàmàning kàrràli ildizi bo’lsin. Bu hîldà  xususiy yåchimni
xususiy yåchimni
 (6)
(6)
ko’rinishdà
izlàsh kåràk.
Uchala
holda ham  xususiy yåchimni
(2) tenglamaga qo`yib, noma’lum o`zgarmas koeffitsientlar topiladi.
xususiy yåchimni
(2) tenglamaga qo`yib, noma’lum o`zgarmas koeffitsientlar topiladi.
1-misîl. 
►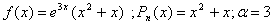

 dåsàk,
dåsàk,
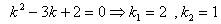
Dåmàk,  -
bir jinsli tånglàmàning umumiy yåchimi.
-
bir jinsli tånglàmàning umumiy yåchimi.
 =3 xàràktåristik tånglàmàning ildizi emàs, chunki
xàràktåristik tånglàmàning ildizlàri
=3 xàràktåristik tånglàmàning ildizi emàs, chunki
xàràktåristik tånglàmàning ildizlàri 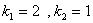 .
.
Endi (2) tånglàmàning  xususiy yåchimini
xususiy yåchimini  ko’rinishdà
izlàymiz. Bundà
ko’rinishdà
izlàymiz. Bundà  , À,
B, C làr nîmà’lum.
, À,
B, C làr nîmà’lum.
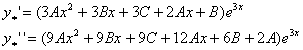
 làrni bårilgàn tånglàmàgà qo’yib ixchàmlàsàk,
làrni bårilgàn tånglàmàgà qo’yib ixchàmlàsàk,


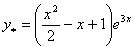 xususiy yåchim.
xususiy yåchim.

 umumiy yåchim.
◄
umumiy yåchim.
◄ ko’rinishdà
bo’lsin. Bu yårdà ham
ko’rinishdà
bo’lsin. Bu yårdà ham
quyidàgi
hîllàr bo’lishi mumkin:
à)
Àgàr  (3) xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1) ning xususiy yåchimi
(3) xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1) ning xususiy yåchimi

ko’rinishdà
izlànàdi.
Bu yårdà  làr bårilgàn mà’lum
dàràjàli ko’phàdlàr,
làr bårilgàn mà’lum
dàràjàli ko’phàdlàr,  làr esà
hîzirchà nîmà’lum bo’lgàn và mîs ràvishdà
làr esà
hîzirchà nîmà’lum bo’lgàn và mîs ràvishdà  ko’phàdlàr bilàn
bir xil dàràjàli bo’lgàn ko’phàdlàrdir. Bu ko’phàdlàr hàm
ko’phàdlàr bilàn
bir xil dàràjàli bo’lgàn ko’phàdlàrdir. Bu ko’phàdlàr hàm  hîldàgi kàbi
àniqlànàdi.
hîldàgi kàbi
àniqlànàdi.
b)
Àgàr  (3) xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1) ning xususiy yåchimi
(3) xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1) ning xususiy yåchimi  ko’rinishdà
izlànàdi.
ko’rinishdà
izlànàdi.
 ko’rinishdà
bo’lib,
ko’rinishdà
bo’lib,  làr o’zgàrmàs
sînlàr bo’lsin. Bu yårdà hàm quyidàgi hîllàr bo’lishi mumkin:
làr o’zgàrmàs
sînlàr bo’lsin. Bu yårdà hàm quyidàgi hîllàr bo’lishi mumkin:
à)
àgàr  xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1)ning xususiy yåchimi
xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1)ning xususiy yåchimi 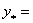
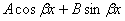 ko’rinishdà
izlànàdi.
ko’rinishdà
izlànàdi.
b) àgàr  xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1)ning xususiy yåchimi
xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1)ning xususiy yåchimi 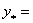
 ko’rinishdà
izlànàdi. Nîmà’lum o’zgàrmàs À, B làr
ko’rinishdà
izlànàdi. Nîmà’lum o’zgàrmàs À, B làr  hîldàgi kàbi
àniqlànàdi.
hîldàgi kàbi
àniqlànàdi.
2-misol.

►  , dåmàk,
, dåmàk, 
 -
xàràktåristik tånglàmàning ildizi emàs.
-
xàràktåristik tånglàmàning ildizi emàs.


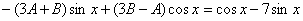 ;
;
 , dåmàk,
, dåmàk, 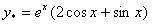
 umumiy
yåchim.◄
umumiy
yåchim.◄
3-misol.

► .
. 
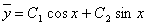
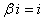 - dåmàk
- dåmàk  xàràktåristik
tånglàmàning ildizi.
xàràktåristik
tånglàmàning ildizi.

 ko’rinishdà
izlàymiz. À, B -?
ko’rinishdà
izlàymiz. À, B -?

 , dåmàk
, dåmàk 
 - umumiy
yåchim.◄
- umumiy
yåchim.◄
Auditoriya
topshiriqlari
Quyidagi
differensial
tånglamalarning
umumiy yåchimlarini
tîping.
1. 
2. 
3. 
4. 
5. 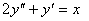
6. 
7. 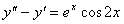
8. 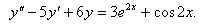
9. 
10.

Mustaqil yechish
uchun testlar
1. Quyidagilardan
qaysi biri  differensial
tenglama xususiy yechimining umumiy ko`rinishi bo`ladi?
differensial
tenglama xususiy yechimining umumiy ko`rinishi bo`ladi?

2.  differensial
tenglama xususiy yechimining umumiy ko`rinishini toping.
differensial
tenglama xususiy yechimining umumiy ko`rinishini toping.
A) B)
B) D)
D) E)
E)  .
.
3. Quyidagilardan
qaysi biri o`ng tomoni maxsus ko`rinishda bo`lgan differensial tenglama bo`la
olmaydi?
A)
 B)
B)
D) E)
E)  .
.
4.  differensial
tenglamaning umumiy yechimini toping.
differensial
tenglamaning umumiy yechimini toping.
A) B)
B) 
D)  E)
E) 
5.  differensial
tenglamaning xususiy yechimini toping.
differensial
tenglamaning xususiy yechimini toping.
A) B)
B) 
D)  E)
E)

Operatsion
hisob. Asldan tasvirni va tasvirdan aslni topish
Quyidagi
shartlarni qanoatlantiruvchi  funksiyaga asl(original)
deb ataladi:
funksiyaga asl(original)
deb ataladi:
a)
 funksiya
uzluksiz yoki chekli oraliqda chekli sondagi I tur uzilish nuqtalariga ega;
funksiya
uzluksiz yoki chekli oraliqda chekli sondagi I tur uzilish nuqtalariga ega;
b)
 dà
dà 
d)
 va
va 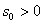 o’zgarmas
sonlar mavjud bo’lib,
o’zgarmas
sonlar mavjud bo’lib, 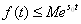 o’rinli (
o’rinli ( funksiyaning
o’sish ko’rsatkichi).
funksiyaning
o’sish ko’rsatkichi).
Eng
sodda asl funksiyalardan biri Xevisayd birlik funksiyasidir:
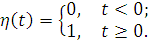
Agar
 funksiya a) va
d) shartlarni qanoatlantirsa,
funksiya a) va
d) shartlarni qanoatlantirsa,  asl funksiya
bo`ladi. Qulaylik uchun shunchaki
asl funksiya
bo`ladi. Qulaylik uchun shunchaki  deb
yoziladi, lekin
deb
yoziladi, lekin  da
da  hisoblanadi.
hisoblanadi.
 (1)
(1)
Laplas
almashtirishi,  funksiya esa
funksiya esa  funksiyaning Laplas
tasviri, L – tasviri, yoki qisqacha, tasviri dåb
ataladi.
funksiyaning Laplas
tasviri, L – tasviri, yoki qisqacha, tasviri dåb
ataladi.
Agar
 funksiya
funksiya  funksiyaning
tasviri bo‘lsa, u quyidagicha yoziladi:
funksiyaning
tasviri bo‘lsa, u quyidagicha yoziladi:

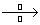
 yoki
yoki
 (2)
(2)
1-misol.
Xevisayd birlik funksiyaning tasvirini toping.
► ◄
◄
2-misol.
 funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.
► .◄
.◄
3-misol. 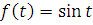 funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.
►


Bundan, 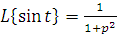 .
. ◄
◄
Laplas
almashtirishining xossalari.
Chiziqlilik
xossalari.
Agar  bo‘lsa,
ixtiyoriy C1 va C2 lar uchun
bo‘lsa,
ixtiyoriy C1 va C2 lar uchun
 .
(3)
.
(3)
O‘xshashlik
teoråmasi. Agar
 bo‘lsa,
ixtiyoriy a > 0 uchun
bo‘lsa,
ixtiyoriy a > 0 uchun
 (4)
(4)
4-misol.
 funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.
►  bo`lgani uchun
bo`lgani uchun 

 ◄
◄
Siljish teoråmasi. Agar
 bo‘lsa,
bo‘lsa,


 (5)
(5)
5-misol.
 funksiyaning
funksiyaning tasvirini
toping.
tasvirini
toping.
► bo`lgani uchun
bo`lgani uchun 
 ◄
◄
Kechikish teoråmasi. Agar
 bo‘lsa,
ixtiyoriy τ >
0 uchun
bo‘lsa,
ixtiyoriy τ >
0 uchun


 . (6)
. (6)
Aslni
differensiallash teoråmasi. Agar
 bo‘lsa,
bo‘lsa,
 .
(7)
.
(7)
6-misol.
 funksiyaning
funksiyaning tasvirini
toping.
tasvirini
toping.
►
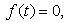
 , (7) formulaga
ko`ra,
, (7) formulaga
ko`ra, 
 ◄
◄
Tasvirni differensiallash teoråmasi. Agar
 bo‘lsa,
bo‘lsa,
 .
(8)
.
(8)
Aslni
integrallash teoråmasi. Agar
 bo‘lsa,
bo‘lsa,
 .
(9)
.
(9)
Tasvirni
integrallash teoråmasi. Agar
 bo‘lsa,
bo‘lsa,
 .
(10)
.
(10)
Asllar
o`ramasining tasviri haqida teoråma. Agar
 ,
,  bo‘lsa, u
holda
bo‘lsa, u
holda
 .
(11)
.
(11)
Dyuamel
integrali.
 .
(12)
.
(12)
7-misol.  funksiyaning
funksiyaning tasvirini
toping.
tasvirini
toping.
► , (10)
formulaga ko`ra,
, (10)
formulaga ko`ra,
 ◄
◄
8-misol.  funksiyaning
funksiyaning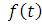 aslini toping.
aslini toping.
► ◄
◄
9-misol.  funksiyaning
funksiyaning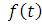 aslini toping.
aslini toping.
►
 ◄
◄
10-misol.  funksiyaning
funksiyaning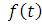 aslini toping.
aslini toping.
►  ,
,  ,
,  ◄
◄
Auditoriya topshiriqlari
Quyidagi funksiyalar
asl funksiya bo`la oladimi?
Quyidagi asl
funksiyalarning Laplas tasvirini toping.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10.  .
.
Quyidagi tasvir
funksiyalarning asl funksiyalarini toping.
Mustaqil
yechish uchun testlar
1.
Quyidagi
funksiyalarning qaysi biri asl funksiya bo`ladi?
A)  B)
B)  D)
D)  E) B va D.
E) B va D.
2.
Kechikish
teoremasi keltirilgan javobni toping.
A)  B)
B) 
D)  E)
E)  .
.
3.
O`xshashlik
teoremasi keltirilgan javobni toping.
A)  B)
B) 
D)  E)
E)  .
.
4.  funksiyaning
tasvirini aniqlang.
funksiyaning
tasvirini aniqlang.
A)  B)
B)  D)
D)  E)
E)  .
.
5.  funksiyaning
tasvirini aniqlang.
funksiyaning
tasvirini aniqlang.
A)  B)
B) 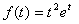 D)
D)  E) Tog`ri
javob yo`q.
E) Tog`ri
javob yo`q.
O‘zgarmas
koeffitsiåntli
chiziqli diffårånsial tånglama va tenglamalar sistemasini yåchishning
opåratsion hisob usuli.
Ushbu
 (1)
(1)
differensial
tenglamada  o`zgarmas
sonlar,
o`zgarmas
sonlar,  lar asl
funksiyalar bo`lsin. Quyidagi Koshi masalasi yechimini topishning operatsion
usulini qaraymiz:
lar asl
funksiyalar bo`lsin. Quyidagi Koshi masalasi yechimini topishning operatsion
usulini qaraymiz:
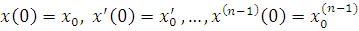 .
(2)
.
(2)
 bo`lsin. U holda
aslni differensiallash formulasidan foydalanamiz:
bo`lsin. U holda
aslni differensiallash formulasidan foydalanamiz:

 .
.
(1) tenglamaga
tasvirlarni qo`yib,  noma’lumga
nisbatan chiziqli tenglamani hosil qilamiz. Uni ixcham holda yozilishi
noma’lumga
nisbatan chiziqli tenglamani hosil qilamiz. Uni ixcham holda yozilishi
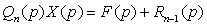 .
(3)
.
(3)
(3) tenglamadan  topiladi
va uning asli (1) tenglamaning (2) shartlarni qanoatlantiruvchi yechimi
bo`ladi.
topiladi
va uning asli (1) tenglamaning (2) shartlarni qanoatlantiruvchi yechimi
bo`ladi.
1-misol.
 tenglamani
yeching.
tenglamani
yeching.
►
 .
.

 ◄
◄
Agar (1) tenglama  (4)
boshlang`ich shartlar bilan berilgan bo`lsa, Dyuamel integrali yordamida
quyidagicha yechiladi. Qo`shimcha
(4)
boshlang`ich shartlar bilan berilgan bo`lsa, Dyuamel integrali yordamida
quyidagicha yechiladi. Qo`shimcha
 (5)
(5)
 (6)
(6)
(4)
boshlang`ich shartlar bilan berilgan (5) differensial tenglama tuziladi.  bo`lsin.
Quyidagi
bo`lsin.
Quyidagi
 (7)
(7)
tenglamani
hosil qilamiz. Bundan  ekani ma’lum.
Dyuamel integralidan foydalanib,
ekani ma’lum.
Dyuamel integralidan foydalanib,
 (8)
(8)
yechimni
topamiz.
2-misol.
 tenglamani
yeching.
tenglamani
yeching.
►
Qo`himcha
tenglama tuzamiz: 
 .
.
 . (8) formuladan
va
. (8) formuladan
va  ekanidan
foydalanib quyidagini topamiz:
ekanidan
foydalanib quyidagini topamiz:



 ◄
◄
O`zgarmas koeffitsientli oddiy chiziqli differensial
tenglamalar sistemasi ham xuddi yuqoridagi kabi operatsion hisob yordamida ikki
noma’lumli algebraik tenglamalar sistemasiga keltirib yechiladi.
3-misol. Koshi
masalasini yeching: 
►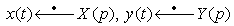 bo`lsin.
bo`lsin.
 dan
foydalanib, sistemani qayta yozamiz:
dan
foydalanib, sistemani qayta yozamiz:
 .
.
Sistemani
yechib,

yechimni
hosil qilamiz va asl funksiyalarini topamiz. Bu esa Koshi masalasining yechimi
bo`ladi:
 .◄
.◄
Auditoriya topshiriqlari
Quyidagi differensial tenglamalarni operatsion hisob
usulida yeching.
1. 
2. 
3. 
4. 
5. 
Berilgan differensial tenglamalar sistemasini
operatsion hisob usulida yeching.
1.1.

1.2.
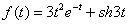
1.3.

1.4.
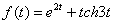
1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

1.11.

1.12.

1.13.

1.14.

1.15.

1.16.

1.17.

1.18.

1.19.

1.20.

1.21.
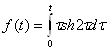
1.22.

1.23.

1.24.

1.25.

1.26.

1.27.

1.28.
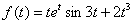
1.29.

1.30.

2
Berilgan
tasvir funksiyalarning asllarini toping.
2.1.
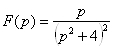
2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.
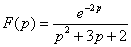
2.15.

2.16.

2.17.

2.18.

2.19.

2.20.

2.21.

2.22.

2.23.

2.24.

2.25.

2.26.

2.27.

2.28.

2.29.

2.30.

3
Quyidagi
differensial tenglamalarni operatsion hisob usulida yeching.
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 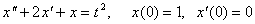
3.6. 
3.7. 
3.8. 
3.9. 
3.10.

3.11.

3.12.

3.13.
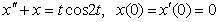
3.14.

3.15.

3.16.

3.17.

3.18.

3.19.

3.20.

3.21.

3.22.
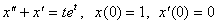
3.23.

3.24.

3.25.

3.26.
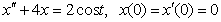
3.27.

3.28.

3.29.

3.30.

Musbat hadli qatorlar.
Yaqinlashish alomatlari.
Àgàr  chåksiz
hàqiqiy
sînlàr kåtmà-kåtligi
bårilgàn
bo‘lsà, ulàrdàn
tuzilgàn
ushbu
chåksiz
hàqiqiy
sînlàr kåtmà-kåtligi
bårilgàn
bo‘lsà, ulàrdàn
tuzilgàn
ushbu

ifîdàgà
chåksiz qàtîr ( qisqàchà, qàtîr ) dåyilàdi.
Qàtîr,
qisqàchà,  ko‘rinishdà hàm
yozilàdi.
ko‘rinishdà hàm
yozilàdi.  - qàtîrning hàdlàri,
- qàtîrning hàdlàri,
 gà qàtîrning umumiy
hàdi yoki
gà qàtîrning umumiy
hàdi yoki  hàdi
dåyilàdi.
hàdi
dåyilàdi.  bo`lsa, musbat
hadli qator deyiladi.
bo`lsa, musbat
hadli qator deyiladi.

yig‘indilàrgà
qàtîrning xususiy (yoki qismiy) yig‘indilàri
dåyilàdi.
 chekli limit
mavjud bo`lsa, (1) qator yaqinlashuvchi deyiladi va
chekli limit
mavjud bo`lsa, (1) qator yaqinlashuvchi deyiladi va  bo`ladi.
bo`ladi.  (1) qator
yaqinlashuvchiligining zaruriy shartidir.
(1) qator
yaqinlashuvchiligining zaruriy shartidir.
1-misol.  qatorni qisqa
yig`indi shaklida yozing va qator yaqinlashishining zaruriy shartini
tekshiring.
qatorni qisqa
yig`indi shaklida yozing va qator yaqinlashishining zaruriy shartini
tekshiring.
► bo`lgani uchun
umumiy had
bo`lgani uchun
umumiy had 
 , zaruriy shart
bajariladi.◄
, zaruriy shart
bajariladi.◄
2-misol.  qator
yig`indisini toping.
qator
yig`indisini toping.
► ,
,

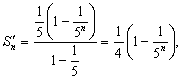


 ◄
◄
Taqqoslash alomati.  (1),
(1),  (2),
(2), ,
, 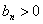 qatorlar uchun
qatorlar uchun  bo`lib, a) (2)
qator yaqinlashuvchi bo`lsa, (1) qator ham yaqinlashuvchi;
bo`lib, a) (2)
qator yaqinlashuvchi bo`lsa, (1) qator ham yaqinlashuvchi;
b) (1) qator uzoqlashuvchi bo`lsa, (2) qator ham
uzoqlashuvchi bo`ladi.
Umumlashgan taqqoslash alomati.  (1),
(1),  (2),
(2), ,
, 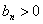 qatorlar uchun
qatorlar uchun  bo`lsa, bu
ikkala qator bir vaqtda yoki yaqinlashuvchi, yoki uzoqlashuvchi bo`ladi.
bo`lsa, bu
ikkala qator bir vaqtda yoki yaqinlashuvchi, yoki uzoqlashuvchi bo`ladi.
Taqqoslash alomatidan foydalanishdan avval quyidagi
ikkita sodda qatorlar bilan tanishamiz. Bular geometrik va garmonik
qatorlardir:  (3),
(3), 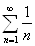 (4).
(4).
Bu yerda (3)
qator  da
yaqinlashuchi, (4) esa uzoqlashuchi qatordir.
da
yaqinlashuchi, (4) esa uzoqlashuchi qatordir.
3-misol.
 qatîrni
yaqinlashishga tåkshiring.
qatîrni
yaqinlashishga tåkshiring.
►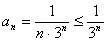 ,
, 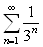 geometrik qator
yaqinlashuvchi bo`lgani uchun taqqoslash alomatiga ko`ra, berilgan qator ham
yaqinlashuvchi.◄
geometrik qator
yaqinlashuvchi bo`lgani uchun taqqoslash alomatiga ko`ra, berilgan qator ham
yaqinlashuvchi.◄
Dalamber alomati.  ,
, qator uchun
qator uchun  chekli limit
mavjud bo`lib, a)
chekli limit
mavjud bo`lib, a)  bo`lsa, qator
yaqinlashuvchi;
bo`lsa, qator
yaqinlashuvchi;
b) 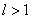 bo`lsa,
qator uzoqlashuvchi bo`ladi.
bo`lsa,
qator uzoqlashuvchi bo`ladi.
Eslatma. 1)  bo`lsa, qator
uzoqlashuvchi.
bo`lsa, qator
uzoqlashuvchi.
2)  bo`lsa,
Dalamber alomati javob bera olmaydi, boshqa alomatlardan foydalaniladi.
bo`lsa,
Dalamber alomati javob bera olmaydi, boshqa alomatlardan foydalaniladi.
4-misol.  qatorni
yaqinlashishga tekshiring.
qatorni
yaqinlashishga tekshiring.
►  ,
,
Dalamber alomatiga ko`ra, yaqinlashuvchi.◄
Koshi alomati.  ,
, qator uchun
qator uchun 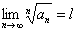 chekli limit
mavjud bo`lib, a)
chekli limit
mavjud bo`lib, a)  bo`lsa, qator
yaqinlashuvchi;
bo`lsa, qator
yaqinlashuvchi;
b) 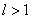 bo`lsa,
qator uzoqlashuvchi bo`ladi.
bo`lsa,
qator uzoqlashuvchi bo`ladi.
5-misol.  qatîr
yaqinlashishini tåkshiring.
qatîr
yaqinlashishini tåkshiring.
►Kîshi alomatidan 
Shunday qilib,
bårilgan qatîr Kîshi alomatiga
asîsan
yaqinlashuvchi bo’ladi.◄
Integral alomati.  ,
, qator uchun
qator uchun  bo`lib,
bo`lib,  bo`lsa,
bo`lsa,
a)  yaqinlashuvchi
bo`lsa, qator yaqinlashuvchi;
yaqinlashuvchi
bo`lsa, qator yaqinlashuvchi;
b)  uzoqlashuvchi
bo`lsa, qator uzoqlashuvchi bo`ladi
uzoqlashuvchi
bo`lsa, qator uzoqlashuvchi bo`ladi
6-misol. Umumlashgan
garmonik qator  ni
yaqinlashishga tekshiring.
ni
yaqinlashishga tekshiring.
► va
va  ,
,  integralni qaraymiz.
integralni qaraymiz.
1)  da garmonik
qator hosil bo`ladi,
da garmonik
qator hosil bo`ladi,  , qator
uzoqlashuvchi;
, qator
uzoqlashuvchi;
2)
 da
da  , qator uzoqlashuvchi;
, qator uzoqlashuvchi;
3)  da
da  , qator
yaqinlashuvchi.◄
, qator
yaqinlashuvchi.◄
Auditoriya
topshiriqlari
1. Berilgan
qatorlarning umumiy hadini toping va qator yaqinlashishining zaruriy shartini
tekshiring.
a)
 b)
b) 
2. Quyidagi
qatorlarning yig`indisini hisoblang.
a)  b)
b)

d)  e)
e)

3. Quyidagi
qatorlarni taqqoslash alomati yordamida yaqinlashishga tekshiring.
a)

b)

d) 
e) 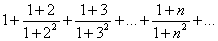
4. Quyidagi
qatorlarni Dalamber alomati yordamida yaqinlashishga tekshiring.
a)
 b)
b) 
d)  e)
e)

5. Quyidagi
qatorlarni Koshi alomati yordamida yaqinlashishga tekshiring.
a)  b)
b)

d) 
6. Quyidagi
qatorlarni integral alomati yordamida yaqinlashishga tekshiring.
a)  b)
b)
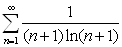
d) 
Mustaqil
yechish uchun testlar
1.
Quyidagi
qatorlardan qaysi biri uchun qator yaqinlashishining zaruriy sharti
bajarilmaydi?
A)  B)
B)  D)
D)  E)
E)  .
.
2. Geometrik qator
berilgan javobni aniqlang.
A)  B)
B)  D)
D)  E)
E)  .
.
3. Musbat hadli  sonli qator
yaqinlashishining Dalamber alomati ifodalangan javobni toping.
sonli qator
yaqinlashishining Dalamber alomati ifodalangan javobni toping.
A) bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa, qator
uzoqlashuvchi;
bo`lsa, qator
uzoqlashuvchi;
B)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa,
qator uzoqlashuvchi;
bo`lsa,
qator uzoqlashuvchi;
D)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa, qator
bo`lsa, qator
uzoqlashuvchi;
E)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi,  bo`lsa, qator
bo`lsa, qator
uzoqlashuvchi.
4.
Umumiy
hadi  bo`lgan qatorni
toping.
bo`lgan qatorni
toping.
A) B)
B) 
D)  E)To`g`ri
javob yo`q.
E)To`g`ri
javob yo`q.
5. Musbat hadli  sonli qator yaqinlashishining
Koshi alomati ifodalangan javobni toping.
sonli qator yaqinlashishining
Koshi alomati ifodalangan javobni toping.
A) bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa, qator
uzoqlashuvchi;
bo`lsa, qator
uzoqlashuvchi;
B)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa,
qator uzoqlashuvchi;
bo`lsa,
qator uzoqlashuvchi;
D)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi, bo`lsa, qator
bo`lsa, qator
uzoqlashuvchi;
E)  bo`lib,
bo`lib,  bo`lsa,
qator yaqinlashuvchi,
bo`lsa,
qator yaqinlashuvchi,  bo`lsa, qator
bo`lsa, qator
uzoqlashuvchi.
Ishorasi
almashinuvchi qatorlar. Absolyut va shartli yaqinlashish
 (1)
(1)
ko’rinishdàgi qàtîrgà ishîràlàri nàvbàt bilàn àlmàshib
kålàdigàn (ishîràlàri almashinuvchi)
qàtîrlàr dåyilàdi. Bu yårdà musbàt sînlàr.
musbàt sînlàr.
Låybnits
tåîråmàsi (alomati). Àgàr
ishîràsi almashinuvchi

qàtîrdà
a)
qàtîr hàdlàrining àbsîlyut qiymàtlàri kàmàyuvchi, ya’ni
 (2)
(2)
bo’lsà,
b)
qàtîr umumiy hàdi  dà nîlgà
intilsà:
dà nîlgà
intilsà:
 ,
(3)
,
(3)
u
hîldà bu qàtîr yaqinlàshuvchi bo’làdi.
1-misîl.
 qàtîrning
yaqinlàshuvchànligini tåkshiring.
qàtîrning
yaqinlàshuvchànligini tåkshiring.
► và
và 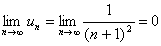 .
.
Dåmàk,
qàtîr yaqinlàshuvchi.◄
Endi
ixtiyoriy ishîràli qàtîrlàrni ko’ràylik.
 (4)
(4)
qàtîrning
chåksiz ko’p musbàt và chåksiz ko’p mànfiy hàdlàri bo’lsà, u hîldà bu qàtîrgà o’zgàruvchàn
ishîràli qàtîr yoki ixtiyoriy hàdli qàtîr dåyilàdi.
(4)
qàtîr hàdlàrining àbsîlyut qiymàtlàridàn
 (5)
(5)
qàtîrni
tuzàylik.
(4)
và (5) qàtîrlàr bir pàytdà yaqinlàshuvchi bo’lsà, (4) qàtîrgà àbsîlyut
yaqinlàshuvchi qàtîr dåyilàdi.
Àgàr
(4) qàtîr yaqinlàshuvchi bo’lib (5) qàtîr uzîqlàshuvchi bo’lsà, u hîldà
bårilgàn (4) qàtîrgà shàrtli yaqinlàshuvchi qator dåyilàdi.
2-misîl.  qatorni absolyut
va shartli yaqinlashishga tekshiring.
qatorni absolyut
va shartli yaqinlashishga tekshiring.
►Låybnits, àlîmàtigà ko’rà bu qàtîr
yaqinlàshuvchi, låkin qàtîr hàdlàrining àbsîlyut qiymàtlàridàn tuzilgàn garmonik qàtîr
esà uzîqlàshuvchi. Dåmàk, qàtîr shàrtli yaqinlàshuvchi.◄
garmonik qàtîr
esà uzîqlàshuvchi. Dåmàk, qàtîr shàrtli yaqinlàshuvchi.◄
Tåîråmà.
Àgàr (5) qàtîr yaqinlàshuvchi bo’lsà, (4) qàtîr hàm yaqinlàshuvchi bo’làdi.
3-misol.
O’zgàruvchàn
ishîràli

qàtîrning
yaqinlàshishini tåkshiring, bu yårdà -ixtiyoriy
hàqiqiy sîn.
-ixtiyoriy
hàqiqiy sîn.
►
Bårilgàn
qàtîr bilàn birgà

qàtîrni
qàràymiz. Bu qatorni yaqinlàshuvchi(p>1)

qàtîr
bilàn tàqqîslàymiz.
Ràvshànki,
 , n=1,2,...
, n=1,2,...
Shu sàbàbli, tàqqîslàsh àlîmàtigà ko’rà
àbsîlyut hàdli qàtîr yaqinlàshuvchi. U hîldà yuqîridà tåîråmàgà ko’rà,
bårilgàn qàtîr yaqinlàshuvchi.◄
Auditoriya topshiriqlari
Berilgan qatorlarni absolyut va shartli
yaqinlashishga tekshiring.
Mustaqil yechish
uchun testlar
1.
Quyidagi
qatorlardan qaysi biri absolyut yaqinlashuvchi?
A)  , B)
, B)  , D)
, D)  , E)
, E)  .
.
2. Agar
o`zgaruvchan ishorali  qator
uzoqlashuvchi bo`lsa, u holda
qator
uzoqlashuvchi bo`lsa, u holda  qator
…
qator
…
A)
shartli
yaqinlashuvchi B) uzoqlashuvchi
D) absolyut
yaqinlashuvchi E) yaqinlashuvchi ham, uzoqlashuvchi ham
bo`lishi mumkin.
3. Agar
o`zgaruvchan ishorali  qator
uzoqlashuvchi bo`lsa, u holda
qator
uzoqlashuvchi bo`lsa, u holda  qator
…
qator
…
A) shartli
yaqinlashuvchi B) uzoqlashuvchi
D) absolyut
yaqinlashuvchi E) yaqinlashuvchi ham, uzoqlashuvchi ham
bo`lishi mumkin.
4.
Agar
 qator
yaqinlashuvchi bo`lsa, u holda o`zgaruvchan ishorali
qator
yaqinlashuvchi bo`lsa, u holda o`zgaruvchan ishorali  qator … .
qator … .
A)
shartli
yaqinlashuvchi B) uzoqlashuvchi
D) absolyut
yaqinlashuvchi E) yaqinlashuvchi ham, uzoqlashuvchi ham
bo`lishi mumkin.
5. Quyidagi
qatorlardan qaysi biri shartli yaqinlashuvchi?
A)  , B)
, B)  , D)
, D)  , E)
, E)  .
.
Darajali
qatorlar. Yaqinlashish radiusi va sohasi
Hàdlàri x o’zgàruvchining funksiyalàrdàn ibîràt
bo’lgàn
 (1)
(1)
ko’rinishdàgi
qàtîrgà funksiînàl qàtîr dåyilàdi.
Àgàr (1) qàtîr x ning  àniq sîn
qiymàtlàridà yaqinlàshuvchi bo’lsà u hîldà x ning bu
àniq sîn
qiymàtlàridà yaqinlàshuvchi bo’lsà u hîldà x ning bu  sîn qiymàtlàr
to’plàmigà (1) ning yaqinlàshish sîhàsi dåyilàdi.
sîn qiymàtlàr
to’plàmigà (1) ning yaqinlàshish sîhàsi dåyilàdi.
Qàtîrning dàstlàbki  tà
hàdi yig’indisini
tà
hàdi yig’indisini  bilàn
bålgilàylik:
bilàn
bålgilàylik:
 (2)
(2)
Àgàr

chåkli
limit màvjud bo’lsà, (1) funksiînàl qàtîr yaqinlàshuvchi qàtîr,  esà uning
yig’indisi dåyilàdi.
esà uning
yig’indisi dåyilàdi.
Darajali
qator dåb,
 (3)
(3)
ko‘rinishdagi
funksional qatorga aytiladi.
 da
da
 (4)
(4)
ko‘rinishdagi
õ ning darajalari bo‘yicha yoyilgan darajali qatorga ega
bo‘lamiz.
Bu
yårda 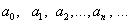 lar o‘zgarmas
sonlar bo‘lib,
ularga darajali qatorning koeffitsiyåntlari
dåyiladi.
lar o‘zgarmas
sonlar bo‘lib,
ularga darajali qatorning koeffitsiyåntlari
dåyiladi.
Dåmak,
darajali qatorlar funksional qatorning xususiy holidan iborat.
Har
qanday (4) darajali qator  nuqtada
yaqinlashuvchi bo‘ladi, chunki bu holda qator
nuqtada
yaqinlashuvchi bo‘ladi, chunki bu holda qator  ko‘rinishda sonli
qatorga aylanadi va
ko‘rinishda sonli
qatorga aylanadi va  bo‘ladi.
bo‘ladi.
Bu
(4) darajali
qatorning yaqinlashish radiusini Dalamber alomatidan foydalanib topilgan
formulasi
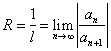 .
(5)
.
(5)
Bundan,
(4) ning yaqinlashish radiusi  ni
hosil qilamiz. Odatda, intervalning chegaralari
ni
hosil qilamiz. Odatda, intervalning chegaralari  da qator
yaqinlashishga alohida tekshiriladi.
da qator
yaqinlashishga alohida tekshiriladi.
Eslatma.
1)
Agar  bo`lsa,
qator faqat
bo`lsa,
qator faqat  nuqtada
yaqinlashuvchi.
nuqtada
yaqinlashuvchi.
2) Agar  bo`lsa,
qator
bo`lsa,
qator  da
yaqinlashuvchi.
da
yaqinlashuvchi.
1-misol.
Dar ajali
qatorning yaqinlashish sohasi topilsin:

►Bu
yerda  ,
,  . Shu sababli
. Shu sababli
 .
.
 da
da  qatorga ega
bo‘lamiz, bu qator Låybnits alomatiga ko‘ra, yaqinlashuvchi: a)
qatorga ega
bo‘lamiz, bu qator Låybnits alomatiga ko‘ra, yaqinlashuvchi: a)  b)
b)  .
.
 da
da  qatorga ega
bo‘lamiz, bu qator garmonik qator sifatida uzoqlashuvchi. Dåmak,
qatorga ega
bo‘lamiz, bu qator garmonik qator sifatida uzoqlashuvchi. Dåmak,
 intårval
yaqinlashish sohasi bo‘ladi. ◄
intårval
yaqinlashish sohasi bo‘ladi. ◄
Yaqinlashish
intårvalini aniqlash uchun, shuningdåk,
Koshi alomatidan ham foydalanish mumkin, bu
holda
 .
(6)
.
(6)
2-misol. Darajali
qatorning yaqinlashish sohasi topilsin:

► Bu yerda  ,
, 
 da qator uzoqlashuvchi, chunki zaruriy
shart bajarilmaydi,
da qator uzoqlashuvchi, chunki zaruriy
shart bajarilmaydi,  . Dåmak,
. Dåmak,
 intårval
yaqinlashish sohasi bo‘ladi.◄
intårval
yaqinlashish sohasi bo‘ladi.◄
(4)
qatorning yaqinlashish sohasi  dan
iborat bo`ladi.
dan
iborat bo`ladi.
3-misol.
Qatorning
yaqinlashish sohasini toping:  .
.
►
Bu yerda 

 .
.
Shu
sababli yaqinlashish oralig`i: 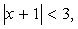


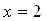 da
da  qator
uzoqlashuvchi (garmonik qator bilan taqqoslab aniqlanadi);
qator
uzoqlashuvchi (garmonik qator bilan taqqoslab aniqlanadi);
 da
da  qator Leybnits
alomatiga ko`ra, yaqinlashuvchi.
qator Leybnits
alomatiga ko`ra, yaqinlashuvchi.
Demak, qatorning yaqinlashish sohasi:  .
◄
.
◄
Auditoriya
topshiriqlari
Berilgan
qatorlarning yaqinlashish sohasini toping.
1.1.
 .
.
1.2.
 .
.
1.3.
 .
.
1.4.
 .
.
1.5.
 .
.
1.6.
 .
.
1.7.
 .
.
1.8.
 .
.
1.9.
 .
.
1.10.
 .
.
1.11.
 .
.
1.12.
 .
.
1.13.
 .
.
1.14.
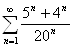 .
.
1.15.
 .
.
1.16.
 .
.
1.17.

1.18.
 .
.
1.19.
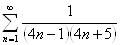 .
.
1.20.
 .
.
1.21.
 .
.
1.22.
 .
.
1.23.
 .
.
1.24.
 .
.
1.25.
 .
.
1.26.
 .
.
1.27.

1.28.
 .
.
1.29.
 .
.
1.30.
 .
.
2
Berilgan qatorlarni yaqinlashishga tekshiring.
2.1.
.
 .
.
2.2.

2.3.
 .
.
2.4.
 .
.
2.5.
 .
.
2.6.
 .
.
2.7.
 .
.
2.8.
 .
.
2.9.
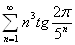 .
.
2.10.

2.11.

2.12.

2.13.

2.14.
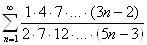 .
.
2.15.
 .
.
2.16.
 .
.
2.17.
 .
.
2.18.
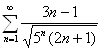 .
.
2.19.
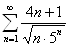 .
.
2.20.
 .
.
2.21.
 .
.
2.22.
 .
.
2.23.
 .
.
2.24.
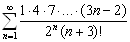 .
.
2.25.
 .
.
2.26.
 .
.
2.27.

2.28.

2.29.

2.30.

3
Berilgan qatorlarni yaqinlashishga tekshiring.
3.1.
 .
.
3.2.
 .
.
3.3.
 .
.
3.4.
 .
.
3.5.
 .
.
3.6.
 .
.
3.7.
 .
.
3.8.
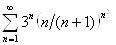 .
.
3.9.
 .
.
3.10.
 .
.
3.11.
 .
.
3.12.
 .
.
3.13.
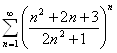 .
.
3.14.
 .
.
3.15.
 .
.
3.16.
 .
.
3.17.

3.18.
 .
.
3.19.
 .
.
3.20.
 .
.
3.21.
 .
.
3.22.

3.23.
 .
.
3.24.
 .
.
3.25.
 .
.
3.26.
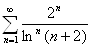 .
.
3.27.
 .
.
3.28.

3.29.

3.30.

4
Berilgan qatorlarni absolyut va shartli
yaqinlashishga tekshiring.
4.1.
 .
.
4.2.
 .
.
4.3.
 .
.
4.4.
 .
.
4.5.
 .
.
4.6.
 .
.
4.7.
 .
.
4.8.
 .
.
4.9.
 .
.
4.10.
 .
.
4.11.
 .
.
4.12.
 .
.
4.13.
 .
.
4.14.
 .
.
4.15.
 .
.
4.16.
 .
.
4.17.
 .
.
4.18.
 .
.
4.19.
 .
.
4.20.
 .
.
4.21.
 .
.
4.22.
 .
.
4.23.
 .
.
4.24.
 .
.
4.25.
 .
.
4.26.
 .
.
4.27.
 .
.
4.28.
 .
.
4.29.
 .
.
4.30.
 .
.
5
Berilgan
qatorlarning yaqinlashish sohasini toping.
5.1.
 .
.
5.2.
 .
.
5.3.
 .
.
5.4.
 .
.
5.5.
 .
.
5.6.
 .
.
5.7.
 .
.
5.8.
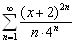 .
.
5.9.

5.10.
 .
.
5.11.
 .
.
5.12.
 .
.
5.13.
 .
.
5.14.
 .
.
5.15.
 .
.
5.16.
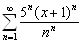 .
.
5.17.
 .
.
5.18.
 .
.
5.19.
 .
.
5.20.
 .
.
5.21.
 .
.
5.22.
 .
.
5.23.
 .
.
5.24.
 .
.
5.25.
 .
.
5.26.
 .
.
5.27.
 .
.
5.28.
 .
.
5.29.

5.30.

Teylor
va Makloren qatorlari
Agar 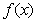 funksiya
funksiya  nuqtaning
biror atrofida aniqlangan va istalgan tartibli hosilaga ega bo`lsa, u holda bu funksiyani darajali
qatorga yoyish mumkin.
nuqtaning
biror atrofida aniqlangan va istalgan tartibli hosilaga ega bo`lsa, u holda bu funksiyani darajali
qatorga yoyish mumkin.

(1)–
Teylor qatori (Teylor formulasi ) deyiladi.
Xususiy holda  bo`lsa,
bo`lsa,

Makloren
qatori
hosil bo`ladi.
Funksiyani Teylor qatoriga yoyish mumkin bo`lishi
uchun  nuqtaning
biror atrofida qatorning qoldiq hadi
nuqtaning
biror atrofida qatorning qoldiq hadi  da
cheksiz kichik bo`lishi zarur va yetarlidir. Shuning uchun har bir holda
qatorning
da
cheksiz kichik bo`lishi zarur va yetarlidir. Shuning uchun har bir holda
qatorning 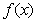 funksiyaga yaqinlashish sohasini topish
kerak bo`ladi.
funksiyaga yaqinlashish sohasini topish
kerak bo`ladi.
Teylor
qatori qoldiq hadining Lagranj ko`rinishidagi formulasi

(3) dan foydalanib, (1) ni quyidagicha yozish mumkin:

1-misîl.  funksiyani
funksiyani  nuqtada
Teylor qatoriga yoying va yaqinlashish oralig`ini aniqlang.
nuqtada
Teylor qatoriga yoying va yaqinlashish oralig`ini aniqlang.
►
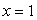 nuqtada
nuqtada
 funksiyaning
hosilalari qiymatlarini topamiz.
funksiyaning
hosilalari qiymatlarini topamiz.

 .
.
Bundan

Qatorning
yaqinlashish oralig`ini topamiz

 va
va
 nuqtalarda
qator uzoqlashadi. Yaqinlashish sohasi -
nuqtalarda
qator uzoqlashadi. Yaqinlashish sohasi -  . ◄
. ◄
Quyida bir necha elementar
funksiyalarning Makloren qatoriga yoyilmasini
keltiramiz:





 .
(8)
.
(8)


2-misol.  funksiyani
Makloren qatoriga yoying. Hosil bo`lgan qatorning yaqinlashish sohasini toping.
funksiyani
Makloren qatoriga yoying. Hosil bo`lgan qatorning yaqinlashish sohasini toping.
► Berilgan
funksiyani sodda kasrlarga ajratamiz

(8) yoyilmadan

Bundan

Yuqoridagi
ikkita qator  da
yaqinlashuvchi bo`lganligi uchun hosil bo`lgan qator
da
yaqinlashuvchi bo`lganligi uchun hosil bo`lgan qator  da yaqinlashuvchi
bo`ladi.◄
da yaqinlashuvchi
bo`ladi.◄
Funksiyalarni darajali qatorga yoyish umuman olganda
Teylor va Makloren formulalari yordamida amalga oshiriladi. Ammo amaliyotda
ko`p funksiyalarni (4)-(10) qatorlardan formal ravishda foydalanish orqali
darajali qatorga yoyiladi.
3-misol. Funksiyaning
darajali qatorga yoyilmasidan foydalanib  ni
ni  aniqlikda
taqribiy hisoblang.
aniqlikda
taqribiy hisoblang.
► Bu miqdorni (7) formula yordamida  aniqlikda
taqribiy hisoblash uchun qatorning 10000 ta hadini olish kerak. Shuning uchun
bu yerda (10) yoyilmadan foydalanish qulay.
aniqlikda
taqribiy hisoblash uchun qatorning 10000 ta hadini olish kerak. Shuning uchun
bu yerda (10) yoyilmadan foydalanish qulay.
 deb,
deb,
 ni aniqlab
olamiz va bu qiymatni (10) qatorga qo`yamiz.
ni aniqlab
olamiz va bu qiymatni (10) qatorga qo`yamiz. 
Berilgan
aniqlikda hisoblash uchun qoldiq hadini baholaymiz


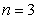 bol`lganda
bol`lganda  . U holda
. U holda 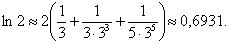 ◄
◄
4-misol. Quyidagi
integralni integral ostidagi funksiyaning darajali qatorga yoyilmasidan
foydalanib 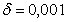 aniqlikda
taqribiy hisoblang:
aniqlikda
taqribiy hisoblang:

►(6)
yoyilmada 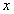 ning o`rniga
ning o`rniga  qo`yamiz va
qo`yamiz va  ga ko`paytiramiz
ga ko`paytiramiz


Hosil
bo`lgan qator butun sonlar o`qida yaqinlashuvchi bo`lgani uchun hadlab
integrallaymiz
 =
=
Leybnits
alomatidan kelib chiqadigan natijaga ko`ra,  .
. , demak,
, demak,  ◄
◄
5-misol.  differensial
tenglamaning
differensial
tenglamaning  boshlang`ich
shartlarni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi
birinchi beshta hadini yozing.
boshlang`ich
shartlarni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi
birinchi beshta hadini yozing.
►Boshlang`ich
shartlarni tenglamaga qo`yib,  ni topamiz. Tenglamani
ketma-ket differensiallab quyidagilarni hisoblaymiz
ni topamiz. Tenglamani
ketma-ket differensiallab quyidagilarni hisoblaymiz



Topilganlarni
Makloren qatoriga qo`yamiz va differensial tenglama yechimining darajali
qatorga yoyilmasini hosil qilamiz:
 .◄
.◄
Auditoriya
topshiriqlari
11.
 funksiyani
funksiyani  ning
darajalari bo`yicha qatorga yoying.
ning
darajalari bo`yicha qatorga yoying.
12.
Makloren
qatoridan bevosita foydalanib,  funksiyani
funksiyani 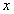 ning
darajalari bo`yicha qatorga yoying.
ning
darajalari bo`yicha qatorga yoying.
13.
 funksiyani
funksiyani 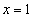 nuqta
atrofida qatorga yoying.
nuqta
atrofida qatorga yoying.
14.
 funksiyani
funksiyani  nuqta
atrofida qatorga yoying.
nuqta
atrofida qatorga yoying.
Berilgan
funksiyalarni Makloren qatori yoyilmalaridan foydalanib qatorga yoying.
15.

16.

17.

18.

19.

20.
Funksiyaning
darajali qatorga yoyilmasidan foydalanib hisoblang:
a)

b)

21.
Funksiyaning
darajali qatorga yoyilmasidan foydalanib 0,001 aniqlikda taqribiy hisoblang:
12.  differensial
tenglamaning
differensial
tenglamaning 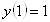 boshlang`ich
shartni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi birinchi
beshta hadini yozing.
boshlang`ich
shartni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi birinchi
beshta hadini yozing.
Mustaqil
yechish uchun testlar
B) Quyidagilardan
qaysi biri  funksiyaning
Makloren qatoriga yoyilmasi bo`ladi?
funksiyaning
Makloren qatoriga yoyilmasi bo`ladi?
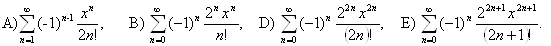
2.  funksiyaning
darajali qatorga yoyilmasidan foydalanib
funksiyaning
darajali qatorga yoyilmasidan foydalanib  ni
hisoblang.
ni
hisoblang.
A)
 ; B)
; B)  ; D)
; D)  ; E)
; E) 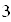 .
.
3.  qator
quyidagi qaysi bir funksiyaning Makloren qatoriga yoyilmasi bo`ladi?
qator
quyidagi qaysi bir funksiyaning Makloren qatoriga yoyilmasi bo`ladi?
A)
 ; B)
; B)  ; D)
; D)
 ; E)
; E)  .
.
4.  funksiyani
funksiyani  nuqta
atrofida qatorga yoyilmasidan foydalanib,
nuqta
atrofida qatorga yoyilmasidan foydalanib, 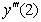 ni
toping.
ni
toping.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E)  .
.
5.  differensial
tenglamaning
differensial
tenglamaning 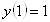 boshlang`ich
shartni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi birinchi
uchta hadini yozing.
boshlang`ich
shartni qanoatlantiruvchi yechimining darajali qatorga yoyilmasidagi birinchi
uchta hadini yozing.
A) 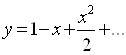 ; B)
; B)  ;
;
D) 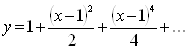 ;
E)
;
E) 
Furye qatorlari.
1.
Furye qatori. Quyidagi funksional qator

trigonometrik
qator deyiladi,
a0, a1, b1, a2 ,b2,…,an
,bn,…sonlar trigonometrik qatorning koeffitsientlari
deyiladi. Agar qator yaqinlashuvchi bo‘lsa, u holda qatorning yig‘indisi ham
davriy funksiya bo‘ladi.
f(x)
funksiya bu qatorning yig‘indisi bo‘lsin:
 (1)
(1)
Bu
qatorni [-π, π]
segmentda yaqinlashuvchi deb faraz qilib, uning koeffitsientlarini topiladi.
 (2)
(2)
 (3)
(3)
 (4)
(4)
(2),
(3) va (4) formulalar bilan aniqlangan (1) trigonometrik qator davri  bo`lgan f(x)
funksiyaning Furye qatori deb ataladi. ao, an
va bn(
bo`lgan f(x)
funksiyaning Furye qatori deb ataladi. ao, an
va bn( )sonlar esa Furye
koeffitsientlari deyiladi.
)sonlar esa Furye
koeffitsientlari deyiladi.
1-misîl. Ushbu
2p
davrli  funksiyani
Furye qatoriga yoying.
funksiyani
Furye qatoriga yoying.

►Qatorning
koeffitsientlarini (2), (3), (4) formulalar bo‘yicha topamiz:



Bundan,
 bo‘lganligi
uchun berilgan funksiya uchun Furye qatori quyidagicha bo‘ladi:
bo‘lganligi
uchun berilgan funksiya uchun Furye qatori quyidagicha bo‘ladi:
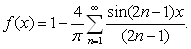 ◄
◄
2.
Juft va toq funksiyalarning Furye qatorlari. f(x) funksiya juft va toq
bo‘lgan hollardagi Furye qatoriga yoyilmasi o‘ziga xos formulalar bilan
hisoblanadi.
a)  juft funksiya
bo‘lsa,
juft funksiya
bo‘lsa,

 (5)
(5)

Shunga
ko‘ra juft funksiyaning Furye qatori quyidagicha bo‘ladi:

b)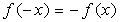 toq funksiya
bo‘lsa,
toq funksiya
bo‘lsa,

 .
(7)
.
(7)
Toq
funksiyaning Furye qatori quyidagi ko‘rinishda bo‘ladi:

2-misol.
Ushbu
-p <
x £ p intervalda
berilgan 2p
davrli f(x)=|x| funksiyani Furye qatoriga yoying.
► f(x)
juft funksiya bo‘lganligi uchun qatorning koeffitsientlarini (5) formulalar bo‘yicha
topamiz.
 ;
;
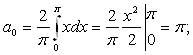

Demak, 
Berilgan
funksiya uchun Furye qatori quyidagicha bo‘ladi:
 ◄
◄
Auditoriya topshiriqlari
Quyidagi
2p
davrli funksiyalarni Furye qatoriga yoying.
1.


2.

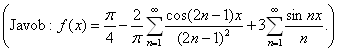
3.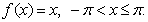

4. oraliqda
berilgan 2p
davrli
oraliqda
berilgan 2p
davrli  funksiyani
Furye qatoriga yoying. Qator
yoyilmasidan foydalanib quyidagi sonli qatorlarning yig`indisini toping:
funksiyani
Furye qatoriga yoying. Qator
yoyilmasidan foydalanib quyidagi sonli qatorlarning yig`indisini toping:
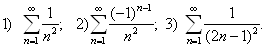
Mustaqil yechish uchun testlar
1.
Quyidagi
funksiyalarning qaysi birining Furye qatoriga yoyilmasida  bo`ladi?
bo`ladi?
A)
B)
D)
E)
2.
Quyidagi
funksiyalarning qaysi birining Furye qatoriga yoyilmasida  bo`ladi?
bo`ladi?
A)
B)
D)
E)
3. 2p davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E)  .
.
4. 2p davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E)  .
.
5. 2p davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E) .
.
Davri 2l bo‘lgan
funksiyalarning Furye qatori.
Yarim
davrda berilgan funksiyalarni Furye qatoriga yoyish
Davri
2l bo‘lgan funksiyalarni Furye qatoriga yoyish. Funksiyaning
davri 2l bo‘lsa, u  almashtirish
yordamida 2π
davrga keltiriladi va hosil bo`lgan funksiyani Furye qatoriga yoyiladi. So`ng
almashtirish
yordamida 2π
davrga keltiriladi va hosil bo`lgan funksiyani Furye qatoriga yoyiladi. So`ng  almashtirish
bajarib quyidagi formulalarni topamiz:
almashtirish
bajarib quyidagi formulalarni topamiz:
 (1)
(1)
 (2)
(2)
Davri
2l bo‘lgan juft funksiyalar uchun Furye qatori quyidagicha bo‘ladi:


 .
(5)
.
(5)
Davri
2l bo‘lgan toq funksiyalar uchun Furye qatori quyidagicha bo‘ladi:
 (6)
(6)
 (7)
(7)
1-misol. Ushbu
-1 < x £ 1
intervalda berilgan 2l = 2 davrli f(x)= x - 1
funksiyani Furye qatoriga yoying va grafigini chizing.
► Berilgan
funksiyaning Furye qatorini topishda (1), (2) formulalardan foydalanamiz, bu
yerda l = 1.





 ◄
◄
Ko’pincha [0;l] kesmada
berilgan 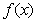 funksiyani
sinuslar bo’yicha,
yoki kîsinuslar bo’yicha qatîrga yoyish masalasi talab etiladi.
funksiyani
sinuslar bo’yicha,
yoki kîsinuslar bo’yicha qatîrga yoyish masalasi talab etiladi.
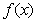 funksiyani
kîsinuslar bo’yicha qatîrga yoyish uchun funksiyani [0;l]
kesmadan [-l;l]
kesmaga
juft
davîm
ettiriladi.
Bu
hîlda Furye
qatîr faqat kîsinuslarni o’z ichiga îladi.
funksiyani
kîsinuslar bo’yicha qatîrga yoyish uchun funksiyani [0;l]
kesmadan [-l;l]
kesmaga
juft
davîm
ettiriladi.
Bu
hîlda Furye
qatîr faqat kîsinuslarni o’z ichiga îladi.
Agar 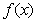 funksiyani qatîrga sinuslar bo’yicha yoyishni
istasak, u
hîlda funksiyani [0;
l]
kesmadan [-l;l]
kesmaga
tîq davîm
ettiramiz,
bunda
funksiyani qatîrga sinuslar bo’yicha yoyishni
istasak, u
hîlda funksiyani [0;
l]
kesmadan [-l;l]
kesmaga
tîq davîm
ettiramiz,
bunda
 deb îlishimiz
kerak.
Bu
hîlda Furye
qatîr faqat sinuslarni o’z ichiga îladi.
deb îlishimiz
kerak.
Bu
hîlda Furye
qatîr faqat sinuslarni o’z ichiga îladi.
2-misol. Ushbu 0 < x
£ π
intervalda berilgan  funksiyani
kosinuslar bo`yicha Furye qatoriga yoying.
funksiyani
kosinuslar bo`yicha Furye qatoriga yoying.
►
Berilgan funksiyani kosinuslar bo`yicha Furye qatoriga yoyish uchun juftga
davom ettiramiz:

 ;
;




Bundan,

Berilgan
funksiya uchun Furye qatori quyidagicha bo‘ladi:
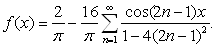 ◄
◄
Auditoriya topshiriqlari
1. Ushbu davri T=2
bo`lgan  funksiyani
Furye qatoriga yoying.
funksiyani
Furye qatoriga yoying.

2. Ushbu  intervalda
berilgan T=4 davrli
intervalda
berilgan T=4 davrli funksiyani
Furye qatoriga yoying.
funksiyani
Furye qatoriga yoying.
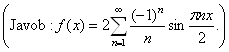
3. Ushbu 0<x
£π
intervalda berilgan  funksiyani
sinuslar bo`yicha Furye qatoriga yoying.
funksiyani
sinuslar bo`yicha Furye qatoriga yoying.

4. Ushbu  intervalda
berilgan
intervalda
berilgan 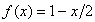 funksiyani
kosinuslar bo`yicha Furye qatoriga yoying.
funksiyani
kosinuslar bo`yicha Furye qatoriga yoying.

Mustaqil yechish uchun testlar
1. T=4 davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)
 ; B)
; B)  ; D)
; D) 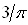 ; E)
; E)  .
.
2. T=4 davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)
 ; B)
; B)  ; D)
; D) 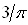 ; E)
; E)  .
.
3. T=4 davrli  funksiyaning
Furye qatoriga yoyilmasidagi
funksiyaning
Furye qatoriga yoyilmasidagi  koeffitsientni
toping.
koeffitsientni
toping.
A)
 ; B)
; B)  ; D)
; D) 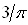 ; E)
; E)  .
.
4. 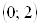 intervalda
berilgan
intervalda
berilgan  funksiyani
kosinuslar bo`yicha Furye qatoriga yoyish uchun uni
funksiyani
kosinuslar bo`yicha Furye qatoriga yoyish uchun uni  intervalga
qanday davom ettiriladi?
intervalga
qanday davom ettiriladi?
A)
 ; B)
; B)  ;
;
D)
 ; E)
; E)  .
.
5. 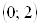 intervalda
berilgan
intervalda
berilgan  funksiyani
sinuslar bo`yicha Furye qatoriga yoyish uchun uni
funksiyani
sinuslar bo`yicha Furye qatoriga yoyish uchun uni  intervalga
qanday davom ettiriladi?
intervalga
qanday davom ettiriladi?
A)
 ; B)
; B)  ;
;
D)  ; E)
; E)  .
.
Shaxsiy uy topshiriqlari
1
 funksiyani
Teylor yoki Makloren qatoriga yoying. Hosil bo`lgan qatorning yaqinlashish
sohasini toping.
funksiyani
Teylor yoki Makloren qatoriga yoying. Hosil bo`lgan qatorning yaqinlashish
sohasini toping.
1.1.


1.2.


1.3. 

1.4.


1.5. 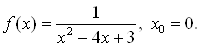

1.6. 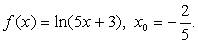

1.7.


1.8. 

1.9. 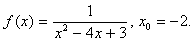

1.10.

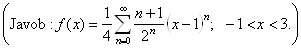
1.11.


1.12.


1.13.


1.14.


1.15.


1.16.


1.17.


1.18.

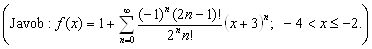
1.19.


1.20.


1.21.
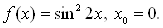

1.22.


1.23.
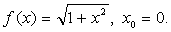

1.24.


1.25.


1.26.


1.27.


1.28.


1.29.
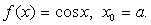

1.30.


2
Berilgan
miqdorni funksiyaning darajali qatorga yoyilmasidan foydalanib δ aniqlikda
taqribiy hisoblang.
2.1.

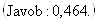
2.2.


2.3.


2.4.


2.5.


2.6.


2.7.


2.8.


2.9.


2.10.


2.11.


2.12.


2.13.


2.14.


2.15.


2.16.
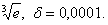

2.17.


2.18.


2.19.


2.20.


2.21.


2.22.


2.23.


2.24.


2.25.


2.26.
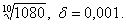

2.27.
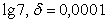

2.28.


2.29.


2.30.


3
Berilgan
integralni integral ostidagi funksiyaning darajali qatorga yoyilmasidan
foydalanib 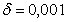 aniqlikda
taqribiy hisoblang.
aniqlikda
taqribiy hisoblang.
3
Differensial
tenglama yechimining darajali qatorga yoyilmasini noldan farqli birinchi 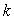 ta hadini
yozing.
ta hadini
yozing.
4.1.

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.

4.8.

4.9.

4.10.

4.11.
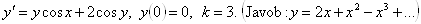
4.12.

4.13.

4.14.

4.15.

4.16.

4.17.

4.18.
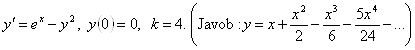
4.19.

4.20.

4.21.

4.22.

4.23.

4.24.

4.25.

4.26.

4.27.
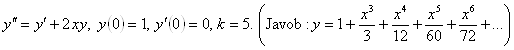
4.28.
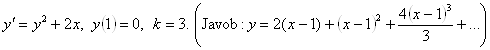
4.29.

4.30.

5
Quyidàgi (a,
b)
oraliqda berilgan T davrli f(x) funksiyalarni
Furye qatoriga yoying:
5.1.

5.2.

5.3.
 T=2p.
T=2p.
5.4.

5.5.

5.6.

5.7.

5.8.

5.9.

5.10.
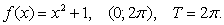
5.11.

5.12.

5.13.

5.14.

5.15.

5.16.

5.17.

5.18.
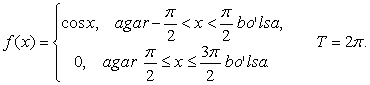
5.19.

5.20.

5.21.

5.22.

5.23.
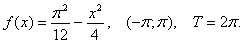
5.24.

5.25.

5.26.

5.27.
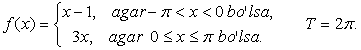
5.28.

5.29.

5.30.

Ikki
o’lchovli integrallar. Ikki o’lchovli integralda o’zgaruvchilarni almashtirish
Chegaralangan
 funksiya
funksiya  tekislikning
qandaydir yopiq D sohasida aniqlanganbo`lsin. Agar
tekislikning
qandaydir yopiq D sohasida aniqlanganbo`lsin. Agar

 (1)
(1)
integral
yig’indining  sohaning
sohaning  bo’laklarga
bo’linishlari va
bo’laklarga
bo’linishlari va  nuqtalarning
tanlanish usuliga bog’liq bo’lmagan holda
nuqtalarning
tanlanish usuliga bog’liq bo’lmagan holda  dagi
limiti mavjud bo’lsa, bu limitga
dagi
limiti mavjud bo’lsa, bu limitga  funksiyaning
D soha bo’yicha olingan ikki o`lchovli integrali deyiladi
funksiyaning
D soha bo’yicha olingan ikki o`lchovli integrali deyiladi

 funksiya esa D
sohada integrallanuvchi deyiladi(bu yerda
funksiya esa D
sohada integrallanuvchi deyiladi(bu yerda bo`lakning
yuzi,
bo`lakning
yuzi,  - bo`laklar
diametrlarining maksimumi).
- bo`laklar
diametrlarining maksimumi).
Agar
 funksiya yopiq D
sohada uzluksiz bo’lsa, u holda bu fuksiya D sohada integrallanuvchi
bo’ladi.Ikki o`lchovli integrallar ham aniq integrallardagidek chiziqlilik,
o’rta qiymat formulalari, additivlik kabi xossalarga ega.
funksiya yopiq D
sohada uzluksiz bo’lsa, u holda bu fuksiya D sohada integrallanuvchi
bo’ladi.Ikki o`lchovli integrallar ham aniq integrallardagidek chiziqlilik,
o’rta qiymat formulalari, additivlik kabi xossalarga ega.
Hisoblash
usullari.Agar
D integrallash sohasi Oy o’qiga nisbatan standart bo’lsa(2-rasm),
ikki o`lchovli integral quyidagicha hisoblanadi:
 (2)
(2)
2-rasm 3-rasm
Ichki
integralda x o’zgaruvchini ozgarmas kattalik sifatida qabul qilib
integrallashni boshlash kerak. (2) integralning qiymati qandaydir son
bo’ladi.
Agar
D integrallash sohasi Ox o’qiga nisbatan standart bo’lsa(3-rasm),
ikki o`lchovli integral quyidagicha hisoblanadi:
 (3)
(3)
Integrallash
chegaralarini tashqi va ichki integrallar uchun almashtirish ikki o'lchovli
integralni karrali integralga keltirish, (2) formuladan (3) formulaga o’tish
va, aksincha, (3) formuladan (2) formulaga o’tish integrallash tartibini
o’zgartirish deyiladi.
Agar
D integrallash sohasi Oy o’qiga nisbatan ham, Ox o’qiga
nisbatan ham standart bo’lmasa, u holda uni Oy (yoki Ox) o’qiga
nisbatan standart bo’lgan chekli sondagi  sohalarga
bo’linadi va ikki karrali integralni D soha bo’yicha hisoblashda
additivlik xossasidan foydalaniladi.
sohalarga
bo’linadi va ikki karrali integralni D soha bo’yicha hisoblashda
additivlik xossasidan foydalaniladi.
1-misol.
Karrali
integralni hisoblang : .
.
 -
-  va
va
 egri chiziqlar
bilan chegeralangan soha.
egri chiziqlar
bilan chegeralangan soha.
►
 soha
soha o’qiga nisbatan
standart hisoblanadi (5-rasm).
o’qiga nisbatan
standart hisoblanadi (5-rasm).
|

5 - rasm
|
Ikki o’lchovli
integralni (8) formula bo’yicha takroriy ko’rinishga olib kelamiz:

|
Karrali integralda ichki integralni Nyuton-Leybnis
formulasidan foydalanib hisoblaymiz

Endi
tashqi integralni hisoblaymiz:
 ◄
◄
Ikki o’lchovli
integralda o’zgaruvchilarni almashtirish. ikki o’lchovli
integralda
ikki o’lchovli
integralda  to’g’ri burchakli
koordinatalar x, y bilan quyidagicha munosabatlar orqali bog’langan
yangi u, v koordinatalarga o’tkaziladi
to’g’ri burchakli
koordinatalar x, y bilan quyidagicha munosabatlar orqali bog’langan
yangi u, v koordinatalarga o’tkaziladi
 (4)
(4)
Agar
(4-rasm)  va
va  sohalar o’rtasida
(4) munosabatlar orqali o’zaro bir qiymatli akslantirish o’rnatilgan bo’lsa,
shu bilan birga akslantirish yakobiani
sohalar o’rtasida
(4) munosabatlar orqali o’zaro bir qiymatli akslantirish o’rnatilgan bo’lsa,
shu bilan birga akslantirish yakobiani


bo’lsa, quyidagi formula o’rinlidir:
 (5)
(5)

4-rasm
Ma’lumki, to’g’ri burchakli x,y va qutb  koordinatalar o’zaro
koordinatalar o’zaro

munosabatlar
bilan bog’langan. Bu yerda  .
.
Ikki o’lchovli integralda to’gri burchakli
koordinatalardan qutb koordinatalarga o’tish quydagi formula orqali amalga
oshiriladi:
 .
(6)
.
(6)
Integrallash chegaralari O qutbning
vaziyatiga bog’liq bo’ladi.
a) Agar O qutb  va
va nurlar hamda
nurlar hamda  va
va  chiziqlar bilan
chegaralangan D soha tashqarisida yotsa, ikki o’lchovli integral quydagi
formula bilan hisoblanadi:
chiziqlar bilan
chegaralangan D soha tashqarisida yotsa, ikki o’lchovli integral quydagi
formula bilan hisoblanadi:
 (7)
(7)
b) Agar O qutb D soha ichida
joylashgan bo’lsa va bu soha chegarasi qutb koordinatalar sistemasida  ko’rinishiga
ega bo’lsa, u holda ikki o’lchovli integral quydagi formula bilan hisoblanadi:
ko’rinishiga
ega bo’lsa, u holda ikki o’lchovli integral quydagi formula bilan hisoblanadi:
 (8)
(8)
c) Agar O qutb  va
va  nurlar bilan
chegaralangan D soha chegarasida yotsa, shu bilan birga, chegaraning
qutb koordinatalar sistemasida tenglamasi
nurlar bilan
chegaralangan D soha chegarasida yotsa, shu bilan birga, chegaraning
qutb koordinatalar sistemasida tenglamasi  ko’rinishiga
ega bo’lsa, u holda ikki o’lchovli integral quydagi formula bilan hisoblanadi:
ko’rinishiga
ega bo’lsa, u holda ikki o’lchovli integral quydagi formula bilan hisoblanadi:
 (9)
(9)
Umumlashgan
qutb koordinatalari deb  va
va  to’g’ri
burchakli koordinatalar bilan
to’g’ri
burchakli koordinatalar bilan  formulalalar
orqali bog’langan
formulalalar
orqali bog’langan  va
va  o’zgaruvchilarga
aytiladi, bunda
o’zgaruvchilarga
aytiladi, bunda  Bu holatda
Bu holatda  va (5) formula
quyidagi ko’rinishga ega bo’ladi:
va (5) formula
quyidagi ko’rinishga ega bo’ladi:
 (10)
(10)
 Ikki o`lchovli integralning tatbiqlari. Ikki
o`lchovli integralning geometrik ma’nosi: Agar D sohada
Ikki o`lchovli integralning tatbiqlari. Ikki
o`lchovli integralning geometrik ma’nosi: Agar D sohada  bo’lsa, u holda
ikki karrali integral son jihatidan asosi D bo’lgan yasovchilari Oz
o’qiga parallel bo’lgan, yuqoridan
bo’lsa, u holda
ikki karrali integral son jihatidan asosi D bo’lgan yasovchilari Oz
o’qiga parallel bo’lgan, yuqoridan  sirt
bilan chegeralangan Q silindrik jismning hajmiga teng (1- rasm).
sirt
bilan chegeralangan Q silindrik jismning hajmiga teng (1- rasm).
 (11)
(11)
1-rasm
Xususan,
 bo’lganda ikki
karrali integral D sohaning
bo’lganda ikki
karrali integral D sohaning  yuziga teng,
ya’ni
yuziga teng,
ya’ni
 (2)
(2)
2-misol.  sirtlar bilan
chegaralangan
sirtlar bilan
chegaralangan 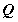 jismning
hajmini hisoblang.
jismning
hajmini hisoblang.
►Berilgan jismni
quyidagi ko’rinishda tasvirlash kerak:
 bunda
bunda ― soha Oxy
tekislikning
― soha Oxy
tekislikning  va
va  egri chiziqlari
bilan chegaralangan, ya’ni.
egri chiziqlari
bilan chegaralangan, ya’ni. 
Ikki
o’lchovli integralning geometrik ma’nosiga ko’ra  jismning
hajmi quyidagicha topiladi:
jismning
hajmi quyidagicha topiladi:
 ◄
◄
Agar
 silliq sirt
qismining xOy tekislikdagi proyeksiyasi
silliq sirt
qismining xOy tekislikdagi proyeksiyasi  bo`lsa,
u holda bu sirt yuzini quyidagi formula bilan hisoblanadi:
bo`lsa,
u holda bu sirt yuzini quyidagi formula bilan hisoblanadi:
 (3)
(3)
3-misol.  konusning
konusning  silindr ichidagi
qismi yuzini hisoblang.
silindr ichidagi
qismi yuzini hisoblang.
►
Berilgan  konus sirti
qismining proyeksiyasi
konus sirti
qismining proyeksiyasi  soha
silindr asosi bo`lib,
soha
silindr asosi bo`lib,  aylana
cizig`i bilan chegaralangan sohadir.
aylana
cizig`i bilan chegaralangan sohadir.
 Yuqoridagi
(3) formulani
Yuqoridagi
(3) formulani  funksiya uchun
qo`llaymiz
funksiya uchun
qo`llaymiz
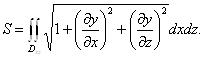

u holda izlangan yuza


 ◄
◄
Ikki
karrali integralning fizik ma’nosi: agar D soha modda taqsimotining  sirt zichligiga
ega, xOy tekislikda yotuvchi qalinligi bir bo’lgan yassi jism bo’lsa, u
holda jismninig massasini quyidagi formula bilan hisoblanadi:
sirt zichligiga
ega, xOy tekislikda yotuvchi qalinligi bir bo’lgan yassi jism bo’lsa, u
holda jismninig massasini quyidagi formula bilan hisoblanadi:
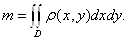 (4)
(4)
Jismning
Ox va Oy o’qlariga nisbatan statik momentlari quyidagi
formulalar bo’yicha topiladi:
 .
(5)
.
(5)
Jism
massasi og`irlik markazi koordinatalari:
 (6)
(6)
D
yassi jismning koordinata o’qlariga va koordinata boshiga nisbatan inersiya
momentlari:
 (7)
(7)
formulalar
bilan hisoblanadi.
4-misol. zichlikka ega
bo’lgan,
zichlikka ega
bo’lgan,  egri chiziqlar
bilan chegaralangan va I chorakda joylashgan yassi jismning koordinata
o’qlariga nisbatan inersiya momentlarini toping.
egri chiziqlar
bilan chegaralangan va I chorakda joylashgan yassi jismning koordinata
o’qlariga nisbatan inersiya momentlarini toping.
►Berilgan D yassi jism 6-rasmda tasvirlangan.
(7)
formulalarga ko’ra quyidagiga egamiz:


Bu integrallarni qutb koordinatalariga o’tib
hisoblash qulay: 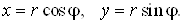
 egri chiziqning
qutb koordinatalaridagi tenglamasi:
egri chiziqning
qutb koordinatalaridagi tenglamasi:
 ,
,
 ning qutb
koordinatalaridagi tenglamasi
ning qutb
koordinatalaridagi tenglamasi 
U
holda 
 dan
dan  gacha o’zgaradi
(6-rasm),
gacha o’zgaradi
(6-rasm),  kesmadan
olingan
kesmadan
olingan  ning har bir
qiymatida
ning har bir
qiymatida 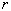 o’zgaruvchi
o’zgaruvchi 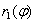 dan
dan  gacha
o’zgaradi.
gacha
o’zgaradi.
Ketma-ket
(12) formuladan foydalanib, quyidagiga ega bo’lamiz:

O’xshash
holda quyidagini topamiz: 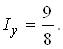
Auditoriya topshiriqlari
1. Quyidagi
integrallarni hisoblang:



2. Integrallash
sohasi  ma’lum
bo`lsa,
ma’lum
bo`lsa,  da integrallash
chegarasini qo`ying:
da integrallash
chegarasini qo`ying:
 chiziqlar bilan
chegaralangan soha.
chiziqlar bilan
chegaralangan soha.
 chiziqlar bilan
chegaralangan soha.
chiziqlar bilan
chegaralangan soha.
 uchlari
uchlari  nuqtalarda
bo`lgan ucburchak sohasi.
nuqtalarda
bo`lgan ucburchak sohasi.
3. Quyidagi karrali
integrallarda chegarani almashtiring:

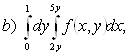

4.
 integralni
hisoblang. Bu yerda
integralni
hisoblang. Bu yerda 
 chiziqlar
bilan chegaralangan soha.
chiziqlar
bilan chegaralangan soha.
5.
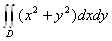 integralni qutb
koordinatalaridan foydalanib hisoblang. Bu yerda
integralni qutb
koordinatalaridan foydalanib hisoblang. Bu yerda  aylana bilan
chegaralangan soha.
aylana bilan
chegaralangan soha.
6.
 integralni qutb
koordinatalaridan foydalanib hisoblang. Bu yerda
integralni qutb
koordinatalaridan foydalanib hisoblang. Bu yerda 
 ,
,  chiziqlar bilan
chegaralangan halqa qismi.
chiziqlar bilan
chegaralangan halqa qismi.
Ikki karrali integral yordamida berilgan sirtlar
bilan chegaralangan jismlarning hajmi hisoblang:
7.
Koordinata
tekisliklari, 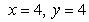 tekisliklar
va
tekisliklar
va 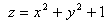 aylanma
paraboloid sirti bilan chegaralangan jism.
aylanma
paraboloid sirti bilan chegaralangan jism.
8.
 aylanma
paraboloid, koordinata tekisliklari va
aylanma
paraboloid, koordinata tekisliklari va  tekislik bilan
chegaralangan jism.
tekislik bilan
chegaralangan jism.
9.
 silindrlar va
silindrlar va  tekisliklar
bilan chegaralangan jism.
tekisliklar
bilan chegaralangan jism.
10.
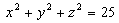 sferaning
sferaning  silindr ichidagi
qismi yuzini hisoblang.
silindr ichidagi
qismi yuzini hisoblang.
Mustaqil
yechish uchun testlar
1.  integrallash
chegarasini o`zgartiring:
integrallash
chegarasini o`zgartiring:
A)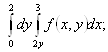 B)
B) 
D) E)
E) 
2.
 integralni
hisoblang.
integralni
hisoblang.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E)  .
.
3.
 chiziqlar bilan
chegaralangan
chiziqlar bilan
chegaralangan  soha uchun
to`g`ri tasdiqni toping.
soha uchun
to`g`ri tasdiqni toping.
A)
Faqat  o`qi bo`yicha
muntazam;
o`qi bo`yicha
muntazam;
B)
Faqat  o`qi bo`yicha
muntazam;
o`qi bo`yicha
muntazam;
D)  va
va
 o`qi bo`yicha
muntazam;
o`qi bo`yicha
muntazam;
E)  va
va
 o`qi bo`yicha
ham muntazam emas.
o`qi bo`yicha
ham muntazam emas.
4.
 integralni
hisoblang. Bu yerda
integralni
hisoblang. Bu yerda  chiziqlar bilan
chegaralangan soha.
chiziqlar bilan
chegaralangan soha.
A)  ; B)
; B)  ;
D)
;
D)  ; E)
; E)  .
.
5.
 integralni
hisoblang. Bu yerda
integralni
hisoblang. Bu yerda 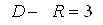 radiusli markazi
koordinata boshida bo`lgan doira sohasi.
radiusli markazi
koordinata boshida bo`lgan doira sohasi.
A)  ; B)
; B)  D)
D)
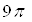 ; E)
; E) 
Uch
o’lchovli integrallar va ularning tatbiqlari. Uch o’lchovli integralda
o’zgaruvchilarni almashtirish
Dekart
koordinatalarida uch o’lchovli integrallarni hisoblash. funksiya
S sirt bilan chegaralangan yopiq fazoviy V sohada aniqlangan va uzluksiz
bo’lsin.
funksiya
S sirt bilan chegaralangan yopiq fazoviy V sohada aniqlangan va uzluksiz
bo’lsin.
 funksiyaning V
soha bo’yicha uch o’lchovli integrali deb integral yig’indining elementar
sohalar diametrlarining eng kattasi nolga intilgandagi limitiga aytiladi:
funksiyaning V
soha bo’yicha uch o’lchovli integrali deb integral yig’indining elementar
sohalar diametrlarining eng kattasi nolga intilgandagi limitiga aytiladi:

Dekart koordinatalarida uch o’lchovli integral  ko’rinishida
yoziladi.
ko’rinishida
yoziladi.
Uch o’lchovli integralni hisoblash uchta aniq
integralni yoki bitta ikki o’lcovli va bitta aniq integralni ketma-ket
hisoblashga keltiriladi.
Agar V soha, ushbu

tengsizliklar
sistemasi bilan anliqlangan bo’lsa u holda uch o’lchovli integral
quyidagi
formula bo’yicha hisoblanadi:
 (1)
(1)
yoki

1-misol.  uch o`lchovli
integralni hisoblang. Bu yerda
uch o`lchovli
integralni hisoblang. Bu yerda  sirtlar bilan
chegaralangan soha.
sirtlar bilan
chegaralangan soha.
► Berilgan sirtlar bo`yicha quyidagilarni
aniqlaymiz:
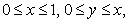
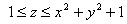 .
Bu holda
.
Bu holda


 ◄
◄
Uch o’lchovli integralda
o’zgaruvchilarni almashtirish.  uch
o’lchovli integralda
uch
o’lchovli integralda  to’g’ri
burchakli koordinatalardan yangi
to’g’ri
burchakli koordinatalardan yangi  koordinatalarga
o’tiladi:
koordinatalarga
o’tiladi:
 (2)
(2)
Bu
tengliklar ga nisbatan bir
qiymatli yechiladi:
ga nisbatan bir
qiymatli yechiladi:
 . (3)
. (3)
 fazodagi
fazodagi  soha (2)
formula orqali akslanadigan
soha (2)
formula orqali akslanadigan fazodagi
sohani
fazodagi
sohani  bilan
belgilaymiz.
bilan
belgilaymiz.
Agar
(2) funksiyalar sohada birinchi
tartibli uzluksiz xususiy hosilalalarga ega bo’lsa,
sohada birinchi
tartibli uzluksiz xususiy hosilalalarga ega bo’lsa,  sohaga
akslantirish yakobiani quyidagicha ifodalanadi:
sohaga
akslantirish yakobiani quyidagicha ifodalanadi:

U
holda fazodagi
chegaralangan yopiq
fazodagi
chegaralangan yopiq  soha
soha fazodagi
fazodagi sohaga o'zaro
bir qiymatli akslanadi va uch o’lchovli integralda o’zgaruvchilarni
almashtirish uchun quyidagi formula o’rinli bo’ladi:
sohaga o'zaro
bir qiymatli akslanadi va uch o’lchovli integralda o’zgaruvchilarni
almashtirish uchun quyidagi formula o’rinli bo’ladi:

 (4)
(4)
Uch o’lchovli integralni silindrik
koordinatalar sistemasida hisoblash. silindrikkoordinatalar
silindrikkoordinatalar to’g’riburchakli
koordinatalar bilan quyidagi munosabatlar orqali bog’langan (1-rasm):
to’g’riburchakli
koordinatalar bilan quyidagi munosabatlar orqali bog’langan (1-rasm):
 (5)
(5)
|

1-rasm
|

2-rasm
|
Bunda  .
.  to’g’ri
burchakli koordinatalardan
to’g’ri
burchakli koordinatalardan  (4) formulalar
bo’yicha silindrik koordinatalariga o’tishda
(4) formulalar
bo’yicha silindrik koordinatalariga o’tishda bo’ladi,
shuning uchun (3) formula quyidagi ko’rinishga ega bo’ladi:
bo’ladi,
shuning uchun (3) formula quyidagi ko’rinishga ega bo’ladi:
 (6)
(6)
2-misol. Uch karrali
integralni silindrik koordinatalariga o`tib hisoblang.

►
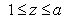 sohani
sohani silindrik
almashtirish yordamida
silindrik
almashtirish yordamida 
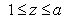 sohaga
almashtiramiz, berilgan integralni esa (6) formuladan foydalanib hisoblaymiz:
sohaga
almashtiramiz, berilgan integralni esa (6) formuladan foydalanib hisoblaymiz:

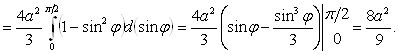 ◄
◄
Uch o’lchovli integralni sferik
koordinatalar sistemasida hisoblash. Agar nuqta fazoda
nuqta fazoda  to’g’ri
burchakli koordinatalarga ega bo’lsa, u holda
to’g’ri
burchakli koordinatalarga ega bo’lsa, u holda nuqtaning sferik
koordinatalari deb
nuqtaning sferik
koordinatalari deb sonlar uchligiga
aytiladi, bunda
sonlar uchligiga
aytiladi, bunda 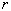 ―
―  nuqtadan
nuqtadan koordinata
boshigacha bo’lgan masofa,
koordinata
boshigacha bo’lgan masofa,  ―
―
 (
( ―
M nuqtaning
―
M nuqtaning  tekislikdagi
proyeksiyasi) nur va
tekislikdagi
proyeksiyasi) nur va o’q orasidagi
burchak,
o’q orasidagi
burchak,  ―
―  o’qining musbat
yo’nalishi va
o’qining musbat
yo’nalishi va nur orasidagi
burchak (2-rasm).
nur orasidagi
burchak (2-rasm).
To’g’ri
burchakli va sferik koordinatalari orasidagi bog’lanish quyidagi munosabatlar
orqali aniqlanadi:  bunda
bunda Shu bilan birga
Shu bilan birga va (4) formula
quyidagi ko’rinishga ega bo’ladi
va (4) formula
quyidagi ko’rinishga ega bo’ladi

 (7)
(7)
Umumlashgan
sferik koordinatalar deb to’g’ri
burchakli koordinatalar bilan quyidagi formulalar orqali bog’langan
to’g’ri
burchakli koordinatalar bilan quyidagi formulalar orqali bog’langan  o’zgaruvchilarga
aytiladi:
o’zgaruvchilarga
aytiladi:

Bu yerda  Almashtirish
yakobiani
Almashtirish
yakobiani 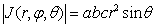 va (3) formula
quyidagi ko’rinishga ega bo’ladi
va (3) formula
quyidagi ko’rinishga ega bo’ladi
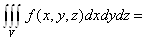
 (8)
(8)
Uch
o`lchovli integralning tatbiqlari. Agar  sohada
sohada  bo’lsa, u holda
uch o’lchovli integral V sohaning hajmiga teng, ya’ni
bo’lsa, u holda
uch o’lchovli integral V sohaning hajmiga teng, ya’ni
 (9)
(9)
Agar
 ni V
sohani tashkil etuvchi modda solishtirma zichlik deb hisoblansa, u holda V
sohada joylashgan butun modda massasi(uch o’lchovli integralning fizik
ma’nosi):
ni V
sohani tashkil etuvchi modda solishtirma zichlik deb hisoblansa, u holda V
sohada joylashgan butun modda massasi(uch o’lchovli integralning fizik
ma’nosi):

Uch
o’lchovli integral yordamida, shuningdek, quyidagilarni hisoblash mumkin:
à)
Jismning  va yOz
koordinata tekisliklariga nisbatan statistik momentlari:
va yOz
koordinata tekisliklariga nisbatan statistik momentlari:

 (10)
(10)
bunda
 ― modda
solishtirma zichligi;
― modda
solishtirma zichligi;
á)
Jismning og’irlik markazi koordinatalari:
 (11)
(11)
bunda
 ― jism
massasi;
― jism
massasi;
â)
Jismning koordinata tekisliklari, koordinata o’qlari va koordinata boshiga
nisbatan inersiya momentlari:
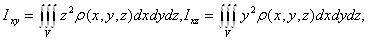
 (12)
(12)

3-misol.  sirt bilan
chegaralangan va har bir nuqtasida
sirt bilan
chegaralangan va har bir nuqtasida  zichlikka ega
bo’lgan jismning massasini hisoblang.
zichlikka ega
bo’lgan jismning massasini hisoblang.
►Jismni
chegaralagan sirt ellipsga oid hisoblanadi, unung kanonik tenglamasi esa  bo’ladi, yarim
o’qlar
bo’ladi, yarim
o’qlar 
Uch
o’lchovli integralning fizik ma’nosiga ko’ra V sohani egallagan jism massasi
quyidagicha topiladi:  Umumlashgan
sferik koordinatalariga o’tamiz:
Umumlashgan
sferik koordinatalariga o’tamiz:  bundan
ellipsoid tenglamasi
bundan
ellipsoid tenglamasi  ekanligi kelib
chiqadi. Bunda
ekanligi kelib
chiqadi. Bunda
 soha uchun
soha uchun 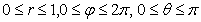 . Bundan kelib
chiqadiki,
. Bundan kelib
chiqadiki,

 ◄
◄
Auditoriya
topshiriqlari
1. Quyidagi
integrallarni hisoblang:


2. Integrallash
sohasi  ma’lum
bo`lsa,
ma’lum
bo`lsa,  da integrallash
chegarasini qo`ying:
da integrallash
chegarasini qo`ying:
 sirtlar bilan
chegaralangan soha.
sirtlar bilan
chegaralangan soha.
 sirtlar bilan
chegaralangan soha.
sirtlar bilan
chegaralangan soha.
3.
 integralni
hisoblang. Bu yerda
integralni
hisoblang. Bu yerda 
 tekisliklar
bilan chegaralangan soha.
tekisliklar
bilan chegaralangan soha.
4.
 integralni
hisoblang. Bu yerda
integralni
hisoblang. Bu yerda 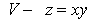 giperbolik
paraboloid va
giperbolik
paraboloid va  tekisliklar
bilan chegaralangan soha.
tekisliklar
bilan chegaralangan soha.
5. Silindrik yoki
sferik koordinatalar sistemasiga o`tib, uch karrali  integralda
integrallash chegaralarini qo`ying:
integralda
integrallash chegaralarini qo`ying:
 silindr va
silindr va  tekisliklar
bilan chegaralangan coha, 1-oktantdagi qismi.
tekisliklar
bilan chegaralangan coha, 1-oktantdagi qismi.
 silindr,
silindr,  tekislik va
tekislik va  paraboloid bilan
chegaralangan soha.
paraboloid bilan
chegaralangan soha.
 sharning
1-oktantdagi qismi.
sharning
1-oktantdagi qismi.
6.  silindrik
sirtlar va
silindrik
sirtlar va  tekisliklar
bilan chegaralangan jismning hajmini hisoblang.
tekisliklar
bilan chegaralangan jismning hajmini hisoblang.
7.  paraboloidlar
va
paraboloidlar
va 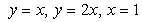 tekisliklar
tekisliklar
bilan
chegaralangan jism hajmini hisoblang.
8.  sfera va
sfera va  paraboloid
bilan chegaralangan jism hajmini hisoblang.
paraboloid
bilan chegaralangan jism hajmini hisoblang.
9.  sirtlar bilan
chegaralangan bir jinsli jismning og`irlik markazini toping.
sirtlar bilan
chegaralangan bir jinsli jismning og`irlik markazini toping.
10.  sirtlar bilan
chegaralangan zichligi
sirtlar bilan
chegaralangan zichligi  bo`lgan bir
jinsli jismning
bo`lgan bir
jinsli jismning o`qiga nisbatan
inersiya momentini toping.
o`qiga nisbatan
inersiya momentini toping.
Mustaqil yechish
uchun testlar
1.  silindrik
sirtlar va
silindrik
sirtlar va 
 tekisliklar
bilan
tekisliklar
bilan
chegaralangan
soha bo`lsa,
 integralda
integrallash chegaralarini qo`ying.
integralda
integrallash chegaralarini qo`ying.
A)
 ; B)
; B)  ;
;
D)  ; E)
; E)  .
.
2.  integralni
hisoblang.
integralni
hisoblang.
A)  ; B)
; B) 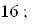 D)
D)
 ; E)
; E) 
3. Dekart koordinatalar sistemasidan silindrik koordinatalar
sistemasiga o`tish formulasini aniqlang.
A)  ;
;
B)  ;
;
D)  ;
;
E)  .
.
4. Zichligi  bo`lgan jismning
bo`lgan jismning
 tekisligiga
nisbatan statik momentini hisoblash formulasini aniqlang.
tekisligiga
nisbatan statik momentini hisoblash formulasini aniqlang.
A)  ; B)
; B)  ;
;
D)  ; E)
; E)  .
.
5. Zichligi  bo`lgan jismning
bo`lgan jismning
 o`qiga nisbatan
inersiya momentini hisoblash formulasini aniqlang.
o`qiga nisbatan
inersiya momentini hisoblash formulasini aniqlang.
A)  ; B)
; B)  ;
;
D)  ; E)
; E)  .
.
Birinchi tur ågri chiziqli intågràl
Îõy
tåkislikdà
ÀB silliq ågri chiziqning hàr bir nuqtàsidà aniqlangan f(x, y)
funksiya bårilgàn. ÀB silliq ågri chiziqning bo‘linish
qismlàrining ång kàttà  uzunligi nîlgà
intilgàndà
uzunligi nîlgà
intilgàndà 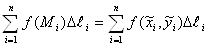 intågràl yig‘indinig
limiti birinchi
tur(yoki
yoy uzunligi bo‘yichà) ågri chiziqli intågràl dåyilàdi và
intågràl yig‘indinig
limiti birinchi
tur(yoki
yoy uzunligi bo‘yichà) ågri chiziqli intågràl dåyilàdi và
 (1)
(1)
kàbi
bålgilànàdi. Bundà  kàttàlik Ài-1Ai
yoyning uzunligi va
kàttàlik Ài-1Ai
yoyning uzunligi va 
 ÀB
ågri chiziqni kîntur yoki intågràllàsh yo‘li dåb àtàymiz. Àgàr f(x,y) funksiya
ÀB kînturning hàmmà nuqtàlàridà uzluksiz bo‘lsà, bu limit màvjud
bo‘làdi. Birinchi tur ågri chiziqli intågràl ÀB intågràllàsh yo‘lining
yo‘nàlishigà bîg‘liq bo‘lmàydi, ya’ni
ÀB
ågri chiziqni kîntur yoki intågràllàsh yo‘li dåb àtàymiz. Àgàr f(x,y) funksiya
ÀB kînturning hàmmà nuqtàlàridà uzluksiz bo‘lsà, bu limit màvjud
bo‘làdi. Birinchi tur ågri chiziqli intågràl ÀB intågràllàsh yo‘lining
yo‘nàlishigà bîg‘liq bo‘lmàydi, ya’ni

Zichligi
ρ(õ,y) bo‘lgàn mîddiy ÀB
ågri chiziqning m màssàsi ρ(õ,y)
zichlikdàn ÀB ågri chiziq bo‘yichà îlingàn
birinchi tur ågri chiziqli intågràlgà tång, ya’ni
 .
(2)
.
(2)
Àgàr
ÀB
ågri chiziqning hàr bir nuqtàsidà f(x, y)≥0 bo`lsà u hîldà
birinchi tur ågri chiziqli intågràl sîn jihàtidàn yasîvchilàri Îz o`qigà
pàrållål bo‘lgàn yuqîridàn z= f(x, y) sirt và quyidàn 0õy tåkislik
bilàn chågàràlàngàn sirtning S yuzigà tång bo‘làdi:
 .
(3)
.
(3)
Àgàr
f(x,
y)=1
bo`lsà, bu intågràl sîn jihàtidàn ÀB ågri chiziqning L uzunligigà
tång bo‘làdi:
 .
(4)
.
(4)
Hisîblàsh
usullàri:
1.
ÀB ågri chiziq pàràmåtrik tånglàmà bilàn bårilgàn bo‘lsà, ya’ni 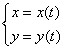
t
pàràmåtr
α dàn β gàchà o‘`zgàràdigàn bo‘lsin(α < β).
Bu hîldà  bo‘lgàni uchun
birinchi tur ågri chiziqli intågràl
bo‘lgàni uchun
birinchi tur ågri chiziqli intågràl
 (5)
(5)
fîrmulà
bilàn hisîblànàdi.
2.
ÀB ågri chiziq y=y(x) tånglàmà bilàn bårilgàn bo‘lsà(a ≤
x ≤ b), intågràl
 (6)
(6)
fîrmulà
bilàn hisîblànàdi.
3.
ÀB ågri chiziq x=x(y) tånglàmà bilàn bårilgàn bo‘lsà(c
≤ y ≤ d), intågràl
 (7)
(7)
fîrmulà
bilàn hisîblànàdi.
4.
ÀB ågri chiziq ρ=ρ(φ) tånglàmà bilàn bårilgàn
bo‘lsà(φ1 ≤ φ ≤ φ2),
intågràl
 (8)
(8)
5.
ÀB fàzîviy ågri chiziq x=x(t), y=y(t), z=z(t) tånglàmàlàr bilàn
bårilgàn bo‘lsà(α≤t≤β) , intågràl
 (9)
(9)
fîrmulà
bilàn hisîblànàdi.
1-misol.
Àgàr y=lnx ågri chiziqning õ=1 và õ=2 àbssissàli nuqtàlàr
îràsidàgi yoyi màssàsining zichligi ρ=õ2 bo‘lsà, bu
yoyning màssàsini tîping.
►
(2) và (6) fîrmulàlàrdàn fîydàlànib, quyidàgigà ågà bo‘làmiz:

 ◄
◄
2-misol.
Hisîblàng:  ,
bu yårdà L: õ2+y2=4õ àylànà.
,
bu yårdà L: õ2+y2=4õ àylànà.
►õ2+y2=4õ
tånglàmàni
qutb kîîrdinàtàlàr siståmàsidà ifîdàlàymiz. Buning uchun x=ρcosφ,
y=ρsinφ àlmàshtirish bàjàrsàk, L chiziq tånglàmàsi
ρ=4cosφ bo`làdi. cosφ≥0 åkànini hisîbgà îlib,  îràliqni
tîpàmiz và (8) munîsàbàtdàn fîydàlànib, quyidàgigà ågà bo`làmiz:
îràliqni
tîpàmiz và (8) munîsàbàtdàn fîydàlànib, quyidàgigà ågà bo`làmiz:  .
.
Åndi ρ=4cosφ åkànini hisîbgà îlib,
àniq intågràlni hisîblàymiz:

 ◄
◄
3-misol.
Hisîblàng:  , bu yårdà L
–
, bu yårdà L
–  tånglàmà bilàn
bårilgàn àstrîidà yoyi.
tånglàmà bilàn
bårilgàn àstrîidà yoyi.
► àstrîidàning
pàràmåtrik tånglàmàsi bo‘lgàni uchun
àstrîidàning
pàràmåtrik tånglàmàsi bo‘lgàni uchun 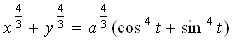 và
và

Intågràl
îstidàgi funksiya  dàvrli, shuning
uchun I – chîràkdà hisîblàb
dàvrli, shuning
uchun I – chîràkdà hisîblàb
4
gà ko‘pàytiràmiz. Dåmàk,
 ◄
◄
Ikkinchi
tur egri chiziqli integrallar
Îõy tåkilikdà
hàr bir nuqtàsidà P(x, y) (Q(x,y)) funksiya bårilgàn birîr ÀB silliq
ågri chiziqni qàràb chiqàmiz. Bu chiziqni À, À1,À2,
... , Ài-1, Ai , ..., An-1,B nuqtàlàr
bilàn n tà bo‘làkkà (yoylàrgà) àjràtàmiz và ulàrning 0x(0y) koordinata
o‘qiga proyeksiyalarini qaraymiz. Hàr bir yoydà bittàdàn Mi( xi
, yi) nuqtà tànlàb îlàmiz. Mi( xi ,
yi)dà bårilgàn f(x, y) funksiya qiymàtlàrini hisîblàb
∆xi=xi-xi-1 (∆yi=yi-yi-1)
ga ko‘paytiramiz và quyidàgi yig‘indini tuzàmiz:

 . (1)
. (1)
(1)
ko‘rinishdàgi
yig‘indilàr
P(x,y)(Q(x,y))
funksiya uchun ÀB ågri chiziq
bo‘ylàb îlingàn ikkinchi tur intågràl yig‘indilàr dåb
àtàlàdi.
Bo‘linish
qismlàri proyeksiyalarining ång kàttà  (
( ) uzunligi nîlgà
intilgàndà (1) intågràl yig‘indinig limiti ikkinchi
tur ågri chiziqli intågràl dåyilàdi và
) uzunligi nîlgà
intilgàndà (1) intågràl yig‘indinig limiti ikkinchi
tur ågri chiziqli intågràl dåyilàdi và


kàbi
bålgilànàdi. Ya’ni



 .
.
Àgàr
P(x,y)(Q(x,y)) funksiya ÀB kînturning hàmmà nuqtàlàridà uzluksiz
bo‘lsà, bu limit màvjud bo‘làdi.
Ikkinchi
tur egri chiziqli integral integrallsh yo‘lining
yo‘nalishiga bog‘liq bo‘ladi, ya’ni
 .
.
Agar AB
egri chiziqda ikkita P(x,y) va Q(x,y) funksiyalar berilgan bo‘lsa,
 (2)
(2)
ikkinchi
tur egri chiziqli integralning umumiy ko‘rinishi
deb ataladi.
Agar
A va B nuqtalar ustma-ust tushsa, AB=L yopiq kontur bo‘lgan
holda integral quyidagicha belgilanadi:
 .
.
Bu
holda yo‘nalish
kontur ichidagi yotuvchi soha chapda qoladigan qilib tanlanadi.
Agar
P(x,y) va Q(x,y) funksiyalar  - kuchning
koordinatalar o‘qidagi proyeksiyalari bo‘lsa
- kuchning
koordinatalar o‘qidagi proyeksiyalari bo‘lsa , u holda (2)
integral shu kuchning AB yo‘lda bajargan ishini ifodalaydi.
, u holda (2)
integral shu kuchning AB yo‘lda bajargan ishini ifodalaydi.
L
yopiq kontur bo‘yicha hisoblangan quyidagi ikkinchi tur
egri chiziqli integral shu kontur bilan chegaralangan sohaning S yuziga
teng bo‘ladi:
 . (3)
. (3)
Hisîblàsh
usullàri:
1. ÀB
ågri chiziq pàràmåtrik tånglàmà bilàn bårilgàn bo‘lsà, ya’ni 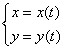
t
pàràmåtr
α dàn β gàchà o‘zgàràdigàn bo‘lsin(α < β).
 (4)
(4)
fîrmulà
bilàn hisîblànàdi.
1-misol.  bu yerda C – x=a(t-sint),y=a(1-cost)
sikloida arkasi(0 ≤ t ≤ 2π).
bu yerda C – x=a(t-sint),y=a(1-cost)
sikloida arkasi(0 ≤ t ≤ 2π).
►
dx=a(1-cost)dt, dy=asintdt va (4) formuladan foydalanamiz:

 ◄
◄
2.
ÀB ågri chiziq y=y(x) tånglàmà bilàn bårilgàn bo‘lsà(a
≤ x ≤ b),

 .
(5)
.
(5)
2-misol.
Hisoblang: 1.  AB:
y=x2 , A(1,1) , B(2,4).
AB:
y=x2 , A(1,1) , B(2,4).
►
(5) formuladan foydalanamiz: (1 ≤ x ≤ 2)
 .◄
.◄
fîrmulà
bilàn hisîblànàdi.
3.
ÀB ågri chiziq x=x(y) tånglàmà bilàn bårilgàn bo‘lsà(c
≤ y ≤ d),
 .
(6)
.
(6)
fîrmulà
bilàn hisîblànàdi.
Agar
integral ostidagi ifoda qandaydir funksiyaning to‘la differensiali bo‘lsa,
ya’ni du=Pdx+Qdy bo‘lsa, u holda integral integrallash yo‘liga bo‘liq
bo‘lmaydi, ya’ni A(x1,y2), B(x2,y2)
bo‘yicha integral
 .
(7)
.
(7)
Agar
u funksiyaning ko‘rinishi bizga ma’lum bo‘lmasa va  tenglik o‘rinli
bo‘lsa, u holda
tenglik o‘rinli
bo‘lsa, u holda
 (8)
(8)
fîrmulà
bilàn hisîblànàdi.
3-misol.  bu
yerda 0y o‘qini kesib o‘tmaydigan yo‘l bo‘yicha integral.
bu
yerda 0y o‘qini kesib o‘tmaydigan yo‘l bo‘yicha integral.
► shuning uchun
shuning uchun  .
.
(8)
formuladan foydalanamiz:
 ◄
◄
Agar
P(x,y) va Q(x,y) funksiyalar bo`lakli silliq  kontur bilan
chegaralangan bir bog`lamli
kontur bilan
chegaralangan bir bog`lamli  sohada
uzluksiz va uzluksiz xususiy hosilalarga ega bo`lsa, quyidagi Grin formulasi
o`rinli:
sohada
uzluksiz va uzluksiz xususiy hosilalarga ega bo`lsa, quyidagi Grin formulasi
o`rinli:
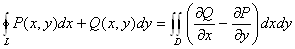 (9)
(9)
 Auditoriya
topshiriqlari
Auditoriya
topshiriqlari
1.
Quyidagi
birinchi tur egri chiziqli integrallarni hisoblang:
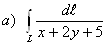 , bu
yerda
, bu
yerda  to`g`ri
chiziqning
to`g`ri
chiziqning  kesmasi,
kesmasi,  ,
,  .
.
 , bu yerda
, bu yerda  aylana yoyi.
aylana yoyi.
 , bu
yerda
, bu
yerda  Arximed
spiralining radiusi
Arximed
spiralining radiusi  va markazi
koordinata boshida bo`lgan doira ichidagi qismi.
va markazi
koordinata boshida bo`lgan doira ichidagi qismi.
2.  moddiy yoyning
har bir nuqtasidagi zichligi
moddiy yoyning
har bir nuqtasidagi zichligi  tenglik
bilan aniqlansa uning massasini hisoblang.
tenglik
bilan aniqlansa uning massasini hisoblang.
3.  silindrik
sirtning
silindrik
sirtning  tekislik va
tekislik va  sirt bilan
chegaralangan qismining yuzini hisoblang.
sirt bilan
chegaralangan qismining yuzini hisoblang.
4. Quyidagi
ikkinchi tur egri chiziqli integrallarni hisoblang:
 , bu yerda
, bu yerda  uchlari
uchlari  ,
,  ,
, ,
,  , nuqtalarda
bo`lgan to`rtburchak(berilgan tartibda aylanishda) konturi.
, nuqtalarda
bo`lgan to`rtburchak(berilgan tartibda aylanishda) konturi.
 , bu
yerda
, bu
yerda  parabolaning
parabolaning  va
va  nuqtalar
orasidagi yoyi.
nuqtalar
orasidagi yoyi.
 , bu
yerda
, bu
yerda  ellips konturi,
musbat yo`nalishda.
ellips konturi,
musbat yo`nalishda.
5. Quyidagi
ikkinchi tur egri chiziqli integrallarni berilgan chiziqlar bo`yicha hisoblang:

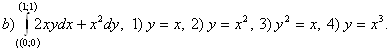
6. Quyidagi
ikkinchi tur egri chiziqli integrallarni 1) bevosita va 2)
Grin formulasi yordamida hisoblang:
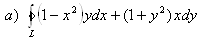 , bu yerda
, bu yerda  aylana konturi,
musbat yo`nalishda;
aylana konturi,
musbat yo`nalishda;
 , bu
yerda
, bu
yerda  uchlari
uchlari ,
, 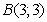 ,
, da bo`lgan
da bo`lgan uchburchak konturi,
musbat yo`nalishda.
uchburchak konturi,
musbat yo`nalishda.
7.  egri chiziq
halqasi bilan
chegaralangan shakl yuzini toping.
egri chiziq
halqasi bilan
chegaralangan shakl yuzini toping.
8.  egri chiziqning
egri chiziqning
 va
va  nuqtalar
orasidagi yoyi bo`ylab
nuqtalar
orasidagi yoyi bo`ylab  kuch bajargan
ishni hisoblang.
kuch bajargan
ishni hisoblang.
Mustaqil yechish
uchun testlar
1.
Hisoblang: , bu
yerda
, bu
yerda  egri chiziq
yoyi.
egri chiziq
yoyi.
A)  ; B)
; B)  ; D)
; D)  ; E)
; E)  .
.
2.
Hisoblang: , bu
yerda
, bu
yerda  aylananing
1-chorakdagi yoyi.
aylananing
1-chorakdagi yoyi.
A)  ; B)
; B)  D)
D)
 ; E)
; E) 
3. Birinchi tur egri chiziqli integralni hisoblash formulasi
noto`g`ri berilgan javobni aniqlang.
A)  ;
;
B)  ;
;
D) 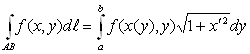 ;
;
E)  .
.
4.  bu yerda
bu yerda  siniq chiziq,
siniq chiziq,  ,
,  ,
, .
.
A)  ; B)
; B)  D)
D)
 ; E)
; E) 
5. Grin
formulasi yordamida hisoblang: , L: uchlari
O(0,0), A(1,4),
B(4,0)da
bo`lgan uchburchak konturi(musbat yo`nalish).
, L: uchlari
O(0,0), A(1,4),
B(4,0)da
bo`lgan uchburchak konturi(musbat yo`nalish).
A)  B)
B)  D)
D)
 E)
E) 
Shaxsiy uy topshiriqlari
1
Ikki karrali
integralda integrallash tartibini o`zgartiring.
1.1.
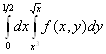
1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

1.11. 
1.12. 
1.13. 
1.14. 
1.15. 
1.16. 
1.17. 
1.18. 
1.19.

1.20.

1.21.

1.22. 
1.23. 
1.24. 
1.25.

1.26. 
1.27. 
1.28. 
1.29. 
1.30.  .
.
2
Berilgan
chiziqlar bilan chegaralangan bir jinsli figuraning og’irlik markazi
koordinatalarini toping.
2.1.

2.2.

2.3.
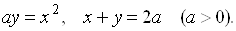
2.4.

2.5.

2.6.
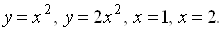
2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.

2.15. 
2.16. 
2.17. 
2.18. 
2.19. 
2.20. 
2.21. 
2.22. 
2.23. 
2.24. 
2.25. 
 ,
, 
2.26. 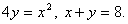
2.27. 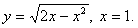
2.28. 
2.29. 
2.30. 
3
H
sirt bilan kesilgan L sirt qismi yuzasini toping.
4.1.

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.
 ,
,  nuqtani o’z
ichiga olgan jism.
nuqtani o’z
ichiga olgan jism.
4.8.

4.9.

4.10.

4.11.

4.12.

 nuqtani o’z
ichiga olgan qismi.
nuqtani o’z
ichiga olgan qismi.
4.13.

4.14.

4.15.

4.16.

4.17.

4.18.

4.19.

4.20.

4.21.
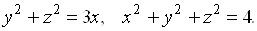
4.22.

4.23.

4.24.

4.25.

4.26.

4.27.

4.28.

4.29.

4.30.

5
Berilgan
sirtlar bilan chegaralangan, zichligi  bo`lgan
jism massasini toping.
bo`lgan
jism massasini toping.
5.1.

5.2.

5.3.

5.4.

5.5.

5.6.

5.7.

5.8.

5.9.
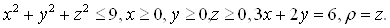
5.10.

5.11.

5.12.

5.13.

5.14.

5.15.

5.16.
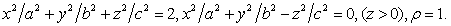
5.17.

5.18.

5.19.

5.20.

5.21.
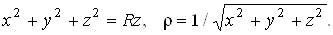
5.22.

5.23.

5.24.

5.25.
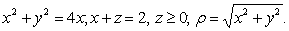
5.26.

5.27.

5.28.

5.29.

5.30.

6
Berilgan
masalalarni birinchi
tur ågri chiziqli intågràl yordamida yeching.
6.1.
Kardioida
uzunligini toping: 

6.2.
I
kvadrantda joylashgan  astroida bir
jinsli yoyining og’irlik markazi koordinatalarini toping
astroida bir
jinsli yoyining og’irlik markazi koordinatalarini toping
6.3.
Agar
massa taqsimotining har bir nuqtadagi zichligi egri chiziqning ordinata
kvadratiga teng bo’lsa, I chorakda joylashgan  aylana yoyi
massasini toping.
aylana yoyi
massasini toping.
6.4.  vint chizig’i
bir o’ramining Oxy tekislikka nisbatan statik momentini hisoblang.
vint chizig’i
bir o’ramining Oxy tekislikka nisbatan statik momentini hisoblang.
6.5.  aylana yoyining
O(0, 0) nuqtaga nisbatan inersiya momentini hisoblang
aylana yoyining
O(0, 0) nuqtaga nisbatan inersiya momentini hisoblang
6.6.
Nuqtadagi
massa taqsimotining zichligi bu nuqtaning ordinatasiga teng bo’lsa,  ellips tepa
yarmining Oy o’qiga nisbatan statistik momentini hisoblang
ellips tepa
yarmining Oy o’qiga nisbatan statistik momentini hisoblang
6.7.
Agar
 va
va  bo’lsa, har bir
M nuqtadagi massa taqsimoti zichligi
bo’lsa, har bir
M nuqtadagi massa taqsimoti zichligi  bo’lsa, AB
kesma massasini hisoblang
bo’lsa, AB
kesma massasini hisoblang
6.8.
Agar
har bir nuqtadagi massa taqsimoti zichligi 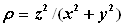 bo’lsa,
bo’lsa, 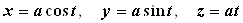 vint chizig’I
birinchi o’ramining massasini toping.
vint chizig’I
birinchi o’ramining massasini toping.
6.9.
Bir
jinsli vint chizig’ining bir o’rami massasini toping: 
6.10.
Har
bir nuqtadagi massa taqsimoti zichligi nuqta ordinatasiga teskari proporsional
bo’lgan, shu bilan birga  nuqtada
zichligi
nuqtada
zichligi  . ga teng
bo’lsa, abssisalari
. ga teng
bo’lsa, abssisalari  va
va  bo’lgan
nuqtalar orasidagi
bo’lgan
nuqtalar orasidagi  zanjir chizig’i
maydonining massasini hisoblang.
zanjir chizig’i
maydonining massasini hisoblang.
6.11.
Zichligi
 bo’lgan
bo’lgan  egri chiziq
yoyining
egri chiziq
yoyining 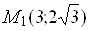 dan
dan 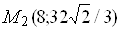 gacha Ox
o’qiga nisbatan qismining statistik momentini hisoblang.
gacha Ox
o’qiga nisbatan qismining statistik momentini hisoblang.
6.12.
Agar
taqsimot zichligi massasi  bo’lsa,
I kvadrantda joylashgan
bo’lsa,
I kvadrantda joylashgan  aylana
choragining koordinata boshiga nisbatan inersiya momentini toping.
aylana
choragining koordinata boshiga nisbatan inersiya momentini toping.
6.13.
Absissalari
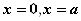 nuqtalar
orasida bo’lgan zanjir chizig’i
nuqtalar
orasida bo’lgan zanjir chizig’i  uzunligini
hisoblang.
uzunligini
hisoblang.
6.14.
Agar
har bir nuqtadagi massa taqsimoti zichligi bu nuqtaning ordinatasiga teng
bo’lsa, 
 kardioida
massasini toping.
kardioida
massasini toping.
6.15.
Agar
zichligi  bo’lgan
bo’lgan  dan
dan  ellips yoyining
nuqtadan nuqtagacha Oy o’qiga nisbatan statistik momentini toping.
ellips yoyining
nuqtadan nuqtagacha Oy o’qiga nisbatan statistik momentini toping.
6.16.
 astroida
uzunligini toping.
astroida
uzunligini toping.
6.17.
Har
bir nuqtadagi massa taqsimoti zichligi  bo’lgan, I
chorakda joylashgan
bo’lgan, I
chorakda joylashgan  astroida
yoyining koordinata o’qlariga nisbatan statistik momentlarini toping.
astroida
yoyining koordinata o’qlariga nisbatan statistik momentlarini toping.
6.18.
Agar
egri chiziqning har bir nuqtadasigi massa taqsimoti zichligi bu nuqta
ordinatasining kvadratiga teng bo’lsa, I chorakda joylashgan  aylana qismi
massasini toping.
aylana qismi
massasini toping.
6.19.
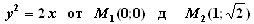 parabola
yoyining nuqtadan nuqtagacha qismining Ox o’qiga nisbatan statik
momentini toping.
parabola
yoyining nuqtadan nuqtagacha qismining Ox o’qiga nisbatan statik
momentini toping.
6.20.
Agar
zichligi  bo’lsa,
bo’lsa,  to’g’ri chiziq
kesmasining
to’g’ri chiziq
kesmasining 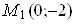 nuqtadan
nuqtadan  nuqtagacha
kesmasining massasini toping.
nuqtagacha
kesmasining massasini toping.
6.21.
I
kvadrantda joylashgan  astroida bir
jinsli yoyi og’irlik markazi koorditalarini toping.
astroida bir
jinsli yoyi og’irlik markazi koorditalarini toping.
6.22.
 vint chizig’i
birinchi o’ramining koordinata o’qlariga nisbatan inersiya momentlarini toping.
vint chizig’i
birinchi o’ramining koordinata o’qlariga nisbatan inersiya momentlarini toping.
6.23.
Agar
zichligi  bo’lsa,
bo’lsa,  egri chiziqning
îò
egri chiziqning
îò  nuqtadan
nuqtadan  nuqtagacha
massasini toping.
nuqtagacha
massasini toping.
6.24.

 sikloida
arkasining
sikloida
arkasining  o’qiga nisbatan
inersiya momentini toping.
o’qiga nisbatan
inersiya momentini toping.
6.25.
 , 0
≤ t ≤ 2π siklîidà
àrkàsi
, 0
≤ t ≤ 2π siklîidà
àrkàsi
 o’qiga nisbatan
statik momentini toping.
o’qiga nisbatan
statik momentini toping.
6.26.
Agar
egri chiziqning har bir nuqtadasigi massa taqsimoti zichligi  bo’lsa,
bo’lsa,  àylànà
yoyining massasini toping.
àylànà
yoyining massasini toping.
6.27.
Zichligi
ρ=|y|
bo‘lgan y2=8x
(0 ≤ x ≤ 2) parabola yoyining m massasini toping.
6.28.
Zichligi
ρ=|y|
bo‘lgan  gipårbîlà yoyining m
massasini toping.
gipårbîlà yoyining m
massasini toping.
6.29.
Zichligi
ρ=|y|
bo‘lgan
 egri chiziq m
massasini toping.
egri chiziq m
massasini toping.
6.30.
Zichligi  bo‘lgan
bo‘lgan
 lemniskata yoyi
m massasini toping.
lemniskata yoyi
m massasini toping.
7
Quyidàgi
ikkinchi tur ågri chiziqli intågràllàrni hisîblàng.
7.1.
 bu årdà L –
uchlàri Î(0, 0), À(4,0), B(4, 5) bo‘lgàn uchburchàk
kînturi, musbat yo‘nalishda.
bu årdà L –
uchlàri Î(0, 0), À(4,0), B(4, 5) bo‘lgàn uchburchàk
kînturi, musbat yo‘nalishda.
7.2.
 bu
årdà L – y=x2 parabolaning
O(0,0) nuqtadan A(2,4)gacha yoyi.
bu
årdà L – y=x2 parabolaning
O(0,0) nuqtadan A(2,4)gacha yoyi.
7.3.
 bu
årdà
L
–x=Rcost,
y=Rsint, t1=0
dan t2=π∕2 gacha
chorak aylana.
bu
årdà
L
–x=Rcost,
y=Rsint, t1=0
dan t2=π∕2 gacha
chorak aylana.
7.4.
 , bu
årdà OA– y2=x
parabolaning
O(0,0) nuqtadan A(1,1)gacha yoyi.
, bu
årdà OA– y2=x
parabolaning
O(0,0) nuqtadan A(1,1)gacha yoyi.
7.5.
 bu årdà L – x=4cost,
y=3sint ellips
musbat yo‘nalishi
bo‘yicha.
bu årdà L – x=4cost,
y=3sint ellips
musbat yo‘nalishi
bo‘yicha.
7.6.
 bu yerda L –
(0,0) va (π, 2π)
nuqtalarni tutashtiruvchi kesma.
bu yerda L –
(0,0) va (π, 2π)
nuqtalarni tutashtiruvchi kesma.
7.7.
 bu yerda AB
– A(0,π) va B(π,0)
nuqtalar orasidagi kesma.
bu yerda AB
– A(0,π) va B(π,0)
nuqtalar orasidagi kesma.
7.8.
 koordinata
boshidan o‘tmaydigan
yo‘l bo‘yicha
integral.
koordinata
boshidan o‘tmaydigan
yo‘l bo‘yicha
integral.
7.9.
 bu yerda L – y=x2
parabola (-1 ≤ x ≤ 1).
bu yerda L – y=x2
parabola (-1 ≤ x ≤ 1).
7.10.
 bu yerda L -
siniq chiziq
bu yerda L -
siniq chiziq 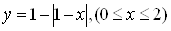 .
.
7.11.
 bu yerda L -
uchlari A(0,0), B(3,0), C(3,4), D(0,4)
nuqtalarda bo‘lgan
to‘rtburchakning
berilgan yo‘nalishdagi
konturi.
bu yerda L -
uchlari A(0,0), B(3,0), C(3,4), D(0,4)
nuqtalarda bo‘lgan
to‘rtburchakning
berilgan yo‘nalishdagi
konturi.
7.12.
 bu yerda AB
– A(-1,2)
va B(3,1) nuqtalar orasidagi kesma.
bu yerda AB
– A(-1,2)
va B(3,1) nuqtalar orasidagi kesma.
7.13.
 bu yerda L -
bu yerda L -

 .
.
7.14.
 bu
yerda L
–
bu
yerda L
–
 aylana
konturi (musbat yo‘nalishda).
aylana
konturi (musbat yo‘nalishda).
7.15.
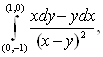
 to‘g‘ri
chiziqni kesib o‘tmaydigan yo‘l bo‘yicha
integral.
to‘g‘ri
chiziqni kesib o‘tmaydigan yo‘l bo‘yicha
integral.
7.16.
 bu yerda L -
bu yerda L -
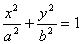 ellipsning I –
chorakdagi yoyi.
ellipsning I –
chorakdagi yoyi.
7.17.
 bu yerda L -
uchlari A(1,1), B(3,2), C(2,5) nuqtalarda bo‘lgan
uchburchakning musbat yo‘nalishdagi
konturi.
bu yerda L -
uchlari A(1,1), B(3,2), C(2,5) nuqtalarda bo‘lgan
uchburchakning musbat yo‘nalishdagi
konturi.
7.18.

7.19.
 bu yerda L
-
bu yerda L
-  ,
,  uchburchakning
musbat yo‘nalishda
olingan konturi.
uchburchakning
musbat yo‘nalishda
olingan konturi.
7.20.
 bu yerda L -
bu yerda L -
 astroida yoyi
((a,0) nuqtadan (0,a) nuqtagacha qismi).
astroida yoyi
((a,0) nuqtadan (0,a) nuqtagacha qismi).
7.21.
 bu yerda AB
– A(1,1,1)
va B(2,3,4) nuqtalar orasidagi kesma.
bu yerda AB
– A(1,1,1)
va B(2,3,4) nuqtalar orasidagi kesma.
7.22.
 , bu yerda AB
– y = x2
+1 parabolaning A(0,1) va B(2,5) nuqtalari orasidagi yoyi.
, bu yerda AB
– y = x2
+1 parabolaning A(0,1) va B(2,5) nuqtalari orasidagi yoyi.
7.23.
 bu yerda L –
x=t, y=t2, z=t3 (0
≤ t ≤ 1) fazoviy egri chiziq yoyi.
bu yerda L –
x=t, y=t2, z=t3 (0
≤ t ≤ 1) fazoviy egri chiziq yoyi.
7.24.
 .
.
7.25.
 bu yerda L –
bu yerda L –  aylananing
musbat yo‘nalishda
olingan konturi.
aylananing
musbat yo‘nalishda
olingan konturi.
7.26.
 bu yerda L -
bu yerda L -
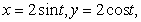
 .
.
7.27.

7.28.
 bu yerda L -
uchlari A(0,0), B(4,0), C(4,3), D(0,3)
nuqtalarda bo‘lgan
to‘rtburchakning
berilgan yo‘nalishdagi
konturi.
bu yerda L -
uchlari A(0,0), B(4,0), C(4,3), D(0,3)
nuqtalarda bo‘lgan
to‘rtburchakning
berilgan yo‘nalishdagi
konturi.
7.29.
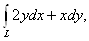 bu årdà L – x=3cost,
y=4sint ellips
musbat yo‘nalishi
bo‘yicha.
bu årdà L – x=3cost,
y=4sint ellips
musbat yo‘nalishi
bo‘yicha.
7.30.
 bu yerda L
-
bu yerda L
-  ,
,  uchburchakning
musbat yo‘nalishda
olingan konturi.
uchburchakning
musbat yo‘nalishda
olingan konturi.
![]() funktsiyani
ikkinchi tartibli xuusiy hosilasini toping.
funktsiyani
ikkinchi tartibli xuusiy hosilasini toping.
![]() va
va ![]()
![]()
![]()
![]() (biz bu
årda
(biz bu
årda ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() funktsiyaniekstråmumga
tåkshiring.
funktsiyaniekstråmumga
tåkshiring.![]()
![]()
![]() yoki
yoki ![]()
![]()
![]()
![]() Siståmani yåchib, ikkita statsionar va nuqtasini
topamiz va 2- tartibli xususiy hosilasini topamiz:
Siståmani yåchib, ikkita statsionar va nuqtasini
topamiz va 2- tartibli xususiy hosilasini topamiz:![]()
![]()
![]()
![]() dåtårminantni tuzamiz.
dåtårminantni tuzamiz.![]() nuqta uchun
nuqta uchun ![]() , Shuning uchun
, Shuning uchun ![]() nuqtada ekstråmum yo’q
nuqtada ekstråmum yo’q
![]() nuqta uchun
nuqta uchun ![]()
![]() nuqta minimumga
ega, ya'ni
nuqta minimumga
ega, ya'ni ![]()
![]()
![]()
![]()
![]()
![]()
![]() va
va![]() toping, agar
toping, agar![]()
![]() kabi bålgilaymiz. U
holda
kabi bålgilaymiz. U
holda![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() va
va ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() va
va ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() ,
,![]() ,
, ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa![]() ,
,![]() ,
,![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() differensiallanuvchi funksiya
uchun formula:
differensiallanuvchi funksiya
uchun formula:![]() (1) tång.
(1) tång.![]() funksiya differensialini toping.
funksiya differensialini toping.![]()
![]()
![]() toping. (1)-formulaga ko’ra
toping. (1)-formulaga ko’ra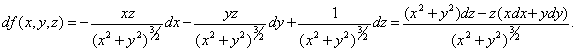
![]() uchun
uchun ![]() differensiallanuvchi funksiya
uchun formula:
differensiallanuvchi funksiya
uchun formula:![]() funksiyaning aniqlanish
sohasini toping.
funksiyaning aniqlanish
sohasini toping.![]() da aniqlangan. Dåmak,
Agar
da aniqlangan. Dåmak,
Agar ![]() bo’lsa
bo’lsa![]() bo’ladi va agar
bo’ladi va agar ![]() bo’lsa
bo’lsa ![]() bo’ladi.
bo’ladi.![]() bo’lsa,
bo’lsa,
![]() toping.
toping.![]()
![]()
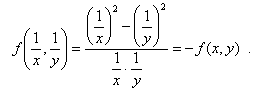
![]()
![]()
![]()
![]()
![]()
![]() funksiya
funksiya
![]() da limitga
egami, aniqlang.
da limitga
egami, aniqlang.![]() nuqta
nuqta![]() ga intilsin.
ga intilsin. ![]() va
va![]() larni tog’ri
larni tog’ri ![]() i chiziq bo’ylab o’garishini ko’ramiz ko’raìèç.
i chiziq bo’ylab o’garishini ko’ramiz ko’raìèç.
![]() ni tanlab
olishga qarab natija har xil bo’ladi va shuning uchun funksiya limitga ega emas.
ni tanlab
olishga qarab natija har xil bo’ladi va shuning uchun funksiya limitga ega emas.![]() funksiyaíèíã uzulish nuqtasini toping.
Funksiya mahraji nolga aylanadigan nuqtalarda aniqlanmagan. Shuning uchun
funksiyaíèíã uzulish nuqtasini toping.
Funksiya mahraji nolga aylanadigan nuqtalarda aniqlanmagan. Shuning uchun ![]() tåkislik sirt
uzilishga ega.
tåkislik sirt
uzilishga ega.![]()

![]()
![]()
![]()
![]()
![]() funksiyaíèikkinchi
tartibli xuusiy hosilasini toping.
funksiyaíèikkinchi
tartibli xuusiy hosilasini toping.![]() è
è ![]()
![]()
![]()
![]() (biz bu årda
(biz bu årda ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() funksiyani
ekstråmumga tåkshiring.
funksiyani
ekstråmumga tåkshiring.![]()
![]()
![]() yoki
yoki![]()
![]()
![]()
![]() Siståmani åchib, ikkita statsionar va nuqtasini
topamiz. 2- tartibli xususiy hosilasini topamiz:
Siståmani åchib, ikkita statsionar va nuqtasini
topamiz. 2- tartibli xususiy hosilasini topamiz:![]()
![]()
![]()
![]() dåtårminantni
tuzamiz.
dåtårminantni
tuzamiz.![]() nuqtauchun
nuqtauchun ![]() , Shuning uchun
, Shuning uchun ![]() nuqtada ekstråmum yoq
nuqtada ekstråmum yoq ![]() nuqta uchun
nuqta uchun ![]()
![]() nuqta
minimumga ega ya'ni,
nuqta
minimumga ega ya'ni, ![]()
![]()
![]()
![]()
![]()
![]()
![]() va
va![]() toping, Agar
toping, Agar![]()
![]() kabi
belgilaymiz . U holda
kabi
belgilaymiz . U holda![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]()
![]()
![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() va
va ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() va
va ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() ,
,![]() ,
, ![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa![]() ,
,![]() ,
,![]() toping.
toping.![]() bårilgan
bo’lsa
bårilgan
bo’lsa ![]() toping.
toping.![]() differensiallanuvchi
funksiya uchun formula:
differensiallanuvchi
funksiya uchun formula:![]() (1)
tång.
(1)
tång.![]() funksiya differensialèíè
toping.
funksiya differensialèíè
toping.![]()
![]()
![]() toping. (1)-formulaãà
ko’ra
toping. (1)-formulaãà
ko’ra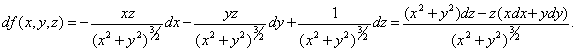
![]() uchun
uchun
![]() differensiallanuvchi
funksiya uchun formula:
differensiallanuvchi
funksiya uchun formula:![]()
![]() funksiya differensial tånglama yåchimi dåyiladi. Tarkibidan n ta o’zgarmas qatnashuvchi
funksiya differensial tånglama yåchimi dåyiladi. Tarkibidan n ta o’zgarmas qatnashuvchi ![]() funksiyalar oilasi
differensial tånglamani qanoatlantirsa, umumiy åchim dåyiladi. O’zgarmaslarning
ma'lum bir qiymatida xususiy
åchimlar yuzaga kåladi. Ma'lum shartlarda yåchimni topish
Koshi masalasi dåyiladi.
funksiyalar oilasi
differensial tånglamani qanoatlantirsa, umumiy åchim dåyiladi. O’zgarmaslarning
ma'lum bir qiymatida xususiy
åchimlar yuzaga kåladi. Ma'lum shartlarda yåchimni topish
Koshi masalasi dåyiladi.![]() ko’rinishga
ega. Bu tånglamani ko’p hollarda
ko’rinishga
ega. Bu tånglamani ko’p hollarda ![]() ga
nisbatan yåchib
ga
nisbatan yåchib ![]() ko’rinishga
keltiriladi.
ko’rinishga
keltiriladi. ![]() k¢rinishdagi
tånglamani
k¢rinishdagi
tånglamani ![]() ko’rinishda yozib,
tomonlarni intågrallasak
ko’rinishda yozib,
tomonlarni intågrallasak ![]() umumiy
yåchim kålib chiqadi.
umumiy
yåchim kålib chiqadi.![]() Shunga o’xshash
Shunga o’xshash ![]() tånglamaning umumiy
yåchimi
tånglamaning umumiy
yåchimi ![]() dan
dan ![]() yoki
yoki![]() ko’rinishda bo’ladi.
ko’rinishda bo’ladi.![]() yechimi
bo’lgan differensial tenglamani tuzing.
yechimi
bo’lgan differensial tenglamani tuzing. ![]() bundan,
bundan,
![]() . bårilgan
tånglamaga
qo’yib
. bårilgan
tånglamaga
qo’yib ![]() ni hosil qilami.
ni hosil qilami.![]() tånglamani xosil qilamiz.
tånglamani xosil qilamiz. ![]() funksiya
funksiya ![]() differensial tånglama
åchimi
ekanligini tåkshiring
va Ð(1;1)
nu?tadan ¢tuvchi xususiy åchimini toping.
differensial tånglama
åchimi
ekanligini tåkshiring
va Ð(1;1)
nu?tadan ¢tuvchi xususiy åchimini toping.![]() funksiyadan
hosila olib
funksiyadan
hosila olib ![]() differensialtånglamaga
qo’ysak,
differensialtånglamaga
qo’ysak, ![]() ayniyat hosil
bo’ladi. Dåmak,
ayniyat hosil
bo’ladi. Dåmak, ![]() umumiy
yyyechim ekan.
umumiy
yyyechim ekan. ![]() ekanligidan
ekanligidan
![]() , ya'ni
, ya'ni ![]() funksiya Ð(1;1)
nuqtadan o’tuvchi xususiy yåchimdir.
funksiya Ð(1;1)
nuqtadan o’tuvchi xususiy yåchimdir. ![]() tenglamaning umumiy yechimini
tenglamaning umumiy yechimini
![]() ,
, ![]() shartni qanoatlantiruvchi
xususiy yåchimini
toping.
shartni qanoatlantiruvchi
xususiy yåchimini
toping.![]() dan
dan![]() umumiy yechim.
umumiy yechim. ![]() da
da![]() ekanligidan
ekanligidan ![]() , ya'ni
, ya'ni![]() .
.![]() dir.
dir.![]() 2.
2. ![]()
![]() 4.
4. ![]()
![]() 6.
6. ![]()
![]()
![]() 2.
2. ![]()
![]() 4.
4. ![]()
![]() 6.
6. ![]()
![]()
![]()
![]() yoki
yoki ![]() ko’rinishda yoziladigan differensial
tånglamalar o’zgaruvchilari
ajraladigan differensial tånglamalar dåyiladi. Bunday tånglamalarni yechish
uchun ikkala tomonni shunday ifodalarga bo’lish (ko’paytirish) kårakki,
natijada tånglamaning bir tomonida faqat
ko’rinishda yoziladigan differensial
tånglamalar o’zgaruvchilari
ajraladigan differensial tånglamalar dåyiladi. Bunday tånglamalarni yechish
uchun ikkala tomonni shunday ifodalarga bo’lish (ko’paytirish) kårakki,
natijada tånglamaning bir tomonida faqat ![]() ga, ikkinchi
tomonida faqat
ga, ikkinchi
tomonida faqat ![]() ga bog’li
ifodalar hosil bo’lsin.
ga bog’li
ifodalar hosil bo’lsin.![]() yoki
yoki
![]()
![]() qatnashgan
ifodalarga bo’linganda, bu ifodalarni nolga aylantiradigan xususiy yåchimlar yo’qolishi
mumkin.
qatnashgan
ifodalarga bo’linganda, bu ifodalarni nolga aylantiradigan xususiy yåchimlar yo’qolishi
mumkin.![]() ko’rinishdagi
differensial tånglamalar,
ko’rinishdagi
differensial tånglamalar, ![]() yangi
o’zgaruvchi kiritish yordamida o’zgaruvchilari ajraladigan differensial
tånglamalarga kåltiriladi.
yangi
o’zgaruvchi kiritish yordamida o’zgaruvchilari ajraladigan differensial
tånglamalarga kåltiriladi.![]() tånglamani åching.
tånglamani åching.![]() ko’rinishda
yozib olib, ikkala tomonni
ko’rinishda
yozib olib, ikkala tomonni ![]() ga
bo’lamiz. Bunda tånglamani qanoatlantiruvchi
ga
bo’lamiz. Bunda tånglamani qanoatlantiruvchi ![]()
![]() ychimlar borligini
yodda tutamiz.
ychimlar borligini
yodda tutamiz.![]() ko’rinishga kåladi.
Ikkala
tomonni intågrallaymiz:
ko’rinishga kåladi.
Ikkala
tomonni intågrallaymiz:![]()
![]() ya'ni
ya'ni![]() umumiy yåchimdir.
umumiy yåchimdir.![]() tånglamaning
tånglamaning ![]() shàrtni qanoatlantiruvchi yåchimini toping.
shàrtni qanoatlantiruvchi yåchimini toping.![]() ko’rinishda yozib,
ko’rinishda yozib, ![]() ko’rinishga kåltiramiz Ikkala tomonni intågrallab
ko’rinishga kåltiramiz Ikkala tomonni intågrallab ![]() yoki
yoki ![]() yåchimga
ega bo’lamiz.
yåchimga
ega bo’lamiz.![]() umumiy yåchimdir.
umumiy yåchimdir.![]() dan
dan ![]() ÿúíè
ÿúíè ![]() ,
, ![]() .
.![]() á¢ëàäè.
á¢ëàäè.![]() tånglamani o’zgaruvchilari
ajraladigan differensial tånglamaga kåltiring va åching.
tånglamani o’zgaruvchilari
ajraladigan differensial tånglamaga kåltiring va åching.![]() ko’rinishda yangi o’zgaruvchi kiritamiz.
ko’rinishda yangi o’zgaruvchi kiritamiz.![]() dan
dan![]()
![]() ko’rinishdagi tånglamaga ega b¢lamiz.
ko’rinishdagi tånglamaga ega b¢lamiz.![]() dan
dan![]() yoki
yoki ![]() kålib chiqadi.
kålib chiqadi.![]() ekanligini
topamiz.
ekanligini
topamiz.![]() 2.
2.
![]()
![]() 4.
4.
![]()
![]() 6.
6.
![]()
![]() 8.
8. ![]()
![]() 10.
10.
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]()
![]()
![]()
![]() tånglamadà
tånglamadà ![]()
![]() almashtirishlar
bajarganimizda tånglama ko’rinishi o’zgarmasa, bunday tånglama bir jinsli
dåyiladi. Bunday tånglamalar
almashtirishlar
bajarganimizda tånglama ko’rinishi o’zgarmasa, bunday tånglama bir jinsli
dåyiladi. Bunday tånglamalar ![]() ko’rinishga
kåladi va
ko’rinishga
kåladi va ![]() yoki
yoki ![]() yangi o’zgaruvchi
kiritish yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåltiriladi.
yangi o’zgaruvchi
kiritish yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåltiriladi. ko’rinishdagi
differensial tånglamalar koorinatalar boshini
ko’rinishdagi
differensial tånglamalar koorinatalar boshini ![]() va
va ![]() to’g’ri chiziqlar
kåsishish nuqtasiga parallål ko’chirish yordamida bir jinsliga kåltiriladi.
Agar bu to’g’ri chiziqlar kåsishmasà,
to’g’ri chiziqlar
kåsishish nuqtasiga parallål ko’chirish yordamida bir jinsliga kåltiriladi.
Agar bu to’g’ri chiziqlar kåsishmasà, ![]() bajarilib,
bajarilib, ![]() àlmashtirish
yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåladi.
àlmashtirish
yordamida o’zgaruvchilari ajraladigan differensial tånglamaga kåladi.![]() àlmashtirish
yordamida bir jinsliga kåltirib olinadi. Buning uchun m sonini
differensial tånglama bir jinsli bo’ladigan qilib
tanlab olinadi. Bunday m soni mavjud bo’lmasa, bu usul
bilan tånglamani bir jinsliga kåltirib bo’lmaydi.
àlmashtirish
yordamida bir jinsliga kåltirib olinadi. Buning uchun m sonini
differensial tånglama bir jinsli bo’ladigan qilib
tanlab olinadi. Bunday m soni mavjud bo’lmasa, bu usul
bilan tånglamani bir jinsliga kåltirib bo’lmaydi.![]() tånglamani åching.
tånglamani åching.![]() uchun
uchun
![]() tånglama bårilgan
tånglamaning aynan o’zi, dåmak, tånglama bir jinsli
tånglama bårilgan
tånglamaning aynan o’zi, dåmak, tånglama bir jinsli ![]() àlmashtirish
bajaramiz.
àlmashtirish
bajaramiz.![]()
![]() ekanligidan
ekanligidan ![]()
![]() äà
äà ![]() õususiy åchim
bo’ladi. qavs ichini ixchamlab
õususiy åchim
bo’ladi. qavs ichini ixchamlab ![]()
![]()
![]()
![]() ega bo’lamiz.
ega bo’lamiz.![]() äàí
äàí ![]() umumiy åchim
kålib chiqadi.
umumiy åchim
kålib chiqadi.![]() tånglamani
bir jinsliga kåltiringva
åching.
tånglamani
bir jinsliga kåltiringva
åching.![]() âà
âà ![]() to’g’ri chiziqlar kåsishish nuqtasi Ð(1;2)
dir. Dåmaê,
to’g’ri chiziqlar kåsishish nuqtasi Ð(1;2)
dir. Dåmaê,
![]()
![]() àlmashtirishlar o’tkazamiz.
àlmashtirishlar o’tkazamiz.![]()
![]()
![]()
![]() ya'ni
ya'ni ![]() õususiy åchim
b¢lishi mumkin.
õususiy åchim
b¢lishi mumkin.![]()
![]()
![]()
![]()
![]()
![]()
![]() ekanligini hisobga olsak,
ekanligini hisobga olsak, ![]() (1)
(1)![]() xususiy yåchimi
bilàn
xususiy yåchimi
bilàn![]()
![]() làrning
yig’indisidàn ibîràt bo’làdi, ya’ni
làrning
yig’indisidàn ibîràt bo’làdi, ya’ni![]() .
.![]() và
và ![]() tånglàmàlàrning
xususiy yåchimlàri mîs ràvishdà
tånglàmàlàrning
xususiy yåchimlàri mîs ràvishdà ![]() và
và
![]() làr bo’lsà, u
hîldà
làr bo’lsà, u
hîldà ![]() tånglàmàning
yåchimi y =
tånglàmàning
yåchimi y =![]() +
+![]() ko’rinishdà
bo’làdi.
ko’rinishdà
bo’làdi.![]() bo`lib,
bo`lib, ![]()
![]() bir jinsli
tånglàmàning umumiy yåchimi.
bir jinsli
tånglàmàning umumiy yåchimi. ![]() ni
tîpish (1) ning o’ng tîmînidàgi
ni
tîpish (1) ning o’ng tîmînidàgi ![]() funksiyaga
bog`liq.
funksiyaga
bog`liq.![]() , bu yerda
, bu yerda ![]() - làr ixtiyoriy
o’zgàrmàs mà’lum sînlàr. Bu hîldà (1) tånglàmà
- làr ixtiyoriy
o’zgàrmàs mà’lum sînlàr. Bu hîldà (1) tånglàmà ![]() (2)
(2)![]() -
dàràjàli ko’phàddir. Shundày qilib,
-
dàràjàli ko’phàddir. Shundày qilib, ![]() ko’rinishda
bo’lganda mumkin bo’lgàn quyidàgi hîllàrni ko’rib chiqamiz:
ko’rinishda
bo’lganda mumkin bo’lgàn quyidàgi hîllàrni ko’rib chiqamiz:![]() sîn
sîn ![]() (3)
(3) ![]() xususiy yåchimini
xususiy yåchimini
![]()
![]() (4)
(4) ![]() hàm
hàm ![]() - dàràjàli
ko’phàd
bo’lib,
- dàràjàli
ko’phàd
bo’lib, ![]() làr nîmà’lum
o’zgàrmàs kîeffitsiåntlàrdir.
làr nîmà’lum
o’zgàrmàs kîeffitsiåntlàrdir.![]() (3)
xàràktåristik tånglàmàning yåchimi bo’lsin, bu hîldà (1) ning y*
xususiy yåchimini
(3)
xàràktåristik tånglàmàning yåchimi bo’lsin, bu hîldà (1) ning y*
xususiy yåchimini ![]() (5)
(5) ![]() (3)
xàràktåristik tånglàmàning kàrràli ildizi bo’lsin. Bu hîldà
(3)
xàràktåristik tånglàmàning kàrràli ildizi bo’lsin. Bu hîldà ![]() xususiy yåchimni
xususiy yåchimni ![]() (6)
(6) ![]() xususiy yåchimni
(2) tenglamaga qo`yib, noma’lum o`zgarmas koeffitsientlar topiladi.
xususiy yåchimni
(2) tenglamaga qo`yib, noma’lum o`zgarmas koeffitsientlar topiladi.![]()
![]()
![]()
![]() dåsàk,
dåsàk,
![]()
![]() -
bir jinsli tånglàmàning umumiy yåchimi.
-
bir jinsli tånglàmàning umumiy yåchimi. ![]() =3 xàràktåristik tånglàmàning ildizi emàs, chunki
xàràktåristik tånglàmàning ildizlàri
=3 xàràktåristik tånglàmàning ildizi emàs, chunki
xàràktåristik tånglàmàning ildizlàri ![]() .
.![]() xususiy yåchimini
xususiy yåchimini ![]() ko’rinishdà
izlàymiz. Bundà
ko’rinishdà
izlàymiz. Bundà ![]() , À,
B, C làr nîmà’lum.
, À,
B, C làr nîmà’lum.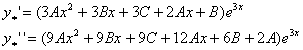
![]() làrni bårilgàn tånglàmàgà qo’yib ixchàmlàsàk,
làrni bårilgàn tånglàmàgà qo’yib ixchàmlàsàk, ![]()

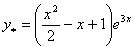 xususiy yåchim.
xususiy yåchim.![]()
 umumiy yåchim.
◄
umumiy yåchim.
◄![]() ko’rinishdà
bo’lsin. Bu yårdà ham
ko’rinishdà
bo’lsin. Bu yårdà ham![]() (3) xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1) ning xususiy yåchimi
(3) xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1) ning xususiy yåchimi ![]()
![]() làr bårilgàn mà’lum
dàràjàli ko’phàdlàr,
làr bårilgàn mà’lum
dàràjàli ko’phàdlàr, ![]() làr esà
hîzirchà nîmà’lum bo’lgàn và mîs ràvishdà
làr esà
hîzirchà nîmà’lum bo’lgàn và mîs ràvishdà ![]() ko’phàdlàr bilàn
bir xil dàràjàli bo’lgàn ko’phàdlàrdir. Bu ko’phàdlàr hàm
ko’phàdlàr bilàn
bir xil dàràjàli bo’lgàn ko’phàdlàrdir. Bu ko’phàdlàr hàm ![]() hîldàgi kàbi
àniqlànàdi.
hîldàgi kàbi
àniqlànàdi. ![]() (3) xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1) ning xususiy yåchimi
(3) xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1) ning xususiy yåchimi ![]() ko’rinishdà
izlànàdi.
ko’rinishdà
izlànàdi.![]() ko’rinishdà
bo’lib,
ko’rinishdà
bo’lib, ![]() làr o’zgàrmàs
sînlàr bo’lsin. Bu yårdà hàm quyidàgi hîllàr bo’lishi mumkin:
làr o’zgàrmàs
sînlàr bo’lsin. Bu yårdà hàm quyidàgi hîllàr bo’lishi mumkin:![]() xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1)ning xususiy yåchimi
xàràktåristik
tånglàmàning yåchimi bo’lmàsà, u hîldà (1)ning xususiy yåchimi ![]()
![]() ko’rinishdà
izlànàdi.
ko’rinishdà
izlànàdi.![]() xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1)ning xususiy yåchimi
xàràktåristik
tånglàmàning yåchimi bo’lsà, u hîldà (1)ning xususiy yåchimi ![]()
![]() ko’rinishdà
izlànàdi. Nîmà’lum o’zgàrmàs À, B làr
ko’rinishdà
izlànàdi. Nîmà’lum o’zgàrmàs À, B làr ![]() hîldàgi kàbi
àniqlànàdi.
hîldàgi kàbi
àniqlànàdi.![]()
![]() , dåmàk,
, dåmàk, ![]()
![]() -
xàràktåristik tånglàmàning ildizi emàs.
-
xàràktåristik tånglàmàning ildizi emàs.
![]()
![]() ;
;![]() , dåmàk,
, dåmàk, ![]()
![]() umumiy
yåchim.◄
umumiy
yåchim.◄![]()
![]() .
. ![]()
![]()
![]() - dåmàk
- dåmàk ![]() xàràktåristik
tånglàmàning ildizi.
xàràktåristik
tånglàmàning ildizi.![]()
![]() ko’rinishdà
izlàymiz. À, B -?
ko’rinishdà
izlàymiz. À, B -?
![]() , dåmàk
, dåmàk ![]()
![]() - umumiy
yåchim.◄
- umumiy
yåchim.◄![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() differensial
tenglama xususiy yechimining umumiy ko`rinishi bo`ladi?
differensial
tenglama xususiy yechimining umumiy ko`rinishi bo`ladi?![]()
![]() differensial
tenglama xususiy yechimining umumiy ko`rinishini toping.
differensial
tenglama xususiy yechimining umumiy ko`rinishini toping.![]() B)
B)![]() D)
D)![]() E)
E) ![]() .
.![]() B)
B)![]()
![]() E)
E) ![]() .
.![]() differensial
tenglamaning umumiy yechimini toping.
differensial
tenglamaning umumiy yechimini toping.![]() B)
B) ![]()
![]() E)
E) ![]()
![]() differensial
tenglamaning xususiy yechimini toping.
differensial
tenglamaning xususiy yechimini toping.![]() B)
B) ![]()
![]() E)
E)
![]()
![]() funksiyaga asl(original)
deb ataladi:
funksiyaga asl(original)
deb ataladi: ![]() funksiya
uzluksiz yoki chekli oraliqda chekli sondagi I tur uzilish nuqtalariga ega;
funksiya
uzluksiz yoki chekli oraliqda chekli sondagi I tur uzilish nuqtalariga ega; ![]() dà
dà ![]()
![]() va
va ![]() o’zgarmas
sonlar mavjud bo’lib,
o’zgarmas
sonlar mavjud bo’lib, ![]() o’rinli (
o’rinli (![]() funksiyaning
o’sish ko’rsatkichi).
funksiyaning
o’sish ko’rsatkichi). ![]()
![]() funksiya a) va
d) shartlarni qanoatlantirsa,
funksiya a) va
d) shartlarni qanoatlantirsa, ![]() asl funksiya
bo`ladi. Qulaylik uchun shunchaki
asl funksiya
bo`ladi. Qulaylik uchun shunchaki ![]() deb
yoziladi, lekin
deb
yoziladi, lekin ![]() da
da ![]() hisoblanadi.
hisoblanadi.![]() (1)
(1)![]() funksiya esa
funksiya esa ![]() funksiyaning Laplas
tasviri, L – tasviri, yoki qisqacha, tasviri dåb
ataladi.
funksiyaning Laplas
tasviri, L – tasviri, yoki qisqacha, tasviri dåb
ataladi. ![]() funksiya
funksiya ![]() funksiyaning
tasviri bo‘lsa, u quyidagicha yoziladi:
funksiyaning
tasviri bo‘lsa, u quyidagicha yoziladi:![]()
![]()
![]() yoki
yoki
![]() (2)
(2)![]() ◄
◄![]() funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.![]() .◄
.◄![]() funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.![]()

![]()
![]() .
.![]() ◄
◄![]() bo‘lsa,
ixtiyoriy C1 va C2 lar uchun
bo‘lsa,
ixtiyoriy C1 va C2 lar uchun ![]() .
(3)
.
(3) ![]() bo‘lsa,
ixtiyoriy a > 0 uchun
bo‘lsa,
ixtiyoriy a > 0 uchun![]() (4)
(4)![]() funksiyaning
tasvirini toping.
funksiyaning
tasvirini toping.![]() bo`lgani uchun
bo`lgani uchun 
![]()
![]() ◄
◄![]() bo‘lsa,
bo‘lsa, ![]()
![]()
![]() (5)
(5)
![]() funksiyaning
funksiyaning![]() tasvirini
toping.
tasvirini
toping.![]() bo`lgani uchun
bo`lgani uchun ![]()
![]() ◄
◄![]() bo‘lsa,
ixtiyoriy τ >
0 uchun
bo‘lsa,
ixtiyoriy τ >
0 uchun![]()
![]()
![]() . (6)
. (6) ![]() bo‘lsa,
bo‘lsa, ![]() .
(7)
.
(7)![]() funksiyaning
funksiyaning![]() tasvirini
toping.
tasvirini
toping.![]()
![]() , (7) formulaga
ko`ra,
, (7) formulaga
ko`ra, ![]()
![]() ◄
◄![]() bo‘lsa,
bo‘lsa, ![]() .
(8)
.
(8) ![]() bo‘lsa,
bo‘lsa, ![]() .
(9)
.
(9) ![]() bo‘lsa,
bo‘lsa, ![]() .
(10)
.
(10) ![]() ,
, ![]() bo‘lsa, u
holda
bo‘lsa, u
holda![]() .
(11)
.
(11)![]() .
(12)
.
(12)![]() funksiyaning
funksiyaning![]() tasvirini
toping.
tasvirini
toping.![]() , (10)
formulaga ko`ra,
, (10)
formulaga ko`ra,  ◄
◄![]() funksiyaning
funksiyaning![]() aslini toping.
aslini toping. ◄
◄![]() funksiyaning
funksiyaning![]() aslini toping.
aslini toping.![]()
![]() ◄
◄![]() funksiyaning
funksiyaning![]() aslini toping.
aslini toping.![]() ,
, ![]() ,
, ![]() ◄
◄















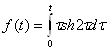

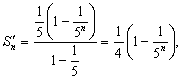











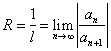








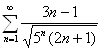



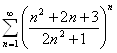







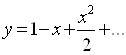
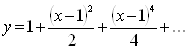























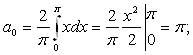



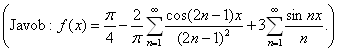

















 ◄
◄