IX-БОБ. ГРАФЛАР НАЗАРИЯСИНИНГ ЭЛЕМЕНТЛАРИ

 

            Бу бобда графлар назариясининг элементлари ёритилган. Бу ерда оддий графлар, графларнинг изоморфлиги, маршрутлар, занжирлар, цикллар, богликлилик, дарахтлар, мультиграфлар, Эйлер графлари, хроматик сон ва хроматик синф, турлар ва турдаги окимлар, Форд-Фалкерсон теоремаси каби масалалар караб чикилган.

 

1-§. Оддий графлар. Таъриф ва мисоллар1

Граф. -Кирралар. -Учлар. -Йуналтирилган, йуналтирилмаган кирра. -Инцидент. -Оддий графлар. -Графнинг тулдирувчиси. -Кисм граф. -Суграф.

 

            Графлар назарияси хозирги замон математикасининг асосий кисмларидан биридир. Кейинги пайтларда турли хил АСУ ва дискрет характерга эга булган хисоблаш курилмаларни лойихалашда (ясашда) графларнинг роли янада ошди. 

 

 

 

 

 

 

 

 

 

 

 


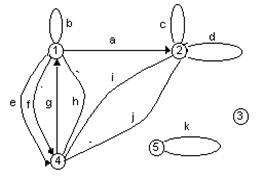1-шакл.

            Графнинг узи нима? Таъриф беришдан аввал куйидаги мисолда тушунтирамиз.

1-шаклда учлари 1,2,3,4,5 ракамлар билан белгиланган доирачалардан, кирралари эса a,b,c,d,e,f,g,h,i,j,k (йуналишга эга ёки йуналишсиз) бу доирачаларни баъзи бирларини туташтирувчи чизиклардан иборат. Кирра а йуналтирилган булиб 1 ва 2 учларни туташтиради (лекин 2 ва 1 учларни туташтирмайди); ёйлар деб аталувчи бу кирраларга e,f,g лар хам мисол була олади. Кирра h йуналтирилмаган булиб, у 1 ва 4, хамда 4 ва 1  учларни туташтиради; звенолар деб аталувчи бундай кирраларга i ва j лар хам киради. Нихоят b,c,d,k  кирралар сиртмоклар деб аталади ва баъзи учни унинг узи билан туташтиради (бу кирралар хам йуналишга эга эмас).

Одатда a,b,e,f,g,h кирраларни 1 учга инцидент деб атайдилар, уз навбатида бу уч шу кирраларнинг хар бирига инцидентдир.Шу билан бирга a,e,f  ёйлар 1 учдан 4 га караб йуналтирилган, g эса аксинча 4 дан 1 га карата йуналтирилгандир. Учинчи ва бешинчи учлар яккаланган дейилади (улар купи билан сиртмокларга инцидент булиши мумкин).

Бу  мисолдаги граф чеклидир: {1,2,3,4,5} учлар ва {a,b,c,d,e,f,g,h,i,j,k}  кирралар тупламларининг иккаласи хам чекли.

            Келгусида оддий графлар мухим урин тутади. Бу синфнинг графлари куйидаги хоссаларга эга: у чекли, барча кирралари ориентирланмаган, сиртмоклари ва каррали кирралари йук (исталган иккита учлар биттадан куп звено билан туташтирилмайди).

Бундай графларга куйидагилар мисол була олади.                         

Петерсен номи билан аталувчи унг томондаги граф кирраларининг доирачалар билан белгиланмаган кесишган жойлари унинг учлари эмасдир.

 

 

 

 

 

 

 


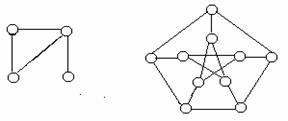
2-шакл.

 

            1-таъриф. Буш  булмаган  учлар туплами ва  кирралар  тупламидан тузилган тартибланган  жуфтлик оддий граф дейилади.

Агар  учлар учун  булса, учлар кушни, агар  булса бу учлар  кушнимас дейилади.

Таърифдан бевосита куринадики, агар учлар сони   булса, у холда кирралар сони  учун куйидаги тенгсизлик уринлидир

Оддий графларнинг куйидаги иккита холини алохида айтиб утамиз:

                -  учли буш граф -

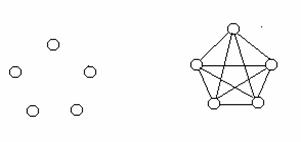
                 -  учли тулик граф -

Куйидаги шаклда  ва  графлар келтирилган

 

 

 

 

 

 

3-шакл.

            2-таъриф. Учлари  графнинг учларидан,  кирралари эса   тупламдан иборат булган  берилган графнинг тулдирувчиси дейилади.

Равшанки, .  ва , бир-бирини тулдирувчи графлардир. Уларга яна мисол келтирамиз

 

 

 

 

 

 

 

 

 

4-шакл.

 

3-таъриф.  Aгар  ва  графлар учун ,  булса, у холда  граф  нинг булаги дейилади.

Масалан,

 

 

 

 

 


                          

 

 

 

 

 

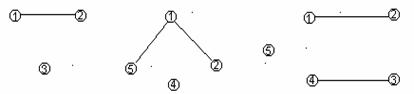
5-шакл.

 

графлар 4-шаклдаги биринчи графнинг булакларидир.

4-таъриф. Агар  графнинг булаги  учун  булса, у холда у кисм граф дейилади.

        Бошкача килиб айтганда кисм графни хосил килиш учун  учлар туплами билан уларнинг камида биттасига инцидент булган кирралар олиб ташланади.

         Масалан, юкоридаги (4-шаклда) келтирилган графнинг кисмларидан баъзилари

 

 

 

 

 

 

 


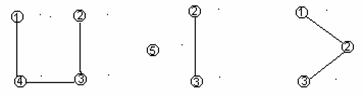6-шакл.

 

шулардан иборат.

5-таъриф. Агар графнинг булаги  учун  булса, у холда у суграф дейилади, яъни суграфларни хосил килиш учун факат кирраларни олиб ташлаш кифоя.

Яна 4-шаклдаги мисолга мурожаат киламиз. Куйидаги          

 

 


                                          

 

 

 

 

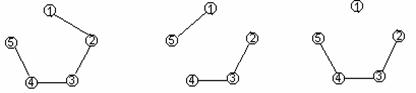7-шакл.

 

графлар унинг суграфларидир.

 

2-§. Графларнинг изоморфлиги

 

Графлар изоморфизми. -Изоморф графлар. -Кушнилик муносабати.

 

          ва  графлар берилган булсин. Кайси холда улар иккаласи битта графни ифодалайди деган саволга жавоб беришга уринамиз.

Бу масала графларнинг изоморфизми тушунчаси билан чамбарчас богликдир.

Таъриф. Агар  ва  графларнинг учлари тупламлари  ва  орасида узаро бир кийматли ва учларнинг кушнилик муносабатини саклайдиган мосликни  урнатиш мумкин булса, яъни  ва уларга мос булган учун   булса, у холда бу графлар изоморф дейилади.

Куйидаги графлар берилган булсин

                  , , бу ерда

                  ,  ;

                  ,  ;

                  ,    ;

                  ,    .                

 

 

 

 

 

 

 


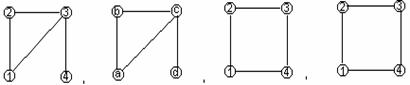       G1             G2               G3               G4

 

8-шакл.

      Умуман олганда бу графларнинг турталаси хар хилдир. , чунки ; , чунки . Лекин куриниб турибдики,  ва  бир хил тузилишга (структурага) эга, шу жумладан,  ва  хам бир хил тузилишга эга. Агар изоморфликни »ва изоморф эмасликни » белгиласак: , , G1 »G3, G1»G4, G2 »G3, G2 »G4  эканлигини курамиз.

     Масалан,  ни куйидагича аниклаш мумкин

                ,   ,   ,  ;

у холда

    ва   ,    ва ,

    ва   ,    ва ,

    ва   ,    ва ,

яъни   шарт бажарилади.

        Укувчига

                

мослик хам  ва  графларнинг изоморфизми эканлигини текширишни тавсия киламиз. Шу билан бирга учларнинг колган 4!- 2=22 мосликларни изоморфизм эмаслигини айтиб утамиз.

 ва  графларнинг изоморфизмини масалан, куйидагича урнатиш мумкин

          1        2        3         4      -   графда

                                

          1        3        2         4       -   графда

(бу графларнинг бошка изоморфизмларини аникланг).  

           эканлигини осонгина аниклаш мумкин: Масалан,   графнинг 4 учи факат битта уч билан кушни,  да эса бундай уч умуман йук.

3-§. Мультиграфлар

 

Параллел кирралар. –Сиртмок. -Инцидентлик матрицаси. –Мультиграф.

 

            Энди умумий холда чекли, ориентирлаштирилмаган графларни киритамиз.

            Таъриф. Граф деб  тартибланган учликга айтилади, бу ерда  - учлар туплами,  - кирралар туплами (иккаласи хам чекли) ва  акслантириш хар бир  кирра учун унинг  учларига тартибланмаган  жуфтликни мос куяди. Агар  булса, у холда  кирра  учдаги сиртмок,  булса у звено дейилади. Агар  ва  учларнинг иккаласи камида битта умумий инцидент киррага эга булса улар кушни дейилади. Хусусий холда, агар  учда камида битта сиртмок булса, у уз-узи билан кушнидир.

            Агар  ва  кирралар учун  булса, у холда улар параллел (каррали) дейилади.

            Агар графнинг учлари  каби тартибланган булса, у холда уни  кушнилик матрицаси ёрдамида бериш мумкин, бу ерда   ва  учларни туташтирувчи кирралар сони. Албатта бу матрица графнинг учларини тартибланишига боглик ва уни параллел кирраларни жойлашиш тартиби аниклигина тиклайди. Инцидентлик матрицаси  буйича графни ягона равишда тиклаш мумкин:

Бу ерда  ва кирралар хам тартибланган деб хисобланади .

 

 

 

 

 

 

 

 

 


                                    

 

 

 

 

 

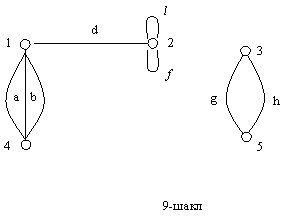Юкоридаги шаклда учлари , кирралари  булган  граф (мультиграф) берилган. Акслантириш  эса куйидагича аникланган: .

            Бу граф учун

 

      .

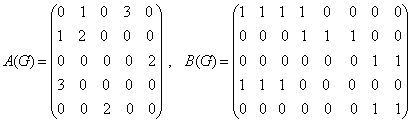4-§. Маршрутлар, занжирлар, цикллар. Богликлилик

 

Маршрут. -Циклик маршрут. -Занжир. -Цикл. -Содда занжир. -Туташтирилган учлар. -Богликли граф. -Кушнилик матрицаси. -Такомиллаштирилган кушнилик матрицаси.

 

1-таъриф. Оддий  графдаги

                                       

кетма-кетлик (бу ерда ; ) узунлиги  тенг булган ва  учларни туташтирувчи маршрут дейилади.

       Агар   ва  булса, маршрут циклик дейилади.  маршрут битта  учдан иборат булади ва у циклик хисобланмайди.

         Маршрутда учлар ва кирраларнинг хар хил булиши талаб килинмайди. Битта уч ёки кирра бир неча марта такрорланиши мумкин.

        2-таъриф. Кирралари хар хил булган маршрут занжир деб аталади. Циклик занжир эса цикл дейилади. Агар занжирда (циклда)   ва  лардан ташкари барча учлари хар хил булса, у холда содда занжир (цикл) дейилади.

 

 

 

 

 

 

 


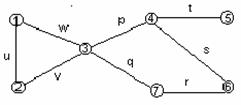10-шакл.

       Юкоридаги графда (10-шакл) 3v2u1w3p4t5t4t5 ва 3w1u2v3p4t5t4t5 маршрутлар бир хил элементлардан тузилган булсада, лекин хар хилдир. Улар циклик эмас ва занжир хам эмасдир. 3w1u2v3p4 маршрут занжир, лекин содда эмас ва циклни ташкил этмайди. 3w1u2v3p4s6r7g3 ва 3v2u1w3p4s6r7g3 хар хил содда булмаган цикллар. 3g7r6s4p3 - маршрут содда циклдир. 1u3v2  кетма-кетлик умуман маршрут эмас.

       3-таъриф.  Агар  графнинг  ва  учлари орасида хеч булмаганда битта занжир мавжуд булса, у холда улар туташтирилган дейилади.

Равшанки, графнинг учлари тупламида берилган “туташтирилганлик” муносабати рефлексивлик, симметриклик, транзитивлик хоссаларига эга. Демак, бу муносабат эквивалентликдир ва графнинг  учлари тупламини  синфларга ажратади. Хар бир синфга тегишли булган учлар узаро туташтирилгандир (турли синфларга тегишли булган учлар орасида занжирлар йук).

 графнинг  кисм графи унинг богликли компонентаси дейилади. Агар  булса, граф богликли дейилади.

            Богликли  графнинг учлари туплами  да масофа тушунчасини киритиш мумкин:  ва  учлар орасидаги масофа деб

                             

га айтилади, бу ерда   занжирнинг узунлиги ва минимум барча  занжирлар буйича олинади (албатта бу минимум содда занжирларда эришилади).

            Киритилган  учун масофанинг барча хоссалари (аксиомалари) бажарилади:

1)     

2)     

3)      .

Демак,  туплам метрик фазони ташкил этади.

 мультиграф берилган булсин, бу ерда ,              ва  кушнилик матрицаси.

Графнинг  ва  учларини туташтирувчи узунлиги  булган турли хил маршрутлар сонини ва узларини аниклаш масаласини караймиз. Бу сон  матрицанинг  элементига тенг.

Хакикатан хам  булганда уз-узидан равшан. Фараз килайлик  узунликдаги  тенг  ва  учларни туташтиручи маршрутлар сони булсин. Унда  ва  учларни туташтирувчи узунликлари  (охиридан олдинги  учни танлаб олган  холда) маршрутлар сони   га тенг, умумий холда эса барча маршрутлар сони матрицалар купайтмаси коидасига асосан  га тенг.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ушбу граф учун

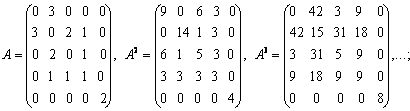
масалан,  уч билан  туташтирувчи узунликлари 2га тенг булган учта маршрут  бор ва бу учларни туташтирувчи узунликлари 3га тенг туккизта маршрут ,, , ,

, , , ,  мавжуд,  учни узи билан богловчи узунлиги 2га тенг туртта маршрут , , ,  бор ва хоказо.

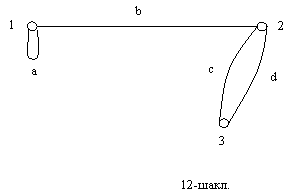            Маршрутларни узларини аниклаш усулини (хисоблашлари куплиги сабабли) содда мисолда курсатамиз.

 

 

 

 

 

 

 

 

 

 

 

            Бу графнинг такомиллаштирилган кушнилик матрицасини тузамиз

,

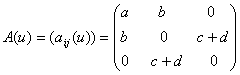бу ерда   ва  учларни туташтирувчи кирраларнинг шартли йигиндиси. Кирралар белгиларини  нокоммутатив (лекин ассоциатив) ярим халканинг ясовчилари деб кабул киламиз.

             матрицанинг кетма-кет даражаларини топамиз

       ,

 

...

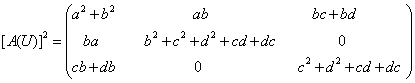       Масалан,  матрицанинг

элементи  билан  туташтирувчи олтита узунлиги 3га тенг булган маршрутларни аниклайди:

,  ,  , 

,  ,   .

            Агар бизни  дан  га  кадамлар билан утиш масаласи кизиктирса, бутун мусбат сонлар ярим халкасига  буль муносабатини киритамиз. У холда, агар  дан  гача камида битта узунлиги  га тенг булган маршрут булса  матрицанинг  элементи 1, акс холда 0 га тенг.

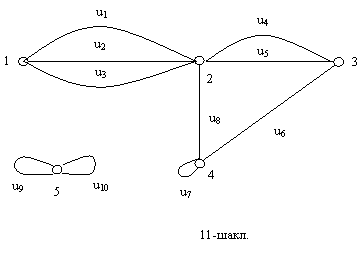
      11-шаклдаги граф учун

 

,

.

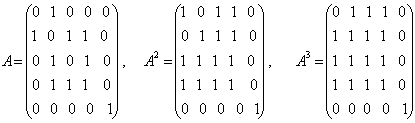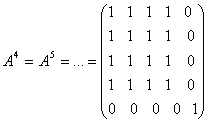            Агар  дан  гача  дан куп булмаган кадамлар билан утиш масаласини курсак, у холда  бирлик матрица) матрицанинг даражаларини караймиз. Юкоридаги мисолда

,   .

 

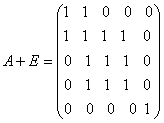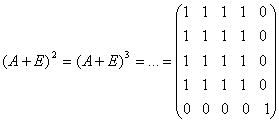            Бу усул билан графнинг барча богликли компонентларини хам топиш мумкин.

 

РЕЖА:

 

            1.Оддий графлар. Таъриф ва мисоллар.

            2.Графларнинг изоморфлиги.

            3.Мультиграфлар.

            4.Маршрутлар, занжирлар, цикллар. Богликлилик.

 

 

 

 

Муаммоли масала ва топшириклар

 

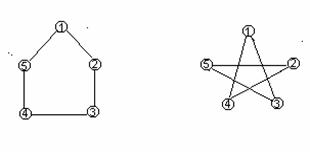
1. 13-шаклда курсатилган иккита графнинг изоморфлигини исботланг.

 

 

 

 

 

 

 

 

 

 


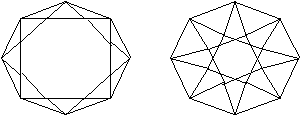13-шакл

 

2. Бир-бири билан аразлаган учта хамсоянинг учта умумий кудуклари бор. Хар бир уйдан хар бир кудукка бир-бири билан кесишмайдиган йул утказиш мумкинми? Жавобингизни изохланг.

 

3. Бешта тугри купкиррали графлар учларининг сони ва даражасини аникланг.

 

4. Тугри купкиррали графлар учун кушнилик ва инцидентлик матрицаларини тузинг.

 

 

Мустакил ишлаш учун саволлар:

 

            1.Оддий графлар. Кирралар, учлар. Йуналтирилган ва йуналтирилмаган кирралар. Инцидент.

            2.Графнинг тулдирувчиси. Кисм граф. Суграф.

            3.Графлар изоморфизми. Изоморф графлар. Кушнилик муносабати.

            4.Мультиграфлар.

            5.Маршрутлар, занжирлар, цикллар. Богликлилик.

 

 

 

 

5-§. Дарахтлар

 

Циклик ва ациклик кирра. -Цикломатик сон. -Дарахт. -Погона учлари. -Графнинг асоси. -Ватар. -Чекли дарахтда кирралар сони учлар сонидан битта

 камлиги хакида.

 

     1-таъриф. Aгар  графнинг  кирраси камида битта циклга тегишли булса, у циклик, акс холда ациклик кирра дейилади.

 граф учун

                     

(бу ерда  нинг кирралари сони,  - учлари cони ва  компоненталари сони) ифода унинг цикломатик сони дейилади.

    Осонгина курсатиш мумкинки:

 

                         

 

                         

 

   Уз-узидан равшанки,

                

    ва факат цикллари булмаган граф учун .

2-таъриф. Барча кирралари ациклик булган богликли граф дарахт дейилади.

Дарахтнинг исталган иккита учлари ягона занжир билан боглангандир. Дарахтнинг исталган  учини танлаб олиб унинг илдизи ёки нолинчи погонали уч деб атаймиз.  га кушни булган барча учларни биринчи погона учлари деймиз ва хоказо -  погонадаги учларга кушни (бошка погоналарга тегишли булмаган) учларни  погона учлари деб атаймиз (14-шакл).

 

                                                           4-погона,

 

                                                           3-погона,

 

                                                           2-погона,

                                                                        

                                                           1-погона,   

                                                                 

                                                           0-погона.

 

                               14-шакл

 

        Дарахтнинг бундай тасвирланишидан келиб чикадики, у четки (факат битта киррага инцидент булган) учларга эга. Масалан, охирги погонанинг учлари.

Богликли  графдан кетма-кет барча циклик кирраларни олиб ташлаймиз. Натижада, хамма кирралари ациклик булган богликли  графни-дарахтни хосил киламиз. Бу дарахт  графнинг асоси дейилади. Графнинг асоси ягона танланмайди, лекин барча ациклик кирралар исталган асосга киради.  асосга нисбатан  булакнинг барча кирралари - ватарлар деб аталади.

 дарахтдан четки учни (автоматик тарзда битта киррани) олиб ташласак, яна дарахтни хосил киламиз. Агар  чекли булса,  кадамлардан кейин битта кирра ва иккита учга эга дарахтни хосил киламиз. Дарахтдан олиб ташланган учлар ва кирралар сони бир хил булганлиги сабабли куйидаги хулосага келамиз: хар кандай чекли дарахтда кирралар сони учлар сонидан битта кам. Аксинчаси хам уринлидир, яъни

Теорема. Чекли богликли  граф дарахт булиши учун, унинг кирралари сони учлари сонидан биттага кам булиши зарур ва етарли.

Учлари  ракамлар билан тартибланган  учли дарахт берилган булсин. Дарахтнинг четки учлари орасидаги энг кичик номерлиси  ва  у билан кушни булган ягона уч  булсин. Дарахтдан  учни, демак  киррани олиб ташлаймиз. Хосил булган дарахтда энг кичик номерли четки  учни ва  киррани олиб ташлаймиз ва хоказо. Бу процессни  марта такрорлаб икки уч ва битта киррали дарахтни хосил киламиз. Олиб ташланган учларни ва лар билан белгилаймиз. Бу иккала  ва  мажмуаларберилган дарахт буйича ягона равишда аникланади, шу билан бирга  нинг барча сонлари хар хил,  ники эса хар хил булиши шарт  эмас (15-шакл).

 

 

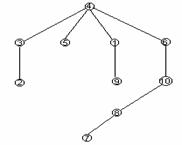
15-шакл.

 

       Бу дарахт учун  ва .

             ва  учлар мажмуалари берилган дарахт буйича ягона аникланади, шу билан бирга биринчи мажмуанинг барча учлари хар хил, иккинчисиники эса хар хил булиши шарт эмас. Шу билан бирга хар кандай   мажмуа битта дарахтга мос келади. Уни куйидагича куриш мумкин.

             тупламнинг  да катнашмаган сонларининг энг кичигини  билан белгилаймиз (бундай сон хамма вакт мавжуд, чунки  да  сонлар бор). Кирра билан  ва  учларни туташтирамиз,  ни  дан,  ни эса  дан учирамиз ва процессни такрорлаймиз:  мажмуада катнашмаган  нинг энг кичик сонини  билан белгилаймиз; ,  учларни кирра билан туташтирамиз ва уларни мос равишда  ва  лардан учирамиз ва хоказо. Охирида  да колган иккита учларни кирра билан туташтирамиз.

            Бундан куринадики, хар кандай  учун  кадамдан кейин ясалган кирралар ичида  га инцидент булганлари йук, лекин  га инцидент булган камида битта кирра мавжуд. Буни назарда тутган холда, процессни тескари тартибда бажариб,  буйича индукцияни куллаб хакикатан хам дарахт хосил булишини курсатамиз (чунки хар гал битта кирра янги, четки уч билан кушилади).

            Шунга ухшаш индукция буйича, лекин тугри тартибда куриб исботлаш мумкинки ушбу дарахтга айнан  мажмуа мос келади.

            Юкоридаги процессдан куринадики хар хил дарахтларга турли хил  жуфтликлар мос келади. Агар  булса, у холда . Хакикатан хам,  ва  булса, у холда  га кирмайди, лекин у  га киради. Шунинг учун хар хил дарахтларга хар хил  куринишдаги мажмуалар мос келади.

            Шундай килиб, куйидаги теорема исбот килинди.

            Теорема (Кэли). Учлар сони тартибланган  та булган дарахтлар сони  га тенг.

( та элементлардан  тадан тузилган барча такрорий уринлаштиришлар сони).

            Албатта булар ичида куплари узаро изоморфдир.

            Масалан,  булганда, учала дарахтлар хам узаро изоморфдир

 

 

 

 

 


                                   ,                             ,

 

 

 

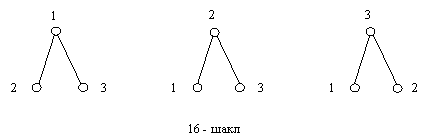
6-§. Эйлер графлари

 

Характеристик вектор. –Жуфт граф. –Эйлер цикли. –Эйлер графи. – Цикломатик сон.

 

            G графнинг барча учларини уз ичида сакловчи кисм графларини караймиз. G нинг барча кирралари  каби тартибланган булсин. G графнинг хар кандай  кисмига 0 ва 1 лардан иборат  улчовли векторни мос куямиз:

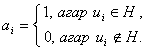
(Н нинг характеристик вектори). Бу мослик узаро бир кийматлидир, шу билан бирга  кисм графларнинг 2 модул буйича йигиндисига уларнинг характеристик векторларининг йигиндиси мос келади. Барча кисм графлар туплами йигинди амалига нисбатан абель группасини ташкил этади. Бу группа  коэффиицентлар майдони устида чизикли фазони ташкил этади (исталган Н кисм графнинг 1 га купайтмаси Н ни беради, 0 га купайтмаси эса буш графдир).

            Куриниб турибдики G граф кисмларининг фазоси уларнинг характеристик векторларининг фазосига изоморф ва  улчовли.

            Агар графнинг барча учларининг даражалари (яъни уларга инцидент булган кирралар сони) жуфт булса, граф хам жуфт дейилади.

            Жуфт графда исталган содда занжирни (циклдан фаркли) унга кирмаган кирра билан давом эттириш мумкин. Хакикатан хам, занжирда охирги учнинг даражаси 1 га тенг, лекин граф жуфт булганлиги сабабли бу учга инцидент булган камида битта кирра мавжуд. Агар граф чекли булса, занжирни кетма-кет давом эттириб, аввал босиб утган учларнинг бирига келамиз, яъни содда циклни хосил киламиз. Бу циклнинг барча кирраларини графдан олиб ташлаймиз. Унинг колган кисми яна жуфт графдир, чунки учларнинг даражалари 2 га камаяди (агар ундан занжир утса) ёки узгармайди (агар занжир утмаса). Бу графда яна циклни ажратамиз ва хоказо. Юкоридаги процессни яна давом этамиз, токи унда бирорта хам цикл колмасин (яъни буш граф хосил булгунча). Шундай килиб, чекли жуфт граф узаро кирралар буйича кесишмайдиган содда цикллар йигиндисига ёйилади. Бундан унинг барча кирралари циклик эканлиги келиб чикади.

            Агар чекли жуфт граф богликли булса, у холда осонгина курсатиш (содда цикллар сони буйича индукцияни куллаб) мумкинки унда барча кирраларини уз ичига олган содда цикл мавжуд. Бундай цикл Эйлер цикли, графнинг узи эса Эйлер графи дейилади.

            Юкорида айтилганлардан куйидаги теорема келиб чикади.

            Теорема. Чекли         богликли граф Эйлер графи булиши учун у жуфт булиши зарур ва етарли.

            Исталган чекли жуфт графнинг хар бир богликли компонентаси Эйлер графидир.

            Ихтиёрий графнинг хар кандай иккита Н1 ва Н2 жуфт кисм графларининг йигиндиси яна жуфт кисм графдир. Хакикатан хам,  учнинг даражаси  Н1+Н2 кисм графда  га тенг. Бу ерда  s1 ва s2  учнинг мос равишда Н1 ва Н2 лардаги даражалари, s12 эса  нинг уларнинг Н1Н2 кесишмасидаги даражаси. Шундай килиб, жуфт кисм графлар туплами барча кисм графлар фазосининг кисм фазосидир. Бу кисм фазонинг улчови  ни аниклаймиз.

            G богликли,  киррали,  учли граф D унинг хтиёрий асоси булсин. Ватарлар сони  га тенг. Хар бир  ватар ягона содда  занжир билан содда циклни хосил килади. Барча циклларнинг векторлари богликмас  системани хосил килади. Чунки хар бир цикл системанинг бошка циклларига тегишли булмаган киррага (узининг ватарига) эга. Демак .

            Иккинчи томондан хар кандай жуфт кисм граф, хусусий холда исталган содда цикл  системанинг цикллари оркали ифодаланади. Хакикатан хам жуфт Н кисм графга ватарлари унга тегишли  системанинг циклларини кушамиз. Хосил булган йигинди бирорта хам ватарга эга эмас. Демак, бу йигинди D дарахтнинг кисм графи, яъни у буш графдир. Акс холда содда циклларга эга жуфт кисм граф (Н ва циклларнинг йигиндиси) дарахтнинг кисм графи булар эди. Бундан  келиб чикади ва юкоридаги тенгсизликни инобатга олган холда .

            Богликли булмаган k компонентали графнинг жуфт кисм графлари фазосининг базиси унинг барча богликли компоненталари базисларининг йигиндисидан иборат. Кирралар ва учлар сони хам компоненталар буйича кушилади. Агар  компонента  кирраларга ва  учларга эга булса, у холда

,    ,     .

            Демак, жуфт кисм графлар кисм фазосининг улчови  графнинг цикломатик сони  га тенг.

            Исталган граф учун  булганлиги сабабли .

            Цикломатик сони нолга тенг булган богликли графлар – дарахтлардир.

 

7-§. Хроматик сон ва хроматик синф

 

Тугри буялган граф. -Хроматик сон. -Хроматик синф. -Бихроматик граф. -Бихроматик булишнинг етарли ва зарурий шарти. -Брукс теоремаси. 

 

            Cиртмоксиз  графнинг хар бир учига (киррасига) берилган ранглардан биттасини мос куямиз. Агар кушни учларга (кушни кирраларга) турли хил ранглар мос куйилган булса, у холда  граф тугри буялган дейилади.

 графнинг учларини (кирраларини) тугри буяш учун керак булган энг кам микдордаги турли хил ранглар сони мос равишда  унинг хроматик сони (хроматик синфи) дейилади.

Хар кандай оддий  граф учун  Тенглик факат Fn учун бажарилади.

Агар графда камида битта кирра булса,   Демак,   тенгсизлик уринли.

Таъриф. Агар  граф учун  булса, у холда  бихроматик дейилади.

            1-теорема. Камида битта киррага эга булган граф бихроматик булиши учун унда узунликлари ток содда циклларнинг булмаслиги зарур ва етарли.

Агар  граф тулик  учли  кисмларга эга булса, унинг хроматик сони  Лекин тескариси тугри эмас.

      Шундай графлар мавжудки, уларда хаттоки  (учбурчак) булмасада исталганча катта хроматик сонга эга.

Хроматик сон ва граф учларининг даражалари (учга инцидент булган кирралар сони) орасидаги богланишни урганамиз.  граф учларининг максимал даражаси  булсин.  билан  булган оддий графларнинг синфини белгилаймиз.

Хар кандай граф учун  эканлигини учлар сони буйича индукция усули билан исботлаш мумкин. Ягона  граф учун .

2-теорема. Камида битта киррага эга булган граф бихроматик булиши учун унда узунликлари ток сонларга тенг содда циклларнинг булмаслиги зарур ва етарлидир.

Зарурийлиги. Графни тугри буялганда цикл учларининг ранглари алмашиб келади, демак узунлиги ток булган содда циклни тугри буяш учун икки ранг етарли эмас. Бундай циклни узида саклаган граф хам бихроматик була олмайди.

Етарлилиги. Аввало шуни таъкидлаймизки, хар кандай дарахт бихроматик графдир. Хакикатан хам, дарахтнинг жуфт погоналаридаги барча учларини битта рангга буяймиз, ток погоналардаги учларни эса иккинчи рангга буяймиз. Натижада у тугри буялган булади, чунки дарахтнинг кирралари факат кушни погоналардаги учларни туташтиради.

Дарахтда      ва  погоналар учларини туташтирувчи содда занжирнинг узунлигининг жуфт-токлиги  соннинг жуфт токлиги билан бир хил. Хусусий холда, бир хил жуфтликдаги погоналарнинг учлари узунлиги жуфт содда занжир билан боглангандир.

Узунлиги ток сонга тенг содда занжирга эга булмаган G графда исталган асосни танлаб оламиз. Бу асосга нисбатан барча ватарлар турли хил жуфтликларга эга булган погоналарнинг учларини туташтиради, акс холда унда узунлиги ток содда занжирлар булар эди. Демак, асоснинг икки ранг билан тугри буялгани бутун графнинг хам тугри буялганидир.

Агар G графда         учли тулик Fc кисм граф мавжуд булса, у холда . Тескариси эса тугри эмас, шундай графлар мавжудки, уларда хатто уч учли тулик кисм графлари (учбурчаклар) йук, лекин хроматик сони исталганча катта.

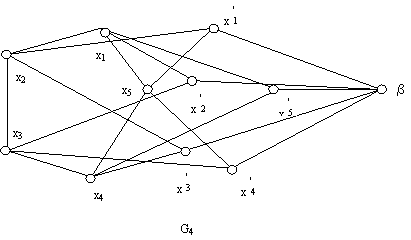
Бунда Gc граф индуктив равишда ясалади. G2 битта киррадан иборат.

 

 

 

 

 

 

 


                

 

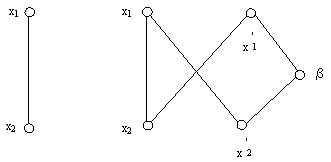     G2                   G3

 

 

 

 

 

 

 

 

 

 

 

 

                             

 

 

 

 

 

 

 

 

 

 

 

 


                                    

 

 

 

 

 

 

 

 

 

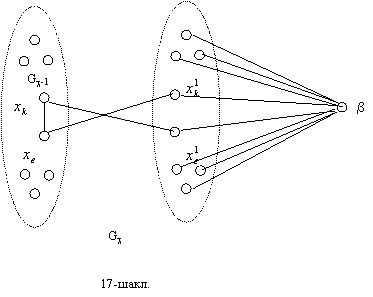Фараз килайлик  учлар тупламида Gc-1 граф курилган булсин. Gc-1 графга  учлар тупламини ва  учни кушамиз. Хар бир  учни  хамда Gc-1 графда  билан кушни булган учлари билан туташтирамиз (1-шакл). Хосил булган Gc графда учбурчаклар йуклигини курсатамиз. Индукция фаразига Gc-1 графда учбурчаклар йук. Агар учбурчак мавжуд булса, у холда  тупламдаги учлар бир-бири билан туташтирилмаганлиги сабабли, унга бу учларнинг купи билан биттаси тегишли;  хам бирорта учбурчакга тегишли эмас, чунки у факат  даги учлар билан туташтирилган.

Агар  учбурчак булса, у холда  учбурчак хам мавжуд булар эди (чунки  ва  учлар  да бир хил кушни учларга эга). Бу эса индукция фаразимизга зид.

Энди  эканлигини курсатамиз.

Равшанки . Фараз килайлик . У холда Gc графни c ранглар билан тугри буяш мумкин: масалан, Gc-1 графни c-1 ранглар билан тугри буяганимиздан кейин хар бир  учни  нинг рангига буяймиз ва  учга колган c рангни берамиз.

Gc  графни      c-1 ранглар билан тугри буяш мумкин эмаслигини курсатамиз. Тескарисини фараз киламиз, яъни Gc граф c-1  ранглар билан тугри буялади ва  учга  ранг тугри келади. Бунда  тупламнинг учлари  дан фаркли рангларга буялган.   рангга буялган учлар кисм туплами булсин. Хар бир  учни  учнинг рангига кайтадан буяймиз. Бу холда  графнинг барча учлари c-2 ранг билан тугри буялган булади. Хакикатан хам  Gc-1 графнинг исталган кирраси булсин. Gc графда  ва  турли рангларга буялганлиги сабабли уларнинг иккаласи бирданига А га тегишли эмас. Агар  булса графни кайта буяганимизда уларнинг ранглари узгармайди ва турли хил булганлигича колади.  Шундай килиб Gc-1 граф индукция фаразимизга зид равишда c-2 ранглар билан тугри буялади.

Хроматик сон ва граф учларининг даражалари орасидаги богланишни аниклаймиз.  билан G граф  учлари даражаларининг энг каттасини белгилаймиз, Гs эса параллел кирраларга эга булмаган ва  графлар синфи.

Учлар сони буйича индукцияни куллаб осонгина курсатиш мумкинки, хар кандай  учун . Хакикатан хам, агар графда учлар сони  дан ошмаса . Фараз килайлик бу тенгсизлик G дан кам учларга эга Гs нинг барча графлари учун уринли булсин. G графдан исталган  учни олиб ташлаймиз (унга инцидент булган барча кирралар билан биргаликда). Индуктив фаразимизга асосан  графни  ранглар билан тугри буяймиз. G графда  учга купи билан  та кушни учлар мавжуд, шунинг учсун камида битта ранг топиладики унга  га кушни булган учларнинг хеч бири буялмаган. Шу рангга  учни буяймиз ва граф G  ранглар билан тугри буялган булади.

Куйидаги теоремадан келиб чикадики Гs синф графлари ичида хроматик сони  тенг булган ягона тулик  учли Fs+1 графдир.

Теорема (Брукс). Агар ва  булса, у холда .

8-§. Турлар ва турдаги окимлар

 

Тур. -Турнинг кутблари. -Кутбли кирра. -Ички кирра. -p-турлар. -Турдаги оким. -Турнинг кесими. -Кесимнинг утказувчанлик кобилияти. -Форд-Фалкерсон теоремаси.

       

Баъзи бир учлари танлаб олинган граф тур деб аталади. Танлаб олинган учлар турнинг кутблари дейилади. Масалан, дарахтни бир кутбли тур деб караш мумкин (унинг илдизи кутбдир).

Турнинг кутбларидан фаркли учлари унинг ички учлари дейилади. Камида битта кутбга инцидент булган кирра кутбли, бошкалари эса ички кирралар дейилади.

Иккита синфларга ажратилган:  та кириш ва  та чикиш кутбларга булинган тур -кутблилик дейилади.(1,1) - кутблилик тур икки кутбли тур дейилади.

Умумий элементларга эга булмаган  ва  турларнинг кутблари мос равишда  ва  булсин.  ва  турларнинг кетма-кет уланишидан хосил килинган  кутбларга эга булган турни  каби белгилаймиз.  ва  турларнинг параллел уланишидан хосил булган ,  кутбларга эга турни эса  каби белгилаймиз (18-шакл).   

18-шакл.

 

Юкоридагига ухшаш ва  турларни аниклаш мумкин.

Бир киррали турлардан параллел ва кетма-кет улаш натижасида хосил булган тур параллел-кетма-кет дейилади. Бундай турларни -турлар деб атаймиз. -турлар индуктив равишда аникланади:

            1. Бир киррали тур -турдир;

        2. Агар  ва  -турлар булса, у холда,  ва  лар хам -турлардир.

-кисман ориентирлаштирилган турнинг хар бир  киррасига утказувчанлик кобилияти деб аталувчи манфий булмаган  сон мос куйилган булсин.

1-таъриф. Куйидаги шартларни каноатлантирадиган  жуфтлик  турдаги оким дейилади:

     1.-турнинг барча звеноларини бирор ориентирлашти-рилиши;

     2.-кирралар тупламида аникланган киймат-лари манфий эмас ва  нинг утказувчанлик кобилиятидан катта булмаган функция. Шу билан бирга барча ички учларда Кирхгоф конуни бажарилади, яъни  учга кирувчи барча кирралар буйича окимларнинг йигиндиси, ундан чикувчи кирралар буйича окимларнинг йигиндисига тенг.

    Бошкача килиб айтганда:

    1)  - турнинг барча кирралари учун;

     2) - барча ички учлар учун, бу eрда  

                  ,

        - ориентирлаштирилишда  учдан чикувчи (мос равишда  га кирувчи) кирралар туплами.

Равшанки, турнинг барча учлари буйича (кутбларни хам инобатга олган такдирда)  ларнинг йигиндиси нолга тенг (чунки  хар бир кирра бирор учдан чикиб бошкасига киради). Шунинг учун

 нинг киймати турдаги окимнинг микдори дейилади.

Кирраларнинг берилган утказувчанлик кобилиятларида  турдан утувчи максимал  окимнинг микдорини аниклаш масаласини курамиз. Бу масаланинг ечими турдаги кесимлар билан богликдир.

2-таъриф. Агар турнинг баъзи бир кирраларини олиб ташлаганимизда, у богликли булмай кутблари турли компонентларига тушиб колса, бу кирралар туплами турнинг кесими дейилади.

 

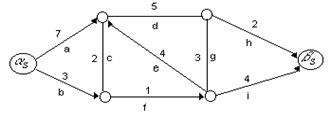
19-шакл.

 

Юкоридаги расмда берилган тур учун 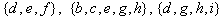 кирралар тупламлари кесимлардир.

Агар кесимдан исталган киррасини олиб ташлаганда кесим булмай колса, у содда дейилади. Масалан,  кесимлар содда,  эса содда эмас.

Богликли турнинг содда кесими уни иккита:  кутбни узида сакловчи чап ва  кутбни узида сакловчи унг кисмларга ажратади. Кесимнинг хар бир кирраси турли кисмларга тегишли булган учларни туташтиради. Агар кесимнинг кирраси звено булса, ёки чапдан унгга караб йуналтирилган булса, у тугри, акс холда тескари дейилади.

3-таъриф. Содда  кесимнинг утказувчанлик кобилияти  деб унинг барча тугри кирраларининг утказувчанлик кобилиятларининг йигиндисига айтилади.

Масалан,  кесимнинг утказувчанлик кобилияти 5+1=6 тенг, - кесимники эса 3+2+3+2=10. Агар  тур богликли булмай кутблари турли компонентларига тегишли булса, у холда ягона содда кесим буш туплам, унинг утказувчанлик кобилияти эса нолга тенг.

Теорема (Форд-Фалкерсон).  турдан утувчи окимнинг максимал киймати  унинг содда кесимларининг минимал утказувчанлик кобилияти  га тенг.

 

 

РЕЖА:

 

            1.Дарахтлар.

            2.Эйлер графлари.

            3.Хроматик сон ва хроматик синф.

            4.Турлар ва турдаги окимлар.

 

Муаммоли масала ва топшириклар

 

1. Т дарахтнинг иккита Т1 ва Т2 кисм дарахтларининг  кесишмаси дарахт булишини исботланг.

            2. Агар i компонента mi кирраларга ва ni учларга эга булса, у холда

,    ,    

булишини исботланг.

                3. Ципломатик сони нолга тенг булган богликли графлар дарахтлар булишини исботланг.

4. Агар ва  булса, у холда  эканлигини исботланг.

5. Форд-Фалкерсон теоремасини исботланг.

 

 

Мустакил ишлаш учун саволлар:

 

            1.Дарахтлар. Циклик ва ациклик кирра. Цикломатик сон.

            2.Графнинг асоси. Ватар. Чекли дарахтда кирралар сони учлар сонидан битта камлиги хакида.

            3.Эйлер графлари.

            4.Хроматик сон ва хроматик синф. Бихроматик граф. Бихроматик булишнинг зарурий ва етарли шарти.

            5.Турлар ва турдаги окимлар. Турнинг кутблари. Кутбли кирра. Ички кирра. Турнинг кесими. Кесимнинг утказувчанлик кобилияти.

            6.Форд-Фалкерсон теоремаси.

 

 

 

 

А Д А Б И Ё Т

 

1.

Алексеев В.Б., Кудрявцев В.Б., Сапоженко А.А., Яблонский С.В. и др. Методическая разработка по курсу “Математическая логика и дискретная математика”. 1980, -135 с.

2.

Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математики. -М.: Наука, 1977.

3.

Гильберт Д., Бернайс П. Основания математики. Логические исчисления и формализация арифметики. -М.: Наука, 1979.

4.

Гёдел К. Совместимость аксиомы выбора и обобщенной континиум-гипотезы с аксиомами теории множеств, УМН, 3, №1, 1948, 96-149 с.

5.

Гейтинг А. Интуиционизм, -М.: МИР, 1965.

6.

Горбатов В.А. Семантическая теория проектирования автоматов. -М.: Энергия, 1979.           

7.

Горбатов В.А., Кафаров В.В., Павлов П.Г. Логическое управление технологическими процессами. -М.: Энергия, 1978.

8.

Горбатов В.А., Останков Б.Л., Фролов С.А. Регулярные структуры автоматного управления /Под ред. В.А.Горбатова. -М.: Машиностроение, 1980.

9.

Горбатов В. А.  Основы дискретной математики. –М.: Высшая школа, 1986, -311 с.

10.

Горбатов В.А., Павлов П.Г., Четвериков В.Н. Логическое управление информационными процессами. -М.: Энергоатомиздат, 1984.

11.

Гиндикин С.Г. Алгебра логики в задачах. –М.: Наука, 1972.

12.

Гаврилов М.А., Девятков В.В., Пупырев Е.И. Логическое проектирование дискретных автоматов. –М.: Наука, 1977, -352 с.

13.

Ёкубов Т. Математик мантик элементлари. -Тошкент: Укитувчи, 1983, 159 б.

14.

Т.Ёкубов, С.Каллибеков. Математик мантик элементлари. Тошкент, Укитувчи, 1996 й, -272 б.

15.

Ершов Ю.Л., Палютин Е.А. Математическая логика. –М.: Наука, 1979.

16.

Журавлёв Ю.И., Мазурик В.П., Столяров Л.Н. Элементы математической логики. –Д.: МФТИ, 1975, -74 с.

17.

33.А.А.Зыков. Основы теории графов. –М.: Наука, 1987, -384 c.

18.

Искандаров Р.И. Математик логика элементлари. Самарканд: СамДУ, 1970, 324б.

19.

Игошин В.И. Математическая логика и теория алгоритмов. Саратов: Изд-во Саратовского университета, 1991.

20.

Игошин В.И. Задачник-практикум по математической логике. -М.:Просвещение, 1986.

21.

Клини С.Математическая логика.-М.:МИР,1973,480с.

22.

Карри Х.Б. Основания математической логики. -М.: МИР, 1969.

23.

Кондаков Н.И. Введение в логику. -М.: Наука, 1967. -466 с.

24.

Каменский М.И., Петрова Л.П., Садовский Б.Н. Математическая логика. –М.: МГУ, 1982, -62 с.

25.

Калбертсон Т. Математика и логика цыфровых устройств. –М.: Просвещение, 1965.

26.

Кудрявцев В.Б. а) Теорема полноты для одного класса автоматов без обратных связей. -Проблемы кибернетики, Вып.8. -М.: Физматгиз, 1962, С.91-116. б) О мощностях множеств предполных множеств некоторых функциональных систем, связанных с автоматами. –Проблемы кибернетики, Вып.13. -М.: Наука, 1965, С.45-74.

27.

Колдуэлл С. Логический синтез релейных устройств. -М.: 1961.

28.

Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. -М.: Наука, 1975.

29.

Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. -Санкт-Петербург: Лань, 1999, 286 с.

30.

Лупанов О.Б. а)О синтезе некоторых классов уп-равляющих систем. Сб. “Проблемы кибернетики”, Вып.10. –М.: Физматгиз, 1963, 88-96 с. б)Об одном подходе к синтезу управляющих систем-принципы локального кодирования. - Проблемы кибернетики, Вып.14. -М.: Наука, 1965, С.31-110. в)Об возможнос-тях синтеза схем из произвольных элементов. -Труды МИАН СССР, 51, 1958, С.158-183.

31.

Ляпунов А.А. О логических схемах программ. -Проблемы кибернетики, Вып.1. -М.: Физматгиз, 1958, С.46-74.

32.

Лазарев В.Г, Пийль Е.И. Синтез управляющих автоматов. -М.: Энергия, 1978.

33.

Мальцев А.И. Алгоритмы и рекурсивные функции. –М.: Наука, 1965.

34.

Мальцев А.И. Алгебраические системы. –М.: Наука, 1970.

35.

Марков А.А. Теория алгорифмов. Труды математического института АН СССР им. В.А.Стеклова, XLII, АН РФ, 1954.

36.

Марков А.А. Невозможность некоторых алгорифмов в теории ассоциативных систем, ДАН СССР, 55, 1947, 587-590 с.

37.

Марков А.А. Невозможность некоторых алгорифмов в теории ассоциативных систем, ДАН СССР, 58, 1947, 353-356 с. 

38.

Матиясевич Ю.В. Диофантовость перечислимых множеств, ДАН СССР, 191, 1970, 279-282 с.

39.

Мендельсон Э. Введение в математическую логику. –М.: Наука, 1976, 320 с.

40.

Михайлов А.Б., Плоткин А.И. Введение в алгебру и математический анализ. Сборник задач. 1. Высказывания. Предикаты. Множества. -Санк-Петербург: 1992.

41.

Новиков П.С. Конструктивная математическая логика с точки зрения классической.-М.:Наука, 1977.

42.

Новиков П.С. Элементы математической логики. –М.: Наука, 1973.

43.

Поспелов Д.А. Логико-лингвистические модели в системах управления. –М.: Энергия, 1981.

44.

Оре О. Теория графов. –М.: Наука, 1980, -336 с.

45.

Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. –М.: МИР, 1972.

46.

Трахтенброт Б.А. Алгоритмы и машинное решение задач. –М.: Физматдиз, 1960.

47.

Тураев Х.Т. Математик мантик ва дискрет математика I-кисм. -Самарканд: СамДУ, 2000, 174 б.; II-кисм. -Самарканд: СамДУ, 2001, 201 б.

48.

Л.Р.Форд., Д.Р.Фалкерсон.-Потоки в сетях. -Москва: Мир, 1966, -276 c.

49.

Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. –М.:Наука, 1960, -400 с.

50.

Шестаков В.И. Математическая логика и автомати-ка. “Математика в школе”, 1958, № 6., 1959, № 1.

51.

Шеннон К.Э. Работы по теории информации и кибернетики. –М.: ИЛ, 1963.

52.

Чёрч А. Введение в математическую логику, том 1, -М.: ИЛ, 1961.

53.

Чудновский Г.В. Диофантовы предикаты, УМН, 25, №4, 1970, 185-186 с.

54.

Чегис И.А., Яблонский С.В. Логические способы контроля работы электрических схем. –М.: Труды МИАН СССР, 51, 1958, С.270-360.

55.

Угрюмов Е.П. Проектирование элементов  и узлов ЭВМ. –М.: Высшая школа, 1987. -318 с.

56.

Яблонский С. В. Введение в дискретную математику. -Москва: Наука, 1979, -272 с.

57.

Яблонский С. В., Лупанов О. Б.  и др. Дискретная математика и математические вопросы кибернетики. Т.I. –М.: Наука, 1974, -312 с.

58.

Яблонский С.В. Основы алгебры логики и теории контактных схем. –М.: Тр. института математики им. Стеклова, 1958, т. 51.

59.

Яблонский С.В. а)Функциональные построения в k-значной логике.–М.:Труды МИАН СССР,51,1958, С.5-142. б) Методические разработки по курсу “Элементы дискретной математики”.-М.:МГУ,1971.

60.

Яблонский С.В., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры логики и классы Поста. -М.: Наука, 1966.

61.

Государственный стандарт Узбекистана. Высшее образование. Требования к обязательному минимуму содержания и уровню подготовки бакалавра по направлению В480100 – Прикладная математика и информатика. –Ташкент: 1999. с.13-14.

62.

Государственный стандарт Узбекистана. Высшее образование. Требования к обязательному минимуму содержания и уровню подготовки бакалавра по направлению В140100 – Математика и информатика. –Ташкент: 1999. с.18.

63.

Государственный стандарт Узбекистана. Высшее образование. Требования к обязательному минимуму содержания и уровню подготовки бакалавра по направлению В522600 – Информатика и информационная технология. –Ташкент: 1999. с.11.

64.

Государственный стандарт Узбекистана. Высшее образование. Требования к обязательному минимуму содержания и уровню подготовки бакалавра по направлению В460100 – Математика. –Ташкент: 1999. с.12.

65.

Кобулов В.К. Ракамли автоматлар. –Ташкент: 1980. –206 б.