Самарканд давлат университети 4

IV-БОБ. ПРЕДИКАТЛАР МАНТИКИ

Куйидаги бобда предикатлар мантики баён этилган. Бу ерда предикат тушунчаси, предикатлар устида мантикий амаллар, умумийлик ва мавжудлик кванторлари, предикатлар мантикининг формуласи ва унинг киймати, предикатлар мантикининг тенгкучли формулалари, предикатлар мантики формуласининг нормал шакли, бажарилувчи ва умумкийматли формулалар, ечилиш муаммоси, хусусий холларда формуланинг умумкийматлилигини топиш алгоритмлари, предикатлар мантикининг математикага тадбики, аксиоматик предикатлар хисоби хакида маълумотлар келтирилади.

1-§. Предикат тушунчаси. Предикатлар устида мантикий амаллар

Предикат. -Предикатлар мантики. -Бир жойли предикат. -Куп жойли предикат. -Предикатнинг чинлик туплами. -Айнан чин предикат. -Айнан ёлгон предикат. -Предикатлар устида мантикий амаллар.

1.1. Предикат тушунчаси

Мантик алгебрасида мулохазалар факатгина чин ёки ёлгон киймат олиши нуктаи назаридан каралади. Мулохазаларнинг на структураси ва хатто на мазмуни каралмайди. Аммо фанда ва амалиётда мулохазаларнинг структураси ва мазмунидан келиб чикадиган хулосалардан (натижалардан) фойдаланилади.

Масалан, «Хар кандай ромб параллелограммдир; -ромб; демак, - параллелограмм». Асос (шарт) ва хулоса мулохазалар мантикининг элементар мулохазалари булади ва уларни бу мантик нуктаи назаридан булинмас, бир бутун деб ва уларнинг ички структурасини хисобга олмасдан каралади. Шундай килиб, мантик алгебраси мантикнинг мухим кисми булишига карамасдан, купгина фикрларни анализ килишга кодир (етарли) эмас.

Шунинг учун хам мулохазалар мантикини кенгайтириш масаласи вужудга келди, яъни элементар мулохазаларнинг ички структурасини хам тадкик эта оладиган мантикий системани яратиш муаммоси пайдо булди.

Бундай система мулохазалар мантикини узининг бир кисми сифатида бутунлайига уз ичига оладиган предикатлар мантикидир.

Предикатлар мантики анъанавий формал мантик сингари элементар мулохазани субъект ва предикат кисмларга булади.

Субъект – бу мулохазада бирор нарса хакида нимадир тасдиклайди; предикат – бу субъектни тасдиклаш.

Масалан, «5 - туб сон» мулохазасида «5» - субъект, «туб сон» - предикат. Бу мулохазада «5» «туб сон булиш» хусусиятига эга эканлиги тасдикланади.

Агар келтирилган мулохазада маълум 5 сонини натурал сонлар тупламидаги узгарувчи билан алмаштирсак, у холда « - туб сон» куринишидаги мулохаза формасига (шаклига) эга буламиз. узгарувчининг бир хил кийматлари (масалан, =13, =3, =19) учун бу форма чин мулохазалар ва узгарувчининг бошка кийматлари (масалан, =10, =20) учун бу форма ёлгон мулохазалар беради.

Аникки, бу форма бир аргументли функцияни аниклайди. Бу функциянинг аниклаш сохаси натурал сонлар туплами ва кийматлар сохаси туплам булади.

1-таъриф. тупламда аникланган ва тупламдан киймат кабул килувчи бир аргументли функцияга бир жойли (бир уринли) предикат деб айтилади.

тупламга предикатнинг аникланиш сохаси деб айтамиз.

предикат чин киймат кабул килувчи хамма элементлар тупламига предикатнинг чинлик туплами деб айтилади, яъни предикатнинг чинлик туплами - тупламдир.

Масалан, «-туб сон» - предикати натурал сонлар тупламида аникланган ва унинг чинлик туплами хамма туб сонлар тупламидан иборат. «» - предикати хакикий сонлар тупламида аникланган ва унинг чинлик туплами . «Параллелограмм диагоналлари бир-бирига перпендикулярдир» - предикатнинг аникланиш сохаси хамма параллелограммлар туплами ва чинлик туплами хамма ромблар туплами булади.

Бир жойли предикатларга юкорида келтирилган мисоллар предметларнинг хусусиятларини ифодалайди.

2-таъриф. Агар тупламда аникланган предикат учун булса, у айнан чин (айнан ёлгон) деб айтилади.

Энди куп жойли предикат тушунчасини аниклаймиз. Куп жойли предикат предметлар орасидаги муносабатни аниклайди.

«Кичик» муносабати икки предмет орасидаги бинар муносабатни ифодалайди. «» (бу ерда ) бинар муносабат икки аргументли функцияни ифодалайди. Бу функция тупламда аникланган ва кийматлар сохаси туплам булади.

3-таъриф. тупламда аникланган ва тупламдан киймат олувчи икки аргументли функцияга икки жойли предикат деб айтилади.

Масалан, «» - икки жойли предикат тупламда аникланган; «» - тугри чизик тугри чизикка перпендикуляр - икки жойли предикат бир текисликда ётувчи тугри чизиклар тупламида аникланган.

- жойли предикат хам худди шундай аникланади.

1-мисол. Куйида берилган мулохазаларнинг кайси бири предикат булишини ва уларнинг чинлик тупламини аникланг. Бир жойли предикатларнинг аникланиш сохаси ва икки жойли предикатлар учун аникланиш сохаси булсин:

1) ; 2) ; 3) ;

4) ; 5) .

Ечим. 1) Берилган ифода бир жойли предикат булади ва ;

2) Ифода билан берилган мулохаза бир жойли предикат булади ва ;

3) Ифода билан берилган мулохаза бир жойли предикат булади ва ;

4) Ифода билан берилган мулохаза предикат булмайди;

5) Берилган ифода икки жойли предикат булади ва .

2-мисол. Куйидаги предикатларнинг кайси бирлари айнан чин булишини аникланг:

1) ; 2) ; 3) ;

4) ; 5) .

Ечим. Равшанки, 1), 3) ва 4) предикатлар айнан чин буладилар. 2) предикатда кийматларида тенгсизлик бузилади. 5) предикатда булса, нинг хамма мусбат кийматларида тенгсизлик ишораси бузилади. Демак, 2) ва 5) предикатлар айнан чин предикатлар була олмайди.

3-мисол. тупламда ва предикатлар берилган булсин. предикатнинг чинлик тупламини топинг ва уни Эйлер доира-лари оркали ифодаланг.

Ечим.

= булганлиги учун

чинлик туплами расмда штрихланган соха сифатида курсатилган

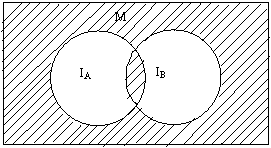1.2. Предикатлар устида мантикий амаллар

Предикатлар хам мулохазалар сингари факатгина чин ва ёлгон (1,0) киймат кабул килганликлари туфайли улар устида мулохазалар мантикидаги хамма мантикий амалларни бажариш мумкин.

Бир жойли предикатлар мисолида мулохазалар мантикидаги мантикий амалларнинг предикатларга татбик этилишини курайлик.

тупламда ва предикатлар аникланган булсин.

4-таъриф. Берилган тупламда аникланган ва предикатларнинг конъюнкцияси деб, факат ва факат нинг кийматларида ва лар бир вактда чин киймат кабул килгандагина чин киймат кабул килиб, колган барча холларда ёлгон киймат кабул килувчи янги предикатга айтилади ва у каби белгиланади.

предикатнинг чинлик сохаси тупламдан, яъни ва предикатлар чинлик сохаларининг умумий кисмидан иборат булади.

Масалан, : « - жуфт сон» ва : « - ток сон» предикатлар учун «-жуфт сон ва -ток сон»: предикатлар конъюнкцияси мос келади ва унинг чинлик сохаси - буш тупламдан иборат булади.

5-таъриф. Берилган тупламда аникланган ва предикатларнинг дизъюнкцияси деб, факат ва факатгина нинг кийматларида аникланган ва предикатлар ёлгон киймат кабул килганда ёлгон киймат кабул килиб, колган барча холларда чин киймат кабул килувчи янги предикатга айтилади ва у каби белгиланади.

предикатнинг чинлик сохаси тупламдан иборат булади.

6-таъриф. Агар хамма кийматларда предикат чин киймат кабул килганда ёлгон киймат ва нинг барча кийматларида предикат ёлгон киймат кабул килганда чин киймат кабул килувчи предикатга предикатнинг инкори деб айтилади ва у каби белгиланади.

Бу таърифдан келиб чикади.

7-таъриф. Факат ва факатгина лар учун бир вактда чин киймат ва ёлгон киймат кабул килганда ёлгон киймат кабул килиб, колган хамма холларда чин киймат кабул киладиган предикатга ва предикатларнинг импликацияси деб айтилади.

Хар бир тайинланган учун

тенгкучлилик тугри булганлигидан уринлидир.

2-§. Умумийлик ва мавжудлик кванторлари

Умумийлик квантори. -Мавжудлик квантори. -Кванторли амаллар билан конъюнкция ва дизъюнкция амаллари уртасидаги муносабат.

тупламда аникланган предикат берилган булсин. Агар ни предикатнинг аргументи урнига куйсак, у холда бу предикат мулохазага айланади.

Предикатлар мантикида яна иккита амал мавжудки, улар бир жойли предикатни мулохазага айлантиради.

2.1.Умумийлик квантори. тупламда аникланган предикат берилган булсин. Хар кандай учун чин ва акс холда ёлгон киймат кабул килувчи мулохаза ифодасини формада ёзамиз. Бу мулохаза энди га боглик булмай колади ва у куйидагича укилади: «Хар кандай учун чин». символ умумийлик квантори деб айтилади. Айтилган фикрларни математик тилда куйидагича ёзиш мумкин:

предикатда ни эркин (озод) узгарувчи ва мулохазада ни умумийлик квантори билан богланган узгарувчи деб айтилади.

2.2.Мавжудлик квантори. предикат тупламда аникланган булсин. Хеч булмаганда бирорта учун предикат чин ва акс холда ёлгон киймат кабул килувчи мулохаза ифодасини шаклда ёзамиз. Бу мулохаза га боглик эмас ва уни куйидагича укиш мумкин: «Шундай мавжудки, », яъни

cимвол мавжудлик квантори деб аталади. мулохазада узгарувчи квантори билан богланган булади.

Масалан, натурал сонлар тупламида предикат берилган булсин: « - туб сон». Кванторлардан фойдаланиб ушбу предикатдан куйидаги мулохазаларни хосил килиш мумкин: - «Хамма натурал сонлар туб сонлар булади»; - «Шундай натурал сон мавжудки, у туб сон булади». Равшанки, биринчи мулохаза ёлгон ва иккинчи мулохаза чин булади.

Маълумки, мулохаза факат айнан чин предикат булгандагина чин киймат кабул килади. мулохаза булса, айнан ёлгон предикат булгандагина ёлгон киймат кабул килади.

Кванторли амаллар куп жойли предикатларга хам кулланилади. Масалан, тупламда икки жойли предикат берилган булсин. Агар предикатга узгарувчи буйича кванторли амалларни кулласак, у холда икки жойли предикатга бир жойли (ёки бир жойли ) предикатни мос килиб куяди.

Бир жойли () предикат факат узгарувчига боглик ва узгарувчига боглик эмас булади. Уларга буйича кванторли амалларни куллаганимизда куйидаги мулохазаларга эга буламиз:

, , , .

Масалан, тугри чизиклар тупламида аникланган : «» предикатни курайлик. Агар предикатга нисбатан кванторли амалларни тадбик этсак, у холда куйидаги саккизта мулохазага эга буламиз:

1. - «Хар кандай тугри чизик хар кандай тугри чизикка перпендикуляр».

2. - «Шундай тугри чизик мавжудки, у хар кандай тугри чизикка перпендикулярдир».

3. - «Хар кандай тугри чизик учун шундай тугри чизик мавжудки, тугри чизиги тугри чизикка перпендикуляр».

4. - «Шундай тугри чизик ва шундай тугри чизик мавжудки, тугри чизик тугри чизикка перпендикуляр».

5. - «Хар кандай тугри чизик хар кандай тугри чизиккга перпендикуляр».

6. - «Хар кандай тугри чизик учун шундай тугри чизик мавжудки, тугри чизик тугри чизиккга перпендикуляр».

7. - «Шундай тугри чизик ва шундай тугри чизик мавжудки, тугри чизик тугри чизикка перпендикуляр».

8. - «Шундай тугри чизик мавжудки, у хар кандай тугри чизикка перпендикуляр».

Бу мисоллардан куриниб турибдики, умумий холда кванторлар тартиби узгариши билан мулохазанинг мазмуни ва демак, унинг мантикий киймати хам узгаради.

Чекли сон элементлари булган тупламда аникланган предикат берилган булсин. Агар предикат айнан чин булса, у вактда мулохазалар хам чин булади. Шу холда мулохаза ва конъюнкция хам чин буладилар.

Агар хеч булмаганда бирорта элемент учун ёлгон булса, у холда мулохаза ва конъюнкция хам ёлгон булади.

Демак,

тенгкучли ифода тугри булади.

Юкоридагидек фикр юритиш йули билан

тенгкучли ифоданинг мавжудлигини курсатиш мумкин.

Бу ердан кванторли амалларни чексиз сохаларда конъюнкция ва дизъюнкция амалларининг умумлашмаси сифатида караш мумкинлиги келиб чикади.

РЕЖА:

1.Предикат тушунчаси. Предикатлар устида

мантикий амаллар.

2.Умумийлик ва мавжудлик кванторлари.

Муаммоли масала ва топшириклар:

1. тупламда иккита : «- туб сон» ва : «- ток сон» предикатлар берилган. Бу предикатларнинг чинлик жадвалини тузинг.

2. тупламда куйидаги предикатлар берилган: : « 5 га булинмайди»; : «- жуфт сон»; : «- туб сон»; : « 3 га каррали».

Куйидаги предикатларнинг чинлик тупламини топинг:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ;

9) ; 10) ; 11) ;

12) ; 13) ; 14) ;

15) ; 16) ;

17) ; 18) ;

19) ; 20) .

3. тупламда : ва : предикатлар берилган булсин. Куйидаги мулохазаларнинг кайси бирлари чин ва кайси бирлари ёлгон эканлигини аникланг:

1) ; 2) ; 3) ; 4) .

4. Куйидаги предикатларнинг кайси бирлари айнан чин кийматга эга б¢лади:

1) , 2) , 3) ,

4) , 5)

Мустакил ишлаш учун саволлар:

1.Предикат тушунчаси. Предикатлар устида ман-

тикий амаллар.

2.Умумийлик ва мавжудлик кванторлари.

3.Бир жойли ва куп жойли предикатлар.

4.Предикатнинг чинлик туплами.

5.Айнан чин ва айнан ёлгон предикатлар.

3-§. Предикатлар мантикининг формуласи. Предикатлар мантики формуласининг киймати. Предикатлар мантикининг тенгкучли формулалари

Предикатлар мантикининг символлари. -Формуланинг таърифи. -Формуланинг киймати тушунчаси. -Тенгкучли формулалар. -Асосий тенгкучли формулалар. -Тенгкучли формулаларнинг исботлари.

Предикатлар мантикида куйидаги символлардан фойдаланамиз:

1. символлар – 1 (чин) ва 0 (ёлгон) кийматлар кабул килувчи узгарувчи мулохазалар.

2. - кандайдир тупламдан киймат олувчи предмет узгарувчилар; - предмет константалар, яъни предмет узгарувчиларнинг кийматлари.

3. - бир жойли узгарувчи предикатлар; , - жойли узгарувчи предикатлар.

4. - узгармас предикатлар символи.

5. - мантикий амаллар символлари.

6. - кванторли амаллар символлари.

7.( , ) (кавс, вергул) – кушимча символлар.

3.1. Предикатлар мантики формуласининг таърифи

1.Хар кандай узгарувчи ёки узгармас мулохаза формула (элементар) булади.

2.Агар --жойли узгарувчи предикат ёки узгармас предикат ва - предмет узгарувчилар ёки предмет константалар булса, у холда формула булади. Бундай формулага элементар формула деб айтамиз. Бу формулада предмет узгарувчилар эркин булади, яъни кванторлар билан богланган булмайди.

3.Агар ва шундай формулаларки, бирорта предмет узгарувчи бирида эркин ва иккинчисида богланган узгарувчи булмаса, у холда , , лар хам формула булади. Бу формулаларда дастлабки формулаларда эркин булган узгарувчилар эркин ва богланган булган узгарувчилар богланган узгарувчилар булади.

4.Агар формула булса, у холда хам формула булади. формуладан формулага утишда узгарувчиларнинг характери узгармайди.

5.Агар формула булса ва унинг ифодасига предмет узгарувчи эркин холда кирса, у холда ва мулохазалар формула булади ва предмет узгарувчи уларга богланган холда киради.

6.1-5 бандларда формулалар деб айтилган мулохазалардан фарк килувчи хар кандай мулохаза формула булмайди.

Масалан, агар ва - бир жойли ва икки жойли предикатлар, - узгарувчи мулохазалар булса, у холда куйидаги мулохазалар формулалар булади:

, , , , .

мулохаза формула булаолмайди, чунки таърифнинг 3-банддаги шарт бузилган: предмет узгарувчи формулага богланган холда кирган ва га эса эркин холда кирган.

Предикатлар мантики формуласининг таърифидан куриниб турибдики, мулохазалар алгебрасининг хар кандай формуласи предикатлар мантикининг хам формуласи булади.

1-мисол. Куйидаги ифодаларнинг кайси бири предикатлар мантикининг формуласи булади? Хар бир формуладаги богланган ва эркин узгарувчиларни аникланг.

1) ;

2) ;

3) ;

4);

5) ;

6) .

Ечим. 1), 2), 4), 6) ифодалар формула буладилар, чунки улар предикатлар мантики формуласининг таърифи асосида хосил этилган. 3) ва 5) ифодалар формула эмас. 3) ифодада амали ва формулаларга нисбатан кулланилган. да предмет узгарувчи эркин ва да булса умумийлик квантори билан богланган. Бу холат формула таърифининг 3-бандига зиддир. Шунинг учун 3) ифода формула булаолмайди. 5) ифодада булса, мавжудлик квантори умумийлик квантори такалган формулага (бу ерда узгарувчи богланган) таркалган. Бу хам таърифга зиддир. 1) формулада у эркин узгарувчи, ва узгарувчилар булса боглангандирлар. 2) формулада предмет узгарувчилар мавжуд эмас. 4) формулада богланган узгарувчи, эса эркин узгарувчидир.

3.2. Предикатлар мантики формуласининг киймати тушунчаси

Энди предикатлар мантики формуласининг киймати тушунчасини аниклайлик.

Качонки предикатлар мантики формуласининг ифодасига кирувчи предикатларнинг аникланиш сохаси туплам берилган булса, шундагина бу формуланинг мантикий киймати хакида суз юритиш мумкин. Предикатлар мантики формуласининг мантикий киймати уч хил узгарувчилар: 1) формулага кирувчи узгарувчи мулохазаларнинг; 2) тупламдаги эркин предмет узгарувчиларнинг; 3) предикат узгарувчиларнинг кийматларига боглик булади.

Уч хил узгарувчилардан хар бирининг маълум кийматларида предикатлар мантикининг формуласи чин ёки ёлгон киймат кабул килувчи мулохазага айланади.

Мисол сифатида куйидаги формулани курайлик:

. (1)

(1) формулада икки жойли предикат тупламда аникланган, бу ерда .

(1) формула ифодасига узгарувчи предикат , ва предмет узгарувчилар лар кирган. Бу ерда ва лар кванторлар билан богланган узгарувчилар, - эркин узгарувчи.

предикатнинг маълум киймати сифатида тайинланган :«» предикатни оламиз, эркин узгарувчи га киймат берамиз. У вактда нинг дан кичик кийматлари учун предикат ёлгон киймат кабул килади, импликация эса нинг хамма кийматлари учун чин булади, яъни мулохаза «чин» кийматга эга булади.

2-мисол. Натурал сонлар туплами да ва предикатлар берилган булсин.

формуланинг киймати куйидаги холларда топилсин:

1) : « сони 3 га булинади», : « сони 4 га булинади», : « сони 2 га булинади» ;

2) : « сони 3 га булинади», : « сони 4 га булинади”, : « сони 5 га булинади».

Ечим. Икки холда хам формула сони 12 га булинади деган тасдикни ифодалайди. Уз навбатида хамма лар учун сони 12 га булинса, у холда сони 2 га хам булинади. Демак, 1) холда формуланинг киймати чин булади.

сонининг 12 га булинишидан айрим лар учун нинг 5 га булиниши, бундан эса 2 - холда формуланинг ёлгон эканлиги келиб чикади.

3-мисол. предикат тупламда аникланган ва : « сони сонидан кичик» булганда формуланинг мантикий кийматини топинг.

Ечим. предикатнинг курсатилган киймати учун : «хар кандай натурал сон учун шундай натурал сон топиладики, у дан катта булади” деган чин мулохазани билдиради. Шу вактнинг узида : «Шундай натурал сон мавжудки, у хар кандай натурал сон дан кичик булади” деган тасдикни билдиради. Бу тасдик ёлгондир. Демак, берилган формуланинг мантикий киймати ёлгон булади.

3.3. Предикатлар мантикининг тенгкучли формулалари

Предикатлар мантикида хам тенгкучли формулалар тушунчаси мавжуд.

1-таъриф. Предикатлар мантикининг иккита ва формулалари уз таркибига кирувчи сохага оид хамма узгарувчиларнинг кийматларида бир хил мантикий киймат кабул килсалар, улар сохада тенгкучли формулалар деб айтилади.

2-таъриф. Агар ихтиёрий сохада ва формулалар тенгкучли булсалар, у холда улар тенгкучли формулалар деб айтилади ва куринишда ёзилади.

Агар мулохазалар алгебрасидаги хамма тенгкучли формулалар ифодасидаги узгарувчи мулохазалар урнига предикатлар мантикидаги формулалар куйилса, у холда улар предикатлар мантикининг тенгкучли формулаларига айланади. Аммо, предикатлар мантики хам узига хос асосий тенгкучли формулаларга эга. Бу тенгкучли формулаларнинг асосийларини куриб утайлик. ва - узгарувчи предикатлар ва - узгарувчи мулохаза булсин. У холда предикатлар мантикида куйидаги асосий тенгкучли формулалар мавжуд:

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

11. ,

12. ,

13. ,

14. ,

15. ,

16. ,

17. .

Бу тенгкучли формулаларнинг айримларини исбот килайлик.

Биринчи тенгкучли формула куйидаги оддий тасдикни (далилни) билдиради: агар хамма лар учун чин булмаса, у холда шундай топиладики, чин булади.

2-тенгкучлилик: агар чин буладиган мавжуд булмаса, у холда хамма лар учун чин булади деган мулохазани билдиради.

3 ва 4 – тенгкучлиликлар 1 ва 2 – тенгкучлиликларнинг иккала тарафидан мос равишда инкор олиб ва икки марта инкор конунини фойдаланиш натижасида хосил булади.

5-тенгкучлиликни исбот килайлик. Агар ва предикатлар бир вактда айнан чин булсалар, у холда предикат хам айнан чин булади ва демак,

, ,

мулохазалар хам чин киймат кабул киладилар.

Шундай килиб, бу холда 5-тенгкучлиликнинг иккала тарафи хам «чин» киймат кабул киладилар.

Энди хеч булмаганда икки предикатдан бирортаси, масалан, айнан чин булмасин. У холда предикат хам айнан чин булмайди ва демак, , , мулохазалар ёлгон киймат кабул киладилар, яъни бу холда хам 5-тенгкучлиликнинг икки тарафи бир хил (ёлгон) киймат кабул киладилар. Демак, 5-тенгкучлиликнинг тугри эканлиги исботланди.

Энди 8-тенгкучлиликнинг тугри эканлигини исбот килайлик. Узгарувчи мулохаза «ёлгон» киймат кабул килсин. У холда предикат айнан чин булади ва , мулохазалар чин буладилар. Демак, бу холда 8-тенгкучлиликнинг иккала тарафи хам бир хил (чин) киймат кабул киладилар.

Энди узгарувчи мулохаза «чин» киймат кабул килсин. Агар бу холда узгарувчи предикат айнан чин булса, у вактда предикат хам айнан чин булади ва демак,

, ,

мулохазалар хам чин киймат кабул киладилар, яъни бу холда 8-тенгкучлиликларнинг иккала тарафи хам бир хил (чин) киймат кабул киладилар.

Агар предикат айнан чин булмаса, у холда предикат хам айнан чин булмайди ва демак,

, ,

мулохазалар ёлгон киймат кабул киладилар.

Шундай килиб, бу холда хам 8-тенгкучлиликларнинг иккала тарафи бир хил (ёлгон) киймат кабул киладилар. Демак, 8-тенгкучлилик уринлидир.

Шуни таъкидлаб утамизки, формула формулага ва формула формулага тенгкучли эмаслар.

Аммо, куйидаги тенгкучлиликлар уринлидир:

Бу тенгкучлиликлардан биринчисини исбот килайлик. Бунинг учун квантор дизъюнкция амалига нисбатан дистрибутив эмаслигини мисолда курсатайлик.

, :«»,

: «»

булсин.

Аникки, сохада ва мулохазалар ёлгон ва демак, бу тенгкучлиликнинг чап томонидаги мулохаза хам ёлгондир. Агар квантор га нисбатан дистрибутив, яъни

булганда эди, чин мулохаза булганлиги учун карама-каршилик хосил буларди.

Демак, булади.

Энди бу тенгкучлиликларнинг унг томони хар доим чап томонидаги мулохаза билан бир хил киймат кабул килишини курсатамиз.

Агар ёки булса, у холда бу тенгкучлилик тугри эканлиги аник, чунки бу холда тенгкучлиликнинг иккала томони хам бир вактда чин киймат кабул киладилар. Бу холда факат эканлигини курсатиш кифоя. Аммо бу охирги тенгкучлилик табиийдир, чунки предмет узгарувчи хам, предмет узгарувчи хам соханинг хар бир элементини киймат сифатида кабул килади.

Энди ва булсин. У холда тенгкучлиликнинг чап тарафи 0 (ёлгон) киймат кабул килади. Унг томонида кванторнинг таъсир сохаси формула булсада, предикатда предмет узгарувчи катнашмаганлиги сабабли, нинг таъсири факат га таркалади. Худди шундай, квантор факат га таъсир этади. Демак, формула хам ёлгон кийматга эга булади.

Келтирилган иккинчи тенгкучлиликни хам худди шундай исбот килиш мумкин ва буни укувчига хавола этамиз.

4-мисол. тенгкучлилик уринли эканлигиникурсатинг.

Ечим. ,

Демак, келтирилган тенгкучлилик уринли экан.

4-§. Предикатлар мантики формуласининг нормал шакли. Бажарилувчи ва умумкийматли формулалар

Формуланинг деярли нормал шакли. -Формуланинг нормал шакли. -Хар кандай формулани нормал шаклга келтириш. -Бажарилувчи формулалар. -Умумкийматли формулалар. - Айнан чин формула. -Айнан ёлгон формула. -Мантик конуни. -Умумкийматли ва бажарилувчи формулалар хакидаги теоремалар.

4.1. Предикатлар мантики формуласининг нормал шакли

1-таъриф. Агар предикатлар мантики формуласи ифодасида факат инкор, конъюнкция, дизъюнкция амаллари ва кванторли амаллар катнашиб, инкор амали элементар формулаларга (предмет узгарувчилар ва узгарувчи предикатларга) тегишли булса, бундай формула деярли нормал шаклда дейилади.

Равшанки, предикатлар мантики ва мулохазалар алгебрасидаги асосий тенгкучлиликлардан фойдаланиб, предикатлар мантикининг хар бир формуласини деярли нормал шаклга келтириш мумкин. Масалан,

формулани деярли нормал шаклга келтирайлик.

Демак,

Предикатлар мантикининг деярли нормал шаклдаги формулалари орасида нормал шаклдаги формулалари мухим рол уйнайди.

Бу формулаларда кванторли амаллар ёки бутунлай катнашмайди, ёки улар мулохазалар алгебрасининг хамма амалларидан кейин бажарилади, яъни нормал шаклдаги формула куйидаги куринишда булади:

, ,

бунда символи урнига ёки кванторларнинг бири тушунилади ва формула ифодасида кванторлар булмайди.

1-теорема. Предикатлар мантикининг хар кандай формуласини нормал шаклга келтириш мумкин.

Исбот. Формула деярли нормал шаклга келтирилган деб хисоблаймиз ва уни нормал шаклга келтириш мумкинлигини курсатамиз.

Агар бу формула элементар формула булса, у холда унинг ифодасида кванторлар булмайди ва, демак, у нормал шакл куринишида булади.

Энди фараз киламизки, теорема купи билан амални камраган формула учун тугри булсин ва уни шу фараз асосида амални камраган формула учун исбот киламиз.

амални уз ичига олган формула ва унинг куриниши шаклда булсин. Бу ерда кванторларнинг бирини ифодалайди.

формула амални уз ичига олганлиги туфайли уни нормал шаклга келтирилган деб хисоблаймиз. У вактда формула таърифга асосан нормал шаклда булади.

формула куринишда булсин, бунда формула нормал шаклга келтирилган ва амални уз ичига олган деб хисобланади. У холда

ва

тенгкучлиликлардан фойдаланиб, инкор амалини предикатлар устига туширамиз. Натижада формулани нормал шаклга келтирган буламиз.

Энди формула куринишда булсин. Бу ерда ва лар нормал шаклга келтирилган формулалар деб каралади.

формулада богланган предмет узгарувчиларни шундай кайта номлаймизки, ва формулалардаги хамма богланган предмет узгарувчилар хар хил булсин. У вактда ва формулаларни куйидаги куринишда ёзиш мумкин:

, ,

, .

ва

тенгкучлиликлардан фойдаланиб, формулани квантор амаллари остига киритамиз, яъни формулани ушбу куринишга келтирамиз:

Сунгра формулани

квантор амаллари остига киритамиз. Натижада формуланинг нормал шаклини хосил киламиз:

куринишидаги формулани нормал шаклга келтиришнинг исботи худди юкорида каби булади.

Агар формулани нормал шаклга келтириш жараёнида ёки куринишдаги ифодаларни куришга тугри келса, у холда

ва

тенгкучлиликлардан фойдаланиш керак булади.

1-мисол. формулани нормал шаклга келтириш талаб этилсин. формулада тенгкучли алмаштиришларни утказиб, уни нормал шаклга келтирамиз:

4.2.Бажарилувчи ва умумкийматли формулалар

2-таъриф. Агар формула ифодасига кирувчи ва сохага оид узгарувчиларнинг шундай кийматлари мавжуд булиб, бу кийматларда формула чин киймат кабул килса, у холда предикатлар мантикининг формуласи сохада бажарилувчи формула деб айтилади.

3-таъриф. Агар шундай соха мавжуд булиб, унда формула бажариладиган булса, у вактда бажарилувчи формула деб айтилади.

Демак, агар бирор формула бажарилувчи булса, бу хали унинг исталган сохада бажарилувчанлигини билдирмайди.

4-таъриф. Агар нинг ифодасига кирувчи ва сохага оид хамма узгарувчиларнинг кийматларида формула чин киймат кабул килса, у холда формула сохада айнан чин формула деб айтилади.

5-таъриф. Агар формула хар кандай сохада айнан чин булса, у холда га умумкийматли формула деб айтилади.

6-таъриф. Агар ифодасига кирувчи ва сохага оид хамма узгарувчиларнинг кийматларида формула ёлгон киймат кабул килса, у холда формула сохада айнан ёлгон формула деб айтилади.

Келтирилган таърифлардан ушбу тасдиклар келиб чикади:

1. Агар умумкийматли формула булса, у холда у хар кандай сохада хам бажарилувчи формула булади.

2. Агар сохада айнан чин формула булса, у холда у шу сохада бажарилувчи формула булади.

3. Агар сохада айнан ёлгон формула булса, у холда у бу сохада бажарилмайдиган формула булади.

4. Агар бажарилмайдиган формула булса, у холда у хар кандай сохада хам айнан ёлгон формула булади.

Демак, предикатлар мантики формулаларини икки синфга ажратиш мумкин: бажарилувчи синфлар ва бажарилмас (бажарилмайдиган) синфлар формулалари.

7-таъриф. Умумкийматли формулага мантик конуни деб айтилади.

Энди бир нечта мисоллар келтирайлик:

1-мисол: формула бажарилувчидир. Хакикатан хам, агар : «» предикат сохада аникланган булса, у холда сохада айнан чин формула булади, демак, бу сохада бажарилувчи формуладир. Аммо, агар учун «» предикат чекли сохада, аникланган булса, у холда сохада айнан ёлгон формула булади ва, демак, сохада бажарилувчимасдир. Равшанки, умумкийматли формула булмайди.

2-мисол. формула бажарилувчидир. Хакикатан хам, агар : «- жуфт сон» предикат учун сохада, аникланган булса, у холда бу формула сохада айнан чин булади, демак, сохада бажарилувчи формуладир.

Аммо, агар : «- жуфт сон» предикат учун сохада аникланган булса, у холда сохада айнан ёлгон формула булади, демак, бу сохада бажарилмас формуладир.

3-мисол. формула исталган ихтиёрий сохада айнан чин булади. Демак, у умумкийматли формула, яъни мантикий конундир.

4-мисол. формула исталган ихтиёрий сохада айнан ёлгон ва шунинг учун хам у бажарилмас формула булади.

Энди предикатлар мантикидаги формулаларнинг умумкийматлиги ва бажарилувчанлиги орасидаги муносабатни куриб утайлик.

2-теорема. умумкийматли формула булиши учун унинг инкори бажарилувчи формула булмаслиги етарли ва зарурдир.

Исбот. Зарурлиги. умумкийматли формула булсин. У холда, равшанки, - исталган сохада айнан ёлгон формула булади ва шунинг учун хам у бажарилмас формуладир.

Етарлилиги. исталган сохада бажарилувчи формула булмасин. У холда бажарилмас формуланинг таърифига асосан исталган сохада айнан ёлгон формуладир. Демак, исталган сохада айнан чин формула булади ва у умумкийматлидир.

3-теорема. бажарилувчи формула булиши учун нинг умумкийматли формула булмаслиги етарли ва зарурдир.

Исбот. Зарурлиги. бажарилувчи формула булсин. У вактда шундай соха ва формула таркибига кирувчи узгарувчиларнинг шундай кийматлар мажмуи (сатри) мавжудки, формула бу кийматлар сатрида чин киймат кабул килади. Аникки, узгарувчиларнинг бу кийматлар сатрида формула ёлгон киймат кабул килади ва, демак, умумкийматли формула булаолмайди.

Етарлилиги. умумкийматли формула булмасин. У вактда шундай соха ва формула таркибига кирувчи узгарувчиларнинг шундай кийматлар сатри мавжудки, формула бу кийматлар сатрида ёлгон киймат кабул килади. Бу кийматлар сатрида формула чин киймат кабул килганлиги учун у бажарилувчи формула булади.

5-мисол. форму-ланинг умумкийматлигини исботланг.

Ечим. формула исталган сохада аникланган деб хисоблаб, тенгкучли алмаштиришларни утказамиз:

яъни формула исталган сохада хар кандай ва бир жойли предикатлар учун айнан чин, демак, у умумкийматли формуладир.

6-мисол. нинг айнан ёлгон формула эканлигини курсатинг.

Ечим. га эгамиз. айнан ёлгон формула эканлигидан, хам айнан ёлгон формула булади.

РЕЖА:

1.Предикатлар мантикининг формуласи.

2.Предикатлар мантики формуласининг кий-

мати.

3.Предикатлар мантикининг тенгкучли фор-

мулалари.

4.Предикатлар мантики формуласининг нормал

шакли.

5.Бажарилувчи ва умумкийматли формулалар.

Муаммоли масала ва топшириклар:

1. Куйидаги ифодаларнинг кайси бири предикатлар мантикининг формуласи булишини аникланг. Хар бир формуладаги эркин ва богланган узгарувчиларни курсатинг.

2. предикат тупламда аникланган ва : «» булсин.

1) Куйида берилган предикатларнинг кайсиси айнан чин ва кайсиси айнан ёлгон эканлигини аникланг:

а) ; б); в); г).

2) Куйидаги мулохазаларнинг кайси бирлари чин ва кайси бирлари ёлгон эканлигини аникланг:

а) ; б) ;

в) ; г) ;

д) ; е) ;

ж) ; з) .

3. Куйидаги тенгкучлиликларни тугри эканлигини исбот килинг:

1);

2);

3);

4);

5);

6);

7);

8);

9);

10);

11).

4. ва ихтиёрий предикатлар булсин. формулага куйида берилган формулалар-нинг кайси бири тенг кучли булади?

1); 2); 3);

4); 5); 6);

7) .

5. Куйида келтирилган формулаларнинг кайси бирлари умумкийматли?

1);

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) ;

14) ;

15) ;

16) ;

17) .

Мустакил ишлаш учун саволлар:

1.Предикатлар мантикининг символлари ва фор-

муласи.

2.Предикатлар мантики формуласининг киймати.

Тенгкучли формулалар. Асосий тенгкучли фор-

мулалар.

3.Формуланинг деярли нормал шакли. Формула-

нинг нормал шакли.

4.Хар кандай формулани нормал шаклга келти-

риш мумкинлиги.

5.Бажарилувчи ва умумкийматли формулалар.

Айнан чин ва айнан ёлгон формулалар.

6.Бажарилувчи ва умумкийматли формулалар ха-

кидаги теоремалар.

5-§. Ечилиш муаммоси. Хусусий холларда формуланинг умумкийматлигини топиш алгоритмлари

Ечилиш муаммоси. -Чекли сохаларда ечилиш муаммоси. -Ёпик формула. -Формуланинг умумий ёпилиши. -Формуланинг мавжудлигини ёпиш. -Таркибида бир турдаги квантор амали катнашувчи нормал шаклдаги формулалар учун ечилиш муаммоси.

5.1. Ечилиш муаммоси

Предикатлар мантикида ечилиш муаммоси мулохазалар алгебрасида кандай куйилган булса, худди шундай куйилади: предикатлар мантикининг исталган формуласи ёки умумкийматли, ёки бажарилувчи, ёки айнан ёлгон (бажарилмас) формула эканлигини аниклаб берувчи алгоритм мавжудми ёки йукми? Бу масала ечилиш муаммоси деб аталади. Агар бундай алгоритм мавжуд булса эди, у (худди мулохазалар алгебрасидагидай) предикатлар мантикидаги исталган формулани айнан чинлигини аниклаб берувчи критерияга келтирилган буларди.

Агар ушбу муаммо мулохазалар алгебраси учун осон ечилган булса, предикатлар мантики учун бу муаммони ечиш катта кийинчиликларга дуч келди. XX асрнинг 30-йилларида алгоритм тушунчасига аник таъриф берилгандан сунг мазкур муаммо умумий холда ижобий хал этилиши мумкин эмаслиги, яъни изланган алгоритм мавжуд эмаслиги маълум булиб колди.

1936 йилда америкалик олим А.Чёрч предикатлар мантикининг ечилиш муаммоси умумий холда алгоритмик ечилмаслигини исботлади, яъни предикатлар мантикининг исталган формуласи кайси (умумкийматли, бажарилувчи ва бажарилмас) синфга киришини аниклаб берадиган алгоритм мавжуд эмаслигини курсатди.

Ечилиш муаммоси предикатлар мантики учун ижобий ечилмасада, предикатлар мантики формулаларининг баъзи синфлари учун бу муаммо ижобий хал этилишини курсатайлик.

5.2. Чекли сохаларда ечилиш муаммоси

Ечилиш муаммоси чекли сохаларда ечилувчидир, яъни ижобий хал булади. Хакикатан хам, бу холда кванторли амалларни конъюнкция ва дизъюнкция амаллари билан алмаштириш мумкин. Натижада предикатлар мантики формуласи мулохазалар алгебраси формуласига келтирилади. Маълумки, мулохазалар алгебраси учун ечилиш муаммоси ечиладигандир.

Масалан, формула икки элементли чекли сохада аникланган булсин. У холда уни ушбу куринишга келтириш мумкин:

Хосил этилган конъюнктив нормал шаклдаги формуланинг хар бир элементар дизъюнкцияси ифодасида битта мулохаза узининг инкори билан биргаликда катнашмокда. Демак, мулохазалар алгебрасининг бу формуласи доимо чин киймат кабул килади, яъни айнан чин булади.

5.3. Таркибида бир турдаги квантор амали катнашувчи нормал шаклдаги формулалар учун ечилиш муаммоси

1-таъриф. Агар предикатлар мантики формуласи таркибида эркин предмет узгарувчилар булмаса, у холда бундай формула ёпик формула деб айтилади.

2-таъриф. Агар предикатлар мантики формуласи таркибида эркин узгарувчилар мавжуд булса, у холда

формула формуланинг умумий ёпилиши ва

формула формуланинг мавжудлигини ёпиш деб айтилади.

1-теорема. Агар предикатлар мантикининг нормал шаклдаги ёпик формуласи, таркибида (ифодасида) факат n та мавжудлик квантори катнашган хамда бир элементли исталган сохада айнан чин булса, у холда у умумкийматли формуладир.

Исбот. Предикатлар мантикининг нормал шаклдаги формуласи

(1)

куринишда булсин, бунда формула ифодасида кванторлар катнашмайди, - мантикий узгарувчи, - бир жойли предикатлар, - икки жойли предикатлар.

Бу формуланинг чинлик киймати унинг таркибида катнашаётган мантикий узгарувчилар ва предикатларга боглик.

Теореманинг шартига асосан бир элементли исталган сохада бу формула айнан чин, яъни

(2)

фомула айнан чин булади.

Аникки, (2) формула мулохазалар алгебрасининг формуласи булади.

(1) формула умумкийматли эмас деб фараз киламиз. У вактда шундай соха ва узгарувчиларнинг шундай кийматлар мажмуаси мавжудки, унда (1) формула ёлгон киймат кабул килади, яъни

. (3)

(3) формуланинг инкорини оламиз:

Бу ердан

(4)

формуланинг сохага оид предмет узгарувчиларнинг кандай олинишидан катъий назар айнан чинлиги келиб чикади.

сохадан ихтиёрий элементни олиб, уни (4) формуладаги предмет узгарувчилар урнига куйиб чикамиз. У холда

Демак,

Бу натижа (2) формуланинг айнан чин эканлигига зиддир ва (1) формула умумкийматли эмас деган фаразимизнинг нотугрилигини курсатади.

Шундай килиб, (1) формула умумкийматлидир.

2-теорема. Агар предикатлар мантикининг нормал шаклдаги ёпик формуласи ифодасида n та умумийлик квантори катнашса ва бу формула купи билан n та элементли хар кандай тупламда (сохада) айнан чин булса, у холда у умумкийматли булади.

Исбот. Предикатлар мантикининг нормал шаклдаги формуласи куйидаги куринишда булсин:

, (5)

бунда - мантикий узгарувчилар, - бир жойли предикатлар, , - икки жойли предикатлар.

(1) формула умумкийматли эмас деб фараз киламиз. У вактда n тадан ортик элементга эга булган соха мавжудки, бунда (1) формула айнан чин булмайди.

Бошкача килиб айтганда, шундай узгарувчиларнинг

кийматлар мажмуаси мавжудки,

. (6)

Бу ердан

Шундай килиб, шундай предмет узарувчиларнинг кийматлари мавжудки,

ва

буладилар.

Демак, сохадан купи билан n та элементи булган шундай сохани ажратиш мумкинки, каерда бу формула айнан чин булмайди. Бу натижа теореманинг шартига зиддир ва у (1) формула умумкийматли эмас деган нотугри фаразимиздан келиб чикди.

Демак, (1) формула умумкийматли формуладир.

Таркибида факат бир жойли (битта предмет узгарувчига боглик булган) предикатлар катнашган формулалар учун ечилиш муаммоси ижобий хал этилиши куйидаги теоремадан куринади.

3-теорема. Предикатлар мантикининг таркибига n та бир жойли предикат кирган формуласи бирор тупламда бажарилувчи булса, у холда бу формула элементлари сони 2ⁿ дан катта булмаган тупламда хам бажарилувчи булади.

Ушбу теоремадан куйидаги натижа келиб чикади.

Натижа. Предикатлар мантикининг таркибига факат n та бир жойли предикат кирган формуласи элементлари сони 2ⁿ дан куп булмаган ихтиёрий тупламда айнан чин булса, у холда бу формула ихтиёрий тупламда хам айнан чин булади.

Куйидаги теорема хам предикат мантикининг катта синфини ташкил килувчи формулалари учун ечилиш муаммосини хал килади.

4-теорема. Агар предикатлар мантикининг формуласи бирор чексиз сохада бажарилувчи булса, у холда у чекли сохада хам бажарилувчи булади.

РЕЖА:

1.Предикатлар мантикида ечилиш муаммоси.

2.Чекли сохаларда ечилиш муаммоси.

3.Таркибида бир турдаги квантор амали катна-

шувчи нормал шаклдаги формулалар учун

ечилиш муаммоси.

Муаммоли масала ва топшириклар:

1. Куйидаги формуланинг умумкийматли эканлигини исботланг:

2. Агар М т¢пламда аникланган А(x) ва В(х) предикатлар чин кийматли б¢лса, у холда уларнинг чинлик т¢пламлари кандай шартларни каноатлантириши керак:

3) ?

3. М={1,2,3,...,20} т¢пламда куйидаги предикатлар берилган:

A(x): «х 5 га б¢линмайди»

B(x): «х жуфт сон»

C(x): «х туб сон»

D(x): «х 3 га каррали»

Куйидаги предикатларнинг чинлик т¢пламини топинг:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

Мустакил ишлаш учун саволлар:

1.Предикатлар мантикида ечилиш муаммоси.

2.Чекли сохаларда ечилиш муаммоси.

3.Ёпик формула. Формуланинг умумий ёпилиши.

Формуланинг мавжудлигини ёпиш.

4.Таркибида бир турдаги квантор амали катна-

шувчи нормал шаклдаги формулалар учун

ечилиш муаммоси.

6-§. Предикатлар мантикининг математикага татбики

Математик таъриф ва теоремаларни предикатлар мантики тили воситаси билан ифодалаш. -Сонлар кетма-кетлиги лимитининг таърифини ифодалаш. -Функциянинг нуктадаги лимитининг таърифини ифодалаш. -Функциянинг нуктадаги узлуксизлиги таърифини ифодалаш. -Усувчи функциянинг таърифини ифодалаш. -Чегараланган функциянинг таърифини ифодалаш. -Карама-карши тасдикларни тузиш. -Тугри, тескари ва карама-карши теоремаларни ифодалаш. -Етарли ва зарурий шартларни ифодалаш.

6.1. Математик мулохазаларни предикатлар мантики формуласи куринишида ёзиш

Куйида асосий математик тушунчалар – таъриф ва теоремаларни предикатлар мантики тили воситаси билан кандай ифодалаш мумкинлигини куриб утамиз.

Хар кандай математик фан шу фанда каралаётган объектлар хакидаги мулохазалар билан иш куради. Мантик ва тупламлар назариясининг символлари хамда берилган фаннинг махсус символлари ёрдамида шундай мулохазалар предикатлар мантикининг формуласи куринишида ифодаланиши мумкин. Предикатлар мантикининг тили математик тушунчалар уртасидаги муносабатни ифодалашга, таъриф, теорема ва исботларни ёзишга имконият яратади. Бу ёзишларни мисолларда курайлик.

1.Сонлар кетма-кетлиги лимитининг таърифи.

Сонлар кетма-кетлиги лимитининг таърифини куйидагича ёзиш мумкин:

Бу ерда уч жойли предикат : фойдаланилган.

2.Функциянинг нуктадаги лимитининг таърифи.

Бу таърифни ушбу шаклда ёзиш мумкин:

Бу ерда : уч жойли предикат фойдаланилган.

3.Функциянинг нуктадаги узлуксизлиги таърифи.

тупламда аникланган функция нуктада узлуксиз деб айтилади, качон булса.

Бу ерда хам уч жойли предикатдан фойдаланилди.

4.Усувчи функциянинг таърифи.

тупламда аникланган функция бу тупламда усувчи функция булади, агар булса.

Бу ерда : икки жойли предикатдан фойдаланилган.

5.Чегараланган функциянинг таърифи.

Аникланиш сохаси булган функция бу сохада чегараланган булади, агар булса.

Бу ерда хам : икки жойли предикатдан фойдаланилган.

Маълумки, математикада куп теоремалар шартли мулохазалар шаклида ёзилади, яъни «Агар булса, у холда булади» тарзида ифодаланади. Масалан, «Агар нукта бурчак биссектрисасида ётган булса, у холда у бурчак томонларидан тенг узоклашган (масофада) булади». Бу теореманинг шарти «Нукта бурчак биссектрисасида ётган» ва хулосаси «Нукта бурчак томонларидан тенг узоклашган» жумлалардан иборат. Куриниб турибдики, теореманинг шарти хам, хулосаси хам тупламда аникланган предикатни ифодалайди. Бу предикатларни учун мос равишда ва лар билан белгилаб, теоремани куйидагича ёзиш мумкин:

Шу сабабли, теореманинг тузилиши (структураси) хакида гапирганда, унда учта кисмни ажратиш керак: 1) теорема шарти: тупламда аникланган предикат; 2) теорема хулосаси: тупламда аникланган предикат; 3) тушунтириш кисми: бу ерда теоремада гап юритилаётган объектлар тупламини ифодалаш керак.

6.2. Карама-карши тасдикларни тузиш

Кандайдир математик тасдик берилган булсин. Унга карама-карши булган тасдик булади.

Предикатлар мантики тенгкучли алмаштиришлар воситаси билан формулага яхши шакл (куриниш) бера олади.

Масалан, чегараланган функциянинг таърифи

формула оркали берилишини курган эдик. Бу формуланинг инкорини олиб ва тенгкучли алмаштиришларни утказиб, чегараланмаган функциянинг таърифини хосил киламиз:

Хосил этилган

формула чегараланмаган функциянинг таърифини ифодалайди.

Келтирилган мисолдан куриниб турибдики, хамма кванторлари олдинда турган предикатлар мантики формуласи оркали ифодаланган тасдикка карама-карши тасдикни ясаш учун хамма кванторларни карама-каршисига (яъни ни га ва ни га) алмаштириш ва кванторлар остида турган предикатнинг инкорини олиш кифоя.

Масалан, тасдикни куйидаги формула ифодалайди:

Энди берилган теореманинг тугрилигини рад этадиган тасдикни ясашни мисолда курайлик.

теорема берилган булсин. Бу теоремани рад этадиган тасдик куйидагича булади:

Охирги формула факат ва булгандагина чин кийматга эгадир.

Демак, теореманинг нотугрилигини исботлан учун шундай элементни курсатиш керакки, бу элемент учун - чин ва - ёлгон киймат кабул килсинлар, яъни контрмисол келтириш керак.

6.3. Тугри, тескари ва карама-карши теоремалар

Куйидаги туртта теоремани куриб утайлик:

, (1)

, (2)

, (3)

. (4)

1-таъриф. Бирининг шарти иккинчисининг хулосаси ва иккинчисининг шарти биринчисининг хулосаси булган жуфт теоремаларга узаро тескари теоремалар деб айтилади.

Масалан, (1) ва (2) теоремалар хамда (3) ва (4) теоремалар узаро тескари теоремалар булади. Бу жуфт теоремаларанинг бирини тугри теорема десак, у холда иккинчисини тескари теорема дейиш керак.

2-таъриф. Бирининг шарти ва хулосаси иккинчисининг шарти ва хулосаси учун мос равишда инкорлари булган жуфт теоремалар узаро карама-карши теоремалар деб айтилади.

(1) ва (3) теоремалар хамда (2) ва (4) теоремалар узаро карама-карши теоремалар булади.

Масалан, (1) : «Агар туртбурчакнинг диагоналлари тенг булса, у холда бу туртбурчак тугри бурчакли булади» теоремага (2) : «Агар туртбурчак тугри бурчакли булса, у холда унинг диагоналлари тенг булади» деган теорема тескари теорема булади. (1) теоремага карама-карши теорема (3) : «Агар туртбурчакнинг диагоналлари тенг булмаса, у холда у тугри бурчакли булмайди» ва (2) теоремага карама-карши теорема (4) : «Агар туртбурчак тугри бурчакли булмаса, у холда унинг диагоналлари тенг булмайди» булади.

Курилган мисолда (1) ва (4) теоремалар бир вактда чин буладилар. (1) теоремага тенг ёнли трапеция контрмисол булади.

Равшанки, тугри ва тескари теоремалар, умуман айтганда, тенгкучли булмайдилар, яъни бири чин, иккинчиси ёлгон булиши мумкин. Аммо, (1) ва (4) теоремалар хамда (2) ва (3) теоремаларнинг тенг кучли формулалар эканлигини осонгина исботлаш мумкин. Хакикатан хам,

Худди шундай (2) ва (3) формулаларнинг тенгкучлилигини исботлаш мумкин:

Бу тенгкучлиликлардан куйидаги хулосага келамиз: агар (1) теорема исбот килинган булса, у холда (4) теорема хам исбот килинган булади ва агар (2) теорема исбот килинган булса, у холда (3) теорема хам исботланган хисобланади.

6.4. Етарли ва зарурий шартлар

Куйидаги теоремани курайлик

. (5)

предикатнинг чинлик туплами тупламдан иборат булади. Демак, бу предикатнинг ёлгонлик туплами тупламдан иборат. Охирги туплам факат булгандагина буш туплам булади.

Шундай килиб, предикат нинг хамма кийматларида предикатнинг чинлик туплами предикат чинлик тупламининг кисм туплами, яъни булганда, шунда ва факат шундагина чин булади. Бу холда предикат предикатдан мантикий келиб чикади деб айтилади. предикатга предикат учун зарурий шарт ва га учун етарли шарт деб айтамиз. Масалан, ушбу «Агар натурал сон булса, у холда бутун сон булади» теоремада : «-бутун сон» предикати : «-натурал сон» предикатидан мантикий келиб чикади ва «-натурал сон» предикати «-бутун сон» предикати учун етарли шарт булади.

Шундай холлар мавжудки, буларда

(6)

ва

(7)

узаро тескари теоремалар чин буладилар.

Бу хол факат , яъни качонки ва предикатлар тенгкучли предикатлар булгандагина мумкин.

Каралаётган холда (1) теоремага асосан предикат предикат учун етарли шарт ва (2) теоремадан предикат предикат учун зарурий шарт эканлиги келиб чикади.

Демак, агар (1) ва (2) теоремалар чин булса, у холда шарт учун хам етарли, хам зарурий шарт булади. Худди шундай бу холатда шарт учун етарли ва зарурий шарт булади.

Биз айрим вактларда «зарур ва етарли» мантикий богловчи урнига «шунда ва факат шунда» мантикий богловчини ишлатамиз.

Бу ерда (1) ва (2) мулохазалар чин булганлиги учун куйидаги мулохаза хам чин булади:

1-мисол. Ушбу теорема: «Агар сони 6 га булинса, у холда сони 3 га булинади» чиндир. Бу ерда предикат : « сони 6 га булинади» ва предикати : « сони 3 га булинади». предикати предикатидан мантикий келиб чикади, яъни . предикати ( сони 6 га булинади) предикати ( сони 3 га булинади) учун етарли шартдир. предикати предикати учун зарурий шартдир. Шу вактнинг узида тескари теорема : «Агар сони 3 га булинса, у холда сони 6 га булинади» нотугридир (ёлгондир). Шунинг учун хам : « сони 3 га булинади» предикати : « сони 6 га булинади» предикат учун етарли шарт ва : « сони 6 га булинади» предикати : « сони 3 га булинади» предикатига зарурий шарт булаолмайди.

6.5.Тескарисини (аксини) фараз килиш усули билан исботлаш

Тескарисини фараз килиш усули билан исботлашни куйидаги схема оркали олиб борадилар:

(8)

теорема нотугри, яъни шундай узгарувчи мавжудки, шарт - чин ва хулоса – ёлгон деб фараз килинади. Агар бу фараздан мантикий фикрлаш натижасида карама-карши тасдик келиб чикса, у холда килинган фараз нотугри эканлиги ва теореманинг тугрилиги хосил булади.

Бу схемадан фойдаланиб (1) теореманинг чинлигини курсатайлик.

Хакикатан хам, (1) теореманинг нотугрилиги (ёлгонлиги) (фараз буйича) ушбу формуланинг чинлигини курсатади:

(1) теоремани нотугри деб кабул килган фаразимиздан келиб чикадиган карама-карши тасдик конъюнкциядан иборат булади, бунда - кандайдир мулохаза. Шундай килиб, тескарисини фараз килиш усули билан исботлаш схемаси куйидаги формуланинг чинлигини исботлашга келтирилади:

Бу охирги формула (8) фомулага тенгкучлидир.

Хакикатан хам,

7-§. Аксиоматик предикатлар хисоби хакида

Аксиоматик предикатлар хисоби. -Предикатлар хисоби аксиомалар системаси. -Умумийлик кванторини киритиш коидаси. -Мавжудлик кванторини киритиш коидаси. -Ечилиш, зидсизлик, туликлилик ва эркинлик муаммолари.

Аксиоматик предикатлар назариясини хам худди аксиоматик мулохазалар назарияси каби яратиш мумкин. Бу ерда куйидагиларни курсатиш зарур:

1.Предикатлар хисоби формуласининг таърифи предикатлар мантики формуласининг таърифи билан бир хил.

2.Предикатлар хисоби аксиомалар системасини танлашни (худди мулохазалар хисобидагидай) хар хил амалга ошириш мумкин. Шундай аксиомалар системасидан биттаси куйидаги: мулохазалар хисобининг ун бир аксиомаси (4 та гурух аксиомалар) ва иккита кушимча аксиома

, ,

аксиомалардан иборат система булиши мумкин, бу ерда узгарувчини уз ичига олмайди.

3.Мулохазалар хисобидаги келтириб чикариш коидасига яна иккита коида кушилади:

а) Умумийлик кванторини киритиш коидаси

;

б) Мавжудлик кванторини киритиш коидаси

агар га боглик булмаса.

4. Хулоса ва исботланувчи формула тушунчалари худди мулохазалар хисобидаги каби аникланади.

5.Худди хамма аксиоматик назариялардагидай ушбу муаммолар курилади:

а) ечилиш,

б) зидсизлик,

в) туликлик,

г) эркинлик.

РЕЖА:

1.Математик мулохазаларни предикатлар ман-

тики формуласи куринишида ёзиш.

2.Карама-карши тасдикларни тузиш.

3.Тугри, тескари ва карама-карши теоремалар.

4.Етарли ва зарурий шартлар.

5.Тескарисини (аксини) фараз килиш усули

билан исботлаш.

6.Аксиоматик предикатлар хисоби хакида.

Муаммоли масала ва топшириклар:

1. Предикатлар мантики тилида куйидаги таърифларни ёзинг:

1) Чизикли тартибланган туплам (тартибланган туплам чизикли деб айтилади, агар шу тупламнинг хар кандай ва элементлари учун ёки , ёки , ёки );

2) Жуфт функция ( жуфт функция деб айтилади, агар унинг аникланиш сохаси координата бошига нисбатан симметрик ва аникланиш сохасининг хар бир элементи учун булса).

2. Куйида берилган жумлалардаги нукталар урнига «зарур, аммо етарли эмас», ёки «етарли, аммо зарур эмас», ёки «зарур эмас ва етарли эмас» ва каерда мумкин булса, «зарур ва етарли» сузларини шундай куйингки, хосил булган мулохазалар чин булсин.

1) Туртбурчак тугри бурчакли булиши учун унинг диагоналларининг узунлиги тенг булиши ....

2) булиши учун булиши ...