III-БОБ. МУЛОХАЗАЛАР ХИСОБИ
Мулохазалар хисоби аксиоматик мантикий система булиб, мулохазалар алгебраси эса унинг интерпретациясидир (талкинидир).
Берилган аксиомалар системаси негизида (базасида) курилган аксиоматик назария деб шу аксиомалар системасига таяниб исботланувчи хамма теоремалар мажмуасига айтилади.
Аксиоматик назария формал ва формалмас назарияларга булинади.
Формалмас аксиоматик назария назарий-тупламий мазмун билан тулдирилган булиб, келтириб чикариш тушунчаси аник берилмаган ва бу назария асосан фикр мазмунига суянади.
Каралаётган аксиоматик назария учун куйидаги шартлар бажарилган булса, яъни:
1)назариянинг тили берилган;
2)формула тушунчаси аникланган;
3)аксиомалар деб аталадиган формулалар туплами берилган;
4)бу назарияда келтириб чикариш коидаси аникланган булса, формал аксиоматик назария аникланган деб хисобланади.
Куйида мулохазалар хисобининг символлари, формуласи, аксиомалар системаси, келтириб чикариш коидалари, формулалар мажмуасидан формулани келтириб чикариш коидаси, дедукция ва умумлашган дедукция теоремалари, айрим мантик конунларининг исботи, мулохазалар алгебраси ва мулохазалар хисоби уртасидаги муносабатлар, мулохазалар хисобида ечилиш, зидсизлик, туликлилик ва эркинлик муаммолари каби масалалар баён этилади.
1-§. Мулохазалар хисоби формуласи тушунчаси
Мулохазалар хисоби. -Мантикий богловчилар. -Символлар. -Формула. -Кисмий формула.
Хар кандай хисобнинг тафсили бу хисобнинг символлари тафсилидан, формулалар ва келтириб чикариш формулалари таърифидан иборат.
Мулохазалар хисобида уч категорияли символлардан иборат алфавит кабул килинади:
Биринчи категория символлари: ![]() . Бу символларни узгарувчилар деб атаймиз.
. Бу символларни узгарувчилар деб атаймиз.
Иккинчи
категория символлари: ![]() ,
, ![]() , ®, - . Булар мантикий богловчилардир. Биринчиси –
дизъюнкция ёки мантикий кушиш белгиси, иккинчиси – конъюнкция ёки мантикий купайтма
белгиси, учинчиси – импликация белгиси ва туртинчиси – инкор белгиси деб аталади.
, ®, - . Булар мантикий богловчилардир. Биринчиси –
дизъюнкция ёки мантикий кушиш белгиси, иккинчиси – конъюнкция ёки мантикий купайтма
белгиси, учинчиси – импликация белгиси ва туртинчиси – инкор белгиси деб аталади.
Учинчи категорияга кавс деб аталадиган ( , ) символ киритилади.
Мулохазалар хисобида бошка символлар йук.
Мулохазалар хисобининг формуласи деб мулохазалар хисоби алфавити символларининг маълум бир кетма-кетлигига айтилади.
Формулаларни белгилаш учун лотин алфавитининг катта харфларидан фойдаланамиз. Бу харфлар мулохазалар хисобининг символлари каторига кирмайди. Улар факатгина формулаларнинг шартли белгилари булиб хизмат килади.
Энди формула тушунчаси таърифини берайлик. Бу тушунча куйидагича аникланади:
1) хар кандай ![]() узгарувчиларнинг
исталган бири формуладир;
узгарувчиларнинг
исталган бири формуладир;
2)
агар ![]() ва
ва ![]() ларнинг хар
бири формула булса, у холда (
ларнинг хар
бири формула булса, у холда (![]()
![]()
![]() ), (
), (![]()
![]()
![]() ), (
), (![]() ®
®![]() ) ва
) ва ![]() лар
хам формулалардир.
лар
хам формулалардир.
3) бошка хеч кандай символлар сатри формула була олмайди.
Узгарувчиларни элементар формулалар деб атаймиз.
Мисол.Формула
таърифининг 1-бандига кура ![]() узгарувчилар
формулалар булади. У вактда таърифнинг 2-бандига мувофик
узгарувчилар
формулалар булади. У вактда таърифнинг 2-бандига мувофик ![]() ,
, ![]() ,
, ![]() ,
, ![]() лар хам формулалардир.
Худди шу тарикада
лар хам формулалардир.
Худди шу тарикада ![]() ,
, ![]() ,
, ![]() лар
хам формулалар булади.
лар
хам формулалар булади.
Куйидагилар формула булаолмаслигини тушунтиринг:
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ®
®![]() .
.
Кисмий формула тушунчасини киритамиз:
1.Элементар формула учун факат унинг узи кисмий формуладир.
2.Агар
![]() формула
булса, у вактда шу формуланинг узи,
формула
булса, у вактда шу формуланинг узи, ![]() формула ва
формула ва ![]() формуланинг
хамма кисмий формулалари унинг кисмий формулалари булади.
формуланинг
хамма кисмий формулалари унинг кисмий формулалари булади.
3.Агар
формула ![]() *
*![]() куринишда булса (бу
ерда ва бундан кейин * урнига
куринишда булса (бу
ерда ва бундан кейин * урнига ![]() ,
, ![]() , ® cимволларнинг
исталганини тушунамиз), у вактда шу формуланинг узи,
, ® cимволларнинг
исталганини тушунамиз), у вактда шу формуланинг узи, ![]() ва
ва ![]() формулалар
хамда
формулалар
хамда ![]() ва
ва ![]() формулаларнинг
барча кисмий формулалари
формулаларнинг
барча кисмий формулалари ![]() *
*![]() формуланинг кисмий
формулалари булади.
формуланинг кисмий
формулалари булади.
Масалан,
![]() формула
учун:
формула
учун:
![]() - нолинчи чукурликдаги
кисмий формула,
- нолинчи чукурликдаги
кисмий формула,
![]() ,
, ![]() - биринчи чукурликдаги
кисмий формулалар,
- биринчи чукурликдаги
кисмий формулалар,
![]() -
иккинчи чукурликдаги кисмий формулалар,
-
иккинчи чукурликдаги кисмий формулалар,
![]() -
учинчи чукурликдаги кисмий формулалар,
-
учинчи чукурликдаги кисмий формулалар,
z – туртинчи чукурликдаги кисмий формула деб аталади.
Формулаларни ёзишда айрим соддалаштиришларни кабул киламиз.
Худди мулохазалар алгебрасидаги каби формулалар ёзувидаги кавсларни тушириб колдиришга
келишамиз. Бу келишувга биноан ![]() ,
, ![]() ,
, ![]() формулаларни
мос равишда
формулаларни
мос равишда ![]() ,
, ![]() ,
, ![]() куринишда
ёзамиз.
куринишда
ёзамиз.
2-§. Исботланувчи формула таърифи. Мулохазалар хисобининг аксиомалар системаси (тизими). Келтириб чикариш коидалари
Исботланувчи формула. -Аксиома. -Келтириб чикариш коидаси. -Урнига куйиш коидаси. -Хулоса коидаси. -Аксиомалар тизими. -Исботлаш.
Энди мулохазалар хисобида исботланувчи формулалар синфини ажратамиз. Исботланувчи формулалар формулалар таърифига ухшаш характерда таърифланади.
Аввал дастлабки исботланувчи формулалар (аксиомалар), ундан кейин эса келтириб чикариш коидаси аникланади. Келтириб чикариш коидаси оркали бор исботланувчи формулалардан янги исботланувчи формулалар хосил килинади.
Дастлабки исботланувчи формулалардан келтириб чикариш коидасини куллаш йули билан янги исботланувчи формулаларни хосил этишга шу формулаларни аксиомалардан келтириб чикариш деб айтилади.
2.1.Мулохазалар хисобининг аксиомалар системаси (тизими)
Мулохазалар хисобининг аксиомалар тизими XI аксиомадан иборат булиб, булар турт гурухга булинади.
Биринчи гурух аксиомалари:
I1 ![]() .
.
I2 ![]() .
.
Иккинчи гурух аксиомалари:
II1 ![]()
II2 ![]()
II3 ![]() .
.
Учинчи гурух аксиомалари:
III1 ![]() .
.
III2 ![]() .
.
III3 ![]() .
.
Туртинчи гурух аксиомалари:
IV1 ![]()
![]() .
.
IV2 ![]()
![]() .
.
IV3 ![]()
![]() .
.
2.2. Келтириб чикариш коидаси
2.2.1.Урнига куйиш коидаси. Агар ![]() мулохазалар хисобининг
исботланувчи формуласи,
мулохазалар хисобининг
исботланувчи формуласи, ![]() -узгарувчи,
-узгарувчи, ![]() мулохазалар
хисобининг ихтиёрий формуласи булса, у вактда
мулохазалар
хисобининг ихтиёрий формуласи булса, у вактда ![]() формула ифодасидаги хамма
формула ифодасидаги хамма
![]() лар
урнига
лар
урнига ![]() формулани куйиш
натижасида хосил этилган формула хам исботланувчи формула булади.
формулани куйиш
натижасида хосил этилган формула хам исботланувчи формула булади.
![]() формуладаги
формуладаги
![]() узгарувчилар
урнига
узгарувчилар
урнига ![]() формулани куйиш
операцияси (жараёни)ни урнига куйиш коидаси деб айтамиз ва уни куйидаги символ
билан белгилаймиз:
формулани куйиш
операцияси (жараёни)ни урнига куйиш коидаси деб айтамиз ва уни куйидаги символ
билан белгилаймиз:
![]() .
.
![]() Зикр
этилган коидага куйидаги аникликларни киритамиз:
Зикр
этилган коидага куйидаги аникликларни киритамиз:
а)
Агар ![]() факат
факат ![]() узгарувчидан
иборат булса, у вактда
узгарувчидан
иборат булса, у вактда ![]() урнига куйиш
урнига куйиш ![]() формулани
беради;
формулани
беради;![]()
б)
Агар ![]() формула
формула ![]() дан
фаркли
дан
фаркли ![]() узгарувчидан иборат булса,
у вактда
узгарувчидан иборат булса,
у вактда ![]() урнига куйиш
урнига куйиш ![]() ни
беради;
ни
беради;
в)
Агар ![]() урнига куйиш аникланган
формула булса, у вактда
урнига куйиш аникланган
формула булса, у вактда ![]() формуладаги
формуладаги ![]() урнига
урнига
![]() формулани
куйиш натижасида урнига куйишнинг инкори келиб чикади, яъни
формулани
куйиш натижасида урнига куйишнинг инкори келиб чикади, яъни ![]() урнига куйиш
урнига куйиш
![]() ни
беради.
ни
беради.
г)
Агар ![]() 1 ва
1 ва ![]() 2
формулаларда урнига куйиш аникланган булса, у вактда
2
формулаларда урнига куйиш аникланган булса, у вактда 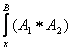 урнига куйиш
урнига куйиш
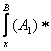
![]() ни
беради.
ни
беради.
Агар
![]() исботланувчи
формула булса, уни
исботланувчи
формула булса, уни ![]() шаклда ёзишга келишамиз.
шаклда ёзишга келишамиз.
У холда урнига куйиш коидасини куйидагича схематик равишда ифодалаш мумкин:
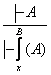
ва
уни «агар ![]() исботланувчи формула булса,
у вактда
исботланувчи формула булса,
у вактда ![]() хам исботланувчи
формула булади» деб укилади.
хам исботланувчи
формула булади» деб укилади.
2.2.2. Хулоса коидаси. Агар ![]() ва А®В лар мулохазалар хисобининг исботланувчи формулалари булса, у холда В хам
исботланувчи формула булади. Бу коида куйидагича схематик равишда ёзилади:
ва А®В лар мулохазалар хисобининг исботланувчи формулалари булса, у холда В хам
исботланувчи формула булади. Бу коида куйидагича схематик равишда ёзилади:
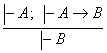 .
.
2.2.3. Исботланувчи формуланинг таърифи.
а) Хар кандай аксиома исботланувчи формуладир;
б) Исботланувчи формуладаги ![]() узгарувчи урнига
ихтиёрий
узгарувчи урнига
ихтиёрий ![]() формулани куйиш
натижасида хосил булган формула исботланувчи формула булади.
формулани куйиш
натижасида хосил булган формула исботланувчи формула булади.
в) ![]() ва
ва ![]() исботланувчи
формулалардан хулоса коидасини куллаш натижасида олинган В формула исботланувчи
формуладир;
исботланувчи
формулалардан хулоса коидасини куллаш натижасида олинган В формула исботланувчи
формуладир;
г) Мулохазалар хисобининг бошка хеч кандай формуласи исботланувчи деб саналмайди.
Таъриф. Исботланувчи формулаларни хосил этиш процесси (жараёни)га исбот килиш (исботлаш) деб айтилади.
1-Мисол. ![]() эканлиги
(импликациянинг рефлексивлиги) исботлансин.
эканлиги
(импликациянинг рефлексивлиги) исботлансин.
Импликациянинг рефлексивлигини исботлаш учун ушбу
![]() - I2
- I2
аксиомадан
фойдаланамиз. Бу ерда ![]() урнига куйишни бажариш
натижасида
урнига куйишни бажариш
натижасида
![]() (1)
(1)
келиб
чикади. ![]() - I2 аксиома ва (1) формулага хулоса коидасини куллаб
- I2 аксиома ва (1) формулага хулоса коидасини куллаб
![]() (2)
(2)
формулани хосил киламиз.
(2) формулага нисбатан куйидаги урнига куйишни
![]() (2)
(2)
бажариш натижасида
![]() (3)
(3)
исботланувчи формулага эга буламиз.
![]()
![]() - IV2 аксиома
ва (3) формулага нисбатан хулоса коидасини куллаш натижасида
- IV2 аксиома
ва (3) формулага нисбатан хулоса коидасини куллаш натижасида
![]() (4)
(4)
исботланувчи
формулага келамиз. Нихоят (4) формуладаги ![]() узгарувчи урнига
узгарувчи урнига ![]() формулани
куйсак
формулани
куйсак
![]()
исботланиши керак булган формула хосил булади.
2-мисол. ![]() эканлигини
исботланг.
эканлигини
исботланг.
![]() - II3 аксиомага нис-батан кетма-кет икки марта урнига куйиш
усулини куллаймиз: аввал
- II3 аксиомага нис-батан кетма-кет икки марта урнига куйиш
усулини куллаймиз: аввал ![]() ни
ни ![]() га ва кейин
га ва кейин ![]() ни
ни ![]() га
алмаштирамиз. Натижада куйидаги исботланувчи формулага эга буламиз
га
алмаштирамиз. Натижада куйидаги исботланувчи формулага эга буламиз
![]() .
(5)
.
(5)
(5)
формулага нисбатан ![]() (5) урнига куйишни
бажариб, куйидагини хосил киламиз
(5) урнига куйишни
бажариб, куйидагини хосил киламиз
![]() .
(5а)
.
(5а)
Энди
![]() (6)
(6)
![]() (7)
(7)
формулаларнинг исботланувчи эканлигини курсатамиз.
Бунинг
учун ![]()
![]() - IV1 аксиомага
нисбатан
- IV1 аксиомага
нисбатан
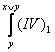
урнига куйишни бажарамиз. Натижада
![]() (8)
(8)
формулага
эга буламиз. (8) формула ва ![]() - III1 аксиомага нисбатан хулоса коидасини ишлатиб, (6) нинг
исботланувчи формула эканлигига ишонч хосил киламиз. Худди шундай (7) нинг хам
исботланувчи формула эканлигини курсатиш мумкин.
- III1 аксиомага нисбатан хулоса коидасини ишлатиб, (6) нинг
исботланувчи формула эканлигига ишонч хосил киламиз. Худди шундай (7) нинг хам
исботланувчи формула эканлигини курсатиш мумкин.
(6) ва (5) формулаларга хулоса коидасини кулласак,
![]() (9)
(9)
исботланувчи формула келиб чикади.
(7) ва (9) формулаларга хулоса коидасини куллаб,
![]()
дастлабки формуланинг исботланувчи эканлигини хосил киламиз.
3-§. Келтириб чикариш коидасининг хосилалари
Хосилавий коидалар. -Бир вактда урнига куйиш коидаси. -Мураккаб хулоса коидаси. -Силлогизм коидаси. -Контрпозиция коидаси.
-Иккимарталик инкорни тушириш коидаси.
Хулоса ва урнига куйиш коидалари сингари келтириб чикариш коидасининг хосилалари хам янги исботланувчи формулалар хосил килишга имкон яратади.
3.1. Бир вактда урнига куйиш коидаси
Таъриф.
Агар ![]() – исботланувчи формула
ва
– исботланувчи формула
ва ![]() мулохазалар хисобининг
ихтиёрий формулалари булса, у вактда
мулохазалар хисобининг
ихтиёрий формулалари булса, у вактда ![]() формуланинг
формуланинг ![]() узгарувчи-лари урнига
бир вактда мос равишда
узгарувчи-лари урнига
бир вактда мос равишда ![]() формулаларни куйиш
натижасида
формулаларни куйиш
натижасида ![]() исботланувчи формулани хосил килиш, бир вактда урнига
куйиш коидаси деб аталади.
исботланувчи формулани хосил килиш, бир вактда урнига
куйиш коидаси деб аталади.
![]() лар
лар
![]()
![]() формулалардаги
бошка узгарувчилардан фарк килувчи узгарувчилар ва
формулалардаги
бошка узгарувчилардан фарк килувчи узгарувчилар ва ![]()
![]() булсин. У холда
булсин. У холда ![]() формулага
формулага ![]() та
кетма-кет урнига куйишни бажарамиз: аввал
та
кетма-кет урнига куйишни бажарамиз: аввал ![]() урнига
урнига ![]() ни,
кейин
ни,
кейин ![]() урнига
урнига ![]() ни
ва хоказо
ни
ва хоказо ![]() урнига
урнига
![]() ни куямиз. Натижада куйидаги исботланувчи формулаларга
эга буламиз:
ни куямиз. Натижада куйидаги исботланувчи формулаларга
эга буламиз: ![]() урнига куйиш
урнига куйиш ![]() ни,
ни,  урнига
куйиш
урнига
куйиш ![]() ни, ......,
ни, ......,  урнига
куйиш
урнига
куйиш ![]() ни беради.
ни беради.
Бундан
кейин ![]() формулага нисбатан яна
формулага нисбатан яна
![]() та
кетма-кет урнига куйишни бажарамиз: аввал
та
кетма-кет урнига куйишни бажарамиз: аввал ![]() урнига
урнига ![]() ни, кейин
ни, кейин ![]() урнига
урнига ![]() ни
ва хоказо
ни
ва хоказо ![]() урнига
урнига ![]() ни куйиб
чикамиз. Бунинг натижасида
ни куйиб
чикамиз. Бунинг натижасида 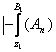 урнига куйишдан
урнига куйишдан ![]() ни,
ни,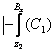 урнига
куйишдан
урнига
куйишдан ![]() ни,.....,
ни,.....,  урнига
куйишдан
урнига
куйишдан ![]() ни хосил киламиз.
ни хосил киламиз.
Демак,
![]() исботланувчи формула
исботланувчи формула ![]() формуладаги
формуладаги ![]() узгарувчилар
урнига бир вактда мос равишда
узгарувчилар
урнига бир вактда мос равишда ![]() формулаларни куйиш
натижасида хосил булади.
формулаларни куйиш
натижасида хосил булади.
Бир вактда урнига куйиш операция (коида)сини куйидагича ифодалаймиз
 (1)
(1)
3.2. Мураккаб хулоса коидаси
Бу коидада
![]()
куринишдаги формулаларга нисбатан иккинчи хосилавий коида ишлатилади ва уни куйидаги тасдик оркали изохлаш мумкин.
1-теорема. Агар ![]() лар ва
лар ва
![]()
![]() (2)
(2)
исботланувчи формулалар булса, у вактда L хам исботланувчи формула булади.
Исбот. Теоремани хулоса коидасини кетма-кет куллаш оркали исботлаш мумкин.
Хакикатан
хам, агар ![]() ва (2) исботланувчи формулалар
булса, у вактда хулоса коидасига асосан
ва (2) исботланувчи формулалар
булса, у вактда хулоса коидасига асосан
![]() (3)
(3)
хам исботланувчи формула булади.
![]() ва
(3) исботланувчи формула булганлиги учун
ва
(3) исботланувчи формула булганлиги учун
![]() (4)
(4)
формула хам исботланувчи булади.
Худди шундай мухокамани давом эттириб, охири ![]() нинг исботланувчи формула эканлигига ишонч хосил киламиз.
нинг исботланувчи формула эканлигига ишонч хосил киламиз.
Мураккаб хулоса коидасини схематик равишда куйидагича ёзиш мумкин:
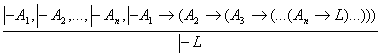 (5)
(5)
3.3. Силлогизм коидаси
2-теорема. Агар ![]() ва
ва ![]() исботланувчи
формулалар булса, у вактда
исботланувчи
формулалар булса, у вактда ![]() формула хам исботланувчи
булади.
формула хам исботланувчи
булади.
Исбот. Теоремани схематик равишда куйидагича ёзамиз
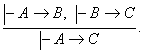 (6)
(6)
![]() - I1 ва
- I1 ва ![]() -I2
аксиомаларга нисбатан куйидаги бир вактда урнига куйиш коидасини
-I2
аксиомаларга нисбатан куйидаги бир вактда урнига куйиш коидасини
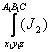 ва
ва
![]()
куллаш натижасида ушбу исботланувчи формулаларни хосил киламиз:
![]()
![]() (7)
(7)
![]() (8)
(8)
Теореманинг шартига асосан
![]() (9)
(9)
![]() (10)
(10)
формулалар исботланувчидир.
(10) ва (8) лардан хулоса коидасига асосан
![]() (11) формулани хосил киламиз. У
вактда (11), (9) ва (7) лардан мураккаб хулоса коидасига асосан
(11) формулани хосил киламиз. У
вактда (11), (9) ва (7) лардан мураккаб хулоса коидасига асосан ![]() эканлиги келиб чикади.
эканлиги келиб чикади.
Агар
![]() ва
ва
![]() исботланувчи
формулалар булса, у вактда
исботланувчи
формулалар булса, у вактда ![]() хам исботланувчи
формула булишига силлогизм коидаси деб айтамиз.
хам исботланувчи
формула булишига силлогизм коидаси деб айтамиз.
3.4.Контрпозиция коидаси
3-теорема.
Агар ![]() исботланувчи
формула булса, у вактда
исботланувчи
формула булса, у вактда ![]() хам исботланувчи формула, яъни
хам исботланувчи формула, яъни
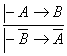 . (12)
. (12)
булади.
Исбот. ![]()
![]() - IV1
аксиомага нисбатан бир вактда урнига куйиш коидаси
- IV1
аксиомага нисбатан бир вактда урнига куйиш коидаси
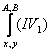
ни куллаб,
![]() (
(![]() ) (13)
) (13)
исботланувчи формулани хосил киламиз.
Теореманинг шартига асосан
![]() (14)
(14)
исботланувчи
формуладир. Шунинг учун (14) ва (13) лардан хулоса коидасига асосан ![]() исботланувчи формула эканлиги келиб чикади.
исботланувчи формула эканлиги келиб чикади.
Агар
![]() исботланувчи формула булса, у вактда
исботланувчи формула булса, у вактда ![]() хам исботланувчи формула булишига контрпозиция коидаси
деб айтамиз.
хам исботланувчи формула булишига контрпозиция коидаси
деб айтамиз.
3.5. Икки карралик инкорни тушириш коидаси
4-теорема. 1) Агар ![]() исботланувчи формула булса, у вактда
исботланувчи формула булса, у вактда ![]() хам
исботланувчи булади.
хам
исботланувчи булади.
2) Агар ![]() исботланувчи формула булса, у вактда
исботланувчи формула булса, у вактда ![]() формула хам исботланувчи, яъни
формула хам исботланувчи, яъни
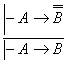 ва
ва 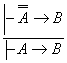 (15)
(15)
булади.
Исбот. ![]()
![]() - IV2 ва
- IV2 ва ![]()
![]() - IV3
аксиомаларга нисбатан урнига куйиш
- IV3
аксиомаларга нисбатан урнига куйиш
![]() ва
ва ![]()
коидаларини куллаб,
![]() ,
(16)
,
(16)
![]() (17)
(17)
исботланувчи формулаларни хосил киламиз.
Теореманинг 1) ва 2) шартига асосан
![]() ,
(18)
,
(18)
![]() (19)
(19)
формулалар исботланувчидир.
Агар
теореманинг 1)-шарти бажарилса, у вактда (17) ва (18) формулалардан силлогизм коидасига
асосан ![]() келиб чикади.
келиб чикади.
Агар
2)-шарти бажарилса, у вактда (16) ва (19) формулалардан ![]() ни келтириб чикарамиз.
ни келтириб чикарамиз.
Агар
![]() (
(![]() ) исботланувчи формула булса, у холда
) исботланувчи формула булса, у холда ![]() хам
исботланувчи формула булишига икки марталик инкорни тушириш коидаси деб
айтамиз..
хам
исботланувчи формула булишига икки марталик инкорни тушириш коидаси деб
айтамиз..
РЕЖА:
1.Мулохазалар хисоби формуласи тушунчаси.
2.Исботланувчи формула таърифи. Мулохазалар
хисобининг аксиомалар системаси (тизими).
Келтириб чикариш коидалари.
3.Келтириб чикариш коидасининг хосилалари.
Муаммоли масала ва топшириклар:
1. Куйидаги ифодаларнинг кайси бирлари мулохазалар хисобининг формулалари булади:
1) ![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() .
.
2. Куйидаги формулаларнинг хамма кисм формулаларини ёзиб чикинг:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ;
;
8) ![]() .
.
3. ![]() ,
, ![]() ,
, ![]()
формулалар учун куйидаги урнига куйишларнинг натижаларини ёзинг:
1)
![]() ;
2)
;
2) ![]() ; 3)
; 3) 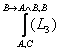 ;
;
4)
 ;
5)
;
5) ![]() ; 6)
; 6) 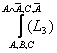 .
.
4. Урнига куйиш коидасини куллаб, куйидаги формулаларнинг исботланувчи эканлигини исботланг:
1) ![]() ;
;
2) ![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)![]() .
.
5. Урнига куйиш ва хулоса кодаларини куллаб, куйидаги формулаларнинг исботланувчи эканлигини аникланг:
1)
![]() ;
2)
;
2) ![]() ;
;
3)
![]() ;
4)
;
4) ![]() ;
;
5) ![]() ;
6)
;
6) ![]() .
.
6. Келтириб чикаришнинг хосилавий коидаларидан фойдаланиб, куйидаги формулаларнинг исботланувчи эканлигини исботланг:
1)
![]() ;
2)
;
2) ![]() ;
;
3)
![]() ;
4)
;
4) ![]() ;
;
5)
![]() ;
6)
;
6) ![]() ;
;
7)
![]() ;
8)
;
8) ![]() .
.
7. Келтириб чикаришнинг хосилавий коидаларини исботланг:
1)
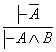 ;
2)
;
2) 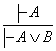 ; 3)
; 3) 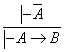 ;
;
4)
![]() ;
5)
;
5) 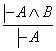 ; 6)
; 6) 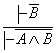 ;
;
7) 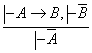 ; 8)
; 8) 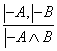 ;
9)
;
9) 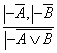 ;
;
10) 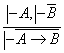 ; 11)
; 11)  ;
12)
;
12) 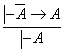 ;
;
13) 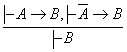 ; 14)
; 14) 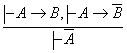 .
.
Мустакил ишлаш учун саволлар:
1.Мулохазалар хисоби формуласи тушунчаси.
Мантикий богловчилар. Символлар. Кисмий
формула.
2.Исботланувчи формула таърифи. Мулохазалар
хисобининг аксиомалар системаси (тизими).
Келтириб чикариш коидалари.
3.Келтириб чикариш коидасининг хосилалари.
4.Бир вактда урнига куйиш ва мураккаб хулоса
коидалари.
5.Силлогизм, контрпозиция ва икки марталик
инкорни тушириш коидалари.
4-§. Формулалар мажмуасидан формулани келтириб чикариш коидаси
Келтириб чикариш коидаси. -Келтириб чикариладиган формуллар синфи. - Исботланувчи формулалар синфи.
![]() чекли формулалар мажмуаси (туплами) берилган булсин.
Бу формулалар мажмуасидан формулани келтириб чикариш тушунчасини берамиз.
чекли формулалар мажмуаси (туплами) берилган булсин.
Бу формулалар мажмуасидан формулани келтириб чикариш тушунчасини берамиз.
Таъриф.
1) Хар кандай ![]() формулалар мажмуаси
формулалар мажмуаси ![]() дан
келтириб чикариладиган формуладир.
дан
келтириб чикариладиган формуладир.
2)
Хар кандай исботланувчи формула ![]() дан келтириб чикарилади.
дан келтириб чикарилади.
3)
![]() ва
ва
![]() лар
лар
![]() формулалар
мажмуасидан келтириб чикарилган формулалар булса, у холда
формулалар
мажмуасидан келтириб чикарилган формулалар булса, у холда ![]() формула хам
формула хам ![]() дан келтириб чикарилади.
дан келтириб чикарилади.
Бирор
![]() формула
формула
![]() формулалар
мажмуасидан келтириб чикариладиган булса, уни символик равишда
формулалар
мажмуасидан келтириб чикариладиган булса, уни символик равишда ![]() шаклда ёзамиз.
шаклда ёзамиз.
Агар
![]() буш туплам ёки
элементлари факат исботланувчи формулалардан иборат булса, у вактда
буш туплам ёки
элементлари факат исботланувчи формулалардан иборат булса, у вактда ![]() дан
келтириб чикариладиган формулалар синфи исботланувчи форму-лалар синфи билан
мос келади. Агар формулалар мажмуаси
дан
келтириб чикариладиган формулалар синфи исботланувчи форму-лалар синфи билан
мос келади. Агар формулалар мажмуаси ![]() нинг хеч булмаганда
битта элементи исботланмайдиган формуладан иборат булса, у холда
нинг хеч булмаганда
битта элементи исботланмайдиган формуладан иборат булса, у холда ![]() дан
келтириб чикари-ладиган формулалар синфи исботланувчи формулалар синфига
нисбатан кенгрок булади.
дан
келтириб чикари-ладиган формулалар синфи исботланувчи формулалар синфига
нисбатан кенгрок булади.
Мисол.
![]() формула
формула ![]() формулалар мажмуасидан келтириб чикарилишини исбот
этинг.
формулалар мажмуасидан келтириб чикарилишини исбот
этинг.
Исбот.
![]() ва
ва
![]() булганлиги
учун формулани келтириб чикариш коидасига асосан
булганлиги
учун формулани келтириб чикариш коидасига асосан
![]() (1)
(1)
![]() (2)
(2)
II3 ва I1
аксиомаларга нисбатан 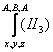 ва
ва ![]() урнига куйишларни
бажарамиз. Натижада исботланувчи формулалар хосил булади. Улар формулани
келтириб чикариш коидасига асосан
урнига куйишларни
бажарамиз. Натижада исботланувчи формулалар хосил булади. Улар формулани
келтириб чикариш коидасига асосан ![]() дан келтирилиб чикарилади,
яъни
дан келтирилиб чикарилади,
яъни
![]() (3)
(3)
![]() (4)
(4)
каби булади.
![]() исботланувчи
формула эканлиги учун
исботланувчи
формула эканлиги учун
![]() (5)
(5)
(5) ва (3) формулалардан хулоса коидасига асосан
![]() (6)
(6)
ни хосил киламиз. Худди шундай (2) ва (4) формулалардан
![]() (7)
(7)
муносабатга келамиз.
(7) ва (6) формулалардан хулоса коидасига асосан
![]() (8)
(8)
келиб чикади. У вактда (1) ва (8) формулалардан
![]() (9)
(9)
ни
хосил киламиз, яъни ![]() формула
формула ![]() формулалар мажмуасидан келиб чикишини курсатдик.
формулалар мажмуасидан келиб чикишини курсатдик.
![]() формулалар мажмуасидан бирорта ихтиёрий формулани
келтириб чикаришда мураккаб хулоса коидасидан хам фойдаланса булади.
формулалар мажмуасидан бирорта ихтиёрий формулани
келтириб чикаришда мураккаб хулоса коидасидан хам фойдаланса булади.
Бу холда (9) муносабатга (5), (7), (1) ва (3) мулохазалар оркали келиш мумкин.
5-§. Келтириб чикариш (исботлаш) тушунчаси.
Дедукция теоремаси. Умумлашган дедукция теоремаси.
Исботлаш тушунчаси. -Келтириб чикаришнинг хоссалари. -Келтириб чикаришнинг асосий коидалари. -Дедукция теоремаси. -Дедукция умумлашган теоремаси. -Конъюнкцияни киритиш коидаси. -Дизъюнкцияни киритиш коидаси.
5.1. Келтириб чикариш (исботлаш) тушунчаси
Таъриф.
Агар ![]() чекли формулалар кетма-кетлигининг
хар кандай хади куйидаги:
чекли формулалар кетма-кетлигининг
хар кандай хади куйидаги:
1)![]() формулалар мажмуасининг бирорта формуласи;
формулалар мажмуасининг бирорта формуласи;
2) исботланувчи формула;
3)![]() кетма-кетликнинг исталган иккита олдинма-кейин келадиган элементларидан хулоса коидасига
асосан хосил килинади деган уч шартнинг бирортасини каноатлантирса, у холда бу
кетма-кетлик
кетма-кетликнинг исталган иккита олдинма-кейин келадиган элементларидан хулоса коидасига
асосан хосил килинади деган уч шартнинг бирортасини каноатлантирса, у холда бу
кетма-кетлик ![]() чекли формулалар мажмуасидан келтириб чикарилган деб
айтилади.
чекли формулалар мажмуасидан келтириб чикарилган деб
айтилади.
Олдинги параграфдаги мисолда курсатилдики, ![]() дан куйидаги формулалар чекли кетма-кетлиги
келтирилиб чикарилади:
дан куйидаги формулалар чекли кетма-кетлиги
келтирилиб чикарилади:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Агар мураккаб хулоса коидасидан фойдалансак, у вактда (исбот) келтириб чикариш формулалари куйидагича булади:
![]()
![]()
![]()
![]()
![]()
![]()
Формулани келтириб чикариш ва формулалар мажмуасидан келтириб чикариш таърифларига асосан келтириб чикаришнинг куйидаги хоссалари хосил булади:
-![]() формулалар мажмуасидан
келтириб чикарилган чекли кетма-кетликнинг бошлангич кисми хам
формулалар мажмуасидан
келтириб чикарилган чекли кетма-кетликнинг бошлангич кисми хам ![]() дан
келтириб чикариладиган булади;
дан
келтириб чикариладиган булади;
-агар ![]() дан келтириб чикарилган
кетма-кетликнинг иккита кушни хадлари (элементлари) орасига
дан келтириб чикарилган
кетма-кетликнинг иккита кушни хадлари (элементлари) орасига ![]() дан келтириб
чикарилган кандайдир бошка кетма-кетлик куйилса, у вактда хосил этилган янги
формулалар кетма-кетлиги хам
дан келтириб
чикарилган кандайдир бошка кетма-кетлик куйилса, у вактда хосил этилган янги
формулалар кетма-кетлиги хам ![]() дан келтириб чикарилиши
мумкин.
дан келтириб чикарилиши
мумкин.
Хакикатан хам, масалан, агар ![]() ва
ва ![]() лар
лар ![]() дан келтириб чикарилса,
у вактда келтириб чикариш таърифига асосан
дан келтириб чикарилса,
у вактда келтириб чикариш таърифига асосан ![]()
![]()
![]() хам
хам ![]() дан
келтириб чикариладиган булади.
дан
келтириб чикариладиган булади.
-![]() формулалар мажмуасидан келтириб чикарилган формулалар кетма-кетлигининг хар кандай хади
формулалар мажмуасидан келтириб чикарилган формулалар кетма-кетлигининг хар кандай хади ![]() дан
келтириб чикариладиган формуладир.
дан
келтириб чикариладиган формуладир.
-агар
![]() Ì
Ì![]() булса, у вактда
булса, у вактда ![]() дан келтириб чикарилган хар кандай формула
дан келтириб чикарилган хар кандай формула ![]() нинг
хам формуласи булади.
нинг
хам формуласи булади.
-![]() формула
формула ![]() дан келтириб чикариладиган формула булиши учун
дан келтириб чикариладиган формула булиши учун ![]() дан келтириб чикарилган ихтиёрий формулалар
кетма-кетлигида бу формуланинг мавжуд булиши етарли ва зарурдир.
дан келтириб чикарилган ихтиёрий формулалар
кетма-кетлигида бу формуланинг мавжуд булиши етарли ва зарурдир.
5.2. Келтириб чикариш коидаси
![]() ва
ва ![]() мулохазалар хисобининг
иккита формулалар мажмуаси булсин.
мулохазалар хисобининг
иккита формулалар мажмуаси булсин. ![]() оркали бу мажмуаларнинг йигиндисини (бирлашмасини)
белгилаймиз, яъни
оркали бу мажмуаларнинг йигиндисини (бирлашмасини)
белгилаймиз, яъни
![]() .
.
Агар
![]() мажмуа
битта
мажмуа
битта ![]() формуладан иборат
булганда хам
формуладан иборат
булганда хам ![]() бирлашмани
бирлашмани ![]() куринишда
ёзамиз.
куринишда
ёзамиз.
Энди келтириб чикаришнинг асосий коидаларини куриб утамиз.
I.
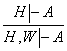 .
.
Бу коида бевосита формулалар мажмуасидан келтириб чикариш коидасидан хосил булади.
II.
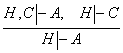 .
.
Исбот. Коиданинг
шартига асосан ![]() формулалар мажмуасидан
формулалар мажмуасидан
![]() формула
келтириб чикарилади. Шунинг учун
формула
келтириб чикарилади. Шунинг учун ![]() дан охирги формуласи
дан охирги формуласи ![]() булган
келтириб чикариш мавжуд:
булган
келтириб чикариш мавжуд:
![]() . (1)
. (1)
Худди шундай ![]() формулалар мажмуасидан
формулалар мажмуасидан ![]() формулани келтириб чикарилиши мумкинлигидан
формулани келтириб чикарилиши мумкинлигидан ![]() дан кейинги формуласи
дан кейинги формуласи ![]() булган келтириб чикариш мавжуд:
булган келтириб чикариш мавжуд:
![]() .
(2)
.
(2)
(1) келтириб чикаришда ![]() формула иштирок этмаган холда, у факат
формула иштирок этмаган холда, у факат ![]() формулалар мажмуасидан келтириб чикарилган
кетма-кетликда булади. Демак,
формулалар мажмуасидан келтириб чикарилган
кетма-кетликда булади. Демак, ![]() дан
дан ![]() формула келтириб чикарилади.
формула келтириб чикарилади.
Агар (1) келтириб чикаришда бирорта формула ![]() булса (масалан формула
булса (масалан формула ![]() ), у холда
), у холда ![]() ва
ва ![]() формулалар орасига (2) ни куямиз. Натижада куйидаги
факат
формулалар орасига (2) ни куямиз. Натижада куйидаги
факат ![]() дан келтириб чикаришни оламиз:
дан келтириб чикаришни оламиз:
![]()
![]()
![]()
![]() .
.
Шундай килиб, Н дан А формула келтириб чикарилади.
III.
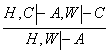 .
.
Исбот. ![]() булганлиги
учун I-коидага асосан
булганлиги
учун I-коидага асосан ![]() . Коиданинг шартига
биноан
. Коиданинг шартига
биноан ![]() , у холда I-коидага
кура
, у холда I-коидага
кура ![]() .
.
II-коидадан
фойдаланиб ![]() ни топамиз.
ни топамиз.
IV.
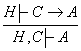 .
.
Исбот. ![]() формула
формула
![]() формулалар
мажмуасидан келтириб чикариладиганлиги сабабли
формулалар
мажмуасидан келтириб чикариладиганлиги сабабли ![]() нинг шундай келтириб
чикариши мавжудки, унинг охирида
нинг шундай келтириб
чикариши мавжудки, унинг охирида ![]() формула туради:
формула туради:
![]() . (3)
. (3)
Энди ![]() формулалар мажмуасига
формулалар мажмуасига ![]() формулани кушиб,
формулани кушиб, ![]() формулалар мажмуасини хосил киламиз. (3) келтириб чикаришга
формулалар мажмуасини хосил киламиз. (3) келтириб чикаришга
![]() формулани кушиб, ушбу келтириб чикаришга эга буламиз:
формулани кушиб, ушбу келтириб чикаришга эга буламиз:
![]() . (4)
. (4)
Уз навбатида бу ![]() формулалар
мажмуасининг келтириб чикариши булади.
формулалар
мажмуасининг келтириб чикариши булади.
(4) нинг охирига ![]() формулани ёзиш мумкин, чунки у хулоса коидасига
асосан
формулани ёзиш мумкин, чунки у хулоса коидасига
асосан ![]() ва
ва ![]() формулалардан хосил килинади.
формулалардан хосил килинади.
Демак, охирги формуласи ![]() булган
булган ![]() формулалар мажмуасининг
формулалар мажмуасининг
![]()
келтириб чикаришига эга буламиз. Бу ердан ![]() эканлиги келиб чикади.
эканлиги келиб чикади.
V. Дедукция теоремаси:  .
.
Аввал ![]() формулалар мажмуасининг хар кандай
формулалар мажмуасининг хар кандай ![]() келтириб чикариши учун
келтириб чикариши учун ![]() нинг тугрилигини математик индукция методидан фойдаланиб исбот киламиз.
нинг тугрилигини математик индукция методидан фойдаланиб исбот киламиз.
1. ![]() хол учун масала тугри.
Хакикатан хам, агар
хол учун масала тугри.
Хакикатан хам, агар ![]() формула
формула ![]() нинг келтириб чикариши булса,
у вактда уч хол булиши мумкин:
нинг келтириб чикариши булса,
у вактда уч хол булиши мумкин:
а) ![]()
б) ![]() – исботланувчи формула,
– исботланувчи формула,
в) ![]() - формула
- формула ![]() нинг узидир.
нинг узидир.
а) ва б) холлар учун ![]() дан куйидаги келтириб
чикаришни ёзиш мумкин:
дан куйидаги келтириб
чикаришни ёзиш мумкин: ![]() ,
, ![]()
![]() . Демак,
. Демак,
![]() .
.
в) хол учун ![]() эканлигини исботлаш керак.
эканлигини исботлаш керак.
Аммо ![]() исботланувчи формуладир.
Шунинг учун уни хар кандай мажмуадан келтириб чикариш мумкин.
исботланувчи формуладир.
Шунинг учун уни хар кандай мажмуадан келтириб чикариш мумкин.
2.Энди исталган ![]() (
(![]() ) чукурликдаги
хар кандай келтириб чикариш учун масала тугри булсин деб хисоблаганда, унинг
) чукурликдаги
хар кандай келтириб чикариш учун масала тугри булсин деб хисоблаганда, унинг ![]() чукурликдаги
келтириб чикариш учун тугрилигини исбот киламиз.
чукурликдаги
келтириб чикариш учун тугрилигини исбот киламиз.
![]() лар
лар ![]() мажмуанинг келтириб чикариши булсин, бу ерда
мажмуанинг келтириб чикариши булсин, бу ерда ![]() . Шунинг учун хам
. Шунинг учун хам ![]() k формулага нисбатан турт хол юз бериши мумкин:
k формулага нисбатан турт хол юз бериши мумкин:
а)![]() Î
Î![]() ,
,
б)![]() – исботланувчи формула,
– исботланувчи формула,
в)![]() формула
формула ![]() нинг узидир,
нинг узидир,
г)![]() формула хулоса коидасига асосан келтириб чикаришдаги
иккита ундан олдин кетма-кет келадиган формулалардан хосил килинади.
формула хулоса коидасига асосан келтириб чикаришдаги
иккита ундан олдин кетма-кет келадиган формулалардан хосил килинади.
а), б), в) холатлар учун исбот тулик равишда ![]() холдаги
исботга мос келади.
холдаги
исботга мос келади.
Шунинг учун г) холни курамиз. Бу холда ![]() формула
формула
![]() ва
ва
![]() формулалардан
хосил килиниб
формулалардан
хосил килиниб ![]() ,
, ![]() формула куринишни
формула куринишни
![]() олади
ва куйидаги тасдиклар тугри булади:
олади
ва куйидаги тасдиклар тугри булади:
![]() (5)
(5)
![]() (6)
(6)
I2 аксиомада

урнига куйишни бажариб, куйидаги исботланувчи формулага эга буламиз:
![]() (7)
(7)
(6), (5) ва (7) лар Н дан келтириб чикариладиган
формулалардир. Уларга мураккаб хулоса коидасини куллаб, ![]() ни хосил киламиз.
ни хосил киламиз.
Энди умумий, яъни ![]() булган холни курайлик. У вактда
булган холни курайлик. У вактда ![]() нинг
нинг ![]() ,
, ![]() келтириб чикариши мавжуд булади. Демак, юкорида исбот
килганимизга асосан
келтириб чикариши мавжуд булади. Демак, юкорида исбот
килганимизга асосан ![]() тасдик тугридир.
тасдик тугридир.
Дедукция теоремасидан мухим ахамиятга эга булган куйидаги натижа келиб чикади.
Умумлашган дедукция теоремаси: 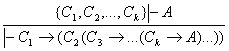 .
.
Исбот. ![]() булсин. Теорема шартига асосан
булсин. Теорема шартига асосан ![]() ёки
ёки ![]() тугрилиги,
тугрилиги,
![]() булганлиги
учун эса
булганлиги
учун эса
![]()
тасдикнинг тугрилиги келиб чикади. Бу ифодага нисбатан яна дедукция теоремасини куллаб,
![]() ни
ни
хосил
киламиз. Бу процедурани ![]() марта такрорлаб, ушбу тасдикка келамиз:
марта такрорлаб, ушбу тасдикка келамиз:
![]() Æ
Æ![]()
Аммо буш тупламдан факатгина исботланувчи формулалар келтириб чикариш мумкин, яъни
![]()
![]() хусусий холда
хусусий холда
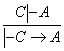 га
га
эга буламиз.
VI. Конъюнкцияни киритиш коидаси:
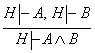 .
.
Исбот. Берилганига кура
![]() ,
(8)
,
(8)
![]() .
(9)
.
(9)
![]() формулалар
мажмуасидан
формулалар
мажмуасидан ![]() формулани келтириб чикариш мумкинлиги, яъни
формулани келтириб чикариш мумкинлиги, яъни
![]()
![]()
![]() . (10)
. (10)
эканлигини курсатган эдик
Келтириб чикаришнинг I коидасига асосан
![]()
![]()
![]() , (11)
, (11)
![]() . (12)
. (12)
Келтириб чикаришнинг II коидасидан фойдаланиб, (11) ва (12) муносабатлардан
![]()
![]()
![]() (13)
(13)
хамда (8) ва (13) дан
![]()
![]()
![]()
ларни хосил киламиз.
VII.Дизъюнкцияни киритиш коидаси:
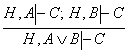 .
.
Исбот. ![]() ;
; ![]() шартлардан
дедукция теоремасига асосан
шартлардан
дедукция теоремасига асосан
![]() ,
(14)
,
(14)
![]() (15)
(15)
формулалар келиб чикади.
III
аксиома ![]() формулалар мажмуасидан
исботланувчи формула сифатида келтириб чикарилади, яъни
формулалар мажмуасидан
исботланувчи формула сифатида келтириб чикарилади, яъни
![]() .
(16)
.
(16)
(14), (15) ва (16) формулаларга мураккаб хулоса коидасини куллаб
![]() (17)
(17)
формулани хосил киламиз.
Энди келтириб чикаришнинг IV коидасини куллаб
![]()
формулага эга буламиз.
6-§. Айрим мантик конунларининг исботи
Мантик конунлари. -Шартларни уриналмаштириш конуни. -Шартларни кушиш конуни. -Шартларни ажратиш конуни.
Дедукция теоремаси бир катор мантик конунларини исботлашга ёрдам беради.
I. Асосларни (шартларни) уриналмаштириш конуни:
![]() (1)
(1)
Исбот.
![]() формулалар
мажмуасидан
формулалар
мажмуасидан ![]() келтириб чикариш келиб
чикади. Демак,
келтириб чикариш келиб
чикади. Демак, ![]() дан
дан ![]() формула
келиб чикади. У холда умумлашган дедукция теоремасига асосан (1) формула
исботланувчи эканлигини хосил киламиз.
формула
келиб чикади. У холда умумлашган дедукция теоремасига асосан (1) формула
исботланувчи эканлигини хосил киламиз.
Асосларни уриналмаштириш конунидан исботланувчи формулалар учун асосларни уриналмаштириш коидаси:
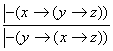
келиб чикади.
Хакикатан хам, агар
![]() (2)
(2)
булса, у вактда (1) ва (2) формулалардан хулоса коидасига асосан
![]()
формула хосил килинади.
II. Асосларни кушиш конуни:
![]()
![]() (3)
(3)
Исбот.
![]() формулалар
мажмуасидан
формулалар
мажмуасидан ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() келтириб чикариш олинади. Бу эса
келтириб чикариш олинади. Бу эса ![]() дан
дан ![]() формула
келиб чикади демакдир. Бу уз навбатида умумлашган дедукция теоремасига асосан
(3) формуланинг исботланувчи эканлигини курсатади.
формула
келиб чикади демакдир. Бу уз навбатида умумлашган дедукция теоремасига асосан
(3) формуланинг исботланувчи эканлигини курсатади.
Асосларни кушиш конунидан исботланувчи формулалар учун асосларни кушиш коидаси:

келиб чикади
Хакикатан хам, агар
![]() (4)
(4)
булса,
у вактда (3) ва (4) формулалардан хулоса коидаларига асосан ![]() эканлигини хосил
киламиз.
эканлигини хосил
киламиз.
III. Асосларни ажратиш конуни:
![]() .
(5)
.
(5)
Исбот. ![]() формулалар мажмуасидан келиб чикадиган
формулалар мажмуасидан келиб чикадиган ![]() келтириб
чикаришни караймиз. Бунда
келтириб
чикаришни караймиз. Бунда ![]() формулалар мажмуасидан
формулалар мажмуасидан
![]() формуланинг
келиб чикиши куриниб турибди. У холда умумлашган дедукция теоремасига асосан
(5) формула исботланувчи эканлигига ишонч хосил киламиз.
формуланинг
келиб чикиши куриниб турибди. У холда умумлашган дедукция теоремасига асосан
(5) формула исботланувчи эканлигига ишонч хосил киламиз.
Асосларни ажратиш конунидан исботланувчи формулалар учун асосларни ажратиш коидаси:
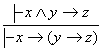
хосил булади.
Хакикатан хам, агар
![]() (6)
(6)
булса,
у вактда (5) ва (6) формулалардан хулоса коидасига асосан ![]() эканлиги
келиб чикади.
эканлиги
келиб чикади.
IV. ![]() .
.
Исбот. I1 ва IV1 аксиомаларда куйидаги урнига ку-йишларни
![]() ва
ва ![]() .
.
бажариш натижасида
![]() (7)
(7)
![]() (8)
(8)
исботланувчи формулаларни хосил киламиз.
(7) ва (8) формулалардан силлогизм коидасига асосан
![]()
формула келиб чикади.
Асосларни бирлаштириш конунидан фойдаланиб,
![]()
формулани хосил киламиз.
Икки карралик инкорни тушириш коидасидан фойдаланиб,
![]()
формулага эга буламиз.
Бу ердан асосларни ажратиш конунини куллаб, исботланиши керак булган (5) формулани келтириб чикарамиз.
V.
![]() .
.
Исбот.
III3
аксиомада z нинг урнига ![]() ни куямиз:
ни куямиз:
![]() . (9)
. (9)
II1 ва II2 аксиомалардан
![]() ,
(10)
,
(10)
![]() (11)
(11)
формулалар келиб чикади.
(10) ва (11) формулаларга контрпозиция коидасини куллаб, ушбу формулаларни хосил киламиз:
![]() ,
(12)
,
(12)
![]() .
(13)
.
(13)
Бу формулаларга икки каррали инкорни тушириш коидасини куллаб, куйидаги формулаларни келтириб чикарамиз:
![]() ,
(14)
,
(14)
![]() .
(15)
.
(15)
Энди (9), (14) ва (15) формулаларга мураккаб хулоса коидасини куллаб,
![]() (16)
(16)
формулага эга буламиз.
Нихоят, (16) формулага аввал контрпозиция коидасини ва сунгра икки мартали инкорни тушириш коидасини куллаб,
![]()
исботланиши лозим булган формулани хосил киламиз.
РЕЖА:
1.Формулалар мажмуасидан формулани келти-
риб чикариш коидаси.
2.Келтириб чикариш (исботлаш) тушунчаси.
Дедукция теоремаси. Умумлашган дедукция
теоремаси.
3.Айрим мантик конунларининг исботи.
Муаммоли масала ва топшириклар:
1. ![]() формулалар
мажмуасидан курсатилган формулаларни келтириб чикариш мумкинлигини курсатинг:
формулалар
мажмуасидан курсатилган формулаларни келтириб чикариш мумкинлигини курсатинг:
1) ![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10) ![]() .
.
2. Умумлашган дедукция теоремасидан фойдаланиб, формулаларнинг исботланувчи эканлигини исботланг:
1) ![]() ;
;
2)
![]() ;
;
3)
![]() .
.
3. Мантик конунларининг тугрилигини курсатинг:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() .
.
4. Шартларни урин алмаштириш, шартларни кушиш ва шартларни ажратиш коидаларидан фойдаланиб, берилганларнинг тугрилигини исботланг:
1) ![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Мустакил ишлаш учун саволлар:
1.Келтириб чикариладиган ва исботланувчи фор-
мулалар синфи.
2.Формулалар мажмуасидан формулани келтириб
чикариш коидаси.
3.Келтириб чикариш (исботлаш) тушунчаси.
Келтириб чикаришнинг хоссалари ва асосий
коидалари.
4.Дедукция теоремаси ва умумлашган дедукция
теоремаси.
5.Конъюнкцияни ва дизъюнкцияни киритиш
коидалари.
6.Мантик конунлари. Шартларни уриналмашти-
риш, кушиш ва ажратиш конунлари.
7-§. Мулохазалар алгебраси ва мулохазалар хисоби уртасидаги муносабатлар
Мулохазалар хисоби формуласининг киймати. -Мулохазалар хисобидаги формулалар билан мулохазалар алгебрасидаги формулалар уртасидаги
муносабатлар. -Умумкийматли формула. -Айнан чин формула. -Келтириб чикариш хакидаги теорема.
Мулохазалар хисоби формулаларини худди мулохаза-лар алгебраси формулалари сифатида караш мумкин. Бунинг учун мулохазалар хисоби узгарувчиларига мулохазалар алгебраси узгарувчилари сингари караймиз, яъни узгарувчилар чин ёки ёлгон (1 ёки 0) киймат олади деб хисоблаймиз.
![]() ва - амалларни мулохазалар алгебрасидагидай аниклаймиз.
ва - амалларни мулохазалар алгебрасидагидай аниклаймиз.
Мулохазалар хисобининг хар бир формуласи, узгарувчилар унинг ифодасига кандай киришидан катъий назар, 1 ёки 0 киймат кабул килади. Унинг киймати мулохазалар алгебрасидаги коидалар буйича хисобланади.
Мулохазалар хисоби формуласининг киймати тушунчасини аниклайлик.
![]() -мулохазалар
хисоби формуласи,
-мулохазалар
хисоби формуласи, ![]() лар эса
лар эса ![]() формула
ифодасига кирувчи узгарувчилар
формула
ифодасига кирувчи узгарувчилар ![]() булсин.
булсин. ![]() лар
оркали мос равишда
лар
оркали мос равишда ![]() узгарувчиларнинг кийматларини
белгилаймиз,
узгарувчиларнинг кийматларини
белгилаймиз, ![]() .
. ![]() вектор 2n
та кийматлар сатрига эга.
вектор 2n
та кийматлар сатрига эга.
Узгарувчиларнинг
битта кийматлар сатри учун ![]() формуланинг киймати
формуланинг киймати ![]() ни куйидагича
аниклаймиз:
ни куйидагича
аниклаймиз:
1.![]() формуланинг энг катта узунликдаги кисмий формуласи
формуланинг энг катта узунликдаги кисмий формуласи ![]() булганда,
булганда, ![]() булади.
булади.
2.Агар
![]() узунликдаги
хамма кисмий формулалари аникланган булса, у вактда
узунликдаги
хамма кисмий формулалари аникланган булса, у вактда ![]() ,
, ![]() ,
, ![]() ,
, ![]() амалларнинг бажарилиши натижасида олинган
амалларнинг бажарилиши натижасида олинган ![]() узунликдаги
кисмий формулалар куйидаги кийматларга эга булади:
узунликдаги
кисмий формулалар куйидаги кийматларга эга булади:
Ra1a2..an(АiLAj)=Ra1a2..an(Аi)LRa1..an(Aj),
Ra1..an(АiVAj)=Ra1..an(Аi)VRa1..an(Aj),
Ra1..an(Аi®Aj)=Ra1..an(Аi)®Ra1..an(Aj),
Ra1..an(![]() )=
)=![]() .
.
Масалан, ![]() формула
формула ![]() узгарувчиларнинг (0,1,1,0) кийматлар
сатрида
узгарувчиларнинг (0,1,1,0) кийматлар
сатрида ![]() 0110
0110![]() кийматга эга.
кийматга эга.
Хакикатан хам, бу формула куйидаги кисмий формулаларга эга:
![]() - биринчи узунликдаги кисмий
формулалар,
- биринчи узунликдаги кисмий
формулалар,
![]() - иккинчи узунликдаги кисмий
формулалар,
- иккинчи узунликдаги кисмий
формулалар,
![]() - учинчи узунликдаги кисмий
формулалар,
- учинчи узунликдаги кисмий
формулалар,
![]() - туртинчи узунликдаги
кисмий формула.
- туртинчи узунликдаги
кисмий формула.
Бу ердан ![]() 0110
0110![]() ,
, ![]() 0110
0110![]() =
=![]() ,
,
![]() 0110
0110![]() ,
,![]() 0110
0110![]() ,
,
![]() 0110
0110![]() =
=![]() 0110
0110![]() 0110
0110![]() ,
,
![]() 0110
0110![]() =
=![]() ,
,![]() 0110
0110![]() ,
,
![]() 0110
0110![]() =0110
=0110![]() 0110
0110![]() ,
,
![]() 0110
0110![]() =
=![]() ,
,
![]() 0110
0110![]() =
=
=![]() 0110
0110![]()
![]() 0110
0110![]()
эканлигини топамиз.
Энди мулохазалар хисоби билан мулохазалар алгебраси уртасидаги муносабатларни аникловчи теоремаларга тухталиб утайлик.
1-теорема. Мулохазалар хисобидаги хар бир исботланувчи формула мулохазалар алгебрасида айнан чин (тавталогия, умумкийматли) формула булади.
Исбот. Теоремани исбот килиш учун куйидаги учта холни куриб чикишга тугри келади:
1)Мулохазалар хисобидаги хар бир аксиома мулохазалар алгебрасидаги айнан чин формуладир.
2)Айнан чин формулаларга урнига куйиш коидасини куллаш натижасида хосил этилган формулалар яна айнан чин формулалар булади.
3)Айнан чин формулаларга хулоса коидасини куллаш натижасида хосил этилган формулалар яна айнан чин формулалар булади.
1-холнинг исботи. Мулохазалар хисоби аксиомаларининг айнан чинлигини исботлаш учун чинлик жадвалидан фойдаланамиз.
а)Ифодасида битта узгарувчиси бор аксиомалар:
|
|
IV2 |
IV3 |
|
1 |
1 |
1 |
|
0 |
1 |
1 |
б)Ифодасида иккита узгарувчиси бор аксиомалар:
|
|
|
I1 |
II1 |
II2 |
III1 |
III2 |
IV1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
в)Ифодасида учта узгарувчиси бор аксиомалар:
|
|
|
|
I2 |
II3 |
III3 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
2-холнинг исботи. Аввал куйидаги леммани исбот киламиз.
Лемма. ![]() ва
ва
![]() формулаларнинг
ифодасига кирувчи хамма узгарувчилар
формулаларнинг
ифодасига кирувчи хамма узгарувчилар ![]() ва бу узгарувчиларнинг
ихтиёрий кийматлар сатри эса
ва бу узгарувчиларнинг
ихтиёрий кийматлар сатри эса ![]() булсин. Агар
булсин. Агар
![]() булса, у холда
булса, у холда ![]()
 =
=![]() булади.
булади.
Исбот. Лемманинг исботини, формуланинг тузилишини хисобга олган холда, индукция методи билан амалга оширамиз.
а)
![]() формула
формула
![]() дан
фарк килувчи
дан
фарк килувчи ![]() узгарувчи булсин. У холда
узгарувчи булсин. У холда
![]() i,
i,
![]()
![]() ;
;
![]()

![]() ,
, ![]() ,
,
яъни лемманинг тасдиги тугри булади.
б) ![]() формула,
формула, ![]() узгарувчи булсин. У вактда
узгарувчи булсин. У вактда
![]() урнига
куйиш
урнига
куйиш ![]() ни беради ва
ни беради ва
![]()
 =
=![]() ,
,
ни оламиз, яъни лемманинг тасдиги яна тугри булади.
в)
![]() хамда
хамда
![]() ва
ва ![]() формулалар учун лемманинг шартлари бажарилсин. У вактда
формулалар учун лемманинг шартлари бажарилсин. У вактда
![]() формула учун лемма тасдигининг тугрилиги куйидаги
тенгликлардан келиб чикади:
формула учун лемма тасдигининг тугрилиги куйидаги
тенгликлардан келиб чикади:
![]()
 =
=![]()
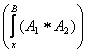 =
=![]()
 =
= ![]()
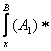
![]()
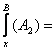
=![]()
![]() =
=![]() =
=![]() .
.
![]()
![]() булган хол учун хам лемманинг тасдиги юкоридагидай
исботланади. Энди 2-холнинг исботига утамиз.
булган хол учун хам лемманинг тасдиги юкоридагидай
исботланади. Энди 2-холнинг исботига утамиз.
Лемма.
![]() -берилган формула,
-берилган формула, ![]() -узгарувчи,
-узгарувчи, ![]() -мулохазалар хисобининг исталган формуласи булсин.
Агар
-мулохазалар хисобининг исталган формуласи булсин.
Агар ![]() айнан чин формула булса, у вактда
айнан чин формула булса, у вактда ![]() формула хам айнан чин формула булади.
формула хам айнан чин формула булади.
Исбот.
![]() лар
лар
![]() ва
ва ![]() формулалар
ифодасига кирувчи узгарувчилар булсин. Узгарувчиларнинг хамма 2n+1 та
формулалар
ифодасига кирувчи узгарувчилар булсин. Узгарувчиларнинг хамма 2n+1 та ![]() кийматлар
сатрида
кийматлар
сатрида ![]() формула чин киймат кабул килишини курсатиш лозим.
формула чин киймат кабул килишини курсатиш лозим. ![]() формула айнан чин формула эмас деб фараз киламиз. У холда
шундай
формула айнан чин формула эмас деб фараз киламиз. У холда
шундай ![]() кийматлар
сатри топилиб,
кийматлар
сатри топилиб,
![]()
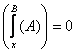
булади.
Бундан уз навбатида лемма шартига асосан ![]() эканлигини топамиз. Аммо бу
эканлигини топамиз. Аммо бу ![]() нинг айнан чин формула эканлигига зиддир. Демак, хамма
киймат-лар сатрида
нинг айнан чин формула эканлигига зиддир. Демак, хамма
киймат-лар сатрида ![]() формула чин киймат кабул килади ва у айнан чиндир.
формула чин киймат кабул килади ва у айнан чиндир.
3-холнинг исботи. Агар ![]() ва
ва ![]() формулалар
айнан чин булса, у холда
формулалар
айнан чин булса, у холда ![]() хам айнан чин формула
булади.
хам айнан чин формула
булади.
Исбот.
![]() лар
лар
![]() ва
ва
![]() формулалар ифодасига кирувчи узгарувчилар булсин.
формулалар ифодасига кирувчи узгарувчилар булсин. ![]() -айнан чин булмаган формула деб фараз киламиз.
У вактда узгарувчиларнинг
шундай
-айнан чин булмаган формула деб фараз киламиз.
У вактда узгарувчиларнинг
шундай
![]() кийматлар сатри мавжуд буладики,
кийматлар сатри мавжуд буладики,
![]() булади.
Бу ердан
булади.
Бу ердан ![]()
![]() =
= ![]()
![]() эканлиги келиб чикади. Бу натижа
эканлиги келиб чикади. Бу натижа ![]() формуланинг
айнан чин эканлигига зиддир. Бу карама-каршилик,
формуланинг
айнан чин эканлигига зиддир. Бу карама-каршилик, ![]() айнан чин формула эканлигини исботлайди.
айнан чин формула эканлигини исботлайди.
2-теорема
(келтириб чикариш хакида). ![]() -мулохазалар хисобининг
бирор формуласи;
-мулохазалар хисобининг
бирор формуласи; ![]() -
-![]() формула ифодасига
кирувчи узгарувчилар ва
формула ифодасига
кирувчи узгарувчилар ва ![]() -узгарувчиларнинг ихтиёрий кийматлар сатри
булсин.
-узгарувчиларнинг ихтиёрий кийматлар сатри
булсин. ![]() оркали чекли формулалар мажмуасини белгилаймиз. Агар
оркали чекли формулалар мажмуасини белгилаймиз. Агар
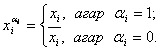
булса,
у холда ![]() формулалар мажмуаси учун:
формулалар мажмуаси учун:
1) ![]() булган холда
булган холда ![]() ;
;
2) ![]() булган холда
булган холда ![]()
булади.
Исбот. Теореманинг исботини формула тузилишига караб индукция методи билан олиб борамиз.
1.
![]() формула
формула ![]() узгарувчи
булсин.
узгарувчи
булсин.
а)Агар
![]() булса,
у вактда
булса,
у вактда ![]() ёки
ёки ![]() , яъни
, яъни ![]() . Демак,
. Демак,
![]() .
.
б)Агар
![]() булса,
у вактда
булса,
у вактда ![]() ёки
ёки ![]() , яъни
, яъни ![]() . Демак,
. Демак, ![]() .
.
2.Энди
фараз киламизки, ![]() ва
ва ![]() формулалар учун теорема тугри деб каралган холда,
формулалар учун теорема тугри деб каралган холда, ![]() формула куйидаги турт куринишнинг бири булсин:
формула куйидаги турт куринишнинг бири булсин:
I. ![]() , II.
, II. ![]() , III.
, III. ![]() , IV.
, IV. ![]() .
.
Хар бир холни алохида куриб утамиз.
1.![]() формула
формула ![]() куринишга эга.
куринишга эга.
а)Агар
![]()
![]() булса, у холда
булса, у холда ![]() ва
ва ![]() келиб
чикади. Бундан килинган фаразимизга кура
келиб
чикади. Бундан килинган фаразимизга кура ![]() ва
ва ![]() .
.
Бу
ердан уз навбатида конъюнкцияни киритиш коидасига асосан ![]() , яъни
, яъни ![]() хосил
булади.
хосил
булади.
б)Агар
![]()
![]() булса, у вактда
булса, у вактда ![]() ёки
ёки ![]() булади.
Масалан,
булади.
Масалан, ![]() дейлик, у холда
фаразга кура
дейлик, у холда
фаразга кура
![]() . (1)
. (1)
II1 аксиомага кура ![]() . Бу ердан контрпозиция коидасига асосан
. Бу ердан контрпозиция коидасига асосан
|-![]() (2)
(2)
келиб чикади.
(1) ва (2) формулалардан хулоса коидасига биноан ![]() ни хосил киламиз, яъни
ни хосил киламиз, яъни ![]() .
.
II.![]() формула
формула ![]() куринишга эга булсин.
куринишга эга булсин.
а)Агар ![]()
![]() булса, у вактда хеч булмаганда
булса, у вактда хеч булмаганда ![]()
![]() ёки
ёки ![]()
![]() булади.
булади. ![]()
![]() булсин, у холда фаразимизга кура
булсин, у холда фаразимизга кура
![]() (3)
(3)
III3 - аксиомага асосан эса
![]() (4)
(4)
келиб чикади.
(3) ва (4) формулалардан хулоса коидасига асосан ![]() ни хосил киламиз, яъни
ни хосил киламиз, яъни ![]() .
.
б)Агар ![]()
![]() булса, у холда
булса, у холда ![]()
![]() ва
ва ![]()
![]() булади. Бу ердан
булади. Бу ердан ![]() ва
ва ![]() келиб
чикади. Уз навбатида конъюнкцияни киритиш коидасига асосан
келиб
чикади. Уз навбатида конъюнкцияни киритиш коидасига асосан
![]() (5)
(5)
га келинади.
Исботланувчи формуладан фойдаланиб
![]() (6)
(6)
ни оламиз.
(5) ва (6) формулалардан хулоса коидасига асосан ![]() ни хосил киламиз, яъни
ни хосил киламиз, яъни ![]() .
.
III. ![]() формула
формула ![]() куринишда булсин.
куринишда булсин.
а)Агар ![]()
![]() булса, ёки
булса, ёки ![]()
![]() , ёки
, ёки ![]()
![]() булади. Масалан,
булади. Масалан, ![]()
![]() булса, у холда
булса, у холда
![]() (7)
(7)
ни хосил киламиз.
Исботланувчи формуладан фойдаланиб ![]() формулани топамиз. Бу формуладан асосларнинг уриналмаштириш
коидасига асосан
формулани топамиз. Бу формуладан асосларнинг уриналмаштириш
коидасига асосан
![]() (8)
(8)
формулани хосил киламиз.
(7) ва (8) формулалардан хулоса коидасига биноан ![]() формулани ёзамиз, яъни
формулани ёзамиз, яъни ![]() .
.
Агар ![]()
![]() булса, у холда
булса, у холда
![]() . (9)
. (9)
I1 - аксиомадан фойдаланиб
![]() (10)
(10)
формулани келтириб чикарамиз.
(9)
ва (10) формулалардан хулоса коидасига кура ![]() келиб чикади, яъни
келиб чикади, яъни ![]() .
.
б)Агар
![]()
![]() булса, у холда
булса, у холда ![]()
![]() ва
ва ![]()
![]() булади. Бу ердан
булади. Бу ердан
![]() , (11)
, (11)
![]()
![]() (12)
(12)
эканлиги келиб чикади. Исботланувчи формула таърифига асосан
![]() .
.
Бу формуладан асосларнинг уриналмаштириш коидасига кура
![]() (13)
(13)
формулани келтириб чикарамиз.
(11) ва (13) формулалардан хулоса коидасига биноан
![]() (14)
(14)
ни хосил киламиз, уз навбатида ундан контрпозиция коидасини куллаб
![]() (15)
(15)
формулани келтириб чикарамиз.
(12)
ва (15) формулалардан хулоса коидасига асосан ![]() формулага эга буламиз, яъни
формулага эга буламиз, яъни ![]() .
.
IV.![]() формула
формула ![]() куринишга эга булсин.
куринишга эга булсин.
а)Агар
![]()
![]() булса, у вактда
булса, у вактда ![]()
![]() булади. Демак,
булади. Демак, ![]() , яъни
, яъни ![]() .
.
б)Агар
![]()
![]() булса, у вактда
булса, у вактда ![]()
![]() булади ва бундан
булади ва бундан
![]() (16)
(16)
келиб чикади.
IV2 аксиомадан фойдаланиб
![]() ®
®![]() . (17)
. (17)
формулани ёзамиз.
(16) ва (17) формулалардан хулоса коидасига асосан ![]()
![]() ни, яъни
ни, яъни ![]()
![]() ни хосил киламиз.
ни хосил киламиз.
3-теорема. Мулохазалар алгебрасининг хар бир айнан чин формуласи мулохазалар хисобида исботланувчи формула булади.
Исбот. ![]() формула теорема шартига асосан айнан чин формула булганлиги
учун
формула теорема шартига асосан айнан чин формула булганлиги
учун ![]()
![]() . Бундан 2-теоремага асосан
. Бундан 2-теоремага асосан
![]() (18)
(18)
келиб
чикади, бу ерда ![]() .
.
![]() кийматлар сатрларининг
сони 2n тага тенг. Шунинг учун (18) формула хамма 2n
та кийматлар сатрида бажарилади.
кийматлар сатрларининг
сони 2n тага тенг. Шунинг учун (18) формула хамма 2n
та кийматлар сатрида бажарилади.
Агар ![]() булса, у вактда, равшан-ки,
булса, у вактда, равшан-ки, ![]() ,
, ![]() ва
ва ![]() ,
, ![]() | булади. Дизъюнкцияни киритиш коидасига асосан бу холда
| булади. Дизъюнкцияни киритиш коидасига асосан бу холда
![]() ,
, ![]() булади. Аммо
булади. Аммо ![]() формула исботланувчи формула булганлиги учун уни
формула исботланувчи формула булганлиги учун уни ![]() ,
, ![]() формулалар мажмуасидан олиб ташлаш мумкин. Демак,
формулалар мажмуасидан олиб ташлаш мумкин. Демак, ![]() .
.
Худди
шундай ![]() ,....,
,...., ![]() ,
, ![]() формулалар мажмуалари учун кетма-кет
формулалар мажмуалари учун кетма-кет ![]() ,
, ![]() ,...,
,...,![]() ,
, ![]() эканлигини исботлаш мумкин. Маълумки,
эканлигини исботлаш мумкин. Маълумки, ![]() муносабат
муносабат ![]() ва
ва ![]() холлар
учун тугридир, яъни
холлар
учун тугридир, яъни ![]() ва
ва ![]() . Бу ердан дизъюнкцияни киритиш коидасига асосан
. Бу ердан дизъюнкцияни киритиш коидасига асосан ![]()
![]() га эга буламиз. Аммо
га эга буламиз. Аммо ![]()
![]() исботланувчи формула булганлиги учун уни ташлаб
юбориш мумкин. Шундай килиб, Æ
исботланувчи формула булганлиги учун уни ташлаб
юбориш мумкин. Шундай килиб, Æ![]() . Демак,
. Демак, ![]() исботланувчи формула экан.
исботланувчи формула экан.
РЕЖА:
1.Мулохазалар алгебраси ва мулохазалар хисо-
би уртасидаги муносабатлар.
2.Мулохазалар хисобидаги формулалар билан
мулохазалар алгебрасидаги формулалар урта-
сидаги муносабатлар.
Муаммоли масала ва топшириклар:
1.
Куйидаги формула ![]() ва узгарувчиларнинг 1)
(0,0,1); 2) (1,0,0) кийматлар сатри берилган.
ва узгарувчиларнинг 1)
(0,0,1); 2) (1,0,0) кийматлар сатри берилган. ![]() формула ва унинг
инкори
формула ва унинг
инкори ![]() ни мос формулалар
мажмуасидан келтириб чикаринг.
ни мос формулалар
мажмуасидан келтириб чикаринг.
2.
Куйидаги формула ![]() ва узгарувчиларнинг 1)
(1,1,1); 2) (1,0,1); 3) (0,1,0) кийматлар сатри берилган.
ва узгарувчиларнинг 1)
(1,1,1); 2) (1,0,1); 3) (0,1,0) кийматлар сатри берилган. ![]() формула ва
унинг инкори
формула ва
унинг инкори ![]() ни мос формулалар
мажмуасидан келтириб чикаринг.
ни мос формулалар
мажмуасидан келтириб чикаринг.
3.
Куйидаги формула ![]() ва узгарувчиларнинг 1)
(1,0,0); 2) (0,1,1); 3) (0,1,0) кийматлар сатри берилган.
ва узгарувчиларнинг 1)
(1,0,0); 2) (0,1,1); 3) (0,1,0) кийматлар сатри берилган. ![]() формула ва
унинг инкори
формула ва
унинг инкори ![]() ни мос формулалар
мажмуасидан келтириб чикаринг.
ни мос формулалар
мажмуасидан келтириб чикаринг.
4. Умумлашган дедукция теоремасидан фойдаланиб, куйидаги формулаларни исботланувчи эканлигини ва улар мулохазалар алгебрасида айнан чин(тавталогия) формулалар эканлигини исботланг:
![]() ,
,
![]()
![]()
5. ![]() формула х1, х2, х3, х4
¢згарувчиларнинг (0,1,1,0) кийматлар сатрида
формула х1, х2, х3, х4
¢згарувчиларнинг (0,1,1,0) кийматлар сатрида ![]() 0110
0110![]() кийматга
эга эканлигини исботланг.
кийматга
эга эканлигини исботланг.
Мустакил ишлаш учун саволлар:
1.Мулохазалар хисоби формуласининг киймати.
2.Мулохазалар алгебраси ва мулохазалар хисоби
уртасидаги муносабатлар.
3.Умумкийматли ва айнан чин формулалар.
4.Келтириб чикариш хакидаги теорема.
5.Мулохазалар хисобидаги формулалар билан му-
лохазалар алгебрасидаги формулалар уртасида-
ги муносабатлар.
8-§. Мулохазалар хисобида ечилиш, зидсизлик, туликлилик ва эркинлик муаммолари
Ечилиш муаммоси. -Зидсизлик муаммоси. -Туликлилик муаммоси. -Эркинлик муаммоси. -Аксиоматик назария. -Тор маънода тулик. -Кенг маънода тулик. -Эркин аксиома. -Эркин аксиомалар системаси. -Тенгкучли формулалар.
Хар кандай аксиоматик назарияни асослаш учун куйидаги туртта:
1) ечилиш;
2) зидсизлик;
3) туликлилик;
4) эркинлик
муаммоларини хал килишга тугри келади.
8.1.Мулохазалар хисобининг ечилиш муаммоси
Мулохазалар хисобидаги ихтиёрий берилган формулани исботланувчи ёки исботланувчи эмаслигини аниклаб берувчи алгоритмнинг мавжудлигини исботлаш муаммоси мулохазалар хисобининг ечилиш муаммоси деб аталади.
1-теорема. Мулохазалар хисоби учун ечилиш муаммоси хал килинувчидир (ечилувчидир).
Исбот. Олдинги параграфда айтилгандай мулохазалар хисобининг исталган формуласини мулохазалар алгебрасининг формуласи сифатида караш мумкин. Демак, бу формуланинг мантикий кийматини узгарувчиларнинг исталган кийматлар сатрида аниклаш мумкин.
![]() -мулохазалар
хисобининг ихтиёрий формуласи,
-мулохазалар
хисобининг ихтиёрий формуласи, ![]() лар эса
лар эса ![]() формуланинг
ифодасига кирувчи узгарувчилар булсин.
формуланинг
ифодасига кирувчи узгарувчилар булсин.
![]()
![]() кийматини
хамма 2n та
кийматини
хамма 2n та ![]() кийматлар сатрида хисоблаб
чикамиз. Агар хамма кийматлар сатрида
кийматлар сатрида хисоблаб
чикамиз. Агар хамма кийматлар сатрида ![]()
![]() булса, у холда
булса, у холда ![]() формула айнан чин булади. Демак, 8-§ даги 3-теоремага
асосан
формула айнан чин булади. Демак, 8-§ даги 3-теоремага
асосан ![]() мулохазалар хисобининг исботланувчи формуласи булади.
мулохазалар хисобининг исботланувчи формуласи булади.
Агар
шундай (![]() ) кийматлар сатри топилиб,
) кийматлар сатри топилиб, ![]() булса, у вактда
булса, у вактда ![]() айнан чин формула булмайди. У холда 8-§ даги
1-теоремага асосан
айнан чин формула булмайди. У холда 8-§ даги
1-теоремага асосан ![]() исботланувчи эмас формуладир.
исботланувчи эмас формуладир.
Шундай килиб, мулохазалар хисобининг исталган формуласини исботланувчи ёки исботланувчи эмаслигини курсатувчи юкорида баён этилган алгоритм мавжуд экан. Демак, мулохазалар хисоби алгоритмик ечилувчи назариядир.
8.2.Мулохазалар хисобининг зидсизлик муаммоси
1-таъриф.
Агар мулохазалар хисобининг ихтиёрий ![]() ва
ва ![]() формулалари бир пайтда исботланувчи формулалар булолмаса,
у холда бундай мулохазалар хисоби зиддиятсиз аксиоматик назария, акс холда эса
зиддиятга эга булган аксиоматик назария деб аталади.
формулалари бир пайтда исботланувчи формулалар булолмаса,
у холда бундай мулохазалар хисоби зиддиятсиз аксиоматик назария, акс холда эса
зиддиятга эга булган аксиоматик назария деб аталади.
Демак,
зиддиятсиз мулохазалар хисобида ![]() ва унинг инкори булган
ва унинг инкори булган ![]() биргаликда исботланувчи формулалар булаолмайдилар.
биргаликда исботланувчи формулалар булаолмайдилар.
Мулохазалар хисобида зидсизлик муаммоси куйидагича куйилади: берилган мулохазалар хисоби зиддиятлилик ёки зиддиятсизми?
2-теорема. Агар мулохазалар хисобида исботланувчи ![]() ва
ва ![]() формулалар мавжудлиги аникланса, у холда бу мулохазалар
хисобида исталган
формулалар мавжудлиги аникланса, у холда бу мулохазалар
хисобида исталган ![]() формула хам исботланувчи формула булади.
формула хам исботланувчи формула булади.
Исбот.
Бундан кейин хар кандай исботланувчи формулани ![]() ва
ва ![]() =
=![]() билан белгилаймиз.
билан белгилаймиз.
1.Аввал
хар кандай ![]() учун
учун
![]() (1)
(1)
формуланинг исботланувчи эканлигини курсатамиз.
Хакикатан хам, I1 - аксиомадан урнига куйиш натижасида
![]() (2)
(2)
ни хосил киламиз.
Аммо шартга кура R исботланувчи формула, яъни
![]() (3)
(3)
У холда (2) ва (3) формулалардан хулоса коидасига асосан (1) формуланинг тугрилиги келиб чикади.
2.Энди хар кандай В учун
![]() (4)
(4)
формуланинг исботланувчи эканлигини тасдиклаймиз.
Хакикатан хам, IV1 - аксиомадан урнига куйиш натижасида
|-![]() (5)
(5)
формула келиб чикади.
Аммо исботлаганимизга асосан
|-(![]() . (6)
. (6)
Уз навбатида (6) ва (5) лардан хулоса коидасига биноан
|-![]() (7)
(7)
формулани хосил киламиз.
Икки
карралик инкор амалини тушириш коидасидан фойдаланиб, ва ![]() ни
ни ![]() билан алмаштирса
билан алмаштирса
![]()
формулага эга буламиз, яъни (4) исботланувчи формуладир.
3.Хар
кандай ![]() учун
учун
![]()
![]() (8)
(8)
формула исботланувчи эканлигини курсатамиз.
Хакикатан хам, I1 ва IV1 аксиомаларга асосан куйидагилар исботланувчи формулалар булади:
![]() , (9)
, (9)
![]() (10)
(10)
(9) ва (10) лардан силлогизм коидасига биноан
![]()
формулани
келтириб чикарамиз. Бу формуладан асосларни бирлаштириш коидасини куллаш
натижасида ![]() формулага келамиз, яъни (8) га эга буламиз.
формулага келамиз, яъни (8) га эга буламиз.
(4) ва (8) лардан силлогизм коидасига асосан
![]() (11)
(11)
формулани хосил киламиз.
Аммо
теореманинг шартига кура ![]() ва
ва ![]() , у холда
, у холда ![]() . Демак,
. Демак, ![]() исботланувчи формула булади.
исботланувчи формула булади.
3-теорема. Мулохазалар хисоби зиддиятсиз назариядир.
Исбот.
Мулохазалар хисобида ![]() ва
ва ![]() лар бир вактнинг узида исботланувчи буладиган хеч кандай
лар бир вактнинг узида исботланувчи буладиган хеч кандай
![]() формула мавжуд эмаслигини курсатамиз.
формула мавжуд эмаслигини курсатамиз.
![]() -мулохазалар хисобининг ихтиёрий формуласи булсин.
Агар
-мулохазалар хисобининг ихтиёрий формуласи булсин.
Агар ![]() исботланувчи формула булса, у вактда 7-§ даги
1-теоремага асосан
исботланувчи формула булса, у вактда 7-§ даги
1-теоремага асосан ![]() айнан чин формуладир ва, демак
айнан чин формуладир ва, демак ![]() - айнан ёлгон формула булади. Шунинг учун хам
- айнан ёлгон формула булади. Шунинг учун хам ![]() исботланувчи формула булмайди.
исботланувчи формула булмайди.
Демак,
бир вактда ![]() ва
ва ![]() лар исботланувчи формулалар булаолмайди. Шунинг учун хам
мулохазалар хисоби зиддиятга эга эмас.
лар исботланувчи формулалар булаолмайди. Шунинг учун хам
мулохазалар хисоби зиддиятга эга эмас.
8.3.Мулохазалар хисобининг туликлилик муаммоси
2-таъриф. Мулохазалар хисобининг аксиомалар системасига шу хисобнинг бирор ихтиёрий исботланмайдиган формуласини янги аксиома сифатида кушишдан хосил буладиган аксиомалар системаси зиддиятга эга булган мулохазалар хисобига олиб келса, бундай мулохазалар хисобига тор маънодаги тулик аксиоматик назария деб айтилади.
3-таъриф. Хар кандай айнан чин формуласи исботланувчи формула буладиган мулохазалар хисобига кенг маънодаги тулик аксиоматик назария деб айтилади.
Демак, мулохазалар хисобининг туликлилик муаммоси иккита масалани хал килиши керак:
1) янги аксиома сифатида кандайдир исботланмайдиган формуласини аксиомалар системасига кушиш натижасида мулохазалар хисобини кенгайтириш мумкинми ёки йукми?
2) мулохазалар алгебрасининг хар кандай айнан чин формуласи мулохазалар хисобида исботланувчи буладими ёки йукми?
Бу масалаларнинг ечими куйидаги теоремаларнинг мазмунидан иборат.
4-теорема. Мулохазалар хисоби тор маънода туликдир.
Исбот. ![]() -мулохазалар хисобидаги ихтиёрий исботланмайдиган
(исботланувчи эмас) формула,
-мулохазалар хисобидаги ихтиёрий исботланмайдиган
(исботланувчи эмас) формула, ![]() –
– ![]() формула таркибига кирувчи узгарувчилар булсин.
формула таркибига кирувчи узгарувчилар булсин.
![]() исботланмайдиган формула эканлигидан у айнан чин
формула эмас. Демак,
исботланмайдиган формула эканлигидан у айнан чин
формула эмас. Демак, ![]() узгарувчиларнинг
шундай
узгарувчиларнинг
шундай ![]() кийматлар сатри
мавжудки,
кийматлар сатри
мавжудки,
![]()
![]() (12)
(12)
булади.
![]() лар
лар
![]() узгарувчиларга
боглик ихтиёрий айнан чин формулалар булсин.
узгарувчиларга
боглик ихтиёрий айнан чин формулалар булсин.
![]() мажмуани (наборни) караймиз. Бу ерда
мажмуани (наборни) караймиз. Бу ерда
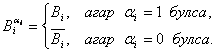
А формулада 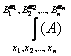 урнига
куйишни бажариб, ушбу
урнига
куйишни бажариб, ушбу
![]() (13)
(13)
формулага эга буламиз.
(12)
формуланинг айнан ёлгон формула эканлигини курсатамиз. ![]() узгарувчиларнинг
ихтиёрий
узгарувчиларнинг
ихтиёрий ![]() кийматлар сатрини
оламиз.
кийматлар сатрини
оламиз. ![]() формула-лар айнан чин
формулалар эканлигидан
формула-лар айнан чин
формулалар эканлигидан ![]() булади. У вактда
булади. У вактда ![]()
![]() =
=![]() уринли.
уринли.
Демак,
![]()
![]() =
=![]() .
.
![]()
Бу ердан ![]() нинг айнан чин формула эканлиги келиб чикади ва у
7-параграфдаги 3-теоремага асосан исботланувчи формула булади.
нинг айнан чин формула эканлиги келиб чикади ва у
7-параграфдаги 3-теоремага асосан исботланувчи формула булади.
Иккинчи тарафдан, агар мулохазалар хисобининг
аксиомалари каторига ![]() формулани янги аксиома
сифатида кушиб куйсак, у холда янги хосил булган мулохазалар хисобида бу
формула аксиома булганлиги учун исботланувчи формула булади. Шу вактнинг узида
янги мулохазалар хисобида
формулани янги аксиома
сифатида кушиб куйсак, у холда янги хосил булган мулохазалар хисобида бу
формула аксиома булганлиги учун исботланувчи формула булади. Шу вактнинг узида
янги мулохазалар хисобида ![]() формула хам исботланувчи формула булади, чунки у
исботланувчи формуладан урнига куйиш коидаси оркали хосил килинган.
формула хам исботланувчи формула булади, чунки у
исботланувчи формуладан урнига куйиш коидаси оркали хосил килинган.
![]() Шундай килиб, янги мулохазалар хисобида иккита
Шундай килиб, янги мулохазалар хисобида иккита ![]() ва
ва ![]() исботланувчи формулаларга эга буламиз. Демак, янги
мулохазалар хисоби зиддиятга эга булган аксиоматик назария экан. Бу ердан унинг
тор маънода туликлиги келиб чикади.
исботланувчи формулаларга эга буламиз. Демак, янги
мулохазалар хисоби зиддиятга эга булган аксиоматик назария экан. Бу ердан унинг
тор маънода туликлиги келиб чикади.
5-теорема. Мулохазалар хисоби кенг маънода туликдир.
Исбот. Биз 7-параграфда (3-теорема) мулохазалар алгебрасининг хар бир айнан чин формуласи мулохазалар хисобида исботланувчи формула эканлигини исбот килган эдик. Демак, мулохазалар хисоби кенг маънода туликдир.
8.4.Мулохазалар хисоби аксиомаларининг эркинлик муаммоси
Хар кандай аксиоматик хисобда аксиомаларнинг эркинлик масаласи, яъни бирорта аксиомани системанинг колган аксиомаларидан келтириб чикариш коидаси оркали хосил этиш мумкинми ёки йукми деган муаммо мавжуд булади.
Агар бирорта аксиома учун бу масала ижобий хал этилса, у холда бу аксиома система аксиомалари руйхатидан чикариб ташланади ва мантикий хисоб бу билан узгармайди, яъни исботланувчи формулалар синфи узгармасдан колади.
4-таъриф. Агар
![]() аксиомани
мулохазалар хисобининг колган аксиомаларидан келтириб чикариш мумкин булмаса, у
шу мулохазалар хисобининг бошка аксиомаларидан эркин аксиома деб аталади.
аксиомани
мулохазалар хисобининг колган аксиомаларидан келтириб чикариш мумкин булмаса, у
шу мулохазалар хисобининг бошка аксиомаларидан эркин аксиома деб аталади.
5-таъриф. Агар мулохазалар хисоби аксиомалар системасининг хар бир аксиомаси эркин булса, у холда мулохазалар хисобининг аксиомалар системаси эркин деб айтилади.
6-теорема. Мулохазалар хисобининг аксиомалар системаси эркиндир.
Исбот. ![]() мулохазалар
хисобининг ихтиёрий аксиомаси булсин.
мулохазалар
хисобининг ихтиёрий аксиомаси булсин.
Бу аксиоманинг эркинлигини исботлаш учун мулохазалар хисобига
нисбатан куйидаги усулни куллаймиз: мулохазалар хисоби узгарувчиларини ![]() ёки
ёки
![]() киймат
кабул килувчи узгарувчилар сифатида караймиз. Бу ерда a чин ролини ва b ёлгон ролини уйнайди.
киймат
кабул килувчи узгарувчилар сифатида караймиз. Бу ерда a чин ролини ва b ёлгон ролини уйнайди.
![]() амалларни шундай аниклаймизки,
куйидаги шартлар уринли булсин:
амалларни шундай аниклаймизки,
куйидаги шартлар уринли булсин:
1. ![]() аксиомадан ташкари
системанинг хамма аксиомалари таркибидаги узгарувчиларнинг барча кийматларида
факат
аксиомадан ташкари
системанинг хамма аксиомалари таркибидаги узгарувчиларнинг барча кийматларида
факат ![]() кийматни кабул килсин.
кийматни кабул килсин.
2. ![]() аксиомадан бошка, аксиомалар
мажмуасидан келтириб чикарилган хар кандай формула хам таркибидаги узгарувчиларнинг
барча кийматларида факат
аксиомадан бошка, аксиомалар
мажмуасидан келтириб чикарилган хар кандай формула хам таркибидаги узгарувчиларнинг
барча кийматларида факат ![]() кийматни кабул килсин.
кийматни кабул килсин.
3. ![]() аксиома таркибидаги узгарувчиларнинг
айрим кийматларида
аксиома таркибидаги узгарувчиларнинг
айрим кийматларида ![]() кийматни кабул килсин.
кийматни кабул килсин.
Агар ![]() аксиомага нисбатан юкорида
келтирилган интерпретация (изохлаш) уринли булса, у холда
аксиомага нисбатан юкорида
келтирилган интерпретация (изохлаш) уринли булса, у холда ![]() аксиома бошка
аксиомалардан эркин эканлиги келиб чикади. Хакикатдан хам, агар
аксиома бошка
аксиомалардан эркин эканлиги келиб чикади. Хакикатдан хам, агар ![]() аксиомани
мулохазалар хисобининг бошка аксиомаларидан келтириб чикариш мумкин булганда
эди, у шартларнинг иккинчисига асосан таркибидаги узгарувчиларнинг барча кийматларида
факат a кийматни кабул килиб, бу эса 3-шартга зид буларди.
Демак,
аксиомани
мулохазалар хисобининг бошка аксиомаларидан келтириб чикариш мумкин булганда
эди, у шартларнинг иккинчисига асосан таркибидаги узгарувчиларнинг барча кийматларида
факат a кийматни кабул килиб, бу эса 3-шартга зид буларди.
Демак, ![]() аксиомани мулохазалар хисобининг
бошка аксиомаларидан келтириб чикариш мумкин эмас ва у системадаги эркин аксиомадир.
аксиомани мулохазалар хисобининг
бошка аксиомаларидан келтириб чикариш мумкин эмас ва у системадаги эркин аксиомадир.
Узгарувчиларининг урнига уларнинг айрим кийматлари куйилганда
хам формулалар маънога эга деб келишамиз. Масалан, ![]() ,
, ![]() ,
, ![]() ва
бошкалар.
ва
бошкалар.
6-таъриф. Таркибидаги
узгарувчиларни ![]() ва
ва ![]() билан
алмаштирганда бир хил киймат кабул килувчи
билан
алмаштирганда бир хил киймат кабул килувчи ![]() ва
ва ![]() формулалар
тенг кучли формулалар деб аталади хамда бу
формулалар
тенг кучли формулалар деб аталади хамда бу ![]() куринишда ёзилади.
куринишда ёзилади.
Тенглик белгиси ![]() мантикий богловчиларга
нисбатан сустрок боглайди деб хисоблаймиз.
мантикий богловчиларга
нисбатан сустрок боглайди деб хисоблаймиз.
Энди II1 - аксиоманинг эркинлигини исбот килайлик.
Бунинг учун конъюнкциядан ташкари колган хамма мантикий
амалларни худди мантик алгебрасидагидай ва конъюнкция амалини ![]() тенглик
оркали аниклаймиз:
тенглик
оркали аниклаймиз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ушбу интерпретация учун юкорида келтирилган учта шартларнинг бажарилишини курсатамиз.
II1 - аксиомадан ташкари мулохазалар хисобининг колган хамма
аксиомалари узгарувчиларнинг барча кийматларида ![]() киймат
кабул килади (бу холни чинлик жадвали оркали курсатиш мумкин).
киймат
кабул килади (бу холни чинлик жадвали оркали курсатиш мумкин).
Хакикатан хам I, III ва IV гурух аксиомаларида конъюнкция амали катнашмайди. Колган мантикий амаллар худди мулохазалар алгебрасидагидай аникланган.
Мулохазалар алгебрасида бу формулалар айнан чин
формулалар булганлигидан, ушбу интерпретацияда узгарувчиларнинг барча кийматларида
улар ![]() киймат
кабул килади.
киймат
кабул килади.
II1, II2 ва II3 - аксиомаларни курайлик.
II2 ва II3
аксиомалар кабул килинган интерпретацияда ![]() формулага тенг булади
ва
формулага тенг булади
ва ![]() ,
, ![]() кийматларда
кийматларда
![]() киймат
кабул килади, яъни хеч качон
киймат
кабул килади, яъни хеч качон ![]() киймат
кабул килмайди.
киймат
кабул килмайди.
Энди айнан ![]() га тенг формулалардан келтириб чикариш коидасига
асосан хосил этилган формулалар хам
га тенг формулалардан келтириб чикариш коидасига
асосан хосил этилган формулалар хам ![]() га тенглигини курсатиш колди, яъни 2-шартнинг
бажарилишини курсатиш керак.
га тенглигини курсатиш колди, яъни 2-шартнинг
бажарилишини курсатиш керак.
Олдинги параграфларда айнан чин формулаларга урнига куйиш ва хулоса коидаларини куллаш натижасида чикарилган формулалар айнан чин формулалар булишини курсатган эдик. Демак, 2-шарт хам бажарилади.
Шундай килиб, мулохазалар хисобининг II1-аксиомаси эркин аксиома экан.
Худди шундай схемадан фойдаланиб, мулохазалар хисобининг I, II, III ва IV-гурухларидаги хар бир аксиоманинг эркинлигини курсатиш мумкин. Демак, мулохазалар хисобининг аксиомалар системаси эркиндир.
РЕЖА:
1.Мулохазалар хисобининг ечилиш муаммоси.
2.Мулохазалар хисобининг зидсизлик муаммоси.
3.Мулохазалар хисобининг туликлилик муаммоси.
4.Мулохазалар хисоби аксиомаларининг эркин-
лик муаммоси.
Муаммоли масала ва топшириклар:
1. Хар кандай аксиоматик назарияни асослаш учун нечта муаммоларни к¢риб чикишга т¢гри келади?
2. А(х) ва В(х) ихтиёрий предикатлар б¢лсин. Куйидаги
формулаларнинг кайси бирлари ![]() формулага тенгкучли
формула б¢лади:
формулага тенгкучли
формула б¢лади:
1)![]() 2)
2) ![]() 3)
3)
![]()
4) ![]() 5)
5) ![]() 6)
6)
![]()
7) ![]()
3. Куйидаги тасдиклар(теоремалар)нинг нот¢грилигини исбот килинг:
1) «Агар функция х0 нуктада узлуксиз б¢лса, у холда у шу нуктада дифференциалланувчи б¢лади».
2) «Агар сонли каторнинг n-хади нолга тенг б¢лса, у холда бу катор якинлашувчи б¢лади».
3) «Агар т¢ртбурчакнинг диагоналлари тенг б¢лса, у холда бу т¢ртбурчак т¢гри бурчакли б¢лади».
4) «Агар [a,b] ёпик интервалда интегралланувчи б¢лса, у холда у шу интервалда узлуксиз б¢лади».
Мустакил ишлаш учун саволлар:
1.Мулохазалар хисобининг ечилиш муаммоси.
2.Мулохазалар хисобининг зидсизлик муаммоси.
3.Мулохазалар хисобининг туликлилик муаммоси
4.Мулохазалар хисоби аксиомаларининг эркин-
лик муаммоси.
5.Аксиоматик назария хакида тушунча.
6.Тор маънода тулик. Кенг маънода тулик.
7.Эркин аксиомалар системаси. Тенг кучли
формулалар.