II-БОБ. МУЛОХАЗАЛАР  АЛГЕБРАСИ

 

1-§. Мулохаза. Мулохазалар устида амаллар

 

Мулохаза. -Абсолют чин (ёлгон) мулохаза. -Кийматлар сатри. -Инкор, конъюнкция, дизъюнкция, эквиваленция ва импликация мантикий амаллар. -Шеффер амали.

 

            Математик мантикнинг ушбу мулохазалар алгебраси деб аталган булимида асосий текшириш объектлари булиб гаплар хизмат килади. Математик мантик хар бир гапнинг маъносига караб, унинг чин, хакконий, тугри ёки ёлгон, нотугри булиши билангина кизикади.

            Масалан: 1. “Тошкент - Узбекистоннинг пойтахти”, “Ой ер атрофида айланади” деган гаплар - чиндир.

2.“Ер ойдан кичик”, “3 > 5”  деган гапларнинг хар бири ёлгондир.

            Шуни хам айтиш керакки, купгина гапларнинг чин ёки ёлгонлигини дархол аниклаш кийин. Масалан, “Бугунги тун кечагидан коронгирок”, деган гап кайси вактда ва кайси жойда айтилишига караб чин хам, ёлгон хам булиши мумкин.

1. Олдимга кел. 2. Уйда булдингми? 3. Янги йил билан. 4. Агар олдин билсам эдим - гаплар чин ёки ёлгон киймат кабул килмайдилар.

            Шундай килиб, математик  мантик: “Хар бир гап чин ёки ёлгон булиш хоссасига эга” деб кабул килади.

            1-таъриф. Факат чин ёки ёлгон киймат кабул кила оладиган дарак гапларга мулохазалар деб айтамиз.

            Демак, хар бир мулохаза маълум холатда чин ёки ёлгон кийматга эга. Бундан кейин, чин кийматни кискача “ч” ва ёлгон кийматни “ё” билан белгилаймиз.

            Мулохазаларни белгилаш учун, асосан, лотин алфавитининг кичик харфлари ишлатилади:

Маълум мулохазалар борки, хамма мумкин булган холатларда (вазиятларда) чин кийматни (ёлгон) кабул киладилар. Бундай мулохазаларга абсолют чин (ёлгон) мулохазалар деб айтилади.

            Мулохазалар алгебрасида одатда, конкрет мулохазалар билангина эмас, балки хар кандай исталган мулохазалар билан шугулланадилар. Бу эса узгарувчи мулохаза тушунчасига олиб келади. Агар узгарувчи мулохазани  деб белгиласак, у холда  конкрет мулохазаларнинг исталганини ифодалайди. Шунинг учун x икки: “ч” ва “ё” кийматли узгарувчини ифодалайди.

             та узгарувчи мулохаза берилган булсин. Буларнинг хар кайсиси чин ва ёлгон кийматларни кабул килади. Шунинг учун куйидаги кийматлар сатрини тузиш мумкин:

ё, ё, ........, ё,

ч, ё, ........, ё,

ё, ч, ........, ё,

.....................

ч, ч, ........, ч.

            Демак, узгарувчилар сони  та булса, у вактда  та кийматлар сатрига эга буламиз.

             та кийматлар сатри.

             та кийматлар сатри.

            Математик мантикда “эмас”, “ёки”, “ва”, “агар..., у вактда”, “шунда ва факат шундагина...., качон....” сузлар (богловчилар) мулохазалар орасидаги мантикий амаллар дейилади. Бу амаллар ёрдамида элементар мулохазалардан мураккаб мулохаза курилади. Мулохазалар устидаги бу амаллар математик мантикнинг элементар кисми булган мулохазалар мантики ёки мулохазалар алгебраси деб аталувчи кисмида урганилади. Хар иккала термин (“мулохазалар мантики” ва “мулохазалар алгебраси”) синоним сифатида ишлатилади, чунки улар мантикнинг маълум кисмини икки нуктаи назардан ифодалайди: бу хам мантик (уз предметига кура), хам алгебра (уз методига кура).

            Мантикий амаллар асосан 5 та булиб, уларнинг таърифлари куйидагичадир.

            1. Инкор амали. Исталган  узгарувчили мулохаза билан бирга  куринишида белгиланган иккинчи узгарувчили мулохаза берилган булсин.

            2-таъриф.  мулохазанинг инкори деб аталган  мулохаза шу билан характерланадики, х мулохаза “ч” кийматни кабул килганда,  мулохаза “ё” кийматни кабул килади ва аксинча.

            Демак, мулохазалар мантикининг энг содда амали бу инкор амали булиб, оддий тилдаги манфий сифатдош “эмас” га тугри келади. Бу амал “—“ символ билан белгиланади. Агар  бирор мулохаза, масалан, “бугун хаво совук” булса, у холда  - янги мураккаб “бугун хаво совук эмас” мулохазадан иборатдир.  мулохаза “ эмас” деб укилади.

            Шунинг учун, агар  чин мулохаза булса, у вактда  ёлгон мулохаза булади, ва аксинча,  ёлгон булса  чиндир.

            Инкор амалининг таъсирини куйидаги чинлик жадвали куринишида тасвирлаймиз:

 

           

            Худди шу жадвални инкор амалининг таърифи сифатида кабул киламиз ва бошка мантикий амаллар учун хам шунга ухшаш жадваллардан фойдаланамиз. Улар чинлик жадвали дейилади. Бу жадваллардан фойдаланиш кулай булиб, улар математик мантикнинг куп булимларида ишлатилади.

            2. Конъюнкция (мантикий купайтма) амали.  ва  узгарувчи мулохазалар устида бажариладиган конъюнкция (лотинча conjunctio - боглайман сузидан) амалини  куринишда ва бу амал натижасида хосил булган янги мураккаб мулохазани  куринишда белгилаймиз.

            3-таъриф. “Ва” богловчисига мос келувчи мантикий амалга конъюнкция амали деб айтамиз.  ва  мулохазаларнинг конъюнкцияси  ва  мулохазалар чин булгандагина чин кийматни кабул килиб, колган холларда эса, ёлгон кийматни кабул килади.

             куринишдаги мулохаза « ва » деб укилади. Куриниб турибдики, бу таъриф “ва” богловчининг маъносига тулик тугри келади. Хакикатан хам “5 сони ток ва туб” мулохаза чин, чунки уни ташкил этувчи “5 сони ток” ва “5 сони туб” хар иккала мулохаза хам чин. “10 сони 5 га булинади ва 7> 9” мулохаза ёлгон, чунки мураккаб мулохазани ташкил этувчиларидан бири, чунончи “7>9” ёлгондир. Конъюнкция таърифини куйидаги чинлик жадвали куринишида ёзиш мумкин:

 

           

            3. Дизъюнкция (мантикий йигинди) амали. Мулохаза мантикида ишлатиладиган учинчи амал “ёки” богловчига тугри келади. Шуни таъкидлаш керакки, “ёки” богловчиси узбек тилида икки хил маънода ишлатилади. Биринчи холда рад этувчи “ёки”, иккинчи холда рад этмайдиган “ёки” маъносида ишлатилади. Бунинг фарки куйидагилардан иборат. Агар  ва  мулохазаларнинг иккаласи хам ёлгон булса, у холда “ ёки ” мулохаза шубхасиз ёлгон булади. Агар  чин ва  ёлгон (ёки  ёлгон ва  чин) булса, у холда “ ёки ” ни чин деб караш керак, бу эса узбек тилидаги “ёки” сузининг маъносига тугри келади. Аммо хар иккала  ва  мулохазалар чин булганда “ ёки ” мулохазалар чин булади. Бу вактда “ ёки ” мулохазага кандай караш керак?

            Масалан, “Бугун якшанба ёки мен кинога бораман” мулохазани олайлик. Агар бугун якшанба ва мен кинога борсам, у холда бу мулохаза чин ёки ёлгонми? Узбек тилида “ёки” богловчиси бир маънода, баъзан эса бошка маънода ишлатилади. Агар юкоридаги мулохазани чин деб карасак, у холда “ёки” ни рад этмайдиган маънода, иккинчи холда “ёки” ни рад этувчи маънода ишлатилаяпти деймиз.

            4-таъриф. Рад этмайдиган  маънода ишлатиладиган “ёки” мантикий амал дизъюнкция (лотинча disjunctio - фарк киламан сузидан) дейилади. Иккита  ва  мулохазанинг дизъюнкцияси “” каби ёзилади ва “ ёки ” деб укилади.

            Икки  ва  мулохазанинг дизъюнкцияси  мураккаб мулохаза булиб, у факат  ва  ёлгон булгандагина ёлгон киймат кабул килиб, колган холларда чин кийматни кабул килади.

            Дизъюнкция амалини куйидаги чинлик жадвали оркали хам ифодалаш мумкин:

 

            4. Импликация амали. Куйидаги мураккаб мулохазаларни курайлик:

            1) “Агар 2´5 = 10 булса, у холда 6´7=42 булади”,  2) “Агар 30 сони 5 га булинса, у холда 5 жуфтдир”,  3) “Агар 3=5 булса, у холда 15=17”, 4) “Агар 4´3=13 булса, у холда 9+3=12”. Бу мулохазаларнинг хаммаси хам 2 та элементар мулохазалардан “агар....., у холда......” богловчи ёрдамида тузилган. Бу богловчи мулохазалар мантикининг импликация (лотинча implicatio - зич боглайман сузидан) амалига тугри келади. Импликация амалини ® куринишида белгилаймиз.

            5-таъриф. Икки  ва  мулохазаларнинг  импликацияси деб шундай мулохазага айтиладики, у факат  чин ва  ёлгон булгандагина ёлгон булиб, колган хамма холларда чиндир.

            “” мулохаза “агар , у холда ” деб укилади. Импликация таърифини куйидаги чинлик жадвали куринишида ёзиш мумкин:

 

 

            Чинлик жадвалидан куринадики, юкоридаги мулохазаларнинг иккинчиси ёлгон булиб, колганлари чиндир. “” импликация  мулохаза асос (шарт, гипотеза, далил) ва у мулохаза эса бу асоснинг окибати деб аталади. Импликация чинлик жадвалининг охирги иккита сатри шуни курсатадики, ёлгон асосдан чин хулоса хам, ёлгон хулоса хам келиб чикар экан, бошкача килиб айтганда “ёлгондан хар бир нарсани кутиш мумкин”.

            Импликация мулохазалар мантикининг мухим амалларидан бири хисобланади. Сузлашув тилида “агар , у холда ” нинг хар хил синонимлари бор: “ булса,  булади”,  “агар  булса, у вактда  булади”, “ дан  хосил булади”, “  дан  келиб чикади”, “, агар  булса”, “  учун етарли шарт” ва хоказо.

            5. Эквивалентлик (тенгкучлилик) амали. Куп мураккаб  мулохазалар элементар мулохазалардан “зарур ва кифоя”, “факат ва факат”, “шунда ва факат шундагина, качонки”, “.......бажарилиши етарли ва зарурдир” каби богловчилари ёрдамида тузилади. Бундай богловчиларга мос келадиган мулохазалар мантикининг амали эквивалентлик дейилади ва ““ каби белгиланади.  мураккаб мулохаза “х эквивалент у” деб укилади.

            6-таъриф. Мураккаб мулохаза  чин булади, агар  ва  лар чин ёки  ва  лар ёлгон булса, бошка холларда у ёлгондир. Бошкача килиб айтганда факат ва факат  ва  мулохазалар бир хил киймат кабул килгандагина  чин булади.

            Бу таърифни куйидаги чинлик жадвали билан ифодалаш мумкин:

 

 

 эквивалентликка “ булса (бажарилса),  булади (бажарилади) ва  булса,  булади” ёки “ дан  келиб чикади ва  дан  келиб чикади” деган мулохаза мос келади, яъни  эквивалентликка математикада зарурий ва етарли шарт хакида айтилган теоремалар мос келади.

Демак,

                      (1)

 

булади. (1) га биноан,  эквивалетликни икки томонли импликация деб аташ мумкин.

            6. Шеффер амали (штрихи). Нихоят, яна бир мантикий амални келтирамиз. У Шеффер амали ёки Шеффер штрихи дейилади ва у “ | “ каби белгиланади. Мураккаб мулохаза “” “ Шеффер штрихи ” деб укилади. Бу амал куйидагича таърифланади:

            7-таъриф. Факат  ва  мулохазалар чин булгандагина,  мулохаза ёлгондир.

Бу таърифни куйидаги чинлик жадвали ёрдамида ифодаласа хам булади:

 

           

Асосий чинлик жадваллари. Юкорида келтирилган чинлик жадваллари, мос равишда, инкор килиш, конъюнкция, дизъюнкция, импликация, эквивалентлик ва Шеффер амалларининг асосий чинлик жадваллари деб айтилади:

 

 

ч	ч	ч	ч	ч	ч	ё
ч	ё	ё	ч	ё	ё	ч
ё	ч	ё	ч	ч	ё	ч
ё	ё	ё	ё	ч	ч	ч

 

                                          

 

                           ч           ё

                                    

                           ё           ч

 

 

Машклар

 

   1.Куйидаги гапларнинг кайси бирлари мулохаза булади:

        1) Тошкент – Узбекистон Республикасининг пойтахти;

            2) ;

3) Ой Марс планетасининг йулдоши;

            4) .

   2.Куйидаги мулохазаларнинг чин ёки ёлгон эканлигини аникланг:

1) ;

2) ;

   3.Куйидаги импликацияларнинг кайси бирлари чин булади:

1) агар  булса, у холда ;

              2) агар  булса, у холда ;

 

2-§. Формулалар. Тенгкучли формулалар

 

Формула. -Чинлик жадвали. -Тенгкучли формулалар. -Эквивалентлик билан тенгкучлилик орасидаги фарк. -Айният.

 

Олдинги параграфда асосан мантикий амалларни урганиб чикдик. Энди бу амаллар орасида богланишлар мавжудлигини курсатамиз. Бунинг учун тенгкучли мулохазалар тушунчасини киритамиз.

                    (1)

 та мулохаза берилган булсин.

            1-таъриф. (1) мулохазаларни инкор, дизъюнкция, конъюнкция, импликация ва эквиваленция мантикий амаллар воситаси билан маълум тартибда бирлаштириб хосил этилган мураккаб мулохазага формула деб айтамиз.

        Масалан:; ;  ;  мураккаб мулохазалар формулалар буладилар. Кавслар мулохазалар устида мантикий амалларнинг кай тартибда бажарилишини курсатади.

            Энди формула тушунчасига математик таъриф берайлик. Бу тушунча куйидагича аникланади.

2-таъриф. 1) хар кандай  мулохазаларнинг исталган бири формуладир;

            2) агар  ва  ларнинг хар бири формула булса, у холда (), (), (®),  («) ва  лар хам формулалардир.

            3) 1 ва 2-бандларда курсатилган ифодалардан ташкари бошка хеч кандай ифода формула була олмайди.

             узгарувчиларни элементар формулалар деб атаймиз.

            Кейинчалик формулани лозим булгандагина  функция шаклида белгилашдан фойдаланамиз.

            Хар кандай формула учун чинлик жадвали тузиш мумкин. Бунинг учун асосий чинлик жадвалларидан кетма-кет фойдаланиш керак.

            Масалан,  формуланинг чинлик жадвали куйидагича булади:

 

 

            Шундай килиб, хар кандай формулага {ч, ё} тупламининг бир элементи мос килиб куйилади.

            3-таъриф.  ва  формулалар берилган булсин. (1) элементар мулохазаларнинг хар бир кийматлари сатри учун  ва  формулаларнинг мос кийматлари бир хил булса,  ва  формулаларга тенгкучли формулалар деб айтилади ва бу  тарзда белгиланади. (1) каторнинг камида битта кийатлари сатри учун  ва  формулаларнинг мос кийматлари бир хил булмаса, у холда  ва  формулаларга тенгкучлимас формулалар деб айтилади ва  куринишда белгиланади.

             ва  формулаларнинг тенгкучли булиш-булмаслиги улар учун тузилган чинлик жадваллари ёрдамида аникланади.

            Мисоллар. 1.  ва  формулалар берилган булсин.

 

            Жадвалдан куриниб турибдики, туртала кийматлар сатри учун  ва  формулаларнинг мос кийматлари бир хил. Демак, таърифга асосан .

            2.  тенглиги исбот этилсин. , .

 

 

            Демак, жадвалга асосан .

 

            3. ,     .

 

 

            Демак, .

            Худди шундай куйидаги тенгкучлиликларни исботлаш мумкин:

            4.  ,              5. ,

            6.,   7. .

            Эквивалентлик билан тенгкучлилик орасидаги фаркни тушуниш учун уларни алгебраик тенглама ва айният билан солиштирамиз. Тенглама (масалан, ) деб шундай харфларнинг айрим кийматлари (масалан, , ) учун бажариб, бошка кийматлар (масалан, , ) учун бажарилмайди. Шунга ухшаш эквивалентлик  деб, шундай (масалан, ) мулохазага айтиладики, унга  харфларнинг уринларига бир хил конкрет мулохазалар куйганда у чин киймат кабул килиб, бошка конкрет кийматлар куйганда ёлгон кийматни кабул килади. Айният деб, шундай тенгликка (масалан, ) айтиладики, унда катнашадиган барча харфлар учун бажарилади. Шунга ухшаш,  мулохазада катнашадиган барча  харфларнинг урнига ихтиёрий конкрет мулохазаларни куйганда у чин киймат кабул килса, бундай мулохаза тенгкучлилик дейилади.

            Алгебрада айний ифодаларни бир-бири билан алмаштириш мумкин булганидек, мантик алгебрасида тенгкучли мулохазаларни (формулаларни) хам бир-бири билан алмаштириш мумкин. Бу эса мураккаб формулаларни (мулохазаларни) соддалаштириш имконини беради.

            Биз тенглама ва айният билан эквивалентлик ва тенгкучлилик орасидаги ухшашликни келтирдик. Энди эса улар орасидаги фаркни курсатамиз. Маълумки, алгебрада хеч кандай алмаштириш ёрдамида тенгликни амаллар ( кушиш, айириш, даражага кутариш, булиш ва хоказо) билан алмаштириб булмайди. Мантик алгебрасида эса эквивалентликни импликация  ёки конъюнкция , дизъюнкция  ва инкор  амаллари оркали ифодалаш мумкинлигини биз юкорида курсатган эдик (1-§ даги (1) формулага каранг). (1) формуланинг тугрилигини чинлик жадвали оркали курсатамиз.

 

 

            Жадвалдан куринадики, охирги икки устуннинг чинлик киймати устма-уст тушади. Шу билан (1) формула исботланади.

            Оддий алгебрада тенглик белгиси «=» куйидаги аксиомаларни каноатлантиради: 1) ихтиёрий а сон учун  (рефлексивлик); 2) агар  булса, у холда  (симметриклик); 3) агар ,  булса, у холда  (транзитивлик) булади.

            Шунга ухшаш, мулохазалар алгебрасида, эквивалентлик таърифидан осонлик билан куриш мумкинки, у рефлексив, симметрик ва транзитив, яъни

            1) ихтиёрий х мулохаза учун ;

            2) ихтиёрий икки  ва  мулохазалар учун, агар    булса, у холда ;

            3) ихтиёрий  учта мулохазалар учун  ва  булса, у холда .

 

Машклар

 

1.Куйидаги формулаларнинг чинлик жадваллари тузилсин:

            1) ;

            2) ;

            3) .

            2.Тенгкучлиликлар исбот этилсин:

            1) ;

            2) ;

            3) ;

            4) ;

5) );

 

            3.Куйидаги формулалар соддалаштирилсин:

            1) ;

            2) ;

            3) ;

            4) ;

 

3-§. Айнан чин, айнан ёлгон ва бажарилувчи формулалар

 

Айнан чин. -Айнан ёлгон. -Тавталогия. -Бажарилувчи формула. -Мантик конунлари. -Ечилиш муаммоси.

 

            1-таъриф. Элементар мулохазаларнинг хамма кийматлар сатрларида факат чин кийматни кабул килувчи формула айнан чин (доимо чин) формула ёки тавтология деб аталади ва  билан белгиланади.

             формуланинг тавтология эканлиги ёки эмаслиги кийматлар жадвалини тузиш оркали билинади.

    Мисоллар:

1. формула тавтологиядир. Хакикатан:

 

           

            2.  формула хам тавталогиядир:

 

            2-таъриф. Элементар мулохазаларнинг хамма кийматлар сатрларида факат ёлгон кийматни кабул килувчи формулалар айнан ёлгон (доимо ёлгон) ёки бажарилмайдиган формулалар дейилади ва  билан белгиланади.

    Масалан,  айнан ёлгон формуладир:

 

 

            Маълумки, айнан чин формуланинг инкори айнан ёлгон формула булади ва аксинча. Айнан чин ва айнан ёлгон формулалар унга кирадиган узгарувчиларга боглик булмай, факат битта киймат кабул килади.

            3-таъриф. Агар  тавтология булса, у холда  ва  лар мантикий эквивалент деб айтилади. Агар  тавтология булса, у холда    нинг мантикий хулосаси деб айтилади.

            Энди Э.Мендельсоннинг [39] китобида баён этилган тавтологияларга тегишли айрим теоремаларни келтирамиз:

            1-теорема. Агар  ва  айнан чин формулалар (тавтологиялар)  булса, у холда  формула хам тавтология булади.

            Исбот.  ва  тавталогиялар булсин.  ва  формулаларнинг таркибига кирувчи узгарувчиларнинг бирор кийматлар сатрида  формула ёлгон киймат кабул килсин.  формула тавтология булганлиги учун узгарувчиларнинг уша кийматлар сатрида  чин киймат кабул килади. У вактда () формула ёлгон киймат кабул килади. Бу натижа () нинг тавтология деган фаразимизга карама-каршидир. Демак,  тавтологиядир.

            2-теорема. Агар  узгарувчиларга боглик булган  формула тавтология ва  формула  формуладан  узгарувчилар урнига мос равишда  формулаларни куйиш натижасида хосил этилган булса, у холда  формула тавтология булади, яъни тавтологияда урнига куйиш яна тавтологияни келтиради.

            Исбот.  тавтология булсин ва  формула таркибига кирувчи узгарувчи мулохазаларнинг ихтиёрий  кийматлар сатри берилган булсин. У вактда  формулалар  (хар бир  ч ёки ё киймат кабул килади) кийматлар кабул киладилар.  Агар  ларга мос равишда  кийматларни берсак, у холда  нинг натижавий киймати  нинг чинлик кийматига мос келади.  тавтология булганлиги учун  формула таркибига кирган узгарувчиларнинг берилган ихтиёрий кийматлар сатрида ч киймат кабул килади. Шундай килиб,  доимо ч киймат кабул килади ва у тавтология булади.

            3-теорема. Агар  формула таркибига бир ёки куп марта кирган  формула урнига  формулани куйиш натижасида  формула хосил этилса, у холда  тавтология булади. Демак,  ва  лар мантикий эквивалент булса, у холда  ва  хам мантикий эквивалент булади.

            Исбот. Агар  ва  формулалар узгарувчиларнинг ихтиёрий кийматлар сатрида карама-карши чинлик кийматларига эга булса, у холда  нинг чинлик киймати ё булади ва натижада  формула ч киймат кабул килади. Агар  ва лар узгарувчиларнинг ихтиёрий кийматлар сатрида бир хил чинлик киймати кабул килсалар, у холда  ва  формулалар хам бир хил чинлик киймати кабул киладилар, чунки теореманинг шартига асосан  формула  формуладан  нинг урнига  ни куйиш натижасида хосил этилган. Демак, бу холда  хам,  хам ч киймат кабул килади. Шунинг учун  формула хам ч киймат кабул килади.

            Демак,  формула тавтология булади.

            4-таъриф. Элементар мулохазаларнинг камида битта кийматлар сатрида чин  киймат кабул килувчи ва айнан чин булмаган формулага бажарилувчи формула деб айтилади.

     Масалан.  1.;  2.;  3.;  4.

формулалар бажарилувчи формулалар хисобланади.

            Айнан чин формулалар катта ахамиятга эга булиб, улар мантик конунларини ифодалайди. Шу муносабат билан куйидаги масала тугилади: шундай методни топиш керакки, у чекли микдордаги амал ёрдамида мантик алгебрасининг ихтиёрий муайан  формуласини айнан чин ёки айнан чин эмаслигини аникласин. Бундай метод ечилувчи метод ёки алгоритм, ёки ечилувчи процедура дейилади. Куйилган масаланинг узи эса “ечилиш  муаммоси” дейилади. Бу муаммо факатгина мулохазалар алгебраси учунгина эмас, балки бошка мантикий системалар учун хам куйилади. У мулохазалар алгебраси учун ижобий равишда ечилади. Бу ерда ечилувчи процедура сифатида чинлик жадвалини олишимиз мумкин, чунки бундай жадвал хар бир муайан формула учун куйилган саволга жавоб беради. Агар берилган формулага мос келадиган жадвалнинг охирги устунида факат “чин” булса, у холда бу формула айнан “чин”, агар охирги устунда хеч булмаганда битта “ёлгон” булса, у холда формула айнан чин эмас булади. Табиийки, амалда бу усулни хар доим бажариб булмайди (чунки формулада  та узгарувчи катнашса, бундай жадвал  та сатрга эга булади). Лекин хар доим чекли микдордаги амал бажариб, принцип жихатдан куйилган саволга жавоб бериш мумкин. Кейинги параграфларда бошка бир ечилувчи процедурани келтирамиз, у берилган формулани нормал шаклга келтиришга асосланган. Нормал шакллар математик мантикнинг бошка масалаларида хам ишлатилади.

 

Машклар

            1. Куйидагиларнинг кайси бирлари айнан чин ва айнан ёлгон формула эканлигини аникланг:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

 

            2. Айнан чин ёки айнан ёлгон формула эканлигини исботланг:

            1) ;

            2) ;

            3) ;

            4) ;

            5) ;

        6) ;

        7) ;

        8) ;

           

4-§. Асосий тенгкучлиликлар

Асосий тенгкучлиликлар. -, , - амаллар катнашган мулохазалар. -Коммутативлик, ассоциативлик ва дистрибутивлик конунлари.

-Идемпотентлик ва ютиш конунлари.

 

            Бу параграфда кенг кулланиладиган тенгкучлиликлар каралади. Аввало, оддий алгебрада маълум булган айниятларга ухшашларини келтирамиз. Маълумки, кушиш ва купайтириш амали куйидаги конуниятларга буйсунади:

1) (кушишнинг коммутативлик конуни);

2)  (кушишнинг ассоциативлик конуни);

3)  (купайтиришнинг коммутативлик конуни);

4)  (купайтиришнинг ассоциативлик конуни);  

5)  (купайтиришнинг йигиндига нисбатан дистрибутивлик конуни).

            Шу айниятларга ухшаш мантик алгебрасида куйидаги  тенгкучлиликлар уринлидир:

                            (3)

                (4)

                            (5)

                (6)

           (7)

            (8)

            Бу тенгкучлиликларни текшириш  учун чинлик жадвалидан фойдаланса булади. Бу ерда биз (8)ни текширадиган жадвални келтиришимиз билан кифояланамиз:

 

 

            Дизъюнкция  амали коммутативлик ва ассоциативлик хоссасига эгадир. (7)-(8) тенгкучлиликлар эса  ва  амалларнинг бир-бирига нисбатан дистрибутив хоссасига эга эканлигини курсатади. Шуни хам таъкидлаш керакки, (8) тенгкучлиликка ухшаш оддий алгебрада айният йук (чунки   айният эмас). Юкоридаги ухшашлик асосида  ни мантикий йигинди,  ни эса мантикий купайтма деб олишимиз мумкин. Бу ухшашликни кучайтириш учун, алгебраик купайтмада нукта × ёзилмаганидек (масалан, ×), мантикий купайтириш белгиси  ни ёзмаймиз, яъни  нинг урнига  ни ёзамиз. Бундан кейин мантикий ифодаларни соддалаштириш, уларда кавсларни камайтириш максадида куйидагича шартлашамиз:

            1) бирор мантикий ифода инкор ишораси остида булса, уни кавссиз ёзамиз, яъни  нинг урнига  ни, ёки  ни ёзамиз.

            2) конъюнкция белгиси дизъюнкция, импликация ва эквивалентлик белгиларига нисбатан  мустахкамрок боглайди деб хисоблаймиз, яъни  урнига ,  урнига ,  урнига  ёзамиз.

            3) дизъюнкция белгиси импликация ва эквивалентлик белгиларига нисбатан мустахкамрок боглайди деб хисоблаймиз, яъни  урнига  ва  урнига  ёзамиз.

            4) импликация белгиси эквивалентлик белгисига нисбатан мустахкамрок боглайди деб хисоблаймиз, яъни  урнига  бу келишувлар мантикий ифодаларни ёзишни соддалаштиради, масалан,

                урнига 

                           ни ёзамиз.

            Юкоридаги (1)-тенгкучлилик ёрдамида  белгисини  ва  белгилари оркали ифодалашимиз мумкин. Энди импликацияни курайлик. Факатгина  чин ва  ёлгон булгандагина  мулохаза ёлгон, бундан эса факатгина  чин (яъни  ёлгон) ва  ёлгон булгандагина  мулохаза ёлгон булиши келиб чикади. Шундай килиб, яна бир тенгкучлиликка эга буламиз:

                           .                      (9)

            Демак, , , , , - белгиларни уз ичига олган ихтиёрий мураккаб мулохазани унга тенгкучли булган шундай мулохаза билан алмаштириш мумкинки, натижада факат , , - белгилар катнашган  мулохазаларга эга буламиз. Бундай алмаштириш мантик алгебрасининг электротехникадаги тадбики учун катта ахамиятга эга, чунки у ерда ишлатиладиган ифодаларда факат учта , , - белгилар катнашади. Энди,  белгини  ва - белгилар оркали ифодалаймиз. Буни икки карра инкорни учириш конуни деб аталувчи  тенгкучлиликдан ва

             ,             (10)

             .             (11)

де Морган конунлари деб аталувчи хамда чинлик жадвали ёрдамида осонгина текшириладиган тенгкучлиликлар ёрдамида бажариш мумкин.

Хакикатан хам,

                  (12)

ва шунга ухшаш

                             (13)

эканлиги келиб чикади.

            Шундай килиб, мантик алгебрасининг ихтиёрий ифодасини унга тенгкучли булган шундай ифода билан алмаштириш мумкинки, охирги ифодада факат  ва - ёки  ва - белгилар катнашади. Шунга ухшаш барча мантик амалларни  ва - амаллар билан алмаштириш мумкин.

            Шуни хам айтиш керакки, барча амалларни факатгина Шеффер штрихи билан алмаштириш хам мумкин:

,  ,      ,    ,    .

Бу тенгкучлиликларни, Шеффер амали таърифидан фойдаланиб, чинлик жадвали ёрдамида осонгина курсатиш мумкин.

            Энди мисол сифатида  ифодани шундай алмаштирамизки, натижада факат ,  ва - белгилар катнашсин. Бунинг учун аввало (9), (2) ва (3) тенгкучлиликлардан фойдаланамиз:

            

              .

            Коммутативлик ва дистрибутивлик конунларидан фойдаланиб, бу ифодани куйидаги куринишда ёзишимиз мумкин:

.

Энди шундай савол тугилади: агар хамма мантикий амаллар иккита (-, ) ёки хатто битта  га келтиришнинг хожати борми?  Сабаб шундаки, факат иккита ёки битта белги оркали алмаштирганда мантикий ифодалар жуда чузилиб кетади ва уни куздан кечириш кийинлашади.

Иккинчи томондан, мантикий хулосаларнинг конуниятларини баён этаётганда, юкорида киритилган , , ,  амаллар катта ахамиятга эга. Бу хусусан  амалига тегишлидир. Яна бир нечта мухим тенгкучлиликларни келтирамиз:

             ё (карама-каршилик конуни)      (14)

             ё (учинчиси истисно конуни)            (15)

             (идемпотентлик конуни)        (16)

             (ютиш конунлари)     (17)

            ё   чч,  ч,  ёё          (18)

            Келтирилгантенгкучлиликлар ихтиёрий мантикий ифодаларни керакли куринишга келтиришга имкон беради.

 

Машклар

 

1.Тенгкучлиликни исботланг:  .

            2.Формулани соддалаштиринг:

.

            3.Берилган формуланинг айнан чинлигини исботланг:

                         

 

5-§. Тенгкучли формулаларга доир теоремалар

 

Теоремалар. -Зарурий ва етарли шартлар.

 

            1-теорема.  ва  формулалар тенгкучли булиши учун  ва  формулалар тенгкучли булиши зарур ва етарли.

            Исбот.  булсин. У вактда хамма холатларда формулалар бир хил кийматга эга буладилар. У холда  ва  формулалар хам чинлик жадвалининг хар бир сатридаги кийматлари бир хил булади. Демак, =.

            Худди шунга ухшаш, = дан  келиб чикади.

            2-теорема.  ва  формулалар тенгкучли булиши учун  формула айнан чин (тавтология) булиши зарур ва етарли.

            Исбот. 1.  булсин. Бу холда, эквивалентлик таърифига асосан,  нинг хамма сатрларидаги кийматлари “ч” дан иборат, демак,  тавтологияни ифодалайди.

            2.  тавтология булсин. У холда  хар бир сатрда “ч” кийматга эга булади. Бундан эса  ва  нинг хар бир сатрдаги кийматлари бир хил, яъни  келиб чикади.

            Мисоллар. 1.  - айнан чин.

                              2.  - айнан чин.

            3-теорема.  айнан чин булиши учун « айнан чин булиши зарур ва етарли.

            Исбот. а)  формула айнан чин булсин. У вактда 2-теоремага асосан =. Демак, 2-теоремага асосан « формуланинг айнан чинлиги келиб чикади.

            б) « айнан чин булсин. Бундан = келиб чикади ва уз навбатида . Демак,  формула айнан чин булади.

            4-теорема.  формуланинг исталган  кисми урнига шу  билан тенгкучли  формулани куйишдан хосил булган янги  формула  билан тенгкучлидир.

            Мисол.   булгани учун

                 .

 

РЕЖА:

 

            1.Мулохаза. Мулохазалар устида мантикий 

           амаллар.

            2.Формулалар. Тенгкучли формулалар.

            3.Айнан чин, айнан ёлгон ва бажарилувчи фор-

           мулалар.

            4.Асосий тенгкучлиликлар.

            5.Тенгкучли формулаларга доир теоремалар.

            6. Т¢пламлар алгебраси билан мулохазалар

   алгебраси ¢ртасидаги муносабат

 

Муаммоли масала ва топшириклар:

 

1. Куйидаги мулохазаларнинг чин ёки ёлгон эканлигини аникланг:

1) ;

2) ;

2. Куйидаги импликацияларнинг кайси бирлари чин булади:

1) агар  булса, у холда ;

              2) агар  булса, у холда ;

3. Куйидаги тенгкучлиликларни исботланг:

 1.  ,           2. ,

 3., 4. .

4. Куйидаги формулаларнинг чинлик жадваллари тузилсин:

1) ;

            2) ;

            3) ;

            4) ;

            5) ;

 

5. Тенгкучлиликлар исбот этилсин:

            1) ;

            2) ;

            3) ;

        4) ;

       5.

 

6. Куйидаги формулалар соддалаштирилсин:

            1) ;

            2) ;

            3) ;

            4) ;

7. Куйидагиларнинг кайси бирлари айнан чин ва айнан ёлгон формула эканлигини аникланг:

7) ;

8) ;

9) ;

10) .

8. Айнан чин ёки айнан ёлгон формула эканлигини исботланг:

1) ;

            2) ;

            3) ;

            4) ;

 

9.  – айнан ёлгон формула булсин.

            эканлигини исбот килинг.

10. Хамма асосий мантикий амалларни

            1) дизъюнкция, конъюнкция ва инкор;

            2) конъюнкция ва инкор;

            3) дизъюнкция ва инкор;

            4) импликация ва инкор

амаллари оркали ифодаланг.

11. Айнан чин ёки айнан ёлгон формула эканлигини исботланг:

            1) ;

        2) ;

            3) .  

 

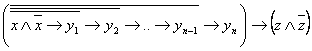Мустакил ишлаш учун саволлар:

 

            1.Мулохаза. Мулохазалар устида кандай манти-

          кий амаллар бажарилади?

            2.Формулалар. Тенгкучли формулаларни келти-

          ринг.

            3.Айнан чин, айнан ёлгон ва бажарилувчи фор-

          мулаларнинг таърифларини келтиринг.

            4.Асосий тенгкучлиликларни исботланг.

            5.Тенгкучли формулаларга доир теоремаларни

          исботланг.

 

6-§. Формулаларнинг нормал шакллари

 

Элементар конъюнкция (дизъюнкция). -КНШ. -ДНШ. -Теоремалар. -Формуланинг доимо чин булишининг етарли ва зарурий шарти.

 

            Тенгкучли алмаштиришлар бажариб, мулохазалар алгебрасининг формулаларини хар хил куринишларда ёзиш мумкин. Масалан, ®ВС формулани  ёки  куринишларда ёза оламиз.

            Мантик алгебрасининг контакт ва реле-контактли схемалар, дискрет техникадаги татбикларида ва математик мантикнинг бошка масалаларида формулаларнинг нормал шакллари катта ахамиятга эга.

            Куйидаги белгилашни киритамиз:

            = ч  эканлиги аник.

            1-таъриф.

                               (1)

куринишдаги формулага элементар конъюнкция деб айтамиз. Бу ерда  ихтиёрий кийматлар сатри ва  узгарувчилар орасида бир хиллари булиши мумкин.

            2-таъриф.

                           (2)

куринишдаги формулага элементар дизъюнкция деб айтамиз. Бу ерда хам  ихтиёрий кийматлар сатри ва  узгарувчилар орасида бир хиллари булиши мумкин.

            3-таъриф. Элементар дизъюнкцияларнинг конъюнкциясига формуланинг конъюнктив нормал шакли (КНШ) ва элементар конъюнкцияларнинг дизъюнкциясига формуланинг дизъюнктив нормал шакли (ДНШ) деб айтилади.

            КНШга  формула ва ДНШга  формула мисол була олади.

            1-теорема. Элементар мулохазаларнинг хар бир  формуласига тенгкучли конъюнктив нормал шаклдаги  формула мавжуд.

            Бу теоремани исботлашда ушбу тенгкучлиликлардан фойдаланамиз:

            1. ;       2. ;      

        3.;    4.;         (3)

5. ;     6. .                   

            Исбот.  формула нормал конъюнктив шаклда булмаса, куйидаги холлар булиши мумкин:

            а)  даги элементар мулохазалар  ва  амаллари билангина бирлаштирилган булса хам, лекин  сунгги амални ифодаламайди. Бу холда  дистрибутивлик конунидан фойдаланиб, сунгги амали  дан иборат тенгкучли  формулага келтирамиз.

            б)  формула -, , , ,  мантикий амаллар воситасида тузилган кандайдир формулани ифодаласин. У холда  га (3) тенгкучлиликларни татбик этиб  билан тенгкучли ва  -, ,  билан ифодаланган  формулани хосил киламиз. Агар  КНШ куринишида булмаса, унга  дистрибутивлик конунини татбик этиб, чекли кадамлардан кейин  билан тенгкучли  конъюнктив нормал шаклдаги формулага келамиз.         

            Изох.  формулани конъюнктив нормал шаклга келтириш жараёнида                    

    ,    ,   ,    ,

    =,    =,   =                  (4)

тенгкучлиликлардан фойдаланиб, уни соддалаштириш мумкин.

            Мисоллар. 1.

                        

                          

                           ;

                        

            Шундай килиб,  формуланинг КНШ биттагина дизъюнктив  хаддан иборат экан.

            2.

         

         

         

           

         

           

           

             формуласи тавтология эканлигини чинлик жадвалига мурожаат килмай туриб аниклаш мумкинми деган саволга куйидаги чинлик аломати деб аталган теорема ижобий жавоб беради.

            2-теорема.  формула доимо чин булиши учун унинг КНШ даги хар бир элементар дизъюнктив хадида камида битта элементар мулохаза билан бирга бу мулохазанинг инкори хам мавжуд булиши зарур ва етарли.

            Исбот: а)  формуланинг

                                                    (5)

КНШ даги хар бир  хадида камида битта элементар мулохаза билан бирга бу мулохазанинг инкори хам мавжуд булсин, яъни  шаклида булсин, у холда  ва  ларга асосан  булади.

Демак,  булади, яъни айнан чин формула булади.

            б) Энди - тавтология булсин ва  унинг КНШ даги шундай элементар дизъюнктив хади булсинки, унда бирорта элементар мулохаза билан бирга унинг инкори катнашмаган булсин. Масалан,  шаклида булсин. Энди, элементар мулохазаларнинг шундай кийматлар сатрини олайликки, бу сатрда  нинг киймати ё,  нинг киймати ч,   нинг киймати ё,......,  нинг киймати ё  булсин. У вактда 

                   ё  ч  ё = ё  ё = ё.

Демак, нинг киймати хам ёлгон булади. Аммо, теореманинг шартига асосан  нинг киймати айнан чиндир. Натижада карама-каршиликка келдик. Демак, элементар дизъюнкцияларнинг хар бир хадида бирорта мулохаза узи ва узининг инкори билан катнашиши шарт.

            Мисол. 1..

                  - айнан чиндир.

     2. - айнан чин формуладир. 

 

 

7-§. Дизъюнктив нормал шакл

 

ДНШ. -Формуланинг доимо ёлгон булишининг етарли ва

зарурий шарти. -Мисоллар.

           

            Эслатиб утамизки, элементар конъюнкцияларнинг дизъюнкциясига формуланинг дизъюнктив нормал шакли (ДНШ) деб айтилади.

            1-теорема. Элементар мулохазаларнинг исталган  формуласини ДНШга келтириш мумкин.

            Исбот. Бунинг учун  формулани КНШга келтирамиз:

 

ва сунгра  нинг инкорини топганимизда формула ДНШ куринишига келади:

   Энди ёлгонлик аломати деб аталган теоремани исботлаймиз.

            2-теорема.  формула айнан ёлгон булиши учун, унинг дизъюнктив нормал шаклидаги хар бир элементар конъюнкция ифодасида камида битта элементар мулохаза билан бирга бу мулохазанинг инкори хам мавжуд булиши зарур ва етарли.

            Исбот. а) -доимо ёлгон булса, у холда  - айнан чин булади. Демак,  нинг КНШ даги хар бир элементар дизъюнкция ифодасида камида битта элементар мулохаза билан бирга унинг инкори хам мавжуд булади. Шунинг учун  нинг ДНШ даги хар бир конъюнктив хадида камида битта элементар мулохаза ва унинг инкори мавжуд булади.

            б) Энди хар бир элементар конъюнкция ифодасида камида битта элементар мулохаза ва унинг инкори мавжуд булсин, яъни

      ..... булсин, у вактда  ва  

.

Демак,  доимо ёлгон формуладир.

         Мисол.                        - айнан чин.

                       - айнан ёлгон.

            3-теорема. Элементар мулохазаларнинг хар бир  формуласи учун ечилиш муаммоси ечиладигандир.

            Исбот. 1.  ни КНШга келтиргандан кейин, айнан чин булиш - булмаслиги дархол аникланади.

            2.  айнан чин булмаса, уни ДНШ га келтириб, айнан ёлгон булиш - булмаслигини аниклаймиз.

            3.  доимо чин ва доимо ёлгон булиш шартларини каноатлантирмаса, у холда бу формула бажарилувчи булади.

            Демак, элементар мулохазалар формуласининг айнан чин, айнан ёлгон ёки бажарилувчи формула булишини чекли кадамлар процессида аниклаш мумкин. Шунинг учун ечилиш муаммоси доимо ижобий хал булади.

 

 

8-§. Мукаммал конъюнктив ва дизъюнктив нормал шакллар

 

МКНШ. -МДНШ. -Тулик ва тугри элементар конъюнкциялар (дизъюнкциялар). -Формулани МКНШ (МДНШ)га келтириш алгоритми.

 

            Мантик алгебрасининг битта формуласи учун бир нечта ДНШ (КНШ) мавжуд булиши мумкин. Масалан,   формулани куйидаги ,  ДНШларга келтириш мумкин. Булар дистрибутивлик ва идемпотентлик конунларини куллаш натижасида хосил килинган.

            Формулаларни бир кийматли равишда нормал шаклда тасвирлаш учун мукаммал дизъюнктив нормал шакл ва мукаммал конъюнктив нормал шакл (МДНШ ва МКНШ) деб аталувчи куринишлари ишлатилади.

             та  элементар мулохазаларнинг

                      (1)

элементар дизъюнкциялари ва

                                 (2)

элементар конъюнкциялари берилган булсин.

            1-таъриф. (1)  элементар дизъюнкция ((2) элементар конъюнкция) тугри элементар дизъюнкция (элементар конъюнкция) деб айтилади, шунда ва факат шундагина, качонки (1)нинг ((2)нинг) ифодасида хар бир элементар мулохаза x_i бир марта катнашган булса.

            Масалан,   ва   элементар дизъюнкциялар ва  ва  элементар конъюнкциялар мос равишда тугри элементар дизъюнкциялар ва элементар конъюнкциялар деб айтилади.

            2-таъриф. (1) элементар дизъюнкция ((2) элементар конъюнкция)  мулохазаларга нисбатан тулик элементар дизъюнкция (элементар конъюнкция) деб айтилади, качонки уларнинг ифодасида  мулохазаларнинг хар биттаси бир матрагина катнашган булса.

            Масалан,  ва  элементар дизъюнкциялар ва , элементар кнъюнкциялар  мулохазаларга нисбатан тулик элементар дизъюнкциялар ва элементар конъюнкциялар булади.

            3-таъриф. Дизъюнктив нормал шакл (конъюнктив нормал шакл) МДНШ (МКНШ) деб айтилади, агар ДНШ (КНШ) ифодасида бир хил элементар конъюнкциялар (элементар дизъюнкциялар) булмаса ва хамма элементар конъюнкциялар (элементар дизъюнкциялар) тугри ва тулик булса.

            Масалан,  ДНШ  мулохазаларга нисбатан МДНШ булади.  КНШ  мулохазаларга нисбатан МКНШ булади.

            Асосий мантикий амалларнинг МДНШ ва МКНШ куринишлари куйидагича булади: а) МДНШ: =; ; ;   ;  .

            б) МКНШ: =; ;

                      ;  ;  .

            1-теорема.  та элементар мулохазанинг айнан чин формуласидан фаркли хар бир  формулани мукаммал конъюнктив нормал шаклга (МКНШ) келтириш мумкин.

            Исбот. Куйидаги исбот тавтологиядан фарк килувчи хар кандай  формулани МКНШ га келтириш алгоритми булади.

            1.Аввало  формулани конъюнктив нормал шаклга келтирамиз. Бунинг учун  формулани конъюнкция, дизъюнкция ва инкор мантикий амаллар оркали ифодалаймиз (инкор амалди факатгина узгарувчилар устида булиши керак). Сунгра дистрибутивлик конунларидан фойдаланиб,  формулани КНШга келтирамиз ва хамма лозим булган соддалаштиришларни бажарамиз.

            2.Агар КНШ ифодасида бир нечта бир хил элементар дизъюнкциялар мавжуд булса, у холда  тенгкучлилик формуласидан фойдаланиб улардан биттасини  ифодасида колдирамиз.

            3.Куйидаги икки усул оркали хамма элементар дизъюнкцияларни тугри элементар дизъюнкцияларга айлантирамиз:

            а) агар бирор элементар дизъюнкция ифодасида бирорта  узгарувчи узининг инкори билан катнашган булса, у холда =ч, ч=ч,  тенгкучлилик формулаларга асосан биз бу элементар конъюнкцияни КНШ ифодасидан олиб ташлаймиз;

            б) агар бирорта узгарувчи элементар дизъюнкция ифодасида бир неча марта катнашган булса (ёки хамма холда инкор ишораси остида эмас, ёки хамма холда инкор ишораси остида), у вактда  формуласига асосан биз улардан факатгина биттасини КНШ ифодасида колдирамиз.

            Натижада, хамма элементар дизъюнкциялар тугри элементар дизъюнкцияларга айланади.

            4. Агар баъзи элементар дизъюнкциялар тулик элементар дизъюнкциялар булмаса, яъни дизъюнктив хадларда элементар мулохазаларнинг баъзилари (ёки уларнинг инкорлари) мавжуд булмаса, у холда бундай  элементар дизъюнкцияларни тулик элементар дизъюнкциялар холатига келтириш керак.

            Масалан, бирор элементар дизъюнкция ифодасида

 ёки  йук деб фараз килайлик. У холда уни  ва  формулалардан фойдаланиб куйидаги

        ......=

         =......

         ......

икки тулик элементар дизъюнкциялар конъюнкциясига келтира оламиз.

Агарда элементар дизъюнкция ифодасида бир нечта  узгарувчилар катнашмаётган булса, у холда унинг ифодасига  = конъюнкцияларни мантикий кушиб, дистрибутивлик конунини куллаймиз. Натижада, битта тулик эмас элементар дизъюнкция урнига  та тулик элементар дизъюнкцияларга эга буламиз.

            5)Туртинчи кадам бажарилиши натижасида КНШ ифодасида бир хил элементар дизъюнкциялар пайдо булади. Шунинг учун яна 2) кадамни ишлатамиз.

            Демак, 1) - 5) кадамлар натижасида КНШ ифодасида бир хил элементар дизъюнкциялар мавжуд булмайди ва хамма элементар дизъюнкциялар тугри ва тулик булади. Таърифга асосан, бундай КНШ мукаммал конъюнктив нормал шакл булади.

            Мисол. 1.  формула куйидаги МКНШ га эга булади.

 

             2.

    

      

      )

    

  

        

3.

 

   

 

  

 

 

 

 мулохазали мукаммал конъюнктив нормал шакл

 

ифодасида  урнига  ни ва аксинча,  урнига  ни куйганимизда

 

биз  мулохазали мукаммал дизъюнктив нормал шаклга эга буламиз.

            Мукаммал дизъюнктив нормал шаклнинг хар бир  хади конъюнктив конституент деб аталади.

 

            2-теорема.  та элементар мулохазаларнинг айнан ёлгон формуласидан фаркли хар бир  формуласини мукаммал дизъюнктив нормал шаклга келтириш мумкин.

 

            Исбот. Берилган формулани  билан белгилаб, аввало  ни мукаммал конъюнктив нормал шаклга келтирамиз

 =  

            Бундан  нинг МДНШ ни топамиз

=

 

            Мисол. =

   

   

 

 

 

9-§. Формулаларнинг асосий хоссалари

 

Чинлик жадвали буйича формулани тиклаш. -Формулани узгарувчилар буйича каторга ёйиш. -Чинлик жадвали буйича формулани МКНШ

(МДНШ)  куринишда ёзиш.

 

      1. Чинлик жадвали буйича формулани тиклаш. Маълумки, берилган формула учун чинлик жадвали тузиш мумкин. Формуланинг чинлик жадвалини тузишни биламиз.

            Энди тескари масала билан шугулланайлик, яъни берилган чинлик жадвали буйича формулани топишни максад килиб куяйлик. Масалан,  ва y элементар мулохазаларнинг куйидаги чинлик жадвалларига эга булган  формулаларни топайлик:

                                                         1-жадвал

 

            Бундан кейин бирор мулохазанинг “чин” кийматини “1” ва “ёлгон” кийматини “0” деб белгилаймиз. Маълумки,

;   ;   ;          (1)

            (1) формулаларнинг хар кайсиси учун жадвалнинг, мос равишда, 1,2,3,4, сатрида “1” киймат ва колган сатрларида “0” киймат туради.

            (1) формулалар икки мулохазали конъюнктив конституентлардан иборат.

            Энди шундай формулаларни топайликки, улар учун жадвалнинг 2 сатрида “1” киймат ва икки сатрида “0” киймат турган булсин. Бу талабга куйидаги формулалар жавоб беради

;    ;

      ;     ва х.к.

            Шундай килиб, ушбу коида уринли: 2 ва 4 - сатрда “1”, 1 ва 3 - сатрларда “0” кийматга эга булган формулани хосил килиш учун, биттасининг “1” киймати худди 2-сатрда ва иккинчисининг “1” киймати худди 4-сатрда турган икки конъюнктив конституент дизъюнкциясини оламиз.

.

            Худди шундай, 1-жадвалдаги учта конъюнктив конституент дизъюнкцияси учта сатрда “1” кийматга ва битта сатрда “0” кийматга эга булган формулани тасвирлайди. Масалан,

.

            Шундай килиб, туртала  конъюнктив конституент дизъюнкцияси турттала сатрда хам “1” кийматга эга, яъни айнан чин

.

            Бу формула - икки мулохазали тулик мукаммал дизъюнктив нормал шаклдан иборат:

            Демак, Е нинг инкори

     ёки

айнан ёлгон формулани ифодалайди. Бу эса икки мулохазали тулик мукаммал конъюнктив нормал шаклдир.

            Шундай килиб, икки  ва  элементар мулохазалар учун чинлик жадвалларига караб мос формулаларни тиклаш масаласи хал килинди.

            Энди берилган чинлик жадвалларига караб учта  элементар мулохазаларнинг формулаларини топиш масаласига утамиз. Бу уч мулохаза учун 2³=8 та кийматлар сатрлари тузилади.

                                                                           2-жадвал

 

 

            2-жадвалнинг сатрларидан биридагина “1” кийматга, колганларида “0” кийматга эга булиш талабига жавоб берувчи формулалар ушбу уч мулохазали хамма 2³=8 та конъюнктив конституентлардан иборатдир:

1.      4.    7. LLz=A₇

 2.      5.    8. LL=A₈

 3.      6.                   (2)

            Бу (2) конъюнктив конституентлардан хар иккитасининг дизъюнкциясини олиб, кийматлари икки сатрда “1”, колганларида “0” булган формулаларни; хар учтасининг дизъюнкциясини олиб, кийматлариуч сатрда “1”, колган сатрларда “0” булган формулаларни хосил киламиз ва  х.к.

            Масалан:

;  ;             ;

; ;             ;

       ;      ; ..................

                                      ; ..................

                          - МДНШ           (3)

                          -МКНШ      (4)

            Бунда саккизтасининг дизъюнкцияси (3) айнан чин формулани ва унинг инкори (4) айнан ёлгон формулани ифодалайди.

             та  элементар мулохазалар учун хам масала худди шу усул билан ечилади.

            Юкорида келтирилган мулохазалардан келиб чикадики, хар бир айнан ёлгон булмаган  аргументли   формулани куйидаги мукаммал дизъюнктив нормал шаклда ёзиш мумкин:

     

                                   (5)

яъни кийматлар сатрида чин кийматга эга булган элементар конъюнкцияларнинг дизъюнкцияси шаклида ёзилади. (5)- формулани куйидагича хам ёзиш мумкин:

      (6)

            Бу ерда  элементар конъюнкцияларнинг дизъюнкцияси хамма 2ⁿ кийматлар сатри буйича олинади.

            Худди шундай айнан чиндан фарк килувчи исталган  формулани куйидаги мукаммал конъюнктив нормал шаклда келтириш мумкин:

     

                                  (7)

ёки

,

                                            (8)

яъни  элементар дизъюнкцияларнинг конъюнкцияси хамма 2ⁿ кийматлар сатри буйича олинади.

            Шундай килиб, (7) ва (8) - формулалар оркали исталган функциянинг чинлик жадвалидан фойдаланиб уни МДНШ ва МКНШ куринишида ёзиш мумкин.

            Мисол. 1.Берилган чинлик жадвалига асосан  формулаларни МДНШ куринишида ёзиш талаб этилсин:

 

                                                 3-жадвал

 

1	1	1	0	1	1	0	1
0	0	1	1	0	1	1	0
0	1	0	0	1	0	1	1
1	0	0	1	1	0	0	0
1	1	0	0	0	1	1	1
1	0	1	1	1	0	0	1
0	1	1	0	0	1	1	0
0	0	0	1	1	0	0	1

 

                                    ,

                                    ,

                                    ,

                                    ,

                                    .

           

Машклар

 

            1.Учинчи жадвалда берилган  формулаларнинг МКНШ куринишини топинг.

            2. Бир, икки ва уч аргументли хар кандай айнан ёлгон булган функцияларнинг ТКНШ куринишини топинг.

 

10-§. Тенгкучлимас формулалар сони

 

n-узгарувчили формулалар сони. -Элементар конъюнкциялар сони.

 

             та элементар

                                                     (1)

мулохазаларнинг нечта узаро тенгкучлимас, яъни хар хил формулалари мавжуд деган масалани куямиз.

            Икки  ва  элементар мулохазалар учун нечта тенгкучлимас формулалар борлигини курайлик.

             ва  нинг 2² = 4 кийматлар сатри учун:

4 та  формулалардан хар кайсисининг кийматларидан биттаси “1” ва учтаси “0” дан иборат устуни мавжуд. Бундай устунлар сони 4 та, яъни .

            Ундан кейин, олтита , , ....,  формулалардан хар кайсисининг кийматлари иккита “1” ва иккита “0” дан иборат устунни хосил килади. Бундай устунлар сони  га тенг. Яна туртта

,   ,   ,  

формулалардан хар кайсисининг кийматлари учта “1” ва битаа “0” дан ташкил этилган устунни беради. Бундай устунлар  тадир. Нихоят, Е формуланинг кийматлари факат “1”  дан тузилган  та устунни ташкил этади.

            Шундай килиб, 1-жадвалда

устун мавжуд булади. Бундан эса худди шунча формула борлиги келиб чикади. Устунларнинг хеч кайси  иккитаси бир хил булмаганлигидан, хеч кайси иккита формула хам узаро тенгкучли эмасдир.

            Демак, икки x ва у мулохазанинг шу 16 та формуласидан ташкари, уларни ифодалайдиган бошка тенгкучли формула йук.

            Бундан,  ва  нинг исталган  формуласи жадвалда келтирилган формулаларнинг бири билан тенгкучли деган хулосага келамиз.

            Масалан,  формулани олсак, ушбу чинлик жадвалидан

 

1	1	0	1	0
1	0	1	0	0
0	1	0	0	0
0	0	1	1	1

 

            = эканлиги маълум булади.

            Юкорида хосил этилган формулалардан 15 таси МДНШ ва 1 таси МКНШ куринишига эга.

            Худди шундай фикр юргизиш йули билан  элементар мулохазаларнинг тенгкучлимас формулалар сони

га тенглиги келиб чикади. Туртта  мулохазаларнинг хар хил формулалар сони га ва, умуман,  та мулохазанинг хар хил тенг кучлимас формулалар сони

яъни  га тенг.

            Шундай килиб, тенгкучлимас n аргументли формулалардан -1 таси МДНШ ва биттаси МКНШ куринишига эга.

 

РЕЖА:

 

            1.Формулаларнинг нормал шакллари.

            2.Дизъюнктив ва конъюнктив нормал шакллар.

  3.Мукаммал конъюнктив ва дизъюнктив нор-

          мал шакллар.

            4.Формулаларнинг асосий хоссалари.

            5.Тенгкучлимас формулалар сони.

 

Муаммоли масала ва топшириклар:

 

1. Куйидаги формулаларни КНШ куринишига келтиринг:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) .

2. Юкорида келтирилган формулаларни ДНШ куринишига келтиринг.

3. Куйидаги формулаларни ДНШ куринишига келтиринг ва айнан ёлгон ёки айнан ёлгон эмаслигини аникланг:

1) ;

2) ;

3) ;

            4) ;

5) ;

            6) .

4. 1 ва 3 бандларда келтирилган формулаларни ТКНШ ва ТДНШ куринишига келтиринг.

5.  функция шунда ва факат шунда чин киймат оладики, качон узгарувчиларнинг факат биттаси  чин киймат олса.  функциянинг чинлик жадвалини тузинг ва уни формула оркали ифодаланг.

6. Чинлик жадвалидан , , , , ,   функциялар-ни ифодаловчи формулаларни топинг ва уларни соддалаштиринг:

 

1	1	1	0	1	1	1	0	1
1	1	0	1	1	1	0	1	0
1	0	1	1	0	0	1	0	0
1	0	0	1	0	0	1	1	1
0	1	1	0	0	0	0	1	0
0	1	0	0	1	1	0	0	1
0	0	1	1	0	1	1	1	1
0	0	0	0	0	0	0	0	1

7. Куйидаги такомил нормал шаклдаги формулаларнинг чинлик жадвалини тузинг ва уларни соддалаштиринг:

            1) ;

            2) ;

            3) ;

            4) .

8. Бир, икки ва уч аргументли хар кандай айнан чин булган функцияларнинг ТДНШ куринишини топинг.

 

 

Мустакил ишлаш учун саволлар:

 

            1.Формулаларнинг нормал шакллари деб нимага

          айтамиз?

            2.Формуланинг дизъюнктив ва конъюнктив нор-

          мал шаклларини ифодаланг.

            3.Формулани мукаммал конъюнктив ва дизъюнк-

       тив нормал шаклларга келтириш алгоритмини

          ёзинг.

            4.Формулаларнинг асосий хоссаларини келти-

          ринг.

            5.Тенгкучлимас формулалар сони нимага тенг?

 

 

11-§. Формуланинг чинлик туплами

 

Чинлик туплами. -Мантикий амалларнинг чинлик тупламлари.

 

            Маълумки,  элементар

мулохазанинг кийматлари 2ⁿ та кийматлар сатрини ташкил этади. Бу  мулохазаларнинг хар бир А формуласи баъзи кийматлар сатрларида “1” кийматни ва баъзиларида “0” кийматни кабул килади.

            Таъриф.  формула “1” киймат кабул килувчи элементар мулохазаларнинг хамма кийматлар сатрларидан тузилган туплам  формуланинг чинлик туплами дейилади.

            Утган параграфларда курганимиздек, элементар мулохазаларнинг  формулаларидан  таси битта кийматлар сатрида “1” кийматни кабул килади. Демак, бундай хар бир формула бир элементли чинлик тупламига эга.

            Худди шунингдек,  формулаларнинг  тасидан хар кайсиси икки элементли чинлик тупламига,  тасидан хар бири уч элементли чинлик тупламига ,........,  формула булса, 2ⁿ элементли чинлик тупламига эгадир.  айнан ёлгон формуланинг чинлик туплами эса Æ буш тупламдан иборат.

             мулохазаларнинг айнан чин формуласига тегишли чинлик тупламини  универсал туплам деб олсак, шу мулохазаларнинг хамма формулаларга тегишли чинлик тупламлари  нинг кисмларини ташкил этади ва бу универсал туплам

 та

кисмларга эга булади.

            Шундай килиб,  та элементар мулохазаларнинг хамма  формулалари билан уларнинг чинлик тупламлари орасида узаро бир     кийматли    мослик урнатилади.

            Хамма узаро тенгкучли формулаларга битта чинлик туплами мос келади.

            Мисоллар. 1.Уч элементар  мулохазанинг  формуласи факат битта (1,0,1) кийматлар сатрида “1” кийматни кабул килади. Шу сабабли, бу формуланинг чинлик туплами ушбу бир элементли  тупламдир.

            2.  формула уч элементли , ,  чинлик тупламига эгадир.

            3. Ушбу  формула айнан чиндир. Шунинг учун унинг чинлик туплами универсал  тупламдан иборат.

             формула  тупламда чин булса, у холда  нинг тулдирувчиси булган  тупламда ёлгон булади. Лекин  нинг  инкори  да чин ва  да ёлгон булади. Худди шундай, айнан чин  формула  да чин, лекин  да ёлгон. Айнан ёлгон  формула эса, аксинча,  да чин ва  да ёлгондир.

             та элементар мулохазалар формулалари билан чинлик тупламлари орасидаги бундай богланиш мулохазалар мантикидаги масалани тупламлар назариясидаги масалага ва, аксинча, тупламлар назариясидаги масалани мулохазалар мантикидаги масалага кучириш имкониятини беради.

            Хакикатан хам:

            1.  формула  тупламда чин ва  формула  тупламда чин булса,  формула кандай тупламда чин булади? Маълумки (конъюнкция таърифига асосан), бу формула  ва  нинг иккаласи хам чин булган тупламда чиндир. Демак,  кесишмада чиндир.

Масалан, ва  формулаларнинг  конъюнкцияси  тупламда чиндир. Шундай килиб, мулохазалар мантикидаги  амалига тупламлар назариясидаги  амали мос келади. (1-шакл).

 

 

                                  U                                         U

 

          

                        Р        Q                      Р        

Q    

 

 

         

             1-шакл.                             2-шакл.

 

2.  формула кандай тупламда чин булади?

    Дизъюнкция таърифига асосан  формула  ва  формулаларнинг камида биттаси чин булган тупламда чиндир. Демак,  тупламда  формула чиндир. Шундай килиб, мулохазалар мантикидаги  амалига тупламлар назариясидаги  амалининг мос келишини курамиз (2-шакл). Юкорида келтирилган  ва  формулалар учун

      3.  импликациянинг чинлик тупламини топайлик.

            Импликация таърифига асосан  формула факат  чин булиб,  ёлгон булган тупламда ёлгондир.

Демак,  айирмада  формула ёлгондир.

            Шундай килиб,  формула  нинг штрихланган булагида ёлгон булиб, колган булагида чиндир (3-шакл).  нинг колган булаги эса  га тенг. Демак,  формула   тупламда чиндир.

 

 

                                                                      U 

                                           

                                                              Q

                                                P

 

                                                                                                     

                              

                               3-шакл.

 

Иккинчи томондан,  формула  да ва  формула  да чин булгани учун,  формула  да чиндир.

            Демак, бизга маълум булган  тенгкучлиликни бошка йул билан исботладик.

            4. (1) мулохазаларнинг исталган  ва  формулаларини олиб,  тенгкучлиликни исботлайлик.  формула  да чин,  формула  да ва  формула  да чин булсин. Шундай килиб,  формула  тупламда чин. Шу сабабли,  айнан чин формула булиб,  дир.

            5. Кандай шартда  тенгкучлилик бажарилади?

            Маълумки,  формула  нинг  дан бошка булагида, демак,  да чин.  шарт буйича  булиши керак. Бундан  ёки  келиб чикади. Бу эса  эканини билдиради.

            6.  формуланинг чинлик тупламини аниклайлик.

            Бу формула  чин ва  ёлгон, шунингдек,  чин ва  ёлгон булган тупламда, яъни  дагина ёлгон булиб,  нинг колган булагида, яъни  да чиндир.

            Шундай килиб,  нинг чинлик туплами  нинг штрихланган булагидан бошка кисми билан тасвирланади (4-шакл):

                                              

                                                U

 

 

                              P            Q

      

 

                               

                                  4-шакл.

 

            Бошка кисмига мос келувчи тупламни топамиз.  ва . Бундан  ва  келиб чикади. Шундай килиб,

Демак,  формула  тупламда чиндир.

            Иккинчи томондан,  туплам  формуланинг чинлик туплами булгани учун, ушбу маълум тенгкучлиликка эга буламиз.

    Куйидаги формулаларга ,  асосан

            7. Формулалар билан тупламлар орасидаги богланишга суяниб, куйидаги теоремани исботлайлик:

            Теорема:  ва  формулалар тенгкучли булиши учун  формула тавтология булиши зарур ва етарли.

    Исбот. а)  булсин. Демак, .  нинг чинлик туплами

         .

Бундан  келиб чикади, яъни  тавтологиядир.

            б)  булсин, у вактда  булади.

Демак, .   Бундан, конъюнкция таърифига асосан  ва .

            Бу ердан, 5-пунктга биноан  ва . Демак,  келиб чикади. Бу уз навбатида  булишини курсатади.

            Шундай килиб, мулохазалар алгебрасидаги ,  - мантикий амалларга мос равишда тупламлар алгебрасидаги , -(купайтма, бирлашма, тулдирувчи) амаллари мос келади. Мулохазалар алгебрасидаги “1”, “0” константаларга тупламлар алгебрасидаги  ва  (универсал ва буш) тупламлар мос келади. Демак, мулохазалар алгебрасидаги бирор ифодада  ни  га,  ни  га, инкорни (-) тулдирувчига, “1” ни универсал  тупламга “0” ни буш  тупламга алмаштирса, тупламлар алгебрасидаги ифода хосил булади ва аксинча.

12-§. Мулохазалар алгебраси функциялари.

Функциялар тенгкучлилиги. Функциялар суперпозицияси

 

Функция. -Функциялар тенгкучлилиги. -0 ва 1 сакловчи функциялар.

-n-аргументли функциялар сони. -Бир рангли суперпозиция.

 

            Маълумки, мантикий амаллар мулохазалар алгебраси нуктаи назаридан чинлик жадваллари билан тулик характерланади. Агарда функциянинг жадвал шаклида берилишини эсга олсак, у вактда мулохазалар алгебрасида хам функция тушунчаси мавжудлигини биламиз.

            1-таъриф. Мулохазалар алгебрасининг  аргументли  функцияси деб, 0 ва 1 киймат кабул килувчи функцияга айтилади ва унинг  аргументлари хам 0 ва 1 киймат кабул килади. Функция  узининг чинлик жадвали билан берилади.

 

 

			...
0	0	0	...	0	0	f(0,0,...,0,0)
1	0	0	...	0	0	f(1,0,...,0,0)
...	...	...	...	...	...	...............
1	1	1	...	1	0	f(1,1,...,1,0)
1	1	1	...	1	0	f(1,1,...,1,1)

 

            Бу жадвалнинг хар бир сатрида аввал узгарувчиларнинг  кийматлари ва шу кийматлар сатрида  функциянинг  киймати берилади. Олдинги параграфларда исбот килган эдикки,  та узгарувчи учун кийматлар сатрларининг сони 2ⁿ ва функцияларнинг сони га тенг булади.

            Мулохазалар алгебрасида асосий элементар функциялар куйидагилардан иборат:

            Агар f(0,0,.....,0)=0 булса, у холда f(x₁,x₂,.....,x_n) функцияга 0 сакловчи функция деб айтилади. Агар  булса, у вактда  функцияга 1 сакловчи функция деб айтамиз.

            n аргументли 0 сакловчи функцияларнинг сони  га ва 1 сакловчи функцияларнинг сони хам   га тенг булади (исбот килишни укувчига хавола этамиз).

            Мулохазалар алгебрасидаги  аргументли 0 сакловчи функциялар тупламини  ва 1 сакловчи функциялар тупламини  билан белгилаймиз.

            2-таъриф.  ва  мулохазалар алгебрасининг функцияси ва  лар хеч булмаганда уларнинг биттасининг аргументлари булсин. Агар  аргументларнинг хамма кийматлари сатри учун f ва g функцияларнинг мос кийматлари бир хил булса, у холда  ва   функциялар тенгкучли функциялар деб айтилади ва  шаклида ёзилади.

            3-таъриф. Агарда куйидаги муносабат

бажарилса, у вактда  аргументга  функциянинг сохта аргументи деб айтилади.

    Агарда  булса, у холда x_i аргументга  функциянинг сохта эмас (мухим) аргументи деб айтилади.

            Мисол.  функция учун у аргументи сохта аргумент булади, чунки .

            Функциянинг аргументлари каторига исталганча сохта аргументларни ёзиш мумкин ва у катордан хамма сохта аргументларни олиб ташлаш мумкин.

            Энди мулохазалар алгебраси функцияларининг суперпозицияси тушунчасини курайлик.

            4-таъриф.  мулохазалар алгебраси функцияларининг чекли системаси булсин.

            Куйидаги икки усулнинг биттаси билан хосил этиладиган  функцияга  системадаги  функцияларнинг элементар суперпозицияси ёки бир рангли суперпозицияси деб айтилади:

            а) кандайдир  функциянинг  аргументини кайта номлаш усули, яъни

бу ерда у,  узгарувчиларнинг бирортаси билан мос тушиши мумкин.

            б) Кандайдир  функциянинг бирор аргу-менти урнига иккинчи бир  функцияни куйиш усули, яъни

 j_e(x_e1,....,x_ek),

            Агар  система функцияларнинг  рангли суперпозициялари синфи  берилган булса, у вактда  булади.

            1-изох. 4-таърифнинг а) кисмига асосан бир хил чинлик жадвалига эга булиб, лекин узгарувчиларнинг белгиланиши билан фарк киладиган функциялар бир-бирининг суперпозицияси булади.

            2-изох. 4-таърифнинг а) кисмига асосан бирор  узгарувчини  билан кайта номласак, натижада кам узгарувчили функцияга эга буламиз. Бу холда  ва  узгарувчилар айнан тенглаштирилди деб айтамиз. Масалан,  ва  функциялардаги  ни  билан кайта номласак, у вактда  ва  функцияларни хосил киламиз.

            3-изох. 4-таърифнинг а) кисмига асосан агар  булса, у холда  ва умуман  булганда .

            5-таъриф. , , , ,  асосий элементар функцияларнинг суперпозициясига формула деб айтамиз.

           

13-§. Буль алгебраси

 

Буль алгебрасининг таърифи. -Мисоллар.

 

            Таъриф. Конъюнкция , дизъюнкция ,  инкор амаллари ва  элементлари аникланган  тупламда шу мантикий амаллар ва  элементлар учун куйидаги аксиомалар

                 ;                                            (1)

                ;                                          (2)

             ;                                               (3)

             ;                                                (4)

        ;                               (5)

          ;                                           (6)

         ;                     (7)

               ;                                     (8)

               =;                                      (9)

                ;                                       (10)

                 ;                               (11)

                 ;                                   (12)

                 ;                            (13)

бажарилса, бундай  тупламга Буль алгебраси деб айтилади.

            Буль алгебрасига куйидаги тупламлар мисол була олади:

1. -кандайдир туплам (масалан, тугри чизикда ётган нукталар туплами ёки натурал сонлар туплами) ва  нинг хамма кисм тупламлардан иборат туплам булсин.  оркали  ва   тупламларнинг    кесишмасини,   оркали  ва  тупламларининг  бирлашмасини,  оркали  тупламнинг  тупламигача  тулдирувчисини, 0 оркали Æ буш тупламни ва 1 оркали  тупламни белгилаб оламиз. У вактда  туплам Буль алгебраси булади, чунки юкорида курсатилган 13 аксиома бажарилади.

            2. Мулохазалар туплами учун ,  ва - амаллари хамда 0 ва 1 элементлари аникланганлиги учун бу тупламни Буль алгебраси деб тахмин килишимиз турган гап. Лекин бунинг учун куйидаги аникликни киритиш керак.  ва  мулохазалар айнан тенг булиши учун  эквивалентлик абсолют чин булиши керак. Ана шундай тушунча киритилган мулохазалар туплами Буль алгебрасига мисол була олади.

РЕЖА:

 

            1.Формуланинг чинлик туплами.

            2.Мулохазалар алгебраси функциялари. Функ-

           циялар тенгкучлилиги. Функциялар суперпо-     

           зицияси.

            3.Буль алгебраси.

 

Муаммоли масала ва топшириклар:

 

1. Куйидаги берилган формулаларнинг чинлик тупламларини  топинг:

 

 ;

        ;

                        ;

            .

;

            ;

            ;

                        ;

            ;

                        .

           

2. Юкорида келтирилган формулалардан тузилган , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,  мураккаб формулаларнинг чинлик тупламини топинг.

3.  ва  функцияларга тенгкучли булган функцияларни топинг.

4. Ёлгон киймат сакловчи ()  аргументли хар хил функцияларнинг сони нечта?

5. Чин киймат сакловчи ()  аргументли хар хил функцияларнинг сони нечта?

6. Куйидаги  ва  хамда  ва  функцияларнинг тенгкучлилигини исботланг.

 

Мустакил ишлаш учун саволлар:

 

            1.Мантикий амалларнинг чинлик тупламлари.

            2.Формуланинг чинлик туплами деб нимага ай-

          тамиз?

            3.Мулохазалар алгебраси функциялари. Качон

          функциялар тенгкучли деб айтилади? Функ-

          циялар суперпозицияси нимадан иборат?

            4.Буль алгебраси таърифини келтиринг.

 

 

14-§. Мантик алгебрасидаги иккитарафлама конун

 

Иккитарафлама функция. -Уз-узига иккитарафлама функция. -Иккитарафлама конун. -Мисоллар. -Теорема. -Лемма.

 

            Энди иккитарафлама (кушма) функция тушунчасини киритамиз.  функцияга иккитарафлама булган функцияни топиш учун  функциянинг чинлик жадвалида хамма узгарувчиларни уларнинг инкорига алмаштириш керак, яъни хамма жойда 1 ни 0 га ва 0 ни 1 га алмаштириш керак.

            1-таъриф. Куйидагича аникланган

функцияга  функциянинг иккитарафлама функцияси деб айтилади.

            2-таъриф. Агар

муносабат бажарилса, у холда га уз-узига иккитарафлама функция деб айтилади.

            Таърифга асосан,  иккитарафлама функция  ва ( кийматлар сатрида карама-карши кийматлар кабул килади.

            Мисоллар. 1. Мулохазалар алгебрасининг асосий элементар функцияларига иккитарафлама булган функцияларни топинг.

            1.  га иккитарафлама функция  булади.

            2.  га иккитарафлама функция  булади.

            3.  га иккитарафлама функция V булади.

            4.  га иккитарафлама функция  булади.

            5.  га иккитарафлама функция  булади.

            6.  га иккитарафлама функция  булади.

            7. f₇=1 га =0 ва f₈=0 га =1 булади.

            Келтирилган мисолнинг ечимидан куриниб турибдики,  ва  функциялар, таърифга асосан, уз-узига иккитарафлама функция булади.

            2.  функциянинг уз-узига иккитарафлама функция эканлигини исбот килинг.

            Демак,  эканлиги учун  уз-узига иккитарафлама функциядир.

            Теорема. Агар  булса, у холда

 булади.

            Исбот.

Теореманинг исботидан иккитарафлама конун келиб чикади.

       Иккитарафлама конун.  функцияларнинг суперпозициясига иккитарафлама булган функция мос равишда  иккитарафлама функциялар суперпо-зициясига тенгкучлидир, яъни агар  формула  функцияни  реализация  этса,  у вактда   формула   функцияни реализация этади.

            Бу формула  формулага иккитарафлама булган формула деб айтилади ва уни ^* деб белгилаймиз. Демак,

.

            Ушбу конундан уз-узига иккитарафлама булган функцияларнинг суперпозицияси яна уз-узига иккитарафлама функция булишлиги келиб чикади, яъни агар  уз-узига иккитарафлама функция булса, у холда () функция хам уз-узига иккитарафлама булади. Хакикатан хам,

()=.

            Агар функция формула оркали ифодаланган ва бу формула уз навбатида , , - мантик амаллари оркали ифодаланган булса, у холда бу функцияга (формулага) иккитарафлама булган функцияни (формулани) топиш учун  ни  га,  ни  га, 1 ни 0 га ва 0 ни 1 га алмаштириш кифоя. Бу принципни тенгкучли формулаларга ишлатганда, яна тенгкучли формулалар хосил киламиз, яъни  булса, у холда .

            Ушбу принцип оркали мантик алгебрасининг бир формуласидан иккинчи формуласига, бир теоремасидан иккинчи теоремасига, бир таърифидан иккинчи таърифига келамиз.

            Масалан, юкорида келтирилган (2), (3), (6), (8), (10), (12) тенгкучли формулаларга ушбу принципни ишлатсак, (4), (5), (7), (9), (11), (13) - тенгкучли формулалар келиб чикади.

            Мантик алгебрасида элементлари  аргументли уз-узига иккитарафлама функциялардан иборат булган тупламни  билан белгилаймиз, унинг элементларининг сони  га тенгдир.

            Энди уз-узига иккитарафлама булмаган функциялар хакидаги леммани куриб чикайлик.

            Лемма. Агар  булса, у холда ундан аргументларининг урнига  ва  функцияларни куйиш усули билан бир аргументли уз-узига иккитарафлама булмаган функция, яъни константани хосил килиш мумкин.

            Исбот.  булганлиги учун, шундай  кийматлар сатри топиладики,  булади.

 функцияни киритамиз ва  деб белгилаб оламиз.

            У вактда куйидаги натижага эга буламиз:

,...,,...,

=,...,.

            Лемма исбот булди.

 

15-§. Мантик алгебрасидаги арифметик амаллар. Жегалкин купхади

 

Арифметик амаллар. -Жегалкин купхади. -Мантикий амалларни арифметик амаллар оркали ифодалаш. -Чизикли функция. -Теорема.

 

            {0,1} Буль алгебрасидаги ху конъюнкция амали оддий арифметикадаги 0 ва 1 сонлар устидаги купайтма амалига мос келади. Аммо 0 ва 1 сонларни кушиш натижаси {0,1} туплам доирасидан четга чикади. Шунинг учун И.И.Жегалкин (3.VIII 1869-28.III 1947) 2 модулига асосан кушиш амалини киритади (И.И.Жегалкин 30-йилларнинг бошида Москва давлат университетида биринчи булиб математик мантик буйича илмий семинар ташкил этган).  ва  мулохазаларнинг 2 модули буйича кушишни  сифатида белгилаймиз ва у куйидаги чинлик жадвали билан берилади:

 

           

Чинлик жадвалидан куриниб турибдики, =. Мантик алгебрасидаги купайтма ва 2 модули буйича кушиш мантик амаллари учун коммутатив, ассоциатив ва дистрибутив арифметик конунлар уз кучини саклайди.

            Буль алгебрасидаги асосий мантикий амалларни киритилган арифметик амаллар оркали куйидагича ифодалаш мумкин:

      1. =;     2. ;     3. ;

      4. ;          5. .

            2 модули буйича кушиш амалининг таърифига асосан  ва  .

            Мантик алгебрасидаги исталган функцияни ягона арифметик купхад шаклига келтириш мумкин. Хакикатан хам, биз олдинги параграфларда исталган функцияни конъюнкция ва инкор мантикий амаллар оркали ифодалаш мумкинлигини курган эдик. Юкорида конъюнкция, дизъюнкция ва инкор мантикий амалларни арифметик амаллар оркали ифодаладик. Демак, исталган функцияни арифметик купхад шаклига келтириш мумкин.

            1-таъриф.  куринишидаги купхадга Жегалкин купхади деб айтилади. Бу ерда хамма  узгарувчилар биринчи даражада катнашади,  кийматлар сатрида хамма  лар хар хил булади, .

            2-таъриф.   куринишидаги функция чизикли функция деб айтилади. Бу ерда .

            Чизикли функциянинг ифодасидан куриниб турибдики,  аргументли чизикли функциялар сони 2^{n+1 га тенг ва бир аргументли функциялар доимо чизикли функция булади.}

            Жегалкин купхади куринишидаги хар бир функциянинг аргументлари сохта эмас аргументлар булади. Хакикатан хам, x₁ шундай аргумент булсин. У вактда ихтиёрий  функцияни куйидаги куринишда ёзиш мумкин:

 

.

 

Бу ерда j функцияси айнан 0 га тенг эмас, акс холда  аргумент  функциянинг (купхаднинг) аргументлари сафига кушилмасди.

Энди  аргументларнинг шундай кийматларини оламизки,  булсин. У вактда  функциянинг киймати  аргументнинг кийматига боглик булади. Демак,  сохта аргумент эмас.

            Мантик алгебрасидаги хамма  аргументли чизикли функциялар тупламини  харфи билан белгилаймиз. Унинг элементларининг сони 2^{n-1 га тенг булади.}

            Теорема. Агар  булса, у холда ундан аргументлари урнига 0 ва 1 константаларни хамда  ва  функцияларни, айрим холда  устига “-“ инкор амалини куйиш усули билан  функцияни хосил этиш мумкин.

 

16-§. Мантик алгебрасидаги монотон функциялар

 

Монотон функция. -Кийматлар сатрининг олдин келиши. -Таъриф. -Монотон функциялар суперпозицияси. -КНШ (ДНШ) куринишидаги функциянинг

монотон функция булиш шарти.

 

            0<1 муносабати оркали {0,1} тупламини тартиблаштирамиз.

            1-таъриф.  ва  кийматлар сатри булсин.  кийматлар сатри  кийматлар сатридан шунда ва факат шундагина олдин келади деб айтамиз, качон  ёки  ва  кийматлар сатри устма-уст тушса, у холда  шаклида ёзамиз.

            2-таъриф.  ва  ихтиёрий кийматлар сатри булсин.  дан  бажарилиши келиб чикса, у холда  функция монотон функция деб айтилади.

            3-таъриф.  дан > муносабат келиб чикса, у холда  номонотон функция деб айтилади.

            Асосий элементар мантикий функциялардан 0, 1, , ,  функциялар монотон функциялар булиб, , , ,  функциялар номонотон функциялардир.

            1-теорема. Монотон функцияларнинг суперпозициясидан хосил килинган функция яна монотон функция булади.

            Исбот.  монотон функциялар системаси ва шу системадаги функциялар суперпозициясидан хосил этилган функция монотон эканлигини исбот килиш керак булсин. 0 рангли суперпозиция учун бу тасдикнинг тугрилиги аник, чунки  системадаги хамма функциялар монотон функциялардир.  рангли суперпозиция учун теоремадаги тасдик тугри булсин. Унинг  рангли суперпозиция учун хам тугрилигини исботлаймиз.

,    булсин.

;

функцияларнинг монотон эканлигини исботлаш лозим. Бу ерда  ва  лар  узгарувчиларнинг бирортаси билан мос келиши мумкин. j функциянинг монотонлигидан  нинг монотон функция эканлиги келиб чикади. F функциянинг монотонлигини исботлаймиз. Бунинг учун F функциянинг иккита g^¢ ва g^¢¢ таккосланадиган кийматлар сатрини куриб чикамиз:

g^¢=(

g^¢¢=(

 булсин. У вактда  эканлигини курсатишимиз керак. Куйидагилар маълум:

, бу ерда  булганда

, бу ерда  булганда 

y монотон функция ва  дан  келиб чикканлигидан  булади. Яъни , чунки j монотон функциядир.

эканлигидан  рангли суперпозиция учун теорема исбот булди.

            Демак, монотон функцияларнингсуперпозициясидан хосил килинган функция яна монотон функциядир.          

            Конъюнкция ва дизъюнкциялар монотон функция булганлиги учун, теоремага асосан, уларнинг суперпозициясидан хосил этилган функция хам монотон булади.

            2-теорема. Агар  булса, у холда ундан аргументлари урнига 0, 1 ва х функцияни куйиш усули билан  функцияни хосил килиш мумкин.

 

РЕЖА:

 

            1.Формуланинг чинлик туплами.

            2.Мулохазалар алгебраси функциялари. Функ-

           циялар тенгкучлилиги. Функциялар суперпо-     

           зицияси.

            3.Буль алгебраси.

 

Муаммоли масала ва топшириклар:

 

1. Мулохазалар алгебрасининг асосий элементар функцияларига иккитарафлама булган функцияларни топинг.

2. Хамма икки аргументли уз-узига иккитараф-лама булган функцияларни топинг.

3.  аргументли уз-узига иккитарафлама булган функцияларнинг сонини топинг.

4.  ва  функцияларга иккитарафлама булган функцияларни топинг.

5. а) ; б) ; в)   формулаларни Жегалкин купхади куринишига келтиринг.

 

6. Функциянинг  Жегалкин купхади куринишидаги ифодаси ягона эканлигини исботланг.

7. Чизикли функцияларнинг кайси бирлари уз-узига иккитарафлама функция булади?

8.  эканлигини исбот этинг.

9. Куйидаги формулаларни Жегалкин купхади куринишига келтиринг:

      ;    ;    .

10. Жегалкин купхади куринишидаги функциянинг хамма аргументлари сохта аргументлар эмаслигини исботланг.

11. Чизикли функцияларнинг кайси бирлари монотон функциялар булади?

12. Ноль (бир) сакловчи монотон функциялар айнан бирга (нолга) тенг эканлигини исботланг.

13. Икки аргументли хамма монотон функцияларни топинг.

14. Куйида келтирилган функцияларнинг кайси бирлари монотон функция эканлигини аникланг:

      а) ; б) ; в) ;  

      г) ;   д) ;   е) .

15. Айнан константадан (0 ёки 1) фарк килувчи функция монотон булиши учун уни конъюнкция ва дизъюнкциялар суперпозицияси оркали ифодалаш етарли ва зарурлигини исботланг.

16. Монотон функцияга иккитарафлама булган функция монотон эканлигини исбот килинг.

17. Факат ва факат ёки константалар, ёки узгарувчилар устида инкор амали булмаган КНШ ва ДНШ куринишида ифода этилган функциялар монотон булишлигини курсатинг.

 

Мустакил ишлаш учун саволлар:

 

            1.Иккитарафлама функция ва уз-узига иккитарафлама функция таърифларини келтиринг.

            2.Мантик алгебрасидаги иккитарафлама конунни  ёзинг.

            3.Мантик алгебрасидаги арифметик амаллар.  Жегалкин купхади.

            4.Мантик алгебрасидаги монотон функциялар.

 

 

17-§. Функционал ёпик синфлар ва Пост теоремаси

 

Тулик функциялар системаси. -Иккитарафлама функциялар системасининг тулик булиш шарти. -Ёпик синфлар. -Хусусий функционал ёпик синф. -Максимал функционал ёпик синф. -Пост теоремаси. -Натижа. -Туплам ёпиги.

-Пост жадвали.

 

            Мантик алгебрасининг  функциялар системаси берилган булсин.

            1-таъриф. Агар мантик алгебрасининг исталган функциясини  системадаги функциялар суперпозицияси оркали ифодалаш мумкин булса, у холда Ф га тулик функциялар системаси деб айтилади.

            Исталган функцияни МКНШ ёки МДНШ куринишида ифодалаш мумкинлигидан  функциялар системасининг туликлиги келиб чикади.  функциялар системаси хам тулик булади, чунки исталган функцияни Жегалкин купхади куринишига келтириш мумкин.

            Куйидаги функциялар системасининг туликлигини исботланг:

а) ;      б) ;      в) ;

    г) ;      д) ;            и) ;

         ж) ;     з) ;    е) .

            Исбот. а). =, яъни дизъюнкция амалини конъюнкция ва инкор амаллари оркали ифодалаш мумкин. Демак, {,} функциялар системаси тулик булади.

            б).== эканлиги маълум. Демак, исталган мантикий функцияни дизъюнкция ва инкор амаллари оркали ифодаласа булади. Шунинг учун {} функциялар системаси туликдир.

            в). Ихтиёрий мантик алгебрасининг функциясини ягона Жегалкин купхади куринишига келтириш мумкинлигидан {} функциялар системасининг туликлиги келиб чикади.

г) ва д). Мантик алгебрасидаги исталган функцияни  ва  Шеффер функциялари оркали ифодалаш мумкин. Хакикатан хам,  

         

ва

        ,

асосий мантикий амалларни Шеффер функцияси оркали ифодалаш мумкин. Демак, {} ва {} функциялар системаси тулик булади.

            и).  булганлиги учун булади. {} тулик система эканлиги в) пунктида исбот килинган эди, демак, {} cистема туликдир.

            Худди шундай бошка функциялар системасининг туликли-гини исбот килиш мумкин.

            1-теорема. Агар  функциялар системаси тулик булса, у холда унга иккитарафлама булган  функциялар системаси хам тулик булади.

            Исбот.  системанинг туликлигини исботлаш учун исталган  функцияни  системасидаги функциялар суперпозицияси оркали ифодалаш мумкинлигини курсатишимиз керак. Бунинг учун аввал  функцияни  cистемасидаги функциялар оркали ифодалаймиз ( система тулик булганлиги учун бу процедурани бажариш мумкин). Кейин иккитарафлама конунга асосан иккитарафлама функциялар суперпозицияси оркали  функцияни хосил киламиз.

            Мисол. Куйидаги функциялар системасининг тулик эмаслигини исботлайлик:

            а) , ;                б) ;         в) ;

            г) ;        д) .

            а).  га тенг. Демак, {} системасидаги функциялар бир аргументли функциялар булади. Бизга маълумки, бир аргументли функцияларнинг суперпозицияси натижасида хосил килинган функция яна бир аргументли функция булади. Натижада, бу системадаги функциялар оркали куп аргументли функцияларни ифодалаб булмайди. Шунинг учун {} тулик система эмас.

            б). {} системасидаги функцияларнинг иккаласи хам монотондир. Монотон функцияларнинг суперпозицияси оркали хосил килинган функция яна монотон булишини исбот килган эдик. Демак, бу иккала функциянинг суперпозицияси оркали монотон булмаган функцияларни ифодалаш мумкин эмас ва натижада, {} система туликмас система булади.

            в). {} cистемасидаги функциялар чизикли функциялардир. Шунинг учун бу функциялар оркали чизиклимас функцияларни ифодалаб булмайди. Демак, {} функциялар системаси тулик эмас.

            г). {} системасидаги функциялар уз-узига иккитарафлама функциялардир. Бу функцияларнинг суперпозициясидан хосил килинган хар кандай функция хам уз-узига иккитарафлама функция булади.

            Демак, {}  функциялар системаси тулик эмас.

            д). {} системадаги функцияларнинг хаммаси монотон функциялар булади. Монотон эмас функциялар бу системадаги функциялар оркали ифодаланмайди. Демак, {} система тулик эмас.

            Шундай килиб, юкорида келтирилган масала ечимининг анализидан куйидаги хулоса келиб чикади.

            Берилган  функциялар системасининг тулик эмаслигини исботлаш учун системадаги функцияларнинг шундай умумий хусусиятини топиш керакки, бу хусусият функциялар суперпозицияси натижасида саклансин.

            Хакикатан хам, у вактда бундай хусусиятга эга булмаган функцияни  системадаги функциялар суперпозицияси оркали хосил килиб булмайди.

            Функцияларнинг бу маълум хусусиятларини текшириш учун одатда функционал ёпик синфлар тушунчасидан фойдаланадилар.

            2-таъриф. Агар  сиcтемадаги функциялар суперпозициясидан хосил булган функция яна шу системанинг элементи булса, у холда бундай системага суперпозицияга нисбатан ёпик система деб айтилади.

            3-таъриф. Суперпозицияга нисбатан ёпик булган хар кандай мантик алгебрасининг функциялар системасига функционал ёпик синф деб айтилади.

            Равшанки, маълум бир хил хусусиятга эга булган функциялар системаси функционал ёпик синфни ташкил этади ва, аксинча, маълум функционал ёпик синфга кирувчи функциялар бир хил хусусиятга эга булган функциялардир. Куйидаги функциялар системаси функционал ёпик синфларга мисол була олади:

            а) бир аргументли функциялар;

            б) хамма мантик алгебрасининг функциялари;

            в)  - чизикли функциялар;

            г)  - уз-узига иккитарафлама функциялар;

            д)  - монотон функциялар;

            е)  - нуль кийматни сакловчи функциялар;

            ж)  - бир кийматни сакловчи функциялар.

            4-таъриф. Буш синфдан ва мантик алгебрасининг хамма функциялари тупламидан фарк килувчи функционал ёпик синфга хусусий функционал ёпик синф деб айтилади.

            Шундай килиб, функциялар системасининг туликлиги учун бу системада хар кандай хусусий функционал ёпик синфга кирмовчи функция топилиши етарли ва зарурдир.

            5-таъриф. Уз-узидан ва мантик алгебрасининг хамма функциялари синфи  дан фарк килувчи функционал ёпик синфларга кирмовчи хусусий функционал ёпик синфга максимал функционал ёпик синф деб айтилади.

            Мантик алгебрасида хаммаси булиб бешта максимал функционал ёпик синф мавжуд:

             - ноль сакловчи функциялар синфи,  - бир сакловчи функциялар синфи,  - уз-узига иккитарафлама функциялар синфи,  - чизикли функциялар синфи.

            Пост теоремаси.  функциялар системасининг туликлиги учун бу системада , , , ,  максимал функционал ёпик синфларнинг хар бирига кирмовчи камида битта функция мавжуд булиши етарли ва зарур (яъни  шунда ва факат шундагина тулик система буладики, качонки у , , , ,  максимал функционал ёпик синфларнинг  бирортасининг хам кисм туплами булмаса).

            Исбот.  тулик система булсин, яъни . Фараз киламизки,  максимал функционал ёпик синфларнинг бирортаси. У вактда  нинг ёпиклигини хисобга олиб,  ни ёзиш мумкин, яъни . Аммо бундай булиши мумкин эмас. Демак,  муносабат бажарилмайди.

            Теореманинг етарлилигининг исботини укувчиларга хавола этамиз.

            Натижа. Мантик алгебрасидаги хар кандай функционал ёпик синф , , , ,  максимал функционал ёпик синфларнинг бирортасининг кисм туплами булади.

            Амалда бирорта  системанинг тулик ёки тулик эмаслигини аниклаш учун Пост жадвалидан фойдаланадилар. Пост жадвали куйидаги куринишда булади:

 

...	...	...	...	...	...

            Жадвалнинг хоналарига уша сатрдаги функция функционал ёпик синфларнинг элементи булса “+” ишора, булмаса “-” ишораси куйилади.

             система тулик функциялар системаси булиши учун, теоремага асосан, жадвалнинг хар бир устунида камида битта “-” ишораси булиши етарли ва зарур.

             функциялар системаси тулик булмаслиги учун , , , ,  максимал функционал ёпик синфларнинг бирортасининг кисм туплами булиши, яъни Пост жадвалининг бирор устуни тулик “+” ишораларидан иборат булиши керак.

            Функциялар системасининг туликлиги тушунчаси билан синфнинг (тупламнинг) ёпиги тушунчаси узаро богланган.

            6-таъриф.  билан  (n аргументли мантик алгебрасининг хамма функцияларини уз ичига олган) тупламнинг бирор кисм тупламини белгилаймиз.  туплам функцияларнинг суперпозициясидан хосил этилган хамма буль функциялари туплами ( туплам функциялари оркали ифодаланган хамма буль функциялари туплам)га  тупламнинг ёпиги деб айтилади ва [] каби белгиланади.

      Мисол. 1. =булсин, у холда []= .

            2. ={} булсин, у вактда  тупламнинг ёпиги хамма  - чизикли функциялар тупламидан иборат булади.

            Туплам ёпиги куйидаги хоссаларга эга:

            1. [] Ê ;

            2. [[]] = [];

            3. агар ₁ Í ₂ булса, у холда [₁] Í [₂] булади;

            4. [_{1  2}] Ê [₁]  [₂].

            7-таъриф. Агар []= булса, у холда  туплам (синф)га функционал  ёпик синф деб айтилади.

            Мисол. 1. = синфи ёпик синф булади.

                      2. ={} cинфи ёпик синф булмайди.

                      3.  - синфи ёпик синф булади.       

            Осонгина куриш мумкинки, хар кандай [] синф ёпик синф булади. Бу хол купгина функционал ёпик синфларни топишга ёрдам беради.

            Туплам ёпиги ва ёпик синф тилида функциялар системасининг туликлиги хакидаги таъриф (аввалги таърифга эквивалент булган таъриф) ни бериш мумкин.

            8-таъриф. Агар []=  булса, у холда  функция-лар системаси тулик деб айтилади.

            Мисол. Куйидаги функциялар системаларининг тулик эмаслигини Пост жадвали оркали исбот килайлик:

            а) ;    б) ;

        в) ;   г) ;

                       д)

 

 

            Жадвалдан куриниб турибдики, юкорида келтирилган хамма функциялар системаси тулик эмас, чунки хар бир система учун жадвалда битта устун факатгина “+” ишораларидан иборат. Шуни таъкидлашимиз керакки, хар бир система учун бу устунлар хар хил. Демак, Пост теоремаси шартидан , , , ,  максимал функционал ёпик синфларнинг бирортасини хам олиб ташлаш мумкин эмас. Бу хулосадан уз навбатида , , , ,  максимал функционал ёпик синфларнинг бирортаси иккинчисининг кисм туплами була олмаслиги келиб чикади.

 

РЕЖА:

 

            1.Функционал ёпик синфлар ва Пост теоремаси.

 

Муаммоли масала ва топшириклар:

 

1. Куйидаги функциялар системаси функционал ёпик синфлар булишини исбот килинг:

            а) бир аргументли функциялар;

            б) хамма мантик алгебрасининг функциялари;

            в)  - чизикли функциялар;

            г)  - уз-узига иккитарафлама функциялар;

            д)  - монотон функциялар;

            е)  - нуль кийматни сакловчи функциялар;

ж)  - бир кийматни сакловчи функциялар.

2. Агар  ва  функционал ёпик синфлар булса, у холда  ва  лар хам функционал ёпик синфлар ва  ни функционал ёпик синф булмаслигини исботланг.

3. Куйидаги максимал функционал ёпик  синфларнинг бирортаси иккинчисининг кисм туплами булмаслигини исботланг.

4. Хар кандай шахсий функционал ёпик синф  максимал функционал ёпик синфларнинг бирортасининг кисм туплами эканлигини исботланг.

5. Ноль сакламовчи функция ёки номонотон функция, ёки ¢з-¢зига иккитарафлама б¢лмаган функция эканлигини исботланг.

 

Мустакил ишлаш учун саволлар:

 

            1.Тулик функциялар системаси.

            2.Функционал ёпик синфлар ва хусусий функционал ёпик синфлар.

            3.Максимал функционал ёпик синф ва Пост теоремаси.

            4.Туплам ёпиги ва Пост жадвали.