УЗБЕКИСТОН РЕСПУБЛИКАСИ ОЛИЙ ВА УРТА МАХСУС ТАЪЛИМ ВАЗИРЛИГИ

АЛИШЕР НАВОИЙ НОМИДАГИ САМАРКАНД ДАВЛАТ УНИВЕРСИТЕТИ

ХОТАМ ТУРАЕВ

МАТЕМАТИК МАНТИК ВА

ДИСКРЕТ МАТЕМАТИКА

Узбекистон Республикаси олий ва урта махсус таълим вазирлиги олий укув юртларининг талабалари учун укув куллан-маси сифатида тавсия этган

Т О Ш К Е Н Т – 2004

Тураев Х.Т. Математик мантик ва дискрет математика: Укув кулланмаси.-Тошкент: Укитувчи нашриёти. 2004. -498 бет.

Китобда тупламлар хакида асосий тушунчалар, муносабатлар, мулохазалар алгебраси, мулохазалар хисоби, предикатлар мантики, математик назариялар, алгоритмлар, математик мантикнинг техникага татбики, математик мантик функцияларини минималлаштириш муаммоси, графлар назариясининг элементлари, турлар ва турдаги окимлар баён килинади.

Мазкур укув кулланмаси олий укув юртларининг математика, амалий математика ва информатика, математика ва информатика, информатика ва информацион технологиялар бакалавриатура йуналишлари буйича таълим олаётган талабаларга мулжалланган.

Китобдан магистрантлар, аспирантлар хамда радиотехника, электротехника ва амалий математика сохаларида ишлаётган мухандис-математиклар ва мутахассислар хам фойдаланишлари мумкин.

Масъул мухаррир- доцент А.М.Мусаев

Такризчилар- УзМУ кафедраси мудири,УзР ФА академиги, профессор Н.Ю. Сатимов, УзМУ профессори А.Пулатов, УзМУ доценти Р. Гуломов, СамДУ кафедраси мудири, профессор А.С.Солеев, СамДУ доценти Г.Э.Эргашев

2004

Ó Тураев Хотам Тураевич

Ó Самарканд давлат университети

Узбекистон Республикаси Мустакиллигининг 13 йиллигига багишланади

СУЗ БОШИ

Дискрет математика - математиканинг бир кисми булиб, мелоддан аввал IV асрда яратила бошланган. Дискрет математика математиканинг такомиллашган сонлар назарияси, алгебра, математик мантик кисмларидан ташкари XX аср урталаридаги илмий-техник тараккиёти туфайли интенсив ривожланаётган функционал системалар назарияси, граф ва турлар назарияси, кодлаштириш назарияси, комбинатор анализ каби булимларни хам уз ичига олади.

Дастлаб факат математик мантик, алгебра, математик анализ, математика асослари, эхтимоллар назарияси, геометрия, топология, сонлар назарияси, моделлар назарияси каби математик фанларда татбик этиб келинган дискрет математика XX асрнинг 40-йилларидан бошлаб хисоблаш математикаси, кибернетика, ахборот назарияси, иктисодиёт, психология, математик лингвистика, тиббиёт фанлари ва дискрет техникада кенг кулланилмокда. Дискрет математика кенг микёсда электр схемаларни лойихалашда ва текширишда, автоматик хисоблаш машиналарини лойихалаш ва программалашда, дискрет автоматларни мантикий лойихалашда, ЭХМ элементлари ва кисмларини лойихалашда, хар хил техник системалар, курилмалар ва автоматик машиналарни анализ ва синтез килишда татбик этилади. Математик мантик фани электрон хисоблаш машиналарининг вужудга келишига ва уни мукаммалаштиришга катта хисса кушди.

Дискрет математика нафакат математик кибернетиканинг фундаменти хисобланади, балки хозирги замон математик таълимнинг мухим бугини хисобланади.

Китобнинг асоси сифатида муаллиф томонидан 1973 йилдан бери Самарканд давлат университети амалий математика ва информатика факультети талабаларига узлуксиз укилаётган маърузалар олинган. Унинг структураси ва мазмунига факультет базасида “Дискрет математика ва унинг татбиклари” мавзусида утказилган Халкаро ва Бутуниттифок илмий анжуманлар, Москва давлат университетининг «Дискрет математика» кафедраси билан укув-услубий сохалардаги хамкорлик хамда факультет талабаларига дискрет математика фанининг етук олимлари А.Дородницын, Ю.Журавлёв, М.Комилов, В.Кудрявцев, А.Зыков ва В.Кобуловлар томонидан укилган маърузаларнинг хам ижобий таъсири бор.

Китоб дискрет математиканинг ривожланиш тарихи (кириш) ва 9 бобдан иборат.

Кулланманинг биринчи бобида тупламлар назариясининг элементлари, муносабатлар, бинар муносабати, функциялар суперпозицияси, тартиблаш муносабати ва панжара хакида тушунчалар берилади.

Иккинчи боби мулохазалар алгебрасига багишланган булиб, унда мулохазалар ва улар устида мантикий амаллар, формулалар, тенгкучли, айнан чин, айнан ёлгон ва бажарилувчи формулалар, тенгкучли формулаларга доир теоремалар, формулаларнинг нормал шакллари, мукаммал дизъюнктив ва конъюнктив нормал шакллар, мулохазалар алгебраси функциялари, Буль алгебраси, мантик алгебрасидаги иккитарафлама конун ва арифметик амаллар, Жегалкин купхади, монотон функциялар, функционал ёпик синфлар ва Пост теоремаси каби масалалар куриб чикилади.

Китобнинг учинчи боби мулохазалар хисобига багишланган булиб, унда мулохазалар хисоби формуласи тушунчаси, исботланувчи формула таърифи, мулохазалар хисобининг аксиомалар системаси (тизими), келтириб чикариш коидалари, келтириб чикариш коидасининг хосилалари булган бир вактда урнига куйиш, мураккаб хулоса, силлогизм, контрпозиция, икки карра инкорни тушириш коидалари, формулалар мажмуасидан формулани келтириб чикариш коидаси, келтириб чикарилган формула (исботлаш) тушунчаси, дедукция ва умумлашган дедукция теоремалари, айрим мантик (асосларни урин алмаштириш, асосларни кушиш, асосларни ажратиш) конунларининг исботи, мулохазалар алгебраси ва мулохазалар хисоби уртасидаги муносабатлар, мулохазалар хисобида ечилиш, зидсизлик, туликлилик ва эркинлик муаммолари каби масалалар куриб чикилади.

Туртинчи бобда предикатлар мантики баён этилган. Бу ерда предикат тушунчаси, предикатлар устида мантикий амаллар, умумийлик ва мавжудлик кванторлари, предикатлар мантикининг формуласи ва унинг киймати, предикатлар мантикининг тенгкучли формулалари, предикатлар мантики формуласининг нормал шакли, бажарилувчи ва умумкийматли формулалар, ечилиш муаммоси, хусусий холларда формуланинг умумкийматлилигини топиш алгоритмлари, предикатлар мантикининг математикага тадбики, аксиоматик предикатлар хисоби хакида маълумотлар келтирилади.

Китобнинг бешинчи боби математик назарияларга багишланган булиб, аксиоматик назария тушунчаси, биринчи тартибли тил, терма ва формулалар, мантикий ва хос (махсус) аксиомалар, келтириб чикариш коидаси, алгебра, геометрия ва анализда мавжуд булган математик назариялар, назарияда исботлаш тушунчаси, тавталогия хусусий холларининг исботланувчанлиги, дедукция теоремаси, назария тилининг интерпретацияси (талкини), берилган интерпретацияда формулаларнинг чинлик кийматлари, назариянинг модели, интерпретациянинг изоморфизмлиги, назариянинг катъийлиги, назариянинг зидсизлик, туликлилик ва ечилиш муаммолари, предикатлар хисобининг зидсизлиги, натурал сонлар назарияси, Гёделнинг туликсизлик хакидаги теоремаси сингари масалалар ёритилган.

Китобнинг олтинчи бобида алгоритмлар назариясининг элементлари атрофлича баён этилган. Бу ерда алгоритм тушунчаси ва унинг характерли хусусиятлари, ечилувчи ва саналувчи тупламлар, Пост теоремаси, алгоритм тушунчасини аниклаш, хисобланувчи функциялар, кисмий рекурсив ва умумрекурсив функциялар, А.Чёрч ва С.Клини тезислари, Тьюринг ташиналари, Тьюринг машинасида алгоритмни реализация килиш, натурал сонларни кушиш алгоритми, Евклид алгоритми, алгоритмлар назариясининг асосий гипотезаси, Марковнинг нормал алгоритмлари, Марков буйича кисман хисобланувчи ва хисобланувчи функциялар, кисмий рекурсив (умумрекурсив) функция билан Марков буйича кисмий хисобланувчи (хисобланувчи) функция уртасидаги муносабат, нормаллаштириш принципи, алгоритмик ечилмовчи муаммолар, математик мантикда келтириб чикарувчанликни таниш муаммоси, уз-узига тадбик этувчанликни таниш муаммоси, каби масаллар курилган.

Китобнинг еттинчи бобида математик мантикнинг техникага тадбиклари келтирилган. Бу ерда реле-контактли схемалар, контактли схемалар ва уларнинг синтези, функционал элементлар ва улардан схемалар ясаш, куптактли схемалар, функционал элементлар системасининг туликлиги, схемаларни минималлаштириш муаммоси, тескари богланиши булмаган автоматлар, чекли автомат хакида умумий тушунчалар, Мили ва Мур автоматлари каби масалалар куриб чикилган. Мантик алгебраси функцияларини схемалар (автоматлар) оркали реализация этиш масаласига алохида ахамият берилган.

Саккизинчи бобда математик мантик функцияларини минималлаштириш муаммоси баён этилган. Бу ерда дизъюнктив нормал шакл (ДНШ)ни соддалаштириш, энг киска ДНШ, кискартирилган ДНШ, тупикли ДНШ, Квайн ДНШ ва минимал ДНШларни ясаш алгоритмлари келтирилган. Аналитик ва геометрик тарздаги алгоритмларнинг эквивалентлиги курсатилган.

Туккизинчи бобда графлар назариясининг элементлари ёритилган. Бу ерда оддий графлар, графларнинг изоморфлиги, маршрутлар, занжирлар, цикллар, богликлилик, дарахтлар, хроматик сон ва хроматик синф, турлар ва турдаги окимлар, Форд-Фалкерсон теоремаси каби масалалар караб чикилган.

Назарий масалаларни баён этишда мисоллардан кенг фойдаланилган, деярли хар бир параграфнинг охирида мустакил ишлаш учун машклар берилган.

Китобда ёритилган масалалар «Математик мантик ва дискрет математика» ва «Математик мантик ва алгоритмлар назарияси» фанларидан ташкари давлат таълим стандартларида курсатилган «Машиналар арифметикаси ва автоматлар назарияси», «Информатика асослари ва хисоблаш техникаси», «ЭХМ ва дастурлаш», «Операцияларни текшириш» каби фанларни укитишда хам мухим ахамият касб этади.

Китобни тайёрлашда америкалик С.Клини ва А.Чёрч, австриялик К.Гёдел, англиялик А.Тьюринг ва Э.Мендельсон хамда россиялик А.А.Марков, А.И.Мальцев, П.С.Новиков, С.В.Яблонский, О.Б.Лупанов, В.Б.Кудрявцев, В.А.Горбатов, С.Г.Гиндикин, А.А.Зыков, Л.Лихтарников ва Т.Сукачёва, узбекистонлик Р.Искандаров, Т.Ёкубов каби математиклар томонидан яратилган монография, дарслик, укув кулланма ва илмий маколалари ва самаркандлик М.Исроиловнинг мулохазалар алгебрасига багишланган кулёзмасидан фойдаланилди.

Олий укув юртлари математика факультетлари талабалари учун узбек тилида ёзилган дастлабки китоблар мархум устозимиз Р.И.Искандаровнинг “Математик логика элементлари” (1970) номли дарслиги ва Т.Ёкубовнинг “Математик логика элементлари” (1983) укув кулланмасидир. Бу китоблар математик мантик фанини укитишда, табиийки, ижобий рол уйнади.

Укувчиларга тавсия этилаётган ушбу китоб “Математик мантик ва дискрет математика” хамда «Математик мантик ва алгоритмлар назарияси» фанлари буйича Рес-

публикамиз давлат таълим стандартларида [61-64] курсатилган укув дастурларига тулик жавоб беради.

Китоб университет ва педагогика институтларида 5460100-математика, 5480100-амалий математика ва информатика, 5140100-математика ва информатика, 5521900-информатика ва информацион технологиялар бакалаврлик йуналишлари хамда 5А460104, 5А480101 ва 5А480107 магистратура мутахассисликлари буйича таълим олаётган талабаларга мулжалланган. Китоб камчиликлардан холи булмаганлиги туфайли, муаллиф китоб хакидаги танкидий фикр ва мулохазаларни миннатдорчилик билан кабул килади ва олдиндан уз ташаккурини изхор этади.

Китобнинг кулёзмаси билан муфассал танишиб, унинг сифатини яхшилаш йулида фойдали курсатма ва маслахатлар берган такризчилар УзР ФА академиги Н.Сатимов, профессорлар А.С.Солеев, А.Пулатов, доцентлар Р.Гуломов ва Г.Эргашевларга, мухаррирлик ишини бажарган доцент А.М.Мусаевга хамда китоб матнини компьютерга киритган ва макетини тузиб нашр этишга тайёрлаган Х.Якубова ва Ф.Муродовларга уз миннатдорчи-лигимни билдираман.

Муаллиф.

КИРИШ

Мантик – мухокама юритишнинг конун-коидалари, усуллари ва формалари хакидаги фан булиб, унинг асосчиси кадимги юнон мутафаккири Аристотель (384-322 й. милоддан аввал) хисобланади. У биринчи булиб дедукция назариясини, яъни мантикий хулоса чикариш назариясини яратиб, мантикий хулоса чикаришнинг формал характерга эга эканлигини курсатди. Аристотельнинг мантикий таълимоти формал мантикнинг (логиканинг) асосини ташкил килади. Формал мантик фикрлашнинг формалари ва конунларини текширади. Шундай килиб, Аристотель мантикий фикрлашнинг асосий конунларини очди.

Аристотель асос солган мантик куп асрлар давомида турли мутафаккирлар, файласуфлар ва бутун фалсафий мактаблар томонидан тулдирилди, узгартирилди ва такомиллаштирилди. Шу жумладан, Абу Наср Фаробий, Абу Али Ибн Сино, Абу Райхон Беруний, Мухаммад ал-Хоразмий, Умар Хайём, Алишер Навоий, Мирзо Бедил каби ватанимиз ва Шаркнинг буюк мутафаккирлари хам узларининг катта хиссаларини кушдилар.

Мантикнинг янгиланишида француз олими Р.Декартнинг (1596-1650) ишлари мухим роль уйнади. Р.Декарт аналитик усулда фикрлашнинг асосий принципларини яратди.

Немис философи ва математиги Г.Лейбниц (1646-1716) биринчи булиб мантикий фикрлашга хисоб характерини бериш зарур деган гоя билан чикди. Бунинг учун, унинг фикрича, хамма илмий тушунчалар ва мулохазаларни асосий мантикий элементларга келтириб, уларни маълум символлар билан белгилаш керак.

Г.Лейбниц гоялари факатгина XIX асрдагина уз ривожини топди. Инглиз олимлари Ж.Буль (1815-1864), Ч.Пирс (1839-1914), Б.Рассел (1872-1970), А.Уайтхед (1861-1947), У.Жевонс (1835-1882), немис олимлари Г.Фрёге (1848-1925), Д.Гильберт (1862-1943), Э.Шрёдер (1853-1910), шотландиялик математик О. де Морган (1806-1871), рус олимлари П.С.Порецкий (1846-1907), В.И.Гливенко (1897-1940), И.И.Жегалкин (1869-1947) ва бошкалар мантик сохасидаги ишлари билан символик ёки математик мантикни (логикани) яратдилар.

Математик мантик асосчиларидан бири булган Ж.Буль (Ж.Буль машхур «Суна» романининг муаллифи Лилиан Войничнинг отасидир) мустакил равишда грек, лотин, немис, француз ва итальян тилларини хамда математикани урганади. 1847 йилда ёзилган «Мантикни математик тахлили», «Мантикий хисоб» ва 1854 йилда ёзган «Фикрлаш конунларини тадкик этиш» китобларида мантикни алгебраик формага келтирди ва математик мантикнинг аксиомалар системасини яратди. Бульнинг мантикий хисоби буль алгебраси деб юритилади.

Ж.Буль мантик ва математика операциялари уртасидаги ухшашликка асосланиб мантикий хулосалаларга алгебраик символикани куллади. У мантик операцияларини формаллаштириш (расмийлаштириш) учун куйидагилар

-предметларни белгилаш учун (x,y,z...) кичик лотин харфларини;

-предметлар сифатини белгилаш учун (X,Y,Z...) катта лотин харфларини;

-кандайдир мулохазага акслантирилган хамма предметлар синфи-1 ни;

-курилиши лозим булган предметлар йуклигининг белгиси 0 ни;

-мулохазаларни мантикий кушишнинг “+” белгисини;

-мулохазаларни мантикий айиришнинг “-” белгисини;

-мулохазалар тенглигининг “=” белгисини киритди.

Символик буль алгебрасида мантикий купайтириш амали, худди алгебраик кийматларни купайтиргандай коммутативлик

xy = yx

ва ассоциативлик

x(yz) = (xy)z

хоссаларига эга. Мантикий кушиш амали хам коммутативлик ва ассоциативлик хоссаларига эга.

x + y = y + x

(x + y) + z = x + (y + z)

Буль алгебрасида йигинди купайтмага нисбатан дистрибутивлик конунига буйсунади

x (y + z) = xy + xz.

Ж.Буль алгебраик символикалар ёрдами билан хамма мантикий операцияларни икки кийматли (1 ва 0) алгебра конунларига буйсунадиган формал (расмий) операцияларга келтиришни уйлади. Буль функциялари ва унинг аргументлари факат икки киймат – «чин» ва «ёлгон» кийматлар кабул килади.

Мантик алгебраси коидалари оркали оддий мулохазалардан мураккаб мулохазаларни хосил этиш мумкин.

Масалан:

хy – бир вактда х ва у хоссаларга эга булган предметлар класси;

х(1-у) – х хоссага эга ва у хоссага эга булмаган предметлар класси;

(1-х)у – у хоссага эга ва х хоссага эга булмаган предметлар класси;

(1-х)(1-у) – х ва у хоссаларга эга булмаган предметлар класси.

Хозирги математик мантик фанини яратишда фундаментал роль уйнаган Буль символик мантикни мукаммаллаштиришга мухтож эди. Масалан, Жевонс фикрича мантикий айириш операциясини айрим нокулайликка олиб келади.

О. де Морган Буль гояларини ривожлантириб, мантик хисобини эхтимоллар назарияси теоремаларини асослашга татбик этди ва символик хисобни яратиш устида ишлади.

Ч.Пирс математикани анализ килишда мантикий муносабатларни курол сифатида ишлатишни асослаб берди. Г.Фрёге ишларидан хабарсиз холда, мантикка квантор тушунчасини киритди.

Г.Фрёге математика принципларини мантик принципларидан келтириб чикариш устида ишлаб, мантик хисобини яратди.

Буль ва О. де Морган асарларида математик мантик узига хос алгебра – мантик алгебраси куринишида шаклланди.

Кейинчалик Буль методлари инглиз олими У.Жевонс, немис математиги Э.Шрёдер (1853-1901) ва рус олими П.С.Порецкий (1846-1907) асарларида уз ривожини топди.

Буль алгебрасини У.Жевонс ва Э.Шрёдерлар мукаммаллаштирдилар. У.Жевонс «Тоза мантик» (1864), «Ухшашларни алмаштириш» (1869) ва «Фан асоси» (1874) китобларида мантик сохасида алмаштириш принципига асосланган узининг назариясини тавсия этди. 1877 йили Э.Шрёдер «Der operationskreis des Logikkalkuls» китобида алгебраик мантик асосларини ёритди.

Математик мантик фанининг ривожланишига рус олими П.С.Порецкийнинг хам катта хизмати бор. Буль, Жевонс ва Шрёдерлар ютукларини умумлаштириб, «Мантикий тенгламаларни ечиш усуллари ва математик мантикнинг тескари усули хакида» (1884) китобида мантик алгебраси аппарати ривожини анча илгари сурди. Америкалик олим А.Блейк П.С.Порецкий методини Э.Шрёдер методидан устун куяди.

П.С.Порецкий системасида куйидаги белгилар кабул килинган:

1) бир-бирига боглик булмаган ва бир-бири билан хеч кандай муносабатда булмаган предметлар классини майда лотин харлфлари a,b,c билан белгилаш;

2) синфларни инкор этиш учун майда лотин харфларидан кейин «эмас» сузини кушиш, яъни а эмас, b эмас ва хоказо каби белгилаш;

3) a,b,c... предметлар синфи хусусиятига эга булмаган предметлар синфини a₁, b₁, c₁... билан;

4) икки ёки купрок синфлар биргаликда бир нечта бир-бирига боглик булмаган хоссаларга эга булишини ab, bc ва хоказо купайтмалар билан белгилаш; Бу операция коммутативлик ва ассоциативлик хоссаларига эга:

ab = ba, (ab) c = a (bc);

5) мантикий кушиш амалини (+) белги билан бегилаш; Бу операция хам коммутативлик ва ассоциативлик хоссаларига эга:

x + y = y + x, x + (y + z) = (x + y) z

6) хеч кандай мазмунга эга булмаган сифат формасини 0 (мантикий 0) билан белгилаш;

7) мумкин булган синфларни уз ичига олган сифат формасини 1 (мантикий 1) билан белгилаш; 0 билан 1 ушбу хоссаларга эга:

а + 0 = а;

а × 1 = а.

8) а синфнинг инкорини а₁ синф билан белгилаш;

9) кушиш, купайтириш ва инкор амалларидан ташкари эквивалентлик амалини киритади ва уни «=» символ билан белгилайди. Бу амал учта коидага буйсунади: 1) агар а=b тенглигига бир хил синфларни кушсак, у холда тенглик бузилмайди, яъни а+с=b+с булади; 2) агар, a=b булса, у холда ad=bd булади; 3) агар, a=b булса, у холда a₁=b₁ булади. Бу ерда a₁=a эмас, b₁=b эмас.

19-асрнинг охирида математик назариялар шундай ривожландики, энди мантик масалалари математиканинг узида хам мухим ахамиятга эга булиб, мавжуд мантикий куроллар математика талабларига жавоб беролмай колди. Айрим математик муаммоларни ечишдаги кийинчиликлар уларнинг мантикий табиатига богликлиги аникланди. Шунинг учун хам математик мантик тор алгебраик доирадан чикиб, жадал равишда ривожлана бошлади. Бу йуналишда биринчи булиб немис математиги Г.Фрёге ва итальян математиги Ж.Пеано (1858-1932) тадкикотлар олиб бордилар, улар математик мантикни арифметика ва тупламлар назариясини асослаш учун кулладилар.

Математик мантикнинг кейинги тараккиёти учун инглиз мантик мутахассислари Б.Рассел ва А.Уайтхеднинг уч томлик «Математика принциплари» (1910-1913 й.), буюк немис математиги Д.Гильбертнинг ишлари, хамда австриялик математик К.Гёделнинг тадкикотлари жуда мухим ахамиятга эга булди. Математик мантикнинг ривожланишида Россия математиклари И.И.Жегалкин, В.И.Гливенко, А.Н.Колмагоров, П.С.Новиков, А.А.Марков ва бошкалар узларининг улкан хиссаларини кушдилар.

1903 йили инглиз философи ва мантикчиси Б.Расселнинг Лондонда нашр этилган «Математика принциплари» китобида мулохазалар ва синфлар хисоб назарияси ишлаб чикилди. Б.Рассел А.Уайтхед билан хамкорликда ёзган 3 томлик «Математика принциплари» китоблари математик мантик фанининг ривожланишида катта роль уйнади. Бу китобларда мулохаза, синф ва предикатлар хисоби деярли тулик аксиомалаштирилди ва формаллаштирилди. Улар хозирги вактда урганилаётган математик мантик куринишини яратдилар.

Д.Гильберт ва немис олими В.Аккерман 1928 йилда «Назарий мантикнинг асосий хусусиятлари» китоблари математик мантикнинг янада ривожланишида мухим роль уйнади. Бу китобнинг муаллифлари мантикий амалларда формализация методини татбик этиб катта ютукка эришдилар. Буль, Шрёдер ва Порецкийнинг мантик алгебраларига таяниб, рус олими И.И.Жегалкин (1869-1947) логик кушиш ва логик купайтириш амалларини куйидагича аниклади: 1) 0+0=0; 0+1=1; 1+0=1; 1+1=0; 2) 0×0=0; 0×1=1×0=0; 1×1=1... Логик кушиш ва купайтириш амалидан а+а=0 ва а×а=а келиб чикади.

Мантикий операцияларнинг символик куринишлари Жегалкин системасида куйидагича булади:

; ; ; ;

Символик мантикка умумийлик ва мавжудлик квантори деган тушунчалар киритди ва предикатлар алгебрасини яратди.

ХХ асрнинг 50-йилларида куп кийматли мантик сохасида илмий изланишлар олиб борилди. Куп кийматли мантикда мулохазалар чекли (3 ва ундан куп) ва чексиз чинлик кийматлари олади. Математик мантикнинг бу булимининг асосчиларидан бири польша олими Я.Лукасевич (1878-1954) хисобланади. У дастлаб уч кийматли (1920), 1954 йилда турт кийматли ва нихоят чексиз кийматли мантикни яратди.

Куп кийматли мантик проблемалари билан Е.Пост, С.Яськовский, Д.Вебб, А.Гейтинг, А.Н.Колмогоров, Д.А.Бочвар, В.И.Шестаков, Г.Рейхенбах, С.К.Клини, П.Детуш-Феврие ва бошка олимлар шугулланганлар.

Конструктив математиканинг ривожланиши конструктив мантик масалаларини ечиш усулларини ишлаб чикиш вазифасини куйди. Бу сохада А.А.Марков, Н.А.Шанин ва шогирдларининг хизматлари каттадир.

Дискрет математиканинг катта булимларидан бири алгоритмлар назарияси хисобланади. Алгоритм сузи IX-асрда яшаган замонасининг буюк математиги ватандошимиз Мухаммад бин-Мусо ал Хоразмий исмининг лотинча Algorithmi формасидан келиб чиккан.

Алгоритмлар назарияси - алгоритмларнинг умумий хусусиятларини ургатувчи дискрет математиканинг бир булимидир.

XX асрнинг 20-йилларида биринчи булиб интуиционистлар вакиллари Л.Брауэр ва немис олими Г.Вейлер (1934) алгоритм тушунчасини урганишга киришганлар. Алгоритмлар назариясининг асосчиларидан бири булган америка олими А.Чёрч 1936 йилда хисобланувчи фукция тушунчасига 1-аникликни киритди ва куйидаги тезисни илгари сурди: натурал аргументларнинг барча кийматларида хамма жойда аникланган хисобланувчи функциялар билан умумий рекурсив функциялар эквивалентдир (бир хилдир). У хисобланувчи функция булмаган функцияни курсатди.

Алгоритмлар назариясининг кейинги ривожланишига америкалик олимлар К.Гёдел, С.К.Клини (1957), Э.Л.Пост (1943-1947), Х.Роджерс (1972), инглиз олими А.Тьюринг (1936-1937), рус олимлари А.А.Марков (1947-1954, 1958, 1967), А.Н.Колмогоров (1953, 1958, 1965), Ю.Л.Ершов (1969-1973), А.И.Мальцев (1965,) Д.А.Трахтенброт (1967, 1970-1974), П.С.Новиков (1952), Ю.В.Матиясевич (1970-1972) ларнинг хизматлари бинихоят каттадир.

Масалан, С.Клини алгоритм ёрдамида хисобланувчи кисмий функциялар кисмий рекурсив функциялардир деган гояни илгари сурди.

Инглиз олими А.Тьюринг ва америка олими Э.Пост (1936) идеаллаштирилган хисоблаш машиналари терминида биринчи булиб, бир-биридан бехабар холда, алгоритм тушунчасига аниклик киритдилар. Пост ва Тьюринг алгоритмик процесслар маълум бир тузилишга эга булган “машина” бажарадиган процесслар эканлигини курсатдилар. Улар уша пайтдаги математикада маълум булган барча алгоритмик процессларни бажара оладиган “машина” лар синфини хосил килиб, улар аник математик терминлар ёрдамида таъриф бердилар. Пост ва Тьюринг ушбу машиналар ёрдамида хисобланувчи барча функциялар синфи барча кисмий рекурсив функциялар синфи билан бир хил эканлигини курсатдилар. Натижада, Чёрч тезисининг яна битта фундаментал тасдиги хосил булди.

С.Клини ва Э.Пост биргаликда рекурсивлик назариясини яратдилар ва рекурсив функциялар назариясини тараккий эттирдилапр. Улар кисман рекурсив функциялар тушунчасини киритдилар.

Дастлаб факат математик мантик, алгебра, математик анализ, математика асослари, эхтимоллар назарияси, геометрия, топология сонлар назарияси, моделлар назарияси каби математика фанларида тадбик этиб келинган алгоритмлар назарияси ХХ асрнинг 40-йилларидан бошлаб хисоблаш математикаси, кибернетека, ахборот назарияси, иктисодиёт, психология, математик лингвистика, тиббиёт фанлари ва дискерт техникада кенг кулланилмокда.

Сунгги даврларда математик мантикни техникага жуда самарали татбик этиш имкониятлари борлиги маълум булди.

Математик мантикни дискрет техникага татбики натижасида унинг техник мантик булими вужудга келди. Бу сохада Е.Пост, В.И.Шестаков, К.Шеннон (1916 й.т.), А.Накашима, М.Ханзава, С.Клини, О.Б.Лупанов (1932 й.т.), С.В.Яблонский (1924 й.т.), В.Б.Кудрявцев, Ю.И.Журавлёв, В.И.Левенштейн, В.В.Глаголев, Ф.Я.Ветухновский, Ю.Л.Васильев ва бошка олимлар уз илмий изланишлари билан унинг тараккий этишига улкан хисса кушганлар.

Биринчи булиб математик мантикни техникага куллашни рус физиги П.Эренфест (1910) ва гидротехника курилишлари буйича етук мутахассис Н.М.Герсевановлар амалга оширганлар.

К.Шеннон хисоблаш машиналарини яратишнинг асосий методи сифатида мантик алгебрасини билган, у информация ва информацияни узатишнинг математик назарияларни яратди, электрон тармоклардаги “1” ва “0” бинар муносабатлар билан математик мантикдаги иккилик (1 ва 0) кийматларининг мос келишини ва кандай килиб “мантик машинасини” яратишни курсатди ва хоказо.

Контакли ва реле-контакли схемаларга мантик алгебрасини татбик этишнинг исботини биринчи булиб рус физиги В.И.Шестаков ва америкалик математик К.Шеннонлар бердилар.

А.Накашима ва М.Ханзава математик мантикни дискрет техника масалаларини ечишда куллаш методларини яратдилар.

С.Клини дискрет курилма моделини (чекли автомат модели) яратгани туфайли, математик мантикни хотирали дискрет курилмаларни лойихалашда ишлатиш имкони юзага келди.

Москва давлат университети дискрет математика мактабининг асосчиларидан бири О.Б.Лупановнинг асосий ишлари математик кибернетика ва математик мантикка багишланган. У мураккаб бошкарувчи системаларнинг асимптотик конуниятларини, контакт схемалар ва функционал элементлардан ясалган схемаларни (умуман асосий бошкарувчи системаларни), энг яхши асимптотик синтез методларини ва локал кодлаш принципини ишлаб чикди.

С.В.Яблонский оптимал схемаларни синтез килиш ва хисоблаш курилмаларини ясаш методини яратди.

Мантик алгебраси кенг микёсда электр схемаларни лойихалашда ва текширишда, автоматик хисоблаш машиналарини лойихалаш ва программалашда, дискрет автоматларни мантикий лойихалашда, ЭХМ элементлари ва кисмларини лойихалашда, хар хил техник системалар, курилмалар ва автоматик машиналарни анализ ва синтез килишда татбик этилади. Математик мантик фани электрон хисоблаш машиналарининг вужудга келишига ва уни мукаммаллаштиришга катта хисса кушди.

Демак, математик мантик, бир томондан, формал мантик муаммоларига математик методларни куллаш натижасида ривожланган булса, иккинчи томондан, математикани асослашга хизмат килувчи фан сифатида ривожланди. Хозирги замон математик мантики автоматика, машина математикаси, бир тилдан иккинчи тилга автоматик тарзда таржима килиш, математик лингвистика, ахборот назарияси ва умуман кибернетика билан богликдир.

Шундай килиб, математик мантик ва дискрет математика 150 йилдан бери ривожланиб келмокда. У математика асослари, алгебра, геометрия, математик анализ, фукционал анализ, топология, эхтимоллар назарияси каби фанларда тадбик этилишидан ташкари кибернетика, иктисодиёт, математик лингвистика, психология, олий нерв системаси, ЭХМ ва дастурлаш, операцияларни текшириш, схемотехника, радиотехника, автоматика, уйинлар назарияси, ахборотлар назарияси сингари фанларда хам кенг кулланилади.

I-БОБ. УМУМИЙ ТУШУНЧАЛАР

1-§. Тупламлар назариясининг асосий тушунчалари

Туплам. -Туплам элементлари. -Тенгкучли тупламлар. -Кисм туплам. -Хос ва хосмас кисм тупламлар. -Буш туплам.

Тупламлар назариясига математик фан сифатида немис математиги Г.Кантор (1845-1918) томонидан асос солинган.

Математикада доимо турли тупламлар билан учрашишга тугри келади. Масалан, тугри бурчакли учбурчаклар туплами, натурал сонлар туплами, тугри чизикда ётувчи нукталар туплами ва хоказо. Умуман туплам тушунчаси айрим-айрим нарсалар, буюмлар, объектларни биргаликда, яъни бир бутун деб караш натижасида вужудга келади.

1-таъриф. Тупламни ташкил этувчи нарсалар, буюмлар, объектлар бу тупламнинг элементлари деб айтилади. Тупламлар, одатда, лотин ёки грек алфавитининг катта харфлари билан белгиланади.

туплам элементлардан тузилганлиги

куринишда ёзилади. Тупламни ташкил этувчи элементлар сони чекли ёки чексиз булиши мумкин. Биринчи холда чекли тупламга, иккинчи холда эса чексиз тупламга эга буламиз.

Масалан:

1) , , ;

2) - чекли тупламлар;

3) ;

4) ;

5) - чексиз тупламлар.

нарса тупламнинг элементи эканлиги ёки куринишда белгиланади. Бирорта нарса тупламнинг элементи эмаслиги ёки куринишда ёзилади.

Масалан:

да , .

ва тупламлар берилган булсин. Агар тупламнинг элементи тупламнинг элементига тенг деб олсак, яъни , бундан битта элемент иккала тупламда хам мавжудлиги келиб чикади.

Масалан, ва тупламларда элементлар иккала тупламда хам мавжуддир.

2-таъриф. тупламнинг хар бир элементи тупламда мавжуд, аксинча, тупламнинг хар бир элементи тупламда хам мавжуд булса, ва тупламларни тенг (тенгкучли) деб атаб, буни ёки белги билан ифодалаймиз.

Демак, иккала ва тупламлар аслида бир тупламдир.

3-таъриф. Агар тупламнинг хар бир элементи тупламда хам мавжуд булса, у вактда нинг кисм туплами деб айтилади ва куйидагича белгиланади.

ёки (1)

Масалан: 1) бутун сонлар хакикий сонлар тупламининг кисм тупламини ташкил этади;

2) вилоятлар республика тупламининг кисм тупламини ташкил этади;

3) ток сонлар бутун сонлар тупламининг кисм тупламидир ва хоказо.

4-таъриф. тупламнинг хамма элементлари тупламда мавжуд булиб, шу билан бирга тупламда га кирмаган элементлар хам бор булса, у вактда - нинг хос кисм туплами дейилади ва

ёки (2)

каби белгиланади.

Демак, ва булса, у вактда

. (3)

(3) тенглик нинг узи узининг кисм туплами булишини курсатади ва бу холатни ифодалаш учун “узининг хосмас кисми” деган иборадан фойдаланамиз.

Масалан: туплам учун , , тупламларнинг хар кайси хос кисмдир.

Одатда, тупламлар назариясида битта хам элементи булмаган тупламлар билан иш куришга тугри келади.

Масалан: тенгламанинг хакикий илдизлари буш тупламни ташкил килади, чунки , яъни тенгламанинг хакикий илдизлари мавжуд эмас.

5-таъриф. Битта хам элементга эга булмаган туплам буш туплам деб аталади ва Æ символ билан белгиланади. Æ буш туплам хар кандай тупламнинг кисм туплами булади ва у хам нинг хосмас кисми дейилади.

2-§. Тупламлар устида амаллар

Тупламларнинг бирлашмаси. -Тупламларнинг кесишмаси. -Тупламларнинг айирмаси. -Тулдирувчи. -Универсал туплам.

ва тупламлар берилган булсин.

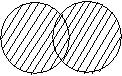
1-таъриф. Берилган тупламларнинг йигиндиси ёки бирлашмаси деб, шу тупламларнинг такрорланмасдан олинадиган хамма элементларидан тузилган ва каби белгиланадиган тупламга айтилади.

А В Агар тупламлар

берилган булса, у холда уларнинг

йигиндиси куйидагича ёзилади:

(1)

1-шакл.

Масалан: , , булса, у вактда

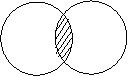
2-таъриф. Берилган , тупламларнинг хамма умумий эле-ментларидан тузилган тупламга , тупламларнинг купайтмаси (кесишмаси ёки умумий кисми) дейилади ва куринишида белгиланади.

A B Агар тупламлар

берилган булса, у холда уларнинг

купайтмаси куйидагича

ёзилади:

. (2)

2-шакл.

Масалан: , булса, у вактда .

Битта хам умумий элементга эга булмаган тупламларнинг кесишмаси Æ буш тупламга тенг булади. Масалан, ток сонлар туплами билан жуфт сонлар тупламининг кесишмаси буш тупламдир.

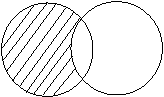
3-таъриф. ва тупламларнинг айирмаси деб, нинг да мавжуд булмаган хамма элементларидан тузиладиган ва ёки куринишида ёзиладиган тупламга айтилади.

А В

3-шакл.

ва булса, у вактда .

4-таъриф. тупламдаги унинг кисм тупламига кирмай колган хамма элементларидан тузилган кисм тупламга нинг тупламигача тулдирувчиси деб айтилади ва куринишда белгиланади.

натурал сонлар туплами ва жуфт сонлар туплами булса, у вактда булади, яъни .

туплам ни гача тулдиради.

Ушбу тенгликларни келтириб чикариш мумкин.

, =. .

5-таъриф. Бирор тупламнинг хос кисми деб каралмаган хар бир тупламни универсал туплам деб атаб, уни харфи билан белгилаймиз.

Таърифга биноан, нинг хамма кисмлари орасида иккита хосмас кисми бор: биттаси нинг узи, иккинчиси Æ буш туплам, колганлари хос кисмлардан иборат.

3-§. Асосий тенгликлар (тенгкучлиликлар)

Асосий тенгкучлиликлар. -Коммутативлик, ассоциативлик, дистрибутивлик конунлари.

универсал тупламнинг кисмлари орасидаги муносабатларни ифодаловчи асосий тенгликлар куйидагилардан иборат:

Тупламлар назариясида тенгликларни исботлашнинг умумий методи тенгликнинг бир томонидаги тупламга тегишли хар бир элемент иккинчи томонидаги тупламда хам мавжуд ва, аксинча, эканлигини курсатишдан иборатдир.

Исбот. туплам нинг тулдирувчиси. Шунинг учун нинг хар бир элементи , демак, . Аксинча, нинг хар бир элементи булгани учун . Демак, .

2. - купайтмага нисбатан коммутативлик конуни.

Исбот. нинг хар бир элементи ва да мавжуд, чунки туплам ва ларнинг умумий элемертларидан тузилган. Демак, нинг элементлари да хам мавжуд. Худди шундай нинг хар бир элементи ва да мавжуд, чунки туплам ва ларнинг умумий элементларидан тузилган. Шунинг учун тупламнинг хар бир элементи тупламнинг хам элементи булади. Демак, =.

3.- купайтмага нисбатан ассоциативлик конуни.

Исбот. булсин. Демак, ва . Бу ердан ва эканлиги келиб чикади. Шунинг учун ва дир. Бу ердан уз навбатида эканлиги келиб чикади. Исботнинг иккинчи кисмини укувчига хавола этамиз.

4. - йигиндига нисбатан коммутативлик конуни.

5.-йигиндига нисбатан ассоциативлик конуни.

4 ва 5 -тенгликларнинг исботлари худди 2 ва 3 - тенгликларни исботлашга ухшаш амалга оширилади.

6. - купайтмага нисбатан дистрибутивлик конуни.

7. - йигиндига нисбатан дистрибутивлик конуни.

6-тенгликнинг исботи: булсин, у вактда ва булади. Бу ердан ва ёки ва келиб чикади. Демак, ёки . Шунинг учун . Энди булсин, у холда ёки булади. Бу ердан ва ёки ва келиб чикади. Демак, .

8. 9. 10.

11. 12. 13.

4-§. Тупламлар алгебраси

Айниятлар. -Теоремалар. -Де Морган конуни. -Жуфт-жуфт эквивалент.

Тупламлар алгебрасида – , Í белгилар уртасидаги узаро муносабатлар куриб чикилади. Тупламлар алгебрасида умуман оддий алгебрадагидай айниятлар - тенгликлар курилади. Бу айниятлар универсал тупламнинг ва унинг хос кисм тупламларининг кандай булишидан катъий назар уз кучини саклайдилар.

1-теорема. универсал тупламнинг исталган кисмлари орасидаги муносабатларни ифодаловчи куйидаги тенгликлар айниятдир:

1. 1^¢.

2. 2^¢.

3. 3^¢.

4. 4^¢.

5. 5^¢

Агар ва булса, у вактда . Ана шу хоссадан фойдаланиб юкорида келтирилган айниятлар исбот этилади, яъни тенгликнинг чап томонидаги хар бир элемент унинг унг томонида хам мавжуд ва аксинча эканлигини курсатиш керак. Биз юкоридаги айниятларнинг айримларини исбот этган эдик.

1 ва 1^¢ - айниятларни мос равишда йигинди ва купайтма амаллари учун ассоциативлик конунлари дейилади. 2 ва 2^¢ - айниятлари эса - коммутативлик конуни ва 3, 3^¢ -айниятлари бул-са, шу амаллар учун дистрибутивлик конуни дейилади.

Ассоциативлик конунига асосан кисм тупламлардан маълум тартибда йигинди амали билан хосил этилган икки туплам тенгдир.

Бу тупламни шаклда белгилаймиз.

Ассоциатив конунига кура кавс белгиси каерда туриши хеч кандай роль уйнамайди. Математик индукция методига асосан

бу ерда , белгилашлар cонларнинг исталган тартибда олинганидан хосил этилган сонларни билдиради.

Шу тарика куйидаги тенгликларни хам келтириб чикариш мумкин:

Курсатилган 1-5 ва 1^¢-5^¢ тенгликлардан куйидаги хулосани хосил киламиз:

1-теоремадаги айниятлар жуфт-жуфт тарзда шундай жойлаштирилганки, бири-иккинчисидан ва хамда ва белгиларни бир вактда узаро жойларини алмаштириш натижасида келиб чикади.

2-теорема. универсал тупламнинг исталган ва тупламлари учун куйидагилар хаклидир:

6. Агар хамма лар учун 6^¢. Агар исталган учун

булса, у вактда булса, у вактда .

7.7^¢. Агар ва булса, у вактда .

8.8^¢. .

9. 9^¢.

10. 10^¢.

11. 11^¢.

12. 12^¢.

13. 13^¢.

2-теореманинг айрим тенгликлари адабиётда махсус номга эгадир. Масалан,10 ва 10^¢ тенгликлар идемпотентлик конуни дейилади,12 ва 12^¢-ютиш конуни,13 ва 13^¢-де Морган конуни деб аталади.

Тупламлар алгебрасида бирор тенгликдан шу тенгликка кирган ни га, ни га, ни га, ни га бирданига алмаштириш натижасида хосил этилган иккинчи тенгликни биринчи тенгликка ва, аксинча, биринчи тенглик иккинчи тенгликка нисбатан иккитарафлама тенглик деб айтилади.

3-теорема. Исталган ва тупламлар учун куйидаги мулохазалар жуфт-жуфт эквивалентдир:

(I) ; (II) ; (III) . (1)

мулохазалар жуфт-жуфт эквивалентдир деган тасдик куйидагини билдиради: исталган ва учун га эквивалентдир. Бу мулохаза уз навбатида факатгина нинг, нинг, ...., нинг тугрилигини келтириб чикаргандагина тугридир.

Исбот: (I) (II) нинг тугрилигини келтириб чикаради.

булсин. Исталган ва учун эканлигини курсатиш керак.

а) булса, у вактда ва дир. Демак, .

б) булсин. У вактда (I.I) га асосан хамдир. Шунинг учун , яъни (I) (II) нинг тугрилигини келтириб чикаради.

Энди булсин, у вактда эканлигини исбот киламиз.

Демак, .

(III) (I) нинг тугрилигини келтириб чикаради.

Ростдан хам ва булишидан . Бу билан исбот якунланади.

РЕЖА:

1.Тупламлар назариясининг асосий тушунча-

лари.

2.Тупламлар устида амаллар.

3.Асосий тенгкучлиликлар.

4.Тупламлар алгебраси.

Муаммоли масала ва топшириклар:

1. а)

б)

эканлиги исбот этилсин.

2. Ушбу тупламларнинг хар иккитаси ва хамда учтасининг кесишмалари ва бирлашмаларини топинг:

, , .

3. туплам учун кисмдир. ни топинг.

4. тенгликни исботланг.

5. 7-13 асосий тенгкучлиликларни исботланг.

Мустакил ишлаш учун саволлар:

1.Тупламлар назариясининг асосий тушунчалари

нимадан иборат?

2.Тупламлар устида кандай амаллар бажарилади?

3.Асосий тенгкучлиликларни ёзинг.

4.Кандай тупламга тупламлар алгебраси деб ай-

тилади?

5.Мулохазаларнинг жуфт-жуфт эквивалентлиги-

нинг шартлари.

5-§. Муносабатлар. Бинар муносабат

Муносабат. -Тартибланган жуфтлик. -Унар ва бинар муносабат. -n-ар муносабат. -Аникланиш сохаси. -Кийматлар сохаси.

Дискрет математикада фундаментал тушунчалардан бири булган муносабатлар тушунчаси предметлар ва тушунчалар орасидаги алокани ифодалайди. Куйидаги туликсиз гаплар муносабатларга мисол була олади:

............кичик .............дан, ...........тенг ............га,

............булинади ...............га ва хоказо.

Бундан кейин муносабатлар тушунчаси тупламлар назарияси нуктаи назаридан туриб урганилади.

Муносабатлар тушунчасини аниклаш учун тартибланган жуфтлик тушунчасига аниклик киритайлик. Маълум тартибда жойлашган икки предметдан тузилган элементга тартибланган жуфтлик дейилади. Математикада тартибланган жуфтлик куйидаги хусусиятларга эга булади деб фарз килинади:

1) Хар кандай (исталган) ва предметлар учун маълум объект мавжуд, кайсиким каби белгиланади, ва ларнинг тартибланган жуфтлиги деб укилади. Хар бир x ва y предметларга ягона тартибланган жуфтлик мос келади.

2)Иккита ва тартибланган жуфтликлар берилган булсин. Агар ва булса, у вактда булади.

Тартибланган жуфтлик куйидаги тупламдир

яъни шундай икки элементли тупламдирки, унинг битта элементи тартибсиз жуфтликдан иборат, иккинчиси эса шу тартибсиз жуфтликнинг кайси аъзоси биринчи хисобланиши кераклигини курсатади.

Тартибланган жуфтлик нинг предмети биринчи координатаси, y предмети булса, иккинчи координатаси деб айтилади.

Тартибланган жуфтликлар терминида тартибланган -ликларни аниклаш мумкин. ва предметларнинг тартибланган учлиги куйидаги тартибланган жуфтликлар шаклида аникланади: . Худди шундай ва предметларнинг тартибланган -лиги , таърифга асосан, тарзда аникланади.

Элементлари тартибланган жуфтликлардан иборат булган тупламга тартибланган жуфтликлар туплами деб айтилади.

Бинар муносабатни тартибланган жуфтликлар туплами сифатида аниклаймиз. Агар бирор муносабатни ифодаласа, у вактда ва ифодаларни узаро алмашувчи ифодалар деб хисоблаймиз. ифодани “предмет предмет га нисбатан муносабатда” деб укилади.

Куйидаги , , белгилар худи ифодадан келиб чиккан.

-ар муносабати тартибланган -ликлар туплами сифатида аникланади. 3-ар муносабатни купинча адабиётда тернар муносабат деб хам юритилади.

Мисоллар. 1. } тартибланган жуфтликлар туплами бинар муносабатга мисол була олади.

2.Агар айният муносабатини билдирса, у вактда дегани ни билдиради.

3.Агар оналик муносабатини билдирса, у вактда <Хуршеда, Ирода> символ Хуршеда Ироданинг онаси эканлигини билдиради.

4.Тернар муносабатига бутун сонлар тупламидаги кушиш амали мисол була олади. ёзувини шаклида хам ёзиш мумкин.

Бундан кейин бинар муносабат термини урнига кискалик учун муносабат терминини ишлатамиз.

cимволини куйидагича тушуниш керак: Шундай лар тупламики, .

айрим y учун туплами муносабатнинг аникланиш сохаси дейилади ва cимволи билан белгиланади. айрим учун туплами муносабатнинг кийматлар сохаси дейилади ва символи билан белгиланади. Бошкача килиб айтганда, муносабатнинг аникланиш сохаси шу муносабатнинг биринчи координаталаридан тузилган тупламга айтилади, иккинчи координаталаридан тузилган тупламга эса, кийматлар сохаси деб айтилади.

Мисол: , , муносабат берилган булсин. У вактда , .

Бирор туплам тартибланган жуфтликлар туплами булсин. Агарда бирор тупламнинг элементи ва y бошка тупламнинг элементи булса, у вактда туплам ва тупламларнинг тугри (декарт) купайтмасидан тузилган туплам дейилади ва

шаклида белгиланади.

Хар бир муносабат айрим олинган тугри купайтманинг кисм туплами булади ва , . Агар булса, у вактда дан га булган муносабат деб айтилади. Агар ва булса, у вактда дан га булган муносабат деб айтилади. дан га булган муносабатни ичидаги муносабат деб айтилади.

кандайдир туплам булсин. У вактда ичидаги муносабатни ичидаги универсал муносабат деб айтилади.

муносабат ичидаги айният муносабати деб айтилади ва ёки символи билан белгиланади. Хар кандай тупламининг ва элементлари учун ифода билан тенг кучлидир.

туплам ва муносабат берилган булсин. У вактда нинг айрим лари учун . Бу тупламга туплам элементларининг - образлари туплами деб айтилади.

Мисоллар. тугри чизикни ва муносабатини шаклларда ёзиш мумкин.

6-§. Эквивалентлик муносабати

Рефлексив, симметрик ва транзитив муносабатлар. -Эквивалентлик синфи.

1-таъриф. Агарда тупламнинг исталган элементи учун булса, у вактда муносабатига тупламидаги рефлексив муносабат деб айтилади; агарда дан келиб чикса, у холда - симметрик муносабат деб айтилади; агарда ва дан келиб чикса, у вактда - транзитив муносабат деб айтилади.

Шу курсатилган учала хоссага эга булган муносабатлар математикада куп учрагани учун, уларга махсус ном куйилган.

2-таъриф. Агарда бирор тупламдаги муносабат рефлексив, симметрик ва транзитив хоссаларга эга булса, у вактда бундай муносабатга шу тупламдаги эквивалентлик муносабати дейилади.

Агарда муносабати тупламдаги эквивалентлик муносабати булса, у вактда .

Мисоллар. Куйидаги хар бир муносабат маълум тупламдаги эквивалетлик муносабатига мисол була олади:

1.Исталган тупламдаги тенглик муносабати.

2.Евклид текислигининг хамма учбурчаклар тупламидаги ухшашлик муносабати.

3.Бутун сонлар тупламидаги модули буйича таккослама муносабати.

4.Узбекистонда яшовчи одамлар тупламидаги “бир уйда яшовчилар” муносабати.

Эквивалентлик муносабати шундай асосий хусусиятга эгаки, у тупламни кесишмайдиган кисм тупламларга булади. Кейинги мисолга, масалан, “бир уйда яшовчилар” муносабати Узбекистонни бир-бири билан кесишмайдиган “бир уйда яшовчилар” кисм тупламларига булади. Бу айтилганларни куйидагича умумлаштириш мумкин.

тупламдаги эквивалентлик муносабати булсин. У вактда тупламининг кисм туплами факат шундагина эквивалентлик синфи ёки эквивалентлик - синфи деб айтилади, качонки тупламининг шундай элементи топилиб, булса.

Шундай килиб, тупламнинг шундай элементи мавжуд булсаки, тенглик бажарилса, у вактда туплам эквивалентлик синфи була олади.

Агарда муносабати тугрисида хеч кандай англашмовчилик тугилмайдиган булса, у вактда туплами шаклида белгиланади, яъни ва юзага келтирган эквивалентлик синфи деб айтилади.

Эквивалентлик синфи куйидаги икки хусусиятга эгадир:

1. - бир синфнинг хамма элементлари узаро эквивалентдир.

2. Агар булса, у вактда .

1-хосса эквивалентлик муносабатининг рефлексивлик хусусиятидан келиб чикади.

2-хоссанинг исботи: булсин, яъни га эквивалент булсин, у вактда . Хакикатан хам, ( ни билдиради) дан ва булганлиги учун муносабатининг транзитив хусусиятига асосан келиб чикади, яъни . Эквивалентлик муносабатининг симметриклик хоссасидан фойдаланиб, ни исбот этиш мумкин. Демак, .

7-§. Функция тушунчаси. Функциялар суперпозицияси

Функция. -Тартибланган жуфтлик. -Функциялар тенглиги. -Бир кийматли функция. -Суперпозиция. -Функцияларнинг функцияси. -Тескари функция.

Функция тушунчасини олдинги параграфларда урганилган терминларда аниклаймиз. Функциянинг графиги тартибланган жуфтликлар тупламидан иборат. Функция билан унинг графиги уртасида хеч кандай фарк йук. Функция шундай муносабатки, унинг икки хил элементининг биринчи координаталари хеч качон тенг булмайди.

Шундай килиб, муносабати куйидаги талабларни каноатлантиргандагина функция була олади:

1. нинг элементлари факатгина тартибланган жуфтликлардан иборат.

2. Агар ва элементлари булса, у вактда .

Мисол: 1. , , фунцкциядир. .

2. , , муносабати функция була олмайди, чунки ва элементларининг биринчи координаталари тенг.

3. функциядир, чунки агар булса, у вактда .

4. функция була олмайди, чунки унинг элементлари мавжуд.

Агар - функция ва булса, яъни булса, у вактда функциянинг аргументи деб айтилади ва ни функциянинг даги киймати ёки элементининг образи дейилади.

ни белгилаш учун , , ёки символларни ишлатадилар. cимволни деб, яъни элементининг -образлари туплами деб караш мумкин.

Икки ва функциялар бир хил элементлардан тузилган булса, бундай функциялар тенг булади , яъни бошкача килиб айтганда, ва булсагина, булади.

Шундай килиб, функция берилган булиши учун аникланиш сохаси ва шу соханинг хар бир элементи учун унинг киймати берилиши керак.

дан келиб чикади.

Агар f функциянинг аникланиш сохаси булса, у вактда функциянинг узгариш сохаси туплами ичида булади деб айтилади ва куйидагича белгиланади:

ёки .

Юкорида курсатилган хамма туплами тупламнинг кисм туплами булади ва уни деб белгилаймиз.

Агар булса, у вактда факатгина бир элементдан иборат булади ва у тупламнинг буш кисм тупламидир.

Агар ва булса, у вактда .

Агар дан келиб чикса, у вактда f бир кийматли функция дейилади.

Иккита ва функциялар берилган булсин. ва функцияларнинг суперпозицияси деб куйидаги шундай мавжудки, ва тупламга айтилади ва символи билан белгиланади. Бу туплам хам функция булади.

Шундай килиб, функцияларнинг суперпозицияси куйидагича булади:

Функцияларнинг суперпозицияси функцияларнинг функцияси деб хам айтилади.

ва булсин, у вактда функция ва функцияларнинг суперпозициясидир.

Суперпозиция амали ассоциативлик конунига буйсунади, яъни

Агар ва булса, у холда ва булади.

Агар бир кийматли функция булса, у вактда дан координаталарини урнини алмаштириш натижасида хосил буладиган функцияга функциясига тескари булган функция деб айтилади ва cимволи билан белгиланади.

Факатгина бир кийматли функциялар учун бажариладиган бу амалга кайтариш амали дейилади.

нинг аникланиш сохаси

8-§. Тартиблаш муносабати

Тартиблаш муносабати. -Антисимметрик муносабат. -Кисман тартиблаш муносабати. -Иррефлексив муносабат. -Чизикли тартиблаш муносабати. -Кисман тартибланган туплам.

1-таъриф. Агар бирор тупламдаги ва элементлари учун муносабат урнига муносабат уринли булишини курсатувчи муносабатга тартиблаш муносабати деб айтилади.

Тартиблаш муносабати ёрдамида элементларни кайтартибда куйиш масаласини хал этиш мумкин. Хакикий сонлар туплами учун < , £ , > , ³ муносабатлари тартиблаш муносабатларига мисол була олади. Тупламлар системаси учун худди шундай ролни Ì, Í муносабатлар уйнайди.

2-таъриф. Агар тупламининг исталган ва элементлари учун бир вактда ва бажарилишидан келиб чикса, бундай r муносабат антисимметрик муносабат деб айтилади.

3-таъриф. туплам ичида рефлексивлик, антисимметрик ва транзитивлик хоссаларига эга булган муносабатга тупламдаги кисман тартиблаш муносабати деб айтилади.

Хар кандай рефлексив ва транзитив муносабатга тартиблаш муносабати деб айтилади.

Кисман тартиблаш муносабати £ символи билан белгиланади. Агар £ муносабати тупламни кисман тартибласа, у вактда тупламнинг исталган ва элементлари учун муносабати бажарилиши хам мумкин, бажарилмаслиги хам мумкин.

Худди шундай, агар ва булса, у вактда деб ёзилади ва дан кичик деб айтилади.

4-таъриф. тупламнинг хар кандай элементи учун муносабат бажарилмаса, у вактда тупламдаги иррефлексив муносабат деб айтилади.

Агар £ муносабати тупламдаги кисман тартиблаш муносабати булса, у вактда < муносабати тупламидаги иррефлексив ва транзитив муносабат булади.

5-таъриф. муносабат кисман тартиблаш муносабати булсин. муносабатнинг аникланиш сохасига карашли хар кандай икки хил ва элементлари учун ёки уринли булса, бундай муносабатга чизикли (оддий) тартиблаш муносабати деб айтилади.

Хакикий сонларни кийматига караб тартиблаш чизикли тартиблаш муносабатига мисол була олади.

6-таъриф. Агар бирор тупламда кисман тартиблаш муносабати берилган булса, бундай тупламга кисман тартибланган туплам деб айтилади ва у тартибланган жуфтликдан иборат булади.

Агар тупламда оддий тартиблаш муносабати берилган булса, у вактда оддий тартибланган туплам деб айтилади ва у хам тартибланган жуфтликдан иборат булади. Бу ерда £ тупламини оддий (чизикли) тартиблайди.

Масалан, агар тупламлар системаси булса, у вактда кисман тартибланган туплам булади.

функцияси тупламининг £ тартиблаш муносабатига ва тупламининг £¹ тартиблаш муносабатига нисбатан шундагина тартибини саклайдиган функция булади, качонки дан келиб чикса, ва тупламлар уртасидаги узаро бир кийматли богланиш ва га кисман тартибланган тупламлар уртасидаги изоморфизм деб айтилади. Агар шундай богланиш мавжуд булса, у вактда курсатилган кисман тартибланган тупламлар изоморфдир.

тупламнинг хамма лари учун булса, у вактда тупламнинг элементи тупламнинг кисман тартиблаш муносабати £ га нисбатан энг кичик элементи деб айтилади. Агар шундай элемент мавжуд булса, у ягонадир.

тупламнинг хеч бир элементи учун муносабати бажарилмаса, у вактда тупламнинг у элементи шу тупламнинг кисман тартиблаш £ муносабатига нисбатан минимал (энг кичик) элементи деб айтилади. Минимал элемент берилган тупламда бир нечта булиши мумкин.

Агар хар кандай учун булса, у вактда тупламнинг элементи шу тупламнинг £ муносабатига нисбатан энг катта элементи деб айтилади. Агар шундай элемент мавжуд булса, у хам ягонадир.

тупламнинг хеч бир элементи учун муносабати бажарилмаса, у вактда тупламнинг у элементи шу тупламнинг £ муносабатига нисбатан максимал элементи деб айтилади.

Агар тупламнинг хар бир буш эмас кисм туплами энг кичик элементга эга булса, у вактда кисман тартибланган тупламга тулик тартибланган туплам деб айтамиз. Масалан, {0,1,2,...}.

Агар кисман тартибланган ва булсин. У вактда исталган учун бажарилса, тупламнинг элементи тупламнинг юкори чегараси деб айтилади.

Худди шундай, агар исталган учун бажарилса, элементи тупламнинг куйи чегараси деб айтилади.

Агар тартибланган туплам булса, у холда унинг кисм туплами хам тартибланган булади. Агар бу тартибланган туплам чизикли булса, у вактда кисм туплам тупламнинг занжири дейилади.

га занжирнинг узунлиги деб айтилади. Бу ерда - чизикли тартибланган кисм тупламнинг куввати. узунликдаги хар бир занжир бутун сонли занжирга изоморфдир.

тупламнинг энг катта элементини билан ва энг кичик элементини билан белгилаймиз.

тартибланган туплам элементининг баландлиги деб ( тупламнинг) занжирлар узунлигининг максимумига айтилади. тартибланган туплам узунлиги деб тупламдаги занжирлар узунлигининг максимумига айтилади, яъни тартибланган тупламнинг узунлиги унинг элементлари баландлиги нинг максимумига тенг булади.

, .

9-§. Панжара хакида тушунчалар

Панжара. -Сигнатура. -Дистрибутивлик критерияси. -Дедекинд (модуляр) панжара. -Дедекиндлик критерияси. -Изоморф. -Изоморфизм.

Кисман тартибланган туплам тушунчасидан фойдаланиб, панжара тушунчасини аниклаймиз.

Таъриф. Тартибланган туплам нинг исталган иккита , элементлари орасида (энг катта куйи ёк) ва (энг кичик юкори ёк) муносабатлар мавжуд булса, бундай туплам панжара деб аталади.

Равшанки, панжара икки тарафлама булган тартибланган туплам хам панжара булади. панжарадан кесишма амалини бирлашмага ва бирлашма амалини кесишма амалига узгартириш керак. Тартибланган тупламнинг хамма кисм тупламлари энг катта куйи ва энг кичик юкори чегарага эга булса, у холда бундай тупламга тулик панжара деб айтилади.

Панжарани сигнатуралари куйидаги хусусиятларга эга булган алгебра сифатида хам аниклаш мумкин:

1. - идемпотентлик;

2. - коммутативлик;

- ассоциативлик;

4. - ютиш.

Панжарага берилган иккала таъриф хам эквивалентдир.

Бундан кейин 0 ва 1 ларни панжаранинг структурали нули ва бири деб биламиз.

Агар хар бир жуфт элементлар билан биргаликда уларнинг йигиндиси ва купайтмаси ларни хам уз ичига олса, у холда га панжаранинг кисм панжараси деб айтилади. Энг катта элементи ва энг кичик элементлардан иборат кисм панжарага I интервал деб айтилади:

I=.

Агар

булса, у холда нол ва бир структурали панжарада иккита ва элементлар кушимча (тулдирувчи) элементлар булади. га кушимча булган элементга панжарадаги элементнинг тулдирувчиси деб хам айтилади.

панжарада умумий тулдирувчига эга булган икки элементга да богланган элементлар деб айтилади.

Панжаралар синфининг энг мухими дистрибутив панжаралардир. Куйидаги айниятларни (хамма ,, лар учун) каноатлантирувчи панжарага

дистрибутив панжара деб айтилади.

Панжаранинг дистрибутивлик критерияси: панжара шунда ва факат шундагина дистрибутив панжара булади, качонки панжаранинг хар бир I интервалида исталган иккита богланган (I да) элементи тенг булса.

Дедекинд (модуляр) панжара деган тушунча киритамиз. панжара шунда ва факат шундагина дедекинд панжараси булади, качонки хамма ,, ва лар учун

муносабат бажарилса.

Панжаранинг дедекиндлик критерияси: панжара дедекинд панжара булиши учун, панжарага изоморф булган кисм панжара мавжуд булмаслиги етарли ва зарур (1,а-шакл):

а) б)

1-шакл.

панжара битта нол баландликдаги элемент, иккита бир баландликдаги элемент, битта икки баландликдаги ва битта уч баландликдаги элементни уз ичига олади.

Панжаранинг модулярлик критериясидан фойдаланиб, дистрибутивлик критериясини кулай хисоблаш шаклини хол учун келтирамиз:

панжара шунда ва факат шундагина дистрибутив булади, качонки у га изоморф булган кисм панжарани уз ичига олмаса, яъни дедекинд булса ва кисм панжарага изоморф булган кисм панжарани уз ичига олмаса (1,б-шакл).

панжара битта нол баландликдаги элементдан, бир баландликдаги учта элементдан ва икки баландликдаги битта элементдан иборат икки узунликдаги учта занжирдан тузилган.

0 ва 1 структурали панжаранинг хар бир элементининг тулдирувчиси мавжуд булсин. У вактда бу панжарада унар операция берилган деса булади. Агар юкорида акс эттирилган хусусиятларга эга булган панжарада

(а)

(б)

(в)

муносабатлар бажарилса, у холда панжарага тулдирувчили (тулдирувчиси бор) панжара деб айтилади.

(а) ва (б) ларга асосан операция билан ва операция билан ифодаланиши мумкин. Демак, тулдирувчили панжарани сигнатураси , - булган алгебра сифатида аниклаш мумкин.

(а)-(б) муносабатлардан куйидагилар келиб чикади ( десак):