Ӯзбекистон почта ва телекоммуникациялар агентлиги

Тошкент электротехника алоқа институти

 

 

 

                                                                                                                           Эхтимоллар назарияси ва

                                                                      статистика кафедраси

 

 

“ Жараёнлар тадқиқоти “ фанидан

амалий ишларни бажариш учун

 

УСУЛИЙ ҚӮЛЛАНМА

 

 

 

Тошкент 2001

Сӯз боши

        

           Усулий қӯлланма Телекоммуникация сохасининг В – 522300 

“ Почта алоқасининг ташкили ва унинг технологияси ” ва В – 341100

“ Алоқа корхоналарида менеджментлик “ йӯналишлари учун Жараёнлар тадқиқоти курсининг дастурига мослаштириб тузилган. У ӯз ичига 3турдаги амалий ишлари тавсифини олган бӯлиб, уларнинг хар бирида қисқача назарий маълумотлар, амалий ишларини бажариш усуллари, хисоб натижаларини тузиш тартиби келтирилган.

          Хар бир амалий топшириқлари параметрларга боғлиқ бӯлиб, талаба параметрлар ӯрнига уларнинг сон қийматларини қӯйиб, топшириқни бажариши керак. Хар бир топшириқ 24 вариантдан иборат. Қӯлланмада к орқали талабанинг вариант тартиб рақами белгиланган.

          Қӯлланма охирида ӯрганилаётган мавзуни тахлил қилиш учун тавсия этиладиган дарсликлар рӯйхати келтирилган. 

 

 

 
 
Режалаштириш ва бошқаришнинг тармоқли усуллари.

 

Тармоқли модел ва унинг асосий элементлари.

Тармокли режалаштириш ва бошкариш (ТРБ) жараёни тармокли график (ТГ) ёрдамида моделлаштиришга асосланади. Тармокли модел айрим узаро богланган ишларни бажариш режаси булиб, тармокларни алохида тури куринишида булади. У график усулида тасвирланади, шу сабабли тармокли график дейилади.

Тармокли моделнинг асосий элементлари ходиса ва иш тушунчаларидир. Ходиса доирача билан, иш эса йуналтирилган кесма билан белгиланади, йуналиш ишлар орасидаги богликликни курсатади.

Тармокли график режалаштиришнинг бошлангич боскичида тузилади. Аввал режалаштирилган жараён алохида ишларга булинади, ишлар сони аникланади ва ходисалар тузилади, уларнинг мантикий богликлиги ва бажарилиш кетма-кетлиги аникланади. Улар ёрдамида хар бир ишнинг давомийлиги бахоланади, сунг тармокли график тузилади.

Тармокли график тартиблаштириш шундан иборатки, бунда ихтиёрий иш олдидаги ходисанинг тартиб раками шу иш охиридаги ходиса тартиб ракамидан кичик булади.

ТГнинг асосий тушунчаларидан бири йулдир. Йул ихтиёрий йуналишлар кема-кетлиги булиб, хар бир йуналишнинг охирги ходисаси кейинги йуналишнинг бошлангич ходисаси билан устма-уст тушади.

Тула йул - бу боши  бошлангич ходиса, охири эса тугаётган ходисадан иботар йулдир.

Критик йул давомийлиги энг катта булган тула йулдир. Бу йулда жойлашган ходиса ва йуналишлар хам критик ходиса ва критик йуналиш дейилади.

 

Тармоқли графикнинг вақт параметрлари

i -ходиса руй беришининг  дастлабки  муддати tД(i) i -ходисага  булган максимал йулнинг давомийлиги билан аникланади:

 

             tД( i ) = max( Lй i )                                                                              (1.1)               

                            Lй i

бунда Lй i  бошлангич ходисадан  i ходисагача  булган  ихтиёрий  йул.

         Агар  j ходиса  бир нечта ундан олдин келадиган йулларга  эга булса, яъни бир нечта олдин  келадиган i ходисаларга эга булса, у холда j ходиса руй беришининг дастлабки муддатини куйидаги формуладан аниклаш кулай булади;

                                              

                 tД(j) = max [ tД(i)+t(i, j)]                                                               (1.2)

 

Ходиса руй беришнинг охирги муддати куйидагича аникланади:

                         

                             t0(i)= tкр -max t(Lci),

                                              Lci

бунда Lсi i ходисадан кейин келадиган охирги ходисагача булган ихтиёрий йул. Агар i ходиса бир нечта кейинги йулларга эга булса, у холда ходиса руй беришининг охирги муддатини куйидаги формула билан хисоблаш кулайдир:

 

                           t0(i)= min [t0(j)-t(i,j)],                                                          (1.3)

 

i ходисанинг  вакт захираси R(i) ходисанинг охирги руй бериш муддатидан дастлабки руй бериш муддатини айирмаси билан аникланади,

 

                                R(i)=t0(i)-tД(i)                                                                  (1.4)

 

Ишнинг вакт захираси 4 турга ажратилади, булар RT(i,j) ишнинг тула вакт захираси:

 

                            RT(i,j)=t0(j)-tД(j)-t(i,j)                                                         (1.5)

 

R1(i,j) -(i,j) ишнинг биринчи тур хусусий вакт захираси:

 

                   R1(i, j)= t0( j)-t0( i) - t( i j) = RT(i,j)- R(i)

 

( i j) ишнинг  иккинчи тур (эркин) вакт захираси RЭ(i,j) ва богликмас вакт захира RД(i,j) мос  равишда куйидаги формулалар оркали аникланади: 

 

                                RЭ(i, j)= tД( j)-tД( i) - t( i, j)                                            (1.6)     

                                                                               

                                   Rб(i, j)= tД( j)-t0( i) - t( i, j)                                          (1.7)

 

Ишнинг  кучланиш коэффициенти.

        Нокритик йулда  жойлашган ишларнинг муддатида  бажарилиши  кийинлик даражасини  ишнинг кучланиш коэффициенти ёрдамида  аникланади.

( i j) ишнинг кучланиш коэффициенти Кн(i,j) деб йулларнинг устма - уст тушмайдиган кисмлари  давомийликларининг нисбатига  айтилади, бу йуллардан бири  (i j) ишдан  утувчи давомийлиги  максимал  булган йул, иккинчиси эса  критик  йулдир,

 

                        t( L max)- t/ k p 

      Кн(i j)= ----------------------                                                                        (1.8)

                         t k p   -  t/ k p

 

бунда t( L max) (i j) ишдан утувчи максимал  йул узунлиги;

 t/ k p - критик  йул  билан  устма-уст тушадиган каралаётган йул  кисмининг  узунлиги.

Тармокли графикни оптималлаштириш.

ТГ ни  шартли равишда хусусий ва комплекс  оптималлаштириш  масалалари турларига  ажратиш мумкин.

Хусусий  оптималлаштириш  турларига комплекс ишни белгиланган нархи буйича уни бажариш  муддатини минималлаштириш ва комплекс иш бажарилиш муддатини билган холда уни  нархини минималлаштириш масалалари киради. Комплекс оптималлаштириш  лойихани нархи ва бажарилиш муддати орасидаги оптимал муносабатни  аниклашдан иборат. Оптималлаштиришнинг вакт-нарх усулини куллашда иш давомийлигини кискартириш унинг нархини усишига пропорционал деб  хисобланади.Хар бир ( i, j) иш t( i, j) давомийлик билан тавсифланади,а( i, j) t( i, j) в( i, j), бунда  а( i, j) ( i, j)ишнинг минимал мумкин булган давомийлиги, в( i,j)(i, j) ишни нормал  шароитда бажарилиш давомийлигидир.(i,j) ишнинг нархи

с(i,j) сmin(i,j) ва сmах(i,j) лар орасида узгаради, бунда сmin(i,j) ишнинг нормал шароитидаги нархи, сmах(i,j) ишни фавкулотда давомийликдаги нахри.

 (i,j) ишни тугри чизикдаги проекциясидан фойдаланиб унинг нархи узгариши D с(i,j) ни аниклаш мумкин.

 

                             D с(i,j)=[b(i,j)-t(i,j)]h(i,j)                                                   (1.9)

 

бунда h(i,j) ишни нормал шароитидаги давомийликка нисбатан тезлаштиришга кетадиган харажат курсаткичидир,

 

                                            

                       сmах(i,j) - сmin(i,j)

        h(i j)= ------------------------                                                                    (1.10)

                          b(i,j) - a(i,j)

 

 

        Хусусий оптималлаштиришнинг оддий тури иш нархини билган холда унинг вакт захираларидан фойдаланишдир. Хар бир ишнинг давомийлиги унинг вакт захираси тугагунча, хеч булмаганда юкори киймат b(i,j) га эришгунча узайтирилади. Бунда лойихани оптималлаштиришгача булган нархи С=åС(i,j) куидаги микдорга камаяди

                i,j                                                        

    

                               DС=åDС(i,j= å [b(i,j)-t(i,j)] h(i,j)

                                                    i,j=1  

 

    

 

 

                                     1-амалий иш.

 

Топшириқ.

1. Расмдаги тармокли графикни тартиблаштиринг ва ундаги ходисаларнинг вакт параметрларини хисобланг. Йуналишлар устидаги сон иш давомийлигини билдиради.

2. Тгнинг барча ишлари вакт параметрини хисобланг.

3. Критик йул ишлари давомийлигини дисперсияси d2(i,j) га тенг. Лойихани Т=Тк суткада бажарилиш эхтимолини бахоланг, бунда:

 

                      

          d2(i,j)=  ,              Тк=tкр+4,                       к=1,2,...25,

 

[а]- а сонининг бутун қисми.

ТГ ишларини кучланиш коэффициентини хисобланг.

 

4. ТГ ни “вакт-нарх” усули билан оптималлаштиринг.(i,j) ишни тезлаштириш харажат курсаткичлари h(i,j) ва нархи с(i,j) (1.12) тенгликларда ва 1.3-жадвалда берилган, иш давомийликларининг чегаралари а(i,j) ва b(i,j) куйидаги формулалар ёрдамида аникланади:

                          a(i,j)=t(i,j)- ,          b(i,j)=t(i,j)+.                               

 

 

                                           m+9                    m+7

                               1                            4                           8

             8                                                       2к+1                        к

                    m+5           m+3                                        2к            

 0                             2                           5                                                        9

                                                                          12                  m+4         

                                   m+5                                             7     

                                                                                                  

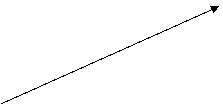
           9                                                   11

                                                                     15       m+2       m+3                  11

                                             

                                           m+1        6             m+1                            17

                                  3                                                  10     

                                                      2m+1                                 

                                                                                            

1.1-расм.

 

 

 

     

{              [ к2],       1£к£ 3

              

              ,      3<к£ 6

 m =

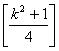             ,  6<к£10

                

             ,   10<к£ 25

                 

 

 

                                        о-вариант ечими

 

1. 1.1-расмдаги тармокли график (ТГ) куришнинг барча тартиб ва коидаларига мос келади, бирок бу график тула тартибланмаган. Куйида тартибланган ТГ келтирилган. 0-вариант учун иш давомийликлари 1.2-расмдаги ТГ иш йуналишлари устида курсатилган.

 

                                                        3                                                              

                          2                                                        7

                                                        4      8                                    5 

                                6

                      1                                               3          4                              10

            8                                     3                                          5                          13    

                                   13                         6   

     0                                                                            6                            6          11

                   

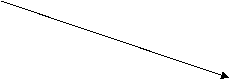
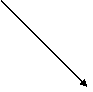
                             9                           7                 9                   8

                                                                                   10                        

                                                                                               13        4

                                                           5                                                   

                                                                                                             9

1.2-расм. Тартибланган тармокли график (ТГ).

 

      Ходиса руй беришининг дастлабки муддатини аниклашда тармокли график буйича  чапдаги ходисадан унгга караб харакатланамиз. (1.1) ёки (1.2) формулага кура i=0 ходиса учун tД(0)=0, i=1 учун tД(1)=tД(0)+t(0,1)=0+8=8c, i=2 ходиса учун tД(2)=tД(1)+t(1,2)=8+9=17c, чунки 2 ходиса учун битта олдинги йул L02:0®1®2 мавжуд; 3 ходиса учун tД(3)=max[tД(0)+t(0,3), tД(1)+t(1,9)]=max(13,12)=13c, i=3 ходиса учун иккита олдинги йул L:0 ®1®3, L:0®3 ва иккита олдинги 0 ва1 ходисалар мавжуд.

 

Худди шу каби колган ходисалар учун хам куйидагиларни хосил киламиз.

 

            tД(4)=max[tД(1)+t(1,4), tД(3)+t(3,4)]=max[8+6,13+10]=23с,

            tД(5)=max[tД(3)+t(3,5), tД(0)+t(0,5)]= max[13+7,0+9]=20 с,

            tД(6)=29 с ва х.к.

 

Критик йулнинг узунлиги охирги 11 ходисанинг дастлабки руй бериш муддатига тенг:

 

tД(11)=tкр=max[tД(9)+t(9,11),tд(10)+t(10,11)]=max[42+17,48+13]=max[59,61]=61 с

 

i- ходиса руй беришини охирги муддатини хисоблашда тармокда тескари йуналиш буйлаб харакат киламиз. (1.3), (1.4) формулаларга кура i=11 ходиса учун  ходиса руй беришининг охирги муддати t0(11) унинг дастлабки руй бериш муддатига тенг булиши керак, акс холда критик йул узунлиги узгариши мумкин.

 

                                t0(11)=tД(11)=61c

 

i=10 ходиса учун t0(10)=tкр-t(10,11)=61-13=48c, i=9 ходиса учун t0(9)=min[t0(10)- t(9,10), t0(11)-t(9,11)]=min[48-6,61-17]=min[42,44]=42c, чунки i=9 ходиса учун иккита кейинги йул мавжуд.

LC9: 9-10-11, 9-11 ва иккита кейинги 10 ва 11 ходисалар мавжуд. Худди юкоридагилар каби куйидагиларга эга буламиз.

 

                         t0(8)= t0(9)-t(8,9)=42-4=38c

                         t0(7)= t0(10)-t(7,10)=48-5=43c

                         t0(5)=min[t0(7)-t(6,7),t0(10)-t(6,10),t0(9)-t(6,9),t0(8)-t(6,8)]=

                                =min[43-4,48-5,42-13,38-8]=29c, ва х.к.

 

Энди (1.5) формула ёрдамида ходисаларнинг  вакт захираларини аниклаймиз,

 

                R(0)=0,     R(1)=t0(1)-tД(1)=9-8=1c,        R(2)=40-17=23c     ва х.к.

 

Масалан 2- ходисанинг  вакт захираси R(2)=23с, 2- ходисани руй бериш муддати 23с га кечикиши мумкинлигини билдиради, бунда умумий лойихани бажариш муддати узгармайди. Куйида 1.1. жадвалда тармокли график ходисаларининг вакт параметрлари келтирилган.

Жадвални тахлил килиш шуни курсатадики, 0 3 5 6 9 10 ва 11 ходисалар вакт захираларига эга эмас. Бу ходисалар критик йул ходисаларидир.

 

 

 

      1.1. жадвал. ТГ ходисаларнинг вакт параметрлари

 

Ходиса раками

Ходисанинг руй бериш муддати

Вакт захи-

 

дастлабки  tД(i)

охирги t0 (i)

раси  R(i)

 

0

1

2

3

4

5

6

7

8

9

10

11

 

 

0

8

17

13

23

20

29

33

37

42

48

61

 

0

9

40

13

26

20

29

43

38

42

48

61

 

0

1

23

0

3

0

0

10

1

0

0

0

 

2. ТГ иш параметрларини хисоблашга утамиз, (i,j) иш параметрларини хисоблашни (1,4) иш учун келтирамиз. (1,4) иш бошланишининг дастлабки муддати tдб (1,4) ишнинг биринчи ходисаси руй беришининг дастлабки муддатига тенг, яъни

                                        tдб(1,4)=tд(1)=8c,

у холда (1,4) иш тугашининг дастлабки муддати

                                        tдт(1,4)=tд(1)+t(1,4)=8+4=12с  

га тенг.

    Иш бошланишининг охирги муддати tоб(1,4)=tо(4)-t(1,4)=26-6=20с,

иш тугашининг охирги муддати эса tот(1,4)=tо(4)=26с га тенг.

Шундай килиб (1,4) иш [ 8,20 ]с  орасида  бошланиши  ва тугаши [ 12, 26 ]c  оралигида булиши керак.

   (1,4) ишнинг тулик вакт  захираси (1.5) формулага кура

                      

                         RT(1,4)=t0(4)-tД(1)-t(1,4)=26-8-6=12с,

 

яъни (1,4) иш муддатини 12с га купайтирш мумкин, бунда комплекс ишнинг бажарилиш муддати узгармайди. Иш параметрларидан хамда (1.4)- (1.7) формулаларидан фойдаланиб, ишларнинг колган параметрларини хам  хисоблаймиз.

Хисоблаш  натижалари куйидаги  жадвалда келтирилган.

 

 

 

 

 

 1. 2-жадвал. ТГ ишларининг вакт параметрлари

 

 

 №

 

 Иш

Ишнинг давомий

Лиги

Ишнинг бошлангич ва охирги муддати

Ишнинг вакт параметрлари

 

(i, j )

t (i,j )

tдб(i, j )

tдт(i, j )

tоб(i, j )

tот(i, j )

RT(i,j)

R1(i,j)

RЭ (i,j)

RБ(i,j)

1

(0,1)

8

0

8

1

9

1

1

0

0

2

(0,3)

13

0

13

0

13

0

0

0

0

3

(0,5)

9

0

9

11

20

11

11

11

11

4

(1,2)

9

8

17

31

40

23

22

0

-

5

(1,4)

6

8

14

20

26

12

11

9

8

6

(1,3)

4

8

12

9

13

1

0

1

0

7

(2,7)

3

17

20

40

43

23

0

13

-

8

(3,4)

10

13

23

16

26

3

3

0

0

9

(3,5)

7

13

20

13

20

0

0

0

0

10

(3,6)

6

13

19

23

29

10

10

10

10

11

(4,7)

8

23

31

35

43

12

9

2

-

12

(4,6)

3

23

26

26

29

3

0

3

0

13

(5,6)

9

20

29

20

29

0

0

0

0

14

(5,8)

10

20

30

28

38

8

8

7

7

15

(5,9)

6

20

26

36

42

16

16

16

16

16

(6,7)

4

29

33

39

43

10

10

0

0

17

(6,10)

5

29

34

43

48

14

14

14

14

18

(6,9)

13

29

42

29

42

0

0

0

0

19

(6,8)

8

29

37

30

38

1

1

0

0

20

(7,10)

5

33

38

43

48

10

0

10

0

21

(8,9)

4

37

41

38

42

1

0

1

0

22

(9,10)

6

42

48

42

48

0

0

0

0

23

(9,11)

17

42

59

44

61

2

2

2

2

24

(10,11)

13

48

61

48

61

0

0

0

0

 

3. ТГ критик йул ишларининг давомийлиги дисперсияси куйидагича булсин,

 

         d2(0,3)=2,5             d2(3,5)=2,1              d2(5,6)=3,2

        d2(6,9)=4,0              d2(9,10)=1,5           d2(10,11)=3,5

 

Лойихани бажариш муддати Т=63с га тенглиги эхтимолини бахолаш талаб килинади.Куйидаги формулалардан      

                                                       d2(L)=åd2(i,j),

    i,j                                                                                                                P(tкр£T)=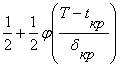

бунда j (Z) Лаплас функцияси,

 

 

      

      _________________________________    ________________     ____

d=Öd2(0,3+d2(3,5)+...+ d2(9,10)+ d2(10,11))  =Ö2,5+2,1...+ 1,5+3,5 =Ö16,8 »4,1     

фойдаланиб,

                              1        1        63-61     1      1       2         1      1      

        P(tкр£ 63) =  ---- + ----- j(-------)= ----+----j(----)= ----+---- j(0,49)=

                              2        2           4,1       2      2     4,1       2      2

        =0,5+0,50,376=0,688»0,69

 

тенгликларни хосил киламиз, яъни 0,69 эхтимол билан лойихани Т=63с да бажариш мумкин.

(1,4) ишнинг кучланиш коэффициенти Кн(1,L1) ни хисоблаймиз. (1,4) ишдан утувчи максимал йул L4 :0®1®4®6®8®10®11 нинг давомийлиги t(Lmax)=t(L4)=49 c га тенг. Бу йул критик йул билан 6®9®10®11 кисмида усма-уст тушади, унинг давомийлиги tкр=13+6+13=32с га тенг. (1.8 ) формулага кура

  49-32       17

Кн(1,4)=--------- = ----= 0,59

  61-32       29

 

Энди тармокли графикни хусусий оптималлаштириш масаласини курамиз. Масалани ечиш учун (i,j) иш давомийликларидан ташкари унинг чегаралари а(i,j) ва b(i,j) хамда ишни тезлаштириш харажат курсаткичлари h(i,j) кийматларини билишимиз керак. Бу кийматлар (1.3) - жадвалда келтирилган.

 

1.3 - жадвал. Тармокли графикни хусусий оптималлаштириш натижалари.

 

 

№

 

Иш

Ишнинг дав. (сут-да)

  а       t       b      

(i,j)    (i,j)   (i,j)

Ишнинг эркин вакт

зах-сиRЭ(i,j)  (сут-да)

Ишнинг нархи

с (i,j)

Ишни тез-ш у-н хар-т коэффиц-т. сум/сут

Лойиха нархини камай-ши (сум)

1

(0,5)

 5        9      14

11

60

8

5*8=40

2

(1,4)

4         6      10

9

28

4

4*4=16

3

(1,3)

3        4        6

1

37

12

1*12=12

4

(2,7)

2        3        7

13

86

6

4*6=24

5

(3,6)

4        6        9

10

92

10

3*10=30

6

(4,7)

3        8       14

2

48

5

2*5=10

7

(4,6)

1        3        6

3

64

12

3*12=36

8

(5,8)

5       10      18

7

15

1

7*1=7

9

(5,9)

3        6       12

16

86

7

6*7=42

10

(6,10)

2        5       10

14

44

5

5*5=25

11

(7,10)

1        5       15

10

74

4

10*4=40

12

(8,9)

2       4        8

1

20

3

1*3=3

13

(9,11)

11     17      23

2

40

4

2*4=8

         ЖАМИ                                                               694                     -                     293            

 

Хар бир (i,j) ишнинг давомийлигини шундай узгартириш керакки, бунда тармок ходисаларнинг дастлабки (кутилаётган) руй бериш муддати узгармай колсин, яъни эркин вакт захираси RЭ(i,j) гача узайтириш керак.Бошлангич холатдаги тармокли графикнинг нархи ундаги барча нархларнинг йигиндисига тенг. Бунга вакт захираларига эга булмаган 1.4-жадвалда келтирилмаган ишлар нархи хам киради.

 

                          С=694+50+45+...+35+10=1216  (сум)

 

1.3-жадвалда факат эркин вакт захирасига эга булган ишлар параметрлари келтирилган. Колган (i,j) ишларнинг нархи куйидагича:

 

с (0,1)=50,         с (0,3)=45,        с (1,2)=82,      с (6,9)=75,

с(3,5)=72,          с(5,6)=50,         с(6,7)=26,       с(6,8)=42.                           (1.12)

с (9,10)=35,       с (10,11)=10,    с (3,4)=55,

Жадвалда эркин вакт захираларининг хаммаси ишнинг давомийлигини узайтиришга фойдаланилган ишлар остида чизилган.

Янги режанинг нархи С-DС=1216-923с га тенг, яъни деярли 25% га камайди. Янги режа 1.3-расмда келтирилган. Янги критик йуллар хосил булганлигига  ишонч хосил килиш кийин эмас, бу йулларнинг узунлиги хам tкр=61с га тенг.

Масалан: 0®1®3®4®7®10®11, 0®3®5®6®8®9®11, 0®3®5®8®9®11, 0®1®3®4®6®7®10®11.

Бу тармокли графикдаги 64 та тулик йулдан 28 таси критик йулдир. Агар ишлар давомийлигининг юкори чегаралари вакт захираларидан тула фойдаланишга имкон берганда, янги режадаги барча тулик йуллар критик йул булар эди. Шундай килиб тармокли графикни оптималлаштириш натижасида янги режа хосил килдик, бунда критик йул узунлиги tкр=61 суткага, лойихани минимал нархи эса 923 сумни ташкил этади.

                                                          7     

                           2                                                        7       15

                                                          10

                                              4                                4 

        8                       10                    6                                                      10        11

 0                1                                                           6               10                  13

            

                                                           10                                                              

                                            3                      

                      14                                                        8            13          6        19 

                                                   7          9     17                   5

     

                                                              5                                               9

                                                                                      12

 

     1.3-расм. Оптималлаштирилган тармокли график.

Оммавий хизмат кӯрсатиш назарияси ёрдамида алоқа корхоналарининг иш жараёнларини оптимал ташкил қилиш.

 

Асосий тушунчалар.

Талаблар тасодифий вақтда келадиган ва уларга хизмат курсатишга мосланган ихтиёрий системага оммавий хизмат курсатиш системаси (ОХКС) дейилади. ОХК назарияси ОХКСларида буладиган тасодифий жараёнлар билан шуғулланади. Хизмат курсатишга мосланган ихтёрий қурилма хизмат курсатиш каналлари дейилади. ОХКСлари бир каналли, куп каналли, талаблар навбатда турадиган ва навбатсиз булиши мумкин. Навбатсиз ОХКСда барча каналлар банд булган пайтда системага келган талаб уни тарк этади ва системанинг кейинги фаолиятида иштирок этмайди. Навбатда турадиган ОХКСда эса барча каналлар банд булган вақтда келган талаб навбатда туриб, бирор канал  бушагунча хизматни кутади. Навбатда турадиган талаблар сони чекли ва чексиз куп булиши мумкин. Талаблар навбати уларни сонидан ташқари талабни навбатда туриш вақти билан хам аниқланади.

Агар системани бир холатдан бошқа холатга утказувчи ходисалар содда оқимдан иборат булса, ОХКСни аналитик усулда текшириш анча қулай булади. Ходисалар орасидаги вақт интерваллари курсаткичли тақсимотга эга булиб, унинг параметри оқим интенсивлигига тенг булган оқим содда оқим дейилади. Биз асосан содда оқимга эга булган ОХКСлари билан шуғулланамиз.

Агар барча ходисалар оқими содда оқимдан иборат булса, ОХКСда булаётган жараён дискрет холатли ва узлуксиз вақтли Марков жараёнини  ташкил этади. Бу жараён учун баъзи бир  шартлар бажарилганда финал стационар холатлар мавжуд булади, у холда холатлар эхтимоли ва бошқа характеристикалар вақтга боғлиқ булмайди.

Системанинг самарадорлик курсаткичлари сифатида қуйидагилар қаралади:

А – ОХКСда бирлик вақт давомида хизмат курсатиладиган талаблар уртача сони ёки системанинг абсолют утказиш қобилияти;

Q – келган талабга хизмат курсатиш эхтимоли ёки нисбий утказиш қобилияти;

Pт – талабни системани тарк этиш эхтимоли,

                                     Рт = 1-Q

- системадаги талабларнинг уртача сони;

- навбатда турган талаблар уртача сони;

- талабни навбатда туриш уртача вақти;

П – талабни навбатда туриш эхтимоли;

Хизмат курсатишни оптимал ташкил қилиш масаласини ечиш учун қуйидаги мақсад функциясини минималлаштириш зарур булади:

                                                           (2.1)

бунда Чi – i қурилмага хизмат курсатувчи ходимлар сони; Кi – хизмат курсатувчи ходимларни алмаштириш коэффициенти; З – бир электромеханикнинг бирлик вақтдаги маоши; - бирлик вақт давомида бир қурилмани носозлиги сабабли корхонани курган зарари. - носоз қурилмаларнинг математик кутулиши; - битта захирадаги қурилмага келтирилган харажат; m – қурил-

малар турининг сони; Ri – захирадаги i-турдаги қурилмалар сони.

 

2 – амалий иш.                                                                                                             Бир каналли хизмат курсатиш системалари.

Фараз қилайлик l талабларнинг кириш оқими интенсивлиги ва  битта талабга хизмат курсатиш (уртача) вақти булсин.

Ро – системада битта хам талаб булмаслик эхтимоли, Рк – эса мумкин булган n та талабдан к тасини системада булиш эхтимоли булсин, к=1,2, ... , n.

қуйидаги муносабатлар турли холат эхтимолларини аниқлайди:

Агар Ро нинг қиймати маълум булса, у холда бу формулалардан фойдаланиб, Рk ларни Р0 орқали ифодалаб уларни йиғиндиси 1га тенглигидан фойдаланамиз:

 

 

 

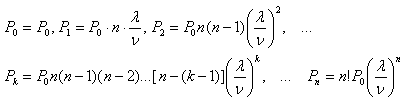
                                                                                                                   (2.2)

Бу тенгликларни унг ва чап қисмларини қушиб қуйидаги тенгликни хосил қиламиз:

бундан Р0 ни, сунгра эса қолган Рk ларни аниқлаймиз.

Рk эхтимолликни билган холда системанинг асосий самарадорлик курсаткичларини хисоблаш мумкин.

Системадаги уртача талаблар сони

ни хизмат курсатиш керак булган қурилмалар сонига булиб, битта қурилмани буш туриш коэффициенти a ни аниқлаймиз:

                                                                                   (2.3)

Қурилмани хизматни кутиш эхтимоли П=1-Ро га тенг.

Хизматни кутаётган қурилмалар уртача сони:

                                                                                                     (2.4)

формула билан аниқланади.

Хизматни кутаётган қурилмаларнинг буш туриш коэффициенти навбат кутаётган талабларни хизмат курсатиладиган талабларга нисбати билан аниқланади:

                                                                            (2.5)

Уртача кутиш вақти хизматни кутаётган қурилмаларнинг уртача сонини хизматга келаётган талабалар сони орасидаги уртача вақтга купайтмасига тенг:

 

                                                                      (2.6)

Хизмат курсатаётган каналнинг буш туриш коэффициенти

                     

га тенг.

Топшириқ

Навбатчи электромеханикнинг зиммасига l та қурилмани назорат қилиш ва қурилмалар ишдан чиққанда уларни тамирлаш юкланган. Хар бир қурилма уртача t минутда тамирлашни талаб қилади. Хар бир қурилмани тамирлаш учун эса мин. вақт сарфланади.Маълумотларни статистик тахлил қилиш натижаси тамирланишга мухтож қурилмаларни содда оқимдан иборат эканлигини тасдиқлайди. Электромеханикнинг хизмат курсатиш жараёни оптимал ташкил қилинсин.

Бунда t=15+қолдиқ.

             қолдиқ+1.

0-вариант ечими

Масалани t=15 мин., l=5 ва мин. булганда ечамиз.

Тақсимот параметрлари:

 бундан

 

(2.2) формулалардан фойдаланиб қуйидаги жадвални хосил қиламиз. Бу маълумотлар кейинги хисоблашлар учун зарур булади.

                                                                                              2.1-жадвал.

k

Pk

Pk/P0

Pk

kPk

(k-1)Pk

0

P0

1

0,4530

0

-

1

5(2/15)P0

0,6667

0,3020

0,3020

0

2

0,3555

0,1611

0,3222

0,1611

3

0,1421

0,0644

0,1932

0,1288

4

0,0378

0,0172

0,0688

0,0516

5

0,0051

0,0023

0,0115

0,0092

 

Жами

2,2072

1,0000

0,8977

0,3507

 

Барча холат эхтимолликлари йиғиндиси 1га тенг.

 бундан         

Бундан электромеханикнинг буш туриш коэффициенти га тенглиги келиб чиқади.

Бир вақтда ишламаётган қурилмаларнинг уртача сони =0,8977 га тенг, буш туриш коэффициенти эса a=0,8977/5=0,18, яъни 18% иш вақтида битта қурилма носозлиги сабабли ишламайди. Хизмат курсатиш эхтимоли

                  П=1-Р0= 1-0,453=0,547

Навбат узунлиги 0,3507. Битта қурилмани навбатда туриш вақти яъни 7% иш вақтида бир қурилма навбатда туриши сабабли ишламайди.

Уртача кутиш вақти

Қурилмани буш туришидан келган зарарни электромеханик-

нинг ойлик маоши билан солиштириб электромеханик назорат қи-

лаётган қурилмалар сонини қанчага қисқартиришни бахолаш мақ-

садга мувофиқдир. 2.2 жадвалда ишламаётган қурилмалар сони ва электромеханикнинг буш булиш вақтларининг математик кутилиш-

лари қурилмалар сонининг турли қийматлари учун (n=1,2,...,5) келтирилган.                                                                           2.2-жадвал

k

Pk/P0

Pk

kPk

(1-k)Pk

 

 

n=1

 

 

0

1

0,8824

0

0,8824

1

0,1333

0,1176

0,1176

-

Жами

1,1333

1,0000

0,1176

0,8824

 

 

n=2

 

 

0

1

0,7679

0

0,7679

1

0,2667

0,2048

0,2048

-

2

0,0356

0,0273

0,0546

-

Жами

1,3022

1,0000

0,2594

0,7679

 

 

n=3

 

 

0

1

0,6576

0

0,6576

1

0,3999

0,2630

0,2630

-

2

0,1066

0,0701

0,1402

-

3

0,0142

0,0093

0,0279

-

Жами

1,5207

1,0000

0,4311

0,6576

 

 

n=4

 

 

0

1

0,5522

0

0,5522

1

0,5332

0,2945

0,2945

-

2

0,2132

0,1177

0,2354

-

3

0,0569

0,0314

0,0942

-

4

0,0076

0,0042

0,0168

-

Жами

1,8109

1,0000

0,6909

0,5522

 

 

n=5

 

 

0

1

0,4530

0

0,4530

1

0,6667

0,3020

0,3020

-

2

0,3555

0,1611

0,3222

-

3

0,1421

0,0644

0,1932

-

4

0,0378

0,0172

0,0688

-

5

0,0051

0,0023

0,0115

-

Жами

2,2072

1,0000

0,8977

0,4530

Агар битта қурилманинг бир соатлик бӯш бӯлиши 3 сумга, электромеханикнинг бир соатлик бӯш бӯлиши ташкилотга 1 сумга туғри келса, у холда умумий зарар қуйидагича бӯлади:

n=1 бӯлганда Э=3ž0,1176+1ž0,8824=1,2352

n=2                  Э=3ž0,2594+1ž0,7679=1,5461

n=3                  Э=3ž0,4311+1ž0,6576=1,9509

n=4                  Э=3ž0,6409+1ž0,5522=2,4749

n=5                  Э=3ž0,8977+1ž0,4530=3,1461

            Натижалар шуни курсатадики, битта электромеханик битта қурилмага хизмат курсатганда харажатлар минимал булади. Назорат қилинаётган қурилмалар сонини ошиши ишлаб чиқариш харажатларини ошишига олиб келади.

 

                                            3 - амалий иш.

Кӯп каналли хизмат кӯрсатиш системалари.

Системани к та қурилмага бир вақтда хизмат курсатиш эхтимолларини аниқловчи формулаларни 2 гурухга ажратамиз.

1. к £ r (к=0,1, ... r). Бунда хизмат курсатиш каналлари талаблар системага келиши билан хизмат курсата бошлайди. Мос эхтимолликлар қуйидагича ифодаланади:

2. к>r (к=r+1,r+2, ... , n). Системага келган талаблар навбатни ташкил қилади,

Р0 эхтимолликни аниқлаш учун барча Рк ларни Р0 орқали ифодалаймиз: к£r булганда

к>r булганда

        

        

         .        .        .        .        .        .        .        .

         .

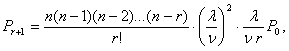
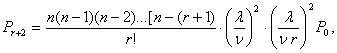
Барча холатлар эхтимоллари йиғиндисини 1га тенглаб, Р0ни аниқлаш учун тенглама хосил қиламиз. Р0ни билган холда барча Ркларни топамиз. (к=1,2, ... ,n). Энди системани сонли характеристикаларини аниқловчи формулаларни келтирамиз.

Системада жойлашган уртача қурилмалар сони:         , битта қурилмани буш туриш коэффициенти: .

Барча хизмат курсатиш каналлари банд ва талабларни навбатда туриш эхтимоли:

Хизматни кутаётган талабларнинг уртача сони ёки навбат узунлиги:

Хизматни кутаётган қурилмани буш туриш коэффициенти:

Талабни хизматни уртача кутиш вақти:

Буш турган хизмат курсатиш каналларининг уртача сони:

Хизмат курсатиш каналларининг буш туриш коэффициенти:

 

         Топшириқ.

Фараз қилайлик битта қурилмани электромеханик уртача хар t минутда тамирлаб туради, тамирлашга сарфланадиган уртача вақт га тенг.

а) Бригадада m электромеханик булиб, улар l та қурилмани назорат қиладилар.

б) l+5 та қурилмани m+1 та электромеханикдан иборат бригада назорат қилади.Бунда t=12 + қолдиқ,    к=1,2,3,…24.

              қолдиққолдиқ

Хизмат курсатиш системанинг иши оптимал ташкил қилинсин.

 

0-    вариант ечими.

Масалани t=15 мин., l=10, мин. ва m=2 га тенг булганда ечимини келтирамиз. Иккала холда хам

              ,                              

а) хол учун холат эхтимоллари (1.3) жадвалда келтирилган. Натижада қуйидагилар хосил қилинган:

1.3-жадвал

k

Pk

Pk/P0

Pk

kPk

k-2

(k-2)Pk

2-k

(2-k)Pk

0

P0

1,0000

0,25813

0

-

-

2

0,51626

1

P1=10P02/15

1,3333

0,34417

0,34417

-

-

1

0,34417

2

0,8000

0,2065

0,41300

-

-

0

0

3

0,42667

0,11014

0,33042

1

0,11014

-

-

4

0,19911

0,0514

0,20560

2

0,1028

-

-

5

0,07964

0,02056

0,10280

3

0,06168

-

-

6

0,02655

0,00685

0,04110

4

0,0274

-

-

7

0,00708

0,00183

0,01281

5

0,00915

-

-

8

0,00142

0,00037

0,00296

6

0,00222

-

-

9

0,00019

0,00005

0,00045

7

0,00035

-

-

10

0,00001

0,00000

0,00003

8

0,00002

-

-

 

Жами

3,874

1,00000

1,45334

 

0,31376

 

0,86043

 

P0=1/3,874=0,25813

 

 

 

 

 

 

 

- бӯш турган қурилмаларнинг ӯртача сони.

 

- битта қурилмани буш туриш коэффициенти.

 

П=1-(Р0+Р1)=0,3977 - қурилмага хизмат курсатиш эхтимоли.

 

=0žР2+(3-2)Р3+(4-2)Р4+(5-2)Р5+(6-2)Р6+ ... +(10-2)Р10=0,31376

– хизматни кутаётган қурилмалар уртача сони ёки навбат узунлиги.

 

- навбатта турган қурилмани буш туриш коэффициенти.

 

 

2Р0+Р1+0žР2=0,86043 –буш турган каналлар уртача сони.

 

- бир канални буш туриш коэффициенти.

 

б) хол учун хисоблашлар (1.4) жадвалда келтирилган:

          Системанинг характеристикалари:                        

 

П=1-(Р0+Р1+Р2)=1-(0,14282+0,28564+0,2666)=0,30494

 

битта қурилма.

 

b=0,26393/15=0,01759

 

0,26393·60/15·4=0,2639 мин.

С=1,26634 , g=1,26634/3=0,4221.

 

 k

Pk

Pk/P0

Pk

kPk

k-3

(k-3)Pk

3-k

(3-k)Pk

0

P0

1,0000

0,14282

0

-

-

3

0,42846

1

P1=15P02/15

2,0000

0,28564

0,28564

-

-

2

0,57128

2

Р2=(14/2)Р12/15

1,86667

0,26666

0,53320

-

-

1

0,26666

3

Р3=(13/3)Р22/15

1,07848

0,15405

0,46215

0

-

0

0

4

Р4=12 Р32/15

0,5752

0,08216

0,32864

1

0,08216

-

-

5

Р5=11 Р42/15

0,28125

0,04017

0,20085

2

0,08034

-

-

6

Р6=10 Р52/15

0,12500

0,01785

0,10710

3

0,05455

-

-

7

Р7=9 Р62/15

0,05000

0,00714

0,04998

4

0,02856

-

-

8

Р8=8 Р72/15

0,01778

0,00254

0,02032

5

0,0127

-

-

9

Р9=7 Р82/15

0,00553

0,00079

0,00711

6

0,00474

-

-

10

Р10=6 Р92/15

0,00147

0,00021

0,0021

7

0,00147

-

-

11

Р11=5 Р102/15

0,00033

0,00005

0,00051

8

0,00037

-

-

12

Р12=4 Р112/15

0,00006

0,00001

0,0001

9

0,00007

-

-

13

Р13=3 Р122/15

0,00001

0

0,00001

10

0,00001

-

-

14

Р14=2 Р132/15

0

0

0

11

-

-

-

15

Р15=Р14 2/15

0

0

0

12

-

-

-

 

Жами

7,00178

1,00003

1,99771

-

0,26393

-

-

2.4-жадвал

Юқоридаги мисоллардаги натижаларни таққослаш мақсадида 2.5- жадвални келтирамиз.                                                          2.5- жадвал

N

m

n

a

П

b

tн

g

5

1

5

0,1795

0,5470

0,0702

1,052

0,453

10

2

5

0,1453

0,3977

0,0314

0,471

0,4302

15

3

5

0,1332

0,3049

0,0176

0,264

0,4221

Биринчи мисолда бир электромеханик 5 та қурилмани назорат қилаётганда ва иккинчи мисолда хам битта электромеханик 5та қурилмага хизмат курсатаётгандаги бир қурилмани буш туриш коэффициентларини солиштирамиз. Иккита электромеханик хизмат курсатаётганда қурилмани буш туриш коэффициенти 0,0342 га, 3 та электромеханик хизмат курсатаётганда эса 0,0463 га, биринчи мисолдагига нисбатан камаяди. Шундай қилиб ишлаб чиқариш бир қурилма учун 3,4 ва 4,6% га мос равишда ортди. Хисоблашлар бригада булиб хизмат қилиш мақсадга мувофиқлигини курсатади.

Фойдаланилган адабиётлар рӯйхати.

1.      В. А. Барсук, Н. М. Губин. Экономико-математические методы и модели в планировании и управлении в отрасли связи. М.1984

2.      А. И. Карасев, Н. Ш. Кремер. Математические методы и модели в планировании. М. Экономика. 1987

3.      Е. Вентцель, Л. А. Овчаров. Прикладные задачи теории вероятностей. М. Радио и связь. 1983

4.      Е. Вентцель. Исследование операции. М.Сов.радио, 1972.-550с.

 

                                              Мундарижа

 

Режалаштириш ва бошкаришнинг тармокли усуллари…………………3

1-амалий иш……………………………………………………………………6

Оммавий хизмат кӯрсатиш назарияси ёрдамида алоқа корхоналарининг иш жараёнларини оптимал ташкил қилиш………..13

2- амалий иш………………………………………………………………….14

3- амалий иш………………………………………………………………….18

 

 

 

 

 

                                                                Жараёнлар тадқиқоти фанидан

амалий ишларни бажариш

 учун усулий қӯлланма .

 

 

 

                                                              Тузувчи: Норхӯжаев О.О.

 

 

                              

Иқтисод факултети услубий кенгашининг

                                                    мажлисида кӯриб чиқилди ва нашрга

                                                    тавсия этилди ( 15.03.2001й, баён №7 )