Узбекское Агентство Почты и Телекоммуникации
Ташкентский Электротехнический Институт Связи
Кафедра Высшей математики
Усманов Р.Н., ст. пр. Шопен И.Л.
Высшая математика
Часть 2
Ташкент 1999
Оглавление.
|
Введение |
|
2 |
|
Лекция 1 |
Функции нескольких переменных. Предел , непрерывности функции нескольких переменных. Частные производные. |
3 |
|
Лекция 2 |
Полный дифференциал. Теорема о дифференцируемости функции двух переменных. Дифференцирование сложной и неявной функции |
5 |
|
Лекция 3 |
Экстремум функции двух переменных. Необходимые и достаточные условия существования экстремума. |
8 |
|
Лекция 4 |
Дифференцирование уравнения. Основные понятия и определения. Дифференцирование уравнения первого порядка. Задача Коши. |
9 |
|
Лекция 5 |
Основные типы дифференциальных уравнений первого порядка. Однородные уравнения первого порядка. Линейные дифференциальные уравнения. Уравнение Бернули. Дифференциальные уравнения в полных дифференциалах. |
11 |
|
Лекция 6 |
Дифференциальные уравнения высших порядков. |
14 |
|
Лекция 7 |
Линейные дифференциальные уравнения n-го порядка. Линейный оператор и его свойства. Решение линейных однородных дифференциальных уравнений второго порядка. |
15 |
|
Лекция 8 |
Решение линейных однородных уравнений n-го порядка. Линейные дифференциальные уравнения с постоянными коэффициентами. |
16 |
|
Лекция 9 |
Решение линейного неоднородного уравнения с правой частью специального вида. Метод вариации произвольных постоянных. |
18 |
|
Лекция 10 |
Операционное исчисление. Основные понятия. Теоремы существования и единственности изображения. |
20 |
|
Лекция 11 |
Основные теоремы операционного исчисления: линейности, подобия, смещения, запаздывания, об интегрировании и дифференцировании оригинала, об интегрировании и дифференцировании изображения. Интеграл Дюамеля. |
21 |
|
Лекция 12 |
Решение линейных дифференциальных уравнений и систем дифференциальных уравнений с постоянными коэффициентами операционным методом. |
23 |
|
Лекция 13 |
Числовые ряды. Сумма ряда. Геометрический ряд и его сходимость. Свойства сходящихся рядов |
25 |
|
Лекция 14 |
Знакоположительные ряды. Необходимое условие сходимости ряда. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения, Даламбера, радикальный признак Коши. |
26 |
|
Лекция 15 |
Интегральный признак Коши. Обобщенный гармонический ряд. Знакопеременные ряды. Признак Лейбница. Абсолютная и условная сходимость знакопеременного ряда. Свойства абсолютно и условно сходящихся рядов. |
29 |
|
Лекция 16 |
Функциональные ряды. Равномерная сходимость функционального ряда. Свойства равномерно сходящихся рядов |
32 |
|
Лекция17 |
Степенные ряды. Радиус и интервал сходимости степенного ряда. Свойства сходящихся степенных рядов. |
33 |
|
Лекция 18 |
Ряды Тейлора и Маклорена. Разложение в ряд Маклорена некоторых элементарных функций. |
35 |
|
Лекция 19 |
Ряды Фурье. Разложение в ряд Фурье по ортогональной системе функций. |
37 |
|
Лекция 20 |
Ряд Фурье для функции с периодом Т=2 |
38 |
|
Лекция 21 |
Разложение в ряд Фурье для четных , нечетных функций и функций, заданных на половине периода. |
40 |
|
Лекция 22 |
Ряд Фурье в комплексной форме. |
42 |
|
Лекция 23 |
Интеграл Фурье. |
43 |
|
Лекция 24 |
Интеграл Фурье для четных и нечетных функций. |
44 |
|
Лекция 25 |
Интеграл Фурье в комплексной форме. Равенства Парсеваля. |
44 |
|
Вопросы |
для самоконтроля |
46 |
|
|
|
|
Содержание:
1. Введение
2. Функции нескольких переменных
3. Дифференциальные уравнения
4. Операционое исчисление
5. Ряды
6. Ряды Фурье и интеграл Фурье
Введение.
Конспект лекций по высшей математике написан в соответствии с рабочей программой изучения курса высшей математики во II семестре по специальности телекоммуникация и телекоммуникационные системы.
В программу курса высшей математики во втором семестре входят разделы:
1. Функции нескольких переменных
2. Дифференциальные уравнения
3. Операционое исчисление
4. Ряды
5. Ряды Фурье и интеграл Фурье
ЛЕКЦИЯ 1
ФУНКЦИИ НЕСКОЛЬКИХ (МНОГИХ) ПЕРЕМЕННЫХ.
Определение функции нескольких переменных.
Функцией двух переменных называется правило или закон, по которому каждой паре чисел (х; у)ÎD соответствует единственное zÎE.
х и у – независимые переменные ÎD; z – зависимая переменная ÎE. Между переменными х и у и в зависимости от их изменения переменной z существует функциональная зависимость, т.е. изменение двух переменных х и у влечёт за собой изменение переменной z. Тогда х,у – аргументы, а z – функция: z=f(x;y), (1)
D – область определения z=f(x;y), Е – область значений z=f(x;y)
Аналогично, если x, y, z – независимые переменные, а их изменение влечёт за собой изменение зависимой переменной u, то закон (правило), по которому происходит эта функциональная зависимость, называется функцией трёх переменных.U=f(x;y;z) (2)
И, в общем, если x, y, z, …, t – n независимых переменных, а U – (n+1) зависимая переменная, то U = f(x; y; z; …;t) – функция нескольких переменных, n переменных.(3)
Так как (х, у) – координаты точки МÎD, то z = f(x, y) = f(M). Аналогично, если (x, y, z, …,t) – координаты т.М в n – мерном пространстве, то U=f(M) – функция зависящая от n – переменных.
Способы задания функции нескольких переменных: аналитический, графический, табличный.
1. Аналитический. Функция задаётся явно, в виде формулы z=f(x; y), либо неявно F(x; y; z) = 0. Например: Z = ln(x2 + y2 – 1) или z2+ax3+lg y = 1
Областью определения функции двух переменных называется множество точек (х, у), удовлетворяющих заданию функции, как правило, это область на плоскости ХОУ.
Например: Z = ln(1- x2 - y2 ),
D(z): 1 – x2 – y2 > 0, x2 + y2 < 1, т.е. областью определения является круг с центром в начале координат и радиуса 1, причём точки, лежащие на окружности не входят в область.
 |
2. Геометрический. Графиком функции двух переменных z=f(x; y) в прямоугольной декартовой системе координат в
пространстве является в общем случае поверхность. Например. Верхняя часть
эллипсоида ![]() является
графиком функции
является
графиком функции ![]() ,
а нижняя его часть графиком функции
,
а нижняя его часть графиком функции ![]()
Предел функции нескольких переменных.
d - окрестностью т.М0 называется круг с центром в т.М0 и радиусом d:
МÎОd (М0) Û ![]()
Число А называется пределом функции z
= f(x; y)
= f(M) при М ® М0, если для любого числа e > 0 найдётся такая d - окрестность точки М0(х0;
у0), что для любой точки М(х; у) этой окрестности (за исключением,
быть может, точки М0) имеет место неравенство ![]() или
или ![]() , т.е.
, т.е. ![]() Û"e>0$ d>0:
Û"e>0$ d>0:
![]() .
.
Функция двух переменных называется бесконечно малой, если её предел равен нулю, т.е.
f(x, y) – называется бесконечно малой при ![]() (или
(или ![]() ), если
), если ![]()
Свойства пределов функций нескольких переменных аналогичны свойствам пределов функций, зависящей от одной переменной.
Непрерывность функции нескольких переменных.
Z = f(x,y) = f(M) называется непрерывной в т.М0, если она в этой
точке определена, т.е. ![]() или
или ![]() , и
, и ![]() .
.
Область состоящая только из внутренних точек, называется открытой областью.
Область состоящая из внутренних точек и всех граничных точек, называется замкнутой областью.
Функция называется непрерывной в D, если она непрерывна в каждой внутренней точке этой области.
Функция называется непрерывной в замкнутой области ![]() , если она непрерывна в
каждой внутренней точке этой области и на её границе.
, если она непрерывна в
каждой внутренней точке этой области и на её границе.
Пусть x получает приращение Dx, а y получает приращение Dy, тогда z = f(x,y) получает полное приращение Dz = f(x + Dx, y + Dy) – f(x, y).
Функция z = f(x,y) называется непрерывной в точке (x, y), если она в этой точке определена и бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, т.е. lim Dz = 0.
Свойства непрерывных функций справедливые для функции одной переменной, аналогично выполняются и для функции, зависящей от нескольких переменных.
В частности, справедлива теорема Вейерштрасса и теорема Коши для функций, непрерывных в замкнутой области.
Если z = f(x,y) непрерывна в замкнутой области ![]() , то
, то
1. Функция достигает в этой области своё наименьшее (m) и своё наибольшее (M) значения.
2.
"(x,
y) Î D: ![]() .
.
Частные производные I порядка.
Рассмотрим функцию z = f(x,y)
1)
Пусть х получает Dх, а у
остаётся неизменным, тогда z получает частное
приращение по х: ![]() .
.
![]() (4)
(4)
Конечный предел отношения частного приращения функции к
вызвавшему это приращение приращению аргумента при условии, что приращение
аргумента стремится к нулю и этот предел не зависит от ![]() называется частной производной I порядка и обозначается (4).
называется частной производной I порядка и обозначается (4).
2)
Пусть у получает приращение Dу;
то ![]()
![]() (5)
(5)
Практически при нахождении частных производных I порядка переменной является та, по которой вычисляется производная, а все остальные буквы, цифры играют роль постоянной.
Частные производные высших порядков.

 - частные производные I
порядка.
- частные производные I
порядка.
 -
частные производные II порядка.
-
частные производные II порядка.
![]() и
и
![]() называются
смешанными производными.
называются
смешанными производными.
Теорема о равенстве смешанных производных.
Пусть z = f(x,y) имеет непрерывные смешанные производные II порядка.
Смешанные производные не зависят от последовательности дифференцирования, т.е.
![]()
Частные производные III порядка –
это частные производные от производных II порядка ![]() и т.д.
и т.д.
Частные производные n – порядка – это частные производные от производных (n – 1) порядка.
ЛЕКЦИЯ 2
Полный дифференциал.
Рассмотрим функцию z = f(x; y).
Dz = f(x+Dx; y+Dy) – f(x; y) - полное приращение функции z = f(x; y).
z = f(x; y) называется дифференцируемой в т.(х; у), если полное приращение этой функции представляется в виде
![]() (6)
(6)
A и B не
зависят от Dx и Dy, а ![]() - бесконечно малое при
- бесконечно малое при 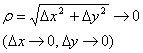 , бесконечно малое
, бесконечно малое ![]() -
бесконечно малое более высокого порядка, чем r,
т.е.
-
бесконечно малое более высокого порядка, чем r,
т.е. ![]()
Теорема о дифференцируемости функции.
Если z = f(x; y) имеет непрерывные частные производные и
![]() (7), то функция z
= f(x; y)
является дифференцируемой в точке (х; у).
(7), то функция z
= f(x; y)
является дифференцируемой в точке (х; у).
Первое слагаемое из (7) является главной частью приращения функции и оно линейно относительно Dx и Dy.
Главная часть приращения функции линейная относительно приращения аргументов называется полным дифференциалом функции z = f(x; y) и обозначается:
![]() (8)
(8)
или Dx=dx, Dy=dy,
то ![]() (9)
(9)
(9) – полный дифференциал функции.
![]() (10)
(10)
(10) – частные дифференциалы функции z
= f(x; y),
причём ![]()
Замечание !!!: ![]()
Если ![]() , то
, то ![]() - полный дифференциал.
- полный дифференциал.
Применение полного дифференциала в приближённых вычислениях.
Пусть z = f(x, y), x = x0 + Dx, y = y0 + Dy, тогда Dz = f(x0+Dx; y0+Dy) – f(x0; y0) и
Dz = dz + w, где w
- бесконечно малая при Dx®0 и Dy®0. Тогда ![]()
![]() (11)
(11)
(11) – формула для приближённого вычисления значения функции.
Дифференцирование сложной функции.
ТЕОРЕМА
Если z = f(x; y), а x = x(t), y = y(t), то z = f(x(t); y(t)) – сложная функция.
Если z = f(x; y) дифференцируема по х и по у, и x(t), и у(t) дифференцируемы по t, то z = f(x(t); y(t)) дифференцируема по t и имеет место формула:
![]() (12)
(12)
Так как z = f(x; y) дифференцируема в (х; у), то ![]() , w - бесконечно малое при
, w - бесконечно малое при ![]() ,
при
,
при ![]() и
и
![]()
Если t получает приращение Dt, то x получает приращение Dx; а y получает приращение Dy и, тогда, z получает приращение Dz, причём Dz представима в виде (7)
По определению производной: ![]() .
.
w -
бесконечно малая более высокого порядка, чем r, т.е. ![]()
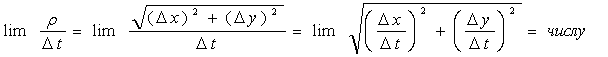
Пусть z = f(x; y); х = х; у = у(х).
Тогда по (12), полагая, что роль t
исполняет х и ![]() ,
получим
,
получим
![]() (13)
– формула полной производной.
(13)
– формула полной производной.
Аналогично, если рассмотреть функцию, зависящую от большего числа переменных.
Например, рассмотрим функцию, зависящую от трёх переменных:
U = f(x, y, z), где x = x(t), y = y(t), z = z(t)
![]() (14)
(14)
Если z = f(x; y; t), x = x(t), y = y(t) Þ полная производная:
![]() (15)
(15)
Пусть z = f(x; y); x = x(U,J); y = y(U,J) z = f(x(U,J); y(U,J))
z = f(x; y) – дифференцируема по х и по у,
а x(U,J) и y(U,J) –
дифференцируемы по U и по J. Тогда функция z
дифференцируема по U и по J, причём ![]() и
и ![]() находится по:
находится по:
![]() (16)
(16)
![]() (17)
(17)
Дифференцирование неявной функции.
Пусть F(x, y) = 0
x2 + y2 +1 = 0 – уравнение связывает х и у, но это уравнение не определяет функцию, заданную неявно, т.к. этому уравнению не удовлетворяет никакая пара действительных чисел (х, у)
Если F(x, y) определена и непрерывна в точке P0
(x0, y0)
и некоторой её окрестности и имеет непрерывные частные производные ![]() и
и
![]() ,
причём F(x0, y0) = 0, а
,
причём F(x0, y0) = 0, а ![]() , то F(x, y) определяет функцию y, заданную неявно, причём существует
, то F(x, y) определяет функцию y, заданную неявно, причём существует ![]() , которая
вычисляется по формуле
, которая
вычисляется по формуле  (18)
(18)
Z
= F(x, y)
= 0 Найдём полную производную от F(x,
y): ![]() , отсюда
, отсюда

![]()
Аналогично, если F(x, y, z) = 0, то
![]() (19)
(19)
![]() (20)
(20)
ЛЕКЦИЯ 3
Экстремум функции двух переменных.
z = f(x, y)
Пусть эта функция определена в точке Р0(x0, y0) принадлежащей некоторой области D и P(x, y)ÎD, D – область определения функции f(x, y)
f(x, y) достигает в точке P0(x0, y0) max, если для всех P(x, y) принадлежащих окрестности точки P0(x0, y0) Þ f(P0) > f(P)
f(x, y) достигает в точке P0(x0, y0) min, если для всех P(x, y) принадлежащих окрестности точки P0(x0, y0) Þ f(P0) < f(P)
Точки максимума и минимума называют точками экстремума функции
Необходимые условия существования экстремума.
Если f(x, y) достигает в точке P0(x0, y0) экстремум, то в точке P0(x0, y0) Þ
![]() ,
,
![]() , в предположении,
что они существуют, либо, если функция в точке P0
определена, а хотя бы одна из частных производных первого порядка в точке P0 не существует. Например, у функции
, в предположении,
что они существуют, либо, если функция в точке P0
определена, а хотя бы одна из частных производных первого порядка в точке P0 не существует. Например, у функции ![]() - экстремум есть, а
частные производные не существуют в точке (0; 0).
- экстремум есть, а
частные производные не существуют в точке (0; 0).
![]() ;
;
![]()
С помощью необходимых условий находятся точки, в которых возможно существование экстремума. Однако, если в этих точках не выполняется достаточное условие существования экстремума, то они не являются точками экстремума, а называются стационарными.
Достаточные условия существования экстремума.
Если в точке Ро выполнено необходимое условие
существования экстремума и в точке Ро(хо,уо)
существуют частные производные второго порядка 
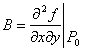

![]()
Если
1) ∆>0, то в точке Ро – экстремум, причем:
если А<0 - максимум
если А>0 - минимум
2) ∆<0, то в точке Ро – экстремума нет
3) ∆=0, то требуются дополнительные исследования.
4)
Задача нахождения наибольшего и наименьшего значения функции в замкнутой области.
Пусть функция z=f(x,y) непрерывна в ограниченной замкнутой области D и дифференцируема внутри этой области.
Тогда она имеет в этой области наибольшее и наименьшее значения, которые достигаются либо внутри этой области, либо на её границе. Если наибольшее и наименьшее значение функция принимает во внутренних точках области D, то эти точки, очевидно, являются точками экстремума функции z=f(x,y). Таким образом, точки, в которых функция имеет наибольшее и наименьшее значения, являются либо точками экстремума функции, либо граничными точками области D.
Мы приходим к следующему правилу нахождения наибольшего и наименьшего значений функции двух переменных.
Для того, чтобы найти наибольшее и наименьшее значения функции z=f(x,y) в ограниченной замкнутой области D, следует найти значения функции в критических точках этой области, а также её наибольшее и наименьшее значения на границе области D. Наибольшее и наименьшее из всех этих значений являются соответственно наибольшим и наименьшим значениями функции z=f(x,y) в заданной области D.
В некоторых случаях при нахождении наибольших и наименьших значений функции двух переменных в ограниченной замкнутой области границу этой области удобно разбить на части, каждая из которых задается своими уравнениями.
ЛЕКЦИЯ 4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Основные понятие и определения.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, функцию у, зависящую от х, и её производные.
F(x, y, y’, …, y(n)) = 0 (1)
(1) является дифференциальным уравнением n – го порядка.
Порядок дифференциального уравнения определяется номером наивысшей производной, входящей в данное уравнение.
(1) может быть представлено в виде
y(n) = f(x; y; y’; …, y(n –1) (2)
(2) – дифференциальное уравнение n-го порядка, разрешённое относительно производной y(n) .
(1) или (2) называются обыкновенными дифференциальными уравнениями, т.е. в эти дифференциальные уравнения входят функция и её производная, как функции, зависящие от одной переменной. Если функция и её производные зависят от большего числа переменных, то дифференциальные уравнения называют дифференциальными уравнениями в частных производных.
y = j(x) – называют решением дифференциального уравнения, если при подстановке в это дифференциальное уравнение j(x) и её соответствующих производных, уравнение обращается в верное равенство, т.е. тождество.
y = j(x, C1, C2, …, Cn) (3), где C1, C2, …, Cn произвольные постоянные, называется общим решением дифференциального уравнения (1) или (2), если она обращает (1) или (2) в тождество.
Общее решение дифференциального уравнения содержит ровно столько произвольных постоянных, каков порядок дифференциального уравнения. Из общего решения при конкретных значениях произвольных постоянных получаются частные решения дифференциального уравнения.
Ф(x, C1, C2, …, Cn) = 0 (4) называют общим интегралом дифференциального уравнения (1) или (2).
Частным интегралом дифференциального уравнения (1) или (2) называют значение полученное из (4) при конкретных значениях произвольных постоянных.
Дифференциальные уравнения первого порядка.
Дифференциальным уравнением первого порядка называют уравнение вида:
![]() (5)
или
(5)
или ![]() (6)
(6)
Так как ![]() , то, если
, то, если ![]() , то
, то ![]() (7)
(7)
(5), (6), (7) - дифференциальные уравнения первого порядка.
y = j(x, C) – общее решение дифференциального уравнения (5), (6), (7)
Решить дифференциальное уравнение, это значит, найти общее решение, либо общий интеграл, и, поскольку, при нахождении общего решения используется действие интегрирование, то иногда слово решить заменяют словом проинтегрировать дифференциальное уравнение. Графиком общего решения является совокупность интегральных кривых. При конкретных значениях С получаем частные решения. Графиком частного решения является интегральная кривая.
Задача Коши.
Задача Коши заключается в нахождении частного решения дифференциального уравнения, удовлетворяющего начальным условиям.
![]() Рассмотрим дифференциальное
уравнение первого порядка y’ = f(x,y) (6)
Рассмотрим дифференциальное
уравнение первого порядка y’ = f(x,y) (6)
и пусть заданы начальные условия: ![]() либо х = х0,
либо х = х0,
у = у0
Теорема Коши. (о существовании и единственности частного решения, удовлетворяющего н.у.)
Если f(x, y) определена и непрерывна в точке (x0,
y0), в этой точке существует непрерывная
частная производная![]() ,
то (6) имеет единственное частное решение удовлетворяющее начальным условиям: y(x0) = y0.
,
то (6) имеет единственное частное решение удовлетворяющее начальным условиям: y(x0) = y0.
y = j(x, C) – общее решение.
При данных начальных условиях из общего решения находим значение для произвольной постоянной С и это значение затем подставляем в формулу общего решения. Этим самым мы определяем частное решение, удовлетворяющее данным начальным условиям. Причём, если f(x, y) удовлетворяет условиям теоремы Коши, то это частное решение единственное и геометрически это значит, что через данную точку (x0, y0) проходит единственная интегральная кривая.
 Рассмотрим дифференциальное уравнение
Рассмотрим дифференциальное уравнение ![]() ,
, ![]() - общее решение.
- общее решение.
Точки в которых не выполняются условия теоремы Коши, а в
данном примере функция ![]() в точке х = 0 функция не определена,
называют особыми точками. Через особые точки проходит бесконечное множество
интегральных кривых, либо не существует ни одной.
в точке х = 0 функция не определена,
называют особыми точками. Через особые точки проходит бесконечное множество
интегральных кривых, либо не существует ни одной.
ЛЕКЦИЯ 5
Основные типы дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения с разделяющимися переменными.
Уравнение вида ![]() (9) или
(9) или ![]() (10) называются дифференциальными
уравнениями с разделяющимися переменными.
(10) называются дифференциальными
уравнениями с разделяющимися переменными.
(10) делим на ![]()
![]()
![]() (11)
(11)
(11) – дифференциальное уравнение с разделёнными переменными. Чтобы найти общее решение этого дифференциального уравнения, проинтегрируем его.
![]() (12)
– общее решение (10) и (11)
(12)
– общее решение (10) и (11)
2. Однородные уравнения I порядка.
f(x,y) – называется однородной функцией m
– го порядка (измерения), если для любого ![]() выполняется равенство
выполняется равенство ![]()
В частности, если m = 0, то ![]() - функция называется
однородной функцией нулевого порядка.
- функция называется
однородной функцией нулевого порядка.
ЗАМЕЧАНИЕ:
1). Если j(x; y) и f(x; y) – однородные функции одного порядка, то
![]() называется
однородной функцией нулевого порядка.
называется
однородной функцией нулевого порядка.
2). Если f(x; y) – однородная функция нулевого порядка, то:
![]() ,
если
,
если ![]() Þ
Þ![]()
y’ = f(x; y) (1) – называется однородным дифференциальным уравнением I порядка, если f(x; y) является однородной функцией нулевого порядка.
(1) Û ![]() (2)
(2)
Для решения (2) употребляется подстановка (3)
(3) ![]() ; U = U(x)
; U = U(x)
(4) y’ = U + U’x; (3) и (4) ® (2)
U + U’x = j(U)
U’x = j(U) – U - дифференциальное уравнение первого порядка с разделяющимися переменными.
![]() или
или ![]() -
дифференциальное уравнение с разделёнными переменными.
-
дифференциальное уравнение с разделёнными переменными.
![]() (5) – общий интеграл (1)
(5) – общий интеграл (1)
3. Линейные дифференциальные уравнения.
Дифференциальное уравнение называется линейным, если функция y и её y’ входят в дифференциальное уравнение линейно, т. е.
![]() ¹ 0
¹ 0
Если ![]()
y’ + P(x)y = Q(x) (6) – линейное дифференциальное уравнение первого порядка.
Если Q(x) = 0, то y’ + P(x)y = 0 (7) – линейное однородное дифференциальное уравнение первого порядка.
Решим (7) Þ![]() ,
, ![]() Þ
Þ
![]() (8)
(8)
(8) – общее решение (7)
Для решения (6) используется метод подстановки: U = U(x) и V = V(x) дифференцируемы и y = UV (9)
y’ = u’v + uv’ (10) (9) и (10) подставим в (6)
u’v + uv’ + p(x)uv =Q(x) или u’v + u(v’ + p(x)v) = Q(x)
пусть v(x)
является решением уравнения (11): ![]() и тогда
и тогда ![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
(14) подставим в (12), получим ![]() , отсюда
, отсюда ![]() и
и
![]() (15)
(15)![]()
![]() (16)
(16)
(16) – общее решение (6)
4. Уравнение Бернулли
Уравнениями Бернулли называются уравнения вида:
y’ + p(x)y = Q(x)ya (17) a ¹0 a¹1
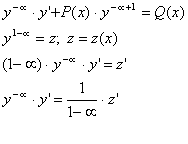
![]()
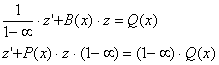 - линейное уравнение ,
дифференциальное уравнение относительно функции z.
- линейное уравнение ,
дифференциальное уравнение относительно функции z.
z=UV z’=U’V+UV’
U’V+UV’+(1-a)P(x)UV=(1-a)Q(x)
Находим U и V, находим z :
![]()
5. Дифференциальные уравнения в полных дифференциалах
M(x, y)dx + N(x, y)dy = 0 (1)
Уравнение (1) называется дифференциальным уравнением в полных дифференциалах, если выполняется условие:
![]() (2)
(2)
если ![]() - 1 равенство
- 1 равенство ![]() - 2 равенство,
то 1 – равенство проинтегрируем по х:
- 2 равенство,
то 1 – равенство проинтегрируем по х:
![]()
![]() (3)
(3)
(3) продифференцируем по у:
![]() ,
но
,
но ![]() Þ
Þ
Þ![]() Þ
Þ ![]()
![]() Þ
Þ
![]() Þ в (3); U(x; y) = c –
решение дифференциального уравнения (1) .
Þ в (3); U(x; y) = c –
решение дифференциального уравнения (1) .
ЛЕКЦИЯ 6
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ.
F (x; y; y’;…; y(n)) – дифференциальное уравнение n – порядка
или y(n) = f(x; y; y’; …; y(n-1))
Общим решением этого уравнения является: y = j(x; c1; c2;…; cn)
Для дифференциального уравнения n – порядка имеет место теорема Коши о существовании и единственности частного решения уравнения при данных n – начальных условиях.
Например для дифференциального уравнения второго порядка.
Теорема Коши: ![]()
начальные условия: 
Если 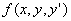 непрерывна
в точке
непрерывна
в точке 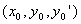 и в этой
точке непрерывна частная производная
и в этой
точке непрерывна частная производная 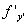 , то существует, причём единственное частное
решение, удовлетворяющее данным начальным условиям
, то существует, причём единственное частное
решение, удовлетворяющее данным начальным условиям 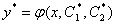 .
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
I. y(n) = f(x) – общее решение такого уравнения находится путём n – кратного интегрирования данного уравнения.
II. Пусть левая часть дифференциального уравнения второго порядка не содержит явно функцию y
F(x; y’; y’’) = 0 (1)
Тогда сделаем подстановку: y’ = z, z = z(x) (2)
и тогда ![]() (3)
(3)
F(x; z; z’) = 0 дифференциальноe уравнениe первого порядка (4)
III. F(x; y’; y’’) = 0 (5)
Уравнение (5) явно не содержит х. Чтобы понизить порядок уравнения, делаем подстановку y’ = p, p = p(y), y = y(x) (6)
![]() (7)
(7)
![]() - дифференциальное уравнение
первого порядка относительно функции р = р(у).
- дифференциальное уравнение
первого порядка относительно функции р = р(у).
ЛЕКЦИЯ 7
ЛИНЕЙНЫЕ дифференциальнЫе уравнениЯ
Уравнения вида y(n) + a1(x)y(n-1) + a2(x)y(n-2) +…+an-1(x)y’ + an(x)y = f(x) (1)
называют линейными дифференциальными уравнениями n – го порядка,
a1(x), a2(x), … ,an(x) - коэффициенты (1)
Если у(х), у’(x), …, y(n), a1(x), a2(x), … , an(x), f(x) – непрерывные функции, то выполняются все условия теоремы Коши и имеется единственное частное решение, удовлетворяющее начальным условиям.
В этом случае, чтобы решить задачу Коши, необходимо задать начальные условия:
 (2)
(2)
При начальных условиях (2) существует, причём единственное частное решение (1), удовлетворяющее начальным условиям (2).
В частности, рассмотрим линейное дифференциальное уравнение второго порядка (3)
(3) y’’ + a1(x)y’ + a2(x)y = f(x) – линейное дифференциальное уравнение второго порядка.
(4) y’’ + a1(x)y’ + a2(x)y = 0 - линейное однородное дифференциальное уравнение второго порядка.
(3) - линейное неоднородное дифференциальное уравнение второго порядка.
Аналогично, если в (1) f(x) = 0, то уравнение будет линейным однородным дифференциальным уравнением n - го порядка, a (1) - линейным неоднородным дифференциальным уравнением n - го порядка.
Линейный оператор и его свойства.
L[y] = y(n) + a1(x)y(n-1) + … + an(x)y – линейный оператор
L[y] = f(x) (1)
L[y] = 0 – линейное однородное дифференциальное уравнение n – го порядка
Линейный оператор обладает следующими свойствами.
1. L[y1+y2] = L[y1] + L[y2]
2. L[Cy] = CL[y], C = const
3. L[C1y1+C2y2] = L[C1y1] + L[C2y2]=C1L[y1]+ C2L[y2]
Решение линейных однородных дифференциальных уравнений второго порядка.
y’’ + a1(x)y’ + a2(x)y = 0 (2)
Пусть y1(x) и y2(x) – частные решения (2)
Тогда y(x) = C1y1(x) + C2y2(x) – решение уравнения (2)
L[y1] = 0, т.к. y1(x) – решение (2), L[y2] = 0, т.к. y2(x) – решение (2), но тогда
L[ y ] = L[C1y1 + C2y2] = 0, т.е. у(х) – решение (2)
Система функций y1(x), y2(x),
…, yn(x) -
называется линейно – независимой, если существуют С1, С2,
…, Сn , что C1y1 + C2y2 + … + Cnyn
= 0 возможно тогда, когда все Сi =
0, ![]() .
.
Теорема (о линейной независимости системы частных решений y1(x), y2(x) уравнения (2))
Пусть y1(x),y2(x) - частные решения (2).
Система y1(x),y2(x) – линейно - независима тогда и только тогда, когда определитель Вронского:
 ,
,
если y1(x), y2(x) – линейно – зависиммы, то W = 0.
1. Пусть y1(x), y2(x) линейно – независимы.
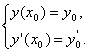 -
начальные условия
-
начальные условия
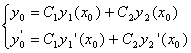 (3)
(3)
Для (2) выполняется условие т. Коши Þ это уравнение имеет единственное частное решение
удовлетворяющее начальным условиям, т.е. в этом случае (3) имеет единственное
решение ![]() , и эта
система имеет единственное решение тогда и только тогда, когда определитель
этой системы ¹ 0 (определитель
Вронского)
, и эта
система имеет единственное решение тогда и только тогда, когда определитель
этой системы ¹ 0 (определитель
Вронского)

2. Пусть y1(x), y2(x) линейно – зависимы, т.е. ay1 + by2 = 0 выполняется, если хотя бы одноиз чисел a или b ¹ 0
Если a ¹ 0 Þ
![]()
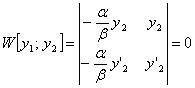 Þ (3) не имеет единственного решения
Þ (3) не имеет единственного решения
ЛЕКЦИЯ 8
Решение линейных однородных дифференциальных уравнений n – го порядка.
y(n)(x) + a1(x)y(n-1) + … + an(x)y = 0
н.у.: 
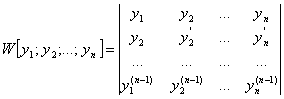
y1(x), y2(x), …, yn(x) – частные решения L[y] = 0 причём y1(x), y2(x), …, yn(x) линейно – независимы и образуют фундаментальную систему решений и тогда общее решение L[y] = 0 представляет собой линейную комбинацию данной фундаментальной системы решений
т.е. y(x) = C1y1(x) + C2y2(x) + … + Cnyn(x)
Решение линейных неоднородных дифференциальных уравнений n – го порядка.
L[y] = f(x) (1) ЛНДУ
L[y] = 0 (2) ЛОДУ, соответствующее (1)
Пусть y(x) = y00 – общее решение однородного уравнения Þ L[y00] º 0
yчн – частное решение неоднородного уравнения (1)
L[yчн] º f(x)
yон – общее решение неоднородного (1) Þ
уон = уоо + учн (3)
L[yон] = L[yоо + учн] = L[y00] + L[yчн] = f(x) Û уон –общее решение (1)
Линейные дифференциальные уравнения с постоянными коэффициентами.
Если а1, а2, …, аn – числа, то y(n) + a1y(n-1) + … + any = f(x) (1) – называется ЛНДУ – n с постоянными коэффициентами.
(2) y(n) + a1y(n-1) +a2y(n-2) + … + any = 0 – называется ЛНДУ – n с постоянными коэффициентами.
(3) y’’ + py’ + qy = f(x) – ЛНДУ- 2
(4) y’’ + py’ + qy = 0 – ЛОДУ- 2
p,q – числа
y’ + qy = 0 – ЛОДУ – 1
![]()
![]()
yчо = e-qx
y00 = Ce-qx
Общее решение (4)
y00 = C1y1 + C2y2 (5), где y1(x) и y2(x) – частные решения (4)
Решение (4) находим в виде
y = ekx
y’ = kekx ; y’’ = k2ekx
Подставим у, у’, y’’ в (4) Þ
k2ekx + pkekx +qekx º 0
ekx(k2 + pk + q) = 0
ekx ¹ 0; k2 + pk + q (6) – характеристическое уравнение для (4)
1) Если D > 0 Þ k1,k2 – различные действительные корни (6)
![]() –
частные решения (4)
–
частные решения (4)
Покажем, что они линейно независимы
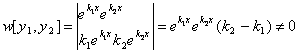
Þ y1, y2 – линейно независимы и общее решение
![]() (7)
(7)
2) Если D = 0 Þ k1 = k2 = k – действительный корень (6)
y1 = ekx; y2 = xekx

y1, y2 – линейно – независимы.
y00 = C1ekx + C2xekx = ekx(C1 + C2x) (8)
3) Если D < 0, то уравнение будет иметь два комплексно – сопряженных корня:
k1 = a + ib; k2 = a - ib;
y1* = e(a + ib)x = eax(cosbx + isinbx) – формулы Эйлера
y2* = e(a - ib)x = eax(cosbx - isinbx)
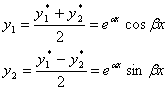
Покажем, что y1 = eaxcosbx и y2 = eaxsinbx линейно независимы
y1’=eaxacosbx - eaxbsinbx
y2’=eaxasinbx + eaxbcosbx
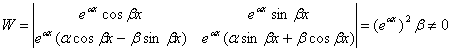
y00 = C1eaxcosbx + C2eaxsinbx = eax(C1cosbx + C2sinbx) (9)
АЛГОРИТМ РЕШЕНИЯ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
1. Составляем характеристическое уравнение (6)
2. Находим корни уравнения (6)
3. По корням уравнения записываем общее решение уравнения (4)
Аналогично решается уравнение более высокого порядка.
ЛЕКЦИЯ 9
РЕШЕНИЕ ЛИНЕЙНОГО НЕОДНОРОДНОГО УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ СПЕЦИАЛЬНОГО ВИДА.
y’’ +py’ +qy = f(x) (3)
yон = уоо + учн учн= ?
k2 + pk + q = 0 (6)
1) f(x) = eaxQn(x), где Qn(x) – многочлен n – степени от (х)
Если a ¹ корню характеристического уравнения (6), то yчн = eax pn(x)
pn(x) – многочлен той же степени что и Qn(x) c неизвестными коэффициентами. Чтобы найти учн, нужно найти неизвестные коэффициенты.
2) f(x) = eaxQn(x)
Если a = корню харрактеристического уравнения (6), то учн = еax pn(x)хr ,
r- кратность корня k = a
3) f(x) = emx(MCosgx + NSingx), если (m ± ig) не является корнем характеристического уравнения (6), то yчн = emx(АCosgx + ВSingx)
A,B – неизвестные коэффициенты
Решение находится в виде (10)
А если (m ± ig) совпадает с корнем характеристического уравнения, то
yчн = emx(АCosgx + ВSingx) (11)
Замечание: если M = Mn(x), N = Ns(x) и (n ³ S), то:
Если m ± ig ¹ корню (6) Þ yчн = emx(An(x)Cosgx + В n(x)Singx) (12)
Если m ± ig = корню (6) Þ yчн = emxx(An(x)Cosgx + В n(x)Singx) (13)
4)Если y’’ + py’ + qy = f1(x) + f2(x), то yчн = yчн1 + yчн2
yчн1 – частное решение по f1(x), yчн2 - частное решение по f2(x), тогда
yон = y00 + yчн1 + yчн2
Метод вариации произвольных постоянных (Метод Лагранжа).
(1) y’’ + py’ + qy = f(x) – ЛНДУ – 2 с постоянным коэффициентом
(2) y’’ + py’ + qy = 0 – ЛОДУ – 2 с постоянным коэффициентом
Пусть y1(x) и y2(x)
– частные решения ЛОДУ – 2 (2). Причём они линейно – независимы, т.е. 
Общее решение (1) будем находить в виде (3) yон = C1(x)y1 + C2(x)y2
Где C1(x), C2(x) – неизвестные функции, которые нужно определить.
y’он = C1’(x)y1 + C1(x)y1’ + C2’(x)y2 + C2(x)y2’
Где C1(x), C2(x) такие, что: C1’(x)y1 + C2’(x)y2 = 0 (4)
y’он = C1(x)y1’ + C2’(x)y2 (5)
y’’он = C1’(x)y1’ + C1(x)y1’’ + C2’(x)y2’ + C2(x)y2’’ (6)
(3), (5), (6) ® в (1)
C1’(x)y1’ + +C1(x)y1’’ + C2’(x)y2’ + C2(x)y2’’+ pC1(x)y1’ + pC2(x)y2’ + qC1(x)y1 + + qC2(x)y2 = f(x)
C1’(x)y1’ + C2’(x)y2’ = f(x) (7)
Для определения C1(x), C2(x) найдём C1’(x), C2’(x) из (8)
 (8)
(8)
Система (8) имеет единственное решение, т.к. определитель этой системы – определитель Вронского, а он не равен нулю. Затем находим C1(x) и C2(x) и, подставляя в (3), находим общее решение (1).
ЛЕКЦИЯ 10
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ (ПРЕОБРАЗОВАНИЕ ЛАПЛАСА)
Основные понятия, определения операционного исчисления.
В основе операционного исчисления рассматриваются f(t) – оригинал, F(p) – изображение.
Определение 1.
f(t) – называется оригиналом, если она удовлетворяет одновременно трём условиям:
1. f(t) º 0, если t<0;
2. Если tÎ[0; ¥) Þ f(t) – кусочно непрерывна.
3. f(t) ограниченного роста Û $ M>0, a>0 Þ " t Î [0; ¥): êf(t) ê£ Meat, a- показатель роста.
Определение 2.
 (1) называется изображением
функции f(t), при условии, что
интеграл в правой части (1) существует.
(1) называется изображением
функции f(t), при условии, что
интеграл в правой части (1) существует.
F(p) – функция комплексного переменного p = s + iw, где S = Rep, w = Imp
Интеграл в правой части (1) называется интегралом Лапласа.
(1) – преобразование Лапласа (прямое преобразование Лапласа)
Теорема о достаточном условии существования изображения.
Если f(t) – оригинал, то существует F(p).
Доказательство:
 =
=  .
.
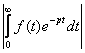 £
£ 
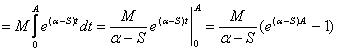
A®¥ и a-S<0, т.е. если S<a, то F(p) существует.
Мы получили, что если f(t) является оригиналом и действительная часть аргумента р больше показателя роста оригинала f(t), то изображение F(p) существует.
Теорема доказана.
ЗАМЕЧАНИЕ.
1. Если F(p) – изображение f(t), то lim F(p)=0; p®¥, если S®¥
Если lim F(p)¹0, то F(p) не является изображением никакой функции.
2. Существуют некоторые функции f(t), которые не являются оригиналом, но тем не менее для них существуют изображения.
Теорема единственности изображения.
Если f1(t) имеет изображение F1(p), а f2(t) имеет изображение F2(p) и если tÎ[0; ¥). f1(t) = f2(t), то F1(p) = F2(p), т.е. если f(t) имеет изображение, то оно единственное.
НАХОЖДЕНИЕ ИЗОБРАЖЕНИЙ НЕКОТОРЫХ ОРИГИНАЛОВ.
То, что f(t) имеет изображение F(p) обозначается следующим образом: f(t)¸F(p)
1. Рассмотрим единичную функцию Хевисайда.
![]()
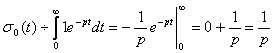
![]()
![]()
2.
f(t)=et; 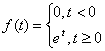

![]()
ЛЕКЦИЯ 11
ОСНОВНЫЕ ТЕОРЕМЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ.
1. Теорема линейности.
Если f(t) имеет изображение F(p), а j(t)¸F(p)
C1,C2 – произвольные числа, то
С1f(t) + C2j(t) ¸ C1F(p) + C2F(p)
2. Tеорема подобия.
Если f(t) ¸ F(p), то f(at) ¸ ![]() ; a – число
; a – число
3. Теорема смещения.
Если f(t) ¸ F(p), то f(t)elt ¸ F(p - l)
4. Теорема запаздывания.
Если f(t) ¸ F(p), то f(t - t) ¸ e-ptF(p); t - число
5. Теорема о дифференцировании оригинала.
Если f(t) ¸ F(p), то f(t) ¸ F(p), то f’(t) ¸ pF(p) – f(0)
Замечание:
1. Если f(t) ¸ F(p), то
f’’(t) ¸ p(pF(p) – f(0)) – f’(0) = p2F(p) – pf(0) – f’(0)
2. Если f(0) = f’(0) = f’’(0) = … = f(n –1)(0) = 0
f’(t) ¸ pF(p), …, f(n)(t) ¸ p(n) F(p)
6. Теорема об интегрировании оригинала.
Если f(t) ¸ F(p), то 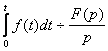 при условии что
интеграл от оригинала существует.
при условии что
интеграл от оригинала существует.
7. Теорема о дифференцировании изображения.
Если f(t) ¸ F(p), то (-1)n tn f(t) ¸ F(n)(p)
(tn f(t) ¸ (-1)n F(n)(p))
8. Теорема об интегрировании изображения.
Если f(t) ¸ F(p), то  , при условии,
что
, при условии,
что ![]() - оригинал.
- оригинал.
9. Теорема о свёртке оригиналов.
Определение. Свёрткой оригиналов называется интеграл: 
Свёртка оригиналов обладает свойством коммутативности, т.е. f(t)*j(x)= =j(x)*f(t), т.е. 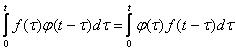
Если f(t) ¸ F(p), j(t)¸F(p), то 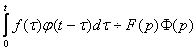
10. Теорема. Интеграл Дюамеля.
Если f(t) ¸ F(p), j(t)¸F(p), то
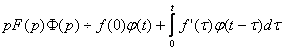 (1)
(1)
 (2)
(2)
 (3)
(3)
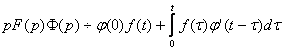 (4)
(4)
Операционный метод решения линейных дифференциальных уравнений с постоянными коэффициентами.
(1) ![]() , где а1, а2,
…, аn – числа.
, где а1, а2,
…, аn – числа.
(1) L[x(t)] = f(t)
Заданы начальные условия (2): 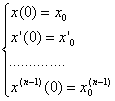
x(t)¸X(p)
x’(t)¸pX(p)-x0
x’’(t)¸p2X(p)-px0-x’0
…………………….
x(n)(t)¸pnX(p)-p(n-1)x0-p(n-1)x0-p(n-2)x’0-…-x0(n-1)
f(t) ¸ F(p)
От (1) в оригиналах перейдём к (3) в изображениях.
(an + an-1p + … + a1p(n-1) + pn)X(p) + (-yn-1(p)) = F(p) (3)
![]() (4), где Аn(p) = an + an-1p + … + a1p(n-1) + pn
(4), где Аn(p) = an + an-1p + … + a1p(n-1) + pn
По изображению (4) находим оригинал x(t), который является решением уравнения (1) при заданных начальных условиях (2).
ЛЕКЦИЯ 12
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОПЕРАЦИОННЫМ МЕТОДОМ, МЕТОДОМ ДЮАМЕЛЯ.
![]()
a1,a2,…an – числа.
L[x(t)]=f(t) (1)
x(0)=x’(0)=x(n-1)(0)=0
f(t)¸F(p)
x(t)¸X(p)
от уравнения (1) с начальными условиями переходим к операторному уравнению (2) A(p)X(p)=F(p) (2)
![]() (3)
(3)
Рассмотрим уравнение (4) L[x(t)]=1, а начальные условия теже самые, тогда
x1(t)¸X1(p); ![]() , получаем операторное уравнение
, получаем операторное уравнение
(5) ![]() , отсюда
, отсюда
![]() (6)
(6)
из (6) найдем ![]() и подставляем в (3), получим
и подставляем в (3), получим
X(p)=pX1(p)F(p).
Применяя формулу Дюамеля, находим 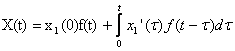 (7)
(7)
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ОПЕРАЦИОННЫМ МЕТОДОМ.
![]()
н.у.: x(0)=x’(0)=1
y(0)=y’(0)=0
x(t)¸X(p) y(t)¸Y(p)
x’(t)¸pX(p)-1 y’(t)¸pY(p)
x’’(t)¸p2X(p)-p-1 y’’(t)¸p2Y(p)
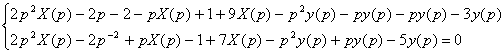
(2p2-p+9)X(p)+(p2+p+p)y(p)=2p+1
(2p2+p+7)X(p)-(p2-p+5)y(p)=2p+3

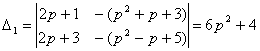
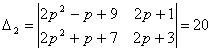

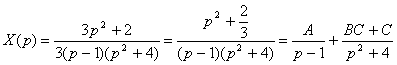
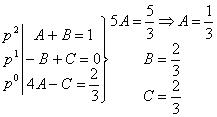
![]()
![]()
![]()

![]()
ЛЕКЦИЯ 13
ЧИСЛОВЫЕ РЯДЫ.
Рассмотрим числовую последовательность { an } = a1, a2,…, an,…
Из членов числовой последовательности { an } составляем выражение:
a1+ a2 +… + an
+ … = ![]() (1)
(1)
(1) – числовой ряд.
an = f(n) (2) – общий, n – ый член ряда (1).
Например an = ![]() , тогда получаем числовой ряд:
, тогда получаем числовой ряд: ![]() , который называется
гармоническим рядом.
, который называется
гармоническим рядом.
Из членов числового ряда (1) составим последовательность частичных сумм ряда (1):
S1 = a1,
S2 = a1+a2,
S3 = a1+a2+a3,
-- -- -- -- -- -- -- --,
Sn = a1+a2+… +an-1+an.
Sn – n-я частичная сумма ряда (1),
{Sn}- последовательность частичных сумм (1)
Если {Sn} имеет конечный предел, т.
е. LimSn =
S ¹ ¥ (3), то ряд (1) называются
сходящимся и S называется суммой ряда (1) и: a1+ a2 +… + an + … = ![]() = S
= S
Если LimSn = ¥, либо не существует, то ряд (1) называется расходящимся, и он суммы не имеет.
О сходимости геометрического ряда.
Рассмотрим геометрический ряд: ![]() (4)
(4)
Составим n-ую частичную сумму этого ряда:
Sn = a + aq + aq2 + … + aqn-1
1) если q = 1 Þ Sn = a + a +…+a = n×a
LimSn = Lim n×a = ¥ Û (4) расходится.
2) если q = -1 Þ Sn = a – a + a – a +…+ (-1)n+1a
Sn = 0, если n – чётное
Sn = a, если n - нечетное
LimSn не существует и, следовательно, ряд (4) расходится.
3) если q ¹ 1 Þ Sn = a + aq +aqn-1 = ![]()
Lim Sn = Lim a(![]() )=[ если
)=[ если ![]() ]
=
]
= 
![]() - сходится и его
- сходится и его ![]()
![]() , если
, если ![]()
![]() -
расходится и S не существует, если
-
расходится и S не существует, если ![]()
Достаточное условие сходимости числовых рядов.
Для того, чтобы ряд (1) сходился, достаточно, чтобы,
последовательность частичных сумм {Sn} этого
ряда была ограниченной, т.е. если $ M>0; и для всех nÎN Þ ![]() .
.
Свойства сходящихся рядов.
10. Если ![]() (1) и
(1) и ![]() (5) сходятся, то
(5) сходятся, то
1)
![]() - сходится
- сходится
2)
Если k – число, то ![]() - сходится
- сходится
Замечания.
Если и ряд (1) и ряд (5) оба расходятся, то ряд ![]() и ряд
и ряд ![]() тоже расходятся.
тоже расходятся.
Если ряд (1) сходится, а ряд (5) расходится, то ![]() - расходится.
- расходится.
20 Рассмотрим ряд a1+a2+…+ak+ak+1+…+an+… (1)
Из ряда (1) отбросим конечное число членов этого ряда и получим ak+1+ak+2+…+an+… (6) – остаток ряда (1) после k членов ряда (1)
a1+a2+…+ak=Аk
Если сходится (1), то сходится и любой остаток этого ряда.
Если сходится остаток (6), то сходится и сам ряд (1).
Если расходится (1), то расходится и остаток этого ряда, а если расходится остаток ряда, то расходится и сам ряд.
ЛЕКЦИЯ 14
ЗНАКОПОЛОЖИТЕЛЬНЫЕ РЯДЫ.
Рассмотрим (1) a1+a2+…+an+…=![]() и пусть ai³0
и пусть ai³0
Необходимое условие сходимости знакоположительного ряда.
Если (1) сходится, то lim an=0 (7) – обратное утверждение неверно, т.е. если lim an=0, то это не означает ещё что ряд сходится, но если lim an¹0 (8), то (1) расходится, а (8) – достаточное условие расходимости ряда.
Теорема.
an=Sn-Sn-1, т.к. (1) сходится Û lim Sn=S и lim Sn-1=S Þ
lim an= lim(Sn-Sn-1)= lim Sn- lim Sn-1=S-S=0
О расходимости гармонического ряда.
(9) ![]() - гармонический ряд.
- гармонический ряд.
![]() ,
однако ряд (9) расходится
,
однако ряд (9) расходится
![]()
![]()
![]()
![]()
![]()
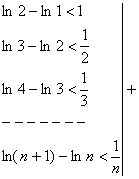
![]() Отсюда:
Отсюда:
![]() , тогда
, тогда ![]()
Если n®¥, то ln (n+1) ®¥, т.е. {Sn} неограниченная, и следовательно ряд (9) расходится.
Достаточные признаки сходимости знакоположительных рядов.
I. Признаки сравнения.
1.
![]() = a1+a2+…+an+… (1)
= a1+a2+…+an+… (1)
![]() = b1+b2+…+bn+… (2)
= b1+b2+…+bn+… (2)
Теорема.
Пусть (2) – сходится. Если для любого nÎN Þ an £ bn (3), то ряд (1) тоже сходится.
An= a1+a2+…+an
Bn= b1+b2+…+bn (2) – сходится Û по определению сходимости. Û
lim Bn=B¹¥ Þ Bn£B
Из (3) Þ An£Bn£B
Получили, что последовательность частичных сумм {An} ограничена Þ по достаточному условию сходимости знакоположительного ряда. Ряд (1) сходится.
2.
![]() (4)
(4)
Известно, что (4) расходится
Если для любого nÎN Þ an³cn (5), то ряд (1) расходится.
Теорема.
An³Cn; Cn=c1+c2+…+cn
lim Cn = ¥ Û (4) расходится, то lim An=¥ и (1) расходится.
3. Предельная форма признаков сравнения.
(1)
![]()
![]() ; (6)
; (6) ![]()
Если $ ![]() , то (1) – сходится,
если сходится (6) и (1) – расходится, если расходится (6).
, то (1) – сходится,
если сходится (6) и (1) – расходится, если расходится (6).
II. Признак Даламбера.
![]() = a1+a2+…+an+an+1+…
(1) ai>0
= a1+a2+…+an+an+1+…
(1) ai>0
Если существует и равен конечному числу предел отношения
последущего члена ряда к предыдущему, т.е. ![]() (7), то
(7), то
1) Если Д<1 Þ (1) сходится.
2) Если Д>1 Þ (1) – расходится.
3) Если Д=1 Þ ответа нет.
Теорема.
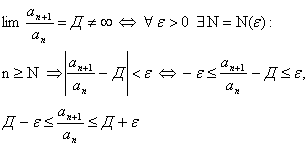
1) Д<1 ![]()
Из (8) Þ an+2£an+1q£anqq Þ
an+2£anq2
an+3£anq3
----------
Рассмотрим два ряда:
(9) an+1+an+2+…
(10) anq+anq2+…
(10) геометрический ряд со знаменателем 0<q<1 Þ сходится, тогда по 1 признаку сравнения ряд (9) сходится.
(9) остаток (1) после первых n – членов ряда, а т.к. сходится остаток ряда, то сходится и сам ряд.
2) Д>1, ![]()
![]()
3) Д=1 Þ ряд (1) может быть либо абсолютно сходящимся, либо абсолютно расходящимся.
В этом случае пользуются другим признаком. Теорема доказана.
Замечание.
1) Если
![]() Þ (1) расходится.
Þ (1) расходится.
2) Признак Даламбера целесообразно использовать в случаях, когда в формуле общего члена присутствуют либо показательная функция, либо факториалы.
III. Радикальный признак Коши.
(1)
![]()
a1>a2>…>an>…
Если $ и = конечному
числу предел ![]() (11),
то:
(11),
то:
1) Если k<1 Þ (1) – сходится
2) Если k>1 Þ (1) – расходится
3) Если k=1 Þ ответа нет
Замечание.
1) Если
![]() , то (1)
расходится.
, то (1)
расходится.
2) Радикальный признак Коши целесообразно применять в случаях, если формула общего члена содержит n – степень выражения.
ЛЕКЦИЯ 15
IV. Интегральный признак Коши.
(1)
![]() ; a1>a2>…>an>…
; a1>a2>…>an>…
Рассмотрим y=f(x), которая положительная, непрерывная, монотонно убывающая, если 1£x£¥ и f(1)=a1, f(2)=a2, …, f(n)=an …, то:
1) Если сходится ![]() , то сходится и сам ряд (1),
, то сходится и сам ряд (1),
2)Если ![]() - расходится, то расходится и (1)
- расходится, то расходится и (1)
доказательство :
1.
дано: ![]() сходится
, то интеграл равен числу J . рассмотрим криволинейную
трапецию , ограниченную х=n и, y=f(x),
x=1, y=0
сходится
, то интеграл равен числу J . рассмотрим криволинейную
трапецию , ограниченную х=n и, y=f(x),
x=1, y=0
![]()
если рассмотреть ступенчатую фигуру из прямоугольников, входящих в трапецию S и которые выходят за пределы трапеции `S

при n®¥ Sn-a1£J Þ Sn£J+a1 т.е. n-ные частичные суммы ряда (1) ограничены.
{Sn}- ограничена и по достаточному условию схдимости ряда (1) сходится
2.
дано![]() расходится, то есть для любых n существует числоM>0, что
расходится, то есть для любых n существует числоM>0, что ![]() >M, тогда Sn >
>M, тогда Sn >![]() +an>M,
то есть последовательность
+an>M,
то есть последовательность ![]() возрастает и неограниченна сверху, то есть
lim Sn =¥, а это означает, что ряд (1) расходится. Теорема доказана.
возрастает и неограниченна сверху, то есть
lim Sn =¥, а это означает, что ряд (1) расходится. Теорема доказана.
Замечание.
О сходимости или расходимости (1) можно судить по сходимости
или расходимости интеграла 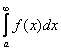 , а – любое целое число >1.
, а – любое целое число >1.
Обобщенный гармонтческий ряд.
 - Этот ряд называется обобщенным
гармоническим рядом, он сходится , если p>1 и
расходится , если p£1.
- Этот ряд называется обобщенным
гармоническим рядом, он сходится , если p>1 и
расходится , если p£1.
О сходимости этого ряда можно судить по сходимости и
расходимости несобственного интеграла ![]() . Этот интеграл сходится ,
если p>1 и расходится , если p£1.
. Этот интеграл сходится ,
если p>1 и расходится , если p£1.
Например:
![]() - сходящийся ряд
- сходящийся ряд
![]()
ЗНАКОПЕРЕМЕННЫЕ РЯДЫ.
Знакопеременными называются ряды, членами которых являются числа любого знака. Частным случаем знакопеременных рядов являются ряды знакочередующиеся, т.е. ряды вида:
(1) a1-a2+a3-a4+…+(-1)n+1an+…=![]()
Признак Лейбница.
Если члены ряда (1) убывают, т.е. a1>a2>…>an>… и lim an=0 (2), то ряд (1) – сходится, причём сумма этого ряда положительна и не превосходит первого числа ряда (1), т.е. 0<S£a1 (3).
Доказательство:
Рассмотрим {Sn} , пусть n=2m Þ S2m=a1-a2+a3-a4+..+a2m-1-a2m
Т.к. сумма конечного числа слагаемых, то их можно группировать S2m= (a1-a2)+(a3-a4)+..+(a2m-1-a2m)
(a1-a2)>0
(a3-a4)>0
(a2m-1-a2m)>0 Þ S2m>0
S2m=a1-[(a2-a3)+(a4-a5)+…+(a2m-2-a2m-1)+a2m]
0<S2m£a1, по свойству пределов предел S2m при m®¥ равен S, где S- число, причем 0<S£a1
пусть n=2m+1Þ S2m+1=S2m+a2m+1
lim S2m+1=lim(S2m+a2m+1)=lim S2m+lim a2m+1=S+0=S, то есть (1) сходится и имеет сумму S.
Абсолютная и неабсолютная (условная) сходимость знакопеременного
числового ряда .
Рассмотрим знакопеременный ряд:
(4) ![]() ,
,
(4) – знакопеременный ряд если члены этого ряда являются числами и положительными и отрицательными.
(5) ![]()
(5) – составлен из абсолютных величин (4)
(5) – знакопеременный ряд.
(4) - называется абсолютно сходящимся, если lim an = 0 и (5) сходится.
(4) – называется неабсолютно (условно) сходящимся, если lim an = 0, а (5) расходится.
(4) расходится, если lim an ¹ 0.
Свойства абсолютно и условно сходящихся рядов.
1. Если сходится ряд из абсолютных величин знакопеременного ряда, то знакопеременный ряд сходится.
2. Абсолютно сходящиеся ряды обладают переместительным и сочетательными свойствами.
3. Условно сходящиеся ряды не обладают свойствами ни переместительным, ни сочетательным, более того, если в условно сходящемся ряде применить сочетательное свойство, то в итоге можно получить даже расходящийся ряд (т. Римана).
4. Абсолютно сходящиеся ряды можно почленно складывать вычитать, умножать. Условно сходящиеся ряды такими свойствами не обладают.
Замечание об оценке сходимости знакопеременного ряда.
a1-a2+a3-a4+…+(-1)n+1an+… (1)
± an+1 ± an+2 ± …(2) – знакопеременный ряд, остаток ряда (1)
Если lim an = 0 и члены ряда убывают, то (2) сходится (по свойству сходящихся рядов).
r – сумма (2)
![]()
ЛЕКЦИЯ 16
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
{fn(x)}=f1(x), f2(x), …, fn(x), … на (a, b)
Из членов этой последовательности составляется ряд.
(1) ![]()
(1) – функциональный ряд.
Рассмотрим последовательность частичных сумм:
S1(x)=f1(x)
S2(x)=f1(x)+f2(x)
--------------------------------
Sn(x)=f1(x)+f2(x)+…+fn(x) (2) – n- ая частичная сумма (1)
(1) называется сходящимся в т. х0Î(a, b), если lim Sn(x0) = S(x0) ¹ ¥
В противном случае (1) расходится в т. х0. Если (1) сходится в т. х0, то т.х0 называется точкой сходимости функционального ряда (1) и число S(x0) называется суммой (1) в т. х0.
Если для всех хÎD Ì (a, b), (1) – сходится, то D называется областью сходимости функционального ряда (1), т.е. если хÎD Þ lim Sn(x)=S(x)¹¥ (4)
lim Sn(x) = S(x) Û " e>0 $ N=N(e, x):
n ³ N Þ ![]()
S(x)-Sn(x)=rn(x)
(1) сходится, если lim rn(x) = 0.
Равномерная сходимость функционального ряда.
(1) называется
равномерно сходящимся в D1, если для любого e > 0 $ N=N(e) для всех х Þ n ³ N Þ ![]()
Понятие равномерной сходимости функционального ряда более жёсткое. Если ряд сходится равномерно, то сходимость этого ряда в общем обеспечена. Но, если ряд просто сходится, то это ещё не значит, что он будет сходится равномерно.
Признак равномерной сходимости функционального ряда. (т. Вейерштрасса)
(5) ![]() ci >
0 - знакоположительный числовой ряд.
ci >
0 - знакоположительный числовой ряд.
U1=f1(x), U2=f2(x), …, Un=fn(x), …
(1) ![]()
(5) – сходится.
Если для любого nÎN Þ ![]() (6) (" xÎD), то (1) равномерно сходится в D.
(6) (" xÎD), то (1) равномерно сходится в D.
(5) – называется мажорантой.
Признак Вейерштрасса: (1) равномерно сходится в D, если в этой области он мажорируется мажорантой.
Свойства равномерно сходящихся функциональных рядов.
![]() (1)
(1)
Пусть f1(x), f2(x), …, fn(x), … непрерывны на (a, b)
Т.1. Если ряд (1), составленный из непрерыных на (a, b) функций, равномерно сходится на (a, b), то сумма этого ряда S(x) – непрерывная функция на (a, b)
Т.2. Пусть f1(x), f2(x), …, fn(x), … дифференцируемы в любой т. xÎ(a, b)
![]() (2)
(2)
Если (1) сходится, а (2) равномерно сходится, то (1) можно почленно дифференцировать, причём сумма (2) равна производной от суммы (1), т.е.:
 (3)
(3)
Равномерно сходящиеся ряды можно почленно дифференцировать.
Т.3. Пусть f1(x), f2(x), …, fn(x), … интегрируемы на [a, b]
Если (1) равномерно сходится на [a, b], то (1) можно почленно интегрировать, причём интеграл от суммы (1) равен сумме ряда, составленного из интегралов от соответствующих членов (1), т.е.:
 (4)
(4)
ЛЕКЦИЯ 17
СТЕПЕННЫЕ РЯДЫ.
Степенные ряды – это частный случай функциональных рядов.
(1) ![]()
(1) – обобщённый степенной ряд или ряд, расположенный по степеням (x-a),
c0, c1, c2, …, cn, … - коэффициенты (1)
Если а = 0, то получим:
(2) ![]() - степенной ряд.
- степенной ряд.
Теорема Абеля.
Если (2) сходится в т.х0 (х0 ¹ 0), то (2) сходится абсолютно для
любых х: ![]() (3)
(3)
Если (2) расходится в т. х1, то (2) расходится,
если х: ![]()
Доказательство.
1) Дано: (2) сходится в т. х0¹0, т.е.
(4)![]()
(4)сходится Þ ![]()
(2) рассмотрим по абсолютной величине, т.е.
(5)
Так как  и
и ![]() , (М – число > 0)
, (М – число > 0)

(6)![]() - сходится, а члены (5) не
превосходят членов (6) Þ
по признаку сравнения (5) сходится, а тогда (2) сходится абсолютно.
- сходится, а члены (5) не
превосходят членов (6) Þ
по признаку сравнения (5) сходится, а тогда (2) сходится абсолютно.
2) Дано: (2) расходится в т. х1.
Предположим, что $ х*>x1 и (2) в т. х* - сходится. Но тогда (2) сходится и в т. х1, а это противоречит условию теоремы.
Теорема доказана.
РАДИУС И ИНТЕРВАЛ СХОДИМОСТИ СТЕПЕННЫХ РЯДОВ.
(1) ![]()
Чтобы решить вопрос об абсолютной сходимости степенного ряда (1) составим ряд из абсолютных величин членов (1):
(2) ![]()
для исследования сходимости (2) используем признак Даламбера.
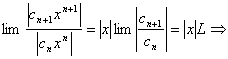 если
если ![]() , то ряд
сходится абсолютно
, то ряд
сходится абсолютно
![]() -
радиус сходимости степенного ряда (1).
-
радиус сходимости степенного ряда (1).
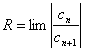 (3)
(3)
![]() (4)
Þ в (-R, R) степенной ряд сходится абсолютно. Вне этого интервала
степенной ряд (1) расходится. Граничные точки x = R и x = -R
исследуются особо. В этих точках, т. е. на границах интервала, степенной ряд может
или сходится, или расходится.
(4)
Þ в (-R, R) степенной ряд сходится абсолютно. Вне этого интервала
степенной ряд (1) расходится. Граничные точки x = R и x = -R
исследуются особо. В этих точках, т. е. на границах интервала, степенной ряд может
или сходится, или расходится.
Замечание:
1) если R = 0, то (1) расходится для всех x, кроме быть может одной точки х = 0.
2) Если R ® ¥ ,то (1) сходится абсолютно для всех х, т. е. в этом случае абсолютной сходимости является (-¥; +¥).
3) Рассмотрим обобщенный степенной ряд (5)
(5) ![]()
R находим по (3), и тогда интегралом сходимости (5) является.
![]()
a – R < x < a + R (6)
Вне интервала (6) степенной ряд (5) расходится, внутри его ряд сходится абсолютно, а граничные точки x = a – R и x = a +R исследуется особо.
4) К ряду (2) и аналогично к ряду (5) можно применять и радикальный признак Коши:
![]()
 (7)
(7)
Все утверждения относительно интервала сходимости (2) и (5) аналогичны предыдущему.
СВОЙСТВА АБСОЛЮТНО СОДЯЩИХСЯ СТЕПЕННЫХ РЯДОВ.
1. Если степенной ряд сходится в (-R, R), то в каждой точке этого интервала сумма ряда непрерывная функция.
2. В каждой внутренней точке интервала сходимости степенного ряда этот ряд можно почленно дифференцировать.
3. Степенной ряд можно почленно интегрировать на любом [a, b] Ì (-R, R).
ЛЕКЦИЯ 18
РЯДЫ ТЕЙЛОРА И МАКЛОРЕНА.
Рассмотрим функцию f(x) непрерывную в т.а и некоторой её окрестности и дифференцируемую в т.а достаточное число раз.
Поставим перед собой задачу: можно ли f(x) представить в виде степенного ряда и всегда ли полученный степенной ряд будет иметь своей суммой данную f(x).
Эту задачу решает ряд Тейлора.
Предположим, что f(x) представима в виде степенного ряда, т.е. имеет место:
(1) f(x)=c0+c1(x-a)+c2(x-a)2+…+cn(x-a)n+…
Найдём, как связаны коэффициенты степенного ряда с f(x)
Полагаем в (1) x=a Þ f(a)=c0
Предположим, что ряд в правой части (1) имеет интервал сходимости некоторую окрестность т. а и тогда этот ряд можно почленно дифференцировать в окрестности т. а.
(2) f’(x)=c1+2c2(x-a)+3c3(x-a)2+…+ncn(x-a)n-1+…
Полагаем в (2) x=a Þ f’(a)=c1
(3) f’’(x)=2c2+2·3c3(x-a)+3·4c4(x-a)2+…+n(n-1)cn(x-a)n-2+…
Полагаем в (3) x=a Þ f’’(a)=2c2 Þ ![]()
![]()
f’’’(x)=2·3c3 + 2·3·4c4(x-a)+…+n(n-1)(n-2)cn(x-a)n-3+… (4)
f’’’(a)=3!c3 Þ ![]() и т.д.
и т.д.
![]() (5)
– коэффициенты Тейлора.
(5)
– коэффициенты Тейлора.
(6) ![]()
ряд (6) – ряд Тейлора для f(x) в окрестности т. а
ТЕОРЕМА ТЕЙЛОРА.
Для того, чтобы f(x) разложить в степенной ряд по степеням (x-a) необходимо и достаточно, чтобы f(x) была определена в т.а и имела непрерывные в этой точке производные до n-го порядка включительно и предел остатка этого ряда, т.е. lim Rn(x) = lim(S(x)-Sn(x))=0, был равен нулю. Для любого х принадлежащего области сходимости ряда (6) сумма ряда равна значению функции f(x) в этой точке и это разложение единственно.
Частным случаем ряда Тейлора является ряд Маклорена (a=0) Þ
(7) ![]() - ряд Маклорена.
- ряд Маклорена.
Разложение в ряд Маклорена некоторых элементарных функций.
1.
![]() (8)
область сходимости xÎ(-¥;
¥)
(8)
область сходимости xÎ(-¥;
¥)
2.
![]() (9) область сходимости xÎ(-¥; ¥)
(9) область сходимости xÎ(-¥; ¥)
3.
![]() (10) область сходимости xÎ(-¥; ¥)
(10) область сходимости xÎ(-¥; ¥)
4. Биноминальный ряд для f(x)=(1+x)m.
![]() (11)
(11)
область сходимости xÎ(-1;1)
Частные случаи биноминальных рядов.
Полагаем в (11) m=-1 Þ ![]() (12)
– геометрический ряд, где область сходимости xÎ(-1;1)
(12)
– геометрический ряд, где область сходимости xÎ(-1;1)
В (12) вместо х подставим –х Þ ![]() (13), область сходимости xÎ(-1;1)
(13), область сходимости xÎ(-1;1)
В (11) ![]() Þ
Þ ![]() (14)
(14)
В (14) вместо х подставим –х2
![]() (15)
(15)
В (12) вместо х подставим х2
![]() (16)
(16)
5. Известно, что степенные ряды можно почленно интегрировать по любому интервалу целиком лежащему в области абсолютной сходимости данного степенного ряда.
Тогда проинтегрировав ряд (12) в пределах (0; x), где xÎ(-1;1)

 на (-1; 1) (17)
на (-1; 1) (17)
Проинтегрируем (13) Þ  (18)
(18)
(17) – (18) Þ
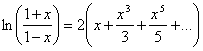 (19)
(19)
Проинтегрируем в (0; х) ряд (16) Þ ![]() (20)
(20)
Проинтегрируем (15) Þ ![]() (21)
(21)
ЛЕКЦИЯ 19
РЯДЫ ФУРЬЕ.
Ортогональные системы функций.
![]() -
называется ортогональной на [a; b],
если выполняется следующие равенства:
-
называется ортогональной на [a; b],
если выполняется следующие равенства:
1) 
2) 
Нормой функции jn(x) называется: 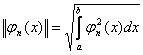 (3)
(3)
В качестве примера ортогональной системы функций рассмотрим тригонометрическую систему функций на [-p; p]
1; cos x; sin x; cos 2x; sin 2x; …; cos nx; sin nx; … - называется тригонометрической системой функций.
1) 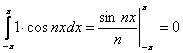
2) 
3) 
4) 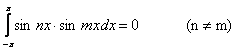
5) 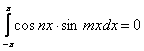 1)
– 5) – условие (1)
1)
– 5) – условие (1)
6) 
7) 
8)  6)
– 8) – условие (2)
6)
– 8) – условие (2)
Мы показали, что тригонометрическая система функций
ортогональна на [-p; p] и в силу периодичности всех
функций, входящих в эту систему, можно утверждать, что эта система функций
ортогональна на любом отрезке длины 2p
и Þ ![]()
![]()
![]()
Наряду с ортогональными системами функций рассматривают ортонормированную систему функций.
Ортонормированной системой функций называют ортогональную систему функций, причём норма каждой из функций входящих в систему равна единице.
Кроме рассматриваемых тригономерических систем функций
рассматриваются ортогональные обобщённые системы тригонометрических функций: 1;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ; …;
; …; ![]() ;
; ![]() ; … на [-p; p].
; … на [-p; p].
Разложение функций в ряд Фурье по ортогональной системе функций.
Рассмотрим систему ортогональных функций {jn(x)} на [a; b].
Пусть имеет место:
f(x) = c1j1(x) + c2j2(x) + … + cnjn(x) + … (4)
Найдём значения коэффициентов ck.
Умножим обе части (4) на jk(x) и проинтегрируем полученное равенство в пределах от a до b:
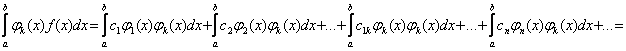
В силу ортогональности все интегралы равны нулю, кроме:
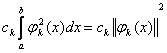 ,
отсюда
,
отсюда 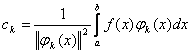 (5) k= 1, 2, 3, …n, …
(5) k= 1, 2, 3, …n, …
(5) – коэффициенты Фурье, а (4) называется рядом Фурье по системам ортогональных функций на [a; b].
ЛЕКЦИЯ 20
Ряд Фурье для функций f(x) с периодом 2p.
(6) ![]()
Каждая из функций, входящая в (6), периодическая с периодом 2p Þ если f(x) является суммой ряда (6), то она обязана быть тоже периодической функцией с периодом 2p.
Предположим, что ряд в правой части (6) равномерно сходится на [-p; p].
Найдём значения коэффициентов a0, an, bn.
Проинтегрируем (6) на [-p; p]

 (7)
(7)
Умножим (6) на cos nx и проинтегрируем на [-p; p]

 (8)
(8)
Аналогично находится bn. Обе части (6) умножаем на sin nx и интегрируем на [-p; p]
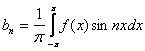 (9)
(9)
(7), (8), (9) – коэффициенты ряда Фурье или ряд Фурье для f(x) с T=2p.
Ряд фурье для f(x) с произвольным периодом.
f(x+2l)=f(x) Û периодическая с T=2l.
Достаточно задать функцию на (-l; l) и на оставшуюся ось ОХ продолжить функцию периодическим образом с T=2l.
(10) ![]()
(11) 
(12) 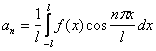
(13) 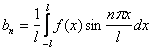
ДОСТАТОЧНОЕ УСЛОВИЕ РАЗЛОЖИМОСТИ f(x) В РЯД ФУРЬЕ (ТЕОРЕМА ДИРИХЛЕ).
f(x) удовлетворяет условиям Дирихле на [-p; p], если она непрерывна на этом отрезке либо имеет конечное число точек разрыва первого рода.
ТЕОРЕМА.
Функцию f(x) удовлетворяющую условиям Дирихле на [-p; p], периодическую с T=2p, можно единственным образом разлагать в ряд Фурье (6) с коэффициентами (7), (8), (9), причём:
1) S(x)=f(x) в точках непрерывности
2) Если
т. х0 – т. разрыва I рода, то S(x0) равна среднему
арифметическому левостороннего и правостороннего пределов функции, т.е. ![]()
3) Значения
суммы ряда на границах отрезка: ![]()
Аналогичная теорема имеет место и для f(x) с произвольным периодом, а именно:
Если f(x) удовлетворяет условия Дирихле на[-l; l ] и периодическая с T=2l, то её можно разложить в ряд Фурье (10) с коэффициентами (11), (12), (13) единственным образом причём:
1) S(x)=f(x) в точках непрерывности.
2) если x0 – точка разрыва первого рода.
![]()
3) ![]()
ЛЕКЦИЯ 21
РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ ЧЁТНЫХ И НЕЧЁТНЫХ ФУНКЦИЙ.
1) f(x) задана на (-p; p), f(x+2p)=f(x) и f(-x)=f(x) для любого xÎ(-p; p).
Известно, что:
Если f(-x) =
f(x) Þ 
Если f(-x) =
- f(x) Þ 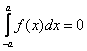
(1) ![]()
(2) 
(3) 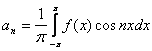
(4) 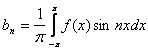
Если f(x) – чётная, то bn = 0, а
(5) 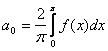
(6) 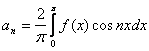
(7) ![]()
Ряд Фурье для чётной функции содержит только косинус и коэффициенты вычисляются по (5) и (6).
2) Если f(x) – нечётная в (-p; p)
f(x+2p)=f(x), f(-x) = - f(x), то a0=0; an=0
(8) 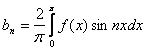
Ряд Фурье для нечётных функций содержит только синус
(9) ![]()
Замечание:
Аналогично, если функция f(x) на (-l; l), T=2l.
Если f(-x)=f(x), то bn=0
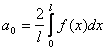

![]()
Если f(-x) = - f(x), то a0=0; an=0
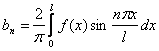
![]()
РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ ФУНКЦИЙ, ЗАДАННЫХ НА ПОЛОВИНЕ ПЕРИОДА.
f(x) à f(x+2p) = f(x); T=2p
f(x) задана либо на (0; p), либо на (-p; 0).
Если f(x) задана на интервале длины, равной периоду и на этом интервале функция удовлетворяет условию Дирихле, то её можно разложить в ряд Фурье, причём это разложение единственно.
Функию заданную на половине интервала можно продолжить на вторую половину интервала так, чтобы на всём интервале длины равной периоду функции, она удовлетворяла условию Дирихле, тогда такую функцию можно разлагать в ряд Фурье, но этот ряд Фурье будет зависеть от продолжения функции на вторую половину интервала. Таким образом функция, заданная на половине интервала, может иметь бесчисленное множество рядов Фурье, каждый из которых зависит от соответствующего продолжения. Но из всего множества продолжений функции можно выделить два продолжения:
1) «Чётное», т.е. функцию зеркально отображают относительно ОУ Þ функция становится чётной ;
2) а если функцию зеркально отобразить относительно начала координат, то на всём интервале она становится нечётной.
Чтобы разложить f(x) в ряд по косинусам, необходимо предварительно продолжить её чётным образом и тогда, её ряд Фурье будет содержать только косинусы. А, чтобы эту функцию разложить в ряд по синусам надо продолжить нечётным образом, и тогда её ряд Фурье будет содержать только синусы.
ЛЕКЦИЯ 22
РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
Пусть f(x) на (-p; p), Т=2p
(1) ![]()
(2) 
(3) 
(4) 
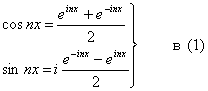
(5) ![]()
(6) 
(7) 
(8) ![]()
Принимая во внимание (6), (7) и (8) и подставляя в (5), получим
(9) ![]()
(9) – ряд Фурье в комплексной форме, коэффициенты которого вычисляются по формуле (6).
Аналогично, если f(x) на (-l; l), T=2l.
(10) ![]()
(11) 
Замечание:
Зная ряд Фурье в действительной форме, можно легко по
формуле ![]() перейти к
комплексной форме.
перейти к
комплексной форме.
Зная ряд Фурье в комплексной форме, можно легко найти коэффициенты an и bn.
an-ibn=2cn
Re Cn – дейтвительная часть cn.
Jm Cn – мнимая часть сn.
an-ibn=2Re cn + i2Jm cn

ЛЕКЦИЯ 23
ИНТЕГРАЛ ФУРЬЕ.
Рассмотрим f(x), определённую для любого х на (-¥; ¥). Пусть эта функция абсолютно интегрируема на любом (-l; l), и она непрерывна либо имеет конечное число течек разрыва первого рода.
Запишем ряд Фурье для этой функции на (-l; l):
(1) 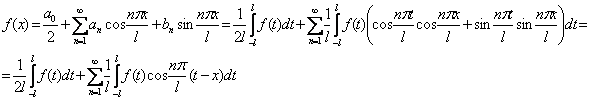
Пусть là¥. Найдём lim (1)
1) 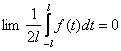
![]() числу,
т.к. функция абсолютно интегрируема.
числу,
т.к. функция абсолютно интегрируема.
2) ![]()
![]()
при lॠ![]()

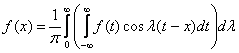 (2)
(2)
(2) – интегральная формула Фурье, а интеграл стоящий в правой части этого равенства называется интегралом Фурье.
Преобразуем (2) к более стандартному виду.
 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
ЛЕКЦИЯ 24
Интеграл Фурье для чётных и нечётных функций.
1) Если f(-x) = f(x) на (-¥; ¥), тогда польхуясь свойствами интегралов о чётности и нечётности функций:
![]()
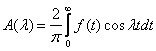 (6)
(6)
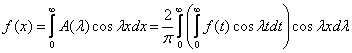 (7)
(7)
2) Если f(-x) = -f(x) на (-¥; ¥)
![]()
 (8)
(8)
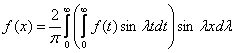 (9)
(9)
(7) – называется cos – преобразованием Фурье.
(9) – называется sin – преобразованием Фурье.
Замечание:
Если функция задана на половине интервала, т.е. на (0; ¥) или (-¥; 0), то для этой функции можно найти и cos – преобразование и sin – преобразование, продолжив предварительно данную функцию на вторую половину интервала чётным или нечётным образом.
ЛЕКЦИЯ 25
Интеграл Фурье в комплексной форме.
Известно
 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
B(1) Þ 
 (4)
(4)
![]()
![]() (5) – преобразование Фурье
(5) – преобразование Фурье
![]() (6)
- преобразование Фурье
(6)
- преобразование Фурье
Подставляя (5) и (6) в (4) Þ
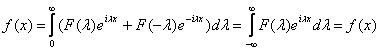 (7)
– интеграл Фурье в комплексной форме (интегральная формула Фурье или обратное
преобразование Фурье).
(7)
– интеграл Фурье в комплексной форме (интегральная формула Фурье или обратное
преобразование Фурье).
Совокупность модулей F(l) образуют амплитудный спектр [½F(l)½] функции f(x). Совокупность аргументов F(l) образуют фазовый спектр f(x)[arg F(l)]. А сама формула (5) называется спектральной функцией.
РАВЕНСТВО ПАРСЕВАЛЯ.
Позволяет определять среднее значение квадрата периодической функции за один период, зная лишь коэффициенты ряда Фурье.
f(x) на [-p; p]; f(x+2p) = f(x)
![]() (1)
(1)
Возведём (1) в квадрат
![]()
Проинтегрируем полученное равенство в пределах [-p; p]
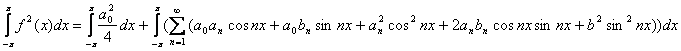 =
=![]() отсюда получаем
равенство Парсеваля.
отсюда получаем
равенство Парсеваля.

Базовый учебник: Пискунов Н.С. Дифференциальное
и интегральное исчисление. Т1, Т2, М: Наука, 1978
Рассмотрено и рекомендовано на заседании
кафедры высшей математики (протокол №1
от 29.09.99 г.)
Составители: доц. Усманов Р.Н., ст. пр. Шопен И.Л.
Ответсвенный редактор: доц. Усманов Р.Н.
Редакционно-корректурная комиссия
Редактор
Корректор