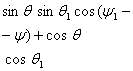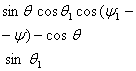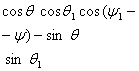VIII-БОБ. НОГОЛОНОМ ТИЗИМЛАР ТУРГУНЛИГИ

 

1-§. Ноголоном тизимлар хакида умумий тушунчалар

 

            «Голоном тизим» ва «ноголоном тизим» деган терминларни (тушунчаларни) 1894 йилда Г.Герц узининг вафотидан кейин нашр этилган машхур китобида таклиф этган эди [110].

            Куп холларда тизимнинг тузилиши унинг айрим кисмларини ихтиёрий равишда харакат килишга йул бермайди, уларнинг харакати ва холати кандайдир узаро богланган бир катор шартларга буйсундирилган булади. Бу холларда механикада тизимга богланишлар куйилган деб айтилади. Бу богланишларнинг муайян куриниши хар хил булади. Богланишлар тизимнинг айрим кисмларининг мумкин булган геометрик жойлашишини чегаралайди. Бундай богланишларни геометрик богланишлар деб айтамиз. Айрим богланишлар тизимнинг кинематик мумкин булган харакатини, яъни тизимнинг айрим кисмларининг тезликларини чегаралаб куяди. Бундай богланишларга кинематик богланишлар деб айтилади. Аникки, хар кандай геометрик богланиш кандайдир кинематик богланишни ифодалайди, аммо акси булмаслиги мумкин, яъни тизимнинг айрим кисмларининг мумкин булган тезликлари орасидаги богланиш унинг мумкин булган холатларини (координаталарини) чегаралаб куймаслиги мумкин.

            Мисол сифатида текислик буйича сирганмай думалаётган дискни куриб утайлик.

            Координата тизими  жойлашган  текислигида думалаётган диск холатини  умумлашган координаталар билан аниклаймиз (8.1-шакл). Бу ерда  - дискнинг текислик билан  уриниш нуктаси координаталари, -фиксацияланган (михланган) диск ободининг нуктасидан  уриниш нуктасигача булган бурчак (айланиш бурчаги),  -  уки билан дискка  нукта оркали утказилган уринма орасидаги бурчак,  - диск текислиги билан  текислиги орасидаги бурчак (дискнинг  га нисбатан огиш бурчаги).

 

 

 

 

 

 

 

 

 

 

 

 

           

8.1-шакл.

 

 

            Дискнинг  текислиги буйича сирганмай думалашидан хар бир моментда дискнинг  текислигига уринадиган нуктанинг тезлиги нолга тенг булиши келиб чикади, яъни  нуктанинг тезлиги , бу ерда , -дискнинг радиуси. Дискнинг ихтиёрий кичик силжиши  координаталарнинг узгариши билан характерланади. Биз уларни  билан белгилаймиз. Радиуси  га тенг  булган диск сирганишсиз думалаётганлиги учун дискнинг холатини аникловчи бешта координатанинг узгариши ихтиёрий булмайди ва доимо иккита шартни каноатлантириши керак:

                                                      (8.1.1)

Шундай килиб, сирганишсиз думалашнинг шарти (8.1.1) тенгламалар системаси билан ифодаланадиган кинематик богланишлардан иборат экан. (8.1.1) тенгламаларни  га булганимизда

                               (8.1.2)

хосил киламиз. (8.1.2) кинематик богланишлар  координаталарнинг мумкин булган кийматларини чегараламайди.

            Шундай килиб,

                   (8.1.3)

тенгламалар билан ифодаланадиган богланишларга геометрик ва

     (8.1.4)

тенгламалар билан ифодаланадиган богланишларга кинематик богланишлар деб айтамиз.. Бу ерда  лар тизимнинг умумлашган координаталари,  лар эса умумлашган тезликлари. (8.1.4) кинематик богланишлар интегралланувчи ва интегралланмовчи булиши мумкин. Интегралланувчи кинематик богланишлар бу геометрик богланишларнинг узидир. Интегралланмовчи кинематик богланишли механик тизимларга ноголоном тизимлар, геометрик богланишли механик тизимларга голоном тизимлар деб айтилади.

            Механикада учрайдиган ноголоном богланишларни, яъни интегралланмовчи кинематик богланишларни одатда куйидагича ёзилади (умумлашган тезликларга нисбатан чизикли богланган):

 .    (8.1.5)

Бундай богланишларга чизикли ноголоном богланишлар деб айтамиз.  булганда улар бир жинсли богланишлар деб айтилади. Агар  ва  ларнинг ифодаларига  очик куринишида кирмаса, улар  вактга боглик эмас деб айтамиз.

             текислиги буйича сирганмасдан думалаётган диск чизикли бир жинсли, вактга боглик булмаган, интегралланмовчи кинематик богланишли ноголоном тизимга мисол була олади.

            Ноголоном тизимлар аналитик механикасини яратиш факат XIX асрнинг охирларида бошланди. Хозирги вактда ноголоном тизимлар харакатининг турли куринишдаги тенгламалари мавжуд. Улардан айримларини келтирамиз.

            Даламбер-Лагранж тенгламаси

                             (8.1.6)

куринишда берилган булсин, бу ерда Т-тизимнинг кинетик энергияси, -умумлашган кучлар. Тизимда факат потенциал кучлар мавжуд булса, яъни  булса, (8.1.6) ни куйидаги куринишга келтириш мумкин:

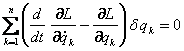                        ,       (8.1.7)

бу ерда  - Лагранж функцияси. Шуни таъкидлаймизки, факат  вариациялар богланмаган булганда, (бу факат голоном тизимлар учун мумкин) (8.1.6) ёки (8.1.7) муносабатлардан бизга маълум Лагранж тенгламаларини хосил килиш мумкин:

                            (8.1.8)

ёки мос равишда

                        .      (8.1.9)

            Ноголоном тизимлар учун (8.1.6) муносабатдан харакатнинг Лагранж формасидаги тенгламаларини хосил килиш мумкин эмас, чунки исталган  умумлашган координаталар учун  вариациялар богланган булади.

                    (8.1.10)

ноголоном богланишлар учун умумлашган координаталар вариацияси  та

                            (8.1.11)

чизикли бир жинсли тенгламаларни каноатлантирадилар. (8.1.6) муносабатдан харакатнинг дифференциал тенгламаларига утиш учун ёки аникмас купайтувчилар усулидан (Лагранж купайтувчилари), ёки богланган вариациялардан кутулиш, яъни уларни кандайдир  та богланмаган вариациялар оркали ифодалашдан фойдаланиш керак. Биринчи холда биз  дифференциал тенгламалар тизимига келамиз. Бу тизим изланаётган  функциялардан ташкари яна  номаълум купайтувчиларни уз ичига олади. (8.1.10) билан биргаликда бу тенгламалар  номаълумлар учун  тулик тенгламалар тизимини ташкил киладилар. Иккинчи холда биз  та тенгламага эга буламиз ва улар (8.1.10) билан биргаликда тулик тизимни ташкил киладилар. Бу дифференциал тенгламаларни интеграллаш курилаётган механик тизимнинг бошлангич холатидан бошланадиган харакатини топишга имкон беради. Бундан ташкари биринчи холда бир вактда тизимга куйилган богланишларнинг реакция кучларини хам топамиз.

            Энди (8.1.11) тенгламаларнинг  хар бирини, умуман айтганда, нолдан фарк килувчи кандайдир  микдорга купайтириб, хосил этилган барча ифодаларни кушамиз. (8.1.6) Даламбер-Лагранж тенгламаларига нолга тенг булган

                                                (8.1.12)

йигиндини кушиб, (8.1.6) га эквивалент

                (8.1.13)

тенгламани хосил киламиз. Бу тенгламада  Лагранж купайтувчилари янги кушимча узгарувчилар буладилар. (8.1.11) тенгламалар чизикли богланмаган, яъни  матрицанинг ранги  тенглиги учун, унинг минорларидан биттаси нолдан фарк килади.

            Аниклик учун

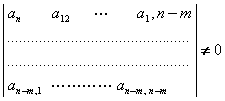                        .    (8.1.14)

дейлик.

            Умумлашган координаталарнинг  вариацияларини ихтиёрий деб караш мумкин, чунки (8.1.11) тенгламалар тизими бу вариацияларнинг исталган кийматлари ва колган  вариацияларнинг аник кийматлари учун бажарилади.

            Энди  Лагранж купайтувчиларини шундай танлаб оламизки, (8.1.13) муносабатдаги богланган  вариациялар олдидаги кавс ичида турган ифодалар нолга тенг булсин.  бундай танлаш мумкин, чунки  чизикли тенгламалар тизими

           

 га нисбатан ((8.1.14) муносабатга асосан) ечилувчидир. Аммо, танлаб олинган  лар учун (8.1.13) тенглама куйидаги ифодага айланади:

            ,

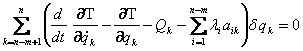бу ерда  вариациялар богланмаган вариациялардир. Шунинг учун барча кавслар нолга тенг булиши керак.

            Шундай килиб, биз харакатнинг Лагранж купайтувчили тенгламасига келдик:

            .  (8.1.15)

            Бу тенгламалар (8.1.10) богланишлар тенгламалари билан биргаликда  номаълум  ва  функцияларга нисбатан  тулик тенгламалар тизимини ташкил килади.  ифода оддий механик маънога эга – булар ноголоном богланишларнинг умумлашган реакция кучлари. Хакикатан хам, - умумлашган реакция кучлари булса, у холда ноголоном тизимнинг харакати худди  умумлашган координаталар, Т кинетик энергияси ва  умумлашган кучлари булган голоном тизимнинг харакатидай булади, яъни ноголоном тизимнинг харакат тенгламасини

                   

куринишда ёзиш мумкин. Бу тенгламаларни (8.1.15) тенгламалар билан солиштирсак,

                                                  (8.1.16)

эканлигига ишонч хосил киламиз.

            Е.Т.Уиттекер ноголоном тизимлар учун (8.1.15) куринишдаги тенгламаларни биринчи булиб Феррер тузган деб айтади [114]. Э.Дж.Раус хам шу турдаги тенгламалардан фойдаланган [82,115-117].

            1899 йилда П.Аппел (P.Appell) голоном ва ноголоном тизимлар харакат тенгламаларининг янги куринишини тавсия этди [107]. У Лагранж тенгламаларидаги Т кинетик энергияга ухшайдиган янги S функция киритди. Бу функцияни кейинчалик тезланиш функцияси деб атадилар. Голоном тизимларда Т кинетик энергия кандай тизимнинг динамикасини характерласа, худди шундай S функция ноголоном тизим динамикасини тулик характерлайди. ¡зининг куриниши билан Аппель тенгламалари содда булса хам муайян масалаларни куришда S функциясини тузиш Т кинетик энергияни топишга нисбатан огиррокдир.

            Ноголоном тизимга куйидаги чизикли богланишлар куйилган булсин:

  .  (8.1.17)

Бу тенглама (8.1.10) ёки (8.1.5) ларни  нисбатан ечиш йули билан хосил этилади ва уларга эквивалентдир.

            Аппель тенгламаси

 (8.1.18)

куринишда булади. Бу ерда - тезланиш энергияси. (8.1.18) тенгламалар богланишларнинг (8.1.17) тенгламалари билан биргаликда n-m та иккинчи тартибли тенгламалар ва m та биринчи тартибли тенгламаларнинг тулик тизимини ташкил киладилар ва n та номаълум  узгарувчиларни топишга имконият яратади.

С.А.Чаплыгин курсатдики, купгина консерватив ноголоном тизимларда  умумлашган координаталарни m та биринчи координаталар вариацияларини богланмаган деб кабул килиб, шундай танлаб олиш мумкинки,  колган n-m координаталар  кинематик интегралланмайдиган

                  (8.1.19)

богланишларнинг  коэффициентлар ифодаларига хам, (8.1.19) богланишларни хисобга олмай тузилган L Лагранж функциясининг ифодасига хам кирмайди. Бундай тизимларни Чаплыгин тизимлари деб атайдилар ва шуниси яхшики, улар учун харакатнинг динамик тенгламаларини интегралланмайдиган кинематик богланишлардан ажратиб олиш мумкин.

С.А.Чаплыгин тенгламалари куйидаги куринишга эга:

 (8.1.20)

            Бу ерда юлдузча билан ифодасидан (8.1.19) богланиш тенгламаларидан  фойдаланиб богланган деб каралаётган умумлашган  тезликлар  чикариб ташланган ифодаларни тушунамиз (масалан, Т^* нинг ифодасида  умумлашган тезликлар катнашмайди.). Бу илмий натижани С.А.Чаплыгин 1895 йили табиатшунослар жамиятида маъруза килиб берди ва мазкур жамиятнинг журналида 1897 йили нашр этган [105]

   1901 йилда П.В.Воронец

         (8.1.21)

интегралланмайдиган кинематик богланишлар билан богланган ноголоном тизимлар харакатининг тенгламаларини тавсия этди [18]:

 . (8.1.22)

Бу ерда

     (8.1.23)

яъни Т ифодасига  лар урнига ифодасини (8.1.21) дан келтириб куйганимизда  функция хосил булади.

   Хусусий холда, агар чикариб ташланган умумлашган тезликларга мос келувчи  кинематик энергия, потенциал энергия П=-U ва ноголоном богланишлар ифодаларига кирмасалар, у вактда координаталар (8.1.22) Воронец тенгламалари С.А.Чаплыгин (8.1.20) тенгламалари билан мос келади. Агар тизимга таъсир этаётган кучлар потенциал кучлар булмаса, у вактда (8.1.22) Воронец тенгламалари куйидагича ёзиладилар:

        (8.1.24)

П.В.Воронец (8.1.22) тенгламаларни Гамильтон-Остроградский вариацион принципидан фойдаланиб топади. У бу принципни умумлаштирди ва ноголоном тизимларга куллашни курсатди. Кейинги ишларида у ноголоном тизимлар харакатининг тенгламаларини квазикоординаталарда яратди.

Умуман айтганда ноголоном тизимлар харакатининг тенгламаларини кайси формада олишимиздан катьий назар (Чаплыгин тизимидан ташкари) тулик тизимни тузиш учун харакат тенгламаларига ноголоном богланишлар тенгламаларини кушиш зарур. Ана шу характери билан ноголоном тизимлар богланмаган координатали голоном тизимлардан фарк килади. Бу холат ноголоном тизимлар харакатининг тургунлигини тадкик этиш масаласини бошкача куйишни такозо килади.

   Ноголоном тизимлар харакати тенгламаларининг бошка формалари Г.Маджи, В.Вольтерра, Г.Ю.Неймарк, Н.Фуфаев ва бошка купгина олимлар томонидан хам яратилган [69,71]. Бу билан кизикувчиларга Ю.И.Неймарк ва Н.А.Фуфаевнинг [71] китобига хамда В.В.Румянцев ва А.В.Карапетяннинг [82,83] илмий маколаларига мурожаат килишларини тавсия этамиз.

   Шуни таъкидлаймизки, ноголоном тизимлар харакатининг назарияси гилдиракли экипажлар харакатининг назарияси [43] ва электромеханик тизимлар назариялари билан чамбарчас богланган. Бу масалалар Ю.И.Неймарк ва Н.А.Фуфаевнинг [71] китобида ва Ю.И.Неймаркнинг [69] маколасида батафсил келтирилган.

   XX асрнинг урталаригача эластик пневматикали гилдиракнинг сирганишсиз думалаши натижасида хосил буладиган ноголоном богланишлар ноголоном тизимлар динамикасига богланмасдан урганиларди. Автомобил, мотоцикл, самолёт шассилари ва темир йул вагонларига доир булган актуал тургунлик масалалари реал гилдирак думалашининг шартларини ва таянч текислик томонидан унга таъсир этадиган реакция кучларини урганиш ва тадкик этиш масаласини кун тартибига куйди.

Ю.И.Неймарк ва Н.А.Фуфаев гилдиракнинг думалашида унга куйиладиган богланишлар (М.В.Келдыш томонидан яратилган) идеал богланишлар эканлигини ва шундай богланишга эга булган тизимларга ноголоном тизимлар харакат тенгламаларини куллаш мумкинлигини курсатдилар [70]. Улар m та баллонли гилдиракка эга булган экипажнинг узгармас тезлик билан тугри чизикли харакатининг дифференциал тенгламалари куйидаги куринишга эга эканлигини курсатдилар

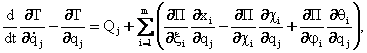
бу ерда  экипажнинг кинетик энергияси,

пневматик шиналар деформациясининг потенциал энергияси,  лар  ракамли шинанинг кинематик параметрлари,  лар  ракамли шинанинг эластиклик коэффициентлари. Кейинчалик бу тенгламаларни экипажнинг эгри чизикли харакатига татбик этдилар.

 

2-§. Ноголоном тизимлар мувозанат холатининг тургунлиги

 

Ноголоном тизимларга багишланган куп илмий ишларга карамасдан уларнинг тургунлигига тааллукли ишлар жуда оздир. Ноголоном тизимларнинг кичик тебранишлари ва тургунлиги масалалари билан Е.Уиттекер, О.Боттема, М.А.Айзерман ва Ф.Р.Гантмахер, А.Н.Обморшев, Н.А.Фу-фаев, Ю.И.Неймарк, В.В.Румянцев, Н.Г.Четаев, И.В.Нико-ленко, А.В.Карапетян, Г.Н.Князев, А.Я.Красинский, И.С.Емельянова ва бошкалар шугулланганлар. Аммо уларнинг ишларидаги тургунликни тадкик этиш усуллари бир-бири билан мос келмас эди. Маълумки, мувозанат холати атрофида потенциал энергия умумлашган координаталарнинг биржинсли квадратик формаси булади деб фараз килиб, Уиттекер чизикли ноголоном богланишларни интеграллади. Бунинг натижасида Уиттекер ноголоном тизимлар мувозанат холатининг тургунлигини текшириш масаласини богланмаган умумлашган координаталари ноголоном богланишлар сонига камайтирилган голоном тизимлар масаласига айлантиради [114]. Боттема [109] биринчи булиб Уиттекер мулохазаларининг мантикка зидлигини пайкади. У аник мисолда ноголоном тизимлар дифференциал тенгламаларининг характеристик детерминанти умумий холда носимметрик эканлигини ва характеристик тенгламаси ноголоном богланишлар сонидан кам булмаган нол илдизларга эга эканлигини курсатди. Шу сабабли Боттема бу ерда тургунлик назариясининг критик холи мавжуд деб айтади. Шунинг учун хам Боттема ноголоном тизимлар мувозанат холатининг тургунлик масаласи хозирча очик колади деган хулосага келди, чунки унгача ихтиёрий сонда нолинчи илдизга эга булган характеристик тенгламали тизимлар учун тургунлик шартлари ишлаб чикилмаган эди.

Кейинчалик А.И.Кухтенко [82], А.Н.Обморшев [76], И.В.Николенко [74] ишларида ноголоном тизимлар тойилган харакатининг чизиклаштирилган дифференциал тенгламалари ва уларга мос характеристик детерминантлари келтирилган ва бу детерминантлар умумий холда симметрик эмаслиги курсатилган.

М.А.Айзерман ва Ф.Р.Гантмахер Боттема тадкик этган масалани охиригача ечиш мумкин эканлигини курсатдилар. Улар бу масалани А.М.Ляпунов ва И.Г.Малкин тулик тадкик этган тургунликнинг махсус холига келишини курсатдилар. Улар ноголоном тизимлар учун ушбу теоремани исбот этдилар [108].

Теорема. Агар тойилган харакат характеристик тенгламасининг, нолга тенг булган илдизларидан ташкари, ноголоном богланишлар сонига тенг булган мувозанат холатлари атрофидаги барча илдизлари чап ярим текисликда ётса, у холда тизимнинг мувозанат холати тургун (аммо ассимптотик тургун эмас) булади. Шу билан тойилмаган харакатга етарли якин булган хар кандай тойилган харакат да куп хиллик мувозанат холатларининг биттасига интилади.

Бу натижага асосланиб, Г.Н.Князев [44] ноголоном богланишлар сонидан характеристик тенгламанинг нолга тенг булган илдизларининг сони катта булган холни факат критик хол деб аташни тавсия этади. ¡зининг ишида у характеристик тенгламанинг нолга тенг булган илдизларининг сони ноголоном богланишлар сонидан биттага ортик булган холни тадкик этди. А.Н.Обморшев умумий холда ноголоном тизимлар кичик тебранишларининг мувозанат холати атрофида чизиклаштирилган дифференциал тенгламаларини ва Чаплыгин системаси учун стационар харакатга нисбатан тебранишлар тенгламасини тузди. Нолга тенг булган илдизлар масаласи хакида у Боттема ноголоном богланишларнинг чизиклаштирилган тенгламаларини интегралланмаганлиги натижасида характеристик тенгламанинг нолга тенг булган  илдизларини олган деган мулохазани билдирди.

Келтирилган адабиётлар обзоридан куриниб турибдики, ноголоном тизимлар мувозанат холатининг тургунлигини тадкик этишда нафакат ягона ёндашиш йуклиги, балки тадкик этиш усуллари хам бир-бирига зид эканлиги маълум булаяпти. Хакикаттан хам, агар Уиттекер чизиклаштирилган ноголоном богланишларни интеграллаб тугри иш килган булса, у вактда бу ишни килмаган ва натижада нолинчи илдизларга эга булган Боттема нохак. Агар Боттема хак булса, у холда Уиттекер ноголоном тизимлар мувозанат холатининг тургунлигини тадкик этишда принципиал хатога йул куйган. Аммо у вактда нолга тенг булган илдизлар табиатини тушунтиришда ноаниклик пайдо булади: Боттема, Айзерман ва Гантмахер нолга тенг булган илдизларнинг пайдо булишини Ляпунов маъносидаги критик хол билан боглаяптилар. Князев бу холатни критик хол деб хисобламаяпти, Обморшев булса, нолга тенг булган илдизларнинг пайдо булишини тушунмаслик сифатида ифодалайди. Агар чизиклаштирилган ноголоном богланишларни интеграллаганда, улар пайдо булмасди деб тушунтиради.

1965-1967 йиллар давомида Ю.И.Неймарк ва Н.А.Фуфаев [71,72,73] ноголоном тизимлар мувозанат холатини тадкик этиш масаласи голоном тизимларнинг мувозанат холатини тадкик этиш масаласидан бутунлай фарк киладиган ва узига хос хусусиятга эга масала эканлигини курсатдилар. Ноголоном тизимда мувозанат холати яккаланган холда булмаслигини (голоном тизимда яккаланган холда булади) ва улар улчами ноголоном богланишлар сонига тенг булган куп хилликни ташкил килишини курсатдилар. Ноголоном тизимнинг бу хусусияти характеристик тенгламада нолга тенг булган илдизларнинг пайдо булишига сабабдир.

Голоном ва ноголоном тизимларнинг стационар харакатини тадкик этишда худди ана шундай холатга дуч келамиз. Биз келгуси бандларда Ю.И.Неймарк ва Н.А.Фуфаев эришган натижаларни баён этамиз [69,71-73]. 

 

2.1.Кичик тебранишлар тенгламасини тузиш. Коэффициентлар матрицасининг хусусияти. Умумий назарияни татбик этиш мумкинлиги. Олинадиган натижаларнинг маъноси

 

   Ноголоном тизимларнинг мувозанат холати атрофидаги кичик тебранишларни урганишда кичик тебранишлар назариясидаги одатий ёндашишдан фойдаланиш мумкин. Бу ёндашиш ноголоном тизимларга хос булган хусусиятларни очишга имконият яратади.

   Конфигурацияси  умумлашган координаталар билан аникланадиган тизимнинг харакати

        (8.2.1)

m (m<n) та ноголоном богланишларга буйсунган деб фараз киламиз. Потенциал ва F диссипатив кучлар таъсир этаётган ноголоном тизим харакатини ифодаловчи тенгламаларни куйидаги куринишда ёзамиз:

  (8.2.2)

бу ерда  номаълум Лагранж купайтувчилари.

(8.2.1) ва (8.2.2) тенгламалар n+m та , номаълум узгарувчиларни вакт функцияси сифатида аниклашга имкон яратади. нукта тизимнинг мувозанат холати деб фараз килайлик. (8.2.1) ва (8.2.2) тенгламалардан куриниб турибдики, мувозанат холатида

        (8.2.3)

муносабат бажарилади, бу ерда V() – тизимнинг потенциал энергияси. (8.2.3) га асосан ноголоном тизимлар мувозанат холатида  микдор, умуман, нолга тенг эмас (голоном тизимларда нолга тенг). Демак, V() функциянинг мувозанат холати атрофидаги катор ёйилмасида чизикли хадлар хам мавжуд булади:

    (8.2.4)

бу ерда

.

Т ва F функциялар ларнинг кичик микдорлари учун худди голоном тизимлардагидай умумлашган  тезликларнинг узгармас коэффициентли квадратик формаси буладилар:

             (8.2.5)

бу ерда

.

 хадларни чизиклаштирганимизда

 

хосил булади, бу ерда

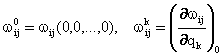               .     (8.2.6)

 аникмас купайтувчиларнинг тизимнинг мувозанат холатидаги кийматлари.

            (8.2.4)-(8.2.6) ифодаларни (8.2.2) га куйиб, куйидагини хосил киламиз

  (8.2.7)

(8.2.3) га асосан . Бу ифодани (8.2.7) га куйганимизда

      (8.2.8)

ни хосил киламиз. Бу тенгламаларга чизиклаштирилган ноголоном

                                                (8.2.9)

богланишларни кушиш керак.

(8.2.8) ва (8.2.9) тенгламалар ноголоном тизимларнинг  мувозанат холат атрофидаги кичик тебранишлар тенгламалари деб аталади. Булар аникмас n+m та , узгарувчиларга нисбатан n+m узгармас коэффициентли чизикли дифференциал тенгламаларни ташкил килади.

   Бу тенгламаларга

куринишдаги ечимларни куйганимизда

  (8.2.10)

характеристик тенгламага келамиз, бу ерда

(8.2.10) характеристик тенгламанинг куринишидан куйидагилар келиб чикади:

            1) характеристик тенгламанинг камида m та илдизи нолга тенг;

            2) (8.2.10) тенглама коэффициентларининг матрицаси симметрик эмас (голоном тизимларда симметрик булади).

            Боттема томонидан биринчи булиб аникланган характеристик тенгламанинг бу хусусиятлари ноголоном тизимнинг узига хос хусусиятларидан биридир.

Ноголоном тизим кичик тебранишларини (8.2.8) ва (8.2.9) чизикли дифференциал тенгламаларга асосланиб тадкик этиш голоном тизим чизикли дифференциал тенгламаларини тадкик этишдан деярли хеч фарк килмайди. Худди голоном тизимлардаги сингари вакт буйича усадиган ечимлар мавжуд булганда тадкикотнинг натижалари факат чекли  вакт оралигида тугри булади.

Бу маънода кичик тебранишлар назариясининг коидалари ноголоном тизимларга бутунлайича ёйилади. (8.2.8) ва (8.2.9) чизиклаштирилган тенгламаларнинг дастлабки ноголоном тизим билан алокаси масаласига келганимизда, бу ерда факат ноголоном тизимга тааллукли узига хос хусусият борлигини курамиз.

Бу узига хос хусусият нолга тенг булган илдизларнинг мавжудлиги ва характеристик тенглама коэффициентлари матрицасининг симметрик эмаслигида намоён булади (консерватив тизим булганда). Бу ерда хар доимги кичик тебранишлар назарияси позицияси билан ёндашиш тургунлик масаласига тулик жавоб бермайди ва нолга тенг булган илдизларнинг табиатини очишга имконият яратмайди. Бу масалалар бир-бири билан чамбарчас богланганлигини курамиз. Ноголоном тизимлар тургунлиги ва кичик тебранишларини батафсил курганимизда нол илдизларнинг нафакат табиатини тушунишни ва балки ноголоном тизимларнинг факат узига хос яна битта хусусиятини: мувозанат холатлари куп хиллиги ва стационар харакатларнинг куп хиллиги мавжуд эканлигини аниклаймиз.

 

2.2. Ноголоном тизимнинг мувозанат холатлари куп хиллиги якинидаги кичик тебранишлар тенгламалари. Мувозанат холатлари куп хиллигининг тургунлиги

 

Харакати

        (8.2.11)

ноголоном богланишларга буйсундирилган  Лагранж функцияли ва  умумлашган кучларга эга булган тизим берилган булсин. Тизимнинг харакат тенгламаларини тузамиз:

 

.                (8.2.12)

(8.2.11) ва (8.2.12) тенгламалар тизими ,  микдорларни бошлангич шартлар ва вактнинг функциялари сифатида аниклашга имконият яратади. (8.2.11) ва (8.2.12) тенгламалардан ноголоном тизимнинг мувозанат холатларини аникловчи тенгламалар тизимини ёзамиз:

,          (8.2.13)

бу ерда

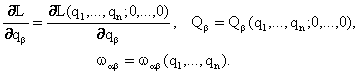
(8.2.13) да тенгламалар сони n ва аникмас узгарувчилар  сони n+m, яъни m та микдорлар ихтиёрий киймат кабул килишлари мумкин. Шу сабабли умумий холда ноголоном тизимнинг мувозанат холатлари куп хиллигига эга буламиз. Мувозанат холатлари куп хиллиги n улчамли конфигурациялар фазосида m улчамли О_m сиртни ташкил килади.

Хакикатан хам, (8.2.13) тенгламалар системасидан фойдаланиб  умумлашган координаталарни  аникмас Лагранж купайтувчилари оркали ифодалаб, О_m сиртнинг параметрик тенгламасини топамиз:

.         (8.2.14)

Шуни таъкидлаймизки, муайян масалаларда (8.2.13) тенгламаларнинг барчаси хам богланмаган булмаслиги мумкин. Бу холларда О_m улчами m дан катта булади. О_m сиртнинг мавжудлиги ноголоном тизимнинг яккаланган мувозанат холатининг тургунлиги хакида гап юритиш мантиксиз эканлигини билдиради, чунки ноголоном тизим яккаланган мувозанат холатга эга эмас. Шу сабабли ноголоном тизимлар кичик тебранишлари хакида масала куйилишининг узи узгариши керак.

   Ноголоном тизимлар кичик тебранишларини яккаланган мувозанат холати атрофида урганмасдан, балки О_m сирт атрофида тадкик этишга масала коррект (тугри) куйилган деб хисоблаш лозим. Демак, ноголоном тизим тургунлиги хакида факат О_m сиртга нисбатан куйиш керак. Яккаланган мувозанат холатига нисбатан ноголоном тизимлар тургунлигини урганиш, масалани нокоррект куйилганини билдиради.

   Юкорида баён этилганларга асосланиб, ноголоном тизим кичик тебранишларининг тенгламаларини О_m мувозанат холатлари сирти атрофида тузамиз.

(8.1.12) тенгламалардан  аникмас купайтувчиларни чикариб, ноголоном тизим дифференциал тенгламаларини нормал формада ёзамиз:

         (8.2.15)

бу ерда оркали , фазавий узгарувчилар белгиланган.  фазавий фазода О_m сирт

тенгламалар билан аникланган булсин, бу ерда  узгарувчилар О_m сиртнинг жорий параметрлари булади.  узгарувчилар катори янги  узгарувчиларни

 

 

муносабат оркали киритамиз, бу ерда - узгарувчиларнинг кандайдир функциялари. Янги u, v узгарувчилар оркали (8.2.15) тенгламаларни куйидагича ёзамиз:

.                  (8.2.16)

(8.2.16) харакат тенгламаларини О_m мувозанат холатлари сирти атрофида чизиклаштирамиз. Бунинг учун (8.2.16) тенгламаларнинг унг тарафидаги функцияларни микдорларнинг кичик кийматлари буйича каторга ёйиб, куйидагини хосил киламиз:

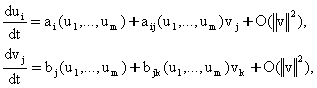     (8.2.17)

бу ерда

                       

- нисбатан иккинчи тартиблидан кам булмаган хадлар. О_m сиртда ,   микдорлар нолга айланиши сабабли (8.2.17) тенгламалардаги  а_i, b_i  коэффициентлар нолга тенг булади.

Шундай килиб, О_m сиртнинг кичик атрофида  ларга нисбатан чизиклаштирилган (8.2.17) тенгламалар системаси

     (8.1.18)

куринишга келади. Хосил килинган тенгламалар О_m мувозанат холатлар сиртининг кичик атрофидаги ноголоном система кичик тебранишларининг тенгламаларидир. (8.2.18) тенгламалар системасига асосан ва  лар кичик микдорлар булганлиги учун  лар вактнинг секин узгарувчи функциялари булади. (8.2.18) системанинг ечимини кетма-кет якинлашиш усулини куллаб излаш мумкин.

            Бу ерда нолинчи якинлашишда  киймати сифатида узгармас  микдорлар олинади. Бу кийматларни (8.2.18) системанинг унг тарафига куйиб,  нинг такрибий кийматларини топиш учун

                                 (8.2.19)

тенгламаларга эга буламиз. (8.2.19) тенгламаларнинг ечимини топишда

                                (8.2.20)

характеристик тенгламага келамиз.  лар (8.2.20) тенгламанинг илдизлари булсин ва соддалик учун уларни хар хил ва нолдан фарк килувчи деб хисоблаймиз. У вактда  учун ечим

                               (8.2.21)

куринишда ёзилади, бу ерда с_к – бошлангич шартлардан топиладиган узгармас сонлар,  - детерминантнинг минорлари (микдорни топиш учун  илдизни  нинг  устун ва охирги сатрини учириш натижасида хосил килинган минорга куйилади). Топилган (8.2.21) ечимни (8.2.18) тенгламалар системасининг биринчи тенгламалар гурухига куйиб,  функцияни аникловчи тенгламаларга эга буламиз. Бу тенгламаларни интеграллаб,

                  (8.2.22)

ечимни топамиз, бу ерда  лар бошлангич шартлардан аникланадиган ихтиёрий узгармас сонлар. Кейин (8.2.22) ифодаларни (8.2.18) системанинг унг тарафига куйиб, келгуси якинлашишни аниклайдиган тенгламаларга эга буламиз. Бу тенгламалар яна икки гурухга булинади.  ни аникловчи тенгламалар экспоненциал коэффициентли 2(n-m) та чизикли дифференциал тенгламалар системасидан иборат булади. Бу жараённи давом эттириб (8.2.18) системанинг исталган зарурий аникликдаги ечимини топиш мумкин.

            Агар бизни факат О_m сиртнинг тургунлиги кизиктирса, у вактда (8.2.18) тенгламалар системасининг аник ечимини топишга зарурият колмайди. Бунинг учун  функциянинг О_m нинг кичик атрофидаги хулкини урганиш кифоядир. Биринчи якинлашишда бу функцияларнинг хулки (8.2.20) характеристик тенгламанинг илдизлари оркали аникланади. Агар барча  илдизларнинг хакикий кисмлари манфий булса, у холда  функциялар ёки экспоненциал сунишни, ёки камаювчи амплитудали тебраниш жараёнини ифодалайдилар. Шунинг учун О_m сиртнинг кичик атрофида булган тасвирловчи нукта  да О_m сиртга интилади. Бу холда О_m мувозанат холатлари сиртини ассимптотик тургун деб айтамиз. Агар  илдизлар орасида хеч булмаганда бирорта илдизининг хакикий кисми мусбат булса, у вактда О_m мувозанат холатлари сирти нотургун булади.

             Илдизлари О_m сиртнинг тургунлигини аниклайдиган (8.2.20) характеристик тенгламани топиш учун u_i, v_i узгарувчиларга утишнинг хожати йук, характеристик тенгламаларнинг нолга тенг булган илдизларининг мохиятини аниклаш максадида янги узгарувчиларга утган эдик. (8.2.20) характеристик тенглама (8.2.10) характеристик тенгламадан нолга тенг булган илдизларни ташлаб юбориш йули билан хосил этилганлигини осонгина куриш мумкин. Нолга тенг булган илдизлар сони, одатда, камида ноголоном богланишлар сонига тенг булади, яъни О_m сиртнинг улчовига тенг булади.

            Изох: Характеристик тенглама нолга тенг булган илдизларининг сони О_m сиртнинг улчовидан катта булган холни критик хол деб караш керак.

            (8.2.18) системадан куриниб турибдики, характерис-тик тенглама нолинчи илдизлари кичик тебранишлар назариясининг критик холига хеч кандай богликлиги йук. Улар m улчамли О_m сиртнинг мавжудлигига богликдир. Шунинг учун О_m сиртнинг тургунлигини текшириш учун нолга тенг булган илдизларни оддийгина ташлаб юбориш керак. Натижада (8.2.20) характеристик тенглама хосил булади ва унга нисбатан тургунликни текширувчи барча критерияларни ишлатиш мумкин, масалан, Раус-Гурвиц, Михайлов, Найквист критерияларини, D-булаклаш усулини ва х.к. Топилган тургунлик шартлари, О_m сиртда тургунлик сохасини ажратишга ва тургунлик сохасининг чегарасини тизим конструктив параметрларининг узгаришига караб узгаришини тадкик этишга шароит яратадилар.

            Шуни таъкидлаймизки, О_m сиртнинг бирорта  нуктаси атрофида ноголоном тизим харакат тенгламаларини чизиклаштириш жараёни шу параграфнинг 1-бандида баён этилган чизиклаштириш жараёни билан тулик мос келади. Аммо бу ерда олинадиган тенгламаларнинг 1-бандда олинган тенгламалардан мухим фарки шундан иборатки,  нукта энди О_m сиртнинг исталган нуктаси булиши мумкин. Шунинг учун хам (8.2.18) тенгламаларнинг a_ij ва b_ij коэффициентлардаги  микдорларни тизимнинг физик параметрлари катори кушимча параметрлар деб караш керак.

            Шундай килиб, олинадиган чизиклаштирилган тенгламалар мувозанат холатлари сиртининг хар бир нуктаси тургунлигини текширишга ва О_m сиртда тургунлик сохасини ясашга имконият яратади. 1-банддаги чизиклаштирилган тенгламалар факат битта (0,0,...,0) нуктанинг тургунлигини текширишга ярайди.

            Бу параграфда баён этилган назариянинг татбикини бир неча мисолларда куриб утайлик.

 

3-§. Ноголоном тизимларнинг мувозанат холати

атрофидаги тургунлигини ва кичик тебранишларини

тадкик этишга доир мисоллар

 

1-мисол. Чаплыгин чанасининг кия текисликдаги харакатининг тургунлиги [71,105]

 

            Каттик жисмнинг кия текисликка параллел харакатини курамиз. Жисм кия текисликка учта оёк билан таянсин. Бу оёклардан иккитаси абсолют силлик, учинчиси булса ярим доиравий тиг билан таъминланган булсин. Бунинг натижасида учинчи оёк тиг текислигига перпендикуляр булган йуналишда харакат килолмайди. Жисм огирлик С марказининг кия текисликдаги проекцияси тиг перпендикуляр булган ва тиг текисликка уринган К нуктадан утувчи тугри чизикда ётган холни куриб утайлик (8.2-шакл).  

            Тизимнинг умумлашган координаталари сифатида К нуктанинг x,y координаталарини          ва жисмнинг кия текисликка перпендикуляр булган тугри чизик атрофида айланиш  бурчакни оламиз. У холда Лагранж функцияси куйидаги куринишда булади:

бу ерда m-жисмнинг массаси, к-инерция радиуси, -текисликнинг киялик бурчаги, -масса марказининг кия текисликдаги проекциясидан К нуктагача булган масофа (8.2-шаклга каранг), -огирлик кучининг тезланиши. Диссипация функциясини куринишда оламиз, бу ерда - сирганиш ва айланишга нисбатан демпфер коэффициентлари. Ноголоном богланиш куйидаги тенглама билан ифодаланади:

                        .              (8.3.1)

                                   

 

                                      

 

 

 

 

 

 

 

 

 

 

 

 

                               8.2-шакл.

 

Жисмнинг харакат тенгламалари куйидаги куринишда буладилар:

    (8.3.2)

(8.3.1) ва (8.3.2) харакат тенгламаларидан  булганда мувозанат холатининг тенгламалари келиб чикади:

.                (8.3.3)

(8.3.3) га асосан курилаётган ноголоном тизимнинг мувозанат холатлари  конфигурация фазосида иккита  ва  текисликни хосил килади. Ноголоном богланишлар сони битта булишига карамасдан (8.3.1) мувозанат холатлари сирти О_m нинг улчови иккига тенг, яъни икки улчовли О₂ сиртга эга буламиз. Улчов бир бирликка ошганлигининг сабаби (ноголоном богланишлар сонига нисбатан) (8.3.3) тенгламаларнинг биринчиси билан учинчиси бир-бирига богланганлигидадир.  лар (8.1.25) тенгламаларни каноатлантирувчи узгарувчиларнинг мувозанат кийматлари,  лар эса етарли кичик микдорлар булсин. У холда

деб кабул килиб, (8.8.1) ва (8.8.2) тенгламаларни  кичик микдорларга нисбатан чизиклаштирамиз:

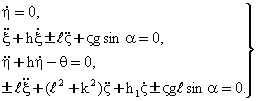                      (8.3.4)

Бу ерда юкори («+») белги  ва куйи «–» белги   текисликка мос равишда олинади. Тенгламаларнинг характеристик тенгламаси

  (8.3.5)

куринишда булади. Мувозанат холатлари сирти икки улчовли булганлиги учун (8.3.5) характеристик тенглама иккита нолга тенг булган илдизга эга (назарияда нолга тенг булган илдизлар сони камида О_m сиртнинг улчовига тенг булиши керак деган эдик).

            О₂ сиртнинг ( ва  текисликларнинг) тургунлиги

      (8.3.6)

характеристик тенглама илдизларининг характери билан аникланади.  текислик учун (8.3.6) тенгламанинг озод хади манфий ишорали булганлиги учун у доимо нотургун булади.  текислик Раус-Гурвиц критериясига асосан

                          (8.3.7)

тенгсизлик бажарилгандагина тургун булади.  параметрлар текислигида тургунлик сохаси ва унинг чегараси 8.3-шаклда курсатилгандай булади, бу ерда  микдори

тенглик билан аникланади (8.3-шакл)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

           

 

            Шундай килиб, h ва h₁ параметрларнинг кийматига караб  текислиги ёки бутунлай тургун, ёки бутунлай нотургун булади. Агар нотургун булса, у холда текисликдан тойдирилган тасвирловчи нукта бу текисликка бошка кайтиб келмайди ёки унинг атрофида усувчи амплитуда билан тебранма харакат килади. Охирги холда К нуктанинг траекторияси худди 8.4-шакл, а) да курсатилгандай булади.

            Агар  текислик тургун булса, у холда К нинг траекторияси 8.4-шакл, б) да ифодалангандай булади.

            Мувозанат холатлари сиртининг ассимптотик тургунлиги хакидаги теоремага асосан (келгуси пунктда курамиз) тургун мувозанат холатлари сиртидан тойдирилган тасвирловчи нукта яна шу сиртга, аммо, умуман айтганда унинг бошка нуктасига  кайтади (8.4-шакл, б)): 8.4-шакл, б) даги (1) нуктадан тойдирилган тасвирловчи нукта янги мувозанат холатига, масалан, 8.4-шакл, б) даги (2) нуктага кайтади.

            (8.3.6) дан куринадики,  булганда (8.3.6) характеристик тенгламада битта нолга тенг булган илдиз пайдо булади. Натижада нолга тенг булган илдизлар сони учга тенг ва у мувозанат холатлар сиртининг улчовидан биттага зиёд булади. Демак,  булганда биз критик холга келамиз.

            Тургунликни тадкик этиш учун харакат тенгламасидаги ночизикли хадларни хисобга олишга тугри келади ():

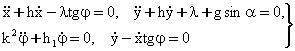          (8.3.8)

булган холда тенгламалар тизимини осонгина текшириш мумкин. Бу холни куриб утайлик.

 хол. (8.3.8) тенгламаларнинг учинчисидан , демак,

                                         

келиб чикади.

            Бу ерда  - бошлангич бурчак. Иккинчи ва туртинчи тенгламалардан фойдаланиб,  ва  узгарувчиларни чикарамиз:

           (8.3.9)

Куйидаги белгилашларни киритамиз:

У холда (8.3.9) тенгламани куйидагича ёзиш мумкин,

Бу тенгламанинг ечими

куринишга эга, бу ерда с – бошлангич шартлардан топиладиган ихтиёрий узгармас сон. (8.3.8) тенгламаларнинг охиргисидан фойдаланиб, х узгарувчига кайтамиз:

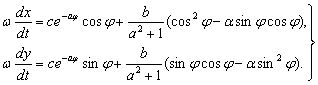     (8.3.10)

Бу тенгламаларни интеграллаганимиздан кейин К нукта траекториясининг параметрик тенгламасига келамиз:

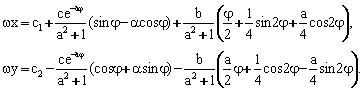(8.3.11)

Бошлангич шартлардан с, с₁, с₂ узгармас сонларни топамиз: t=0 булганда  Бу микдорларни (8.3.10) ва (8.3.11) ларга куйиб,

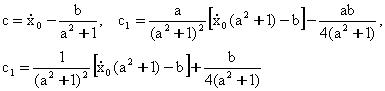
ларни хосил киламиз.

            Агар  комплекс узгарувчи киритсак, у холда К нукта харакати ушбу конунга буйсунади

бу ерда

Бу харакатнинг траекториясини график усулда хосил килиш мумкин. Бунинг учун  ва  векторларни кушиш керак.

            Шундай килиб,  холатда (8.3.8) тенгламаларни интеграллаш шуни курсатаяптики,  булмаган хар кандай бошлангич шартларда жисм бошлангич холатидан исталган узокликка кетади. Бу холда жисмнинг харакати куйидагилардан иборат:

            1) горизонтал йуналиш билан  бурчак ташкил киладиган тугри чизик буйича узгармас тезликдаги силжишдан;

            2)   бурчак тезликли сунувчи айланишдан;

3) 2 бурчак тезлик билан айланишдан.

Демак,  холда мувозанат холат доимо нотургун.

             хол. Бу холда (8.3.8) тенгламаларнинг учинчисидан  бурчакнинг узгариш конунини топамиз:

бу ерда  нинг бошлангич кийматлари.  булганлиги учун  хар кандай кийматга эга булиши мумкин. Жисм факат  булгандагина тургун мувозанат холатда булади. Демак,  булганда,  мувозанат холати нотургундир.

 

2-мисол. Нотекис горизонтал текисликдаги шарнинг

харакати [71]

 

            Марказий эллипсоид инерцияси айланиш эллипсоиди булган биржинсли булмаган шар нотекис горизонтал текисликда думалансин ва айлансин. Куйидаги холни куриб

 

 

 

 

 

 

 

 

 

 

 

 

 

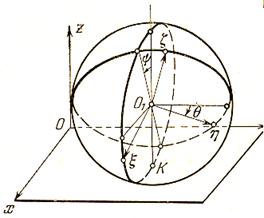                                                8.5-шакл.

 

утамиз: шарнинг масса маркази геометрик марказига тугри келмасин; эллипсоид инерция симметрия уки шарнинг геометрик маркази оркали утсин.

            Жисмнинг конфигурациясини бешта умумлашган координаталар оркали аниклаймиз: x,y – текислик билан шар уринган К нуктанинг координаталари, -Резал бурчаклари, -жисмнинг  динамик симметрия уки атрофидаги бурилиш бурчаги (8.5-шакл).

             уки хар доим xoz текислигига параллел.  ва  текисликлар уклари орасидаги косинус бурчаклари куйидаги жадвал оркали аникланади:

                                                                                                                                                                        8.1-жадвал.

 

Сирганишсиз думаланиш шарти куйидагидан иборат: . Бу тенгликка

ифодаларни куйиб, ноголоном богланишларнинг тенгламаларини топамиз

            (8.3.12)

Лагранж функциясининг ифодасини тузамиз:

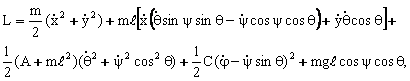
бу ерда m–жисмнинг массаси, -шар маркази билан унинг масса маркази орасидаги масофа, С–айланиш уки буйича инерция моменти, А-марказий экваториал инерция моменти, g–огирлик кучининг тезланиши.

            Куйидаги ифода оркали диссипация кучини киритамиз:

бу ерда  думалаш ва айланиш буйича ковушкок ишкаланиш коэффициентлари. Диссипация кучининг ифодасига нинг компоненталарини куйиб ва (8.8.12) фойдаланиб,

 

 

ни хосил киламиз. Аникмас купайтувчили харакат тенгламасини ёзамиз:

 

бу ерда

                       

 

            F, L ва a_ik ларнинг кийматини харакат тенгламасига куйиб, нотекис горизонтал шар харакатининг тенгламасини хосил киламиз:

 

(8.3.13)

бу ерда . (8.3.12) ва (8.3.13) тенгламалардан куриниб турибдики, шарнинг мувозанат холатида куйидаги муносабатлар бажарилади:

     (8.3.14)

Бу муносабатлар тизимнинг  беш улчовли конфигурацияда уч улчовли мувозанат холатларининг сиртларини ажратади:

1) ва 2) сиртларни хамда 3) ва 4) сиртларни бир хил конфигурацияларни акс этаётганликлари учун айнан тенглаштириш керак.

             сиртнинг тургунлик шартларини топиш учун (8.3.12) ва (8.3.13) харакат тенгламаларини бу сиртнинг бирорта мувозанат холати атрофида чизиклаштирамиз. Штрихлар билан узгарувчиларнинг уларнинг мувозанат кийматларидан етарлича кичик микдорда тойилишларини белгилаб, тойилган харакатнинг

(8.3.15)

тенгламаларни хосил киламиз. Бу ердан куйидаги характеристик тенгламани келтириб чикарамиз:

  .   (8.3.16)

(8.3.16) тенгламанинг учта нолга тенг булган илдизи борлиги мувозанат холатлари сирти уч улчовли булганлиги учундир. Сиртнинг тургунлигини

        (8.3.17)

характеристик тенгламанинг илдизлари аниклайди. Бу ердан ,  булганда,  сиртнинг доимо тургунлиги келиб чикади.

             сиртнинг характеристик тенгламасини топиш учун (8.3.16) муносабатда ­ни  га алмаштирамиз.  булганда хосил килинган характеристик тенгламада озод хаднинг ишораси манфий, демак,  сирт доимо нотургун булади.

 

4-§. Ноголоном тизимлар мувозанат холатлари сиртининг

ассимптотик тургунлиги хакидаги теорема

 

            Ноголоном тизимлар мувозанат холатининг тургунлигини О_m сиртдан етарли кичик тойилишга нисбатан тадкик этилгандагина маънога эга булишини аниклаб олдик.  узгарувчиларни вактинча параметрлар сифатида караб, (8.2.18) тизимнинг иккинчи гурух тенгламаларини биринчи гурух тенгламаларига богламасдан караш табиийдир. Бу ёрдамчи тизимнинг характеристик тенгламаси (8.2.20) ифода билан аникланади.

             параметрларнинг бирор  сохасида

                            (8.4.1)

тенгламалар системасининг  мувозанат холати ассимптотик тургун булсин, яъни

                                             (8.4.2)

бу ерда  эса  узгарувчиларнинг бошлангич кийматлари. У вактда ноголоном тизим мувозанат холатлари сиртининг ассимптотик тургунлиги тугрисидаги Ю.И.Неймарк ва Н.А.Фуфаевнинг куйидаги теоремаси уринли булади [71].

            Теорема.  бошлангич кийматлар шундай танлаб олинган булсинки,  микдорлар (8.4.1) тенгламаларнинг ­ ассимптотик тургунлик сохасининг ичида ётсин,  кийматлар етарлича кичик булсин. У вактда ноголоном тизимнинг

                   (8.4.3)

харакат тенгламаларига асосан

лимитик муносабатлар бажарилади, бу ерда  аммо, умуман айтганда, . Шу билан бирга  узгарувчилар учун

                                                (8.4.4)

бахолаш уринли булади, бу ерда   

            Исбот. (8.4.3) тенгламаларни факат

                                            (8.4.5)

тенгсизликлар (-етарли кичик сон), ва  бажарилганда,

                       (8.4.6)

куринишда ёзамиз. Агар (8.4.5) муносабатлар  учун бажарилса, у вактда (8.4.6) тенгламаларнинг ечими учун

                                           (8.4.7)

куринишдаги бахолашни курсатиш мумкин. Хакикатан хам, [67] асосан (8.4.1) тенгламалар системаси учун шундай аник-мусбат ишорали  квадратик форма мавжуд буладики,

                                    (8.4.8)

муносабат бажарилади ва бунда  нинг хар кандай етарли кичик узгаришлари учун куйидаги тенгсизлик уринлидир:

                .                     (8.4.9)

(8.4.8) ва (8.4.9) лардан куйидагини хосил киламиз:

ва, демак,

.

Шундай килиб, (8.4.7) каби бахолаш тугридир. (8.4.7) тенгсизликдан

муносабат келиб чикади, шунинг учун

                  .                    (8.4.10)

Дастлабки пайтда (8.4.5) шарт  ва куйидаги тенгсизлик

                        (8.4.11)

бажарилсин. Ечим вактга нисбатан текис узлуксиз булганлиги учун (8.4.5) шарт  учун кандайдир  ораликда бажарилади. Шу  вакт оралигида (8.4.7) ва (8.4.8) бахолашлар уринли булади. (8.4.7), (8.4.10) ва (8.4.11) ларга асосан  микдор (8.4.5) тенгсизликни  учун каноатлантиради. Бу мулохазани давом эттириб, шундай хулосага келамиз, бу тенгсизликлар  вакт оралигида, яъни хамма  лар учун хам бажарилади ва теорема шу билан исбот булади.

 

5-§. Доимо таъсир этувчи кичик кучларга (тойдирувчиларга) нисбатан тургунлик

 

            Ноголоном тизим мувозанат холатлари сирти О_m ассимптотик тургун булсин. Тизимга кичик микдордаги тойдирувчи кучлар доимо таъсир этганда, О_m сиртнинг ассимптотик тургунлиги сакланадими ёки у нотургун буладими? - деган саволга куйидаги теорема жавоб беради [71].

            Теорема. Мувозанат холатлар ассимптотик тургунлик сохаси  да исталган  учун шундай  курсатиш мумкинки, дан кичик хар кандай доимо таъсир этувчи кучлар  компоненти  сохада тургунча фазавий нукта мувозанат холатлари тупламининг  атрофидан ташкарига чикмайди ва хамма вакт шундай доимий таъсир этувчи исталганча кичик кучлар топиладики, фазавий нукта мувозанат холатлари сирти буйлаб  сохада хар кандай олдиндан берилган эгри чизик буйича силжийди.

            Бу теоремадан ушбу фикр келиб чикади:

            Агар мувозанат холатлари тупламининг богламли тармоги хамма нукталари ассимптотик тургун булса, у холда доимо таъсир этувчи етарли кичик тойдирувчи кучларга нисбатан у тургун, агар бу богламли тармокда нотургун нукталар мавжуд булса, у нотургун булади.

            Исбот. Доимий таъсир этувчи тойдирувчи кучлар мавжудлигида харакат тенгламаси О_{m ­}сирт атрофида куйидаги куринишга эга:

      (8.5.1)

Теореманинг биринчи тасдигини исботлаш учун Ляпунов функциясидан фойдаланамиз. Бу функцияни (8.5.1) тенгламалар системасининг иккинчи гурух тенгламалари учун тузамиз, бу ерда  лар параметр сифатида каралади. Асимптотик тургунлик сохаси  да коэффициентлари  ларга боглик шундай мусбат квадратик форма  мавжудки, баъзи  лар учун

тенгсизлик бажарилади ва (8.4.1) га асосан

 булганда, яъни мувозанат холатлари сиртида V=0 ва (8.5.1) тенгламалар системасига асосан

            ,              (8.5.2)

булади, бу ерда А ва В – баъзи узгармас сонлар ва . Агар  булса, (8.5.2) муносабатдан

келиб чикади. Демак,  нинг етарли кичик кийматларида харакати (8.5.1) тенгламалар системаси билан ифодаланадиган  фазавий нукта  узгарувчилар  ассимптотик тургунлик сохасининг элементи булиб турган пайтда мувозанат холатлари сиртининг  радиусли атрофидан чикмайди. Бу тасдик теореманинг биринчи кисмининг исботидир.

            Теореманинг иккинчи кисмини исбот килиш учун куйидагини аниклаш керак: хар кандай кичик тойдирувчи кучлар учун  микдор хар доим усишини ва колган  узгарувчиларнинг киймати узгармасдан колишини исботлаш керак. 

     булсин. У холда (8.5.1) системанинг иккинчи гурух тенгламаларидан

тенгсизликнинг бажарилиши келиб чикади ва биринчи m та тенгламалардан талаб этиладиган  ва  тойдирувчиларни топамиз

 .

 

 

6-§. Керкговен-Витгоф масаласи [71]

 

            Бу масалани Уиттекер узининг «Аналитическая динамика» китобида куйидаги холда курган: ярим сфера куринишидаги огир бир жинсли жисм узининг каварик томони билан пастга каратилган холда гадир-будурли горизонтал текисликда мувозанатда турибди. Бу ярим сферанинг юкори текислигига иккинчи ярим сфера куйилган. Иккинчи ярим сферанинг биринчи ярим сферанинг юкори текислиги билан уринган нуктаси биринчи ярим сферанинг марказига мос келади. Масала куйидагича куйилади: кичик тебранишларни ва тизимнинг мувозанат холати атрофидаги тургунлик шартларини аниклаш.

            Харакат тенгламаларини мувозанат холати (яккаланган мувозанат холат деб каралган) атрофида чизиклаштириб, Уиттекер тизимнинг консерватив тургунлик шартини куйидаги тенгсизлик сифатида топади:

                        ,                    (8.6.1)

бу ерда R ва m лар куйи ярим сферанинг радиуси ва массаси,  лар юкори ярим сферанинг радиуси ва массаси. Куйида ушбу масалани ноголоном тизимлар мувозанат холатининг тургунлик назарияси нуктаи назаридан караб чикамиз. Бу ерда, кисман, куйидагилар курсатилади:

            1) курилаётган тизим олти улчовли мувозанат холатлари сиртига эга;

            2) энергиянинг диссипация булишини хисобга олмаганда, характеристик тенгламанинг нолга тенг булган илдизларининг сони мувозанат холатлари сиртининг улчовидан икки бирликка катта булади.

Шундай килиб, юкорида ифодаланган икки ярим шардан иборат тизимни куриб утамиз. Учта координата тизимини киритамиз (8.6-шакл):

Оxyz – кузгалмас  тизими, z=0 текислиги куйи ярим сфера думаланадиган нотекис горизонтал текисликка мос келади; -координата боши куйи ярим сферанинг маркази билан мос келадиган  тизим. Бу тизимнинг  уки куйи ер ярим сферанинг диаметрал текислигига перпендикуляр булиб йуналган,  уки булса,  текислигига параллел булган вертикал текисликда ётади;  -  тизимга ухшаш аммо, юкори ярим сферага таълукли кузгалувчи  тизим. Ярим шарлар конфигурациясини унта умумлашган координата аниклайди (8.7-шакл):  - ярим сфера горизонтал текислик билан уринган  нуктанинг координаталари;  -  укларининг холатини белгиловчи Резал бурчаклари (8.7-шаклга каранг); -куйи ярим шарнинг  уки атрофидаги айланиш бурчаги;  - ярим шарлар уринган                                                                                                                                                                     8.2-жадвал.

 

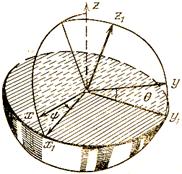
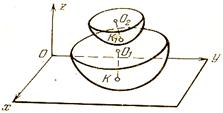
 нуктанинг координаталари (8.6-шаклга каранг);  -  укларининг холатини  тизимга нисбатан белгиловчи Резал бурчаклари; - юкори ярим шарларнинг  уки атрофида айланиш бурчаги. ,  ва  координата системалари орасидаги косинус бурчаклари куйидаги жадваллар билан аникланади:

 

 

 

 

 

 

 

 

 

 

 

 

 

          8.6-шакл.                       8.7-шакл.

 

                                            8.3-жадвал

 

Куйи ярим сферанинг горизонтал текисликдаги сирганишсиз думаланишининг шарти

                                      (8.6.2)

булади, бу ерда  нуктанинг тезлиги,  - куйи ярим сферанинг оний бурчак тезлиги.  ва  векторларнинг  тизимдаги компонентларини топамиз;

Бу ифодаларни (8.6.2) куйиб, куйи ярим сферанинг горизонтал текисликда сирганишсиз думаланиш шартини ифодалайдиган ноголоном богланишларни топамиз: 

     (8.6.3)

Юкори ярим сферанинг куйи ярим сфера диаметрал текислиги буйича сирганмасдан думаланиш шарти

                     (8.6.4)

ифода билан аникланади, бу ерда  нуктанинг тезлиги, -юкори ярим сферанинг оний бурчак тезлиги. (8.6.4) муносабатга 

              

ифодаларни куйиб,

              

ни ёки  координата системасида 

     (8.6.5)

хосил киламиз, бу ерда  векторнинг  оний бурчак тезлиги билан айланаётган   координата тизимига нисбатан хосиласи.   

(8.6.5) формулага

      

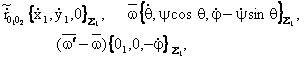
(8.6.6)

ифодаларни куйиб, юкори ярим сферанинг куйи ярим сфера диаметрал текислиги буйича сирганмай думалашини ифодаловчи яна иккита ноголоном богланишларнинг тенгламаларини хосил киламиз:

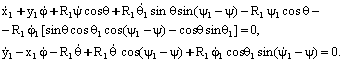    (8.6.7)

Лагранж функциясининг ифодаси куйидаги куринишга эга:

  

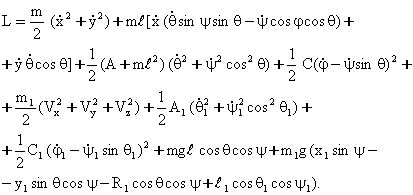
Бу ерда  ва  мос равишда куйи ва юкори ярим сфераларнинг массаси,  лар айланиш уклари буйича инерция моментлари,  лар масса марказларидан ярим сфералардан хар бир экваториал текисликларигача булган масофа,  лар сферик сиртларнинг радиуслари,

Диссипация функциясини куйидаги куринишда киритамиз:

       ,

бу ерда  лар думаланиш ва айланишлар буйича демпфер коэффициентлари,  векторнинг  координата тизими укларига нисбатан проекциялари,  лар  векторнинг  координата системаси укларига нисбатан проекциялари. Бу проекцияларни умумлашган координата ва тезликлар билан ифодалаб хамда (8.6.3), (8.6.6) ва (8.6.7) формулалардан фойдаланиб  нинг

  (8.6.8)

ифодасини топамиз.

Аникмас купайтувчили харакат тенгламаларини ёзамиз:

 ,   (8.6.9)

бу ерда

     (8.6.9) тенгламалардан аникмас  купайтувчиларни чикариб ташлаб ва

                  

алмаштиришни киритиб, хосил килинган харакат тенгламаларини ушбу куринишда ёзамиз:

(8.6.10)

(8.6.10) системадаги кейинги иккита тенгламани янги тенгламалар билан алмаштирамиз. Янги тенгламалар шу иккита тенглама билан (8.6.10) нинг колган тенгламалари комбинациясидан иборат. Бунинг учун (8.6.10) системанинг биринчи тенгламасини  га, иккинчисини  га ва охиргидан олдингисини  га  купайтирамиз ва хосил булган ифодаларни кушамиз. Худди шу тарзда (8.6.10) нинг учинчи тенгламасини  га, туртинчисини   га, охиргисини  га купайтирамиз ва хосил булган тенгламаларни кушамиз. Натижада куйидаги тенгламаларни хосил киламиз:

         

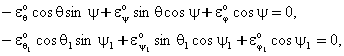
бу ерда

Шундай килиб, каралаётган тизимнинг харакат тенгламалари куйидаги куринишда булади:

  

 

             (8.6.11)

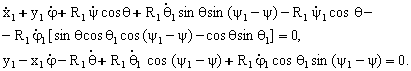                 Бу тенгламалар унта  микдорларни вакт функцияси сифатида аниклашга имконият яратадиган тулик системадир. (8.6.11) тенгламаларда барча вакт буйича олинган хосилаларни нолга тенглаштириб, мувозанат холатларини аниклайдиган ва бир-бирига богланмаган туртта тенгламаларга эга буламиз:

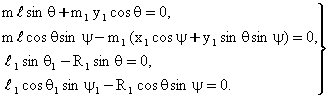   (8.6.12)   

       Бу тенгламалардан куриниб турибдики, каралаётган тизимнинг ун олти улчовли фазавий фазосида мувозанат холатлари олти улчамли сиртни ташкил килади.

       Мувозанат холатлари сирти  нинг тургунлик шартларини аниклаш учун тизимнинг характеристик тенгламасини тузамиз. Хисоблашни кискартириш учун  ларни етарли кичик микдорлар деб хисоблаб,  сиртнинг  нуктасининг кичик атрофини караб, шу атрофида (8.6.11) харакат тенгламаларини чизиклаштирамиз. Чизиклаштириш пайтида тенглама коэффициентларининг ифодасидаги кичик микдорлар купайтмасини ташлаб кетамиз. Умумлашган координаталарни мувозанат холатидаги микдорларидан тойилганини штрих билан белгилаб, чизиклаштирилган харакат тенгламаларини ёзамиз:

 

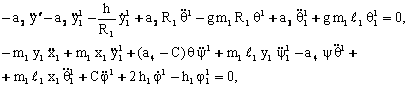
         (8.6.13)

                            

бу ерда

 

(8.6.3) тенгламалар системасига

           

ечимларни куйиб, характеристик тенгламанинг куйидаги куринишига келамиз: 

 

                                                                               (8.6.14)

            Бу ерда куйидаги белгилашлар киритилган:

(8.6.14) дан куриниб турибдики, характеристик тенглама олтита нолинчи илдизга эга. Бунинг сабаби мувозанатлар холатининг сирти О₆ олти улчовли эканлигидадир. (8.6.14) нинг колган илдизлари О₆ сиртнинг тургунлигини аниклайдилар. О₆ сиртнинг  нуктасининг етарлича кичик атрофида бу тенглама куйидаги куринишда булади:

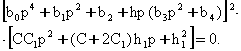             (8.6.15)

Бу ерда  коэффициентлар тизимнинг физик параметрлари оркали куйидагича ифодаланади:

(8.6.16)

            Бу коэффициентлар тизимнинг умумлашган координаталарига боглик эмас. Агар (8.6.15)  деб олсак, у вактда Е.Уиттекер тадкик этган холга келамиз. Бу холда характеристик тенглама куйидаги куринишда булади:

                        .             (8.6.17)

Бу тенглама кушимча яна иккита нолга тенг булган илдизга эга ва шунинг учун тургунлик назариясининг критик холига келамиз. Агар  купайтувчини ташлаб юборсак, у холда хосил буладиган

                                             (8.6.18)

тенглама, Уиттекер тенгламаси билан мос келади [114, 253-бет], бу ерда  коэффициентлар бир жинсли ярим шарлар учун хисобланган. (8.6.18) тенгламага асосан иккита бир жинсли ярим шарлар учун консерватив тургунлик шарти

                                                           (8.6.19)

тенгсизликнинг бажарилишига келтирилади. (8.6.1) билан (8.6.19) тенгсизликларни солиштирганимизда (8.6.19) нинг ишораси (8.6.1) нинг ишорасига карама-карши эканлигини курамиз. Уиттекернинг (8.6.1) муносабатидаги ишоранинг тескари булгани Ю.И.Неймарк ва Н.А.Фуфаевларнинг фикри буйича типографиянинг хатоси булиши мумкин. Аммо (8.6.17) муносабатдаги иккита нолга тенг булган илдизни хисобга олмаслик умуман нотугридир.

            (8.6.15) муносабатда  ва  булсин. Агар

                (8.6.20)

тенгламалар системаси барча илдизларининг хакикий кисми манфий ишорали булса, у вактда (8.6.15) га асосан О₆ сиртнинг  мувозанат нуктаси асимптотик тургун булади. Бунинг учун куйидаги тенгсизликларнинг бажарилиши зарурдир ((8.6.16) га асосан доимо ):

                            (8.6.21)

 булганда (бир жинсли ярим шар учун бу доимо бажарилади)  булади. Бундан ташкари  дан  келиб чикади.

            Шунинг учун асимптотик тургунлик шарти

                                  (8.6.22)

тенгсизликларнинг бажарилишига келтирилади. Кейинги тенгсизлик  ёки  ва  булганларида бажарилади. (8.6.22) шартларнинг охиргиси бажарилса, у вактда ковушкок ишкаланиш кучини  киритиш консерватив тургун тизимни асимптотик тургун тизимга айлантириш учун етарлидир.

 

7-§. Лагранж теоремасини ноголоном тизимларга куллаш

 

            Ю.И.Неймарк ва Н.А.Фуфаев 1965 йилда ноголоном тизимлар тургунлигини факат мувозанат холатларининг  сиртига нисбатан куйиш мумкинлигини исботлаб берган эдилар. Яккаланган мувозанат холати атрофида ноголоном тизимнинг тургунлигини тадкик этиш масалани нокоррект куйилганини билдиради, чунки ноголоном тизимларда яккаланган мувозанат холат мавжуд эмас [71,72].

            Бу илмий  натижага В.В.Румянцев ва унинг шогирдлари бошкача карайдилар [82,83]. Уларнинг фикрича: тургунлик  умумий назарияси буйича алохида олинган мувозанат холатининг тургунлигини хам, (яккаланган мувозанат холатлари булмаса хам), мувозанат холатлари сиртининг тургунлигини хам тадкик этиш мумкин. Мувозанат холатлари сиртининг айрим нукталари тургун ва бошкалари нотургун булишлари мумкин.

            Демак, хозирги пайтда ноголоном тизимлар мувозанат холатларини тадкик этиш масаласида бир-бидан фаркли иккита эркин фикр (гоя) мавжуд. Олдинги параграфларда Ю.И.Неймарк ва Н.А.Фуфаевнинг илмий натижалари баён этилган эди. Бу параграфда В.В.Румянцев мактабининг илмий натижалари шархлов тарикасида баён этилади.

            Лагранж теоремасини ва унинг тескарисини ноголоном тизимларга татбик килиш масаласини 1967 йилда, бизнингча, биринчи булиб В.В.Румянцев куйди [84].  У ноголоном тизимлар мувозанат холатининг тургунлиги ва нотургунлигининг етарли шартларини топди хамда диссипатив кучларнинг тургунликка таъсирини урганди [85].

             умумлашган координаталарга эга булган ноголоном механик тизимни курамиз. Бу тизимнинг  умумлашган тезликлари  та

                             (8.7.1)

интегралланмайдиган кинематик богланишлар билан чегараланган булсин, бу ерда . Тизимга  потенциал кучлардан ташкари

                                   

хусусиятга эга  диссипатив кучлар хам таъсир этсин. Хусусан, диссипатив кучлар  булиши мумкин, бу ерда F Релей функцияси ва у куйидагича аникланади:

                                    .

            Агар (8.7.1) ноголоном богланишлар тенгламаларини  та умумлашган тезликларга нисбатан ечсак ( булгани учун буни амалга ошириш мумкин), у холда бу тенглама (8.7.1) ни куйидаги куринишда ёзиш мумкин

          .      (8.7.2)

Ноголоном тизимнинг харакат тенгламаларини Воронец тенгламалари куринишида ёзамиз:

,  (8.7.3)

бу ерда

     ,

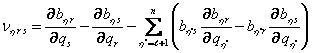 ва  лар (8.7.2) муносабат оркали мос равишда  ва  ларнинг ифодаларидан  ларни чикариб ташлаш натижасида хосил килинади:

      

(8.7.3) ва (8.7.2) лар  та  узгарувчиларга нисбатан  тартибли тенгламалар системаси булиб,

                                   

энергия тенгламаси ва диссипатив кучлар таъсир этмаганда

                                      

энергия интегралига эга булади.

            Агар кинетик энергия, диссипатив ва  куч функцияси хамда (8.7.2) ноголоном богланишларнинг коэффициентлари охирги  та умумлашган координаталарга боглик булмасалар, у холда (8.7.3) тенгламаларни (8.7.2) ноголоном богланишлар тенгламаларисиз куриш мумкин. Бундай холда ноголоном тизимларни Чаплыгин тизимлари деб, куйидаги

     (8.7.4)

                                   

тенгламаларни эса Чаплыгин тенгламалари деб айтайдилар (Ю.И.Неймарк ва Н.А.Фуфаев таърифи).

            Координата бошини мувозанат холати деб кабул килиб ва бу нуктада богланишларнинг коэффициентлари хамда  куч функцияси (, бу ерда П-потенциал энергия) нолга тенг булсин. Куйидаги теорема мавжуд.

            7.1-теорема  (В.В.Румянцев [84]). Агар мувозанат холати атрофида потенциал энергия аник-мусбат ишорали булса ( куч функцияси аник-манфий ишорали булса), у вактда диссипатив кучлар таъсир этса-этмаса мувозанат холати тургун булади.

            Бу теореманинг исботи тургунлик хакидаги Ляпунов теоремасидан келиб чикади. Ляпунов функцияси сифатида  олинади. (8.7.2) ва (8.7.3) ларга нисбатан олинган  ёки нолга тенг (диссипатив кучлар йук), ёки –2Ф тенг ва мусбат эмас (диссипатив кучлар таъсир этади) булади.

            Теорема 7.1 ни (диссипатив кучлар таъсири йугида) Лагранж теоремасининг ноголоном тизимларга татбик этилиши сифатида караш мумкин ва уни умумлаштириш мумкин.

            7.2-теорема (В.В.Румянцев [84]). Агар мувозанат холатининг етарли кичик атрофида  куч функцияси мусбат киймат кабул кила олса ва

                                  (8.7.5)

сохада

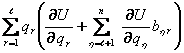                                    (8.7.6)

ифода  узгарувчиларнинг аник-мусбат функцияси булса, у вактда мувозанат холати нотургундир.

            Бу теореманинг исботи Четаевнинг нотургунлик хакидаги теоремасидан келиб чикади. Бунинг учун Четаев функциясини

                                   

куринишида олиш керак.

            7.3.-теорема (В.В.Румянцев [84,85]). Агар мувозанат холатда  хамда мувозанат холатнинг етарли кичик атрофида  функциянинг квадратик кисми ва (8.7.6) ифода  узгарувчиларга нисбатан аник-манфий ишорали булса, у вактда умумлашган тезликларга нисбатан тулик диссипацияли кучлар таъсири остидаги тизимнинг мувозанат холати  узгарувчиларга нисбатан асимптотик тургун булади.

            Теореманинг исботи [80, 86] да берилган.

            Юкорида баён этилган натижаларнинг ривожи А.В.Карапетяннинг [36-38] ишларида берилган. У Ляпунов-Малкин, Айзерман-Гантмахер теоремалари ва Ляпуновнинг биринчи якинлашиш усулидаги нотургунлик хакидаги теоремаларидан фойдаланиб, ноголоном тизимлар мувозанат холатининг тургунлигини тадкик этишни координаталари ноголоном богланишлар сонига камайтирилган ва нопотенциал позицион кучлар (дастлабки таъсир этаётган кучлардан ташкари) таъсири остидаги голоном тизим мувозанат холатининг тургунлигини тадкик этиш масаласига келтиради.

            7.1-лемма (А.В.Карапетян [36]). Ноголоном тизимнинг нолинчи               

                    (8.7.7)

мувозанат холати (координата боши) асимптотик тургун (экспоненциал нотургун) булса, унинг

   (8.7.8)

мувозанат холати хам тургун (нотургун)дир. Бундан ташкари, биринчи холатда, хар кандай тойилмаган харакатга етарли якин булган тойдирилган харакат  да

                           (8.7.9)

мувозанат холатлар сиртининг бирорта мувозанат холатига  интилади.

            Шу лемма оркали Карапетян ноголоном тизим мувозанат холатининг тургунлигини текшириш масаласини юкорида акс эттирилган голоном тизим мувозанат холатининг тургунлигини текширишга келтирган.

            (8.7.8) системада кушимча нопотенциал

                                   

кучлар мавжуд (келтирилган кучлар деб айтилади).

            Агар

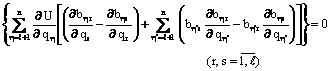     (8.7.10)

шарт бажарилса, у вактда .

            Ушбу леммадан фойдаланиб, куйидаги теоремаларни исбот килиш мумкин.

            7.4-теорема (А.В.Карапетян [36]). Агар  матрицанинг барча хоc (характеристик) кийматлари мусбат булса, у вактда (8.4.10) шарт бажарилганда консерватив ноголоном тизимнинг (8.4.7) мувозанат холати биринчи якинлашишда тургун булади ва бу мувозанат холат тизимга етарли кичик кийматли тулик диссипацияли кучларни кушиш билан Ляпунов буйича тургун булади.

            7.5-теорема. Агар матрица хеч булмаганда битта манфий ишорали хос (характеристик) кийматга эга булса, у вактда (8.7.10) шарт бажарилганда диссипатив кучлар тизимга таъсир этса-этмаса хам ноголоном тизимнинг (8.7.7) мувозанат холати нотургун булади.

            Изох. Агар мувозанат холатда  ёки барча  лар нолга айланса, у вактда (8.7.10) шартлар бажарилади. Бу шартлар бажарилган вактда  матрица манфий ишорали хос кийматлар эга булган холда ноголоном тизим мувозанат холатининг нотургунлигини олдин В.В. Румянцев исбот килган эди [84].

            Бу теоремаларнинг исботи  холлар учун Томсон-Четаевнинг [102] (8.7.8) формадаги тизимлар мувозанат холатининг тургунлигига диссипатив кучларнинг таъсири хакидаги теоремаларидан келиб чикади.

            7.6-теорема (А.В.Карапетян [36]). Агар куйидаги:

            1)        

            2)

            3) матрицанинг барча хос кийматлари манфий деган шартларнинг бирортаси бажарилса, консерватив ноголоном тизимнинг (8.7.7) мувозанат холати нотургун булади.

            (2) ёки (3) шарт бажарилганда мувозанат холатини хеч кандай диссипатив кучлар оркали стабиллаштириш мумкин эмас.

            Э.М.Красинская-Тюменева ва А.Я.Красинскийнинг [45] илмий ишида нопотенциал позицион кучларнинг мувозанат холатига таъсири тадкик этилган.

 

8-§. Ноголоном тизимларнинг циклик координаталари.

Масаланинг куйилиши

 

            Консерватив ноголоном тизимлар стационар харакатларини тадкик этишда Лагранж координаталарида тузилган харакат тенгламаларидан хам, квазикоординаталарда тузилган харакат тенгламаларидан хам фойдаланиш мумкин. Биз бу параграфда Лагранж координаталарида тузилган ушбу харакат тенгламаларидан фойдаланамиз:

                        ,      (8.8.1)

                .    (8.8.2)

Бу ерда  - Лагранж функцияси, Т-тизимнинг кинетик энергияси, U-куч функцияси (U=-П, П-потенциал энергия).

            Лагранж координаталаридаги харакат тенгламаларидан фойдаланганда, стационар харакат сифатида шундай харакатни тушунамиз: бу харакатда позицион координаталар, циклик координаталарнинг тезликлари дастлабки кийматларини саклайдилар, циклик координаталарнинг узлари эса, вакт буйича чизикли равишда узгарадилар [114].

            Голоном тизимларда Лагранж функциясининг ифодасига ошкора равишда кирмаган координаталарга циклик координаталар ва колганларига позицион координаталар деб айтилади. Циклик координаталарга мос келган умумлашган кучлар нолга тенг булади.

            Ноголоном тизимлар учун циклик координаталарнинг бир неча хил таърифлари мавжуд. Уларни шартли равишда уч гурухга булиш мумкин.

            Биринчи гурухга циклик интегралларнинг мавжудлигини таъминлайдиган таърифларни киритамиз. Улардан энг умумийроги куйидагидир.

            1-таъриф (А.С.Сумбатов [89]). Агар  координаталарнинг тезлиги  богланишлар тенгламасига кирмаса ва Лагранж функциясидан бу координата буйича олинган хусусий хосиланинг богланишларни хисобга олиб топилган киймати нолга тенг булса, у вактда  га ноголоном тизимнинг циклик координатаси деб айтилади.

            Демак,  циклик координата булганда,

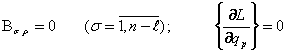            .   (8.8.3)

Бу ерда ва бундан кейин ифодалар фигурали кавсга олинган булса, бу ифода (8.8.1) ни инобатга олиб хисобланганлигини билдиради.

            (8.8.3) шартлар бажарилса, (8.8.1) ва (8.8.2) харакат тенгламалари куйидаги куринишдаги циклик интегралга эга буладилар:

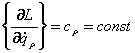                                    .             (8.8.4)

Бу ерда циклик координаталар (8.8.4) тенгламалар ифодасига ошкора равишда кириши мумкин (масалан, бу координатага боглик булиши мумкин булган богланишлар коэффициентлари оркали). 1-таъриф олдин киритилган ушбу таърифни умумлаштиради.

            2-таъриф (Л.Н.Семенова [87]). Агар

                   (8.8.5)

бажарилса, у вактда  га циклик координата деб айтамиз.

            (8.8.5) тенгламалар

                                                       (8.8.6)

куринишдаги интегралга эга буладилар. Бу тенгламалар ифодасига хам  циклик координата ошкора равишда катнашиши мумкин.

            Агар  та узгармас  микдорлар

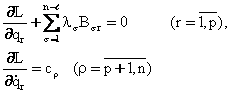                             (8.8.7)

 та тенгламалар системасини каноатлантирса, у вактда 2-таъриф маъносидаги  циклик координата  учун (8.8.1) ва (8.8.2) харакат тенгламалари куйидаги куринишли ечимга эга буладилар:

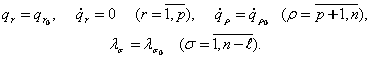(8.8.8)

(8.8.6) ва (8.8.7) ифодалардаги  та узгармас  ихтиёрий (эркин) булганликлари учун бу холда стационар харакатлар  дан кам булмаган улчовга эга булган сиртни ташкил килади.  та циклик координаталар ва  та ноголоном богланишлар йигиндиси  сонини беради. Демак, стационар харакатлар сиртининг улчами циклик координаталар ва ноголоном богланишлар сонларининг йигиндисидан кам булмаслиги керак.

            Иккинчи гурухга стационар харакатлар мавжудлигини таъминлайдиган циклик координаталар таърифларини киритамиз. Булардан энг умумийроги куйидаги И.Е.Емельянова ва Н.А.Фуфаев берган таърифдир.

            3-таъриф (И.Е.Емельянова ва Н.А.Фуфаев [29,30]). Агар ноголоном богланишларни хисобга олиб тузилган харакат тенгламаларининг ифодаларига  координатанинг узи ошкор равишда кирмасдан факат унинг тезланиши ва, мумкин, тезлиги кирса, у вактда  га циклик координата деб айтилади.

            Бу таъриф аввалги хамма таърифларни, шу жумладан, 1 ва 2 – таърифларни хам умумлаштиради.

            4-таъриф (Ю.И.Неймарк ва Н.А.Фуфаев [71,73]). Агар

               (8.8.9)

бажарилса, у вактда  циклик координата деб атаймиз.

            3 ва 4-таърифлар маъносидаги циклик координаталар мавжудлигида харакат тенгламаларининг циклик интеграллари булмаслиги мумкин. Масалан, (8.8.9) шартлар бажарилганда

                          

ва (8.8.8) куринишдаги стационар харакатлари булади. (8.8.9) шартларда (8.8.8)даги  узгармаслар куйидаги  та тенгламалар системасини каноатлантиради:

                             (8.8.10)

            (8.8.10) тенгламалар системасининг  нисбатан нолга тенг булмаган ечими мавжуд булганда, стационар харакатлар улчови бирдан кам булмаган сиртни ташкил киладилар [71,73], чунки (8.8.10) системанинг охирги  та тенгламалари  холда бир-бирига богланган булади.

            1 ва 2 – таърифлар буйича харакат тенгламаларининг циклик координаталарга богликлиги хамда 3 ва 4 – таърифларга асосан циклик интегралларнинг мавжуд эмаслигига карамасдан хар икки холда хам Раус буйича циклик узгарувчилар инкор этилмайди.

            Агар М.Ф.Шульгин ва А.В.Карапетян берган ушбу таърифни кабул килсак, у вактда Раус буйича циклик узгарувчиларни инкор этиш мумкин.

            5-таъриф (М.Ф.Шульгин, А.В.Карапетян [38,106]). Агар

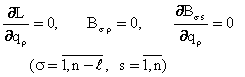                      (8.8.11)

шартлар бажарилса, у вактда  циклик координата деб аталади.

             - координаталар учун (8.8.11) шартлар бажарилганда харакат тенгламалари ифодасида циклик координаталар ошкора равишда катнашмайди ва харакат тенгламалари (8.8.6) куринишдаги циклик интегралга эга буладилар.

                                   

муносабат оркали Раус функциясини киритамиз (унг тарафидаги  циклик тезликлар (8.8.6) формулалар оркали функция ифодасидан чикарилган). У вактда (8.8.1) ва (8.8.2) ноголоном тизимлар харакат тенгламаларини куйидаги куринишга келтирса булади:

            ,   (8.8.12)

                 ,        (8.8.13)

                        .       (8.8.14)

            (8.8.12) ва (8.8.13) тенгламаларни (8.8.14) тенгламаларга богламасдан алохида куриш мумкин.

            Уларни  умумлашган координатали ва  та интегралланмайдиган кинематик богланишлар билан богланган келтирилган ноголоном тизимлар харакатининг аникмас купайтувчилар катнашган Лагранж тенгламалари сифатида караш мумкин. Тизимнинг динамик хусусиятини R Раус функцияси аниклайди. Бу ерда дастлабки тизимнинг ((8.8.1) ва (8.8.2)) стационар харакатларига келтирилган тизимнинг мувозанат холатлари мос келади. Мувозанат холатларининг тургунлигини олдинги параграфларда баён этилган усуллар билан тадкик этиш мумкин.

            Шуни таъкидлаймизки, 1,3 ва 4-таърифлар маъносидаги циклик координатали ноголоном тизимлар стационар харакатларининг тургунлиги умумий холда тадкик этилган эмас.

9-§. Голоном ва ноголоном тизимлар стационар харакатларининг тургунлиги [71,73]

 

            Голоном ва ноголоном тизимларнинг стационар харакатлари фазавий фазода ва конфигурация фазосида кандайдир улчовли сиртни ташкил килади. Шунинг учун хам стационар харакатлар тургунлигини текширишда ноголоном тизимлар мувозанат холатларини тадкик этишдаги холатга (ситуацияга) келамиз.

            Аввал голоном тизимлар стационар харакатларини куриб утайлик.

                

Лагранж функцясига эга булган  умумлашган координатали голоном тизим берилган булсин. Бу ерда -умумлашган координаталар сони,  та охирги координаталар циклик координаталар булсин. Тизимга туликмас диссипатив

                                   

кучлар таъсир этсин. Бу кучларнинг ифодасида циклик тезликлар мавжуд булмасин. Бундай тизимнинг харакат тенгламалари

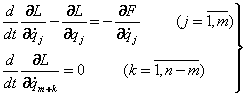                           (8.9.1)

куринишда булади.  алмаштириш киргизиб, (8.9.1) тизимни куйидаги куринишда ёзамиз:

            .      (8.9.2)

Бу тенгламалар тасвирловчи нуктанинг харакатини  улчовли Ф фазавий фазода ифодалайди. Фазонинг координата уклари буйича  микдорлар йуналган. Таъриф буйича стационар харакат деб шундай харакатга айтамизки, унда ноциклик(позицион) координаталар ва циклик координаталарга мос келган тезликлар узгармас (дастлабки) кийматни саклайдилар. Демак, стационар харакатда

           

муносабатларга эга буламиз, яъни стационар харакат Ф фазавий фазога мувозанат холати булиб аксланади. Шундай килиб, стационар харакатлар тургунлиги масаласи Ф фазавий фазодаги мувозанат холатларининг тургунлик масаласига айланади. Мувозанат тенгламаси

                                   

 та  номаълум узгарувчиларга нисбатан  та тенгламалар системасини ифодалайди. Бу ердан бевосита умумий холда  улчовли стационар харакатлар сиртини (Ф фазода  улчовли мувозанат холатлари сиртини) хосил киламиз. Шунинг учун хам 2-§ даги натижаларга асосан тизимнинг характеристик тенгламаси  та нол илдизларга эга булади ва стационар харакатлар сиртининг тургунлигини характеристик тенгламанинг колган  та илдизларининг характери аниклайди. Хакикатан хам  алмаштиришларни киритиб,  стационар кийматлардан етарли кичик микдордаги  тойилишларга нисбатан харакат тенгламасини тузамиз:

            (8.9.3)

Бу ердан тизимнинг характеристик тенгламаси  та нол илдизга эга эканлиги куриниб турибди, Колган  илдизларнинг хакикий кисмлари манфий булишининг шартлари стационар харакатлар сиртининг асимптотик тургунлик сохаларини аниклашга ва асимптотик тургунлик сохаси чегарасининг тизим конструктив параметрларининг узгаришига кандай богликлигини аниклаб беради.

            Энди ноголоном тизим стационар харакатининг тургунлигини куриб утамиз. Лагранж функцияси ва диссипация функциясининг ифодаларида  умумлашган координаталарнинг охирги  таси мавжуд булмасин деб фараз киламиз. Тизимнинг Лагранж функцияси

                        ,

бу ерда -Лагранж функцияси ифодасига кирмаган координаталар сони. Бу координаталарни циклик координаталар деб атаймиз. Ноголоном богланишлар

               (8.9.4)

муносабатлар билан ифодалансин, бу ерда . Диссипация функцияси

                              (8.9.5)

куринишда булсин. Унинг ифодасида циклик координаталарга мос келган тезликлар катнашмайди. У вактда бундай тизимнинг харакат тенгламалари куйидаги куринишда булади:

            ,  (8.9.6)

          .        (8.9.7)

 белгилашни киритиб ва (8.9.7) дан фойдаланиб, (8.9.6), (8.9.7) ва (8.9.4) харакат тенгламаларини куйидаги куринишда ёзамиз:

            ,    (8.9.8)

                   ,             (8.9.9)

  ,   (8.9.10)

бу ерда

              .

            Хосил  килинган тенгламалар  та тенгламалар тизимини ташкил этади. Бу тизимдан

               

та микдорлар вакт функцияси сифатида топилади.           Стационар харакатда

            .

Буларни (8.9.8) – (8.9.10) тенгламаларга куйиб, ноголоном тизимларнинг куйидаги стационар харакатлари тенгламаларини хосил киламиз:

                                    ,                     (8.9.11)

                                    ,                         (8.9.12)

   .   (8.9.13)

(8.9.11) – (8.9.13) тенгламалар  тенгламалар тизимини ташкил килади. Бу тизимдан  та  микдорларни аниклаймиз. Агар (8.9.11) – (8.9.13) тизимни ташкил этаётган тенгламаларнинг хаммаси хам богланмаган булмаса (аъни айримлари бир-бирига богланган булса), у вактда аникланиши лозим булган микдорларнинг сони тенгламалар сонидан катта булади. Бу холда олдинги натижаларга асосан стационар харакатлар сиртига эга буламиз. Курсатиш мумкинки, (8.9.11) – (8.9.13) тенгламалар системасининг хеч булмаганда битта тенгламаси богланмаган эмас. Хакикатан хам, агар (8.9.12) тенгламаларнинг ха бирини мос равишда  купайтириб барчасини кушсак, у холда (8.9.13) асосан айнан нолни хосил киламиз.

            Демак, (8.9.11) – (8.9.13) тенгламалар тизимининг богланмаган (эркин) тенгламалар сони барча тенгламалар сонидан хеч булмаганда биттага кам булади.

            Шунинг учун хам ноголоном тизимлар стационар харакатлари хеч булмаганда бир улчамли сиртни ташкил киладилар.

            Шундай килиб, ноголоном тизимлар стационар харакатлари холатини текширишда ноголоном тизимлар мувозанат холатларини текширишдагига холатга монанд холатга келамиз. Демак, иккинчи параграфда баён этилган назарияни бу ерда хам татбик этиш мумкин.

            Келгуси параграфда муайян голоном ва ноголоном тизимлар стационар харакатларининг тургунлигини ушбу праграфда баён этилган назария асосида текширамиз.

10-§. Муайян голоном ва ноголоном тизимлар стационар

харакатларининг тургунлигини тадкик этиш

 

            Ушбу параграфда Ю.И.Неймарк ва Н.А.Фуфаев томонидан муайян голоном ва ноголоном тизимлар стационар харакатларини урганиш учун утказган тадкикот натижаларини келтирамиз [71,73].

 

 

1-мисол. Айланаётган ясси маятник

 

            Шарнирга осилган ва укка нисбатан симметрик булган жисмни курамиз. Шарнир вертикал подшипникка махкамланган (8.8-шакл).

           

 

 

 

 

 

 

 

 

 

 

 

           

                              8.8-шакл.

 

Подшипникдаги ишкаланишни хисобга  олмаймиз ва шарнирдаги ишкаланиш ковушкок деб хисоблаймиз. Жисмнинг инерция буйича харакатини урганамиз.  - тизимнинг умумлашган координаталари, С-жисмнинг ук буйича инерция моменти, А-осилган ук буйича жисмнинг экваториал инерция моменти, -шарнир укидан жисмнинг масса марказигача булган масофа, -огирлик кучининг тезланиши булсин. Лагранж функцияси  ва диссипация функцяси F ларнинг ифодаларини топамиз:

           

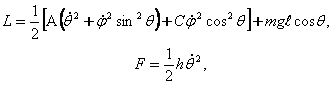
бу ерда -шарнирдаги ковушкок ишкаланишнинг коэффициенти.

            Куйидаги улчовсиз микдорларни киритамиз:

            ,

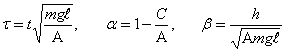бу ерда -параметр мусбат микдор,  параметр булса –1 дан +1 гача ораликда исталган киймат кабул килиши мумкин.

             деб белгилаб, курилаётган тизимнинг харакат тенгламасини ёзамиз:

               (8.10.1)

Стационар харакатлар тенгламаси

                                     (8.10.2)

куринишда булади. Бу ердан стационар харакатлар сирти бир улчовли ва учта тармокдан иборат эканлиги келиб чикади: I) , II) , III).    ва   булганлиги учун  текисликнинг биринчи квадрантини курамиз, бу ерда  (8.9-шакл).

            Стационар харакатлар тармокларининг тургунлигини тадкик этиш учун (8.10.1) тизимнинг характеристик тенгламасини тузамиз:

   (8.10.3)

Бу ерга  куйиб, I тармок учун характеристик тенгламани хосил киламиз:

                                    .

Бу тенгламадан I тармокнинг тургунлик шартини топамиз:

                                    .

 булганда I тармок доимо тургун. Агар  булса, у вактда I тармок факат  сохада тургун булади.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

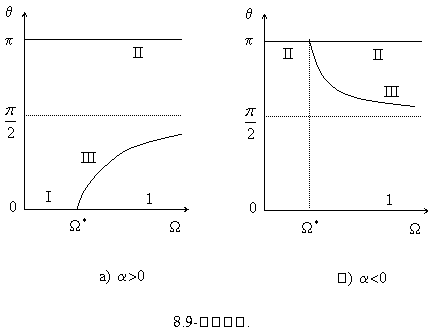            II тармокнинг характеристик тенгламасини топиш учун  (8.10.3) га  ни куямиз:

                                    .

II тармокнинг тургунлик шарти

                                   

дан иборат булади. Бу ердан  холатда II тармокнинг нотургунлиги ва  холда II тармок факат  сохада тургун булиши келиб чикади.

 

 

 

 

 

 

 

 

 

 

 

 

 

           

                                                8.10-шакл.

 

            III тармокнинг характеристик тенгламасини топиш учун (8.10.3) тенгламага  ни куямиз:

.

Гурвиц критериясига асосан тургунлик шартини топамиз:

                                    .

Бу ердан  да III тармокнинг доим тургунлиги,  холда агар  булса – нотургунлиги келиб чикади.

             кийматлар учун III тармокда

тургунлик сохаси мавжуд. Бу интервалдан ташкарида III тармок нотургун.  Олинган натижалар 8.3-шаклда ифодаланган. Бу ерда доирачалар билан тургун стационар харакатлар ва юлдузчалар билан нотургун стационар харакатлар белгиланган.

            Изох. Агар  деб кабул килсак, у вактда мажбурий айланишдаги (масалан, чексиз кувватга эга булган мотор оркали) тургунлик масаласига келамиз.

            У вактда харакат тенгламаси (8.10.1) тизимнинг биринчи тенгламасидан иборат булади. Бу ерда  ва  берилган параметр. Стационар харакатларнинг тенгламаси аввалгидай (8.10.2) дан иборат. Аммо стационар харакатлар тармокларининг тургунлик шартлари бироз узгаради. Тизимнинг характеристик тенгламаси

                       

куринишда булади. Тармокларнинг тургунлик шартлари

                                   

лардан иборат. Бу ердан I ва II тармоклар учун тургунлик шартлари аввалгидай булиши, III тармок учун эса

булиши келиб чикади. Демак,  булган холда аввалгидай III тармок тургун ва  да доим нотургун булади. Худди мана шу мухим натижа билан тизимнинг мажбурий айланиш динамикаси айнан шу тизимнинг эркин харакати динамикасидан фарк килади.

 

 

 

 

2-мисол. Нотекис горизонтал текисликдаги диск харакатининг тургунлиги

 

            Радиуси , массаси  тенг булган диск сирганмасдан нотекис горизонтал текисликда думалаб харакат килсин. Диск конфигурациясини (холатини) бешта умумлашган координата аниклайди:  - текислик билан диск уринган нуктанинг декарт координаталари ва учта  Эйлер бурчаклари (8.11-шакл). Дискнинг текислик буйича  сирганишсиз думалаши иккита ноголоном богланишларга олиб келади:

                                 (8.10.4)

 Лагранж функциясини (8.10.4) ноголоном богланишлар тенгламаларини хисобга олмасдан тузамиз

            Курилаётган тизимга туликмас диссипацияли F куч таъсир этсин ва унинг куриниши

                                               

каби булсин, бу ерда  - ковушкок ишкаланишнинг коэффициенти.

            Диск харакатининг тенгламаларини куйидаги куринишда ёзамиз:

 (8.10.5)

            (8.10.4) ва (8.10.5) тенгламалар системасидан  ларни чикариб ташлаб ва

                                   

белгилашларни киритиб, дискнинг куйидаги харакат тенгламасини хосил киламиз:

(8.10.6)

            (8.10.6) тенгламалар  фазода тасвирловчи нуктанинг харакатини ифодалайдилар. Дискнинг стационар харакати бу фазога мувозанат холати булиб аксланади. (8.10.6) системадан икки улчовли стационар харакатлар сиртини ифодалайдиган мувозанат холатларининг тенгламасини топамиз:

            .      (8.10.7)

 

 

 

 

 

 

 

 

 

 

 

 

 

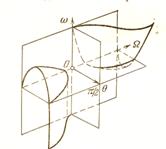         8.11-шакл.                           8.12-шакл.

             интервалда (8.10.7) сирт 8.12-шаклда курсатилгандек булади. Бу сиртда  тугри чизикнинг нукталари дискнинг тугри чизик буйлаб думаланишига мос келади (диск текислиги вертикал холатда).  тугри чизикнинг нукталари дискнинг кузгалмас вертикал диаметр атрофидаги айланишига мос келади. (8.10.7) сиртнинг колган барча нукталари дискнинг шундай айланма харакатларига мос келадики, дискнинг горизонтал текислик билан уринган нуктаси айлана чизади ва  микдорлар (8.10.7) ни каноатлантирадиган узгармас кийматларини саклайдилар.

            (8.10.7) стационар харакатлар сиртининг асимптотик тургунлик шартларини топамиз. Бунинг учун

           

деб олиб, (8.10.6) харакат тенгламаларини  етарли кичик микдорларга нисбатан чизиклаштирамиз.  лардан нол индексларни ташлаб,

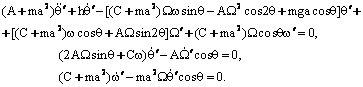(8.10.8)

хосил киламиз. (8.10.8) тизимнинг характеристик тенгламаси

                                                (8.10.9)

куринишда булади, бу ерда 

Стационар харакатлар сирти икки улчовли булганлиги сабабли (8.10.9) характеристик тенгламанинг иккита нол илдизлари бор. Асимптотик тургунлик шартлари куйидаги тенгсизликлардан иборат:

                                           ,                    (8.10.10)

(8.10.11)

            (8.10.10) муносабатга асосан ковушкок ишкаланиш коэффициенти  мусбат булиши керак. (8.10.11) тенгсизлик тургунлик сохасининг чегарасини топишга имкон беради

(8.10.12)

            Тайинланган  киймат учун  параметрлар буйича эллипс хосил киламиз. Бу эллипснинг ярим уклари  да нолга интилади.  булганда

                       

ни оламиз. Бу ердан дискнинг тугри чизикли харакати  факат

                       (8.10.13)

кийматларда, дискнинг кузгалмас вертикал диаметр атрофида айланиш харакати эса

                                          (8.10.14)

тенгсизлик бажарилганда тургун булиши келиб чикади. (8.10.12) сиртнинг (8.10.7) стационар харакатлар сирти билан кесишиши (8.10.7) сиртда тургунлик сохасининг чегарасини аниклайди. Бу чегара 8.13-шаклда курсатилган.

            Стационар харакатлар сиртининг асимптотик тургунлигининг маъноси куйидагидан иборат: асимптотик тургун стационар харакат тойилганда тизимда сунувчи тебранишлар (ёки экспоненциал сунувчи жараён) вужудга келади. Натижада, умуман айтганда, аввалгидан фарк киладиган стационар харакат тикланади. Масалан, дискнинг тугри чизикли думаланиши тойилганда умумий холда шундай стационар харакат тикланадики, дискнинг горизонтал текислик билан уринган нуктаси радиуси   булган бирор айлана буйича харакат килади.

 

 

 

 

				8.14-шакл.

 

 

 

 

 

 

 

 

 

 

 

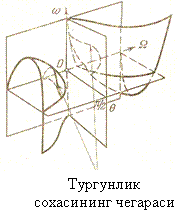
               8.13-шакл.                                        

 

             холи. Дискнинг уз уки буйича айланишининг бурчак тезлиги  доимо узгармас булсин деб фараз киламиз. У вактда ноголоном богланишлар тенгламасининг ва L Лагранж функциясининг ифодаларига кирувчи  микдор энди координата булмай, балки тизимнинг бошка физик параметрлари катори параметр булади. Дискнинг харакат тенгламаси (8.10.4) тенгламалар тизимидан ва охирги тенгламасиз (8.10.5) тизимдан иборат булади. Бу тенгламалардан  микдорларни чикариб ва  деб белгиласак, дискнинг харакат тенгламасини куйидаги куринишга келади:

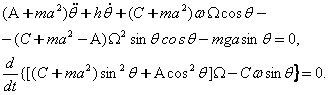    (8.10.15)

(8.10.15) тенгламалар тасвирловчи нуктанинг  текисликдаги харакатини ифодалайди. (8.10.15) га асосан мувозанат холатлари  текисликнинг куйидаги эгри чизигида жойлашган:

.(8.10.16) Шундай килиб, курилаётган холда дискнинг стационар харакатлари бир улчовли сиртни хосил килади. 8.14-шаклда  бир нечта тайинланган кийматлари учун (8.10.16) эгри чизиклар чизилган.

             нинг манфий кийматлари учун 8.14-шаклдаги эгри чизикларни мос равишда  укига нисбатан кузгудаги аксини олиш керак. (8.10.16) стационар харакатлар сиртининг асимптотик тургунлик шартларини топамиз. Бунинг учун (8.10.15) тенгламалар тизимини  лардан етарли кичик микдорга тойилган  микдорларга нисбатан чизиклаштирамиз:

(8.10.17)

            Бу тизимнинг характеристик тенгламаси

                                   

куринишда булади, бу ерда

Асимптотик тургунлик шартлари

                                                    (8.10.18)

дан иборат. Бу ердан  тугри чизикли харакатнинг тургун булиши учун

                                          

тенгсизлик бажарилиши лозимлиги келиб чикади. Бу охирги диск думаланишининг тургунлик шарти (8.10.13) билан бир хилдир. (8.10.13) шартда  микдор тайинланган эмас.

             холи. Бу холда диск консерватив тизимни ташкил килади. (8.10.9) характеристик тенгламанинг иккита илдизи (нол илдизларни хисобга олмасдан) ёки хакикий (ва у вактда диск харакати нотургун), ёки кушма соф мавхум буладилар. Охирги холда тизим одатда консерватив тургун деб хисобланади. Аммо биринчи якинлашиш буйича тургунлик назарияси нуктаи назаридан охирги хол Ляпуновнинг махсус холига киради ва шунинг учун уни алохида текширишга тугри келади.

РЕЖА:

1. Ноголоном  ва голоном тизимлар хакида умумий тушунчалар.

2. Ноголоном тизимлар мувозанат холатининг тургунлиги.Кичик тебранишлар        тенгламасини тузиш. Коэффициентлар матрицасининг хусусияти. Умумий назарияни татбик этиш мумкинлиги.

3. Ноголоном тизимнинг мувозанат холатлари сирти якинидаги кичик тебранишлар тенгламалари. Мувозанат холатлари сиртининг тургунлиги.

4. Чаплигин чанасининг кия текисликдаги харакатининг тургунлиги.

5. Нотекис горизонтал текисликдаги шарнинг харакати.

6. Ноголоном тизимлар мувозанат холатлари сиртининг ассимптотик тургунлиги хакидаги теорема.

7. Доимо таъсир этувчи кичик кучларга (тойдирувчиларга) нисбатан тургунлик

8. Керкговен-Витгоф масаласи.

9. Лагранж теоремасини ноголоном тизимларга куллаш.

10. Ноголоном тизимларнинг циклик координаталари. Масаланинг куйилиши.

11. Голоном ва ноголоном тизимлар стационар харакатларининг тургунлиги.

12. Айланаётган ясси маятникнинг тургунлигини тадкик этиш.

13. Нотекис горизонтал текисликдаги диск харакатининг тургунлиги.

 

            Таянч иборалар. Голоном тизим, ноголоном тизим, кинематик богланишлар, геометрик богланишлар, Лагранж функцияси, кинетик энергияси, Лагранж купайтувчили тенглама, Воронец тенгламаси, Аппел тенгламаси, Неймарк ва Фуфаевлар тенгламаси, ноголоном тизимлар мувозанат холатларининг сирти, ноголоном тизимлар стационар харакати, кичик тебранишлар, теоремалар, Чаплигин чанаси, шар харакати, мувозанат холатлари сиртининг ассимптотик тургунлиги, Лагранж теоремаси, Румянцев теоремаси, Карапетян теоремаси, ноголоном тизимларнинг циклик координаталари, Сумбатов, Семёнова, Емельянова ва Фуфаев, Неймарк ва Фуфаев, Шульгин, Карапетян тарифлари, келтирилган ноголоном тизимлар.

 

Такрорлаш учун саволлар:

 

1.      Ноголоном тизимлар хакида умумий тушунчалар. Ноголоном тизимлар харакатининг тенгламалари.

2.      Ноголоном тизимлар мувозанат холатлари сиртиинг тургунлиги хакидаги теорема.

3.      Ноголоном тизимлар мувозанат холатлари сиртиинг ассимптотик тургунлиги.

4.      Доимо таъсир этувчи ктчтк кучларга нисбатан ноголоном тизимларнинг тургунлиги.

5.      Лагранж теоремасини ноголоном тизимларга куллаш. Румянцев ва Карапетян теоремалари.

6.      Ноголоном тизимларнинг циклик координаталари хакидаги таърифлар.

7.      Голоном ва ноголоном тизимлар стационар харакатларининг тургунлиги. 

 

 

 

А Д А Б И Ё Т

 

1.	Андронов А.А., Витт А.А., Хайкин С.Э., Теория колебаний, М., Физматгиз, 1959, 915 с.
2.	Андронов А.А., Вознесенский И.Н., О работах Д.К.Максвелла, И.А.Вышнеградского и В.Стодолы в области теории регулирования машин, Собрание трудов А.А.Андронова, М., Изд. АН СССР, 1956, С.490-522.
3.	Айзерман М.А., Теория автоматического регулирования двигателей, Уравнения движения и устойчивость, М., Наука, 1966, 542 с.
4.	Айзерман М.А., Об одной проблеме, касающейся устойчивости «в большом» динамических систем, Успехи матем. Наук, Т.IV, вып.4, 1949.
5.	Айзерман М.А., Гантмахер Ф.Р., Абсолютная устойчивость регулируемых систем, Изд. АН СССР, 1963.
5,а.	Атажанов Б., Красинская Э.М., О стабилизации стационарных механических систем, Прикладная математика и механика, Т.52, Вып.6, 1988, С.902-908.
5,б.	Атажанов Б., Красинская Э.М., К устойчивости стационарных движений неголономных систем //Изв.АН УзССР, Сер.техн.наук,1985, № 1, С.41-46.
5,в.	Атажанов Б., Красинская Э.М., К устойчивости стационарных движений неголономных систем //Изв.АН УзССР, Сер.техн.наук,1985, № 6, С.39-43.
6.	Артемьев Н.А., Осуществимые движения, Изв. АН СССР, сер. матем., № 3, 1939.
7.	Андреев В.Д., Теория инерциальных навигации. Автономные системы, М., Наука, 1966.
8.	Барбашин Е.А., Введение в теории устойчивости, М., Наука, 1967, 223 с.
9.	Барбашин Е.А., О построении периодических движений, ПММ, Т.25, вып.2, 1961; Программное регулирование систем со случайными параметрами, ПММ, Т.25, вып.5, 1961.
10.	Барбашин Е.А., Красовский Н.Н., Об устойчивости движения в целом, ДАН СССР, Т.86, вып.3, 1952.
11.	Барбашин Е.А., Об устойчивости решения одного нелинейного уравнения третьего порядка, ПММ, Т.16, вып.5, 1952.
12.	Баутин Н.Н., Поведение динамических систем вблизи границы области устойчивости, М., Гостехиздат, 1949.
13.	Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А., Введение в теорию нелинейных колебаний, М., Наука, 1976.
14.	Бутенин Н.В., Автоколебания стенда с автопилотом, Труды ЛВВА, Т.3, 1943.
15.	Болотин В.В., Неконсервативные задачи теории упругой устойчивости, Физматгиз, Москва, 1961.
16.	Ведров В.С., Об устойчивости движения, Труды ЦАГИ, вып.327, 1937.
17.	Вышнеградский И.А., О регуляторах прямого действия (1876), Сб. «Теория автоматичесокго регулирования», Изд. АН СССР, 1949.
18.	Воронец В.П., Об уравнениях движения для неголономных систем, Матем.сб., 1901, Том 22, вып. 4.
19.	Вкроч И., Интегральная устойчивость, Чехосл. Мат. Жур., Т.9, № 1, 1959.
20.	Гантмахер Ф.Р., Теория матриц, М.: -Наука,1967,576 с.
21.	Гермаидзе В.Е., Красовский Н.Н., Об устойчивости при постоянно действующих возмущениях, ПММ, Т.21, вып.6, 1957.
22.	Горшин С.И., Об устойчивости движения при постоянно действующих возмущениях. Критические случаи, Изв. АН Казахской ССР, № 56, сер.мат. и мех. Вып.2, 1948.
23.	Горшин С.И., Об устойчивости движения с постоянно действующими возмущениями, Изв. АН Казахской ССР, № 58, 1948.
24.	Диментберг Ф.М., Изгибные колебания вращающихся валов, Изд.АН СССР, Москва, 1959.
25.	Дубошин Г.Н., К вопросу об устойчивости движения относительно постоянно действующих возмущений, Труды ГАИШ, Т.XIV, вып.1, 1940.
26.	Дубошин Г.Н., Основы теории устойчивости движения, М.,Изд.МГУ, 1952, 318 с.
27.	Еругин Н.П., Об одной задаче теории устойчивости систем автоматического регулирования, ПММ, Т.XVI, вып.5, 1952.
28.	Еругин Н.П., Качественное исследование интегральных кривых системы дифференциальных уравнений, ПММ, Т.14, вып. 5, 1950; О некоторых вопросах теории устойчивости движения и качественной теории дифференциальных уравнений, ПММ, Т.14, вып.6, 1950.
29.	Емельянова И.С., Фуфаев Н.А., Об устойчивости стационарных движений, В сб.: Теория колебаний, Прикл.мат и киберн., Горький, 1974, С.3-9.
30.	Емельянова И.С., К определению циклических координат и стационарных движений механических систем, В сб.: Динамика систем, Вып.3, Горький, 1974, С.117-130.
31.	Емельянова И.С., Об устойчивости стационарных движений и состояний равновесия неголономных механических систем, В сб.: Вопр.прикл.мат. и мех., Вып.4, Чебоксары, 1975, С.149-158.
32.	Жуковский Н.Е., О прочности движения, Ученые зп. МГУ, отдел физ.-мат., вып.4, 1882;  Собрание сочинений, Т.1., Гостехиздат,1948.
33.	Зубов В.И., Методы А.М.Ляпунова и их применение, Изд. ЛГУ, 1957.
34.	Кай И.Я., Красовский Н.Н., Об устойчивости систем со случайными параметрами, ПММ, Т.24, вып.5, 1960.
35.	Капица П.Л., Устойчивость и переход через критические обороты быстровращающихся роторов при наличии трения, ШТФ, IX, вып.2., 1939.
36.	Карапетян А.В., Об устойчивости равновесия неголономных систем, Прикл.мат и мех., 1975, 39, № 6, С.1135-1140.
37.	Карапетян А.В., О распространении теоремы Лагранжа на неголономные системы Чаплыгина, Теория и приложения механики, 1979, 10, № 2, С.11-16.
38.	Карапетян А.В., Некоторые задачи устойчивости движения неголономных систем, В сб.: Теория устойчтвости и ее приложения, Новосибирск, 1979, С.184-190.
39.	Красовский Н.Н., Некоторые задачи теории устойчивости движения, М., Физматгиз, 1959.
40.	Красовский Н.Н., Об устойчивости решений системы двух дифференциальных уравнений, ПММ, Т.17, вып.6, 1953; Об устойчивости движения в целом при постоянно действующих возмущениях, ПММ, 18, вып.1, 1954.
41.	Красинский  А.Я., Ронжин В.В., К стабилизации установившихся движений механических систем с циклическими координатами. Прикладная математика и механика, Том.52, вып.4, 1988, С.542-548.
41,а	Красинский  А.Я., Ронжин В.В., Об оптимальной стабилизации установившихся движений голономных систем. //Всесоюзн.науч.конф. «Метод функций А.М.Ляпунова в современной математике», Тез.докл.,Харьков: Изд-во Харьк. ун-та, 1986. С.95.
41,б	Красинский  А.Я., О математическом моделировании в задачах оптимальной стабилизации установившихся движений. //Всесоюз. Школа-семинар «Математическое моделирование в науке и технике». Тез.докл.,Пермь: УНЦ АН СССР, 1986, С.184-185.
41,в	Красинский  А.Я.,  К стабилизации установившихся движений систем с циклическими координатами. Прикладная математика и механика, Том.56, вып.6, 1992, С.939-950.
41,г	Красинский  А.Я., Об устойчивости и стабилизации положений равновесия неголономных систем, Прикладная математика и механика, Том.52, вып.2, 1988, С.194-202.
42.	Крылов А.Н., О вращательном движении продолговатого снаряда во время полета, Собрание трудов, Т.IV, Изд. АН СССР, 1937.
43.	Келдыш М.В., Шимми переднего колеса трехколесного шасси, Труды ЦАГИ, № 564, 1945.
44.	Князев Г.Н., Об устойчивости  неголономных  систем в критических случаях, Вопросы аналитической и прикладной механики, Сб.статей, Оборонгиз, 1963.
45.	Красинская-Тюменева Э.М., Красинский А.Я., О влиянии структуры сил на устойчивость равновесия неголономных систем, В сб.: Вопросы вычислительной и прикладной математики, вып.45, Ташкент, 1977, С.172-185.
45,а	Красинская Э.М., К стабилизации стационарных движений механических систем, Прикладная математика и механика, Т.47, вып.2, 1983, С.302-309.
45,б	Красинская Э.М., Ронжин В.В., К стабилизации стационарных движений голономных механических систем, //Изв.АН УзССР, Сер.техн.наук, 1983, Вып.1, С.33-36.
46.	Крейн М.Г., Наймарк М.А., Метод симметрических и эрмитовых форм в теории отделения корней алгебраических уравнений, Харьков, 1936.
47.	Летов А.М., Устойчивость нелинейных систем автоматического регулирования, М., Гостехиздат, 1955.
48.	Лурье А.И., Об устойчивости одного класса регулируемых систем, ПММ, Т.XV, вып.5, 1951.; О характере границ области устойчивости регулируемых систем, ПММ, Т.XV, вып.2, 1951.
49.	Лурье А.И., Некоторые нелинейные задачи теории автоматического регулирования, Гостехиздат, 1951.
50.	Лурье А.И., Постников В.Н., К теории устойчивости регулируемых систем, МПП, 8, вып.3, 1944.
51.	Лагранж Ж., Аналитическая механика, Т.1-2, М.-Л., Гостехиздат, 1950; Lagrange J.L., Mecanique analitique. Paris, 1788.
52.	Ляпунов А.М., Общая задача об устойчивости движения, М.: -Гостехиздат,1950.
53.	Малкин И.Г., Теория устойчивости движения, М., Наука, 1966, 530 с.
54.	Малкин И.Г., Проблема существования функций Ляпунова, Изв. Казанского физ. мат. об-ва, Т.IV (1929-1930), Т.V (1931); Об устойчивости движения в смысле Ляпунова, Матем.сб. Т.3, вып.1, 1938.
55.	Малкин И.Г., Об устойчивости при постоянно действующих возмущениях, ПММ, Т.VIII, № 3, 1944.; Об устойчивости систем автоматического регулирования, ПММ, Т.16, вып.4, 1952.
56.	Малкин И.Г., Некоторые задачи теории нелинейных колебаний, М., Гостехиздат, 1956.
57.	Матросов В.М. Об устойчивости движения, ПММ, Т.XXVI, вып.5, 1962.
58.	Максвелл Д.К., О регуляторах, (1868), Сборник «Теория автоматического регулирования», Изд. АН СССР, 1949.
59.	Матросов В.М., К вопросу устойчивости гироскопических систем с диссипацией, Труды Казанского авиац. Института, вып.45, 1959.
60.	Меркин Д.Р., Введение в теорию устойчивости движения, М., Наука, 1971, 312 с.
61.	Меркин Д.Р., Гироскопические системы, М., Гостехиздат, 1956.
62.	Михайлов А.В., Автоматика и телемеханика, Т.3, 1938.; Журнал технической физики, № 6, 1938.
63.	Неймарк Ю.И. Динамические системы и управляемые процессы, М., Наука, 1978, 336 с.
64.	Неймарк Ю.И., Об условиях самовозбуждения и стабилизации, Горький, Ученые зап. ГГУ, вып.28, сер.ф.-м.наук, 1955.
65.	Неймарк Ю.И., Устойчивость линеаризованных систем, Ленинград, Изд. ЛВВКА, 1949.
66.	Неймарк Ю.И., О допустимости линеаризации при исследовании устойчивости, ДАН СССР, Т.127, № 5, 1959.
67.	Неймарк Ю.И., О некоторых общих свойствах функции Ляпунова, Горький, Изв. Вузов Радиофизика, Т.4, вып.2, 1961.
68.	Неймарк Ю.И., Метод точечных отображений в теории нелинейных колебаний.
69.	Неймарк Ю.И, Динамика неголономных систем, В сб. «Механика в СССР за 50 лет», Том 1, Москва, Наука, 1968, 171-178 с.
70.	Неймарк Ю.И, Фуфаев Н.А., К вопросу о путевой устойчивости экипажей на баллонных колесах, ДАН СССР, 1966, Том 170, № 3, С.533-536.
71.	Неймарк Ю.И, Фуфаев Н.А., Динамика неголономных систем, М., Наука, 1967, 519 с.
72.	Неймарк Ю.И., Фуфаев Н.А., Устойчивость состояний равновесия неголономных систем, Прикладная математика и механика, 1965, 29, № 1, 46-53; Об устойчивости состояний равновесия неголономных систем, ДАН СССР, 1965, 160, № 4, С.781-784.
73.	Неймарк Ю.И., Фуфаев Н.А., Об устойчивости стационарных движений голономных и неголономных систем, Прикл.мат.и мех., 1966, 30, № 2, С.236-242.
74.	Николенко И.В., Об устойчивости установившихся движений неголономных систем П.В. Воронца, Прикл.мех., 1968, 4, № 4, С.84-89.
75.	Николаи Е.Л., Теоретическая механика, ч.3., ГОНТИ, 1939.
76.	Обморшев А.Н., Колебания и устойчивость неголономных систем, В сб.: Механика, Москва, 1955, С.75-96; Колебания линейных неголономных систем около состояния установившегося движения, Ивз.АН СССР, Отд.тех.наук, Мех.и машиностроение, 1961, № 5, С.84-89.
77.	Плисс В.А., Некоторые проблемы теории устойчивости движения в целом, Изд. ЛГУ, 1958.
78.	Понтрягин Л.С., Обыкновенные дифференциальные уравнения, М.: -Наука, 1965, 332 с.
79.	Пуанкаре А., О кривых, определяемых дифферен-циальными уравнениями, Москва, Гостехиздат, 1947.
80.	Румянцев В.В., Об устойчивости движения по отношению к части переменных, Вестник МГУ, № 4, 1957.
81.	Румянцев В.В., Об устойчивости стационарных движений спутников, Математические методы в динамике космических аппаратов, вып. 4, Изд. ВЦ АН СССР, 1969.
82.	Румянцев В.В., Карапетян А.В., Устойчивость движений неголономных систем, /Итоги науки и техники, Общая механика, Том 3, вып.7, М., ВИНИТИ, 1977.
83.	Румянцев В.В., Карапетян А.В., Устойчивость консервативных и диссипативных систем /Итоги науки и техники, Общая механика, Том 6,  М., ВИНИТИ, 1983.
84.	Румянцев В.В., Об устойчивости движения неголономных систем, Прикл.мат. и мех., 1967, 31, № 2, С.260-271.
85.	Румянцев В.В., Метод функции Ляпунова в теории устойчивости движения, В сб. «Механика в СССР за 50 лет», Том 1, Москва, Наука, 1968, С. 7-66.
86.	Румянцев В.В., Об асимптотической устойчивости и неустойчивости движения по отношению к части переменных, Прикл.мат и мех., 1971, 35, № 1, С.138-143.
87.	Семенова Л.Н., О теореме Рауса для неголономных систем, Прикл.мат и мех., 1965, 29, № 1, С.156-157.
88.	Султанов Р.М., Некоторые свойства матриц с элементами из некоммутативного кольца, Баку, Труды сектора матем. АН Аз ССР, 2, 1946, С.11-17.
89.	Сумбатов А.С., О линейных интеграллах неголономных систем, Вестник МГУ, Мат., Мех. 1972, № 6, С.77-83.
90.	Тамм И.Е., Основы теории электричества, Изд. 5-е, Гостехиздат, М., 1954.
91.	Тураев Х.Т., Фуфаев Н.А., Мусарский Р.А., Теория движения систем с качением, Ташкент, ФАН, 1987, 158 с.
92.	Тураев Х.Т., Моделирование и исследование динамики колесных транспортных машин с деформируемыми шинами, Ташкент, ФАН, 1995, 168 с.
93.	Тураев Х.Т., Урунбаев Э., Программа «Автоматизация исследования устойчивости движения колесно-транспортных машин», Свидетельство об официальной регистрации программы для ЭВМ, № DGU 00305, ГКНТ РУз, Государственное патентное ведомство, 28.02.2000.
94.	Тураев Х.Т., Урунбаев Э., Программно-инструментальная система «AVTO» для автоматизации исследования устойчивости движения колесных транспортных машин, Доклады Международной конференции «Проблемы управления и информатики», Бишкек, 19-22 сентября, 2000, С.285-290.
95.	Тураев Х.Т., Урунбаев Э., Алгоритм развертывания определителя n-го порядка с полиномиальными элементами, Материалы Международной конференции The third international workshop on computer algebra in scientific computing CASC-2000, Samarkand, Uzbekistan, October 5-9, 2000, C.93-96.
96.	Тураев Х.Т., Урунбаев Э., Алгоритм определения рациональной области устойчивости и рациональных значений конструктивных параметров колесных транспортных машин. International scientific and practical conference «INNOVATION-2000», The scientific articles, Bukhara, September 5-7, 2000, С.296-298.
97.	Урунбаев Э., Программа нахождения рациональной области устойчивости движения и рациональных значений конструктивных параметров динамических систем, Сведетельство об официальной регистрации программы для ЭВМ, № DGU 00475, ГКНТ РУз, Государственное патентное ведомство, 15.11.2001; Программа исследования области устойчивости движения систем с качением. Сведетельство об официальной регистрации программы для ЭВМ, № DGU 00476, ГКНТ РУз, Государственное патентное ведомство, 15.11.2001;                                                                   Программа раскрытия определителя n-го порядка, Сведетельство об официальной регистрации программы для ЭВМ, № DGU 00477, ГКНТ РУз, Государственное патентное ведомство, 15.11.2001.
98.	Хуа Ло-ген, Розенфельд Б.А., Геометрия прямоугольных матриц и ее применения к вещественной проективной и неевклидной геометрии, Изв.высших уч.зав. СССР, Математика, 1, 1957, С.233-246.
99.	Циммерман Г.К., Разложение нормы матрицы по произведениям норм её строк, Научные записки Николаевского Гос.пед.института, №4,1953,130-135 с.
100.	Четаев Н.Г., Об устойчивых траекториях динамики, Ученые записки Казанского гос. Ун-та, кн. 4, Вып.1, 1936.
101.	Четаев Н.Г., Одна теорема о неустойчивости, ДАН СССР, Т.1, № 9, 1934.
102.	Четаев Н.Г., Устойчивость движения, Гостехиздат, 1956; Устойчивость движения. Работы по аналитической механике, М., Изд. АН СССР, 1962.
103.	Четаев Н.Г., К вопросу об обращении теоремы Лагранжа, Сб. научн. Трудов Казанск. Авиационного ин-та, № 2, 1934.
104.	Четаев Н.Г., Об устойчивости вращательных движений снаряда, ПММ, Т.Х, вып.1, 1946.
105.	Чаплыгин С.А., О движении тяжелого тела вращения на горизонтальной плоскости, Тр.отд. физ.наук Обществе любителей естествознания, 1897, 9; Собр.соч., Том 1, М. –Л., Гостехиздат, 1948; Т.4, М. –Л., Гостехиздат, 1949.
106.	Шульгин М.Ф., О некоторых дифференциальных уравнениях аналитической динамики и их интегрировании, Труды САГУ, 1958, 144, С.183.
107.	Appell P., Sur une forme generale des equations de la dynamique, C.r. Acad. Sei., 1899, 129, 423-427; - Перевод: Аппель П., Теоретическая механика, Т.2, Москва, Физматгиз, 1960.
108.	Aiserman M.A., Gantmacher F.R., Stabilität der Gleichgewichtsiage in einem nichtholonomen System., Z. angew. Math. Und Mech., 1957, 37, № ½, 74-75.
109.	Bottema O., On the small vibrations of nonholonomic systems. Proc. Kon. Ned. akad. wet., 1949, 52, № 8, C. 848-850.
110.	Hertz H., Die Prinzipen der Mechanik in neuem Zusammenhange dargestellt. Leipzig, 1894. – Перевод: Герц Г., Принципы механики, изложенные в новой связи, М., Изд. АН СССР, 1959.
111.	Herrman G., Stability of Equilibrium of Elastic Systems Subjected to Nonconservative Forces. Applied Mechanics Reviews, 20, № 2, 1967.
112.	Thomson W., Tait P., Treatise on Natural Philosophy, Т.1, 1879.
113.	Cahen G., Elements de calcul matriciel, Paris, 1955.
114.	Whittaker E.T., Atreatise on the analytical dynamics of particles and rigid bodies. Cambridge, Univ., Press, 1904. – Перевод: Уиттекер Е.Т., Аналитическая динамика, М. –Л., ОНТИ, 1937.
115.	Routh E.J. An elementary treatise on the dynamics of a system of  rigid bodies. Cambridge, 1860.
116.	Routh E.J. The advanced part of a treatise on the dynamics of a system of rigid bodies. London, 1884.
117.	Routh E.J. A treatise on the stability of a given state of motion. London: McMilland and Co., 1877.
118.	Раус Э. Дж. Динамика системы твердых тел: Пер. с англ. Т.1., М.: Наука, 1983, 463 с.
119.	Lejeune-Dirichlet G. Über die Stabilität der Gleichgewichtslagen. J. Reine und angew. Math., 1846, 32, 85-88. Перевод: Лежен Дирихле Г. Об устойчивости равновесия. В кн.: Лагранж Ж. Аналитическая механика. Т.1, М.: Гостехиздат, 1950, С.537-540 (Доп.II).
120	Тураев Х.Т., Урунбаев Э., Математические модели движения  автомобиля в случае больших величин кине-матических параметров шин и теории увода.  ДАН РУз, № 11, ФАН,Ташкент, 1999, 37-40 с.
121	Тураев Х.Т., Урунбаев Э., Математические модели движения  авто-мобиля в случае достаточно больших ско-ростей   движения и гипотезы увода.  ДАН РУз, №9, ФАН, Ташкент, 1999, 28-33 с.
122	Тураев Х.Т., Урунбаев Э., Автоматизация моделирования и  исследования устойчивости движения автомобиля. Материалы Международной научной конференции, посвященной 1200-летию Ахмада ибн Мухаммада ал-Фергани. 28-30 сентября 1998г. Ташкент, ТГТУ, 1999, С.146-150.
123	Тураев Х.Т., Урунбаев Э., Математическая модель движения  автомобиля с учетом упругости  и деформируемости пневматика. Материалы Международной научной конференции, посвященной 1200-летию Ахмада ибн Мухаммада ал-Фергани. 28-30 сентября 1998г. Ташкент, ТГТУ, 1999, С.150-155.
124	Тураев Х.Т., Урунбаев Э., Теория качения деформируемого колеса. Вестник СамГУ, № 1,Самарканд,1999,С.21-29.
125	Тураев Х.Т., О работе Горьковской школы А.А.Андронова по теории устойчивости систем с качением. Тезисы докладов V-Международной конференции “Нелинейные колебания  механических систем”, Нижний Новгород, 13-16 сентября  1999 г.
126	Тураев Х.Т., Математические модели и устойчивость движения автомобиля. Тезисы докладов V- Международной конференции “Нелинейные колебания механических систем”, Нижний Новгород, 13-16 сентября 1999 г.
127	Тураев Х.Т., Урунбаев Э., Программно-инструментальная система «AVTO» для автоматизации исследования устойчивости движения колесных транспортных машин. Доклады Международной конференции «Проблемы управления и информатики», Бишкек, 19-22 сентября, 2000, С.285-290.
128	Тураев Х.Т., Урунбаев Э., К вопросу о влиянии конструктивных параметров на устойчивость прямолинейного движения автомобиля. Материалы Международной научно-технической конференции «Развитие и эффективность автомобильно-дорожного комплекса в Центрально-азиатском регионе», Ташкент, 1-3 ноября, 2000, Часть-1, С.108-114.
130	Тураев Х.Т., Урунбаев Э., Алгоритм определения рациональной области устойчивости и рациональных значений конструктивных параметров колесных транспортных машин. International scientific and practical conference  «INNOVATION-2000», The scientific articles, Bukhara, September 5-7, 2000, С.296-298.
131	Тураев Х.Т., Урунбаев Э., Программа «Автоматизация исследования устойчивости движения колесно-транспортных машин». Свидетельство об официальной регистрации программы для ЭВМ, №DGU 00305, ГКНТ РУз, Государственное патентное ведомство, 28.02.2000.
132	Тураев Х.Т., Урунбаев Э., Уравнения колебаний кузова движущегося четырехколесного экипажа по горизонтальной и наклонной плоскости. ДАН РУз, №4,Ташкент.-ФАН,2002.
133	Тураев Х.Т., Урунбаев Э., Уравнения колебаний кузова экипажа с учётом бокового увода колёс. ДАН РУз, №6, Ташкент.-ФАН. 2002.
134	Б.Атаджанов, А.Красинский, Х.Тураев, Ф. Муродов, Э.Урунбоев, Математическая модель криволинейного движения автомобиля с учетом упругости и деформируемости шин. 1.Кинематика системы. Сборник научн.статей. Междун. научн. конф. ”Инновация-2001.”Ташкент, 2002, С.158-161 .
135	Б.Атаджанов, А.Красинский, Х.Тураев, Э.Ўрунбоев. Динамика автомобиля на балонных колесах. Доклады научной конференции “Современные проблемы алгоритмизации и программирования”, Ташкент, 5-7 сентября, 2001, С.76-80.
136	Б.Атаджанов, А.Красинский, Х.Тураев. Стабилизация установившихся движений механических систем с дифференциальными связями. Доклады научной конференции  «Современные проблемы алгоритмизации и програмирование», Ташкент, 5-7 сентября, 2001, С.80-82.
138	Тураев Х.Т., Урунбаев Э. Янги информацион технологиялар асосида дастурий таъминотнинг хисоблаш тизимини яратиш тамойиллари., Самарканд:- СамДУ илмий тадкикотлар ахборотномаси, 2003, 5-сон.
139	Э.Урунбаев. Амалий дастурий таъминот яратишда янги информацион технологияларни куллаш., Тошкент:-Информатика ва энергетика муаммолари Узбекистон журнали, 2003, 4-сон.
140	Тураев Х.Т., Урунбаев Э. Динамик тизимлар харакатининг математик модели ва тургунлигини тадкик этишни автоматизациялаш. Тошкент:-Информатика ва энергетика муаммолари Узбекистон журнали, 2003, 5-сон.
141	Тураев Х.Т., Урунбаев Э. Механик тизимлар харакатининг математик моделини келтириб чикариш алгоритми. Самарканд:- «Таълим тизимида информацион технологияларни куллашнинг долзарб муаммолари» Халкаро илмий конференция тезислари, 2003й 14-16 октябр.
142	Тураев Х.Т., Урунбаев Э. Механик тизимлар харакатининг тургунлигини тадкик этишнинг алгоритми. Самарканд:- «Таълим тизимида информацион технологияларни куллашнинг долзарб муаммолари» Халкаро илмий конференция тезислари, 2003й 14-16 октябр.
143	Ким И., Муродов Ф. D-булаклаш усулига асосан динамик тизимлар харакатининг тургунлик сохасини аниклаш жараёни. Самарканд:- «Таълим тизимида информацион технологияларни куллашнинг долзарб муаммолари» Халкаро илмий конференция тезислари, 2003й 14-16 октябр.
144	Муродов Ф. Математическая модель прямолинейного движения в случае одинаковых поворота передних колес вокруг оси шкворней с учётом продольной деформации шин. Ташкент:- Тезисиы докладов I-республиканской научной конференции магистрантов, 2003г, 27-29 май, 24-26 с.
145	Красинская Э.М. К стабилизации стационарных движений механических систем. Ташкент:- Прикладная математика и механика. Том 47, вып. 2, 1983г, С. 302-309.

 

Русча – узбекча лугат

 

Автоматическое регулирование	автоматик созлаш
ветвь	буток, шох
Возмущающий	Тойдирувчи (кузгатувчи)
возмущение	тойиш, тойилиш,     тойдириш
возмущенное состояние	тойилган холат
Возмущенный	тойилган, тойдирилган (кузгатилган)
возмущенный системы	Системанинг тойилиши
возникать	хосил булмок
Волчок	Пилдирок
Восстанавливающий	тикловчи, тикламок
Вспомогательный	Ёрдамчи
Выкладка	исботдаги амаллар, хисоблар, хисоблаш
Вынужденный	Мажбурий
Выпуклый	Каварик
Вязкий	Ковушок
Вязкость	Ковушоклик
Грань	Ёк
Делитель	булувчи, булгич
Дополнение	тулдириш, кушимча, тулдирма
Ёмкость	Сигим
затухание	суниш
Изгиб	Эгилиш
изображать	Тасвирламок
Изображение	тасвирлаш, тасвирланиш
Изолированный	яккаланган, ажратилган, ажралган
Исследование	текшириш, урганиш, тадкик, тадкикот
Исследовать	текширмок, урганмок, тадкик килмок
Касательная	Уринма
Касательный	уринувчи, уриниб утган, уринма
Катушка	Галтак
Качание	тебраниш, чайкалиш, тебратиш
Качение	Думалаш
Классификация	классификация, синфларга ажратиш
Кососимметрический	кийшик симметрик
Круг	доира, айлана
Крутизна	тиккалик, тиклик
Момент	момент, он, лахза, пайт
наибольший общий делитель	энг катта умумий булувчи
Накладывать	устма-уст куймок
Накладываться	Куйилмок
Наклон	огмалик, огиш, нишаблик, кия
Напряжение	Кучланиш
Образец	намуна, нусха
Обход	атрофлаб айланиш, айланиб чикиш, айланиб утиш
Обычно	Одатда
Ограничение	чек куймок
Однородный	бир жинсли, турдош
Описание	тавсифлаш, таърифлаш
описание математическое	математик тасвир, мат.модель
Описать	тасвирламок, тавсифламок
Опора	Таянч
Особенность	узига хос хусусият, хослик
Особый	мухим, алохида, махсус, айрим
Отклонение	четга чикиш, четланиш, четлашиш, огиш
Отнесение	оид килиш, оидлик
Отнесенные	оид килинган, оид
Отображение	аксланиш, акслатиш
Отсчёт	санок, хисоб, санаш, хисоблаш, санок боши
Очевидный	ойдин, куриниб турган, равшан, аник, аён
Перемещение	силжиш, сурилиш, кучиш
Плоский	Ясси
поверхности уровня	паст-баландлик сирти
Поверхность	Сирт
Подход	Ёндашиш
положение (состояние)	вазият, хол - ахвол, холат
Поправочный	тузатувчи, тугриловчи
Последовательно	кетма-кет
Предел	лимит, чек, чегара
Преобразование	алмаштириш, узгартириш
Преобразованный	алмаштирилган, узгартирилган, келтирилган
Приближение	Якинлашиш
Признак	аломат, белги
Прилегать	ёнида булмок, чегарадош булмок, ёнма-ён, ёндош жойлашмок
Прилегающий	ёндош булган, ёндош, ёнма-ён туташган
Приращение	Орттирма
Продукт	Махсулот
Пространство	Фазо
Равномерно	текис, бир маромда, бир текис
разностное диф.уравнение	айирмали диф.тенглама
Разностный	айирмали
Рассеивание	сочилиш, таркалиш
Ребро	Кирра
Регулирование	ростлаш, тартибга олиш
Регулировка	Ростлаш
Регулируемый	созланадиган, ростланадиган
Регулярно	мунтазам, доимий равишда
Регулярность	Мунтазамлик
Регулятор	Ростлагич
Связанность	богланганлик, богликлик
Связанный	богланган, боглик
Связка	богланиш, богланма
Сетка	тур
Сечение	Кесим
Следящий	Кузатувчи
Содержать	камрамок, уз ичига олмок
Соприкасание	уриниш, эгилиш
Соприкосновение	уриниш, тегиш, ёпишиш
Стабилизация	стабилизация, стабилизациялаш, стабилизацияланиш, баркарорланиш
Строгий	Катъий
Структура	структура, тузилиши
Существенный	катъий, мухим, жиддий
Сущность	мохият
Трактовать	изохламок, талкин килмок
Усиление	кучайтиш, кучайтириш
Усилитель	кучайтиргик, кучайгич
ускорять, ускорить	тезлатмок, тезлаштирмок
Условия	шарт
Установившийся	карор топган, баркарор, стационар, урнашган
Устойчивость	тургунлик, баркарорлик
Участок	кисм, булак, парча
Чётность	Жуфтлик
Явно	ошкор равишда, очикдан – очик