VII-БОБ. ХАРАКАТ ТУРГУНЛИГИГА КУЧЛАР ТАРКИБИНИНГ ТАЪСИРИ
1-§. Математик таркибига караб кучларни синфларга
ажратиш [60]
К¢п холларда тизимга таъсир этаётган кучларнинг таркибига караб унинг тургун ёки нотургун эканлигини аниклаш мумкин. Шунинг учун хам кучларнинг математик таркибига караб уларни синфларга ажратишни берамиз.
![]() ва
ва
![]() микдорларга
нисбатан харакатнинг тургунлигини тадкик этиш тойилган харакатнинг ушбу
микдорларга
нисбатан харакатнинг тургунлигини тадкик этиш тойилган харакатнинг ушбу
![]() (7.1.1)
(7.1.1)
матрицавий
дифференциал тенгламани тахлил килишга келтирилади деб хисоблаймиз. Бу ерда ![]() -
-
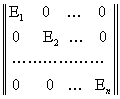
![]() элементлари
б¢лган устун-матрица;
элементлари
б¢лган устун-матрица; ![]() - ¢згармас
коэффициентли
- ¢згармас
коэффициентли ![]() тартибли берилган
квадрат матрицалар;
тартибли берилган
квадрат матрицалар; ![]() -
- ![]() элементли,
элементли,
![]() ва
ва ![]() ларни
камида иккинчи даражада ¢з ичига олган хамда барча
ларни
камида иккинчи даражада ¢з ичига олган хамда барча ![]() б¢лганда
нолга айланувчи устун-матрица. Бундан ташкари
б¢лганда
нолга айланувчи устун-матрица. Бундан ташкари ![]() симметрик матрица
симметрик матрица ![]() ва
ва
![]() (7.1.2)
(7.1.2)
аник-мусбат ишорали функция, чунки
 (7.1.3)
(7.1.3)
(7.1.1)
тенгламага бирор моддий тизимни мос килиб к¢йиш мумкин. У вактда ![]() лар
тизимнинг координаталари,
лар
тизимнинг координаталари, ![]() лар тезликлари
ва (7.1.2) квадратик
лар тезликлари
ва (7.1.2) квадратик
форма
унинг кинетик энергияси б¢лади. К¢п холларда бу квадратик форма хакикатан
хам реал тизимнинг кинетик энергияси б¢лади, аммо айрим холларда ![]() харакат
тенгламаларини ¢згартириш натижасида хам хосил б¢лиши мумкин (Раус
тенгламаларида ¢згартириш киритганимизда хосил б¢лган эди:
харакат
тенгламаларини ¢згартириш натижасида хам хосил б¢лиши мумкин (Раус
тенгламаларида ¢згартириш киритганимизда хосил б¢лган эди: ![]() ,
бу ерда
,
бу ерда ![]() -квадратик форма).
-квадратик форма).
(7.1.1)
тенгламанинг ![]() ва
ва ![]() устун
– матрицаларини (мос ишора билан олганда) кучлар сифатида талкин килиш мумкин.
Улар айрим холларда реал кучларни ифодалайди ва айрим холларда тойилган харакат
тенгламаларини келтириб чикаришда хосил б¢ладиган хадларни ифодалайди.
устун
– матрицаларини (мос ишора билан олганда) кучлар сифатида талкин килиш мумкин.
Улар айрим холларда реал кучларни ифодалайди ва айрим холларда тойилган харакат
тенгламаларини келтириб чикаришда хосил б¢ладиган хадларни ифодалайди.
Келгусида
соддалик учун (7.1.2) квадратик форма кинетик энергия деб аталади, ![]() ва
ва
![]() матрицалар –
тизимга таъсир этаётган кучлар,
матрицалар –
тизимга таъсир этаётган кучлар, ![]() ларни
¢згарувчилар ва уларнинг вакт б¢йича олинган
ларни
¢згарувчилар ва уларнинг вакт б¢йича олинган ![]() хосилаларини
эса тезликлар деб айтамиз.
хосилаларини
эса тезликлар деб айтамиз.
![]() ва
ва
![]() матрицаларни
симметрик ва кийшик симметрик матрицаларга ажратамиз:
матрицаларни
симметрик ва кийшик симметрик матрицаларга ажратамиз:
![]() ,
, ![]() ,
(7.1.4)
,
(7.1.4)
бу ерда В ва С симметрик матрицалар хамда G ва P кийшик симметрик матрицалар куйидагича аникланади
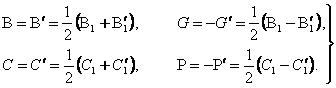 (7.1.5)
(7.1.5)
(7.1.4) ифодаларни (7.1.1) тенгламага к¢йсак
![]() (7.1.6)
(7.1.6)
ни хосил киламиз.
![]() симметрик
матрицали
симметрик
матрицали ![]() куч потенциал ёки
консерватив куч,
куч потенциал ёки
консерватив куч,
![]() (7.1.7)
(7.1.7)
квадратик форма эса тизимнинг потенциал энергияси деб аталади.
![]() кучлар
реал огирлик, эластиклик кучлар потенциалининг чизикли кисмини (ночизикли
потенциал кучлар кисми
кучлар
реал огирлик, эластиклик кучлар потенциалининг чизикли кисмини (ночизикли
потенциал кучлар кисми ![]() матрица ифодасига
киради) ифодалайди.
матрица ифодасига
киради) ифодалайди.
![]() симметрик матрица ёрдамида
симметрик матрица ёрдамида
![]() (7.1.8)
(7.1.8)
квадратик
формани тузамиз. У манфий б¢лмаган холда таркалиш (сочилиш) функцияси ёки
Релейнинг диссипатив функцияси деб, уз навбатида бу функцияга мос ![]() кучларга
диссипатив кучлар деб аталади.
кучларга
диссипатив кучлар деб аталади.
Агар F квадратик форма мусбат б¢лишдан ташкари яна аник-мусбат ишорали хам б¢лса, у холда диссипация т¢лик, акс холда эса т¢лик эмас деб айтилади.
Агар
F функция манфий кийматлар хам кабул килса, бу ![]() матрицага
кирувчи кучлар орасида тезлатувчи кучлар мавжудлигини билдиради. Одатда
диссипатив кучлар, жисмларнинг табиий равишда каршилик к¢рсатадиган мухитида
харакат килганида, омик каршилиги бор электр занжирларида ва х.к. холларда хосил
б¢лади. Коида б¢йича тезлатувчи кучлар махсус курилмалар оркали хосил
килинади.
матрицага
кирувчи кучлар орасида тезлатувчи кучлар мавжудлигини билдиради. Одатда
диссипатив кучлар, жисмларнинг табиий равишда каршилик к¢рсатадиган мухитида
харакат килганида, омик каршилиги бор электр занжирларида ва х.к. холларда хосил
б¢лади. Коида б¢йича тезлатувчи кучлар махсус курилмалар оркали хосил
килинади.
![]() тезликларга
чизикли богланган ва
тезликларга
чизикли богланган ва ![]() кийшик симметрик
матрицаси бор
кийшик симметрик
матрицаси бор ![]() кучлар гироскопик
кучлар деб аталади. К¢пинча бу кучлар гироскопи бор тизимларда ва бошка,
масалан, автомобил, самолёт, биологик популяция, ¢згармас магнит майдонида
электроннинг харакати каби тизимларда хам мавжуд б¢лиши мумкин.
кучлар гироскопик
кучлар деб аталади. К¢пинча бу кучлар гироскопи бор тизимларда ва бошка,
масалан, автомобил, самолёт, биологик популяция, ¢згармас магнит майдонида
электроннинг харакати каби тизимларда хам мавжуд б¢лиши мумкин.
![]() координата
чизикли богланган ва
координата
чизикли богланган ва ![]() кийшик симметрик
матрицаси бор
кийшик симметрик
матрицаси бор ![]() кучларнинг баркарор
аник номи йук.
кучларнинг баркарор
аник номи йук.
Г.Циглер уларни циркуляцион кучлар деб атади, гироскопик тизимлар назариясида уларни радиал коррекция кучлари деб, к¢пинча эса уларни яна ноконсерватив кучлар, псевдогироскопик кучлар деб хам атайдилар. Бизлар бундан кейин уларни (бу термин унча т¢гри эмаслигини билган холда) ноконсерватив (консерватив эмас) кучлар деб атаймиз. Ноконсерватив кучлар табиий равишда мавжуд б¢лиши ва махсус курилмалар оркали хосил этилиши мумкин.
![]() кучларни
ночизикли кучлар деб атаймиз. Бу кучлар ёйилмасида
кучларни
ночизикли кучлар деб атаймиз. Бу кучлар ёйилмасида ![]() ва
ва ![]() лар
камида иккинчи даражада катнашади хамда
лар
камида иккинчи даражада катнашади хамда ![]() ва
ва ![]() б¢лганда
бу ёйилма нолга тенг б¢лади.
б¢лганда
бу ёйилма нолга тенг б¢лади.
Мисол. Тойилган харакатнинг тенгламаси
![]()
к¢ринишда
берилган б¢лсин. Бу тенгламаларда ![]() матрицалар мос
равишда
матрицалар мос
равишда
![]()
каби аникланади. Тизимнинг кинетик энергиясини тузамиз:
![]() .
.
Т
квадратик форма учун Сильвестр критерияси бажарилади: ![]() ,
, ![]() .
Демак, у аник – мусбат ишорали.
.
Демак, у аник – мусбат ишорали.
![]() ва
ва
![]() матрицаларнинг
сатр ва устунларини мос равишда жойларини алмаштириб, уларнинг транспонирланган
матрицаларнинг
сатр ва устунларини мос равишда жойларини алмаштириб, уларнинг транспонирланган
![]() ва
ва ![]() матрицаларини
топамиз:
матрицаларини
топамиз:
![]() .
.
![]() ва
ва
![]() матрицаларни
симметрик ва кийшик симметрик матрицаларга ажратамиз:
матрицаларни
симметрик ва кийшик симметрик матрицаларга ажратамиз:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Энди Релей функцияси F ва потенциал энергия П топамиз:

Релей
функцияси (F) хам мусбат киймат (масалан, ![]() ва
ва ![]() б¢лганда),
хам манфий киймат кабул килиши мумкин (масалан,
б¢лганда),
хам манфий киймат кабул килиши мумкин (масалан, ![]() ва
ва ![]() б¢лганда).
Шунинг учун хам
б¢лганда).
Шунинг учун хам ![]() кучлар орасида хам
диссипатив, хам тезлатувчи кучлар мавжуд. Гироскопик (
кучлар орасида хам
диссипатив, хам тезлатувчи кучлар мавжуд. Гироскопик (![]() ),
потенциал (
),
потенциал (![]() ) ва ноконсерватив
(
) ва ноконсерватив
(![]() ) кучларнинг
матрицалари мос равишда куйидагича б¢лади:
) кучларнинг
матрицалари мос равишда куйидагича б¢лади:
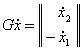 ,
, 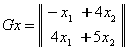 ,
,
 .
.
![]() ,
,
![]() тойилмаган харакатнинг
тургунлигини тадкик этишдан олдин
тойилмаган харакатнинг
тургунлигини тадкик этишдан олдин
![]()
формула
оркали янги ![]() ¢згарувчиларга
¢тамиз, бу ерда
¢згарувчиларга
¢тамиз, бу ерда ![]() -матрица. Бу формулани
(7.1.6) тенгламага к¢йиб, куйидагини хосил киламиз
-матрица. Бу формулани
(7.1.6) тенгламага к¢йиб, куйидагини хосил киламиз
![]() .
.
Бу
тенгламанинг икки томонини чапдан ![]() матрицанинг
транспонирланган
матрицанинг
транспонирланган ![]() матрицасига
к¢пайтирамиз
матрицасига
к¢пайтирамиз
![]() , (7.1.9)
, (7.1.9)
бу
ерда ![]() - устун-матрица ва
унинг элементларининг ифодасига
- устун-матрица ва
унинг элементларининг ифодасига ![]() ва
ва ![]() ларнинг
биринчидан юкори даражалари киради.
ларнинг
биринчидан юкори даражалари киради.
Эслатиб ¢тамизки, А ва С матрицалар симметрик, бундан ташкари А-аник-мусбат ишорали. Чизикли алгебрадан куйидаги теорема маълум:
Агар
![]() тартибли А ва С
матрицалар симметрик ва А матрица аник-мусбат ишорали б¢лса, у вактда:
тартибли А ва С
матрицалар симметрик ва А матрица аник-мусбат ишорали б¢лса, у вактда:
1) ![]() (7.1.10)
(7.1.10)
характеристик тенгламанинг барча илдизлари хакикий;
2)
Доимо шундай хосмас ![]() матрица
топиладики,
матрица
топиладики,
![]() ,
, ![]() (7.1.11)
(7.1.11)
б¢лади, бу ерда Е – бирлик матрица ва
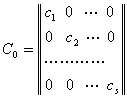 (7.1.12)
(7.1.12)
диагонал
матрица, бунда ![]() лар мос равишда
(7.1.10) тенгламанинг илдизларига тенг.
лар мос равишда
(7.1.10) тенгламанинг илдизларига тенг.
Теореманинг 2) кисмидан куйидаги келиб чикади: агар иккита квадратик форма
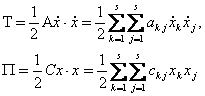
берилган ва бунда Т аник-мусбат ишорали б¢лса, у вактда доимо шундай
![]()
алмаштириш
топиладики (![]() - хосмас матрица),
янги ¢згарувчиларда Т ва П ларнинг ифодалари
- хосмас матрица),
янги ¢згарувчиларда Т ва П ларнинг ифодалари
![]() , (7.1.13)
, (7.1.13)
![]() (7.1.14)
(7.1.14)
к¢ринишни олади.
![]() хосмас
матрица б¢лсин. У вактда А ва С матрицалар симметрик ва А-аник-мусбат
ишорали эканлиги учун, теоремага асосан, (7.1.11) муносабатлар бажарилади.
хосмас
матрица б¢лсин. У вактда А ва С матрицалар симметрик ва А-аник-мусбат
ишорали эканлиги учун, теоремага асосан, (7.1.11) муносабатлар бажарилади.
Бу
ерда ![]() матрица симметрик,
матрица симметрик,
![]() ва
ва ![]() матрицалар
эса кийшик симметрик б¢ладилар.
матрицалар
эса кийшик симметрик б¢ладилар.
Хакикатан хам матрицалар назариясидаги
![]() (7.1.15)
(7.1.15)
формулаларга асосан
![]()
![]()
ёки
В симметрик матрица б¢лганлиги учун ![]() ва
ва
![]() .
.
Демак,
![]() симметрик матрица
б¢лади.
симметрик матрица
б¢лади.
Агар симметрик В матрица ¢рнига кийшик симметрик G (ёки Р) олсак, у вактда
![]()
ёки
G нинг кийшик симметрик матрица эканлигини ва улар учун
![]() тенглик мавжудлигини
хисобга олиб,
тенглик мавжудлигини
хисобга олиб,
![]()
ни
хосил киламиз. Демак, ![]() хам кийшик
симметрик матрица б¢лади. Худди шундай
хам кийшик
симметрик матрица б¢лади. Худди шундай ![]() хам кийшик симметрик
матрица эканлигини исботлаш мумкин.
хам кийшик симметрик
матрица эканлигини исботлаш мумкин.
Келтирилган
мулохазаларни ва ![]() ни хисобга олиб,
(7.1.9) тенгламани куйидаги к¢ринишда ёзиш мумкин:
ни хисобга олиб,
(7.1.9) тенгламани куйидаги к¢ринишда ёзиш мумкин:
![]() ,
(7.1.16)
,
(7.1.16)
бу
ерда ёзувни соддалаштириш учун ![]() ,
, ![]() ва
ва
![]() матрицалар мос
равишда дастлабки
матрицалар мос
равишда дастлабки ![]() харфлар билан белгиланган.
харфлар билан белгиланган.
Агар юкорида келтирилган теоремани А ва В ёки В ва С (С-т¢лик диссипацияга эга деб хисоблаб) матрицаларга к¢лласак, у вактда яна (7.1.9) тенгламанинг иккита янги формасини ёзиш мумкин:
![]() ,
(7.1.17)
,
(7.1.17)
![]() ,
(7.1.18)
,
(7.1.18)
бу
ерда ![]() ва
ва ![]() -
хакикий элементли диагонал матрицалар
-
хакикий элементли диагонал матрицалар
 ,
, 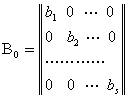 .
.
Шундай
килиб, ![]() алмаштириш ёрдами
билан (7.1.6) тенгламани учта (7.1.16), (7.1.17) ва (7.1.18) к¢ринишдаги хакикий
формаларнинг бирортасига келтириш мумкин. Бу алмаштиришда потенциал, диссипатив,
гироскопик ва ноконсерватив кучлар яна ¢ша таркибда (структурада) ги
кучларга айланадилар. Аникки,
алмаштириш ёрдами
билан (7.1.6) тенгламани учта (7.1.16), (7.1.17) ва (7.1.18) к¢ринишдаги хакикий
формаларнинг бирортасига келтириш мумкин. Бу алмаштиришда потенциал, диссипатив,
гироскопик ва ноконсерватив кучлар яна ¢ша таркибда (структурада) ги
кучларга айланадилар. Аникки, ![]() ва
ва ![]() ларга
нисбатан тургунликдан (нотургунликдан)
ларга
нисбатан тургунликдан (нотургунликдан) ![]() ва
ва ![]() ларга
нисбатан тургунлик (нотургунлик) келиб чикади. Шунинг учун хам бизларни (7.1.6)
тенгламани (7.1.16), (7.1.17) ва (7.1.18) тенгламаларнинг бирортасига
келтирадиган
ларга
нисбатан тургунлик (нотургунлик) келиб чикади. Шунинг учун хам бизларни (7.1.6)
тенгламани (7.1.16), (7.1.17) ва (7.1.18) тенгламаларнинг бирортасига
келтирадиган ![]() алмаштиришнинг
¢зи кизиктирмайди. Бизга шундай алмаштиришнинг мавжудлигини билиш кифоядир.
алмаштиришнинг
¢зи кизиктирмайди. Бизга шундай алмаштиришнинг мавжудлигини билиш кифоядир.
Дастлабки
В ва С матрицалар билан улардан хосил килинган ![]() ва
ва ![]() матрицалар
¢ртасида
матрицалар
¢ртасида
![]() ,
, ![]() (7.1.19)
(7.1.19)
муносабатлар
мавжуд, бу ерда ![]() - алмаштириш
матрицасининг детерминанти. Хакикатан хам,
- алмаштириш
матрицасининг детерминанти. Хакикатан хам, ![]() формулани (7.1.11)
формулаларнинг иккинчисига к¢ллаб,
формулани (7.1.11)
формулаларнинг иккинчисига к¢ллаб,
![]()
ни
хосил киламиз. Иккинчидан, ![]() эканлигини хисобга
олиб, бу муносабатдан
эканлигини хисобга
олиб, бу муносабатдан
![]()
ни
хосил киламиз, бу ерда ![]() . Бу ерда С0
диагонал матрица, шунинг учун
. Бу ерда С0
диагонал матрица, шунинг учун
![]() ,
,
демак,
![]() .
(7.1.20)
.
(7.1.20)
Худди шундай (7.1.19) формулаларнинг биринчисини хам исботлаш мумкин.
Тезлатувчи
куч б¢лмаса В матрицанинг ![]() элементлари
орасида манфийлари й¢к ва т¢лик диссипация холатида барча
элементлари
орасида манфийлари й¢к ва т¢лик диссипация холатида барча ![]() лар
мусбат б¢лади. Агар тезлатувчи кучлар мавжуд булса, у холда
лар
мусбат б¢лади. Агар тезлатувчи кучлар мавжуд булса, у холда ![]() элементлар
орасида манфийлари хам б¢лади. П потенциал энергиянинг минимумида барча
элементлар
орасида манфийлари хам б¢лади. П потенциал энергиянинг минимумида барча ![]() коэффициентлар
мусбат, максимумида эса манфий б¢лади.
коэффициентлар
мусбат, максимумида эса манфий б¢лади.
2-§. Факат потенципал кучлар таъсири остидаги тизим харакатининг тургунлиги. Тургунлик коэффициентлари
Каралаётган
тизимга факатгина ![]() потенциал кучлар таъсир
этаётган б¢лсин ва колган барча кучларга нисбатан, улар йук, яъни
потенциал кучлар таъсир
этаётган б¢лсин ва колган барча кучларга нисбатан, улар йук, яъни ![]() деб
фараз киламиз. У холда (7.1.16) фойдаланиб, тойилган харакат тенгламасини куйидаги
к¢ринишда ёзиш мумкин:
деб
фараз киламиз. У холда (7.1.16) фойдаланиб, тойилган харакат тенгламасини куйидаги
к¢ринишда ёзиш мумкин:
![]() .
(7.2.1)
.
(7.2.1)
![]() диагонал
матрица эканлигини хисобга олиб, (7.7.1) матрицали-тенгламани скаляр тенгламалар
к¢ринишида ёзиш мумкин:
диагонал
матрица эканлигини хисобга олиб, (7.7.1) матрицали-тенгламани скаляр тенгламалар
к¢ринишида ёзиш мумкин:
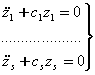 (7.2.2)
(7.2.2)
Бу
ерда ![]() ларга нормал
координаталар деб айтилади. (7.2.2) тенгламалар бир-бири билан богланмаган
ва хар бири алохида интегралланади:
ларга нормал
координаталар деб айтилади. (7.2.2) тенгламалар бир-бири билан богланмаган
ва хар бири алохида интегралланади:
 (7.2.3)
(7.2.3)
бу
ерда ![]() ва
ва ![]() -
¢згармас сонлар. Равшанки, биринчи холда
-
¢згармас сонлар. Равшанки, биринчи холда ![]() , иккинчи холда эса
, иккинчи холда эса
![]() характеристик
сонлардир.
характеристик
сонлардир.
(7.2.3)
дан к¢риниб турибдики, агар барча ![]() б¢лса,
б¢лса, ![]() ва
ва
![]() тойилмаган харакат
тойилмаган харакат
![]() координата ва
координата ва ![]() тезликларга
нисбатан тургун б¢лади (демак,
тезликларга
нисбатан тургун б¢лади (демак, ![]() ва
ва ![]() ларга
нисбатан хам). Хар бир
ларга
нисбатан хам). Хар бир ![]() га (агар у мавжуд
б¢лса) нотургун
га (агар у мавжуд
б¢лса) нотургун ![]() координата т¢гри
келади ва, демак,
координата т¢гри
келади ва, демак, ![]() б¢лганда,
тойилмаган харакат нотургун б¢лади (чунки
б¢лганда,
тойилмаган харакат нотургун б¢лади (чунки ![]() б¢лса,
б¢лса, ![]() характеристик
сонларнинг бири мусбат). У вактда
характеристик
сонларнинг бири мусбат). У вактда ![]() ночизикли
функцияларнинг кандай б¢лишидан катъий назар тойилмаган харакат нотургун
б¢лади (Ляпуновнинг теорема В га асосан). Шунинг учун хам
ночизикли
функцияларнинг кандай б¢лишидан катъий назар тойилмаган харакат нотургун
б¢лади (Ляпуновнинг теорема В га асосан). Шунинг учун хам ![]() сонлар
тизимнинг тургунлик коэффициентлари ва манфий ишорали
сонлар
тизимнинг тургунлик коэффициентлари ва манфий ишорали ![]() лар
сонига тургунлик даражаси деб айтилади. Бу таърифлар француз олими
Пуанкаре томонидан берилган.
лар
сонига тургунлик даражаси деб айтилади. Бу таърифлар француз олими
Пуанкаре томонидан берилган.
Келгусида
бизни факат ![]() нотургун
коэффициентлар сонининг, улар жуфт ёки токлигигина кизиктиради.
нотургун
коэффициентлар сонининг, улар жуфт ёки токлигигина кизиктиради.
(7.1.19) формулаларнинг
![]() (7.2.4)
(7.2.4)
иккинчисидан
фойдаланиб, тизим тургунлик даражасининг жуфтлигини аниклаш мумкин. Бу ерда
нормал координаталарга ¢тишнинг хожати й¢к. Хакикатан хам, агар
манфий коэффициентлар ![]() сони жуфт
б¢лса, у вактда
сони жуфт
б¢лса, у вактда ![]() к¢пайтманинг
ишораси мусбат б¢лади (
к¢пайтманинг
ишораси мусбат б¢лади (![]() коэффициентлар
орасида нолга тенглари й¢к деб фараз киламиз) ва (7.2.4) тенгликдан
коэффициентлар
орасида нолга тенглари й¢к деб фараз киламиз) ва (7.2.4) тенгликдан ![]() эканлиги
келиб чикади. Агар манфий ишорали
эканлиги
келиб чикади. Агар манфий ишорали ![]() коэффициентлар
сони ток б¢лса, у холда
коэффициентлар
сони ток б¢лса, у холда ![]() к¢пайтманинг
ишораси «ток» б¢лади, ва, демак,
к¢пайтманинг
ишораси «ток» б¢лади, ва, демак, ![]() . Шундай килиб,
оддий коидани хосил киламиз: дастлабки тойилган харакат дифференциал
тенгламаларида потенциал кучлари матрицаси С нинг детерминанти мусбат
б¢лса, тизим нотургунлик даражаси жуфт,
. Шундай килиб,
оддий коидани хосил киламиз: дастлабки тойилган харакат дифференциал
тенгламаларида потенциал кучлари матрицаси С нинг детерминанти мусбат
б¢лса, тизим нотургунлик даражаси жуфт, ![]() б¢лганда эса,
ток б¢лади.
б¢лганда эса,
ток б¢лади.
Бу коидани иккита мисолга татбик этиб к¢рамиз.
1-мисол. Тойилган харакат тенгламаси
![]() (7.2.5)
(7.2.5)
к¢ринишда б¢лсин. Координатага чизикли богланган кучларнинг матрицаси
![]()
симметрик б¢лганлиги учун (7.7.5) тизим потенциал тизим б¢лади. Бу матрицанинг детерминанти
![]()
манфий. Шунинг учун тенгламаларни нормал к¢ринишга келтирмасдан тизим ток даражали нотургунликка эга деб айтиш мумкин. Координаталар сони иккита б¢лганлиги учун битта тургун ва битта нотургун координата мавжуд б¢лади.
2-мисол. Тойилган харакат тенгламаси
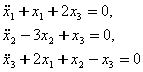 (7.2.6)
(7.2.6)
к¢ринишда берилган б¢лсин. Бу тизим учун потенциал кучлар матрицаси
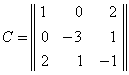
симметрик. Шунинг учун (7.7.6) потенциал тизимдир. Бу матрицанинг детерминанти
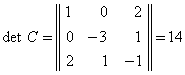
мусбат. (7.7.6) тенгламалар системасини нормал холга келтирмасдан тасдиклаш мумкинки, агар тизим нотургун координаталарга эга б¢лса, у вактда уларнинг сони жуфт б¢лади. С матрицанинг бош диагонал минорлари учун
![]()
Бу ерда Сильвестер детерминантларидан (потенциал энергия квадратик форма эканлигини эсланг) бири манфий б¢лганлиги учун координаталар орасида нотургунлари мавжуд б¢лади. Унинг сони жуфт б¢лиши керак, барча координаталар сони эса учта. Шунинг учун хам тизим битта тургун ва иккита нотургун координатага эга.
3-§. Потенциал тизим харакатининг тургунлигига
диссипатив ва гироскопик кучларнинг таъсири
Реал шароитларда потенциал тизимга диссипатив кучлар таъсир килади. Бу кучлар каршилик мухити хисобидан ёки махсус ¢рнатилган курилмалар оркали таъсир курсатади.
Бундан ташкари шундай тизимлар хам мавжудки, уларга потенциал ва диссипатив кучлардан ташкари гироскопик кучлар хам таъсир этади.
Дастлаб
факат потенциал кучлар таъсири остидаги ![]() ва
ва ![]() тойилмаган
харакат нотургун деб фараз киламиз. Шундай савол тугилади: потенциал кучларга
гироскопик кучларни к¢шиб харакатни стабиллаштириш (баркарорлаш) мумкинми?
Оддий мисоллар к¢рсатадики, айрим холларда буни амалга ошириш мумкин. Хакикатан
хам,
тойилмаган
харакат нотургун деб фараз киламиз. Шундай савол тугилади: потенциал кучларга
гироскопик кучларни к¢шиб харакатни стабиллаштириш (баркарорлаш) мумкинми?
Оддий мисоллар к¢рсатадики, айрим холларда буни амалга ошириш мумкин. Хакикатан
хам,
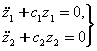 (7.3.1)
(7.3.1)
потенциал
тизим ![]() ва
ва ![]() б¢лганда
нотургундир. Тизимга, мос равишда
б¢лганда
нотургундир. Тизимга, мос равишда ![]() ва
ва ![]() гироскопик
кучларни к¢шиб,
гироскопик
кучларни к¢шиб,
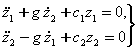 (7.3.2)
(7.3.2)
ни хосил киламиз. (7.3.2) система тизимнинг ечимини
![]()
к¢ринишида излаймиз. Унинг характеристик тенгламаси
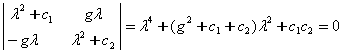
к¢ринишда
б¢лади. Бу тенгламада ![]() факат жуфт даражалари
билан катнашаётганлиги учун хар бир
факат жуфт даражалари
билан катнашаётганлиги учун хар бир ![]() илдизга
илдизга ![]() илдиз
жавоб беради. Шунинг учун агар хеч б¢лмаганда бирорта илдизнинг хакикий кисми
нолга тенг б¢лмаса, у вактда хакикий кисми мусбат б¢лган илдиз
топилади. Бундан шу келиб чикадики, характеристик тенгламанинг барча илдизлари
соф мавхум ва
илдиз
жавоб беради. Шунинг учун агар хеч б¢лмаганда бирорта илдизнинг хакикий кисми
нолга тенг б¢лмаса, у вактда хакикий кисми мусбат б¢лган илдиз
топилади. Бундан шу келиб чикадики, характеристик тенгламанинг барча илдизлари
соф мавхум ва ![]() нисбатан илдизлар
– манфий хакикий сонлар б¢лгандагина тизим тургун б¢лади. Бунинг
учун уз навбатида характеристик тенгламанинг коэффициентлари
нисбатан илдизлар
– манфий хакикий сонлар б¢лгандагина тизим тургун б¢лади. Бунинг
учун уз навбатида характеристик тенгламанинг коэффициентлари
![]()
![]()
![]()
шартларни
баражиши зарур ва етарли. Бу учта тенгсизликни (фаразга асосан ![]() ва
ва
![]() ) битта
) битта
![]() (7.3.3)
(7.3.3)
шартга келтириш мумкин.
Шундай
килиб, агар ![]() коэффициент
(7.3.3) шартни каноатлантирса, у вактда нотургун (7.3.1) потенциал тизим
коэффициент
(7.3.3) шартни каноатлантирса, у вактда нотургун (7.3.1) потенциал тизим ![]() ва
ва
![]() гироскопик
кучларни к¢шиш натижасида стабиллашади (баркарорлашади).
гироскопик
кучларни к¢шиш натижасида стабиллашади (баркарорлашади).
Табиийки, иккинчи савол хам уринли: хар доим гироскопик кучларни к¢шиш усули билан нотургун потенциал тизимни стабиллаштириш (баркарорлаштириш) мумкинми? Гироскопик стабиллаштиришнинг зарурий шартларидан бирини куйидаги Томсон ва Тет теоремаси беради. Томсон ва Тет ¢з теоремаларини 1879 йили исбот килганлар [112]. Етарли шартлар [60,102] ишларда ишлаб чикилган.
Теорема (Томсон ва Тетларнинг биринчи теоремаси). Агар потенциал тизим тойилмаган харакатининг нотургунлиги ток даражали б¢лса, у вактда харакатни хеч кандай гироскопик кучлар билан стабиллаштириш (баркарорлаштириш) мумкин эмас.
Исбот. Потенциал тизим
![]() (7.3.4)
(7.3.4)
нотургунлиги
ток даражада б¢лсин. Тизимга ихтиёрий ![]() гироскопик кучларни к¢шиб,
гироскопик кучларни к¢шиб,
![]() (7.3.5)
(7.3.5)
тизимни
хосил киламиз . ![]() - диагонал ва
- диагонал ва ![]() кийшик
симметрик матрицалар эканлигини хисобга олиб, характеристик тенгламани тузамиз:
кийшик
симметрик матрицалар эканлигини хисобга олиб, характеристик тенгламани тузамиз:
![]()
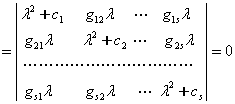 .
.
Детерминантни
ёйиб, ![]() даражаси б¢йича хадларни гурухлаганимиздан кейин
даражаси б¢йича хадларни гурухлаганимиздан кейин
![]()
характеристик
тенгламага эга б¢ламиз. Бу тенгламанинг озод хади (уни топиш учун детерминантга
![]() к¢йиш
кифоя)
к¢йиш
кифоя)
![]()
каби топилади. Теореманинг шартига асосан манфий
ишорали ![]() коэффициентларнинг
сони ток, шунинг учун хам
коэффициентларнинг
сони ток, шунинг учун хам ![]() (
(![]() деб фараз килинади). Бундан ¢з навбатида, характеристик тенглама
илдизларидан хеч б¢лмаганда биттасининг хакикий кисми мусбат б¢лиши
келиб чикади. Гироскопик кучларнинг
деб фараз килинади). Бундан ¢з навбатида, характеристик тенглама
илдизларидан хеч б¢лмаганда биттасининг хакикий кисми мусбат б¢лиши
келиб чикади. Гироскопик кучларнинг ![]() озод хад ишорасига
таъсири й¢клигидан,
озод хад ишорасига
таъсири й¢клигидан, ![]() ва
ва ![]() тойилмаган
харакатнинг нотургунлиги (7.3.4) тизимга хар кандай гироскопик кучларни к¢шганда
хам сакланади.
тойилмаган
харакатнинг нотургунлиги (7.3.4) тизимга хар кандай гироскопик кучларни к¢шганда
хам сакланади.
Эслатма. Ночизикли тизимлар учун хам теорема ¢з кучини
саклайди. Чунки Ляпуновнинг иккинчи теоремасига асосан характеристик тенглама
илдизларидан хеч б¢лмаганда биттасининг хакикий кисми мусбат б¢лганда
![]() ночизикли функциянинг кандай б¢лишидан катъий
назар, тойилмаган харакат нотургундир.
ночизикли функциянинг кандай б¢лишидан катъий
назар, тойилмаган харакат нотургундир.
Энди тургун потенциал тизимнинг харакатига гироскопик ва диссипатив кучларнинг таъсирини к¢риб ¢тайлик.
Теорема (Томсон ва Тетнинг иккинчи теоремаси). Агар потенциал тизимнинг 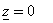 ва
ва  тойилмаган харакати тургун б¢лса, у вактда ихтиёрий гироскопик ва
диссипатив (т¢лик диссипацияли б¢лиши шарт эмас) кучлар к¢шилганда
хам тизимнинг тургун харакати сакланади.
тойилмаган харакати тургун б¢лса, у вактда ихтиёрий гироскопик ва
диссипатив (т¢лик диссипацияли б¢лиши шарт эмас) кучлар к¢шилганда
хам тизимнинг тургун харакати сакланади.
Исбот. ![]() тургун потенциал тизимга
тургун потенциал тизимга ![]() гироскопик
ва
гироскопик
ва ![]() диссипатив
кучларни к¢шганимизда
диссипатив
кучларни к¢шганимизда
![]() (7.3.6)
(7.3.6)
хосил
киламиз. Бу тенгламанинг иккала томонини хам ¢нг тарафдан ![]() векторга к¢пайтирамиз:
векторга к¢пайтирамиз:
![]() . (7.3.7)
. (7.3.7)
Биринчи параграфдаги (7.1.8) ![]() формулага
асосан
формулага
асосан ![]() бу ерда F
диссипация функцияси. Бундан ташкари G кийшик симметрик матрица учун
бу ерда F
диссипация функцияси. Бундан ташкари G кийшик симметрик матрица учун ![]() к¢пайтма
нолга тенг б¢лади (чунки бу матрицалар учун
к¢пайтма
нолга тенг б¢лади (чунки бу матрицалар учун ![]() ,
, ![]() ва
ва ![]() ). Алмаштириш натижасида
хосил килинган (7.1.16) тенгламани к¢раётганимиз учун бу ерда
). Алмаштириш натижасида
хосил килинган (7.1.16) тенгламани к¢раётганимиз учун бу ерда
![]() ва
ва ![]() .
.
У вактда, куйидаги уз-узидан аён булган
![]()
тенгликларни хисобга олиб, (7.3.7) тенгламани
![]() (7.3.8)
(7.3.8)
к¢ринишда ёзиш мумкин.
Теореманинг шартига асосан потенциал тизим тургун
б¢лгани учун барча ![]() ва П потенциал энергия
ва П потенциал энергия
![]() координаталарга
нисбатан аник-мусбат ишорали б¢лади.
координаталарга
нисбатан аник-мусбат ишорали б¢лади.
Демак, ![]() координата ва
координата ва ![]() тезликларга
нисбатан
тезликларга
нисбатан ![]() т¢лик энергия
аник-мусбат ишоралидир. Шундай килиб, (7.3.8) тенгликка асосан
т¢лик энергия
аник-мусбат ишоралидир. Шундай килиб, (7.3.8) тенгликка асосан ![]() гироскопик
кучлар ва
гироскопик
кучлар ва ![]() диссипатив
кучларнинг характерлари кандай б¢лишидан катъий назар аник-мусбат ишорали
диссипатив
кучларнинг характерлари кандай б¢лишидан катъий назар аник-мусбат ишорали ![]() функциядан
(7.3.6) тойилган харакат дифференциал тенгламасига нисбатан вакт б¢йича
олинган т¢лик хосиласи мусбат б¢лмайди. Булардан Ляпуновнинг тургунлик
хакидаги теоремасига асосан
функциядан
(7.3.6) тойилган харакат дифференциал тенгламасига нисбатан вакт б¢йича
олинган т¢лик хосиласи мусбат б¢лмайди. Булардан Ляпуновнинг тургунлик
хакидаги теоремасига асосан ![]() ва
ва ![]() тойилмаган
харакатнинг тургунлиги келиб чикади.
тойилмаган
харакатнинг тургунлиги келиб чикади.
Томсон ва Тетнинг иккинчи теоремасида тургун потенциал тизимга ихтиёрий гироскопик ва диссипатив кучлар к¢шилади деб айтилган. Энди к¢шилган диссипатив кучлар ихтиёрий б¢лмасдан, балки т¢лик диссипацияли диссипатив кучлар б¢лган холни к¢риб ¢тайлик. Бу холда F диссипатив кучлар аник-мусбат ишорали функция б¢лади.
Теорема (Томсон ва Тетнинг учинчи теоремаси). Агар ![]() ва
ва
![]() тойилмаган харакат
биргина потенциал кучлар таъсирида тургун б¢лса, у вактда ихтиёрий гироскопик
кучлар ва т¢лик диссипацияли диссипатив кучларни к¢шганимизда у
асимптотик тургун булади.
тойилмаган харакат
биргина потенциал кучлар таъсирида тургун б¢лса, у вактда ихтиёрий гироскопик
кучлар ва т¢лик диссипацияли диссипатив кучларни к¢шганимизда у
асимптотик тургун булади.
Исбот.
Исботдаги амаллар (хисоблаш) оддийрок б¢лиши учун ![]() деб кабул
килиб (ихтиёрий
деб кабул
килиб (ихтиёрий ![]() учун исбот
¢хшаш) (7.3.6) матрицавий тенгламани скаляр формада ёзамиз:
учун исбот
¢хшаш) (7.3.6) матрицавий тенгламани скаляр формада ёзамиз:
![]() (7.3.9)
(7.3.9)
Янги
![]()
¢згарувчилар киритиб, иккита иккинчи тартибли (7.3.9) тенгламаларни т¢ртта биринчи тартибли тенгламалар к¢ринишида ёзамиз
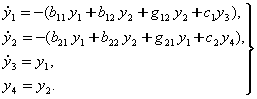 (7.3.10)
(7.3.10)
Куйидаги квадратик формани караймиз
![]() ,
(7.3.11)
,
(7.3.11)
бу
ерда ![]() -бирор мусбат сон.
-бирор мусбат сон.
(7.3.11) квадратик форма коэффициентларининг матрицасини тузамиз
 . (7.3.12)
. (7.3.12)
Бу матрицанинг бош диагонал минорларини ![]() билан
белгилаймиз, бу ерда
билан
белгилаймиз, бу ерда ![]() 1, 2, 3, 4 кийматларни
кабул килади.
1, 2, 3, 4 кийматларни
кабул килади. ![]() б¢лганда
б¢лганда
![]() (7.3.13)
(7.3.13)
га эга б¢ламиз.
Теорема шартига асосан тизим факат потенциал кучлар
таъсирида тургун б¢лгани учун ![]() ,
, ![]() ва,
демак, барча
ва,
демак, барча ![]() лар учун
лар учун ![]() .
.
![]() детерминант
детерминант ![]() параметрга
нисбатан узлуксиз б¢лгани учун
параметрга
нисбатан узлуксиз б¢лгани учун ![]() нинг етарли кичик кийматлари
учун барча
нинг етарли кичик кийматлари
учун барча ![]() лар мусбат
б¢ладилар.
лар мусбат
б¢ладилар. ![]() нинг бундай кийматларида
(7.3.12) матрицанинг бош диагонал минорлари нолдан катта, яъни бу матрица учун
Сильвестр критериясининг шартлари бажарилади ва, демак,
нинг бундай кийматларида
(7.3.12) матрицанинг бош диагонал минорлари нолдан катта, яъни бу матрица учун
Сильвестр критериясининг шартлари бажарилади ва, демак, ![]() функция
аник-мусбат ишорали б¢лади.
функция
аник-мусбат ишорали б¢лади.
![]() функциядан вакт
б¢йича т¢лик хосила оламиз
функциядан вакт
б¢йича т¢лик хосила оламиз
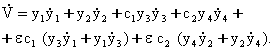
Бу тенгламадаги ![]() лар ¢рнига
уларнинг кийматларини (7.3.10) дан келтириб к¢ямиз, хадларни гурухлаймиз
ва
лар ¢рнига
уларнинг кийматларини (7.3.10) дан келтириб к¢ямиз, хадларни гурухлаймиз
ва ![]() хисобга
олганимизда
хисобга
олганимизда
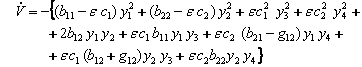 (7.3.14)
(7.3.14)
хосил
киламиз. ![]() функция
коэффициентларининг матрицасини тузамиз
функция
коэффициентларининг матрицасини тузамиз

 (7.3.15)
(7.3.15)
Бу матрица бош диагонал минорларини ![]()
![]() билан
белгилаймиз.
билан
белгилаймиз. ![]() етарли кичик сон
деб фараз килиб,
етарли кичик сон
деб фараз килиб, ![]() ларни топамиз
ларни топамиз
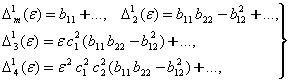 (7.3.16)
(7.3.16)
бу
ерда нукталар билан ¢з ифодасида ![]() ни янада юкорирок
даражаларини ((7.3.16) да ёзилганларга нисбатан) саклайдиган холлар
ифодаланган.
ни янада юкорирок
даражаларини ((7.3.16) да ёзилганларга нисбатан) саклайдиган холлар
ифодаланган.
Релейнинг диссипация функцияси
![]()
аник-мусбат ишорали (шартга асосан диссипация т¢лик) ва, демак, унинг коэффициентлари Сильвестр шартлари
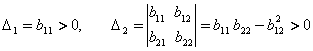
ни каноатлантиради.
Шундай килиб, ![]() ни танлаб олиш
й¢ли билан бир вактда
ни танлаб олиш
й¢ли билан бир вактда ![]() функцияни аник-мусбат ишорали ва унинг вакт
б¢йича олинган
функцияни аник-мусбат ишорали ва унинг вакт
б¢йича олинган ![]() т¢лик хосиласини
аник-манфий ишорали килиш мумкин.
т¢лик хосиласини
аник-манфий ишорали килиш мумкин.
Шунинг учун хам Ляпуновнинг Б теоремасига асосан
![]()
тойилмаган харакат асимптотик тургундир ва шу билан теорема исботи якунланади. Келтирилган исбот Н.Г.Четаевга тегишли [102]. Нотургун потенциал тизимни айрим холларда гироскопик кучлар оркали стабиллаштириш мумкинлигини бу параграфнинг бошида к¢рсатган эдик. Биз бу холда диссипатив кучларни хисобга олмаган эдик. Энди диссипатив кучларнинг гироскопик стабиллаштириш жараёнидаги ролини к¢риб ¢тамиз.
Теорема (Томсон ва Тетнинг
т¢ртинчи теоремаси). Потенциал кучлар таъсирида нотургун
б¢лган 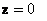 ва
ва 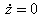 тойилмаган
харакат хар кандай гироскопик ва т¢лик диссипацияли диссипатив кучларни к¢шганимизда
хам нотургунлигича колади.
тойилмаган
харакат хар кандай гироскопик ва т¢лик диссипацияли диссипатив кучларни к¢шганимизда
хам нотургунлигича колади.
Исбот.
Потенциал кучлар таъсирида ![]() ва
ва ![]() тойилмаган
харакат нотургун б¢лгани учун
тойилмаган
харакат нотургун б¢лгани учун ![]() коэффициентлар
орасида хеч б¢лмаганда битта манфий ишоралиси топилади. Шунинг учун хам
коэффициентлар
орасида хеч б¢лмаганда битта манфий ишоралиси топилади. Шунинг учун хам ![]() ларни
шундай танлаб олиш мумкинки, (7.3.11) ифода билан аникланган
ларни
шундай танлаб олиш мумкинки, (7.3.11) ифода билан аникланган ![]() функция
манфий б¢лсин.
функция
манфий б¢лсин. ![]() ларнинг ишоралари
кандай б¢лишидан катъий назар ((7.3.16) минорларнинг бош хадлари ёки
ларнинг ишоралари
кандай б¢лишидан катъий назар ((7.3.16) минорларнинг бош хадлари ёки ![]() га
боглик эмас, ёки уни квадрати билан ¢з ифодасида сакланади) ихтиёрий
етарли кичик
га
боглик эмас, ёки уни квадрати билан ¢з ифодасида сакланади) ихтиёрий
етарли кичик ![]() ларда
ларда ![]() аник-мусбат ишорали функция б¢лади. Шундай килиб,
Ляпуновнинг B-теорема шартлари т¢лик бажарилгани учун
тойилмаган харакат нотургундир.
аник-мусбат ишорали функция б¢лади. Шундай килиб,
Ляпуновнинг B-теорема шартлари т¢лик бажарилгани учун
тойилмаган харакат нотургундир.
Исбот этилган теоремадан куйидаги келиб чикади: агар нотургун потенциал тизимни гироскопик кучлар оркали стабиллаштирсак хам етарли кичик т¢лик диссипацияли диссипатив кучлар вактнинг ¢тиши билан эришилган тургунликни бузади. Шунинг учун хам Томсон ва Тет факат потенциал кучлар таъсири остида мавжуд б¢лган тургунликни абадий тургунлик ва гироскопик стабиллаштириш оркали эришилган тургунликни муваккат тургунлик деб аташни таклиф этганлар.
4-§. Томсон ва Тет теоремаларининг татбикига
доир мисоллар
1-мисол. Пилдирок тургунлиги
Пилдирок ¢ки ![]() нинг холатини
нинг холатини ![]() ва
ва
![]() бурчаклар билан
аниклаймиз. Тизимнинг масса маркази
бурчаклар билан
аниклаймиз. Тизимнинг масса маркази ![]() таянч нуктадан юкорида
турганлиги сабабли иккала
таянч нуктадан юкорида
турганлиги сабабли иккала ![]() ва
ва ![]() координаталар
пилдирок айланмаётганда нотургун б¢лади (7.1-шакл,а).
координаталар
пилдирок айланмаётганда нотургун б¢лади (7.1-шакл,а).
Шундай килиб пилдирокнинг нотургун координаталар сони
жуфт ва Том ва Тетнинг биринчи теоремасидаги зарурий шарт бажарилади. Пилдирок
тойилган харакатининг ![]() ва
ва ![]() ларга
нисбатан дифференциал тенгламаларини иккинчи бобда топган эдик:
ларга
нисбатан дифференциал тенгламаларини иккинчи бобда топган эдик:
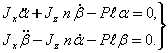 (7.4.1)
(7.4.1) ![]()
(7.4.1) тенгламаларни
![]()
нотургун
потенциал тизимга мос равишда ![]() ва
ва ![]() гироскопик
кучларни к¢шиш натижасида хасил этилган деб караш мумкин.
гироскопик
кучларни к¢шиш натижасида хасил этилган деб караш мумкин.
Агар ![]() деб кабул килсак, y вактда
(7.4.1) тенгламалар системаси (7.3.2) тенгламалар системаси билан мос келади.
Гироскопик стабиллаштириш шарти (7.3.3) бу мисол учун
деб кабул килсак, y вактда
(7.4.1) тенгламалар системаси (7.3.2) тенгламалар системаси билан мос келади.
Гироскопик стабиллаштириш шарти (7.3.3) бу мисол учун
![]()
ёки
![]()
к¢ринишда б¢лади. Бу шартни китобнинг иккинчи бобида (ночизикли тизим учун) хам топган эдик.
 |
Агар масса маркази С осилиш нуктасидан пастда
жойлашган б¢лса (гироскопик маятник, 7.1-шакл, б), у вактда ![]() ва
ва
![]() координаталар тургун
б¢лади. Бу холатда Томсон ва Тетнинг иккинчи теоремасига асосан хар кандай
координаталар тургун
б¢лади. Бу холатда Томсон ва Тетнинг иккинчи теоремасига асосан хар кандай
![]() бурчак тезлик учун
бурчак тезлик учун
![]() ва
ва ![]() координаталар
тургун б¢лади. Томсон ва Тетнинг т¢ртинчи теоремасига асосан пилдирокнинг
тургунлиги муваккат ва гироскопик маятникнинг тургунлиги абадийдир.
координаталар
тургун б¢лади. Томсон ва Тетнинг т¢ртинчи теоремасига асосан пилдирокнинг
тургунлиги муваккат ва гироскопик маятникнинг тургунлиги абадийдир.
2-мисол. Инерциал навигация тизимининг тургунлиги
Харакат килаётган объектнинг (сув ости кема, самолёт,
космик кема, ракета ва х.к) координаталарини ¢лчаш учун инерциал навигация
тизимидан фойдаланиш мумкин. Бу тизим оркали одатда объектнинг чизикли
тезланишини ва инерциал тизим хисобига нисбатан бурчак тезлигини
¢лчайдилар. Бу максад учун уч гироскопли платформа (у абсолют бурчак
тезлигининг компонентларини ¢лчайди) ва учта ![]() акселерометрдан
(улар нъютонометр деб хам аталади) фойдаланиш мумкин (7.2-шакл).
акселерометрдан
(улар нъютонометр деб хам аталади) фойдаланиш мумкин (7.2-шакл).
Тойилмаган харакатда платформанинг О нуктаси
¢згармас тезлик билан Ернинг параллели б¢йлаб харакат килади деб
фараз киламиз. Ерни т¢гри шар сифатида кабул киламиз ва платформа билан каттик
богланган ![]() ¢клар
географик ориентирланган (
¢клар
географик ориентирланган (![]() ¢ки шаркка
й¢налтирилган,
¢ки шаркка
й¢налтирилган, ![]() ¢ки - шимолга,
¢ки - шимолга,
![]() ¢ки - вартикал
равишда юкорига). В.Д.Андреев платформанинг ориентацияси бузилмайди деган шарт
билан О нуктанинг тойилган харакатининг куйидаги дифференциал тенгламаларини
топган [7]:
¢ки - вартикал
равишда юкорига). В.Д.Андреев платформанинг ориентацияси бузилмайди деган шарт
билан О нуктанинг тойилган харакатининг куйидаги дифференциал тенгламаларини
топган [7]:
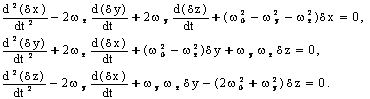 (7.4.2)
(7.4.2)
Бу тенгламаларда ![]() -
- ![]() тизимда О нуктанинг тойилмаган харакатдаги
координаталари (О1 - Ер маркази,
тизимда О нуктанинг тойилмаган харакатдаги
координаталари (О1 - Ер маркази, ![]() ,
, ![]() ,
, ![]() ¢клар мос равишда
¢клар мос равишда ![]() ,
, ![]() ,
, ![]() ¢кларга параллел),
¢кларга параллел), ![]()
![]() координаталарнинг
тойилган харакатдаги тойилиши,
координаталарнинг
тойилган харакатдаги тойилиши, ![]() - платформа абсолют бурчак тезлигининг
- платформа абсолют бурчак тезлигининг ![]() ва
ва ![]() ¢кларидаги проекциялари (к¢рилаётган харакатда
¢кларидаги проекциялари (к¢рилаётган харакатда
![]() ),
), ![]() бу ерда
бу ерда ![]() - Ернинг
гравитацион ¢згармаси,
- Ернинг
гравитацион ¢згармаси, ![]() - тойилмаган харакатда
Ер марказидан О нуктагача б¢лган масофа.
- тойилмаган харакатда
Ер марказидан О нуктагача б¢лган масофа.
Кулайлик учун
![]() (7.4.3)
(7.4.3)
деб вакт масштабини ¢згартирамиз ва куйидаги ¢лчовсиз параметрларни киритамиз
![]() (7.4.4)
(7.4.4)
(7.4.3) ва (7.4.4) ларни (7.4.2) к¢йганимизда тойилган харакатнинг тенгламаси куйидаги к¢ринишда б¢лади:
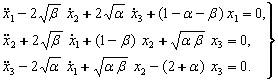 (7.4.5)
(7.4.5)
Бу ерда устида нукталар куйилган ![]() лар билан
лар билан ![]() б¢йича хосилалар белгиланган.
б¢йича хосилалар белгиланган.
Агар Томсон ва Тет теоремаларини татбик этсак, у вактда
![]() харакатнинг
тургунлигини тадкик этиш соддалашади.
харакатнинг
тургунлигини тадкик этиш соддалашади.
![]() лар билан чизикли
богланган кучлар коэффициентларининг матрицаси
лар билан чизикли
богланган кучлар коэффициентларининг матрицаси
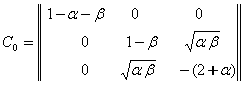 (7.4.6)
(7.4.6)
симметрик. Шунинг учун хам (7.4.5) тенгламаларни
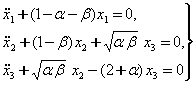 (7.4.7)
(7.4.7)
потенциал тизимга
![]()
гироскопик кучларни мос равишда к¢шиш натижасида хосил килинган деб караш мумкин.
![]() нормал координата
(7.4.7) тизимнинг биринчи тенгламасидагина катнашади (иккинчи ва учинчи тенгламалар
билан богланган эмас).
нормал координата
(7.4.7) тизимнинг биринчи тенгламасидагина катнашади (иккинчи ва учинчи тенгламалар
билан богланган эмас).
 |
|||
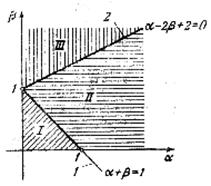 |
|||
7.2-шакл. 7.3-шакл.
Агар
![]() (7.4.8)
(7.4.8)
б¢лса,
у вактда ![]() координата тургун,
агар
координата тургун,
агар
![]() (7.4.9)
(7.4.9)
б¢лса – нотургундир.
![]() текислигида
текислигида ![]() координатанинг тургунлик
сохаси биринчи квадрантда
координатанинг тургунлик
сохаси биринчи квадрантда ![]() т¢гри чизикнинг пастида ва нотургунлик сохаси шу
т¢гри чизикнинг юкорисида жойлашган (7.3-шакл).
т¢гри чизикнинг пастида ва нотургунлик сохаси шу
т¢гри чизикнинг юкорисида жойлашган (7.3-шакл).
(7.4.7) тизимнинг иккинчи ва учинчи тенгламаларини к¢ришга ¢тамиз. Потенциал кучлар коэффициентларининг матрицасини тузамиз
 .
.
Бу матрицанинг бош диагонал минорларини топамиз:
![]() .
.
![]() т¢гри чизикнинг пастида
т¢гри чизикнинг пастида ![]() , шунинг учун хам
, шунинг учун хам ![]() ва
ва ![]() координаталар орасида биттаси тургун ва иккинчиси
нотургун; бу чизикнинг юкорисида
координаталар орасида биттаси тургун ва иккинчиси
нотургун; бу чизикнинг юкорисида ![]() ва, демак, иккала координата хам нотургун (чунки у
ерда
ва, демак, иккала координата хам нотургун (чунки у
ерда ![]() ) (7.3-шакл).
) (7.3-шакл).
Айтилганлардан куйидагилар келиб чикади:
1.
I сохада ![]() координата тургун,
координата тургун, ![]() ва
ва ![]() координаталардан биттаси тургун, иккинчиси нотургун,
яъни бу сохада факат битта координата нотургун б¢лади.
координаталардан биттаси тургун, иккинчиси нотургун,
яъни бу сохада факат битта координата нотургун б¢лади.
2.
II сохада иккита координата нотургун (![]() тургун булган холда
тургун булган холда ![]() ва
ва ![]() лардан биттаси).
лардан биттаси).
3. III сохада учала координата хам нотургун.
Томсон ва Тетнинг биринчи теоремасига асосан I ва III сохаларда нотургун харакатни гироскопик стабиллаштириш мумкин эмас. II сохада гироскопик стабиллаштиришни амалга ошириш мумкинми? Буни аниклаш учун (7.4.5) тенгламалар тизимининг характеристик тенгламасини тузамиз:
 (7.4.10)
(7.4.10)
детерминантни очиб ва хадларни гурухлаб, куйидаги тенгламага келамиз:
![]() , (7.4.11)
, (7.4.11)
бу ерда
![]() (7.4.12)
(7.4.12)
(7.4.11)
характеристик тенгламада ![]() факат жуфт
даражада катнашганлиги сабабли харакатнинг тургун б¢лиши учун унинг барча
илдизлари соф мавхум б¢лишлари зарур ва етарли. Бу дегани,
факат жуфт
даражада катнашганлиги сабабли харакатнинг тургун б¢лиши учун унинг барча
илдизлари соф мавхум б¢лишлари зарур ва етарли. Бу дегани, ![]() га
нисбатан (7.4.11) тенглама илдизлари манфий ва хакикий б¢лишлари керак.
Бунинг учун
га
нисбатан (7.4.11) тенглама илдизлари манфий ва хакикий б¢лишлари керак.
Бунинг учун ![]() коэффициентлар
Гурвиц шартлари
коэффициентлар
Гурвиц шартлари
![]() (7.4.13)
(7.4.13)
хамда
![]() га нисбатан кубик
илдизларнинг хакикий б¢лиши шартларини каноатлантириши керак.
га нисбатан кубик
илдизларнинг хакикий б¢лиши шартларини каноатлантириши керак.
Шу максадда ![]() алмаштириш оркали
(7.4.11) тенгламани
алмаштириш оркали
(7.4.11) тенгламани
![]()
к¢ринишга келтирамиз ва
![]()
тенгсизликнинг
бажарилишини талаб киламиз. Агар бу тенгсизлик ифодасидаги ![]() ва
ва ![]() лар
¢рнига уларнинг
лар
¢рнига уларнинг ![]() ,
, ![]() ва
ва
![]() коэффициентлар оркали
ифодаларини келтириб к¢йсак, куйидаги тенгсизликка эга б¢ламиз:
коэффициентлар оркали
ифодаларини келтириб к¢йсак, куйидаги тенгсизликка эга б¢ламиз:
![]() . (7.4.14)
. (7.4.14)
Бу
шартни ![]() ва
ва ![]() параметрлар
оркали ифодалаш учун (7.4.12) формулаларни (7.4.13) ва (7.4.14) даги
параметрлар
оркали ифодалаш учун (7.4.12) формулаларни (7.4.13) ва (7.4.14) даги ![]() ,
,
![]() ва
ва ![]() лар
¢рнига келтириб к¢ямиз ва II сохадан гироскопик стабиллаштиришни
амалга ошириш мумкин б¢лган кисмини ажратиб оламиз. Аввало
лар
¢рнига келтириб к¢ямиз ва II сохадан гироскопик стабиллаштиришни
амалга ошириш мумкин б¢лган кисмини ажратиб оламиз. Аввало ![]() ва
ва
![]() параметрларнинг
мусбатлигини эслатиб ¢тамиз. Демак,
параметрларнинг
мусбатлигини эслатиб ¢тамиз. Демак, ![]() тенгсизлик
автоматик равишда бажарилади ((7.4.12)нинг биринчи хадига каранг).
тенгсизлик
автоматик равишда бажарилади ((7.4.12)нинг биринчи хадига каранг).
Бундан ташкари II сохада ![]() хамда
(1) ва (2) т¢гри чизикларда
хамда
(1) ва (2) т¢гри чизикларда ![]() (7.3 ва
7.4-шаклларга каранг). II сохада турган
(7.3 ва
7.4-шаклларга каранг). II сохада турган

эгри
чизикларнинг б¢лагини чизамиз (бу сохадан ташкарида стабиллаштириш мумкин
эмас). Шуни таъкидлаймизки, учала эгри чизик хам (1) ва (2) т¢гри чизикларни
![]() ва
ва ![]() нукталарда
кесиб ¢тади. Хакикатан хам, бу т¢гри чизикларда
нукталарда
кесиб ¢тади. Хакикатан хам, бу т¢гри чизикларда ![]() хамда
хамда ![]() ва
ва
![]() функциялар
функциялар ![]() билан
бир вактда бирданига нолга айланадилар (
билан
бир вактда бирданига нолга айланадилар (![]() б¢лганда,
б¢лганда, ![]() ).
).
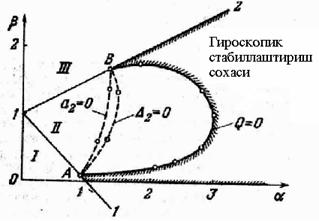
7.4-шакл.
Осонгина
аниклаш мумкинки, ![]() ва
ва ![]() эгри
чизикларнинг чап тарафида
эгри
чизикларнинг чап тарафида ![]() ва
ва ![]() функциялар
манфий, ¢нгида эса мусбатдир. Бундан ташкари
функциялар
манфий, ¢нгида эса мусбатдир. Бундан ташкари ![]() эгри чизикнинг чап
томонида
эгри чизикнинг чап
томонида ![]() ва ¢нг тарафида
ва ¢нг тарафида
![]() . Шундай килиб, II сохада
. Шундай килиб, II сохада
![]() эгри чизикнинг
¢нг тарафида бирданига барча (7.4.13) ва (7.4.14) тенгсизликлар бажарилади
ва, демак, бу сохада гироскопик стабиллаштиришни амалга ошириш мумкин (
эгри чизикнинг
¢нг тарафида бирданига барча (7.4.13) ва (7.4.14) тенгсизликлар бажарилади
ва, демак, бу сохада гироскопик стабиллаштиришни амалга ошириш мумкин (![]() ва
ва ![]() эгри чизиклар II сохани
факат 7.4-шаклда к¢рсатилган чизиклар буйича кесадилар);
эгри чизиклар II сохани
факат 7.4-шаклда к¢рсатилган чизиклар буйича кесадилар); ![]() эгри
чизикнинг бир кисми (7.4-шаклда к¢рсатилганидан бошкаси) II сохада
жойлашгану, лекин
эгри
чизикнинг бир кисми (7.4-шаклда к¢рсатилганидан бошкаси) II сохада
жойлашгану, лекин ![]() ва
ва ![]() эгри
чизикларда чап тарафда б¢лади (бу ерда
эгри
чизикларда чап тарафда б¢лади (бу ерда ![]() ва
ва ![]() ).
).
3-мисол. Гироскопик бир рельсли вагон
XX асрнинг биринчи чорагида бир рельсли вагон ва икки гилдиракли автомобилларнинг экспериментал нусхалари пайдо б¢лди. Уларнинг масса маркази рельсдан (й¢лдан) юкорида жойлашган эди (7.5-шакл). Вагоннинг (автомобилнинг) вертикал холати нотургун ва уни стабиллаштириш учун гироскопдан фойдаланилган.
Вагоннинг вертикал холатини стабиллаштириш учун
тизимнинг параметрлари каноатлантириши лозим б¢лган муносабатларни аниклашдан
олдин масалани сифат жихатдан к¢риб ¢тамиз. Вагоннинг масса маркази
рельсдан юкорида туради. Шунинг учун вертикалдан вагоннинг огишини
белгилайдиган ![]() бурчаги нотургун
координата б¢лади.
бурчаги нотургун
координата б¢лади.
 |
7.5-шакл.
Томсон ва Тетнинг биринчи теоремасига асосан факат
нотургун координаталарнинг сони жуфт б¢лгандагина тойилмаган харакатни
гироскопик стабиллаштириш мумкин. Бундан шу нарса келиб чикадики, тизимнинг
иккинчи координатаси ![]() (гироскоп
¢рнатилган халканинг бурилиш бурчаги) хам нотургун координата
б¢лиши керак. Шу максадда халканинг юкори кисмига L юкни
¢рнатганлар. Шундай килиб тизим иккита
(гироскоп
¢рнатилган халканинг бурилиш бурчаги) хам нотургун координата
б¢лиши керак. Шу максадда халканинг юкори кисмига L юкни
¢рнатганлар. Шундай килиб тизим иккита ![]() ва
ва ![]() нотургун
координатага эга б¢лади ва уни гироскопик стабиллаштириш мумкин б¢либ
колади.
нотургун
координатага эга б¢лади ва уни гироскопик стабиллаштириш мумкин б¢либ
колади.
Вагон ва халка билан гироскоп тебранишлари натижасида хосил
б¢ладиган каршилик кучларини хисобга оламиз (бу кучлар мухитнинг каршилиги
ва таянч нукталаридаги ишкаланиш натижасида юзага келади). Томсон ва Тетнинг
т¢ртинчи теоремасига асосан бу кучлар гироскопик стабиллаштиришни
бузадилар (чунки гироскопсиз тизим нотургун). Шунинг учун хам стабиллаштиришни
амалга ошириш учун бошка хил куч киритиш керак. Шу максадда К халканинг айланиш
¢ки N га махсус электромагнит курилма ¢рнатганлар. Бу курилма
![]() тезлатувчи момент
яратади. Момент айланиш бурчак тезлигига пропорционал б¢либ халканинг
айланиш томонига й¢налган б¢лади (тебранишлар назариясида бундай
моментлар ва кучларни манфий ишкаланиш деб атайдилар).
тезлатувчи момент
яратади. Момент айланиш бурчак тезлигига пропорционал б¢либ халканинг
айланиш томонига й¢налган б¢лади (тебранишлар назариясида бундай
моментлар ва кучларни манфий ишкаланиш деб атайдилар).
Томсон ва Тет теоремалари оркали бир рельсли гироскопик вагоннинг тургунлигини таъминлайдиган кучларнинг характерини аниклагандан кейин сонли анализга ¢тамиз. Бунинг учун тизимнинг тойилган харакат дифференциал тенгламаларидан фойдаланамиз [75]:
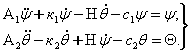 (а)
(а)
Бу ерда
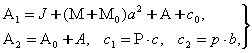 (б)
(б)
![]() ва
ва
![]() халканинг инерция
моментлари,
халканинг инерция
моментлари, ![]() -унинг массаси,
-унинг массаси, ![]() –гироскопнинг
экваториал инерция моменти,
–гироскопнинг
экваториал инерция моменти, ![]() –унинг массаси,
–унинг массаси, ![]() –вагоннинг
рельс ¢кига нисбатан инерция моменти,
–вагоннинг
рельс ¢кига нисбатан инерция моменти, ![]() –вагоннинг огирлиги,
–вагоннинг огирлиги,
![]() –к¢шимча
–к¢шимча ![]() юкнинг
огирлиги,
юкнинг
огирлиги, ![]() –гироскопнинг кинетик
моменти,
–гироскопнинг кинетик
моменти, ![]() –вагонга таъсир
этаётган каршилик кучининг коэффициенти,
–вагонга таъсир
этаётган каршилик кучининг коэффициенти, ![]() -
- ![]() тезлатувчи
момент яратувчи курилма характеристикасининг тиклиги;
тезлатувчи
момент яратувчи курилма характеристикасининг тиклиги; ![]() ва
ва ![]() ¢згармас
сонларнинг микдори 7.5-шаклда к¢риниб турибди,
¢згармас
сонларнинг микдори 7.5-шаклда к¢риниб турибди, ![]() –бутун
тизимнинг масса маркази (
–бутун
тизимнинг масса маркази (![]() юкдан ташкари),
юкдан ташкари), ![]() ва
ва
![]() - ночизикли
кучлар.
- ночизикли
кучлар.
(а) тенгламаларни
![]()
нотургун
потенциал тизимга ![]() ва
ва ![]() гироскопик
кучларни,
гироскопик
кучларни, ![]() диссипатив кучни,
диссипатив кучни, ![]() тезлатувчи
кучни хамда
тезлатувчи
кучни хамда ![]() ва
ва ![]() ночизикли
кучларни мос равишда к¢шиш натижасида хосил этилган деб караш мумкин.
ночизикли
кучларни мос равишда к¢шиш натижасида хосил этилган деб караш мумкин.
Биринчи
якинлашиш тенгламаларининг (улар ![]() ва
ва ![]() ларни
ташлаш натижасида хосил б¢лади) характеристик тенгламасини тузамиз:
ларни
ташлаш натижасида хосил б¢лади) характеристик тенгламасини тузамиз:
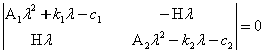 .
.
Детерминантни ёйиб ва хадларни гурухлаганимиздан кейин
![]()
ни хосил киламиз, бу ерда
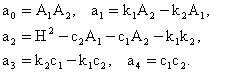 (в)
(в)
Т¢ртинчи
тартибли тизим учун Гурвиц критериясини ёзамиз (![]() ):
):
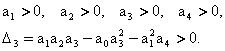
Биз
к¢раётган холда ![]() >0 ва
>0 ва ![]() шартлар
уз-узидан бажарилади, яна
шартлар
уз-узидан бажарилади, яна ![]() дан
дан ![]() бажарилиши,
колган
бажарилиши,
колган ![]() ва
ва ![]() шартлардан
эса куйидагилар келиб чикади:
шартлардан
эса куйидагилар келиб чикади:
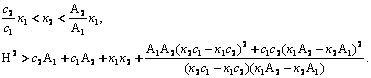 (г)
(г)
Биринчи шарт курилма характеристикасининг тиклик
коэффициенти ![]() нинг ¢згариш
чегарасини, иккинчи шарт
нинг ¢згариш
чегарасини, иккинчи шарт ![]() кинетик моментнинг
к¢йи чегарасини аниклайди. (г) шартларнинг бажарилиши характеристик
тенглама илдизларидан барчасининг хакикий кисми манфий б¢лишини
таъминлайди. У вактда Ляпуновнинг биринчи якинлашиш усулидаги биринчи
теоремасига асосан бир рельсли вагон тойилмаган харакати ассимптотик тургун
б¢лади.
кинетик моментнинг
к¢йи чегарасини аниклайди. (г) шартларнинг бажарилиши характеристик
тенглама илдизларидан барчасининг хакикий кисми манфий б¢лишини
таъминлайди. У вактда Ляпуновнинг биринчи якинлашиш усулидаги биринчи
теоремасига асосан бир рельсли вагон тойилмаган харакати ассимптотик тургун
б¢лади.
(в) формулалардан к¢риниб турибдики, агар ![]() б¢лса
(тезлатувчи момент ¢рнига оддий каршилик кучи юзага келади),
б¢лса
(тезлатувчи момент ¢рнига оддий каршилик кучи юзага келади), ![]() коэффициент
манфий ва Томсон ва Тетнинг т¢ртинчи теоремасига асосан тизим нотургун
б¢либ колади. Демак, тизим тургун б¢лиши учун албатта тезлатувчи
момент мавжуд б¢лиши зарур.
коэффициент
манфий ва Томсон ва Тетнинг т¢ртинчи теоремасига асосан тизим нотургун
б¢либ колади. Демак, тизим тургун б¢лиши учун албатта тезлатувчи
момент мавжуд б¢лиши зарур.
5-§. Факат гироскопик ва диссипатив кучлар таъсири
остидаги харакатнинг тургунлиги
Шу вактгача тизимга гироскопик ва диссипатив кучлар потенциал кучлар билан биргаликда таъсир этаётган холлар к¢риб ¢тилди. Аммо амалда шундай тизимлар мавжудки, уларда диссипатив ва гироскопик кучлар потенциал кучларсиз таъсир курсатадилар. Ана шундай тизимларнинг тургунлигини ушбу параграфда ¢рганамиз.
5.1.Факат гироскопик кучлар таъсир этадиган хол
Даставвал тизимга факат гироскопик кучлар таъсир этади ва унинг тойилган харакатининг тенгламаси
![]() (7.5.1)
(7.5.1)
к¢ринишга келтирилган деб фараз киламиз.
Бу хол учун Д.Р.Меркин томонидан яратилган теоремаларни келтирамиз [61].
1-теорема. Агар тизимга факат
гироскопик кучлар таъсир этса, у вактда унинг ![]() ва
ва
![]() тойилмаган харакати
тезликларга нисбатан доим тургун б¢лади.
тойилмаган харакати
тезликларга нисбатан доим тургун б¢лади.
Исбот. (7.5.1) тенгламанинг
иккала тарафини ¢нг томондан ![]() матрицага
к¢пайтирамиз:
матрицага
к¢пайтирамиз:
![]() . (7.5.1¢)
. (7.5.1¢)
![]() кийшик симметрик матрица учун
кийшик симметрик матрица учун ![]() б¢лишини хисобга
олиб, (7.5.1¢) тенгламадан
б¢лишини хисобга
олиб, (7.5.1¢) тенгламадан
![]()
ни хосил киламиз. Бу тенгламани интеграллаб
![]() (7.5.2)
(7.5.2)
ни оламиз, бу ерда ![]() -¢згармас
сон.
-¢згармас
сон. ![]() функция тургунлик хакидаги
Ляпунов теоремасининг хамма шартларини каноатлантиради, чунки у аник-мусбат
ишорали ва ундан вакт б¢йича (7.5.1) тойилган харакат тенгламаларига нисбатан
олинган т¢лик хосиласи
функция тургунлик хакидаги
Ляпунов теоремасининг хамма шартларини каноатлантиради, чунки у аник-мусбат
ишорали ва ундан вакт б¢йича (7.5.1) тойилган харакат тенгламаларига нисбатан
олинган т¢лик хосиласи ![]() айнан нолга тенг.
айнан нолга тенг.
Теорема чизикли автоном тизим учун
яратилган эди. В.В.Румянцев гироскопик куч ![]() вактдан
ошкора равишда боглик б¢лганда чизикли ноавтоном тизимлар учун хам 1-теорема
¢з кучини саклашини к¢рсатади (теореманинг исботи
вактдан
ошкора равишда боглик б¢лганда чизикли ноавтоном тизимлар учун хам 1-теорема
¢з кучини саклашини к¢рсатади (теореманинг исботи ![]() тенгликка
суянган). Бу тенглик вактдан ошкора равишда боглик б¢лган исталган
тенгликка
суянган). Бу тенглик вактдан ошкора равишда боглик б¢лган исталган ![]() кийшик симметрик матрица учун бажарилади [80].
кийшик симметрик матрица учун бажарилади [80].
Харакат тургунлиги факат тезликлар тургунлиги билангина эмас, балки координаталар тургунлиги билан хам аникланади. Куйидаги теоремада координата ва тезликлар мажмуасига нисбатан (7.5.1) тизим харакати тургунлигининг зарур ва етарли шарти келтирилган.
2-теорема. Факатгина гироскопик кучлар таъсири остида б¢лган чизикли автоном тизимнинг тойилмаган харакати координаталар б¢йича тургун б¢лиши учун гироскопик кучлар матрицасининг детерминанти нолга тенг б¢лмаслиги етарли ва зарур.
Исбот. Дастлаб агар ![]() б¢лса,
у вактда
б¢лса,
у вактда ![]() тойилмаган харакат
тойилмаган харакат
![]() координата
б¢йича тургун б¢лишини к¢рсатамиз (олдинги теоремада
координата
б¢йича тургун б¢лишини к¢рсатамиз (олдинги теоремада ![]() нинг хар кандай
кийматида тизим тезликларга нисбатан тургунлигини исбот килган эдик).
нинг хар кандай
кийматида тизим тезликларга нисбатан тургунлигини исбот килган эдик).
(7.5.1) тенгламани вакт б¢йича бир марта интеграллаймиз:
![]() (7.5.3)
(7.5.3)
бу ерда
![]() .
(7.5.4)
.
(7.5.4)
Янги ![]() ¢згарувчи
матрицага куйидаги
¢згарувчи
матрицага куйидаги
![]() (7.5.5)
(7.5.5)
формула оркали ¢тамиз
(шарт б¢йича ![]() хосмас
матрица, шунинг учун хам
хосмас
матрица, шунинг учун хам ![]() мавжуд
б¢лади). (7.5.5) формулани (7.5.3) тенгламага к¢йиб, куйидагини хосил
киламиз
мавжуд
б¢лади). (7.5.5) формулани (7.5.3) тенгламага к¢йиб, куйидагини хосил
киламиз
![]()
бунда ![]() айниятни
хисобга олиб,
айниятни
хисобга олиб,
![]() (7.5.6)
(7.5.6)
тенгламага келтирамиз.
1-теоремага асосан харакат ![]() тезликларга
нисбатан тургун. (7.5.1) ва (7.5.6) тенгламалар куриниши б¢йича бир хил
б¢лганлиги учун харакат
тезликларга
нисбатан тургун. (7.5.1) ва (7.5.6) тенгламалар куриниши б¢йича бир хил
б¢лганлиги учун харакат ![]() га нисбатан
хам тургун б¢лади. (7.5.4) ва (7.5.5) тенгликларга асосан харакат
га нисбатан
хам тургун б¢лади. (7.5.4) ва (7.5.5) тенгликларга асосан харакат ![]() координатага
нисбатан тургун деган хулосага келамиз. (
координатага
нисбатан тургун деган хулосага келамиз. (![]() ва
ва ![]() ларнинг
модул б¢йича етарли кичик кийматлари учун
ларнинг
модул б¢йича етарли кичик кийматлари учун ![]() матрицанинг
элементлари хам кичик б¢лади).
матрицанинг
элементлари хам кичик б¢лади).
Энди теореманинг зарурий шартини исбот киламиз.
Бунинг учун ![]() б¢лганда
тизимнинг нотургунлигини к¢рсатиш кифоя. (7.5.1) дифференциал
тенгламасининг характеристик тенгламани тузамиз:
б¢лганда
тизимнинг нотургунлигини к¢рсатиш кифоя. (7.5.1) дифференциал
тенгламасининг характеристик тенгламани тузамиз:
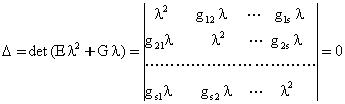 (7.5.7)
(7.5.7)
Хар бир сатрдан умумий к¢пайтувчи ![]() ни
чикариб:
ни
чикариб:

хосил булган детерминантни ![]() даражалари
б¢йича ёямиз:
даражалари
б¢йича ёямиз:
![]() .
.
Равшанки,
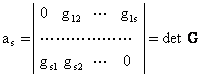 .
.
![]() муносабатдан ва
кейинги икки тенгликдан (7.5.7) характеристик тенгламанинг камида
муносабатдан ва
кейинги икки тенгликдан (7.5.7) характеристик тенгламанинг камида ![]() та
нолинчи илдизлари борлиги келиб чикади.
та
нолинчи илдизлари борлиги келиб чикади.

характеристик матрицанинг элементар б¢лувчиларини тадкик этишга ¢тамиз. Асосий тадкикотни давом эттиришдан олдин матрицанинг элементар б¢лувчиси, энг катта умумий б¢лувчиси ва инвариант к¢пайтувчиси деган тушунчаларга аниклик киритайлик.
Элементлари бирор ![]() параметрнинг
параметрнинг
![]() к¢пхади
б¢лган квадрат матрицани к¢райлик:
к¢пхади
б¢лган квадрат матрицани к¢райлик:
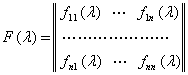 (7.5.8)
(7.5.8)
Бундай матрицалар ![]() -матрицалар деб
айтилади.
-матрицалар деб
айтилади.
![]() оркали (7.5.8)
матрицанинг барча
оркали (7.5.8)
матрицанинг барча ![]() тартибли
минорларининг энг катта умумий б¢лувчисини белгилаймиз, унинг катта
хади олдидаги коэффициентини бирга тенг деб танлаб оламиз.
тартибли
минорларининг энг катта умумий б¢лувчисини белгилаймиз, унинг катта
хади олдидаги коэффициентини бирга тенг деб танлаб оламиз. ![]() к¢пхадининг
к¢пхадининг
![]() к¢пхадга
б¢линишини осонгина к¢рсатиш мумкин. Энг катта умумий б¢лувчи
к¢пхадга
б¢линишини осонгина к¢рсатиш мумкин. Энг катта умумий б¢лувчи ![]() топишда
куйидаги коидага риоя килиш фойдали:
топишда
куйидаги коидага риоя килиш фойдали:
агар бирор ![]() тартибли минор
¢згармас микдорга тенг б¢лса, у вактда
тартибли минор
¢згармас микдорга тенг б¢лса, у вактда ![]() (чунки бу минор
(чунки бу минор ![]() га
б¢линиши керак,
га
б¢линиши керак, ![]() эса
эса ![]() ларга
б¢линади).
ларга
б¢линади).
![]() (7.5.9)
(7.5.9)
к¢пхадга (7.5.8) матрицанинг инвариант к¢пайтувчиси деб айтилади. Равшанки,
![]()
ва у ¢згармас
к¢пайтувчигача аникликда ![]() га тенг
б¢лади:
га тенг
б¢лади:
![]() (7.5.10)
(7.5.10)
Хар бир ![]() инвариант
к¢пайтувчини к¢пайтувчиларга ёямиз:
инвариант
к¢пайтувчини к¢пайтувчиларга ёямиз:
![]() ,
,
бу ерда ![]() лар
лар
![]() (7.5.11)
(7.5.11)
тенгламанинг хар хил илдизлари. Равшанки,
![]() .
.
Бундан ташкари ![]() , агар
, агар ![]() б¢лса
(чунки
б¢лса
(чунки ![]() инвариант
к¢пайтувчи
инвариант
к¢пайтувчи ![]() га б¢линади).
га б¢линади).
![]() ифодасига
к¢пайтувчи б¢либ кирган ва ¢згармас сондан фарк килувчи
ифодасига
к¢пайтувчи б¢либ кирган ва ¢згармас сондан фарк килувчи ![]() хадга
хадга
![]() - матрицанинг
элементар б¢лувчиси деб айтилади. Уларнинг умумий сонини
- матрицанинг
элементар б¢лувчиси деб айтилади. Уларнинг умумий сонини ![]() ва
б¢лувчиларнинг ¢зини
ва
б¢лувчиларнинг ¢зини ![]() билан белгилаймиз.
билан белгилаймиз.
![]() сонларнинг орасида
бир-бирига тенглари хам б¢лиши мумкин (
сонларнинг орасида
бир-бирига тенглари хам б¢лиши мумкин (![]() к¢пайтувчилар
хар хил
к¢пайтувчилар
хар хил ![]() инвариант
к¢пайтувчиларнинг ифодасига кириши мумкин).
инвариант
к¢пайтувчиларнинг ифодасига кириши мумкин).
Куйидаги мисолда юкорида баён этилганларни тушунтирамиз.
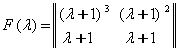 (7.5.12)
(7.5.12)
матрица учун т¢ртта биринчи тартибли минорни ёзиш мумкин:
![]()
Уларнинг энг катта умумий б¢лувчиси
![]()
б¢лади. (7.5.30) матрица учун битта иккинчи тартибли минор мавжуд
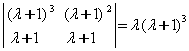 .
.
Бу минорнинг энг катта умумий б¢лувчиси ![]() .
(7.5.9) формуладан фойдаланиб, инвариант к¢пайтувчиларни топамиз:
.
(7.5.9) формуладан фойдаланиб, инвариант к¢пайтувчиларни топамиз:
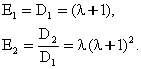
(7.5.12) матрицанинг элементар б¢линувчиларини топамиз:
![]() .
.
Уларнинг илдизлари
![]()
б¢ладилар. Бу илдизлар, албатта,
![]()
тенгламанинг илдизлари хам б¢ладилар.
![]() илдиз
илдиз ![]() тенгламанинг
уч каррали илдизидир. Шу илдизнинг ¢зи битта элементар б¢лувчи учун
оддий ва бошкаси учун икки каррали илдиз б¢лади.
тенгламанинг
уч каррали илдизидир. Шу илдизнинг ¢зи битта элементар б¢лувчи учун
оддий ва бошкаси учун икки каррали илдиз б¢лади.
матрица (![]() - (7.5.8)
матрицанинг инвариант к¢пайтувчилари) (7.5.8) матрицанинг нормал диагонал
формаси деб айтилади. Масалан, (7.5.12) учун
- (7.5.8)
матрицанинг инвариант к¢пайтувчилари) (7.5.8) матрицанинг нормал диагонал
формаси деб айтилади. Масалан, (7.5.12) учун
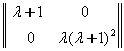
нормал диагонал форма
б¢лади. Хар кандай ![]() -матрицани чекли
сондаги элементар алмаштиришлар оркали нормал диагонал форма к¢ринишига
келтириш мумкин.
-матрицани чекли
сондаги элементар алмаштиришлар оркали нормал диагонал форма к¢ринишига
келтириш мумкин.
Энди асосий тадкикотимизга кайтамиз. Характеристик
матрицанинг барча минорларининг энг катта умумий б¢линувчисини ![]() билан
белгилаймиз. Аникки,
билан
белгилаймиз. Аникки, ![]() га б¢линади,
га б¢линади, ![]() га
б¢линади ва х.к. (чунки бу матрицанинг барча элементи умумий
га
б¢линади ва х.к. (чунки бу матрицанинг барча элементи умумий ![]() к¢пайтувчига
эга). Шунинг учун барча инвариант к¢пайтувчилар
к¢пайтувчига
эга). Шунинг учун барча инвариант к¢пайтувчилар
![]()
![]() га б¢линади,
яъни хар бир
га б¢линади,
яъни хар бир ![]() инвариант
к¢пайтувчи хеч б¢лмаганда битта нол илдизга эга б¢лади. (7.5.10)
формуладан фойдаланиб, куйидагини ёзамиз:
инвариант
к¢пайтувчи хеч б¢лмаганда битта нол илдизга эга б¢лади. (7.5.10)
формуладан фойдаланиб, куйидагини ёзамиз:
![]()
Бу тенгламанинг чап тарафи камида ![]() та
нолинчи илдизга эга, ¢нг тарафида турган
та
нолинчи илдизга эга, ¢нг тарафида турган ![]() та инвариант
к¢пайтувчининг хеч б¢лмаганда биттаси карраси бирдан катта нол илдизга
эга б¢лади.
та инвариант
к¢пайтувчининг хеч б¢лмаганда биттаси карраси бирдан катта нол илдизга
эга б¢лади.
Бу хол тизимнинг нотургунлигини
исботлайди, чунки хеч б¢лмаганда битта хакикий кисми нолга тенг илдиз, мос
элементар б¢лувчининг каррали илдизи б¢лса (![]() ), у вактда
топилмаган харакат нотургун б¢лади.
), у вактда
топилмаган харакат нотургун б¢лади.
1-изох. Агар тизимга факат
гироскопик кучлар таъсир этиб, у ток сондаги координаталарга эга б¢лса, у
вактда бундай тизимнинг тойилмаган харакати доимо нотургун б¢лади (агар ![]() ток
сон б¢лса, у холда
ток
сон б¢лса, у холда ![]() )
)
2-изох. ![]() нинг
исталган кийматида тойилмаган харакат тезликларга нисбатан тургун
б¢лганлиги учун тизим нотургунлигининг исботидан
нинг
исталган кийматида тойилмаган харакат тезликларга нисбатан тургун
б¢лганлиги учун тизим нотургунлигининг исботидан ![]() б¢лганда
тизим факат координата б¢йига тургунликни й¢котиши келиб чикади.
б¢лганда
тизим факат координата б¢йига тургунликни й¢котиши келиб чикади.
3-изох. Агар ![]() б¢лса,
тизимнинг характеристик детерминанти
б¢лса,
тизимнинг характеристик детерминанти ![]() та нолинчи илдизга
эга б¢лади. Тизим тургунлигидан элементар б¢лувчилар учун бу илдизларнинг
оддийлиги келиб чикади.
та нолинчи илдизга
эга б¢лади. Тизим тургунлигидан элементар б¢лувчилар учун бу илдизларнинг
оддийлиги келиб чикади.
4-изох. (7.5.1) тенглама
к¢п холларда ночизикли тизимнинг гироскопик кучлар таъсири остидаги
биринчи якинлашиш тенгламасини ифода этади. Албатта, ![]() б¢лган
холда биринчи якинлашиш тенгламалари оркали аникланган тизимнинг тургунлигидан
дастлабки ночизикли тизимнинг тургунлиги келиб чикади.
б¢лган
холда биринчи якинлашиш тенгламалари оркали аникланган тизимнинг тургунлигидан
дастлабки ночизикли тизимнинг тургунлиги келиб чикади.
5.2.Гироскопик ва диссипатив кучлар
Диссипатив кучларнинг тизимга таъсирини ¢рганишдан олдин детерминантлар назариясининг биз учун зарур буладиган бир натижасини келтирамиз.
![]() тартибли иккита
тартибли иккита ![]() ва
ва
![]() квадрат матрица
берилган б¢лсин.
квадрат матрица
берилган б¢лсин.
Бунда ![]() аник ишорали
диагонал ва
аник ишорали
диагонал ва ![]() кийшик симметрик
матрица деб оламиз.
кийшик симметрик
матрица деб оламиз. ![]() матрицанинг детерминантини
тузамиз
матрицанинг детерминантини
тузамиз
![]() .
.
У вактда куйидаги тасдиклар ¢ринлидир:
1. ![]() матрица хосмас
матрицадир, яъни
матрица хосмас
матрицадир, яъни
![]() (7.5.13)
(7.5.13)
2. Агар ![]() матрица аник-манфий
ишорали б¢лса, у холда
матрица аник-манфий
ишорали б¢лса, у холда
![]() (7.5.14)
(7.5.14)
3. Агар ![]() матрица аник-мусбат
ишорали б¢лса, у вактда
матрица аник-мусбат
ишорали б¢лса, у вактда
![]() -жуфт
б¢лганда
-жуфт
б¢лганда ![]() , (7.5.15)
, (7.5.15)
![]() -ток
б¢лганда
-ток
б¢лганда ![]() .
(7.5.16)
.
(7.5.16)
Энди диссипатив кучларнинг таъсирини ¢рганамиз.
3-теорема. Агар тизимга гироскопик кучлардан ташкари т¢лик дисспацияли диссипатив кучлар хам таъсир этса, у вактда тойилмаган харакат тезликларга нисбатан асимптотик тургун ва координаталарга нисбатан тургун б¢лади.
Исбот. Теореманинг шартига асосан факат гироскопик ва т¢лик диссипацияли кучлар мавжудлигини хисобга олиб, тойилган харакат дифференциал тенгламаларни (7.1.17) к¢ринишга келтирамиз:
![]() (7.5.17)
(7.5.17)
Бу тенгламада ![]() - аник-мусбат
ишорали диагонал матрица,
- аник-мусбат
ишорали диагонал матрица, ![]() -кийшик симметрик
матрица. Бу тенгламанинг иккала тарафини хам ¢нг томондан
-кийшик симметрик
матрица. Бу тенгламанинг иккала тарафини хам ¢нг томондан ![]() матрицага
к¢пайтирамиз:
матрицага
к¢пайтирамиз:
![]()
сунгра биринчи к¢шилувчини
узгартириб ва ![]() эканлигини хисобга
олиб, уни
эканлигини хисобга
олиб, уни
![]()
к¢ринишда ёзамиз. Бу тенгламани скаляр к¢ринишда куйидагича ёзиш мумкин.
![]() .
.
![]()
функция асимптотик тургунлик
хакидаги Ляпунов теоремасининг шартларини каноатлантиради – у ![]() тезликларга
нисбатан аник-мусбат ишорали хамда вакт б¢йича (7.5.17) тенгламаларга
нисбатан олинган т¢лик хосиласи
тезликларга
нисбатан аник-мусбат ишорали хамда вакт б¢йича (7.5.17) тенгламаларга
нисбатан олинган т¢лик хосиласи ![]() тезликларнинг аник-манфий
ишорали функциясидир (теорема шартига асосан диссипация т¢лик ва, демак,
барча
тезликларнинг аник-манфий
ишорали функциясидир (теорема шартига асосан диссипация т¢лик ва, демак,
барча ![]() ). Шундай килиб, харакат
). Шундай килиб, харакат
![]() тезликларга
нисбатан асимптотик тургун б¢лади.
тезликларга
нисбатан асимптотик тургун б¢лади.
Теореманинг иккинчи кисмини исботлашга ¢тамиз. (7.5.17) тенгламани бир марта вакт б¢йича интеграллаймиз:
![]() ,
(7.5.18)
,
(7.5.18)
бу ерда ¢згармас матрица ![]() куйидаги
тенглик билан аникланади
куйидаги
тенглик билан аникланади
![]() .
(7.5.19)
.
(7.5.19)
(7.5.13) муносабатга асосан ![]() матрица
хосмас, демак, тескари матрица
матрица
хосмас, демак, тескари матрица ![]() мавжуд.
мавжуд.
![]() (7.5.20)
(7.5.20)
тенглик билан аникланадиган
янги ![]() ¢згарувчи
матрица киритамиз, у холда (7.5.18) тенглама куйидаги к¢ринишга келади
¢згарувчи
матрица киритамиз, у холда (7.5.18) тенглама куйидаги к¢ринишга келади
![]() ,
,
сунгра ![]() эканлигини хисога
олиб,
эканлигини хисога
олиб,
![]() (7.5.21)
(7.5.21)
ни хосил киламиз.
Теореманинг биринчи кисмига асосан ![]() тезликларга
нисбатан харакат асимптотик тургун. (7.5.17) ва (7.5.21) тенгламалар бир хил куринишда
эканлигидан харакатнинг у га нисбатан асимптотик тургунлиги келиб чикади.
(7.5.20) ва (7.5.19) тенгликларга асосан харакат z
га нисбатан тургун (асимптотик тургун эмас) деган хулосага келамиз.
тезликларга
нисбатан харакат асимптотик тургун. (7.5.17) ва (7.5.21) тенгламалар бир хил куринишда
эканлигидан харакатнинг у га нисбатан асимптотик тургунлиги келиб чикади.
(7.5.20) ва (7.5.19) тенгликларга асосан харакат z
га нисбатан тургун (асимптотик тургун эмас) деган хулосага келамиз.
Изох. В.М.Матросов 1959 йилда ушбу теорема ночизикли тизимлар учун хам ¢з кучини саклашини исбот килди [59].
Мисол. ¡згармас магнит майдонида электрон харакатнинг тургунлигини тадкик этиш
![]() б¢лганда
электрон харакатнинг тенгламаси куйидаги к¢ринишда б¢лади:
б¢лганда
электрон харакатнинг тенгламаси куйидаги к¢ринишда б¢лади:
![]() .
(7.5.22)
.
(7.5.22)
Бу ерда ![]() -электрон
тезлигининг вектори,
-электрон
тезлигининг вектори, ![]() -электрон
массаси,
-электрон
массаси, ![]() -унинг
заряди,
-унинг
заряди, ![]() -ёруглик
тезлигига тенг б¢лган электродинамик ¢згармас сон (
-ёруглик
тезлигига тенг б¢лган электродинамик ¢згармас сон (![]() ),
),
![]() -магнит
майдонининг кучланганлиги [90].
-магнит
майдонининг кучланганлиги [90].
К¢згалмас координаталар тизимининг ¢клари б¢йича бу тенгламанинг проекцияларини ёзамиз:
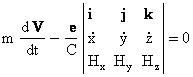 .
.
Бу ердан
 (7.5.23)
(7.5.23)
ни хосил киламиз.
Бу тенгликларда ![]() тезликларга
нисбатан чизикли богланган кучлар матрицаси
тезликларга
нисбатан чизикли богланган кучлар матрицаси

кийшик симметрикдир. Демак,
бу кучлар гироскопик кучлардир. Бошка кучлар мавжуд эмас. Демак, 1-теоремага
асосан электроннинг тойилмаган харакати ![]() тезликларга
нисбатан тургун б¢лади ва 2-теореманинг изохига асосан электроннинг
тойилмаган харакати
тезликларга
нисбатан тургун б¢лади ва 2-теореманинг изохига асосан электроннинг
тойилмаган харакати ![]() координаталар
б¢йича нотургун б¢лади (координаталар сони 3 та (ток сон)
б¢лганлиги учун).
координаталар
б¢йича нотургун б¢лади (координаталар сони 3 та (ток сон)
б¢лганлиги учун).
Агар ![]() ¢кини
¢кини ![]() векторига
параллель килиб ¢тказсак, у холда
векторига
параллель килиб ¢тказсак, у холда ![]() ва (7.5.23) тенгламалар
куйидаги к¢ринишга келади:
ва (7.5.23) тенгламалар
куйидаги к¢ринишга келади:

Биринчи ва иккинчи тенгламалар учинчисига боглик эмас. Шунинг учун уларни алохида к¢рамиз. Бу тенгламалар учун гироскопик коэффициентлар матрицасининг детерминанти

нолдан фарк килади. Шунинг
учун хам 2-теоремага асосан электроннинг харакати ![]() ва
ва ![]() координаталарга
нисбатан тургун б¢лади. Учинчи тенгламадан
координаталарга
нисбатан тургун б¢лади. Учинчи тенгламадан ![]() келиб чикади ва бу
ердан
келиб чикади ва бу
ердан ![]() координата
б¢йича харакатнинг нотургунлиги келиб чикади.
координата
б¢йича харакатнинг нотургунлиги келиб чикади.
6-§. Харакатнинг тургунлигига ноконсерватив
кучларнинг таъсири
6.1.Факат ноконсерватив кучлар таъсиридаги харакат
Дастлаб тизимнинг харакати факат
ноконсерватив кучлар таъсири остида содир б¢лади деб фараз киламиз, бу холда
координаталарга нисбатан чизикли богланган ноконсерватив ![]() кучларнинг
кучларнинг
![]() матрицаси
симметрик б¢лади.
матрицаси
симметрик б¢лади.
1-теорема. Биргина
ноконсерватив кучлар таъсири остидаги тизимнинг ![]() тойилмаган харакати,
ночизикли хадларнинг кандай б¢лишидан катъий назар, нотургун б¢лади.
тойилмаган харакати,
ночизикли хадларнинг кандай б¢лишидан катъий назар, нотургун б¢лади.
Исбот. Теореманинг шартлари
б¢йича тойилмаган харакат тенгламасини (7.1.16) к¢ринишга келтириш мумкин
(![]() ):
):
![]() (7.6.1)
(7.6.1)
Бу ерда ![]() -кийшик симметрик
матрица,
-кийшик симметрик
матрица, ![]() - элементлари
- элементлари ![]() ва
ва
![]() ларнинг биринчидан
юкори даражаларидан иборат устун-матрица ва
ларнинг биринчидан
юкори даражаларидан иборат устун-матрица ва ![]() .
.
![]() (7.6.2)
(7.6.2)
характеристик тенгламани
к¢рамиз. (7.5.1) ![]() тизимнинг тезликларга
нисбатан тургунлигидан
тизимнинг тезликларга
нисбатан тургунлигидан
![]()
тенгламанинг ((7.5.7) тенглама) нолга тенг б¢лмаган илдизлари соф мавхум сонлардир. Бу
![]() (7.6.3)
(7.6.3)
тенгламанинг нолдан фаркли
илдизлари ![]() к¢ринишида
б¢лади демакдир, бу ерда
к¢ринишида
б¢лади демакдир, бу ерда ![]() -мусбат хакикий
сон.
-мусбат хакикий
сон. ![]() эканлигини
осонгина к¢рсатиш мумкин. Демак, агар
эканлигини
осонгина к¢рсатиш мумкин. Демак, агар ![]()
![]() нинг
илдизи б¢лса, у холда
нинг
илдизи б¢лса, у холда ![]() хам бу
тенгламанинг илдизи б¢лади. Шунинг учун хам агар хакикий кисми нолдан фаркли
илдиз мавжуд б¢лса, у вактда хакикий кисми мусбат б¢лган илдиз мавжуд
б¢лиши керак. Бу харакатнинг нотургунлигини к¢рсатади.
хам бу
тенгламанинг илдизи б¢лади. Шунинг учун хам агар хакикий кисми нолдан фаркли
илдиз мавжуд б¢лса, у вактда хакикий кисми мусбат б¢лган илдиз мавжуд
б¢лиши керак. Бу харакатнинг нотургунлигини к¢рсатади.
(7.6.2) тенглама (7.6.3) тенгламадан ![]() ни
ни
![]() га (P матрицаси худди G матрицаси сингари
кийшик симметрик матрицадир) алмаштириш натижасида б¢лади. Шунинг учун
(7.6.2) тенгламанинг
га (P матрицаси худди G матрицаси сингари
кийшик симметрик матрицадир) алмаштириш натижасида б¢лади. Шунинг учун
(7.6.2) тенгламанинг ![]() га нисбатан нолга
тенг б¢лмаган илдизлари
га нисбатан нолга
тенг б¢лмаган илдизлари
![]()
к¢ринишдадир.
Бу ердан
![]()
ни топамиз.
Шундай килиб, (7.6.2) характеристик тенгламанинг илдизлари орасида хакикий кисми мусбат б¢лган илдизлар мавжуд.
Демак, ![]() тойилмаган харакат
нотургундир.
тойилмаган харакат
нотургундир.
6.2. Ноконсерватив ва потенциал кучлар
таъсиридаги харакат
Энди тизимга бир вактда потенциал ва ноконсерватив кучлар таъсир этаётган холни к¢риб ¢тайлик. Тойилмаган харакат тенгламасини (7.1.16) к¢ринишда оламиз:
![]() ,
,
бу ерда ![]() -диагонал,
-диагонал, ![]() -кийшик
симметрик матрицалар. Характеристик тенглама
-кийшик
симметрик матрицалар. Характеристик тенглама
![]()
к¢ринишда б¢лади. ![]() бу
тенгламада квадрати билан катнашаётганлигидан детерминантнинг ёйилмаси
бу
тенгламада квадрати билан катнашаётганлигидан детерминантнинг ёйилмаси
![]() (7.6.4)
(7.6.4)
к¢ринишда б¢лади. Бу тенгламада
![]() .
(7.6.5)
.
(7.6.5)
(7.6.4) тенгламанинг чап тарафи ![]() ни -
ни -![]() га алмаштириш билан ¢згармайди. Шунинг учун бу тенгламанинг
га алмаштириш билан ¢згармайди. Шунинг учун бу тенгламанинг ![]() га
нисбатан барча илдизлари соф мавхум ва
га
нисбатан барча илдизлари соф мавхум ва ![]() нисбатан хакикий
манфий сон б¢лишлари зарур.
нисбатан хакикий
манфий сон б¢лишлари зарур.
Бу параграфнинг 1-теоремасига асосан тизим
консерватив кучларсиз (![]() ) нотургун. Шунинг
учун тургун потенциал тизимга ноконсерватив кучларни к¢шиш билан айрим холларда
тургунликни бузиш мумкин деган фикрга бориш мумкин. Ноконсерватив кучлар потенциал
тизимнинг тургунлигини бузиш, билан бир каторда нотургун потенциал тизимни
стабиллаштириши хам мумкинлигини мисолда к¢рсатамиз.
) нотургун. Шунинг
учун тургун потенциал тизимга ноконсерватив кучларни к¢шиш билан айрим холларда
тургунликни бузиш мумкин деган фикрга бориш мумкин. Ноконсерватив кучлар потенциал
тизимнинг тургунлигини бузиш, билан бир каторда нотургун потенциал тизимни
стабиллаштириши хам мумкинлигини мисолда к¢рсатамиз.
Икки эркинлик даражасига эга б¢лган тизимни к¢риб ¢тайлик. Тойилган харакат тенгламаси куйидаги к¢ринишга келтирилган б¢лсин:
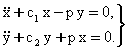 (7.6.6)
(7.6.6)
Бу тенгламаларни
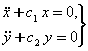 (7.6.7)
(7.6.7)
потенциал тизимга
ноконсерватив куч - ![]() ва
ва
![]()
кийшик симметрик матрицали ![]() кучни
к¢шиш натижасида хосил б¢лган деб караш мумкин.
кучни
к¢шиш натижасида хосил б¢лган деб караш мумкин.
(7.6.6) тизимнинг характеристик тенгламасини тузамиз:
![]() .
(7.6.8)
.
(7.6.8)
Агар иккала илдиз хам ![]() га
нисбатан хакикий ва манфий б¢лса, у холда тизим тургун б¢лади. Бунинг
учун (7.6.8) тенгламаларнинг коэффициентлари ва дискриманти нолдан катта
б¢лишини талаб килиш зарур:
га
нисбатан хакикий ва манфий б¢лса, у холда тизим тургун б¢лади. Бунинг
учун (7.6.8) тенгламаларнинг коэффициентлари ва дискриманти нолдан катта
б¢лишини талаб килиш зарур:
![]() .
.
Кейинги тенгсизликни соддалаштириб, тургунлик шартларини куйидаги холга келтирамиз:
![]() .
(7.6.9)
.
(7.6.9)
![]() б¢лганда,
яъни ноконсерватив кучлар катнашмаганда, бу шартлар
б¢лганда,
яъни ноконсерватив кучлар катнашмаганда, бу шартлар ![]() ларга
айланади. Бу тенгсизликларни бевосита (7.6.7) тенгламалардан хам хосил килиш
мумкин.
ларга
айланади. Бу тенгсизликларни бевосита (7.6.7) тенгламалардан хам хосил килиш
мумкин. ![]() ва
ва ![]() параметрлар
текислигида потенциал тизимнинг тургунлик сохаси тулик биринчи квадрантни
эгаллайди.
параметрлар
текислигида потенциал тизимнинг тургунлик сохаси тулик биринчи квадрантни
эгаллайди. ![]() б¢лгандаги тургунлик
сохаси 7.6-шаклда к¢рсатилган. Тургунлик сохасининг чегараси (1) т¢гри
чизик,
б¢лгандаги тургунлик
сохаси 7.6-шаклда к¢рсатилган. Тургунлик сохасининг чегараси (1) т¢гри
чизик, ![]() гиперболанинг
тармоклари хамда гиперболанинг учларига уриниб ¢тадиган (2) ва (3) (
гиперболанинг
тармоклари хамда гиперболанинг учларига уриниб ¢тадиган (2) ва (3) (![]() )
т¢гри чизиклардан иборат. Расмдан к¢риниб турибдики, потенциал тизим
тургунлик сохасининг анча кисми ноконсерватив кучларни к¢шганимиздан кейин
нотургунлик сохасига ((2) ва (3) т¢гри чизиклар орасидаги соха) айланади.
Расмдан яна к¢ринаяптики, каралаётган (7.6.6) тизимнинг тургунлик сохасининг
бир кисми иккинчи ва т¢ртинчи квадрантларда жойлашган, у ерда потенциал
(7.6.7) тизим нотургун. Шундай килиб, ноконсерватив кучлар потенциал тизим тургунлигини
бузиши мумкин ва айрим холларда улар потенциал тизимни стабиллаштириши хам
мумкин.
)
т¢гри чизиклардан иборат. Расмдан к¢риниб турибдики, потенциал тизим
тургунлик сохасининг анча кисми ноконсерватив кучларни к¢шганимиздан кейин
нотургунлик сохасига ((2) ва (3) т¢гри чизиклар орасидаги соха) айланади.
Расмдан яна к¢ринаяптики, каралаётган (7.6.6) тизимнинг тургунлик сохасининг
бир кисми иккинчи ва т¢ртинчи квадрантларда жойлашган, у ерда потенциал
(7.6.7) тизим нотургун. Шундай килиб, ноконсерватив кучлар потенциал тизим тургунлигини
бузиши мумкин ва айрим холларда улар потенциал тизимни стабиллаштириши хам
мумкин.
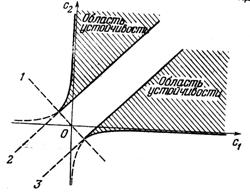 |
7.6-шакл.
Икки эркинлик даражасига эга б¢лган
бу мисолдан к¢ринадики, агар Пуанкаре коэффициентлари ![]() ва
ва ![]() лар
тенг б¢лса (
лар
тенг б¢лса (![]() ), у вактда хар кандай
к¢шилган -
), у вактда хар кандай
к¢шилган -![]() ва
ва ![]() ноконсерватив
кучлар потенциал тизимнинг тургунлигини бузадилар. Ихтиёрий эркинлик даражасида
ва барча
ноконсерватив
кучлар потенциал тизимнинг тургунлигини бузадилар. Ихтиёрий эркинлик даражасида
ва барча ![]() Пуанкаре коэффициентларининг
тенглигида
Пуанкаре коэффициентларининг
тенглигида ![]() хар кандай
ноконсерватив кучларнинг к¢шилиши потенциал тизим тургунлигини бузишини
к¢рсатиш мумкин. Эслатиб ¢тамиз, тургун потенциал тизим учун Пуанкаренинг
тургунлик коэффициентлари
хар кандай
ноконсерватив кучларнинг к¢шилиши потенциал тизим тургунлигини бузишини
к¢рсатиш мумкин. Эслатиб ¢тамиз, тургун потенциал тизим учун Пуанкаренинг
тургунлик коэффициентлари ![]() тизим хусусий
тебранишлар частотасининг квадратига тенг б¢лади. Шунинг учун хусусий
частоталари тенг б¢лган тургун потенциал тизимга ноконсерватив кучлар к¢шилганда
тизимнинг тургунлиги бузилади. Тургунликнинг бузилиш сабаби характеристик
тенглама илдизлари орасида хакикий кисми мусбат б¢лган илдизларнинг пайдо
б¢лишидир. Шунинг учун тургунликни хатто ночизикли кучлар ёрдами билан хам
тиклаш мумкин эмас.
тизим хусусий
тебранишлар частотасининг квадратига тенг б¢лади. Шунинг учун хусусий
частоталари тенг б¢лган тургун потенциал тизимга ноконсерватив кучлар к¢шилганда
тизимнинг тургунлиги бузилади. Тургунликнинг бузилиш сабаби характеристик
тенглама илдизлари орасида хакикий кисми мусбат б¢лган илдизларнинг пайдо
б¢лишидир. Шунинг учун тургунликни хатто ночизикли кучлар ёрдами билан хам
тиклаш мумкин эмас.
6.3. Ноконсерватив, потенциал ва диссипатив кучлар
таъсиридаги харакат
Энди потенциал ва ноконсерватив кучларга
таъсир этаётган тизимга диссипатив кучларни к¢шганимизда тургунликнинг
¢згаришини к¢риб ¢тайлик. Бунинг учун (7.6.6) тизимга ![]() ва
ва
![]() кучларни к¢шамиз,
бу ерда
кучларни к¢шамиз,
бу ерда ![]() ва
ва ![]() мусбат
сонлар:
мусбат
сонлар:
 (7.6.10)
(7.6.10)
Тизимнинг характеристик тенгламаси

к¢ринишга эга. Детерминантни ёйиб, соддалаштирганимиздан кейин
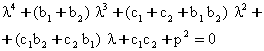
ни хосил киламиз. Бу тенглама учун Гурвиц критериясини ёзамиз:
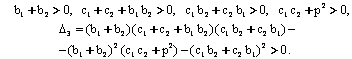 (7.6.11)
(7.6.11)
Охирги тенгсизликни
![]() (7.6.12)
(7.6.12)
к¢ринишга келтирамиз.
Диссипатив кучлар баъзи шартлар
бажарилганда нотургун (7.6.6) тизимни стабиллаштириш мумкинлигини
к¢рсатамиз. Хакикатан хам, ![]() б¢лганда
Гурвиц критерияси (7.6.11)
б¢лганда
Гурвиц критерияси (7.6.11)
![]()
к¢ринишда б¢лади.
Фаразимиз б¢йича ![]() .
Шунинг учун биринчи т¢ртта тенгсизлик уз-узидан бажарилади, охирги тенгсизлик
эса диссипатив кучлар
.
Шунинг учун биринчи т¢ртта тенгсизлик уз-узидан бажарилади, охирги тенгсизлик
эса диссипатив кучлар
![]() (7.6.13)
(7.6.13)
шартни каноатлантирганда бажарилади.
Шундай килиб, потенциал ва ноконсерватив
кучлар таъсири остидаги нотургун тизимни (![]() б¢лганда харакат
доимо нотургун (7.6-шакл)га каранг) диссипатив кучлар оркали стабиллаштириш
мумкин.
б¢лганда харакат
доимо нотургун (7.6-шакл)га каранг) диссипатив кучлар оркали стабиллаштириш
мумкин.
Диссипатив коэффициентлар ![]() б¢лганда
(7.6.6) тургун система хар кандай
б¢лганда
(7.6.6) тургун система хар кандай ![]() киймат учун
асимптотик тургун б¢лади. -Хакикатдан хам, бу холда Гурвиц критерияси,
киймат учун
асимптотик тургун б¢лади. -Хакикатдан хам, бу холда Гурвиц критерияси,

(7.6.6) тизимнинг тургун б¢лишининг шарти
(7.6.9) га асосан, уз-узидан бажарилади. Бу натижа тизим ночизикли
б¢лганда хам ¢з кучини саклайди (чунки ![]() ).
).
Энди потенциал ва нокосерватив кучлар
таъсири остидаги тизимнинг тургунлигини диссипатив кучлар бузиб юборишини
к¢рамиз. Хакикатдан хам, (7.6.9) тургунлик шарти бажарилсин. ![]() ва
ва
![]() деб фараз киламиз.
У холда (7.6.12) шарт
деб фараз киламиз.
У холда (7.6.12) шарт
![]()
к¢ринишга келади,
демак, тизим нотургундир. ![]() ,
, ![]() хол
т¢ликсиз диссипацияга мос келади. Аммо, олинган натижа т¢лик
диссипация б¢лган хол учун хам ¢з кучини саклайди.
хол
т¢ликсиз диссипацияга мос келади. Аммо, олинган натижа т¢лик
диссипация б¢лган хол учун хам ¢з кучини саклайди.
6.4.Умумий хол
Умумий холни к¢ришга ¢тамиз, яъни тизимга бирданига потенциал, гироскопик, диссипатив, ноконсерватив тезлатувчи ва ночизикли кучлар таъсир этади деб фараз киламиз.
Харакат тенгламасини (7.1.17) к¢ринишда оламиз:
![]() .
(7.6.14)
.
(7.6.14)
(7.6.14) нинг характеристик тенгламасини топамиз:
![]() (7.6.15)
(7.6.15)
уни ёйиб ёзсак
![]()
к¢ринишга келади. ![]() ва
ва ![]() параметрларни
киритамиз ва куйидаги ёрдамчи тенгламани караймиз:
параметрларни
киритамиз ва куйидаги ёрдамчи тенгламани караймиз:
![]() . (7.6.16)
. (7.6.16)
(7.6.15) тенглама (7.6.16) тенгламадан ![]() б¢лганда
хосил б¢лади, яъни
б¢лганда
хосил б¢лади, яъни ![]() .
.
(7.6.16) детерминантни куйидаги к¢ринишда ёзамиз:
![]() =
(7.6.17)
=
(7.6.17)
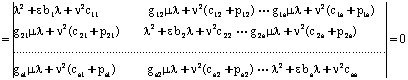
бу
ерда ![]() ёки матрица формасида
ёки матрица формасида
![]() , (7.6.18)
, (7.6.18)
каерда
штрих транспонирлаш белгисини билдиради. (7.6.17) детерминантни очиб, ![]() даражаси
буйича гурухлаб чикамиз:
даражаси
буйича гурухлаб чикамиз:
![]() . (7.6.19)
. (7.6.19)
![]() коэффициентлар
коэффициентлар
![]() параметрларнинг
бутун рационал функциялари ва
параметрларнинг
бутун рационал функциялари ва ![]() . (7.6.17) детерминант
. (7.6.17) детерминант
![]() параметрларга
нисбатан биржинсли, шунинг учун хам
параметрларга
нисбатан биржинсли, шунинг учун хам ![]() да
да ![]() ва
ва
![]() ларнинг даража курсаткичлари
йигиндиси
ларнинг даража курсаткичлари
йигиндиси ![]() га тенг булиши керак.
(7.6.19) характеристик тенглама коэффициентлари [61]:
га тенг булиши керак.
(7.6.19) характеристик тенглама коэффициентлари [61]:
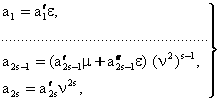 (7.6.20)
(7.6.20)
куринишга эга,
бу
ерда ![]() ва
ва ![]() лар ва
лар ва ![]() ларнинг функциялари ва уларнинг ифодаларида
ларнинг функциялари ва уларнинг ифодаларида ![]() ва
ва
![]() параметрлар катнашмайди.
параметрлар катнашмайди.
 (7.6.21)
(7.6.21)
Бу тенгликлардан фойдаланиб, харакат тургунлигининг зарурий шартларини ифодалайдиган теоремаларни осонгина исботлаш мумкин [61].
2-теорема.
Ночизикли хадлар мавжуд булмаганда ![]() , диссипатив кучларсиз тизим асимптотик тургун булаолмайди.
, диссипатив кучларсиз тизим асимптотик тургун булаолмайди.
Исбот.
Теорема шартлари буйича ![]() (
(![]() коэффициентлари нафакат диссипатив кучларни, балки
тезлатувчи кучларни хам характерлайди ва тезлатувчи кучлар учун
коэффициентлари нафакат диссипатив кучларни, балки
тезлатувчи кучларни хам характерлайди ва тезлатувчи кучлар учун ![]() ). Демак, Гурвиц шартлари бажарилмайди ва тизим
асимптотик тургун булмайди.
). Демак, Гурвиц шартлари бажарилмайди ва тизим
асимптотик тургун булмайди.
3-теорема.
Агар ![]() (координатага чизикли богланган кучларнинг коэффициентларидан
тузилган детерминант манфий) булса, у холда тизим хар кандай гироскопик,
диссипатив, тезлатувчи ва ночизикли кучлар таъсирида нотургун булади.
(координатага чизикли богланган кучларнинг коэффициентларидан
тузилган детерминант манфий) булса, у холда тизим хар кандай гироскопик,
диссипатив, тезлатувчи ва ночизикли кучлар таъсирида нотургун булади.
Исбот.
Бу холда ![]() га тенг булган (7.6.15) тенгламанинг озод хади манфий
булади
га тенг булган (7.6.15) тенгламанинг озод хади манфий
булади ![]() ва, демак, характеристик тенглама илдизлари орасида хеч
булмаганда битта илдизнинг хакикий кисми мусбат булади. Шунинг учун нотургунлик
хакидаги Ляпунов теоремасига асосан тизим нотургун булади.
ва, демак, характеристик тенглама илдизлари орасида хеч
булмаганда битта илдизнинг хакикий кисми мусбат булади. Шунинг учун нотургунлик
хакидаги Ляпунов теоремасига асосан тизим нотургун булади.
1-изох.
![]() нинг ишорасини (7.1.5) тенглама оркали аниклаш осонрок
булади.
нинг ишорасини (7.1.5) тенглама оркали аниклаш осонрок
булади.
2-изох.
Томсон ва Тетнинг 1-теоремаси ушбу
теореманинг натижаси булади. Хакикатан хам, агар нотургун консерватив тизим ![]() ток даражага эга булса, у вактда
ток даражага эга булса, у вактда ![]() булади.
булади.
4-теорема.
Агар тизимга консерватив ва ночизикли
кучлар таъсир этмаса ![]() , у вактда
, у вактда
1) координаталар сони ток булган холда хеч кандай гироскопик, диссипатив, тезлатувчи ва ноконсерватив кучлар таъсири билан тизимни асимптотик тургун килиш мумкин эмас;
2) координаталар сони жуфт булган холда тизимни асимптотик тургун килиш учун диссипатив кучлардан ташкари гироскопик кучларни хам кушиш зарур.
Исбот.
Агар консерватив кучлар йук ![]() ва координаталар сони ток булса, у холда
ва координаталар сони ток булса, у холда ![]() (ток тартибли кийшик симметрик матрицанинг детерминанти
булганлиги учун). (7.6.21) нинг охирги тенглигига асосан (7.6.19) характеристик
тенгламанинг озод хади нолга тенг булади ва, демак, асимптотик тургунлик учун
зарур булган Гурвиц критерияси бажарилмайди. Шундай килиб, тизим асимптотик тургун
булмайди.
(ток тартибли кийшик симметрик матрицанинг детерминанти
булганлиги учун). (7.6.21) нинг охирги тенглигига асосан (7.6.19) характеристик
тенгламанинг озод хади нолга тенг булади ва, демак, асимптотик тургунлик учун
зарур булган Гурвиц критерияси бажарилмайди. Шундай килиб, тизим асимптотик тургун
булмайди.
Теореманинг
иккинчи кисмини исбот килишдан олдин шуни таъкидлаймизки, 2-теоремага асосан
диссипатив кучларни кушиш зарур. Гироскопик кучлар кушилмаганда ![]() асимптотик тургунлик булмаслигини курсатамиз. Хакикатан
хам, бу холда (7.6.16) тенглама ва (7.6.21) даги
асимптотик тургунлик булмаслигини курсатамиз. Хакикатан
хам, бу холда (7.6.16) тенглама ва (7.6.21) даги ![]() коэффициент (
коэффициент (![]() деб фараз киламиз):
деб фараз киламиз):
 (7.6.22)
(7.6.22)
куринишда булади.
![]() детерминантда
сатрларни устунларга алмаштирамиз (бундан детерминантнинг киймати узгармайди):
детерминантда
сатрларни устунларга алмаштирамиз (бундан детерминантнинг киймати узгармайди):
![]() .
(7.6.23)
.
(7.6.23)
![]() ларни
хисобга олиб,
ларни
хисобга олиб,
![]()
хосил
киламиз, яъни ![]() . Демак,
. Демак, ![]() сони
(7.6.22) тенгламаларда жуфт даражаси билан катнашади. Бунга асосланиб шундай
хулосага келамиз:
сони
(7.6.22) тенгламаларда жуфт даражаси билан катнашади. Бунга асосланиб шундай
хулосага келамиз: ![]() жуфт сон булганда
жуфт сон булганда ![]() коэффициент
ва у билан бирга
коэффициент
ва у билан бирга ![]() нолга тенг булади,
демак, Гурвиц критерияси бажарилмайди ва тизим харакати асимптотик тургун булмайди.
нолга тенг булади,
демак, Гурвиц критерияси бажарилмайди ва тизим харакати асимптотик тургун булмайди.
Демак, харакатни асимптотик тургун килиш учун диссипатив кучлар билан биргаликда гироскопик кучлар хам тизимга таъсир килиши керак.
5-теорема. Агар тойилган харакатнинг потенциал энергияси максимумга эга булса, у вактда
1) координаталар сони ток булган холда, тизимга таъсир этаётган ночизикли кучлар кандай булишидан катъий назар, тизим харакатини хеч кандай гироскопик, диссипатив, тезлатувчи ва ноконсерватив кучлар билан стабиллаштириш мумкин эмас;
2) координаталар сони жуфт ва тизим тулик диссипацияли кучлар таъсирида булганда уни стабиллаштириш учун ночизикли кучлар кандай булишидан катъий назар бир вактда гироскопик ва ноконсерватив кучларни кушиш зарур.
Исбот. Тойилган харакат тенгламасини (7.1.18) куринишда оламиз:
![]() . (7.6.24)
. (7.6.24)
(7.6.24) тенгламанинг характеристик тенгламасини тузамиз:
![]() . (7.6.25)
. (7.6.25)
Детерминантни
ёйиб, ![]() нинг даражалари буйича
гурухлаб чикамиз
нинг даражалари буйича
гурухлаб чикамиз
![]() (7.6.26)
(7.6.26)
(7.6.26)
тенгламанинг ![]() озод хадини
((7.6.25) да
озод хадини
((7.6.25) да ![]() тенглаштириб)
топамиз:
тенглаштириб)
топамиз:
![]() .
.
Теореманинг
шартига асосан ![]() диагонал
матрицанинг барча элементлари манфий (потенциал энергия максималга эга) ва
диагонал
матрицанинг барча элементлари манфий (потенциал энергия максималга эга) ва ![]() кийшик
симметрик матрица.
кийшик
симметрик матрица.
Агар
![]() кийшик симметрик
матрица ва
кийшик симметрик
матрица ва ![]() аник-мусбат
ишорали матрица булса, у вактда
аник-мусбат
ишорали матрица булса, у вактда
![]() -
жуфт булганда
-
жуфт булганда ![]() ,
,
![]() -
ток булганда
-
ток булганда ![]()
булишини олдин курган эдик.
Шунга
асосан ток сонли координаталар учун ![]() . Демак, характеристик
тенглама илдизлари орасида хеч булмаганда хакикий кисми мусбат булган битта
илдиз мавжуд. Ноконсерватив, диссипатив ва тезлатувчи кучларнинг озод хад
. Демак, характеристик
тенглама илдизлари орасида хеч булмаганда хакикий кисми мусбат булган битта
илдиз мавжуд. Ноконсерватив, диссипатив ва тезлатувчи кучларнинг озод хад ![]() ишорасига
таъсири йуклигидан улар воситасида тизим харакатини стабиллаштириш мумкин эмаслиги
келиб чикади, яъни теореманинг биринчи кисми исботланади.
ишорасига
таъсири йуклигидан улар воситасида тизим харакатини стабиллаштириш мумкин эмаслиги
келиб чикади, яъни теореманинг биринчи кисми исботланади.
Теореманинг иккинчи кисмини исботлашга утамиз. Агар потенциал энергия максимумга эга ва тизим тулик диссипацияли диссипатив кучлар таъсири остида булганда факат гироскопик кучларни кушганимизда Томсон ва Тетнинг туртинчи теоремасига асосан тизим харакати нотургун булади. Шунинг учун хам теоремани исбот килиш учун потенциал энергия максимумга эга ва тулик диссипацияли кучлар таъсири остидаги тизимга факат ноконсерватив кучларни кушганимизда тизим яна нотургун булишини курсатиш кифоя.
Потенциал энергияси максимал булган ва тулик диссипацияли кучлар таъсири остидаги тизимга ноконсерватив кучларни кушайлик.
У вактда (7.6.25) характеристик тенглама куйидагича
![]()
ёки
кейинчалик бирга тенглаштириладиган иккита ![]() ва
ва ![]() параметрларни
киритганимиздан кейин
параметрларни
киритганимиздан кейин
![]() (7.6.27)
(7.6.27)
куринишни олади.
![]() детерминантни
очикрок ёзамиз
детерминантни
очикрок ёзамиз
 (7.6.28)
(7.6.28)
![]()
детерминантнинг сатрларини устунларга алмаштирамиз
![]() .
.
![]() ва
ва
![]() матрицаларнинг
симметрик ва
матрицаларнинг
симметрик ва ![]() нинг кийшик
симметрик эканликларини хисобга олиб,
нинг кийшик
симметрик эканликларини хисобга олиб, ![]() тенгликларни
ёзамиз. Шунинг учун
тенгликларни
ёзамиз. Шунинг учун
![]() .
.
Демак,
(7.6.28) детерминант ифодасида ![]() параметр факат
жуфт даражаларда катнашади.
параметр факат
жуфт даражаларда катнашади. ![]() нинг (7.6.28)
ифодасидан фойдаланиб,
нинг (7.6.28)
ифодасидан фойдаланиб, ![]() коэффициентни
(7.6.26) дан топамиз. (7.6.28) детерминантда
коэффициентни
(7.6.26) дан топамиз. (7.6.28) детерминантда ![]() сони бош
диагоналда турган
сони бош
диагоналда турган ![]() коэффициентнинг купайтувчиси
булиб катнашади. Шунинг учун
коэффициентнинг купайтувчиси
булиб катнашади. Шунинг учун ![]() детерминантнинг
ёйилган ифодасида
детерминантнинг
ёйилган ифодасида ![]() нинг биринчи
даражаси олдидаги
нинг биринчи
даражаси олдидаги ![]() коэффициентнинг ифодаси
коэффициентнинг ифодаси
![]() куринишда булади,
бу ерда
куринишда булади,
бу ерда ![]() нинг ифодаси
нинг ифодаси ![]() ва
ва
![]() ларга боглик.
Киритилган
ларга боглик.
Киритилган ![]() ва
ва ![]() параметрларни
хисобга олиб,
параметрларни
хисобга олиб, ![]() коэффициентни
коэффициентни ![]() даражалари
буйича жойлашган купхад сифатида ифодалаш мумкин:
даражалари
буйича жойлашган купхад сифатида ифодалаш мумкин:
![]() . (7.6.29)
. (7.6.29)
Бу
ерда ![]() факат жуфт
даражада катнашиши хисобга олинган.
факат жуфт
даражада катнашиши хисобга олинган. ![]() олдида купайтувчи
сифатида факат
олдида купайтувчи
сифатида факат ![]() параметр турибди.
Шунинг учун
параметр турибди.
Шунинг учун ![]() бош диагоналда
турган хадлардан ташкил топади:
бош диагоналда
турган хадлардан ташкил топади:
![]() . (7.6.30)
. (7.6.30)
Колган
![]() коэффициентларнинг
тузилиши куйидагича булади (
коэффициентларнинг
тузилиши куйидагича булади (![]() -жуфт сон):
-жуфт сон):
![]() , (7.6.31)
, (7.6.31)
бу
ерда ![]() нинг барча
нинг барча ![]() сонлардан
иборат бирлашмасига таркатилган,
сонлардан
иборат бирлашмасига таркатилган, ![]() матрицанинг диагонал
минорлари (матрицадан
матрицанинг диагонал
минорлари (матрицадан ![]() индексли сатр ва
устунларни учириш йули билан хосил килинади). (7.6.31) ва (7.6.30) йигиндилар
ифодасидаги хар бир хад битта мусбат
индексли сатр ва
устунларни учириш йули билан хосил килинади). (7.6.31) ва (7.6.30) йигиндилар
ифодасидаги хар бир хад битта мусбат ![]() купайтувчи (диссипация
тулик), ток сонли манфий
купайтувчи (диссипация
тулик), ток сонли манфий ![]() купайтувчи (
купайтувчи (![]() ва
ва ![]() сонлар жуфт ва
сонлар жуфт ва ![]() мавжуд)
ва манфий булмаган
мавжуд)
ва манфий булмаган ![]() купайтувчига (кийшик
симметрик детерминант булганлиги учун) эга булади. Шунинг учун барча
купайтувчига (кийшик
симметрик детерминант булганлиги учун) эга булади. Шунинг учун барча ![]() ва
ва
![]() , чунки
, чунки ![]() ва
ва
![]() - ток сон. Шарт буйича
- ток сон. Шарт буйича
![]() .
.
Демак,
![]()
ва (7.6.26) характеристик тенгламанинг хеч булмаганда битта илдизининг хакикий кисми мусбат ишорали булади.
Шундай
килиб, агар жуфт координатали потенциал тизимнинг потенциал энергияси максимум
(![]() ) ва тулик
диссипацияли диссипатив кучларга эга булса, у вактда факат ноконсерватив
кучларни кушганимизда
) ва тулик
диссипацияли диссипатив кучларга эга булса, у вактда факат ноконсерватив
кучларни кушганимизда ![]() тойилмаган харакат
нотургун булади. Бу теореманинг иккинчи кисмининг исботидир.
тойилмаган харакат
нотургун булади. Бу теореманинг иккинчи кисмининг исботидир.
1-мисол.
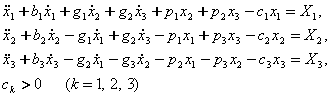
тизим
![]() ва
ва ![]() ларнинг
хар кандай кийматларида хам нотургун, чунки бу ерда
ларнинг
хар кандай кийматларида хам нотургун, чунки бу ерда ![]() потенциал
энергия
потенциал
энергия ![]() кийматларда
координата бошида максимумга эга ва координаталар сони токдир.
кийматларда
координата бошида максимумга эга ва координаталар сони токдир.
2-мисол.
![]()
тизимни
бир вактда гироскопик ва ноконсерватив кучларни мувофик равишда кушиш йули
билан стабиллаштириш мумкин, чунки ![]() потенциал энергия
потенциал энергия ![]() ва
координаталар сони жуфт булганда координата бошида максимумга эга ва диссипация
тулик.
ва
координаталар сони жуфт булганда координата бошида максимумга эга ва диссипация
тулик.
7-§. Ноконсерватив кучлар таъсири остидаги тизим харакатининг тургунлигини тадкик этишга
доир мисоллар
Кизикарли ва техникада жуда хам зарур буладиган ноконсерватив кучлар таъсири остидаги тизим тургунлиги хакидаги масалалар эластиклик назариясида куплаб учрайди. Бу ерда бундай масалаларнинг уч турини курсатиш мумкин. Биринчиси кузатувчи кучлар деб аталадиган кучлар таъсиридаги эластик тизимлар билан богланган.
Кузатувчи куч (момент) – таъсир чизиги стержен эластик укининг уринмасига мос келувчи куч (момент). Бундай кучлар, кисман, реактив курилмаларда ёнувчи махсулотларнинг ажралиб чикишида пайдо булади. Бундай тизимларни тадкик этишни биринчи булиб 1928 йилда Е.Л.Николаи бошлаган.
Иккинчи тур масалалар айланувчи валлар тургунлиги ва учинчи тури моддий мухитда харакат килувчи эластик жисмларнинг тургунлиги масалаларига оиддир. Биринчи тур масалаларни тадкик этиш усуллари ва олинган натижалар шархи Г.Херманнинг [111] китобида ва 2-3 тур масалаларни ечиш усуллари ва олинган натижалар кисман В.В.Болотиннинг [15] китобида берилган.
Эластик жисмлардан иборат тизимлардан ташкари, шундай курилмалар, хусусан, гироскопик тизимлар мавжудки, уларда ноконсерватив кучларни махсус асбоблар оркали вужудга келтирадилар (утувчи жараёнларни тезлатиш максадида килинади).
Бу параграфда оддийрок масалаларни куриб утамиз.
1-мисол. Ташки ишкаланиш кучи таъсири остида айланаётган вал нотургунлиги
Тажриба курсатаяптики, гидродинамик мухитдаги ишкаланишнинг борлиги ва демпферланишнинг йуклигида кобигда айланаётган ротор нотургун ён харакатга эга булади. Бу холатни биринчи булиб П.Л.Капица тадкик этган эди [35].
7.7-шаклда
халкавий 2 кобикда ![]() бурчак тезлиги билан айланаётган массаси
бурчак тезлиги билан айланаётган массаси ![]() га тенг булган 1 ротор ифодаланган.
га тенг булган 1 ротор ифодаланган.
Ротор билан кобик орасидаги фазо гидродинамик мухит билан, масалан, газ билан тулдирилган. Агар ротор маркази О1 билан кобик маркази О устма-уст (мос) тушса, у вактда газ билан содир буладиган ишкаланиш факатгина тормозлайдиган момент хосил килади. Бу моментнинг ротор укининг холатига таъсири йук. Ротор О1 нинг уки силжиши натижасида ноконсерватив кучлар пайдо булишини курсатамиз.
 |
7.7-шакл.
Мисол
учун ротор О1 маркази ![]() уки
буйича унг тарафга ОО1=
уки
буйича унг тарафга ОО1=![]() микдорга силжисин деб фараз киламиз. Газнинг холатига
роторнинг айланиши таъсир этади ва у V1 ва V2
тезликларга эга булади. Ротор маркази О1 силжиган томонда кобиг
билан ротор уртасидаги масофа кам булганлиги ва доиравий харакатдаги газнинг микдори
узгармаслиги учун V2>V1. Шунинг учун чап ва унг тарафда ротор сиртининг газ
билан ишкаланиши хар хил булади. Равшанки, ротор тезлиги билан газ тезлиги
орасидаги айирма каерда катта булса, роторнинг уша сиртида ишкаланиш купрок булади.
Ротор маркази унг тарафга силжийди деган фаразимиздан унинг чап тарафи унг
тарафига нисбатан купрок газ билан ишкаланади. Бунинг натижасида
микдорга силжисин деб фараз киламиз. Газнинг холатига
роторнинг айланиши таъсир этади ва у V1 ва V2
тезликларга эга булади. Ротор маркази О1 силжиган томонда кобиг
билан ротор уртасидаги масофа кам булганлиги ва доиравий харакатдаги газнинг микдори
узгармаслиги учун V2>V1. Шунинг учун чап ва унг тарафда ротор сиртининг газ
билан ишкаланиши хар хил булади. Равшанки, ротор тезлиги билан газ тезлиги
орасидаги айирма каерда катта булса, роторнинг уша сиртида ишкаланиш купрок булади.
Ротор маркази унг тарафга силжийди деган фаразимиздан унинг чап тарафи унг
тарафига нисбатан купрок газ билан ишкаланади. Бунинг натижасида ![]() кучи
пайдо булади.
кучи
пайдо булади.
![]() кучни
куйидаги хол учун топамиз: 1) газнинг тезлиги етарли катта ва 2) унинг харакатини
тулигинча турбулент харакат деб кабул киламиз; 3) бундан ташкари, роторнинг ишкаланиши
биринчи якинлашишда газнинг ковушоклигига боглик эмас деб фараз киламиз. Ротор
билан кобик марказлари устма-уст тушган холатдаги ротор билан кобик орасидаги
масофани (ораликни)
кучни
куйидаги хол учун топамиз: 1) газнинг тезлиги етарли катта ва 2) унинг харакатини
тулигинча турбулент харакат деб кабул киламиз; 3) бундан ташкари, роторнинг ишкаланиши
биринчи якинлашишда газнинг ковушоклигига боглик эмас деб фараз киламиз. Ротор
билан кобик марказлари устма-уст тушган холатдаги ротор билан кобик орасидаги
масофани (ораликни) ![]() билан белгилаймиз.
Ротор маркази
билан белгилаймиз.
Ротор маркази ![]() уки буйича ОО1=
уки буйича ОО1=![]() микдорга силжиди деб фараз киламиз. О1 нуктадан
микдорга силжиди деб фараз киламиз. О1 нуктадан ![]() укига q бурчак остида О1М тугри чизикни утказамиз. Ротор билан кобик
орасидаги КМ масофани
укига q бурчак остида О1М тугри чизикни утказамиз. Ротор билан кобик
орасидаги КМ масофани ![]() билан белгилаймиз
(7.7-шаклга каранг). ОМО1 учбурчакдан косинуслар теоремасига асосан
(кобик радиуси ОМ=R+e, бу ерда R-ротор радиуси)
билан белгилаймиз
(7.7-шаклга каранг). ОМО1 учбурчакдан косинуслар теоремасига асосан
(кобик радиуси ОМ=R+e, бу ерда R-ротор радиуси)
![]() ,
,
ёки кавсларни очиб
![]()
ни
хосил киламиз. ![]() ва
ва ![]() микдорларни
R га нисбатан етарли кичик деб кабул килиб,
иккинчи тартибли
микдорларни
R га нисбатан етарли кичик деб кабул килиб,
иккинчи тартибли
хадларни инобатга олмаймиз:
![]()
Бу ердан
![]() .
(7.7.1)
.
(7.7.1)
Ротордаги
силжимаган газнинг уртача тезлигини ![]() деб кабул киладилар,
яъни ротор перифериясида ётган нукталар тезлигининг ярми сифатида кабул кабул килинади.
Ротор силжиган пайтда газнинг V уртача
тезлиги ораликларда узгаради. Аммо исталган кесим буйича утаётган газнинг микдори
силжишгача булган микдорга тенг булади. Демак
деб кабул киладилар,
яъни ротор перифериясида ётган нукталар тезлигининг ярми сифатида кабул кабул килинади.
Ротор силжиган пайтда газнинг V уртача
тезлиги ораликларда узгаради. Аммо исталган кесим буйича утаётган газнинг микдори
силжишгача булган микдорга тенг булади. Демак
![]()
бу
ерда ![]() -роторнинг калинлиги.
(7.7.1) муносабатдан фойдаланиб ва
-роторнинг калинлиги.
(7.7.1) муносабатдан фойдаланиб ва ![]() га кискартириб,
га кискартириб,
![]() (7.7.2)
(7.7.2)
ни хосил киламиз.
Катта
тезликларда роторнинг ташки сирти ![]() элементларга
таъсир этаётган ишкаланиш кучи
элементларга
таъсир этаётган ишкаланиш кучи ![]() тахминан нисбий тезликнинг квадратига
тахминан нисбий тезликнинг квадратига ![]() ва
атроф мухитнинг
ва
атроф мухитнинг ![]() зичлигига
пропорционал булади. Бу куч роторга уринма булиб йуналган (7.7-шакл). Унинг
зичлигига
пропорционал булади. Бу куч роторга уринма булиб йуналган (7.7-шакл). Унинг ![]() укидаги
проекциясини олиб ва q буйича 0 дан 2p гача интегралласак
укидаги
проекциясини олиб ва q буйича 0 дан 2p гача интегралласак
![]()
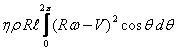
ни
хосил киламиз, бу ерда ![]() - ишкаланиш
коэффициенти. (7.7.2) дан V ни топиб
- ишкаланиш
коэффициенти. (7.7.2) дан V ни топиб ![]() ифодасига куйсак
ифодасига куйсак
![]()
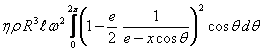 (7.7.3)
(7.7.3)
ни
хосил киламиз. Силжишнинг ![]() микдорини
микдорини ![]() ораликнинг микдорига нисбатан кичик деб кабул киламиз.
У вактда интеграл остидаги ифодани
ораликнинг микдорига нисбатан кичик деб кабул киламиз.
У вактда интеграл остидаги ифодани ![]() буйича каторга ёйиб, биринчи даражали хадлар билан каноатланиб,
маълум алмаштиришлардан кейин
буйича каторга ёйиб, биринчи даражали хадлар билан каноатланиб,
маълум алмаштиришлардан кейин
![]() (7.7.4)
(7.7.4)
ифодани
хосил киламиз. Худди шундай ![]() ни топамиз
ни топамиз
![]() . (7.7.5)
. (7.7.5)
Роторга
![]() ва
ва ![]() ишкаланиш кучларидан ташкари
ишкаланиш кучларидан ташкари ![]() эластиклик кучи таъсир килади. Унинг координата уклари
буйича проекциялари
эластиклик кучи таъсир килади. Унинг координата уклари
буйича проекциялари
![]() ,
,
бу
ерда ![]() -ротор валининг эгилиш буйича каттиклик коэффициенти
(7.8-шаклда
-ротор валининг эгилиш буйича каттиклик коэффициенти
(7.8-шаклда ![]() ва
ва ![]() кучлар ифодаланган).
кучлар ифодаланган).
 |
Масса марказининг харакати хакидаги теоремадан фойдаланиб, О1 нуктанинг харакат тенгламасини тузамиз:
![]()
Бу
ерда ![]() ва
ва ![]() -
-
![]() ва
ва ![]() ларни
биринчидан юкори даражада уз ифодасида сакловчи ночизикли кучлар. Бу тенгламага
ларни
биринчидан юкори даражада уз ифодасида сакловчи ночизикли кучлар. Бу тенгламага
![]() ларнинг кийматларини
куйиб, М массага кискартириб, бир кисм хадларни чап тарафга утказганимизда
ларнинг кийматларини
куйиб, М массага кискартириб, бир кисм хадларни чап тарафга утказганимизда
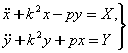 (7.7.6)
(7.7.6)
ни хосил киламиз. Бу ерда
![]() . (7.7.7)
. (7.7.7)
(7.7.6)
тенгламалар системасидаги ![]() ва
ва ![]() кушилувчилар
потенциал кучларни,
кушилувчилар
потенциал кучларни, ![]() ва
ва ![]() кушилувчилар
ноконсерватив кучларни,
кушилувчилар
ноконсерватив кучларни, ![]() ва
ва ![]() лар
ночизикли кучларни ифодалайдилар. (7.7.6) тенгламаларнинг чап тарафи (7.6.6)
тенгламалар билан мос келади. (7.6.6) тенгламалар учун куйидагини курсатган
эдик: агар
лар
ночизикли кучларни ифодалайдилар. (7.7.6) тенгламаларнинг чап тарафи (7.6.6)
тенгламалар билан мос келади. (7.6.6) тенгламалар учун куйидагини курсатган
эдик: агар ![]() ва
ва ![]() коэффициентлар
тенг булса (бизнинг хозирги мисолимизда
коэффициентлар
тенг булса (бизнинг хозирги мисолимизда ![]() ), у вактда хар кандай
), у вактда хар кандай
![]() кийматларда ва хар
кандай
кийматларда ва хар
кандай ![]() ва
ва ![]() ночизикли
кучларда харакат нотургун булади. Шунинг учун хам ишкаланиш каршилик кучи мавжуд
булмаса, гидродинамик мухитда айланаётган ротор укининг ён харакати доимо нотургун
булади.
ночизикли
кучларда харакат нотургун булади. Шунинг учун хам ишкаланиш каршилик кучи мавжуд
булмаса, гидродинамик мухитда айланаётган ротор укининг ён харакати доимо нотургун
булади.
![]() деб
кабул килиб, нотургун харакатнинг характерини чукуррок урганамиз. Бунинг учун
(7.7.6) тенгламалар системасининг иккинчи тенгламасини
деб
кабул килиб, нотургун харакатнинг характерини чукуррок урганамиз. Бунинг учун
(7.7.6) тенгламалар системасининг иккинчи тенгламасини ![]() га купайтирамиз
ва иккала тенгламани хадма-хад кушамиз:
га купайтирамиз
ва иккала тенгламани хадма-хад кушамиз:
![]()
ёки
![]() ,
(7.7.8)
,
(7.7.8)
бу
ерда ![]() комплекс узгарувчи
комплекс узгарувчи
![]() .
(7.7.9)
.
(7.7.9)
(7.7.8) тенгламанинг ечимини
![]() (7.7.10)
(7.7.10)
куринишида
излаймиз, бу ерда А-бирор комплекс сон. ![]() ни (7.7.8) га куйиб,
ни (7.7.8) га куйиб,
![]()
хосил киламиз. Бу ердан
![]() .
(7.7.10)
.
(7.7.10)
![]() деб
хисоблаймиз ва
деб
хисоблаймиз ва ![]() комплекс сондан
комплекс сондан ![]() гача
аниклик билан илдиз чикарамиз.
гача
аниклик билан илдиз чикарамиз.
![]() .
(7.7.11)
.
(7.7.11)
(7.7.8) тенгламанинг умумий ечими
![]() ,
(7.7.12)
,
(7.7.12)
булади, бу ерда А ва В – интеграллаш узгармаслари. Иккинчи кушилувчи вакт утиши билан модул буйича камайиб кетади, уни хисобга олмасак,
![]() (7.7.13)
(7.7.13)
ни
хосил киламиз. Таъриф буйича ![]() О1 нуктанинг
комплекс координатаси булади. О1 нуктанинг кутб
О1 нуктанинг
комплекс координатаси булади. О1 нуктанинг кутб ![]() ва
ва ![]() координаталари
билан
координаталари
билан ![]() узгарувчи
орасидаги богланиш
узгарувчи
орасидаги богланиш
![]()
тенглик билан аникланади. Демак,
![]() . (7.7.14)
. (7.7.14)
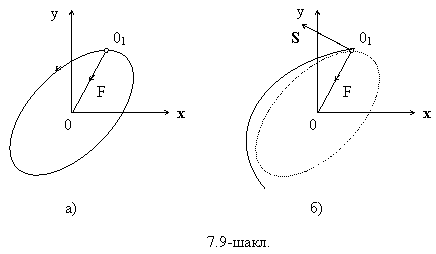
Шундай
килиб, О1 нукта логарифмик спирал оркали харакат килади ва ротор
марказининг мувозанат холати нотургун фокус булади. Ноконсерватив ![]() кучлар
таъсири остида нотургун харакатнинг пайдо булишининг физик маъносини осонгина
тушунтириш мумкин. Ноконсерватив
кучлар
таъсири остида нотургун харакатнинг пайдо булишининг физик маъносини осонгина
тушунтириш мумкин. Ноконсерватив ![]() кучлар йук деб
фараз килайлик. У вактда эластик F кучи таъсири остида роторнинг О1 маркази
эллипс буйича харакат килади (7.9-шакл,а).
кучлар йук деб
фараз килайлик. У вактда эластик F кучи таъсири остида роторнинг О1 маркази
эллипс буйича харакат килади (7.9-шакл,а).
Энди
О1 нуктага ![]() кучи таъсир этсин.
Бу куч ОО1 тугри чизикка перпендикуляр ва эллипснинг ташкарисига караб
йуналган булади (7.9-шакл,б). Бу кучнинг таъсири остида О1 нукта
эллипсдан чикиб, логарифмик спирал буйича харакат кила бошлайди.
кучи таъсир этсин.
Бу куч ОО1 тугри чизикка перпендикуляр ва эллипснинг ташкарисига караб
йуналган булади (7.9-шакл,б). Бу кучнинг таъсири остида О1 нукта
эллипсдан чикиб, логарифмик спирал буйича харакат кила бошлайди.
Ротор укининг ён харакатини стабиллаштириш учун халкавий демпфер урнатадилар.
Демпфер
каршилик кучи хосил килади. Бу куч тезликларга пропорционал ва демпфер
коэффициентлари бир хилдир: ![]() . Шунга кура
(7.7.6) харакат тенгламалари куйидаги
. Шунга кура
(7.7.6) харакат тенгламалари куйидаги
куринишни олади.
Асимптотик тургунлик шарти (7.6.13) дан фойдаланиб,
![]()
ни хосил киламиз. Бу тенгсизлик демпферга куйиладиган асосий талабни ифода килади.
2-мисол. Ички ишкаланиш кучи таъсири остида
айланаётган вал нотургунлиги
1-мисолда айланаётган валнинг нотургунлигига ташки ишкаланиш кучлари сабабчи эканлигини курсатган эдик. Бу мисолда айланаётган валнинг нотургунлигига ички ишкаланиш кучлари (вал материалида гистерезис борлиги, вал билан унга махкам урнатилган диск орасидаги ишкаланиш туфайли хосил буладиган кучлар) хам сабабчи булиши мумкин. Масалани оддий модел учун ечамиз [60]. Кенг маънода куйилган масалани В.В.Болотин [15] ва Ф.М.Диментберг [24] китобларидан укишни тавсия этамиз.
7.10-шаклда
узгармас ![]() бурчак тезлиги билан айланаётган ва массаси М га тенг
булган вал ифодаланган. Оддийлик учун валга ротор силжишсиз ва кийшайтирилмасдан
урнатилган деб фараз киламиз. ОХY координата тизими кузгалмас, О
бурчак тезлиги билан айланаётган ва массаси М га тенг
булган вал ифодаланган. Оддийлик учун валга ротор силжишсиз ва кийшайтирилмасдан
урнатилган деб фараз киламиз. ОХY координата тизими кузгалмас, О![]() тизим
тизим ![]() бурчак
тезлиги билан айланади. Дастлаб факат ички ишкаланиш кучларини хисобга оламиз.
Ротор О1 укининг мувозанат холати О дан силжиши натижасида куйидаги
кучлар хосил булади (7.10-шаклда бу кучларнинг компоненталари курсатилган):
бурчак
тезлиги билан айланади. Дастлаб факат ички ишкаланиш кучларини хисобга оламиз.
Ротор О1 укининг мувозанат холати О дан силжиши натижасида куйидаги
кучлар хосил булади (7.10-шаклда бу кучларнинг компоненталари курсатилган):![]()
1.![]() кучи – валнинг эластиклик кучи, проекциялари
кучи – валнинг эластиклик кучи, проекциялари ![]() ва
ва ![]() ,
бу ерда
,
бу ерда ![]() - валнинг эгилиш буйича
каттиклик коэффициенти;
- валнинг эгилиш буйича
каттиклик коэффициенти;
2.Ички
ишкаланиш кучи Ф. Бу куч вал силжишининг нисбий тезлигига боглик булади ва
унинг проекциялари ![]() ва
ва ![]() .
.
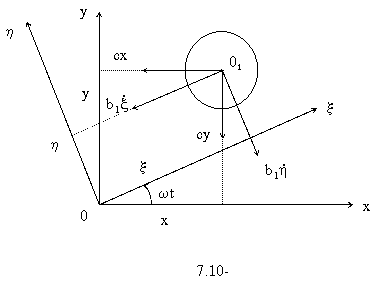 |
Тойилган харакат тенгламасида
 (7.7.15)
(7.7.15)
куйидаги
![]()
алмаштиришни киритамиз.
Бу ердан
![]()
ни хосил киламиз. Бу ифодаларни (7.7.15) га к¢йиб, айрим соддалаштиришлардан кейин
![]() (7.7.16)
(7.7.16)
тенгламаларни хосил киламиз, бу ерда
![]() (7.7.17)
(7.7.17)
Коэффициентларнинг
физик маъноси: ![]() - валнинг ён
эластик тебранишининг доиравий частотаси,
- валнинг ён
эластик тебранишининг доиравий частотаси, ![]() - ички ишкаланиш
коэффициентининг масса бирлигига нисбати.
- ички ишкаланиш
коэффициентининг масса бирлигига нисбати.
(7.7.16)
тенгламалардан куринадики, ротор айланишида ![]() ички ишкаланиш ва
ички ишкаланиш ва ![]() диссипатив
кучлардан ташкари ноконсерватив кучлар хам юзага келади. Ноконсерватив кучлар
коэффициентларидан тузилган матрица
диссипатив
кучлардан ташкари ноконсерватив кучлар хам юзага келади. Ноконсерватив кучлар
коэффициентларидан тузилган матрица

кийшик симметрик булади.
Асимптотик
тургунлик шарти (7.6.13) дан фойдаланиб, биз кураётган мисол учун асимптотик
тургунлик шартини топамиз (бу холда ![]()
![]()
![]() ):
):
![]() .
.
Бу ердан
![]() .
(7.7.18)
.
(7.7.18)
Шундай
килиб, айланаётган ротор укининг тургунлиги учун унинг айланиш бурчак тезлиги ![]() эластик
тебранишлар доиравий частотаси
эластик
тебранишлар доиравий частотаси ![]() дан кичик булиши керак.
Агар
дан кичик булиши керак.
Агар ![]() булса, у вактда
ички ишкаланиш кучи таъсири остида ротор укининг харакати нотургун булади.
булса, у вактда
ички ишкаланиш кучи таъсири остида ротор укининг харакати нотургун булади.
Энди ташки кучлар каршилигини (мухит ковушкок деб хисоблаймиз) хисобга оламиз. У вактда тойилган харакат тенгламаси (7.7.16) куйидаги куринишга эга булади:
 (7.7.19)
(7.7.19)
Бу
тенгламаларда ![]() - ташки ковушкок
ишкаланиш коэффициентининг масса бирлигига нисбати. Асимптотик тургунлик шарти
(7.6.13) бу хол учун куйидаги куринишда булади:
- ташки ковушкок
ишкаланиш коэффициентининг масса бирлигига нисбати. Асимптотик тургунлик шарти
(7.6.13) бу хол учун куйидаги куринишда булади:
![]()
ёки
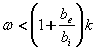 .
(7.7.20)
.
(7.7.20)
Агар
айланиш бурчак тезлиги ![]() унг тарафдаги
ифодадан катта булса, у холда ротор укининг харакати нотургун булади.
унг тарафдаги
ифодадан катта булса, у холда ротор укининг харакати нотургун булади.
3-мисол. Радиал коррекцияли гировертикал
Авиацияда радиал коррекцияли гировертикаллар куп кулланилади.
Курилманинг тузилиши ва ишлаш принципини [60,61] китоблардан укишингизни тавсия этамиз.
Лагранж тенгламаларидан фойдаланиб, гировертикал ук харакатининг дифференциал тенгламаларини топиш мумкин:
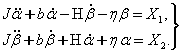 (7.7.21)
(7.7.21)
 |
7.11-шакл.
Бу
тенгламаларда ![]() - гироскопнинг экваториал инерция моменти, Н-унинг
кинетик моменти,
- гироскопнинг экваториал инерция моменти, Н-унинг
кинетик моменти, ![]() - каршилик кучининг коэффициенти,
- каршилик кучининг коэффициенти, ![]() ва
ва ![]() -
- ![]() ва
ва ![]() ларнинг биринчидан юкори даражаларини уз ифодасида сакловчи
ночизикли кучлар,
ларнинг биринчидан юкори даражаларини уз ифодасида сакловчи
ночизикли кучлар, ![]() - ташки халканинг айланиш бурчаги,
- ташки халканинг айланиш бурчаги, ![]() - кобикнинг айланиш бурчаги.
- кобикнинг айланиш бурчаги.
![]() ва
ва ![]() лар – гироскопик,
лар – гироскопик, ![]() ва
ва ![]() лар эса ноконсерватив кучлар (гироскопияда уларни радиал
коррекция кучлари деб атайдилар). (7.7.21) тизимнинг характеристик тенгламасини
тузамиз:
лар эса ноконсерватив кучлар (гироскопияда уларни радиал
коррекция кучлари деб атайдилар). (7.7.21) тизимнинг характеристик тенгламасини
тузамиз:
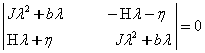
ёки детерминантни ёйиб чикганимиздан сунг
![]()
булади.
Бу тенгламанинг хамма коэффициентлари мусбат булганлиги учун Гурвиц критерияси факат
![]()
тенгсизликнинг
бажарилишига келтирилади. Бу тенгсизликка ![]() коэффициентларнинг
кийматларини куйиб соддалаштирганимизда
коэффициентларнинг
кийматларини куйиб соддалаштирганимизда
![]() (7.7.22)
(7.7.22)
тенгсизликка
эга буламиз. Каршилик кучи мавжуд булмаганда ![]() , бу шарт тескари
маънога эга булади, яъни
, бу шарт тескари
маънога эга булади, яъни ![]() ва тизим нотургун.
Демак, тизим тургун булиши учун каршилик кучининг мавжуд булиши
ва тизим нотургун.
Демак, тизим тургун булиши учун каршилик кучининг мавжуд булиши ![]() зарур.
(7.7.22) тенгсизликдан асимптотик тургунлик шартини топамиз:
зарур.
(7.7.22) тенгсизликдан асимптотик тургунлик шартини топамиз:
![]() .
(7.7.23)
.
(7.7.23)
Гироскоп
![]() кинетик моменти
кинетик моменти ![]() га
нисбатан жуда катта микдордир. Шу туфайли демпфер коэффициенти
га
нисбатан жуда катта микдордир. Шу туфайли демпфер коэффициенти ![]() учун
унинг куйи чегараси жуда хам кичик сондир. Амалий нуктаи назардан тизимнинг тургун
булиши учун хавонинг каршилиги, таянч нукталардаги ишкаланишлар етарли.
учун
унинг куйи чегараси жуда хам кичик сондир. Амалий нуктаи назардан тизимнинг тургун
булиши учун хавонинг каршилиги, таянч нукталардаги ишкаланишлар етарли.
РЕЖА: |
|
1. Математик таркибига караб кучларни синфларга ажратиш |
|
2. Факат потенциал кучлар таъсири остидаги тизим харакатининг тургунлиги. Тургунлик коэффициентлари |
|
3. Потенциал тизим харакатининг тургунлигига диссипатив ва гироскопик кучларнинг таъсири |
|
4. Томсон ва Тет теоремаларининг татбикига доир мисоллар |
|
5. Факат гироскопик ва диссипатив кучлар таъсири остидаги харакатнинг тургунлиги |
|
6. Харакатнинг тургунлигига ноконсерватив кучларнинг таъсири |
|
7. Ноконсерватив кучлар таъсири остидаги тизим харакатининг тургунлигини тадкик этишга доир мисоллар |
Таянч иборалар. Математик таркиби, куч, синф, потенциал кучлар, харакат тургунлиги, тургунлик коэффициентлари, потенциал тизим, диссипатив ва гироскопик кучлар, Томсон ва Тет теоремалари, ноконсерватив кучлар, мисоллар
Такрорлаш учун саволлар
|
1. Математик таркибига караб кучларни синфларга ажратиш нимадан иборат? |
|
2. Факат потенциал кучлар таъсири остидаги тизим харакатининг тургунлиги кандай булади. Тургунлик коэффициентлари деб нимани тушунасиз? |
|
3. Потенциал тизим харакатининг тургунлигига диссипатив ва гироскопик кучлар кандай таъсир килади? |
|
4. Томсон ва Тет теоремаларининг татбикига доир мисоллар келтиринг. |
|
5. Факат гироскопик ва диссипатив кучлар таъсири остидаги харакатнинг тургунлиги кандай булади? |
|
6. Харакатнинг тургунлигига ноконсерватив кучларнинг таъсирини изохлаб беринг. |
|
7. Ноконсерватив кучлар таъсири остидаги тизим харакатининг тургунлигини тадкик этишга доир мисоллар келтиринг. |