VI-БОБ. РАУС – ГУРВИЦ МУАММОСИ
1-§. Раус – Гурвиц муаммоси пайдо булишининг тарихи
IV–бобда куриб утдикки, Ляпуновнинг 1-теоремасига асосан
![]() (6.1.1)
(6.1.1)
дифференциал тенгламалар системасининг мувозанат холати (тойилмаган харакати) асимптотик тургун булиши учун
![]()
характеристик
тенгламанинг барча ![]() илдизлари (яъни
илдизлари (яъни ![]() матрицанинг
барча характеристик сонлари) нинг хакикий кисми манфий булиши етарли ва зарур.
Бу ерда
матрицанинг
барча характеристик сонлари) нинг хакикий кисми манфий булиши етарли ва зарур.
Бу ерда ![]() - ёйилмаси камида
иккинчи даражали хадлар билан бошланадиган функция.
- ёйилмаси камида
иккинчи даражали хадлар билан бошланадиган функция.
Шунинг учун хам берилган алгебраик тенгламанинг барча илдизларининг хакикий кисми манфий ишорали булишининг етарли ва зарур шартларини топиш масаласи механик, электрик, автоматик бошкариш ва ростлаш (регулирование) системаларининг тургунлик масаласини тадкик этиш учун фундаментал ахамиятга эгадир.
Бу масаланинг мухимлигини биринчи булиб XIX асрнинг иккинчи ярмида машиналарни ростлаш назариясининг асосчилари булган англиялик физик, Кембридж университетининг профессори Д.К.Максвелл (1831-1879) ва россиялик мухандис-математик, Петербург технология институтининг профессори И.А.Вышнеградский (1931-1895) лар курсатган эдилар [17,58]. Улар узларининг ростлагичларга (регуляторларга) багишлаган ишларида юкорида айтилган етарли ва зарурий шартларни учинчи даражали алгебраик тенгламалар учун топдилар ва тадкикотларида фойдаландилар.
1868 йилда Максвелл Лондон математиклар жамияти олдига ана шу етарли ва зарурий шартларни юкори даражали алгебраик тенгламалар учун топиш масаласини куяди. Бу масала аслида француз математиги Эрмит томонидан хал этилган эди [88]. Аммо унинг натижалари амалий сохаларда ишлаётган тадкикотчилар фойдалана оладиган холатга келтирилмаган эди. Шунинг учун хам Эрмитнинг бу иши кенг таркалмади.
1875
йилда англиялик механик Раус [115-117], Штурм теоремаси ва Коши индекслари
назариясидан фойдаланиб, дастлаб туртинчи ва бешинчи даражали алгебраик тенгламалар
учун ва 1877 йилда («Устойчивость заданного состояния движения» китобида) ихтиёрий
даражали алгебраик тенгламалар учун унг ярим текисликда ![]() ётган
илдизлар сони
ётган
илдизлар сони ![]() ни топиш
алгоритмини яратди.
ни топиш
алгоритмини яратди. ![]() булганда, бу
алгоритм тургунлик критериясини беради.
булганда, бу
алгоритм тургунлик критериясини беради.
Бу критерия ихтиёрий даражали характеристик тенглама илдизларининг хакикий кисми манфий булишининг етарли ва зарурий шартларини беради.
1890-йилларда словак мухандис-тадкикотчиси, Цюрих политехника институти профессори, газ ва пар турбиналар назариясининг асосчиси Аурель Стодола (1859-1942), Максвелл ва Раус ишларидан бехабар холда, алгебраик тенгламанинг барча илдизларининг хакикий кисми манфий булишининг етарли ва зарур шартларини топишни Цюрих политехника институти профессори, математик А.Гурвицдан илтимос килади. 1895 йилда А.Гурвиц [20] 15 йил олдин Раус томонидан ечилган масалани, француз математиги Эрмитнинг ишларига асосланиб, уша масаланинг иккинчи марта ечимини беради. Аммо Гурвиц Раус ечимини кайтармайди. У масаланинг ечимини элегант детерминант шаклида ёзилган тенгсизликлар сифатида беради. Гурвицнинг бу критерияси форма жихатидан Раус критериясидан фарк килсада, мазмун жихатидан у билан мос келади. Хозирги вактда бу тенгсизликларни Раус-Гурвиц тенгсизликлари ёки Раус-Гурвиц критерияси деб атайдилар.
Аммо Гурвиц критерияси яратилгунча, хозирги замон тургунлик назариясининг асосчиси А.М.Ляпунов узининг машхур диссертациясида [52] характеристик тенглама барча илдизларининг хакикий кисми манфий булиши учун кандай етарли ва зарурий шартлар бажарилиши кераклигини курсатадиган теорема яратди. Бу шартлар ростлаш назариясида кенг кулланилади.
1914 йилда француз математиклари Льенар ва Шипарлар томонидан янги тургунлик критерияси яратилди [20]. Льенар-Шипар тургунлик критериясида детерминант тенгсизликлар сони Раус-Гурвиц критериясидагига нисбатан тахминан икки марта кам.
Шу жихатдан уларнинг критерияси Раус-Гурвиц критериясидан устун туради.
Автоматика, радиотехника, бошкариш ва ростлаш назарияларида пайдо булган янги тургунлик масалаларини ечиш учун Найквист, Михайлов, Попов критериялари хамда Неймаркнинг D-булаклаш усули яратилди [62,65,63].
2-§. Коши индекси ва Штурм теоремаси
Раус-Гурвиц муаммосини урганишни Коши индексини куришдан бошлаймиз [20].
1-таъриф.
Коши индекси деб, хакикий рационал ![]() функциянинг киймати
аргументнинг
функциянинг киймати
аргументнинг ![]() дан
дан ![]() гача
узгариш пайтида
гача
узгариш пайтида ![]() дан
дан ![]() га
утишдаги узилишлар
га
утишдаги узилишлар ![]() дан
дан ![]() га
утишдаги узилишлар сонининг айирмасига айтилади. Бу ерда
га
утишдаги узилишлар сонининг айирмасига айтилади. Бу ерда ![]() ,
, ![]() -
хакикий сонлар ёки
-
хакикий сонлар ёки ![]() . Узилишлар сонини хисоблашда
. Узилишлар сонини хисоблашда
![]() нинг четки
(чегаравий)
нинг четки
(чегаравий) ![]() ва
ва ![]() кийматлари
хисобга олинмайди. Коши индексини
кийматлари
хисобга олинмайди. Коши индексини ![]() белги билан белгилаймиз.
белги билан белгилаймиз.
Ушбу
таърифга асосан, агар ![]() - хакикий сонлар,
- хакикий сонлар, ![]() -
хакикий кутбларга эга булмаган рационал функция булганда
-
хакикий кутбларга эга булмаган рационал функция булганда
![]()
булса, у холда
![]() (6.2.1)
(6.2.1)
ва умуман
![]() . (6.2.2)
. (6.2.2)
Бу
ерда ![]() (
(![]() - хакикий сон) одатдагидек
- хакикий сон) одатдагидек ![]() ва
ва ![]() булишига
мос равишда
булишига
мос равишда ![]() ёки 0 кийматлар кабул
килувчи ишора функция.
ёки 0 кийматлар кабул
килувчи ишора функция.
Изох. Рационал функцияни чексизликка айлантирадиган аргументнинг кийматига шу функциянинг кутби (полюси) деб айтилади.
Хусусан, агар ![]() хаки-кий купхад
хаки-кий купхад ![]() да
да
![]() ;
; ![]() ва
купхаднинг
ва
купхаднинг ![]() илдизлари орасида
факат биринчи
илдизлари орасида
факат биринчи ![]() таси хакикий булса,
у холда
таси хакикий булса,
у холда
![]() ,
,
бу
ерда ![]() - хакикий кутбларга
эга булмаган хакикий рационал функция.
- хакикий кутбларга
эга булмаган хакикий рационал функция.
Шунинг учун хам
![]()
индекс
![]() интервал орасидаги
интервал орасидаги
![]() функциянинг хар
хил хакикий илдизларининг сонига тенг булади.
функциянинг хар
хил хакикий илдизларининг сонига тенг булади.
Ихтиёрий
хакикий рационал ![]() функцияни
функцияни

куринишда
ифодалаш мумкин, бунда барча ![]() ва
ва ![]() лар
хакикий сонлар
лар
хакикий сонлар ![]() ;
; ![]() функция
эса хакикий кутбларга эга эмас.
функция
эса хакикий кутбларга эга эмас.
У вактда
![]() (6.2.3)
(6.2.3)
ва умуман
![]() (6.2.4)
(6.2.4)
Агар
![]() булса, у холда
булса, у холда ![]() индексни
индексни
![]() узлуксиз функциянинг
ортирмаси оркали ифодалаш мумкин:
узлуксиз функциянинг
ортирмаси оркали ифодалаш мумкин:
![]() (6.2.5)
(6.2.5)
Изох.
(6.2.3) формулада ![]() ток булган
сонларга мос келувчи
ток булган
сонларга мос келувчи ![]() кийматлар учунгина
жамлаш (сумма) белгиси ишлатилади. (6.2.4) да эса, факат
кийматлар учунгина
жамлаш (сумма) белгиси ишлатилади. (6.2.4) да эса, факат ![]() ва
ва ![]() ток
сонларга мос келувчи
ток
сонларга мос келувчи ![]() лар буйича жамлаш
амалга оширилади. Агар
лар буйича жамлаш
амалга оширилади. Агар ![]() ва
ва ![]() булса,
у холда (6.2.5) формула хар кандай рационал
булса,
у холда (6.2.5) формула хар кандай рационал ![]() каср учун тугри булади,
чунки бу холда
каср учун тугри булади,
чунки бу холда ![]() .
.
![]() индексни хисоблаш
усулларидан бири Штурмнинг классик теоремасига асосланади.
индексни хисоблаш
усулларидан бири Штурмнинг классик теоремасига асосланади.
![]() (6.2.6)
(6.2.6)
хакикий
купхадлар катори берилган булиб, бу катор ![]() (
(![]() ва
ва ![]() булиши хам мумкин)
интервалга нисбатан куйидаги икки хоссага эга деб хисоблаймиз:
булиши хам мумкин)
интервалга нисбатан куйидаги икки хоссага эга деб хисоблаймиз:
1.Бу
функцияларнинг бирортаси, масалан, ![]() ни нолга
айлантирувчи хар кандай
ни нолга
айлантирувчи хар кандай ![]() кийматда у билан кушни
(ёнма-ён) иккита
кийматда у билан кушни
(ёнма-ён) иккита ![]() ва
ва ![]() функцияларнинг
кийматлари нолдан фарк килади ва карама-карши ишораларга эга булади, яъни
функцияларнинг
кийматлари нолдан фарк килади ва карама-карши ишораларга эга булади, яъни ![]() дан
дан
![]()
![]()
![]() келиб
чикади.
келиб
чикади.
2.(6.2.6)
каторнинг охирги ![]() функцияси
функцияси ![]() интервалда
нолга тенг булмайди, яъни
интервалда
нолга тенг булмайди, яъни ![]() лар учун
лар учун ![]() .
.
Бундай
(6.2.6) купхадлар каторига ![]() интервалдаги Штурм
катори деб айтилади.
интервалдаги Штурм
катори деб айтилади.
Тайинланган
![]() киймат учун
(6.2.6) катордаги ишора узгаришлари сонини
киймат учун
(6.2.6) катордаги ишора узгаришлари сонини ![]() деб белгилаймиз.
деб белгилаймиз.
Бу
ерда агар ![]() ва
ва ![]() булса,
у холда 1-хоссага асосан
булса,
у холда 1-хоссага асосан ![]() ни аниклаш
жараёнида (6.2.6) катордаги нол кийматларни ташлаб юбориш ёки уларга исталган
ишорани бериш мумкин. Агар
ни аниклаш
жараёнида (6.2.6) катордаги нол кийматларни ташлаб юбориш ёки уларга исталган
ишорани бериш мумкин. Агар ![]() чекли сон булса, у
холда
чекли сон булса, у
холда ![]() ни
ни ![]() деб
караш керак, бу ерда
деб
караш керак, бу ерда ![]() шундай мусбат
кичик сонки,
шундай мусбат
кичик сонки, ![]() интервалда бирорта
хам
интервалда бирорта
хам ![]() функция нолга
айланмайди. Худди шундай, агар
функция нолга
айланмайди. Худди шундай, агар ![]() чекли сон булса, у
вактда
чекли сон булса, у
вактда ![]() ни
ни ![]() деб
караш керак, бу ерда
деб
караш керак, бу ерда ![]() сон юкорида айтилгандай
аникланади.
сон юкорида айтилгандай
аникланади.
У
вактда ![]() нинг
нинг ![]() дан
дан
![]() гача узгариши
давомида
гача узгариши
давомида ![]() нинг микдори факат
(6.2.6) катордаги бирорта функциянинг нол кийматдан утишида узгариши мумкин.
Аммо, биринчи хоссага асосан
нинг микдори факат
(6.2.6) катордаги бирорта функциянинг нол кийматдан утишида узгариши мумкин.
Аммо, биринчи хоссага асосан ![]() микдор
микдор ![]() функция
нол кийматдан утганда узгармайди,
функция
нол кийматдан утганда узгармайди, ![]() функция нол кийматдан
утаётганда эса, (6.2.6) каторнинг ишора узгаришлари сони
функция нол кийматдан
утаётганда эса, (6.2.6) каторнинг ишора узгаришлари сони ![]() нисбатнинг
нисбатнинг
![]() дан
дан ![]() (ёки
аксинча) утишига караб биттага камаяди ёки ошади.
(ёки
аксинча) утишига караб биттага камаяди ёки ошади.
Шунинг учун куйидаги Раус теоремаси уринлидир.
1-теорема
(Раус). Агар ![]() интервалда
интервалда
![]()
Штурм
катори ва ![]() бу катордаги ишора
узгаришлари сони булса, у холда
бу катордаги ишора
узгаришлари сони булса, у холда
![]() .
(6.2.7)
.
(6.2.7)
Изох. Штурм
каторидаги барча хадларни битта ихтиёрий ![]() купхадга купайтирамиз.
Шундай хосил килинган янги купхадлар каторига Штурмнинг умумлашган катори деб
айтилади. (6.2.6) каторнинг барча хадларини битта купхадга купайтирилиши
(6.2.7) муносабатнинг на чапдаги ва на унгдаги кисмини узгартирмаслиги туфайли
Штурмнинг умумлашган катори учун хам Штурм теоремаси уз кучини саклайди.
купхадга купайтирамиз.
Шундай хосил килинган янги купхадлар каторига Штурмнинг умумлашган катори деб
айтилади. (6.2.6) каторнинг барча хадларини битта купхадга купайтирилиши
(6.2.7) муносабатнинг на чапдаги ва на унгдаги кисмини узгартирмаслиги туфайли
Штурмнинг умумлашган катори учун хам Штурм теоремаси уз кучини саклайди.
![]() ва
ва ![]() -
ихтиёрий купхадлар хамда
-
ихтиёрий купхадлар хамда ![]() нинг даражаси
нинг даражаси ![]() нинг
даражасидан кичик булмасин. У вактда Евклид алгоритми воситаси билан шундай умумлашган
Штурм катори тузиш мумкинки, у
нинг
даражасидан кичик булмасин. У вактда Евклид алгоритми воситаси билан шундай умумлашган
Штурм катори тузиш мумкинки, у ![]() ва
ва ![]() функциялар
билан бошланади.
функциялар
билан бошланади.
Хакикатан хам, ![]() ни
ни ![]() га
булишдан хосил булган колдикни -
га
булишдан хосил булган колдикни - ![]() билан,
билан, ![]() ни
ни
![]() га булишдан хосил
булган колдикни -
га булишдан хосил
булган колдикни - ![]() билан белгилаб ва
шу сингари давом эттириб, куйидаги каторни хосил киламиз:
билан белгилаб ва
шу сингари давом эттириб, куйидаги каторни хосил киламиз:
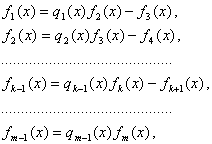 (6.2.8)
(6.2.8)
бу
ерда ![]() ва
ва ![]() хамда
шу тарзда тузилган (6.2.6) каторнинг барча функцияларининг энг катта умумий булувчиси.
Агар
хамда
шу тарзда тузилган (6.2.6) каторнинг барча функцияларининг энг катта умумий булувчиси.
Агар ![]() булса, у холда
(6.2.8) га асосан хосил булган (6.2.6) катор 1 ва 2 – хоссаларни каноатлантиради
ва у Штурм катори булади. Агар
булса, у холда
(6.2.8) га асосан хосил булган (6.2.6) катор 1 ва 2 – хоссаларни каноатлантиради
ва у Штурм катори булади. Агар ![]() купхад
купхад ![]() интервалда
илдизга эга булса, у холда (6.2.6) умумлашган Штурм катори булади, чунки унинг
барча хадларини
интервалда
илдизга эга булса, у холда (6.2.6) умумлашган Штурм катори булади, чунки унинг
барча хадларини ![]() га булишдан кейин
у Штурм катори булади.
га булишдан кейин
у Штурм катори булади.
Демак,
исталган ![]() рационал
функциянинг индексини Штурм теоремаси оркали аниклаш мумкин. Бунинг учун
рационал
функциянинг индексини Штурм теоремаси оркали аниклаш мумкин. Бунинг учун ![]() ни
ни
![]() куринишда ёзиш
кифоя, бу ерда
куринишда ёзиш
кифоя, бу ерда ![]() - купхадлар ва
- купхадлар ва ![]() нинг
даражаси
нинг
даражаси ![]() купхаднинг
даражасидан катта. Агар
купхаднинг
даражасидан катта. Агар ![]() ва
ва ![]() лар
учун умумлашган Штурм катори тузилса, у холда
лар
учун умумлашган Штурм катори тузилса, у холда
![]() .
.
![]() нинг
нинг
![]() интервалдаги хар
хил илдизларининг сонини Штурм теоремаси оркали аниклаш мумкин, чунки бу сон
интервалдаги хар
хил илдизларининг сонини Штурм теоремаси оркали аниклаш мумкин, чунки бу сон ![]() га
тенг эканлигини биз курган эдик.
га
тенг эканлигини биз курган эдик.
3-§. Раус алгоритми. Махсус холлар. Мисоллар
3.1.Раус алгоритми
Фараз килайлик ![]()
![]() комплекс
аргумент функцияси сифатида ушбу
комплекс
аргумент функцияси сифатида ушбу
![]()
куринишда аникланган булсин.
 |
Хакикий
купхаднинг унг ярим текисликда ![]() ётган
илдизларининг сонини аниклаш Раус масаласини ташкил килади.
ётган
илдизларининг сонини аниклаш Раус масаласини ташкил килади.
Аввал
![]() купхаднинг мавхум укда
илдизлари ётмаган холни курайлик, яъни
купхаднинг мавхум укда
илдизлари ётмаган холни курайлик, яъни ![]() нинг нол ва соф
мавхум илдизлари булмаган холни куриб утамиз.
нинг нол ва соф
мавхум илдизлари булмаган холни куриб утамиз.
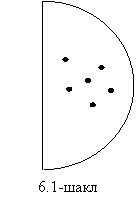
Унг
ярим текисликда маркази нолда ва радиуси ![]() га тенг булган
ярим айлана чизамиз, шу ярим айлана хамда мавхум ук билан чегараланган сохани курамиз
(6.1-шакл).
га тенг булган
ярим айлана чизамиз, шу ярим айлана хамда мавхум ук билан чегараланган сохани курамиз
(6.1-шакл).
![]() нинг
етарли катта кийматларида
нинг
етарли катта кийматларида ![]() нинг хакикий кисми
мусбат булган барча илдизлари шу соханинг ичида ётади. Шунинг учун хам соханинг
чегараси айланиб утилганда (контурини)
нинг хакикий кисми
мусбат булган барча илдизлари шу соханинг ичида ётади. Шунинг учун хам соханинг
чегараси айланиб утилганда (контурини) ![]() аргументнинг орттирмаси
аргументнинг орттирмаси
![]() га тенг булади. Хакикатан
хам, агар
га тенг булади. Хакикатан
хам, агар ![]() булса, у холда
булса, у холда ![]() .
Агар
.
Агар ![]() нукта курилаётган
соханинг ичида ётган булса, у вактда
нукта курилаётган
соханинг ичида ётган булса, у вактда ![]() ; агар бу соханинг
ташкарисида ётган булса, у холда
; агар бу соханинг
ташкарисида ётган булса, у холда ![]() . Иккинчи тарафдан,
. Иккинчи тарафдан,
![]() нинг
нинг ![]() радиусли
ярим айлана буйича айланиб утишгандаги орттирмаси
радиусли
ярим айлана буйича айланиб утишгандаги орттирмаси ![]() да
да ![]() нинг
орттирмаси билан аникланади ва у
нинг
орттирмаси билан аникланади ва у ![]() га тенг булади.
Шунинг учун хам
га тенг булади.
Шунинг учун хам ![]() нинг мавхум ук буйича
(
нинг мавхум ук буйича
(![]() ) орттирмаси
) орттирмаси
![]() (6.3.1)
(6.3.1)
га тенг булади.
![]() купхадни
ихтиёрий комплекс сонга купайтирганимизда (6.3.1) формуладаги
купхадни
ихтиёрий комплекс сонга купайтирганимизда (6.3.1) формуладаги ![]() узгармайдиганлиги
туфайли
узгармайдиганлиги
туфайли
![]() , (6.3.2)
, (6.3.2)
бу ерда
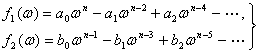 (6.3.3)
(6.3.3)
Коши индексидан фойдаланиб, (6.2.5) ва (6.3.2) формулалардан куйидагини топамиз:
![]() .
.
Шунинг учун хам (6.3.1) формуладан
![]() . (6.3.4)
. (6.3.4)
(6.3.4)
муносабатнинг чап тарафидаги ифоданинг индексини аниклаш учун Штурм теоремасига
мурожаат киламиз. (6.3.3) даги тенгликлар билан аникланадиган ![]() ва
ва
![]() функциялардан
фойдаланиб, Евклид алгоритми ёрдамида (Раусга ухшатиб) умумлашган Штурм каторини
тузамиз:
функциялардан
фойдаланиб, Евклид алгоритми ёрдамида (Раусга ухшатиб) умумлашган Штурм каторини
тузамиз:
![]() . (6.3.5)
. (6.3.5)
Энди
регуляр (мунтазам) холни курамиз: ![]() . Бу холда (6.3.5) катордаги
хар бир функциянинг даражаси олдинги функциянинг даражасидан бир бирликка кам
ва охирги
. Бу холда (6.3.5) катордаги
хар бир функциянинг даражаси олдинги функциянинг даражасидан бир бирликка кам
ва охирги ![]() нинг даражаси нолга
тенг.
нинг даражаси нолга
тенг.
Изох. Регуляр холда (6.3.5) оддий (умумлашмаган) Штурм катори булади.
Евклид алгоритмидан фойдаланиб, куйидагиларни топамиз:
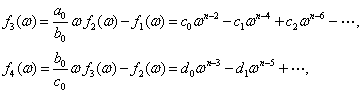
бу ерда
 (6.3.6)
(6.3.6)
Колган
![]() купхадларнинг
коэффициентлари хам худди шундай аникланади.
купхадларнинг
коэффициентлари хам худди шундай аникланади.
Шуни таъкидлаймизки,
![]() (6.3.7)
(6.3.7)
купхадларнинг хар бири жуфт ёки ток функция ва ёнма-ён турганлари доимо хар хил жуфтликда буладилар.
Раус схемасини тузамиз:
 (6.3.8)
(6.3.8)
(6.3.6) формулаларга асосан бу схеманинг хар бир сатри олдинги икки сатрлардан куйидаги коида билан аникланади:
Юкори сатрдаги сонлардан куйи сатрдаги мос сонларни шундай сонга купайтириб айириш керакки, биринчи айирма нолга айлансин. Бу нолга тенг булган айирмани ташлаб, изланаётган кейинги сатр хосил килинади.
Регуляр хол шу билан характерланадики, юкорида берилган коидани кетма-кет ишлатиш натижасида хосил этилган
![]()
каторда
нолга тенг сонни учратмаймиз ва бу сонлар ![]() та булади.
та булади.
 |
6.2 ва 6.3 – шаклларда ![]() ва
ва ![]() холлар
учун регуляр схеманинг скелети берилган
холлар
учун регуляр схеманинг скелети берилган
Бу шаклларда схеманинг элементлари нукта оркали ифодаланган.
Регуляр
холда ![]() ва
ва ![]() купхадларнинг
энг катта умумий булувчиси
купхадларнинг
энг катта умумий булувчиси ![]() булади. Шунинг
учун хам бу купхадлар бирданига нолга айланмайдилар, яъни хакикий
булади. Шунинг
учун хам бу купхадлар бирданига нолга айланмайдилар, яъни хакикий ![]() лар
учун
лар
учун ![]() . Демак, регуляр холда
(6.3.4) формула уринлидир. Бу формуланинг чап тарафига Штурм теоремасини (
. Демак, регуляр холда
(6.3.4) формула уринлидир. Бу формуланинг чап тарафига Штурм теоремасини (![]() интервалда) куллаб ва (6.3.7) катордан фойдаланиб, (6.3.4) га асосан куйидагини
интервалда) куллаб ва (6.3.7) катордан фойдаланиб, (6.3.4) га асосан куйидагини
![]() (6.3.9)
(6.3.9)
хосил киламиз.
Изох.
![]() булганда,
булганда, ![]() нинг
ишораси катта коэффициентнинг ишораси билан бир хил,
нинг
ишораси катта коэффициентнинг ишораси билан бир хил, ![]() булганда
эса бу ишорадан
булганда
эса бу ишорадан ![]() купайтувчи билан
фарк килади.
купайтувчи билан
фарк килади.
Бу ерда
![]()
Демак,
![]() (6.3.10)
(6.3.10)
(6.3.9) ва (6.3.10) тенгликлардан
![]() (6.3.11)
(6.3.11)
ни хосил киламиз.
Шундай килиб, регуляр хол учун куйидаги тасдикни исбот килдик.
2-теорема
(Раус). ![]() унг ярим
текисликда ётган хакикий
унг ярим
текисликда ётган хакикий ![]() купхаднинг
илдизларининг сони Раус схемасининг биринчи устунидаги ишора узгаришлари сонига
тенг булади.
купхаднинг
илдизларининг сони Раус схемасининг биринчи устунидаги ишора узгаришлари сонига
тенг булади.
Куйидаги
амалиётда зарур булган хусусий холни курайлик: ![]() купхаднинг барча
илдизларининг хакикий кисми манфий булсин. Бу холда
купхаднинг барча
илдизларининг хакикий кисми манфий булсин. Бу холда ![]() купхад
соф мавхум илдизларга эга эмас. Шунинг учун хам (6.3.4) ва, демак, (6.3.9)
формулалар уринлидир.
купхад
соф мавхум илдизларга эга эмас. Шунинг учун хам (6.3.4) ва, демак, (6.3.9)
формулалар уринлидир. ![]() булганлиги учун
(6.2.17) формулани куйидагича ёзамиз:
булганлиги учун
(6.2.17) формулани куйидагича ёзамиз:
![]() . (6.3.12)
. (6.3.12)
Аммо,
![]() ва
ва ![]() .
Шунинг учун хам (6.3.12) формула
.
Шунинг учун хам (6.3.12) формула ![]() ва
ва ![]() булгандагина
уринли. У холда (6.3.11) муносабатдан куйидаги келиб чикади:
булгандагина
уринли. У холда (6.3.11) муносабатдан куйидаги келиб чикади:
Раус критерияси. Хакикий ![]() купхаднинг барча
илдизларининг хакикий кисми манфий булиши учун Раус алгоритми бажарилганда,
Раус схемасининг биринчи устунидаги барча элементлар нолдан фарк килиши ва бир
хил ишорали булиши етарли ва зарур.
купхаднинг барча
илдизларининг хакикий кисми манфий булиши учун Раус алгоритми бажарилганда,
Раус схемасининг биринчи устунидаги барча элементлар нолдан фарк килиши ва бир
хил ишорали булиши етарли ва зарур.
Раус
теоремаси (6.3.4) формулага асосланган. Бу формуланинг узи, мавхум укда ![]() купхаднинг
илдизлари ётмайди деган фараз натижасида келтириб чикарилганди. Агарда
купхаднинг
илдизлари ётмайди деган фараз натижасида келтириб чикарилганди. Агарда
![]()
![]() купхаднинг
купхаднинг
![]() та илдизи унг ярим
текисликда ва
та илдизи унг ярим
текисликда ва ![]() та илдизи мавхум укда
ётган булса, у холда (6.3.4) формула куйидаги куринишга эга булади ([20], 475
б.):
та илдизи мавхум укда
ётган булса, у холда (6.3.4) формула куйидаги куринишга эга булади ([20], 475
б.):
![]() (6.3.13)
(6.3.13)
Бу муносабат (6.3.4) формуланинг умумлашмаси булади.
3.2. Махсус холлар. Мисоллар
Биз
хозиргача регуляр холни куриб утдик. Бу холда Раус схемасидаги ![]() элементларнинг бирортаси хам нолга тенг булмайди.
элементларнинг бирортаси хам нолга тенг булмайди.
Аммо,
амалий масалаларни Раус алгоритми оркали ечиш жараёнида ![]() катордаги
бирор
катордаги
бирор ![]() сон нолга тенг булиши мумкин, яъни
сон нолга тенг булиши мумкин, яъни ![]() .
. ![]() турган сатрга Раус алгоритмини куллаб булмайди, чунки
навбатдаги сатр элементларини топишда
турган сатрга Раус алгоритмини куллаб булмайди, чунки
навбатдаги сатр элементларини топишда ![]() га булишга тугри келади. Бунинг натижасида махсус
хол юзага келади:
га булишга тугри келади. Бунинг натижасида махсус
хол юзага келади:
Махсус холлар икки турга булинади:
1. ![]() турган сатрдаги сонлар орасида нолга тенг булмаган
сонлар хам топилади. Бу (6.3.5) каторнинг
бирор жойида даража курсатгичи бирдан купрок камайганини билдиради.
турган сатрдаги сонлар орасида нолга тенг булмаган
сонлар хам топилади. Бу (6.3.5) каторнинг
бирор жойида даража курсатгичи бирдан купрок камайганини билдиради.
2.
![]() турган сатрдаги барча сонлар нолга тенг буладилар. У вактда бу сатр
турган сатрдаги барча сонлар нолга тенг буладилар. У вактда бу сатр ![]() - сатр булади. Бу ерда
- сатр булади. Бу ерда ![]() - (6.2.6) умумлашган Штурм каторидаги хадлар сони. Бу
холда (6.3.5) катордаги функциялар даражаси хамма вакт бирга камаяди, аммо
охирги
- (6.2.6) умумлашган Штурм каторидаги хадлар сони. Бу
холда (6.3.5) катордаги функциялар даражаси хамма вакт бирга камаяди, аммо
охирги ![]() функциянинг даражаси нолдан катта.
функциянинг даражаси нолдан катта.
Икки холда хам (6.3.5) катордаги функциялар сони ![]() булади. Оддий Раус алгоритми махсус хол учун ярамаганлиги
туфайли, Раус 1- ва 2- махсус холларда схемани давом эттириш учун алохида
(махсус) коидалар беради.
булади. Оддий Раус алгоритми махсус хол учун ярамаганлиги
туфайли, Раус 1- ва 2- махсус холларда схемани давом эттириш учун алохида
(махсус) коидалар беради.
Биринчи
махсус холда Раус буйича ![]() урнига
ихтиёрий аник ишорали етарли кичик
урнига
ихтиёрий аник ишорали етарли кичик ![]() сонини куйиб, схемани давом эттириш керак. Бу холда
схеманинг биринчи устунидаги кейинги элементлар
сонини куйиб, схемани давом эттириш керак. Бу холда
схеманинг биринчи устунидаги кейинги элементлар ![]() нинг рационал функциялари булади. Бу элементларнинг
ишораси
нинг рационал функциялари булади. Бу элементларнинг
ишораси ![]() нинг “кичиклиги” ва ишораси билан аникланади. Агар бу
элементларнинг бирортаси яна
нинг “кичиклиги” ва ишораси билан аникланади. Агар бу
элементларнинг бирортаси яна ![]() га нисбатан хам нолга тенг булса, у холда бу
элементни бошка кичик
га нисбатан хам нолга тенг булса, у холда бу
элементни бошка кичик ![]() сон билан алмаштириб, алгоритмни давом эттирамиз.
сон билан алмаштириб, алгоритмни давом эттирамиз.
Мисол.
![]() булсин.
булсин.
Раус схемаси (![]() кичик параметр билан) куйидагича булади:
кичик параметр билан) куйидагича булади:

Энди иккинчи турдаги махсус холни куриб утамиз. Раус схемасида элементларнинг кийматлари
![]()
шаклда булсин. Бу хол учун умумлашган Штурм каторининг охирги купхади
![]()
куринишни олади.
Раус нолга тенг булган ![]() урнига
урнига ![]() ни
куйишни таклиф килади, яъни нолга тенг булган
ни
куйишни таклиф килади, яъни нолга тенг булган ![]() урнига мос равишда
урнига мос равишда
![]()
ларни ёзиб, алгоритмни давом эттиришни тавсия этади.
Мисол.
![]()
купхад берилган булсин. Бу купхад учун Раус схемаси куйидагича:

Изох. Биринчи устундаги элементларнинг ишорасини узгартирмасдан, айрим олинган сатрнинг барча элементларини бирорта бир хил сонга купайтириш мумкин. Бу изохдан схемани тузишда фойдаланилди.
4-§. Раус-Гурвиц теоремаси
Олдинги параграфда коэффициентлари муаян сонлар булган хакикий купхаднинг унг ярим текисликда ётган илдизларининг сонини топишнинг Раус алгоритмини баён этдик.
Агарда
купхаднинг коэффициентлари параметрларга боглик булса ва параметрларнинг кайси кийматларида
![]() 0нинг у ёки бу кийматга эга эканлигини топиш талаб
этилса (механик ёки электрик системаларни лойихалашда худди шундай масала куйилади),
у холда
0нинг у ёки бу кийматга эга эканлигини топиш талаб
этилса (механик ёки электрик системаларни лойихалашда худди шундай масала куйилади),
у холда ![]() микдорларни берилган купхаднинг коэффициентлари оркали
ифодалаш максадга мувофикдир. Бу масалани ечиб, биз
микдорларни берилган купхаднинг коэффициентлари оркали
ифодалаш максадга мувофикдир. Бу масалани ечиб, биз ![]() сонини топиш методини, хусусан, Гурвиц томонидан
яратилган тургунлик критериясини хосил киламиз.
сонини топиш методини, хусусан, Гурвиц томонидан
яратилган тургунлик критериясини хосил киламиз.
![]()
купхад
берилган булсин. Куйидаги ![]() -тартибли квадрат
матрицага
-тартибли квадрат
матрицага
 (6.4.1)
(6.4.1)

Гурвиц матрицаси деб айтилади.
Регуляр
холни куриб утамиз, яъни ![]() булсин. Н
матрицанинг иккинчи, туртинчи, .... сатрларидан мос равишда
булсин. Н
матрицанинг иккинчи, туртинчи, .... сатрларидан мос равишда ![]() га купайтирилган
биринчи, учинчи, .... сатрларни айириб, куйидаги матрицага эга буламиз:
га купайтирилган
биринчи, учинчи, .... сатрларни айириб, куйидаги матрицага эга буламиз:
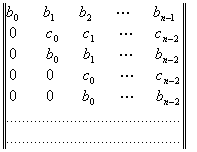 .
.
Бу
ерда ![]() - ноллар билан тулдирилган
Раус схемасининг учинчи сатр элементлари
- ноллар билан тулдирилган
Раус схемасининг учинчи сатр элементлари
![]() .
.
Хосил
булган матрицанинг учинчи, бешинчи, .... сатрларидан мос равишда олдиндан ![]() га
купайтирилган иккинчи, туртинчи, .... сатрларни айирамиз. Натижада ушбу
га
купайтирилган иккинчи, туртинчи, .... сатрларни айирамиз. Натижада ушбу

матрицани хосил киламиз.
Бу жараённи давом эттириб, охири учбурчакли

матрицага
келамиз. Бу матрица Раус матрицаси деб айтилади. Бу матрицани Раус схемасидан
((6.3.8) га каранг): 1) биринчи сатрни ташлаш; 2) сатрларни, уларнинг биринчи
элементлари бош диагоналларда ётадиган килиб унгга суриш; 3) ![]() -
тартибли квадрат матрицага келгунча ноллар билан тулдириш йули билан олинади.
-
тартибли квадрат матрицага келгунча ноллар билан тулдириш йули билан олинади.
1-таъриф.
Агар хар кандай ![]() лар учун
лар учун ![]() ва
ва
![]() матрицаларнинг
биринчи
матрицаларнинг
биринчи ![]() сатрларига мос
келган
сатрларига мос
келган ![]() -тартибли минорлари
тенг, яъни
-тартибли минорлари
тенг, яъни
![]()
булса, бу матрицалар тенг кучли матрицалар деб аталади.
Матрицанинг кандайдир сатридан кайсидир олдинги
сатрини ихтиёрий сонга купайтириб айирганимизга, биринчи ![]() сатрларининг
сатрларининг
![]() -минорининг киймати
узгармагани учун 1-таърифга асосан Гурвиц матрицаси Н ва Рауслар матрицаси R
тенг кучли булади:
-минорининг киймати
узгармагани учун 1-таърифга асосан Гурвиц матрицаси Н ва Рауслар матрицаси R
тенг кучли булади:
![]() (6.4.2)
(6.4.2)
Н
ва R матрицаларнинг тенг кучлилиги туфайли R
матрицанинг барча элементларини (яъни Раус схемасининг элементларини) Гурвиц
матрицаси Н нинг минорлари оркали ифодалаш мумкин. Хакикатан хам, (6.4.2) даги ![]() га
кетма-кет 1, 2, 3, ... кийматлар бериб, куйидагини хосил киламиз:
га
кетма-кет 1, 2, 3, ... кийматлар бериб, куйидагини хосил киламиз:
 (6.4.3)
(6.4.3)
ва хоказо.
Бу ердан Раус схемасининг элементларини тузамиз:

Н матрицанинг кетма-кет бош минорлари Гурвиц детерминантлари деб айтилади. Биз уларни куйидагича белгилаймиз:
 (6.4.5)
(6.4.5)
1-изох. (6.4.3) формулаларга асосан
![]() (6.4.6)
(6.4.6)
ни
хосил киламиз. Агар ![]() купхаднинг
коэффициентлари муаян сонлардан иборат булса, у холда (6.4.5) формулалар Гурвиц
детерминантларини хисоблашнинг энг осон йулини беради. Бу хисоблашлар Раус схемасини
тузишга келтирилади.
купхаднинг
коэффициентлари муаян сонлардан иборат булса, у холда (6.4.5) формулалар Гурвиц
детерминантларини хисоблашнинг энг осон йулини беради. Бу хисоблашлар Раус схемасини
тузишга келтирилади. ![]() лардан биринчи
лардан биринчи ![]() та
та
![]() ларнинг нолга тенг
эмаслиги келиб чикади ва аксинча. Бу холда Раус схемасининг учинчи сатридан
бошлаб
ларнинг нолга тенг
эмаслиги келиб чикади ва аксинча. Бу холда Раус схемасининг учинчи сатридан
бошлаб ![]() та кетма-кет
келаётган сатрлари аникланган булади. Улар учун (6.4.4) формулалар уринлидир.
та кетма-кет
келаётган сатрлари аникланган булади. Улар учун (6.4.4) формулалар уринлидир.
2-изох.
Регуляр хол (хамма ![]() лар маънога эга ва
нолга тенг булмаган хол)
лар маънога эга ва
нолга тенг булмаган хол)
![]()
тенгсизликлар билан характерланади.
3-изох.
Раус схемасининг элементларини Раус алгоритми воситаси билан аниклашдан кура
(6.4.4) формулалар оркали топиш умумийрокдир. Масалан, агар ![]() булса,
у холда Раус алгоритми берилган купхаднинг коэффициентларидан иборат булган
биринчи икки катордан ташкари бошка бирор нимани бермайди. Аммо, агар
булса,
у холда Раус алгоритми берилган купхаднинг коэффициентларидан иборат булган
биринчи икки катордан ташкари бошка бирор нимани бермайди. Аммо, агар ![]() булса
хам бошка
булса
хам бошка ![]() детерминантлар
нолдан фарк килса, у холда биз (6.4.4) формулалар оркали
детерминантлар
нолдан фарк килса, у холда биз (6.4.4) формулалар оркали ![]() лардан
ташкил топган сатрини чеклаб, Раус схемасидаги бошка барча сатрларни аниклашимиз
мумкин.
лардан
ташкил топган сатрини чеклаб, Раус схемасидаги бошка барча сатрларни аниклашимиз
мумкин.
(6.4.6) формулаларга асосан
![]()
ва шунинг учун хам
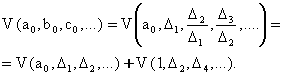
Демак, куйидагини тасдиклаш мумкин.
Раус-Гурвиц теоремаси.
![]() хакикий
купхаднинг унг ярим текисликда ётган илдизларининг сони
хакикий
купхаднинг унг ярим текисликда ётган илдизларининг сони ![]()
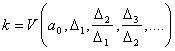 (6.4.7)
(6.4.7)
формула билан ёки
![]() (6.4.8)
(6.4.8)
ифода оркали аникланади.
4-изох. Келтирилган Раус-Гурвиц теоремаси
![]()
регуляр
хол учун тугридир. Гурвиц детерминантларининг айрим ![]() лари
нолга тенг булган махсус холларда бу формулалардан кандай фойдаланиш йулини
кейинги параграфда берамиз.
лари
нолга тенг булган махсус холларда бу формулалардан кандай фойдаланиш йулини
кейинги параграфда берамиз.
![]() хакикий
купхаднинг качон барча илдизлари
хакикий
купхаднинг качон барча илдизлари ![]() чап ярим текисликда
ётишини курамиз. Бу холда, Раус критериясига асосан, барча
чап ярим текисликда
ётишини курамиз. Бу холда, Раус критериясига асосан, барча ![]() лар нолдан
фарк килишлари ва бир хил ишорали булишлари керак.
лар нолдан
фарк килишлари ва бир хил ишорали булишлари керак.
Регуляр
хол учун (6.4.7) дан ![]() булганда, куйидаги
критерияни хосил киламиз:
булганда, куйидаги
критерияни хосил киламиз:
Раус-Гурвиц критерияси.
![]()
![]()
хакикий купхаднинг барча илдизларининг хакикий кисми манфий булиши учун
 (6.4.9)
(6.4.9)
тенгсизликларнинг бажарилиши етарли ва зарур.
5-изох.
Агар ![]() булса, у холда бу
тенгсизликлар куйидагича ёзилади:
булса, у холда бу
тенгсизликлар куйидагича ёзилади:
![]() . (6.4.10)
. (6.4.10)
Агар
![]() куринишда булса, у холда
куринишда булса, у холда ![]() булганда (6.4.10) Раус-Гурвиц шартларини детерминантлар
билан ифодаланган куйидаги тенгсизликлар оркали бериш мумкин:
булганда (6.4.10) Раус-Гурвиц шартларини детерминантлар
билан ифодаланган куйидаги тенгсизликлар оркали бериш мумкин:
 (6.4.11)
(6.4.11)
Барча илдизларининг хакикий кисми манфий булган хакикий купхадга Гурвиц купхади деб айтилади.
5-§. Орландо формуласи. Раус-Гурвиц теоремасидаги
махсус холлар
Амалий
масалаларни ечаётганда, Гурвиц детерминантларининг айримлари нолга тенг булиши
мумкин. Бу холларда ![]() детерминантни катта коэффициент
детерминантни катта коэффициент ![]() ва
ва ![]() (
(![]() купхаднинг коэффициентлари ихтиёрий комплекс сонлар хам
булиши мумкин) купхаднинг
купхаднинг коэффициентлари ихтиёрий комплекс сонлар хам
булиши мумкин) купхаднинг ![]() илдизлари билан ифодаловчи куйидаги Орландо формуласи
[20,99] керак булиб колади:
илдизлари билан ифодаловчи куйидаги Орландо формуласи
[20,99] керак булиб колади:
![]() (6.5.1)
(6.5.1)
![]() булганда, бу формула
булганда, бу формула ![]() квадрат тенгламадаги бизга маълум булган
квадрат тенгламадаги бизга маълум булган ![]() ни топиш
ни топиш ![]() формуласига келади.
формуласига келади.
(6.5.1) формула ![]() - даражали
- даражали ![]() купхад учун тугри деб фараз киламиз ва уни
купхад учун тугри деб фараз киламиз ва уни ![]() - даражали
- даражали

купхад учун хам тугрилигини исбот киламиз.
Шу максадда ![]() - тартибли
- тартибли
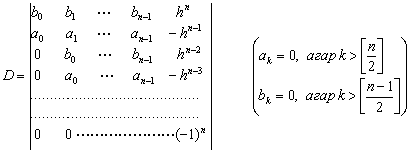
ёрдамчи
детерминантни тузамиз. D нинг биринчи сатрини ![]() га купайтирамиз ва
унга иккинчи сатрни
га купайтирамиз ва
унга иккинчи сатрни ![]() га, учинчи сатрни
га, учинчи сатрни ![]() га,
туртинчи сатрни
га,
туртинчи сатрни ![]() га ва х.к. купайтириб
кушамиз. У вактда биринчи сатрнинг охиргисидан бошка хамма элементлари нолга
айланади. Охирги элементи
га ва х.к. купайтириб
кушамиз. У вактда биринчи сатрнинг охиргисидан бошка хамма элементлари нолга
айланади. Охирги элементи ![]() га тенг булади. Бу
ердан
га тенг булади. Бу
ердан
![]()
лиги келиб чикади.
Бошка
тарафдан D нинг хар бир сатрига (охиргисидан ташкари) кейингисини
h га купайтирган холда кушиб, ![]() купхаднинг
купхаднинг
![]() га купайтирилган
га купайтирилган ![]() -тартибли
-тартибли
![]() Гурвиц
детерминантини хосил киламиз:
Гурвиц
детерминантини хосил киламиз:
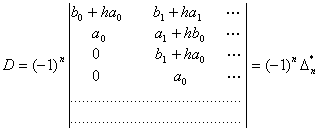 .
.
Демак,
![]() .
.
Бу формуладаги ![]() ни (6.5.1) ифода
билан алмаштириб ва
ни (6.5.1) ифода
билан алмаштириб ва ![]() деб кабул килиб,
деб кабул килиб,
![]()
формулани хосил киламиз.
Шундай килиб, математик индукция усули оркали Орландо формуласининг ихтиёрий даражали купхад учун тугрилигини исбот килдик.
Орландо
формуласидан: ![]() купхаднинг иккита
илдизининг йигиндиси нолга тенг булгандагина,
купхаднинг иккита
илдизининг йигиндиси нолга тенг булгандагина, ![]() булиши келиб чикади.
булиши келиб чикади.
![]() эканлигидан
(бу ерда
эканлигидан
(бу ерда ![]() купхаднинг озод хади
ва
купхаднинг озод хади
ва ![]() ) (6.5.1) формуладан
) (6.5.1) формуладан
![]() (6.5.2)
(6.5.2)
ифодани хосил киламиз.
(6.5.2)
формуладан ![]() нинг нолга айланиши
учун
нинг нолга айланиши
учун ![]() купхаднинг узи билан
бирга унга карама-карши сон хам илдиз буладиган
купхаднинг узи билан
бирга унга карама-карши сон хам илдиз буладиган ![]() илдизи мавжуд булишининг
етарли ва зарурлиги келиб чикади, яъни агар
илдизи мавжуд булишининг
етарли ва зарурлиги келиб чикади, яъни агар ![]() нинг илдизи булса,
у холда
нинг илдизи булса,
у холда ![]() хам
хам ![]() нинг
илдизи булиши етарли ва зарурдир.
нинг
илдизи булиши етарли ва зарурдир.
Махсус
холда Гурвиц детерминантларининг айримлари нолга тенг булади. Бу холда ![]() ва,
демак,
ва,
демак, ![]() деб фараз киламиз.
деб фараз киламиз.
Хакикатан
хам, агар ![]() булса, у холда
булса, у холда ![]() купхад
шундай
купхад
шундай ![]() илдизга эга буладики,
илдизга эга буладики,
![]() хам унинг илдизи булади.
Агар
хам унинг илдизи булади.
Агар
![]()
булганда,
![]() деб кабул килсак,
у холда
деб кабул килсак,
у холда ![]() тенгликдан
тенгликдан ![]() нинг
келиб чикиши хакида хулоса киламиз. Демак,
нинг
келиб чикиши хакида хулоса киламиз. Демак, ![]() сон
сон ![]() ва
ва
![]() купхадларнинг энг
катта умумий булувчиси
купхадларнинг энг
катта умумий булувчиси ![]() нинг илдизи булади.
нинг илдизи булади.
![]() деб кабул килиб,
деб кабул килиб, ![]() купхад
учун Раус-Гурвиц масаласини
купхад
учун Раус-Гурвиц масаласини ![]() купхад учун
Раус-Гурвиц масаласига келтирамиз. Бу купхад учун Гурвицнинг охирги детерминанти
нолга тенг эмас. Демак, доимо
купхад учун
Раус-Гурвиц масаласига келтирамиз. Бу купхад учун Гурвицнинг охирги детерминанти
нолга тенг эмас. Демак, доимо ![]() деб хисоблашимиз
мумкин.
деб хисоблашимиз
мумкин.
Махсус хол учун Раус-Гурвиц теоремасига кушимча булган куйидаги тасдик мавжуд.
Теорема.
Агар Гурвиц детерминантларидан айримлари нолга тенг булса (аммо ![]() ),
у холда
),
у холда ![]() хакикий купхаднинг
унг ярим текисликда ётган илдизларининг сони
хакикий купхаднинг
унг ярим текисликда ётган илдизларининг сони

формула
оркали аникланади. Бу ерда хар бир каторасига нолга тенг булган ![]() детерминантлар
гурухи учун (
детерминантлар
гурухи учун (![]() - хамма вакт ток
сон)
- хамма вакт ток
сон) ![]() нинг кийматини хисоблашда
нинг кийматини хисоблашда
 , (6.5.3)
, (6.5.3)
формуладан фойдаланиш керак, бу ерда
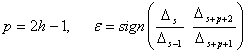
ва
![]() булганда,
булганда,![]()
![]() ни
ни ![]() га,
га, ![]() булганда
эса
булганда
эса ![]() га алмаштириш
керак.
га алмаштириш
керак.
Бу теореманинг исботини Гантмахер [20] китобининг 490-493 бетларидан топиш мумкин.
6-§. Льенар ва Шипарнинг тургунлик критерияси [20]
![]()
![]()
![]()
хакикий
коэффициентли купхад берилган булсин. ![]() купхаднинг барча
илдизларининг хакикий кисми манфий булишлигининг зарур ва етарли шартини
ифодаловчи Раус-Гурвиц критерияси куйидагича ёзилади:
купхаднинг барча
илдизларининг хакикий кисми манфий булишлигининг зарур ва етарли шартини
ифодаловчи Раус-Гурвиц критерияси куйидагича ёзилади:
![]() (6.6.1)
(6.6.1)
бу ерда
![]()

![]()
i – тартибли
Гурвиц детерминанти ![]() .
.
Агар
(6.6.1) шарт бажарилса, у вактда  купхаднинг барча
коэффициентлари мусбат ишорали, яъни
купхаднинг барча
коэффициентлари мусбат ишорали, яъни
![]() (6.6.2)
(6.6.2)
булади
(6.6.2) шарт, (6.6.1) шартдан фаркли уларок, ![]() купхад
илдизларининг барчаси
купхад
илдизларининг барчаси ![]() чап ярим текисликда
ётишлигининг зарурий шарти хисобланади.
чап ярим текисликда
ётишлигининг зарурий шарти хисобланади.
Аммо
(6.6.2) шартнинг бажарилиши натижасида (6.6.1) шартлар бир-бирига боглик булиб колади.
Масалан, n=4 булганда Раус-Гурвиц шарти битта ![]() шартга;
n=5 булганда иккита
шартга;
n=5 булганда иккита ![]()
![]() n=6 булганда
иккита
n=6 булганда
иккита ![]() ,
, ![]() шартларга
келтирилади.
шартларга
келтирилади.![]()
Бу холат француз математиклари Льенар ва Шипар томонидан тадкик этилди ва улар 1914 йили Раус-Гурвиц критериясидан фарк киладиган тургунлик критериясини яратдилар.
Льенар ва Шипар критерияси.
![]()
![]()
хакикий купхад илдизларидан хаммасининг хакикий кисми манфий булиши учун ушбу;
1) ![]()
2) ![]()
3) ![]()
4) ![]()
туртала шартдан исталган биттасининг бажарилиши зарур ва етарли.
1),
2), 3) ва 4) шартлар Гурвиц шартларига нисбатан маълум кулайликка эга, чунки
уларда карийб 2 марта кам тенгсизликлар мавжуд (Гурвиц тенгсизликларига нисбатан).
![]() ва
ва ![]() тенгсизликларга
нисбатан, амалда
тенгсизликларга
нисбатан, амалда ![]() куринишдаги
тенгсизликлардан фойдаланиш маъкул, чунки бу тенгсизликларда кичик тартибли
детерминантлар катнашади.
куринишдаги
тенгсизликлардан фойдаланиш маъкул, чунки бу тенгсизликларда кичик тартибли
детерминантлар катнашади.
Бу
критериядан барча коэффициентлари (хатто факат ![]() лардан бир кисми)
мусбат булган
лардан бир кисми)
мусбат булган ![]() хакикий купхаднинг
барча илдизларининг хакикий кисми манфий булганда Гурвицнинг (6.6.1) детерминант
тенгсизликлари эркин булаолмаслиги келиб чикади, яъни жуфт тартибли Гурвиц
детерминантларининг мусбатлигидан ток тартибли Гурвиц детерминантларининг
мусбатлиги келиб чикади ва аксинча.
хакикий купхаднинг
барча илдизларининг хакикий кисми манфий булганда Гурвицнинг (6.6.1) детерминант
тенгсизликлари эркин булаолмаслиги келиб чикади, яъни жуфт тартибли Гурвиц
детерминантларининг мусбатлигидан ток тартибли Гурвиц детерминантларининг
мусбатлиги келиб чикади ва аксинча.
Льенар ва Шипар 1) шартни махсус квадратик формалардан фойдаланиб топганлар [20] (критериянинг исботи [20] нинг 509-512 бетларида келтирилган). Улар эришган айрим асосий натижаларни М.Г.Крейн ва М.А.Наймаркнинг [46] фундаментал обзорида топиш мумкин.
Льенар ва Шипар критериясидан куйидаги натижа келиб чикади:
Агар
![]() хакикий купхаднинг
барча коэффициентлари
хакикий купхаднинг
барча коэффициентлари
![]()
шартларни
каноатлантирса ва ![]() булса, у вактда бу
купхаднинг
булса, у вактда бу
купхаднинг ![]() унг ярим текисликда
ётган илдизларининг сони
унг ярим текисликда
ётган илдизларининг сони ![]()
![]()
формула оркали аникланади.
7-§. Тургунлик ва нотургунлик ходисаларини
текширишга физик ёндашув
Нотургунлик ва уз-узидан тебранма харакатнинг хосил булиши фан ва техниканинг куп тармоклари учун бенихоят кенг кизикиш уйготади. Бошкариш тизимларида, радиотехник тизимларда, химик ва биологик жараёнларда, иктисодиётда, энергетикада, курилиш тармокларида, харакатланувчи ва бошка купгина тизимларда нотургунлик ва тебранма харакат пайдо булади. Баъзи холларда нотургунлик ва уз-узидан тебранма харакат зарар ходиса сифатида пайдо булади ва у билан карши курашишга тугри келади. Масалан, самолёт канотининг тебранма харакати (флаттери) ёки автомобил олдинги гилдиракларининг автотебранма харакати шулар жумласидандир. Шу каби бошка холларда, аксинча, уз-узидан тебранма харакатни хосил этиш максад килиб куйилади. Радиотехник хамда квантли генераторларда, соатларда, музика асбоблари ва х.к..
Агар курилаётган динамик системанинг харакат тенгламаси тугри тузилган булса, у холда амалиётда хосил буладиган купгина масалаларнинг харакат тургунлигини тадкик этиш характеристик тенглама илдизларини текширишга келтирилишини курган эдик. Аммо, урганилаётган тизимни тугри идеаллаштириш ва харакатнинг чизикли тенгламалари бизни кизиктираётган масалаларни тугри (адекват) акс эттириши учун нотургунлик ва тебранма харакат хосил булишининг сабабини ва механизмини билиш зарур ёки хар холда фойдалидир. Мумкин булган нотургунликнинг механизмини ва сабабини билиш нафакат тугри идеаллаштириш учун, балки айрим холларда тебранма харакат ва нотургунлик пайдо булмаслиги учун каралаётган тизим конструкциясига кандай узгартиришлар киритиш кераклигини хам курсатади. Бундай маълумотни билиш жуда хам зарурдир (фойдалидир), чунки харакат тенгламаларини тадкик этиш натижалари тизим конструкциясига кандай узгартиришлар киритиш кераклигини аниклаб бермайди ва энг яхши холда тизим параметрларининг кийматини кандай танлаш зарурлиги хакида маълумот олиш мумкин холос.
Шунинг учун хам курилаётган система харакатида пайдо булиши мумкин булган тебранма харакат хамда нотургунликнинг механизми ва сабабини олдиндан урганиб билиш катта амалий ахамиятга эгадир.
Нотургунлик ва уз-узидан тебранма харакат пайдо булишининг механизми ёки механизмлари деб нимани тушунамиз?
Улар, хар бир муаян хол учун узига хос: масалан, скрипка торида пайдо буладиган тебранма харакат учун – манфий ишкаланиш кучининг мавжуд булиши, ростлагич тизимларда пайдо буладиган тебранма харакат учун – манфий ишкаланиш кучининг мавжуд булиши, ростлагич тизимларда пайдо буладиган тебранма харакат учун – тескари богланиш контуридаги кераксиз фаза муносабатларининг мавжудлиги, химик жараёнларда – температуранинг ошиши ва хоказо. Аммо, айрим тизимлар синфи учун нотургунлик пайдо булишининг механизмларини олдиндан курсатиш мумкин.
Бундайлардан бири сифатида бир-бирига таъсир этадиган осцилляторлар тизимини курсатиш мумкин.
7.1.Осциллятор сифатида тавсифлаш
![]() лар бирор склероном богланишли
голоном тизимнинг умумлашган координаталари булсин. Бундай тизимнинг харакат
тенгламаси куйидаги куринишда булади
лар бирор склероном богланишли
голоном тизимнинг умумлашган координаталари булсин. Бундай тизимнинг харакат
тенгламаси куйидаги куринишда булади
![]() ,
(6.7.1)
,
(6.7.1)
бу ерда
![]() -
-
тизимнинг кинетик энергияси,
![]() -
-
умумлашган кучлар.
(6.7.1) дан куриниб турибдики, тизимнинг мувозанат холатида
![]() . (6.7.2)
. (6.7.2)
Бунда ![]() лар (6.6.2) ни каноатлантирувчи
тизимнинг мувозанат холати ва унинг атрофида (6.7.1) тенгламаларни чизиклаштириш
мумкин булсин.
лар (6.6.2) ни каноатлантирувчи
тизимнинг мувозанат холати ва унинг атрофида (6.7.1) тенгламаларни чизиклаштириш
мумкин булсин.
Чизикли тенгламаларни хосил этиш учун (6.7.1) тенгламаларни тузишдан олдин
![]()
функцияни Маклорен каторига ёйиш ва бу каторнинг
![]()
иккинчи тартибли хадлари билан каноатланиш мумкин, бу ерда ![]() ,
яъни кинетик энергия
,
яъни кинетик энергия ![]() умумлашган
тезликлар буйича узгармас коэффициентли квадратик формадир.
умумлашган
тезликлар буйича узгармас коэффициентли квадратик формадир.
Консерватив тизимлар учун ![]() - потенциал
энергия булганда,
- потенциал
энергия булганда,
![]()
уринли. Мувозанат холатида эса
![]() . (6.7.3)
. (6.7.3)
Бу холда хам чизикли тенгламаларни тузишгача ![]() потенциал
энергияни мувозанат холати атрофида Маклорен каторига ёйиш ва унда окибатда харакат
тенгламасига таъсири булмаганлиги учун узгармас хадни ташлаб юбориш мумкин.
(6.7.3) га асосан ёйилмада чизикли хадлар катнашмайди. Демак,
потенциал
энергияни мувозанат холати атрофида Маклорен каторига ёйиш ва унда окибатда харакат
тенгламасига таъсири булмаганлиги учун узгармас хадни ташлаб юбориш мумкин.
(6.7.3) га асосан ёйилмада чизикли хадлар катнашмайди. Демак, ![]() нинг
ёйилмаси
нинг
ёйилмаси ![]() умумлашган
координаталарга нисбатан иккинчи даражали хад билан бошланади. У вактда юкори
даражали кичик хадларни ташлаб юборгандан кейин куйидагини топамиз
умумлашган
координаталарга нисбатан иккинчи даражали хад билан бошланади. У вактда юкори
даражали кичик хадларни ташлаб юборгандан кейин куйидагини топамиз
![]() ,
,
бу ерда
 .
.
Шундай килиб, потенциал энергия ![]() умумлашган
координаталарга нисбатан узгармас коэффициентли квадратик форма булади.
умумлашган
координаталарга нисбатан узгармас коэффициентли квадратик форма булади.
![]() ва
ва ![]() ларнинг
такрибий олинган ифодаларига асосан консерватив тизимнинг мувозанат холати атрофидаги
харакатининг чизиклаштирилган (бундан кейин чизикли) тенгламалари
ларнинг
такрибий олинган ифодаларига асосан консерватив тизимнинг мувозанат холати атрофидаги
харакатининг чизиклаштирилган (бундан кейин чизикли) тенгламалари
![]() (6.7.4)
(6.7.4)
куринишда булади.
Агар тизимга ковушкок ишкаланиш кучлари хам таъсир этса, у холда
![]()
диссипация функциясини (Релей функциясини) киритиб, уларни хисобга олиш мумкин. Бу холда (6.7.1) тенгламалардаги умумлашган кучлар
![]()
ифодалар билан аникланади.
Харакатнинг чизикли тенгламаларини хосил килиш
учун ![]() функцияни
функцияни ![]() ларга
нисбатан мувозанат холати атрофида Маклорен каторига ёйиб, иккинчи даражали хадлар
билан чегараланамиз
ларга
нисбатан мувозанат холати атрофида Маклорен каторига ёйиб, иккинчи даражали хадлар
билан чегараланамиз
![]() ,
,
бу ерда ![]() ва
ва ![]() .
Шундай килиб, диссипация функцияси
.
Шундай килиб, диссипация функцияси ![]() хам
хам ![]() умумлашган
тезликларга нисбатан узгармас коэффициентли квадратик форма булади.
умумлашган
тезликларга нисбатан узгармас коэффициентли квадратик форма булади.
Демак, агар тизимда ковушкок ишкаланиш кучлари хам катнашса, у холда чизиклаштирилган (6.7.1) тенгламалар
![]() (6.7.5)
(6.7.5)
куринишда булади.
(6.7.5) тенгламалар тизимнинг мувозанат холати
атрофидаги кичик тебранма харакатининг тенгламалари деб айтилади. Ихтиёрий умумлашган
кучлар таъсири остидаги тизимнинг харакат тенгламаси хам (6.7.5) куринишда булади,
аммо бу ерда ![]() муносабатлар
умуман бажарилмаслиги мумкин.
муносабатлар
умуман бажарилмаслиги мумкин.
Агар каралаётган (6.7.5) тизимнинг ![]() координатасидан
ташкари колган барча координаталарини нолга тенглаштирсак (белгилаб куйсак), у холда
у биринчи эркинлик даражасига эга булган тизимга айланади ва куйидаги иккинчи
тартибли чизикли тенглама билан ифодаланади
координатасидан
ташкари колган барча координаталарини нолга тенглаштирсак (белгилаб куйсак), у холда
у биринчи эркинлик даражасига эга булган тизимга айланади ва куйидаги иккинчи
тартибли чизикли тенглама билан ифодаланади
![]() . (6.7.6)
. (6.7.6)
Бундай тизимни осциллятор (парциал осциллятор)
сифатида караймиз ва у ![]() умумлашган координатага
мувофикдир.
умумлашган координатага
мувофикдир.
![]() ва
ва ![]() ларни
мос равишда унинг (
ларни
мос равишда унинг (![]() осцилляторнинг) массаси,
ишкаланиш коэффициенти ва каттиклик (эластиклик) коэффициенти деб айтамиз. Масалан,
барча
осцилляторнинг) массаси,
ишкаланиш коэффициенти ва каттиклик (эластиклик) коэффициенти деб айтамиз. Масалан,
барча ![]() ва
ва ![]() коэффициентлари
мусбат булган пружинага осилган юкнинг ковушкок мухитдаги тебранма харакатининг
математик модели шундай парциал осцилляторга мисол була олади.
коэффициентлари
мусбат булган пружинага осилган юкнинг ковушкок мухитдаги тебранма харакатининг
математик модели шундай парциал осцилляторга мисол була олади.
(6.7.5) тизимнинг ![]() -тенгламасини куйидаги
куринишда ёзамиз
-тенгламасини куйидаги
куринишда ёзамиз
![]() (6.7.7)
(6.7.7)
ва уни
![]() (6.7.8)
(6.7.8)
куч таъсири остидаги ![]() парциал осцилляторнинг
харакат тенгламаси сифатида караймиз. Бу
парциал осцилляторнинг
харакат тенгламаси сифатида караймиз. Бу ![]() куч
куч ![]() осцилляторга
таъсир этаётган барча колган осцилляторлар таъсирининг йигиндисидан иборат. Бу
ерда
осцилляторга
таъсир этаётган барча колган осцилляторлар таъсирининг йигиндисидан иборат. Бу
ерда ![]() осциллятор
осциллятор ![]() осцилляторга
осцилляторга
![]() (6.7.9)
(6.7.9)
куч билан таъсир этади. Худди шундай ![]() осциллятор
осциллятор
![]() осцилляторга
осцилляторга
![]() (6.7.10)
(6.7.10)
куч билан таъсир этади.
Бу иккита осцилляторларнинг узаро таъсирларини координата, тезлик ва тезланишлар буйича узаро хамда йуналтирилган таъсирларга буламиз (1.1-жадвалга каранг).
1.1-жадвал
|
Узаро таъсир этувчи кучлар (богланишлар) |
Координата буйича |
Тезлик буйича |
Тезланиш буйича |
|
Узаро |
эластиклик |
ишкаланиш
гироскопик |
инерцион |
|
йуналтирилган |
|
|
|
Узаро координата буйича таъсир этаётган эластик кучлар куйидаги потенциал функция билан ифодаланади
![]() .
.
Узаро ва ишкаланиш кучлар
![]()
диссипатив функция оркали ифодаланади ва инерцион узаро таъсирлар инерциал кучлар билан биргаликда
![]()
кинетик энергияни беради.
Осцилляторлар орасидаги узаро таъсирлар кандайдир йул билан узаро ва йуналтирилган таъсирларга булинган булсин.
Узаро таъсирлар (богланишлар) нинг коэффициентлари
сифатида ![]() ,
, ![]() ,
,
![]() ларни саклаймиз ва
йуналтирилган богланишлар коэффициентларини мос равишда
ларни саклаймиз ва
йуналтирилган богланишлар коэффициентларини мос равишда ![]() ,
, ![]() ва
ва
![]() лар оркали белгилаймиз.
Бунга мувофик (6.7.5) тенгламалар системасини куйидагича ёзамиз
лар оркали белгилаймиз.
Бунга мувофик (6.7.5) тенгламалар системасини куйидагича ёзамиз
![]() . (6.7.11)
. (6.7.11)
(6.7.11) тенгламаларнинг хар бирини ![]() га купайтириб
кушамиз ва оддий алмаштиришлардан кейин куйидаги муносабатга келамиз
га купайтириб
кушамиз ва оддий алмаштиришлардан кейин куйидаги муносабатга келамиз
![]() , (6.7.12)
, (6.7.12)
бу ерда ![]() -кинетик энергия,
-кинетик энергия, ![]() -диссипатив
функция,
-диссипатив
функция, ![]() -потенциал энергия
-потенциал энергия
![]()
ва ![]() лар
лар
![]()
каби аникланадиган функциялардир.
![]() микдорни тизимнинг
энергияси деб айтамиз.
микдорни тизимнинг
энергияси деб айтамиз. ![]() микдорини узгартирмайдиган
узаро таъсир этувчи кучларга консерватив, доимо камайтирувчилари- диссипатив, купайтувчи узаро таъсир этувчи
кучларга актив кучлар деб айтамиз. Энергиянинг узгаришини ифодаловчи (6.7.12)
тенгламадан бевосита куйидагилар келиб чикади.
микдорини узгартирмайдиган
узаро таъсир этувчи кучларга консерватив, доимо камайтирувчилари- диссипатив, купайтувчи узаро таъсир этувчи
кучларга актив кучлар деб айтамиз. Энергиянинг узгаришини ифодаловчи (6.7.12)
тенгламадан бевосита куйидагилар келиб чикади.
1) хусусий ва узаро эластик, инерциал хамда гироскопик кучлар консерватив кучлар булади;
2) ![]() функциянинг киймати
мусбат булганда хусусий ва узаро ишкаланиш кучлар диссипатив ва
функциянинг киймати
мусбат булганда хусусий ва узаро ишкаланиш кучлар диссипатив ва ![]() нинг
киймати манфий булганда – актив кучлар булади.
нинг
киймати манфий булганда – актив кучлар булади.
3) барча йуналтирилган кучлар актив кучлардир, чунки ![]() формалар
манфий кийматлар кабул килиши мумкин. Йуналтирилган ва манфий ишорали ишкаланиш
кучлари актив булганлиги учун уларни реализация килиш учун ташки энергия манбаи
талаб этилади.
формалар
манфий кийматлар кабул килиши мумкин. Йуналтирилган ва манфий ишорали ишкаланиш
кучлари актив булганлиги учун уларни реализация килиш учун ташки энергия манбаи
талаб этилади.
7.2.Богланишларнинг геометрик схемаси ва
нотургунликнинг структуравий шартлари
Энди узаро таъсирларнинг геометрик схемаси
деган тушунчани киритамиз. Бунинг учун хар бир парциал осцилляторни нукта билан
белгилаймиз. Агар ![]() ва
ва ![]() осцилляторлар
орасида узаро богланишлар (таъсирлар) мавжуд булса, у холда уларга мос келувчи
нукталарни эгри чизик кесмаси билан туташтирамиз. Агар улар орасида йуналтирилган
богланишлар мавжуд булса, у холда уларга мос келувчи нукталарни йуналтирилган
богланишнинг йуналишини ифодаловчи стрелкали эгри чизик кесмаси билан туташтирамиз.
Бундай кесмани йуналтирилган кесма деб айтамиз. Шундай усул билан хосил килинган
геометрик схемага (нукта хамда бу нукталарни бирлаштирувчи йуналтирилмаган ва йуналтирилган
кесмалар мажмуасига) осциллятор сифатида ифодаланган тизим богланишларининг геометрик
схемаси деб айтилади.
осцилляторлар
орасида узаро богланишлар (таъсирлар) мавжуд булса, у холда уларга мос келувчи
нукталарни эгри чизик кесмаси билан туташтирамиз. Агар улар орасида йуналтирилган
богланишлар мавжуд булса, у холда уларга мос келувчи нукталарни йуналтирилган
богланишнинг йуналишини ифодаловчи стрелкали эгри чизик кесмаси билан туташтирамиз.
Бундай кесмани йуналтирилган кесма деб айтамиз. Шундай усул билан хосил килинган
геометрик схемага (нукта хамда бу нукталарни бирлаштирувчи йуналтирилмаган ва йуналтирилган
кесмалар мажмуасига) осциллятор сифатида ифодаланган тизим богланишларининг геометрик
схемаси деб айтилади.
Бу геометрик схеманинг йуналтирилган богланишлари факатгина стрелка билан курсатилган йуналиш буйича, йуналтирилмаганлари эса, исталган йуналишда утадилар.
Таъриф. Йуналтирилмаган ва хеч булмаганда битта йуналтирилган богланишлардан иборат узаро кесишмовчи кесмалардан иборат ёпик контурга цикл деб айтилади.
Геометрик схема ва киритилган тушунчалардан фойдаланиб, Нижний Новгород давлат университетининг профессори академик Ю.И.Неймарк куйидаги теоремаларни яратди [64].
1-теорема. Агар тизимнинг ![]() энергияси
энергияси
![]() ва
ва![]() узгарувчиларнинг аник мусбат ишорали функцияси булса, у холда тизим нотургун булиши
учун цикл ёки манфий ишкаланиш кучининг мавжуд булиши зарур ва етарли.
узгарувчиларнинг аник мусбат ишорали функцияси булса, у холда тизим нотургун булиши
учун цикл ёки манфий ишкаланиш кучининг мавжуд булиши зарур ва етарли.
2-теорема. Агар ![]() кинетик
энергия
кинетик
энергия ![]() узгарувчиларнинг
аник мусбат ишорали функцияси ва
узгарувчиларнинг
аник мусбат ишорали функцияси ва ![]() потенциал энергия
потенциал энергия ![]() узгарувчиларнинг
узгарувчан ишорали функцияси булса, у холда система тургун булиши учун ёки
манфий ишорали ишкаланиш кучи, ёки циклнинг мавжуд булиши зарурдир.
узгарувчиларнинг
узгарувчан ишорали функцияси булса, у холда система тургун булиши учун ёки
манфий ишорали ишкаланиш кучи, ёки циклнинг мавжуд булиши зарурдир.
Бу теоремалар куйидаги оддий фактни ифодалайдилар: биринчи холда тизимни нотургун килишга керак булган ташки энергия келиши учун ва иккинчи холда тизимни мувозанат холатига келтириш учун манфий ишкаланиш кучи ёки цикл мавжуд булишининг зарурлигини билдиради.
Худди шундай тизимдан энергияни чикариб юбориш учун мусбат ишкаланиш кучи ёки циклнинг мавжуд булиши зарурдир.
1-теореманинг исботини келтирамиз. Агар тизимда манфий ишкаланиш кучи ва йуналтирилган богланишлар мавжуд булмаса, у холда (6.7.12) га асосан
![]() (6.7.13)
(6.7.13)
булади. Шу туфайли учун хам ![]() функция
аник мусбат ишорали функция булганлиги учун Ляпунов теоремасига асосан
тизимнинг мувозанат холати тургун булади. Демак, тизим мувозанат холатининг
нотургун булиши учун манфий ишкаланиш кучи ёки йуналтирилган богланишларнинг
мавжуд булиши зарурдир.
функция
аник мусбат ишорали функция булганлиги учун Ляпунов теоремасига асосан
тизимнинг мувозанат холати тургун булади. Демак, тизим мувозанат холатининг
нотургун булиши учун манфий ишкаланиш кучи ёки йуналтирилган богланишларнинг
мавжуд булиши зарурдир.
Тизимда йуналтирилган богланишлардан бошка манфий
ишкаланиш кучи хам, цикл хам мавжуд булмасин. Бу холда хам тизим мувозанат холати
нотургун булмаслигини курсатамиз. Хакикатан, агар тизим мувозанат холати нотургун
булганда эди, бу холат тизим параметрларининг хар кандай етарлича кичик микдорда
узгаришларида хам сакланарди. Шу сабабли ![]() диссипатив
функцияни аник
диссипатив
функцияни аник
 |
мусбат ишорали деб караш мумкин. Тизимдаги осцилляторлар
сони ![]() дан кам булган хол
учун юкоридаги тасдик тугри булсин.
дан кам булган хол
учун юкоридаги тасдик тугри булсин. ![]() осциллятордан
иборат тизимни курамиз.
осциллятордан
иборат тизимни курамиз. ![]() геометрик
схемадаги кандайдир йуналтирилган богланиш ва
геометрик
схемадаги кандайдир йуналтирилган богланиш ва ![]() -
- ![]() буйича тушиш
мумкин булган осцилляторлар булсин. Цикл мавжуд булмаганлиги учун
буйича тушиш
мумкин булган осцилляторлар булсин. Цикл мавжуд булмаганлиги учун ![]() га
хамма осцилляторлар кирмайди.
га
хамма осцилляторлар кирмайди. ![]() га кирмаган осцилляторлар
тизимини
га кирмаган осцилляторлар
тизимини ![]() билан белгилаймиз.
билан белгилаймиз.
![]() осцилляторлар
осцилляторлар ![]() осцилляторларга
таъсир эта олмайди (6.4-шаклга каранг) ва, демак, фаразимизга асосан
осцилляторларга
таъсир эта олмайди (6.4-шаклга каранг) ва, демак, фаразимизга асосан ![]() тизим
тургун, яъни унинг исталган тойилиши сунувчидир.
тизим
тургун, яъни унинг исталган тойилиши сунувчидир. ![]() осцилляторлар
тизими
осцилляторлар
тизими ![]() та осциллятордан
кам булган тизимни ифодалайди ва унга
та осциллятордан
кам булган тизимни ифодалайди ва унга ![]() осцилляторлар тизими
таъсир этади. Аммо
осцилляторлар тизими
таъсир этади. Аммо ![]() га таъсир этувчи
кучлар нолга интилади, чунки
га таъсир этувчи
кучлар нолга интилади, чунки ![]() даги тебранма харакат
маълум давр ичида сунади. Демак,
даги тебранма харакат
маълум давр ичида сунади. Демак, ![]() нинг хам тебранма харакати
сунади. Шундай килиб, тизимнинг мувозанат холати тургун булади. Демак, тизим мувозанат
холати нотургун булиши учун манфий ишорали ишкаланиш кучи ёки цикл мавжуд булиши
етарлидир.
нинг хам тебранма харакати
сунади. Шундай килиб, тизимнинг мувозанат холати тургун булади. Демак, тизим мувозанат
холати нотургун булиши учун манфий ишорали ишкаланиш кучи ёки цикл мавжуд булиши
етарлидир.
Энди 2-теореманинг исботини келтирамиз. ![]() функция
манфий киймат кабул килиши мумкин, лекин тизимда манфий ишкаланиш кучи ва цикл
мавжуд эмас деб фараз килайлик. Бу холда тизим тургун була олмаслигини курсатамиз.
Бир осцилляторли тизим учун бу тасдик тугридир. Бу тасдикни купи билан
функция
манфий киймат кабул килиши мумкин, лекин тизимда манфий ишкаланиш кучи ва цикл
мавжуд эмас деб фараз килайлик. Бу холда тизим тургун була олмаслигини курсатамиз.
Бир осцилляторли тизим учун бу тасдик тугридир. Бу тасдикни купи билан ![]() осциллятордан
иборат тизим учун тугри деб
осциллятордан
иборат тизим учун тугри деб ![]() осциллятордан
иборат тизимни караймиз. Худди олдингидай бу тизимдан
осциллятордан
иборат тизимни караймиз. Худди олдингидай бу тизимдан ![]() осциллятордан
кам сонли
осциллятордан
кам сонли ![]() кисм тизимни
ажратиб оламиз. Агар ажратиб олинган
кисм тизимни
ажратиб оламиз. Агар ажратиб олинган ![]() кисм тизим учун
кисм тизим учун ![]() функциянинг
мос кисми
функциянинг
мос кисми ![]() манфий ишорали киймат
кабул кила олса, у холда
манфий ишорали киймат
кабул кила олса, у холда ![]() тизим нотургун булади
(Ляпуновнинг теорема В га асосан) ва, демак, бутун
тизим нотургун булади
(Ляпуновнинг теорема В га асосан) ва, демак, бутун ![]() тизим хам
нотургун булади. Агар
тизим хам
нотургун булади. Агар ![]() функциянинг
функциянинг ![]() кисми
манфий ишорали киймат кабул кила олмаса, у холда
кисми
манфий ишорали киймат кабул кила олмаса, у холда ![]() кисм тизимга мос
келувчи унинг
кисм тизимга мос
келувчи унинг ![]() кисми манфий киймат
кабул килади. Бу холда
кисми манфий киймат
кабул килади. Бу холда ![]() тизим тургун ва
тизим тургун ва ![]() тизим
булса нотургун булади. Бу ердан яна бутун
тизим
булса нотургун булади. Бу ердан яна бутун ![]() тизимнинг нотургунлиги
келиб чикади.
тизимнинг нотургунлиги
келиб чикади.
Шундай килиб, ![]() кинетик энергияси
аник мусбат ишорали функция булган бир-бирига богланган осцилляторлар тизими
нотургун булиши учун ёки
кинетик энергияси
аник мусбат ишорали функция булган бир-бирига богланган осцилляторлар тизими
нотургун булиши учун ёки ![]() функция манфий киймат
кабул кила олиши, ёки манфий ишкаланиш кучи мавжуд, ёки цикл мавжуд булиши керак.
функция манфий киймат
кабул кила олиши, ёки манфий ишкаланиш кучи мавжуд, ёки цикл мавжуд булиши керак.
Бу хулосага асосан айтиш мумкинки, бир-бирига богланган осцилляторлар сифатида тавсифланиши мумкин булган тизимларнинг нотургун булишининг асосий сабаблари ва механизмлари куйидагилардан иборат:
а) статистик тургунликнинг бузилиши, яъни ![]() функция
мусбат аник ишоралиликни йукотиб узгарувчан ишорали функцияга айланиши;
функция
мусбат аник ишоралиликни йукотиб узгарувчан ишорали функцияга айланиши;
б) манфий диссипациянинг хосил булиши, яъни манфий ишкаланиш кучлари хисобидан тизимга ташки манбадан энергия келиши;
в) тизимга энергияни олиб кела оладиган (йуналтирилган богланиши булган) ёпик циклнинг мавжуд булиши.
Шуни хам эътироф этиш керакки, статистик нотургун
тизимни б) ва в) механизмлар оркали тургун килиш мумкин, яъни манфий киймат кабул
кила оладиган ![]() функцияли тизимни
тургун килиш учун манфий ишкаланиш кучлар ёки цикл мавжуд булиши керак.
функцияли тизимни
тургун килиш учун манфий ишкаланиш кучлар ёки цикл мавжуд булиши керак.
Шундай килиб, а), б) ва в) механизмлардан бирортаси
мавжуд булгандагина каралаётган тизим нотургун булиши мумкин. Шу билан бирга
айтиш жоизки, нотургунлик хакикатан хам пайдо булиши учун бу механизмлар микдор
жихатдан канча булиши аник эмас. Бу саволга жавоб бериш учун тизим параметрлари
кийматларини кайси ораликда узгартиришимиз мумкинлигини аниклаштиришимиз керак.
Уз-узидан хам маълум ва осонгина текшириш мумкинки, агар ![]() функция узгарувчан
ишорали булса ва б) хамда в) механизмлар мавжуд булмаса, у холда тизим нотургун
булади; агар тизимда хос манфий ишкаланиш кучи мавжуд булса, у холда унинг микдорини
етарлича катта килиш хисобидан нотургунликка келиш мумкин; тизимда цикл мавжуд
булса, у холда доимо йуналтирилган богланиш таркибига кирган параметрларни
танлаб олиш йули билан уни нотургун килиш мумкин [64,69].
функция узгарувчан
ишорали булса ва б) хамда в) механизмлар мавжуд булмаса, у холда тизим нотургун
булади; агар тизимда хос манфий ишкаланиш кучи мавжуд булса, у холда унинг микдорини
етарлича катта килиш хисобидан нотургунликка келиш мумкин; тизимда цикл мавжуд
булса, у холда доимо йуналтирилган богланиш таркибига кирган параметрларни
танлаб олиш йули билан уни нотургун килиш мумкин [64,69].
Шундай килиб, нотургунликни келтириб чикарувчи механизмларнинг параметрларини етарлича узгартириш йули билан тизимни нотургун килиш мумкин ва шу маънода уларнинг мавжуд булиши тизимнинг нотургун булиши учун етарлидир.
8-§. Чизиклаштирилган тизимларда нотургунликнинг
пайдо булишига доир мисоллар
1-мисол. Автомобилнинг бошкарилувчи олдинги гилдираклари харакатининг нотургунлиги сабаблари
Автомобил уз харакати давомида маълум тезликка етгандан кейин бошкарилувчи олдинги гилдиракларида уз-узидан тебранма харакат бошланади. Бу тебранма харакат натижасида автомобил шиналари тез ейилади, олдинги подвеска ва бошкариш тизимининг кисмлари ишдан чикади, автомобил харакатининг нотургун булиши ва хатто бошкарувни йукотиш хавфи пайдо булади. Шунинг учун хам автомобил харакатининг тургунлигини тадкик этиш масаласи мухим амалий ахамиятга эгадир.
Автомобилнинг бошкарилувчи гилдираклари, рул бошкаруви ва олдинги подвескадан иборат тизим харакатининг тургунлик масаласини курайлик.
Бу тизимнинг увод гипотезасига асосан харакат тенгламаси куйидагича булади [92]:
 (6.8.1)
(6.8.1)
Бу ерда ![]() -олдинги гилдиракларнинг
шкворен уки атрофида айланиш бурчаги,
-олдинги гилдиракларнинг
шкворен уки атрофида айланиш бурчаги, ![]() - олдинги
подвесканинг гилдираклар билан биргаликда автомобилнинг буйлама уки атрофида айланиш
бурчаги,
- олдинги
подвесканинг гилдираклар билан биргаликда автомобилнинг буйлама уки атрофида айланиш
бурчаги, ![]() -шквореннинг буйлама
бурчаги,
-шквореннинг буйлама
бурчаги, ![]() -автомобилнинг
тезлиги. Колган параметрларнинг физикавий (механик) маъноси [92] да келтирилган
(6.5-шакл).
-автомобилнинг
тезлиги. Колган параметрларнинг физикавий (механик) маъноси [92] да келтирилган
(6.5-шакл).
 |
6.5-шакл
(6.8.1) тизимни иккита бир-бирига богланган
осцилляторлар тизими сифатида караш мумкин: ![]() ва
ва ![]() .
Бу осцилляторларда масса (инерция), мусбат ишкаланиш кучи ва эластиклик
(шиналар, рессор ва бошкарув органларининг эластиклиги) мавжуд. Гилдиракларнинг
айланиши ва
.
Бу осцилляторларда масса (инерция), мусбат ишкаланиш кучи ва эластиклик
(шиналар, рессор ва бошкарув органларининг эластиклиги) мавжуд. Гилдиракларнинг
айланиши ва ![]() бурчакнинг
мавжудлигидан бу осцилляторлар орасида гироскопик ва инерцион богланишлар мавжуд
(тенгламалардаги таги битта чизик билан чизилган хадлар). Бундан ташкари улар уртасида
бурчакнинг
мавжудлигидан бу осцилляторлар орасида гироскопик ва инерцион богланишлар мавжуд
(тенгламалардаги таги битта чизик билан чизилган хадлар). Бундан ташкари улар уртасида
![]() дан
дан ![]() га
караб координата буйича йуналтирилган богланиш мавжуд (таги икки марта чизилган
хад), чунки
га
караб координата буйича йуналтирилган богланиш мавжуд (таги икки марта чизилган
хад), чунки ![]() бурчакнинг узгариши
натижасида олдинги гилдираклар бурилади ва натижада автомобилнинг буйлама уки (
бурчакнинг узгариши
натижасида олдинги гилдираклар бурилади ва натижада автомобилнинг буйлама уки (![]() уки) буйича момент хосил килувчи гилдиракларга таъсир этувчи ён реакция кучи
пайдо булади. Гироскопик ва инерцион богланишлар йуналтирилган богланиш билан
биргаликда циклни ташкил этадилар. Демак, 1-теоремага асосан курилаётган тизим
потенциал нотургун тизимдир, яъни йуналтирилган богланишнинг параметрларини
шундай танлаб олиш мумкинки, тизим нотургун булади. Йуналтирилган богланишни реализация
этиш учун ташки энергия манбаи зарурдир. Курилаётган тизим учун доимий ташки
энергия манбаи булиб автомобил двигатели хизмат килади ва сирганишсиз харакат килаётган
гилдираклар «ташки» алока (богланиш) вазифасини бажаради. У асосий тизимни
энергия манбаи билан боглайди.
уки) буйича момент хосил килувчи гилдиракларга таъсир этувчи ён реакция кучи
пайдо булади. Гироскопик ва инерцион богланишлар йуналтирилган богланиш билан
биргаликда циклни ташкил этадилар. Демак, 1-теоремага асосан курилаётган тизим
потенциал нотургун тизимдир, яъни йуналтирилган богланишнинг параметрларини
шундай танлаб олиш мумкинки, тизим нотургун булади. Йуналтирилган богланишни реализация
этиш учун ташки энергия манбаи зарурдир. Курилаётган тизим учун доимий ташки
энергия манбаи булиб автомобил двигатели хизмат килади ва сирганишсиз харакат килаётган
гилдираклар «ташки» алока (богланиш) вазифасини бажаради. У асосий тизимни
энергия манбаи билан боглайди.
Шундай килиб, увод гипотезасига асосан олдинги гилдираклар
харакат нотургунлигининг асосий сабаби тизимда циклнинг мавжудлигидир. Бу цикл ![]() ва
ва
![]() лар осцилляторлар орасидаги
узаро гироскопик ва инерцион богланишлар хамда
лар осцилляторлар орасидаги
узаро гироскопик ва инерцион богланишлар хамда ![]() дан
дан ![]() га
караб йуналтирилган богланишдан иборат.
га
караб йуналтирилган богланишдан иборат.
Тизимнинг геометрик схемасидан (6.6-шакл) куринадики,
харакатни тургун килиш учун ёки ![]() ва
ва ![]() лар
орасидаги узаро богланишларни, ёки
лар
орасидаги узаро богланишларни, ёки ![]() дан
дан ![]() га
караб йуналтирилган богланишни йук килиш керак.
га
караб йуналтирилган богланишни йук килиш керак. ![]() дан
дан ![]() га
каратиб йуналтирилган богланишни факат абсолют каттик гилдиракларга утиш хисобида
йук килиш мумкин, яъни гилдиракларга эластик шиналар кийдирмаслик йули билан
эришиш мумкин. Албатта, буни амалга ошириш ноуриндир.
га
каратиб йуналтирилган богланишни факат абсолют каттик гилдиракларга утиш хисобида
йук килиш мумкин, яъни гилдиракларга эластик шиналар кийдирмаслик йули билан
эришиш мумкин. Албатта, буни амалга ошириш ноуриндир. ![]() ва
ва ![]() лар
орасидаги узаро богланишларни богланмаган параллелограмм ёки свечали подвескага
утиш йули билан йукотиш мумкин. Шунинг учун хам барча тез юрар енгил машиналар
богланмаган подвеска билан жихозланган.
лар
орасидаги узаро богланишларни богланмаган параллелограмм ёки свечали подвескага
утиш йули билан йукотиш мумкин. Шунинг учун хам барча тез юрар енгил машиналар
богланмаган подвеска билан жихозланган.
 |
Демак, увод гипотезаси асосида богланган подвескадан богланмаган подвескага утиш оркали автомобил олдинги гилдиракларининг харакатини тургун килиш мумкин (чунки бу холда цикл мавжуд булмайди).
Шундай килиб, Ю.И.Неймаркнинг теоремалари тизимнинг харакат тенгламаларини тадкик этмасдан туриб, конструкцияга узгартиришлар киритиш йули билан унинг харакатини тургун килишга имкон яратади.
2-мисол. Гиростабиллаштирилган бир рельсли вагон [63]
Бир рельсли вагон харакатини стабиллаштириш
учун вагон ичига икки эркинлик даражасига эга булган тез айланадиган гироскоп урнатилади
(6.7-шакл). Вагон-гироскоп тизими харакатини гироскоп айланишининг бурчак
тезлиги узгармас булган холда икки ![]() ва
ва ![]() бурчаклар билан
ифодалаш мумкин. Бурчакларга мос келган осцилляторлар манфий эластикликка (кайишкокликка)
эгадирлар. Вагоннинг масса маркази унинг таянч нуктасидан юкорида жойлашганлиги
учун у манфий эластикликка эга булади. Гироскоп рамкасининг айланиш бурчаги
бурчаклар билан
ифодалаш мумкин. Бурчакларга мос келган осцилляторлар манфий эластикликка (кайишкокликка)
эгадирлар. Вагоннинг масса маркази унинг таянч нуктасидан юкорида жойлашганлиги
учун у манфий эластикликка эга булади. Гироскоп рамкасининг айланиш бурчаги ![]() буйича манфий
эластиклик
буйича манфий
эластиклик ![]() юк оркали сунъий
равишда эришилади.
юк оркали сунъий
равишда эришилади. ![]() ва
ва ![]() осцилляторлар орасида
анчагина катталикдаги гироскопик богланиш мавжуд.
осцилляторлар орасида
анчагина катталикдаги гироскопик богланиш мавжуд.
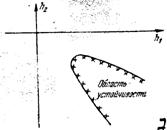 |
|||
 |
|||
6.7-шакл. 6.8-шакл.
Каралаётган тизимнинг харакат тенгламаси куйидагича:
 (6.8.2)
(6.8.2)
(6.8.2) тизимнинг характеристик тенгламаси
 (6.8.3)
(6.8.3)
куринишда булади. (6.8.3) тенгламадан куриниб турибдики,
агар ![]() ва
ва ![]() булса, у холда
тизимнинг тойилмаган харакати нотургундир. Шунга карамасдан
булса, у холда
тизимнинг тойилмаган харакати нотургундир. Шунга карамасдан ![]() ёки
ёки ![]() параметрларнинг
бирортаси манфий ишорали булганда тизимнинг колган параметрларини шундай танлаб
олиш мумкинки, каралаётган тизимнинг тойилмаган харакати тургун булади
(6.8-шакл).
параметрларнинг
бирортаси манфий ишорали булганда тизимнинг колган параметрларини шундай танлаб
олиш мумкинки, каралаётган тизимнинг тойилмаган харакати тургун булади
(6.8-шакл).
9-§. Тургунлик сохаларини ясаш. Ю.И.Неймаркнинг D-булаклаш усули [63,65]
Юкорида утказилган мулохазалардан маълумки, чизикли тизимлар мувозанат холатининг тургунлигини тадкик этиш масаласи купхад ва аналитик функциялар илдизларининг комплекс узгарувчилар текислигида кандай жойлашишига боглик.
Купгина техник масалаларда параметрларнинг шундай кийматларини танлаб олиш керакки, курилаётган тизимнинг харакати асимптотик тургун булсин. Масалан, конструктив параметрларнинг кандай кийматларида кема, самолет ва ракеталар олдиндан берилган йуналиш буйича тургун харакат киладилар? Турбина ва генераторларнинг параметрларини шундай танлаб олиш керакки, улар берилган иш режимини тургун саклаб колсинлар ва хоказо.
Агар
характеристик тенгламанинг даражаси ![]() булса, у вактда
тургунлик сохасини Гурвиц критерияси ёрдами билан топиш мумкин.
булса, у вактда
тургунлик сохасини Гурвиц критерияси ёрдами билан топиш мумкин. ![]() холлар
учун бу критериядан фойдаланиш огир кечади. Аникланиши лозим булган параметрларнинг
сони иккидан куп булмаган хол учун Нижний Новгородлик олим Ю.И.Неймарк
томонидан ихтиёрий
холлар
учун бу критериядан фойдаланиш огир кечади. Аникланиши лозим булган параметрларнинг
сони иккидан куп булмаган хол учун Нижний Новгородлик олим Ю.И.Неймарк
томонидан ихтиёрий ![]() даражали
характеристик тенгламалар учун тургунлик сохасини ясаш усули ишлаб чикилди
[65]. Ушбу усулни (D-булаклаш усули деб айтилади) изохлашга утамиз.
даражали
характеристик тенгламалар учун тургунлик сохасини ясаш усули ишлаб чикилди
[65]. Ушбу усулни (D-булаклаш усули деб айтилади) изохлашга утамиз.
![]() (6.9.1)
(6.9.1)
комплекс
узгарувчи ![]() ва хакикий
ва хакикий ![]() параметрларнинг
аналитик функцияси булсин.
параметрларнинг
аналитик функцияси булсин. ![]() комплекс узгарувчи
текислигида кандайдир G соха берилган булсин.
комплекс узгарувчи
текислигида кандайдир G соха берилган булсин. ![]() параметрлар
фазосини
параметрлар
фазосини ![]() сохаларга булаклаб
чикамиз. Бу ерда
сохаларга булаклаб
чикамиз. Бу ерда ![]() соха
соха ![]() та
илдизи G соха ичида ва
та
илдизи G соха ичида ва ![]() та илдизи G соха
ташкарисида ётган (6.9.1) функцияларга мос келади.
та илдизи G соха
ташкарисида ётган (6.9.1) функцияларга мос келади. ![]() ва
ва ![]() лар
¢рнида чексизлик хам келиши мумкин. Тургунлик назарияси учун G сохаси
сифатида
лар
¢рнида чексизлик хам келиши мумкин. Тургунлик назарияси учун G сохаси
сифатида ![]() бирлик доиранинг
ташкарисида ётган соха, ёки
бирлик доиранинг
ташкарисида ётган соха, ёки ![]() унг ярим текисликнинг
олинадиган холлар кизикиш уйготади.
унг ярим текисликнинг
олинадиган холлар кизикиш уйготади.
![]() параметрлар
буйича тургунлик сохаси
параметрлар
буйича тургунлик сохаси ![]() нинг хар хил кийматларига
мос келувчи
нинг хар хил кийматларига
мос келувчи ![]() сохаларнинг
бирлашмасидан (йигиндисидан) иборат булади. Параметрлар фазосини хар хил
сохаларнинг
бирлашмасидан (йигиндисидан) иборат булади. Параметрлар фазосини хар хил ![]() ва
ва
![]() ларга мос келувчи
ларга мос келувчи ![]() сохаларга
булаклаш G сохага нисбатан
сохаларга
булаклаш G сохага нисбатан ![]() параметрлар
фазосини D-булаклаш деб айтилади.
параметрлар
фазосини D-булаклаш деб айтилади.
G соха чизикдан иборат булиши хам мумкин, масалан, хакикий ук ёки мусбат хакикий ярим ук, биринчи холда D – булаклаш параметрлар фазосини турли сондаги хакикий ва комплекс илдизларга мос келувчи сохаларга булаклайди.
D – булаклашни урганиш ва ундан амалда фойдаланиш учун куйидаги интерпретациядан (талкиндан) фойдаланамиз.
![]() (6.9.2)
(6.9.2)
муносабат
комплекс текисликнинг z нукталарига параметрлар фазосининг ![]() нуктани
мос килиб куювчи Т нуктавий акслантиришни ифодаласин [68]. Агар z нуктага
нуктани
мос килиб куювчи Т нуктавий акслантиришни ифодаласин [68]. Агар z нуктага
![]() нуктаси жавоб
берса, у вактда бу параметрларнинг ушбу кийматида (6.9.2) тенглама z
илдизга эга эканлигини билдиради.
нуктаси жавоб
берса, у вактда бу параметрларнинг ушбу кийматида (6.9.2) тенглама z
илдизга эга эканлигини билдиради.
Умумий
холда Т хам ва унга тескари булган Т-1 акслантириш хам бир кийматли
булмайдилар. Хар бир ![]() нуктага
нуктага ![]() параметрлар
фазосида
параметрлар
фазосида ![]() улчовли гиперфазо
тугри келади (
улчовли гиперфазо
тугри келади (![]() фазонинг улчовидан
2 бирлик кам улчовли фазо). Параметрлар фазосининг хар бир
фазонинг улчовидан
2 бирлик кам улчовли фазо). Параметрлар фазосининг хар бир ![]() нуктасига
(бу нуктага параметрларнинг
нуктасига
(бу нуктага параметрларнинг ![]() кийматлари мос келади)
(6.9.1) аналитик функциянинг барча
кийматлари мос келади)
(6.9.1) аналитик функциянинг барча ![]() илдизлари тугри
келади. Агар
илдизлари тугри
келади. Агар ![]() G сохадаги
G сохадаги
![]() илдизларнинг сони
ва
илдизларнинг сони
ва ![]() G соха
тулдирувчиси булган сохадаги илдизлар сони булса, у холда
G соха
тулдирувчиси булган сохадаги илдизлар сони булса, у холда ![]() . (6.9.1)
функция
. (6.9.1)
функция ![]() -даражали купхад ва
-даражали купхад ва
![]() унинг
коэффициентлари булсин, яъни
унинг
коэффициентлари булсин, яъни
![]() .
.
Хар
бир (![]() ) нуктага
) нуктага ![]() та
та
![]() илдизлар мос
келади. Маълумки,
илдизлар мос
келади. Маълумки, ![]() параметрларни
параметрларни ![]() илдизларнинг
кийматлари оркали ифодалаш мумкин, чунки
илдизларнинг
кийматлари оркали ифодалаш мумкин, чунки
![]() (6.9.3)
(6.9.3)
Бу ердан
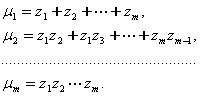 (6.9.4)
(6.9.4)
Энди
унг ярим текисликда ёки ихтиёрий G сохага нисбатан D-булаклашни куриб
утамиз. ![]() соханинг хар бир
соханинг хар бир ![]() нуктасига
m та
нуктасига
m та ![]() нукталар мос
келади, булардан
нукталар мос
келади, булардан ![]() таси G сохада
ва
таси G сохада
ва ![]() таси G сохадан
ташкарида ётади. Хусусан,
таси G сохадан
ташкарида ётади. Хусусан, ![]() соханинг хар бир
соханинг хар бир ![]() нуктасига
G соханинг
нуктасига
G соханинг ![]() та
та ![]() нукталари
мос келади ва, аксинча, G соханинг
нукталари
мос келади ва, аксинча, G соханинг ![]() та ихтиёрий
та ихтиёрий ![]() нукталарига
факат битта
нукталарига
факат битта ![]() нукта мос келади (
нукта мос келади (![]() ларнинг хар бири
ларнинг хар бири ![]() нуктага
аксланади). Демак, параметрлар фазосининг
нуктага
аксланади). Демак, параметрлар фазосининг ![]() сохаси
сохаси ![]() та
G сохаларнинг топологик купайтмасига топологик эквивалентдир.
та
G сохаларнинг топологик купайтмасига топологик эквивалентдир.
Агар
G соха богланишли булса, у холда ![]() соха хам
богланишли булади. Агар G соха бир богланишли булса, у вактда
соха хам
богланишли булади. Агар G соха бир богланишли булса, у вактда ![]() соха
на факат богланишли булади, балки
соха
на факат богланишли булади, балки ![]() -улчовли Евклид
фазосига ухшаш (гемеоморф) булади.
-улчовли Евклид
фазосига ухшаш (гемеоморф) булади.
Худди
шундай ![]() соха
соха ![]() та
G соха ва унинг
та
G соха ва унинг ![]() та тулдирувчиларининг
(чегарасиз) топологик купайтмасига топологик эквивалентдир. Бу ердан, хусусан
бирлик доира ёки унг ярим текисликка нисбатан D-булаклаш утказилганда
барча
та тулдирувчиларининг
(чегарасиз) топологик купайтмасига топологик эквивалентдир. Бу ердан, хусусан
бирлик доира ёки унг ярим текисликка нисбатан D-булаклаш утказилганда
барча ![]() сохалар
сохалар ![]() -улчовли
Евклид фазосига ухшаш (гемеоморф) булиши келиб чикади.
-улчовли
Евклид фазосига ухшаш (гемеоморф) булиши келиб чикади.
![]() нуктанинг
бирор D сохадан иккинчи сохага утиши учун шу
нуктанинг
бирор D сохадан иккинчи сохага утиши учун шу ![]() нуктага
мос келувчи
нуктага
мос келувчи ![]() илдизлардан биттаси
ёки бир нечтаси G сохага унинг чегарасини кесиб кириши ёки ундан чикиб
кетиши керак. Демак,
илдизлардан биттаси
ёки бир нечтаси G сохага унинг чегарасини кесиб кириши ёки ундан чикиб
кетиши керак. Демак, ![]() параметрлар
фазосида D-булаклашнинг чегараси
параметрлар
фазосида D-булаклашнинг чегараси ![]() нукталардан
иборат. Бу нукталар учун G соханинг чегарасига тааллукли бирор
нукталардан
иборат. Бу нукталар учун G соханинг чегарасига тааллукли бирор ![]() кийматда
кийматда
![]() (6.9.5)
(6.9.5)
муносабат
уринли булади. Шунинг учун хам ![]() нукта комплекс узгарувчи
текислигидаги G соханинг чегараси буйлаб юрганида (6.9.5) тенгламани
нукта комплекс узгарувчи
текислигидаги G соханинг чегараси буйлаб юрганида (6.9.5) тенгламани ![]() параметрлар
фазосидаги D-булаклашнинг параметрик тенгламаси сифатида караш мумкин.
параметрлар
фазосидаги D-булаклашнинг параметрик тенгламаси сифатида караш мумкин.
Параметрлар
фазоси икки улчовли булганда, яъни икки хакикий ![]() ва
ва ![]() параметрлар
фазосида ёки битта
параметрлар
фазосида ёки битта ![]() комплекс параметр
фазосида (бу параметрлар (6.9.1) функция ифодасига чизикли равишда кирганда) D-булаклашни
осонгина ясаш мумкин.
комплекс параметр
фазосида (бу параметрлар (6.9.1) функция ифодасига чизикли равишда кирганда) D-булаклашни
осонгина ясаш мумкин.
10-§. Бир комплекс параметр текислигида тургунлик
сохасини ясаш
Ихтиёрий
![]() даражали купхад берилган
ва унинг коэффициентлари
даражали купхад берилган
ва унинг коэффициентлари ![]() комплекс параметрга
чизикли тарзда богланган булсин. Бу холда уни куйидаги
комплекс параметрга
чизикли тарзда богланган булсин. Бу холда уни куйидаги
![]() (6.10.1)
(6.10.1)
куринишда ёзиш мумкин.
![]() комплекс
параметр текислигининг хар бир
комплекс
параметр текислигининг хар бир ![]() нуктасига G соханинг
ичида
нуктасига G соханинг
ичида ![]() та ва бу соханинг
ташкарисида
та ва бу соханинг
ташкарисида ![]() та илдизи мавжуд булган
(6.10.1) купхад мос келади. Шундай килиб
та илдизи мавжуд булган
(6.10.1) купхад мос келади. Шундай килиб ![]() текислиги G сохада
(6.10.1) к¢пхад турли
текислиги G сохада
(6.10.1) к¢пхад турли ![]() сондаги илдизларга
эга булган D(
сондаги илдизларга
эга булган D(![]() ) сохаларга булакланади.
Бир D(
) сохаларга булакланади.
Бир D(![]() ) сохадан иккинчи
сохага утиш учун (6.10.1) купхад илдизларининг биттаси G соханинг
чегарасини кесиб утиши керак. G соха чегарасининг параметрик тенгламасини
) сохадан иккинчи
сохага утиш учун (6.10.1) купхад илдизларининг биттаси G соханинг
чегарасини кесиб утиши керак. G соха чегарасининг параметрик тенгламасини
![]() (6.10.2)
(6.10.2)
куринишда
ёзишга эришдик деб фараз килайлик, бу ерда ![]() параметр бирор интервалда
узгаради. У вактда D-булаклаш чегарасининг параметрик тенгламаси
параметр бирор интервалда
узгаради. У вактда D-булаклаш чегарасининг параметрик тенгламаси
![]() (6.10.3)
(6.10.3)
куринишда
булади. (6.10.3) эгри чизик ![]() текисликни бир
нечта сохаларга булаклайди. Бу сохаларнинг хар бирида (6.10.1) купхад
илдизларининг сони
текисликни бир
нечта сохаларга булаклайди. Бу сохаларнинг хар бирида (6.10.1) купхад
илдизларининг сони ![]() бир хил булади. Бу
сохаларнинг бирорта нуктасида (6.10.1) купхад илдизларининг сони
бир хил булади. Бу
сохаларнинг бирорта нуктасида (6.10.1) купхад илдизларининг сони ![]() ни
топиш керак. Агар
ни
топиш керак. Агар ![]() - текисликнинг D-булаклашини,
- текисликнинг D-булаклашини,
![]() комплекс параметр
текислиги G ни
комплекс параметр
текислиги G ни ![]() текисликка
текисликка
![]() (6.10.4)
(6.10.4)
муносабат
оркали Т нуктавий акслантириш сифатида каралса, у вактда ![]() сонини
топиш осонлашади. Бу холда D-булаклашнинг (6.10.3) N чегараси, G соха
чегарасини (6.10.4) формула оркали
сонини
топиш осонлашади. Бу холда D-булаклашнинг (6.10.3) N чегараси, G соха
чегарасини (6.10.4) формула оркали ![]() текислигига
акслантириш натижасида хосил булади.
текислигига
акслантириш натижасида хосил булади. ![]() нуктасига
нуктасига ![]()
 |
текислигида
![]() та
та ![]() илдизлар
мос келади. Агар
илдизлар
мос келади. Агар ![]() булса, у вактда бу
илдизларнинг
булса, у вактда бу
илдизларнинг ![]() таси
таси ![]() G сохада
ва
G сохада
ва ![]() таси G сохадан
ташкарида ётадилар.
таси G сохадан
ташкарида ётадилар. ![]() нукталарнинг хар
бири (6.10.4) формула оркали
нукталарнинг хар
бири (6.10.4) формула оркали ![]() нуктага аксланади.
Бу холда
нуктага аксланади.
Бу холда ![]() нукталарнинг
нукталарнинг ![]() атрофлари
атрофлари
![]()
![]() нуктанинг
нуктанинг
![]() атрофига айланади
(6.9-шакл).
атрофига айланади
(6.9-шакл).
![]() нукта
D(
нукта
D(![]() ) cоханинг биридан иккинчисига утиши учун
) cоханинг биридан иккинчисига утиши учун ![]() илдизларнинг
бири ёки бир нечтаси G соханинг чегарасини кесиб утиши керак.
илдизларнинг
бири ёки бир нечтаси G соханинг чегарасини кесиб утиши керак.
![]() илдиз
G соханинг чегарасида ётган булсин (6.10-шакл).
илдиз
G соханинг чегарасида ётган булсин (6.10-шакл).
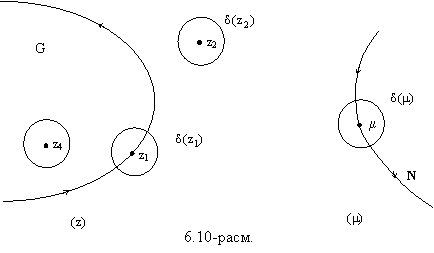
У
вактда унга мос ![]() нукта N чегаранинг
бир булагида ётади. N чегаравий эгри чизикнинг бу бир булаги
нукта N чегаранинг
бир булагида ётади. N чегаравий эгри чизикнинг бу бир булаги ![]() нукта
ётган G соханинг бир булагининг аксидир. Бу ерда
нукта
ётган G соханинг бир булагининг аксидир. Бу ерда ![]() атроф
атроф
![]() атрофга айланади.
(6.10.4) аксланиш конформлик хусусиятига эга, яъни
атрофга айланади.
(6.10.4) аксланиш конформлик хусусиятига эга, яъни ![]() кичик атрофни
кичик атрофни
![]() атрофга айланиши
унинг радиал чузилишидан ва бирор бурчакка бурилишидан иборат булади. G соха
доимо чап тарафда колиши шарти билан G соханинг чегарасида мусбат йуналишни
танлаб оламиз.
атрофга айланиши
унинг радиал чузилишидан ва бирор бурчакка бурилишидан иборат булади. G соха
доимо чап тарафда колиши шарти билан G соханинг чегарасида мусбат йуналишни
танлаб оламиз. ![]() нукта G соха
чегарасида мусбат йуналиш буйича караб харакат килганда унга мос булган
нукта G соха
чегарасида мусбат йуналиш буйича караб харакат килганда унга мос булган ![]() нукта
N чегаравий эгри чизик буйича харакат килади. Унинг бу
харакат йуналишини мусбат йуналиш сифатида кабул киламиз.
нукта
N чегаравий эгри чизик буйича харакат килади. Унинг бу
харакат йуналишини мусбат йуналиш сифатида кабул киламиз. ![]() нукта G соханинг
чегарасини чап тарафдан унг тарафга караб кесиб утсин. Бу вактда аксланишнинг
конформлик хусусиятига асосан унга мос булган
нукта G соханинг
чегарасини чап тарафдан унг тарафга караб кесиб утсин. Бу вактда аксланишнинг
конформлик хусусиятига асосан унга мос булган ![]() нукта хам N
эгри чизикнинг чап тарафдан унг тарафга караб кесиб утади.
нукта хам N
эгри чизикнинг чап тарафдан унг тарафга караб кесиб утади. ![]() нукта
чегаравий эгри чизикни чап тарафдан унг тарафга кесиб утганда у G сохадан
чикиб кетади, яъни G соха ичидаги илдизлар сони биттага камаяди. Бу холда
нукта
чегаравий эгри чизикни чап тарафдан унг тарафга кесиб утганда у G сохадан
чикиб кетади, яъни G соха ичидаги илдизлар сони биттага камаяди. Бу холда ![]() га
мос келувчи
га
мос келувчи ![]() нукта D(
нукта D(![]() ) сохадан D(
) сохадан D(![]() ) сохага утади. Шундай килиб,
) сохага утади. Шундай килиб, ![]() нукта N
эгри чизикни чап тарафдан унг тарафига караб кесиб утса,
нукта N
эгри чизикни чап тарафдан унг тарафига караб кесиб утса, ![]() сони биттага камаяди. Демак, D(
сони биттага камаяди. Демак, D(![]() ) сохаларни топиш учун
) сохаларни топиш учун ![]() сонини
сонини ![]() комплекс текисликнинг
исталган бир нуктасида топиш кифоя. Колганларини юкорида баён этилган коидага
асосан топиш мумкин, яъни D-булаклашнинг N чегарасини
комплекс текисликнинг
исталган бир нуктасида топиш кифоя. Колганларини юкорида баён этилган коидага
асосан топиш мумкин, яъни D-булаклашнинг N чегарасини ![]() нукта
чап тарафдан унг тарафга караб кесиб утса,
нукта
чап тарафдан унг тарафга караб кесиб утса, ![]() сони биттага камаяди ва унг томондан чап томонга караб
кесиб утса,
сони биттага камаяди ва унг томондан чап томонга караб
кесиб утса, ![]() сони биттага купаяди деган коидага асосан барча
мавжуд булган D(
сони биттага купаяди деган коидага асосан барча
мавжуд булган D(![]() ) сохалар топилади. Бу коидани амалда куллаш яна хам кулай
булиши учун N эгри чизикни мусбат йуналишда айланиб, уни чап тарафдан
штрихлаб чикамиз. Агар N эгри чизикнинг айрим булакларини бир неча марта
айлансак, у холда шунча марта уша булакни штрихлаймиз.
) сохалар топилади. Бу коидани амалда куллаш яна хам кулай
булиши учун N эгри чизикни мусбат йуналишда айланиб, уни чап тарафдан
штрихлаб чикамиз. Агар N эгри чизикнинг айрим булакларини бир неча марта
айлансак, у холда шунча марта уша булакни штрихлаймиз.
N
эгри чизик бир марта штрихланган булсин. У вактда N эгри чизикни кесиб
утишда ![]() сонининг узгаришини куйидагича ифодалаш мумкин: N
эгри чизикни штрихланган тарафдан штрихланмаган тарафга кесиб утишда
сонининг узгаришини куйидагича ифодалаш мумкин: N
эгри чизикни штрихланган тарафдан штрихланмаган тарафга кесиб утишда ![]() сони биттага камаяди ва штрихланмаган тарафдан
штрихланган тарафга утишда
сони биттага камаяди ва штрихланмаган тарафдан
штрихланган тарафга утишда ![]() сони биттага купаяди.
сони биттага купаяди.
Шундай
килиб, ![]() эгри чизик билан
чегараланган ихтиёрий G сохага нисбатан
эгри чизик билан
чегараланган ихтиёрий G сохага нисбатан ![]() купхадлар текислигини
D – булаклаш учун куйидаги коидадан фойдаланамиз:
купхадлар текислигини
D – булаклаш учун куйидаги коидадан фойдаланамиз:
1.![]() эгри чизик (6.10.4) муносабат оркали
эгри чизик (6.10.4) муносабат оркали ![]() текислигига акслантирилади.
Шу тарзда хосил этилган N эгри чизикнинг мусбат йуналиши топилади ва у штрихланади.
текислигига акслантирилади.
Шу тарзда хосил этилган N эгри чизикнинг мусбат йуналиши топилади ва у штрихланади.
2.N
эгри чизик ![]() текислигини булаклаган
сохалардан биттасини D(
текислигини булаклаган
сохалардан биттасини D(![]() ) деб фараз килиб, колган сохалар штриховка коидасига
асосан топилади. Энг кичик ва энг катта
) деб фараз килиб, колган сохалар штриховка коидасига
асосан топилади. Энг кичик ва энг катта ![]() сонига даъвогар сохалар топилади.
сонига даъвогар сохалар топилади.
3.![]() текислигида бирорта купхади учун кушимча мулохазалар юритиб, унинг G соха
ичида ва ундан ташкарисида ётган илдизларининг сони топилади.
текислигида бирорта купхади учун кушимча мулохазалар юритиб, унинг G соха
ичида ва ундан ташкарисида ётган илдизларининг сони топилади.
G соханинг
![]() чегарасини
чегарасини ![]() текисликка
акслантириш учун унинг (6.10.2) параметрик тенгламасидан фойдаланиш кулайдир.
Бу холда N эгри чизикнинг параметрик тенгламаси (6.10.3) куринишда
булади. Агар G соха бирлик доира ёки чап ярим текислик булса,
текисликка
акслантириш учун унинг (6.10.2) параметрик тенгламасидан фойдаланиш кулайдир.
Бу холда N эгри чизикнинг параметрик тенгламаси (6.10.3) куринишда
булади. Агар G соха бирлик доира ёки чап ярим текислик булса, ![]() чегаравий
эгри чизик (6.10.2) куринишда ёзилади, бу ерда мос равишда
чегаравий
эгри чизик (6.10.2) куринишда ёзилади, бу ерда мос равишда
![]() ва
ва![]() (6.10.5)
(6.10.5)
булиб унинг акси булган N эгри чизик мос равишда
![]() ёки
ёки ![]() (6.10.6)
(6.10.6)
куринишда
ёзилади, бу ерда хакикий параметр ![]() мос равишда 0 дан
мос равишда 0 дан ![]() гача
ва -¥ дан +¥ гача узгаради. Бу холда
гача
ва -¥ дан +¥ гача узгаради. Бу холда ![]() нинг
усиши билан N эгри чизикдаги
нинг
усиши билан N эгри чизикдаги ![]() нуктанинг узгариш
йуналиши мусбат йуналиш булади.
нуктанинг узгариш
йуналиши мусбат йуналиш булади.
Биз
юкорида ихтиёрий ![]() даражали купхаднинг
коэффициентлари бир комплекс параметрдан чизикли тарзда богланган хол учун шу
комплекс параметр текислигида D-булаклашни ясашнинг умумий назариясини ифодалаб бердик.
даражали купхаднинг
коэффициентлари бир комплекс параметрдан чизикли тарзда богланган хол учун шу
комплекс параметр текислигида D-булаклашни ясашнинг умумий назариясини ифодалаб бердик.
Энди
умумий назарияни тушуниш осон булиши учун ихтиёрий ![]() даражали
даражали
![]() (6.10.7)
(6.10.7)
характеристик
тенгламанинг ![]() коэффициентлари
коэффициентлари ![]() комплекс
параметрга чизикли равишда богланган
комплекс
параметрга чизикли равишда богланган ![]() хол учун D-булаклашни
ясашни куриб утайлик.
хол учун D-булаклашни
ясашни куриб утайлик.
(6.10.7)
характеристик тенгламанинг барча ![]() илдизларининг хакикий
кисми манфий буладиган
илдизларининг хакикий
кисми манфий буладиган ![]() параметрнинг кийматлар
сохасини (агар бу соха мавжуд булса) топиш талаб этилсин.
параметрнинг кийматлар
сохасини (агар бу соха мавжуд булса) топиш талаб этилсин.
Бу
![]() комплекс узгарувчи
текислигида барча илдизлар чап ярим текисликда ётиши керак демакдир. (6.10.7)
характеристик тенгламани
комплекс узгарувчи
текислигида барча илдизлар чап ярим текисликда ётиши керак демакдир. (6.10.7)
характеристик тенгламани
![]() (6.10.8)
(6.10.8)
куринишда
ёзамиз. Бу тенгламадан ![]() параметрни топамиз:
параметрни топамиз:
![]() .
(6.10.9)
.
(6.10.9)
(6.10.9)
муносабат ![]() ни
ни ![]() нинг
функцияси сифатида аниклайди.
нинг
функцияси сифатида аниклайди. ![]() га хар хил киймат
бериб,
га хар хил киймат
бериб, ![]() ни кийматларини (хакикий
ёки комплекс) топишимиз мумкин.
ни кийматларини (хакикий
ёки комплекс) топишимиз мумкин.
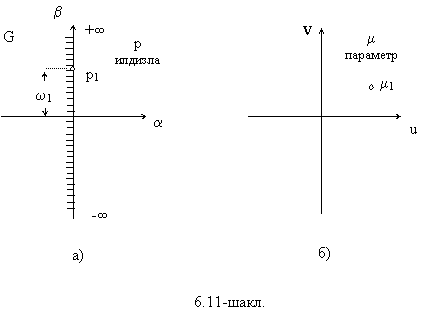
G соханинг
штрихланган чегарасини (6.11-шакл,а) ![]() комплекс параметр
текислигига нуктавий акслантириш учун
комплекс параметр
текислигига нуктавий акслантириш учун ![]() деб оламиз, бу
ерда
деб оламиз, бу
ерда ![]() ,
, ![]() хакикий
сон ва
хакикий
сон ва ![]() дан
дан ![]() гача
киймат кабул килади.
гача
киймат кабул килади. ![]() нинг бу кийматини
(6.10.9) га куйиб
нинг бу кийматини
(6.10.9) га куйиб
![]()
ни хосил киламиз ва бу муносабатнинг унг томонини хакикий ва мавхум кисмларга ажратамиз
![]() . (6.10.10)
. (6.10.10)
![]() комплекс параметр эканлигини хисобга олсак, (6.10.10)
тенгламадан
комплекс параметр эканлигини хисобга олсак, (6.10.10)
тенгламадан
![]() (6.10.11)
(6.10.11)
D-булаклашнинг
чегараси булган N эгри чизикнинг параметрик тенгламасини хосил киламиз.
Шундай килиб, D-булаклашнинг чегараси ![]() илдизлар текислиги
илдизлар текислиги
![]() мавхум укининг
мавхум укининг ![]() комплекс
параметр текислигидаги аксидир. (6.10.11) муносабатга асосан
комплекс
параметр текислигидаги аксидир. (6.10.11) муносабатга асосан ![]()
![]() га
нисбатан жуфт функция ва
га
нисбатан жуфт функция ва ![]() - ток функция.
- ток функция.
Мисол.
![]() (6.10.12)
(6.10.12)
характеристик
тенглама берилган булсин. Бу тенгламадан ![]() ни топамиз
ни топамиз
![]() . (6.10.12¢)
. (6.10.12¢)
Бу
ердан ![]() ва
ва ![]() (6.10.12¢) тенгламадаги
(6.10.12¢) тенгламадаги ![]() урнига
урнига ![]() ни
куйиб,
ни
куйиб,
![]() (6.10.13)
(6.10.13)
муносабатни хосил киламиз. Бу ердан

(6.10.13) муносабатни хакикий ва мавхум кисмларга ажратиб, D-булаклашнинг чегараси N эгри чизикнинг параметрик тенгламасини топамиз:
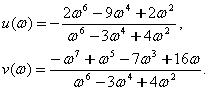 (6.10.14)
(6.10.14)
Энди
умумий холга кайтайлик. ![]() илдизлар текислигининг
мавхум укида ётган кандайдир
илдизлар текислигининг
мавхум укида ётган кандайдир ![]() 1 нуктани
оламиз.
1 нуктани
оламиз. ![]() текислигининг
текислигининг ![]() 1
нуктасига
1
нуктасига ![]() 1=
1=![]() 1
координата тугри келади (6.11-шакл,а). (6.10.11) параметрик тенгламага
1
координата тугри келади (6.11-шакл,а). (6.10.11) параметрик тенгламага ![]() кийматни
куйиб,
кийматни
куйиб, ![]() текислигида унга
мос келган
текислигида унга
мос келган ![]() нуктани ясаймиз
(6.11-шакл,б).
нуктани ясаймиз
(6.11-шакл,б).
Агар
![]() га -¥ дан +¥ гача киймат берсак, у вактда
га -¥ дан +¥ гача киймат берсак, у вактда ![]() текислигида
кандайдир эгри чизикни хосил киламиз. Бу эгри чизик
текислигида
кандайдир эгри чизикни хосил киламиз. Бу эгри чизик ![]() илдизлар
текислиги мавхум укининг
илдизлар
текислиги мавхум укининг ![]() комплекс параметр
текислигидаги акси булади. Шундай килиб топилган эгри чизик (1.12-расм,а да курсатилгандай
булсин деб фараз киламиз) D-булаклашнинг чегараси деб айтилади.
комплекс параметр
текислигидаги акси булади. Шундай килиб топилган эгри чизик (1.12-расм,а да курсатилгандай
булсин деб фараз киламиз) D-булаклашнинг чегараси деб айтилади.

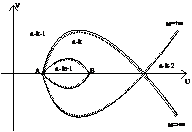
а) б)
6.12-шакл
D-булаклашнинг
чегарасини (![]() га мос келган нуктадан
га мос келган нуктадан
![]() мос келган нуктагача
булган ораликни) чап тарафдан штрихлаймиз (6.12-шакл,а).
мос келган нуктагача
булган ораликни) чап тарафдан штрихлаймиз (6.12-шакл,а). ![]() жуфт функция
ва
жуфт функция
ва ![]() ток функция булганлиги
учун D–булаклашнинг чегарасини ясашда
ток функция булганлиги
учун D–булаклашнинг чегарасини ясашда ![]() ни 0 дан
+¥ гача узгартириш етарли.
ни 0 дан
+¥ гача узгартириш етарли. ![]() нинг -¥ дан 0 гача булган кийматларига мос келувчи чегарани хосил килиш учун
ясалган чегаранинг
нинг -¥ дан 0 гача булган кийматларига мос келувчи чегарани хосил килиш учун
ясалган чегаранинг ![]() текисликнинг
текисликнинг ![]() укига
нисбатан кузгудаги аксини олиш кифоядир.
укига
нисбатан кузгудаги аксини олиш кифоядир.
D-булаклаш
чегарасида ётган ![]() нукталарга
нукталарга ![]() илдизлар
текислигидаги
илдизлар
текислигидаги ![]() нукталар, яъни
характеристик тенгламанинг соф мавхум илдизлари мос келади.
нукталар, яъни
характеристик тенгламанинг соф мавхум илдизлари мос келади. ![]() текисликнинг
текисликнинг
![]() хакикий укида (D-булаклаш
чегарасида ётмаган) ётган
хакикий укида (D-булаклаш
чегарасида ётмаган) ётган ![]() 1 нуктани
оламиз ва унинг кийматини (6.10.7) характеристик тенгламага келтириб куямиз:
1 нуктани
оламиз ва унинг кийматини (6.10.7) характеристик тенгламага келтириб куямиз:
![]() , (6.10.15)
, (6.10.15)
бу
ерда ![]() коэффициентлар хакикий
сонлар. (6.10.15) характеристик тенгламанинг коэффициентларидан
коэффициентлар хакикий
сонлар. (6.10.15) характеристик тенгламанинг коэффициентларидан
 (6.10.16)
(6.10.16)
Гурвиц
детерминантини тузамиз. Маълумки, ![]() илдизлар
текислигининг унг ярим текислигида ётган илдизлар сони
илдизлар
текислигининг унг ярим текислигида ётган илдизлар сони
![]() (6.10.17)
(6.10.17)
катордаги
ишораларнинг узгариш сонига тенг, бу ерда ![]() Гурвиц детерминантининг
бош минорлари. Шу коидадан фойдаланиб
Гурвиц детерминантининг
бош минорлари. Шу коидадан фойдаланиб ![]() 1 нуктага
мос булган (6.10.15) характеристик тенгламанинг унг ярим текисликда ётган илдизларининг
сонини топамиз. (6.10.15) тенгламанинг унг ярим текисликда ётган илдизларининг
сони
1 нуктага
мос булган (6.10.15) характеристик тенгламанинг унг ярим текисликда ётган илдизларининг
сонини топамиз. (6.10.15) тенгламанинг унг ярим текисликда ётган илдизларининг
сони ![]() тенг деб фараз килайлик.
тенг деб фараз килайлик.
Мисол.
(6.10.12) характеристик тенгламадаги ![]() =
=![]() 1
параметрнинг киймати 4 га тенг булсин, яъни
1
параметрнинг киймати 4 га тенг булсин, яъни ![]() 1=4. У
вактда
1=4. У
вактда ![]() 1=4 ни
(6.10.12) тенгламага куйиб, куйидагини хосил киламиз:
1=4 ни
(6.10.12) тенгламага куйиб, куйидагини хосил киламиз:
![]() . (6.10.15¢)
. (6.10.15¢)
Бу тенгламанинг Гурвиц детерминанти
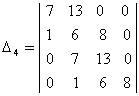 (6.10.16¢)
(6.10.16¢)
куринишда булади. Бу ердан
![]()
хосил киламиз ва (6.10.17) катордаги ишора алмашинишлар
+, +, +, -, + (6.10.17¢)
куринишда булади. (6.10.17¢) катордаги ишоралар узгариш сони 2 га тенг.
Демак,
![]() текислигининг
текислигининг ![]() 1=4
нуктасига мос келувчи характеристик тенгламанинг
1=4
нуктасига мос келувчи характеристик тенгламанинг ![]() илдизлар текислигининг
унг ярим текислигида ётган илдизларининг сони
илдизлар текислигининг
унг ярим текислигида ётган илдизларининг сони ![]() га тенг, яъни 2 та
илдизининг хакикий кисми мусбат ишорали булади. Шундай килиб, (6.10.15¢) характеристик тенгламанинг 2 та илдизи чап ярим
текисликда ва 2 та илдизи унг ярим текисликда ётади, яъни 2 илдизининг хакикий кисми
манфий ва 2 илдизининг хакикий кисми мусбат ишорали булади (яъни D(2,2)).
га тенг, яъни 2 та
илдизининг хакикий кисми мусбат ишорали булади. Шундай килиб, (6.10.15¢) характеристик тенгламанинг 2 та илдизи чап ярим
текисликда ва 2 та илдизи унг ярим текисликда ётади, яъни 2 илдизининг хакикий кисми
манфий ва 2 илдизининг хакикий кисми мусбат ишорали булади (яъни D(2,2)).
Энди
умумий холни карашни давом этайлик. Унг ярим текисликда ётган илдизларнинг
сони ![]() га тенг булгани
учун чап ярим текисликда ётган илдизларнинг сони
га тенг булгани
учун чап ярим текисликда ётган илдизларнинг сони ![]() тенг булади,
демак,
тенг булади,
демак, ![]() .
. ![]() нуктадан
нуктадан
![]() нуктага утиш учун D-булаклаш
чегарасини штрихланмаган тарафдан штрихланган тарафга кесиб утганимиз учун бу
нуктага мос келган характеристик тенгламанинг
нуктага утиш учун D-булаклаш
чегарасини штрихланмаган тарафдан штрихланган тарафга кесиб утганимиз учун бу
нуктага мос келган характеристик тенгламанинг ![]() та илдизи чап ярим
текисликда ётади.
та илдизи чап ярим
текисликда ётади. ![]() дан
дан ![]() га
утиш учун чегарани штрихланган тарафдан штрихланмаган тарафга караб кесиб утамиз,
демак, бу нуктада
га
утиш учун чегарани штрихланган тарафдан штрихланмаган тарафга караб кесиб утамиз,
демак, бу нуктада ![]() та илдиз чап ярим
текисликда ётганини топамиз.
та илдиз чап ярим
текисликда ётганини топамиз. ![]() дан
дан ![]() нуктага
утишда биз D-булаклаш чегарасини кесмаймиз (бу илдизлар текислигида
биз мавхум укни кесиб утмаймиз деган мулохаза билан тенгкучлидир). Демак,
нуктага
утишда биз D-булаклаш чегарасини кесмаймиз (бу илдизлар текислигида
биз мавхум укни кесиб утмаймиз деган мулохаза билан тенгкучлидир). Демак, ![]() нуктада
хам чап ярим текисликда ётган илдизлар
нуктада
хам чап ярим текисликда ётган илдизлар ![]() та булади.
та булади.
Шундай
килиб, D-булаклашнинг чегараси бутун ![]() текисликни
сохаларга булаклаб ташлайди. Бу сохаларнинг хар бирида характеристик
тенгламанинг маълум микдордаги илдизлари чап ярим текисликда ётади. 1.12-расмда
келтирилган мисолда D-булаклаш чегараси
текисликни
сохаларга булаклаб ташлайди. Бу сохаларнинг хар бирида характеристик
тенгламанинг маълум микдордаги илдизлари чап ярим текисликда ётади. 1.12-расмда
келтирилган мисолда D-булаклаш чегараси ![]() текисликни 4 сохага
булаклаб ташлаган:
текисликни 4 сохага
булаклаб ташлаган: ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
Агар
.
Агар ![]() б¢лса,
б¢лса, ![]() соха
тургунлик сохаси булади ва
соха
тургунлик сохаси булади ва ![]() параметрнинг
параметрнинг ![]() интервалдаги
барча кийматларида (6.10.7) характеристик тенгламанинг хамма илдизларининг хакикий
кисми манфий ишорали булади, яъни барча илдизлари
интервалдаги
барча кийматларида (6.10.7) характеристик тенгламанинг хамма илдизларининг хакикий
кисми манфий ишорали булади, яъни барча илдизлари ![]() илдизлар текислигининг
чап ярим текислигида ётади.
илдизлар текислигининг
чап ярим текислигида ётади.
11-§. D-булаклаш усули билан икки хакикий параметр
текислигида тургунлик сохасини ясаш
Ихтиёрий
![]() -даражали купхаднинг
коэффициентлари
-даражали купхаднинг
коэффициентлари ![]() ва
ва ![]() хакикий
параметрлар билан чизикли тарзда богланган булсин. У вактда бу купхадни
хакикий
параметрлар билан чизикли тарзда богланган булсин. У вактда бу купхадни
![]() (6.11.1)
(6.11.1)
куринишда
ёзиш мумкин. ![]() ва
ва ![]() параметрларнинг
кандай кийматларида (агар бундай кийматлар мавжуд булса) (6.11.1) купхаднинг
барча илдизлари чап ярим текисликда ётади деган саволга жавоб беришимиз керак.
Бу масалани ечиш учун D-булаклаш усулидан фойдаланамиз. Худди, аввалги бир
параметрли холдагидай
параметрларнинг
кандай кийматларида (агар бундай кийматлар мавжуд булса) (6.11.1) купхаднинг
барча илдизлари чап ярим текисликда ётади деган саволга жавоб беришимиз керак.
Бу масалани ечиш учун D-булаклаш усулидан фойдаланамиз. Худди, аввалги бир
параметрли холдагидай ![]() илдизлар текислигининг
хар бир нуктасига (
илдизлар текислигининг
хар бир нуктасига (![]()
![]() )
параметрлар текислигининг бирорта нуктаси мос келади.
)
параметрлар текислигининг бирорта нуктаси мос келади.
(![]()
![]() )
параметрлар текислигида D-булаклаш утказиш учун
)
параметрлар текислигида D-булаклаш утказиш учун ![]() илдизлар текислигининг
мавхум укини (
илдизлар текислигининг
мавхум укини (![]()
![]() ) параметрлар
текислигига акслантирамиз. Бунинг учун
) параметрлар
текислигига акслантирамиз. Бунинг учун
![]() (6.11.2)
(6.11.2)
тенгламага
![]() куямиз, сунгра хакикий
ва мавхум кисмларга ажратиб, мос равишда нолга тенглаштирамиз:
куямиз, сунгра хакикий
ва мавхум кисмларга ажратиб, мос равишда нолга тенглаштирамиз:
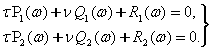 (6.11.3)
(6.11.3)
(6.11.3)
муносабатни ![]() ва
ва ![]() ларга
нисбатан ечиб, D-булаклашнинг чегараси N нинг
параметрик тенгламасини топамиз:
ларга
нисбатан ечиб, D-булаклашнинг чегараси N нинг
параметрик тенгламасини топамиз:
![]() (6.11.4)
(6.11.4)
бу ерда
![]() .
.
Мисол.
![]() (6.11.5)
(6.11.5)
купхад берилган булсин. (6.11.5) купхадни
![]() (6.11.6)
(6.11.6)
куринишга келтириш мумкин. Бу ердан
![]()
(6.11.6)
тенгламага ![]() куйиб, хакикий ва
мавхум кисмларга ажратамиз:
куйиб, хакикий ва
мавхум кисмларга ажратамиз:
![]() .
.
Комплекс сон нолга тенг булиши учун унинг хакикий ва мавхум кисмлари нолга тенг булиши керак, яъни

Бу
ердан ![]() ва D-булаклашнинг
чегараси N нинг параметрик тенгламаси
ва D-булаклашнинг
чегараси N нинг параметрик тенгламаси
![]()
куринишда булади.
(6.11.4)
формулалар ![]() дагина тугри булади.
дагина тугри булади.
![]() да икки хол: 1)
ёки
да икки хол: 1)
ёки ![]() , ёки
, ёки ![]() ;
2)
;
2) ![]() булиши мумкин. 1) хол
хеч кандай ахамиятга эга эмас, чунки бу холга мос келувчи
булиши мумкин. 1) хол
хеч кандай ахамиятга эга эмас, чунки бу холга мос келувчи ![]() нукта чексиз
узоклашади («чексизликка кетади»). 2) хол, аксинча, махсус хол хисобланади, чунки
бу холда (6.11.3) тенгламалар бир-бирига чизикли богланган булади. Бу махсус холни
тугдираётган
нукта чексиз
узоклашади («чексизликка кетади»). 2) хол, аксинча, махсус хол хисобланади, чунки
бу холда (6.11.3) тенгламалар бир-бирига чизикли богланган булади. Бу махсус холни
тугдираётган ![]() нуктага энди битта
нукта эмас, балки бутун бир тугри чизик мос келади демакдир. Бу тугри чизик
(6.11.3) тенгламаларнинг исталган биттаси билан ифодаланади ва уни махсус тугри
чизик деб атаймиз.
нуктага энди битта
нукта эмас, балки бутун бир тугри чизик мос келади демакдир. Бу тугри чизик
(6.11.3) тенгламаларнинг исталган биттаси билан ифодаланади ва уни махсус тугри
чизик деб атаймиз.
Агар
купхаднинг катта ![]() ва озод хадлари
ва озод хадлари ![]()
![]() ва
ва
![]() параметрларга боглик
булса, уларни нолга тенглаштириб мос равишда
параметрларга боглик
булса, уларни нолга тенглаштириб мос равишда ![]() ва
ва ![]() кийматларга
мос келувчи махсус тугри чизикларга эга буламиз:
кийматларга
мос келувчи махсус тугри чизикларга эга буламиз:
![]() (6.11.7)
(6.11.7)
![]() (6.11.8)
(6.11.8)
Шундай
килиб, умумий холда D-булаклашнинг чегараси N эгри чизикдан
ва айрим махсус тугри чизиклардан иборат булади. (6.11.4) формулалар D-булаклашнинг
N эгри чизигини аниклайди. ![]() мусбат йуналишда
узгарганда (-¥ дан +¥ гача) (
мусбат йуналишда
узгарганда (-¥ дан +¥ гача) (![]() ,
,![]() )
нукта хам N эгри чизик буйлаб мусбат йуналишда харакат килади.
)
нукта хам N эгри чизик буйлаб мусбат йуналишда харакат килади. ![]() хол
учун махсус тугри чизиклар аникланади.
хол
учун махсус тугри чизиклар аникланади. ![]() ва
ва ![]() лар
лар
![]() га нисбатан жуфт
функциялар булганлиги туфайли
га нисбатан жуфт
функциялар булганлиги туфайли ![]() нинг (0,+¥) интервалдаги кийматлари учун D-булаклашнинг N чегарасини
ясаш кифоя.
нинг (0,+¥) интервалдаги кийматлари учун D-булаклашнинг N чегарасини
ясаш кифоя. ![]() нинг (-¥,0) интервалдаги кийматларида (
нинг (-¥,0) интервалдаги кийматларида (![]() ,
,![]() )
нукта N чегаранинг
)
нукта N чегаранинг ![]() =+¥ нуктага мос келган
=+¥ нуктага мос келган ![]() нуктасидан
нуктасидан ![]() нуктага
мос келган
нуктага
мос келган ![]() нуктасигача харакат
килиб келади, яъни N чегаравий эгри
чизик буйлаб
нуктасигача харакат
килиб келади, яъни N чегаравий эгри
чизик буйлаб ![]() нинг
нинг ![]() узгариш
кийматларида (
узгариш
кийматларида (![]() ,
,![]() )
нукта икки марта юради.
)
нукта икки марта юради.
(![]() ,
,![]() ) текислигида D-булаклашнинг чегаралари утказилгандан кейин штрихлаш коидасидан фойдаланиб, уларни штрихлаб чикиш керак. Штрихлаш коидасини асослаш учун
) текислигида D-булаклашнинг чегаралари утказилгандан кейин штрихлаш коидасидан фойдаланиб, уларни штрихлаб чикиш керак. Штрихлаш коидасини асослаш учун ![]() нуктанинг
нуктанинг ![]() атрофини
атрофини ![]() нуктанинг
нуктанинг ![]() атрофига аксланишини куриб утамиз.
Бу аксланиш (6.11.2) ёки (6.11.3) формулалар
оркали амалга оширилади.
атрофига аксланишини куриб утамиз.
Бу аксланиш (6.11.2) ёки (6.11.3) формулалар
оркали амалга оширилади. ![]() ва
ва ![]() булсин,
булсин,
![]() ва
ва ![]() нинг
бу кийматларини (6.11.2) га куйиб ва айрим уриналмаштиришларни утказгандан
кейин
нинг
бу кийматларини (6.11.2) га куйиб ва айрим уриналмаштиришларни утказгандан
кейин
![]() (6.11.9)
(6.11.9)
ни
хосил киламиз. Бу ерда куп нукталар ![]() ларга нисбатан
етарлича кичик иккинчи тартибли хадларни билдиради ва
ларга нисбатан
етарлича кичик иккинчи тартибли хадларни билдиради ва
![]() ,
,
чунки
![]() нукта
нукта ![]() нуктага
аксланади.
нуктага
аксланади. ![]() ни
ни ![]() лар
билан богловчи муносабатни биринчи якинлашишда куйидаги куринишда ёзиш мумкин:
лар
билан богловчи муносабатни биринчи якинлашишда куйидаги куринишда ёзиш мумкин:
![]() ,
(6.11.10)
,
(6.11.10)
![]() .
(6.11.11)
.
(6.11.11)
![]() нинг
атрофини
нинг
атрофини ![]() нинг атрофига
акслантиришни кетма-кет (6.11.10) формула оркали
нинг атрофига
акслантиришни кетма-кет (6.11.10) формула оркали ![]() нинг атрофини
нинг атрофини ![]() комплекс
узгарувчининг ёрдамчи текислигидаги
комплекс
узгарувчининг ёрдамчи текислигидаги ![]() нуктанинг
нуктанинг ![]() атрофига
акслантиришдан ва (6.11.11) формула оркали
атрофига
акслантиришдан ва (6.11.11) формула оркали ![]() нинг атрофини
нинг атрофини ![]() нинг
атрофига акслантиришдан иборат деб караш мумкин (6.13-шакл). Биринчи (6.11.10)
акслантириш конформ булади. Иккинчи чизикли акслантиришни хакикий ва мавхум
нинг
атрофига акслантиришдан иборат деб караш мумкин (6.13-шакл). Биринчи (6.11.10)
акслантириш конформ булади. Иккинчи чизикли акслантиришни хакикий ва мавхум

кисмларга ажратиб ёзамиз
![]() (6.11.12)
(6.11.12)
бу
ерда ![]() ва
ва ![]() -
-
![]() нинг хакикий ва
мавхум кисмлари,
нинг хакикий ва
мавхум кисмлари, ![]() ва
ва ![]() -
мос равишда
-
мос равишда ![]() ва
ва ![]() нинг
хакикий ва мавхум кисмлари.
нинг
хакикий ва мавхум кисмлари. ![]() нукта унинг атрофини
икки кисмга булувчи
нукта унинг атрофини
икки кисмга булувчи ![]() чегарада ётган булсин
деб фараз киламиз (1.13-шакл). Шу расмда
чегарада ётган булсин
деб фараз киламиз (1.13-шакл). Шу расмда ![]() чегарани айланиб утишнинг
мусбат йуналиши курсатилган.
чегарани айланиб утишнинг
мусбат йуналиши курсатилган. ![]() атроф конформ
равишда
атроф конформ
равишда ![]() атрофга алмашади
(1.13-шакл). Бу аксланиш натижасида
атрофга алмашади
(1.13-шакл). Бу аксланиш натижасида ![]() чегаранинг чап
тарафи мос равишда
чегаранинг чап
тарафи мос равишда ![]() текислигидаги
текислигидаги ![]() эгри
чизикнинг чап тарафига утади. Навбатдаги
эгри
чизикнинг чап тарафига утади. Навбатдаги ![]() атрофни
атрофни ![]() атрофга
чизикли акслантиришда
атрофга
чизикли акслантиришда ![]() атроф сикилиши ёки
чузилиши мумкин ва яна агар (6.11.12) чизикли алмаштиришнинг
атроф сикилиши ёки
чузилиши мумкин ва яна агар (6.11.12) чизикли алмаштиришнинг ![]() детерминанти
манфий ишорали булса, у холда кузгуда аксланиш юз бериши мумкин (6.14-шакл).
детерминанти
манфий ишорали булса, у холда кузгуда аксланиш юз бериши мумкин (6.14-шакл).
Бунинг
маъноси куйидагидан иборат: иккинчи чизикли акслантиришда агар ![]() булса,
у вактда
булса,
у вактда ![]() эгри чизикнинг чап
тарафи N чегаравий эгри чизикнинг чап тарафига (6.14-шакл,а)
ва, аксинча, агар
эгри чизикнинг чап
тарафи N чегаравий эгри чизикнинг чап тарафига (6.14-шакл,а)
ва, аксинча, агар ![]() булса, у вактда N
нинг унг тарафига утади (6.14-шакл,б).
булса, у вактда N
нинг унг тарафига утади (6.14-шакл,б).
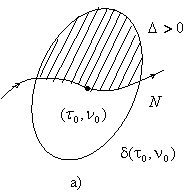 |
|||
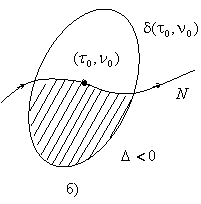 |
|||
|
Утказилган
текширишлар D-булаклашнинг N чегарасини
штрихлаш коидасини аниклайди: N эгри чизикнинг мусбат йуналиши буйлаб айланиб, агар ![]() булса,
унинг чап тарафини ва агар
булса,
унинг чап тарафини ва агар ![]() булса, унинг унг
тарафини штрихлаш керак. Бир марта штрихланган N эгри чизикни
штрихланган
булса, унинг унг
тарафини штрихлаш керак. Бир марта штрихланган N эгри чизикни
штрихланган
 |
6.15-шакл.
тарафига
кесиб утганимизда чап ярим текисликда ётган илдизлар сони ![]() биттага
ошади ва, аксинча, штрихланмаган тарафига утгаминизда
биттага
ошади ва, аксинча, штрихланмаган тарафига утгаминизда ![]() сони
биттага камаяди (6.15-шакл).
сони
биттага камаяди (6.15-шакл).
D-булаклашнинг
чегараси, N эгри чизикдан ташкари, L махсус тугри
чизиклардан хам иборат булиши мумкин. L махсус тугри чизикларни
штрихлаш коидаси N эгри чизикни штрихлаш коидасидан фарк килади, чунки L да
айланишнинг мусбат йуналиши деган тушунчани акниклаш мумкин эмас. Бунинг сабаби
L факат биттта ![]() нуктанинг образи булади. Шунга карамасдан махсус тугри
чизикларни штрихлаш коидаси N эгри чизикни кай тарзда штрихланганлигидан келиб чикади.
нуктанинг образи булади. Шунга карамасдан махсус тугри
чизикларни штрихлаш коидаси N эгри чизикни кай тарзда штрихланганлигидан келиб чикади.
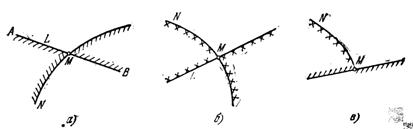 |
6.16-шакл.
N эгри чизикнинг
штрихланган тарафи G сохага ёндош булган эгри чизик тарафининг акси булганлигидан
L махсус чизикнинг штрихланган тарафи чегаравий ![]() нуктанинг
G соха нукталаридан иборат ярим атрофининг аксидан иборат
булади.
нуктанинг
G соха нукталаридан иборат ярим атрофининг аксидан иборат
булади.
6.16-шаклда N эгри чизик билан L махсус чизикнинг баъзи узаро жойлашишлари курсатилган.
D-булаклашнинг
хамма чегараларини ясаганимиздан кейин (![]() ,
,![]() )
текислиги бир нечта сохаларга булинади (6.17-шакл.)
)
текислиги бир нечта сохаларга булинади (6.17-шакл.)
6.17-шаклда L1, L2, L3 – махсус тугри чизиклар, N – D булаклашнинг чегаравий эгри чизиги.
Хар
бир соханинг нукталарига мос келган (6.11.2) купхадларнинг илдизлар текислигининг
чап ва унг ярим текисликда ётган илдизларининг сони бир хил булади. Бир сохадан
иккинчи бир сохага утганда чап ва унг ярим текисликда ётган илдизларнинг сони узгаради.
Бирор соханинг кандайдир нуктасига мос келган (6.11.2) купхаднинг унг ярим текисликда
ётган илдизларининг сони ![]() ни аниклайлик.
Бунинг учун шу соханинг ихтиёрий М(
ни аниклайлик.
Бунинг учун шу соханинг ихтиёрий М(![]() ,
,![]() )
нуктасининг
)
нуктасининг ![]() ва
ва ![]() координаталарининг
кийматини (6.11.2) га келтириб куямиз:
координаталарининг
кийматини (6.11.2) га келтириб куямиз:
![]() (6.11.13)
(6.11.13)
(6.11.13) купхадни ушбу куринишда ёзиш мумкин
![]() ,
(6.11.14)
,
(6.11.14)
бу
ерда ![]() аникланган хакикий
сонлар. (6.11.12) тенгламанинг Гурвиц детерминанти
аникланган хакикий
сонлар. (6.11.12) тенгламанинг Гурвиц детерминанти

 |
6.17-шакл.
куринишда булади. Ушбу детерминант бош минорларидан
![]() (6.11.15)
(6.11.15)
каторни
тузамиз. Бу катордаги ишоралар узгариш сони (6.11.13) (ёки (6.11.14)) купхаднинг
унг ярим текисликда ётган илдизларининг сонига тенг. Унг ярим текисликда ётган
илдизларнинг сони ![]() га тенг булсин. У
вактда (
га тенг булсин. У
вактда (![]() ,
,![]() )
текислиги D-булаклаш 1.17-шаклда курсатилгандай булади:
)
текислиги D-булаклаш 1.17-шаклда курсатилгандай булади: ![]() -I соха,
-I соха,
![]() -II соха,
-II соха,
![]() -III
соха,
-III
соха, ![]() -IV соха,
-IV соха,
![]() -V соха
ва
-V соха
ва ![]() -VI соха.
-VI соха.
Агар
![]() булса, у вактда III
ва IV сохалар тургунлик сохалари булади. Демак,
булса, у вактда III
ва IV сохалар тургунлик сохалари булади. Демак, ![]() ва
ва
![]() ларнинг бу сохаларда
ётган барча кийматлари учун (6.11.2) характеристик тенглама билан ифодаланадиган
хамма динамик системаларнинг харакати асимптотик тургун булади.
ларнинг бу сохаларда
ётган барча кийматлари учун (6.11.2) характеристик тенглама билан ифодаланадиган
хамма динамик системаларнинг харакати асимптотик тургун булади.
Шундай
килиб, ![]() ва
ва ![]() хакикий
параметрлар текислигида тургунлик сохасини ясаш учун куйидаги алгоритмдан фойдаланиш
керак:
хакикий
параметрлар текислигида тургунлик сохасини ясаш учун куйидаги алгоритмдан фойдаланиш
керак:
1. ![]() (6.11.2¢)
(6.11.2¢)
тенгламага
![]() ни куйиб, хакикий
ва мавхум кисмларини ажратгандан сунг, уларни мос равишда нолга тенглаштирилади:
ни куйиб, хакикий
ва мавхум кисмларини ажратгандан сунг, уларни мос равишда нолга тенглаштирилади:
 (6.11.3¢)
(6.11.3¢)
2.
(6.11.3¢) тенгламалар системасидан ![]() ва
ва ![]() лар
топилади
лар
топилади
![]() ,
(6.11.4¢)
,
(6.11.4¢)
бу ерда
![]() .
.
3.![]() хол учун
хол учун ![]() га 0 дан +¥ гача киймат бериб, (6.11.4¢) асосан, (
га 0 дан +¥ гача киймат бериб, (6.11.4¢) асосан, (![]() ,
,![]() )
текислигида D-булаклашнинг N чегаравий эгри
чизиги ясалади.
)
текислигида D-булаклашнинг N чегаравий эгри
чизиги ясалади.
4.![]() ва
ва ![]() кийматларга мос келувчи
(агар мавжуд булса) L1 ва L2 махсус тугри чизикларни хамда
кийматларга мос келувчи
(агар мавжуд булса) L1 ва L2 махсус тугри чизикларни хамда ![]() хол учун
хол учун
![]() кийматига мос келувчи
L3 махсус тугри
чизик (
кийматига мос келувчи
L3 махсус тугри
чизик (![]() ,
,![]() )
текислигида ясалади (1.17-шаклга каранг).
)
текислигида ясалади (1.17-шаклга каранг).
5.Штрихлаш
коидаси буйича N эгри чизикнинг мусбат йуналиши буйича айланганимизда ![]() булса,
унинг чап тарафи ва
булса,
унинг чап тарафи ва ![]() булса, унг томони
штрихланади. N эгри чизикнинг штрихланганлигига караб L1, L2 ва L3
махсус тугри чизиклар штрихлаб чикилади.
N эгри чизик билан L махсус тугри
чизикларнинг штрихланган тарафлари бир-бирига караган булиши керак.
булса, унг томони
штрихланади. N эгри чизикнинг штрихланганлигига караб L1, L2 ва L3
махсус тугри чизиклар штрихлаб чикилади.
N эгри чизик билан L махсус тугри
чизикларнинг штрихланган тарафлари бир-бирига караган булиши керак.
6.(![]() ,
,![]() )
текисликнинг исталган М(
)
текисликнинг исталган М(![]() 1,
1,![]() 1)
нуктасининг
1)
нуктасининг ![]() 1 ва
1 ва ![]() 1
координаталарини (6.11.2¢) тенгламага куйиб, бу тенгламанинг Гурвиц
детерминантини тузилади ва (6.11.15) катордаги ишора узгаришлар сони (унг ярим
текисликда ётган илдизлар сонини) аникланади.
1
координаталарини (6.11.2¢) тенгламага куйиб, бу тенгламанинг Гурвиц
детерминантини тузилади ва (6.11.15) катордаги ишора узгаришлар сони (унг ярим
текисликда ётган илдизлар сонини) аникланади.
7.М(![]() 1,
1,![]() 1)
нукта ётган сохадан D-булаклаш чегараларини бошка сохаларга кесиб утиб (
1)
нукта ётган сохадан D-булаклаш чегараларини бошка сохаларга кесиб утиб (![]() ,
,![]() )
текислик D-булаклаб чикилади.
)
текислик D-булаклаб чикилади.
8.Агар
сохалар ичида D(![]() ) соха (n-характеристик тенгламанинг даражаси) мавжуд булса, у холда
бу D(
) соха (n-характеристик тенгламанинг даражаси) мавжуд булса, у холда
бу D(![]() ) соха тургунлик сохаси булади.
) соха тургунлик сохаси булади. ![]() ва
ва ![]() ларнинг
тургунлик сохасидаги барча кийматлари учун динамик системанинг харакати асимптотик
тургун булади.
ларнинг
тургунлик сохасидаги барча кийматлари учун динамик системанинг харакати асимптотик
тургун булади.
Мисол.
![]() (6.11.2¢¢)
(6.11.2¢¢)
купхад
учун (![]() ,
,![]() )
хакикий параметрлар текислигини D-булаклаш утказиш талаб этилсин. Уни алгоритм буйича
бажарамиз.
)
хакикий параметрлар текислигини D-булаклаш утказиш талаб этилсин. Уни алгоритм буйича
бажарамиз.
1.Алгоритмнинг биринчи кадамига асосан

2.N эгри чизикнинг параметрик тенгламаси:
![]()
ва
![]() .
.
3.![]() текислигида N эгри чизикни ясаймиз.
текислигида N эгри чизикни ясаймиз.
4.![]() мос келувчи L1 махсус тугри
чизик мавжуд эмас,
мос келувчи L1 махсус тугри
чизик мавжуд эмас, ![]() мос келувчи L2 махсус тугри чизик
мос келувчи L2 махсус тугри чизик ![]() тугри чизикдан
иборат булади.
тугри чизикдан
иборат булади. ![]() мос келувчи L3 махсус тугри чизик хам мавжуд эмас.
мос келувчи L3 махсус тугри чизик хам мавжуд эмас.
5.![]() нинг -¥ дан 0 гача узгаришда
нинг -¥ дан 0 гача узгаришда ![]() ва
ва ![]() нинг
0 дан +¥ гача узгаришида
нинг
0 дан +¥ гача узгаришида ![]() булганлиги учун N
эгри чизикнинг мусбат йуналиши буйича айланиб уни чап тарафдан икки марта
штрихлаб чикамиз (6.18-шаклга каранг). L2 ни шундай бир марта штрихлаймизки, унинг штрихланган
тарафи N нинг штрихланган тарафига караган булсин (6.18-шаклга
каранг).
булганлиги учун N
эгри чизикнинг мусбат йуналиши буйича айланиб уни чап тарафдан икки марта
штрихлаб чикамиз (6.18-шаклга каранг). L2 ни шундай бир марта штрихлаймизки, унинг штрихланган
тарафи N нинг штрихланган тарафига караган булсин (6.18-шаклга
каранг).
6.(![]() ,
,![]() )
текислигида ётган ихтиёрий М(2,1) нуктанинг
)
текислигида ётган ихтиёрий М(2,1) нуктанинг ![]() ва
ва ![]() координаталарини
(6.11.2¢¢) купхадга келтириб куямиз:
координаталарини
(6.11.2¢¢) купхадга келтириб куямиз:
![]() .
.
 |
6.18-шакл.
Бу тенгламанинг Гурвиц детерминанти

ва (6.11.15) катор
2, 3, ![]() ,
1 (6.11.15¢)
,
1 (6.11.15¢)
куринишда булади. (6.11.15¢) каторда ишора узгаришлар сони 0 га тенг булади. Демак, бу нукта учун илдизлар текислигининг унг ярим текислигида бирорта хам илдиз ётмайди, яъни характеристик тенгламанинг хамма илдизларининг хакикий кисми манфий булади. М(2,1) нукта ётган сохада D(3.0) булади.
7.D(3.0) сохадан бошка сохаларга D-булаклашнинг чегараларини кесиб утганимизда 1.18-шаклда курсатилган D-булаклашга келамиз.
Шундай
килиб, ![]() ва
ва ![]() нинг
D(3.0) сохадаги барча кийматларида курилаётган динамик
система харакати асимптотик тургун булади.
нинг
D(3.0) сохадаги барча кийматларида курилаётган динамик
система харакати асимптотик тургун булади.
12-§. Михайлов критерияси [60,62]
![]() (6.12.1)
(6.12.1)
характеристик
тенглама берилган булсин. ![]() параметр киритиб,
умумийрок
параметр киритиб,
умумийрок
![]() (6.12.2)
(6.12.2)
тенгламалар
синфини караймиз. Бу тенгламадан ![]() булганда (6.12.1)
келиб чикади. (6.12.1) тенгламага
булганда (6.12.1)
келиб чикади. (6.12.1) тенгламага ![]() куйиб,
куйиб, ![]() параметр
буйича D-булаклашни утказамиз.
параметр
буйича D-булаклашни утказамиз.
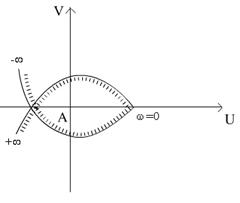 |
6.19-шакл.
А
тургунлик сохаси булсин (6.19-шакл). Агар ![]() нукта А соханинг
ичида ётса, у холда (6.12.1) характеристик тенгламанинг барча илдизларининг хакикий
кисми манфий ишорали булади. N эгри чизикни штрихламасдан А соха тургунлик сохаси булиши
ёки булмаслигини аниклайдиган коидани курсатиш мумкин. Бу коидани А.В.Михайлов
яратган ва автоматик регуляторлар назариясида куп ишлатилади. Бунинг учун
нукта А соханинг
ичида ётса, у холда (6.12.1) характеристик тенгламанинг барча илдизларининг хакикий
кисми манфий ишорали булади. N эгри чизикни штрихламасдан А соха тургунлик сохаси булиши
ёки булмаслигини аниклайдиган коидани курсатиш мумкин. Бу коидани А.В.Михайлов
яратган ва автоматик регуляторлар назариясида куп ишлатилади. Бунинг учун ![]() холни,
яъни (6.12.1) тенгламани куриб утамиз. (6.12.1) нинг даражаси
холни,
яъни (6.12.1) тенгламани куриб утамиз. (6.12.1) нинг даражаси ![]() га
тенг ва
га
тенг ва ![]() лар унинг
илдизлари булсин. У вактда
лар унинг
илдизлари булсин. У вактда
![]() . (6.12.3)
. (6.12.3)
(6.12.3)
муносабатга ![]() ни куямиз:
ни куямиз:
![]() .
.
Агар
![]() илдизлар текислигида
илдизлар текислигида ![]() нуктани белгилаб олсак, у холда
нуктани белгилаб олсак, у холда ![]() вектор
вектор ![]() нуктадан мавхум укда ётган
нуктадан мавхум укда ётган ![]() нуктага йуналтирилган булади.
нуктага йуналтирилган булади. ![]() нукта чап ярим текисликда ётган булсин. У вактда
нукта чап ярим текисликда ётган булсин. У вактда ![]() ни -¥ дан +¥ гача узгартирганимизда (
ни -¥ дан +¥ гача узгартирганимизда (![]() ) векторнинг аргументи
) векторнинг аргументи ![]() га купаяди. Шунинг учун агар барча
га купаяди. Шунинг учун агар барча ![]() илдизлар
чап ярим текисликда ётса, у вактда
илдизлар
чап ярим текисликда ётса, у вактда ![]() нинг -¥ дан +¥ гача узгаришида
нинг -¥ дан +¥ гача узгаришида ![]() вектор аргументининг орттирмаси (хамма (
вектор аргументининг орттирмаси (хамма (![]() ) векторлар аргументи орттирмаларининг йигиндисига
тенг)
) векторлар аргументи орттирмаларининг йигиндисига
тенг) ![]() га тенг булади. Агар
га тенг булади. Агар ![]() илдиз унг ярим текисликда ва
илдиз унг ярим текисликда ва ![]() илдиз чап ярим текисликда ётса, у вактда аргументлар
орттирмасининг йигиндиси
илдиз чап ярим текисликда ётса, у вактда аргументлар
орттирмасининг йигиндиси ![]() тенг булади.
тенг булади.
![]() ни 0 дан +¥ гача узгартириш
билан кифояланамиз. У вактда
ни 0 дан +¥ гача узгартириш
билан кифояланамиз. У вактда ![]() характеристик вектор аргументининг узгариши 2 мартага
камаяди (
характеристик вектор аргументининг узгариши 2 мартага
камаяди (![]() нинг -¥ дан +¥ гача узгаришига нисбатан) ва тургун тизим учун унинг киймати
нинг -¥ дан +¥ гача узгаришига нисбатан) ва тургун тизим учун унинг киймати
![]() тенг булади. Шуни кайд килиш керакки,
тенг булади. Шуни кайд килиш керакки, ![]() нинг усиши билан чап ярим текисликда ётган барча
нинг усиши билан чап ярим текисликда ётган барча ![]() илдизлар учун хамма (
илдизлар учун хамма (![]() ) векторларнинг аргументлари ва, демак, тургун система
) векторларнинг аргументлари ва, демак, тургун система
![]() характеристик векторининг хам аргументи монотон
равишда усади.
характеристик векторининг хам аргументи монотон
равишда усади.
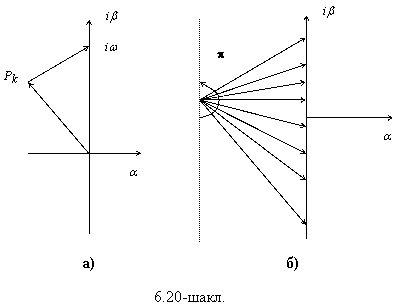 |
Шундай
килиб, А тургунлик сохаси булиши учун ![]() тенгламани
тенгламани ![]() параметр буйича D-булаклаш
чегараси
параметр буйича D-булаклаш
чегараси ![]() булганда,
координата бошидан унг тарафда булган хакикий укдан бошланиб
булганда,
координата бошидан унг тарафда булган хакикий укдан бошланиб ![]() нинг
+¥ гача усиши билан
нинг
+¥ гача усиши билан ![]() нинг радиус вектори соат стрелкаси йуналишига карама-карши
айланиб
нинг радиус вектори соат стрелкаси йуналишига карама-карши
айланиб ![]() квадрат оркали утиши керак.
квадрат оркали утиши керак.
Келтирилган натижавий мулохазани Михайлов критерияси сифатида ифодалаймиз.
Михайлов
критерияси. Тизим харакатининг тургун булиши учун 1) характеристик векторнинг
модули ![]() нинг барча
нинг барча ![]() кийматларида
нолдан фарк килиши ва 2) бу векторнинг аргументи
кийматларида
нолдан фарк килиши ва 2) бу векторнинг аргументи ![]() булганда нолга
тенг булиб,
булганда нолга
тенг булиб, ![]() нинг 0 дан +¥ гача монотон равишда узгаришида у монотон тарзда 0 дан
нинг 0 дан +¥ гача монотон равишда узгаришида у монотон тарзда 0 дан ![]() гача
усиши зарур ва етарлидир (
гача
усиши зарур ва етарлидир (![]() - характеристик
тенгламанинг даражаси).
- характеристик
тенгламанинг даражаси).
Мисол.
![]()
характеристик
тенгламаси булган динамик системанинг тургунлигини текшириш талаб этилсин.
Бунинг учун тенгламага ![]() нинг урнига
нинг урнига ![]() куямиз
ва хакикий ва мавхум кисмларини ажратамиз
куямиз
ва хакикий ва мавхум кисмларини ажратамиз
![]() .
.
Бу ердан
 (6.12.4)
(6.12.4)
(![]() )
текислигида
)
текислигида ![]() векторнинг годографини (6.12.4) тенгламалар системасига
асосан ясаймиз. Бу годограф 6.21-шаклда келтирилган.
векторнинг годографини (6.12.4) тенгламалар системасига
асосан ясаймиз. Бу годограф 6.21-шаклда келтирилган.
Расмдан куриниб турибдики, ![]() да годограф
да годограф ![]() хакикий
укнинг мусбат кисмини кесади ва
хакикий
укнинг мусбат кисмини кесади ва ![]() нинг 0 дан +¥ гача узгаришида унинг аргументи
нинг 0 дан +¥ гача узгаришида унинг аргументи ![]() га тенг булади,
яъни годограф 3 квадрант оркали утади.
га тенг булади,
яъни годограф 3 квадрант оркали утади.
 |
Кейинги икки параграфда баён этилган D-булаклаш усулини техникавий масалаларни ечишда татбик килинишини куриб утамиз.
13-§. Автомобил олдинги гилдираклари харакатининг тургунлигини D-булаклаш усули оркали тадкик этиш [92]
13.1. Харакатнинг математик модели
Автомобил олдинги гилдираклари харакатининг математик моделини гилдиракли транспорт машиналари харакатининг
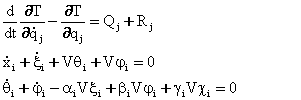 (6.13.1)
(6.13.1)
умумий тенгламаларидан фойдаланиб тузамиз [91].
Бу
ерда ![]() -тизимнинг умумлашган
координаталари, Т-тизимнинг кинетик энергияси,
-тизимнинг умумлашган
координаталари, Т-тизимнинг кинетик энергияси, ![]() -тизимга таъсир
этаётган умумлашган кучлар,
-тизимга таъсир
этаётган умумлашган кучлар, ![]() -шиналарнинг деформацияланиши
натижасида хосил бўладиган умумлашган реакция кучлари, V-автомобил харакатининг
тезлиги,
-шиналарнинг деформацияланиши
натижасида хосил бўладиган умумлашган реакция кучлари, V-автомобил харакатининг
тезлиги, ![]() -шинанинг кинематик
параметрлари,
-шинанинг кинематик
параметрлари, ![]() -шинанинг ён деформацияси,
-шинанинг ён деформацияси,
![]() -шинанинг
бурчак(бурилиш) деформацияси,
-шинанинг
бурчак(бурилиш) деформацияси, ![]() -шинанинг вертикал
ўкка нисбатан огиш бурчаги,
-шинанинг вертикал
ўкка нисбатан огиш бурчаги, ![]() -гилдирак ўрта текислигининг
абциссаси,
-гилдирак ўрта текислигининг
абциссаси, ![]() - гилдиракнинг
шкворня ўки бўйича бурилиш бурчаги.
- гилдиракнинг
шкворня ўки бўйича бурилиш бурчаги.
Каралаётган тизим уч кисмдан иборат: богланган подвеска, бошкариладиган олдинги гилдираклар ва рул бошкаруви.
Унинг
харакатини ![]() умумлашган координаталар
оркали аниклаймиз, бу ерда
умумлашган координаталар
оркали аниклаймиз, бу ерда ![]() - олдинги ¢книнг
гилдираклар билан биргаликда автомобилнинг б¢йлама ¢ки атрофида
бурилиш бурчаги,
- олдинги ¢книнг
гилдираклар билан биргаликда автомобилнинг б¢йлама ¢ки атрофида
бурилиш бурчаги, ![]() - гилдиракнинг
шкворня ўки бўйлаб бурилиш бурчаги,
- гилдиракнинг
шкворня ўки бўйлаб бурилиш бурчаги, ![]() - шинанинг ён
деформацияси,
- шинанинг ён
деформацияси, ![]() -шинанинг бурчак
деформацияси (1.5-шакл).
-шинанинг бурчак
деформацияси (1.5-шакл).
Тизимнинг
Т кинетик энергияси ва унга таъсир этаётган ![]() умумлашган кучлар
мос равишда куйидагича аниланади [92].
умумлашган кучлар
мос равишда куйидагича аниланади [92].
![]() , (6.13.2)
, (6.13.2)
![]() . (6.13.3)
. (6.13.3)
Бу ерда
![]() - тизимнинг автомобил бўйлама ўки бўйича инерция моменти,
- тизимнинг автомобил бўйлама ўки бўйича инерция моменти,
![]() - иккита гилдиракнинг шкворня ўки бўйича инерция моменти,
- иккита гилдиракнинг шкворня ўки бўйича инерция моменти,
![]() ,
, ![]() -
-
тизимнинг
![]() бурчаги бўйича
бурчак каттиклиги,
бурчаги бўйича
бурчак каттиклиги, ![]() - рул бошкарувининг бурчак каттиклиги,
- рул бошкарувининг бурчак каттиклиги,
![]()
- ![]() координата
бурчаги бўйича ковушкок ишкаланиш коэффициенти,
координата
бурчаги бўйича ковушкок ишкаланиш коэффициенти, ![]() - рул бошкарувидаги ковушкок ишкаланиш коэффициенти,
- рул бошкарувидаги ковушкок ишкаланиш коэффициенти, ![]() - стержен курилмасининг бурчак каттиклиги, Срс -
рессор эластиклигининг коэффициенти, Сш - шинанинг радиал каттиклиги,
Lрс-тизим
масса марказидан рессоргача бўлган масофа,
- стержен курилмасининг бурчак каттиклиги, Срс -
рессор эластиклигининг коэффициенти, Сш - шинанинг радиал каттиклиги,
Lрс-тизим
масса марказидан рессоргача бўлган масофа, ![]() - шина, рессор ва амортизаторлар ички каршилигининг
коэффициентлари,
- шина, рессор ва амортизаторлар ички каршилигининг
коэффициентлари, ![]() -стержен курилмасининг ковушкок ишкаланиш
коэффициенти, А-гилдиракнинг ступица ва тормоз барабанлари билан биргаликдаги
унинг диаметри бўйича инерция моменти, В1-олдинги ўкнинг марказий
инерция моменти, С-гилдиракнинг ўз айланиш ўки бўйича инерция моменти,
-стержен курилмасининг ковушкок ишкаланиш
коэффициенти, А-гилдиракнинг ступица ва тормоз барабанлари билан биргаликдаги
унинг диаметри бўйича инерция моменти, В1-олдинги ўкнинг марказий
инерция моменти, С-гилдиракнинг ўз айланиш ўки бўйича инерция моменти, ![]() - шкворнянинг марказидан гилдирак марказигача бўлган
масофа, L1-подвеска
массасининг марказидан шкворнягача бўлган масофа,
- шкворнянинг марказидан гилдирак марказигача бўлган
масофа, L1-подвеска
массасининг марказидан шкворнягача бўлган масофа, ![]() - гилдирак радиуси,
- гилдирак радиуси, ![]() - гилдирак айланишининг бурчак тезлиги,
- гилдирак айланишининг бурчак тезлиги, ![]() - гилдирак ва ступицанинг массаси,
- гилдирак ва ступицанинг массаси, ![]() - шкворнянинг бўйлама бурчаги.
- шкворнянинг бўйлама бурчаги.
Шинанинг
деформацияланиши натижасида хосил бўладиган ![]() умумлашган реакция
кучлари
умумлашган реакция
кучлари
 (6.13.4)
(6.13.4)
муносабати оркали аникланади, бу ерда
![]() (6.13.5)
(6.13.5)
деформацияланган
шиналарнинг потенциал энергияси, ![]() - шинанинг
эластиклик коэффициентлари, 1 индекс чап шинага, 2 индекс ўнг шинага тегишли, N-олдинги
подвескага таъсир этадиган вертикал реакция кучи.
- шинанинг
эластиклик коэффициентлари, 1 индекс чап шинага, 2 индекс ўнг шинага тегишли, N-олдинги
подвескага таъсир этадиган вертикал реакция кучи. ![]() лар
тизимнинг
лар
тизимнинг ![]() умумлашган координаталари
билан
умумлашган координаталари
билан
![]() (6.13.6)
(6.13.6)
муносабатлар
оркали богланган. (6.13.5) ва (6.13.6) муносабатлардан фойдаланиб, ![]() умумлашган
реакция кучларини топамиз:
умумлашган
реакция кучларини топамиз:
![]() (6.13.7)
(6.13.7)
бу ерда
![]()
(6.13.2), (6.13.3), (6.13.6) ва (6.13.7) муносабатларни (6.13.1) тенгламаларга кўйиб, автомобил олдинги гилдираклари харакатининг математик моделини хосил киламиз:
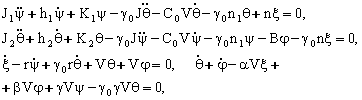 (6.13.8)
(6.13.8)
бу ерда
![]()
(6.13.8)
тенгламалар тасвирловчи нукта харакатини ![]() олти ўлчовли фазода
ифодалайди.
олти ўлчовли фазода
ифодалайди.
13.2. Харакатнинг тургунлигини D-булаклаш усули
оркали тадкик этиш
Автомобил
олдинги гилдираклари харакатининг тургунлигини К1=¥ хол учун тадкик этамиз. Бу холда ![]() ва (6.13.8)
дифференциал тенгламалар
ва (6.13.8)
дифференциал тенгламалар
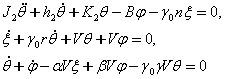 (6.13.9)
(6.13.9)
кўринишга келади. Агар автомобил тезлиги V га боглик бўлган
![]() (6.13.10)
(6.13.10)
параметрларни ажратсак, у вактда (6.13.9) дифференциал тенгламаларнинг характеристик тенгламаси
![]() (6.13.11)
(6.13.11)
кўринишда
бўлади. (t,n) текислигида D-бўлаклаш
ўтказиш учун (6.13.11) тенгламага ![]() ни кўямиз.
Тенгламанинг хакикий ва мавхум кисмларини ажратиб, уларни мос равишда нолга
тенглаштирамиз
ни кўямиз.
Тенгламанинг хакикий ва мавхум кисмларини ажратиб, уларни мос равишда нолга
тенглаштирамиз ![]() :
:
![]() (6.13.12)
(6.13.12)
(6.13.12)
алгебраик тенгламаларни ![]() ва
ва ![]() ларга
нисбатан ечиб, D-бўлаклаш N чегаравий эгри чизигининг
параметрик тенгламасини топамиз:
ларга
нисбатан ечиб, D-бўлаклаш N чегаравий эгри чизигининг
параметрик тенгламасини топамиз:
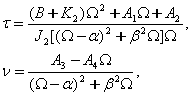 (6.13.13)
(6.13.13)
бу ерда
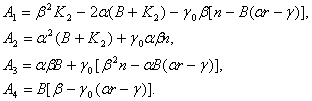 (6.13.14)
(6.13.14)
Амалдаги
олдинги подвеска конструкциялари учун ![]() учун топилган
(6.13.13) ифоданинг сурати нолга айланмайди ва (6.13.13) N
эгри чизикнинг кўриниши 1-расмдагидек бўлади, бу ерда
учун топилган
(6.13.13) ифоданинг сурати нолга айланмайди ва (6.13.13) N
эгри чизикнинг кўриниши 1-расмдагидек бўлади, бу ерда ![]() ва
ва ![]() асимптота
ушбу муносабат билан аникланади:
асимптота
ушбу муносабат билан аникланади:
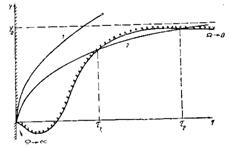 |
![]() .
.
6.22-шакл.
N эгри чизикдан
ташкари ![]() хам D-бўлаклашнинг
махсус тўгри чизиги (чегараси) бўлади. Бу тўгри чизик
хам D-бўлаклашнинг
махсус тўгри чизиги (чегараси) бўлади. Бу тўгри чизик ![]() кийматга
мос келади ва (6.13.11) тенгламадан топилади.
кийматга
мос келади ва (6.13.11) тенгламадан топилади. ![]() кийматга мос келадиган
тўгри чизик мавжуд эмас. (6.13.12) алгебраик системанинг детерминанти
кийматга мос келадиган
тўгри чизик мавжуд эмас. (6.13.12) алгебраик системанинг детерминанти
![]()
тенг
бўлади. Штрихлаш коидасига асосан N эгри чизикни ва L¥ махсус тўгри чизикни штрихлаб чизамиз (6.22-шаклга каранг).
D (4,0) тургунлик сохаси N эгри чизикдан
юкорида ва ![]() махсус тўгри чизикдан
ўнгда жойлашган бўлади. (6.13.10) га асосан
махсус тўгри чизикдан
ўнгда жойлашган бўлади. (6.13.10) га асосан ![]() ярим текисликда
ярим текисликда
![]() (6.13.15)
(6.13.15)
параболани
ўтказамиз. Подвеска, рул бошкаруви ва шиналар параметрларининг муносабатларига караб,
тургунлик сохасининг чегараси билан (6.13.15) парабола бир-бирига нисбатан икки
хил жойлашиши мумкин (1.22-шакл). Биринчи холда ((1) эгри чизик) кўрилаётган тизимнинг
харакати автомобилнинг барча мумкин бўлган тезликларида тургун бўлади. Иккинчи холда
((2) эгри чизик) (![]() ) тезликлар
интервали мавжудки, бу интервалда тизим харакати нотургун бўлади. Тизимнинг
барча тезликларда тургун бўлиши учун лозим бўлган
) тезликлар
интервали мавжудки, бу интервалда тизим харакати нотургун бўлади. Тизимнинг
барча тезликларда тургун бўлиши учун лозим бўлган ![]() минимал демпфер
коэффициенти (6.13.15) парабола билан (6.13.13) N эгри чизикларнинг
уриниш шартидан келиб чикади.
минимал демпфер
коэффициенти (6.13.15) парабола билан (6.13.13) N эгри чизикларнинг
уриниш шартидан келиб чикади.
Бу ясашдан фойдаланиб, тизимнинг барча конструктив параметрларининг тургунлик чегарасига таъсирини ўрганиш мумкин.
14-§. Самолёт олдинги шасси харакатининг тургунлигини
D-булаклаш усули оркали тадкик этиш [92]
Иккинчи мисол сифатида самолёт олдинги шасси харакатининг тургунлигини D-бўлаклаш усули оркали тад-кик этамиз. Бу тизим харакатининг математик модели
 (6.14.1)
(6.14.1)
кўринишда
бўлади [92]. Бу ерда А-стойка билан гилдиракнинг ![]() уки бўйича инерция
моменти, В -
уки бўйича инерция
моменти, В - ![]() ўки бўйича инерция
моменти, D-
ўки бўйича инерция
моменти, D-![]() ва
ва ![]() ўклар
бўйича марказий инерция моменти,
ўклар
бўйича марказий инерция моменти, ![]() - гилдирак айланишининг
бурчак тезлиги, N - гилдиракка тушадиган юк,
- гилдирак айланишининг
бурчак тезлиги, N - гилдиракка тушадиган юк, ![]() - шинанинг
кинематик параметрлари,
- шинанинг
кинематик параметрлари, ![]() - шинанинг
эластиклик коэффициенти,
- шинанинг
эластиклик коэффициенти, ![]() бурчак бўйича каттиклик
коэффициенти,
бурчак бўйича каттиклик
коэффициенти, ![]() - демпфер коэффициенти,
- демпфер коэффициенти,
![]() ларнинг маъноси
1.23-шаклда келтирилган.
ларнинг маъноси
1.23-шаклда келтирилган.
![]() хол
учун (6.14.1) дифференциал тенгламалар системаси
хол
учун (6.14.1) дифференциал тенгламалар системаси
 (6.14.2)
(6.14.2)
кўринишга келади. (6.14.2) тизимнинг характеристик тенгламаси

![]() (6.14.3)
(6.14.3)
кўринишда
бўлади. Агар ![]() ўзгарувчи ўрнига
янги
ўзгарувчи ўрнига
янги ![]()
![]() ўзгарувчи
киритсак, у вактда (6.14.3) характеристик тенглама куйидаги кўринишда бўлади:
ўзгарувчи
киритсак, у вактда (6.14.3) характеристик тенглама куйидаги кўринишда бўлади:
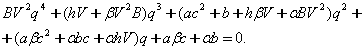 (6.14.4)
(6.14.4)
D-бўлаклашнинг
параметрлари сифатида ![]() ларни олиб,
(6.14.4) характеристик тенгламани куйидаги кўринишда ёзиш мумкин:
ларни олиб,
(6.14.4) характеристик тенгламани куйидаги кўринишда ёзиш мумкин:
![]() .
(6.14.5)
.
(6.14.5)
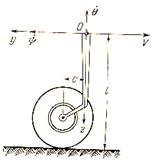 |
6.23-расм.
Бу
тенгламага ![]() ни кўйиб, хакикий
ва мавхум кисмларга ажратиб, уларни мос равишда нолга тенглаштирамиз:
ни кўйиб, хакикий
ва мавхум кисмларга ажратиб, уларни мос равишда нолга тенглаштирамиз:
![]() (6.14.6)
(6.14.6)
(6.14.6) алгебраик тенгламалар системасидан N эгри чизикнинг параметрик тенгламасини топамиз:
![]() (6.14.7)
(6.14.7)
Бу ерда

t ифодасининг сурати
барча c>0 учун мусбат илдизга эга эмас. D-бўлаклаш
чегарасини штрихлаш учун лозим бўлган (6.14.6) тизимнинг детерминанти ![]() га
тенг бўлади. 6.24-шаклда
га
тенг бўлади. 6.24-шаклда ![]() ва
ва ![]() ,
,
![]() ва
ва ![]() холлар
учун D-бўлаклаш чегараси ясалган.
холлар
учун D-бўлаклаш чегараси ясалган.
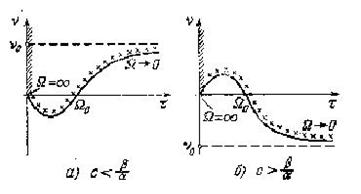 |
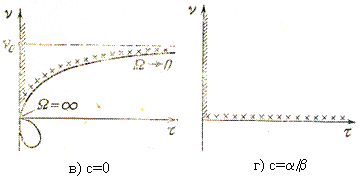 |
6.24-шакл.
Бу
ерда ![]() , асимптота
, асимптота ![]() .
Тургунлик сохаси N эгри чизикдан юкорида ва
.
Тургунлик сохаси N эгри чизикдан юкорида ва ![]() махсус
тўгри чизикдан ўнгда жойлашган (6.24-шаклга каранг).
махсус
тўгри чизикдан ўнгда жойлашган (6.24-шаклга каранг).
15-§. Ёпик тизим ва очик тизим харакатлари ўртасидаги богланиш. Динамик тизимларни оператор оркали
ифодалашда кўзгалмас нукта принципи
Статик тургун тизим нотургун бўлиши учун факат ташки манбадан тизимга энергия келтирадиган механизм мавжуд бўлиши керак. Ёпик циклга кирувчи манфий ишкаланиш кучи, йўналтирилган таъсир этувчи куч(богланиш) ва кечикувчи йўналтирилган богланишлар бундай механизмларга мисол бўла олади. Аммо энергия келтирувчи механизмнинг мавжудлиги тизимнинг нотургун бўлишини билдирмайди. Тизим нотургун бўлиши учун унга етарлича интенсив тарзда энергия келиши керак. Бу ўз навбатида координаталар ва бу координаталар бўйича таъсир этадиган йўналтирилган кучларнинг ўзгариши ўртасида кулай фазавий муносабат мавжуд бўлишини такозо килади. Бу муносабатларни кўриш учун тизимда L йўналтирилган богланишни (6.25-шакл,а) ажратиб, уни узамиз ва натижада L1 кириш ва L2 чикишга эга бўлган тизимга эга бўламиз (6.25-шакл, б).
Дастлабки тизимни (6.25-шакл,а) доимо кириши чикишига тенг бўлган очик тизим деб караш мумкин. Бу хар хил мумкин бўлган киришли очик тизимнинг харакати кириши чикишига тенг бўлган ёпик тизимнинг харакатини ўз ичига олади демакдир.
Чизикли
тизимнинг исталган харакатини (L йўналтирилган богланишнинг ![]() микдорининг
ўзгариши кўзда тутилаяпти)
микдорининг
ўзгариши кўзда тутилаяпти)
![]() (6.15.1)
(6.15.1)
кўринишдаги
харакатларнинг суперпозицияси сифатида караш мумкин. Шунинг учун кириши ![]() бўлган очик тизимнинг
бўлган очик тизимнинг ![]() чикиши нимага тенг
бўлишини кўрайлик. Дастлаб умумийрок масалани караймиз.
чикиши нимага тенг
бўлишини кўрайлик. Дастлаб умумийрок масалани караймиз.
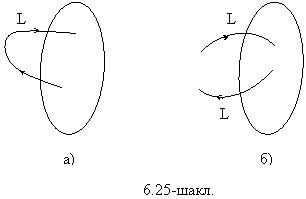 |
![]() -чизикли тизимнинг
ихтиёрий кириши,
-чизикли тизимнинг
ихтиёрий кириши, ![]() -унинг чикиши
бўлсин.
-унинг чикиши
бўлсин. ![]() ва
ва ![]() лар
орасида кандай богланиш мавжуд?
лар
орасида кандай богланиш мавжуд?
Чизикли
тизимлар кенг синфларининг тасвирланишида нолинчи бошлангич шартларда киришнинг
![]() тасвири билан чикишнинг
тасвири билан чикишнинг
![]() тасвири ўртасидаги
муносабатни
тасвири ўртасидаги
муносабатни
![]() (6.15.2)
(6.15.2)
кўринишда ёзиш мумкин.
Бу
ерда ![]() -узатиш коэффициенти
деб айтилади. Масалан,
-узатиш коэффициенти
деб айтилади. Масалан, ![]() кириш ва
кириш ва ![]() чикиш
орасидаги богланиш бирор
чикиш
орасидаги богланиш бирор
![]() (6.15.3)
(6.15.3)
дифференциал муносабат оркали берилган бўлсин. (6.15.3) га нисбатан Лаплас алмаштиришини кўллаб
![]() ,
,
ёки
![]() (6.15.4)
(6.15.4)
ни хосил киламиз. Бу ерда
![]() .
.
Агар
![]() билан
билан ![]() орасидаги
богланиш
орасидаги
богланиш
![]() (6.15.5)
(6.15.5)
айирмали
дифференциал тенглама кўринишида берилган бўлса, у вактда ![]() -алмаштиришни
кўллаб,
-алмаштиришни
кўллаб,
![]() (6.15.6)
(6.15.6)
ни хосил киламиз. Бу ерда
![]() .
.
Маълумки,
![]() функциянинг Лаплас
алмаштириши
функциянинг Лаплас
алмаштириши ![]() комплекс
ўзгарувчининг аналитик функцияси бўлади ва куйидаги Лаплас интеграли билан аникланади:
комплекс
ўзгарувчининг аналитик функцияси бўлади ва куйидаги Лаплас интеграли билан аникланади:
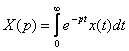 (6.15.7)
(6.15.7)
ва
![]() ,
, ![]() ,
,
![]() , ...
кетма-кетликнинг
, ...
кетма-кетликнинг ![]() -алмаш-тириши бўлса
-алмаш-тириши бўлса
![]() комплекс
ўзгарувчининг функцияси бўлиб,
комплекс
ўзгарувчининг функцияси бўлиб,
кўринишда
ёзилади. Бу ерда ![]() ва мос равишда
ва мос равишда ![]() -
сасланиш (жавоб бериш) функциялари деб аталади.
-
сасланиш (жавоб бериш) функциялари деб аталади. ![]() жавоб бериш
функцияси К узатиш коэффициентининг оригинали бўлади.
жавоб бериш
функцияси К узатиш коэффициентининг оригинали бўлади.
Бу
чекинишдан кейин тизимга ![]() кўринишдаги кириш
таъсир этганда унинг чикиши нимага тенг бўлишини кўрайлик.
кўринишдаги кириш
таъсир этганда унинг чикиши нимага тенг бўлишини кўрайлик. ![]() нинг
тасвири
нинг
тасвири ![]() бўлади.
Шунинг учун чикишнинг тасвири
бўлади.
Шунинг учун чикишнинг тасвири ![]() кўринишда
бўлади.
кўринишда
бўлади. ![]() -кўпхадлар нисбати
деб караб, чикишнинг тасвирини оддий тасвирларга ёямиз ва унга мос бўлган
оригинални
-кўпхадлар нисбати
деб караб, чикишнинг тасвирини оддий тасвирларга ёямиз ва унга мос бўлган
оригинални
![]() (6.15.11)
(6.15.11)
кўринишда
топамиз. Чикиш оригиналининг ![]() биринчи хади
мажбурий тебранишга мос келади. Бу тебраниш худди тизим киришига берилган
таъсирдай
биринчи хади
мажбурий тебранишга мос келади. Бу тебраниш худди тизим киришига берилган
таъсирдай ![]() конуни билан харакат
килади ва ундан ўзгармас
конуни билан харакат
килади ва ундан ўзгармас ![]() кўпайтувчи билан
фарк килади. Чикиш оригиналининг колган хадлари эркин тебранишлардан иборат. Бу
эркин тебранишларнинг
кўпайтувчи билан
фарк килади. Чикиш оригиналининг колган хадлари эркин тебранишлардан иборат. Бу
эркин тебранишларнинг ![]() «частоталари»
«частоталари» ![]() узатиш
коэффициентининг илдизлари (кутблари) бўладилар.
узатиш
коэффициентининг илдизлари (кутблари) бўладилар. ![]() коэффициентлар
умумий холда бошлангич шартларга боглик. (6.15.11) ифодада улар нолинчи
бошлангич шартларга тўгри келади. Нолга тенг бўлмаган бошлангич шартларда
уларнинг кийматлари бошкача бўлади.
коэффициентлар
умумий холда бошлангич шартларга боглик. (6.15.11) ифодада улар нолинчи
бошлангич шартларга тўгри келади. Нолга тенг бўлмаган бошлангич шартларда
уларнинг кийматлари бошкача бўлади.
Келтирилган
мулохазалардан кўриниб турибдики, чизикли тизимнинг чикиши (тойилган ёки тойилмаган)
(6.15.11) ифода кўринишида ифодаланади ва ![]() - коэффициентларнинг
киймати бошлангич шартларга боглик. Кисман, бошлангич шартларни шундай танлаб
олиш мумкинки, барча
- коэффициентларнинг
киймати бошлангич шартларга боглик. Кисман, бошлангич шартларни шундай танлаб
олиш мумкинки, барча ![]() -коэффициентлар
нолга тенг бўлсин. У вактда
-коэффициентлар
нолга тенг бўлсин. У вактда ![]() киришга эга бўлган
тизимнинг чикиши
киришга эга бўлган
тизимнинг чикиши ![]() га тенг бўлади.
га тенг бўлади.
Энди
дастлаб кўйилган масалага кайтишимиз мумкин: очик тизимнинг (йўналтирилган богланиши
узилган тизимнинг) барча мумкин бўлган харакатлари билан дастлабки ёпик тизим харакатлари
орасидаги богланишни аниклайлик. Бу масалани куйидагича кўйиш мумкин: кириш ![]() ва
чикиш
ва
чикиш ![]() орасидаги богланиши
орасидаги богланиши
![]() (6.15.12)
(6.15.12)
кўринишда бўлган очик тизим мавжуд бўлсин, бу ерда S-бошлангич шартлар. Унга мос бўлган ёпик тизимнинг харакати очик тизимнинг
![]() (6.15.13)
(6.15.13)
холга
тўгри келадиган харакатидан иборат бўлади. Кириш билан чикиш орасидаги богланишни
аниклайдиган очик тизимнинг L оператори бўйича ёпик тизимнинг харакати хакида нима
айтиш мумкин? Масаланинг бундай кўйилиши хам хозир кўрилаётган чизикли тизимларга,
хам ночизикли тизимларга тааллукли, у хам тургунлик масалаларини тадкик этишда,
хам бошка масалаларга, масалан, даврий харакатларни излашга ишлатилади. Бу
умумийликни ва куршаб олинадиган масалаларнинг кенглигини кўрсатиш учун таъкидлаймизки,
агар L операторни функциялар фазосини тасвирловчи сифатида карасак,
у вактда бу тасвир учун ёпик тизимнинг харакатлари L операторнинг кўзгалмас
нукталари бўлади. Шунинг учун хам ёпик ва очик тизимлар орасидаги богланишни
динамик тизимларни операторли тасвирлашнинг кўзгалмас нукта принципи деб аташ
мумкин. Кўзгалмас нукта принципини чизикли тизимлар тургунлигини ёки нотургунлигини
тадкик этишда татбик этишнинг маъноси шундан иборатки, бизни ёпик тизимнинг ![]() кўринишидаги
харакатлари кизиктиради ва шундай кўринишдаги киришлар учун тизимнинг чикиши
кўринишидаги
харакатлари кизиктиради ва шундай кўринишдаги киришлар учун тизимнинг чикиши
![]() (6.15.14)
(6.15.14)
кўринишда
ифодаланади, бу ерда хар бир ![]() учун S бошлангич шартларни шундай танлаб олиш мумкинки,
учун S бошлангич шартларни шундай танлаб олиш мумкинки, ![]() коэффициентларнинг
барчаси нолга айланади. Маълумки, бизни кизиктираётган кўринишдаги эркин харакатлар
коэффициентларнинг
барчаси нолга айланади. Маълумки, бизни кизиктираётган кўринишдаги эркин харакатлар
![]() нинг факат
нинг факат
![]() (6.15.15)
(6.15.15)
муносабатни каноатлантирувчи кийматлари учун мавжуд бўлади.
Агар (6.15.13) тенглик факат хакикий кисми ![]() манфий
бўлган
манфий
бўлган ![]() кийматлар учун бажарилса,
у вактда чизикли ёпик тизим тургун бўлади ва бу тенглик хеч бўлмаганда битта хакикий
кисми мусбат бўлган
кийматлар учун бажарилса,
у вактда чизикли ёпик тизим тургун бўлади ва бу тенглик хеч бўлмаганда битта хакикий
кисми мусбат бўлган ![]() учун холда
бажарилса, у вактда чизикли тизим нотургун бўлади. Бу холларнинг кайси бири
мавжуд бўлишини Найквист критерияси хал килиб беради.
учун холда
бажарилса, у вактда чизикли тизим нотургун бўлади. Бу холларнинг кайси бири
мавжуд бўлишини Найквист критерияси хал килиб беради.
16-§. Найквист критерияси [63,65]
![]() (6.16.1)
(6.16.1)
формула
оркали ![]() комплекс параметр
текислигини W текислигига акслантирамиз.
комплекс параметр
текислигини W текислигига акслантирамиз.
Агар бу аксланиш
![]() (6.16.2)
(6.16.2)
ярим текисликни W текислигининг W=1 нуктадан ташкарида ётган D сохасига акслантирса, у холда тизим тургун бўлади. Аксинча, агар W=1 нукта D соханинг ичида ётса, у вактда тизим нотургун бўлади.
W
текислигидаги D соханинг чегараси ![]() текислигидаги
текислигидаги ![]() ярим
текисликнинг чегараси бўлган мавхум ўкнинг аксидир. Бу чегаранинг тенгламаси
ярим
текисликнинг чегараси бўлган мавхум ўкнинг аксидир. Бу чегаранинг тенгламаси
![]() (6.16.3)
(6.16.3)
кўринишга
эга, бу ерда ![]() ,
, ![]() .
.
(6.16.3)
эгри чизик куйидаги физик маънога эга. Тизим киришига частотаси ![]() бўлган
гармоник тебраниш берилсин, яъни
бўлган
гармоник тебраниш берилсин, яъни ![]() бўлсин. У вактда
(6.15.13) асосан тизимнинг чикишида хам маълум тарзда танлаб олинган бошлангич
шартларда
бўлсин. У вактда
(6.15.13) асосан тизимнинг чикишида хам маълум тарзда танлаб олинган бошлангич
шартларда ![]() микдорга тенг
бўлган гармоник тебранма харакат пайдо бўлади. Шунинг учун хам
микдорга тенг
бўлган гармоник тебранма харакат пайдо бўлади. Шунинг учун хам
![]()
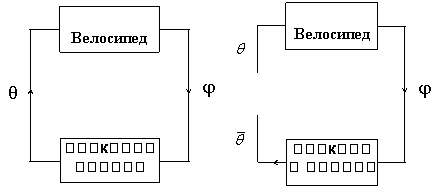
![]()
чикиш
ва киришдаги гармоник кисмини богловчи амплитуда - фазавий частота характеристикасини
англатади: ![]() нинг модули чикиш
ва киришдаги амплитудаларнинг нисбатини, аргументи бўлса-чикиш ва киришдаги
фазалар орасидаги силжишни билдиради.
нинг модули чикиш
ва киришдаги амплитудаларнинг нисбатини, аргументи бўлса-чикиш ва киришдаги
фазалар орасидаги силжишни билдиради.
Мисол. Юкорида баён этилган мулохазаларни оддий велосипед моделининг тургунлигини тадкик этишга татбик этамиз. Бу оддий модел [63]
![]() , (6.16.4)
, (6.16.4)
![]() (6.16.5)
(6.16.5)
тенглама
билан ифодаланади. Бу ерда ![]() - велосипед текислиги билан вертикал ¢к орасидаги
бурчак (киялик бурчаги),
- велосипед текислиги билан вертикал ¢к орасидаги
бурчак (киялик бурчаги), ![]() - рулнинг бурилиш бурчаги,
- рулнинг бурилиш бурчаги, ![]() -велосипеднинг тезлиги,
-велосипеднинг тезлиги, ![]() -етарлича кичик микдорлар,
-етарлича кичик микдорлар, ![]() -велосипед параметрлари.
-велосипед параметрлари.
(6.16.5) ифода рул бошкариш конунини ифодалайди. Велосипед рулни бошкариш конунини руёбга чикарувчи этадиган бошкариш тизими билан биргаликда ёпик тизимни ташкил этади (6.26-шакл).
Агар
6.27-шаклда к¢рсатилгандай богланишлардан биттасини узсак, у вактда очик
тизимнинг ![]() дан
дан ![]() га
узайтириш коэффициентини (6.16.4) ва (6.16.5) тенгламалардан топиш мумкин ва у
га
узайтириш коэффициентини (6.16.4) ва (6.16.5) тенгламалардан топиш мумкин ва у
 (6.16.6)
(6.16.6)
га тенг б¢лади.
Хакикатан хам, тасвирлашга ¢тганимиздан кейин (6.16.4) велосипед харакати тенгламасидан
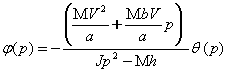 (6.16.7)
(6.16.7)
ва (6.16.5) бошкариш конунидан
![]() (6.16.8)
(6.16.8)
келиб
чикади. (6.16.7) ифодани ![]() ¢рнига
(6.16.8) га келтириб к¢йсак,
¢рнига
(6.16.8) га келтириб к¢йсак, ![]() ва
ва ![]() тасвирлар
орасидаги богланишни топамиз:
тасвирлар
орасидаги богланишни топамиз:
![]() ,
,
бу
ерда ![]() (6.16.6) ифодага
тенг.
(6.16.6) ифодага
тенг.
Бошкариладиган
велосипед харакати тургунлиги ![]() нукта D соха
ичида ёки ташкарисида ётишига боглик б¢лади. D сохани топиш
учун
нукта D соха
ичида ёки ташкарисида ётишига боглик б¢лади. D сохани топиш
учун ![]() текислигининг
¢нг яримини W текислигига
текислигининг
¢нг яримини W текислигига
![]() (6.16.9)
(6.16.9)
воситасида
акслантирамиз. ![]() текислиги мавхум
¢кининг акси D соханинг чегарасидан иборат. Уни топиш учун (6.16.9)
га
текислиги мавхум
¢кининг акси D соханинг чегарасидан иборат. Уни топиш учун (6.16.9)
га ![]() ни к¢ямиз, хосил
булган ифодани хакикий ва мавхум кисмларга ажратамиз:
ни к¢ямиз, хосил
булган ифодани хакикий ва мавхум кисмларга ажратамиз:
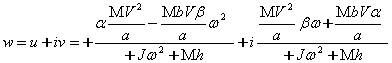 .
.
Бу ердан W текислигидаги D соха чегарасининг ушбу
 (6.16.10)
(6.16.10)
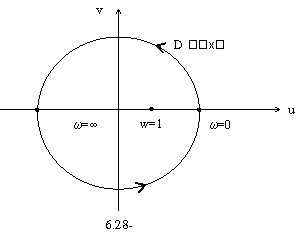 параметрик тенгламасини топамиз. 6.28-шаклда
параметрик тенгламасини топамиз. 6.28-шаклда ![]() хол
учун
хол
учун
D соха
келтирилган. Бу ерда курсатилганича ![]() б¢лганда тизимнинг
харакати тургун,
б¢лганда тизимнинг
харакати тургун, ![]() да эса нотургун
б¢лади. Тизим параметрларининг узлуксиз ¢згариши натижасида D соханинг
чегараси
да эса нотургун
б¢лади. Тизим параметрларининг узлуксиз ¢згариши натижасида D соханинг
чегараси ![]() нукта оркали
¢тганда тургун харакатдан нотургун харакатга ¢тилади. (6.16.10) параметрик
тенглама, тизим параметрлари ¢згариши унинг тургунлигига кандай тарзда
таъсир этишини тадкик этишга имконият яратади.
нукта оркали
¢тганда тургун харакатдан нотургун харакатга ¢тилади. (6.16.10) параметрик
тенглама, тизим параметрлари ¢згариши унинг тургунлигига кандай тарзда
таъсир этишини тадкик этишга имконият яратади.
17-§. Тургунлик критериялари ва алгоритмлари.
![]() -
ва
-
ва ![]() - утиш. Мавхум укнинг
чап ва унг тарафида
- утиш. Мавхум укнинг
чап ва унг тарафида
ётган илдизлар сонини топиш алгоритми
Купхадларни
D-булаклаш структурасини билиш тургунликни тадкик этиш
алгоритмларини яратишга маълум имкониятлар яратади. Бу алгоритмларни яратиш гоясини
куйидагича изохлаш мумкин: каралаётган купхадлар (функциялар) фазосида ![]() йул
танланади. Бу йул дастлабки функцияга мос келувчи
йул
танланади. Бу йул дастлабки функцияга мос келувчи ![]() нуктадан чекли
нуктадан чекли ![]() нуктага
боради.
нуктага
боради. ![]() нуктага мос келувчи
функция кайси
нуктага мос келувчи
функция кайси ![]() сохага мансублиги
аникланган ёки осонгина аникланади. Бу йул шундай танлаб олинадики, хар бир
сохага мансублиги
аникланган ёки осонгина аникланади. Бу йул шундай танлаб олинадики, хар бир ![]() нуктадан
нуктадан
![]() нуктага утишда каралаётган
нуктага утишда каралаётган
![]() сохада ётган илдизлар
сонининг узгаришини аниклаш мумкин булсин. Купхадлар учун бу йулни шундай
танлаймизки,
сохада ётган илдизлар
сонининг узгаришини аниклаш мумкин булсин. Купхадлар учун бу йулни шундай
танлаймизки, ![]() нуктадан
нуктадан ![]() нуктага
утишда
нуктага
утишда ![]() га мос келувчи купхаднинг
даражаси камайсин. Бу гоянинг кандай амалга ошишини
га мос келувчи купхаднинг
даражаси камайсин. Бу гоянинг кандай амалга ошишини ![]() - ва
- ва ![]() -
утишлар оркали тушунтирамиз.
-
утишлар оркали тушунтирамиз.
Ю.И.Неймарк томонидан ишлаб чикилган ![]() -
ва
-
ва ![]() - утиш деб
аталадиган мавхум укнинг чап ва унг тарафида ётган илдизлар сонини топиш
алгоритмини баён этамиз [63].
- утиш деб
аталадиган мавхум укнинг чап ва унг тарафида ётган илдизлар сонини топиш
алгоритмини баён этамиз [63].
![]()
![]() - даражали купхад ва
- даражали купхад ва
![]() (6.17.1)
(6.17.1)
булсин, бу ерда
![]()
хакикий купхадлар. ![]() купхадни
купхадни
![]() ёки
ёки ![]() (6.17.2)
(6.17.2)
жадвалларнинг бирортаси оркали ифодалаймиз.
Масалан, ![]() купхад
купхад
 ёки
ёки ![]()
жадваллар оркали ифодаланади.
Теорема.
 (6.17.3)
(6.17.3)
купхаддан
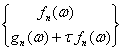 (6.17.4)
(6.17.4)
купхадга утишда чап ва унг ярим текисликда
ётган илдизларнинг сони узгармайди, бу ерда ![]() -ихтиёрий хакикий сон.
-ихтиёрий хакикий сон.
Исбот. Соддалик учун ![]() ва
ва ![]() купхадларнинг умумий хакикий
илдизлари мавжуд булмасин деб фараз киламиз.
купхадларнинг умумий хакикий
илдизлари мавжуд булмасин деб фараз киламиз. ![]() нинг узлуксиз узгариши
натижасида (6.17.4) купхаднинг чап ва унг ярим текисликларида ётган илдизларининг
сони факат
нинг узлуксиз узгариши
натижасида (6.17.4) купхаднинг чап ва унг ярим текисликларида ётган илдизларининг
сони факат ![]() комплекс узгарувчининг
мавхум укни кесиб утиши натижасида узгариши мумкин, яъни агар (6.17.4) купхаднинг
комплекс узгарувчининг
мавхум укни кесиб утиши натижасида узгариши мумкин, яъни агар (6.17.4) купхаднинг
![]() мавхум илдизи ёки
(6.17.1) га асосан
мавхум илдизи ёки
(6.17.1) га асосан ![]() ва
ва ![]() купхадларнинг янги умумий
хакикий илдизи пайдо булса, бу хол юз беради. Аммо бундай умумий илдизнинг
пайдо булиши мумкин эмас, чунки
купхадларнинг янги умумий
хакикий илдизи пайдо булса, бу хол юз беради. Аммо бундай умумий илдизнинг
пайдо булиши мумкин эмас, чунки ![]() ва
ва ![]() лардан
лардан ![]() ва
ва ![]() эканликлари келиб чикади.
Умуман, агар
эканликлари келиб чикади.
Умуман, агар ![]() ва
ва ![]() ларнинг коэффициентлари
шундай узлуксиз узгарсаки,
ларнинг коэффициентлари
шундай узлуксиз узгарсаки, ![]() ва
ва ![]() купхадларнинг умумий хакикий
илдизи пайдо булмаса, у холда
купхадларнинг умумий хакикий
илдизи пайдо булмаса, у холда  купхаднинг чап ва унг
ярим текисликда ётган илдизлари сони узгармай колади. Бундай утишлар жоиз (мумкин
булган) утишлар деб айтилади. Айтилганларга кура
купхаднинг чап ва унг
ярим текисликда ётган илдизлари сони узгармай колади. Бундай утишлар жоиз (мумкин
булган) утишлар деб айтилади. Айтилганларга кура ![]() лар учун
лар учун
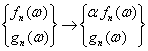 ва
ва  (6.17.5)
(6.17.5)
утишлар жоиз булади.
(6.17.3) дан (6.17.4) га жоиз утишни ![]() -утиш деб айтамиз.
-утиш деб айтамиз. ![]() купхадни
купхадни ![]() га купайтириш
га купайтириш
 купхаддан
купхаддан  купхадга
купхадга
утиш билан эквивалентдир. Шунинг учун

![]()
 (6.17.6)
(6.17.6)
утиш хам жоиздир.
Энди ![]() , яъни
, яъни ![]() булсин. Агар
булсин. Агар ![]() нинг 0 дан бирор кийматигача
узлуксиз узгаришида
нинг 0 дан бирор кийматигача
узлуксиз узгаришида ![]() киймат нолга
айланмаса, у холда
киймат нолга
айланмаса, у холда
![]() (6.17.7)
(6.17.7)
утиш жоиз утиш булади. Бу утишни ![]() -утиш деб айтамиз.
-утиш деб айтамиз.
Хакикатан хам, ![]() ва
ва ![]() муносабатлардан
муносабатлардан ![]() ва
ва ![]() , ёки
, ёки ![]() ва
ва ![]() муносабатлар, яъни
муносабатлар, яъни ![]() келиб чикади.
келиб чикади.
Агар ![]() булса, у холда
булса, у холда ![]() -утишда купхад
илдизларининг кандай узгаришини кузатайлик.
-утишда купхад
илдизларининг кандай узгаришини кузатайлик.
Ушбу

жадвал
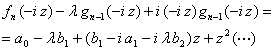 (6.17.8)
(6.17.8)
купхадни ифодалайди. ![]() булган умумий холда
булган умумий холда ![]() да (6.17.8) купхаднинг
битта илдизи нолга интилади. Бу илдиз
да (6.17.8) купхаднинг
битта илдизи нолга интилади. Бу илдиз ![]() булсин. Уни (6.17.8)
га асосан
булсин. Уни (6.17.8)
га асосан
![]()
куринишда ёзиш мумкин ва бу ердан
![]() (6.17.9)
(6.17.9)
булишлигини топамиз.
Охирги (6.17.9) ифодадан куриниб турибдики, ![]() нинг хакикий кисмининг
ишораси
нинг хакикий кисмининг
ишораси ![]() нинг ишораси билан
бир хил, яъни
нинг ишораси билан
бир хил, яъни ![]() нолдан
нолдан ![]() гача узгарган пайтда
нолга айланувчи
гача узгарган пайтда
нолга айланувчи ![]() илдиз
илдиз ![]() булганда унг ярим
текисликдан ва
булганда унг ярим
текисликдан ва ![]() да - чап ярим текисликдан
утади.
да - чап ярим текисликдан
утади.
Ушбу натижани ![]() параметр буйича купхадни
D-булаклаш (6.17.8) йули
билан хам олиш мумкин. Хакикатан хам, (6.17.8) купхадни
параметр буйича купхадни
D-булаклаш (6.17.8) йули
билан хам олиш мумкин. Хакикатан хам, (6.17.8) купхадни ![]() комплекс параметр буйича
D-булаклаш натижасида хосил
буладиган N эгри чизикнинг параметрик тенгламаси
комплекс параметр буйича
D-булаклаш натижасида хосил
буладиган N эгри чизикнинг параметрик тенгламаси
![]()
куринишда булади ва бу
чизик хакикий укни ![]() га мос келадиган
га мос келадиган ![]() нуктада
кесади.
нуктада
кесади. ![]() кийматнинг усиши
натижасида N эгри
чизик пастдан юкорига караб интилади ва чап тарафидан штрихланади.
кийматнинг усиши
натижасида N эгри
чизик пастдан юкорига караб интилади ва чап тарафидан штрихланади.
Бу ердан ![]() нинг уз хакикий ук буйлаб
нинг уз хакикий ук буйлаб ![]() дан чекли
дан чекли ![]() кийматгача
узлуксиз монотон узгаришида дастлабки
кийматгача
узлуксиз монотон узгаришида дастлабки ![]() купхад
купхад ![]() купхадга
утиб, шу билан бирга агар
купхадга
утиб, шу билан бирга агар ![]() булса, нолга тенг
булган илдиз унг ярим текисликдан ва
булса, нолга тенг
булган илдиз унг ярим текисликдан ва ![]() - чап ярим
текисликдан утади (6.29-шакл).
- чап ярим
текисликдан утади (6.29-шакл).
![]() -
даражали
-
даражали

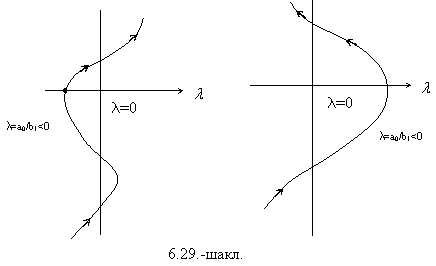
купхад берилган булсин. ![]() - утиш оркали
бу купхаддан
- утиш оркали
бу купхаддан

купхадга ва ![]() -утиш
оркали
-утиш
оркали

купхадга утамиз. ![]() кийматда
бу кейинги купхад
кийматда
бу кейинги купхад ![]() купхадга утади.
Олдинги мулохазаларга асосан
купхадга утади.
Олдинги мулохазаларга асосан ![]() купхаднинг унг
ярим текисликда ётган
купхаднинг унг
ярим текисликда ётган ![]() илдизларининг сони
илдизларининг сони
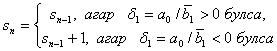 (6.17.10)
(6.17.10)
га тенг булади.
Шундай килиб, ![]() -даражали
-даражали ![]() купхаднинг унг ва чап
ярим текисликларда ётган илдизларининг сонини топиш масаласини
купхаднинг унг ва чап
ярим текисликларда ётган илдизларининг сонини топиш масаласини ![]() - даражали
- даражали ![]() купхаднинг худди
шундай масаласига келтирдик.
купхаднинг худди
шундай масаласига келтирдик.
Мисол.
![]() (6.17.11)
(6.17.11)
туртинчи даражали купхаднинг унг ва чап ярим текисликларда ётган илдизларининг сонини топиш талаб этилсин.
(6.17.11) га ![]() ни куйиб, уни хакикий
ва мавхум кисмларга ажратамиз:
ни куйиб, уни хакикий
ва мавхум кисмларга ажратамиз:
![]() .
.
Бу ердан

Демак, (6.17.11) купхадни куйидаги жадвал оркали ифодалаш мумкин
![]() .
.
![]() -утишдан
фойдаланиб ва
-утишдан
фойдаланиб ва ![]() деб олиб, охирги купхаддан
деб олиб, охирги купхаддан
![]() (6.17.12)
(6.17.12)
купхадга келамиз, бу ерда ![]() . (6.17.12) купхадга
. (6.17.12) купхадга ![]() -утишни куллаб (
-утишни куллаб (![]() ),
),
![]() (6.17.13)
(6.17.13)
купхадга келамиз.
Энди (6.17.13) купхадга ![]() -утишни бажариб,
-утишни бажариб,
![]() (6.17.14)
(6.17.14)
купхадга келамиз, каерда ![]() . Бу жараённи давом
эттириб, куйидагиларни хосил киламиз:
. Бу жараённи давом
эттириб, куйидагиларни хосил киламиз:
![]() ,
,
![]() .
.
![]() - ва
- ва ![]() -утишлар натижасида
биз
-утишлар натижасида
биз ![]() купхаддан
купхаддан ![]() купхадга келдик ва бу
утишлар жараёнида
купхадга келдик ва бу
утишлар жараёнида ![]() ,
, ![]() ,
, ![]() ,
, ![]() эканликларини аникладик.
эканликларини аникладик.
Демак, ![]() купхаддан
купхаддан ![]() купхадга утишда унг
ярим текисликдан битта илдиз (
купхадга утишда унг
ярим текисликдан битта илдиз (![]() ) ва чап ярим текисликдан
учта илдиз (
) ва чап ярим текисликдан
учта илдиз (![]() ,
, ![]() ,
, ![]() ) нолга айланади.
Шунинг учун хам
) нолга айланади.
Шунинг учун хам ![]() купхаднинг битта илдизининг
хакикий кисми мусбат ва учта илдизининг хакикий кисми манфий ишорали булади.
купхаднинг битта илдизининг
хакикий кисми мусбат ва учта илдизининг хакикий кисми манфий ишорали булади.
18-§. Купхад илдизлари хакикий кисмининг манфий ва мусбат ишоралилари сонини топишнинг детерминантли критериялари
![]() купхаднинг унг ва
чап ярим текисликларда ётган илдизларининг сонини топиш учун
купхаднинг унг ва
чап ярим текисликларда ётган илдизларининг сонини топиш учун ![]() -
ва
-
ва ![]() -утишлардан
фойдаланиб,
-утишлардан
фойдаланиб, ![]() купхаднинг
жадвалидан
купхаднинг
жадвалидан ![]() купхаднинг
жадвалига,
купхаднинг
жадвалига, ![]() дан
дан ![]() га
ва хоказо
га
ва хоказо ![]() дан
дан ![]() га
утамиз ва
га
утамиз ва ![]() ларнинг
ишораларини аниклаймиз. Демак,
ларнинг
ишораларини аниклаймиз. Демак, ![]() купхаднинг унг ва
чап ярим текисликда ётган илдизларининг сонини топиш масаласини
купхаднинг унг ва
чап ярим текисликда ётган илдизларининг сонини топиш масаласини ![]() ларнинг
ишораларини аниклаш масаласига келтирилади.
ларнинг
ишораларини аниклаш масаласига келтирилади.
![]() ларнинг
кийматларини топиш учун бажариладиган барча кетма-кет утишларни бажармаслик максадида
ушбу
ларнинг
кийматларини топиш учун бажариладиган барча кетма-кет утишларни бажармаслик максадида
ушбу
![]()
![]()
![]()
![]()
![]()
![]()
![]() а0
a1 a2 a3 ¼ an 0
0 ¼ 0
а0
a1 a2 a3 ¼ an 0
0 ¼ 0
B2 b0 b1 b2 b3 ¼ bn 0 0 ¼ 0
![]()
![]() A2n= 0 а0 a1 a2
a3 ¼ an 0 ¼ 0
A2n= 0 а0 a1 a2
a3 ¼ an 0 ¼ 0
B4 0 b0 b1 b2 b3 ¼ bn 0 ¼ 0 (6.18.1)
![]()
![]() ¼¼¼¼¼¼¼¼¼¼¼¼¼¼
¼¼¼¼¼¼¼¼¼¼¼¼¼¼
0 0 0 0 0 ¼¼ a0 a1 ¼ an
B2n 0 0 0 0 0 ¼¼ b0 b1 ¼ bn
![]()
матрицани курамиз.
(6.18.1) ифодани

купхаднинг матрицаси деб айтамиз. ![]() купхаддан
купхаддан ![]() купхадга утишда
(6.18.1) матрицанинг кандай узгаришини кузатамиз.
купхадга утишда
(6.18.1) матрицанинг кандай узгаришини кузатамиз. ![]() -утишда
-утишда ![]() матрицанинг
2,4,6,... жуфт сатрларига 1,3,5,... ток сатрларининг
матрицанинг
2,4,6,... жуфт сатрларига 1,3,5,... ток сатрларининг ![]() сонига купайтирилган
мос элементлари кушилади. Бу жараён натижасида (6.18.1) матрицанинг жадвалида
чизик билан ажратиб курсатилган
сонига купайтирилган
мос элементлари кушилади. Бу жараён натижасида (6.18.1) матрицанинг жадвалида
чизик билан ажратиб курсатилган ![]() детерминантларнинг
киймати узгармайди ва
детерминантларнинг
киймати узгармайди ва ![]() матрицанинг узи булса
куйидаги
матрицанинг узи булса
куйидаги
а0 a1 a2 a3 ¼ an 0 0 ¼ 0
B2
b0 ![]()
![]()
![]() ¼
¼ ![]() 0
0 ¼ 0
0
0 ¼ 0
![]()
![]()
![]() 0 а0 a1 a2 ¼ an
0 ¼ 0
0 а0 a1 a2 ¼ an
0 ¼ 0
B4
0 0 ![]()
![]() ¼
¼ ![]() 0
¼ 0
(6.18.2)
0
¼ 0
(6.18.2)
![]()
![]()
![]() ¼¼¼¼¼¼¼¼¼¼¼¼¼¼
¼¼¼¼¼¼¼¼¼¼¼¼¼¼
0 0 0 a0 a1 ¼ an
![]() B2n
0 0 0 0
B2n
0 0 0 0 ![]() ¼
¼ ![]()
A2n-2 A2n-4
куринишга эга булади. Навбатдаги ![]() -утишда 3,5,7,... ток
сатрлардан
-утишда 3,5,7,... ток
сатрлардан ![]() га купайтирилган
2,4,6,... жуфт сатрларнинг мос элементлари айрилади. Бу холда хам
га купайтирилган
2,4,6,... жуфт сатрларнинг мос элементлари айрилади. Бу холда хам ![]() детерминантларнинг кийматлари
узгармайди. (6.18.2) да
детерминантларнинг кийматлари
узгармайди. (6.18.2) да ![]() оркали ифодаланган
ифода
оркали ифодаланган
ифода ![]() купхаднинг матрицаси
булади ва
купхаднинг матрицаси
булади ва ![]() детерминантнинг
детерминантнинг ![]() киймати
киймати ![]() нинг кийматига тенг булади.
нинг кийматига тенг булади.
![]() матрицанинг узи булса,
матрицанинг узи булса,
![]() - ва
- ва ![]() - утишлардан кейин куйидаги
- утишлардан кейин куйидаги
а0 a1 a2 a3 ¼ an 0 0 ¼ 0
![]() 0
0 ![]()
![]()
![]() ¼
¼ ![]() 0
0 ¼ 0
0
0 ¼ 0
![]()
![]() 0 0
0 0 ![]()
![]() ¼
¼ ![]() 0
¼ 0
0
¼ 0
0
0 ![]()
![]() ¼
¼ ![]() 0
¼ 0
0
¼ 0
¼¼¼¼¼¼¼¼¼¼¼¼¼¼
0 0 0 ¼ ![]()
![]() ¼¼
¼¼ ![]()
0 0 0 ¼ ![]()
![]() ¼¼
¼¼ ![]()
A2n-2
куринишни олади. ![]() купхаддан
купхаддан ![]() купхадга утиш учун
купхадга утиш учун ![]() матрицага
матрицага ![]() - ва
- ва ![]() - утишларни куллаймиз,
- утишларни куллаймиз,
![]() матрицагача бу
жараённи давом эттириб, ушбу
матрицагача бу
жараённи давом эттириб, ушбу
 (6.18.3)
(6.18.3)
келамиз. Бу матрицанинг ифодасидан куриниб турибдики,
![]() ,
, ![]()
ва, демак, ![]() лар орасидаги манфий
микдорларнинг сони
лар орасидаги манфий
микдорларнинг сони
![]() (6.18.4)
(6.18.4)
детерминантлар каторидаги ишора узгаришлар сонига тенг булади.
![]() (6.18.5)
(6.18.5)
хакикий коэффициентли купхад учун юкорида келтирилган мулохазаларни
бошкачарок олиш бориш мумкин. Бунда ![]() матрица урнига
матрица урнига
B1 а1 a0 0 0 ¼ 0
B2 a3 a2 a1 a0 ¼ 0
An = B3 а5 a4 a3 a2 ¼ 0
¼¼¼¼¼¼¼¼
Bn 0 0 0 0 ¼ an
куринишдаги матрицадан фойдаланиш мумкин. Бу ерда хам хакикий купхаднинг унг ярим текисликдаги илдизларининг сони
 (6.18.6)
(6.18.6)
катордаги ишора узгаришлар
сонига тенглигини курсатиш мумкин. Демак, купхаднинг барча илдизлари чап ярим
текисликда ётиши учун (6.18.6) катордаги хамма ![]() булиши зарур ва
етарлидир. Бу тасдик Раус-Гурвиц критериясининг узгинасидир ва биз буни бошка йул
билан топдик.
булиши зарур ва
етарлидир. Бу тасдик Раус-Гурвиц критериясининг узгинасидир ва биз буни бошка йул
билан топдик.
Шундай килиб,
комплекс ва хакикий коэффициентли купхадлар учун тургунликнинг детерминантли
критериялари мос равишда (6.18.4) ва (6.18.6) детерминантларнинг мусбат булишидан
иборат экан. Аммо тургунлик сохасининг чегарасини факат ![]() ва мос равишда
ва мос равишда ![]() детерминатлар аниклайди.
Тургунлик сохасининг чегарасида
детерминатлар аниклайди.
Тургунлик сохасининг чегарасида ![]() =0 ва
=0 ва ![]() =0 булади.
=0 булади.
Хакикий к¢пхадлар учун ![]() тенглама билан аникланадиган
тургунлик сохасининг чегараси
тенглама билан аникланадиган
тургунлик сохасининг чегараси ![]() б¢лганлиги учун
икки кисмга б¢линади: иккита соф мавхум илдизга мос келувчи
б¢лганлиги учун
икки кисмга б¢линади: иккита соф мавхум илдизга мос келувчи ![]() га ва битта хакикий 0
илдизга мос келувчи
га ва битта хакикий 0
илдизга мос келувчи ![]() га.
га.
|
РЕЖА:
|
|
1. Раус-Гурвиц муаммоси пайдо булишининг тарихи хакида. |
|
2. Коши индекси ва Штурм теоремаси. |
|
3. Раус алгоритми. Махсус холлар. Мисоллар. |
|
4. Раус-Гурвиц теоремаси. |
|
5. Орландо формуласи. Раус-Гурвиц теоремасидаги махсус холлар. |
|
6. Льенар ва Шипарнинг тургунлик критерияси. |
|
7. Тургунлик ва нотургунлик ходисаларини текширишга физик ёндашув. |
|
8. Чизиклаштирилган тизимларда нотургунликнинг пайдо булишига доир мисоллар. |
|
9. Тургунлик сохаларини ясаш. Ю.И.Неймаркнинг D-булаклаш усули. |
|
10. Бир комплекс параметр текислигида тургунлик сохасини ясаш. |
|
11. D-булаклаш усули билан икки хакикий параметр текислигида тургунлик сохасини ясаш. |
|
12. Михайлов критерияси. |
|
13. Автомобил олдинги гилдираклари харакатининг тургунлигини D-булаклаш усули оркали тадкик этиш. |
|
14. Самолёт олдинги шасси харакатининг тургунлигини D-булаклаш усули оркали тадкик этиш. |
|
15. Ёпик тизим ва очик тизим харакатлари уртасидаги богланиш. Динамик тизимларни оператор оркали ифодалашда кузгалмас нукта принципи. |
|
16. Найквист критерияси. |
|
17. Тургунлик критериялари ва алгоритмлари. t- ва n- утиш. Мавхум укнинг чап ва унг тарафида ётган илдизлар сонини топиш алгоритми. |
|
18. Купхад илдизлари хакикий кисмининг манфий ва мусбат ишоралилари сонини топишнинг детерминантли критериялари. |
Таянч иборалар. Раус – Гурвиц муаммоси, Коши индекси, Штурм катори ва теоремаси, Раус алгоритми, махсус хол, Раус –Гурвиц теоремаси, Арландо формуласи, Льенар ва Щипар критерияси, тургунлик ва нотургунлик ходисаларига физик ёндашув, богланишларнинг геометрик схемаси, Неймарк теоремалари, нотургунликнинг пайдо булишига доир мисоллар, тургунлик сохаси, Неймаркнинг D- булаклаш усули, Михайлов критерияси, Найквист критерияси, ёпик ва очик тизимлар, кузгалмас нукта принципи, t- ва n- утиш, мавхум укнинг чап ва унг тарафида ётган илдизлар сонини топиш алгоритми, детерминантли критериялар.
Такрорлаш учун саволлар:
1. Раус – Гурвиц муаммоси нимадан иборат? Коши индекси ва Штурм теоремаси.
2. Раус алгоритми ва теоремаси. Махсус холлар.
3. Раус –Гурвиц теоремаси.
4. Раус –Гурвиц теоремасидаги махсус холлар. Арландо формуласи.
5. Льенар ва Щипарнинг тургунлик критерияси.
6. Богланишларнинг геометрик схемаси ва нотургунликнинг структуравий шартлари.
7. Автомобильнинг бошкарилувчи олдинги гилдираклари харакатининг нотургунлиги сабаблари.
8. Гиростабиллаштирилган бир рельсли вагоннинг тургунлиги.