V-БОБ. БАРКАРОР ХАРАКАТЛАР УЧУН КРИТИК ХОЛЛАРНИ ТАДКИК ЭТИШ
1-§. Характеристик тенглама. Битта нол илдизга эга булган хол.
Дифференциал тенгламаларни махсус куринишга келтириш
Тойилган
харакат дифференциал тенгламалари системаси куйидаги ![]() - тартибли
система булсин
- тартибли
система булсин
![]() , (5.1.1)
, (5.1.1)
бу
ерда ![]() - узгармас сонлар,
- узгармас сонлар,
![]() - координата боши
(мувозанат холати) атрофида
- координата боши
(мувозанат холати) атрофида ![]() узгарувчиларнинг даражалари
буйича каторга ёйилувчи функция. Катор камида иккинчи даражали хаддан
бошланади. (5.1.1) системанинг биринчи якинлашиш тенгламалари
узгарувчиларнинг даражалари
буйича каторга ёйилувчи функция. Катор камида иккинчи даражали хаддан
бошланади. (5.1.1) системанинг биринчи якинлашиш тенгламалари
![]() (5.1.2)
(5.1.2)
куринишда
булади. (5.1.2) биринчи якинлашиш тенгламалари системаси характеристик
тенгламасининг битта илдизи нолга ва колган ![]() та илдизларининг хакикий
кисми манфий булсин.
та илдизларининг хакикий
кисми манфий булсин.
(5.1.2)
тенгламаларнинг бирорта ![]() узгарувчиси урнига
куйидаги алмаштириш
узгарувчиси урнига
куйидаги алмаштириш
![]()
оркали
![]() узгарувчини
киритамиз. Бу ерда
узгарувчини
киритамиз. Бу ерда ![]() кандайдир узгармас
сонлар. Бу узгармас сонларни шундай танлаб оламизки, алмаштирилган тенглама
кандайдир узгармас
сонлар. Бу узгармас сонларни шундай танлаб оламизки, алмаштирилган тенглама
![]()
куринишга эга булсин.
Демак, биз куйидаги тенгликка келамиз
![]() .
.
Энди
![]() олдидаги
коэффициентларни нолга тенглаштириб, куйидаги бир жинсли чизикли алгебраик тенгламалар
системасини хосил киламиз
олдидаги
коэффициентларни нолга тенглаштириб, куйидаги бир жинсли чизикли алгебраик тенгламалар
системасини хосил киламиз
![]() . (5.1.3)
. (5.1.3)
(5.1.2)
системанинг характеристик тенгламаси нол илдизга эга эканлиги учун (5.1.3)
системанинг детерминанти нолга тенг булади ва, демак, бу система хамма ![]() лар
нолга тенг булмаган ечимга эга. Аниклилик учун
лар
нолга тенг булмаган ечимга эга. Аниклилик учун ![]() деб фараз килайлик.
У холда
деб фараз килайлик.
У холда ![]() ни
ни ![]() узгарувчи
урнига кабул килишимиз мумкин. Колган
узгарувчи
урнига кабул килишимиз мумкин. Колган ![]() узгарувчиларни келгусида
узгарувчиларни келгусида
![]() билан белгилаймиз.
билан белгилаймиз.
Шундай килиб, (5.1.2) тенгламаларни
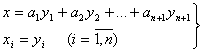 (5.1.4)
(5.1.4)
алмаштиришлар ва
![]()
белгилашлар киритиб,
![]()
куринишга
келтирамиз, бу ерда ![]() - узгармас сонлар.
Бу системанинг ушбу
- узгармас сонлар.
Бу системанинг ушбу
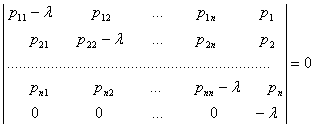
характеристик
тенгламаси ![]() ва
ва
 (5.1.5)
(5.1.5)
тенгламаларга ажралади.
Характеристик
тенглама чизикли алмаштиришларга нисбатан инвариант булганлиги ва курилаётган холда
у ![]() та хакикий кисми
манфий ишорали илдизга эга булганлиги учун (5.1.5) тенглама илдизларининг хамма
хакикий кисми манфий булади.
та хакикий кисми
манфий ишорали илдизга эга булганлиги учун (5.1.5) тенглама илдизларининг хамма
хакикий кисми манфий булади.
Агар (5.1.4) алмаштиришларни (5.1.1) га нисбатан кулласак, у холда (5.1.1) тенгламалар куйидаги куринишга келади
 (5.1.6)
(5.1.6)
бу
ерда ![]() ва
ва ![]() -
-
![]() узгарувчиларнинг
аналитик функциялари ва уларнинг ёйилмаси камида иккинчи даражали хаддан бошланади.
узгарувчиларнинг
аналитик функциялари ва уларнинг ёйилмаси камида иккинчи даражали хаддан бошланади.
Характеристик тенгламаси битта нол илдизга эга булган критик холда тойилган харакатнинг дифференциал тенгламалари (5.1.6) куринишга эга булади. Булђуси тадкикотларни биз шу дифференциал тенгламаларга нисбатан олиб борамиз.
Изох.
Бундан кейин ![]() узгарувчини критик
узгарувчи,
узгарувчини критик
узгарувчи, ![]() узгарувчиларни эса
нокритик узгарувчилар деб атаймиз. Шунга мувофик (5.1.6) системанинг биринчи
тенгламасини критик тенглама, колган
узгарувчиларни эса
нокритик узгарувчилар деб атаймиз. Шунга мувофик (5.1.6) системанинг биринчи
тенгламасини критик тенглама, колган ![]() та тенгламаларини
эса нокритик тенгламалар деб атаймиз.
та тенгламаларини
эса нокритик тенгламалар деб атаймиз.
2-§. Биринчи тартибли система учун масалани
тадкик этиш
Дастлаб
![]() булган холни курайлик.
Бу хол учун тойилган харакат дифференциал тенгламаси
булган холни курайлик.
Бу хол учун тойилган харакат дифференциал тенгламаси
![]() (5.2.1)
(5.2.1)
куринишда
булади, бу ерда ![]() ва
ва ![]() -
кандайдир узгармас сонлар.
-
кандайдир узгармас сонлар.
Курилаётган
хусусий холда турђунлик масаласи осонгина ечилади: агар ![]() жуфт сон
булса, у холда тойилмаган харакат нотурђун ва
жуфт сон
булса, у холда тойилмаган харакат нотурђун ва ![]() ток сон булса, у холда
ток сон булса, у холда
![]() да тойилмаган харакат
асимптотик турђун,
да тойилмаган харакат
асимптотик турђун, ![]() да эса нотурђун булади.
да эса нотурђун булади.
 |
Хакикатан хам, агар ![]() жуфт сон булса, у холда
(5.2.1) тенгламанинг унг тарафидаги функция координата бошининг атрофида
жуфт сон булса, у холда
(5.2.1) тенгламанинг унг тарафидаги функция координата бошининг атрофида ![]() нинг
ишорасига мос келадиган киймат кабул килади (2-бобдаги 4-леммага асосан).
нинг
ишорасига мос келадиган киймат кабул килади (2-бобдаги 4-леммага асосан).
Шунинг
учун хам (5.2.1) тенгламага асосан ![]() уки буйича харакат
килаётган тасвирловчи нукта харакатининг тезлиги нуктанинг дастлабки пайтда
координата бошининг чапида ёки унгида туришидан катъий назар, маълум йуналишга
эга булади.
уки буйича харакат
килаётган тасвирловчи нукта харакатининг тезлиги нуктанинг дастлабки пайтда
координата бошининг чапида ёки унгида туришидан катъий назар, маълум йуналишга
эга булади.
Демак,
агар тасвирловчи нукта дастлабки лахзада ![]() булганда
координата бошининг унгида ва
булганда
координата бошининг унгида ва ![]() булганда чапида
турса, у холда бу нукта
булганда чапида
турса, у холда бу нукта ![]() функциянинг аник
ишорали сохасидан чикгунга кадар координата бошидан узоклашади (5.1,а-шакл ).
Шундай килиб, бу холда тойилмаган харакат,
функциянинг аник
ишорали сохасидан чикгунга кадар координата бошидан узоклашади (5.1,а-шакл ).
Шундай килиб, бу холда тойилмаган харакат, ![]() нинг ишораси кандай
булишидан катъий назар, нотурђун булади.
нинг ишораси кандай
булишидан катъий назар, нотурђун булади.![]()
Агар
![]()
![]() ток сон
булса, у холда тасвирловчи нукта тезлигининг йуналиши координата бошидан утганда
узгаради. Бу хол учун
ток сон
булса, у холда тасвирловчи нукта тезлигининг йуналиши координата бошидан утганда
узгаради. Бу хол учун ![]() да, нукта
координата бошидан узоклашади (5.1,б-шакл) ва
да, нукта
координата бошидан узоклашади (5.1,б-шакл) ва ![]() булганда, у,
аксинча, координата бошига якинлашади (5.1,в-шакл). Демак,
булганда, у,
аксинча, координата бошига якинлашади (5.1,в-шакл). Демак, ![]() булганда,
тойилмаган харакат нотурђун,
булганда,
тойилмаган харакат нотурђун, ![]() эса асимптотик
турђун булади.
эса асимптотик
турђун булади.
Курилаётган масала учун осонгина Ляпунов функциясини тузиш мумкин.
а) ![]() - ток сон булсин,
у холда
- ток сон булсин,
у холда
![]()
деб оламиз. Унинг вакт буйича олинган тулик хосиласи
![]() =
=![]()
га
тенг булади. ![]() ва
ва ![]() функцияларнинг
иккаласи хам аник ишорали. Агар
функцияларнинг
иккаласи хам аник ишорали. Агар ![]() булса, у холда
иккаласи хам бир хил ишорали ва, демак,
булса, у холда
иккаласи хам бир хил ишорали ва, демак, ![]() функция теорема В
нинг хамма шартларини каноатлантиргани учун тойилмаган харакат нотурђун булади.
Агар
функция теорема В
нинг хамма шартларини каноатлантиргани учун тойилмаган харакат нотурђун булади.
Агар ![]() булса, у холда
булса, у холда ![]() ва
ва
![]() ларнинг ишоралари
бир-бирига карама-карши ва, демак,
ларнинг ишоралари
бир-бирига карама-карши ва, демак, ![]() функция теорема Б
нинг хамма шартларини каноатлантиради. Шундай килиб, бу холда тойилмаган харакат
асимптотик турђун булади.
функция теорема Б
нинг хамма шартларини каноатлантиради. Шундай килиб, бу холда тойилмаган харакат
асимптотик турђун булади.
б)
![]() - жуфт сон булганда,
Ляпунов функциясини
- жуфт сон булганда,
Ляпунов функциясини ![]() шаклда излаймиз. У
вактда
шаклда излаймиз. У
вактда ![]() аник ишорали
функция булади.
аник ишорали
функция булади. ![]() функция кийматининг
ишораси булса,
функция кийматининг
ишораси булса, ![]() кандай киймат кабул
килишидан катъий назар,
кандай киймат кабул
килишидан катъий назар, ![]() кийматининг
ишораси билан бир хил булиши мумкин. Демак,
кийматининг
ишораси билан бир хил булиши мумкин. Демак, ![]() да хам,
да хам, ![]() да
хам
да
хам ![]() функция теорема В
нинг хамма шартларини каноатлантиради, яъни тойилмаган харакат нотурђун булади.
функция теорема В
нинг хамма шартларини каноатлантиради, яъни тойилмаган харакат нотурђун булади.
3-§. ![]() - тартибли система
учун масалани хусусий холда тадкик этиш
- тартибли система
учун масалани хусусий холда тадкик этиш
Энди
![]() деб фараз киламиз.
Шу билан бирга, биз (5.1.6) дифференциал тенгламаларнинг унг тарафидаги
функциялар айрим кушимча шартларни каноатлантиради деб фараз киламиз. Ушбу
деб фараз киламиз.
Шу билан бирга, биз (5.1.6) дифференциал тенгламаларнинг унг тарафидаги
функциялар айрим кушимча шартларни каноатлантиради деб фараз киламиз. Ушбу
 (5.3.1)
(5.3.1)
белгилашларни
киритамиз, бу ерда ![]() узгармас сонлар.
У холда кушимча шартлар куйидагилардан иборат:
узгармас сонлар.
У холда кушимча шартлар куйидагилардан иборат:
1)
![]() айнан нолга тенг булмайди,
айнан нолга тенг булмайди,
2)
![]() ,
,
3)
(5.1.6) тенгламалардаги барча ![]() булсин.
булсин.
Бу шартлар бажарилганда турђунлик масаласи бирданига ечилади:
Агар ![]() - жуфт сон булса ,
у холда тойилмаган харакат доимо нотурђун булади.
- жуфт сон булса ,
у холда тойилмаган харакат доимо нотурђун булади.
Агар ![]() - ток сон булса, у
холда
- ток сон булса, у
холда ![]() булганда
тойилмаган харакат нотурђун ва
булганда
тойилмаган харакат нотурђун ва ![]() булганда – асимптотик
турђун булади.
булганда – асимптотик
турђун булади.
Бошкача килиб айтганда, масаланинг ечими
![]()
битта дифференциал тенглама билан ифодаланган тойилган харакат мувозанат холатининг турђунлик масаласининг ечими билан бир хил булади.
Шундай килиб, юкорида келтирилган 3 та шартлар бажарилганда, турђунлик масаласини ечиш учун хамма нокритик тенгламаларни ва критик тенгламадаги хамма нокритик узгарувчиларга бођлик булган хадларни ташлаб юбориб, хосил булган бир узгарувчили битта дифференциал тенгламани тадкик этиш етарлидир.
Келтирилган тасдикни исботлаш учун тойилган харакатнинг
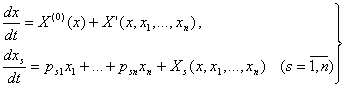 (5.3.2)
(5.3.2)
дифференциал
тенгламалари учун Ляпуновнинг теорема Б ёки теорема В ларини каноатлантирувчи ![]() функцияни
тузиш керак булади, бу ерда
функцияни
тузиш керак булади, бу ерда
![]()
нуктада нолга айланувчи функция булиши лозим.
Демак,
шундай ![]() ни топиш керакки,
унинг (5.3.2) га нисбатан вакт буйича олинган тулик хосиласи
ни топиш керакки,
унинг (5.3.2) га нисбатан вакт буйича олинган тулик хосиласи ![]() аник
ишорали функция булсин.
аник
ишорали функция булсин.
а)
Аввал ![]() - ток сон булган холни
куриб утайлик.
- ток сон булган холни
куриб утайлик.
![]() куйидаги
муносабатни каноатлантирувчи
куйидаги
муносабатни каноатлантирувчи ![]() узгарувчиларнинг
квадратик формаси булсин:
узгарувчиларнинг
квадратик формаси булсин:
![]() . (5.3.3)
. (5.3.3)
(5.1.5) характеристик тенглама илдизларининг барчаси хакикий
кисми манфий булганлигидан 4-бобдаги 1-теоремага асосан бундай ![]() форма
мавжуд ва у аник манфий ишорали булади.
форма
мавжуд ва у аник манфий ишорали булади.
Ляпунов функциясини куйидаги куринишда танлаб оламиз:
![]() , (5.3.4)
, (5.3.4)
бу
ерда ![]()
![]() узгарувчиларнинг
чизикли формаси.
узгарувчиларнинг
чизикли формаси. ![]() чизикли формаларни
шундай танлаймизки,
чизикли формаларни
шундай танлаймизки, ![]() функциянинг
(5.3.2) системага кура вакт буйича олинган тулик хосиласи
функциянинг
(5.3.2) системага кура вакт буйича олинган тулик хосиласи
![]() (5.3.5)
(5.3.5)
куринишга
эга ва аник мусбат ишорали функция булсин. Бу ерда ![]() ва
ва ![]() узгарувчиларнинг
кандайдир функциялари булиб, уларнинг
узгарувчиларнинг
кандайдир функциялари булиб, уларнинг ![]() нуктадаги киймати
нолга тенг.
нуктадаги киймати
нолга тенг.
![]() функцияни
куриб утайлик.
функцияни
куриб утайлик. ![]() - квадратик
форманинг аник манфий ишорали эканлигини юкорида айтиб утган эдик. Шунинг учун хам
- квадратик
форманинг аник манфий ишорали эканлигини юкорида айтиб утган эдик. Шунинг учун хам
![]() булса,
булса, ![]() узгарувчиларнинг
узгарувчиларнинг
![]() (5.3.6)
(5.3.6)
квадратик
формаси хам аник манфий ишорали, шунга биноан (5.3.4) формула билан аникланадиган
![]() функция хам аник
манфий ишорали булади.
функция хам аник
манфий ишорали булади.
Шундай
килиб, ![]() булганда
булганда ![]() -
аник мусбат ишорали ва
-
аник мусбат ишорали ва ![]() - аник манфий
ишорали функциялар буладилар ва, демак,
- аник манфий
ишорали функциялар буладилар ва, демак, ![]() функция
Ляпуновнинг теорема Б сининг хамма шартларини каноатлантиради. Бу ердан тойилмаган
харакатнинг асимптотик турђунлиги келиб чикади.
функция
Ляпуновнинг теорема Б сининг хамма шартларини каноатлантиради. Бу ердан тойилмаган
харакатнинг асимптотик турђунлиги келиб чикади.
Агар
![]() булса, у холда
(5.3.6) квадратик форма ва, демак,
булса, у холда
(5.3.6) квадратик форма ва, демак, ![]() функция узгарувчан
ишорали ва шунга кура
функция узгарувчан
ишорали ва шунга кура ![]() хам аник ишорали
функция булади. Шундай килиб, бу холда
хам аник ишорали
функция булади. Шундай килиб, бу холда ![]() функция теорема В
нинг хамма шартларини каноатлантиради ва тойилмаган харакат нотурђун булади.
функция теорема В
нинг хамма шартларини каноатлантиради ва тойилмаган харакат нотурђун булади.
б)
Энди ![]() жуфт сон булсин.
Бу холда
жуфт сон булсин.
Бу холда ![]() узгармас соннинг кандай
ишорали булишидан катъий назар, тойилмаган харакат нотурђун булишини курсатамиз.
Бунинг учун
узгармас соннинг кандай
ишорали булишидан катъий назар, тойилмаган харакат нотурђун булишини курсатамиз.
Бунинг учун ![]() функцияни куйидаги
куринишда излаймиз:
функцияни куйидаги
куринишда излаймиз:
![]() , (5.3.7)
, (5.3.7)
бу
ерда ![]() - (5.3.3)
муносабатни каноатлантирувчи аник манфий ишорали квадратик форма,
- (5.3.3)
муносабатни каноатлантирувчи аник манфий ишорали квадратик форма, ![]()
![]() узгарувчиларнинг
кандайдир чизикли формалари. Бу формаларни шундай танлаб оламизки,
узгарувчиларнинг
кандайдир чизикли формалари. Бу формаларни шундай танлаб оламизки, ![]() нинг
хосиласи куйидаги куринишга
нинг
хосиласи куйидаги куринишга
![]() (5.3.8)
(5.3.8)
эга
булсин, бу ерда ![]() -
- ![]() нинг
функцияси ва
нинг
функцияси ва ![]() ларнинг функцияси
ва
ларнинг функцияси
ва ![]() .
.
Агар
![]() етарлича кичик сон
булса, у холда
етарлича кичик сон
булса, у холда ![]() - аник мусбат
ишорали функция булади. Ёйилмаси чизикли хадлар билан бошланадиган
- аник мусбат
ишорали функция булади. Ёйилмаси чизикли хадлар билан бошланадиган ![]() функция
эса, равшанки, узгарувчан ишорали, демак,
функция
эса, равшанки, узгарувчан ишорали, демак, ![]() функция теорема В
нинг хамма шартларини каноатлантиради хамда тойилмаган харакат нотурђун булади.
функция теорема В
нинг хамма шартларини каноатлантиради хамда тойилмаган харакат нотурђун булади.
Шундай килиб, курилаётган хол учун хамма тасдикларни исбот килдик.
Тасдикларнинг туларок исботини Г.Н.Дубошиннинг [26, 180-186 бетлар] ва И.Г.Малкиннинг [53, 94-101 бетлар] китобларидан топиш мумкин. Бу китобларда нима учун Ляпунов функциясини (5.3.4) ва (5.3.7) куринишларда излашни тушунтирувчи мулохазалар келтирилган.
4-§. ![]() - тартибли система
учун масалани умумий холда тадкик этиш
- тартибли система
учун масалани умумий холда тадкик этиш
Турђунлик масаласини умумий хол, яъни (5.1.6) тойилган харакат тенгламаларининг унг тарафидаги функцияларни чегараловчи хеч кандай шартлар куйилмаган холда куриб утамиз.
Масалани умумий холда ечиш учун (5.1.6) тенгламалар системасини олдинги парараграфдаги чегараловчи шартлар бажариладиган куринишга келтирамиз. Шу максадда
![]() (5.4.1)
(5.4.1)
тенгламалар
системасини караймиз. Бу тенгламаларнинг чап кисми ![]() нуктада
нолга айланади. (5.4.1) тенгламаалар системасидан
нуктада
нолга айланади. (5.4.1) тенгламаалар системасидан ![]() узгарувчиларни
узгарувчиларни ![]() узгарувчининг
функциялари сифатида аниклаймиз. Бу системанинг
узгарувчининг
функциялари сифатида аниклаймиз. Бу системанинг ![]() узгарувчиларга
нисбатан функционал детерминанти
узгарувчиларга
нисбатан функционал детерминанти ![]() нуктада нолдан фаркли.
Хакикатан хам,
нуктада нолдан фаркли.
Хакикатан хам,
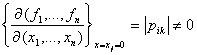 ,
,
чунки
(5.1.5) характеристик тенгламанинг нолга тенг илдизи мавжуд эмас. Шунинг учун хам
ошкормас функцияларнинг мавжудлиги хакидаги теоремага асосан (5.4.1) системанинг
ягона ечими мавжуд ва ![]() функциялар
функциялар ![]() да
нолга айланиб, улар
да
нолга айланиб, улар ![]() нинг даражалари буйича
каторга ёйилади хамда бу катор
нинг даражалари буйича
каторга ёйилади хамда бу катор ![]() нинг етарлича
кичик кийматларида якинлашувчи булади.
нинг етарлича
кичик кийматларида якинлашувчи булади.
Айтилган функциялар
![]() (5.4.2)
(5.4.2)
булсин, яъни
![]() . (5.4.3)
. (5.4.3)
Энди (5.1.6) тенгламаларда узгарувчиларни куйидагича алмаштирамиз
![]() . (5.4.4)
. (5.4.4)
У холда

ёки (5.4.3) га асосан
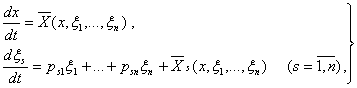 (5.4.5)
(5.4.5)
бу ерда
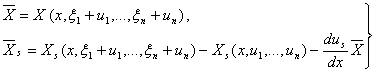 (5.4.6)
(5.4.6)
лар -![]() узгарувчиларнинг
аналитик функциялари. Бу функцияларнинг ёйилмаси камида иккинчи даражали хадлардан
бошланади.
узгарувчиларнинг
аналитик функциялари. Бу функцияларнинг ёйилмаси камида иккинчи даражали хадлардан
бошланади.
Эски узгарувчилар бирданига нолга айланганларида, шунда ва факат шундагина янги узгарувчилар бир вактда нолга айланадилар. Шунинг учун эски узгарувчиларга нисбатан турђунлик масаласи янги узгарувчиларга нисбатан турђунлик масаласига эквивалентдир. Демак, курилаётган умумий холда турђунлик масаласини тадкик этиш учун (5.4.5) системани куришимиз кифоя булади.
(5.4.5) тенгламалар системаси олдинги параграфда курилган чегараловчи шартлардан иккинчи ва учинчисини каноатлантиради.
Хакикатан
хам, (5.4.5) системанинг охирги ![]() та тенгламасида
барча
та тенгламасида
барча ![]() .
. ![]() ва
ва
![]() функциялар учун
(5.4.6) га асосан
функциялар учун
(5.4.6) га асосан
 (5.4.7)
(5.4.7)
тенгликларни
хосил киламиз. Бу ердан куриниб турибдики, ![]() функция ёйилмасидаги
биринчи хаднинг даражаси
функция ёйилмасидаги
биринчи хаднинг даражаси ![]() нинг ёйилмасидаги
энг паст даражали хадникидан кам эмас, яъни
нинг ёйилмасидаги
энг паст даражали хадникидан кам эмас, яъни ![]() .
.
Демак,
агар ![]() булса, у холда
(5.4.5) система олдинги параграфдаги барча чегараловчи шартларни каноатлантиради.
Шунинг учун хам
булса, у холда
(5.4.5) система олдинги параграфдаги барча чегараловчи шартларни каноатлантиради.
Шунинг учун хам ![]() булган холда, биз
турђунлик масаласини ечиш учун олдинги параграфда олинган натижалардан фойдаланишимиз
мумкин.
булган холда, биз
турђунлик масаласини ечиш учун олдинги параграфда олинган натижалардан фойдаланишимиз
мумкин.
Агар
![]() булса, у холда
(5.4.7) га асосан
булса, у холда
(5.4.7) га асосан ![]() ва олдинги
параграфдаги шартлар бажарилмайди. Бу холни адабиётда махсус хол деб айтадилар
ва уни махсус тадкик этиш керак булиб колади.
ва олдинги
параграфдаги шартлар бажарилмайди. Бу холни адабиётда махсус хол деб айтадилар
ва уни махсус тадкик этиш керак булиб колади.
Хозир
биз номахсус холни курамиз. Бу холда, олдинги параграфдаги натижаларга асосан,
биз (5.4.5) системадаги факат биринчи тенгламани куришимиз, ![]() ларга
бођлик булган хамма хадларни ташлаб юборишимиз ва шу ишларнинг натижасида хосил
этилган
ларга
бођлик булган хамма хадларни ташлаб юборишимиз ва шу ишларнинг натижасида хосил
этилган
![]() (5.4.8)
(5.4.8)
ёки (5.4.7) нинг биринчи тенгламасига асосан
![]() (5.4.9)
(5.4.9)
тенгламани тадкик этишимиз керак. Бу тенглама учун турђунлик масаласи унинг унг тарафидаги функция ёйилмасидаги кичик хади оркали хал булади. Агар бу кичик хаднинг даража курсаткичи ток ва унинг олдидаги коэффициент манфий сон булса, у холда тойилмаган харакат асимптотик турђун булади. Колган хамма холларда тойилмаган харакат нотурђун булади.
Шундай килиб, качон характеристик тенглама битта нол илдизга ва колган илдизларининг хакикий кисми манфий булса, у холда турђунлик масаласини ечиш учун куйидаги алгоритмдан фойдаланиш керак:
1.Тойилган харакат тенгламасини (5.1.6) куринишга келтириш керак.
2.Нокритик
тенгламаларнинг унг тарафини нолга тенглаштириб, хосил этилган (5.4.1)
тенгламаларни ![]() ларга нисбатан
ечиш керак.
ларга нисбатан
ечиш керак.
3.Критик
тенглама унг тарафидаги функция ифодасидаги ![]() ларни топилган
ларни топилган ![]() нинг
функцияси
нинг
функцияси ![]() билан алмаштириш
керак.
билан алмаштириш
керак.
4.Уриналмаштириш натижасида:
а)
агар ![]() булса, у холда хосил
этилган
булса, у холда хосил
этилган
![]()
тенглама учун турђунлик масаласини ечамиз.
Бунинг
учун унинг унг тарафидаги функция ёйилмасининг энг кичик даражали хадини курамиз.
Бу хад ![]() булсин. Агар
булсин. Агар ![]() -
ток сон ва
-
ток сон ва ![]() булса, у холда
тойилмаган харакат асимптотик турђун булади. Колган барча холларда тойилмаган харакат
нотурђун булади.
булса, у холда
тойилмаган харакат асимптотик турђун булади. Колган барча холларда тойилмаган харакат
нотурђун булади.
б)
![]() булса, у холда
махсус холга дуч келамиз. Бу масаланинг ечимини кейинги параграфлардан берамиз.
булса, у холда
махсус холга дуч келамиз. Бу масаланинг ечимини кейинги параграфлардан берамиз.
5-§. Мисоллар
Биз
кураётган критик холда турђунлик масаласини ечиш учун олдинги параграфда баён
этилган алгоритмнинг 2-бандига асосан (5.4.1) тенгламаларни ![]() ларга
нисбатан ечиш керак. Бу ечимни топиш учун уни ушбу
ларга
нисбатан ечиш керак. Бу ечимни топиш учун уни ушбу
![]() (5.5.1)
(5.5.1)
катор
сифатида излаймиз, каерда ![]() - аникланмаган
коэффициентлар. Бу коэффициентларни аниклаш учун (5.5.1) каторни (5.4.1) га куямиз
ва бир хил даражали
- аникланмаган
коэффициентлар. Бу коэффициентларни аниклаш учун (5.5.1) каторни (5.4.1) га куямиз
ва бир хил даражали ![]() узгарувчилар
олдидаги коэффициентларни нолга тенглаштирамиз. Биринчи даражали
узгарувчилар
олдидаги коэффициентларни нолга тенглаштирамиз. Биринчи даражали ![]() олдидаги
коэффициентни нолга тенглаштириб, ушбу тенгламалар
олдидаги
коэффициентни нолга тенглаштириб, ушбу тенгламалар
![]() (5.5.2)
(5.5.2)
системасини
хосил киламиз. Бу системадан ![]() коэффициентлар топилади.
коэффициентлар топилади.
Бу
тенгламалар чизикли, нолдан фарк килувчи детерминантга эга ва шунинг учун хам
битта ва факат битта ечимга эга. Худди шундай, ![]() узгарувчилар
олдидаги коэффициентларни нолга тенглаштириб,
узгарувчилар
олдидаги коэффициентларни нолга тенглаштириб, ![]() коэффициентларни
топиш учун куйидаги тенгламалар системасини хосил киламиз:
коэффициентларни
топиш учун куйидаги тенгламалар системасини хосил киламиз:
![]() ,
(5.5.3)
,
(5.5.3)
бу
ерда ![]() ларга нисбатан кандайдир
купхад.
ларга нисбатан кандайдир
купхад.
(5.5.3)
тенгламалар ![]() коэффициентларни
кетма-кет топишга имкон беради.
коэффициентларни
кетма-кет топишга имкон беради.
![]() коэффициентларни
аниклаб булгандан кейин,
коэффициентларни
аниклаб булгандан кейин, ![]() функциянинг
функциянинг ![]() узгарувчилари
урнига (5.5.1) каторни куйиш лозим.
узгарувчилари
урнига (5.5.1) каторни куйиш лозим. ![]() нинг ёйилмасидаги
нинг ёйилмасидаги ![]() га
нисбатан энг кичик даражали хади турђунлик масаласини хал килади. Бизни катордаги
факат энг кичик даражали хад кизиктиргани учун умумий холда хисоблашлар утказаётганда
амалий нуктаи назардан (5.5.1) катордаги факатгина
га
нисбатан энг кичик даражали хади турђунлик масаласини хал килади. Бизни катордаги
факат энг кичик даражали хад кизиктиргани учун умумий холда хисоблашлар утказаётганда
амалий нуктаи назардан (5.5.1) катордаги факатгина ![]() хадни
аниклаш кифоядир, чунки ушбу хад
хадни
аниклаш кифоядир, чунки ушбу хад ![]() функциянинг ёйилмасидаги
энг кичик даражали хадни аниклайди. Агар (5.5.1) каторни
функциянинг ёйилмасидаги
энг кичик даражали хадни аниклайди. Агар (5.5.1) каторни ![]() функция
ифодасига куйганимизда,
функция
ифодасига куйганимизда, ![]() ва
ва ![]() функцияларнинг
коэффициентлари орасидаги кандайдир муносабатларга асосан энг кичик даражали хад
нолга тенг булиб колса, у холда (5.5.1) катордаги
функцияларнинг
коэффициентлари орасидаги кандайдир муносабатларга асосан энг кичик даражали хад
нолга тенг булиб колса, у холда (5.5.1) катордаги ![]() хадни ва айрим вактларда
юкори даражали хадларни хам хисобга олишга туђри келади.
хадни ва айрим вактларда
юкори даражали хадларни хам хисобга олишга туђри келади.
Шуни
хам таъкидлаб утамизки, агар (5.5.2) тенгламалардаги барча ![]() булса, у
холда
булса, у
холда ![]() ва, демак,
ва, демак, ![]() нинг
ёйилмаси камида иккинчи даражали хадлардан бошланади. Умуман, агар барча
нинг
ёйилмаси камида иккинчи даражали хадлардан бошланади. Умуман, агар барча ![]() функциялар
ифодасида
функциялар
ифодасида ![]() - даражалигича хадлар
йук ва бу функциялардан бирортасининг ифодасида
- даражалигича хадлар
йук ва бу функциялардан бирортасининг ифодасида ![]() - тартибли хад катнашса,
у холда (5.5.1) ёйилма
- тартибли хад катнашса,
у холда (5.5.1) ёйилма ![]() - тартибли хаддан
бошланади.
- тартибли хаддан
бошланади.
Бу изохлардан кейин бир нечта мисолларни курайлик.
1-мисол. Тойилган харакат тенгламалари куйидаги куринишга келтирилган булсин
 (5.5.4)
(5.5.4)
бу
ерда ![]() - айрим узгармас
сонлар. (5.5.4) системанинг биринчи якинлашиш тенгламалари
- айрим узгармас
сонлар. (5.5.4) системанинг биринчи якинлашиш тенгламалари
 (5.5.5)
(5.5.5)
куринишга эга. (5.5.5) нинг характеристик тенгламасини тузамиз:

ёки
![]() .
.
Бу тенглама ушбу илдизларга эга:
![]() ,
,
ва, демак, бу ерда критик холга дуч келдик.
(5.5.5) тенгламаларнинг биринчи интеграли
![]() .
.
(5.5.4)
тенгламалардаги ![]() узгарувчи урнига
янги
узгарувчи урнига
янги ![]() узгарувчини
узгарувчини
![]()
муносабат оркали киритиб, уни куйидаги махсус куринишга келтирамиз ((5.1.6) га каранг):
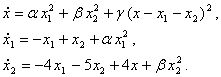 (5.5.6)
(5.5.6)
Энди
![]() ва
ва ![]() узгарувчиларга
нисбатан ечилиши лозим булган куйидаги алгебраик тенгламалар системасини
тузамиз ((5.4.1) га каранг):
узгарувчиларга
нисбатан ечилиши лозим булган куйидаги алгебраик тенгламалар системасини
тузамиз ((5.4.1) га каранг):
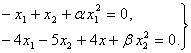 (5.5.7)
(5.5.7)
Биринчи тенгламадан
![]() (5.5.8)
(5.5.8)
ни топиб, иккинчи тенгламага келтириб куямиз
![]() . (5.5.9)
. (5.5.9)
Бу тенгламанинг ечимини ушбу катор сифатида излаймиз ((5.4.2) га каранг):
![]() (5.5.10)
(5.5.10)
Бу
каторни (5.5.9) даги ![]() урнига куйиб ва
урнига куйиб ва ![]() нинг
даражалари олдидаги коэффициентларни нолга тенглаштиргандан сунг, куйидаги тенгламаларга
келамиз:
нинг
даражалари олдидаги коэффициентларни нолга тенглаштиргандан сунг, куйидаги тенгламаларга
келамиз:

Бу тенгламалардан кетма-кет барча коэффициентларни топамиз:
 (5.5.11)
(5.5.11)
(5.5.11)
ни (5.5.10) га куйиб аввал ![]() ни ва кейин
ни ва кейин ![]() ни
(5.5.8) га куйиб
ни
(5.5.8) га куйиб ![]() ни топамиз
ни топамиз

Энди
топилган ![]() ва
ва ![]() ларнинг
ифодаларини
ларнинг
ифодаларини
![]()
функцияга келтириб куйсак, куйидаги ифодани хосил киламиз:

Бу ифодани олдинги параграфда баён этилган назария асосида тадкик этсак, куйидаги натижаларга эришамиз:
а)
Агар ![]() булса, у холда
тойилмаган харакат ((5.5.6) нинг мувозанат холати) нотурђун булади.
булса, у холда
тойилмаган харакат ((5.5.6) нинг мувозанат холати) нотурђун булади.
б)
Агар ![]() булса, у холда
булса, у холда
![]()
муносабат учун тойилмаган харакат нотурђун,
![]()
тенгсизлик бажарилганда эса асимптотик турђун булади.
в) Хакикий коэффициентлар учун
![]()
тенглик бажарилмайди.
2-мисол. Ляпунов тавсия этган мисолни куриб утайлик [34]
Тойилган харакат дифференциал тенгламалари куйидаги куринишда берилган булсин:
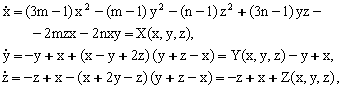 (5.5.12)
(5.5.12)
бу
ерда ![]() ва
ва ![]() -
айрим узгармас сонлар.
-
айрим узгармас сонлар.
Бу тенгламалар системаси (5.1.6) махсус куринишга эга ва унинг биринчи якинлашиш тенгламаларининг характеристик тенгламаси
![]()
илдизларига эга.
Олдинги
параграфда баён этилган назарияга асосан (5.5.12) системанинг иккинчи ва учинчи
тенгламаларини нолга тенглаштириб, улардан ![]() ва
ва ![]() ларни
ларни
![]() нинг функцияси
сифатида топиш керак:
нинг функцияси
сифатида топиш керак:
![]() (5.5.13)
(5.5.13)
Бунинг учун (5.5.13) системадаги тенгламаларни кушиб ва айириб
![]()
ларни
хосил киламиз. Энди ![]() янги узгарувчиларни
янги узгарувчиларни
![]() (5.5.14)
(5.5.14)
муносабат оркали киритиб, сунгги тенгламаларни
![]() (5.5.15)
(5.5.15)
соддарок
куринишга келтирамиз. (5.5.15) дан ![]() ни чикариб ташлаб,
ни чикариб ташлаб,
![]() га нисбатан учинчи
даражали (кубик) тенгламага келамиз
га нисбатан учинчи
даражали (кубик) тенгламага келамиз
![]() .
.
Бу
тенгламанинг чап тарафи ![]() да нолга айланади
ва унинг ечимини
да нолга айланади
ва унинг ечимини
![]()
катор
куринишида излаймиз. ![]() коэффициентларни
топиб,
коэффициентларни
топиб,
![]()
га келамиз. Бу ифодани (5.5.15) системанинг иккинчи тенгламасига куйиб,
![]()
ни
аниклаймиз. ![]() ва
ва ![]() ларнинг
ифодасини (5.5.14) га куйиб,
ларнинг
ифодасини (5.5.14) га куйиб, ![]() ва
ва ![]() ларни
топамиз:
ларни
топамиз:
![]()
![]() ва
ва
![]() ларнинг бу
ифодаларини (5.5.12) системанинг унг тарафидаги
ларнинг бу
ифодаларини (5.5.12) системанинг унг тарафидаги ![]() функциянинг
функциянинг ![]() ва
ва
![]() узгарувчилари урнига
куйиб, куйидаги каторни хосил киламиз:
узгарувчилари урнига
куйиб, куйидаги каторни хосил киламиз:
![]() (5.5.16)
(5.5.16)
![]() функциянинг
ифодасини тадкик килиб куйидаги натижаларга эришамиз:
функциянинг
ифодасини тадкик килиб куйидаги натижаларга эришамиз:
а) Агар ![]() булса, у холда
тойилмаган харакат нотурђун булади.
булса, у холда
тойилмаган харакат нотурђун булади.
б) Агар ![]() булса, у холда
булса, у холда ![]() куйидаги
куринишга келади:
куйидаги
куринишга келади:
![]()
Бу
ердан: агар ![]() (демак,
(демак, ![]() )
булса, тойилмаган харакатнинг нотурђун,
)
булса, тойилмаган харакатнинг нотурђун, ![]() булганда эса
асимптотик турђун булиши келиб чикади.
булганда эса
асимптотик турђун булиши келиб чикади.
в)
![]() да,
да, ![]() булади,
яъни махсус холга келамиз. Бу холни келгуси параграфларда куриб утамиз.
булади,
яъни махсус холга келамиз. Бу холни келгуси параграфларда куриб утамиз.
3-мисол. Тойилган харакат тенгламалари
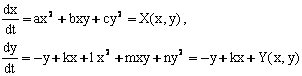
куринишда
булсин, каерда ![]() - узгармас сонлар
[52].
- узгармас сонлар
[52].
Ушбу
![]()
тенгламани тузиб, унинг ечимини
![]()
катор
сифатида излаймиз. Бу каторни ![]() нинг ифодасига куйиб,
нинг ифодасига куйиб,
![]()
ни хосил киламиз, бу ерда
![]()
Тойилмаган харакат турђун булиши учун
![]() (5.5.16)
(5.5.16)
булиши зарурдир.
Бу
шарт бажарилган деб фараз киламиз. У вактда ![]() коэффициентни карашга
туђри келади. Бунинг учун
коэффициентни карашга
туђри келади. Бунинг учун ![]() ни хисоблаш керак:
ни хисоблаш керак:
![]() .
(5.5.17)
.
(5.5.17)
Бу ерда икки хол булиши мумкин.
а)
![]() , у холда агар
, у холда агар ![]() булса,
тойилмаган харакат
булса,
тойилмаган харакат ![]() да нотурђун булади.
Агар
да нотурђун булади.
Агар ![]() булса, у холда
булса, у холда ![]() коэффициентни
куришга туђри келади. Бу холда
коэффициентни
куришга туђри келади. Бу холда ![]() булса, тойилмаган харакат
нотурђун булади. Агар
булса, тойилмаган харакат
нотурђун булади. Агар ![]() булса, у холда
булса, у холда ![]() ва
ва
![]() , демак,
, демак, ![]() булади
ва биз махсус холга дуч келамиз.
булади
ва биз махсус холга дуч келамиз.
б)
Энди ![]() булсин. У вактда
(5.5.17) га асосан (А) тенглама
булсин. У вактда
(5.5.17) га асосан (А) тенглама ![]() ечимга эга булади.
Бу ечим (5.5.16) га асосан
ечимга эга булади.
Бу ечим (5.5.16) га асосан ![]() функцияни айнан
нолга айлантиради, яъни
функцияни айнан
нолга айлантиради, яъни ![]() . Демак, яна махсус
холга келамиз.
. Демак, яна махсус
холга келамиз.
4-мисол. Куйидаги дифференциал тенгламалар
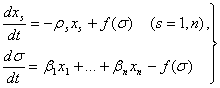 (5.5.18)
(5.5.18)
билан
ифодаланган ростланадиган (созланадиган) системанинг турђунлигини тадкик этайлик.
Бу ерда ![]() ва
ва ![]() -
узгармас сонлар ва
-
узгармас сонлар ва ![]() ,
, ![]() -
кандайдир
-
кандайдир
![]() (5.5.19)
(5.5.19)
шартни каноатлантирувчи узлуксиз функция.
Агар
![]() аналитик функция булса
ва унинг ёйилмаси камида иккинчи даражали хаддан бошланса, у холда (5.5.18)
система тойилмаган харакатининг турђун булиши учун
аналитик функция булса
ва унинг ёйилмаси камида иккинчи даражали хаддан бошланса, у холда (5.5.18)
система тойилмаган харакатининг турђун булиши учун
![]() (В)
(В)
шартнинг бажарилиши зарур эканлигини 1951 йилда А.И.Лурье курсатган [48]. Агар етарли кичик бошланђич тойилишлар учун тойилмаган харакатнинг турђунлиги талаб этилса, у холда бу шарт етарли хам булади [48].
Хакикатан хам,
![]()
булсин,
бу ерда ![]() . (5.5.19) шартдан
. (5.5.19) шартдан ![]() -ток
сон ва
-ток
сон ва ![]() эканлиги келиб чикади.
Биринчи якинлашиш
эканлиги келиб чикади.
Биринчи якинлашиш
 (5.5.20)
(5.5.20)
системасининг
характеристик тенгламаси ![]() та манфий -
та манфий - ![]()
![]() илдизга
ва битта нол илдизга эга. (5.5.20) система
илдизга
ва битта нол илдизга эга. (5.5.20) система
![]()
биринчи
интегралга эга. Бу интегрални ![]() урнига янги узгарувчи
сифатида кабул килиб, (5.5.18) системани (5.1.6) куринишга келтирамиз:
урнига янги узгарувчи
сифатида кабул килиб, (5.5.18) системани (5.1.6) куринишга келтирамиз:
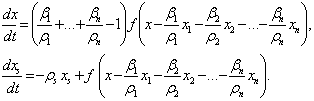 (5.5.21)
(5.5.21)
Бу ерда

Демак,
![]() ва
ва ![]() функцияларнинг
ёйилмаларида
функцияларнинг
ёйилмаларида ![]() нинг энг кичик
даражалари тенг. Шундай килиб,
нинг энг кичик
даражалари тенг. Шундай килиб, ![]() ,
, ![]() ва
ва
![]() шартлар
бажарилаяпти ва 3-§ даги натижалар (5.5.21) система учун хам тааллукли.
шартлар
бажарилаяпти ва 3-§ даги натижалар (5.5.21) система учун хам тааллукли.
Тойилмаган
харакат турђун булиши учун ![]() ёйилмасидаги энг
кичик даражали хаднинг даражаси ток ва коэффициентининг ишораси манфий булиши
керак. Биринчи шарт бажарилаяпти (
ёйилмасидаги энг
кичик даражали хаднинг даражаси ток ва коэффициентининг ишораси манфий булиши
керак. Биринчи шарт бажарилаяпти (![]() - ток сон). Иккинчи
шартнинг бажарилиши учун (В) шарт бажарилиши лозим. Демак, (В) шарт бажарилса,
у холда тойилмаган харакат турђун булади.
- ток сон). Иккинчи
шартнинг бажарилиши учун (В) шарт бажарилиши лозим. Демак, (В) шарт бажарилса,
у холда тойилмаган харакат турђун булади.
6-§. Махсус холда турђунлик масаласини тадкик этиш
Энди махсус холни курамиз. Демак, ![]() функция
ифодасидаги
функция
ифодасидаги ![]() узгарувчилар урнига
узгарувчилар урнига
![]() тенгламаларни каноатлантирувчи
тенгламаларни каноатлантирувчи
![]() функцияни куйганимизда
функцияни куйганимизда
![]() булсин. Бу холда
булсин. Бу холда
 (5.6.1)
(5.6.1)
тенгламалар системасини
![]()
белгилашлар ёрдами билан хосил этилган
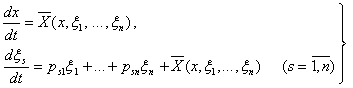 (5.6.2)
(5.6.2)
тенгламалар системасидаги ![]() ва
ва ![]() лар
учун
лар
учун
![]() (5.6.3)
(5.6.3)
булади. Бу муносабатлар бевосита

муносабатлардан келиб чикади.
Аммо, (5.6.2) тенгламалар системаси, (5.6.3) муносабатлар бажарилганда,
![]() (5.6.4)
(5.6.4)
ечимга эга, бу ерда ![]() - ихтиёрий узгармас
сон. Демак, (5.6.1) тенгламалар системаси куйидаги
- ихтиёрий узгармас
сон. Демак, (5.6.1) тенгламалар системаси куйидаги
![]() (5.6.5)
(5.6.5)
ечимга эга. Системанинг тривиал ечими ![]() (5.6.5)
ечимлар оиласининг орасида булади ва у
(5.6.5)
ечимлар оиласининг орасида булади ва у ![]() кийматга мос
келади.
кийматга мос
келади.
Маълумки, курилаётган динамик системанинг тойилмаган баркарор харакати тривиал ечимга мос келади. Худди шундай динамик системанинг бошка баркарор харакатлари (5.6.5) ечимга мос келадилар. Шундай килиб, махсус холда тадкик этилаётган тойилмаган харакат баркарор харакатлар оиласига мансуб булади.
Бу тасдикнинг акси хам туђри, яъни махсус холда баркарор харакат тойилмаган харакат булади (бу тасдикнинг исботи И.Г.Малкин [53] китобининг 109-111 бетларида келтирилган).
Масалан, олдинги бобларда курилган кузђалган нукта
атрофида инерция буйича айланаётган каттик жисм ихтиёрий ![]() параметрга
бођлик булган учта баркарор харакатлар оиласига эга:
параметрга
бођлик булган учта баркарор харакатлар оиласига эга:
![]()
бу ерда ![]() - оний бурчак
тезлиги векторининг бош инерция уклари буйича йуналган координата укларидаги
проекциялари.
- оний бурчак
тезлиги векторининг бош инерция уклари буйича йуналган координата укларидаги
проекциялари.
Шундай килиб, махсус холда тойилмаган харакат
баркарор харакатлар оиласига мансуб булади, бунда ![]() узгарувчиларга
нисбатан бу оила (5.6.5) муносабат билан, ва
узгарувчиларга
нисбатан бу оила (5.6.5) муносабат билан, ва ![]() узгарувчиларга
нисбатан эса, (5.6.4) формулалар билан аникланади.
узгарувчиларга
нисбатан эса, (5.6.4) формулалар билан аникланади.
Махсус холда тойилмаган харакат доимо турђун.
Турђунлик бу холда асимптотик булмайди. Аммо, тойилмаган харакатга етарлича якин
булган хар кандай тойилган харакат ![]() да тойилмаган харакатга
интилмасдан, юкорида курсатилган баркарор харкатлар оиласининг бирорта харакатига
барибир интилади. Бошкача килиб айтганда,
да тойилмаган харакатга
интилмасдан, юкорида курсатилган баркарор харкатлар оиласининг бирорта харакатига
барибир интилади. Бошкача килиб айтганда, ![]() ,
, ![]() бошланђич
кийматлари етарли кичик булган хар кандай
бошланђич
кийматлари етарли кичик булган хар кандай ![]() тойилган харакатлар
учун
тойилган харакатлар
учун
![]()
муносабат уринлидир, бу ерда ![]() - танланган
тойилган харакатга бођлик булган узгармас сон.
- танланган
тойилган харакатга бођлик булган узгармас сон.
Тойилмаган харакатнинг худди шундай хусусиятига тойилмаган харакатга етарлича якин булган оиланинг барча баркарор харакатлари хам эга булади.
Келтирилган мулохаза Ляпуновнинг умумий теоремасининг хусусий холи хисобланади. Бу теоремани И.Г.Малкин 1938 йилда умумлаштирган ва унинг бошкача исботини берган. Биз бу ерда уша теоремани келтирамиз.
Тойилган харакат дифференциал тенгламалари куйидаги куринишда булсин:
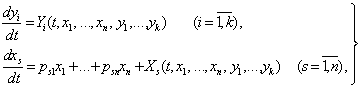 (5.6.6)
(5.6.6)
бу ерда ![]() - барча
- барча ![]() да
чегараланган функция,
да
чегараланган функция, ![]() га бођлик булган
координата боши атрофида
га бођлик булган
координата боши атрофида ![]() узгарувчиларнинг
аналитик функциялари, шу узгарувчилар буйича ёйилмаси камида иккинчи даражали хаддан
бошланади. Бу ерда яна
узгарувчиларнинг
аналитик функциялари, шу узгарувчилар буйича ёйилмаси камида иккинчи даражали хаддан
бошланади. Бу ерда яна
![]()
муносабат уринли, яъни факатгина ![]() да
да ![]() ва
ва
![]() функциялар нолга
айланадилар.
функциялар нолга
айланадилар.
![]() коэффициентлар
шундайки,
коэффициентлар
шундайки,
 (5.6.7)
(5.6.7)
тенглама факат хакикий кисми манфий булган илдизларга эга.
(5.6.6) тенгламалар системасининг куйидаги хусусий ечими мавжуд
![]()
![]() .
(5.6.8)
.
(5.6.8)
Бу ечим ![]() га ихтиёрий
га ихтиёрий ![]() узгармас
сон (параметр)ларга бођлик ва тадкик этилаётган тойилмаган харакатни уз ичига
олган баркарор харакатлар оиласини аниклайди. Агар
узгармас
сон (параметр)ларга бођлик ва тадкик этилаётган тойилмаган харакатни уз ичига
олган баркарор харакатлар оиласини аниклайди. Агар ![]() ва
ва ![]() лар
лар
![]() га бођлик булмаса
ва
га бођлик булмаса
ва ![]() булса, у холда
(5.6.6) система махсус холда (5.6.2) системага айланади.
булса, у холда
(5.6.6) система махсус холда (5.6.2) системага айланади.
Теорема. Агар тойилган харакатнинг дифференциал тенгламалар системаси (5.6.6) куринишга эга булса, у холда тойилмаган харакат турђун булади. Бу ерда тойилмаган харакатга етарлича якин хар кандай тойилган харакат вактнинг чегараланмай усиши билан (5.6.8) оиланинг бирорта баркарор харакатига интилади.
Агар ![]() параметрларнинг кийматлари
етарлича кичик булса, у холда (5.6.8) оиладаги барча баркарор харакатлар шу
хусусиятга эгадир.
параметрларнинг кийматлари
етарлича кичик булса, у холда (5.6.8) оиладаги барча баркарор харакатлар шу
хусусиятга эгадир.
Теореманинг исботи И.Г.Малкин [53] китобининг 114-118 бетларида келтирилган.
Келгуси параграфда биз иккинчи критик холни, яъни характеристик тенглама жуфт соф мавхум илдизга эга булган холни тадкик этамиз.
7-§. Жуфт соф мавхум илдизлар холи. Тойилган харакат тенгламаларини махсус куринишга келтириш
Куйидаги ![]() - тартибли
тенгламалар системасини куриб утамиз:
- тартибли
тенгламалар системасини куриб утамиз:
![]() , (5.7.1)
, (5.7.1)
бу ерда хар бир ![]() узгарувчиларга
нисбатан координата бошининг бирор атрофида аналитик функция,
узгарувчиларга
нисбатан координата бошининг бирор атрофида аналитик функция, ![]() ларнинг
даражалари буйича ёйилмаси эса камида иккинчи тартибли хаддан бошланади.
Биринчи якинлашиш
ларнинг
даражалари буйича ёйилмаси эса камида иккинчи тартибли хаддан бошланади.
Биринчи якинлашиш
![]() (5.7.2)
(5.7.2)
системасининг характеристик тенгламаси
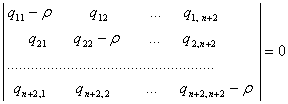 (5.7.3)
(5.7.3)
жуфт соф мавхум ![]() илдизга ва
илдизга ва ![]() та
хакикий кисми манфий булган илдизларга эга булсин.
та
хакикий кисми манфий булган илдизларга эга булсин.
Куйидаги

алмаштиришлар воситасида иккита кандайдир ![]() узгарувчилар
урнига янги
узгарувчилар
урнига янги ![]() ва
ва ![]() узгарувчиларни
киритамиз, бу ерда
узгарувчиларни
киритамиз, бу ерда ![]() ва
ва ![]() -
узгармас сонлар. Бу узгармас сонларни шундай танлаб оламизки, (5.7.2)
системанинг иккита тенгламаси
-
узгармас сонлар. Бу узгармас сонларни шундай танлаб оламизки, (5.7.2)
системанинг иккита тенгламаси
![]()
куринишга келсин. Демак, биз

муносабатларга эга булишимиз керак. Бу муносабатларнинг
икки тарафидаги бир хил даражали ![]() лар олдидаги
коэффициентларни тенглаштириб,
лар олдидаги
коэффициентларни тенглаштириб, ![]() ва
ва ![]() ларга
нисбатан
ларга
нисбатан ![]() та чизикли бир
жинсли тенгламалар системасини хосил киламиз:
та чизикли бир
жинсли тенгламалар системасини хосил киламиз:
 (5.7.4)
(5.7.4)
Агар ![]() ва
ва ![]() номаълумлар
урнига
номаълумлар
урнига ![]() комплекс
номаълумларни киритсак, у холда
комплекс
номаълумларни киритсак, у холда ![]() та тенгламали
системага келамиз. Хакикатан хам, (5.7.4) даги иккинчи гурух тенгламаларни
та тенгламали
системага келамиз. Хакикатан хам, (5.7.4) даги иккинчи гурух тенгламаларни ![]() га
купайтириб мос равишда биринчи гурух тенгламаларига кушсак,
га
купайтириб мос равишда биринчи гурух тенгламаларига кушсак, ![]() та бир
жинсли чизикли тенгламалар системасига келамиз:
та бир
жинсли чизикли тенгламалар системасига келамиз:
![]()
Шартга асосан (5.7.3) тенглама ![]() илдизга
эгалигидан хосил этилган системанинг
илдизга
эгалигидан хосил этилган системанинг ![]() детерминанти нолга
тенг булади. Демак, бу система
детерминанти нолга
тенг булади. Демак, бу система ![]() ларга нисбатан
нотривиал ечимга эга. Бу ечимларни хакикий ва мавхум кисмларини ажратиб,
(5.7.4) системанинг ечимини хосил киламиз.
ларга нисбатан
нотривиал ечимга эга. Бу ечимларни хакикий ва мавхум кисмларини ажратиб,
(5.7.4) системанинг ечимини хосил киламиз.
Шундай килиб, топилган ![]() ва
ва ![]() ларни
ларни
![]() ларнинг иккитаси
сифатида кабул килиб, колганларини
ларнинг иккитаси
сифатида кабул килиб, колганларини ![]() билан белгиласак,
(5.7.2) система куйидаги куринишга келади:
билан белгиласак,
(5.7.2) система куйидаги куринишга келади:
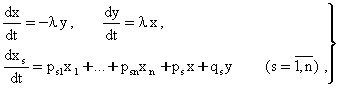
бу
ерда ![]() - кандайдир узгармас
сонлар. Агар айтилган алмаштиришларни (5.7.1) га нисбатан кулласак, улар куйидаги
куринишга келади:
- кандайдир узгармас
сонлар. Агар айтилган алмаштиришларни (5.7.1) га нисбатан кулласак, улар куйидаги
куринишга келади:
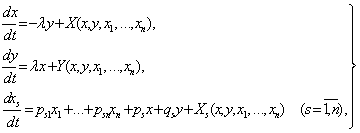 (5.7.6)
(5.7.6)
бу
ерда ![]() - худди
- худди ![]() ларга
ухшаш функциялар.
ларга
ухшаш функциялар.
Хосил этилган тенгламалар системаси курилаётган холни келгусида тадкик этиш учун асос булиб хизмат килади.
Хар
кандай чизикли системанинг характеристик тенгламаси чизикли алмаштиришлар
натижасида узгармайди. Шунинг учун хам (5.7.6) нинг биринчи якинлашиш тенгламалари
системасининг характеристик тенгламаси (5.7.3) характеристик тенглама билан мос
келиши керак. Аммо (5.7.6) система чизикли кисмининг характеристик тенгламаси ![]() илдизларни
берувчи
илдизларни
берувчи ![]() ва
ва
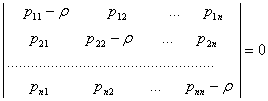 (5.7.7)
(5.7.7)
тенгламаларга ажралади. Демак, (5.7.7) тенгламанинг барча илдизларининг хакикий кисми манфий булади.
Биз
курилаётган иккинчи критик холни дастлаб ![]() хол учун куриб утамиз.
хол учун куриб утамиз.
8-§. Иккинчи тартибли система. Масалани ечишнинг биринчи усули
![]() булганда
тойилган харакат дифференциал тенгламалари иккинчи тартибли системадан иборат булади:
булганда
тойилган харакат дифференциал тенгламалари иккинчи тартибли системадан иборат булади:
![]() (5.8.1)
(5.8.1)
бу
ерда ![]() ва
ва ![]() ларнинг
ёйилмаси камида иккинчи даражали хаддан бошланади.
ларнинг
ёйилмаси камида иккинчи даражали хаддан бошланади.
(5.8.1) куринишдаги тенгламалар системаси билан аникланадиган интеграл эгри чизикларнинг хусусиятларини биринчи булиб франциялик олим А.Пуанкаре урганган [79]. Унинг тадкикотларига таяниб, тойилмаган харакатнинг нафакат характерини текшириш, балки координата боши атрофида (5.8.1) тенгламаларнинг интеграл эгри чизиклари «хулкининг» умумий тасвирини хам бериш мумкин.
Шу максад учун ушбу алмаштиришлар
![]() (5.8.2)
(5.8.2)
оркали
![]() ва
ва ![]() кутб
координаталарини киритамиз.
кутб
координаталарини киритамиз.
(5.8.2) муносабатлардан
![]() (5.8.3)
(5.8.3)
тенгламалар келиб чикади.
(5.8.3)
тенгламаларни ![]() буйича дифференциаллаб,
буйича дифференциаллаб,
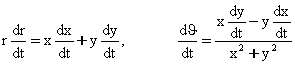
ни хосил киламиз. Бу ердан (5.8.1) системага асосан
![]()
ёки
![]() ва
ва ![]() ларни
(5.8.2) ифодалари билан алмаштирсак, куйидаги тенгламалар хосил булади:
ларни
(5.8.2) ифодалари билан алмаштирсак, куйидаги тенгламалар хосил булади:
 (5.8.4)
(5.8.4)
бу
ерда ![]() ва
ва ![]() ларнинг
функциялари, улар етарли кичик
ларнинг
функциялари, улар етарли кичик ![]() лар учун
лар учун ![]() нинг
даражалари буйича якинлашувчи каторга ёйилади хамда
нинг
даражалари буйича якинлашувчи каторга ёйилади хамда
![]() .
.
Бу
каторларнинг коэффициентлари даври ![]() га тенг булган
га тенг булган ![]() нинг
даврий функцияларидан иборат. Уларнинг хар бири
нинг
даврий функцияларидан иборат. Уларнинг хар бири ![]() ва
ва ![]() ларга
нисбатан оддий купхаддир. Шунинг учун хам уларни косинус ва синусларнинг чекли
йиђиндиси деб караш мумкин.
ларга
нисбатан оддий купхаддир. Шунинг учун хам уларни косинус ва синусларнинг чекли
йиђиндиси деб караш мумкин.
Интеграл
эгри чизикларнинг тенгламасини хосил этиш учун (5.8.4) дан ![]() вактни
чикариб ташлаб, куйидагини хосил киламиз:
вактни
чикариб ташлаб, куйидагини хосил киламиз:
![]() , (5.8.5)
, (5.8.5)
бу
ерда ![]() ва
ва ![]() ларга
нисбатан купхад.
ларга
нисбатан купхад.
(5.8.5)
тенгламанинг унг тарафида турган катор ![]() нинг етарлича
кичик кийматларида якинлашувчи булади.
нинг етарлича
кичик кийматларида якинлашувчи булади.
(5.8.5)
тенгламанинг ![]() тривиал ечими
мавжуд. Демак, интеграл эгри чизикларнинг биттасига координата боши мос келади.
(5.8.5) тенгламанинг унг тарафи координата боши атрофида аналитик булгани учун
бу атрофнинг хар бир нуктасидан (дифференциал тенгламалар ечимининг мавжудлиги
ва ягоналиги хакидаги теоремага асосан) битта ва факат битта интеграл эгри чизик
утади. Бу ердан координата боши атрофидаги бирор нуктадан чикаётган исталган
интеграл эгри чизик координата бошини хеч качон кесмаслиги келиб чикади.
тривиал ечими
мавжуд. Демак, интеграл эгри чизикларнинг биттасига координата боши мос келади.
(5.8.5) тенгламанинг унг тарафи координата боши атрофида аналитик булгани учун
бу атрофнинг хар бир нуктасидан (дифференциал тенгламалар ечимининг мавжудлиги
ва ягоналиги хакидаги теоремага асосан) битта ва факат битта интеграл эгри чизик
утади. Бу ердан координата боши атрофидаги бирор нуктадан чикаётган исталган
интеграл эгри чизик координата бошини хеч качон кесмаслиги келиб чикади.
(5.8.5) тенгламанинг унг тарафи аналитик эканлигидан яна бу тенгламанинг
![]() (5.8.6)
(5.8.6)
бошланђич
шарт билан аникланадиган унинг хар кандай ![]() ечими
ечими ![]() параметрнинг
даражалари буйича каторга ёйилиши келиб чикади:
параметрнинг
даражалари буйича каторга ёйилиши келиб чикади:
![]() (5.8.7)
(5.8.7)
Агар
![]() етарлича кичик булса,
(5.8.7) катор якинлашувчи булади. Бу каторнинг якинлашиш радиуси
етарлича кичик булса,
(5.8.7) катор якинлашувчи булади. Бу каторнинг якинлашиш радиуси ![]() нинг
узгариш интервалига бођлик. Аммо, бу интервал хар канча катта булмасин, шундай
етарли кичик
нинг
узгариш интервалига бођлик. Аммо, бу интервал хар канча катта булмасин, шундай
етарли кичик ![]() сони топиладики,
барча
сони топиладики,
барча ![]() лар учун (5.8.7) катор
якинлашувчи булади. Биз
лар учун (5.8.7) катор
якинлашувчи булади. Биз ![]() сонини шунчалик
кичик деб хисоблаймизки,
сонини шунчалик
кичик деб хисоблаймизки, ![]() лар учун (5.8.7) катор
якинлашувчи булсин.
лар учун (5.8.7) катор
якинлашувчи булсин.
![]() коэффициентларни
топиш учун (5.8.7) каторни (5.8.5) тенгламанинг икки тарафига хам куямиз ва бир
хил даражали
коэффициентларни
топиш учун (5.8.7) каторни (5.8.5) тенгламанинг икки тарафига хам куямиз ва бир
хил даражали ![]() лар олдидаги
коэффициентларни тенглаштирамиз. (5.8.7) ни (5.8.5) га куйганимиздан кейин
унинг унг тарафида хосил буладиган каторнинг
лар олдидаги
коэффициентларни тенглаштирамиз. (5.8.7) ни (5.8.5) га куйганимиздан кейин
унинг унг тарафида хосил буладиган каторнинг ![]() даражалари
олдидаги коэффициентларни
даражалари
олдидаги коэффициентларни ![]() билан белгиласак, куйидаги
тенгликка келамиз:
билан белгиласак, куйидаги
тенгликка келамиз:
![]() (5.8.8)
(5.8.8)
Бу ерда ![]() лар
лар ![]()
![]() лар
буйича купхадлар булиб, коэффициентлари
лар
буйича купхадлар булиб, коэффициентлари ![]() ларга бођлик ва
ларга бођлик ва ![]() аргументнинг
аргументнинг
![]() даврли функциялари
(
даврли функциялари
(![]() ва
ва ![]() ларга
нисбатан купхадлар)дир. Хусусан,
ларга
нисбатан купхадлар)дир. Хусусан,
![]() .
.
![]() функцияларни аникловчи
тенгламалар куйидаги куринишда буладилар:
функцияларни аникловчи
тенгламалар куйидаги куринишда буладилар:
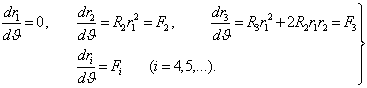 (5.8.9)
(5.8.9)
Бундан ташкари, (5.8.6) дан куйидаги бошланђич шартларни хосил киламиз
![]() (5.8.10)
(5.8.10)
Демак,
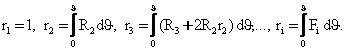 (5.8.11)
(5.8.11)
Шундай килиб, оддий квадратурада кетма-кет барча ![]() функциялар
аникланадилар.
функциялар
аникланадилар. ![]() функция учун биз
даврий функциянинг квадратурасига эга буламиз. Бундай квадратураларнинг
келгусида биз доимо фойдаланадиган битта умумий хусусиятини курсатиб утамиз.
функция учун биз
даврий функциянинг квадратурасига эга буламиз. Бундай квадратураларнинг
келгусида биз доимо фойдаланадиган битта умумий хусусиятини курсатиб утамиз.
![]() кандайдир узлуксиз
кандайдир узлуксиз
![]() даврли даврий функция
булсин, у холда
даврли даврий функция
булсин, у холда
 , (5.8.12)
, (5.8.12)
ифодаланиш
уринли, бу ерда ![]() -
- ![]() даврли
даврий функция,
даврли
даврий функция, ![]() эса куйидагича аникланадиган
эса куйидагича аникланадиган
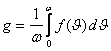 (5.8.13)
(5.8.13)
узгармас сон.
Агар
![]() куйидаги
куйидаги
![]() ,
,
Фурье
каторига ёйилса у холда ![]() нинг (5.8.13)
формула билан аникланиши равшан булиб колади. Хакикатан хам,
нинг (5.8.13)
формула билан аникланиши равшан булиб колади. Хакикатан хам,
бу холда куйидагига эгамиз:
![]() .
.
Бу ердан курилаётган хол учун (5.8.12) формуланинг туђрилиги янада аён булади.
Энди
![]() коэффициентни курайлик.
коэффициентни курайлик.
![]() даврий функция
эканлиги учун
даврий функция
эканлиги учун ![]() ёки (5.8.12) куринишда
булади, ёки даврий (агар
ёки (5.8.12) куринишда
булади, ёки даврий (агар ![]() булса) функция булади.
Иккинчи холда
булса) функция булади.
Иккинчи холда ![]() функция даврий булади
ва шунинг учун хам
функция даврий булади
ва шунинг учун хам ![]() ёки (5.8.12) куринишга
эга, ёки даврий функция булади. Шу тарзда давом эттирсак, биз икки хол мавжуд
эканлигига икрор буламиз: 1)
ёки (5.8.12) куринишга
эга, ёки даврий функция булади. Шу тарзда давом эттирсак, биз икки хол мавжуд
эканлигига икрор буламиз: 1) ![]() индекс хар канча
катта булмасин, барча
индекс хар канча
катта булмасин, барча ![]() коэффициентлар
коэффициентлар ![]() даврли
даврий функциялар булади, 2) ёки бу коэффициентлар орасида даврий эмас функциялар
мавжуд. Агар
даврли
даврий функциялар булади, 2) ёки бу коэффициентлар орасида даврий эмас функциялар
мавжуд. Агар ![]() биринчи давриймас
коэффициентлар булса, у холда
биринчи давриймас
коэффициентлар булса, у холда
 (5.8.14)
(5.8.14)
уринли,
бу ерда ![]() даврли даврий
функция.
даврли даврий
функция.
 |
5.1-шакл.
а)
Барча ![]() функциялар даврий.
Бу холда
функциялар даврий.
Бу холда ![]() нинг каторнинг якинлашиши
сохасидаги битта кийматларида (5.8.7) ечим даврий ва, демак,
нинг каторнинг якинлашиши
сохасидаги битта кийматларида (5.8.7) ечим даврий ва, демак, ![]() ва
координата бошининг етарлича кичик атрофида барча интеграл эгри чизиклар ёпик хамда
бу нуктани камраб оладилар (5.1-шакл). Пуанкаре бундай координата бошини
(мувозанат холатини) марказ (центр) деб атади ва илмий адабиётда шу атама кабул
килинган.
ва
координата бошининг етарлича кичик атрофида барча интеграл эгри чизиклар ёпик хамда
бу нуктани камраб оладилар (5.1-шакл). Пуанкаре бундай координата бошини
(мувозанат холатини) марказ (центр) деб атади ва илмий адабиётда шу атама кабул
килинган.
б)
![]() коэффициентлар
орасида даврий эмаслари хам мавжуд. Шундай коэффициентлардан биринчиси
коэффициентлар
орасида даврий эмаслари хам мавжуд. Шундай коэффициентлардан биринчиси ![]() булсин,
у холда
булсин,
у холда ![]() учун (5.8.14)
формула уринли булади, бу ерда
учун (5.8.14)
формула уринли булади, бу ерда ![]() ва барча
ва барча ![]() коэффициентлар
даврийдир.
коэффициентлар
даврийдир.
Ушбу
 (5.8.15)
(5.8.15)
алмаштириш воситасида (5.8.5) тенгламани узгартирамиз. (5.8.8) муносабатга асосан куйидагини хосил киламиз:
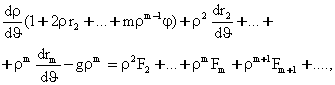
ёки (5.8.9) ни хисобга олиб,
![]()
га эга буламиз.
Бу ердан
![]() (5.8.16)
(5.8.16)
ни
хосил киламиз. (5.8.15) алмаштиришнинг коэффициентлари даврий булганлиги учун ![]() лар
лар
![]() нинг
нинг ![]() даврли
функцияларидир.
даврли
функцияларидир.
(5.8.16)
тенгламадан ![]() хосила координата
бошининг етарли кичик атрофида
хосила координата
бошининг етарли кичик атрофида ![]() нинг ишорасига мос
булган (узгармас) ишорани саклашлиги келиб чикади. Агар
нинг ишорасига мос
булган (узгармас) ишорани саклашлиги келиб чикади. Агар ![]() булса, у
холда
булса, у
холда ![]() да
да ![]() функция
узлуксиз камайиб, нолга интилади. (5.8.15) алмаштиришларга асосан
функция
узлуксиз камайиб, нолга интилади. (5.8.15) алмаштиришларга асосан ![]() радиус-вектор
хам худди шундай хусусиятга эга булади. Демак, координата бошининг етарлича
кичик атрофида жойлашган барча интеграл эгри чизиклар спираллардан иборат. Улар
координата боши атрофида чексиз куп марта айланиб, логарифмик спирал сингари
асимптотик равишда унга якинлашади. Пуанкаре бундай координата бошини фокус деб
атаган ва биз хам бундан кейин шундай деб атаймиз (5.2-шакл).
радиус-вектор
хам худди шундай хусусиятга эга булади. Демак, координата бошининг етарлича
кичик атрофида жойлашган барча интеграл эгри чизиклар спираллардан иборат. Улар
координата боши атрофида чексиз куп марта айланиб, логарифмик спирал сингари
асимптотик равишда унга якинлашади. Пуанкаре бундай координата бошини фокус деб
атаган ва биз хам бундан кейин шундай деб атаймиз (5.2-шакл).

![]()
5.2-шакл.
![]() булганда
хам интеграл эгри чизикларнинг хулки худди юкорида баён этилгандай булади. Факат
бу холда
булганда
хам интеграл эгри чизикларнинг хулки худди юкорида баён этилгандай булади. Факат
бу холда ![]() да спираллар
координата бошидан узлуксиз равишда узоклашади.
да спираллар
координата бошидан узлуксиз равишда узоклашади.
Энди
турђунлик масаласини курайлик. Марказ холида бошланђич пайтда етарли кичик булган
![]() ва у билан бирга
ва у билан бирга ![]() ва
ва
![]() лар доимо етарлича
кичиклигини саклаганликлари учун тойилмаган харакат турђун булсада, асимптотик
турђунмас.
лар доимо етарлича
кичиклигини саклаганликлари учун тойилмаган харакат турђун булсада, асимптотик
турђунмас.
Координата
боши фокус булган холни курайлик. (5.8.4) системанинг иккинчи тенгламаси курсатадики,
координата бошининг етарли кичик атрофида ![]() нинг киймати (
нинг киймати (![]() ва
ва ![]() ) модул буйича
) модул буйича ![]() дан
кичик булса,
дан
кичик булса, ![]() хосила бирор
мусбат сондан катта булади. Демак,
хосила бирор
мусбат сондан катта булади. Демак, ![]() нинг усиши билан
нинг усиши билан ![]() нинг
киймати хам усади ва агар интеграл эгри чизик координата бошининг етарлича
кичик атрофида колса,
нинг
киймати хам усади ва агар интеграл эгри чизик координата бошининг етарлича
кичик атрофида колса, ![]() да
да ![]() хам
чексиз чегараланмаган холда усади. Охирги хол айнан
хам
чексиз чегараланмаган холда усади. Охирги хол айнан ![]() булганда
юз беради. Бу холда
булганда
юз беради. Бу холда ![]() нинг усиши билан
интеграл эгри чизиклар координата бошига якинлашадилар ва
нинг усиши билан
интеграл эгри чизиклар координата бошига якинлашадилар ва ![]() да унга
асимптотик равишда интиладилар. Демак,
да унга
асимптотик равишда интиладилар. Демак, ![]() булганда,
тойилмаган харакат асимптотик турђун булади (5.2-шаклга каранг).
булганда,
тойилмаган харакат асимптотик турђун булади (5.2-шаклга каранг).
![]() булганда,
интеграл эгри чизиклар
булганда,
интеграл эгри чизиклар ![]() нинг усиши ва,
демак,
нинг усиши ва,
демак, ![]() нинг хам усиши
билан координата бошидан узоклашади. Барча интеграл эгри чизиклар бошланђич шартларга
бођлик булмаган холда координата бошининг атрофини (бошланђич вактда уша ерда булганлигига
карамасдан) ташлаб кетадилар. Бу ердан тойилмаган харакатнинг нотурђунлиги
келиб чикади.
нинг хам усиши
билан координата бошидан узоклашади. Барча интеграл эгри чизиклар бошланђич шартларга
бођлик булмаган холда координата бошининг атрофини (бошланђич вактда уша ерда булганлигига
карамасдан) ташлаб кетадилар. Бу ердан тойилмаган харакатнинг нотурђунлиги
келиб чикади.
Демак,
марказ булган холда тойилмаган харакат турђун, аммо асимптотик турђун эмас.
Фокус холида, ![]() булса, тойилмаган харакат
асимптотик турђун,
булса, тойилмаган харакат
асимптотик турђун, ![]() булганда эса
нотурђун булади.
булганда эса
нотурђун булади.
Шундай килиб, бизни кизиктираётган холда турђунлик масаласини ечиш учун куйидаги алгоритмдан фойдаланиш керак:
1. (5.8.1) тенгламалар системасини (5.8.2)
алмаштиришлар ва ![]() вактни чикариб битта (5.8.5) тенгламага келтирамиз.
вактни чикариб битта (5.8.5) тенгламага келтирамиз.
2. (5.8.5) тенгламанинг
![]()
ечимини
катор куринишида излаймиз, бу ерда ![]() . Бу каторни (5.8.5) га куйиб ва чап ва унг тарафдаги
бир хил даражали
. Бу каторни (5.8.5) га куйиб ва чап ва унг тарафдаги
бир хил даражали ![]() ларнинг коэффициентларини тенглаштириб,
ларнинг коэффициентларини тенглаштириб, ![]() функцияларни кетма-кет квадратурада аниклашга имкон
берадиган тенгламаларни хосил киламиз. Бу ерда барча
функцияларни кетма-кет квадратурада аниклашга имкон
берадиган тенгламаларни хосил киламиз. Бу ерда барча ![]() лар ёки даврий функциялар, ёки
лар ёки даврий функциялар, ёки ![]() орасида
даврий эмас функциялар хам мавжуд булиши мумкин.
орасида
даврий эмас функциялар хам мавжуд булиши мумкин.
Биринчи холда тойилмаган харакат турђун булади, аммо асимптотик турђун эмас.
Иккинчи
холда  лар орасида
биринчи даврий эмас коэффициент
лар орасида
биринчи даврий эмас коэффициент  булса, у албатта
(5.8.14) формулалар оркали аникланади. Агар
булса, у албатта
(5.8.14) формулалар оркали аникланади. Агар 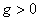 булса, тойилмаган харакат
нотурђун,
булса, тойилмаган харакат
нотурђун, 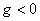 булганда эса – асимптотик
турђун булади.
булганда эса – асимптотик
турђун булади.
Мисол. Тойилган харакатнинг дифференциал тенгламалари
![]() (5.8.17)
(5.8.17)
куринишда
булсин. Бу ерда ![]() - узгармас сонлар.
- узгармас сонлар.
(5.8.17) тенгламани
![]() (5.8.18)
(5.8.18)
тенгламалар системасига келтириб,
![]()
алмаштиришларни киритамиз. У вактда бу тенгламалар
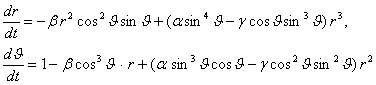
куринишга
келадилар. Бу тенгламалардан ![]() ни чикариб,
ни чикариб,
![]()
ни хосил киламиз. Бу тенгламанинг ечимини
![]()
катор
сифатида излаймиз, бу ерда ![]() . Бир хил даражали
. Бир хил даражали ![]() олдидаги коэффициентларни тенглаштириб,
олдидаги коэффициентларни тенглаштириб,
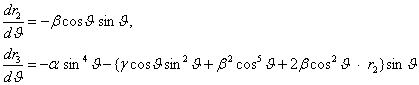
тенгламаларни хосил киламиз. Бу ердан
 ,
,
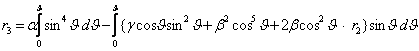 ва
ва ![]() даврий,
даврий,
![]() эса даврий
эмаслиги келиб чикади.
эса даврий
эмаслиги келиб чикади.
![]() функция
функция
![]()
формула оркали аникланади, бу ерда
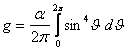 ,
,
ва ![]() - даврий
функция.
- даврий
функция.
Демак,
![]() булганда,
тойилмаган харакат нотурђун,
булганда,
тойилмаган харакат нотурђун, ![]() булганда эса – асимптотик
турђун булади.
булганда эса – асимптотик
турђун булади.
9-§. Иккинчи тартибли система. Ляпунов функциясини тузиш усули билан масалани ечиш
Ляпунов томонидан тавсия этилган усул билан масалани ечишни курсатамиз. Бу усул (5.8.1) тенгламалар системаси учун Ляпунов функциясини тузишга асосланади.
Дастлаб
куйидаги масалани курамиз. ![]() ва
ва ![]() узгарувчиларга
нисбатан берилган
узгарувчиларга
нисбатан берилган ![]() - тартибли форма булсин.
(5.8.1) системанинг биринчи якинлашиш
- тартибли форма булсин.
(5.8.1) системанинг биринчи якинлашиш
![]() (5.9.1)
(5.9.1)
тенгламаларига
кура вакт буйича олинган тулик хосиласи ![]() формага тенг булган
формага тенг булган
![]() формани излаймиз.
Бошкача килиб айтганда,
формани излаймиз.
Бошкача килиб айтганда,
![]() (5.9.2)
(5.9.2)
тенгламани
каноатлантирувчи ![]() формани топиш
керак. Бу масала 4-бобнинг 2-§идаги 2-теореманинг хусусий холи булади. Уша ерда
олинган натижаларга кура
формани топиш
керак. Бу масала 4-бобнинг 2-§идаги 2-теореманинг хусусий холи булади. Уша ерда
олинган натижаларга кура

формаларни
(5.9.2) га куйиб ва ухшаш хадлар олдидаги коэффициентларни тенглаштириб, ![]() ларни
топиш учун куйидаги чизикли тенгламаларни хосил киламиз:
ларни
топиш учун куйидаги чизикли тенгламаларни хосил киламиз:
![]() (5.9.3)
(5.9.3)
бу
ерда ![]() - айрим узгармас
сонлар.
- айрим узгармас
сонлар.
Бу системанинг детерминанти нолга тенг булмаса, у ягона ечимга эга. Демак, (5.9.3) система ягона ечимга эга булиши учун
 (5.9.4)
(5.9.4)
тенглама нолга тенг булган илдизга эга булмаслиги керак.
Аммо, 4-бобнинг 2-§даги 1-теоремасига асосан (5.9.4) тенгламанинг барча илдизлари
![]() (5.9.5)
(5.9.5)
формула
билан аникланади. Бу ерда ![]() ва
ва ![]() лар
лар
![]() (5.9.6)
(5.9.6)
муносабат билан бођланган хар кандай манфиймас бутун сонлар.
Агар
![]() - ток сон булса, у
холда (5.9.5) ни нолга айлантирадиган (5.9.6) муносабат билан бођланган
- ток сон булса, у
холда (5.9.5) ни нолга айлантирадиган (5.9.6) муносабат билан бођланган ![]() ва
ва
![]() ларнинг хеч кандай
жуфтлиги мавжуд эмас. Демак,
ларнинг хеч кандай
жуфтлиги мавжуд эмас. Демак, ![]() - ток сон булганда,
(5.9.4) детерминант нолдан фарк килади ва (5.9.3) система (5.9.2) тенгламани каноатлантирувчи
битта ва факат битта
- ток сон булганда,
(5.9.4) детерминант нолдан фарк килади ва (5.9.3) система (5.9.2) тенгламани каноатлантирувчи
битта ва факат битта ![]() формани аниклаб
берувчи ягона ечимга эга.
формани аниклаб
берувчи ягона ечимга эга.
Энди
![]() - жуфт сон булсин
деб фараз киламиз. Бу холда
- жуфт сон булсин
деб фараз киламиз. Бу холда ![]() булади ва (5.9.6)
ни каноатлантиради.
булади ва (5.9.6)
ни каноатлантиради.
Факатгина
ана шу жуфтлик комбинацияда (5.9.5) ифода нолга айланади. Демак, бу холда
(5.9.4) тенглама нолга тенг илдизга эга ва (5.9.3) системанинг детерминанти
нолга тенг булади. Аммо, бу детерминантнинг ![]() - тартибли бирорта
хам минори нолга тенг эмас. Хакикатан хам, барча
- тартибли бирорта
хам минори нолга тенг эмас. Хакикатан хам, барча ![]() - тартибли
минорлар нолга тенг булганда, (5.9.4) тенгламанинг нолга тенг илдизи хеч булмаганда
икки каррали буларди, чунки у нафакат
- тартибли
минорлар нолга тенг булганда, (5.9.4) тенгламанинг нолга тенг илдизи хеч булмаганда
икки каррали буларди, чунки у нафакат ![]() ни, балки
ни, балки ![]() ни
хам нолга айлантирган буларди.
ни
хам нолга айлантирган буларди.
(5.9.3)
системанинг детерминанти нолга тенг булгани учун бу система, умуман айтганда,
ечилмовчидир. Бу холда (5.9.3) тенгламанинг чап тарафидаги хадлар узаро чизикли
бођланган булади, яъни шундай бирортаси нолдан фарк килувчи ![]() сонлар
мавжудки, (5.9.3) системанинг чап тарафидаги хадларни бу сонларга купайтириб сунгра
кушсак, биз айнан нолни хосил киламиз. (5.9.3) система ечилувчи булиши учун
унинг унг тарафидаги хадлар хам шу чизикли бођланишда булиши зарур, яъни куйидаги
айният бажарилиши лозим
сонлар
мавжудки, (5.9.3) системанинг чап тарафидаги хадларни бу сонларга купайтириб сунгра
кушсак, биз айнан нолни хосил киламиз. (5.9.3) система ечилувчи булиши учун
унинг унг тарафидаги хадлар хам шу чизикли бођланишда булиши зарур, яъни куйидаги
айният бажарилиши лозим
![]() . (5.9.7)
. (5.9.7)
Бу шарт (5.9.3) системанинг ечилувчи булиши учун
етарли хамдир, чунки ![]() детерминантнинг
нолга тенг булмаган
детерминантнинг
нолга тенг булмаган ![]() - тартибли минорлари
хам мавжуд ва шунинг учун хам бу системанинг чап тарафи факат битта чизикли
муносабат билан бођланган.
- тартибли минорлари
хам мавжуд ва шунинг учун хам бу системанинг чап тарафи факат битта чизикли
муносабат билан бођланган.
Шундай килиб, ![]() - жуфт сон булганда,
(5.9.2) тенгламани каноатлантирувчи
- жуфт сон булганда,
(5.9.2) тенгламани каноатлантирувчи ![]() форма факат
форма факат ![]() форманинг
коэффициентлари (5.9.7) муносабат билан бођланган булсагина мавжуддир.
форманинг
коэффициентлари (5.9.7) муносабат билан бођланган булсагина мавжуддир.
Шунинг учун хам ![]() - жуфт сон булган хол
учун масаланинг куйилишини сал узгартирамиз.
- жуфт сон булган хол
учун масаланинг куйилишини сал узгартирамиз.
Энди (5.9.2) тенгламани эмас, балки
![]() (5.9.8)
(5.9.8)
тенгламани
каноатлантирувчи ![]() формани излаймиз.
Бу ерда
формани излаймиз.
Бу ерда ![]() - бирор узгармас
сон. Уни шундай танлаб оламизки, (5.9.8) тенглама ечимга эга булсин.
- бирор узгармас
сон. Уни шундай танлаб оламизки, (5.9.8) тенглама ечимга эга булсин.
Энди (5.9.3) система ушбу
![]()
системага
айланади, бу ерда ![]() -
- ![]() форманинг
коэффициентлари. Системанинг ечилувчи булишининг шарти
форманинг
коэффициентлари. Системанинг ечилувчи булишининг шарти
![]() (5.9.9)
(5.9.9)
куринишга келади.
![]() узгармас
сон (5.9.9) тенгламадан бир кийматли равишда аникланади. Уни топиш учун (5.9.9)
тенгламани тузиш шарт эмас, уни (5.9.8) тенгламадан фойдаланиб, топиш мумкин.
Бунинг учун
узгармас
сон (5.9.9) тенгламадан бир кийматли равишда аникланади. Уни топиш учун (5.9.9)
тенгламани тузиш шарт эмас, уни (5.9.8) тенгламадан фойдаланиб, топиш мумкин.
Бунинг учун ![]() ва
ва ![]() форма
аникланган деб хисоблаймиз. Уларни (5.9.8) га куйиб, хар кандай
форма
аникланган деб хисоблаймиз. Уларни (5.9.8) га куйиб, хар кандай ![]() ва
ва
![]() ларнинг кийматларини
каноатлантирувчи, айниятга келамиз. Хусусан,
ларнинг кийматларини
каноатлантирувчи, айниятга келамиз. Хусусан, ![]() кийматларда хам у
айният булади. (5.9.8) га
кийматларда хам у
айният булади. (5.9.8) га ![]() ларни куйиб, хосил
булган айниятни
ларни куйиб, хосил
булган айниятни ![]() га купайтириб, 0
дан
га купайтириб, 0
дан ![]() оралиђида интеграллаймиз.
У холда
оралиђида интеграллаймиз.
У холда

ва, демак,
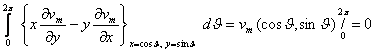
![]()
ларни хисобга олиб, куйидагини хосил киламиз
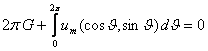 . (5.9.10)
. (5.9.10)
Шундай
килиб, узгармас сон ![]() билан
билан ![]() форма коэффициентлари уртасидаги муносабатни топдик.
Агар (5.9.8) тенглама ечимга эга булса, у холда бу муносабатнинг бажарилиши
зарур булади. Исбот килинганга кура бундай муносабат битта булади ва, демак, у
(5.9.9) муносабат билан бир хил булади.
форма коэффициентлари уртасидаги муносабатни топдик.
Агар (5.9.8) тенглама ечимга эга булса, у холда бу муносабатнинг бажарилиши
зарур булади. Исбот килинганга кура бундай муносабат битта булади ва, демак, у
(5.9.9) муносабат билан бир хил булади.
(5.9.10)
формула ![]() узгармас
сонни бирданига топишга имконият беради.
узгармас
сонни бирданига топишга имконият беради.
Энди куйилган масалани хал килишга утамиз. Тойилган харакат дифференциал тенгламаларини куйидаги куринишда ёзамиз:
 (5.9.11)
(5.9.11)
бу
ерда ![]() ва
ва ![]() функциялардаги
функциялардаги ![]() - тартибли хадлар мажмуаси. Бу система учун теорема Б
ёки теорема В ни каноатлантирувчи Ляпунов функциясини тузамиз. Бу функция
- тартибли хадлар мажмуаси. Бу система учун теорема Б
ёки теорема В ни каноатлантирувчи Ляпунов функциясини тузамиз. Бу функция
![]() (5.9.12)
(5.9.12)
куринишда
булсин, бу ерда ![]() - бирон-бир
- бирон-бир ![]() - тартибли форма
- тартибли форма ![]() .
.
![]() формаларни шундай танлаб оламизки,
формаларни шундай танлаб оламизки, ![]() нинг (5.9.11) тенгламаларга кура вакт буйича олинган
тулик хосиласи
нинг (5.9.11) тенгламаларга кура вакт буйича олинган
тулик хосиласи
 (5.9.13)
(5.9.13)
аник ишорали функция булсин.
(5.9.13) тенгламанинг унг тарафидаги ифода 3-тартибли хадлардан бошланади. Бу хадлар куйидагилардан иборат:
 (5.9.14)
(5.9.14)
бу
ерда ![]() формаларга бођлик булган
формаларга бођлик булган ![]() - тартибли форма. Демак, агарда
- тартибли форма. Демак, агарда ![]() формаларни кайсидир шартлардан аниклай олсак, у холда
формаларни кайсидир шартлардан аниклай олсак, у холда
![]() форма хам аник булади.
форма хам аник булади.
Маълумки,
![]() функция аник ишорали булиши учун унинг ёйилмаси жуфт
тартибли хаддан бошланиши зарур. Шунинг учун хам
функция аник ишорали булиши учун унинг ёйилмаси жуфт
тартибли хаддан бошланиши зарур. Шунинг учун хам ![]() формани шундай танлаб олиш керакки, (5.9.14)да учинчи
тартибли хадлар нолга айлансин, яъни
формани шундай танлаб олиш керакки, (5.9.14)да учинчи
тартибли хадлар нолга айлансин, яъни
![]()
муносабат бажарилсин. Шундай ![]() формани
танлаб олгандан кейин,
формани
танлаб олгандан кейин, ![]() формани энди
шундай танлаймизки,
формани энди
шундай танлаймизки, ![]() ифодасидаги
ифодасидаги ![]() туртинчи
тартибли хадлар мажмуаси аник ишорали форма булсин, яъни бу хадлар мажмуасини
аник ишорали
туртинчи
тартибли хадлар мажмуаси аник ишорали форма булсин, яъни бу хадлар мажмуасини
аник ишорали ![]() формага
тенглаштирамиз
формага
тенглаштирамиз
![]()
![]() ,
,
бу ерда ![]() .
.
Биз хозир (5.9.8) турдаги тенгламани каноатлантирувчи
жуфт тартибли форма хакида гап юритаяпмиз. Бу форма мавжуд булиши учун ![]() аникланган
сон булиши керак. Бу сонни (5.9.10) га
асосан куйидагича
аникланган
сон булиши керак. Бу сонни (5.9.10) га
асосан куйидагича
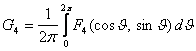
топамиз.
Шундай килиб топилган ![]() микдор
нолга тенг булмасин.
микдор
нолга тенг булмасин.
У холда
![]()
функциянинг тулик хосиласи
![]()
юкори
тартибли хадлар аник ишорали функция булади. Бу функция билан ![]() нинг ишораси бир хил,
нинг ишораси бир хил, ![]() функциянинг узи эса, аник мусбат ишорали булади.
Шунинг учун хам, Б ва В теоремаларга асосан, тойилмаган харакат
функциянинг узи эса, аник мусбат ишорали булади.
Шунинг учун хам, Б ва В теоремаларга асосан, тойилмаган харакат ![]() булганда нотурђун ва
булганда нотурђун ва ![]() булганда асимптотик турђун булади.
булганда асимптотик турђун булади.
Аммо,
![]() микдор нолга тенг булиши хам мумкин. Бу холда (5.9.13)
ифоданинг ёйилмаси 5-тартибли хаддан бошланади.
микдор нолга тенг булиши хам мумкин. Бу холда (5.9.13)
ифоданинг ёйилмаси 5-тартибли хаддан бошланади. ![]() функция аник ишорали булиши учун бу хадларни нолга
айлантириш керак. Бунинг учун
функция аник ишорали булиши учун бу хадларни нолга
айлантириш керак. Бунинг учун ![]() формани шундай танлаб олиш керакки,
формани шундай танлаб олиш керакки, ![]() булсин.
Бу охирги тенглама (5.9.2) куринишда булади ва ундан
булсин.
Бу охирги тенглама (5.9.2) куринишда булади ва ундан ![]() ни шу усул билан топганимиздан кейин,
ни шу усул билан топганимиздан кейин, ![]() ни шундай танлаймизки,
ни шундай танлаймизки, ![]() нинг ифодасидаги олтинчи тартибли хадлар аник ишорали
нинг ифодасидаги олтинчи тартибли хадлар аник ишорали
![]() формага тенг булсин.
формага тенг булсин.
Шундай
килиб, ![]() ни топиш учун куйидаги тенгламага эга буламиз
ни топиш учун куйидаги тенгламага эга буламиз
![]()
![]() ,
,
бу ерда
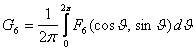 .
.
Агар
![]() булса, у холда
булса, у холда
![]()
функциянинг
тулик хосиласи ![]() юкори тартибли хадлар аник ишорали форма,
юкори тартибли хадлар аник ишорали форма, ![]() функциянинг узи эса, аввалгидай, аник мусбат ишорали
булади. Бу ерда хам тойилмаган харакат
функциянинг узи эса, аввалгидай, аник мусбат ишорали
булади. Бу ерда хам тойилмаган харакат ![]() булганда нотурђун,
булганда нотурђун, ![]() да эса асимптотик турђун булади.
да эса асимптотик турђун булади.
Агар
![]() булса,
булса, ![]() формаларни топишни яна давом эттириш керак. Худди олдин
баён этилган тарзда иш тутиб, яъни (5.9.13) даги ток тартибли хадларни нолга тенглаштириб,
жуфт тартибли хадларни
формаларни топишни яна давом эттириш керак. Худди олдин
баён этилган тарзда иш тутиб, яъни (5.9.13) даги ток тартибли хадларни нолга тенглаштириб,
жуфт тартибли хадларни ![]() формага тенглаштириб ва
формага тенглаштириб ва ![]() ни
ни
 (5.9.15)
(5.9.15)
формула
оркали аниклаб, биз мумкин булган икки холнинг биттасига дуч келамиз: 1) ёки ![]() индекснинг канчалик катта булишидан катъий назар
барча
индекснинг канчалик катта булишидан катъий назар
барча ![]() лар нолга тенг булади, 2) ёки биз охири шундай
лар нолга тенг булади, 2) ёки биз охири шундай ![]() га келамизки,
га келамизки, ![]() булади.
булади.
Агар
иккинчи холга дуч келсак, у холда турђунлик масаласи ![]() нинг ишораси билан хал булади: тойилмаган харакат
нинг ишораси билан хал булади: тойилмаган харакат ![]() булганда нотурђун ва
булганда нотурђун ва ![]() булганда асимптотик турђун булади.
булганда асимптотик турђун булади.
Энди
барча ![]() коэффициентлар нолга тенг булсин деб фараз килайлик.
Албатта, барча коэффициентларни хисоблаб чикиш йули билан бунга ишониш анча
мураккаб масала, бирок кандайдир усул билан буни тасдикласак, у холда турђунлик
масаласи осонгина ечилади. Хакикатан хам, бу холда координата боши марказ булади.
Демак, тойилмаган харакат турђун, аммо асимптотик турђун эмас. (5.9.11)
тенгламаларнинг умумий ечимининг даври бошланђич шартларга бођлик булган даврий
функция булади.
коэффициентлар нолга тенг булсин деб фараз килайлик.
Албатта, барча коэффициентларни хисоблаб чикиш йули билан бунга ишониш анча
мураккаб масала, бирок кандайдир усул билан буни тасдикласак, у холда турђунлик
масаласи осонгина ечилади. Хакикатан хам, бу холда координата боши марказ булади.
Демак, тойилмаган харакат турђун, аммо асимптотик турђун эмас. (5.9.11)
тенгламаларнинг умумий ечимининг даври бошланђич шартларга бођлик булган даврий
функция булади.
Баён
этилган турђунликни тадкик этиш усулини амалда куллаш учун ![]() коэффициентларни ёки (5.9.15) формулалар оркали аниклаш
керак, ёки бевосита бу формулани келтириб чикарадиган усулдан фойдаланиш
мумкин. Бунинг учун
коэффициентларни ёки (5.9.15) формулалар оркали аниклаш
керак, ёки бевосита бу формулани келтириб чикарадиган усулдан фойдаланиш
мумкин. Бунинг учун ![]() нинг ифодасидаги
нинг ифодасидаги ![]() - тартибли хадларни аниклаб, уларни
- тартибли хадларни аниклаб, уларни ![]() га тенглаштириб, хосил булган тенгламаларга
га тенглаштириб, хосил булган тенгламаларга ![]() ларни куйиб, 0 дан
ларни куйиб, 0 дан ![]() оралиђида интеграллаш керак. Бу ерда
оралиђида интеграллаш керак. Бу ерда ![]() форма чикариб ташланади, шунинг учун биз уни
форма чикариб ташланади, шунинг учун биз уни ![]() ифодасидаги
ифодасидаги ![]() - тартибли хадни аниклашда хисобга олмаслигимиз
мумкин.
- тартибли хадни аниклашда хисобга олмаслигимиз
мумкин.
1-мисол. Олдинги параграфда тадкик этилган
![]()
системани курайлик. ![]() функцияни
функцияни
![]()
каби олиб, ![]() формани шундай
танлаймизки,
формани шундай
танлаймизки, ![]() нинг ифодасидаги
учинчи тартибли хадлар нолга тенг булсин. Демак,
нинг ифодасидаги
учинчи тартибли хадлар нолга тенг булсин. Демак,
![]()
тенгламани хосил киламиз. Бу ифодага
![]()
ни куйиб, сунгра ухшаш хадлар олдидаги коэффициентларни тенглаштириб, куйидаги тенгламаларга келамиз:
![]() .
.
Бу ердан
![]()
эга буламиз. ![]() формани аниклаш
учун туртинчи тартибли хадларни
формани аниклаш
учун туртинчи тартибли хадларни ![]() га тенглаштириб, куйидагини
хосил киламиз:
га тенглаштириб, куйидагини
хосил киламиз:
![]() . (5.9.16)
. (5.9.16)
![]() узгармас
сонни аниклаймиз. Агар у нолга тенг булмаса,
узгармас
сонни аниклаймиз. Агар у нолга тенг булмаса, ![]() ни аниклаш керак булмай колади ва барча хисоблашлар
шу билан тамом тугайди. Агар
ни аниклаш керак булмай колади ва барча хисоблашлар
шу билан тамом тугайди. Агар ![]() нолга тенг булса, у холда
нолга тенг булса, у холда ![]() ни хам,
ни хам, ![]() ни хам ва шундай булиши хам мумкинки, навбатдаги юкори
тартибли формаларни хам аниклашга туђри келади.
ни хам ва шундай булиши хам мумкинки, навбатдаги юкори
тартибли формаларни хам аниклашга туђри келади. ![]() ни аниклаш учун (5.9.16) га
ни аниклаш учун (5.9.16) га ![]() ларни куйиб,
ларни куйиб, ![]() буйича 0 дан
буйича 0 дан ![]() оралиђигача интеграллаймиз. Бу амални бажаришда
оралиђигача интеграллаймиз. Бу амални бажаришда ![]() хадларни
хисобга олмаслик мумкин, чунки улар бу амални бажариш жараёнида тушиб коладилар.
Шундай килиб, куйидагини хосил киламиз:
хадларни
хисобга олмаслик мумкин, чунки улар бу амални бажариш жараёнида тушиб коладилар.
Шундай килиб, куйидагини хосил киламиз:
 .
.
Агар
![]() булса, у холда тойилмаган харакат асимптотик турђун,
агар
булса, у холда тойилмаган харакат асимптотик турђун,
агар ![]() булса, у нотурђун булади.
булса, у нотурђун булади.
Агар
![]() булса, у холда олдинги параграфда курсатганимиздай,
координата боши марказ булиб, тойилмаган харакат турђун булади.
булса, у холда олдинги параграфда курсатганимиздай,
координата боши марказ булиб, тойилмаган харакат турђун булади.
10-§. Иккинчи тартибли система. Масалани ечишнинг
учинчи усули
![]() (5.10.1)
(5.10.1)
тенгламалар билан ифодаланган системанинг турђунлик масаласини ечишнинг Ляпунов томонидан курсатилган учинчи усулини куриб утамиз.
8-§
да курсатган эдикки, (5.10.1) система учун координата боши ёки марказ, ёки фокус
булиб, уларнинг кайси бири мавжуд булишини аниклаш турђунлик масаласининг асосий
вазифаси булади. Агар координата боши марказ булса, у холда тойилмаган харакат турђун
булади; агар фокус булса, у холда тойилмаган харакатнинг турђун ёки нотурђун булиши
8-§ да киритилган ![]() узгармас
соннинг ишораси билан аникланади.
узгармас
соннинг ишораси билан аникланади.
Уша
ерда курсатган эдикки, координата боши марказ булган холда ва факат шу холда
(5.10.1) тенгламаларнинг умумий ечими даврий булади. Шундай килиб, турђунлик
масаласини хал килиш учун (5.10.1) тенгламаларнинг умумий ечими даврий буладими
ёки йукми эканлигини аниклашга харакат килишимиз керак. Бу ечим даврий булса,
тойилмаган харакат турђун ва агар даврий булмаса, у холда ![]() узгармас
соннинг ишорасини аниклаш масаласини хал килишимиз керак булади.
узгармас
соннинг ишорасини аниклаш масаласини хал килишимиз керак булади.
Бунинг учун
![]() (5.10.2)
(5.10.2)
бошланђич
шартларни каноатлантирувчи (5.10.1) системанинг ![]() ечимини курамиз, бу ерда
ечимини курамиз, бу ерда ![]() - етарлича кичик ихтиёрий узгармас сон.
- етарлича кичик ихтиёрий узгармас сон.
Агар координата боши марказ булса, у холда бу ечим даврий булиб, унинг даври
![]() (5.10.3)
(5.10.3)
формула
((5.8.20) формулага каранг) билан аникланади. Бу ерда ![]() лар айрим узгармас сонлар ва
лар айрим узгармас сонлар ва ![]() нинг етарли кичик кийматларида (5.10.3) катор якинлашувчидир.
нинг етарли кичик кийматларида (5.10.3) катор якинлашувчидир.
Хакикатан
хам координата боши марказ булсин деб фараз килайлик. Бу холда (5.10.1)
тенгламаларда ![]() узгарувчини
узгарувчини
![]() узгарувчи
билан куйидагига
узгарувчи
билан куйидагига
![]() (5.10.4)
(5.10.4)
алмаштирамиз. Шу йусинда хосил килинган
 (5.10.5)
(5.10.5)
тенгламаларнинг
(5.10.2) бошланђич шартларни каноатлантирувчи ечими даврий ва унинг даври ![]() га тенг булади.
га тенг булади.
(5.10.5)
тенгламаларнинг унг тарафидаги ифодалар ![]() га нисбатан аналитик функциялардир. Шунинг учун хам
бу тенгламаларнинг хар кандай ечими
га нисбатан аналитик функциялардир. Шунинг учун хам
бу тенгламаларнинг хар кандай ечими ![]() га нисбатан аналитик булади. Бундан ташкари хар бир
бундай ечим узининг
га нисбатан аналитик булади. Бундан ташкари хар бир
бундай ечим узининг ![]() бошланђич кийматларига (бизда
бошланђич кийматларига (бизда ![]() ) нисбатан хам аналитик булади. Бу мулохазани курилаётган
даврий ечимга куллаб, у
) нисбатан хам аналитик булади. Бу мулохазани курилаётган
даврий ечимга куллаб, у ![]() га нисбатан аналитик деган хулосага келамиз.
га нисбатан аналитик деган хулосага келамиз.
Демак, бу ечим куйидаги куринишга эга
 (5.10.6)
(5.10.6)
бу
ерда унг тарафдаги каторлар етарли кичик ![]() учун якинлашувчи. Бу ечим даври
учун якинлашувчи. Бу ечим даври ![]() га тенг булган даврий функция булганлиги учун барча
га тенг булган даврий функция булганлиги учун барча ![]() лар хам даври
лар хам даври ![]() га тенг булган даврий функциялар булади. Бундан ташкари,
(5.10.2) бошланђич шартлардан
га тенг булган даврий функциялар булади. Бундан ташкари,
(5.10.2) бошланђич шартлардан
![]() ,
, ![]() (5.10.7)
(5.10.7)
ни хосил киламиз.
Шундай
килиб, агар коррдината боши марказ булса, у холда (5.10.5) тенгламалар (бу ерда
![]() - айрим аникланган узгармас сонлар) (5.10.6) куринишли
- айрим аникланган узгармас сонлар) (5.10.6) куринишли
![]() даврий функцияларга бођлик булган ечимга эга булади.
Агар,
даврий функцияларга бођлик булган ечимга эга булади.
Агар, ![]() узгармас
сонларни кандай килиб олишимиздан катъий назар, (5.10.5) система
узгармас
сонларни кандай килиб олишимиздан катъий назар, (5.10.5) система ![]() даврий функцияларга бођлик булган (5.10.6) даврий
ечимга эга булмаса, у холда бу координата боши фокус эканлигини билдиради.
даврий функцияларга бођлик булган (5.10.6) даврий
ечимга эга булмаса, у холда бу координата боши фокус эканлигини билдиради.
(5.10.6)
ни (5.10.5) га куйиб, ![]() нинг бир хил даражалари олдидаги коэффициентларни
тенглаштириб,
нинг бир хил даражалари олдидаги коэффициентларни
тенглаштириб, ![]() ва
ва ![]() функциялар каноатлантириши керак булган тенгламаларни
хосил киламиз. Шу йул билан биринчи навбатда
функциялар каноатлантириши керак булган тенгламаларни
хосил киламиз. Шу йул билан биринчи навбатда
![]()
система хосил килинади, бу ердан (5.10.7) бошланђич шартларни хисобга олганда,
![]()
ечимга эга буламиз. Сунгра
 (5.10.8)
(5.10.8)
системани
хосил киламиз, бу ерда ![]() ва
ва ![]() функциялар ифодасидаги даражали хадлар мажмуаси.
функциялар ифодасидаги даражали хадлар мажмуаси.
Шунга
ухшаш тенгламаларни ![]() ва
ва ![]()
![]() функциялар учун хам топамиз. Бу тенгламаларнинг унг
тарафидаги функциялар ифодасида
функциялар учун хам топамиз. Бу тенгламаларнинг унг
тарафидаги функциялар ифодасида ![]() узгармас
сонлар катнашади. Биз факат
узгармас
сонлар катнашади. Биз факат ![]() узгармас
сон катнашувчи тенгламалар системасини ёзамиз
узгармас
сон катнашувчи тенгламалар системасини ёзамиз
![]() , (5.10.9)
, (5.10.9)
бу
ерда ![]() ва
ва ![]() -
- ![]() ларга нисбатан купхадлар. Бу купхадларнинг коэффициентлари
факат
ларга нисбатан купхадлар. Бу купхадларнинг коэффициентлари
факат ![]() узгармас
сонларга бођлик.
узгармас
сонларга бођлик.
(5.10.8) тенгламалар куйидаги куринишга келади
![]() , (5.10.10)
, (5.10.10)
бу
ерда ![]() ва
ва ![]() -
- ![]() даврга эга булган
даврга эга булган ![]() нинг даврий функциялари. Бу тенгламаларнинг даврий
ечимларини топиш масаласи юзага келади. Бу биринчи даражали эркинликка эга булган
чизикли системанинг мажбурий тебранишларини аниклаш масаласидир. Биз кураётган холда
резонанс ходисаси мавжуд, чунки эркин тебранишлар даври тойдирувчи кучнинг
даври билан бир хил. Шунинг учун хам (5.10.10) тенгламалар умумий холда даврий
ечимга эга эмас. Улар даврий ечимга эга булишлари учун
нинг даврий функциялари. Бу тенгламаларнинг даврий
ечимларини топиш масаласи юзага келади. Бу биринчи даражали эркинликка эга булган
чизикли системанинг мажбурий тебранишларини аниклаш масаласидир. Биз кураётган холда
резонанс ходисаси мавжуд, чунки эркин тебранишлар даври тойдирувчи кучнинг
даври билан бир хил. Шунинг учун хам (5.10.10) тенгламалар умумий холда даврий
ечимга эга эмас. Улар даврий ечимга эга булишлари учун ![]() ва
ва ![]() функциялар айрим шартларни каноатлантиришлари керак.
функциялар айрим шартларни каноатлантиришлари керак.
![]() ва
ва ![]() функцияларнинг Фурье каторига ёйилмаси куйидаги куринишда
булсин:
функцияларнинг Фурье каторига ёйилмаси куйидаги куринишда
булсин:

бу ерда
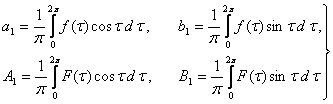 (5.10.11)
(5.10.11)
Изланаётган даврий ечимнинг Фурье каторига ёйилмаси куйидагича булсин:

![]() ва
ва
![]() ларнинг кийматларини
(5.10.10) га куйганимизда,
ларнинг кийматларини
(5.10.10) га куйганимизда, ![]() ларни ва коэффициентларни
аниклашга имкон берадиган куйидаги тенгламаларни топамиз:
ларни ва коэффициентларни
аниклашга имкон берадиган куйидаги тенгламаларни топамиз:
![]()
Бу
тенгламалардан барча ![]() лар учун
лар учун ![]() ларни
топиш мумкин. Агар
ларни
топиш мумкин. Агар ![]() булганда
булганда
![]()
муносабатлар бажарилмаса, у холда бу тенгламалар ечилмовчидир.
Бу муносабатлар бажарилса, у вактда куйидагиларни топамиз
![]()
бу
ерда ![]() ва
ва ![]() -
ихтиёрий узгармас сонлар.
-
ихтиёрий узгармас сонлар.
Шундай килиб, (5.10.11) ни инобатга олган холда, куйидаги хулосага келамиз:
1.(5.10.10) системанинг даврий ечими булиши учун
 (5.10.12)
(5.10.12)
муносабатларнинг бажарилиши етарли ва зарур.
2.Агар бу муносабатлар бажарилса, у холда айтилган даврий ечим куйидаги куринишда булади
![]() (5.10.13)
(5.10.13)
бу
ерда ![]() ва
ва ![]() -
ихтиёрий узгармас сонлар,
-
ихтиёрий узгармас сонлар, ![]() лар -
лар - ![]() даврли
даврий функциялар. Таркибида иккита ихтиёрий узгармас сонлар катнашувчи бу ечим
(5.10.10) системанинг умумий ечими булади.
даврли
даврий функциялар. Таркибида иккита ихтиёрий узгармас сонлар катнашувчи бу ечим
(5.10.10) системанинг умумий ечими булади.
3.Агар
(5.10.12) муносабатлар бажарилмаса, у холда (5.10.10) тенгламалар даврий ечимга
эга эмас. ![]() ва
ва ![]() хадларга
хадларга
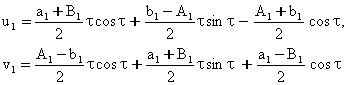
хусусий ечимлар мос келади ва (5.10.10) нинг умумий ечими
 (5.10.14)
(5.10.14)
куринишда
эга, бу ерда ![]() ва
ва ![]() лар
– даврий функциялар,
лар
– даврий функциялар, ![]() ва
ва ![]() лар
эса ихтиёрий узгармас сонлардир.
лар
эса ихтиёрий узгармас сонлардир.
Шундан
сунг, барча ![]() функциялар даврий
ва барча
функциялар даврий
ва барча ![]() узгармас сонлар хам
аникланган деб фараз киламиз. У вактда (5.10.9) тенгламаларнинг
узгармас сонлар хам
аникланган деб фараз киламиз. У вактда (5.10.9) тенгламаларнинг ![]() ва
ва
![]() ларни аникловчи унг
тарафидаги хадлар
ларни аникловчи унг
тарафидаги хадлар ![]() нинг аникланган
даврий функциялари буладилар. Демак, бу тенгламалар (5.10.10) куринишга эга.
Шунинг учун хам
нинг аникланган
даврий функциялари буладилар. Демак, бу тенгламалар (5.10.10) куринишга эга.
Шунинг учун хам ![]() ва
ва ![]() лар
даврий функциялар булиши учун куйидаги
лар
даврий функциялар булиши учун куйидаги
 (5.10.15)
(5.10.15)
муносабатларнинг, (5.10.12) га асосан, бажарилиши етарли ва зарур.
Бу
муносабатларнинг биринчиси ![]() узгармас сонни аниклайди.
Иккинчи муносабат бажарилиши хам, бажарилмаслиги хам мумкин. Агар у
бажарилмаса, (5.10.5) тенгламалар,
узгармас сонни аниклайди.
Иккинчи муносабат бажарилиши хам, бажарилмаслиги хам мумкин. Агар у
бажарилмаса, (5.10.5) тенгламалар, ![]() узгармас сонларни кандай
килиб олишимиздан катъий назар, даврий ечимга эга булмайди. Демак, бу холда
координата боши фокус булади.
узгармас сонларни кандай
килиб олишимиздан катъий назар, даврий ечимга эга булмайди. Демак, бу холда
координата боши фокус булади.
Шундай
килиб, координата боши марказ булиши учун (5.10.15) шартнинг иккинчиси хар кандай
![]() учун бажарилиши
зарурдир.
учун бажарилиши
зарурдир.
Агар
биз кандайдир усул билан иккинчи шартнинг бажарилишини аникласак, у вактда
барча ![]() ,
, ![]() функциялар
даврий булади. Шу билан бирга функцияларнинг барчаси (5.10.13) куринишга эга ва
хар бирининг ифодасига кирувчи иккита ихтиёрий узгармас сонлар бир кийматли
равишда бошланђич
функциялар
даврий булади. Шу билан бирга функцияларнинг барчаси (5.10.13) куринишга эга ва
хар бирининг ифодасига кирувчи иккита ихтиёрий узгармас сонлар бир кийматли
равишда бошланђич ![]() шартлардан аникланади.
Бу холда (5.10.6) каторлар, илгари аниклаганимиздек, якинлашувчи булади ва
(5.10.1) системанинг даврий ечимини ифодалайди. Шу асосда координата боши
марказ ва тойилмаган харакат турђун деган хулосага келамиз.
шартлардан аникланади.
Бу холда (5.10.6) каторлар, илгари аниклаганимиздек, якинлашувчи булади ва
(5.10.1) системанинг даврий ечимини ифодалайди. Шу асосда координата боши
марказ ва тойилмаган харакат турђун деган хулосага келамиз.
Аммо, ![]() ва
ва ![]() функцияларни
аниклаш жараёнида бирор
функцияларни
аниклаш жараёнида бирор ![]() индекс учун (5.10.15)
муносабатларнинг иккинчиси бажарилмайдиган холга келиб колиши мумкин. Бу холда,
олдин айтганимиздек, координата боши фокус булади. Шунинг учун хам турђунлик
масаласини хал килиш учун 8-§ да киритилган
индекс учун (5.10.15)
муносабатларнинг иккинчиси бажарилмайдиган холга келиб колиши мумкин. Бу холда,
олдин айтганимиздек, координата боши фокус булади. Шунинг учун хам турђунлик
масаласини хал килиш учун 8-§ да киритилган ![]() узгармас соннинг
ишорасини аниклаш зарурияти туђилади. Бу узгармас сон ушбу
узгармас соннинг
ишорасини аниклаш зарурияти туђилади. Бу узгармас сон ушбу
 , (5.10.16)
, (5.10.16)
формула
оркали аникланади, бу ерда ![]() ифодасида
ифодасида ![]() олдидаги
коэффициент,
олдидаги
коэффициент, ![]() ифодасида
ифодасида ![]() олдидаги
коэффициент.
олдидаги
коэффициент.
(5.10.16)
формуланинг туђрилигини исбот килайлик. Бунинг учун ![]() нинг
нинг ![]() ёки
шунга тенг булган
ёки
шунга тенг булган ![]() пайтдаги кийматини
курамиз. Биз
пайтдаги кийматини
курамиз. Биз ![]() нинг кийматини аникловчи
(5.10.3) катор
нинг кийматини аникловчи
(5.10.3) катор ![]() - даражали хадда
узилади деб фараз киламиз. (5.10.14) га асосан
- даражали хадда
узилади деб фараз киламиз. (5.10.14) га асосан ![]() ва
ва ![]() лар
учун тенгламаларнинг умумий ечими куйидагича булади
лар
учун тенгламаларнинг умумий ечими куйидагича булади
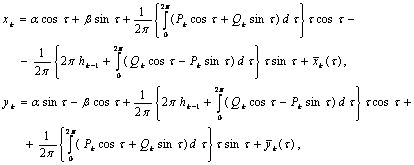
бу
ерда ![]() - даврий
функциялар. Яна давом этиб
- даврий
функциялар. Яна давом этиб ![]() ва
ва ![]() лар
учун (5.10.7) бошланђич шартлардан куйидагини хосил киламиз
лар
учун (5.10.7) бошланђич шартлардан куйидагини хосил киламиз
![]()
ва, демак,
![]() . (5.10.17)
. (5.10.17)
Барча
![]() функциялар даврий
эканлигини, (5.10.7) бошланђич шартларни ва уларга мос булган (5.10.17) ни
эътиборга олиб, (5.10.6) дан куйидагини хосил киламиз
функциялар даврий
эканлигини, (5.10.7) бошланђич шартларни ва уларга мос булган (5.10.17) ни
эътиборга олиб, (5.10.6) дан куйидагини хосил киламиз
 (5.10.18)
(5.10.18)
Шу
микдорнинг узини 8-§ да олинган натижаларга асосан хам топа оламиз. Уша
натижаларга кура ![]() булганда (5.8.7),
(5.8.10) ва (5.8.14) лар асосида
булганда (5.8.7),
(5.8.10) ва (5.8.14) лар асосида ![]() учун ва, демак,
учун ва, демак, ![]() учун
хам куйидагини топамиз
учун
хам куйидагини топамиз
![]() (5.10.19)
(5.10.19)
(5.10.18)
ва (5.10.19) формулаларнинг иккаласида хам ![]() узгармас сон
узгармас сон ![]() ва
ва
![]() нинг
нинг ![]() пайтдаги
кийматини ифодалайди. Бу формулаларни солиштириш курсатадики,
пайтдаги
кийматини ифодалайди. Бу формулаларни солиштириш курсатадики, ![]() ,
чунки
,
чунки ![]() да кутб бурчаги
да кутб бурчаги ![]()
![]() дан
дан
![]() дан кам
дан кам
булган
тартибли микдорга (![]() га нисбатан) фарк килади
ва
га нисбатан) фарк килади
ва ![]() хакикатан хам
(5.10.16) формула оркали аникланади.
хакикатан хам
(5.10.16) формула оркали аникланади.
Одатдагидек
турђунлик масаласи ![]() нинг ишораси билан
ечилади.
нинг ишораси билан
ечилади. ![]() булганда,
тойилмаган харакат нотурђун ва
булганда,
тойилмаган харакат нотурђун ва ![]() булганда, асимптотик
турђун булади.
булганда, асимптотик
турђун булади.
Шундай килиб, турђунлик масаласини ечиш учун биз куйидаги алгоритмдан фойдаланишимиз лозим:
1.(5.10.4) алмаштиришлар оркали (5.10.1) тенгламалар системасини (5.10.5) куринишига келтирамиз ва унинг ечимини
 (5.10.20)
(5.10.20)
куринишда
излаймиз. Бу ерда ![]() - ихтиёрий узгармас
сон,
- ихтиёрий узгармас
сон, ![]() лар булса –
(5.10.7) бошланђич шартларни каноатлантирувчи
лар булса –
(5.10.7) бошланђич шартларни каноатлантирувчи ![]() даврли
даврли ![]() нинг
даврий функциялари.
нинг
даврий функциялари.
2.
![]() ва
ва ![]() функцияларни
топиш учун (5.10.9) тенгламаларни хосил киламиз. Агар (5.10.15) муносабатлар бажарилса,
у холда (5.10.9) тенгламаларнинг ечими даврий булади. Бу муносабатларнинг
биринчиси
функцияларни
топиш учун (5.10.9) тенгламаларни хосил киламиз. Агар (5.10.15) муносабатлар бажарилса,
у холда (5.10.9) тенгламаларнинг ечими даврий булади. Бу муносабатларнинг
биринчиси ![]() узгармас сонни бир
кийматли равишда топишга имкон яратади, иккинчи муносабат булса, бажарилиши хам
мумкин, бажарилмаслиги хам мумкин. Биринчи холда (5.10.9) тенгламаларнинг
бошланђич шартлар билан аникланадиган даврий ечими мавжуд. Агар бу даврий ечим
узгармас сонни бир
кийматли равишда топишга имкон яратади, иккинчи муносабат булса, бажарилиши хам
мумкин, бажарилмаслиги хам мумкин. Биринчи холда (5.10.9) тенгламаларнинг
бошланђич шартлар билан аникланадиган даврий ечими мавжуд. Агар бу даврий ечим ![]() индекснинг
исталганча катта барча кийматлари учун мавжуд булса, у холда тойилмаган харакат
турђун, (5.10.20) ва (5.10.3) каторлар якинлашувчи булади хамда улар мос
равишда даврий ечимни ва (5.10.1) тенгламаларнинг даврини ифода этадилар.
индекснинг
исталганча катта барча кийматлари учун мавжуд булса, у холда тойилмаган харакат
турђун, (5.10.20) ва (5.10.3) каторлар якинлашувчи булади хамда улар мос
равишда даврий ечимни ва (5.10.1) тенгламаларнинг даврини ифода этадилар.
3.Агар ![]() ,
, ![]() ларни
хисоблаш жараёнида биз шундай
ларни
хисоблаш жараёнида биз шундай ![]() индексга дуч
келсакки, унинг учун (5.10.15) муносабатларнинг иккинчиси бажарилмаса, у холда
тойилмаган харакат
индексга дуч
келсакки, унинг учун (5.10.15) муносабатларнинг иккинчиси бажарилмаса, у холда
тойилмаган харакат ![]() булганда
нотурђун,
булганда
нотурђун, ![]() булганда эса
асимптотик турђун булади. Узгармас сон
булганда эса
асимптотик турђун булади. Узгармас сон ![]() (5.10.16) формула
оркали аникланади.
(5.10.16) формула
оркали аникланади.
Келтирилган алгоритм (5.10.1) тенгламалар системасининг даврий ечимини (агар у мавжуд булса) ва унинг даврини топишнинг энг кулай усулини беради.
Ечимларнинг узлари булса амалда кулланиш учун энг кулай шаклда (формада) ифодаланадилар. Бу ечимлар чизиклимас тебранишлар назариясида мухим ахамиятга эга.
Охирида шуни таъкидлаймизки, узгармас сон 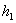 доимо нолга тенг булади.
Бу бевосита (5.10.15) ва (5.10.8) лардан келиб чикади. Исбот килиш мумкинки,
умуман биринчи нолга тенг булмаган
доимо нолга тенг булади.
Бу бевосита (5.10.15) ва (5.10.8) лардан келиб чикади. Исбот килиш мумкинки,
умуман биринчи нолга тенг булмаган  узгармас
сонларнинг индекси жуфт булади.
узгармас
сонларнинг индекси жуфт булади.
1-мисол. Олдинги параграфда тадкик этилган
![]()
системани яна караймиз. Бу ерда
![]()
алмаштиришни бажариб, куйидагини хосил киламиз

Системанинг
ечимини (5.10.20) куринишда излаймиз. Уни системага куйиб, чап ва унг тарафдаги
бир хил даражали ![]() лар олдидаги
коэффициентларни тенглаштириб,
лар олдидаги
коэффициентларни тенглаштириб, ![]() ва
ва ![]() ларни
аникловчи куйидаги тенгламаларга келамиз:
ларни
аникловчи куйидаги тенгламаларга келамиз:

![]() ва
ва
![]() ларни аникловчи
тенгламалар резонанс берувчи гармоникаларга эга эмас ва шунинг учун хам
ларни аникловчи
тенгламалар резонанс берувчи гармоникаларга эга эмас ва шунинг учун хам ![]() ва
ва
![]() даврий функциялар
булади.
даврий функциялар
булади. ![]() ва
ва ![]() функциялар
эса даврий булмайди, чунки (5.10.16) га асосан узгармас сон
функциялар
эса даврий булмайди, чунки (5.10.16) га асосан узгармас сон ![]() куйидаги
куйидаги
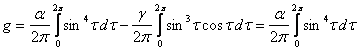
куринишга
эга ва у нолга тенг эмас. Турунлик масаласини ![]() нинг ишораси хал килади:
нинг ишораси хал килади:
![]() булганда тойилмаган
харакат нотурђун,
булганда тойилмаган
харакат нотурђун, ![]() да эса, асимптотик
турђун булади.
да эса, асимптотик
турђун булади.
2-мисол. Математик маятникнинг куйи мувозанат холати атрофидаги тебранма харакатининг дифференциал тенгламаси
![]() (5.10.21)
(5.10.21)
куринишига
эга, бу ерда ![]() .
.
Бу тенгламанинг куйидаги энергия интеграли мавжуд
![]() ,
,
бу
ерда ![]() . Демак, координата
боши
. Демак, координата
боши ![]() марказ булади.
Шунинг учун хам мувозанат холати турђун ва (5.10.21) тенгламанинг умумий ечими даврий
функция булади. Шу ечимни топайлик, бунинг учун
марказ булади.
Шунинг учун хам мувозанат холати турђун ва (5.10.21) тенгламанинг умумий ечими даврий
функция булади. Шу ечимни топайлик, бунинг учун
![]() (5.10.22)
(5.10.22)
алмаштириш ёрдамида (5.10.21) тенгламани
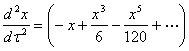
![]() (5.10.23)
(5.10.23)
куринишга келтирамиз. Бу тенгламанинг ечимини
![]() (5.10.24)
(5.10.24)
катор
куринишида излаймиз. Бу ерда ![]() -
-![]() бошланђич шартни каноатлантирувчи
бошланђич шартни каноатлантирувчи ![]() даврли
даврли ![]() нинг
даврий функцияси. (5.10.22) каторда узгармас сон
нинг
даврий функцияси. (5.10.22) каторда узгармас сон ![]() факат жуфт даражаларда
ва (5.10.24) каторда булса, ток даражаларда катнашаяпти, чунки (5.10.21) тенглама
факат жуфт даражаларда
ва (5.10.24) каторда булса, ток даражаларда катнашаяпти, чунки (5.10.21) тенглама
![]() ни -
ни -![]() га алмаштирганимизда узгармайди.
га алмаштирганимизда узгармайди.
(5.10.24)
ни (5.10.23) тенгламага куйгандан сунг, чап ва унг тарафдаги бир хил даражали ![]() лар
олдидаги коэффициентларни тенглаштириб,
лар
олдидаги коэффициентларни тенглаштириб, ![]() ларни аникловчи
тенгламаларни топамиз.
ларни аникловчи
тенгламаларни топамиз.
![]() .
(5.10.25)
.
(5.10.25)
(5.10.25)
тенглама даврий ечимга эга булиши учун ![]() олдидаги
коэффициент нолга айланиш зарур. Бу тасдикдан
олдидаги
коэффициент нолга айланиш зарур. Бу тасдикдан
![]()
ни ва бошланђич шартни хисобга олиб, (5.10.25) тенгламадан куйидагини хосил киламиз:
![]() .
.
Шундай
килиб, ![]() ни топиш учун куйидаги
тенгламага эгамиз:
ни топиш учун куйидаги
тенгламага эгамиз:
![]() .
.
Бу ердан
![]() ,
, ![]() .
.
натижага келамиз. Шу якинлашиш билан чегараланиб куя коламиз.
Шундай килиб, (5.10.21) тенгламанинг даврий ечими ва бу ечимнинг даври куйидаги формулалар билан аникланади:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Бу
ерда ![]() - тебранма харакатнинг
бошланђич амплитудаси. Бошланђич тезлик нолга тенг.
- тебранма харакатнинг
бошланђич амплитудаси. Бошланђич тезлик нолга тенг. ![]() ни
ни ![]() га
алмаштириб (
га
алмаштириб (![]() - ихтиёрий узгармас
сон), (5.10.21) тенгламанинг умумий ечимини хосил киламиз.
- ихтиёрий узгармас
сон), (5.10.21) тенгламанинг умумий ечимини хосил киламиз.
11-§. ![]() - тартибли
системани хусусий холда
- тартибли
системани хусусий холда
тадкик этиш
Келгусида бизга 4-боб, 2-§ да баён этилган
2-теореманинг бевосита умумлашмаси булган битта ёрдамчи мулохаза керак булади. ![]() узгарувчиларнинг
узгарувчиларнинг
![]() -тартибли
-тартибли ![]() та
та
![]() формалари берилган
булсин. Кандай шартлар бажарилганда,
формалари берилган
булсин. Кандай шартлар бажарилганда,
![]()
![]() (5.11.1)
(5.11.1)
муносабатни
каноатлантирувчи яна бошка ![]() та
та ![]() -тартибли
-тартибли
![]() формалар мавжуд булади
деган масалани ечишга туђри келади, бу ерда
формалар мавжуд булади
деган масалани ечишга туђри келади, бу ерда ![]() -айрим узгармас
сонлар.
-айрим узгармас
сонлар.
Шу
максадда ![]() лар оркали
лар оркали
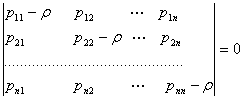 (5.11.2)
(5.11.2)
тенгламанинг
илдизларини ва ![]() лар оркали,
лар оркали,
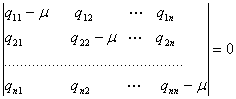 (5.11.3)
(5.11.3)
тенгламанинг илдизларини белгилаб оламиз.
Юкорида айтилган шартларни аниклаб берувчи куйидаги теорема уринли.
Теорема. Агар (5.11.2) ва (5.11.3) тенгламалар илдизлари орасида хеч кандай
![]() (5.11.4)
(5.11.4)
куринишдаги
муносабат мавжуд булмаса, у холда (5.11.1) тенгламаларни каноатлантирувчи битта
ва факат битта ![]() -тартибли
-тартибли ![]() формалар
системаси мавжуд булади. Бу ерда
формалар
системаси мавжуд булади. Бу ерда ![]() лар –
лар –
![]() (5.11.5)
(5.11.5)
муносабат билан бођланган манфиймас бутун сонлар.
Исбот.
Математик индукция усулидан фойдаланамиз. Шунинг учун дастлаб ![]() холни
куриб утамиз. Демак, битта
холни
куриб утамиз. Демак, битта
![]() (5.11.6)
(5.11.6)
тенглама
берилган, бу ерда ![]() -тартибли форма.
(5.11.3) нинг факат битта
-тартибли форма.
(5.11.3) нинг факат битта ![]() илдизи булади.
илдизи булади.
![]()
булганлиги учун (5.11.6) тенгламани
![]() .
.
куринишда ёзиш мумкин
Агар куйидаги
![]() (5.11.7)
(5.11.7)
муносабат бажарилса, у холда 4-боб, 2-§ да баён этилган теоремага асосан бу тенглама ягона ечимга эга.
Бу
ерда ![]() - манфиймас
бутун сонлар,
- манфиймас
бутун сонлар, ![]() лар эса
лар эса

тенгламанинг илдизлари.
Аммо равшанки,
![]() ,
(5.11.8)
,
(5.11.8)
демак, (5.11.7) муносабат
![]() (5.11.9)
(5.11.9)
куринишни
олади. Бу ердан теореманинг ![]() хол учун туђрилиги
келиб чикади.
хол учун туђрилиги
келиб чикади.
Худди
шу усулда теорема ![]() та номаълум
функциялар учун хам туђри деб кабул килиб, уни
та номаълум
функциялар учун хам туђри деб кабул килиб, уни ![]() та номаълум
функциялар учун хам туђрилигини исботлаш мумкин. Теорема исботининг бу кисми
билан кизикканларга [53] китобнинг 151-152 бетларини укишга тавсия этамиз.
та номаълум
функциялар учун хам туђрилигини исботлаш мумкин. Теорема исботининг бу кисми
билан кизикканларга [53] китобнинг 151-152 бетларини укишга тавсия этамиз.
1-мисол. Куйидаги система берилган булсин
 (5.11.10)
(5.11.10)
Бу
ерда ![]() - олдиндан
берилган ихтиёрий
- олдиндан
берилган ихтиёрий ![]() -тартибли формалар,
-тартибли формалар,
![]() -мусбат сон.
(5.11.2) тенглама барча илдизларининг хакикий кисми манфий булсин деб фараз киламиз.
-мусбат сон.
(5.11.2) тенглама барча илдизларининг хакикий кисми манфий булсин деб фараз киламиз.
Бу
холда (5.11.10) система битта ва факат битта ![]() -тартибли форма куринишидаги
-тартибли форма куринишидаги
![]() ечимга эга булади.
ечимга эга булади.
Хакикатан
хам, курсатиш мумкинки, курилаётган холда (5.11.3) тенгламанинг илдизлари агар ![]() -жуфт
сон булса,
-жуфт
сон булса,
![]()
ва
![]() -ток сон булса,
-ток сон булса,
![]()
дан
иборат булади. Равшанки, бу холда бир вактда нолга тенг булмаган хар кандай манфиймас
бутун ![]() сонлар учун
(5.11.4) муносабат бажарилмайди. Демак, хар кандай
сонлар учун
(5.11.4) муносабат бажарилмайди. Демак, хар кандай ![]() учун
теоремани ишлатиш мумкин.
учун
теоремани ишлатиш мумкин.
Энди
![]() - тартибли
системани
- тартибли
системани ![]() хол учун тадкик
этамиз. Тойилган харакатнинг дифференциал тенгламалари (7-§ га каранг)
хол учун тадкик
этамиз. Тойилган харакатнинг дифференциал тенгламалари (7-§ га каранг)
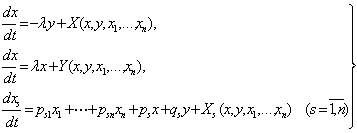 (5.11.11)
(5.11.11)
куринишда
ва ![]() коэффициентлар шундайки,
коэффициентлар шундайки,
 (5.11.12)
(5.11.12)
характеристик тенглама барча илдизларининг хакикий кисми манфий булади.
Бу ерда (5.11.11) система учун турђунлик масаласини хусусий холда тадкик этамиз. Кейин умумий холни тадкик этиш хам шу хусусий холга келтирилишини курсатамиз.
![]() ва
ва
![]() функцияларнинг
функцияларнинг ![]() узгарувчи-ларга
бођлик булган барча хадларини ташлаб юбориб, бу функцияларнинг
узгарувчи-ларга
бођлик булган барча хадларини ташлаб юбориб, бу функцияларнинг ![]() ва
ва
![]() ларга бођлик булган
колган кисмини мос равишда
ларга бођлик булган
колган кисмини мос равишда ![]() ва
ва ![]() билан
белгилаб оламиз, яъни
билан
белгилаб оламиз, яъни
![]() ,
, ![]() ,
,
![]() .
.
Куйидаги иккинчи тартибли системани караймиз:
![]() . (5.11.13)
. (5.11.13)
Бу
система учун турђунлик масаласини ечганда, биз икки холнинг биттасига дуч
келамиз: 1) умумий хол, яъни качон масала ![]() ва
ва ![]() лар
ёйилмаларидаги чекли сондаги хадлар билан хал этилади (координата боши фокус булган
хол); 2) махсус хол, качон турђунлик масаласи
лар
ёйилмаларидаги чекли сондаги хадлар билан хал этилади (координата боши фокус булган
хол); 2) махсус хол, качон турђунлик масаласи ![]() ва
ва ![]() лар
ёйилмаларидаги жуда хам катта даражали хадларни куришни талаб этади (марказ холи).
лар
ёйилмаларидаги жуда хам катта даражали хадларни куришни талаб этади (марказ холи).
Шу
холларнинг биринчиси юз берган дейлик. (5.11.13) система турђунлигини ечиш
масаласи ![]() ва
ва ![]() лар
ёйилмаларидаги энг купи билан 2N-1 даражали хадларга бођлик булсин. Бу сон (даража)
доимо ток булишини 9-§ да курсатган эдик. Каралаётган холда (5.11.11)
тенгламалар учун куйидаги икки шарт бажарилади деб фараз киламиз:
лар
ёйилмаларидаги энг купи билан 2N-1 даражали хадларга бођлик булсин. Бу сон (даража)
доимо ток булишини 9-§ да курсатган эдик. Каралаётган холда (5.11.11)
тенгламалар учун куйидаги икки шарт бажарилади деб фараз киламиз:
1.Барча ![]() ва
ва ![]() узгармас
сонлар нолга тенг.
узгармас
сонлар нолга тенг.
2.![]() функцияларнинг
ёйилмаси камида 2N-1 даражали хадлар билан бошланади.
функцияларнинг
ёйилмаси камида 2N-1 даражали хадлар билан бошланади.
Агар бу икки шарт бажарилса, у холда ![]() - тартибли (5.11.11) системанинг турђунлик масаласи
иккинчи даражали (5.11.13) системанинг турђунлик масаласига эквивалентдир,
яъни: агар (5.11.13) система мувозанат холати (тойилмаган харакат) нотурђун булса,
у холда (5.11.11) системанинг хам мувозанат холати нотурђун булади ва, аксинча,
(5.11.13) системанинг турђунлиги (5.11.11) системанинг турђунлигини келтириб чикаради.
- тартибли (5.11.11) системанинг турђунлик масаласи
иккинчи даражали (5.11.13) системанинг турђунлик масаласига эквивалентдир,
яъни: агар (5.11.13) система мувозанат холати (тойилмаган харакат) нотурђун булса,
у холда (5.11.11) системанинг хам мувозанат холати нотурђун булади ва, аксинча,
(5.11.13) системанинг турђунлиги (5.11.11) системанинг турђунлигини келтириб чикаради.
Шундай килиб, юкорида келтирилган икки шарт
бажарилганда, турђунлик масаласини хал килиш учун нокритик илдизларга мос келадиган
хамма тенгламаларни (![]() ларга нисбатан
тузилган тенгламаларни) ташлаб юбориш ва критик илдизларга мос келган
тенгламалардаги (
ларга нисбатан
тузилган тенгламаларни) ташлаб юбориш ва критик илдизларга мос келган
тенгламалардаги (![]() ва
ва ![]() ларга
нисбатан тузилган тенгламалардаги) нокритик узгарувчиларга бођлик булган хадларни
хам ташлаб юбориш керак булади.
ларга
нисбатан тузилган тенгламалардаги) нокритик узгарувчиларга бођлик булган хадларни
хам ташлаб юбориш керак булади.
Келтирилган мулохазаларни исботлаш учун худди
характеристик тенгламанинг битта илдизи нолга тенг булган холдагидай иш
тутамиз. Шу максадда (5.11.11) тенгламалар системаси учун Ляпунов функциясини
(5.11.13) система учун алохида тузилган Ляпунов функцияси ва (5.11.11)
системанинг нокритик тенгламалари (охирги ![]() та тенгламалар)
учун тузилган Ляпунов функцияларининг йиђиндиси сифатида топамиз. Бу
функциянинг (5.11.11) тенгламаларга кура вакт буйича олинган тулик хосиласи аник
ишорали функция булиш керак.
та тенгламалар)
учун тузилган Ляпунов функцияларининг йиђиндиси сифатида топамиз. Бу
функциянинг (5.11.11) тенгламаларга кура вакт буйича олинган тулик хосиласи аник
ишорали функция булиш керак.
9-§ да курсатдикки, (5.11.13) система учун Ляпунов функцияси
![]()
куринишда
булади, бу ерда ![]() ва
ва ![]() ларнинг
ларнинг
![]() - тартибли формалари.
Бу функциянинг (5.11.13) тенгламаларга кура вакт буйича олинган тулик хосиласи
- тартибли формалари.
Бу функциянинг (5.11.13) тенгламаларга кура вакт буйича олинган тулик хосиласи
![]() куринишда
булади , бу ерда
куринишда
булади , бу ерда ![]() функция
функция ![]() нуктада
нолга айланади. (5.11.13) система учун турђунлик масаласи
нуктада
нолга айланади. (5.11.13) система учун турђунлик масаласи ![]() нинг
ишораси билан ечилади: тойилмаган харакат
нинг
ишораси билан ечилади: тойилмаган харакат ![]() булганда нотурђун
ва
булганда нотурђун
ва ![]() булганда асимптотик
турђун булади.
булганда асимптотик
турђун булади.
Биз (5.11.11) тенгламалар учун хам шу натижа уз кучини саклашини курсатишимиз керак.
(5.11.12)
характеристик тенглама барча илдизларининг хакикий кисми манфий булганлиги
сабабли олдиндан берилган ![]() аник мусбат
ишорали форма учун
аник мусбат
ишорали форма учун
![]()
![]() (5.11.14)
(5.11.14)
муносабатни
каноатлантирувчи аник манфий ишорали ![]() квадратик форма мавжуд.
квадратик форма мавжуд.
Куйидаги
![]() (5.11.15)
(5.11.15)
функцияни курамиз. Бу функциянинг (5.11.11) тенгламалар системасига кура вакт буйича олинган тулик хосиласи
![]()
![]()

![]()
![]()
![]()
куринишда
булади. Бу ерда ![]() лар
лар ![]() лар
ёйилмасидаги
лар
ёйилмасидаги ![]() узгарувчиларга
бођлик булган хадлар мажмуаси хамда улар
узгарувчиларга
бођлик булган хадлар мажмуаси хамда улар ![]() да нолга айланади.
да нолга айланади.
Агар
![]() ва
ва ![]() функциялар
айнан нолга айланганида эди,
функциялар
айнан нолга айланганида эди, ![]() нинг хосиласи
нинг хосиласи
![]() (5.11.16)
(5.11.16)
куринишга
эга буларди. Бу ерда ![]() узгарувчиларнинг
аналитик функциялари ва
узгарувчиларнинг
аналитик функциялари ва ![]() да нолга айланади.
Бу хосила, равшанки,
да нолга айланади.
Бу хосила, равшанки, ![]() та
та ![]() узгарувчиларнинг
аник мусбат ишорали функциялари буларди. Аммо, юкорида келтирилган (5.11.16)
муносабат, умуман айтганда, бажарилмайди ва шунинг учун хам
узгарувчиларнинг
аник мусбат ишорали функциялари буларди. Аммо, юкорида келтирилган (5.11.16)
муносабат, умуман айтганда, бажарилмайди ва шунинг учун хам ![]() аник
мусбат ишорали дея олмаймиз ва у куйидаги куринишга эга:
аник
мусбат ишорали дея олмаймиз ва у куйидаги куринишга эга:
 (5.11.17)
(5.11.17)
Бу
ерда ![]() функция энди
функция энди ![]() ларга
хам бођлик булади ва
ларга
хам бођлик булади ва ![]() ,
, ![]() эса
шундай хадларнинг мажмуасики, уларни на
эса
шундай хадларнинг мажмуасики, уларни на
![]() (5.11.18)
(5.11.18)
гурух хадларга ва на
![]()
гурух хадларга кушиб булмайди.
![]() функцияни
туликрок тадкик этайлик. Бу функциянинг ёйилмасида учинчи даражали хадлардан пасти
йук, чунки
функцияни
туликрок тадкик этайлик. Бу функциянинг ёйилмасида учинчи даражали хадлардан пасти
йук, чунки ![]() нинг ифодасида
ягона иккинчи даражали хадлар (5.11.14) ифода булади.
нинг ифодасида
ягона иккинчи даражали хадлар (5.11.14) ифода булади. ![]() функциянинг
ёйилмасида
функциянинг
ёйилмасида ![]() узгарувчилардан
эркин булган хадлар хам йук, чунки бу хадларнинг барчаси
узгарувчилардан
эркин булган хадлар хам йук, чунки бу хадларнинг барчаси ![]() нинг
нинг
![]()
![]()
таркибий ифодасида булади ва, демак, уларни (5.11.18) га киритиш мумкин.
![]() ларга нисбатан
чизикли булган хадлардан
ларга нисбатан
чизикли булган хадлардан ![]() нинг ифодасида факат
нинг ифодасида факат
![]() ва
ва ![]() ларга
нисбатан тартиби 2N дан паст булган хадлар мавжуд булади. Шу турдаги хадларнинг
колган кисмини (5.11.18) га киритиш мумкин.
ларга
нисбатан тартиби 2N дан паст булган хадлар мавжуд булади. Шу турдаги хадларнинг
колган кисмини (5.11.18) га киритиш мумкин. ![]() ларга нисбатан
иккинчи даражали ва ундан юкори даражали хадларнинг барчасини (5.11.17) га
киритиш мумкин ва шунинг учун хам улар
ларга нисбатан
иккинчи даражали ва ундан юкори даражали хадларнинг барчасини (5.11.17) га
киритиш мумкин ва шунинг учун хам улар ![]() нинг ифодасида йук.
нинг ифодасида йук.
Шундай килиб, юкорида келтирилган мулохазалардан келиб
чикадики, ![]() функция
функция
![]() ,
(5.11.19)
,
(5.11.19)
куринишга
эга, бу ерда ![]() ва
ва ![]() ларга
нисбатан
ларга
нисбатан ![]() - тартибли
формалар. Уларнинг коэффициентлари
- тартибли
формалар. Уларнинг коэффициентлари ![]() ларга нисбатан
чизикли формалар буладилар.
ларга нисбатан
чизикли формалар буладилар. ![]() ифодасида
ифодасида ![]() функциянинг
булиши унинг аник ишорали эканлигини бузади. Шунинг учун хам биз
функциянинг
булиши унинг аник ишорали эканлигини бузади. Шунинг учун хам биз ![]() функция
ифодасига шундай хадларни киритишимиз керакки,
функция
ифодасига шундай хадларни киритишимиз керакки, ![]() нинг ифодасида
нинг ифодасида ![]() га
кирувчи хадлар, яъни
га
кирувчи хадлар, яъни ![]() ларга нисбатан
чизикли ва
ларга нисбатан
чизикли ва ![]() ларга нисбатан 2N дан
кичик даражали хадлар булмасин. Шу максадда
ларга нисбатан 2N дан
кичик даражали хадлар булмасин. Шу максадда ![]() нинг ифодасига кушимча
нинг ифодасига кушимча
![]() (5.11.20)
(5.11.20)
хадларни
киритамиз. Бу ерда ![]() ,
, ![]() эса
эса
![]() ларнинг чизикли
формалари. Бунинг натижасида
ларнинг чизикли
формалари. Бунинг натижасида ![]() нинг ифодасида
пайдо буладиган янги кушилувчи хадлар унинг аник ишорали форма булишини бузадиган
нинг ифодасида
пайдо буладиган янги кушилувчи хадлар унинг аник ишорали форма булишини бузадиган
![]() функциянинг йуколишини
таъминлайди.
функциянинг йуколишини
таъминлайди.
Шундай
килиб, биз (5.11.11) тенгламалар системаси учун ![]() функцияни
функцияни
![]()
![]()
ёки
![]()
![]()
тарзда оламиз ва унинг вакт буйича олинган тулик хосиласи
![]()
куринишда
булади. Бу ерда ![]() ва
ва ![]() лар
лар
![]() да нолга
айланадилар,
да нолга
айланадилар, ![]() узгарувчиларнинг
аналитик функцияси, ёйилмаси камида учинчи даражали хадлардан бошланади.
узгарувчиларнинг
аналитик функцияси, ёйилмаси камида учинчи даражали хадлардан бошланади. ![]() функция
аник мусбат ишорали форма булади.
функция
аник мусбат ишорали форма булади.
![]() функция
аник манфий ишорали форма эканлигидан
функция
аник манфий ишорали форма эканлигидан ![]()
![]() та
та
![]() узгарувчиларга нисбатан
агар
узгарувчиларга нисбатан
агар ![]() булса, аник манфий
ишорали ва агар
булса, аник манфий
ишорали ва агар ![]() булса, узгарувчан
ишорали форма булади. Бу ердан Б ва В теоремаларга асосан худди иккинчи тартибли
(5.11.14) системадагидай (5.11.11) тулик системанинг хам тойилмаган харакати
булса, узгарувчан
ишорали форма булади. Бу ердан Б ва В теоремаларга асосан худди иккинчи тартибли
(5.11.14) системадагидай (5.11.11) тулик системанинг хам тойилмаган харакати ![]() да
асимптотик турђун,
да
асимптотик турђун, ![]() да эса нотурђун булади
деган хулосага келамиз. Шундай килиб бизни кизиктирувчи тасдик исботланди.
да эса нотурђун булади
деган хулосага келамиз. Шундай килиб бизни кизиктирувчи тасдик исботланди.
12-§. ![]() -тартибли системани
умумий
-тартибли системани
умумий
холда тадкик этиш
Олдинги параграфда ![]() - тартибли
системани хусусий холда курган эдик. Умумий холда масалани ечиш учун (5.11.11)
системани шундай куринишга келтирамизки, унинг учун олдинги параграфда куйилган
иккита шарт бажарилсин. Шу максад билан уз навбатида бу системани шундай узгартирамизки,
у (5.11.11) куринишни сакласин, аммо нокритик узгарувчиларга мос келган хар бир
тенгламанинг унг тарафидаги ёйилмада хамма нокритик узгарувчиларга бођлик булган
хадларни ташлаганимиздан кейин ёйилманинг колган кисми етарли катта даражали хадлардан
бошлансин.
- тартибли
системани хусусий холда курган эдик. Умумий холда масалани ечиш учун (5.11.11)
системани шундай куринишга келтирамизки, унинг учун олдинги параграфда куйилган
иккита шарт бажарилсин. Шу максад билан уз навбатида бу системани шундай узгартирамизки,
у (5.11.11) куринишни сакласин, аммо нокритик узгарувчиларга мос келган хар бир
тенгламанинг унг тарафидаги ёйилмада хамма нокритик узгарувчиларга бођлик булган
хадларни ташлаганимиздан кейин ёйилманинг колган кисми етарли катта даражали хадлардан
бошлансин.
Бунинг
учун (5.11.11) системадаги ![]() узгарувчилар урнига
янги
узгарувчилар урнига
янги ![]() узгарувчиларни куйидаги
алмаштиришлар оркали киритамиз
узгарувчиларни куйидаги
алмаштиришлар оркали киритамиз
![]() , (5.12.1)
, (5.12.1)
бу
ерда ![]() ва
ва ![]() ларнинг
аналитик функцияси ва
ларнинг
аналитик функцияси ва ![]() . Узгартирилган
тенгламалар
. Узгартирилган
тенгламалар
 (5.12.2)
(5.12.2)
куринишда булади.
![]() оркали
оркали
![]() нокритик узгарувчиларга
бођлик булмаган
нокритик узгарувчиларга
бођлик булмаган ![]() даги барча хадларни
белгилаб оламиз, яъни
даги барча хадларни
белгилаб оламиз, яъни

Энди ![]() функцияларни
шундай танлаб оламизки,
функцияларни
шундай танлаб оламизки, ![]() функциянинг
ёйилмаси камида
функциянинг
ёйилмаси камида ![]() - тартибли хадлардан
бошлансин. Бу ерда
- тартибли хадлардан
бошлансин. Бу ерда ![]() - етарли катта
сон. У вактда (5.12.2) система олдинги параграфдаги икки шартни каноатлантирадиган
куринишни олади ва турђунлик масаласини ечиш учун бу системанинг
- етарли катта
сон. У вактда (5.12.2) система олдинги параграфдаги икки шартни каноатлантирадиган
куринишни олади ва турђунлик масаласини ечиш учун бу системанинг ![]() ва
ва
![]() критик узгарувчиларга
мос келган тенгламалар унг тарафидаги
критик узгарувчиларга
мос келган тенгламалар унг тарафидаги ![]() нокритик узгарувчиларга
бођлик булган хадларни ташлаб, хосил булган иккинчи тартибли системани курамиз:
нокритик узгарувчиларга
бођлик булган хадларни ташлаб, хосил булган иккинчи тартибли системани курамиз:
 (5.12.4)
(5.12.4)
Бу
системани тадкик этиш жараёнида икки холга дуч келамиз. ![]() сони хар
канча катта булмасин, (5.12.4) система учун турђунлик масаласи
сони хар
канча катта булмасин, (5.12.4) система учун турђунлик масаласи ![]() дан
кичик тартибли хадлар воситаси билан ечилмайдиган хол булиши мумкин. Бу махсус холга
туђри келади ва биз уни кейинчалик алохида куриб утамиз.
дан
кичик тартибли хадлар воситаси билан ечилмайдиган хол булиши мумкин. Бу махсус холга
туђри келади ва биз уни кейинчалик алохида куриб утамиз.
Аммо,
шундай холлар хам мавжудки ва биз буни умумий хол деб атаймиз, етарли катта ![]() сонлар
учун (5.12.4) системанинг турђунлик масаласи
сонлар
учун (5.12.4) системанинг турђунлик масаласи ![]() - тартиблидан катта
булмаган хадлар оркали ечилади, чунки
- тартиблидан катта
булмаган хадлар оркали ечилади, чунки ![]() дан юкори тартибли
булган хадлар турђунликка таъсири булмайди. Бу холда (5.11.11)
дан юкори тартибли
булган хадлар турђунликка таъсири булмайди. Бу холда (5.11.11) ![]() -
тартибли система учун турђунлик масаласи (5.12.4) иккинчи тартибли система
билан хал булади: агар (5.12.4) система учун тойилмаган харакат нотурђун булса,
у холда (5.11.11) система учун у нотурђун булади ва (5.12.4) система учун хам
асимптотик турђун булса, у холда (5.11.11) система учун хам асимптотик турђун булади.
-
тартибли система учун турђунлик масаласи (5.12.4) иккинчи тартибли система
билан хал булади: агар (5.12.4) система учун тойилмаган харакат нотурђун булса,
у холда (5.11.11) система учун у нотурђун булади ва (5.12.4) система учун хам
асимптотик турђун булса, у холда (5.11.11) система учун хам асимптотик турђун булади.
Хакикатан
хам, шарт буйича (5.12.4) система учун турђунлик масаласи ![]() - тартибли
хаддан катта булмаган хадлар билан хал этилгани учун ва (5.12.3) функциянинг
ёйилмаси камида
- тартибли
хаддан катта булмаган хадлар билан хал этилгани учун ва (5.12.3) функциянинг
ёйилмаси камида ![]() - тартибли хадлар
билан бошланганлиги туфайли (5.12.2) система олдинги параграфдаги хамма
(иккита) шартларни каноатлантиради. Уша параграфда олинган натижаларга асосан
(5.12.4) система (5.12.2) система учун ва, демак, (5.11.11) система учун хам тулик
турђунлик масаласини хал килади.
- тартибли хадлар
билан бошланганлиги туфайли (5.12.2) система олдинги параграфдаги хамма
(иккита) шартларни каноатлантиради. Уша параграфда олинган натижаларга асосан
(5.12.4) система (5.12.2) система учун ва, демак, (5.11.11) система учун хам тулик
турђунлик масаласини хал килади.
Энди
(5.12.3) ифодасидаги ![]() - тартиблигача булган
барча хадларни нолга айлантирадиган
- тартиблигача булган
барча хадларни нолга айлантирадиган ![]() функцияларни топиш
йулини курсатамиз. Шу максад учун уни
функцияларни топиш
йулини курсатамиз. Шу максад учун уни
![]() (5.12.5)
(5.12.5)
куринишда
излаймиз, бу ерда ![]() ва
ва ![]() узгарувчиларнинг
узгарувчиларнинг
![]() - тартибли формалари.
У вактда (5.12.3) муносабатдаги биринчи тартибли хадлар
- тартибли формалари.
У вактда (5.12.3) муносабатдаги биринчи тартибли хадлар
![]() (5.12.6)
(5.12.6)
ва
![]() -тартибли хадлар
мажмуаси
-тартибли хадлар
мажмуаси
![]() (5.12.7)
(5.12.7)
куринишга
эга булади. Бу ерда ![]() ларга бођлик булган
ларга бођлик булган
![]() - тартибли
формалар.
- тартибли
формалар.
(5.12.3)
ифодада биринчи даражали хадлар катнашмаслиги учун ![]() чизикли
формани шундай танлаб олиш керакки,
чизикли
формани шундай танлаб олиш керакки, ![]() булсин ва (5.12.3)
ифодадаги функциялар ёйилмаси камида
булсин ва (5.12.3)
ифодадаги функциялар ёйилмаси камида ![]() -даражали хадлар билан
бошланиши учун
-даражали хадлар билан
бошланиши учун
![]() (5.12.8)
(5.12.8)
тенгламалар бажарилиши керак.
![]() функция
факат
функция
факат ![]() буладиган
буладиган ![]() ларга
бођлик булганлигидан (5.12.8) тенгламалар
ларга
бођлик булганлигидан (5.12.8) тенгламалар ![]() дан бошлаб
дан бошлаб ![]() ларни
кетма-кет топишга имкон беради.
ларни
кетма-кет топишга имкон беради. ![]() ни топиш учун унг
тарафи аник булган тенгламаларни хосил киламиз, чунки (5.12.6) га асосан
ни топиш учун унг
тарафи аник булган тенгламаларни хосил киламиз, чунки (5.12.6) га асосан ![]() .
(5.12.3) ёйилмалар камида
.
(5.12.3) ёйилмалар камида ![]() - тартибли хад
билан бошланишлари учун (5.12.5) каторнинг
- тартибли хад
билан бошланишлари учун (5.12.5) каторнинг ![]() - тартиблигача булган
хадларини аниклашга туђри келади.
- тартиблигача булган
хадларини аниклашга туђри келади.
Барча
![]() хадлар аникланган
деб хисоблайлик. У вактда
хадлар аникланган
деб хисоблайлик. У вактда ![]() ларни топиш учун
биз унг тарафи аник булган (5.12.8) тенгламаларни хосил киламиз. Бу тенгламаларнинг
куриниши олдинги параграфдаги (5.11.1) тенгламаларники кабидир. Хозирги холда
(5.11.1) тенгламанинг илдизлари
ларни топиш учун
биз унг тарафи аник булган (5.12.8) тенгламаларни хосил киламиз. Бу тенгламаларнинг
куриниши олдинги параграфдаги (5.11.1) тенгламаларники кабидир. Хозирги холда
(5.11.1) тенгламанинг илдизлари ![]() ва (5.11.3)
тенгламанинг илдизлари (5.11.2) нинг
ва (5.11.3)
тенгламанинг илдизлари (5.11.2) нинг ![]() илдизларидан
иборат булади. Энди (5.11.4) муносабат
илдизларидан
иборат булади. Энди (5.11.4) муносабат
![]()
куринишни
олади ва у хеч кандай манфиймас бутун ![]() ,
, ![]() сонлар
учун бажарилмаслиги учун 11-§ даги теоремага асосан (5.12.18) система
сонлар
учун бажарилмаслиги учун 11-§ даги теоремага асосан (5.12.18) система ![]() индекс
кандай булишидан катъий назар
индекс
кандай булишидан катъий назар ![]() ечимга эга булиши
керак. Бу ечимни аникмас коэффициентли формалар шаклида излаш маъкул. Аникмас
коэффициентларни топиш учун чизикли бир жинслимас алгебраик тенгламалар хосил
килинади.
ечимга эга булиши
керак. Бу ечимни аникмас коэффициентли формалар шаклида излаш маъкул. Аникмас
коэффициентларни топиш учун чизикли бир жинслимас алгебраик тенгламалар хосил
килинади.
Энди
амалий масалаларни ечишда (5.12.5) каторнинг нечта хадини топишимиз лозимлиги хакида
тухталиб утайлик. Агар иккинчи даражали система учун турђунлик масаласи чекли
даражали хадлар билан ечилса, у холда бу даража доимо ток сон эканлигини
олдинги параграфларда айтган эдик. Амалда деярли купинча учинчи даражали хадлар
билан масала ечилади. Демак, (5.12.3) ёйилмада биринчи ва иккинчи даражали хадлар
булмаслиги керак. Бунинг учун (5.12.5) ![]() функцияларнинг
ёйилмасида факат
функцияларнинг
ёйилмасида факат ![]() биринчи тартибли
ва
биринчи тартибли
ва ![]() иккинчи тартибли хадларни
олиш кифоя. Бундай хадлар оркали аникланувчи
иккинчи тартибли хадларни
олиш кифоя. Бундай хадлар оркали аникланувчи ![]() функцияларни
(5.12.4) тенгламаларга куйиб, улар учун турђунлик масаласини ечамиз. Агар
масала учинчи даражали хадлар билан ечилмаслиги маълум булса ва, демак, хеч булмаганда
туртинчи ва бешинчи даражали хадларни куришга туђри келса, у холда
функцияларни
(5.12.4) тенгламаларга куйиб, улар учун турђунлик масаласини ечамиз. Агар
масала учинчи даражали хадлар билан ечилмаслиги маълум булса ва, демак, хеч булмаганда
туртинчи ва бешинчи даражали хадларни куришга туђри келса, у холда ![]() ва
ва
![]() формаларни хам аниклашга
туђри келади. Агар бешинчи даражали хадлар билан хам (5.12.4) учун турђунлик
масаласи хал булмаса, у холда янади юкори даражали формаларни аниклаш керак булади.
формаларни хам аниклашга
туђри келади. Агар бешинчи даражали хадлар билан хам (5.12.4) учун турђунлик
масаласи хал булмаса, у холда янади юкори даражали формаларни аниклаш керак булади.
(5.12.4)
тенгламалар (5.11.11) тенгламаларнинг биринчи ва иккинчисидан ![]() узгарувчиларни
узгарувчиларни
![]() функциялар билан
алмаштириш натижасида олинганлигини эслатиб утамиз.
функциялар билан
алмаштириш натижасида олинганлигини эслатиб утамиз.
(5.12.8) тенгламаларни хосил килиш учун хусусий хосилали
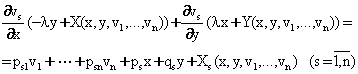 (5.12.9)
(5.12.9)
тенгламаларнинг ечимини (5.12.5) катор куринишда топиш керак.
Шунинг учун хам айтилган барча мулохазалар курилаётган холда турђунлик масаласини ечиш учун бизни куйидаги алгоритмга олиб келади:
1. (5.11.11) тенгламалар холида турђунлик масаласинии ечиш учун хусусий хосилали (5.12.9) тенгламалар системаси тузилади ва унинг ечими (5.12.5) каторлар сифатида изланади.
2.
Бундай каторлар доимо мавжуд ва ягона булади. (5.11.11) ситеманинг дастлабки
иккита тенгламасидаги ![]() узгарувчиларни
(5.12.5) каторлар билан (
узгарувчиларни
(5.12.5) каторлар билан (![]() функциялар билан)
алмаштириб, иккинчи даражали (5.12.4) система хосил килинади.
функциялар билан)
алмаштириб, иккинчи даражали (5.12.4) система хосил килинади.
3. (5.12.4) система учун турђунлик масаласи чекли сондаги хадлар билан ечилади деб фараз килинади. У вактда агар (5.12.4) система учун тойилмаган харакат нотурђун булса, у холда (5.11.11) система учун хам у нотурђун булади. Агар (5.12.4) система учун тойилмаган харакат асимптотик турђун булса, у холда (5.11.11) система учун хам у асимптотик турђун булади. Турђунлик масаласи ечиш учун (5.12.5) каторлардаги хадларнинг нечтасини олиш масаласини биз юкорида айтиб утган эдик.
Изох. Битта нол илдизга эга булган критик хол хамда жуфт соф мавхум илдизларга эга булган критик холлар учун тойилган харакат тенгламалари аналитик булмаганда, турђунлик масаласининг ечими [16] да берилган.
1-мисол. Куйидаги системанинг
 (5.12.10)
(5.12.10)
турђунлик
масаласини ечиш талаб этилган булсин. Бу ерда ![]() функциянинг ёйилмаси
камида учинчи даражали хадлар билан бошланади деб фараз киламиз. Хусусий хосилали
функциянинг ёйилмаси
камида учинчи даражали хадлар билан бошланади деб фараз киламиз. Хусусий хосилали
![]()
дифференциал тенгламани тузамиз ва унинг ечимини
![]()
катор
сифатида излаймиз. Бу ерда ![]() -
- ![]() -
тартибли форма. Аввал
-
тартибли форма. Аввал ![]() ва
ва ![]() формаларни
топамиз. Юкори тартибли формаларни заруриятга караб аниклаймиз.
формаларни
топамиз. Юкори тартибли формаларни заруриятга караб аниклаймиз. ![]() ва
ва
![]() ларни топиш учун
ларни топиш учун
![]() ,
,
![]()
тенгламаларга
эгамиз. Биринчи тенглама ![]() ни беради. Буни
иккинчи тенгламага куйиб,
ни беради. Буни
иккинчи тенгламага куйиб,
![]() (5.12.11)
(5.12.11)
хосил
киламиз. ![]() ни куйидаги
ни куйидаги
![]()
ифода куринишида излаймиз. Буни (5.12.11) га куйиб, А, В, С аникмас узгармас сонларни топиш учун
-А+В+С=0, А+2В=1, -2В+С=1
тенгламаларни хосил киламиз. Бу ердан
![]()
эканлигини топамиз (А=1, В=0, С=1).
Энди
(5.12.10) системанинг дастлабки иккита тенгламасидаги ![]() урнига
урнига
![]()
ни куйиб, иккинчи тартибли
 (5.12.12)
(5.12.12)
системани
хосил киламиз. Бу ерда ![]() ва
ва ![]() лар
ёйилмаси камида туртинчи даражали хадлар билан бошланадиган формалар.
лар
ёйилмаси камида туртинчи даражали хадлар билан бошланадиган формалар.
(5.12.12) система учун турђунлик масаласини ечамиз. Бунинг учун турђунликни ечишнинг иккинчи усулидан фойдаланамиз (9-§ га каранг). (5.12.12) система учун
![]()
аник мусбат ишорали Ляпунов функцияси мавжуд. Бу функциянинг (5.12.12) системага кура вакт буйича олинган тулик хосиласи
![]()
![]() кийматлар
учун аник ишорали функция булади. (5.12.12) системанинг тойилмаган харакати ва,
демак, (5.12.10) системанинг хам тойилмаган харакати
кийматлар
учун аник ишорали функция булади. (5.12.12) системанинг тойилмаган харакати ва,
демак, (5.12.10) системанинг хам тойилмаган харакати ![]() да
нотурђун,
да
нотурђун, ![]() да эса асимптотик
турђун булади.
да эса асимптотик
турђун булади.
![]() да
турђунлик масаласи учинчи даражали хадлар билан ечилмайди. Аммо,
да
турђунлик масаласи учинчи даражали хадлар билан ечилмайди. Аммо,![]()
![]() функция таркибидаги
функция таркибидаги ![]() ,
, ![]() ва
юкори тартибли хадларни топишнинг хожати йук, чунки
ва
юкори тартибли хадларни топишнинг хожати йук, чунки ![]() да
(5.12.10) нинг дастлабки иккита тенгламасининг ифодасида
да
(5.12.10) нинг дастлабки иккита тенгламасининг ифодасида ![]() узгарувчи
катнашмайди, демак,
узгарувчи
катнашмайди, демак, ![]() хол махсус холга
мансуб булади.
хол махсус холга
мансуб булади.
2-мисол. Иккинчи мисол сифатида А.И.Лурье тадкик этган автоматик ростлаш (регулирование) системасининг битта масаласини куриб утайлик [48]. Система харакатининг (ростланадиган объект, улчагич, сервомотор ва б.к.) дифференциал тенгламалари
 (5.12.13)
(5.12.13)
куринишда
булсин. Бу ерда ![]() - узгармас сонлар,
- узгармас сонлар,
![]() - чизиклимас функция
ва
- чизиклимас функция
ва ![]() .
.
![]()
![]() нинг
аналитик функцияси ва у
нинг
аналитик функцияси ва у
![]()
куринишга эга дейлик.
(5.12.13) нинг биринчи якинлашиш системаси
![]() (5.12.14)
(5.12.14)
куринишда булади.
Бу
системанинг ![]() мувозанат холатининг
турђунлиги учун
мувозанат холатининг
турђунлиги учун
 (5.12.15)
(5.12.15)
характеристик
тенглама барча илдизларининг хакикий кисми манфий булиши етарлидир. Шуни
таъкидлаймизки, турђунлик сохасининг кулами илдизлар хакикий кисмининг сон микдорига
бођлик. Агар (5.12.15) тенгламанинг хеч булмаганда айрим илдизларининг хакикий
кисми микдор жихатдан кичик булса, у холда турђунлик сохаси нуктаи назардан тадкик
этилаётган мувозанат холатини нотурђун деб караш мумкин. Шундай килиб, критик холни
тадкик этиш масаласига келамиз. Бу масалани (5.12.13) системага нисбатан курамиз.
Бу ерда (5.12.15) характеристик тенглама жуфт соф ![]() мавхум илдизларга
ва колган
мавхум илдизларга
ва колган ![]() таси хакикий кисми
манфий булган илдизлар деб фараз киламиз.
таси хакикий кисми
манфий булган илдизлар деб фараз киламиз.
(5.12.15) тенгламанинг хамма илдизлари оддий (карралимас) булсин.
Куйидаги чизикли алмаштиришларни киритамиз
![]() . (5.12.16)
. (5.12.16)
Бу
ерда ![]() коэффициентлар
коэффициентлар
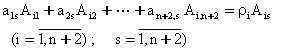
тенгламалардан аникланади, яъни
![]() ,
,
бу
ерда ![]() - (5.12.15) детерминантнинг
- (5.12.15) детерминантнинг
![]() - сатр ва
- сатр ва ![]() -
устун буйича алгебраик тулдирувчиси,
-
устун буйича алгебраик тулдирувчиси, ![]() - ихтиёрий узгармас
сон. (5.12.16) алмаштириш (5.12.14) тенгламаларни
- ихтиёрий узгармас
сон. (5.12.16) алмаштириш (5.12.14) тенгламаларни
![]()
куринишга, (5.12.13) системани эса
![]()
куринишга
келтиради. Бу ерда ![]() узгармас сон
узгармас сон
![]()
шартни каноатлантиради деб фараз киламиз ва
![]()
куринишга
эга булади (![]() - айрим узгармас
сонлар).
- айрим узгармас
сонлар).
![]() ва колган
ва колган ![]() та
илдизнинг хакикий кисми манфий булсин. У вактда
та
илдизнинг хакикий кисми манфий булсин. У вактда
![]()
деб кабул килиб, система харакатининг тенгламаларини
 (5.12.17)
(5.12.17)
куринишга келтирамиз.
Бу
ерда ![]() ва
ва ![]() -
-
![]() коэффициентнинг хакикий
ва мавхум кисми (
коэффициентнинг хакикий
ва мавхум кисми (![]() коэффициент
коэффициент ![]() га
кушма комплекс булади).
га
кушма комплекс булади).
![]()
тенгламаларни тузиб, уларнинг ечимини
![]() (5.12.18)
(5.12.18)
катор
тарзида излаймиз. Одатдагидек, (5.12.18) асосида олдинги тенглама воситасида ![]() функция
учун
функция
учун
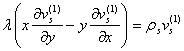
тенгламани
хосил киламиз. Бу ердан ![]() эканлиги келиб чикади.
Шунинг учун хам
эканлиги келиб чикади.
Шунинг учун хам ![]() функция учун тенглама
функция учун тенглама
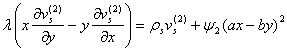
куринишда
булади. ![]() функцияни
функцияни
![]()
куринишда
излаймиз. Буни олдинги тенгламага куйиб, ![]() ва
ва ![]() лар
олдидаги коэффициентларни тенглаштириб, сунгра хосил булган тенгламаларни
лар
олдидаги коэффициентларни тенглаштириб, сунгра хосил булган тенгламаларни ![]() ларга
нисбатан ечиб, куйидагиларга эга буламиз:
ларга
нисбатан ечиб, куйидагиларга эга буламиз:
![]() ,
,
![]() ,
,
![]() .
.
Масалани
биринчи усул билан ечамиз. Бунинг учун ![]() форма ифодасига
форма ифодасига ![]() ,
,
![]() ларни куямиз. У холда,
ларни куямиз. У холда,
![]() коэффициентларнинг
ифодасини хисобга олиб, куйидагини хосил киламиз:
коэффициентларнинг
ифодасини хисобга олиб, куйидагини хосил киламиз:
![]() ,
,
бу ерда
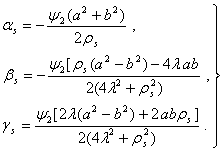 (5.12.19)
(5.12.19)
(5.12.17)
системанинг дастлабки иккита тенгламасидаги ![]() лар урнига
(5.12.18) каторни куямиз, кутб координаталарига утиб,
лар урнига
(5.12.18) каторни куямиз, кутб координаталарига утиб, ![]() ни чикаргандан
сунг, куйидагини хосил киламиз
ни чикаргандан
сунг, куйидагини хосил киламиз
![]() (5.12.20)
(5.12.20)
Бу ерда
![]()
![]() ,
,
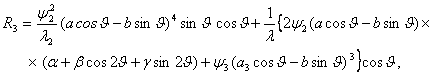
![]() .
.
Охирги учта ифодани хисобга олиб, (5.12.19)га асосан куйидагиларга эга буламиз:
 (5.12.21)
(5.12.21)
Бу ерда
![]() .
.
(5.12.20) тенгламанинг ечимини
![]()
катор
шаклида излаймиз. Буни (5.12.20) га куйиб, унг ва чап томондаги бир хил
даражали ![]() лар олдидаги коэффициентларни
тенглаштириб,
лар олдидаги коэффициентларни
тенглаштириб,

ифодаларни хосил киламиз.
![]() функция
даврий булади. Шунинг учун
функция
даврий булади. Шунинг учун

ифода хам даврий функциядир. Шунга кура
![]() даврий функция
даврий функция
ифодадаги
![]() узгармас сон
узгармас сон
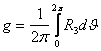
формула оркали аникланади. Бу ердан
![]()
ёки, (5.12.21) ни хисобга олиб,
![]()
ни
топамиз. Агар ![]() нинг ифодасига
кирган микдорларни (5.12.13) системадаги коэффициентлар оркали ифодаласак ва
унча мухим булмаган
нинг ифодасига
кирган микдорларни (5.12.13) системадаги коэффициентлар оркали ифодаласак ва
унча мухим булмаган ![]() мусбат купайтувчини
ташлаб юборсак, у холда А.И.Лурье курсатганидек, куйидагини хосил киламиз:
мусбат купайтувчини
ташлаб юборсак, у холда А.И.Лурье курсатганидек, куйидагини хосил киламиз:
 , (5.12.22)
, (5.12.22)
бу
ерда ![]() - (5.12.15)
детерминантнинг
- (5.12.15)
детерминантнинг ![]() булгандаги киймати.
булгандаги киймати.
13-§. ![]() - тартибли
системани махсус холда
- тартибли
системани махсус холда
тадкик этиш
Тойилган харакат дифференциал тенгламалари куйидаги куринишда берилган булсин:
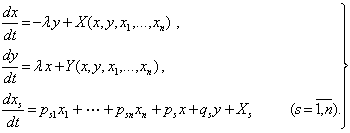 (5.13.1)
(5.13.1)
Энди махсус холни куришга утамиз. Турђунлик масаласини тадкик этишнинг олдинги параграфларда баён этилган коидасига асосан куйидаги хусусий хосилали
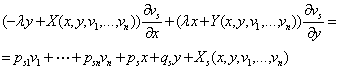 (5.13.2)
(5.13.2)
дифференциал тенгламаларни тузамиз.
Бу тенгламаларни куйидаги формал каторлар каноатлантириши мумкин
![]() (5.13.3)
(5.13.3)
Бу
каторлардаги ![]() хадлар билан кифояланиб,
(5.13.1) системанинг дастлабки иккита тенгламасидаги
хадлар билан кифояланиб,
(5.13.1) системанинг дастлабки иккита тенгламасидаги ![]() узгарувчиларни
узгарувчиларни
![]() бутун рационал
функциялар билан алмаштириб, куйидаги иккинчи тартибли системани хосил киламиз:
бутун рационал
функциялар билан алмаштириб, куйидаги иккинчи тартибли системани хосил киламиз:
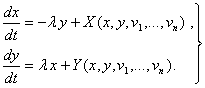 (5.13.4)
(5.13.4)
(5.13.4)
система учун турђунлик масаласи ![]() - даражалидан (
- даражалидан (![]() - етарли катта сон) юкори булмаган хадлар билан хал этилиши мумкин. Бу олдин курилган
умумий хол булади. Бу холда (5.13.1) система учун турђунлик масаласи (5.13.4)
система билан ечилади.
- етарли катта сон) юкори булмаган хадлар билан хал этилиши мумкин. Бу олдин курилган
умумий хол булади. Бу холда (5.13.1) система учун турђунлик масаласи (5.13.4)
система билан ечилади.
Аммо,
шундай холлар мавжудки, ![]() сони канчалик
катта булмасин, ва, демак, (5.13.3) каторда олинган хадлар сони хар канча катта
булмасин, (5.13.4) система учун турђунлик масаласи
сони канчалик
катта булмасин, ва, демак, (5.13.3) каторда олинган хадлар сони хар канча катта
булмасин, (5.13.4) система учун турђунлик масаласи ![]() дан
кичик тартибли булган хадлар билан ечилмайди. Бу холда системадаги
дан
кичик тартибли булган хадлар билан ечилмайди. Бу холда системадаги ![]() дан
юкори даражали булган хадларни узгартириб, хохишимизга караб, тойилмаган харакатни
турђун ёки нотурђун килишимиз мумкин. Бу хол махсус хол деб айтилади. Олдинги
параграфда баён этилган турђунликни ечиш коидаси (алгоритми) махсус холни тадкик
этишга ярамайди.
дан
юкори даражали булган хадларни узгартириб, хохишимизга караб, тойилмаган харакатни
турђун ёки нотурђун килишимиз мумкин. Бу хол махсус хол деб айтилади. Олдинги
параграфда баён этилган турђунликни ечиш коидаси (алгоритми) махсус холни тадкик
этишга ярамайди.
Шундай
булсада, биз махсус холда хам (5.13.1) системанинг турђунлик масаласи иккинчи
тартибли (5.13.4) системанинг турђунлик масаласига эквивалент эканлигини курсатамиз.
Бунинг учун (5.13.4) тенгламалардаги ![]() функциялар
(5.13.3) каторнинг чекли сондаги хадларинигина эмас, балки бутун каторни
ифодалаши керак. У вактда, равшанки, (5.13.3) катор якинлашувчи булгандагина,
(5.13.4) система маънога эга булади. Бу катор хакикатан хам якинлашувчи буладими?
функциялар
(5.13.3) каторнинг чекли сондаги хадларинигина эмас, балки бутун каторни
ифодалаши керак. У вактда, равшанки, (5.13.3) катор якинлашувчи булгандагина,
(5.13.4) система маънога эга булади. Бу катор хакикатан хам якинлашувчи буладими?
Бу масала А.М.Ляпунов томонидан хал килинган. У бу катор узоклашувчи булиши хам мумкинлигини курсатган. Масалан,
![]()
тенглама учун (5.13.3) формал катор
![]()
куринишга эга ва узоклашувчидир.
Аммо, бундан (5.13.3) каторлар доимо узоклашувчи булади деган хулоса келиб чикмайди. Махсус холлар учун (5.13.3) каторлар албатта якинлашувчи булиши Ляпунов томонидан исбот этилган.
Демак, Ляпунов тасдиђига асосан (5.13.4)
система аникланган, яъни маънога эга булади. Бу система учун турђунлик масаласи
чекли сондаги хадлар билан хал этилмаслиги туфайли 8-10-§ лардаги натижаларга
асосан координата боши ![]() (5.13.4)
тенгламалар учун марказ булади. (5.13.4) тенгламалар билан ифодаланувчи
тойилмаган харакат турђун (аммо асимптотик турђун эмас) ва умумий ечим даврий
функция булади.
(5.13.4)
тенгламалар учун марказ булади. (5.13.4) тенгламалар билан ифодаланувчи
тойилмаган харакат турђун (аммо асимптотик турђун эмас) ва умумий ечим даврий
функция булади.
Бу даврий ечимни куйидаги куринишда ифодалаш мумкин:
 (5.13.5)
(5.13.5)
Бу ерда ![]() даврли
даврли ![]() нинг
даврий функциялари ва
нинг
даврий функциялари ва ![]() ,
, ![]() -
айрим аник аникланган узгармас сонлар,
-
айрим аник аникланган узгармас сонлар, ![]() -
- ![]() нинг
бошланђич киймати булган ихтиёрий узгармас сон. (5.13.5) даги хамма каторлар
нинг
бошланђич киймати булган ихтиёрий узгармас сон. (5.13.5) даги хамма каторлар ![]() нинг
етарли кичик кийматлари учун якинлашувчи булади.
нинг
етарли кичик кийматлари учун якинлашувчи булади.
Махсус холда худди шундай холат (5.13.1) ![]() -
тартибли система учун хам мавжуд: бу система хам
-
тартибли система учун хам мавжуд: бу система хам ![]() нинг бошланђич киймати
булган ихтиёрий битта узгармас сонга бођлик даврий ечимга эга булади. Бу система учун
нинг бошланђич киймати
булган ихтиёрий битта узгармас сонга бођлик даврий ечимга эга булади. Бу система учун ![]() тойилмаган харакат хам турђун булади. Бу холда даврий
ечимдаги
тойилмаган харакат хам турђун булади. Бу холда даврий
ечимдаги ![]() ва
ва ![]() лар (5.13.5) формулалар билан аникланади,
лар (5.13.5) формулалар билан аникланади, ![]() лар эса,
лар эса,
![]() (5.13.6)
(5.13.6)
формула
билан аникланади, бу ерда ![]() - (5.13.3) билан
аникланадиган функциялар.
- (5.13.3) билан
аникланадиган функциялар.
Бу
тасдикларни исбот килишдан олдин шуни таъкидлаймизки, агар ![]() функциялар
(5.13.4) тенгламаларнинг бирор хусусий ечими булса, у холда
функциялар
(5.13.4) тенгламаларнинг бирор хусусий ечими булса, у холда ![]() ,
,
![]() функциялар
(5.13.1) системанинг бирор хусусий ечимини аниклайдилар. Хакикатан хам, бу
функцияларни (5.13.1) системага куйсак, (5.13.2) ва (5.13.4) ларга асосан,
системадаги тенгламаларнинг айниятга айланишига ишонч хосил киламиз. Бу ердан
бевосита келиб чикадики, (5.13.1) система (5.13.5) ва (5.13.6) формулалар оркали
аникланадиган даврий ечимга эга.
функциялар
(5.13.1) системанинг бирор хусусий ечимини аниклайдилар. Хакикатан хам, бу
функцияларни (5.13.1) системага куйсак, (5.13.2) ва (5.13.4) ларга асосан,
системадаги тенгламаларнинг айниятга айланишига ишонч хосил киламиз. Бу ердан
бевосита келиб чикадики, (5.13.1) система (5.13.5) ва (5.13.6) формулалар оркали
аникланадиган даврий ечимга эга.
Энди
![]() - тартибли (5.13.1) система учун тойилмаган харакат
турђун эканлигини курсатамиз. Бунинг учун системадаги
- тартибли (5.13.1) система учун тойилмаган харакат
турђун эканлигини курсатамиз. Бунинг учун системадаги ![]() узгарувчилар
урнига
узгарувчилар
урнига
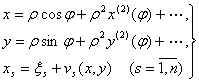 (5.13.7)
(5.13.7)
алмаштиришлар
билан янги ![]() узгарувчиларни
киритамиз. У вактда (5.13.1) системанинг дастлабки иккита тенгламаси куйидаги куринишни
олади:
узгарувчиларни
киритамиз. У вактда (5.13.1) системанинг дастлабки иккита тенгламаси куйидаги куринишни
олади:
 (5.13.8)
(5.13.8)
бу
ерда ![]() ёйилмасида озод хадлар булмаган
ёйилмасида озод хадлар булмаган ![]() узгарувчиларнинг
аналитик функциялари. Бу ёйилмаларнинг коэффициентлари
узгарувчиларнинг
аналитик функциялари. Бу ёйилмаларнинг коэффициентлари ![]() даврли
даврли ![]() нинг даврий функциялари булади.
нинг даврий функциялари булади.
(5.13.8)
тенгламаларни ![]() ва
ва ![]() ларга нисбатан ечамиз.
ларга нисбатан ечамиз.
![]() ва
ва ![]() нисбатан чизикли тенгламаларнинг
нисбатан чизикли тенгламаларнинг ![]() детерминанти куйидаги куринишда булади
детерминанти куйидаги куринишда булади
![]() Бу ердан
Бу ердан ![]() микдорнинг
микдорнинг ![]() га нисбатан аналитиклиги келиб чикади. Бу микдорнинг
га нисбатан аналитиклиги келиб чикади. Бу микдорнинг ![]() даражалари буйича ёйилмасининг коэффициентлари
даражалари буйича ёйилмасининг коэффициентлари ![]() га нисбатан даврийдир. Демак,
га нисбатан даврийдир. Демак,
 (5.13.9)
(5.13.9)
ни
хосил киламиз, бу ерда ![]() ва
ва ![]() лар -
лар - ![]() ва
ва ![]() ларга ухшаш функциялар, яъни
ларга ухшаш функциялар, яъни ![]() ва
ва ![]() ларга нисбатан аналитик,
ларга нисбатан аналитик, ![]() га нисбатан даврий ва
га нисбатан даврий ва ![]() да нолга айланади.
да нолга айланади.
![]() лар урнига (5.13.7) ни куйгандан кейин (5.13.1)
системанинг охирги
лар урнига (5.13.7) ни куйгандан кейин (5.13.1)
системанинг охирги ![]() та тенгламалари
та тенгламалари
![]() (5.13.10)
(5.13.10)
куринишга
келади. Бу ерда ![]() лар
лар![]() даврли
даврли ![]() га нисбатан
аналитик функциялар, уларнинг ёйилмаси камида иккинчи даражали хадлардан
бошланади. Бу ёйилмаларнинг коэффициентлари
га нисбатан
аналитик функциялар, уларнинг ёйилмаси камида иккинчи даражали хадлардан
бошланади. Бу ёйилмаларнинг коэффициентлари ![]() даврли
даврли ![]() нинг
даврий функциялари булади.
нинг
даврий функциялари булади.
(5.13.1)
системанинг (5.13.5) ва (5.13.6) даврий ечимининг ифодаси янги ![]() узгарувчиларда
куйидаги куринишга келади:
узгарувчиларда
куйидаги куринишга келади:
![]() . (5.13.11)
. (5.13.11)
Демак, (5.13.9) ва (5.13.10) тенгламалар (5.13.11) хусусий ечимга эга. Бунинг учун
![]()
муносабатларнинг бажарилиши зарурдир.
Аммо
бу холда (5.13.9) системанинг биринчи тенгламаси ва (5.13.10) тенгламалардан
иборат ![]() - тартибли система
(бу ерда
- тартибли система
(бу ерда ![]() нинг бирор аникмас
функцияси) биз 6-§ да курган (битта нол илдизга эга булган махсус хол)
нинг бирор аникмас
функцияси) биз 6-§ да курган (битта нол илдизга эга булган махсус хол)
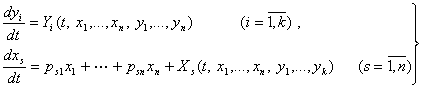
системанинг
((5.6.2) га каранг) хусусий холи булади. 6-§ даги натижаларга асосан юкорида
айтилган ![]() - тартибли
системанинг
- тартибли
системанинг ![]() тойилмаган харакати турђун булади. У вактда (5.13.7)
алмаштиришнинг характерига асосан (5.13.1) системанинг
тойилмаган харакати турђун булади. У вактда (5.13.7)
алмаштиришнинг характерига асосан (5.13.1) системанинг ![]() тойилмаган харакати хам турђун булади.
тойилмаган харакати хам турђун булади.
Шундай килиб, махсус холда тойилмаган харакатнинг турђунлигини ва тойилган харакат тенгламаларининг (5.13.5) ва (5.13.6) формулалар билан аникланадиган даврий ечими мавжудлигини исбот килдик.
Демак, махсус холда турђунлик масаласи осонгина ечилади. Аммо, афсуски, хозиргача курилаётган хол марказ эканлигини аниклайдиган бирорта умумий усул мавжуд эмас. Хакикатан хам, агар биз махсус холга эга булсак, у вактда (5.13.4) тенгламаларда канчалик куп хадларни курмайлик, янада юкори даражали хадлар каралганда фокус холига келмаслигимизга бизда ишонч булмайди.
Аммо, битта умумий аломатни курсатиш мумкинки, агар у бажарилса, курилаётган хол албатта марказ булади.
(5.13.1) система
![]() (5.13.12)
(5.13.12)
куринишдаги
биринчи интегралга эга булсин, бу ерда ![]() узгарувчиларнинг
аналитик функцияси, унинг ёйилмаси камида учинчи даражали хадлардан бошланади.
Агар (5.13.1) система (5.13.12) биринчи интегралга эга булса, у холда курилаётган
хол албатта марказ булишини курсатамиз.
узгарувчиларнинг
аналитик функцияси, унинг ёйилмаси камида учинчи даражали хадлардан бошланади.
Агар (5.13.1) система (5.13.12) биринчи интегралга эга булса, у холда курилаётган
хол албатта марказ булишини курсатамиз.
Хакикатан
хам, (5.13.12) муносабатдаги ![]() узгарувчилар
урнига (5.13.2) нинг формал ечими булган (5.13.3) каторни
узгарувчилар
урнига (5.13.2) нинг формал ечими булган (5.13.3) каторни ![]() ни
ни![]() келтириб куйсак, (5.13.4) системанинг формал биринчи
интегралини хосил киламиз, яъни каторнинг барча
келтириб куйсак, (5.13.4) системанинг формал биринчи
интегралини хосил киламиз, яъни каторнинг барча
![]() ,
,
каби хадлари йуколади, бу ерда
![]() .
.
У
вактда (5.13.4) система учун (9-§ даги мулохазаларга асосан) ![]() нукта марказ булади ва шу билан бизнинг тасдиђимиз
исботланади.
нукта марказ булади ва шу билан бизнинг тасдиђимиз
исботланади.
Ляпунов бу тасдикнинг аксининг хам туђрилигини исботлаган, яъни (5.13.1) система албатта (5.13.12) куринишдаги биринчи интегралга эга булиши зарурлигини курсатган.
Бундан ташкари, агар (5.13.1) система (5.13.12) куринишдаги биринчи интегралга эга булса, у холда

характеристик
тенгламанинг илдизларининг хакикий кисми манфий булиши ёки булмаслигидан катъий
назар (5.13.1) система (5.13.5) ва (5.13.6) формулалар билан аникланадиган
даврий ечимга эга булишини хам Ляпунов исботлаб берган. Энг мухими бу
илдизларнинг бирортаси хам ![]() куринишга эга булмаслиги
керак, бу ерда
куринишга эга булмаслиги
керак, бу ерда ![]() - бутун мусбат сон
ёки нол.
- бутун мусбат сон
ёки нол.
Курсатилган даврий ечимлар чизиклимас тебранишлар назариясида мухим рол уйнайди [56].
14-§. Турђунлик сохасининг «хавфли» ва «хавфсиз»
чегаралари
Энди турђунлик сохасининг «хавфли» ва «хавфсиз» чегаралари хакида тухталиб утамиз [12]. Бу масала «амалий» турђунлик тушунчаси билан бевосита бођланган.
Тойилган харакатнинг тенгламаси
![]() (5.14.1)
(5.14.1)
куринишда
берилган булсин, бу ерда ![]() - ёйилмаси камида
иккинчи даражали хадлар билан бошланадиган
- ёйилмаси камида
иккинчи даражали хадлар билан бошланадиган ![]() узгарувчиларнинг
функцияси.
узгарувчиларнинг
функцияси.
(5.14.1) система параметрлари фазосининг
![]() (5.14.2)
(5.14.2)
муносабат
билан аникланадиган сохасини курайлик. Бу ерда ![]() - биринчи якинлашиш
системаси характеристик тенгламасининг илдизлари. Бу илдизлар система параметрларининг
функцияларидир. (5.14.2) соха тадкик этилаётган тойилмаган харакатга нисбатан
турђунлик сохасидир, чунки (5.14.2) муносабат бажарилганда тойилмаган харакат
асимптотик турђун булади. Аксинча, акалли бирорта
- биринчи якинлашиш
системаси характеристик тенгламасининг илдизлари. Бу илдизлар система параметрларининг
функцияларидир. (5.14.2) соха тадкик этилаётган тойилмаган харакатга нисбатан
турђунлик сохасидир, чунки (5.14.2) муносабат бажарилганда тойилмаган харакат
асимптотик турђун булади. Аксинча, акалли бирорта ![]() илдизнинг хакикий кисми
мусбат булган параметрлар фазосининг барча нукталар мажмуаси нотурђунлик сохани
ташкил этади.
илдизнинг хакикий кисми
мусбат булган параметрлар фазосининг барча нукталар мажмуаси нотурђунлик сохани
ташкил этади.
Турђунлик
сохасини нотурђунлик сохасидан ажратадиган чегара параметрлар фазосининг
(5.14.2) тенгсизликларнинг хеч булмаганда бирортаси тенгликка айланадиган параметрлар
фазосининг барча нукталар мажмуасидан иборат, яъни чегарада ![]() ларнинг хеч
булмаганда айримлари критик илдизлар булади. Параметрларнинг чегара нукталарига
мос келувчи кийматларида тойилмаган харакат
ларнинг хеч
булмаганда айримлари критик илдизлар булади. Параметрларнинг чегара нукталарига
мос келувчи кийматларида тойилмаган харакат ![]() функциянинг ифодасига
караб турђун хам, нотурђун хам булиши мумкин.
функциянинг ифодасига
караб турђун хам, нотурђун хам булиши мумкин.
Система
параметрлари турђунлик сохасида ётади деб фараз килайлик, у холда барча ![]() илдизларнинг
хакикий кисми манфий ва тойилмаган харакат асимптотик турђун булади. Бу холда хар
кандай бошланђич шартлар учун барча
илдизларнинг
хакикий кисми манфий ва тойилмаган харакат асимптотик турђун булади. Бу холда хар
кандай бошланђич шартлар учун барча ![]() функциялар нолга
айланган такдирда хам тойилмаган харакат турђун булади. Аммо, агар
функциялар нолга
айланган такдирда хам тойилмаган харакат турђун булади. Аммо, агар ![]() функцияларнинг
баъзилари нолдан фаркли булса, у холда, умуман айтганда, бошланђич шартлар
маълум чегарадан чикмаган холдагина тойилмаган харакат турђун булади. Агар
характеристик тенглама илдизларининг хакикий кисмлари (микдор жихатдан) кичик булса,
яъни турђунлик сохасининг чегарасига якин булса, у холда мумкин булган
бошланђич тойилишларнинг максимал микдори етарли кичик булади. Агар хакикатан хам
шундай холат юз берса, у холда амалий нуктаи назардан бу системани нотурђун система
деб карашга туђри келади.
функцияларнинг
баъзилари нолдан фаркли булса, у холда, умуман айтганда, бошланђич шартлар
маълум чегарадан чикмаган холдагина тойилмаган харакат турђун булади. Агар
характеристик тенглама илдизларининг хакикий кисмлари (микдор жихатдан) кичик булса,
яъни турђунлик сохасининг чегарасига якин булса, у холда мумкин булган
бошланђич тойилишларнинг максимал микдори етарли кичик булади. Агар хакикатан хам
шундай холат юз берса, у холда амалий нуктаи назардан бу системани нотурђун система
деб карашга туђри келади.
Худди шундай холат система параметрлари нотурђунлик сохасида ётганда хам содир булиши мумкин (агар система чегарага жуда якин булса). Бу холда бошланђич тойилишларнинг максимал микдори жуда кичик булганда Ляпунов буйича тойилмаган харакат нотурђун булишига карамасдан, амалий нуктаи назардан уни турђун деб караш мумкин.
Мисол сифатида куйидаги дифференциал тенгламалар билан ифодаланган
![]() (5.14.3)
(5.14.3)
динамик
системанинг турђунлигини текширайлик, бу ерда ![]() - айрим узгармас
сон. Бу системанинг
- айрим узгармас
сон. Бу системанинг ![]() мувозанат холати
мавжуд ва у нотурђун, чунки биринчи якинлашиш
мувозанат холати
мавжуд ва у нотурђун, чунки биринчи якинлашиш ![]() системасининг
характеристик тенгламаси илдизи
системасининг
характеристик тенгламаси илдизи ![]() га тенг, яъни
мусбат сон. (5.14.3) системанинг умумий ечими
га тенг, яъни
мусбат сон. (5.14.3) системанинг умумий ечими
 (5.14.4)
(5.14.4)
куринишда
булади, бу ерда ![]() . (5.14.4) ифодага
асосан
. (5.14.4) ифодага
асосан ![]() да хам,
да хам, ![]() да
хам
да
хам ![]() хакикий кийматга
эга булади.
хакикий кийматга
эга булади.
Икки холда хам
![]() .
(5.14.5)
.
(5.14.5)
Бу
ердан яна бир марта ![]() мувозанат холатининг
нотурђунлиги келиб чикади, чунки бошланђич пайтда тойилиш хар канча кичик булмасин,
у маълум бир пайтда бирор тайин сондан катта булади, масалан,
мувозанат холатининг
нотурђунлиги келиб чикади, чунки бошланђич пайтда тойилиш хар канча кичик булмасин,
у маълум бир пайтда бирор тайин сондан катта булади, масалан, ![]() дан.
Аммо, бошка тарафдан, курилаётган масалада
дан.
Аммо, бошка тарафдан, курилаётган масалада ![]() нинг киймати
амалий жихатдан кичик булса, у холда
нинг киймати
амалий жихатдан кичик булса, у холда ![]() мувозанат холатидан
мувозанат холатидан
![]() га тенг микдорда
тойилиш амалий ахамиятга эга эмас ва бу мувозанат холати
га тенг микдорда
тойилиш амалий ахамиятга эга эмас ва бу мувозанат холати ![]() нинг хар
кандай бошланђич кийматлари учун амалий турђун деб айтилади.
нинг хар
кандай бошланђич кийматлари учун амалий турђун деб айтилади.
Аксинча, агар дифференциал тенглама
![]()
куринишда
булса, у холда характеристик тенгламанинг илдизи ![]() тенг, яъни манфий
булади ва шунинг учун хам
тенг, яъни манфий
булади ва шунинг учун хам ![]() мувозанат холати
(тойилмаган харакат) Ляпунов буйича асимптотик турђун булади. Аммо,
мувозанат холати
(тойилмаган харакат) Ляпунов буйича асимптотик турђун булади. Аммо, ![]() жуда
хам кичик сон булса, у холда амалий нуктаи назардан бундай тойилмаган харакатни
нотурђун деб карашга туђри келади, чунки агар
жуда
хам кичик сон булса, у холда амалий нуктаи назардан бундай тойилмаган харакатни
нотурђун деб карашга туђри келади, чунки агар ![]() нинг бошланђич киймати
нинг бошланђич киймати
![]() дан катта булса, у
вактда
дан катта булса, у
вактда ![]() булади. Хакикатан хам,
булади. Хакикатан хам,
![]() кийматлари учун
кийматлари учун ![]() тенгсизлик
уринлидир.
тенгсизлик
уринлидир.
Шундай килиб, амалий нуктаи назардан мухим булган динамик системанинг турђунлик сохасининг чегараси якинидаги хулки хакидаги масала келиб чикади. Бу масалани Нижний Новгородлик олим Н.Н.Баутин тадкик этган [12]. У турђунлик сохаси чегарасининг ёки битта илдиз, ёки иккита илдиз критик булган кисмларини тадкик этди. Иккинчи холда иккала илдиз хам нолдан фарк килади, яъни соф мавхум илдизлар деб каралган. Биринчи холда, битта критик илдиз булганлиги учун у, албатта, нолга тенг булади. Динамик системанинг турђунлик сохаси чегараси якинидаги хулки унинг чегаранинг узидаги хулки билан аникланишини Н.Н.Баутин исботлаган.
Хар икки холда хам тойилган харакат дифференциал тенгламаларини
![]() (5.14.6)
(5.14.6)
куринишда
ёзиш мумкин. Бу ерда ![]() - айрим узгармас
сонлар,
- айрим узгармас
сонлар, ![]() лар эса шундай узгармас
сонларки,
лар эса шундай узгармас
сонларки,
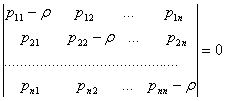 (5.14.7)
(5.14.7)
характеристик
тенгламанинг ёки битта илдизи нолга тенг, ёки иккита илдизи жуфт соф мавхум
илдиз булиб, колган барча илдизларининг хакикий кисми манфий ишорали булади. ![]() микдор
кичик кийматли параметр булиб, системанинг турђунлик сохасининг чегарасига кай
даражада якинлигини ифодалайди. Бу параметр шунчалик кичик деб хисобланадики,
микдор
кичик кийматли параметр булиб, системанинг турђунлик сохасининг чегарасига кай
даражада якинлигини ифодалайди. Бу параметр шунчалик кичик деб хисобланадики,
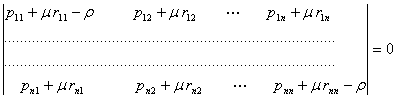
характеристик
тенгламанинг хакикий кисми манфий илдизларининг сони (5.14.7) нинг хакикий кисми
манфий илдизларининг сонига тенг, яъни ёки ![]() , ёки
, ёки ![]() тенг
булади. Бу тенгламанинг колган илдизларининг хакикий кисми хам манфий, хам
мусбат булиши, яъни (5.14.6) система хам турђунлик сохасида, хам нотурђунлик сохасида
булиши мумкин.
тенг
булади. Бу тенгламанинг колган илдизларининг хакикий кисми хам манфий, хам
мусбат булиши, яъни (5.14.6) система хам турђунлик сохасида, хам нотурђунлик сохасида
булиши мумкин.
а) Турђунлик сохасининг чегарасида курилаётган (5.14.6) система асимптотик турђун булсин. Бошкача килиб айтганда,
![]() (5.14.8)
(5.14.8)
системанинг
тойилмаган харакати асимптотик турђун булсин. У вактда, олдинги параграфларда курдикки,
битта нолга тенг илдизга эга булган холда хам, жуфт соф мавхум илдизга эга булган
холда хам (5.14.8) система учун Ляпуновнинг Б теоремасини каноатлантирувчи ![]() функция
мавжуд булади. Аниклик учун, бу функция аник мусбат ишорали булсин. У холда
унинг вакт буйича олинган тулик хосиласи
функция
мавжуд булади. Аниклик учун, бу функция аник мусбат ишорали булсин. У холда
унинг вакт буйича олинган тулик хосиласи
![]() (5.14.9)
(5.14.9)
аник
манфий ишорали функциядир. Теорема Б нинг геометрик талкинидан фойдаланамиз. ![]() ёпик
сиртлар системасини курамиз
ёпик
сиртлар системасини курамиз
 |
Координата
бошига (мувозанат холатига) етарлича якин жойлашган бу сиртларни (5.14.8) нинг
интеграл эгри чизиклари ташкаридан ичкарига караб кесиб утади (5.2-шакл). ![]() ва
ва
![]() шу сиртларнинг
иккитаси булсин. Бу сиртлардан биринчисини, (иккинчисининг ичида ётган деб каралади),
яъни
шу сиртларнинг
иккитаси булсин. Бу сиртлардан биринчисини, (иккинчисининг ичида ётган деб каралади),
яъни ![]() ) координата бошига
етарлича якин жойлаштиришимиз мумкин. Иккинчисини булса, аксинча, сиртлар
оиласидаги энг катта сиртга якин килиб оламиз. Бу катта сиртни хам (5.14.8)
нинг интеграл эгри чизиклари ташкаридан ичкарига караб кесади.
) координата бошига
етарлича якин жойлаштиришимиз мумкин. Иккинчисини булса, аксинча, сиртлар
оиласидаги энг катта сиртга якин килиб оламиз. Бу катта сиртни хам (5.14.8)
нинг интеграл эгри чизиклари ташкаридан ичкарига караб кесади.
Энди
![]() функциядан
(5.14.6) га кура вакт буйича тулик хосила оламиз
функциядан
(5.14.6) га кура вакт буйича тулик хосила оламиз
![]() . (5.14.10)
. (5.14.10)
![]() функция аник
манфий ишорали булганлиги учун
функция аник
манфий ишорали булганлиги учун ![]() ва
ва ![]() сиртлар
орасидаги барча нукталарда
сиртлар
орасидаги барча нукталарда ![]() тенгсизлик
бажарилади. (
тенгсизлик
бажарилади. (![]() - нолдан фарк килувчи
мусбат сон). Бу ердан, агар
- нолдан фарк килувчи
мусбат сон). Бу ердан, агар ![]() етарли кичик сон булса,
у холда бу нукталардан (5.14.10) ифода хам манфий ишорали кийматлар кабул килиши
келиб чикади. Демак, етарли кичик
етарли кичик сон булса,
у холда бу нукталардан (5.14.10) ифода хам манфий ишорали кийматлар кабул килиши
келиб чикади. Демак, етарли кичик ![]() учун
учун ![]() ва
ва
![]() сиртлар орасида
жойлашган барча сиртларни (5.14.6) тулик системанинг интеграл эгри чизиклари
ташкаридан ичкарига караб кесиб утадилар. (5.14.6) система турђунлик сохасидами
ёки нотурђунлик сохасидами эканлигига карамасдан бу холат узгармай колади.
сиртлар орасида
жойлашган барча сиртларни (5.14.6) тулик системанинг интеграл эгри чизиклари
ташкаридан ичкарига караб кесиб утадилар. (5.14.6) система турђунлик сохасидами
ёки нотурђунлик сохасидами эканлигига карамасдан бу холат узгармай колади.
Демак,
агар (5.14.6) системани ифодаловчи ![]() нукта
нукта ![]() ва
ва
![]() сиртлар орасига
тушиб колса, у холда у координата бошига караб якинлашади (хеч булмаганда
сиртлар орасига
тушиб колса, у холда у координата бошига караб якинлашади (хеч булмаганда ![]() сирт
билан чегараланган сохагача). Агар
сирт
билан чегараланган сохагача). Агар ![]() етарли кичик булса
(яъни система турђунлик сохасининг чегарасига етарли якин булса), у вактда бу
сохани етарлича кичик килиш мумкин.
етарли кичик булса
(яъни система турђунлик сохасининг чегарасига етарли якин булса), у вактда бу
сохани етарлича кичик килиш мумкин.
Агар
бу холда система нотурђунлик сохасида булса хам, биз тойилмаган харакатни амалий
турђун деб карашимиз мумкин, чунки дастлабки пайтда етарли кичик булган тойилишнинг
усишига карамасдан у амалда анча кичиклигича колади (етарли кичик ![]() учун
етарлича кичик булади). Бундан ташкари, агар бошланђич тойилишлар унча кичик булмаса
хам, улар кичрая бошлайди ва охирида етарли кичик булиб колади (етарли кичик
учун
етарлича кичик булади). Бундан ташкари, агар бошланђич тойилишлар унча кичик булмаса
хам, улар кичрая бошлайди ва охирида етарли кичик булиб колади (етарли кичик ![]() учун
етарлича кичик булади). Факат бошланђич тойилишлар
учун
етарлича кичик булади). Факат бошланђич тойилишлар ![]() сирт чегараланган
сиртдан ташкари чикадиган холдагина улар вакт утиши билан камаймаслиги мумкин.
сирт чегараланган
сиртдан ташкари чикадиган холдагина улар вакт утиши билан камаймаслиги мумкин.
Агар
система турђунлик сохасида булса, у холда ![]() функцияни шундай
танлаб олиш мумкинки, нафакат (5.14.9) ифода, балки (5.14.10) ифода хам манфий
ишорали булади.
функцияни шундай
танлаб олиш мумкинки, нафакат (5.14.9) ифода, балки (5.14.10) ифода хам манфий
ишорали булади.
Демак,
![]() деб кабул килиш
мумкин. Тойилмаган харакат асимптотик турђун булади. Бу холда бошланђич жоиз
тойилишлар учун аник чекли чегара мавжуд булади. Бу чекли чегара
деб кабул килиш
мумкин. Тойилмаган харакат асимптотик турђун булади. Бу холда бошланђич жоиз
тойилишлар учун аник чекли чегара мавжуд булади. Бу чекли чегара ![]() га,
яъни системанинг турђунлик сохасининг чегарасига якинлигига бођлик эмас.
га,
яъни системанинг турђунлик сохасининг чегарасига якинлигига бођлик эмас.
Шундай килиб, агар турђунлик сохасининг чегарасида система асимптотик турђун булса, у холда бу чегаранинг якинидаги турђунлик (агар у мавжуд булса) «амалий» нотурђунликка ута олмайди. Аксинча, агар чегаранинг якинида нотурђунлик мавжуд булса, у холда уни амалий нуктаи назардан турђун деб караш мумкин.
Юкорида келтирилган мулохазалар турђунлик сохасининг чегарасида исталганча сондаги критик илдизлар мавжуд булганда хам уз кучини саклайди ([35]нинг 310-317 бетларига каранг).
б)
Энди турђунлик сохаси чегарасининг курилаётган кисмида тойилмаган харакат
нотурђун булсин. У вактда икки холда хам (5.14.8) система учун Ляпуновнинг В теоремаси шартларини каноатлантирувчи ![]() функция
мавжуд ва демак, (5.14.9) ифода олдингидай аник ишорали булади.
функция
мавжуд ва демак, (5.14.9) ифода олдингидай аник ишорали булади. ![]() функциянинг
узи булса, координата бошининг етарли кичик атрофида (5.14.9) ифоданинг ишораси
билан бир хил ишорали киймат кабул килиши мумкин. Аниклик учун (5.14.9) ифода
аник мусбат ишорали булсин ва
функциянинг
узи булса, координата бошининг етарли кичик атрофида (5.14.9) ифоданинг ишораси
билан бир хил ишорали киймат кабул килиши мумкин. Аниклик учун (5.14.9) ифода
аник мусбат ишорали булсин ва ![]() сохани курамиз
(5.3-шакл). Бу соха
сохани курамиз
(5.3-шакл). Бу соха ![]() сирт билан
чегараланган. Бу сохада
сирт билан
чегараланган. Бу сохада ![]() сиртлар оиласини
чизамиз, бу ерда
сиртлар оиласини
чизамиз, бу ерда ![]() . (5.14.9) хосила
мусбат булганлиги учун (5.14.8) системанинг интеграл эгри чизиклари бу сиртларни
. (5.14.9) хосила
мусбат булганлиги учун (5.14.8) системанинг интеграл эгри чизиклари бу сиртларни
![]() нинг усиши томон
кесадилар (5.3-шаклга каранг).
нинг усиши томон
кесадилар (5.3-шаклга каранг). ![]() сиртлар оиласидан
иккита
сиртлар оиласидан
иккита ![]() ва
ва ![]() сиртларни
ажратамиз. Бу ерда
сиртларни
ажратамиз. Бу ерда ![]() ни исталганча
кичик килиб олиш мумкин. Демак,
ни исталганча
кичик килиб олиш мумкин. Демак, ![]() сирт
сирт ![]() сиртга
етарли якин булади. (5.14.9) функция аник мусбат ишорали булганлиги учун
сиртга
етарли якин булади. (5.14.9) функция аник мусбат ишорали булганлиги учун ![]() ва
ва
![]() сиртлар орасидаги
сохада у нолдан фарк килувчи мусбат аник куйи чегарага эга булади.
сиртлар орасидаги
сохада у нолдан фарк килувчи мусбат аник куйи чегарага эга булади.
 |
У
вактда агар ![]() нинг киймати
етарли кичик булса, бу сохада хам (5.14.10) хосиланинг киймати мусбат булади.
Демак,
нинг киймати
етарли кичик булса, бу сохада хам (5.14.10) хосиланинг киймати мусбат булади.
Демак, ![]() ва
ва ![]() сиртлар
орасида жойлашган барча
сиртлар
орасида жойлашган барча ![]() сиртларни нафакат
(5.14.8) системанинг интеграл эгри чизиклари, балки (5.14.6) системанинг хам
интеграл эгри чизиклари
сиртларни нафакат
(5.14.8) системанинг интеграл эгри чизиклари, балки (5.14.6) системанинг хам
интеграл эгри чизиклари ![]() нинг усиши томон кесиб
утадилар. Шунинг учун хам ифодаловчи нукта
нинг усиши томон кесиб
утадилар. Шунинг учун хам ифодаловчи нукта ![]() ва
ва ![]() сиртлар
орасидаги сохага тушгандан кейин
сиртлар
орасидаги сохага тушгандан кейин ![]() сиртнинг ташкарисига
чиккунча координата бошидан доимо узоклашади.
сиртнинг ташкарисига
чиккунча координата бошидан доимо узоклашади. ![]() сирт координата
бошидан чекли масофада туради. Равшанки, амалий нуктаи назардан тойилмаган харакат
хеч булмаганда нотурђун булади. Хакикатан хам, агар тойилмаган харакат хатто
турђун булса хам (бу хол агар (5.14.6) система турђунлик сохасида булгандагина
юз беради), жоиз бошланђич тойилишлар сохаси шундай кичик булиши керакки,
сирт координата
бошидан чекли масофада туради. Равшанки, амалий нуктаи назардан тойилмаган харакат
хеч булмаганда нотурђун булади. Хакикатан хам, агар тойилмаган харакат хатто
турђун булса хам (бу хол агар (5.14.6) система турђунлик сохасида булгандагина
юз беради), жоиз бошланђич тойилишлар сохаси шундай кичик булиши керакки, ![]() сирт
ундан ташкарида жойлашган булиши керак. Амалда
сирт
ундан ташкарида жойлашган булиши керак. Амалда ![]() сирт, етарли кичик
сирт, етарли кичик
![]() учун координата
бошига етарлича якин жойлашган булади.
учун координата
бошига етарлича якин жойлашган булади.
Шундай килиб, турђунлик сохасининг чегарасида тойилмаган харакат нотурђун булиб, агар система бу чегара якинида булса (турђунлик ёки нотурђунлик сохасида эканлигига карамасдан) доимо етарли кичик бошланђич тойилиш топиладики, улар вактнинг утиши билан усади ва натижада тойилган харакат тойилмаган харакатдан сезиларли даражада фарк килади, яъни тойилмаган харакат нотурђун булади.
Барча баён этилган мулохазалар шуни курсатаяптики, система турђунлик сохасининг чегарасига етарли якин турганда тойилмаган харакатнинг амалий турђун ёки нотурђун булиши шу системанинг чегарада Ляпунов буйича турђун ёки нотурђун булишига бођлик экан:
1.Агар турђунлик сохасининг чегарасида система асимптотик турђун булса, у холда чегарага якин сохада у амалий турђун булади.
2.Агар турђунлик сохасининг чегарасида система нотурђун булса, у холда чегарага якин сохада у амалий нотурђун булади.
Шу сабабли, тойилмаган харакат турђун булган турђунлик сохасининг чегарасига «хавфсиз» чегара ва нотурђун булган чегарага «хавфли» чегара деб айтилади. «Хавфли» ва «хавфсиз» чегараларни топиш масаласи критик холларда турђунликни тадкик этиш масаласига келтирилади.
Мисол. Автопилотли самолёт харакатининг турђунлиги
Мисол сифатида автопилотли самолётнинг харакатини ифодаловчи
 (5.14.11)
(5.14.11)
дифференциал
тенгламалар системасини куриб утамиз. Бу тенгламалар 1943 йилда Н.В.Бутенин
томонидан келтириб чикарилган эди [14]. Бу ерда ![]() - самолётнинг кидириш
(рыскание) бурчаги,
- самолётнинг кидириш
(рыскание) бурчаги, ![]() - рулни буриш бурчаги,
- рулни буриш бурчаги,
![]() - рул билан бошкариладиган
сервомоторнинг параметри,
- рул билан бошкариладиган
сервомоторнинг параметри, ![]() - сервомоторнинг
характеристикаси,
- сервомоторнинг
характеристикаси, ![]() - узгармас мусбат
сонлар, шу билан бирга
- узгармас мусбат
сонлар, шу билан бирга ![]() - самолётнинг
табиий демпфери,
- самолётнинг
табиий демпфери, ![]() - рул курилмасини
ва
- рул курилмасини
ва ![]() - самолётнинг
статик турђунлигини характерлайди,
- самолётнинг
статик турђунлигини характерлайди, ![]() - сунъий демпфер
коэффициенти,
- сунъий демпфер
коэффициенти, ![]() эса тескари алока
коэффициенти.
эса тескари алока
коэффициенти.
Сервомоторнинг характеристикасини куйидагича кабул киламиз
![]() .
.
У вактда куйидаги янги узгарувчиларни
![]()
киритиб, (5.14.11) системани куйидаги
 (5.14.12)
(5.14.12)
куринишга келтирамиз.
Биринчи якинлашиш системасининг характеристик тенгламаси
![]() (5.14.13)
(5.14.13)
куринишда булади. Бу ерда
![]() . (5.14.14)
. (5.14.14)
(5.14.13) характеристик тенгламанинг барча илдизларининг хакикий кисми манфий булиши учун
![]() (5.14.15)
(5.14.15)
тенгсизликларнинг бажарилиши етарли ва зарурдир. Бу тенгсизликлар система параметрларининг фазосида турђунлик сохасини аниклайдилар. Бу соханинг чегарасида (5.14.15) тенгсизликларнинг хеч булмаганда бирортаси тенгликка айланиши керак. (5.14.14) дан куриниб турибдики, факат охирги тенгсизлик тенгликка айланиши мумкин. Шундай килиб, турђунлик сохасининг чегараси
![]() (5.14.16)
(5.14.16)
тенглама билан аникланади.
Агар
(5.14.16) муносабат бажарилса, у холда (5.14.13) характеристик тенглама жуфт
соф ![]() илдизга эга булади. Демак, “хавфли” ва “хавфсиз”
чегара кисмларини топиш учун (5.14.12) системани иккинчи критик хол учун ечишга
туђри келади.
илдизга эга булади. Демак, “хавфли” ва “хавфсиз”
чегара кисмларини топиш учун (5.14.12) системани иккинчи критик хол учун ечишга
туђри келади.
(5.14.12)
тенгламалар системаси А.И.Лурье тадкик этган (5.12.17) системанинг хусусий холидир
(12-§ га каранг). Шунинг учун хам биз ![]() ни топиш учун (5.12.22) формуладан фойдаланишимиз мумкин.
Биз кураётган холда
ни топиш учун (5.12.22) формуладан фойдаланишимиз мумкин.
Биз кураётган холда
![]()
булганлиги учун (5.12.22) формула куйидагини беради
![]() .
.
Улчовсиз
![]()
параметрлар
киритганимиздан кейин ![]() нинг ишораси
нинг ишораси
![]()
микдорнинг ишорасига мос келади.
 |
Агар
![]() булса, у холда тойилмаган харакат асимптотик турђун булади
ва агар
булса, у холда тойилмаган харакат асимптотик турђун булади
ва агар ![]() булса, у холда у нотурђун булади.
булса, у холда у нотурђун булади.
![]() микдорни куйидаги куринишда ёзамиз:
микдорни куйидаги куринишда ёзамиз:
![]() .
.
![]() ва
ва ![]() параметрларни узгармас деб хисоблаб (фиксациялаб), А
ва В параметрлар текислигининг биринчи квадрантини курамиз (чунки А ва В параметрлар
факат мусбат киймат кабул киладилар).
параметрларни узгармас деб хисоблаб (фиксациялаб), А
ва В параметрлар текислигининг биринчи квадрантини курамиз (чунки А ва В параметрлар
факат мусбат киймат кабул киладилар). ![]() деб фараз киламиз.
деб фараз киламиз.
Бу шарт учун турђунлик сохасининг чегараси булган ![]() эгри чизик 5.4-шаклда курсатилгандай булади.
эгри чизик 5.4-шаклда курсатилгандай булади. ![]() эгри чизик
эгри чизик ![]() эгри
чизикни
эгри
чизикни ![]() нуктада кесади. Бу нукта турђунлик сохаси
чегарасининг “хавфли” кисмини “хавфсиз” кисмидан ажратиб турадиган нуктадир.
нуктада кесади. Бу нукта турђунлик сохаси
чегарасининг “хавфли” кисмини “хавфсиз” кисмидан ажратиб турадиган нуктадир. ![]() булганда,
булганда, ![]() эгри чизикнинг унг томонида
эгри чизикнинг унг томонида ![]() микдорнинг киймати манфий булади. Шунинг учун хам
турђунлик сохаси чегарасининг
микдорнинг киймати манфий булади. Шунинг учун хам
турђунлик сохаси чегарасининг ![]() кисми
“хавфсиз” ва
кисми
“хавфсиз” ва ![]() кисми
“хавфли” булади.
кисми
“хавфли” булади. ![]() булганда, чегаранинг “хавфли” ва “хавфсиз” кисмлари узаро
жойларни узгартирадилар.
булганда, чегаранинг “хавфли” ва “хавфсиз” кисмлари узаро
жойларни узгартирадилар. ![]() булганда,
булганда, ![]() эгри чизик биринчи квадрантда ётмайди.
эгри чизик биринчи квадрантда ётмайди.
|
РЕЖА: |
|
1. Характеристик тенглама. Битта нол илдизга эга булган хол. Дифференци- ал тенгламаларни махсус куринишга келтириш. |
|
2. Биринчи тартибли система учун масалани тадкик этиш. |
|
3. |
|
4. |
|
5. Махсус холда турђунлик масаласини тадкик этиш. |
|
6. Жуфт соф мавхум илдизлар холи. Тойилган харакат тенгламаларини мах- сус куринишга келтириш. |
|
7. Иккинчи тартибли система. Масалани ечишнинг биринчи усули. |
|
8. Иккинчи тартибли система. Ляпунов функциясини тузиш усули билан ма- салани ечиш. |
|
9. Иккинчи тартибли система. Масалани ечишнинг учинчи усули. |
|
10. |
|
11. |
|
12. |
|
13. Турђунлик сохасининг «хавфли» ва «хавфсиз» чегаралари. |
Таянч иборалар. Характеристик тенглама, тенгламаларнинг махсус куриниши, биринчи тартибли система учун масалани тадкик этиш, (n+1)- тартибли система учун масалани хусусий ва умумий холда тадкик килиш, масалани ечишнинг алгоритми, мисоллар, махсус хол, жуфт соф мавхум илдизлар холи, масалани ечишнинг усуллари, автоматик ростлаш системаси, турђунлик масаласини ечишнинг алгоритми, муаян динамик системаларни тадкик этиш, «хавфли» ва «хавфсиз» чегаралар.
Такрорлаш учун саволлар:
1. Битта нол илдизга эга булган хол учун дифференциал тенгламаларнинг махсус куриниши.
2. Биринчи тартибли система учун масалани тадкик килинг.
3. Хусусий холда (n+1) – тартибли системани тадкик килинг.
4. Умумий холда (n+1) – тартибли системани тадкик килинг.
5. Битта нол илдизга эга булган муаян динамик системаларни тадкик килинг.
6. Махсус холда турђунлик масаласини тадкик килинг.
7. Жуфт соф мавхум илдизлар холи. Харакат тенгламаларини махсус куринишга келтириш.
8. Иккинчи тартибли системалар учун масалани ечишнинг биринчи усули.
9. Ляпунов функциясини тузиш усули билан масалани ечинг.
10. (n+2) – тартибли системани хусусий холда тадкик этинг.
11. (n+2) – тартибли системани умумий холда тадкик этинг.
12. (n+2) – тартибли системани махсус холда тадкик этинг.
13. Турђунлик сохасининг «хавфли» ва «хавфсиз» чегаралар.
14.