IV-БОБ. БАРКАРОР ХАРАКАТЛАР УЧУН БИРИНЧИ ЯКИНЛАШИШ УСУЛИ БУЙИЧА ТУРГУНЛИК КРИТЕРИЯЛАРИ

Куп холларда, асосан амалиётда, харакатнинг тургунлигини биринчи якинлашиш тенгламалари асосида тадкик киладилар. Аммо, китобнинг 1-бобида курсатгани-миздек, биринчи якинлашиш тенгламалари харакат тургунлиги хакида умуман нотугри хулосалар бериши мумкин. Шунинг учун хам шундай шартларни топиш масаласи тугиладики, бу шартлар бажарилганда, биринчи якинлашиш тенгламалари асосида харакат тургунлиги хакида тугри жавоб бериш мумкин булсин. Бошкача килиб айтганда, кандай шартлар бажарилганда, биринчи якинлашиш тенгламалари асосида тургунлик хакида олинган натижалар тугри булади деган муаммо пайдо булади. Бу муаммо XIX асрнинг иккинчи ярмида пайдо булди ва уни россиялик олим А.М.Ляпунов (6.VI.1857 – 3.XI.1918) 1892 йили узининг докторлик диссертациясида автоном системалар ва баъзи бир ноавтоном системалар учун ечди.

Бу бобда баркарор харакатлар учун биринчи якинлашиш усули буйича тургунлик мезонларини (етарли ва зарур шартларни) баён этамиз.

1-§. Биринчи якинлашиш тенгламалари

Бирор система тойилган харакатининг дифференциал тенгламалари куйидаги куринишда берилган булсин

. (4.1.1)

Бу ерда - узгармас сонлар, вактга боглик булмаган узгарувчиларнинг функциялари ва

(4.1.2)

сохада уша узгарувчилар даражалари буйича каторга ёйилувчи ва ёйилмаси биринчи хадининг даражаси иккидан кам булмаслиги керак.

(4.1.1) системанинг биринчи якинлашиш тенгламалари

. (4.1.3)

Бу тенгламаларнинг хусусий ечимлари куйидаги куринишда изланади:

, (4.1.4)

бу ерда , - узгармас сонлар. (4.1.4) ларнинг вакт буйича хосиласи

(4.1.5)

га тенг булади. ва ларнинг кийматларини (4.1.4) ва (4.1.5) лардан (4.1.3) га келтириб куйиб ва нолга тенг булмаган умумий купайтувчига кискартириб, хадларни гурухлаганимиздан кейин

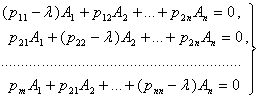(4.1.6)

аникмас узгармас сонларга нисбатан бир жинсли чизикли алгебраик тенгламалар системасига келамиз. Бу система нолдан фарк килувчи ечимга (акс холда хамма ) эга булиши учун унинг детерминанти нолга айланиши зарур:

. (4.1.7)

Бу ердан куйидагини хосил киламиз

, (4.1.8)

бунда коэффициентлар (4.1.3) тенгламалардаги коэффициентларнинг функциялари булади . (4.1.7) ни характеристик детерминант ва (4.1.8) ни (4.1.3) биринчи якинлашиш тенгламалари системасининг га нисбатан характеристик тенгламаси деб атаймиз.

Алгебранинг асосий теоремасига асосан (4.1.8) характеристик тенглама та илдизларга эга булади.

а) Агар характеристик тенглама илдизлари орасида карралилари булмаса (яъни бир-бирига тенг эмас), у холда хар доим шундай хосмас чизикли алмаштириш

(4.1.9)

мавжудки (бу ерда - кандайдир узгармас сонлар), у (4.1.3) биринчи якинлашиш тенгламаларини куйидаги куринишга келтиради

(4.1.10)

узгарувчиларга каноник узгарувчилар деб айтамиз. Агар (4.1.9) алмаштиришларни (4.1.1) тойилган харакат тенгламаларига нисбатан кулласак, у холда куйидагини хосил киламиз:

(4.1.11)

бу ерда - ночизикли хадлар, ёйилмаси ларга нисбатан камида иккинчи даражали хадлардан бошланади.

Характеристик тенгламанинг хар кандай комплекс илдизига битта кушма илдиз мос келади (, - хакикий узгармас сонлар). Уларга ва комплекс – кушма каноник узгарувчилар мос келадилар, бу ерда ва - t нинг хакикий функцияси. Характеристик тенгламанинг хакикий илдизларига хакикий каноник узгарувчилар мос келади.

(4.1.9) алмаштиришнинг коэффициентлари узгармас сонлар булганликлари учун тойилмаган харакатнинг узгарувчиларга нисбатан тургунлигидан (нотургунлигидан) каноник узгарувчиларга нисбатан тургунлиги (нотургунлиги) келиб чикади ва аксинча.

Курилаётган системанинг тойилган харакат дифференциал тенгламалари (4.1.3) куринишда булсин ёки каноник узгарувчиларда – (4.1.10) куринишда, яъни чизикли булсин. лар бир-бирига тенг булмаганликлари учун (оддий илдизлар), (4.1.10) тенгламалар хам бир-бирига боглик эмас. Улар осон интегралланади ва умумий ечим куйидаги куринишга эга:

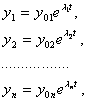(4.1.12)

бу ерда - ларнинг t=0 пайтдаги (бошлангич) кийматлари.

характеристик тенгламанинг илдизи булсин. Агар ва булса, комплекс илдизга, ва булса соф мавхум илдизга, ва булса, хакикий илдизга, булганда эса нол илдизга эга буламиз. Маълумки,

ёки хар кандай ва t лар учун булишини хисобга олиб,

(4.1.13)

ни хосил киламиз. да (4.1.13) тенгликдан куйидагилар келиб чикади:

а) агар булса, у холда ,

б) агар булса, у холда

, (4.1.14)

в) агар булса, у холда .

Демак, агар характеристик тенгламанинг илдизлари оддий булсалар, у холда (4.1.12) умумий ечим ва (4.1.14) муносабатлардан чизикли автоном система харакатининг тургунлиги хакидаги куйидаги теоремалар келиб чикади:

1.Агар характеристик тенгламанинг барча илдизларининг хакикий кисми манфий ишорали булса (), у холда тойилмаган харакат асимптотик тургун булади ( да хамма );

2.Агар характеристик тенглама илдизларидан хеч булмаганда биттасининг хакикий кисми мусбат булса, у холда тойилмаган харакат нотургун булади ( да хеч булмаганда битта );

3.Агар характеристик тенглама илдизларидан бирор кисмининг хакикий кисми нолга тенг ва колганларининг хакикий кисми манфий булса, у холда тойилмаган харакат тургун (асимптотик эмас) булади (барча лар чегараланган ва уларнинг бир кисми нолга интилади).

б)Характеристик тенгламанинг бирорта илдизи каррали булсин. Бу илдизга аввалгидай

(4.1.4,а)

ечим мос келади, бу ерда хам лар (4.1.6) тенгламаларни каноатлантиради. Аммо бу холда илдизга (4.1.3) тенгламанинг (4.1.4,а) дан фарк килувчи бошка хусусий ечимлари хам мос келади. Бу ечимлар

(4.1.15)

куринишда булиб, бу ерда - бирор t га нисбатан купхад [78]. Бу купхадларнинг даражаси хеч качон дан катта эмас, аммо дан кичик булиши мумкин.

Бу ерда детерминантнинг ((4.1.7) га каранг) ранги га тенгми ёки ундан кичик булишига караб, икки хол юз бериши мумкин.

Изох. Асосий детерминантдан сатр ва устунни учиришдан хосил булган детерминант - тартибли минор деб аталади. Агар дан кичик тартибли барча минорлари нолга тенг булган холда, акалли битта - тартибли минори нолдан фаркли булса, бу детерминантнинг ранги га тенг деб айтилади.

детерминантнинг ранги га тенг булсин, у холда (4.1.3) тенгламанинг куйидаги та ечими мавжуд булади:

(4.1.16)

Бу ечимлар чизикли богланмаган (эркиндир). Охиргиси (4.1.4,а) га мос булади. Демак, каррали илдизга бир гурух ечим мос келяпти.

Агар детерминантнинг ранги га тенг булса, у холда каррали илдизга та чизикли богликмас ечимлар мос келади, аммо энди бу ечимлар икки гурухга булинади:

(4.1.17)

бу ерда , -тартибли, эса -тартибли купхад.

Умуман, агар детерминантнинг ранги га тенг булса, у холда каррали илдизга аввалгидай та чизикли богликмас ечимлар мос келади ва бу ечимлар (4.1.17) га ухшаган та гурухга булинади.

детерминантнинг ранги дан кичик булолмайди. Акс холда, илдизнинг карраси дан катта буларди [78]. Шунинг учун хам каррали илдизга мос келувчи ечимлар гурухининг сони дан катта була олмайди. Агар гурухлар сони га тенг булса, у холда хар бир гурух битта ечимдан иборат ва хамма ечимлар (4.1.4,а) куринишда булади.

Шундай килиб, барча холларда хам (4.1.3) тенгламаларнинг каррали илдизига мос келган хусусий ечимлари сони шу илдиз неча каррали булса, шунча булади.

Бу ечимларни топиш, чизикли алгебраик тенгламалар системасини ечиш масаласига келтирилади. Н.Г.Четаев томонидан бундай тенгламаларни тузишнинг энг содда усули курсатилган [102].

(4.1.8) характеристик тенгламанинг хамма илдизларини топгандан кейин, биз (4.1.3) тенгламаларнинг чизикли богликлимас та хусусий ечимини топамиз. Бу ечимларни деб белгилаб (биринчи индекс – функция ракамлари, иккинчи индекс – ечим раками), (4.1.3) тенгламанинг умумий ечимини топамиз:

, (4.1.18)

бу ерда - ихтиёрий узгармас сонлар ва улар дастлабки (бошлангич) шартлардан топилади. Агар кайси бир ечимда нинг бошлангич киймати етарли кичик микдор булса, у холда бу ечимга мос келган сон хам етарлича кичик сон булади.

Характеристик тенгламанинг баъзи илдизларининг хакикий кисми нолга тенг ва барча колган илдизларининг хакикий кисми манфий ишорали булсин. У вактда бу илдизлар ёки нолга тенг, ёки соф мавхум сонга тенг буладилар. Хар бир нолга тенг булган илдизга, агар у оддий илдиз булса ёки илдиз каррали булганда хам унга мос келган ечимларнинг гурухлар сони илдиз каррасига тенг булса, у холда

(4.1.19)

ечим мос келади. Акс холда (4.1.3) системага

(4.1.20)

ечим мос келади ((4.1.15) га каранг), бу ерда - купхадлар. Хар бир соф мавхум илдизга, агар у оддий илдиз ёки каррали хамда унга мос келган ечимларнинг гурухлар сони илдиз каррасига тенг булса, у холда

(4.1.21)

ечим мос келади, бу ерда - хакикий узгармас сонлар (). Агар илдизлар каррали булсалар ва уларга мос келган ечимлар гурухларининг сони илдизнинг каррасидан кичик булса, у холда (4.1.3) система шу илдизларга мос келган

(4.1.22)

ечимга эга булади, бу ерда ва - купхадлар ().

(4.1.19) ёки (4.1.21) куринишдаги ечимларнинг борлиги харакат тургунлигини бузмайди, чунки ечимга кирувчи хамма функциялар чегараланган, (4.1.20) ёки (4.1.22) куринишдаги ечимларнинг мавжудлиги эса нотургун харакатга олиб келади.

Шундай килиб, агар характеристик тенглама илдизлари орасида каррали илдизлар мавжуд булса, у холда икки хол юз беради:

а) агар каррали илдизга мос келган (4.1.3) тенгламалар ечимларининг гурухлари сони илдизнинг каррасига тенг булса, у холда тойилмаган харакат тургунлигини тадкик этиш натижалари худди характеристик тенглама хамма илдизлари оддий илдизлар булгандаги каби булади, яъни юкорида келтириб чикарилган 1-3 теоремалар уз кучини саклайди.

б) агар каррали илдизга мос келган (4.1.3) тенгламалар ечимларининг гурухлари сони илдизнинг каррасидан кичик булса, у холда характеристик тенгламанинг хамма илдизлари оддий илдизлар булганда олинган натижалардан, бу хол учун факат 1-2 теоремаларгина уз кучини саклайди ва 3-теорема эса уз кучини йукотади, яъни тойилмаган харакат нотургун булади.

Демак, агар тойилган харакатнинг дифференциал тенгламалари (4.1.3) куринишда булса, у холда биз куйидаги натижаларга келамиз:

1.Тойилмаган харакат асимптотик тургун булиши учун, характеристик тенгламанинг барча илдизларининг хакикий кисмлари манфий булиши етарли ва зарурдир;

2.Агар характеристик тенгламанинг илдизлари орасида хеч булмаганда биттасининг хакикий кисми мусбат булса, у холда тойилмаган харакат нотургун булади;

3.Агар характеристик тенглама хакикий кисми мусбат илдизларга эга булмай, хакикий кисми нолга тенг булган оддий ёки каррали илдизларга эга ва каррали илдизлар холида хар бир илдизга мос келган ечимларнинг гурухлари сони, шу илдизнинг каррасига тенг булса, у холда тойилмаган харакат тургун булади. Агар характеристик тенгламанинг хакикий кисми нолга тенг хар бир каррали илдизига мос ечимларнинг гурухлари сони шу илдизнинг каррасидан кичик булса, у холда тойилмаган харакат нотургун булади.

Шундай килиб, чизикли системанинг тойилмаган харакати тургунлигини текшириш масаласи чизикли тойилган харакат тенгламалари характеристик тенгламасининг илдизларини текшириш масаласига, яъни алгебраик масалага келтирилди. Бу ерда Ляпуновнинг иккинчи усулини куллашнинг хожати йук. Шунга карамасдан биз (4.1.3) тенгламалар учун Ляпунов функциясини ясаш усулларини урганамиз, чунки бу функциялар булажак тадкикотларимизда фундаментал рол уйнайди. Бунинг учун айрим ёрдамчи мулохазалар билан танишишга тугри келади.

2-§. Баъзи ёрдамчи мулохазалар

Фараз килайлик, функция - тартибли форма булсин. Бу форманинг (4.1.3) тенгламаларга нисбатан вакт буйича олинган тулик хосиласини курамиз:

. (4.2.1)

функция хам - тартибли форма булади.

(4.2.2)

муносабатни каноатлантирувчи V формани топишни максад килиб куямиз, бу ерда -узгармас сон. Изланаётган форманинг коэффициентлари кандайдир тенгламалар системасини каноатлантириши керак. Бу системани (4.2.2) тенгламанинг чап ва унг тарафидаги ухшаш хадларнинг коэффициентларини тенглаштириш йули билан хосил киламиз. Бу системани хосил этишни булган хол, яъни

(4.2.3)

учун курсатамиз.

(4.2.3) ни (4.2.2) га куйиб ва чап хамда унг тарафдаги лар олдидаги коэффициентларни тенглаштириб, коэффициентлар каноатлантириши лозим булган куйидаги тенгламалар системасини топамиз:

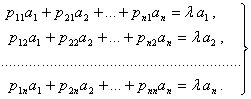
Бу чизикли бир жинсли тенгламалар системаси нолдан фаркли ечимга эга булиши учун унинг детерминанти

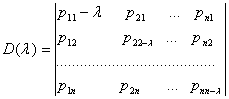
нолга тенг булиши етарли ва зарурдир. Шундай килиб, (4.2.2) тенгламани (4.2.3) чизикли форма каноатлантириши учун характеристик тенгламанинг илдизи булиши етарли ва зарур. Характеристик тенгламанинг хар бир илдизига битта (4.2.3) чизикли форма мос келади. Агар характеристик тенглама та хар хил илдизга эга булса, у холда (4.2.2) муносабатни каноатлантирувчи та чизикли формага эга буламиз.

Энди булсин, яъни . билан -тартибли форма хадларининг сонини, яъни аникмас коэффициентларнинг сонини белгилаймиз.

Бу сон

(4.2.4)

тенглик оркали аникланишини 2-бобда курган эдик, бу ерда

, (4.2.5)

лар манфиймас бутун сонлар. V форманинг узгарувчилари олдидаги коэффициентларни лар билан белгилаймиз. Уларни (4.2.2) тенгламага куйгандан сунг, чап ва унг тарафдаги ухшаш хадлар олдидаги коэффициентларни тенглаштириб, ларни аниклаш учун куйидаги бир жинсли чизикли тенгламаларни хосил киламиз:

, (4.2.6)

бу ерда лар коэффициентларнинг чизикли комбинациясидан иборат узгармас сонлар. Масалан, ва булганда, (4.2.6) система куйидаги куринишга эга:

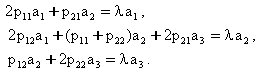
(4.2.6) система нолдан фарк килувчи ечимга эга булиши учун куйидаги тенгламани

(4.2.7)

каноатлантириши етарли ва зарурдир.

Шундай килиб, - тартибли форма V (4.2.2) тенгламанинг ечими булиши учун алгебраик тенглама (4.2.7) нинг илдизи булиши етарли ва зарурдир.

(4.2.7) тенгламанинг илдизлари билан характеристик тенглама илдизлари орасидаги оддий муносабатни Ляпуновнинг куйидаги теоремаси аниклаб беради.

1-теорема. (4.2.7) тенгламанинг барча илдизлари

(4.2.8)

формула оркали аникланади, бу ерда - характеристик тенглама илдизлари, - куйидаги

. (4.2.9)

муносабат билан богланган манфиймас бутун сонлар.

Теореманинг исботини Н.Г.Малкиннинг [53, 64-66 бетлар] ва Н.Г.Дубошиннинг [26, 152-154 бетлар] китоб-ларидан топиш мумкин.

Берилган - форма - тартибли булсин. Куйидаги

(4.2.10)

тенгламани каноатлантирувчи - тартибли формани аниклаймиз.

V форманинг коэффициентларини ва берилган форманинг коэффициентларини билан белгилаймиз. коэффициентларни аниклаш учун (4.2.10) тенгламанинг чап ва унг тарафидаги ухшаш хадларнинг коэффициентларини тенглаштириб, куйидаги алгебраик тенгламалар системасини хосил киламиз:

. (4.2.11)

Бу тенглама (4.2.6) дан факат унг тарафидаги ифода билан фарк килади, яъни (4.2.6) даги урнига (4.2.11) да турибди.

(4.2.11) системанинг детерминанти

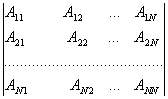
билан мос келади ((4.2.7)га каранг). Агар нолга тенг булмаса, у холда (4.2.11) тенгламанинг ягона битта ечими бор ва, демак, (4.2.10) ни каноатлантирувчи ягона V форма мавжуд булади. Аммо, купхаднинг хамма илдизлари (4.2.8) тенглама оркали аникланади. Шундай килиб куйидаги Ляпунов теоремасига келамиз:

2-теорема. Агар характеристик тенгламанинг илдизлари шундай булсаки, (4.2.10) муносабат билан богланган манфий бутун сонларнинг хеч бир кийматида (4.2.8) нолга айланмаса, у холда олдиндан берилган - тартибли форманинг кандай булишидан катъий назар (4.2.10) тенгламани каноатлантирувчи битта ва факат битта уша тартибли форма мавжуд булади.

3-§. Узгармас коэффициентли чизикли тенгламалар системаси учун Ляпунов функциясини тузиш

Узгармас коэффициентли чизикли тенгламалар системаси

(4.3.1)

учун Ляпунов функциясини тузиш усулларини куриб утамиз.

1.Тойилмаган харакат асимптотик тургун булсин. Бу хол факат характеристик тенгламанинг хамма илдизларининг хакикий кисми манфий булгандагина юз беради. Курилаётган холда 2-бобдаги теорема Б нинг хамма шартларини каноатлантирувчи функция мавжуд буладими? Бунга куйидаги теорема ижобий жавоб беради.

1-теорема. Агар характеристик тенгламанинг барча илдизларининг хакикий кисми манфий булса, у холда олдиндан берилган аник ишорали форма кандай булишидан катъий назар

(4.3.2)

тенгламани каноатлантирувчи битта ва факат битта уша тартибли форма мавжуд буладики, у албатта ишораси нинг ишорасига тескари булган аник ишорали форма булади.

Исбот. Характеристик тенгламанинг хамма илдизларнинг хакикий кисми манфий булганлигидан бир вактда нолга тенг булмайдиган манфиймас бутун сонларнинг хеч бир кийматида (4.2.8) микдор нолга тенг булмайди. Шунинг учун хам 2-§ даги 2-теоремага асосан (4.3.2) ни каноатлантирувчи битта ва факат битта форма мавжуд булади. Энди, агар аник ишорали форма булса, у холда V хам ишораси нинг ишорасига тескари булган аник ишорали форма булишини исбот килишимиз керак.

Аниклилик учун, - аник манфий ишорали форма булсин. V формани курамиз. Уч хол булиши мумкин: 1) V форма манфий ишорали кийматлар кабул килиши мумкин; 2) V – узгармас мусбат ишорали форма; 3) V – аник мусбат ишорали форма.

Агар биринчи хол юз берса, у холда V функция теорема В нинг хамма шартларини каноатлантирган булади ва, демак, тойилмаган харакат нотургун булади. Бу шартга зиддир.

Иккинчи хол хам булиши мумкин эмас. Хакикатан хам, ни (4.3.1) ни каноатлантирувчи функция сифатида караб, унинг бошлангич кийматини шундай танлаб оламизки, булсин. Бу мумкин, чунки шарт буйича V узгармас ишорали форма (аник ишорали форма эмас). Аммо манфий булгани учун V камаювчи функция булади ва, демак, V манфий ишорали функция булиб колади. Бу унинг узгармас мусбат ишорали функция эканлигига зиддир. Демак, бу хол хам булиши мумкин эмас.

Шундай килиб, факат учинчи хол колади.

Демак, V – аник мусбат ишорали форма булади. Исбот этилганига кура V функция теорема Б нинг хамма шартларини каноатлантиради ва, демак, курилаётган хол учун Ляпунов функцияси булади.

Шундай килиб, узгармас коэффициентли чизикли тенгламалар системасининг характеристик тенгламасининг барча илдизларининг хакикий кисми манфий булган холда Ляпунов функциясини тузиш учун ихтиёрий тартибли аник ишорали формани олиш керак ва вакт буйича олинган тулик хосиласи бу формага тенг булган иккинчи формани излаш керак булади. Олдинги параграфда курдикки, бу масала алгебраик тенгламалар системасини ечишга келтирилади. Агар олдиндан олинган форма катта тартибли булса, у холда хисоблаш жараёни мураккаб булади. Шунинг учун хам форма сифатида доимо кандайдир аник ишорали квадратик формани, масалан, лар квадратларининг йигиндисини олиш маъкулдир,

2.Характеристик тенглама илдизларининг хеч булмаганда биттасининг хакикий кисми мусбат булсин. У вактда (4.3.1) тенгламалар учун тойилмаган харакат нотургун булади. Теорема В ёки теорема Г шартларини каноатлантирувчи Ляпунов функциясининг мавжудлиги ва уни топишнинг йулини куйидаги Ляпунов теоремалари курсатиб беради.

2-теорема. Агар характеристик тенгламанинг илдизлари орасида хеч булмаганда битта хакикий кисми мусбат ишорали илдиз мавжуд булса ва агар бу илдизлар шундай булсаки,

(4.3.3)

микдор

(4.3.4)

муносабат билан богланган манфиймас бутун сонларнинг хеч бир кийматида нолга айланмаса, у холда олдиндан берилган -тартибли аник ишорали форма кандай булишидан катъий назар (4.3.2) тенгламани каноатлантирувчи уша тартибли битта ва факат битта V форма мавжуд булади ва у ишораси га тескари булган узгармас ишорали (кисман, аник ишорали) форма булмаслиги мумкин.

Исбот. Фараз килайлик, ихтиёрий -тартибли аник ишорали форма булсин. Аниклик учун, у аник мусбат ишорали деб хисоблаймиз. Олдинги параграфнинг 2-теоремасига асосан (4.3.2) тенгламани каноатлантирувчи битта ва факат битта уша тартибли V форма мавжуд булади. Биз бу форманинг на аник манфий ишорали ва на узгармас манфий ишорали форма булолмаслигини исбот килишимиз керак. Хакикатан хам, агар V аник манфий ишорали форма булганида эди, у холда V теорема Б нинг хамма шартларини каноатлантирган ва, демак, тойилмаган харакат асимптотик тургун буларди. Аммо, бу мумкин эмас, чунки тойилмаган харакат нотургун.

Иккинчи тарафдан, V узгармас манфий ишорали форма булолмайди (характеристик тенглама илдизлари кандай булишидан катъий назар). Бунга ишониш учун, худди олдинги теоремани исбот килгандай, V формани бошлангич кийматлари нолга айлантирадиган (4.3.1) тенгламанинг бирорта ечимини куриш кифоя. Бу ечим учун, мусбат ишорали булганлиги сабабли, V функция усади ва мусбат кийматлар кабул килади. Бу шартга зиддир. Шундай килиб, теорема тулик исбот этилди.

Теоремадаги V функция теорема В нинг хамма шартларини каноатлантирувчи Ляпунов функциясидир.

Изох. Исбот этилган теорема факатгина (4.3.3) ифода нолга айланмайдиган хол учун V функцияни тузиш усулини беради. Аммо бу шарт бажарилмаслиги мумкин. Масалан, характеристик тенгламанинг айрим илдизлари нолга тенг булганда, (4.3.3) ифода нолга айланади ва, демак, теорема В ни каноатлантирадиган V функция мавжуд булмайди. Аммо, бу холда теорема Г ни каноатлантирувчи функция мавжуд. Бу функциянинг мавжудлигини ва унинг куринишининг кандай булишини куйидаги теорема курсатиб беради.

3-теорема. Агар характеристик тенгламанинг илдизлари орасида хеч булмаганда битта хакикий кисми мусбат булган илдиз мавжуд булса, у холда олдиндан берилган ихтиёрий - тартибли аник ишорали форма кандай булишидан катъий назар, доимо

(4.3.5)

муносабатни каноатлантирувчи уша тартибли V форма хамда мусбат сон топилади ва V ишораси нинг ишорасига тескари булган узгармас ишорали форма булмаслиги мумкин.

Теореманинг исботини И.Г.Малкиннинг [53,70-71 бетлар] китобидан топиш мумкин.

Кейинги икки параграфда исбот этилган теоремаларнинг мухимлиги шундан иборатки, характеристик тенглама илдизларининг хусусиятларини билган холда, биз баъзи тенгламаларни каноатлантирувчи V функциянинг мавжудлигини аниклаймиз ва бу уша тенгламанинг ечимини топиш заруриятидан бизни халос этади.

Исбот этилган теоремаларни куллаш учун факатгина илдизларни билишни ёки уларнинг хусусиятларини аниклашни талаб килинади. Бу эса алгебраик масалани ечиш билан хал этилади.

4-§. Биринчи якинлашиш буйича тургунлик хакидаги

Ляпунов теоремалари

Энди биз Ляпуновнинг асосий теоремаларини исбот кила оламиз. Бу теоремалар тойилмаган харакатнинг тургунлигини тадкик этиш масаласини баъзи алгебраик тенгламаларнинг илдизларини текшириш масаласига келтиради.

Тойилган харакатнинг дифференциал тенгламалари

(4.4.1)

куринишда берилган булсин, бу ерда функция

(4.4.2)

сохада ларнинг даражалари буйича каторга ёйилади ва бу каторнинг бошлангич хадининг даражаси иккидан кам булмайди, эса узгармас сонлар. (4.4.1) тенгламалар системасининг биринчи якинлашиш тенгламалари системаси

(4.4.3)

куринишда, (4.4.3) системанинг характеристик тенгламаси эса

(4.4.4)

куринишга эга булади, бу ерда лар коэффициентларнинг функциялари булади.

1-теорема. Агар биринчи якинлашиш тенгламалари системасининг характеристик тенгламасининг барча илдизларининг хакикий кисми манфий булса, у холда тойилган харакатнинг дифференциал тенгламаларидаги юкори даражали хадларнинг кандай булишидан катъий назар тойилмаган харакат асимптотик тургун булади.

Исбот. Характеристик тенгламанинг хамма илдизларининг хакикий кисми манфий булсин. У вактда 3-§ даги 1-теоремага асосан

тенгламани каноатлантирувчи V форма мавжуд булади ва у албатта аник мусбат ишорали булади (чунки унинг ишораси нинг ишорасига тескари булиши керак). Бу форманинг (4.4.1) тойилган харакатнинг дифференциал тенгламаларига асосан вакт буйича олинган тулик хосиласини топамиз:

функциянинг ёйилмаси камида учинчи тартибли хад билан бошланганлиги туфайли, функция, 2-бобдаги 4-леммага асосан, функцияларнинг кандай булишидан катъий назар аник манфий ишорали булади.

Шундай килиб, V функция (4.4.2) сохада аник мусбат ишорали функция ва аник манфий ишорали функциядир. Демак, V функция теорема Б нинг хамма шартларини каноатлантиради ва тойилмаган харакат асимптотик тургун булади. Теорема исботланди.

2-теорема. Агар характеристик тенгламанинг илдизлари орасида хеч булмаганда битта хакикий кисми мусбат ишорали илдиз мавжуд булса, у холда тойилган харакатнинг дифференциал тенгламаларидаги юкори даражали хадларнинг кандай танлаб олинишидан катъий назар тойилмаган харакат нотургун булади.

Исбот. Характеристик тенглама илдизлари орасида хеч булмаганда биттасининг хакикий кисми мусбат булсин. У вактда 3-§ даги 3-теоремага асосан

тенгламани каноатлантирувчи V форма ва сон мавжуд ва V форма мусбат кийматлар кабул килиши мумкин.

Бу формадан (4.4.1) тойилган харакат тенгламаларига асосан вакт буйича олинган тулик хосила

куринишга эга, бу ерда

функция 2-бобдаги 4-леммага асосан аник мусбат ишоралидир.

Шундай килиб, V функция мусбат кийматлар кабул килганлиги ва W функция аник мусбат ишорали булганлиги учун V функция Ляпуновнинг теорема Г сини каноатлантиради ва, демак, функцияни кандай танлаб олишимиздан катъий назар тойилмаган харакат нотургун булади.

1 ва 2 – теоремаларга мос равишда тескари теоремалар исботланган.

1¢ - теорема. Агар функцияларнинг кандай танлаб олинишидан катъий назар тойилмаган харакат асимптотик тургун булса, у холда биринчи якинлашиш дифференциал тенгламаларининг характеристик тенгламаларининг барча илдизларининг хакикий кисми манфий булади.

2¢ - теорема. Агар функцияларни кандай танлаб олишимиздан катъий назар тойилмаган харакат нотургун булса, у холда биринчи якинлашиш тенгламаларининг характеристик тенгламаларининг илдизлари орасида хеч булмаганда биттасининг хакикий кисми мусбат булади.

Исбот этилган Ляпуновнинг иккала теоремаси амалиёт учун жуда хам мухим ахамиятга эга, чунки бу теоремалар качон тургунлик масалаларини биринчи якинлашиш тенгламалари асосида тадкик этиш мумкинлигини курсатади. Бу кейинги масала бир неча бор таъкидлаганимиздек, соф алгебраик масалага, яъни узгармас коэффициентли алгебраик тенглама илдизларининг хусусиятларини тадкик этиш масаласига келтирилади.

Шуни хам таъкидлаш керакки, бу теоремалар ёрдамида биз Ляпунов функциясини топиш ёки уни тузиш имкониятига эга булиш билан бирга, асимптотик тургунлик сохасини топиш ва кайси вакт оралигида система асимптотик тургун ёки нотургун булиши мумкин деган масалаларни хам хал килиш имкониятига эга буламиз.

Энди характеристик тенглама илдизлари орасида хакикий кисми мусбат ишоралиси булмасдан, айримларининг хакикий кисми нолга тенг булганда, тургунлик масаласи кандай ечилишини курайлик.

Эслатиб утамизки, бу хол учун биринчи якинлашиш тенгламаларини тадкик этиш натижасида тойилмаган харакат ёки тургун (аммо асимптотик тургун эмас), ёки нотургун булади деган хулосага келган эдик.

Тойилган харакатнинг ночизикли дифференциал тенгламалари учун бу хулоса уз кучини саклайдими ёки йукми деган саволларга жавоб беришга тугри келади.

Бу саволга Ляпуновнинг куйидаги теоремаси жавоб беради.

3-теорема. Агар биринчи якинлашиш тенгламаларининг характеристик тенгламаси хакикий кисми мусбат ишорали илдизларга эга булмасдан, хакикий кисми нолга тенг илдизлари бор булса, у холда тойилган харакатнинг дифференциал тенгламаларидаги функцияларни шундай танлаб олиш мумкинки, хохишимиз буйича тойилмаган харакат тургун ёки нотургун булади.

Демак, биринчи якинлашиш тенгламалари буйича тургун булган харакат аслида нотургун булиши мумкин ва аксинча. Бу холда, тойилмаган харакатнинг тургун ёки нотургун булиши тойилган харакат тенгламаларидаги юкори даражали хадларга тулик боглик экан.

Шундай килиб, тойилган харакатнинг дифференциал тенгламалари

куринишда булганда, тургунлик масалаларини тадкик этишни икки категорияга булиш мумкин:

1) нокритик хол, бу ерда тургунлик масалалари биринчи якинлашиш тенгламалари оркали ечилади;

2) критик хол, бу ерда тургунлик масалаларини ечиш учун юкори тартибли хадларни жалб этиш лозим булиб колади. Характеристик тенгламанинг хакикий кисми мусбат ишорали илдизлари йук ва хакикий кисми нолга тенг булган илдизлари бор булгандагина критик хол мавжуд булади. Математик нуктаи назардан критик холни, бир истисно хол сифатида куриш мумкин. Аммо механик нуктаи назардан бу холлар жуда хам мухимдир.

5-§. Теоремаларнинг татбикига доир мисоллар

1-мисол. Кузгалмас нукта атрофида инерция буйича

айланаётган каттик жисм харакатининг тургунлиги

Кузгалмас нукта атрофида инерция буйича айланаётган каттик жисм харакатининг тургунлик масаласини курайлик. Агар каттик жисмни бошлангич пайтда махкамланган нуктадаги бирорта бош инерция уки атрофида айлантирсак, у холда маълум вакт давомида шу ук атрофида текис айланади. Бу айланма харакатнинг тургунлигини текширамиз.

Координата уклари сифатида махкамланган нуктадаги бош инерция укларини оламиз. Тойилмаган харакат уки атрофидаги айланма харакатга мос келсин. Тойилган харакат дифферецниал тенгламаларини биз 1-боб 2-§ да тузган эдик ва улар куйидаги

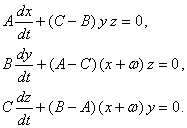(4.5.1)

куринишга эга.

(4.5.1) системанинг характеристик тенгламаси

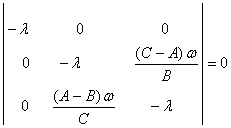
куринишда, бу ердан эса

. (4.5.2)

(4.5.2) муносабатдан куриниб турибдики, характеристик тенгламанинг битта илдизи нолга тенг ва иккитаси куйидаги тенглик билан топилади

. (4.5.3)

Агар ёки , яъни айланма харакат урта инерция уки атрофида юз бераётган булса, у холда иккала илдиз хам хакикий кийматга булади ва албатта биттаси мусбатдир. Демак, тойилмаган харакат нотургун булади.

Агар айланма харакат кичик ёки катта инерция уки атрофида содир булаётган, яъни агар , ёки , тенгсизликлар уринли булса, у холда иккала илдиз хам соф мавхумдир. Шундай килиб, битта илдиз нолга тенг ва иккитасининг хакикий кисми нолга тенг булаяпти. Демак, биз критик холга дуч келдик ва биринчи якинлашиш тенгламалари билан тургунлик масаласи хал булмайди.

Учта критик илдизга эга булган системани тадкик этиш жуда хам огир масала. Аммо, биз кураётган масала учун бу осон ечилади. (4.5.1) тенгламалар системаси биринчи интегралга эга:

Бу интеграл ва ларга нисбатан аник ишорали. Бу ердан ва узгарувчиларга нисбатан системанинг тургунлиги келиб чикади. У вактда (4.5.1) системанинг

биринчи интегралидан (энергия интеграли) системанинг га нисбатан тургунлиги келиб чикади.

Шундай килиб, системанинг урта инерция уки атрофидаги айланма харакати нотургун, катта ва кичик инерция уклари атрофидаги айланма харакатлари эса тургун булади.

2-мисол. Снаряднинг айланма харакати тургунлигининг

зарурий шарти

Иккинчи бобда снаряд баркарор харакати (снаряд айланма харакати) тургунлигининг ва ларга нисбатан етарли шарти аникланган эди:

. (4.5.4)

Бу тенгсизликка карама-карши булган тенгсизлик бажарилганда, снаряд айланма харакати (баркарор харакати) нотургун булишини курсатамиз.

Тойилган харакатнинг дифференциал тенгламаларини тузамиз. Снаряд айланма харакатининг кинетик ва потенциал энергиялари куйидаги куринишга эга эди (2-боб, 11-§ га каранг)

Харакатнинг нотургунлигини курсатиш учун тойилган харакатнинг бирорта траекторияси сферадан чикиб кетишини курсатиш етарли. Бунинг учун

(4.5.5)

биринчи интеграл узининг кийматини саклайдиган лахзадаги тойилишларни курамиз.

Биринчи якинлашиш тенгламаларини тузиш учун Т кинетик ва П потенциал энергияларни ва ларнинг даражалари буйича (факат иккинчи даражали хадларни саклаган холда) каторга ёямиз. У холда узгармас хадгача (сон) аникликда куйидагига эга буламиз:

Лагранж тенгламаси ва (4.5.5) биринчи интегралдан фойдаланиб, ва , ларга нисбатан тойилган харакатнинг биринчи якинлашиш дифференциал тенгламаларини хосил киламиз:

(4.5.6)

(4.5.6) системанинг характеристик тенгламаси

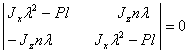
ёки

. (4.5.7)

куринишда булади.

Гурвиц критериясини бу характеристик тенгламага ишлатиб булмайди, чунки ва уларнинг бирортаси карама-карши маънога эга эмас. Шунинг учун тургунлик масаласини бошка усул билан ечамиз.

(4.5.7) характеристик тенгламанинг хар бир илдизига илдиз жавоб беради (номаълум факат жуфт даражада булгани учун). Шунинг учун хам агар бирорта илдизнинг хакикий кисми нолга тенг булмаса , у холда албатта хакикий кисми мусбат ишорали булган илдиз мавжуд булади. Демак, бу холда Ляпуновнинг биринчи якинлашиш буйича 2-теоремасига асосан тойилмаган харакат нотургун булади. Бундан уз навбатида снаряд тойилмаган харакатининг тургун булиши учун (4.5.7) характеристик тенгламанинг барча илдизлари соф мавхум булиши зарур, яъни куринишга эга булиши керак ва га нисбатан илдизлар хакикий манфий сонлар булиши лозим. Аммо, бунинг учун (4.5.7) тенгламанинг га нисбатан D дискриминанти

тенгсизликни каноатлантириши зарур.

Бу ердан куриниб турибдики, агар (4.5.4) тенгсизликка (тургунликнинг етарли шартига) карама-карши тенгсизлик бажарилса (яъни булса), у холда D < 0 ва, демак, тойилмаган харакат нотургун булади.

Шундай килиб,

шарт тойилмаган харакат тургунлигининг нафакат етарли шарти ва балки зарурий шарти хам булади.

3-мисол. Лампали генератор тургунлигининг шарти

Иккинчи бобда лампали генератор тойилган харакатининг куйидаги ночизикли дифференциал тенгламаларини

(4.5.8)

топган эдик. Тойилмаган харакатнинг асимптотик тургун булишининг шартини Ляпуновнинг иккинчи усули асосида аникланган эди. Бу мисолда биз ушбу шартни Ляпуновнинг биринчи якинлашиш усулидаги теоремалар оркали аниклаймиз.

функциянинг даражаси буйича каторга ёйилмаси

куринишда эди. Бу ифодани (4.5.8) тенгламалар системасидаги урнига куйиб ва факат чизикли хадларни колдирганимиздан кейин, куйидаги биринчи якинлашиш дифференциал тенгламаларини

хосил киламиз. Бу тенгламаларнинг

характеристик тенгламасини

куринишга келтирамиз.

Гурвиц критерияси буйича доимо

шарт бажарилганда, лампали генераторнинг мувозанат холати (тойилмаган харакати) ток ва кучланишларга нисбатан асимптотик тургун булади. Агар булса, у холда мувозанат холат нотургун булади.

Агар булса, у холда характеристик тенглама иккита соф мавхум кийматли илдизларга эга булиб, тургунлик масаласини биринчи якинлашиш тенгламалари оркали хал килиш мумкин эмас.

Бу ечимни шу масаланинг 2-бобдаги ечими билан солиштирганимизда Ляпуновнинг биринчи якинлашиш усулидаги теоремалари тургунликни тадкик этишни анча соддалаштирганини курамиз.

РЕЖА:

1. Биринчи якинлашиш тенгламалари. Баъзи ёрдамчи мулохазалар.

2. Узгармас коэффициентли чизикли тенгламалар системаси учун Ляпунов

функциясини тузиш.

3. Биринчи якинлашиш буйича тургунлик хакидаги Ляпунов теоремалари.

4. Теоремаларнинг татбикига доир мисоллар.

Таянч иборалар. Чизикли система, автоном ва ноавтоном системалар, биринчи якинлашиш усули, биринчи якинлашиш тенгламалари, теоремалар, детерминант ранги, m – тартибли форма, тенгламанинг ечими, чизикли тенгламалар системаси учун Ляпунов функциясини тузиш, Ляпунов теоремалари, мисоллар.

Такрорлаш учун саволлар:

1. Автоном ва ноавтоном системалар хакида тушунчалар.

2. Биринчи якинлашиш тенгламаларини тузиш.

3. Чизикли автоном система харакатининг тургунлиги хакидаги теоремалар.

4. Чизикли тенгламани каноатлантирувчи V (х₁,......х_n) форманинг мавжуд булишининг шартлари.

5. Узгармас коэффициентли чизикли тенгламалар системаси учун Ляпунов функциясини тузиш усуллари.

6. Биринчи якинлашиш буйича тургунлик хакидаги Ляпунов теоремалари.

7. Кузгалмас нукта атрофида инерция буйича айланаётган каттик жисм харакатининг тургунлиги.