III-БОБ. КОНСЕРВАТИВ СИСТЕМАЛАР МУВОЗАНАТ ХОЛАТИ ВА СТАЦИОНАР ХАРАКАТЛАРИНИНГ ТУРГУНЛИГИ

 

1-§. Мувозанат  холатининг тургунлиги хакидаги

Лагранж теоремаси

 

Агар тойилган харакат дифференциал тенгламалари

                            (3.1.1)

 биринчи интегралга эга булса,  аник ишорали функция, у холда Ляпунов теоремаси тойилмаган харакатнинг тургунлигини исботлашга имконият яратади. Хакикатан хам, бу холда  ва  функция Ляпунов теоремасининг хамма шартларини каноатлантиради. Бу ердан тойилмаган харакатнинг тургунлиги келиб чикади. Худди шу холат билан голоном консерватив системалар мувозанат холатининг тургунлигини тадкик этаётганда дуч келамиз.

            1788 йилда француз олими Ж.Лагранж (1736-1813) узининг “Аналитик механика” китобида ихтиёрий голоном консерватив система мувозанат холати тургунлигининг етарли шартларини топди [51].

            Голоном ва стационар богланишларга эга булган механик системани курайлик. Системанинг холатини  умумлашган эркин координаталар аникласин. Равшанки, бундай системанинг мувозанат холатида умумлашган кучлар нолга тенг булади:

                   .         (3.1.2)

            Агар  умумлашган кучлар  координаталар ва  тезликларга боглик булса, у холда системанинг мувозанат холатларини топиш учун (3.1.2) тенгликларда

 

ни киритиб, хосил булган тенгламаларни  ларга нисбатан ечиш керак.

            Консерватив системалар учун

                                   ,                (3.1.3)

бу ерда П-системанинг  потенциал энергияси.

(3.1.3) га асосан (3.1.2) тенгламалар куйидаги куринишга эга

                  .    (3.1.4)

            Бу тенгламаларни  ларга нисбатан ечганимизда, мувозанат холатларни аниклаймиз. Бундай мувозанат холатлар бир нечта ва уларнинг айримлари тургун, айримлари эса нотургун булиши мумкин. Масалан, оддий математик маятник иккита мувозанат холатига эга: куйи мувозанат холати тургун ва юкори мувозанат холати нотургун булади.

            Системанинг бирорта мавжуд булган мувозанат холатини курамиз. Бу холатда потенциал энергия нолга тенг булсин. Бунга хар доим эришиш мумкин, чунки потенциал энергия доимо аддитив узгармасгача аникликда топилади. Бундан ташкари мувозанат холатида  булсин. Мувозанат холатининг тургунлигини  координаталар ва  тезликларга нисбатан куриб утамиз. У вактда Лагранжнинг

        (3.1.5)

тенгламалари тойилган харакатнинг тенгламалари булади. Тенгламалар сони  ва улар

                                               (3.1.6)

энергия интегралига эга булади, T-системанинг кинетик энергияси. Голоном консерватив системалар учун

                           (3.1.7)

                           (3.1.8)

булади, бу ерда

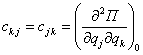                        ,         (3.1.9)

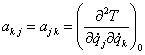                        .         (3.1.10)

            Лагранж-Дирихле теоремаси. Агар голоном стационар богланишларга эга булган консерватив системасининг яккаланган (изолированный) мувозанат холатида потенциал энергия минимумга эга булса, у холда бу мувозанат холат тургун булади.

            Исбот. Курилаётган мувозанат холатида потенциал энергия минимумга эга булсин. У холда  мувозанат холатининг исталганча кичик атрофида П потенциал энергиянинг кийматлари мусбат булади. Бу мувозанат холатининг кичик атрофида П потенциал энергия  узгарувчиларнинг аник мусбат ишорали функцияси булишини курсатади. Бошка томондан, голоном ва стационар богланишли консерватив системанинг (3.1.8) кинетик энергияси  умумлашган тезликларнинг аник мусбат ишорали квадратик формаси булади. Демак, (3.1.6) га асосан     системанинг тулик энергияси

                                               (3.1.11)

 умумлашган координаталар ва  умумлашган тезликларнинг аник мусбат ишорали функциясидан иборатдир. функциянинг вакт буйича тулик хосиласи, (3.1.6) га асосан, нолга тенг, яъни . Шундай килиб,  функция Ляпунов теоремасининг хамма шартларини каноатлантиргани учун курилаётган механик системанинг   мувозанат холати тургун булади.

            Лагранж-Дирихле теоремаси хаётда кенг кулланилади. Уни амалда куллаш учун Т ва П функцияларни (3.1.7) ва (3.1.8) куринишларга келтиргандан кейин Сильвестер критериясидан фойдаланиш керак. Агар  коэффициентлар Сильвестер критериясини каноатлантирса, у холда (3.1.7) нинг квадратик кисми  узгарувчиларнинг аник мусбат ишорали функцияси, демак, П потенциал энергия хам мувозанат холати атрофида аник мусбат ишорали функция булади. Бу потенциал энергиянинг минимум кийматга эга хамда, Лагранж теоремасига асосан, система мувозанат холатининг тургун эканлигини билдиради.

            Лагранж - Дирихле теоремаси факатгина консерватив система мувозанат холати тургунлигининг етарли шартини аниклайди: агар яккаланган мувозанат холатида потенциал энергия минимумга эга булса, у холда бундай мувозанат холат тургун булади.

            Аммо системанинг мувозанат холатида потенциал энергия максимумга эга булса, у холда бундай мувозанат холат нотургун буладими ёки йукми деган саволга бу теорема жавоб бермайди.

            Амалиётда жуда хам зарур булган бу саволга Ляпунов узининг икки теоремаси билан жавоб беради. Бу теоремаларни исботсиз келтирамиз [52]:

Ляпуновнинг биринчи теоремаси. Агар яккаланган мувозанат холатида потенциал энергия минимумга эга булмаса ва унинг мавжуд эмаслиги потенциал энергия ёйилмасидаги юкори тартибли хадларни жалб этмасдан факат иккинчи тартибли хадлар билан аникланса, у холда мувозанат холат нотургун булади.

            Ляпуновнинг иккинчи теоремаси. Агар яккаланган мувозанат холатида потенциал энергия максимумга эга булса ва бу холат потенциал энергия ёйилмасида мавжуд булган хадларнинг энг кам юкори даражали хадлари билан аникланса, у холда мувозанат холат нотургун булади.

            Н.Г.Четаев Ляпуновнинг бу иккала теоремасини умумлаштириб, куйидаги теоремани исбот этди [102]:

 

Теорема. Агар  узгарувчиларнинг аналитик функцияси булган потенциал энергия яккаланган мувозанат холатида минимумга эга булмаса, у холда мувозанат холат нотургун булади.

 

2-§. Лагранж – Дирихле теоремасининг татбикига доир мисоллар

 

            Энди Лагранж-Дирихле теоремасининг татбикларини куриб утамиз.

 

            1-мисол. Курилаётган система маятниклар иккилигидан иборат булсин. Мос равишда  ва  массали  ва  жисмлар моддий нукталар сифатида каралади. Стерженлар массаси, хавонинг каршилиги ва горизонтал цилиндрик таянчлардаги ишкаланишларни хисобга олмаймиз. Маятникларнинг юкори вертикал холатида  ва  каттиклик коэффициентларга эга булган спирал пружиналар табиий деформацияланмаган холатда булади. Маятникларнинг  ва  массалари хамда уларнинг  ва  узунликлари берилган булсин (3.1-шакл). Пружиналарнинг  ва  каттиклик коэффициентларини шундай танлаб олиш керакки, маятникларнинг юкори мувозанат холати тургун булсин.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


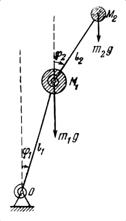                                   3.1-шакл

 

            Системанинг богланишлари идеал, голоном ва стационар. Системага таъсир этаётган актив кучлар потенциал кучлардир. Шунинг учун бу масалага Лагранж теоремасини татбик этиш мумкин. Маятникларнинг холатини  ва  бурчаклар оркали аниклаймиз. Системанинг П потенциал энергияси пружиналарнинг П1 ва огирлик кучининг П2 потенциал энергияларидан иборат булади:

                              П=П1+П2­,              (3.2.1)

бу ерда

                   ,    (3.2.2)

   .

(3.2.2) ифодаларни (3.2.1) га куйиб системанинг

потенциал энергиясини хосил киламиз. Косинус функциясининг Маклорен каторига ёйилмаси

                              

дан фойдаланиб ва баъзи соддалаштиришлардан кейин

    (3.2.3)     

ифодани хосил киламиз, бу ерда нукталар билан  ва  ларни уз ичига олган иккинчи тартибли хадлардан юкори булган хадлар белгиланган.

            Ушбу

           ,    ,

                                            (3.2.4)

белгилашларни киритамиз. (3.2.4) ни (3.2.3) га куйиб, потенциал энергиянинг куйидаги

                    (3.2.5)

куринишини хосил киламиз. Сильвестер критерияси шартлари бу мисол учун куйидаги куринишга эга:

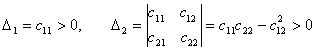     .   (3.2.6)

             ларнинг (3.2.4) даги кийматларини (3.2.6) га куйиб, куйидагиларга эга буламиз:

 .

            Бу тенгсизликларни  ва  ларга нисбатан ечиб,

      (3.2.7)

ифодаларни хосил киламиз. Ушбу

                      (3.2.8)

белгилашларни киритиб, (3.2.7) тенгсизликларни куйидаги

                        (3.2.9)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


куринишга келтирамиз. (3.2.9) даги иккинчи тенгсизликда ифода алмаштиришларни амалга оширамиз:

  

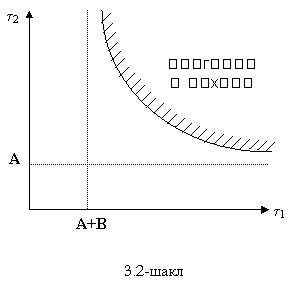
Энди тургунликнинг (3.2.9) етарли шарти куйидаги куринишга эга булади

                 

(3.2) шаклда системанинг юкори мувозанат холатининг тургунлик сохаси курсатилган.

            Тургунлик сохасининг чегараси

                       

ифодалар билан аникланади.

2-мисол. Масса маркази таянчдан юкорида турган физик маятникнинг мувозанат холати нотургун булади. Бу холатни баркарорлаштириш учун жисм билан таянч уртасига спирал пружина урнатилган. Бу спирал пружина маятникнинг  огиш бурчагига пропорционал булган тикловчи момент яратади. Мувозанат холатини баркарорлаштириш учун пропорционаллик коэффициентнинг кийматини кандай танлаб олиш керак?

Ечим. Жисмга таъсир этаётган кучларнинг потенциал энергияси

                             

га тенг булади, бу ерда -жисмнинг массаси, -масса маркази  билан маятникнинг тебраниш уки О орасидаги масофа , -изланаётган пружинанинг каттиклик коэффициенти.

 

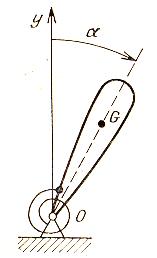
                                       3.3-шакл.

 

            Мувозанат холатида

                           .

Параметрларнинг хар кандай кийматида хам бу тенгламанинг ечими , яъни физик маятникнинг мувозанат холати  булади.

                           

булганда, потенциал энергия мувозанат холатида минимумга эга булади. Бу ердан

                                      

булгандагина, мувозанат холатининг тургун (баркарор) булиши келиб чикади.

 

3-§. Циклик координаталар. Раус алмаштириши

 

Шундай механик системалар синфи мавжудки, уларнинг кинетик энергияси ошкор равишда баъзи координаталарга боглик булмайди ва бу координаталарга мос келган умумлашган кучлар нолга тенг булади. Бундай координаталар циклик координаталар, колганлари эса позицион ёки ноциклик координаталар деб аталади. Масалан, Ер сунъий  йулдоши учун  - циклик координата,  ва  лар – позицион координаталар, коник (конуссимон) маятник учун  - циклик координата,  эса – позицион координата булади. Пилдирок учун  ва  - позицион,  - циклик координатадир.

Бирор динамик система учун  - позицион ва  -циклик координаталар булсин. Циклик координаталар учун Лагранж тенгламасини тузамиз

          (3.3.1)

T кинетик энергия циклик координата таърифига асосан ошкора равишда  га боглик булмагани учун

                               .

Бундан ташкари, циклик координаталарга мос келган  умумлашган кучлар нолга тенг, яъни

                              .             (3.3.2)

Шундай килиб, циклик координаталар учун (3.3.1) Лагранж тенгламалари

               (3.3.3)

куринишга келади. Бу тенгламалар куйидаги

                  (3.3.4)

биринчи интегралларга эга, яъни циклик координаталарга мос келган умумлашган импульслар бутун харакат давомида узгармас булиб колади.

            Позицион координаталар учун Лагранж тенгламаларини алмаштиришда (3.3.4) биринчи интеграллардан фойдаланиш мумкин.

Бу алмаштиришлар Раус томонидан курсатилгани учун унинг номи билан юритилади. Биз бу ерда факат олинган натижаларни келтирамиз. Натижаларнинг исботини Д.Р.Меркин ва Н.Г.Четаевларнинг [60,102] китобларидан топасиз.

            Т кинетик энергия тезликларга нисбатан квадратик форма булгани учун (3.3.4) биринчи интегралларнинг унг тарафи  циклик тезликларга нисбатан чизикли булади.  та биринчи интеграллардан  ларни  ва  лар оркали ифодалаймиз ва уларни Т циклик энергиянинг ифодасига киритиб, хосил булган янги ифодани Т* билан белгилаймиз. Бундан кейин  Раус функциясини

                                               (3.3.5)

формула оркали аниклаб оламиз.

            Бу формулада  циклик тезликлар уларнинг (3.3.4) биринчи интеграллардан топилган ифодалар билан алмаштирилган деб каралади.  позицион координаталар учун тенгламалар (системага таъсир этаётган кучлар потенциал кучлар деб фараз килинади; акс холда тенгламанинг унг тарафида  умумлашган кучлар туради)

                         (3.3.6)

куринишга келади.

            Раус функцияси факат  ва  ларга боглик булиб,  циклик координата ва  циклик тезликка боглик булмайди. Шунинг учун хам позицион координаталар буйича содир булаётган харакатни (циклик координаталарни инобатга олмагандай булиб) (3.3.6) тенгламалар асосида  тадкик килиш мумкин. Шу сабабли циклик координаталар буйича юз бераётган харакатни ошкормас харакат ва позицион координаталар буйича содир булаётган харакатни ошкор харакат деб айтамиз.

            Энди  Раус функциясининг структурасини (тузилишини) куриб утайлик. Хамма бажарилган алмаштиришлар натижасида хосил этилган ва (3.3.5) формула билан аникланадиган  Раус функцияси учта хаднинг йигиндисидан иборат булади:

                         ,            (3.3.7)

бу ерда  - ифодасида  позицион тезликлар иккинчи даражада катнашувчи хадлар йигиндиси, яъни

                       ,          (3.3.8)

- ифодасида  позицион тезликлар биринчи даражада катнашувчи хадлар йигиндиси, яъни

                            ,              (3.3.9)

 - ифодаси  позицион тезликларга боглик булмаган хадлар йигиндиси. Бу тенгликларда  хамда  ва    позицион координаталар ва  узгармас сонларга боглик функциялар.  квадратик форма аник мусбат ишорали булади [61].

(3.3.6) тенгламаларга R Раус функциясининг ифодасини (3.3.7) дан келтириб куямиз:

   .

 нинг  богликмаслигини хисобга олиб ва алохида кушилувчиларга ажратиб гурухлаганимиздан кейин

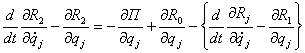      (3.3.10)

ифодага келамиз. (3.3.9) фоормуладан фойдаланиб, унг томонда кавс ичидаги ифодани алмаштирамиз

                         .

 коэффициентнинг  лар оркали t вактга нисбатан мураккаб функция эканлигини хисобга олиб,

                      

ни топамиз. (3.3.9) формулада  индексни  га алмаштириб,  буйича дифференциаллаймиз

          .

Демак,

    ,

бу ерда  гироскопик коэффициентлар

                                   (3.3.11)

тенглик билан аникланади.

            Энди (3.3.10) тенгламаларни куйидаги куринишга келтириш мумкин

,    (3.3.12)

бу ерда

                              .                     (3.3.13)

            (3.3.12) тенгламаларни бирор келтирилган система деб караш мумкинки, унда  ва  функциялар мос равишда кинетик ва потенциал энергия вазифасини бажарадилар. Бу системанинг умумлашган кучлари

                       (3.3.14)

тенгликлар билан аникланади, бу ерда  - гироскопик кучлар деб аталади. Гироскопик коэффициентларнинг аникланишига кура ((3.3.11) га каранг), уларнинг матрицаси кийшик симметрик булади, яъни

                   .                (3.3.15)

            Агар гироскопик кучлар йук булса (бу холат, одатда,  да юз беради), у холда системани гироскопик богланмаган деб атаймиз. Гироскопик кучларнинг асосий хусусияти шундан иборатки, хакикий силжишдаги уларнинг бажарган иши нолга тенг булади. Бу хусусият уларга Томсон ва Тет берган [112] таърифнинг асосини ташкил этади.

            (3.3.12) келтирилган системанинг дифференциал тенгламаларидан энергия интегралини хосил килиш мумкин

            .      (3.3.16)

Бу интегралнинг физик маъноси равшандир: келтирилган системага таъсир этаётган гироскопик кучлар иш бажармайди ва, демак, улар умумий энергия балансини узгартирмайдилар.

 

4-§. Стационар (баркарор) харакатлар тургунлиги

 

            Маълум шароитда  циклик ва  позицион координаталари булган моддий система стационар харакат килиши мумкин. Стационар харакатда хамма позицион координаталар ва циклик тезликлар бошлангич кийматларига тенг булган узгармас кийматга эга булади. Бу стационар харакат мавжуд булиши учун зарур булган шарт куйидаги мулохазалардан келиб чикади.

            Таърифга асосан стационар харакатда барча позицион координаталар кийматларини узгармас холда саклайдилар, яъни

                   .

            Бу келтирилган системанинг мувозанатда (харакатсиз) туришини билдиради. Уз навбатида бунинг учун системага таъсир этаётган хамма умумлашган кучлар нолга, яъни

                          

булиши, ёки стационар харакатда (келтирилган система мувозанатда) барча  лар учун  булишини хисобга олганда

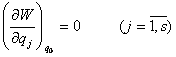                   .         (3.4.1)

булиши зарур ва етарлидир.

            Келтирилган системанинг потенциал энергияси  ((3.3.13) га каранг) эканлигини хисобга олиб, (3.4.1) шартларга бошкача куриниш бериш мумкин:

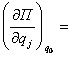
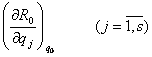            .        (3.4.2)

            Шундай килиб, стационар харакат мавжуд булиши учун  позицион координаталарнинг бошлангич кийматлари  та (3.4.1) шартларни каноатлантириши ва хамма позицион тезликларнинг бошлангич кийматлари нолга тенг булишлари ( ва  булганда хамма  циклик тезликлар узгармас кийматларини саклайдилар) етарли ва зарурдир.

             нинг ифодасига (3.3.4) циклик интегралларнинг  узгармас сонлари кирганликлари туфайли  нинг стационар харакатларининг киймати  ни уз ичига олган  циклик тезликларга боглик булади.

            Стационар харакатни тойилмаган харакат сифатида караб, унинг тургун булишининг шартларини аниклаймиз. Умумийликни бузмасдан, стационар харакатда хамма  позицион координаталар нолга тенг, яъни (3.4.1) тенгламаларнинг ечимлари  деб кабул килишимиз мумкин. У холда келтирилган системанинг (3.3.12) тенгламалари  позицион координаталар ва позицион тезликларга нисбатан тойилган харакатнинг дифференциал тенгламалари булади. Стационар харакатнинг тургунлиги хакидаги бир катор теоремаларни Раус исбот килган. Бу ерда улар орасидан куп таркалган ва амалиётда мухим булган биттасини келтирамиз.

           

Раус теоремаси. Агар стационар харакатда келтирилган системанинг  потенциал энергияси минимумга эга булса, у холда, хеч булмаганда (3.3.4) циклик интегралларнинг кийматини бузмайдиган тойилишлар учун, стационар харакат  позицион координаталар ва  тезликларга нисбатан тургун булади.

           

Исбот. Берилган моддий системанинг стационар харакати пайтида келтирилган система мувозанатда (харакатсиз) булади. Бундан ташкари келтирилган система учун (3.3.16) энергия интеграли мавжуд. Шу туфайли Раус теоремасини исбот килиш учун Лагранж теоремасининг исботини кайтариш етарли.

            Келтирилган Раус теоремаси факатгина (3.3.4) циклик интегралларнинг кийматини бузмайдиган тойилишлар учун тугридир. Ляпунов Рауснинг бу теоремасидаги камчиликни тузатадиган теоремани яратди. Биз уни исботсиз келтирамиз.

           

Теорема. Агар келтирилган система  потенциал энергияси хам курилаётган стационар харакатга мос келувчи  кийматлар учун хам  кийматлар учун минимумга эга, бу ерда   етарлича кичик микдор, хамда  ни минимумга айлантирувчи  узгарувчиларнинг кийматлари  микдорларнинг узлуксиз функциялари булса, у холда стационар харакат  позицион координаталар ва  тезликларга нисбатан тургун булади.

            Ляпунов Раус теоремасини умумлаштирган уз теоремасининг исботини келтирмайди.

             узлуксиз функция булган хол учун В.В.Румянцев бу теоремани исбот килади [81]. [81] китобда стационар харакатлар тургунлик назарияси деярли тулик келтирилган. Китобдаги куп натижалар В.В.Румянцев томонидан олинган.

            Таъкидлаш зарурки, стационар харакатларнинг тургунлигига потенциал энергия минимумга эга булмаган холда хам эришиш мумкин (гироскопик кучлар ёрдами билан). Шунинг учун хам Лагранж теоремасига тескари булган Ляпунов ва Четаев теоремаларини стационар харакатга куллаш мумкин эмас.

            Аммо, гироскопик богланмаган системалар учун куйидаги теорема тугридир.

           

Теорема. Агар гироскопик богланмаган системанинг яккаланган стационар харакати учун (3.3.4) циклик интегралларнинг махкамланган кийматларида  ларнинг аналитик функцияси булган  минимум кийматга эга булмаса, у холда стационар харакат нотургун булади.

           

Изох. Раус теоремасини амалий масалаларни ечишда фойдаланиш учун теорема шартлари бажарилганда,  функциянинг аник мусбат ишорали эканлигини аниклаш етарли, бу ерда  нинг стационар харакатдаги киймати  деб олинган. Шунинг учун хам бу функцияни каторга ёйиш ва Сильвестер критериясидан фойдаланиш керак.

5-§. Раус теоремасининг татбикига доир мисоллар

 

            Китобнинг 2-бобида конуссимон маятник ва Ер Сунъий йулдоши стационар харакатларининг тургунлигини Четаев усули билан исбот килган эди. Энди Раус теоремасини татбик этиб шу натижаларни оламиз.

 

1-мисол. Конуссимон маятник стационар харакатининг тургунлиги

 

            Олдин конуссимон (коник) маятникнинг куйидаги кинетик ва потенциал энергиялари топилган эди:

          .

            Бу ифодалардан куриниб турибдики,   - циклик координата (у кинетик энергия ифодасига факат  бурчак тезлиги оркали кираяпти ва потенциал энергия ифодасида йук) ва  - позицион координата. (3.3.4) формулага асосан, циклик интегрални тузамиз

                     (3.5.1)

Бу ердан  топиб, Т кинетик энергия ифодасига киритамиз

         .

(3.3.5) формуладан фойдаланиб,  Раус функциясини топамиз

    

ёки

                     .

(3.3.7), (3.3.8) ва (3.3.9) формулаларга асосланиб

      

хосил киламиз.  булганлиги учун курилаётган система гироскопик богланмаган булади. Энди келтирилган системанинг  потенциал энергиясини топамиз

               .      (3.5.2)

            Баркарор харакатдаги  бурчакнинг кийматини  билан,  циклик тезликнинг кийматини  билан белгилаймиз. Стационар харакат мавжуд булишининг (3.4.1) шарти куйидаги куринишга эга булади:

           .      (3.5.3)

ёки алмаштиришлар утказгандан кейин

                   .           (3.5.4)

га келади.

            Бу формула (3.5.3) тенгламанинг бир параметрлик ечимлар оиласини аниклайди ва (3.5.4) га мос келадиган конуссимон маятник бурчак тезлигининг киймати (3.5.1) тенгликдан аникланади:

                     (3.5.5)

(3.5.4) ва (3.5.5) тенгликлардан  параметрини чикарсак, ушбу тенгликка келамиз

                             .

Бу тенглик конуссимон маятник стационар харакати мавжуд булишининг шарти хисобланади ва олдин биз уни элементар мулохазалар оркали топган эдик.

            Энди маятник стационар харакатини тойилмаган харакат сифатида кабул килиб, унинг тургунлигини  Раус теоремаси ёрдами билан тадкик киламиз.

            Бунинг учун  ни  нинг (3.5.2) ифодасига киритамиз ва  айирмани  нинг даражалари буйича каторга ёйамиз:

          

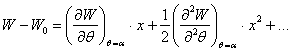
ёки (3.5.3) ни хисобга олиб,

                  

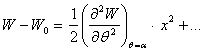
ни хосил киламиз, бу ерда нукталар билан  нинг даражалари иккинчидан юкори булган хадлар белгиланган. 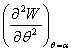 ни топиб урнига куйганимиздан кейин

         

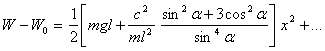
га эга буламиз.

             олдидаги купайтувчи мусбатлиги учун  функция стационар харакатда минимумга эга. Бундан ташкари, хар кандай  учун (3.5.4) ечим (3.5.1) интегралдаги  узгармас сондан узлуксиз боглик. Циклик тезлик  хам  кийматларда  дан узлуксиз боглик булади. Шунинг учун хам Раус теоремаси ва умумлашган Ляпунов теоремасига асосан конуссимон маятник стационар харакати  ва  узгарувчиларга нисбатан тургундир.

 

 

 

2-мисол. Ер Сунъий йулдоши масса марказининг

стационар харакати тургунлиги [81]

 

            2-бобда Ер Сунъий йулдошининг кинетик ва потенциал энергиялари куйидаги куринишда топилган эди

          .

Бу ифодалардан куриниб турибдики,  - циклик ва  - позицион координаталар.  циклик координатага куйидаги биринчи интеграл мос келади:

            .          (3.5.6)

Бу тенгликдан  ни топиб, Т кинетик энергияси ифодасига келтириб куямиз

    .

(3.3.5) формуладан фойдаланиб, Раус функциясини тузамиз

 

ёки

                .

Бу ифодадан, (3.3.7) га асосан , ,  . Демак,  булганлиги учун система гироскопик богланмаган. (3.3.13) га асосан келтирилган системанинг потенциал энергиясини топамиз

    .           (3.5.7)

Стационар харакат мавжуд булишининг шарти ((3.4.1) га каранг)

  (3.5.8)

куринишда булади. Бу тенгламалар бир параметрли ечимлар оиласига эга:

                  ,            (3.5.9)

                    .              (3.5.10)

Бу ечимларга мос келувчи Ер Сунъий йулдоши масса марказининг радиус-вектори айланишининг бурчак тезлиги (3.5.6) интегралдан аникланади

                 .         (3.5.11)

Ер сунъий йулдошининг,  текислигида  радиусли   айлана буйлаб, узгармас бурчак тезлиги билан килаётган чин харакати, унинг стационар харакати булади. (3.5.9) ва (3.5.10) лардан куйидагини топамиз

                        .

Бу формулани аввал оддий физик мулохазалар йули билан топган эдик.

Сунъий йулдош стационар харакатини тойилмаган харакат сифатида кабул килиб, унинг тургунлигини Раус теоремаси ва Ляпуновнинг умумлашган теоремаси оркали текширамиз.

 ни кабул килиб, уни (3.5.7) ифодага куямиз ва  айирмани  ва  ларнинг даражалари буйича каторга ёямиз:

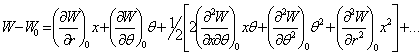
ёки (3.5.8) ифодаларни хисобга олиб,

  

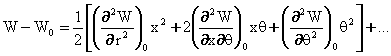
ни хосил киламиз, бу ерда

 

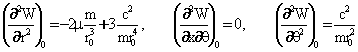.(3.5.12)

(3.5.12) ни  айирманинг ифодасига куйиб,

             

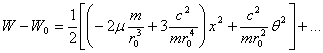
ни хосил киламиз.

Баркарор харакатда, (3.5.9) ифодага асосан  булганлиги учун

                   

Бу ифодадан куриниб турибдики, стационар харакатда  функция минимумга эга. Бундан ташкари, хар кандай  учун (3.5.9) ечим узгармас  га узлуксиз боглик. Шунга кура, хамда Раус теоремаси ва Ляпуновнинг умумлашган теоремасига асосан стационар харакат тургун булади.    

 

РЕЖА:

     1. Мувозанат холатининг тургунлиги хакидаги Лагранж теоремаси.

     2. Лагранж – Дирихле теоремасининг татбикига доир мисоллар.

     3. Циклик координаталар. Раус алмаштириши.

     4. Стационар (баркарор) харакатлар тургунлиги.

     5. Раус теоремасининг татбикига доир мисоллар.

            Таянч иборалари. Голоном ва консерватив системалар, стационар харакат, мувозанат холати, Лагранж – Дирихле теоремаси, Ляпунов теоремаси, Четаев теоремаси, мисоллар, физик маятниги, циклик координата, позицион координата, ошкор ва ошкормас харакатлар, Раус функцияси, стационар харакатнинг тургунлиги.

 

Такрорлаш учун саволлар:

 

1.      Лагранж – Дирихле теоремаси. Теореманинг татбикига доир мисоллар.

2.      Консерватив системалар мувозанат холатининг нотургунлиги хакидаги Ляпунов теоремалари.

3.      Циклик ва ноциклик координаталар. Руаус алмаштириши. Ошкор харакатлар.

4.      Стационар харакатлар тургунлиги хакидаги Раус теоремаси.

5.      Конуссимон маятник стационар харакатининг тургунлиги.

6.      Ер сунъий йулдоши масса марказининг стационар харакати тургунлиги.