II-БОБ. БАРКАРОР ХАРАКАТЛАР УЧУН ЛЯПУНОВНИНГ ИККИНЧИ УСУЛИ
1-§. Ляпунов функциялари. Аник ишорали ва узгарувчан ишорали функцияларнинг аломатлари
Биз бундан кейин факат баркарор (стационар) харакатларни куриб утамиз. Бу хол учун тойилган харакатнинг дифференциал тенгламалари
![]()
![]() (2.1.1)
(2.1.1)
куринишда
булади. ![]() функция ошкора
равишда
функция ошкора
равишда ![]() вактдан боглик
эмас. Ляпунов узининг тадкикотларида
вактдан боглик
эмас. Ляпунов узининг тадкикотларида ![]() функцияни
функцияни ![]() узгарувчиларнинг
даражалари буйича каторга ёйилувчи ва бу катор
узгарувчиларнинг
даражалари буйича каторга ёйилувчи ва бу катор
![]()
![]() (2.1.2)
(2.1.2)
сохада
якинлашувчи деб фараз килган эди. Бу ерда Н–узгармас кичик сон. Аммо Ляпуновнинг
иккинчи усулининг хамма холлари ва уларга боглик булган исботлар умумийрок фаразлар
учун хам уз кучини саклайди. Аникроги, ![]() функциянинг
аналитиклигини (2.1.2) сохада узлуксиз ва (2.1.1) тенгламалар (2.1.2) сохадаги
функциянинг
аналитиклигини (2.1.2) сохада узлуксиз ва (2.1.1) тенгламалар (2.1.2) сохадаги ![]() ларнинг
хар бир бошлангич
ларнинг
хар бир бошлангич ![]() кийматлар
системаси учун ягона ечимга эга булишлигини таъминловчи шартлар билан алмаштириш
мумкин.
кийматлар
системаси учун ягона ечимга эга булишлигини таъминловчи шартлар билан алмаштириш
мумкин.
1.1.Ляпунов функциялари
![]() узгарувчиларга боглик
булган
узгарувчиларга боглик
булган ![]() функцияни курайлик.
Бу функция координата бошини камраб олган
функцияни курайлик.
Бу функция координата бошини камраб олган
![]()
![]() (2.1.3)
(2.1.3)
сохада аникланган, бир кийматли, узлуксиз, узлуксиз
хусусий хосилаларга эга ва ![]() деб фараз киламиз.
Бу ерда
деб фараз киламиз.
Бу ерда ![]() етарлича кичик
мусбат сон ва
етарлича кичик
мусбат сон ва ![]() .
.
1-таъриф. (2.1.3)
сохада факатгина бир хил ишорали кийматлар кабул килувчи ![]() функция
аник ишорали деб айтилади. Агар (2.1.3) сохада
функция
аник ишорали деб айтилади. Агар (2.1.3) сохада ![]() факат мусбат кийматлар
кабул килса, у аник мусбат ишорали, факат манфий кийматлар кабул килганда эса
аник манфий ишорали функция деб аталади.
факат мусбат кийматлар
кабул килса, у аник мусбат ишорали, факат манфий кийматлар кабул килганда эса
аник манфий ишорали функция деб аталади.
2-таъриф. Агар
![]() функция (2.1.3) сохада
факатгина бир хил ишорали кийматлар кабул килиб, шунинг билан бирга координата
бошидан ташкари бошка
функция (2.1.3) сохада
факатгина бир хил ишорали кийматлар кабул килиб, шунинг билан бирга координата
бошидан ташкари бошка ![]() нукталарда хам нолга
айланса, у холда бундай функция узгармас (узгармас мусбат ёки узгармас манфий)
ишорали деб аталади.
нукталарда хам нолга
айланса, у холда бундай функция узгармас (узгармас мусбат ёки узгармас манфий)
ишорали деб аталади.
3-таъриф.
(2.1.3) сохада аник ишорали хам, узгармас ишорали хам булмаган ![]() функцияга
узгарувчан ишорали деб аталади. Демак, таърифга биноан узгарувчан ишорали
функция (2.1.3) сохада хам мусбат, хам манфий ишорали кийматлар кабул килади.
функцияга
узгарувчан ишорали деб аталади. Демак, таърифга биноан узгарувчан ишорали
функция (2.1.3) сохада хам мусбат, хам манфий ишорали кийматлар кабул килади.
Берилган таърифларни мисолларда
тушунтирайлик. Тушуниш осон булиши учун ![]() деб оламиз.
деб оламиз.
У вактда
![]() ,
,
![]()
функциялар аник мусбат ишорали
булади. Бу функциялар учун (2.1.3) тенгсизликдаги ![]() сони
исталганча катта булиши мумкин.
сони
исталганча катта булиши мумкин.
![]()
функция ![]() нинг
исталганча етарли кичик кийматлари учунгина аник мусбат ишорали булади.
нинг
исталганча етарли кичик кийматлари учунгина аник мусбат ишорали булади.
![]() ,
, ![]()
лар узгармас ишорали
функциялардир. Хакикатан хам биринчи функция ![]() ,
, ![]() ва
иккинчиси
ва
иккинчиси ![]() ва ихтиёрий
ва ихтиёрий ![]() кийматларда
нол киймат кабул килади.
кийматларда
нол киймат кабул килади.
![]() ,
, ![]()
лар узгарувчан ишорали функциялар булади.
1.2. Функцияларнинг аник ишоралилик ва узгарувчан ишоралилик аломатлари
Ляпуновнинг
иккинчи усулини амалий масалаларни ечишга татбик этиш учун ![]() функциянинг
аник ишорали ва узгарувчан ишорали эканлигини аниклайдиган критерияларни билиш
зарур. Афсуски, хозиргача бундай турдаги умумий критериялар мавжуд эмас ва
умумий холда бу масала жуда хам мураккабдир. Аммо, куплаб хусусий холлар учун бу
масала бирор содда критерия ёрдамида хал этилади. Буларнинг айримларини (баъзан
исботсиз) келтирамиз.
функциянинг
аник ишорали ва узгарувчан ишорали эканлигини аниклайдиган критерияларни билиш
зарур. Афсуски, хозиргача бундай турдаги умумий критериялар мавжуд эмас ва
умумий холда бу масала жуда хам мураккабдир. Аммо, куплаб хусусий холлар учун бу
масала бирор содда критерия ёрдамида хал этилади. Буларнинг айримларини (баъзан
исботсиз) келтирамиз.
m-тартибли
бир жинсли ![]() форма берилган булсин.
У вактда ихтиёрий
форма берилган булсин.
У вактда ихтиёрий ![]() учун
учун
![]()
бажарилишидан равшанки, агар V аник ишорали функция булса, у холда бутун фазода хам (нафакат
мувозанат холати атрофида) функциянинг аник ишоралилик хусусияти сакланади.
Худди шундай, агар V функция узгарувчан ишорали булса,
у холда бутун фазода хам у узгарувчан ишорали булади. Уз-узидан куриниб турибдики,
![]() -тартибли форма
учун, аник ишоралилик факатгина m жуфт сон булгандагина
юз бериши мумкин.
-тартибли форма
учун, аник ишоралилик факатгина m жуфт сон булгандагина
юз бериши мумкин.
1-лемма. Хар кандай ток тартибли форма узгарувчан ишорали функция булади.
Агар m жуфт сон булса, у холда V
аник ишорали хам, узгарувчан ишорали хам булиши мумкин. Узгарувчиларнинг сони
иккидан катта ![]() булганда, иккинчи
тартиблидан юкори булган формалар учунок юкорида айтилган икки холнинг кайси
бири мавжуд булишини аниклаш анча мураккаб масаладир. Иккинчи тартибли форма
учун (узгарувчилар сони исталганча булиши мумкин) бу масала жуда хам оддий
равишда куйидагича ечилади.
булганда, иккинчи
тартиблидан юкори булган формалар учунок юкорида айтилган икки холнинг кайси
бири мавжуд булишини аниклаш анча мураккаб масаладир. Иккинчи тартибли форма
учун (узгарувчилар сони исталганча булиши мумкин) бу масала жуда хам оддий
равишда куйидагича ечилади.
Ушбу
![]() (2.1.4)
(2.1.4)
квадратик форма берилган булсин. Маълумки, (2.1.4) формани
![]() (2.1.5)
(2.1.5)
куринишга келтирадиган детерминанти нолга тенг булмаган чексиз куп
![]()
![]() (2.1.6)
(2.1.6)
чизикли алмаштиришлар мавжуд.
1.Агар
![]() коэффициентларнинг
барчаси нолга тенг эмас ва бир хил ишорали булса, у холда V
форма аник ишорали булади. Хакикатан хам, бу холда V
факатгина
коэффициентларнинг
барчаси нолга тенг эмас ва бир хил ишорали булса, у холда V
форма аник ишорали булади. Хакикатан хам, бу холда V
факатгина ![]() булгандагина нолга
айланади. Бу хол, (2.1.6) нинг детерминанти нолга тенг булмаганлиги учун, факат
булгандагина нолга
айланади. Бу хол, (2.1.6) нинг детерминанти нолга тенг булмаганлиги учун, факат
![]() булгандагина юз
беради.
булгандагина юз
беради.
2.Агар
![]() коэффициентларнинг
бир кисми нолга тенг булиб, колганлари бир хил ишорали булса, у холда V
форма узгармас ишорали булади.
коэффициентларнинг
бир кисми нолга тенг булиб, колганлари бир хил ишорали булса, у холда V
форма узгармас ишорали булади.
3.Агар
![]() коэффициентлар
орасида мусбат ишоралиси хам, манфий ишоралилари хам топилса, у холда V
форма узгарувчан ишорали булади.
коэффициентлар
орасида мусбат ишоралиси хам, манфий ишоралилари хам топилса, у холда V
форма узгарувчан ишорали булади.
Нолдан
фарк килувчи ![]() коэффициентларнинг
сони ва бу коэффициентлар каторидаги ишораларнинг узгариш сони (2.1.6) алмаштиришнинг
кандай танланишига боглик эмас.
коэффициентларнинг
сони ва бу коэффициентлар каторидаги ишораларнинг узгариш сони (2.1.6) алмаштиришнинг
кандай танланишига боглик эмас.
Сильвестер критерияси ёрдамида берилган квадратик форманинг аник ишорали ёки узгарувчан ишорали эканлиги аникланади.
Сильвестер теоремаси. (2.1.4) квадратик форма аник мусбат ишорали булиши учун унинг коэффициентларидан тузилган
 (2.1.7)
(2.1.7)
матрицанинг хамма
![]() ,
,
 , . . . ,
, . . . , 
бош минорлари мусбат булиши етарли ва зарурдир.
Ушбу теореманинг исботи Ф.Р.Гантмахернинг [20] китобида келтирилган. Сильвестер критериясидан квадратик форманинг аник манфий ишорали булишининг етарли ва зарурий шартини чикариш мумкин:
(2.1.4) квадратик форма аник манфий ишорали булиши учун
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
. . . (2.1.8)
,
. . . (2.1.8)
тенгсизликларнинг бажарилиши етарли ва зарурдир.
1-мисол. Мисол сифатида куйидаги функцияни курамиз
![]() .
.
Бу
функцияни ![]() ва
ва ![]() даражалари
буйича каторга ёямиз:
даражалари
буйича каторга ёямиз:
![]() ,
, ![]() ,
,
бу
ерда нукталар билан ![]() ва
ва ![]() ларга
нисбатан иккидан юкори даражали булган хадлар белгиланган.
ларга
нисбатан иккидан юкори даражали булган хадлар белгиланган. ![]() ва
ва ![]() ларнинг
ёйилмаларини V функциянинг ифодасига куйиб соддалаштиришлардан сунг
ларнинг
ёйилмаларини V функциянинг ифодасига куйиб соддалаштиришлардан сунг
![]()
функцияни хосил киламиз. Бу функциянинг квадратик формани ташкил этадиган барча хадларининг коэффициентларидан
![]()
матрицани тузамиз. Бу матрицанинг бош диагонал минорлари
![]() ,
, ![]()
тенг
булади. ![]() ,
, ![]() булгани
учун, Сильвестр критериясига асосан, V функция аник мусбат ишорали булади.
булгани
учун, Сильвестр критериясига асосан, V функция аник мусбат ишорали булади.
![]() функция
ихтиёрий m-тартибли форма булсин. Энди
функция
ихтиёрий m-тартибли форма булсин. Энди ![]() ва
етарли кичик килиниши мумкин булган А мусбат узгармас сон учун
ва
етарли кичик килиниши мумкин булган А мусбат узгармас сон учун
![]() (2.1.9)
(2.1.9)
тенгсизликни
каноатлантирувчи ихтиёрий ![]() функцияни караймиз.
Куйидаги тасдик уринли.
функцияни караймиз.
Куйидаги тасдик уринли.
2-лемма.
Агар V m-тартибли
аник ишорали форма булса, у холда (2.1.3) сохада (2.1.9) тенгсизликни каноатлантирувчи
![]() функция учун,
унинг кандай танлаб олинишига боглик булмаган холда
функция учун,
унинг кандай танлаб олинишига боглик булмаган холда
![]()
![]()
![]() (2.1.10)
(2.1.10)
форма
хам ишораси V нинг ишораси билан бир хил булган аник ишорали форма
булади. Бу ерда (2.1.9) да иштирок этувчи А етарли кичик мусбат узгармас сон ва
факат ![]() форма коэффициентларига
боглик деб хисобланади.
форма коэффициентларига
боглик деб хисобланади.
Агар V узгарувчан ишорали форма ва юкоридаги шартлар уринли булса, у холда U форма хам узгарувчан ишорали булади.
Исбот. Даставвал
![]() . (2.1.11)
. (2.1.11)
буладиган ихтиёрий хакикий сонлар учун
![]() ,
, ![]()
деб белгилаймиз.
У холда
![]()
![]()
![]()
га эга буламиз.
V аник ишорали, масалан, аник мусбат ишорали форма булсин. ![]() микдорлар (2.1.3)
сохада ётиши учун
микдорлар (2.1.3)
сохада ётиши учун ![]() ни етарли кичик
сон деб хисоблаб, (2.1.9) ва (2.1.11) лар асосида
ни етарли кичик
сон деб хисоблаб, (2.1.9) ва (2.1.11) лар асосида
![]() (2.1.12)
(2.1.12)
муносабатни ёза оламиз.
Айтайлик ![]() сон
сон ![]() форманинг
куйи чегараси булсин, яъни
форманинг
куйи чегараси булсин, яъни
![]() .
(2.1.13)
.
(2.1.13)
Мусбат ишорали ![]() форма (2.1.11)
сферада факат мусбат кийматлар кабул килганлигидан
форма (2.1.11)
сферада факат мусбат кийматлар кабул килганлигидан ![]() албатта мусбат сон
булади. Факат V форманинг коэффициентларига боглик булган А сони агар
албатта мусбат сон
булади. Факат V форманинг коэффициентларига боглик булган А сони агар
![]() сонидан кичик
сонидан кичик ![]() булса,
у холда (2.1.3) соханинг координата бошидан ташкари хамма нукталарида, (2.1.12)
ва (2.1.13) ларга асосан,
булса,
у холда (2.1.3) соханинг координата бошидан ташкари хамма нукталарида, (2.1.12)
ва (2.1.13) ларга асосан, ![]() функция факат
мусбат кийматлар кабул килади. Демак, агар V – аник ишорали
функция булса ва
функция факат
мусбат кийматлар кабул килади. Демак, агар V – аник ишорали
функция булса ва ![]() (2.1.9)
тенгсизликни каноатлантирса, у холда
(2.1.9)
тенгсизликни каноатлантирса, у холда ![]() функция хам аник
ишорали булади.
функция хам аник
ишорали булади.
V – узгарувчан ишорали форма булганда, у (2.1.11) сферада хам мусбат, хам манфий ишорали кийматлар кабул килади.
![]() ва
ва ![]()
шундай
кийматларнинг ихтиёрий иккитаси булсин. Агар ![]() ва
ва ![]() деб
кабул килинса,
деб
кабул килинса, ![]() канчалик кичик булмасин,
канчалик кичик булмасин,
![]() ва
ва ![]()
лар бажарилади. Демак, U форма узгарувчан ишорали булади. Шундай килиб, лемма тулик исбот булди.
2-леммага асосланган куйидаги тасдикларни исботсиз келтирамиз.
3-лемма. Форманинг аник ишорали ёки узгарувчан ишорали эканлиги унга коэффициентлари етарли кичик булган хар кандай уша тартибли формани кушиш билан узгармайди.
Энди
![]()
![]()
![]() (2.1.14)
(2.1.14)
булсин. Бу ерда Vm m – тартибли форма, V* эса m дан катта тартибли форма.
4-лемма. Агар Vm аник ишорали форма булса, у холда (2.1.14) билан аникланадиган V хам аник ишорали форма булади ва агар Vm узгарувчан ишорали форма булса, у холда V хам узгарувчан ишорали форма булади.
Шундай килиб, аналитик функцияларнинг аник ишорали ёки узгарувчан ишорали эканлигини унинг ифодасидаги энг кичик тартибли хадларнинг мажмуаси аниклайди.
Масалан,
икки аргументли ![]() функция аник
ишорали ва
функция аник
ишорали ва
![]()
функция узгарувчан ишорали функция булади.
Агар форма ифодасидаги энг кичик тартибли хадларнинг мажмуаси узгармас ишорали булса, у холда унинг аник ишорали ёки узгарувчан ишорали эканлиги масаласини ёйилмасидаги юкори тартибли хадлар мажмуаси хал килади.
Масалан,
![]() ва
ва ![]() аргументли
куйидаги туртта функцияни курайлик:
аргументли
куйидаги туртта функцияни курайлик:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Бу
функцияларнинг биринчиси узгармас мусбат ишорали форма, унга 3-тартибли ![]() хадни
кушиб, иккинчи функцияни хосил киламиз ва у узгарувчан ишорали булади. Хосил
этилган функцияга
хадни
кушиб, иккинчи функцияни хосил киламиз ва у узгарувчан ишорали булади. Хосил
этилган функцияга ![]() туртинчи тартибли хадларни
кушиб, учинчи функцияни хосил киламиз ва у аник ишоралидир. Учинчи
функцияга
туртинчи тартибли хадларни
кушиб, учинчи функцияни хосил киламиз ва у аник ишоралидир. Учинчи
функцияга ![]() олтинчи тартибли хадни
кушиб туртинчи функцияни хосил киламиз ва у узгарувчан ишорали форма булади.
олтинчи тартибли хадни
кушиб туртинчи функцияни хосил киламиз ва у узгарувчан ишорали форма булади.
Бу мисолнинг ечимидан ушбу натижа келиб чикаяпти: агар бирор функция хамма аргументларининг формаси булмаса, у холда унга юкори тартибли хадларни кушиш натижасида унинг аник ишорали ёки узгарувчан ишорали эканлигини бузиш мумкин.
5-лемма.
Агар ![]() функция аник
ишорали булса, у холда шундай мусбат
функция аник
ишорали булса, у холда шундай мусбат ![]() сони топиладики,
барча
сони топиладики,
барча ![]() булганда V=с
сиртлар, координата боши О га нисбатан ёпик булади.
булганда V=с
сиртлар, координата боши О га нисбатан ёпик булади.
 |
Келгусида
биз ![]() функциянинг
характерини тадкик этилаётган дифференциал тенгламаларнинг траекториялари буйлаб
урганамиз ва бу тадкик натижасида курилаётган система траекторияларининг характери
хакида хам хулоса чикарамиз. Бундай максад учун ишлатиладиган
функциянинг
характерини тадкик этилаётган дифференциал тенгламаларнинг траекториялари буйлаб
урганамиз ва бу тадкик натижасида курилаётган система траекторияларининг характери
хакида хам хулоса чикарамиз. Бундай максад учун ишлатиладиган ![]() функцияларини
Ляпунов функциялари деб аташ кабул килинган.
функцияларини
Ляпунов функциялари деб аташ кабул килинган.
2-§. Харакат тургунлиги хакидаги Ляпуновнинг
биринчи теоремаси
Энди
Ляпуновнинг харакат тургунлигига багишланган асосий теоремаларини куриб утамиз.
 функциянинг
функциянинг 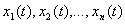 аргументлари
тойилган харакат дифференциал тенгламаларининг ечимлари деб каралади. У холда
бу функциянинг вакт буйича тойилган харакат дифференциал тенгламаларига кура
олинган тулик хосиласи
аргументлари
тойилган харакат дифференциал тенгламаларининг ечимлари деб каралади. У холда
бу функциянинг вакт буйича тойилган харакат дифференциал тенгламаларига кура
олинган тулик хосиласи
![]()
![]()
га тенг булади. Бу ифодани кискача
![]() (2.2.1)
(2.2.1)
куринишда ёзамиз. (2.2.1) ифодадан куриниб турибдики,
![]() .
.
Ляпуновнинг тургунлик хакидаги биринчи теоремаси куйидагича ифодаланади.
Теорема
А. Агар тойилган харакат дифференциал тенгламалари учун шундай аник
ишорали ![]() функция топиш
мумкин булсаки, унинг вакт буйича бу тенгламаларга кура олинган тулик хосиласи
ёки V функциянинг ишорасига тескари булган узгармас ишорали
функция, ёки айнан нолга тенг булса, у холда тойилмаган харакат тургун булади.
функция топиш
мумкин булсаки, унинг вакт буйича бу тенгламаларга кура олинган тулик хосиласи
ёки V функциянинг ишорасига тескари булган узгармас ишорали
функция, ёки айнан нолга тенг булса, у холда тойилмаган харакат тургун булади.
Исбот.
Умумийликни бузмасдан, ![]()
![]()
![]() (2.2.2)
(2.2.2)
сохада аник мусбат ишорали функция деб фараз киламиз. Шу сохада, теореманинг шартига кура,
![]() (2.2.3)
(2.2.3)
тенгсизлик бажарилади.
![]() - ихтиёрий етарли
кичик мусбат сон ва
- ихтиёрий етарли
кичик мусбат сон ва ![]() булсин.
булсин. ![]() билан
билан
![]() сонларнинг энг
каттасини белгилаймиз, яъни
сонларнинг энг
каттасини белгилаймиз, яъни
![]() ,
,
сунгра
![]() (2.2.4)
(2.2.4)
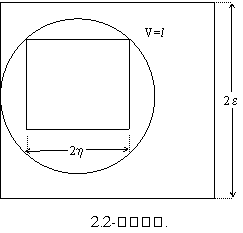 |
муносабат
билан богланган ![]() микдорларининг
барча кийматлари мажмуасини курамиз, яъни маркази координата боши билан
устма-уст тушадиган ва кирралари координата укларига параллель булган хамда
томони
микдорларининг
барча кийматлари мажмуасини курамиз, яъни маркази координата боши билан
устма-уст тушадиган ва кирралари координата укларига параллель булган хамда
томони ![]() га тенг келадиган
га тенг келадиган ![]() -улчовли
куб ёкларида ётган хамма нукталарни караймиз.
-улчовли
куб ёкларида ётган хамма нукталарни караймиз.
![]() функциянинг
(2.2.4) шарт учун аник куйи чегараси
функциянинг
(2.2.4) шарт учун аник куйи чегараси ![]() булсин, яъни
булсин, яъни
![]() . (2.2.5)
. (2.2.5)
(2.2.2) сохада V факат мусбат киймат
кабул килганлиги учун ![]() булади. V
(2.2.2) сохада узлуксиз булганлигидан унинг (2.2.4) тупламдаги аник куйи
чегараси бу функциянинг шу тупламда кабул киладиган кийматларидан биттаси булади.
булади. V
(2.2.2) сохада узлуксиз булганлигидан унинг (2.2.4) тупламдаги аник куйи
чегараси бу функциянинг шу тупламда кабул киладиган кийматларидан биттаси булади.
Энди бошлангич киймати 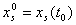
![]() (2.2.6)
(2.2.6)
шартни
каноатлантирадиган тойилган харакат дифференциал тенгламаларининг ечими ![]() ни
курамиз.
ни
курамиз. ![]() сони
сони ![]() дан
кичик ва у шунчалик кичик булсинки,
дан
кичик ва у шунчалик кичик булсинки,
![]() (2.2.7)
(2.2.7)
тенгсизлик
бажарилсин. ![]() сонини ана шундай
танлаб олиш мумкин, чунки V узлуксиз функция ва
сонини ана шундай
танлаб олиш мумкин, чунки V узлуксиз функция ва ![]() .
. ![]() ечимларни
ечимларни
![]() функциянинг ифодасига
куйиб,
функциянинг ифодасига
куйиб, ![]() вактга боглик булган
вактга боглик булган
![]() га эга буламиз. Бу
функция, (2.2.3) муносабатга асосан, (2.2.2) сохада камаювчи функция булади.
Демак,
га эга буламиз. Бу
функция, (2.2.3) муносабатга асосан, (2.2.2) сохада камаювчи функция булади.
Демак, ![]() нинг (2.2.2) сохада
ётадиган хамма кийматлари учун
нинг (2.2.2) сохада
ётадиган хамма кийматлари учун
![]()
![]() .
(2.2.8)
.
(2.2.8)
Бу
муносабатдан барча ![]() лар учун
лар учун
![]()
![]() (2.2.9)
(2.2.9)
нинг
бажарилиши келиб чикади. Хакикатан хам, ![]() булганидан ва
булганидан ва ![]() нинг
узлуксизлигидан хеч булмаганда
нинг
узлуксизлигидан хеч булмаганда ![]() нинг
нинг ![]() 0
га якин кийматлари учун (2.2.9) тенгсизликлар бажарилади. Агар бу тенгсизликлар
бажарилмаса, у холда вактнинг шундай
0
га якин кийматлари учун (2.2.9) тенгсизликлар бажарилади. Агар бу тенгсизликлар
бажарилмаса, у холда вактнинг шундай ![]() пайти топиладики,
шу пайтда
пайти топиладики,
шу пайтда ![]() ларнинг хеч булмаса
бирортасининг микдори
ларнинг хеч булмаса
бирортасининг микдори ![]() га тенг булади. Бошкача
килиб айтганда, шундай
га тенг булади. Бошкача
килиб айтганда, шундай ![]() пайт мавжуд буладики,
шу пайтда (2.2.4) муносабат бажарилади ва, демак, (2.2.5) га
асосан
пайт мавжуд буладики,
шу пайтда (2.2.4) муносабат бажарилади ва, демак, (2.2.5) га
асосан
![]()
булиши
керак. Аммо бундай булиши мумкин эмас, чунки ![]() булганлигидан
(2.2.4) туплам (2.2.2) сохада ётади, демак,
булганлигидан
(2.2.4) туплам (2.2.2) сохада ётади, демак, ![]() учун (2.2.8)
тенгсизлик бажарилади.
учун (2.2.8)
тенгсизлик бажарилади.
Шундай
килиб, (2.2.6) шартни каноатлантирувчи тойилган харакат дифференциал
тенгламаларининг хамма ![]() ечимлари барча
ечимлари барча ![]() лар
учун (2.2.9) тенгсизликларни каноатлантиради. Демак, тойилмаган харакат
(тойилган харакатнинг мувозанат холати) тургун булади.
лар
учун (2.2.9) тенгсизликларни каноатлантиради. Демак, тойилмаган харакат
(тойилган харакатнинг мувозанат холати) тургун булади.
Изох.
Теореманинг келтирилган исботидан, берилган ![]() сони учун амалий
масалалар учун зарур булган
сони учун амалий
масалалар учун зарур булган ![]() сонини топиш алгоритми
келиб чикади:
сонини топиш алгоритми
келиб чикади:
1.Берилган
![]() сонига асосан
(2.2.4) тупламда
сонига асосан
(2.2.4) тупламда ![]() функциянинг аник куйи
чегараси
функциянинг аник куйи
чегараси ![]() топилади.
топилади.
2.![]() сонини топилган
сонини топилган ![]() сонига асосан
шундай танлаш лозимки,
сонига асосан
шундай танлаш лозимки, ![]() тенгсизликларнинг
бажарилишидан
тенгсизликларнинг
бажарилишидан ![]() келиб чиксин.
келиб чиксин.
![]() сонини топиш
усулини курсатайлик.
сонини топиш
усулини курсатайлик.
![]() -
мусбат ишорали квадратик форма булсин. V квадратик
формага мос келувчи
-
мусбат ишорали квадратик форма булсин. V квадратик
формага мос келувчи
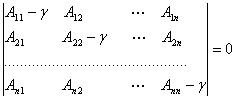 (А)
(А)
характеристик
тенгламани тузамиз. Алгебрадан маълумки, бу тенгламанинг хамма илдизлари хакикий
ва мусбат сонлардир. ![]() узгарувчилар
узгарувчилар
![]() ёки
ёки ![]()
шартларни
каноатлантирганда V функциянинг аник куйи чегараси (энг минимал киймати) ![]()
![]() (В)
(В)
формула
оркали аникланади, бу ерда ![]() -(А) тенглама илдизларининг
энг кичик кийматли илдизи.
-(А) тенглама илдизларининг
энг кичик кийматли илдизи.
Худди
шундай, V нинг аник юкори чегараси (энг максимал киймати) ![]() ва
ва
![]() сони
сони
![]() ,
, ![]()
формулалар
оркали аникланади. Бу ерда ![]() - (А) нинг энг
катта кийматли илдизи. Бу тасдикларнинг исботини Г.Н.Дубошиннинг [26] (89-91 бетлардан)
топасиз.
- (А) нинг энг
катта кийматли илдизи. Бу тасдикларнинг исботини Г.Н.Дубошиннинг [26] (89-91 бетлардан)
топасиз.
Агар
![]() тенглик билан аникланса,
у холда
тенглик билан аникланса,
у холда ![]() ва
ва ![]()
![]() ,
, ![]()
формулалар
билан аникланадилар, бу ерда ![]() коэффициентларнинг
энг кичиги,
коэффициентларнинг
энг кичиги, ![]() эса коэффициентларнинг
энг каттаси.
эса коэффициентларнинг
энг каттаси.
Агар
![]() булса, у холда
булса, у холда
![]()
булади.
1-мисол. Тойилган харакат дифференциал тенгламалари
![]()
куринишда берилган булсин. Аник мусбат ишорали
![]()
функцияни олиб, унинг тойилган харакат тенгламаларига кура вакт буйича тулик хосиласини топамиз:
![]()
![]() .
.
V аник мусбат
ишорали функция ва унинг вакт буйича олинган тулик хосиласи ![]() узгармас
манфий ишорали функция булгани учун теореманинг хамма шартларини каноатлантирадилар.
Демак,
узгармас
манфий ишорали функция булгани учун теореманинг хамма шартларини каноатлантирадилар.
Демак, ![]() тойилмаган харакат
тургун булади.
тойилмаган харакат
тургун булади.
2-мисол. Тойилган харакат тенгламалари
![]()
![]()
куринишда булсин. Агар V функцияни
![]()
куринишда олсак, у холда унинг тойилган харакат тенгламаларига нисбатан вакт буйича олинган тулик хосиласи
![]()
булади.
V аник мусбат ишорали ва ![]() узгармас манфий
ишорали функциялар, шунинг учун теорема А га асосан, тойилмаган харакат тургун
булади.
узгармас манфий
ишорали функциялар, шунинг учун теорема А га асосан, тойилмаган харакат тургун
булади.
3-мисол. Куйидаги тойилган харакатнинг тенгламалари берилган булсин
![]() ,
,
![]() ,
,
![]() .
.
V функцияни
![]()
куринишда оламиз. Унинг вакт буйича тойилган харакат тенгламаларига асосан олинган тулик хосиласи
![]()
булади.
V –
аник мусбат ишорали функция ва ![]() - узгармас манфий
ишорали функция булганлигидан, исбот килинган теоремага асосан, тойилмаган харакат
тургун булади.
- узгармас манфий
ишорали функция булганлигидан, исбот килинган теоремага асосан, тойилмаган харакат
тургун булади.
Ихтиёрий
![]() сон учун V
функциянинг аник куйи чегараси (энг минимал киймати)
сон учун V
функциянинг аник куйи чегараси (энг минимал киймати) ![]() ва
ва ![]() эканлигини
топамиз.
эканлигини
топамиз.
Демак, агар бошлангич
![]()
шартни
каноатлантирувчи ![]() ,
, ![]() ва
ва
![]() ларни олсак, у холда
хамма
ларни олсак, у холда
хамма ![]() лар учун
лар учун ![]()
тенгсизликка эга буламиз.
3-§. Харакатнинг асимптотик тургунлиги хакидаги
Ляпунов теоремаси
Куйида баён этиладиган харакатнинг асимптотик тургунлиги хакидаги Ляпуновнинг теоремаси унинг биринчи теоремасини тулдиради.
Теорема
Б. Агар тойилган харакат дифференциал тенгламалари учун шундай аник
ишорали ![]() функция топилиб,
унинг бу тенгламаларга нисбатан вакт буйича олинган тулик хосиласи V
нинг ишорасига тескари аник ишорали функция булса, у холда тойилмаган харакат
асимптотик тургундир.
функция топилиб,
унинг бу тенгламаларга нисбатан вакт буйича олинган тулик хосиласи V
нинг ишорасига тескари аник ишорали функция булса, у холда тойилмаган харакат
асимптотик тургундир.
Исбот. Худди биринчи теоремани исбот килгандаги-дай
![]() аник мусбат ишорали
функция булсин.
аник мусбат ишорали
функция булсин.
Демак,
теореманинг шартига асосан ![]() - аник манфий
ишорали функция булади, яъни (2.2.2) сохада
- аник манфий
ишорали функция булади, яъни (2.2.2) сохада
![]() ,
, ![]()
муносабатлар бажарилади.
![]()
![]() дан
кичик ихтиёрий мусбат сон булсин. Курилаётган хол учун биринчи
теореманинг шартлари тулик бажарилади ва, демак, тойилмаган харакат тургун булади.
Шу сабабли хам хар кандай етарли кичик мусбат
дан
кичик ихтиёрий мусбат сон булсин. Курилаётган хол учун биринчи
теореманинг шартлари тулик бажарилади ва, демак, тойилмаган харакат тургун булади.
Шу сабабли хам хар кандай етарли кичик мусбат ![]() сон учун шундай
мусбат
сон учун шундай
мусбат ![]() сон топиладики,
тойилган харакат дифференциал тенгламаларининг хар кандай
сон топиладики,
тойилган харакат дифференциал тенгламаларининг хар кандай ![]() ечимлари
учун
ечимлари
учун ![]() пайтда
пайтда
![]() (2.3.1)
(2.3.1)
бажарилишидан
барча ![]() лар учун
лар учун
![]() (2.3.2)
(2.3.2)
тенгсизликнинг бажарилиши келиб чикади.
Энди теорема шарти бажарилганда тойилмаган харакатнинг асимптотик тургун булишини, яъни
![]()
![]() (2.3.3)
(2.3.3)
эканлигини курсатамиз.
Хакикатан хам, курилаётган ![]() ечимлар
доимо (2.3.2) сохада ётганлиги учун теореманинг шартига асосан
ечимлар
доимо (2.3.2) сохада ётганлиги учун теореманинг шартига асосан ![]() функциянинг
вакт буйича олинган тулик хосиласи t нинг хамма кийматлари учун
(нолга айланмасдан) манфий булади.
функциянинг
вакт буйича олинган тулик хосиласи t нинг хамма кийматлари учун
(нолга айланмасдан) манфий булади. ![]() аник ишорали
функция булганлиги учун факат координата бошида нол киймат кабул килади.
аник ишорали
функция булганлиги учун факат координата бошида нол киймат кабул килади.
Шундай
килиб, ![]() доимо манфий,
демак,
доимо манфий,
демак, ![]() функция монотон
камаювчи булади. Шунинг учун хам бу функция
функция монотон
камаювчи булади. Шунинг учун хам бу функция ![]() да кандайдир
да кандайдир ![]() лимитга
(ундан доимо катта булга холда) интилади, яъни доимо
лимитга
(ундан доимо катта булга холда) интилади, яъни доимо
![]() . (2.3.4)
. (2.3.4)
булади.
![]() эканлигини исбот киламиз.
Тескарисини фараз килайлик. Демак,
эканлигини исбот киламиз.
Тескарисини фараз килайлик. Демак, ![]() ва V аник
мусбат ишорали функция булганлигидан
ва V аник
мусбат ишорали функция булганлигидан ![]() булади. V
функция узлуксиз функция эканлиги учун (2.3.4) тенгсизликдан
булади. V
функция узлуксиз функция эканлиги учун (2.3.4) тенгсизликдан
![]() (2.3.5)
(2.3.5)
келиб
чикади, бу ерда ![]() - кандайдир мусбат
сон. Уз навбатида
- кандайдир мусбат
сон. Уз навбатида ![]() аник манфий
ишорали функция булганлигидан (2.3.5) га асосан
аник манфий
ишорали функция булганлигидан (2.3.5) га асосан
![]()
ни
хосил киламиз. Бу ерда ![]() - бирор мусбат
сон. Демак, хамма
- бирор мусбат
сон. Демак, хамма ![]() лар учун
лар учун
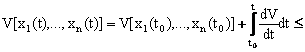
![]() (2.3.6)
(2.3.6)
га эга буламиз.
Бирок бунинг булиши мумкин эмас, чунки (2.3.6) тенгликнинг унг тарафидаги ифода
билан бирга V функция t нинг етарли катта кийматларида
манфий булиб колади. Теореманинг шартига асосан эса ![]() мусбат
ишорали функциядир. Биз карама-каршиликка келиб колдик.
мусбат
ишорали функциядир. Биз карама-каршиликка келиб колдик.
Демак
![]()
ва
![]() аник ишорали
функция эканлигидан
аник ишорали
функция эканлигидан
![]()
булади. Демак, теорема шарти бажарилганда, тойилмаган харакат асимптотик тургун булади.
Изох. Тойилган харакат
дифференциал тенгламаларининг ![]() ечимлари учун
ечимлари учун ![]() шартнинг
бажарилишини таъминлай оладиган
шартнинг
бажарилишини таъминлай оладиган ![]() бошлангич кийматларнинг
энг катта сохасини асимптотик тургунлик сохаси деб атаймиз.
бошлангич кийматларнинг
энг катта сохасини асимптотик тургунлик сохаси деб атаймиз.
Келтирилган
исботдан равшанки, бу соха хеч качон ![]() сохадан кичик булмайди.
сохадан кичик булмайди.
![]() сонини берилган
сонини берилган ![]() сонига
асосан топиш алгоритми 2-§ даги изохда берилган.
сонига
асосан топиш алгоритми 2-§ даги изохда берилган.
1-мисол. Тойилган харакат дифференциал тенгламалари
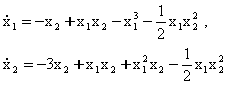
лар булсин. V функцияни куйидаги куринишда оламиз
![]() .
.
Бу функциянинг коэффициентларидан тузилган
матрицанинг бош минорлари Сильвестер критерияси шартларини каноатлантирганлиги
учун у аник мусбат ишоралидир, яъни ![]() .
.
V функциянинг вакт буйича тулик хосиласи
![]()
куринишда булади.
![]() ифодасидаги
ифодасидаги ![]() ва
ва
![]() ларнинг урнига
тойилган харакат тенгламаларидан кийматларини келтириб куйиб, соддалаштирганимиздан
кейин
ларнинг урнига
тойилган харакат тенгламаларидан кийматларини келтириб куйиб, соддалаштирганимиздан
кейин
![]()
га эга буламиз. Бу функция коэффициентларидан тузилган
![]()
матрицани
карайлик. Бу ерда узгарувчилар сифатида ![]() ва
ва ![]() лар
олинган. А нинг бош минорлари
лар
олинган. А нинг бош минорлари
![]() .
.
Демак,
Сильвестер критериясига асосан ![]() функция
функция ![]() ва
ва
![]() узгарувчиларга (шунинг
учун хам
узгарувчиларга (шунинг
учун хам ![]() ва
ва ![]() ларга)
нисбатан аник манфий ишорали функция булади, яъни
ларга)
нисбатан аник манфий ишорали функция булади, яъни ![]() булади.
булади.
Шундай килиб, V – аник мусбат ишорали ва ![]() -аник
манфий ишорали функциялар булганликларидан, теорема Б га асосан, тойилмаган харакат
асимптотик тургун булади.
-аник
манфий ишорали функциялар булганликларидан, теорема Б га асосан, тойилмаган харакат
асимптотик тургун булади.
2-мисол. Тойилган харакат тенгламалари куйидагича булсин

Ляпунов функциясини
![]()
куринишда оламиз. Унинг вакт буйича тойилган харакат тенгламаларига кура олинган тулик хосиласи
![]()
булади.
V функция ![]() ва
ва ![]() узгарувчиларнинг
хамма кийматларида аник мусбат ишоралидир,
узгарувчиларнинг
хамма кийматларида аник мусбат ишоралидир, ![]() функция эса
функция эса
![]()
сохада
аник манфий ишорали булади. Демак, V ва -![]() функциялар
учун
функциялар
учун
![]()
сохада
![]() ва
ва ![]() муносабатлар
уринли, яъни теорема Б нинг хамма шартлари каноатлантирилади ва шунинг учун хам
тойилмаган харакат асимптотик тургун булади. Бу мисолда
муносабатлар
уринли, яъни теорема Б нинг хамма шартлари каноатлантирилади ва шунинг учун хам
тойилмаган харакат асимптотик тургун булади. Бу мисолда ![]() деб олиш
мумкин, у холда
деб олиш
мумкин, у холда ![]() вактда бошлангич
вактда бошлангич
![]()
шартни
каноатлантирувчи хамма ![]() ва
ва ![]() ечимлар
учун
ечимлар
учун
![]()
![]()
муносабат бажарилади.
3-мисол. Куйидаги тенгламалар системаси берилган булсин
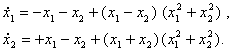
V функцияни
![]()
куринишда олиб, ундан вакт буйича тулик хосила оламиз
![]()
V аник мусбат ишорали функция, ![]() функцияси
булса,
функцияси
булса,
![]()
сохада манфий ишоралидир. Шунинг учун агар бошлангич кийматни
![]()
тенгсизликни
каноатлантирадиган килиб танласак, у холда ![]() булади. Бу ердан
булади. Бу ердан ![]() ва
тойилмаган харакатнинг асимптотик тургун эканлиги келиб чикади.
ва
тойилмаган харакатнинг асимптотик тургун эканлиги келиб чикади.
4-§. Харакатнинг батамом асимптотик тургунлиги хакидаги Барбашин - Красовскийлар теоремалари
Ляпунов
кичик тойилишлар учун асимптотик тургунликнинг етарли шартларини яратди. Бошкача
килиб айтганда, Ляпунов теоремаси факатгина ![]() бошлангич вактда
динамик система харакатига таъсир этадиган тойдирувчи кучлар микдори етарлича
кичик булган холлар учун тугридир, яъни
бошлангич вактда
динамик система харакатига таъсир этадиган тойдирувчи кучлар микдори етарлича
кичик булган холлар учун тугридир, яъни
![]() (2.4.1)
(2.4.1)
тенгсизликдаги
![]() етарли кичик мусбат
сон булиши керак. Аммо, амалиётда (масалан, бошкарув жараёнларида, кузатувчи
системаларида, автоматик регуляторларда ва б.к.). динамик системага таъсир
этадиган тойдирувчи кучларнинг микдори (демак,
етарли кичик мусбат
сон булиши керак. Аммо, амалиётда (масалан, бошкарув жараёнларида, кузатувчи
системаларида, автоматик регуляторларда ва б.к.). динамик системага таъсир
этадиган тойдирувчи кучларнинг микдори (демак, ![]() ларнинг микдори хам)
катта булиши мумкин. Бу холлар учун Ляпунов теоремаси уз кучини йукотади.
ларнинг микдори хам)
катта булиши мумкин. Бу холлар учун Ляпунов теоремаси уз кучини йукотади.
Е.А.Барбашин, Н.П.Еругин, В.А.Плисс ва Н.Н.Красовскийлар 1950-1955 йиллар давомида хар кандай катталикдаги тойилишлар учун асимптотик тургунликнинг етарли шартларини ишлаб чикдилар [9,10,27,28,40,77].
Бу холларда (2.4.1) бошлангич ![]() тойилишлар
сохасининг куламини бахолаш масаласи мухимдир. Шунинг учун хам тойилмаган харакатнинг
асимптотик тургунлиги хакидаги таърифни тулдириш лозим булиб колади.
тойилишлар
сохасининг куламини бахолаш масаласи мухимдир. Шунинг учун хам тойилмаган харакатнинг
асимптотик тургунлиги хакидаги таърифни тулдириш лозим булиб колади.
1-таъриф. Агар
G масаланинг шарти буйича ![]() бошлангич
тойилишлар ётиши мумкин булган
бошлангич
тойилишлар ётиши мумкин булган ![]() узгарувчиларнинг
олдиндан берилган узгариш сохаси булиб, тойилмаган харакат
узгарувчиларнинг
олдиндан берилган узгариш сохаси булиб, тойилмаган харакат ![]() тургун
ва
тургун
ва
![]() (2.4.2)
(2.4.2)
муносабат
G сохадаги хамма ![]() лар учун
бажарилса, у холда тойилмаган харакат кенг куламда асимптотик тургун дейилади.
лар учун
бажарилса, у холда тойилмаган харакат кенг куламда асимптотик тургун дейилади.
Айрим холда, G соха
![]() (2.4.3)
(2.4.3)
тенгсизлик билан хам аникланиши мумкин, каерда N – берилган мусбат сон.
2-таъриф.
Агар тойилмаган харакат тургун булса ва (2.4.2) муносабат хар кандай бошлангич
![]() тойилишлар учун
бажарилса, у холда тойилмаган харакат батамом асимптотик тургун деб аталади.
тойилишлар учун
бажарилса, у холда тойилмаган харакат батамом асимптотик тургун деб аталади.
Ляпуновнинг асимптотик тургунлик хакидаги теоремасини кенг куламда ва батамом асимптотик тургунлик холлар учун умумлаштириш мумкин. Куйида Е.А.Барбашин ва Н.Н.Красовскийларнинг шу масалага багишлаган теоремаларини (асимптотик тургунлик критерияларини) исботсиз келтирамиз.
Теорема Б1. Агар тойилган харакат дифференциал тенгламалари учун
![]() (2.4.4)
(2.4.4)
сохада
аник ишорали ![]() функция топилиб,
унинг тойилган харакат тенгламаларига асосан вакт буйича олинган
функция топилиб,
унинг тойилган харакат тенгламаларига асосан вакт буйича олинган ![]() тенгсизликни
каноатлантирувчи тулик хосиласи хам (2.4.4) сохада V
нинг ишорасига тескари аник ишорали функция булса, у холда тойилмаган харакат
тенгсизликни
каноатлантирувчи тулик хосиласи хам (2.4.4) сохада V
нинг ишорасига тескари аник ишорали функция булса, у холда тойилмаган харакат
![]() (2.4.5)
(2.4.5)
сохадаги
![]() бошлангич
тойилишларга нисбатан кенг куламда асимптотик тургун булади.
бошлангич
тойилишларга нисбатан кенг куламда асимптотик тургун булади.
Бу
ерда ![]() билан
билан ![]()
![]() шарт
бажарилгандаги
шарт
бажарилгандаги ![]() функциянинг
аник куйи чегараси,
функциянинг
аник куйи чегараси, ![]() билан эса
билан эса ![]() шарт
учун
шарт
учун ![]() функциянинг
аник юкори чегараси белгиланган.
функциянинг
аник юкори чегараси белгиланган.
Теорема
Б2. Агар тойилган харакат дифференциал тенгламалари учун
шундай мусбат ишорали ![]() функция топилиб,
унинг тойилган харакат тенгламаларига кура вакт буйича олинган тулик хосиласи хамма
функция топилиб,
унинг тойилган харакат тенгламаларига кура вакт буйича олинган тулик хосиласи хамма
![]() лар учун манфий
ишорали функция хамда
лар учун манфий
ишорали функция хамда
![]()
булса, у холда тойилмаган харакат батамом асимптотик тургун булади.
Теоремадаги
![]() шартни куйидагича
тушуниш лозим: хар кандай
шартни куйидагича
тушуниш лозим: хар кандай ![]() сони учун
сони учун ![]() сонини
танлаб олиш мумкинки,
сонини
танлаб олиш мумкинки, ![]() тенгсизлик
бажарилсин. У вактда теорема Б2 нинг тугрилиги теорема Б1
дан келиб чикади. Бу шартнинг батамом тургунлик масалалари учун мухимлигини
Н.П.Еругин узининг [27] ишида курсатган эди.
тенгсизлик
бажарилсин. У вактда теорема Б2 нинг тугрилиги теорема Б1
дан келиб чикади. Бу шартнинг батамом тургунлик масалалари учун мухимлигини
Н.П.Еругин узининг [27] ишида курсатган эди.
5-§. Тургунлик хакидаги теоремаларнинг
геометрик талкини
Харакат тургунлиги хакидаги Ляпуновнинг теорема-
ларига содда геометрик талкин бериш мумкин. Бу талкин нафакат теоремаларнинг асосий мазмунларини тушунишга ёрдам беради, балки купгина техник масалаларни ечишда хам фойдаланилади.
Биз куйида келтираётган геометрик талкинни И.Г.Малкин 1929-1931 йилларда Казан физика-математика жамиятида ифодалаган эди [54].
Дастлаб
Ляпуновнинг биринчи теоремасида соддалик учун ![]() деб фараз киламиз.
Аник ишорали
деб фараз киламиз.
Аник ишорали ![]() функция мавжуд
ва бу функция учун
функция мавжуд
ва бу функция учун ![]() булсин.
булсин.
![]() (2.5.1)
(2.5.1)
сиртларни
ясаймиз, бу ерда ![]() -нолдан етарлича
кичик фарк киладиган узгарувчи мусбат параметр. 1-параграфда курсатилган
эдики, (2.5.1) сиртлар ёпик ва координата бошини камраб олади,
-нолдан етарлича
кичик фарк киладиган узгарувчи мусбат параметр. 1-параграфда курсатилган
эдики, (2.5.1) сиртлар ёпик ва координата бошини камраб олади, ![]() булганда
эса нуктага айланади (координата боши). Агар
булганда
эса нуктага айланади (координата боши). Агар ![]() булса, у холда
булса, у холда ![]() сирт
тулик
сирт
тулик ![]() сиртнинг ичида
ётади.
сиртнинг ичида
ётади.
Бошлангич
![]() вактда координата
боши атрофининг бирор нуктасидан чикаётган
вактда координата
боши атрофининг бирор нуктасидан чикаётган
![]() (2.5.2)
(2.5.2)
тойилган
харакат дифференциал тенгламаларининг бирор интеграл эгри чизигини курамиз. Бу
интеграл эгри чизик t нинг усиши билан хеч качон (2.5.1) сиртларнинг
бирортасини ичкарисидан ташкарига караб кесиб утмайди. Хакикатан хам, агар
бирор нуктада бу кесишув юз берса эди, у холда бу нуктада ёки унинг атрофида ![]() функция
мусбат хосилага эга буларди,
функция
мусбат хосилага эга буларди,
чунки
биринчи (2.5.1) сиртни камраб олган иккинчи (2.5.1) сиртга утишда ![]() функция
усади. Аммо,
функция
усади. Аммо, ![]() эканлигидан,
бундай булиши мумкин эмас. Шундай килиб, агар бошлангич вактда бирор интеграл
эгри чизик бирор (2.5.1) сиртнинг ичида булса, у холда у
эканлигидан,
бундай булиши мумкин эмас. Шундай килиб, агар бошлангич вактда бирор интеграл
эгри чизик бирор (2.5.1) сиртнинг ичида булса, у холда у ![]() вактларда
хам унинг ичида колади.
вактларда
хам унинг ичида колади.
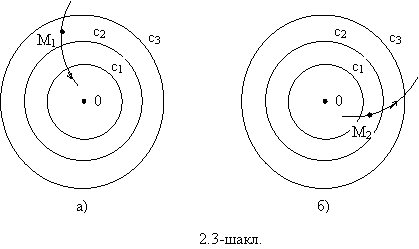
![]() нинг
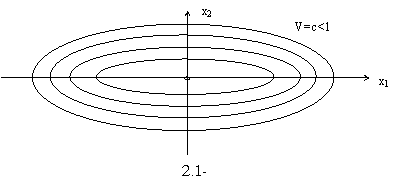
етарлича кичик кийматларида (2.5.1) сирт координата бошини камраб олганидан,
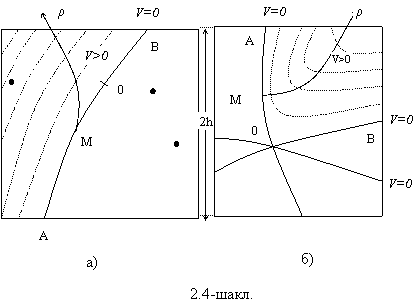
тойилмаган харакатнинг тургунлиги келиб чикади ( 2.3-шаклга каранг).
нинг
етарлича кичик кийматларида (2.5.1) сирт координата бошини камраб олганидан,
тойилмаган харакатнинг тургунлиги келиб чикади ( 2.3-шаклга каранг).
Агар ![]() функция аник
манфий ишорали булса, у холда координата бошининг етарли кичик атрофидан чикаётган
хар бир интеграл эгри чизик (2.5.1) сиртларни ташкаридан ичкарига караб кесиб утади,
чунки
функция аник
манфий ишорали булса, у холда координата бошининг етарли кичик атрофидан чикаётган
хар бир интеграл эгри чизик (2.5.1) сиртларни ташкаридан ичкарига караб кесиб утади,
чунки ![]() функция узлуксиз
камайиши керак. У холда интеграл эгри чизиклар узлуксиз координата бошига якинлашади.
Демак, тойилмаган харакат асимптотик тургун булади.
функция узлуксиз
камайиши керак. У холда интеграл эгри чизиклар узлуксиз координата бошига якинлашади.
Демак, тойилмаган харакат асимптотик тургун булади.
Шундай
килиб, Ляпуновнинг иккинчи усули геометрик нуктаи назаридан тургунликни
текширишни координата бошини камраб (ураб) олган (2.5.1) сиртларни ясашга келтирилади.
Агар (2.5.2) тенгламаларнинг интеграл эгри чизиклари ![]() вактларда
бу сиртларни ташкаридан ичкарига караб кесиб утсалар, у холда тойилмаган харакат
тургун, интеграл эгри чизиклар (2.5.1) сиртларни ичкаридан ташкарига караб
кесиб утганда эса, тойилмаган харакат нотургун булади. Кандайдир мулохазалар
асосида юкорида айтилган хусусиятларга эга булган сиртлар мавжудлигини аникласак,
у холда тургунлик масаласи осонгина ечилади.
вактларда
бу сиртларни ташкаридан ичкарига караб кесиб утсалар, у холда тойилмаган харакат
тургун, интеграл эгри чизиклар (2.5.1) сиртларни ичкаридан ташкарига караб
кесиб утганда эса, тойилмаган харакат нотургун булади. Кандайдир мулохазалар
асосида юкорида айтилган хусусиятларга эга булган сиртлар мавжудлигини аникласак,
у холда тургунлик масаласи осонгина ечилади.
6-§. Харакатнинг нотургунлиги хакидаги Ляпуновнинг
биринчи теоремаси
Энди харакатнинг нотургунлиги хакидаги Ляпунов теоремаларини куриб утамиз. Унинг биринчи теоремаси куйидагича таърифланади.
Теорема
В. Агар тойилган харакат
дифференциал тенгламалари учун шундай ![]() функция топилиб,
унинг тойилган харакат тенгламаларига кура вакт буйича олинган тулик хосиласи
аник ишорали функция булиб, функциянинг узи эса ишораси
функция топилиб,
унинг тойилган харакат тенгламаларига кура вакт буйича олинган тулик хосиласи
аник ишорали функция булиб, функциянинг узи эса ишораси ![]() никига
тескари булган узгармас ишорали функция булмаса, у холда тойилмаган харакат
нотургун булади.
никига
тескари булган узгармас ишорали функция булмаса, у холда тойилмаган харакат
нотургун булади.
Исбот.
![]() функция
функция
![]() (2.6.1)
(2.6.1)
сохада
аник ишорали булсин. ![]() ни шундай етарли
кичик мусбат сон деб фараз киламизки, тойилган харакатнинг (2.5.2) дифференциал
тенгламалари (2.6.1) сохада
ни шундай етарли
кичик мусбат сон деб фараз киламизки, тойилган харакатнинг (2.5.2) дифференциал
тенгламалари (2.6.1) сохада ![]() ларнинг хар бир
ларнинг хар бир ![]() бошлангич
кийматлари учун ягона ечимга эга булсин. Яна, аниклик учун,
бошлангич
кийматлари учун ягона ечимга эга булсин. Яна, аниклик учун, ![]() дейлик.
дейлик.
![]() канча
кичик сон булмасин,
канча
кичик сон булмасин,
![]() (2.6.2)
(2.6.2)
сохада
ётувчи ![]() ечимларнинг шундай
бошлангич
ечимларнинг шундай
бошлангич ![]() кийматлари
топилиб, маълум бир
кийматлари
топилиб, маълум бир ![]() вактда
вактда ![]() ечимлар
(2.6.1) сохадан чикиб кетиши, яъни
ечимлар
(2.6.1) сохадан чикиб кетиши, яъни ![]() булишини курсатиш
мумкин. Шу билан тойилмаган харакатнинг нотургунлиги исботланади.
булишини курсатиш
мумкин. Шу билан тойилмаган харакатнинг нотургунлиги исботланади.
Шу
максадда, ![]() ларнинг кийматларини
шундай танлаб оламизки, нафакат (2.6.2) тенгсизлик бажарилсин, балки
ларнинг кийматларини
шундай танлаб оламизки, нафакат (2.6.2) тенгсизлик бажарилсин, балки
![]() (2.6.3)
(2.6.3)
хам булсин.
Кийматлари
(2.6.2) ва (2.6.3) тенгсизликларни каноатлантирувчи ![]() ларни
танлаб олиш мумкин, чунки теореманинг шартига асосан V функция узгармас
манфий ишорали эмас ва, демак, координата бошининг етарли кичик атрофида V
функция мусбат кийматлар кабул кила олади. Энди (2.5.2) тенгламаларнинг (2.6.2)
ва (2.6.3) тенгсизликларни каноатлантирувчи бошлангич
ларни
танлаб олиш мумкин, чунки теореманинг шартига асосан V функция узгармас
манфий ишорали эмас ва, демак, координата бошининг етарли кичик атрофида V
функция мусбат кийматлар кабул кила олади. Энди (2.5.2) тенгламаларнинг (2.6.2)
ва (2.6.3) тенгсизликларни каноатлантирувчи бошлангич ![]() кийматларга
мос келувчи
кийматларга
мос келувчи ![]() ечимини курамиз.
Бу ечим кандайдир t вактда албатта (2.6.1) сохадан чикиб кетади. Бу тасдикни
исбот килиш учун тескарисини фараз киламиз, яъни хамма
ечимини курамиз.
Бу ечим кандайдир t вактда албатта (2.6.1) сохадан чикиб кетади. Бу тасдикни
исбот килиш учун тескарисини фараз киламиз, яъни хамма ![]() вактларда
вактларда
![]() ечимлар (2.6.1)
тенгсизликни каноатлантирсин. У вактда хар доим
ечимлар (2.6.1)
тенгсизликни каноатлантирсин. У вактда хар доим ![]() булади ва, демак,
булади ва, демак, ![]() функция
доимо усади.
функция
доимо усади.
Шунинг учун
![]()
![]() (2.6.4)
(2.6.4)
ёзишга хаклимиз. Бу ердан албатта
![]() (2.6.5)
(2.6.5)
келиб
чикади, бу ерда ![]() - бирор мусбат
сон. Агар
- бирор мусбат
сон. Агар ![]() булса, у холда
булса, у холда ![]() узлуксиз
функция ва
узлуксиз
функция ва ![]() булганлиги
учун
булганлиги
учун ![]() нинг етарли кичик киймати
учун (2.6.4) тенгсизлик бажарилмаслиги мумкин.
нинг етарли кичик киймати
учун (2.6.4) тенгсизлик бажарилмаслиги мумкин.
![]() мусбат
ишорали функция булганлиги сабабли (2.6.5) тенгсизликдан курилаётган
мусбат
ишорали функция булганлиги сабабли (2.6.5) тенгсизликдан курилаётган ![]() ечимлар
учун хар доим
ечимлар
учун хар доим
![]()
тенгсизлик
бажарилади, бу ерда ![]() етарли кичик
мусбат сон. Демак,
етарли кичик
мусбат сон. Демак,
![]()
![]()
![]() (2.6.6)
(2.6.6)
булади.
(2.6.6) муносабатдан ![]() функциянинг чексиз
усиши келиб чикади. Аммо, бу
функциянинг чексиз
усиши келиб чикади. Аммо, бу ![]() ечим (2.6.1) сохадан
чикмайди деган фаразимизга тугри келмайди. Демак, фаразимиз нотугри экан. Бу
тойилмаган харакатнинг нотургун эканлигини билдиради.
ечим (2.6.1) сохадан
чикмайди деган фаразимизга тугри келмайди. Демак, фаразимиз нотугри экан. Бу
тойилмаган харакатнинг нотургун эканлигини билдиради.
7-§. Харакатнинг нотургунлиги хакидаги Ляпуновнинг
иккинчи теоремаси
Энди Ляпуновнинг харакат нотургунлиги хакидаги иккинчи теоремасини исбот киламиз.
Теорема
Г. Агар шундай ![]() функция топилиб,
унинг тойилган харакат тенгламаларига асосан вакт буйича олинган тулик хосиласи
(2.6.1) сохада
функция топилиб,
унинг тойилган харакат тенгламаларига асосан вакт буйича олинган тулик хосиласи
(2.6.1) сохада
![]() (2.7.1)
(2.7.1)
куринишга
эга хамда, бунда ![]() узгармас мусбат
сон,
узгармас мусбат
сон, ![]() эса, ёки айнан
нол, ёки узгармас ишорали функция булса ва агар охирги холда
эса, ёки айнан
нол, ёки узгармас ишорали функция булса ва агар охирги холда ![]() функция
функция
![]() нинг ишорасига
тескари булган узгармас ишорали булмаса, у холда тойилмаган харакат нотургун булади.
нинг ишорасига
тескари булган узгармас ишорали булмаса, у холда тойилмаган харакат нотургун булади.
Исбот. Аниклик
учун ![]() булсин. У холда
(2.7.1) муносабатдан
булсин. У холда
(2.7.1) муносабатдан
![]() (2.7.2)
(2.7.2)
ни
хосил киламиз. Худди теорема В дагидек ![]() ечимнинг
ечимнинг ![]() даги
бошлангич кийматларини шундай танлаб оламизки,
даги
бошлангич кийматларини шундай танлаб оламизки,
![]() ,
,
![]() (2.7.3)
(2.7.3)
тенгсизликлар
бир вактда бажарилсин, бу ерда ![]() - исталганча кичик
мусбат сон. Шу шартлар бажарилганда,
- исталганча кичик
мусбат сон. Шу шартлар бажарилганда, ![]() ечим вакти келиб
(2.6.1) сохадан чикиб кетишини курсатамиз. Аксини, яъни (2.6.1) тенгсизликлар
доимо бажарилади деб фараз киламиз. У холда (2.7.2) тенгсизликлар доимо
бажарилади ва
ечим вакти келиб
(2.6.1) сохадан чикиб кетишини курсатамиз. Аксини, яъни (2.6.1) тенгсизликлар
доимо бажарилади деб фараз киламиз. У холда (2.7.2) тенгсизликлар доимо
бажарилади ва ![]() булганлиги учун
(2.7.2) га асосан
булганлиги учун
(2.7.2) га асосан ![]() доимо мусбат булиб
колади, яъни
доимо мусбат булиб
колади, яъни ![]() . Демак,
. Демак, ![]() усувчи
функция булади. У вактда (2.7.2) тенгсизликдан
усувчи
функция булади. У вактда (2.7.2) тенгсизликдан
![]()
![]() (2.7.4)
(2.7.4)
ни хосил киламиз. Бу ердан
![]() (2.7.5)
(2.7.5)
муносабат
келиб чикади. (2.7.5) нинг булиши мумкин эмас, чунки (2.6.1) сохада ![]() функция
чегараланган. Шундай килиб, (2.6.1) тенгсизлик курилаётган
функция
чегараланган. Шундай килиб, (2.6.1) тенгсизлик курилаётган ![]() ечим
учун бузилади. Бу холат тойилмаган харакатнинг тургун эмаслигини курсатади.
ечим
учун бузилади. Бу холат тойилмаган харакатнинг тургун эмаслигини курсатади.
8-§. Теорема В нинг геометрик талкини.
Н.Г.Четаев теоремаси
Теорема В га хам, худди теорема А ва Б лар учун булганидек, геометрик талкин бериш мумкин.
Соддалик
учун ![]() деб оламиз ва
аввал
деб оламиз ва
аввал ![]() функцияни аник
ишорали эмас деб хисоблаймиз. Бу холда
функцияни аник
ишорали эмас деб хисоблаймиз. Бу холда ![]() эгри чизик
координата бошидан утадиган битта ёки бир нечта хакикий тармокка (шохга) эга булади
(2.4-шакл).
эгри чизик
координата бошидан утадиган битта ёки бир нечта хакикий тармокка (шохга) эга булади
(2.4-шакл).
![]() функция аник
мусбат ишорали булсин. Теорема шартига асосан координата боши атрофида камида
битта
функция аник
мусбат ишорали булсин. Теорема шартига асосан координата боши атрофида камида
битта ![]() соха булади. Бу соха
соха булади. Бу соха
![]() эгри чизиклар
билан чегараланган булади. 2.4,6-шаклдаги АОВ сектор уша сохаларнинг биттасини
ифодалайди, пунктирланган чизиклар эса
эгри чизиклар
билан чегараланган булади. 2.4,6-шаклдаги АОВ сектор уша сохаларнинг биттасини
ифодалайди, пунктирланган чизиклар эса ![]() эгри чизикларни билдиради.
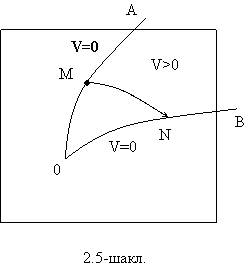
Соха чегарасининг ихтиёрий М нуктасидан чикаётган МР интеграл эгри чизикни курайлик.
М нуктани координата бошига жуда хам якин килиб олиш мумкин.
эгри чизикларни билдиради.
Соха чегарасининг ихтиёрий М нуктасидан чикаётган МР интеграл эгри чизикни курайлик.
М нуктани координата бошига жуда хам якин килиб олиш мумкин. ![]() булганлиги
учун бу интеграл эгри чизик t нинг усиши билан албатта
булганлиги
учун бу интеграл эгри чизик t нинг усиши билан албатта ![]() эгри чизиклар оиласини ичкаридан ташкарига (С нинг усадиган
томонига) караб кесиб утади ва
эгри чизиклар оиласини ичкаридан ташкарига (С нинг усадиган
томонига) караб кесиб утади ва ![]() чегарадан узоклашади. Равшанки, интеграл эгри чизиклар
хамма вакт координата бошидан узоклаша боради ва агар бирор t вактда
чегарадан узоклашади. Равшанки, интеграл эгри чизиклар
хамма вакт координата бошидан узоклаша боради ва агар бирор t вактда
![]() соханинг иккинчи чегарасига етиб бормаса (2.4-шакл),
окибатда (2.6.1) сохадан чикиб кетади.
соханинг иккинчи чегарасига етиб бормаса (2.4-шакл),
окибатда (2.6.1) сохадан чикиб кетади.
Аммо,
![]() соханинг иккинчи чегарасини кесиши мумкин эмас, чунки
агар бирор
соханинг иккинчи чегарасини кесиши мумкин эмас, чунки
агар бирор ![]() нуктада содир булса эди, (2.5-шакл) у холда бу нуктада,
равшанки,
нуктада содир булса эди, (2.5-шакл) у холда бу нуктада,
равшанки, ![]() буларди (чунки
буларди (чунки ![]() функция
мусбат кийматдан нол кийматга узгариши учун албатта камайиши, яъни
функция
мусбат кийматдан нол кийматга узгариши учун албатта камайиши, яъни ![]() булиши
керак).
булиши
керак).
 |
Шундай килиб, координата бошига исталганча якин булган нуктадан чикувчи ва маълум вактда (2.6.1) сохадан чикиб кетувчи интеграл эгри чизиклар мавжуд экан. Демак, тойилмаган харакат тургун булмайди.
Теоремани исбот килишда ![]() аник ишорали
функция булганда хам хеч нарса узгармайди. Бу холда координата бошининг бутун
атрофи
аник ишорали
функция булганда хам хеч нарса узгармайди. Бу холда координата бошининг бутун
атрофи ![]() соха булади.
соха булади.
Келтирилган геометрик талкин Н.Г.Четаевга Ляпу-новнинг бу теоремасини умумлаштиришга имкон беради.
Хакикатан хам, юкорида юритилган мулохазаларда ![]() нинг
аник ишорали функция эканлиги хеч кандай рол уйнагани йук. Агар «аник ишорали»
иборани «
нинг
аник ишорали функция эканлиги хеч кандай рол уйнагани йук. Агар «аник ишорали»
иборани «![]() функция
функция ![]() соханинг хамма нукталарида мусбат ишорали киймат
соханинг хамма нукталарида мусбат ишорали киймат ![]() кабул
килади» деган ибора билан алмаштирсак хам юкорида юритилган мулохазалар узгармайди.
Шундай килиб, 1934 йилда Н.Г.Четаев яратган куйидаги теоремага келамиз
[100-102].
кабул
килади» деган ибора билан алмаштирсак хам юкорида юритилган мулохазалар узгармайди.
Шундай килиб, 1934 йилда Н.Г.Четаев яратган куйидаги теоремага келамиз
[100-102].
 |
Н.Г.Четаев
теоремаси. Агар тойилган харакат
дифференциал тенгламалари учун шундай ![]() функцияни топиш
мумкин булиб:
функцияни топиш
мумкин булиб:
1)
координата бошининг исталганча кичик атрофида ![]() буладиган соха мавжуд
ва унинг чегарасида
буладиган соха мавжуд
ва унинг чегарасида ![]() ;
;
2)
![]() соханинг хамма нукталарида
соханинг хамма нукталарида
![]() булса, у холда тойилмаган
харакат тургун булмайди.
булса, у холда тойилмаган
харакат тургун булмайди.
Н.Г.Четаев теоремасининг аник аналитик исботини [101] китобдан топиш мумкин.
1-мисол. Тойилган харакат дифференциал тенгламалари
![]()
куринишда
берилган булсин. ![]() тойилмаган харакатнинг
тургун эмаслиги курсатамиз. Бунинг учун Ляпунов функциясини
тойилмаган харакатнинг
тургун эмаслиги курсатамиз. Бунинг учун Ляпунов функциясини
![]() (2.8.1)
(2.8.1)
куринишда
оламиз. Бу функция учун ![]() соха мавжуд ва
унинг чегарасида
соха мавжуд ва
унинг чегарасида ![]() (2.6-шакл).
(2.6-шакл).
![]() функциядан
тойилган харакат тенгламаларига асосан вакт буйича олинган тулик хосиласи
функциядан
тойилган харакат тенгламаларига асосан вакт буйича олинган тулик хосиласи
![]() (2.8.2)
(2.8.2)
булади.
![]() функция барча
функция барча ![]() ва исталган
ва исталган ![]() лар учун мусбат, демак,
лар учун мусбат, демак, ![]() сохада
сохада ![]() булади (2.5-шаклга каранг). У холда Четаев
теоремасига асосан тойилмаган харакат нотургундир.
булади (2.5-шаклга каранг). У холда Четаев
теоремасига асосан тойилмаган харакат нотургундир.
Шуни
таъкидлаймизки, танлаб олинган ![]() функция Четаев теоремасининг шартларига буйсунсада,
Ляпунов теоремасининг шартларини каноатлантирмайди (чунки
функция Четаев теоремасининг шартларига буйсунсада,
Ляпунов теоремасининг шартларини каноатлантирмайди (чунки ![]() холларда
холларда
![]() булади).
булади).

2.6-шакл.
Изох. 2-7 параграфларда келтирилган теоремалар (А, Б, В ва Г теоремалар) Ляпуновнинг иккинчи усули билан харакат тургунлигини тадкик этишнинг фундаменти хисобланади. Уларни исботлашда тойилган харакатнинг дифференциал тенгламаларига кирган хамма узгарувчиларга нисбатан тойилмаган харакат тургунлиги тадкик этилаяпти деб каралади. 1957 йилда В.В.Румянцев Ляпуновнинг иккинчи усулини узгарувчиларнинг факат бир кисмига нисбатан харакат тургунлигини тадкик этишни талаб этадиган динамик системаларга жорий этди [80].
9-§. Интеграллар богланмаси воситасида Ляпунов функциясини тузиш
Ляпуновнинг иккинчи усули теоремаларини татбик этиш, аник хусусиятларга эга булган функцияни топишни такозо килади. Афсуски, хозиргача бундай функцияларни топишнинг умумий усули мавжуд эмас. Шундай булсада, куп холларда тойилган харакат тенгламаларининг интеграллари аник булганда, улардан фойдаланиб Ляпунов функциясини ясаш мумкин булиб колади.
Тойилган харакат дифференциал тенгламалари
![]() (2.9.1)
(2.9.1)
куйидаги
![]() (2.9.2)
(2.9.2)
интегралга
келтирилган ва бу интеграл учун ![]() айирма
айирма ![]() узгарувчиларнинг
мусбат ишорали функцияси булсин. У холда Ляпунов функцияси сифатида
узгарувчиларнинг
мусбат ишорали функцияси булсин. У холда Ляпунов функцияси сифатида
![]() (2.9.3)
(2.9.3)
ни олиш мумкин.
Хакикатан
хам, ![]() функциянинг тойилган харакат тенгламаларига нисбатан
вакт буйича олинган тулик хосиласи (2.9.2) муносабатга асосан айнан нолга тенг
булади, яъни
функциянинг тойилган харакат тенгламаларига нисбатан
вакт буйича олинган тулик хосиласи (2.9.2) муносабатга асосан айнан нолга тенг
булади, яъни ![]() . Демак,
. Демак, ![]() функция Ляпуновнинг харaкат тургунлиги хакидаги
биринчи теоремасининг (теорема А) хамма шартларини каноатлантиради.
функция Ляпуновнинг харaкат тургунлиги хакидаги
биринчи теоремасининг (теорема А) хамма шартларини каноатлантиради.
Айрим холларда тойилган харакат дифференциал тенгламалари бир нечта
![]()
![]() (2.9.4)
(2.9.4)
интегралларга
эга булиши мумкин. Бу ерда ![]() - узгармас сонлар ва
- узгармас сонлар ва ![]() ларнинг бирортаси хам мусбат ишорали функция эмас. Бу
хол учун Н.Г.Четаев
ларнинг бирортаси хам мусбат ишорали функция эмас. Бу
хол учун Н.Г.Четаев ![]() функцияни (2.9.4) интеграллар богланмаси оркали
излашни тавсия этди [101,102]. Умумий куринишда бу богланма куйидагича
ифодаланади
функцияни (2.9.4) интеграллар богланмаси оркали
излашни тавсия этди [101,102]. Умумий куринишда бу богланма куйидагича
ифодаланади
![]() (2.9.5)
(2.9.5)
мумкин
булса, у холда бу функция теорема А нинг хамма шартларини каноатлантирарди
(чунки ![]() хам
тойилган харакат дифференциал тенгламаларининг интеграли булади).
хам
тойилган харакат дифференциал тенгламаларининг интеграли булади).
Интеграллар богланмаси оркали Ляпунов функциясини ясашнинг Четаев усули анча самарлидир. Аник масалаларни Четаев усулидан фойдаланиб тадкик этишда куйидаги эслатмаларни хисобга олиш тавсия этилади:
1.![]() та
та ![]() ва
ва ![]() коэффициентлардан бирортасини ихтиёрий равишда
танлаш, масалан,
коэффициентлардан бирортасини ихтиёрий равишда
танлаш, масалан, ![]() деб олиш мумкин.
деб олиш мумкин.
2.Купинча
хамма ![]() деб кабул килиб,
деб кабул килиб, ![]() функцияни факат чизикли интеграллар богланмаси оркали
ясаш мумкин.
функцияни факат чизикли интеграллар богланмаси оркали
ясаш мумкин.
Чизикли интеграллар богланмаси етарли булмаган холдагина V функцияни ясашга квадратик интегралларни жалб этиш максадга мувофик.
3.Куп холларда тойилган харакат тенгламаларининг интегралларини тенгламаларнинг узларини тузмасдан умумий англаш (тушуниш) (масалан, механиканинг умумий теоремаларидан фойдаланиб) асосида тузиш мумкин. Ортикча алмаштиришлардан кочиб, бу усулдан кенг фойдаланиш керак.
10-§. Хосиласи узгармас ишорали булган Ляпунов функцияларига асосланган критериялар
Ляпуновнинг Теорема Б да келтирилган асимптотик тургунлик
критерияси тойилган харакат дифференциал тенгламаларига нисбатан вакт буйича
олинган тулик хосиласи ![]() аник ишорали булган
аник ишорали булган ![]() Ляпунов функциясига таянади. Аммо техникада, асосан
кенг куламда ва батамом тургунликни тадкик этиш лозим булган чизиклимас системалар
холида баъзан шундай мусбат ишорали
Ляпунов функциясига таянади. Аммо техникада, асосан
кенг куламда ва батамом тургунликни тадкик этиш лозим булган чизиклимас системалар
холида баъзан шундай мусбат ишорали ![]() функцияни ясаш мумкинки, унинг хосиласи
функцияни ясаш мумкинки, унинг хосиласи ![]() факат узгармас манфий ишорали функция булади (аник
манфий ишорали функция булмайди). Шу вактнинг узида хосиласи аник манфий
ишорали функция буладиган Ляпунов функциясини ясаш катта кийинчиликлар тугдиради.
Шу боисдан хам шундай умумий критерияни топиш зарурияти тугилдики, бу критерия
шартлари бажарилганда хосиласи узгармас ишорали функция булган Ляпунов функцияси
учун тойилмаган харакат хар кандай бошлангич шартлар учун асимптотик тургун булсин.
факат узгармас манфий ишорали функция булади (аник
манфий ишорали функция булмайди). Шу вактнинг узида хосиласи аник манфий
ишорали функция буладиган Ляпунов функциясини ясаш катта кийинчиликлар тугдиради.
Шу боисдан хам шундай умумий критерияни топиш зарурияти тугилдики, бу критерия
шартлари бажарилганда хосиласи узгармас ишорали функция булган Ляпунов функцияси
учун тойилмаган харакат хар кандай бошлангич шартлар учун асимптотик тургун булсин.
ХХ асрнинг 40-60 йилларида бир катор шундай критериялар тавсия этилди.
Критерияни ифодалаган дастлабки теоремалар унг тарафидаги функциялар ошкор равишда t вактга боглик булмаган дифференциал тенгламалар системаси (автоном системалар) учун исбот этилди [8,10]. Унчалик узгаришсиз бу критериялар вакт буйича даврий булган системалар учун умумлаштирилди. Кейинчалик иккита ва ундан ортик Ляпунов функцияларидан фойдаланиш хисобига ноавтоном (но-стационар) системалар учун шунга ухшаш критериялар исбот этилди [57].
Биз бу ерда Ляпуновнинг асимптотик тургунлик ва нотургунлик теоремаларининг умумлаштирилиши булган Е.А.Барбашин ва Н.Н.Красовскийларга мансуб теоремаларни исботсиз келтирамиз. Уларнинг исботи Е.А.Барбашин, И.Г.Малкин ва Н.Н.Красовскийларнинг китобларида келтирилган [8,39 (464-466 бетлар), 53].
Тойилган харакат дифференциал тенгламалари
![]() (2.10.1)
(2.10.1)
куринишда берилган булсин.
Бу ерда ![]() функция
функция
![]() ёки
ёки ![]() (2.10.2)
(2.10.2)
сохада
аникланган, узлуксиз ва узлуксиз хусусий хосилаларга эга хамда ![]() деб хисобланади.
деб хисобланади.
![]() Ляпунов функциясининг (2.10.1) тенгламаларга нисбатан
вакт буйича олинган тулик хосиласи
Ляпунов функциясининг (2.10.1) тенгламаларга нисбатан
вакт буйича олинган тулик хосиласи ![]() узгармас
манфий ишорали функция булсин. (2.10.2) сохадаги
узгармас
манфий ишорали функция булсин. (2.10.2) сохадаги
![]() буладиган хамма нукталар мажмуасини (тупламини) М
билан белгилаймиз.
буладиган хамма нукталар мажмуасини (тупламини) М
билан белгилаймиз. ![]() мувозанат холати бу тупламнинг элементи булмайди, бу
ерда хар доим
мувозанат холати бу тупламнинг элементи булмайди, бу
ерда хар доим ![]() .
.
Куйидаги асимптотик тургунлик хакидаги критерияни келтирамиз.
Барбашин - Красовский теоремаси. Агар (2.10.1) тойилган харакат дифференциал
тенгламалари учун шундай (2.10.2) сохада аник мусбат V функция
топилиб, унинг хосиласи ![]() куйидаги:
куйидаги:
1) М соха ташкарисида ![]()
2) М сохада ![]() шартларни каноатлантирса, у холда тойилмаган харакат
асимптотик тургун булади.
шартларни каноатлантирса, у холда тойилмаган харакат
асимптотик тургун булади.
Энди тойилмаган харакатнинг нотургунлиги хакидаги умумлашган теоремани келтирамиз.
Теорема. Агар (2.10.1) тойилган харакат дифференциал
тенгламалари учун шундай ![]() функцияни топиш мумкин булиб, унинг хосиласи
функцияни топиш мумкин булиб, унинг хосиласи ![]() М-
М-![]() вакт ичида системанинг
вакт ичида системанинг ![]() бутун траекториясига эга булмаган
бутун траекториясига эга булмаган ![]() нукталар мажмуаси булганда куйидаги
нукталар мажмуаси булганда куйидаги
1) М соха ташкарисида ![]()
2) М сохада ![]()
шартларни
каноатлантирса ва агар координата бошининг ихтиёрий атрофида шундай нукталар
топилсаки, улар учун ![]() булса, у холда тойилмаган харакат нотургун булади.
булса, у холда тойилмаган харакат нотургун булади.
11-§. Ляпуновнинг харакат тургунлиги хакидаги теоремасининг татбикига доир мисоллар
1-мисол. Коник (конуссимон) маятник харакатининг тургунлиги
Узунлиги ![]() га тенг булган
вазнсиз ипга осилган
га тенг булган
вазнсиз ипга осилган ![]() массали моддий нуктанинг
стационар (баркарор) харакатини куриб утайлик. Бу нукта горизонтал жойлашган
доира буйича огирлик кучи таъсири остида узгармас тезлик билан харакат килсин
(2.7,а-шакл).
массали моддий нуктанинг
стационар (баркарор) харакатини куриб утайлик. Бу нукта горизонтал жойлашган
доира буйича огирлик кучи таъсири остида узгармас тезлик билан харакат килсин
(2.7,а-шакл).
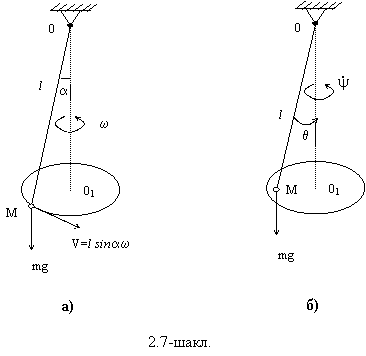
О нуктага махкамланган маятникнинг ипи стационар харакатда
доирали конус чизади. ОО1 вертикал ук билан ип орасидаги бурчакни ![]() билан,
ипнинг вертикал ук атрофида айланишининг бурчак тезлигини
билан,
ипнинг вертикал ук атрофида айланишининг бурчак тезлигини ![]() билан
белгилаймиз. Стационар харакатда
билан
белгилаймиз. Стационар харакатда ![]() бурчак, ип
узунлиги
бурчак, ип
узунлиги ![]() ва бурчак тезлиги
ва бурчак тезлиги ![]() орасирида
куйидагича муносабат борлигини олдинги параграфларда курган эдик:
орасирида
куйидагича муносабат борлигини олдинги параграфларда курган эдик:
![]() .
(2.11.1)
.
(2.11.1)
Маятникнинг
доира буйлаб стационар харакатини тойилмаган харакат сифатида кабул киламиз. Бу
харакатга кандайдир етарлича кичик тойдирувчи кучлар таъсир килсин. Тойилган харакатда
ОО1 вертикал билан ип орасидаги бурчакни ![]() , ОО1
ук атрофида айланишининг бурчак тезлигини
, ОО1
ук атрофида айланишининг бурчак тезлигини ![]() деб олиб, куйидаги
белгилашни киритамиз
деб олиб, куйидаги
белгилашни киритамиз
![]() . (2.11.2)
. (2.11.2)
Тойилмаган
харакатни ![]() ва
ва ![]() ларга
нисбатан тургунлигини урганамиз. Маятникнинг кинетик ва потенциал энергиялари
ларга
нисбатан тургунлигини урганамиз. Маятникнинг кинетик ва потенциал энергиялари
![]()
куринишда булади.
Маятникка
таъсир этаётган огирлик кучи потенциал куч ва ![]() циклик координата
(Т кинетик энергия
циклик координата
(Т кинетик энергия ![]() координатага боглик
эмас ва умумлашган куч
координатага боглик
эмас ва умумлашган куч ![]() ) эканлиги учун
иккита харакат интеграли (
) эканлиги учун
иккита харакат интеграли (![]() ва
ва ![]() -
узгармас сонлар) га
-
узгармас сонлар) га
![]() ,
,
![]() . (2.11.3)
. (2.11.3)
эга буламиз.
Бу ерда ![]() ва
ва ![]() купайтувчиларни
кулайлик учун киритдик.
купайтувчиларни
кулайлик учун киритдик.
(2.11.3) нинг иккинчи формуласи ОО1 вертикал укка нисбатан маятник харакат микдорининг моменти булади.
(2.11.2) муносабатлардан фойдаланиб, (2.11.3) интегралларни куйидаги куринишда ёзамиз:
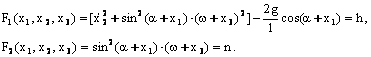 (2.11.4)
(2.11.4)
(2.11.4) интегралларни динамиканинг умумий теоремаларидан фойдаланиб топдик. Албатта, аввал тойилган харакат дифференциал тенгламаларини тузиб (1-бобдаги (1.3.14) формулага каранг) кейин (2.11.4) интегралларни топиш мумкин эди.
Энди
маятник стационар харакатининг ![]() ва
ва ![]() ларга
нисбатан тургунлигини текширайлик. Топилган интегралларнинг бирортаси хам
ларга
нисбатан тургунлигини текширайлик. Топилган интегралларнинг бирортаси хам ![]() ,
,
![]() ва
ва ![]() узгарувчиларга
нисбатан аник ишорали функция эмас. Шунинг учун хам
узгарувчиларга
нисбатан аник ишорали функция эмас. Шунинг учун хам ![]() ва
ва ![]() деб
белгилаб, Четаев усулига асосан (2.11.4) интегралларнинг чизикли богламасини
тузамиз:
деб
белгилаб, Четаев усулига асосан (2.11.4) интегралларнинг чизикли богламасини
тузамиз:

![]() кийматда
кийматда
![]() функция нолга тенг
булиши учун
функция нолга тенг
булиши учун ![]() ва
ва ![]() хадларни
киритдик.
хадларни
киритдик. ![]() муносабатни
(2.11.1) даги киймати билан алмаштирамиз ва
муносабатни
(2.11.1) даги киймати билан алмаштирамиз ва ![]() функцияни
функцияни ![]() ,
,
![]() ва
ва ![]() узгарувчиларнинг
даражалари буйича каторга ёямиз.
узгарувчиларнинг
даражалари буйича каторга ёямиз.
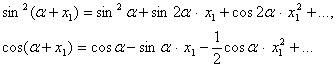
(бу
ерда нукталар оркали юкори тартибли хадлар белгиланган) ифодаларни ![]() функциянинг
ифодасига куйиб ва хадларни гурухлаб
функциянинг
ифодасига куйиб ва хадларни гурухлаб
![]() (2.11.5)
(2.11.5)
ни
хосил киламиз. Равшанки, ![]() функция аник
мусбат ишорали булиши учун унинг ёйилмасида биринчи даражали хадлар булмаслиги
зарурдир. Шунинг учун хам (2.11.5) ифодадаги
функция аник
мусбат ишорали булиши учун унинг ёйилмасида биринчи даражали хадлар булмаслиги
зарурдир. Шунинг учун хам (2.11.5) ифодадаги ![]() ,
, ![]() ва
ва
![]() ларга нисбатан биринчи
тартибли хадларни нолга айлантириш учун
ларга нисбатан биринчи
тартибли хадларни нолга айлантириш учун ![]() деб кабул киламиз.
деб кабул киламиз.
У
холда ![]() функция куйидаги куринишга
эга булади:
функция куйидаги куринишга
эга булади:
![]() (2.11.5¢)
(2.11.5¢)
(2.11.5¢) нинг квадратик кисми коэффициентлари Сильвестер критерияси
шартларини каноатлантиргани учун ![]() ,
, ![]() ва
ва
![]() ларнинг етарли
кичик кийматларида
ларнинг етарли
кичик кийматларида ![]() мусбат ишорали
функция булади.
мусбат ишорали
функция булади. ![]() нинг вакт буйича
олинган тулик хосиласи, (2.11.4) интегралларга кура, айнан нолга тенг, яъни
нинг вакт буйича
олинган тулик хосиласи, (2.11.4) интегралларга кура, айнан нолга тенг, яъни ![]() булади.
Демак, Ляпуновнинг теорема
булади.
Демак, Ляпуновнинг теорема ![]() сига асосан тойилмаган
харакат
сига асосан тойилмаган
харакат ![]() ,
, ![]() ва
ва
![]() ларга нисбатан тургундир.
ларга нисбатан тургундир.
2-мисол. Ер сунъий йулдоши стационар харакатининг тургунлиги
Ер Сунъий йулдоши радиуси ![]() булган
айлана буйича узгармас тезлик билан харакат килиш мумкинлигини 1-бобнинг
3-параграфида курсатгандик. Бу харакатнинг параметрлари
булган
айлана буйича узгармас тезлик билан харакат килиш мумкинлигини 1-бобнинг
3-параграфида курсатгандик. Бу харакатнинг параметрлари
![]() (2.11.6)
(2.11.6)
шартни каноатлантириши керак эди.
Сунъий
йудошнинг тойилган харакатдаги холатини ![]() сферик координаталар
билан аниклаймиз (1.4-шакл).
сферик координаталар
билан аниклаймиз (1.4-шакл).
Сунъий йулдошнинг кинетик ва потенциал энергиялари
![]()
ифодалар билан аникланади.
Сунъий
йулдошга таъсир этаётган тортиш кучи потенциал ва ![]() циклик координата
булганлиги учун иккита харакат интеграли (
циклик координата
булганлиги учун иккита харакат интеграли (![]() ва
ва ![]() -
узгармас сонлар)
-
узгармас сонлар)
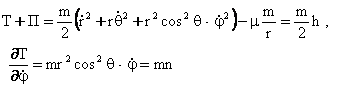 (2.11.7)
(2.11.7)
мавжуд булади.
Сунъий
йулдошнинг доиравий орбита буйича стационар харакатининг ![]() ва
ва ![]() узгарувчиларга
нисбатан тургунлигини тадкик киламиз. Куйидаги белгилашларни киритамиз
узгарувчиларга
нисбатан тургунлигини тадкик киламиз. Куйидаги белгилашларни киритамиз
![]()
Киритилган янги узгарувчилар буйича топилган интегралларни куйидаги куринишда ёзиш мумкин:
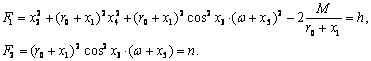 (2.11.8)
(2.11.8)
Бу мисолда хам биз тойилган харакат дифференциал тенгламаларининг иккала интегралини умумий мулохазаларга таяниб топдик.
Энди сунъий йулдош тойилмаган харакатининг тургунлигини текширамиз.
Топилган
интегралларнинг бирортаси хам ![]() ,
, ![]() ,
,
![]() ,
, ![]() ва
ва
![]() узгарувчиларнинг
аник мусбат ишорали функцияси булмайди. Шунинг учун хам Ляпунов функциясини бу
интегралларнинг богланмалари сифатида излаймиз:
узгарувчиларнинг
аник мусбат ишорали функцияси булмайди. Шунинг учун хам Ляпунов функциясини бу
интегралларнинг богланмалари сифатида излаймиз:
![]() ,
,
бу
ерда ![]() ва
ва ![]() -
узгармас сонлар.
-
узгармас сонлар. ![]() ва
ва ![]() интегралларнинг
кийматларини (2.11.8) дан
интегралларнинг
кийматларини (2.11.8) дан ![]() нинг ифодасига
келтириб куямиз
нинг ифодасига
келтириб куямиз
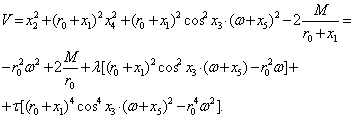 (2.11.9)
(2.11.9)
Бу
ифоданинг унг тарафидаги тригонометрик функцияларни ва ![]() касрни
касрни ![]() ларга
нисбатан мувозанат холати атрофида каторга ёямиз:
ларга
нисбатан мувозанат холати атрофида каторга ёямиз:
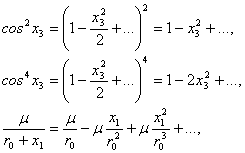
бу ерда нукталар билан юкори тартибли хадлар белгиланган.
Стационар
харакатда ![]() ва
ва ![]() параметрлар
параметрлар
![]() шартни каноатлантиришини
хисобга олиб, топилган ифодаларни (2.11.9) га куямиз. У холда соддалаштиришлардан
кейин куйидагини хосил киламиз
шартни каноатлантиришини
хисобга олиб, топилган ифодаларни (2.11.9) га куямиз. У холда соддалаштиришлардан
кейин куйидагини хосил киламиз
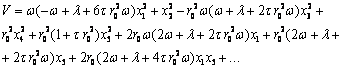 (2.11.10)
(2.11.10)
![]() аник
мусбат ишорали функция булиши учун унинг ифодасида узгарувчиларга нисбатан
биринчи тартибли хадлар булмаслиги зарурлигини биламиз. Шунинг учун (2.11.10)
ифодада
аник
мусбат ишорали функция булиши учун унинг ифодасида узгарувчиларга нисбатан
биринчи тартибли хадлар булмаслиги зарурлигини биламиз. Шунинг учун (2.11.10)
ифодада ![]() ва
ва ![]() ларга
нисбатан биринчи тартибда булган хадларнинг коэффициентларини нолга тенглаштирамиз
ларга
нисбатан биринчи тартибда булган хадларнинг коэффициентларини нолга тенглаштирамиз
![]() .
(2.11.11)
.
(2.11.11)
Демак,
![]() аник мусбат ишорали
функция булиши учун
аник мусбат ишорали
функция булиши учун ![]() ва
ва ![]() узгармас
сонлар (2.11.11) шартни каноатлантиришлари керак. Бу ердан
узгармас
сонлар (2.11.11) шартни каноатлантиришлари керак. Бу ердан
![]() (2.11.12)
(2.11.12)
ни топамиз.
![]() нинг бу кийматини
(2.11.10) га куйиб, куйидагини хосил киламиз
нинг бу кийматини
(2.11.10) га куйиб, куйидагини хосил киламиз
![]()
Бу
ифодадаги квадратик хадларни иккита гурухга ажратамиз, яъни ![]() функцияни
функцияни
![]() куринишда ёзамиз,
бу ерда
куринишда ёзамиз,
бу ерда
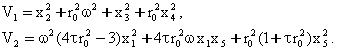
![]() функция
функция
![]() ,
, ![]() ва
ва
![]() узгарувчиларга
нисбатан аник мусбат ишорали функциядир. Демак,
узгарувчиларга
нисбатан аник мусбат ишорали функциядир. Демак, ![]() функция аник
мусбат ишорали функция булиши учун
функция аник
мусбат ишорали функция булиши учун ![]() функция хам
функция хам ![]() ,
,
![]() узгарувчиларга
нисбатан мусбат ишорали функция булиши керак. Бунинг учун
узгарувчиларга
нисбатан мусбат ишорали функция булиши керак. Бунинг учун ![]() нинг
шундай кийматини топиш керакки,
нинг
шундай кийматини топиш керакки, ![]() функция
функция ![]() ва
ва
![]() ларга нисбатан аник
мусбат ишорали функция булсин. Шу максадда Сильвестер критериясидан фойдаланамиз.
ларга нисбатан аник
мусбат ишорали функция булсин. Шу максадда Сильвестер критериясидан фойдаланамиз.
![]() нинг ифодасидаги
нинг ифодасидаги ![]() ва
ва
![]() узгарувчиларнинг
коэффициентларидан тузилган матрицани
узгарувчиларнинг
коэффициентларидан тузилган матрицани
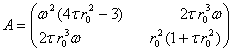
караймиз. Бу ердан
![]() (2.11.13)
(2.11.13)
Булардан куриниб турибдики,
![]() (2.11.14)
(2.11.14)
булганда,
(2.11.13) даги иккала тенгсизлик хам бажарилади. Демак, ![]() функция
функция ![]() ва
ва
![]() узгарувчиларга нисбатан
мусбат ишорали функция ва у билан бирга
узгарувчиларга нисбатан
мусбат ишорали функция ва у билан бирга ![]() функция хам
функция хам ![]() узгарувчиларга
нисбатан мусбат ишорали функция булади.
узгарувчиларга
нисбатан мусбат ишорали функция булади.
Шундай
килиб, ![]() функция
функция ![]() узгарувчиларга
нисбатан мусбат ишорали функция булиши учун
узгарувчиларга
нисбатан мусбат ишорали функция булиши учун ![]() ва
ва ![]() узгармас
сонлар мос равишда (2.11.12) ва (2.11.14) шартларни каноатлантиришлари
етарлидир. Бу холда Ер сунъий йулдошининг стационар харакати
узгармас
сонлар мос равишда (2.11.12) ва (2.11.14) шартларни каноатлантиришлари
етарлидир. Бу холда Ер сунъий йулдошининг стационар харакати ![]() ,
,![]() узгарувчиларга нисбатан тургун булади. В.В.Румянцев хам узининг [81] илмий
ишида бошка усул билан шу натижани олган. В.В.Румянцев узининг бу ишида сунъий
йулдошнинг бошка стационар харакатларининг тургунлигини хам текширган ва
Сизларга мазкур илмий иш билан танишиб чикишни тавсия этамиз.
узгарувчиларга нисбатан тургун булади. В.В.Румянцев хам узининг [81] илмий
ишида бошка усул билан шу натижани олган. В.В.Румянцев узининг бу ишида сунъий
йулдошнинг бошка стационар харакатларининг тургунлигини хам текширган ва
Сизларга мазкур илмий иш билан танишиб чикишни тавсия этамиз.
Изох. Тургунлик масалаларини икки гурухга булиш мумкин:
1. Куп амалий масалаларда курилаётган харакат тургун буладими, асимптотик тургун буладими ёки нотургун буладими деган саволларга жавоб беришга тугри келади. Хозир курилган мисоллар айнан шу гурух масалаларга тааллукли эди.
2. Аммо техникада купинча бошка турдаги масалалар учрайди. Динамик система параметрларининг айрим кийматларида тойилмаган харакат нотургун эканлиги маълум булади. Шу сабабли куйидаги масала келиб чикади: система параметрлари кандай танланганда, унинг тойилмаган харакати тургун ёки асимптотик тургун булади? Бу саволга жавоб бериш алгоритмларини топиш жуда хам мухим илмий ва техникавий ахамиятга эгадир.
Энди иккинчи гурух масалаларига доир мисолни куриб утамиз.
3-мисол. Снаряднинг айланма харакати тургунлигининг
етарли шартлари
Маълумки, айланмаётган пилдирок (волчок) йикилади ва тик (вертикал холатда) туриши учун уни каттик айлантириш, яъни унга етарлича катта микдорда хусусий айланма тезлик бериш керак. Худди шундай, хар кандай айланмайдиган снаряд тез орада нишонга етмасдан йикилиб тушади. Табиий савол тугилади: пилдирокка (снарядга) кандай тезлик бериш керакки, у йикилиб тушмасин.
Масса маркази горизонт билан етарлича кичик бурчак ташкил этадиган траектория буйича йуналган чузик снаряднинг айланма харакати билан вертикал ук атрофида айланиб харакат киладиган пилдирокнинг дифференциал тенгламалари бир хил булганлиги учун улардан бири учун харакат тургунлигини тадкик этиш кифоя.
 |
а) б)
2.8-шакл.
Биз пилдирок айланма харакатининг тургунлигини текширамиз.
Хусусий
бурчак тезлиги ![]() га тенг пилдирокка
икки ташки куч, (каршилик кучини хисобга олмаймиз) масса марказига куйилган огирлик
кучи
га тенг пилдирокка
икки ташки куч, (каршилик кучини хисобга олмаймиз) масса марказига куйилган огирлик
кучи ![]() ва
ва ![]() таянчнинг
реакция кучи
таянчнинг
реакция кучи ![]() (2.8,а-шакл)
таъсир этади. Кузгалмас
(2.8,а-шакл)
таъсир этади. Кузгалмас ![]() (
(![]() ук вертикал холатда) координата укларига нисбатан пилдирокнинг симметрия уки
ук вертикал холатда) координата укларига нисбатан пилдирокнинг симметрия уки ![]() нинг
холатини
нинг
холатини ![]() ва
ва ![]() бурчаклар
билан аниклаймиз (2.8,б-шакл). Пилдирокнинг кузгалмас вертикал ук
бурчаклар
билан аниклаймиз (2.8,б-шакл). Пилдирокнинг кузгалмас вертикал ук ![]() билан
устма-уст тушадиган
билан
устма-уст тушадиган ![]() симметрия уки
атрофида
симметрия уки
атрофида ![]() бурчак тезлиги
билан текис айланишини унинг тойилмаган харакати сифатида кабул киламиз. Тойилмаган
харакатда
бурчак тезлиги
билан текис айланишини унинг тойилмаган харакати сифатида кабул киламиз. Тойилмаган
харакатда
![]() .
.
Тойилган
харакатда бу микдорларнинг хаммаси узгаради. ![]() укларни киритамиз
(2.8,б-шакл) ва
укларни киритамиз
(2.8,б-шакл) ва ![]() уч ёкнинг кузгалмас
уч ёкнинг кузгалмас
![]() укларга нисбатан
айланишининг
укларга нисбатан
айланишининг ![]() бурчак тезлигининг
проекцияларини мос равишда
бурчак тезлигининг
проекцияларини мос равишда ![]() ва
ва ![]() билан
белгилаймиз. 2.8,б-шаклдан фойдаланиб,
билан
белгилаймиз. 2.8,б-шаклдан фойдаланиб,
![]()
ларни
топамиз. Пилдирок айланишининг бурчак тезлиги ![]() нинг проекциялари
нинг проекциялари ![]() ва
ва
![]() лар куйидаги
лар куйидаги
![]()
тенгликлар билан аникланади.
Энли пилдирокнинг кинетик энергиясини топамиз
![]() ,
,
бу
ерда ![]() - пилдирокнинг
экваториал,
- пилдирокнинг
экваториал, ![]() - аксиал инерция
моментлари.
- аксиал инерция
моментлари.
Пилдирокнинг потенциал энергияси
![]() ,
,
булиб,
бу ерда ![]() - пилдирокнинг огирлиги,
- пилдирокнинг огирлиги,
![]() - масса маркази
- масса маркази ![]() билан
таянч нуктаси
билан
таянч нуктаси ![]() орасидаги масофа.
орасидаги масофа.
Бу
мисолда хам, олдинги иккита мисолдагидек, тойилган харакат дифференциал тенгламаларини
тузмасдан туриб, учта интеграл топиш мумкин. Иккита интеграл осонгина топилади:
энергия интеграли ва ![]() циклик координатага
мос келувчи интеграл (иккинчи интеграл пилдирок харакат микдорининг
циклик координатага
мос келувчи интеграл (иккинчи интеграл пилдирок харакат микдорининг ![]() укига
нисбатан моментидир):
укига
нисбатан моментидир):
 (2.11.15)
(2.11.15)
Учинчи интеграл пилдирок харакат микдорининг к¢згалмас
![]() ¢кга нисбатан
моментидан иборат:
¢кга нисбатан
моментидан иборат:
![]() .
(2.11.16)
.
(2.11.16)
Бу интегрални ошкора к¢ринишда ёзиш учун куйидаги маълум тенгликлардан фойдаланамиз
![]() (2.11.17)
(2.11.17)
2.8,б-шакл дан фойдаланиб,
![]() (2.11.18)
(2.11.18)
ифодаларни хосил киламиз. (2.11.17) ва (2.11.18) ларни (2.11.16) га к¢йиб, учинчи интегрални топамиз
![]() (2.11.19)
(2.11.19)
Пилдирок
айланма харакатининг тургунлигини ![]() ва
ва ![]() узгарувчиларга
нисбатан урганамиз. Куйидаги тенгликлар билан янги
узгарувчиларга
нисбатан урганамиз. Куйидаги тенгликлар билан янги ![]() узгарувчиларни
узгарувчиларни
![]()
киритамиз.
Янги узгарувчилар оркали тойилган харакат дифференциал тенгламаларининг интегралларини ифодалаймиз
 (2.11.20)
(2.11.20)
Бу интегралларнинг бирортаси хам аник ишорали функция булмаганлиги учун интегралларнинг чизикли богланмаларини тузамиз
![]() , (2.11.21)
, (2.11.21)
бу
ерда ![]() ва
ва ![]() -
аникмас узгармас коэффициентлар
-
аникмас узгармас коэффициентлар ![]() ни хисобга олган холда,
ни хисобга олган холда,
![]() ва
ва ![]() ларнинг
ифодаларини (2.11.20) дан (2.11.21) га куйиб,
ларнинг
ифодаларини (2.11.20) дан (2.11.21) га куйиб, ![]() узгарувчиларнинг
даражалари буйича каторга ёямиз. Хадларни даражалари буйича гурухлаб, куйидагига
эга буламиз:
узгарувчиларнинг
даражалари буйича каторга ёямиз. Хадларни даражалари буйича гурухлаб, куйидагига
эга буламиз:
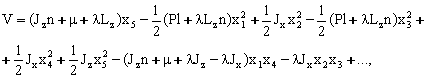 бу
ерда нукталар билан юкори тартибли хадлар белгиланган.
бу
ерда нукталар билан юкори тартибли хадлар белгиланган.
![]() функциянинг
аник ишорали булиши учун биринчи тартибли
функциянинг
аник ишорали булиши учун биринчи тартибли ![]() узгарувчи олдидаги
коэффициентни нолга тенглаштириш лозим:
узгарувчи олдидаги
коэффициентни нолга тенглаштириш лозим:
![]() .
(2.11.22)
.
(2.11.22)
(2.11.22)
ни инобатга олганда, ![]() функция куйидаги куринишга
келади:
функция куйидаги куринишга
келади:
![]() (2.11.23)
(2.11.23)
бу ерда
![]() .
(2.11.24)
.
(2.11.24)
(2.11.23)
ифода билан аникланадиган ![]() нинг квадратик кисмини
учта функцияга ажратамиз, яъни
нинг квадратик кисмини
учта функцияга ажратамиз, яъни
![]()
бунда

![]() функцияси
функцияси
![]() га нисбатан аник
мусбат ишоралидир,
га нисбатан аник
мусбат ишоралидир, ![]() ва
ва ![]() лар
бир хил структурага (тузилишга) эга. Шунинг сабабли умумий назарияга асосан
пилдирок тойилмаган харакатининг
лар
бир хил структурага (тузилишга) эга. Шунинг сабабли умумий назарияга асосан
пилдирок тойилмаган харакатининг ![]() ва
ва ![]() узгарувчиларга
нисбатан тургунлигини аниклаш учун
узгарувчиларга
нисбатан тургунлигини аниклаш учун ![]() функциянинг
функциянинг ![]() ва
ва
![]() ларга нисбатан аник
мусбат ишорали функция булишининг шартини (уша шартларда
ларга нисбатан аник
мусбат ишорали функция булишининг шартини (уша шартларда ![]() функция
функция ![]() ва
ва
![]() ларга нисбатан аник
мусбат ишорали функция булади) топиш етарли.
ларга нисбатан аник
мусбат ишорали функция булади) топиш етарли.
![]() функция учун
Сильвестер шартини ёзамиз:
функция учун
Сильвестер шартини ёзамиз:
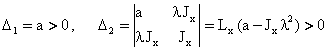 .
.
(2.11.24) ифодадан фойдаланиб, бу шартларни куйидаги куринишга келтирамиз:
![]() . (2.11.25)
. (2.11.25)
(2.11.25) муносабатни каноатлантирувчи ![]() сонини
танлаб олиш масаласини ойдинлаштириш колди.
сонини
танлаб олиш масаласини ойдинлаштириш колди.
Агар ![]() квадратик учхаднинг
дискриминанти
квадратик учхаднинг
дискриминанти
![]()
мусбат
булса, у холда ![]() нинг иккала
нинг иккала ![]() ва
ва
![]() илдизлари хам хакикий
ва хар хил булади.
илдизлари хам хакикий
ва хар хил булади. ![]() функциянинг
графигидан (2.9–шакл) куриниб турибдики, бу холда
функциянинг
графигидан (2.9–шакл) куриниб турибдики, бу холда ![]() тенгсизликни каноатлантирувчи
хамма
тенгсизликни каноатлантирувчи
хамма ![]() лар учун
лар учун ![]() булади,
яъни (2.11.25) нинг иккинчи шарти бажарилади. Агар
булади,
яъни (2.11.25) нинг иккинчи шарти бажарилади. Агар ![]() булса, у
холда иккала илдиз хам манфий булади (2.9–шаклга каранг). Агар
булса, у
холда иккала илдиз хам манфий булади (2.9–шаклга каранг). Агар ![]() булса,
у холда иккала
булса,
у холда иккала ![]() ва
ва ![]() илдизлар
мусбат булади.
илдизлар
мусбат булади.
![]() нинг
бу кийматлари учун (2.11.25) нинг биринчи шарти хам бажарилишини курсатамиз.
Бунинг учун
нинг
бу кийматлари учун (2.11.25) нинг биринчи шарти хам бажарилишини курсатамиз.
Бунинг учун ![]() да бу шартни катта
илдиз каноатлантиришини курсатиш етарли.
да бу шартни катта
илдиз каноатлантиришини курсатиш етарли.
![]()
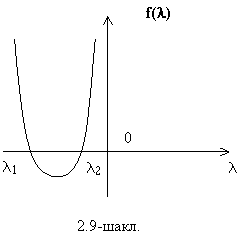 |
Элементар тенгсизлик
![]()
дан фойдаланиб,
![]() (2.11.26)
(2.11.26)
тенгсизликни
хосил киламиз. Шу билан (2.11.25) даги биринчи тенгсизликнинг бажарилиши исботланди
(![]() да кичик
да кичик ![]() илдизни
куриш керак).
илдизни
куриш керак).
Шундай
килиб, пилдирокнинг тойилмаган харакатида ![]() бурчак тезлик
бурчак тезлик ![]() шартни
уринли килса, яъни
шартни
уринли килса, яъни
![]() (2.11.27)
(2.11.27)
булса,
![]() ва
ва ![]() орасида
жойлашган
орасида
жойлашган ![]() лар учун
лар учун ![]() функция
мусбат ишорали булади.
функция
мусбат ишорали булади.
Бу
функциянинг тойилган харакат тенгламаларига нисбатан вакт буйича олинган тулик хосиласи
(2.11.26) интегралларга асосан нолга тенг булади. Демак, (2.11.27) шарт пилдирок
вертикал холатининг ![]() ларга нисбатан тургунлигининг
етарли шарти булади.
ларга нисбатан тургунлигининг
етарли шарти булади.
Снаряд айланма харакати тургунлигининг етарли шарти (2.11.27) ни (адабиётда бу шарт Маневский-Крылов шарти деб юритилади) биринчи булиб Н.Г.Четаев исбот килган [42,102].
Изох. Айрим вактларда Четаев усули (интеграллар богланмаси) буйича мусбат ишорали функцияни ясаш мумкин булмайди. Бу холда интегралларнинг бошка хил комбинацияларини куриш керак. Агар интеграллар богланмаси оркали тургунликнинг шартини аниклаш имконияти булмаса, бу хали тойилмаган харакат нотургун деган мулохазани билдирмайди. Бу холда тургунлик масаласини хал килиб бера оладиган бошка усулларни ишлатиш керак булади.
12-§. Асимптотик тургунлик хакидаги теореманинг татбигига доир мисоллар
1-мисол. Лампалик генераторнинг тургунлик шарти
Индуктив тескари алокали ва тур занжирида тебраниш контури булган лампалик генераторнинг оддий схемасини куриб утайлик (2.10-шакл) [1].
Кирхгоф конунларидан фойдаланиб, занжирдаги токнинг йуналишини ва конденсаторнинг мусбат кутбининг холатини хисобга олиб (турдаги токни эътиборга олмаган холда) турдаги токнинг куйидаги тенгламаларини хосил киламиз
![]() (2.12.1)
(2.12.1)
бу
ерда ![]() - турдаги
кучланиш,
- турдаги
кучланиш, ![]() - занжирдаги ток,
- занжирдаги ток, ![]() -
уз-узига индукция коэффициенти,
-
уз-узига индукция коэффициенти, ![]() - анод токи,
- анод токи, ![]() -
тескари алокадаги электр юритувчи куч,
-
тескари алокадаги электр юритувчи куч, ![]() -конденсатор сигими,
-конденсатор сигими,
![]() - занжирнинг каршилиги.
- занжирнинг каршилиги.
![]() галтак оркали окаётган
анод токининг контурга таъсири остида
галтак оркали окаётган
анод токининг контурга таъсири остида ![]() электр юритувчи
куч (э.ю.к.) хосил булади. Анод токи факат турнинг кучланишига
электр юритувчи
куч (э.ю.к.) хосил булади. Анод токи факат турнинг кучланишига ![]() боглик
деб фараз килиб (катта коэффициентли кучайтириши булган триодлар учун бу жуда
яхши бажарилади),
боглик
деб фараз килиб (катта коэффициентли кучайтириши булган триодлар учун бу жуда
яхши бажарилади),
![]() (2.12.2)
(2.12.2)
ни
хосил киламиз, бу ерда ![]() - лампа токи
- лампа токи ![]() нинг
тиклик характеристикаси (2.11-шакл).
нинг
тиклик характеристикаси (2.11-шакл). ![]() нинг кийматини
(2.12.2) дан (2.12.1) куйганимизда, харакатнинг дифференциал тенгламалари
нинг кийматини
(2.12.2) дан (2.12.1) куйганимизда, харакатнинг дифференциал тенгламалари
![]() (2.12.3)
(2.12.3)
куринишга келади.
Кучланиш
![]() ва
ва ![]() токка
нисбатан
токка
нисбатан ![]() ,
, ![]() мувозанат
холатнинг тургунлигини текширамиз. Бунинг учун Ляпунов функциясини
мувозанат
холатнинг тургунлигини текширамиз. Бунинг учун Ляпунов функциясини
![]() (2.12.4)
(2.12.4)
куринишда
танлаймиз, бу ерда ![]() - кандайдир хакикий
сон.
- кандайдир хакикий
сон. ![]() функциянинг
коэффициентларининг
функциянинг
коэффициентларининг
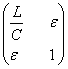
матрицасидан фойдаланиб, Сильвестер критериясининг
![]() (2.12.5)
(2.12.5)
шартларини
топамиз. Биринчи шарт доимо бажарилади, иккинчиси булса, ![]() сонининг
модули буйича етарлича кичик кийматлари учун бажарилади.
сонининг
модули буйича етарлича кичик кийматлари учун бажарилади.
![]() функциянинг
тойилган харакат дифференциал тенгламаларига нисбатан вакт буйича олинган тулик
хосиласи
функциянинг
тойилган харакат дифференциал тенгламаларига нисбатан вакт буйича олинган тулик
хосиласи
![]() (2.12.6)
(2.12.6)
куринишда
булади. (2.12.3) тенгламалардан ![]() ва
ва ![]() ларнинг
кийматини (2.12.6) га келтириб куйганимизда
ларнинг
кийматини (2.12.6) га келтириб куйганимизда
![]()
ни хосил киламиз. Бу ифоданинг кавсларини очиб ва хадларини гурухлаганимизда
![]()
келиб
чикади. ![]() функцияни
функцияни ![]() нинг
даражалари буйича каторга ёямиз:
нинг
даражалари буйича каторга ёямиз:
![]() (2.12.7)
(2.12.7)
ва
буни ![]() нинг ифодасидаги
нинг ифодасидаги ![]() урнига
куямиз
урнига
куямиз
![]() (2.12.8)
(2.12.8)
бу
ерда нукталар билан ![]() ва
ва ![]() ларга
нисбатан юкори тартибли булган хадлар белгиланган ва
ларга
нисбатан юкори тартибли булган хадлар белгиланган ва ![]() .
.
![]() функция
квадратик кисмининг коэффициентларидан тузилган
функция
квадратик кисмининг коэффициентларидан тузилган
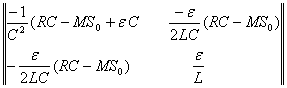
матрицанинг бош диагонал минорларини топамиз:
 (2.12.9)
(2.12.9)
1.Системанинг параметрлари
![]() (2.12.10)
(2.12.10)
тенгсизликни каноатлантирсин.
![]() нинг ихтиёрий
кичик сонлигидан фойдаланамиз. Уни
нинг ихтиёрий
кичик сонлигидан фойдаланамиз. Уни ![]() деб кабул килиб ва
модули буйича етарли даражада кичик килиб оламизки, (2.12.5) шартдаги
деб кабул килиб ва
модули буйича етарли даражада кичик килиб оламизки, (2.12.5) шартдаги ![]() ва
(2.12.9) формуладаги
ва
(2.12.9) формуладаги ![]() ва
ва ![]() лар
куйидаги шартни каноатлантирсин:
лар
куйидаги шартни каноатлантирсин:
![]() (2.12.11)
(2.12.11)
(2.12.11)
шартларнинг бажарилишини доимо таъминлаш мумкин, чунки бу дитерминантлар
ёйилмасидаги иккинчи хадлар биринчи хадларига нисбатан ![]() буйича юкори
тартиблидир.
буйича юкори
тартиблидир. ![]() нинг бу кийматида
(2.12.4) тенглик билан аникланадиган
нинг бу кийматида
(2.12.4) тенглик билан аникланадиган ![]() мусбат ишорали
функция булади (Сильвестер критериясининг шартлари бажарилади:
мусбат ишорали
функция булади (Сильвестер критериясининг шартлари бажарилади: ![]() )
ва (2.12.8) формула билан аникланадиган
)
ва (2.12.8) формула билан аникланадиган ![]() аник манфий
ишорали функция булади (бу ерда хам Сильвестер критериясининг шартлари
бажарилади:
аник манфий
ишорали функция булади (бу ерда хам Сильвестер критериясининг шартлари
бажарилади: ![]() ). Демак (2.12.10)
шарт бажарилса, у холда теорема Б га асосан системанинг
). Демак (2.12.10)
шарт бажарилса, у холда теорема Б га асосан системанинг ![]() мувозанат
холати кучланиш
мувозанат
холати кучланиш ![]() ва ток
ва ток ![]() ларга
нисбатан асимптотик тургун булади.
ларга
нисбатан асимптотик тургун булади.
2.Энди системанинг параметрлари
![]() (2.12.12)
(2.12.12)
шартни каноатлантирсин.
Бу холда 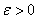 ва уни етарлича
кичик килиб оламизки,
ва уни етарлича
кичик килиб оламизки,
![]() (2.12.13)
(2.12.13)
тенгсизликлар
бажарилсин. ![]() сонининг бу кийматида
сонининг бу кийматида
![]() функция ва унинг хосиласи
функция ва унинг хосиласи
![]() аник мусбат ишорали
функция буладилар. Харакатнинг нотургунлиги хакидаги Ляпунов теоремасига
асосан системанинг
аник мусбат ишорали
функция буладилар. Харакатнинг нотургунлиги хакидаги Ляпунов теоремасига
асосан системанинг ![]() мувозанат холати нотургун
булади.
мувозанат холати нотургун
булади.
Шундай килиб, мувозанат холатининг асимптотик тургун
ёки нотургун булиши системанинг параметрларини конструктор томонидан кандай килиб
танлаб олишига боглик экан: агар (2.12.10) шартлар бажарилса, у холда ![]() ва
ва
![]() ларга нисбатан мувозанат
холати асимптотик тургун булади, (2.12.12) шартлар бажарилганда ток
ларга нисбатан мувозанат
холати асимптотик тургун булади, (2.12.12) шартлар бажарилганда ток ![]() ва
кучланиш
ва
кучланиш ![]() ларга нисбатан мувозанат
холат нотургун булади.
ларга нисбатан мувозанат
холат нотургун булади.
![]() хол
амалий ахамиятга эга булмаганлиги учун биз уни тадкик этмадик.
хол
амалий ахамиятга эга булмаганлиги учун биз уни тадкик этмадик.
Бу мисол фаннинг техника тараккиётига катта хизмат килишини яна бир бор курсатади.
2-мисол. Ночизикли потенциал куч ва каршилик кучи таъсири остидаги биринчи даражали эркинликка эга булган система мувозанат холатининг тургунлиги
Система холатини битта ![]() умумлашган
координата билан аниклаймиз.
умумлашган
координата билан аниклаймиз. ![]() нинг кийматлари
мувозанат холатига нисбатан хисобланади. Системанинг кинетик ва потенциал
энергиялари куйидагича аникланади деб хисоблаймиз
нинг кийматлари
мувозанат холатига нисбатан хисобланади. Системанинг кинетик ва потенциал
энергиялари куйидагича аникланади деб хисоблаймиз
![]() ,
, ![]() ,
(2.12.14)
,
(2.12.14)
бу
ерда ![]() - системанинг
келтирилган массаси, уни узгармас деб хисоблаймиз,
- системанинг
келтирилган массаси, уни узгармас деб хисоблаймиз, ![]() - узгармас
коэффициент,
- узгармас
коэффициент, ![]() (
(![]() булган) мусбат бутун сон. Системага потенциал кучдан ташкари тезликка пропорционал
булган
булган) мусбат бутун сон. Системага потенциал кучдан ташкари тезликка пропорционал
булган ![]() каршилик кучи
таъсир килади
каршилик кучи
таъсир килади
![]() ,
(2.12.15)
,
(2.12.15)
бу
ерда ![]() - мусбат узгармас
сон. Тойилмаган харакат сифатида
- мусбат узгармас
сон. Тойилмаган харакат сифатида ![]() ,
, ![]() мувозанат
холатини оламиз. Лагранж тенгламаси
мувозанат
холатини оламиз. Лагранж тенгламаси
![]()
дан фойдаланиб, тойилган харакат тенгламасини тузамиз
![]() (2.12.16)
(2.12.16)
ва нормал системага утиш учун янги узгарувчилар киритамиз
![]() .
.
(2.12.16) тенгламага янги узгарувчиларни киритамиз:
![]() ,
, ![]() ,
(2.12.17)
,
(2.12.17)
бу
ерда шартга асосан ![]() . Ляпунов функцияси
сифатида тулик механик энергияни оламиз
. Ляпунов функцияси
сифатида тулик механик энергияни оламиз
![]() .
.
У янги узгарувчиларда
![]() .
(2.12.18)
.
(2.12.18)
куринишга эга.
![]() нинг вакт буйича
олинган тулик хосиласи
нинг вакт буйича
олинган тулик хосиласи
![]()
ни топамиз.
Бу ерга ![]() ва
ва ![]() ларнинг
ифодаларини тойилган харакат тенгламаларидан келтириб куямиз
ларнинг
ифодаларини тойилган харакат тенгламаларидан келтириб куямиз
![]()
ва соддалаштиргандан сунг
![]() .
(2.12.19)
.
(2.12.19)
га келамиз.
Энди мумкин булган холларни курамиз.
а)
![]() ва
ва ![]() -
ток сон булсин. Бу холда
-
ток сон булсин. Бу холда ![]() функция
функция ![]() ва
ва
![]() узгарувчиларга нисбатан
мусбат ишорали,
узгарувчиларга нисбатан
мусбат ишорали, ![]() эса
эса ![]() ва
ва
![]() ларга нисбатан узгармас
манфий ишорали функция булади. Теорема А га кура мувозанат холати тургундир.
ларга нисбатан узгармас
манфий ишорали функция булади. Теорема А га кура мувозанат холати тургундир. ![]()
![]() ва
ва
![]() ларга нисбатан аник
манфий ишорали функция булмаганлиги туфайли, теорема Б ни ишлатиш мумкин эмас.
ларга нисбатан аник
манфий ишорали функция булмаганлиги туфайли, теорема Б ни ишлатиш мумкин эмас.
Барбашин
– Красовский теоремасига мурожаат киламиз. ![]() аник мусбат
ишорали функция. Бундан ташкари бу функция
аник мусбат
ишорали функция. Бундан ташкари бу функция ![]() шартни каноатлантиради.
шартни каноатлантиради.
![]() факат
факат ![]() (
(![]() ук) тугри чизикда нолга айланади. Бу тугри чизик тасвирловчи нуктанинг бутун
траекторияси булмайди, чунки
ук) тугри чизикда нолга айланади. Бу тугри чизик тасвирловчи нуктанинг бутун
траекторияси булмайди, чунки ![]() ,
, ![]() функциялар
(2.12.17) тенгламаларнинг иккаласини айниятга айлантирмайди. Шундай килиб,
Барбашин – Красовский теоремасининг хамма шартлари бажарилади ва, демак,
функциялар
(2.12.17) тенгламаларнинг иккаласини айниятга айлантирмайди. Шундай килиб,
Барбашин – Красовский теоремасининг хамма шартлари бажарилади ва, демак, ![]() ва
ва
![]() ток сон булганда
мувозанат холати
ток сон булганда
мувозанат холати ![]() ва
ва ![]() ларга
нисбатан асимптотик тургун булади.
ларга
нисбатан асимптотик тургун булади.
б)
![]() ва
ва ![]() жуфт
сон булсин.
жуфт
сон булсин. ![]() функцияни куйидаги куринишда аниклаймиз
функцияни куйидаги куринишда аниклаймиз
![]() . (2.12.20)
. (2.12.20)
У холда
![]() . (2.12.21)
. (2.12.21)
![]() ва
ва ![]() жуфт
сон булганда,
жуфт
сон булганда, ![]() соха мавжуд булади (2.12-шакл).
соха мавжуд булади (2.12-шакл).
![]() сохада
сохада ![]() булганлиги учун
булганлиги учун ![]() хамма
жойда тасвирловчи нукта траекторияси
хамма
жойда тасвирловчи нукта траекторияси ![]() сиртни уткир бурчак остида ичкаридан ташкарига караб
кесиб утади.
сиртни уткир бурчак остида ичкаридан ташкарига караб
кесиб утади.
(![]() сохада
сохада ![]() сиртлар ёпик
эмас).
сиртлар ёпик
эмас). ![]() ва
ва ![]() холда
хам тасвирловчи нукта траекторияси
холда
хам тасвирловчи нукта траекторияси ![]() сиртларни
ичкаридан ташкарига кесиб, координата бошидан узоклашади. Демак,
сиртларни
ичкаридан ташкарига кесиб, координата бошидан узоклашади. Демак, ![]() ва
ва
![]() жуфт сон булганда,
мувозанат холати нотургун булади.
жуфт сон булганда,
мувозанат холати нотургун булади.
Худди
шундай, ![]() булганда мувозанат
холатининг нотургунлигини курсатиш мумкин.
булганда мувозанат
холатининг нотургунлигини курсатиш мумкин.
Шундай
килиб, курилаётган система ![]() ва
ва ![]() -
ток сон булгандагина бутунлайига асимптотик тургун булиб, колган хамма холларда
нотургун булади.
-
ток сон булгандагина бутунлайига асимптотик тургун булиб, колган хамма холларда
нотургун булади.
3-мисол. Автоматик ростлаш системасининг тургунлиги назариясининг битта масаласи хакида
Масаланинг куйилиши. 1949 йилда М.А.Айзерман томонидан битта чизиклимас элементга эга булган автоматик ростлаш системасининг (система автоматического регулирования) тургунлиги хакидаги куйидаги масала куйилди [3-5].
Автоматик ростлаш системасининг харакати
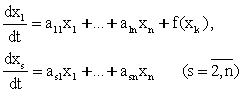 (2.12.22.)
(2.12.22.)
дифференциал
тенгламалар оркали ифодалансин, бу ерда ![]() - узгармас сонлар.
(2.12.22) система билан биргаликда
- узгармас сонлар.
(2.12.22) система билан биргаликда
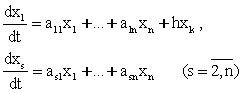 (2.12.23)
(2.12.23)
чизикли системани хам курамиз. (2.12.23) система характеристик тенгламасининг барча илдизларининг хакикий кисми
![]() (2.12.24)
(2.12.24)
интервалда
ётган ![]() нинг хамма кийматларида
манфий ишорага эга, яъни (2.12.23) системанинг мувозанат холати асимптотик тургун
булсин.
нинг хамма кийматларида
манфий ишорага эга, яъни (2.12.23) системанинг мувозанат холати асимптотик тургун
булсин.
![]() ва
барча
ва
барча ![]() лар учун
лар учун
![]() ёки
ёки ![]() (2.12.25)
(2.12.25)
тенгсизликни
каноатлантирувчи хар кандай бир кийматли ва узлуксиз ![]() функция
учун (2.12.22) системанинг
функция
учун (2.12.22) системанинг ![]() мувозанат холати
бутунлайига асимптотик тургун буладими ёки йукми деган муаммо пайдо булади.
мувозанат холати
бутунлайига асимптотик тургун буладими ёки йукми деган муаммо пайдо булади.
Бошкача килиб айтганда, агар ![]() эгри
чизикнинг графиги
эгри
чизикнинг графиги ![]() ва
ва ![]() тугри
чизиклар оралигида жойлашган булса (2.13-шакл), у холда бу (2.12.22) системанинг
тугри
чизиклар оралигида жойлашган булса (2.13-шакл), у холда бу (2.12.22) системанинг
![]() мувозанат холати
батамом асимптотик тургун булиши учун етарлими?
мувозанат холати
батамом асимптотик тургун булиши учун етарлими?
Бу муаммо М.А.Айзерман томонидан куйилди [4] ва жуда хам куп математик ва механикларнинг тадкикотларига сабаб булди.
1950 йилда бу масала иккинчи тартибли системалар учун Н.П.Еругин томонидан тулик урганилди [28]. У узининг тадкикотларида дифференциал тенгламаларнинг сифат назариясидан фойдаланди. 1952 йилда И.Г.Малкин хам Ляпуновнинг иккинчи усулига таяниб, бу муаммони иккинчи тартибли системалар учун куриб чикди [55]. В.А.Плисс Айзерман муаммосини учинчи тартибли системалар учун тадкик этди [77]. Н.П.Еругин, И.Г.Малкин ва В.А.Плиссларнинг изланишлари купгина келгуси илмий тад-кикотларга йул очди.
 |
Биз бу ерда Н.П.Еругин ва И.Г.Малкинларнинг натижаларини келтирамиз. Дастлаб ночизиклилиги биринчи координатага боглик булган иккинчи тартибли
![]() (2.12.26)
(2.12.26)
системани куриб утайлик. Унинг биринчи якинлашиш
![]() (2.12.27)
(2.12.27)
тенгламалари учун характеристик тенглама
![]() (2.12.28)
(2.12.28)
куринишга эга булади. Бу тенглама илдизларининг хакикий кисми
![]() (2.12.29)
(2.12.29)
тенгсизликларни
каноатлантирувчи ![]() нинг хамма кийматларида
манфий ишорали булади.
нинг хамма кийматларида
манфий ишорали булади.
(2.12.27) система учун Ляпунов функциясини
![]() (2.12.30)
(2.12.30)
шартни
каноатлантирувчи ![]() квадратик форма
сифатида танлаймиз.
квадратик форма
сифатида танлаймиз.
(2.12.30)
дан фойдаланиб, ![]() ва
ва ![]() узгармас
коэффициентларни аниклаганимиздан кейин Ляпунов функцияси
узгармас
коэффициентларни аниклаганимиздан кейин Ляпунов функцияси
![]() (2.12.31)
(2.12.31)
куринишга
эга булади. (2.12.29) шартлар ![]() нинг аник мусбат
ишорали функция ва
нинг аник мусбат
ишорали функция ва ![]() нинг узгармас
манфий ишорали функция булишларини таъминлайди.
нинг узгармас
манфий ишорали функция булишларини таъминлайди.
Энди
(2.12.31) функция асосида (2.12.26) система учун Ляпунов функциясини тузамиз.
(2.12.26) система (2.12.27) системадан факат ![]() функция урнида
функция урнида ![]() чизикли
эмас функция турганлиги билан фарк килади. (2.12.31) ифодасида
чизикли
эмас функция турганлиги билан фарк килади. (2.12.31) ифодасида ![]() коэффициент
коэффициент
![]() нинг олдида
турибди. Агар
нинг олдида
турибди. Агар ![]() ифодани
ифодани 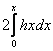 интеграл
сифатида карасак, у холда (2.12.26) система учун Ляпунов функциясини
интеграл
сифатида карасак, у холда (2.12.26) система учун Ляпунов функциясини
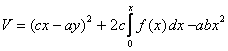 (2.12.32)
(2.12.32)
куринишда танлаш табиийдир. Бу функциянинг (2.12.26) системага нисбатан вакт буйича олинган тулик хосиласи
![]()
га тенг.
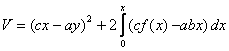 булганлигидан
булганлигидан ![]() нинг
аник мусбат ишорали функция булишининг шарти
нинг
аник мусбат ишорали функция булишининг шарти ![]() да
да
а) ![]()
дан иборат. а) шарт ушбу
б) ![]()
шарт
билан биргаликда ![]() нинг узгармас
манфий ишорали функция булишини таъминлайди. Равшанки,
нинг узгармас
манфий ишорали функция булишини таъминлайди. Равшанки, ![]() тупламда
тупламда
![]() булади ва
системанинг бутун траекториялари йук.
булади ва
системанинг бутун траекториялари йук. ![]() функция чексиз
катта булиши учун
функция чексиз
катта булиши учун ![]() да
да
с) 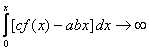
бажарилишини талаб килиш етарли.
а), б) ва с) шартлар, Барбашин-Красовский теоремасига асосан, (2.12.26) система мувозанат холатининг батамом асимптотик тургун булишини таъминлайди.
Агар с) шарти бажарилмаса, у холда (2.12.26) нинг мувозанат холати хар кандай бошлангич шартларда асимптотик тургун булмаслигини Н.Н.Красовский томонидан курсатилган [39].
Энди ночизикли иккинчи координатага боглик булган иккинчи тартибли
![]() (2.12.33)
(2.12.33)
системани куриб утамиз. Бу системанинг биринчи якинлашиш
![]() (2.12.34)
(2.12.34)
тенгламалари учун характеристик тенглама
![]()
куринишга эга.
Бу тенглама илдизларининг хакикий кисми манфий булиши учун
![]()
тенгсизликларнинг бажарилиши етарли ва зарурдир.
![]() булсин,
у холда
булсин,
у холда
![]() .
(2.12.35)
.
(2.12.35)
Бундан
ташкари ![]() нинг етарли катта кийматлари
учун
нинг етарли катта кийматлари
учун ![]() тенгсизлик бажарилади
деб фараз киламиз, бу ерда
тенгсизлик бажарилади
деб фараз киламиз, бу ерда ![]() - исталганча кичик
мусбат сон.
- исталганча кичик
мусбат сон.
Хусусан,
агар ![]() булса, у холда
булса, у холда ![]() функция
чегараланмаган. Аммо,
функция
чегараланмаган. Аммо, ![]() да, (2.12.35)
асосан
да, (2.12.35)
асосан ![]() ,
, ![]() булади
ва (2.12.33) системани бевосита интеграллаш натижаси шуни курсатадики,
мувозанат холати хар кандай бошлангич шартларда ва хар кандай
булади
ва (2.12.33) системани бевосита интеграллаш натижаси шуни курсатадики,
мувозанат холати хар кандай бошлангич шартларда ва хар кандай ![]() функция
учун асимптотик тургун булади.
функция
учун асимптотик тургун булади.
Энди
![]() деб хисоблаб куйидаги
функцияни караймиз:
деб хисоблаб куйидаги
функцияни караймиз:
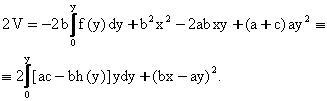 (2.12.36)
(2.12.36)
(2.12.35) шартга асосан ![]() аник мусбат
ишорали функция булади.
аник мусбат
ишорали функция булади. ![]() нинг (2.12.33) на
нисбатан вакт буйича тулик хосиласини оламиз:
нинг (2.12.33) на
нисбатан вакт буйича тулик хосиласини оламиз:
![]() .
.
Энди ![]() урнига (2.12.35)
ни каноатлантирадиган
урнига (2.12.35)
ни каноатлантирадиган ![]() ни куйиб,
ни куйиб, ![]() лар
учун
лар
учун
![]() (2.12.37)
(2.12.37)
ни хосил киламиз.
Бу ердан, агар (2.12.33) тенгламалардаги функция (2.12.35) шартни каноатлантирса, у холда мувозанат холат хар кандай бошлангич шартларда хам асимптотик тургун булади деган натижага келамиз.
Демак, (2.12.26) ва (2.12.33) системалар учун М.А.Айзерман муаммоси доимо ижобий хал булади.
бу
ерда ![]() - аникмас узгармас сонлар.
- аникмас узгармас сонлар.
Агар
![]() ва
ва ![]()
![]() узгармас
сонларни
узгармас
сонларни ![]() мусбат ишорали функция буладиган килиб танлаб олиш
мусбат ишорали функция буладиган килиб танлаб олиш
РЕЖА: |
|
1. Ляпунов функциялари. Аник ишорали ва узгарувчан ишорали функцияларнинг аломатлари. |
|
2. Харакат тургунлиги хакидаги Ляпуновнинг теоремалари. |
|
3. Харакатнинг батамом асимптотик тургунлиги хакидаги Барбашин – Красовскийлар теоремалари. |
|
4. Тургунлик хакидаги теоремаларнинг геометрик талкини. |
|
5. Харакатнинг нотургунлиги хакидаги Ляпуновнинг теоремалари. |
|
6. Теорема В нинг геометрик талкини. Н.Г.Четаев теоремаси. |
|
7. Интеграллар богланмаси воситасида Ляпунов функциясини тузиш. Хосиласи узгармас ишорали булган Ляпунов функцияларига асосланган критериялар. |
|
8. Харакат тургунлиги хакидаги теоремаларнинг татбикига доир мисоллар. |
Таянч иборалар. Ляпунов функциялари, Аник ишорали ва узгарувчан ишорали функциялар, Сильвестр критерияси, функцияларнинг аник ишоралилик ва узгарувчан ишоралилик аломатлари, харакат тургунлиги хакидаги теоремалар, Четаев теоремаси, Барбашин – Красовский теоремалари, геометрик талкин, Ляпунов функциясини тузиш, Теоремаларнинг татбиги, лампалик генератор, автоматик ростлаш системаси.
Такрорлаш учун саволлар:
1.Аник ишорали, узгармас ишорали ва узгарувчан ишорали функцияларнинг таърифлари.
2.Функцияларнинг аник ишоралилик ва узгарувчан ишоралилик аломатлари.
3.Харакат тургунлиги ва нотургунлиги хакидаги Ляпунов теоремалари.
4.Барбашин – Красовскийлар теоремалари.
5.Тургунлик хакидаги теоремаларнинг геометрик талкини.
6.Четаев теоремаси.
7.Интеграллар богланмаси воситасида Ляпунов функциясини тузиш.
8.Хосиласи узгармас ишорали булган Ляпунов функцияларига асосланган критериялар.
9.Коник маятник, Ер сунъий йулдоши стационар харакатларининг тургунлиги.
10.Снаряднинг айланма харакати тургунлигининг етарли шартлари.