УЗБЕКИСТОН РЕСПУБЛИКАСИ ОЛИЙ ВА УРТА МАХСУС ТАЪЛИМ ВАЗИРЛИГИ
АЛИШЕР НАВОИЙ НОМИДАГИ САМАРКАНД ДАВЛАТ УНИВЕРСИТЕТИ
ХОТАМ ТУРАЕВ
ХАРАКАТНИНГ
ТУРГУНЛИК НАЗАРИЯСИ
Узбекистон Республикаси олий ва урта махсус таълим вазирлиги республика олий укув юртларининг талабалари учун укув кулланмаси сифатида тавсия этган.
Т О Ш К Е Н Т– 2004
Тураев Х.Т. Харакатнинг тургунлик назарияси: Укув кулланмаси. –Тошкент: Укитувчи нашриёти.2004.-596 бет.
Китобда харакат тургунлик назариясининг умумий тушунчалари ва таърифлари, баркарор харакатлар учун Ляпуновнинг иккинчи усули, консерватив системалар мувозанат холати ва стационар харакатларининг тургунлиги, баркарор харакатлар учун биринчи якинлашиш усули буйича тургунлик критериялари, баркарор харакатлар учун критик холларни тадкик этиш баён килинади.
Мазкур китоб олий укув юртларининг 5480100–амалий математика ва информатика, 5460100– математика, 5440200–механика бакалавриатура йуналишлари ва 5А480103–амалий математика ва ахборот технологиялари, 5А460106–тизимли тахлил ва автоматик бошкарув, 5А440201–назарий механика мутахассисликлари буйича магистратурада таълим олаётган талабалар учун махсус курсдан укув кулланмаси сифатида ёзилган.
Китобдан аспирантлар, илмий ходимлар хамда радиотехника, амалий механика, автоматлаш ва бошкарув тизимлари сохаларида ишлаётган мухандис-математиклар ва мутахассислар хам фойдаланишлари мумкин.
Масъул мухаррир: доц. А.М.Мусаев
Такризчилар: УзМУ оптимал бошкарув назарияси кафедраси профессори, физика-математика фанлари доктори А.Я.Красинский, СамДУ амалий ва назарий механика кафедраси профессори, физика-математика фанлари доктори О.М.Дусматов, СамДУ амалий ва назарий механика кафедраси доценти Ф.Сатторов, ТДТУ «Автоматика ва телемеханика» кафедраси мудири И.Х.Сиддиков.
2004
Ó Тураев Хотам Тураевич
Ó Самарканд давлат университети
Узбекистон Республикаси Мустакиллигининг 13 йиллигига багишланади
СУЗ БОШИ
Азиз укувчиларга тавсия этилаётган ушбу китоб назарий механика курсини тулдирувчи укув адабиёти сифатида ёзилган.
Рус ва бошка хорижий тилларда тургунлик назариясига багишланган куп ажойиб адабиётлар ёзилиб, нашр этилган, масалан, А.М.Ляпунов [52], А.А.Андронов [1], И.Г.Малкин [53], Н.Н.Красовский [39], Е.А.Барбашин [8], Н.Г.Дубошин [26], Ю.И.Неймарк ва Н.А.Фуфаев [71] каби таникли олимларнинг китоблари шулар жумласидандир. Афсуски, хозиргача узбек тилида тургунлик назариясига багишланган бирорта хам укув адабиёти (дарслик, укув кулланма, монография) ёзилмаган. Олий укув юртларида тургунлик назариясидан дарслар 3-5 курсларда махсус курс сифатида асосан рус тилида олиб борилар эди. Мустакиллик шарофати туфайли олий укув юртларининг узбек гурухларида барча курслар (умумий ва махсус курслар) давлат тилида укитиладиган булди. Шунинг учун хам муаллиф ушбу кулланмани узбек тилида биринчи булиб ёзишга жазм килди.
Укув кулланма асосан юкори курс талабаларига ва магистрантларга мулжалланган. Унда барча олий укув юртларида укитиладиган математика курсидан ташкарига чикмайдиган математик аппарат фойдаланилган.
Мазкур кулланмада асосан автоном тизимлар харакатининг тургунлиги ёритилган. Келтирилган назарий масалаларни баён этишда мисоллардан кенг фойдаланилган. Тургунлик назариясини биринчи булиб укиётган талабалар амалий масалаларни ечиш учун татбик этаётганда доимо кийинчиликларга дуч келишини хисобга олиб, фан ва техниканинг хар хил сохаларидан мисоллар танланиб, уларнинг ечиш йуллари курсатилган.
Кулланма саккиз бобдан иборат, биринчи бобда тургунлик назариясига оид умумий тушунчалар ва таърифлар келтирилган.
Иккинчи бобда баркарор харакатлар учун Ляпуновнинг иккинчи усули ёритилган. Иккинчи усулнинг асосий фундаменти хисобланган Ляпуновнинг тургунлик, асимптотик тургунлик ва нотургунлик хакидаги теоремалари, харакатнинг батамом асимптотик тургунлиги хакидаги Барбашин-Красовский теоремалари, Н.Г.Четаев теоремаси, хосиласи узгармас ишорали булган Ляпунов функцияларига асосланган Барбашин-Красовский критерияси ва теоремаларнинг татбигига доир хар хил мисоллар келтирилган.
Учинчи бобда консерватив тизимлар мувозанат холати ва (баркарор) стационар харакатларининг тургунлиги тадкик этилган. Мувозанат холатининг тургунлиги хакидаги Лагранж-Дирихле теоремаси, мувозанат холатининг нотургунлиги хакидаги Ляпунов теоремаси, циклик координаталар, Раус теоремаси ва теоремаларнинг татбигига доир мисоллар ёритилган.
Китобнинг туртинчи бобида баркарор харакатлар учун биринчи якинлашиш усусли буйича тургунлик критериялари каралади. Бу ерда биринчи якинлашиш тенгламалари, узгармас коэффициентли чизиклаштирилган тенгламалар тизими учун Ляпунов функциясини тузиш, харакатнинг тургунлиги хакидаги Ляпунов теоремалари ва бу теоремаларнинг татбигига доир мисоллар келтирилган.
Китобнинг бешинчи бобида баркарор харакатлар учун критик холларни тадкик этиш баён этилган. Бу ерда битта нол илдизга эга булган хол, жуфт соф мавхум илдизлар холи хамда тургунлик сохасининг «хавфли» ва «хавфсиз» чегаралари курилган. Назарий натижалар муайян динамик тизимларни текширишга татбик этилган.
Олтинчи бобда Раус-Гурвиц муаммоси ёритилган. Бунда Коши индекси хакидаги тушунча, Штурм теоремаси, Раус алгоритми, Раус-Гурвиц теоремаси, махсус холлар, Орландо формуласи, Льенар ва Шипар критерияси, богланишларнинг геометрик схемаси, Неймаркнинг тургунлик ва нотургунлик хакидаги теоремалари, Неймаркнинг D-булаклаш усули, бир комплекс параметр ва икки хакикий параметр текислигида тургунлик сохасини ясаш, Найквист критерияси, Михайлов критерияси, критерияларнинг татбигига доир мисоллар каралган.
Китобнинг еттинчи бобида кучлар таркибининг харакат турнгунлигига таъсири урганилган. Бу ерда математик таркибига караб кучларнинг тури (классификацияси), тургунлик коэффициентлари, потенциал тизим харакатининг тургунлигига диссипатив ва гироскопик кучларнинг таъсири, Томсон ва Тет теоремалари, факатгина гироскопик ва диссипатив кучлар таъсиридаги харакатнинг тургунлиги, харакатнинг тургунлигига ноконсерватив кучларнинг таъсири ёритилган, теоремаларнинг техникавий тизимлар харакатининг тургунлигини тадкик этишга доир мисоллар каралади.
Саккизинчи бобда ноголоном тизимлар мувозанат холатлари ва стационар харакатларининг тургунлигини тадкик этиш масалалари келтирилган. Шу масалаларга багишланган Ю.И.Неймарк ва Н.А.Фуфаев, В.В.Румянцев, А.В.Карапетян теоремалари куриб чикилади.
Нижний Новгородда 1966-1973 йиллар давомида академик А.А.Андронов мактабида профессорлар Ю.И.Неймарк ва Н.А.Фуфаевлар илмий рахбарлигида таълим олиб кайтгандан сунг, 1973 йилдан бошлаб Самарканд давлат университети амалий математика факультетининг 3-5 курс талабаларига муаллиф томонидан махсус курс сифатида узлуксиз укилаётган маърузалар матни китобнинг асоси сифатида олинган. Унинг тузилиши ва мазмунига хурматли устозларим В.К.Кобилов, Ю.И.Неймарк ва Н.А.Фуфаевлар томонларидан факультет талабаларига укилган маърузаларнинг хам ижобий таъсири бор.
Китобни тайёрлашда россиялик А.А.Андронов, А.М.Ляпунов, М.А.Айзерман ва Ф.Р.Гантмахер, Ю.И.Ней-марк ва Н . А.Фуфаев, В. В.Румянцев, А. В.Карапетян,
Г.Н.Дубошин, Е.А.Барбашин, Д.Р.Меркин, Н.Н.Красовский, И.Г.Малкин, Н.Г.Четаев, И.С.Емельянова ва узбекистонлик М.Ф.Шульгин, А.Я.Красинский, Э.М.Красинская, Б.Атажанов, Х.Тураев каби олимлар томонидан яратилган монография, укув кулланмаси ва илмий маколалардан фойдаланилди.
Мазкур укув кулланмаси олий укув юртларининг 5480100–амалий математика ва информатика, 5460100– математика, 5440200–механика бакалавриатура йуналишлари ва 5А480103–амалий математика ва ахборот технологиялари, 5А460106–тизимли тахлил ва автоматик бошкарув, 5А440201–назарий механика мутахассисликлари буйича магистратурада таълим олаётган талабаларга мулжалланган.
Муаллиф китоб нафакат олий укув юртларининг талабаларига, балки уз ишида тургунлик назариясидан фойдаланувчи аспирантларга, мухандисларга ва илмий ходимларга хам фойдали булади деб ишонади.
Харакатнинг тургунлик назарияси биринчи марта узбек тилида ёзилгани учун камчиликлардан холи эмаслиги туфайли муаллиф китоб хакидаги танкидий фикр ва мулохазаларни миннатдорчилик билан кабул килади ва олдиндан уз ташаккурини изхор этади.
Китоб матнининг кулёзмаси билан муфассал танишиб, унинг мазмунини ва сифатини яхшилаш йулида фойдали курсатма ва маслахатлар берган такризчилар ¡збекистон миллий университети профессори А.Я.Красинский, Самарканд давлат университети профессори О.М.Дусматов ва доценти Ф.Сатторов ва Тошкент давлат техника университети «Автоматика ва телемеханика» кафедраси мудири И.Х.Сиддиковларга, мухаррирлик ишини бажарган доцент А.Мусаев хамда китоб матнини компьютерга киритган ва макетини тузган кафедрамиз ходимлари Ф.Муродов ва Х.Якубоваларга уз миннатдорчилигимни билдираман.
Муаллиф
КИРИШ
Механикада биринчи булиб тургунлик муаммоси тизимнинг мувозанат холатини урганиш учун пайдо булди. Оддий кузатишлардан маълумки, тизимнинг айрим мувозанат холатлари кичик тойилишларда тургун ва бошкалари етарли кичик тойдирувчи кучлар таъсирида нотургун булади. Масалан, маятникнинг куйи мувозанат холати оний равишда таъсир этувчи кичик тойдирувчи куч таъсирида тургун, юкори мувозанат холати - нотургун. Бу оддий мисолда албатта тургунлик масаласи элементар равишда ечилади, аммо умумий холда кандай шартлар бажарилганда тизимнинг мувозанат холатлари тургун булади деган масала доимо аник булмайди. 1644 йилда огирлик кучи таъсири остидаги жисмлар тизимининг мувозанат холатининг тургунлик критериясини умумий холда Е.Торичелли таърифлаб берди. 1788 йилда Ж.Лагранж ихтиёрий консерватив голоном тизим мувозанат холатининг тургунлигини аникловчи етарли шартларни ифодалади [51]. Бу теореманинг катъий исботи Г.Лежен-Дирихлега тегишли [119].
ХIХ асрнинг урталарида фан ва техникада жисмнинг нафакат мувозанат холатини, балки харакатининг хам тургунлигини аниклаш муаммоси пайдо булди.
Масалан, кам кувватли буг машиналарида урнатилган марказдан кочувчи регуляторлар (ростлагичлар) двигателнинг берилган айланишини тургун холда сакларди. Машиналар кувватининг ошиши билан олдинги схемада тайёрланган регуляторлар двигател айланишини катъий тартибга солиб турсаларда, бу айланишни кучайтириб, нотургун иш режимини яратардилар. ¡ша замондаги мухандис ва техниклар учун тушунарли булмаган бу ходиса двигателсозлик саноатида катта кризис тугдирди ва куп мамлакатлар олимларини бу муаммони ечишга жалб этишни талаб килди.
Дж.К.Максвелл (1868 й.), И.А.Вышнеградский (1876-1877 йиллар) ва бошка олимларнинг тадкикотлари, бу масаланинг ечими учун хам, ростлаш назариясининг умумий тараккиёти учун хам, харакат тургунлигининг критерияларини аниклаш лозимлигини курсатди.
XIX асрнинг охирларида харакат тургунлиги масалаларини умумий холда изохловчи ишлар пайдо булди.
1868 йилда Дж.К.Максвел «О регуляторах» деган илмий ишида машина-регулятор тизими харакатининг дифференциал тенгламаларини тузиб, кичик тебранишлар назариясига асосан тенгламаларни баркарор харакат атрофида чизиклаштиради. Максвел буйича машина-регулятор тизимининг баркарор харакати тургун булиши учун характеристик тенглама илдизларининг хакикий кисми манфий булиши керак. Максвел учинчи даражали характеристик тенгламалар учун илдизларнинг хакикий кисми манфий булишининг етарли ва зарур шартларини топади [58]. 1868 йилнинг узида у Лондон математиклар жамияти олдига ихтиёрий даражали тенгламалар учун бундай шартларни топиш масаласини куяди. Максвел куйган муаммони бир неча йилдан кейин Э.Дж.Раус туртинчи ва бешинчи даражали тенгламалар учун ечди. 1877 йилда у Максвел ва Стокс тавсиясига асосан ёзган «Устойчивость заданного состояния движения» ишида бу масалани ихтиёрий даражали характеристик тенгламалар учун ечади.
1877-1884 йилларда Э.Дж.Раус [116,117] циклик координатали консерватив голоном тизимлар стационар харакатининг тургунлик шартларини, 1879 йилда эса У.Томсон (лорд Кельвин) ва П.Тет гироскопик ва диссипатив кучларнинг харакат тургунлигига таъсирини урганиб, бир катор теоремалар яратдилар [112].
1876 йилда И.А.Вышнеградский узининг «О регуляторах прямого действия» ишида марказдан кочувчи регулятор билан таъминланган буг машинаси харакатининг тургунлигини тадкик этади [17]. У кичик тебранишлар назариясини куллаб, машина ва регулятор орасидаги муносабатни тугри акс этдирувчи харакатнинг тенгламаларини тузиб, тизим харакатининг тургунлигини текшириш масаласини учинчи даражали характеристик тенгламани текширишга, яъни алгебраик масалага келтиради. У характеристик тенглама илдизларининг хакикий кисми манфий ишорали булиши учун етарли ва зарур булган шартларни топди. Бу шартларнинг ажойиб геометрик талкинини берди. Шунинг учун хам И.А.Вышнеградскийни уз-узини автоматик ростлаш назариясининг асосчиси деб хисоблайдилар.
1882 йилда Н.Е.Жуковский узининг докторлик диссертациясида [32] хар хил усуллардан фойдаланиб, харакат тургунлигининг бир катор умумий масалаларини урганади.
1893 йилда словак мухандиси, Цюрих политехникуми профессори А.Стодола И.А.Вышнеградскийнинг чизикли назариясини регуляторлар харакатини тадкик этишга куллар экан, юкори даражали алгебраик тенгламаларда барча илдизларнинг хакикий кисми манфий ишорали булишининг шартларини топиш заруриятига дуч келди. Максвелл ва Раус ишларидан бехабар холда у узининг дусти Цюрих политехникумининг математиги А.Гурвицдан хакикий коэффициентли n-тартибли алгебраик тенгламада барча илдизларнинг хакикий кисми манфий булишининг етарли ва зарур шартларини топишни илтимос килади. Тахминан 25 йил аввал Максвел куйган масалани ва 15 йил олдин Раус ечган масалани Гурвиц француз олими Эрмит ишларига таяниб, 1893 йилда кайтадан ечади:
купхад барча илдизларининг хакикий кисми манфий булиши учун
Гурвиц детерминантининг бош минорлари мусбат булиши
етарли ва зарурдир (яъни 
). Гурвицнинг бу критерияси шакл жихатидан Раус
критериясидан фарк килсада, мазмунан у билан бирдир. Хозирги вактда бу
тенгсизликларни Раус-Гурвиц тенгсизликлари (критерияси) деб атайдилар.
Агар Гурвиц детерминантининг бош минорлари
мусбат булса, у холда купхаднинг барча коэффициентлари 
булади. Бу холни француз математиклари Льенар ва
Шипар тадкик этиб, 1914 йилда янги тургунлик критериясини кашф этишга муяссар буладилар.
Уларнинг критерияси буйича хисоб-китоблар Раус-Гурвиц критериясига нисбатан карийб
икки баробар камаяди.
Юкорида номлари келтирилган олимларнинг баъзи натижалари ва тадкик этиш усуллари хозирги кунда хам уз ахамиятини йукотгани йук.
¡ша вактдаги ишларнинг асосий камчилиги куйидагилардан иборат: тойилган харакатнинг тенгламаларини тадкик этишда муаллифлар тойилган харакатнинг чизиклаштирилган тенгламаларини текшириб, юкори тартибли хадларнинг харакатга таъсирини хисобга олмас эдилар. Масалан, агарда тойилган харакатнинг тенгламалари
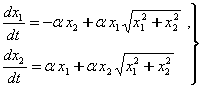(а)
куринишда булса, бу тенгламаларни
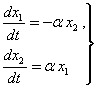(б)
тенгламалар тизими билан алмаштириб, харакатнинг тургун ёки нотургун эканлигини (а) тенгламалар билан эмас, балки (б) тенгламалар тизими оркали аниклашни тавсия этилган. Аммо (б) тенгламаларга асосланиб харакатнинг тургунлиги хакида олинган натижа (а) тенгламалар тизими буйича олинган натижага умуман олганда мос келмайди.
1892 йилда А.М.Ляпунов узининг “Общая задача об устойчивости движения” номли докторлик диссертация-сида хозирги замон тургунлик назариясининг асосини яратди [52]. Тургунликнинг умумий таърифи берилди, тургунликни тадкик этишнинг иккита усули яратилди (усулларнинг асосини у берган тургун, асимптотик тургун ва нотургун харакатлар хакидаги теоремалар ташкил этади), биринчи якинлашиш буйича харакатнинг тургун ва нотургунлиги хакидаги теоремалар тавсия этилди, характеристик сонлар назарияси ишлаб чикилди, оддий критик холларда харакатнинг тургунлик масалаларининг ечими топилди. Хусусан, А.М.Ляпунов биринчи булиб, Лагранж теоремасининг тескарисини топиш масаласини куйиб, икки хусусий хол учун унинг ечимини берди ва х.к.
Н.Г.Четаев [101-104] хам харакатнинг тургунлик назариясига катта хисса кушди: нотургунлик хакида умумий теорема яратди, нобаркарор харакатларнинг нотургунлиги хакидаги теоремаларни ишлаб чикди, Ляпунов функциясини тузишнинг эффектив усулини берди, Лагранж теоремасининг тескарисини бир катор холлар учун яратди ва х.к.
Ляпуновдан кейин харакатнинг тургунлик назарияси турли йуналишлар буйича ривожланди. Ляпунов куллаган усуллар чукурлаштирилди ва у олган натижалар ойдинлаштирилди, Ляпунов томонидан тургунлик назариясига киритилган тушунчалар кенгайтирилди. Жумладан, куп олимларнинг эътибори чекли вакт оралигида, бошлангич шартлар катта булганда, узлуксиз таъсир этувчи тойдирувчи кучлар хамда тасодифий кучлар таъсир этаётганда тургунлик шартларини топишга каратилган эди.
Узлуксиз таъсир этувчи тойдирувчи кучлар таъсири остидаги харакатларнинг тургунлигига оид 1936-1955 йиллар давомида олиб борилган тадкикот ишларида Н.Г.Четаев, И.Г.Малкин, И.Л.Массера, Е.А.Барбашин, Н.Н.Красовский, В.Е.Гермаидзе ва К.П.Персидскийларнинг хизматлари бенихоят каттадир.
Е.А.Барбашин, Н.П.Еругин, В.А.Плисс ва Н.Н.Кра-совскийлар 1950-1955 йиллар давомида хар кандай катталикдаги тойилишлар учун асимптотик тургунликнинг етарли шартларини ишлаб чикдилар.
1957 йилда В.В.Румянцев Ляпуновнинг иккинчи усулини узгарувчиларнинг факат бир кисмига нисбатан харакат тургунлигини тадкик этишни талаб киладиган динамик тизимларга жорий этди.
1949 йилда Н.Н.Баутин тургунлик сохасининг чегараси якинида динамик тизимнинг хулкини тадкик этиб, тургунлик сохасининг «хавфли» ва «хавфсиз» чегаралари деган тушунчаларни киритди.
Автоматика, радиотехника, бошкариш ва ростлаш назарияларида пайдо булган янги тургунлик масалаларини ечиш учун Найквист, Михайлов, Попов критериялари хамда Неймаркнинг D-булаклаш усули яратилди.
Динамик тизимларда содир этилиши мумкин булган нотургунликнинг механизмини ва сабабини билиш факатгина тугри идеаллаштириш учун эмас, балки айрим холларда тебранма харакат ва нотургунлик пайдо булмаслиги учун тизим конструкциясига кандай узгартиришлар киритиш кераклигини билиш учун хам зарурдир. Бу кейинги холат жуда хам катта амалий ахамиятга эга. Ю.И.Неймарк 1955 йилда тургунлик ва нотургунлик ходисаларини текширишга физика нуктаи назардан ёндашиб, иккита теорема яратди ва бу теоремалар оркали динамик тизимда юз бериши мумкин булган нотургунликнинг механизмини ва сабабини курсатди, харакат тургунлигига кучлар таркибининг таъсирини изохлаб берди.
Ноголоном тизимлар тургунлиги ва кичик тебранишлари масаласи буйича Е.Уитеккер, О.Боттема, М.А.Ай-зерман ва Ф.Р.Гантмахер, А.Н.Обморшев, Г.Н.Князев, Ю.И.Неймарк ва Н.А.Фуфаев, В.В.Румянцев, А.В.Карапетян, А.Я.Красинский, И.Е.Емельянова, Б.Атажанов, Х.Т.Тураев ва бошкалар шугулланганлар.
ХХ асрнинг 60-йилларигача олимлар уртасида ноголоном тизимлар мувозанат холатларининг тургунлигини тадкик этиш масаласида ягона ёндашиш йук булиб, хатто, тургунликни текшириш усуллари борасида хам бир катор карама-каршиликлар бор эди.
1965 йилда Ю.И.Неймарк ва Н.А.Фуфаев ноголоном тизимларда мувозанат холатлари яккаланган холда мавжуд булмаслиги ва улар улчови камида ноголоном богланишлар сонига тенг булган (купхиллик) сирт ташкил килишларини курсатдилар. Ноголоном тизимлар харакати тенгламаларининг характеристик тенгламалари: 1) m та нол илдизга эга, бу ерда m – ноголоном богланишлар сони; 2) унинг коэффициентларидан тузилган матрица симметрик (голоном тизимларда симметрик булади) эмас.
Ноголоном тизимларда мувозанат холатлари сиртининг мавжудлиги сабабли улар харакатининг тургунлигини мувозанат холатлари сиртига нисбатан куйиш (яккаланган мувозанат холати атрофида эмас) лозим.
Ноголоном тизимларнинг стационар харакатлари худди голоном тизимларникидай фазавий фазо ва конфигурациялар фазосида бирор улчамли сиртни ташкил килади. Шунинг учун бу ерда хам стационар харакатлар
сиртининг тургунлиги тадкик этилгандагина масала коррект куйилган булади.
Э.Урунбаев харакатнинг тургунлигини ЭХМ воситаси билан тадкик этиш усулларини яратди. У детерминантнинг элементлари полиномиал хадлар булган холда уни ёйиш усули, Гурвиц, Льенар ва Шипар, Михайлов ва Найквист критериялари, умумлашган Штурм катори хамда D-бу-лаклаш усули асосида тизим параметрлари текислигида тургунлик сохаларини ясашни автоматлаштириш усуллари ва курилаётган тизим конструктив параметрларининг тургунлик сохаларининг чегараларига таъсирини урганиш учун хисоблаш экспериментларини утказиш услубини ишлаб чикди [93-97].
Тургунлик назарияси физикада, химияда, астрономияда, биологияда, радиоэлектроникада, техникада кенг кулланилади.
Шуни таъкидлаймизки, тургунлик назарияси хали хам мукаммал холга келтирилган эмас, унда ечилмаган масалалар жуда куп. У йилдан-йилга ривожланиб бормокда. Бу ривожланишга бутун дунё олимлари, шу жумладан, ¡збекистон олимлари хам уз хиссаларини кушмокдалар. Имконият чегараланганлиги боис барча номларни келтиришнинг иложи йуклигидан куплари хакида китоб матнида айтиб утамиз.
I-БОБ. УМУМИЙ ТУШУНЧАЛАР ВА ТАЪРИФЛАР
1-§. Харакатнинг тургунлик назарияси предмети хакида
Харакатнинг тургунлик назарияси – моддий система (тизим) харакатига тойдирувчи (кузгатувчи) омилларнинг таъсирларини тадкик этиш билан шугулланувчи фандир. Тойдирувчи омиллар (факторлар) сифатида – материал система харакатига таъсир этувчи асосий кучларга нисбатан етарлича кичик булган ва шунинг учун хам харакатнинг математик моделини тузишда хисобга олинмайдиган кучларга каралади. Бу кучларнинг таъсир этиш тартиби аслида аник эмас. Улар бир онда таъсир килиши мумкин, натижада материал системанинг дастлабки холати - координата ва тезликларнинг дастлабки киймати бир озгина узгаради. Шунингдек тойдирувчи омиллар система харакатига узлуксиз таъсир этиши хам мумкин. Бунинг натижасида биз тузган математик модел аслидан фарк килади, чунки унда кичик тузатувчи хадлар хисобга олинмаган булади.
Аникки, кичик тойдирувчи омилларнинг материал система харакатига таъсири хар хил харакатлар учун бир хил булмайди. Айрим харакатларга уларнинг таъсири билинмас даражада, яъни тойилган харакатнинг тойилмаган харакатдан фарки озгина булади. Аксинча, бошка харакатларга тойдирувчи факторларнинг таъсири сезиларли даражада булиб, тойдирувчи кучлар канчалик кичик булмасин, тойилган харакат тойилмаган харакатдан анча фарк килади. Биринчи турдаги харакатга тургун ва иккинчи турдаги харакатга нотургун (тургун эмас) харакат деб айтамиз.
Харакатнинг тургунлик назарияси – курилаётган харакатнинг тургун ёки нотургун эканлигини аниклаб берувчи белгиларни (аломатларни) топиш (урнатиш) билан шугулланади. Хаётда тойдирувчи омиллар доимо мавжуд булганлиги учун харакатнинг тургунлиги масаласи бенихоят катта назарий ва амалий ахамиятга эгадир.
Харакатнинг тургунлик масаласи билан купгина буюк математик ва механиклар шугулланган. Мувозанат холатининг тургунлиги тугрисидаги теоремани 1788 йилда Лагранж яратган эди [51]. Бу ишга асосланиб Раус олиб борган изланишлар айрим хусусий холларда харакатнинг тургунлик белгиларини топишга туртки берди. Тургунлик масалалари билан У.Томсон ва П.Г.Тэт (1810), Дж.К.Макс-велл (1868), И.А.Вышнеградский (1877), Н.Е.Жуковский (1882), Стодола, Гурвицлар хам шугулландилар. Бу олимлар уз тадкикотларида харакатнинг хусусий холларинигина караганлар ва унча асосланмаган усуллардан фойдаланганлар. Масаланинг биринчи катъий ечими француз олими Пуанкарега тааллукли. Аммо Пуанкаренинг натижалари хусусий характерга эга эди.
1892 йилда Харков шахрида А.М.Ляпунов «Общая задача об устойчивости движения» мавзусида докторлик диссертациясини химоя килди. Бу диссертацияда харакатнинг тургунлик масаласи кенг маънода куйилди ва уни ечишнинг катъий усуллари курсатилди. Ляпуновнинг бу иши тургунликни тадкик этишда келгуси хамма илмий изланишлар учун асос булди.
Юкорида биз харакатнинг тургун ва нотургунлиги тушунчаларини схематик равишда ифодаладик. Бу тушунчаларга аник таъриф биринчи булиб А.М.Ляпунов томонидан берилган [52].
Мазкур китоб Ляпунов маъносидаги харакатнинг тургунлик назарияси ва унинг татбиклари масалаларига багишланади.
2-§. Тургун харакат. Тойилган харакатнинг
дифференциал тенгламаси
2.1.Тургун харакатнинг таърифланиши
Харакатнинг тургунлиги хакидаги тушунча мувозанат холатининг тургунлиги тугрисидаги тушунчанинг бевосита умумлашмасидир.
умумлашган
координаталар билан аникланган ва 
эркинлик даражасига
эга булган ихтиёрий динамик системани куриб утайлик. Фараз киламизки, курилаётган
система 
мувозанат холатига
эга булсин. Демак, харакат тенгламаси 
хусусий ечимга эга
булади. Ушбу
, 
бошлангич шартларни каноатлантирувчи системанинг харакатини курайлик.
Агар
хамма шундай турдаги харакатлар учун вактнинг 
кийматида 
бошлангич
четланишлар ва 
бошлангич
тезликлар етарлича кичик
мусбат 
сонидан кичик булганда
координаталар четланиши (огиши) 
ва 
тезликларнинг
абсолют микдори хамма вакт 
исталганча кичик
мусбат 
сонидан кичиклигича
колса, у холда мувозанат холати тургун деб айтилади. Акс холда мувозанат холати
нотургун деб айтилади. Маятникнинг куйи ва юкори вертикал холати мос равишда
тургун ва нотургун мувозанат холатига оддий мисол була олади.
Тургунлик таърифидан куйидаги иккита асосий тасдик келиб чикади:
1)Мувозанат холатининг тургун ёки нотургунлиги унга якин харакатларнинг характерига караб аникланади.
2)Мувозанат холати тургун булиши учун системанинг бу
мувозанат холатидан бошлангич тойилиши ва бошлангич тезлигини шундай танлаб
олиш зарурки, уларнинг хар бири берилган исталганча кичик сондан кичик була
олсин. Масалан, 1.1-шаклда курсатилган маятникнинг юкори мавозанат холати 
бурчак
хар канча кичик булишига карамасдан, харакатнинг бошлангич шартларини кандай килиб
олишимиздан катъий назар, маятникнинг мувозанат холатдан тойилишини бурчакдан
кичик килиб булмайди.
 |
Мувозанат холатининг тургунлигини кандай аниклаган булсак, худди шундай харакатнинг Ляпунов буйича тургунлиги аникланади.
Куйидаги математик модел (дифференциал тенгламалар) билан аникланган ихтиёрий динамик системани курайлик:
.
(1.2.1)
Бу ерда 
- харакат
билан боглик булган параметрлар, масалан, координата ва тезликлар ёки умумоан
шу микдорларга боглик булган функциялар.
Курилаётган системанинг 
хусусий ечимига
мос келган харакатини тойилмаган харакат деб, системанинг 
дан
фарк килувчи колган барча 
харакатларини тойилган
харакатлар деб айтамиз.
-
айирмаларнинг кийматлари тойилишлар деб айтилади.
1-таъриф. Агар хар кандай кичик 
сон
учун шундай мусбат 
сони мавжуд булсаки,
барча 
тойилган
харакатлар учун бошлангич лахзада
(1.2.2)
муносабатнинг бажарилишидан барча 
лар учун
(1.2.3)
тенгсизликнинг
бажарилиши келиб чикса, у холда тойилмаган харакат 
микдорларга
нисбатан тургун деб айтилади.
Тойилмаган
харакат тургун булмаса, у нотургун деб айтилади. Шундай килиб, харакатнинг
нотургун булиши учун шундай мусбат кичик сон мавжуд булиши
ва хар кандай исталганча кичик сон учун (1.2.2)
муносабатни каноатлантирувчи бирорта тойилган харакат учун хеч булмаганда бирор
пайт 
да (1.2.3)
тенгсизликнинг бажарилмаслиги (тенгликка айланиши) етарлидир.
2-таъриф.
Агар тойилмаган харакат микдорларга
нисбатан тургун булса ва шундай исталганча кичик 
сони мавжуд булсаки,
пайтда
(1.2.4)
муносабатнинг бажарилишидан лар учун
(1.2.5)
булишлиги
келиб чикса, у холда тойилмаган харакат микдорларга
нисбатан асимптотик тургун деб айтилади.
3-таъриф. Агар 
да тойилган
харакат тойилмаган харакатга
га нисбатан текис
интилса, у холда тойилмаган харакат га нисбатан текис
асимптотик тургун деб айтилади.
4-таъриф.
Агар тойилган харакат тойилмаган
харакатга да 
бошлангич
шартларга нисбатан текис интилса, у холда тойилмаган
харакат бошлангич
шартларга нисбатан текис асимптотик тургун деб айтилади.
Агар
(1.2.1) система автоном булса, яъни унг тарафидаги 
функциялар
ошкор равишда t га боглик булмасалар, у холда
тойилмаган харакат доимо бошлангич шартларга нисбатан текис асимптотик тургун булади.
Бу натижага 1949 йилда И.Л.Массер эришган [53].
5-таъриф.
Агар тойилмаган
харакат Ляпунов буйича тургун булиб ва (1.2.5) муносабат исталган бошлангич
шартлар учун бажарилса, у холда тойилмаган харакат батамом асимптотик тургун
дейилади.
Шундай килиб, куйидаги тушунчаларга эга булдик:
тургунлик тушунчаси,
асимптотик тургунлик тушунчаси,
бошлангич вактга ва бошлангич шартларга
нисбатан текис асимптотик тургунлик тушун- часи,
батамом асимптотик тургунлик тушунчаси.
2.2.Тойилган харакатнинг дифференциал тенгламалари
Тургунликни
тадкик этиш учун (1.2.1) дифференциал тенгламаларда узгарувчилар
урнига янги 
узгарувчилар
киритамиз:
.
(1.2.6)
Бу
ерда - тойилмаган харакатга
мос келувчи (1.2.1) нинг хусусий ечими, - тойилган харакатга
мос келувчи (1.2.1) нинг хусусий ечими, 
- тойилишнинг
микдори.
Янги узгарувчиларга нисбатан (1.2.1) дифференциал тенгламаларнинг куриниши куйидагича булади:
,
(1.2.7)
бу ерда
. (1.2.8)
Худди шу (1.2.7) тенгламага тойилган харакатнинг дифференциал тенгламалари деб айтилади.
Равшанки,
(1.2.8) муносабатга кура 
тривиал ечим тойилмаган
харакатга мос келувчи тойилган харакатнинг мувозанат холати булади.
Шундай
килиб, (1.2.6) муносабат оркали янги узгарувчилар
киритилганлиги туфайли, тойилган харакат-нинг 
мувозанат холатига
(1.2.1) тенгламанинг тойилмаган
харакати мос келади ва аксинча. Демак, тойилмаган
харакатнинг тургунлик масаласи (1.2.7) дифференциал тенгламалар билан аникланувчи
тойилган харакат мувозанат холатининг тургунлик масаласига келтирилди. Бундан уз
навбатида тойилган харакатнинг мувозанат холати тургун (асимптотик тургун)
лигидан, тойилмаган харакатнинг хам тургун (асимптотик тургун) булишлиги келиб
чикади.
Янги
узгарувчилар
учун (1.2.2), (1.2.3), (1.2.4) ва (1.2.5) муносабатлар мос равишда куйидаги куриниш-ларга
эга булади:
,
(1.2.9)
,
(1.2.10)
,
(1.2.11)
.
(1.2.12)
Энди
(1.2.7) система мувозанат холати
учун тургунлик таърифини берайлик.
6-таъриф.
Агар хар кандай исталганча кичик сон учун шундай мусбат
сони танлаб олиш
мумкин булсаки, хамма тойилган харакатлар учун бошлангич вактда
(1.2.9) муносабатнинг бажарилишидан лар учун (1.2.10)
тенгсизликнинг бажарилиши келиб чикса, у холда тойилмаган харакат (тойилган харакатнинг
мувозанат холати)
тургун деб айтилади.
7-таъриф.
Агар тойилмаган харакат тургун ва сонини шундай
танлаш мумкин булсаки, барча (1.2.11) тенгсизликни каноатлантирувчи тойилган харакатлар
учун (1.2.12) муносабат бажарилса, у холда тойилмаган харакат асимптотик тургун
деб айтилади.
Худди шу тарзда текис асимптотик тургун ва батамом асимптотик тургун тушунчаларини хам келтириш мумкин.
Энди тойилган харакат тенгламасини тузишга оид мисоллар куриб чикайлик.
3-§. Тойилган харакатининг тенгламаларини
тузишга доир мисоллар
1-мисол. Математик маятник тойилган харакатининг тенгламаси
Математик маятник тебранма харакатининг дифференциал тенгламаси
ёки
(1.3.1)
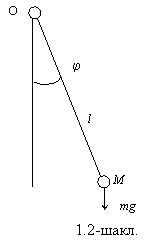куринишда булишини биламиз, бу ерда 
-
маятникнинг вертикал укдан огиш бурчаги. 
, 
бошлангич
шартларни каноатлантирувчи харакатнинг 
ва 
ларга
нисбатан тургунлигини текшириш масаласини курайлик (1.2-шакл). Берилган бошлангич
шартларга мос келувчи (1.3.1) динамик системанинг хусусий ечими 
куринишда
булади, бунда 
- бирор даврий
функция (аналитик куриниши бизга зарур эмас).
Ушбу 
янги узгарувчини
киритиб, (1.3.1) дан куйидаги дифференциал тенгламани хосил киламиз:
,
ёки 
ни х буйича
каторга ёйиб,
(1.3.2)
га келамиз. У математик маятник тойилган харакатини ифодаловчи изланган дифференциал тенгламадир.
2-мисол. Кузгалмас нукта атрофида инерция буйича айланаётган каттик жисм тойилган харакатининг тенгламаси
Маълумки, кузгалмас нукта атрофида инерция буйича айланаётган каттик жисмнинг дифференциал тенгламаси куйидаги система куринишида булади (назарий механикага доир ихтиёрий укув кулланмани куринг):
(1.3.3)
бу ерда 
- оний бурчак
тезликнинг жисм махкамланган нуктадаги бош инерция укларига мос келувчи кузгалувчи
координаталар системасидаги проекциялари, А, В, С лар эса
шу укларга нисбатан инерция моментларидир.
(1.3.3) тенгламалар
., 
(1.3.4)
хусусий ечимга ва яна колган икки укларга мос келувчи
худди шундай 
иккита хусусий
ечимларга эга.
(1.3.3) харакатни тойилмаган харакат сифатида кабул килиб ва куйидаги янги
узгарувчиларни (1.3.3) га куйсак, тойилган харакатнинг дифференциал тенгламалари системасига келамиз:
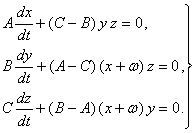(1.3.5)
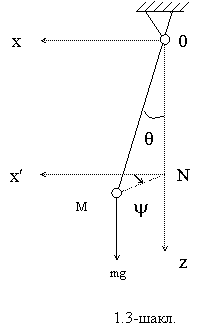
3-мисол. Коник (конуссимон) маятник тойилган харакатининг дифференциал тенгламалари
Дастлаб
О нуктада вазнсиз ОМ ипда осилган 
массали М моддий
нуктани курайлик. Ипнинг узунлиги 
га тенг булсин. М
моддий нуктанинг холатини 
ва 
бурчаклар
оркали аниклаймиз (1.3-шаклга каранг).
 |
Бу сферик маятникнинг кинетик ва потенциал энергиялари мос равишда
, 
(1.3.6)
булади. Ушбу
, 
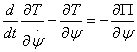
Лагранж тенгламаларидан фойдаланиб, сферик маятник харакатининг дифференциал тенгламаларини тузамиз
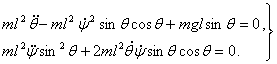(1.3.7)
(1.3.7) система бир мунча соддалаштиришлардан сунг,
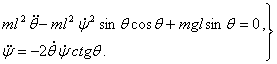(1.3.8)
куринишга келади.
(1.3.8) системани биринчи тартибли нормал дифференциал тенгламалар системасига келтириш учун куйидаги
, 
,
.
(1.3.9)
янги узгарувчиларни киритамиз.
Янги узгарувчиларда сферик маятник харакатининг дифференциал тенгламалари системаси
, (1.3.10)
куринишга келади.
Энди горизонтал жойлашган айлана буйлаб узгармас тезликда харакат килаётган маятник (конуссимон маятник)ни курайлик. Бу холда
,
,
(1.3.11)
булади.
, 
ва
ларнинг бу кийматларини
(1.3.10) га куйиб, ушбу конуссимон маятник параметрлари каноатлантириши лозим булган
(1.3.12)
муносабатни топамиз.
(1.3.11) тенгликлар билан аникланган харакатни тойилмаган харакат сифатида кабул киламиз. У холда юкорида баён этилган назарияга асосан
, 
,
. (1.3.13)
(1.3.13) тенгликлар билан аникланадиган ,
, ларнинг
кийматларини (1.3.10) системага куйиб ( ва 
ларнинг
узгармас сонлар эканлигини хисобга олиб), тойилган харакатнинг дифференциал
тенгламалари системасини хосил киламиз:
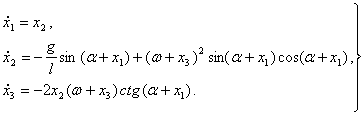(1.3.14)
(1.3.14) система дифференциал тенгламаларнинг
унг тарафидаги функциялар ((1.3.12) тенгликни хисобга олганимизда) 
нуктада
нолга айланади, яъни 
шартлар
бажарилади. Бу функцияларни мувозанат холати атрофида 
, 
ва
лар буйича каторга
ёйиб ва факат чизикли хадларни колдириб, куйидаги биринчи якинлашиш
тенгламалари системасини хосил киламиз ((1.3.12) тенгликни хисобга олганда)
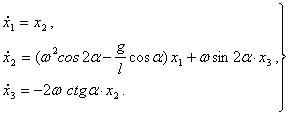(1.3.15)
4-мисол. Ер сунъий йулдоши массаси марказининг тойилган харакатининг дифференциал тенгламалари
Ер сунъий йулдошига факат Ернинг тортиш кучлари таъсир этади деб фараз киламиз. Бу кучларнинг тенг таъсир этувчиси F сунъий йулдош массасининг марказига таъсир этади ва унинг модули
(1.3.16)
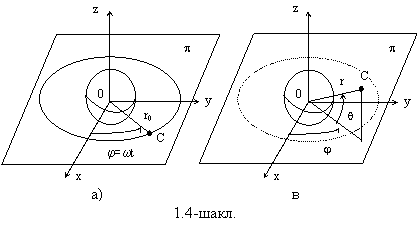
бутун олам тортилиш конуни билан аникланади деб кабул киламиз.
Бу ерда 
- Ернинг
гравитацион параметри, R – Ер шарининг радиуси, g – Ер тортиш
кучининг тезланиши, М – Ер массаси, f -
гравитацион доимийси, r=OC – Ер маркази О дан сунъий йулдош массаси маркази С
гача булган масофа, m – сунъий йулдош массаси.
Ер сунъий йулдоши массаси марказининг (
)
текисликда ётган ва радиуси r0 булган
доира буйича текис харакатини курамиз (3.3,а-шакл). Бундай харакат Ер сунъий йулдошининг
баркарор (стационар) харакати деб хам айтилади. Сунъий йулдош баркарор харакатининг
параметрларини каноатлантирувчи шартни бевосита Ньютоннинг
, (
ёки 
) (1.3.17)
иккинчи конунидан фойдаланиб топамиз, бу ерда 
-
сунъий йулдош радиус – вектори r0 айланишининг баркарор (стационар) харакатидаги бурчак
тезлиги.
Сунъий йулдошнинг баркарор харакатига вактда
кандайдир тойдирувчи кучлар оний равишда таъсир этди деб фараз килайлик.
Масалан, ракетанинг охирги боскичидан сунъий йулдошнинг ажралиши пайтида унинг
радиуси r0 булган
доира буйича текис харакат килишга шароит яратиб берадиган шартлар озгина
бузилиши мумкин. Натижада, сунъий йулдошнинг харакати тойилган булади, хусусан,
энди у доира буйича харакат килмайди, радиус-вектор айланишининг бурчак тезлиги
булади, харакат ()
текисликда юз бермайди ва х.к.
Ер сунъий йулдошининг тойилган харакати дифференциал
тенгламаларини келтириб чикариш учун Oxyz
координаталар системасини шундай тузамизки, унинг xy координата
текислиги () текислик билан устма-уст
тушсин. Ер сунъий йулдоши массаси марказининг тойилган харакатдаги холатини 
,,
сферик координаталар оркали аниклаймиз (3.3,б-шакл). Сунъий йулдошнинг кинетик
ва потенциал энергиялари мос равишда
, 
(1.3.18)
тенгликлар оркали аникланади.
Сунъий йулдошнинг баркарор (стационар) харакати
тургунлигини 
ва 
микдорларга
нисбатан урганамиз.
Бунинг учун унинг тойилган харакати тенгламасини Лагранжнинг
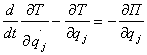
(1.3.19)
тенгламасидан фойдаланиб тузамиз. Аввал координата
учун тенгламани тузишда зарур буладиган хосилаларни (1.3.18) дан фойдаланиб
топамиз:
, 
,
, 
Бу ифодаларни координата учун
(1.3.19) тенгламага куйиб,
(А)
ни хосил киламиз. Тойилган харакат тенгламасини тузиш
учун, коидага асосан, 
, 
деб
кабул киламиз ва уларни (А) га куйиб, сунгра m га булиб юбориб,
(1.3.20)
ни хосил киламиз. Худди шу тарзда иш юритиб,
,
(1.3.21)
тенгламаларни хам келтириб чикарамиз. Энди (1.3.20) ва (1.3.21) тойилган харакат тенгламаларини нормал дифференциал тенгламалар куринишига келтирамиз. Бунинг учун
, 
,
, 
,
янги узгарувчиларни киритамиз. Буларни (1.3.20) ва (1.3.21) тенгламаларга куйиб ва уларни хосилалар буйича ечиб, Ер сунъий йулдошининг тойилган харакати дифференциал тенгламаларининг нормал куринишига эга буламиз:
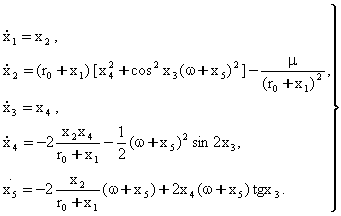(1.3.22)
Бу тенгламаларнинг унг тарафидаги функциялар 
координата
бошида ((1.3.17) ни хисобга олганда) нолга айланадилар, яъни шарт
бажарилади.
(1.3.22) тенгламалар системасининг биринчи якинлашиш тенгламалари куйидаги куринишда булади:
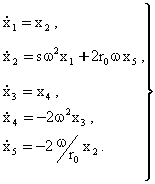(1.3.23)
Бу тенгламаларни чикаришда (1.3.17) тенглик инобатга олинган.
4-§. Баркарор (стационар) ва баркарормас
(ностационар) харакатлар
Яна умумий холга, яъни тойилган харакатнинг (1.2.7) тенгламасига кайтайлик.
Тойилган харакат тенгламасидаги 
функциялар
вактнинг 
булган ихтиёрий кийматлари
учун мувозанат холатини камраб олувчи
(1.4.1)
сохада аникланган, узлуксиз ва узлуксиз хусусий хосилаларга
эга, яъни шу сохада 
аргументларнинг
голоморф (аналитик) функциялари булсин. Бу ерда Н - ихтиёрий етарлича
кичик мусбат сон. Шу шартда уларни
(1.4.2)
каторга ёйиш мумкин. Бу ерда
, 
,
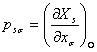(1.4.3)
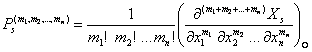, (1.4.4)
, 
,
, о
белгиси эса хосила олингандан кейин 
лар урнига ни
куйишни билдиради.
(1.4.2) ифодани куйидагича ёзиш мумкин:
, (1.4.5)
бу ерда
, (1.4.6)
.
(1.4.7)
Бу йигинди хамма бутун манфий булмаган ва шартни
каноатлантирувчи 
сонлар буйича
олинади. Шундай килиб, 
ларга нисбатан
чизикли булган хадлар мажмуасини, 
ларга нисбатан –
даражали хадлар мажмуасини билдиради. 
купхаддаги хар хил
ухшаш булмаган хадлар сони
га тенг. Масалан, 
купхаддаги, яъни 
узгарувчили
квадратик формадаги хар хил хадлар сони
га тенг булади.
функциялар умумий холда
ошкора равишда 
га боглик булиши
мумкин. Шунинг учун хам (1.4.2) даги коэффициентлар вактнинг
узлуксиз функциялари булади. Бу холда тойилмаган харакатни баркарормас (ностационар)
харакат деб атаймиз.
Амалда функциялар ошкора
равишда га боглик булмайдиган
холлар хам учрайди. Бунинг натижасида (1.4.2) ёйилмадаги коэффициентлар хакикий
узгармас сонлар булади. Бу холда тойилмаган харакатни баркарор (стационар) харакат
деб атаймиз. Баркарор ва баркарормас деган тушунчаларни А.М.Ляпуновнинг узи
киритган эди. Бирок айрим муаллифлар бу сузлар урнига мос равишда стационар ва
ностационар (стационар эмас) деган атамаларни ишлатадилар. Масалан, тойилган харакатнинг
(1.3.23) дифференциал тенгламалари ошкор равишда вактга боглик
эмас. Шунинг учун бу харакат баркарор харакат булади. Куп амалий масалалар
худди шундай холга келтирилади.
Тебранма харакатни ифода этувчи
дифференциал тенгламаларнинг унг тарафидаги функциялар га
нисбатан даврий функциялардир. Масалан, 1-мисолдаги математик маятникнинг харакатини
ифодаловчи (1.3.14) тенгламанинг унг тарафидаги функция га нисбатан
даврий, чунки тенглама ифодасида катнашувчи даврий функция.
5-§. Узлуксиз таъсир этадиган тойдирувчи кучлар
таъсиридаги харакатнинг тургунлиги хакида
Юкорида танишилган Ляпунов киритган таърифларда тойилмаган харакатнинг тургунлиги бошлангич шартларнинг тойилишига нисбатан курилади, яъни тургунлик масаласи оний равишда таъсир этадиган тойдирувчи факторларга нисбатан каралади. Аммо реал механик (физик ва б.) система микдор жихатидан унча катта булмаган доимий таъсир этиб турувчи кучлар таъсири остида булади. Системанинг харакат тенгламасини тузаётганда бу кучларни амалий жихатдан хисобга олиш деярли мумкин эмас. Шунинг учун хам тойилмаган харакатнинг тургунлигини узлуксиз таъсир этиб турадиган тойдирувчи факторларга нисбатан тадкик этиш мухим амалий ахамиятга эгадир. Бу эса уз навбатида математик нуктаи назардан, тургунликни тадкик этиш жараёнида нафакат бошлангич шартларнинг тойилишини, балки харакат тенгламасининг тойилишини хам хисобга олиш кераклигини англатади.
Узлуксиз таъсир этиб турадиган тойдирувчи факторлар таъсиридаги харакатнинг тургунлигига оид 1936-1955 йиллар давомида олиб борилган тадкикот ишларида Н.Г.Четаев, И.Г.Малкин, И.Л.Массера, Е.А.Барбашин, Н.Н.Красовский, В.Е.Гермаидзе ва К.П.Персидскийларнинг бенихоят хизматлари каттадир ([53] нинг 20-21, 302-307 бетларига каранг) [8,11,21-23,25,40,53,55,102].
Узлуксиз таъсир этиб турадиган тойдирувчи факторлар таъсиридаги харакат тургунлигининг куйидаги таърифини берамиз.
Динамик системага оний равишда тойдирувчи факторлар таъсир этгандаги харакат тенгламаси
(1.5.1)
куринишда эканлигини курган эдик.
Динамик системага тойдирувчи факторлар узлуксиз таъсир этиб турганда харакат тенгламаси куйидагича булади:
,
(1.5.2)
бу
ерда 
- тойдирувчи
факторларни ифодаловчи номаълум функциялар. Улар етарлича кичик ва (1.5.2)
тенгламанинг курилаётган тойилмаган харакат атрофидаги ечимини таъминловчи
баъзи умумий шартларни каноатлантирувчи функциялардир.
8-таъриф.
Агар хар кандай исталганча кичик сон учун шундай
иккита бошка мусбат 
ва 
сонлар
топилиб, 
; 
сохада
(1.5.3)
тенгсизликларни
каноатлантирувчи 
функцияларнинг кандай
булишидан катъий назар (1.5.2) тенгламаларнинг хар кандай ечими yчун вактнинг
лахзасида
(1.5.4)
муносабатнинг бажарилишидан булганда
(1.5.5)
тенгсизликларнинг
хамма вакт бажарилиши келиб чикса, у холда узлуксиз таъсир этадиган тойдирувчи
факторлар таъсиридаги тойилмаган харакат
((1.5.1) тенгламанинг хусусий ечими) тургун деб айтилади.
Шу тарзда аникланган узлуксиз тойдирувчи факторлар таъсиридаги тойилмаган харакатнинг тургунлик тушунчаси Ляпунов буйича тургунлик тушунчасининг бевосита умумлашмаси булиб, катта амалий ахамиятга эгадир.
Биринчи карашда Ляпуновнинг тургунлик назарияси кийматсизлангандек куриниши мумкин. Аммо аслида бундай эмас, чунки, биринчидан, Ляпунов яратган усуллар узлуксиз таъсир этадиган тойдирувчи омиллар таъсиридаги тойилмаган харакатларнинг тургунлигини тадкик этишда хам ярайди;
Иккинчидан, амалий жихатдан энг зарур холларда тойдирувчи омиллар узлуксиз таъсир этиб тургандаги тургунлик масаласи бевосита Ляпунов маъносидаги тургунлик масаласига келтирилади. Учинчидан, карор топган (стационар) ва даврий харакатларнинг асимптотик тургунлиги тойдирувчи факторлар узлуксиз таъсир этиб тургандаги харакатнинг тургун булиши учун етарли шарт эканлиги исботланган [53].
Юкорида келтирилган мулохазалардан шу нарса келиб чикадики, тургунликнинг Ляпунов берган таърифи мухим амалий ахамиятга эга. Аммо амалий масалаларда динамик система харакатининг нафакат тургунлигини, балки бошлангич тойилишнинг мумкин булган сохасини хам аниклаш талаб этилади. Кейинги масала билан А.М.Ляпунов шугулланган булмаса хам, у яратган усуллар бу масалани ечишга имконият яратади.
Юкорида берилган асосий таърифларни изохлаш учун бир нечта оддий мисоллар курайлик.
1-мисол. Тойилган харакатнинг тенгламаси куйидаги куринишда булсин:
,
, (1.5.6)
бу
ерда - хакикий узгармас
сон. Тенгламаларнинг унг тарафидаги 
ва 
функциялар
вактга боглик эмас
хамда 
ва 
ларнинг
барча хакикий кийматлари учун голоморфдирлар. Демак, тойилмаган харакат баркарор
харакатдир. (1.5.6) дифференциал тенгламаларнинг умумий ечими
,
(1.5.7)
куринишда
булади. Бу ерда 
, 
лар
ва ларнинг
вактга мос
келувчи бошлангич кийматлари (бошлангич тойилиш) дир.
(1.5.7) тенгламалардан
(1.5.8)
эга
буламиз. Шунинг учун хам хар кандай мусбат сони учун шундай 
сони
топиладики, вактда ,
ларнинг
тенгсизликни
каноатлантиришидан, (1.5.8) га асосан, да
тенгсизликнинг бажарилиши келиб чикади. Демак,
тойилмаган харакат, яъни (1.5.6) тенгламаларнинг 
мувозанат холати
тургун булади.
2-мисол. Тойилган харакатнинг тенгламаси куйидаги куринишда булсин
, 
,
(1.5.9)
бу ерда - хакикий узгармас
сон. Бу тенгламаларнинг умумий ечими
,
(1.5.10)
куринишга эга. Бу ерда , -
вактга мос
келувчи ва ларнинг
бошлангич кийматлари. (1.5.10) ифодасидан куриниб турибдики, (1.5.9)
дифференциал тенгламаларнинг мувозанат холати
(тойилмаган харакат) тургун эмас, чунки ва ларнинг
исталганча кичик кийматлари учун хам ва ларнинг
киймати билан биргаликда
чегараланмаган холда усади ва тенгсизлик бажарилмайди.
6-§. Тургунлик масаласини ечишнинг усуллари хакида
Агарда тойилган харакатнинг дифференциал тенгламаларини интеграллаш мумкин булганда эди, тургунлик масаласини тадкик этишда хеч кандай кийинчиликларга дуч келинмасди. Аммо бундай холлар жуда хам оз учрайди, амалий масалаларда эса деярли учрамайди. Шунинг учун хам тадкикотчилар дифференциал тенгламаларни интегралламасдан, тургунлик масаласини ечиш усулларини топиш устида ишладилар. Ляпуновдан олдин утган тадкикотчилар асосан чизиклаштириш усулидан фойдаланар эдилар. Бу усул куйидагидан иборат.
Тойилган харакатнинг тенгламаси
(1.6.1)
берилган, 
функциялар эса 
(Н–етарлича
кичик мусбат сон) сохада аникланган, узлуксиз ва узлуксиз хусусий хосилаларга
эга булсин. 
булганлиги учун (1.6.1)
динамик системанинг мувозанат холати (тойилмаган харакат) булади. 
функцияларни
шу мувозанат холати атрофида (голоморфлиги учун) узгарувчиларнинг даражалари
буйича каторга ёйиб, (1.6.1) системани куйидаги куринишда ёзамиз:
,
(1.6.2)
бу ерда 
- функциялар
ёйилмасидаги даражаси биринчидан юкори булган хадларнинг мажмуасидан иборат,
яъни чизикли эмас функция. Тургунлик масаласи курилаётганда, одатда (1.6.2)
нинг ечими узгарувчиларнинг
етарлича кичик бошлангич кийматлари учунгина каралади. Табиийки, бундай холда ечимларнинг
характери (1.6.2) тенгламалардаги биринчи даражали хадлар билан аникланади деб уйлаш
мумкин. Бошкача килиб айтганда, тургунлик масаласини ечиш учун
(1.6.3)
чизикли тенгламани тадкик этиш кифоя деган хулосага келиш мумкин. (1.6.3) дифференциал тенгламаларга (1.6.2) тенгламалар системасининг биринчи якинлашиш тенгламалари деб айтилади.
Томсон ва Тет, Раус, Гурвиц,
Н.Е.Жуковский, Максвелл, Вишнеградскийлар тургунлик масалаларини худди шу
усулдан фойдаланиб тадкик этган эдилар [17,32,112, 116,117]. Бу холда масала
анча соддалашади ва баркарор (карор топган) харакатлар учун 
коэффициентлар
узгармас сонлар булганлигидан (1.6.3) дифференциал тенгламаларни ёпик шаклда
интеграллаш мумкин.
Аммо бу йусинда масалани ечилиши катъий эмас ва умуман айтганда, нотугри булиши мумкин. Аслида (1.6.2) чизиклимас (ночизикли) тенгламаларни (1.6.3) чизикли тенгламалар билан алмаштириш, бир масалани иккинчи бир масала билан алмаштириш деган суздир. Бунда алмаштирилган иккинчи масала биринчисига умуман боглик булмай колиши хам мумкин. Иккинчидан, тойилмаган харакат аслида нотургун булса хам, биринчи якинлашиш тенгламаларини тадкик этиш натижасида тургун булиб чикиб колиши хам мумкин ва аксинча. Бу холатни куйидаги мисолда кузатса булади.
1-мисол. Тойилган харакатнинг дифференциал тенгламалари куйидаги куринишда булсин
, 
,
(1.6.4)
бу ерда 
–узгармас сон. Бу
тенгламаларнинг ихтиёрий ечимлари 
ва 
лар
дейлик. Даставвал (1.6.4) тенгламаларни хисобга олиб, 
ифоданинг
хосиласини оламиз
. (1.6.5)
Бунда икки хол булиши мумкин.
1.
булсин. У вактда 
булади
ва, демак, функция нинг
усиши билан усади. Бу функциянинг усиши натижасида ва (1.6.5) нинг унг томонига
асосан унинг вакт буйича олинган хосиласи хам усади. Шундай килиб, бошлангич 
ва
шартлар етарли
кичик булганда хам функция нинг
усиши билан усади, демак, тойилмаган харакат нотургун булади.
2.
булсин. Бу холда
тойилмаган харакат асимптотик тургун булади, чунки 
ва функция
мусбат колган холда, доимо камаяди ва 0 га интилади, яъни 
. Демак,
тойилмаган хааркатнинг тургун ёки нотургун булиши динамик система параметрининг
ишорасига боглик экан.
Иккинчидан, (1.6.4) динамик системанинг биринчи якинлашиш тенгламалари
, 
(1.6.6)
куринишда булади. (1.6.6) тенгламаларнинг умумий ечими
, 
(1.6.7)
куринишда булади, бу ерда , лар
ва ларнинг
пайтдаги бошлангич
кийматларидан иборат.
Етарлича кичик сон
учун шундай 
сонни танлаб
оламизки, да 
,
тенгсизликларнинг
бажарилиши ва (1.6.7) тенгламаларга асосан булганда хамма вакт
,
нинг бажарилиши келиб чикади. Демак, тойилмаган харакат
биринчи якинлашишда тургун булади. Аммо бу тургунлик, (1.6.7) га асосан,
асимптотик булмайди. Юкорида биз курдикки, реал система (1.6.4) да
асимптотик тургун ва да нотургун булади.
Шундай килиб, тойилмаган харакатнинг характерини (1.6.4) дифференциал
тенгламалардаги юкори даражали хадлар аниклайди.
Бошка томондан яна шундай холлар мавжудки, уларда биринчи якинлашишда тургунлик масаласи тулик ечилади. Шунинг учун хам биринчи якинлашишда тургунликнинг етарли ва зарурий шартларини аниклаш масаласи пайдо булади. Бу масалани дастлаб Ляпунов куйган ва баркарор (стационар) хамда даврий харакатлар учун унинг тулик ечимини берган. Ляпунов томонидан баркарормас (ностационар) харакатларнинг кенг синфи учун хам тургунлик масаласи ечиб берилган.
Шундай килиб, Ляпунов биринчи булиб тургунлик масалаларини ечиш учун:
1) качон биринчи якинлашиш системасини тадкик этиш кифоя эканлигини;
2) качон тойдирилган харакат тенгламаларидаги юкори даражали хадларни хисобга олган холда тадкикотни утказиш кераклигини курсатди.
Куйилган масалаларни ечиш учун Ляпунов махсус усуллар яратди. Тургунлик масалаларини ечишнинг хамма усулларини у икки категорияга булади. Биринчи категорияга тойдирилган харакат тенгламаларининг умумий ёки хусусий ечимларини бевосита топиш усулларини киритади. Бу ечимларни одатда каторлар куринишида излайдилар. Биринчи категориядаги хамма усуллар мажмуасини Ляпунов биринчи усул деб атайди.
Аммо тургунлик масалаларини ечишнинг бошка
усулларини хам курсатиш мумкин. Бу усулларда тойдирилган харакат
тенгламаларининг умумий ёки хусусий ечимларини топиш талаб этилмайди. Бу ерда
махсус хусусиятларга эга ва 
узгарувчиларга боглик
булган кандайдир функциялар изланади. Маълум шартларни каноатлантирувчи бундай
функцияларнинг мавжудлиги тургунлик масаласини хал килади. Иккинчи категориядаги
хамма усуллар мажмуасини Ляпунов тургунликни тадкик этишнинг иккинчи усули
деб атайди.
Иккинчи усулнинг асоси сифатида Ляпунов узи яратган ва исбот этган бир нечта асосий теоремаларни олади. Бу теоремалар шундай самарадор булиб чикдики, уларнинг ёрдамида тургунлик масаласини биринчи якинлашиш усули билан осонгина хал этиш мумкин булди. Шу билан бирга уларнинг ёрдамида кандай холларда биринчи якинлашиш усули билан тургунлик масаласи ечилмаслиги ва масалани ечиш учун тенгламадаги юкори даражали хадларни хисобга олиш кераклиги аникланади.
Куйида Ляпуновнинг иккинчи усули учун негиз булиб хизмат килувчи асосий теоремалар ва уларнинг татбиклари ёритилади.
|
РЕЖА: 1. Харакатнинг тургунлик назарияси предмети хакида. 2. Тургун харакат. Тойилган харакатнинг дифференциал тенгламси. 3. Тойилган харакатнинг тенгламасини тузишга доир мисоллар. 5. Узлуксиз таъсир этадиган тойдирувчи кучлар таъсиридаги харакатнинг тургунлиги хакида. 6. Тургунлик масаласини ечишнинг усуллари хакида. |
Таянч иборалар. Тургун харакат, нотургун харакат, тойилган харакат, тойилмаган харакат, тойдирувчи кучлар, асимптотик тургун, математик маятник, коник маятник, Ер сунъий йœлдоши, баркарор харакат, баркарормас харакат.
Такрорлаш учун саволлар:
1. Харакатнинг тургунлик назарияси фани нимани œрганади?
2. Тургун ва нотургун харакатларнинг таърифи.
3. Тойилган харакатнинг дифференциал тенгламаси.
4. Тургунлик масаласини ечишнинг кандай усуллари мавжуд?
5. Кандай харакат баркарор харакат деб айтилади?
6. Баркарормас харакатнинг таърифи.