|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
O‘ZBEKISTON ALOQA VA AXBOROTLASHTIRISH
AGENTLIGI TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
|
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
|
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
7 |
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
5 |
1 |
4 |
2 |
4 |
2 |
1 |
3 |
1 |
0 |
6 |
1 |
2 |
1 |
4 |
2 |
2 |
0 |
2 |
4 |
||
|
2 |
2 |
1 |
2 |
2 |
5 |
6 |
|
8 |
6 |
7 |
5 |
8 |
4 |
5 |
8 |
9 |
2 |
9 |
7 |
||
|
2 |
3 |
1 |
4 |
5 |
6 |
6 |
3 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
||
|
4 |
6 |
0 |
2 |
1 |
3 |
3 |
1 |
2 |
5 |
3 |
1 |
2 |
2 |
4 |
4 |
4 |
3 |
2 |
5 |
||
|
2 |
5 |
1 |
2 |
3 |
0 |
3 |
0 |
5 |
1 |
2 |
1 |
3 |
0 |
4 |
0 |
2 |
2 |
1 |
0 |
KIRISH
Ko‘p sonli masalalarni yechishda matematik usullarni qo‘llash chegarasining ortib borishi matematik statistikadan samaraliroq foydalanishni taqozo etadi. Bu hol albatta tabiiydir, chunki iqtisodiy-texnik o‘zgarishlarni bashorat qilishning asosini tashkil etuvchi axborotni yig‘ish va qayta ishlashda birinchi navbatda matematik statistikaning usullari muhimdir.
Tadbiqiy statistikaning asosiy masalalaridan biri mumkin bo‘lgan ko‘p sonli modellar orasidan tekshirilayotgan tizimni yaxshiroq aks ettiradigan modellarni tanlash. Modellarni tuzatish va ularni tajriba asosida tekshirish, ya’ni tadqiqotchi qiziqayotgan, tahlil qilinayotgan tizimning elementlari orasidagi bog‘liqlik va munosabatlarning matematik ifodasi odatda bir vaqtda foydalaniladigan ikki turdagi ma‘lumotlarga asoslanadi:
a) tekshirilayotgan munosabatlarning tabiati va tavsifi haqidagi aprior ma‘lumotlar;
b) tahlil qilinayotgan tizimning ishlash jarayoni va natijasini tavsiflaydigan dastlabki statistik ma‘lumotlar.
Agar tadqiqotchi a) turdagi aprior ma‘lumotlardan yoki xar ikkala turdagi ma‘lumotlardan foydalanib tizim holatini tahlil qilsa, modelning matematik ifodasiga kiradigan parametrlarning son qiymatlarini aniqlashda yoki b) turdagi statistik ma‘lumotlarni to‘ldirish maqsadida ularni sun’iy holda hosil qilishda tadqiqotchiga matematik modellashtirish elementlari bilan bir qatorda EXMga murojat qilish kerak bo‘ladi.
Shu sababli talabalarni statistik ma‘lumotlarni qayta ishlashga o‘rgatishda EXMga kiritilgan statistik dasturlar paketidan foydalanishni o‘rgatish muhimdir.
Oliy matematikaning yakunlovchi qismida ehtimollar nazariyasi va matematik statistika o‘tiladi va o‘quv rejasi bo‘yicha uchinchi yoki to‘rtinchi semestrlarda o‘qitiladi. O‘quv rejasiga mos ravishda oliy matematikaning 4-qismida (ehtimollar nazariyasi va matematik statistika) V-522220 telekommunikatsiya, V-5521900 informatika va axborot texnologiyalari,V-5522000 radiotexnika, V-5522100 televideniya, radioaloqa va radioeshittirish yo‘nalishlari uchun 64 soat ajratilgan, undan 32 soat ma‘ruzaga, 16 soat amaliy mashg‘ulotga, 16 soat laboratoriya ishlari, V-5340100 iqtisod va V-5340200 menejment yo‘nalishlariga 58 soat ajratilgan, undan 30 soat ma‘ruzaga, 28 soat amaliy mashg‘ulotga,V-5140900 kasbiy pedagogika va V-5840200 pochta xizmati yo‘nalishlari uchun 62 soat ajratilgan,undan 32 soat ma‘ruzaga va 30 soat amaliy mashg‘ulotga.
Ushbu o‘quv uslubiy qo‘llanma matematik statistikaning to‘rtta bo‘limiga bag‘ishlangan bo‘lib ular: statistik ma’lumotlarning dastlabki tahlili, noma’lum parametrlarini baholash, statistik taxminlarni tekshirish nazariyasi va korrelyatsion-regression taxlili laboratoriya ishlaridan iborat.
Laboratoriya ishlarini bajarishdan maqsad talabalarni matematik statistika usullarini va Excel dasturidan foydalanishni o‘rgatishdan iborat.
Qo‘shimcha ma‘lumotlarni keltirilgan adabiyotlardan va kafedra o‘qituvchilari tomonidan tayyorlangan ma‘ruzalar matnidan olish mumkin.
Ushbu uslubiy qo‘llanma «Statistik dasturlar paketidan foydalanish tartibi» bo‘limini o‘z ichiga oladi, bunda statistik dasturlardan foydalanish mukammal keltirilgan.
Qo‘llanmada statistik tahlilda zarur bo‘lgan har xil koeffitsiyentlarni hisoblashda kerak bo‘lgan jadvallar ilovalarda keltirilgan. Laboratoriya ishlarini bajarishda zarur bo‘lgan tanlanmalar har bir talaba uchun alohida variant qilib keltirilgan. Undan tashqari talabalar ushbu laboratoriya ishini universitetimiz saytining www.tatu.uz oliy matematika kafedrasiga tegishli ma‘lumotlar qismida ham tanishib chiqishlari mumkin. Ushbu qo‘llanmadan telekommunikatsiya, informatika va axborot texnologiyalari, radiotexnika, televideniye, radioaloqa va radioeshittirish, iqtisod va boshqarish fakultetlari talabalari foydalanishlari mumkin.
1-§. 1-laboratoriya ishi.
Tanlanma ma‘lumotlarning dastlabki statistik tahlili
Ehtimollar
nazariyasida o‘rganilayotgan tasodifiy jarayonning matematik modeli sifatida {W,
,P} ehtimollik fazosi qaraladi, bunda W - elementar hodisalar fazosi deb ataluvchi
biror to‘plam, – W elementar hodisalar
fazosining to‘plam osti to‘plamlaridan biror qoidaga ko‘ra ajratilgan tasodifiy
hodisalar to‘plami, P to‘plamdagi
tasodifiy hodisalar ehtimoli. Xar bir tayin holat uchun P ehtimollik o‘lchovi
to‘la aniqlanadi. Ehtimollar nazariyasining asosiy vazifasi mavjud ehtimollik
fazosi qonuniyatlarini ochib berish, xususan murakkab hodisalarning
ehtimollarini aniqlashga imkon beruvchi usullarni ishlab chiqishdan iboratdir.
Biroq
amaliyotda tayin tajribalarni o‘rganishda P ehtimollik ba’zi bir noaniqliklarga
ega bo‘ladi. Ko‘p hollarda aytish mumkinki, P ehtimollik biror ehtimollar
sinfining elementi bo‘ladi. Bu sinf da berilishi mumkin bo‘lgan barcha ehtimolliklarni o‘z ichiga oladi.
Agar sinf
berilgan bo‘lsa, u holda ehtimollikning statistik modeli yoki qisqacha
statistik modeli berilgan deyiladi. Shunday qilib statistik model
o‘rganilayotgan tajribani ehtimollik modelida ehtimollikni berishda u yoki bu
noaniqlik bo‘lgandagi holatni yoritadi. Matematik statistikaning vazifasi bu
noaniqliklarni kuzatilayotgan tajriba ma‘lumotlari asosida kamaytirishdan
iborat.
Shunday qilib matematik statistikada barcha mulohazalar statistik ma’lumotlarga, ya’ni kuzatilgan tajriba natijalariga asoslanadi. Ko‘p hollarda esa dastlabki statistik ma’lumotlar R taqsimotga ega bo‘lgan X tasodifiy miqdor ustida o‘tqazilgan tajribalar natijasi bo‘ladi. Bu holda tajriba tasodifiy miqdor ustida n ta sinov o‘tqazishdan iborat bo‘lib, i-sinov natijasi Xi tasodifiy miqdor bilan aniqlanadi, i=1,2,…,n. X1,Õ2,…,Xn – to‘plamga tanlanma deyiladi, n- tanlama hajmi. Biz kuzatishlar bir-biriga bog‘liqsiz bo‘lgan holni qaraymiz. Shu sababli X1,X2,…,Xn larni n ta bog‘liqsiz, bir xil taqsimlangan tasodifiy miqdorlar deb qarash mumkin. Tayin o‘tqazilgan tajriba natijalari X1,X2,…,Xn tanlanma hisoblanadi, uni x1, x2,.., xn lar orqali belgilaymiz.
Ma‘lumki x1,
x2,…,xn sonlar kuzatilayotgan X tasodifiy miqdorning
qiymatlar to‘plamidan bo‘ladi, shu sababli ular
variantalar deyiladi. Faraz qilaylik 
kuzatilayotgan X tasodifiy miqdorning barcha qiymatlar to‘plami bo‘lsin. bosh
to‘plam deyiladi, x1,x2,…,xn qiymatlarni bosh
to‘plam dan
qaytariladigan tanlashlar sxemasi bo‘yicha olingan, hajmi n bo‘lgan tanlanma
deb qarash mumkin. Tanlanmani o‘sib borish yoki kamayib borish tartibida
yozilishiga variatsion qator deyiladi. Variatsion qatorning uchta turi mavjud:
ranjirlangan, diskret, oraliq variatsion qatorlar. Variatsion qatorni ko‘pincha
taqsimot qatori ham deyiladi. Ranjirlangan qator tanlanma hajmi kichik
bolganda bu tanlanmaning alohida qiymatlari x1,x2,…,xn
larni o‘sish (kamayish) tartibida joylashishidan iboratdir, x(1)≤x(2)≤x(3)
≤…..≤x(n). Agar variantalar soni yetarlicha katta
bo‘lib, xmin va xmax lar o‘rtasidagi farq kichik bo‘lsa,
ranjirlangan qator juda katta bo‘ladi. Agar belgi qiymatlari bir nechta bo‘lsa, u holda diskret variatsion qator tuziladi.
Diskret variatsion qator, ikkita qatordan tashkil topgan bo‘lib, birinchi qatorda belgining x1,x2,…,xs turli variantalari ikkinchi qatorda esa shu variantalarga mos ularning chastotalari ni yoki nisbiy chastotalari ni/n joylashgan bo‘ladi. Agar tanlanma hajmi katta bo‘lib, xmin va xmax o‘rtasidagi farq yetarlicha katta bo‘lsa, u holda oraliq variatsion qator tuziladi.
Oraliq variatsion qator ikkita qatordan tuzilgan bo‘lib, birinchi qatorda o‘rganilayotgan belgining oraliqlaridan, ikkinchisi esa bu oraliqlarga tegishli variantalar chastotasi yoki nisbiy chastotalaridan tuzilgan. Tanlanmaning statistik taqsimoti deb variantalar va ularga mos chastotalar yoki nisbiy chastotalar ro‘yxatiga aytiladi. Tanlanmaning statistik taqsimotini oraliqlar va ularning chastotalari yordamida ham berish mumkin. Ehtimollar nazariyasida taqsimot deganda tasodifiy miqdorning qabul qilishi mumkin bo‘lgan qiymatlari bilan bu qiymatlar ehtimollari orasidagi moslik tushuniladi, matematik statistikada esa kuzatilgan variantalar va ularga mos chastotalar yoki nisbiy chastotalar orasidagi moslik tushuniladi.
Faraz qilaylik birorta bir jinsli ob‘yektlar to‘plamining miqdor yoki sifat belgilarini o‘rganish talab qilinayotgan bo‘lsin.
Empirik taqsimot funktsiya.
Faraz qilaylik diskret variatsion qator berilgan (1-jadval)
1-jadval
|
|
|
|
…. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Bu yerda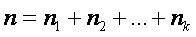 
, 
dan kichik variantalar soni bo‘lsin , bunda
boshqa so‘z bilan aytganda, 
X tasodifiy miqdor ustida n ta kuzatish o‘tqazilgandagi 
hodisaning ro‘y berishlari chastotalar soni.
Ta‘rif. Tanlamaning empirik taqsimot funktsiyasi Fn(u) deb n(u)/n nisbatga aytiladi, ya‘ni
(1.1)
Empirik
taqsimot funktsiya 
taqsimot
funktsiyaning barcha xossalarini qanoatlantiradi. Faraz qilaylik 
kuzatilayotgan X tasodifiy miqdorning noma‘lum taqsimot funktsiyasi
bo‘lsin. Odatda
ni X
tasodifiy miqdorning nazariy taqsimot funktsiyasi deyiladi. Shuni aytib o‘tish
kerakki, tayin tajriba o‘tqazilguncha empirik taqsimot funktsiyani tasodifiy
miqdor deb qarash kerak, chunki u 
tanlamaning funktsiyasi xisoblanadi. Kuchaytirilgan katta sonlar
qonunidan Glivenko teoremasi kelib chiqadi.
Glivenko
teoremasi. Ixtiyoriy 
>0 son uchun quyidagi munosabat o‘rinli 
Shunday qilib empirik taqsimot funksiya 
“taqriban” nazariy
taqsimot funktsiyaga tengdir. Empirik funktsiya zinapoyasimon funktsiya
bo‘lib, 
nuqtalarda
sakrashlarga ega, 
nuqtadagi sakrash
qiymati 
ga teng,
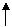Fn(x)
____________
(n1+n2)/n
n1/n
x1 x2
xk
1-rasm
Empirik fuktsiya
bilan
nazariy taqsimot funktsiya ning
farqi shundan iboratki, (X<x)
hodisaning ehtimolini, empirik taqsimot funktsiya esa xuddi shu hodisaning nisbiy chastotasini aniqlaydi.
Misol. Tanlanmaning berilgan diskret variatsion qatori bo‘yicha empirik taqsimot funktsiyani yasang.
xi |
2 |
6 |
10 |
ni |
12 |
18 |
20 |
n=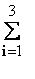 
ni
=12+18+20=50
 |
Fn(x)
1
0.6
0.24
x
0 2 6 10
2-rasm.
Poligon va gistogramma. 
nuqtalarni tutashtiruvchi siniq chiziq chastotalar poligoni
deyiladi. 
nuqtalarni
tutashtiruvchi siniq chiziqqa nisbiy chastotalar poligoni deyiladi.
Chastotalar
gistogrammasi deb asoslari 
uzunlikdagi
guruh oraliqlari, balandliklari esa 
nisbatlarga teng bo‘lgan to‘g‘ri to‘rtburchaklardan iborat
pog‘onaviy figuraga aytiladi.
 |
 |
/
/
………………………….
3-rasm
Hosil bo‘lgan
figuraning yuzasi n ga teng. Xususan oraliqlar qadamlari bir xil ham
bo‘lishi mumkin 
Nisbiy
chastotalar gistogrammasi deb asoslari uzunlikdagi oraliqlar, balandliklari esa 
nisbatga teng bo‘lgan to‘g‘ri to‘rtburchaklardan iborat pog‘onaviy
figuraga aytiladi. Nisbiy chastotalar gistogrammasining yuzasi birga teng.
Boshqa so‘z bilan aytganda nisbiy chastotalar poligoni va gistogrammasi
nazariy taqsimot funktsiya zichlik
funktsiyasining geometrik bahosi xisoblanadi.
Tanlanmaning sonli xarakteristikalari.
Nazariy taqsimotning sonli xarakteristikalari kabi X1,X2,….,Xn tanlanmaning empirik taqsimot funktsiyasining ham sonli xarakteristikalari kiritiladi. Tanlanma momentlar quyidagicha aniqlanadi:
Ranjirlangan variatsion qator berilgan holda:
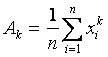
tartibli
tanlanma moment. (1.3)
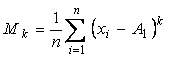
tartibli
markaziy moment. (1.4)
Ko‘p hollarda
ishlatiladigan 
va 
xarakteristikalar aloxida harflar bilan belgilanadi.
-
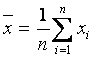tanlanma o‘rta
qiymat, (1.5)
- tanlanma
dispersiya, (1.6)
=
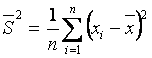- tanlanma
o‘rtacha kvadratik chetlanish. (1.7)
Agar diskret variatsion qator berilgan bo‘lsa tanlanma momentlar quyidagicha hisoblanadi:
j- tartibli tanlanma
moment, (1.8)
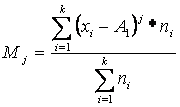j- tartibli markaziy moment (1.9)
tanlanma o‘rta qiymat (1.10)
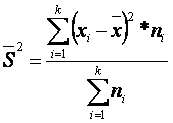tanlanma
dispersiya (1.11)
Oraliqli variatsion qatorlarda ham tanlanma momentlar diskret variatsion qatorlar uchun berilgan formulalar orqali topiladi, bunda xi variantalar sifatida oraliq o‘rtalari olinishi mumkin. Diskret va oraliqli variatsion qatorlarda hisoblashni soddalashtirish uchun
(1.12)
(1.13)
formulalardan foydalanish mumkin, bunda C- umuman olganda ixtiyoriy son, lekin hisoblashni soddalashtirish uchun eng ko‘p qatnashgan xi ni olgan ma’qul, k- xi larning o‘zgarish qadami.
2. Tanlanma modasi M0. Ranjirlangan variatsion qatorlarda M0 aniqlanmaydi. Diskret variatsion qatorlarda eng katta chastotali varianta M0 bo‘ladi, agar eng katta chastotali varianta ikkita bo‘lsa, u holda variatsion qator bimodal qator hisoblanadi va h.k. Agar kuzatishlar oraliqli variatsion qator ko‘rinishida berilgan bo‘lsa, u holda moda
(1.14)
formula bilan hisoblanadi, bu yerda XMo-eng ko‘p qatnashgan oraliq - moda oralig‘ining quyi chegarasi, nMo- moda oralig‘i chastotasi, nMo+1- moda oralig‘idan bitta keyingi oraliq chastotasi, nMo-1- moda oralig‘idan bitta oldingi oraliq chastotasi, k-moda oraliq uzunligi.
Ranjirlangan
variatsion qatorlarda 
quyidagi formula bilan aniqlanadi:
(1.15)
bu erda n-tanlanma hajmi, [a]- a sonning butun qismi.
Diskret variatsion qator mediana yig‘ma chastotalar tanlanma hajmining yarmi erishiladigan yoki
yig‘ma nisbiy chastotalar 0,5 ga erishiladigan 
variantaga aytiladi.
Oraliq
variatsion qator uchun quyidagicha
formula bilan aniqlanadi: 
(1.16)
Bu yerda 
oraliqli variatsion qatorda yig‘ma chastotalar tanlanma hajmining
yarmi erishiladigan oraliq yoki yig‘ma nisbiy chastotalar 0,5 ga erishiladigan
oraliq - mediana oralig‘ining boshi, 
- mediana oralig‘ining chastotasi, 
mediana oralig‘i chastotasigacha bo‘lgan chastotalar yig‘indisi,
ya‘ni 
,
k-mediana oralig‘i uzunligi.
1-topshiriq
A va B tanlanmalar bo‘yicha quyidagi masalalarni yeching
- variatsion qator tuzing
- nisbiy va yig‘ma chastotalarni hisoblang;
- variatsion qatorning grafiklarini chizing (poligon va gistogramma);
- empirik taqsimot funktsiyani tuzing va uning grafigini chizing;
- variatsion qatorning sonli xarakteristikalarini hisoblang: tanlanma o‘rta qiymat, tanlanma dispersiya, o‘rtacha kvadratik chetlanish, moda, mediana;
- EXM da statistik dasturlardan foydalanib yuqorida qayd etilgan topshiriqlarni bajaring; olingan natijalar ma’nosini yozing.
- Tanlanmalarni www.tatu.uz saytining oliy matematika kafedrasiga tegishli ma‘lumotlar qismidan yoki [7] adabiyotdan oling.
2-§. 2- laboratoriya ishi.
Taqsimot parametrlarining statistik baholarini topish usullari
Aytaylik o‘rganilayotgan belgining taqsimoti nazariy mulohazalardan aniqlangan bo‘lsin. Bu taqsimotni aniqlaydigan parametrlarni baholash masalasi yuzaga kelishi tabiiydir.
Ta’rif. Nazariy taqsimot noma’lum parametrining statistik baxosi deb tanlanmadan olingan ixtiyoriy funktsiyaga aytiladi.
Statistik baxolar baxolanayotgan parametrni yaxshi yaqinlashtirib berishi uchun ular ma’lum talablarni qanoatlantirishlari lozim.
Faraz qilaylik 
nazariy taqsimotning noma’lum 
parametri bahosi bo‘lsin va hajmi n ga teng bo‘lgan tanlanma
bo‘yicha 
baho
topilgan bo‘lsin. Endi bosh to‘plamdan hajmi n ga teng bo‘lgan boshqa
tanlanma hosil qilamiz va bu tanlanma bo‘yicha 
bahoni
topamiz va hokazo. 
sonlar
bir xil bo‘lishi shart emas. Shunday qilib 
bahoni
tasodifiy miqdor deb, sonlarni
esa uning mumkin bo‘lgan qiymatlari deb qarash mumkin.
Boshqa tomondan, ta‘rifdan kelib chiqadiki bitta parametr uchun bir nechta yoki cheksiz ko‘p statistik baxolar tuzish mumkin. Shu sababli barcha baholar sinfi ichidan «yaxshi» larini ajratish, ya’ni shunday statistika ajratish kerakki, ularning qiymatlari u yoki bu ma’noda noma’lum parametrning haqiqiy qiymati atrofida joylashgan bo‘lsin.
Ta‘rif. Siljimagan baho deb, tanlanma hajmi n ixtiyoriy bo‘lganda
ham matematik kutilishi baholanayotgan 
parametrga teng bo‘lgan statistik bahoga
aytiladi,
(2.1)
agar bu shart
bajarilmasa, u holda bu bahoga siljigan baho deyiladi va siljish 
ayirma
sifatida aniqlanadi.
Aynan bitta parametr uchun bir nechta siljimagan baholarni tuzish mumkin.
Masalan,
noma’lum parametr kuzatilayotgan tasodifiy miqdor X ning matematik kutilishi
bo‘lsin, ya’ni, 
shunday qilib
(eslatib
o‘tamizki tanlanma bu 
tasodifiy
miqdorning 
ta
nusxasidir).
Statistik baho sifatida esa quyidagini olamiz.
(2.2)
Bu yerda 
o‘zgarmas sonlar va ular uchun 
tenglik o‘rinli bo‘lsin,
Shunday qilib, (2.2) noma’lum matematik kutilma uchun siljimagan baho bo‘ladi.
Xususan
bo‘lsa, u holda
(2.3)
Agar
bo‘lsa, u holda
(2.4)
demak o‘rta
qiymat (matematik kutilma) 
uchun siljimagan baho
tanlanma o‘rta qiymat bo‘lar ekan. Xuddi shunday 
dispersiyani
tanlanma dispersiya 
orqali baholash mumkin.
Umumiylikka zarar yetqazmasdan 
deb olamiz (
bo‘lgan holda 
…,
tasodifiy
miqdorlarga o‘tiladi), u holda 
bo‘ladi.
.
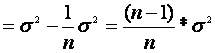Shunday qilib tanlanma
dispersiya dispersiya uchun
siljigan baho bo‘ladi. Siljish 
ga teng bo‘lib, bundan
ko‘rinib turibtiki 
da siljish nolga
intiladi. Demak yetarlicha katta n hajmli tanlanmalarda tanlanma
dispersiyani dispersiyaning taxminan
siljimagan bahosi deb qabul qilish mumkin. Kichik hajmli tanlanmalarda
dispersiyaning siljimagan bahosi sifatida quyidagicha aniqlanadigan
to‘g‘rilangan dispersiya ishlatiladi:
(2.5)
Haqiqatdan ham 
siljimagan
baho bo‘ladi, chunki
(2.6)
bo‘ladi.
Yuqoridagi misolda ko‘rsatilganidek bitta parametrga bir nechta siljimagan baho tuzish mumkin, bu baholar ichidan yaxshisini topish uchun statistik bahodan effektivlik sharti talab qilinadi.
Effektiv baxo. 
bilan
noma’lum parametrning
barcha siljimagan baholari to‘plamini belgilaymiz. Faraz qilaylik
, 
bo‘lsin,
Agar 
bo‘lsa, u holda 
baho 
bahoga nisbatan effektivroq deyiladi.
Siljimagan baholar to‘plamidagi (tanlama hajmi n berilganda) dispersiyasi eng kichik bo‘lgan statistik bahoga tekis effektiv baho deyiladi.
(2.7) O‘quvchiga tanlanma o‘rta
qiymat X1 statistikaga nisbatan effektivroq baho bo‘lishini
tekshirishni taklif qilamiz.
Eslatma: tekis effektiv baho har doim mavjud bo‘lavermaydi, chunki to‘plam infimiumi har doim ham bu to‘plamga tegishli bo‘lmaydi.
Katta xajmli tanlanmalar qaralganda statistik baholarga asoslilik talabi qo‘yiladi.
Ta’rif 
uchun
(2.8)
bo‘lsa, 
statistik
baho 
parametr uchun asosli
baho deyiladi.
Demak asosli
baho baholanayotgan parametr 
ga 
da ehtimol bo‘yicha yaqinlashadigan statistik bahoga aytiladi.
Noma’lum parametrlarni baholashning bir nechta usullari mavjud. Baholashning momentlar va eng katta o‘xshashlik usullarini ko‘rib chiqamiz.
Momentlar
usuli. Faraz qilaylik kuzatilayotgan tasodifiy
miqdorning taqsimot funktsiyasi
noma’lum 
parametrga,
ya’ni 
ta noma’lum parametrga bog‘liq bo‘lsin. Momentlar usulining
mantiqiy asosi shundan iboratki, parametrlar shunday bo‘lishi kerakki
taqsimotning nazariy momentlari mos tanlanma momentlariga teng bo‘lishi kerak.
-
tartibli boshlang‘ich va markaziy momentlarni mos ravishda quyidagicha belgilaymiz
Nazariy taqsimot
parametrga bog‘liq
bo‘lganligi sababli, nazariy momentlar ham 
parametrga bog‘liq bo‘ladi, 
Agar noma’lum parametrlar soni ta bo‘lsa, u holda quyidagi ta tenglamalar tizimini tuzamiz.
(2.9)
bunda 
j-tartibli
tanlanma momentlar.
Agar (2.9) tenglamalar tizimining yechimi 
mavjud bo¢lsa, u holda 
yechim noma’lum parametrga momentlar usulida olingan baho deyiladi.
Shuni ta’kidlab o‘tamizki momentlar usulida bir xil ma’noli momentlar tenglashtirilishi kerak. Masalan, agar noma’lum parametrlar matematik kutilma va dispersiya bo’lsa, u holda tabiiyki quyidagi tenglamalar tizimini hosil qilamiz
(2.10)
Eng katta o‘x shashlik usuli
Belgilash kiritamiz: 
agar
tasodifiy miqdor X diskret bo‘lsa, X uzluksiz tasodifiy miqdor bo‘lsa 
tasodifiy miqdorning zichlik funktsiyasi. U holda quyidagicha
tuzilgan funktsiyaga
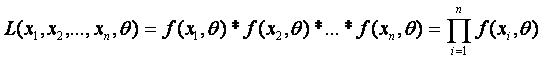(2.11)
O‘xshashlik funktsiyasi deyiladi. Eng katta o‘xshashlik usulining
mohiyati shundan iboratki, noma’lum parametrga eng katta ehtimolli tanlanma
asosida baxo tuzish kerak, ya’ni parametrni
shunday tanlash kerakki, o‘xshashlik funktsiyasi eng katta qiymat qabul qilsin,
demak agar parametrning qabul
qilishi mumkin bo‘lgan qiymatlar to‘plamini 
deb belgilasak
quyidagi shartni bajarilishini talab qilamiz
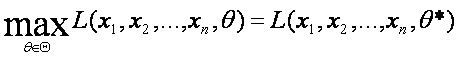(2.12)
Faraz qilaylik, barcha 
lar
uchun 
va
o‘xshashlik funktsiyasi 
bo‘yicha
differentsiallanuvchi bo‘lsin. Yuqorida aytilganlarga ko‘ra, parametrning eng
katta o‘xshashlik bahosi deb, quyidagi tenglamaning
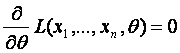(2.13)
yechimiga
aytiladi. Bizga ma’lumki funktsiya va uning logarifmining statsionar nuqtalari
ustma-ust tushadi, shuning uchun (2.13) tenglama quyidagi tenglamaga teng
kuchlidir.
(2.14)
agar noma’lum parametr 
bo‘lsa, ya’ni 
ta
noma’lum parametr bo‘lsa, u holda quyidagi tenglamalar tizimiga ega bo‘lamiz
(2.15)
yoki unga teng kuchli tenglamalar tizimi
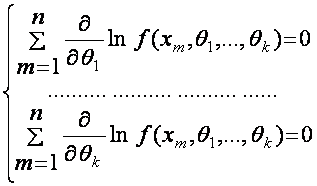(2.16)
Bu tenglamalar tizimining yechimiga noma’lum parametrga eng katta o‘xshashlik usulida topilgan baho deyiladi.
Oraliq baxo. Ishonchlilik oralig‘i.
Tanlanmadagi variantlar kam takrorlangan holdagina, tanlama berilganlari guruhlanadi, shu bilan birga guruhlar soni guruhlash usuliga bog‘liq bo‘lmasligi kerak. Nuqtaviy baho deb, bitta son bilan aniqlanadigan bahoga aytiladi. Yoqirida ko‘rilgan barcha baholar nuqtaviy baholar, chunki ular sonlar o‘qida bitta sonni aniqlaydi. Hajmi unchalik katta bo‘lmagan tanlanma uchun (n<30) nuqtaviy baho baholanayotgan parametrdan farq qilishi mumkin, ya‘ni qo‘pol xatoliklarga olib kelishi mumkin. Shu sababli hajmi kichik bo‘lgan tanlanmalarda oraliqli baholardan foydalanish maqsadga muvofiqdir.
Oraliq baho deb, ikkita
son - oraliq uchlari bilan aniqlanadigan bahoga aytiladi. Faraz qilaylik
- noma’lum parametrning
bahosi bo‘lsin (
o‘zgarmas yoki
tasodifiy miqdor bo‘lishi mumkin). Barcha nuqtaviy baholar tanlanma asosida
baholanadi, lekin tanlanmalar tasodifiy bo‘lganligi uchun baholar ham tasodifiy
miqdor bo‘lib, asl parametrlardan
farq qiladi. Bahoning aniqliligini 
deb
belgilasak, u holda 
bo‘ladi,
tushunarliki qanchalik kichik
bo‘lsa, baho
shunchalik aniq bo‘ladi. Statistik usullar baho tengsizlikni
qanoatlantiradi deb qat’iy davo qilishga imkon bermaydi, har qanday aniqlikni
qandaydir 
ehtimol
bilan olish mumkin:
(2.17)
va tengsizlikni
unga teng kuchli bo‘lgan 
tengsizlik
bilan almashtirsak (2.17) quyidagi ko‘rinishni oladi
(2.18)
(2.18) shart 
oraliq parametr qiymatini berilgan 
ishonchlilik ehtimoli bilan qoplashini bildiradi. oraliqqa
ishonchklilik oralig‘i deyiladi, -
ehtimollikka ishonchlilik ehtimoli ham deyiladi. Ko‘p hollarda birga yaqin qilib tanlanadi (masalan 0,95; 0,98, 0.99 va h.k.).
Eslatma. Baholanayotgan parametr emas, balki ishonchlilik oralig‘i tasodifiy miqdor
bo‘lganligi uchun, q ning berilgan oraliqqa tushish ehtimoli haqida emas, balki
ishonchlilik oralig‘i q ni qoplash ehtimoli haqida gapirish to‘g‘riroq bo‘ladi.
Dispersiyasi 
ma’lum bo‘lgan normal taqsimotning noma‘lum matematik kutilmasi 
uchun ishonchlilik oralig‘i
Aytaylik, bosh to‘plam parametrlari va bo‘lgan
normal taqsimotga ega bo‘lsin, ya’ni kuzatilayotgan X tasodifiy miqdor normal
taqsimlangan va 
noma’lum
bo‘lib, 
ma’lum
bo‘lsin. Bu 
kabi
belgilanadi.
Noma’lum parametrning
statistik bahosi sifatida tanlanma o‘rta qiymatini olamiz. Ma’lumki, o‘zaro
erkli normal taqsimlangan tasodifiy miqdorlarning yig‘indisi normal taqsimotga
ega bo‘lib, uning parametrlari mos parametrlar yig‘indisiga teng bo‘ladi, ya‘ni
bizning holda 
.
Shunday qilib
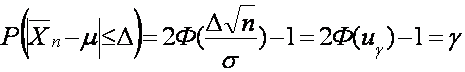(2.19)
Bu yerda 
âà 
- standart normal taqsimot funktsiya.
(2.19) tenglikka asosan
(2.20)
Shunday qilib q parametr uchun
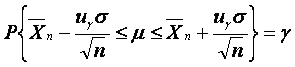(2.21)
va g ishonchlilik ehtimoli bilan
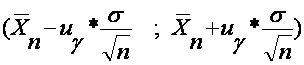(2.22)
oraliq noma’lum 
parametrni
qoplaydi, bu yerda 
quyidagi
tenglama yechimidir
(2.23)
va normal taqsimot funktsiyasi uchun EXM dagi statistik dasturlar orqali aniqlanadi yoki keltirilgan adabiyotlardagi ilovalardan foydalanib topiladi.
taqsimot (Pirson taqsimoti)
Aytaylik 
(
=1,2,…,
) lar
erkli normal tasodifiy miqdorlar bo‘lib, shu bilan birga ularning matematik
kutilmalari 0 ga, o‘rtacha kvadratik chetlanishlari 1 ga teng bo‘lsin, u holda
bu miqdorlar kvadratlari yig‘indisi:
(2.24)
erkinlik darajali («xi
kvadrat») qonun bo‘yicha taqsimlangan deyiladi, agar bu miqdorlar bitta
chizikli munosabat bilan bog‘langan, masalan,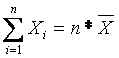 
bo‘lsa, u holda erkinlik darajalari soni 
bo‘ladi.
Erkinlik darajalari soni ortishi bilan taqsimot normal taqsimotga sekin yaqinlashadi.
taqsimot (Styudent
taqsimoti)
Z normal tasodifiy miqdor, shu bilan birga 
, 
, V esa
erkinlik
darajali qonun
bo‘yicha taqsimlangan va Z ga bog‘liq bo‘lmagan miqdor bo‘lsin, u holda
(2.25)
miqdor 
taqsimot
yoki erkinlik
darajali Styudent (ingliz statistigi V. Gosset taxallusi) taqsimoti deb
ataladigan taqsimotga ega. Erkinlik darajalari soni ortishi bilan Styudent
taqsimoti normal taqsimotga tez
yaqinlashadi.
Dispersiyasi noma’lum bo‘lgan normal taqsimotning noma’lum matematik kutilmasi uchun ishonchlilik oralig‘i
Aytaylik 
bo‘lsin,
bu holda yuqorida keltirilgan formulalardan foydalana olmaymiz, chunki bu holda
ishonchlilik oralig‘i noma’lum parametr 
ga bog‘liq. Shuning uchun ham baho sifatida quyidagi statistikani
tanlaymiz:
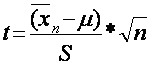(2.26)
bu yerda 
to‘grilangan tanlama dispersiya.
Ma’lumki, t-statistika erkinlik darajasi 
ga teng bulgan Styudent taqsimotiga
(t-taqsimot) ega.
Oraliqli bahoni tuzish uchun quyidagi munosabat bajarilishini talab etamiz
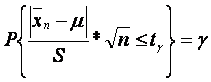(2.27)
Bu tenglamadan 
miqdor
berilgan 
âà 
bo‘yicha
Styudent taqsimoti uchun EXM da mavjud statistik dasturlar bo‘yicha yoki
keltirilgan adabiyotlardagi ilovalardan foydalanib topiladi. Agar Y tasodifiy
miqdor Styudent taqsimotiga ega bo‘lsa, u holda
(2.28)
tenglamaning yechimi sifatida aniqlanadi. Odatda jadvalda 
ning qiymatlari beriladi, shuning uchun quyidagi tenglamaning
(2.29)
yechimi sifatida topiladi. Shunday qilib, noma’lum 
parametr uchun quyidagi oraliq bahoga ega bo‘lamiz.
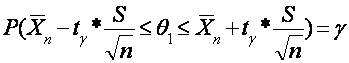(2.30)
Bundan kelib chiqadiki, noma’lum matematik kutilma uchun ishonchlilik oralig‘i
(2.31)
ni hosil qilamiz. (2.30) va (2.22) oraliqlar o¢xshashdir, bu yerda
(2.32)
Normal taqsimotning dispersiyasi uchun
ishonchlilik oralig‘i
Aytaylik 
bo‘lsin,
u holda
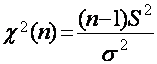(2.33)
tasodifiy miqdor erkinlik darajasi 
ga teng bo‘lgan 
-taqsimotga
(Pirson taqsimoti) ega bo‘ladi. 
tasodifiy
miqdor faqat manfiy bo‘lmagan qiymatlarni qabul qiladi. Berilgan ishonchlilik
ehtimoli bo‘yicha
shunday 
ni
topish mumkinki, unda
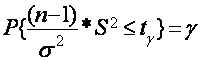(2.34)
munosabat o‘rinli bo‘ladi, bu yerda miqdor
(2.35)
tenglamaning yechimi bo‘lib, -taqsimot (Pirson taqsimoti) jadvalidan yoki EXM dagi mavjud
statistik dastur paketidan aniqlanadi, bunda tasodifiy miqdor bo‘lib, erkinlik darajasi 
ga teng bo‘lgan taqsimotga
ega. Biroq ishonchlilik oralig‘ini tuzish uchun shunday 
sonlarni topish kerakki
(2.36)
tenglik o‘rinli bo‘lishi kerak. Bunday 
sonlar cheksiz ko‘pdir. Bunday sonlarning yagona juftligini topish
uchun quyidagi «simmetriklik sharti» ni kiritamiz:
(2.37)
taqsimot jadvalidan (ilova 4) va (2.37) formula orqali 
ni topamiz. 
ni topish
uchun qarama-qarshi hodisa ehtimolidan foydalanamiz:
(2.38)
o‘rniga uning (2.33) ifodasini qo‘yib va elementar
almashtirishlarni bajarib, ushbu
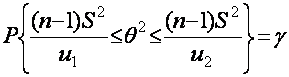(2.39)
tenglikni hosil qilamiz.
Noma‘lum dispersiya 
uchun ishonchlilik
oralig‘ini aniqlovchi tengsizlikni har ikki tomonidan kvadrat ildiz olib,
noma‘lum o‘rtacha kvadratik chetlanish ni g ishonchlilik ehtimoli
bilan qoplaydigan
(2.40)
ishonchlilik oralig‘ini hosil qilamiz.
Tanlanma hajmini aniqlash
Shu vaqtgacha biz hajmi berilgan statistik ma’lumotlarning tahlili bilan shug‘ullandik. Yetarlicha aniq natijalar olish uchun tanlanmaning minimal hajmini aniqlash masalasi muhimdir.
Normal taqsimotning dispersiyasi ma’lum bo‘lganda noma’lum o‘rta qiymat uchun ishonchlilik oralig‘ini aniqlashda (2.20) formuladan foydalanish mumkin, u holda quyidagi
(2.41)
tenglikka ega bo‘lamiz.
Agar normal taqsimotning dispersiyasi noma‘lum bo‘lsa, u holda ishonchlilik oralig‘ini aniqlash uchun zarur bo‘lgan tanlanma hajmi (2.32) dan aniqlanadigan quyidagi
(2.42)
formula bo‘yicha aniqlanadi.
Shuni ta‘kidlab o‘tamizki, dispersiya ma‘lum bo‘lganda berilgan ishonchlilik ehtimoli bilan matematik kutilmani qoplaydigan ishonchlilik oralig‘ini tuzishga zarur bo‘lgan tanlanma hajmini tanlanmani hosil qilishdan avval (2.41) formuladan aniqlash mumkin. Biroq (2.42) formulaga ko‘ra yechilayotgan masalada zarur bo‘lgan tanlanma hajmini, noma’lum dispersiya uchun siljimagan baho hisoblangan tanlanmani qayta tahlil qilingandan so‘ng korrektlashtirish mumkin.
2–topshiriq.
Quyidagi masalalarni yechishda Tanlanmalarni universitetimiz www.tatu.uz saytining oliy matematika kafedrasiga tegishli ma‘lumotlar qismidan yoki [7] adabiyotdan oling va 1-laboratoriya ishida olingan ma‘lumotlardan foydalaning.
2.1. masala. D tanlanmaning F3 va F4 ustunlari bo‘yicha bosh
to‘plamning o‘rta qiymati 
,
dispersiyasi 
va
o‘rtacha kvadratik chetlanishi 
lar
uchun siljimagan 
, 
va S baholarni
hisoblang.
2.2. masala. C tanlanmaning ikkinchi X, Y, Z uchligi ustunlari
bo‘yicha bosh to‘plamning o‘rta qiymati m, dispersiyasi va
standart chetlanishi lar
uchun siljimagan baholarni hisoblang.
2.3. masala. A, B, C tanlanmaning X, Y, Z ustunlari va D
tanlanmaning F3 va F4 ustunlari bo‘yicha bosh to‘plamning o‘rta qiymati m, dispersiyasi va standart chetlanishi 
lar uchun berilgan
ishonchlilik ehtimoli bilan ishonchlilik oraliqlarini tuzing.
V-variant nomeri (talabaning jurnal bo‘yicha nomeri)
2.4. masala. 2.1, 2.2-masalalardagi
tanlanmalar qo‘llanilingan deb hisoblab, o‘rta qiymat 
uchun ishonchlilik oralig‘i uzunligi 
va ishonchlilik
ehtimoli 
bo‘lgan
ishonchlilik oralig‘ini tuzish uchun tanlanmaning minimal hajmi n ni
aniqlang, bu yerda
3-§. 3- laboratoriya ishi.
Statistik taxminlarni tekshirish
Matematik statistikaning asosiy vazifalaridan biri - statistik taxminlarni tekshirishning ratsional usullarini ishlab chiqishdan iborat.
Statistik taxmin, bu tajribada kuzatilayotgan tasodifiy miqdor
noma’lum taqsimotining ko‘rinishi yoki uning xossalari haqidagi ixtiyoriy
tasdiq, yoki ma’lum taqsimotning noma’lum parametrlari haqidagi ixtiyoriy
farazdir. Bunday taxminlar nazariy tushunchalar yoki tanlanma kuzatishlarning
statistik tahlili asosida ilgari suriladi. Masalan, X tasodifiy miqdor Puasson
taqsimotiga ega; normal taqsimotga ega bo‘lgan tasodifiy miqdor 
yoki 
o‘rta
qiymatga ega.
Taqsimotning noma‘lum parametri haqidagi taxminlar oddiy va murakkab bo‘ladi. Oddiy taxminda
noma‘lum parametr bitta
tayin qiymat qabul qilishini ta‘kidlaydi. Murakkab taxminda parametr qiymatlar to‘plamidan qiymat qabul qilishi ta‘kidlanadi (
, 
, 
). Tekshirilayotgan taxmin 
harfi bilan belgilanadi. Bizning maqsadimiz tanlama qiymatlari
tekshiralayotgan taxminni tasdiqlashini tekshirishdan iborat.
Tekshirilishi kerak bo‘lgan taxmin nolinchi (asosiy) taxmin deyiladi. Ko‘p hollarda nolinchi
taxminni rad etuvchi ixtiyoriy 
taxmin
alternativ (qarama-qarshi) taxmin ishlab chiqiladi. Oddiy taxmin deb faqat
bitta taxminni o‘z ichiga olgan taxminga aytiladi. Murakkab taxmin deb chekli
yoki cheksiz sondagi oddiy taxminlardan iborat taxminga aytiladi. Shunday
qilib, tekshirish natijasida faqat bitta taxmin qabul qilinadi yoki , mos
ravishda ikkinchisi rad etiladi.
Taxmin bosh to‘plamdan olingan tanlanmalar asosida tekshiriladi, tanlanma tasodifiy bo‘lganligi uchun xatoliklarga yo‘l qo‘yilib, noto‘g‘ri xulosalar qabul qilinishi mumkin. Xatoliklar ikki turga bo‘linadi. Agar taxmin to‘g‘ri bo‘la turib, u rad etilsa 1-tur xatolikka yo‘l qo‘yilgan bo‘ladi. Agar taxmin noto‘g‘ri bo‘la turib, u qabul qilinsa 2-tur xatolikka yo‘l qo‘yilgan bo‘ladi. Bu xatolarning oqibatlari har xil bo‘lishi mumkin, masalan «binoni qurish davom ettirilsin» degan to‘g‘ri qaror rad etilgan bo‘lsa, u holda 1-tur xatolik moddiy zararga olib keladi, agar binoning ag‘darilib tushish xavfiga qaramasdan «qurilish davom ettirilsin» degan qaror qabul qilingan bo‘lsa, u holda ikkinchi tur xatolik kishilarning halokatiga olib kelishi mumkin. Birinchi tur xato ikkinchi tur xatoga nisbatan og‘irroq oqibatlarga olib keladigan misollar ham keltirish mumkin.
1-eslatma. To‘g‘ri qaror ham ikki holda qabul qilinishi mumkin:
1) taxmin qabul qilinadi, u aslida ham to¢g¢ri edi;
2) taxmin rad etiladi, u aslida ham noto‘g‘ri edi.
Shunday qilib, ayrim tanlanmalar bo‘yicha to‘g‘ri qaror qabul qilinadi, boshqalari bo‘yicha noto‘g‘ri qaror qabul qilinadi. Qaror esa statistika yoki statistik tasnif deb ataluvchi tanlanmadan olingan biror bir funktsiyaning qiymati asosida qabul qilinadi. Bu statistika qiymatlar to‘plamini ikkita kesishmaydigan to‘plamlarga ajratishi mumkin:
taxmin
qabul qilinadigan (rad etilmaydigan) statistikaning qiymatlar to‘plam ostisi
taxminning qabul qilinish sohasi deyiladi.
taxmin
qabul qilinmaydigan (rad etiladigan), taxmin qabul qilinadigan statistikaning qiymatlar to‘plam ostisiga
kritik soha deyiladi. Taxminlarni tekshirganda tushunarliki noto‘g‘ri qaror qabul
qilish ehtimolini kamaytirish maqsadga muvofiqdir. Birinchi tur xatoga yo‘l
qo‘yish ehtimolini 
orqali
belgilash qabul qilingan; u ahamiyatlilik darajasi deyiladi. Ahamiyatlilik
darajasi ko‘pincha 0,05, 0,01 ga teng qilib olinadi. Lekin ko‘p holda 1-tur
xatoligi ehtimolining kamayishi 2-tur xatoligi ehtimolining oshishiga olib
keladi. 2 tur xatoligi 
bilan
belgilanadi. Shuning uchun ham statistika âà ehtimolliklar minimal bo‘ladigan qilib tanlanadi. Ushbu qo‘llanmada
taxmin
har doim oddiy deb faraz qilinadi, shuning uchun ham to‘g‘ri taxminda statistika taqsimoti ma‘lum. Eng yaxshi statistikani
tanlash usullari ko‘rib chiqilmagan. Statistikaning kritik sohasini aniqlash
uchun ahamiyatlilik darajasi va
alternativ taxminning ko‘rinishi e’tiborga olinadi.
Noma’lum parametr ning
qiymati haqidagi asosiy taxmin quyidagicha:
Alternativ taxmin esa
quyidagi ko‘rinishlardan biri bo‘lishi mumkin:
, 
, 
Mos ravishda chap tomonlama, o‘ng tomonlama yoki ikkitomonlama kritik sohalarni olish mumkin. Kritik sohaning chegaraviy nuqtalari statistikaning taqsimot jadvallaridan aniqlanadi.
Statistik taxminni tekshirish bosqichlari quyidagilardan iborat
1) âà taxminlar aniqlanadi;
2) Statistika tanlanadi va ahamiyatlilik darajasi beriladi;
3) Ahamiyatlilik darajasi , alternativ taxmin va
jadvallar
orqali kritik soha aniqlanadi;
4) Tanlanma bo‘yicha statistika qiymati hisoblanadi;
5) Statistika qiymati kritik soha bilan taqqoslanadi;
6) Qaror qabul qilish: agar statistika qiymati kritik sohaga
kirmasa, u holda taxmin
qabul qilinadi, rad
etiladi, agar kritik sohaga kirsa, u holda taxmin rad etiladi, taxmin
qabul qilinadi.
Ayrim hollarda altevnativ taxmin ni aniqlashdan oldin statistika qiymatini xisoblash uchun bosh
to‘plam parametrlarining siljimagan baholarini topishni talab etadigan 4)
bosqichni bajarish maqsadga muvofiqdir. Masalan 
taxmin tekshirilayapti va o‘rta qiymat uchun siljimagan baxo 
bo‘lsa, u holda ko‘rinib turibtiki alternativ taxmin 
yoki 
ko‘rinishda
qilib tanlab olish kerak.
Statistik taxminni tekshirish natijalariga quyidagicha
interpretatsiya beriladi: agar taxmin
qabul qilinsa, u holda bu isbotlangan hisoblanadi, agar taxmin qabul qilinsa, u holda kuzatish natijalariga zid emasligini tan olgan bo‘lamiz, lekin
qaror qabul qilishdan oldin yana qo‘shimcha tadqiqot o‘tqazish kerak bo‘ladi.
Pirsonning 
tasdiqlash alomati
Bosh to‘plam X taqsimoti
haqidagi taxminni qanday tekshirish kerakligini ko‘rib chiqaylik. Aytaylik bosh
to‘plam qandaydir noma’lum taqsimotga ega bo‘lsin. Bosh to‘plamdan tanlanma
olamiz. Tanlanmaga asoslanib yoki boshqa mulohazalarni e’tiborga olib bosh
to‘plamning aniq 
taqsimot funksiyasi
haqidagi taxminni tuzamiz. Bu taqsimotni nazariy deb ataymiz. Tanlanma asosida
taqsimotning empirik funktsiyasi 
ni topishimiz mumkin.
Agar empirik taqsimot nazariy taqsimotga yaqin bo‘lsa bosh to‘plamning
taqsimoti haqidagi 
taxminni qabul qilamiz.
Bunday taxminlarni tekshirish uchun bir necha tasdiqlash alomatlari mavjud
bo‘lib, ulardan biri Pirsonning tasdiqlash alomatini keltiramiz. tasdiqlash alomatida X bosh to‘plamning o‘zgarish
sohasi umuman olganda turli xil uzunliklarga ega bo‘lgan 
ta
oraliqqa bo‘lamiz. Tanlanma bo‘yicha shu oraliqlar asosida variatsion qator
tuzamiz. Agar ayrim oraliqlarda ni chastota juda kichik bo‘lsa (5
dan kichik), u holda bu oraliqlarni qo‘shni oraliqlar bilan bilashtiramiz.
Tanlanma asosida nazariy taqsimot parametrlarining baholarini hisoblaymiz. Shu
bilan nazariy taqsimot funktsiya to‘laligicha aniqlanadi. Endi nazariy taqsimot
asosida X tasodifiy miqdorning 
oraliqdan qiymat qabul
qilish ehtimolliklari 
larni hisoblaymiz:
(3.1)
bunda 
.
Keyin nazariy chastotalarni hisoblaymiz 
(n-tanlanma hajmi).
Agar nazariy va empirik chastotalar 
va 
lar
yetarlicha bir-biridan farq qilsa taxminni qabul qilamiz. taxminni
tekshirish uchun quyidagi statistikadan foydalanamiz:
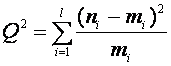(3.2)
tasodifiy
miqdor erkinlik darajasi 
bo‘lgan 
- taqsimotga ega, bu erda 
oraliqlar
soni, r- tanlanma asosida baholari topilgan nazariy taqsimotning parametrlar
soni.
qanchalik katta
bo‘lsa, shunchalik nazariy va empirik taqsimotlar mutanosiblashmagan bo‘ladi. statistikaning yetarlicha katta qiymatlarida taxminni
rad etish kerak. Shuning uchun faqat o‘ng tomonlama kritik sohadan
foydalanamiz.
Agar 
bo‘lsa, taxminni rad etishga asos bor.
Agar 
bo‘lsa, taxminni qabul qilishga asos bor. 
kritik nuqta avvaldan berilgan ahamiyatlilik darajasi 
va erkinlik darajasi lar asosida keltirilgan
adabiyotlardagi taqsimot
uchun ilovalardan yoki EXM da mavjud dasturlar paketidan foydalanib topiladi.
Bosh to‘plamning normal taqsimlanganligi
haqidagi taxminni tasdiqlash alomati yordamida tekshirish
qoidasi
1.
Taxmin qilinayotgan
taqsimot parametrlarining bahosi topiladi, ya‘ni 
va 
lar hisoblanadi.
2.
Taqsimot parametrlari
bahosi normal taqsimot zichlik funktsiyasiga qo‘yilib, zichlik funktsiyaning
bahosi -
topiladi.
(3.3)
3. Tasodifiy miqdor X ning i-oraliqqa tushish
ehtimoli 
ni quyidagi
formula yordamida hisoblanadi:
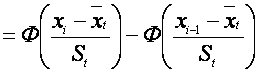(3.4)
bu yerda 
- normal
taqsimot funktsiya va uning qiymatlari adabiyotlarda keltirilgan ilovalardan
yoki EXM da mavjud dasturlar paketidan foydalanib topiladi.
4. Nazariy chastotalar 
(n-tanlanma
hajmi, - X tasodifiy miqdorning
i-oraliqqa tushish ehtimoli) hisoblanadi.
5. 
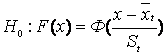taxminni tekshirish uchun quyidagi statistika
qiymatini hisoblaymiz:
(3.5)
6. Avvaldan berilgan ahamiyatlilik darajasi va erkinlik darajasi
lar asosida keltirilgan adabiyotlardagi taqsimot uchun ilovalaridan yoki EXM dagi mavjud
dasturlar paketidan foydalanib kritik nuqta topiladi.
6. Agar bo‘lsa, bosh to‘plamning normal
taqsimlanganligi haqidagi 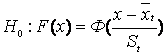taxmin qabul qilinadi.
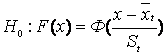Agar bo‘lsa, taxminni rad etishga asos
bor.
Normal taqsimot o‘rtacha kvadratik chetlanishi ma’lum bo‘lganda, uning o‘rta qiymati haqidagi taxminni tekshirish
Faraz qilaylik, bosh to‘plam 
va 
parametrli normal
taqsimotga ega 
, bu
yerda -ma’lum, a ahamiyatlilik darajasida 
taxminni tekshirish kerak. Alternativ
taxmin sifatida 
, 
, 
taxminlardan biri olingan bo¢lsin.
Statistika sifatida quyidagi tasodifiy miqdor
(3.6)
olinadi. H0 taxmin to‘g‘ri
bo‘lganda Z tasodifiy miqdor standart normal taqsimotga (0 va 1 parametrli)
ega 
.
Kritik nuqtani adabiyotlarda keltirilgan normal taqsimot funktsiya uchun ilovalardan yoki EXM dagi mavjud dasturlar paketidan foydalanib topiladi.
Agar alternativ taxmin ko‘rinishda bo‘lsa, u holda quyidagi shartni
bajaruvchi chap tomonlama kritik sohadan foydalanamiz:
(3.7)
Jadval faqat musbat qiymatlar uchun berilgan, shuning uchun
(3.8)
Formulani e’tiborga olib, 
kritik
nuqtani
(3.9)
tenglikdan topamiz, u holda kritik soha
(3.10)
ko‘rinishda bo‘ladi.
Agar alternativ taxmin ko‘rinishda bo‘lsa, u holda quyidagi shartni
bajaruvchi o‘ng tomonlama kritik soha olinadi:
(3.11)
kritik nuqtani
topish uchun asosan quyidagi tenglikdan foydalaniladi
(3.12)
Bu erdan kritik soha ko‘rinishini topamiz
(3.13)
Agar alternativ taxmin 
ko‘rinishda bo‘lsa, u holda quyidagi shartni
bajaruvchi ikki tomonlama kritik soha olinadi:
(3.14)
Mutlaq miqdor ta’rifiga ko‘ra
(3.15)
(3.11) va (3.12) formulalarga ko‘ra jadvaldan foydalanish shartini olamiz:
(3.16)
Shunday qilib bu holda kritik soha 
ko‘rinishda
bo‘ladi.
3- topshiriq.
Bu paragrafning masalalarida tanlanma normal taqsimotga ega bo‘lgan bosh to‘plamdan olingan va ularni universitetimiz www.tatu.uz saytining oliy matematika kafedrasiga tegishli ma‘lumotlar qismidan yoki [7] adabiyotdan oling.
3.1-masala. C
tanlanmaning birinchi X ustuni bo‘yicha 
ahamiyatlilik darajasiga
ko‘ra o‘rta qiymat haqidagi 
taxminni Í1:
M alternativ taxminga
qarshi tekshiring, o‘rtacha kvadratik chetlanish 
berilgan, ahamiyatlilik
darajasi quyidagicha:
, 
,
(3.17)
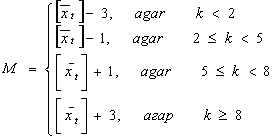
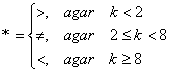(3.18)
ning
butun qismi, V – talabaning
jurnaldagi tartib raqami.
3.2-masala. B tanlanma bo‘yicha ahamiyatlilik darajasiga ko‘ra bosh
to‘plamni normal taqsimotga ega ekanligi haqidagi taxminni tekshiring, bunda
k= qoldiq 
,
4-§. 4-laboratoriya ishi.
Regressiya egri chiziqlarini yasash
Ikkita tasodifiy miqdor funktsional bog‘lanish bilan, yoki statistik deb ataladigan boshqa tur bog‘lanish bilan bog‘langan bo‘lishi, yoki o‘zaro bog‘lanmagan bo‘lishi mumkin.
Masalan Y=φ (x) funktsional bog‘lanishda, tasodifiy miqdorlardan biri (x) ning o‘zgarishi bilan ikkinchi tasodifiy miqdor (Y) ning o‘zgarishi kuzatiladi. Statistik bog‘lanishda tasodifiy miqdorlardan birining o‘zgarishi ikkinchisining taqsimoti o‘zgarishiga olib keladi. Xususan, statistik bog‘liqlik miqdorlardan birining o‘zgarishi ikkinchisining o‘rta qiymatining o‘zgarishida ko‘rinadi; bu holda statistik bog‘lanish korrelyatsion bog‘lanish deb ataladi. Korrelyatsion bog‘lanish tasodifiy miqdorlar orasidagi bog‘lanishni o‘rganadi. Statistik bog‘lanish yana regression bog‘lanishni, ya‘ni tasodifiy va tasodifiy bo‘lmagan miqdorlar orasidagi bog‘lanishni ham o‘rganadi.
Korrelyatsion bog‘lanishning ikki asosiy masalasi
1. Korrelyatsion bog‘lanish formasini aniqlash, ya‘ni regressiya funktsiyasining ko‘rinishini (chiziqli, kvadratik, ko‘rsatkichli va h.k.) topish. O‘rganilayotgan ikki miqdor orasida bog‘lanish bormi, agar bor bo‘lsa qanday?
2. Korrelyatsion bog‘lanishning zichligini aniqlash. Y ning X ga korrelyatsion bog‘liqligining zichligi Y qiymatlarining Yx shartli o‘rtacha qiymat atrofida tarqoqligining kattaligi bo‘yicha baholanadi. Ko‘p tarqoqlik Y ning X ga kuchsiz bog‘liqligidan yoki bog‘liqlik yo‘qligidan darak beradi. Kam tarqoqlik ancha kuchli bog‘liqlik borligini ko‘rsatadi. Korrelyatsion bog‘liqlik ta‘rifini aniqlashtiramiz, buning uchun shartli o‘rtacha qiymat tushunchasini kiritamiz.
Shartli o‘rtacha qiymat Yx deb Y ning X=x qiymatga mos qiymatlarining arifmetik o‘rtacha qiymatlariga aytiladi. Agar har bir x qiymatiga shartli o‘rtacha qiymatning bitta qiymati mos kelsa, u holda ravshanki shartli o‘rtacha qiymat x ning funktsiyasidir; bu holda Y tasodifiy miqdor X miqdorga korrelyatsion bog‘liq deyiladi.
Y ning X ga korrelyatsion bog‘liqligi deb, Yx shartli o‘rtacha qiymatning x ga funktsional bog‘liqligiga aytiladi:
Yx= f(x)
Yuqoridagi tenglama Y ning X ga regressiya tenglamasi deyiladi; f(x) funktsiya Y ning X ga regressiyasi, uning grafigi esa Y ning X ga regressiya chizig‘i deyiladi. Xy shartli o‘rtacha qiymat va X ning Y ga bog‘liqligi shunga o‘xshash aniqlanadi: Xy=φ (u) X ning Y ga regressiya tenglamasi.
Agar f(x) va φ(u) funktsiyalarning ikkalasi ham chiziqli bo‘lsa, u holda korrelyatsiya chiziqli deyiladi. O‘rganilayotgan miqdorlar orasidagi bog‘liqlik ko‘rinishini topishni tanlanma korrelyatsiya koeffitsiyenti osonlashtiradi:
(4.1)
bu ifoda chiziqli korrelyatsiya koeffitsiyentining bahosidir:
(4.2)
Agar X va Y bog‘lanmagan bo‘lsa, u holda r=0.
Teskari tasdiq esa to‘g‘ri emas va har doim ham bajarilmaydi.
Agar X va Y – chiziqli bog‘liq bo‘lsa, ya‘ni Y=a*X+b bo‘lsa, u holda
(4.3)
Demak, tanlanma korrelyatsiya koeffitsiyenti birga yaqin
bo‘lsa, u holda chiziqli regressiya funktsiyasini izlash kerak. Agar 
nolga yaqin bo‘lsa, u holda X va Y orasida chiziqli bog‘lanish
yo‘q, lekin boshqa ko‘rinishdagi bog‘lanish mavjud bo‘lishi mumkin, ya‘ni bu
holda chiziqli bo‘lmagan regressiya funktsiyasini izlash kerak.
Faraz qilaylik, X va Y chiziqli korrelyatsion bog‘lanish bilan bog‘langan bo‘lsin. Bu to‘g‘ri chiziqlar tenglamasini topish uchun n ta tajriba o‘tqazilgan bo‘lsin, u holda n ta sonlar juftligi: (x1,u1), …, (xn,un) vujudga keladi. Bu sonlar juftligiga (x,u) tasodifiy miqdorning barcha mumkin bo‘lgan qiymatlari bosh to‘plamidan olingan tasodifiy tanlanma sifatida qarashimiz mumkin. Aniqlik uchun, Y ning X ga regressiya to‘g‘ri chizig‘ining tanlanma tenglamasini izlaymiz, ya‘ni izlanayotgan tenglamani quyidagicha yozishimiz mumkin:
Y = k*X + b
Y ning X ga regressiya to‘g‘ri chizig‘ining burchak koeffitsiyentini Y ning X ga tanlanma regressiya koeffitsiyenti deyish va uni ρyx orqali belgilash qabul qilingan. Shunday qilib, Y ning X ga regressiya to‘g‘ri chizig‘ining
Y = ρyx x + b (4.4)
ko‘rinishdagi tenglamasini izlaymiz.
O¢z oldimizga ρyx va b parametrlarni shunday tanlashni vazifa qilib qo‘yaylikki, kuzatish ma’lumotlari bo‘yicha XOY tekislikda yasalgan (x1,u1), (x2,u2), …, (xn,un) nuqtalar iloji boricha (4.4) to‘g‘ri chiziq yaqinida yotsin. (4.4) chiziqli empirik formulani topish uchun bir necha xil usullar mavjud: «Tortilgan ip», «yig‘indilar», «eng kichik kvadratlar» usullari.
«Eng kichik kvadratlar» usulida ushbu Yi – yi (i=1, 2, ..., n) ayirmani chetlanish deb ataymiz, bu yerda Yi – (4.4) tenglama bo‘yicha hisoblangan va kuzatilayotgan xi ga mos ordinata, yi esa xi ga mos kuzatilayotgan ordinata.
va b parametrlarni
chetlanishlarning kvadratlari yig‘indisi minimal bo‘ladigan qilib tanlaymiz
(eng kichik kvadratlar usulining mazmuni shundan iborat).
Har bir chetlanish izlanayotgan parametrga bog‘liq bo‘lgani uchun chetlanishlarning kvadratlari yig‘indisi ham bu parametrlarning F funktsiyasi bo‘ladi:
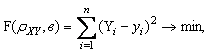yoki
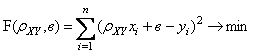(4.5)
(4.5) funktsiya minimumini izlash uchun tegishli xususiy hosilalarni nolga tenglaymiz:
(4.6)
Bu tizimni yechib, izlanayotgan parametrlarni topamiz va ularni (4.4) ga qo‘yib, izlanayotgan regressiya tenglamasini topamiz. Shuni eslatib o‘tish joizki, tenglamani ixtiyoriy ko‘rinishda qidirish mumkin, faqat bu parametrlar tenglamada chiziqli ravishda qatnashishi talab qilinadi.
«Tortilgan ip» usulida barcha natijalar korrelyatsion maydon nuqtalari ko‘rinishda tasvirlanadi.
Shuning uchun fikran bu nuqtalar orasidan ipni shunday tortish kerakki uning ikki tomonida taqriban bir xil sondagi nuqtalar yotsin. Tortilgan ip ustida yotuvchi, koordinatalari (x1,y1) va (x2,y2) bo‘lgan ikki nuqtani olamiz, bu nuqtalar tanlanmada qatnashgan bo‘lishi shart emas, lekin bir-biridan yetarlicha uzoqlikda bo‘lishi kerak. Bu koordinatalarni (4.4) ga qo‘yib
(4.7)
tenglamalar tizimiga ega bo‘lamiz, ρxy va b noma’lumlarga nisbatan tenglamalar tizimni yechib, (4.4) empirik tenglama formulasini olamiz.
Yig‘indilar
usulida quyidagicha mulohaza yuritiladi. Kuzatishlar jadvali ko‘rinishida
ifodalangan, ikki o‘lchovli tanlanma berilgan bo‘lsin. (4.4) empirik formula
topilgan deb faraz qilaylik. Unga X tasodifiy miqdorning tanlanmadagi qiymatini
qo‘yamiz va Y tasodifiy miqdorning mos qiymatlarini 
, i
= 1, 2, ..., n ko‘rinishda yozib, Y ning o‘lchangan va xisoblangan qiymatlari
orasidagi chetlanishni topamiz:
(4.8)
Barcha tanlanmalar uchun chetlanishlar yig‘indisi nolga teng bo‘lishini talab qilish tabiiy hol:
(4.9)
ρxy âà b koeffitsiyentlarni topish uchun bitta tenglama olindi. Ikkita tenglamaga ega bo‘lish uchun, kuzatishlar jadvalini ikki qismga ajratamiz. Faraz qilaylik, birinchi qismda r kuzatishlar bor, u holda ikkinchi qismda (n-r) ta kuzatishlar mavjud bo‘ladi. Jadvalning ikkala qismida ham (4.9) shart bajarilishini talab qilamiz. Natijada quyidagi chiziqli tenglamalar tizimiga ega bo‘lamiz:
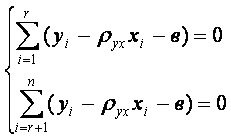(4.10)
Mos hadlarni ajratib, quyidagini olamiz:
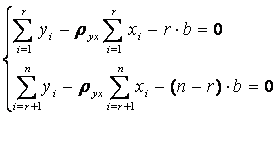(4.11)
Bundan ko‘rinib turibdiki, jadvalning ikkala qismida ham xi va yi qiymatlarini qo‘shish va keyin (4.11) tizimni yechish kerak.
X va Y tasodifiy miqdorlarning o‘zaro bog‘liqlik zichligini ifodalovchi kattalik determinatsiya koeffitsiyenti hisoblanadi va u quyidagicha formula bilan hisoblanadi:
(4.12)
«Eng kichik kvadratlar» usuli eng aniq, lekin eng mashaqqatli usul hisoblanadi. «Tortilgan ip» usuli eng sodda, shu bilan birga eng noaniq usul ham hisoblanadi.
4-topshiriq:
Topshiriqda zarur bo‘lgan C tanlanma berilganlarini [7] adabiyotdan yoki universitetimiz www.tatu.uz saytining oliy matematika kafedrasiga tegishli ma‘lumotlar qismidan oling.
4.1-masala. C tanlanmaning ikkinchi X,Y,Z ustunlari bo‘yicha ikki o‘lchovli XY, XZ, YZ tanlanmalar uchun korrelyatsion maydonlarni quring.
4.2-masala. 4.1-masala natijalari asosida “Tortilgan ip”, “Yig‘indilar”, “Eng kichik kvadratlar” usullarida mos pegressiyaning chiziqli funktsiyalarini toping.
Ushbu vazifani Excel dasturlar paketidan foydalanib ham bajaring va olingan natijalarni taqqoslang.