MINISTRY OF INFORMATION TECHNOLOGIES
AND COMMUNICATIONS OF THE REPUBLIC OF UZBEKISTAN
TASHKENT UNIVERSITY OF INFORMATION TECHNOLOGIES
The Faculty "Telecommunication technologies"
The Department "Technologies
of mobile communication"
THE USEGE MATLAB PROGRAM
IN EDUCATIONAL PROCESS
on the subject of "Mobile Communication Systems"
guidelines
Tashkent 2016
Matlab system is a powerful tool for solving engineering problems. It is a versatile software package which allows to solve a wide range of tasks from symbolic computation to complex engineering calculations.
When developing personal settings in Matlab system for managing work on specific tasks, and often just in solving problems require specific skills that can be attributed to programming skills. Although Matlab is neither medium nor programming language, it still provides a basic agent present in most programming languages.
This handbook will enable students to become acquainted with these basic resources and to acquire the skills to use them.
Introduction
The system MatLAB established by MathWork Inc. (USA, Neytik, Massachusetts). Although for the first time this system began to be used at the end of the 70s, the heyday of its application began in the late 80s. Recent versions of MatLAB, - is highly developed systems that contain a huge collection of procedures and functions necessary for engineers and scientists to perform complex numerical calculations, modeling the behavior of the technical and physical systems, processing the results of these calculations in a visual form.
MatLAB system (short MATrix LABoratory - Matrix Laboratory) is an interactive computer system to perform the engineering and scientific calculations, focused on working with data arrays. The system suggests the possibility of recourse to the programs that are written in FORTRAN and C.
An attractive feature of the system is that it contains a built-in matrix and complex arithmetics. The system supports operations with vectors, matrices and arrays of data, the calculation of the rank and condition numbers of matrices, supports algebraic polynomials, solution of nonlinear equations and optimization problems, the integration of functions in quadrature, numerical integration of differential and difference equations, the construction of various types of graphs and ect. It supports a comfortable operating environment, which allows to address the problems and get solutions in the usual mathematical form.
The main object of MatLAB system - rectangular numeric array (matrix), which allows integrated elements. Using matrix does not require an explicit size. The system allows us to solve many computational problems in significantly less time than that required for writing the respective programs on the language FORTRAN, BASIC and C.
MatLAB system performs operations with vectors and matrices, even in the immediate calculation mode without any programming. It can be used as a powerful calculator, which along with the usual arithmetic and algebraic operations may be used such complex operations as matrix inversion, the calculation of its own values and vectors, solving systems of linear algebraic equations, and more. However, the main characteristic feature of the system is its "openness" that is easy to modify and adapt it to specific user tasks. The user can enter any new command, operator, or function, and then use them as easy as built-in operators and functions.
The basic set of words of the system includes: special characters; arithmetic and logical operations; arithmetic, trigonometric and some special mathematical functions; features fast Fourier transform and filtering; vector and matrix functions; means for work with complex numbers; Operators charting in Cartesian and polar coordinate systems, three-dimensional surfaces, etc.
MatLAB system has its own programming language. Recording of programs in the system is conventional, and therefore common to most users of personal computers. And in addition, the system makes it possible to edit the program by any familiar user of text editor.
MatLAB have opportunities to work with the signals for the calculation and design of analog and digital filters for the construction of their frequency, pulse and transient characteristics. The presence and the means for spectral analysis and synthesis, in particular for implementing the direct and inverse Fourier transform. This system is quite useful for the design of electronic devices.
The work in MatLab environment can be carried out in two modes:
• In calculator mode, when the calculation carried out immediately after dialing the next operator or MatLab command;
• by calling the name of the program, written in MatLAB, language pre-compiled and stored on disk.
In both modes the user has access to virtually all the computing capabilities of the system, including the withdrawal of information in graphical form. Program mode allows saving developed computational algorithms and thus repeating calculations with input data.
MATLAB system
MATLAB system consists of the main parts of:
MATLAB language. It is the language of matrices and high-level arrays with flow control, functions, data structures, input-output and features of object-oriented programming. This allows a program to "small scale" for the rapid creation of roughing programs, and in the "large" to create large and complex applications.
MATLAB environment. This is a set of tools and accessories, works with the user or the MATLAB programmer. It includes tools for managing the variables in the MATLAB workspace, input and output, as well as the creation, control and debug M-files and MATLAB applications.
Managed schedule. This graphic system MATLAB, which includes high-level commands and for rendering two-dimensional data, image processing, graphic animation and illustrated.
The software interface. This is a library that allows you to write programs in C and Fortran, which interact with MATLAB. It includes facilities for calling programs from MATLAB (dynamic link), calling MATLAB as a computational tool for read-write file.
Description of MATLAB environment
MATLAB system is an interactive system for performing engineering and scientific calculations, focused on working with data arrays.
In MATLAB system the following major functional elements can be shown:
1. Command Window for interactive input commands from the keyboard.
2. The workspace that contains the data that produced the work. The data is presented in the form of variables - arrays.
3. Libraries of (Toolboxes) MATLAB functions and commands, including standard MATLAB commands.
4. m-file editor for creating and editing scripts and MATLAB functions.
5. Reference MATLAB system.
The easiest way to work with MATLAB commands is their input in the command window and receive a response interactively. However, the interactive input commands from the keyboard is not always convenient, so it provides the ability to write scripts.

Figure. 1. Interface MATLAB environment
All variables in MATLAB system are represented as arrays.
Therefore, each variable has the following properties:
1. The dimension of the array is the number of measurements (for the vector dimension is 1 - dimensional array; for a rectangular matrix - 2 - two-dimensional array).
2. The array length - the number of elements in the array.
3. The size of the array in each dimension.
4. Type of data array elements (Table 1).
Scalar variables in MATLAB system are represented as arrays of length. When you create a numeric variable The default data type is a numeric floating-point number (double type). The variables of numerical type can take values except numeric values Inf, -Inf and NaN, which means infinity, negative infinity, and not a numerical value, respectively.
Table 1. Data Types of MATLAB environment
|
Type |
Description
|
|
int8 int16 int32 int64 |
8, 16, 32, 64 - bit signed integers |
|
uint8 uint16 uint32 uint64 |
8, 16, 32, 64 - bit integer without sign |
|
single double |
Floating point numbers with a single and double precision |
|
logical |
Binary numbers: 1 (true) 0 (false) |
|
char |
symbolic variables |
|
cell |
An array of different types of data cells
|
There are also reserved variables of MATLAB environment and control functions that are shown in Tables 2 and 3.
Table 2. The reserved environment variables of MATLAB
|
Name of the variable |
Description |
|
pi |
It contains the value of "pi" |
|
i, j |
Integrated unit |
|
eps |
The relative accuracy of the numerical values of the floating-point |
|
ans |
It contains the result of the last command |
|
% |
The symbol indicating the start of a comment, the entire string after this symbol can contain any text |
|
; |
Symbol for the transition to the next step without displaying the results of the team in the dialog window |
|
Inf |
Note infinity (e.g., is the result of dividing by zero) |
|
Nan
|
Specifying a non-numeric value (for example, the uncertainty of zero divided by zero) |
Table 3. Control functions
|
Name to functions or commands |
Description
|
|
help |
Displays the description of the function or command in the command window |
|
lookfor |
It displays a list of functions, including the description of the keyword |
|
which |
It gives the path m-file, which contains the specified function |
|
load |
Loads variables MATLAB working area of the file * .mat |
|
save |
Saves variables in the MATLAB workspace file * .mat |
|
clear |
It removes the variables in the workspace (for example: clear all) |
|
clc |
Scrape down the command window |
|
echo |
Enable / disable result output enabled by default |
Creation and work with variables
In creation a variable in MATLAB system it is not necessary to explicitly define the variable name, data type or dimension of the array.
When MATLAB meets a new variable name, automatically creates with the same name, and the required amount of memory allocates the variable automatically.
For this purpose the brackets can be used to carry out the union of scalars or arrays, with the result in an array as well (see. Table 4 Examples).
The elements within the brackets may be separated by a comma or semicolon, depending on whether the measurement is performed on any association. The MATLAB System assumed that rectangular matrix (two-dimensional arrays) first measurement determines the number of rows and the second dimension - the number of columns. When you use square brackets comma divides the line, and a semicolon separates the columns.
Target arrays consisting of equidistant range numbers may be accomplished by a colon a: b: c. This indicates the value of the first element of the array a, b, and increments of the maximum possible value (the minimum possible, if b is negative) in the array.
There are also a number of functions that allow you to create and fill the arrays of different sizes (see. Table 5).
Table 4. Examples of creating variables
|
Commands |
Description |
|
NumVar = 0.0321;
|
This command creates a numeric variable called NumVar, and whose value is the number of 0.0321 |
|
Text = ‘Òåêñò’;
|
The command creates a symbolic variable named Text, and whose value is the string 'text' |
|
A = [1; 2];
|
This command creates a variable named A, and whose value is an array of size 2X1: 1 2 |
|
B = [1, 2];
|
This command creates a variable named B, and whose value is an array of size 1X2: 1 2 |
|
D = 1:5;
|
The command creates a variable with the name of D, and whose value is an array of size 1X5: 1 2 3 4 5 |
|
F = zeros(2, 3);
|
This command creates a variable named F, and whose value is an array of size 2X3, filled with zeros |
Table 5. Functions of creating basic arrays
|
Name to functions or commands |
Description
|
|
eye
|
It creates an identity matrix, for example, eye team (2) creates a matrix of size 2X2: 1 0 0 1 |
|
ones(m, n) |
Creating an array of size mxn filled units |
|
zeros(m, n) |
Creating an array of size mxn filled with zeros |
|
rand(m, n)
|
Creating an array of size mxn filled with random numbers, uniformly distributed in the interval (0, 1) |
|
randn(m, n)
|
Creating an array of size mxn filled with random numbers normally distributed with zero mean and unit variance |
Access to the individual array elements is performed by specifying the index in parentheses. The indices (numbers) for different measurements separated by a comma. Thus, if the two-dimensional array is created with the name of Matrix, access to element of the array, which is located at the intersection of m-th row and the n-th column, as follows:
Element = Matrix (m, n);
Access can receive not only a single element of the array, but also to the whole block. For this set no individual indexes and index arrays. For example, the command
Block = Matrix ([2, 3], [4, 5])
Block write variable square matrix formed from the Matrix array elements, which are located at the intersection of row 2 and 3 and 4 and column 5 Matrix array.
Also, instead of indexes can indicate special characters. colon symbol indicates that you need to take the whole range of indices on the measure. End symbol indicates that it is necessary to take the last item on this measurement.
For example the command
Vector = Matrix (:, end)
writes in variable Vector Matrix last column of the array.
Table 6 shows the main functions to determine the parameters of variables.
Table 6. Basic functions to determine the parameters of variables
|
Name to functions or commands |
Description
|
|
length(A) |
Specifies the length of the vector A |
|
ndims(A) |
Specifies the number of dimensions of an array A numel (A) Specifies the number of elements of A |
|
size(A) |
Specifies the size of the array A |
|
disp(A) |
It displays the value of the variable A in the command window |
|
isscalar(A)
|
It determines whether a variable is a scalar A |
Mathematical expressions and functions
Most of the functions in the MATLAB system are designed to work with arrays. Therefore, the mathematical functions such as sin, log, in the MATLAB system can be as an argument to pass an array of numeric values. In this case the result is calculated for each element separately. The exceptions are specialized to work with matrices functions that do not operate element-wise.
Tables 7 and 8 are operators MATLAB environment and some elementary mathematical functions.
Table 7. Operators of the ambience MATLAB
|
Operators |
Description |
|
( ) |
Set the order of evaluation |
|
* / |
multiplication and division operations |
|
^ |
Involution |
|
` |
Operation transpose |
|
+ - |
Addition and subtraction |
|
< > |
Operator less or more |
|
<= >= |
The operator or equal to and less than or equal |
|
= ~= |
The operator is equal and unequal |
|
& |
"And" operator |
|
| |
"Or" operator |
|
~ |
"Not" operator |
Table 8. Some basic mathematical functions
|
Name to functions or commands |
Description
|
|
sin |
Calculates sine |
|
cos |
Calculates cosine |
|
tan |
Calculates tangent |
|
atan |
Calculates arctangent |
|
exp |
Involution |
|
log |
Natural logarithm |
|
sqrt |
Root square |
|
round |
Truncation of the number before integer |
Graphic commands and functions
MATLAB system is convenient to display data in graphical form. To this end a number of high-level functions. These functions allow you to construct a histogram, graphic lines and surfaces. At the same time, they are automatically put up the display options. But any display options schedules can be changed using special low-level functions.
create a separate window to display graphic information. Such a window can be created command figure. Each high-level function displays the graphical information in the current graphic window. At the same time the contents of the window is rewritten. If this window is not created, the higher-level functions automatically create it.
Low-level functions work with the current graphics window. They are designed to modify the display parameters, and to display the individual graphic elements.
Table 9. Some high-level graphics functions
|
Name to functions or commands |
Description |
|
plot |
Build lines or dots on a linear scale |
|
loglog |
Build lines or points on a logarithmic scale |
|
polar |
Build a line or point in polar coordinates |
Table 10. Some low-level graphics functions
|
Name to functions or commands |
Description |
|
figure |
Graphical window |
|
title |
Name the chart |
|
xlable |
The label on the X axis |
|
axis |
Zooming axis |
|
subplot |
Split window into several areas |
When working with graphic functions need to understand object - oriented graphics structure. To display the graphic elements created a number of objects:
1. Graphical window (figure).
2. The coordinate system (axes).
3. Various graphical elements (line, patch, text, surface, image, light).
Each of these objects placed in line identifier (handle - handle). Knowledge of object identifier allows you to read and modify the properties of an object using the get and set functions.
Consider the example of using the concepts introduced above for writing a program in MATLAB.
An example of the use of MATLAB program
for generating a binary signal using
amplitude modulation
the signal program can be as follows:
% Is the sampling rate
SamplingRate = 1000;
% Define the sampling period
SamplingPeriod = 1 / SamplingRate;
% Ask information sequence of bits
Bits = [1, 0, 0, 1, 1, 0, 1, 0, 1, 1];
% Determine the number of bits transmitted
NoBits = length (Bits);
% Sets the duration of one bit in seconds
TBit = 1;
% Determine the length of the entire sequence of bits in seconds
SignalDuration = T * NoBits;
% Forming an array of values of the time, in seconds, the length of the array corresponds to the number of discrete signal generated in
Time = 0: SamplingPeriod: SignalDuration;
% Form a signal sequence of bits, using the interpolation function
SignalBits = interp1 (0.5: NoBits, Bits, Time, 'nearest', 'extrap');
% Of the set period of the carrier sinusoidal signal in seconds
TSin = 0.1;
% Determined by the frequency of the carrier sinusoidal signal in hertz
SinRate = 1 / TSin;
% Forming a carrier sinusoidal signal
SignalSin = sin (2 * pi * SinRate * Time);
% Modulate carrier sine wave signal bit sequence
ModulatedSignal = SignalBits * SignalSin.;
close all% close the window for drawing open earlier
% Draw a graph of the signal sequence of bits
H = figure; % Create Drawing window
set (gcf, 'Units', 'normalized'); % Determine
set (H, 'Position', [0.1 0.63 0.8 0.25]); % Window position
plot (Time, SignalBits); % Draw signal
axis ([0 SignalDuration -0.5 1.5]); % Change the display scale
title ( 'Bits signal'); % Determines the title of the chart
xlabel ( 'Time, seconds'); % Specifies the label of the time axis
% Draw a graph of sine wave
H = figure; % Create Drawing window
set (gcf, 'Units', 'normalized'); % Determine
set (H, 'Position', [0.1 0.33 0.8 0.25]); % Window position
plot (Time, SignalSin); % Draw signal
axis ([0 SignalDuration -1.5 1.5]); % Change the display scale
title ( 'Sinusoidal signal'); % Determines the title of the chart
xlabel ( 'Time, seconds'); % Specifies the label of the time axis
% Draw a graph of the modulated signal
H = figure; % Create Drawing window
set (gcf, 'Units', 'normalized'); % Determine
set (H, 'Position', [0.1 0.03 0.8 0.25]); % Window position
plot (Time, ModulatedSignal); % Draw signal
axis ([0 SignalDuration -1.5 1.5]); % Change the display scale
title ( 'Modulated signal'); % Determines the title of the chart
xlabel ( 'Time, seconds'); % Specifies the label of the time axis
The results are graphically display a sequence of bits, and modulated sinusoidal signals are represented in Figures 2.3and 4.

Fig.2. Graphical display of the signal sequence of bits

Figure 3. The result is a graphic display of the sinusoidal signal
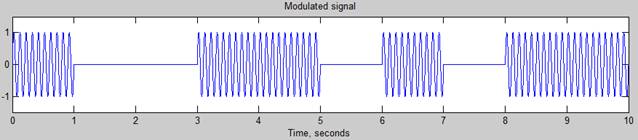
Figure 4. Result graphical representation of the modulated signal
In conclusion it can be noted that Matlab is a convenient tool for modeling and visualization of designed objects, and can be used in the educational process.
Literature
1. Ìàêñèìåé È.Â. Èìèòàöèîííîå ìîäåëèðîâàíèå íà ÝÂÌ.-Ì.: Ðàäèî è ñâÿçü. 1988 ã.
2. Ëóçèíà Ë.È. Êîìïüþòåðíîå ìîäåëèðîâàíèå. Ó÷åáíîå ïîñîáèå. Òîìñê 2001 ã.
3. Àíóôðèåâ È, Ñìèðíîâ À. Matlab 7. Ïîëíîå ðóêîâîäñòâî. Ñàíêò-Ïåòåðáóðã, 2005 ã.
4. Âàñèëüåâ Â.Â.Ìàòåìàòè÷åñêîå è êîìïüþòåðíîå ìîäåëèðîâàíèå ïðîöåññîâ è ñèñòåì. Ó÷åáíîå ïîñîáèå. Óêðàèíà, 2008 ã.
THE
USAGE MATLAB PROGRAM
IN EDUCATIONAL PROCESS
on the subject of "Mobile Communication Systems"
guidelines
The work is considered in the Faculty
"Telecommunications
Technologies"
(protocol__________)
The
work was considered and approved at the meeting
department of TMÑ
(protocol__________)
Compiled by Senior Lecturer. Hatamov A.P.
Editor Ibraimov R.R.
Corrector Rakhmatullayeva D.P.
Offset paper. Order number ¹
Circulation
Printed TUIT
Tashkent 700084, ul. A.Timura
- 108