1. Графики функций

1.1. Основные правила построения количественных графиков

Чаще всего приходится иметь дело с функциональной зависимостью между двумя величинами. Такую зависимость представляют обычно в виде кривой линии в прямоугольной системе координат. Реже строят полярные графики (рис.1.1).

Рис.1.1. Угловое распределение вторичных ионов , рассеянных на в форме полярной диаграммы.

Когда необходимо изобразить зависимость, связывающую более двух переменных, пользуются номограммами (рис.1.2) и треугольными графиками (рис.1.3).

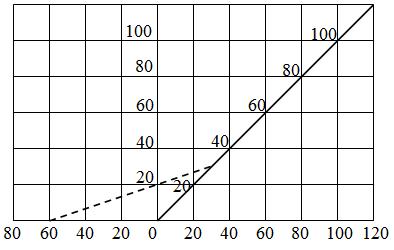
Рис.1.2. Оптические характеристики тонкой линзы (номограмма)

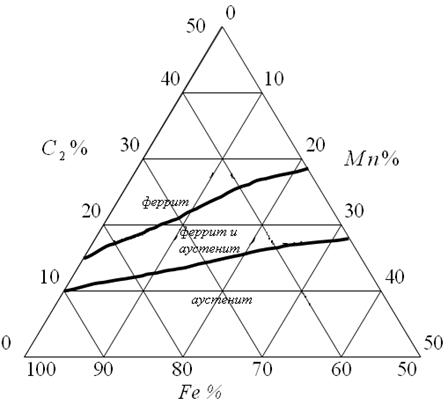
Рис.1.3. Металлографические фазы в сплавах (треугольный график).

Впредь будем рассматривать простейшие графики, представляющие в прямоугольной системе координат связь между двумя величинами. При построении количественных графиков необходимо выполнение ряда требований.

1. Масштаб на осях координат следует выбирать так, чтобы наносимая кривая занимала все координатное поле. На рис.1.4,а показан пример плохо выбранного масштаба. На рис.1.4,б – масштаб выбран хорошо.

Рис.1.4. Температурная зависимость коэффициента катодного распыления вольфрама ионами с энергией 2600 эВ.

2. Не нарушая условия 1, масштабы следует выбирать так, чтобы полученная кривая возможно более приближалась к прямой линии. Выполнение этого правила важно для отыскания аналитического вида представляемой функции. Чтобы получить график в виде прямой линии, иногда удобно пользоваться специальной шкалой. Например, если предполагается, что искомая функция является экспонентой, то кривую удобно представить в полулогарифмическом масштабе: по оси абсцисс откладывается независимая переменная Х, по оси ординат ln Y. В таких случаях удобно пользоваться специальной полулогарифмической бумагой.

Пример. Задана таблица пар значений (Х, Y).

Таблица 1.1

Х	5	6	8	9
Y	4,81	5,31	8,1	14,6

На рис.1.5,а по данным таблицы 1 кривая построена в линейном масштабе, на рис.1.5,б использована полулогарифмическая шкала.

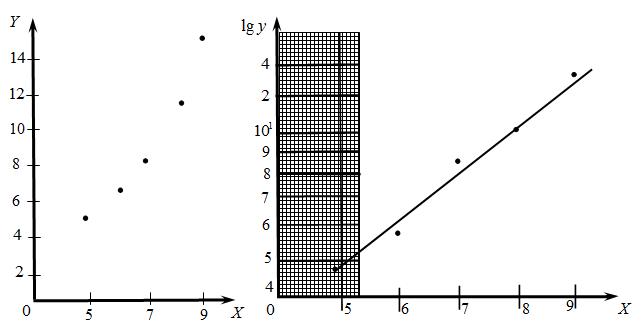
а) Линейная шкала б) Полулогарифмическая шкала

Рис.1.5. Виды линейной и полулогарифмической шкал

3. Если имеем малое число точек или неясен закон, связывающий переменные величины, нанесённые точки следует соединить отрезками прямых линий.

4. Если имеется достаточное количество точек, проводят плавную кривую. При проведении плавной кривой следует придерживаться общих правил:

I) Кривая должна быть плавной с малым числом перегибов;

II) Кривая должна проходить насколько возможно ближе ко всем нанесённым точкам;

III) Кривая не обязательно должна проходить через каждую определённую точку.

1.2. Графическое дифференцирование

Существует ряд методов выполнения графического дифференцирования. Ниже приводится один из более точных – метод секущей. Прежде всего, тщательно выполняется построение кривой y=f(x). Далее находится наклон кривой в заданной точке (х₀, у₀). Он определяется предельным положением секущей, проводимой через точку (х₀, у₀) и соседние точки А₁, А₂ … А_i, когда А_i стремится к (х₀, у₀). Для этой цели на кривой выбирают 5-6 точек так, чтобы их абсциссы отстояли от х₀ на Δх₁, Δх₂=2Δх₁ (рис.1.6).

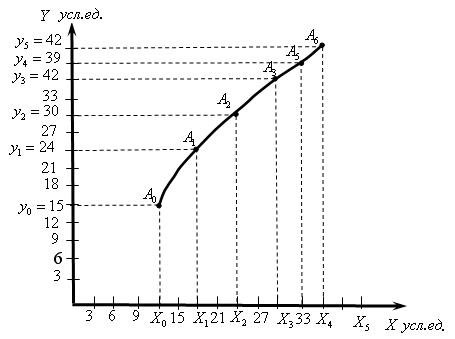
Рис.1.6. Графическое дифференцирование.

По графику находим соответствующие изменения ∆у (в условных единицах)

∆у₁=24 -15=9; ∆у₂=30 -15=15; ∆у₃=36 -15=21;

∆у₄=39 -15=24; ∆у₅=42 -15=27.

Отношение ∆у_i/∆х_i выражает наклон секущей, проходящей через заданную точку (х₀, у₀) и точку А_i.

Строим зависимость ∆у_i /∆x_i =f(∆x_i)

; ; ; ; .

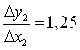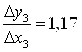Значение (Δу/Δх) для Δх=0 даёт наклон секущей. Это значение находят методом экстраполяции (рис.1.7).

Рис.1.7.Использование метода экстраполяции.

Следует иметь в виду, что величина наклона зависит от масштаба и является отвлеченным числом. Единицы, в которых выражается производная, есть частное от деления единиц измерения у на единицы измерения х. Т.о. производная

Здесь масштабный коэффициент графика, т.е. отношение физических величин, принятых на графике за единицы масштабов по осям у и х.

В заключение следует обратить внимание, что графическое дифференцирование применяется в тех случаях, когда нужно найти производную в небольшом числе точек экспериментальной кривой.

Самостоятельная работа № 1

Задана зависимость яркости В накаленного вольфрама от его температуры. (табл.1.2).

Таблица 1.2

ТК

В^св/cм²

ТК

В^св/cм²

2000

2100

2200

2300

2400

2500

20.0

35.0

61.0

100.1

156.0

234.0

2600

2700

2800

2900

3000

345

495

390

950

1270

Определить методом секущей величину Tdb/Bdt для Т₁=2000К, Т₂=2500К, Т₃ =3000К.

1.3. Графическое интегрирование

Рассмотрим метод средних ординат на конкретном примере.

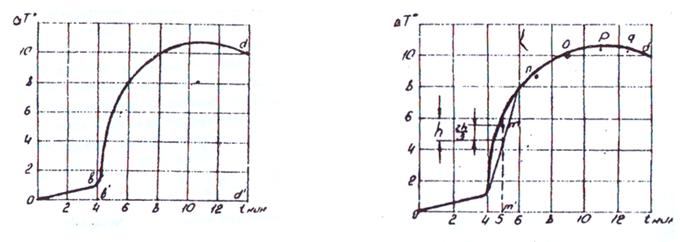
Рис. 1.8. Кривая зависимости температуры калориметра от времени.

Рис.1.9.Определение средней ординаты.

На рис.1.8 приведена кривая зависимости температуры калориметра от времени. Нагретый образец внесен в калориметр на 4 –ой минуте (начало эксперимента). После 14 минут калориметр остывает вместе с образцом (окончание эксперимента). По оси ординат отложена разность температур калориметрической жидкости и кожуха калориметра. Требуется определить разность температур начала и конца опыта. Для этого нужно найти площадь криволинейной трапеции.

Будем искать среднюю ординату криволинейной трапеции. Восстановим ординаты в точках 4,6,8,10,12,14 мин. Этим мы разобьем площадь всей фигуры на 5 криволинейных трапеций. Требуется найти среднюю ординату криволинейной трапеции, ограниченной ординатами в точках 4 и 6 мин. Для этого соединим отрезком прямой точки пересечения кривой с выбранными ординатами ( рис.1.9).

Затем на ординате в точке 5 мин отметим точку m, находящуюся на расстоянии 2/3 от проведенного отрезка прямой (теорема Симпсона). Отрезок будет искомой средней ординатой рассматриваемой криволинейной трапеции.

Аналогично точке m находим положения точек n, o, p, q для других криволинейных трапеций.

Далее начинаем объединять криволинейные трапеции попарно (рис.1.10). Определяем верхний конец r средней ординаты, для трапеции, заключенной между ординатами в точках 4 мин. и 8 мин.

Точка r находится на пересечении ординаты в точке 6 мин (середина интервала 4-8 мин) и отрезка прямой, соединяющего точки m и n.

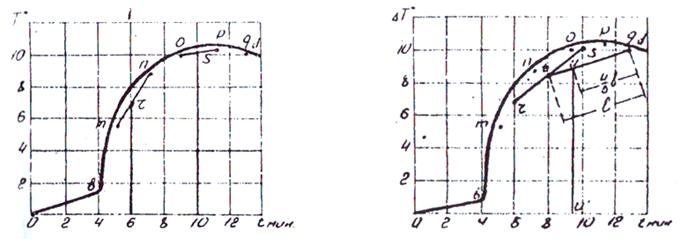
Рис. 1.10. Определение верхнего конца средней ординаты.

Рис. 1.11. Нахождение вершины средней ординаты для трапеции.

Точно так же определяется верхний конец S средней ординаты для трапеции между ординатами в точках 8 мин и 14 мин. Следующий этап – нахождение вершины t средней ординаты для трапеции, заключенной между ординатами в точках 4 мин и 12 мин. (рис. 1.11.)

Площадь между ординатами в точках 12 мин. и 14 мин. присоединяется следующим образом. Соединяем точки t и q. Поскольку интервал времени для последней трапеции составляет 1/5от общего интервала, то на отрезка tq находим точку u, для которой 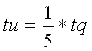. Ордината является средней для площади, заключенной между ординатами в точках 4 мин и 14 мин. Т.о., искомая площадь равна ≈ 900 мин. град. Искомая разность температур определяется по найденной площади фигуры и известным параметрам калориметра.

2.МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ТАБЛИЧНЫХ ДАННЫХ

2.1. Сглаживание методом разностей

Таблица обычно представляет результат измерения неизвестной прежде функциональной зависимости некоторой переменной величины y от значений независимой переменной величины х. Для того, чтобы ход изменения y сделать более плавным таблицу следует сгладить. Одним из наиболее точных способов сглаживания таблиц является метод разностей. Для удобства математической обработки данных значения независимой переменных х следует выбирать так, чтобы их последовательность образовывала арифметическую прогрессию.

Х₀, Х₁= Х₀+l, Х₂=Х₁+l=Х₀+2l, …, Х_n=Х₀+nl (2.1)

Эти значения независимой переменной (аргумент функции) назовем «целыми», а l шагом таблицы. Получающиеся при таких изменениях аргумента приращения функции назовем первыми разностями. Первые разности обозначим:

δу_1/2=у₁ – у₀, δ у_1+1/2=у₂-у₁, …, δy_n _½= у_n-у_n_-1(2.2)

Индексы при разностях означают, что последние относят не к краям соответствующих интервалов х, а их серединам: Х_1/2=Х_о+l/2_, Х₁+_1/2=Х₀+3/2, …

Сущность сглаживания мы поясним на примере.

При определении энергетической зависимости коэффициента рассеяния ионов калия на поликристаллической платине получены данные, приведенные в первом и втором столбцах табл.2.1. Находим первые разности (табл.2.2).

Таблица 2.1

Е_о,эВ	К_р⁺
1	2	3	4	5	6
100	0,65
200	0,50
300	0,45
400	0,38
500	0,36
600	0,39
700	0,27
800	0,25
900	0,23
1000	0,22
1100	0,20

Таблица 2.2

Е_о,эВ	К_р⁺	SK_p+
1	2	3	4	5	6
100	0,65
200	0,50	-0,15
300	0,45	-0,6
400	0,38	-0,7
500	0,36	-0,2
600	0,39	-0,6
700	0,27	-0,3
800	0,25	-0,2
900	0,23	-0,2
1000	0,22	-0,1
1100	0,20	-0,2

Наносим полученные значения δК_p⁺ в системе координат δК_p⁺- Е_o_.По полученным точкам проводим плавную кривую (рис.2.1).

Рис.2.1. Построение графика.

По полученному графику находим сглаженные значения первых разностей с прежней точностью (второй знак после запятой). Записываем их в 4 столбец табл. 2.3.

Таблица 2.3

Е_о,эВ	К_р⁺	SK_p⁺	(δК_p⁺)
1	2	3	4	5	6
100	0,65
200	0,50	-0,15	-0,13
300	0,45	-0,6	-0,8
400	0,38	-0,7	-0,6
500	0,36	-0,2	-0,4
600	0,39	-0,6	-0,3
700	0,27	-0,3	-0,3
800	0,25	-0,2	-0,2
900	0,23	-0,2	-0,2
1000	0,22	-0,1	-0,1
1100	0,20	-0,2	-0,2

Вычисляем сглаженные значений (К_p⁺)

Таблица 2.4

Е_о_,эВ	К_р⁺	SK_p⁺	(δК_p⁺)	(К_p⁺)
1	2	3	4	5	6
100	0,65			0,65
200	0,50	-0,15	-0,13	0,52
300	0,45	-0,6	-0,8	0,44
400	0,38	-0,7	-0,6	0,38
500	0,36	-0,2	-0,4	0,34
600	0,39	-0,6	-0,3	0,31
700	0,27	-0,3	-0,3	0,28
800	0,25	-0,2	-0,2	0,26
900	0,23	-0,2	-0,2	0,24
1000	0,22	-0,1	-0,1	0,23
1100	0,20	-0,2	-0,2	0,22

Для оценки качества проделанного сглаживания используют вторые разности,

определяемые по следующему правилу:

δ²у₁=δу_1+1/2– δу_{1/2 ,}δ²y=δу_2+1/2- δу_1+1/2….(2.3)

В рассматриваемом примере вторые разности для сглаженных значений (К_р⁺)

приведены в 6^ом столбце табл.2.5.

Таблица 2.5

Е_о_,эВ	К_р⁺	SK_p⁺	(δК_p⁺)	(К_p⁺)
1	2	3	4	5	6
100	0,65			0,65
200	0,50	-0,15	-0,13	0,52	-0,05
300	0,45	-0,6	-0,8	0,44	-0,02
400	0,38	-0,7	-0,6	0,38	-0,02
500	0,36	-0,2	-0,4	0,34	-0,01
600	0,39	-0,6	-0,3	0,31	0
700	0,27	-0,3	-0,3	0,28	-0,01
800	0,25	-0,2	-0,2	0,26	0
900	0,23	-0,2	-0,2	0,24	-0,2
1000	0,22	-0,1	-0,1	0,23	-0,01
1100	0,20	-0,2	-0,2	0,22	0

Малость вторых разностей указывает на плавность изменения оглаженной функции К_p⁺=f(E_o) Однако, если того требует точность проведенного эксперимента, можно провести дополнительное сглаживание по вторым разностям.

Техника сглаживания та же:

1. Строится график зависимости δ²К_p⁺ = f(E_o)

2. Находятся сглаженные значения вторых разностей

3. Cглаживаются первые разности

4. По cглаженным первым разноcтям и получают дважды cглаженные значения.

Самостоятельная работа № 2

В табл.2.6 приведены экспериментальные данные по зависимости эффекта Джоуля-Томсона для воздуха (в ^оС/атм)

Таблица 2.6

Т^оС Р_ат	0	50	100	150	200	2500
1	0,2746	0,1956	0,1355	0,0961	0,0645	0,0409
20	0,2577	0,1830	0,1258	0.0883	0,0580	0,0356
60	0,2200	0,1571	0,1062	0,0732	0,0453	0,0254
100	0,1822	0,1310	0,0884	0,0600	0,0344	0,0165
140	0,1446	0,1070	0,0726	0,0482	0,0250	0,0092
180	0,1097	0,0829	0,0580	0,0376	0,0174	0,0027
220	0,0795	0,0609	0,0449	0,0291	0,0116	-0,0025

Задание:

1. Сгладить таблицу по давлениям

2. Установить, требуется ли после этого сглаживание по температурам.

Самостоятельная работа № 3

В табл.2.7 приведены результаты измерения температурной зависимости теплоемкости платины при постоянном объеме.

Таблица 2.7

Т	С_p	Т	С_p
100	6,130	900	6,785
200	6,250	1000	6,2831
300	6,355	1100	6,884
400	6,454	1200	6,930
500	6,545	1300	6,969
600	6,610	1400	7,010
700	6,678	1500	7,046
800	6,731	1600	7,079

Задание:

Провести сглаживание таблицы по вторым разностям.

2.2. Интерполяция и экстраполяция

Интерполяция состоит в нахождении значений функции при промежуточных, не содержащихся в таблице значениях аргумента.

Существует несколько способов интерполяции:

Линейная интерполяция

В этом случае истинная функция заменяется линейной таким образом, чтобы обе функции совпадали на границах интересующего нас интервала Х_к≤Х≤Х_к+1Интерполяция производится по формуле:

У=Y_к₊(Y_к₊₁- Y_к)/l_*S=(1- S/l)Y_k+ S/l *Y_k+1(2.4)

Здесь l - постоянный шаг таблицы, S=X - X_к, где Х –то значение аргумента, для которого производится интерполяция

Пример

Требуется найти силу тока, который нагреет в вакууме длинную вольфрамовую нить радиусом 62 мкм до 2500 К Имеется I=f (r) для Т=2500 К

r, мкм	30	40	50	60	80	100
I, А	0,690	1,065	1,485	1,950	3,000	4,200

r, мкм	30	40	50	60	80	100
I, А	0,690	1,065	1,485	1,950	3,000	4,200

I = (1-S/l)*1₄+S/l*I₅

l=20мкм, S=62мкм - 60мкм=2мкм, S/l =0,1

I=(1-0,1)*1,950+0,1*3000=2,055(A)

Квадратичная интерполяция по формуле Ньютона

В этом случае истинная функция заменяется квадратичной так, чтобы обе функции совпадали на границах интересующего нас интервала Х_к<Х<Х_к+1.

Формула Ньютона имеет вид:

(2.5)

Пример

Возьмем ту же задачу, что и для линейной интерполяции.

r, мкм	30	40	50	60	80	100
I, А	0,690	1,065	1,485	1,950	3,000	4,200

δI_4+1/2=I₅- I₄=1,050

δI_5+1/2=I₆- I₅=1,200

δ²I₅=δI_5+1/2- δI_4+1/2= 0,150

S=2 мкм , l=20 мкм, S/l ₌0,01

I=1,950+1,050*0,1+0,150 *0,1(0,1-1)=2,0483 (А)

Квадратичная интерполяция по формуле Бесселя

Недостатком формулы Ньютона является ее несимметричность относительно заданного аргумента Х_к<Х<Х_к+1/2, а использовании значения функции У_к, У_к+1,Ук₊₂.

Этот недостаток устраняется формулой Бесселя

(2.6)

Пример

Рассмотрим ту задачу, что и в двух предыдущих случаях

r, мкм	30	40	50	60	80	100
I, А	0,690	1,065	1,485	1,950	3,000	4,200

Для того чтобы сохранить шаг таблицы постоянным ( l =20 мкм ) в нужном интервале, опустим третью пару значений.

r, мкм	30	40	60	80	100
I, А	0,690	1,065	1,950	3,000	4,200

r, мкм	30	40	60	80	100
I, А	0,690	1,065	1,950	3,000	4,200

δI_2+1/2= I₃- I₂ = 0,885

δI _3+1/2=I₄- I₃=1,050

δI _4+1/2=I₅- I₄=1.200

δ ²I₃= δI_3+1/2- δI _2+1/2=0,165

δ ²I₄= δI_4+1/2 – δI _3+1/2=1,150

I=1,065+1,950 + 1,050*(0.1-1) + 0,165+0,150 *0.1*(0.1-1)=2.0479(A)

2 2 4

Интерполяция методом Лагранжа

Для этого метода таблица может иметь произвольный шаг l.

Искомую функцию представляют в виде степенного ряда

Y=a+bx+cx²+dx³+m (2.7)

Для небольших интервалов изменения аргумента можно ограничиться тремя членами в (2.7) (опять квадратичная интерполяция). В этом случае выбираются из таблицы три точки (х₁, у₁), (х₂, у₂), (х₃, у₃), достаточно близкие к заданному значению аргумента Х. Постоянные а, в, с определяются из системы уравнений, полученных при подстановке в (2.7) выбранных точек.

В форме определителя уравнение (2.7) записывается

Y 1 X X²

Y₁ 1 X₁ X₁²= 0

Y₂ 1 X₂ X₂²

Y₃ 1 X₃ X₃²

Или через миноры

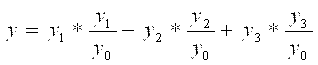, где Y_i – миноры.

Например:

Пример

Возьмем ту же задачу, что и прежде.

r, мкм	30	40	60	80	100
I, А	0,690	1,065	1,950	3,000	4,200

I 1 r r²

I₃ 1 r₃ r₃²= 0

I₄ 1 r₄r₄²

I₅1 r₅ r₅²

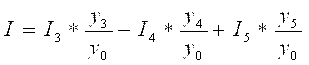
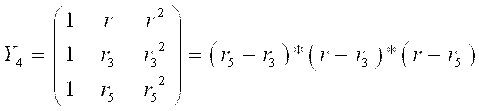
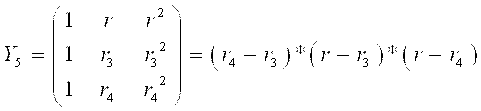
I =2,047 А

Экстраполяцией называют операцию определения функции при значениях независимой переменной, лежащих за пределами таблицы. Экстраполяция производится теми же методами. Однако, следует помнить, что достоверность экстраполяции в сильной степени зависит от того, насколько уверенно найденную экспериментальную зависимость можно распространить за переделы области эксперимента.

3.ПРЕСТАВЛЕНИЕ ДАННЫХ С ПОМОЩЬЮ УРАВНЕНИЙ

3.1. Выбор вида эмпирической формулы

Уравнение, представляющее экспериментальные данные, называется эмпирическим, если оно не было получено теоретически. Для нахождения формы зависимости данные опыта наносят на график в виде точек, проводят плавную кривую, а затем, пользуясь принципами аналитической геометрии, подбирают вид уравнения для этой кривой. Чтобы облегчить использование этого метода и повысить его точность, рекомендуется, когда это возможно, выбирать такую систему координат, в которой экспериментальная кривая возможно ближе приближается к прямой линии.

После того, как сделано предположение о виде функции, необходимо проверить пригодность выбранной формулы.

Графический способ проверки

1-й этап. Для предполагаемого соотношения f(х,у,a,b) = 0, следует подобрать две не содержащие произвольных постоянных «а» и «в» функции F₁ и F₂, с помощью которых может быть записано уравнение:

F₁=A+ВF₂(3.1)

2-й этап. Функции F₁ и F₂вычисляют для четырех-пяти далеко отстоящих пар значений (Х,У).

3-й этап. Строят график зависимости F₁ от F₂ .Если получается прямая линия, то это значит, что выбранное уравнение пригодно для описания данных.

Пример

Задана таблица значений (Х,У)

Таблица 3.1

Х	1	4	6	9
У	1,78	3,74	5,31	10,87

Будем искать формулу типа у =ае ^вх

Функции F₁ и F₂выбираем в виде F₁=lgY , F₂=x

Тогда А=lga; B=b*lg e; lgY =lga +(b*lge) x

Таблица 3.2

Х	1	4	6	8
У	1,78	3,74	6,31	10,97
Lg Y	0,250	0,537	0,725	1,040

На рис.3.1 видно, что экспериментальные точки хорошо укладываются на прямую линию.

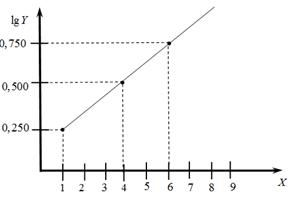
Рис. 3.1. Расположение экспериментальных точек.

Графическим способом можно проверить большое число уравнений.

Y=ax y=a+bx y=aх^в y=e ^(a+bx)

y=ae^bx y=ax^b Y=х/( a+bx)

Нельзя пользоваться графическим способом проверки уравнений

Y=a(1-e^bx) y=x^a+bx и др.

Табличный способ проверки

Этот метод удобен в том случае, когда выбранное уравнение содержит более двух произвольных постоянных.

1-й этап. Нанесение экспериментальных данных в виде точек на график.

2-й этап. Построение таблицы по этому графику с постоянным шагом l.

3-й этап. Вычисление последовательных разностей до некоторого определенного порядка (зависящего от вида уравнения).

Критерием пригодности уравнения является постоянство старших разностей (табл.3.3).

Таблица 3.3

№/№	Предполагаемый вид формулы	Критерий пригодности
1	y=a+bx+cx+cx²+…+qxⁿ	δⁿy=const
2		δⁿy=const
3	Y²=a+bx+cx+cx²+…+qxⁿ	δⁿ(y²)=const
4	Lg y=a+bx+cx+cx²+…+qxⁿ	δⁿ(lgy)=const
5	y=a+blgx+c(lgx)²+cx²+…	δy=const
6	y=ab^x; y=ae^bx	δ(lgy)=const
7	y=a+bx+cd^x; y=a+bx+ce^dx	δ(lgδ²y)=const
8	y=a+bx^c	δ(lgδy)=const
9	y=axe^bx	δ(lgy-δlgx)=const

Пример:

Имеем уравнение y=a+bx+cx+cx²+dx³

y+Δу=а+b(х+l)+c(x+l)²+d(x+l)³

Δу=(bl+cl²+dl³)+(2cl+3dl²)x+3dlx²

Так как l=const; Δу=а'+b'х+с'х²; Δ²у=а'+b'х

Отсюда Δ³у=а'"= const.

Последнее равенство показывает, что если справедливо исходное уравнение и l=const, то табличные разности третьего порядка будут постоянными.

3.2. Определение коэффициентов уравнения

Графический метод

1. Уравнение с двумя произвольными коэффициентами. В этом случае коэффициенты могут быть определены в процессе проверки пригодности формулы описанным ранее графическим способом.

2. уравнение с тремя произвольными коэффициентами. Задача состоит в исключении одного коэффициента и после этого применении пункта 1.

Пример 1.

Уравнение y=a+bx+cx₀²

Начало координат переносят в такую точку (Х₀, Y₀) кривой, чтобы можно было освободиться от свободного члена уравнения. Связь новых координат со старыми будет Х′=Х-Х₀ и Y′=Y-Y_0,а уравнение перепишется

y=b′x+c′x′² или

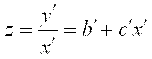(3.2)

В переменных Z^′, Х′ имеем уравнение прямой с двумя произвольными коэффициентами. Коэффициенты исходного уравнения связаны с b′ и c′ простыми соотношениями:

С=С′ b=b′-2c′х₀ a=y₀-b′x₀+c^′x₀²

Пример 2

Уравнение у=а +вх^с

Задача остается прежний – исключить один коэффициент. Для этого на экспериментальной кривой выбираем 3 далеко отстоящих точки (Х₁ У₁); (Х₂ У₂); (Х₃ У₃), так чтобы

Тогда

Отсюда

Теперь введем новую переменную Z=Y-A

Z=bx^c

Т.о., исходное уравнение сведено к уравнению с двумя коэффициентами.

Если кривая, изображающая зависимость lgZ=f(lgX) не является точной прямой и обращена вогнутостью вниз, то значит, что найденное значение а слишком мало. Поправка вносится новым выбором трех исходных точек.

Метод избранных точек

Отыскание постоянных коэффициентов выбранного уравнения проводится по следующей схеме.

1. Строится график У=f (x)

2. На кривой выбирается n точек (х_i, у_i). (n=числу определяемых коэффициентов)

3. Подставляя эти точки в выбранное уравнение, получаем систему n уравнений с n неизвестными.

4. Решая эту систему уравнений, находим коэффициенты. Если выбранное уравнение линейно относительно определяемых коэффициентов, то пункты 3 и 4 можно совместить применением определителей.

Пример. Дана таблица экспериментальных значений X_i иY_i(первые два столбца табл.3.4).

Таблица 3.4

Х	У	Lg Y
0,125	1,595
0,250	2,239
0,325	2,995
0,450	6,625
0,575	12,97
0,675	27,93
0,750	53,88
0,850	141,7
0,925	320,8
0,975	571,3

Будем искать уравнение в виде

y=ae^bx^+сх2 (3.3)

Чтобы построить кривую с достаточной степенью точности целесообразно перейти в полулогарифмическую шкалу (третий столбец табл.3.5).

Таблица 3.5

Х	У	Lg Y
0,125	1,595	0,2028
0,250	2,239	0,350
0,325	2,995	0,4764
0,450	6,625	0,7502
0,575	12,97	1,1096
0,675	27,93	1,4459
0,750	53,88	1,7314
0,850	141,7	2,1514
0,925	320,8	2,5062
0,975	571,3	2,7569

lnY=lna+bx+cx²

LgY=lga+0,4343bx+0,4343cx²=a′+b′x+c′x²

Строим график LgY =f(x) и выбираем три точки (рис.3.3) и записываем определитель (рис.3.2).

Рис. 3.2. Построение графика LgY =f(x).

Lg y 1 X X²

0,356 1 0,250 (0.250)

1,031 1 0,550 (0.250) = 0

2,158 1 0,850 (0.850)

Однако, это уравнение сильно упростится, если мы сделаем замену переменных

Z 1 X′ X′²

-0,675 1 -1 1

0 1 0 0 =0

1,127 1 1 1

1 -1 1 -0,675 -1 1 -0,675 1 1 -0.675 1 -1

Z 1 0 0 - 0 0 0 +x^′0 1 0 -x^′20 1 0 =0

1 1 1 1,127 1 1 1,127 1 1 1,127 1 1

LgН =0,1388+0,2411x +2,5111x ²

Y=1,377^e ^10,5552^x^+5,782^x²

Метод последовательных приближений

Если искомое уравнение линейно относительно коэффициентов или может быть приведено к такому виду, полученное каким-либо способом уравнение может быть улучшено методом последовательных приближений.

Пусть мы получили для уравнения у=а+вх+сх² значения а′,в′,с′ и.т.д., по которым можно определить y′. Улучшение уравнения выполняется по следующей схеме.

1. Для различных х_iзависимости у – у_i =Δ_i

2. Строят график зависимости у – у_i=f(х).

3. Находят уравнение этой кривой одним из описанных способов

4. Это поправочное уравнение прибавляют к уравнению первого приближения.

Так как получат уравнение второго приближения. Очевидно, наилучшим (n-тым ) приближением будет такое, когда кривая полученная в пункте 2 совпадает с осью Х.

Пример.

Получим уравнение второго приближения для задачи, решенной в предыдущим пункте. Будем считать полученное выше уравнение первым приближением. В двух столбцах табл.3.6 приведены значения lgY′ и lgY- lgY′.

Таблица 3.6

Х	У	lgY	lgY′	Δ= lgY- lgY′.
0,125	1,595	0,2028	0,2028	- 0,0054
0 ,250	2,239	0,3500	0,2559	- 0 ,0059
0 ,325	2,995	0,4764	0,4824	-0 ,0060
0 ,450	5,685	0,7502	0 ,7557	-0,0055
0 ,575	12,97	1,1069	1,1076	- 0 ,0007
0 ,675	27,95	1,4459	1,4456	- 0 ,0004
0,750	53,88	1,7314	1,7320	-0 ,0006
0 , 850	141,7	2,1514	2,1579	- 0 ,0065
0 ,925	320,8	2,5062	2,5103	- ,0041
0 ,975	571,3	2,7569	2,7610	- 0,0041

На рис.3.3 приведена зависимость Δ=f(x).

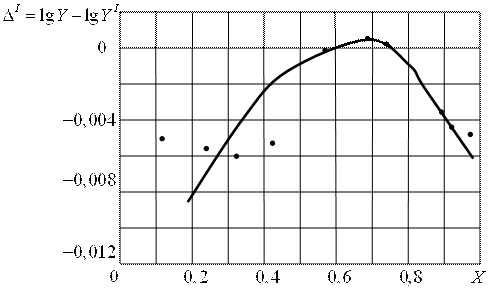
Рис.3.3. Зависимость Δ=f(x).

Выбираем три точка (0,3-0,0060) (0,6-0,0004) ,(0,9-0,0040)

Δ^I1 х х²

-0,0060 1 0,3 0,09 =0

-0,0004 1 0,6 0,36

-0,0040 1 0,9 0,81

1 0,3 0,09 0,0060 0,3 0,09 0,0060 1 0,09 0,0060 1 0,3

Δ^I 1 0,6 0,36 + 0,0004 0,6 0,36 - 0,0004 1 0,36 *0,0004 1 0,6 х²=0

1 0,9 0,81 0,0040 0,9 0,81 0,0040 1 0,81 0,00401 1 0,9

Δ^I = -0,0184+0,0580x-0,0467x²

Lgy^II=Lgy¹+ Δ^I =(0,1388+А^I)+(0,2411+b^I)x+(2,5111+c^I)x²

Lgy^II=0,1204+0,2991x +2,4644x²

В четвертом приближении

Lgy ^IV =0,1273+0,2753x + 2,4822x²

Y^IV=1,3406 e^{(0,6325x+6,7170x 2)}

Самостоятельная работа № 4

Э.д.с. Е стандартной термопары (90% Pt – 10% Rh) при температуре холодного спая О^оС представлена как функция температуры Т (табл.3.7).

Таблица 3.7

Т^oC	Е мв	Т^оС	Е мв
0	0,000	1000	9,569
200	1,436	1200	11,924
400	3,850	1400	14,312
600	5,222	1600	16,674
800	7,330

Используя критерий постоянства старших разностей, определить какова должна быть степень многочлена относительно Т-О^о С чтобы с помощью этого многочлена можно было достаточно точно описать зависимость Е =f (Т-О^оС)

Самостоятельная работа № 5

Построить эмпирическую формулу угловой замисимости коэффициента рассеяния ионов С₃⁺ с энергией 1 кэВ на поликристаллическом вольфраме. получить второе приближение.

λ	К_p⁺
0	0,4
10	0,42
20	0,48
30	0,52
40	0,57
50	0,60
60	0,64

Самостоятельная работа № 6

Построить эмпирическую формулу угловой зависимости коэффициента рассеяния ионов С₃⁺ с энергией 1 кэВ на поликристаллическом молибдене. Получить второе приближение.

λ	К_p⁺
0	0,18
10	0,21
20	0,25
30	0,32
40	0,36
50	0,44
60	0,56

ЛИТЕРАТУРА

1.Налимов В.В., Теория эксперимента , М., Наука, 1971, 207 стр.

2.Блохин В.Г., Глудкин О.П., Гуров А.И., Ханин М.А., Современный эксперимент ( подготовка, проведение, анализ результатов) ,М., Радио и связь,1997,230 стр.

3. Международный семинар Белл лаборатории. Технологии и услуги
следующего века, М., 1994.

МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ

НАУЧНЫХ ИССЛЕДОВАНИЙ

Рассмотрено на заседании кафедры МАТ

«___» __________ 2014 года (протокол №___)

и рекомендовано к печати

Рекомендовано к печати научно-методическим

советом ТУИТ (протокол №___ от__________)

Составитель: Т.Д.Раджабов

Ответственный редактор: к.т.н., доцент Р.Ибраимов

Корректор: С.Х. Абдуллаева