МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Факультет «Телекоммуникационные технологии»

Кафедра «Технологии мобильной связи»

Методическое пособие на тему

«Использование программы Matlab в учебном процессе»

Составитель ст.преп. Хатамов А.П.

Ташкент 2015

Система Matlab представляет собой мощное средство решения инженерно-технических задач. Она является универсальным программным продуктом, позволяющим решать широкий спектр задач от символьных вычислений до сложных инженерных расчетов.

При разработке собственных настроек в системе Matlab для управления работы над специфическими задачами, а зачастую и просто при решении задач требуются определенные навыки, которые можно отнести к навыкам программирования. И хотя Matlab не является ни средой, ни языком программирования, она все же предоставляет собой базовые средства, присутствующие в большинстве языков программирования.

Данное методическое пособие позволит студентам познакомиться с этими основными средствами и приобрести навыки их использования.

Введение

Система MatLAB создана фирмой MathWork Inc. (США, г. Нейтик, штат Массачусетс). Хотя впервые эта система начала использоваться в конце 70-х лет, расцвет ее применения начался в конце 80-х. Последние версии MatLAB, - это чрезвычайно развитые системы, которые содержат огромную совокупность процедур и функций, необходимых инженеру и научному работнику для осуществления сложных численных расчетов, моделирования поведения технических и физических систем, оформления результатов этих расчетов в наглядном виде.

Система MatLAB (сокращение от MATrix LABoratory - матричная лаборатория) представляет собой интерактивную компьютерную систему для выполнения инженерных и научных расчетов, ориентированную на работу с массивами данных. Система предполагает возможность обращения к программам, которые написаны на языках FORTRAN и C.

Привлекательной особенностью системы является то, что она содержит встроенную матричную и комплексную арифметику. Система поддерживает выполнение операций с векторами, матрицами и массивами данных, расчет ранга и чисел обусловленности матриц, поддерживает работу с алгебраическими полиномами, решение нелинейных уравнений и задач оптимизации, интегрирование функций в квадратурах, численное интегрирование дифференциальных и разностных уравнений, построение разнообразных видов графиков и т.д. В ней реализована удобная операционная среда, которая позволяет формулировать проблемы и получать решения в обычной математической форме.

Основной объект системы MatLAB - прямоугольный числовой массив (матрица), который допускает комплексные элементы. Использование матриц не требует явного указания их размеров. Система позволяет решать многие вычислительные задачи за значительно меньшее время, чем то, которое необходимо для написания соответствующих программ на языках FORTRAN, BASIC и C.

Система MatLAB выполняет операции с векторами и матрицами даже в режиме непосредственных вычислений без какого-либо программирования. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции, как обращение матрицы, вычисление ее собственных значений и векторов, решение систем линейных алгебраических уравнений и многое другое. Тем не менее, характерная основная особенность системы – ее "открытость", то есть легкость ее модификации и адаптации к конкретным задачам пользователя. Пользователь может ввести в систему любую новую команду, оператор или функцию и пользоваться потом ими так же просто, как и встроенными операторами и функциями.

В базовый набор слов системы входят: спецзнаки; знаки арифметических и логических операций; арифметические, тригонометрические и некоторые специальные математические функции; функции быстрого преобразования Фурье и фильтрации; векторные и матричные функции; средства для работы с комплексными числами; операторы построения графиков в декартовой и полярной системах координат, трехмерных поверхностей и т.п.

Система MatLAB имеет собственный язык программирования. Запись программ в системе является традиционной и потому обычной для большинства пользователей персональных компьютеров. И вдобавок система дает возможность редактировать программы при помощи любого привычного для пользователя текстового редактора.

MatLAB имеет широкие возможности для работы с сигналами, для расчета и проектирования аналоговых и цифровых фильтров, для построения их частотных, импульсных и переходных характеристик. В наличии и средства для спектрального анализа и синтеза, в частности, для реализации прямого и обратного преобразования Фурье. Благодаря этому система довольно удобна для проектирования электронных устройств.

Робота в среде MatLab может осуществляться в двух режимах:

· в режиме калькулятора, когда вычисления осуществляются сразу после набора очередного оператора или команды MatLab;

· путем вызова имени программы, написанной на языке MatLAB, предварительно составленной и записанной на диске.

В обоих режимах пользователю доступны практически все вычислительные возможности системы, в том числе по выводу информации в графической форме. Программный режим позволяет сохранять разработанные вычислительные алгоритмы и, таким образом, повторять вычисления при входных данных.

Система MATLAB

Система MATLAB состоит из основных частей:

Язык MATLAB. Это язык матриц и массивов высокого уровня с управлением потоками, функциями, структурами данных, вводом-выводом и особенностями объектно-ориентированного программирования. Это позволяет как программировать в "небольшом масштабе" для быстрого создания черновых программ, так и в "большом" для создания больших и сложных приложений.

Среда MATLAB. Это набор инструментов и приспособлений, с которыми работает пользователь или программист MATLAB. Она включает в себя средства для управления переменными в рабочем пространстве MATLAB, вводом и выводом данных, а также создания, контроля и отладки М-файлов и приложений MATLAB.

Управляемая графика. Это графическая система MATLAB, которая включает в себя команды высокого уровня для визуализации двух- и трехмерных данных, обработки изображений, анимации и иллюстрированной графики.

Программный интерфейс. Это библиотека, которая позволяет писать программы на Си и Фортране, которые взаимодействуют с MATLAB. Она включает средства для вызова программ из MATLAB (динамическая связь), вызывая MATLAB как вычислительный инструмент и для чтения-записи файлов.

Знакомство со средой MATLAB

Система MATLAB является интерактивной системой для выполнения инженерных и научных расчетов, ориентированной на работу с массивами данных.

В системе MATLAB можно выделить следующие основные функциональные элементы:

1. Командное окно для интерактивного ввода команд с клавиатуры.

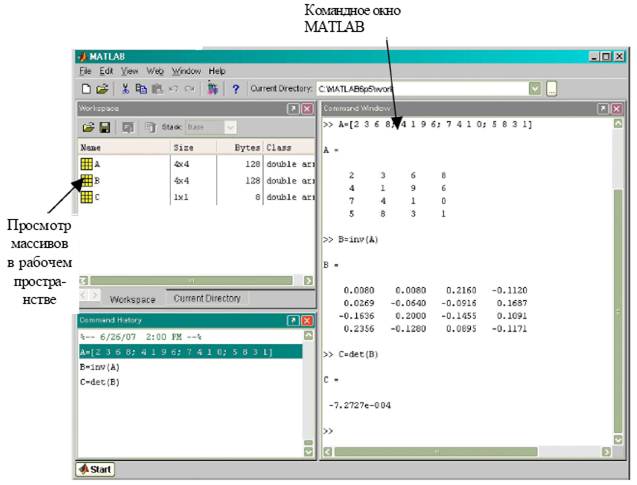
Рис. 1. Интерфейс среды MATLAB

2. Рабочее пространство, содержащее данные, с которыми производится работа. Данные представляются в виде переменных -массивов.

3. Библиотеки (Toolboxes) функций и команд MATLAB, включая стандартные команды MATLAB

4. Редактор m-файлов, предназначенный для создания и редактирования скриптов и функций MATLAB.

5. Справочная система MATLAB.

Простейшим способом работы с командами MATLAB является их ввод в командном окне и получение ответа в интерактивном режиме. Однако интерактивный ввод команд с клавиатуры не всегда удобен, поэтому предусмотрена возможность написания скриптов (сценариев).

Все переменные в системе MATLAB представляются в виде массивов.

Поэтому каждая переменная обладает следующими свойствами:

1. Размерность массива – количество измерений (для вектора

размерность равна 1 – одномерный массив; для прямоугольной матрицы – 2 – двумерный массив).

2. Длина массива – количество элементов массива.

3. Размер массива по каждому измерению.

4. Тип данных элементов массива (таблица 1).

Скалярные переменные в системе MATLAB представляются как массивы единичной длины. При создании числовой переменной тип данных по умолчанию устанавливается в числовой с плавающей точкой (тип double). Переменные числового типа могут принимать кроме числовых значений значения Inf, -Inf и NaN, которые означают бесконечность, минус бесконечность и не числовое значение соответственно.

Таблица 1. Типы данных среды MATLAB

Тип	Описание
int8 int16 int32 int64	8, 16, 32, 64 – битные знаковые целые числа
uint8 uint16 uint32 uint64	8, 16, 32, 64 – битные без знаковые целые числа
single double	Числа с плавающей точкой с единичной и с двойной точностью
logical	Двоичные числа: 1 (истина), 0 (ложь)
char	Символьные переменные
cell	Массив ячеек разных типов данных

Также имеются зарезервированные переменные среды и управляющие функции MATLAB (таблицы 2 и 3).

Таблица 2. Зарезервированные переменные среды MATLAB

Имя переменной	Описание
pi	Содержит значения числа «пи»
i, j	Комплексная единица
eps	Относительная точность числовых значений с плавающей точкой
ans	Содержит результат выполнения последней команды
%	Символ, обозначающий начало комментария, вся строка после этого символа может содержать любой текст
;	Символ, обозначающий переход к следующему действию без отображения результатов команды в диалоговое окно
Inf	Указание бесконечности (например, возникает в результате деления на ноль)
Nan	Указание нечислового значения (например, неопределенность ноль деленный на ноль)

Таблица 3. Управляющие функции

Название функции или команды	Описание
help	Выводит описание функции или команды в командное окно
lookfor	Выводит список функций в описание которых входит ключевое слово
which	Дает путь m-файла в котором содержится указанная функция
load	Загружает переменные рабочей области MATLAB из файла *.mat
save	Сохраняет переменные рабочей области MATLAB в файл *.mat
clear	Удаляет переменные в рабочей области (пример: clear all)
clc	Отчищает командное окно
echo	Включает/выключает вывод результата, по умолчанию включен

Создание и работа с переменными

При создании переменных в системе MATLAB нет необходимости определять явно имя переменной, тип данных или размерность массива.

Когда MATLAB встречает новое имя переменной, автоматически создается переменная с таким именем и автоматически выделяется необходимое количество памяти.

Для этого могут использоваться скобки, которые осуществляют объединение скаляров или массивов, при этом в результате получается также массив (см. примеры в таблице 4).

Элементы внутри скобок могут быть разделены запятой, либо точкой запятой, в зависимости от того, по какому измерению осуществляется объединение. В системе MATLAB принято, что для прямоугольных матриц (двумерных массивов) первое измерение определяет число строк, а второе измерение – число столбцов. При использовании квадратных скобок запятая разделяет строки, а точка с запятой разделяет столбцы.

Задание массивов состоящих из диапазона равноотстоящих чисел может быть осуществлено с помощью символа двоеточия a:b:c. При этом указывается значение первого элемента массива a, шаг приращения b и максимально возможное значение (минимально возможное, если b отрицательно) в массиве.

Также существует ряд функций, которые позволяют создавать и заполнять массивы разного размера (см. таблицу 5).

Таблица 4. Примеры создания переменных

Команды

Описание

NumVar = 0.0321;

Команда создает числовую переменную с именем NumVar, и значением которой является число 0.0321

Text = ‘Текст’;

Команда создает символьную переменную с именем Text, и значением которой является строка ‘Текст’

A = [1; 2];

Команда создает переменную с именем A, и значением которой является массив размером 2X1:

B = [1, 2];

Команда создает переменную с именем B, и значением которой является массив размером 1X2:

1 2

D = 1:5;

Команда создает переменную с именем D, и значением которой является массив размером 1X5:

1 2 3 4 5

F = zeros(2, 3);

Команда создает переменную с именем F, и значением которой

является массив размером 2X3, заполненный нулями

Таблица 5. Функции создания элементарных массивов

Название функции или команды	Описание
eye	Создает единичную матрицу, например, команда eye(2) создаст матрицу размером 2X2: 1 0 0 1
ones(m, n)	Создание массива размером mxn заполненного единицами
zeros(m, n)	Создание массива размером mxn заполненного нулями
rand(m, n)	Создание массива размером mЧn заполненного случайными числами равномерно распределенными в интервале (0; 1)
randn(m, n)	Создание массива размером mЧn заполненного случайными числами нормально распределенными с нулевым средним и единичной дисперсией

Доступ к отдельным элементам массива осуществляется с помощью указания индексов в скобках. Индексы (номера) по разным измерениям отделяются запятой. Таким образом если создан двухмерный массив с именем Matrix, то доступ к элементу массива, который находится на пересечении m-ой строки и n-ого столбца осуществляется следующим образом:

Element = Matrix(m, n);

Доступ получить можно не только к отдельному элементу массива, но и к целому блоку. Для этого задаются не отдельные индексы, а массивы индексов. Например команда

Block = Matrix([2, 3], [4, 5]);

запишет в переменную Block квадратную матрицу, образованную из элементов массива Matrix, которые расположены на пересечении 2 и 3 строки и 4 и 5 столбца массива Matrix.

Кроме того, вместо индексов можно указывать специальные символы. Символ двоеточия указывает, что необходимо взять весь диапазон индексов по данному измерению. Символ end указывает, что необходимо взять последний элемент по данному измерению.

Например команда

Vector = Matrix(:, end);

запишет в переменную Vector последний столбец массива Matrix.

В таблице 6 приведены основные функции для определения параметров переменных

Таблица 6. Основные функции для определения параметров переменных

Название функции или команды	Описание
length(A)	Определяет длину вектора A
ndims(A)	Определяет количество измерений массива A numel(A) Определяет количество элементов массива A
size(A)	Определяет размер массива A
disp(A)	Выводит значение переменной A в командное окно
isscalar(A)	Определяет, является ли переменная A скаляром

Математические выражения и функции

Большинство функций в системе MATLAB предназначены для работы с массивами. Поэтому математическим функциям, таким как sin, log, в системе MATLAB можно в качестве аргумента передавать массив числовых значений.

При этом результат вычисляется для каждого элемента массива отдельно. Исключением являются специализированные для работы с матрицами функции, которые работают не поэлементно.

В таблицах 7 и 8 приведены операторы среды MATLAB и некоторые элементарные математические функции.

Таблица 7. Операторы среды MATLAB

Операторы	Описание
( )	Задают порядок вычислений
* /	Операции умножения и деления
^	Возведение в степень
`	Операция транспонирования
+ -	Сложение и вычитание
< >	Операnтор меньше или больше
<= >=	Операnтор меньше или равно и больше или равно
= ~=	Операnтор равно и неравно
&	Оператор «и»
\|	Оператор «или»
~	Оператор «не»

Таблица 8. Некоторые элементарные математические функции

Название функции или команды	Описание
sin	Вычисляет синус
cos	Вычисляет косинус
tan	Вычисляет тангенс
atan	Вычисляет арктангенс
exp	Возведение в степень
log	Натуральны логорифм
sqrt	Корень квадратный
round	Округление числа до целого

Графические команды и функции

Система MATLAB удобна для вывода данных в графическом виде. Для этого существует ряд высокоуровневых функций. Эти функции позволяют построить гистограммы, графики линий и поверхностей. При этом они автоматически выставляют параметры отображения. Но любые параметры отображения графиков могут быть изменены с помощью специальных низкоуровневых функций.

Для отображения графической информации создается отдельное окно. Такое окно может быть создано командой figure. Каждая высокоуровневая функция выводит графическую информацию в текущее графическое окно. При этом содержимое окна перезаписывается. Если такое окно не создано высокоуровневые функции автоматически создают его.

Низкоуровневые функции работают с текущим графическим окном. Они предназначены для изменения параметров отображения, а также для вывода отдельных графических элементов.

Таблица 9. Некоторые высокоуровневые графические функции

Название функции или команды	Описание
plot	Строит линии или точки в линейном масштабе
loglog	Строит линии или точки в логарифмическом масштабе
polar	Строит линии или точки в полярных координатах

Таблица 10. Некоторые низкоуровневые графические функции

Название функции или команды	Описание
figure	Графическое окно
title	Имя графика
xlable	Метка по оси X
axis	Изменение масштаба по оси
subplot	Разделения окна на несколько областей

При работе с графическими функциями необходимо понимать объект - ориентированную структуру графики. Для вывода графических элементов создается ряд объектов:

1. Графическое окно (figure).

2. Система координат (axes).

3. Различные графические элементы (line, patch, text, surface, image, light)

Каждому из этих объектов ставиться в соответствие идентификатор (дескриптор - handle). Знание идентификатора объекта, дает возможность читать и изменять свойства объекта с помощью функций get и set.

Рассмотрим пример использования введенных выше понятий для написания программы в MATLAB.

Пример использования функции MATLAB

Формирование радиосигнала с использованием двоичной

амплитудной модуляции (BASK).

% Задаем частоту дискретизации

SamplingRate = 1000;

% Определяем период дискретизации

SamplingPeriod = 1/SamplingRate;

% Задаем информационную последовательность битов

Bits = [1, 0, 0, 1, 1, 0, 1, 0, 1, 1];

% Определяем количество передаваемых битов

NoBits = length(Bits);

% Задаем длительность одного бита в секундах

TBit = 1;

% Определяем длительность всей последовательности битов в секундах

SignalDuration = T * NoBits;

% Формируем массив значений времени в секундах, длина массива соответствует количеству дискрет в создаваемом сигнале

Time = 0 : SamplingPeriod : SignalDuration;

% Формируем сигнал последовательности битов, используя функцию интерполяции

SignalBits = interp1(0.5 : NoBits, Bits, Time, 'nearest', 'extrap');

% Задаем период несущего синусоидального сигнала в секундах

TSin = 0.1;

% Определяем частоту несущего синусоидального сигнала в герцах

SinRate = 1/TSin;

% Формируем несущий синусоидальный сигнал

SignalSin = sin( 2 * pi * SinRate * Time );

% Модулируем несущий синусоидальный сигнал сигналом последовательности бит

ModulatedSignal = SignalBits .* SignalSin;

close all % закрываем окна для рисования открытые ранее

% Рисуем график модулированного сигнала

H = figure; % Создаем окно для рисования

set(gcf,'Units', 'normalized'); % Определяем

set(H, 'Position', [0.1 0.03 0.8 0.25]);% положения окна

plot(Time, ModulatedSignal); % Рисуем сигнал

axis([0 SignalDuration -1.5 1.5]); % Изменяем масштаб отображения

title('Modulated signal'); % Задаем название графика

xlabel('Time, seconds'); % Задаем метку временной оси

% Рисуем график синусоидального сигнала

H = figure; % Создаем окно для рисования

set(gcf,'Units', 'normalized'); % Определяем

set(H, 'Position', [0.1 0.33 0.8 0.25]);% положения окна

plot(Time, SignalSin); % Рисуем сигнал

axis([0 SignalDuration -1.5 1.5]); % Изменяем масштаб отображения

title('Sinusoidal signal'); % Задаем название графика

xlabel('Time, seconds'); % Задаем метку временной оси

% Рисуем график сигнала последовательности бит

H = figure; % Создаем окно для рисования

set(gcf,'Units', 'normalized'); % Определяем

set(H, 'Position', [0.1 0.63 0.8 0.25]);% положения окна

plot(Time, SignalBits); % Рисуем сигнал

axis([0 SignalDuration -0.5 1.5]); % Изменяем масштаб отображения

title('Bits signal'); % Задаем название графика

xlabel('Time, seconds'); % Задаем метку временной оси

Результаты программы графиков модулированного и синусоидального сигнала а также сигнала последовательности бит наглядно представлен на рисунках 2,3 и 4.