Узбекское агентство связи и информатизации

 

 

Ташкентский университет информационных технологий

 

 

 

 

 

Кафедра: Телевидения и радиовещания

 

 

 

 

 

Учебное пособие-практикум

по дисциплине «Цифровое телевидение»

для магистрантов ФРРТ специальностей

5А522005 (Радиотехника)

5А522105 (Системы мобильной связи)

 

 

 

Ташкент 2005 г.

 

 

СОДЕРЖАНИЕ

 

 

Предисловие

3

Общие замечания

3

Список литературы

3

1. Информационная оценка параметров ТВ изображений

4

2. Квантование сигналов изображения

6

3. Кодирование

9

4. Дискретное преобразование Фурье (ДПФ) и дискретно-косинусное

преобразование (ДКП)

13

5. Нерекурсивные и рекурсивные цифровые фильтры

17

6. Выбор параметров АЦП

23

7. Расчет ширины полосы передаваемых частот и скорости передачи

последовательности символов

24

8. Задачи для практических занятий: условия задач и их решение

26

8.1. Расчетные формулы

26

8.2. Условия задач

28

8.3. Решение задач

29

9. Контрольные вопросы

32

9.1. Контрольные вопросы по первому модулю

32

9.2. Контрольные вопросы по второму модулю

33

9.3. Контрольные вопросы к итоговому контролю

34

 

 

ПРЕДИСЛОВИЕ

         Учебное пособие-практикум предназначено для проведения практических аудиторных занятий и контрольных работ по дисциплине «Цифровое телевидение», разработано согласно Рабочей программе по специальности 5А522005 (Радиотехника) и 5А522105 (Системы мобильной связи). Утверждено на заседании кафедры Телевидения и радиовещания (Протокол №5 от 21.07.04), на методическом совете ФРРТ (Протокол №1 от 6.09.04) по программе подготовки магистрантов.

В подготовке данного пособия и рабочей программы по данной дисциплине активное участие принимали магистранты Ибраева С., Игнатьева О., Четин А., которым авторы выражают свои благодарности.

 

ОБЩИЕ ЗАМЕЧАНИЯ

         Практические занятия по дисциплине «Цифровое телевидение» состоят из аудиторных и контрольных работ.

         Целью практических занятий является помощь магистрантам в практическом исследовании и изучении параметров и информационных характеристик систем обработки, кодирования, передачи и хранения цифровых сигналов в ТВ системах.

 

СПИСОК ЛИТЕРАТУРЫ

1.     Самойлов В.Ф., Хромой Б.Н. Телевидение. Учебник для ВУЗов. Москва: Связь 1975г.

2.     Телевидение. Учебник для ВУЗов под ред. Джакония В.Е. Москва: Связь 1986г.

3.     Зубарев Ю.Б., Глориозов Т. Передача изображений. Учебник для ВУЗов связи. Москва: Связь 1982г.

4.     Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах. Москва: Связь 1978г.

5.     Зубарев Ю.Б. и др. Цифровое ТВ вещание. Основы, методы, системы. Москва: НИИР 2001г.

6.     Локшин Б.А., Цифровое телевизионное вещание. Москва: Компания «Сайрус систем» 2001г.

7.     Кривошеев М. и др. Интерактивное телевидение. Москва: Радио и связь 2000г.

8.     Таджибаев Ш.З. Цифровое телевидение. Ташкент: РИСО 1998г.

9.     Смирнов А.В. Основы цифрового телевидения. Москва: Горячая линия – Телеком 2001г.

10. Аезгаус Г.Г. и др. Справочник по вероятностным расчетам. Москва: Воениздат 1970г.

11. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. Пер. с англ. – М.: 1978 – 848c.

12. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. Пер. с англ. – Москва: ''Мир'', 1982г. – 428с.

13. Хемминг Р.В. Цифровые фильтры. Пер. с англ. – Москва: ''Недра'', 1987г. – 221с.

14. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.И. Цифровая обработка сигналов. – Москва: Радио и связь, 1990г. – 256с.

15. Канасевич Э.Р.  Анализ временных последовательностей в геофизике. - Москва: Недра, 1985г. - 300с.

16. Никитин А.А.  Теоретические основы обработки геофизической информации. Учебник для вузов. - Москва: Недра, 1986г. - 342с.

17. Материалы сервера: http://dspdav.nm.ru/

18. Материалы сервера: http://prodav.narod.ru/dsp/

19. Материалы сервера: http://center.neic.nsk.su/

 

 

1. Информационная оценка параметров ТВ изображений

Кодирование источника сообщений и сокращение избыточности видеосигнала

(кодирование с сокращением избыточности ТВ сигналов).

Проблема теоретического плана дальнейшего развития общей теории ТВ.

Оценка статистических свойств изображения, создание математических моделей и

разработка на их основе алгоритмов обработки изображений с целью сокращения

избыточности и повышения качества изображений, лучшего использования канала связи.

 

Теория информации изучает количественные закономерности передачи, хранения и обработки информации. Она позволяет оценить эффективность различных систем связи и установить условия согласования источника сообщений (информации) с каналом связи и получателем сообщений.

Количественная мера для сравнения способности различных систем передавать информацию была предложена Хартли в 1927г. Эта мера была названа им информационной емкостью и определена соотношением:

,   (1.1)

где m – число различных состояний системы. При m=2, a=2, C=1 бит/с, (1.2).

         Информационная емкость не характеризует полностью источник информации. Важно знать какое количество информации может быть произведено источником за единицу времени. Для этого вводят понятие производительности источника информации R, определяемое выражением:

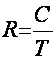,   (1.3)

где Т – время, в течение которого источник в состоянии выработать информацию, равную его накопительной емкости.

         Производительность характеризует предельные возможности источника информации. Количество информации I в сообщении о некотором событии А, согласно Шеннону, определяется вероятностью этого события P{A}.

,   (1.4)

         Знак минус перед логарифмом поставлен потому, что всегда , а информация должна быть положительной: 0 £ P{A} £ 1

Среднее количество информации, приходящееся на одну посылку в сообщении, может служить мерой эффективности кодирования сообщения. Эта величина называется энтропией и определяется как математическое ожидание. Для P{A}=0, вероятность события 0 – Р0, а количество информации при этом I=I0, а при P{A}=1, I=I1, тогда на основании (1.4) заменим:

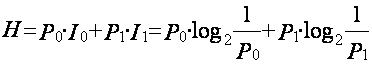,   (1.5)

         Если сообщение имеет больше чем 2 состояния, тогда энтропия определяется по формуле:

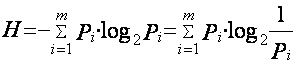,   (1.6)

где Pi – априорная вероятность i-го состояния; m – общее число возможных состояний.

H ® Hmax при Pi = , в этом случае .

Объем информации I, который способен пропустить канал связи равен:

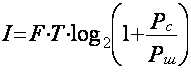,   (1.7)

где F – полоса пропускания канала связи; Т – время передачи сообщения; Рс и Рш – соответственно мощности сигнала и шума.

         Формула выведена в предположении, что помехи представляют собой белый шум и сигнал имеет такую же статическую структуру.

Используя формулы (1.1)-(1.7) произведем информационную оценку различного рода изображений согласно предложению Хартли.

Рассмотрим элементарное изображение черно-белого ТВ, как наиболее простое, имеющее число m градаций яркости каждого элемента. Информационная емкость элемента разложения определяется из соотношения (1.1):

,   (1.8)

Информационная емкость изображения, состоящего из N элементов кадра:

,   (1.9)

Информационная емкость изображения состоящего из q последовательностей кадров:

,   (1.10)

Тогда ,   (1.11) - минимальное возможное количество информации в ТВ изображении.

         Знание количества информации помогает эффективно строить ТВ систему, но этого не достаточно, нужно знать энтропию, т.е. среднее количество информации, приходящееся на кадр или на элемент для данного класса визуального сообщения, однако это очень сложно. Теория информации развита применительно к одномерному сигналу, а источники ТВ изображений являются многомерными.

         Пример. Для фрагмента N=16´16=256, m=3, цвета серый, белый и черный. При этом Сэ = log 2 3 = 1,58 бит, а Ск = 256´1,58 = 404 бит.

Способы описания изображений:

1способ. Условимся, что абонентам передаем индекс элемента и цвета и представим их I как Iэл и Iцвет, т.е. сведения об элементе изображения и цвете, которым нужно его закрасить:

,   (1.12)

где Iпр – сведения о пространственном положении; Iя – сведения о положении яркости.

Для того чтобы указать положение любого элемента необходимо пронумеровать его двоичным кодом с числом разрядов равным log 2 N.

,   (1.13)

Чтобы закодировать яркость элемента, необходимо log 2 m двоичных разрядов:

,   (1.14)

Таким образом ,   (1.15)

Для нашего примера N=16´16, m=3, Irc = 256´8+256´1,58 = 2048+400 = 2440 бит. Нетрудно заметить, что второе слагаемое в (1.15) есть Ск = N´log 2 m = 400 бит.

         2 способ. Указываем абоненту только цвет сверху вниз и слева направо, тогда: Irc = = Iя = N´log 2 m = Cк = 256´1,58 = 404 бит, что в 6 раз меньше, чем в предыдущем случае.

         Канал имеет шум, нужно ввести избыточность против шума. При большом числе элементов это может привести к ошибкам. Поэтому целесообразно вносить в сообщение избыточность для повышения надежности приема.

         3 способ. Аналогичен второму способу, но в канале каждой строки для повышения надежности передачи сообщения сообщается дополнительная информация в конце строки и в конце кадра. По этому способу работают современные системы ТВ, в которых дополнительная информация о конце строки и кадра передается по каналам строчных и кадровых синхроимпульсов.

         4 способ. Предложим абоненту взять бумагу серого цвета и на ней записать элементы серым 5, 10 и т.д., и белым от 10, 15 и т.д. Этот способ требует расписание не всех, а только l элементов из N. Поскольку не все элементы расписаны, то необходимо передать контрольным каналом рассматриваемое число элементов.

,   (1.16)

 

2. Квантование сигналов изображения

         Большую роль в процессе преобразования видеоинформации в цифровую форму играет операция дискретизации параметров сигналов изображения, которая в отличие от многомерной (в общем случае) пространственной дискретизации и дискретизации во времени является одномерной и обычно называется квантованием по уровню.

         Под квантованием подразумевается процесс представления динамического диапазона изменения сигнала конечным числом дискретных уровней. Квантование по уровню представляет собой процесс сокращения избыточной информации. Его применение обуславливается не только техническими, но и психофизиологическими причинами, в частности тем, что:

1.     наличие помех при обработке или передаче информации влияет на параметры видеоинформации;

2.     представление непрерывно изменяющейся видеоинформации конечным числом допустимых уровней позволяет уменьшить воздействие помех, хотя способствует возникновению шума квантования;

3.     получатель видеоинформации обладает ограниченной контрастной чувствительностью.

Дискретизация видеоинформации путем ее квантования по уровню реализуется в совокупности с рассмотренной дискретизацией в пространстве и во времени.

Важность вопросов квантования особенно возрастает при повышении требований к скорости передачи цифровых видеосигналов.

Представление непрерывной входной величины в квантованную по уровню осуществляется в соответствии с характеристикой квантования с равномерным или неравномерным распределением уровней SАi и порогов Di квантования. Характеристика квантования одномерного сигнала приведена на рис. 2.1.

 

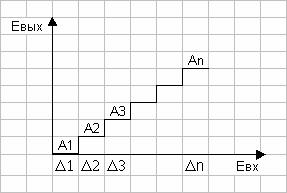
Рис. 2.1. Характеристика квантования.

 

         Расстояние между соседними уровнями квантования называется шагом квантования, а расстояние между соседними порогами квантования называется интервалом квантования, т.е. является интервалом округления до входящего в него уровня квантования. Математически характеристику квантования униполярного входного сигнала можно записать как:

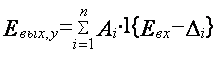,   (2.1)

где Евх, Евых – входной и выходной сигналы; Аi (i = 1, 2, 3, …, n) – шаги квантования выходного сигнала; Di – пороги квантования входного сигнала; 1{*} – единичная функция, для которой выполняется условие:

.

Аналогично можно записать характеристику квантования биполярного сигнала:

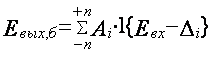,   (2.2)

При неравномерном распределении уровней и порогов квантования выражение (2.2) приводится к виду:

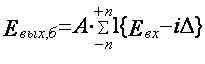,   (2.3), т.к. Аi = А = const, а Di = iD.

Распределение порогов квантования входного и уровней квантования выходного сигналов связаны с максимальными значениями Евхmax, Евыхmax соотношениями:

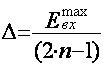,   ,   (2.4)

где 2n – обозначает общее число уровней квантования в общем случае биполярного сигнала.

         Характеристика квантования по своему значению является разновидностью амплитудной характеристики Евых = F(Евх). Кроме характеристики квантования имеется понятие коэффициента усиления (рис. 2.2) при квантовании, который определяет как отношение:

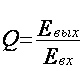,   (2.5)

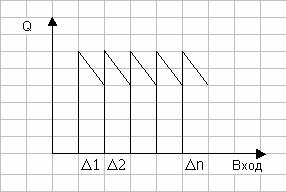
Рис. 2.2. Характеристика усиления при квантовании.

 

Используя формулу (2.3) выражение (2.5) можно записать в виде:

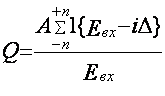,   (2.6)

При равномерном квантовании при  характеристика Евых = F(Евх) преобразуется в линейную и , тогда как при неравномерном квантовании при  – в нелинейную, следовательно , т.е. var.

Соотношение между характеристикой квантования и коэффициентом усиления подобно соотношению между фазовой характеристикой и характеристикой времени распространения фазы в ТЛЭЦ.

 

Шум квантования.

В результате представления сигнала конечным числом уровней квантования в восстановленном изображении возникает шум квантования, обусловленный различием между исходным и квантованным сигналами и имеющий характер нелинейных искажений. Шум квантования на изображении проявляется различным образом, что зависит от пространственной временной характеристики видеоинформации. Например, при больших уровнях шума квантования плавные изменения яркости изменяются скачкообразно и проявляются лишние контура и т.д.

Шум квантования сигнала можно изменять в значительных пределах. Для уменьшения мощности шума квантования могут быть использованы:

1.     выбор шага квантования, как можно больше числа уровней сигнала К = Кmax;

2.     выбор переменного шага при К = const;

3.     использование статистических характеристик обрабатываемых сигналов путем соответствующего преобразования;

4.     использование различных форм маскирования помех квантования с помощью дополнительных сигналов (случайных, детерминированных или их комбинаций);

5.     в ТВ технике – выбор соответствующей связи частоты дискретизации с частотой строк ТВ развертки fдис и с частотой цветовой поднесущей fцпод.

,   (2.6) где р – гармоники сигнала fцпод.

Наиболее часто используется для дискретизации величина р = 3, тогда при fцпод = 4,21 (4,41) МГц, fдис = 3´4,21 (4,41) = 12,63 (13,23) МГц.

 

3. КОДИРОВАНИЕ СИГНАЛОВ

Под кодированием источника сообщений понимается обработка видеоинформации только в сигнальной области. Она включает в себя нестандартные формы кодирования источника сигнала, которые основаны на более эффективном кодировании с помощью нестандартных способов сокращения различных видов избыточности сигнала. Его цель – выражение цифрового сигнала минимальным количеством двоичных символов в единицу времени с тем, чтобы сузить полосу пропускания канала, сократить время передачи или уменьшить среднюю мощность сигнала в канале.

Различают статистическую избыточность, избыточность по восприятию, структурную и спектральную избыточность. По теории вероятностей избыточность является следствием определенных корреляционных связей. Корреляция означает, что некоторый элемент изображения более или менее существенно зависит от соседей в пространстве и во времени.

1.     Структурная избыточность – итог особенностей стандарта разложения или, по иному, преобразования изображения в ТВ сигнал. В нем, например, периодически передаются неизменные по форме элементы сигнала: гасящие импульсы строк и полей. В цифровом ТВ сигнале нет необходимости предавать эти импульсы по каналу связи, т.к. они могут быть восстановлены в декодере по опорным сигналам синхронизации. Устранение из состава цифрового ТВ сигнала гасящих импульсов строк и полей снижает скорость передачи видеоданных примерно на 23%.

2.     Под статистической избыточностью понимают корреляционные связи между соседними (по вертикали и горизонтали) отсчетами ТВ сигнала. Сразу же надо подчеркнуть, что снижение избыточности в этом случае до определенных пределов обратимо, т.е. без потерь информации. Примером такого «беспроигрышного» кодирования служит предсказание на основе дискретно-косинусного преобразования (ДКП).

3.     Спектральная избыточность проявляется как результат излишне высокой частоты дискретизации. В частности, принятая ортогональная структура дискретизации ТВ изображения в общем случае не является оптимальной в частотном пространстве. Используя интерполяцию и передискретизацию определенным образом выбранных групп отсчетов ТВ сигнала можно, в принципе, видоизменить спектральный состав и снизить частоту дискретизации. Такая обработка обычно необратима и, как правило, ведет к некоторому снижению качества восстановленного ТВ изображения.

4.     Избыточность по восприятию связана с особенностями зрения человека. Например, цветовое разрешение нашего зрения ниже яркостного. Эта особенность учтена во всех стандартных аналоговых системах цветного кодирования. В NTSC, PAL,     SECAM цветовое разрешение существенно понижено по отношению к яркостному. То же самое зафиксировано в цифровом стандарте 4:2:2, где, по определению, две цветоразностные компоненты представлены таким же по объему информационным массивом, что и один яркостной сигнал. Учитывая эту особенность нашего зрения по восприятию мелких деталей цветного изображения, можно в несколько раз сократить полосу частот при передаче и кодировании сигналов цветности.

Если предположить наличие идеального канала передачи (не влияющего на поток сообщений), то кодирование источника сообщений вместе с соответствующим декодированием можно представить как процесс передачи сообщения через эквивалентный четырехполюсник (рис. 3.1).

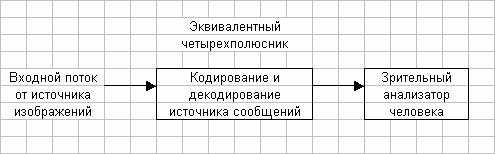
Рис. 3.1. Передача сообщения через эквивалентный четырехполюсник.

 

         Оптимальное использование рассматриваемого канала передачи сообщений соответствует случаю, когда эквивалентный четырехполюсник и зрительный анализатор наблюдателя характеризуются одинаковой пропускной способностью. Под пропускной способностью подразумевается количество информации, которое данный канал обрабатывает за единицу времени. Если пропускная способность эквивалентного четырехполюсника меньше, чем пропускная способность зрительного анализатора, то в сообщении, принятом получателем, возникают потери информации. Если пропускная способность эквивалентного четырехполюсника превышает пропускную способность зрительного анализатора, то четырехполюсник не оптимален. Таким образом, сокращение психофизиологической избыточности сообщения выполняется с целью оптимального согласования процесса кодирования источника с параметрами получателя сообщений с точки зрения пропускной способности.

         Условие оптимального согласования заключается в таком сокращении объема передаваемой в сообщении информации, при котором не проявится ухудшение качества сообщения при его получении. Возможность сокращения психофизиологической избыточности сообщения основано на предположении, что производительность источника сообщений превышает пропускную способность получателя сообщений. Это условие выполняется для видеоинформации. Более того, например, в современных телевизионных системах критерий качества задается для наиболее критичных изображений. Следствием этого является то, что пропускная способность телевизионного канала в среднем намного выше, чем того требует зрительный анализатор человека.

         Если для сокращения избыточности сообщения используются его статистические свойства, то говорят о сокращении статистической избыточной информации. Дискретный источник сообщений генерирует отдельные реализации сообщения как конечную последовательность элементов {Si}, выбираемых из конечного множества элементов {Xk}, k = 1, 2, 3, …, n, называемых алфавитом источника (рис. 3.2).

 

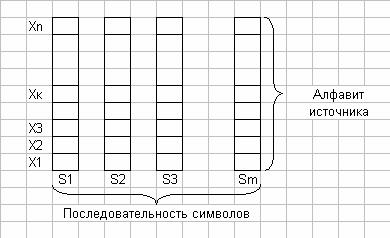
Рис. 3.2. Алфавит источника.

 

         Элементы последовательности, образуемые посредством выбора из алфавита источника, называются символами. В последовательности символов (реализации) элементы алфавита могут быть произвольным образом повторяться, так что один и тот же элемент алфавита различается только местом, которое он занимает в последовательности. Применительно к телевидению отдельные элементы алфавита источника представляют собой дискретные значения яркости, которые может принимать элемент изображения. Последовательность символов, таким образом, определяет дискретное во времени изменение видеоинформации.

         Статистическая избыточность источника сообщений определяется в общем случае соотношением:

,   (3.1)

т.е. разностью между максимальной энтропией источника Hmax, соответствующей алфавиту элементов источника с одинаковой вероятностью появления и статистически независимыми друг от друга символами, и энтропией источника Н, как правило, с различной вероятностью появления элементов алфавита и с различной статистической зависимостью между символами. Выражение для статистической избыточности определяет величину избыточной информации, которую можно устранить, исключив статистические взаимосвязи. Эта величина принципиально различна для источников сообщений различных типов и для источников с различными статистическими свойствами.

         При разработке системы компрессии (сжатия) изображений с использованием ДКП, следует учесть, что величина коэффициента сжатия (Ксж) зависит от значений битовых размеров коэффициента трансформант и границ зон с минимальным среднеарифметическим (СА) и среднеквадратическим отклонением (СКО). Это требует предварительного аналитического определения этих параметров с целью количественной оценки эффективности ВИС с использованием предложенных алгоритмов быстрого ДКП и отбора коэффициентов трансформант посредством компьютерного моделирования.

         Каждый блок, включающий в себя N´N отсчетов сигнала яркости Lm(k,l) подвергается двухмерному унитарному ДКП., в результате которого получаются блоки (матрицы) спектральных коэффициентов F(u,v) той же размерности, что и блоки изображения.

F(u,v) = 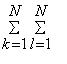Lm(k,l) ´ W(k,l,u,v),   (3.2)

где W(k,l,u,v) – ядро прямого преобразования; Lm(k,l) – отсчеты сигнала яркости; k и l – номера строки и столбца в блоке изображения; u и v номера строк и столбцов в блоке спектральных коэффициентов.

         Дисперсия F(u,v) в среднем убывает с увеличением номеров u и v. Для сокращения цифрового потока F(u,v) подвергается избирательному квантованию: коэффициенты, обладающие большой дисперсией, квантуют на больше число уровней, а малой дисперсией – на меньшее число уровней или отбрасывают. При избирательном квантовании используются два способа отбора коэффициентов – зональный и пороговый. В первом случае блоки F(u,v) разбиваются на зоны, а для каждой зоны назначают число уровней квантования L(u,v). Число разрядов двоичного кода, отводимое на передачу каждого из блоков F(u,v) зоны равно:

n(u,v) = log2L(u,v),   (3.3)

Минимум дисперсии шума определяется по формуле:

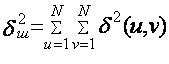,   (3.4)

где d 2(u,v) – дисперсия шума, возникающая при квантовании F(u,v).

Ограничение на общее число бит, затраченных на передачу блока, характеризуется значением:

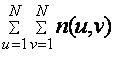= N2 ´ ng ,   (3.5)

Коэффициент сжатия системы компрессии с ДКП при зональном способе отбора коэффициентов трансформант без учета шумов квантования:

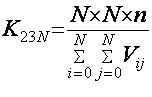,   (3.6)

где N 2 – число отсчетов фрагментов; n – битовый размер отсчетов (разрядность кода) исходного изображения; Vij – средний битовый размер коэффициента трансформант i-строки j-столбца фрагмента NxN.

Коэффициент сжатия K23N  для N=16 и n=8, принятые с точки зрения получения наибольшего значения при простой аппаратурной реализации и программного обеспечения без учета шумов квантования согласно формуле (3.6) можно записать в виде:

,   (3.7)

Во втором случае из N 2 спектральных коэффициентов каждого блока выбирают М наибольших, которые квантуют на одно и тоже число уровней L = 2 ´ n, где n – число разрядов кода, отводимое на передачу каждого из них.

M´(2´log 2 N + n) = N2´ng ,   (3.8)

Выбирая M и n, можно будет обеспечивать минимум отводимых разрядов.

         Принятые по каналу связи блоки спектральных коэффициентов F(u,v) подвергаются обратному унитарному преобразованию, в результате которого блок за блоком восстанавливается изображение.

Степень сжатия цифрового потока определяется при пороговом способе отбора коэффициентов трансформант из выражения:

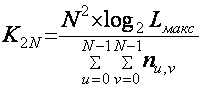,   (3.9)

где N – линейный размер блока преобразования, выраженный в числе отсчетов.

Выбор числа двоичных единиц, используемых для передачи каждого из спектральных коэффициентов матрицы, следует производить в соответствии со следующим правилом:

,   (3.10)

где Fn – порог, определяемый экспериментальным путем.

Немаловажным при нахождении величины К2N при ДКП является знание величины порога ограничения Fn. Естественно, чтобы К2N изменялось с изменением типа сюжетов необходимо изменить величину Fn. Такое возможно путем введения управляющих воздействий на различные параметры системы.

 

4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (ДПФ)

И ДИСКРЕТНО-КОСИНУСНОЕ ПРЕОБРАЗОВАНИЕ (ДКП)

         Одним из наиболее распространенных средств обработки как одномерных, так и многомерных сигналов, в том числе и изображений, является ортогональное преобразование. Особенно велика роль ортогональных преобразований в решении задачи уменьшения скорости передачи символов в ЦТВ, и, следовательно, уменьшения полосы частот канала и объема памяти устройств для архивного хранения.

         Сущность ортогональных преобразований заключается в представлении исходного сигнала в виде суммы ортогональных базисных функций. Функции X(t) и Y(t) называются ортогональными на отрезке (t1, t2), если их скалярное произведение равно нулю:

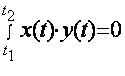,   (4.1)

Это определение может быть распространено и на дискретные сигналы, представляемые последовательностями чисел. Дискретные сигналы X(n) и Y(n), имеющие по N отсчетов, называются ортогональными, если выполняется условие:

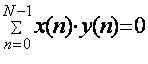,   (4.2)

Одним из наиболее известных примеров применения ортогонального преобразования является разложение периодического сигнала X(t) в ряд Фурье:

,   (4.3)

где v0 = 2×p / Т; Т – период повторения сигнала.

Действительные коэффициенты ряда Фурье ak и bk определяются соотношениями:

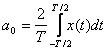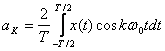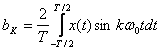,   ,   ,   (4.4)

В комплексной форме разложение в ряд Фурье имеет вид:

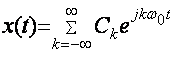,   (4.5)

где  - комплексная амплитуда гармоники.

Дискретное преобразование Фурье (ДПФ) имеет вид:

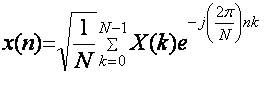, n = 0, 1, 2, …, N-1,   (4.6)

где коэффициент ДПФ X(k) определяется соотношением:

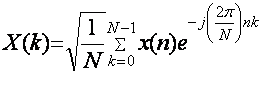, k = 0, 1, 2, …, N-1,   (4.7)

         Нахождение коэффициентов X(k) по формуле (4.7) обычно называют прямым преобразованием, а получение сигнала по этим коэффициентам в соответствии с формулой (4.6) – обратным ДПФ.

         Чтобы иметь дело только с действительными числами обычно используют разложение с помощью дискретно-косинусного преобразования (ДКП), определяемого соотношением:

,   (4.8)

где коэффициенты ДКП определяются по формулам:

,   , k = 1, 2, …, N-1,   (4.9)

Нахождение C(k) по x(n) называют прямым ДКП, а представление сигнала x(n) по C(k) – обратным ДКП.

Ядро преобразований при переходе от ДПФ к ДКП определяется как:

, где W = exp,   (4.10)

Формула (4.10) отражает взаимосвязь между ядрами ДПФ и ДКП. Аналитическое выражение для ортогонального ДКП, отражающее взаимосвязь между ДКП и ДПФ можно записать в виде:

,   ,   (4.11)

где k’Î {1, 2, …, N}, A(i) = 0, i Î {1, 2, …, N-1}.

После проведения соответствующих математических преобразований выражение для ортогонального преобразования упрощается:

,   , k’Î {1, 2, …, N-1},   (4.12)

что соответствует записи без дополнительного условия A(i) = 0, i Î {N, N+1, …, 2N-1}.

Соотношения (4.11) и (4.12) описывают два равноценных способа определения одномерных коэффициентов F(0) и F(k) ДКП. В соответствии с (4.11) спектральные коэффициенты одномерного ДКП порядка N найдем исходя из N спектральных коэффициентов ДПФ порядка 2N. Из основной формулы преобразования с ядром [Fk] (4.12) получаем выражение спектральной матрицы столбца вектора:

[F] = [Fk]×[A],   (4.13)

где [Fk], [A] – матрицы – столбцы векторов Fk, и A соответственно строки матрицы преобразования исходного сигнала.

Существуют достаточные теоретические предпосылки для практической реализации способов построения алгоритмов быстрого преобразования Фурье (БПФ), отличающихся друг от друга числом операций умножения (ОУ), сложения (ОС) и вычитания (ОВ), и рассчитанных на выполнение различных задач. БПФ – один из алгоритмов для вычисления ДПФ, заключающийся в устранении избыточных операций (ИО). Ниже приводятся результаты аналитического представления разработанных алгоритмов быстрого дискретно-косинусного преобразования (БДКП) для порядка N = 4 и N = 8, и их сравнение с прямым преобразованием Фурье. Формулу одномерного ДКП можно записать следующим образом:

, (4.14)

где C(x) – нормирующий множитель, C(0) = , C(W) = 1 при W = 1, 2, 3, …, N-1.

Для случая ДКП порядка N = 4 и N = 8 она примет соответствующий вид:

,   ,   (4.15)

Используя формулу (4.15) определим выражение для расчета конкретно каждого из четырех и восьми косинусных коэффициентов соответственно:

F(0) = (A(0) + A(1) + A(2) + A(3))

F(1) = (0,923×А(0) + 0,382×А(1) – 0,3892×А(2) - 0,924×А(3))

F(2) = (A(0) - A(1) - A(2) + A(3))

F(3) = (0,923×А(0) - 0,382×А(1) + 0,3892×А(2) - 0,924×А(3))

На общий множитель 0,5 при вычислении каждого косинусного коэффициента можно при прямом преобразовании не умножать, учтя это при обратном косинусном преобразовании. Тогда разложение матрицы ДКП порядка N = 4  будет записано следующим образом:

,   (4.16)

Применим для (4.16) эффективный алгоритм расчета БДКП, основанный на прямом разложении ядра ДКП на произведение более простых матриц. Это можно осуществить следующим образом:

[F4] = [B4]×[E4],   (4.17) где 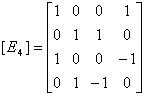,   (4.18)

При прямом преобразовании умножению сигнальной матрицы [A] слева на матрицу разложения [B4] соответствует образованная пара значений сигнала (А(0)+А(3)), (А(1)+А(2)), (А(0)-А(3)), (А(1)-А(2)).

,   (4.19)

При последующем умножении слева полученного промежуточного результата на матрицу [B4] находим результирующие спектральные коэффициенты F(x):

F(0) = (A(0) + A(3) + A(1) + A(2))

F(1) = [0,923×(А(0) - А(3)) + 0,382×(А(1) –А(2))]

F(2) = 0,707[(A(0) - A(3) - A(1) + A(2))]

F(3) = [0,382×(А(0) – A(3)) - 0,923×(А(1) + А(2))]

Сравнение количества необходимых операций, производимых согласно алгоритму БДКП, показывает, что этот алгоритм расчета отличается меньшим на единицу числом умножений. Проведя аналогичные расчеты и сравнение обратного четырех точечного косинусного преобразования, можно установить, что предлагаемый вариант, по сравнению с базовым, также обеспечивает уменьшение на единицу числа умножений. Аналогично произведем расчет коэффициентов трансформанты для N = 8.

F(0) = (A(0)+A(1)+A(2)+A(3)+А(4)+А(5)+А(6)+А(7))

F(1) = (0,981×А(0)+0,831×А(1)+0,555×А(2)+0,195×А(3)-0,195×А(4)-0,555×А(5)-0,831×А(6)-0,981×А(7))

F(2) = (0,923×А(0)+0,382×А(1)-0,382×А(2)-0,923×А(3)-0,923×А(4)-0,382×А(5)+0,382×А(6)-0,923×А(7))

F(3) = (0,831×А(0)-0,195×А(1)-0,981×А(2)-0,555×А(3)+0,555×А(4)-0,981×А(5)+0,195×А(6)-0,831×А(7))

F(4) = (0,707×А(0)-0,707×А(1)-0,707×А(2)+0,707×А(3)+0,707×А(4)-0,707×А(5)-0,707×А(6)+0,707×А(7))

F(5) = (0,555×А(0)-0,981×А(1)+0,195×А(2)+0,831×А(3)-0,831×А(4)-0,195×А(5)+0,981×А(6)-0,555×А(7))

F(6) = (0,382×А(0)-0,923×А(1)+0,923×А(2)-0,382×А(3)-0,382×А(4)+0,923×А(5)-0,923×А(6)-0,832×А(7))

F(7) = (0,195×А(0)-0,555×А(1)+0,831×А(2)-0,981×А(3)+0,981×А(4)-0,831×А(5)+0,555×А(6)-0,195×А(7))

Применение эффективного алгоритма БДКП, основанного на прямом разложении ядра ДКП на произведение более простых матриц для коэффициентов трансформанты F(x) позволяют выразить их следующими аналитическими выражениями:

F(0) = (A(0)+A(1)+A(2)+A(3)+А(4)+А(5)+А(6)+А(7))

F(1) = (0,981×(А(0)-А(7))+0,831×(А(1)-А(6))+0,195×(А(3)-А(4))+0,555×(А(2)-А(5)))

F(2) = (0,923×(А(0)-А(3)-А(4)-А(7))+0,382×(А(1)-А(2)-А(5)+А(6))

F(3) = (0,831×(А(0)-А(7))+0,195×(А(6)-А(1))+0,555×(А(4)-А(3))+0,981×(А(2)-А(5)))

F(4) = (А(0)-А(1)-А(2)+А(3)+А(4)-А(5)-А(6)+А(7))

F(5) = (0,555×(А(0)-А(7))+0,981×(А(6)-А(1))-0,195×(А(2)-А(5))+0,831×(А(3)-А(4)))

F(6) = (0,381×(А(0)-А(3)-А(4)+А(7))+0,923×(А(2)-А(1)+А(5)-А(6))

F(7) = (0,195×(А(0)-А(7))+0,831×(А(2)-А(5))+0,981×(А(4)-А(3))+0,555×(А(6)-А(1)))

         Сравнивая алгоритмы вычисления F(x) на основе БДКП порядка N = 8, в обеих вариантах построения можно выявить общее количество арифметических операций сложения, умножения и вычитания. Здесь имеет место существенный выигрыш в количестве выполненных операции умножения, сложения, что снижает время вычисления коэффициентов почти в два раза. Данные вычисления сведены в таблицу:

Таблица 4.1. Данные вычисления коэффициентов трансформанты

на основе предложенного алгоритма БДКП

Варианты алгоритмов

вычисления коэффициентов

Наименование арифметических операций и их количество

Сложение

Умножение

Вычитание

Общее число

операций

Прямое вычисление коэффициентов быстрого косинусного преобразования Фурье

29

64

27

120

Быстрое косинусное преобразование Фурье с прямым разложением ядра ДКП на произведение простых матриц

24

26

29

79

Результаты сравнения

5

38

-2

41

 

Проведя аналогичные расчеты и сравнения для обратного восьмиточечного косинусного преобразования можно установить, что предлагаемый вариант по сравнению с базовым вариантом обеспечивает уменьшение 41 арифметических операций, в том числе 38 операций умножения и позволяет вдвое уменьшить время обработки цифрового ТВ сигнала. Следовательно, представляется возможность создать эффективные системы компрессии видеоданных со значительно простой аппаратурной реализацией и несложным программным обеспечением.

 

5. НЕРЕКУРСИВНЫЕ И РЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ

Выделяют три основных группы частотных фильтров. Схематические частотные характеристики фильтров приведены на следующих рисунках 5.1. Между частотными интервалами пропускания и подавления сигнала существует зона, которая называется переходной.

1.     ФНЧ - фильтры низких частот (пропускание низких, подавление высоких частот во входном сигнале) (рис. 5.1.1),

 

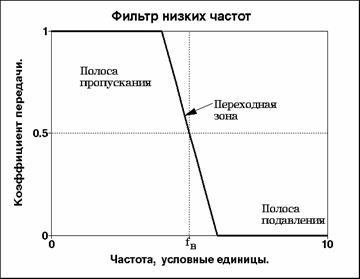
Рис. 5.1.1. Частотная характеристика ФНЧ.

 

2.     ФВЧ - фильтры высоких частот (пропускание высоких, подавление низких частот) (рис. 5.1.2),

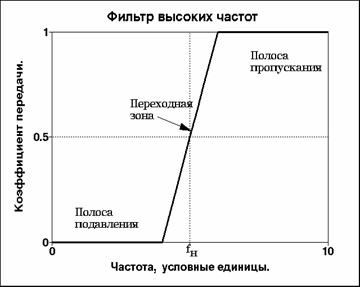
Рис. 5.1.2. Частотная характеристика ФВЧ.

 

3.     ПФ - полосовые фильтры (пропускание определенных частот с подавлением остальных частот сигнала) (рис. 5.1.3).

 

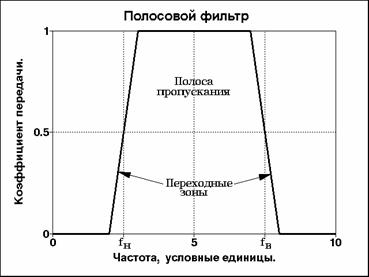
Рис. 5.1.3. Частотная характеристика ПФ.

 

Среди последних в отдельную группу иногда выделяют РФ - режекторные фильтры, понимая под ними фильтры с подавлением узкой полосы частот во входном сигнале, и СФ – селекторные фильтры, обратные РФ.

В общем виде линейное разностное уравнение М-го порядка имеет вид:

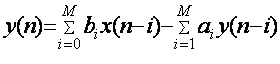, n ³ 0,   (5.1),

где {bi}, {ai} - коэффициенты, описывающие конкретную систему, причем aM ¹ 0.

         Решение разностного уравнения можно произвести методом прямой подстановки, имея набор начальных условий и входную последовательность. Например, разностное уравнение следующего вида:

y(n) = x(n) – 3y(n-1), n ³ 0,   (5.2)

с начальным условием y(-1) = 0 и входной последовательностью:

x(n) = n2 + n,   (5.3)

по методу прямой подстановки имеет решение:

y(0) = x(0) – 3y(-1) = 0; y(1) = x(1) – 3y(0) = 2; y(2) = x(2) – 3y(1) = 0;

y(3) = x(3) – 3y(2) = 12; y(4) = x(4) – 3y(3) = 16 и т.д.

         Для получения решения в явном виде можно использовать аналитический метод, основанный на получении двух решений разностного уравнения: однородного и частного. Однородное решение получается путем подстановки нулей вместо всех членов, содержащих элементы входной последовательности и определения при этом отклика системы. Частное решение получают, подбирая вид выходной последовательности при заданной входной. Для определения произвольных постоянных однородного решения используются начальные условия.

         В нерекурсивных цифровых фильтрах (НЦФ) текущее значение отклика y(n) зависит только от текущего значения и конечного числа предшествующих значений входной последовательности x(n). При этом длина импульсной характеристики фильтра (отклика на единичный отсчет) является конечной и определяется количеством звеньев задержки.

Практика проектирования НЦФ базируется, в основном, на синтезе фильтров низких частот. Все другие виды фильтров могут быть получены из фильтров низких частот соответствующим преобразованием. Так, например, фильтр высоких частот может быть получен инверсией фильтра низких частот  -  вычислением разности между исходным сигналом и результатом его фильтрации низкочастотным НЦФ. Применяется также способ получения фильтров высоких частот из низкочастотных фильтров путем реверса частоты в передаточной функции низкочастотного фильтра, т.е. заменой переменной w на переменную w' = p-w (при DТ = 1).

Полосовой фильтр может реализоваться последовательным применением ФНЧ и ФВЧ с соответствующим перекрытием частот пропускания. Полосовой режекторный фильтр также может быть получен методом инверсии полосового фильтра. Одночастотные режекторные фильтры обычно выполняются на основе простых рекурсивных цифровых фильтров, более эффективных для данных целей.

Идеальным полосовым фильтром называется фильтр, имеющий единичную амплитудно-частотную характеристику в полосе от определенной нижней частоты wн до определенной верхней частоты wв, и нулевой коэффициент передачи за пределами этой полосы (для цифровых фильтров - в главном частотном диапазоне).

         Наибольшее распространение имеет прямая структурная форма фильтра. Этой форме соответствует разностное уравнение:

y(n) = h(0)x(n) + h(1)x(n-1) + … + h(N-1)x(n-N+1),   (5.4)

Характеристикой фильтра является передаточная функция 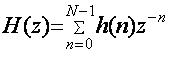,   (5.5)

На рис. 5.2 представлена структурная схема такой  нерекурсивной цепи со звеньями задержки z –1 (Т), масштабными множителями h (-0,8; 2; -1) и сумматором.

 

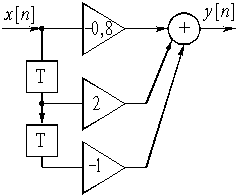
Рис. 5.2. Структурная схема нерекурсивной цепи.

 

         Найдем ее выходную последовательность и передаточную функцию. Выходная последовательность y(n) в соответствии с уравнением (5.4) имеет вид:

y(n) = h(0)x(n) + h(1)x(n-1) +  h(2)x(n-2) =

=  -0,8x(n) + 2x(n-1) – x(n-2),   (5.6)

Передаточную функцию цепи найдем, используя уравнение (5.5) или непосредственно по схеме:

H(z) = h(0) + h(1)z –1 + h(2)z –2 = -0,8 + 2z –1 – z –2,   (5.7)

При построении таких фильтров удобна последовательная форма. В этом случае Z – преобразование импульсной характеристики представляется в виде произведения Z – преобразования, соответствующего системе первого порядка:

, i = 1, 2, …,m,   (5.8)

или второго порядка:

, i = 1, 2, …,m,   (5.9)

Тогда передаточная функция имеет вид:

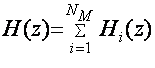,   (5.10),

причем величина NM  равна целой части выражения (N-1)/2.

Пусть {h(n)} – физически реализуемая последовательность конечной длины, заданной на интервале 0 ≤ n ≤ (N-1) с Z – преобразованием (5.5). Преобразование Фурье от {h(n)} составит:

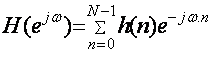,   (5.11)

и оно является периодическим по частоте с периодом  2p, т.е. при m = 0, ±1, ±2, ±3,… имеем:

,   (5.12)

В случае только действительной последовательности:

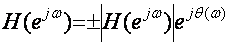,   (5.13)

Знаки “±” необходимы, так как H(ejw) = H*(ejw), (5.14), где H*(ejw) - действительная функция, принимающая положительные и отрицательные значения.

Требование линейности фазовой характеристики:

Q(w) = - aw;  -p ≤ w ≤ p,   (5.15),

где a - постоянный коэффициент, значение a определяется из уравнения:

,   (5.16),

удовлетворяющего следующим условиям:

a = (N-1) / 2, h(n) = h[(N-1)-n], 0 ≤ n ≤ (N-1),   (5.17)

Таким образом, при заданном значении коэффициента a импульсная характеристика должна обладать вполне определенной симметрией. Если N – нечетное число, то a - целое число и задержка в фильтре равна целому числу интервалов дискретизаций. Например, для N = 11, a = 5 и центр симметрии для h(n) приходится на пятый отсчет. Для четного N, например, N = 10, a = 4.5, а центр симметрии лежит между отсчетами.

В рекурсивном цифровом фильтре значение процесса на выходе определяется не только конечным числом значений входного процесса, но также и предшествующими величинами выходного процесса. На рис. 5.3 представлена структурная схема рекурсивного цифрового фильтра со звеньями задержки z -1, масштабными множителями h и сумматорами.

 

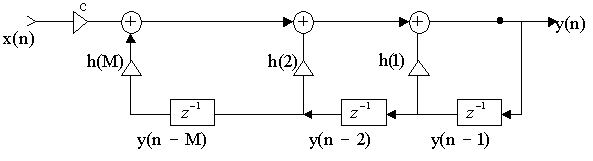
Рис. 5.3. Структурная схема рекурсивного цифрового фильтра.

 

В этом случае:

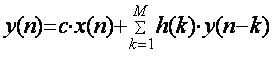,   (5.18)

Рекурсивные фильтры имеют определенную "память" по значениям предыдущих отсчетов, которая, в пределе, может быть бесконечной. С учетом этого фактора рекурсивные фильтры получили название фильтров с бесконечной импульсной характеристикой (БИХ-фильтров), в отличие от нерекурсивных фильтров, всегда имеющих конечную импульсную характеристику (КИХ-фильтры). Реакция рекурсивного фильтра на сигнал с учетом "памяти" исключает возможность создания фильтров с четным импульсным откликом, и частотные характеристики рекурсивных фильтров всегда являются комплексными.

Синтез рекурсивных фильтров, как и НЦФ, выполняется на базе фильтров низких частот (ФНЧ). Другие типы фильтров (ФВЧ - высоких частот, ПФ - полосовые, РФ - режекторные) образуются на основе ФНЧ путем частотного преобразования.

Фильтр использует М значений выходного процесса и только одно входного. В рекурсивном цифровом фильтре более общего вида число значений выходного процесса не меняется, а число значений входного процесса со звеньями задержки, масштабными множителями и сумматорами возрастает. Преобразование Фурье равенства (5.18) дает:

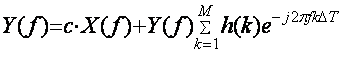,   (5.19)

Причем сумма содержит многочлен по степеням комплексной экспоненты         exp(-j2pfkDT). Обозначая последнее выражение символом z, переходим к Z – преобразованию. Как следует из формулы (5.19), частотная характеристика рассматриваемого цифрового рекурсивного фильтра имеет вид:

,   (5.20)

Таким образом, изучение свойств частотной характеристики сводится к определению положения и характера полюсов в знаменателе выражения (5.20).

Простейший рекурсивный фильтр низких частот (ФНЧ) может быть задан следующим разностным уравнением:

y(n) = (1-a)x(n) + a.y(n-1),   (5.21)

Для расчета удобно использовать частотную характеристику, которая для рассматриваемого рекурсивного ФНЧ имеет вид:

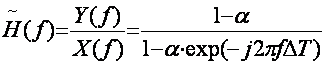,   (5.22)

с модулем: 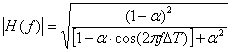,   (5.23)

и фазой: ,   (5.24),

где DТ – интервал между отсчетами.

Импульсная функция этого фильтра имеет вид:

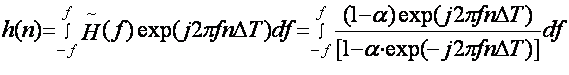,  (5.25)

В настоящее время существует достаточно большое количество видов рекурсивных частотных фильтров и их различных модификаций. Наиболее известный из них - фильтр Баттеруорта (рис.5.4). Он имеет монотонную гладкую АЧХ во всем частотном диапазоне. При том же порядке многочленов фильтров (равном количестве полюсов) большую крутизну обеспечивают фильтры Чебышева – прямой и инверсный, однако при этом в полосе пропускания (для инверсного – в полосе подавления) у фильтров Чебышева появляются равноволновые пульсации (с одинаковой амплитудой пульсаций). Еще более крутые срезы характеристик (при равноволновых пульсациях как в полосах пропускания, так и в полосе подавления) реализуются с использованием эллиптических функций.

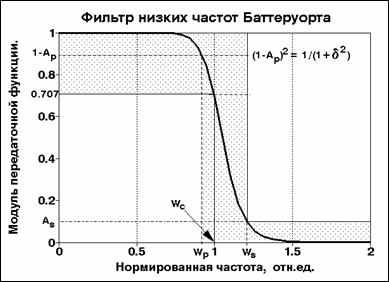
Рис. 5.4. АЧХ фильтра Баттеруорта.

 

Одно из важнейших свойств рекурсивных фильтров - возможность получения узких переходных зон при конструировании частотных фильтров. Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчетов для текущих вычислений может приводить к накапливанию ошибок.

 

6. ВЫБОР ПАРАМЕТРОВ АЦП

Основными параметрами преобразования являются:

1.     частота выборок или число отсчетов в единицу времени;

2.     число уровней квантования (число разрядов кода на одну выборку).

Частота выборок определяется теоремой Котельникова (теоремой отсчетов), исходя из ширины спектра преобразуемого сигнала. Для телевизионного сигнала вещательного ТВ DF = 6 МГц, fвыб ³ 2×DF ³ 12 МГц.

         Значительно более сложно представляется выбор необходимого числа уровней квантования. Число уровней квантования определяет точность преобразователя, а в некоторой степени и его быстродействие, т.к. с увеличением числа уровней растет число разрядов кода на выборку, т.е. число операций, проводимых с сигналом за время одного преобразования. С этой точки зрения необходимо стремиться к уменьшению числа уровней квантования. Уменьшение числа уровней квантования применительно и для уменьшения требуемой пропускной способности канала связи.

         В то же время малое число уровней квантования приводит к появлению ложных контуров на восстановленных изображениях, когда наблюдатель начинает замечать различие в яркостях соседних уровней квантования. Появление ложных контуров снижает эстетическую ценность изображений, что не допустимо в вещательном ТВ.

         Теоретическое определение числа уровней квантования в соответствии с законом Вебера – Вехнера может быть сделано по формуле:

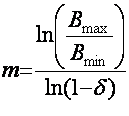,   (6.1),

где Вmax и Bmin – максимальная и минимальная яркости экрана кинескопа; d - пороговый контраст (d = 0,015 ¸ 0,02).

При контрасте d = 0,02 и отношении яркостей экрана Вmax/Bmin = 100, теоретическое число уровней квантования m » 230.

         Таким образом, число разрядов при двоичном коде а = 2, практически выбирается порядка 7 ¸ 8. Скорость передачи полного цифрового сигнала цветного ТВ можно представить как:

,   (6.2),

где n1, n2, n3 – разрядность кодов сигнала яркости (Uy), цветоразностных сигналов (Ub-y или Ur-y) и сигнала звука; fвя, fвц, fзв – верхние граничные частоты сигнала яркости, цветоразностных сигналов и сигнала звука.

1.     При n1 =  n2 = n3 = 8, fвя = 2×fвц = 6 МГц, fзв = 20 кГц,

Vп = 2×6×8×106+2×(2×3×8×106)+2×20×8×103 = (96+96) ×106+0,32×106=192,32´106 бит/с.

2.     При n3 = 16, Vзв = 0,64´106 бит/с.

3.     При n3 = 24, Vзв = 0,96´106 бит/с.

4.     При n3 = 32, Vзв = 1,28´106 бит/с.

 

7. РАСЧЕТ ШИРИНЫ ПОЛОСЫ ПЕРЕДАВАЕМЫХ ЧАСТОТ

И СКОРОСТИ ПЕРЕДАЧИ ПОСЛЕДОВАТЕЛЬНОСТИ СИМВОЛОВ

При образовании цифрового сигнала ТВ программ композитным и компонентным кодированием цветного ТВ стандарта «SEKAM» и кодирования звукового сопровождения ТВ с последующей их транспортировки в едином цифровом потоке применяются два вида стыка: параллельный – для внутренней подачи цифровых сигналов в АСК ТЦ или с использованием способа солитонной оптоволоконной сети дальней связи; и последовательный – для трансляции сигналов программ ТВ в едином транспортном потоке. Поэтому важно знать ширину полосы передаваемых частот, пропускную способность высокочастотного тракта подачи в зависимости от используемого тракта и объема цифровых данных, подлежащих передаче. В каждом случае сигналы синхронизации передаются байтно, отдельно от информационных сигналов.

Пусть периодическая последовательность импульсов прямоугольной формы, передаваемых по каналам связи имеет вид (рис. 7.1):

 

Рис. 7.1. Форма сигнала несущей цифровой информации U{0;1}.

 

Из рисунка видно, что длительность посылок U{0} и U{1} и период тактирования связаны через выражение:

Т = 2´Ти ,   (7.1),

где Т – полный период для рассматриваемого случая передачи двоичных сигналов U{0;1}; Ти – длительность символов (элементарных посылок пикселей) U{0} или U{1}.

         Спектр такого сигнала содержит постоянную составляющую, основную гармонику и постоянно убывающие нечетные гармоники этой частоты, спектр его не ограничен (рис. 7.2):

 

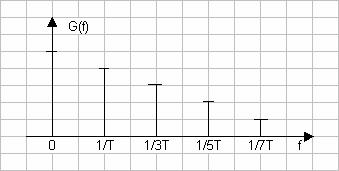
Рис. 7.2. Спектр сигнала.

 

         Если ограничить полосу частот такого сигнала с помощью ФНЧ с достаточно крутым срезом АЧХ, форма импульсов будет искажена, т.к. часть частотных составляющих спектра окажется подавленной.

         Искажения проявятся в виде увеличения длительности нарастания и спада импульса и возникновения колебательного переходного процесса. Это будет причиной ограничения допустимой частоты передаваемого импульсного сигнала, т.е. ограничения скорости передачи двоичных символов по каналу связи.

         Длительность нарастания импульса tн связана с верхней граничной частотой ФНЧ fв соотношением:

tн = 1 / (2´fв) ,   (7.2)

 

         Если длительность входного импульса Ти < tн, то амплитуда импульса на выходе ФНЧ станет уменьшаться. Этот случай показан на рис. 7.3 штриховой линией:

 

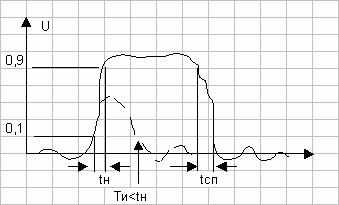
Рис. 7.3. Уменьшение амплитуды импульса на выходе ФНЧ.

 

При достаточно малой длительности Ти их амплитуда на выходе канала связи сравнимой с уровнем помех, что приведет к ошибкам работы приемного устройства. Колебательные явления переходных процессов возникающих при передаче также ограничивают частоту передаваемых по каналу связи импульсов.

Если эта частота слишком велика, колебательный переходный процесс, созданный одним импульсом, будет накладываться на следующий импульс. Возникает помеха, называемая интерференционной, которая может привести к ошибкам приема. Изложенные причины приводят к известному еще с ранних работ по теории связи условию: по каналу связи с шириной полосы пропускания DF можно передавать в виде двухуровневых импульсов 2´DF бит информации за 1 сек., т.е. эффективность использования полосы частот канала связи составляет:

g = (2´DF) / DF = 2 (бит/с)/Гц ,   (7.3)

 

Следовательно, для передачи двоичных символов со скоростью 243 Мбит/с необходим канал связи с шириной полосы частот 121,5 МГц. Тогда как для стандарта формата 4:2:2 скорость передачи определяются как:

Vпс = fдя´nя + 2´fдц´nц ,   (7.4)

        

При fдя = 13,5 МГц, fдц = fдя / 2 = 6,75 МГц, nя = nц = 8 (Рекомендация 601), скорость передачи Vпс = 216 Мбит/с, ширина полосы частот канала Df = 108 МГц. Аналогично можно определить для других стандартов формата цифрового ТВ вещания.

         Ясно, что ни стандартный канал ТВ вещания, имеющий ШПП 8 МГц, ни спутниковый канал, имеющий ширину полосы 27 МГц, не пригодны для передачи цифрового ТВ сигнала. Это относится и к видеосвязи даже при пониженной частоте кадров, а для передачи ТВ сигналов ВЧ и ПЧ необходима еще более широкая полоса частот или сокращение информационной избыточности.

 

8. Задачи для практических занятий: Условия задач и их решение

 

8.1. Расчетные Формулы

1) Скорость передачи сигнала в цифровой форме: ,

где fд – частота дискретизации;

, где Fмакс – граничная частота исходного сигнала.

К – число двоичных символов в одном дискретном отсчете.

, где m – число уровней квантования исходного сигнала.

2) При равномерном расположении тактовых импульсов внутри интервала дискретизации минимальная полоса частот цифрового канала, предназначенного для передачи цифровой информации со скоростью С определяется по формуле:

3) Физический объем сигнала: ,

где Tc – длительность сигнала; Fc – ширина спектра;

Dc – динамический диапазон уровней сигнала.

,

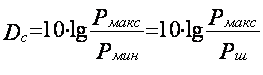где Рмакс и Рмин – максимальное и минимальное значение мощности сигнала;

Рш – значение мощности шумов в канале.

 

4) Физический объем канала: ,

где Тк – время использования канала; Fк – полоса пропускаемых каналом частот;

Dк – динамический диапазон уровней, пропускаемых каналом с допустимыми искажениями.

 

5) Количество информации I(ai), содержащееся в символе ai, выбираемом из ансамбля {ai} (i = 1, 2, 3,…, K, K – объем алфавита) с вероятностью Р(аi), определяется как

, причем .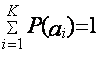

6) Среднее количество информации (энтропия источника), приходящееся на один символ, выдаваемый дискретным источником независимых сообщений с объемом алфавита К:

.

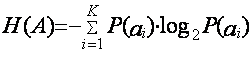7) Избыточность дискретного источника: .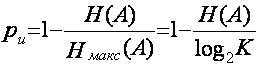

Если источник без памяти и все символы равновероятны, то  и избыточность .

8) Если в единицу времени источник выдает в среднем Vи символов, то среднее количество информации, создаваемое источником в единицу времени (производительность дискретного источника):

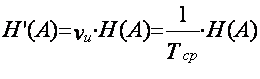, где Тср – средняя длительность одного символа.

9) Средняя вероятность ошибки при оптимальном кодировании: ,

где Т – длительность сигнала, соответствующего последовательности символов источника достаточно большой длины; [C-H’(A)] – определяет запас пропускной способности канала.

 

10) Максимальный объем информации, который может быть передан по непрерывному каналу с пропускной способностью С:

, где Тк – время использования канала.

11) Если число разрядов во всех кодовых комбинациях n=const, то код называется равномерным. Число кодовых комбинаций равномерного кода:

, где m – основание кода; n – число разрядов в кодовой комбинации.

12) Каждую букву из ансамбля {ai} (i = 1, 2, 3,…, K, K – объем алфавита) можно закодировать при условии:

, где m – основание кода; n – число разрядов в кодовой комбинации.

Код, для которого , называется примитивным (код без избыточности). Для корректирующих кодов справедливо неравенство: .

При этом часть кодовых комбинаций используется для кодирования (эти кодовые комбинации называются разрешенными их число равно К), а другая часть при кодировании не используется. Число неиспользованных при кодировании комбинаций, называемых запрещенными, равно N – K.

13) Избыточность кода можно оценить соотношением: ,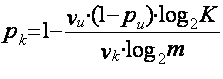

где Ри – избыточность источника;

Vи и Vк – скорость выдачи символов источником и кодером соответственно.

 

14) Избыточность равномерного m – позиционного n – разрядного кода при Ри = 0:

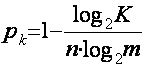, где 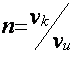 - число символов кода на один символ источника.

15) Средняя длина кодовых комбинаций экономного кода не может быть меньше величины Nмин, которая согласно теореме Шеннона об оптимальном кодировании в каналах без шумов определяется по формуле:

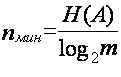, где m – основание кода.

16) Избыточность оптимального по Шеннону кода определяется соотношением:

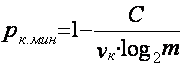, где С – пропускная способность канала.

8.2. Условия Задач

1. Верхняя граничная частота ТВ сигнала равна 6 МГц. Число уровней квантования исходного сигнала равно 256. Найти скорость передачи цифрового потока и минимальную полосу частот цифрового канала.

2. При дискретизации цветного изображения был применен стандарт 4:2:2. Найти суммарную скорость передачи цифрового потока и минимальную полосу частот цифрового канала для двух значений числа двоичных символов в кодовой комбинации одного отсчета равных 8 и 10.

3. Во сколько раз отличаются скорости передачи цифрового потока и минимальные полосы частот цифрового канала при использовании стандартов 4:1:1 и 2:1:1. Число двоичных символов К в кодовой комбинации одного отсчета равно 10.

4. Сигнал с полосой 100 кГц передается по каналу связи в течение 30 с. Максимальная мощность сигнала 120 мВт, мощность шума 9,5 мВт. Найти физический объем сигнала.

5. Найти мощность сигнала, который может быть передан по каналу связи с физическим объемом 106 и полосой 10 кГц. Время использования канала 10 с. В канале действует шум с равномерной спектральной плотностью мощности    Gш=10-4 мВт/Гц.

6. Определить количество информации, содержащееся в каждом из символов источника при их независимом выборе. Источник без памяти выдает символы из ансамбля А={ai} (i=1, 2, 3, 4) c вероятностями Р(а1)=0,25; Р(а2)=0,16; Р(а3)=0,36; Р(а4)=0,23. Найти энтропию и избыточность источника.

7. Источник без памяти выдает символы из ансамбля А={ai} (i=1, 2, 3, 4, 5) с вероятностями Р(а1)=0,175; Р(а2)=0,045; Р(а3)=0,038; Р(а4)=0,6; Р(а5)=0,142. Средняя длительность одного символа равна 0,3 с. Определить избыточность дискретного источника и среднее количество информации, создаваемое источником в единицу времени.

8. Источник сообщений без памяти и объемом алфавита 12 выдает символы с равной вероятностью. Средняя длительность одного символа равна 0,15 с. Найти среднее количество информации, создаваемое источником в единицу времени и среднее количество символов.

9. За время равное 106 с источник выдал 107 бит информации двоичными посылками длительностью 10 мс. Во сколько раз изменилось время передачи и количество посылок для передачи того же объема информации после устранения избыточности (т.е. каждый символ источника несет 1 бит информации). Определить избыточность источника.

10. Найти запас пропускной способности канала связи при условии, чтобы вероятность ошибки не превысила величину 10-6. Длительность кодовой комбинации равна 0,2 с. Во сколько раз изменится запас пропускной способности канала, если при неизменной вероятности ошибки длительность кодовой комбинации увеличится в 3 раза?

11. Дискретный источник выдает символы из ансамбля А={ai} с объемом 10. Какое минимальное число разрядов должны иметь кодовые комбинации равномерного примитивного двоичного кода, предназначенного для кодирования символов данного ансамбля? Найти скорость передачи и минимальную полосу частот цифрового канала необходимую для передачи ТВ сигнала с граничной частотой 6,5 МГц с таким числом разрядов.

12. Источник сообщений выдает символы из ансамбля А={ai}, объем ансамбля К=64, энтропия источника Н(А)=3 бит/символ. Найти минимальное количество кодовых символов необходимых при кодировании символов источника в канале без шумов равномерным примитивным двоичным кодом и при оптимальном кодировании. Какое избыточное количество символов приходится тратить на один символ источника при использовании равномерного примитивного двоичного кода по сравнению с оптимальным кодом?

13. Производят АЦП первичного непрерывного сигнала. Число уровней квантования К=1024. Каждый уровень кодируется равномерным двоичным кодом. Найти число разрядов в кодовой комбинации, если избыточность кода Рк=0, если отдельные отсчеты сигнала независимы. Определить избыточность кода при увеличении числа разрядов на 4.

14. Источник сообщений выдает символы из ансамбля А={ai} (i=1, 2, 3, 4) с вероятностями Р(а1)=0,25; Р(а2)=0,15; Р(а3)=0,4; Р(а4)=0,2. Средняя длительность одного символа Тср=0,2с. Найти избыточность источника и избыточность равномерного кода, если скорость выдачи символов кодером Vк=15.

15. Источник без памяти с объемом алфавита К=3 выдает символы из ансамбля с вероятностями Р(а1)=0,28; Р(а2)=0,53 и Р(а3)=0,19. Найти избыточность источника и число символов кода на один символ источника n = Vк / Vи, при условии, что избыточность кода Рк=0.

 

8.3. РЕШЕНИЕ ЗАДАЧ

Задача 1.

1. Из условия fд³2×Fмакс Þ fд³12 МГц выбираем fд = 13,5 МГц.

2. k = log 2 m = log 2 256 = 8.

3. По формуле (1) вычислим: С = 13,5´8 = 108 Мбит/с.

4. По формуле (2) находим: Dfц = 0,5´108 = 54 МГц.

 

Задача 2.

1. При стандарте 4:2:2 коэффициенту 4 соответствует частота дискретизации 13,5 МГц, коэффициенту 2 – частота 6,75 МГц.

2. Используя формулу (1) найдем суммарную скорость передачи цифрового потока:

при k = 8, C = 13,5´8+6,75´8+6,75´8 = 216 Мбит/с.

при k = 10, C = 13,5´10+6,75´10+6,75´10 = 270 Мбит/с.

3. По формуле (2) вычислим минимальную полосу частот цифрового канала:

при k = 8, Dfц = 0,5´216 = 108 МГц.

при k = 10, Dfц = 0,5´270 = 135 МГц.

 

ЗАДАЧА 3.

1. Коэффициенту 1 соответствует частота дискретизации 3,375 МГц, коэффициенту 2 – частота 6,75 МГц, коэффициенту 4 – 13,5 МГц.

2. Используя формулу (1) найдем суммарную скорость передачи цифрового потока:

при стандарте 4:1:1, C1 = 13,5´10+3,375´10+3,375´10 = 202,5 Мбит/с.

при стандарте 2:1:1, C2 = 6,75´10+3,375´10+3,375´10 = 135 Мбит/с.

3. По формуле (2) вычислим минимальную полосу частот цифрового канала:

при стандарте 4:1:1, Dfц1 = 0,5´202,5 = 101,25 МГц.

при стандарте 2:1:1, Dfц2 = 0,5´135 = 67,5 МГц.

4. Найдем отношение этих величин: =1,5 и =1,5.

 

ЗАДАЧА 4.

1. Dc = 10´lg = 10´lg = 11.

2. По формуле (3) вычислим физический объем сигнала: Vc = 30´100´103´11 = 33´106.

 

Задача 5.

1. Dc = 10´lg(Рмакс / Рш) ® Рмакс = Рш´10Dc / 10.

2. Из формулы (4) получим: .

3. Рш = Gш´Fк = 10-4´10-3´104 = 10-3 Вт или Рш = 1 мВт.

4. Рмакс = Рш´10Dc / 10 = 10-3´1010 / 10 = 10-2 Вт или Рмакс = 10 мВт.

 

Задача 6.

1. По формуле (5) находим:

I(a1) = - log 2 0,25 = - lg0,25 / lg2 = 2 бит.   I(a2) = - log 2 0,16 = 2,64 бит.

I(a3) = - log 2 0,36 = 1,47 бит.   I(a4) = - log 2 0,23 = 2,12 бит.

2. По формуле (6) вычислим энтропию источника:

Н(А) = 0,25´2+0,16´2,64+0,36´1,47+0,23´2,12 = 1,941 бит/символ.

3. Из формулы (7) избыточность дискретного источника равна:

Ри =  = 1-0,971 = 0,029.

 

Задача 7.

1. По формуле (5) находим:

I(a1) = - log 2 0,175 = - lg0,175 / lg2 = 2,51 бит.

Соответственно: I(a2) = 4,47 бит.   I(a3) = 4,72 бит.   I(a4) = 0,74 бит.   I(a5) = 2,82 бит.

2. По формуле (6) вычислим энтропию источника:

Н(А) = 0,44+0,201+0,179+0,442+0,4 = 1,663 бит/символ.

3. Из формулы (7) избыточность дискретного источника равна:

Ри =  = 1-0,716 = 0,283.

4. Производительность дискретного источника вычислим по формуле (8):

Н’(А) = Н(А) / Тср = 1,663 / 0,3 = 5,543 бит/с.

 

ЗАДАЧА 8.

1. Если источник без памяти выдает все символы с равной вероятностью, то избыточность дискретного источника Ри=0 и Н(А) = Нмакс(А) = log 2 К = log 2 12 = 3,585 бит/символ.

2. Производительность дискретного источника вычислим по формуле (8):

Н’(А) = Vи ´ Н(А) = Н(А) / Тср = 3,585 / 0,15 = 23,9 бит/с.

3. Из формулы (8): Vи =  =  = 6,66 символов.

 

ЗАДАЧА 9.

1. Первоначальное количество посылок: .

2. Количество информации в одном символе: = 0,1 бит/символ.

3. Количество посылок после устранения избыточности: =107.

4. Время передачи: Т2 = n2´t = 10´10-3´107=105 с.

5. Найдем отношение величин Т и n:  и .

6. Избыточность источника: .

 

ЗАДАЧА 10.

1. Из формулы (9) получим [C - H’(A)] =  =  = 100.

2. Из условия равенства вероятностей ошибки следует равенство степеней: Т´[C - H’(A)]1= = 3´Т´[C - H’(A)]2. Следовательно, запас пропускной способности канала [C - H’(A)] уменьшится в 3 раза.

 

ЗАДАЧА 11.

1. Из теоретических сведений (12) для равномерного примитивного двоичного кода выполняется условие 2n = K. Тогда n = log 2 K / log 2 2 = log 2 10 = 3,32, т.к. n может быть только целым числом, то n = 4.

2. Из условия fд³2×Fмакс Þ fд³13 МГц выбираем fд = 13,5 МГц.

3. По формуле (1) вычислим: С = 13,5´4 = 54 Мбит/с.

4. По формуле (2) находим: Dfц = 0,5´54 = 27 МГц.

 

ЗАДАЧА 12.

1. Из теоретических сведений (12) при кодировании равномерным примитивным двоичным кодом выполняется условие 2n = K. Тогда n1 = log 2 K / log 2 2 = log 2 64 = 6.

2. По формуле (15) при оптимальном кодировании n2 = H(A) / log 2 2 = 3.

3. Количество избыточных символов при использовании равномерного примитивного двоичного кода: Dn = n1 – n2 = 6 – 3 = 3.

 

ЗАДАЧА 13.

1. Т.к. отдельные отсчеты сигнала независимы, то избыточность источника Ри=0, а т.к. и избыточность кода Рк=0, то из формулы (13): , где n = Vк / Vи, получим n = log 2 K / log 2 2 = log 2 1024 = 10.

2. По формуле (14) вычислим избыточность равномерного кода при увеличении числа разрядов на 4: = 1 - 0,714 = 0,285.

 

ЗАДАЧА 14.

1. По формуле (5) находим количество информации, содержащееся в каждом символе:

I(a1) = - log 2 0,25 = - lg0,25 / lg2 = 2 бит.

Соответственно: I(a2) = 2,73 бит.   I(a3) = 1,32 бит.   I(a4) = 2,32 бит.

2. По формуле (6) вычислим энтропию источника:

Н(А) = 0,25´2+0,15´2,73+0,4´1,32+0,2´2,32 = 1,904 бит/символ.

3. Из формулы (7) вычислим избыточность дискретного источника: Ри =  = 0,048.

4. Из формулы (8) среднее количество символов, выдаваемое источником в единицу времени равно Vи = 1 / Тср = 1 / 0,2 = 5.

5. Избыточность кода вычислим по формуле (13): Рк = 1 -  = 0,365.

 

ЗАДАЧА 15.

1. По формуле (5) находим количество информации, содержащееся в каждом символе:

I(a1) = - log 2 0,28 = - lg0,28 / lg2 = 1,83 бит.

Соответственно: I(a2) = 0,91 бит.   I(a3) = 2,39 бит.

2. По формуле (6) вычислим энтропию источника:

Н(А) = 0,28´1,83+0,53´0,91+0,19´2,39 = 1,455 бит/символ.

3. Из формулы (7) вычислим избыточность дискретного источника: Ри =  = 0,272.

4. Т.к. избыточность кода Рк=0, то из формулы (13) получим:

n =  = 0,728´1,585 = 1,15.

 

9. КОНТРОЛЬНЫЕ ВОПРОСЫ

 

9.1. Контрольные вопросы по первому модулю

1.     Что такое компонентное кодирование ТВ сигнала? Найти скорость передачи двоичных символов для формата ПЦТС 4:2:2.

2.     Что такое композитное кодирование ТВ сигнала? Найти скорость передачи двоичных символов для формата ПЦТС 4:2:2.

3.     Как передаются сигналы синхронизации ТВ развертки в цифровом ТВ по стандарту и рекомендации ITU-В656?

4.     Варианты интерфейса. Что такое параллельный видеостык? Как осуществляется передача цифрового ТВ сигнала и сигнала синхронизации?

5.     Варианты интерфейса. Последовательный видеостык. Как осуществляется передача цифрового ТВ сигнала и сигнала синхронизации ПЦТС?

6.     Что такое ошибка квантования? Дисперсия шума квантования при равномерном квантовании и равновероятных значениях сигнала U{1;0}.

7.     По какому закону определяется пороговое превышение яркости объекта, называемое фоном, при котором объект различается наблюдателем?

8.     Передаточная характеристика тракта и ее учет при АЦП полного цветного ТВ сигнала. Параметры АЦП при равномерном квантовании с числом двоичных разрядов n и N.

9.     Дискретизация сигналов изображения. Цифровые ТВ сигналы согласно ITU-R ВТ 601 формата 4:2:2, 4:2:0 и их методы передачи двоичных символов.

10. Дискретизация сигналов изображения. Цифровые ТВ сигналы согласно ITU-R ВТ 601 формата 4:1:1, 4:4:4 и их методы передачи двоичных символов.

11. Квантование цифровых ТВ сигналов согласно рекомендации 601.

12. Передача цифрового ТВ сигнала и сигнала синхронизации согласно рекомендации 601 при n = 8 и n = 10.

13. Формирователи цифровых ТВ сигналов на студиях ТЦ с аналоговым и цифровым ГК.

14. Выделение тактовых импульсов из передаваемого последовательно цифрового сигнала.

15. Схема построения последовательного видеостыка по рекомендации ITU-R ВТ 656.

16. Стандарты цифровых ТВ сигналов CIF, 4 CIF, 16 CIF и их параметры.

17. Стандарты цифровых ТВ сигналов SQCIF, QCIF.

18. Как определяется ширина полосы частот ТВ канала связи при передаче цифрового сигнала в последовательной форме?

19. Избыточность ТВ сигнала и их использование для снижения скорости передачи.

20. Виды избыточности ТВ сигнала и их применение при кодировании ЦТВ.

21. Требования, предъявляемые к каналам связи в системе цифрового ТВ.

22. В какой последовательности кодируется по стандарту JPEG блоки цветного изображения?

23. Почему квантование коэффициентов ДКП создает менее заметные искажения, чем квантование самого изображения?

24. Каким образом в стандарте JPEG осуществляется управление степени сжатия?

25. В чем состоит сущность кодирования с переменной длиной кодовых слов?

26. Что означает термин «гибридное кодирование» применительно к стандартам MPEG-1, MPEG-2?

27. Зачем перед кодированием по MPEG-1, MPEG-2 выполняется перестановка кадров в ОЗУ (GOP) (B,P,F)?

28. Чем различаются кадровый и полевой режимы кодирования в MPEG-1, MPEG-2?

29. Почему для В кадров достигается наибольшая степень сжатия?

30. Каково назначение БЗУ в кодере MPEG-2?

31. Что такое масштабируемость?

32. Что такое уровни и профили MPEG-2?

33. Что имеют общего и чем различаются уровни кодирования звуковой информации в стандартах MPEG-1, MPEG-2?

34. В чем сущность адаптивного распределения битов?

35. Каково назначение психоакустической модели?

36. Как выделяются данные разных ТВ программ из транспортного потока MPEG-2?

 

9.2. Контрольные вопросы по второму модулю

1.     Что такое видео и аудио объекты MPEG-4?

2.     Какие методы используются для передачи изображений человеческих лиц?

3.     Опишите процесс декодирования потока данных MPEG?

4.     Какие методы применяются для кодирования речевых сигналов в системах цифрового ТВ вещания?

5.     Где могут быть применены рекомендации Н261 и Н263?

6.     В чем состоит сходство и различие стандартов Долби ЛС-3, MPEG-2 и Audio Layer3?

7.     Что такое сотовое ТВ?

8.     Виды модуляции, используемые в DVB-C и DVB-S.

9.     Что затрудняет развитие наземного цифрового ТВ вещания?

10. От чего зависит скорость передачи двоичных символов полезной информации в канале DVB?

11. Что такое одночастотная сеть цифрового ТВ вещания?

12. Что нового могут дать цифровые методы прикладному ТВ?

13. Какие преимущества обеспечивает нелинейный монтаж по сравнению с линейным?

14. Для чего могут использоваться видеосерверы?

15. Какими способами могут быть организованы обратные каналы в системах интерактивного ТВ?

16. Для чего могут быть полезны кабельные модели?

17. Что является основным содержанием стандарта MPEG-7?

18. Назовите основные параметры формата ТВЧ.

19. Что такое скремблирование и для чего оно применяется?

20. Чем отличается ВИС от ТВС?

21. Чем отличается МВИС от ВИС?

22. Чем отличается интерактивное цифровое ТВ от цифрового ТВ вещания?

23. Что такое условный доступ в цифровом ТВ и СКТВ?

24. Принцип формирования транспортного потока данных для цифрового ТВ вещания с компрессией.

25. Почему ДПФ содержит конечное число частотных составляющих?

26. Почему ДКП во многих случаях удобнее применять чем ДПФ?

27. Нарисовать структурные схемы нерекурсивного и рекурсивного цифровых фильтров.

28. Написать формулу, описывающую действие двумерного нерекурсивного цифрового фильтра.

29. Чем различаются матрицы двумерного фильтра верхних частот и двумерного фильтра Лапласа и воздействия указанных фильтров на изображение?

30. Почему при разложении сигнала на частотные поддиапазоны количество отсчетов в каждом поддиапазоне может быть уменьшено?

31. Каковы свойства квадратурных зеркальных фильтров?

32. Что происходит с изображением при выполнении вэйвлет-преобразования?

33. За счет чего может быть достигнуто сжатие изображения с помощью вэйвлет-преобразования?

34. В чем состоит оценка движения методом соответствия блоков?

35. Что такое линейное предсказание?

36. Почему использование ДИКМ позволяет уменьшить скорость передачи двоичных символов в канале связи?

37. Какими средствами может быть обеспечена помехоустойчивость передачи информации с использованием ДИКМ?

38. Как выполняются кодирование и декодирование в системах передачи с векторным квантованием?

 

9.3. Контрольные вопросы к итоговому контролю

1.     Основные особенности, этапы развития, современное состояние и проблемы цифрового ТВ. Обобщенные модели обработки, хранения и передачи видеоинформации, модели цифровой системы передачи, видеоинформационной системы, системы интерактивного ТВ. Цифровой ТВ сигнал.

2.     Преобразование аналогового ТВ сигнала в цифровой (дискретизация, квантование, кодирование), цифро-аналоговое преобразование, импульсно-кодовая модуляция, структура дискретизации видеосигналов, оценка возможности передачи цифрового потока видеоданных.

3.     Цифровые ТВ сигналы согласно рекомендации ITU-R BT-601, дискретизация, квантование, формирователи цифровых ТВ сигналов, параллельный и последовательный видеостык.

4.     Другие стандарты цифровых ТВ сигналов – SQCIF, QCIF, CIF, 4CIF, 16CIF. Передача цифровых ТВ сигналов форматов и файлов DCX, TIFF, DNG, JPEG-M по каналам связи, сокращение избыточности ТВ сигналов, задача сжатия передаваемой и хранимой видеоинформации.

5.     Эффективные методы цифровой обработки и кодирования ТВ сигналов и изображений, дискретное преобразование Фурье (ДПФ), дискретное косинусное преобразование Фурье (ДКПФ).

6.     Цифровая фильтрация сигналов, рекурсивные и нерекурсивные фильтры, обработка и передача сигналов с разложением на частотные поддиапазоны, вейвлет-преобразование, оценка и компенсация движения.

7.     Дифференциальная импульсно-кодовая модуляция (ДИКМ), принцип кодирования с предсказанием, дельта-модуляция (ДМ), принцип ДМ, адаптивные ДМ, векторное квантование, фрактальное кодирование ТВ сигналов, преобразование звуковых сигналов в цифровую форму.

8.     Методы сжатия изображения и звуковых сигналов, сжатие неподвижных изображений по стандарту JPEG, разбиение изображений на блоки, ДКП, квантование коэффициентов ДКП, энтропийное кодирование, формат, практическая реализация и варианты JPEG.

9.     Стандарты сжатия движущихся изображений и звукового сопровождения MPEG-1, MPEG-2, макроблок и его формирование, кодер видеоинформации, поток видео- и аудиоданных MPEG-2, декодирование движущихся изображений, декодеры видео- и аудиоинформации стандарта MPEG-2.

10. Стандарт кодирования звуковой и видеоинформации MPEG-4, оценка кодирования аудио объектов, формирование потока видео- и аудиоданных, декодирование видео- и аудиоинформации, перспективы применения MPEG-4 в вещании.

11. Стандарт описания метаданных MPEG-7, новый стандарт компрессии видеоданных Windows Media 9 Series, стандарты сжатия аудиоданных, основные характеристики, области применения практическая реализация.

12. Интеграция функций ТВ приемников и ПК при приеме цифрового ТВ, цифровое прикладное ТВ, система наблюдения и измерения параметров удаленных объектов, оценка качества изображения при восстановлении компрессированного видеосигнала и измерение параметров видеоканала.

13. Особенности эффективного цифрового кодирования ТВ сигнала в системах с повышенной и высокой четкостью, повышенного качества.

14. Особенности цифрового кодирования изображений и сигналов вещательной системы цветного ТВ PAL, методы цифрового кодирования при формировании, передаче и хранении ТВ программ, алгоритмы расчета переходных помех, амплитудных и разовых искажений.

15. Проблемы и пути решения передачи цифрового ТВ сигнала по сети Интернет, средства защиты доступа к сетевым ресурсам, проколы.

16. Использование цифровой вещательной сети для дистанционного обучения, параметры и информационные характеристики прямого и обратного каналов, использование стандартных протоколов обмена данными.

17. Вопросы формирования и передачи данных пользователя и дополнительной информации в транспортном потоке семейства стандартов MPEG (от MPEG-1 до MPEG-10).

18. Использование цифровой обработки ТВ сигналов в аппаратурно-студийном комплексе (АСК), методы и средства обработки ТВ сигналов используемые для коррекции временных искажений, видеозаписи, архивирования, шумоподавления и преобразования ТВ стандартов.

19. Применение цифровой обработки изображений, компонентов, восстановление, снижение искажений изображений, повышение качества изображения и распознавание образов.

20. Кодирование источника сообщений, сокращение избыточности видеосигнала.

21. Преобразование аналоговых звуковых и видеосигналов в цифровую форму, теорема отсчетов, дискретизация сигналов изображения, теорема многомерной дискретизации.

22. Квантование сигналов изображения, характеристики, шумы, число уровней квантования, определение оптимального уровня квантования.

23. Цифровое кодирование квантованных отсчетов сигнала изображения, характеристики цифрового кодирования.

24. Кодирование с преобразованием, одно- и двухмерное быстрое преобразование Фурье, ДКП, алгоритмы БДКП для цифрового кодирования, алгоритмы быстрого ДКП Фурье, применение БДКП для сигналов изображения и звукового сопровождения ТВ.

25. Оценка коэффициентов сжатия при кодировании источников изображения на основе алгоритмов быстрого ДКП при зональной, пороговой, адаптивной фильтрации или отборах коэффициентов трансформанты, кодирование трансформанты и декодирование с преобразованием.

26. Цифровая фильтрация сигналов изображения и звукового сопровождения, рекурсивные и одномерные фильтры.

27. Международный стандарт цифрового кодирования, параметры системы компонентного цифрового кодирования.

28. Эффективное кодирование ТВ сигнала и сигнала звукового сопровождения, оценка качества воспроизводимого компрессированного изображения, определение значения КНИ, при котором достигается заданное или приемлемое слуховое восприятие.

29. Цифровая обработка ТВ сигналов и сигналов звукового сопровождения в АСК, оценка качества изображений и измерение параметров видеоканалов.

30. Эффективное кодирование ТВ сигналов в системе с высокой четкостью.

31. Эффективное кодирование ТВ сигналов в системе с повышенной четкостью.

32. Эффективное кодирование ТВ сигналов в системе с повышенным качеством.

33. Передача цифрового сигнала по сетям Интернет, защита, доступ, ресурсы, протоколы.

34. Цифровое кодирование изображений и сигналов вещательной системы цветного ТВ стандарта PAL.

35. Цифровая вещательная сеть дистанционного обучения, параметры, информационные характеристики прямого и обратного каналов, используемые протоколы.

36. Передача данных пользователя и дополнительной информации в транспортном потоке семейства стандартов MPEG.

37. Цифровая обработка ТВ сигналов в АСК, методы и средства цифровой обработки, преобразование стандартов.

38. Цифровая обработка изображения с помощью ПК, восстановление качества, снижение искажений, повышение качества изображения, методы и средства.

39. Сотовые системы ТВ, проблемы, пути решения.

40. Разработка универсального цифрового ТВ приемника.

41. Наземное цифровое ТВ вещание, пути реализации.

42. Цифровая ТВ сеть в видении магистранта.

43. Условный доступ в системе цифрового ТВ вещания.

44. Дистанционное образование через сеть цифрового ТВ вещания с предоставлением каналов обмена через ТЛФ линию, оптическое волокно.

45. Анализ эффективных алгоритмов, позволяющих функционировать системе в комплексе сжатие-шифрование для цифрового ТВ вещания для дистанционного обучения.

46. Методы оценки качества изображения, контроль и измерение параметров цифровых вещательных ТВ каналов.

47. Средства оперативного контроля и тестирования параметров цифровых ТВ каналов с цифровой компрессией сигнала.

48. Средства измерения параметров и обнаружения ошибок передачи в цифровом канале без компрессии.

49. Оценка качества изображения в ТВ каналах с цифровой компрессией.

50. Прикладное цифровое ТВ, его применение и перспективы.

 

Дополнительные вопросы подготовлены по рефератам и докладам, а также по применению в магистерских диссертациях элементов новых цифровых технологий.

 

 

 

 

Учебное пособие-практикум

по дисциплине «Цифровое телевидение»

для магистрантов ФРРТ специальностей

5А522005 (Радиотехника)

5А522105 (Системы мобильной связи)

 

Работа рассмотрена и рекомендована к печати на заседании кафедры Телевидения и радиовещания, Пр №      от

 

Составитель: Махмудов Э.Б.

Редактор: Таджибаев Ш.З.

 

Редакционно-корректурная группа: к.т.н. Гаврилов И.А.,

Крапивницкая Л.Н., Ахмедова А.Х.

Редактор: Крапивницкая Л.Н.

Корректор: Ахмедова А.Х.
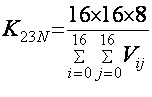