ЎЗБЕКИСТОН РЕСПУБЛИКАСИ АЛОҚА ,АХБОРОТЛАШТИРИШ ВА ТЕЛЕКОММУНИКАЦИЯ ТЕХНОЛОГИЯЛАРИ ДАВЛАТ ҚЎМИТАСИ
Тошкент ахборот технологиялари университети
“Ахборот технологиялари” факультети
“АМАЛИЙ МАТЕМАТИК ДАСТУРЛАР ПАКЕТИ”
фанидан тажриба ишларини бажариш бўйича
УСЛУБИЙ КЎРСАТМА
Тошкент- 2013
Услубий кўрсатма “Амалий математик дастурлар пакети” (MATLAB) фанидан таълим олувчи талабаларга мўлжалланган бўлиб, мазкур фандан тажриба ишларини бажариш услуби ва топшириқлар ўрин олган. Тажриба ишларига мўлжалланган барча мавзулар мисоллар воситасида кенг ёритиб берилган. Ҳар бир тажриба иши қуйидагиларни ўз ичига олган: ишдан мақсад, тажриба ишининг қисқача назарий қисми, топшириқлар.
Тузувчилар: Ф.-м.ф.н. Рахманов А.Т.,
ф.-м.ф.н Акбарова М.Х.,
т.ф.н. Керимов К.Ф.
Тақризчилар: Проф.,т.ф.д. Якубов М.С. ,
доцент, т.ф.н. Худайбердиев М.Х.
Услубий кўрсатма Ахборот технологияси дастурий таъминоти кафедрасининг 2013 йил 15 январда ўтказилган мажлисида кўрилган ва тасдиқланган.
Ахборот технологиялари факультети илмий-услубий кенгаши рухсати билан чоп этилди( № 7- баённома, 2013).
Тошкент ахборот технологиялари университети, 2013 йил
Мундарижа
КИРИШ................................................................................................................4
ТАШКИЛИЙ-УСЛУБИЙ КЎРСАТМАЛАР ..................................................5
1-тажриба иши. MATLAB ИНТЕРФЕЙСИ БИЛАН ТАНИШУВ. МАТРИЦАЛАРНИ ШАКЛЛАНТИРИШ ВА УЛАР УСТИДА АМАЛЛАР..........................................................................................................6
2-тажриба иши. MATLABДА СИМВОЛЛИ ЎЗГАРУВЧИЛАР БИЛАН ИШЛАШ............................................................................................................26
3- тажриба иши. MATLABДА ДАСТУРЛАШ. СЦЕНАРИЙ
ФАЙЛЛАРИ (СКРИПТ) ВА ФАЙЛ -ФУНКЦИЯЛАРНИ ТУЗИШ...........38
4-тажриба иши. MATLABда графикларни чизиш............................45
5-тажриба иши. Кузатув натижаларини бошланғич қайта ишлаш............................................................................................................58
ФОЙДАЛАНИЛГАН АДАБИЁТЛАР...........................................................71
кириш
Амалий математик дастурлар пакети бўлган MATLAB(Matrix laboratory) тизими нейрон тўри, электротехник қурилмаларни моделлаштириш, мураккаб математик масалаларни ечиш, физик жараёнларни компьютерда моделлаштириш каби кўплаб соҳаларда қўллаш учун яратилган. Инглиз тилидаги интеллектуал маҳсулот бўлган MATLAB тизими ҳозирги кунда илмий – техникавий ҳисоблашлар учун мукаммал ва кенг оммалашган тизим бўлгани сабабли, уни ўрганиш ва айниқса математика, физика, амалий математика, дастурлаш асослари каби фанларини ўқитиш жараёнида қўллаш табиийки, таълим самарасини янада оширади
Ушбу услубий кўрсатманинг асосий вазифаси қуйидагиларни ўргатиш ва амалда қандай қўллашни кўрсатишдан иборат:
1.MATLABда маълумотларни (сонли ва символли) матрица кўринишида киритиш , шакллантириш ва турли амалларни бажара олиш;
2.Фойдаланувчи функцияларини киритиш ва тузиш ;
3.Маълумотларни статистик қайта ишлаш;
4.Натижаларни визуализациялаш.
Кўрсатилган вазифаларни бажариш учун батафсил назарий маълумот амалий мисоллар билан биргаликда келтирилган.
Фанни ўқитилишидан мақсад: талабаларга кучли моделлаштириш тили бўлган MATLAB тизимини ўргатиш.
Тажриба машғулотларини ўтказишдан мақсад: аниқ масалаларни ечиш орқали назарий билимларни мустахкамлаш ва уларни амалиётда қўллаш кўникмаларини ҳосил қилиш.
Тажриба машғулотлари 16 соат хажмида белгиланган ва 5 та мавзу асосида бирлаштирилган.
Мазкур услубий кўрсатма тажриба машғулотларини бажариш ва ўзлаштириш учун ҳар бир мавзуга мос назарий маълумотлар ва мисоллар асосида шакллантирилган.
ТаШКИЛИЙ-УСЛУБИЙ КЎРСАТМАЛАР
1. Ҳар бир тажриба ишини бажаришдан олдин, тайёрланиши лозим бўлган тажриба ишига оид мавзулар бўйича маслаҳатлар (консультация) ўтказилади.
2. Ҳар бир тажриба иши хажми, уни тайёрлаш ва бажариш тартиби шундай тузилганки, барча талабалар берилган топшириқларни тайёрлашлари ва ҳисоботларни ўз вақтида топширишлари имкони эътиборга олинган.
3. Талабалар навбатдаги тажриба ишини бажаришга олдиндан тайёрланиб борадилар.
4. Талабалар 1000 В гача бўлган тажриба қурилмаларида ишлаш учун техника хавфсизлигини ўрганишлари шарт.
5. Талаба тажриба ишига тайёргарлик кўриш даврида мазкур кўрсатма ва тавсия этилаётган адабиётлардан фойдаланган ҳолда керакли назарий материалларни ўрганишлари, зарурий ҳисоблашларни амалга оширишлари ва назорат саволларига жавоб беришлари шарт..
6. Тайёр бўлмаган талабалар тажриба ишларини бажаришига рухсат берилмайди.
7. Машғулот мобайнида ҳисобот топширмаган талабалар, кейинчалик ўқитувчи белгилаган вақтда топширадилар.
8. Тажриба ишларини ўз вақтида топширмаган талабалар кейинчалик ўқитувчи билан вақтни келишган ҳолда топширадилар.
9. Ҳар бир тажриба иши талаба томонидан мустақил равишда тайёрланади. Ҳар бир талаба шахсий тарзда ҳисобот топширади. Ҳисоботни электрон хужжат ёки текст кўринишда топширилиши мумкин.
10. Талабалар билимлари тажриба машғулоти ва ҳисобот топшириш мобайнида ўқитувчи томонидан текширилади.
11. Ҳисобот топшириш даврида талаба назорат саволлари орқали аниқланувчи хажм асосида назарий билимларини ҳамда бажарилаётган ишнинг моҳиятини тушунишини кўрсатиши керак.
1-Тажриба иши. MATLAB ИНТЕРФЕЙСИ БИЛАН ТАНИШУВ. МАТРИЦАЛАРНИ ШАКЛЛАНТИРИШ ВА УЛАР УСТИДА АМАЛЛАР
Ишдан мақсад: Matlab тизими имкониятларини ўрганиш,матрицалар ва улар устида амалларни тадқиқ қилиш.
Қўйилган масала: MATLAB тизими менюлари, оддий ҳисоблашлар, ўзгарувчиларнинг турлари, матрицалар ва уларга доир мисолларни MATLAB тизимида ишлаб чиқиш .
Иш тартиби:
Ø Тажриба иши тавсифини ўрганиш;
Ø Берилган топшириқни MATLAB тизимида ҳал қилиш;
Ø Хисоботни тайёрлаш.
1.1. MATLAB матрицали тизимнинг вазифаси
Жадал суръатлар билан ривожланиб бораётган компьютерлашган математик тизимлар (КМТ), айниқса, сонли ҳисоблашларга йўналтирилган тизимлар орасида MATLAB матрицали математик тизим алоҳида ажралиб туради. MATLAB тизимини ташкил қилувчи пакетлар сони кўплиги унинг жуда кўплаб соҳа масалаларини ҳал қилишга жорий этиш имкониятини беради. Ҳозирги кунга келиб MATLAB тизими замонавий математик ва илмий-техникавий дастурий таъминоти соҳасида деярли жаҳон стандарти бўлиб қолди.
MATLAB – математик ва илмий-техник ҳисоблашларни амалга оширишга мўлжалланган, узоқ вақт давомида ишлаб чиқилган ва текширилган, автоматлаштирилган тизимлардан бири бўлиб, у матрица ва матрицавий амалларни кенгайтирилган талқини устига қурилган. Мазкур тушунча унинг номида ўз аксини топган, яъни MATLAB – matrix laboratory – матрицали лаборатория. Маълумки, жуда кўплаб дастурлаш тилларида матрицаларни эълон қилиш ва улар устида амаллар бажариш цикллар орқали амалга оширилади. Бу эса дастурни ишлашини секинлаштиради ва баъзи бир амалларни бажаришни мураккаблаштиради. MATLABда асосий объект сифатида матрицалардан фойдаланиш цикллар сонини кескин камайтиради.
MATLAB тизимини яратишдаги асосий мақсадлардан бири бўлиб, техник ва математик ҳисоблашларга йўналтирилган, фойдаланувчи учун қулай ва сонли усулларни амалга ошириш учун тадбиқ этиб келинаётган анъанавий дастурлаш тиллари имкониятларидан устунроқ дастурлаш тилини яратиш ҳисобланади. Мазкур тизимни яратишда ҳисоблашлар тезлигини оширишга ҳамда тизимнинг турли ҳил масалаларини ҳал қилишга мослашувчанлигига катта эътибор қаратилган.
MATLAB тизими дастурлашнинг учта асосий концепциясини амалга оширади:
· Модулларни, яъни процедура ва функцияларни, яратишга асосланган процедура модулли дастурлаш;
· Объектга йўналтирилган дастурлаш (айниқса, тизимнинг графикли воситаларини жорий қилиш аҳамиятли);
· Фойдаланувчининг графикли интерфейсини яратишга йўналтирилган визуаль-йўналтирилган дастурлаш (GUI-Graphics User Interface).
Умуман олганда, MATLAB дастурлаш тили интерпретаторлар синфига киради. Демак, тизимнинг ҳар бир командаси номи бўйича аниқланади ва зудлик билан жорий қилинади. Бу эса ихтиёрий дастурий кодни қисм-қисм бўйича текширишни осонлаштиради.
Тизимнинг асосий афзалликларидан бири бу унинг очиқлиги ва кенгайтириш мумкинлигидир.
Тизимнинг жуда кўплаб команда ва функциялари матнли форматдаги m-файл (кенгайтмаси .m) ва C/C++ файллари кўринишида бўлиб, барча файлларни модификация қилиш мумкин.
1.2. MATLABда оддий ҳисоблашлар
MATLAB тизими шундай ишлаб чиқилганки, ҳисоблашларни, фойдаланувчи дастурини тайёрламасдан тўғридан-тўғри бажариш мумкин. Бунда MATLAB суперкалькулятор вазифасини бажариб, қаторли команда режимида ишлайди. Масалан, >>2+3, ans=5; >>2*3, ans=6 ва хоказо.
Тизимда ишлаш мулоқатли (диалогли) тавсифга эга бўлиб, “савол берилди – жавоб олинди” қоидаси бўйича ишланади,яъни фойдаланувчи клавиатура ёрдамида ҳисобланиши лозим бўлган ифодани киритади, таҳрир қилади (агар лозим бўлса) ва киритишни ENTER клавиатурасини босиш билан якунлайди.
Умуман олганда, маълумотларни киритиш ва ҳисоблашларни амалга ошириш қуйидагича амалга оширилади:
· Бошланғич маълумотларни киритишни кўрсатиш учун >> белгидан фойдаланилади;
· Маълумотлар оддий ёзувли таҳрир ёрдамида киритилади;
· Бирор бир ифода ҳисоблаш натижасини блокировка қилиш учун мазкур ифодадан кейин ; (нуқта вергул) қўйилади;
· Ҳисоблашлар натижасини кўрсатувчи ўзгарувчи аниқланмаган бўлса, у ҳолда MATLAB тизими бундай ўзгарувчи деб ans олади;
· Ўзлаштириш амали сифатида жуда кўплаб дастурлаш тиллари каби := белги эмас, балки математикадаги оддий = ни ўзи олинади;
· Созланган функциялар (масалан, sin) ёзма харфлар билан ёзилади ҳамда уларнинг аргументлари оддий қавслар ичида ёзилади;
· Ҳисоблашлар натижаси янги қаторда >> белгисиз чиқади;
· Мулоқат “Савол берилди – жавоб олинди” кўринишида амалга ошади.
Маълумки, жуда кўплаб математик тизимларда, агар v сон эмас, вектор бўлса, у ҳолда sin(v) ва exp(v) каби ифодаларни ҳисоблаб бўлмайди, яъни тизим бундай ифодаларни хато деб беради. MATLABда эса агар берилган ўзгарувчи вектор(матрица) бўлса, натижа ҳам мазкур ўлчамдаги вектор(матрица) бўлади.
Командали режимда бир қатордаги белгиларнинг максимал сони – 4096, m – файлларда эса чегараланмаган.
Маълумки, ўзгарувчилар компьютер хотирасида, яъни ишчи соҳа (Workspace) да маълум бир жой эгаллайди. Ишчи соҳани кераксиз ўзгарувчилардан тозалаш учун clear функциясининг турли хил кўринишларидан фойдаланилади, масалан:
· clear - барча аниқланган ўзгарувчиларни йўқотиш;
· clear x - аниқланган x ўзгарувчини йўқотиш;
· clear a b c - аниқланган бир неча ўзгарувчиларни йўқотиш.
1.3. Тизим ўзгарувчилари ва константалари
Барча математик тизимлар каби MATLABнинг ҳам марказий тушунчаси математик ифодалардир. Маълумки, улар устида амаллар бажарилаётганда асосан уларнинг сонли қийматларидан фойдаланилади (кам холатларда белги кўринишларидан ҳам фойдаланилади).
MATLABда ифодалар бир қатор кўринишида ифодаланиб, сонларни бутун қисмларини ажратиш учун вергулдан эмас, балки нуқтадан фойдаланилади. Қуйида баъзи бир ифодаларни MATLAB ва оддий математикадаги ифодаланишини 1-жадвалда кўриб чиқамиз:
1-жадвал.
|
MATLABда |
Математикада |
|
2+3; |
2+3 |
|
2^3*sqrt(y)/2; |
|
|
2.301*sin(x); |
2,301sin(x) |
|
4+exp(3)/5 |
|
Математик ифодалар сонлар, константалар, ўзгарувчилар, операторлар, функциялар ва турли ҳил махсус белгилар устига қурилади.
1.4.Ҳақиқий ва комплекс сонлар
Сон - MATLAB тилининг энг оддий объектларидан бири бўлиб, у миқдорий маълумотларни ифодалаб беради. Сонлар бутун, каср, фиксирланган ва сузувчи нуқтали бўлиши мумкин. Уларни яхши маълум бўлган илмий шаклда, яъни мантисса ва сон тартибини кўрсатган ҳолда ифодалаш мумкин:
0
-3
2.301
123.456е-24
-234.456е10
Сон тартибини мантиссадан ажратиш учун улар орасига е белгиси қўйилади. “+” ишора сонлар олдига қўйилмайди, “-” ишора эса қўйилади ва у унар минус деб номланади. Сонларда белгилар орасига пробел (бўш жой) қўйиш рухсат этилмайди.
Бундан ташқари сонлар комплекс бўлиши мумкин: z=Re(z)+Im(z)*i. Бундай сонлар Re(z) ҳақиқий ва Im(z) мавхум қисмга эга бўладилар. Мавҳум қисм квадрати -1 га тенг бўлган, i ёки j кўпайтувчига эга бўлади:
3i
2+3j
-3.141i
-123.456+2.7e-3i
real(z) функция комплекс соннинг бутун қисмини, imag(z) эса мавхум қисмини ажратиб беради. Комплекс соннинг модулини abs(z) функция, бурчагини(фазасини) angle(z) функция ҳисоблаб беради. Масалан:
>> i
Ans=0+1.000i
>>z=2+3i
Z=2.000+3.000i
>>abs(z)
Ans=3.6056
>>real(z)
Ans=2
>>Imag(z)
Ans=3
>>angle(z)
Ans=0.9828
1.5. Сонларни ифодалаш форматлари
MATLABда сонларни форматини (шаклини) аниқлаштириш учун
>>format name
командасидан фойдаланилади, бу ерда name форматнинг номи.
Турли ҳил форматларни намойиш қилиш учун узунлиги иккига тенг бўлган x=[4/3, 1.234e-6] векторни кўриб чиқамиз:
2-жадвал.
|
format short |
1.3333 |
0.000 |
|
format short e |
1.3333E+000 |
1.2345E-006 |
|
format long |
1.333333333333338 |
0.000001234500000 |
|
format long e |
1.333333333333338E+000 |
1.234500000000000E-006 |
|
format bank |
1.33 |
0.00 |
Мазкур форматларни берилиши фақатгина натижавий маълумотларни кўринишига таъсир этади, холос. Барча ҳисоблашлар икки карра аниқлик форматида амалга оширилади, сонларни киритиш эса фойдаланувчи учун қулай бўлган ихтиёрий шаклда киритилиши мумкин.
1.6. Константа (ўзгармас) ва тизим ўзгарувчилари
Константа (ўзгармас) – бу олдиндан аниқланган сонли ёки белгили қиймат бўлиб, у ноёб ном (идентификатор) билан тақдим этилади. Сонлар (масалан, 1, -2 ва 1.23) номсиз сонли константа ҳисобланади.
MATLABда бошқача кўринишдаги константаларни тизим ўзгарувчилари деб аташ қабул қилинган, сабаби, бир томондан тизим юкланаётган вақтда улар берилади, иккинчи томондан улар дастурларда қайта аниқланиши мумкин. MATLAB тизимида ишлатиладиган асосий тизим ўзгарувчилари қуйидагилар:
· i ёки j мавхум бирлик (улардан квадрат илдиз олинса -1 га тенг бўлади);
· pi – сони, p=3,1415926… ;
· eps - сонлар устида амаллар бажарилгандаги хатолик (2-52);
· realmin - сузувчи нуқтали энг кичик сон (2-1022);
· realmax - сузувчи нуқтали энг катта сон (21023);
· inf - машина чексизлик қиймати;
· ans - энг охирги амални натижасини сақловчи ўзгарувчи;
· NaN - маълумотни сонли тавсифга эга эмаслигини кўрсатади (Not-a-number);
Белгили константа – бу апостроф ичига олинган белгилар занжири. Масалан, ‘Hello my friend’, ‘Salom’, ‘2+3’.
1.7. Дастурлардаги матнли шарҳлар
MATLAB тизими, асосан, мураккаб ҳисоблашларни амалга оширишга мўлжалланганлиги сабабли, бажарилаётган амаллар таърифини ошкорлиги, шаффофлиги катта аҳамиятга эга. Бунга, хусусан, матнли шарҳлар ёрдамида эришиш мумкин. Дастурларда матнли шарҳлар % белги ёрдамида қаторнинг ихтиёрий жойидан киритилади, масалан:
% It is factorial function.
MATLABнинг янги версияларида матнли шарҳни кириллчада ҳам киритиш имкониятлари мавжуд.
Одатда, m-файлларнинг дастлабки қаторларида биринчи позициядан бошлаб, ушбу файл амалга оширувчи вазифалар таърифлари шарҳ сифатида келтириб ўтилади. Мазкур таърифларни кўриш учун қуйидаги буйруқдан фойдаланилади:
>>help Файл номи
Агар матнли шарҳлар тўла-тўкис келтирилган бўлса, m-файл яхши ёзилган ҳисобланади. Сабаби, бундай кўринишдаги шарҳларсиз хаттоки, дастурий модулларни ишлаб чиққан дастурчининг ўзи хам ёзилган модул қандай вазифани бажариб бериши мумкинлигини ёддан чиқариб қўйиши мумкин.
1.8. Ўзгарувчилар ва уларга қийматларни ўзлаштириш
Ўзгарувчилар – бу номга эга бўлган объектлар бўлиб, баъзи-бир, одатда турли хил қийматларни сақлаш имкониятига эга маълумотлардир. Ушбу маълумотларга боғлиқ равишда ўзгарувчилар сонли ёки белгили, векторли ёки матрицали бўлиши мумкин. Ўзгарувчилар математика ва дастурлашда кенг тарқалган объектлар бўлиб ҳисобланади.
MATLAB дастурлаш тилида ўзгарувчига маълум бир қийматларни бериш учун ўзлаштириш (=) амалидан фойдаланилади:
<ўзгарувчи номи> = <ифода>
Ўзгарувчилар тури олдиндан эълон қилинмайди. Улар ўзгарувчиларга ўзлаштирилаётган ифодалар қийматлари орқали аниқланади. Демак, агар ифода вектор ёки матрица бўлса, у ҳолда ўзгарувчи шунга мос бўлади.
Ўзгарувчи номи (идентификатор) ихтиёрий сондаги белгилардан ташкил топган бўлиши мумкин, аммо фақатгина дастлабки 31 таси эслаб қолинади ва шулар орқали идентификация қилинади. Ўзгарувчи номи бошқа ўзгарувчилар, функциялар, процедуралар номи билан устма-уст тушмаслиги лозим, яъни ном ноёб бўлиши лозим. Гарчи ўзгарувчи номи харфдан бошланиши лозим бўлсада, орасида харфлар, рақамлар ва _ белгидан (подчеркивание) иборат бўлиши мумкин. Лекин, ўзгарувчи номларига бўш жойларни (пробелларни) ва махсус белгиларни, масалан +, -, *, / ва бошқаларни қўйиш мумкин эмас.
1.9. MATLABнинг операторлари ва созланган функциялари
Оператор – бу маълумотлар устида бажариладиган маълум бир амалларни бажариш учун ишлатиладиган махсус белгилаш (операнда). Масалан, оддий арифметик операторларга мисол қилиб қуйидагиларни олиш мумкин: йиғинди +, айирма -, кўпайтириш *, бўлиш /. Операторлар операндалар (маълумотлар) билан бирга ишлатилади. Масалан, 2+3*4 ифодада * кўпайтириш, + эса қўшиш оператори, 2,3 ва 4 эса операнда ҳисобланади.
Шуни таъкидлаб ўтиш лозимки, кўплаб операторлар матрицали операторларга тегишли бўлиб, жиддий тушунмовчиликларга сабаб бўлиши мумкин. Масалан, * - кўпайтириш ва / - бўлиш операторлари икки массив, вектор ёки матрицаалрнинг кўпайтмаси ва бўлинмасини ҳисоблайди. Бир қатор шундай махсус операторлар мавжудки, масалан, .\ , .* ва ./ операторлар, мос равишда, массивларда элементлар бўйича кўпайтириш ва бўлишни(ўнгдан ва чапдан) англатади.
Қуйида келтириладиган мисоллар юқорида айтиб ўтилган амалларни тушунтириб беради:
>>v1=[2 4 6 8 ]
V1 = 2 4 6 8
>>V2=[1 2 3 4 ]
V2 = 1 2 3 4
>>v1.*v2
ans=2 8 18 32
>>v1./v2
ans=2 2 2 2
MATLABдаги барча операторлар рўйхатини кўриш учун help ops операторидан фойдаланилади.
Функция – ўзининг аргументлари устида маълум бир шакл алмаштиришларни бажарувчи ва мазкур шакл алмаштириш натижаларини қайтариш хусусиятига эга бўлган ноёб номли объектдир. Натижани қайтариш – функциянинг бошқа объектлардан ажратиб турувчи хусусиятидир.
Функциялар умумий ҳолда бир нечта аргументларга эга бўлиши мумкин. Агар функция битта эмас, бир нечта натижавий қийматларни қайтарадиган бўлса, у ҳолда у қуйидагича ёзилади:
[Y1, Y2, …] = func(X1, X2, …),
бу ерда Y1, Y2, … - чиқиш параметрлар рўйхати, X1, X2, …-эса кириш параметрлар (аргументлар) рўйхати.
Элементар функциялар рўйхати билан help elfun буйруқ(команда)ни бериш орқали, махсус функциялар рўйхати билан эса help specfun орқали танишиш мумкин. Умуман олганда, функциялар созланган (ички) ва ташқи, яъни m-функциялар бўлади. Созланган функцияларга жуда кенг тарқалган элементар функциялар киради, масалан, sin(x), exp(x) ва бошқалар. Созланган функциялар MATLAB тизими ядросида сақланади, шу сабабли, улар орқали ҳисоблашлар жуда хам тез амалга оширилади. Ташқи функцияларни бериш учун махсус m-файлларни таҳрир қилувчи редактордан фойдаланилади.
1.10. Икки нуқта (:) операторини қўллаш
Маълумки, кўп ҳолларда тартибланган сонлар кетма-кетлигини шакллантириш зарурати пайдо бўлади. Бундай кўринишдаги кетма-кетликлар, масалан, графиклар ёки жадвалларни яратишда керак бўлади. Бунинг учун MATLAB тизимида : (икки нуқта) операторидан фойдаланилади. Тартибланган кетма-кетлик қуйидаги кўринишда ҳосил қилинади:
<бошланғич қиймат>: <қадам>: <сўнги қиймат>
Бундай конструкцияни тадбиқ қилиш дастурий циклларни беришни кескин камайтиради.
Агар қадам берилмаган бўлса, у ҳолда унинг қийматини автоматик тарзда 1 деб ҳисобланади. Агар қадам мусбат бўлиб, бошланғич қиймат сўнги қийматдан кичик бўлса, у ҳолда дастур хатолик ҳақида маълумот беради.
Мисоллар кўриб чиқайлик:
>>1:5
ans= 1 2 3 4 5
>>i=0:2:10
i = 0 2 4 6 8 10
>>j=10:-2:2
j= 10 8 6 4 2
>>0:pi/2:2*pi
ans = 0 1.5708 3.1416 4.7124 6.2832
>>1:-0.2:0
Ans = 1.0000 0.8000 0.6000 0.4000 0.2000 0
>>5:2
ans=Empty matrix: 1-by -0
MATLAB тизимида маълумотлар вектор ёки матрица кўринишида қуйидагича берилиши мумкин:
1) вектор- қатор:
>>V=[1 2 3] % ёки V=[1, 2, 3]
V= 1 2 3
2) вектор –устун:
>>V=[1; 2; 3]
V=
1
2
3
3) Матрица:
>>M=[1, 2, 3; 4, 5, 6; 7, 8, 9]
M=
1 2 3
4 5 6
7 8 9
Вектор ва матрица элементлари ифодалардан ёки функциялардан ташкил топган бўлиши мумкин. Вектор ва матрица элементларига уларнинг индексларини кўрсатиш орқали мурожаат қилинади, яъни
>> M(2,3)
ans = 6
Агар, масалан, M(i,j) элементга бирор бир x қийматни ўзлаштириш лозим бўлса, у ҳолда M(i,j)=x деб ёзилади.
>> M(2,3)=11;
>> M
M = 1 2 3
4 5 11
7 8 9
Умуман олганда, MATLAB тизимида индекс сифатида i,j лар ўрнига I ва J лардан фойдаланиш тавсия этилади.
Бир индексли M(I) ифода берилган матрицани бир қаторга ёйилгандаги қийматини аниқлаб беради. Масалан:
>> M=[1, 2, 3; 4, 5, 6; 7, 8, 9]
M = 1 2 3
4 5 6
7 8 9
>> M(6)
ans = 8
>> M(6)=111;
>> M
M = 1 2 3
4 5 6
7 111 9
MATLABнинг 2007b
версиясида nxn ўлчамли матрица билан ишлаш мумкин бўлиб, бунда максимал 
(олдинги
версияларда эса 
бўлган). Бундай
ҳолда мазкур катталикдаги матрицаларни ўз ичига олувчи файлларнинг хажми
18 Гб гача бўлиши мумкин.
1.11. Комплекс элементли вектор ва матрицаларни аниқлаш
Бундай кўринишдаги вектор ва матрицаларни қуйидагича бериш мумкин:
>> CM=[1, 2; 3, 4] + i*[5, 6; 7, 8]
Ёки
>> CM=[1+5*i, 2+6*i; 3+7*i, 4+8*i]
CM =
1.0000 + 5.0000i 2.0000 + 6.0000i
3.0000 + 7.0000i 4.0000 + 8.0000i
1.12. Матрицалар устида алмаштиришлар
1. Матрицаларни бирлаштириш (конкатенация қилиш) мумкин. Бунинг учун cat(1,A,B) ёки [A;B] ва cat(2,A,B) ёки [A,B] командаларидан фойдаланилади. Масалан, бизга М матрица берилган бўлсин:
1 3 4
M = 5 7 8
3 5 6
4 6 7
>> B=[M M+16; M+32 M+16]
B =
1 3 4 17 19 20
5 7 8 21 23 24
3 5 6 19 21 22
4 6 7 20 22 23
33 35 36 17 19 20
37 39 40 21 23 24
35 37 38 19 21 22
36 38 39 20 22 23
2. Буриш амалларини бажариш учун MATLABда қуйидаги командалардан фойдаланилади:
fliplr (A) – А матрицада вертикал ўққа нисбатан устунлар алмаштирилади.
flipud (A) – А матрицада горизонтал ўққа нисбатан қаторлар алмаштирилади.
rot90 (A) – А матрицани соат стрелкасига қарши 90° га буради.
rot90 (A, k) – A матрицани 90*k градусга буради (k – бутун сон).
3. Матрицани сатр ёки устунларини ажратиб олиш ва ўчириш мумкин. Масалан, берилган М матрицанинг бирор бир i- устун ёки j-сатрни ўчириш талаб этилган бўлсин. У ҳолда ушбу амал қуйидагича амалга оширилади (икки нуқта (:) операторидан фойдаланилган ҳолда): M(:, i) команда М матрицанинг i-устунини, M(j, :) команда М матрицанинг j-қаторини ажратиб олади:
>> M(3,:)
ans=3 5 6
>>c=M(:,2)
с=3
7
5
6
Агар бирор устун ёки қаторни ўчириш лозим бўлса, [] – белгисидан фойдаланилади:
>> M(:, 3)=[ ]
M = 1 3
5 7
3 5
4 6
>> M(2, :)=[ ]
M= 1 3 4
3 7 8
4 6 7
Олинган натижаларни таҳлил қилишда фойдаланувчи ўзини қизиқтирган матрица ёки массив ҳақида баъзи -бир маълумотларга эга бўлиши лозим бўлади. Бунинг учун MATLABда бир қанча махсус функциялар мавжуд:
1. size(M) – иккита элементга эга бўлган вектор ҳосил бўлиб, биринчи элемент М матрица қаторлар сонини, иккинчиси эса устунлар сонини кўрсатади.
2.
length(A) – А
вектор узунлигини аниқлаб беради (агар А матрица бўлса, у ҳолда 
.)
3. ndims(M) – М матрица ўлчовини аниқлаб беради.
4. isempty(M) – берилган М массивни “бўшликка” текширади. Агар массив элементлари йўқ бўлса, у 1 қийматни, акс ҳолда 0 қийматни қайтаради.
5. isequal(A,B) – берилган иккита А ва В массивни эквивалентликга текширади. Улар эквивалент дейилади, яъни 1 қийматни беради, агар хар иккала массив ўлчови бир ҳил ва элементлар қийматлари устма-уст тушса, акс ҳолда 0 қийматни қайтаради.
6. isnumeric(A) – берилган А массивни турини мантиқий аниқлайди, агар сонли тур бўлса 1 қийматни, акс ҳолда 0 қийматни қайтаради.
1.13. MATLABда арифметик ва мантиқий амаллар
MATLABда арифметик амаллар икки турга бўлинади:
- скаляр тур – бу скаляр миқдорлар устида бажариладиган оддий амаллар;
- матрицали тур – матрицалар устида бажариладиган амаллар. Уларни бажариш қоидалари оддий амалларни бажариш қоидаларидан фарқ қилади.
Скаляр турдаги арифметик амаллар: (+) қўшиш; (-) айриш; (*) кўпайтириш; (/) чапдан ўнгга бўлиш; (\) ўнгдан чапга бўлиш (яъни a\b- b ни a га нисбати каби тушунилади); (^) даражага ошириш. Скаляр миқдорлар устида амаллар 3- жадвалда келтирилган устиворлик қоидасига асосан бажарилади.
3- жадвал.
|
устиворлик |
Амаллар |
|
1 |
Оддий қавс |
|
2 |
Даражага ошириш, чапдан-ўнга |
|
3 |
Кўпайтириш ва бўлиш, чапдан-ўнга |
|
4 |
Қўшиш ва айриш, чапдан-ўнга |
Матрицали турдаги арифметик амаллар:
1. (+) қўшиш ва (-) айириш. Ушбу амал фақатгина қўшилаётган ёки айрилаётган матрицаларнинг ўлчамлари тенг бўлгандагина ўринли бўлади (агар қўшилувчиларнинг бирортаси скаляр бўлса, MATLAB тизими скаляр миқдорни ўлчамлари берилган матрицага тенг бўлган ўлчамли, элементлари эса берилган скаляр миқдорга тенг матрица деб ҳисоблайди);
2. (*) кўпайтириш: Матрицани матрицага кўпайтиришнинг бир неча кўринишлари мавжуд:
а)алгебрадаги матрицани матрицага кўпайтириш: 
, бунда 
ва
бўлиб,
;
б) A.*B – А нинг ҳар бир элементи В нинг мос элементига кўпайтирилади, яъни
.
3. Бўлиш: а) A./B – А
нинг ҳар бир элементи В нинг мос элементига бўлинади, яъни 
.
б) A.\B – В нинг ҳар бир элементи А нинг
мос элементига бўлинади, яъни 
.
4. Даражага ошириш: A.^B – A нинг ҳар бир элементи B нинг мос
элементига тенг даражага кўтарилади, яъни 
.
Икки вектор-қаторнинг скаляр (ички) кўпайтмаси деб (a*b') га , ташқи кўпайтмаси деб (b'*a) га айтилади.('-транспонирлашни англатади)
Назорат саволлари
1. MATLABнинг асосий объектлари нима?
2. MATLABда сонларнинг қандай форматлари бор?
3. Матрица, вектор-устун ва вектор-қаторни таърифланг.
4. Матрицаларни хосил қилиш усулларини айтинг ва мисоллар келтиринг
5.Матрицалар устида бажариладиган қандай амаллар бор?
6.Арифметик амаллар бажарилишини устуворлик қоидаси қандай?
7.Матрицалар устида кўпайтириш амали қандай бажарилади?
8.Икки нуқта (:)командаси вазифаларини тушунтиринг.
9.MATLABда қандай солиштириш ва мантиқий амаллар мавжуд?
10.Матрицани транспонирлаш нима?
11.flipud ва fliplr командалари нима учун хизмат қилади?
12.Махсус матрицаларни ҳосил қилувчи командаларни келтиринг.
Топшириқлар
1. Элементлари cosnx кўринишида бўлган (4х4) матрицани х=π/2 да хисобланг. (n=1, …,16). Уни Паскальнинг мос тескари матрицаси билан таққосланг ва натижанинг ўлчовини кўрсатинг.
2. Ўлчови 5 га тенг бўлган Гильберт матрицасига Паскаль матрицасини кўпайтиринг. Кўпайтманинг элементлари йиғиндисини топинг ва натижани format short да чиқаринг.
3. Паскаль ва “сехрли” матрица берилган. Уларнинг мос элементлари таққосланиб, катталаридан янги матрица хосил қилинсин. Массив йиғиндиси ва ўлчовлари аниқлансин.
4. Берилган матрица жуфт сатрдаги элементларини тескариси билан, тоқ учтундаги элементларини тоқ сатр элементларига алмаштириб матрица ясанг. Янги матрицанинг ўртадаги сатр ва устунни ўчириб, натижани пастдан юқорига буринг.
5. Берилган икки матрицани бирлаштириш орқали янги матрица ҳосил қилинг.
6. Берилган матрицани бошидаги учта сатри ва сўнги бешта устунидан иборат бўлган матрица ҳосил қилинг.
7. Берилган “сеҳрли” матрицадан индекслари йиғиндиси жуфт бўлганлари ўрнига 0 жойлаштириш орқали янги матрица шакллантиринг.
8. Берилган “сеҳрли” матрицадан индекслари йиғиндиси тоқ бўлганлари ўрнига 5 жойлаштириш орқали янги матрица шакллантиринг.
9. Берилган “сеҳрли” матрицанинг тоқ сатр ва жуфт устундаги элементлари ўрнига 9 ни жойлаштириш орқали янги матрица шакллантиринг.
10. Берилган “сеҳрли” матрицанинг жуфт сатр ва тоқ устундаги элементлари ўрнига -1 ни жойлаштириш орқали янги матрица шакллантиринг.
11.
Берилган
“сеҳрли” матрицанинг элементлари 
дан катта бўлса, у
ҳолда улар ўрнида 1, элементлари дан кичик бўлса, у
ҳолда улар ўрнида -1, акс ҳолда улар ўрнида 0 бўлган янги матрица
шакллантиринг.
12. Берилган Гильберт матрицадан индекслари йиғиндиси жуфт бўлганлари ўрнига 0 жойлаштириш орқали янги матрица шакллантиринг.
13. Берилган Гильберт матрицадан индекслари йиғиндиси тоқ бўлганлари ўрнига 5 жойлаштириш орқали янги матрица шакллантиринг.
14. Берилган Гильберт матрицанинг тоқ сатр ва жуфт устундаги элементлари ўрнига 9 ни жойлаштириш орқали янги матрица шакллантиринг.
15. Берилган Гильберт матрицанинг жуфт сатр ва тоқ устундаги элементлари ўрнига -1 ни жойлаштириш орқали янги матрица шакллантиринг.
16. Берилган Гильберт матрицанинг элементлари 0,7 дан катта бўлса, у ҳолда улар ўрнида 1, элементлари 0,4 дан кичик бўлса, у ҳолда улар ўрнида -1, акс ҳолда улар ўрнида 0 бўлган янги матрица шакллантиринг.
17. Ўлчови 5 бўлган Паскал матрицасига тескари матрицани шакллантиринг ва шакллантирилган матрица бош диагоналига 0 жойлаштиринг.
18. Берилган Гильберт матрицанинг элементлари ўрнига мазкур матрица детерминантини қўйиш орқали матрица хосил қилинг.
19. Берилган матрицадан жуфт сатрда турган элементлар ўрнига ушбу элементлар квадратига, тоқ сатрда турган элементлар ўрнига эса ушбу элементлар кубига тенг бўлган матрица шакллантиринг.
20. Берилган матрицанинг тоқ устуни билан жуфт устунларини ўрнини алмаштириш орқали матрица шакллантиринг.
21. Берилган матрицанинг тоқ сатри билан жуфт сатрларини ўрнини алмаштириш орқали матрица шакллантиринг.
22. Берилган матрицанинг тоқ элементлари ўрнига 1 ва жуфт элементлари ўрнига 0 қўйиш орқали янги матрица шакллантиринг.
23. Берилган матрицанинг мусбат элементлари ўрнига 1 қўйиш орқали янги матрицани шакллантиринг.
24. Берилган матрицанинг манфий элементлари ўрнига 0 қўйиш орқали янги матрицани шакллантиринг.
25. Берилган матрицанинг манфий элементларини шу элемент тескариси билан алмаштириш орқали янги матрицани шакллантиринг.
26. Берилган матрицанинг мусбат элементларини шу элемент тескариси билан алмаштириш орқали янги матрицани шакллантиринг.
27. Бир хил ўлчамли иккита, Паскаль ва “сеҳрли” матрица берилган бўлсин. Ушбу матрицаларнинг мос элементлари таққосланиб, шу элементларнинг катталаридан ташкил топган янги матрица шакллантиринг.
28. Бир хил ўлчамли иккита, Паскаль ва “сеҳрли” матрица берилган бўлсин. Ушбу матрицаларнинг мос элементлари таққосланиб, шу элементларнинг кичикларидан ташкил топган янги матрица шакллантиринг.
29. Берилган матрицанинг манфий элементларини шу элемент қарама-қаршиси билан алмаштириш орқали янги матрицани шакллантиринг.
30. Берилган сехрли ва Паскаль матрицаларининг тескарисини топинг. Тўғри сехрли ва унга мос тескари матрицаларни асосий диагоналга, тўғри паскаль ва унга мос тескари матрицаларни иккинчи диагоналга жойлаб, янги матрица ҳосил қилинг ҳамда ҳосил бўлган матрицани детерминантини, тескарисини аниқланг.
Ҳосил қилинган маълумотларни экранга ва қоғозга чиқаринг.
2-Тажриба иши. MATLABДА СИМВОЛЛИ ЎЗГАРУВЧИЛАР БИЛАН ИШЛАШ
Ишдан мақсад: Matlab тизимида символли ўзгарувчилар билан ишлаш имкониятларини ўрганиш,
Қўйилган масала: MATLAB тизимида ифодалар устида амаллар бажариш, функцияларни киритиш ва қийматларини ҳисоблаш , тенгламаларни ечиш.
Иш тартиби:
Ø Тажриба иши тавсифини ўрганиш;
Ø Берилган топшириқни MATLAB тизимида ҳал қилиш;
Ø Хисоботни тайёрлаш.
2.1. Символли ўзгарувчилар
MATLABда математик ҳисоблашларни, символли ўзгарувчилар ва улар қатнашган ифодаларни, функцияларни киритиш ва улар устида амаллар бажариш учун махсус созланган функциялар ва командалар ёрдамида бажариш мумкин.
Маълумки, символли ўзгарувчилар синфи сонли ўзгарувчилар синфидан тубдан фарқ қилади. Чунки сонли ўзгарувчилар ёрдамида фақат арифметик ифодалар қийматлари хисобланса, символли ўзгарувчилар ёрдамида алгебраик ифодалар устида хар хил алмаштиришлар ва амаллар бажариш мумкин. Символли ўзгарувчиларни киритишдан олдин sym ёки syms командалари орқали эълон қилиш керак:
% ёки
a b c
Агар уларнинг қийматини чиқариш командасини берсак, система хатолик ҳақида ахборот беради:
>>c
??? Undefined function or variable ‘c’
2.2. Символли функциялар ва ифодалар
Функцияни эълон қилиш учун
>>
командасидан фойдаланилади.
Масалан, командалар ойнасида 
функция кўринишини хосил қилиш мумкин:
>>
Функцияни бериш учун бошқа командалардан хам фойдаланса бўлади.
Бу холда функция аниқланишида ишлатилаётган
барча ўзгарувчилар аввал эълон қилинади. Масалан, функцияни
аниқлаш ва унда 
, 
, 
, 
, 
каби
алмаштиришларни бажариш керак бўлса, қуйидагича командалардан
фойдаланилади:
a b c x
, , ,
Натижалар экранга чиқади :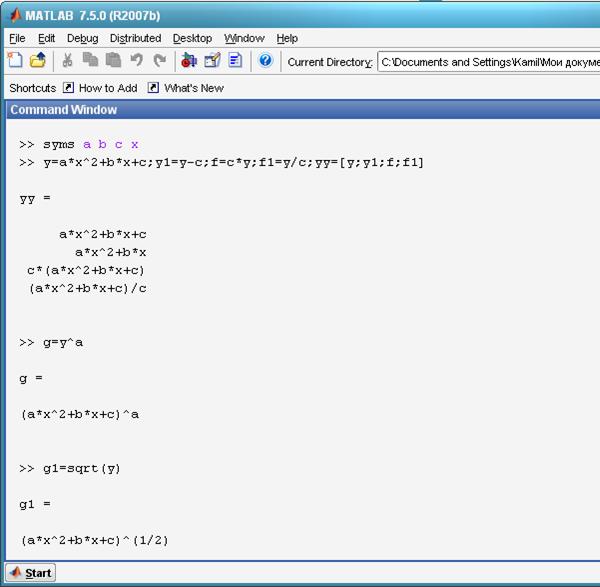 
1 - расм. Символли ифодаларни командалар ойнасида кўриниши. Р ифодани туб қўпайтувчиларга ажратиш учун factor(Р), тўла ёйиш учун expand(Р), кўрсатилган а параметр бўйича ёйиш учун collect(Р,’a’), соддалаштириш учун simplify(Р) ва ўрнига қўйиш учун subs(Р, ‘а’ ,’в’) командалари ишлатилади.
1-мисол. 
кўпхадни а ва 
нинг даражалари бўйича ва тўла ёйинг.
Бу вазифани қуйидаги командалар кетма-кетлиги ҳал қилиб беради:
a b c
;
Натижа.
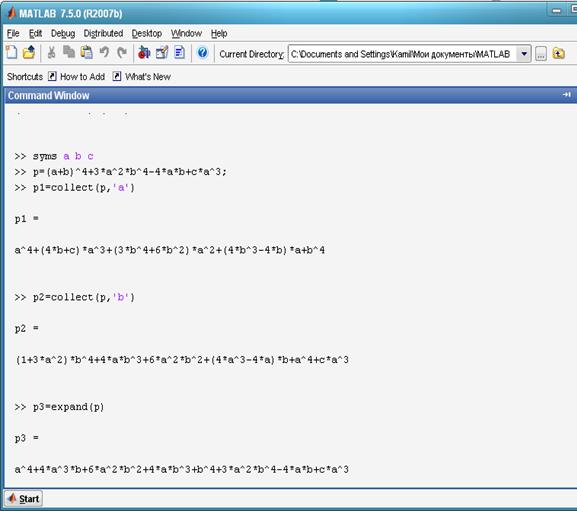
2 - расм. Символли командаларни қўлланилиши.
2-мисол. 
кўпҳадни
кўпайтувчиларга ажратинг, 
алмаштиришни
бажаринг ва уни соддалаштиринг.
;
Натижа:
3 - расм. Соддалаштириш командаларининг кўриниши.
Юқорида келтирилган командалардан фойдаланиб, мураккаб ифодаларни қийматларини ҳисоблаш ҳам мумкин.
Мисол.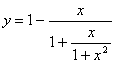 
ифодани
соддалаштиринг ва 
да ҳисобланг.
х
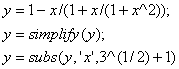
4- расм. Каср функцияни соддалаштириш.
2.3. Cимволли ўзгарувчилар ёрдамида aлгебраик тенгламаларни ечиш
MATLAB тизимида символли ўзгарувчилар ёрдамида график чизиш ва алгебраик тенгламаларни ечиш имконияти хам мавжуддир. Функция нолларини топиш учун fzero, fsolve, solve, график равишда топиш учун эса ezplot ва кўпхад нолларини топиш учун roots командалари ишлатилади.
Мисол. y=x5-2x3+2x-0,2 полиномни илдизлари топилсин . Бунинг учун символли ўзгарувчилардан фойдаланиб ezplot(y) ёрдамида график қурамиз ва функция ноли жойлашган оралиқни тахминан аниқлаймиз. Бизнинг мисолда бу оралиқ [0;1,5] бўлади. Ечимни аниқлаш учун қуйидаги командалар кетма-кетлигини ёзамиз ва графикни ҳосил қиламиз(5-расм):
syms x
y=x^5-2*x^3+2*x-0.2;
H=ezplot(y, [0;1,5]); % у функция графигини чизиш командаси
grid on; % координаталар текислигида тўр чизиш
ylabel(‘y’); % оу ўқини белгилаш
xlabel(‘x’); % ох ўқини белгилаш
title(‘Funksiya y=x^5-2*x^3+2*x-0.2’) % график сарлавҳаси
5 -расм. Функциянинг бошланғич графиги.
Энди график ойнада Zoom In кнопкасини ишлатиб, графикни масштаблаймиз ва керакли аниқликдаги ечимни аниқлаймиз. Графикни масштаблашда, уни ОХ ўқини тахминан кесиб ўтаётган нуқтада бажаришимиз лозим бўлади. Керакли аниқликка эришиш учун масштаблаш бир неча марта бажарилиши мумкин. Масштаблашни 5-расмдаги графикда бир неча марта бажариб, қуйидагини оламиз(6-расм):
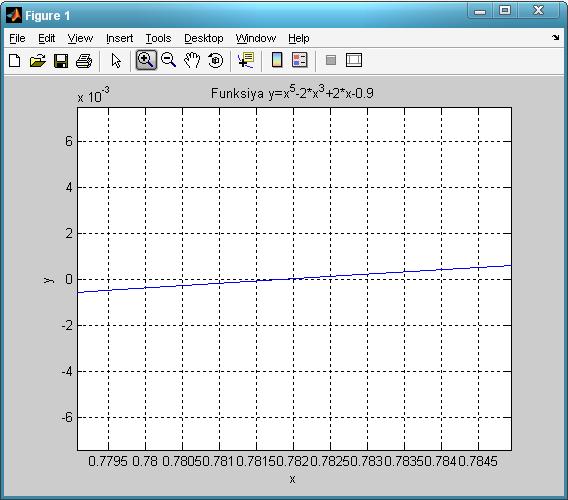
6 -расм. Масштабланган график.
Бу расмдан кўриниб турибдики, тенгламани тақрибий ечими х=0,7820 бўлади.
Тенгламани ечиш учун MATLABнинг созланган функцияси solve дан ҳам фойдаланиш мумкин. Бу функция ечимни аналитик формада топиб беради. Ундан кейин эса ечимни кўрсатилган аниқликда ифодалаб берувчи vpa(y,n) (n-вергулдан кейинги рақамларлар сони) функциясини қўллаш керак.
Агар тенглама тўрт ва ундан юқори тартибли, иррационал ёки транцендент бўлса, solve функцияси ечимни тақрибий сонли қийматини аниқлаб беради. Юқоридаги тенгламада ҳам худди шундай ечимлар аниқланган.
Энди масалани қуйидагича қўямиз: x5 -2x3+2x-0.9=0 тенгламани ечимини символли ўзгарувчилар ёрдамида solve функциясини қўллаб топинг ва аргументнинг шу қийматида y=x5-2x3+2x-0.9 полином қийматини ҳам аниқланг.
Бунинг учун қуйидаги командалар кетма-кетлиги етарли:
syms x ;
y=x^5-2*x^3+2*x-0.9; x=solve(y,x)
7 - расм. y=x5-2x3+2x-0.9 функция нолларини топиш.
Бу усул ёрдамида олинган ҳақиқий тақрибий ечим (7-расмда х векторнинг 1-координатаси), юқорида график усулда топилган ечим билан бир хил эканлиги кўриниб турибди.
Алгебраик тенгламаларни ечиш учун мўлжалланган бошқа функциялар қуйидаги форматларда қўлланилади:
1) [x, f]=fzero(‘F’,х0) – х ечимни ва шу нуқтадаги функция қийматини қайтаради; бу ерда F – тенглама чап томонини қийматини баҳоловчи файл-функциянинг ёки тенглама чап томони бўлиши мумкин, х0 эса
[a b] вектор ёки [a ,b] оралиққа тегишли сон, F(a)*F(b)<0;
2) [x, f]=fsolve(‘F’,x1) – бу ерда х ечим, f эса шу нуқтадаги функция қиймати, х1 – бошланғич нуқталардан тузилган массив.
3) R=roots(a) – p полиномнинг илдизларини тақрибий қийматларини беради (а – полином коэффициентлардан тузилган вектор).
Юқорида келтирилган функция форматларидан кўриниб турибдики, ezplot(y), ezplot(y, [x1, x2]) командалари fsolve, fzero функциялари билан бирганликда ишлатилса, ечимни аниқлаш жараёни универсал бўлади. Таъкидлаш жоизки, fsolve ва solve функциялари чизиқли бўлмаган тенгламалар системаларини ечишда ҳам қўлланилади.
Назорат саволлари
1.Символли ў згарувчилар қандай эълон қилинади?
2.Қандай функциялар ёрдамида ифодани тўла ёйиш,соддалаштириш,кўпайтирувчиларга ажратиш мумнин?
3.Ифодада қатнашаётган ўзгарувчини бошқа параметрга алмаштириш учун нима қилиш керак?
4.Кўпҳад илдизини қандай функция ёрдамида топиш мумкин?
5.Қайси функция тенгламанинг илдизини график усулда топади?
6. fzero ва fsolve функцияларнинг вазифаларини тушунтиринг.
7. solve функциясининг қўлланиш форматини изоҳлаб беринг.
8.Нима учун тенглама илдизини аниқловчи функцияларни биргаликда
қўллаш керак?
9.Қайси функцияни бошланғич қадам сифатида ишлатиш мумкин?
10. ezplot функцияси қандай ечимни топади?
Топшириқлар
1.х=0, 2, 4, 6, 8, 10 массивни яратинг. Ушбу 
ўзгарувчини киритинг ва 
да мос матрицани
тузинг ва уни транспонирланг.
2.х=0, 
массивни яратинг.
Ушбу 
ва 
ўзгарувчиларини
киритинг. Мос Y ва Z матрицаларни =1,
=2
да ҳосил қилинг ва уларни кўпайтмасини ҳисобланг.
3.Агар 
бўлса, k=lg
y ва m=ln(y+1) амалларни бажаринг. =1
ва х=0,5 да натижани узун формат билан чиқаринг.
4.Ушбу 
алгебраик
ифодани нинг
даражалари бўйича ёйинг. ва
ни
0.5 ва 1.5 қийматларга алмаштириб, ифода қийматини
қисқа форматда чиқаринг.
5.Ушбу 
тригонометрик
ифодани кўпайтувчиларга ажратинг. 
да 
да
қийматини ҳисобланг. Ҳосил бўлган векторнинг элементлар
йиғиндисини рационал кўринишда чиқаринг.
6.
ифодани 
да
соддалаштиринг. Р (0), Р (1) ларни ҳисобланг. Натижалар квадратлари
йиғиндисини рационал форматда чиқаринг.
7.=(5,6,7) бўлганда символли ўзгарувчи 
учун
қийматларни subs
командаси ёрдамида банк форматида чиқаринг, х нинг қийматлари
йиғиндисини ва кўпайтмасини топинг.
8.Ушбу 
тригонометрик
ифодани тўла ёйинг. ни
- га алмаштириб, натижани 
ва 
да
узун формат билан чиқаринг.
9.
кўпхад
илдизларини roots функция орқали аниқланг. Илдизларга мос функция
қийматларини 0.001 аниқликда чиқаринг.
10.
функциянинг нолларини roots функцияси орқали топинг . Илдизларга мос
функция қийматларини йиғиндисининг кубини топинг. Натижани ва
функция нолларини рационал кўринишда чиқаринг.
11.
функциянинг
нолларини fzero функция ёрдамида топинг. Илдизларнинг ва уларга мос функция
қийматларининг ўрта арифметигини ҳисобланг.
12.
функциянинг нолларини fzero функцияси ёрдамида аниқланг (бошланғич
нуқталар сифатида -1 ва 0 ни қаранг). Илдизлар ва уларга мос
функция қийматларининг мос ўрта геометригини чиқаринг.
13.
функция
нолларини fzero функцияси орқали топинг (бошланғич нуқта
сифатида 0 ва 1 ни қаранг). Илдизлар ва уларга мос функция
қийматларининг квадратларини ҳисобланг.
14.
тенгламанинг ечимини топинг (бошланғич нуқта сифатида -3, -1, 1 ни
олинг. Функция мос қийматларини ҳисобланг).
15.Ушбу 
ифодани
кўпайтувчиларга ажратинг. 
ва бўлса,
ифоданинг қийматини ҳисобланг ва натижаларининг тафовутини
аниқланг.
16.Ушбу 
тригонометрик
ифодани кўпайтувчиларга ажратинг. Агар 
бўлса, у нинг
қийматини топинг. Натижанинг квадрат илдизини банк форматида
чиқаринг.
17.
тенгламани
ечинг. Илдизларнинг йиғиндисини узун форматда чиқаринг.
Бошланғич нуқта сифатида -3, -5, 0, 4 ни олинг.
18.
нинг
ечимини fzero функцияси ёрдамида топинг (бошланғич нуқталар
сифатида 0 ва 1 ни олинг). Ечимларга мос функция қийматларини
аниқланг ва уларнинг ўрта арифметигини топинг.
19.
тенглама
ечимларини топинг. Ечимларга мос функция қийматларини аниқланг.
Уларнинг ўрта геометригини ҳисобланг. Бошланғич нуқта
сифатида -1, 0, 1 ни олинг.
20.
тенгламани
ечимларини топинг. Чап томондаги ифоданинг илдизларга мос қийматларини
аниқланг.
21. 13-мисолда келтирилган функция нолларини solve ва vpa функциялардан фойдаланиб 10^-5 аниқликда топинг.
22. 14-мисолда келтирилган тенгламани solve ва vpa функциялардан фойдаланиб 10^-4 аниқликда топинг.
23. функция
нолларини roots ҳамда solve ва vpa функцияларидан фойдаланиб
керакли аниқликда топинг ва мос нолларни солиштиринг.
24. 19 ва 23 мисоллардаги функциялар йиғиндисини, айирмасини ва кўпайтмасини нолларини roots ҳамда solve функциялардан фойдаланиб топинг.
25. тенглама
ечимларини 10^(-7) аниқликда топинг.
Илова. Топилган ечимларни ezplot функцияси ёрдамида текширинг ва хулоса қилинг. Ҳосил қилинган маълумотларни экранга ва қоғозга чиқаринг.
3-Тажриба иши. MATLABДА ДАСТУРЛАШ. СЦЕНАРИЙ ФАЙЛЛАРИ (СКРИПТ) ВА ФАЙЛ ФУНКЦИЯЛАРНИ ТУЗИШ
Ишдан мақсад: MATLABда M-файлларни яратиш ва улардан фойдаланишни ўрганиш ҳамда уларни тадқиқ қилиш.
Қўйилган масала: Берилган масалалар учун скрипт ва файл -функциялар яратиш.
Иш тартиби:
Ø Тажриба иши тавсифини ўрганиш;
Ø Берилган топшириқни MATLAB тизимида ҳал қилиш;
Ø Ҳисоботни тайёрлаш.
3.1. MATLABда файллар
MATLABда 2 турдаги файллар мавжуд:
Файл-сценарий - янги м-файлда ёзилган MATLAB командалари кетма кетлигидан иборат бўлади;
Файл-функция - аниқ номга эга функция бўлиб, фойдаланувчи томонидан аниқланган бўлади.
Script-файл деб аталувчи файл-сценарийлар кириш ва чиқиш параметрлари бўлмаган ва янги m-файлда ёзилган бир нечта командалар қаторининг тўпламидир. Улар қуйидаги таркибга эга бўлади:
· %Асосий изоҳ;
· %Қўшимча изоҳ;
· Бир нечта командаларни ўз ичига олувчи файлнинг қобиғи.
Файл-сценарий қуйидаги хоссаларга эга бўлади:
· Кириш ва чиқиш аргументлари бўлмайди;
· Ишчи соҳадаги маълумотлар билан ҳам ишлайди;
· Бажарилиш вақтида компиляция бўлмайди;
· Файл кўринишга келтирилган, сессиядагига ўхшаш амаллар кетма-кетлигидан иборат бўлади.
Файл-сценарийларга ном бериб сақланади, уларга командалар ойнасидан номи терилиб мурожаат қилинади. Масалан, берилган х векторнинг йиғиндиси а дан ошмайдиган биринчи к та координатасини топиш керак бўлсин. Бу масалани sikl деб номланган 8-расмдаги файл-сценарий ечиб беради.
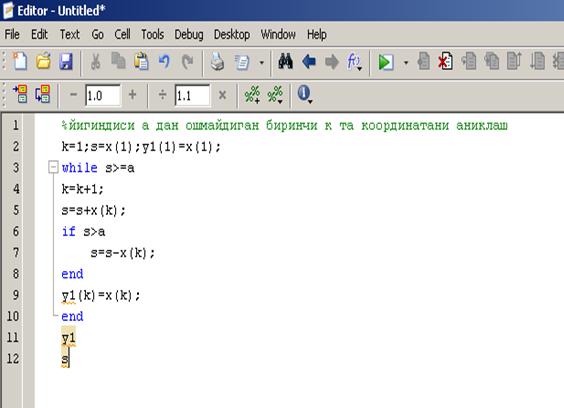
8-расм. sikl номли файл-сценфрий кўриниши.
Юқоридаги файлга командалар ойнасидан қуйидагича мурожат қилиб натижа олинади:
>>a=30; x=[1 4 2 7 8 9 23 11 7 ];
>>sikl
3.2. Фойдаланувчи функцияси
MATLAB тизимида гарчи 1000 дан ортиқ созланган функциялар (ўнлаб кенгайтма пакетларда аниқланган функцияларни ҳисобламаганда) бўлса-да, фойдаланувчи учун яна қандайдир функциялар зарур бўлиб қолиши мумкин. MATLAB тизимининг дастурлаш тили фойдаланувчи учун бундай функцияларни яратишнинг бир қатор имкониятларини беради. Бунда фойдаланувчи янги функцияни ҳосил қилиб MATLAB каталогига қўшиб қўйиш имкониятига эга. Янги функцияни ташкил қилувчи команда ва функциялар матнли м-файлларда жойлашган бўлади. Шунинг учун м-файл-функция деб аталади.
Янги ҳосил қилинган, бир нечта командалар кетма-кетлигидан иборат функция ўзининг номига, кириш параметрлари деб аталувчи аргументларига ва локал характердаги ўзгарувчиларга эга бўлиб, унга параметрларига қиймат берган холда номи орқали мурожаат қилиш мумкин бўлади.
Функция ҳосил қилинаётган м-файлнинг бошланғич қаторлари матнли шарҳлардан иборат бўлиб, шу функциянинг моҳиятини, хоссаларини очиб берувчи бўлиши керак. Ундан кейинги биринчи қаторда аниқланган функция номи м-файлнинг кенгайтмасиз номи билан бир хил бўлиши керак. Умумий кўринишда м-файл- функция ҳар доим function сўзидан бошланиб, қуйидагича бўлади:
function y=<функция номи>
Функция номидан кейин оддий қавс ичига аргументлар (параметрлар) вергул(,) билан ажратиб ёзилади. Масалан, m-файл таҳрир ойнасида sc2.m ном билан файл яратамиз:
function y=sc2(x,y)
y=sin(x).^2+cos(y).^2
Мазкур усулда яратилган функцияга мурожаатни MATLAB командалар ойнасидан амалга ошириш sc2(x,y) кўринишда бўлиб, x ва y ўрнига мос қийматлар қўйилади. Масалан:
>>sc2(1,2)
>>sc2([2 3],[1 1])
ans=1.1187 0.3118
Фойдаланувчи функциясини inline ва handle функцияси ёрдамида ҳам яратиш мумкин. Фойдаланувчи ўз учун зарур бўладиган функцияни яратишда inline функцияси аргументига апостроф ичида бир ёки бир неча ўзгарувчили ифодани ёзиши лозим бўлади.
Мисол. 
функцияни
ҳосил қилинсин. Бу MATLABда қуйидагича амалга оширилади:
>>sc2=inline(‘sin(x).^2+cos(y).^2’)
sc2=
Inline function:
sc2(x,y)= sin(x).^2+cos(y).^2.
Handle функция (баъзан аноним функция деб ҳам аталади) @ белги ёрдамида яратилади:
>>fh=@sc2;
Бундай функцияга ижрочи feval(fh,x,y) функция орқали мурожаат қилиш мумкин:
>>feval(fh,1,2)
ans=0.8813
ans=0.8813
>>feval(fh,[2 3],[1 1])
ans=1.1187 0.3118
Назорат саволлари
1. Ишчи файллар қандай аниқланади?
2. Файлларнинг қандай тоифаларини биласиз?
3. Ишчи файлларнинг хусусиятларини айтинг.
4. Файлларга қандай кенгайтма берилади?
5.
функцияни қийматларини ҳисобловчи ишчи файл
яратинг.
6. Ишчи файлларга қандай номлар бериш мумкин?
7. Маълумотларни қандай тоифаларни биласиз?
8. М-файл функция нима?
9.М-файл функция қандай хоссаларга эга?
10.Локал ва глобал ўзгарувчиларни тушунтириб беринг.
Топшириқлар
1.
ифода
қийматини ҳисобловчи функция яратинг (inline ва handle ёрдамида).
2.
ифода
қийматини ҳисобловчи файл- сценарий ва файл -функция ёзинг.
3.
ифода
қийматини ҳисобловчи файл функция ва файл- сценарий ёзинг.
4.
ифода
қийматини ҳисобловчи аноним функция ёзинг.
5.
-cosx ифода
қийматини ҳисобловчи функция яратинг (inline ва handle ёрдамида).
6.
+ctgx ифода
қийматини ҳисобловчи файл-сценарий ва файл-функция ёзинг.
7.
+tgx ифода
қийматини ҳисобловчи файл функция ва файл- сценарий ёзинг.
8.
-sinx ифода
қийматини ҳисобловчи аноним функция ёзинг.
9. Тўғри тўртбурчакнинг периметрини ва юзини ҳисобловчи файл сценарий ёзинг.
10. Учбурчакнинг периметрини ва юзини ҳисобловчи файл сценарий ёзинг.
11. Ромб юзини ва баландлигини ҳисобловчи файл сценарий ёзинг.
12. Доирани юзини ва айлана узунлигини ҳисобловчи файл функция яратинг.
13. Айлана радиусини ва узунлигини квадратини ҳисобловчи файл функция ёзинг.
14. Учбурчак баландлигини ва медианасини ҳисобловчи файл сценарий ёзинг.
15. Учбурчак биссектрисасини ва периметрини ҳисобловчи аноним функция ёзинг.
16. Учбурчак медианасини ва юзининг квадратини ҳисобловчи файл функция ёзинг.
17. Цилиндр хажмини ва сиртини ҳисобловчи функция яратинг (inline ёрдамида).
18. Агар учбурчак томонлари берилган бўлса, у ҳолда учбурчак юзини ва бурчакларини ҳисобловчи файл функция ёзинг.
19. Икки нуқта орасидаги масофани ҳисоблаш ва шу нуқталар орқали аниқланувчи векторни топиш функциясини ишлаб чиқинг.
20. Шар сиртини ва учбурчакли пирамида хажмини ҳисобловчи файл сценарий ёзинг.
21. Шар хажмини ва мунтазам кўпбурчак юзини ҳисобловчи файл функция ёзинг.
22. Трапеция ўрта чизиғини ва юзини ҳисобловчи аноним функция ёзинг.
23.
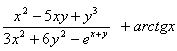ифода
қийматини ҳисобловчи функция яратинг (inline ёрдамида).
24.
ифода
қийматини ҳисобловчи файл сценарий ёзинг.
25.
ифода
қийматини ҳисобловчи файл функция ёзинг.
26.
ифода
қийматини ҳисобловчи аноним функция ёзинг.
Ҳосил қилинган маълумотларни экранга ва қоғозга чиқаринг.
4-тажриба иши. MATLABда графикларни чизиш
Ишдан мақсад: MATLABнинг график командаларини ишлашини ўрганиш ва тадқиқ қилиш.
Қўйилган масала: MATLABнинг график командалари ёрдамида икки ва уч ўлчовли графикларни чизиш.
Иш тартиби:
Ø Тажриба иши тавсифини ўрганиш;
Ø Берилган топшириқни MATLAB тизимида ҳал қилиш;
Ø ҳисоботни тайёрлаш.
4.1. MATLABда оддий график
MATLAB тизимининг энг катта хусусиятларидан бири, унда график чизиш имкониятини мавжудлигидир. Биз MATLABда икки вектор графигини чизишнинг энг содда ва умумий командалари билан танишамиз.Бу ерда шуни таъкидлаш лозимки, MATLABда вектор деганда, координаталари бўйича аниқланган оддий алгебраик векторни ҳам тушуниш мумкин, ёки ўзгарувчининг кетма-кет ҳосил қилинган қийматларидан иборат векторни ҳам тушуниш мумкин.
MATLABда графикларни ҳар хил координата системаларда қуриш мумкин. Булардан тўғри бурчакли декарт координаталари системаси, поляр координаталари, сферик ва цилиндрик системаларни келтириш мумкин. Ундан ташқари координаталарни бир системадаги кўринишидан бошқа кўринишга ўтказиш мумкин.
Бирор бир системада график чизиш учун умумий бўлган баъзи командаларни келтирамиз:
Ø plot(x,y)-х ва y векторларнинг декарт текислигидаги графигини ҳосил қилади;
Ø plot(x,y1,х,у2)-битта график ойнада у1 ва у2 функциялар графикларини чизади;
Ø plot(y)-y нинг y -вектор элементлари номерларга нисбатан графигини ясайди;
Ø semilogх(x,y)- “х”ни логарифмини “ y” га нисбатан графигини ясайди;
Ø semilogy(x,y)-“х”ни “y” нинг логарифмига нисбатан графигини ясайди;
Ø loglog(x,y)-“х”ни логарифмини “y” ни логарифмига нисбатан графигини ясайди;
Ø grid -координаталар системасида тўрни ҳосил қилади;
Ø title (‘матн’)- график тепасига матн ёзади;
Ø xlabel (‘матн’)- “матн”ни “х” ўқи остига ёзади;
Ø ylabel (‘матн’)- “матн”ни “ y ” чап томонига ёзади;
Ø text(x,y,’матн’)- “матн”ни (х, y) нуқтадан бошлаб ёзади;
Ø polar(theta, r) - r вa theta векторларнинг поляр координаталар системасида графигини ясайди (бу ерда theta фақат радианларда берилади);
Ø bar(x) ёки stairs(x)- “х” векторнинг гистограммасини ясайди;
Ø bar(x,y) ёки stairs(x,y)-“у” вектор элементларини гистограммасини “х” векторнинг элементларига мос тўпламга жойлаштириб чизади;
Ø subplot(m,n,k)-график ойнани m*n та ойначаларга бўлади, k-ойнача номери;
Декарт координаталар системасида график чизиш (х, y) жуфтлигининг қийматларини аниқлаб, ҳосил бўлган нуқталарни кесмалар билан туташтириш орқали ҳосил қилинади. Демак (х, y) жуфтликлар сони қанчалик кўп бўлса, график ҳам шунчалик силлиқ ва аниқроқ бўлади. Жуфтликлар аввалдан берилган бўлиши ёки маълум функциянинг аргументи ва қийматларидан ҳисоблаб ҳосил қилиниши мумкин. Масалан, у=log2(x) функциянинг хє[0,4] даги графигини чизиш керак бўлса, қуйидаги комадалар кетма-кетлиги етарли бўлади(9-расм):
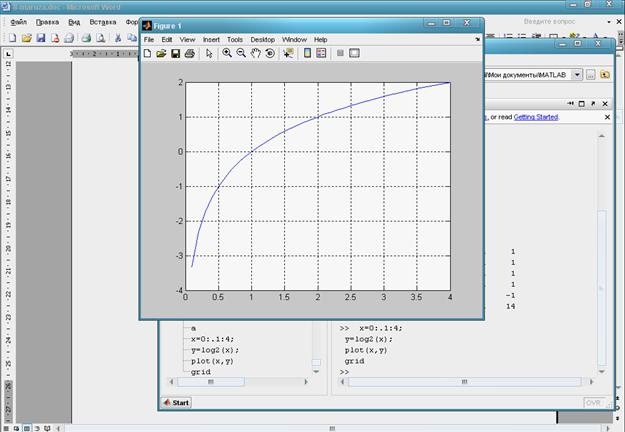
9- расм. у=log2(x) функциянинг хє[0,4] даги графиги.
plot(x,y)- командаси график ойнани очади ва унда (x,y) жуфтликлар ҳосил қилган графикни чизади. Янги командани эълон қилиш учун курсорни командалар ойнасига ўтказишимиз керак. Қайта чизмаслик учун … (уч нуқта -қаторнинг давоми) белгисини ишлатиш мумкин.
>> plot(x,y)...
>> grid,...
>> title('кўрсаткичли функция'),...
>> xlabel('x'),...
>> ylabel('exp(x)'),...
Кўпинча график командалар М-файлга жойлаштирилади (ишчи файл ёки файл функциялар). Бу усул хатоликларни тўғрилаш учун яхши имконият беради.
4.2. Гистограммалар
Амалий ҳисоблашларда бирор вектор таркибини тасвирлайдиган устунли диаграммалар деб аталувчи гистограммалар кўп учрайди. Бунда векторнинг ҳар бир элементи баландлиги унинг қийматига мос бўлган устун шаклида кўрсатилади. Устунлар тартиб рақамларига ва энг баланд устуннинг максимал қийматига нисбатан маълум масштабга эга бўлади. Бундай графиклар bar(a) командаси ёрдамида қурилади(10-расм):
>> a=[2 4 6 8 10 12];
>> bar(a)
10- расм. а
векторнинг гистограммаси.
Бундан ташқари гистограмма қуришнинг яна бошқа усули ҳам мавжуд бўлиб, бу hist функцияси ёрдамида амалга оширилади:
· N=hist(Y)- автоматик танланган 10 интервалли вектор қийматини қайтаради;
· N=hist(Y,M)-ҳудди юқоридаги каби, фақат М (М-скаляр) интарвалда қайтаради;
Мисол(11-расм.)
>> x=-3:0.2:3; y=randn(1000,1);
>> hist(y,x); h=hist(y,x)
h =
Columns 1 through 13
2 3 4 5 4 12 20 22 30 32 39 56 73
Columns 14 through 26
64 66 88 81 71 72 60 47 33 35 25 20 12
Columns 27 through 31
8 7 3 3 3
11- расм. hist(y,x) командаси ёрдамида чизилган гистограмма.
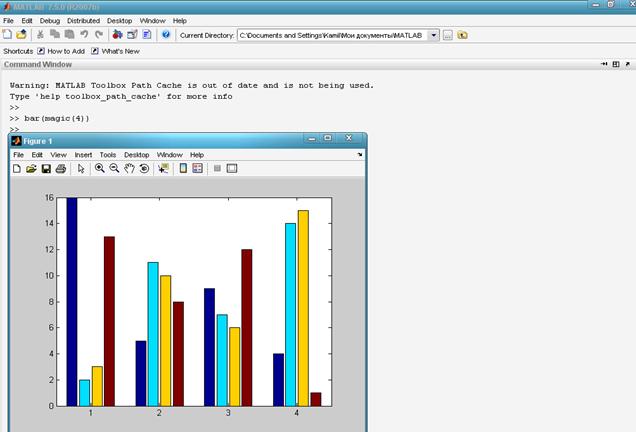
12- расм. Матрицанинг гистограммаси.
Юқоридаги 12-расмда bаr командасини матрицага қўлланиши кўрсатилган. Унда кетма-кет келган 1, 2, 3, 4 рақамлари матрицанинг қаторларини билдиради. Бундай гистограмма-графикни уч ўлчовли фазода bаr3 командаси ёрдамида чизиш мумкин.
4.3.Поляр координаталарда график
Поляр координаталар тизимида ихтиёрий нуқта худди радиус-вектор охири каби бошланғич координатлар тизимидан чиқиб, RHO узунликка ва THETA бурчакка эгалигини кўрсатади. RHO(THETA) функция графигини қуриш учун қуйида келтирилган буйруқлардан фойдаланилади.THETA бурчаг одатда 0 дан 2*pi гача ўзгаради. Поляр координаталар тизимида функция графигини қуриш учун polar(…) типидаги буйруқдан фойдаланилади :
· polar(theta,rho)-поляр координаталар тизимида радиус-вектор охирининг ўз ҳолатидаги rho узунлик билан theta бурчакни кўрсатувчи графикни қуради;
Қуйидаги мисолни кўрамиз:
>> angle=0:.1*pi:3*pi;
>> r=exp(angle/10);
>> polar(angle,r),...
>> title('polar koordinatida grafik');
>> grid on
13- расм. Поляр координатасида функция графиги.
4.4. Уч ўлчовли графика
Уч ўлчовли фазода чизиқнинг графигини чизиш учун plot3(x,y,z) буйруғидан фойдаланилади. Бунда x,y,z-векторлар бир хил сондаги координаталарга эга бўлиши керак. Масалан,
>> t=-5*pi:pi/60:10*pi;
>> plot3(t,sin(t),cos(t))
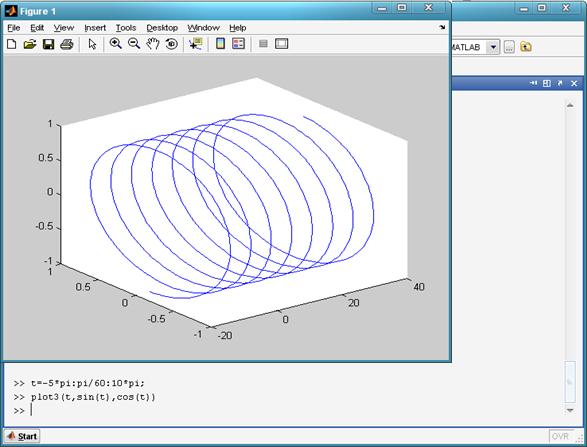
14- расм. Уч ўлчовли фазода чизиқнинг графиги.
Бундан ташқари хар хил сиртларни хосил қилиш учун қуйидаги командалардан фойдаланиш мумкин:
· mesh-уч ўлчовли сиртни “тўр” сифатида чизади;
· surf-уч ўлчовли сиртни чизади.
Meshgrid функцияси ёрдамида x,y ларнинг қийматларидан фойдаланиб, x,y матрицалар ҳосил қилинади. Агар x,y ларнинг қийматлари бир хил тўпламда бўлса, meshgrid функциянинг аргументида 1 та аргумент қиймати кўрсатилса етарли; x,y ларнинг қийматлари хар хил тўпламда ўзгарса, meshgrid функциянинг аргументида иккита тўплам кўрсатилади. Масалан,
Z=
, 
, x,yє[-8,8] бўлсин. У ҳолда
>>[x,y]=meshgrid(-8:.5:8);
>> R=sqrt(x.^2+y.^2)+eps;
>> z=sin(R)./R;
>> mesh(z)
15- расм. Уч ўлчовли фазода сиртнинг графиги.
Мисол. MATLAB да 3та цилиндрни радиусини катталаштириш тартиби билан ёнма-ён жойлаштиринг.
Бу вазифани бажариш учун MATLAB командалар ойнасидан ёки м-файлдан фойдаланиш мумкин. Биз командалар ойнасини ишлатамиз. Учта график битта ойнада ҳосил қилиниши учун график ўқларни ушлаб турувчи hold командасидан, цилиндр ҳосил қилиш учун cylinder(R,N), surf(x,y,z)
командалар форматларидан фойдаланамиз. Цилиндрларни ёнма-ён жойлаштириш учун surf(x,y,z) функциянинг талаб қилинган йўналиш бўйича аргумент қийматларини ўзгартирамиз. Қуйида ушбу командалар кетма-кетлиги келтирилган:
>> hold on
>> [x,y,z]=cylinder(1,20);
>> surf(x,y,z,x);
>> [x,y,z]=cylinder(2,20);
>> surf(x,y+3,z,x);
>> [x,y,z]=cylinder(3,20);
>> surf(x,y+8,z,x);
Натижа график ойнада чиқади:
16-расм. Цилиндрларнинг графиги.
Графикни қуйидаги ранглар билан ҳосил қилиш мумкин:
y ---------- сариқ m---------- сиёхранг
c -----------хаворанг r -----------қизил
g -----------яшил b -----------тўқ кўк
w ---------- оқ k -----------қора
Назорат саволлари
1. MATLABда график чизишнинг қандай имкониятлари мавжуд?
2. Loglog(x,y) қандай графикни ясайди?
3. Гистограммалар қандай буйруқ ёрдамида қурилади?
4. Поляр координаталарда график ясаш қандай амалга оширилади?
5. Meshgrid қандай функция?
6. Бир нечта графиклар қандай ҳосил қилинади?
7. Цилиндр ва сфера уч ўлчовли фазода қандай қурилади?
Топшириқлар 4.1.
Қуйидаги функцияларни икки ва уч ўлчовли фазода графикларини чизинг ( битта график ойнада,ойначаларга бўлиб , турли рангларда, турли маркерларда ва х.к.). Оралиқни мустақил танланг.
1.
ва 
2.
ва 
3.
ва 
4.
ва 
5.
ва 
6.
ва 
7.
ва 
8.
ва 
9.
ва 
10.
ва 
11.
ва 
12.
ва 
13.
ва 
14.
ва 
15.
ва 
16.
ва 
17.
ва 
18.
ва
19.
ва 
20.
ва 
21.
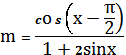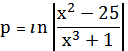ва 
+
22.z =(x^2)sin(y)+(y^2)cos(x) ва y=x3 – 3x2
23. z = xsin(y)+ycos(x) ва y = xlnх
24. z =xsinx +y siny ва y = (2x - 1)/(2+x2)
25. z =( 2sin2xy + 3cos3xy) ва y = 
Топшириқлар 4.2.
1. z=х+3 сиртни уч ўлчовли фазода графигини чизин г (оралиқни мустақил танланг). Шу сиртнинг устига иккита сфера жойлаштиринг.
2. Цилиндрнинг сирт графигини чизинг ва уни икки ёнига иккита сфера жойлаштиринг.
3. Сфера графиги устига цилиндрнинг графигини жойлаштиринг.
4.
z=
параболоид
ичига сферани жойланг.
5. Цилиндрнинг устига сферани жойланг.
6.
Цилиндрни 
га
оғган ҳолатини графигини чизинг.
7. Параллелпипедни графигини чизинг, уни икки ёнига биттадан сфера жойлаштиринг.
8.
z=y+2 текислик сиртни ясанг ва унинг устига z=
элипсоидни
учлари билан жойланг.
9.
z=
сиртнинг
чуқурликларига биттадан сфера жойланг.
10. z=х+y сиртнинг устига цилиндрни жойланг.
11. Иккита цилиндрнинг орасига бир нечта сфераларни жойланг.
12. Иккита цилиндрни шундай жойлангки ,бири ерда тургандек, иккинчиси устидан йиқилиб кетаётгандек бўлсин.
13. Иккита та цилиндрни ўзаро перпендикуляр қилиб жойланг.
14. Учта сферани устма-уст қилиб жойланг.
15. Иккита паралел цилиндрлар устига учинчи цилиндрни ёпиқ қилиб жойланг.
16. Учта сферани ёнма-ён қилиб жойланг.
17.
Ўзаро бурчак
остида кесишувчи цилиндрларни ясанг.
18.
Иккита цилиндрни 
бурчак
остида кесишган ҳолатини чизинг.
19.
функция
сиртини аниқланг ва унинг ёнига цилиндрни жойлаштиринг.
20. 2 та цилиндрнинг графигини устма-уст жойланг.
21. Катта цилиндрнинг ичига кичик цилиндрнинг ярмини жойланг.
22. Цилиндрнинг ичига сферани ярмидан каттарок кисмини жойланг.
23.
сиртни
қуринг ва унинг ичига цилиндрни жойлаштиринг..
24. Иккита сфера ва учта цилиндрни оралатиб жойлаштиринг..
25.
сиртни
ясанг ва унинг устига иккита сферани жойлаштиринг.
5-Тажриба иши. Кузатув натижаларини бошланғич қайта ишлаш
Ишдан мақсад: Кузатув ва тажриба натижаларини бирламчи қайта ишлашни ўрганиш ва тадқиқ қилиш.
Қўйилган масала: MATLABда кузатув ва тажриба натижаларига асосланган ҳолда жараённи тузилмавий ва параметрик идентификация қилиш.
Иш тартиби:
Ø Тажриба иши тавсифини ўрганиш;
Ø Берилган топшириқни MATLAB тизимида ҳал қилиш;
Ø ҳисоботни тайёрлаш.
5.1. Статистик қайта ишлаш муаммосига кириш
Фараз қилайлик, тадқиқот натижасида бирор бир 
миқдорнинг
қийматларига
миқдорнинг
қийматлари
мос қўйилган бўлсин. У холда ва миқдорларни
боғловчи 
боғликликни
аналитик кўриниши топилсин.
Агар берилган катталиклар орасидаги аналитик боғлиқлик тажрибалар натижасида аниқланса, у ҳолда бундай боғлиқлик эмпирик боғлиқлик ёки эмпирик қонуният деб аталади.
Эмпирик қонуниятларни аниқлашни иккита босқичга ажратиш мумкин:
· эмпирик формулани (қонуниятни) танлаш (тузилмавий идентификация);
· танланган формуладаги коэффициентларни аниқлаш (параметрик идентификация).
Келгусидаги барча тадқиқотлар учун бошланғич
маълумотлар сифатида иккита ва массивлардан
фойдаланамиз. Бу ерда берилган массивлар мос равишда ва элементларга
эга бўлиб, ҳар бир 
элементга 
элемент
мос қўйилади (
).
5.2. Тузилмавий идентификация қилиш усули
Тузилмавий идентификация қилиш учун бир ёдошувни кўрамиз. Фараз
қилайлик, изланаётган 
функция иккита 
ва
параметрларга
эга бўлган бир ўзгарувчили функция бўлсин. У ҳолда эмпирик
боғлиқлик, асосан, қуйидаги функциялар ичидан танлаб олинади:
1.
- чизиқли
функция;
2.
- кўрсаткичли
функция;
3.
- каср-чизиқли
функция;
4.
- логарифмик функция;
5.
(
да
параболик боғлиқлик, 
да гиперболик
боғлиқлик, 
да чизиқли
боғлиқлик) - даражали функция;
6.
- гиперболик функция;
7.
- каср-чизиқли
функция.
Тузилмавий идентификация ўтказишнинг бошланғич босқичи
бўлиб берилган бошланғич маълумотларнинг графигини қуриш
ҳисобланади ( ва массивларнинг
элементлари бўйича). Навбатдаги вазифа эса баъзи бир қўшимча
ҳисоблашларни бажаришдан иборат бўлади. Масалан, массивда
етарлича ишончли ва имкон қадар бир-биридан узоқда жойлашган иккита
нуқтани танлаб оламиз. Соддалик учун массивнинг четки нуқталарини яъни
ва
ни
қарайлик. Ушбу катталиклар учун ўрта арифметик - 
, ўрта
геометрик - 
, ўрта гармоник - 
қийматларни
аниқлаб оламиз. Қурилган графикдан, MATLABда график имкониятларидан
фойдаланиб, эркли ўзгарувчининг
хисобланган 
, 
, 
қийматларига
мос равишда эрксиз ўзгарувчи
қийматлари аниқланади:
,
,
.
Ҳозирча олиб борилган ҳисоблашларда 
аналитик
боғлиқлик номаълум.
Юқоридаги каби ҳисоблашларни массив
учун ҳам бажарамиз, яъни 
, 
ва
.
, 
, 
, 
, 
ва
ларга
эга бўлгандан кейин қуйидаги оғишларни ҳисоблаймиз:
,
,
,
,
,
,
.
Энди юқорида ҳисобланган оғишларни энг кичигини
аниқлаб оламиз: 
.
Энг кичик оғишни аниқлаб олгандан сўнг тузилмавий идентификацияни қуйидаги қоида асосида амалга ошириш мумкин:
1.
агар 
бўлса, у ҳолда
аналитик боғлиқлик − чизиқли функция;
2.
агар 
бўлса, у ҳолда
аналитик боғлиқлик − кўрсаткичли функция;
3.
агар 
бўлса, у ҳолда
аналитик боғлиқлик − каср-чизиқли
функция;
4.
агар 
бўлса, у ҳолда
аналитик боғлиқлик −- логарифмик функция;
5.
агар 
бўлса, у ҳолда
аналитик боғлиқлик − даражали функция;
6.
агар 
бўлса, у ҳолда
аналитик боғлиқлик −- гиперболик функция;
7.
агар 
бўлса, у ҳолда
аналитик боғлиқлик −- каср-чизиқли
функция.
5.3. Параметрик идентификация қилиш усуллари
ва ўзгарувчиларини
боғловчи функцияни ташқи кўриниши аниқланиб олингандан кейин
мазкур функция таркибига кирувчи ва параметрларни
қийматини аниқлаб олиш лозим бўлади.
Умуман олганда, мазкур параметрларни аниқлашнинг бир қанча усуллари мавжуд. Лекин реал масалалар ҳал қилинаётганда, кўпинча, қуйидаги усуллар қўлланилади:
· танланган нуқталар усули;
· ўрта қиймат усули;
· кичик квадратлар усули.
5.4. Танланган нуқталар усули
Номаълум параметрларни аниқлашда танланган нуқталар усули энг содда усул бўлиб, ҳисоблашлар минимал бўлади. Бироқ мазкур усулнинг аниқлиги графикни қуриш аниқлигига кучли боғлиқ бўлади. Бу эса унинг камчилиги бўлиб ҳисобланади.
Танланган нуқталар усулининг мазмун-моҳияти
қуйидагича: қурилган эгри чизиқда ихтиёрий иккита 
ва
нуқта
танланади ҳамда қуйидагича тенгламалар системаси тузилади:
.
Мазкур тенгламалар системаси изланаётган ва параметрларга
нисбатан ҳал қилинади.
5.5. Кичик квадратлар усули (ККУ)
Кичик квадратлар усули танланган нуқталар усулига нисбатан анча аниқ ечимни бериб, бунда усул график қурилишига боғлиқ бўлмайди. Аммо бу усулнинг камчилиги ҳисоблашларнинг кўплигидир.
ККУ ни қараб чиқишдан олдин баъзи бир тушунчаларни
келтириб ўтайлик. Фараз қилайлик, миқдорга
тажрибавий миқдор ва
танланган функциянинг 
нуқтадаги
қиймати 
мос келади.
Тажрибавий қиймат билан мазкур функция қийматлари орасидаги
фарқни кўрамиз, яъни
. (1)
ККУда ва параметрларни аниқлаш учун (1) қийматлар квадратлари
йиғиндиси минимал бўлиши лозим, яъни:
.
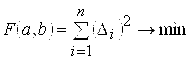функциянинг ва
параметрлар
бўйича хусусий хосилаларини ҳисоблаймиз ва функция экстремумга эришишнинг
шартига кўра ҳосил бўлган хусусий ҳосилаларни нолга тенглаймиз:
,
,
Функциянинг ўрнига берилган қийматларни келтириб қўямиз:
.
Юқоридаги тенгламалар системасидан a ва b параметрларнинг қиймати аниқланади.
5.6. MATLABда берилганларни статистик қайта ишлаш функциялари
1. mean(x)- x вектор элементларини ўрта қийматини қайтаради, ёки x матрица бўлса устуннинг ўрта қийматларидан тузилган қатор векторни қайтаради;
2. median(x)- худди mean(x) каби , фақат x векторнинг (матрицанинг) медианасини қайтаради;
3. std(x)- x вектор ўрта квадратик хатолигини қайтаради, x матрица учун қаторларни ўрта квадратик хатоликларидан тузилган вектор қаторни қайтаради;
4. hist(x)- x вектор элементларини гистограммасини чизади. Ўнта нуқта максимум ва минимум орқали масштабланади;
5. hist(x,n)- n тa нуқтанинг гистограммасини максимум ва минимумга нисбатан масштабда чизади;
6. max(x)- x вектор элементларини максимумини ёки x матрица бўлса устунларнинг максимумлардан иборат вектор қаторни қайтаради;
7. min(x)- худи max(x) каби фақат минимумни қайтаради;
8. sort(x)- x вектор кooрдинаталарини ўсиш тартибида жойлаштиради;
9. sum(x)- x вектор элементлари йиғиндисини қайтаради. x матрица бўлса, матрицанинг мос устун элементлари йиғиндисини қайтаради;
10. prod(x)- худди sum(x) каби, фақат кўпайтма қайтаради.
Назорат саволлари
1. Эмпирик боғлиқликнинг структурали идентификация масаласи алгоритми қандай?
2. Танланган нуқталар усулини келтиринг.
3. ККУ ни тушунтириб беринг.
4. MATLABда статистик қайта ишлаш функцияларини барчасини келтиринг.
5. Бошланғич маълумотларни бирламчи қайта ишлаш масаласининг қўйилиши қандай?
Топшириқлар
Қуйида берилган кузатув натижаларига кўра жараённи тузилмавий ва параметрик идентификация қилинг.
, 
бу ерда 
қадам, 
-талабанинг
журналдаги тартиб рақами.
1. x=1:δ:t,
2. y=5:ω:40,8 .
1-вариант
|
5.00 |
6.05 |
7.11 |
8.16 |
9.21 |
10.26 |
11.32 |
12.37 |
13.42 |
14.47 |
15.53 |
16.58 |
17.63 |
18.68 |
19.74 |
20.79 |
21.84 |
22.89 |
|
23.95 |
25.00 |
26.05 |
27.11 |
28.16 |
29.21 |
30.26 |
31.32 |
32.37 |
33.42 |
34.47 |
35.53 |
36.58 |
37.63 |
38.68 |
39.74 |
40.79 |
|
2-вариант.
|
6.00 |
11.05 |
20.34 |
37.44 |
68.93 |
126.91 |
233.64 |
430.15 |
791.94 |
1458.00 |
2684.26 |
4941.88 |
9098.29 |
16750.47 |
30838.58 |
56775.60 |
|
104527.14 |
192440.48 |
354294.00 |
652275.64 |
1200876.99 |
2210883.65 |
4070364.04 |
7493774.43 |
13796469.97 |
25400095.16 |
46763036.89 |
86093442.00 |
158502981.15 |
291813109.68 |
537244727.93 |
|
3-вариант
|
0.20 |
0.16 |
0.14 |
0.12 |
0.10 |
0.09 |
0.08 |
0.08 |
0.07 |
0.06 |
0.06 |
0.06 |
0.05 |
0.05 |
0.05 |
|
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.04 |
0.03 |
0.03 |
0.03 |
0.03 |
0.03 |
0.03 |
0.03 |
|
|
4-вариант
|
3.00 |
3.97 |
4.62 |
5.11 |
5.51 |
5.83 |
6.12 |
6.36 |
6.58 |
6.78 |
6.96 |
7.13 |
7.28 |
|
7.42 |
7.55 |
7.68 |
7.80 |
7.91 |
8.01 |
8.11 |
8.21 |
8.30 |
8.38 |
8.47 |
8.55 |
|
5-вапиант
|
.2.00 |
.9.26 |
25.41 |
54.00 |
98.59 |
162.74 |
250.00 |
363.93 |
508.07 |
686.00 |
901.26 |
|
1 1157.41 |
1 1458.00 |
1 1806.59 |
2 2206.74 |
2 2662.00 |
3 3175.93 |
3752.07 |
4394.00 |
5 5105.26 |
558 89.41 |
6750.00 |
6-вариант
|
5.00 |
3.75 |
3.24 |
2.95 |
2.78 |
2.66 |
2.57 |
2.50 |
2.45 |
2.40 |
2.37 |
2.34 |
2.31 |
2.29 |
2.27 |
2.26 |
2.24 |
2.23 |
2.22 |
7-вариант
|
0.20 |
0.27 |
0.31 |
0.34 |
0.37 |
0.38 |
0.39 |
0.40 |
0.41 |
0.42 |
0.43 |
0.43 |
0.44 |
0.44 |
0.44 |
0.45 |
8-вариант
|
5.00 |
7.50 |
10.00 |
12.50 |
15.00 |
17.50 |
20.00 |
22.50 |
25.00 |
27.50 |
30.00 |
32.50 |
35.00 |
37.50 |
9-вариант
|
6.00 |
11.27 |
21.16 |
39.73 |
74.61 |
140.11 |
263.11 |
494.08 |
927.81 |
1742.30 |
3271.81 |
6144.00 |
10-вариант
|
0.20 |
0.13 |
0.09 |
0.07 |
0.06 |
0.05 |
0.04 |
0.04 |
0.03 |
0.03 |
11-вариант
|
2.00 |
3.62 |
4.66 |
5.44 |
6.05 |
6.56 |
7.00 |
7.38 |
7.71 |
|
8.02 |
8.29 |
8.54 |
8.78 |
8.99 |
9.19 9.38 |
9.56 |
9.73 |
9.89 |
12-вариант
|
3.00 |
9.39 |
19.33 |
32.82 |
49.86 |
70.46 |
94.60 |
122.29 |
|
153.53 |
188.33 |
226.67 |
268.56 |
314.01 |
363.00 |
415.54 |
471.64 |
13-вариант
|
5.00 |
4.09 |
3.75 |
3.57 |
3.46 |
3.39 |
3.33 |
3.29 |
3.26 |
3.24 |
3.21 |
3.20 |
3.18 |
3.17 |
14-вариант
|
0.20 |
0.25 |
0.27 |
0.28 |
0.29 |
0.30 |
0.30 |
0.31 |
0.31 |
0.31 |
0.31 |
0.31 |
15-вариант
|
7.00 |
10.00 |
13.00 |
16.00 |
19.00 |
22.00 |
25.00 |
28.00 |
31.00 |
34.00 |
16-вариант
|
12.00 |
28.54 |
67.88 |
161.45 |
384.00 |
913.31 |
2172.23 |
5166.47 |
12288.00 |
29225.95 |
69511.43 |
165326.96 |
393216.00 |
|
935230.53 |
2224365.60 |
5290462.80 |
12582912.00 |
29927376.96 |
71179699.22 |
169294809.51 |
402653184.00 |
957676062.58 |
2277750374.98 |
5417433904.26 |
12884901888.00 |
|
17-вариант
|
0. 14 |
0.11 |
0.09 |
0.08 |
0.07 |
0.06 |
0.06 |
0.05 |
0.05 |
0.04 |
0.04 |
0.04 |
0.04 |
0.03 |
0.03 |
0.03 |
0.03 |
0.03 |
0.03 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
18-вариант
|
4.00 |
5.33 |
6.24 |
6.94 |
7.51 |
7.99 |
8.40 |
8.76 |
9.08 |
9.38 |
9.64 |
9.88 |
10.11 |
10.32 |
10.52 |
10.70 |
|
10.87 |
11.04 |
11.19 |
11.34 |
11.48 |
11.62 |
11.75 |
11.87 |
11.99 |
12.10 |
12.21 |
12.32 |
12.42 |
12.52 |
12.62 |
|
19-вариант
|
3.00 |
16.28 |
53.26 |
132.71 |
278.94 |
521.80 |
896.63 |
1444.33 |
2211.30 |
3249.47 |
4616.31 |
6374.79 |
8593.42 |
11346.24 |
14712.80 |
18778.19 |
23633.01 |
29373.39 |
|
36100.99 |
43923.00 |
52952.11 |
63306.57 |
75110.12 |
88492.05 |
103587.16 |
120535.78 |
139483.77 |
160582.50 |
183988.89 |
209865.36 |
238379.87 |
269705.90 |
304022.44 |
341514.04 |
382370.73 |
|
20-вариант
|
7.00 |
5.67 |
5.00 |
4.60 |
4.33 |
4.14 |
4.00 |
3.89 |
3.80 |
3.73 |
3.67 |
3.62 |
3.57 |
3.53 |
|
3.50 |
3.47 |
3.44 |
3.42 |
3.40 |
3.38 |
3.36 |
3.35 |
3.33 |
3.32 |
3.31 |
3.30 |
3.29 |
3.28 |
|
3.27 |
3.26 |
3.25 |
3.24 |
3.24 |
3.23 |
3.22 |
3.22 |
3.21 |
3.21 |
3.20 |
|
|
|
21-вариант
|
0.14 |
0.20 |
0.23 |
0.25 |
0.26 |
0.27 |
0.28 |
0.28 |
0.29 |
0.29 |
0.29 |
0.30 |
22-вариант
|
11.00 |
15.17 |
19.33 |
23.50 |
27.67 |
31.83 |
36.00 |
40.17 |
44.33 |
48.50 |
52.67 |
56.83 |
61.00 |
65.17 |
23-вариант
|
30.00 |
119.04 |
472.36 |
1874.37 |
7437.60 |
29512.82 |
117108.54 |
464693.34 |
|
1843929.59 |
7316817.44 |
29033547.50 |
115206766.83 |
457146999.54 |
1813985280.00 |
7197996704.25 |
28562060081.58 |
24-вариант
|
0.09 |
0.07 |
0.06 |
0.05 |
0.04 |
0.03 |
0.03 |
0.03 |
0.03 |
0.02 |
|
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.01 |
0.01 |
0.01 |
|
25-вариант
|
6.00 |
8.55 |
10.24 |
11.49 |
12.50 |
13.33 |
14.05 |
14.67 |
15.23 |
15.73 |
16.18 |
|
16.60 |
16.99 |
17.34 |
17.68 |
17.99 |
18.28 |
18.56 |
18.82 |
19.07 |
19.31 |
19.54 |
26-вариант
y =
|
5.00 |
92.06 |
648.73 |
2823.56 |
9191.33 |
24632.80 |
57429.05 |
120570.43 |
233280.00 |
422751.64 |
726102.69 |
1192541.16 |
|
1885747.58 |
6235892.74 |
8857805.00 |
12340358.42 |
16896102.54 |
22774740.15 |
30267225.70 |
39710078.29 |
51489909.23 |
66048164.21 |
83886080.00 |
|
27-вариант
|
11.00 |
8.78 |
7.76 |
7.17 |
6.79 |
6.52 |
6.32 |
6.17 |
6.05 |
5.95 |
5.87 |
5.80 |
5.74 |
5.69 |
|
5.65 |
5.61 |
5.58 |
5.55 |
5.52 |
5.49 |
5.47 |
5.45 |
5.43 |
5.41 |
5.40 |
5.38 |
5.37 |
5.36 |
28-вариант
|
0.09 |
0.11 |
0.13 |
0.14 |
0.15 |
0.15 |
0.16 |
0.16 |
0.16 |
0.17 |
0.17 |
0.17 |
0.17 |
0.17 |
0.18 |
0.18 |
|
0.18 |
0.18 |
0.18 |
0.18 |
0.18 |
0.18 |
0.18 |
0.18 |
0.18 |
0.19 |
0.19 |
0.19 |
0.19 |
0.19 |
0.19 |
|
Қадам шундай танланадики, натижада х ва у тажрибавий векторлар узунлиги бир хил бўлсин.
ФОЙДАЛАНИЛГАН АДАБИЁТЛАР
1.Дяконов В. П.MATLAB 7.*/Р2006/Р2007 ўқув қўлланма.:М.2008.695c.
2. Маthematica. Wолфрам, Стефен, 1959.
3.Дяконов В. П., Абраменкова И. В., Круглов В. В. MATLAB 5 с пакетами расширений. – М.: Нолидж, 2001.
4.Потемкин В. Г. Сиcтема MATLAB: Справочное пособие. – М.: Диалог_МИФИ, 1997.
5.Т.Дадажонов ,М.Муҳитдинов MATLAB асослари.-Т.”Фан” .2008.632б
6.В.В.Мещеряков. Задачи по математике с MATLAB & SIMULINK,-М.:”ДИАЛОГ-МИФИ”.2007.528с.