O’ZBEKISTON ALOQA, AXBOROTLASHTIRISH VA TELEKOMMUNIKATSIYA TEXNOLOGIYALARI DAVLAT QO’MITASI

 

TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI

 

 

 

 

Teleradioeshittirish tizimlari

kafedrasi

 

 

 

 

 

 

 

 

 

 

ELEKTROMAGNETIZM

 

fanidan

 

ma’ruza mashg’ulotlari bo’yicha o’quv qo’llanma

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

TOSHKENT 2014
MUNDARIJA

bet

KIRISH…………………………………………………………………………..4

1. ELEKTROSTATIKA…………………………………………………………5

1.1.         Elektr zaryadi.................................................................................................5

1.2.         Elektrostatik maydon kuchlanganligi...........................................................6

1.3.         Elektrostatik maydonning uyurmasiz tavsifi................................................7

1.4.         Elektr potentsiali............................................................................................8

1.5.         Elektrostatik maydonning grafik tasviri........................................................9

1.6.         Dielektrikning qutblanishi va elektr induktsiyasi.........................................9

1.7.         Gauss teoremasi.............................................................................................10

1.8.         Elektrostatik maydonda o’tkazgichlar..........................................................10

1.9.         Elektrostatik maydonda chegaraviy shartlar................................................11

1.10.    Elektrostatik maydon energiyasi...................................................................12

2. ELEKTROMAGNIT MAYDONDA ELEKTR TOKI

2.1.    Tok va o’tkazuvchanlik toki zichligi............................................................15

2.2.    O’tkazuvchanlik toki zichligining divergentsiyasi......................................15

2.3.    Differentsial shakldagi Om qonuni...............................................................16

2.4.    To’liq elektr toki............................................................................................17

3. MAGNIT MAYDONI

3.1.   Magnit maydonni tavsiflovchi asosiy kattaliklar.........................................19

3.2.   Magnit oqimi va uning uzluksizligi...............................................................20

3.3.   Magnit maydonining skalyar potentsiali.......................................................22

3.4.   Magnit maydonining  vektor potentsiali.......................................................22

3.5.   Magnit maydonidagi chegaraviy shartlar......................................................22

3.6.   Magnit maydoni energiyasi...........................................................................23

3.7.   Magnit maydonning hisoblash usullari........................................................24

4. MAKSVELL TENGLAMALARI TIZIMI

4.1.   Maksvelning birinchi tenglamasi..................................................................26

4.2.   Maksvelning ikkinchi tenglamasi..................................................................26

4.3.   Maksvellning uchinchi tenglamasi................................................................27

4.4.   Maksvellning to’rtinchi tenglamasi..............................................................28

4.5.   Elektromagnit maydonning to’liq tenglamalar tizimi..................................28

4.6.   To’liq tokning uzluksizligi tenglamasi..........................................................30

5. MONOXROMATIK MAYDON UCHUN MAKSVELL TENGLAMALARI

5.1. Kompleks vektorlar. Maksvell tenglamalarining kompleks shakllari…………..........................................................................31

5.2.   Kompleks dielektrik singdiruvchanlik. Yo’qotishlar burchagi....................32

5.3.   Monoxromatik maydon uchun chetki manba’larni xisobga oluvchi

tenglamalar tizimi………………….……………………………......……...33

6. ELEKTROMAGNIT MAYDON ENERGIYASI VA QUVVATI

6.1.   Asosiy gipoteza……………………………………………………...……..36

6.2.   Eneriya balansi……………………………………………………...……...36

6.3.   Elektromagnit maydon  vektorlarining  oniy  qiymatlari uchun

         Poyting teoremasi…....................................................................................37

6.4.   Elektromagnit maydonning kompleks vektorlari uchun Poynting

         teoremasi……................................................................……………….…39

7. ELEKTROMAGNIT TO’LQINLARNING NURLANISHI

7.1.   Elementar elektr tebratgich..........................................................................41

7.2.   Elementar elektr tebratgich maydoni tuzilishining taxlili..........................42

8. YASSI ELEKTROMAGNIT TO’LQINLAR

8.1.   Yassi elektromagnit to’lqin parametrlari.....................................................48

8.2.   Elektromagnit to’lqinning qutblanishi........................................................50

9. MUXITLAR CHEGARASIDAGI TO’LQINLI JARAYONLAR

9.1.   Elektromagnit to’lqinning muxitlar chegarasidan o’tishi va

akslanishi......................................................................................................54

9.2.   Yassi elektromagnit to’lqinning ikkinchi muxitga to’liq o’tishi.

Bryuster burchagi..........................................................................................58

10. YUZA EFFEKTI

10.1. Yuza effekti xodisasi.....................................................................................60

10.2. O’tkazgichning yuza qarshiligi va undagi energiya yo’qotishlari...............61

11. YO’NALTIRUVCHI TIZIMLAR

11.1. Yo’naltiruvchi tizimlarning sinflanishi.........................................................62

11.2. Bir to’lqinli rejimni hosil qilish uchun to’lqinning ishchi

         uzunligini tanlash...........................................................................................65

11.3. To’lqino’tkazgichdagi amplitudaviy taqsimotning turlari...........................66

KIRISH

 

Elektromagnetizm nazariyasi asosida elektromagnit maydoni tushunchasi yotadi. Elektromagnit maydon esa materiyaning aloxida, muxim ko’rinishi bo’lib, bir-birini shartli ravishda to’ldiruvchi va doimo birga mavjud bo’luvchi elektr va magnit maydonlarining yig’indisi xisoblanadi.

Zamonaviy telekommunikatsiya sohasida  radiotexnik tizimlarning hissasi tobora yuksalmoqda. SHu bilan birgalikda, foydalanilayotgan radiochastota spektrining yuqoriroq tebranishlar soxasiga siljishi kuzatilmoqda. Masalan, sun’iy yo’ldoshli aloqa tizimlari 4...6 GGs diapazonining imkoniyatlarida to’la foydalanib, endi 11...14 GGs chastota diapazoniga ko’chib o’tgan. Koinot stantsiyalari esa 20...30 GGs diapazonida faoliyat yuritish uchun katta amaliy saloxiyatga ega.

Signallarni tashuvchi chastotalarning oshib borishi uning yordamida ko’psonli kanallarni uzatish imkonini beradi, ya’ni, foydalanilayotgan diapazon hajmini kengaytirishga ta’sir ko’rsatadi. SHu nuqtai  nazardan  ham 3000 GGs chastotali optik diapazonining imkoniyatlari juda ham yuqoridir. Zamonaviy telekommunikatsiya sohasida optik tolali aloqa tizimlarining asosiy o’rinni egallab borishi xam ana shu omil bilan bog’liq. OTAT ning asosiy elementi sifatida qurilmalarni bog’lovchi kvarts tolasini e’tirof etish lozim. Ammo, harakatdagi ob’ektlar bilan aloqa o’rnatishda OTAT asosiy aloqa turi sifatida namoyon bo’la olmaydi. CHunki, xarakatdagi ob’ekt uchun erkin tarqaluvchi radioto’lqinlardan foydalanish qulayroq. Masalan, uyali aloqa tizimlarida 450, 800, 900, 1800, 2100, 2500 MGs chastota spektrlaridan keng foydalaniladi.

Zamonaviy telekommunikatsiya tizimlaridan keltirilgan misollar shuni ko’rsatadiki, yuqori chastotali spektrlardan foydalanish rivojlanuvchan yo’nalishdir. O’ta yuqori  chastotali (shuningdek optik) texnikaning nazariy zaxirasi Maksvell tenglamalariga asoslangan va unda vektorli algebra, vektorlar tahlili elementlaridan foydalaniladi.

Erkin fazodagi, O’YUCH qurilmalaridagi, xamda uzatish liniyalaridagi to’lqinli jarayonlarni kvant fizikasi darajasida o’rganish talab etilmaydi. Ularni cheksiz fazodagi uzluksiz maydonlar ko’rinishida taxlil qilish etarli. Bunday  kuzatuvni  makroskopik  kuzatuv deyiladi. Bu kabi engillashtirilgan nazariyani esa klassik elektrodinamika deyiladi.

Ushbu o’quv qo’llanma Elektromagnetizm fanining nazariy asoslarini qamrab olgan va texnik elektrodinamika sohasining boshqa qismlarini o’rganishda nazariy zaxira vazifasini bajaradi.

 

 

 

 

1. ELEKTROSTATIKA

1.1. Elektr zaryadi

 

Elektr zaryadini cheksiz bo’linuvchan deb hisoblash mumkin va «zaryad zichligi» tushunchasi orqali ifodalanadi. Agar «q» zaryad fazoda taqsimlangan bo’lsa, unda zaryadning xajmiy zichligi

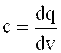,                                                    (1.1)

zaryad esa quyidagicha aniqlanadi

.                                                 (1.2)

Agar «q» zaryad «S» yuzada taqsimlangan bo’lsa, unda yuzadagi zaryad zichligi

,                                                       (1.3)

u holda umumiy zaryad

,                                                 (1.4)

ifoda yordamida aniqlanadi.

Zaryadning chiziqli zichligi

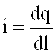,                                                     (1.5)

bu erda dl – zaryad taqsimlangan chiziqning bir qismi.

Shunga ko’ra zaryad

.                                                   (1.6)

Bir hil ishorali ikkita nuqtaviy zaryad bir-birini itaradi. Itarish kuchi  vakumda Kulon qonuni asosida aniqlanadi.

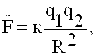                                               (1.7)

bu erda

q₁ va q₂  - nuqtaviy zaryad

k - proportsionallik koeffitsiyenti.

,                            (1.8)

bu erda  e₀ - elektr doimiysi

.                        (1.9)

Agar zaryadlangan jismlar birjinsli izotrop muhitda joylashgan bo’lsa,

                                       (1.10)

bu erda       e - muhitning nisbiy dielektrik singdiruvchanligi.

q zaryadga  ta’sir etuvchi kuch vektor ko’rinishida quyidagicha yoziladi

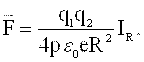                                     (1.11)

 

1.2. Elektrostatik maydon kuchlanganligi

 

Elektr maydon kuchlanganligi bu sinov zaryadi q nolga intilgan holda unga ta’sir etayotgan  kuch  va zaryad o’rtasidagi munosabat orqali aniqlanadigan tushunchadir.

.                                                  (1.12)

Nuqtaviy zaryadning elektr maydon kuchlanganligi

                                              (1.13)

Ikkita nuqtaviy zaryadnining o’zaro ta’sir kuchi

                                              (1.14)

Agar maydonda sinov zaryadi q mavjud bo’lmasa, u holda mexanik ta’sir kuchi nolga teng, ammo har bir nuqtadagi maydon kuchlanganligi E noldan farq kiladi.

Elektr siljishi yoki elektr induktsiyasi D deb birjinsli va  izotrop muhitlarda elektr maydon kuchlanganligiga proportsional bo’lgan kattalikka aytiladi.

  - vakuumda

 - muxitda

SI tizimida [] = [Kl/m² ]

Agarda maydon bir necha zaryadlar tomonidan yuzaga keltirilayotgan bo’lsa, unda fazoning istalgan nuqtasidagi umumiy kuchlanganlik quyidagi geometrik yig’indiga teng

.                  (1.15)

Umuman, elektrostatik maydonni harakatsiz hajmiy, yuza va chiziqli zaryadlar xosil qila oladi.

V hajm, S yuza va l chiziqlarni dv,ds,dl larga bo’lib, quyidagini yozish mumkin

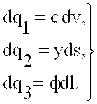                                     (1.16)

Bu erda q – hajmiy zaryad zichligi, σ –yuza zaryadi zichligi, τ- chiziqli zaryad zichligi.

Shunda

,                          

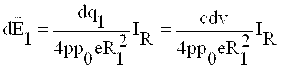,                       (1.17)

,                         

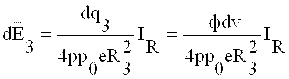Geometrik vektorlar  ni V xajm bo’yicha, ni S yuza bo’yicha, ni esa l chiziq bo’yicha qo’shib quyidagiga ega bo’lamiz

.                                               (1.18)

Keltirilgan tenglama, zaryadlarning fazodagi taqsimoti aniq bo’lganda, elektr maydon kuchlanganligi vektorini xisoblash imkonini beradi. Xisoblashlar, vektorning proektsiyalarini osonroq xisoblab olish mumkin bo’lgan tizimni aniqlashga qaratilgan bo’lishi lozim.

 

1.3. Elektrostatik maydonning uyurmasiz tavsifi

 

Maydon kuchi bilan q zaryadni bir nuqtadan ikkinchi nuqtaga siljitilganda bajariladigan ish quyidagi ifoda orqali aniqlanadi

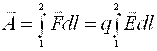.                                           (1.19)

Maydon kuchining yopiq egri chiziq bo’yicha bajargan ishi nolga teng. Buning uchun   vektorining tsirkulyatsiyasi nolga tengligini isbotlash kerak.

,                                                  (1.20)

Nuqtaviy  zaryad holatida

                                      (1.21)

Madomiki, quyidagi ifodalar o’rinli ekan

 

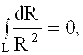
demak, keltirilgan (1.20) ifoda, chindan xam o’rinli.

Stoks teoremasidan foydalanib quyidagi tenglamani xosil qilamiz

                                           (1.22)

Bu tenglama elektrostatik maydonning uyurmasiz ekanligini ifodalaydi.

 

1.4. Elektr potentsiali

 

Elektr maydoni uyurmasiz bo’lganligi uchun (), skalyar funktsiya j ni topish mumkin. Bunda funktsiyaning «+» yoki «-» ishora bilan olingan gradienti elektr maydon kuchlanganligi vektoriga teng.

grad j = ± E.                                                      (1.23)

Maydonlar nazariyasida «-» ishora tanlanadi va bu maydon kuchlanganligi j ning so’nishi tomoniga yo’nalganligini ko’rsatadi. Skalyar funktsiya j ni potentsial funktsiya  yoki shunchaki  potentsial deyiladi.

 Istalgan nuqtadagi potentsial quyidagicha aniqlanishi mumkin

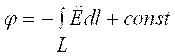.                              (1.24)

Bunda integrallash doimiysi nol potentsialli nuqtani berish orqali aniqlanadi. SI tizimida [φ]=[V].

Potentsiallar farqi esa

.                                            (1.25)

Nuqtaviy zaryad potentsiallar farqi integrallash usuliga bog’liq emas. Nuqtaviy zaryad maydonining potentsiali

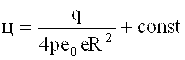.                                     (1.26)

Xarakatsiz hajmiy, yuza va chiziqli zaryadlarning maydon potentsiallari

.          (1.27)

 

Potentsialni aniqlagandan so’ng elektr maydon kuchlanganligi «E» ni xisoblab olsa bo’ladi. Buning uchun quyidagi ifodadan foydalanish lozim

E = - grad j.                                              (1.28)

 

Hajmiy zaryadlar maydonida «E» vektori doimo uzluksiz va tugallangan. YUza zaryadlari maydonida «E» doimo tugallangan, biroq «S» yuzada uzilishlarga duch keladi. CHiziqli  zaryadlar maydonida esa, «E» vektori zaryadlar taqsimalangan l  chiziqda  cheksizlikka aylanadi.

1.5. Elektrostatik maydonning grafik tasviri

 

Elektrostatik maydon  ekvipotentsial yuza va maydon vektori chiziqlari orqali tasvirlanadi. Ekvipotentsial yuzalar j = const tenglamasi yordamida aniqlanadi. Doimiy qiymatni o’zgartirish orqali ekvipotentsial yuzalar guruxini xosil qilish mumkin. Tasvirlashda ekvipotentsial yuzalar shunday joylashtiriladiki, bunda yonma-yon joylashgan qo’shni yuzalar potentsiallar farqi bir hil qiymatga ega bo’lishi lozim.

 

j₂=j₁ + Dj :                                                       

j₃ =j₂ + Dj =j₁ + 2 Dj:                                      (1.29)

j_n+1 =j_n + Dj =j₁ + n Dj.                                  

                           

Ekvipotentsial yuzalar yaqin joylashgan joyda maydon kuchlanganligi yuqori bo’ladi va ular o’zaro kesishmaydi..Elektr maydon kuch chiziqlari ekvipotentsial yuzaning urunmatashkil etuvchisi bilan mos keladi va to’g’ri burchak ostida kesishadi. Vektor chiziqlarining differentsial tenglamasi

[E dl] = 0.                                        (1.30)

Dekart koordinatlar tizimida

 

E_y dz - E_z dy = 0 :       E_z dx - E_x dz = 0:       E_x dy - E_y dx = 0.          (1.31)

 

Ekvipotentsial yuzalarning bittasi to’g’ri burchakli bo’laklarga bo’linadi. Bo’laklarning o’lchamini shunday tanlash lozimki, bunda maydon vektorining barcha bo’laklar orqali oqimi bir xil qiymatga ega bo’lsin. CHizmada xar bir bo’lakka bittadan vektor chizig’i o’tkaziladi va bu chiziq xar bir bo’lakning markazidan o’tishi kerak. Maydonning kuchlanganlik yuqori bo’lgan hududlarida vektor chiziqlari soni ko’payadi, ya’ni zichroq joylashtiriladi. Elektrostatik maydonda E vektorining chiziqlari tutashmagan, egri, xamda ular musbat zaryaddan manfiy zaryad tomonga yo’nalgan bo’ladi. Bunda musbat va manfiy zaryadlar kuch chiziqlarining boshlanish va tugash nuqtalari sifatida namoyon bo’ladi.

 

1.6. Dielektrikning qutblanishi va elektr induktsiyasi

 

Dielektrikda elektr maydon kuchlanganligining «ε» marta o’zgarishi dielektrikning qutblanishi natijasida yuz beradi. Tashqi maydon ta’siri ostida dielektrik o’zining neytrallik hususiyatini yo’qotadi va qutblanadi. Kutblanish paytida namoyon bo’lgan zaryadlar erkin zaryadlar deb ataladi. Bog’langan zaryadlar tashqi maydon yo’nalishiga teskari bo’lgan maydon xosil qiladi. SHuning uchun xam «E» ning qiymati kamayadi. Dielektrikning qutblanish darajasi kutblanish vektori R orqali tavsiflanadi.

,                                            (1.32)

 

bunda  K_E – dielektrik ta’sirchanlik.

Qutblanganlik havoda elektr induktsiyasi vakuumdagiga nisbatan  qanchaga farq qilishini ko’rsatadi.

 

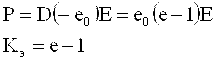.                               (1.33)

 

SI tizimida  [R] = [Kl/m²].

 

1.7. Gauss teoremasi

 

Elektr induktsiyasi vektori D ning chegaralangan ixtiyoriy S yuza orqali oqimi, shu yuza bilan chegaralangan hajmda joylashgan q erkin zaryadlarning algebraik yig’indisiga teng

.                                           (1.34)

Integral shakldagi Gauss teoremasi. Elektr induktsiya vektori oqimini Ostragradskiy teoremasiga ko’ra almashtirib, quyidagi ifodani xosil qilamiz

.                                 (1.35)

Zaryad hajmiy taksimotga ega bo’lganda

.                                                (1.36)

Gauss teoremasiga ko’ra

,

.                                  (1.37)

Differentsial shakldagi Gauss teoremasi. V – hajm ihtiyoriy ravishda tanlangan edi va tenglik uning barcha kiymatlarida xam o’rinli bo’ladi. Bu holda:

div D = r

.                                             (1.38)

Keltirilgan tengliklarga ko’ra, elektr maydon manbaalari faqatgina elektr zaryadlari ta’sir etayotgan joydagina mavjud bo’lishini aytish mumkin.

 

1.8. Elektrostatik maydonda o’tkazgichlar

 

Agar o’tkazgichga zaryad kiritsak, yuzaga keladigan itarilish kuchlari ta’siri ostida zaryad o’tkazgich bo’ylab xarakatlana boshlaydi. Xarakatlanish o’tkazgichning ustki cheksiz yupqa qatlamida amalga oshadi va barcha zaryadlar aynan shu qatlamda jamlanadi. O’tkazgichning ichida esa elektr maydon kuchlanganligi E nolga teng bo’ladi. O’tkazgichning yuzasidagi barcha ntsqtalarda toklar bir xil potentsialga ega bo’lishi kerak, ya’ni o’tkazgich yuzasi ekvipotentsial sirtni hosil qiladi.

Tashqi maydon ta’sirida erkin elektronlar o’tkazgich bo’ylab xarakatlanadi. Bunda o’tkazgichning bir qismida «-» zaryadlar, ikkinchi qismida esa «+» zaryadlar to’planadi. O’tkazgich ichida maydon mavjud emas. Atrofi dielektrik bilan qoplangan o’tkazgichning yuzasi elektrostatik maydon chegarasi bo’lib xizmat qiladi. Bu texnikada radioaparaturani elektrostatik ekranlash (tashqi ta’sirlardan saqlash) maqsadida  ishlatiladi.

 

1.9. Elektrostatik maydonda chegaraviy shartlar

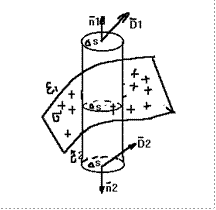
Dielektrik o’tkazuvchanlik ε₁ va ε₂ bo’lgan ikki muhitlar chegarasini ko’rib chiqamiz. Aytaylik, muxitlar chegarasida qandaydir qiymatga ega bo’lgan yuza zaryadi mavjud bo’lsin. Yopiq tsilindrsimon S yuzani tengma-teng ravishda ikki muxitda joylashtiramiz. Gauss teoremasiga ko’ra

.                           (1.39)

D vektorining oqimini uchta vektorlar oqimi yig’indisi orqali ifodalaymiz

 

.                  (1.40)

 

Agar  yuzani kichik o’lchamli deb qabul qilsak, u holda bu maydonning barcha nuqtasida D vektori bir xil qiymatga ega deyishimiz mumkin, ya’ni

 

         ò D₁ ds = D_1n DS,

                                                                               ^DS

         ò D₂ ds =  - D_2n DS.

                                                                              ^DS

Agar tsilindrning balandligini nolga intiltirib,  yuzalarni dielektriklar chegarasiga keltirsak, tsilindrning yon tomoni bo’yicha yuzaga keladigan vektor oqimi nolga teng bo’ladi, u holda

yoki

.                                (1.41)

 

Elektr induktsiyasining normal tashkil etuvchilari ikki o’tkazmaydigan  muhitlar chegarasida sakrashga uchraydi. Bu sakrash qiymati chegara bo’ylab taqsimlangan erkin yuza zaryadlari zichligiga teng. Agar s = 0 bo’lsa,

,

e₀ e₁E_1n  = e₀ e₂E_2n.                                                                               (1.42)

 

D vektorning normal tashkil etuvchisi muxitlar chegarasida uzluksiz. Ikkinchi chegaraviy shartni xosil qilish uchun esa yopiq L chiziqni ikki muxitlarda teng qiymatlarda joylashtirishimiz kerak bo’ladi.

Agar 2-3 va 1-4 kesmalarni kamaytirib, pirovardida ularni nolga tenglasak, Dl kesmasini esa chegara yuzasida joylashtirsak

 

E₁tDl - E₂tDl = 0,

E₁t  = E₂t

yoki

D₁t / e₁  = D₂t / e₂.

 

O’tkazgich bo’lmagan ikki muxitlar chegarasida elektr maydoni kuchlanganligi vektorining urunma tashkil etuvchilari o’zaro teng. Agar Ikki muhitlar chegarasida potentsiallar uzluksiz

j₁  =  j_2.

Agar muhitlardan biri o’tkazgich bo’lsa, u holda chegaraviy shartlar o’zgaradi.

Agar birinchi muhit dielektrik, ikkinchi muxit esak o’tkazgich bo’lsa, chegaraviy shartlar quyidagicha yoziladi

 

E₂ = 0     D₂ = 0     j₂ = const

D_1n = D₁ = s      yoki    e₀e E₁  = s

E₁t = 0     D₁t = 0.

 

1.10. Elektrostatik maydon energiyasi

 

Umumiy xolda, elektrostatik maydon energiyasi quyidagicha aniqlanadi

.                                              (1.43)

 

Bu ifoda faqat ta’sirlashish energiyasini xisobga oladi. Nuqtaviy zaryadning xususiy energiyasi rasman cheksizga teng. CHunki, cheklangan miqdorli bu zaryadni bir nuqtaga jamlash uchun cheksiz katta ishni bajarish talab etiladi. Bu formuladan foydalanish uchun, zaryadlar orasidagi masofa ularni tashuvchi jismlar o’lchamidan ancha katta bo’lgan masofada joylashgan bo’lishi lozim.

Elektrostatik maydon energiyasini quyidagi ifoda yordamida yozish mumkin

 

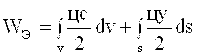.                                            (1.44)

 

Vektorlar taxlili kursidan quyidagi ma’lum

 

div (jD) = j div D +  Dgrad j.                                    (1.45)

 

YUqoridagi formuladan foydalanib, quyidagini yozish mumkin

 

,                  (1.46)

 

Madomiki , quyidagi ifodalar o’rinli ekan,

divD =r,    gradj = - E,

ò div (jD) dV = ò  jD dS,

                                     ^{V                                       S}

demak,

,                     (1.47)

 

DdS = -DdS = - sdS.

 

U holda

,                                (1.48)

 

 

va elektr maydon energiyasi

 

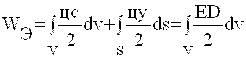.                         (1.49)

 

Birjinsli va izotrop muhitlarda

 

D =   e₀e E ,                                       (1.50)

 

demak,

 

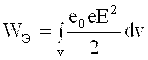,                                            (1.51)

Bu tenglamaning fizik ma’nosi quyidagicha, elektr maydoni energiya tashuvchisi bo’lib xizmat qiladi va energiya butun fazoda xajmiy zichlik bilan taqsimlangan.

.                                (1.52)

 

Elektr maydon kuchlanganligi noldan farqli bo’lgan xollarda maydon kuchlari maydon energiyasi xisobiga ish bajarishi mumkin.

 

2. ELEKTROMAGNIT MAYDONDA ELEKTR TOKI

2.1. Tok va o’tkazuvchanlik toki zichligi

 

Dq zaryadning berilgan yuza orqali ma’lum bir Dt vaqt ichida oqib o’tish nisbati tok o’lchovi sifatida hizmat qiladi. Bunda Dt®0 ga intiladi.

 

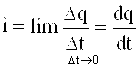.                                              (2.1)

 

Tok skalyar kattalikdir [i]=[A].

Tok zichligi – bu vektor kattalik J bo’lib, zaryadlar harakat yo’nalishiga perpendikulyar joylashtirilgan yuzadan oqib o’tuvchi tokning shu yuza o’lchamiga nisbatiga aytiladi. Bunda yuzaning maydoni nolga intiltiriladi.

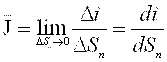.                               (2.2)

 

J vektorining yo’nalishi musbat zaryadlarning harakati yo’nalishi bilan bir xilda tanlanadi.

Tok va tok zichligi quyidagi munosabat bilan bog’langan

 

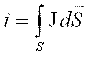.                                               (2.3)

 

Tok zichligi SI tizimida [ J ] = [A¤m²].

Ayrim hollarda, o’tkazuvchining faqat yuza qismidan oqib o’tuvchi yuza toklari ko’rib chiqiladi

 

.                                               (2.4)

 

SI tizimida [h] = [A¤m].

 

2.2. O’tkazuvchanlik toki zichligining divergentsiyasi

 

O’zgarmas toklar faqatgina yopiq zanjirlarda mavjud bo’ladi. J vektorining kuch chiziqlari uzluksiz va div J=0. Ixtiyoriy yopiq yuza bo’yicha o’zgarmas tokning oqimi doimo nolga teng.

O’zgaruvchan toklar yopiq bo’lmagan zanjirlarda xam mavjud bo’la oladi. Demak, o’zgaruvchan maydonlarda o’tkazuvchanlik toki oqadigan zanjirlar tutashmagan bo’lishi xam mumkin. O’tkazuvchanlik toki zichligi vektori J ning kuch chiziqlari tugallanadigan joyda zaryadlar to’planadi. SHu vektorning yopiq yuza bo’yicha oqimi noldan farqli bo’la oladi.

Aytaylik, S yuza bilan chegaralangan V xajmda q zaryad joylashtirilgan bo’lsin. Uning xajmiy zichligi  r orqali berilgan. Agar o’tkazuvchanlik toki i yuzadan chiqsa, unda q zaryad kamayadi.

Tokni uning zichligi, zaryadni esa xajmiy zichlik orqali ifodalaylik

 

,

.

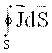
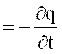Ostragradskiy teoremasi asosida J vektorining oqimini almashtirib

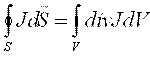
quyidagini xosil qilamiz

 ,

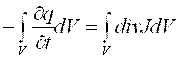yoki

.

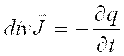O’tkazuvchanlik toki zichligining divergentsiyasi zaryadlar xajmiy zichligining kamayish tezligiga teng. O’tkazuvchanlik tokining zichligi o’z manbasiga ega bo’lishi mumkin. Uning oqib kirish chiziqlari (stoklari) vaqt bo’yicha o’zgaruvchan xajmiy zaryadlar ko’rinishida bo’ladi.

 

2.3. Differentsial shakldagi Om qonuni

 

Birjinsli izotrop o’tkazgichdagi o’tkazuvchanlik toki zichligi J elektr maydoni kuchlanganligi E ga to’g’ri proportsional.

                                                 (2.5)

Bu tenglama differentsial ko’rinishidagi Om qonuni nomi bilan yuritiladi.

O’tkazgichdan tok uzluksiz ravishda oqib turishi uchun zaryadlarni harakatga keltiruvchi elektr maydon bo’lish shart. Bunday maydonni yuzaga keltirish mumkin va u noelektrostatik jarayonlar (kimyoviy va termoelektrostatik) tomonidan qo’llab quvvatlanadi. Bu jarayonda ishtirok etayotgan maydon chetki elektr maydon deb ataladi. CHetki elektr maydonning kuchlanganligi

.                                               (2.6)

Natijaviy maydon kuchlanganligi

 

.                                          (2.7)

 

O’tkazgichning chetki kuchlar mavjud bo’lgan hududlarida Om qonuni kuyidagicha yoziladi

 

.                                       (2.8)

 

Bunda σ – solishtirma o’tkazuvchanlik.

SI tizimida [s]=[Sm/m].

 

2.4. To’liq elektr toki

 

O’tkazgich muxitdagi elektr toki maydon kuchlari ta’siri ostida yuzaga keladigan erkin elektr zaryadlarining tartibli xarakatidir. Bu tok o’tkazuvchanlik toki deb ataladi.

Om qonuniga ko’ra

Agar zaryadlangan jism yoki zarralar o’tkazgich bo’lmagan muxit yoki vakuumda V tezlik bilan xarakatlansalar, ular ko’chish tokini yuzaga keltiradi.

Chetki elektr maydoni ta’siriga kiritilgan dielektrikning molekulalari xarkatlanib, qutblanish tokini yuzaga keltiradi.

bu erda - qutblanish vektori.

Ba’zi bir muxitlarda =e₀k_e tenglik o’rinli. Bu xolda

YUqorida aytib o’tilgan uchchala tok turlari xam elektr zaryadlarining siljishini ifodalaydi. Xar bir tok o’zining magnit maydoniga ega.

Maksvell elektr toki deb tokning vakuumdagi vaqt bo’yicha o’zgarishini aytishni taklif etgan

Siljish tokining boshqa turdagi toklardan farqi shundagi, bu tok issiqlik yo’qotishlarini  (qizish xisobiga yuzaga keladigan energiya yo’qotishlari) yuzaga keltirmaydi.

To’liq elektr toki deb – magnit maydonini yuzaga kelishida qatnashadigan archa turdagi toklarning yig’indisiga aytiladi

I_to’l=I + I_ko’ch + I_qutb + I_0sil.

Vakuumdagi qutblanish va siljish toklari yig’indisini dielektrikdagi siljish toki deb ataladi.

Bu xolatda tok zichligi

J_to’liq = J_o’tk + J_sil= sE +.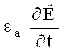

Ko’chish tokini ko’rib chiqish shart emas. YAxshi o’tkazuvchanlikka ega bo’lgan muxitda I >> I_sil, kam yo’qotishli dielektrikda esa I_sil >> I. Yarimo’tkazgich muxitlarda ikkala toklar xam o’zaro teng qiymatlarga ega bo’ladi.

 

3. MAGNIT MAYDONI

3.1. Magnit maydonni tavsiflovchi asosiy kattaliklar

 

Magnit maydonni tavsiflovchi asosiy kattaliklar shundan iboratki ular o’z ta’siri ostidagi harakatlanayotgan zaryadlangan jismga  va tok oqayotgan harakatsiz o’tkazgichga kuch bilan ta’sir kiladi.  Magnit maydonni  magnit induktsiyasi vektori orqali tavsiflanadi.  vektorining  yo’nalishi va qiymatini bilgan xolda, u tomonidan hosil kilinishi mumkin bo’lgan hodisalarni aniqlash mumkin.  vektorini  tok oqayotgan konturga ta’sir etayotgan kuch orqali aniqlash mumkin. Tokning chiziqli qismiga ta’sir ko’rsatuvchi kuchni quyidagi formula bilan aniqlash mumkin.

 

.                                        (3.1)

 

SI tizimida []= [Tl].

Tok va u tomonidan bo’shliqda qo’zg’atilgan induktsiya orasidagi bohliqlikning differtsial ko’rinishi quyidagicha

 

,                                   (3.2)

bu erda       J – tok zichligi

dV – elementar hajm

R – vektor aniqlanadigan nuqtagacha bo’lgan masofa

m₀ – magnit doimiysi m₀=4p×10^-7 Gn/m.

 

Agar o’tkazgichning ko’ndalang kesimi o’tkazgich uzunligi va kuzatish nuqtasigacha bo’lgan masofadan kichik bo’lsa  (bu erda o’tkazgich chiziqli)

 

[ ]dv=[ ] =[()]=I[].                   (3.3)

 

Tenglamani integrallab quyidagi ifodani xosil qilamiz

 

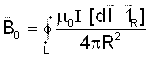.                                            (3.4)

Agar, tokli kontur biror muhitda joylashgan bo’lsa, unda magnit induktsiyasining qiymati ₀ dan m marta farq qiladi

 

                                            (3.5)

m - nisbiy magnit singdiruvchanlik.

Magnit maydon kuchlanganligi quyidagicha aniqlanadi

 

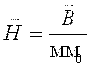.                                              (3.6)

 

Magnit maydon kuchlanganligi muhit xossalariga bog’lik emas. Tokli o’tkazgich uchun Bio-Savar-Laplas qonuni quyidagicha

 

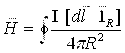 .                                       (3.7)

 

Muhitning xususiy makroskopik maydonini M vektori bilan tavsiflash mumkin. U magnitlanish vektori deb atalladi. Bu vektor bir xil kuchlanganlikka ega bo’lgan magnit maydoni ta’sir etayotgan muxitda va vakuumda magnit induktsiyasi vektorlari o’zaro qanchaga farq qilishini (=mm₀ muhitdagi magnit induktsiyasi, =m₀ vakuumdagi magnit induktsiyasi) ko’rsatadi.

 

-₀=m₀,                                                (3.8)

M=k_m.                                                    (3.9)

 

bu erda k_m –magnit ta’sirchanlik

 

=m₀M+m₀=m₀(1+ k_m)= mm₀.                      (3.10)

 

YUqoridagilarga ko’ra, m=1+ k_m

SI birliklar tizimida []=[A/m], [M]=[A/m].

3.2. Magnit oqimi va uning uzluksizligi

 

Magnit induktsiyasi vektorining oqimi quyidagicha yoziladi

 

F=.                                          (3.11)

SI tizimida [F] = [Vb].

YOpiq yuza orqali magnit oqimi  doimo nolga teng.

 

.                                         (3.12)

 

Ostragradskiy teoremasidan foydalanib quyidagi ifodani yozish mumkin

 

.                                 (3.13)

Bu tenglama istalgan hajm uchun o’rinli va shunga asosan

 

div=0.                                                    (3.14)

 

Keltirilgan tenglama magnit oqimining uzluksizlik printsipi bo’lib, differentsial shaklda yozilgan. Bu magnit maydonining istalgan nuqtasida  xam keluvchi (stok) va ketuvchi (istok) magnit induktsiya kuch chiziqlarining mavjud emasligini ifodjalaydi. Magnit induktsiyasi  chiziqlari hech qachon uzilmaydi va ular  doimo o’z-o’ziga tutashgan.

 vektorining yopiq kontur bo’yicha tsirkulyatsiyasi va konturdagi  tok bilan miqdoriy aloqasi to’liq tok qonuni orqali aniqlanadi.

 

I      .                                              (3.15)

 

Biron-bir muxitda uncha katta bo’lmagan kontur olamiz va unda  vektorini tsirkulyatsiyasini ko’rib chiqamiz.

    J_o’tk    D      J

Di =J  D=J_o’tk D

 

 

 

Ifodaning ikkala tomonini D ga bo’lib, yuzaning maydonini nolga intiltiramiz D®0.

,

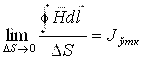rot_p =J_o’tk,

 

rot =J.

 

rot =J tenglama to’liq tok qonunining differentsial shakli xisoblanadi.

H vektori kuzatilayotgan nuqtada maydonga uyurmali ko’rinish bera oladigan funktsiya sifatida ko’rib chiqilishi mumkin.

 

3.3. Magnit maydonining skalyar potentsiali

 

Rotori noldan farq qiluvchi maydonni uyurmali maydon deyiladi. O’zgarmas tok  yuzaga keltirayotgan maydonda rot =J bo’lganligi, va bu erda  J¹0 tenglik bajarilganligi uchun vektorining maydoni uyurmali bo’ladi. Agar  J=0  va rot=0 bo’lsa, magnit maydonni potentsial maydon sifatida qo’rib chiqish lozim.

Bunday xollarda

=-grad j_M,

chunki

div=divmm₀=0,

 

div=0,

 

div gradj_M=0.                                           (3.16)

yoki Ѳj_M=0 – toksiz tarmoqlar uchun Laplas tenglamasi.

Birinchi va ikkiinchi nuqtalardagi skalyar magnit potentsiallari farqini shu nuqtalar orasidagi magnit kuchlanishining tushushi deb ataladi.

U_M12=j_M1-j_M2=.                                (3.17)

 

“Magnit kuchlanishning tushishi” va  “magnit kuchlanish” orasidagi farqni tushunib olish kerak. Birinchisi faqat   dan   bo’yicha tanlangan yo’l orqali chiziqli integralash bilan, ikkinchisi esa nafaqat shu integral bilan, balki,  shu yo’lda mavjud bo’lgan EYUK bilan xam aniqlanadi.

 

3.4. Magnit maydonining vektor potentsiali

 

Magnit maydonini hisoblash uchun vektor potentsialidan foydalaniladi

=rot .

Magnit induktsiyasini vektor potentsialidan olingan rotor sifatida tasvirlash uchun ixtiyoriy rotorning divergentsiyasi nolga teng ekanligi xaqidagi ayniyat asos bo’lib xizmat qiladi

div =0  ekan, demak div rot =0.

Ixtiyoriy konturni yorib o’tayotgan magnit oqimi va magnit induktsiyasini topish uchun vektor potentsialidan foydalanish ma’qul.

 

3.5. Magnit maydonidagi chegaraviy shartlar

 

Magnit maydoni uchun N_1t=N_2t shart o’rinli. Bu shart mnpq yassi konturi bo’ylab chiziqli  integralni tuzish orqali keltirib chiqarilgan.  Konturning np va mq  tomonlar mn va pq  tomonlarga nisbatan juda xam kichik. Konturning mn va pq tomonlarini dl deb belgilab quyidagini xosil qilamiz

H₁sina₁dl-H₂sina₂dl=0,                   (3.18)

H₁sina₁=H_1t   H₂sina₂=H_2t

Demak,  H_1t=H_2t shart chindan xam o’rinli. Agar ikki muxitlar chegarasida yuza toklari oqayotgan bo’lsa, bu shart bajarilmaydi. Bunday xollarda

H₁sina₁dl - H₂sina₂dl = J_sdl ,

H_1t - H_2t = J_s.

 

J_s zichlikka ega bo’lgan yuza toki mavjud bo’lganda maydonning urunma tashkil etuvchisi muxitlar chegarasida uzilishga uchraydi, ya’ni sakrab o’zgaradi.

Magnit maydoni uchun

V_1p=V_2p

Bu ifoda magnit oqimi printsipidan kelib chiqadi

=0

Ikki muhitlar chegarasida uncha katta bo’lmagan yassi paralipiped xosil qilaylikda, undagi oqimlarni xisoblaylik. Xisob-kitoblarni paralellepipedning quyi V_1p DS va yuqori V_2p  DS chekkalari uchun amalga oshirmiz. Natijada quyidagi tengliklar xosil bo’ladi

 

-V_1p DS+ V_2p  DS=0,                       

V_1p= V_2p,                                                                     

.                              (3.19)

 

 

3.6. Magnit maydoni energiyasi

 

dl elementar maydonni kesib o’tayotgan magnit oqimi dF=d ga teng. To’la oqim esa

 

F=.                                          (3.20)

 

d yuzani chegaralovchi konturda kuch naychalarini chizamiz.  vektorining magnit maydondagi chiziqlari doimo o’zaro tutashgan bo’lganligi uchun, kuch naychalari xam yopiq (tutashgan) bo’ladi. Ular magnit maydoni bilan band bo’lgan V hajmni to’ldiradi. Agar nay o’qini  L bilan belgilasak, u holda

Maydon energiyasi esa

,

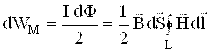yoki

,

u holda

.                          (3.21)

Agar =rot ekanligini hisobga olsak

,

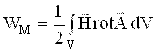 biroq,

div[]=rot-  rot.

SHunday ekan,

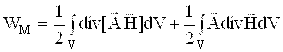
tenglamani yozish mumkin.

 

Ostrogradskiy teoremasiga ko’ra

.                                    (3.22)

Magnit maydoni cheksiz hajmni egallaganligi uchun S ni cheksiz katta R radiusli sharning yuzasi deb qarash mumkin. [] vektor masofa funktsiyasi sifatida  dan tezroq, yuza esa R²  dan  sekinroq o’sib boradi. O’unday ekan, R®¥ xolatida

.

U xolda, Maksvellning  (rot=J)  birinchi tenglamasiga ko’ra  

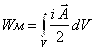                                               (3.23)

tenglamani hosil qilamiz.

 

3.7. Magnit maydonning hisoblash usullari

 

Magnit maydonini hisoblash ko’pincha N vektorni aniqlashga taqaladi. 

Bunda, tok ыiymatlari va tok oqayotgan o’tkazgichlarning joylashuvi berilishi shart. Agar maydon ferromagnitsiz muhitda ta’sir etayotgan bo’lsa,

mm₀»m₀=4p10^-7 Gn/m .                               (3.24)

 

Agar N ni hisoblash katta matematik qiyinchiliklar tug’dirsa, u holda  vektor potentsial tushunchasini kiritish qulay. Vektor potentsialini aniqlash orqali maydon kuchlanganligini topish mumkin. Magnit maydonini hisoblashda quyidagi usullardan foydalanish mumkin:

·                   Integral ko’rinishdagi to’liq tok qonuni qo’llash;

·                   Maksvelning birinchi tenglamasini qo’llash;

·                   Vektor potentsiali uchun Puasson – Laplas tenglamasini qo’llash;

·                   Ko’zguli tasvir usuli;

·                   Konform o’zgarishlar usuli;

·                   grafik xisoblash usulini.

 

4. MAKSVELL TENGLAMALARI TIZIMI

4.1. Maksvelning birinchi tenglamasi

 

To’liq tok qonuniga asosan

.                           (4.1)

 

Bu tenglama Stoks teoremasi asosida o’zgartirilgach, quyidagi ko’rinishga keladi

 

 .                            (4.2)

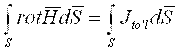
Natijada

yoki

Ushbu tenglamaning fizik ma’nosi shundaki, uyurmali magnit maydoni xam o’tkazuvchanlik toklari tufayli, xam vaqt mobaynida o’zgaruvchan elektr maydonlari tufayli yuzaga keladi.

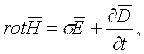
Ideal dielektriklar uchun solishtirma elektr o’tkazuvchanlik s = 0 ga teng.

u holda to’liq dielektrik singdiruvchanlik muhiti e=const uchun Maksvelning birinchi tenglamasini vaqt davomida o’zgaruvchan elektr maydoni va magnit maydoni kuchlanganligining fazoda o’zgarishi o’rtasidagi bog’liqlikni o’rnatadi va elektromagnit maydon doimo xarakatda ekanligini isbotlaydi.

 

4.2. Maksvelning ikkinchi tenglamasi

 

Bu tenglama konturda xosil qilingan elektromagnit induktsiya qonunining differentsial ko’rinishi bo’lib, quyidagicha aniqlanadi

.                                                 (4.3)

S yuza hamda L kontur ko’zg’almas va shaklan o’zgarmas deb tasavvur qilatslik. U xolda, Stoks teoremasiga ko’ra

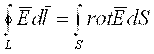,                                  (4.4)

Shunday ekan,

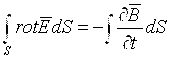                               (4.5)

yoki

 

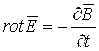.                                   (4.6)

 

Bu tenglamaning fizik ma’nosi shundan iboratki, uyurmali elektr maydoni o’zgaruvchan magnit maydonini qo’zg’atadi. rotE¹0 bo’lganligi uchun, E vektorining kuch chiziqlari yopiq bo’lishi mumkin va ular V vektori chiziqlarini qamrab olishi kerak.

Magnit singdiruvchanlik m=const bo’lgan muhitlar uchun esa

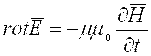.                         (4.7)

 

Shunday qilib, Maksvelning ikkinchi tenglamasi N vektorining vaqt bo’yicha o’zgarishi bilan E vektorining fazoda o’zgarishi o’rtasidagi bog’liqlikni o’rnatadi.

 

4.3. Maksvellning uchinchi tenglamasi

 

Maksvellning uchinchi tenglamasi Gauss qonunining o’zgaruvchan jarayonlar xolati uchun umumlashtirilgan ko’rinishi xisoblanadi. Gauss qonuni ixtiyoriy yopiq S yuza orqali elektr siljishi vektori oqimining shu yuzada jamlangan Q zaryad bilan bog’laydi

,                                                         (4.8)

Maksvellgacha bu tenglama faqatgina o’zgarmas maydonlarga nisbatan qo’llanilar edi. Maksvell esa bu tenglamani o’zgaruvchan maydonlarda xam qo’llash mumkin degan fikr bilan chiqdi. Q zaryad S yuzada ixtiyoriy taqsimlangan bo’lishi mumkin. shuning uchun, umumiy xolda

bu erda       V- S yuzada joylashgan xajm;

                   ρ – zaryadning xajmiy zichligi.

Zaryadning xajmiy zichligi esa

_{YUqoridagilarni xisobga olgan xolda, quyidagi tenglamani xosil qilamiz}

                                                            _(4.9)

Bu tenglamani Maksvellning integral shakldagi uchinchi tenglamasi deb atashadi. Ostragradskiy teoremasiga asosan bu tenglamani differentsial shakli quyidagicha

                                   (4.10)

Maksvellning uchinchi tenglamasidan quyidagi fizik ma’no kelib chiqadi; Elektr siljish vektorining yopiq yuza bo’yicha oqimi shu yuzada taqsimlangan zaryadlarning xajmiy zichligiga teng va elektr maydoni kuch chiziqlari musbat zaryadlardan manfiy zaryadlar tomonga yo’nalgan bo’ladi.

 

4.4. Maksvellning to’rtinchi tenglamasi

 

Maksvellning integral shakldagi to’rtinchi tenglamasi magnit maydoni uchun Gauss qonuni bilan mos keladi. Unga ko’ra, B vektorining ixtiyoriy S yuza orqali oqimi nolga teng

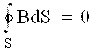.                                    (4.11)

Bu esa, V vektorining faqatgina yuzaga kiruvchi yoki yuzadan chiquvchi kuch chiziqlari mavjud emas, ular doimo yuzani yorib o’tishini ifodalaydi.

Ushbu tenglama Maksvellning integral shakldagi to’rtinchi tenglamasi nomi bilan yuritiladi. Uning differentsial shakliga Maksvellning uchinchi tenglamasidagi kabi, Ostragradskiy-Gauss teoremasini qo’llagan xolda o’tish mumkin. Natijada

div B = 0.                               (4.12)

Bu tenglama esa Maksvellning to’rtinchi tenglamasini differentsial shakli. Unga ko’ra, tabiatda magnit zaryadlari mavjud emas va V vektorining (magnit maydonining) kuch chiziqlari  doimo o’ziga-o’zi tutashgan.

 

4.5. Elektromagnit maydonning to’liq tenglamalar tizimi

 

Elektromagnit maydonni to’rtta D, E, B, H vektor kattaliklar bilan tavsiflanadi. Doimiy singdiruvchanlikka ega bo’lgan muhitlar uchun 

D=ee₀E,               B=m₀mH                                  (4.13)

 

SHuning uchun xam, hisoblashlarda ikki vektorni aniqlash kifoya qiladi. Odatda,`E va `N vektorlari Maksvel tenglamalaridan aniqlanadi

`E  va`N ni aniqlash uchun yuqoridagi tenglamalarning o’zi etarli emas. SHuning uchun, vektorlarning divergentsiyalarini ham aniqlash kerak. Gaussning differentsial shakldagi teoremasiga ko’ra div`D=r.

e  doimiy qiymatga ega bo’lganda

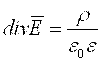                                              (4.14)

Magnit maydonning asosiy hususiyati bu uning solenoidalligi (div`B=0). Agar m doimiy bo’lsa, div`H=0.

Aniq masalalarni echishda boshlang’ich chegaraviy shartlari inobatga olish lozim.

Ikki muhitlar chegarasida e, m  va  s ning qiymatlari sakrab, keskin o’zgaradi. Demakki, chegara yuzasida magnit maydon vektori uzluksizligining uzilishi o’rin tutadi. Vaqt bo’yicha doimiy maydon uchun olingan chegaraviy shartlar elektromagnit maydon vektorlarining oniy qiymatlari uchun ham axamiyatini yo’qotmaydi.

 

                         (4.15)

 

Elektromagnit maydonning asosiy tenglamalaridan quyidagi fizik ma’no kelib chiqadi:

-         magnit maydoni doimo uyurmalidir va u harakatlanayotgan zaryadlar bilan xam, vaqt bo’yicha o’zgaruvchan elektr maydoni bilan xam qo’zg’aladi.

 

Elektr va magnit maydonlari doimiy o’zaro bir-biri bilan almashib turuvchi jarayon bo’lib,  yagona elektromagnit maydoning ikki tomoni sifatida namoyon bo’ladi. Elektromagnit maydon doimo xarakatda va o’zi bilan energiya zahirasini olib yuradi.

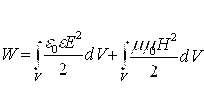                         (4.16)

Vaqt bo’yicha doimiy jarayonlarda maydon tenglamasi ikki bir-biridan mustaqil tizimlarga ajraladi

elektr maydon uchun  rotE=0, dive₀eE=r

magnitostatistik maydon uchun rotH=J, divm₀m`H=0.

 

4.6. To’liq tokning uzluksizligi tenglamasi

 

Bu tenglama Maksvellning birinchi tenglamasidan xosil qilinadi. Buning uchun tenglamaning ikkalal tomoniga nisbatan divergentsiya amalini qo’llash lozim, ya’ni

                               (4.17)

vektorlar taxliliga ko’ra, rotordan olingan divergentsiya nolga teng degan ayniyat mavjud. Shuning uchun

                                              (4.18)

vektor divergentsiyasining nolga tengligi, uning kuch chiziqlari yopiq ekanligini anglatadi. SHunday ekan, to’liq tokning kuch chiziqlari uzluksiz. Bu xolat aloxida ikki yoki undan ko’p simlardan tashkil topgan antennalarda nima uchun tok oqib o’tishi va yopiq zanjir xosil bo’lishini tushuntiradi. Bunday tizimda, o’tkazuvchanlik tokining kuch chiziqlari fazo orqali siljish tokining kuch chiziqlari yordamida  tutashadi va antennada tok oqishi uchun sharoit yaratadi. Xuddi shunday xodisa mobil va radiotelefonlarda xam kuzatiladi.

 

5. MONOXROMATIK MAYDON UCHUN ELEKTROMAGNIT MAYDON TENGLAMALARI

5.1. Kompleks vektorlar. Elektromagnit maydon tenglamalarining kompleks shakllari

 

Yuqorida yozilgan tenglamalar maydon vektorlarining oniy qiymatlari uchun yozilgan, ya’ni, ular maydonning vaqt bo’yicha ixtiyoriy o’zgarishi uchun o’rinli. Agar vektorlar vaqt bo’yicha doimiy davrli sinusoidal qonun bo’yicha o’zgarsa, bunday maydonlar monoxromatik deb ataladi. Bunday maydonlar uchun kompleks vektorlarni keritish, ya’ni, kompleks amplitudalar usulini qo’llash o’rinli. Bu usulda oniy qiymatlar o’rniga formal kattaliklarni qo’llaniladi. Masalan, N = H_msin(t+_n) o’rniga N_me^jt ko’rinishdagi kompleks kattalik yoziladi.

Quyidagi tenglamaga ko’ra, I_m kompleks miqdorning mavxum qismini ko’rsatadi

EMM bo’yicha ko’p adabiyotlarda, vaqt bo’yicha kosinusoidal qonun bo’yicha o’zgaradigan maydonlarni monoxromatik maydon deb ataladi. U xolda,

ya’ni, kompleks miqdorning moddiy qismi qo’llaniladi.

Oniy qiymatlardan kompleks qiymatlarga o’tish garmonik fizik jaryonlarni matematik usulda ko’rib chiqishni osonlashtiradi. Bunda differentsiallash va integrallash amallari ularni (jw) ko’paytuvchisiga ko’paytirish yoki bo’lish amallari bilan almashtiriladi. Bu erda  - ko’rib chiqilayotgan chastota garmonikasi.

Masalan, siljish tokining zichligini quyidagicha almashtirish mumkin

Quyidagi tenglama o’rniga

                                (5.1)

mana bu tenglamadan foydalaniladi

.

Uni umumiy ko’paytuvchisiga qisqartirib quydagi ko’rinishga ega bo’lamiz

 

                             (5.2)

 

(5.1) dagi Maksvellning birinchi tenglamasi real mavjud bo’lgan maydonlar uchun yozilgan. (5.2) tenglama esa (5.1) ning matematik shakli xisoblanadi va faqatgina garmonik maydon uchun, ya’ni, signalning bitta spektral tashkil etuvchisi uchun yozilgan. SHuni yodda tutish kerakki, EMM tenglamalarining kompleks shakllari maydon vektorlarining garmonik o’zgarishlari uchun, xususiy xolat sifatida namoyon bo’ladi. Maksvellning qolgan tenglamalari kompleks shaklda quyidagi ko’rinishga ega bo’ladi

Vektorlarning kompleks shakllari ularning ustida nuqta belgisi kiritilganligi bilan farqlanadi. Kompleks shakldagi tenglamalardan xosil bo’lgan javoblarning real qismi to’g’ri javob sifatida qabul qilinadi.

 

5.2. Kompleks dielektrik singdiruvchanlik. Yo’qotishlar burchagi

 

(5.2) ga elektrodinamikaning uchinchi moddiy tenglamasini qo’yib, quyidagini xosil qilamiz

Tenglamaning o’ng tomonini matematik o’zgartirib

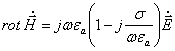                               (5.4)

tenglamaga ega bo’lamiz.

Elektromagnit jarayonlarni taxlil qilishda yangi koeffitsiyent – kompleks dielektrik singdiruvchanlikning kiritilishi tenglamalarni soddalashtirish imkonini beradi.

                                   (5.5)

Shunday ekan, tenglama quyidagi ko’rinishga keladi

formulani algebraik va ko’rsatmali shakllarda yozish mumkin

                                 (5.5.a)

                                 (5.5.b)

Eyler formulasi asosida o’zgartirishlar bajarilganidan so’ng, yana bir asosiy tenglamaga ega bo’lamiz

                                             

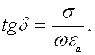                                              (5.6)

(5.6) ni dielektrik yo’qotishlar burchagining tangensi deb ataydilar. Elektr maydonining energiya yo’qotishlari o’tkazuvchanlik toklari va muxitdagi siljish toklari xisobiga yuzaga keladilar. tg parametri siljish toki xisobiga xosil bo’ladigan yo’qotishlarni, ya’ni, tashqi elektr maydoni ta’siri ostida yuzaga keladigan xarakat tufayli paydo bo’ladigan yo’qotishlarni ko’rsatadi.

Kompleks o’tkazuvchanlik tokining zichligi moduli quyidagiga teng

 

Siljish toki zichligining moduli esa

Ularning nisbati bizga yo’qotishlar burchagi tangensini beradi

Shunga ko’ra, bu parametr muxitda o’tkazuvchanlik toki siljish tokidan qancha katta qiymatga ega ekanligini ko’rsatadi va muxitlarni o’tkazgich va dielektriklarga bo’lish mezoni bo’lib xizmat qiladi.

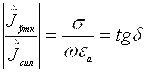
Agar tg >10 (tg  » 1) bo’lsa, bunday muxitni katta yo’qotishli muxit yoki o’tkazgich muxit deb ataydilar.

Agar tg <0,l (tg  « 1) bo’lsa, bunday muxitni kichik yo’qotishli muxit deb ataydilar, ya’ni bu muxit dielektrikka xos.

Agarda bu parametr qiymati 0,1<tg <l0 (tg  ≈ 1)  oraliqda joylashgan bo’lsa, bunday muxitni yo’qotishli yoki yarimo’tkazgich muxit deb ataydilar. Toza va quruq xavoni vakuumga yaqin deb xisoblash mumkin va u yo’qotishlarni yuzaga keltirmaydi (tg = 0). Amalda qo’llaniladigan sifatli dielektriklar radiochastota diapazonida (f = 30 GGs gacha) tg = 10^-2…10^-4 qiymatga egadirlar.

 

5.3. Monoxromatik maydon uchun chetki manba’larni xisobga oluvchi tenglamalar tizimi

 

(5.1) va (5.2) tenglamalarida qatnashuvchi maydon orqali shu muhitda vujudga keltirilgan va  toklari yo’q. Bu toklar maydonning manba’lari bo’lib hisoblanmaydi, balki ular uning ta’siri ostida paydo bo’lgan. Shu vaqtning o’zida EMM chetdan olinadigan energiya hisobiga qandaydir maydon tomonidan vujudga keladi. Bunday manba sifatida ko’pincha radiouzatgichning kuvvatli chiqish kaskadi yordamida antennada yuzaga keladigan tok hisoblanadi. Antennaning toki chetki resurs (transformatorli yordamchi stantsiya) ning quvvati orqali aniqlanadi va muhitda ko’rilayotgan maydon vektorlari funktsiyasi hisoblanmaydi. Elektromagnit maydon manbasini chetki kuch deb atash qabul qilingan. Chetki kuch - bu EMM ni hisoblashda boshlang’ich miqdor hisoblanadigan funktsiyadir. Bu kuch ko’pincha J_silj tokining zichligi orqali ifodalanadi. U Maksvellning 1-tenglamasini o’ng tarafida qatnashadi.

        

                                  (5.7)

 bo’lganligi sababli, birinchi tenglama kompleks shaklda quyidagi ko’rinishga ega

 

 

Qolgan tenglamalar esa

                             (5.8)

                                       (5.9)

(5.8) tenglamada qayta magnitlanishda yuzaga keladigan yo’qotishlarni hisobga olishda qo’llaniladigan kompleks magnit o’tkazuvchanlik qatnashadi. Ammo O’YUCH texnikasida faqatgina bir magnit modda — noyob xususiyatlarga ega magnitlangan ferritgina qo’llaniladi. Radiotexnikada qo’llaniladigan boshqa modalar magnit  xossasiga ega emas va magnit yo’qotishlarini yuzaga keltirmaydi. SHuning uchun (5.8) tenglamasida bundan keyin m o’rniga m_a ni yozamiz.

(5.7) tenglamasida chetki mabalarning mavjudligi uni bir jinsli emas qilib qo’yadi. CHetki manbalarsiz tenglama esa bir jinsli hisoblanadi.

 

                              (5.10)

 

SHuni payqash qiyin emaski, agan  ni  ga, e_a ni esa m_a ga  almashtirsak 1-tenglama 2-tenglamadan, 2-tenglama esa 1-tenglamadan xosil qilinishi mumkin. Maksvell tenglamalarining bu xussusiyati ikki taraflamalik printsipi deb ataladi. Uning yordamida, echilgan ikki taraflamali masalalar javoblarining mos keluvchi simvollarini almashtirish yo’li bilan ba’zi bir tenglamalarning echilishini olish uchun qo’llaniladi.

Elektrodinamikaning ba’zi bir masalalari, shuningdek agar tenglamalar tizimiiga chetki magnit toki J_chetm  kirgizilsa ham soddalashadi. Tabiatda real mavjud magnit zaryadlar yo’qligi sababli, fizik nuqtai nazardan  soxta miqdor hisoblanadi. U holda Maksvellning bir jinsli bo’lmagan tenglamalari ham shakl jihatdan simmetrik bo’ladi

 

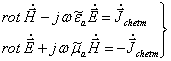                               (5.11)

 

Maksvellning simmetrik bir jinsli va bir jinsli bo’lmagan (5.10) va (5.11) tenglamalari yordamida, vektorlar va parametrlar o’rnini almashtirish yo’li bilan, ikki taraflamali masalalarning amallaridan foydalanib bir qator masalalarning echimi olinadi.

 

6. ELEKTROMAGNIT MAYDON ENERGIYASI VA QUVVATI

6.1. Asosiy gipoteza

 

EMM - materiyaning o’ziga xos turi sifatida ish bajarishga qodir. Masalan, u zaryadlangan zaryadlarni xarakatga keltira oladi. Makroskopik maydondagi energetik nisbatlarni ko’rib chiqilayotganda, ularning orasida aloqa o’rnatuvchi quyidagi ikki taxmindan foydalaniladi.

1.                Elektromagnit energiya fazoda hajiy zichlik bilan taqsimlangan

 

w=w_e+w_m=1/2 (E*D+H*B),   J/m³

 

bu erda w_e=(E*D)/2 va w_m=(N*V)/2 — elektr va magnit maydon energiyalarining hajmiy zichliklari.

2.                Elektromagnit energiya oqimining zichligi elektr va magnit maydon kuchlanganliklarining vektor ko’paytmasiga teng

 

П=[ExH], Vt/m²

 

Bu erda П — energiya harakatining yo’nalishini ko’rsatuvchi va miqdori bo’yicha uning oqimi zichligiga teng bo’lgan Poynting vektori. Vektorning o’lchov birligi uning quvvat zichligiga tengligini, ya’ni harakat yo’nalishiga perpendikulyar joylashgan 1 m² maydondan o’tuvchi to’lqin quvvatini ko’rsatadi.

 

6.2. Eneriya balansi

 

EMM energiyaning saqlanish qonuniga bo’ysunadi. SHuning uchun S yuza bilan chegaralangan har qanday V hajmda kelayotgan va undan chiqayotgan energiyalar tengligi sharti bajariladi. Berilgan vaqt laxzasida hajmdagi energiya qiymatini quyidagi tenglamani integrallash orqali aniqlash mumkin

 

Vaqt o’tishi bilan energiya qiymati bir qator sabablarga ko’ra o’zgaradi:

— energiya boshqa turlarga aylanadi. Radioto’lqinlarni qabul qiluvchi qurilmaning kirish zanjirida elektronlarning EMM ta’siri ostida issiqlik harakati hajmdagi (iste’molchi uchun foydali) energiya yo’qotishlariga olib keladi. Energiyaning sarflanish tezligi uning yo’qotishlar quvvati deb ataladi;

— chetki (begona) manba’larning energiyasi hisobiga to’lib boradi. Masalan, berilgan hajmda joylashgan antennaning nurlashi xisobiga maydon energiyasi ko’payadi. Bunda, energiya ko’payishining tezligi chetki kuchlar quvvati R_chet ga teng;

—                          xajmdan nurlanadi yoki hajm tashqarisidagi manba’lar energiyasi hisobiga to’ladi. Hajmdan chiquvchi elektromagnit oqimini nurlanish deb ataymiz. Nurlanish quvvati “oqim” operatori orqali aniqlanadi:

 

                                          (6.2)

 

Yodingizda bo’lsa, elektromagnit maydon vektori dS shu yuzani o’rab turuvchi hajmga tashqi normal bo’yicha yo’nalgan. Agar П va dS vektorlarining yo’nalishlari qarama –qarshi (ya’ni quvvat oqimi hajm ichiga yo’nalgan) bo’lsa, u holda quvvatning manfiy qiymatiga ega bo’lamiz. Unda R_S miqdorni nurlanish quvvati deb emas, balki kirish quvvati deb atash lozim bo’ladi. Lekin, bunday atama elektrodinamikada ishlatilmaydi, balki faqat nazarda tutiladi.

Biz berilgan hajmdagi energiyaning vaqt bo’yicha o’zgarish (dW/dt) sabablarining barchasini qo’rib chiqdik. Demak

 

bu erda       P_chetki – chetki manba’ quvvati,

         R_y – yo’qotishlar quvvati (iste’mol qilingan),

         R_Σ – nurlanish quvvati.

 

(6.3) ifoda berilgan hajmdagi EMM quvvati balansining umumiy fizik tenglamasi hisoblanadi.

 

6.3. Elektromagnit maydon vektorlarining  oniy  qiymatlari uchun Poyting teoremasi

 

(6.3) tenglamaga  (6.2) va (6.1) ifodalarni qo’ysak quyidagi tenglamani xosil qilamiz

 

 

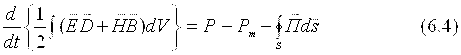
P_chetki bilan R_y  ning tarkibini taxlil qilaylik. EMM ning energiya yo’qotishlari zaryadlarning maydon ta’siri ostidagi harakatiga bog’liq. SHu bilan birga, qo’zg’almas zaryadlar yo’qotishlarga olib kelmaydi. Zaryadlarning harakatini elektromagnit maydon ro’yobga chiqaradi, ya’ni magnit maydoni bu xarakatga ta’sir ko’rsatmaydi. Chunki, uning ta’sir etish kuchi

xarakatning tezligi vektori V ga perpendikulyar, yo’qotishlar quvvati esa skalyar ko’paytma xisoblanadi

 

 

Bu tenglikning to’g’riligi olingan miqdorning o’lchov birligi ([(Kl*V/m)*m/s]=[(A*s*V/m)*m/s]=A*V=Vt) bilan xam tasdiqlanadi.  Hajmning har bir nuqtasidagi energiya balansini ko’rib chiqish uchun ham yo’qotishlar quvvatining hajmiy zichligi va chetki kuchlar tushunchalari kiritiladi

 

(6.5) formulada yo’qotishlarning hajmiy zichligini xosil qilinadi

 

 

Bu erda r*V elektr tokining zichligi vektorini ifodalaydi. SHuning uchun yo’qotishlar quyidagi miqdor bilan ta’riflanadi

 

 

         (6.6) tenglamani quyidagi ko’rinishga xam keltirish mumkin

 

 

(6.7) tenglama Joul-Lents qonunining diferentsial shakli xisoblanadi.

(6.6) skalyar ko’paytma musbat hamda manfiy miqdor bo’lishi mumkinligi sababli, R_y>0 holati maydon energiyasining zaryadlar harakatini hosil qilishiga sarflanishini ifodalaydi. J va E qarama-qarshi yo’nalgan bo’lsa, EMM chetki manba’lardan energiya oladi. SHuning uchun

 

 

Unda (6.4) ifodadan integral shakldagi EMM energiyasining saqlanish qonuni xosil qilish mumkin

 

               (6.9)

 

Hajmning kamaytirilishi, ya’ni fazodagi nuqtachalik kichik o’lchamga o’tkazilishi yo’li bilan  qonunning  differentsial shaklini xosil qilinadi

                       (6.10)

Bunda ED=, NV= ko’paytmalari ochib berilgan va Ostragradskiy – Gauss teoremasi qo’llanilgan.

=

Poyting teoremasi shuni isbotlaydiki, hajmda to’plangan EMM quvvati foydali ish bajarish uchun sarflangan xamda tashqaridan oqim ko’rinishida olingan chetki  manbalar quvvatlarning algebraik yig’indisiga teng. Quvvat balansi tenglamasi EMM nazariyasida  katta ahamiyatga ega. Xususan, bu tenglama elektrodinamik masalalar javoblarining to’g’riligini tekshiruvchi  universal apparat hisoblanadi. (6.9) va (6.10) tenglamalari vektorlarining oniy qiymatlari uchun yozilgan. SHuning uchun xam ular har qanday o’zgaruvchi maydon uchun o’rinli. Garmonik maydonlar uchun esa ular ancha soddaroq ko’rinishga ega.

 

6.4. Elektromagnit maydonning kompleks vektorlari uchun Poynting teoremasi

 

Garmonik jarayonlarning fizik mohiyati davr davomidagi o’rtacha energetik xarakteristikalarni aniqlash imkonini beradi. O’zgaruvi tok zanjirida  tenglik qo’llanilgani kabi, EMM nazariyasida kompleks yo’qotishlar va nurlanish quvvatlari tushunchalari kiritiladi. SHu bilan birga, shuni ham nazarda tutish kerakki, quvvatning xarakteri fazalar yig’indisiga emas, balki tebranishlar fazasining o’lchov birligiga bog’liq. Skalyar ko’paytmadagi ikkinchi ko’paytma kompleks xolda bog’langan miqdor sifatida olinadi

 

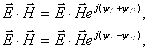
SHuning uchun, EMM elektr va magnit energiyalarining o’rtacha zichligi mos ravishda quyidagilarga teng

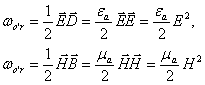
Yo’qotishlar quvvatining o’rtacha xajmiiy zichligi esa

 

 

CHetki kuchlar quvvatining o’rtacha zichligi

 

Bunda  — chetki kuchlar quvvatining kopleks hajmiy zichligi.

Kompleks Poynting vektori quyidagi ko’rinishdagi ko’paytma sifatida aniqlanadi

 

Kompleks vektor oqimi aktiv va mavxum qismlarni o’z ichiga oladi.

Energiya oqimi zichligining bir davrdagi o’rtacha qiymati kompleks vektorning moddiy qismiga teng, ya’ni

CHeklangan S yuzali fazoning hajmidan chiquvchi nurlanish quvvvati quyidagi integral ko’rinishida aniqlanadi

 

EMM nazariyasi bo’yicha o’quv qo’llanmalarida, (6.11) ifodadagi E va N lar ostida vektorlarning amplituda qiymatlari fahmlanadi. U holda (6.12) tenglama quyidagi ko’rinishda yoziladi

 

 

Shunday qilib garmonik (monoxromatik) maydon uchun energiya balansi tenglamasi (5.9) ning moddiy qismi quyidagi ko’rinishga ega bo’ladi

 

(6.10) tenglamasi esa

 (6.15) tenglamasi (6.10) ga parametrlarning kompleks qiymatlarini qo’yish yo’li kompleks tenglamaning moddiy qismi uchun yozilgan

Energiya balansi tenglamasi quvvatning mavxum qismi uchun  ayrim hollarda (6.15) tenglamasiga o’xshab yoziladi.

 

7. ELEKTROMAGNIT TO’LQINLARNING NURLANISHI

 

7.1. Elementar elektr tebratgich

 

Elementar elektr tebratgich deb – butun uzunligi bo’ylab doimiy amplituda va fazaga ega bo’lgan va o’lchamlari ishchi to’lqin uzunligidan ancha kichik  bo’lgan sim  bo’lagiga aytiladi.

Bu tebratgich, nurlatuvchi tizimlarni taxlil qilishda katta qulayliklar yaratadigan ideallashtirilgan tizim hisoblanadi. Ideallashtirilgan deyilishiga sabab esa, butun uzunligi bo’yicha o’zgarmas to’lqin amplitudasi va fazasiga ega bo’lgan tebratgichni yaratish mumkin bo’lmaganligidir.

Elementar elektr tebratgichni o’rganish, antennaning to’lqin nurlatish jarayonini tushunish uchun judda xam muxim. Tok oqayotgan har qanday o’tkazgichni elementar elektr tebratgichlardan tashkil topgan nurlantiruvchi tizim deb xisoblash mumkin. Bunda, toklar orqali xosil qilinadigan maydoni aniqlashda superpozitsiya usullaridan foydalanish, ya’ni antennani elementar tebratgichlarning yig’indisi sifatida ko’rib chiqish mumkin.

 

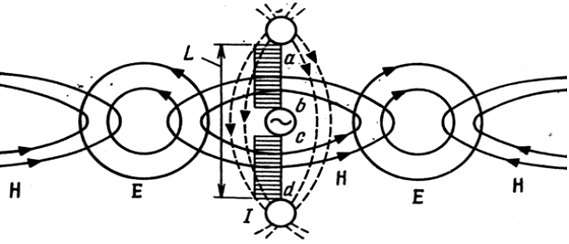
7.1-rasm. Gerts dipoli yordamida elektromagnit to’lqinlarning xosil qilinishi

 

 parametrlari bilan tavsiflanuvchi, cheksiz bir jinsli izotrop o’tkazmas muxitda joylashgan elementar elektr tebratgichning maydonini taxlil qilamiz. Tebratgichdagi tokni ma’lum qonun bo’yicha o’zgaruvchi chetki tok deb xisoblaymiz.  Tebratgichlar tomonidan xosil qilinuvchi maydon kompleks amplitudalar usuli bilan ko’rib chiqilayotgani sababli  I_chet tokining o’rniga kompleks kattalik kirgizamiz.

SHunday qilib, masalan berilgan tok taqsimlanish maydonini topishga aylanadi. Birinchi vektor potentsiali  ni topamiz. Buning uchun sferik koordinatalar tizimi (r, φ, θ) dan foydalanamiz. Uning qutb o’qi     (o x z) tebratgichning o’qi bilan mos keladi, koordinatalar boshi esa uning markazida turadi.

                                    (7.1)

bunda        

 vektori   vektori potentsiali bilan   nisbati bilan bog’langan.

 vektorini  formulasi orqali topish mumkin, ammo magnit maydon kuchlanganligini topib  vektorini Maksvellning birinchi tenglamasidan topish osonroq

.                                              (7.2)

 

7.2. Elementar elektr tebratgich maydoni tuzilishining taxlili

 

Tebratgichning EMM tuzilishini taxlil qilishda uning atrofidagi fazo 3 zonaga bo’linadi

1)         uzoq yoki to’lqinli zona (kr»1);

2)         yaqin zona (kr«1);

3)         oraliq zona (kr ≈ 1).

7.2-rasm. Elementar tebratgichning maydon tashkil etuvchilarini aniqlash

 

Uzoq zona ko’rsatib o’tilganidek 2πr » λ sharti bilan xarakterlanadi. Formulalarni solishtirishdan  ifodalarida k=2π/λ va  ekanligini hisobga olgan xolda quyidagiga ega bo’lamiz

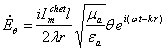                                 (7.3)

 

                                (7.4)

SHunday qilib, uzoq  zonada elektr maydon kuchlanganligi faqat  tashkil etuvchisiga, magnit maydon kuchlanganligi esa  tashkil etuvchisiga va  va  vektorlari bir xil fazaga ega. Maydon vektorlari fazasi vibratorning markazidan ular xisoblanadigan nuqtagacha bo’lgan r masofa bilan aniqlanadi. Teng fazalar yuzalari markazi koordinatalar boshida joylashgan kontsentrik sferalarni xosil qiladi. Teng fazalar yuzalaridan hohlagan bittasini tanlab olamiz va vaqt o’tishi bilan unga nima bo’lishini kuzatib turamiz. Maydon fazasi r₀ koordinatali nuqtada t₀  vaqt laxzasida  ga teng. t₁=t₀+ laxzada huddi o’sha r₀  nuqtada u φ₀ dan o’zgacha bo’ladi. r₁=r₀+ koordinatali nuqtada t₁ laxzada faza uchun matematik ifodani yozib, shu ifodani φ₀  ga qayta tenglashtirib   ga ega bo’lamiz. SHunga muvofiq,  da teng fazalar yuzasi  oraliqqa siljiydi, t₁ laxzada  esa r+ radiusga ega sferani ifodalaydi. Teng fazalar yuzasining siljish tezligi

.                       (7.5)

Shunday qilib, elementar elektr tebratgich uzoq zonada sferasimon to’lqin tarqatuvchi xisoblanadi. To’lqinning xarakatlanish tezligi shu muxitdagi yorug’lik tezligiga teng. Maydon tashkil etuvchilarining  nisbatlari doimiy kattalikka teng

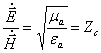.                                          (7.6)

Bu nisbat qarshilik o’lchamligiga ega va muhitning to’lqinli qarshiligi deb ataladi. Vakuum holatida muhitning to’lqinli qarshiligi  Om ga teng.

Yaqin zona. Yaqin zonada 2πr « λ. Ammo tebratgich maydoni uchun xisob formulalari r » l taxmindan kelib chiqqan xolda yozilgan. SHuning uchun xam yaqin zona l « r « λ / 2 π tengsizliklar bilan harakterlanadi.

YAqin zona uchun maydon quyidagi tashkil etuvchilarga ega

                          (7.7)

                                      (7.8)

                                            (7.9)

 vektorining oniy qiymatlariga o’tib, quyidagilarga ega bo’lamiz

                           (7.10)

YAqin zonadagi tebratgichning elektr maydoni taxliliga o’tamiz. Tebratgichdagi tokning o’zgarishi uning oxirlaridagi zaryadlar kattaliklarining o’zgarishiga olib keladi. YAqin zonada tebratgich maydoni quyidagi tashkil etuvchilar orqaligina aniqlanadi

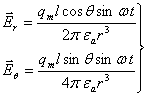                                  (7.11)

YAqin zonadagi tashkil etuvchilarni taxlilidan kelib chiqqan xolda shuni aytishm mumkinki, bu erda maydon ko’proq reaktiv xarakterga ega, ya’ni, tebratgichga bog’liq bo’lgan, nurlanmaydigan energiya katta qiymatga erishadi.

Oraliq zona yaqin zonadan uzoq zonaga o’tish zonasi hisoblanadi. SHunga muvofiq, oraliq zonada to’lqin tarqalishini taxlil qilishda, yuqoridagi tashkil etuvchilarning xar birini xisobga olishimiz lozim. Bu xolatda nurlanish maydoni va reaktiv (tebratgichda qolib ketadigan) maydon  bir xil tartibga (darajaga) ega bo’ladi.

Xar bir nurlantiruvchi tizim elektromagnit maydon energiyasini biron bir yo’nalishda jamlash xususiyatiga ega. Elementar elektr tebratgich xam o’zi nurlatayotgan maydonni ma’lum qonuniyat asosida biron yo’nalishda nurlatadi. Bu xususiyat nurlatgichning yo’nalganlik tavsifi orqali ifodalanadi. Yo’nalganlik tavsifi deb  vektori kompleks amplitudalarining θ va φ burchak koordinatalariga bog’liqligiga aytiladi. Yo’nalganlik tavsifining grafik ko’rinishigi ifodasi yo’nalganlik diagrammasi deb ataladi. Elementar elektr tebratgichgichning yo’nalganlik tavsifi quyidagicha aniqlanadi

 

                                     (7.12)

 

Turli tizimlarning yo’nalganlik tavsiflarini va diagrammalarini yagona masshtabda tasvirlash va ularni solishtirish uchun qiymatlarni me’yorlashtirish amalga oshiriladi. Bunday me’yorlashtirish quyidagi ifoda yordamida amalga oshiriladi

                                          (7.13)

Garmonik tebranishning amplitudasi faqat musbat qiymatlarga ega. SHuning uchun (7.13) formulada  ning modul qiymati ishlatilgan. Yo’nalganlik tavsifi qutbli yoki to’g’ri burchakli koordinatalar tizimida tasvirlanadi. Me’yorlangan qiymatli yo’nalganlik diagrammasining tasviri quyidagi ko’rinishga ega.

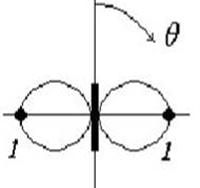
7.3-rasm. Elementar elektr tebratgichning qutbiy koordinatalar tizimida tasvirlangan E-tekislikdagi yo’nalganlik diagrammasi

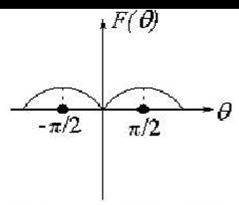
7.4-rasm. Elementar elektr tebratgichning to’g’riburchakli koordinatalar tizimida tasvirlangan E-tekislikdagi yo’nalganlik diagrammasi

 

(7.13) formuladan ko’rinib turibdiki, azimutal amplituda φ burchakka bog’liq emas, ya’ni nurlatgich  φ burchak oralig’ida bir xil nurlatadi (7.5-rasm).

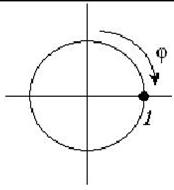
7.5-rasm. Elementar elektr tebratgichning qutbiy koordinatalar tizimida tasvirlangan H- tekislikdagi yo’nalganlik diagrammasi

 

7.6-rasm. Elementar elektr tebratgichning to’g’riburchakli koordinatalar tizimida tasvirlangan H-tekislikdagi yo’nalganlik diagrammasi

 

Garmonik toklarning nurlatish quvvati quyidagi formula orqali aniqlanadi

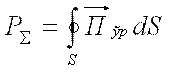                                         (7.14)

 

Shunday qilib, antenna, sirtida quvvat oqimi zichligining taqsimlangan o’rtacha qiymatiga ega bo’lgan sfera bilan o’ralgan. U xolda quvvat, (3.6) formula o’zgartirilgandan so’ng quyidagicha ifodalanadi

                              (7.15)

 

Demak, nurlatish quvvati nurlatgichning uzunligi va to’lqin uzunligi orasidagi munosabatga bog’liq. Joul-Lents qonuniga asosan, elektr sxemasida sarflanayotgan quvvatni quyidagicha xam ifodalash mumkin

,                               (7.16)

bu erda

.                             (7.17)

R_Σ Om birligida o’lchanadigan kattalik bo’lib, tebratgichning nurlanish qarshiligi deb ataladi. Erkin fazoda uni xisoblash ifodasi quyidagicha

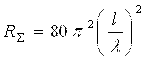                                     (7.18)

Nurlatish quvvati va nurlatish qarshiligi ifodalarini taxlil qilib, shuni anglash mumkinki, elementar elektr nurlatgichning nurlatish quvvatini oshirish uchun qo’shimcha energiya sarflash o’rniga uning nurlatish qarshilishigini oshirishning o’zi kifoya bo’ladi. Bu tebratgich modeli ideallashtirilgan bo’lganligi sababli xam, unda tebratgich uzunligi l ning to’lqin uzunligi λ ga nisbati oshirilganda xam faza va amplitudaning bir xilda qolishi ta’minlanadi. Ammo, real sharoitda, buni amalga oshirish mumkin emas. Shuning uchun xam, antennalarning o’lchamlari to’lqin uzunligiga uzviy bog’liq.

8. YASSI ELEKTROMAGNIT TO’LQINLAR

 

8.1. Yassi elektromagnit to’lqin parametrlari

 

Amaliyotda, elektromagnit maydonlarni xisoblash talab etilganda, biron bir matematik modeldan foydalanish katta axamiyatga ega. CHunki, aynan shu model yordamida elektromagnit to’lqinlarning real sharoitda tarqalishini ifodalab berish mumkin. Ana shulardan biri yassi elektromagnit to’lqin modeli bo’lib, uning yordamida ko’pgina to’lqinli jarayonlarni xisoblash mumkin. Keling, avval yassi elektromagnit to’lqin xaqida biroz tushunchaga ega bo’laylik. Bunda, avvalambor, to’lqin fronti yoki to’lqinli yuza tushunchasini bilib olish lozim. To’lqin fronti deb shunday sirtga aytiladiki, bunda, uning xar bir nuqtasida maydon kuchlanganligi vektorlarining fazalari bir xil qiymatga ega bo’ladi. Maydonni xosil qilayotgan nurlantiruvchining shakliga ko’ra, to’lqin fronti tsilindrsimon, sferasimon yoki boshqa shaklga ega bo’lishi mumkin.  SHuni xam ta’kidlash lozimki, ixtiyoriy nurlantiruvchi tizim tomonidan xosil qilingan to’lqin fronti, undan juda xam katta masofada sverasimon shaklga ega bo’ladi. Ana shu xolatga chuqurroq nazar tashlaydigan bo’lsak, quyidagini anglashimiz mumkin. Radioaloqa liniyalarida, deyarli barcha xollarda, qabul qiluvchi antenna katta masofada joylashgan bo’ladi. Bunda, maydonning to’lqin uzunligi ana shu masofadan o’n marta kichik bo’lsa, bu xolatni uzoqqa tarqalish deb xisoblash mumkin. Amalda esa bu shart deyarli xar doim bajariladi. Agar to’lqin frontining sferik tarqalishini xisobga oladigan bo’lsak, qabul qiluvchi antenna bu frontning o’zining o’lchamiga teng bo’lgan juda xam kichik bo’lagini qabul qiladi. Sferaning juda kichik bo’lagini esa, biz doimo yassi deb qabul qilishimiz mumkin. SHu sababdan xam, yassi elektromagnit to’lqin modelining o’rni axamiyatli. Vektorlar xosil qiladigan monoxromatik maydonning to’lqinli yuzasi o’zaro parallel joylashgan, yoki ular bir tekislikda yotuvchi to’lqinni yassi to’lqin deb ataydilar. To’lqin frontining barcha nuqtalarida maydon vektorlarining qiymatlari bir xil bo’lgan yassi to’lqinni birjinsli yassi to’lqin deb ataydilar.

CHeksiz birjinsli muxitda tarqalayotgan yassi garmonik elektromagnit to’lqin quyidagi tenglama yordamida ifodalanishi mumkin

           (8.1)

Maydon vektorining oniy qiymatlari uchun ifodasi quyidagi ko’rinishga ega

     (8.2)

YAssi elektromagnit to’lqinning erkin fazoda tarqalish xolatida ettita parametrlari bilan tavsiflanadi. Bu parametrlar to’lqinning o’tkazgich, yarimo’tkazgich va dielektrik xossasiga ega bo’lgan muxitlarda tarqalish xolatlari uchun aloxida yoziladi. Avvalgi paragraflarda  aytib o’tilganidek, muxitning o’tkazuvchanlik xossalari bo’yicha sinflanishi tg  parametri orqali amalga oshiriladi

.

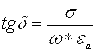Quyida keltirilgan formulalar yassi elektromagnit to’lqin parametrlarining ifodalaridir.

1.        γ – to’lqin tarqalishining kompleks qoeffitsienti. Bu matematik parametr ifodalarni soddalashtirish va o’zgartirish uchun qo’llaniladi

                                       (8.3)

2.        α – susayish koeffitsiyenti. Bu parametr to’lqinning 1 m masofa bosib o’tganda yuzaga keladigan energiyaning so’nishini ko’rsatadi.

 

                            (8.4)

3.        β – faza koeffitsiyenti. Bu kattalik to’lqinning 1 m masofa bosib o’tganida o’z fazasini qancha burchakka o’zgartirishini ifodalaydi.

 

             (8.5)

4.        v_f – faza tezligi. Bu parametr to’lqli yuzaning xarakatlanish tezligini ifodalaydi, boshqacha qilib aytganda, maydon vektorining tebranish tezligini ko’rsatadi.

                                             (8.6)

5.        v_g – guruxiy tezlik. Bu parametr energiyaning tarqalish tezligini ko’rsatadi

                                   (8.7)

6.        λ – to’lqin uzunligi. Bu parametr bir to’liq davr mobaynida to’lqin tomonidan bosib o’tilgan masofani ko’rsatadi

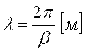                                        (8.8)

7.        Z_c – muxitning tavsifiy qarshiligi. Bu parametr maydon vektorlarining kompleks amplitudalari nisbati orqali aniqlanadi

                                 (8.9)

Vakuum xolatida muxitning tavsifiy qarshiligi 120π Omga teng bo’ladi. Real muxitlar uchun esa u kompleks xarakterga ega bo’lib, quyidagicha aniqlanishi mumkin

                                 (8.10)

 

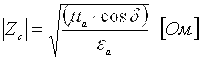                       (8.11)

Yuqorida keltirilganlardan shuni anglash mumkinki, yassi elektromagnit to’lqinni faqatgina fazoning cheklangan qismidagina xosil qilish mumkin. Biroq, ko’pgina amaliy masalalarni echishda, tashqi maydonni fazoning barcha nuqtalarida xam to’laligicha yassi deb qabul qilinadi. Bu esa elektrodinamik masalalarning echimini osonlashtiradi.

 

8.2. Elektromagnit to’lqinning qutblanishi

 

Tarqalish muhiti parametri  tg δ   dielektrik yo’qotishlarning tangens burchagi deb ataladi

.

 

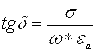Bu burchak qiymati berilgan materialdagi erkin zaryadlarning harakati va moddaning qutblanishi oqibatida elektromagnit maydon energiyasining yo’qotishlar darajasini hisoblash uchun ishlatiladi. σ  qancha katta bo’lsa,  tg δ  ham shuncha katta bo’ladi, yo’qotishlar ham katta bo’ladi. Agar maydon chastotasi ω ortsa,  tg δ  kamayadi, yo’qotishlar ham kamayadi, muhit dielektrikka yaqinroqdir. Agar chastota kamaysa,  tg δ  ortadi, yo’qotishlar ham ortadi, muhit o’tkazgichga yaqinroqdir. Yo’qotishlarning qiymati maydonning tebranish chastotasiga bog’liq, bir muhit turli chastotalarda dielektrik yoki o’tkazgich bo’lishi mumkin.

To’lqin yoki to’lqin tarqalish jarayoni elektromagnit to’lqinning tarqalishi natijasida fazoda energiya uzatilishining hosil bo’lishidan iboratdir. Agar  E  va  H  vektorlarning amplitudasi ko’ndalang koordinataga bog’liq bo’lmasa, to’lqin bir jinsli deb ataladi.

Fazoda  c (s – yorug’lik tezligi, 3*10⁸ m/s ga teng) tezlik bilan harakatlanuvchi garmonik maydon yugurma to’lqin deb ataladi. Tarqalish o’qi bo’ylab fazaning

y = wt - kz                                                             (8.12)

 

ko’rinishdagi chiziqli o’zgarishi yugurma to’lqinga xosdir,

bunda  - to’lqin soni yoki cheksiz muhitda to’lqin tarqalish doimiysi;  – tsiklik chastota.

To’lqin tarqalishining yana bir turi turg’un to’lqin hisoblanadi, u qarama–qarshi tarqalayotgan ikki to’lqinning ustma-ust,

ya’ni    y₁ = wt - kz    va    y₂ = wt + kz    fazalar farqi bilan tushishidan hosil bo’ladi.

Bu to’lqinlarning maydonlari yig’indisi

 

E = E₁ + E₂ = E₀₁ cos (wt – kz -j₁) + E₀₂ cos (wt + kz - j₂)            (8.13)

 

Agar  E₀₁ = E₀₂ = E₀  va  j₁ = j₂= j   bo’lsa,  u xolda

E = E₀ cos kz  cos (wt + j).                                (8.14)

 

(8.4) formula orqali ifodalangan maydon vaqtning har onida va fazoning istalgan nuqtasida garmonik taqsimotning o’zgarmas qolishi bilan tavsiflanadi va bu jarayon turg’un to’lqin deb ataladi.

Qutblanish deganda fazoning berilgan nuqtasida  E  yoki  H  vektorning uzunligi va yo’nalishi o’zgarishi tushuniladi. Qutblanish jarayoni qutblanish tekisligi tushunchasi bilan bog’liqdir. E vektorining tarыalish yo’nalishi bo’ylab xosil qiladigan tekisligi qutblanish tekisligi deb ataladi.

 

 

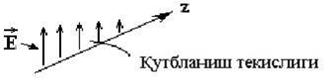
8.1-rasm. Qutblanish tekisligining shakllanishi

 

Qutblanish - elektromagnit to’lqinni tavsiflovchi juda xam muxim kattalik xisoblanadi. Elektromagnit to’lqinning erkin fazoda tarqalish vaqtida uch turdagi qutblanish turlari e’tirof etiladi. Qutblanish turlarini (2.3) va (2.4) formulalar orqali ifodalangan maydonlar misolida ko’rib chiqish qulaydir.

 

1.     Chiziqli qutblangan to’lqin deb fazoning istalgan nuqtasida vaqt o’tishi bilan E yoki H vektorlarining tebranishlar yo’nalishi o’zgarmas bo’lib qolishiga aytiladi.

 

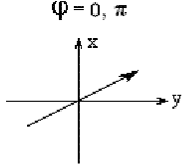
8.2-rasm. Chiziqli qutblanishning grafik tasviri

 

2.     Aylana bo’yicha qutblangan to’lqin deb fazoning istalgan nuqtasida E yoki H  vektorining bir tekis aylanishiga aytiladi, ya’ni vektor bir T davr vaqt mobaynida o’z uchi bilan aylana hosil qiladi.

 

 

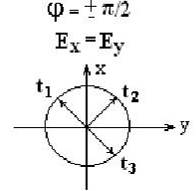
8.3-rasm. Aylanali qutblanishning grafik tasviri

 

3.     Ellipssimon qutblangan to’lqin deb fazoning istalgan nuqtasida E yoki H  vektorining aylanishiga aytiladi, ya’ni vektor bir T davr vaqt mobaynida o’z uchi bilan ellips hosil qiladi. Ellipssimon qutblanishda ortogonal tashkil etuvchi vektorlarning fazalar farqi j   0, p, p/2, -p/2  qiymatlardan tashqari istalgan qiymatni olishi mumkin. Ellipsning o’lchamlari va o’qlari yo’nalishlari j  kattalikka bog’liqdir.

 

8.4-rasm. Ellipssimon qutblanish turining grafik tasviri

 

Bundan tashqari, vektorning aylanish yo’nalishi qutblanishning turini aniqlaydi va chapga (LZ) aylanadigan yoki o’ngga (RZ) aylanadigan aylanali qutblanish turlari yuzaga keladi. Aylanish yo’nalishi uzatuvchi antennadan qabul qiluvchi antenna tomon yo’nalishida aniqlanadi. Bunda soat millari yo’nalishi bo’yicha xarakatlanuvchi vektor o’ng tomonli aylanali qutblanishni yuzaga keltiradi.

Ellipssimon qutblanish (EQ) atayin yuzaga keltirilmaydi, chunki EQ da signal qabul qilish quvvati aylanasimon qutblanishdagi (AQ) signal qabul qilish quvvatidan kamroq. SHuni esda tutish kerakki, AQ li antenna (nurlatgich) maydonning shu turli qutblanishini faqatgina nurlatgich o’qi yo’nalishida ishlab chiqaradi. Boshqa yo’nalishlarda bu maydon ellipssimon qutblanish sifatida qabul qilinadi. YAna shuni esda tutish kerakki, bir turdagi qutblanishga ega bo’lgan antenna ideal xolatda boshqa turdagi qutblanish signalini qabul qilmasligi lozim. Real sharoitda esa bu qutblanishlar susaygan xolda qabul qilinadi.

AQ li to’lqinlar radiotexnika va aloqada keng qo’llaniladi. AQ li to’lqinlarni vujudga keltirishda shuni nazarda tutish kerakki, bunday to’lqin E (H) vektorning fazoda ortogonal bo’lgan, bir xil amplitudali va tebranishnig faza siljishi 90⁰ ni tashkil qilgan ikki chiziqli qutblangan to’lqinlarning qo’shilishi natijasidir.

O’z navbatida, chiziqli qutblangan to’lqinni  harakatning qarama-qarshi yo’nalishiga va E (H) vektorning bir xil amplitudalariga ega bo’lgan, aylanasimon qutblanishli ikki to’lqinning superpozitsiyasi sifatida tasvirlashimiz mumkin.

SHaxar sharoitida tarqatiladigan elektromagnit to’lqinlar uchun joyning qurilishini xisobga olgan xolda qutblanish turi tanlanadi. Masalan, televizion signallarning shaxar sharoitida vertikal elektr ustunlari, ko’p qavatli binolarning armaturali karkaslari tomonidan qo’shimcha susayishlarini oldini olish maqsadida, gorizontal qutblanish turidan foydalaniladi. Buni antennani er sirtiga nisbatan gorizontal joylashtirish orvali xosil qilinadi. YUqorida aytib o’tilganidek, antennaning chiqishidagi qutblanish turi uning o’qi bo’ylabgina o’z xolatini saqlaydi. SHaxar sharoitida signallar ko’pgina to’siqlar va binolarning devorlaridan akslanishi xisobiga, qabul nuqtasiga ma’lum burchak ostida, dastlabki xolatidan og’gan xolda kelishi mumkin. Bunda signalni qabul qilishda uning energiyasi to’liq iste’mol qilina olmaydi. SHuning uchun xam antennaning er sirtiga nisbatan joylashuvini o’zgartirib, signal satxining maksimal qiymatiga ko’ra uni sozlash yaxshi natija beradi.

9. MUXITLAR CHEGARASIDAGI TO’LQINLI JARAYONLAR

 

9.1. Elektromagnit to’lqinning muxitlar chegarasidan o’tishi va akslanishi

 

Yassi elektromagnit to’lqin e_a1 va m_a1 parametrli muhitdan parametrlari e_a2 va m_a2 (bu erda e_a va m_a - muhitning absolyut dielektrik va magnit singdiruvchanliklari) bo’lgan yassi chegaraga tushganda qisman bu chegaradan qaytadi va qisman esa tarqalish yo’nalishini o’zgartirgan holda ikkinchi muhitga o’tadi. xou tekisligini ikkita muhit chegarasi deb qabul qilamiz.

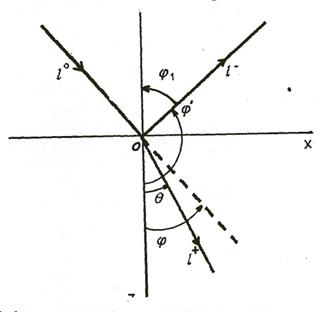
9.1-rasm. To’lqinning muhitlar chegarasidan qaytishi va o’tishining geometrik tasviri

 

Muhitlar chegarasiga normal o’q (Z o’qi) orqali o’tayotgan XOZ tekisligi hamda tushayotgan to’lqinining  tarqalish yo’nalishi tushish tekisligi deb ataladi.

Qaytgan va o’tgan (singan) to’lqinlar ham yassi bo’ladi, hamda ularning tarqalish yo’nalishlari  va  ham tushish tekisligida joylashadi.

Tushayotgan to’lqinning tarqalish yo’nalishi hamda muhitlar chegarasi normali o’rtasidagi φ burchagi (burchak Z o’qining musbat yo’nalishidan boshlab hisoblanadi) tushish burchagi deb ataladi.

Qaytuvchi (akslangan) to’lqinning tarqalish yo’nalishi va normal o’rtasidagi bo’linish chegarasi tomon yo’nalgan j' burchagi qaytish burchagi deyiladi. Ammo, geometrik optikada qaytish burchagi j₁ deb, j' burchakni 180⁰ gacha to’ldiradigan burchakka aytiladi.

  O’tuvchi (sinuvchi) to’lqinning tarqalish yo’nalishi bilan normal o’rtasidagi bo’linish chegarasi tomon yo’nalgan q burchagi sinish burchagi deyiladi.

j, j' va  q burchaklarning qiymatlari o’rtasidagi bog’liqlik Snellius qonunlari orqali ifodalanadi:

j¢ = p - j ,                                                      (9.1)

 

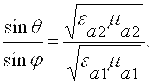                                        (9.2)

 

Tushuvchi to’lqinning elektr maydoni kuchlanganligi vektori  tarqalish yo’nalishiga perpendikulyar bo’ladi, va umumiy holda tushish tekisligiga nisbatan turlicha joylashishi mumkin. Biroq u doimo ikkita o’zaro perpendikulyar vektorlar yig’indisi ko’rinishida tasvirlanishi mumkinligi sababli, ikkita holatni, ya’ni  vektori tushish tekisligida joylashgan va tushish tekisligiga perpendikulyar joylashgan holatlarni ko’rib chiqish kifoya.

Birinchi holda to’lqinning qutblanishi paralel deb ataladi. Bunda  vektori koordinatalar o’qida ikkita proektsiyaga ( va ),  esa faqat  proektsiyaga ega bo’ladi (9.2.b-rasm).

Qaytgan va singan i  to’lqinlar ham tushish tekisligida joylashadi. Ikkinchi holda, to’lqinning qutblanishi normal qutblanish deb ataladi. Bunda  vektori bitta  proektsiyaga,  esa ikkita  va  proektsiyalarga ega bo’ladi. Qaytgan  va singan  to’lqinlar ham tushish tekisligiga perpendikulyar holda joylashgan bo’ladi.

Qaytgan  va tushuvchi  to’lqinlar kompleks amplitudalarining nisbati qaytish koeffitsiyenti R deb ataladi, ya’ni

.                                                  (9.3)

 

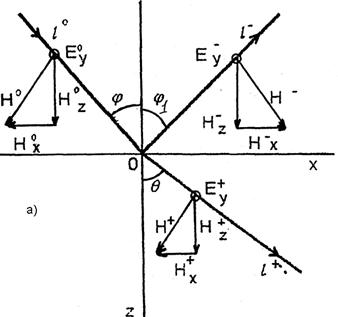
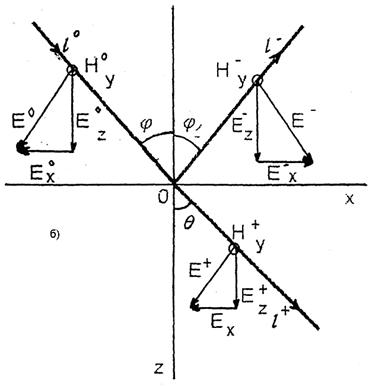
9.2-rasm. Normal va parallel qutblanishda

vektorlarning proektsiyalari

 

Singan  va tushuvchi  to’lqinlar kompleks amplitudalarining nisbatlari o’tish koeffitsiyenti χ deb ataladi, ya’ni

.                                        (9.4)

Bu o’rinda R va c umumiy holatda kompleks qiymatlar ekanini ta’kidlab o’tishimiz lozim. Ularning modullari tegishli to’lqinlar amplitudalarining munosabatlarini tavsiflaydi, argumentlari esa muhitlar chegarasida ushbu maydonlar o’rtasidagi fazalar siljishini bildiradi.

Parallel qutblanish holatida

,                    (9.5)

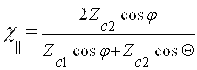,                     (9.6)

 

Normal qutblanish holatida esa

 

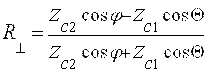,                  (9.7)

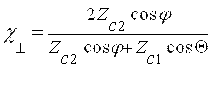,                           (9.8)

Bu erda Z_c1=, Z_c2= - birinchi va ikkinchi muhitlarning to’lqin qarshiliklaridir. (9.5)…(9.8) ifodalarni ko’pincha Frenel formulalari deb ataydilar.

YAssi elektromagnit to’lqin yassi o’tkazgich yuzasiga tushganda undan qaytadi. Bu xolatda esa, o’tkazgichlardagi to’lqin qarshiligini quyidagicha aniqlanadi

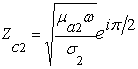
bu erda w = 2p f -tsiklik chastota, s -muhitning o’tkazuvchanligi.

Ideal o’tkazgich uchun (s=¥) to’lqin qarshiligi nolga teng. SHuning uchun yassi to’lqin dielektrikdan ideal o’tkazgich yuziga tushganda, tushish burchagidan qat’iy nazar, (9.5)....(9.8) formulalaridan quyidagi tenglik kelib chiqadi

 

R_|| = 1,   R_^ = -1,                c_|| = c_^ = 0                              (9.9)

 

Demak, to’lqin to’liq qaytadi va ideal o’tkazgich ichida maydon bo’lmaydi.

Real metallar chekli o’tkazuvchanlikka ega. Biroq metallarning o’tkazuvchanligi katta (tahminan 10⁶–10⁷ Sm/m) bo’lgani sababli, metallarning to’lqin qarshiligi barcha radiodiapazonlarda nolga yaqin bo’ladi. Demak, har qanday tushish burchaklarida ham qaytish koeffitsentining moduli kichik tomonga 1 dan ko’p ham farq qilmaydi.

 

9.2. Yassi elektromagnit to’lqinning ikkinchi muxitga to’liq o’tishi. Bryuster burchagi

 

Yassi elektromagnit to’lqin havoda joylashgan d qalinlikli yassi dielektrik qatlamiga tushganda (9.3-rasm), tushgan to’lqin qisman qaytadi va qisman ikkinchi qatlamga o’tadi. Qatlamning pastki chegarasiga etgach, to’lqin yana qisman qaytadi, qisman esa qatlamdan chiqadi. Qatlamning pastki chegarasidan qaytgan to’lqin ustki chegaraga kelib tushadi, bu erda u yana qisman qaytadi,  qisman esa qatlamdan chiqadi va h.k. Shunday qilib, qatlamdan qaytgan to’lqin bir xil yo’nalishda (Z-o’qiga nisbatan j’ burchakda) tarqalayotgan hisobsiz to’lqinlarning ustma-ust taxlanishini bildiradi. Bu to’lqinlar qatlam ichidagi to’lqinning qaytish soniga bog’liq bo’lgan amplitudalari va fazalari bilan bir-biridan farq qiladi.

Qatlamdan o’tgan to’lqin haqida ham xuddi shunday xulosa chiqarish mumkin.

 

 

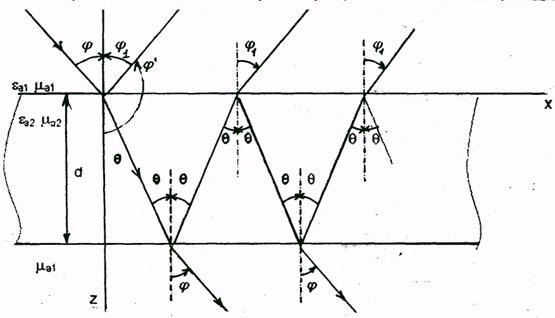
9.3-rasm. YAssi elektromagnit to’lqinning dielektrik

qatlamiga tushishi

 

Shuni ham ta’kidlashimiz kerakki, qatlamdan o’tgan to’lqinning tarqalish yo’nalishi tushayotgan to’lqin yo’nalishiga mos keladi. Qaytgan to’lqinni tashkil qiluvchi barcha to’lqinlarning kompleks amplitudalarini jamlasak, to’lqinning qatlamdan qaytish koeffitsiyenti R va o’tish koeffitsiyentlari c uchun quyidagi ifodalarga ega bo’lamiz

R = ,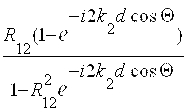

c = ,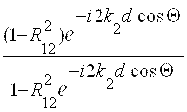

 

bu erda R₁₂ - to’lqinning havodan qatlam chegarasiga tushayotgandagi qaytish koeffitsiyenti bo’lib, u parallel qutblanishda (9.5) formula yordamida, normal qutblanishda esa (9.7) formula yordamida aniqlanadi.

k₂ = ,  burchak esa Snelliusning (9.2) da keltirilgan ikkinchi qonunidan aniqlanadi.

Qaytish va o’tish koeffitsiyentlarining modullari quyidagi ifodalar yordamida aniqlanadi

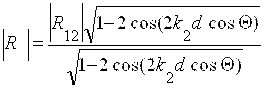,                 (9.10)

 

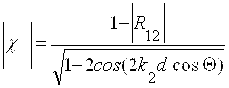.                        (9.11)

Agar ikkala muhit ham dielektrik bo’lib,  m_a1=m_a2=m₀ bo’lsa, unda normal qutblangan to’lqinning qaytish koeffitsiyenti, tushish burchagi j qanday bo’lishidan qat’iy nazar, nolga teng bo’lmaydi. Parallel qutblanishda esa Bryuster burchagi deb ataluvchi

                                   (9.12)

burchak mavjud bo’lib, bunda qaytish koeffitsiyenti nolga teng va to’lqin ikkinchi muhitga to’liq o’tadi.

Demak, parallel qutblangan yassi elektromagnit to’lqin dielektrik qatlamiga Bryuster burchagi ostida tushganda, uning qatlamdan to’liq o’tishi kuzatiladi. Buni (9.10), (9.11) ifodalardan ko’rishimiz mumkin. Bu sharoitlarda R₁₂ qaytish koeffitsiyenti nolga teng bo’lgani uchun, qatlamdan qaytish va o’tish koeffitsiyentlari mos holda 0 va 1 ga teng.

 

10. YUZA EFFEKTI

 

10.1. Yuza effekti xodisasi

 

Avvalgi bo’limlarda aytib o’tilganidek, o’zgaruvchan elektromagnit maydonning kuchlanganligi, demak, uning tok zichligi xam metall ichida eksponentsial qonun bo’yicha kamayib boradi. O’ta yuqori chastotalarda barcha tok, o’tkazgichning sirti yaqinida jamlanadi. Bu xodisani yuza effekti yoki skin effekt deb ataladi.

Yuza effekti natijasida o’tkazgichning ko’ndalang kesimi kamayadi, ya’ni, samarali foydalanilayotgan kesim geometrik kesimdan kam bo’lib qoladi. Bu esa o’tkazgichning aktiv qarshiligini oshishiga olib keladi. YUqori chastotalarda bu qarshilik simning doimiy tok xolatidagi qarshiligidan juda ko’p marta katta bo’lishi mumkin. Bundan tashqari, yuza effekti o’tkazgichning ichida jamlangan magnit energiyasini, va buning natijasi o’laroq, simning ichki induktivligini kamaytiradi. Bundan ko’rinadiki, agar simning diametri qanchalik katta bo’lsa, yuza effekti shunchalik kamroq namoyon bo’ladi. YUza effektining ta’siri ostida simning markaziy qismidan foydalanilmas ekan, buni o’tkazgichlarni tayyorlashda xisobga olish lozim. SHuning uchun xam, yuqori chastotalarda, metallni iqtisod qilish uchun to’la simlar ichi bo’sh (naysimon) simlar bilan almashtiriladi.

Yuza effekti xodisasi ko’pgina radiotexnik qurilmalar va elementlarni tashqi maydon ta’siridan muxofazalash imkonini beradi. Buning uchun metall ekranlardan foydalaniladi. Agar ximoyalovchi ekran qurilmani to’liq o’rab turgan bo’lsa va uning qalinligi etarlicha bo’lsa, tashqi maydonning ta’sirini deyarli yo’qotish mumkin. Agar ekran qurilmani to’la qoplamagan bo’lsa, yoki uning qalinligi etarlicha bo’lmasa, tashqi elektromagnit maydon difraktsiya xodisasi tufayli qobiqdan kirishi mumkin. SHuni xam ta’kidlash lozimki, doimiy va past chastotali maydon xollarida metall ekranlar qurilmani elektr maydonidan saqlashi mumkin. Biroq, agar ekran paramagnit yoki diamagnit materialdan tayyorlangan bo’lsa, u magnit maydoni uchun to’siq bo’la olmaydi.

Metalldan tayyorlanadigan ekran elektromagnit ta’sirlardan to’liq ximoyalashi uchun, ekran listining qalinligi ma’lum qiymatdan kichik bo’lmasligi kerak. Bunda, maydonning metallga singish chuqurligi parametridan foydalaniladi. Maydonning metallga singish chuqurligi deb shunday masofaga aytiladiki, bunda maydon kuchlanganligi e marta kamayadi. Singish chuqurligi maydonning susayish koeffitsiyentiga teskari kattalik xisoblanadi va uni quyidagicha xisoblash mumkin

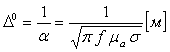                                (10.1)

Bu erda α – to’lqin amplitudasining 1 m masofa bosib o’tgandagi susayishi.

O’ta yuqori chastota diapazonida bu parametr juda xam kichik qiymatlarga erishadi.

 

10.2. O’tkazgichning yuza qarshiligi va undagi energiya yo’qotishlari

Yuza effektini ko’rib chiqish vaqtida, albatta, yuza qarshiligi parametrini xam xisobga olish zarur. Chunki, bu xodisa tufayli, samarali foydalanilayotgan yuza kamayadi va uning to’lqinga bo’lgan qarshiligi ortadi. O’tkazgich sirtida elektr maylonining urunma tashkil etuvchisi  va ekvivalent yuza toki zichliklari bir xil yo’nalgan. Demak, ular orasida quyidagi bog’liqlik mavjud

Proportsionallik koeffitsiyenti Z_s ni o’tkazgichning yuza qarshiligi deb ataydilar. Chegaraviy shartlarga ko’ra, Z_s uchun quyidagi ifodani yozish mumkin

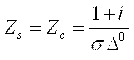                             (10.2)

Yuza qarshiligining aktiv tashkil etuvchisi esa

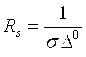                                       (10.3)

Bu ifodadan shuni anglash mumkinki, fazoni to’ldirib turuvchi o’tkazgichning yuza effekti ta’siri ostida erishgan qarshiligi yuza effekti mavjud bo’lmagan Δ⁰ qalinlikka ega bo’lgan metall bilan bir xil qiymatga ega bo’ladi.

Shuni xam ta’kidlash kerakki, elektromagnit to’lqinning metallda tarqalishi vaqtida yuzaga keladigan energiya yo’qotishlari kompleks quvvat orqali ifodalanadi. Kompleks yo’qotishlar quvvatini esa ekvivalent yuza toki va yuza qarshiligi yordamida ifodalash mumkin

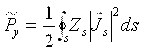.                                    (10.4)

Ideal o’tkazgich sirtidagi chegaraviy shartlardan kelib chiqqan xolda (), kompleks quvvatni xisoblash uchun magnit maydon vektorining urunma tashkil etuvchisi qiymatini bilishning o’zi kifoya. Avval aytilganidek, metallning sirtidagi maydon tuzilishi ideal o’tkazgich sirtidagi maydon tuzilishiga juda xam o’xshash. SHuning uchun, yo’qotishlar quvvatini xisoblanilayotganda shart bajariladi deb qabul qilinadi. Bu taxmin xisoblashlar xajmini kamaytirgani xolida, muxandislik amaliyoti uchun etarlicha aniqlikdagi natijalarni bera oladi.

11. YO’NALTIRUVCHI TIZIMLAR

 

11.1. Yo’naltiruvchi tizimlarning sinflanishi

 

Elektromagnit tebranishlarning tarqalish hududini chegaralovchi va oqimni berilgan yo’nalishga yo’naltiruvchi qurilma uzatish liniyasi deb ataladi. Bu liniyalar energiyani manbadan qabul qilgichga uzatish uchun qo’llaniladi, masalan uzatkichdan antennaga, antennadan qabul qilgich kirishiga va hokazo. Soddalashtirish uchun, yo’naltiruvchi tizim ideal o’tkazuvchi sirtga ega deb xisoblansa, shu sirt orqali to’lqinlarning yo’nalish jarayonini o’tkazgichdagi tok va zaryadlar orasidagi bog’liqlik orqali tushuntirsa bo’ladi.

  Uzatish liniyalarini ikki guruhga ajratish mumkin: ochiq uzatish liniyalari va yopiq uzatish liniyalari (to’lqino’tkazgichlar). To’lqino’tkazgich bir yoki bir necha tutashtirilgan o’tkazuvchi kontur ko’rinishidagi ko’ndalang kesimli o’tkazuvchi sirtlardan iborat uzatish liniyasidir. To’lqino’tkazgich maydoni tashqi qobiq bilan ekranlanadi.

Bo’sh to’lqino’tkazgichlardagi to’lqinlarni tadqiq qilish quyidagi shartlar bilan bajariladi:

1)    to’lqino’tkazgichning ichki yuzasi ideal o’tkazuvchi (σ = ∞);

2)    to’lqino’tkazgichning ichi vakuumdir.

Bu cheklovlar masalaning mohiyatini o’zgartirmagan xolda maydon taxlilini osonlashtiradi, chunki to’lqin o’tkazgichlar yuqori solishtirma elektr o’tkazuvchanlikka ega bo’lgan metalldan tayyorlanadi, to’lqin o’tkazgich havosi esa o’zining parametrlari bo’yicha vakuumga o’xshashdir.    

Detsimetrli va santimetrli diapazonlarda asosan yopiq turdagi uzatish tarmoqlari qo’llaniladi. Bu tarmoqlarda butun energiya tashqi muhitdan temir qobiq bilan ajratilgan maydonda jamlangan bo’ladi.

Koaksial to’lqin o’tkazgich, to’g’ri burchakli, aylanali va ellipssimon to’lqin o’tkazgichlar asosiy, keng qo’llaniladigan yopiq turdagi uzatish tarmoqlaridir.

Yo’naltiruvchi tizimlarda T turkumli to’lqinlar (ko’ndalang elektromagnit to’lqinlar), H turkumli to’lqinlar (ko’ndalang elektr yoki bo’ylama magnitli to’lqinlar), E turkumli to’lqinlar (ko’ndalang magnitli yoki bo’ylama elektr to’lqinlar) tarqatilishi mumkin. Shuni qayd etib o’tish kerakki, T turkumli to’lqinlar faqat bir-biridan ajratilgan (o’zgarmas tok energiyasini uzatsa bo’ladigan) ikkita va undan ko’p o’tkazgichga ega yo’naltiruvchi tizimlarda tarqatilishi mumkin.

Har qanday yo’naltiruvchi tizimolarda (E va H turkumlariga mansub) to’lqinlarning juda ko’p turlari mavjud bo’lishi mumkin. Ularning miqdori l_i to’lqining ishchi uzunligining tanlanishiga bog’liq bo’ladi. Ammo to’lqinlar uzunliklarining shunday bir sohasi mavjudki, unda, ya’ni l_i to’lqinining ishchi uzunligi asosiy turga mansub to’lqinining l_kr kritik uzunligidan katta yoki unga teng (l_i ³ l_kr) bo’lgan to’lqin o’tkazgichda elektromagnit to’lqinlarning tarqalishi mumkin emas (ajratilgan soha). Maksimal kritik uzunlikka ega bo’lgan to’lqin shu to’lqin o’tkazgichdagi asosiy to’lqin deb ataladi. To’lqino’tkazgichni to’ldiruvchi materialning nisbiy dielektrik singdiruvchanligidan kelib chiqib, to’lqinning ishchi uzunligi quyidagi shartdan keltirib chiqarilishi lozim

bu erda l - generator to’lqinining uzunligi (erkin fazodagi to’lqin uzunligi).

Havoda e = 1 va  l_i = l shart bajariladi.

11.1 va 11.2-rasmlarda to’g’ri burchakli va aylanali to’lqin o’tkazgichlarda N₁₀ va N₁₁ turiga mansub asosiy to’lqinlar uchun, 11.3-rasmda esa – koaksial to’lqin o’tkazgichda T turkumli to’lqinlar uchun elektr va magnit maydonlarining oniy tarqalish manzaralari keltirilgan. Bu rasmlarda «bizdan» ketgan kuchlanish chiziqlari krestchalar bilan, «bizga» qarab keluvchi chiziqlar esa – doirachalar bilan ko’rsatilgan.

 

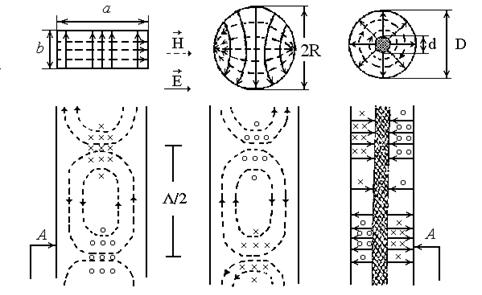
Bir to’lqinli rejimda to’lqin o’tkazgichdagi to’lqin qarshiligi Z_t, faza v_f va guruhiy v_gur tezliklar hamda yo’naltiruvchi tizimdagi to’lqin uzunligi L miqdorlarini quyidagi formulalar bo’yicha hisoblash mumkin.

To’g’ri burchali to’lqino’tkazgich uchun:

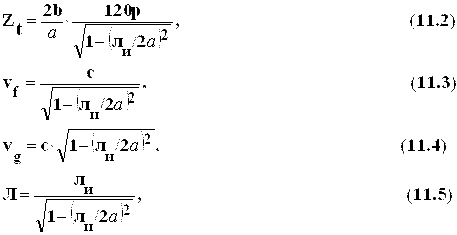
Koaksial to’lqino’tkazgich uchun:

 

bu erda       c – vakuumdagi yorug’lik tezligi;

         a ­– to’g’ri burchakli to’lqin o’tkazgich keng devorining ichki hajmi;

         b – to’g’ri burchakli to’lqin o’tkazgich tor devorining ichki hajmi;

         D – koaksial kabel to’qimasining (ekran qobig’ining) ichki diametri;

         d – koaksial kabel markaziy simining tashqi diametri.

 

To’g’ri burchakli to’lqin o’tkazgichdagi to’lqin uzunligi L erkin fazodagi to’lqin uzunligi l dan kattaligi quyidagi oddiy fizik holat bilan izohlanadi. Elektromagnit to’lqinlar to’lqin o’tkazgichda uning devorlariga urilib qaytishi natijasida tarqaladi (11.4-rasmga qarang). Bunda, to’lqin fronti to’lqinning tarqalish yo’nalishi bo’ylab l_i masofani bosib o’tib, ayni vaqtda to’lqin o’tkazgich bo’ylab L ga teng bo’lgan masofani bosib o’tadi.

 

11.2. Bir to’lqinli rejimni hosil qilish uchun to’lqinning ishchi uzunligini tanlash

 

 

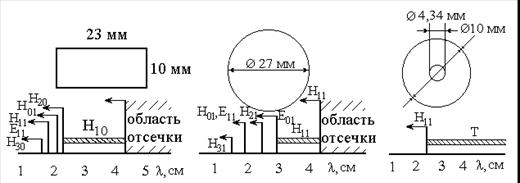
11.5…11.7-rasmlarda to’g’ri burchakli, aylanali va koaksial to’lqino’tkazgichlar uchun l_i shkalasi bo’yicha to’lqinlar kritik uzunliklarining taqsimlanishi keltirilgan. Birto’lqinli rejim holatida to’lqino’tkazgich bo’ylab asosiy to’lqin tarqaladi. 11.5-rasmdan ko’rinib turganidek, to’lqinining kritik uzunligi l_kr^N10=2a bo’lgan N₁₀ to’lqini to’g’ri burchakli to’lqino’tkazgich uchun asosiy to’lqin hisoblanadi. To’g’riburchakli to’lqino’tkazgichda oliy tartibdagi birinchi to’lqin – kritik uzunligi  l_kr^N20=­a bo’lgan N₂₀ to’lqinidir. Binobarin, birto’lqinli rejim quyidagi shart bajarilgan holda kuzatiladi

a < l < 2a.                                                        (11.10)

Aylanali to’lqino’tkazgich (11.6-rasm) uchun N₁₁ to’lqini asosiy to’lqin (l_kr^N11=3,41R), E₀₁ to’lqini esa – oliy tartibdagi birinchi to’lqin (l_kr^E01=2,62R) hisoblanadi. SHunday qilib, bir to’lqinli rejim quyidagi shart bajarilgan holda kuzatiladi

2,62R<l_r<3,41R.                                              (11.11)

Koaksial to’lqino’tkazgichda (11.7-rasm) T turkumiga mansub to’lqin asosiy to’lqin (l_kr^T=¥), kritik uzunligi l_kr^N11»p(D+d)/2 bo’lgan N₁₁ to’lqini esa – oliy tartibdagi birinchi to’lqin hisoblanadi, ya’ni bir to’lqinli rejim quyidagi shart bajarilgan holda kuzatiladi

p(D+d)/2< l_r < ¥.                                                (11.12)

Amalda, nisbatan uzun to’lqinlar, ya’ni asosiy turga mansub to’lqinning kritik uzunligiga yaqin sohada energiya susayishi ko’p bo’lganligi uchun, to’lqinning ishchi uzunligi miqdori to’lqinning kritik uzunligidan 20...30% kam olinadi.

 

11.3. To’lqino’tkazgichdagi amplitudaviy taqsimotning turlari

 

To’lqino’tkazgich bo’ylab amplitudaviy taqsimotga to’lqino’tkazgichning chiqishida o’rnatilgan yuklama xususiyatining ta’sirini ko’rib chiqamiz. To’lqino’tkazgich o’qi bo’ylab birto’lqinli rejim bilan birga maydonning taqsimlanishi shakllanadi. Bu taqsimot uzun chiziq (liniya) rejimida ishlaydigan odatdagi ikkisimli tarmoqda maydonning taqsimoti bilan bir xil bo’ladi.

Agar to’lqino’tkazgich uchiga qisqatutashuvchi yuklama o’rnatilgan bo’lsa, tushuvchi to’lqinga nisbatan faza bo’ylab 180° ga surilgan qaytgan (akslangan) to’lqin yuzaga keladi. Akslangan to’lqin amplitudasi tushuvchi to’lqin amplitudasiga tengdir. Bu ikki to’lqinning tutashishi natijasida turg’un to’lqin (turg’un to’lqin rejimi) yuzaga keladi. Turg’un to’lqin rejimidagi ampli­tudaviy taqsimot 11.8-rasmda uzluksiz chiziq bilan ko’rsatilgan. Maydon jadalligining ikki qo’shni minimumlari o’rtasidagi masofasi to’lqino’tkazgichdagi to’lqin uzunligining yarmiga teng. Qisqatutashuvchi yuklama qarshiligi to’lqino’tkazgichning tavsifiy  qarshiligiga teng bo’lgan moslashgan (muvofiqlashtirilgan) yuklamaga almashtirilganida, yuklamadan akslangan to’lqin bo’lmaydi va to’lqino’tkazgichda yuguruvchi to’lqin rejimi qaror topadi. Bunda amplitudaviy taqsimot maydonning to’lqino’tkazgich bo’ylab amplituda miqdorining o’zgarmasligi bilan tavsiflanadi (11.8-rasmdagi punktir chiziq).

 

Yuklamadan tushuvchi to’lqinning bir qismi akslangan hollarda to’lqin o’tkazgichda aralash rejim qaror topadi. Bu rejimning amplitudaviy taqsimoti 11.9-rasmda ko’rsatilgan. To’lqino’tkazgichdagi amplitudaviy taqsimotni yuguruvchi to’lqin koeffitsiyenti miqdori YUTK=E_min/E_max bilan tavsiflash qulaydir. Amalda qo’llaniladigan moslashtirilgan yuklamalarning YUTK si 0,65-0,85 oraliqlarda bo’ladi. Bunda, ko’rsatkichning 1 ga yaqinlashishiga intilinadi.

 

 

ADABIYOTLAR

 

1.     Volman V.I., Pimenov YU.V, Texnicheskaya elektrodinamika, - M: Radio i Svyaz, 2002 g.

2.     Vitevskiy V.I., Pavlovskaya E.A. Elektromagnitnыe volnы v texnike svyazi. - M.: Radio i svyaz, 1995.

3.     Nikolskiy V.V., Nikolskaya T.I. Elektrodinamika i rasprostranenie radiovoln. – M.: Nauka, 1989.

4.     Fedorov N.N. Osnovы elektrodinamiki. – M.: Vыsshaya shkola, 1980.

5.     Golshteyn L.D., Zernov N.V. Elektromagnitnыe polya i volnы. – M.: Sov. radio, 1971.

6.     Sbornik zadach po kursu "Elektrodinamika i rasprostranenie radiovoln" / Pod red. S.I. Baskakova. - M: Vыsshaya shkola, 1981.

 

 

«Elektromagnetizm» fanidan ma’ruza mashg’ulotlari bo’yicha o’quv qo’llanma TRET kafedrasi majlisida ko’rib chiqilgan va nashrga tavsiya etilgan («_3__»___05_ 2014 y dagi № _32___ - bayonnoma).

TATU IUK majlisining «____» ____ 2014 y. dagi №_____ - bayonnomasi asosida nashrga tavsiya etilgan.

 

Muallif:                   Shaxobiddinov A.SH.

 

Mas’ul muxarrir:     Aripova U.X.

 

Taxririy-musaxxixlik xay’ati:

Muharrir: Abduazizov A.A.

Musaxxix: Radjabova Z.