УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра «Сети и системы передачи данных»

ЦИФРОВАЯ СХЕМОТЕХНИКА

Методическое указание к лабораторным работам для студентов направления 5522000-«Радиотехника»

Ташкент 2008

Авторы: Д. Ю. Юнусов, Р. П. Абдурахманов, Х. Ю. Аббасханова,

А. К. Ядгаров

«ЦИФРОВАЯ СХЕМОТЕХНИКА»/ТУИТ. 103 стр. Ташкент, 2008.

Курс "Цифровая схемотехника" (ЦС) состоит в изучении принципов построения и применения цифровых устройств различной функциональной сложности – от цифровых логических элементов (ЛЭ) до микропроцессоров (МП).

В данном методическом пособии изучается построение различных цифровых устройств на основе логических элементов.

Рецензенты

Начальник отдела РРТ Уз АСИ

«Перспективы развития широкополосного доступа»,

к.т.н., доцент Ю.К. Камалов.

Зав. кафедрой «ТУТ»

ТУИТ к. т. н., доцент Р. И. Исаев

Корректор: Д. У. Доспанова

ВВЕДЕНИЕ

Цель курса "Цифровая схемотехника" (ЦС) состоит в изучении принципов построения и применения цифровых устройств различной функциональной сложности – от цифровых логических элементов (ЛЭ) до микропроцессоров (МП). Курс ЦС включает изучение теоретического материала (в согласованности с рабочей программой) и выполнение цикла лабораторно-практических работ.

Курс ЦС состоит из двух частей. В первой части основное внимание уделяется структурам и принципам построения цифровых устройств небольшой сложности. Для закрепления знаний по первой части курса студентам предлагается выполнить 6 лабораторных работ. Во второй части рассматриваются принципы организации цифровых устройств высокой сложности, в частности МП и МПС, а также некоторые вопросы их применения.

ЛАБОРАТОРН ЫЕ РАБОТЫ № 1, 2

СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ, ВЫХОДНЫЕ ПАРАМЕТРЫ ЦИФРОВЫХ ЭЛЕМЕНТОВ, МОДЕЛИ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

Цель работы: изучить методы синтеза комбинационных дискретных автоматов на интегральных элементах; получить навыки в сборке, наладке и экспериментальном исследовании синтезируемых схем.

Основные теоретические сведения

Поведение любого дискретного устройства определяется изменением во времени некоторых физических величин на его входах , выходах и внутри самого устройства . Для рассматриваемых в данном курсе устройств такими величинами являются потенциалы на входных и выходных полюсах, а также в некоторых внутренних точках устройств являются то, что во времени могут быть выделены интервалы, на которых все эти входные, исходные и внутренние величины (переменные)сохраняют свои постоянные значения. Указанные интервалы носят название тактов работы дискретных устройств. Значения переменных в интервалах определяют правила, по которым осуществляется работа авторов и определяется их внутренняя организация.

Поставив в соответствие последовательности тактов автомата ряд чисел, например, от 0 и k, получим дискретное автоматное время.

Таким образом, в каждый момент автоматного времени входные, выходные и внутренние переменные имеют вполне определенные значения. Набор входных, выходных и внутренних переменных в некоторый момент времени называется входным, выходным внутренним состоянием устройства.

Наиболее общей моделью автомата является абстрактный автомат, представляющий собой совокупность шести объектов:

-множество входных состояний, наборов X={x1, x2… xn}, где n-число входов автомата, связывающих его с объектом управления;

-множество выходных состояний, наборов Z= {z1, z2… zm}, где m-число выходов автомата;

-множество внутренних состояний, S= {s1, s2… s k};

-функций переходов, δ, S (t+1) = δ [S (t), X (t)];

-функции выходов, λ, Z (t) = λ [S (t), X (t)];

-начального состояния автомата S1 Є S.

Если функции δ и λ заданы на всем множестве Х и S, то автомат называется полностью заданным, в противном случае – не полностью заданным.

Для задания автомата необходимо иметь формальные средства описания, как правил функционирования, так и внутренней структуры автомата. Известно несколько таких методов описания, каждый из них имеет свои возможности границы применения. Выбор метода описания в первую очередь определяется особенностью поведения и структурой автомата. Сложность автомата определяется наличием во внутренней структуре элементов, хранящих внутренние состояния автомата - элементов памяти.

В виду отсутствия у комбинационных элементов внутренних состояний упрощается задача описания структуры и функционирования. Для задания автомата достаточно указать соответствие между значениями входных и выходных наборов. Если комбинационный автомат имеет n входов и m выходов, то достаточно указать m-зависимостей функций от n аргументов:

Z1=λ1(x1, x2… xn)

Z2=λ2(x1, x2… xn)

Zm=λm(x1, x2… xn)

Указанная система из m функций описывает автомат, у которого аргументы и функции могут принимать любое число значений. Ограничимся рассмотрением автоматов, у которых число значений функций и аргументов не превышает двух, т.е.

Xi=0, 1 для i=1, n

Zi=0, 1, для j=1, m

Общая задача исследования дискретных автоматов состоит из двух взаимосвязанных задач - анализа и синтеза.

Анализ работы КДА производится в 2 этапа. Сначала из схемы удаляют все вспомогательные элементы, не влияющие на логику работы схемы и выполняющие функции согласования, формирования и др. После этого останутся только логические элементы, по которым сопоставляется система функций:

Z ₁… Z _m

Задача синтеза обратная задаче анализа и не однозначна. В общем случае КДА представляется в виде (n,m) полесника, поведение которого описывается системой из m функций. Такая схема может быть построена двумя способами. Во-первых, раздельной реализацией каждой функции в виде одновыводной схемы, т.е., в виде совокупности из m (n,1)-полесников и совместной реализацией всей системы в целом. Во-вторых, совместной реализацией отдельных ее частей в виде многовходовой схемы, в последнем случае некоторые элементы или даже целые фрагменты схемы используются для реализации нескольких функций.

Решение задач анализа и синтеза невозможно без представления КДА в виде совокупности определенных элементов, объединенных между собой в схему. Во всех КДА необходимо определить тот набор элементов, из которого может быть построен любой автомат. Кроме того, необходимо определить математический аппарат, который будет описывать функционирование КДА в процессе переработки информации, описывать работу отдельных его элементов и соединение элементов в схему.

Для описания законов функционирования КДА используется математический аппарат булевых функций. Функция от двоичных переменных f (X₁,X₂,…..,X_n) называется булевой, если она также, как ее аргументы, принимает только два значения 0 и1. Любая булевая функция может быть задана таблицей истинности, карт Карно и т.д. Естественно, возникает вопрос, существует ли такой набор булевых функций, из которых методом суперпозиции можно получить любую булевую функцию?

Система булевых функций называется функционально полной, если для любой булевой функции f (X₁,X₂,…..,X_n) может быть построена равная ей функция путем суперпозиции переменных Х₁,Х₂,….,Х_n и функцией системы W взятых в любом конечном числе экземпляров каждая. В математической логике доказывается, что если система булевых функций содержит функции.

I. f₁= x₁*x₂; f₁=x₁ x₂; fg = x

II. f₂=x₁*x₂

III. f_g=x₁ v x_2,

то она является функционально полной.

Техническим аналогом булевой функции является комбинационная схема, выполняющая соответствующие этой функции преобразования информации. Уровни напряжений и токов, соответствующие принятому в схеме представлению сигналов 0 и I,могут рассматриваться как технические аналоги функции константы 0 и I.Элементарные логические операции над двоичными переменными реализуются схемами, которые называются логическими элементами. Число видов логических элементов соответствует числу аргументов.

Помимо логических элементов булевая функция может быть реализована на релейных контактных элементах. Аргументы функции в этом случае, сопоставлены с контактами соответствующих реле, а логические операции определяются правилами соединения контактов. Параллельному соединению контактов соответствует дизъюнкция, а последовательному – конъюнкция.

Синтез одновыходного КДА

Задача синтеза одновыходной логической схемы сводится к задаче синтеза (n,I) полюсника. Сначала задается некоторая булевая функция Y=f(x1,x2,….,xn), которая приводится к совершенной нормальной форме и затем, тем или иным способом, минимизируется. После этого можно перейти к составлению функциональной схемы, вырабатывающих на выходе функцию преобразовав ее предварительно в базис “И-НЕ”.

Исследование КДА производится при помощи программы ANALYSE , путем построения автомата и подачей всех возможных значений наборов переменных X1,X2,…..,Xn, от 0000 и I I I I, и исследованием полученной таблицы состояний исследуемого автомата.

Синтез многовыходовых КДА

Синтез многовыходового КДА есть синтез (n,m) полесника, поведение которого, как указывалось выше, описывается системой из m функций. Если рассматривать задачу синтеза этих функции как задачу о разделенном синтезе для каждой функции, то синтез (n,m)- полюсника ничем принципиально не отличается, и в общем случае такой подход не приводит к оптимальному решению. Существует несколько достаточно общей методов синтеза (n,m)полесников, однако все они не дают однозначного оптимального решения. В основе всех способов лежит идея использования одной функции или ее части для получения другой функции. Например, пусть заданы функции:

f₁= f₂=; f₂=

Очевидно, что при синтезе можно использовать соотношение

f₂=f₁_;f₃=f₂

Это значительно сократит объем необходимого оборудования. Наиболее наглядно и удобно для синтеза многовыходовых КДА применяется карта Карно.

f₁=

f₂=

f₃=

табл. 1.1.

Вариант

f₁

F₂

f₃

0,1,3,5,(7,12,13)

1,2,6,7,11,(12,13)

2,3,5,8,(10,13,14)

3,4,5,6,(7,8,9)

4,5,6,(7,8,9,10)

5,6,7,8,9,10,(11)

6,7,8,9,(10,11,12)

7,8,9,10,11,(12,13)

8,9,10,(11,12,13,14)

7,8,9,10,11,12,(13,14)

2,3,4,(5,6,7,8)

1,2,3,(4,5,6,7,8)

0,1,2,3,(4,5,6)

0,2,4,6,8,(10,12)

2,4,6,8,(10,12,14)

1,3,5(7,9,11,14)

3,5,7,9,11,(15)

0,1,2,3,11,(12,13)

0,1,2,3,(4,5,6)

0,1,2,(3,7,8,9)

0,1,2,3,8,(9,10)

0,1,3,(9,10,11)

0,1,2,3,10,11,(12)

0,1,2,3,(12,13,14)

0,1,3,13,(14,15)

2,4,6,8,9,(10,11)

2,4,6,(8,10,11)

2,4,(8,12,13)

2,4,(6,8,12,13,14)

1,3,5,7,(9,11,13)

6,7,8,9,10,(11)

10,11,12,(13,14,15)

9,10,(11,12,13,14)

8,9,(10,11,12,13)

7,8,9,10,(11,12)

6,7,(8,9 ,10,11)

5,6,(7,8,9,10)

4,5,6,7,(8,9)

3,4,5,(6,7,8)

2,3,4,5,6,(7)

1,2,3,(4,5,6)

0,1,(2,3,4,5)

0,1,2,(3,4,6)

1,2,3,4,(5,6)

2,3,4,(5,6,7)

3,4,5,6,(7,8)

4,5,7,(8,9)

5,6,7,(8,9,10)

6,7,8,9,(10,11)

7,8,9,10,(11,12)

8,9,(10,11,12,13)

9,10,11,12,(13,14)

10,11,12,(13,14,15)

0,2,4,6,(8,10)

2,4,(6,8,10,12)

4,6,8,(10,12,14)

1,3,5,6,(9,11)

3,5,7,(9,11,14)

5,7,9,11,(12,15)

0,2,(5,8,12,15)

2,4,6,(7,8)

0,1,2,3.(4)

0,1,2,(3,5)

2,3,4,(5,6)

3,4,5,(6,7)

4,5,(6,7,8)

5,6,7,(8,9)

6,7,8,9,(10)

7,8,(9,10,11)

8,9,10,11(12)

9,10,11,(12,13)

10,11,(12,13,14)

11,12,13,(14,15)

0,2,4,6,(8)

2,4,6,(8,10)

4,6,(8,10,12)

6,8,10,(12,14)

1,3,(5,7,9)

3,5,7,9,(11)

5,7,(9,11,13)

7,9,11,(13,15)

0,1,(3,5,6)

0,1,4,(5,8)

1,2,7,(8,9)

1,2,8,(9,10)

1,2,(9,10,11)

1,2,10,(11,12)

1,2,11,(12,13)

1,2,(12,13,14)

3,5,(7,8,10)

В качестве примера рассмотрим вариант № 30

f₁= 1,3,5,7,(9,11,13); f₂ = 0,2,(5,8,12,15); f₃ = 3,5,(7,8,10)

1) Таблица истинности 2) СНДФ

x₃

x₂

x₁

x₀

f₁

f₂

f₃

0000111100001111

0011001100110011

0101010101010101

010101010~0~0~00

10100~00~000~00~

0001010~~0~00000

f₁ = x₀x₁x₂x₃Vx₀x₁x₂x₃Vx₀x₁x₂x₃V

Vx₀x₁x₂x₃V x₀x₁x₂x₃Vx₀x₁x₂x₃Vx₀x₁x₂x

0 0 0

f₂ = x₀x₁x₂x₃Vx₀x₁x₂x₃V

Vx₀x₁x₂x₃Vx₀x₁x₂x₃Vx₀x₁x₂x₃Vx₀x₁x₂x₃

0 0 0 0

f₃ = x₀x₁x₂x₃Vx₀x₁x₂x₃V Vx₀x₁x₂x₃Vx₀x₁x₂x₃Vx₀x₁x₂x

0 0 0

3) Диаграмма времени

х₀

x₁

x₂

x₃

__f₁____________________________~___~___~_______________

__f₂_________________~________~_______~____________~____

__f₃_______________________~_~___~______________________

4) Таблица Карта Карно

X₁________

X₀________

	1	1
	1	1

f₁= X₀X₃

X₂

X₃

f2 = X₀ X₂ X₃

X₂

X₃

1

X₂

X₃

f3 = X₁ X₂ X₃V X₀ X₁ X₃

Рис 1.1. Этапы синтеза комбинационного дискретного автомата.

Табл. 1.2.

Функ-ция	Название функций	СНДФ	Представ-ление в базисе И, ИЛИ, НЕ	Обозна-чение функции	Название логичес-кого элемента
f₀	Константа нуля	__	0	0	Генератор нуля
f₁	Конъюнкция	Х₁Х₂	Х₁Х₂	Х₁Х₂	Элемент И
f₂	Обратный запрет	Х₁Х₂	Х₁Х₂	Х₁= Х₂	Запрет
f₃	Повторение X₁	Х₁Х₂V Х₁Х₂	Х₁	Х₁	__
f₄	Запрет	Х₁Х₂	Х₁Х₂	Х₁= Х₂	Запрет
f₅	Повторение X₂	Х₁Х₂VХ₁Х₂	Х₂	Х₂	__
f₆	Сложение по модулю(неравно-значность)	Х₁Х₂VХ₁Х₂	Х₁Х₂V Х₁Х₂	Х₁Х₂	МОД-2
f₇	Дизъюнкция	Х₁Х₂VХ₁Х₂V VХ₁Х₂	Х₁V Х₂	Х₁V Х₂	Элемент ИЛИ
f₈	Ф-ция Вебба (стрелка Пирса)	Х₁Х₂	Х₁V Х₂	Х₁ Х₂	Элемент ИЛИ
f₉	Эквивалент-ость	Х₁Х₂V Х₁Х₂	Х₁Х₂V Х₁Х₂	Х₁ Х₂	Эквивалент-ость
f₁₀	Инверсия	Х₁Х₂V Х₁Х₂	Х₂	Х₂	Элемент НЕ
f₁₁	Инверсия X₁	Х₁Х₂V Х₁Х₂	Х₁	Х₁	Элемент НЕ
f₁₂	Обратная импликация	Х₁Х₂V Х₁Х₂V VХ₁Х₂	Х₁V Х₂	Х₁ Х₂	импликация
f₁₃	Функция Шеффера (Штрих Шеффера)	Х₁Х₂V Х₁Х₂V VХ₁Х₂	Х₁ Х₂	Х₁ Х₂	Элемент И-НЕ

Содержание отчета

1. Синтез заданных схем.

2. Схемы одно и многовыходовых КДА, Схемы дешифратора и мультиплексора, схемы исследований.

3. Временные диаграммы работы и значения задержек сигналов.

4. Выводы.

Контрольные вопросы

1. Какие функции называются булевыми?

2. Какая система функций называется функционально полной?

3. В чем состоят задачи анализа, синтеза дискретных устройств(КДА)?

4. Какой автомат является полностью заданным?

5. Какая логическая операция лежит в основе минимизации?

6. Какой автомат называется синхронным, асинхронным?

7. Как определить число состояний КДА?

8. Для чего необходимо синтезировать КДА

ЛАБОРАТОРНЫЕ РАБОТЫ № 3, 4

ПОСТРОЕНИЕ КОМБИНАЦИОННЫХ ДИСКРЕТНЫХ АВТОМАТОВ В УНИВЕРСАЛЬНЫХ БАЗИСАХ “И-НЕ”, “ ИЛИ – НЕ”

Цель работы: Изучение построения комбинационных дискретных автоматов в универсальных базисах “и-не”, “ или – не”.

Основные теоретические сведения.

Перевод в базис И - НЕ.

Перевод функций, записанных в общем базисе И, ИЛИ, НЕ, в базис “И– НЕ” проводится с целью упрощения выполнения функций, использования однотипной элементной базы: микросхем И – НЕ.

Определим правила перевода функций, записанных в общем базисе, в базис И–НЕ. Такое преобразование проводится после минимизации системы функций (вар. 30)

, ,

Для Функций Шеффера справедливы следующие соотношения:

Правило Де Моргана для перевода функции в базис И – НЕ

Для построения схемы на интегральных элементах в базисе "И – НЕ" необходимо функции, содержащие более одной переменной, привести к такому виду, при котором каждая конъюнкция и вся функция должна содержать знак инверсии, характеризующий операцию "НЕ", а отдельные конъюнкции связаны между собой операцией логического умножения, соответствующей схеме "И". Для приведения функции к такому виду присваиваем знак двойной инверсии отдельным частям или функции. При этом функция не меняется, т.к. отрицание отрицания есть отсутствие отрицания. Для рассматриваемого примера функции будут иметь следующий вид:

Один знак инверсии используется для устранения в функции операции логического сложения, которая не может быть реализована в базисе "И – НЕ". При инверсии функции изменяется операция между членами функции (логическое сложение заменяется на логическое умножение ) и присваивается знак инверсии каждой конъюнкции. Схема, соответствующая данным функции, приведена на рис.1, где для упрощения входы выходных схем "И – НЕ" объединены. Роль инверторов играют элементы "И – НЕ" с объединенными входами.

В результате можно сформировать простой алгоритм перевода функций, записанных в дизъюнктивной форме в базис Шеффера:

1. Заключить слагаемые в скобки.

2. Заменить знаки сложения и умножения на штрих Шеффера.

3. Одиночные слагаемые инвертировать.

4. При необходимости заменить инверсии переменных по одному из правил:

Перевод в базис ИЛИ – НЕ

Перевод функций, записанных в общем базисе И, ИЛИ, НЕ проводится в 6азис ИЛИ – НЕ с целью упрощения выполнения функций, использования однотипной элементной базы: микросхем ИЛИ – НЕ.

Определим правила перевода функций, записанных в общем базисе, в базис ИЛИ – НЕ. Такое преобразование проводится после минимизации системы функций (вар. 30).

Для функций Пирса справедливы следующие соотношения:

Правило Де Моргана для перевода в базис ИЛИ – НЕ

Для построения схемы на интегральных элементах в базисе ИЛИ – НЕ необходимы функции, содержащие более одной переменной, привести к такому виду, при котором каждая дизъюнкция и вся функция должна содержать знак инверсии, характеризующий операцию “НЕ”, а отдельные дизъюнкции связаны между собой операцией логического сложения, соответствующей схеме “ИЛИ”. Для приведения функции к такому виду присваиваем знак двойной инверсии отдельным частям или всей функции. При этом функция не меняется, т.к. отрицание отрицания есть отсутствие отрицания. Для рассматриваемого примера функции будут иметь вид:

Один знак инверсии используется для устранения в функции логического умножения, которая не может быть реализована в базисе “ИЛИ -НЕ”. При инверсии функции изменяется операция между членами функции , логическое умножение заменяется на логическое сложение и присваивается знак инверсии каждому члену дизъюнкции. Схема, соответствующая данным функции, приведена на рис. 2, где для реализации инверторов в базисе “ИЛИ – НЕ” на один из входов подается логический нуль.

В результате можно сформировать алгоритм перевода функций, записанных в конъюнктивной форме в базис Пирса:

Заключить слагаемые в скобки.

1. Заменить знаки умножения и сложения на стрелку Пирса.

2. Одиночные слагаемые не инвертировать.

3. Заменить инверсии переменных по одному из правил:

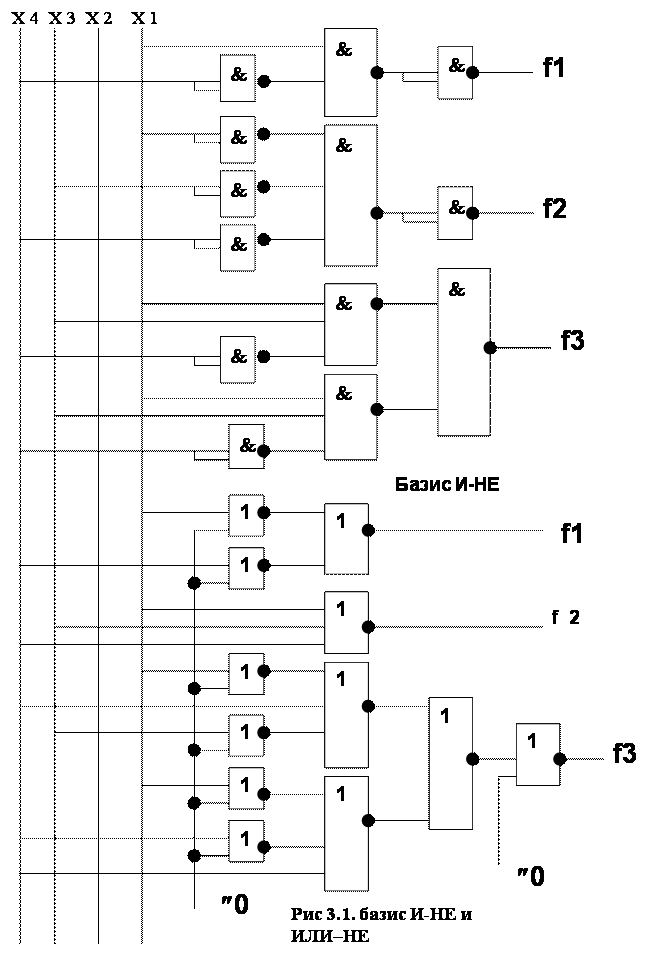Содержание отчета

1. Синтез КДА согласно заданного варианта в общем базисе. (смотреть варианты работы № 1)

2. Перевод КДА в базис И- НЕ, ИЛИ НЕ.

3. Построение схем КДА в базисе И- НЕ, ИЛИ- НЕ.

4. Заключение.

Контрольные вопросы

1. Функции и операции булевой алгебры.

2. Законы и правила булевой алгебры.

3. Способы описания логических схем.

4. Правила перевода в базисе И- НЕ.

ЛАБОРАТОРНЫЕ РАБОТЫ № 5, 6

СИНТЕЗ ДВОИЧНЫХ И ПРИОРИТЕТНЫХ ДЕШИФРАТОРОВ

Цель работы: Ознакомление со способами синтеза различных дешифраторов и шифраторов, построение схем двоичных и приоритетных дешифраторов, а также приобретение навыков в сборке и отладке дешифраторов и шифраторов.

Основные теоретические сведения

Для обратного преобразования двоичных чисел в небольшие по значению десятичные числа используются дешифраторы (называемые также декодерами). Входы дешифратора предназначаются для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.

Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.

На рис. 5.1,а приведено символическое изображение дешифратора. Символ DС образован из букв английского слова De Сoder. Слева показаны входы, на которых отмечены весовые коэффициенты двоичного кода справа — выходы, пронумерованные десятичными числами, соответствующие отдельным комбинациям входного двоичного кода. На каждом выходе образуется уровень лог.1 при строго определенной комбинации входного кода. Дешифратор может иметь парафазные входы для подачи наряду с входными переменными их инверсий, как показано на рис. 5.1,6.

Рис. 5.1 Парафазные входы и выходы дешифратора.

По способу построения различают линейные и прямоугольные дешифраторы. Рассмотрим построение дешифратора, осуществляющего преобразование, заданное табл. 5.1.

Таблица 5.1

Выходной код 8421				Номер выхода ( в десятичной системе)
X₈	X₄	X₂	X₁	Номер выхода ( в десятичной системе)
0	0	0	0	0
0	0	0	1	1
0	0	1	0	2
0	0	1	1	3
0	1	0	0	4
0	1	0	1	5
0	1	1	0	6
0	1	1	1	7
1	0	0	0	8
1	0	0	1	9

В линейном дешифраторе выходные переменные формируются по (5.1) либо (5.2). При выполнении дешифратора на элементах И-НЕ пользуются (5.2), получая инверсии выходных функций. В этом случае каждой комбинации входного кода будет соответствовать уровень лог.О на строго определенном выходе, на остальных выходах устанавливается Уровень лог.1. На рис. 5.2, а, б показана структура дешифратора, построенного на элементах И-НЕ, и его изображение в схемах. Структура имеет особенности, характерные для дешифраторов в интегральном исполнении:

-для уменьшения числа входов формирование инверсий входных переменных осуществляется в самом дешифраторе;

-подключенные непосредственно к входам дополнительные инверторы уменьшают нагрузку со стороны дешифратора на его входные цепи.

Дешифратор с 16 выходами для дешифрирования всех возможных комбинаций четырехразрядного двоичного кода 8421 можно построить на двух рассмотренных дешифраторах с 10 выходами. На рис. 5.З показана структура такого дешифратора. В каждом из дешифраторов используется по восемь выходов, которые и образуют требуемые 16 выходов.

А)

Б)

Рис. 5.2. Структура дешифратора, построенного на элементах И-НЕ.

Рис. 5.3. Прямоугольный дешифратор.

Прямоугольный дешифратор. Рассмотрим принцип построения прямоугольного дешифратора на примере дешифратора с 4 входами и 16 выходами.

Разобьем входные переменные х₈ ,x₄ ,х₂,x₁ на две группы по две переменные в каждой: х₈ ,x₄ и х₂,x₁

Каждую пару переменных используем в качестве входных переменных отдельного линейного дешифратора на четыре выхода, как показано на рис. 5.4,а. Выходные переменные линейных дешифраторов определяются следующими выражениями:

Yо=X₈·X4, Yо=X₂·X₁,

Y₁=X₈·X₄, Y₁=X₂·X₁,

Y₂=X₈X_4, Y₂=X₂·X₁,

Y₃=X₈·X₄, Y3=X₂·X₁,

Эти дешифраторы выполняют функции первой ступени дешифратора. Выходные переменные у₀ , у₁ , ... , у₁₅ прямоугольного дешифратора можно представить логическими выражениями, используя в них в качестве аргументов выходные переменные y'₀,... у'₃ и у"₀ ,... у"₃ линейных дешифраторов:

y₀=x₈·x₄·x₂·x₁=y₀’·y₀”,

y₁=x₈·x₄·x₂·x₁=y₀’·y₁”,

y₂=x₈·x₄·x₂·x₁=y₀’·y₂”,

………………………

y₁₅=x₈·x₄·x₂·x₁=y₀’·y₃”.

Эти логические операции выполняются в отдельном дешифраторе второй ступени, называемом матричным и состоящим из двухвходовых элементов. На рис. 5.4,6 показано условное обозначение матричного дешифратора, где помеченные десятичными числами две группы входов служат для подключения к выходам двух предварительных ступеней дешифрации. На рис. 5.4,6 представлена структура прямоугольного дешифратора с использованием символов линейного и матричного дешифраторов.

Могут быть построены прямоугольные дешифраторы с числом ступеней, больше двух. Применение прямоугольного дешифратора может оказаться более выгодным, чем линейного дешифратора, в тех случаях, когда велико число входов и нежелательно использовать требующиеся для построения линейного дешифратора элементы с большим числом входов. Однако прохождение сигналов последовательно через несколько ступеней приводит в прямоугольном дешифраторе к большей задержке распространения сигнала.

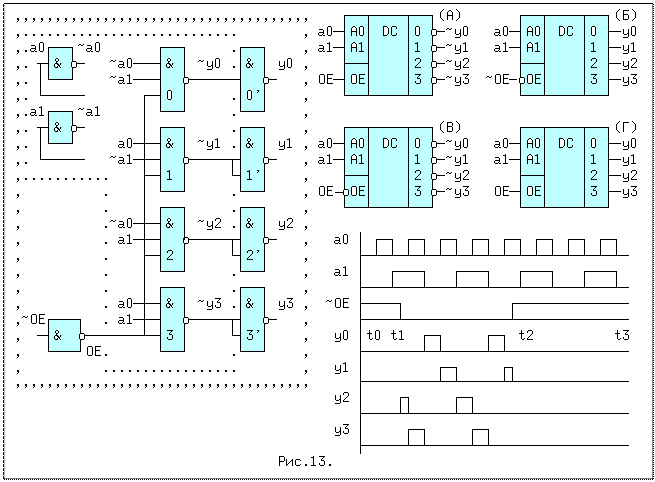
Дешифратор (ДШ) преобразует двоичный код на входах в активный сигнал на том выходе, номер которого равен десятичному эквиваленту двоичного кода на входах. В полном дешифраторе количество выходов m = 2ⁿ, где n - число входов. В неполном ДШ m < 2ⁿ. По определению полный ДШ должен генерировать 2ⁿ выходных ЛФ, определенных на всех наборах из n - входных переменных, т.е. минтермов. Рассмотрим ДШ с n=2 и m=4, называемый также дешифратором "2 в 4" и дополним его входом разрешения выходов OE. Активным уровнем сигнала на прямых входах/выходах будет 1, а на инверсных - 0. По этому определению заполним таблицу истинности, где величина x может принимать любые значения.

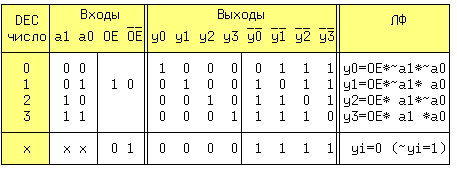
tabl-dc.gif (4484 bytes)

Таблица Карно для выхода y0 и 3-х входных переменных будет иметь вид:

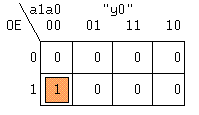
karno-dc.gif (1826 bytes)

Прямоугольник, составленный из 1-ных клеток содержит только одну такую клетку, поэтому логическая функция выхода y0 будет иметь вид: y0 = OE*~a1*~a0. Аналогично получены остальные три уравнения. Преобразуем полученные для yi уравнения с помощью аксиомы двойного отрицания к базису И-НЕ: y0 = ~(~(OE*~a1*~a0)). Решению соответствует схема на рис.13.

Схема обведенная "..." имеет условное обозначение (A), а схема в запятых - обозначение (Б). Возможны также еще 2 комбинации прямых и инверсных входов и выходов В и Г.

рис. 5.5. Дешифраторы и временные диаграммы их работ.

Пояснить работу ДШ можно с помощью временных диаграмм для схемы (Б). Во время действия сигнала ~OE=1 на нижних входах элементов И-НЕ(0..3) присутствует OE=0, и независимо от значений a0,a1, выходные значения ~yi=1, а yi=0, что и видно из рис.5.5. В эти отрезки времени t0..t1 и t2..t3 выходы "запрещены", т.е. на прямых выходах yi устанавливается пассивный уровень "0", а на инверсных выходах пассивная "1". В интервале t1..t2 сигнал ~OE=0(OE=1) и значения yi зависят только от переменных a1,a0. Если код на входах A1A0=10, что соответствует десятичной двойке, на входах второго элемента И-НЕ соберутся 3 логических "1". Сигнал ~y2=0, а y2=1, что видно на диаграмме y2. Вместо инвертора OE,может применяться более сложная схема,показанная на рис.5.6. Здесь OE=1 в случае,когда ~OE1 = ~OE2 = 0 и OE3 = 1.

Рис. 5.6. Дешифратор "3 в 8" типа.

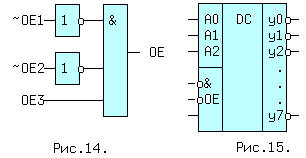
ris14-15.gif (3022 bytes)

Такая схема применяется в дешифраторе "3 в 8" типа 1533ИД7(555ИД7), условное обозначение которого приведено на рис.5.6. Дешифраторы широко применяются в вычислительной технике, как часть больших интегральных схем, для выбора одного из нескольких внешних устройств (ВУ) при обмене данными между ним и микропроцессором. В этом случае на входы ai подаются сигналы, называемые адресом ВУ, а входы называются адресными.

ШИФРАТОРЫ

Шифратор (Ш) может быть неприоритетным, если допускается подача только одного активного сигнала и может быть приоритетным, если допускается подача одновременно нескольких активных сигналов на входы. Неприоритетный Ш осуществляет преобразование десятичного номера активного входа в двоичный эквивалент этого номера. Для неприоритетного шифратора "4 в 2" таблица истинности имеет вид (рис. 5.7.):

Рис. 5.7. Таблица истинности шифратора «4 в 2».

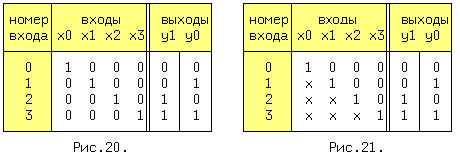
ris20-21.gif (4289 bytes)

В приоритетном Ш производится преобразование максимального десятичного номера активного входа в двоичный эквивалент этого номера. Для такого Ш входные сигналы, лежащие снизу от единичной диагонали, по определению не известны ("x" может быть 0 или 1). Следовательно полная таблица истинности, вместо нижних трех строчек должна содержать еще 2+4+8=14 строк см. рис.5.7. Комбинация 0000 на входах не определена.

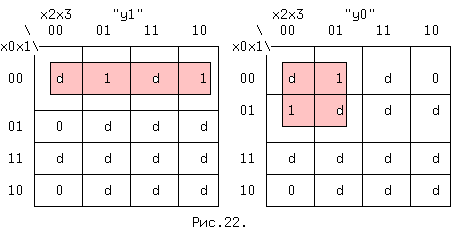
Для синтеза схемы неприоритетного Ш для каждого выхода составим таблицу Карно. Четыре входных переменных дают 2⁴=16 комбинаций из которых по определению заданы в таблице только 4. Остальные 12 неопределенных (запрещенных) комбинаций в таблицах Карно отметим символом d. Так как появление этих комбинаций на входах не предусмотрено (по определению), то в соответствующие клетки т.Карно можно подставлять любые значения, в том числе такие, которые позволяют наиболее полно минимизировать ЛФ. Два из четырех вариантов приведены на рис.5.7. В обоих случаях две величины d доопределены до 1.




 
  
  
   
    
    
    Рис. 5.8. Карты Карно.

Из приведенных таблиц находим y1 и y0:

      -- --   -------          -- --   -------

 y1 = x0*x1 = x0 + x1  и  y0 = x0*x2 = x0 + x2.




 
  
  
   
    
    
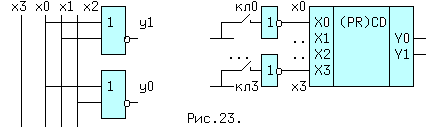
    Рис. 5.9. Неприоритетный шифратор.

Реализация и условное обозначение неприоритетного Ш приведены на рис.5.9. Переменная x3 оказалась "обделенной", но это произошло из-за того, что если нет сигнала ни на одном из первых трех входов, то он неизбежно должен присутствовать, по определению, на оставшемся, т.е. на третьем. Переменная x3, вместе с остальными может быть использована для формирования функции x0 + x1 + x2 + x3 равной 0, когда не активен ни один из входов, что может сигнализировать, например, о неисправности источников сигналов.

Шифраторы применяются в контроллерах прерываний работы микропроцессора внешними устройствами, в параллельном преобразователе напряжения в код и для кодирования номера клавиши. Последнее применение показано на рисунке. Если нажата клавиша кл3, то на выходе ей будет соответствовать код 11(BIN) = 3(DEC).

таблица 5.9. Варианты для выполнения лабораторных работ

№	код	№	код	№	код	№	код	№	код
1-16	1248	4-19	1235	7-22	1245	10-25	1225	13-28	1234
2-17	1237	5-20	1247	8-23	1136	11-26	1227	14-29	1135
3-18	1236	6-21	1246	9-24	1226	12-27	1228	15-30	1136

Содержание отчета

1. Синтез заданных схем.

2. Схему дешифратора и мультиплексора, схемы исследований.

3. Временные диаграммы работы и значения задержек сигналов.

4. Выводы.

Контрольные вопросы

1. Какие функции называются булевыми?

2. Какая система функций называется функционально полной?

3. В чем состоят задачи анализа, синтеза дешифраторов и шифраторов?

4. Какой автомат является полностью заданным?

5. Какая логическая операция лежит в основе минимизации?

6. Какой автомат называется синхронным, асинхронным?

7. Как определить число состояний шифраторов и дешифраторов?

8. Для чего необходимо синтезировать дешифратор и шифратор?

ЛАБОРАТОРНАЯ РАБОТА № 7

СИНТЕЗ МУЛЬТИПЛЕКСОРОВ И ДЕМУЛЬТИПЛЕКСОРОВ

Цель работы: Ознакомление с принципами синтеза мультиплексоров и демультиплексоров, приобретение навыков в отладке и сборке мультиплексорных систем.

Основные теоретические сведения

Устройство, которое осуществляет выборку одного из нескольких входов и подключает его к своему выходу, называется мультиплексором. Мультиплексор имеет несколько информационных входов (D₀,D₁...), адресные входы (А_о,А₁,...), вход для подачи стробирующего сигнала С и один выход Q. На рис. 7.1, показано символическое изображение мультиплексора с четырьмя информационными входами.

Рис.7.1 Мультиплексор.

Каждому информационному входу мультиплексора присваивается номер, называемый адресом. При подаче стробирующего сигнала на вход С мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу.

Таким образом, подавая на адресные входы адреса различных информационных входов, можно передавать цифровые сигналы с этих входов на выход Q. Очевидно, число информационных входов n_i и число адресных входов n_a связаны соотношением п_i =2^na .Функционирование мультиплексора определяется табл. 7.1.

Таблица 7.1

Адресные входы		Стробирующий сигнал	Выходы
А₁	А₀	С	Q
X	X	0	0
0	0	1	D₀
0	1	1	D₁
1	0	1	D₂
1	1	1	D₃

При отсутствии стробирующего сигнала (С =0) связь между информационными входами и выходом отсутствует (Q = 0). При подаче стробирующего сигнала (С = I) на выход передается логический уровень того из информационных входов Z), номер которого i в двоичной форме задан на адресных входах. Так, при задании адреса а₁a₀=11₂=3₁₀ на выход Q будет передаваться сигнал информационного входа с адресом З₁₀ , т.е. D_з.

По этой таблице можно записать следующее логическое выражение для выхода Q:

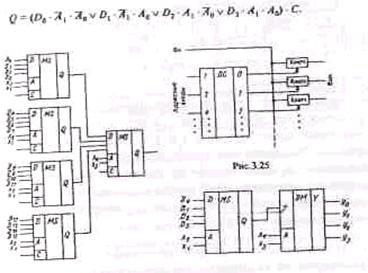
Рис. 7.2. Мультиплексорное дерево.

Построенная по этому выражению принципиальная схема мультиплексора приведена на рис. 7.1,6.

В тех случаях, когда требуется передавать на выходы многоразрядные входные данные в параллельной форме, используется параллельное включение мультиплексоров по числу разрядов передаваемых данных.

Мультиплексорное дерево. Максимальное число информационных входов мультиплексоров, выполненных в виде интегральных схем, равно 16. Если требуется построить мультиплексорное устройство с большим числом входов, можно объединить мультиплексоры в схему так называемого мультиплексорного дерева. Такое мультиплексорное дерево, построенное на четырехвходовых мультиплексорах, показано на рис. 7.2. Схема состоит из четырех мультиплексоров первого уровня с адресными переменными х₁ х₂ и мультиплексора второго уровня с адресными переменными Х₃ Х₄. Мультиплексорное устройство имеет 16 входов, разбитых на четверки, которые подключены к отдельным мультиплексорам первого уровня. Мультиплексор второго уровня, подключая к общему выходу устройства выходы отдельных мультиплексоров первого уровня, переключает четверки входов. Внутри четверки требуемый вход выбирается мультиплексором первого уровня. По такой схеме, используя восьмивходовые мультиплексоры, можно построить мультиплексорное устройство, имеющее 64 входа.

На первом и втором уровнях мультиплексорного дерева можно использовать мультиплексоры с разным числом входов. Если на первом уровне такого дерева используются мультиплексоры с числом адресных переменных п_а1 на втором — с числом переменных n_а2, то общее число входов мультиплексорного дерева п₁ = 2 ^na1+na2 , а число мультиплексоров в схеме составит 2 ^nа2 + 1.

Демультиплексор имеет один информационный вход и несколько выходов и осуществляет коммутацию входа к одному из выходов, имеющему заданный адрес (номер). На рис. 7.2 показана структура демультиплексора. Она включает в себя дешифратор, выходы которого управляют ключами. В зависимости от поданной на адресные входы кодовой комбинации, определяющей номер выходной цепи, дешифратор открывает соответствующий ключ, и вход демультиплексора подключается к определенному его выходу.

Объединяя мультиплексор с демультиплексором, можно построить устройство, в котором по заданным адресам один из входов подключается к одному из выходов. Таким образом, может быть выполнена любая комбинация соединений входов с выходами. Например, при комбинации значений адресных переменных х₁ = I, Х₂ == 0, Х₃ = О, Х₄ ⁼ О вход D₂ окажется подключенным к выходу Уо.

Если требуется большое число выходов, то может быть построено демультиплексорное дерево.

Мультиплексор передает сигнал с одного из информационных входов xi на единственный выход y, причем, номер этого входа равен десятичному эквиваленту двоичного кода на адресных входах ai. Если имеется вход разрешения выхода OE, то "0" на этом входе должен перевести выход в пассивное состояние (последняя строчка таблицы.5). Рассмотрим мультиплексор "4 в 1", имеющий 4 информационных входа и log4 = 2 адресных входов.

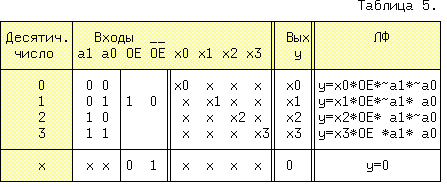
tabl5.gif (4454 bytes)

Величина x может принимать любые значения. Количество входных переменных равно 7, и таблица истинности должна иметь 128 строк. В табл.5 в 4-x основных строках упаковано 64 исходных (с учетом значений x0 ... x3) и в последней строке, остальные 64 строчки. Анализ 0 строки, приводит к выводу,что y=x0, если a1=0 И a0=0 И OE=1, независимо от переменных x1 ... x3. Поэтому для этого входного набора можно записать: y=x0*OE*~a1*~a0. Аналогично записывается y для остальных трех наборов переменных. Общее решение тогда будет иметь вид:

y = OE(x0*~a1*~a0 + x1*~a1*a0 + x2*a1*~a0 + x3*a1*a0)

Применяя аксиомы двойного отрицания и двойственности к правой части уравнения получим:

y = ~(OE*x0*~a1*~a0)+ ... +~(OE*x0*a1*a0),

Выражению соответствует схема, приведенная на рисунке:

Рис. 7.3. Условное обозначение и механический аналог мультиплексора.

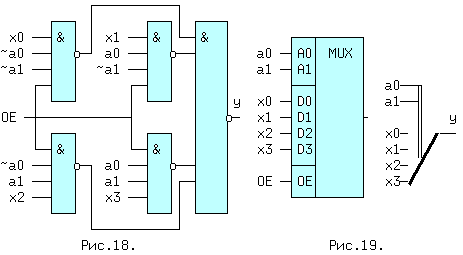
ris18-19.gif (4944 bytes)

а ее условное обозначение и механический аналог на рис. 7.3. Если на адресные входы подать комбинацию a1a0 = 11(BIN) = 3(DEC), то к выходу y будет подключен вход D3, при условии, если OE=1. Мультиплекcор может иметь инверсный выход, а также третье состояние этого выхода, которое отмечается на схеме ромбом с поперечной чертой.

Мультиплексоры находят широкое применение в вычислительной технике, например, многие выводы у микропроцессоров "мультиплексированы", т.е. к одному выходу подключается несколько внутренних источников различных сигналов. Это могут быть сигналы линий шины данных и шины адреса, передаваемые последовательно во времени, что позволяет сократить общее число выводов микропроцессора. Если сравнить выражения (16) и (12), то можно увидеть их тождественность, при fi = xi и OE = 1. Следовательно, с помощью мультиплексора с "n" адресными входами можно реализовать любую ЛФ с "n" переменными, подавая на инфрмационные входы мультиплексора значения fi.

Устройство передающее сигнал с информационного входа на один из выходов, причем номер этого выхода равен десятичному эквиваленту двоичного кода на адресных входах, называется демультиплексором (ДМ). В качестве ДМ может использоваться дешифратор, у которого вместо сигнала OE подается информационный сигнал x. Например, если на входы подать код a1a0=10(BIN)=2(DEC), то сигнал x появится на выходе y2, а на остальных выходах yi=0. На рис.7.4. даны условное обозначение ДМ "1 в 4" и его механический аналог.

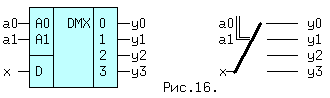
ris16.gif (2212 bytes)

Рис. 7.4. Условное обозначение ДМ "1 в 4" и его механический аналог.

На рис.7.5. показано соединение двух ДШ "3 в 8" для получения одного ДШ "4 в 16", или двух демультиплексоров "1 в 8" для получения одного "1 в 16".

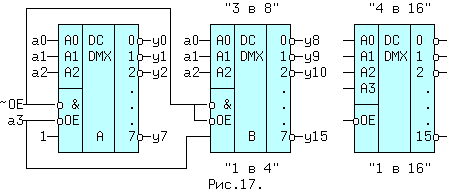
ris17.gif (4836 bytes)

Рис.7.5. Соединение двух дешифраторов "3 в 8".

При пассивном значении ~OE=1 сигнал OE=0 (рис.14) и на всех выходах yi будет "1", независимо от значений сигналов ai. Если ~OE=0 (активный уровень), то какой из дешифраторов работает зависит только от сигнала a3. Так если a3=0, то на всех разрешающих входах ДШ (A) будут активные уровни, а на прямом разрешающем входе OE дешифратора (B) сигнал a3 равный нулю переведет все выходы в состояние 1 (см. табл.4), т.е. работоспособным будет ДШ (A). Когда a3=1, наоборот работоспособным становится дешифратор (B), потому что для инверсного входа ~OE дешифратора (A) этот сигнал запрещает его выходы. Комбинации сигналов a3 и a2..a0, это видно из первых колонок таблицы, образуют последовательность двоичного кода 0000 ... 0111 (0 ... 7) для дешифратора (A) и последовательность 1000 ... 1111 (8 ... 15) для ДШ (B). Поэтому нумерация выходов yi, получившегося ДШ "4 в 16" сквозная от 0 до 15. На рис.7.5, справа приведено условное обозначение, получившегося дешифратора - демультиплексора (в справочниках они так часто и называются и помещаются в один раздел).

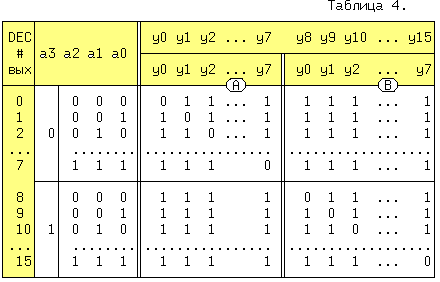
tabl4.gif (5562 bytes)

таблица 7.4. Варианты для выполнения лабораторных работ

№	входы	№	входы	№	входы	№	входы	№	входы
1	4	4	5	7	6	10	7	13	8
2	9	5	10	8	11	11	12	14	13
3	14	6	15	9	16	12	2	15	3

таблица 7.5. Варианты для выполнения лабораторных работ

№	выходы	№	выходы	№	выходы	№	выходы	№	выходы
16	4	19	5	22	6	25	7	28	8
17	9	20	10	23	11	26	12	29	13
18	14	21	15	24	16	27	2	30	3

Содержание отчета

1.Синтез заданных схем.

2.Схему одно и многовыходовых КДА, Схему мультиплексора и демультиплексора, схемы исследований.

3.Временные диаграммы работы и значения задержек сигналов.

4.Выводы.

Контрольные вопросы

1.Какие функции называются булевыми?

2.Какая система функций называется функционально полной?

3.В чем состоят задачи анализа, синтеза дискретных устройств(КДА)?

4.Какой автомат является полностью заданным?

5.Какая логическая операция лежит в основе минимизации?

6.Какой автомат называется синхронным, асинхронным?

7.Как определить число состояний мультиплексоров и демультиплексоров?

8.Для чего необходимо синтезировать мультиплексоры и демультиплексоры?

ЛАБОРАТОРНАЯ РАБОТА № 8

СИНТЕЗ СХЕМ КОНТРОЛЯ И СРАВНЕНИЯ, МАЖОРИТАРНЫХ ЭЛЕМЕНТОВ

Цель работы: В цифровых системах автоматики, в частности, в устройствах управления коммутации и передачи данных, широкое применение находят схемы контроля и сравнения, мажоритарные элементы. Целью данной работы является изучение принципов построения и синтеза схемы контроля и сравнения, мажоритарные элементы.

Основные теоретические сведения

Сравнивающее устройство представляет собой комбинационный автомат, выполняющий главным образом сравнение двух и много разрядных двоичных слов, в которых каждый разряд имеет определённый вес. На рис 8.1. приведёна таблица истинности и карты Карно для сравнения двух разрядных двоичных слов.

После минимизации получим систему булевых функций сравнивающего устройства.

Поскольку для реализации СУ требуется большое число логических элементов с четырьмя входами, то для уменьшения, согласно таблице истинности можно написать следующее эквивалентное представление:

Тогда системы булевых функций с учётом в базисе И-НЕ имеют вид:

F A>B = [A1/(B1/B1)] / [A0/(B1/B1) /(B0/B0)] /[A1/A1/(B0/B0)]

F A<B = [(A1/A1)/B1] / [(A1/A1)/(A0/A0)/B0]/[(A0/A0)/B0/B1]

FA=B = [(FA>B/FA>B)/(FA<B/FA<B)]/[(FA>B/FA>B)/(FA<B/FA<B)]

Рис. 8.1. Таблица истинности и карты Карно сравнивающего устройства.

В цифровых системах автоматики, в частности, в устройствах управления коммутации и передачи данных, широкое применение находят различного рода устройства преобразования кодов, которые выполняют различные функции преобразования управляющей информации. При этом в цифровых устройствах представление информации производится в виде взвешенных двоичных, двоично-десятичных, циклических и других специальных кодах. Существующее множество кодов предназначено для обеспечения удобства перевода чисел из десятичной системы в двоичную, простоты выполнения арифметических операций и контроль результатов вычислений, набор кода влияет также на аппаратурные затраты реализуемых схем цифровых устройств и на надежность выполнения ими заданных алгоритмов функционирования.

При проектировании цифровых устройств наибольшее раcпроcтранение получил двоично-десятичный взвешенный код 8421, который образуется путем естественного представления каждой десятичной цифры двоичным взвешенным кодом. Рассмотрим синтез комбинационных преобразователей кодов на примерах преобразования двоично-десятичного кода 8221 в широко применяемые в цифровых устройствах двоично-десятичные коды 2421.

Код Айкена, код с избытком 3, циклический код, код 2 из 5, а также кодов Джонсона.

Коды о избытком 3 применяются для кодирования декад при двоично-десятичном представлении чисел. Особенностью данного кода является то, что он самодополняющий, т.е. дополнительное до 9 чисел в каждой декаде подучается заменой нулей на единицы и наоборот, в каждом двоичном разряде. Конструкция этого кода (таблица 3.4) заключается в перечислении двоичных эквивалентов десятичных чисел от 0 + 3= 3 до 9 + 3 = 12.

Другим примером самодополняющего кода является код Айкена, где цифры 2,4,2,1 символизируют веса отдельных разрядов существующих АТС.

В существующих АТС применяется код 2 из 5. Преимущество данного метода состоит в простоте обнаружения ошибок, поскольку единичное искажение любого символа может быть распознано.

В циклическом коде Джонсона переход к последующему числу осуществляется путем последовательной замены 0 на I, начиная, справа, до заполнения всех разрядов единицами, а затем заменой 1 на 0 до заполнения 0. Ошибки с помощью кода Джонсона обнаруживаются, когда один или несколько 0 оказываются между 1 или наоборот.

Рис.8.2. Схема сравнения.

Рассмотрим синтез комбинационных преобразователей кодов на примерах преобразования двоично-десятичного бинарного кода 842І в широко применяемых в цифровых устройствах двоично-десятичные коды 2421, и кода 2 из 5. Выполним синтез схемы преобразования в код 2421 на основе карт Карно (рис.8.1). С целю минимизации определим значения функций на некоторых избыточных наборах входных состояний.

Таблица 8.1. Таблица состояний для преобразователей кодов

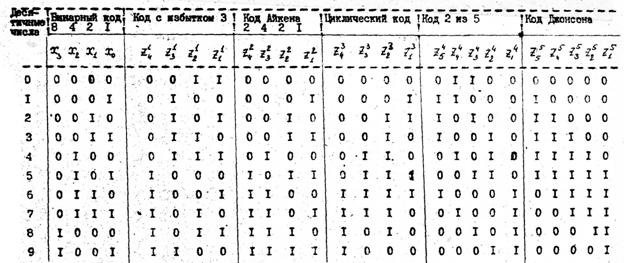
В соответствии с таблицей 8.1 получаем минимальную дизъюнктивную нормальную форму для наших четырех функций:

Полученные функции преобразуем в удобную для реализации на логических элементах форму в базисе И-НЕ

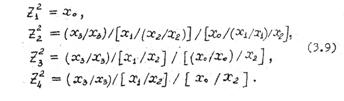
Логическая схема преобразователя кода 8421 в код 2421 приведена на нижеследующем рисунке.

В качестве последнего примера, иллюстрирующего принципы построения схем преобразователей кодов, рассмотрим преобразователь кода 8421 в код 2 из 5, приведенный в таблице 8.1.

Построив карты Карно можно получить результаты минимизации,

которые могут быть реализованы на логических элементах.

Кроме рассмотренных типов преобразователей кодов, существует множество других. В частности, для упрощения структур и облегчения взаимодействия с устройствами ввода и потребителями информации существуют различные преобразователи арифметических кодов. Как будет рассматриваться в дальнейшем, арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными. Однако с целью упрощения цифровых систем для выполнения сложения, умножения, деления обычно применяется алгоритмы, не используемые в обычной десятичной арифметике.

Обычно вычитание в цифровых системах реализуют с помощью сложения, представляя вычитаемое в одном из специальных кодов. Одной из разновидностей таких кодов является обратный код числа А2 , который получается заменой всех 0 в числе на 1 и наоборот

Недостатком использования обратного кода является образование циклического переноса, который приводит к повышению операции сложения, что существенно увеличивает время выполнения действий. Поэтому во многих случаях предпочтительнее использовать дополнительный код числа А2 , который образуется из обратного прибавлением 1 к младшему разряду (табл.8.2.). При использовании дополнительного кода отпадает необходимость в циклическом переносе и перенос, который может возникать в знаковом разряде числа, не учитывается. В дополнительном коде представляются все отрицательные числа.

Таблица 8.2.

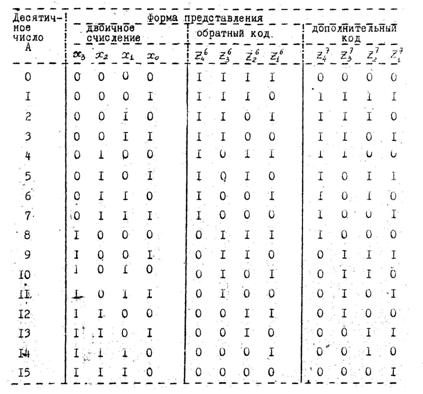
Содержание отчета:

4. Синтез заданных схем.

5. Схему контроля, Схему построенных мажоритарных элементов.

6. Временные диаграммы работы и значения задержек сигналов.

7. Выводы.

Контрольные вопросы

9. Какие функции называются булевыми?

10. Какая система функций называется функционально полной?

11. В чем состоят задачи анализа, синтеза схемы контроля и сравнения, мажоритарных элементов.?

12. Какой автомат является полностью заданным?

13. Какая логическая операция лежит в основе минимизации?

14. Какой автомат называется синхронным, асинхронным?

15. Как определить число состояний ?

16. Для чего необходимо синтезировать схемы контроля и сравнения, мажоритарные элементы.

ЛАБОРАТОРНАЯ РАБОТА № 9

СИНТЕЗ СУММАТОРОВ

Цель работы: В ЭВМ сумматор является центральным узлом арифметико-логического устройства (АЛУ) и от его быстродействия зависит производительность компьютера. Поэтому, целью данной работы является ознакомление со способами синтеза различных сумматоров.

Основные теоретические сведения

Сумматор осуществляет арифметическое суммирование n-разрядных кодов X=(x(n-1),..,x0) и Y=(y(n-1),..,y0). Правила сложения двух одноразрядных двоичных чисел:

0(+)0=0

0(+)1=1(+)0=1

1(+)1=0 и перенос 1 в старший разряд.

Операция (+) называется – сумма по модулю два (переключательная функция F6). Устройство, реализующее эти правила называется одноразрядным полусумматором и имеет два входа и два выхода. Сложение трех одноразрядных чисел производится следующим образом:

0(+)0(+)0=0

0(+)0(+)1=1

0(+)1(+)1=0 и перенос 1 в старший разряд

1(+)1(+)1=1 и перенос 1 в старший разряд.

Устройство, реализующее эти правила называется одноразрядным полным сумматором (ОПС) и имеет три входа и два выхода. Таблица истинности ОПС приведена на рис. 9.1., слева.

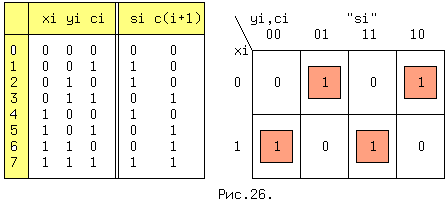
ris26.gif (4407 bytes)

Рис.9.1. Таблица истинности ОПС.

xi,yi - одноименные двоичные разряды чисел X и Y, ci - перенос из предыдущего разряда, si - частичная сумма по модулю два и c(i+1) - перенос в следующий разряд. Значения c(i+1) совпадают со значениями функции мажоритарности , поэтому воспользуемся готовым решением:

c(i+1) = xi*yi + xi*ci + yi*ci.

Таблица Карно для si приведена на рис.26 справа. Из таблицы находим: si = xi*~yi*~ci + ~xi*~yi*ci + xi*yi*ci+ ~xi*yi*~ci = ~yi(xi*~ci + ~xi*ci) + yi(xi*ci + ~xi*~ci) = ~yi(xi (+) ci) + yi(xi*ci + ~xi*~ci). Выражение в последней скобке необходимо преобразовать, используя соотношение двойственности.

xi*ci + ~xi*~ci = ~(xi*ci) * ~(~xi*~ci) = (~xi+~ci) * (xi+ci) =

~xi*xi + ~xi*ci + ~ci*xi + ~ci*ci = ~xi*ci + xi*~ci =

~(xi (+) ci) = ~F6 = F9.

С учетом последнего выражения

si = ~yi(xi (+) ci) + yi~(xi (+) ci) = yi (+) (xi (+) ci) = yi (+) xi (+) ci

Схема одноразрядного полного сумматора соответствующая уравнениями и ее условное обозначение приведены на рис.9.2.

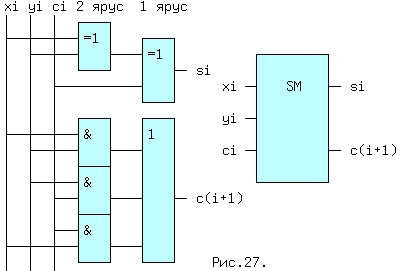
ris27.gif (4069 bytes)

Рис.9.2. Схема одноразрядного полного сумматора

Сумматор с последовательным переносом для сложения n- разрядных двоичных чисел показан на схеме (рис.9.3.). К его недостатку относится большое время задержки, в наихудшем случае, когда от сложения x0,y0 возникает сквозной перенос через все разряды до выхода s(n-1). При двухъярусной схеме одноразрядного сумматора, задержка сигнала от входов до выходов составит 2tзд.р., если считать задержку в каждом ярусе одинаковой. Суммарная величина задержки будет равна:

tзд.р.посл.сумматора = n*2tзд.р.

При сложении многоразрядных чисел задержка выходного сигнала на выходе последнего разряда становится недопустимо большой.

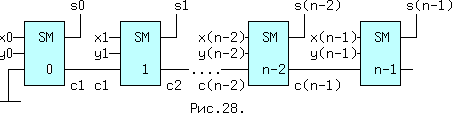
ris28.gif (2964 bytes)

Рис. 9.3. Сумматор с последовательным переносом.

В ЭВМ сумматор является центральным узлом арифметико-логического устройства (АЛУ) и от его быстродействия зависит производительность компъютера. Поэтому применяются сумматоры с параллельной схемой переноса. Выражение (18) для младшего разряда можно преобразовать, используя тождество для для функции ИЛИ: x + y = ~x*y + x*~y + xy. В правой части равенства СДНФ ф-ии ИЛИ. Тогда

c1 = x0*y0 + x0*c0 + y0*c0 = x0*y0 + c0(x0 + y0) =

x0*y0 + c0(~x0*y0 + x0*~y0 + x0*y0) =

x0*y0(с0 +1) + c0(~x0*y0 + x0*~y0) =

x0*y0 + с0(x0 (+) y0). (21)

Уравнениям соответствует схема на рис.9.4.

Рис.9.4. Схема сумматора.

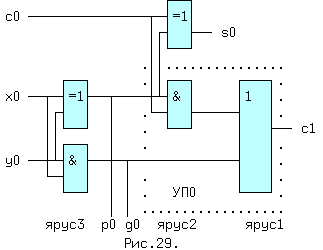
ris29.gif (3267 bytes)

Если в каждом разряде сумматора использовать такой одноразрядный сумматор, то никакого выигрыша в скорости не будет. Узел обведенный точками называется узлом переноса (УП), а функции gi и pi называются функциями генерации переноса и распространения переноса. С учетом этого можно записать:

c1 = g0 + p0*c0, с2 = g1 + p1*c1 =

= g1 + p1*g0 + p1*p0*c0,

с3 = g2 + p2*c2 =

= g2 + p2*g1 + p2*p1*g0 + p2*p1*p0*c0,

и так далее. Выражения - это еще последовательный сумматор, т.к. c3 зависит от c2, c2 зависит от c1, а c1 зависит от c0. Вышеприведенные выражения соответствуют уже параллельному, т.к. величина ci снимается с выхода предыдущего разряда, в котором она формируется параллельно из всех первичных переменных. Схемы узлов переноса УП1 и УП2 приведены на рис. 9.5.

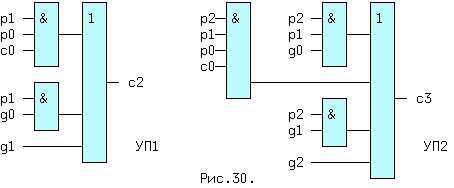
ris30.gif (3585 bytes)

Рис. 9.5. Схемы узлов переноса УП1 и УП2.

Из рис.9.4. и 9.5. видно, что узел сложения в каждом разряде остается неизменным, а изменяется только узел переноса, причем задержка сигнала от входов xi, yi до c(i+1) остается неизменной и для 3-ярусной схемы равна 3tзд.р.. Суммарная задержка в каждом разряде увеличится на время прохождения сигнала от входа ci до si, т.е. на величину tзд.р., и составит: tзд.р.паралл.сумматора = 4tзд.р. независимо от количества разрядов. За это приходится платить усложнением узла переноса от разряда к разряду.

Таблица 9.1. Варианты

№ варианта	Число разрядов	Список команд	Код операнда
№ варианта	Число разрядов	Список команд	А	В
1-16	2	А + В; А – 1; В + 1; Ā.	01	11
2-17	3	А – В; А – 1 ; В – 1 ; А.	010	011
3-18	4	А+В; А – 1; А – В – 1; В.	0101	0111
4-19	2	А – В; В – 1; А+В+1; Ā.	10	11
5-20	3	А+В; А+1;А – В+1; В.	101	010
6-21	4	А – В; А – 1; А+В – 1; А.	0111	0011
7-22	2	А+В; В+1;А – В – 1; В.	11	01
8-23	3	А – В; А – 1; А+В+1; Ā.	011	101
9-24	4	А+В; А+1;А – В +1; В.	1111	0010
10-25	2	А – В; В+1;А+В – 1; А.	11	10
11-26	3	А+В; А+1; А – В – 1; В.	111	101
12-27	4	А – В; В – 1; А+В+1; Ā.	0101	1010
13-28	2	А+В; А – 1; А+В – 1; В.	01	01
14-29	3	А – В; В+1;А – В +1; Ā.	110	011
15-30	4	А+В; А+1;А-В – 1; В.	0111	0110

Содержание отчета

1. Синтез заданных схем.

2. Схему одно и многовыходовых КДА, Схему сумматора, схемы исследований.

3. Временные диаграммы работы и значения задержек сигналов.

4. Выводы.

Контрольные вопросы

1. Какие функции называются булевыми?

2. Какая система функций называется функционально полной?

3. В чем состоят задачи анализа, синтеза сумматоров?

4. Какой автомат является полностью заданным?

5. Какая логическая операция лежит в основе минимизации?

6. Какой автомат называется синхронным, асинхронным?

7. Как определить число состояний сумматоров?

8. Для чего необходимо синтезировать сумматор?

ЛАБОРАТОРНЫЕ РАБОТЫ № 10, 11

СИНТЕЗ КБЯ, ДБЯ И МНОГОТАКТНЫХ ДИСКРЕТНЫХ АВТОМАТОВ

Цель работы: В цифровых устройствах для хранения информации используют триггеры. Триггеры – элементарные автоматы, содержащие элементарную запоминающую бистабильную ячейку (БЯ) памяти и схемы управления состоянием БЯ. Целью данной работы является изучение функционирования и синтез различных триггеров.

Основные теоретические сведения

В цифровых устройствах для хранения информации используют триггеры. Триггеры – элементарные автоматы, содержащие элементарную запоминающую бистабильную ячейку (БЯ) памяти и схемы управления состоянием БЯ.

Обобщенная схема триггера состоит из: Хı, . . . ,Хn - информационные входы; Сı, . . . , Сm- входы синхронизации, или тактовые входы; Vı, . . . , Vk – управляющие входы; Sy, Rу – установочные входы; f1, f 2 – информационные входы БЯ; Q, Q - выходы.

Коммутационные входы используются для внешних соединений в программируемых универсальных триггерах.

Классификация триггеров может быть проведена по признакам логического функционирования и способу записи информации.

По логическому функционированию различают триггеры типов RS, JK, T, D, DV, TV и комбинированные.

По способу записи информации различают асинхронные (нетактируемые) и синхронные (тактируемые) триггеры. В нетактируемых переход в новое состояние вызывается изменениями информационных входных сигналов. В тактируемых такой переход происходит только при подачи специальных тактовых сигналов С (clock).

В зависимости от числа тактовых сигналов управления различают многотактные и однотактные триггеры.

По способу восприятия тактовых сигналов триггеры делятся на управляемые уровнями и управляемые фронтами. Управление уровнями означает, что при одном уровне триггер находится в определенном режиме (например, воспринимает входные сигналы), а при другом переходит в иной режим (например, изменяет состояние). При управлении фронтами разрешение на переключение триггера дается в момент перепада тактового сигнала (на его фронте или спаде).

Управляемые уровнем триггеры делятся на одноступенчатые и двухступенчатые. В одноступенчатом поступлении соответствующего уровня разрешает полное переключение в новое состояние. Двухступенчатые триггеры состоят из входного и выходного каскадов и управляются таким образом, что переход в новое состояние происходит в обеих ступенях поочередно.

К параметрам триггера можно отнести параметры логических элементов, на которых выполнен триггер: Коб – коэффициент объединения по входу; К раз – коэффициент разветвления по выходу, уровни «0» и «1», входные и входные токи и т.д.

Специфическими параметрами триггера, в отличие от логических элементов, являются:

Разрешающее время триггера tраз – наименьший интервал времени между входными сигналами минимальной длительности, вызывающими бесперебойное переключение триггера. Принято считать, что триггер переключается бесперебойно, если любое значение выходного сигнала, определяемое правилами работы, иметь длительность, не меньшую среднего времени задержки распространения tзр одного логического элемента схемы.

Минимальная длительность входного сигнала

tи = ∑ tзр

i=1

где k – количество элементов в цепочке от входа информационного или тактового сигнала до входа элемента, на котором замыкается триггерное кольцо обратной связи.

Время задержки переключения триггера

tз.пер=∑ tзр

i=1

где m – количество элементов в цепочке от входа информационного или тактового сигнала до выхода элемента, на котором подтверждается состояние триггера.

Из определения tи и tз.пер следует m = k + 1.

Триггеры характеризуются функцией переходов или связи внутренних переменных для момента времени tn+ı со значениями входных и выходных переменных для момента времени tn , называемых характеристическими уравнениями

Qn+ı = f (Xn ,Qn).

Для всех триггеров имеются состояния входов, под воздействием которых происходит изменения состояния триггеров Qn →Qn+ı всех четырех видов:

0→0 , 0→1 , 1→0 , 1→1.

Правила функционирования триггеров могут быть заданы: в виде таблице переходов триггера, т.е. таблицы информационных значений входных сигналов, внутренних состояний и выходных сигналов триггера; в виде характеристических уравнений.

Триггеры используются для построения регистров, счетчиков, делителей частоты, в формирователях импульсов и т.д.

В большинстве серий интегральных микросхем содержатся триггеры различных типов. Ниже рассмотрены лишь простейшие, но наиболее распространенные типы триггеров.

Студенты должны синтезировать триггер со специальными функциями, которым не удовлетворяют имеющиеся в наличие триггеры, т.е. возникает задача проектирования произвольного триггера.

Канонический метод структурного синтеза применительно к триггерам позволяет свести задачу их синтеза к задаче структурного синтеза комбинационных схем (КС) управления. Результатом канонического метода структурного синтеза является система логических уравнений, выражающая зависимость выходных сигналов триггеров и функций возбуждения БЯ (f1, f2) от сигналов на входе триггера и сигналов с выходов БЯ памяти.

Бистабильная ячейка памяти

Функционирование БЯ описывается в виде таблицы переходов (таб.10.3).

Таблица 10.3.

Qn+ı

Как видно из таб.1, при f1=f2=1 БЯ хранит старое состояние, при f1=0 и f2=1 устанавливается в единичное состояние, при f1=1 и f2=0 – в нулевое; комбинация сигналов f1=f2=0 запрещена, поэтому для нее отмечено неопределенное состояние (×). Определим характеристическое уравнение БЯ с помощью метода карт Карно (рис.10.3).

f1 f2

Рис.10.3. Карта Карно для БЯ памяти.

Объединяя единицы, как показано на карте, и относя к ним неопределенные состояния, отмеченные крестиками, получаем характеристическое уравнение

Qn+ı = f1 V f2Qn.

Структурное уравнение для базиса И – НЕ получаем, взяв двойную инверсию правой части характеристического уравнения

Qn+ı = f1 V f2Qn = f1∙ f2Qn

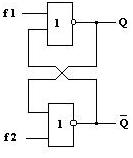Схемы БЯ в базисе И-НЕ и ИЛИ-НЕ показаны на рис.3.3

а) б)

Рис.10.4 Схемы БЯ в базисе И-НЕ (а) и ИЛИ-НЕ (б)

RS – ТРИГГЕР

Асинхронный RS – триггер - двухвходовый триггер с раздельным управлением по каждому входу: при подаче сигнала на вход S триггер устанавливается единичное состояние, при подаче сигнала на вход R – в нулевое состояние; одновременная подача сигналов на оба входа запрещается; если же такая ситуация возникает , то безразлично, в каком состояние будет находиться триггер. Описание функционирования RS-триггера представлено в виде таблицы переходов (табл. 10.4).

Таблица 10.4

Qn+ı

Как видно из табл.10.4, при нулевых выходных сигналах триггер хранит старое состояние.

Триггеру типа RS соответствует карта Карно (рис.5).

S R

Рис.10.5 Карта Карно RS-триггера.

Из карты Карно, получаем характеристическое уравнение в базисе И-НЕ

Qn+ı= S v RQn = S · RQn

Характеристическое уравнение в базисе ИЛИ-НЕ имеет вид

Qn+ı = R v (S v Qn)

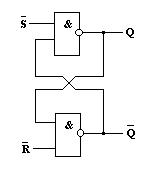
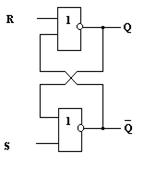
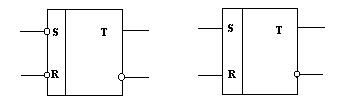
По полученным уравнениям строим схемы RS – триггера (рис.10.6).

а) б)

Рис.10.6. Схемы RS-триггеров в базисе И-НЕ (а) , ИЛИ-НЕ(б) и их условные обозначения.

На временной диаграмме (рис.10.7) иллюстрируется предельный динамический режим работы RS –триггера.

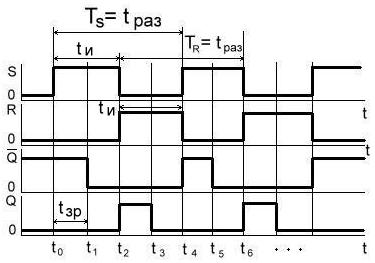
Рис.10.7. Предельный динамический режим работы RS – триггера.

При анализе режима предполагается, что логические элементы являются идеальными элементами задержки на время tзр , не искажающими фронты входных и выходных сигналов. Пусть до момента времени t0 триггер находился в состоянии «0», а S=R=0. В момент времени t0 сигнал S изменил свое значение с 0 на 1. В момент времени t1=t0 + tзр выходной сигнал изменился с 1 на 0. Нулевые сигналы, действующие на R входе и на выходе Q в момент времени t2 = t1 + tзр , обеспечат появление сигнала 1 на выходе Q. В этот же момент можно снять сигнал 1 со входа S, а сигнал 1 с выхода Q подтвердит сигнал на выходе Q в момент времени t3 = t2 + tзр . Тогда с учетом данного выше определения бесперебойного переключения триггера можно записать

tи = 2tзр ; tз.пер = 3tзр .

Из временной диаграммы видно, что

tраз = Ts = T R = 4tзр.

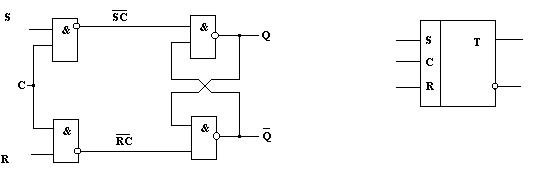
а) б)

Рис.10.8. Схема синхронного RS-триггера (а) и его условное

обозначение (б).

а) б)

Рис. 10.9. Схема двухступенчатого RS- триггера (а) и его условное обозначение (б).

В синхронном триггере при С=0 на входах БЯ действуют единичные сигналы и БЯ хранит старое состояние. Если С=1, то БЯ получает нулевой сигнал установки от того входа (S или R), на котором действует единица. При отсутствии единиц триггер сохраняет старое состояние. Таким образом, переключение разрешается только при подачи единицы на вход С.

Двухступенчатые триггеры называют также триггерами с внутренней задержкой и триггерами типа MS (master – slave), отражая наличие в триггере входной (главной) и выходной ступени, копирующей состояние входной. Триггеры типа MS надежно работают по сравнению с одноступенчатыми триггерами.

JK – ТРИГГЕР

Триггер типа JK- универсален, с раздельной установкой нулевого и единичного состояний. Вход J (Jerk – внезапное включение) для установки триггера в состояние 1 и вход K (Kill – внезапное отключение) для установки – 0. В отличие от RS-триггера в нем не запрещена одновременная подача сигналов на оба входа. При этом JK-триггер инвертирует старое состояние (табл.5)

Табл. 10.5

Qn+ı

Триггеру типа JK соответствует карта Карно (рис.10.10). Объединяя единицы, как показано на карте, получим характеристическое уравнение

Qn+ı = J Qn V K Qn

Рис. 10.10. Карта Карно для JK- триггера.

Схема синхронного JK – триггера показана на рис.11.

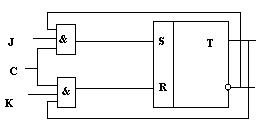Рис. 10.11. Схема синхронного JK- триггера.

Т- ТРИГГЕР

Триггер типа Т называется триггером со счетным входом Т (Toggle – релаксатор). Он изменяет свое состояние на противоположное каждый раз, когда на его вход приходит очередной сигнал (табл. 10.6).

Таблица 10.6

Qn+ı

Карта Карно для Т-триггера имеет вид

С помощью этой карты получаем характеристическое уравнение

Qn+ı = T Qn V T Qn

Рис. 10.12 Схема Т-триггера

D - ТРИГГЕР

Триггер типа D(elay – задержка) принимает информацию по одному входу. Его состояние повторяет входной сигнал, но с задержкой, определяемой тактовым сигналом (табл.7).

Таблица 10.7

Qn+ı

Из карты Карно(рис.13) имеем Qn+ı = D.

Рис. 10.13. Карта Карно D-триггера.

Схема D– триггера имеет вид ( рис.14)

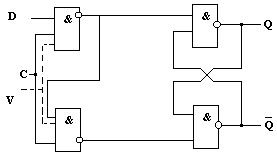Рис. 10.14. Схема D-триггера.

Триггер типа DV получается при добавлении в рассмотренную схему вход V, параллельно входу тактового сигнала С. При V=1 триггер работает обычным образом, а при V=0 триггер находится в режиме сохранения состояния.

Синтез произвольного триггера

Необходимо разработать синхронный двухвходовый триггер, функционирующий в соответствии с табл. 10.8 на базе БЯ.

Таблица 10.8.

Е1

Е2

Структура синтезируемого триггера в общем виде представлена на рис.15.

Рис. 10.15. Структура произвольного триггера.

Задача синтеза триггера заключается в построении комбинационной схемы (КС), преобразующей входные сигналы (Е1 и Е2) во выходные (f1 и f2) так, чтобы БЯ реализовала переходы произвольного триггера в соответствии с табл. 10.9.

Составление таблицы истинности КС осуществляется с учетом таблицы переходов синтезируемого триггера (табл. 10.8) и управляющей таблицы КБЯ (табл. 10.9).

Таблица 10.9.

Qn+ı

Таблица истинности (табл.10) содержит 16 наборов входных переменных (четыре входа – С, Е1, Е2, Qn) . Пятый столбец (Qn+ı) таблицы заполняется на основании таблицы переходов синтезируемого триггера (табл. 10.9), а шестой (f1) и седьмой (f2) столбцы – на основании управляющей таблицы БЯ ( табл. 10.9).

Таблица 10.10

Е1

Е2

Qn+ı

Из принципа работы синхронного триггера известно, что при С=0 триггер сохраняет старое состояние (Qn+ı=Qn), а при С=1 - работает в соответствии с таблицей переходов .

Карты Карно для f1 и f2 приведены на рис. 10.16 и 10.17.

Qn Е2

Е1

1

С

1

Рис. 10.16. Карта Карно для f1.

Qn Е2

С

~

Рис. 10.17. Карта Карно для f2.

Из карт Карно определяем

f1 = C + Е2 + Qn = C∙Е2∙Qn

f2 = C + Е1 + Qn = C∙Е1∙Qn

На основании полученных выражений строим схему произвольного триггера (рис. 10.18).

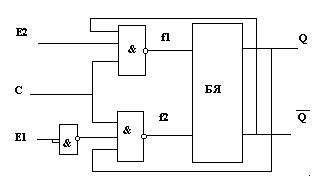Рис. 10.18. Схема произвольного триггера.

Студенты в соответствии таблицы вариантов должны синтезировать произвольный триггер (табл. 10.11).

Таблица 10.11

№

Е1

Е2

Qn+ı

№

Е1

Е2

Qn+ı

–Qn

Содержание отчета

1. Синтез заданных схем.

2. Схему произвольного триггера, схемы исследований.

3. Временные диаграммы работы и значения задержек сигналов.

4. Выводы.

Контрольные вопросы

1. Какие функции называются булевыми?

2. Какая система функций называется функционально полной?

3. В чем состоят задачи анализа, синтеза произвольного триггера?

4. Какой автомат является полностью заданным?

5. Какая логическая операция лежит в основе минимизации?

6. Какой автомат называется синхронным, асинхронным?

7. Как определить число состояний триггеров?

8. Для чего необходимо синтезировать произвольный триггер?

ЛАБОРАТОРНАЯ РАБОТА № 12

Синтез триггера на базе другого триггера

Цель работы: В практике построения цифровых устройств часто возникает задача синтеза триггера заданного типа на базе триггера другого типа.

Основные теоретические сведения

Пусть, имеется Т – триггер. Требуется построить RS-триггер. Функциональная схема RS-триггера, построенного на базе Т-триггера показана на рис.12.1.

Рис.12.1 Функциональная схема синтезируемого RS- триггера.

Из предыдущего раздела известно, что задача синтеза триггера сводится к задаче синтеза комбинационной схемы (КС). Таблица истинности КС составляется на основании совместного рассмотрения таблицы переходов RS –триггера (табл.3) и управляющей таблицы Т – триггера (табл.12.1.)

Таблица 12.1.

Qn Qn+ı

S R

J K

0 0

0 1

1 0

1 1

0 ~

1 0

0 1

~ 0

0 ~

1 ~

~ 1

~ 0

Таблица истинности КС (табл.12.2.) содержит 8 наборов входных переменных (S,R,Qn). Значение Qn+ı (четвертый столбец) определяется на основании таблицы переходов для RS – триггера, а значение Т (пятый столбец) – на основании управляющей таблицы Т – триггера.

Таблица 12.2.

Qn+ı

Карта Карно для функции Т имеет вид (рис. 12.2.)

Qn R

Рис.12.2. Карта Карно для функции Т.

Из карты Карно находим

Т = SQn v RQn

Функция Т в базисе И-НЕ имеет вид

T = SQn · RQn

На основании полученного выражения строим схему синтезируемого RS – триггера в базисе И-НЕ

Студенты должны синтезировать триггер заданного типа на основе триггера другого типа в соответствии таблицы вариантов (табл.12.3.).

Рис. 12.3. Синтезированный RS – триггер

Таблица 12.3.

Номер варианта

Тип исходного триггера

Тип синтезируемого триггера

Содержание отчета

1. Цель работы.

2. Постановка задачи.

3. Этапы синтеза и временная диаграмма работы произвольного триггера.

4. Этапы синтеза и временная диаграмма работы триггера заданного типа.

5. Заключение.

Контрольные вопросы

1. Что такое триггеры? Перечислите области их использования.

2. Приведите классификацию триггеров по определяющим признакам.

3. Какими параметрами и характеристиками определяется работа триггера?

4. Что такое элементарная запоминающая (бистабильная) ячейка?

5. Какими способами можно описать закон функционирования триггера?

6. Перечислите типы триггеров?

7. Перечислите разновидности RS – триггера?

8. Что такое асинхронные и синхронные триггеры?

9. Опишите работу универсального JK – триггера.

10. Опишите работу Т – триггера.

11. Опишите работу D – триггера.

12. Опишите работу двухступенчатого триггера.

13. Из каких этапов состоит синтез произвольного триггера на основе БЯ ?

14. Из каких этапов состоит синтез триггера заданного типа на основе триггера другого типа?

15. Приведите примеры использования триггеров.

ЛАБОРАТОРНЫЕ РАБОТЫ № 13, 14

СИНТЕЗ УНИВЕРСАЛЬНЫХ И СДВИГОВЫХ РЕГИСТРОВ

Цель работы: Регистры представляют собой совокупность соединенных определенным образом триггеров и вспомогательных схем, обеспечивающих выполнения некоторых операций. Целью данной работы является изучение функционирования и выполнение синтеза различных регистров, таких как, универсальные или сдвиговые регистры.

Основные теоретические сведения

Регистром называется устройство, предназначенное для приема, запоминания и выдачи информации, а также для выполнения над принятой информацией некоторых логические преобразования.

По выполняющим функциям регистры подразделяются на следующие типы:

1) с параллельной записью и параллельным считыванием информации;

2) с последовательной записью и параллельным считыванием информации (параллельно-последовательное преобразование информации)

3) с параллельной записью и последовательным считыванием (параллельно-последовательный преобразователь);

4) регистры сдвига (влево, вправо, циклический).

Регистр представляет собой совокупность соединенных определенным образом триггеров и вспомогательных схем, обеспечивающих выполнения некоторых операций, среди которых могут бать:

× Установка регистра в исходное состояние

× Прием информации их другого устройства

× Передача информации в другое устройство

× Сдвиг содержимого регистра

На рисунке 13.1. показана схема n разрядного регистра с параллельной записи информации.

При сигнале на входе С=1 в регистр записывается информация, содержащая на входах Д. При подаче сигнала 0 на вход R, регистр устанавливается в исходное состояние, т.е. на всех входах регистра будут нули.

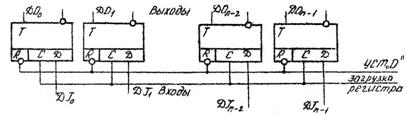
Рис. 13.1. Схема n разрядного регистра

В цифровых автоматах часто возникает задача хранения нескольких двоичных слов в непосредственной близости от устройства переработки информации, Для этого организуется массив регистров, в котором информация может передаваться из одного регистра в другой. Для обеспечения высокой скорости межрегистрового обмена, информация передается параллельным кодом, т.е. одновременно все n-разрядов.

На рис. 13.2. показана схема массива из n-регистров. Для обеcпечения межрегистрового обмена схема содержит n-мультиплексоров (М5), с помощью которых обеспечивается доступ к выходам любого регистра, Количество мультиплексоров определяется разрядностью регистра.

Подавая на управляющие входы мультиплексоров код адреса регистра передатчика, на шине данных (ШД) может получить его содержимое.

Для записи информации с ШД в необходимый регистр, нужно подать. на его вход С сигнал I - разрешения записи. Для формирования сигнала используется дешифратор (ДС), на входы которого подается код адреса регистра приемника. Число входов ДС определяется как:

K=log2(m+1)

гдe m - количество регистров.

Если К получается дробным, то его следует округлить до ближайшего большего целого числа

В исходном состоянии на входах мультиплексоров и дешифратора подан код, состоящий из одних нулей, (00, ,0), поэтому не один из регистров не выбран. Часто в цифровых автоматах требуется производить сдвиг содержимого регистра влево или вправо на определенное число разрядов. Эту операцию выполняет регистры сдвига.

Регистр сдвига, в котором для хранения информации используется n-триггера, называется n-разрядим регистром сдвига. Принято считать крайний левый разряд старшим, а правый - младшим. Старший разряд имеет номер 0, младший (n-1). В связи о этим говорят о правом и левом сдвиге

В общем случае операция сдвига в регистре состоит в передаче информации из i-го триггера j+i, затем иp, j-і-го в і-й триггер. Освобождающиеся разряды могут заполняться нулями .или принимать информацию извне.

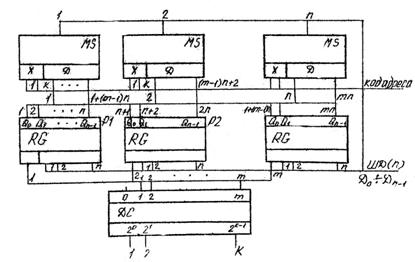
Рис. 12.2. Схема регистра сдвига.

Сдвиг информации может теряться или передаваться в другие устройства автомата для переработки.

Иногда старший разряд соединяется с младшим, т.е. регистр замыкается в кольцо. В этом случаи можно осуществлять циклический сдвиг информации.

Основная особенность триггеров и комбинационных схем состоит в том, что они должны допускать возможность в самом простом случае выдачу информации в следующий триггер и одновременно прием из предыдущего. Особе значение имеет при этом тип используемого триггера. На рис. 12.3. приведены схемы регистров сдвига на однокаскадных, и двухкаскадных триггерах.

Рис. 12.3. Схема регистра сдвига.

Для сдвига информации в регистре на однокаскадных триггерах используются две шины сдвига (а) ШС1 и ШС2. Для записи информации из четных триггеров в нечетные служит шина ШС1, а из нечетных в четные шина ШС2. Нечетный триггер служит для хранения информации при выполнении операции сдвига. В первом такте сигнал сдвига подается на шину ШС1, а во втором на шину ШС2.

В схеме регистра на двух каскадных триггерах необходима только одна шина сдвига (б). Работу регистра на двух каскадных триггерах можно проследить по временной диаграмме, показанной на рис. 12.4..

Рис. 12.4. Временная диаграмма.

По временной диаграмме может быть определено быстродействие регистра - Тсдв. Значение Тсдв равно интервалу между моментом поступления сдвигового импульса до момента завершения переходного процесса в схеме. Из временной диаграммы (рис. 12.4.) значение определяется как Тсдв=t_ф +t_зфт +t_u_.

Если требуется сдвинуть информацию на К разрядов, то нужно сделать К раз последовательный сдвиг. Для сокращения времени выполнения этой операции схема регистра дополняется мультиплексорами. Число разрядов на которое нужно произвести сдвиг, определяется кодом, подаваемым на управляющие входы мультиплексоров. На рис. 12.5. приведена схема регистра сдвига, допускающая сдвиг информации на 1, 2, … d разрядов. Перед началом сдвига на управляющих входах мультиплексорах устанавливается код числа разрядов, на которые нужно сдвинуть хранимое в регистре число. В результате мультиплексор коммутирует вход i-го триггера с выходом необходимого (i-k)-го триггера, затем подает импульс сдвига на шину ШС и операция завершена.

Рис. 12.5. Схема регистра сдвига.

Используя мультиплексоры, можно построить реверсивные регистры сдвига, т.е. такие, которые допускают сдвиг информации, как и налево, так и направо. Для этого необходимо часть входов мультиплексоров соединить с триггерами, находящихся не только с права, но и слева. Тогда часть кода будет определять сдвиг вправо, а другая сдвиг влево.

В современных цифровых автоматах, как правило, регистры сдвига имеет возможность параллельной записи и считывания информации. Для этого каждый триггер снабжен необходимыми логическими схемами для реализации логических функций схемы. На рис. 12.6. приведена схема такого регистра.

Рис. 12.6. Схема регистра сдвига.

Если на входе последовательно-параллельный сигнал 1, то при подачи сигнала на ШС происходит сдвиг информации или последовательная запись.

Если сигнал последовательно-параллельный равен 0, то в регистр записывается информация, содержащаяся на входах Ji , т.е. происходит параллельная запись информации.

Такой регистр можно использовать как последовательно-параллельный преобразователь информации и наоборот (параллельно-последовательный).

Синтез регистров cдвига

Общая функциональная схема регистра сдвига приведена на рис. 12.7.

Рис. 12.7. Схема регистра сдвига.

На входы комбинационной схемы (КС) поступают сигналы с выходов триггеров регистра и внешние сигналы управления Уі , і=1,m которые определяют цепи сдвига от одних триггеров к другим и запрещают работу остальных цепей. Сигналы с выходов КС подаются на входы триггеров. Функции возбуждения входов I -го триггера можно записать в следующем виде:

При заданных типах триггеров задача проектирования регистра сводится к составлению функций возбуждения входов каждого триггера и минимизации найденных выражений.

Известно, что функционирование любого триггера можно задать с помощью Таблицы переходов. Однако, непосредственное использование этой таблицы для синтеза создает ряд трудностей, которые могут быть обойдены, если преобразовать ее в матрицу переходов. Элементы матрицы переходов q Q(t) представляют собой значения сигнала Ек, под воздействием которого триггер К переходит из состояния Q{t) в Q(t).

Каждый элемент матрицы может быть равен 0, I или его значение
может быть неопределенным.

Рассмотрим процедуру преобразования таблицы переходов в матрицу для JK – триггера.

Для JK – триггера из таблицы 13.1. получим упрощенную таблицу переходов (табл. 13.2.).

На следующих этапах синтеза регистра необходимо определить число управляющих шин и уточнить функции возбуждения триггеров с учетом матрицы переходов и требований, предъявляемых к проектируемому регистру.

Таблица 13.1.

t			t+1
J	K	Q(t)	Q(t+1)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Таблица 13.2.

Q(t)->Q(t+1)	J	K
0->0	0	~
0->1	1	~
1->0	~	1
1->1	~	0

Очевидно, достаточно рассмотреть выражения для одного триггера, поскольку схема регистра состоит из одинаковых схем, т.е. она регулярна.

Рассмотрим пример синтеза. Необходимо синтезировать реверсивный регистр сдвига (регистр, имеющий возможность сдвига влево и вправо), Так как число выполняемых операций не превышает 2, то достаточно иметь одну шину управления;

Строим таблицу переходов, при этом будем считать, что при У=0 осуществляется сдвиг на один разряд вправо, и У =1 на один разряд влево.

Таблица 13.3.

t				t+1	t
Y	Q_i-1	Q_i	Q_i+1	Q_i	J_i	K_i
0	0	0	0	0	0	~
0	0	0	1	0	0	~
0	0	1	0	0	~	1
0	0	1	1	0	~	1
0	1	0	0	1	1	~
0	1	0	1	1	1	~
0	1	1	0	1	~	0
0	1	1	1	1	~	0
1	0	0	0	0	0	~
1	0	0	1	1	1	~
1	0	1	0	0	~	1
1	0	1	1	1	~	0
1	1	0	0	0	0	~
1	1	0	1	1	1	~
1	1	1	0	0	~	1
1	1	1	1	1	~	0

Левые пять столбцов таблицы 13.3. представляют собой таблицу переходов для і-го триггера, проектируемого регистра. Следующие 2 столбца определяют функции возбуждения триггера при условии, что регистр строится на JK – триггерах, Рассмотрим первую строку таблицы 3. для триггера. При У =0 триггер і (состояние Q = 0) должен осуществить переход 0—0 в соответствии с матрицей переходов для JK – триггера J = 0, а K = ~ , Аналогично заполняются остальные строки таблицы для триггера.

Таким образом функции возбуждения триггеров заданы и необходимо произвести минимизацию, для этого следует воспользоваться картами Карно.

На рис. 12.8. Приведены карты для функций возбуждения JK – триггера:

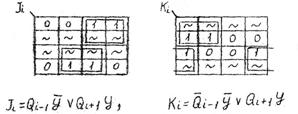
рис. 12.8.

На рис. 12.9. Карта Карно реверсивного регистра сдвига.

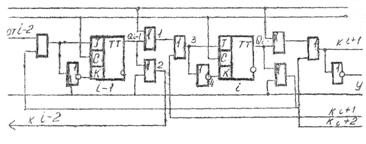
рис. 12.9. Схема реверсивного регистра сдвига на триггерах.

Учитывая того, что синтез регистров проводится на подобия синтеза счетчиков, более подробно данный процесс приводится в разделе синтез синхронного счетчика (см. таблицу 15.1. синтеза синхронного счетчика).

Итак, рекомендуется следующий порядок синтеза регистра:

1. Выписать исходные данные для синтеза.

2. Построить граф переходов.

3. Построить таблицу переходов и на основании ее анализа с помощью управляющей таблицы соответствующего триггера определить значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

4. Определить схему реализации регистра.

Таблица 13.4 Варианты.

№	Операция сдвига	Тип триггера	Код
1	Влево 1 разряд, вправо 1 разряд	D	0001
2	Влево 1 разряд, вправо 2 разряд	JK	0010
3	Влево 1 разряд, вправо 3 разряд	RS	0011
4	Влево 1 разряд, вправо 4 разряд	SR	0100
5	Влево 2 разряд, вправо 1 разряд	T	0101
6	Влево 2 разряд, вправо 2 разряд	D	0110
7	Влево 2 разряд, вправо 3 разряд	JK	0111
8	Влево 2 разряд, вправо 4 разряд	RS	1000
9	Влево 3 разряд, вправо 1 разряд	SR	1001
10	Влево 3 разряд, вправо 2 разряд	T	1010
11	Влево 3 разряд, вправо 3 разряд	D	1011
12	Влево 3 разряд, вправо 4 разряд	JK	1100
13	Влево 4 разряд, вправо 1 разряд	RS	1101
14	Влево 4 разряд, вправо 2 разряд	SR	1110
15	Влево 4 разряд, вправо 3 разряд	T	1111
16	Влево 4 разряд, вправо 4 разряд	D	0001
17	Влево 1 разряд, вправо 1 разряд	JK	0010
18	Влево 1 разряд, вправо 2 разряд	RS	0011
19	Влево 1 разряд, вправо 3 разряд	SR	0100
20	Влево 1 разряд, вправо 4 разряд	T	0101
21	Влево 2 разряд, вправо 1 разряд	D	0110
22	Влево 2 разряд, вправо 2 разряд	JK	0111
23	Влево 2 разряд, вправо 3 разряд	RS	1000
24	Влево 2 разряд, вправо 4 разряд	SR	1001
25	Влево 3 разряд, вправо 1 разряд	T	1010
26	Влево 3 разряд, вправо 2 разряд	D	1011
27	Влево 3 разряд, вправо 3 разряд	JK	1100
28	Влево 3 разряд, вправо 4 разряд	RS	1101
29	Влево 4 разряд, вправо 1 разряд	SR	1110
30	Влево 4 разряд, вправо 2 разряд	T	1111

Содержание отчета

1. Цель работы;

2. Постановка задачи;

3. Этапы синтеза регистра;

Контрольные вопросы:

1. Назначение и применение регистра.

2. Реализация регистров различного типа.

3. Реверсивные регистры.

ЛАБОРАТОРНЫЕ РАБОТЫ № 15, 16

СИНТЕЗ СЧЁТЧИКОВ

Цель работы: В данной работе требуется синтезировать синхронный счетчик с произвольным коэффициентом счета на основе триггеров заданного типа. Целью работы является построение схемы формирования блокирующего сигнала аварийной тревоги и временной диаграммы работы счётчика.

Основные теоретические сведения

Счетчиком называют устройство, сигналы, на выходе которого в определенном коде отображают число импульсов, поступивших на счетный вход. Счетчики подразделяются на два класса: синхронные (управляемые временем) и асинхронные (управляемые событием).

Главным образом применяются счетчики с циклически повторяющейся последовательностью состояний, которые называют счетчиками по модулю. Термин модуль (коэффициент счета Ксч) используется также для обозначения числа различных состояний в счетной последовательности.

Счетчики синтезируют из элементов памяти, таких, как триггеры и элементов комбинационной логики.

Принцип построения счетчиков с произвольными (недвоичными) коэффициентами счета состоит в исключении некоторых устойчивых состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика. Обратные связи образуют введением дополнительных логических цепей, соединяющих входы и выходы соответствующих триггеров.

Число избыточных состояний М для любого счетчика определяется из следующего выражения:

M = 2ⁿ – Ксч,

где n – количество триггеров в счетчике, Ксч – требуемый коэффициент счета, 2ⁿ – число устойчивых состояний двоичного счетчика.

Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения:

n = ] log₂ Ксч [,

где ] log₂ Ксч [– двоичный логарифм заданного коэффициента пересчета Ксч, округленный до большего целого числа.

Один из методов синтеза счетчиков заключается в построении таблицы переходов, в первых столбцах которой будут отражены текущие состояния триггеров счетчика, а затем – следующие за ними состояния. Анализ таблицы позволяет установить те переходы, которые должны быть сделаны триггерами, входящими в состав счетчика. Затем с помощью управляющей таблицы соответствующего триггера (управляющие таблицы JK, D, T –триггеров представлены на рис. 15.1.) находятся значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

Рассмотрим порядок синтеза на примере синхронного двоично-десятичного счетчика. Предположим, что для реализации счетчика выбран JK-триггер.

На рис. 15.2. показан граф переходов двоично-десятичного счетчика, а в таблице 15.1.– таблица переходов.

Q^t

Q^t+1

Q^t

Q^t+1

Q^t

Q^t+1

б)

в)

Рис. 15.1. Управляющие таблицы а) JK-триггера, б) D-триггера, в) T-триггера

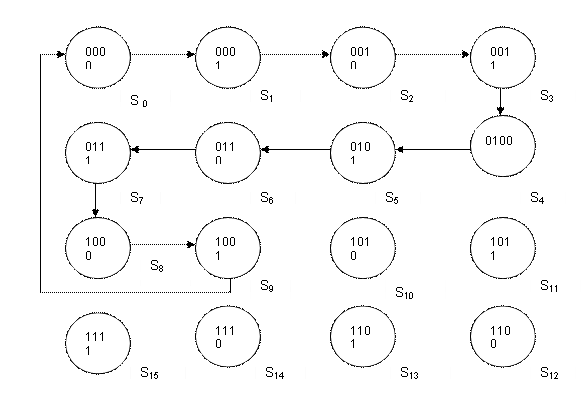
Рис. 15.2. Граф переходов двоично-десятичного счетчика

Граф счетчика изображается в виде совокупности вершин, каждой из которых ставится в соответствие одно из внутренних состояний автомата, и дуг, соединяющих вершины графа и соответствующих переходам между состояниями. Вершины изображаются кружочками, а дуги стрелками. Направленность графа, которая отображается дугами, позволяет проследить последовательность переключений состояний автомата. В каждую вершину графа вписывается символ внутреннего состояния, которому соответствует данная вершина.

Таблица 15.1.

Q^t₄

Q^t₃

Q^t₂

Q^t₁

Q^t+1₄

Q^t+1₃

Q^t+1₂

Q^t+1₁

J₄

K₄

J₃

K₃

J₂

K₂

J₁

K₁

В правой части таблицы 15.1. приведены значения входных сигналов четырех триггеров. Для поиска этих значений были проанализированы те переходы, которые должны быть сделаны, а затем с помощью управляющей таблицы (см. рис. 15.1.) определены соответствующие значения J и K входов триггеров.

На рис 15.3. приведены карты Карно для логических функций, которым должны соответствовать сигналы, присутствующие на управляющих входах триггеров[1].

J₄ Q₂ K₄ Q₂

Q₁ Q₁

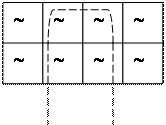Q₃ Q₃

d

d

1

d

d

~

~

Q₄ Q₄

J₃ Q₂ K₃ Q₂

Q₁ Q₁

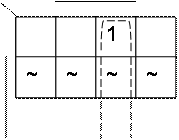Q₃ Q₃

Q₄ Q₄

J₂ Q₂ K₂ Q₂

Q₁ Q₁

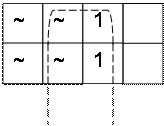Q₃ Q₃

Q₄ Q₄

Рис. 15.3. Карты Карно для логических функций комбинационной логики двоично-десятичного счетчика

После минимизации методом карт Карно для входов J и K были получены следующие выражения:

J₄ = Q₁ Q₂ Q₃; K₄ = Q₁;

J₃ = Q₁ Q₂; K₃ = Q₁ Q₂;

J₂ = Q₁ Q₄; K₂ = Q₁.

Просмотр столбцов J₁ и K₁ в табл.1 показывает, что все значения равны либо ~, либо 1. И, так как неиспользуемые состояния могут также участвовать в процессе упрощения, то все ячейки карт Карно для J₁ и K₁ оказываются заполненными символами “~”, “1” и “d”. Следовательно, J₁=K₁=1. На рис. 15.4 показана реализация двоично-десятичного счетчика.

Если счетчик из-за неисправности окажется в одном из запрещенных (неиспользуемых) состояний, то его работа может быть прервана специальным синхросигналом и также может быть подан сигнал тревоги. Обнаружить то, что счетчик находится в запрещенном состоянии, позволяет схема, реализующая выражение, описывающее функцию неиспользуемых состояний:

f_Н = Q₂ Q₄ + Q₃ Q₄

Функция получена f_Н в результате охвата контурами клеток с записанными в них знаками d, обозначающими, как уже указывалось, неиспользуемые состояния счетчика.

Выражение, описывающее новый сигнал синхронизации, имеет вид:

C´ = f_Н · C

Следовательно, когда f_Н = 1, то C´ = 0, и синхроимпульсы будут отсутствовать до тех пор, пока счетчик не выйдет из запрещенного состояния.

Важным методом представления состояния счетчиков является временная диаграмма, которая используется при анализе и наладке. Временная диаграмма двоично-десятичного счетчика, схема которого представлена на рис. 15.4, заданного графом переходов рис. 15.2 и таблицей переходов табл. 15.1. приведена на рис. 15.5.

2⁰ 2¹ 2² 2³

Q₁ Q₂ Q₃ Q₄

TT

T₁

J

C

K

TT

T₂

J

C

K

TT

T₃

J

C

K

TT

T₄

J

C

K

«1»

«1» Q₁ Q₂ Q₃ Q₄

&

&

&

&

&

&

Q₁ Q₁ Q₃

Q₄

Q₂

Рис. 15.4. Схема реализации двоично-десятичного счетчика

s₀ s₁ s₂ s₃ s₄ s₅ s₆ s₇ s₈ s₉ s₀

Рис. 15.5. Временная диаграмма двоично-десятичного счетчика

Все изменения состояний триггеров происходят во время формирования отрицательных фронтов тактовых импульсов, что обусловлено применением двухступенчатых триггеров. На временных диаграммах выходов Q₁ … Q₄ присутствуют двоичные цифры, характеризующие состояние (текущее) счетчика.

Итак, рекомендуется следующий порядок синтеза счетчика:

5. Выписать исходные данные для синтеза.

6. Построить граф переходов.

7. Построить таблицу переходов и на основании ее анализа с помощью управляющей таблицы соответствующего триггера определить значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

8. Определить схему реализации синтезируемого счетчика.

9. Начертить временную диаграмму синтезированного счетчика.

Таблица 15.2. Варианты.

№

Тип счётчика

Тип триггера

Модуль счёта

Суммирующий

Вычитающий

Суммирующий

Вычитающий

Суммирующий

Вычитающий

Суммирующий

Вычитающий

Суммирующий

Вычитающий

Суммирующий

Вычитающий

Суммирующий

Суммирующий Вычитающий

Суммирующий

Вычитающий

Содержание отчета

1. Цель работы;

2. Постановка задачи;

3. Этапы синтеза двоично-десятичных счетчиков;

4. Временные диаграммы двоично-десятичных счетчиков;

5. Двоично-десятичные счетчики с произвольным коэффициентом счета.

Контрольные вопросы:

1. Назначение и применение двоично-десятичных счетчиков.

2. Реализация двоично-десятичных счетчиков различного типа.

3. Суммирующие и вычитающие двоично-десятичные счетчики.

4. Реверсивные двоично-десятичные счетчики.

5. Двоично-десятичные счетчики с различным коэффициентом деления.

ЛАБОРАТОРНЫЕ РАБОТЫ № 17, 18

СИНТЕЗ ПРОГРАММИРУЕМЫХ ЛОГИЧЕСКИХ МАТРИЦ

Цель работы: В общем случае программируемые логические матрицы представляют собой логическую схему для преобразования комбинаций. Целью данной работы является изучение способов синтеза ПЛМ, построение схем и логических программируемых матриц

Основные теоретические сведения

Синтез логических устройств на программируемых логических матрицах. В настоящее время успехи микроэлектроники и создание элементов четвертого поколения в виде больших интегральных схем (БИС) открывают новые перспективы и возможности при создании различных цифровых устройств дискретной автоматики.

Создаваемые современные БИС обладают универсальностью и специализацией, которые допускают "программируемым" поведением и выполнением в данном конкретном случае требуемых функций. Представителями БИС указанного типа являются программируемые логические матрицы (ПЛМ). В общем случае программируемые логические матрицы представляют собой логическую схему для преобразования комбинаций X = x1, x2, …, xn входного двоичного кода в cоответcтвующие комбинации У = y1, y2,…, ym выходного двоичного кода. Структурная схема простейшей ПЛМ (рио. І7.1.а) состоит из двух матриц МІ и М2. Условное обозначение ПЛМ приведено иа рис. 17.1.6.

Рис 17.1. Условное обозначение ПЛМ.

Число входов х1,…, хn и выходов y1,…,ym в ПЛМ ограничено и зависит от степени интеграции БИС. Инверсные входы х1,…, хn л образуются непосредственно в буфере ПЛМ, выполняющем инверсию НЕ. В матрице М1 формируются l конъюнкций yi =f(х1,…, хn), i=1,…,l от прямых и инверсных входных переменных, сопоставленных с прямыми и инверсными входами ПЛМ. Выходы Z1,…,Zl матрицы М1, которым соответствуют образованные в МІ конъюнкции являются входами матрицы М2, ,в которой конъюнкции Z1,…,Zl логически Суммируются, образуя дизъюнктивные нормальны формы (ДНФ) функций y1,…,ym описывающих сигналы на одноименных выходах матрицы М2[9]. При этом в ПЛМ допускается настройка (программирование) и МІ, и'М2 путем изменения состава входов в логические элементы как И, так и ИЛИ. Если рассматривать построенную внутреннюю структуру ПЛМ, приведенную на рис. 17.1., то ее можно представить в видов системы вертикальных и горизонтальных шин , в каждой точке пересечения которых стоит элемент (диод, транзистор и т.п.), соединяющий соответствующие горизонтальную и вертикальную шины (рио. 17.2.). В зависимости от шины применяемых элементов различают биполярные ПЛИ и МОП (металл, окисел, полупроводник) ПЛМ. На рис. 17.3., а представлены возможные элементы в МІ и М2 ПЛМ, а на рис. 17.3.– МОП ПЛМ.

Рис 17.2-17.3(а,б) Возможные элементы в МІ и М2 ПЛМ.

Характеристики некоторых ПЛМ приведены в таблице 17.1. В зависимости от способа настройки (программирования) элементов матриц МІ и М2 различают два основных типа ПЛМ: 1) программируемые в процессе изготовления; 2) программируемые пользователем.

В ПЛМ первого типа информация заносится в матрицы путем подключения элементов к шинам благодаря металлизации нужных участков схемы, что выполняется с помощью фотошаблона (маски). Никаких изменений в схеме пользователь в этом случае в ходе эксплуатации ПЛМ сделать не сможет. Подобным способом изготовляются ПЛМ, встраиваемые в микропроцессор БИС, автономные ПЛМ стандартного микропрограммного обеспечения.

Таблица 17.1.

ПЛМ второго типа поставляются не до программированными и их функциональная ориентация производится пользователем с помощью специального оборудования, причем существует ПЛМ с однократной записью информации и перепрограммируемые ПЛМ, в которых записанная информация может быть стерта ультрафиолетовыми или рентгеновскими лучами.

Рассмотрим методику синтеза цифровых автоматов на ПЛМ. Для синтеза на ПЛМ как при синтезе обычных логических элементов предварительно производится минимизация этих функций. В качестве примера рассмотрим синтез преобразователя кода 8421 в код 242І заданный после минимизации формулами. Реализацию рассмотрим на биполярной ПЛМ. Следует отметить, что при минимизации системы функций необходимо стремиться получить не минимальные, а кратчайшие ДНФ, причем такие, которые имели бы большее число одношаговых конъюнкций.

Прежде чем реализовать полученную систему ДНФ на ПЛМ, удобно составить сокращенную таблицу соответствия (табл. 17.2.).

В таблице 17.2. строки соответствуют горизонтальным шинам матрицы М1 и М2

В левой части таблицы (МІ) единицами отмечаются переменные Xi , если они входят в минтерм Zk2 без инверсии; нулями - переменные Xi, если они входят Zk2 с инверсией, косыми крестами (*) - переменные Хi, не входящие в минтерм Zk2..

В правой части таблицы (соответствующей матрице М2) единицами в каждом столбце отмечены минтермы Zk2, входящие в качестве дизъюнкции в соответствующие функции Zk2. Реализация преобразователя на ПЛМ показана на рис. 17.4.

Таблица 17.2.

Рис 17.4. Преобразователи на ПЛМ.

Содержание отчета

1. Синтез заданных схем.

2. Схему ПЛМ, схемы исследований.

3. Временные диаграммы работы и значения задержек сигналов.

4. Выводы.

Вопросы для самоконтроля и задачи

1. Составьте таблицу состояния и с ее помощью опишите работу

2. одноразрядного комбинационного сумматора.

3. Объясните разницу между сумматорами с последовательным и ускоренным переносом.

4. Проведите синтез четырехразрядного сумматора с ускоренным переносом.

5. Проведите синтез мультиплексора 8x1.

6. Проведите синтез дешифратора 1x8.

7. Напишите систему булевых выражений для мультиплексоров 8x1 и

8. демультиплексоров 1х8.

9. Приведите схему передачи информации с использованием мультиплексоров и демультиплексоров для четырехразрядного слова.

10. Напишите систему булевых выражений, реализуемых в полном двухкаскадном дешифраторе 4x16.

11. Проведите синтез полного матричного дешифратора 4x16.

12. Проведите синтез трехразрядного сравнивающего устройства.

13. Спроектируйте на элементах И-НЕ схему преобразования кода 2 из 5 и код Джонсона.

14. Опишите особенности, перечислите преимущества и области применения ПЛМ

15. Проведите синтез на ПЛМ преобразователя кода 2 из 5 в код Джонсона.

СПИСОК ЛИТЕРАТУРЫ

1. Преснухин Л.Н., Воробьев Н.В., Шишкевич А.А. Расчет элементов цифровых устройств. М.: Высш.шк., 1991, 526 с.

2. Угрюмов Е.П. Цифровая схемотехника. Учеб. пособие для вузов.- 2- изд. перераб. и доп.-СПб. БХВ – Петербург. 2005.-800 с.:ил.

3. Калабеков Б.А. Цифровые устройства и микропроцессорные системы. Учебник.-М.:Горачая линия- Телеком.,2003 г.-336.

4. Суворов В.И., Юнусов Д.Ю. Методическое руководство по лабораторно-практическим занятиям по курсу «Основы цифровой техники и микропроцессоры» (№ 47). ТЭИС, 1984, 118 с.

5. Хокинс Г. Цифровая электроника для начинающих: Пер. с англ. М.: Мир, 1986, 232 с.

6. Гольденберг Л.М. и др. Цифровые устройства и микропроцессорные системы. Задачи и упражнения: Учеб. пособие для вузов. М.: Радио и связь, 1992, 256с.

7. Абдурахманов Р.П., Баширов Р.В., Амирсаидов У.Б. Задания к контрольной работе и методические указания к их выполнению по курсу «Цифровая и вычислительная техника». ТЭИС, 1995, 30 с.

8. Преснухин Л.Н., Воробьев Н.В., Шишкевич А.А. Расчет элементов цифровых устройств. – М.: Высш.шк., 1991. – 526 с.

9. Угрюмов Е.П. Проектирование элементов и узлов ЭВМ . – М.: Высш.шк., 1987. – 318 с.

10. Суворов В.И., Юнусов Д.Ю. Методическое руководство по лабораторно-практическим занятиям по курсу «Основы цифровой техники и микропроцессоры» (№ 47). – ТЭИС, 1984. – 118 с.

11. Гольденберг Л.М. Цифровые устройства и микропроцессорные системы.

12. Задачи и упражнения.: Учеб. Пособие для вузов. М.: Радио и связь, 1992.

13. Гольденберг Л.М. Цифровые устройства на интегральных схемах в связи. М.: Радио и связь, 1979, 232 с.

14. Абдурахманов Р.П., Баширов Р.В., Амирсаидов У.Б. Задания к контрольной работе и методические указания к их выполнению по курсу «Цифровая и вычислительная техника». – ТЭИС, 1995. – 30 с.

15. Преснухин Л.Н., Воробьев Н.В., Шишкевич А.А. Расчет элементов цифровых устройств. – М.: Высшая школа, 1991. – 526 с.

16. Угрюмов Е.П. Проектирование элементов и узлов ЭВМ . – М.: Высшая школа., 1987. – 318 с.

17. Суворов В.И., Юнусов Д.Ю. Методическое руководство по лабораторно-практическим занятиям по курсу «Основы цифровой техники и микропроцессоры» (№ 47). – ТЭИС, 1984. – 118 с.

18. Абдурахманов Р.П., Баширов Р.В., Амирсаидов У.Б. Задания к контрольной работе и методические указания к их выполнению по курсу «Цифровая и вычислительная техника». – ТЭИС, 1995. – 30 с.