УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра Системы телематика

Джураев Р.Х., Джаббаров Ш.Ю., Умирзаков Б.М., Хамраев Э.А

Помехоустойчивые коды в телекоммуникационных

системах

Учебное пособие

Ташкент 2008

УДК 621.391

Авторы: Джураев Р.Х., Джаббаров Ш.Ю., Умирзаков Б. М., Хамраев Э.А

В учебном пособии рассмотриваются теоретические основы кодирования и применения помехоустойчивых кодов в телекоммуникационных системах. Описываются принципы построения помехоустойчивых кодов, даны их классификация и сравнительные характеристики, приведены алгоритмы кодирования и декодирования основных помехоустойчивых кодов (Голея, БЧХ, Файра и Рида – Соломона).

Учебное пособие предназначено для бакалавров и магистров, изучающих вопросы помехоустойчивого кодирования, а также для специалистов по защите информации от ошибок.

ОГЛАВЛЕНИЕ

	Введение …………………………………………………………….	4
1.	Методы повышения верности на основе помехоустойчивых кодов…................................................	6
1.1.	Классификация и основные параметры помехоустойчивых кодов………………………………………………………………......	6
2.	Принципы построения циклических кодов………..	26
2.1.	Определение циклических кодов и их свойства……………………	26
2.2.	Мажоритарное декодирование………………………………………	32
2.3.	Принципы обнаружения и исправления ошибок помехоустойчивыми кодами………………………………………...	34
2.4.	Способы исправления ошибок на основе синдрома ошибок, свойства цикличности и анализ веса остатка………………...……..	37
3.	Помехоустойчивые коды для коррекции независимых ошибок………………………………………..	42
3.1.	Принцип кодирования и декодирования кода Голея………………	44
3.2.	Принцип построения кода БЧХ……………………………………...	52
3.3.	Принцип кодирования и декодирования кода БЧХ………………..	53
4.	Помехоустойчивые коды для коррекции пакетов ошибок……………………………………………………………...	80
4.1.	Принцип построения кода Файра……………………………………	80
4.2.	Принцип кодирования и декодирования кода Файра……………...	81
4.2.1	Принцип кодирования кода Файра…………………………………	81
4.2.2	Принцип декодирования кода Файра………………………………	82
4.3.	Принцип кодирования и декодирования кода Рида-Соломона……	88
4.3.1	Принцип кодирования кода Рида-Соломона………………………	88
4.3.2	Принцип декодирования кода Рида-Соломона……………………..	89
4.4.	Алгоритм программной реализации кода Голея…………………...	91
4.5.	Алгоритм программной реализации кодера и декодера кода БЧХ.	94
4.5.1	Алгоритм программной реализации кодера кода БЧХ……………	94
4.5.2	Алгоритм программной реализации декодера кода БЧХ………….	95
4.6.	Алгоритм программной реализации кодера и декодера кода Файра………………………………………………………………….	96
4.6.1	Алгоритм программной реализации кодера кода Файра …………	96
5.2.	Алгоритм программной реализации декодера кода Файра………..	97
4.7.	Алгоритм программной реализации кодера и декодера кода Рида-Соломона ……………………………………………………………..	99
4.7.1	Алгоритм программной реализации кодера кода Рида-Соломона………...................................................................................	99
4.7.2	Алгоритм программной реализации декодера кода Рида-Соломона………...................................................................................	100
	СПИСОК ЛИТЕРАТУРЫ……………………………………………	104

Введение

Происходящие в последние десятилетия динамичные изменения в различных сферах деятельности общества характеризуются лавинообразным ростом объемов самой различной информации: социально – политической, производственной, научной, культурной и др. Международная практика показывает, что информационный потенциал в обществе начинает все большие определять его экономический потенциал наравне с материальным производством. Экономическое развитие такого общества будет целиком определяться результатами интеллектуальной деятельности. Это связано с возрастающей ролью информации, которая становится определяющей в развитии различных сфер деятельности общества.

Общемировой тенденцией является быстрое развитие информационно – коммуникационных технологий (ИКТ) и их интенсивное внедрение во все сферы общественной жизни с целью предоставления разнообразных услуг. Широкое использование ИКТ ведет к появлению новых форм социальной и экономической деятельности: дистанционное образование, телемедицина, телеработа, электронная торговля и др.

В последние годы сфера связи и информатизации становится одной из важнейших инфраструктур страны и ей принадлежит особая роль во многих сферах деятельности общества. Важной задачей является создание и развитие инфокоммуникационной инфраструктуры и её основы – телекоммуникационных сетей и систем.

Вследствие создания современных телекоммуникационных сетей и систем обеспечивается широкая доступность разнообразной информации, которая становится основным производственным ресурсом и основным товаром в обществе. Именно достоверная информация все больше определяет эффективность работы в различных сферах деятельности общества.

Передаваемая в виде различных сигналов информация может представлять собой речь, данные, видеоизображение или любую их комбинацию, называемую мультимедийной.

Тенденция к увеличению количества передаваемой по сети телекоммуникаций мультимедийной информации неизбежно приводит к возрастанию информационных потоков, а резкий рост потребностей в обмене мультимедийной информацией – вызвал необходимость создания современных высокоскоростных телекоммуникационных систем.

Известно, что уровень требований, предъявляемых к современным системам и сетям телекоммуникаций постоянно повышается по следующим основным причинам:

- расширение числа видов услуг, в которых заинтересованы пользователи;

- высокая пропускная способность и хорошая масштабность;

- повышение уровня требований к качеству обслуживания (прежде всего, к достоверности приема и ко времени доставки информации).

Поэтому одной из важнейших задач при построении современных телекоммуникационных систем является обеспечения высокой достоверности информации в процессе её передачи, хранения и обработки.

В современных телекоммуникационных системах обеспечение достоверности приема 10^-6÷10^-9 невозможно без применения помехоустойчивых кодов с высокой обнаруживающей и исправляющей способностью. Таким образом, помехоустойчивое кодирование является одним из основных путей решения задачи повышения достоверности в телекоммуникационных системах.

1. Методы повышения верности на основе помехоустойчивых кодов

1.1 Классификация и основные параметры помехоустойчивых кодов

Проблема повышения верности обусловлена несоответствием между требованиями, предъявляемыми при передаче данных и качеством реальных каналов связи. В сетях передачи данных требуется обеспечить верность не хуже 10^-6 – 10^-9, а при использовании реальных каналов связи и простого (первичного) кода указанная верность не превышает 10^-2 - 10^-5.

Вследствие этого глубокое изучение статистических характеристик реальных каналов связи таких, как помехи, ошибки должно предшествовать анализу и проектированию систем передачи информации. Так как выбор метода борьбы с ошибками, базируется на той или иной модели источника ошибок, то в соответствии с установленной моделью тот или иной метод должен быть ориентирован на борьбу с наиболее вероятными ошибками. Таким образом, правильный выбор метода повышения верности в значительной степени зависит от адекватности принятой за основу модели источника помех, искажений, ошибок, характеристикам канала связи.

Можно выделить следующие из известных основных направлений повышения верности передачи информации по каналам связи:

· Сокращение числа и уменьшение интенсивности действия источников помех и искажений на основе использования мер эксплуатационно-профилактического характера;

· Повышение помехоустойчивости передачи и приема самих сигналов, за счет использования более совершенных способов передачи и модемов, включая вероятностные методы обнаружения ошибок;

· Повышение помехоустойчивости передачи сообщений за счет использования помехоустойчивых кодов.

Анализ современного состояния и тенденций развития методов повышения достоверности показывает, что решение задачи по созданию высокоэффективных систем передачи информации видится на путях использования как инвариантного, так и адаптивного подхода. Рассмотрим вначале способы передачи, которые инвариантны (нечувствительны) относительно действия основных видов помех действующих в канале связи. Известно, что одной из актуальных задач теории и техники связи является увеличение скорости передачи информации по проводным и радиоканалам с ограниченной полосой пропускания.

Ее решение возможно как на основе параллельной передачи с помощью многоканальных (многочастотных) модемов и на основе последовательной передачи с помощью одноканальных (одночастотных) модемов. Анализ результатов исследований показывает, что основное достоинство использования при передаче данных многоканальных модемов заключается в нечувствительности (инвариантности) к воздействию перерывов и кратковременных занижении уровня сигналов. Подобные методы при сохранении высокой скорости передачи информации позволяют значительно уменьшить скорость манипуляции.

Преимущество параллельной передачи, заключающейся в том, что она осуществляется с намного меньшими скоростями, чем последовательная, и поэтому может быть основана на использовании более простых методов модуляции.

Анализ эффективности использования многоканальных модемов для высокоскоростной передачи дискретной информации по проводным каналам связи, показывает, что по отношению к воздействию флуктуационной помехи многоканальной и одноканальные модемы практически эквивалентны. В то же время при наличии скачков уровня импульсных помех следует ожидать, что параллельный способ передачи будет обеспечивать большую помехоустойчивость и меньше пакетирование ошибок.

В отличие от вышерассмотренного способа, базирующегося на инвариантном подходе к борьбе с помехами, в настоящее время широкое использование при проектировании систем передачи информации находит принцип адаптации. Различают три направления адаптации систем передачи информации: системы с параметрической адаптацией, системы с адаптацией стратегии управления и системы с непараметрической адаптацией.

К первому относятся с адаптацией следующих параметров:

1. Дискретных сигналов (мощности, длительности, формы, спектра);

· Модемов (глубины модуляции, ограничения спектра);

· Фильтров (ограничения ширины полосы, оценивая амплитуды сигналов);

· Кодеков (основания кода, его длины, избыточности);

· Фазирования (шага, угла и времени корреляции).

2. Ко второму направлению относятся следующие системы с адаптацией стратегии управления:

· Подбора формы сигналов;

· Переключения алгоритмов модуляции и демодуляции;

· Переключения алгоритмов фильтрации;

· Переключения алгоритмов фазирования;

· Переключения алгоритмов повышения верности передачи;

· Переключения алгоритмов системной передачи и приема;

· Переключением каналов.

К третьему направлению относятся системы с непараметрической адаптацией:

· Методом самонастройки всех режимах и алгоритмов узлов;

· Методом самоперестройки всех режимов и алгоритмов узлов;

· Методом обучения алгоритмов преобразования и обработки сигналов;

· Методом системной (автоматической) настройки, перестройки обучения алгоритмов.

Как указывалось ранее для направления, связанного с повышением помехоустойчивости передачи информации за счет использования помехоустойчивых кодов возможны два пути построения эффективных систем с кодированием, известны коды, предназначенные для исправления пачек ошибок. Для каналов с медленно меняющимися параметрами иногда используют адаптивное кодирование.

Второй путь заключается в том, что исходные каналы преобразуются к некоторому «стандартному» дискретному каналу, для которого оптимальные коды известны. Простейшим примером этого разнесения символов, входящих в один кодовый блок. При этом символы, входящие в одну кодовую комбинацию, передаются не непосредственно друг за другом, а перемежаются символами других кодовых комбинации. Если интервал между символами, входящими в одну кодовую комбинацию, сделать длиннее «памяти» (интервала корреляции) канала, то в пределах комбинации группирования не будет и можно декодировать, как в канале без памяти. Дальнейшим шагом является разработка и применение методов построения адаптивных систем, позволяющих обеспечить высокую верность передачи сообщений в каналах с переменными параметрами при неполной априорной информации о сигналах и помехах. Недостатком присущим методом декорреляции является постоянная задержка при передаче сообщений, величина которой зависит от интервала корреляции ошибок и скорости передачи.

Подробный анализ, проведенный показывает, что корректирующее кодировании использует по существу все виды избыточности сигналов – временную, частотную и энергетическую. Если длина кодовой комбинации не фиксирована (скорость передачи информации не фиксирована), то для корректирования ошибок используют временную избыточность – кроме информационных символов, дополнительно вводят еще ряд символов, называемых проверочными. С помощью информации фиксированно ввести проверочные символы в кодовую комбинацию бинарного кода, можно лишь уменьшая длительность элементарных сигналов, что ведет к расширению их спектра. В этом случае корректирующее кодирование использует частотную избыточность. Чтобы отношение сигнал/шум с уменьшением длительности импульсов не падало, необходимо увеличить амплитуду импульсов. Увеличивая амплитуду укороченного импульса, можно настолько увеличить его энергию, что вероятность ошибки при его приеме уменьшится по сравнению с вероятностью при приеме импульса не укороченной длительности. Так вводиться энергетическая избыточность (корректирующая способность кода улучшается в результате повышения энергии импульсов).

Анализ принципов адаптивного кодирования, показывает на возможность использования нескольких методов адаптивного преобразования помехоустойчивых кодов:

· Изменение соотношения между числом информационных символов при постоянной длине кода

· Изменение числа информационных символов при постоянном числе избыточных символов.

· Преобразование кода путем изменения длины кода и числа проверочных символов.

· Преобразование кодов путем изменения числа избыточных символов при постоянной информационной части. Такое преобразование можно выполнить специальным подбором цепочки образующих полиномов.

Основной причиной ошибок являются помехи в непрерывном канале, а также его не идеальность. Причиной ошибок могут быть также неправильные действия персонала, осуществляющего как эксплуатацию различных участков канала связи, так и самой аппаратуры ПДС.

Условно, разобьем методы повышения верности на три группы. В первую группу включим меры эксплуатационного и профилактического характера, направленные на улучшение качественных показателей канала связи: повышение стабильности работы генераторного оборудования, резервирование электропитания систем передачи, выявление неисправного оборудования и его элементов и своевременная их замена, повышение культуры технического обслуживания и, в частности, принятие специальных мер предосторожности при проведении измерительных и профилактических работ на каналах во время передачи дискретных сообщений и т. п. Опыт показывает, что указанные мероприятия позволяют, уменьшит коэффициент ошибок в среднем в 5 раз.

Ко второй группе мероприятий относятся мероприятия, направленные на увеличение помехоустойчивости передачи единичных элементов. Речь идет о таких мерах, как повышения отношения сигнал – помеха за счет увеличения амплитуды длительности, или спектра частот полезного сигнала, применение более помехоустойчивых методов модуляции и сложных сигналов на приеме и т. п. Применение большинства из перечисленных методов наталкивается на серьезные трудности. Так сколько – нибудь существенно увеличить амплитуду сигналов, передаваемых по физической линии, нельзя из–за опасности возникновения недопустимых переходов на соседние цепи. Если передача дискретных сообщений осуществляется по каналу ТЧ, то мощность дискретных сигналов ограничивается из–за необходимости не допустить перегрузку групповых усилителей. Увеличение длительности единичных элементов с одновременным введением интегрирования на приеме позволяет понизить вероятность ошибки на элемент; однако получить удовлетворительную верность при работе по каналам все же не представляется возможным, не говоря уже о неизбежном при этом снижении скорости передачи. Заметного эффекта можно достичь за счет использования сложных сигналов.

К третьей группе мер по повышению верности передачи дискретных сообщений относятся меры, связанные с введением избыточности в передаваемую по дискретному каналу последовательность. Следует заметить, что, используя эти методы, можно добиться существенного повышения верности. При выборе способа введения избыточности следует исходить из того, что заданную верность передачи необходимо получить при минимальной избыточности. Должны приниматься во внимание и вопросы, связанные со сложностью реализации способа.

История кодирования, контролирующего ошибки, началась в 1948 г. публикацией знаменитой статьи Клода Шеннона. Шеннон показал, что с каждым каналом связано измеряемое в битах в секунду и называемое пропускной способностью канала число С, имеющее следующее значение. Если требуемая от системы связи скорость передачи информации R (измеряемая в битах в секунду) меньше С, то, используя коды, контролирующие ошибки, для данного канала можно построить такую систему связи, что вероятность ошибки на выходе будет сколь угодно мала. В самом деле, из шенноновской теории информации следует тот важный вывод, что построение слишком хороших каналов является расточительством; экономически выгоднее использовать кодирование. Фактически в работе Шеннона утверждается, что мощность сигнала, шум в канале и полоса частот ограничивают лишь скорость передачи, а не ее точность. Шеннон, однако, не указал, как найти подходящие коды, а лишь доказал их существование. В пятидесятые годы много усилий было потрачено на попытки построения в явном виде классов кодов, позволяющих получить обещанную сколь угодно малую вероятность ошибки, но результаты были скудными. В следующем десятилетии решению этой увлекательной задачи уделялось меньше внимания; вместо этого исследователи кодов предприняли длительную атаку по двум основным направлениям.

Первое направление носило чисто алгебраический характер и преимущественно рассматривало блоковые коды. Первые блоковые коды были введены в 1950 г., когда Хэмминг описал класс блоковых кодов, исправляющих одиночные ошибки. Коды Хэмминга были разочаровывающе слабы по сравнению с обещанными Шенноном гораздо более сильными кодами. Несмотря на усиленные исследования, до конца пятидесятых годов не было построено лучшего класса кодов. В течение этого периода без какой-либо общей теории были найдены многие коды с малой длиной блока. Основной сдвиг произошел, когда Боуз и Рой-Чоудхури [1960] и Хоквингем [1959] нашли большой класс кодов, исправляющих кратные ошибки (коды БЧХ), а Рид и Соломон [1960] нашли связанный с кодами БЧХ класс кодов для недвоичных каналов. Хотя эти коды остаются среди наиболее важных классов кодов, общая теория блоковых кодов, контролирующих ошибки, с тех пор успешно развивалась.

Открытие кодов БЧХ привело к поиску практических методов построения жестких или мягких реализации кодеров и декодеров. Первый хороший алгоритм был предложен Питерсоном. Впоследствии мощный алгоритм выполнения описанных Питерсоном вычислений был предложен Берлекэмпом и Месси, и их реализация вошла в практику, как только стала доступной новая цифровая техника. Второе направление исследований по кодированию носило скорее вероятностный характер. Ранние исследования были связаны с оценками вероятностей ошибки для лучших семейств блоковых кодов, несмотря на то, что эти лучшие коды не были известны. С этими исследованиями были связаны попытки понять кодирование и декодирование с вероятностной точки зрения, и эти попытки привели к появлению последовательного декодирования. В последовательном декодировании вводится класс неблоковых кодов бесконечной длины, которые можно описать деревом и декодировать с помощью алгоритмов поиска по дереву. Наиболее полезными древовидными кодами являются коды с тонкой структурой, известные под названием сверточных кодов. Эти коды можно генерировать с помощью цепей линейных регистров сдвига, выполняющих операцию свертки информационной последовательности. В конце 50-х годов для сверточных кодов были успешно разработаны алгоритмы последовательного декодирования. Интересно, что наиболее простой алгоритм декодирования - алгоритм Витерби - не был разработан для этих кодов до 1967 г. Применительно к сверточным кодам умеренной сложности алгоритм Витерби пользуется широкой популярностью, но для более мощных сверточных кодов он не практичен.

В 70-х годах эти два направления исследований опять стали переплетаться. Теорией сверточных кодов занялись алгебраисты, представившие ее в новом свете. В теории блоковых кодов за это время удалось приблизиться к кодам, обещанным Шенноном: были предложены две различные схемы кодирования (одна Юстесеном, а другая Гоппой), позволяющие строить семейства кодов, которые одновременно могут иметь очень большую длину блока и очень хорошие характеристики. Обе схемы, однако, имеют практические ограничения. Между тем к началу 80-х годов кодеры и декодеры начали появляться в конструкциях цифровых систем связи и цифровых систем памяти.

К настоящему времени разработано много различных помехоустойчивых кодов, отличающихся друг от друга основанием q, расстоянием d, избыточностью, структурой, функциональным назначением, энергетической эффективностью, корреляционными свойствами, алгоритмами кодирования и декодирования, формой частотного спектра. 

Связь между кодами можно проиллюстрировать как на рис. 1.1.

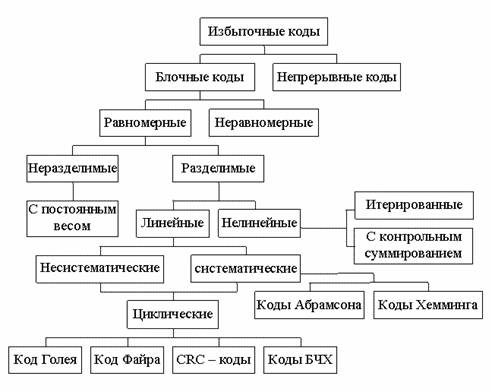
Рис. 1.1. Классификация помехоустойчивых кодов

Как видно, все помехоустойчивые (избыточные) коды делятся на два класса: блочные коды и непрерывные коды. В блочных кодах передаваемая информационная последовательность разбивается на отдельные блоки кодовые комбинации, которые кодируются и декодируются независимо друг от друга. В непрерывных кодах, называемых также рекуррентными сверточными, или цепными передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы, размещаются в определённом порядке между информационными.

Блочные коды делятся на равномерные и неравномерные. Широкое практическое применение нашли равномерные коды. Равномерные блочные коды делят на разделимые и неразделимые. В разделимых кодах информационные элементы и проверочные элементы во всех кодовых комбинациях занимают одни и те же позиции.

Поэтому разделимые коды обычно обозначают как (n, k), где n-разрядность кода; k-число информационных элементов. В неразделимых кодах деление на информационные и проверочные элементы отсутствует. Эти коды служат только для обнаружения ошибок на основании изменения веса.

Разделимые коды делятся на линейные (систематические) и нелинейные (несистематические). Линейные получили своё название потому, что их проверочные элементы представляют собой линейные комбинации информационных элементов. Большую и важную подгруппу линейных кодов образуют циклические коды.

В циклических кодах каждое слово содержит все свои циклические перестановки, т.е. если (x_n-1, x_n-2, ...x₁, x₀) - слово кода, то и (x_n-2, ...x₁, x₀, x_n-1), ...., (x₀, x_n-1, x_n-2, ..., x₁) - слова кода. Циклические коды важны как с точки зрения математического описания, так и для построения и реализации кода. К циклическим кодам относятся такие коды, как коды Файра, код Голея, коды Боуза–Чоудхури - Хоквингема, коды Рида-Соломона, CRC-коды.

Линейные отличаются от нелинейных замкнутостью кодового множества относительно некоторого линейного оператора, например сложения или умножения слов кода, рассматриваемых как векторы пространства, состоящего из кодовых из кодовых слов-векторов. Линейные коды упрощают его построение и реализацию. При большой длине практически могут бить использованы только линейные коды. Вместе с тем часто нелинейные коды обладают лучшими параметрами по сравнению с линейными. Для относительно коротких кодов сложность построения и реализации линейных и нелинейных кодов примерно одинаково.

Как линейные, так и нелинейные коды образуют обширный классы, содержащие много различных конкретных видов помехоустойчивых кодов. Среди линейных блочных кодов наибольшее значение имеют коды с одной проверкой на чётность, М-коды, ортогональные, биортогональные, Хэмминга, БЧХ, Голея, квадратично - вычетные (КВ), Рида-Соломона. К инверсным относят коды с контрольной суммой, инверсные, с постоянным весом, перестановочные с повторением и без повторения.

Рассмотренные коды могут быть использованы как для обнаружения, так и для исправления ошибок. Следует, однако, иметь в виду, что всякий избыточный код всегда имеет большую избыточность, что необходимо для обнаружения и исправления ошибок, потому что избыточностью обладают все кодовые комбинации, а ошибки содержат только некоторые из них. А так как избыточность, необходимая для обнаружения ошибок, меньше избыточности, необходимой для исправления, то для избежания излишней избыточности часть ограничивается применением кодов с обнаружением ошибок, а повышение верности осуществляют, используя обратную связь.

Для повышения верности передачи ДС коды используют в следующих режимах: исправления ошибок, исправления и обнаружения ошибок. Режим исправления ошибок в системах передачи данных используют редко. Он применяется в тех случаях, когда обратная связь невозможна или явно не целесообразна, например, при жёстких требованиях и допустимой задержке и большом времени распространении символов.

Для обнаружения ошибок в основном используются коды двух типов: циклические и итеративные (матричные), что обусловлено простотой аппаратурной или программной реализации кодирования и декодирования.

Для кодирования и декодирования информации любыми видами кодов необходимо знать их параметры. С помощью вычислений и измерений находятся параметры кодов, затем они используются при выборе кодов предназначенных для передачи, хранения и обработки информации:

1.     Длина кода n-число разрядов составляющих кодовую комбинацию.

2.     Основание кода m-отличающихся друг от друга значений импульсных признаков используемых в кодовых комбинациях. В качестве значений импульсных признаков используются 0 и 1.

3.     Мощность кода N_p-число кодовых комбинаций используемых для передачи сообщения.

4.     Полное число кодовых комбинаций N-число всех возможных кодовых комбинаций равное mⁿ:

N=mⁿ (1.1)

Или в двоичной системе

N=2ⁿ (1.2)

5.   Число информационных символов k-количество символов кодовой комбинации предназначенных для передачи сообщения. Очевидно что:

N_p=2^k (1.3)

6.    Число проверочных разрядов r-количество разрядов кодовой комбинации необходимых для коррекции ошибок. Это число характеризует избыточность кода.

В теории кодирования под избыточностью кода R-понимают относительную избыточность, равную отношению числа проверочных символов к длине кода.

(1.4)

В общем случае эта формула может быть приведена к виду:

R=1- (1.5)

Скорость передачи кодовой комбинации отношение числа информационных символов к длине кода

R’= (1.6)

Так как n= k+r то,

R’=1-R (1.7)

7.    Вес кодовой комбинации ω- количество единиц в кодовой комбинации.

8.    Кодовое расстояние d-между двумя кодовыми комбинациями, число одноимённых разрядов с различными символами. Практически кодовое расстояние выражается как вес суммы по модулю два кодовых комбинаций. Если произошло t ошибок и если расстояние от принятого слова до каждого другого кодового слова больше t, то декодер исправит ошибки, приняв ближайшее к принятому кодовое слово в качестве принятого. Это всегда будет так, если

d2t+1 (1.8)

9. Весовая характеристика кода W(ω)-число кодовых комбинаций веса ω.

10.  Вероятность необнаружения ошибки P_н.о.- это вероятность такого события при котором принятая кодовая комбинация отличается от переданной, а свойство данного кода не позволяет определить наличия ошибок.

Одной из важнейших задач построения помехоустойчивых кодов с заданными характеристиками является установление соотношения между его способностью обнаруживать или исправлять ошибки и избыточностью.

Существуют граничные оценки, связывающие d₀, n и k.

Граница Хэмминга, которая близка к оптимальной для высоко скоростных кодов, определяется соотношениями:

для q - ного кода

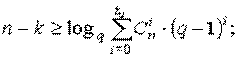
для двоичного кода

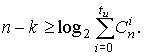
Граница Плоткина, которую целесообразно использовать для низкоскоростных кодов определяется соотношениями:

для q-ного кода

для двоичного кода

Границы Хэмминга и Плоткина являются верхними границами для кодового расстояния при заданных n и k, задающими минимальную избыточность, при которой существует помехоустойчивый код, имеющий минимальное кодовое расстояние и гарантийно исправляющий t_u - кратные ошибки.

Граница Варшамова - Гильберта (нижняя граница), определяемая соотношениями:

и ,

показывает, при каком значении n - k определено существует код, гарантировано исправляющий ошибки кратности t_u.

Требования, предъявляемые к помехоустойчивым кодам и их характеристики.

Под кодеком понимаются программные и аппаратные средства, реализующие заданный (n, к) код.

Задача практического использования циклического кода разбивается на три основных этапа:

1. Задание кода, т. е выбор такого множества кодовых слов, посредством которых будет вестись передача;

2. Кодирование, т.е. разработка алгоритма и аппаратуры, реализующей этот алгоритм кода;

3. Декодирование, т. е разработка алгоритма и аппаратуры, реализующей этот алгоритм декодера.

К корректирующим кодам предъявляются следующие требования:

- коды должны иметь минимально необходимое число проверочных символов (разрядов) для обнаружения или для исправления ошибок заданной кратности;

- схемы кодирующих и декодирующих устройств должны содержать минимальное число элементов;

- правила построения кодов должны быть простыми, обеспечивающими построение кодов любой длины, исправляющих ошибки любой кратности;

- переход от кода, обнаруживающего заданную кратность ошибок, к коду, обнаруживающему большую или меньшую кратность ошибок, должен осуществляться несложным изменением схем кодирующих и декодирующих устройств.

В зависимости от назначения телекоммуникационной системы к кодам предъявляются дополнительные требования. (Под кодеком понимаются программные и аппаратные средства, реализующие заданный код):

- скорость передачи информации, в канале может быть от сотен бит/с, до десятков миллионов бит/с;

- ошибки могут быть одиночными, многократными одиночными, одиночными пакетами, многократными пакетами;

- длина блока - от нескольких десятков до десятков тысяч бит;

- вероятность ошибочного декодирования бита должна быть, по крайней мере, не выше 10^-9.

Перечисленным выше требованиям в наибольшей степени удовлетворяют циклические коды, которые являются универсальными, наиболее экономичными и обладают хорошими корректирующими способностями.

Так как развитие кодов, контролирующих ошибки, первоначально стимулировалось задачами связи, терминология теории кодирования проистекает из теории связи. Построенные коды, однако, имеют много других приложений. Коды используются для защиты данных в памяти вычислительных устройств и на цифровых лентах и дисках, а также для защиты от неправильного функционирования или шумов в цифровых логических цепях. Коды используются также для сжатия данных, и теория кодирования тесно связана с теорией планирования статистических экспериментов.

Приложения к задачам связи носят самый различный характер. Двоичные данные обычно передаются между вычислительными терминалами, между летательными аппаратами и между спутниками. Коды могут быть использованы для получения надежной связи даже тогда, когда мощность принимаемого сигнала близка к мощности тепловых шумов. И поскольку электромагнитный спектр все больше и больше заполняется создаваемым человеком сигналами, коды, контролирующие ошибки, становятся еще более важным инструментом, так как позволяют линиям связи надежно работать при наличии интерференции. В военных приложениях такие коды часто используются для защиты против намеренно организованной противником интерференции.

Во многих системах связи имеется ограничение на передаваемую мощность. Например, в системах ретрансляции через спутники увеличение мощности обходится очень дорого. Коды, контролирующие ошибки, являются замечательным средством снижения необходимой мощности, так как с их помощью можно правильно восстановить полученные ослабленные сообщения. Передача в вычислительных системах обычно чувствительна даже к очень малой доле ошибок, так как одиночная ошибка может нарушить программу вычисления. Кодирование, контролирующее ошибки, становится в этих приложениях весьма важным. Для некоторых носителей вычислительной памяти использование кодов, контролирующих ошибки, позволяет добиться более плотной упаковки битов. Другим типом систем связи является система с многими пользователями и разделением по времени, в которой каждому из данного числа пользователей заранее предписаны некоторые временные окна (интервалы), в которых ему разрешается передача. Длинные двоичные сообщения разделяются на пакеты, и один пакет передается в отведенное временное окно. Из-за нарушения синхронизации или дисциплины обслуживания некоторые пакеты могут быть утеряны. Подходящие коды, контролирующие ошибки, защищают от таких потерь, так как утерянные пакеты можно восстановить по известным пакетам.

Связь важна также внутри одной системы. В современных сложных цифровых системах могут возникнуть большие потоки данных между подсистемами. Цифровые автопилоты, цифровые системы управления процессами, цифровые переключательные системы и цифровые системы обработки радарных сигналов - все это системы, содержащие большие массивы цифровых данных, которые должны быть распределены между многими взаимно связанными подсистемами. Эти данные должны быть переданы или по специально предназначенным для этого линиям, или посредством более сложных систем с шинами передачи данных и с разделением по времени. В любом случае важную роль играют методы кодирования, контролирующего ошибки, так как они позволяют гарантировать соответствующие характеристики.

Применение и требования к помехоустойчивым кодам в современных телекоммуникационных системах. Одним из основных способов обеспечения достоверности передачи информации по каналам связи является использование помехоустойчивых кодов, обнаруживающих и исправляющих ошибки.

Применение того или иного кода зависит тип ошибок. Например, код Хэмминга служит для исправления ошибок, код БЧХ для исправления многократных одиночных независимых ошибок, код Файра для одиночных пакетов ошибок и код РС для многократных пакетов ошибок.
Циклические широко применяются в различных системах, таких как система космической связи, системы цифрового телевидения, в цифровом радиовещании, в сотовой и транкинговой связи, в системах передачи данных. Эти коды также используются для устранения ошибок в полупроводниковых ЗУ, в накопителях на магнитных дисках и лазерных дисках, позволяющих обеспечить высокую надежность хранения информации. Например, в технологии ATM используются коды БЧХ (BCH – Bose – Chaudhuri - Hoquenghem), в цифровой транкинговой связи стандарта APCO 25 кодов Хэмминга, кодов Рида-Соломона и кодов Голея, а также циклических кодов контроля чётности (CRC - Cyclic Redundancy Check) в радиоканалах подвижной связи GSM PLMN блочных и свёрточных кодов, в цифровом телевидении и при записи информации на магнитные диски кодов РС.

В системах АТМ очень успешно используются циклические коды БЧХ для обнаружения и исправления ошибок в заголовке. Кроме кодов БЧХ также используются другие коды, использование которых зависит от типов ошибок в каналах связи и которые могут исправлять различные комбинации ошибок в зависимости от избыточности. Тип ошибок во многом зависит от способа передачи информации и от физической природы канала.

В технологиях ATM из-за ошибок в основном происходит потеря ошибок, который называется "эффектом размножения". При этом эффекте из-за ошибок в заголовке информационный пакет может быть доставлен не тому получателю. Для защиты заголовка ячейки АТМ наиболее целесообразным является использование кодов БЧХ. Эти коды с большим выбором длины и с широким спектром возможностей по исправлению ошибок при ограниченном количестве набора значений n, k, t.

В ячейке АТМ заголовок составляет 5 октетов. Под поле контроля ошибок отведено 8 бит. Этого вполне достаточно для исправления ошибок и обнаружения 89% многобитовых ошибок. Каждый передатчик АТМ ячеек подсчитывает значение поля контроля ошибок в заголовке для первых четырёх октетов заголовка и заносит результат в пятый октет (в поле контроля ошибок в заголовке). Значение поля определяется как остаток от деления (по mod2) произведения x⁸ на содержимое заголовка ячейки (без поля контроля заголовка) на производящий полином x⁸+x²+x+1. Оборудование передатчика подсчитывает этот остаток и прибавляет к нему по mod2 фиксированную комбинацию 01010101. Эта сумма и записывается в поле контроля ошибок заголовка. Все эти вышеуказанные операции реализуются оборудованием приёма ячеек АТМ с помощью адаптивного механизма.

После запуска приёмник находится в режиме коррекции. Если обнаружена однобитовая ошибка, то ячейка стирается. В обоих случаях приёмник переключается в режим детектирования. В этом состоянии приёмника каждая ячейка с обнаруженной одиночной или множественной ошибкой в заголовке стирается. Если ошибок в заголовке не обнаружено, то механизм переходит в состояние коррекции.

В цифровой транкинговой связи стандарта APCO25 основными методами кодирования являются:

- блочное кодирование;

- решёточное кодирование;

- перемежение;

При блочном кодировании информации используются следующие виды корректирующих кодов:

- коды Хэмминга;

- коды Рида-Соломона;

- коды Голея;

- циклические коды контроля чётности (CRC-коды).

Коды Хэмминга используются при кодировании речевых сообщений (речевых кадров, синхрослова шифрования, слова управления каналом связи), коды Рида-Соломона и Голея для преамбулы и маркёра конца сообщения, а коды контроля чётности используются в основном для кодирования данных и формируются путём вычисления остатка от деления исходного информационного блока, представленного в виде полинома, на порождающий полином и сложения по mod 2 с определённым инверсным полиномом. Например, для кодирования речевой информации используются 3 вида кодов Рида – Соломона с параметрами (36, 20, 17), (24, 16, 9) и (24, 12, 13). Все они являются укороченными и получаются из кода длиной 63 путей вычеркивания левых наиболее информативных символов.

Блочное кодирование в APCO25 является систематическим, т.е. первые k символов кодового слова представляют собой повторение информационного блока, а последние (n - k) символов являются проверочными.

В стандарте APCO25 используются три разновидности кода Голея:

- стандартный код Голея с параметрами (23, 12, 7);

- расширенный (24, 12, 8);

- укороченный (18, 6, 8).

Стандартный код Голея генерируется порождающим полиномом:
G(x)=x¹¹+x¹⁰+x⁶+x⁵+x⁴+x³+x²+1,
который при записи в восмиричном виде можно представить числом 6165.
Расширенный код Голея (24, 12, 8) образуется добавлением к стандартному одного бита контроля чётности. Укороченный код Голея (18, 6, 8) получается вычислением левых наибольших шести битов из расширенного кода.
В радиоканалах подвижной связи GSM PLMN используется свёрточное и блочное кодирование с перемежением. Перемежение обеспечивает преобразование пакетов ошибок в одиночные. Свёрточное кодирование является мощным свойством борьбы с одиночными ошибками, а блочное кодирование используется для обнаружения нескорректированных ошибок.

Блочный код (n, k, t) преобразует k информационных символов путём добавления символов чётности (n-k), а также корректировать t ошибочных символов.

Одной из основных характеристик свёрточного кодирования является величина k, которая называется длиной кодового ограничения, и показывает, на какое максимальное число выходных символов влияет данный информационный символ. Так как сложность декодирования свёрточных кодов по наиболее выгодному, с точки зрения реализации, алгоритму Витерби возрастает экспоненциально с увеличением длины кодового ограничения, то типовые значения k малы и лежат в интервале 3-10. Другой недостаток СК заключается в том, что они не могут обнаруживать ошибок. Поэтому в стандарте GSM для внешнего обнаружения ошибок используется блочный код на основе свёрточного кода (2, 1, 5). Наибольший выигрыш обеспечивают СК только при одиночных (случайных) ошибках в канале. В канале с замираниями, что имеет место в GSM PLMN, необходимо использовать СК совместно с перемежением.

В подвижной связи стандарта GSM используются следующие помехоустойчивые коды:

- циклический код (53, 50), с кодовым расстоянием d₀ = 3;

- сверточный код (2, 1);

- перемежение (в речевом режиме).

- код Файра (х²³ + 1)(х¹⁷ + х⁹ + 1), k = 184; r = 40;

- сверточный код (2, 1).

Первые три кода имеют вероятность не обнаружения ошибок порядка 10^-3 . Четвертый и пятый коды используется для передачи данных.

- В системах CDMA используются следующие коды:

- сверточный код;

- каскадное кодирование;

- код Рида – Соломона → перемежение → сверточный код;

- Турбокодирование;

- специальное кодирование.

Сверточные коды используются для кодирования речи. Второй и третий коды для кодирования данных, четвертый и пятый коды используются для передачи данных.

Кодирование речи имеет ряд принципиальных особенностей: необходимо обеспечить интерактивную связь в режиме реального времени, при которой задержка, связанная с обработкой информации, не должна превышать допустимой величины.

Для этого на первом этапе производится декорреляция пакетов ошибок, в результате которой они преобразовываются в одиночные ошибки. На втором этапе сигнал обрабатывается с помощью классических методов борьбы со случайными ошибками, что приводит к их полному подавлению. Для борьбы с замираниями и возникновением, связанных с ними, пакетов ошибки служит процедура перемежения, которая состоит в перестановке символов кодируемой последовательности её модуляции и восстановлении исходной последовательности после демодуляции. Данная операция не вносит избыточности, а только изменяет порядок следования импульсов. Чем больше глубина перемежения, то есть максимальное расстояние, на которое разносятся соседние символы входящей последовательности, тем больше задержка.

Код БЧХ (63,44), используемый в системе спутникового цифрового радиовещания, позволяет исправить две или три ошибки, обнаружить и замаскировать 5 или 4 ошибки на каждый кодовый блок из 63 символов.

Так, например, в английском стандарте TACS исключаются коды параметрами (63,51), (40,28), (48,36); в стандарте AMPS (США) – (63,51), (40,28), (48,36); в стандарте HCMTS (Япония) - (63,51), (15,11),(43,31); в стандарте С-450 (Германия) – (15,7).

Повышение производительности вычислительных систем существенно увеличило объем хранимой и передаваемой информации. Недопустимость ошибок, а в ряде случаев сама природа данных, требует использование, как оборудования, так и программных процедур обнаружения и исправления ошибок обмена. Так в системе IBM 3370 используется кодек, реализующий код Рида – Соломона (174, 172,3), в этой системе также применяется кодек, реализующий код Рида – Соломона (61,50), а фирмами Motorola и Fairchild сконструирован кодек кодов БЧХ, рассчитанный на скорость передачи информации 30 Мбит/с.

В системах цифровой записи и воспроизведения на компакт-дисках и магнитных лентах основную долю ошибок составляют ошибки типа «лотерея пакета». Для уменьшения влияния пакетов ошибок на качество записи и воспроизведения используют помехоустойчивое каскадное кодирование, являющееся эффективным средством борьбы с такими ошибками. Для того чтобы можно было обнаружить и исправить ошибки даже в самых неблагоприятных ситуациях, характеризующая способность кодов даже обнаружение и исправление ошибок выбирается с большим запасом. Кроме того, в цифровых магнитофонах записываемый поток имеет блочную структуру. Такая организация (формат) записи требует применения помехоустойчивых кодов блочной структуры.

В системах записи- воспроизведения на подвижные носители ошибки считывания обуславливаются царапинами и другими дефектами носителя, в устройствах полупроводниковой памяти замыканиями и отрывами межкомпонентных соединений и т.к.

В системах записи воспроизведения информации (как правило, двоичной) роль канала играет носитель информации: магнитная лента, диск, грампластинка, полупроводниковые запоминающие устройства.

В цифровых магнитофонах формата Prodigi (от англ. Professesional Digital), R – DAT (Rotary head Digital Audio Tape), S – DAT (Stationary head Digital Audio Tape) используются коды Рида – Соломона: двойной код С1(32,28) и С2(36,26), (40,32) и (29, 27).

На Рис.1.2. приведена типовая структурная схема систем телепередачи и записи - воспроизведения информации.

Рис.1.2.

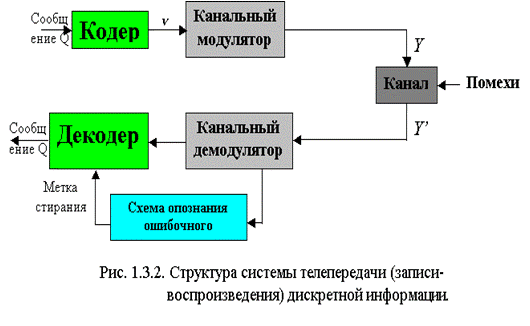
Кодер, который состоит из внешнего кодера, интерливера и внутреннего кодера, преобразует сообщение Q в кодовое слово, которое подвергается канальной модуляции в системах телепередачи модулятор вырабатывает физические сигналы Y, предназначенные для пересылки по некоторому каналу связи.

Декодер, который состоит из внутреннего декодера, деинтерливера т внешнего декодера, исправляет стирания и ошибки. Если их число не превышает условия

d ≥ 2τ + υ + 1,

где d - кодовое расстояние кода, τ - число стираний, υ -число ошибок.
Повысить кодовое расстояние d кода можно при каскадировании. Кодер и декодер на Рис.1.2. изображены двухкаскадными. Сообщение на первом шаге кодируется внешним (n₁, k₁, d₁)-кодом, а на втором внутренним (n₂, k₂, d₂)-кодом. Параметры результирующего (n, k, d)-кода: n=n₁·n₂; k=k₁·k₂; d=d₁·d₂, что позволяет создавать высоко помехоустойчивые коды (12,13,46).

Интерливер и деинтерливер предназначены для перемежения и деперемежения, что позволяет трансформировать весьма длинные пакеты ошибок в отдельные независимые.

Как упоминалось выше для повышения d - кодового расстояния выполняется кодирование, а при каскадировании целесообразно использовать коды Рида - Соломона над полем GF (2r).

В цифровых системах коммутации, а точнее в ОКС №7 тоже используются коды БЧХ. Обнаружение ошибок осуществляется с помощью 16 проверочных битов, передаваемых в конце каждого сигнала. Проверочные биты формируются АТС, которая передаёт сигнал. Проверочные биты получаются путём применения образующего полинома к информации в сигнале.

Используется следующий образующий полином: x¹⁶+x¹²+x⁵+1. В соответствии с рекомендацией МСЭ Х.25/2. Он выбран так, чтобы обнаруживать пакеты ошибок при передаче.

Проверочные биты образуются из остатка от деления по mod 2 2x^k(x¹⁵+x¹⁴+x¹³+x¹²+...+x²+x+1) на образующий полином x¹⁶+x¹²+x⁵+1, где k-количество битов в сигнальной единице между последним битом открывающего флага и первым проверочным битом и остатка после умножения на x¹⁶ и деления на образующий полином x¹⁶+x¹²+x⁵+1 содержимого сигнальной единицы также между последним битом открывающего флага и первым проверочным битом.

В линейных трактах STM-16, STM-64, STM-256 введена упреждающая коррекция ошибок - Forwork Error Correction – FEC.

FEC обслуживает сетевой слой мультиплексных секций. В пункте приема выполняется декодирование, т.е. контроль и коррекция ошибок. Используемый код (укороченный) код БЧХ обеспечивает коррекцию 3-х ошибок в блоке, состоящий из 4320 информационных бит. Упреждающая коррекция ошибок является полезной возможностью при организации мощных линейных трактов, позволяющей увеличить длину участка регенерации. При передаче сигнал подвергается дополнительной обработке (кодированию), результаты которой записываются в заголовке мультиплексной и регенерационной секций (MSON и RSON). На приеме в точке окончания мультиплексной секции осуществляется декодирование, т.е. контроль и коррекция ошибок. Эта процедура позволяет существенно снизить коэффициент ошибок (k_ош). Например, считающиеся нормальным в системе SDH значение 10^-10 за счет применения FEC удается получить при исходном k_ош = 10^-5.

Задача практического использования циклического кода разбивается на 3 этапа:

- задание кода, т.е. выбор такого множества кодовых слов, посредством которых будет вестись передача;

- кодирование, т.е. разработка алгоритма и аппаратуры, реализующей этот алгоритм кода;

- декодирование, т.е. разработка алгоритма и аппаратуры, реализующей этот алгоритм декодера.

К корректирующим кодам предъявляются следующие требования:

- коды должны иметь минимально необходимое число проверочных символов (разрядов) для обнаружения или для исправления ошибок заданной кратности;

- схемы кодирующих и декодирующих устройств должны содержать минимальное число элементов;

- правила построения кодов должны быть простыми, обеспечивающими построение кодов любой длины, исправляющих ошибки любой кратности;

- переход от кода, обнаруживающего заданную кратность ошибок, к коду, обнаруживающему большую или меньшую кратность ошибок, должен осуществляться несложным изменением схем кодирующих и декодирующих устройств.
Этим требованиям в наибольшей степени удовлетворяют циклические коды, которые являются универсальными, наиболее экономичными и обладают хорошими корректирующими способностями.

В зависимости от назначения схемы к кодекам предъявляются дополнительные требования:

а) длина кода от нескольких десятков до десятков тысяч бит;

б) ошибки могут быть одиночными, многократными одиночными, одиночные пакеты, многократные пакеты;

в) вероятность ошибочного декодирования бита должна быть не выше 10^-9, повторение передачи не разрешается;

г) скорость передачи (v_прд) информации в канале может быть от сотен тысяч до млн. бит/с;

д) кодек должен работать в непрерывном режиме, в темпе поступления информации из канала; иногда допускается постоянная задержка до десятков длин блока.

Перечисленным выше требованиям в наибольшей степени удовлетворяют циклические коды, которые являются универсальными, наиболее экономичными и обладают хорошими корректирующими способностями.

2. ПРИНЦИПЫ ПОСТРОЕНИЯ ЦИКЛИЧЕСКИХ КОДОВ

2.1. Определение циклических кодов и их свойства

Циклические коды являются подклассом в классе линейных кодов, удовлетворяющим дополнительном сильному структурному требованию. В силу этой структуры поиск хороших кодов, контролирующих ошибки, в классе циклических кодов оказался наиболее успешным. При этом в качестве математического аппарата, облегчающего поиск хороших кодов, была использована теория полей Галуа. Вне класса циклических кодов теория полей Галуа помогает мало; большинство завершённых построений, использующих идеи этой теории, относятся к циклическим кодам.

Важность циклических кодов обусловлена также, тем, что заложенные в основу их определения идеи теории полей Галуа приводят к процедурам кодирования и декодирования, эффективным как с алгоритмической, так и с вычислительной точки зрения. Поэтому нужно знать свойства полей Галуа.

Полем называется множество с двумя определёнными на нём операциями - сложением и умножением.

Существуют следующие примеры полей:

1. R: множество вещественных чисел;

2. С: множество комплексных чисел;

3. Q: множество рациональных чисел.

 Все эти поля содержат бесконечное число элементов. Но нас интересуют поля с конечным числом элементов. Конечное поле названное в честь французского математика Галуа обозначается GF(q), где q- это конечное множество элементов обладающих свойством поля.

Множество p(x) и элементы поля GF(p^m) обладают целым рядом свойств, используемых при построении и описании циклических кодов.

Свойство 1: Элементы поля GF(p^m) отличные от нуля образуют мультипликативную группу порядка p^m-1. Поэтому для любого элемента поля имеет место равенство ^p-1=1.

Это свойство выполняется и для нулевого элемента поля. Очевидно, что ненулевые элементы поля являются корнями многочлена x^p-1, а все элементы поля являются корнями многочлена x^p-x.

Свойство 2: Всегда в поле GF(p^m) всегда существует первообразный элемент , элемент порядка p^m-1. любой ненулевой элемент поля может быть представлен как степень одного и того же первообразного элемента , т.е. мультипликативная группа поля Галуа циклична. Важную роль при кодировании циклическими кодами имеют следующие свойства:

Свойство 3: Любой приводимый по модулю p многочлен p(x) степени m, если он существует, есть делитель по этому модулю двучлена x^p-x.

Следующие свойства позволяют определить элементы поля, являющиеся корнями многочлена p(x), если известно, что один из этих корней .

Свойство 4: В простом поле GF(p) имеет место равенство (a+b)^p=a^p+b^p.

Свойство 5: Для простого модуля p справедливо сравнение

[p(x)]^p=p(x^p)(mod p), где p(x)-произвольный многочлен, коэффициенты которого принадлежат простому полю GF(p).

Свойство 6: Если элемент поля поля GF(p^m) есть корень неприводимого по модулю p многочлена p(x) степени m, то остальными корнями p(x) будут элементы ^p, ^p, …., ^p. Следующие свойства имеют важную роль в теории циклических кодов.

Свойство 7: Если k- делитель n, то многочлен x^k-1 является делителем многочлена x^n-1.

Свойство 8: Для того чтобы неприводимый по модулю многочлен p₁(x) степени k является делителем двучлена x^p-1, то степень k должна быть делителем числа m, и наоборот.

Свойство 9: Поля Галуа GF(p^m), образованные различными неприводимыми примитивными многочленами степени m изоморфны, т.е. для любого простого числа p и любого примитивного многочлена p(x) степени m существует только одно поле Галуа GF(p^m).

Выше мы рассмотрели все необходимые свойства полей Галуа, необходимых для изучения циклических кодов. Приступим теперь к изучению самих циклических кодов.

Циклическим кодом называется линейный блоковый (n,k) - код, который характеризуется свойством цикличности, т.е. сдвиг влево на один шаг любого разрешённого кодового слова даёт также разрешенное кодовое слово, принадлежащее этому же код и у которого, множество кодовых слов представляется совокупностью многочленов степени (n-1) и менее, делящихся на некоторый многочлен g(x) степени r=n-k, являющийся сомножителем двучлена x+1. Многочлен g(x) называется порождающим. Как следует из определения, в циклическом коде кодовые слова представляются в виде многочленов: a(x)=a+…+axгде, n-длина кода, a-коэффициент из поля GF(p). Длина циклического кода называется примитивной и сам код называется примитивным, если его длина n=q-1 над GF(p). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным.

Общее свойство кодовых слов циклического кода-это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена x-1 на многочлен g(x) является проверочный многочлен h(x). При кодировании циклического кода (n,k)-кода построение кода сводится к тому, чтобы к информационным элементам a,a…,aисходного k-элементного кода добавить (n-k) полученных определённым образом избыточных элементов. Причём в каждой комбинации n-элементного циклического кода информационные и избыточные элементы будут занимать определённые позиции.

При декодировании циклического кода используется многочлен ошибок e(x) и синдромный многочлен S(x). Остаток S(x) от деления (x) на g(x) называется синдромом. Так как S(x)= (x)+g(x)l(x), а p(x)= (x)+e(x), то e(x)=[l(x)+q(x)]g(x)+S(x), то есть синдром S(x) равен остатку от деления принятого многочлена (x) на g(x). Синдром S(x), вычисленный по принятому многочлену (x), содержит информацию о векторе ошибок e(x).

Синдромный многочлен зависит непосредственно от многочлена ошибок e(x). Это положение используется при построении таблицы синдромов, применяемой в процессе декодирования.

В процессе декодирования по принятому кодовому слову вычисляется синдром, затем в таблице находится соответствующий многочлен e(x), суммирование которого с принятым кодовым словом даёт исправленное кодовое слово.

Итак мы ввели следующие многочлены:

Порождающий многочлен g(x) deg g(x)=n-k,

Проверочный многочлен h(x) deg h(x)=k,

Кодовый многочлен p(x) deg p(x)=n-1,

Многочлен ошибок e(x) deg e(x)=n-1,

Принятый многочлен (x) deg (x)=n-1,

Синдромный многочлен S(x) deg S(x)=n-k-1

Информационный многочлен i(x) deg i(x)=k-1.

Теперь перечислим некоторые свойства циклических кодов, которые необходимо знать при кодировании и декодировании, чтобы упростить число выполняемых операций.

Свойство 1: Циклический код в полиномиальном его представлении можно определить как множество многочленов степени n-1 и меньше, каждый из которых делится без остатка на некоторый порождающий многочлен g(x).

Свойство 2: Циклический код длины n с порождающим многочленом g(x) существует тогда и только тогда, когда делит x-1.

Свойство 3: пусть d-минимальное кодовое расстояние циклического кода. Каждому многочлену ошибок веса меньшее, чем d/2 соответствует единственный синдромный многочлен.

Для задания циклических кодов в основном используются два способа задания циклического кода - используя корни порождающего многочлена g(x) и в виде порождающей и проверочной матрицы.

Предположим, нам дан циклический код C(g(x)) длиной n=2-1. Мультипликативная группа поля GF(2) содержит n=2-1 элементов и является циклической группой {} порядка 2-1(здесь -примитивный элемент поля). Но каждый элемент конечной группы в степени, равной порядку группы, равен единице. Поэтому все 2-1 ненулевые элементы поля GF(2) и только они являются корнями многочлена x-1. Порождающий многочлен циклического кода длиной n=2-1 должен без остатка делить многочлен x-1, следовательно, корни многочлена должны содержаться среди корней многочлена x-1, т.е. лежать в поле GF(2). Обозначим эти корни через , где (n-k)- степень многочлена g(x). Если p(x)C(g(x))-кодовый многочлен, то по определению многочлен p(x) делится без остатка на g(x). Отсюда следует, что p()=…=p()=0, т.е. каждый многочлен содержит среди своих корней.

Для задания циклического кода, таким образом, нет нужды задавать все корни порождающего многочлена g(x). Рассмотрим разложение многочлена g(x) на неприводимые множители-многочлены f(x),…,f(x) с коэффициентом из поля GF(2): g(x)= f(x),…,f(x). Обозначим через -какой-нибудь корень многочлена f_ij. Тогда для того чтобы многочлен p(x) являлся кодовым, необходимо и достаточно, чтобы p(_i)=p(_i)=…=p(_i)=0.

Кроме вышерассмотренного описания циклического кода в виде многочлена код также можно описать в виде порождающих и проверочных матриц.

Имеется много способов формирования этих матриц. Прежде всего, проверочную матрицу можно формировать в расширении поля, так как показано ниже. Предположим, что проверочная матрица линейного кода содержит n столбцов и что число n-k строк этой матрицы делится на m. Каждая группа из m строк такой матрицы может быть представлена в виде одной строки содержащей элементы из GF(q^m). Таким образом, первые m строк становятся одной строкой (₁₁,…,_1n), а матрица H сводится к матрице

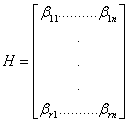
C r=(n-k)/m строками. Вместо [(n-k)m]-матрица над GF(q) мы получили (rn)-матрицу над GF(q).

Если нулями g(x) являются элементы _iGF(q^m) при j=1,…,r, то

, ( 2.1)

Что в матричном виде можно переписать как

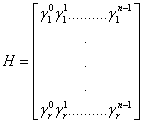(2.2)

Если заменить эту (r n) матрицу над GF(q) на (rm n)-матрицу, заменяя каждый элемент вектором столбцом коэффициентов многочлена, представляющего над GF(q), то некоторые строки этой матрицы могут быть зависимы и, следовательно, являются излишними. Удаление наименьшее число строк, необходимое для построения матрицы с линейно независимыми строками приведёт к проверочной матрице.

Вышеупомянутая процедура проясняет связь между корнями многочлена и проверочной матрицей кода, но она слишком сложна для исправления. По порождающему многочлену можно построить необходимые матрицы, даже не переходя в расширение поля. Одним из способов сделать это является построение порождающей матрицы непосредственно по порождающему многочлену.

Рассмотренные способы задания циклических кодов вытекают из методов задания линейных кодов с учётом специфики, связанной с цикличностью.

Циклические коды, задаваемые с помощью корней порождающего многочлена, получили название кодов Боуза-Чоудхури-Хоквингема (БЧХ). Если при задании циклических кодов порождающей или проверочной матрицей значительно облегчает построение кодирующих и декодирующих устройств, то с помощью корней порождающего многочлена позволяет сравнительно легко оценить корректирующие свойства этих кодов.

Корректирующие свойства ЦК могут быть определены на основе двух следующих теорем:

Теорема 1: Для любых значений m и t существует циклический код длиной n=2^m-1, исправляющий все ошибки кратности t и менее и содержащий не более mt проверочных разрядов.

Теорема 2 (БЧХ): Если среди корней порождающего многочлена g(x) циклического кода длиной n=2^m-1 содержится d₀-1 последовательных степеней ^b, ^b+1, …, ^b+d-2, то кодовое расстояние этого кода не менее d₀.[1]

Для построения циклического кода, обнаруживающего одиночные ошибки, достаточно, чтобы выбранный порождающий многочлен кода g(x) состоял больше чем из одного члена. Одиночной ошибке соответствует многочлен ошибок e(x)=xⁱ ,где i- указывает место ошибки. Для обнаружения такой ошибки необходимо, чтобы многочлен e(x) не делился на g(x) без остатка. Одночлен xⁱ нельзя разделить без остатка на многочлен, имеющий более одного члена. Простейшим подходящим многочленом является g(x)=1+x. При таком порождающем многочлене p(x) кодовый многочлен должен делиться на , т.е p(x)=(1+x)q(x).

Введём понятие о показателе порождающего многочлена g(x)-наименьшем целом положительном числе l, для которого x^l+1 делится на g(x). Если g(x)- многочлен степени m, то его показатель равен l=2^m-1. Например, нам дан циклический код n=2^m-1, k=2^m-m-1, порождённый многочленом g(x) степени m. Этот код обнаруживает все двоичные ошибки. Действительно многочлен двойной ошибки имеет вид e(x)= xⁱ+x^j, где i<jn. Многочлен ошибок останется не обнаруженным только в том случае, если он делится на g(x). Но e(x)=xⁱ(1+x^j-i) не может делиться на g(x), поскольку степень i-jn-1, т.е. меньше показателя многочлена g(x). Таким образом, многочлен двоичной ошибки всегда обнаруживается. Следовательно, такой циклический (n, k)-код позволяет обнаружить все одиночные и двойные ошибки.

При наличии пакетов ошибок длиной m=n-k многочлен ошибок имеет вид e(x)= x^j+…+xⁱ, где j-i=m+1. Вынося xⁱ за скобку, получим e(x)=xⁱ(x^m-1+…+1). Так как степень многочлена в скобках меньше m, то многочлен e(x) не делится на многочлен g(x), степень которого m, что и обеспечивает обнаружение пакетов ошибок длиной, меньшей или равной m.

Для исправления обнаруженной ошибки код строится таким образом, чтобы многочлены ошибок давали при делении на g(x) различные остатки. Исправление ошибок производиться в следующей последовательности: (x) делим на g(x) и находим остаток (синдром) S(x), здесь (x)- это принятая из ДК(дискретный канал) кодовая комбинация, которая образовалось при воздействии ошибок в ДК на информационную кодовую комбинацию p(x)=q(x)g(x)=x^n-km(x)+r(x); по S(x) находим e(x); складывая (x)+ e(x) , получаем p(x). Следовательно, основной операцией, выполняемой в процессах кодирования и декодирования циклического кода, является операция вычисления синдрома.

Посмотрим теперь, что кодовое расстояние рассмотренного выше циклического кода обнаруживающего двойные ошибки не менее 3. если бы существовало кодовое слово веса 2, то существующий кодовый многочлен имел бы вид f(x)=xⁱ+x^j, но такой многочлен не может делиться на g(x). Кодовое веса 1 также не может существовать, в противном случае многочлен g(x) делил бы одночлен xⁱ, что, очевидно, невозможно. Следовательно, кодовое расстояние d₀3, поэтому рассматриваемый код исправляет любую одиночную ошибку.

Для исправления многократных ошибок большое применение нашли циклические коды БЧХ.

2.1. Мажоритарное декодирование

При мажоритарном декодировании используются принципы решения по большинству (мажоритарный принцип), который часто позволяет упростить задачу исправления многократных ошибок. Рассмотрим реализацию мажоритарного принципа декодирования.

Пусть система проверок задана с помощью проверочной матрицы Н. Для кодового вектора А должно удовлетворяться равенство АНТ=О, эквивалентное системе r проверок на четность:

(2.3)

Систему проверок можно видоизменять, используя линейные комбинации из вышеприведенных равенств. Предположим, что удалось так подобрать эти комбинации, что некоторый символ aj входит во все проверки, а каждый из остальных символов входит в проверки по одному разу. Тогда aj можно выразить несколькими способами:

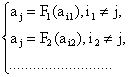(2.4)

Данная система называется системой раздельных проверок. Если выполняется соотношение l≥2t+1, то исправляются все ошибки кратности t. Действительно, каждый символ входит только в одну проверку. Если искажено t символов, то искажено t проверок. Чтобы принять правильное решение относительно символа a_j, надо иметь t+1 неискаженную проверку. Таким образом, общее число проверок l≥2t+1.

Рассмотрим циклический код (7,4) с образующим полиномом Р(х)=х³+х²+1. Проверочный полином этого кода имеет вид

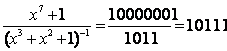
На основе проверочного полинома строим проверочную матрицу:

H=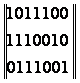

которая определяет систему проверок

a₆+a₄+a₃+a₂ =0;

a₆+a₅+a₄+a₁ =0;

a₅+a₄+a₃+a₀ =0;

На основе этих проверок построим новую систему проверок, используя первое и второе равенства, а также суммы первого с третьим и второго с третьим:

a₆+a₄+a₃+a₂ =0;

a₆+a₅+a₄+a₁ =0;

a₆+a₅+a₂+a₀ =0,

a₆+a₃+a₁+a₀=0,

a₆ + a₆ =0.

Для декодирования единичного элемента а₆ система линейных уравнений имеет вид:

a₆ = a₄ + a₃ + a₂,

a₆ = a₅ + a₄ + a₁,

a₆ = a₅ + a₂ + a₀,

a₆ = a₃ + a₁ + a₀,

a₆ = a₆.

Из системы видно, что одиночная ошибка нарушит не более двух уравнений и безошибочное значение единичного элемента а₆ определяется с помощью мажоритарного элемента на пять входов. Аналогично декодируются и остальные символы:

a_i=a_4+i+1+a_3+i+1+a_2+i+1,

a_i=a_5+i+1+a_4+i+1+a_1+i+1,

a_i=a_5+i+1+a_2+i+1+a_0+i+1,

a_i=a_3+i+1+a_1+i+1+a_0+i+1,

a_i=a_i

Индексы рассчитываются по модулю 7. Принятая ошибочная комбинация имеет вид:

110 0 110

a₆ a₅ a₄ a₃ a₂ a₁ a₀

Решим систему уравнений для единичного элемента

a₆=a₄+a₃+a₂=0+0+1=1,

a₆=a₅+a₄+a₁=1+0+1=0,

a₆=a₅+a₂+a₀=1+1+0=0,

a₆=a₃+a₁+a₀=0+1+0=1,

a₆=a₆=1.

Анализ результатов показывает, что большинство a₆=l, соответственно a₆=1. Аналогичным образом определяются другие единичные элементы. После декодирования мажоритарным методом принятая комбинация имеет вид: 10 0 0 1 10.

2.3. Принципы обнаружения и исправления ошибок помехоустойчивыми кодами

Идея построения циклических кодов базируется на использовании неприводимых многочленов. Неприводим называется многочлен, который не может бить представлен в виде произведения многочленов низших степеней, т. е. такой многочлен делится только на самого себя или на единицу и не делится ни на какой другой многочлен. На такой многочлен делится без остатка двучлен .

Неприводимые многочлены в теории циклических кодов играют роль образующих полиномов. В приложении 2 представлены все неприводимые полиномы до 9-й степени включительно, которые обозначены , где i-порядковый номер неприводимого полинома данной степени m при расположении по признаку возрастания соответствующих им двоичных чисел. Чтобы понять принцип построения циклического кода, умножаем комбинацию простого k-значного кода Q(x) на одночлен , а затем делим на образующий полином P(x), степень которого равна r. В результате умножения Q(x) на степень каждого одночлена, входящего в Q(x), на образующий полином получается частное C(x) такой же степени, как и Q(x). Результат умножения и деления можно представить как

где R(x)-остаток от деления Q(x), на Р(х).

Частное C(x) имеет такую же степень, как и кодовая комбинация Q(x) простого k-значного кода. Следует заметить, что степень остатка не может быть больше степени образующего полинома, т. е. его наивысшая степень может быть равна (r-1). Следовательно, наибольшее число разрядов остатка R(x)не превышает числа r.

Умножая обе части равенства (4.3) на P(x) и производя некоторые перестановки, получаем:

(2.5)

В (2.5) знак минус перед R(x) заменен знаком плюс, так как вычитание по модулю два сводится к сложению.

Таким образом, кодовая комбинация циклического n-значного кода может быть получена двумя способами.

1). Умножение кодовой комбинации Q(x) простого кода на одночлен и добавления к этому произведению остатка R(x), полученного в результате деления произведения на образующий полином P(x);

2). Умножения кодовой комбинации C(x) простого - значного кода на образующий полином P(x);

При построении циклических кодов первым способом расположение информационных символов во всех комбинациях строго упорядочено – они занимают к старших разрядов комбинации, а остальные () разрядов отводятся под проверочные (контрольные).

При втором способе образования циклических кодов информационные и контрольные символы в комбинациях циклического кода не отделены друг от друга, что затрудняет процесс декодирования. Поэтому в основном применяют первый способ построения циклического кода.

Пример. Дано , и образующий полином третьей степени . Следовательно, кодовые комбинации циклического кода будут иметь по семь разрядов. Требуется записать произвольную кодовую комбинацию циклического кода (7,4) первым способом. Возьмем произвольную четырехразрядную комбинацию 0111. т.е. . Найдем произведение . Произведем деление:

Следовательно, остаток R(x)=1.

Таким образом, в соответствии со сформулированным выше правилом найдем комбинацию, принадлежащую циклическому коду (7,4):

или в двоичной форме .

Операция образования циклического кода непосредственно производится при записи исходных кодовых комбинаций в виде двоичных чисел.

Пример дано и образующий полином . Следовательно, кодовые комбинации циклического кода будут иметь семь разрядов . Возьмем произвольное четырехразрядное двоичное число Q(1,0)=0001. Найдем произведение . Произведем деление

.

В результате деления получится остаток R(1.0)=101. Следовательно, комбинация циклического кода (7,4) запишется следующим образом:

.

Пример давно P(1.0)=1101 – образующий полином. Построит циклический код из простого четырехзначного кода, вторым способом. В качестве исходного используем простую комбинацию C(1.0)=0011. Операция умножения этой комбинации на образующий полином Р(1,0)=1101 запишется следующим образом:

Итак, простую четырех символьную комбинацию C(1.0)=0011 можно представить семи символьным циклическим кодом

Результаты расчетов для всего множества кодовых комбинаций этого кода сведенны в таблице 2.1.

Таблица 2.1

Простой четырех символьный код C(x)	Образующий полином P(x)	Циклический (7,4) код
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	1101	0000000 0001101 0011010 0010111 0110100 0111001 0101110 0100011 1101000 1100101 1110010 1111111 1011100 1010001 1000110 1001011

2.4. Способы исправления ошибок на основе синдрома ошибок, свойства цикличности и анализ веса остатка

Синдром циклического кода, как и в любом систематическом коде, определяется суммой по модулю два, принятых проверочных элементов и элементов первичной группы, сформированных из принятых элементов информационной группы.

В циклическом коде для определения синдрома следует разделить приятую кодовую комбинацию на кодовую комбинацию производящего полинома. Если все элементы приняты без ошибок, остаток R(x) от деления равен нулю. Наличие ошибок приводит к тому, что остаток R(x)≠0.

Для определения номеров элементов, в которых произошла ошибка, существует несколько методов. Один из них основан на свойстве, которое заключается в том, что R(х), полученный при делении принятого многочлена H(x) на P_r(x), равен R(x), полученному в результате деления соответствующего многочлена ошибок E(x) на P_r(x).

Многочлен ошибок E(x)=A(x)+H(x) , где A(x)– исходный многочлен циклического кода. Так, если ошибка произошла в а₁, то при коде (9.5) E₁(0,1)=100000000, ошибка в а₂ соответствует E₂(0,1)=010000000 и т.д., остаток от деления E(0,1) на P_r(0,1)=10011=R1(0,1) для данного 9-элементного кода всегда одинаков, он не зависит от вида предаваемой комбинации. В рассматриваемом примере R(0,1)=0101. Наличие ошибки в других элементах (a₂, a₃, …) приведет к другим остаткам. Остатки зависят только от вида P_r(x) и n. Для n=9 и P₄(0,1)=10011 будет следующее соответствие:

Таблица.2.2

Элемент с ошибкой	a1	a2	a3	a4	a5
Синдром	0101	1011	1100	0110	0011

Указанное однозначное соответствие можно использовать для определения места ошибки. Синдром не зависит от переданной кодовой комбинации, но в нем сосредоточена вся информация о наличии ошибок. Обнаружение и исправление ошибок в систематических кодах может производиться только на основе анализа синдрома.

На основании приведенного свойства существует следующий метод определения места ошибки. Сначала определяется остаток R₁(0,1), соответствующий наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде (более низком), то такой же остаток получится в произведении принятого многочлена и x, т.е. H(x)x. Это служит основанием для следующего приема, суть которого ясна из следующего примера.

Пример: Предположим, задан код (11,7) в виде кодовой комбинации 10110111100. Здесь последние четыре разряда проверочные и получены на основе использования производящего многочлена P(0,1)=100011. Принята кодовая комбинация 10111111100. Определить ошибочно принятый элемент.

Вычисляем R(x) как остаток от деления E(x)=10000000000 на 10011. Произведя деление, получим 0111. Далее делим принятую комбинацию на P_r(x) и получаем остаток R(0,1). Если R(0,1)=R₁(0,1), то ошибка в старшем разряде. Если нет, то дописываем «0» и продолжаем деление. Номер ошибочно принятого разряда (отсчет слева направо) на единицу больше числа приписанных нулей, после которых остаток окажется равным 0111. Проведем процесс деления, отмечая штрихом получаемые остатки R₁(0,1), R₂(0,1), R₃(0,1), R₄(0,1):

(2.6)

В данном примере для этого пришлось дописать четыре нуля. Это означает, что ошибка произошла в пятом элементе, т.е. исправленная кодовая комбинация будет имееть вид

. (2.7)

На основе свойства цикличности, предполагается, что ошибка произошла в старшем разряде. Определяется остаток, соответствующий вектору ошибок:

(2.8)

если остатки совпадают, то ошибка произошла в старшем разряде; если не совпадают, то дописывается 0 в комбинацию R(x) и продолжается деление, пока остатки не совпадут.

Важным свойством циклических кодов является то, что все они строятся с помощью образующего полинома Р(х). приведем методику построения циклического кода. Образующий полином Р(х) принимает участие в образовании каждой кодовой комбинации, поэтому комбинация кода делится на образующий полином без остатка. Однако без остатка делятся только те многочлены (комбинации), которые принадлежат данному коду, т.е. образующий полином позволяет выбрать разрешенные кодовые комбинации из всех возможных. Если же при делении принятой кодовой комбинации циклического кода на образующий многочлен будет получен остаток, значит, имеет место ошибка. Таким образом, остатки от деления принятой комбинации на образующий полином являются опознавателями ошибок циклических кодов. Но данные остатки еще не указывают непосредственно на место ошибки в кодовой комбинации.

В циклических кодах идея исправления ошибок основывается на следующем: ошибочная комбинация после переделанного числа циклических сдвигов «подгоняется» под остаток таким образом, чтобы в сумме с остатком она давала бы исправленную комбинацию. Остаток при этом представляет собой разницу между искаженными и правильными символами, а единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами комбинациями. «Подгоняют» искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть равно числу ошибок tи, исправляемых данным кодом (код исправляет три ошибки и в искаженной комбинации три ошибки) или меньше tи (код исправляет три ошибки, в принятой комбинации – одна ошибка).

Таким образом, для обнаружения и исправления ошибочного разряда производят следующие операции.

1) Принятую комбинацию делят на образующий полином;

2) Подсчитывают количество единиц в остатке (вес остатка). Если

где t_и – допустимое число исправляемых данным кодом ошибок, принятую комбинацию складывают по модулю два с получением остатком. Сумма дает исправленную комбинацию. Если то

3) Производят циклический сдвиг принятой комбинации влево на один разряд. Комбинацию, полученную в результате циклического сдвига, делят на образующий полином Р(х) . В результате повторного деления делимое суммируют с остатком, затем

4) Производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делимого с последним остатком. Полученная комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес то

5) Повторяют операцию из пункта 3 до тех пор, пока не будет достигнуто

В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатком от деления этой комбинации на образующий многочлен, а затем

6) Производят циклический сдвиг вправо ровно на столько разрядов, на сколько сдвинута суммируемая с последним остатком комбинация относительно принятой комбинации. В результате получим исправленную комбинацию.

Пример. При передаче комбинации 1001110 циклического кода, исправляющего одиночные ошибки (t_и=1), полученного с помощью образующего полинома произошла ошибка в четвертом разряде. Принятая комбинация имеет вид 1000110. Процесс исправления ошибки следующий:

Делим принятую комбинацию на образующий полином:

(2.9)

2. Сравниваем вес полученного остатка w с числом исправляемых ошибок t_и=1, т. е.

3. Производим циклический сдвиг принятой комбинации на один разряд влево и деление на P(x):

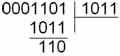(2.10)

4. Повторяем п. 3 до тех пор, пока небудет получено

(2.11)

5.Складываем по модулю два последнее делимое с последним остатком:

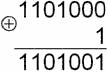(2.12)

6. Производим циклический сдвиг комбинации, полученный в результате суммирования последнего делимого с последним остатком, вправо на четыре разряда (так как перед этим мы четырежды сдвигали принятую комбинацию влево): Как видим, последняя комбинация соответствует переданной, т.е. не содержит ошибки.

3. Помехоустойчивые коды для коррекции независимых ошибок

В настоящее время среди многих корректирующих кодов широкое применение получили систематические коды особенно их подкласс – циклические коды. Циклическим кодом называется такой код, который вместе с каждым словом а = (a₀,a₁,…, a_n-1,a_n-2) содержит слово ă = (a_n-1, a₀, a₁, …, a_n-2) получающееся из а циклическим сдвигом в право на одну позицию. Характерной особенностью систематических (циклических) кодов является то, что информационные и проверочные разряды кодовой комбинации связанны между собой зависимостями, описываемые линейными уравнениями.

Код Голея занимает уникальное и важное место в теории кодирования. В силу такой хорошей сфере не удивительно, что код Голея тесно связан со многими математическими объектами, и поэтому его можно использовать для перехода от изучения теории кодирования к глубоким задачам теории групп и других областей математики. Дело в том, что код Голея относится к классу совершенных кодов, для которых выполняется следующее условие:

2^k=2ⁿ/(C_n⁰+C_n¹+C_n^t) или 2^k (C_n⁰+C_n¹+…+C_n^t)=2ⁿ , (3.1.)

где n - количество разрядов в кодовой комбинации

k - количество информационных разрядов в кодовой комбинации

Определим код Голея как двоичный циклический код через его порождающий многочлен.

Пусть g(x) и g(x) следующие взаимные многочлены:

g(x)= x¹¹ +х¹⁰+х⁶+х⁵+х⁴+х²+1 (3.2)

g(x)= x¹¹+х⁹+х⁷+х⁶+х⁵+х+1. (3.3)

Простым вычислением проверяется, что

(x-l)g(x)g(x)=x²³-l (3.4)

так что в качестве порождающего многочлена циклического (23,12)-кода можно использовать g(x), так и g(x). Как было сказано выше, минимальное расстояние кода не может быть больше 7. Ниже перечисленные утверждения совместно означают, что минимальный вес кода равен, по меньшей мере, 7.

1. в коде нет слов веса 4 или меньше;

2. в коде нет слов веса 2, 6, 10, 14, 18 и 22;

3. в коде нет слов веса 1, 5, 9, 13. 17 и 21.

Все веса слов в коде Голея исчерпываются числами: 0, 7, 8, 11, 12, 15, 16 и 23. Просчитанное на ЭВМ число слов каждого веса приведено в таблице 3.1.

Для кодирования используются три разновидности кода Голея:

• стандартный код Голея с параметрами (23, 12, 7);

• расширенный - (24, 12, 8);

• укороченный - (18, 6, 8).

Расширенный код Голея (24, 12, 8) образовался добавлением к стандартному одного бита контроля четности. Укороченный код (18, 6, 8) получается путем вычитания левых наибольших шести битов из расширенного кода.

Таблица 3.1.

Веса слов кода Голея

Вес	Число слов
	(23,12)-код	(24,12)-код
0	1	1
7	253	- 759
8	506
11	1288	2576
12	1288
15	506	759
16	253
23	1	0
24	-	1
	4096	4096

Длина вектора ошибок равна 23, а вес не превосходит 3. Длина синдромного регистра равна 11. Если данная конфигурация ошибок не вылавливается, то она не может быть циклически сдвинута так, чтобы все три ошибки появились в 11 младших разрядах. Можно убедиться, что в этом случае по одну сторону от одной из трех ошибочных позиций стоит, по меньшей мере, пять, а по другую сторону - по меньшей мере, шесть нулей. Следовательно, каждая исправляемая конфигурация ошибок может быть с помощью циклических сдвигов приведена к одному из трех следующих видов (позиции нумеруются числами от 0 до 22):

1. все ошибки (не более трех) расположены в 11 старших разрядах;

2. одна ошибка занимает пятую позицию, а остальные расположены в 11 старших разрядах;

одна ошибка занимает шестую позицию, а остальные расположены в 11 старших разрядах. Таким образом, в декодере надо заранее вычислить величины:

S⁵(x)=R_g(x)[xⁿV] и S⁶(x)=R_6(x)[xⁿV] (3.5)

Тогда ошибка вылавливается, если вес S(x) не превышает 3 или вес S(x)-Ss(x) либо S(x)-Se(x) не превышает 2. В декодере можно исправлять все три ошибки, если эти условия выполнены, либо исправлять только две ошибки в младших 11 битах, дожидаясь удаления из регистра третьего ошибочного бита. Разделив х¹⁶ и х¹⁷ на образующий полином g(x)=x¹¹+х¹⁰+х⁶+х⁵+х⁴+х²+1, получаем: S⁵(x)=x⁹+x⁸+x⁶+x⁴+x²+x

(в двоичной форме 01100110110) S⁶(x)=x¹⁰+x⁹+x⁷+x⁶+x³+x²

(в двоичной форме 00110011011)

Следовательно, если ошибка содержится в пятой или шестой позициях, то синдром соответственно равен (01100110110) или (00110011011). Наличие двух дополнительных ошибок в 11 старших разрядах приводит к тому, что в соответствующих позициях два из этих битов заменяются на противоположные.

3.1. Принцип кодирования и декодирования кода Голея

Задачей кодирующего устройства является преобразование k-элементной комбинации (a₀ a₁…a_k-1) исходного без избыточного кода в n-элементную комбинацию (а₀, а₁, a₂, … , a_n-1) избыточного циклического (n,k)-кода. Таким образом, каждая комбинация циклического кода содержит (n-k) избыточных элементов. Под кодированием в широком смысле слова подразумевается представление сообщений в форме, удобной для передачи данных по каналам связи.

Так как код Голея является разновидностью циклических кодов, то к нему применимы следующие методы кодирования:

1-й метод: Деление на образующий полином g(х)

x^r j(x) R(x)

---------- = Q(x) + ---------- (3.6)

g(х) g(х)

Видоизменив уравнение, получим:

Q(x)g(x) = x^r j(x) + R(x), (3.7)

где j (х) - кодовая комбинация,

r - степень образующего полинома.

Данный метод кодирования основан на следующем:

1. кодовую комбинацию а=(а₀, a₁, ..., а_k-1) сдвигаем па х^r разрядов влево (сдвиг аналогичен умножению на х^r);

2. полученную в результате сдвига комбинацию a=(а_k-1, ..., а_n-1), делим на образующий полином g(x);

3. полученный остаток от деления R(x) размещаем на позициях (а₀,, ..., а_n-1) кодовой комбинации.

Пример.

Для кодирования комбинации (110101101101), которой соответствует многочлен

j(х)= x¹¹ +х¹⁰+х⁸+х⁶+х⁵+х³+ х²+1, умножим сначала на х¹¹ , а затем разделим х^r j(х) на образующий полином g(x) и найдем остаток R(x). В результате деления находим, что

R(x)= x¹⁰+х⁹+х⁸+х⁶+х⁵+х⁴+ х³+x² . Кодовый многочлен образуется путем сложения х^гj(х) и R(x) согласно (2.2.2).

x^rj(х)+R(_Х)=х²²+_Х²¹+_Х¹⁹+х¹⁷+х¹⁶+х¹⁴+х¹³+_Х¹¹+х¹⁰+х⁹+х⁸+х⁶+х⁵+х⁴+х³+х² (3.8)

Этому многочлену соответствует комбинация циклического кода, в которой

110101101101, 11101111100

Информационная часть Проверочная часть

2-й метод: Умножение на образующий полином g(x)

F(x) ≤ p(x)g(x) (3.9)

Данный метод основан на умножении кодовой комбинации j(х) на образующий полином g(x). В результате получается комбинация несистематического кода, т.е. комбинация, в которой нельзя определить информационные и проверочные разряды.

Пример.

Необходимо умножить многочлен j(x)= x¹¹ +х¹⁰+х⁸+х⁶+х⁵+х³+ х²+1 на g(x)=x¹¹+x⁹+x⁷+x⁶+x⁵+x+1. Умножение осуществляется с использованием сложения по модулю 2. В результате получаем:

j(x)g(x)=x²²+x^2l+x²⁰+x¹⁸+x¹⁶+x¹⁵+x¹⁴+x¹³+x¹⁰+x⁸+x⁷+x⁶+x⁴+x²+x+l. (3.10)

Этому многочлену соответствует комбинация циклического кода:

11101011110010111010111.

3-й метод: Использование производящей и проверочной матриц. Этот метод основан на использовании производящей g(x) и проверочной Н(х) матриц.

Как и всякий линейный код, циклический код задается парой матриц: производящей и проверочной. Производящую матрицу можно представить двумя подматрицами: информационной и проверочной. Информационная подматрица имеет k столбцов (т.е. матрица размером kxk), а проверочная - n столбцов. Установлено, что в качестве информационной под матрицы удобно брать единичную матрицу. Количество информационных разрядов k кода Голея равно 12, следовательно, размерность информационной подматрицы Е(х)=2х12. Она имеет вид:

Для построения проверочной подматрицы, которую обозначим как C_r,k, прибегнем к следующему способу: выбираем комбинацию Q(x), содержащую только одну единицу, и делим ее на образующий полином g(x) с получением остатка R(x), который в результате и есть строка проверочной подматрицы.

Допустим, единичный вектор равен 00000000000100000000000, тогда первая строка подматрицы С₁(х) получается следующим образом:

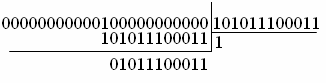
C₁(x)=R(x)= 01011100011 (3.11)

Аналогичным образом, сдвигая каждый раз единицу в следующий разряд информационной комбинации, получаем последующие строки проверочной подматрицы С(х).

Данную операцию проводим i=1¸k раз.

Таким образом, проверочная подматрица имеет вид:

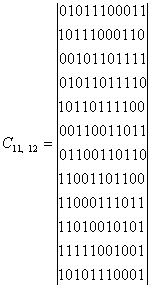
Полученная подматрица С_11,12 приписывается справа к единичной подматрице E_{12, 12} в результате чего получается производящая матрица G_{23, 12}.

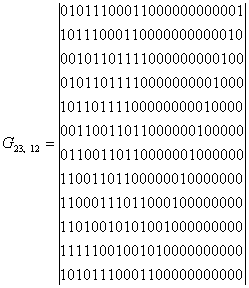
Теперь, для кодирования любой комбинации j(х) достаточно выбрать из нее разряды, равные 1, и сложить по модулю 2 соответствующие номерам выбранных разрядов строки матрицы G_23,12

В циклических кодах, а именно в кодах Голея, процесс кодирования сводится к определению r проверочных разрядов. Каждый проверочный разряд определяется с помощью проверочного соотношения, а определение r проверочных разрядов требует r проверочных соотношений, которые записываются одно под другим в виде проверочной матрицы Н_n,r

Проверочная матрица Н может быть построена с помощью проверочного полинома:

h(x)=(xⁿ+l)/g^-1(x), (3.12)

где g^-1 (x) - полином, сопряженный с образующим полиномом или обратный ему.

h(х)=(х²³+1)/(х¹¹+х⁹+х⁷+х⁶+х⁵+х+1)^-1 = х¹²+х¹¹+х¹⁰+х⁹+х⁸+х⁵+х²+1 (3.13)

что в двоичной форме: 1111100100101.

Последующие строки проверочной матрицы Н получаются с помощью циклического сдвига полученной комбинации, проверочного полинома.

В результате проверочная матрица имеет вид:

Также проверочную матрицу в каноническом виде можно получить из производящей матрицы. Образование этой матрицы производится путем замены строк производящей матрицы на столбцы.

Процесс образования схематично показан стрелками на рис. 3.1.

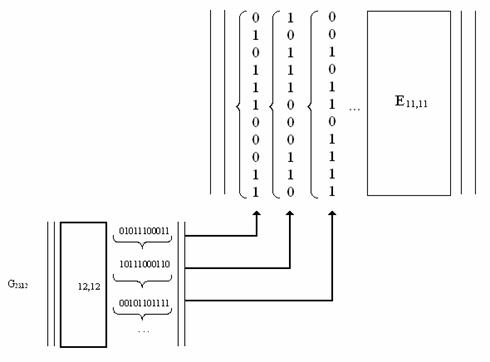
рис. 3.1 Схема образования проверочной матрицы Н

G_23,12- производящая матрица

E_12,12- информационная подматрица

H_23,11 - проверочная матрица

В результате проверочная матрица имеет вид:

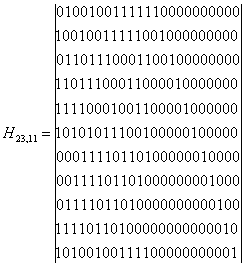
Проверочная матрица обычно используется при построении кодирующих и декодирующих устройств, поскольку она определяет алгоритм нахождения проверочных разрядов по информационным символам.

Пример.

С помощью проверочной матрицы Н определим проверочные символы при комбинации:

(110101101101).

Для вычисления первого проверочного разряда берем первую строку проверочной матрицы:

B₁=а₂ а₅ а₈ а₉ а₁₀ а₁₁ a₁₂= 1001101=0

B₂=а₁₁ а₄ а₇ а₈ а₉ а₁₀ а₁₁=1110110=1

B₃=а₂ а₃ а₅ а₆ а₇ а₁₁ а₁₂=1001101=0

B₄=а₁ а₂ а₄ а₅ а₆ а₁₀ а₁₁=1110110=1

B₅=а_] а₂ а₃ а₄ а₈ а₁₁ а₁₂=1101001=0

B₆⁼а₁а₃ а₅ а₇ а₈ а₉ а₁₂=1001011=0

B₇=а₄ а₅ а₆ а₇ а₉ а₁₀ а₁₂=1011111=0

B₈=а₃ а₄ а₅ а₆ а₈ а₉ а₁₁=0101010=1

B₉=а₂ а₃ а₄ а₅ а₇ а₈ а₁₀ = 1010101=0

B₁₀=а₁₁ а₂ а₃ а₄ а₆ а₇ а₉ = 1101111=0

B₁₁=а₁а₃ а₆ а₉ а₁₀ а₁₁ а₁₂=1011101=1

Таким образом, комбинация линейного кода имеет вид:

(11010110110101010001001).

Задачей декодера является обратное преобразование принятой поэлементной комбинации циклического кода в исходную k-элементную комбинацию. При этом эффективность циклического кода оценивается его способностью корректировать возникающие при передаче по каналу ошибки.

Декодирование кода Голея можно производить двумя методами:

• декодером Меггита;

• на основе алгоритма Берлекмпа-Месси (в данном случае код Голея рассматривается как разновидность БЧХ).

Декодером Меггита можно однозначно определить и исправить трехкратные ошибки, а алгоритм Берлекемпа-Месси исправляет только двухкратные ошибки. Также необходимо учесть простоту и сравнительную дешевизну аппаратного исполнения декодера Меггита по сравнению с декодером БЧХ. Поэтому в настоящее время в качестве декодера кода Голея используется декодер Меггита.

Принцип работы декодера Меггита основан на «вылавливании» ошибок, расположенных в старших разрядах. При этом должно выполняться следующее условие: длина информационной части не должна превышать длины синдромов ошибок.

Декодер Меггита проверяет синдромы только для тех конфигураций ошибок, которые расположены в старших разрядах. Декодирование ошибок в остальных позициях основано на циклической структуре кода и осуществляется позднее. Соответственно таблица синдромов содержит только те синдромы, которые соответствуют многочленам ошибок с ненулевым коэффициентом e_n_i. Если вычисленный синдром находится в этой таблице, то e_n_i исправляется. Затем принятое слово циклически сдвигается и повторяется процесс нахождения возможной ошибки в предшествующей по старшинству позиции (e_n-i *0). Этот процесс повторяется последовательно для каждой компоненты; каждая компонента проверяется на наличие ошибки, и если ошибка найдена, то она исправляется.

Опишем декодер Меггита для (23,12)-кода Голея.

Длина вектора ошибок равна 23, а вес не превосходит 3. Длина синдромного регистра равна 11. Если данная конфигурация ошибок не вылавливается, то она не может быть циклически сдвинута так, чтобы все три ошибки появились в 11 младших разрядах. Можно убедиться, что в этом случае по одну сторону от одной из трех ошибочных позиций стоит, по меньшей мере, пять, а по другую сторону - по меньшей мере, шесть нулей. Следовательно, каждая исправляемая конфигурация ошибок может быть с помощью циклических сдвигов приведена к одному из трех следующих видов (позиции нумеруются числами от 0 до 22):

1. все ошибки (не более трех) расположены в 11 старших разрядах;

2. одна ошибка занимает пятую позицию, а остальные расположены в 11 старших разрядах;

3. одна ошибка занимает шестую позицию, а остальные расположены в 11 старших разрядах. Таким образом, в декодере надо заранее вычислить величины:

S⁵(x)=R_g(x)[xⁿV] и S⁶(x)=R_6(x)[xⁿV]. (3.14)

Тогда ошибка вылавливается, если вес S(x) не превышает 3 или вес S(x)-Ss(x) либо S(x)-Se(x) не превышает 2. В декодере можно исправлять все три ошибки, если эти условия выполнены, либо исправлять только две ошибки в младших 11 битах, дожидаясь удаления из регистра третьего ошибочного бита.

Разделив х¹⁶ и х¹⁷ на образующий полином

g(x)=x¹¹+х¹⁰+х⁶+х⁵+х⁴+х²+1, получаем S⁵(x)=x⁹+x⁸+x⁶+x⁴+x²+x (в двоичной форме 01100110110), S⁶(x)=x¹⁰+x⁹+x⁷+x⁶+x³+x² (в двоичной форме 00110011011). Следовательно, если ошибка содержится в пятой или шестой позициях, то синдром соответственно равен (01100110110) или (00110011011). Наличие двух дополнительных ошибок в 11 старших разрядах приводит к тому, что в соответствующих позициях два из этих битов заменяются на противоположные.

Декодер отслеживает синдром, отличающийся от нулевого синдрома не более чем в трех позициях, а также синдром, отличающийся от выписанных двух синдромов не более чем в двух позициях.

Пример.

Допустим, что передавалось кодовое слово

С(х)= 10101010101001100001011.

При передаче часть символов исказилась: V(x)=C(x)+e(x). Многочлен ошибок равен: е(х)=00100000001000000010. Тогда принимаемое слово: V(x)==lo8oi010100001100001o5l, где искаженные символы обозначены значком (*). Определяем синдром S(x)=10011000111.

Рассмотрим второй этап декодирования (где r⁶(x)=x'⁶mod g(x)=00110011011, г (х)=х mod g(x)=01100110110). В каждом цикле шаги а,б,в,г -вычисления. На 17 цикле вес Wa=2 и осуществляется исправление ошибок суммированием по модулю 2 содержимого буферного устройства (старшие разряды) с синдромом и 6 символ заменяется на обратный. В это время искаженные два символа находятся в старших разрядах n-разрядах буферного устройства, а третий - в 6 разряде буфера.

Операция вычисления очередного синдрома выполняется следующим образом: анализируется старший разряд синдрома, и если он равен единице, то производится сдвиг содержимого синдрома на 1 разряд влево и суммирование по модулю 2 с образующим полиномом g(x), в противном случае осуществляется только сдвиг синдрома влево.

3.2. Принцип построения кода БЧХ

Одним из наилучших среди известных неслучайных кодов, для которых предложены удобные алгоритмы кодирования и декодирования являются коды БЧХ (Боуза-Чоудхури-Хеквингема). Коды БЧХ представляют собой большой класс циклических кодов, исправляющих независимые ошибки кратности t и менее. Для кодов БЧХ характерны все основные свойства циклических кодов.

Свойство 1. Циклический код в полиномиальном его представление можно определить как множество многочленов степени n-1 и меньше, каждый из которых делится без остатка на некоторый многочлен P(x), называемый образующим или порождающим многочленом кода.

Свойство 2. Если кодовая комбинация а_i, a₃,…, a_n-i, a_n принадлежит циклическому коду, то и комбинация, полученная из предыдущей в результате циклического сдвига её элементов, например (а_n, a₁, a₂, …, a_n-1, a_n, … a_n-2), также принадлежит этому циклическому коду.

Коды БЧХ определяются величинами n, k, d, g(x),

где: n - количество элементов в кодовой комбинации,

k – количество информационных элементов кода БЧХ,

d – количества проверочных разрядов кода БЧХ,

g(x) – порождающий многочлен кода БЧХ.

Построение кодов предложенных Боузом-Чоудхури основано на следующем. Мультипликативная группа поля Галуа GF(2^m) содержит n=2^m-1 элементов и является циклической группой {a} порядка 2^m-1(здесь а – примитивный элемент поля Галуа). Но каждый элемент конечной группы в степени, равной порядку группы, равен единице (т.е. a^m = 1). Поэтому все 2^m-1 ненулевые элементы поля GF(2^m) являются корнями многочлена 1-(2^m-1)-1. Порождающий многочлен циклического кода длинной n=2^m-1 должен без остатка делить многочлен х=2^m-1, следовательно, корни многочлена g(x) должны содержаться. Например, для кода n = 2^m-1=15 производящий многочлен является делителем многочлена z = 2^m-1, т.е.

x^15-1 = g₁(x) ×g₂(x) ×g₃(x) ×g₄(x)(x-1) (3.15)

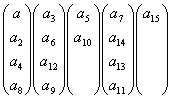
Здесь под неправильным делителем g(x) выписаны их корни, т.к. среди корней g₁(x) и g₄(x) содержаться две последовательные степени а, то, что они могут быть выбраны в качестве порождающих многочленов с d₀ ≥ = 3. g₁(x) и g₄(x) имеют соответственно вид:

g₁(x)=x⁴+x²+x+1 (3.16)

g₄(x)=x⁴+x³+ x²+x+1 (3.17)

т.к. deg g₁(x)=4 (т.е. максимальная степень g₁(x)), то длина информационных разрядов равна n-k=4, отсюда k=n-4=15-4=11 получаем код БЧХ (15,11) способный исправить однократную ошибку. Для получения большего n-k=4 необходимо взять в качестве производящего многочлена произведение g₂(x) и g₄(x), содержащие четыре последовательные степени a: a¹¹, a¹², a¹³, a¹⁴.

deg (g₂(x), g₄(x))=8 отсюда n-k=8 и k=15-8=7. Получаем код БЧХ (15,7) с d_0≥5, который может исправлять 2-х кратные ошибки.

Примитивные двоичные коды БЧХ, таким образом, строятся для любого числа n=2^m-1 и любого t=2^m-1, определяется кодовое расстояние d₀>=2t+1, число проверочных символов должно быть равно или меньше mt, число информационных символов k=n-deg(g(x)).

3.3. Принцип кодирования и декодирования кода БЧХ

Параметры кода БЧХ выбираются следующим образом:

1) Выбирается число n, исходя из формулы n=2^m-1, где m – любое целое число.

2) Определяется количество ошибок, которые необходимо исправить

(3.18)

отсюда код БЧХ должен иметь вид d₀>2t+1.

3) В зависимости от величины d₀ вычисляется

g(x)=НОКm₁(x),…m_2t(x),

где m₁(x) … m_2t(x) – минимальные неприводимые многочлены (т.е. m₁(x) = g₁(x))

4) Число проверочных символов вычисляется по формуле: r = m · t.

5) Количество информационных символов k вычисляется по формуле

K = n – r = (2^m – 1) – r (3.19)

Существует несколько способов кодирования кода БЧХ:

1) Любой циклический код задается порождающим многочленом.

Отношение (3.20) называется проверочным многочленом.

(3.20)

Поскольку g(x) и h(x) однозначно определяют друг друга, код БЧХ может быть задан порождающей и проверочными матрицами.

Для циклического кода (n,k) с порождающим многочленом g(x) можно найти k линейно независимых кодовых комбинаций образующих порождающую матрицу |G|.

В неканоническом виде |G’| имеет вид.

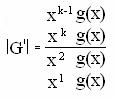
После преобразования эта матрица приводится к канонической форме |G|:

|G| = |J_k·A_k2|,

где J_k – единичная матрица размерности k x k,

A_k2 – матрица коэффициентов уравнений проверок, связывающих значений информационных и проверочных разрядов.

Для того, что бы закодировать простую комбинацию, необходимо умножить эту комбинацию на матрицу |G|, т.е. сложить по mod 2 строки порождающей матрицы |G| номера, которых соответствуют ненулевым элементам простого кода.

Полученный код является несистематическим, т.е. код, в котором нельзя разделить информационные разряды от проверочных.

Построить систематический код можно с помощью проверочной матрицы |H|. Проверочная матрица имеет вид:

|H| = |B^t, I_n-1| (3.21)

где B^t – значение матрицы проверочных соотношений размерностью k x k

I_n-1 – единичная матрица размерностью (n - k) x k.

2) Другой способ кодирования кода БЧХ состоит в следующем:

Необходимую кодовую комбинацию a(x) = a₀….a_k-1 сдвигаем на x_n-k разрядов влево. Получим число

X^n-k a(x) = X^n-k(a₀=…=a_k-1 X^k-1)=a₀ X^n-1+…+ a_k-1 X^n-1 (3.22)

Разделим теперь многочлен X^n-k a(x) на g(x) и запишем делимое в виде

X^n-k a(x) = g(x)q(x) + r(x) (3.23)

где q(x) – частное,

r(x) – остаток от деления на g(x).

Так как степень многочлена g(x) = n – k, то степень r(x) = n – k – 1.

Тогда:

X^n-k a(x) + r(x) = g(x)q(x) (3.24)

Отсюда получаем искомую кодовую комбинацию разделимого кода БЧХ.

Отличие кодов БЧХ от других циклических кодов состоит в том, что согласно определению коды БЧХ работают с неприводимыми многочленами в поле GF(q), которые могут иметь корни в некотором расширении.

Если q является степенью числа (q = q^m), то элементами поля являются все многочлены степени m-1, коэффициенты которых лежат в простом поле GF(р). Поля, которые являются расширением в простом поле GF(q), называются полем Галуа. Элемент поля GF(q^m)представляет собой m разрядный вектор с q элементами.

Алгоритм декодирования БЧХ состоит из нескольких этапов:

1) Вычисление синдрома.

2) Вычисление многочлена локатора ошибок.

3) Нахождение корней многочлена локатора ошибок.

4) Исправление ошибок.

Рассмотрим каждый этап.

1) Вычисление синдрома при декодировании можно выполнить двумя способами: с помощью проверочной матрицы H^т или по формуле (3.25)

S_j = 2^n-1 ea^2(m+j) (3.25)

где е - ошибки, а – элементы поля Галуа

Рассмотрим оба способа.

1.1 С помощью проверочной матрицы Н. Использование проверочной матрицы H^т основано на факте:

G· H^т =0, (3.26)

где G –каноническая матрица, H^т - транспонированная контрольная матрица. Поэтому если принятое слово принадлежит кодовому множеству, т.е. в нем отсутствуют ошибки, то

Х· H^т =0 (3.27)

1.2 Второй способ основан на вычислении синдромов по (i₁, i₂, … ,i_v).

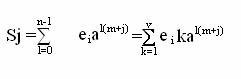(3.28)

где v – количество ошибок по позициям (i₁, i₂, … ,i_v);

а – элементы поля Галуа.

Для двоичных кодов БЧХ синдромы четных определяются как квадраты предыдущих нечетных синдромов, т.е. S₂ = S₁² и т.д. Если же все синдромы равны S₁ – S_q, то ошибок нет.

2) Зная значения синдромов, необходимо определить многочлен локаторов ошибок Л|Z|, т.к.

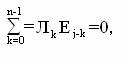(3.29)

то, решив её можно определить место расположения ошибок. Данная система уравнений называется ключевыми уравнениями. Известны два наиболее удачных алгоритма вычисления ключевого уравнения Питерсона и Берлекампа – Месси.

Для многочлена локаторов ошибок Л|Z| необходимо определить последовательность минимальной длины L, чтобы посредством уравнений

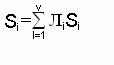(3.30)

она порождала известную последовательность S₁, S₂ … S_2t синдрома. Величина L должна быть минимальной, потому что она равна числу
ошибок, но так как ошибки в канале независимы и равновероятны, то
наиболее вероятным вектором - ошибкой должен быть вектор
минимального веса, ибо этот вес есть кратность ошибки.

Основная черта алгоритма Берлекампа - Месси состоит в следующем: вначале находим самый короткий регистр сдвига L, порождающий с S₁ по S₀. Далее проверяем, порождает ли этот регистр также S₂. Если порождает, то этот регистр по-прежнему остается наилучшим решением, и нужно продолжать проверять, порождает он следующие символы синдрома. На каком-то шаге очередной символ уже не будет порождаться, в этот момент нужно изменить регистр таким образом, чтобы он:

а) правильна, предсказал следующий символ S;

б) не менял предсказаний предыдущих символов;

в) увеличивал длину на максимально возможную величину.

Этот процесс нужно продолжать до тех пор, пока не будут
порождены первые 2t символа синдрома.

3. Определение локаторов ошибок и, следовательно, корней многочлена локаторов ошибок можно выполнить с помощью процедуры Ченя. Согласно процедуре Ченя, корнем ключевого уравнения должен быть элемент поля Галуа, удовлетворяющий условию (3.31)

Л(а^-1) = 0, (3.31)

где i-ошибочный символ. Отсюда:

.

Таким образом, для обнаружения местоположения ошибок необходимо перебрать все элементы поля Галуа GF (2ⁿ) и, если n(а^-1) = 0, то обратный элемент а¹ и будет являться локатором ошибок и укажет место положения ошибки.

4. Зная место положения, ошибок, производят исправление ошибок согласно формуле:

С^(х) = r(х) + с(х),

где с^ (х) - исправленная кодовая комбинация,

r(х) - принятая кодовая комбинация,

с(х) - вычисленные местоположения ошибок.

Пример реализации кода БЧХ.

В этом примере рассматривается декодирование циклического (7,4,3) кода Хемминга с порождающим многочленом g(x) = х³+х+1. Схема вычисления синдрома показана на Рисунке 3.2. Принимаемые символы накапливаются в регистре сдвига и одновременно вводятся в схему деления на g(x). После приема седьмого бита содержимое этого регистра сдвигается на один разряд в каждом такте, а схема деления модифицирует синдром и проверяет совпадение с полиномом х⁶ mod(l+х+х³)= 1+х² ↔ 101 (в двоичной записи).

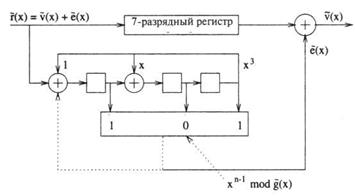
Рис.3.2. Синдромный декодер двоичного циклического (7,4,3) кода Хэмминга.

Как только на выходе схемы проверки появится 1, будет исправлена ошибка в позиции х⁶. В тот же самый момент исправление вводится по обратной связи в схему деления и, тем самым, обнуляет остаток от деления. Нулевой остаток может рассматриваться как сигнал об успешном завершении декодирования. Проверка на нулевой остаток схемы деления позволяет обнаруживать некоторые аномалии по окончании процедуры декодирования. Перейдем теперь к изучению циклических кодов, исправляющих многократные ошибки, для которых задача декодирования может рассматриваться как решение системы уравнений. По этой причине здесь необходимо знакомство с полем, в котором будут выполняться операции умножения, сложения и деления. Циклические коды имеют хорошую алгебраическую структуру. Позднее будет показано, что эффективная реализация мощных алгоритмов декодирования достигается при использовании арифметики конечного поля, когда известно размещение корней порождающего многочлена кода.

Напомним, что порождающий полином всегда может быть представлен произведением двоичных неприводимых многочленов:

Алгебраическая структура циклических кодов выражается, в частности, в возможности определения корней каждого из многочленов в некотором поле разложения (которое является расширением поля, которому принадлежат коэффициенты многочлена). В интересующем нас случае поле разложения неприводимого многочлена является полем Галуа. В литературе поля Галуа называют также конечными полями, имея в виду конечное число принадлежащих ему элементов. Стандартным обозначением является GF(q), где q число элементов поля.

В общем случае число элементов поля есть степень простого числа, однако ниже будут рассматриваться только поля характеристики 2, когда q = 2^m.

Пример. В этом примере мы напомним читателям, что они хорошо знакомы с понятием «поле разложения». Рассмотрим поле действительных чисел. Известно, что в этом поле многочлен х²+1 неприводим. Однако в поле комплексных чисел он раскладывается в произведение (х+i) (х-i), где i = .

Таким образом, комплексное поле является полем разложения (т.е. расширением) поля вещественных чисел!

Использование арифметики GF(2^m) в процедурах декодирования позволяет заменить сложные комбинационные схемы практичными процессорными архитектурами, пригодными для решения уравнения (2.8). Ниже приводятся инструменты, необходимые для решения систем уравнений, которые возникают при декодировании циклических кодов.

Поле Галуа GF(2^m) изоморфно (с точностью до знака «+») линейному пространству {0, 1}^m. Другими словами, каждому элементу GF(2^m) соответствует единственный m - мерный вектор .

В конечном поле имеется примитивный элемент , степени которого порождают все ненулевые элементы поля, т.е. Элемент α является корнем неприводимого двоичного полинома р(х), р(α) = 0. Наименьшее положительное целое n, для которого αⁿ = 1, равно 2^m-1. Все элементы поля удовлетворяют уравнению βⁿ =1, n = 2^m -1 (Другими словами, все ненулевые элементы поля совпадают с корнями степени n из единицы).

Наименьшее положительное целое z, для которого β^z = 1, равно одному из делителей 2^m-1. Это число z называют порядком элемента. Примитивными элементами поля являются все такие элементы β = αⁱ, 0 < i < 2^m - 2, для которых i взаимно просто с числом 2^m -1.

Неприводимый многочлен называют примитивным, если его корни имеют максимальный порядок, т.е. 2^m - 1. Все корни неприводимого многочлена имеют одинаковый порядок. Периодом многочлена называют наименьшее число z, при котором р(х) делит бином x^z- l, z /(2^m - 1). Период неприводимого многочлена совпадает с порядком его корней.

Пример. Примитивный полином р(х) = х3 + х + 1 порождает поле GF(2³). Примитивный элемент поля обозначим α, р(α) = α³ + α + 1 = 0. В таблице показаны три способа представления элементов поля GF(2³).

Степень	Полином	Вектор	Степень	Полином	Вектор
-	0	000	α^3	1 + α	011
1	1	001	α^4	α + α^2	110
α	α	010	α^5	1 + α + α^2	111
α^2	α^2	100	α^6	1 + α^2	101

Для сложения элементов в GF(2^m) наиболее удобно векторное представление. При этом используется поразрядное сложение по модулю два. Однако для умножения в поле наиболее удобно степенное представление. В этом случае умножение сводится к сложению показателей степени элементов по модулю 2^m - 1. Действительно, так как равенство αⁿ =1, n=2^m - 1, выполняется для всех элементов поля, то αⁿ+1 = α, αⁿ+2 = α², и т.д. Таким же способом находим, что α-1 = α^-1+n = α^n-1.

В примере 2.8 α^-1 = α⁶. В общем случае, обратный элемент β^-1 = αb элемента β = α^k определяется из сравнения b + k ≡ 0 mod (2^m - 1). Таким образом, b = 2^m – 1- k. Наконец, для реализации сложений в степенном представлении полезно использовать равенство р(α) = 0. Например, в примере 27 имеем

α³ = α³ + (α³ + α + 1) = α + 1.

Полиномиальное представление может быть удобным, когда требуется реализация вычислений по модулю некоторого полинома. Примером этого может служить декодирование циклических кодов, где требовалось вычисление

xⁱ mod g(x).

Дополнительного пояснения требует только операция деления, или точнее, вычисление обратного элемента по неприводимому модулю. Пусть f(x) некоторый (ненулевой) вычет, тогда его обратным элементом φ(х) = (f(x))^-1 называется решение сравнения f(x) φ(x)-g(x)p(x)= 1 ≡ 1 mod p(x).

Решение этого сравнения можно найти с помощью алгоритма Евклида для вычисления наибольшего общего делителя многочленов или вычисления подходящей дроби для отношения [р(х) /f(x)].

Удобным способом реализации умножений и сложений в конечном поле является применение таблиц с различной интерпретацией их входного адреса. Эти таблицы позволяют легко переходить от полиномиального к степенному представлению элементов поля и наоборот.

Таблица анти - логарифмов (точнее, степеней) A(i) удобна для реализации сложения. Выходом таблицы является двоичный вектор, записанный как целое число, A(i), соответствующее элементу αⁱ. Таблица логарифмов (или индексов) L(i) удобна для реализации умножения в конечном поле. Эта таблица выдает значение показателя степени примитивного элемента альфа, α^L(i), соответствующего двоичному вектору, представленному целым числом i. Справедливо следующее равенство:

α^L(i) = A(i)

Рассмотрим пример использования таблиц для реализации арифметики конечного поля.

Пример. Рассмотрим поле GF(23) с порождающим многочленом

р(α) = α³ + α+1 и α⁷=1. Таблицы логарифмов и антилогарифмов имеют вид:

Адрес входа i	Анти - логарифм A(i)	Логарифм L(i)
0	1	-1
1	2	0
2	4	1
3	3	3
4	6	2
5	7	6
6	5	4
7	0	5

В приведенной таблице имеются две особые точки. Нулевой элемент конечного поля не может быть представлен степенью примитивного элемента. Так что в столбце «Анти-логарифм» не должно быть нулевого элемента поля, а в столбце «Логарифм» нулевому элементу поля не должно быть сопоставлено какое-либо число. Таким образом, при работе с этими таблицами требуется специальная проверка на нулевой элемент поля в результате вычислений или в исходных данных.

Рассмотрим вычисление элемента γ = α(α³ + α⁵)³ в векторной форме. Учитывая свойства поля GF(23), находим последовательно:

α³ + α⁵= 110111 = 001 = α², γ= α(α²)³ =α¹⁺⁶= α⁷ = α⁰ =1

С использованием таблиц эти вычисления выглядят следующим образом:

γ=A(L(A(3) A(5))3+l)=A(L(37) 3+1)=A(L(4) 3+1)=A(23+l)=A(7)=A(0)=1.

Таблицы логарифмов и степеней (анти - логарифмов) используются для реализации арифметики конечного поля и GF(2^m).

Минимальным многочленом φ_i(х) элемента αⁱ называется многочлен минимальной степени, корнем которого является данный элемент поля. Следующие свойства минимальных многочленов легко могут быть доказаны. Минимальный многочлен φ_i(х) элемента αⁱ имеет двоичные коэффициенты и является неприводимым над GF(2) = {0,1}. Более того, корнями этого многочлена являются αⁱ, α²ⁱ, α⁴ⁱ, ..., α^τ, где τ = 2^k и k делит m. Эти элементы называются сопряженными с αⁱ элементами поля. Степени сопряженных элементов поля образуют циклотомический смежный класс: С_i={i,2i,4i,...,2^k-1i}

Очевидно, что степень минимального многочлена равна числу элементов (мощности) соответствующего циклотомического смежного класса, т.е.

deg [φ_i(х)]=

Циклотомические смежные классы (называемые также циклическими множествами) обладают свойством расщепления множества вычетов целых чисел Z_n по модулю n = 2^m - 1. Таким образом, циклотомические смежные классы не пересекаются. Иначе, их пересечение Ø, является пустым множеством, а их объединение равно всему множеству, т.е. U_i C_i = Z_n.

Пример. Циклотомическими множествами по модулю 7 являются:

C₀ ={0}

С₁ ={1,2,4}

С₃ ={3,6,5}

Сs	Сопряженные элементы	Минимальный многочлен φs(x)
С0 = {0} С1 = {1,2,4} С3 = {3,6,5}	1 α, α^2, α^4 α^3, α^6, α^5	Φ0,(х)=x+1 Φ1,(х)=x^3+ x+1 Φ3,(х)= x^3+ x^2 +1

Примитивный элемент α поля GF(2^m) (как и все другие) удовлетворяет уравнению αⁿ=1. Все ненулевые элементы поля являются некоторой степенью примитивного элемента. Таким образом, бином степени n=2^m-1 имеет следующее разложение на неприводимые двоичные сомножители в двоичном поле:

,

где М - число циклотомических классов, и следующее полное разложение на сомножители первой степени в поле GF(2^m)

(+1)= (x+α^j) (3.32)

Важно отметить, что степень минимального многочлена, φ_i(х) равна мощности (т.е. числу элементов множества) циклотомического класса С_i. Отсюда следует способ нахождения всех неприводимых делителей бинома (хⁿ-1).

1. Найти все циклотомические классы по модулю 2^m-1.

2. Для каждого циклотомического класса C_s вычислить минимальный многочлен

φ_s (x)= (3.33)

Этот способ может быть использован для построения порождающих многочленов циклических кодов. Он используется в программе моделирования БЧХ кодов для построения порождающего многочлена кода, заданного его корнями.

Пример. Рассмотрим поле GF(2³), порождаемое примитивным многочленом р(х) = х³+х +1. Корни каждого из делителей бинома х⁷ + 1 показаны в таблице.

Коды БЧХ это двоичные коды, конструкция которых определяется заданием их нулей, т.е. корней порождающего их многочлена:

БЧХ код с кодовым расстоянием d_min ≥2t_d+1 является циклическим кодом, порождающий многочлен g(x) которого имеет 2t_d последовательных корней в точках α^b, α^b+l, ..., α^b+δ , где δ = 2t_d - 1.

Таким образом, порождающий многочлен двоичного (n, k, d_min) кода БЧХ имеет вид:

G(х) = HOК{φ_b (х), φ_b+1(x), ... , },

а длина и размерность кода равны, соответственно,

n = НОК{n_b, n_b+1,..., }

k = n-deg [g(x)].

Двоичный БЧХ код, заданный таким образом, имеет конструктивное кодовое расстояние равное 2t_d + 1. Однако, следует заметить, что истинное кодовое расстояние может быть больше конструктивного.

Пример. Над полем GF(2³), порождаемым примитивным многочленом р(х) = х³ + х + 1, для параметров t_d = 1 и b = 1 многочлен g(х) = HОК{φ₁,(х), φ₂} = х³+х +1 порождает двоичный (7,4,3) код БЧХ. На самом деле, это двоичный циклический код Хемминга! Заметим, что вес Хемминга этого порождающего многочлена равен 3 и, следовательно (в данном случае, но не всегда), конструктивное и истинное расстояние кода совпадают.

Пример. Рассмотрим поле GF(2⁴), порождаемое примитивным многочленом р(х) = х⁴ + х + 1, и параметры t_d = 3, b = 1. Тогда многочлен

g(x) = HОК{ φ₁,(х), φ₃ (х)} = (х⁴ + х + 1)(х⁴ + х³ + х² + х + 1)= х⁸ +х⁷ +х⁶ +х⁴ +1

порождает двоичный (15,7,5) код БЧХ, исправляющий две ошибки.

Пример. В поле GF(2⁴) , порождаемом примитивным многочленом

р(х) = х⁴ + х + 1, и параметры t_d = 3, b = 1, многочлен

g(x)=НОК{ φ₁,(х),φ₃(х),φ₅ (х)}=(х⁴+х+1)(х⁴+х³+х²+х+1)(х²+х+1)=х¹⁰+х⁸+х⁵+х⁴+х²+х + 1

порождает двоичный (15,5,7) код БЧХ, исправляющий три ошибки.

Рассмотрим нижнюю границу минимального расстояния кодов БЧХ известную как граница БЧХ. Это полезно не только тем, что позволяет оценить корректирующие способности кода в общем случае, но и тем, что выделяет особые свойства кодов БЧХ. Напомним, что элементы α^b, α^b+1, ..., α^b+δ ,

где δ = 2t_d -1, являются корнями порождающего многочлена g(x) и что все кодовые слова v кода БЧХ, ассоциированные с полиномами v(x), кратны порождающему многочлену кода. Следовательно

v(x) C↔v(αⁱ)=0,b<i<b + 2t_d-1 (3.34)

Таким образом, на основании (3.34), все кодовые слова

удовлетворяют следующей системе 2t_d уравнений (в матричной форме)

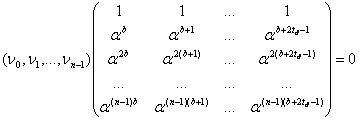(3.35)

Соответственно, проверочная матрица двоичного БЧХ кода имеет вид

(3.36)

Эта проверочная матрица обладает следующим свойством: любая ее 2t_d х 2t_d подматрица, т.е. образованная любыми 2t_d столбцами, является матрицей Вандермонда. Следовательно, любые 2t_d столбцов проверочной матрицы линейно независимы. Отсюда следует, что минимальное кодовое расстояние этого кода удовлетворяет неравенству d > 2t_d + 1. Этот результат можно интерпретировать следующим образом:

Граница БЧХ. Если порождающий многочлен g(x) циклического (n,k,d) кода имеет последовательных корней, например, α^b, α^b+1 ,..., α^b+, то d ≥2+ 1.

Класс циклических полиномиальных кодов включает циклические коды Рида-Маллера, коды БЧХ и Рида-Соломона, коды над конечными геометриями. Задание полиномиальных кодов связано с наложением условий на их корни (нули) следующим образом.

Пусть α примитивный элемент поля GF(2^ms). Пусть s положительное целое число и b делитель 2^s — 1. Тогда α^h является корнем порождающего полинома g(x) полиномиального кода порядка μ, если и только если b делит h и где 0 < j <

где для любого целого i,

функция Wα (s) определена как (α (s) = 2^s) - ичный вес целого числа i, т.е.

Согласно этому определению коды БЧХ и Рида-Соломона являются полиномиальными с параметрами b = m = 1. Коды Рида-Маллера являются подкодами полиномиальных кодов с параметром s=1. Коды над конечными геометриями возникают как дуальные к полиномиальным кодам. Ниже даются свойства нулей конечно-геометрических кодов.

Пусть α примитивный элемент поля GF(2^ms). Пусть h неотрицательное целое меньше 2^ms - 1. Тогда α^h является корнем порождающего многочлена g(x) ЕГкода порядка (μ,s), длины 2ms— 1, если и только если

,

где

Для s = 1 ЕГ коды совпадают с циклическими РМ*_m,μ кодами и, следовательно, ЕГ коды можно рассматривать как обобщенные коды РМ (Рида-Маллера).

Пусть, а примитивный элемент поля GF(2^(m+1)s). Пусть h неотрицательное целое меньше 2^(m+1)s -1. Тогда α^h является корнем порождающего многочлена g(x) ПГкода порядка (μ, s), длины (2^ms-1)/(2^s - 1), если и только если h делится на 2^s-1 и ,

где и

Главной идеей в декодировании БЧХ кодов является использование элементов конечного поля для нумерации позиций кодового слова (или, эквивалентно, в порядке коэффициентов ассоциированного многочлена). Такая нумерация показана на Рисунке 2.5. для вектора r = (r₀, r₁, ... , r_n-1), соответствующего многочлену r(х).

Позиции ошибок могут быть найдены из решения системы уравнений в поле GF(2^m). Эти уравнения можно получить, вводя многочлен ошибок е(х) и учитывая нули кода α^j для b < j < b + 2t_d -1, как показано ниже.

Пусть r(х) = v(x) + e(x) представляет полином, ассоциированный с принятым словом, где многочлен ошибок определен как

(3.37)

где v < td число ошибок в принятом слове. Множества и называют значениями ошибок и локаторами ошибок, соответственно, где e_j{0, 1} для двоичных БЧХ кодов и α GF(2^m).

Синдромы определены как значения принятого полинома r(х) в нулях кода:

.

.

.

Это определение эквивалентно s = Нr, где проверочная матрица Н определена в (3.36).

Введем многочлен локаторов ошибок

(3.38)

корни которого равны обратным величинам локаторов ошибок. Тогда справедливо следующее соотношение между коэффициентами многочлена локаторов ошибок и синдромами:

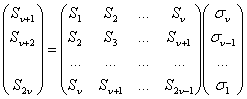(3.39)

Решение ключевого уравнения, представленного в (3.39), требует довольно интенсивных вычислений в процедуре декодирования БЧХ кодов. Известны следующие методы решения ключевого уравнения:

1. Алгоритм Берлекемпа-Мэсси (ВМА). Этот алгоритм был предложен Берлекемпом и Мэсси. По числу операций в конечном поле этот алгоритм обладает высокой эффективностью. ВМА обычно используется для программной реализации или моделирования кодов БЧХ и PC.

2. Евклидов алгоритм (ЕА). Из-за высокой регулярности структуры этого алгоритма его широко используют для аппаратной реализации декодеров БЧХ и PC кодов.

3. Прямое решение. Этот алгоритм, предложенный Питерсоном, находит коэффициенты многочлена локаторов ошибок прямым решением системы (3.39) как системы линейных уравнений. Алгоритм Питерсона используется для декодирования недвоичных кодов БЧХ и PC. В действительности, так как сложность обращения матрицы растет как куб корректирующей способности кода, прямой алгоритм может быть использован только для малых значений td.

На Рисунке 3.2 показана блок-схема декодера БЧХ кодов (как двоичных, так и недвоичных). Декодер состоит из логических схем и обрабатывающих блоков, реализующих следующие задачи:

• Вычислить синдромы, вычисляя значения принятого полинома в нулях кода

S_i=r(αⁱ), i = b, b +1,...,b + 2t_d-1 (3.40)

• Найти коэффициенты многочлена локаторов ошибок σ(х).

Рис.3.2. Архитектура БЧХ декодера

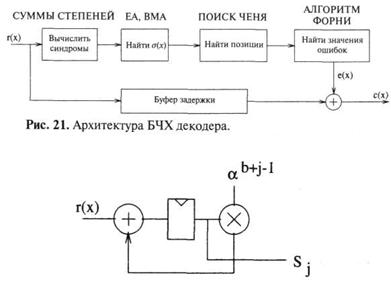
Рис.3.3. Пример схемы вычисления синдрома.

• Найти обратные величины корней σ(х), т.е. позиции ошибок j₁, j₂, ... , j.

• Найти значения ошибок (этап ненужный для двоичных кодов).

• Исправить принятое слово на вычисленных позициях для вычисленных значений ошибок.

Одним из преимуществ использования арифметики над конечным полем GF(2^m) является возможность применения относительно простых логических схем и вычислительных блоков. Например, на Рисунке 3.3 показана схема вычисления синдромов S_j. Умножение в поле GF(2m) также реализуется относительно простой логической схемой.

Алгоритм Берлекэмпа-Мэсси лучше всего рассматривать как итеративный процесс построения минимального линейного регистра (сдвига) с обратной связью (ЛРОС), аналогичного показанному на рисунке 3.4, который генерирует известную последовательность синдромов S₁ S₂,...,.

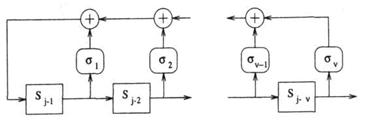
Рис. 3.4. ЛРОС с отводами σ₁, σ₂, ..., σ_ν и выходом S₁ ,S₂ , ..., S_2ν .

Целью ВМА является построение многочлена (обратной связи) σ⁽ⁱ⁺¹⁾(x) наименьшей степени, удовлетворяющего следующему уравнению, выведенному из (3.39):

(3.41)

Решение этой задачи эквивалентно условию, что многочлен

является многочленом обратной связи ЛРОС, который генерирует ограниченную последовательность синдромов.

Несовместность (рассогласование, расхождение, различие) на i-ой итерации, определенная как

является мерой соответствия синдромной последовательности и генерируемой ЛРОС и содержит корректирующий множитель для вычисления σ⁽ⁱ⁺¹⁾ на следующей итерации. Возможны два случая:

• Если d_i = 0, то уравнение (2.18) удовлетворяется с равенством

(3.42)

• Если d_i 0, то решение на следующей итерации имеет вид

(3.43)

где является решением на m-ой итерации такое, что — 1 < m < i, d_m 0 и разность () максимальна.

Итеративное вычисление σ⁽ⁱ⁺¹⁾(x) продолжается, пока не удовлетворятся одно или оба условия: либо, либо i = 2t_d- 1.

Начальными условиями алгоритма являются:

(3.44)

Заметим также, что в Алгоритме Берлекэмпа-Мэсси используются программные инструкции (если — то). По этой причине ВМА не слишком удобен для аппаратной реализации. Тем не менее, по числу операций в конечном поле GF(2^m) этот алгоритм весьма эффективен. Эта версия алгоритма реализована в большинстве программ на языке Си для моделирования БЧХ кодов.

Пример. Пусть Сдвоичный (15, 5, 7) код БЧХ, исправляющий три ошибки из Примера 2.14. Для проверки вычислений и просто для справки приводится степенное и векторное представление элементов поля GF(16), порожденное примитивным многочленом р(х) = 1 + х + х⁴:

Таблица элементов поля GF(2⁴), p(x) = 1 + x + х⁴:

Степень	0	1	α	α2	α3	α4	α5	α6
Вектор	0000	0001	0010	0100	1000	0011	0110	1100
Степень	α ^7	α^8	α^9	α^10	α^11	α^12	α^13	α^14
Вектор	1011	0101	1010	01111	1110	1111	1101	1001

Порождающий многочлен кода С равен g(x) = х¹⁰ + х⁸ + х⁵ + х⁴ +х² + х + 1. Предположим, что информационный полином равен u(х) = х+х²+х⁴. Тогда соответствующее ему кодовое слово равно

v(x) = х + х² + х³ + х⁴ + х⁸ + х¹¹ + х¹² + х¹⁴.

Пусть принятое слово равно

r(х) = 1+х + х² + х³ + х⁴ + х⁶ + х⁸ + х¹¹ + х¹⁴,

соответствующее вектору r=v+e, полученному в результате передачи слова v по ДСК. (Вектору е соответствует многочлен ошибок е(х) = 1 + х⁶ + х¹². Хотя декодеру этот вектор ошибок неизвестен, он используется здесь для упрощения вычисления синдромов.

Таким образом, σ(х) = 1 + α х + α⁷ х² +α³х³.

То, что на нечетных шагах алгоритма d_i = 0 в предыдущем примере не случайность. Для двоичных кодов БЧХ это закономерность. С тем же результатом можно было выполнять только четные шаги алгоритма. Единственное изменение состоит в замене правила остановки на следующее

В результате снижается сложность декодирования.

Впервые этот алгоритм был рассмотрен Питерсоном. Решение ключевого уравнения (2.16) может быть найдено с помощью стандартной техники решения системы линейных уравнений. Это решение дает коэффициенты σ(х). Применению этой техники мешает только то, что неизвестно действительное число ошибок в принятом слове. По этой причине приходится проверять гипотезу о том, что действительное количество ошибок в принятом слове равно v. Предположим, что не все синдромы S_i, 1≤i≤2t равны нулю. Очевидно, что принятое слово совпадает с одним из кодовых, если все синдромы равны нулю. Тогда процедура декодирования на этом завершается!

Декодер начинает с предположения о том, что возникло максимальное число ошибок, v_max = t_d. Он вычисляет определитель Δ_i для i =v_max = t_d

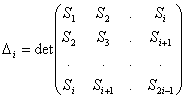(3.45)

и сравнивает его с нулем. Если определитель равен нулю, то действительное число ошибок меньше, чем предполагалось. Значение i уменьшается на единицу и снова проверяется определитель. Процедура повторяется, если это необходимо, пока i >1. Как только окажется, что определитель не равен нулю, вычисляется обратная матрица для матрицы синдромов и вычисляются значения σ₁ , σ₂, ..., σ_v, где v = i. В случае, когда Δi = 0, для i = 1, 2,..., t_d, декодирование считается безуспешным и регистрируется обнаружение неисправляемой комбинации ошибок.

Пример. В этом примере полином локаторов ошибок для (15, 5, 7) БЧХ кода из Примера 2.15 находится с помощью PGZ алгоритма. Предположим для начала, что имеется i = t_d = 3 ошибки. Определитель Δ₃ вычисляется (с использованием алгебраического дополнения) следующим образом:

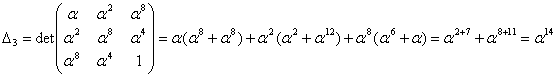
Так как Δ₃ 0, то подтверждается предположение о том, что в принятом слове три ошибки. Подставляя синдромы, найденные в примере, в ключевое уравнение (3.39), получаем:

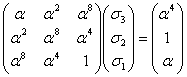(3.46)

Напомним, что (Δ₃)-1 = α^-14 = α. Решение уравнения (3.46) имеет вид:

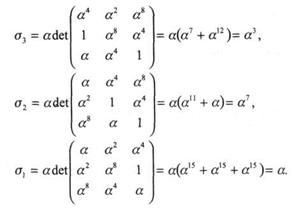
Таким образом, получили σ(х) = 1 + αх + α⁷х² +α³х³, что совпадает с результатом, полученным по алгоритму БМ в примере.

В основе этого алгоритма лежит хорошо известная процедура нахождения наибольшего общего делителя (НОД) двух полиномов (или целых чисел). Ниже рассматривается применение ее для декодирования БЧХ кодов.

Определим полином значений ошибок как Λ(х) = σ(x)S(x), где синдромный полином имеет вид

(3.47)

Из уравнения (3.39) следует, что

(3.48)

Задача декодирования может быть переформулирована как задача определения многочлена Λ(х), удовлетворяющего уравнению (3.48). Это решение может быть найдено применением расширенного алгоритма Евклида к многочленам r₀(x) = x^d, d = 2t_d + 1 и r₁(x) = S(x). Если на j-ом шаге алгоритма получено решение

такое, что deg[r_j(x)]≤t_d, то Λ(х) = r_j(х) и σ_i(x) = b_j(x). Заметим, что для задачи декодирования полином α_i(х) не представляет интереса, так как решение (3.48) ищется по модулю x^d.

Расширенный алгоритм Евклида вычисления НОД состоит в следующем.

Расширенный алгоритм Евклида: Вычисление НОД (r₀(x), r₁(x))

• Вход: r₀(х), r₁(х), deg [r₁(x)] ≥ deg [r₁(x)],

• Начальные условия: α₀ (х) = 1, b₀(x) = 0, α₁(x) = 0, b₁(х) = 1.

• На шаге j (j ≥ 2) применить длинное деление к многочленам

r_j-2(x) и r_j-1(x), r_j-2(x)= q_j (x) r_j-1(x)+r_j(x), 0deg[r_j(x)]<deg[r_j-1(x)]

• Вычислить

α_j(x)= α_j-2(x)-q_j(x)α_j-1(x), b_j(x)= b_j-2(x)- q_j(x)b_j-1(x)

• Остановить вычисления на итерации last = j_last, когда deg[r_last(x)] = 0.

Выход: НОД(r₀(х), r₁x)) = r_k(x), где k наибольшее ненулевое целое такое, что

r_k(х) 0 и k <J_last.

Пример. В этом примере вычисляется полином локаторов ошибок σ(х) для (15, 5, 7) кода БЧХ из примера по алгоритму Евклида.

• Начальные условия:

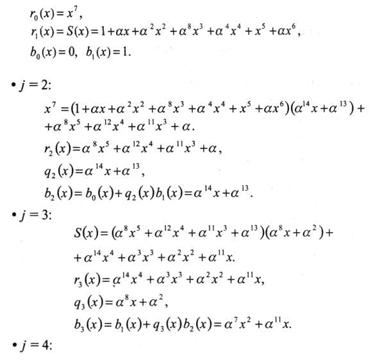
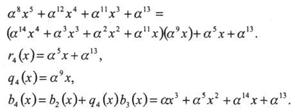
Так как deg[r₄(x)]=1≤3, алгоритм останавливается. Очевидно, что многочлен σ(х) = b₄(х)=α¹³(1+αх+α⁷х² +α³ x³)

имеет те же самые корни, что и многочлены, найденные алгоритмами ВМА и PGZ, и отличается только константным множителем.

Последний пример показывает, что в общем случае многочлен локаторов ошибок, полученный алгоритмом Евклида, может отличаться на константный множитель от решения, полученного алгоритмами ВМА и PGZ. Для декодирования представляют интерес только корни этих полиномов, а не их коэффициенты. Таким образом, все три метода находят требуемый многочлен локаторов ошибок.

Для поиска корней σ(х) на множестве локаторов позиций кодовых символов используется метод проб и ошибок, получивший название метод Ченя. Для всех ненулевых элементов βGF(2m), которые генерируются в порядке 1,α, α², .. проверяется условие σ(β^-1)=0. Этот процесс легко реализуется аппаратно. На самом деле, поиск корней (факторизация) многочленов над GF(2^m) является увлекательной математической задачей, которая еще ждет своего решения.

Для двоичных кодов БЧХ исправление ошибок на позициях j₁,...,j_ν соответствующих найденным корням, сводится к инвертированию символов, принятых на этих позициях, т.е. после чего, выдается восстановленное кодовое слово ύ (x).

Пример. Продолжая Пример 2.16, находим, что корни многочлена локаторов ошибок равны: 1, α⁹ = α^-6 и α³ = α^-12. Другими словами, получено следующее разложение многочлена на множители

σ(х) = (1 + x)(1 + α⁶х)(1+ α¹²х)

Соответственно, восстановленный многочлен ошибок равен

е(х) = 1 + х⁶ + х¹² и (x) = x + x² +x³ +х⁴+х⁸+х¹¹+х¹²+х¹⁴

Три ошибки исправлены.

Существует много ситуаций, когда решение о принятом символе не может считаться надежным. Рассмотрим, например, передачу двоичных символов по каналу с АБГШ с двоичной фазовой манипуляцией, т.е. с отображением 0→+1 и 1→-1. Если значение принятого сигнала слишком близко к нулю, то возможно, более разумно, с точки зрения минимизации вероятности ошибки декодирования, отказаться от решения о принятом символе. В таких случаях принятый символ «стирается», а такое решение называют стиранием. Подобные стирания представляют собой простейшую форму мягкого решения.

Введение стираний, по сравнению с исправлением только ошибок, обладает тем преимуществом, что декодеру известны позиции, с ненадежными символами. Пусть d минимальное кодовое расстояние, v число ошибок и μ число стираний в принятом слове. Тогда минимальное Хеммингово расстояние по нестертым позициям снижается, по меньшей мере, до величины d-μ. Следовательно, корректирующая способность равна [(d-μ — 1 )/2] и справедливо следующее соотношение

(3.49)

Последнее неравенство, на уровне интуиции, означает, что исправление ошибок требует вдвое больше усилий (и избыточности), чем исправление стираний, поскольку позиции стираний известны.

Для двоичных линейных кодов, включая коды БЧХ, стирания и ошибки могут быть исправлены следующим ниже методом.

1. Записать нули на стертые позиции и декодировать полученное слово в кодовое слово обозначенное v₀(x).

2. Записать единицы на стертые позиции и декодировать в кодовое слово v₁ (x).

3. Выбрать из v₀(x) и v₁(x) в качестве результата декодирования кодовое слово, ближайшее к принятому слову по нестертым позициям. Иначе говоря, в качестве результата декодирования выбирается слово, потребовавшее наименьшего числа исправлений.

Таким образом, любая допустимая по условию (3.49) комбинация стираний и ошибок исправляется за две попытки исправления ошибок.

Пример 2.19. Рассмотрим циклический (7, 4, 3) код Хемминга с порождающим многочленом g(x)=1+х+х³ и конечное поле GF(23) с примитивным элементом а, удовлетворяющим условию р(α)=1+α+α³. Предположим, что передано слово v(x) =х+х²+х⁴ и что приемник ввел два стирания. Так как d =3 > μ , то эти стирания могут быть исправлены. Пусть r(х) = ƒ+ х + х² + ƒх³ + х⁴ полином, ассоциированный с принятым словом, где через ƒ обозначены стирания.

Первая попытка: декодируем принятое слово при ƒ = 0, r₀(х) = х + х² + х⁴. Синдромы для него равны: S₁ = r₀(α) = 0 и S₂ = (S₁)² = 0. Следовательно,

v₀(x) = r₀(х) = х + х² + х⁴.

Вторая попытка: теперь декодируем при ƒ =1, r₁{х) = 1 + х + х² + х³ + х⁴,

S₁= α и S₂ = α². Уравнение (3.39) имеет в этом случае вид: ασ₁ = α². В результате получаем σ (х) = 1 + α х, е(х) =х и кодовое слово v₁(x) =r₁(х) +е(х) = 1+х² +х³ + х⁴, которое отличается от принятого слова r(х) в одной нестертой позиции. В качестве результата декодирования выбираем слово v₀(x). Таким образом, исправлены два стирания.

Следует напомнить, что для исправления только стираний линейным кодом (при точном отсутствии ошибок) достаточно найти решение системы линейных уравнений rН^T=0. Решение этой системы единственно, если число стираний меньше кодового расстояния. Кроме того, этим методом можно исправить многие из комбинаций с числом стираний больше кодового расстояния (но не более числа проверок), хотя решение может быть не всегда единственным.

В общем случае, распределение весов двоичного линейного (n,k) кода С может быть найдено перечислением всех 2^k кодовых слов и подсчетом их веса Хемминга. Обозначим A_w число кодовых слов веса Хемминга w. Тождество Мак-Вильяме связывает распределение весов линейного кода, А(х) = А₀+А₁х+А₂х²+...+А_nxⁿ, с распределением весов дуального ему

(n, n-k) кода С^┴,

В(х) = B₀ + В₁х + В₂Х² +... + В_nхⁿ, следующим соотношением:

(3.50),

которое может быть записано и в обращенной форме:

(3.51)

Таким образом, для кодов с высокой скоростью проще сначала подсчитать распределение весов дуального кода, а затем вычислить А(х) по формуле (3.50).

Для некоторых классов кодов может быть использована решетчатая структура кода. Для кодов меньшей длины распределение весов нетрудно посчитать с помощью тождества Мак-Вильяме. Далее вводится определение расширенного циклического кода. Двоичный расширенный циклический код получается из циклического кода добавлением, в начале (или, наоборот, в конце) каждого кодового слова, общей проверки на четность. Расширенный код уже не является циклическим. Пусть Н проверочная матрица циклического кода, тогда проверочная матрица Н _ext расширенного кода равна

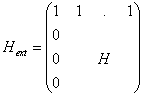(3.52)

Для расширенных БЧХ кодов известно, что A^(ext)_n+1-w = A^(ext)_w. Эти данные полезны для нахождения распределения весов двоичного циклического БЧХ кода длины до 127. Это делается с помощью следующего результата:

Пусть С двоичный циклический (n,k) БЧХ код с распределением весов А(х), полученный исключением общей проверки из двоичного расширенного (n+1, k) с распределением весов A^(ext)(x). Тогда для четного веса w справедливо соотношение:

(n+1)A_w-1=wA^(ext)_w

wA_w=(n + l-w)A_w-l (3.53)

Пример. Рассмотрим двоичный расширенный (8,4,4) код Хемминга. Этот код имеет проверочную матрицу

легко проверить, что A^(ext)(х)=1+14х⁴+х⁸. Для распределения весов двоичного циклического (7,4,3) кода Хэмминга получаем с помощью (3.53)

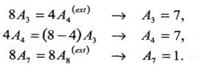
Известный спектр весов кода позволяет оценить его вероятности ошибки. Распределение весов и граница объединения дают хорошую оценку вероятности ошибки кода при передаче двоичных сигналов по каналу с АБГШ.

В качестве примера граница объединения посчитана для расширенных кодов БЧХ длины от 8 до 64. Результаты представлены на рисунках 3.5 — 3.9. На рисунке 3.9. представлена граница объединения для канала с общими Релеевскими замираниями и распределения весов для БЧХ кода длины 8. Граница посчитана с помощью метода Монте-Карло при замене коэффициента A_w на wA_w/n чтобы учесть двоичные ошибки. Границы для других кодов могут быть получены аналогичным способом.

Границы объединения для вероятности ошибки на информационный бит (BER) расширенных БЧХ кодов длины 8.

Рис.3.5. Оценки (BER) по границе объединения для расширенных БЧХ кодов длины 8. Двоичный канал с АБГШ.

Границы объединения для вероятности ошибки на информационный бит (BER) расширенных БЧХ кодов длины 16.

Рис.3.6. Оценки (BER) по границе объединения для расширенных БЧХ кодов длины 16. Двоичный канал с АБГШ.

Границы объединения для вероятности ошибки на информационный бит (BER) расширенных БЧХ кодов длины 32.

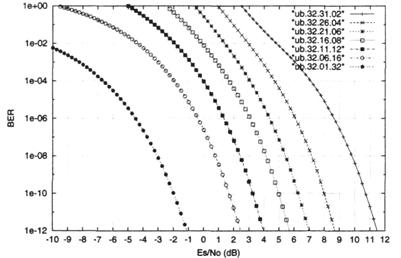
Рис. 3.7. Оценки (BER) по границе объединения для расширенных БЧХ кодов длины 32. Двоичный канал с АБГШ.

Границы объединения для вероятности ошибки на информационный бит (BER) расширенных БЧХ кодов длины 64.

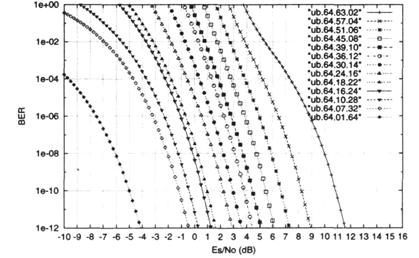
Рис.3.8. Оценки (BER) по границе объединения для расширенных БЧХ кодов длины 64. Двоичный канал с АБГШ.

Границы объединения для расширенных БЧХ кодов длины 8 в канале с общими Релеевскими замираниями.

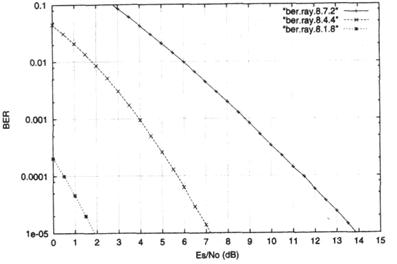
Рис.3.9. Оценки (BER) по границе объединения для расширенных БЧХ кодов длины 8. Двоичный канал с общими Релеевскими замираниями.

Прежде чем выбирать конкретный алгоритм мягкого декодирования имеет смысл использовать распределение весов кода и границу объединения для предварительной оценки эффективности, достижимой в заданном канале. Для каналов с АБГШ и Релеевскими замираниями граница объединения дает точный ответ для вероятности ошибки на бит менее 10^-4.

4. Помехоустойчивые коды для коррекции пакетов ошибок

4.1. Принцип построения кода Файра

Экспериментальные исследования каналов связи показали, что ошибки символов при передаче по каналу связи, как правило, группируются в пакеты различной длительности. Под пакетом ошибок длиной L понимают такой вид комбинации ошибок, в котором между соседними разрядами, пораженными ошибками содержится b < L - 2 разряда.

Пакеты ошибок возникают в результате воздействия на канал передачи помех импульсного характера, длительность которых больше длительности одного символа. При этих условиях ошибки независимы, они возникают пакетами, общая длительность которых соответствует длительности помех. Существуют специально сконструированные коды для обнаружения и исправления пакетов ошибок. Код Файра есть наиболее известный циклический код, исправляющий одиночные пакеты ошибок, причем для этого требуется небольшое число проверочных символов.

Образующий полином кода Файра определяется как:

P(x)=g(x)(x^c +1),

где g(x) - неприводимый многочлен степени t, принадлежащий степени m, причем с не кратно m.

Многочлен g(x) называется неприводимым, если его нельзя разложить на множители. Однако, этот многочлен всегда можно разложить на множители, используя элементы из некоторого расширения.

Порядком m элемента β конечного поля называется наименьшее значение m, для которого β^m = 1 , β является корнем многочлена х^m- 1. Если β является также корнем некоторого неприводимого многочлена у(х), то g(x) должен быть делителем х^m- 1, с - простое число, которое не делится на m без остатка. Наименьшее значение m, для которого произвольный многочлен g(х) без кратных корней делит х^m- 1совпадает с наименьшим общим кратным порядков корней g(х). Поэтому m является длиной самого короткого цикла, порожденного регистром с обратными связями, определяемыми многочленом g(х).

Для любого t существует, по крайней мере, один неприводимый многочлен g(х) степени t, принадлежащий показателю степени m = 2^t -1. Например: если g(х)=х³ +x² +1 (t=3) то m= 2^t -1 =7 и число может принимать значения, которые делятся на 7, то есть 15, 16, 17, 18, 19, 20, 22 и т.д.

Длина кода Файра равна наименьшему общему кратному чисел с и m

n = НОК (с, m) т, е. такому, что g(х) делит х^m-1 .

Число проверочных символов r = с + t.

Число информационных символов k =n - с -t.

Длина "b" исправляемого пакета ошибок удовлетворяет неравенству:

с≥b + d-1, t≥b

Код Файра может быть использован в режиме одновременного исправления пакета ошибок длины ≤b, и обнаружения пакета ошибок длины, d≥b причем должны выполняться неравенства:

с≥b + d - 1, t≥b

Наличие сомножителя x^c +1 в многочлене Р(х) достаточно для обнаружения одиночной пачки ошибок длины "с" или меньше и для полного определения значений ошибок в пачках длины не превосходящей "b".

Дополнительная информация, требуемая для определения положения пачки ошибок, обеспечивается сомножителем g (x).

Пример: Пусть К=63, b=3, d=9, т.е. требуется построить код, исправляющий пакет ошибок длиной в 3 и меньше разрядов и одновременно обнаруживающий пакет ошибок длиной 9 и меньше разрядов Тогда t≥b = 3, c≥b + d-1 =3 + 9-1 =11. Выбираем неприводимый многочлен третьей степени, g(х)=х³+х²+1. Порядок корней такого многочлена равен 7. Числа, соответствующие с и m, взаимно простые.

Следовательно: n = НОК (с, m) = НОК(11, 7) = 77. Образующий многочлен заданного кода имеет вид: Р(х)=( х³+х² +1)* (х¹¹ + 1) Таким образом, при заданных корректирующих возможностях (b=3; d=9) код Файра имеет n=77, k=63, с + t = 14

4.2. Принцип кодирования и декодирования кода Файра

4.2.1. Принципы кодирования кода Файра

Так как коды Файра относятся к классу циклических кодов, то они обладают всеми свойствами последних. Построение кода Файра ведется по тем же правилам, что и построение любого циклического кода. Как известно, кодовая комбинация циклического кода может быть получена двумя способами:

1 ) Умножением k-элементной комбинации простого кода на образующий полином Р(х).

2) Умножением кодовой комбинации простого кода на одночлен хr и добавлением к этому произведению остатка от деления произведения G(x) х^r на Р(х).

Циклический код, как и всякий систематический код, однозначно определяется подобранными определенным образом исходными кодовыми комбинациями. Эти комбинации записываются в виде производящей матрицы из k строк и n столбцов. Для формирования строк производящей матрицы по второму способу образования циклического кода берут не произвольные комбинации неизбыточного кода G(x), а лишь те из них, которые содержат 1 в одном разряде. Именно эти комбинации умножаются на хrи находится остаток от деления G(x) х^r / Р(х), равный Ri(x)

Соответствующая строка матрицы записывается в виде Gi(x)х^r+Ri(x). При этом вся матрица разбивается на две подматрицы G_n,k=| E^t_k T,C_r,к|, где E^t_k -единичная транспонированная матрица; C_r,k - подматрица с числом столбцов r и строк k, образованная остатками от деления Ri(x)

Производящая матрица дает возможность получить первые к комбинаций кода. Остальные 2^k- 1-комбинаций получаются суммированием по модулю 2 строк производящей матрицы во всех возможных сочетаниях. Последняя комбинация кода является нулевой. Рассмотрим построение кода Файра с параметрами n=9; k=4. Для построения данного кода выберем образующий полином Р(х) =(х² + х + 1)(х³ + 1) = х⁵ + х⁴ + х³ + х² + 1 Для этого кода t=2; m= 2^t -1 = 22 -1 = 3, с=3; r = c + t = 3 + 2 = 5

По второму способу построения построим производящую матрицу

Все остальные комбинации получаются путем суммирования по модулю два - строк производящей матрицы во всех возможных сочетаниях.

4.2.2. Принципы декодирования кода Файра

Код Файра позволяет исправить любой одиночный пакет ошибок длиной b и менее и одновременно обнаружить любой пакет ошибок длиной t≥b, появившиеся в пределах n - элементной кодовой комбинации. Известны два метода исправления ошибок кодом Файра. Рассмотрим каждый из них. Пусть на передаваемый кодовый вектор {f (x)} воздействует пакет ошибок { хⁱ В(х)}, здесь {} обозначают смежный класс, а член в скобках представитель смежного класса.

В(х) представляет собой многочлен описывающий пакет ошибок, а множитель хⁱ показывает разряд с которого начинается пакет. Если принимаемый вектор принадлежит коду, то при делении на образующий полином остаток будет равен 0. Если же остаток не равен 0, то вектор содержит информацию об ошибках:

{хⁱ В(х) = g(x)S(x) + R(x)}, где R(x)- многочлен остатка степени меньшей n-k. Задача исправления ошибок состоит в том, чтобы по виду остатка R(x) найти

хⁱ В(х). Тогда исправление сведется к суммированию по модулю 2 принятого вектора с хⁱ В(х). Можно показать, что если хⁱ В(х) принадлежит k-классу исправляемых пакетов ошибок, то {хⁱ В(х) }={х^n-i R₁(х)} , где{R₁(х)} ={х^j R(х)} и i = n-j

Следовательно, в качестве вектора ошибок берется остаток R₁(х) и считается, что эта комбинация расположена в принимаемом кодовом слове, начиная с (n- i) - го разряда.

Сформируем алгоритм декодирования. Он состоит из следующих этапов:

1) Принятая комбинация делится на Р(х); Если деление будет произведено без остатка, то ошибки в принимаемой комбинации отсутствуют или не обнаруживаются. Если же имеется остаток R(x), то переходят ко второму этапу:

2) Остаток от деления R(x) умножается на хⁱ(i= 1,2,3,..., n) и делится на Р(х).

3) Проверяется будет ли остаток R₁(х) исправимой комбинацией. Если степень искажений принятой n - разрядной кодовой комбинации такова, что она может быть исправлена, то полученный в результате остаток R(x) степени, меньшей или равной r, будет расположен в конце регистра-делителя, а в остальных "с" разрядах регистра делителя будут 0. Операция деления хⁱ R(х) на Р(х) продолжается до такого значения i, при котором R₁(n) будет исправимой комбинацией, но не более чем n раз. Отсутствие признака исправляемости комбинации указывает на то, что степень искажения принятой комбинации превышает исправляющую возможность кода.

4) Если после i шагов остаток R₁(x) окажется исправимой комбинацией, то для исправления ошибок необходимо принятую комбинацию сложить по модулю 2 с полученным остатком, начиная с j= (n - i) разряда.

Существует еще один способ исправления ошибок кодом Файра. Пусть в канале связи имеет место одиночный пакет ошибок, непревосходящий b. При этом на выходе канала связи будет получен полином: F(x)=f(x)+х^I B(х)

где f(x)- кодовый полином, кратный Р(х);

В(х) - полином в степени, соответствующей пакету ошибок;

I- номер разряда кодового слова, определяющий начало пакета ошибок.

Декодирование разбивается на следующие этапы:

1) Производится вычисление остатков от деления принятого полинома F(x) на полиномы g(х) и (х^c+1) при этом получаются остатки B₁(x) и В₂(х), соответственно.

2) Производится умножение B₁(x) и В₂(х) на последовательные степени х и вычисление на каждом таком шаге остатков от деления результатов на полиномы g(х) и (х^c+1), соответственно. При этом каждый раз производится сравнение новых остатков.

3) Этап второй осуществляется до тех пор, пока вышеназванные остатки не совпадут. Полученный в результате совпадения остаток определяет вид пакета ошибок. Для нахождения местоположения пакета ошибок (I) может быть использован аппарат теории сравнений. Пусть i и j - показатели степеней х, при которых соответствующие остатки совпадают, тогда

I = -(iD₁ +jD₂) mod n

Если два числа a и b дают один и то же остаток при делении на число n, то говорят что a и b сравнены по модулю n и обозначают a= b mod n где:

D1=1 mod m; D1=0 mod c;

D2=1 mod c; D2=0 mod m;

Наряду с кодами Файра к числу кодов, наиболее подходящий для исправления пакетов ошибок относятся коды Рида–Соломона (РС). Коды Рида–Соломона представляют частный случай не двоичных (в общем случае с основанием q) циклических кодов БЧХ. Образующий полином кода Рида–Соломона определяется соотношением

g(x) = (x – α) * (x – α²) * (x – α);

где α – это корни многочлена, d₀-кодовое расстояние.

PС - коды являются недвоичными кодами и для работы с ними необходимо знать поле Галуа типа GF(2^m), где m - расширение поля Галуа, построенное по полю примитивного многочлена степени m .

Полем называют множество элементов, на котором определены две операции. Одна из них называется сложением и обозначается a+b, а другая – умножением и обозначается a · b, даже если эти операции не являются обычными операциями сложения и умножения чисел. Для того чтобы множество элементов, на котором заданы операции сложения и умножения, было, полем, необходимо, чтобы по каждой из этих операций выполнялись все групповые аксиомы, а также выполнялся дистрибутивный закон, т. е. для трех любых элементов поля а, b, с были справедливы равенства а · (b+с) = а · b+а · с и (b+с) · а = b · а+с · а. Кроме того, по каждой операции группа должна быть коммутативной, т. е. должно выполняться, а + b = b + a и а · b = b· а. Следует заметить, что групповые свойства по операции умножения справедливы для всех ненулевых элементов поля. Поля с конечным числом элементов q называют полями Галуа по имени их первого исследователя Эвариста Галуа и обозначают GF(q). Число элементов поля q называют порядком поля. Конечные поля используются для построения большинства известных кодов и их декодирования. В зависимости от значения q различают простые или расширенные поля. Поле называют простым, если q – простое число. Для обозначения простых чисел будем использовать символ p. Простое поле образуют числа по модулю p: 0, 1, 2,…, p–1, а операции сложения и умножения выполняются по модулю p. Наименьшее число элементов, образующих поле, равно 2. Такое поле должно содержать 2 единичных элемента: 0 относительно операции сложения и 1 относительно операции умножения. Это поле GF(2),или двоичное. Правила сложения (a) и умножений (б) для элементов GF(2)приводятся ниже:

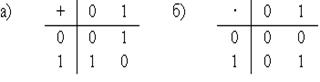
GF(3) –троичное поле с элементами 0, 1, 2. Для него правила сложения и умножения приводятся ниже:

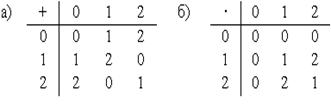
Формирование таблиц производится приведением результата сложения или умножения чисел, записанных во главе строк или столбцов, по модулю p, т. е. в качестве результата операции принимается остаток от деления полученного числа на p. Анализируя состав таблиц, легко убедиться, что 0 и 1 как единичные элементы по операции сложения и умножения не изменяют значения других элементов поля по соответствующей операции. Кроме того, видно, что для каждого элемента по операции сложения и для ненулевых элементов по операции умножения имеются обратные. Ниже приведены правила сложения и умножения для элементов GF(4) при попытке построить это поле из чисел 0, 1, 2, 3 по предыдущей конструкции.

Изучим возможность построения полей с элементами в виде последовательностей чисел. Определим условия, при которых последовательности длины m с элементами из поля GF(p) образуют поле. Рассмотрим последовательности длины 4 с элементами из GF(2). Такие последовательности можно складывать как векторы, и нулевым элементом по операции сложения является 0000. Для задания операции умножения сопоставим каждой последовательности многочлен от a:

Умножение таких многочленов может дать степень, большую, чем 3, т. е. последовательность, не принадлежащую рассматриваемому множеству. Например, (1101) · (1001) <--> (1+a+a³) · (1+a³) = 1+a+a⁴+a⁶. Для того чтобы свести ответ к многочлену степени не более 3, положим, что α удовлетворяет уравнению степени 4, например,

Π(a) = 1+a+a⁴ = 0, или a⁴ = 1+a.

тогда

a⁵ =a+a², a⁶ =a²+a³;

1+a+a⁴+a⁶ = 1+a+1+a+a²+a³ = a²+a³.

Это эквивалентно делению на многочлен 1+a+a⁴ и нахождению остатка от деления:

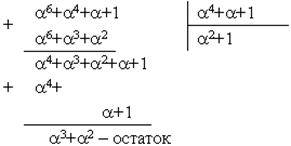
Таким образом, имеет место аналогия при формировании поля из чисел и последовательностей чисел (многочленов). Эта аналогия распространяется и на то, что для обратимости введенной операции умножения (чтобы система элементов в виде последовательностей длины m или многочленов степени меньшей m, образовывала поле) многочлен Π(a ) должен быть неприводим над полем своих коэффициентов. Поле, образованное многочленами над полем GF(р) по модулю неприводимого многочлена p(x) степени m, называется расширением поля степени m над GF(p) или расширенным полем. Оно содержит p^m элементов и обозначается GF(p^m).

     Поле, образованное шестнадцатью двоичными последовательностями длины 4, или многочленами степени 3 и менее с коэффициентами из GF(2) по модулю многочлена x⁴+x+1, неприводимого над GF(2), является примером расширенного поля GF(2⁴), которое может быть обозначено также GF(16) Важнейшим свойством конечных полей является следующее. Множество всех ненулевых элементов конечного поля образует группу по операции умножения, т. е. мультипликативную группу порядка q–1. Рассмотрим совокупность элементов мультипликативной группы, образованную некоторым элементом a и всеми его степенями a²,a³ и т. д. Так как группа конечна, должно появиться повторение, т. е. aⁱ = a^j. Умножая это равенство на (aⁱ)^–1 = (a^–1)ⁱ, получим 1 = a^j-i. Следовательно, некоторая степень a равна 1.

Наименьшее положительное число e, такое, что a^e= 1, называется порядком элемента a. Совокупность элементов 1, a, a²,…,a^e–1 образует подгруппу, поскольку произведение любых двух элементов принадлежит этой совокупности, а элемент, обратный a^j, равен a^e–j и тоже входит в эту совокупность. Группа, которая состоит из всех степеней одного из ее элементов, называется циклической группой. Из рассмотренного свойства конечных полей вытекают два важных следствия. Первое из них утверждает, что многочлен x^q–1–1 имеет своими корнями все q–1 ненулевых элементов поля GF(q), т. е.

(4.1)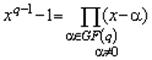

В поле GF(q) элемент a, имеющий порядок e = q–1, называется примитивным. Отсюда следует, что любой ненулевой элемент GF(q) является степенью примитивного элемента. Второе следствие из рассмотренного свойства утверждает, что любое конечное поле GF(q) содержит примитивный элемент, т. е. мультипликативная группа GF(q) является циклической. В табл.2.1 представлены различными способами элементы GF(2⁴).

Таблица 4.1

Элементы поля Галуа GF(2⁴).

Последовательность длины 4	Многочлен	Степень	Логарифм
1	2	3	4
0000	0	0	–¥
1000	1	1	0
0100	a	a	1
0010	a^2	a^2	2
0001	a^3	a^3	3
1100	1+a	a^4	4
0110	a+a^2	a^5	5
0011	a^2+a^3	a^6	6
1101	1+a+a^3	a^7	7
1010	1+a^2	a^8	8
0101	a+a^3	a^9	9
1110	1+a+a^2	a^10	10
0111	a+a^2+a^3	a^11	11
1111	1+a +a^2+a^3	a^12	12
1011	1+a^2+a^3	a^13	13
1001	1+a^3	a^14	14

Поле GF(2⁴), представленное в табл.2.1 построено по модулю x⁴+x+1. Примитивный элемент поля a является корнем этого многочлена. Многочлен, корнем которого является примитивный элемент, называется примитивным многочленом. Если в качестве Π(x) выбрать примитивный неприводимый многочлен степени m над полем GF(2),то получим поле GF(2^m) из всех 2^m двоичных последовательностей длины m.

4.3. Принцип кодирования и декодирования кода Рида-Соломона

4.3.1. Принципы кодирования кода Рида-Соломона

Коды БЧХ являются большим классом легко строящихся кодов с произвольной длиной блока и скоростью. Одним из важных подклассов кодов БЧХ являются PС-коды. PС-коды являются недвоичными кодами и для работы с ними необходимо знать поле Галуа типа GF(2^m), где m - расширение поля Галуа, построенное по полю примитивного многочлена степени m . Коды PС могут исправлять как одиночные ошибки, так и пакеты ошибок. Благодаря простоте аппаратной реализации PС-коды получили широкое применение в технике связи. Наиболее часто эти коды используются при построении каскадных кодов, где они используются как внешние коды. Коды PC являются циклическими кодами, поэтому им характерны все свойства циклических кодов. Кодирование циклического кода производится с помощью порождающего многочлена, если k/n > 0,5, и с помощью проверочного многочлена в противном случае. Кодирование кодов РС производится как и для обычного циклического кода: делением информационной последовательности, сдвинутой на хr разрядов влево на порождающий многочлен с выделением остатка. Затем полученный остаток добавляют к информационной части. Порождающий многочлен для РС-кодов, можно определить по формуле: g(x) = П (х-α^r) = (x-α)(x-α²).. (x-α^2t). Степень многочлена равна 2t , откуда следует, что параметры кода связаны соотношением n-k = 2t.

Для кода PС с параметрами n =15, k =9 показатель k/n =0,6, следовательно, процесс кодирования будет производиться с помощью порождающего многочлена g(x). Рассмотрим на примере вычисление порождающего многочлена для кода PС с параметрами (15,9). Порождающий многочлен для данного кода будет 6 степени n-k=15-9=6

g(x)=(x+α)(x+α²)(x+α³)(x+α⁴)(x+ α ⁵)(x+ α ⁶)=x⁶+ α¹⁰x⁵+ α¹⁴x⁴+ α ⁴x³+ α ⁶x²+ α⁹x+ α⁶

Минимальное кодовое расстояние d=n-k+1=15-9+1=7. Следовательно, данный код может исправить 3 ошибки, т.к. t = (n-k)/2= 7-1/2=3. Зная параметры кода и поле Галуа можно перейти к кодированию. Допустим, передается кодовая комбинация вида α x⁷+ α ⁸x⁶. Разделим эту комбинацию на порождающий многочлен и остаток от деления добавим к данной комбинации

ax⁷+a⁸x⁶ x⁶+a¹⁰x⁵+a¹⁴x⁴+a⁴x³+a⁶x²+a⁹x+a⁶

Å ax+a⁷

ax⁷+a¹¹x⁶+a¹⁵x⁵+a⁵x⁴+a⁷x³+a¹⁰x²+a⁷x

a⁷x⁶⁺a ¹⁵x⁵+a⁵x⁴+a⁷x³+a¹⁰x²+a⁷x

Å

a⁷x⁶⁺a ¹²x⁵+a⁶x⁴+a¹¹x³+a¹³x²+ax+a¹³

a⁸x⁵⁺a ⁹x⁴+a⁸x³+a⁹x²+a¹⁴x+a¹³

Таким образом, в канал поступит кодовая комбинация в виде:

α х⁷+ α ⁸х⁶+ α ⁸х⁵+ α х⁴+ α ⁸х³+ α ⁹х²+ α ¹⁴х+ α ¹³.

4.3.2. Принципы декодирования кода Рида-Соломона

Вследствие помех, действующих в канале связи, любая кодовая комбинация может быть поражена ошибками. Информацию о наличии ошибок в кодовой комбинации дают синдромы, т.е. проверочные соотношения. Предположим, что была передана кодовая комбинация f(х). В процессе передачи по каналу связи произошли ошибки, и была принята комбинация:

f(x)=f(x)+e(x),

где е (х) - вектор ошибок.

Вектор ошибки можно задать перечнем его ненулевых комбинаций и позиций, на которых они расположены. Эти позиции будут определяться номерами позиций ошибок. Каждая нулевая компонента вектора ошибок е(х) описывается парой элементов: У_i и X_i, где У_i - величина ошибки, а X_i- номер позиции ошибки. Здесь У_i- элемент GF(q), a X_i- элемент GF(qm). Если произошло t ошибок, то е(х) имеет t ненулевых компонент и требует для описания t пар (у_i, х_i). Тогда

е(αⁱ)= ∑ у_i x_i= S_i

Значение S_i =е(αⁱ) задается проверками 0 ≤ i ≤ 2t₀-1.

Таким образом, синдромы ошибок связаны с ошибками уравнением:

S_i= ∑ y_ix , 0≤ j ≤ 2t-1

Эти уравнения являются нелинейными, поэтому любой метод решения этих уравнений составляет основу процедуры исправления ошибок. Для решения этих уравнений используется метод, предложенный Берлекэмпом. Наиболее трудным этапом в этом методе является нахождение многочлена локаторов ошибок. Многочлен вида: Т(x)=То+T_i+..T_n-1 = П(1-X_i), называется многочленом локаторов ошибок (локаторами ошибок называются элементы поля GF(q), равные x₁=αⁱⁱ ,…, x_t=a^it). Многочлен локаторов ошибок может иметь вид:

Т(x)=Т_tx^t+T_t-1x^x-1+…+T_ix+ имеющий корни x_i^-1, i=1,…,t.

Допустим, что величины Т_t,Т_t-1,…,Т₁ известны, тогда записав

S_J= - ∑ T_i S _j-1, где j =t+1….2t

можем трактовать её следующим образом: по компонентам S_j-t,S_j-t+1,…,S_j-1 вычисляется следующая компонента S_j c помощью величин Т_t,Т_t-1,…,Т_1. Однако декодеру известны не величины Т_t,Т_t-1,…,Т₁ их-то как раз надо найти, а компоненты синдрома S₁,S₂, S_2t. Поэтому нахождение многочлена локаторов ошибок Т(х), производится следующим образом. Определяют последовательность минимальной длины L , чтобы посредством уравнений Si=∑ T_iS_j-i, она порождала известную последовательность S₁,S₂, S_2t компонент синдрома. Величина L должна быть минимальной, потому что она равна числу ошибок, но т.к. ошибки в канале связи независимы и равновероятны, то наиболее вероятным вектором-ошибкой должен быть вектор минимального веса, ибо этот вес и есть кратность ошибки.

Теперь на основе вышеизложенного сформулируем алгоритм Берлекэмпа-Месси – построение многочлена локаторов ошибок Т(х). Пусть определены компоненты синдрома S₁,S₂, S_2tи пусть при начальных условиях То(х)=1, Во(х)=1, Lo=0 выполняется равенство:

∆_n=∑ T_j^(n-1)S_n-j , (4.2)

где ∆_n - погрешность вычисления.

∆_n вычисляется элементом поля GF(2^m),n=1,2…,2t- число шагов искания, В₀(х) - добавочный элемент. Если ∆_n=0 и условие 2L_n-1≤n-1 не выполняется, то L_n-L_n-1 и, B_n(х)∆_n^-1.T_n-1(x) Если условие 2L_n-1≤n-1 не выполняется, то L_n-L_n-1 и, B_n=B_n-1(x). Тогда многочлен Т_2t(х) является многочленом наименьшей степени.

После вычисления многочлена локаторов ошибок отыскиваются корни многочлена локаторов ошибок. Это делается посредством процедуры Ченя. Она состоит в последовательной подстановке всех элементов поля GF(2^m) в многочлен локаторов ошибок Т(х). Его корнями являются те элементы, которые при подстановке их в Т(х) обращают его в "0". Обратные значения корней многочлена локаторов ошибок являются локаторами ошибок и указывают позицию, на которой произошла ошибка.

Следующим этапом декодирования кодов PС является нахождение значений ошибок У₁,У₂,...,У_t. Для нахождения значений ошибок используется алгоритм Форни. Для описания алгоритма Форни представим многочлен локаторов ошибок в виде:

Т(х)=T_tx^t+T_t-1x^t-1+…+T₁x+1, (4.3)

имеющим корни x_j^-1 , i=1,…,t.

Определим синдромный многочлен:

S(x)=∑S_jx^j= ∑∑ У_jx_i^j x^j. (4.4)

Теперь по синдромному многочлену S(x) можно записать многочлен значения ошибок:

Ω(X)=S(x)*T(x)(modx^2t) (4.5)

Указание mod х^2t означает, что все члены, в которых Х входит в степень 2t или более равны нулю. Данный многочлен можно выразить следующим образом: и в таком виде использовать для определения значений ошибок У_j:

У_j=Ω(X)/T¹(x) (4.6)

где T¹(x) - производная многочлена Т (х).

Исходя из вышеизложенного общий алгоритм определения наличия ошибок и их исправления состоит из выполнения ряда пунктов:

1. Вычисление синдромов ошибок S(x)

2. Вычисление многочлена локаторов ошибок Т(х) с использованием алгоритма Берлекэмпа-Месси.

3. Нахождение корней многочлена локаторов ошибок (Х₁, ... , Х_2t) с использованием процедуры Ченя.

4. Нахождение значений ошибок (У₁,У₂ ... , У_2t) при помощи алгоритма Форни.

5. Исправление ошибок.

4.4. Алгоритм программной реализации кода Голея

Программные методы реализации помехоустойчивого кодирования передаваемой информации обладает по сравнению с аппаратурным такими преимуществами, как большая гибкость и меньшее время разработки.

Одна из основных задач программной реализации состоит в выборе наиболее экономичных алгоритмов кодирования. Рассмотрим отдельный алгоритм кодирования циклических кодов, а именно кода Голея, применительно к ПК.

Алгоритм кодирования кода Голея аналогичен кодированию циклического кода. В данном алгоритме использован метод сдвига информационной части комбинации на r разрядов влево и деление полученной комбинации на образующий полином g(x) с получением остатка R(x). Затем полученный остаток R(x) добавляется к информационной части кодовой комбинации.

Алгоритм кодирования состоит в следующем:

1. Начало программы кодирования.

2. Объявление меток и всех переменных в программе.

3. Ввод параметров кода Голея:

п - длина кодовой комбинации, k - количество информационных символов,

r - количество проверочных разрядов.

4. Ввод образующего полинома кода Голея g(x).

5. Ввод значения исправляющей способности кода Голея t.

6. Ввод информационной части кода Голея.

7. Вывод на печать образующего полинома g(x).

8. Вывод на печать значений n, k, r, t

9. Вывод на печать информационной части кодовой комбинации.

10. Вычисление длины кодовой комбинации по формуле: n₁=k₁+r, где k₁ -длина введенной информационной части комбинации.

11. Сдвиг информационной части на r разрядов влево.

12. Деление полученной комбинации на образующий полином g(x) с выделением остатка R(x).

13. Произведем замену нулей на значение выделенного остатка R(x).

14. Вывод на печать закодированной комбинации кода Голея.

15. Ввод значений ошибок С(х) в данную кодовую комбинацию.

16. Вывод на печать искаженной кодовой комбинации.

Алгоритм декодирования кода Голея основан на использовании модифицированного кодера Меггита, основанного на вылавливании ошибок с использованием двух дополнительных многочленов, равных х mod g(x) и х mod g(x). Алгоритм декодирования состоит в следующем:

1. Вычисление синдрома для данной кодовой комбинации с помощью процедуры ОСТ.

2. Если синдром S(x)=0, то выводится на печать сообщение об отсутствии ошибок и осуществляется переход на конец цикла программы. Если нет, то - переход к блоку 3.

3. Вывод на печать сообщения о наличии ошибок.

4. 1-0, начало вылавливания ошибок по декодеру Меггита.

5. Сдвиг на i разрядов влево кодовой комбинации.

6. Добавление к полученной кодовой комбинации r нулей (kkk).

7. Вычисление синдрома полученной комбинации с использованием процедуры ОСТ.

8. Обращение к процедуре БЕС, где происходит вычисление веса синдрома.

9. Если полученный вес синдрома W(x)<3, то считаем, что выловлены все ошибки, которые находились в 11 старших разрядах. Если нет, то переход к блоку 13.

10. Полученный синдром складывается по модулю 2 со сдвинутой кодовой комбинации.

11. Полученная комбинация сдвигается на i первоначальному виду.

12. Вывод на печать исправленной кодовой комбинации и переход на конец программы.

13. Так как полученный вес W(x)>3, то комбинация (kkk) складывается по модулю 2 со значением x¹⁶mod g(x).

14. Обращение к процедуре ОСТ, где происходит вычисление синдрома полученной комбинации.

15. Обращение к процедуре БЕС, где происходит вычисление веса полученного синдрома.

16. Если вес синдрома W(x)<t-l, то считаем, что:

17. Ошибки произошли в 11 старших разрядах и в пятом проверочном разряде. Если нет, то переход к блоку 20.

18. Сложение по модулю 2 синдрома с кодовой комбинацией и инвертирование пятого проверочного разряда.

19. Вывод на печать исправленной кодовой комбинации и переход к концу программы.

20. Так как W(x)>t-l, то комбинация (kkk) складывается по модулю 2 со значением x17mod g(x).

21. Обращение к процедуре ОСТ, где происходит вычисление синдрома.

22. Обращение к процедуре БЕС, где происходит вычисление веса полученного синдрома.

23. Если вес W(x)<t-l, то считаем, что:

24. Ошибки произошли в 11-ти старших и в шестом проверочном разрядах. Если нет, то переход к блоку 27.

25. Сложение по модулю 2 синдрома с кодовой комбинацией и инвертирование шестого проверочного разряда.

26. Вывод на печать исправленной кодовой комбинации.

27.I=I+1,

28. Если I > 23, то переход к блоку 30. Если нет, то к блоку 5.

29. Вывод на печать о невозможности исправить ошибки.

30. Конец программы.

4.5. Алгоритм программной реализации кодера и декодера кода БЧХ

4.5.1. Алгоритм программной реализации кодера кода БЧХ

Алгоритм программной реализации кодера кода БЧХ состоит в том, что первоначально моделируется поле Галуа. Затем вводятся параметры кода БЧХ и на основе элементов поля Галуа производится кодирование кодовой комбинации по методу деления на образующий полином с выделением остатка, который затем добавляется к информационным разрядам.

Алгоритм кодирования разбит на следующие этапы:

1) Начало программы;

2) Объявление методов используемых в программе и всех переменных, используемых в данной программе;

3) Ввод параметров поля Галуа величина расширения неприводимых в полном для данного расширения;

4) Вычисление элементов поля Галуа;

Вычисление поля Галуа основано на двух основных положениях:

а) каждый последующий элемент поля Галуа равен произведению предыдущего элемента на примитивный элемент α;

б) степень элементов поля Галуа после данного умножения должна
быть меньше степени неприводимого многочлена. Для этого используется
операция сложения двух чисел по mod m.

5) Вывод на печать элементов поля Галуа;

6) Ввод параметров кода БЧХ;

N - длина кодовой комбинации,

К - длина информационной части,

R - длина проверочной части,

7) Ввод исправляющей способности t, для данного кода БЧХ;

(4.7)

8) Ввод значения неприводимого многочлена для данного кода БЧХ;

9) Ввод информационной части кодовой комбинации длины не более kl;

10) Определение длины информационной части кодовой комбинации
вычисление параметров кодовой комбинации;

11) Вывод на печать значения n, k, r, g(x), t, kl;

13) Вычисление длины кодовой комбинации по формуле: N = k2 + r;

14) Сдвиг информационной части кодовой комбинации на r разрядов влево;

15) Деление полученной комбинации на образующий многочлен с выделением остатка. Принцип деления аналогичен делению для двоичных
кодов, только вместо нулей и единиц используются элементы поля Галуа.
Соответственно сложение и умножение производится по mod m;

16) r нулей в данной комбинации заменяются выделенным остатком;

17) Вывод на печать закодированной кодовой комбинации для данного
кода БЧХ.

4.5.2. Алгоритм программной реализации декодера кода БЧХ

Алгоритм декодирования основан на вычислении многочлена локаторов ошибок с использованием алгоритма Берлекампа - Месси. Для этого в закодированную ранее кодовую комбинацию вводятся ошибки не превыше значения tl.

1) Ввод стираний;

2) Выбор этапа алгоритма исправления ошибок и стираний. Если
первый этап алгоритма, то на стертое место записывается f. Если второй,
то дописывается 0;

3) Ввод количества ошибок + стираний не более t≥t+2S;

4) Ввод местоположения ошибок;

5) Вывод на печать местоположения ошибок;

6) Вывод на печать искаженной кодовой комбинации;

7) Вычисление значений синдромов для данной кодовой комбинации;
Количество синдромов должно быть равно 2t;

8) Сравнения всех значении синдромов с нулем. Если все синдромы = 0, то выводится сообщение 0 об отсутствии ошибки. Если хотя бы один
синдром не равен 0, то выводится сообщение о наличии ошибки и переход
к вычислению многочленов локаторов ошибок по алгоритму Б-М;

9) Ввод начальных условии, необходимых для работы алгоритму

10) Расчет навязки по формуле;

d_n=∑^ i ∙ S_n-i (4.8)

Если dn<0, то рассчитывается только добавка

D_n(z)=Z D_n-1(Z) (4.9)

Если d_n≠ 0, то считается ^ n (Z)

11) Многочлен локаторов ошибок считается по следующим формулам,

^n (Z) = ^ _n-1 (Z) + D_n-1(Z) (4.10)

12) Расчет длины α_n регистр сдвига
при d_n= 0 α_n=α_n-1
при d_n≠ 0 α_n = α_n-1+1

13) При α_n > α_n-1 добавка считается по формуле (4.11);

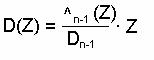(4.11)

14) При n=2t вывод на печать многочлена локаторов ошибок

15) Вычисление местоположения ошибок с использованием процедуры
Ченя. Принцип процедуры Ченя основан на подставление всех элементов
поля Галуа в многочлен локаторов ошибок и сравнения полученных
результатов с нулем. Если получится 0, то обратное значение этого
элемента указывает местоположение ошибки.

16) Исправление ошибок по формуле: С (х) + r (х) = с (х), где: С (х) - искаженная кодовая комбинация, R (х) - вектор ошибки.

17) Вывод на печать исправленной комбинации.

18) Конец.

4.6. Алгоритм программной реализации кодера и декодера кода Файра

4.6.1. Алгоритм программной реализации кодера Файра

Алгоритм кодирования кода Файра аналогичен кодированию обычного циклического кода. В данной программе реализован метод сдвига информационной части комбинации на r разрядов влево и деление полученной комбинации на Р(х) - образующий полином, с выделением остатка R(x). Затем данный остаток добавляется к информационной части кодовой комбинации.

Алгоритм кодирования состоит в следующем:

1. Начало программы кода Файра.

2. Объявление меток, констант и переменных

З. Ввод параметров кода n, k, r.

4. Ввод неприводимого многочлена g(х) и его степени r.

5. ВЫВОД на печать значений g(х), r.

6. ВВОД степени дополнительного многочлена m.

7. m кратно r, если да, то переход к пункту 6, если нет - к пункту 8.

8. Вычисление дополнительного многочлена (х^c +1).

9. Вывод на печать значения (х^c +1).

10. Ввод общего полинома Р(х).

11. Вывод на печать полинома Р(х).

12. Ввод информационной части кода Файра.

13. Определение параметров r₁, k₁ для данной кодовой комбинации.

14. Сдвиг информационной части комбинации на r разрядов влево.

15.Обращение к подпрограмме деления, где происходит деление информационной части на образующий полином Р(х).

16. Присоединение к информационной части кодовой комбинации ОСТ полученного в результате деления.

17. Вывод на печать закодированной информации.

4.6.2. Алгоритм программной реализации декодера Файра

Алгоритм декодирования кода Файра с образующим полиномом

Р(х) = g(х)(х^c+1) основан на вычислении и сравнивании остатков, полученных при делении на полиномы g(х) и (х^c+1) , для нахождения местоположения пакета ошибок (I) может быть использован аппарат теории сравнения.

Алгоритм состоит в следующем:

1. Ввод начала пакета, т.е. определяется место, где начнется искажение информации (кодовой комбинации).

2. Ввод значения пакета (х^c +1).

3. Искажение пакета начинается с mb.

4. Вывод на печать ошибочной комбинации.

5. Обращение к подпрограмме деления, где кодовая комбинация делится на Р(х).

6. Если остаток от деления равен 0, то переход к пункту 24, если нет - к пункту 25.

7. Вывод на печать информации об отсутствии ошибок и переход на конец программы.

8. Вывод на печать сообщения о наличии ошибки в кодовой комбинации.

9. Обращение к подпрограмме деления, где происходит деление кодовой комбинации на образующий полином Р(х).

10. Значение ОСТ запоминается в ячейке памяти ОСТ.

11. Обращение к подпрограмме деления, где происходит деление кодовой комбинации на образующий полином (х^c +1)

12.ОСП сравнивается с ОСТ, если они равны, то исправление пакета ошибок с местоположением равным 1 и величины пакета равной ОСТ. Если нет, то переход к блоку 13.

13. i = I

14. Сдвиг ОСТ на i разряда влево.

15. Обращение к подпрограмме деления, где происходит деление сдвинутого на i разрядов влево ОСТ на образующий полином g(х),

16. i₁=I.

17. СДВИГ на i₁разрядов влево. Обращение к подпрограмме деления, где происходит деление сдвинутого на i₁ разрядов влево значения на образующий полином (х^c +1).

18. Сравнение остатков OCT₁ и ОСТ, если они равны, то переход к пункту 22, если нет, то к пункту 19.

19. i_I=i + I

20. i_I> n_I, если да, то к пункту 21, если i_I< n_I то к пункту 14.

21. Вывод на печать сообщения о невозможности исправления ошибок и переход на 12.

22. Вывод на печать значений ОСТ и OCT₁

23. Вывод на печать i_I и i.

24. Вычисление D₁, D₁=1 mod m, D₁ =0 mod с

25. Вычисление D₂, D₂ =1 mod c, D₂=0 mod m

26. Определение начала местоположения пакета ошибок по вычисленным значениям D₁ и D₂

27. Исправление кодовой комбинации пакетом ошибок, равным ОСТ.

28. Вывод на печать исправленной кодовой комбинации.

Использование кода Файра в цифровых системах

Циклические коды Файра, исправляющие одиночные пакеты ошибок, широко применяются в различных системах, таких как системы цифровой связи, системы цифрового телевидения, системы цифрового радиовещания, системы цифровой магнитной записи. Эти коды также успешно используются для устранения ошибок в полупроводниковых ЗУ, в накопителях на магнитных дисках и лентах, позволяющих обеспечить высокую надежность хранения информации. Один из основных способов обеспечения высокой верности передачи сообщений по каналам связи с группирующимися ошибками является использование кодов Файра, обнаруживающих и исправляющих ошибки. Так, например, в многоканальной аппаратуре «Думка» используется укороченный циклический код Файра (252, 232) с образующим полиномом

g(х) = (х¹³ + 1)(х⁷ + х³ + 1). Он позволяет исправлять в пределах блока одиночный пакет с числом ошибок не более семи. Для защиты от ошибок в каналах управления систем подвижной связи стандарта GSM используется укороченный циклический код Файра (224,184) с образующим полиномом

g(х)=(х²³ +1)(х¹⁷ + х³ + 1). Используемый код позволяет исправлять одиночный пакет ошибок с числом ошибок не более 17. Повышение производительности вычислительных систем существенно увеличило объем хранимой и предаваемой информации. Недопустимость ошибок, а в ряде случаев сама природа данных, требуют использования, как оборудования, так и программных процедур обнаружения и исправления ошибок обмена. Коды Файра позволяют исправлять одиночные пакеты ошибок при передаче информационных массивов. Так как создание специализированных кодеков не всегда экономически оправдано, актуальным является разработка эффективных программных методов кодирования и декодирования кода Файра. В системах цифровой записи и воспроизведения на компакт - дисках и магнитных лентах основную долю ошибок составляют ошибки типа «потеря пакета». Это связано с тем, что канал записи-воспроизведения при прохождении сигналов вносит временные искажения и в нем наблюдается группирование ошибок (вызванных выпадениями сигнала). Длинные последовательности ошибок, которые вызываются грубым повреждением диска или крупным дефектом ленты, исправить гораздо сложнее, чем случайные ошибки. Поэтому важной задачей техники цифровой записи является использование кодовой защиты информации. Последняя заключается в нахождении оптимальных параметров кодов для обнаружения и коррекции ошибок в одно - и многодорожечных каналах и сбоев синхронизации. Эффективность практической реализации кодовой защиты зависит от адекватности характера группирования ошибок в этих каналах и свойств корректирующих кодов Файра. Кроме того, в цилиндрических магнитных доменах ЗУ, используемых в электронно-вычислительной аппаратуре применяются средства коррекции ошибок. При этом характер отказов ЦМД ЗУ (сбои в считанных и хранимых данных) достаточно благоприятен для использования корректирующих кодов. Пакетный характер ошибок из-за сбоев ЦМД ЗУ обусловил использование с целью повышения их надежности кодов Файра, исправляющих произвольно расположенные одиночные пакеты ошибок. Применение кодов Файра обеспечивает значительное уменьшение вероятности отказа ЦМД ЗУ и увеличение средней наработки на отказ, т. е. повышение их безотказности. Диагностирование ЗУ методом сигнатурного анализа на базе кода Файра является еще одним из применений этого кода. Обеспечивая быстрый поиск места неисправности с точного до микросхемы, диагностирование позволяет уменьшить время восстановления работоспособного состояния ЗУ и, как следствие этого повысить коэффициент его готовности.

4.7. Алгоритм программной реализации кодера и декодера кода

Рида-Соломона

4.7.1. Алгоритм программной реализации кодера кода Рида-Соломона

Его сущность состоит в том, что первоначально моделируется поле Галуа. Затем вводятся параметры кода РС и на основе элементов поля Галуа осуществляется кодирование. Кодирование производится по методу деления информационной последовательности, сдвинутой на r разрядов влево, на порождающий многочлен кода РС с выделением остатка. После этого r нулей заменяем полученным остатком.

Алгоритм кодирования разбит на следующие этапы:

Начало программы.

1. Объявление всех переменных и меток, используемых в программе.

2. Ввод параметров поля Галуа: m - величина расширения данного поля, g(х) - неприводимый многочлен для данного расширения m; a - примитивный элемент для данной величины m.

3. Задается количество элементов поля Галуа, в зависимости от величины m.

4. Задается начальное условие для вычисления элементов поля Галуа.

5. Осуществляется вычисление элементов поля Галуа по принципу: каждый последующий элемент поля равен произведению предыдущего элемента на примитивный элемент a.

6. Проверяется условие: старшая степень элемента поля Галуа после умножения должна быть меньше степени неприводимого многочлена, т.е. deg α (I)< deg g (x). Если условие не выполняется, то следующий элемент поля Галуа вычисляется с помощью операции по модулю два данного элемента с неприводимым многочленом поля Галуа. Эта операция осуществляется в блоке 7.

8. Вывод на печать всех элементов поля Галуа.

9. Ввод параметров кода PС: n - длина блока; r - проверочная часть блока; k - информационная часть блока; g(x) - неприводимый многочлен с вышеприведенными параметрами. А также ввод количества элементов информационной части кодовой комбинации (К2).

10. Ввод значений кодовой комбинации K1(I).

11. Производится расчет кодового расстояния α.

12. Производится расчет исправляющей способности t .

13. Осуществляется вывод на печать α, и t.

14. Расчет длины кодовой комбинации, в зависимости от введенных ранее количества элементов информационной части.

15. Сдвиг значений информационной части кодовой комбинации К1 на r разрядов влево. В результате сдвига получаем кодовую комбинацию №2.

16. Производится деление полученной комбинации №2 на неприводимый многочлен данного кода g(х) с выделением остатка R(x). Принцип деления аналогичен делению для двоичных кодов, только вместо нулей и единиц используются элементы поля Галуа. И, следовательно, сложение и умножение производится по модулю m .

17. Замена r нулей на полученный остаток R(x). В результате этой операции получим закодированную комбинацию n1.

18. Вывод на печать параметров кода n,k, неприводимый многочлен q(x), а также закодированную комбинацию n1.

4.7.2. Алгоритм программной реализации декодера кода Рида-Соломона

      Алгоритм декодирования основан на вычислении многочлена локаторов ошибок Т(х) с использованием алгоритма Берлекэмпа-Месси (Б-М). Для этого в закодированную ранее кодовую комбинацию n1 необходимо ввести ошибки, не превышающие значение t.

1(19). Осуществляется ввод количества ошибок – t1 .

2(20). Осуществляется ввод местонахождения ошибок в комбинации n1 .

3(21). Осуществляется ввод значений ошибок В(α).

4(22). Выводится на печать местонахождение ошибок и их значения.

5(23). Производится операция внесения ошибок в комбинацию n1 , в зависимости от их местоположения. В результате этой операции получим комбинацию n2.

6(24). Выводится на печать искаженная комбинация n2.

Следующий этап - вычисление синдромов ошибок.

7(25). Задается количество синдромов J=1,2t.

8(26). Задается количество элементов, составляющих синдром n2.

9(27). Вычисление значений синдромов S по формуле:

Sj = Σ УjXj, где Уj- значение элемента поля Галуа (α), Xj- его местоположение.

10(28). Производится проверка значений синдромов Sj. Если все синдромы равны 0, то комбинация не содержит ошибок, и мы переходим к пункту 11(29), который осуществляет вывод на печать комбинации n2, и следовательно, выход из программы. Если хотя бы один из синдромов не равен "0", то существует ошибка, и, следовательно, её необходимо обнаружить и исправить.

12(30). Производится вычисление синдромного многочлена S(x). Затем переходим к вычислению многочлена локаторов ошибок по алгоритму Б-M.

13(31). Вводим начальные условия для алгоритма Б-М.

14(32). Задаем № шага искания по алгоритму Б-М.

15(33). Вычисляем погрешность ∆n.

16(34). Проверяем значения этой погрешности. Если ∆_n≠0 то многочлен Т(х) вычисляется по формуле в пункте 17(35): T_n(x)=T_n-1(x) +∆_nx B_n-1(x). Если ∆_n =0, то многочлен Т_n(х) равен предыдущему многочлену Т_n-1 (x) пункт 18(36).

19(37). Проверяется условие 2 L_n-1≤ n-1, где L - число ошибок, h - шаг искания. Если данное условие не выполняется, то переходим к пункту 21(39), который показывает, что количество ошибок L остается равным предыдущему значению L_n-1. Если условие выполняется, то переходим к пункту 20(38), который покажет, что количество ошибок увеличилось.

22(40). Производим проверку n=2t, которая указывает, что число шагов искания многочлена локаторов ошибок не должно превышать 2t. Если условие выполняется, то переходим к пункту 23(41).

23(41). Проверяем степень многочлена Т(х). Она не должна превышать количество найденных ошибок. Если условие не выполняется, то на печать выводится сообщение о том, что в принятом слове более t ошибок, и затем, конец программы. Если условие в пункте 23(41) выполняется, то в пункте 24(42) вычисляется многочлен значений ошибок Ω (x).

25(43). Находится производная от многочлена Т(х).

26(44). Выводится на печать многочлен Т(х).

27(45). Начало цикла определяет местоположение ошибки согласно процедуры Ченя.

28(46).Определяется количество проверок, необходимых для нахождения корней многочлена Т(х).

29(47). Задание начального элемента поля Галуа для вычисления корней.

30(48). Вычисляются номера позиций, на которых произошла ошибка. Для этого используется процедура Ченя, при которой все элементы поля Галуа подставляются в многочлен Т(х).

31(49).Осуществляется проверка многочлена Т(х). Если многочлен Т(х)=0, то данная величина является корнем и переходим к пункту 34(52), который вычисляет обратное значение корня многочлена Т(х). Это значение указывает номер позиции ошибки.

32(50). Переход к следующему элементу поля Галуа.

33(51). Все ли элементы поля Галуа участвуют в процедуре нахождения корней многочлена локаторов ошибок.

35(52). Переход к нахождению следующего корня многочлена локаторов ошибок.

36(54). Все ли корни многочлена определены.

37(55). Задается количество происшедших ошибок.

38(56). Задание начального элемента для вычисления значений ошибок.

39(57). Вычисление значений ошибок.

40(58). Исправление ошибок в комбинации n2. Для этого необходимо сложить по mod m значение ошибок с вычисленным значением ошибок.

41(59). Вывод на печать исправленной комбинации.

42(60). Конец программы.

Список литературы

1. Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир,1986.

2. Варгаузин В. Помехоустойчивое кодирование в пакетных сетях.- «Телемултимедиа»,2005г,№4стр.3.

3. Вернер М. Основы кодирования – ТЕХНОСФЕРА – Москва, 2006, с.127 – 129, 200 – 201.

4. Золотарев В. В., Овечкин Г. В. Помехоустойчивое кодирование. Методы и алгоритмы. М.: Горячая линия-Телеком,2004.

5. Кларк Дж., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. М: Радио и связь, 1987.

6. Конопелько В.К., Липницкий., В.А. Теория норма синдромов и перестановочное декодирование помехоустойчивых кодов. Изд. 2е - Москва,: Едиториал УРСС, 2004.-176 с.

7. Назаров А.Н., Симонов М.В. ATM: Технология высокоскоростных сетей. М.: Эко - Трендз, 1997.-232с

8. Морелос - Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение – ТЕХНОСФЕРА – Москва, 2005, с.67 – 127.

9. Абдуллаев Д.А., Арипов М.Н. Передача дискретных сообщений в задачах и упражнениях: Учеб. Пособие для вузов. – М.: Радио и связь. 1985.-128с.

10. Джураев Р.Х., Джаббаров Ш.Ю Хатоликлар пакетини тўғриловчи айра ва Рид-Соломон кодларини ўрганиш. Худдатли электралоқа тизимлари ва тармоқлари фанидан амалиёт машғулотларига услубий кўрсатма. ТАТУ, Тошкент 2005.

11. Джураев Р.Х., Джаббаров Ш.Ю Циклические коды БЧХ и Рида Соломона. Методические указания к практическим занятиям по курсу «Системы телематики». ТУИТ, Ташкент 2001.

12. Джураев Р.Х Циклические коды Файра. Методические указания к практическим занятиям по курсу «Передача дискретных сообщений». ТЭИС, Ташкент 1998.

Помехоустойчивые коды в телекоммуникационных системах

Учебное пособие по направлению образования «5522200 - телекоммуникация»

Рассмотрено и рекомендовано к изданию на заседании научно - методического Совета ТУИТ от « 30 » 06 2008 г, протокол № 32

Составители:

ст. преп. Джураев Р.Х

ст. преп. Джаббаров Ш.Ю

Умирзаков Б.М.,

Хамраев Э.А

Ответственный редактор:

Камалов Ю.К.

Корректор: Абдуллаева С.Х