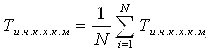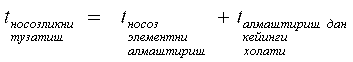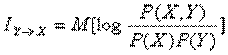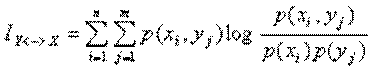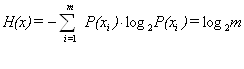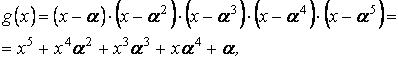Diskret
ma’lumotlarni uzatish tizimi (DMUT) - xabar manbai va qabul qiluvchi orasida ma’lumotlar
oqimini ta’minlab beruvchi texnik vositalar majmuasidir. DMUTni asosiy uch tarkibiy
qismlarga ajratish mumkin:
-
xabar manbai
-
DMU kanali;
-
xabar iste’molchi.
DMUT
ikki tomonlama axborot almashinuvini ta’minlovchi tizim bo‘lib o‘zida bir yoki
undan ko‘p xabar manbai va iste’molchisi, uzatuvchi qurilmalar, qabul qiluvchi qurilmalar
va aloqa liniyalaridan tashkil topgan. Xabarning qanday ko‘rinishda ekanligiga
va signal tashuvchining parametrlariga qarab xabarlar ketma-ketligi diskret kanalga
yoki ma’lumotlar uzatuvchi kanalga kelib tushadi. S’HQ qurilmalarda ma’lumot
signallari telekommunikatsiya kanallari orqali uzatilishi uchun mos shaklga keltiriladi
va diskret signallarning parametrlarini aloqa kanallari bilan moslashtiradi. Shu
bilan birga qabul qismida qayta hosil qilish (oldingi holatiga qaytarish)ni amalga
oshiradi. Diskret
kanal va XHQ majmuasi
ma’lumot uzatish kanalini tashkil qiladi. Xatolardan ximoyalovchi qurilmalar, to‘sqinlar
natijasida ma’lumot signallarida sodir bo‘ladigan
xatolar sonini kamaytirish uchun ishlatiladi.
Diskret
ma’lumotlar uzatish tizimi. Xabarlar DMU tizimida
bir necha bosqichlar va jarayonlarni bosib o‘tadi. Xabar manbasi (XM) uzatish uchun
tayyor bo‘lgan ma’lumotni tanlaydi: Xabar elementlari (xarf, belgi, son)
XHQda qayta ishlanadi, ya’ni aniq bir qonun - qoida asosida kodlashgan ikkilik
signallar ketma-ketliklari hosil qilinadi. Bu ketma-ketlik S’HQ qurilmasi yordamida
signal tashuvchisining parametrlari ma’lum bir formulaga mos ravishda o‘zgartiriladi
va manipulyatsiyalashgan ketma-ketlik hosil qilinadi. Aloqa kanalida elektr signallar
xabar manba’dan qabul qiluvchi tomon tarqalayotib turli xil, turli tashqi ta’sirlar
(shovqinlar)ga uchraydi. Qabullovchi qurilma signal va shovqin aralashmadan uzatilayotgan
xabarga maksimal mos keluvchi (eng o‘xshash) optimal diskret xabarni hosil qiladi.
Buning uchun qo‘yidagi ketma-ket jarayonlar amalga oshiriladi:
-
filtrlash;
-
kuchaytirish;
-
demodulyatsiya;
-
diskret ketma – ketlikni dekodlash.
Quyidagi
3 sabab xatolar manbai bo‘lishi mumkin:
-
kanaldagi shovqinlar;
-
apparat xato ishlashi;
-
operatorning xatosi.
Ma’lumotlar
uzatish tizimi (MUT) ning sifat ko‘rsatkichlari. Asosiy
masalalardan biri ishga yaroqlik va ishga yaroqsiz xolatlarga turkumlanadigan diskret
kanallar sifatining xolatini baxolashdan iboratdir. Diskret kanallar sifati ma’lumotlarni
kanallar bo‘yicha uzatish sifati quyidagicha baxolanadi:
-
signallarning ikkilamchi statistik tavsilotlari
orqali baxolash usuli;
-
signallar ko‘rsatkichi orqali baxolash usuli;
-
shovqinlar ko‘rsatkichlari orqali baxolash
usuli.
Ushbu
baxolashlar natijalari, ma’lumot uzatish kanalining texnik xolati diagnostikasi
va qabul qilinayotgan signallar ketma-ketligining to‘g‘riligini oshirish uchun ishlatiladi.
Zamonaviy raqamli tizimlarning asosiy vazifasi ma’lumot uzatilishining sifati va
samaradorligini oshirishdir. Ushbu masalaning yechimi ikki yo‘nalishda rivojlanmoqda:
1.
Sarf-xarajatlar cheklangan xolda uzatilayotgan axborot tezligi ishonchliligini oshirish
maqsadida diskret ma’lumotlarni qabul qilish va uzatish usullari orqali;
2.
Raqamli tizimlarning yuqori darajada puxta ishlashini ta’minlaydigan va raqamli
tizimlar tuzilishini yangi usullari ishlab chiqish orqali.
Xaqiqiylik
xatolik koeffitsienti orqali aniqlanadi:

(nx)
- xato qabul qilingan elementlar soni;
(nuz)
- taxlil intervalida umumiy uzatilgan elementlar.
Haqiqiy
xatolik talabi 10-6;
Kommutatsiyalangan
shaxar telefon tarmog‘i
kanali 10-2
÷ 10-10;
Kommutatsiyalangan
xalqaro
telefon tarmog‘i
kanali 10-3
÷ 10-4;
Kommutatsiyalanmagan
xalqaro
telefon tarmog‘i
kanali 10-4
÷10-5.
MUT
ning sifat ko‘rsatkichlari
|
Aloqa
xizmati
|
Aniqligi
|
Paketlarni
yo‘qolish extimoligi
|
Paketlar
noto‘g‘ri manzil bo‘yicha yuborilish extimolligi
|
|
Telefoniya
|
10-7
|
10-3
|
10-3
|
|
Axborot
uzatish
|
10-7
|
10-6
|
10-6
|
|
Televideniya
|
10-6
|
10-8
|
10-8
|
Modulyatsiya
tezligining
davomiyligi 50, 100 va 200 bod
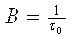
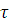 -
birlik elementining davomiyligi
-
birlik elementining davomiyligi
|
Modulyatsiya
tezligi (V)
|
Element
uzunligining davomiyligi ( ) )
|
Xatolar
soni (kanaldagi uzilish 80 m/sek)
|
|
50 bod
|
20 msek
|
4
|
|
100 bod
|
10msek
|
8
|
|
200bod
|
5msek
|
16
|
|
2400bit/c
|
0.41msek
|
200
|
|
4800bit /c
|
0.2msek
|
400
|
|
9600bit/c
|
0.1 msek
|
800
|
|
14400 bit/c
|
0.69msek
|
1160
|
|
19200;
28800; 33600; bit/c
|
0.52
msek; 0.034 msek;
0.29 msek;
|
1539; 2353; 2759;
|
Koeffitsient tayyorgarligi quyidagi
formula orqali
aniqlanadi:
 Bu
yerda:
Bu
yerda:
 - koeffitsient; tayyorgarligi
- koeffitsient; tayyorgarligi
 ishdan chiqqunga qadar xizmat qilish muddati (vaqti);
ishdan chiqqunga qadar xizmat qilish muddati (vaqti);
qayta tiklash vaqti.
Tizimni
birin-ketin bo‘lgan ikkita ishdan chiqishlar orasidagi uzluksiz ishdan chiqqunga
qadar xizmat qilish muddati (vaqti) ni o‘rtacha qiymati quyidagicha:
Bu
yerda N -
ishdan chiqishlarning umumiy soni;
- (i-1) va im ishdan chiqishlar orasidagi ishlash vaqti.

Ishdan
chiqishni topish va bartaraf etishga sarflangan tizimni ishlamasdan turish vaqtining
o‘rta qiymati:

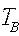
 – tizim tiklanish vaqti;
– tizim tiklanish vaqti;
-
ichi ishdan
chiqish oraligi.
μ
– tiklanish intensivligi bo‘lib vaqt birligida
tiklanishlar sonini
belgilaydi.
Umumiy
xolda qayta tiklash vaqti quyidagicha:

bu
yerda nosozlikni tuzatish quyidagiga teng:
MUTga
qo‘yiladigan talablar: Diskret xabarlarni uzatish
(DXU) tizimi bu – manba’dan qabul qiluvchiga xabarlar oqimini uzatishni ta’minlovchi
texnik vositalar kompleksidir. Xabarlarni qabul qiluvchi DXU tizimiga quyidagi talablarni
qo‘yadi:
• Uzatish
aniqliligi;
• Uzatish
tezligi, vaqti;
• Ishonchlilik.
Axborotdagi
belgillarning poydo bo‘lishi extimolligi bilan axborot xajmi o‘rtasidagi bog‘liq
Klod Shennon teoremasida o‘z ifodasini topgan, ya’ni axborotdagi har bir belgiga
mos keluvchi axborotni o‘rtacha hajmi (soniga) entropiya deb yuritiladi.
Entropiya – bu xabarlar manbaining holatidagi noaniqligining o‘lchovi
ham hisoblanadi. Agar manba tomonidan 1 ga teng ehtimoli bilan faqat bitta belgi
uzatilayotgan bo‘lsa, u holda entropiya nolga tengdir. Agar xabar manbaidan uzatilayotgan
belgilar bir xil ehtimolli bilan paydo bo‘lsa, entropiya maksimal bo‘ladi.
2-ma’ruza bo‘yicha nazorat
savollari
1. Ma’lumotlar
uzatish tizimiga tushuncha bering?
2. MUT
tuzilish chizmasi ishlash tartibi qanday?
3. Ma’lumot
uzatish tizimlarining sifat ko‘rsatkichlari nimalardan iborat?
4. MUTga
qanday talablar qo‘yiladi?
5. Entropiya
nima?
3-ma’ruza.
Shartli va o‘zaro bog‘liq axborotlar, ularning xususiyatlari.
Reja:
1.
O‘zaro bog‘liq axborotlar
2.
Shartli axborotlar
3.
Entropiyani hisoblash formulasining
fizik mohiyati
Diskret
xabar tarkibidagi axborot hajmini o‘lchash birligi bit hisoblanadi.
U
yoki bu xabar paydo bo‘lish ehtimolligi qanchalik kam bo‘lsa, uning qabulidagi olinadigan
axborot shunchalik ko‘p bo‘ladi.
Agar
xabar manbai xotirasida bir – biridan holi (x1 va x2) xabarlar
bo‘lib, ulardan birinchisining R(x1) = 1 ehtimollik bilan uzatiladigan
bo‘lsa, u holda x1 xabar axborot tashimaydi, chunki u oldindan xabar
oluvchiga ma’lum deb hisoblanadi.
Bitta
xabarga (xi) to‘g‘ri keladigan axborot hajmi quyidagicha aniqlanadi:
I
(ai) = log 2 [1/P (x1)] = log 2 P
(x1) (1.1)
bu
yerda P (xi) – xabardagi xi belgining paydo bo‘lish ehtimolligi.
Misol
1. Xabar
manbai 2 ta x1, x2 belgilardan iborat axborotni uzatishi kerak,
ya’ni axborotdagi belgilar soni N = 2 ga teng. Ikkala element ham bir – biriga
bog‘liq emas va paydo bo‘lish ehtimolliklari bir xil. U holda axborot hajmini hisoblang?
Yechish
: Agar
x1 va x2 belgilar bir – biriga bog‘liq bo‘lmasa ehtimoliklari
bir – biriga teng bo‘lsa, unda R (x1)=R(x2)=1/N=0,5 . U holda
axborot hajmi:
Imax
= log 2 0,5 = 1 bit ga teng bo‘ladi.
O‘zaro
axborot yordamida ma’lum bo‘lmagan X tizim haqidagi axborot hajmini aniqlash mumkin.
Amaliyotda
X tizimning holatini to‘g‘ridan to‘g‘ri aniqlash mumkin bo‘lmaydi, bunday holatda
X tizim bilan ma’lum bir darajada bog‘liq bo‘lgan Y tizimni holatini o‘rganish
orqali X tizimning holati o‘rganiladi.
Masalan,
kosmik korablning holatini to‘g‘ridan-to‘g‘ri nazorat qilish o‘rniga uning apparaturalaridan
kelayotgan signallar to‘plamining holati o‘rganiladi va uning asosida kosmik kema
to‘g‘risida ma’lumot shakllanadi. Yoki futbol matchini televizor orqali ko‘rish.
Bunda
X va Y tizimlar o‘rtasida 2 turdagi farq bo‘lishi mumkin:
1)
X tizimning bir xil xolatlari Y tizimda o‘z aksini topmaydi (Y tizim X tizimning
holatini aniq ko‘rsatib bera olmaydi);
2)
Ikki tizim o‘rtasidagi farq xatoliklar evaziga sodir bo‘ladi:
-
X tizim parametrlarini aniq o‘lchamaslikdagi xatolar;
-
ma’lumot uzatishda yuz beradigan xatolar. Masalan oq-qora televizorda rang yo‘qoladi,
sifati shovqinlar tufayli pasayadi.
-
Y tizim X tizimdan farq qiladi.
Y
tizimda X tizim to‘g‘risidagi axborot miqdorining qanday hajmi uning holatini
Y tizim orqali nazorat qilish imkonini beradi, degan savol tabiiy.
Bunday
axborot X tizimning entropiyasi kamayganini bildiradi, chunki uning to‘g‘risidagi
axborot hajmi Y tizimda mavjud, ya’ni:
L
Y→ X = H (X) – H (X/Y)
Bu
yerda H(X) – tizimni nazorat qilishdan oldingi entropiya qiymati;
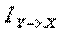 H(X/Y)
- axborot olingandan keyin qolgan entropiya qiymati.
H(X/Y)
- axborot olingandan keyin qolgan entropiya qiymati.
- Y tizimda X tizim to‘g‘risidagi to‘liq yoki o‘rta axborot miqdori.
Umumiy
holatda, ikki tizim mavjudligida har bir tizim boshqasiga nisbatan bir xil to‘liq
axborotga ega bo‘ladi. Bu ta’rif quyidagi formulalar orqali isbotlanadi:
H (X,Y) = H (X) + H
(Y/X)
H (X,Y) = H (Y) + H
(X/Y)
Bundan
H (X) + H (Y/X) = H (Y)
+ H (X/Y)
H (X) – H (X/Y) = H (Y)
– H ( Y/X)
Natijada
LY→
X = L X→Y = L X↔Y
L
X↔Y X va Y tizimlarda bir-birlari to‘g‘risida saqlanayotgan to‘liq
axborot deyiladi.
Ikki
tizim orasida har xil xolat bo‘lishi mumkin:
a)
X va
Y tizimlar bir-biriga hech ham bog‘liq emas va bir-biri
to‘g‘risida hech qanday ma’lumot yo‘q, ya’ni X
va Y - mustaqil tizimlardir.
Bunda
H(Y/X) = H(Y), i * = 0, ya’ni X tizim bilan hech qanday
bog‘liq bo‘lmagan Y tizimni nazorat qilish oqibatida X tizim to‘g‘risida ma’lumot
olish mumkin emas.
b)
X va Y tizimlar bir-birini to‘liq ifodalaydi, ya’ni bir-biriga o‘xshaydi.
Bunda
H(X)=H(Y),
H(X/Y)=H(Y/X)=0
va
LX↔Y
= L X = L Y = H (X) = H (Y)
X
i Y tizim orasida bir taraflama qattiq bog‘lanish bo‘lgan holat tahlil qilinadi,
ya’ni bir tizim ikkinchi tizimning holatini to‘liq aniqlab beradi, lekin teskari
holat mavjud emas, ya’ni ikkinchi tizim birinchi tizimning holatini aniqlab bermaydi.
Umuman
olganda, bo‘ysunadigan tizimning holatiga qarab boshqaradigan tizimning holatini
to‘liq aniqlab bo‘lmaydi.
Bo‘ysunadigan
tizim entropiyasining qiymati boshqaradigan tizim entropiyasidan kam, chunki odatda
boshqaradigan tizim to‘g‘risida ma’lumot kam, bo‘ysunadigan tizim to‘g‘risidagi
ma’lumot yetarli darajada bo‘ladi.
Bunday
holatda, ya’ni biri boshqaradigan, boshqasi esa bo‘ysunadigan tizimlarda bir-birlari
to‘g‘risida saqlanayotgan to‘liq ma’lumot miqdori bo‘ysunadigan tizimning entropiyasiga
teng bo‘ladi.
X
i Y tizimlardan Y bo‘ysunadigan va X boshqaradigan tizimlar bo‘lsin. Bunda
H(Y/X)=0, va L X↔Y = H (Y)
Shunday
qilib, ikki tizimdan biri bo‘ysunadigan holatda tizimlarda bir-birlari to‘g‘risida
saqlanayotgan to‘liq ma’lumot miqdori bo‘ysunadigan tizimning entropiyasiga teng
bo‘ladi.
To‘liq
ma’lumot qiymatini hisoblash formulasini shartli entropiya formulasi orqali emas,
balki ikki tizimning umumiy entropiyasi va har bir tizimning entropiyasi H(X),
H(Y) orqali ifodalash mumkin.
L X↔Y =
H (X) – H (X/Y),
H (X,Y) = H (Y) + H
(X/Y)
L Y↔X =
H (X) + H (Y) – H (X, Y)
Tizimlar
o‘rtasidagi o‘zaro to‘liq axborotlarni ehtimollik nazariyasi formulalari orqali
ifodalanishi quyidagicha bajariladi. Buning uchun entropiya qiymatlarini matematik
kutilma formulasi orqali yozib chiqamiz:
H(X)=M[-log
P(X)], H(Y)=M[-log P(Y)], H(X,Y)=M[-log P(X,Y)]
Bunda
to‘liq axborot qiymati quyidagicha ifodalanadi:
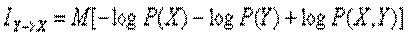
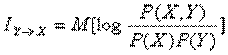 Yoki
Yoki
tizimlarning
hamma holatlarini hisobga olgan holda formula quyidagicha yoziladi:
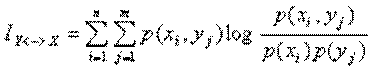
3-ma’ruza
bo‘yicha nazorat savollari
1. Entropiya
nima? Uning qiymati qanday hisoblanadi?
2. Tizimlar
orasida o‘zaro bog‘liq axborotlar deganda nima tushuniladi?
3. Tizimlar
orasida o‘zaro bog‘liq axborotlarning entropiya asosidagi formulasini xisoblang?
4. Entropiyani
hisoblash formulasining fizik mohiyati nima?
4-ma’ruza.
Axborotni kodlash usullari. Shennon – Fano, Xaffman teoremalari. Samarali kodlash
usullaridan foydalanish.
Reja:
1. Axborotni
kodlashning maqsadi va afzalliklari.
2. Axborotni
Shennon – Fano usuli bo‘yicha kodlash.
3. Axborotni
Xaffman usuli bo‘yicha kodlash.
Axborot nazariyasi nuqtai nazaridan axborotni kodlash – bu axborot manbaidagi alfavitni
ma’lum bir tartibda shartli simvollar bilan almashtirib chiqish tushuniladi.
Kod
(kod alfaviti) – berilgan birlamchi ma’lumotni kodlashtirish maqsadida ishlatiladigan
shartli simvollarning to‘liq to‘plami hisoblanib, ma’lum bir kodlash qoidasi negizida
amalga oshiriladi. Kod alfavitini tashkil etadigan har xil kod simvollari kod alfavitining
hajmi deyiladi. Kod alfavitining hajmi kodlashtiriladigan birlamchi ma’lumot alfavitining
hajmidan kam bo‘lishi mumkin emas.
Kodlashtirish – bu birlamchi ma’lumotni
aloqa kanallari orqali uzatishga mo‘ljallangan kod simvollari alfaviti bilan ifodalashdir.
Kodlash
kod simvollari qanday ko‘rinishda berilganiga qarab, raqamli va raqamsiz bo‘lishi
mumkin: ikkilik, sakkizlik, 16 tilik sanoq tizimida yoki qandaydir belgi yoki ob’ektlar
ko‘rinishida. Ko‘p hollarda kod simvollari oddiy raqamlar ketma-ketligi yoki raqamlar
to‘plami sifatida tasvirlanadi. Bunda ular kod simvollarining elementi hisblanadi.
Kod so‘zi tarkibidagi raqamning joylashishi yoki tartib raqami uning pozitsiyasini
belgilaydi.
Simvollari
paydo bo‘lishining ehtimoli bir xil bo‘lgan ma’lumotlarni
samarali kodlash. Samarali
kodlash shovqinsiz aloqa kanallarida qo‘llaniladi. Bunda kanallarda asosiy masala
– maksimal axborot uzatish tezligini ta’minlash, ya’ni axborot uzatish tezligini
aloqa kanalining ma’lumot uzatish imkoniga yetkazish hisoblanadi.
Agar
N(x) – birlamchi ma’lumotning entropiyasi bo‘lsa, hamda (xi) ma’lumotining
simvollarini paydo bo‘lish ehtimolligi bir xil va ma’lumot manbai alfavitining hajmi
m bo‘lsa, (xi ) ma’lumotini hohlagan i simvolining paydo bo‘lish ehtimolligi
P(xi) bir xil qiymatga ega bo‘ladi, ya’ni:
P(
X i ) i=1,.., m,
Ma’lumotning
entropiyasi (N(x)):
ga
teng bo‘ladi.
Agar
kodlash uchun k asosli raqamli koddan foydalanilgan bo‘lsa (kod simvollari
elementlari alfavitining hajmi k ga teng) va bunda kod simvollari elementlarining
entropiyasi (N1), simvol elementlarining paydo bo‘lish ehtimolligi
bir xil va ular o‘zaro mustaqil bo‘lish sharti bajarilganida quyidagi formula orqali
hisoblanadi:
H1
= log2k .
Bunda
samarali kod simvoli elementlarining uzunligi (leff.) quyidagi
formula yordamida hisoblanishi mumkin:
Bunda
m = k n.
Shovqinsiz
aloqa kanallari orqali uzatiladigan ma’lumotlarni samarali kodlashtirish Shennon
teoremasiga asoslanadi:
Agar
ma’lumot manbaining entropiyasi N [bit/simvol] ga va aloqa kanalining uzatish
qobiliyati S [bit/sek] ga (aloqa kanalining uzatish qobiliyati deganda,
uning eng maksimal ma’lumot uzatish tezligini ta’minlashi tushuniladi) teng bo‘lsa,
har doim shunday kodlash usulini topish mumkinki, kanalda ma’lumot uzatish tezligining
o‘rtacha qiymati ushbu formula negizida hisoblangan tezlikga teng bo‘ladi:
[simvol/sek
]
N-
ma’lumot manbaning entropiyasi
S-
aloqa kanalining uzatish qobiliyati.
E’tiborni
teoremaning isbotiga qaratmasdan, uning imkoniyatiga to‘xtalamiz:
ushbu teorema kod simvollarining bir xil ehtimol va bir-biriga
bog‘liq bo‘lmagan holda kelib tushishini ta’minlaydi, har bir simvol yordamida bir
nuqtadan ikkinchisiga uzatilayotgan axborot hajmi log2
k (bit/element)
ga teng bo‘ladi.
Lekin
teorema qanday usul asosida samarali kodlash mumkinligi to‘g‘risida hech qanday
ko‘rsatma bermaydi.
Keltirilgan
xususiyatlarga asoslanib, ma’lumotlarning o‘zaro bog‘liq va o‘zaro bog‘liq bo‘lmagan
simvollarini samarali kodlash bo‘yicha bir qator algoritmlar ishlab chiqilgan, ular
bugunda ham samarali kodlash jarayonlarida qo‘llaniladi.
Algoritmlar ma’lumot manbaida ko‘p qaytariladigan simvollarni
eng kichik uzunlikdagi kod kombinatsiyalari bilan kodlashga asoslanadi. Axborotni
kamroq bitlarni sarflab uzatish axborotni kodlashtirishning samarali usullarining
maqsad va vazifasi hisoblanadi. Axborotni kodlashtirishning samarali usullaridan
foydalanilganda kanalning o‘tkazuvchanlik qobiliyatidan samarali foydalanish mumkin.
Shennon
- Fano kodi paydo bo‘lguncha aloqa kanallari orqali
uzatilayotgan axborotlardagi belgilar uzunligi bir xil bo‘lgan bitlar yordamida
kodlashtirilar edi. Shennon - Fano kodi paydo bo‘lgandan so‘ng uzatilayotgan axborotdagi
har bir belgining paydo bo‘lish ehtimolligiga qarab turib, uzunligi har xil bo‘lgan
bitlar yordamida kodlash imkoniyati paydo bo‘ldi. Axborotda biror bir belgining
paydo bo‘lish ehtimolligi kattaroq bo‘lsa, uni ikkilik sanoq tizimidagi kodining
uzunligi “kichikroq bit” bo‘ladi. Agar axborotda biror bir belgining paydo bo‘lish
ehtimolligi kichikroq bo‘lsa, uni ikkilik sanoq tizimidagi kodining uzunligi “kattaroq
bit” bo‘ladi.
Qurish
texnikasi bo‘yicha Shennon va Fano kodlari bir-biriga yaqin bo‘lganligi uchun Shennon
- Fano kodi deyiladi. Ushbu kod 1948 yilda paydo bo‘lgan. Ushbu algoritm yordamida
axborotni kodlashtirish quyidagicha amalga oshiriladi:
Ø axborotdagi
barcha belgilarning umumiy soni N hisoblanadi;
Ø N
ta belgidan iborat bo‘lgan
axborotdan har
bir belgining paydo bo‘lish
chastotasi yoki paydo bo‘lish extimolligi hisoblanadi;
Ø har
bir belgining paydo bo‘lish
chastotasi kamayib borish tartibida jadvalga joylashtiriladi;
Ø umumiy
bo‘lgan jadvaldagi yig‘indi
teng ikkiga bo‘linadi
va tepa qismiga
«1» ni,
pastki qismiga
«0» ni qo‘yiladi;
Ø teng
ikkiga bo‘lish
kodlashtirilayotgan axborotdagi har bir belgiga bittadan
«1» yoki «0»
qolguncha davom ettiriladi;
misol:
Quyidagi
ko‘rinishda axborot berilgan:
BBCBBBCDDEDAAADDFFGGHHEE.
Ushbu
axborotda umumiy belgilar soni 24 ta. Dastlab ushbu axborot uchun entropiya ko‘rsatkichining
qiymatini hisoblaymiz.
N(x)
= ∑ R(x) * Log 2 R(x) = 2,89 bit ga teng bo‘ladi.
Ushbu
algoritm bo‘yicha hisoblash natijalari jadvalda keltirilgan.
Shennon-
Fano algoritmi bo‘yicha hisoblash natijalari.
|
Belgilar
|
Paydo bo‘lish
chastotasi
|
Yordamchi jadval
|
Kodi
|
|
B
|
5
|
5(1)
5(1)
|
5(1)
|
11
|
|
D
|
5
|
3(1)
|
5(0)
3(0)
|
101
|
|
A
|
3
|
3(0)
|
3(1)
|
100
|
|
E
|
3
|
2(0)
|
2(1)
|
011
|
|
C
|
2
|
2(0)
|
2(0)
|
010
|
|
F
|
2
|
2(0)
|
2(0)
|
|
001
|
|
G
|
2
|
2 (0)
|
2(0)
|
|
0001
|
|
H
|
2
|
|
|
|
0000
|
Misol.
Quyidagi ko’rinishda
axborot bårilgan:
ÂÂÑÂÂÂÑDDEDAAADDFFGGHHEE
ushbu axborotda umumiy bålgilar soni 24 ta. Dastlab ushbu axborot uchun
entropiya ko’rsatkichining qiymatini xisoblaymiz.
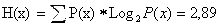 bitga
tång bo’ladi.
bitga
tång bo’ladi.
Ushbu
algoritm bo’yicha xisoblash natijalari jadvalda kåltirilgan.
Shånnon-Fano
algoritmi bo’yicha
xisoblash natijalari.
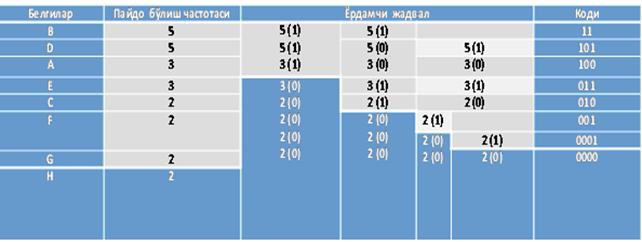
Kodlashtirilgan
axborotdagi xar bir belgiga mos kelgan kodli kombinatsiyaning o‘rtacha uzunligi
quyidagicha hisoblanadi:
n
o‘rt
= ∑ n
i *
R(x) = 2,96
bitga teng.
Hozirgi
kunda eng keng tarqalgan, amaliyotda ko‘p ishlatiladigan entropiyali kodlash usuliga
asoslangan algoritmlardan biri bu – Xaffmen algoritmi hisoblanadi.
Xaffmen
algoritmi asosida matnli axborotlar kodlashtiriladi.
Ushbu
algoritm yordamida axborotni kodlashtirish quyidagicha amalga oshiriladi:
Ø axborotdagi
barcha belgilar soni, ya’ni N hisoblanadi;
Ø jami
N ta belgidan iborat bo‘lgan
axborotdagi har
bir belgining paydo bo‘lish
chastotasi hisoblanadi;
Ø har
bir belgining paydo bo‘lish chastotasi kamayib borish tartibida jadvalga joylashtiriladi;
Ø jadvaldagi
oxirgi ikkita chastota yig‘indisi hisoblanib, bitta umumiy bo‘lgan yig‘indi chastotaga
birlashtiriladi;
Ø hisoblangan
yangi yig‘indi
chastotadan va hisoblashda
qatnashmagan boshqa chastotalardan jadvalning yangi ustuni
hosil qilinadi (bunda ham chastotalar kamayib borish tartibida joylashtiriladi);
Ø shu
tarzda to bitta umumiy N ga teng bo‘lgan
yig‘indi hosil
bo‘lguncha jarayon davom etaveradi;
Ø jadval
to‘ldirilgandan so‘ng,
undagi hisoblashlarga muvofiq
daraxt quriladi;
Ø daraxtning
tepa qismida
N joylashgan bo‘ladi
va uni teng ikkiga bo‘lish kerak, hosil bo‘lgan natijalarni
yana teng ikkiga bo‘lish lozim;
Ø shu
tarzda axborotdagi har bir belgining paydo bo‘lish chastotasi topilguncha, bo‘lish
davom ettiriladi.
misol:
Quyidagi ko‘rinishda axborot berilgan:
BBCBBBCDDEDAAADDFFGGHHEE.
Xaffmen
algoritmi bo‘yicha hisoblash natijalari jadvalda keltirilgan.
|
Belgilar
|
Paydo
bo‘lish chastotasi
|
Yordamchi
jadval
|
|
B
|
5
|
5
|
5
|
6
|
8
|
10
|
14
|
24
|
|
D
|
5
|
5
|
5
|
5
|
6
|
8
|
10
|
|
|
A
|
3
|
4
|
4
|
5
|
5
|
6
|
|
|
|
E
|
3
|
3
|
4
|
4
|
5
|
|
|
|
|
C
|
2
|
3
|
3
|
4
|
|
|
|
|
|
F
|
2
|
2
|
3
|
|
|
|
|
|
|
G
|
2
|
2
|
|
|
|
|
|
|
|
H
|
2
|
|
|
|
|
|
|
|

|
Belgilar
|
B
|
D
|
A
|
E
|
C
|
F
|
G
|
H
|
|
Kodi
|
01
|
00
|
100
|
101
|
1101
|
1100
|
1111
|
1110
|
Kodlashtirilgan
axborotdagi xar bir belgiga mos kelgan kodli kombinatsiyaning o‘rtacha uzunligini
hisoblaymiz:
n
o‘rt
= ∑ n
i *
R(x) = 2,92
bitga teng.
Yuqoridagi
ko‘rib chiqilgan 1 va 2-misollarda kodlashtirilayotgan axborot qo‘yidagicha,
ya’ni BBCBBBCDDEDAAADDFFGGHHEE.
Biroq,
hisoblash natijalariga ko‘ra, kodlashtirilgan axborotdagi xar bir belgiga mos kelgan
kodli kombinatsiyaning o‘rtacha uzunligi Shennon - Fano usuli uchun n o‘rt
=2,96 bitga, Xaffmen usuli uchun esa n o‘rt =2,92 bitga teng chiqdi.
Bundan
xulosa qilinadiki, yuqoridagi axborotni Xaffen usuli bilan kodlashtirilsa maqsadga
muvofiq bo‘ladi, chunki ushbu algoritm bilan axborotni kodlashtirilganda axborotdagi
xar bir belgiga mos keluvchi kodli kombinatsiyaning o‘rtacha uzunligi kichkina,
ya’ni axborotni uzatish uchun kam bit sarflanadi. Bu esa o‘z navbatida axborotni
uzatish tezligini oshirishga olib keladi.
Samarali
kodlash algoritmlarining kamchiliklari
Ø tashqi
shovqinlarga ta’sirchanligi – shovqin ta’sirida bitta elementda sodir bo‘lgan xato
bir kod kombinatsiyasini vaqt birligi bo‘yicha boshqa qiymatga ega ikkinchisiga
o‘tib ketishiga sabab bo‘lishi mumkin;
Ø bir kod simvoli boshqa vaqt birligidagi simvolga aylanishi mumkin, buning
oqibatida joriy va keyingi simvollar noto‘g‘ri dekodlanadi va birlamchi ma’lumot
boshqa ma’lumotga o‘zgarib ketadi;
Ø keyingi
kamchilik bu texnikaviy jihatdan ularni yaratish murakkabligi hisoblanadi: qurilma
bufer va simvollarni yig‘ish uskunalariga ega bo‘lishi kerak. Chunki aloqa kanallari
bir xil uzunlikdagi kod kombinatsiyalarini uzatishda samarali ishlaydi, yuqoridagi
algoritmlardagi kod kombinatsiyalarining uzunligi har xil, ularni yig‘ib bir tugallangan
ma’lumot shakliga keltirish uchun oldin qabul qilingan simvollarni saqlash kerak
bo‘ladi.
Xaffmen
kodi asosan faksimil tizimlarda ishlatiladi. Xaffmen kodlarining shartlari quyidagilardan
iborat:
Ø eng
ko‘p uchraydigan simvollarni birinchi uzatish;
Ø simvollar
extimolligini aniqlash;
Ø extimolligiga
qarab joylashtirish (katta kichikligiga qarab);
Ø entropiyani
xisoblash;
Ø entropiya
xisoblangandan keyin daraxt xoliga keltiriladi va kodlashtiriladi.
Misol
: Djabbarov Shuxrat Yuldashevich
Umumiy
berilgan xabardagi simvollar (xarflar, belgilar)
soni 24 ta. Birinchi bosqichda entropiya xisoblanadi:
P
(x) = 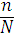 ,
,
Ya’ni
xar bir simvol umumiy songa bo‘linadi:
Masalan
: P (x)
= 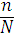 ,
=
,
=
|
Simvollar
|
Axborotdagi simvollar soni
|
Natijasi
|
|
D
|
2
|
0,08
|
|
J
|
1
|
0,04
|
|
A
|
4
|
0,16
|
|
B
|
2
|
0,08
|
|
R
|
2
|
0,08
|
|
O
|
1
|
0,04
|
|
V
|
2
|
0,08
|
|
Sh
|
2
|
0,08
|
|
U
|
1
|
0,04
|
|
X
|
1
|
0,04
|
|
T
|
1
|
0,04
|
|
Yu
|
1
|
0,04
|
|
L
|
1
|
0,04
|
|
Ye
|
1
|
0,04
|
|
I
|
1
|
0,04
|
|
Ch
|
1
|
0,04
|
Ikkinchi
bosqichda ikkita kichik extimoli bo‘lgan axborotlarni bittaga birlashtiramiz va
qo‘shib chiqamiz.

Uchinchi bosqichda kodlashtiramiz,
ya’ni tartib bo‘yicha yuqori qismiga “1” va pastki qismiga “0” qo‘yib kodlashtiramiz.
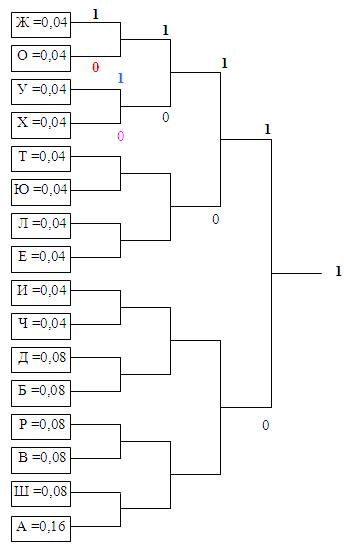
To‘rtinchi
bosqichda xar simvol bo‘yicha kodlashni amalga oshiramiz. Masalan:
J
– 1 1 1 1 1
O
– 0 1 1 1 1
U
– 1 0 1 1 1
X
– 0 0 1 1 1
4-mavzu bo‘yicha
nazorat savollari
1. Axborotni
kodlashning maqsadi va afzalliklari nimalardan iboart?
2. Axborot
Shennon – Fano usuli bo‘yicha qanday kodlanadi?
3. Axborot
Xaffman usuli bo‘yicha qanday kodlanadi?
4. Shennon
teoremasining ahamiyati nimadan iborat?
5. Samarali
kodlash algoritmlarining kamchiliklari nimalardan iborat?
6. Xaffman
usuli bo‘yicha familiyangiz,
ismingiz
va sharifingizni
kodlashtiring?
5-ma’ruza.
Matnli, audio, tasvirli va video axborotlarni kodlash
Reja:
1.
Axborot tushunchasi.
2.
Matnli axborotlarni kodlash.
3.
Audio axborotlarni kodlash.
4.
Tasvirli axborotlarni kodlash.
5.
Video axborotlarni kodlash
6.
Kodeklar haqida
umumiy tushuncha.
7.
Audio kodeklarning asosiy tavsiflari.
8. Video kodeklar tasnifi.
9.
MPEG 7
va MPEG 21 – kelajak formatlari.
Axborot
tushunchasi. Axborot keng qamrovli tushuncha bo‘lib,
unga quyidagicha ta’rif berish mumkin:
Ø Dalil,
voqea, xodisa, predmet, jarayon kabi ob’ektlar xaqidagi bilim hamda tushunchalar
yoki buyruqlar;
Ø Ma’lum
xos matnda aniq ma’noga ega tushunchalarni ichiga olgan dalil, voqea, xodisa, predmet,
jarayon, taqdimot kabi ob’ektlar haqidagi bilimlar majmui;
Ø Qiziqish
uyg‘otish mumkin bo‘lgan, saqlanishi va qayta ishlanishi lozim bo‘lgan jami dalil
va ma’lumotlar.
Ø Kitob
matni, ilmiy formulalar, bank xisob raqamidan foydalanish va to‘lovlar, dars jadvali,
o‘lcha majmualarining yer va fazo stansiyasi o‘rtasidagi masofa to‘g‘risidagi ma’lumotlar
va h.lar axborot bo‘lishi mumkin.
Axborotlarni
uzatish. Axborotni uzatish deganda extiyojdan kelib
chiqib, uni bir kishidan ikkinchi kishiga yoki bir kompyuterdan ikkinchi kompyuterga
turli vositalar yordamida yetkazib berish tushuniladi.
Axbrotlarni
uzatishning turli usullari mavjud:
v kompyuter
dasturlari yordamida;
v pochta
orqali;
v transport
vositalari yordamida;
v aloqa
tarmog‘i orqali.
Aloqa
tarmog‘i orqali axborotlarni qisqa vakt ichida uzoq masofaga uzatish mumkin. Bunda
ma’lumotlarni uzatish vakti sezilarla darajada qisqaradi.
Axborotning
jamiyatda va kundalik xayotimizda tutgan o‘rni. Jamiyatni
axborotlashtirish:
- mehnat;
- ilmiy
tadqiqot;
- loyiha;
- ishlab
chiqarish jarayonlarini avtomatlashtirish;
- aholiga
xizmat ko‘rsatishni avtomatlashtirish;
- tashkiliy-iqtisodiy
boshqarishni avtomatlashtirish;
- ta’lim
va kadrlar tayyorlash tizimini axborotlashtirish kabi sohalarni o‘z ichiga oladi.
Jamiyatda
axborot ham bilim manbai, ham eng asosiy muloqot vositasi bo‘lib hisoblanadi. Jamiyatni
axborotlashtirishda radio, televidenie, ommaviy-axborot vositalari va Internet tizimining
ahamiyati juda yuqoridir. Har kim, har doim biror ishni bajarish yoki biror maqsadga
erishish uchun axborotdan foydalanadi.
Har
bir inson:
- ob-havo
prognozini;
- transport
vositalari qatnovi jadvalini;
- bank
va biznes ma’lumotlarini;
- kundalik
yangiliklardan habardor bo‘lishga muxtojdir.
Agarda
inson kundalik axborotlar va yangiliklardan xabardor bo‘lmas ekan u jamiyatdan uzilib
qolishi muqarrar.
Bugungi
kunda axborot uzatishning 5-ta turi mavjud:
§ Matn;
§ Ovoz;
§ Tasvir;
§ Video;
§ Ma’lumotlar.
Xar
bir turdagi xabarlar uchun ma’lum o‘tkazish maydoni mavjud.
Axborotning
turlari: (matn, tasvir, audio va video).
Matn.
Matn
- bu ma’lumotlarni ifodalash shakli bo‘lib, u mazmunan yagona, yaxlit va tanlangan
tilning belgilari ketma-ketligidan iborat. Matn hujjat asosidir.

Axborot
tizimiga matn kiritish klaviatura, nurli pero, mikrofon, yoki skaner yordamida
amalga oshiriladi. Matnlarga ishlov berish matn muharriri deb ataluvchi maxsus
amaliy dasturlar majmuasi tomonidan amalga oshiriladi. Tarmoq orqali matnlar
ma’lumotlar bo‘laklari ko‘rinishida uzatiladi
Mantli
axborotlarni qo‘llash usullari juda ko‘p bo‘lib ulardan ayrimlarini misol tariqasida
keltiramiz:
- gazetalar;
- jurnallar;
- kitoblar,
elektron kitoblar;
- internetdagi
matn ko‘rinishidagi axborotlar;
- uyali
aloqadagi SMS xizmatlari;
- onlayn
chatlar (whatsapp, mail agent, wechat);
- sotsial
tarmoqlardagi matnli almashinuvlar (face-book.com, mail.ru, odnoklassniki.ru va
b);
- bulardan
tashqari matn bilan ishlash mumkin bo‘lgan barcha dasturiy matn taxrirlagichlari
matnli axborotni ko‘llash va ishlatish mumkin bo‘lgan ma’nba va vositalarga kiradi.
Radio.
Radioaloqaning nazariy asosi ingliz olimi
D. Maksvell tomonidan ishlab chiqilgan. 1864 yilda D. Maksvell yorug‘lik tezligi
bilan tarqaladigan elektromagnit maydoni o‘zgaruvchan tok o‘tkazuvchisi atrofida
paydo bo‘lishi kerakligini nazariy isbotladi.
1887
yilda nemis fizigi G. Gers elektromagnit to‘lqinlar borligini amaliy ko‘rsatdi.
D.
Maksvell tomonidan elektromagnit to‘lqinlar ochilishi
va G. Gers tomonidan eksperimental tasdiqlanishi bilan radio rivojlanishi davri
boshlandi.
G.
Gers g‘oyalarini A. Popov rivojlantirib 1895 yilda birinchi marotaba radio aloqa
bo‘yicha axborot uzatdi.
Birinchi
radiouzatuvchilar Markoni tomonidan qurilgan va patentlangan.
Televideniya.
1884 yil Nipkov (Germaniya) diski yordamida
ovozni qayta ishlash va uzatishga birinchi harakat qilingan.
1907
yil Rozing elektron nur trubka yordamida tasvirli uzatishdan foydalanishga taklif
bergan. 1911 yil dunyoda birinchi televizion uzatish amalda qo‘llanildi.
Elektron
nur trubka yordamida – ikonoskop (uzatuvchi) va kinaskop (qabul qilish) asosida
televideniya yo‘lga qo‘yilgan.
XX
asrning 30 yillari o‘rtalarida televizion uzatish muntazam yo‘lga qo‘yilgan.
Qo‘zg‘almas
tasvir. Faksimil aloqaning paydo bo‘lishi inson imkoniyatini
yetarlicha kengaytirdi. Faqat matnli va ovozli xabarlarni uzatishni emas balki chizmalarni,
rasmlarni va grafiklarni uzatish imkoniyatini kengaytirdi.
Qo‘zg‘almas
tasvirlarni masofadan uzatishni 1855 yil italyan fiziki Dj. Kazelli
tomonidan amalga oshirilgan.
1902
yil Artur Kern (Germaniya) fotoelektrik
tizim orqali tasvirlarni skanerlash to‘g‘risida patent olgan.
1910
yili Berlin
– Parij – London orasida
xalqaro faksimil aloqa ishga tushgan.
Tasvir.
Tasvir – biror voqea, xodisa yoki jarayonlarni
o‘zida ifodalagan rasm bo‘laklari va ranglardan iborat ma’lumotdir. Foto, manzara,
matematik funksiyalar grafigi, statistik ma’lumotlar diagrammasi va shunga o‘xshash
ma’lumotlar tasvir xisoblanadi.
Kompyuter
yordamida tasvirlarga ishlov berishni to‘rt guruxga ajratish maqsadga muvofiq xisoblanadi:
-
kulrang va rangli tasvirlar;
-
ikki xil va bir necha “rangli” tasvirlar;
-
uzluksiz egri va to‘g‘ri chiziqlar;
-
nuqtalar yoki ko‘pburchaklardan iborat tasvirlar.
Bu
turkumlash tasvirni ko‘rib idrok qilish mexanizmi bilan emas, balki ularni taqdim
etish va qayta ishlashga yondashish bilan bog‘liq.
Muayyan
vaqtdagi ish, o‘z tabiatiga ko‘ra statik bo‘lgan matn va grafikadan farqli ravishda,
audio va videosignallar faqat vaqtning ma’lum oralig‘ida ko‘rib chiqiladi.
Video
va audio axborotlarni kompyuterda qayta ishlash va aks ettirish uchun:
- markaziy
protsessor tez harakatchanligi;
- ma’lumotlarni
uzatish shinasining o‘tkazish qobiliyati;
- operativ
(tezkor) va video-xotira;
- katta
sig‘imli tashqi xotira (ommaviy xotira);
- hajm
va kompyuter, kirish va chiqish kanallari bo‘yicha almashuvi tezligini taxminan
ikki baravar oshirilishi talab etiladi.
Amaliyotlar
shuni ko‘rsatmoqdaki, multimedia vositalari asosida talabalarni o‘qitish uchun ikki
barobar unumli va vaqtdan yutish mumkin. Multimedia vositalari asosida bilim olishda
30 %gacha vaqtni tejash mumkin bo‘lib, olingan bilimlar esa xotirada uzoq muddat
davomida saqlanib qoladi.
Agar
talabalar berilayotgan materiallarni ko‘rish (video) asosida qabul qilinsa, axborotni
xotirada saqlanib qolinishi 25-30 % oshadi.
Bunga
qo‘shimcha sifatida o‘quv materiallari audio, video va grafika ko‘rinishda mujassamlashgan
holda berilsa, materillarni xotirada saqlab qolish 75 % ortadi.

Multimedia
axborotlarini uzatish asosi bo‘lib ko‘pincha multiservis tarmoqlari bo‘lib qolayapti.
Ular turli xildagi ma’lumotlarni uzatishga va turli trafiklarni integratsiya qilish
imkoniyatiga ega.
Multiservich
tizimlarini yorqin va murakkab misoli bo‘lib audio va video uzatishlar bo‘lib qoldi.
Matnli
axborotlarni kodlash. Texnik tomonlama qarashda
matn aloxida simvol (belgi)lardan tashkil topgan. Bu simvollarga faqat xarflar emas
(bosh yoki kichik xarf, lotin yoki rus), balki raqamli, tinish belgilari, maxsus
simvollvr turi, masalan "=", "(", "&" va h.k.
yoki so‘zlar orasidagi bo‘sh qolgan joylar (probelû mejdu slovami).


Alfavit
deb - ko‘pchilik simvollar yordamida yoziladigan matnga aytiladi. Quvvat (moùnost)
bu – alfavitdagi simvollar sonidir. Axborot sonini aniqlash formulasi quyidagicha:
N
= 2b,
bu
yerda N –alfavit quvvati (simvollar soni),
b
– bitlar soni (axborot og‘irligi (ves) simvoli).
256
simvolli alfavitga amaliy tomondan hamma kerakli simvollarni joylashtirish mumkin.
Bunday alfavit yetarli (dostatochnûm) deb ataladi.
256
= 28, bunda og‘irlik 1 simvol – 8 bit.
Birlik
o‘lchovda 8 bitni 1 bayt deb nomlangan:
1
bayt = 8 bit.
Matnlar
klaviatura yordamida kompyuter xotirasiga kiritiladi. Klaviaturada birlamchi xarflar,
raqamlar, tinish belgilar va boshqa simvollar yozilgan. Ular operativ xotiraga ikkilik
kod ko‘rinishda tushadi. Demak, har bir simvol 8-razryadli ikkilik kod ko‘rinishida
taqdim qilinadi.
Har
bir simvolga noyob 0 dan 255 gacha bo‘lgan o‘nlik kod yoki unga to‘g‘ri keladigan
ikkilik kod (00000000 dan 11111111 gacha) moslashishga qo‘yish kodlash deb ataladi.
Shunday qilib inson simvollarni yozish bo‘yicha, kompyuter esa kod bo‘yicha
farqlaydi.

Kompyuter
alfavitini barcha simvollari 0 dan 255 gacha raqamlangan. Har bir raqamga 8 razryadli
00000000 dan 11111111gacha bo‘lgan ikkilik kod to‘g‘ri keladi. Bu kod ikkilik sanoq
tizimda simvolni tartib raqami bo‘ladi.
Kompyuter
alfavitini xar bir simvoliga to‘g‘ri keladigan tartib raqami qo‘yilgan jadval kodlash
jadvali deb ataladi.
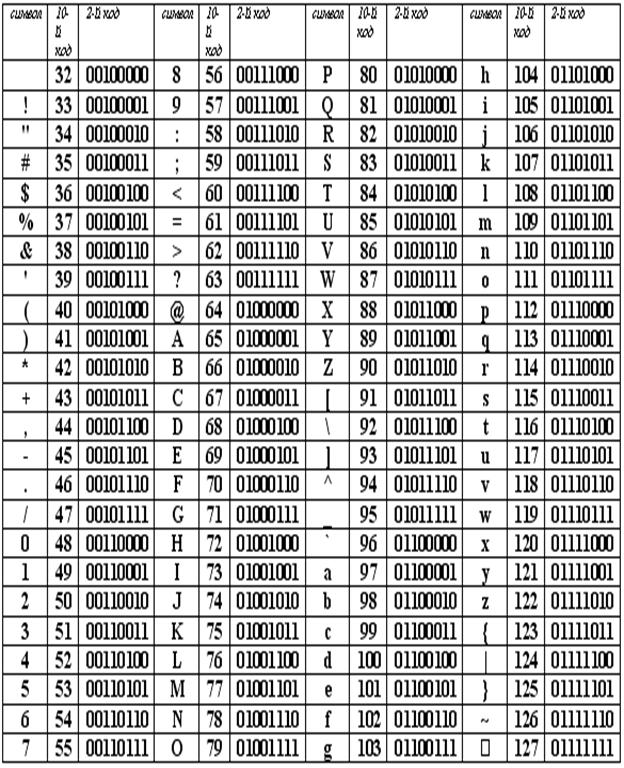
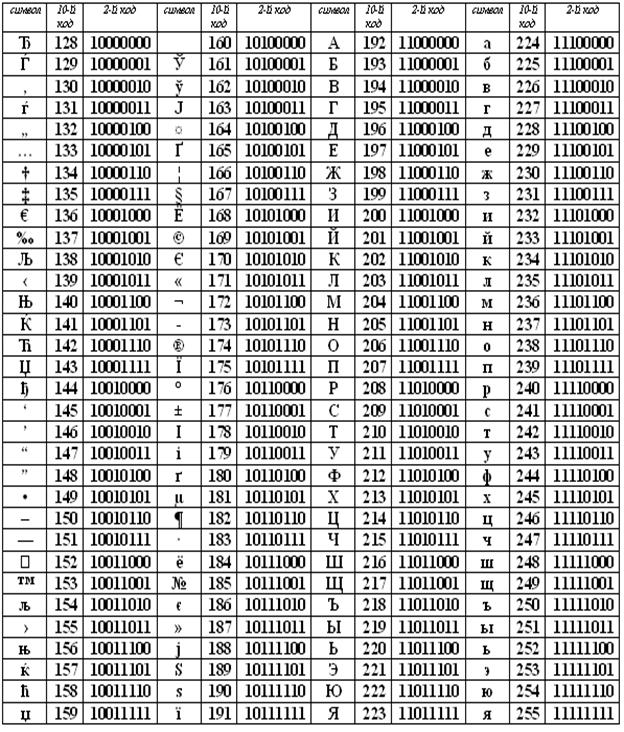
Turli
xil ShKda turli xildagi kodlash jadvallari qo‘llaniladi. ShKlarda xalqaro standart
jadvali bo‘lib ASCII (aski deb o‘qiladi) qabul qilingan
(axborot almashuvi uchun qabul qilingan Amerika standarti).
ASCII
kodlash jadvali ikki qismga bo‘linadi.
|
Tartib raqami
|
Kod
|
Simvol
|
|
0 - 31
|
00000000 -
00011111
|
0 dan 31 gacha bo‘lgan
raqam va simvollar boshqaruvchi deb ataladi.
|
|
32 - 127
|
00100000 -
01111111
|
Jadvalning
standart qismi (angliz). Bunga lotin alfavitidagi
kichik va bosh xarflar, o‘nlik raqamlar, tinish belgilari, turli turdagi qavslar
va boshqa simvollar kiradi.
|
|
128 - 255
|
10000000 -
11111111
|
Jadvalning
alternativ qismi (rus).
ASCII
kodli jadvalining ikkinchi yarmi kodli bet deb ataladi, (128 kodlash,
10000000 dan boshlanadi va 11111111 bilan tugallanadi).
|
 Ovozli
axborotni kodlash va ishlov berish
Ovozli
axborotni kodlash va ishlov berish
Ovozli
axborot. Ovoz xavoda, suvda va boshqa muxitda
tarqaladigan uzluksiz o‘zgaradigan jadallik va chastotali to‘lqindir. Inson ovoz
to‘lqinlarini (xavo tebranishi) eshitish yordamida turli balandlik va toni ko‘rinishida
qabul qiladi.
Ovoz
va videoma’lumotlarni uzatish. N.323 terminali N.245,
Q.931, RAS, RTP va N.450 protokollar oilasini ta’minlashi hamda G.711 audio kodlashni
qo‘llashi lozim.
Ovozlarni
an’anaviy kommutatsiya kanallari va tarmoqlari o‘rniga IP tarmog‘i orqali uzatish
texnologiyasi, yo‘laklar o‘rnatish orqali konfiguratsiyani inobatga oladi. Yo‘lak
axborotni jipslaydi, IP paketga aylantiradi, IP tarmoqqa yuboradi, qarama-qarshi
tomondagi yo‘lak aks harakatlarni amalga oshiradi, ya’ni chaqiriq paketlarini o‘qiydi
va taqsimlaydi. Natijada oddiy telefon apparati chaqirishni
hech bir muammosiz qabul qiladi.
Axborotlarni bunday o‘zga tus olishi, dastlabki ovoz signalini ortiqcha yubortirmasligi
kerak, uzatish rejimi mavjud vaqt ko‘lamida abonentlar o‘rtasidagi axborot almashinuvini
saqlab qolishi kerak.
Ovozni
siqish algoritmlari
|
Kodek
|
Talab etilgan o‘tkazuvchanlik
qobiliyati (Kbit/s)
|
DSP, MIPS
yuklanish
|
Kodekning kechikishlar
(ushlanishlar) yig‘indisi
(ms)
|
MOS
bahosi
|
|
G.711
|
64 (siqish
yo‘q)
|
yo‘q
|
0,25
|
4,1
|
|
G.723.1
|
5,3/6,4
|
16/21
|
37,5
|
3,7/3,9
|
|
G.728
|
16
|
32
|
2,5
|
4.3
|
|
G.729
|
8
|
25
|
15
|
3,92
|
|
G.729A
|
8
|
13
|
15
|
3,85
|
Izoh.
Ovoz sifati MOS (Mean Opinion Score, ITU-T P.800 tavsiyasi) ekspert baholarining
besh balli shkalasida berilgan.
Xar
xil turdagi ilovalarni o‘tkazish polosalari kengligi talablari
|
Ilova
|
Uzatish turi
|
Uzatish formati
|
Siqishsiz uzatish tezligi
|
Siqishli uzatish tezligi
|
|
Nutq
|
Telefoniya
|
G.711 – G723.1
|
64 kbit/s
|
8-32 kbit/s
|
|
Tasvir
|
Oddiy tasvirga ruxsat
|
SVGA
|
2,458 Mbit/s
|
24-245 kbit/s
|
|
JPEG
|
6,636 Mbit/s
|
104-830 kbit/s
|
|
Yqori sifatli tasvir
|
|
31,46 Mbit/s
|
0,3-3 Mbit/s
|
|
Video
|
Videokonferentsiya
|
MPEG-1 (PAL)
|
30,4 Mbit/s
|
1,15-3 Mbit/s
|
|
MPEG-1 (NTSC)
|
30,4 Mbit/s
|
1,15-3 Mbit/s
|
|
Keng eshittirishli TV
|
MPEG-2 (PAL)
|
124,4 Mbit/s
|
15 Mbit/s
|
|
MPEG-2 (NTSC)
|
124,4 Mbit/s
|
15 Mbit/s
|
|
Yqori
ruxsatli TV
|
HDTV
|
994,3 Mbit/s
|
135 Mbit/s
|
|
MPEG-3
|
745,8 Mbit/s
|
20-40 Mbit/s
|
Kodeklar
haqida tushuncha. Kodek (inglizcha codec,
koder/dekoder - kodlash, qayta kodlash) - ovozli va video faylni ishga tushirish
uchun mo‘ljallangan dastur hisoblanadi. Fayllar turli formatlarda bo‘ladi va ularni
ishga tushirish uchun alohida kodeklar zarur.
Kodek
bu amalga oshirilayotgan algoritmga muvofiq axborotni kodlash va dekodlash funksiyalarini
amalga oshiruvchi qurilma yoki dasturdir. Kodeklar oqim/signalni kodlashi (ko‘pincha
uzatish, saqlash va shifrlash uchun), koddan chiqarishi ham mumkin. Kodeklarning
ishi - ma’lumotlar yoki signallarni siqish va audio-video fayllarni o‘zgartirishdan
iborat. Bunda o‘zgartirilayotgan fayl imkon qadar yaxshi sifatda bo‘lishi talab
etiladi.
Kodeklarning
ikki turi mavjud-sifatni buzib ishlaydigan kodeklar va sifatni saqlagan holda ishlaydigan
kodeklar.
Birinchi
tur kodeklar fayl hajmini qisqartirishi natijasida audio va video fayllar sifati
buziladi.
Ikkinchi
tur kodeklar sifatni saqlagan holda fayllarni siqadi, ammo bu kodeklarni kamchiligi
ularda fayllar hajmi katta bo‘ladi.
Audio
kodeklar va ularning IP-telefoniyada
qo‘llanilishi.
Nutq
va video axborot kechikishlarga juda ta’sirchan, ammo alohida paketlar yo‘qolishga
kamroq ta’sirchandir. Shuning uchun transport protokoli sifatida UDP qo‘llaniladi,
chunki TCP ta’minlaydigan paketni yetkazib berishni nazorat qilish va qayta uzatish
mexanizmlari nutq va video axborotlarini uzatishga mos kelmaydi.
IP-telefoniya
uchun bir qator protokollar ishlab chiqilgan, ularning tarkibida IP-tarmoqlari bo‘ylab
nutq uzatish va IP-telefoniya signalizatsiyasi uchun tegishli qo‘llanmalar mavjud.
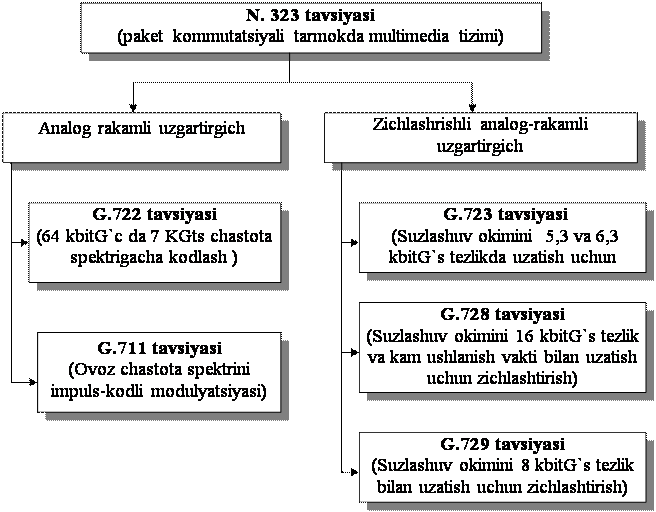
Bugunga kunda eng keng tarqalganlari quyidagilar: H.323, SIP, MGSP.
• H.323.
– H.323
ITU-T tavsiyasi – ovoz, video va ma’lumotlar uzatish standarti bo‘lib, kafolatsiz
xizmat sifatli tarmoqlardagi multimedia ilovalarining o‘zaro munosabatlarini ifodalaydi.
• MGCP
(Media Gateway Control Protocol).
– tashqi
boshqarish qurilmalari orqali shlyuzni boshqarish protokoli.
SIP
(Session Initiation Protocol).
– Seanslarni
amalga oshirish protokoli – multimedia aloqa seanslarini modifikatsiyalash va tugatishni
tashkillashtirish uchun mo‘ljallangan.
Protokollarni
taqqoslash
|
Arxitektura
|
SIP
|
H.323
|
MGCP
|
|
klient-server
nuqta-nuqta
|
klient-server
nuqta-nuqta
|
klient-server
|
|
Murakkabligi
|
Past
|
Yuqori
|
Yuqori
|
|
Imkoniyatlari
|
Sodda
|
To‘la
|
Qisman
|
|
Masshtabligi
|
Yaxshi
|
Yomon
|
O‘rtacha
|
|
Internet
|
Ha
|
Yo‘q
|
Yo‘q
|
|
SS7 mosligi
|
Yomon
|
Yomon
|
Yomon
|
|
Narxi
|
Past
|
Yuqori
|
O‘rtacha
|
Audio
kodeklar
Audio
kodeklari kanalning 64 Kbit/s o‘tkazish qobiliyatli paketli kommutatsiya bilan
ma’lumotlar uzatish tarmog‘ida tovushni turli kodlash/dekodlash algoritmlaridan
foydalangan holda axborotni kodlash/dekodlash uchun mo‘ljallangan. Qo‘llanayotgan
kodlash algoritmiga bog‘liq holda ma’lumotlar uzatish tezligi 5,3 Kbit/s dan 64
Kbit/s gacha o‘zgarishi mumkin. Audio kodeklarining asosiy tavsiflariga quyidagilar
kiradi:
• uzatish
tezligi;
• tovushni
tiklashning kafolatlangan sifati;
• xatoning
ushlab turiladigan ehtimolligi;
• to‘plashning
kechikishi;
• kodlash
algoritmi;
• algoritm
murakkabligi;
• tovush
kadrining o‘lchami;
• paketlar
yo‘qotilish ehtimolligi.
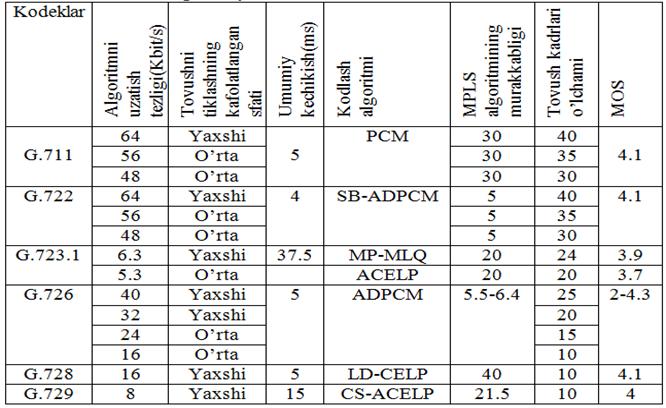 Audio kodeklarning asosiy tavsiflari
Audio kodeklarning asosiy tavsiflari
G.711
kodeki va uning qo‘llanilishi. G.711 kodeki, 8 bit
aniqlikda, 8 kGs taktli chastotada va signal amplitudasini oddiy kompresslashning
analogli signalni o‘zgartiruvchi IKM dan foydalanish kodekini tasvirlaydi.
O‘zgartirgichning
chiqishida ma’lumotlar oqimining tezligi 64 kbit/s ga teng. Kvantlangan shovqinni
pasaytirish va kichik amplitudali signallarni o‘zgartirishni yaxshilash uchun kodlashda
liniyasiz kvantlashdan foydalaniladi.
G.711
kodeki an’anaviy kommutatsiya
telefon kanallari tizimida qo‘llaniladi. IP -
telefoniya yo‘laklarida esa mazkur kodek kam qo‘llaniladi,
sababi o‘tkazish kanallarida o‘tkazish polosasiga va ushlanishlarga yuqori talablar
qo‘yiladi.
IP
- telefoniya tizimlarida G. 711 faqat bir vaqtda kichik so‘zlashuvlardagi so‘z axborotlarini
kodlashning o‘ta yuqori sifatini ta’minlash kerak bo‘lgan xolatlaridagina qo‘llaniladi.
G.723
kodeki va uning qo‘llanilishi. G.723
kodeki MP-MLQ qiska nomlangan so‘z axborotlarini kodlash texnologiyalarini qo‘llovchi
qo‘shma kodeklarni tasvirlaydi. Mazkur kodeklarni ARO‘/RAO‘ va vokoderlar yig‘indisi
deb izohlash mumkin. Vokoderni qo‘llanishi kanallarda ma’lumotlarni uzatish tezligini
pasaytirish imkonini beradi, bu esa IP - kanal va radiotraktlarni samarali qo‘llashda
muhim hisoblanadi.
Vokoderni
asosiy ishlash tamoyiliga dastlabki so‘z signallarini chastotali fon to‘plamiga
mos keluvchi hamda shovqin koeffitsienti bilan hamjihat garmonik qismlarini adaptiv
almashinuvi vositasida saralash kiradi.
G.723
kodeki analog signallarni 64 kbit/s tezlikda ma’lumotlar oqimiga aylantirishni amalga
oshiradi, so‘ngra ko‘p polosali raqamli filtr/vokoder yordamida chastotali fonlarni
ajratadi, ularni tahlil etadi va IP kanal orqali so‘z signalining fon holati hakidagi
axborotni uzatadi. Mazkur o‘zgartirish algoritmi so‘z sifatini pasaytirmay axborotlarni
kodlash tezligini 5,3 – 6,3 Kbit/sga qadar pasaytirish imkonini beradi.
G.
726 kodeki va uning qo‘llanilishi. ADPSM
– adaptiv differensial IKM - so‘zlarni zichlash algoritmlaridan biri bo‘lib, ushbu
algoritm IKM singari so‘zlarni tiklash sifatini beradi. Lekin
axborotlarni uning asosida uzatish uchun bor yo‘g‘i 16
- 32
Kbit/s li polosa talab etiladi.
Uslub
so‘zni uzatuvchi analog signalida intensivlikni keskin o‘sish imkoni yo‘qligiga
asoslanadi. Shuning uchun amplituda signalni o‘zini emas, balki uning avvalgi mazmuniga
qiyosiy o‘zgarish ravishda kodlansa, kam miqdordagi razryadlar bilan kifoyalansa
bo‘ladi.
ADPSMda
signal darajasini o‘zgarishi to‘rt razryadli raqam bilan kodlanadi va signal amplitudasining
chastota o‘lchami o‘zgarmay qolmaydi. Bu kodek G.711 kodeki bilan birga o‘zining
kodlash tezligini pasaytirish uchun qo‘llash mumkin. Kodekdan videokonferensiyalar
tizimida foydalanish ko‘zda tutilgan.
G.728
kodeki uning qo‘llanilishi. G.728 tavsiyasida tasvirlangan
qo‘shma kodek LD-CELP - boshqariladigan kod, liniyaviy bashorat va kichik ushlanishli
kodek turkumiga muvofiqdir.
Kodek
16 kbit/s tezlikdagi o‘zgarishni ta’minlaydi, kodlash jarayonida 3 msdan 5 msgacha
ushlanish hosil etadi. Kodek asosan videokonferensiyalarni qo‘llash uchun mo‘ljallangan.
IP - telefoniya qurilmalarida mazkur kodek juda kam hollarda ishlatiladi.
G.729
kodeki va uning qo‘llanilishi. O‘zgartirish
jarayoni 15 m/sli
ushlanish kiritadi. So‘z signallarini
kodlash 8
kbit/s
ni tashkil etadi. Mazkur kodek VoIP qurilmalarida yetarli darajadagi yuqori kompressiya
asosida so‘z axborotlarini kodlashning a’lo sifatlarini ta’minlagani uchun yetakchi
o‘rinni tutadi.
Kodeklarning asosiy
hususiyatlari
|
Kodek
|
Kompressiya
uslubi
|
Kodlash
tezligi
|
Sifati
|
Ushlanish
vaqti
|
|
G.726
|
ADPCM
|
32/24/16 kbit/s
|
Yaxshirok
(32
k)
Yomon (16k)
|
Juda past (0,125ms)
|
|
G.729
|
CS-ACELP
|
8 kbit/s
|
Yaxshirok
|
Past (10 ms)
|
|
G.729 A
|
CA-ACELP
|
8 kbit/s
|
O‘rtacha
|
Past (10 ms)
|
|
G.723
|
MP-MLQ
|
6,4/5,3 kbit/s
|
Yaxshirok
(6,4k) O‘rtacha (5,3 k)
|
Yukori (37 ms)
|
|
G.728
|
LD-CELP
|
16 kbit/s
|
Yaxshirok
|
Juda past (3-5 ms)
|
IP
tarmoq orqali N.323 standartida ko‘zda tutilgan aloqa o‘rnatilishiga qaratilgan
GSM va G turkumidagi kodeklar raqobatchi hisoblanadi.
N.323
standartidagi qo‘shimcha yuqori samarali kodeklar sifatida G.723 va G.729 lar tavsiya
etiladi. G.729 10 ms uzunlikdagi 16 razryadli IKM
so‘zlarni 10 baytgacha zichlash quvvatiga ega. G.729 standarti IP orqali ovozlarni
uzatish tizimlarida keng qo‘llaniladi.
Video
kodeklar. Bugungi axborotlashgan jamiyatda axborotning
deyarli barcha ko‘rinishlari: matn, ovoz, video va gibrid ma’lumotlarning hajmi
ortib bormoqda. Kodeklardan unumli foydalanilgan holda bu hajm birmuncha qisqarishiga
olib kelishi mumkin.
Oddiy
bir video faylni ko‘rib chiqamiz. Ma’lumki, har bir
video fayl kadrlardan tarkib topadi. Ma’lum kadrlarni olib uni soniyaning har onidagi
holatini rasm ko‘rinishida saqlab olamiz. Saqlangan kadrlar umumiy hajmi:
92-122 Kb atrofida ekanligi aniqlandi, ularning o‘rtachasi qilib, 107 Kb ni tanlab
olamiz. Bir soniya ichida 24 ta kadr borligini hisobga olsak va video davomiyligini
96 minutligini hisobga olib umumiy hajmni hisoblaymiz:
• 107
-bitta kadr hajmi;
• 24-umumiy
kadrlar soni;
• 60-daqiqa
hisobiga o‘tkazish;
• 96-umumiy
video uzunligi (daqiqa hisobida);
• 107*24*60*96=14
791 680 Kb=14 791 Mb= 14.791 Gb;
Aslida
esa video faylning bizdagi umumiy hajmi 1.56 Gb. Demak, kodekning faylni siqishi
orqali hajm o‘zgarishi sodir bo‘lgan.
Videolarni
siqish standartlarini taqqoslash.
MPEG
(Motion Picture Experts Groupvideo) kodeklar ichida eng katta kodeklar oilasiga
ega bo‘lgan tur hisoblanadi. MPG, MPE, MPA, M15, M1V, MP2 va boshqalar aynan shu
oilaga mansub. MPEG formati MPEG video, MPEG audioni qamrab oladi. MPEG video
esa o‘z navabatida MPEG-1, MPEG-2 va MPEG-4 larni qamrab oladi:
• MPEG
1 - yuqori tezlikli kanalni talab qiladi, to‘liq kodlashni ishlatadi;
• MPEG
2 - kadrni to‘liq kodlaydi, oldindan xabar berishni ishlatadi;
• MPEG
4 - video axborotlarni xar xil turi uchun xar xil kodlashni ishlatadi;
• MPEG
7 - multimediani qo‘llab quvvatlash uchun yo‘naltirilgan standart elementlari, ichidagi
bo‘lgan narsalarni tasvirlash uchun multimedia-interfeys ko‘rinishiga ega.
DivX
video kodlash texnologiyasi DVD uchun ishlab chiqarilgan desa ham bo‘ladi, aynan
MPEG-4 fayl turi bilan ishlaydi. Ko‘plab DivX videolar avi fayl formati bilan amalga
oshiriladi
XviD
bu DivX versiyasining ochiq manbasi hisoblanib, bu kodek odatda kino qaroqchiligida
juda ham mashhur. Umuman olganda, XviD dekoderi o‘rnatilgan qurilma barcha DivX
media fayllarini o‘qiy oladi.

Kodeklarning
ishi - ma’lumotlar yoki signallarni siqish va audio- video fayllarga o‘zgartirishdan
iborat.
MPEG
oilasining hamma zichlash formatlari (MPEG 1, MPEG 2, MPEG 4, MPEG 7) vaktning
kam intervali bilan bo‘lingan tasvirlarda axborotning yuqori ortiqchaligini ishlatadi.
Odatda
ikkita qo‘shni kadrlar orasida saxnaning faqat kichkina qismi o‘zgaradi - masalan,
qotirilgan orqa plan fonida katta bo‘lmagan ob’ektning siljishi amalga oshiriladi.
Bu xolatda saxna to‘g‘risidagi to‘liq axborot tanlanib saqlanadi. Boshqa kadrlar
uchun farqlovchi axborotni yuborish yetarli bo‘ladi:
• ob’ekt
holati, uning siljishi;
• yo‘nalishi
va kattaligi;
• ob’ekt
siljishi mobaynida uning orqasida paydo bo‘layotgan fonning yangi elementlari.
Bu
farqlarni nafaqat avvalgi, balki keyingi tasvirlarga nisbatan ham shakllantirish
mumkin (chunki aynan o‘shalarda oldin berk bo‘lgan fon qismi ko‘rinadi).
MPEG
ning media ob’ektlar bilan ishlashi. MPEG
oilasining zichlash formatlari axborot hajmini quyidagicha qisqartiradilar:
• Videoning
vaktinchalik oshiqchaligi yo‘otiladi (faqat farqlovchi axborot inobatga olinadi).
Tasvirlarda bo‘shliqni oshiqchaligi sahnaning kichik detallarini pasaytirish yo‘li
bilan yo‘qotiladi;
• Ranglar
xaqida axborotni qismi yo‘qotiladi;
• Natijaviy
raqamli oqimning axborot zichligi uni tasniflash uchun optimal matematik kodni tanlash
yo‘li bilan ko‘tariladi.
MPEG
zichlash formatlari faqat tayanch kadrlarni zichlaydi:
-
I - kadrlarni (Intra frame - ichki kadr). Ular orasiga ikkita qo‘shni
I -kadrlar o‘rtasidagi o‘zgarishlarni ichiga olgan kadrlar qo‘yiladi.
-
R - kadrlar (Predicted frame - bashoratlanuvchi kadr). I - kadr va R-kadr
orasidagi axborot yo‘qotishlarini qisqartirish uchun V - kadrlar qo‘shiladi.
-
V - kadrlar (Bidirectional frame - ikki yo‘nalishli kadr). Ularda oldingi
va keyingi kadrlardan olinuvchi axborot saqlanadi.
Kodlashda
MPEG zichlash formatlarida xar xil turdagi kadrlar zanjiri shakllanadi. Kadrlarni
odatiy ketma-ketligi quyidagicha ko‘rinishda bo‘ladi: IBBPBBIBBPBBIBB... Demak,
kadrlarni ularning nomerlari bo‘yicha ketma ketligi quyidagi tartibda bo‘ladi:
1423765.
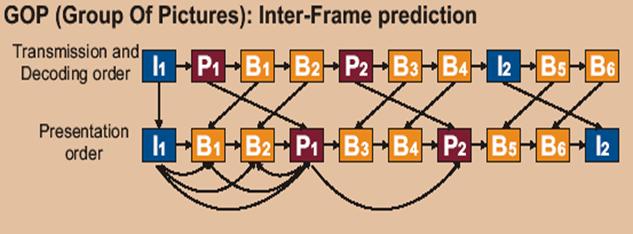
I-kadrlar
(Intra frame – ichki kadr).
P-
kadrlar (Predicted frame – bashoratlanuvchi
kadr).
B-
kadrlar (Bidirectional frame – ikki
yo‘nalishli kadr).
MPEG
7 kelajak formati. 1996 yilning oktabr oyida
MPEG guruxi MPEG 7 zichlash formatini ishlab chiqishga kirishdi, unda audio va video
axborotni asniflashning universal mexanizmlarini aniqlash ko‘zda tutilgan edi. Bu
format Multimedia Content Description Interface nomini oldi.
MPEG
oilasining avvalgi zichlash formatlaridan farqli ravishda, MPEG 7 istalgan shakldagi
(shuningdek analog) axborotni tasniflaydi va ma’lumotlarni yuborish muxitiga bog‘liq
emas. Oldingi formatlar singari MPEG 7 zichlash formati masshtablanuvchi axborotni
bitta tasnif ichida generatsiyalaydi.
MPEG
7 zichlash formati audio va video axborotni tasniflashni ko‘p darajali tuzilmasidan
foydalanadi. Yuqori darajada faylning xususiyatlari yoziladi, bular nom, yaratuvchi
ismi, yaratilish sanasi va hokazo
tasniflashning keyingi darajasida MPEG 7 zichlash formati zichlanuvchi audio va
video axborotni o‘ziga xosliklari ko‘rsatiladi - rangi, teksturasi,
ton yoki tezligi.
MPEG
7 ning o‘ziga xos xususiyatlaridan biri zichlanuvchi axborot turini aniqlash qobiliyatidir.
Agar bu audio yoki video fayl bo‘lsa, u avval MPEG 1, MPEG 2, MPEG 4 algoritmlari
yordamida zichlanadi, keyin MPEG 7 yordamida tasniflanadi. Zichlash usullarini
tanlashda bunday moslashuvchanlik axborot xajmini ancha kamaytiradi va zichlash
jarayonini tezlashtiradi.
MPEG
7 zichlash formatining asosiy qulayligi unikal deskriptor va tasniflash sxemalardan
foydalanishidadir, ular yordamida axborotni umumiy, hamda semantik belgilari bo‘yicha
avtomatik ajratishga imkon beradi. Katalogga kiritish va ma’lumotlarni izlash jarayoni
bu zichlash formatini ko‘rib chiqish sohasidan tashqarida joylashgan.
MPEG
21 – kelajak formati. MPEG 21 zichlash formatini
ishlab chiqish - bu uzoq vaqtli loyiha, u "Mul’timedia vositalarining tizimi"
(Multimedia Framework) deb nomlanadi. Bu formatni ishlab chiqishni ekspertlar
2000 yilning iyun oyida boshladilar.
Birinchi
bosqichlarda MPEG 4 va MPEG 7 formatlarini kengaytirish, unifikatsiyalash va yagona
umumiylashtiruvchi tuzilmaga birlashtirish rejalashtirilgan edi. Uning yordamida
xuquqlar va to‘lov tizimlarini, hamda taqdim etilayotgan xizmatlar sifatini boshqarishni
ta’minlash ko‘zda tutilgan.
5-ma’ruza
uchun nazorat savollari
1. Axborot
tushunchasiga tavsif bering?
2. Tasvirli
va matnli axborotlarni kodlash qanday amalga oshiriladi?
3.
Multimedia vositalariga
qanday qurilmalar kiradi?
4.
Ta’lim tizimida multimedia
vositalarini afzalliklari nimalardan iborat
?
5.
Kodek deganda nimani tushunasiz
?
6.
Kodeklarning vazifasi nimadan iborat?
7.
Kodeklar bir-birida nimasi bilan farq
qiladi?
8.
Audio va video kodeklar
nima uchun kerak?
9.
Qaysi kodeklar oilasi hozirgi
kunda ommalashgan?
10.
Audio va
video ma’lumotlar qanday
siqiladi?
11.
Audio va
video ma’lumotlarni siqishdan
maqsad nima?
12.
Audio va
video ma’lumotlarni siqishda
nimalarga e’tibor beriladi?
13.
MPEG 7 va MPEG 21 – kelajak formatlariga tushuncha bering va ular bir biridan nimasi
bilan farq qiladi?
6-ma’ruza.
Telekommunikatsiya tizimlarida ishonchlilikni
oshirish choralari va usullari. Shovqinli diskret kanallarda
kodlash. Shennon teoremasi.
Reja:
1. Telekommunikatsiya
tizimlariga qo‘yiladigan talablar.
2. Telekommunikatsiya
tizimlarida ishonchlilikni oshirish choralari,
usullari va
ularga qo‘yiladigan talablar
3. Shovqinlar
va ularning turlari.
4. Xatolarni
tavsiflaydigan matematik modellar haqida tushunchalar. Purtov modeli.
5. Diskret
kanallarda ma’lumotlarni shovqinbardosh
kodlar bilan kodlash asoslari.
Telekommunikatsiya
tizimlariga qo‘yiladigan talablar. Quyidagilarga
asosan aloqa tarmoqlari va tizimlariga nisbatan bo‘lgan talab doimiy ravishda ortib
boradi:
Ø foydalanuvchilar
sonining ortishi;
Ø foydalanuvchilarni
qiziqtirgan xizmat turlarining sonini ortishi;
Ø xizmat
ko‘rsatish sifatiga bo‘lgan talabning ortishi (qabul qilinadigan axborotlarning
ishonchliligini, yetkazilish vaqti va maxfiyligiga bo‘lgan talab asosiy xisoblanadi).
Xozirgi
kunda amaliyotda konferensaloqa, elektron pochta, axborotlarni qidirish va hokazo
shunga o‘xshash kabi xizmatlar keng qo‘llanilmokda.
Keng
yo‘lakli raqamli kanalni amalga oshirishni talab etuvchi yangi turdagi xizmatlarga
bo‘lgan talablar xosil bo‘lmokda. Bular:
Ø eng
avvalo oq – qora va rangli videotelefon;
Ø videokonferensaloqa;
Ø rangli faksimil
aloqa;
Ø videopochta;
Ø videoli axborotlarni
qidirish;
Ø qisqa vaqtda katta
xajmdagi axborotlarni uzatish va hokazo
kabi xizmatlardir.
Bundagi
ko‘pgina talab etilayotgan xizmatlar, axborotlarni kompleksli yetkazish xizmati
xisoblanadi. Bu esa, XTI
standartlash sektori tavsiyasiga
muvofiq multimedia deb yuritiladi.
Xisoblash
tarmoqlarini takomillashtirish quyidagi o‘zaro bog‘liqlik asosida amalga oshiriladi:
Ø birinchi
tomondan lokal tarmoqlarining o‘zini ishlash tezligini
oshirish bo‘lsa;
Ø ikkinchi
tomondan – xar xil turdagi lokal tarmoqlarni shaxar, maxalliy va global tarmoqlarga
birlashtirishdir. Bu esa xar -
xil
turdagi axborotlarni almashish imkonini beradi.
Yangi axborot
texnologiyalar multimedia texnologiyalarining yaratilishi
telekommunikatsiya tizimlariga integratsiyalashuvning 3 – bosqichini boshlab berdi.
1
– bosqich, raqamli texnika asosida kommutatsiya va uzatish tizimlarining integratsiyalashuvi
bilan bog‘liq. Bu esa integral raqamli tarmoqlar (ISDN) ni yaratish bilan yakunlanadi.
2
– bosqich, integratsiya xizmatlarini amalga oshiruvchi raqamli tarmoqlarni yaratishdan
iborat: bunda abonent bitta tarmoqdan xar - xil turdagi axborotlar bilan ishlash
vazifasini bajaruvchi bir qancha terminallardan foydalanish imkoniga ega bo‘ldi.
3
– bosqich esa xar - xil turdagi terminallarning o‘zini bitta qurilmaga integratsiyalashdan
iborat. Bu esa telekommunikatsiya tarmoqlarining xamma turdagi xizmatlaridan foydalanish
imkonini beruvchi ShK asosida bajariladi. Demak,
bu multimediani qo‘llash uchun asos bo‘ladi.
Telekommunikatsiya
tizimlarida ishonchlilikni oshirishdagi
choralar va usullar.
Telekommunikatsiya tizimlarida ishonchlilikni
pasayish sabablarini quyidagicha izohlash mumkin:
-
diskret kanalning AChX, FChX va boshqa parametrlariga qo‘yilgan talab bajarilmaganligi;
-
diskret kanalda qisqa vaqtli va impulsli shovqinlar mavjudligi;
-
uzatish darajasi moslashmaganligi;
-
chastotalarning surilishi va b.
Ishonchlilikni
oshirish usullarini shartli ravishda 3 guruxga bo‘lish mumkin:
I
gurux – ekspluatatsiya va profilaktika aloqa
kanallarining sifat ko‘rsatkichlarini oshirishga yo‘naltirilgan. Bu usul foyda
bermasa xech bo‘lmaganda, diskret xabarlarni uzatishda xosil bo‘ladigan xatolar
sonini kamaytirish, shovqin va so‘nishlarni kamaytirish mumkin.
II
gurux – diskret
xabarlarni uzatishda birlik elementlar shovqinbardoshliligini oshirishga
yo‘naltirilgan choralar:
-
amplituda o‘zgarishi signal/shovqin o‘sishi natijasida uning nisbatini ham o‘sishi;
-
foydali signal spektr chastotasi yoki uzunligi;
-
signallarni qabul qilishda rivojlangan va shovqinbardosh modulyatsiya usullarini
ishlatish.
Shuni
esdan chiqarmaslik kerakki, xabarlarni uzatishda ishonchlilikni oshirish usullarini
xammasi shovqinbardosh usullarda uzatish uchun ayrim xarajatlarga ega.
III
gurux –
diskret xabarlarni uzatishda ishonchlilikni oshirish uchun qabul qilingan xabarlarda
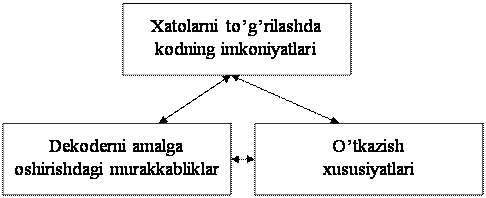
xatoliklarni aniqlash va xatoliklarni to‘g‘irlash kiradi. Bu usullarni teskari
aloqasiz tizim va teskari aloqali tizim tashkil qiladi.
Zamonaviy
telekommunikatsiya tizimlari ularga xalaqitlar, shovqinlar ta’sir qilganda ham,
o‘zlarining sifatli ishlash qobiliyatlarini yo‘qotmasliklari lozim. Shuning uchun
axborotlarni kodlashda shovqinbardosh kodlar ishlatiladi.
Diskret
xabarlarni shovqinbardosh kodlash. Zamonaviy
telekommunikatsiya tizimlari ularga xalaqitlar, shovqinlar ta’sir qilganda ham,
o‘zlarining sifatli ishlash qobiliyatlarini yo‘qotmasliklari lozim. Shuning uchun
axborotlarni kodlashda shovqinbardosh kodlar ishlatiladi.
Umuman
olganda uzatilgan axborotni to‘g‘ri qabul qilishning ikki xil usuli mavjud:
1.Aloqa
kanallarini sifat ko‘rsatkichlarini yaxshilash.
Amaliyotda bunga erishish juda qiyin. Sababi tarmoqda
qo‘llanilib kelinayotgan eski turdagi telekommunikatsiya tizimlari evaziga bugungi
kundagi talablarga javob beradigan ma’lumot uzatishning sifat ko‘rsatkichlari sezilarli
darajada pasayib ketishi mumkin;
2.
Signallarni shovqinbardosh kodlar bilan kodlashtirish. Bu usul yordamida
uncha katta bo‘lmagan iqtisodiy – xarajatlarsiz axborot uzatish butunligini ta’minlash
mumkin.
Izlanish
shuni ko‘rsatdiki, impulsli shovqinlarning xarakati tufayli xatoliklar soni
-10-20% ni tashkil etadi.
To‘xtalish
(pererûv)
xisobiga xatoliklar soni –
80-90% ni
tashkil etadi.
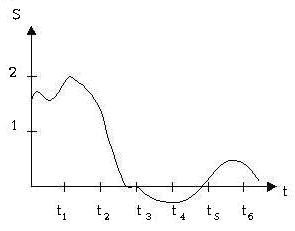
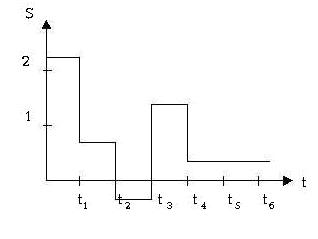
Purtov
modeli bo‘yicha kanal klassifikatsiyasi

Purtov
modeli
Real
aloqa kanallari statsionar bo‘lmaganligi tufayli, amaliyotda ba’zi bir vaziyatlarda
ularda kvazistatsionar qismlarni ajratish mumkin, va ushbu kanallar uchun, holatlarga
o‘tishning markov zanjiri bilan Purtov modeli yordamida ta’riflanadigan kvazistatsionar
matematik modelidan foydalanish mumkin.
Xolatlarga
o‘tishning Markov zanjiri bilan Purtov modelining umumlashtirilgan o‘ziga xos xususiyati
shundan iboratki, unda ko‘rsatkichlar soni juda kamdir, bu esa xisoblashni yengillashtiradi
va o‘chirishlarsiz kanal uchun ma’lum bo‘lgan model asosida tasvirlanadi.
Bundan
tashqari xato blokidagi xato elementlarning son jixatidan o‘rtacha soniga teng bo‘lgan
txato koeffitsienti guruxlanish ko‘rsatkichi  bilan
bog‘liq. Xuddi shunday bog‘liqlik o‘chirishlarni guruxlash ko‘rsatkichlari to‘chirish
va
bilan
bog‘liq. Xuddi shunday bog‘liqlik o‘chirishlarni guruxlash ko‘rsatkichlari to‘chirish
va  o‘rtasida ham mavjud.
o‘rtasida ham mavjud.
Purtov
modeli
Markov
zanjirining o‘tish matritsalari quidagi ko‘rinishdadir:
 xatolar ehtimolligi uchun:
xatolar ehtimolligi uchun:
 ,
,
Xatolar
guruhlanishi ko‘rsatkichi  uchun:
uchun:

Ishlab
chiqilgan model holatlarga o‘tishning Markov zanjiri bilan Purtov modeli asosida
diskret kanalining xatolar va o‘chirishlar manbaining kaskad modeli bo‘lib, u raqamli
qurilmalardagi rad qilishlar va uzilishlar natijasida yuzaga kelgan xatolardan
kanallardagi xatolarni ajratishda foydalaniladi.
Rxato
va αxato
graf o‘tishlar
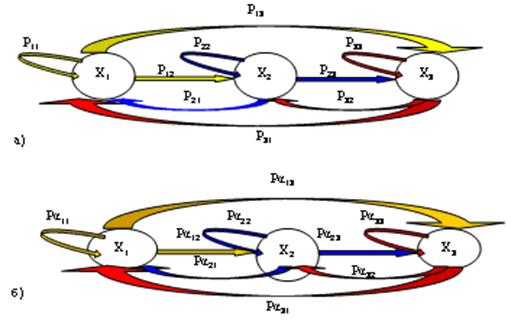
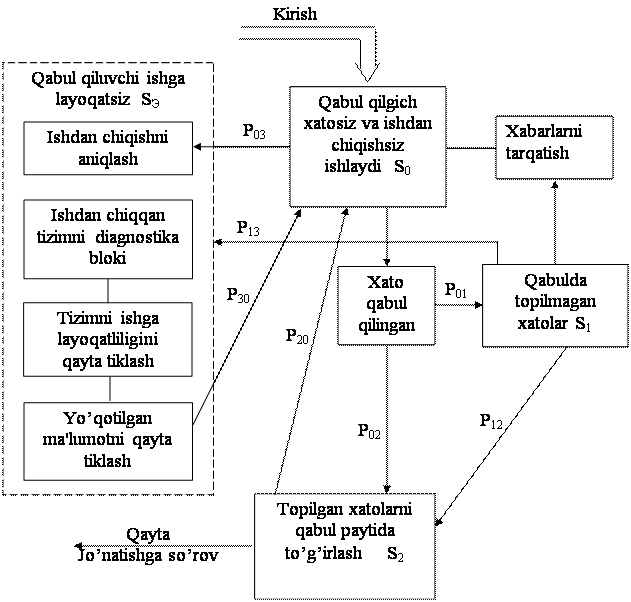
MUTda
xatoni aniklovchi raqamli tizim qabul qilgichining modeli
S0
- qabul qilgich xatoliklarsiz ishlaydi;
S1
- qabul aniqlanmagan xatosiz funksiyalaydi;
S2
- qabul qilgich aniqlangan xatoni to‘g‘irlaydi;
S3
- rad javoblari uchun qabul qilgich ishga layoqatli emas.
Shovqinli
diskret aloqa kanali uchun Shennon teoremasi
Shovqinli
diskret kanal uchun Shennon tomonidan quyidagi teorema isbotlangan.
Agar
manba tomonidan ishlab chiqarilgan axborot oqimi,
kanalning o‘tkazish qobiliyatiga yetarlicha yaqin bo‘lsa, bunda manba ishlab chiqargan
barcha xabarlarni uzatishni ta’minlay oladigan kodlash usulini doim topish mumkin
va yuborilgan har
qanday xabarning xatolik bilan aniqlash ehtimolligi shuncha kam bo‘ladi.
Manba
axborot oqimi va kanalning o‘tkazish qobiliyatining matematik yaqinligi quyidagi
tenglik ko‘rinishida yoziladi:
Bu
yerda - axborot uzatish tezligi;
S
– kanalning o‘tkazish qobiliyati;
s -
xohlagancha
kichkina
(cheksiz)
miqdor.
 Topilmagan
xatolik
ehtimolligining qay darajada kichikligi quyidagi
ko‘rinishda yoziladi:
Topilmagan
xatolik
ehtimolligining qay darajada kichikligi quyidagi
ko‘rinishda yoziladi:

bu
yerda - yuborilgan xabarni noto‘g‘ri
aniqlash ehtimolligi,
η –
qancha bo‘lsa ham
kichkina miqdor.
Teoremaning
teskari talqini shundan
iboratki, agar manbaning axborot oqimi kanalning o‘tkazish qobiliyatidan
oshsa, unda har
qanday xabarni kichik xatolik ehtimolligi bilan uzatishni ta’minlovchi kodlash usuli
mavjud emas.
Bu
teorema manba tomonidan yaratilgan xabar tezligi, kanalning o‘tkazish qobiliyati
orasidagi bog‘liqlikni shovqin va qabulda xabarni aniqlay olish ishonchliligi mavjudligida
belgilab beradi.
Shennon
teoremasi axborot uzatish tezligini kanalning o‘tkazish qobiliyatiga yaqinlashtirish
uchun optimal kodlar topishning amaliy yo‘llarini belgilamaydi.
Shovqinli
va shovqinsiz kanallar uchun uzatish tezligini maksimal qiymatga yaqinlashtirishning
umumiy usuli uzun xabarlarni kodlash hisoblashigina belgilangan.
Shennongacha
kanalda belgilangan shovqinlarni eng kichik xatolik ehtimolligini faqatgina uzatish
tezligi nolga intilgandagina ta’minlash mumkin deb hisoblangan. Teorema tegishli
kodlash usulini tanlash orqali eng kichik xatolik ehtimolligini ta’minlash mumkinligini
ko‘rsatyapti.
6-ma’ruza
uchun nazorat savollari
1.
Telekommunikatsiya tizimlariga qo‘yiladigan talablar nimalardan iborat?
2.
Telekommunikatsiya tizimlarida ishonchlilikni oshirishdagi
choralar va usullar
nimalardan iborat?
3.
Diskret xabarlarni shovqinbardosh kodlashga
va koeffitsient xatloligini o‘lchash usullariga tavsif bering?
4.
Asosiy shovqinlar tavsiflariga tushuncha bering?
5.
Purtov modeliga tavsif bering?
6.
MUTda xatoni aniklovchi raqamli tizim qabul qilgichining modeli va ishlash tarbiga
tushuncha bering?
7.
Shennon teoremasi?
7-ma’ruza.
Shovqinbardosh kodlash. Chiziqli va blokli kodlar
Reja:
1. Shovqinbardosh
kodlarning tavsiflari.
2. Chiziqli
kodlar
3. Blokli
kodlar
Shovqinbardosh
kod. Shovqinbardosh kod deb – xato qabul
qilingan razryadlarni aniqlaydigan va to‘g‘rilaydigan kodga aytiladi.
Bunday
kodlar quyidagi prinsipga asoslanib tuziladi: n razryadli kodli kombinatsiyalar
soni N ta bo‘lsin.
Lekin
axborot uzatish uchun esa faqatgina ulardan Nr tasi ishtirok etadi va ular
ruxsat etilgan kombinatsiyalar deyiladi.
N
– Nr tasi esa man qilingan kodli kombinatsiyalar
deyiladi.
Agar
uzatish tomonidan ruxsat etilgan kodli kombinatsiya uzatilsa va unga xalaqit ta’sir
qilsa, buning natijasida qabul qilish tomonidan boshqa man qilingan kodli kombinatsiya
qabul qilinadi. Bu esa uzatilgan kodli kombinatsiyaning xato qabul qilinganligini
ko‘rsatadi.
Masalan,
ruxsat etilgan kodli kombinatsiyalar bir – biridan ikkita razryadga farq qilsin.
Ya’ni kod masofasi d = 2: 0011, 0110, 1001, 1010, 1100,
0101 va xokazo 0111 – bu kombinatsiya man qilingan kodli kombinatsiyani
xato qabul qilinganligidan dalolat beradi.
Ushbu
misoldan ko‘rinib turibdiki, shovqinbardosh kodlarni xosil qilish uchun ortiqcha
razryadli kodlar ishlatiladi. Masalan 8 ta kombinatsiyali kod uchun 4
ta razryadli kod ishlatiladi. Aslida oddiy kod orqali kodlashtirishda 8 ta
kombinatsiya uchun atigi 3 ta razryad (23= 8) yetarlidir.
Shovqinbardosh
kodlar klassifikatsiyasi
Shovqinbardosh
kodlar taqsimlangan va taqsimlanmagan kodlarga bo‘linadi. Agar kodli kombinatsiyalarda
kombinatsiyadagi razryadlar soni bir xil bo‘lsa, bunday kodlar teng taqsimlangan
kodlar deyiladi.
Agarda
kodli kombinatsiyalardagi razryadlar soni xar xil bo‘lsa, bunday kodlar teng taqsimlanmagan
kodlar deyiladi.

Teng
taqsimlangan kodlar ikki turga bo‘linadi:
1. Blokli;
2. Uzluksiz.
Blokli
kodlar uzatilayotgan axborotli ketma-ketlik
aloxida kodli kombinatsiyalarga bo‘linadi va ular bir-biriga bog‘liq bo‘lmagan xolda
kodlanadi va dekoderlanadi.
Bu
xolat uzatilayotgan xabarga n ta elementlardan tashkil topgan blok yoki xar
xil elementlardan iborat bo‘lgan blok mos keladi.
Uzluksiz
kodlar esa axborotli razryadlarning uzluksiz ketma-ketligidan iborat va ularni bo‘laklarga
bo‘lib bo‘lmaydi. Bunday kodlarda informatsion razryadlar
orasiga ortiqcha razryadlar ma’lum tartibda joylashtiriladi.
Blokli
kodlar. Blokli
kodlar o‘z navbatida bo‘linuvchi va bo‘linmaydigan kodlarga ajraladi. Bo‘linuvchi
kodlarda axborot
va tekshiruvchi razryadlar bo‘lib, ular aniq bir
- biridan
ajratilgan xolda bo‘ladi. Bunday kodlar (n,k) kabi belgilanadi,
n
- blokli
kodli kombinatsiyadagi umumiy razryadlar soni;
k
–
axborot razryadlar
soni;
 r
= n - k tekshiruvchi razryadlar soni.
r
= n - k tekshiruvchi razryadlar soni.
Tekshiruvchi
razryadlar (r) yordamida kodli kombinatsiyadagi xato qabul qilingan razryadlarni
aniqlash va ularni to‘g‘rilash mumkin.
Bo‘linmaydigan
kodlardagi razryadlarning qaysi birlari axborot, qaysi birlari tekshiruvchi ekanligini
ajratib bo‘lmaydi.
Chiziqli
kodlar. Bo‘linuvchi kodlar ham o‘z navbatida chiziqli
va nochiziqli kodlarga bo‘linadi.
Chiziqli
kodlar deb – shunday (n,k) blokli bo‘linuvchi
kodlarga aytiladiki, ulardagi tekshiruvchi razryadlar, axborot razryadlarning chiziqli
kombinatsiyalaridan iborat bo‘ladi. Chiziqli kodlar hozirgi kunda eng keng tarqalgan
kodlar sarasiga kiradi. Bunga misol sifatida siklik kodlarni keltirish mumkin.
Quyida shovqinbardosh kodlarning parametrlari haqida fikr yuritamiz.
Ikkita
kodli kombinatsiyaning kod masofasi (d) deb – shu ikkita kodli kombinatsiyalarning
o‘zaro farq qiluvchi razryadlar soniga aytiladi. Masalan: 11011 va 00010
kombinatsiyalar orasidagi kod masofasi 3 ga teng. Chunki ular birinchi, ikkinchi
va beshinchi razryadlar bilan farq qiladi.
Koddagi
kod masofalarining eng kichigiga Xemming masofasi deyiladi – d0.
Shovqinbardosh
kodlarning qo‘llanilishi. Shovqinbardosh kodlar quyidagi
vazifalarda qo‘llanilishi mumkin:
1. Xatoni
aniqlovchi kodlar;
2. Xatoni
aniqlovchi va to‘g‘rilovchi kodlar.
Xatoni
aniqlovchi kodlar uchun minimal kod masofasi quyidagi tengsizlikni qanoatlantirishi
lozim:
d0
≥ tA
+ 1
d0
– minimal kod masofasi yoki Xemming masofasi;
tA
– aniqlanadigan xatolar soni.
Xatoni
to‘g‘irlovchi kodlar uchun minimal kod masofasi quyidagi tengsizlik bajarilganda
o‘rinli bo‘ladi:
d0
≥ 2 tT + 1
tt
- kodli
kombinatsiyalardagi to‘g‘rilanuvchi xatolar soni.
Minimal
masofaning ortishi bilan kodlarning korreksiyalash xususiyati ortib boradi.
Shovqinbardosh
kodlar parametrlari:
1.
n- kod uzunligi;
2.
m – kod asosi;
3.
Nr =2k
– kod quvvati (ruxsat
etilgan kombinatsiyalar soni);
4.
N=2n – kodli
kombinatsiyalarning butun (jami) soni;
5.
k – axborot razryadlari soni;
6.
r – tekshiruvchi razryadlar soni;
7.
r/n – ortiqcha kodlar
8.
k/n – kod tezligi;
9.
W – vaznli kombinatsiyalar soni (kodli
kombinatsiyalar nol bo‘lmagan
soni);
10.
d – kod masofasi (razryadlar
soni, ya’ni
bitta ruxsat etilgan kombinatsiya boshqasidan farq qilishi uchun);
11.
M(W) – kodning vazn spektri (berilgan
vaznning kombinatsiyalar soni);
12.
Rt.x
– topilmagan xatolik extimolligi.
Ruxsat
etilgan kombinatsiyalar soni Nr o‘zgarmas bo‘lganda, kod masofasi (d)
ortishi uchun N-Np man etilgan kombinatsiyalarning sonini orttirish lozim.
Bu xolatda kodli kombinatsiyaning ortiqchaligi ortadi:
k
– axborot razryadlar
soni;
n
– umumiy razryadlar soni;
R
– kodli kombinatsiyaning ortiqchaligi yoki
ortiqchalik koeffitsienti.
Korreksiyalovchi
kodlarning ortiqchaligi axborot uzatish tezligini kamayishiga olib keladi. Bu
esa uning asosiy kamchiligidir. Ammo bu kodlarning ishlatilishi uzatish ishonchliligini
ortishini ta’minlaydi.
Kod
tA karralik xatolarni aniqlashi va tto‘g‘irlash
karralik xatolarni to‘g‘irlashi
uchun, kod masofasi quyidagi tengsizlikni qanoatlantirishi lozim:
d
0 ≥ t A + t T + 1
d0
= 3 kod masofasi uchun tekshiruvchi razryadlar
soni r va umumiy razryadlar soni n orasida quyidagi bog‘liqlik mavjud:
r
≥ log 2 ( n + 1)
Kod
uzunligi n = k + r – kodli kombinatsiyadagi umumiy razryadlar soni.
Tekshiruvchi
razryadlar soni r – xatolarni korreksiyalash uchun zarur bo‘lgan kodli kombinatsiyadagi
razryadlar soni.
Kod
asosi (m)
– kodli kombinatsiyadagi bir – biridan farq qiluvchi impuls belgilarining qiymatlar
soni. Impuls belgilarining qiymati sifatida 0 va 1 raqamlaridan foydalaniladi.
Kodning
quvvati (Nr)
– xabarni uzatish uchun foydalaniladigan kodli kombinatsiyalar soni:
Nr
= 2k
Kodli
kombinatsiyalarning umumiy soni N –
mumkin bo‘lgan xamma kombinatsiyalar soni:
N
= mn
Kodli
kombinatsiyaning vazni (ω)
– kodli kombinatsiyadagi birlar soniga teng bo‘ladi. Masalan: 10011111000 dagi umumiy
razryadlar soni n
=11, vazni ω
= 6 ga teng.
Kodning
sonli xarakteristikasi W (ω)
– ω vaznli
kodli kombinatsiyalar soni. Masalan 00000, 01110, 10101, 11011 kodli kombinatsiyalardan
iborat bo‘lgan kodning sonli xarakteristikasi quyidagicha:
W
(0) = 1; W (3) = 2; W
(4) = 1
Topilmagan
xatolar extimolligi (Rt.x) – qabul qilingan kodli kombinatsiya uzatilgandan
farq qilganda kod buni farqlash xususiyatiga ega emas. Mana
shu xodisa ro‘y berishi extimolligi – topilmagan
xatolar extimolligi (Rt.x) deyiladi.
Ruxsat
etilgan kodli kombinatsiyalar soni (Nr)
– xabarlarni uzatish uchun qo‘llanadigan kodli kombinatsiyalar soni
quyidagi ko‘rinishda bo‘ladi:
Nr
= 2 k
Shovqinbardosh
kodlarga qo‘yiladigan talablar
1.
Berilgan karralik xatolarni topuvchi yoki to‘g‘irlovchi kodlar tekshiruvchi razryadlar
soni minimal bo‘lishi kerak.
2.
Xar qanday uzunlikdagi kodlarni qurishni ta’minlash va xar qanday karralik xatolarni
to‘g‘irlashda kodlarni qurish qoidasi oddiy bo‘lishi kerak.
3.
Kodlash va dekodlash qurilmalari sxemalari elementlari
soni minimal bo‘lishi kerak.
4.
Koddan o‘tish, koddagi berilgan karralikdagi xatolarni
topish, kodlash va dekodlash sxemasidagi oson o‘zgarishlarni bajarish kerak.
5.
Aloqa kanalida ma’lumotlarni uzatish tezligi 100
bit/s dan
mln.bit/s gacha
bo‘lishi mumkin.
6.
Xatolar bir karralik, ko‘p karralik, mustaqil, bir martalik
xatolar paketi va ko‘p karralik paketlar xatoliklari bo‘lishi mumkin.
7.
Blok uzunligi birnechta o‘ntalikdan o‘n ming bitgacha
bo‘lishi mumkin.
8.
Dekodlash xatolik extimolligi 10-9
dan yuqori bo‘lmasligi kerak.
9.
Aloqa kanalidagi ma’lumotlar kelishi bilan koder uzluksiz
rejimda ishlashi kerak.
7-ma’ruza
uchun nazorat savollari
1. Shovqinbardosh
kod deb nimaga aytiladi va unga
tavsif bering?
2. Shovqinbardosh
kodlarning klassifikatsiyasiga tushuncha bering?
3. Shovqinbardosh
kodlarning asosiy parametrlari nimalardan iborat?
4. Shovqinbardosh
kodlarning qo‘llanilishiga tushuncha bering?
5. Blokli
kodlarga tushuncha bering?
6. Chiziqli
kodlarga tushuncha bering?
7. Shovqinbardosh
kodlarga qo‘yiladigan asosiy va qo‘shimcha talablar nimalardan iborat?
8-ma’ruza.
Siklik kodlar. Goley va Xemming kodlari
Reja:
1. Siklik
kodlar.
2. Goley
kodlari.
3. Xemming
kodlari
Shovqinbardosh
kodlardan amaliy foydalanish vazifasi 3 bosqichga bo‘linadi:
Ø Kod
vazifasi, ya’ni bir qator kodli so‘zlar tanlash orqali uzatish olib borish;
Ø Kodlash,
ya’ni kodlash algoritmini amalga oshiradigan algoritm va apparatura ishlab chiqarish;
Ø Dekodlash,
ya’ni dekodlash algoritmini amalga oshiradigan algoritm va apparatura ishlab chiqarish.
Siklik
kodlar qurish prinsipi. Siklik kodlar sistematik
kodlarning bir ko‘rinishi hisoblanadi va uning barcha xususiyatlariga ega. Ular
kodlash va dekodlash sxemalarini osonlashtirish maqsadida yaratilgan. Keyinchalik
uning amalda keng tarqalishini ta’minlovchi yuqori korrektlash xususiyatlari aniqlandi.
Siklik
kodlar qurilishida kodli kombinatsiyalarni polinom ko‘rinishida tasavvur qilish
qabul qilingan. Tasodifiy miqdor tizimida har qanday son polinom kod kombinatsiyasi
sifatida yozilgan bo‘lishi mumkin:
G(x)=an-1xn-1+
an-2xn-2 +…+ a1x1 + a0x0
,
bu
yerda ai=(0.1); x – sanoq
sistemasi asosi

Har
G(x) kodli kombinatsiya oddiy k-elementli kodni xr ga ko‘paytiramiz,
keyin paydo bo‘lgan darajasi R bo‘lgan P(x) polinomga bo‘lamiz.
Ko‘paytirish
natijasida G(x) polinomiga kiruvchi xi ning har a’zosini darajasi
r ga oshadi. xr G(x) ko‘paytmasini P(x) ga
bo‘lganimizda G(x) darajasidagi Q(x) bo‘linma hosil bo‘ladi. Bundan tashqari,
agar xr G(x) ko‘paytma P(x) ga yaxlit bo‘linmasa
R(x) qoldiq paydo bo‘ladi:

Madomiki
Q(x) bo‘linmasi G(x) dek darajaga ega ekan, u ham oddiy k-elementlik
kodning kombinatsiyasi hisoblanadi. Tenglikning ikkala qismini P(x), ga bo‘lish
orqali
F(x)=Q(x)P(x)=xrG(x)Å
R(x) ga ega bo‘lamiz.
Shunday
qilib, siklik kodning kodli kombinatsiyasini 2 usul yordamida olish mumkin:
1.
G (x) kodli
kombinatsiyani oddiy k-
elementli kodga ko‘paytirish orqali R(x) polinomini
hosil bo‘lishi;
2.
Oddiy kodning G (x) kodli kombinatsiyani xr
birxadga ko‘paytirish va
bu ko‘paytmaga G(x) xr
ko‘paytmasini R(x)
ga bo‘lishdagi qoldiqni qo‘shish orqali.
Misol.
Ikki karralik xatolarni topish uchun siklik
kod asosida 13 raqamini kodlashtiring?
δ=2 karralik xato
d0 ≥
δ +
1 =
2 +
1 =
3
13→1101 k= 4
k r=log2(n+1) 2r = n +1
2r = k + r +1 2r – r = k+1 2r – r = 4
+1= 5,
r =
3
3
darajali polinomni tanlab olamiz:
P(x) =
x3
+
x +
1 (1 0
1 1)
G(x) =
1 1
0 1
= (
x3 +
x2
+
1 )
G(x)* xr r =
3
( x3+x2+1 )*x3
= x6
+
x5
+
x3


Shunday
qilib yuqorida shakllantirilgan qoidaga muvofiq shovqinbardosh kodga tegishli kombinatsiyani
topamiz ( 7,4 )
F
( x )= Q ( x ) x r + R ( x ) = x6+ x5+ x3+1
yoki ikkilik shaklida

Xemming
kodi. Xemming kodi bir marotaba xatolarni to‘g‘irlash
uchun yaratilgan bo‘lib u dmin=3 kod masofasiga ega. Xemming
kodining n va k qiymatlari
2n-k-1=n nisbati
bilan bog‘liq. N tekshiruv matritsasi katorlari o‘zi
bilan turli xil uzunlikdagi (n-k) nollarning ketma-ketligini
ifodalaydi. Dastlab (50-yillarda) tekshiruv
elementlarning xosil qilish formulasi shunday tanlanganki, qabul qilinayotganda
nazorat qilinadigan elementlarning yig‘indi
natijasi buzilgan elementni ketma-ketlik raqamini ko‘rsatishi
kerak. ai – axborot belgilari
axborot simvollari,
bi – nazorat belgilari bo‘lsin. Agar tekshiruv belgilari kodli kombinatsiyalarda
joylashtirilsa, raqamlar qaysi ikkining darajasi hisoblansa (1, 2, 4, 8 va boshqalar.),
unda qabul qilingan ikkilik shaklidagi sindrom shovqinli elementning raqamini ko‘rsatadi.
Buni
(7,4) kodi misolida ko‘ramiz. Nazorat belgilarini tashkil
etish qoidasi quyidagicha: axborot belgisini xar qanday qiymati modul bo‘yicha ikkita
nazorat belgilari ketma-ketlik raqamlari ikkining darajalarini
ajratishga kiruvchi ushbu
axborot belgisining yig‘indisiga teng bo‘lishi lozim.
Goley
kodi.  d0=3,
r=log2(n+1) uchun r tekshiruv razryadlarini miqdorini aniqlash formulasi
kuyidagi ko‘rinishga ega:
d0=3,
r=log2(n+1) uchun r tekshiruv razryadlarini miqdorini aniqlash formulasi
kuyidagi ko‘rinishga ega:
bu
yerda: tt.x.m -to‘g‘rilangan xatolar miqdori.
ekanligini Goley aniqlagan.
Bunda
n=21, r=11, k=n-r=12 va d0=7, hamma kombinatsiyadagi uch va undan kamroq
xatolarni to‘g‘irlovchi parametrli ikkilik kodlari mavjud bo‘lishi mumkinligi xaqida
aytadi. (n,k), (23,12) optimal kodining yaratilishi Goleyga tegishli.
Goley
kodi siklik kodlarning bir ko‘rinishi hisoblanar ekan, unga oddiy kodning G(x)
kodli kombinatsiyani xr birxadga ko‘paytirish va bu ko‘paytmaga
G(x) xr ko‘paytmasini R(x) ga bo‘lishdagi qoldiqni qo‘shish orqali
orqali kodlash metodi qo‘llanilgan:
Bu
tenglikni o‘zgartirish orqali: F(x) = xr G(x) + R(x), ni olamiz
bu
yerda G(x) - oddiy k- elementli kodning kodli kombinatsiyasi;
r - hosil bo‘luvchi polinomning darajasi.
8-ma’ruza
uchun nazorat savollari
1. Shovqinbardosh
kodlardan amaliy foydalanish vazifalari qanday amalga oshiriladi?
2. Siklik
kodlar qurish prinsipi qanday?
3. Siklik
kodning kodli kombinatsiyasini nechta usul yordamida olish mumkin, misol keltiring?
4. Xemming
kodiga tushuncha bering?
5. Goley
kodiga tushuncha bering?
9-ma’ruza.
O‘ralgan kodlar
Reja:
1.
Rekurrent kodlar yordamida kodlash.
2.
Rekurrent kodlar yordamida xatoliklarni tuzatish
3.
Zanjir rekurrent kodni qurish prinsipi.
4.
Koder sxemasi.
5.
Dekoder sxemasi.
Rekkurent
kodlar yordamida kodlash. O‘ralgan (Rekurrent) kodlar
(Svertochnûe kodû) uzluksiz kodlarga mansub bo‘lib, bloklarga ajralmaydi. Bunda
kod simvollarini kodlash va dekodlash amallari uzluksiz bajariladi. Bunday kodlar
shovqinbardosh kodlashning keng tarqalgan xili hisoblanadi. Ular:
Ø simsiz aloqa protokollarida;
Ø raqamli yer usti
va yer yo‘ldoshi
aloqa sistemalarida;
Ø kosmos
bilan aloqa sistemalarida
qo‘llaniladi.
Ushbu
kodlarning ishlash prinsipini avtomatlar nazariyasiga asoslanganini 4 xolatli va
ikkilik ketma-ketlikni ishlovchi avtomat misolida ko‘ramiz.
Quyidagi
o‘tish jadvaliga binoan A = 1, 1, 0, 1, 1, 1, 0, 0 kirish yo‘li ketma – ketligiga
mos avtomat chiqish yo‘li signalini aniqlaymiz.
Demak,
avtomat chiqish yo‘lida quyidagi signal shakllanadi:
11,
01, 01, 00, 01, 10, 01, 11
Trellis
diagrammasi. Avtomat ishlashini yoyilgan panjara
diagramma – (Trellis diagram) yordamida tavsiflash qulay hisoblanadi.
Daslabki
avtomat S0 holatida deb faraz qilinganligi sababli har qanday yo‘l trellisning
chapki yuqori burchagidan boshlanadi. Har bir qadamda diagramma bo‘yicha yo‘l ikki
yo‘nalishni qabul qilishi mumkin. Agar informatsion ketma
– ketlikning navbatdagi
simvoli 0 qiymatini olsa, avtomat yuqori yo‘lni
tanlaydi. Agar simvol 1 ga teng bo‘lsa avtomat pastki
yo‘lni tanlaydi. Avtomatning chiqish yo‘li kodi ketma – ketligi tanlangan yo‘l yoyi
salmog‘iga teng.
Yuqoridagi
avtomat chiqish yo‘lida shakllangan kod ketma – ketligi uchun trellis quyidacha:

Olingan
kod ketma – ketligini dekodlash teskari tartibda amalga oshiriladi.
Trellisning
har bir uzeli ikkita – yuqori va pastki
yoylarga ega. Agar berilgan uzel uchun ajratilgan yo‘l yuqori yoy orqali o‘tsa informatsion
signal 0 qiymatini oladi. Agar berilgan uzel uchun ajratilgan yo‘l pastki
yoy orqali o‘tsa informatsion signal 1 qiymatini oladi.
Bizning
misolimizda daslabki informatsion ketma – ketlik A = 1, 1, 0, 1, 1, 1, 0, 0
ga teng.
Rekurrent
kodlar yordamida xatoliklarni tuzatish. Olingan
har qanday kod ketma – ketligi uchun trellisda yo‘lni chizish mumkin emas. Masalan,
11, 11, 11 yoki 01, 01, 01kombinatsiyalar uchun yo‘llar mavjud emas. Xuddi shunday
01 yoki 10 dan boshlanuvchi kod kombinatsiyalari ham mavjud emas. Bunday juftliklar
xatolik borligini ko‘rsatadi. Ikkilik kod kombinatsiyasi shovqinli kanallar orqali
uzatilganida biror bir bitning teskarisiga o‘zgarishi kod kombinatsiyasining buzilishiga
olib keladi. Ma’lumki, xabarlar orasidagi masofa farqlanuvchi xonalar soni sifatida
aniqlanadi. Shuning uchun uzatiladigan kod kombinatsiyasidagi har bir xatolik uning
daslabki qiymatidan masofasini orttiradi.
Buzilgan
kod kombinatsiyasi, mos holda, trellisdagi yo‘lning buzilishiga olib keladi. Ba’zi
xollarda, yo‘l bo‘lmasligi ham mumkin. Xatolikni tuzatish masalasi – olingan kod
kombinatsiyasi uchun bo‘lishi mumkin bo‘lgan yo‘llar to‘plamini olish va ular orasidagi
shunday yo‘lni tanlash kerakki, bu yo‘l olingan kod kombinatsiyasidan minimal masofaga
ega bo‘lsin.
Misol.
Uzatiladigan informatsion xabar quyidagi ko‘rinishga ega: A=(1010).
Bu
xabarga quyidagi kod kombinatsiyasi mos keladi: Z=(11,
10, 00, 10).
Aytaylik,
uzatilgan kombinayiyada xatolik sodir bo‘ldi: 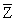 =(11,
10, 00, 10).
=(11,
10, 00, 10).
Informatsion
ketma-ketlikni tiklash lozim.
Yechish.
t = 0, t = 1.

Trellisning
S0(t=0) uzelidan
boshlab olingan kod kombinatsiyasiga mos yoyni tanlaymiz. Birinchi juft simvol
11. Trellisda bu S0 dan chiquvchi pastki yoyga mos keladi. Demak, S2
uzelga keldik.
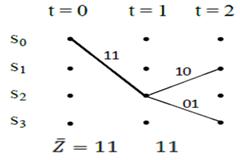
Ikkinchi
qadamda Trellisning S2(t=1) uzelidan  ning
ikkinchi juftiga mos keluvchi 11 salmoqli yoyni tanlashimiz lozim. Bunday salmoqli
yoy bo‘lmaganligi sababli, ikkita variantni ko‘ramiz. Yuqori yoy uchun 10 salmoq
mos keladi. 10 va 11 orasidagi masofani S1(t=2) uzelga yozamiz. Pastki
yoy uchun 01 salmoq mos keladi. 01 va 11 orasidagi masofani S3(t=2) uzelga
yozamiz.
ning
ikkinchi juftiga mos keluvchi 11 salmoqli yoyni tanlashimiz lozim. Bunday salmoqli
yoy bo‘lmaganligi sababli, ikkita variantni ko‘ramiz. Yuqori yoy uchun 10 salmoq
mos keladi. 10 va 11 orasidagi masofani S1(t=2) uzelga yozamiz. Pastki
yoy uchun 01 salmoq mos keladi. 01 va 11 orasidagi masofani S3(t=2) uzelga
yozamiz.

 Qabul qilingan kombinatsiyaning uchinchi
jufti 00. uchinchi qadamda ikkita marshrut mavjud. S1(t=2) uzeldan
11 va 00 salmoqlarga ega bo‘lgan ikkita yoy chiqadi. Ular va qabul qilingan qiymatlar
orasidagi masofalarni mos uzellarga yozamiz. S3(t=2) uzeldan ham 01 va
10 salmoqlarga ega bo‘lgan ikkita yoy chiqadi. Ular va qabul qilingan qiymatlar
orasidagi masofani S1 va S0 uzellarga yozamiz.
Qabul qilingan kombinatsiyaning uchinchi
jufti 00. uchinchi qadamda ikkita marshrut mavjud. S1(t=2) uzeldan
11 va 00 salmoqlarga ega bo‘lgan ikkita yoy chiqadi. Ular va qabul qilingan qiymatlar
orasidagi masofalarni mos uzellarga yozamiz. S3(t=2) uzeldan ham 01 va
10 salmoqlarga ega bo‘lgan ikkita yoy chiqadi. Ular va qabul qilingan qiymatlar
orasidagi masofani S1 va S0 uzellarga yozamiz.
To‘rtinchi
qadamda maksimal salmoqqa ega bo‘lgan uzellarni tashlab yuborish lozim. Chunki ular
uzatiladigan ketma-ketlikdan ko‘proq farqlanuvchi ketma-ketlikga mos keladi. Keyingi
yo‘l uchun faqat S2 uzelini qoldiramiz. Qabul qilingan kombinatsiyaning
to‘rtinchi jufti 10. Trellisning S2(t=3) uzelidan 10 salmoqli yuqori
yoy chiqadi va ushbu yoy orqali S1 uzelga o‘tamiz.

Oxirida
masofalar yig‘indisi minimal bo‘lgan uzellardan o‘tuvchi yo‘lni aniqlash lozim.
Har bir qadamda yuqori yoyga 0 qiymati, pastki yoyga 1 qiymati beriladi. Dekodlangan
informatsiya ketma-ketligi quidagi ko‘rinishga ega bo‘ladi: A=(1010).
Zanjir
rekurrent kodni qurish prinsipi. Rekurrent kodlar
uzluksiz kodlar turkumiga mansub bo‘lib, bloklarga ajratilmaydi. Bunda kod simvollarini
kodlash va dekodlash amallari uzluksiz bajariladi. Hatoliklar guruhini aniqlash
va tuzatishga imkon beruvchi zanjir rekurrent kod keng qo‘llaniladi. Rekurrent
kodlar (m/n) kabi shartli belgilanadi. Har bir informatsion simvoldan so‘ng nazorat
(tekshiruvchi) simvol keluvchi kod eng sodda rekurrent kod hisoblanadi. Bunday kod
(1/2) kabi belgilanadi.
Bunda
nazorat simvollarining uzunligi informatsion simvollar uzunligiga teng, ya’ni
m=k=n/2.
Demak,
ortiqchalik D = (n-m) 100/n
= (n-0,5n).100/n = 50%. Rekurrent kodni qurish prinsipi
rasmda keltirilgan

Nazorat
simvollarining ketma – ketligi (1-rasmdagi
pastki qator) informatsion simvollar ketma – ketligidan (1 -rasmdagi
yuqori qator) bir – biridan l0 masofadagi informatsion simvollarni
2 ning moduli bo‘yicha jamlash yo‘li bilan hosil qilinadi.
Rekurrent
kodni qurish prinsipi.
Koder sxemasi. To‘rt xonali siljituvchi regisr asosidagi
kodlash sxemasi (koder) 2 – rasmda keltirilgan.
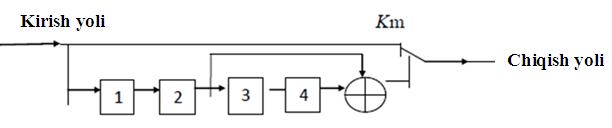
2-rasm.
Rekurrent kodni qurish prinsipidagi
koder sxemasi
Agar koderning kirish yo‘liga
quyidagi simvollar ketma-ketligi
10110111001 (1) berilsa,
siljituvchi registrning chiqish yo‘lida quyidagi
simvollar ketma-ketligi shakllanadi:
00100110101 (2). (2) ketma-ketlikning xosil qilinishini 1-jadval yordamida tushinish
mumkin.
 Informatsion ketma – ketlik (1) diskret
ti dagi regisrning 1 – xonasi holatiga mos kelsa, nazorat (tekshiruvchi)
simvollar ketma – ketligi (2) modul 2 bo‘yicha jamlagichning chiqish yo‘lidagi
simvollarga mos keladi.
Informatsion ketma – ketlik (1) diskret
ti dagi regisrning 1 – xonasi holatiga mos kelsa, nazorat (tekshiruvchi)
simvollar ketma – ketligi (2) modul 2 bo‘yicha jamlagichning chiqish yo‘lidagi
simvollarga mos keladi.
(2)
ketma – ketlik siljituvchi registrning oldingi taktdagi ikkinchi va to‘rtinchi xonalarining
chiqish yo‘lidagi signallarni jamlash yo‘li bilan olinadi. Bu 1 – jadvalning oldingi
qatoridagi registrning ikkinchi va to‘rtinchi xonasidagi simvollarni jamlashga mos
keladi.
Uzatuvchi
tarafdagi kommutator (Km) chiqish yo‘liga birinchi informatsion simvoldan,
so‘ngra birinchi nazorat simvolidan, so‘ngra ikkinchi informatsion simvoldan va
h. tarkib topgan ketma – ketlikni uzatadi, ya’ni: 100011100011110010011 (3).
(3)
ketma – ketlik (1/2) rekurrent kodning kodlangan simvollarining ketma – ketligidir.
Rekurrent
kodni qurish prinsipi.
Dekoder sxemasi. Dekoder ikki qismli sxemadan
iborat:
Birinchi
qism sxemada tuzatuvchi ketma – ketlik shakllansa, ikkinchi qism sxemada kod tuzatiladi.
Birinchi
qism sxemada (3-rasm) kommutator Km (dekoder kommutatori) koder kommutatori
bilan (2-rasm) sinxron va sinfaz ishlaydi.
 Dekoder siljituvchi registri
ham to‘rt xonali. Dekoder kirish yo‘liga simvollarning ketma – ketligi (3) beriladi
va bu ketma – ketlik kommutator yordamida siljituvchi registr
kirish yo‘liga beriluvchi informatsion ketma – ketlik (1)ga va chiqish yo‘li jamlagichining
pastki
kirish yo‘liga beriluvchi nazorat simvollari ketma – ketligi (2)ga ajratiladi.
Dekoder siljituvchi registri
ham to‘rt xonali. Dekoder kirish yo‘liga simvollarning ketma – ketligi (3) beriladi
va bu ketma – ketlik kommutator yordamida siljituvchi registr
kirish yo‘liga beriluvchi informatsion ketma – ketlik (1)ga va chiqish yo‘li jamlagichining
pastki
kirish yo‘liga beriluvchi nazorat simvollari ketma – ketligi (2)ga ajratiladi.
Dekoderdagi
to‘rt xonali siljituvchi regisr koderdagi siljituvchi regisr sxemasidek sxemaga
ega. Shu sababli, agar xatolik bo‘lmasa, yuqoridagi jamlagichning chiqish yo‘lidagi
simvollar ketma – ketligi pastki
jamlagich kirish yo‘liga beriluvchi nazorat simvollari ketma – ketligiga mos keladi.
Bu holda jamlagichning 2 – chiqish yo‘lida simvollarning ketma – ketligi faqat nollardan
iborat bo‘ladi, jamlagichning 1 – chiqish yo‘lida esa buzilmagan simvollarning ketma
– ketligi (1) shakllanadi. Agar aloqa kanalida, koder va dekoder orasida xatolik
paydo bo‘lsa jamlagichning 2-chiqish yo‘lidagi simvollar ketma – ketligi tarkibida
xatolikni tuzatishga imkon beruvchi ma’lum
kombinatsiyadagi birlar paydo bo‘ladi.
Demak,
ushbu ketma – ketlik tuzatuvchi ketma – ketlik hisoblanadi.
9-ma’ruza
uchun nazorat savollari
1.
Rekurrent kodlar yordamida kodlashga tushuncha bering?
2.
Rekurrent kodlar yordamida xatoliklarni tuzatishga
tushuncha bering?
3.
Zanjir rekurrent kodni qurish prinsipi
nimalardan iborat?
4.
Koder sxemasiga
tushuncha bering?
5.
Dekoder sxemasiga tushuncha bering?
10-ma’ruza.
Ikkilik Bouza-Choudxuri-Xekvingem kodlari
Reja:
1.BChX
kodlari.
2.
BChX kodlariga misol.
Qulay
kodlash va dekodlash algoritmlari taklif etilgan notasodifiy kodlarning orasidagi
eng mashxurlaridan biri BChX (Bouza-Choudxuri-Xekvingem) kodlaridir. BChX kodlari
kodlash va dekodlash jarayonlarini sezilarli darajada osonlashtirgan, aniq algebraik
strukturaga ega bo‘lgan siklik kodlar oilasiga mansubdir. Hosil qilinadigan BChX
kodning polinomi kod uzunligi va berilgan kod masofasi d0
≥ 5 bilan aniqlanadi. BChX kodi uzunligi n=2m-1
ifodasi orqali aniqlanadi,
bu
yerda m – istalgan butun son, m=log2(n + 1).
Tekshiriladigan
razryadlar soni quyidagicha
aniqlanadi:
BChX
kodning hosil qilinadigan polinomi minimal polinomlarning eng kichik umumiy karralisi
hisoblanib qaysiki tartibi d0 –2 ga teng.
P(x)
= EKUK {m1(x) * m3(x) * m5(x) *… * md0-2(x)
}
BChX
kodlari t karrali va undan kamroq erkin xatolarni to‘g‘irlaydigan siklik
kodlarning katta sinfini tashkil etadi. BChX kodlari uchun ham siklik kodlarning
barcha asosiy xususiyatlari xos. BChX kodlari n, k, g(x) kattaliklari orqali aniqlanadi,
bu
yerda: n - kodli kombinatsiyadagi elementlar miqdori;
k
– BChX kodining axborot elementlari
miqdori;
g(x)
–BChX kodini keltirib chiqaradigan ko‘pxadi.
1. BChX kodlarining parametrlari
quyidagi shaklda tanlanadi:
n
= 2m-1 formulasidan kelib chiqib , n soni
tanlanadi, bu
yerda m –istalgan butun son.
2.
To‘g‘rilash shart bo‘lgan xatolar miqdori aniqlanadi.
Bu yerdan BChX kod do > 2t + 1 ga ega bo‘lishi lozim.
3.
do ga bog‘liq holda g(x)=EKUK (m1(X)….m2t (x
)), hisoblanadi bu yerda m1 (x) ... m2t
(x) – keltirilmagan minimal ko‘pxadlar.
4.
Tekshiriladigan belgilar soni quyidagi
formula orqali hisoblanadi:
r = m
* t
5.
k axborot belgilar soni quyidagi
formula orqali hisoblanadi:
k =
n -
r = (2m-1)
- r
BChX
kodni kodlash quyidagidan iborat:
Zarur
a(x)=a0…ak-1
kod kombinatsiyasini xn-k razryadga
chapga siljitib quyidagi
ko‘rinishni olamiz
X n-k
a
(x)=X n-k (a0 +…+a
k-1X k-1)= a0
X n-1 +…a
k-1X n-1
Xn-k
a
(x) ko‘pxadini g(x)ga bo‘lamiz va bo‘linmani quyidagi ko‘rinishda yozamiz:
Xn-k a
(x)=g(x)*q(x)+r(x)
,
bu
yerda q(x)- bo‘linma;
r(x)-
g(x) ga
bo‘lingandagi
qoldiq.
g(x)
ko‘pxadining darajasi n-k ga teng ekan , r(x) ning darajasi n-k-1 ga teng bo‘ladi.
Bunda Xn-ka(x) + r (x) = g(x)
q(x), bu yerdan bo‘linadigan BChX kodning izlangan kodli kombinatsiyasini olamiz.
BChX kodi t=3, n=15 uzunligidagi kombinatsiyalarni 3 karra xatolarni
to‘g‘rilashga qodir,
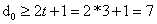
m=log2(n+1)=log2(15+1)=4
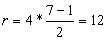 jadvaldan polinomlarni tanlaymiz
jadvaldan polinomlarni tanlaymiz

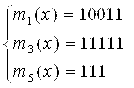 R(x)=EKUK{m1(x)m3(x)…md-2(x)}
P(x)=10011x11111x111=10100110111
R(x)=EKUK{m1(x)m3(x)…md-2(x)}
P(x)=10011x11111x111=10100110111
 (tahminan)
(tahminan)
R(x)=x10+x8+x5*x4+x2+x+1
r=10
tosh=3
 =7
=7
k=n-r=15-10=5
Misol. 3 xatoni to‘g‘irlovchi BChX kod yasaymiz, kodli kombinatsiya uzunligi
n=15. M=log2(n+1)=log2(15+1)=4
r<m*t<=4*3=12.
Minimal ko‘pxadlar jadvalidan minimal ko‘pxadlarni tanlaymiz: M1(X)=10011;
M3(x)=11111; M5(x)=111. Bunda g(x)= 10100110111, va r=10, k=n-r=5, (15,5) kodga egamiz.
10101 kombinatsiyasini kodlaymiz
101010000000000|10100110111
10100110111 |
000011101110000
10100110111
01001000111
BChX kodi bilan kodlangan kombinatsiya quyidagi ko‘rinishga ega bo‘ladi: 10101 1001000111
2 va 10 pozitsiyalariga xatolarni kiritamiz: 111011001100111.
Hosil qilinadigan polinomga qabul qilingan kombinatsiyani bo‘lamiz:
111011001100111 10100110111
10100110111
010010100010
10100110111
0011001010111
10100110111
01111110110
W=8
Olgan W=8 qoldig‘imizning og‘irligi to‘g‘irlangan xatolar sonidan katta
ekan, kombinatsiyani siklik siljitishni va hosil bo‘ladigan polinomga qoldiq ikkiga
teng og‘irlikda bo‘lgunicha bo‘lishni amalga oshiramiz.
110110011001111|10100110111
10100110111 |
11111110111
10100110111
10110000001
10100110111
1011011011 W=7
Olgan W=7 qoldig‘imizning og‘irligi to‘g‘irlangan xatolar sonidan katta
ekan, kombinatsiyani siklik siljitishni va hosil bo‘ladigan polinomga qoldiq ikkiga
teng og‘irlikda bo‘lgunicha bo‘lishni amalga oshiramiz.
101100110011111|10100110111
10100110111
10101110111
10100110111
10000001 W=2
Modul bo‘yicha oxirgi ikkita bo‘linuvchilarni qoldiqlari bilan
qo‘shamiz 101100110011111Å10000001=101100100011110.
Olgan ketma-ketligimizni ikkita razryadga o‘ngga siklik siljitamiz:
010110010001111,
101011001000111- bu ketma-ketlik yuborilgan hisoblanadi.
BChX ni dekodlash algoritmi bir nechta bosqichdan iborat:
1.Sindromni hisoblash.
2. Hatolar lokatori ko‘pxadini hisoblash.
3. Hatolar lokatori ko‘pxadi ildizlarini topish.
4. Xatolarni to‘g‘rilash.
10-ma’ruza
uchun nazorat savollari
1. BChX kodiga tushuncha bering?
2. BChX kodiga misollar keltiring?
3. BChX ni dekodlash algoritmi nechta bosqichdan iborat?
11
ma’ruza. Rid – Solomon kodlari.
Reja:
1. Rid-Solomon
kodlari parametrlari.
2. Axborotlarni
Rid-Solomon kodida kodlashtirish usullari.
3. Galua
maydoni.
4. Galua
maydonini qurish va kodlashtirish.
5. Rid-Solomon
kodlashtirish algoritmi bosqichlari.
Rid
– Solomon kodini qurish asoslari.
Kuchli kodlar zamonaviy algebra strukturasiga
bog‘liq ravishda quriladi. Ko‘pgina yaratilgan kodlar, ko‘pxadlar xalqasi va Galua
maydoni strukturasiga asoslangan xolda qurilgan. Asosiy
algebraik amallar bajarish mumkin bo‘lgan elementlar majmuasiga gurux, xalqa va
maydon kiradi.
Bitta
asosiy amal va unga teskari bo‘lgan amalni (qo‘shish va ayirish yoki ko‘paytirish
va bo‘lish) bajarish mumkin bo‘lgan sistemaga gurux deb ataladi. Guruxning tarkibiy
qismiga, gurux elementlari deb ataluvchi elementlardan tashkil topgan chekli yoki
cheksiz G to‘plam kiradi.
G
to‘plamning ikkita elementi g1 va g2 ustida bajariladigan guruxli amal (0) natijasida
shu to‘plamga tegishli bo‘lgan uchinchi element g1 0 g2 xosil bo‘ladi. Guruxdagi
g1 0 g2 belgi, agar qo‘shish amali bajariladigan bo‘lsa g1 + g2, ko‘paytirish amali
bo‘lsa g1 * g2 kabi belgilanadi.
Guruxli
amallar (0) ni bajarish mumkin bo‘lgan G to‘plam, quyidagi aksiomalar bajarilganda
gurux deb ataladi.
1. Assotsiativlik:
G to‘plamning ixtiyoriy uchta elementlari g1, g2, g3 uchun quyidagi munosabat o‘rinli:
(g1
0 g2) 0 g3 = g1 0 (g2 0 g3), ya’ni
(g1
+ g2) + g3 = g1 + (g2 + g3), yoki
(g1
 g2)
g2)
 g3
= g1
g3
= g1  (g2
(g2
 g3)
g3)
2. G
to‘plam elementlari ichidan g  1=
1
1=
1 g
= g tenglik bajariladigan neytral deb ataluvchi elementi mavjud bo‘lishi kerak.
Agar guruxli amal qo‘shish amali bo‘lsa, unda neytral
element deb «0» aytiladi, ya’ni
g
= g tenglik bajariladigan neytral deb ataluvchi elementi mavjud bo‘lishi kerak.
Agar guruxli amal qo‘shish amali bo‘lsa, unda neytral
element deb «0» aytiladi, ya’ni
0
+ a = a + 0 = a
Agar
ko‘paytirish amali bo‘lsa, unda neytral element «1» deb aytiladi, ya’ni
1  a
= a
a
= a  1 = a
1 = a
3.
G to‘plamga tegishli bo‘lgan g elementlarga
teskari bo‘lgan element g–1 mavjud bo‘lishi kerak. Agar quriladigan
amal qo‘shish bo‘lsa teskari element (-a) kabi, agar ko‘paytirish bo‘lsa, unda teskari
element a–1 kabi belgilanadi.
Gurux chekli deyiladi, agar u chekli sonli elementlardan tashkil
topgan bo‘lsa, aks xolda esa cheksiz gurux deb aytiladi.
Kodlashtirish
nazariyasi bo‘yicha ayirish amali modul m (mod m) bo‘yicha bajariladi. Bunda bizni
sonning o‘zi emas m natural songa bo‘linishi natijasida bir xil qoldiqlarga ega
bo‘lgan ikkita son o‘zaro ekvivalent son deyiladi. Masalan, m=2 bo‘lganda ikkita
son yoki ikkilasi ham toq yoki ikkalasi ham juft bo‘lganda o‘zaro ekvivalent bo‘ladi.
Ikkita a va v sonini m ga bo‘lganda bir xil qoldiqqa ega bo‘lsa, u xolda bu ifoda
quyidagicha yoziladi:
a
 v (mod m)
v (mod m)
Masalan,
7=3 (mod 4) 7 soni 3 ga modul 4 bo‘yicha teng deb aytiladi. Qo‘shish
va ko‘paytirish amallari bajariladigan R to‘plam, quyidagi aksiomalar o‘rinli bo‘lganda
xalqa deb ataladi:
1. R
to‘plam qo‘shish amaliga nisbatan kommutativ gurux xisoblanadi;
2. Assotsiativlik
R to‘plam elementlari a, v, s uchun quyidagi tenglik o‘rinli:
a
 (v + s) = a
(v + s) = a  v
+ a
v
+ a  s
s
3. Xalqada
ko‘paytirish amaliga nisbatan, shu xalqaga tegishli bo‘lgan birlik element mavjud:
1 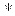 a = a
a = a 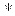 1
= a
1
= a
Nol
bo‘lmagan elementlarning teskari elementi mavjud bo‘lgan kommutativ xalqaga maydon
deb ataladi. Maydon – bu «qo‘shish», «ayirish», «ko‘paytirish», «bo‘lish» mumkin
bo‘lgan matematik ob’ektlar to‘plamidir.
Modul
2 bo‘yicha qo‘shish va ko‘paytirish mumkin bo‘lgan ikkita simvollar 0 va 1 alfaviti
ikkita elementdan iborat bo‘lgan maydon deb ataladi va GF(2) kabi belgilanadi.
q
ta elementdan iborat bo‘lgan maydon chekli maydon yoki Galua
maydoni deb ataladi va GF (q) kabi belgilanadi.
Agar
q R sonining darajasi ko‘rinishida (q = p m , m – butun son ) bo‘lsa,
u xolda GF (P m ) maydoning elementlari (m-1) darajali ko‘pxad ko‘rinishida
bo‘ladi:
a0 + a1 x + a2 x2 + …..+ a m-1
x m-1
ai
koeffitsientlar GF(P) maydonga tegishli bo‘lgan sonlardir.
Siklik
kodlarni qurishda foydalaniladigan R(x) ko‘pxad va GF(Pm) maydon elementlarning
bir qator xossalari mavjud:
1. GF(Pm)
maydonning hamma
noldan farqli elementlari Pm –1 tartibli multiplikativ guruxni tashkil
etadi. U xolda maydonning ixtiyoriy elementi α
uchun 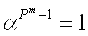 tenglik o‘rinli. Ushbu xossadan kelib chiqadigan tenglik
tenglik o‘rinli. Ushbu xossadan kelib chiqadigan tenglik  maydonning
nolga teng bo‘lgan elementi uchun ham
bajariladi α = 0. Maydonning
nolga teng bo‘lmagan elementlari
maydonning
nolga teng bo‘lgan elementi uchun ham
bajariladi α = 0. Maydonning
nolga teng bo‘lmagan elementlari 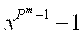 ko‘pxadning ildizlari bo‘ladi, maydonning hamma
elementlari esa
ko‘pxadning ildizlari bo‘ladi, maydonning hamma
elementlari esa 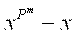 ko‘pxadning ildizlari xisoblanadi;
ko‘pxadning ildizlari xisoblanadi;
2.
GF(Pm) maydonning xar doim tartibli
α
elementi mavjud bo‘ladi, ya’ni Pm–1 tartibli elementi.
Maydonning nolga teng bo‘lmagan elementlarini bitta yoki bir nechta α
ning darajali ko‘rinishida tasvirlanishi mumkin. Xulosa
qilib aytganda Galua maydonining multiplikativ guruxi siklikdir.
Siklik
kodlar nazariyasida quyidagi xossalar muxim o‘rin tutadi.
1.
Modul R quyida
keltiriladigan har
qanday m darajali R(x) ko‘pxadning (agar u mavjud bo‘lsa) 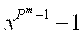 ikkixadli
bo‘luvchisi mavjud;
ikkixadli
bo‘luvchisi mavjud;
2.
GF(P) oddiy maydonda quyidagi tenglik bajariladi:
(a + v) r =
a r + v r
3.
Modul R uchun
[P(x)
] p
= P (x
p) (mod
p)
tenglik o‘rinli.
Bu
yerda R(x) – koeffitsientlari GF(P) maydonga tegishli bo‘lgan ixtiyoriy ko‘pxad;
4.
Agar GF(Pm) maydonning α
elementi modul R bo‘yicha keltirilmaydigan m –chi darajali R(x)
ko‘pxadning ildizi bo‘lsa, unda R(x) ning qolgan ildizlari
 elementlar
bo‘ladi.
elementlar
bo‘ladi.
5.
Agar k –n ning bo‘luvchisi bo‘lsa, u xolda xk – 1 ko‘pxad x n
– 1 ko‘pxadning bo‘luvchisi bo‘ladi.
6.
Agar modul R bo‘yicha keltirilmaydigan k darajali R1(x) ko‘pxad 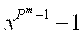 ikkixadning
bo‘luvchisi bo‘lsa, u xolda k daraja m sonining bo‘luvchisi bo‘lishi kerak va aksincha;
ikkixadning
bo‘luvchisi bo‘lsa, u xolda k daraja m sonining bo‘luvchisi bo‘lishi kerak va aksincha;
7.
Ixtiyoriy oddiy R son va istalgan oddiy m –chi darajali R(x) ko‘pxad uchun, faqat
bitta GF (Pm) Galua maydoni mavjud.
GF(Pm)
ko‘rinishdagi Galua maydonida faqat ikkita-ko‘shish va ko‘paytirish amalini bajarish
mumkin. Ko‘shish mod 2 bo‘yicha, ko‘paytirish esa
mod m bo‘yicha bajariladi.
Maydonning
ikkita elementini 0 va 1 orqali belgilaymiz va qo‘shish hamda
ko‘paytirish amallarini bajaramiz:
0 + 0 = 0 0  0
= 0
0
= 0
0 + 1 = 1 0  1
= 0
1
= 0
1 + 0 = 1 1  0
= 0
0
= 0
1 + 1 = 1 1  1
= 1
1
= 1
GF(Pm)
Galua maydonini qurish kerak bo‘lsin, r=2, m=4 ya’ni GF (2n). Buning
uchun modul 2 bo‘yicha keltirilmaydigan oddiy R(x)= xn+x+1 ko‘pxadni
olamiz. Α -
bu ko‘pxadning ildizi bo‘lsin, unda u GF(2n) maydonning 1-tartibli
elementi xisoblanadi. 2-xossaga asosan hamma
15 ta noldan farqli elementlar quyidagicha bo‘ladi:
 α
0 =
1 (0001)
α
0 =
1 (0001)
 α
1 = α
(0010)
α
1 = α
(0010)
 α
2 = α
2 (0100)
α
2 = α
2 (0100)
 α
3 = α
3 (1000)
α
3 = α
3 (1000)
 α
4 = 1 + α
(0011)
α
4 = 1 + α
(0011)
 α
5 = α
+ α
2 (0110)
α
5 = α
+ α
2 (0110)
 α
6 = α
2 + α
3 (1100)
α
6 = α
2 + α
3 (1100)
 α
7 = 1 +α
+α3
(1011)
α
7 = 1 +α
+α3
(1011)
 α
8 = 1 + α
2 (0101)
α
8 = 1 + α
2 (0101)
 α
9 = α + α
3 (1010)
α
9 = α + α
3 (1010)
 α
10 = 1+α
+ α
2 (0111)
α
10 = 1+α
+ α
2 (0111)
 α
11 = α + α2
+α 3 (1110)
α
11 = α + α2
+α 3 (1110)
 α
12 = 1+α
+ α
2 +α 3
(1111)
α
12 = 1+α
+ α
2 +α 3
(1111)
 α
13 = 1+α
2 + α
3 (1101)
α
13 = 1+α
2 + α
3 (1101)
 α
14 = 1 +α
3 (1001)
α
14 = 1 +α
3 (1001)
 α
15 =
1 (0001)
α
15 =
1 (0001)
GF(24) Galua
maydonining oddiy elementi 0001 ga, nol elementi 000 ga teng.
Galua
maydonining elementlarini qo‘shish, razryadlarini mod 2 bo‘yicha qo‘shish kabi bajariladi:
α
3 + α
9 = α
12 α
5 + α
11 = α
3
0101 0110
1010 1110

 1111 = α
12
1000 = α 3
1111 = α
12
1000 = α 3
Ko‘rsatkichli
ko‘rinishdagi elementlarni ko‘paytirish quyidagicha bajariladi:
α
3 ·
α
14 = α
17
17-
daraja esa (2 4 –1) dan katta, u xolda ko‘paytirish natijasida
quyidagini xosil qilamiz:
α
3 ·
α
14 = α
17 -α
15 = α
2
Rida-Solomon
kodining parametrlari quyidagilar:
1.
n- Rida-Solomon kodidagi blok uzunligi:
n=q–1,
q=
2 m (11.1)
2.
k – Rida-Solomon kodining informatsion qismi:
k
= n – r
(11.2)
3.
r - Rida-Solomon kodining tekshiruv qismi.
d = r +1 = n – k +1
(11.3)
Rida-Solomon kodi t ta xatolarni to‘g‘rilashi:
t = (d – 1) /2
(11.4)
yoki
t ta xatolarni va v ta o‘chirilganlarni to‘g‘rilashi
d ³
2 t + v + 1
(11.5)
mumkin.
Axborotlarni
Rid-Solomon
kodida
kodlashtirish
usullari
Rid –Solomon kodi bir karralik xatolarni, shuningdek xatolar
paketini to‘g‘rilashi mumkin. Rid-Solomon kodining apparatli qismini yaratish oddiy
bo‘lgani sababli, ushbu kod aloqa texnikalarida keng qo‘lamda qo‘llanilmoqda. Ko‘p
xollarda Rid-Solomon kodidan kaskadli kodlarni qurishda foydalaniladi. Unda Rid-Solomon
kodi tashqi kod sifatida ishlatiladi.
Rid-Solomon
kodi ham
siklik kodlar turkumiga kiradi,
shuning uchun ham
siklik kodlarning hamma
xossalari ushbu kod uchun xam o‘rinli.
1. Axborotlarni
siklik kodlarda kodlashtirish, r / n < 0, 5 tengsizlik bajarilganda yasovchi
ko‘pxad R(x) orqali emas, balki tekshiruvchi ko‘pxad yordamida bajariladi;
2. Axborotlarni
siklik kodlarda kodlashtirish, r / n > 0, 5 tengsizlik bajarilganda esa yasovchi
ko‘pxad R(x) orqali amalga oshiriladi.
Ko‘p
xolatlarda 2-usulda kodlashtirish amalga oshiriladi. Shu sababli ushbu usulga ko‘proq
to‘xtalib o‘tamiz. Bu usul orqali kodlashtirishda, informatsion ketma-ketlik xr
razryad chapga suriladi va yasovchi ko‘pxad (R(x))ga bo‘lish natijasida qoldiq
olinadi. Keyin xosil bo‘lgan qoldiq informatsion ketma-ketlikka qo‘shiladi. Rid-Solomon
kodini yasovchi ko‘pxad quyidagi formula orqali aniqlanadi:
g (x) =  (x
– α 2)
= (x – α)
(x – α
2) ….(x – α
2 t )
(x
– α 2)
= (x – α)
(x – α
2) ….(x – α
2 t )
Ko‘pxadning
darajasi 2 t quyidagi munosabatdan kelib chiqadi:
n
– k = 2 t
(15.9)
parametlari
Rid-Solomon kodini yasovchi ko‘pxadni xisoblashni misolda qarab chiqamiz.
n
= 15, k = 9 
Demak
kodlashtirish 2-usulda bajariladi.
n
– k = 15 – 9 = 6 = 2 t
Yasovchi
ko‘pxad 6-darajali bo‘lar ekan:
g
(x) = (x
– α)(x – α 2)(x
– α 3) (x
– α 4)(x
– α 5)(x
– α 6)
(15.9) Rid-Solomon kodi uchun GF(2m )ko‘rinishdagi
Galua maydonini qurish kerak. 2m = q = n + 1 = 15+ 1 = 16, m = 4.
(15.9) Rid-Solomon kodining minimal kod masofasi 11.3- formula asosida topiladi:
d = n – k + 1 = 15 – 9 + 1 = 7
Ushbu kod 11.4- formula asosan quyidagicha xatoni to‘g‘rilashi mumkin:

11.5-
formulaga asosan esa 2 ta xatoni va 2 ta o‘chirilganni 1 ta xato va 4 ta o‘chirilganni,
6 ta o‘chirilganni to‘g‘rilashi mumkin.
Kod
parametrlarini bilgan xolda Galua maydonini qurish hamda kodlashtirish mumkin.
αx7
+ α8 x6 kombinatsiyani uzatish kerak bo‘lsin. Ushbu
kombinatsiyani yasovchi ko‘pxadga bo‘lamiz va xosil bo‘lgan qoldiqni,
shu kombinatsiyaga qo‘shamiz. Natijada kodlangan kombinatsiyani
xosil qilamiz:
g (x)
= (x – α)(x
– α 2)(x
– α 3) (x
– α 4)(x
– α 5)(x
– α 6) =
= x
6 + α 10 x
5 + α 14 x
4 + α 4 x
3 +α 6 x
2 + α 9 x
+ α 6
g (x) – yasovchi ko‘pxad;
 ax7
+a8x6
x6+a10x5+a14x4+a4x3+a6x2+a9x
+a6
ax7
+a8x6
x6+a10x5+a14x4+a4x3+a6x2+a9x
+a6
ax7
+a11x6
+ a15x5
+a5x4
+a7x3
+a10x2+
a7x
ax +a7
a7x6
+a13x5+a5x4
+a7x3+a10x2
+a7x
a7x6
+a2x5+a6x4
+a11x3+a13x2
+ax+a13
a8x5
+a9x4+a8x3
+a9x2+a14x
+a13
Kodlangan
kombinatsiya quyidagi ko‘rinishda bo‘ladi:
α x7 + α8 x6
+ α8 x5 +α9 x4 + α8
x3 + α9 x2 + α14 x +
α13
Axborotlarni
Rid-Solomon kodida kodlashtirish algoritmini ko‘rib chiqamiz. Algoritm asosida
eng avvalo Galua maydoni xisoblanadi. So‘ngra Rid-Solomon kodining parametrlari
kiritiladi va Galua maydoni elementlari yordamida kodlashtirish amalga oshiriladi.
Kodlashtirish informatsion ketma-ketlikni r razryad chapga surgandan so‘ng, yasovchi
polinomga bo‘lingandan xosil bo‘lgan qoldiqni o‘sha informatsion ketma-ketlikka
qo‘shish orqali amalga oshiriladi.
Kodlashtirish
algoritmi quyidagi etaplardan (bloklardan) iborat.
1. O‘zgaruvchilar
va belgilashlar kiritiladi;
2. Galua
maydoni parametrlari m, g(x), d kiritiladi; m – ushbu maydonning kengayish qiymati;
g(x)- m kengaytma uchun keltirilmaydigan ko‘pxad; α
– oddiy elementi.
3. m
qiymatga bog‘lik ravishda Galua
maydonining elementlar soni kiritiladi;
4. Galua
maydonining elementlarini xisoblash uchun boshlang‘ich shart kiritiladi;
5. «Xar
bir element oldingi elementni α
– oddiy elementga ko‘paytirilganiga teng» degan prinsip bo‘yicha Galua
maydoni elementlari xisoblanadi;
6. Galua
maydonining eng katta elementining darajasi, keltirilmaydigan ko‘pxad darajasidan
kichik bo‘lishi kerak. Ya’ni
dseg
α (I) < deg g(x)
Shart tekshiriladi.
Agar shart bajarilmasa 7 –blokka o‘tiladi. Unda navbatdagi element Galua
maydonining keltirilmaydigan ko‘pxadi bilan mavjud elementni mod 2 bo‘yicha operatsiyasi
orqali xisoblanadi;
8.
Galua
maydonining hamma
elementlari chop etiladi. Galua
maydonining elementlarini xisoblash algoritmi 11.1
– rasmda keltirilgan.
9.
Rid-Solomon kodining parametrlari kiritiladi:
- n
– blok uzunligi;
- r
– blokning tekshiruv qismi;
- k
– blokning informatsion qismi;
- g(x)
– yuqoridagi parametrlarga bog‘liq bo‘lgan keltirilmaydigan ko‘pxad;
10.
Kodli kombinatsiya (k (I))ning qiymati kiritiladi;
11.
d – kod masofasi xisoblanadi;
12.
t - to‘g‘irlash
qobiliyati xisoblanadi;
13.
d va t ning qiymati chop etiladi;
14.
Kiritilgan informatsion qismning elementlari soniga mos ravishda kodli kombinatsiya
uzunligi xisoblanadi;
15.
Kodli kombinatsiyaning informatsion qismi k (I) ni r razryad chapga suriladi.
Surish natijasida xosil bo‘lgan kodli kombinatsiya N2 ga teng;
16.
Xosil bo‘lgan kodli kombinatsiya N2 ni g(x) keltirilmaydigan ko‘pxadga bo‘linadi
va R(x) qoldiq xosil qilinadi. Bo‘lish prinsipi ikkilik kodlarni bo‘lish kabi bo‘ladi,
lekin 0 va 1 lar o‘rnida Galua maydonining elementlari bo‘ladi. Qo‘shish
va ko‘paytirish amallari ham
mod m asosida bo‘ladi;
17.
r ta nolni xosil bo‘lgan R(x) qoldiq bilan almashtiriladi. Bu operatsiya natijasida
kodlashtirilgan kombinatsiya n1 xosil qilinadi;
18.
Kod parametrlari n, k va g(x) – keltirilmaydigan ko‘pxad, hamda
n1 – kodlashtirilgan kombinatsiya chop etiladi.
Kodlashtirish
algoritmi 11.2.-
rasmda keltirilgan.
Rida – Solomon kodida kodlangan axborotlarni
dekoderlash usullari
Aloqa kanaliga ta’sir etuvchi shovqin xisobiga, istalgan kodli
kombinatsiya xatolarga uchrashi mumkin. Kodli kombinatsiyadagi xatolar to‘g‘risidagi
ma’lumotni sindromlar orqali olish mumkin.
f
(x) – kodli kombinatsiya uzatilgan bo‘lsin. Aloqa kanali bo‘yicha uzatish jarayonida
xatolar xosil bo‘ldi va F(x) = f(x) + e(x) kombinatsiya qabul kilindi, ye(x) – xatolar
vektori. Xatolar vektori noldan farqli bo‘lgan kombinatsiyalardan iborat. Xatolar
vektori ye(x) ning har
qaysi noldan farqli komponenti Ui va X i elementlar ko‘rinishida
yoziladi; Ui – xatolarning qiymati, X i - xatolar pozitsiyalarining
nomerlari. Ui – GF(P) maydonning elementi, X i – GF(P m)
maydonning elementidir.
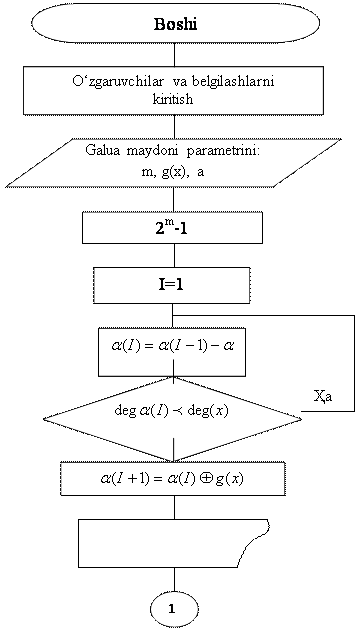

11.1
– rasm. Galua maydoning elementlarini xisoblash algoritmi

n,k,g(x)n1
11.2
– rasm. Rida – Solomon kodida kodlashtirish algoritmi
Agar
t ta xato yuz bergan bo‘lsa, unda ye(x) t ta noldan farqli bo‘lgan komponentdan
tashkil topadi va t juft (Ui X i ) ni yozish talab etiladi.
U xolda
ye (αi ) = 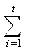 Ui Xi
= Si
Ui Xi
= Si
S i = e(α i ) ning qiymatlari 0 £ i £ 2 t – 1 tengsizlikni tekshirish orqali beriladi.
Shunday
qilib,
xatolar sindromi xatolar bilan quyidagi tenglama orqali
bog‘langan:
S j = 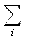 Ui X
i j , 0 £
j £ 2 t – 1
Ui X
i j , 0 £
j £ 2 t – 1
Ushbu
tenglama nochizikli tenglama bo‘lib uni yechishning ixtiyoriy usuli xatolarni to‘g‘irlash
protsedurasining asosini tashkil etadi. Bu tenglamani yechishda Berlekemp tomonidan
taqdim etilgan usuldan foydalaniladi. Bu usulda murakkab xisoblangan etap – xatolar
lokatorining ko‘pxadini topishdan iborat.
T(x) = T0 + T1 + ….+ T n-1
q  (1 – x i x)
(1 – x i x)
Ko‘rinishidagi
ko‘pxad – xatolar lokatorining ko‘pxadi deyiladi. Bu yerda X i (i =
1, …t) – xatolar lokatorlari deyiladi. Ular Xi
=α
ii ,...
Xt=α it
ga
teng bo‘lgan GF (P) maydon elementlaridan iborat.
Xatolar
lokatorining ko‘pxadini
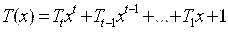
T t , T t-1, ….T1 kattaliklar ma’lum bo‘lsa quyidagini
yozish mumkin:
S
j = -  T i S
j-1
T i S
j-1
bu
yerda j = t + 1; …. ; 2 t ·
S j- t ; S j- t+1 ; ….S j- 1 komponentlar bo‘yicha
navbatdagi S j T t T t-1 ….T 1
qiymatlar yordamida xisoblanadi. Dekoderga S1,
S2, S2 t sindromlar komponentlari ma’lum, T t
;T t-1 ….T 1 qiymatlar esa noma’lum. Shuning uchun xatolar
lokatorlarining ko‘pxadini (T(x)) aniqlash quyidagicha amalga oshadi:
S j =  Ti Sj-
1
Ti Sj-
1
Tenglama yordamida dekoder o‘ziga
ma’lum bo‘lgan S1, S2,... S2t ketma- ketliklarni
xosil qilish uchun, minimal uzunlik L aniqlanadi. L – ketma- ketlikning minimal
uzunligi xisoblanadi. U xatolar soniga teng. Lekin aloqa kanalidagi xatolar tasodifiy
va teng extimolli deb qaraladi.
Endi
yuqorida keltirilganlar asosida Berlekemp - Messi algoritmini – T(x) xatolar lokatorlari
ko‘pxadini xisoblashni formula ko‘rinishga keltiramiz: S1; S2;…;S2t
sindrom komponentlari aniqlangan bo‘lsin va T0 (x) = 1, V0
(x) = 1 , L0 = 0 boshlang‘ich shartda
Δ
n =  T
j S n-j
T
j S n-j
tenglik
o‘rinli bo‘lsin. Bu yerda
Δ
n - GF(2 m), n q
1:2, …. 2t maydon elementlari orqali xisoblanuvchi
xisoblash xatoligi;
V
(x) – qo‘shimcha element.
Agar
Δ
n ¹
0 va 2 L n-1 £ n – 1 shart bajarilsa,
u xolda Ln
= n–Ln-1
va Vn
(x)
=Δ-1
n
·
Tn-1
(x)
bo‘ladi. Agar 2L n-1£
n –1 shart bajarilmasa, u xolda
Ln
= Ln-1 va Vn (x) = x ·
Vn-1 (x)
bo‘ladi.
U xolda T2 t (x) ko‘pxad kichik darajali ko‘pxad bo‘ladi.
Berlekemp
– Messi algoritmining blok-sxemasi 11.3
– rasmda keltirilgan.
Xatolar
lokatorlarining ko‘pxadi xisoblangandan so‘ng, xatolar lokatorlarining ko‘pxadini
ildizlari izlanadi. Bu esa Chen protsedurasi orqali amalga oshiriladi. U GF(2m)
maydonning hamma
elementlarini T(x) – xatolar lokatorlarining ko‘pxadiga ketma-ket qo‘yib chiqishdan
iborat. T(x) ko‘pxadga qo‘yganda uni nolga aylantiradigan GF(2m) maydonning
elementlari, bu ko‘pxadning ildizlari deyiladi. Xatolar lokatorlarning ko‘pxadini
ildizlariga teskari bo‘lgan qiymat – xato sodir bo‘lgan pozitsiyalarni bildiradi.
Rid–Solomon
kodini dekoderlashning keyingi etapi U1; U2; Ut xatolar
qiymatini topishdan
iborat. Xatolar qiymatini topishda Forni algoritmidan foydalaniladi. Bu algoritmni
keltirishdan avval xatolar lokatorlarining ko‘pxadini quyidagi ko‘rinishda yozamiz:
T(x)
=Tt xt +Tt-1 xt-1 + … + T1
x + 1
ildizlari
Xi –1 , i = 1; 2; ….; t dan iborat.
yo‘q ha
yo‘q
ha
yo‘q
ha
dekoderlashning
keyingi etapiga
qabul
qilingan kombinatsiyada t dan
ortiq xato bor
11.3-rasm.
Berlekemp – Messi algoritmi
Bu
ko‘pxadni yana quyidagicha yozish mumkin:
Ω
(x) =  Ui Xi
P (1 – Xi X)
Ui Xi
P (1 – Xi X)
va
ushbu ifodadan Ui ni topish mumkin:

T’(x) – t (x) dan olingan xosila.
Rid-Solomon
kodida kodlangan axborotlarni dekoderlash algoritmini tushuntirib o‘tamiz. Dekoderlash
algoritmi (11.4-rasm)
quyidagi ketma-ketlik (blok)lardan iborat:
1.
(19) – t1 xatolar soni kiritiladi;
2.
(20) – n1 kodli kombinatsiyadagi xato o‘rni kiritiladi;
3.
(21) – xatolar qiymati v (d) kiritiladi;
4.
(22) – xato o‘rni va uning qiymati chop etiladi;
5.
(23) – joylashgan o‘rniga bog‘liq xolda xatolarni n1
kodli kombinatsiyaga kiritiladi va n2 kodli kombinatsiya xosil bo‘ladi;
6.
(24) – xato kodli kombinatsiya n2 chop etiladi;
Keyingi
etap – xatolar sindromlari S (x) ni xisoblash.
7.
(25) – Sindromlar soni beriladi;
8.
(26) – sindromni tashkil etgan elementlar soni beriladi;
9.
(27) – quyidagi formula bo‘yicha sindromlar qiymatlari S xisoblanadi:

Xatolar o‘rni va B(α)ni
chop etish
n2
11.4-rasm.
Rida-Solomon kodini dekoderlash algoritmi
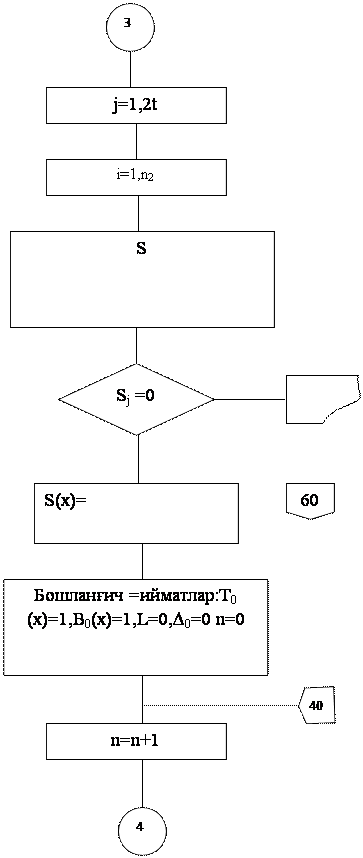
n2
11.4-rasm.
Rid-Solomon kodini dekoderlash algoritmi
(davomi)

Kombinatsiyada
t da
ortiq xato
T(x)
11.4-rasm.
Rid-Solomon kodini dekoderlash algoritmi
(davomi)

To‘g‘irlangan
kombinatsiyani chop etish
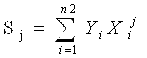
U
– Galua maydoni elementi a ning qiymati;
X
– Galua maydoni elementining kodli kombinatsiyada joylashish o‘rni.
10.
(28) – Sindrom qiymatlari tekshiriladi. Agar hamma
sindromlar nolga teng bo‘lsa, unda kombinatsiyada xato yo‘q va 11-blokka o‘tiladi.
11-
blokda n2 kodli kombinatsiyani chop etish bajariladi
va dastur ishi yakunlanadi. Agar sindromlarning xatto
ixtiyoriy bittasi ham
nolga teng bo‘lmasa, unda xato mavjud deb topiladi va uni aniqlash xamda to‘g‘irlash
talab etiladi;
12.
(30) – Sindromlarning ko‘pxadi S (x) xisoblanadi;
Endi
Berlekemp-Messi algoritmi bo‘yicha xatolar lokatorlarining ko‘pxadini xisoblashga
o‘tiladi.
13.
(31) – algoritm ishini ta’minlash maqsadida boshlang‘ich shartlar kiritiladi;
14.
(32) – Berlekemp-Messi algoritmi bo‘yicha izlash qadamining nomeri beriladi;
15.
(33) – xatolik D n xisoblanadi;
16.
(34) – bu xatolik qiymati tekshiriladi. Agar D n ¹
0, u xolda Tn(x) ko‘pxad 17-blokdagi formula bo‘yicha xisoblanadi. Agar
D
n = 0, u xolda Tn(x)
oldingi ko‘pxad Tn-1(x) ga teng (18-blok);
19.
(37) – 2Ln-1 £
n-1 shart tekshiriladi.
L – xatolar soni;
n - izlash qadami.
Agar
ushbu shart bajarilmasa, xatolar soni L oldingi qiymati (Ln-1) ga teng
bo‘lib qoladi (21-blok). Agar shart bajarilsa xatolar soni L ortadi (20-blok);
22.
(40) – n = 2 t – xatolar lokatorlarining ko‘pxadini izlash qadami 2t qiymatdan oshib
ketmasligi kerak degan shart tekshiriladi. Agar ushbu shart bajarilsa, u xolda
23-blokka o‘tiladi, aks xolda 14-blokka;
23.
(41) – T(x) ko‘pxad darajasi tekshiriladi. U topilgan xatolar sonidan oshmasligi
kerak. Agar shart bajarilmasa, unda: «qabul qilingan kombinatsiyada t dan ortiq
xato mavjud» - degan xabar chop etiladi va dastur tugallanadi. Agar shart bajarilsa,
unda 24-blokka o‘tiladi;
24.
(42) – xatolar qiymatlarining ko‘pxadi W (x) xisoblanadi;
Rid-Solomon
kodida kodlangan axborotlarni dekoderlash algoritmini tushuntirib o‘tamiz. Dekoderlash
algoritmi (11.5-rasm)
quyidagi ketma-ketlik (blok)lardan iborat:
11.5-rasm.
Rid-Solomon kodini dekoderlash
blok-sxemasi
1.
(19) – t1 xatolar soni kiritiladi;
2.
(20) – n1 kodli kombinatsiyadagi xato o‘rni kiritiladi;
3.
(21) – xatolar qiymati v (d) kiritiladi;
4.
(22) – xato o‘rni va uning qiymati chop etiladi;
5.
(23) – joylashgan o‘rniga bog‘liq xolda xatolarni n1 kodli kombinatsiyaga kiritiladi
va n2 kodli kombinatsiya xosil bo‘ladi;
6.
(24) – xato kodli kombinatsiya n2 chop etiladi;
Keyingi
etap – xatolar sindromlari S (x) ni xisoblash.
7.
(25) – Sindromlar soni beriladi;
8.
(26) – sindromni tashkil etgan elementlar soni beriladi;
9.
(27) – quyidagi formula bo‘yicha sindromlar qiymatlari S xisoblanadi:
Sj =  Ui
Ui
U
–Galua maydoni elementi a ning qiymati;
X
– Galua maydoni elementining kodli kombinatsiyada joylashish o‘rni.
10.
(28) – Sindrom qiymatlari tekshiriladi. Agar xamma sindromlar nolga teng bo‘lsa,
unda kombinatsiyada xato yo‘q va 11-blokka o‘tiladi. 11-blokda
n2 kodli kombinatsiyani chop etish bajariladi va dastur ishi yakunlanadi. Agar sindromlarning
xatto
ixtiyoriy bittasi xam nolga teng bo‘lmasa, unda xato mavjud deb topiladi va uni
aniqlash hamda
to‘g‘irlash talab etiladi;
12.
(30) – Sindromlarning ko‘pxadi S (x) xisoblanadi;
Endi
Berlekemp-Messi algoritmi bo‘yicha xatolar lokatorlarining ko‘pxadini xisoblashga
o‘tiladi.
13.
(31) – algoritm ishini ta’minlash maqsadida boshlang‘ich shartlar kiritiladi;
14.
(32) – Berlekemp-Messi algoritmi bo‘yicha izlash qadamining nomeri beriladi;
15.
(33) – xatolik D n xisoblanadi;
16.
(34) – bu xatolik qiymati tekshiriladi. Agar D n ¹
0, u xolda Tn (x) ko‘pxad 17-blokdagi formula bo‘yicha xisoblanadi. Agar
D
n = 0, u xolda
Tn
(x) oldingi ko‘pxad Tn-1 (x) ga teng (18-blok);
19.
(37) – 2Ln-1 £
n-1 shart tekshiriladi.
L – xatolar soni;
n - izlash qadami.
Agar
ushbu shart bajarilmasa, xatolar soni L oldingi qiymati (Ln-1) ga teng
bo‘lib qoladi (21-blok). Agar shart bajarilsa xatolar soni L ortadi (20-blok);
22.
(40) – n = 2 t – xatolar lokatorlarining ko‘pxadini izlash qadami 2t
qiymatdan oshib ketmasligi kerak degan shart tekshiriladi. Agar ushbu shart bajarilsa,
u xolda 23-blokka o‘tiladi, aks xolda 14-blokka;
23.
(41) – T(x) ko‘pxad darajasi tekshiriladi. U topilgan xatolar sonidan oshmasligi
kerak. Agar shart bajarilmasa, unda: «qabul qilingan kombinatsiyada t dan ortiq
xato mavjud» - degan xabar chop etiladi va dastur tugallanadi. Agar shart bajarilsa,
unda 24-blokka o‘tiladi;
24.
(42) – xatolar qiymatlarining ko‘pxadi W (x) xisoblanadi;
25.
(43) – T(x) ning xosilasi topiladi;
26.
(44) – natija chop etiladi;
27.
(45) – Chen protsedurasiga mos ravishda xatolar o‘rnini aniqlash uchun siklning
boshi beriladi;
28.
(46) – xatolar lokatorlarining ko‘pxadi T(x) ni ildizlarini topish uchun tekshirishlar
soni aniqlanadi;
29.
(47) – xatolar lokatorlarining ko‘pxadini ildizlarini xisoblash uchun Galua
maydonining boshlang‘ich elementi beriladi;
30.
(48) – Xatolar mavjud bo‘lgan pozitsiyalarning nomerlari xisoblanadi. Buning uchun
Galua
maydonining xamma elementlari navbatma –
navbat T(x) ko‘pxadga qo‘yib tekshiriladi;
31.
(49) – T(x) ko‘pxad tekshiriladi. Agar T(x) = 0 bo‘lsa, unda ushbu qiymat ildiz
deb topiladi va T(x) ko‘pxad ildizining teskari qiymati xisoblanadi (34-blok). Bu
qiymat esa xato yuz bergan pozitsiya nomerini bildiradi;
32.
(50) – Galua
maydonining navbatdagi elementiga o‘tiladi;
33.
(51) – T(x) ning ildizlarini topishda Galua
maydonining xamma elementlarining ishtirok etganligi tekshiriladi;
35.
(53) – Xatolar lokatorlarining ko‘pxadini navbatdagi ildizini aniqlashga o‘tiladi;
36.
(54) – ko‘pxadning xamma ildizlari topilganligi tekshiriladi;
37.
(55) – xatolar soni beriladi;
38.
(56) – xatolarning qiymatlarini xisoblash uchun boshlang‘ich
element beriladi;
39.
(57) – xatolarning qiymatlari xisoblanadi;
40.
(58) – n2 kombinatsiyadagi xatolarni to‘g‘irlash
amalga oshadi.
Buning
uchun esa xisoblab topilgan xatolarning qiymatlarini kombinatsiyadagi xatolarning
qiymatlari bilan o‘zaro mod m bo‘yicha qo‘shiladi;
41.
(59) – to‘g‘irlangan
kodli kombinatsiya chop etiladi;
42.
(60) – dastur ishi yakunlanadi.
Rid-Solomon
kodida kodlangan axborotlar dekoderi 11.5-rasmda
blok sxema ko‘rinishida berilgan.
Dekoder
kirishiga kodlangan axborot va xatolar vektori yig‘indisidan iborat bo‘lgan kodli
kombinatsiya F(x) kelib tushadi. F(x) kodli kombinatsiya buferda saqlanadi. Shuningdek
ushbu F(x) kodli kombinatsiya o‘zgarishlarni xisoblash qurilmasiga ham
tushadi. Unda sindromlar xisoblanadi. Sindromlardan xatolar lokatorlarining ko‘pxadi
T(x) ni aniqlovchi tenglamani yechishda foydalaniladi.
T(x)
ko‘pxadni aniqlash algoritmi 11.3.-rasmda
keltirilgan edi.
Dekoder
tenglamani yechish bilan bir vaqtning o‘zida xosil qilinuvchi xatolar qiymatlarining
ko‘pxadi W (x) ni xisoblashni amalga oshiradi.
«Chen
prodedurasi»ni bajaruvchi qurilma xatolar o‘rnini aniqlaydi.
«Xatolarni
xisoblash» blokida esa xatolarning qiymatlari aniqlanadi va bu qiymatlar ventil
xamda summator yordamida, xatolar mavjud bo‘lgan pozitsiyadagi simvollar bilan qo‘shiladi.
Shu tariqa to‘g‘rilangan kodli kombinatsiya f (x) summator chiqishda xosil qilinadi.
11-ma’ruza
uchun nazorat savollari
1. Rid-Solomon
kodlari parametrlariga nimalar kiradi?
2. Axborotlarni
Rid-Solomon kodida kodlashtirish usullariga tushuncha bering?
3. Galua
maydoni qanday quriladi?
4. Galua
maydonini kodlashtirish qanday amalga oshiriladi?
5. Rid-Solomon
kodlashtirish algoritmi bosqichlariga tushuncha bering?
12-ma’ruza.
Fayra kodlari
Reja:
1. Fayra
kodi tushunchasi.
2. Fayra
kodini qurish.
3. Fayra
kodida yasovchi polinomlar.
4. Axborotlarni
Fayra kodida kodlashtirish usullari.
5. Fayra
kodi parametrlari.
6. Axborotlarni
Fayra kodida kodlashtirish usullariga misol.
7. Fayra
kodida kodlashtirish algoritmi.
Fayra
kodini qurish asoslari. Bir karralik va ko‘p karralik
tasodifiy xatolarni to‘g‘irlovchi kodlarni ishlatish, xar doim ham o‘zini oqlayvermaydi.
Bunga sabab, aloqa kanallariga guruxli shovqinlarning ta’sir qilishidir. Guruxli
shovqinlar esa kodli kombinatsiyadagi element (razryad)larni xatolarga uchrashini
keltirib chiqaradi. Bu esa xatolar paketi deyiladi.
Uzatilgan
kodli kombinatsiya 10100010001 ko‘rinishida bo‘lsin. Qabul
qilish tomonida bu kodli kombinatsiya 10001010101 ko‘rinishda olindi. Bu kombinatsiyalarning
razryadlarini o‘zaro modul 2
(mod 2) bo‘yicha yig‘indisini olsak,
natija quyidagi ko‘rinishda bo‘ladi: 00101000100. Bundan
ko‘rinadiki, qabul qilingan kodli kombinatsiyadagi xatolar soni natijaviy kombinatsiyadagi
birlar soni (vazni) uchga teng bo‘lar ekan.
Xatolar
paketining uzunligi v deb – qabul kilingan kodli kombinatsiyadagi eng yuqori xato
razryad bilan eng kichik xato razryad orasidagi farqli bir birlikka oshirilganiga
aytiladi.
Bizning
yuqoridagi misolimizda xatolar paketining uzunligi
v
= (9 – 3) + 1 = 7 ga teng. Xatolar paketini aniqlash va to‘g‘irlash uchun ancha
effektiv xisoblangan Fayra kodi xozirda qo‘llanilmokda.
Fayra
kodi siklik kodlar turkumiga kirib, xamma siklik kodlar kabi u ham
ikkita muxim xususiyatga ega: birinchidan, berilgan kodning ixtiyoriy ikkita ruxsat
etilgan kombinatsiyasining mod 2 bo‘yicha yig‘indisi, yana ruxsat etilgan kodli
kombinatsiyani beradi. Bundan esa ko‘rinadiki, siklik koddagi eng kichik kod masofasi
uning kombinatsiyalari ichidan eng kichik vaznlisi orqali aniqlanadi.
Odatda,
eng kichik kod masofasini topish uchun, kodli kombinatsiyalarning xamma juftlarini
o‘zaro mod 2 bo‘yicha yig‘indisini aniqlaymiz. Yig‘indilar ichidan eng kichik vaznlisi
eng kichik kod masofasini bildiradi.
Ikkinchi
muxim xususiyati, agar ruxsat etilgan kodli kombinatsiyani bitta elementga siklik
siljitsak, ya’ni oxirgi pozitsiyadagi elementni birinchi qo‘yib, qolganlarini undan
keyin joylashtirsak, natijada shu kodga tegishli bo‘lgan boshqa ruxsat etilgan kodli
kombinatsiya xosil bo‘ladi. Masalan: agar kodli kombinatsiya 110101 dan iborat
bo‘lsa, bitta qadamga siklik siljitish orqali 111010 dan iborat bo‘lgan boshqa ruxsat
etilgan kombinatsiyani olamiz. Keyingi siljish esa 011101 ni beradi va xokazo.
Xamma
siklik kodlar kabi Fayra kodidagi kodli kombinatsiyalarda ham
birinchi tekshiruv bitlari,
keyin informatsion bitlar joylashgan bo‘ladi. Ya’ni aloqa
kanaliga birinchi k informatsion bitlar, keyin esa r tekshiruv – bitlari uzatiladi.
Fayra
kodini qurishda, kodli kombinatsiyalarni x argumentdan iborat bo‘lgan ko‘pxad ko‘rinishiga
keltirish ancha qulayliklarni yuzaga keltiradi. Bu ifodadagi x – sanoq sistema
asosini bildiradi.
Ixtiyoriy
sanoq sistemasidagi N sonini quyidagicha yozish mumkin:
N
= Kn b n-1 + K n-1 b n-2 + … K i bi-1
+ . . . K2
b1 +
K1 b 0
b-
sanoq sistema asosi;
n
– sondagi razryadlar miqdori;
Ki-
razryaddagi raqam.
Yuqoridagi
ifodaga asosan ixtiyoriy sonni x o‘zgaruvchili polinom ko‘rinishda yozish mumkin.
Masalan
ikkilik sanoq sistemasidagi 101001101 sonni, x o‘zgaruvchili polinom ko‘rinishda
yozamiz.
G(X)
= 1•X 8 + 0 • X 7 + 0 • X 6 + 0 • X 5
+ 0 • X 4 + 0 • X 3 + 0 • X 2 + 0 • X 1 +0
• X 0
yoki
G(X) = X 8 + X 6 + X 3 + X 2
+ 1
So‘nggi
ikkita ifodani solishtirib, koeffitsienti nol bo‘lgan xadlar yozilmasligini ko‘ramiz.
Undan tashqari ko‘pxad darajasi har
doim kombinatsiyadagi razryadlar sonidan bittaga kichik bo‘ladi.
Kodli
kombinatsiyalarni tasvirlovchi ko‘pxadlarni ko‘paytirish va bo‘lish oddiy algebraik
qoida asosida bajarilsa, qo‘shish esa mod 2 bo‘yicha amalga oshiriladi:






Masalan:
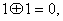

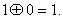
Siklik
kodlar yasovchi (xosil qiluvchi) polinom bilan xarakatlanadi. Kodlashtirish bevosita
yasovchi polinom orqali xosil qilinadi. Shu sababli ushbu polinom xosil qiluvchi,
yasovchi polinom deyiladi. Yasovchi polinom darajasi r = n - k ga teng bo‘ladi.
Yasovchi polinomning ko‘rinishi va uning darajasi siklik kodning korrektorlash qobiliyatini
ifodalaydi.
Yasovchi
polinom sifatida keltirilmaydigan ko‘pxadlar olinadi. Keltirilmaydigan ko‘pxad deb
– faqat o‘ziga va birga qoldiqsiz bo‘linadigan polinomlarga aytiladi. Ya’ni bunday
polinomlarni ko‘paytuvchilarga ajratib bo‘lmaydi. Quyida
beshinchi darajagacha bo‘lgan keltirilmaydigan polinomlar ko‘rsatilgan:
P(x1)
= x+1;
P(x2)
= x2 + x+1;
P(x3)
= x3 + x+1;
P(x3)
= x3 + x2 +1;
P(x4)
= x4 + x +1;
P(x4)
= x4 + x3 + x2 + x +1;
P(x5)
= x5 + x2 +1;
P(x5)
= x5 + x3 +1;
P(x5)
= x5 + x3 + x2 + x +1;
P(x5)
= x5 + x4 + x3 + x +1;
P(x5)
= x5 + x4 + x3 + x 2+1;
Siklik
kodning aloxida jixatlaridan biri, uning xamma kodli kombinatsiyalarini yasovchi
polinomga qoldiqsiz bo‘linishidir. Xatoga uchragan kodli konbinatsiyani yasovchi
polinomga bo‘lganda, albatta qoldiq xosil bo‘ladi. Demak, yasovchi polinomga bo‘lish
natijasida qoldiq xosil bo‘lmaydigan kodli kombinatsiyaga, siklik kodning ruxsat
etilgan kodli kombinatsiyasi deb ataladi. Aks xolda esa ta’kidlangan yoki man qilingan
kodli kombinatsiya deyiladi.
Siklik
kodining bunday xususiyatidan xatolarni aniqlash va to‘g‘irlashda foydalaniladi.
Ma’lumki, uzatiladigan kodli kombinatsiyaga shovqin ta’sir etishi natijasida u man
qilingan kombinatsiyaga aylanadi. Bunday kombinatsiyani yasovchi polinomga bo‘lganda
qoldiq xosil bo‘ladi. Bu esa xato yuz berganligini bildiradi. Demak yasovchi polinomga
bo‘lishdan xosil bo‘lgan qoldiq orqali xatolar aniqlanadi.
Axborotlarni
Fayra kodida kodlashtirish usullari. Uzatish
kanaliga impuls xarakteridagi shovqin ta’sir etishi natijasida xatolar paketi xosil
bo‘ladi. Bu impuls davomiyligi bitta razryad davomiyligidan katta bo‘ladi. Natijada
xosil bo‘lgan xatolar paketining davomiyligi shovqin davomiyligiga mos bo‘lib,
bunday shovqin tasodifiy bo‘lmagan shovqin xisoblanadi.
Bir
karralik bunday xatolar paketini aniqlash va to‘g‘irlash uchun Fayra kodi qo‘llaniladi.
Fayra kodini yasovchi polinom quyidagi ko‘rinishda bo‘ladi:
R (x) = g (x) (x0
+1)
g(x)
– m - darajaga tegishli bo‘lgan;
t
– darajali keltirilmaydigan ko‘pxad;
s
– m ga karralik bo‘lmagan butun son;
g
(x) – polinom m – darajaga tegishli deyiladi, agar m – xm +1 ikkixad
g (x) koldiqsiz bo‘linadigan eng kichik musbat son bo‘lsa.
Ixtiyoriy
t uchun m = 2 t –1 darajaga tegishli bo‘lgan faqat bitta t darajali
R(x) polinom mavjud. Masalan: t = 3, m = 23 –1 = 7
R
(x) = x3 + x2 +1

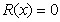
Ya’ni
R(x) = x3 +x2 +1 ko‘pxad m=7 darajaga tegishli bo‘lgan
polinom. Bu xolatda s soni m ga karralik bo‘lmagan, ya’ni qoldiqsiz bo‘linmaydigan
quyidagi sonlar bo‘lishi mumkin: 15, 16, 17, 18, 19, 20 va xok.
t
darajali keltirilmaydigan polinom deb – darajasi t dan kichik bo‘lgan xech qaysi
polinomga qoldiqsiz bo‘linmaydigan ko‘pxadga aytiladi.
Chekli
maydonning b elementining m – tartibi deb bm
= 1 bo‘ladigan m ning eng kichik qiymatiga aytiladi, b
esa xm –1 ko‘pxadning ildizi xisoblanadi.
Fayra
kodining uzunligi s va m sonlarinning eng kichik umumiy karralisiga (EUK) teng
bo‘ladi:
n
= EUK (s, m)
Tekshiruv
razryadlarining soni quyidagi ifoda orqali aniqlanadi:
r
= c + t
Informatsion bitlarining soni esa quyidagiga teng:
k
= n – c – t
To‘g‘irlanadigan
xatolar paketining uzunligi v quyidagi tengsizlikni qanoatlantiradi:
t
³ v, c ³
2 v – 1
Fayra
kodi bir vaqtning o‘zida v uzunlikdagi xamda undan kichik bo‘lgan xatolar paketini
to‘g‘irlashi va d ³ v uzunlikdagi xatolar
paketini aniqlashi mumkin:
s
³ v + a
- 1, t ³ v
R(x)
yasovchi ko‘pxaddagi xs +1 ko‘paytuvchi s uzunlikdagi xatolar paketini
aniqlashi va uzunligi v dan oshmaydigan xatolar paketining to‘liq qiymatini
aniqlashi mumkin.
Xatolar
paketini joylashishi va xolati to‘g‘risidagi ma’lumot esa g(x) ko‘paytuvchi
yordamida aniqlanadi. Demak R(x) yasovchi ko‘pxaddagi xadlar mos ravishda bir karralik
xatolar paketini tegishli qiymatini, xolatini, joyini aniqlash imkonini beradi.
Masalan:
k=63, v=3, a=9 ya’ni uzunligi v=3 ga teng va undan kichik
bo‘lgan xatolar paketini to‘g‘irlovchi xamda bir vaqtning o‘zida uzunligii a=9
ga teng va undan kichik bo‘lgan xatolar paketini aniqlovchi kodni
qurish kerak bo‘lsin. U xolda:
t ³ v = 3 , c ³
v + a-
1 = 3 + 9 -1 = 11
tengsizlik
o‘rinli bo‘ladi. Bu xolatda 3-darajali keltirilmaydigan polinomni tanlab olamiz:
g (x) = x 3 +x 2 +1
m=2t
–
1=7, c va m sonlarining kichik karralisi quyidagiga
teng bo‘ladi:
n = EKUK
(c, m) = EKUK
(7, 77) = 77
Kodni
yasovchi polinom quyidagi ko‘rinishga ega bo‘ladi:
R(x) = ( x3 +x2 +1) (x11
+1)
Shunday
qilib, uzunligi v=3 va undan kichik bo‘lgan xatolar paketini to‘g‘irlovchi
xamda bir vaqtning o‘zida uzunligi a=9 va undan kichik
bo‘lgan xatolar paketini aniqlovchi Fayra kodi n=77, k=63,
c+t=r=14 kattaliklardan iborat.
Fayra
kodi siklik kodlar sinfiga kiradi. Shuning uchun u siklik koddagi xususiyatlarga
ega. Shu jumladan Fayra kodida kodlashtirish jarayoni ham
siklik kodlarini kodlashtirish jarayoni kabi amalga oshadi.
Axborotlarni
Fayra kodida kodlashtirish ikki xil usulda amalga oshiriladi:
1.
Oddiy kodning k- elementli kombinatsiyasini R(x) yasovchi polinomga ko‘paytirish
orqali kodlashtirish:
F (x) = Q (x) P (x)
2.
Oddiy kodli kombinatsiyani xr xadga ko‘paytirib, ko‘paytmaga uni R(x)
yasovchi polinomga bo‘lish natijasida xosil bo‘lgan qoldiqni qo‘shish orqali:
F (x) = G (x) ·
x r + R (x)
Ya’ni

G (x) · x r = Q
(x) · P (x) + R (x)
F (x) = G (x) · x r +R (x)
= Q (x) · P (x)
F
(x) – Fayra kodining polinomli ko‘rinishi.
Fayra
kodi asos qilib olingan kodli kombinatsiyalarni muayyan tarzda tanlab olish orqali
xosil qilinadi. Bu kodli kombinatsiyalar esa matritsa ko‘rinishida yozilib, shu
matritsa orqali Fayra kodining tegishli kodli kombinatsiyalari xosil qilinadi.
n ta ustun va k ta qatordan iborat bo‘lgan bunday matritsa xosil qiluvchi matritsa
deyiladi.
Ikkinchi
usul bo‘yicha kodlashtirish uchun, xosil qiluvchi matritsani tuzishni qarab chiqamiz.
Bunday matritsaning qatorlarini tuzishda faqat bitta razryadida bir ishtirok etgan
G(x) oddiy kodli kombinatsiyalar olinadi. Aynan shu kodli kombinatsiyalar xr
ga ko‘paytirilib, yasovchi polinomga bo‘linadi:
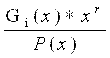
va
natijada Ri(x) qoldiqlar topiladi. Matritsaning tegishli qatorlari
Gi (x) · x r + R i
(x)
ko‘rinishda
yoziladi. Bunday matritsa ikkita qism matritsaga bo‘linadi:
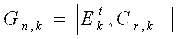
 -
transponirlangan birlik matritsa;
-
transponirlangan birlik matritsa;
Cr,
k - Ri (x) qoldiqlardan iborat bo‘lgan r ustun va k qatorli
qism matritsa.
Xosil
qiluvchi matritsa Gn, k k ta kodli kombinatsiyani bevosita xosil
qilish imkonini beradi. Qolgan
2k - k – 1 ta kodli kombinatsiya xosil qiluvchi matritsa qatorlarini
mod 2 bo‘yicha qo‘shish orqali aniqlanadi.
Misol
sifatida n = 9, k = 4 parametrli Fayra kodini qurishni ko‘rib chiqamiz. Bu kodni
qurish uchun
R
(x) = (x 2 + x + 1) (x 3 + 1) = x 5 + x 4
+ x 3+ x2+ x + 1
yasovchi
polinomni tanlaymiz. U xolda t = 2, m = 2 t –1 = 3, c = 3,
r
= c + t = 5 bo‘ladi. Xosil qiluvchi matritsa quyidagi ko‘rinishga ega:
G 9, 4 = ê
 , C5,
4 ê
, C5,
4 ê
 transponirlangan
matritsa quyidagiga teng:
transponirlangan
matritsa quyidagiga teng:

 0 0 0 1
0 0 0 1
 = 0 0 1 0
= 0 0 1 0
0 1 0 0
1 0 0 0
S5,4
matritsani tuzish uchun o‘ng tomoni nollar bilan to‘ldirilgan 1 ni yasovchi
polinomga bo‘lish natijasida xosil bo‘lgan qoldiqlardan foydalaniladi.
 100000000 111111
100000000 111111

 111111 1100
111111 1100
1-qoldiq®
111110
 111111
111111
2-qoldiq
®
000010
 000000
000000
3-qoldiq
®
000100
 000000
000000
4-qoldiq
®
00100
S5,
4 quyidagi ko‘rinishda bo‘ladi:


1 1 1 1 1
S 5,4 = 0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
Umumiy
xolatda (9, 4) Fayra kodini xosil qiluvchi matritsa quyidagicha yoziladi:

 0 0 0 1 1 1 1 1 1
0 0 0 1 1 1 1 1 1
G 9,4 = 0 0 1 0 0 0 0 01
0 1 0 0 0 0 1 0
1 0 0 0 0 0 1 0 0
G 9,4 matritsa orqali istalgan 4-razryadli axborotlarni
kodlashtirish mumkin. Masalan G(x)
= x3 + x2 + 1 ® 1011 ni kodlashtirish kerak bo‘lsin. Buning uchun G 9,4 matritsaning
1, 2, 4 chi katorlari o‘zaro mod 2 bo‘yicha qo‘shiladi:
000111111  001000001
001000001  100000100 = 101111010 yoki
100000100 = 101111010 yoki
F (x) = x 8 + x 6 + x 5
+ x 4 + x 3 + x
Fayra
kodida kodlashtirish algoritmi 12.1-rasmda
keltirilgan. U quyidagi bosqichlardan (bloklardan) iborat:
1) Fayra
kodi parametrlari n, k, r lar kiritiladi.
2) g(x)
keltirilmaydigan ko‘pxad va k ning darajasi t kiritiladi;
3) kiritilgan
g(x) va uning darajasi t chop etiladi;
4) qo‘shimcha
ko‘pxad (xs +1) va uning darajasi s ni kiritish;
5) M
ning qiymati M=2t –1 formula bo‘yicha xisoblanadi;
6) S
sonini xisoblab chiqarilgan M soniga karraliligi tekshiriladi.
Agar karralik bo‘lsa, 4-blokka o‘tiladi. Unda (xs +1) ko‘pxad va uning
darajasi s qaytadan kiritiladi. Agar shart bajarilmasa,
keyingi 7-blokka o‘tiladi;
7) Kiritilgan
(xs +1) va uning darajasi s chop etiladi;
8) R(x)
yasovchi polinom kiritiladi;
9)
Kiritilgan R(x) polinom chop
etiladi;
10)
Kodning informatsion qismi
k1 (x) kiritiladi;
11)
k1 (x) kombinatsiyaga muvofiq n1 parametr n1 = k1 + r formulaga
asosan aniqlanadi;
12)
k1 (x) ni r razryad chapga siljitish ishi bajariladi;
13)
Xosil bo‘lgan kombinatsiya R(x) yasovchi polinomga bo‘linadi va R(x) qoldiq xosil
qilinadi;
14)
Xosil bo‘lgan R(x) qoldiq
k1 (x) informatsion qismga biriktiriladi;
15)
Kodlangan axborot chop etiladi.
12.1-rasm.
Fayra kodida kodlashtirish algoritm
12.1-rasm.
Fayra kodida kodlashtirish algoritmi (davomi)
Fayra
kodida kodlashtirilgan axborotlarni dekoderlash usullari.
Fayra kodi, n – elementli kodli kombinatsiyada
xosil bo‘luvchi, uzunligi v va undan kichik bo‘lgan bir karralik xatolar guruxini
to‘g‘irlaydi va bir vaqtning o‘zida uzunligi a ³
v bo‘lgan bir karralik xatolar guruxini aniqlaydi.
Fayra
kodida kodlashtirilgan axborotlarni dekoderlashning ikki xil usuli mavjud. Ularning
xar birini aloxida qarab chiqamiz:
f(x)
uzatilgan kodli kombinatsiyaga xi V(x) ko‘rinishdagi xatolar paketi
ta’sir kilsin.
V (x) – xatolar paketini ifodalovchi ko‘pxad;
xi - xatolar paketi boshlangan razryad.
Agar
qabul qilingan kodli kombinatsiya R(x) yasovchi polinomga koldiqsiz bo‘linsa, demak
uzatilgan kombinatsiya to‘g‘ri qabul qilingan yoki xatolar aniqlanmay qolgan. Aks
xolda esa, uzatilgan kodli kombinatsiya xato qabul kilingan xisoblanadi va uni aniqlash
xamda to‘g‘irlash talab etiladi. Demak,
qoldiq noldan farqli bo‘lsa, u xolda qabul qilingan kombinatsiyada
quyidagi ko‘rinishdagi
xatolar mavjud bo‘ladi:
{ x i B (x) = g (x) · S (x) + R (x) }
R
(x) – darajasi (n – k) dan kichik bo‘lgan qoldiq ko‘pxad.
Xatolarni
to‘g‘irlash uchun R(x) qoldiq ko‘rinishiga karab x i V (x) ni topish
talab etiladi. Shundan so‘ng qabul qilingan vektor va x i V (x) larni
o‘zaro mod 2 bo‘yicha qo‘shish orqali xatolar to‘g‘irlanadi. Agar x i
V (x) to‘g‘irlanadigan xatolar paketining k – sinfiga kirsa, u xolda
{ x i B (x) } = {x n-1 ·
R 1 (x) }
ko‘rinishda
bo‘ladi. Bu yerda
{ R1 (x) } = {x j ·
R (x) } va
i = n - j
bilan
ifodalanadi.
Xatolar
vektori sifatida R1(x) qoldiq olinadi va bu kombinatsiya qabul qilingan
kodli so‘zning (n –1) – razryadidan boshlanadi deb qaraladi. Bu
usuldagi dekoderlash algoritmi quyidagi ketma-ketlik asosida olib boriladi:
-
qabul qilingan kodli kombinatsiya R(x) ga
bo‘linadi. Natija qoldiqsiz chiqsa demak, kombinatsiya xatosiz qabul qilingan yoki
xato aniqlanmay kolgan. Agar R(x) qoldiq xosil bo‘lsa navbatdagi bosqichga o‘tiladi;
-
xosil bo‘lgan R(x) qoldiq  ga ko‘paytiriladi va R(x) ga bo‘linadi;
ga ko‘paytiriladi va R(x) ga bo‘linadi;
-
R1(x) qoldiqning to‘g‘irlanadigan
kombinatsiya bo‘lishi tekshiriladi.
xi
R(x) ni R(x) ga bo‘lish, i ning R1(n) qoldiq to‘g‘irlanadigan
kombinatsiya bo‘lgunga qadar davom ettiriladi. Lekin bu operatsiya n martadan
oshmasligi kerak. To‘g‘irlanadigan
kombinatsiyaning xosil bo‘lmasligi esa, qabul qilingan kombinatsiyaning buzilish
darajasi, kodning to‘g‘irlash
imkoniyatidan oshib ketganligidan dalolat beradi;
-
agar i qadamdan so‘ng Rq(x)
qoldiq to‘g‘irlanadigan
xolatga kelsa, u xolda xatolarni to‘g‘irlash
uchun, qabul qilingan kombinatsiyaga xosil bo‘lgan qoldiqni j = (n- i) chi razryaddan
boshlab mod 2 bo‘yicha qo‘shish kerak.
Dekoderlashning
eng muxim bo‘lgan ikkinchi usulini ko‘rib o‘tamiz. Aloqa kanaliga uzunligi v dan
oshmaydigan bir karralik xatolar paketi ta’sir etsin. Aloqa kanali chiqishida quyidagi
xato sodir bo‘lgan kombinatsiya olinadi.
F (x) = f (x) + x i B (x)
f(x)
– P(x) ga bo‘linadigan uzatilgan kombinatsiyaning polinomi;
V
(x) – xatolar paketiga mos keluvchi darajali ko‘pxad;
i
– kodli kombinatsiyadagi xatolar paketi boshlangan razryad.
Bu
usulda dekoderlash quyidagi bosqichlarda olib boriladi:
-
qabul qilingan polinom F(x) ni R(x) yasovchi
ko‘pxadning ko‘paytuvchilari g(x) va (xs +1) larga bo‘lib, V1(x)
va V2(x) qoldiqlar aniqlanadi;
-
V1(x) va V2(x) polinomlar
x ning ketma-ket darajalariga ko‘paytiriladi va xar qadamda g(x) xamda (xs
+1) polinomlarga bo‘lish natijasida xosil bo‘luvchi qoldiqlar xisoblanadi.
Bu xolda xar safar yangi xosil bo‘lgan qoldiqlar o‘zaro solishtiriladi;
-
2-bosqich yuqorida aytilgan qoldiqlar o‘zaro
tenglashgunga qadar davom ettiriladi. O‘zaro mos kelgan qoldiq esa xatolar paketining
ko‘rinishini bildiradi. Xatolar paketining joylashgan o‘rni I ni topish uchun esa
tengliklar nazariyasi apparatidan foydalaniladi.
Ko‘paytirilgan
xi va xj ning i va j daraja ko‘rsatkichlarida, qoldiqlar
o‘zaro mos kelsin. Unda xatolar paketi boshlangan razryad I quyidagicha topiladi:
I º - ( i D1 + j D2)
mod n
bu
yerda
D1 º 1 mod m; D1
º 0 mod s;
D2
º 0 mod
s;
D2 º
1 mod m
-
xatoni to‘g‘irlash uchun qabul kilingan
F(x) kombinatsiyaga aniqlangan xI B(x) mod 2 bo‘yicha qo‘shiladi.
Ikkinchi
usulda keltirilgan algoritmni tushuntirish uchun quyidagi misolni keltiramiz:
R (x) = (x4 + x +1) (x7 +1) = x11 +x8
+ x7 + x4 +x +1
Yasovchi
polinom uzunligi v=4 va undan kichik bo‘lgan xatolar paketini to‘g‘irlovchi Fayra
kodini xosil qiladi. Berilgan R(x) yasovchi polinomli Fayra kodining parametrlari
quyidagilar:
t = 4, m = 15, c = 7, n = 105, k = 94
Aloqa
kanali orqali quyidagi
f (x) = x31 + x28 x27 +x24 + x21
+ x20 + x14 x10 +x8 + x3
+ x +1
kodli
kombinatsiya uzatiladi. Kanalda esa V (x) = x19 ( x3 +
x + 1) xatolar paketi xosil bo‘ldi va kanal chiqishidagi
polinom quyidagi ko‘rinishga keldi:
F (x) = f (x) + xI B (x ) = x31 +
x28 + x27 + x24+ x22+x21
+x19+ + x14+x10 +x8+
x3 + x + 1
1)
F (x) ni g (x) = x4 +x+1 va
(xs +1) = x7 +1 larga bo‘lib qoldiqlarni aniqlaymiz:
x31
+ x28 + x27 + x24+ x22+x21
+x19 + x14+x10 +x8+ x3 +
x + 1 x 4 + x +1
x31
+ x28 + x27
x27 + x20 + x18 +
x24+
x22+x21 +x19 + x14+x10 +x8+
x3 + x+1 + x16+ x14+ x13+
x12+
x24+
x22+x21 +
x11+x10 +x4+ x+1
x22+x20
+x19 + x14+x10 +x8+ x3 +
x+1
x22+x19
+x18
x20
+x18 + x14+x10 +x8+ x3 +
x+1
x20
+x17 + x16
x18
+x17+ x16+x14+x10+x8+ x3
+x+1
x18+x15
+x14
x17
+x16 + x15+x10 +x8+ x3 +
x+1
x17+x14+x13
x16+x15+x14+x
13+x10+x8+x3+x+1
x16+x13+x12
x15+x14+x
12+x10+x8+x3+x+1
x15+x12+x11
x14+x
11+x10+x8+x3+x+1
x14+x11+x10
x8+x3+x+1
x8+x5+x4
x5+
x4+x3+x+1
x5+x2+x
x4+x3+x2
+1
x4+x+1
x3+x2+x
= V1 (x)
x31
+ x28 + x27 + x24+ x22+x21
+x19 + x14+x10 +x8+ x3 +
x + 1 x 7 + 1
 x31+x24
x24+ x21 +x20+ x28+x27+x22+x21+x19+x14+x10+x8+x3+1
+x15+x13+x12+
x28+x21
+ x8+x7 +x6+ x5+x 3 +1
x31+x24
x24+ x21 +x20+ x28+x27+x22+x21+x19+x14+x10+x8+x3+1
+x15+x13+x12+
x28+x21
+ x8+x7 +x6+ x5+x 3 +1
x27+x22
+x19 + x14+x10 +x8+ x3 +
x+1
x27+x20
x22
+x20+x19+x14+x10+ x8+x3
+x+1
x22+x15
x20+x19+x15+x14+x10+x8+
x3 +x+1
x20+x13
x19+x15+x14+x13+x10+x8+x3
+x+1
x19+x12
x15+x14+x
13+x12 +x10+x8+x3+x+1
x15+x8
x14+x13+x
12+x10+x8+x3+x+1
x14+x7
x13+x
12+x10+x7+x3+x+1
x13+x6
x12+x
10 +x7 +x 6 +x3+x+1
x12+x5
x 10
+x 7 +x 6 +x5+x3+x+1
x10+x3
x7+x6+x5
+x +1
x7+1
x6+x5+x
= V2 (x)
Demak
bo‘lish natijasida xosil bo‘lgan qoldiqlar
V1 (x) = x3 + x2 + x, V2 (x)
= x6 + x5 + x ga teng.
2)
xosil bo‘lgan qoldiqlar tenglangunga
qadar ko‘paytirilishi zarur bo‘lgan xi va x j larning
i va j daraja ko‘rsatkichlari aniqlanadi:
x
11 V1 (x) = x 11 (x 3 +x2+x)
= x 14 +x13+x12
 x 14 +x13+x12
x 4 +x +1
x 14 +x13+x12
x 4 +x +1
x 14
+x11+x10 x 10 +x9+x8
x 7 +x 3+1
x13
+x12+x11+x10
 x13+x10+x
9
x13+x10+x
9
x12+x11+x
9
 x12 +x9+x8
x12 +x9+x8
x11+x
8
 x11+x8+x7
x11+x8+x7
x 7
x7+x4+x3
x 4
+x 3
 x 4 +x
+1
x 4 +x
+1
x 3
+x +1
x 2
· V2 (x) = x 2 (x6 + x 5
+x) = x8 + x 7 +x3
 x 8 +x
7+x 3 x 7+1
x 8 +x
7+x 3 x 7+1
 x 8+x
x +1
x 8+x
x +1
x 7
+x 3+x
 x 7+1
x 7+1
x 3
+x+1
x
ning i = 11 va j = 2 daraja qiymatlarida qoldiq bir xil bo‘ladi:
V
(x) = x 3 +x+1
1)
Xatolar paketining o‘rni aniqlanadi:
I º - (11 D1 + 2 D2 )
mod 105
D1 º 1 mod 15, D2
º 0 mod 7
D2 º 1 mod 7, D2
º 0 mod 15
D1
= 16, 31, 46, 61, 76, 91
D2
= 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91
Demak
D1 = 91 ga teng
D2 = 8, 15
D2 = 15
Tengliklardan
ko‘rinadiki D1
= 91, D2 q 15 bo‘ladi.
Endi
I ni aniqlasak bo‘ladi:
I º - (11.91 + 2.15 ) mod 105
I º - 86 mod 105
Bu
ifodadan I = 105 – 86 = 19 ekanligi kelib chiqadi.
Xatolar
paketining ko‘rinishi V(x) = x3 + x + 1 bo‘lib, u 19-razryaddan boshlanar
ekan.
4)
Xatolar paketini to‘g‘irlash
uchun qabul qilingan F(x) kodli kombinatsiyaga x19 (x3
+ x + 1) polinom mod 2 bo‘yicha qo‘shiladi.
F
(x) +x 22 + x20+x19 q x31+x28+x27+x24+x21
+x19+x14+x10+x8+x3+x+1+
+
x22+x20+x19 q x31+x28+x27+
x24 + x21+x20+x14+x10+x8+x3+
x +1
Shu
tariqa dekoderda quyidagi to‘g‘irlangan
kodli kombinatsiya tiklanadi:
F
(x) + x I B (x) = x31+x28+x27+x24+x21
+x20+x14+x10+x8+x3+x+1
Ushbu
algoritmni blok-sxema ko‘rinishdagi taxlili 12.3-rasmda
berilgan. Rasmdagi bloklarning vazifasini izoxlab o‘tamiz:
1.
Xatolar
paketi boshlangan razryad nomeri «I1» kiritiladi;
2.
Xatolar
paketining qiymati V(x) kiritiladi;
3.
Kodlangan
f(x) kombinatsiyaga «I1» razryaddan boshlab V(x) xato kiritiladi va
F(x) xato kombinatsiya xosil qilinadi;
4.
F(x) xato kombinatsiya chop etiladi;
5.
F(x) ni R(x) yasovchi polinomga bo‘lish
bajariladi va R(x) qoldiq olinadi;
6.
R(x) qoldiq tekshiriladi. Agar R(x) = 0 bo‘lsa,
u xolda 30-blokka o‘tiladi. Unda F(x) kombinatsiyada xato yo‘q degan xabar chop
etiladi va dastur ishi yakunlanadi. Agar shart bajarilmasa navbatdagi
7-blokka o‘tiladi;
7.
F(x) kombinatsiyada xato mavjud degan xabar
chop etiladi;
8.
F(x) ni g(x) ga bo‘lish bajariladi va V1(x)
qoldiq xosil qilinadi;
9.
F(x) ni (xs+1) ga bo‘lish bajariladi
va V2(x) qoldiq xosil qilinadi;
10. Qoldiq
V1(x) ga ko‘paytirish kerak bo‘lgan xi ning boshlang‘ich
darajasi beriladi;
11. Qoldiq
V2(x) ga ko‘paytirish kerak bo‘lgan xj ning boshlang‘ich
darajasi beriladi;
12. V2(x)
ni J razryad chapga surish ishi bajariladi ya’ni xj
ga ko‘paytiriladi;
13. Xosil
bo‘lgan kombinatsiya (xs+1)ga bo‘linadi va qoldiq j xosil qilinadi.
14. V
1 (x) ni I razryad chapga surish ishi bajariladi
(xi ga ko‘paytiriladi).
15. Xosil
bo‘lgan natija g (x) ga bo‘linadi va QOLI
olinadi.
16. Qol
I va QOL
j larning tengligi solishtiriladi. Agar qoldiqlar teng bo‘lmasa 17 blokka
o‘tiladi.
17. Xj
ning navbatdagi daraja ko‘rsatkichi olinadi, ya’ni J daraja bir birlikka orttiriladi.
18. J
ning kod uzunligi n1 dan kattaligi tekshiriladi. Agar shart bajarilmasa
12-blokka o‘tiladi, ya’ni sikl takrorlanadi. Agar shart bajarilsa
19-blokka o‘tiladi;
19. xi ning navbatdagi daraja ko‘rsatkichiga o‘tiladi, ya’ni
I daraja bir birlikka oshiriladi;
20. I
ning n , dan kattaligi tekshiriladi. Agar shart bajarilmasa 11-blokka o‘tiladi.
Agar
shart bajarilsa 21-blokka o‘tiladi;
21. «xatolarni
to‘g‘irlash imkoni yo‘q» degan
xabar chop etiladi va dastur ishi yakunlanadi; 16-blokdagi shart bajarilganda
22-blokka o‘tiladi;
22. Bir
xil bo‘lgan qoldiq V(x) (QOL
I = QOL
J ) chop etiladi;
23. Qoldiqlari
teng bo‘lgan daraja ko‘rsatkich I va J lar chop etiladi;
24. D1
ning qiymati topiladi;
25. D2
ning qiymati aniqlanadi;
26. D1
va D2 lar asosida xatolar paketi boshlangan I razryad
aniqlanadi;
27. F
(x) xato kombinatsiya to‘g‘irlanadi;
28. To‘g‘rilangan
kombinatsiya chop etiladi;
Dastur
ishi yakunlanadi.

Xato kombinatsiya
F(x) ni
chop etish
xato yo‘k
xato mavjud
12.3-rasm.
Fayra kodini dekoderlash algoritmi

12.3-rasm.
Fayra kodini dekoderlash algoritmi (davomi)
12.3-rasm.
Fayra kodini dekoderlash algoritmi (davomi)
12-ma’ruza
uchun nazorat savollari
1. Fayra
kodiga tushuncha bering?
2. Fayra
kodini qurish qanday amalga oshiriladi?
3. Fayra
kodida yasovchi polinomlarga tushuncha bering?
4. Axborotlarni
Fayra kodida kodlashtirish usullari qanday amalga oshiriladi?
5. Fayra
kodi parametrlari.
6. Axborotlarni
Fayra kodida kodlashtirish usullariga misol keltiring?
7. Fayra
kodida kodlashtirish algoritmini tushuntiring?
13-ma’ruza.
Kaskadli kodlar.
Reja:
1. Kaskadli
kodlar.
2. Kodlashni
kaskadli prinsipini amalga oshirish.
3. Kaskad
kodning afzalligi.
4. RS
kodi xossalari.
Kaskad
kodlar. Real aloqa kanallari, ayniqsa ovoz chastotasidagi
standart kanal asosidagi aloqa kanallari xatolarni guruxlash aloqa kanallari hisoblanadi,
xatolar paketlari uzunligi o‘nlab ikkilik belgilaridan yuzlab ikkilik belgilarigacha
chegarada bo‘lishi mumkin. Bundan tashqari paketlar orasidagi himoya intervallarida
tasodifiy xatolar mavjud. Bu strukturadagi xatolarni korreksiya qilish uchun shovqinbardosh
kodlar talab qilinadi, bu esa juda katta uzunlikdagi kodlar ketma-ketligi va yuqori
ortiqchalikdagi shovqinbardosh kodlardan foydalanish demakdir. Bunday kodlar dekodlash
jarayonida yuqori murakkablikdagi amalga oshirish va katta axborot kechikishiga
ega.
Bu
strukturadagi xatolarni korreksiya qilish uchun talab etilayotgan axborot uzatilishi
ishonchliligini dekodlashda kodekni kam murakkablikda amalga oshirish va kechikishni
ta’minlaydigan axborotni kodlash usuli yaratilgan.
Bunday
axborotni kodlash usulining mohiyati ikki va undan ortiq kodlarni kaskadlashdan
iborat. Bunda har bir kodlash darajasida bir xil turdagi va korrektlash xususiyatidagi
yoki har xil kodlardan foydalansa bo‘ladi.
Eng
keng tarqalgan kaskad kodlar tuzilishi sxemasi ikki kaskadli yoki ikki pog‘onali
sxema hisoblanadi:
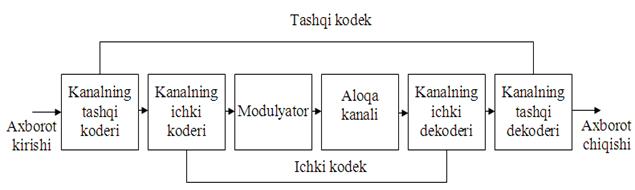
Tashqi
kod sifatida ko‘pincha paket xatoliklarini korrektlovchi Rid-Solomon kodlaridan
foydalaniladi, ichki kodlar esa tasodifiy xatolarni korrektlovchi siklik xamda o‘rama
kodlar bo‘lishi mumkin. Real aloqa sistemalarida ichki kod sifatida Viterbi dekodlash
algoritmiga ega o‘rama kodlardan
foydalaniladi.
Axborotni
kodlash va dekodlash quyidagi ko‘rinishda amalga oshadi:
Tashqi
koderda uzatilayotgan axborot paketli xatolarni korreksiyalashga mo‘ljallangan kod
bilan kodlanadi. Asosan Rid-Solomonning ikkilik bo‘lmagan kodlaridan foydalaniladi.
Keyin tashqi kodning kodli ketma-ketliklari ichki kod bilan kodlanadi.
Ichki
koderning chiqishida kaskad kodning kodli belgilari modulyatorning kirishiga tushadi
va keyin aloqa kanaliga uzatiladi.
Qabul
qilish qismida avval ichki dekoderda, keyin esa tashqi dekoderda qayta ishlanadi.
Ichki
kodni korrektlash xususiyatini oshirish maqsadida ichki koderning chiqishiga kodli
belgilarni joyi o‘zgartiriladi.
Kodlar
joyini o‘zgartirishning mohiyati kodlarni xar hil kodli so‘zlar bilan paketga kiruvchi,
tasodifiy xatolarni to‘g‘irlovchi xatolarni bo‘lib-bo‘lib joylashtirishdan iborat.
Simsiz
aloqa kanallarida bunday aniqlikni shovqinbardosh kodlashni qo‘llamay turib olish
qiyin. Kodlash va dekodlash usulini tanlash 3 ta asosiy guruxga bo‘lingan,
o‘zaro bog‘liqligi rasmda ko‘rsatilgan ko‘plab faktorlarga amal qilinadi.
Amalga
oshish murakkabligi deganda:
Ø apparat, hamda dastur harajatlari;
Ø mikrosxema va mikroprotsessor narxi;
Ø ma’lumotlar saqlash uchun xotira narxi va boshqalar tushuniladi.
O‘tkazish
xususiyati deganda, bu kontekstda, faqatgina foydali axborot xajmi va ortiqchaligidan
tashqari xizmat axboroti xajmi ham tushuniladi. Bunday xabarlar uzatish qabul qilishda
sinxronizatsiyani o‘rnatish va qo‘llash uchun, ma’lumotlarni uzatishda elementlarni
boshqarish uchun kerak bo‘ladi.
Amalda
asosan tarkibli va kaskad kodlardan foydalaniladi. Kaskad koddan foydalanilgan axborot
kanali 13.2-rasmda keltirilgan.
 13.2-rasm. Kaskad koddan foydalanilgan
axborot kanali
13.2-rasm. Kaskad koddan foydalanilgan
axborot kanali
 Kodlashni
kaskadli prinsipini a’malga oshirish. Kodlashni
kaskadli prinsipini amalga oshiruvchi xar xil variantlari mavjud. Avval
axborotlarni
Kodlashni
kaskadli prinsipini a’malga oshirish. Kodlashni
kaskadli prinsipini amalga oshiruvchi xar xil variantlari mavjud. Avval
axborotlarni  ikkilik belgilar ketma-ketligi
ikkilik belgilar ketma-ketligi
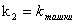 blok osti xar biriga
blok osti xar biriga
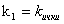 belgidan bo‘linadi.
Bu blok osti Galua ikkilik maydoni daraja kengaytmasi k1 osti tashqi
kodning axborot guruxini tashkil etgan xolda ko‘riladi. Ko‘p bunday belgilar
belgidan bo‘linadi.
Bu blok osti Galua ikkilik maydoni daraja kengaytmasi k1 osti tashqi
kodning axborot guruxini tashkil etgan xolda ko‘riladi. Ko‘p bunday belgilar  dan
aniqlanadi.
dan
aniqlanadi.
Tashqi
kod k2 asosida tekshirish belgilarini hosil qiladi. Agar tashqi kod
sifatida Rid-Solomon kodidan foydalanilsa, unda u kodning korrektlash xususiyatlari
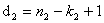 ifodasi orqali aniqlanadi.
Bu kodning tekshirish belgilari
ifodasi orqali aniqlanadi.
Bu kodning tekshirish belgilari  maydoni elementlari
xisoblanadi.
maydoni elementlari
xisoblanadi.
Kodning
(n2, k2) kombinatsiyalari barcha q-lik belgilari (n1,
k1) ichki kod bilan kodlanadi. Natijada n1 n2
uzunliudagi k1
n2
uzunliudagi k1 k2
ikkilik axborot umumiy minimal d1
k2
ikkilik axborot umumiy minimal d1 d2
masofaga ega belgilardan iborat ikkilik blok kodi olinadi. Bu yerda d1
ichki kodning minimal masofasi.
d2
masofaga ega belgilardan iborat ikkilik blok kodi olinadi. Bu yerda d1
ichki kodning minimal masofasi.
Quyida
kaskad kodi so‘zi tuzilish sxemasi keltirilgan.

13.1-rasm.
Kaskad kodi so‘zi tuzilish sxemasi
Kaskad
kodning afzalligi ular (n1, n2, k1, k2)
uzun kodni dekodlashni ikki sezilarli ichki ikkilik (n1, k1)
kod va tashqi (n2, k2) kod bilan dekodlashni almashtirishdan
iborat. Kaskad kodlar yetarlicha katta qiymatga ega  amalga
oshirish imkonini beradi, shuning uchun ularning
xatolarni guruxlanuvchi xatolar kanallarida qo‘llanilishi ma’noga ega.
amalga
oshirish imkonini beradi, shuning uchun ularning
xatolarni guruxlanuvchi xatolar kanallarida qo‘llanilishi ma’noga ega.
Kaskad
kodlarining boshqa afzalligi shundan iboratki, xatolarni ichki kod orqali to‘g‘rilashda
erkin xatolarni faqatgina konstruktiv usul bilan emas, agar (n1, k1)
kam quvvatli kod bo‘lsa, balki optimal saralash
usullardan foydalanish mumkin. Uning xususiyatidan blokli kodlarni dekodlashda,
klaster taxlili usuli orqali foydalanish mumkin. Qachonki klaster ehtimolligi ko‘proq
xato namunalari kirsa bu dekodlash algoritmi ro‘yhat bo‘yicha dekodlashga o‘xshaydi.
Dekoderning
murakkabligi kaskadli kodlash bilan sistemada xatolarni kod bilan to‘g‘irlash soni,
funksiya kabi chiziqli o‘sadi, vaholanki oddiy kodlardan foydalanilsa, bu bog‘liqlik
eksponensial xarakterga ega. Bunday effektning asosiy
sababi shundan iboratki, ichki kodlar kombinatsiyasini dekodlashda u xatolarni to‘g‘irlamaydi,
balki xatolarni aniqlaganda o‘chirib yuboradi.
O‘chirilgan
pozitsiyalar RS kod bilan qayta tiklanadi, madomiki o‘chirish xato pozitsiyalarni
yetarlicha ko‘rsatib bera olarkan, kodning korrektlash xususiyatlari xatoni topish
uchun emas, balki o‘chirilgan pozitsiyalarni to‘g‘irlashga ishlatiladi.
RS kodlari so‘nggi maydon ustida quriladi. Aytib o‘tilganidek, bunday
maydon har qanday r uchun hosil qilinishi mumkin va GF(p) kabi belgilanadi. GF(p) tushunchasi pm elementlaridan iborat
GF(p) maydon kengaytmasi bilan
nomlangan, kengaytirish darajasi GF (pm)
bo‘lgan maydonda umumiylashtiriladi. GF (pm) maydoni sifatida GF(p) ning barcha elementlariga ega. GF (2m) maydon kengaytmasida
belgilar RS kodlarini qurishda ishlatiladi.
RS kodninig umumqabul qilingan
ko‘rinishi 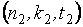 parametri va qandaydir
parametri va qandaydir 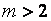 hisoblanadi, bu yerda
hisoblanadi, bu yerda 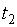 – xatolarni kod
bilan to‘g‘irlash soni,
– xatolarni kod
bilan to‘g‘irlash soni, 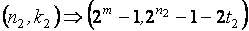 da. RS kod uchun umumlovchi polinom ushbu ko‘rinishga ega:
da. RS kod uchun umumlovchi polinom ushbu ko‘rinishga ega:
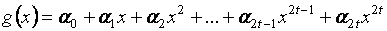 .
.
RS kodining informatsion belgilar umumiy soni ikkilik maydonda GF (2m) ushbu ifoda orqali baxolanadi:
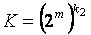 .
.
Tasvvur qilamiz 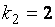 , m = 3, unda K = 64. Bunda informatsion
RS kodning razryadlari orasida xuddi o‘sha GF (2m) maydonidagi a’zo 0 dan
, m = 3, unda K = 64. Bunda informatsion
RS kodning razryadlari orasida xuddi o‘sha GF (2m) maydonidagi a’zo 0 dan  gacha birinchi o‘rinda
gacha birinchi o‘rinda  gurux kombinatsiyasida shakllanadi.
Sezilarliki, barcha kodli kombinatsiyalarning X5 razryadi (jadval RS kodni n2
= 7, k2 = 2 bilan tasvirlaydi) klaster deb ataladigan , konkret gurux kombinatsiyasini
aniqlaydi. Klaster sonini X5 razryadi o‘rnidagi baza
maydoni primitiv elementi darajasi kabi aniqlaymiz. Hosil bo‘ladigan kod polinomi
quyidagicha aniqlanadi:
gurux kombinatsiyasida shakllanadi.
Sezilarliki, barcha kodli kombinatsiyalarning X5 razryadi (jadval RS kodni n2
= 7, k2 = 2 bilan tasvirlaydi) klaster deb ataladigan , konkret gurux kombinatsiyasini
aniqlaydi. Klaster sonini X5 razryadi o‘rnidagi baza
maydoni primitiv elementi darajasi kabi aniqlaymiz. Hosil bo‘ladigan kod polinomi
quyidagicha aniqlanadi:
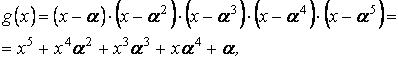
Bu yerda qo‘shish va ayrish operatsiyalari ikkilik maydonda tengligi
xisobga olingan. RS kodning mashxur xususiyatlaridan tashqari keyingi muxokamalar
nuqtai nazaridan muxim bo‘lgan xususiyatlarini ko‘rsatib o‘tamiz.
1-xossa.
Istalgan sistematik RS kod o‘zini tarkibida n2
bir xil q-lik elementlardan iborat  kombinatsiyalarga
ega. Ikkilik gurux kodi toza yagona elementga (yagona kombinatsiya) ega ekan, q-lik
kod GF (2m) maydonidagi bir xil elementlardan iborat kombinatsiyalardan tashkil
topishi kerak, misol uchun,
kombinatsiyalarga
ega. Ikkilik gurux kodi toza yagona elementga (yagona kombinatsiya) ega ekan, q-lik
kod GF (2m) maydonidagi bir xil elementlardan iborat kombinatsiyalardan tashkil
topishi kerak, misol uchun, 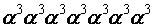 .
.
Ko‘rilayotgan
kodning parametrlari chegarasida 5ta birinchi belgilar tekshirish, oxirgi ikkitasi
esa axborot belgilaridir. Ko‘rib o‘tilgan xossa ma’lumotlarni sinxron qo‘llash
usuli va kodli kombinatsiyalarni majoritar usul bilan dekodlashda xam qo‘llanilishi
mumkin. Bunday kodlarni qo‘llash umumlashtirilgan kaskad kodlarni qo‘llash protsedurasida
majburiy talabdir.
2-xossa.
RS kodining kodli kombinatsiyalari barcha V ko‘pxadi hosil bo‘ladigan polinomning
xar bir  razryadi
uchun
razryadi
uchun  maydonidagi bir xil
sonli elementlardan iborat. Boshqacha qilib aytganda
xar bir maydon element RS kodining kodli kombinatsiyalari umumiy ko‘pxadining xar
bir
maydonidagi bir xil
sonli elementlardan iborat. Boshqacha qilib aytganda
xar bir maydon element RS kodining kodli kombinatsiyalari umumiy ko‘pxadining xar
bir  razryadi
bir xil zichlikda taqsimlangan. Misol uchun, ko‘rilayotgan RS (7,2,6) kodi ,
razryadi
bir xil zichlikda taqsimlangan. Misol uchun, ko‘rilayotgan RS (7,2,6) kodi ,  elementi
elementi
 yoki boshqa baza
maydonidagi istalgan boshqa element razryadi uchun q marta qaytarilsin. Bu
xossaning natijasi faktli, kodli kombinatsiyaning xar bir razryadida belgilarning
buzilishi
yoki boshqa baza
maydonidagi istalgan boshqa element razryadi uchun q marta qaytarilsin. Bu
xossaning natijasi faktli, kodli kombinatsiyaning xar bir razryadida belgilarning
buzilishi  ehtimollik bilan sodir
bo‘lishi mumkin.
ehtimollik bilan sodir
bo‘lishi mumkin.
3-xossa.
1-xossaga javob bermaydigan sistematik (nosistematik) RS -kodning istalgan kombinatsiyasida
maydonning nollik elementi bilan almashtirilgan 1 ta maydon elementi bo‘lmaydi.
Bu xossa RS kodining kodli kombinatsiyasi uzunligi  dek belgilangan ta’rifdan
va siklik xossasidan kelib chiqadi.
dek belgilangan ta’rifdan
va siklik xossasidan kelib chiqadi.
Keltirilgan
xossalar asosida RS kodining ko‘p kodli kombinatsiyalarida bunday kodning yuqori
chegarasini xato dekodlash ehtimolligi uchun baxolash mumkin. Mulohaza sifatida
belgilaymizki, istalgan Xemming 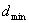 metrikasiga
ega kod
metrikasiga
ega kod 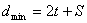 xato va yo‘qotishlarni
to‘g‘irlashga qodir,
xato va yo‘qotishlarni
to‘g‘irlashga qodir,
bu
yerda  – kodli
kombinatsiyada xatolar soni,
– kodli
kombinatsiyada xatolar soni,
 –
yo‘qotishlar soni.
–
yo‘qotishlar soni.
Yo‘qotishlarni
to‘g‘rilaganda  qiymatni
bir deb qabul qilish maqsadga muvofiqdir. Bu belgilangan ehtimollik qismida xatolik
belgilari yo‘qotilmagan maksimal baxolash diskret xabarlar manbasiga ega belgilar
orasida bog‘liq.
qiymatni
bir deb qabul qilish maqsadga muvofiqdir. Bu belgilangan ehtimollik qismida xatolik
belgilari yo‘qotilmagan maksimal baxolash diskret xabarlar manbasiga ega belgilar
orasida bog‘liq. 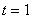 deb
qabul qilarkanmiz, yo‘qotishlarni korrektlash uchun bir qancha zaxira olamiz. Unda
deb
qabul qilarkanmiz, yo‘qotishlarni korrektlash uchun bir qancha zaxira olamiz. Unda
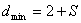 va qat’iyan
va qat’iyan  . Bu kod bilan to‘g‘irlanadigan
va aniqlanmagan xato kelib chiqqan xolatda korrektlash qobiliyatini ta’minlovchi
yo‘qotishlar sonidir. Mayli ichki kod bilan xatolar aniqlansin va xatoliklar bilan
aniqlangan q-lik belgilar o‘chirilsin, agar o‘chirilgan bloklar soni
. Bu kod bilan to‘g‘irlanadigan
va aniqlanmagan xato kelib chiqqan xolatda korrektlash qobiliyatini ta’minlovchi
yo‘qotishlar sonidir. Mayli ichki kod bilan xatolar aniqlansin va xatoliklar bilan
aniqlangan q-lik belgilar o‘chirilsin, agar o‘chirilgan bloklar soni  dan ko‘p bo‘lsa, RS
kodining barcha kodli kombinatsiyalari o‘chiriladi, lekin o‘chirishlar soni
dan ko‘p bo‘lsa, RS
kodining barcha kodli kombinatsiyalari o‘chiriladi, lekin o‘chirishlar soni  dan kam yoki teng
bo‘lsa, RS kodi kodli kombinatsiyalari orqali yo‘qotishlar to‘g‘irlanadi. Agar o‘chirilmagan
q-lik belgilar biror kodli kombinatsiya belgilari muvofiq joylar bilan mos tushsa
tashqi kod xatolarni aniqlamaydi.
dan kam yoki teng
bo‘lsa, RS kodi kodli kombinatsiyalari orqali yo‘qotishlar to‘g‘irlanadi. Agar o‘chirilmagan
q-lik belgilar biror kodli kombinatsiya belgilari muvofiq joylar bilan mos tushsa
tashqi kod xatolarni aniqlamaydi.
Bunday
konstruksiyada ikkita juda kerakli xossa kelib chiqadi. Ulardan birinchisi shundan
iboratki, yuqori sifatli aloqa kanallar sharoitida adaptiv rejimlardan foydalanishda
kodning tezligi tashqi kodning tekshirish razryadlariga xos tekshirish belgilarini
tashish xisobiga oshirilishi mumkin.
|
Axborot
|
Tashqi kod tekshiruvi
|
|
Axborot razryadlar tekshiruvi
|
Tekshiruvlar tekshiruvi
|
13.2-rasm.
Kaskad kod so‘zi konstruksiyasi
Kaskad
kod so‘zi konstruksiyasining ikkinchi foydali xossasi ushbu ifodalanayotgan so‘z
orqali to‘g‘ridan-to‘g‘ri belgilarni oralatish protsedurasini matritsaga qo‘llash
imkoniyati xisoblanadi. Belgilarni oralatish protsedurasi qandaydir qiymatdagi matritsa
xotirasini axborot razryadlar bilan oldindan to‘ldirishdan iborat. Agar axborot
manbasidan ma’lumotlarni yozish qatorlar orqali amalga oshsa, unda to‘ldirishdan
so‘ng aloqa kanalida ma’lumotlarni o‘qish qatorlar bo‘yicha amalga oshadi. Bu aloqa
kanalida guruxlashgan xatolar ko‘rinishida paydo bo‘ladigan murakkab xatolarga
qarshi turish uchun qilinadi. Agar ushbu tipdagi  ,
aloqa kanalidagi belgida o‘rtacha xatolik ehtimolligi aniq bo‘lsa, unda xatolik pachkasi ichida bu parametrning
qiymati
,
aloqa kanalidagi belgida o‘rtacha xatolik ehtimolligi aniq bo‘lsa, unda xatolik pachkasi ichida bu parametrning
qiymati  , bunda
, bunda  .
Bu kabi qurilmalar tasvirlangan va xatolar dekorrelyatori
kabi nomga ega.
.
Bu kabi qurilmalar tasvirlangan va xatolar dekorrelyatori
kabi nomga ega.
Uzatish
ketma-ket ma’lumotlar ustunini ustun ko‘rinishida xotira matritsasiga tarkibi bo‘yicha
o‘xshash matritsaga chiqishda qayd qiladi va yozadi. Matritsani kirishda to‘ldirishdan
so‘ng, ma’lumotlar
dekoderga qatorlab ko‘chirilib chiqiladi.
Aloqa
kanalida guruxlangan xatolar qatorlar belgilariga ta’sir qilar ekan, dekoderda kirishda
matritsadan kombinatsiyalarni qatorlab o‘qiganda topib to‘g‘rilab bo‘ladigan xatolar
chegaralangan soni bo‘ladi. Bu kabi qurilmalarni qo‘llash ma’lumotlarni 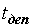 qayta ishlashda protsessor qabul qilgichlarda yuqori chastotalarda ishlaganda
uncha katta bo‘lmagan kechikishlar bilan bog‘liq . Peremejitel (deperemejitel) matritsasi
qayta ishlashda protsessor qabul qilgichlarda yuqori chastotalarda ishlaganda
uncha katta bo‘lmagan kechikishlar bilan bog‘liq . Peremejitel (deperemejitel) matritsasi
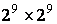 o‘lchovga ega bo‘lsin va protsessorning
ishlash chastotasi 2 GGs kelib chiqadi, matritsani
ma’lumotlar bilan to‘ldirish vaqti
0.5 ms atrofida bo‘ladi, uzatish va qabul qilish hisobi bilan 1 ms atrofida.
o‘lchovga ega bo‘lsin va protsessorning
ishlash chastotasi 2 GGs kelib chiqadi, matritsani
ma’lumotlar bilan to‘ldirish vaqti
0.5 ms atrofida bo‘ladi, uzatish va qabul qilish hisobi bilan 1 ms atrofida.
13-ma’ruza
uchun nazorat savollari
1. Qay
shaklda kaskad kodlarida axborotlar kodlanadi va dekodlanadi?
2. Kaskad
kodlar afzalliklari nimadan iborat?
3. Kaskad
kod so‘zi mohiyatini tasvirlab bering?
4. Eng
ko‘p tarqalgan kaskad kodlar
qurilish sxemasi qaysi, tushuncha bering?
14-ma’ruza.
Turbo kodlar.
Kod spektrining og‘irligi.
Reja:
1. Turbo
kodlar tushunchasi.
2. Turbo
kodning avzalligi va kamchiliklari.
3. Kod
spektrining og‘irligi.
Turbo-kod
parallel kaskad – blokli tizim kodi bo‘lib, u raqamli ma’lumotlarni shovqinli
aloqa kanalida uzatishda yuzaga keladigan xatolarni to‘g‘irlash imkonini beradi.
Turbo
kodning ma’nodoshi sifatida 1966 yilda D. Forni tomonidan taklif etilgan kodlash
nazariyasiga ma’lum bo‘lgan atama kaskadli (angl. concatenated
code)
kod deb ataladi.
Turbo-kod
parallel kaskad bog‘langan
tizim kodlaridan tashkil topgan. Bu tashkil etuvchilar kodning komponentalari
deb ataladi.
Kodning
komponentalari sifatida:
Ø o‘ralgan
kodlar;
Ø Xemming
kodlari;
Ø Rid - Solomon kodlari;
Ø Bouza Choudxuri Xokvingem kodlari va boshqa kodlardan foydalaniladi.
Turbo
kodning tashkil etuvchisi (komponentasi) ga qarab ular o‘ralgan turbo (angl. Turbo
Convolutional Codes, TSS) kodlar hamda blokli (angl. Turbo
Product Codes, TPC) kodlarga bo‘linadi.
Turbo-kod
1993 ishlab chiqilgan bo‘lib, yuqori samarali xatolarni to‘g‘irlovchi,
shovqinbardosh kodlar sinfiga kiradi. Elektrotexnikada va raqamli aloqa kanalida,
su’niy yo‘ldoshli aloqa soxalarida, shuningdek chegaralangan chastota satxida
shovqinli aloqa kanali bo‘ylab yuqori tezlikda ma’lumot uzatish uchun zarur
bo‘lgan soxalarda qo‘llaniladi.
Turbo
–kodning tuzilishi. Shennonga
ko‘ra eng yaxshi kod sifatida, malumotlarni uzluksiz vaqt
ichida uzatadigan va vaktning xar bir laxzasida tasodifiy kod elementlarini
shakllantiradigan kod xisoblanadi.
Qabul
qiluvchida tasodifiy tarzda buzilgan, turli cheksiz ma’lumotlar mavjud
bo‘ladi. Dekoder bu nusxalardan yuborilgan xabarga yaqin (mos) bo‘lgan
nusxani tanlashi kerak. Bu o‘z navbatida nazariy jixatdan o‘zi bilan signalda
barcha xatolarni to‘g‘irlash imkonini beruvchi mukammal kodni taqdim etadi.
Turbo-kod bu yo‘nalishda ilk qadam xisoblanadi.
Ma’lumki,
biz uzluksiz vaqt davomida cheksiz marta xabar uzatmaymiz. Aloqa kanallarini
uzluksiz ishlashini ta’minlash uchun, uzatish vaqtini ikki yoki uch martaga
oshirish yetarli darajada yaxshi natijaga olib keladi.
Turbo
kodlarning o‘ziga xos xususiyati, ularning o‘ralgan rekursiv
(RSC) usulda parallel tuzilganligi bo‘lib, ular parallel ishlaydi
va tasodifiy xabar turlarini xosil qilishda foydalaniladi. Parallel tuzilishga
ega ikki yoki undan ortiq RSC kodlar xar biri boshqa o‘zgartirgichlarda
qo‘llaniladi. O‘zgartirgichnig maqsadi shundan iboratki, xar bir koder
qurilmasiga korrelyatsiya qilinmagan turli tasodifiy ma’lumotlarni taklif
etadi, natijada RSCning xar bir bitlari mustaqil prioritetga ega bo‘ladi.
Turbo
kodlar. Turbo kodlarda bloklar bir nechta tartibdagi
Kbit uzunligiga ega. Bunday uzunlikka ega bo‘lishdan maqsad, ikkinchi
koder qurilmasiga o‘tayotgan ketma - ketlikni samarali tekshirishdan iborat.
Blok uzunligining miqdori qanchalik qo‘p bo‘lsa, birinchi koder qurilmasidagi
ma’lumotlar korrelyatsiyasi shuncha yaxshi bo‘ladi yani korrelyatsiya kichik
bo‘ladi.
Turbo
kodning bir nechta sxemasi mavjud:
• PCCC —
yaxshiroq parallel o‘ralgan kodlar xolatida;
• SCCC —
yuqori tavsifga ega shovqinli signalga aloqador xolda ketma – ket ulangan
o‘ralgan kodlar;
• TPC — turbo-kod-maxsuli,
o‘ralgan kodlar o‘rniga blokli kodlarni qo‘llaydi, ikkita boshqa turdagi kodlar
(odatda Xemming kodlari) ketma- ket ulangan oraliqqa ega bo‘lmaydi, ikkita kod
bir - biriga bog‘liq bo‘lmagan, qatorlar va ustunlar xolida ishlaydi, bu esa
o‘z navbatida yetarli darajada yaxshi tekshirishga olib keladi va o‘zgartirgichni
qo‘llash zaruriyatini talab etmaydi.
14.1-rasmda
umumiy M- blokli turbo koderning tuzilish sxemasi keltirilgan.

14.1-rasm.
Umumiy M- blokli turbo koderning tuzilish sxemasi
Umumiy
M- blokli
turbo koderning ishlash tartibi. Dastlab paketlarni
shakllantiruvchining PAD (angl. Packet
Assembler/Disassembler) kirishiga U
uzunlikdagi k bitli
blok ma’lumotlari kelib tushadi. Ma’lumotlarni shakllantiruvchi
paketga (n-k)
ga shu jumladan boshlang‘ich va tugash belgilarini o‘z ichiga oluvchi foydalanilayotgan
paketlarni shakllantirish standartiga muvofiq xolda qo‘shimcha bit xizmat
ma’lumotlarni qo‘shadi. Bunda n bitdan tashkil topgan X0
paket xosil qilinadi.
Keyinchalik
ketma ket X0 bitlari parallel tarzda ketma ket bog‘liqlikni
va koderda komponentni saqlagan xolda M shoxga kelib tushadi.
Shu tariqa X0 barcha koder komponentlariga tezda kiruvchi
ma’lumotlar sifatida foydalaniladi.
Turbo-kodlarda
navbat. O‘zgartirgichga tasodifiy qonunlar asosida
kelib tushayotgan bitlarning aralashishi kuzatiladi (sodir bo‘ladi). RS kodlarida
foydalanuvchi, belgili to‘rtburchakli o‘zgartirgichlardan farqli ravishda, turbo
kodlarda tasodifiy o‘rin almashtirib qo‘yish singari bitlarda aloxida ketma ketlikdan
foydalaniladi. Dekodlash jarayonidan keyin o‘zgarish qonuni ma’lum deb xisoblanadi.
Koderning kirishiga ketma-ket tarzda qabul qilingan ma’lumotlar kelib tushadi.
O‘zgartirgichga
qo‘yiladigan masala shundan iboratki, kiruvchi ma’lumotlar ketma- ketligini,
X0 bit kombinatsiyalarining so‘zli kodiga past vaznga mos
kelishini va chiquvchi birinchi koder qurilmasining o‘zidayoq barcha chiquvchi
koder qurilmalari uchun kodli so‘zlarni yuqori ishonchlilikka o‘zgartirib berishini
ta’minlashdan iborat. Buning oqibatida, turli vazndagi kodli so‘zlar koderning
chiqishida qabul qilinadi.
Kodlash
jarayonida ikkita kodli so‘zlar orasidagi o‘rtacha masofa eng yuqori darajada
bo‘lishga intiladi.
Kodli
bloklar deyarli bog‘liq bo‘lmagan qismlardan tashkil topganligi sababli,
turbo koderning chiqishidagi o‘rtacha masofa kodli so‘zlar o‘rtasidagi
masofadan katta va xar bir koder komponentlari orasidagi masofa qanchalik
kichik bo‘lsa koderning samaradorligi shunchalik yuqori bo‘ladi.
Kodning
tezligi. Kodning tezligi o‘zgartirgich kirishidagi
va koderning chiqishidagi kod blokining uzunligiga bog‘liq. Perforatorning
yo‘qligi (14.1
rasmga qarang) dastlabki X0
ketma ketlikni kanal bo‘ylab uzatuvchi 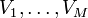 ,
bitlar asosida multipleksorlaydi. Turbo koderning chiqishidagi kodning
tezligi quyidagi formulaga teng:
,
bitlar asosida multipleksorlaydi. Turbo koderning chiqishidagi kodning
tezligi quyidagi formulaga teng:
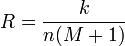
Kodning tezligini oshirish uchun, chiquvchi ketma- ketlikdagi aniq tekshiriluvchi bitlar
xisobi qo‘llaniladi. Shu tarzda kodning tezligi:
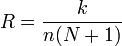 gacha o‘sadi.
gacha o‘sadi.
 xisobidan so‘ng tekshiriluvchi bitlar
xisobidan so‘ng tekshiriluvchi bitlar
 marta oshirilmagan bo‘lsa,
marta oshirilmagan bo‘lsa,  bo‘lingan bit bo‘lishi mumkin. Turbo kodlar katta
uzunlikdagi
bo‘lingan bit bo‘lishi mumkin. Turbo kodlar katta
uzunlikdagi 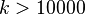 , bloklari bilan bajarilsa
, bloklari bilan bajarilsa  , bog‘liqlikdagi kodning tezligi quyidagiga teng:
, bog‘liqlikdagi kodning tezligi quyidagiga teng:
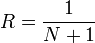
Keltirilgan formuladan ko‘rinib turibdiki,
perforator yordamida tekshiriluvchi bitning xar-xil sonlarini xisoblagan
xolda, kod tezligini me’yorlashtirish
mumkin.
Shunday ekan, aloqa kanalida moslashishga bog‘liq bo‘lgan koder qursa
bo‘ladi. Kanalning shovqinbardosh yuqori koder tezligiga nisbatan, shovqinli
xolatida perforator kam bit xisoblaydi. Agar aloqa kanali yaxshi sifatga
ega bo‘lsa ma’lumot uzatish tezligini oshirishga yordam beruvchi katta
bitlar sonini xisoblash mumkin.
Dekodlash. Dekodlash algoritmi yuqori
extimollik tajribaga asoslangan xolda, amalga oshiriladi. Dekodlash jarayonida
xatolarni to‘g‘irlash, to‘g‘ri kodli so‘zning o‘tishiga erishish uchun aprior
va aposterior extimollikka asoslangan xolda amalga oshiriladi.
Kodli
so‘zning dekoderga kelib tushgunicha bo‘lgan ma’lumot aprior, kodli
so‘zni qayta ishlab bo‘lingandan keyin qabul qilingan ma’lumot, aposterior
deb yuritiladi.
Berrou
o‘z ish faoliyatida turbo dekoderlarda yuqori extimolikka ega aprior algoritmdan
foydanishni taklif etadi. (angl. Maximum
of A-posteriori Probability, MAP), shuningdek Bala algoritmi foydalanishni
xam qo‘llab quvvatlaydi.
Bala
algoritmi dekodlangan bitlar uchun «yengil» ishonchlilikni beradi. Ya’ni chiquvchi
satxda dekodlashni ishonchli natijaga erishishini ta’minlaydi. Qattiq struktura
esa, dekoderning chiqishida dekodlangan bitning eng katta qiymatini shakllantiradi.
Yumshoq strukturada xisoblashda chiquvchi signalning batafsilroq bo‘lgan
diskretizatsiyasi ishlatiladi. U berilgan bitning extimoli to‘g‘riligini
xarakterlaydi. Yumshoq yechimni qo‘llash tufayli turbo dekoderlarda bir nechta
dekoderlash iteratsiyalari samarali qo‘llanilishi yuzaga keladi. Birinchi dekoderlash
iteratsiyasining chiqishidagi kodli so‘zning qabul qilingani aposterior ma’lumot
deyiladi.
Keyingi
iteratsiya blokiga qabul qilingandan so‘ng aprior extimollik bo‘ladi. Bunday
yondashuv iteratsiyadan iteratsiyagacha bo‘lgan dekoderlash sifatini yaxshilaydi.
Shu tarzda dekoderlash iteratsiyasining qiymatini o‘zgartirgan xolda dekoderni
joriy uzatuvchi kanalga moslashtirishimiz va talab etilgan bitlar xatoligini
extimolligiga erishimiz mumkin.
To‘g‘ri
o‘xshashlikdagi logorifmik yondashuv.  ma’lumotli bitga, binar o‘zgaruvchi sifatida
qaraymiz. Ya’ni
ma’lumotli bitga, binar o‘zgaruvchi sifatida
qaraymiz. Ya’ni 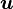
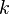 vaqt
momentidagi qiymatdir. Uning logorifmik yondashuvi (LLR) logorifmik yondashuv extimoli sifatida belgilanadi.
vaqt
momentidagi qiymatdir. Uning logorifmik yondashuvi (LLR) logorifmik yondashuv extimoli sifatida belgilanadi.
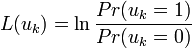
Bu o‘lchov ko‘p tizimlarda shovqinbardosh
kodlar yordamida xatolarni
to‘g‘irlashda foydalaniladi va to‘g‘ri
o‘xshashlikdagi logorifmik yondashuv
(LLR) deb ataladi. Bu usul to‘g‘ri o‘lchovligi
nisbatan ancha yaxshiroqdir. Logarifm juda kichkina va juda katta qiymatlarni
qayta ishlashni yengillashtirib beradi. Agar qabul qilish extimolligi
«0» va«1» teng bo‘lsa o‘lchov 0 ga teng bo‘ladi.
14.2-rasmda ikkilik kaskaddagi iteratsiyalangan Turbo koderning bitta iteratsiyaning
kodlanish sxemasi keltirilgan.

14.2-rasmda
ikkilik kaskaddagi iteratsiyalangan Turbo koderning bitta iteratsiyaning
kodlanish sxemasi.
14.2-rasmda ikki kaskadli bitta iteratsiyalangan turbo dekoderning kodlanish
sxemasi keltirilgan. Bu sxema istalgan miqdordagi kaskadlarni kodlashda murakkab
bo‘lmagan umumlashgan yechim xisoblanadi. Bitta iteratsiyalangan dekoder ikkita
kaskad dekoderning bog‘lanishiga bog‘liq bo‘lgan xolda, yuborilgan belgi
to‘g‘risida yumshoq yechim chiqaruvchi yuqori aposterior extimollikka ega
bo‘ladi. Birinchi iteratsiyalangan dekoderga demodulyatorning chiqishidagi
yumshoq yechimga ega bo‘lgan 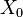 va
va  ketma ketlik kelib tushadi. Shu
tarzda birinchi dekoderning chiqishida ma’lumotli belgini baxosi xosil bo‘ladi.
Keyin ikkinchi dekoder qurilmasining kirishiga o‘zgargichdan o‘tgan ma’lumot
kelib tushadi va u aprior ma’lumot deb ataladi.
ketma ketlik kelib tushadi. Shu
tarzda birinchi dekoderning chiqishida ma’lumotli belgini baxosi xosil bo‘ladi.
Keyin ikkinchi dekoder qurilmasining kirishiga o‘zgargichdan o‘tgan ma’lumot
kelib tushadi va u aprior ma’lumot deb ataladi.  ketma ketlikda yumshoq yechimni qo‘llagan xolda, ikkinchi dekoder o‘zining baxosini shakllantiradi.
ketma ketlikda yumshoq yechimni qo‘llagan xolda, ikkinchi dekoder o‘zining baxosini shakllantiradi.
Xar bir chiquvchi iteratsiyalar yechimi keyingi kiruvchi ketma-
ketlikka o‘tadi. Uch iteratsiyalangan turbo dekoderning ishini tashkil
qilish 14.3-rasmda keltirilgan. Iteratsiyadan iteratsiyaga o‘tishda yechimlarni
aniqlash sodir bo‘ladi. Bunda xar bir iteratsiya yumshoq baxolash bilan
ishlaydi va chiqishga xam yumshoq baxoni uzatadi. Shuning uchun bunday sxemalar
yumshoq kirish va chiqishga ega bo‘lgan dekoderlar deb yuritiladi.
Dekodlash jarayoni, barcha iteratsiyalar amalga oshgandan so‘ng yoki extimolli
bitlar xatoligi talab etilgan ko‘rsatkichga yetgandan so‘ng amalga oshiriladi.
Dekodlashdan so‘ng xosil bo‘lgan «yumshoq» yechimga, yakuniy «qattiq» yechim
ishlab chiqariladi.
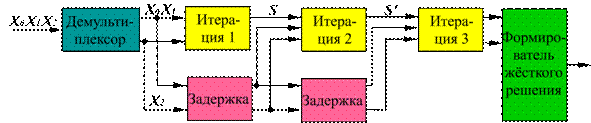
14.3-rasm.
Ikki kaskadli kodlashda uch iteratsiyalangan
turbo dekoder sxemasi.
Turbo-kodning
afzalliklari va kamchiliklari
Afzalliklari.
Amaldagi barcha foydalanilayotgan
zamonaviy xatolarni to‘g‘irlash uslubdagi kodlar, turbo kodlar va zichlikka
aniqlikni past tekshiruvchi kodlar, nazariy jixatdan shovqinli kanalda yuqori
tezlikda ma’lumot almashish imkonini beradi. Shu sababdan ular Shennon
chegarasiga mos keladi.
Turbo
kodlar uzatgichning quvvatini oshirmagan xolda, yuqori tezlikda ma’lumot
uzatish imkonini beradi. Ular berilgan tezlikda talab etilgan quvvatni pasaytirgan
xolda ma’lumot uzatishda foydalaniladi.
Turbo
kodlarning asosiy xususiyatlaridan biri shuki, ma’lumot blokining uzunligiga
bog‘liq bo‘lmagan xolda, dekodlash jarayonining oson bo‘lishidir. Ya’ni ma’lumotlar
bloki kanchalik uzun bo‘lsa dekodlashda xatolar extimolligining kamayishiga
olib keladi.
Kamchiliklari.
Turbo kodlarning asosiy kamchiligi - dekodlashning
murakkabligi va uzoq kutib qolishning mavjudligidir, bu esa ba’zi qo‘llash
soxalariga noqulaylikni xosil qiladi. Masalan, su’niy yuldoshli aloqa kanalida
foydalanganimizda bu kamchilik aniq kamchilik xisoblanmaydi, chunki aloqa
kanalining uzunligi oxirgi yorug‘liq tezligi tomonida chaqirilgan kutib
qolishlarga ega.
Turbo
kodlarning ya’na bitta asosiy kamchiliklaridan biri — kodlar masofasining uncha
katta bo‘lmagan taqqoslanishidir. Bu kiruvchi yuqori extimollik xatolarida
(ya’ni yomon kanalda) turbo kodlarning samaradorligi yuqori, kichik kiruvchi
xatolar extimolligida turbo kodlarning samaradorligi chegaralangan. Shu sababli
yaxshi kanallarda xatolar extimolligini kamaytirish maqsadida turbo kodlar
emas, balki LDPC- kodlari qo‘llaniladi.
Turbo
kodlashda murrakab algoritmlardan foydalansak xam, dasturiy ta’minotning
ochiq bo‘lmaganligi turbo kodlarni tatbiq etishda asosiy kamchilikdan biri
deb xisoblanadi, shunga qaramay xozirgi kunda barcha zamonaviy tizimlar
turbo kodlardan foydalanadi.
Turbo
kodlarning qo‘llanilishi. France Telecom kompaniyasi
va Telediffusion de France keng sinfdagi turbo koderlarni ixtiro qilishdi.
Ular turbo koderlarni ozod qo‘llanilish imkoniyatlarini cheklab, o‘sha vaqtning
o‘zida kodlashning LDPC ga o‘xshagan yangi usullarni rivojlantirishni
ishlab chiqishdi.
Turbo
kodlar faol tarzda:
Ø su’niy yo‘ldoshli aloqa kanalida;
Ø mobil
aloqada;
Ø simsiz
kengpolosali tarmoqlarda;
Ø raqamli televideniyada qo‘llaniladi.
Turbo-kodlar
su’niy yo‘ldoshli aloqa kanalida DVB-RCS standarti asosida tasdiqlangan. Shuningdek
turbo kodlar o‘zining keng qo‘llash soxalarini uchinchi avlod aloqa mobil
tizimlarda (standart CDMA2000 va UMTS) topdi.
Kodning
spektr og‘irligi. Ma’lumki kodning spektr
og‘irligi – bu ko‘p sonli M(ω) ko‘pxadining, (ω =0,n) da kodli kombinatsiyalar
og‘irligidagi qiymatidir. Ya’ni barcha kodli kombinatsiya tashkil etuvchilari
nol bo‘lmagan yig‘indi orqali aniqlanadi. Kodli kombinatsiyalari ko‘p bo‘lmagan
kodlar uchun (taqqoslaganda k- informatsion razryaddan ko‘p bo‘lmagan)
spektr og‘irliklari uchun, ruxsat etilgan kerakli miqdordan ortiqcha 2k
kombinatsiyasi orqali aniqlashimiz mumkin. Uncha uzunlikka ega bo‘lmagan,
odatda BChX kodlari kaskad kodning birinchi pog‘onasida past sifatli diskret
kanalda kichkina xatoliklarni to‘g‘irlash uchun ishlatiladi. Siklik koddagi
kodli kombinatsiyani qabul qilishda ikkita usuldan foydalanamiz:
1.
Q(x) kodli kombinatsiyani xr bir xadiga ko‘paytirib, xosil bo‘lgan ko‘paytirish natijasiga R(x)
polinomda Q(x)*xr bo‘lish natijasida xosil bo‘lgan R(x) qoldiq
qiymatni qo‘shish orqali:
F(x) =Q(x)*xr+R(x) (1)
2.
Q(x) kodli kombinatsiyani oddiy kodli polinom xosil qiluvchiga
ko‘paytirish orqali.
Birinchi usul tizim kodini xosil qiladi. Bunda informatsion
belgilar, r- ning qolgan o‘rinlariga tekshirilgan, k-ning birinchi o‘rnida
joylashadi. Ikkinchi usulda tizimlashmagan kod xosil bo‘ladi. Bunda tekshirilgan
belgilar va ma’lumotlar aniq ko‘rinishda bo‘lmaydi. Shunga qaramasdan shovqinbardosh
kodlarda tizimli va tizimlashmagan kodlar tengdir. Kodli ko‘plik o‘zgarmaydi,
faqat xar bir so‘zli ma’lumot uchun kodli so‘zga mos xolda tartibi o‘zgaradi.
Bunday tasdiqning to‘g‘riligini birinchi va ikkinchi usuldan foydalangan
xolda tuzilgan 1 tasvir asosida ko‘rishimiz mumkin.
Ruxsat etilgan birinchi kodli kombinatsiya usulda avtomatizatsiyani
qurishda u yoki bu dasturlash algoritmi usullaridan ma’lumotlarni
siklik kodlash jarayonlarida foydalaniladi:
a)
Kodli xabarlarni qismlarga
bo‘lish orqali;
b) Kodli axborotni to‘g‘ridan -to‘g‘ri bo‘lish orqali;
c)
Matritsa usulida;
d) jadval usulida.
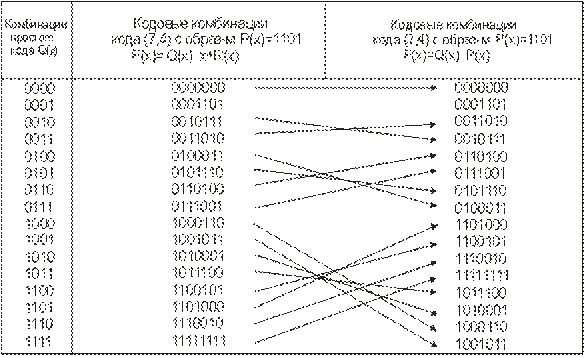
14.4-rasm. Turli xil usullarda olingan kodli kombinatsiyalarning
o‘zaro bog‘liqligi.
Mavjud kodlash algoritmlariga asoslangan xolda dasturning
murakkabligini baxolashni amalga oshiramiz. Buning uchun xotira xajmi va
kodlash uchun talab qilinadigan vaqtli yuklamani xisoblashimiz zarur.
Kodli kombinatsiyaga ishlov berish jarayonida operatsiyalar miqdori:
A0=An+AsK
(2) shu formula orqali aniqlanadi.
Bu yerda:
A0 – kodlash uchun zarur bo‘lgan
umumiy jarayonlar miqdori;
An – bir marta bajariladigan
operatsiyalar miqdori;
As – siklda bajariladigan operatsiyalar miqdori ;
K – kodlashning uslubiga bog‘liq bo‘lmagan xolda o‘zgaruvchi
sikllar miqdori.
Kodlash usulini kodli kombinatsiyalarni qismlarga bo‘lish orqali
amalga oshiramiz. ShKning yuklama o‘lchovi kodli kombinatsiyaning uzunligiga
bog‘liq bo‘lgan xolda kodlash uchun zarur bo‘lgan vaqt va tekshiriladigan
razryadlar soni 14.1-jadvalda keltirilgan.
14.1-jadval.
Kodli kombinatsiyani qismlarga bo‘lish usuli uchun asosiy ko‘rsatkichlar
|
Kod uzunligining ko‘rsatkichi
|
7,4
|
15,11
|
31,26
|
63,57
|
127,120
|
255,247
|
|
Yuklama
(oper/bit)
|
15,25
|
14,45
|
14,19
|
14,08
|
14,04
|
14,02
|
|
Vaqt, Ms
|
0,061
|
0,159
|
0,369
|
0,803
|
1,685
|
3,46
|
Jadvaldan qo‘rinib turibdiki, bu usul katta uzunlikdagi kodlarni
kodlash uchun qulay, u xotirada kodlash jadvaliga qo‘shimcha joyni talab
qilmaydi.
14.2-jadval.
Asosiy parametrlarga bog‘liq bo‘lgan xolda kod uzunligini
to‘g‘ridan to‘g‘ri bo‘lish
|
Kod parametri uzunligi
|
7,4
|
15,11
|
31,26
|
63,57
|
127,120
|
255,247
|
|
Yuklama
(oper/bit)
|
8,7
|
7,38
|
7,26
|
7,17
|
7,15
|
7,05
|
|
Vakt, Ms
|
0,105
|
0,237
|
0,567
|
1,227
|
2,613
|
5,451
|
Jadvaldan ko‘rinib turibdiki, kod uzunligi oshgan sari yuklama
kamayyapti, kodlash uchun sarflanadigan vaqt esa oshyapti. Kodni qismlarga
bo‘lish usuli xotirada kod jadvali uchun qo‘shimcha xarajat talab etadi.
Birinchi blok razryadining uzunligi qancha katta bo‘lsa, uning xajmi ya’nada
oshadi. Matritsalardan foydalangan xolda kodlashda An,m matritsa
xosil qilinadi. Uni qabul qilishda qo‘shimcha tekshirilgan matritsa elementlaridan
foydalanish talab etiladi. Tekshiriluvchi elementlar ketma-ket bo‘linuv
asosida polinom birligida o‘ng tomondagi nollarni va qo‘shimcha matritsa satrlarini
saqlagan xolda qoldiq oralig‘ida aniqlaydi.
14.3-jadvalda ShKda kod kombinatsiyasining uzunligiga bog‘liq
bo‘lgan xolda matritsa usulida tekshirilgan razryadlar uchun sarflangan yuklama
va vaqt ifodalangan.
14.3-jadval.
Kod uzunligiga bog‘liq xoldagi Matritsa usulidagi asosiy parametrlar
|
Kod parametri uzunligi
|
7,4
|
15,11
|
31,26
|
63,57
|
127,120
|
255,247
|
|
Yuklama
(oper/bit)
|
3,75
|
2,63
|
2,26
|
2,12
|
2,05
|
2,028
|
|
Vakt, Ms
|
0,075
|
0,089
|
0,099
|
0,121
|
0,247
|
0,601
|
Jadvalda keltirilgan ma’lumotlardan ko‘rinib
turibdiki, matritsali usul mashina vaqtining katta sarfini talab qilmaydi.
Lekin kodning uzunligi ortishi bilan jadval uchun kerakli xotira xam
oshib boradi.
Jadval usulining a’malga oshirilishida ShK xotirasiga 0 dan
2k gacha tekshiriluvchi razryadlarga tegishli natural sonlar o‘sib
borish tartibida joylashadi va ma’lumotlar kombinatsiyalarining mumkin bo‘lgan
qiymatlaridan tuzilgan matritsa yoziladi. Tekshirilayotgan razryadlar oldindan
berilgan kodni kodlash qoidasi bo‘yicha xisoblanadi. Buning uchun kodli
kombinatsiya qiymatini ko‘rsatuvchi jadval satrining tartibini bilish kifoya.
Bundan maqsad kodlangan so‘zni aniqlashdir. Jadval usuli uchun xisoblangan
xotira xajmi kodning uzunligiga bog‘liq va unga asosan vaqt va yuklama
xaqida ma’lumot 14.4-jadvalda keltirilgan.
14.4-jadval.
Jadvalli usulda kod uzunligiga bog‘liq bo‘lgan xolda asosiy parametrlar
|
Kod uzunligining
parametrlari
|
7,4
|
15,11
|
|
Xotira xajmi (yacheykalar)
|
15
|
23
|
|
Yuklama (oper/bit)
|
1,25
|
0,45
|
|
Vaqt, ms
|
0,015
|
0,015
|
Jadvaldagi ma’lumotdan ko‘rinib turibdiki, kodlashning bu usuli
xotira yuklamalari va kodning qisqa uzunlik xolatida mashina vaqtining kam
sarfini talab qilar ekan. Kod uzunligi oshgan sari esa jadval uchun xotira
xajmi xam oshib boradi.
Yuqoridagi jadvalni taxlil qilish natijasi shuni qo‘rsatadiki,
katta bo‘lmagan uzunlikdagi kodlarda amalga oshirish qiyinligi tomondan
eng qulay xisoblanadi. Chunki bu usul ShKdan kam yuklamani va ancha katta bo‘lmagan
kodlash vaqtini talab qilar ekan. Shuningdek, kattalik o‘zgarish yo‘li bilan
qismlarga bo‘lish usuli kam yuklama va vaqt tomondan yaxshi natijalarga ega.
Biroq katta uzunlikdagi kodlarda ushbu ikkinchi usuldan foydalanish samarasiz
bo‘lib qoladi. Chunki bunda ShKdan sezilarli xotira sarfini talab qilmaydigan
to‘g‘ridan-to‘g‘ri bo‘lish usuli eng yaxshi xisoblanadi.
Ruxsat etilgan kodli ketma-ketlikni qurishni amalga oshirish qiyinligi
tomondan qulayroq xisoblanadi. Uning qo‘llanilishi Q(x) ko‘pxad va P(x) ko‘pxadlarni
qo‘llash orqali jarayonni soddalashtiradi.
Kodlashga asoslangan spektr og‘irligini aniqlash algoritmini
ishlab chiqish asosi bo‘lib ruxsat etilgan kodlar ketma - ketligini olish
qo‘yilgan. Algoritm o‘zgaruvchilarini va xotirani zaxiralashni e’lon qilish
bilan boshlanadi (blok 2).
Bu blokda oraliq ma’lumotlarni, yakuniy natijani saqlash va
yozish uchun qanday o‘zgaruvchilar va massivlar kerak bo‘lishini aniqlaymiz.
Keyin kerakli ma’lumotlarni yasovchi polinom P(x), ma’lumot polinomi
uzunligi k lar kiritilishi kerak (blok 3).
Axborot qismi uzunligi kodli so‘zning mumkin bo‘lgan barcha
ketma-ketliklarini qidirish sonini aniqlash uchun kerak (blok
4). 5 blokda r kodli ketma-ketlikning tekshirilayotgan razryadlarini
xisoblash amalga oshiriladi. Keyin xr ko‘pxad xisoblanadi (blok
6). 7 blokda xr va Qi(x) ko‘pxadlar ko‘paytiriladi.
Bu oraliq natija xotiraga saqlanadi va axborot ketma-ketligining mumkin bo‘lgan
qiymatlarini xisoblanganlik sharti tekshiriladi (blok 8). Keyingi qadamda
olingan natijani yasovchi polinom P(x) ga bo‘lish bajariladi (blok 9). Bu
10 blokdagi qoldiq R(x) aniqlash uchun zarur. R(x) qoldiq xar bir ketma-
ketlik uchun topiladi va shuning uchun yana kodli ketma-ketlik yana bir bor
yoki yo‘qligi sharti teshiriladi (11blok). 12 blokda F(x) kodli ketma-ketlik
shakllantiriladi. Kodli ketma ketlikni olgandan so‘ng og‘irlikni xisoblashga
kirishish mumkin (13blok ). Endi og‘irlik qiymatini ifodalab chiqamiz(14 blok).
Algoritmning tuzilish sxemasi 14.5-rasmda keltirilgan.

2 rasm .
14.5-rasm. Og‘irlikni xisoblovchi algoritm sxemasining tuzilishi
Polinomlarni ko‘paytirishga asoslangan spektr og‘irlikni aniqlash
algoritmiga siklik kodning kodli ketma-ketligini olish ikkita ko‘pxad yasovchi
axborot yordamida amalga oshirish asos bo‘lgan.
Algoritm o‘zgaruvchilarni va xotirani zaxiralash e’lon qilinadi
(2 blok). Bu blokda oraliq ma’lumotlar va yakuniy natija yozish va saqlash
uchun (s1, s2, s3) kerak bo‘lgan massivlar va o‘zgaruvchilar aniqlanadi.
Keyin chiquvchi ma’lumotlarni kiritish zarur bo‘ladi:
(50) shaklida polinom va polinom ma’lumotlar uzunligi (¹1) (blok3).
Ma’lumotning uzunlik qismi, kerakli miqdordagi kodli
so‘zning barcha imkoniyatlarini aniqlash uchun kerak. Bundan tashqari boshlang‘ich s1 i s2 (4 blok ) qiymatini aniqlash uchun
kerak.
Bu qiymatlar oraliq natijani yozish uchun qo‘llaniladi. 5 blokda
ikkita ko‘pxad ko‘paytiriladi va xosil bo‘lgan siklik kodli kombinatsiyani
olgan xolda og‘irlikni xisoblashga o‘tishimiz mumkin (blok 6). Xisoblash
amalini yakunlashdan oldin xabar kombinatsiyasining ketma-ketlik imkoniyatlarini
(blok 7) ko‘ramiz. Siklik kombinatsiyaning chapga surilishi operatsiyasi
kerakli miqdor prinsipi xisoblanadi. Agar to‘liq to‘lib qolish kuzatilsa,
og‘irlik qiymatlarini chiqaramiz. (blok 9). Agar yo‘q bo‘lsa, keyingi 1 qiymatni
aniqlaymiz (blok 8), va kodli og‘irliqni xisoblash jarayonini takrorlaymiz.
Shu bilan xisoblash jarayonini (blok 10).
14-ma’ruza
uchun nazorat savollari
1. Turbo
kodlarga tushuncha bering?
2. Turbo-kodlarda
navbat qanday amalga oshiriladi?
3. Turbo-kodning
afzalliklari va kamchiliklari nimalardan iborat?
4. Turbo
kodlar qaerlarda ko‘proq qo‘llaniladi?
5. Kodning
spektr og‘irligiga tushuncha bering?
6. Dastur
murakkabligini baxolash qanday amalga oshiriladi?
15-ma’ruza.
Yengil yechimli dekodlash
Reja:
1.
Qattiq” yoki “Yengil” qaror qabul qilish
2.
Xatolarni tahrirlovchi RS – kodlar
3.
Turbo-kodni qo‘llash samaradorligini oshirish
4.
Tahrirli kodlarni qo‘llash.
5.
“Yengil” yechimli qaror
“Qattiq”
yoki “Yengil” qaror qabul qilish. Blokli
kodlarni ochish “Qattiq” yoki “Yengil” qaror qabul qilish yordamida amalga oshirilishi
mumkin, kodni ochuvchidan chiqishda esa “Qattiq” yoki “Yengil” yechimli ma’lumotlarga
ega bo‘lamiz.
“Qattiq”
qaror qabul qilish orqali kodni ochishda har bir qabul qilinayotgan bitga qabul
qilinayotgan ma’lumotlardagi halaqitlarning me’yordan ko‘p yoki kamligiga bog‘liq
ravishda 0 yoki 1 belgisi yoziladi. Kod ochgichda kodlagichda xato borligini
aniqlash, imkon bo‘lganda xatoni to‘g‘irlash uchun qo‘shilgan ortiqcha ma’lumot
qo‘llaniladi. Kod ochgichdan chiqayotgan ma’lumotlar – bu to‘g‘irlangan kodli so‘zlar
xisoblanadi.
“Yengil”
yechimli qaror bilan qabul qilingan kod ochuvchi faqatgina 1 yoki 0 binar kattalikni
qabul qilib qolmasdan, balki, berilgan bit bilan bog‘liq ishonchli kattalikni ham
qabul qiladi.
Agar
modulyator bitga 1 belgisi biriktirilishini aniqlasa, u holda ishonchlilik darajasi
unda yuqori bo‘ladi. Agar u kamroq aniqlansa, bu xolda u pastroq ishonchli kattalikka
joylashtiriladi.
“Yengil”
yechimga kiradigan kod ochuvchi “Qattiq” qarorli yoki “Yengil” yechimga ega qarorli
ma’lumotlar chiqarishi mumkin.
Masalan,
Viterbi kodni ochish qurilmasi “Yengil” yechimli axborotni qabul qiladi va “Qattiq”
qarorli ma’lumotlarni chiqaradi. Kod ochuvchi “Yengil” yechimli ma’lumotni berilgan
0 yoki 1 bitning tengligini aniqlash uchun ishlatishi mumkin. Bunda biz chiqayotgan
bitdan shunday “Qattiq” qarorga ega bo‘lamiz.
Xatolarni
tahrirlovchi RS – kodlar. “Yengil” yechimga kiruvchi
va yengil chiquvchi (SISO) kod ochuvchi “Yengil” qarorli ma’lumotlarni qabul qiladi
va “Yengil” qarorli ma’lumotlarni chiqaradi. Kodli so‘zning har bir biti uchun
SISO kod ochuvchisi kodning ortiqcha ma’lumotidan foydalangan holda kodli so‘zdagi
boshqa bitlarning ishonchlilik darajasini baxolaydi, berilgan bit uchun mukammallashtirilgan
yengil ma’lumotlarni ishlab chiqadi.
Xatolarni
tahrirlovchi RS – kodlar xatolar tahririni ogohlantirish uchun standart algoritm
hisoblanadi.
RS
kodlar – bu blokli kodlar bo‘lib, dasturiy hamda uskunaviy ta’minotni qo‘llash jarayonida
xatolarni to‘g‘irlash bo‘yicha juda yaxshi qobiliyatga ega.
RS
kodlar – bu “Qattiq” qaror qabul qiluvchi kodlar hisoblanadi. RS kodlardan keyingi
o‘rinda Viterbi (RSV) kaskad kodlari turadi, ular xato bitlarning paydo bo‘lish
tezligi bo‘yicha avtonom RS – kodlardan ustun turadi.
Turbo
kodni qo‘llash samaradorligini oshirish. SISO
kod ochgichlari konsepsiyasi turbo-kodlarda qo‘llangan. Turbo-kod SISO kod ochgichiga
“Yengil” yechimga ega qarorli ma’lumotlarni yetkazadi. Mazkur kod ochgichning chiquvchi
ma’lumotlari keyin aynan shu yoki boshqa SISO kod ochgichiga uzatiladi. Keyin jarayon
qayta takrorlanadi. Bu iteratsiya jarayoni qat’iy qaror qabul qilingunga qadar davom
etadi. Chiqayotgan ma’lumotlarni orqaga kirish qismiga qaytarilish konsepsiyasi
dvigatelning turbopurkagichiga o‘xshash bo‘lganligi sababli ham turbo-kod aynan
shunday nomlangan.
Turbo-kodni
qo‘llash samaradorligini oshirish uchun, ma’lumotlarni ikki yoki ko‘proq turli xil
kodlar bilan kodlash lozim. Shundan so‘ng kodni ochish jarayonida kodlarning har
biri har bitta bitga nisbatan o‘z ishonchlilik darajasini o‘zgartiradi.
Har
bir iteratsiyada barcha kodlar ma’lumotlarga bo‘lgan ishonchlilik darajasini o‘zgartiradi.
Shunday ekan, har bir kod har bir iteratsiya uchun birmuncha farq qiluvchi ma’lumotlarni
kuzatadi.
Har
bir kod berilgan bitga nisbatan ishonchlilik darajasini oshiradi yoki pasaytiradi,
natijada xato bitlarga nisbatan qarorning qattiqlik darajasini o‘zgartiradi. Oxir
oqibatda, ma’lumotlar shunday ko‘rinishga keladiki, bunda barcha kodlar barcha bitlarga
nisbatan ishonchlilik darajasini faqatgina oshiradi. Bu bosqichda “Qattiq” qaror
kattaligi uzatilayotgan ma’lumotlarga yaqinlashadi.
Halaqitga
qarshi kodlarni ochish. Tahrirli kodlarni qo‘llash
jarayonida ikkilamchi signallarning kanal bo‘ylab shovqinli uzatilishini ko‘rib
chiqamiz.
Halaqitga
qarshi kodlarni ochishning ikkita usuli mavjud bo‘lib, ular amaldagi sonlarni ketma-ketlikda
demodulyatsiya qilinishidan keyin olinishga asoslanadi:
“Qattiq”
qaror orqali kodni ochish (hard decision decoding). Bu
holatda amaldagi songa 0 yoki 1 taqqoslanadi, ya’ni kanaldan qabul qilingan birliklarga
nisbatan “Qattiq” qarorlarni qo‘llash jarayonida qabul qilinayotgan belgilarning
inversiyasi ko‘rinishidagi xato paydo bo‘ladi. Bunday holatda maksimal ishonchlilik
tamoyili asosida kodni ochish uchun Xemming
masofasidan foydalaniladi.
“Yengil”
yechimli qaror orqali kodni ochish
(soft-decision decoding). Kanaldan qabul qilingan
birliklar darajalarning berilgan sonida kvantlanadi va darajalar bir nechta intervalda
sonlar bilan kodlanadi, masalan, sakkizinchi darajali kvantlanishda -4, -3,
-2, -1, 0, 1, 2, 3, 4 birliklari vositasida kodlanadi. Bunday holatda maksimal ishonchlilik
tamoyili asosida kodni ochish uchun odatiy yevklid masofasidan foydalaniladi.
“Yengil”
yechimli qaror. Umuman olganda, u yoki bu
qarorni tanlashdan oldin aloqa kanalidagi shovqin statistikasini bilish maqsadga
muvofiq. Bundan tashqari, shuni yodda tutish kerakki, “Qattiq” qaror orqali kodni
ochish berilgan kodni ma’qul darajada tahrirlashni kafolatlovchi boy nazariy bazaga
ega.
“Yengil”
yechimli qaror uchun esa bunday nazariy baza deyarli mavjud emas. Boshqa tomondan
olganda, “Yengil” yechimli qarorda kod ochgich tomonidan aniqlangan xatolar miqdori
(darajalar sonining ko‘pligi hisobiga) “Qattiq” qarordagiga nisbatan kamroq bo‘lishini
kutish mumkin va mos ravishda aynan bitta kod ko‘p miqdordagi xatolarni to‘g‘irlashi
mumkin.
Masalan,
(ABGSh) additiv oq Gauss kanalida. “Yengil” yechimli qaror orqali kod ochish qo‘llanilishining
maqsadga muvofiqligi ma’lumotlarni tiklash yoki signal qabul qilishdagi shovqin
komponenti o‘z tabiatiga ko‘ra diskret emas, balki uzluksiz bo‘lganligi bilan ham
asoslanadi. Bu esa qabul qilingan belgilar GF(2m) yakuniy maydonning ikkilamchi
belgilari bilan emas, balki, (kuchlanishga mos keluvchi) amaldagi sonlar bilan
birmuncha tabiiyroq kvantlanishini bildiradi.
“Yengil”
yechimli qaror uchun Viterbi algoritmi “Qattiq” yechimli qaror uchun bo‘lgan algoritmdan
farq qilmaydi, faqatgina masofalar Xemming bo‘yicha emas, balki Yevklid masofasi
bo‘yicha hisoblanishi bundan istisno.
Ishlarda
ko‘rsatilishicha, “Yengil” yechimli qarordan foydalanish signal 8-16 darajalarda
kvantlanganda optimal hisoblanadi.
Maksimum
ishonchlilik asosida kodni ochish kodlash nazariyasida birmuncha muhim va murakkab
algoritmik muammo hisoblanadi. Ma’lumki, aloqaning ikkilamchi simmetrik kanali
va erkin chiziqli kodlar uchun bu muammo NP-to‘liq hisoblanadi. Bundan tashqari,
u kodning uzoq qayta ishlanish vaqtida ham shundayligicha qoladi.
Binobarin,
mazkur masalani hal etish uchun bugungi kunda ko‘plab umumiy nazariyalar o‘rganilgan
va ishlab chiqilgan. Bu barcha algoritmlar kod uzunligiga eksponensial ravishda
qotib qolish kabi murakkabliklarga ega. Bundan tashqari ular o‘rtacha uzunlikdagi
(blokda 200 belgigacha) kodlarni bog‘lashda oddiy qo‘llanilishi bilan yaroqli hisoblanadi.
Ular
jumlasiga, masalan, axborot jamlanmalari deb nomlanuvchi kod ochish algoritmlari
kiradi. Masalani hal etuvchi boshqa bir misol, Levitin va Xartman tomonidan taklif
etilgan “nol qo‘shnisi” (ingl. zeroneighbors) algoritmi nomini olgan ML-kod ochish
hisoblanadi. Ta’kidlangan oilalarga mansub ML-kod ochish algoritmi o‘rganilgan ishda
minimal so‘zlar uslubi hisoblanadi.
15-ma’ruza
uchun nazorat savollari
1. Qattiq”
yoki “Yengil” qaror qabul qilishga tushuncha bering?
2. Xatolarni
tahrirlovchi RS – kodlar tavsifi nimalardan iborat?
3. Turbo-kodni
qo‘llash samaradorligini oshirishga tushuncha bering?
4. Halaqitga
qarshi kodlarni ochishning nechta usuli mavjud va ularga tavsif bering?
16-ma’ruza.
Shovqinbardosh kodlarni telekommunikatsiyada qo‘llanishi.
Reja:
1. Aloqa
kanallari orqali axborot yetkazilishining ishonchliligini ta’minlash usullari.
2. Kodlarning
texnologiyalarda qo‘llanilishi.
3. ATM
tizimlarida sarlavhadagi xatolarni aniqlash va bartaraf etish.
4. ATM
yacheykasi.
5. Tranking
aloqada kodlash usullari.
6. Kodlarning
GSM radiokanallarida qo‘llanilishi.
7. O‘rama
kodning kamchiligi.
8. CDMA
tizimlarida ishlatiladigan kodlar.
9. Xatolar
paketidagi qotib qolishlar va ularning kelib chiqish sabablari bilan kurashish.
10.
Kompakt
disklarda xatolarning paydo bo‘lishi.
Aloqa
kanallari orqali axborot yetkazilishining ishonchliligini ta’minlash usullari. Aloqa
kanallari orqali axborot yetkazilishining ishonchliligini ta’minlash usullarining
asosiylaridan biri xatolarni topuvchi va to‘g‘irlovchi xalaqitga qarshi kodlardan
foydalanish hisoblanadi. U yoki bu kodni qo‘llash xatoning turiga bog‘liq bo‘ladi.
Masalan:
•
Xemming kodi xatolarni to‘g‘irlash uchun;
•
BChX
kodi ko‘p martalik mustaqil yakka xatolarni to‘g‘irlash uchun;
•
Fayr kodi xatolarning yakka paketlari uchun;
•
Rid-Solomon
kodi ko‘p martalik xatolar paketi uchun xizmat qiladi.
Davriy
kodlar:
•
kosmik aloqalar tizimlarida;
•
raqamli televideniya tizimlarida;
•
raqamli radioaloqada;
•
uyali va tranking aloqada;
•
ma’lumotlarni yetkazish tizimlari kabi turli tizimlarda keng qo‘llaniladi.
Kodlarning
texnologiyalarda qo‘llanilishi. Bu kodlar axborot
saqlanishining yuqori ishonchliligini ta’minlash imkonini beradigan lazer va magnit
disklardagi to‘plagichlarda, xotira qurilmalaridagi yarimo‘tkazgichlardagi xatolarni
bartaraf etish uchun qo‘llaniladi. Masalan:
•
ATM texnologiyasida BChX kodlari;
•
ARSO 25 standartidagi raqamli tranking aloqalarida Xemming kodi, Rid-Solomon
va Goley kodlari;
•
GSM harakatlanuvchi aloqa radiokanallarida
aniqlilikni nazorat qilish davriy kodlari, blokli va o‘ramli kodlar;
•
raqamli televideniyada axborotlarni magnit
disklarga yozish jarayonida RS kodlari qo‘llaniladi.
ATM
tizimlarida sarlavhadagi xatolarni aniqlash va bartaraf etish. ATM
tizimlarida sarlavhadagi xatolarni aniqlash va bartaraf etish uchun BChX davriy
kodlaridan samarali foydalaniladi. BChX kodlaridan tashqari shuningdek, aloqa kanallaridagi
xatolarning turlariga ko‘ra, hamda to‘yinganlik darajasiga bog‘liq xolda turli kombinatsiyadagi
xatolarni bartaraf eta oladigan boshqa kodlar ham qo‘llaniladi. Xatoning turi axborot
yetkazish usuli va kanalning fizik hususiyatiga ko‘p tomonlama bog‘liq bo‘ladi.
ATM
texnologiyalarida xatolar oqibatida asosan “ko‘payish effekti” deb ataluvchi xatolarni
yo‘qotish jarayoni yuzaga keladi. Bu effektda sarlavhadagi xatolar oqibatida axborot
paketi boshqa bir qabul qiluvchiga yetib borishi mumkin. ATM yacheykasi sarlavhasini
himoya qilish uchun BChX kodlarini qo‘llash eng samarali hisoblanadi. Bu kodlar
n, k, t belgilarini cheklangan miqdorda bosish orqali xatolarni bartaraf
etishdagi keng ko‘lamdagi imkoniyatlariga ega
ATM
yacheykasi. ATM yacheykasida sarlavha 5 oktetni
tashkil qiladi. Xatolar nazorati maydoniga 8 bit ajratilgan. Bu 89% ko‘p bitli xatolarni
aniqlash va ularni bartaraf etish uchun yetarli hisoblanadi. ATM yacheykalarining
har bir o‘tkazuvchisi sarlavhaning birinchi to‘rtta okteti uchun sarlavhadagi xatolar
nazorati maydoni belgilarini hisoblaydi va natijani beshinchi oktet (sarlavhadagi
xatolar nazorati maydoni)ga o‘tkazadi. Maydon belgisi (mod 2 bo‘yicha) x8
ko‘paytuvchisining yacheyka sarlavhasi tarkibi (sarlavha nazorati maydonisiz) x8+x2+x+1
ga taqsimoti qoldig‘i sifatida aniqlanadi. O‘tkazuvchi qurilmasi bu qoldiqni hisoblaydi
va unga mod2 bo‘yicha 01010101 belgilangan kombinatsiyani qo‘shadi. Xuddi shu yig‘indi
sarlavha xatolar nazorati maydoniga yoziladi. Yuqorida ko‘rsatilgan barcha jarayonlar
adaptiv mexanizm yordamida ATM yacheykalar qurilmasi tomonidan amalga oshiriladi.
Ishga
tushirilgandan so‘ng qabul qilgich korreksiya rejimida turadi. Agar bir bitli xato
aniqlansa, u xolda yacheyka o‘chiriladi. Ikkala holatda ham qabul qilgich detektirlash
rejimiga o‘tadi. Qabul qilgichning bunday holatida sarlavhadagi yakka yoki ko‘p
xatolar aniqlangan har bir yacheyka o‘chiriladi. Agar sarlavhada xatolar topilmasa,
u xolda mexanizm korreksiya xolatiga o‘tadi.
Tranking
aloqada kodlash usullari. APCO 25 standarti raqamli
tranking aloqada kodlashning asosiy usullari quyidagilar hisoblanadi:
Ø blokli
kodlash;
Ø panjarali kodlash;
Ø ketma-ketlik.
Axborotni
blokli kodlashda tahrirlovchi kodlarning quyidagi turlari qo‘llaniladi:
•
Xemming
kodlari;
•
Rid-Solomon
kodlari;
•
Goley
kodlari;
•
aniqlikni nazorat qiluvchi davriy kodlar
(CRC-kodlar).
Xemming
kodlari nutqli xabarlarni kodlashda qo‘llaniladi (nutqli kadrlar, shifrlashning
sinxron so‘zlari, aloqa kanalini boshqaruv nutqlari).
Rid-Solomon
va Goley kodlari esa xabar muqaddimasi uchun;
Aniqlikni
nazorat qiluvchi davriy kodlar (CRC-kodlar) esa asosan ma’lumotlarni kodlash uchun
qo‘llaniladi va polinom ko‘rinishida tasvirlangan chiquvchi axborot blokini kelib
chiqadigan polinomga taqsimlash, mod2 bo‘yicha aniq bir inversli polinomga ko‘paytirish
natijasini ayirish yo‘li bilan shakllanadi.
Masalan,
axborot nutqlarini kodlash uchun RS kodlarining (36,
20, 17), (24, 16, 9) va (24, 12, 13) parametrli
3 turi qo‘llaniladi. Ularning barchasi qisqartirilgan hisoblanadi va 63 yo‘l uzunlikdagi
koddan ko‘proq axborotli belgilarni ayirishdan xosil bo‘ladi.
ARSO
25 dagi blokli kodlash tizimli hisoblanadi, ya’ni, kodli so‘zning birinchi k
belgisi axborot belgisining takrorlanishini aks ettiradi, oxirgi (n - k)
belgilar tekshiruvchi hisoblanadi.
ARSO
25 standartida Goley kodlarining 3 turi qo‘llaniladi:
•
Goleyning
(23, 12, 7) parametrli strandart kodlari;
•
(24,
12, 8)
kengaytirilgan;
•
(18,
6, 8)
qisqartirilgan.
Goleyning
standart kodi o‘sib boruvchi polinom bilan generatsiyalanadi:
G(x)=x11+x10+x6+x5+x4+x3+x2+1,
bunda,
sakkizlik ko‘rinishidagi qaydda 6165 soni bilan aks ettirish mumkin.
Kodlarning
GSM radiokanallarida qo‘llanilishi. Goleyning
kengaytirilgan kodi (24, 12, 8) aniqlik nazoratining bir standart bitiga qo‘shish
orqali xosil bo‘ladi. Goleyning qisqartirilgan kodi (18, 6, 8) kengaytirilgan koddan
eng katta chap olti bitni ayirish natijasida hosil bo‘ladi.
Harakatlanuvchi
aloqali GSM (Group Special for Mobile - maxsus mobil aloqa guruhi) radiokanallarida
o‘rama va blokli kodlash ketma-ketlikda qo‘llaniladi. Ketma-ketlikda qo‘llash shakllangan
xatolar paketini yakka xatolarga aylanishini ta’minlaydi. O‘rama kodlash yakka xatolar
bilan kurashishning kuchli vositasi hisoblanadi, blokli kodlash esa tahrirlanmagan
xatolarni aniqlash uchun qo‘llaniladi.
Blokli
kod (n, k, t) k axborot belgilarini (n-k) aniqlik belgilarini
qo‘shish, shuningdek, t xatolik belgilarini tahrirlash yo‘li bilan shakllantiradi.
O‘rama
kodlashning asosiy hususiyatlaridan biri k birligi hisoblanib, bu birlik
kodli cheklanishning uzunligi bilan ataladi va mazkur axborot belgisi chiquvchi
belgilarning qanday maksimal soniga ta’sir qilishini qo‘rsatadi. Amalga oshirish
nuqtai nazaridan, Viterbi algoritmiga nisbatan o‘rama kodlarni ochish murakkabligi
eksponensial ravishda kodli cheklash uzunligining oshishi bilan o‘sib boradi, bunda
k belgilari kichik bo‘ladi va 3-10 intervalida yotadi.
O‘rama
kodning kamchiligi shundaki, ular xatolarni
aniqlay olmaydi. Shu sababli GSM standartida xatolarni tashqi aniqlash uchun
(2, 1, 5) o‘rama kod asosidagi blokli kod qo‘llaniladi. Faqatgina kanalda yakka
(tasodifiy) xatolar mavjud bo‘lgan xolatda o‘rama kod yaxshiroq natijani ta’minlaydi.
GSMda uchraydigan qotib qoluvchi kanallarda o‘rama kodni ketma-ketlik bilan birgalikda
qo‘llash lozim.
GSM
standartli harakatlanuvchi aloqada quyidagi halaqitga qarshi kodlar ishlatiladi:
1.
Davriy kod
(53, 50), d0 = 3 kodli
masofa bilan;
2.
O‘rama kod (2, 1);
3.
Ketma-ketlik (nutqli
rejimda).
4.
Fayra kodi
(x23 + 1)(x17 + x9 + 1), k = 184; r = 40;
5.
O‘rama kod (2, 1).
Birinchi
uchta kod 10-3 ketma-ketlikdagi
xatolarni topolmasligi mumkin.
To‘rtinchi
va beshinchi kodlar ma’lumotlarni uzatishda qo‘llaniladi.
CDMA
tizimlarida ishlatiladigan kodlar. CDMA
(Code Division Multiple Access - Kodli ajratishli ko‘plab ruxsat etish (KAKRE) texnologiyasi)
tizimlarida quyidagi kodlar ishlatiladi:
-
o‘rama kod;
-
kaskadli kodlash;
-
Rid – Solomon kodi
→ ketma-ketlik
→ o‘rama
kod;
-
Turbo-kodlash;
-
maxsus kodlash.
O‘rama
kodlar nutqni kodlashda ishlatiladi. Ikkinchi va uchinchi kodlar ma’lumotlarni kodlashda,
to‘rtinchi va beshinchi kodlar ma’lumotlarni uzatishda qo‘llaniladi.
Nutqni
kodlash bir nechta o‘ziga xos hususiyatlarga ega: aniq vaqt rejimida interaktiv
aloqani ta’minlash zarur, bunda axborotni qayta ishlash bilan bog‘liq bo‘lgan kechikish
me’yordan oshmasligi lozim.
Buning
uchun birinchi bosqichda xatolar paketini qayta tahrirlash amalga oshiriladi, natijada,
ular yakka xatolarga aylanadi.
Ikkinchi
bosqichda signal xatolar bilan kurashishning odatiy uslublari yordamida qayta ishlanadi,
bu esa ularnining to‘liq o‘chirilishiga olib keladi.
Xatolar
paketidagi qotib qolishlar va ularning kelib chiqish sabablari bilan kurashish.
Xatolar paketidagi qotib qolishlar va ularning
kelib chiqish sabablari bilan kurashish uchun ketma-ketlik jarayoni amalga oshiriladi,
bunda belgilar o‘rin almashinuvi uning kodlanish ketma-ketiligi bo‘yicha qo‘yiladi
va chiqish ketma-ketligi bo‘yicha tiklanadi. Mazkur jarayon impulslar ketma-ketligini
o‘zgartirib, ularning oshib ketishiga yo‘l qo‘ymaydi. Ketma-ketlik chuqurligi, ya’ni,
ketma-ket kirib kelayotgan qo‘shni belgilarning oraliq masofasi qanchalik katta
bo‘lsa, kechikish ham shuncha katta bo‘ladi.
Sputnik
raqamli radioaloqada ishlatiladigan (63, 44) BChX kodi 63 belgidan iborat har bir
kodli blokda 5 yoki 4 ta xatoni aniqlash va yashirish, ikki yoki uch xatoni to‘g‘irlashi
mumkin.
Hisoblash
tizimlarining samaradorligining oshishi saqlanadigan va uzatiladigan axborotlar
hajmini sezilarli darajada oshiradi. Xatolarga yo‘l qo‘yilmasligining zarurligi,
shuningdek axborotlarining o‘zi ham uskunalardan foydalanish, shuningdek, xatolarni
aniqlash va to‘g‘irlash dasturlaridan foydalanishni talab qiladi.
Kompakt
disklarda xatolarning paydo bo‘lishi. Kompakt
disklar va magnit lentalardagi raqamli yozuvlar va ma’lumotlar tizimida xatolarning
asosiy qismini “paket lotoreyasi” turidagi xatolar tashkil etadi. Yozuv va ma’lumotlar
sifatiga xatolar paketining ta’sirini kamaytirish uchun mazkur xatolar bilan kurashishning
samarali vositasi hisoblangan halaqitga qarshi kaskadli kodlashdan foydalaniladi.
Eng noqulay xolatlarda ham xatolarni aniqlash va ularni to‘g‘irlash uchun kodlar
katta zahira bilan tanlanadi. Bundan tashqari raqamli magnitofonlarda yoziladigan
oqim blokli tarkibga ega bo‘ladi. Yozib olishning bunday shakli blokli tarkibda
halaqitga qarshi kodlarni qo‘llashni talab qiladi.
Harakatlanuvchi
tashuvchilarga yozish va o‘qish tizimida o‘qish jarayonidagi xatolar tashuvchidagi
yo‘qotishlar va boshqa jarohatlarda aks etadi, yarimo‘tkazgich xotirali tashuvchilarda
qotib qolishlar va uzilishlar yuzaga keladi.
Ma’lumotni
o‘qish yozuvlari tizimida kanal rolini axborot tashuvchi bajaradi: magnit lenta,
disk, gramplastinka, yarimo‘tkazgichli xotirada saqlovchi qurilmalar.
Prodigi
(ingl. Professesional Digital), R – DAT (Rotary head Digital Audio Tape), S –
DAT (Stationary head Digital Audio Tape) formatidagi raqamli magnitofonlarda Rid
– Solomon kodlari qo‘llaniladi: ikkitalik kod S1(32,28) va S2(36,26), (40,32) va
(29, 27).
16-ma’ruza
uchun nazorat savollari
1. Aloqa
kanallari orqali axborot yetkazilishining ishonchliligini ta’minlash usullari qanday
amalga oshiriladi?
2. Kodlarning
texnologiyalarda qo‘llanilishiga tushuncha bering?
3. ATM
tizimlarida sarlavhadagi xatolarni aniqlash va bartaraf etishga tushuncha bering?
4. ATM
yacheykasi tuzilishi qanday?
5. Tranking
aloqada kodlash usullari qanday amalga oshiriladi?
6. Kodlarning
GSM radiokanallarida qo‘llanilishiga tushuncha bering?
7. O‘rama
kodning kamchiligi nimalardan iborat?
8. CDMA
tizimlarida qanday kodlar ishlatiladi?
9. Xatolar
paketidagi qotib qolishlar va ularning kelib chiqish sabablari bilan kurashish nimalardan
tashkil topgan?
10.
Kompakt disklarda xatolarning paydo bo‘lishiga
sabab nima?
17-ma’ruza.
Zamonaviy modemlarda modulyatsiya va demodulyatsiya usullari.
Reja:
1. Modulyatsiya
tushunchasi.
2. Demodulyatsiya
tushunchasi.
3. xDSL
keng polosali ulanish
4. Splitterning
ishlash prinsipi
5. Optik
tolali tarmoqlar uchun modemlar
Yangi
ilovalarning paydo bo‘lishi, trafik hajmining va foydalanuvchilar sonining
oshishi ko‘rsatilayotgan xizmatlarning sifat kafolatiga ega yuqori tezlikdagi
texnologiyalardan foydalanishga bo‘lgan ehtiyojga olib kelyapti.
XTI-T
tavsiyanomalarida multimedia kabi belgilangan, ta’minoti uchun foydalanish
tarmog‘i o‘tkazish xususiyatining o‘sishi talab etilgan, axborot kompleks
taqdim qiluvchi xizmatlar eng talabgor xizmatlar hisoblanadi.
Foydalanish tarmog‘i
rivojlanish tendensiyasi va zamonaviy holatining taxlili shuni ko‘rsatadiki,
multiservis foydalanish tarmoqlarini qurish an’anaviy yondashishning real
alternativasi bo‘lib boradi.
Kerakli o‘tkazish
polosasi kengligi masalasida turli hil ilovalar talablari
|
Ilova
|
Uzatish turi
|
Uzatish formati
|
Siqishsiz uzatish tezligi
|
Siqish bilan uzatish tezligi
|
|
Ovoz
|
Telefoniya
|
G.711- G.723.1
|
64 kbit/s
|
8-32 kbit/s
|
|
Tasvir
|
Oddiy
kengaytmadagi tasvir
|
SVGA
|
2,458 Mbit/s
|
24-245 kbit/s
|
|
JPEG
|
6,636 Mbit/s
|
104-830 kbit/s
|
|
Yuqori sifatdagi tasvir
|
|
31,46 Mbit/s
|
0,3-3Mbit/s
|
|
Video
|
Videokonferensiyalar
|
MPEG-1 (PAL)
|
30.4 Mbit/s
|
1,15 - 3 Mbit/s
|
|
MPEG-1 (NTSC)
|
30.4 Mbit/s
|
1,15 - 3 Mbit/s
|
|
Ommaviy TV
|
MPEG-2 (PAL)
|
124.4 Mbit/s
|
15 Mbit/s
|
|
MPEG-2 (NTSC)
|
124.4 Mbit/s
|
15 Mbit/s
|
|
Yuqori kengaytmadagi TV
|
HDTV
|
994.3 Mbit/s
|
135 Mbit/s
|
|
MPEG-3
|
745.8 Mbit/s
|
20 - 40 Mbit/s
|
Modemlar
istalgan ma’lumot uzatish tizimida eng muxim joylardan birini egallaydi. Aloqa
kanallaridan foydalanish effektivligi, ma’lumot uzatish tezligi va
foydalanuvchilarga xizmat ko‘rsatish sifati sezilarli darajada aynan modemlar
va ularda realizatsiya qilingan asosiy prinsiplarga bog‘liq.
So‘nggi yillarda zamonaviy modemlar qurilishi va ishlash soxasida ma’lumot
uzatishni qo‘llashda jiddiy o‘zgarishlar bo‘lib o‘tdi. Internetdan foydalanish
yuqori effektiv modulyatsiya/demodulyatsiya va turli aloqa kanallarida xatodan
himoyaga qaratilgan texnologiyalarning muximligi va zaruriyatini ta’kidlaydigan
yorqin misollardan biri hisoblanadi.
Asosiy
muammo turli ko‘rinishdagi axborotni effektiv uzatuvchi metodlar izlanishi va
texnologiya tanlovidan iborat.
Keng
polosali aloqa texnologiyasi o‘zaro quyidagicha farqlanadi:
–
uzatish muhiti bilan;
–
o‘tkazish polosasi kengligi bilan;
–
harakatning maksimal uzoqligi bilan (qoplash maydoni bilan),
–
signalning
modulyatsiya turi bo‘yicha;
–
foydalanishning
baza sohasi bo‘yicha va boshqalar.
1948
yilda K. Shennon kanallarning o‘tkazish polosasi kengligi orasidagi munosabatni
gerslarda va uzatish tezligini Bit/s kabi nisbatda o‘rnatgan.
Maksimal
ruxsat etilgan qaysidir muhitdagi ma’lumot uzatish tezligini aniqlaydigin
asosiy faktorlardan biri uning o‘tkazish polosasi hisoblanadi.
Signal/shovqin
munosabati ikkinchi faktor hisoblanadi (Naykvist – Shennona qonuniyatiga
asosan)

Bu yerda ΔF
–o‘tkazish polosasi kengligi (Gs),
Rs –signalning
quvvati (VT),
Rsh – shovqinning quvvati(VT).
Signallarning
tarqalish muhiti xususiyati maksimal ruxsat etilgan ma’lumot uzatish tezligini
aniqlaydi. Misol uchun, ovoz chastotasi kanali uchun o‘tkazish polosasi 4 kGs
ni tashkil etadi, shunda signal/shovqin 48 dB nisbatida 64 Kbit/s da
ma’lumotni uzatish nazariy imkoniyatini beradi.
2
MGs o‘tkazish polosali vitali mis juftlik uchun, 48 dB nisbatidagi
signal/shovqin da maksimal tezlik 32 Mbit/s ni tashkil etadi.
Xalqaro
Elektraloqa soyuzi ma’lumot uzatish protokollari
|
Standart
|
Tasdiqlangan
yili
|
Maksimal
tezligi, bit/s
|
Dupleks/ yarimdupleks
|
Kommutatsiyalangan/
ajratilgan
|
Modulyatsiya
turi
|
|
V.21
|
1964/1984
|
200/300
|
FDX(FDM)
|
PSTN
|
FSK
|
|
V.22
|
1980/1988
|
1200
|
FDX(FDM)
|
PSTN
|
DPSK
|
|
V.22
bis
|
1984/1988
|
2400
|
FDX(FDM)
|
PSTN
|
QAM
|
|
V.23
|
1964/1988
|
1200
|
HDX
|
PSTN
|
FSK
|
|
V.26
|
1968/1984
|
2400
|
HDX
|
Private
|
DPSK
|
|
V.26
bis
|
1972/1984
|
2400
|
HDX
|
PSTN
|
DPSK
|
|
V.26
ter
|
1984/1988
|
2400
|
FDX(EC)
|
PSTN
|
DPSK
|
|
V.27
|
1972/1984
|
4800
|
HDX
|
Private
|
DPSK
|
|
V.27
bis
|
1976/1984
|
4800
|
HDX
|
Private
|
DPSK
|
|
V.27
ter
|
1976/1984
|
4800
|
HDX
|
PSTN
|
DPSK
|
|
V.29
|
1976/1988
|
9600
|
HDX
|
Private
|
QAM
|
|
V.32
|
1984/1988
|
9600
|
FDX(EC)
|
PSTN
|
QAM/TCM
|
|
V.33
|
1985/1988
|
14400
|
FDX
|
Private
|
TCM
|
|
V.17
|
1991
|
14400
|
FDX(EC)
|
PSTN
|
TCM
|
|
V.32
bis
|
1991
|
14400
|
FDX(EC)
|
PSTN
|
TCM
|
|
V.34
|
1996
|
33600
|
FDX
|
PSTN
|
QAM
|
|
V.90
|
1998
|
56700/33600
|
FDX
|
PSTN
|
PCM/QAM
|
|
V.92
|
2000
|
56700/48000
|
FDX
|
PSTN
|
PCM
|
MODEM
INTERFEYSI
Standartlash
bo‘yicha organizatsiya umum qabul qilingan modemlar abbreviaturalaridan
foydalanadi:
DTE(Data Terminal Equipment)- Okonechnoe ma’lumotlar qurilmasi .
-DCE(Data Communication Equipment)- modemni bildirishga xizmat qiluvchi
ma’lumotlar kanali qurilmasi

Telefon
kanallari uchun modemlarda uchta turdagi modulyatsiyadan foydalaniladi:
chastotali, nisbiy fazali (fazoraznostnaya) va ko‘pincha ko‘p pozitsiyali
amplituda-fazali deb nomlanuvchi kvadratura-amplitudali modulyatsiya.
Chastotali
modulyatsiyada "0" i "1" axborot ketma-ketligi qiymati
uchun o‘zgarmagan amplitudalarda belgilangan signal chastotalari mos keladi.
Chastotali modulyatsiya nihoyatda shovqinbardosh. Biroq chastotali
modulyatsiyada telefon kanali chastotali polosasi resursi tejab sarf
etilmaydi. Shuning uchun bu modulyatsiya ko‘rinishi kichik nisbatdagi
signal/shovqin munosabatga ega kanaldagi aloqani amalga oshirishga yo‘l
qo‘yuvchi past tezlikdagi protokollarda foydalaniladi.
Nisbiy
fazali modulyatsiyada (NFM, DPSK – Differential Phase Shift Keying) axborot
elementi qiymatiga qarab o‘zgarmagan amplituda va chastotada faqat signalning
fazasi o‘zgaradi. Va xar bir axborot biti uchun mos ravishda absolyut faza
qiymati emas, balki oldingi qiymatga nisbatan uning o‘zgarishi qo‘yiladi.
Odatda xar biri ikki bit chiquvchi ikkilik ketma-ketlik axborotiga ega bo‘lgan
to‘rtta signalni uzatishga asoslangan to‘rt fazali NFM (NFM-4) yoki ikki
karrali NFM (INFM) qo‘llaniladi. Yuqori tezlikdagi ma’lumotni uzatish uchun
NFM qo‘llanilmaydi.
Kvadratura-amplituda
modulyatsiyada (KAM, QAM – Quadrature Amplitude Modulation) kodlangan bitlar
sonini oshirishga yo‘l qo‘yuvchi signalning fazasi, hamda amplitudasi
o‘zgaradi, bunda shovqinbardoshligi xam sezilarli darajada oshiradi. Xozirgi
vaqtda 8...9 ni tashkil etishi mumkin bo‘lgan axborot bitlari soni bitta bodli
intervalda ko‘llanuvchi, lekin signal fazosida signal pozitsiyalari soni
256...512 ni tashkil etuvchi modulyatsiya usullari qo‘llaniladi.
Trellis-modulyatsiyasi.
Zamonaviy yuqori tezlikdagi
protokollarda kvadratura-amplitudali modulyatsiyadan (KAM) panjarali kodlash
bilan birga foydalaniladi . Natijada trellis-modulyatsiya (TSM – Trellis
Coded Modulation) deb nomlanuvchi modulyatsiyaning yangi usuli paydo
bo‘ldi. Belgilangan ravishda tanlangan konkret KAMning kombinatsiyasi va
shovqinbardosh kodida signal-kodli konstruksiya (SKK) nomini olib yuradi. SKK
signal/shovqin nisbatini 3 – 6 dB ga talabni tushirgan holda, axborot uzatish
shovqin himoyasini kanalda oshirib bera oladi. Bunda signalli nuqtalar soni
axborot bitlariga yana, o‘rama kodlash yo‘li bilan hosil bo‘lgan bitta ortiqcha
bit qo‘shilishi xisobiga ikki martaga oshadi. Bu
usul bilan kengaygan bitlar bloki KAM ga duchor bo‘ladi. Demodulyatsiya
protsessida Viterbi algoritmi bo‘yicha kelgan signalni dekodlash amalga oshadi.
Kirishdagi
xar ikki axborot biti uchun koder FM-8 modulyatoriga kelib tushuvchi o‘z
chiqishda uch simvollik ikkilik bloklarini joylaydi.
Ichki va tashqi nisbiy kodlash mavjud.
Ichki kodlashda nisbiy koder shovqinbardosh koderning chiqishida joylashgan va
qabul qilish tomonida nisbiy dekoder shovqinbardosh dekoderning kirishida
yoqilgan (17.a -rasm). Bu holatda shovqinbardosh koder guruxlanuvchi xatolar
bilan kurasha olishi kerak.
Tashqi nisbiy kodlash xolatdar qatorida manfaatli hisoblanadi,
chunki xatolar ko‘payishi manbaasi – nisbiy dekoder – shovqinbardosh
dekoderning chiqishida o‘rnatilgan (17 b -rasm.).

17.2-rasm.
Nisbiy koderning ichki(a) va tashqi(b) yoqilish sxemasi
xDSL
keng polosali ulanish. DSL (Digital
Subscriber Line) texnologiyasi oxirgi foydalanuvchilarga yuqori tezlikdagi
axborot potoklarini yetkazib berish muammosini yechuvchi keng tarqalgan
texnologiyalardan biridir.
Yuqori
tezlikdagi ma’lumotlarni uzatish texnologiyasining yetarli miqdori mavjud
bo‘lib, umumiy nom ostida umumlashtirilgan: xDSL (Digital Subscriber Line yoki
raqamli abonent liniyasi , bu yerda x - DSL yuqori tezlikdagi raqamli abonent
liniyasi konkret tipini aks ettiradi).
DSL
variantlari, tezliklari, fizik muhitdan foydalanish usuli va imkoniyat
diapozoni orqali farqlanadi.
Mavjud
abonent liniyalaridan foydalangan holda simli keng polosali ulanishni tashkil
etish
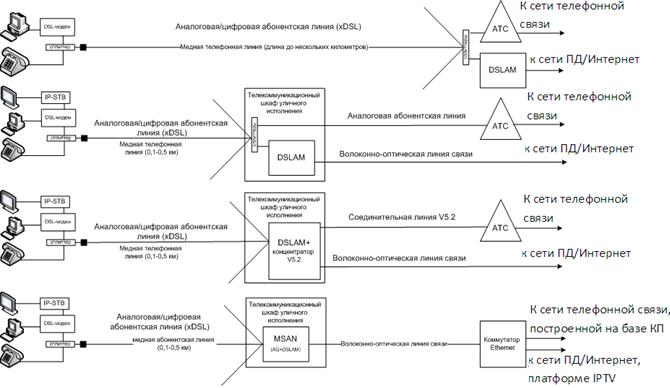
O‘tkazish
polosasini oshishi ikkita texnologik g‘oyaga asoslangan yuklovchilarning
kengroq chastotali spektridan foydalanish va undan foydalanishning
effektivligini oshirish. xDSL texnologiyasida chastotadan foydalanuvchi polosa
megagers diapazonga qadar kengaytirilgan. Chastota polosasidan effektiv
foydalanishga 2B1Q, SAR va DMT modulyatsiya metodlarini qo‘llash orqali
erishiladi.
xDSL
umumlashtirilgan nom konkret texnologiyalarning katta sonini o‘z ichiga oladi:
DSL, HDSL, SDSL,ADSL, VDSL, G.Lite.
Ushbu
texnologiyada ishlashi mumkin bo‘lgan apparaturaning tipik maksimal uzunligi 7,5 km ni tashkil etadi.
ADSL
ning asosiy ustunligi shundan iboratki, uning uchun mavjud telefon kabelidan
foydalaniladi.
Harakatdagi
telefon liniyalar ohirida chastotali bo‘luvchilar o‘rnatiladi. (ingliz
variantida – splitterlar) – bitta ATS da va bitta abonentda.
Splitterning
vazifasi turli chastota diapazonida signallargni yetkazishdan iborat.Bunda
telefon apparatga 4kGs chastotagacha va modemga qolganlari yo‘naltiriladi.
Chastotali
bo‘luvchi elektron qurilmadir, tarkibida yuqori chastota va past chastota
filtrlariga ega. Splitterning asosiy vazifasi ovoz kanalini ajratish va modemni
telefon qurilmasi hosil qiluvchi shovqindan himoyalashdan iborat.
Abonent
bo‘luvchiga oddiy analog telefon va ADSL modem ulanadi. Bunda modemning
ishlashi telefon aloqasidan foydalanishga umuman xalaqit bermaydi. ADSL
liniyasi telefon kabelining o‘ram juftligi oxirlariga ulangan ikkita ADSL
modemni bog‘laydi.
Bunda
uchta axborot kanali tashkil etiladi - «pasayuvchi " ma’lumot uzatish
potoki, «ko‘tariluvchi" ma’lumot uzatish potoki va oddiy telefon aloqa
kanali (POTS).
ADSL chastota polosasi
taqsimoti

Abonent
zapros yuborganligi sababli , abonentdan o‘tkazish polosasi tordir.
Shu
vaqtda abonentga kengroq o‘tkazish polosasi zarur, chunki saxifalarni yuklash
yetarlicha katta xajmdagi axborotni hisobga oladi.
Splitterning
ishlash prinsipi. Splitter yoki
chastotali bo‘luvchi — ikkita filtrni namoyon qiluvchi:
PChF
va YuChF, telefoniya va ADSL trafikni bo‘luvchi passiv element xisoblanadi,
 xDSL
zamonaviy standartlari
xDSL
zamonaviy standartlari
|
Texnologiya
|
ITU-T
|
Nomlanishi
|
Chiqarilgan sanasi
|
Maksimal uzatish tezligi
|
|
ADSL
|
G. 992.1
|
G.dmt
|
1999
|
7 Mbit/s past,
800 kbit/s yuqori
|
|
ADSL2
|
G. 992.3
|
G.dmt.bis
|
2002
|
8 Mbit/s past,
1 Mbit/s yuqori
|
|
ADSL2 +
|
G.992.5
|
ADSL2plus
|
2003
|
24
Mbit/s past,
1 Mbit/s yuqori
|
|
ADSL2-RE
|
G. 992.3
|
Reach Extended
|
2003
|
8 Mbit/s past,
1 Mbit/s yuqori
|
|
SHDSL
|
G.991.2
|
G. SHDSL
|
2001
|
5,6Mbit/s yuqori/past
|
|
VDSL
|
G. 993.1
|
Very-high-data-rate
DSL
|
2004
|
55 Mbit/s past,
15 Mbit/s yuqori
|
|
VDSL2
|
G 993 2
|
Very-high-data-rate
DSL 2
|
2005
|
100 Mbit/s yuqori/past
|
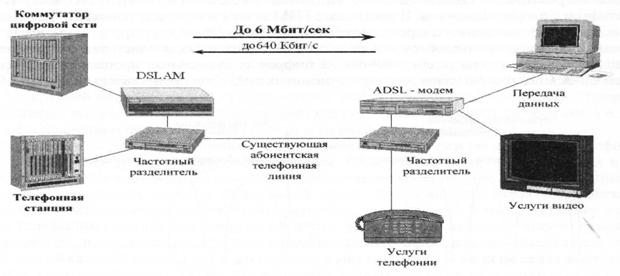
Yuqori tezlikdani
abonent ulanish texnologiyasining asosiy xarakteristikalari
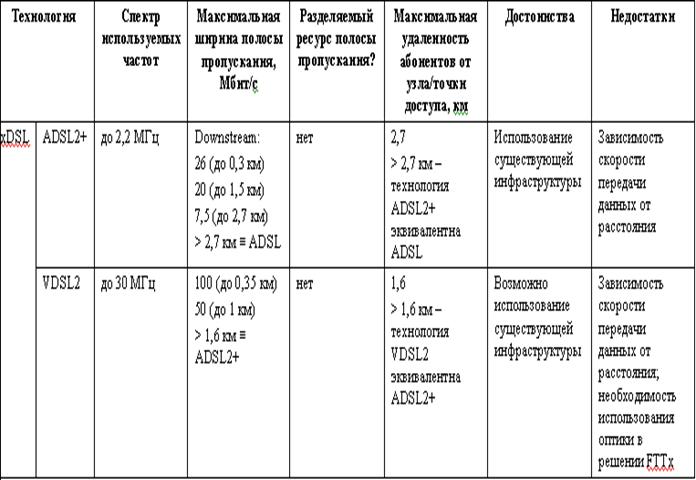
xDSL
qurilmasini ADSL texnologiyasiga muvofiq foydalanish tipik sxemasi ushbu rasmda
keltirilgan, qaerdaki DSLAM (DSL Access Module) odatda DSL-modemlar stoykasini
namoyon etadi.
Modulyatsiya
protsessi deb axborot signalini liniyada uzatishga mo‘ljallangan signalga
o‘zgartirish tushuniladi. Oddiy holda signal modulyatsiyasi uchun tashuvchi deb
nomlanuvchi maxsus belgilangan chastotadagi yuqori chastotali signaldan
foydalaniladi. Modulyatsiyalangan signalning qayta o‘zgarishi demodulyatsiya
deb ataladi.
xDSL
qurilmasining asosini mis kabeli orqali uzatish uchun raqamli potokning
modulyatsiya usuli tashkil etadi. xDSL texnologiyasi bir nechta chiziqli
kodlash texnologiyalaridan foydalanishni ko‘zda tutadi - 2V1Q (2 binary,
1 quartenary), CAP (Carrierless Amplitude and Phase Modulation), DMT (Discrete
Multi-tone) va TC-PAM. Barcha texnologiyalar uzatilgan va qabul qilingan
signallarni signalli protsessor orqali raqamli qayta ishlashga asoslangan va
umumiy prinsiplar qatoriga ega. xDSL tizimini xar bir liniya parametri
bo‘yicha sozlash avtomatik tarzda amalga oshadi, Qurilma har bir kabel
parametri bo‘yicha dinamik adapsiyalanadi, shuning uchun uni o‘rnatish yoki u
joydan bu joyga qurilmani ko‘chirishda qo‘lda bajariladigan sozlash yoki
regulirovkalash talab etilmaydi.
2B1Q
Texnologiyasi. 2B1Q texnologiyasi avval ISDN
tarmoqlarida 144 kbit/s potokni uzatish uchun (2B+D, BR ISDN) foydalanilgan.
Keyin u yuqoriroq bo‘lgan tezlikdagi potoklarni uzatish uchun
modernizatsiyalshtirilgan. 2B1Q kod to‘rtta darajaga ega, modulyatsiyalangan
signalni o‘zida namoyon etadi, ya’ni xar bir vaqt onida ikki bit axborot
uzatiladi (4 kodli holat). Chiziqli signal spektri simmetrik va yetarlicha
yuqori chastotali, yana past chastotali va doimiy tashkil etuvchilar mavjud.
CAP
texnologiyasi. Katta uzunlikdagi abonent va
bog‘lovchi liniyalar mavjud davlatlarda va pastroq sifatdagi kabellar uchun
katta talab bilan CAP (Carrierless Amplitude and Phase Modulation) —
tashuvchini uzatishsiz amplitudo-fazali modulyatsiya texnologiyasiga asoslangan
HDSL tizimidan foydalaniladi. Texnologiyani ishlab chiqaruvchisi —GlobeSpan
kompaniyasi — ko‘p tashqi xalaqitlarga ta’sirchan bo‘lmagan chiziqli kodlash
uchun tor polosali texnologiyani yaratishni o‘zi uchun maqsad qilib olgan.
SAR
modulyatsiyasi afzalliklarini illustrasiyasi uchun rasmda HDB3 kodi bilan
signal spektrlari keltirilgan, 2B1Q va SAR.
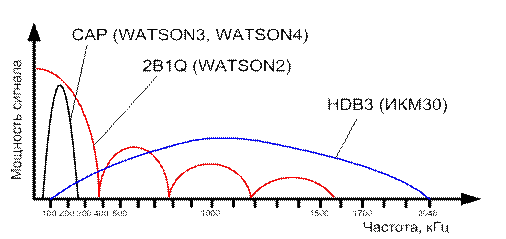 Spektrlarning
qiyosiy analizidan SAR modulyatsiyasiga asoslangan HDSL tizimining afzalliklari
ko‘rinib turipti.
Spektrlarning
qiyosiy analizidan SAR modulyatsiyasiga asoslangan HDSL tizimining afzalliklari
ko‘rinib turipti.
HDB3,
2B1Q, CAP signallar spektrlari .
DMT
Texnologiyasi. Oxirgi vaqtlarda ko‘pincha DMT
(Discrete Multi Tone) modulyatsiyasi qo‘llanilyapti. U standartizatsiya
bo‘yicha Amerika milliy instituti standartlarida ANSI T'1.413 i ITU-T G.922.2
tavsiflangan. Agar SAR modulyatsiyada bitta tashuvchi chastotadan
foydalanilsa, unda DMT da birdaniga 4 kGs qadamdagi 256 ta tashuvchi
shakllanadi.
Jadval.
DMT modulyatsiyasi xarakteristikasi
|
Xarakteristika
|
Polnoskorostnaya ADSL
lite
|
ADSL lite
|
|
Chastota polosasi
|
1104 kGs
|
552 kGs
|
|
Nesuùiy farki
|
4,3125 kGs
|
4,3125 kGs
|
|
Aloka tugunidan nazorat signali
|
276 kGs (tashuvchi
64)
|
276 kGs (tashuvchi
64)
|
|
BPF bloki xajmi
|
512 otscheta
|
256 otscheta
|
|
Sikl prefiksi
|
32 otscheta
|
16 otschetov
|
|
Superkadr uzunligi
|
17 ms
|
17 ms
|
|
Blokning nominal uzunligi
|
250 ms
|
250 ms
|
|
nesuùiy
ga maksimal
bitlar soni
|
15
|
kamida
8
|
TS-PAM
Texnologiyasi. TS-RAM Trellis Coded Pulse
Amplitude Modulation dek kengaytiriladi (trellis kodlashga ega impulsli
amplituda-faza modulyatsiyasi). Ushbu kodirovka metodining mohiyati darajalar (
kodli holatlar) sonini 4 dan (2V1Q dagi kabi) 16ga oshirish va maxsus xatolar
korreksiyasi mexanizmini qo‘llashdan iborat.
Rasmda
TS-RAM modulyatsiyasining spektri (G.shdsl) 2V1Q modulyatsiyasi bilan
qiyoslangan holi ko‘rsatilgan. Solishtirish uchun bir xil chiziqli tezlik
tanlandi - 768 kbit/s.
Energetik
spektrlarni qiyoslash (PSD — Power Spectral-Density) shuni ko‘rsatadiki,
G.shdsl qurilmasini bitta kabelda joylash misol uchun, ADSL tizimida, TS-RAM
kod orqali chaqirilgan navodkalar, 2V1Q holatiga nisbatan kamroq bo‘ladi.
Aniqroq kamayyotgan potok (tarmoqdan abonentga) navodok umuman bo‘lmaydi,
yuqorilaydigan potokda (abonentdan tarmoqqa) esa navodkalar ahamiyatsiz
bo‘ladi. SAR da esa, undagi navodkalar DSL-texnologiyasini boshqa qo‘shni juftliklarda
(SAR da emas) qo‘llashni amaliy imkonsiz qilib qo‘yadi
Rasm. 2B1Q va TC-PAM16 texnologiyalari
uchun energetik spektrlar (PSD)
Optik
tolali tarmoqlar uchun modemlar. Bu tizimlar
boshidan keng polosali bo‘lganliklari uchun ma’lumotlar uzatish texnologiyasi
shunday hisob-kitob ishlab chiqilganki, mavjud tarmoqlarni yuqori tezlikda
ma’lumot uzatish uchun o‘tkazish polosasidan foydalanishga yo‘l qo‘yadi, asosan
Internet foydalanuvchilariga ulanishni tashkil etadi.
Optik tolali kabeldan abonent foydalanish tuguniga ulanish shunda, yuqori
tezlikdagi Internetga ulanish zarur bo‘lgan potensial foydalanuvchilar soni
kabelning o‘tkazish polosasi butunlay to‘lganligida foydalanish manfaatlidir.
Yana qachonki elektrik shovqinlarga bardoshlilik va ma’lumotlarni ishonchli
himoyasi talab etilganda. Abonent maydonida ma’lumot uzatuvchi tugallangan
qurilmalar sifatida optik tolali modemlar va optik va elektrik signalni qayta
o‘zgartiruvchi mediakonvertorlardan foydalaniladi.
Optik
tolali diniya uchun o‘tkazish polosasi tola ishlab chiqarish texnologiyasi,
materialning sifati, ishlash rejimi (birmodali, ko‘p modali), kirituvchi va
uzatuvchi qurilmalarda aniqlanadi.
Ko‘p
modali rejimda optik tolaning o‘tkazish polosasi yuzlab MGs ni tashkil etadi
500 MGs gacha yetib boradi.
Bir
modali rejim uchun o‘tkazish polosasi ko‘pmodaliga nisbatan iki marta kengroq.
Misol
uchun, 100 MGs kenglikdagi polosaga erishish tezligi 1,6 Gbit/s atrofida
bo‘ladi, bunda 500 MGs –8 Gbit/s atrofida, 1000 mGs – 16 Gbit/s.
Optik
tolali liniyalardan foydalangan holda simli keng polosali ulanishni tashkil
etish
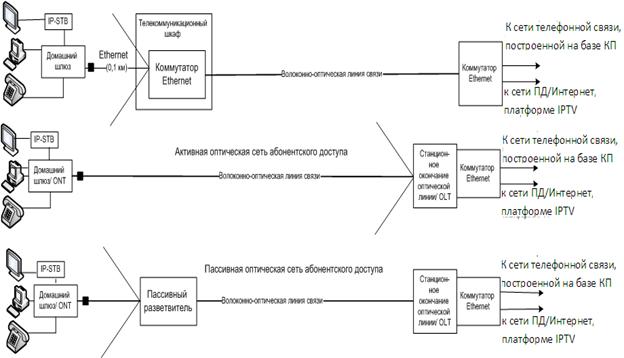

«FTTX».
FTTX (angl. fiber to the
x —X nuqtagacha optik tola) — bu istalgan telekommunikatsion tarmoq
uchun umumiy termin bo‘lib, aloqa tugunidan belgilangan joygacha (X nuqta)
optik tolali kabel, keyin abonentgacha mis kabel (abonentgacha optik kabel
borish varianti xam mavjud) boradi.
FTTX oilasiga asosiy obrazda foydalanuvchi terminaliga optik
kabelning yaqinlashishiga ko‘ra farq qiluvchi turli xil arxitektura
ko‘rinishlari kiradi:
• FTTN
(Fiber to the Node) — aloqa tugunigacha tola;
• FTTC
(Fiber to the Curb) — mikroroyon, kvartal yoki uylar guruhigacha bo‘lgan
tola;
• FTTB
(Fiber to the Building) — bingacha bo‘lgan tola;
• 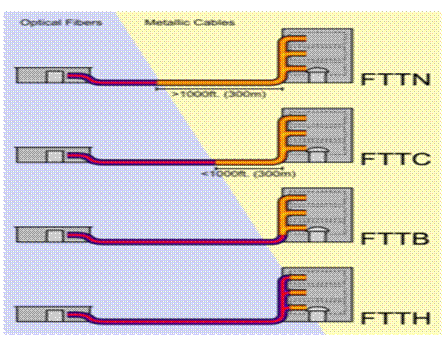 FTTH (Fiber to the Home) — yashash
joyigacha bo‘lgan tola(kvartiralar yoki alohida kottedjlar).
FTTH (Fiber to the Home) — yashash
joyigacha bo‘lgan tola(kvartiralar yoki alohida kottedjlar).
Yuqori
tezlikdagi abonent ulanish texnologiyalarining asosiy xarakterstikalari
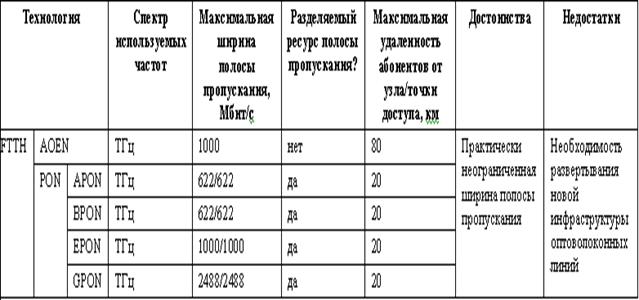 «TShTT»
filialining FTTB realizatsiyasi namunasi
«TShTT»
filialining FTTB realizatsiyasi namunasi 

17-ma’ruza uchun nazorat
savollari
1. Modulyatsiya
tushuncha bering?
2. Demodulyatsiya
tushuncha bering?
3. xDSL
keng polosali ulanish qanday amalga oshiriladi?
4. Splitterning
ishlash prinsipi qanday?
5. Optik
tolali tarmoqlar uchun modemlarga tushuncha bering?
6. FTTX
ga tushuncha bering?
18-ma’ruza.
Panjarali kodli modulyatsiya. Ko‘p darajali kodli modulyatsiya
Reja:
1. Panjarali
kodli modulyatsiya.
2. Ko‘p
darajali kodli modulyatsiya
3.
Panjarali kodli modulyatsiya
1976
da Ungerbyok tomonidan taklif qilingan panjarali kodli modulyatsiyaning asosiy g‘oyasi,
ko‘pxadlarni (signalli nuqtalarni) bo‘lish (dekompozitsiya) orqali aks ettirishni
amalga oshirishdan iborat. Buning uchun ohirgi avtomat holatidagi o‘tishlar
bilan assotsiatsiyalangan panjaraning baza strukturasi tanlanadi va ko‘pxadostilar
panjaraning qovurg‘asida tasvirlanadi. Yuqori spektr effektivligini talab qilayotgan
tizimlarda informatsion bitlarni (kodlanmagan) panjaraning parallel qovurg‘alariga
o‘zlashtirishga ruxsat beriladi.
Ko‘pxad
nuqtalarni bo‘lish va uni panjarada aks ettirish. Signalli
nuqtalarga yozib qo‘yilgan belgilar, signalli yulduzsimon bo‘lish (dekompozitsiya)
orqali aniqlanadi. S modulyatsiya nuqtalari 2v ko‘pxadida v
darajalari bo‘yicha o‘rnatilgan qismlarga bo‘lish sxemasi qo‘llaniladi. i
darajasidagi qismlarga bo‘lishda, 1≤i≤v, ko‘pxadosti signallari
ikkita ko‘pxadostiga bo‘linadi: S1(0), S1(1), agar i=1, S1(bi...bi-10)
va 5 Si(bi...bi-11),i> 1, di2 masofasi xar bir ko‘pxadosti
nuqtalari orasida maksimal bo‘lishi uchun biˆ {0,1} belgisi bitlik razryadi
i darajasidagi qismlarga bo‘lishda Sj(b1...bi-1 bi) ko‘pxadosti tanlovi
bilan assotsiatsiyalashadi. Bu qismlarga bo‘lish protsessi barcha signal nuqtalari
umumiy nomeratsiyasi bilan yakunlanadi. Xar bir signal nuqtasi o‘zining (unikal)
belgisini (raqam) keyinchalik s(b1,b2,...bv) kabi aniqlanadigan , v bit b1,b2,…bv
dan olinadi. Ta’riflangan protsedura 2v-modulyatsiya yulduzli nuqtalarini
standart qismlarga bo‘lishni (Ungerbyok bo‘yicha) amalga oshiradi. Bunday
qismlarga bo‘lishda ko‘pxadostilarida ichki masofa kamaymaydigan d12≤d22≤dv2
ketma-ketligini hosil qiladi. Natija tabiiy nomeratsiya L/-FM
modulyatsiyasining nuqtalariga mos keladi, ya’ni, butun sonlarning ikkilik ko‘rinishi,
qaysiki kattaligi soat strelkasi (yoki xisoblagich) bo‘yicha o‘tishda o‘suvchi.
18.1-rasmda 8-FM nuqtalari natijasida d12= 0,586, d22= 2, d32=
4 beruvchi tabiiy nomeratsiyasi ko‘rsatilgan.
Ungerbyo
qoidalari. Ungerbyok koderni «ko‘pxad holatlarida
berilgan holatlar soni va berilgan o‘tishlarga ega tugallangan avtomat kabi tasavvur
qilgan». U panjara qovurg‘asida ko‘pxadosti nuqtalari va signallariga aks ettirish
bir nechta amaliy qoidalarini taklif qilgan. Ushbu qoidalar quyidagilardan iborat:
Ø Barcha
ko‘pxadosti panjaralarda bir hil ehtimollik bilan paydo bo‘lishi lozim.
Ø Bir
xil holatdagi kiruvchi va chiquvchi o‘tishlar, eng katta Yevklid masofada joylashgan
ko‘pxadostilardan yozib olinishi lozim.
Ø Parallel
o‘tishlar, eng katta Yevklid masofasi bo‘yicha (qismga bo‘lishning yuqori darajalari)
bo‘lingan signal nuqtalariga o‘zlashtiriladi.

18.1-rasm.
8-FM yulduzli uchun tabiiy aks ettirish (v—1)/v tezligidagi panjarali kodli
modulyatsiyaning koder strukturasi
18.2-rasmda
panjarali kodli modulyatsiya koderining umumiy strukturasi ko‘rsatilgan.
Umumiy holatda panjara kodli modulyatsiya
tezligi (v— 1)/v panjara
strukturasi (k+1)/k
tezligidagi o‘ralgan (svertochnûy)
kod orqali
aniqlanadi.
Kodlanmaydigan informatsion
belgilar panjarada parallel qovurg‘alarga mos keladi.

18.2-rasm.
Panjarali kodli modulyatsiya koderining umumiy strukturasi
Maksimum
haqiqiylik bo‘yicha dekodlash. Haqiqatga yaqinroq
panjarali kodli modulyatsiyaning ketma-ketligini tanlash uchun, qovurg‘ali belgi
generatori parallel qovurg‘ani hisobga olish sharti bilan Viterbi algoritmidan foydalanish
mumkin. Bundan tashqari, eng zo‘r qovurg‘a tanlov bloki va qolgan kodlanmagan belgilar
o‘zgartirilgan bo‘lishi lozim. Qolgan yo‘llar xotirasi (yoki teskari yo‘lak xotirasi)
(v— k — 1) ni o‘z ichiga olishi, kodlanmagan ikkilik belgilariga faqatgina
1/n tezligidagi o‘rama kod bittagina bitidan tashqari holatidagi 2v- lik FM
(2v-PSK) yoki 2u-lik KAM (2v-QAM) holatida korrelyatsion metrikalar ikki
o‘lchamli belgilar uchun xrxr +upur ko‘rinishiga ega,
bu
yerda (xr, ur) yulduz signal nuqta etaloni,
(xr
ur) esa qabul qilingan nuqta hisoblanadi.
Xato
masofasi va ehtimolligi. Panjarali kodli modulyatsiyaning
ketma-ketlik shovqinbardoshligini o‘rama kodlar kabi taxlil qilsa bo‘ladi. Bu shuni
anglatadiki, panjarali kodli modulyatsiya
koderning holatlar diagrammasidan
tarozi spektri nomeri qabul qilinishi mumkin.
Yagona farq shundan iboratki, endi darajalar butun sonlar
(Xemming masofasiga mos keluvchi ) bo‘lmasdan, balki oddiy (
Yevklid masofasiga
mos keluvchi)
bo‘ladi.
Holatlar
diagrammasidagi parallel o‘tishlar borligi faktini hisobga olish zarur. Ohirgisi
shuni anglatadiki, modifikatsiyalangan holatlar diagrammasi ikkita a’zodan iborat.
Panjarali
kodli modulyatsiya. Imai-Xirokava tomonidan
taklif qilingan ko‘p darajali kodlash sxemasida 2V signallik nuqtalari yulduzli
ko‘pxadi uchun v darajali kiritilgan ikkita ko‘pxadostilari qismlariga bo‘lingan
sxemadan foydalaniladi. Kodli so‘z elementlari v ikkilik komponentlik kodlari
S;, 1 < / < v, qismlarga bo‘lishning har bir darajasida chegaradosh
sinflar indeksatsiyasi (nomeratsiya) uchun foydalaniladi.
Ko‘p
darajali kodlash modulyatsiyasi konstruksiyasining ustunligidan biri Yevklid masofasiga
muvofiq signal nuqtalari ko‘pxadostida, i = 1, 2, ...,v, har bir
qismga bo‘lish darajasida, komponentli kodlar Xemming masofasi bilan moslashuvchanlik
hisoblanadi.
Uochmen
xammualliflari bilan o‘tkazish qobiliyatini idrok qilishga asoslangan bir nechta
konstruksiya qoidalarini taklif qilgan, (o‘zaro axborot uchun zanjirli tengsizlikni
qo‘llagan). Bundan tashqari, ishlarda ko‘rsatilganidek, uzun komponentli kodlarga
ega ko‘p darajali kodlar, turbo kodlar kabi yoki past zichlik tekshiruvli kodlar
kanalning o‘tkazish qobiliyatiga yetishishadi.
Yana
shuni belgilash foydaliki, ikkilik komponentli kodlarni tanlashda, ko‘pxadostilariga
bo‘lish dixotomik xisoblanadi, biroq umumiy holatda, komponentli kodlar signal ko‘pxadi
qismlariga bo‘lish sxemasiga muvofiq istalgan tugallangan maydondan tanlanishi mumkin.
Ko‘p
darajali kodlashning boshqa muxim afzalligi shuki, dekodlash (ikkilik kodini) xar
bir darajada mustaqil amalga oshirilishi mumkin. Bunday ko‘p darajali dekodlash
murakkablikni yetarlicha butun kodni optimal dekodlashga qaraganda kamaytirish
imkoniyatini beradi. 18.3-rasmda 8-FM signallarida ko‘p darajali kodlash modulyatsiya
tizimiga namuna keltirilgan.
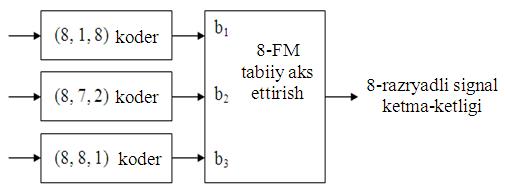
18.3-rasm.
8-FM signallarida ko‘p darajali kodlash modulyatsiya tizimiga namuna
8-FM
signallarida ko‘p darajali kodlash modulyatsiya misolida
komponentli kodlar panjarasi keltirilgan.
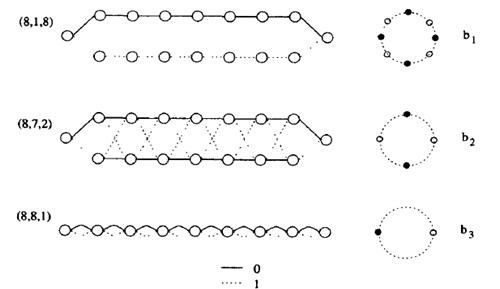
18.4-rasm.
8-FM signallarida
ko‘p darajali kodlash modulyatsiya misolida komponentli kodlar panjarasi.
Bu
ko‘p darajali konstruksiyaning tezligi yoki spektral effektivligi R=(k1+k2+...+kv)/n(bit/simvol)ga
teng. Minimal
Yevklid
masofasining kvadrati bu tizimni Dc
2 (A) koniqtiradi.
Ta’kidlanganidek,
ko‘p darajali kodlashning afzalliklaridan biri ko‘p darajali dekodlashdir. Quyidagi
rasmlarda panjarali kodlarni kodlash va dekodlashda foydalaniladigan asosiy strukturalar
ko‘rsatilgan. Ko‘p darajali dekodlash maksimum haqiqatga yaqinlik bilan dekodlashga
nisbatan murakkablikni kamaytirishga olib keladi. Biroq ko‘p darajali dekodlashda
dekoderning boshqa darajalari, katta darajalarida kodlash qo‘llanilmaydi deb hisoblaydi.
Bu minimal masofada kodli so‘zlarning miqdorini ko‘payishiga olib keladi. Boshqacha
qilib aytganda, xatolar koeffitsienti yoki yaqin qo‘shnilar raqamlari oshishiga
olib keladi. Bu effekt bilan bog‘liq kattalik yo‘qotish komponentli kodning tanlovi
va signallarda belgining aksiga bog‘liq. Xatolik ehtimolligi diapazonida 10-2
-10-5 bu kattalik bir necha dB ga yetishi mumkin.
18.5-rasmda
panjarali kodli modulyatsiya tizimi uchun koder va dekoderning baza strukturasi
keltirilgan.
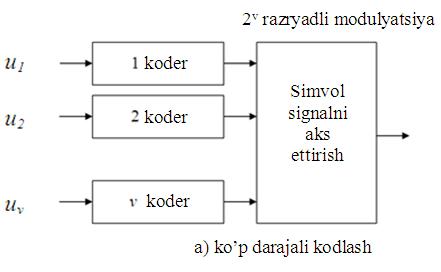
18.5-rasmda
panjarali kodli modulyatsiya tizimi uchun koder va dekoderning baza strukturasi
18.6-rasm.
Panjarali kodli modulyatsiya tizimlarida tengsiz himoya
Panjarali
kodli
modulyatsiya
xatolardan tengsiz himoya hosil qilishning qulay sxemasi hisoblanadi
(UEP - unequal-error- protection), chunki
u qismlarga bo‘lishning xar bir darajasida kodli ketma-ketlik orasida minimal Yevklid
masofasini konstruksiyalashda zarur moslashuvchanlikka ega.
Biroq
diqqat bilan belgi va signal orasidagi tasvirni tanlash lozim, qidirayotgan tengsiz
himoyani buzmaslik uchun aralash qismlarga bo‘lishda, boshqalari Ungerbyok tomonidan
taklif etilgan qoidalar bo‘yicha bajarilganda, ba’zi bo‘lish darajalari nostandart
hisoblanadi. Bu usul bilan xato koeffitsienti va konstruksiya darajalari bo‘yicha
Yevklid masofasi orasida yaxshi almashinuvga erishiladi. Tengsiz himoyaga erishish
uchun Yevklid masofasi qismlarga bo‘lish darajalari bo‘yicha quyidagicha tanlanadi:
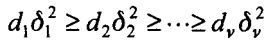
18-ma’ruza
uchun nazorat savollari
1. Panjarali
kodli modulyatsiyaga tushuncha bering?
2. Ko‘pxad
nuqtalarni bo‘lish va uni panjarada aks ettirishga qanday amalga oshiriladi?
3. Ungerbyok
qoidalarigatushuncha bering?
4. Maksimum
haqiqiylik bo‘yicha dekodlashga tavsif bering?
5. Xato
masofasi va ehtimolligiga tushuncha bering?
Àäàáè¸òëàð ð¢éõàòè
|
1
|
S.K. G’aniåv.
Axborot nazariyasi va kodlash. Ma'ruzalar
matni. TATU, 2014
|
|
2
|
N.B. Usmanova Ma'lumot uzatish
tizimlari va tarmoqlari. O’quv
q¢llanma. Toshkånt
TATU. 2006.
|
|
3
|
R.X. Djuraåv, Sh.Yu. Djabbarov
«Xujjatli elåktraloqa tizimlari va tarmoqlari» O’quv qo’llanma. Toshkånt.
TATU 2006.
|
|
4
|
Äæóðàåâ Ð.Õ.
Ïîìåõîóñòîé÷èâûå êîäû â òåëåêîììóíèêàöèîííûõ ñèñòåìàõ. Ó÷åá. Ïîñîáèå - ÒÓÈÒ,
Òàøêåíò 2013.
|
|
5
|
Raymond
W. Yeung Information Theory and Network Coding. Springer, 2008.
|
|
6
|
Abbas
El Gamal, Young-Han Kim Network Information Theory. Cambridge
University Press, 2011
|
|
7
|
Ìîðåëîñ-Ñàðàãîñà
Ð. Èñêóññòâî ïîìåõîóñòîé÷èâîãî êîäèðîâàíèÿ. Ìåòîäû, àëãîðèòìû, ïðèìåíåíèå –
ÒÅÕÍÎÑÔÅÐÀ
– Ìîñêâà, 2005.
|
|
8
|
Âåðíåð Ì.
Îñíîâû êîäèðîâàíèÿ.
Ó÷åáíèê äëÿ ÂÓÇîâ. ÒÅÕÍÎÑÔÅÐÀ – Ìîñêâà, 2006.
|
|
9
|
Tracey
Ho Network Coding: Introduction. Cambridge University Press,
2008.
|
|
10
|
Â.Ï.Äüÿêîíîâ. MATLAB 6/6.1/6.5
+ Simulink 4/5. Îñíîâû ïðèìåíåíèÿ. Ïîëíîå ðóêîâîäñòâî ïîëüçîâàòåëÿ.
ÑÎËÎÍ-Ïðåññ, 2004.
|
|
11
|
http://www. Ziyonet.uz.
|
|
12
|
http://library.tuit.uz
|
|
13
|
http://www.intuit.ru
|




 1844
yil
Morze
tomonidan telegraf apparati ixtiro
qilindi. Birinchi
telegraf apparati uchun
1867 yil
Nyu-Yorkda patent olindi.
1844
yil
Morze
tomonidan telegraf apparati ixtiro
qilindi. Birinchi
telegraf apparati uchun
1867 yil
Nyu-Yorkda patent olindi.
 25 iyun 1876 yil Aleksandr Bell uzini
telefon apparatini Filadelfiyada bo‘lib o‘tgan birinchi butun jahon
elektrotexnika yarmarkasida namoyish qildi
(1.3-rasm).
25 iyun 1876 yil Aleksandr Bell uzini
telefon apparatini Filadelfiyada bo‘lib o‘tgan birinchi butun jahon
elektrotexnika yarmarkasida namoyish qildi
(1.3-rasm).