ЎЗБЕКИСТОН РЕСПУБЛИКАСИ АЛОҚА, АХБОРОТЛАШТИРИШ ВА ТЕЛЕКОММУНИКАЦИЯ ТЕХНОЛОГИЯЛАРИ ДАВЛАТ ҚЎМИТАСИ
ТОШКЕНТ АХБОРОТ ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ
КОМПЬЮТЕР ИНЖИНИРИНГ ФАКУЛЬТЕТИ
«Информатика асослари»кафедраси
«ДАСТУРЛАШ АСОСЛАРИ» КУРСИ ЛАБОРАТОРИЯ ИШЛАРИ УЧУН УСЛУБИЙ ҚЎЛЛАНМА
(1 қисм)
Тошкент-2013
ТАТУ “Информатика асослари” кафедраси мудири проф. Ш.А.Назировнинг раҳбарлиги остида.
Муаллифлар: доц.ХайдароваМ.Ю., ассис.Д.З.Ганиходжаева, ассис.М.З.Маҳкамова, ассис. Ш.Реджебов
“Дастурлаш асослари” курси лаборатория ишлари учун услубий қўлланма “Компьютер инжиниринг” факультетининг илмий-методик кенгашида кўриб чиқилди ва нашр қилинишига рухсат берилди.
“Дастурлаш асослари” курси лаборатория ишлари учун топшириқлар ва услубий қўлланма 1 курс талабаларига 1 семестр учун- 2013 йил.
Такдим этилаётган ушбу иш тўрт йил (2009-2013) давомида ёзилди. Бу иш ўз ичида 8 та лаборатория иши ва 1 семестрнинг назариясини тўлиқ қамраб олади.
2011 йилдан ўқув дастурига ўзгартиришлар киритилганлиги сабабли ва « Дастурлаш асослари» фани барча йўналиш талабаларига ўтилиши муносабати билан қўлланмадан барча факультет талабалари фойдаланиш -лари тавсия этилади.
1- Курс талабалари биринчи семестрда умумий информатиканинг асосий тушунчалари ва С++ дастурлаш тилидан бошланғич маълумотларни оладилар, жумладан :
- Ахборот тушунчаси, унинг турлари , ўлчаш, кодлаш;
- Ҳисоблаш машиналарининг асослари ва архитектураси;
- Алгоритмлар ва уларни тавсифлаш усуллари;
- С++ алгоритмик тилида процедурали дастурлаш.
Қўлланмадаги хар бир лаборатория ишида маълум бир мавзуни ёритилган.
Ҳар бир лаборатория иши услубий кўрсатмалар мисолларини бажариш йўллари , дастурлар билан бойитилган. Муаллифларнинг фикрича талаба ўзи мустақил равишда қўлланма ёрдамида керакли мавзуни ўзлаштира олади. Бундан ташқари қўлланмада иқтидорли талабалар учун алоҳида топшириқлар ҳам мавжуд.
Ушбу қўлланма 2013 йил 8 апрель куни кафедра мажлисида муҳокама килинди ва № сонли буйруқ билан нашрга рухсат берилди.
( № __________ буйруқ _______________ 2013 йил )
Рецензент
АТДТ кафедраси доценти
Т.ф.н. Латипова Н.
Тошкент ахборот технологиялари университети 2013й.
КИРИШ
Ўзбекистон Республикасининг мустақиллик йилларида ахборот технологияларининг ривожига алоҳида аҳамият берилмоқда. Барча ўқув тизимлари учун янги ўқув стандартлари қабул қилинган, бу эса ўз навбатида ўқув жараёнининг сифатини оширишга хизмат қилмоқда.
Қуйидаги берилган методик қўлланма ўқув ишчи дастури асосида “Дастурлаш асослари” фанидан “Информатика асослари” кафедраси бўйича 8та лаборатория ишларини ўз ичига олади ва ўқув юкламаси бўйича 54 соатга мўлжаллангандир. Лаборатория ишлари қуйидагиларни ўз ичига олади:
- Шахсий компьютер архитектураси;
- Ахборотни сақлаш усуллари, ахборотларни кодлаш, шифрлаш, дешифрлаш ва ахборот хавфсизлиги;
- Мантиқий алгебранинг асосий функциялари;
- Саноқ системалари;
- Алгоритмнинг турли структуралари (чизиқли, цикл ва тармоқли);
- С++ даги турли структурадаги дастурлар (чизиқли, цикл ва тармоқли);
- С++ тилида массивлар билан ишлаш(бир ўлчамли);
Ушбу методик қўлланманинг Тошкент ахборот технологиялари университетининг барча йўналиш талабалари ўқув жараёнига қўлланилиши бизнинг ҳаётдаги мақсадимиз, яъни “Миллий кадрлар тайёрлаш дастури” ни амалга оширилишига ўз ҳиссасини қўшади деган умиддамиз.
№ 1 Лаборатория иши
Электрон хисоблаш машиналарининг(ЭХМ) архитектураси,дастурий таъминоти.
Ишнинг максади
1. Компьютернинг асосий қурилмалари ва уларнинг вазифалари билан танишиш.
Топшириқ
1. Берилган саволларга жавоб бериш ва дафтарга “Компьютерларнинг асосий қурилмалари” мавзусида хисобот тайёрлаш. «Орион» ўргатувчи дастуридан(лаборатория дарсида ўқитувчи бошчилиги асосида) ва қўшимча материалдан фойдаланинг. (1 иловага қаранг).
Саволларга жавобни ёзма хисобат тарзида ифодалаш керак.
1. Фон Нейман принципи ва ЭХМ архитектураси. Хисоблаш машиналарнинг асосий қурилмалари.
2. Компьютернинг бошқариш қурилмаси , таркиби, вазифаси, ишлаш принципи.
3. Компьютерларнинг хотираси, турлари, хар бирининг ишлаш принципи.
4. Киритиш ва чоп этиш қурилмалари, турлари, хар бирининг ишлаш принципи.
5. Асосий қурилмаларнинг ўзаро боғлиқлиги, Компьютерни дстурий бошқариш принципи.
6. Компьютер турлари ва вазифалари.
Ҳисобот таркиби
Хисобот қуйидагилардан иборат бўлиши керак:
1) Лаборатория ишининг номи.
2) Лаборатория ишига толшириқ.
3) «ШК асосий қурилмалари» мавзусида конспект.
Назорат саволлари
1. Ҳисоблаш системаси архитектураси нима ?
2. «Фон-Нейман» тамойилига асосланган компьютер архитектурасини тавсифлаб беринг.
3. Кўп даражали хотира ташкили нима учун ишлатилади?
4. Регистр нима?
5. Процессор нима , унинг вазифаси?
6. Периферик қурилма турлари , мисол келтиринг.
7. Шахсий компьютер дастурий таъминотининг таркиби.
8. Компьютердаги операцион тизим таркиб ва вазифаси.
9. Процессор асоси транзистордан ташкил топган ЭХМ авлоди.
10. Мониторнинг вазифаси ва турлари.
11. АЛУ ( арифметик мантиқий қурилманинг вазифаси ).
12. ЭҲМ қурилмаларининг ишини назорат қилувчи ва дастур бажарилишини кузатувчи ЭҲМнинг асосий қисми.
13. ЭҲМ операцион тизимининг қулайликлари: тармоққа ЭҲМнинг уланиши, ҳамда бир нечта ЭҲМларнинг ҳисоблаш ресурсларининг тўплаши ва уларни биргаликдаги фойдалануви.
14. Ишчи станциялар учун ҳисобланувчи асосий операцион тизим ва мэйнфрейм ва миниЭҲМларда фойдаланиладиган операцион тизим.
15.Компьютернинг аппарат ва дастурий қисмларини бошқарувчи тизим.
16. Бошқа дастурларнинг бажарилиши, фойдаланувчи билан мулоқотни ташкиллаштирувчи, оператив хотирани тақсимловчи ва х.к. ишларни бажарувчи дастурлар коплекси.
17. Кэш хотирани ишлаш принципи.
18. Компьютернинг асосий иккита хотираси.
19. Мониторнинг рангли ойнасидаги тасвирни шаклланиши.
20. Ташқи хотира вазифаси. Ташқи хотирадаги қурилма хиллари.
№ 2 Лаборатория иши
Ахборотни сақлаш усуллари. Ахборот ўлчов бирлиги. ШЭҲМда маълумотларни кўрсатиш. Кодлаш ва шифрлаш, ҳимоялаш, антивирус ҳимояси ҳақидаги асосий тушунчалар.
Ишнинг мақсади
1.Ахборотни сақлаш усулларини ўрганиш.
2.Асосий ахборот бирликлари билан танишиш.
3.ШЭҲМда маълумотларни берилиши.
4.Ахборотни кодлашни асосий усулларини ўрганиш.
5.Ахборотни шифрлашни асосий усулларини ўрганиш.
6.Ахборот хавфсизлиги асосий усулларини ўрганиш.
7.Антивирус ҳимояси асосий тушунчалари билан танишиш.
Топшириқ
1а жадвал
|
№ |
вариантлар |
||||||||||||||||||||||||
|
1. |
Томошабинлар залида иккита томошабинлар креслосининг тўғри бурчакли қисми: бири 10га 12, бошқаси 17га 8.Автоматлаштирилган тизимда хар бир жойни кодлаш учун минимал миқдорда неча бит керак бўлади. |
||||||||||||||||||||||||
|
2. |
Узунлиги олти символли «+» ва «-»символларининг неча хил турлари мавжуд бўлади. |
||||||||||||||||||||||||
|
3. |
Узунлиги ўнта символли «а» ва «б» символларининг неча хил турлари мавжуд бўлади. |
||||||||||||||||||||||||
|
4. |
Морзе алифбоси радиоалоқа учун нуқта ва тире комбинацияларини ишлатиб символларни кодлайди. Морзе алифбосидан фойдаланиб узунлиги учдан бешгача бўлган сигналларни (нуқта ва тире), неча хил турдаги символлардан(сон, ҳарф,пунктир белгилар ва х.к.) кодлаш мумкин. |
||||||||||||||||||||||||
|
5. |
Unicode кодлашда ҳар бир символга ўн олти бит ажратилади. Шу кодлашдаги йигирма тўртта символли сўзнинг ахборот ҳажмини аниқланг. |
||||||||||||||||||||||||
|
6. |
Ёритгичли табло лампочкалардан иборат. Ҳар бир лампочка уч хил кўринишда бўлиши мумкин («ёқилган», «ўчирилган» ва «ёниб ўчадиган»). Лампочкаларнинг энг ками билан қанчаси таблода туриши керак, яъни уларни ёрдами билан 8 хилдаги сигналларни узатиш мумкин бўлсин. |
||||||||||||||||||||||||
|
7. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, Жан Жак Руссонинг айтган сўзларини ахборот ҳажми нимага тенглигини аниқланг: Тысячи путей ведут к заблуждению, к истине – только один.
|
||||||||||||||||||||||||
|
8. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, Алексей Толстойнинг айтган сўзларини ахборот ҳажми нимага тенглигини аниқланг: Не ошибается тот, кто ничего не делает, хотя это и есть его основная ошибка. |
||||||||||||||||||||||||
|
9. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, Рене Декартнинг айтган сўзларини ахборот ҳажми нимага тенглигини аниқланг: Я мыслю, следовательно, существую. |
||||||||||||||||||||||||
|
10. |
Ҳар бир символ ўн олти бит билан кодланишини ҳисобга олган ҳолда, Пушкиннинг айтган сўзларини ахборот ҳажми Unicode кодида нимага тенглигини аниқланг: Привычка свыше нам дана: Замена счастию она.
|
||||||||||||||||||||||||
|
11. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, Пушкиннинг айтган тўртлигини ахборот ҳажми нимага тенглигини аниқланг: Певец-Давид был ростом мал, Но повалил же Голиафа!
|
||||||||||||||||||||||||
|
12. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилганларни ахборот ҳажми нимага тенглигини аниқланг: Мой дядя самых честных правил, Когда не в шутку занемог, Он уважать себя заставил И лучше выдумать не мог. |
||||||||||||||||||||||||
|
13. |
Автоматик қурилма ўзбек тилида келган ахборот маълумотини қайта кодлайди,яъни 8-битли кодни 16 битли Unicode.даги кодга айлантирди.Бунда ахборот маълумоти 2048 байтга кўпайди.Қайта кодлашдан олдинги ахборот маълумоти ҳажми қандай бўлган. |
||||||||||||||||||||||||
|
14. |
Ҳар бир символни 16 битга кодланишини ҳисобга олган ҳолда Unicode даги ёзилган қуйида келтирилган ахборот ҳажмини кўрсатинг: Олти литрда 6000 миллилитр.
|
||||||||||||||||||||||||
|
15. |
Ҳар бир символни 16 битга кодланишини ҳисобга олган ҳолда қуйида келтирилган ахборот ҳажмини кўрсатинг: Ишонганга толе ёр бўлур! |
||||||||||||||||||||||||
|
16. |
Ҳар бир символни бир байтга кодланишини ҳисобга олган ҳолда қуйида келтирилган ахборот ҳажмини кўрсатинг: Белеет Парус Одинокий В Тумане Моря Голубом! |
||||||||||||||||||||||||
|
17. |
Автоматик қурилма ўзбек тилида келган ахборот маълумотини қайта кодлади,яъни 16-битли Unicode.даги кодни 8-битли КОИ-8 кодга айлантирди.Бунда ахборот маълумоти 800 битга камайди. Ахборот маълумоти узунлиги символларда қандай бўлади. |
||||||||||||||||||||||||
|
18. |
Жадвалда ASCII кодини бир қисми келтирилган:
Символ «р»ни 16ли коди қандай? |
||||||||||||||||||||||||
|
19. |
Жадвалда кодлашни бир қисми келтирилган:
Символ «я»ни 16ли коди қандай?
|
||||||||||||||||||||||||
|
20. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Интилганга толе ёр! |
||||||||||||||||||||||||
|
21. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Рим рақамлари – нопозицион саноқ системасига киради! |
||||||||||||||||||||||||
|
22. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Қуёш ёритарди, бироқ қиздирмас эди. |
||||||||||||||||||||||||
|
23. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Баҳор – йилнинг энг яхши фасли. |
||||||||||||||||||||||||
|
24. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Мен фасллар ичидан баҳорни ёқтираман. |
||||||||||||||||||||||||
|
25. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Қўйчивон кўп бўлса, қўй ҳаром ўлади. |
||||||||||||||||||||||||
|
26. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Етти ўлчаб,бир кес. |
||||||||||||||||||||||||
|
27. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Жангдаги ёлғиз жангчи, жангчи эмас. |
||||||||||||||||||||||||
|
28. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Гўзал бўлиб эмас, балки бахтли бўлиб туғилгин. |
||||||||||||||||||||||||
|
29. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Юз сўм пулинг бўлмасин, юзта дўстинг бўлсин. |
||||||||||||||||||||||||
|
30. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Яхшилик қил, қайтар дунё. |
||||||||||||||||||||||||
|
31. |
Ҳар бир символ бир байт билан кодланишини ҳисобга олган ҳолда, қуйида келтирилган гапнинг ахборот ҳажмини аниқланг: Ўқиш, ўқиш ва яна ўқиш! |
Жадвал 1б
|
№ |
вариантлар |
|
1. |
Компьютер тармоғи. Структура тармоғи. |
|
2. |
Computer NetWork, net - тармоқ, work - иш |
|
3. |
Локал тармоқлар (Local Area Network, LAN) |
|
4. |
Глобал тармоқлар(Wide Area Network, WAN); |
|
5. |
Шаҳар тармоқлари(Metropolitan Area Network, MAN). |
|
6. |
Клиент - бир хил хизматларни сўровчи объект (компьютер ёки программа) |
|
7. |
Сервер - бир хил хизматларни кўрсатувчи объект (компьютер ёки программа) |
|
8. |
«Умумий шина» топологияли тармоқ |
|
9. |
«Юлдуз» топологияли тармоқ |
|
10. |
«Айлана» топологияли тармоқ |
|
11. |
Қадимий кўринишли топологияли тармоқ |
|
12. |
Аралашма топологияли тармоқ |
|
13. |
Шинали структура тармоғи |
|
14. |
Юлдуз кўринишли структура тармоғи |
|
15. |
Айлана структура тармоғи |
|
16. |
Шина ва юлдуз кўринишли тармоқ |
|
17. |
Аралашма топологияси |
|
18. |
Алоқа тармоғи ва интерфейс |
|
19. |
Трансивер (transceiver)
|
|
20. |
Такрорловчи (Repeater) |
|
21. |
Концентратор (Hub) |
|
22. |
Мост (Bridge) |
|
23. |
Коммутатор (Switch) |
|
24. |
Маршрутизатор (Router) |
|
25. |
Кабель алоқа тармоғи |
|
26. |
Симсиз алоқа тармоғ |
|
27. |
Тармоқ картаси |
|
28. |
SMTP (Simple Mail Protocol) |
|
29. |
TCP IP протокол |
1б жадвалидаги топшириқларни бажарилишига доир методик кўрсатмалар
Сир сақланишида Юлий Цезарь томонидан келтирилган "Записках о галльской войне" (эрадан олдинги 1 асрда)асаридаги асосий рольни шифрлаш эгаллайди. Бу ҳақда Гай Светоний шундай ёзади: “...унинг Цицеронга бўлган хатларида ва яқин уйдагиларга ёзган хатларида сирли хат ёзишдан фойдаланар эди, яъни ҳарфларни шундай ўзгартирар эдики, улардан бир сўз ясаб бўлмас эди. Уларни ўқиш учун, ҳар сафар биринчи ҳарф ўрнига тўртинчи ҳарфни қўйиб ўқиш керак бўлар эди, масалан А ни ўрнига D ва х.к.” Шу йўл билан Цезарь, ҳарфларни керакли ҳарфларга алмаштирар, бунда кейинги қатор ўзида учта ҳарф чап тарафга сурилган очиқ матнни кўрсатар эди.
INFORMATIKA сўзини Цезарь усули бўйича учта позицияга шифрлаймиз. INFORMATIKA сўзи ANCII (1чи кўрсаткичга қаранг) кодидаги сонли кетма кетлигига тўғри келади (73,78,70,79,82,77,65,84,73,75,65).Ҳар бир сонга 3 ни қўшамиз ва қуйидаги кетма кетликка эга бўламиз. (76,81,73,82,85,80,68,87,76,78,68).Бу сонларга ANCII кодидаги қуйидаги шифрланган сўз мос келади LQIRUPDWLND.
Энди эса шифрланган сўз XQLYHUVLWHW берилган бўлсин. Бу сўзга мос равишда ANCII кодида қуйидаги сонли кетма-кетлик тўғри келади(88,81,76,89,72,85,86,76,87,72,87). Ҳар бир сондан 3 ни олиб ташласак, қуйидаги сонли кетма-кетлик юзага келади (85,78,73,86,69,82,83,73,84,69,84). ANCII жадвалидаги код орқали UNIVERSITET сўзи юзага келади. Бу процесс дешифрлаш дейилади.
Назорат саволлари
1. Юлий Цезарь томонидан яратилган шифрлаш усули ҳақида.
2. Ўз фамилиянгизни Цезарь усули ёрдамида шифрланг.
3. Ахборот технологиялари сўзини дешифрланг.
4. Йигирма тўртта символдан иборат бўлган ахборот ҳажмини аниқланг.
5.Кодлаш ва унинг асосий қўлланилиши.
Лаборатория иши № 3
ЭХМ нинг арифметик асослари. Саноқ системаси(2,8,16), улардаги амаллар. Лаборатория иши бажарилишидаги топшириқлар.Бир саноқ системасидан иккинчи саноқ системасига ўтиш.
Ишнинг мақсади
1. 2-, 8- ва 16- системаларидаги арифметик хисоблашларни ўрганиш
2. Бир саноқ системасидан иккинчисига ўтишни ўрганиш.
Топшириқ
2. Маъруза ва амалиёт дарсларида олинган маълумотларга асосланиб, ўз вариантингиз учун қуйидагиларни
а) 1 жадвалдан ўз вариантинг кўчириб олинг, (а) иккилик саноқ системасида ва (б) саккизлик саноқ системасида тўртта арифметик амал (+, -, *, /) бажаринг (а);
б) 2 жадвалдан ўз вариантингизни олинг , бир саноқ системасидан иккинчисига ўтинг :
· Иккилик саноқ системасида берилган Х2 сонини 10, 8 ва 16 ,2 саноқ системасига махсус , позицион ва бўлиш қоидаларига асосан ўтказинг;
· Ўнлик сон ўнлик саноқ системасида берилган У10 сонини в 2, 8 ва 16 саноқ системасига позицион ва бўлиш қоидаларига асосан ўтказинг;
Ҳисобот таркиби
Хисобот қуйидагилардан иборат бўлиши керак:
1) Лаборатория ишининг номи.
2) Лаборатория ишига топшириқ.
3)1 жадвалда келтирилган топшириқ ечими( иккилик ва саккизлик саноқ системаларида тўрт арифметик амал)
4)2 жадвалда келтирилган топшириқ ечими (Бир саноқ системасидан иккинчисига ўтиш)
5)Назорат саволларига тайёргарлик
.
№1 лаборатория иши топшириқлари
1 Жадвал
|
№ |
Задания |
|
1. |
а)
б)
|
|
2. |
а) б)
|
|
3. |
а)
б)
|
|
4. |
а)
б) |
1 Жадвал давоми
5. |
а) б)
|
|
6. |
а)
б)
|
|
7. |
а)
б)
|
|
8. |
а)
б) |
1 Жадвал давоми
|
9. |
а)
б)
|
|
10. |
а)
б)
|
|
11. |
а)
б)
|
|
12. |
а)
б)
|
1 Жадвал давоми
|
13. |
а)
б)
|
|
14. |
а)
б)
|
|
15. |
а)
б)
|
|
16. |
а)
б) |
1 Жадвал давоми
|
17. |
а)
б)
|
|
18. |
а)
б)
|
|
19. |
а)
б)
|
|
20. |
а)
б)
|
1 Жадвал давоми
|
21. |
а)
б)
|
|
22. |
а)
б)
|
|
23. |
а)
б)
|
|
24. |
а)
б)
|
1 Жадвал давоми
|
25. |
а)
б)
|
|
26. |
а)
б)
|
|
27. |
а)
б)
|
|
28. |
а)
б)
|
1 Жадвал давоми
|
29. |
а)
б)
|
|
30. |
а)
б)
|
2 жадвал
|
№ |
X2 |
Y10 |
|
1. |
100011,01 |
409,7 |
|
2. |
110011,01 |
2041,2 |
|
3. |
1010110,11 |
408,6 |
|
4. |
1011,01 |
250,3 |
|
5. |
100001,10 |
179,8 |
|
6. |
101101,11 |
405,1 |
|
7. |
111111,11 |
364,3 |
|
8. |
10001,10 |
198,1 |
|
9. |
101100,11 |
273,1 |
|
10. |
111110,11 |
157,3 |
|
11. |
1011001,11 |
126,08 |
|
12. |
100101,11 |
441,03 |
|
13. |
101011,10 |
251,6 |
|
14. |
101111,11 |
102,5 |
|
15. |
1011011,10 |
205,1 |
|
16. |
1011011,01 |
409,6 |
|
17. |
1011110,01 |
307,9 |
|
18. |
101000,11 |
126,03 |
|
19. |
110001,01 |
226,08 |
|
20. |
111101,11 |
493,01 |
|
21. |
1011011,01 |
199,6 |
|
22. |
101101,11 |
375,3 |
|
23. |
101001,11 |
266,8 |
|
24. |
111101,11 |
399,3 |
|
25. |
110101,11 |
181,01 |
|
26. |
110100,01 |
411,03 |
|
27. |
1110111,11 |
299,06 |
|
28. |
1101101,011 |
198,0325 |
|
29. |
1000111,001 |
997,1 |
|
30. |
1001001,11 |
203,7 |
2А Жадвали
|
№ |
вариантлар |
|
1. |
а) 12; в) 18; с) F16; сонларидан кейин қайси бутун сонлар келади |
|
2. |
1011012 дан 1100002 гача иккилик соноқ системасидаги бутун сонларни ёзинг |
|
3. |
Иккилик жуфт сони қайси сон билан тугайди? |
|
4. |
Бир хил типдаги сонлардан иборат учлик ва бешлик саноқ системасида кўпайтириш жадвалини тузинг |
|
5. |
Қуйидаги келтирилган қўшиш амали қайси саноқ системасида бажарилган?Ҳар бир системанинг асосини топинг:
|
|
6. |
2023 дан 10003гача учлик системасидаги бутун сонларни ёзинг |
|
7. |
Қуйидаги келтирилган қўшиш амали қайси саноқ системасида бажарилган?Ҳар бир системанинг асосини топинг:
|
|
8. |
Иккилик тоқ сони қайси сон билан тугайди? |
|
9. |
Қуйидаги келтирилган сонларни ўсиш тартибида жойлаштиринг: o а) 748, 1100102, 7010, 3816;
|
|
10. |
Учлик ва бешлик саноқ системасидаги бир хил типдаги сонларни кўпайтириш жадвалини тузинг |
|
11. |
а) 1012; в)78; с) 1F16; сонларидан кейин қайси бутун сонлар келади.
|
|
12. |
Қуйидаги келтирилган мисолни ечинг: o а) 2568 + 10110,12 . (608 + 1210) - 1F16; o б) 1AD16 - 1001011002 : 10102 + 2178;
|
|
13. |
Ўнлик сонни энг каттасини учта сон билан ёзинг: А)иккилик системасида;В)ўн олтилик системасида; |
|
14. |
Қуйидаги ккелтирилган сонларни камайиш тартибида ёзинг: o а) 748, 1100102, 7010, 3816;
|
|
15. |
Қуйидаги ккелтирилган сонларни ўсиш тартибида ёзинг:
б) 6E16, 1428, 11010012, 10010 |
|
16. |
148 дан 208гача бўлган саккизлик системасидаги бутун сонларни ёзинг |
|
17. |
Ҳисоблаш қонунини ҳисобга олган ҳолда биринчи 20та бутун сонни ўнлик, иккилик, учлик, бешлик ва саккизлик саноқ системасида ёзинг |
|
18. |
Қуйидаги келтирилган қўшиш амали қайси саноқ системасида бажарилган?Ҳар бир системанинг асосини топинг:
|
|
19. |
21 + 24 = 100 амали қайси саноқ системасида |
|
20. |
а) 1112; в) 378; с) FF16;сонларидан кейин қайси бутун сонлар келади
|
|
21. |
Қуйидаги ккелтирилган сонларни ўсиш тартибида ёзинг: o г) 10010, 11000002, 6016, 1418.
|
|
22. |
2816 дан 3016гача ўн олтилик системасидаги бутун сонларни ёзинг |
|
23. |
Қайси саноқ системасида қуйидаги келтирилган амаллар тўғри o а) 20 + 25 = 100; o б) 22 + 44 = 110?
|
|
24. |
а) 11112; в) 1778; с) 9AF916; сонларидан кейин қайси бутун сонлар келади |
|
25. |
Учлик бутун сон қайси сон билан тугалланиши мумкин |
|
26. |
Ўнлик 59 сони эквивалент бошқа саноқ системасидаги 214 сонига. Шу система асосини топинг. |
|
27. |
Энг катта ўнлик сонни қайси учта сон билан ёзиш мумкин: А) саккизлик саноқ системасидаги; В) иккилик саноқ системасидаги; |
|
28. |
Ўнлик 86 сони эквивалент бошқа саноқ системасидаги 126 сонига. Шу система асосини топинг. |
|
29. |
а)1010112; В)77778; С)CDEF16; сонларидан кейин қайси бутун сонлар келади |
|
30. |
Қуйидаги ккелтирилган сонларни ўсиш тартибида ёзинг: o в) 7778, 1011111112, 2FF16, 50010;
|
1 Жадвалдаги топшириқларни бажариш учун услубий кўрсатмалар
Компьютер билан мулоқатда бўлиш учун мутахассислар қайси ҳисоб тизимларидан фойдаланишади? Ўнлик санок системасидан ташқари 2 рақамининг бутун даражали бўлган асосли системалардан кенг фойдаланилади, масалан:
· Иккилик саноқ (0, 1 раками фойдалинилади);
· Саккизлик саноқ ( 0, 1, ..., 7 ракамлари фойдаланилади);
· Ўн олтилик саноқ ( 0, 1, ..., 9 ракамлари учун биринчи бутун нольдан тўққизгача рақамлар ишлатилади. Кейинги рақамлар эса ўндан – ўн бешгача, — A, B, C, D, E, F символлари рақамлар ўрнига ишлатилади).
3жадвал
|
|
|
Иккилик саноқ системаси барча саноқ системалари ичида айниқса содда ва шу билан бирга қизиқарли бўлгани учун компьютерларнинг арифметик асосини ташкил этади.
|
|
Позицион ҳисоблаш системаларда арифметик амаллари қандай амалга оширилади?
ҚЎШИШ
Ҳисоб қоидасидан фойдаланиб, қўшиш жадвалларини тузиш осон. Иккилик ва саккизлик саноқ системаларида қўшиш қоидалари 4 жадвалда келтирилган.
4 жадвал
|
Иккилик саноқ системасида қўшиш
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10
|
Саккизлик саноқ системасида қўшиш
|
Мисол 1. Турли саноқ системаларида 15 ва 6 рақамларини қўшамиз.
Ўнлик с.с.: 1510 + 610 Иккилик с.с.: 11112 + 1102 Саккизлик с.с.: 178 + 68
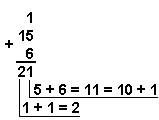
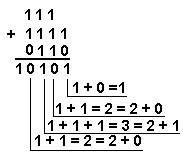

Мисол 2. 141,5 ва 59,75 сонларини қўшамиз.
Ўнлик с.с.: 141,510 + 59,7510 Иккилик с.с.: 10001101,12 + 111011,112

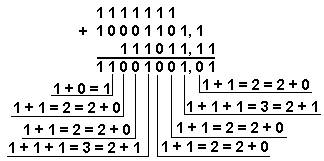
Жавоб: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
А й и р и ш
Мисол 3. 102, 108 ва 1016 сонларидан бирни айирамиз
Иккилик саноқ: 102-12 саккизлик саноқ: 108 + 18 Ўн олтилик саноқ: 1016-116

4 Мисол . 1002, 1008 ва 100 16 ракамларидан бирни айирамиз.
Иккилик санок: 1002 - 12 Саккизлик саноқ: 1008 + 18 Ўн олтилик саноқ: 10016 -116
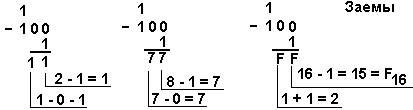
5 Мисол. 201,25 рақамидан 59,75 рақамини айирамиз..
Ўнлик саноқ : 201,2510 – 59,7510 Иккилик саноқ: 11001001,012 – 111011,112
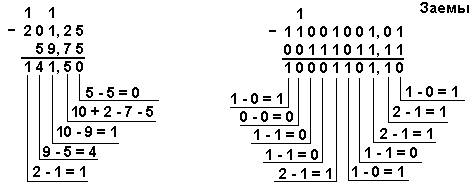
Саккизлик с.с. : 311,28 + 73,68 Ўн олтилик с.с: С9,416 – 3В,С16
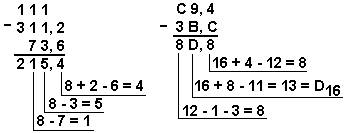
Жавоб: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Кўпайтириш
Кўп хонали рақамларни хар хил позицион саноқ системаларида кўпайтириш амалини бажараётган вақтда , рақамларни устун шаклида оддий ўнлик сонларни кўпайтириш алгоритмидан фойдаланиш мумкин. Лекин бу холатда кўпайтириш ва қўшиш кўрилаётган саноқ системасининг қўшиш ва кўпайтириш жадвалларига мос равишда амалга оширилади.
|
Икклик санок системасида кўпайтириш
|
Саккизлик санок системасида кўпайтириш
|
6 Мисол. 5 ва 6 сонларни.кўпайтирамиз
Ўнлик санок системаси: ![]() Иккили саноқ
системаси:
Иккили саноқ
системаси: ![]() Саккизлик саноқ системаси:
Саккизлик саноқ системаси:![]()
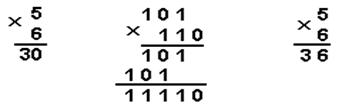
Жавоб: ![]()
Текшириш . Олинган кўпайтмани ўнлик саноқ системасига ўгирамиз.
![]()
![]()
7 Мисол. 115ва 51 ракамларни купайтирамиз.
Ўнлик саноқ
системаси: ![]()
Иккилик санок
системаси: ![]()
Саккизлик санок системаси қуйидаги сонларни кўпайтирамиз
![]()

Жавоб: 115 . 51 = 586510 = 10110111010012 = 133518
Бўлиш
Барча позицион системасида бўлиш ўнлик саноқ системасида бурчакли бўлиш қоидалари каби бўлади.
8 Мисол. 30 сонни 6 га бўламиз.
Ўнлик саноқ
системаси: ![]() Иккили саноқ системаси:
Иккили саноқ системаси: ![]() Саккизлик
саноқ системаси :
Саккизлик
саноқ системаси :![]()
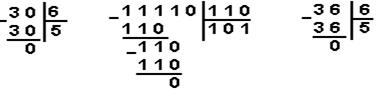
Жавоб: ![]()
9 Мисол. 5865 сонни 115 га буламиз..
Ўнлик
саноқ системаси: ![]() Иккили
саноқ системаси:
Иккили
саноқ системаси: ![]()
2-Жадвалдаги топшириқларга услубий кўрсатма.
Бу топшириқлардан фойдаланиш учун қуйидаги қоидаларидан фойдаланиш керак: «Махсус қоида », «Бўлиш қоидаси »ва «Позиция қоидаси».
Махсус қоида . Бу қоида факатгина улардаги асос , улардан бирига, бошқасига эса бутун даражали асос ҳисобланган ҳисоб системаси учунгина ишлатилади, масалан, 8=23 ,16=24 ,яъни иккили санок системаси, саккизлик саноқ системаси ва ўн олтилик саноқ системаси учун. Қоида хар бир саккизлик рақамини учта (триада), ўн олтилик рақамларини эса тўртта (тетрада) иккилик рақамлари билан кетма-кетликда алмаштиришдан иборат. Тескари ўтказиш хам тўғри хисобланади.
Масалан:
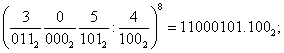
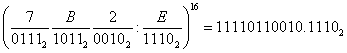
Иккилидан саккизлик (ўн олтилик) саноқ системасига ўтиш учун шундай қилиш керак: нуқтадан чапга ва ўнгга харакатланаётганда иккилик саноқ рақамини 3(4) разрядлар гуруҳларига бўлиб, зарурият бўлса четдаги чап ва ўнг гуруҳларини нол билан тўлдирилади.Кейин эса 3(4) разрядли гурухни мос келадиган саккизлик (ўн олтилик) рақами билан алмаштиришади.
Масалан:
1) 1101111001.11012 саккизлик саноқ системасига ўтказиш
![]()
2) 11111111011.1001112 ўн олтилик саноқ системасига ўтказиш
![]()
Позиция қоидаси. Позицион хисоблаш системасида хохлаган сонни системанинг асоси даражаси бўйича жойлаштириш мумкин. Масалан:
![]()
![]()
![]()
Бу жойлаштиришнинг хар бир рақам ва хар бир сонни ўтказиш учун , ўтказилаётган шу ҳисоб системасига мос келадиган рақам ва сон билан алмаштиринг Ҳисобни янги системада бажариб кидирилаётган сонни топамиз.
![]()
![]()
![]()
2,8,16-лик саноқ системасидан 10-лик саноқ системасига ўтамиз:
Масалан,
Разрядлар 3 2 1 0 -1
Рақам 1 0 1 1, 12=1*23+1*21+1*20+1*2-1=11,510
Разрядлар 2 1 0 -1
Рақам 2 7 6, 58=2*82+7*81+6*80+5*8-1=190,62510
Разрядлар 2 1 0
Рақам 1 F 316=1*162+15*161+3*160=49910
Бўлиш қоидаси. Ўтказилиши керак бўлган сонни навбат билан
ўтказилаётган система асосига қолдик система асосидан кичик бўлгунча давом эттирамиз. Агар махалий сон булинмадан катта бўлса унда хам анологик харакатларни давом эттирамиз..Кетма-кетликдаги колдикларни ва охирги бўлинма ўнгдан чапга томон ёзиб, қидирилаётган сонни топамиз.
Каср сонларни бир саноқ системасидан бошқа саноқ системасига ўтказганда соннинг бутун қисмини алоҳида қонун-қоидага мувофиқ ва каср қисмини алоҳида қонун-қоидага мувофиқ равишда ўтказилади.
Мисол

16 мисол
Ўнлик саноқ системасидаги 75 сонини иккилик, саккизлик, ўн олтилик саноқ системаларига бўлиш қоидаси ёрдамида ўтказамиз:
Иккилик с.с саккизлик с.с ўн олтилик с.с.
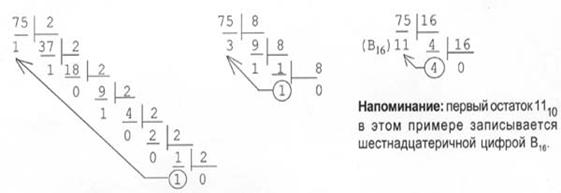
Жавоб: 7510 = 1 001 0112 = 1138 = 4B16
17 мисол
Ўнлик саноқ системасида берлган 0,36 сонини иккилик, саккизлик, ўн олтилик саноқ системаларига ўтказамиз

«Махсус қоида », «Бўлиш қоидаси »ва «Позиция қоидаси» ёрдамида сонларни 2, 8, 10, 16 саноқ системаларига ўтказиш жадвали келтирилган (6 жадвал)

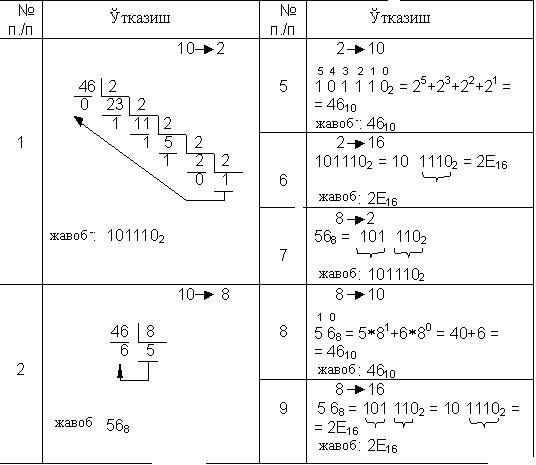
Бутун сонларни бир саноқ системасидан иккинчисига ўтказишнинг умумий
жадвали
6 жадвал
![]()
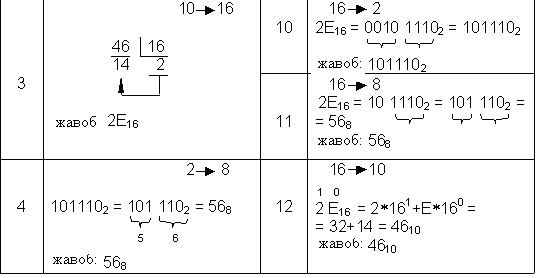
Назорат саволлари
1. Саноқ системаси деб нимага айтилади?
2. Позиция коидаси. Ёрдамида сонларни бир саноқ системасидан иккинчисига ўтказишни гапириб беринг.
3. «Махсус қоида », қандай системаларда уларни қўллаш мумкин, мисол келтиринг.
4. Каср сонларни бир саноқ системасидан иккинчи бир саноқ қандай ўтказилади:
а) кўпайтириш( бўлиш ) қоидасига кўра
б) Позиция коидасига кўра
в) Махсус қоидага кўра
5.Ўтказинг :1643 10- >2 ; 34.27 8 - >2 - >16 ; 1ADF16 - >2 - >8 ; 101110112 - >16 .
№4 лаборатория иши
Турли структурали алгоритмлар.Барча турдаги алгоритмлар ткрларидан фойдаланган ҳолда алгоритмлар тузиш.
Ишнинг мақсади
1.Турли кўринишдаги алгоритмлар билан танишиш
2. Турли структурали алгоритмларни тузишни урганинг. (чизикли, тармоқланувчи ва такрорланувчи(цикли)).
3.Масалаларнинг математик изохлаб беришни билиш.
4. Топшириқни таърифлаб беришни ўрганиш
Топширик
1. 9, 10 жадвалдан(жадвалнинг ракамини укитувчидан билиб оласиз), ўз вариантингизга мос топшириқни кўчириб олинг,маълумотларга асосланиб берилган топшириклар учун, тузинг:
1) масаланинг математи қўйилиши;
чизиқли структурали алгоритм:
а) блок – схема;
б) псевдокод
в) Насси диаграммасини.
2. 11, 12. жадвалдан(жадвалнинг ракамини укитувчидан билиб оласиз), ўз вариантингизга мос топшириқни кўчириб олинг,маълумотларга асосланиб берилган топшириклар учун, тузинг:
Тармоқланувчи структурали алгоритм:
а) блок – схема;
б) псевдокод
в) Насси диаграммасини.
3. 13-18. жадвалдан(жадвалнинг ракамини укитувчидан билиб оласиз), ўз вариантингизга мос топшириқни кўчириб олинг,маълумотларга асосланиб берилган топшириклар учун, тузинг:
Такрорланувчи структурали алгоритм:
а) блок – схема;
б) псевдокод
в) Насси диаграммасини.
Алгоритмни аниқлаш
Алгоритм – масалани ечимини топишда аниқ натижага эришишда ҳаракатларнинг тартибланган кетма-кетлигини белгиловчи кўрсатмалар тўпламидир.Илгари «тартибланган»сўзининг ўрнига «кетма-кетлик» сўзи ишлатиларди, лекин компьютерларнинг ривожланиши натижасида «кетма-кетлик» сўзининг ўрнига «тартибланган» сўзи ишлатила бошланди.Бу алгоритмнинг кўрсатмалари бошқа кўрсатмалар ёки уларнинг натижалари билан боғлиқлигини кўрсатади.Шунинг учун, баъзи бир кўрсатмалар бошқа кўрсатмалар ишига боғлиқ бўлганлиги туфайли, уларнинг иши тугаллангандан сўнггина бажарилиши керак.Мустақил кўрсатмалар ёки кўрсатмалар иши тугалланганлиги сабабли мустақил бўлган кўрсатмалар иши , ўз ишларини мустақил, параллел ёки бир хил вақтда бажаришлари мумкин, агарда буни процессор ва операцион система фойдалануви йўл берса.
Алгоритмларнинг формал хусусиятлари
Алгоритмни ҳар хил аниқлашда аниқ ва ноаниқ формасида қуйидаги умумий талабларни ўз ичига олади.
Дискретлилик – алгоритм масалани ечилиш жараёнини оддий қадамма қадам бажарилиш кетма-кетлигини ўз ичига олиши керак. Бунда алгоритмнинг ҳар бир қадамини бажарилишига маълум бир вақт талаб қилинади, яъни чиқаётган маълумотларнинг қайта ишлови натижада вақт бўйича дискрет бўлади.
Аниқлилик (детерминированность). Ҳар доим системанинг ҳолатига қараб ишнинг кейинги қадами аниқланади. Шунда, алгоритм чиқаётган бир хил маълумот учун бир хил жавобни беради.Замонавий трактовкада хар хил реализацияда худди шу алгоритмни ўзида изоморф графи бўлиши керак. Бошқа тарафдан эса, эҳтимоллик алгоритмлари мавжуд бўлиб, уларнинг ҳар бир кейинги қадами системанинг ҳолатидан ва ихтиёрий сон генерациясидан келиб чиқади. Бироқ, “Чиқарилаётган маълумотлар” рўйхатида эҳтимоллик алгоритми ихтиёрий сонларни генерация усулини тадбиқида оддий ҳолат бўлиб қолади.
Тушунарлилик – фақат бажарувчи учун бўлиб, унинг буйруқлар системасига кирадиган алгоритмларини буйруқларини ўз ичига олади.
Тамомийлик – топширилган маълумотни чиқиши алгоритм ишини тамомлаши керак ва охирги қадам учун натижани бериши керак.Бошқа тарафдан эса эҳтимоллик алгоритми ҳеч қачон натижа бермаслиги мумкин, бу эҳтимоллик 0 га тенг бўлади.
Оммавийлик (универсаллилик). Алгоритм чиқаётган маълумотларни хар хил тўпламига қўлланилиши керак.
Натижавийлик – аниқ натижаларда алгоритмнинг тамомланиши.
Алгоритм хатоликларни ташкил этади, агар у нотўғри натижа берса ёки умуман натижа бермаса.
Алгоритм хатоликларни ташкил этмайди, агар у чиқадиган маълумотлар учун тўғри натижа берса.
Алгоритм турлари
Аниқ амалий масалалар ечими учун мўлжалланган амалий алгоритмлар алоҳида ўрин эгаллайди. Алгоритм тўғри саналади, қачонки у масаланинг талабларига жавоб берса(масалан, ҳақиқатга яқин натижани берса).Алгоритм (дастур) хатоликларга эга, агар у баъзи бир чиқувчи маълумотларга нотўғри натижани берса, узилса, жавоб бермаса ва умуман ҳеч қандай натижа бермаса. Алгоритм турлари худди мантиқий-математик масалалар каби инсон фаолияти компоненталари ва тенденцияларини акслантиради, алгоритмларни ўзи эса қўйилган мақсадга, бошланғич масала шартига, унинг ечимларига, ижро этувчининг ҳаракатларини аниқлашга боғлиқ равишда қуйидагиларга бўлинади:
Механик алгоритмлар, ёки бошқача қилиб айтганда детерминлашган, қаттиқ(масалан, машина, двигатель ишининг алгоритми ва ҳ.к.);
Эгилувчан алгоритмлар, масалан стохастик, яъни эҳтимоллашган ва эвристик. Механик алгоритм, ягона ва ишонарли кўрсаткичларни белгилаб,шу билан бирга талаб қилинган ва қидирилган натижани ягона қийматини таъминлаб, аниқ ҳаракатларни беради, агарда шу алгоритм ишлаб чиқариш учун масалани ечиш жараёнидаги шартлари бажарилса.
Эҳтимоллилик (стохастик) алгоритми дастурга масаланинг аниқ бир натижага олиб келадиган бир неча хил йўллар ва усуллар билан ечишни беради.
Эвристик алгоритми(грекча “эврика” сўзидан) – бу шундай алгоритмки, бунда дастур ишини охирги натижасига эришиш аниқланмаган, шунингдек ишнинг кетма-кетлиги кўрсатилмаган, бажарувчининг ҳаракатлари очиб берилмаган. Эвристик алгоритмларга, мисол учун инструкция ва аввалдан ёзилган рўйхат киради. Бу алгоритмларда универсал мантиқий процедуралар ва уларнинг аналогияларга, ассоцияцияларга ва аввалги ўхшаш масалаларни ечишга асосланган ҳал этиш усуллари ишлатилади.
Чизиқли алгоритм – бир-бирининг кетидан кетма-кет бажариладиган буйруқлар(кўрсаткичлар) тўплами.
Тармоқланувчи алгоритм – ҳеч бўлмаганда битта шарти бор алгоритм, яъни текшириш натижасида алгоритмни параллел тармоқларга ажралиши.
Циклик алгоритми - янги маълумотлар устида бир ҳаракатнтнг бир неча бор такрорланишини кўзда тутадиган алгоритм.Циклик алгоритмларга кўпинча ҳисоблаш усуллари, варианларни танлаш киради.Цикл дастурлар – бу шундай дастурларки бунда буйруқлар кетма-кетлиги бир неча бор бажарилиши мумкин(янги чиқаётган маълумотлар учун), то маълум бир шартни бажаргунгача.
Ёрдам берувчи (бўйсинувчи) алгоритм (процедура) – Аввалдан ва бутунлигича фойдаланиладиган, аниқ масалани алгоритмлаш учун ишлаб чиқилган алгоритм. Баъзи бир ҳолатларда хар хил маълумотлар учун бир хил буйруқлар ткетма-кетлиги учраганда, ёзувни қисқартириш мақсадида ёрдамчи алгоритмлар ажратилади. Алгоритмлашга тайёрлашни хамма этапларида алгоритмнинг структурали кўриниши ишлатилади.
Алгоритмнинг структурали блок-схема, граф-схемаси – алгоритмнинг бири-бири билан стрелка ёрдамида боғланган блокларининг- график символларининг график кўриниши, яъни уларнинг ҳар бири алгоритмнинг бир қадамига тўғри келади. Блок ичида ҳаракатнинг кўриниши берилади. Алгоритмнинг график кўриниши масалани дастурлашдан олдин уни ечимини кенг кўриниши учун фойдаланилади, бунда кўз хотираси дастур ёзилиш жараёнини осонлаштиради, юзага келиши мумкин бўлган хатоликларни олдини олади, ахборотни қайта ишлаш жараёнини тўла тушунишга олиб келади.
Ҳатто шундай дейиш мумкин:” Ташқи алгоритм ўзида шундай схемани мужассам этганки – у ўзини ичида шу масалани ечишда, ҳисоблашда, келаётган ахборотни машинага киритишда ва босмага чиқаришда шаклларни ичига киритиладиган масалани ечимини ўзида мужассам этади.
Алгоритмларга мисоллар киритамиз:
Энг катта умумий бўлувчи ва энг кичик умумий каррали
а ва b нинг энг катта умумий бўлувчиси(ЭУБ(НОД))ни топишни биз ҳаммамиз мактабда ўрганганмиз. Яъни бу, а ва b қолдиқсиз бўлинадиган энг катта бутун сон d. Ҳеч қандай қийинчиликсиз ҳар бир ўқувчи айтиши мумкин ЭУБ(12,18)=6 га. Агар бу икки сондан бири 0 га тенг бўлсачи? Агар
а ва b манфий бўлсачи? Бу ҳақда мактаб дарсларида хар биримиз ўйлаб кўрганмиз.Бу саволларга жавоб бериши учун умумий бўлувчини нима эканлигини аниқлаштириб оламиз.
1-аниқлаштириш. а ва b қолдиқсиз бўлинадиган 0га тенг бўлмаган энг катта бутун сон d. Бу қуйидагича бўлади: d= ЭУБ (a,b). Агар иккита сон ҳам нолга тенг бўлса ЭУБ(0,0)=0. Булардан келиб чикиб қуйидаги тенгликка эга бўламиз:
ЭУБ(a,b)= ЭУБ(b,a),
ЭУБ(a,b)= ЭУБ(-a,b)
ЭУБ(a,0)=|a|
Айтиш мумкин нима учун ЭУБ (-12,18) тенг 6га, нега -6га эмас? -12 ва 18 , 6га ва -6га бўлинади. Буни жавоби осон: ЭУБ – бу энг катта умумий бўлувчи, 6 сони эса -6 дан катта .
Энг катта умумий бўлувчи ва энг кичик каррали бир-бири билан чамбарчас боғлиқдир.
2-аниқлаштириш. а ва b сонларининг Энг кичик умумий каррали(ЭУК(НОК))си а ва b сонларининг энг кичик умумий бўлинувчисидир.
Арифметиканинг асосий теоремаси шуни кўрсатадики, ҳар қандай натурал сон n ни оддий сонлар кўпайтмаси сифатида тасвирлаш мумкин:
![]()
Натурал сонларнинг бундай кенгайтмаси каноник дейилади.Бундан қуйидаги келиб чиқади, агар
![]() бўлса, қуйидагича
бўлади
бўлса, қуйидагича
бўлади
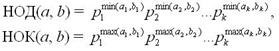
Мисол 1. a = 24 ва b = 18 сонларини кўриб чиқамиз.Уларни оддий кўпайтма шаклида ёзиб оламиз 24 = 23·3, 18 = 2·32. Шунингдек
НОД(24, 18) = 2min(3,1) · 3min(1,2) = 21 · 31 = 6,
НОК(24, 18) = 2max(3,1) · 3max(1,2) = 23 · 32 = 8 · 9 = 72
Худди шундай сонларни каноник усулда ёзилишини биз мактабда ЭУБ ва ЭУК ни топиш учун ўрганганмиз.Бироқ, бу усул алгоритмни ҳисоблашни реализациясида у даражада эффектли эмас.
Кейинги яққол фактни кўриб чиқамиз. Агар ЭУБ(a, b) = d, унда a ва b , d.га бўлинади. a – b фарқи ҳам d га бўлинади. ЭУБ ни ҳисоблашни рекуррентлиги
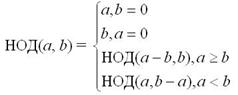
Мисол 2. a = 32, b = 12 бўлсин, унда
НОД(32, 12) = НОД(32 – 12, 12) = НОД(20, 12) = НОД(20 – 12, 12) = НОД(8, 12) =
= НОД(8, 12 – 8) = НОД(8, 4) = НОД(8 – 4, 4) = НОД(4, 4) = НОД(4 – 4, 4) = НОД(0, 4) = 4
Бу ҳисоблаш усули оптимал ҳисобланмайди.Масалан, НОД(1000000, 2)ни топиш учун 500000 ҳисоблаш операциясини бажариш керак бўлади. ЭУБ(НОД) ни ҳисоблашни тезроқ амалга ошириш учун айирма операциясини бўлинмадан қолган қолдиқни олишга алмаштирамиз:
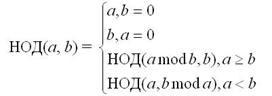
Мисол 3. a = 78, b = 14. ,бўлсин, унда
НОД(78, 14) = НОД(78 mod 14, 14) = НОД(8, 14) = НОД(8, 14 mod 8) = НОД(8, 6) =
= НОД(8 mod 6, 6) = НОД(2, 6) = НОД(2, 6 mod 2) = НОД(2, 0) = 2
Шартлар сонини иккига қисқартириш эвазига юқоридаги рекурентликни соддалаштирамиз:
![]()
Агар a < b, то НОД(a, b) = НОД(b, a mod b) = НОД(b, a), яъни функция аргументлари келтирилади. Кейинги функция чақирилишида ЭУБ(НОД) биринчи аргумент иккинчисидан катта бўлади. Фақат иккинчи аргумент b ноль бўлиши мумкин.
Мисол 4. a = 14, b = 78. бўлсин, унда
НОД(14, 78) = НОД(78, 14) = НОД(14, 8) = НОД(8, 6) = НОД(6, 2) = НОД(2, 0) = 2
Си дастурлаш тилида gcd (Greatest Common Divisor) функциясини реккурентликдан фойдаланган ҳолда ЭУБни ҳисоблашни амалга оширамиз.Бунда % белгиси Си да бўлишдан қолган қолдиқ операциясини олишни билдиради.
int gcd(int a, int b)
{
if (b == 0) return a;
return gcd(b, a % b);
}
Эслатиб ўтамиз, Си да шартли оператор қуйидаги синтаксисга эга :
if (<шартли ифода>) <ифода 1>; else <ифода 2>;
Агар (<шартли ифода>) рост бўлса, у ҳолда <ифода 1>; бажарилади, акс ҳолда <ифода 2>; бажарилади.
Тернар шартли оператори қуйидаги синтаксисга эга:
<шартли ифода > ? <ифода 1> : <ифода 2>;
Ва у семантик жиҳатдан оператор if..then..else дан фарқ қилади. Агар<шартли ифода > рост бўлса, у ҳолда оператор қийматни қайтаради, бунда <ифода 1> қайтади, акс ҳолда <ифода 2> қайтади.
Тернар оператордан фойдаланган ҳолда gcd функциясини қуйидагича ёзиш мумкин:
int gcd(int a, int b)
{
return (!b) ? a : gcd(b, a % b);
}
Теорема. Иккита сони НОД ва НОК қуйидагиларни ўз ичига олади:
a · b = НОД(a, b) · НОК(a, b)
lcm (Lowest Common Multiple) ҳисоблаш функцияси НОК қуйидагиларни ўз ичига олади:
int lcm(int a, int b)
{
return a / gcd(a, b) * b;
}
a * b / gcd(a, b) ифодасини ҳисоблашига аҳамият берсак, тўлишиш юзага келади, a / gcd(a, b) * b да эса келмайди. Бу ерда a, b и lcm(a, b) ифодаси int типининг чегарасида ётиши кўзда тутилади.
Оддий сонларнинг алгоритмини топиш
2 3 5 7 11 13 17 19 23 29 31… $250.000…
Бу анча олдин, университетда Pascal дастурлаш тилини ўрганишга бошлаганимизда бўлган эди, уйга вазифа қилиб оддий сонларни топиш алгоритмини яратиш керак эди.
Алгоритмни Pascal тилидаги намунаси билан берамиз. Дастур фойдаланувчидан N сонини ва ҳамма содда сонларни N кирган ҳолда қидиришини сўрайди. Биринчи тестдан сўнг N= «кўп» ни киритиш умиди юзага келди. Дастур ишларди, аммо кутилгандан анча секин ишларди. Табиийки, буни сабаби кўп сонли текширишларда (N*N/2тартибида) эди, шунинг учун ортиқчаликдан халос қилинди. Натижада, бири бирига ўхшаш 5та алгоритм юзага келди ва улар бирига қараганда иккинчиси тезроқ ишларди. Буни Листинг 1 да кўрсатамиз.
# Листинг 1# киритамиз N
n = input("n=")
# содда сонларни сақлаш учун бўш рўйхат яратамиз
lst = []# ва k да бўлувчилар сонини сақлаймиз
k = 0# 2 дан N гача бўлган сонларни босиб ўтамиз
foriinxrange(2, n+1):
# 2дан жорийгача бўлган сонларни босиб ўтамизforjinxrange(2, i):
# бўлувчилар сонини қидирамизifi % j ==0:
k = k + 1 # агар бўлувчи бўлмаса, сонни рўйхатга қўшамизifk ==0:
lst.append(i)else:
k = 0# рўйхатни экранга чиқарамиз
print lst
Тушунарлики, ҳар бир рақамни бўлувчисини санашга ҳеч қандай эғтиёж йўқ., шунинг учун k ўзгарувчини ўз вазифасидан озод қилиш мумкин. Ҳақиқатда, ҳеч бўлмаганда битта бўлувчи бўлса, бу рақам оддий бўлмайди.
Листинг 2 ни кўрамиз
# Листинг 2n = input("n=")
lst = []foriinxrange(2, n+1):
forjinxrange(2, i):
ifi % j ==0:
# агар бўлувчи топилса,соддасон эмас. breakelse:
lst.append(i)print lst
break конструкцияси ички циклни якунини ясашга ёрдам беради ва ташқи итерацияга ўтишга ёрдам беради.
Савол туғилади:” нега 4 га бўлиш керак, агар сон 2 га бўлинмаса?”. Шундай хулосага келамизки, бўлувчиларни бўлинмадан ошиб кетмайдиган содда сонлар орасидан қидириш керак.Бизнинг алгоритм Листинг 3 (га қаранг) га айланади.
# Листинг 3n = input("n=")
lst=[]foriinxrange(2, n+1):
# (lst) рўйхати бўйича содда сонларни босиб ўтамизforjinlst:
ifi % j ==0:
breakelse:
lst.append(i)print lst
Сўнгра сонлар
назариясини эслаймиз ва тушунамизки, шундай сонларни танлаймизки, у илдиздан
ошиб кетмаслиги керак. Мисол учун, агар М сонини pi бўлувчиси бўлса, у
ҳолда qi бўлувчиси бўладики, бунда pi * qi = M. Яъни, ўхшашини топиш
учун, кичигини топиш керак. Ҳамма ўхшашликлар орасида, кўрилган максимал
кичик ўхшашлик - pi и qi га тенг бўлган ўхшашлик, яъни pi * pi = M => pi =
sqrt(M). Листинг 4 ни кўрамиз.
# Листинг 4
frommathimportsqrt
n = input("n=")
lst=[]foriinxrange(2, n+1):
forjinlst:
ifj > int((sqrt(i)) +1):
lst.append(i) breakif(i % j ==0):
breakelse:
lst.append(i)print lst
Листинг 4 коди N=10000да 1000 марта биринчи вариантга нисбатан тезроқ бажарилади.Яна ҳам тез бажариш йўли бу,фақат 1,3,7 ёки 9 га(бошқалари 2 ва 5 га бўлинадиганлари) тамом бўладиган сонларни текширишдир.Листинг 5 га қараймиз.
# Листинг 5
frommathimportsqrt
n = input("n=")
lst=[]foriinxrange(2, n+1):
if(i >10):
if(i%2==0)or(i%10==5):
continueforjinlst:
ifj > int((sqrt(i)) +1):
lst.append(i) breakif(i % j ==0):
breakelse:
lst.append(i)print lst
Листинг 5 даги озгина ўзгартириш эвазига тезликни оширамиз.
# Листинг 6
frommathimportsqrt
n = input("n=")
lst=[2]
foriinxrange(3, n+1,2):
if(i >10)and(i%10==5):
continueforjinlst:
ifj > int((sqrt(i)) +1):
lst.append(i) breakif(i % j ==0):
breakelse:
lst.append(i)print lst
Натижа: Охирги листингдаги дастур биринчи вариантга нисбатан 1300 баравар тезроқ бажарилади.Мен ўз олдимга шу масалани максимал даражада тез еча оладиган дастур тузишни мақсад қилмаган эдим, бу энди бошлаётган дастурчилар учун тўғри тузилган алгоритм сизнинг дастурларингизни оптималлаштиришда ўз ролини ўйнашини исботи эди.
P.S.
Листинг 7 камчиликларини ҳисобга олган ҳолда қуйидагиларга эга
бўламиз:
# Листинг 7n=input("n=")
lst=[2]
foriinxrange(3, n+1,2):
if(i >10)and(i%10==5):
continueforjinlst:
ifj*j-1> i:
lst.append(i) breakif(i % j ==0):
breakelse:
lst.append(i)print lst
N=10000да, вақт:
time 1 = 26.24
time 2 = 3.113
time 3 = 0.413
time 4 = 0.096
time 5 = 0.087
time 6 = 0.083
time 7 = 0.053
Решето Эратосфена:
# Листинг 8
n = input("n=")
a = range(n+1)
a[1] =0
lst = [] i = 2while i <= n:ifa[i] !=0:
lst.append(a[i])forjinxrange(i, n+1, i):
a[j] = 0 i += 1print lst
натижалар n = 1 000 000да:
time 7 = 7.088
time 8 = 1.143
Тескари матрица тузиш алгоритми
А-берилган матрица бўлсин, биз уни тескарисини топамиз. n ва k – сатр ва устунлар сони.
1.Олдин А квадрат матрицами йўқми, n ва k лар бир-бирига мослигини текширамиз.
2. Сўнгра А матрицанинг аниқловчиси нолга тенг эмаслигини текширамиз. Агар у нолга тенг бўлса матрицанинг тескариси бўлмайди.
3. Матрица Invга мос nxn ўлчамдагини ҳосил қиламиз.
4. Сўнгра элементар ўзгартиришлар: матрица сатрларини қўшиш, сатрларни сонга кўпайтириш , сатр ва устунларни ўзгартириш орқали А ни бир ўлчовли массив ҳолатига келтирамиз. Шу билан бирга шунга параллел равишда Inv матрицасига ўзгартиришлар киритамиз.( худди шу сатр ва устунларни алмаштириш, тахлаш ва худди шу сонга кўпайтириш).
Натижада матрица Inv А матрицасининг тескариси бўлади.
Алгоритмнинг тўртинчи қадамини кўриб чиқамиз.
Бу цикл матрица А нинг сатрлар сонларига қараб бўлади. Ҳар бир циклнинг итерацияси қуйидагича тузилган:
1. Ҳар бир итерацияда биз элемент A(i,i) га қараймиз. Агар у нолга тенг бўлса, биз матрица А да нолга тенг бўлмаган элементни қидирамиз.Яъни уни А матрицасининг тўғри бурчагида (i, i, n, n) қидирамиз. Агар у топилса, у ҳолда унинг координатлари (i2, j2) ни i-чи сатрни i2-чи сатрга , j-чи устунни j2-чи устунга алмаштирамиз. Худди шуларни Inv. матрицасида ҳам қиламиз.
2. А ва Inv матрицасини i-чи сатрини элемент A(i, i) га бўламиз.(бўлиш мумкин, чунки у биринчи қадамдаёқ нолга тенг эмас эди). Шунинг учун A(i, i) элементи 1га тенг.
3. А матрицанинганиқ коэффициентли i-чи сатрга бўлиш орқали, бошқа сатрлардаги (i, i) индексли элементдан тепа ва пастдаги элементларни нолга айлантирамиз. Худди шу коэффициент билан Inv матрицасини i-чи сатрини бошқа сатрларга бўламиз.
Мисол
![]()
Inv матрицасини ёзамиз
![]()
Иккинчи саирдаги 3 коэффициентлини оламиз.
![]()
-2 га иккинчи сатрни бўламиз
![]()
Биринчи сатрдан иккинчи 2 коэффициентлини оламиз
![]()
Матрицанинг тескариси қуйидагича бўлади
![]()
Назорат саволлари.
1.Алгоритм турлари.
2. break оператори ёрдамида дастур тузиш.
3. Содда сонлар топиш алгоритми.
4. Тармоқланувчи алгоритмлар.
№5 Лаборатория иши
Алгоритмлар. Чизикли структурали дастурлар.
Borland C++ ва Builder 6 муҳитида ишлаш.
Ишнинг максади
1. Хар хил кўринишдаги алгоритмлар билан танишиш
2. Хар хил тузилишдаги алгоритмларни тузишни ўрганинг. (чизиқли, тарқалувчан ва циклли).
3.Масалаларнинг математик кўрсатмаларини изоҳлаб беришни билиш.
4. Чизиқли тузилмаларининг энг содда дастурларини тузишни ўрганинг.
Топшириқ
1. 7 , 8, 9, 10 № жадвалларидан вариантингиз рақами бўйича топшириқни кўчиринг . (жадвалнинг ракамини ўқитувчидан билиб оласиз),берилган топшириқлар учун, тузинг:
а) масаланинг математик кўрсатмасини;
б) блок – схемасини;
в) Насси диаграммасининг псевдокоди.
2. С дастурлаш мухити билан танишинг, Менюнинг кулланиладиган асосий командаларининг кулланилишини дафтарингизга ёзиб олинг. (лаборатория машгулотларида бажарилади).
3. 9,10 жадвалдаги топшириқлари учун С++ га дастур тузинг, ШК жойлаштиринг ва олинган натижаларни ўқитувчига кўрсатинг.
Ҳисобот таркиби
Хисобот куйидагиларни ўз ичига камраб олиши керак:
1) Лаборатория ишининг номи.
2) Лаборатория ишига топшириклар.
3) масаланинг математик кўрсатмасини, (7,8) Блок-схемалар (Т 5, Т6) учта куринишдаги алгоритмлар
4) С++ мухитидаги менюнинг асосий командаларининг курсатмасини тасвирлаб беринг .
4) Натижалари билан чизикли тузилишнинг иккита дастури.
7 Жадвал
|
вариантнинг раками |
А ва В формулалар учун |
х, y |
|
1 |
2 |
3 |
|
1 |
A= B=x(arctgA+e-(x-1)) |
x = 3 y = -1,4 |
|
2 |
|
x=2 y=3.1 |
|
3 |
B=(1+tg2 |
x= -2,3 y= 2,7
|
|
4 |
|
x=-5,3 y=2,5 |
|
5 |
|
x=1,6 y=-6,2 |
|
6 |
|
x=4 y=3,4 |
|
7 |
|
x=3,6 y=5,5 |
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
Қўшимча ўзгарувчиларни киритишдан фойдаланиш орқали берилган параметрлар бўйича ҳисоблаш
Таблица 8
|
№ |
Задание |
Параметры |
|
|
|
1 |
2 |
3 |
|
|
|
1. |
|
|
|
|
|
2. |
|
|
|
|
|
3. |
|
|
|
|
|
4. |
|
|
|
|
|
5. |
|
|
|
|
|
6. |
|
|
|
|
|
7. |
|
|
|
|
|
1 |
2 |
3 |
|
|
|
8. |
|
|
|
|
|
9. |
|
|
||
|
10. |
|
|
||
|
11. |
|
|
||
|
12. |
|
|
||
|
13. |
|
|
||
|
14. |
|
|
||
|
15. |
|
|
||
|
16. |
|
|
||
|
17. |
|
|
||
|
18. |
|
|
||
|
19. |
|
|
||
|
20. |
|
|
||
|
21. |
|
|
||
|
22. |
|
|
||
|
23. |
|
|
||
|
24. |
|
|
||
|
25. |
|
|
||
|
26. |
|
|
||
|
27. |
|
|
||
|
28. |
|
|
||
|
29. |
|
|
||
|
30. |
|
|
||
9 Жадвал
|
1 |
Тўғрибурчакли учбурчакнинг иккита катети берилган.Учбурчакнинг бурчагини ва гипотинузасини топинг.
|
|
2 |
Ғишт h баландлигидан тушади. Унинг ер билан тўқнашиш вактида ва бу содир бўлган вактидаги тезликни аниқланг.
|
|
3 |
c гипотинузаси ва тўғрибурчакли учбурчакнинг тегишли a бурчаги маълум. Учбурчакнинг майдонини топинг.
|
|
4 |
Квадратнинг диагонали маълум .Квадратнинг периметр ва майдонини ҳисобланг.
|
|
5 |
Катта томондан диагоналнинг ўртасидаги бурчак , ва тўгрибурчакнинг диагонали маълум . Тўғрибурчакнинг майдонини ҳисобланг.
|
|
6 |
Метал куймоғи цилиндр шаклига эга , S устки майдони, h баландлиги, r қалинлиги. Куймокнинг массасини хисобланг.
|
|
7 |
Гишт параллепипед шаклига эга h баландлиги, тугрибурчак асосида d диагоналига эга. Маълум асосдаги диагоналлари a бурчаги остида кесишади. Ғиштнинг ҳажмини ва устки қисмининг майдонини аниқланг.
|
|
8 |
Учбурчакда a катети ва S майдони маълум. Иккинчи b катетини, a ва b бурчакларини, с гипотинузасини топинг. |
|
9 |
S квадратнинг майдони маълум. a квадратининг томонини , d диагоналини ва квадрат атрофига чизилган айлананинг юзасини топинг.
|
|
10 |
S квадратининг юзаси маълум. Унинг ичига ва ташқарисига чизилган айлананинг юзасини ҳисобланг.
|
|
11 |
V кубнинг ҳажми маълум. Унинг ичига ва ташқарисига чизилган шарларнинг ҳажмини ҳисобланг.
|
|
12 |
Агар асосда d диагоналли ва a диагоналларини орасида учбурчак, тўғри учбурчак бўлса, h баландлигида пирамиданинг хажмини хисобланг. Баландлиги h, асоси d диагоналли тўғри бурчакли тўртбурчак бўлган ва диагоналлар орасидаги бурчак a бўлган пирамиданинг ҳажмини ҳисобланг.
|
|
13 |
Уй 4 подъезд ва K қаватдан иборат. Биринчи подъезда 3 хонадон, Иккинчи ва учинчи подъездларининг майдонларида иккита хонадон, тўртинчида эса тўртталиги аниқ бўлса, уйдаги хонадонларнинг сонини аниқланг.
|
|
14 |
(V) пирамиданинг ҳажми аник .Асосида d диагоналли тўғриучбурчак , асосидаги a. бурчагининг остида кесишганлиги аник, унинг баландлигини ҳисобланг.
|
|
15 |
A ва B шахарларнинг орасида L масофа. Из города A шахардан В шахарга V1 тезлигида велосипедчи чиққан, B шахардан A шахарга эса V2 тезлигида пиёда чиққан. Улар қачон учрашишлигини ва А шахардан қанча масофа узоқликда бўлишларини ҳисобланг.
|
|
16 |
A ва B шахарларнинг орасида масофа L. A шахардан В шахарга V1 тезлигида енгил автомобильйўлга чиққан, B шахардан эса A шахарга тескари томонга V2 (V2<V1) тезлиги билан мотоциклчи йўлга чиққан . Качон автомобиль мотоциклга етиб боради ва улар А шахридан қанча масофа узоқликда бўлишларини ҳисобланг.
|
|
17 |
Тўғриучбурчак d диагоналига эгалиги , ҳамда диагоналлар орасидаги бурчак a га тенглиги аниқ. Бир томоннинг атрофида тўғриучбурчак айланма йўли билан ҳосил бўладиган цилиндрнинг ҳажмини аниқланг.
|
|
18 |
Учбурчак с гипотинузага ва a бурчагига эга.Катетлар атрофида айланма йўли билан ҳосил бўладиган конусларнинг ҳажмини аникланг.
|
|
19 |
h баландлигидан m массали ғишт тушди. Ер билан тўқнашган вақтда унинг кинетик энергияси кандай бўлади.
|
|
20 |
Иккита тўғри чизиқ берилган: биринчиси y=kx+b тенгламага эга ,иккинчиси эса (x1,x2) ва (y1,y2) нуқталардан ўтади.Тўғри чизиқларнинг кесишишган нуқтасини топинг.
|
|
21 |
Цилиндирнинг ҳажмини ва майдонини аниқланг. Цилиндрнинг баландлиги h , S асосида жойлашган айлананинг ҳажми..
|
|
22 |
Тенгламани ечинг:
|
|
23 |
Арифметик прогрессияни n чи хадини суммасини ва n-чи хадининг кийматини хисоблангго .
|
|
24 |
n чи хадининг геометрик прогрессияси суммасини ва n- чи хадини қийматини ҳисобланг.
|
|
25 |
Тенг ёнтомонли учбурчагида асоси ва ундаги бурчаги аниқ. Ён томонининг кўпайтмасини ва учбурчакнинг майдонини топинг. .
|
|
26 |
h баландлигидан V0 бошланғич тезлик билан ғиштни ташлашди У қачон ва қайси тезликда тушади.
|
|
27 |
Агар цилиндрнинг S сиртини юзасига тенг бўлса , асосдаги айлана ёйининг узунлиги L тенг бўлса унинг ҳажми қандай.
|
|
28 |
Агар цилиндрнинг V сиртини юзасига тенг бўлса , асосдаги айлана ёйининг узунлиги L тенг бўлса унинг ҳажми кандай.
|
|
29 |
Параллепипеднинг асосида Р периметрли квадрат бўлса унинг сиртини юзаси S га тенг булса параллепипеднинг ҳажмини топинг.
|
|
30 |
m массали жисмни вертикал ҳолатда тепага V0 тезлиги билан h баландликдан ташлашишди. Қайси , баландликга уни кўтарилишини аниқланг.
|
Учбурчакмасаласи.
Кўрсатма : АВС (расм.1) ихтиёрий учбурчак учун белгилашлар киритамиз

Расм. 1.
![]() – учбурчак томонларининг узунлиги.
– учбурчак томонларининг узунлиги.
![]() –
– ![]() мос равишда томонларига тескари ётган бурчаклари
мос равишда томонларига тескари ётган бурчаклари
![]() – учбурчакнинг юзаси ва периметри.
– учбурчакнинг юзаси ва периметри.
![]() –учбурчакнинг ичига ва
ташқарисига чизилган айланаларининг радиуслари.
–учбурчакнинг ичига ва
ташқарисига чизилган айланаларининг радиуслари.
Учбурчакнинг берилган учта параметрига асосланиб, қолган еттита параметрни аниқланг.
10 жадвал
|
№ |
Чикиш маълумотлари |
Хисобланаётган ўсиб боришлар |
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
|
16. |
|
|
|
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
|
21. |
|
|
|
22. |
|
|
|
23. |
|
|
|
24. |
|
|
|
25. |
|
|
|
26. |
|
|
|
27. |
|
|
|
28. |
|
|
|
29. |
|
|
|
30. |
|
|
№ 4,5 лаборатория ишига услубий кўрсатмалар
Алгоритмни график шаклида блок,схема ёки диаграмма кўринишида ифодалаш мумкин. (маъруза матнига қаранг).
8 Жадвалдан мисолларни ечиш намунаси.
Масаланинг қўйилиши:Берилган а ва α қийматлар учун У нинг қийматини хисобланг

![]()
![]()
Матн шаклидаги алгоритмлар
Мисолни ечиш учун қуйидаги белгилашлар киритамиз:
![]() ва тенгламани куп содда
тенгламаларга булиб ташлаймиз. Чунки
ва тенгламани куп содда
тенгламаларга булиб ташлаймиз. Чунки ![]() 4 маротаба учратамиз , ва уни b ўрнига
белгилаймиз :
4 маротаба учратамиз , ва уни b ўрнига
белгилаймиз :
1) ![]()
2) ![]()
3) ![]()
4) 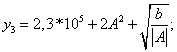
5) ![]()
6) ![]()
 Алгоритмни блок схема кўриниши à
Алгоритмни блок схема кўриниши à
С++ да икки усулда дастурни тузамиз.
1. усул
#include <stdio.h> // киритиш -чикариш-стандарти
#include <conio.h> // экран билан ишлаш стандарти
#include <math.h> // математик функцциярнинг стандарти
void main ( ) //бош дастур
{
float A = -4.6;
float а,b,y, y1, y2, y3, y4 ; // узгарувчан турининг эълони
clrscr( ) ; // экранни тозалаш
printf(“а=”); // а= экранга чикаради
scanf(“%f”,&а); // а кийматини киритинг
b = pow (A,2) + pow (a,2);
y1 = pow( (atan (a/b) + a/2 * log10 (b)), 2) ;
y2 = pow(sin(b),3) + 7.6 ;
y3 = ( 2.3 e5 + 2 * pow(a,2) + sqrt(b / fabs(A)) ) ; y4 = y2/y3+A ;
y = y1+y4 ;
printf(“y=%f”,y); // у кийматини чикаради
getch( ); //натижалар ойнасини ушлаб колади
}
Дастурнинг натижалари :
a= 1.3
y =-3.716167
2. усул
# include <iostream.h>
# include <math.h>
int main()
{
float a = 1.3, A = -4.6;
float b,y, y1, y2, y3, y4 ;
b = pow (A,2) + pow (a,2);
y1 = pow( (atan (a/b) + a/2 * log10 (b)), 2) ;
y2 = pow(sin(b),3) + 7.6 ;
y3 = ( 2.3 e5 + 2 * pow(a,2) + sqrt(b / fabs(A)) ) ; y4 = y2/y3+A ;
y = y1+y4 ;
cout << "y = " << y ;
return 0;
}
Дастурнинг натижалари: y=-3.716167
10 Жадвалдаги мисолларни ечиш наъмунаси
у катталикнинг қийматини қуйидаги шартга асосан хисобланг. a,b,c ўзгарувчиларнинг қийматини талаба клавиатурадан киритади:
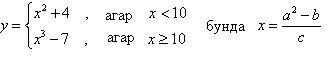
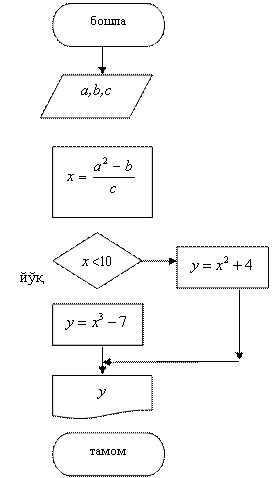
3 расмда ушбу масаланинг ечими блок – схема ва Насси диаграммаси кўринишида ифода этилган.
Блок – схема Диаграмма Насси
 |
|
a,b,c кирит |
|
|
|
|
|
|
|
Y чоп эт |
|
тамом |
![]()
![]()
![]()
![]()
![]()
![]()
|
x =1 |
|
|
dx=0.5 |
|
|
R =1 |
|
|
k =0 |
|
|
R>0.02 бўлгунча |
|
|
|
|
|
|
|
|
|
Z чоп этинг |
|
|
k = k+ 1
|
|
|
х = х+dx |
|
K чоп этинг |
|
|
тамом |
|
Алгоритм Насси диаграммаси кўринишида
16жадвалдан мисол ечиш наъмунаси.
Берилган: x=1; dx=0.5. Қуйидаги
формула бўйича Z ни хисобланг: ![]() .
.
Считать Z ни илдиз остидаги ифода 0.02 бўлгунга қадар хисобланг. k - Z ўзгарувчининг неча маротаба хисобланишлар сони.Экранга x, Z, k ўзгарувчилар қийматини чоп этинг.
Дастур тузишда математик ифодаларни ёзилишини осонлаштириш учун 11 Жадвалда С/С++ тилида керакли математик функцияларнинг ёзилиши кўрсатилган
Таблица 11
|
Функция |
С++даги ёзилиши |
|
|
pow(x,y) |
|
|
sqrt(x) |
|
|
exp(x) |
|
lg x |
log10(x) |
|
ln x |
log(x) |
|
th x |
tanh(x) |
|
ch x |
cosh(x) |
|
sh x |
sinh(x) |
|
tg x |
tan(x) |
|
cos x |
cos(x) |
|
sin x |
sin(x) |
|
arctg x |
atan(x) |
|
arcsin x |
asin(x) |
|
arccos x |
acos(x) |
|
|
fabs(x) |
|
abs(x) |
|
|
Х ни у даги қолдиғини қайтаради |
fmod(x,y) |
|
Тепасини яхлитлайди |
ceil(x) |
|
Пастини яхлитлайди |
floor(x) |
|
1,3*103 |
1.3Е3 |
|
1,3*10-17 |
1.3Е-17 |
10 жадвалдан масалани ечиш намунаси:
АВС учбурчагида a,b томонлари ва S майдони берилган булсин. . P, R, r. Ни хисобини бажариш учун дастурни тузиш талаб килинади.
Хисоблаш формулалари сифатида куйидагиларни эслатамиз:
![]() (1) / синулар теоремаси /
(1) / синулар теоремаси /
![]() (2) / косинуслар теоремаси /
(2) / косинуслар теоремаси /
![]() (3) /периметр/
(3) /периметр/
![]() (4 /)яримрпериметр/
(4 /)яримрпериметр/
![]() (5) ;
(5) ; ![]() (6);
(6); ![]() (7);
(7);
![]() (8) / Герон формуласи/
(8) / Герон формуласи/
Хисоблаш формулаларининг кетма-кетлигини тузиш.
(7) формуладан ![]() . Аниклаймиз.
. Аниклаймиз.
Шунда ![]() ва формуласи буйича
(2) хисоблаймиз
ва формуласи буйича
(2) хисоблаймиз ![]() .
.
 Кетма кетликда
Кетма кетликда ![]() , формулалар буйича (4), (6)
топамиз
, формулалар буйича (4), (6)
топамиз
![]()
![]()
|
Форму-лалар |
|
|
|
|
|
|
R |
C |
r |
|
дастур |
A |
B |
S |
G |
G1 |
P |
R |
C |
R1 |
Дастурнинг намунаси :
#include<stdio.h>
#include<conio.h>
#include<math.h>
int main()
{
float A,B,C,S,G; //узгарувчанларнинг эълони
float G1,P,R,R1;//узгарувчанларнинг эълони
printf("Введите A,B,S:");//матнни босмага чикарамиз
scanf("%f%f%f",&A,&B,&S); //Киритилган маълумотларни узлаштирамиз
G=2*S/(A*B);//Хисоблашлар
G1=sqrt(1-G*G); //хисоблашлар
C=sqrt(A*A+B*B-2*A*B*G1); //хисоблашлар
P=A+B+C; //хисоблашлар
R=A*B*C/(4*S); //хисоблашлар
R1=2*S/P; //хисоблашлар
printf(" P = %.2f\n R = %.2f\n R1 = %.2f\n",P,R,R1);// чоп килинган натижа
getch();// клавишига босилишини кутамиз
}
Дастурнинг натижалари :
Киритинг A,B,S: 5 6 7
P = 13.82
R = 3.02
R1 = 1.01
Назорат саволлари:
1. С++ га дастури кайси булимлардан иборат?
2. Таъриф эълондан нима билан фарк килади?
3. С++ бажарилаётган дастурнинг яратилишини боскичларини санаб беринг..
4. препроцессор нима?
5. Препроцессорнинг дериктиваси нима? Препроцессорнинг дериктиваси мисолини келтиринг.
6. Матнни босмага чикарадигин дастурни тузинг. « С++ даги Менинг биринчи дастурим »
7.Форматли катор нима? Printf функциясининг формат катори уз ичига нимани олади? Scanf функциясининг формат катори уз ичига нимани олади ?
8. Бошлангич спецификацияси нима? Бошлангич спецификациясининг хар хил турдаги маълумотлар учун мисоллар келтиринг.
9. printf( функцияси билан нималар киритилади"\nРакамларнинг урта арифметик :кетма кетлиги %10.5fга тенг \nМусбат элементларининг кетма кетлигидаги микдори %10.5d ",S/n,k га тенг).
10 . << операцияси ёрдамида 3 саволнинг натижасини кандай ёзиб олиши мумкин ?
11 . х ва у узгарувчанларнинг киритилиши кандай бажариш мумкин ,бунда x туридаги long int, double турида эса scanf функцияси ёрдамида >> операцияси ёрдамида?
№ 6 Лаборатория иши
Тармоқланувчи программалар структураси.Алгебранинг мантиқ элементлари
.Танлов операторлари.
Ишнинг максади
1.Тармоқланувчи структурасининг дастурини тузишни ўрганинг
2.Ўрганилаётган тилнинг ва бошқарувчилар тилининг конструкцияси билан ўрганиш нинг аник такдимоти билан танишиш.
3. Танлов операторини қўллаб дастурлар тузишни ўрганинг.
Топшириқ
1) 2 № лаборатория ишида ишлаб чиққан алгоритм мисоллари учун ПК га дастур тузинг ва унинг натижаларини олинг.(№6,7,8. ёки ўқитувчининг берган вазифаси буйича №).
2) №7 жадвалдан ўзингизнинг вариантингиздан рақам буйича вазифани ёзиб олинг.
а) Z ўзгарувчини хисоблаш учун логик операторнинг ўзлаштиришини ёзиб олинг..
б) ундаги операцияларни бажарилишининг тартибини кўрсатинг.
в) вычислить значения Z кийматиниберилган ўзгарувчан кийматлар учун аниқланг.
г) составить программу вычисления Z хисоблаш дастурини тузинг, натижаларни олинг.
3) 8 № жадвалдан ўзингизнинг вариант рақами буйича топшириқларни кўчириб олинг, агар (X;Y) нуқта координаталари билан берилган жойга тегишли бўлса логик ўзгарувчан Z киймати TRUE, ўзлаштирувчи логик тенгламани ёзинг.
Атрофни графикада тасвирланг. (X;Y) нуқтани координаталари билан берилган атрофни тегишлилигини текшириш дастурини тузинг.
4)* 9 № жадвалдан ўзингизнинг вариант рақами бўйича топшириқларни кўчириб олинг, функциянинг қийматини топиш учун танлов операторини ишлатган холда дастурни тузинг, ПК ишлатинг, олинган натижаларни ўқитувчингизга кўрсатинг.
Ҳисоботнинг мазмуни
Ҳисобот қуйидагилардан иборат бўлиши керак:
1) Лаборатория ишининг номи.
2) Лаборатория иши учун топширик.
3) 1 пункт учун дастурлар топшириқ ва жавоблари билан, ҳамда ўқитувчининг имзоси.
4) 7 № жалвалдаги топшириқларнинг бажарилиши (услубий кўрсатмалар қаранг)
5) 8 № жадвалдан берилган атроф график тасвири билан, логик тенглама, дастур ва натижалар.
12 Жадвал
Функцияларни хисоблаш
|
№ |
Функции |
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
19. |
|
|
20. |
|
|
21. |
|
|
22. |
|
|
23. |
|
|
24. |
|
|
25. |
|
|
26. |
|
|
27. |
|
|
28. |
|
|
29. |
|
|
30. |
|
13 Жадвал
|
1. |
a,b,c учта рақамдан энг катта квадратни топинг, қийматни босмага чиқаринг: N=1, агар –a энг катта бўлса; N=2, агар-b энг катта бўлса; N=3, агар -c энг катта бўлса; |
|
2. |
x0, y0 нукта координаталари билан бирга r радиусли айланага тушадими, аниқланг. r²=x²+y² айлананинг тенгламаси. Агар нуқта айлананинг ичида бўлса , ва N=0 айланадан ташқари бўлса N=1 эгалласин. |
|
3. |
х,у Координаталар билан нуқта кайси квадратда жойлашганини аниқланг , ва босмага квадратнинг рақамини чиқаринг. |
|
4. |
a, b хақиқий сонлар берилган. агар a≥b бу рақамларни иккига кўпайтиринг ва уларни агар шарт бажарилмаса абсолют қийматлари билан алмаштиринг ,. |
|
5. |
a,b хақиқий иккита сон берилган.. “a, b дан катта” матнни ва биринчи сонни чиқаринг, агар у иккинчисидан катта бўлса ва агар бундай бўлмаса иккала сон ва матн “a, b дан кичик”,.. |
|
6. |
Иккита хақиқий сон берилган. Биринчи сонни нол билан алмаштиринг, агар у кичик бўлса ёки иккинчисига тенг бўлса ,акс холда уни ўзгартирмасдан қолдиринг. |
|
7. |
Учта хақиқий сон берилган. (І;3) интервалига тегишли сонларни улардан тангланг.
|
|
8. |
x,y (x ≠ y) хақиқий сонлар берилган. Бу иккита сондан кичигини ярим микдор билан алмаштиринг, каттасини эса иккига купайтиринг. |
|
9. |
Учта хақиқий сон берилган. Манфий бўлмаган қийматларни квадратга ўтказинг. |
|
10. |
a, b, c. Хақиқий сонлар берилган. a<b<c тенгсизликлар бажарилаётганлигини текширинг. Агар шартлар бажарилаётган бўлса “a<b<c” босмага чиқаринг.Акс холда « Шартлар бажарилмаяпти» деб босмага чиқаринг. |
|
11. |
a,b,c учта хақиқий сонлар берилган.Уларни иккига кўпайтиринг ,агар a≥b≥c, ва уларни агар бундай бўлмаса абсолют қийматлар билан алмаштиринг. |
|
12. |
Учта хақиқий сонлар берилган. Улардан манфий қийматларни квадратга чиқаринг. |
|
13. |
x,y,z хақиқий сонлар берилган. (x,y,z) max топинг. |
|
14. |
x, y, z.хақиқий сонлар берилган. max ( x+y+z, x×y×z) min ((x+y+z)/2, x×y×z)+1 ҳисобланг.
|
|
15. |
Агар x,y,z жуфт ҳисоби хар хил хақиқий сонларнинг миқдори 1 дан кичик бўлса,бунда бу учта сондан энг кичигини иккита бошқа ярим миқдорли сон билан алмаштиринг, акс ҳолда х ва у ярим микдорли иккита қолган қийматни алмаштиринг. . |
|
16. |
x,y,z хақиқий мусбат сонлар берилган. x,y,z. томонлар узунлиги билан учбурчак борлигини аниқланг. |
|
17. |
a,b,c.учта ҳаракатдаги сонлар берилган. Уларни иккига кўпайтиринг ,агар a≤b≤c ,ундай бўлмаса уларни квадрат билан алмаштиринг. |
|
18. |
x,y (x≠y). ҳақиқий сонлар берилган.Булардан иккита кичик сонни уларнинг суммаси билан алмаштиринг , каттасини эса учга кўпайтиринг. |
|
19. |
x,y,z хақиқий сонлари уч жуфт ҳисоби ундан катта бўлса шу уч сондан каттарок сонни ярим суммалига алмаштиринг ёки х ва у катталарини қолган икки ярим суммалининг қийматига алмаштиринг. |
|
20. |
Учта хақиқий сонлар берилган. Улардан интервалига тегишли бўлмаганларини топинг.(- І;5) |
|
21. |
Айлананинг S1
ва квадратнинг S2 .юзалари
берилган.Квадрат айланага жойлашдими йўқми аниқланг. S= |
|
22. |
Айлананинг S1 ва квадрата S2 .майдони берилган. Айлана квадрат ичига сиғадими,йўқми, аниқланг. |
|
23. |
(х, у,z).координаталари
билан нуқта берилган. Нукта |
|
24. |
(х, у,z)
координатолари билан нуқта берилган. Нуқта |
|
25. |
(х, у,z)
координатали нуқта
берилган.. |
|
26. |
x,y,z хақиқий сонлар берилган . (x,y,z) min топинг. |
|
27. |
А хақиқий сон берилган. Агар f(x) бўлса ,ҳисобланг
ва босмага чиқаринг.
|
|
28. |
Учта хақиқий сон берилган. f(a) ни тангланг ва босмага чиқаринг
,агар |
|
29. |
Хақиқий сон берилган. Ҳисобланг ва босмага чиқаринг,агар F(x)=
|
№13
жадвалга ![]()
![]()
Х қийматининг берилган. Берилган интервалдаги х қийматидан у ва S га мос келадиган 10 қийматни ҳисобланг, S ни ҳисоблаш учун иккита вариант тайёрланг:а)берилган қўшилувчининг миқдори билан ҳисобланг в) Е берилган аниқлик билан.
#include<iostream.h>
#include<conio.h>
#include <math.h>
float zy(float );// прототиплар
float zs(float ,int );// 3-х
float zc(float ,float );// функцияларни
void main()
{
clrscr(); float x=0.1,e=0.00001;
float y,s1,s2;
while(x<=1.1 )
{
y=zy(x); // zy функциясига мурожаат , У хисобланувчи
s1=zs(x,20); // S хисобланувчи функциясига мурожаат (n-берилган)
s2=zc(x,e); // S хисобланувчи функциясига мурожаат, (E- берилган)
cout<<"x="<<x<<" fun= "<<y;
cout<<" sum="<<s1<<" sum2="<<s2<<"\t"<<endl;
x+=0.1;}
getch();}
float zy(float t) //функцияси zy , У хисоблайди
{float y; //cout<< exp(t); cout<< "e--"<< exp(-t)<<endl;
y=(exp(t)-exp(-t))/2; return y;}
float zs(float t,int m) // zs функцияси , S хисоблайди, берилган n
{ int n; float s=t;float a=t;
for(n=1;n<=m;n++)
{a=a*t*t/(2*n*(2*n+1)); s+=a;} return s; }
float zc(float t,float m) // функцияси zc, S хисоблайди
// аниклиги берилган m.
{ int n=0; float s=t;float a=t;
while(a>m)
{ n++;
a=a*t*t/(2*n*(2*n+1)); s+=a;}
cout<<" "<<n<<endl;
return s;
}
14 Жадвал
|
1. |
Ўртадаги нуқтада О(x0, y0) ва R0 радиусли айлана , А(x1, y1) нуқта берилган.. Нуқта айлананинг ичида жойлашганми,йўқми, аниқланг. |
|
2. |
x0, y0 нуқта ва R0 радиусда айлана ва y=ax+b тугри чизик берилган.. Тўғри чизик билан айлананинг кесишадими йўқми аниқланг.Агар кесишишса ,кесиш нуқтасини аникланг. |
|
3. |
у=аx2+bx+с ва у=dx2+ex + ¦ параболаси кесишини аниқланг Агар кесишса кесиш нуқтасини аниқланг.. |
|
4. |
A и B пунктларнинг ўртасида L км. Масофа. А пунктдан В пунктга V0, тезлиги билан автомобиль чиқди, B пунктдан A пунктига эса V1 .тезлиги билан автомобиль чиқди. В пунктидан S км масофасида жойлашган C пунктига қайси бири тезроқ келади? (С пункти Aва B пунктларининг ўртасида жойлашган). |
|
5. |
A, B ва C пунктлари битта тўғри чизикда жойлашган , B пункти м A ва C пунктларнинг ўртасида. A ва B пунктларнинг ўртасидаги масофаси L.га тенг. B ва C уртасидаги масофа S. га тенг.А пунктидан С пунктига V0 , тезлиги билан автомобилист чиқди, B пунктидан C пунктига эса V1 .тезлиги билан мотоциклист чиқди. C пунктига ким биринчи етиб келади? |
|
6. |
h1 баландлигидан жисм тушаяпти. h2 (h2<h1) баландлигидан вертикал холатда V0 . тезлигида бошка ғишт ташланди. Қайси жисм ерга вохлироқ тушишини аниқланг. |
|
7. |
h1 баландлигидан ғишт тушаяпти. h2 (h2>h1) баландлигидан вертикал тарзда бошқа ғиштни V0 . тезлигида ташлашди . Қайси ғишт ерга биринчи тушишини аниқланг. Определите, какой кирпич упадет раньше. |
|
8. |
h1 баландлигидан ғишт тушаяпти. h2 (h2>h1) баландлигидан вертикал тарзда бошқа ғиштни V0 . тезлигида ташлашди . Ғиштнинг кайси бирида ерга тегаётганда тезлиги кўпрок бўлишини аниқланг.. |
|
9. |
у=cx2+dx+f ват угри y=ax+b кесишини аниқланг. Агар кесишишса кайси нукталарда кесишини аниқланг. |
|
10. |
|
|
11. |
y=ax4+bx3+cx2+dx+f ва y=gx4+bx3+fx2+dx+l қийшиқ ва тўғриларни y=ux+v и y=mx+k .ларни кесиш нуқтаси тўғри келишини аниқланг. |
|
12. |
Берилган тўғрибурчакли учбурчагининг юзаси катталигини аниқланг: · гипотенуза c, бурчак a; · катет a , тегишли бурчак b · баландлик h, бурчак g. |
|
13. |
А=(а1,а2,а3) и B=(b1,b2,b3) векторнинг коллинеарностини текширинг. Улардан қайси бири узонроқ ва неча маротабага,уларнинг йўналишини аниқланг. |
|
14. |
Кайси қийматда x ва y векторлари A=a1i+a2j+xk ва B=yi+b2j+b3k коллинеар ва векторларнинг қайси бири қисқалигини аниқланг. |
|
15. |
A(a1,a2,a3), B(b1,b2,b3) и C(c1,c2,c3) учта нукта берилган.. Кайси нуқталар ўртасида масофа камрок бўлишини аниқланг. |
|
16. |
Иккита тўғри y=a1x+b1 и y=a2x+b2. Тенгламалари берилган.Тўғри тенгламалар кесишадими ёки параллел бўладими аниқланг. |
|
17. |
(х,у) Координаталари билан М нуктаси берилган. Бу нуқта координаталарнинг боши ёки координата ўқларида ётганлигини аниқланг. |
|
18. |
(x, y) координаталари билан М нуқтаси берилган. Бу нуқта координатанинг бошими,ёки қайси координата бурчагида жойлашганлигини аниқланг. |
|
19. |
A(x1,y1) ва B(x2,y2) нукталар берилган. y=ax+b. Битта тўғри чизикда жойлашганми йўқми, аниқланг. |
|
20. |
M(x,y) нуктанинг координаталари аниқ.Бу нуқта тўғрилардан бирига тегишлими йўқми аниқланг y=a1x+b1; y=a2x-b2. |
|
21. |
Иккита жуфт тўғри берилган бўлсин y = a1x + b1 y = a3x + b3 y = a2x + b2 y = a4x + b4 |
|
22. |
Қайси тўғриларни ўртасида бурчаг катта, аниқланг? |
|
23. |
Иккита тўғрини тенгламаси аниқ y=a1x+b1 и y=a2x+b2. Бу тўғрилар параллелми ёки перпендикулярлигини аниқланг, агар йўқ бўлса, улар ўртасидаги бурчакни топинг. |
|
24. |
y=x3-3x.функция берилган , экстремум функциясининг нуқтасини аниқланг. |
|
25. |
y=x4-2x2.функцияси аник. [a, b].берилган интервалидаги бу функциянинг максимум ва минимумини аниқланг. |
|
26. |
ABC ва DFG: A(a1, a2), B(b1, b2), C(c1, c2), D(d1, d2), F(f1, f2), G(g1, g2)иккита учбурчакнинг тепалик координаталари берилган.Қайси учбурчакнинг периметри каттароғини аниқланг. . |
|
27. |
a (ax, ay, az), b (bx, by, bz ), c (cx, cy, cz) и d (dx, dy, dz ), f (fx, fy, fz), g (gx, gy, gz). учта векторда хосил булган иккита параллепипед берилган.Кайси параллепипеднинг хажми кичик, аникланг? |
|
28. |
иккита неколлинеара1(x1, y1, z1) ва a2(x2, y2, z2) векторлар берилган.. Векторларнинг перпендикулар шартини текширинг, агар улар бажарилмаса улар ўртасидаги бурчакни текширинг. |
|
29. |
a(ax,aу) ва b(bx,by) векторлардан ҳосил бўлган иккита параллелограмма берилган., c(cx,cу) и d(dx,dy). Қайси параллелограмманинг юзаси катталигини аниқланг |
|
30. |
Квадратнинг қайси катталигини аниқланг: d диагоналли,, S1 юза ёзилган айлана билан, S1 тасвирланган айлананинг юзаси ; Қайси бири катталигини аниқланг Барча муҳим чиқиш маълумотларни дисплейдан экранга чиқаринг. |
15 Жадвал
|
№ |
Топшириқлар |
Параметрлар |
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
|
16. |
|
|
|
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
|
21. |
|
|
|
22. |
|
|
|
23. |
|
|
|
24. |
|
|
|
25. |
|
|
|
26. |
|
|
|
27. |
|
|
|
28. |
|
|
|
29. |
|
|
|
30. |
|
|
16 Жадвал
|
№ |
Топшириқ: Агар нуқта (Х,У.)координаталари билан берилган атрофга тегишли бўлса унда логик тенгламани ўзлаштирувчан логик Z узгарвчанни TRUE қийматини ёзиб олинг.
|
|
1. |
M (x;y) координата бошида ёки ярим текисликдаги бирламчи айлананинг маркази билан иккинчи чоракка тегишли х=у тўғри чизиқнинг қуйида ётади. |
|
2. |
M(x;y) координата бошида ёки кейин у=о; у=3; бирламчи айлананинг маркази билан ички бўлимига тегишли. |
|
3. |
M(x;y) координата бошида ёки ётган ярим текисликнинг у=х+2 тўғри чизиқнинг қуйида ётган R=2 айлананинг маркази билан ички бўлимига тегишли. |
|
4. |
М(x;y) , y=x2 ички бўлимининг параболага у=3 тўғридан қуйида ётган тўртинчи чоракка тегишли. |
|
5. |
M(x;y) , x=2 дан у=3 гача ёки учинчи чоракка тегишли чизиқ. |
|
6. |
M(x;y) координата бошида ёки у=-/х/ график тенгламасидан қуйида ётган бирламчи айлананинг маркази билан тепасининг яримисига тегишли. |
|
7. |
М(х ;у) , (х-2)2+у2=4 айлананинг ички булимига ва х=2 дан х=3 гача тегишли.. |
|
8. |
М( х ;у) , х2+у2=4 айлананинг ички булимига ва у=х тўғри дан юқорида ёки унинг тўртинчи чоракка тегишли. |
|
9. |
М(х;у) , у=1 дан у=3 гача ,у=х тугри чизикнинг чапрогида ётган туртинчи чоракка ёки яримчизикка тегишли. . |
|
10. |
М(х;у) 3 радиуси билан айлананинг бўлими ва марказнинг координата бошида ва y=x2 у=-2 дан у=1гача чизиққа тегишли.. |
|
11. |
М(х;у) ,y=x2 x=y2-1 парабола билан чекланган ва x2+y2=4 айлананинг ёки тўртинчи чоракдаги айлананинг ташқи кўринишига тегишли. . |
|
12. |
М(х;у) (0;-3) бирламчи айлананинг марказининг ташқи кўриниши билан ёки унинг биринчи чорагига тегишли. |
|
13. |
М(х;у) , |
|
14. |
М(х;у) у=2;х=1 тўғри чизиқ ўртасида бириктирилган ва парабола у=0,5х2.га тегишли. |
|
15. |
М(х;у) ,у = cos(2x) и y=0,5x2.тўғри чизиқ ўртасида бириктирилган атрофга тегишли. |
|
16. |
М(х;у) , x = -1 ,y= - 1, x = y2 -1 чизиқлар билан чекланган атрофга тегишли. |
|
17. |
М(х;у), у=-х2 ва у=-3 чизиқлар билан чекланган атроф ёки иккинчи чоракка тегишли.. |
|
18. |
М(х;у) , у=0; х=1; х=-1;у=cosх. Чизиклар билан чекланган атрофга тегишли. |
|
19. |
М(х;у) , R=2
радиуси билан ва координата бошида маркази билан |
|
20. |
М(х;у), у=х и у=х3 чизиқлар билан чекланган атрофга тушади.. |
|
21. |
М(х;у) ,у=х2-1 и х2+у2=4 чизиқлар билан чекланган ёки иккинчи чоракка тегишли. |
|
22. |
М(х;у) , у=0; у=-2; х2+у2=9 чизиқлар ўртасида бириктирилган атрофга тегишли. |
|
23. |
М(х;у) ,х=2; х=3; х=2у2.чизиқлар билан чекланган атрофга тегишли. |
|
24. |
М(х;у) , х2+(у2+1)=9 айлананинг ички бўлимига ёки иккинчи чоракка тегишли. |
|
25. |
М(х;у) , х2+у2=9 и у=х2+1.қийшиқ чизиқлар билан чекланган атрофга тегишли. |
|
26. |
М(х;у) , у=2x, у=1; х=5. қийшик чизиқлар билан чекланган атрофга тегишли. |
|
27. |
М(х;у) , |
|
28. |
М(х;у) , у=0,5х; у=2; у=-0,5х2 чизиқлар билан чекланган атрофга тегишли.. |
|
29. |
М(х;у) , у=2х; у=х2+5. чизиқлар билан чекланган атрофга тегишли. |
|
30. |
М(х;у) , у=х; у=х2; и у=3 чизиқлар билан чекланган атрофга тегишли. |
№6 лаборатория ишини бажариш учун услубий курсатмалар
Жадвалдаги берилган масалани ечиш мисоли
Шароитни текшириб у кийматини топинг, a,b,c кийматлари талабанинг узи клавиатурадан олади :

Куйида блок –схема келтирилган, Насси диаграммаси ва бу масалани ечиш учун дастур.
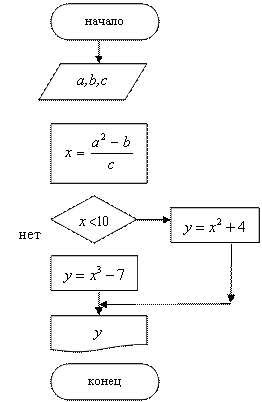 Блок – схема Насси Диаграммаси
Блок – схема Насси Диаграммаси
|
Ввод a,b,c |
|
|
|
|
|
|
|
Вывод y |
|
конец |
![]()
![]()
![]()
![]()
![]()
#include <stdio.h> // киритиш ва чикариш стандарти
#include <conio.h> // экран билан ишлаш учун стандарт
#include <math.h> // математик функциялар стандарти
void main ( ) // бош дастур
{
float x,y,a,b,c; // узгарувчан турлар учун эълон
clrscr( ) ; // экранни тозалаш
printf(“ vvedi a,b,c”); // vvedi a,b,c экранга чикаради
scanf(“%f%f %f ”,&a,&b,&c); // кийматларни киритиш a,b,c
x=(pow(a,2)-b)/c; //кийматларни хисоблайди х
![]() if
(x<10) {y= pow(x,2)+4; printf(“x<10”);}
if
(x<10) {y= pow(x,2)+4; printf(“x<10”);}
else {y= pow(x,3)-7; printf(“x>=10”);}
printf(“ y=%f”,y); // вывод у
getch( );
}
Дастурнинг натижалари:
vvedi a,b,c vvedi a,b,c
2 7 9 9 2 4
x<10 y=4.111111 x>=10 y=7696.734375
Танлов оператори - бу шартли оператор ва утказгич. .
1. Шартли оператор бутун ва кискартирилган шаклга эга. (б.6,7,8 жадвалга).
if (тенглама –шарт ) оператор; /кискартирилган шакл/
шартли-тенглама сифатида арифметик тенгламалар ишлатилиши мумкин.
Агар шартли тенгламани киймати нулдан фарк килса.
(тугри), унда оператор бажарилади . Масалан:
if (x<y&&x<z)min=x;
if ( тенглама-шарти ) оператор1; //тулик шакл
lse оператор2;
Агар тенглама-шартини киймати нулдан фарк килса, 1 оператори амалга оширилади. Тенгламанинг киймати нулга тенг булса уни оператор 2 бажаради. Масалан:
if (d>=0)
{
x1=(-b-sqrt(d))/(2*a);
x2=(-b+sqrt(d))/(2*a);
cout<< “\nx1=”<<x1<<“x2=”<<x2;
}
else cout<<“\n Ечими йук ”;
2.Утказгич куп танловни аниклайди р (к таб.9).
switch (выражение)
{ case константа1 :
оператор1 ;
case константа2 : оператор2 ;
. . . . . . . . . . .
[default: операторы;]
}
Мисол:
#include <iostream.h>
void main()
{
int i;
cout<<"\nEnter the number";
cin>>i;
switch(i)
{ case 1:cout<<"\nthe number is one";
case 2:cout<<"\n2*2="<<i*i;
case 3: cout<<"\n3*3="<<i*i;break;
case 4: cout<<"\n"<<i<<" is very beautiful!";
default:cout<<"\nThe end of work";
}
}
Дастурнинг иш натижалари
1. 1киритиш вактида киритилади :
The number is one
2*2=1
3*3=1
2. 2 киритиш вактида киритилади:
2*2=4
3*3=4
3. 3Киритиш вактида , киритилади :
3*3=9
4. 4 Киритиш вактида киритилади :
The end of work
«Логик алгебранинг элементлари »мавзунинг конспектини ўкиб чикиб , ( жадвалдаги топширикларни бажаришга киришинг .Қуйида бажариш мисоли келтирамиз.
Логик тенгламада бажариш тартибини куйиб чикамиз ва (х=1,у=1) зарур хисоботларни амалга оширамиз.

Жавоб: Z=TRUE
Логик тенгламани ёрдами билан чизиклар билан шаккилланган атрофни тасвирлаб беринг: y=2-x2 , y=-1; y=1, буни шундай амалга оширинг М (x, y) нуктаси атрофга тегишли ва акс холда алдамчи булиши мумкин. принадлежит области, и ложным в противном случае ( 10 жадвал).
Берилган чизикларни тугрибурчак координатолар системасида ташкил киламиз: : параболани y=2-x2, тугри чизикни y=-1, тугри y=1, ва шу атрофни штрихлаймиз , M (x, y) нуктасига тегишли (расм. 1.)
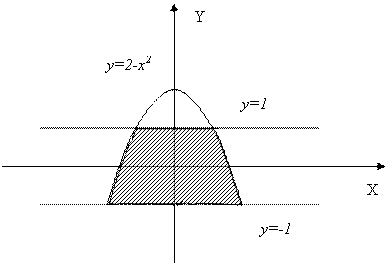 |
Z узгарувчан учун логик тенгламани ёзиб оламиз, барча нукталар учун штрихли атрофни TRUE кийматини кабул килади :
![]()
Бунда куриниб турибдики яримтексликларнинг кесишиши атрофини курсатади, улар эса ташкил килинган чизиклар билан чекланилади.
Дастурнинг намунаси:
#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{
float x,y; int z;
clrscr();
puts("Vvedite koord. tochki M :");
printf("enter x="); scanf("%f",&x);
printf("enter y="); scanf("%f",&y);
z=(y>2-pow(x,2)&&(y>-1)&&(y<1));
if (z) {printf(" prinadlegit");}
else {printf("ne prinadlegit");}
getch();
}
Дастурнинг натижалари :
|
Vvedite koord. tochki M :
|
Vvedite koord. tochki M :
|
Vvedite koord. tochki M :
|
|
enter x=-1
|
enter x=0
|
enter x=-1
|
|
enter y=-5
|
enter y=0
|
enter y= 2
|
|
ne prinadlegit
|
Prinadlegit
|
ne prinadlegit
|
![]() I) X1 ва
Y1 координатоларга боглик TRUE кийматига
тегишли тенгламани ёзиб олинг, агар нукта штрихли атрофга ва FALSE
тегишли булмаса .Берилган нукта учун бу тенгламани хисобланг ва натижани
босмага чикаринг.
I) X1 ва
Y1 координатоларга боглик TRUE кийматига
тегишли тенгламани ёзиб олинг, агар нукта штрихли атрофга ва FALSE
тегишли булмаса .Берилган нукта учун бу тенгламани хисобланг ва натижани
босмага чикаринг.
17 жадвал
|
1) |
Кидирилаётган нуктанинг координаталари : (0.5;0,5).
|
2) |
Кидирилаётган нуктанинг координаталари:(1.5;0.5).
|
|
3) |
Кидирилаётган нуктанинг координаталари (0.2;0.9).
|
4) |
Кидирилаётган нуктанинг координаталари: (0.75;-0,3).
|
|
5) |
Кидирилаётган нуктанинг координаталари: (0.2;0.45).
|
6) |
Кидирилаётган нуктанинг координаталари: (0.0;0.0).
|
|
7) |
Кидирилаётган нуктанинг координатолари: (1.5;0.0).
|
8) |
Кидирилаётган нуктанинг координатолари: (-0.5;0.9).
|
|
9) |
Кидирилаётган нуктанинг координаталари: (0.5;-2,5).
|
10) |
Кидирилаётган нуктанинг координаталари: (1.0;1.5).
|
|
II) Атрофни логик кўринишида тасвирланг.
|
|||
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
|
11) |
|
12) |
|
|
13) |
|
14) |
|
|
15) |
|
16) |
|
|
17) |
|
18) |
|
|
19) |
|
20) |
|
Назорат саволлари
.
1.Шартли ўтказиш оператори нима учун мўлжалланган?
2.Шартли ўтказиш операторнинг ёзиш шакллари кандай?
3. Ташкиллаштирилган оператор качон ва кандай кўлланилади?
4.Шартли ўтказиш операторини блок-схемасини чизиб беринг ва тушунтиринг. .
5.Танлов оператори нима учун мўлжалланган?
6. Бир вақтни ўзида танлов оператори ёрдамида бир неча йуналишлар бажарилиши мумкинми? .
7.Ўзгарувчаннинг қийматининг қанча операторни ёзиб олиш мумкин?
8.Асосий логик операциялар ҳақида гапириб беринг.
9. Муносабатлар операцияси ҳақида гапириб беринг.
10. Логик тенгламада ҳаракатларнинг тартиби ҳақида гапириб беринг.
№ 7 Лаборатория иши
Цикл структурасининг алгоритмлари ва дастурлари.
Ишнинг максади
1.Алгоритмларни шакллантириш, такрорлаш, ҳисоблагич билан бошқариш.
Такрорлаш назорат қиймати билан бошқариш, бошқарувчи операторлар киритилган.
2.Циклнинг операторини ўрганинг. .
3.Цикл структурасининг дастурларини тузишни ўрганинг.
Топширик
1. Ўзингизнинг вариантингиздаги топшириқлар учун алгоритмларни ишлаб чиқинг
2. Уларга дастурларни ёзинг. 10,11 жадвалдаги топшириқларни бажариш вақтида учта оператор циклни хаммасини ишлатиш керак . В гурухида бу учта алохида дастур бўлиши мумкин , А гурухларида эса бу мажбурий алохида функциялар бўлиши керак (main()) Асосий дастур тегишли дастурнинг функциясини танлаш учун менюнингг мазмунида бўлиши керак.
3. Дастурларни кўриб чиқиш ечимини олинг ва ўқитувчининг имзосини қўйдириб олинг.
4. Топшириқнинг барча пунктлари бажарилгандан сўнг , ҳисоботни тайёрланг, ишни ҳимояланг ва баллни қўлга киритинг.
Ҳисоботнинг мазмуни
Ҳисобот қуйидагилардан иборат бўлиши керак::
1. Лаборатория ишининг номи
2. Лаборатория ишига топшириқ
3. Барча топшириқлар пунктига алгоритмлар ва дастурлар, топшириқларнинг жавоблари ва бажарилганлиги ҳақида ўқитувчининг имзоси.
4. Ҳимоядан кейин санаси ва бахони ўқитувчининг имзоси билан.
Топшириқларнинг шартлари:
11 жадвалдаги F(x) функциясининг қийматини ҳисоблаш учун дастурини тузинг, [a,b] кесимида h. кадами билан. Натижани жадвал шаклида тақдим этинг, биринчи устун аргумент қийматида , иккинчиси тегишли функциянинг қиймати.
12№ жадвал учун.
18 Жадвал
|
вариантнинг раками |
Функциялар F(x) |
Параметрлар |
m |
|
|
А |
b |
|||
|
1. |
x-sin(x) |
0 |
π/2 |
10 |
|
2. |
sin(x) |
π/4 |
π/2 |
10 |
|
3. |
-cos(2x) |
π/3 |
2π/3 |
10 |
|
4. |
tg(x) |
0 |
π/4 |
10 |
|
5. |
ctg(x) |
π/4 |
π/2 |
10 |
|
6. |
arcsin(x) |
0 |
1 |
10 |
|
7. |
arccos(x) |
0.5 |
1 |
10 |
|
8. |
arctg(x) |
2 |
7 |
10 |
|
9. |
sin(x)-cos(x) |
0 |
π/2 |
10 |
|
10. |
x sin(x) |
0 |
π/3 |
10 |
|
11. |
sin(1/x) |
π/8 |
π/2 |
10 |
|
12. |
cos(1/x) |
π/4 |
π/2 |
10 |
|
13. |
sin(x2) |
π/6 |
2π/3 |
10 |
|
14. |
cos(x2) |
π/3 |
3π/2 |
10 |
|
15. |
sin(x)+tg(x) |
0 |
π/4 |
10 |
|
16. |
cos(x)+ctg(x) |
π/4 |
π/2 |
10 |
|
17. |
tg(x/2) |
0 |
2π/3 |
10 |
|
18. |
tg(x/2)+cos(x) |
π/2 |
3π/4 |
10 |
|
19. |
ctg(x/3)+sin(x) |
π/4 |
π/2 |
10 |
|
20. |
sin(x/4)/2 |
π/2 |
π |
10 |
|
21. |
sin2x |
π/8 |
π/4 |
10 |
|
22. |
2cosx-1 |
π/4 |
π/2 |
10 |
|
23. |
ctgx+1 |
π/4 |
π/2 |
10 |
|
24. |
sin(1/x)+2 |
π/8 |
π/4 |
10 |
|
25. |
x cos(1/x)+2 |
π/8 |
π/2 |
10 |
|
26. |
|
π/6 |
2π/3 |
10 |
|
27. |
x2sin2x+1 |
π/2 |
3π/4 |
10 |
|
28. |
|
0 |
π/2 |
10 |
|
29. |
sin2x-cos2x |
0 |
π/3 |
10 |
|
30. |
7sin2x-1/2cosx |
π/2 |
3π/4 |
10 |
18 А Жадвал
|
|
1. a)
2. a)
3. a)
4. a)
5. a)
6. a)
7. a)
m!+7; b)
8. a)
(m+1)!; b)
|
Вариантлар
10.
a) ;
b)
;
b)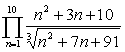 c)
c) 
11.
a)  ;
b)
;
b) ;
c)
;
c) 
12. а) 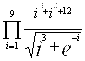 ; b)
; b)  ; c)
; c)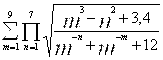 ;
;
13. a) ![]() ; b)
; b) ![]() ; c)
; c)![]()
14. a) ![]() ; b)
; b) 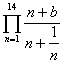 ; c)
; c)![]()
15. a) ![]() ; b)
; b)![]() ; c)
; c)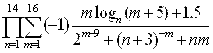
16. a)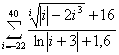 ; b)
; b)![]() ; c)
; c)![]()
![]() 17. a)
17. a)![]() ; b)
; b)![]() ; c)
; c)![]()
![]()
18. a) ![]() ; b)
; b) 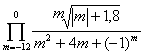 c)
c)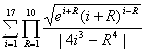
Вариантлар
19. a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
20. a) ![]() ; b)
; b) ![]() c)
c) ![]()
![]()
21. a) ![]() b)
b)![]() ; c)
; c) ![]()
22. a) ![]() ; b)
; b)![]() c)
c)![]()
23. a) ![]() ; b)
; b)![]() ; c)
; c)![]()
24. a)![]() b)
b)![]() c)
c)
![]()
25. a)![]() b)
b)![]() c)
c)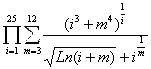
Вариант![]() лар
лар
26. a)![]() b)
b)![]() c)
c)![]()
27. a)![]() b)
b)![]() c)
c)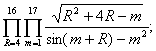
28. а)![]() b)
b)![]() c)
c)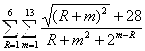
29. а)![]() b)
b)![]() c)
c)![]()
30. а)
m!; b)![]() c)
c)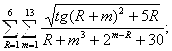
19 Жадвал
|
№ |
Микдор |
a, b диапазони |
y-функцияси |
N |
|
1. |
|
|
|
10 |
|
2. |
|
|
|
40 |
|
3. |
|
|
|
40 |
|
4. |
|
|
|
10 |
|
5. |
|
|
|
40 |
|
6. |
|
|
|
25 |
|
7. |
|
|
|
10 |
|
8. |
|
|
|
20 |
|
9. |
|
|
|
30 |
|
10 |
|
|
|
25 |
|
11 |
|
|
|
10 |
|
12 |
|
|
|
35 |
|
13 |
|
|
|
10 |
|
14 |
|
|
|
20 |
|
15 |
|
|
|
30 |
|
16.. |
|
|
|
20 |
|
17. |
|
|
|
20 |
|
18. |
|
|
|
50 |
|
19. |
|
|
|
20 |
|
20. |
|
|
|
30 |
|
21. |
|
|
|
40 |
|
22. |
|
|
|
35 |
|
23. |
|
|
|
15 |
|
24. |
|
|
|
40 |
|
25. |
|
|
|
20 |
|
26. |
|
|
|
20 |
|
27. |
|
|
|
40 |
|
28. |
|
|
|
40 |
|
29. |
|
|
|
40 |
|
30. |
|
|
|
20 |
20 Жадвал
|
1. у қийматини ҳисобланг, х ( |
|
2. z ,қийматини ҳисобланг ,хар бир
қийматига тегишли х ( |
|
1.
t ,қийматини ҳисобланг х ( |
|
4.
у, қийматини ҳисобланг, х ( |
|
5.
z ,қийматини ҳисобланг, х ( |
|
6.
t ,қийматини ҳисобланг х ( |
|
7. t ,кўпайтмасини, t³a.манфий миқдорини.Назорат ҳисоботини a=3.72, xn=1, xk=3, dx=0.2.амалга оширади |
|
8.
y,қийматини ҳисобланг х ( |
|
9.
z,қийматини ҳисобланг, х ( |
|
10.
t, қийматини ҳисобланг х ( |
|
11.
у, қийматини ҳисобланг, х ( |
|
12.
z,қийматини ҳисобланг, х ( |
|
13.
t, қийматини ҳисобланг х ( |
|
14.
у, қийматини ҳисобланг, х ( |
|
15.
z,қийматини ҳисобланг х ( |
|
16.
t қийматини ҳисобланг, х ( |
|
17.
У қийматини ҳисобланг , х ( |
|
18.
Z қийматини ҳисобланг, х ( |
|
19.
t,қийматини ҳисобланг, х ( |
|
20.
у, қийматини ҳисобланг, х ( |
|
21.
z, қийматини ҳисобланг, х ( |
|
22.
t, қийматини ҳисобланг, х ( |
|
23.
у,қийматини ҳисобланг.хар бир қиймати тегишли х ( |
|
24 z ,қийматини ҳисобланг хар бир қиймати тегишли х ( |
|
25 t,қийматини ҳисобланг , х ( |
|
26. у,қийматини
ҳисобланг, х ( |
|
27. z, қийматини ҳисобланг, х ( |
|
28. t, қийматини ҳисобланг, х ( |
|
29. у,қийматини ҳисобланг, х ( |
|
30. z,қийматини ҳисобланг, х ( |
21 Жадвал
Номаълум кайтарилувчи сони билан циклларни дастурлаш
|
|
1. а =4; dа=-0.5 берилган.. S ни , S = 2.79ln(a3+a+1) формула асосида ҳисобланг.. S ни логарифм белгисидан 1 дан кўпайгунича ҳисобланг. . S ҳисобланувчилар k –миқдорини аниқланг. a, S, k.ни экранга чиқаринг. |
|
2.
q =3; dq=-0.2 берилган. Fни q, F, k.ни экранга чиқаринг. |
|
3.
x=2; dx=-0.2 берилган. Z ни |
|
4.
а = 1.2; x =1;dx= 0.5 берилган. Z ни |
|
5. а =5; dа=-0.5
берилган.. Z ни |
|
6. а=3.7; x=2; dx=0.2 берилган. Z ни Z=0.5cos(x)+ln(a/x3 +1/x). формуласи бўйича ҳисобланг. Z ни логарифм белгисидан 03 дан кўпайгунга қадар ҳисобланг. k – ҳисобланувчилар миқдорини ҳисобланг. Z. Экранга чиқаринг x, Z, k. |
|
7. x=1; dx=0.5.берилган. Z ни Z = q(cos(3x)+sin(5x)), где q = ex-1 + x формуласи бўйича ҳисобланг.. q < 400 бўлгунга қадар ҳисобланг.. k – ҳисобланувчилар миқдорини ҳисобланг. Z. Экранга чиқаринг x, q, Z, k. |
|
8. x=1; dx=0.5.
берилган. Z ни |
|
9. x=-1.5;dx=0.5.берилган.
Z ни |
|
10. b=1; db=-0.2.
берилган. Z ни |
|
11. x=2; dx=-0.2.берилган.
Z ни Илдиз ости тенгламаси 0 дан кўпайгунга қадар ҳисобланг. k –ҳисобланувчилар миқдорини аниқланг. . Z.Экранга чиқаринг x, Z, k. |
|
12. а=5; dа=-0.5 берилган. Z ни Z = ln(1+0.8a)cos(a). формуласи бўйича ҳисобланг. Z ни логарифм белгисидаги тенглама 0 дан кўпайгунга қадар ҳисобланг. k –ҳисобланувчилар миқдорини аниқланг Z. Экранга чиқаринг a, Z, k. |
|
13. x=3; dx =-0.2
берилган.. Z ни |
|
14 x=4; dx =-0.3.берилган. Zни Z = ln(5x-5)sin(x). Формуласи бўйича ҳисобланг. Z ни логарифм белгиси остидаги тенглама 0 дан кўпайгунга қадар ҳисобланг. k – ҳисобланувчилар миқдорини аниқланг.Z.Экранга чиқаринг x, Z, k. |
|
15. x =1; dx=0.2
берилган. Z ни |
|
16. а=2; dа=0.5берилган..
Zни |
|
17. b=3; db= -0.3берилган..
Z ни |
|
18. x=2; dx=0.4. берилган. Z ни |
|
19. с =3.2; а=1; dа=0.3берилган.
Z ни |
|
20. x=3; dx=-0.4.берилган.
Z ни |
|
21. x =0; dx=0.5.берилган.
Z ни |
|
22. а=1; dа=0.4.
берилган. Z ни |
|
23. x =6; dx=-0.5.берилган. Z ни Z = cos(x)ln(x2-0.5x).формуласи бўйича ҳисобланг. Z ни логарифм белгиси остидаги тенглама 0 кўпайгунга қадар ҳисобланг. k – ҳисобланувчилар миқдорини аниқланг. Z. экранга чиқаринг x, Z, k. |
|
24. x=5;.dx=-0.4.
берилган. Z ни |
|
25. b=1; db=0.2.берилган.
Z ни |
|
26. x=1; dx=0.2.берилган Z ни Z = x2ln(1+ex). Формуласи бўйича ҳисобланг. Z ни логарифм белгиси остидаги тенглама 2.5. камайгунга қадар ҳисобланг. k –ҳисобланувчилар миқдорини аниқланг Z.Экранга чиқаринг x, Z, k. |
|
27. а=4; dа=-0.5. берилган. Z ни Z ни илдизости тенгламаси 0 дан кўпайганга қадар ҳисобланг . Определить k - количество вычисленных Z. Экранга чиқаринг a, Z, k. |
|
28. x=5; dx=1.
берилган. Z ни |
|
29. x=6; dx=-0.4.берилган.
Z ни |
|
30. x=1; dx=0.5. Z
берилган . Z ни илдизости тенгламаси 0.02. кўпайгунга қадар ҳисобланг. k – ҳисобланувчиларни миқдорини аниқланг Z. Экранга чиқаринг x, Z, k. |
z кийматини хисобланг, х
(![]() ,хар
бир кийматига тегишли x ўзгарувчан қадам dx)тенг
,хар
бир кийматига тегишли x ўзгарувчан қадам dx)тенг ![]() . Формуласи бўйича. Аниқланг
. Формуласи бўйича. Аниқланг ![]() , n бор жойда z
айирилган миқдор. Назорат ҳисобини a=5.27, xn=1,
xk=10, dx=1. Амалга оширинг
, n бор жойда z
айирилган миқдор. Назорат ҳисобини a=5.27, xn=1,
xk=10, dx=1. Амалга оширинг
16 жадвалдан топширикларни бажараётган вактда учта цикл операторини хаммасини ишлатиш керак В гурухларида – учта алохида дастур булиши мумкин, А-гурухларида эса мажбурий алохида функциялари. (main()) Асосий дастур тегишли дастурнинг функциясини танлаш учун менюнинг мазмунига кириши керак.
У кийматини хисобланг : У=6.25x5 +1.85x4+2.74x3-10.5x2-10x+3;
Горнер схемасидан фойдаланинг
Y=(((6.25x+1.85)x +2.74)x -10.5)x +3;
# include<iostream.h>
# include<conio.h>
void main()
{
clrscr();
const float a[6]={6.25,1.83,2.74,-10.5,-10,3};//koefitsienti
int i=0 ; //indeks koefits
float x,p=1.0; // p-dlia proizvedenie
cout<<"vvedi x";
cin >>x;
while(i<6)
{
p=p*x+a[i]; i++; //telo sikla
}
cout<< "\n mnogochlen pri x= "<<x<<" raven="<<p<<endl;
cout<<"enter ";
getch();
}
22 Жадвал
|
ε айрим сони ва рақамли қатор берилган..Модули катта ёки ε тенг бўлган қаторнинг қисмларини суммасини топинг. Каторнинг умумий қисми қуйидаги кўринишга эга: |
|||
|
1. |
an = (-1)n-1 / nn |
7. |
an=n!/nn |
|
2. |
an=1/2n+1/3n |
8. |
an=2nn!/nn |
|
3. |
an=(2n-1)/2n |
9. |
an=3nn!/(2n)! |
|
4. |
an=1/((3n-2)(3n+1)) |
10. |
an=n!/3nn |
|
5. |
an=10n/n! |
11. |
an=n!/(2n)! |
|
6. |
an=n!/(2n)! |
12. |
an=2n/(n-1) |
|
│an-an-1 │<ε шарти бажариладиган кетма-кетликни энг кичик рақамини топинг.Экранга барча элементларни ва шу рақамни чиқаринг. ai ,где i=1,2,…,n;
|
|||
|
13. |
an=arctg an-1+1, a1=0 |
18. |
an=(2+an-1²)/2an-1, a1=1, a2=2; |
|
14. |
an=2+1/an-1, a1=2 |
19. |
an=nln n/(ln n)n; |
|
15. |
an=1/2 tgan-1, a1=0,5 |
20. |
an=e-a -1, a1=0: |
|
16. |
an=1/(2n)n |
21. |
an=x/(2an-12, a1=x; |
|
17. |
an=1/2 cosan-1, a1=0,5 |
22. |
an=(2+an-1²)/2an-1, a1=1, a2=2; |
|
Элементнинг кетма кетлигини ракамини энг кичигини топинг шу учун М , шарти бажарилади. Барча элементларни ва шу рақамни экранга чиқаринг ai , где i=1,2,…,n. |
|||
|
23. |
an=1/2 (an-1+2/an-1), a1=1, M:│an²-2 │<ε |
||
|
24. |
an=(-1)nn/2n, M:│an│<ε |
||
|
25. |
an=((-1)n2n)/n!, M:│an│<ε |
||
|
26. |
an=1/(n+1)², M: an<ε |
||
|
27. |
қаторнинг суммасини ҳисоблаш учун дастур тузинг
|
||
|
28. |
қаторнинг суммасини ҳисоблаш учун дастур тузинг
|
||
|
29. |
Тарқалувчи қаторнинг чексиз қўшиладиган сонларни аниқланг
|
||
|
30. |
қатордаги суммани ҳисоблаш учун дастурни тузинг
|
||
x=1;
dx=0.5.Берилган. Z
![]() .формула
буйича ҳисобланг.
.формула
буйича ҳисобланг.
Z шундай ҳисоблангки илдизли тенглама 0.02 дан катта бўлсин . Аниқланг, k ҳисобланувчиларнинг миқдори Z. Экранга чикаринг x, Z, k.
(while).
#include<iostream.h>
#include<conio.h>
#include <math.h>
void main ()
{float x =1, dx=0.5 ,R =1, Z ; //R=1 циклни бошлаш учун
int k =0;
while (R>0.02)
{ R=x/(x+1);
Z= log(x)* sqrt(R); // ![]()
cout<<“Z=“ <<Z<<endl;
K++;
X+=dx;
} cout<<” Col_Z=”<<K<<endl;
getch();
}
Таблица 23
|
№ |
Формулалар |
Параметрлар |
|||
|
a |
b |
|
|
||
|
1 |
|
2,8 |
-3,5 |
0,3 |
(0,3;2,9) |
|
2 |
|
-1,3
|
0,6 |
0,1 |
(0,3;1,5) |
|
3 |
|
3,4 |
-3,3 |
0,4 |
(0,1;1,8) |
|
4 |
|
-1,7 |
3,2 |
0,4 |
(0,4;3,2) |
|
5 |
|
0,7 |
-1,5 |
0,9 |
(3,5;9,8) |
|
6 |
|
-3,4 |
-1,2 |
0,4 |
(0,3;10)
|
|
7 |
|
0,5 |
-1,7 |
1,1 |
(3,1;8,8) |
|
8 |
|
2,4
|
-0,9 |
0,5 |
(0,2;1,7)
|
|
9 |
|
3,8 |
7,9 |
2,1 |
(1,4;4,1) |
|
10 |
|
3,8 |
-2,5 |
0,3 |
(1,5;5,7) |
|
11 |
|
1,8 |
-3,3 |
0,2 |
(0,2;1,4) |
|
12 |
|
1,8 |
2,5 |
1,1 |
(3,1;8,6) |
|
13 |
|
-0,3 |
-4,3 |
0,1 |
(0,5;0,9) |
|
14 |
|
1,8 |
1,3 |
0,1 |
(1,1,;1,6) |
|
15 |
|
0,4 |
2,5 |
0,1 |
(0,1;0,8) |
|
16 |
|
7,1 |
1,8 |
0,7 |
(1,4;4,1) |
|
17 |
|
1,4 |
3,8 |
0,2 |
(0,5;1,7) |
|
18 |
|
0,4 |
0,2 |
0,2 |
(0,2;1) |
|
19 |
|
0,8 |
2,4 |
0,2 |
(0,1;1,1) |
|
20 |
|
2,4 |
8,2 |
0,9 |
(3,5;9,8) |
|
21 |
|
0,8 |
1,4 |
0,5 |
(0,3;2,3) |
|
22 |
|
1,7 |
-3,1 |
0,5 |
(1,4;1,8) |
|
23 |
|
1,7 |
-4,1 |
0,3 |
(2,5;7,5) |
|
24 |
|
0,5 |
-1,3 |
0,1 |
(0,4;1,4)
|
|
25 |
|
-4,7 |
0,5 |
0,4 |
(0,5;8,5) |
|
26 |
|
7,7 |
-4,4
|
0,3 |
(0,3;6,4) |
|
27 |
|
1,1 |
0,7 |
0,2 |
(0,5;2,4) |
|
28 |
|
-1,9
|
0,7 |
0,3 |
(0,3;2,5) |
|
29 |
|
2,8 |
-3,6 |
0,2 |
(0,7;1,9) |
|
30 |
|
2,4 |
-0,9 |
0,5 |
(0,2;1,7) |
№7. Лаборатория ишини бажариш учун услубий кўрсатмалар.
Лаборатория ишини бажаришдан олдин конспектдаги «Цикллар» мавзусини , ўқиб чиқинг.. Ўкитувчининг ёрдамида амалий машғулотларда машқ қилиш масалаларини бажаринг. .
Қуйида келтирилган дастурдаги мисоллари ишни бажаришга ёрдам беришади.
18№ жадвалга.. F(x) функциясининг қийматини ҳисоблаш учун дастурни тузинг. [a,b] кесимида , h кадами билан. Натижаларни жадвал асосида келтиринг.Аргументнинг қиймати устун шаклида , иккинчиси эса функциянинг қийматини мос келиши.
|
Функциялар F(x) |
Параметрлар |
m |
|
|
x/cosx |
π/2 |
Π |
10 |
#include<conio.h>
|
pi=3.1415 |
|
|
a=pi*0.5 |
|
|
b=pi |
|
|
m=10 |
|
|
h=abs(b-a)/m |
|
|
i=1 ; x=a |
|
|
натижа h |
|
|
гача i £ m |
|
|
|
fx=x/cos(x) |
|
|
натижа x , fx |
|
|
х = х + h |
|
|
i= i+ 1 |
|
тамом |
|
#include<math.h>
#include<stdio.h>
void main()
{ clrscr();
float fx,x,h,pi=3.1415;
float a=pi*0.5,b=pi/4;
float m=10;int i;
h=abs(b-a)/m;x=a;
printf("h=%.2f\n",h);
printf(" F(x)=x/cosx\n");
printf("--------------------\n");
printf(" x | F(x)\n");
printf("--------------------\n");
for (i=1;i<=m;i++)
{fx=x/cos(x);
printf("%6.2f | %6.2f\n",x,fx);
x+=h; Блок-схема
}
printf("--------------------\n");
getch();
}
h=0.10
F(x)=x/cos(x)
--------------------
x | F(x)
--------------------
1.57 | 33904.47
1.67 | -16.74
1.77 | -8.92
1.87 | -6.33
1.97 | -5.06
2.07 | -4.32
2.17 | -3.84
2.27 | -3.53
2.37 | -3.30
2.47 | -3.15
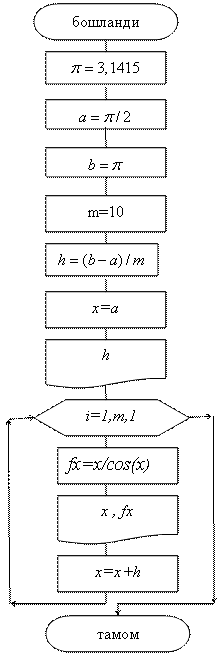
Горнер схемаси бўйича функцияни ҳисоблашга мисол
У ифодани топинг : У=6.25x5 +1.85x4+2.74x3-10.5x2-10x+3;
Горнер схемасидан фойдаланинг
Y=(((6.25x+1.85)x +2.74)x -10.5)x +3;
# include<iostream.h>
# include<conio.h>
void main()
{
clrscr();
const float a[6]={6.25,1.83,2.74,-10.5,-10,3}; //koefitsienti
int i=0 ; //indeks koefits
float x,p=1.0; // p-dlia proizvedenie
cout<<"vvedi x";
cin >>x;
while(i<6)
{
p=p*x+a[i]; i++; //telo сikla
} cout<< "\n mnogochlen pri x= "<<x<<" raven="<<p<<endl;
cout<<"enter ";
getch();
}
20 Жадвалдаги топширикни бажариш мисол
x=1; dx=0.5.
Z берилган: формула бўйича
: ![]() .
Z шундай хисоблангки илдизли тенглама 0.02 дан катта булсин . Аникланг
k хисобланувчилар микдори Z. Экранга чикаринг x, Z,
k.
.
Z шундай хисоблангки илдизли тенглама 0.02 дан катта булсин . Аникланг
k хисобланувчилар микдори Z. Экранга чикаринг x, Z,
k.
Дастур
#include<iostream.h>
|
x =1 |
|
|
dx=0.5 |
|
|
R =1 |
|
|
k =0 |
|
|
пока R>0.02 |
|
|
|
|
|
|
|
|
|
Вывод Z |
|
|
k = k+ 1
|
|
|
х = х+dx |
|
Вывод k |
|
|
конец |
|
#include<conio.h>
#include <math.h>
void main ()
{float x =1, dx=0.5 ,R =1, Z ; //R=1 для начала цикла
int k =0;
while (R>0.02)
{ R=x/(pow(x,3)+1);
Z= log(x)* sqrt(R); // ![]()
cout<<“Z=“ <<Z<<endl;
k++;
x+=dx;
} cout<<” Col-vo_Z=”<<k<<endl;
getch();
}
Формула асосида берилган кўп маротабали Zни ҳисоблаш учун кўп маротабали циклни ташкил этиш итерацион бўлиши керак, яъни цикл сони номаълум. (while).шарти билан циклдан фойдаланамиз.
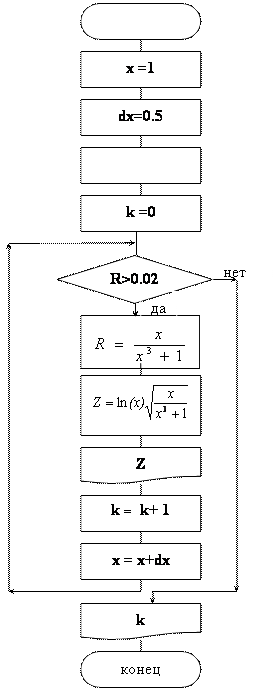

19 Жадвалдаги топширикни бажариш мисол
![]()
![]()
Берилган х интервалда У ва S га мос келувчи 10 ифодани ҳисоблаш керак, Sни ҳисоблаш учун иккита вариант тайёрлаш керак:а)берилган йиғиндилар сони билан ҳисоблаш в) Енинг аниқ қийматида.
#include<iostream.h>
#include<conio.h>
#include <math.h>
float zy(float );// прототипы
float zs(float ,int );// 3-х
float zc(float ,float );// функций
void main()
{
clrscr(); float x=0.1,e=0.00001;
float y,s1,s2;
while(x<=1.1 )
{
y=zy(x); // У ни ҳисобловчи zy функциясига мурожаат
s1=zs(x,20); // S ни ҳисобловчи функциясига мурожаат (n-берилган)
s2=zc(x,e); // S ни ҳисобловчи функциясига мурожаат (Е-берилган)
cout<<"x="<<x<<" fun= "<<y;
cout<<" sum="<<s1<<" sum2="<<s2<<"\t"<<endl;
x+=0.1;}
getch();}
float zy(float t)
{float y; //cout<< exp(t); cout<< "e--"<< exp(-t)<<endl;
y=(exp(t)-exp(-t))/2; return y;}
float zs(float t,int m) { int n; float s=t;float a=t;
for(n=1;n<=m;n++)
{a=a*t*t/(2*n*(2*n+1)); s+=a;} return s; }
float zc(float t,float m)
{ int n=0; float s=t;float a=t;
while(a>m)
{ n++;
a=a*t*t/(2*n*(2*n+1)); s+=a;}
cout<<" "<<n<<endl; return s; }
. 18 Жадвалдаги топшириқни бажаришга мисол
18 жадвалдаги топшириқларни бажариш вақтида учта цикл операторини хаммасини ишлатиш керак В гурухларида – учта алохида дастур бўлиши мумкин, А-гурухларида эса мажбурий алохида функциялари. (main()) Асосий дастур тегишли дастурнинг функциясини танлаш учун менюнинг мазмунига кириши керак. А ва В иккала гурухда хам вариантнинг иккитадан бирини арифметик тенгламани F1() ва F2() функция шаклида номлари билан расмийлаштирилиши лоъзим.. Қуйида аналогик масалалар учун 12 жадвалдаги масалаларга дастур келтирилган.

Формуланинг ракамини ва Х ва У кийматини дастур экранга чикаради
#include<iostream.h>
#include<stdio.h>
#include<conio.h>
#include<math.h>
float f1(float z)
{ float a=3.246;
cout<<" formula 1 ";
return z*z-а;
}
float f2(float z)
{ float b= 6.46;
cout<<" formula 2 ";
return z*z*z-b;
}
float ffor(float xn,float xk,float h)
{ float x,y;
for(x=xn;x<=xk;x+=h)
{ if (x<3.0) y=f1(x);else y=f2(x);
cout<< x<<” “<< y<<"\n" ; }
return 0;
}
void fwhile(float xn,float xk,float h)
{ float x,y;
x=xn;
while(x<=xk)
{ if (x<3.0) y=f1(x);else y=f2(x);
cout<<x<<” “<< y<<"\n" ;
x+=h;}
}
void fdo(float xn,float xk,float h)
{ float x,y;
x=xn;
do
{
if (x<3.0) y=f1(x);else y=f2(x);
cout<< x<<” “<< y<<"\n" ;
x+=h;
}
while(x<=xk);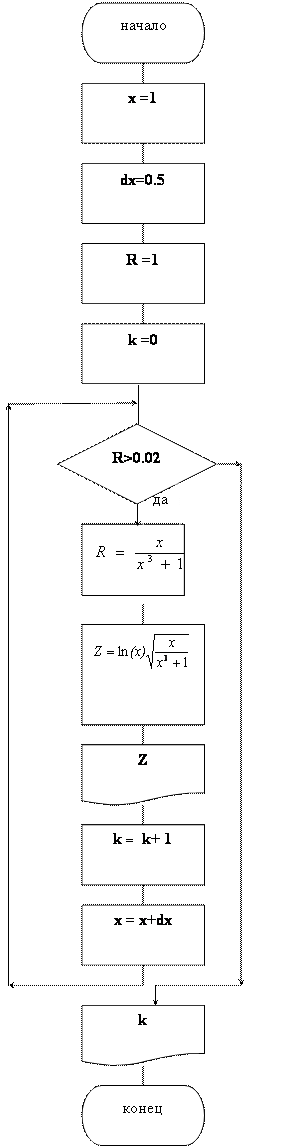
}
void main()
{float xn,xk,h,y;
int n;
xn=1.7; xk=5.3; h=0.4;
clrscr(); puts("vvedi--1,esli for");
puts("vvedi--2,esli while");
puts("vvedi--3,esli do");
cin>>n;cout<<"\n";
if (n== 1) ffor(xn,xk,h); //sikl s parametrom
if (n== 2) fwhile(xn,xk,h); //sikl s predusloviem
if (n== 3) fdo(xn,xk,h); //sikl s postusloviem
getch();
}
Назорат саволлари
1.Кайси холатларда ишлатилади ва кандай килиб ёзилади:
а)Параметр билан цикл оператори ;
б)кириш сўзи билан цикл оператори
2)Алгоритмларда цикллар кандай тасвирланади? Мисоллар келтиринг.
3.Дастурлашдаги цикл нима?
4.Цикллар киритилган бўлиши мумкинми?
5. С++ даги кийматнинг структураси кандай?
6. Дастурда функцияларга мурожаат кандай амалга оширилади?
7. return операторнинг муложааси кандай,Кайтариш киймати кандай аникланади?
8. Менюни ишлатиш йули билан дастурнинг фрагментини ёзинг.
9. Прототип нима (прообраз, сигнатура)киймати ва уни ишлатилиши?
10. Натурал сонларнинг кетма кетлигини тўсатдан кандай ташкил килади?
Лаборатория иши № 8
Массивлар . Берилган массивдан янги массив ҳосил қилиш.Бир ўлчамли массивда элементни киритиш ва уни олиб ташлаш.
Ишнинг максади: дарснинг назарий қисмини мустаҳкамлаш ва массивлар хақида маълумотлар бериш.
Топшириқ: масалаларга мос алгоритм ва дастурлар тузиш. (Ўқитувчи томонидан таркатилади):
1. Бир ўлчамли массив
а) жадвал.1 б) жадвал.2 в) жадвал.3 .
· Топширилган жавобларнинг ҳаммасини ўқитувчи текшириши лозим.
Ҳисоботнинг мазмуни
Ҳисобот қуйидагилардан иборат бўлиши керак:
1. Лаборатория ишининг номи
2. Лаборатория ишига топшириқ
3. Барча топшириқлар пунктига алгоритмлар ва дастурлар, топшириқларнинг жавоблари ва бажарилганлиги ҳақида ўқитувчининг имзоси.
4. Ҳимоядан кейин санаси ва бахони ўқитувчининг имзоси билан.
Топшириқларнинг шартлари:
жадвал 1
2 жадвал
|
|
Бир ўлчовли массивлар(ихтиёрий ўлчамли массив) |
|
1 |
U(K) массиви берилган. [a,b], интервалига тегишли бўлган элементлар сонини аниқланг ва экранга чоп этинг. |
|
2 |
Р(N) массиви берилган .D массивга унинг максимал ва минимал элементидан ташқари бўлган элементларни ёзинг |
|
3 |
X(N) массивининг ўрта арифметик ва ўрта геометрик қий -матларини аникланг. X массивининг ўрта арифметик қийма-тидан катта ва ўрта геометрик қийматдан кичик бўлган эле-ментлар сонини аниқланг ва чоп этинг. |
|
4 |
У(K) массивининг мусбат, тоқ индексли элементларининг йиғиндисини топинг. |
|
5 |
Z(K) массивининг манфий , жуфт индексли элементларининг кўпайтмасини топинг. |
|
6 |
H(N) массивининг ўрта арифметик қийматидан кичик бўл -ган элементларининг кўпайтмасини топинг. |
|
7 |
H(N) массивининг энг катта ва энг кичик элементларини топинг ва массивда улардан қайси бири аввал жойлашгани-ни аниқланг. |
|
8 |
Берилган иккита X=(X1,X2,...,Xn) ва Y=(Y1,Y2,...,Yn) векторнинг скаляр кўпайтмасини топинг. |
|
9 |
X(N) массив берилган. X массив элементларини камайиб бориш тартибида жойланг. |
|
10 |
X(N) массивининг мусбат элементларидан Y массивини ташкил этинг, сўнгра Y массив элементларини ўсиб бориш тартибида ёзинг |
|
11 |
Х(N) массивининг Xi>M,.шартини қаноатлантирувчи элементлар йиғиндисини ҳисобланг.( бунда М=махX - minX). |
|
12 |
Y(K) массивдан X массивига манфий элементларни кўчи -риб ёзинг . Х массивдаги энг кичик элементни биринчи элемент билан ўрнини алмаштиринг.
|
|
13 |
2 жадвал
X(N) ва Y(K ) иккита массив берилган. Х ва Y массивлари-нинг мусбат элементларидан Z массивни ташкил этинг . Z массивининг максимал элементини ва унинг индексини аниқланг. |
|
14 |
X(N) массиви берилган. Унинг элементларини тескари тартибда жойлаштиринг. Массивнинг тоқ индексли элемент-ларининг кўпайтмасини ҳисобланг. |
|
15 |
X(N) массив берилган. Унинг жуфт индексли элементларни Z массивга кўчириб ёзинг. Z массивдаги максимал ва минимал элементларининг ўрнини ўзаро алмаштиринг. |
|
16 |
Х(К)массив берилган. Х массивдаги манфий элементлар- ни Z массивига кўчириб ёзинг. Ҳосил бўлган Z массивини камайиб бориш тартибида жойланг. |
|
17 |
Z (N) массиви берилган. Y массивни шундай ташкил этинг-ки , Y массивида аввал мусбат, кейин манфий , ва нуль элементлари жойлашсин. |
|
18 |
Z массивидаги манфий элементлар купайтмасини, ҳамда йиғиндисини ҳисобланг. |
|
19 |
Z(К ) массивининг максимал ва минимал элементидан бошқа барча элементларидан X массивини хосил қилинг. Х массивининг ўрта геометрик қийматидан кичик бўлган эле -ментлари сонини топинг . |
|
20 |
X(N) массивидаги хамма мусбат элементларидан Z масси –вини хосил қилинг ва Z массив элементларини камайиб бориш тартибида жойланг. |
|
21 |
X(K) массивлари берилган. Х массивидаги барча мусбат элементлари индексидан L массивини хосил қилинг. |
|
22 |
X(N) и Y(N) массивларининг манфий элементларидан D массивини хосил қилинг. D массив элементларини ўсиб бориш тартибида жойланг. 3 та минимал элементларни чоп этинг. |
|
23 |
X(N) ва Y(K) массивлари берилган. D массивини шундай ташкил этингки, унда Х массивининг 3та ва У массивининг 4 та энг катта элементлари ёзилган бўлсин . D массиви элемент-ларининг купайтмаси хисобланг. |
|
24 |
X(N) массивнинг модул бўйича энг катта элементини топинг ва уни биринчи элементи билан ўрнини алмаштиринг. |
|
25 |
Х(N) ва Y(N ) массивнинг мусбат элементларининг йиғин-дисини ва манфий элементларининг купайтмаси хисобланг. |
|
26 |
Х(N) ва Y(N) массивлари берилган. Аi=Xi+ Yi. формуласи ёрдамида массив ташкил этинг. А массивнинг ўрта ариф –метик қийматидан кичик бўлган элементлар сонини ,хамда энг катта ва энг кичик элементлар орасидаги фарқни хисобланг. 2 жадвал |
|
27 |
X(N) бирор тўғри чизиққа тегишли бўлган нуқталар координаталар тўпламидан иборат массив бўлсин. Шу массивга тегишли бўлган , қайси икки нуқта орасидаги масофа энг катта эканлигини аниқланг. |
|
28 |
X(N) массиви берилган. X(N) массиви ўрта арифметик қийматини аниқланг ва массив биринчи элементининг ўрни билан алмаштиринг. |
|
29 |
X(N) массиви берилган. Уларни камайиб бориш тартибида Y(N ) массивига жойланг. X(N), Y(N ) массивларнинг модул бўйича энг катта элементининг индексини аниқланг . |
|
30 |
Z(N) массиви берилган. Унинг элементларининг модули бўйича ўсиб бориш тартибида жойланг. |
3 Жадвал
|
|
Бир ўлчовли массивлар билан ишлаш ( А гурух) |
|
1. |
x=(x1,
x2, …, xn) массивининг мусбат
элементларини y=(y1, y2,…,yk)
массивга кетма кет ёзинг. Мусбат элементлари сони - k ни
аниқланг. |
|
2. |
А
= (a1, a2, …, an) массивнинг жуфт индекслари элементларини В = (b1, b2,…,
bk) массивига кетма кет ёзинг. Массивнинг жуфт элементларининг сони k –ни топинг. |
|
3. |
х=(х1,…,хn) массивининг биринчи 5та мусбат элементларини Y=(y1, y2, …, y5) массивига кетма кет ёзинг.
|
|
4. |
х=(х1, х2,…, хn) массив элементларининг xiє[1, 2] шартни бажарувчи элементларини y
=(y1, y2,…, yk) массивига кетма кет ёзинг. |
|
5. |
x =(x1, x2,…, xn) массиви элементларини тескари тартибда Y =(y1, y2,…, yn) массивга ёзинг. Y массивининг жуфт индексли элементларининг кўпайтмасини ҳисобланг. |
|
6. |
X =(x1, x2,…, x25) массивининг элементларини 1, 4, 9, 16, 25 индексли элементларидан Y=(y1, y2,…, y5) массивини ҳосил қилинг.
3 Жадвал
|
|
7. |
X=(x1,x2,…, xn) массивининг мусбат элементларини Y=(y1,y2,…, yk) массивига ёзинг. Ундаги К-мусбат элементларининг сонини аникланг. Y массивнинг жуфт индекси элементларининг кўпайтмасини ҳисобланг. |
|
8. |
X=(x1,x2,…, x16) массивининг элементларини тескари тартибда Y=(y1,y2,…, y16) массивига ёзинг. S=y1+y4+y9+y16 ҳисобланг. |
|
9. |
X=(x1,x2,…,x12 ) массив элементларини 3та позиция ўнгга суринг ва Y=(y1,y2,…, y12) массивига ёзинг. Бунда X массивининг охирги 3та элементи Y массивнинг бошига кўчади. Яни (y1,y2,…, y12)=(x10,x11,x12,x1,x2,…x9). Y массивнинг жуфт индексли элементларининг кўпайтмасини хисобланг. |
|
10. |
X=(x1,x2,…,xn) массивидаги
манфий элементларини Y=(y1,y2,…,yk) массивига
кетма кет ёзинг. Манфий элементларнинг сонини аниқланг. |
|
11. |
X=(x1,x2,…, xn) массивнинг тоқ индексли элементларини Y=(y1,y2,…,
yk ) га кетма кет ёзинг. Бу ерда k–тоқ элементлар
сони. |
|
12. |
X=(x1,x2,…,xn) массивинин биринчи 8та манфий элементларини Y=(y1,y2,…, y8) массивига кетма кет ёзинг.
|
|
13. |
X=(x1,x2,…, xn) массивнинг xi є [2,3] шартини қаноатлантирувчи элементларини Y=(y1,y2,…, yk) массивига кетма кет ёзинг. k –шартни қаноатлантиручи элементлар сони.
|
|
14. |
X=(x1,x2,…, xn ) массив элементларини тескари тартибда Y=(y1,y2,…, yn) массивига ёзинг. Y массивининг ток индексли элементларининг кўпайтмасини хисобланг. |
|
15. |
X=(x1,x2,…, x36) массивининг 1, 4, 9,16,25, 36 индексли элементларини кетма кет тарзда Y=(y1,y2,…, y6) массивига ёзинг.
|
|
16. |
3 Жадвал
X=(x1,x2,…, xn) массивнинг мусбат элементларидан Y=(y1,y2,…, yk) массивини хосил қилинг . Y массив элементлари k – сонини аникланг. Y массивнинг тоқ индексли элементларининг кўпайтмасини ғисобланг. |
|
17. |
X=(x1,x2,…, x25) массив элементларини тескари тартибда Y=(y1,y2,…, y25) массивига ёзинг.. P=y1*y4*y9*y16*y25 ҳисобланг. |
|
18. |
X=(x1,x2,…,x15) массив элементларини 4 позиция чапга суриб Y=(y1,y2,…, y15), массивига ёзинг. Бунда Х массивининг бошидаги 4 элементи Y массивнинг охирига ўтказилади. яъни (y1,y2,…, y15)=(x5,x6,…,x15,x1,x2,x3,x4). Y массивининг тоқ индексли элементлари кўпайтмасини ҳисобланг. |
|
19. |
X=(x1,x2,…, xn) массивнинг мусбат элементларини кетма кет тартибда Y=(y1,y2,…, yk) массивиги ёзинг. Y массивнинг элементлар сони - k , максимал элементи ва унинг тартиб рақамини аниқланг. |
|
20. |
X=(x1,x2,…, xn) массивнинг жуфт индексли элементларини кетма кет тартибда Y=(y1,y2,…, yk) массивга ёзинг. Бунда k – жуфт индексли элементлар сони. Y массивнинг модуль бўйича минимал элементини ва унинг индексин топинг. |
|
21. |
X=(x1,x2,…, xn) массивининг биринчи еттита мусбат элементларини кетма кет тартибида Y=(y1,y2,…, y7) ёзинг. Y массивининг максимал элементини ва унинг тартиб ракамини топинг. |
|
22. |
X=(x1,x2,…, xn) массивнинг xiє [1.5, 2.5] шартни қаноатлантирувчи элементларини кетма кет тартибда Y=(y1,y2,…, yk) ёзинг. Y массивининг элементлари сонини - k энг катта элементини ва унинг индексини аниқланг. |
|
23. |
X=(x1,x2,…, xn) массивнинг элементларини тескари тартибда Y=(y1,y2,…, yn ) массивга ёзинг. Y массивнинг максимал элементини ва унинг индексини аниқланг. |
|
24. |
X=(x1,x2,…, x16 ) массивнинг 1, 4, 9, 16 индексли элементларини кетма кет тартибда Y=(y1, y2, y3 ,…, yn ) массивга ёзинг. Y массивнинг модуль буйича энг кичик элементини ва унинг индексини аниқланг. |
|
25. |
X=(x1,x2,…, x10) массив элементларини икки позиция ўнг томонга суриб, Y=( y1, y2 ,…,y10 ) массивига ёзинг. Бунда X массивининг охирги 2 та элементи Y массивнинг бошига кўчади. Яъни ( y1, y2, …, y10 )=( x9 ,x10 , x1,x2,…, x8). Y массивнинг модуль буйича минимал элементини ва унинг индексини аниқланг. |
|
26. |
3 Жадвал X=(x1,x2,…,xn) массивининг минимал элементини ва унинг индексини аниқланг. X массивининг энг кичик элементини (-1) билан алмаштиринг ва кетма кет тарзда Y=( y1, y2, … , yn ),массивига ёзинг. |
|
27. |
X=(x1,x2,…, xn) массивининг энг катта элементини ва унинг индексини аниқланг. Массивнинг энг катта элементини x1 билан ўзаро ўрнини алмаштириб, Y=(y1,y2,…,yn) массивига ёзинг. |
|
28. |
X=(x1,x2,…, xn) массивнинг энг кичик элементи ва унинг тартиб рақамини аниқланг. Массивнинг энг кичик элементини x1 билан ўзаро ўрнини алмаштириб, Y=(y1,y2,…,yn) массивига ёзинг. |
|
29. |
X=(x1,x2,…,
xn) массивнинг хар бир учинчи элементини Y= ( y1
, y2 ,… yk га ёзинг. |
|
30. |
X=(x1,x2,…, xn) массивининг xi
|
}
Биринчи лаборатория ишини бажариш учун кўрсатмалар.
1. Маъруза ва керакли адабиётлардан « массивлар» мавзусини ўқинг. Дастурда массивлар кандай тавсифланишини ва инициализация-қилишни эсланг. масалан:
int a[100];
char b[40];
Массивларни индекслаш нолдан бошланади . Яъни массивдаги 1 элемент a[0],
охиргиси эса a[99], бўлади. Массив кўп ўлчамли ҳам бўлиши мумкин.
Масалан: 2 ўлчамли int v[3][7] массивни 3та int тоифали 7та элементдан
иборат бир ўлчамли массив сифатида тассавур қилишимиз мумкин. Буни график кўринишда қуйидагича тасаввур қилишимиз мумкин:
|
v[0] |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
v[1] |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
v[2] |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
1- топшириқ
Берилган (-14; 5; 3;2;6;8;-4;3;11;2;5;6;-7;8) элементлардан иборат массивнинг жуфт индексли элементларини В массивга, тоқ индексли элементларини С массивга жойланг ва натижани сатр кўринишида чоп этинг.
#include <stdio.h>
#include <conio.h>
#define SIZE 7 // X массивнинг ўлчами
Void main()
{ clrscr(); // экранни тозалаш
int X[SIZE]={_14.5, 3.2,6.8,-4.3,11.2,5.6,-7,8}; //берилган массив
int m = 0, k=0; // янги массивнинг элементлар сони
int i; // индекс
printf (“ B C ”) // сарлавҳа
//массив индексларини аниқлаш
for (i = 0; i < SIZE; i++)
if (i % 2} {C[m]=X[i] ; printf(“ %.2f \n “,C[m]); m++;
}
else
{B[k] =X[i] ;k++; printf(“ %.2f “,B[k]); }
printf("\n тугаши учун <Enter>" босинг);
getch();}
- 2 жадвалга мисол.
5 та элементдан иборат бир ўлчамли массив элементларини клавиатурадан киритинг ва нолдан фарқли элементлар сонини аниқланг.
//дастур:
// нолдан фарқли элементлар сонини аниқланг
// ( номер буйича элементларга кириш)
#include <stdio.h>
#include <conio.h>
#define SIZE 5 // массив ўлчами
void main()
{
int a[SIZE]; //массив
int n = 0; // нолдан фарқли элеменлар сони
int i; // индекс
printf("\n бутун сонли массив элементларини киритинг.\n");
printf("хар бир сони киритишдан кейин ");
printf(" <Enter>\n ни босинг");
for (i = 0; i < SIZE; i++)
{
printf("a[%i] ->",i+l) ;
scanf("% i", &a[i]);
if (a[i] != 0) n++;
}
printf(" %i массивдаги нолдан фарқли элементлар сони\n", n);
printf("\п тугатиш учун <Enter>" босинг);
getch();
}
3. 3 жадвалга топшириқлар
Иккинчи тартибли квадрат матрицанинг дискрименантини аниқловчи дастур тузинг. Дастур ишлаш жараёнида тавсия этилаётган экран кўриниши қуйида келтирилган.
2 тартибли матрицани киритинг.
элементлар киритилгандан кейин <Enter> босинг
-> 5 -7
-> 1 3
матрицани аниклаш
5.00 -7.00
1.00 3.00 тенг 22.00
Юқорида келтирилган мисол дастури:
// 2 тартибдаги матрицанинг детерменантини аниклаш
#include <stdio.h>
#include <conio.h>
void main ()
{ float a[2][2]; // матрица
float det; // (детерминант) аникловчи
int i,j; // массив индекси
printf("\n2 тартибдаги матрицани киритинг.\n");
printf("элементлар киритилгандан кейин <Enter>\n"босинг);
for (i = 0; i < 2; i++)
{
printf("->");
scanf("%f%f", &a[i][0], &a[i][l]); } det = a[0] [0] * a[l]
[1] - a[0] [1] * a[l] [0];
printf("матирцани аникловчи\п") ;
for (i = 0; i < 2;
i++)
printf ("%f %f\n", a[i][0], a[i][l]);
printf("тенг %f ",
det);
printf("\n тугаши учун <Enter>"босинг);
getch(); }
Назорат саволлари
1) Массив элементлари ҳақида маълумот беринг.
2) Массивнинг аниқ элементига мурожаат қилувчи сон қандай аталади?
3) Массив ўлчамини эълон қилишга қулай,___________фойдаланиш.
4) Дастур бўлакларидан хатоликни топинг
а) #include <iostream.h> ;
б) arraySize = 10;// ўзгарувчи arraySize – const каби эълон қилинган
в) int b [ 10] = { 0 };
for (int i =0; i<=10; i++) b[ I ] = 1;
г) a[2] [2] = { {1,2},{3 ,4 } }; a[1,1] = 5;
5)Ихтиёрий йўл билан массивларни эълон қилиш, аниқлаш.
6) Индекс ўзгарувчиси, у қайси ҳолатда фойдаланилади?
АДАБИЁТЛАР
1. Сборник заданий для лабораторных и арифметических работ по курсу «Информатика» 1 часть. Методическая разработке – Т.: ТЭИС, 2000.
2. Практикум работы на бейсик ДВК2-2М. методическая разработка – Т.: ТЭИС, 1989.
3. Т.А.Павловская С/С++. Программирование на языке высокого уровня.
4. Информатика. Фани бўйича лаборатория ишларини бажариш учун ўқув-услубий қўлланма 1-қисм – Т.: ТАТУ, 2009.
5. Динман М.И. С++ Освой на примерах- СПб.:БХВ, - Петербург, 2006
МУНДАРИЖА
Кириш..........................................................................................................................................2
1. № 1 Лаборатория иши.
Электрон хисоблаш машиналарининг(ЭХМ) архитектураси. ....................4
1.1. Топшириқлар............................................................................................4
1.2. Назорат саволлари...................................................................................5
2. № 2 Лаборатория иши.
Ахборотни сақлаш усуллари. Ахборот ўлчов бирлиги. ШЭҲМда маълумотларни кўрсатиш. Кодлаш ва шифрлаш, ҳимоялаш, антивирус ҳимояси ҳақидаги асосий тушунчалар.............................................................6
2.1Топшириқлар.......................................................................................6
2.2. 1а жадвал............................................................................................6
1б жадвал............................................................................................9
3. № 3Лаборатория иши
ЭХМ нинг арифметик асослари. Саноқ системаси(2,8,16), улардаги амаллар. Лаборатория иши бажарилишидаги топшириқлар....................11
1.1.Топшириқ..............................................................................................................................11
1.2.жадвал....................................................................................................................................13
1.3.жадвал....................................................................................................................................20
1.4. 2а жадвал........................................................................................................21
1.4. 3жадвал...........................................................................................................24
1.4.4жадвал............................................................................................................25
1.5.6 жадвал...........................................................................................................33
1.6. Назорат саволлари.........................................................................................34
4. №4 лаборатория иши.
Турли структурали алгоритмлар.....................................................................35
1.1. Топшириқлар.....................................................................................35
1.2. Назорат саволлари.............................................................................52
5. №5 Лаборатория иши
Алгоритмлар. Чизикли структурали дастурлар..........................................53
1.1. Топшириқлар...............................................................................................53
1.2. 7 жадвал........................................................................................................54
1.3. 8 жадвал........................................................................................................57
1.4. 9 жадвал........................................................................................................60
1.5. 10 жадвал.....................................................................................................64
1.6. Назорат саволлари.......................................................................................72
6. № 6 Лаборатория иши
Тармоқланувчи программалар структураси.Алгебранинг мантиқ Элементлари.Танлов операторлари................................................................70
1.1. Топшириқлар..............................................................................................73
1.2. 12 жадвал....................................................................................................74
1.3. 13 жадвал...................................................................................................78
1.4. 14 жадвал..................................................................................................82
1.5. 15 жадвал..................................................................................................85
1.6. 16 жадвал.................................................................................................87
1.7. №6 Лаборатория ишини бажариш бўйича услубий кўрсатмалар.....89
1.8. 17 жадвал.................................................................................................94
1.9. Назорат саволлари..................................................................................98
7. № 7 Лаборатория иши
Цикл структурасининг алгоритмлари ва дастурлари.......................................................92
1.1.Топшириқлар........................................................................................................99
1.2. 18 жадвал..........................................................................................................100
1.3. 18А....................................................................................................................101
1.4 19 жадвал...........................................................................................................105
1.6. 20 жадвал..........................................................................................................106
1.7. 21 жадвал...........................................................................................................111
1.8. 22 жадвал...........................................................................................................115
1.9. №7 Лаборатория ишини бажариш бўйича услубий кўрсатмалар.............120
2.0. Назорат саволлари........................................................................................130
8. № 8Лаборатория иши Массивлар . Функциялар..........................................................115
1.1.Топшириқлар......................................................................................................130
1.2. 1 жадвал................................................................................................................131
1.3. 2 жадвал............................................................................................................135
1.4 3 жадвал............................................................................................................137
1.5. №8 Лаборатория ишини бажариш бўйича услубий кўрсатмалар............141
1.6. Назорат саволлари.......................................................................................144
АДАБИЁТЛАР.........................................................................................................................145
Дастурлаш асослари курси лаборатория
ишлари учун услубий қўлланма
ТАТУ “Компьютер инжиниринг” факультетининг илмий-методик кенгашида кўрилди ва нашрга тавсия этилди.
_____-йил ________
Протокол №______
Тузувчилар: доц.М.Ю.Хайдарова, асс.Д.З.Ганиходжаева, асс.М.З.Маҳкамова,Ш.Реджебов
Жавобгар мухаррир
проф. Ш.А. Назиров
корректор :Толипова О.
Формат 60х84 1/16
Заказ № ____ Тираж _____
ТАТУ қошидаги «ALOQACHI»
нашриёт марказида босмадан чиқди.
Тошкент Амир Темур кўчаси, 108.
1





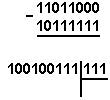
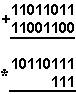

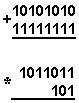
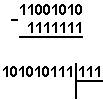

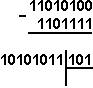
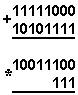
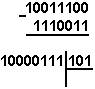

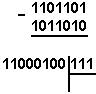
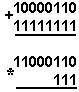
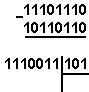
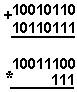
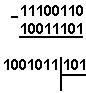
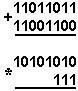

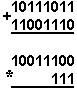

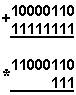
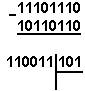

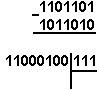
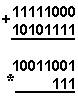

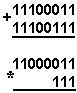


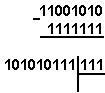




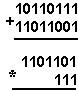
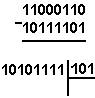
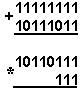
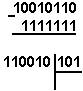

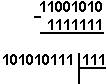

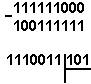
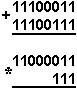

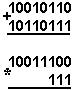
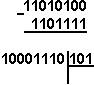

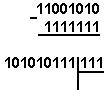
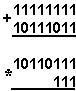
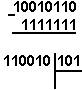

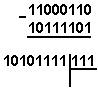
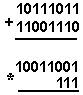
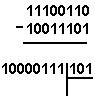

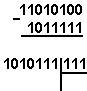
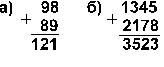
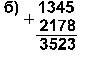
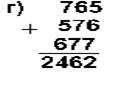

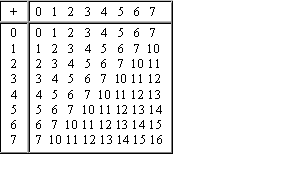
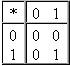






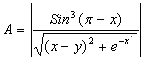
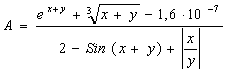
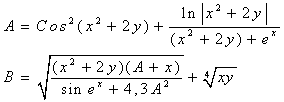
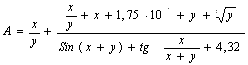


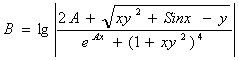














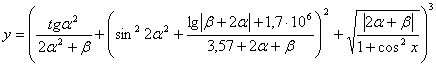

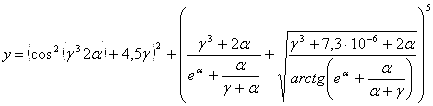
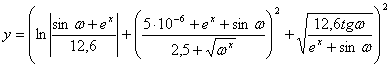

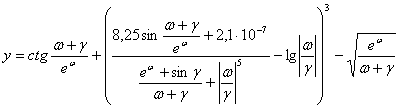


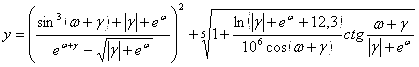

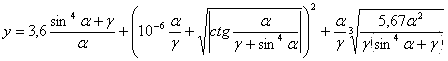


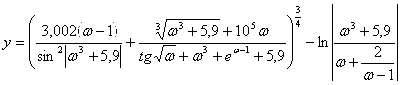
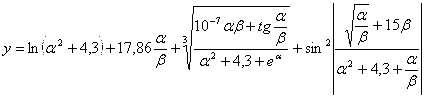

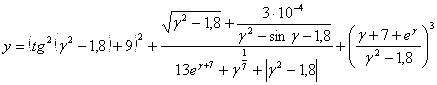
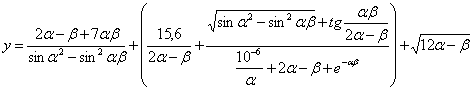
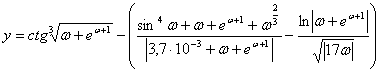

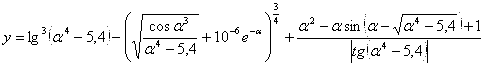
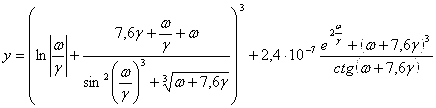



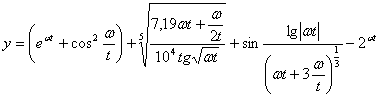

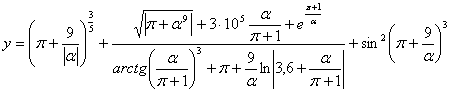

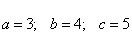
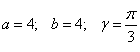
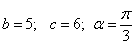
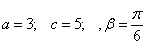
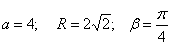


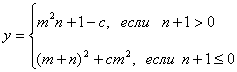
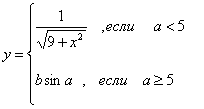
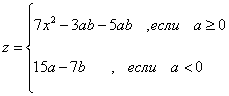
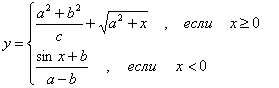
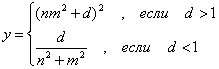

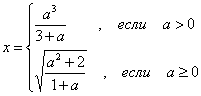
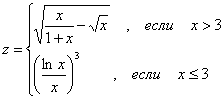
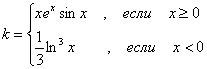
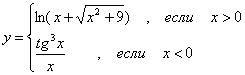
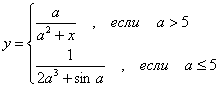

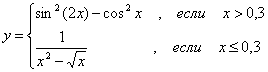
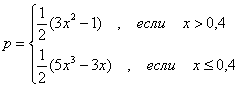
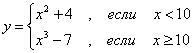
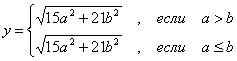
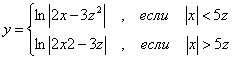
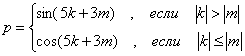
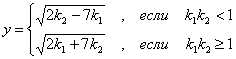

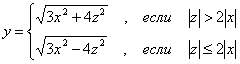
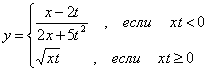
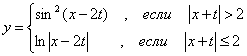
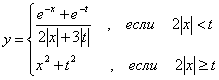
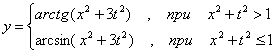
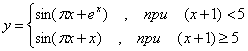
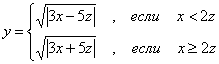
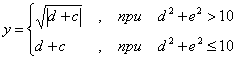
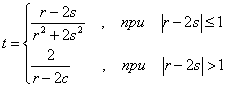
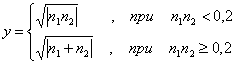
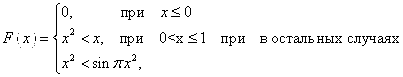
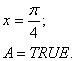

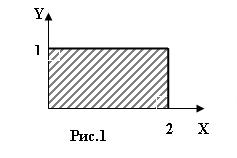
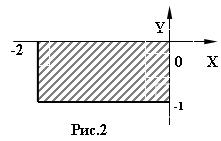
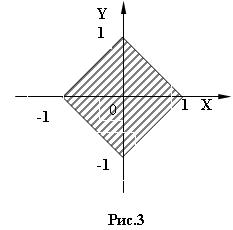
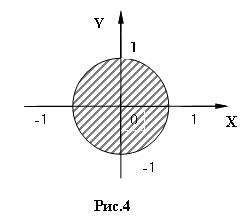
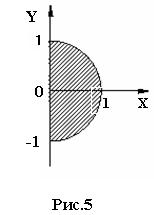
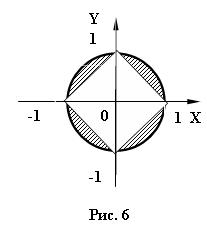
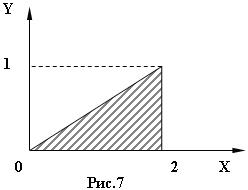
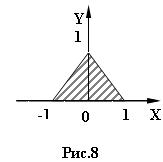
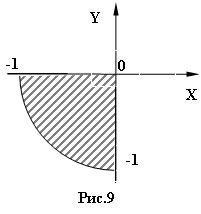
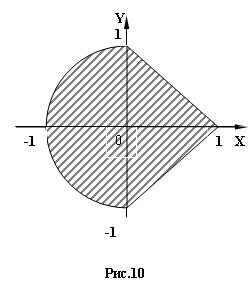
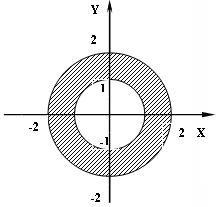
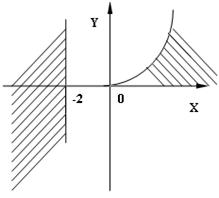
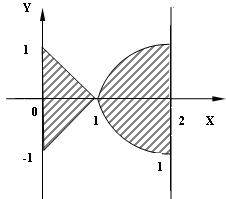
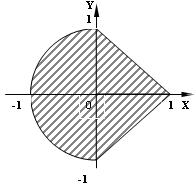
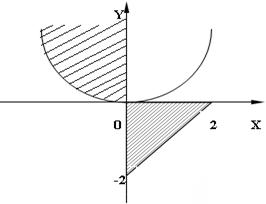
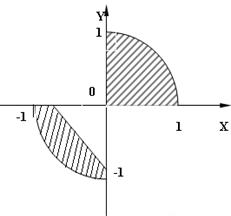
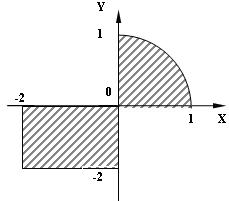
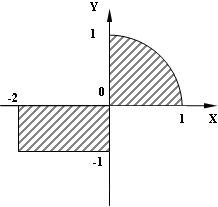
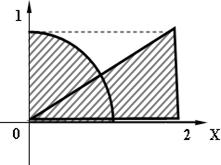
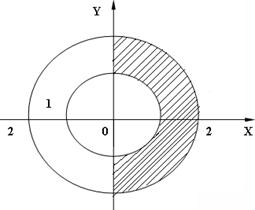
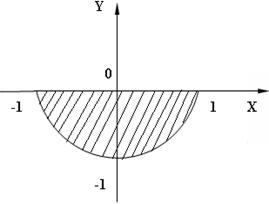
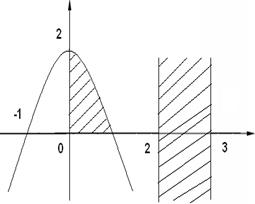
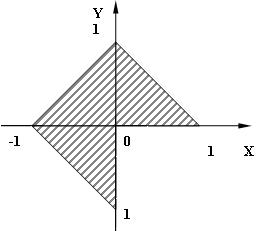
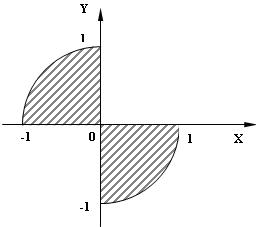
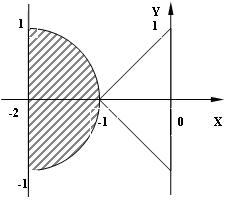


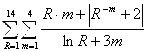
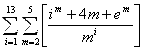

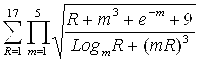
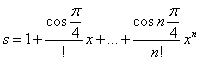
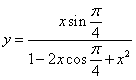
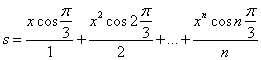
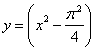
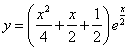
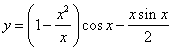

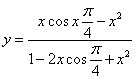

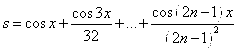

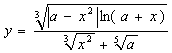 . Формуласи
буйича
. Формуласи
буйича  .формуласи буйича
.формуласи буйича  формуласи б
формуласи б формула буйича.
формула буйича. 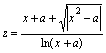 .
. 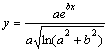 .формула б
.формула б
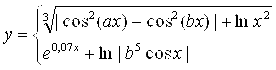
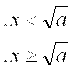

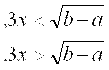
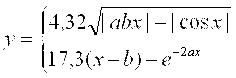
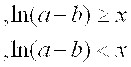

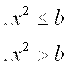
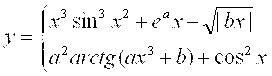

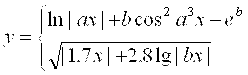
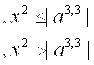

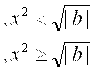

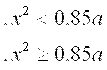
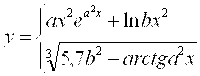
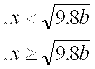


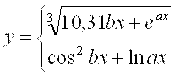
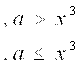

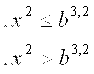
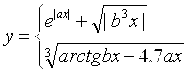
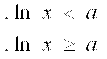
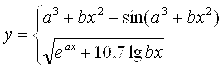
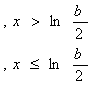
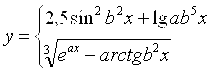

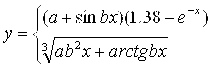
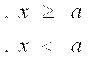
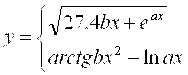
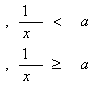
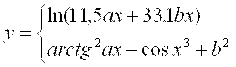

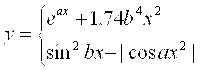

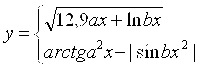
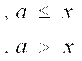

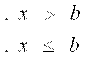
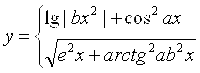
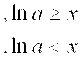


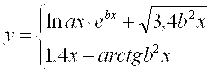
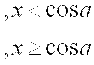
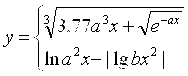





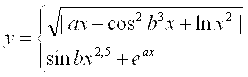
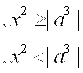
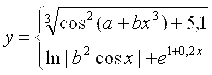

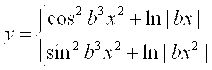
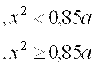

 ни хисобланг.
ни хисобланг.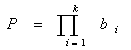 ни
ни 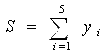 ни хисобланг.
ни хисобланг.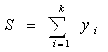

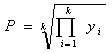 ни
ни