УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Основы теории управления
Методические указания к выполнению лабораторных работ
Ташкент 2012
Авторы :Когай В.Н., Турсунбаев Ф.К., Яковлева Ю.А., Азимова У.А.
«Основы теории управления» ТУИТ. 33 с. Ташкент, 2011
Методические указания по курсу «Основы теории управления» предназначены для студентов направлений 55221900-«Информатика и информационные технологии», 5323500-«Безопасность информации»,5811200-«Сервис (Информационный сервис)»,5811100-«Сервиспредприятий»,5140900-«Профессиональное образование (информатика и ИТ)» учебным планом предусмотрено проведение лабораторных занятий на 6-м семестре обучения.
Методические указания разработаны с целью закрепления материала курса, изучения методов проектирования систем управления.
Предусматривается знакомство иизучениесо средой MATLAB, управление потоками, ознакомление с динамическими характеристиками систем автоматического управления и получение навыков исследования линейных динамических моделей, ознакомление с частотными характеристиками систем автоматического управления.
Лабораторные занятия включают в себя также исследования линейных динамических моделей, наблюдаемости, управляемости и вычисление граничных коэффициентов устойчивости систем.
Рецензенты:
д.т.н., профессор, в.н.с. института
“Математики и информационных технологии”
АН Республики Узбекистан Исмаилов М.А.
д.т.н., проф.зав. кафедры «Электронная
комерция» ТУИТ Якубов М.С.
Ташкентский Университет Информационных Технологий, 2012
Введение
Теория управления – это наука, разрабатывающая и изучающая методы и средства систем управления и закономерности, протекающих в них процессах.
Современная теория управления занимает одно из ведущих мест в технических науках и в то же время относится к одной из отраслей прикладной математики, тесно связанной с вычислительной техникой.
Теория управления на базе математических моделей позволяет изучать динамические процессы в автоматических системах, устанавливать структуру и параметры составных частей системы для придания реальному процессу управления желаемых свойств и заданного качества. Она является фундаментом для специальных дисциплин, решающих проблемы автоматизации управления и контроля технологических процессов, проектирования следящих систем и регуляторов, автоматического мониторинга производства и окружающей среды, создания автоматов и робототехнических систем[2,3].
Задачей лабораторных работ является закрепление теоретического материала дисциплины «Основы теории управления» и получение практических навыков по созданию, принципов организации, функционированию и проектированию технических и информационных систем управления.
С этой целью по курсу основы теория управления подлежит к выполнению следующие лабораторные работы:
Лабораторная работа №1
Лабораторная работа №2
Лабораторная работа №3
Лабораторная работа №4
Лабораторная работа №5
Лабораторная работа №6
Лабораторная работа №1
Тема: Знакомство со средой MATLAB. Вычисления в командном режиме.
Цель работы: освоить основные подходы работы в среде Matlab.
1.1 Краткие теоретические сведения.
MATLAB - это высокоэффективный язык инженерных и научных вычислений [1]. Он поддерживает математические вычисления, визуализацию научной графики и программирование с использованием легко осваиваемого операционного окружения, когда задачи и их решения могут быть представлены в нотации, близкой к математической.
Наиболее известные области применения системы MATLAB:
⁃ математика и вычисления;
⁃ разработка алгоритмов;
⁃ вычислительный эксперимент, имитационное моделирование, макетирование;
⁃ анализ данных, исследование и визуализация результатов;
⁃ научная и инженерная графика;
⁃ разработка приложений, включая графический интерфейс пользователя.
1.1.1 Работа с панелью инструментов
Средства панели инструментов
Панель инструментов (рисунок 2) дает наиболее простой и удобный (особенно для начинающих пользователей) способ работы с системой MATLAB. При этом основные команды вводятся указанием курсором мыши на нужную кнопку с нажатием левой клавиши мыши. Кнопки имеют изображение, явно подсказывающее их назначение.
![]()
Рисунок 2 - Часть окна системы MATLAB с меню и панелью инструментов
Назначение всех кнопок панели инструментов:
New M-file (Новый m-файл) — выводит пустое окно редактора m-файлов;
Openfile (Открыть файл) — открывает окно для загрузки m-файла;
Cut (Вырезать)— вырезает выделенный фрагмент и помещает его в буфер;
Сору (Копировать)— копирует выделенный фрагмент в буфер;
Paste (Вставить)— переносит фрагмент из буфера в текущую строку ВВОДА
Undo (Отменить)— отменяет предшествующую операцию;
Redo (Повторить) — восстанавливает последнюю отмененную операцию;
Simulink — открывает окно браузера библиотек Simulink;
Help (Помощь)— открывает окно справки.
Набор кнопок панели инструментов обеспечивает выполнение наиболее часто необходимых команд и вполне достаточен для повседневной работы с системой.
Вызов окна открытия нового файла
Кнопка New M-file открывает окно редактора/отладчика m-файлов. Это окно показано на рисунок 3.
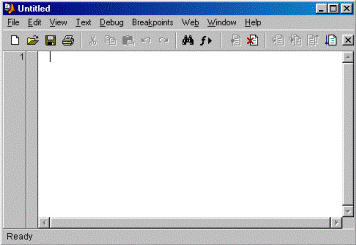
Рисунок 3 - Пустое окно редактора/отладчика m-файлов
По умолчанию файлу дается имя Untitled, которое впоследствии (при записи файла) можно изменить на другое, отражающее тему задачи. Это имя отображается в титульной строке окна редактирования m-файла, которое размещается в окне редактора/отладчика и видно на рисунке 3. В редакторе/отладчике можно редактировать несколько m-файлов, и каждый из них будет находиться в своем окне редактирования, хотя активным может быть только одно окно, расположенное поверх других окон.
1.1.2 Работа с меню. Команды, операции и параметры
Открытая позиция строки меню содержит различные операции и команды. Выделенная команда или операция исполняется при нажатии клавиши Enter (Ввод). Выполнение команды можно также осуществить щелчком мыши или нажатием на клавиатуре клавиши, соответствующей выделенному символу в названии команды.
Между командами и операциями нет особых отличий, и в литературе по информатике их часто путают. Мы будем считать командой действие, которое исполняется немедленно. А операцией — действие, которое требует определенной подготовки, например открытие окна для установки определенных параметров.
Параметр (option)— это значение определенной величины, действующее во время текущей сессии. Параметрами обычно являются указания на применяемые наборы шрифтов, размеры окна, цвет фона и т. д.
Меню системы
Перейдем к описанию основного меню системы MATLAB 6.0. Это меню (см. рисунок 1) выглядит довольно скромно и содержит всего шесть
пунктов:
•File — работа с файлами;
•Edit — редактирование сессии;
•View — вывод и скрытие панели инструментов;
•Web — доступ к Интернет-ресурсам;
•Windows — установка Windows-свойств окна;
•Help — доступ к справочным подсистемам.
Подменю File
Подменю File содержит ряд операций и команд для работы с файлами.
Оно показано на рисунке 5. Число операций и команд значительно сокращено по сравнению с тем же меню у предшествующей версии системы MATLAB.
Теперь меню File содержит следующие операции:
•New - открывает подменю с позициями:
•M-file — открытие окна редактора/отладчика m-файлов;
•Figure — открытие пустого окна графики;
•Model — открытие пустого окна для создания Simulink-модели;
•GUI — открытие окна разработки элементов графического интерфейса пользователя.
•Open — открывает окно загрузки файла.
•CloseCommandWindows — закрывает окно командного режима работы (оно при этом исчезает с экрана).
•Importdata — открывает окно импорта файлов данных.
•SaveWorkspaceAs... — открывает окно записи рабочей области в виде файла с заданным именем.
•SetPath — открывает окно установки путей доступа файловой системы.
Preferences... — открывает окно настройки элементов интерфейса.
•Print... — открывает окно печати всего текущего документа.
•PrintSelection... — открывает окно печати выделенной части документа.
•Exit — завершает работу с системой.
Загрузка и сохранение файлов
Команды Open... (Открыть) и Importdata... (Импортировать данные) выводят стандартные окна (см. рис. 5.5) для загрузки m-файлов и файлов данных. Команда SaveWorkspaceAs... (Сохраните рабочую область как...) открывает стандартное окно записи файлов с расширением .mat. Они хранят определения переменных, массивов, функций пользователя и иных объектов, созданных в ходе текущей сессии работы. Эти команды в силу общеизвестности в более подробных комментариях не нуждаются.
Установка путей доступа файловой системы
Команда SetPath... (Установить путь) открывает окно редактора путей доступа файловой системы. Это окно показано на рисунке 6 .
Окно дает список папок с файлами системы MATLAB. Имеется возможность переноса папок вверх или вниз по списку, уничтожения их и переименования. По умолчанию задается правильная установка путей доступа, так что данными возможностями стоит пользоваться только в особых обстоятельствах, например при случайном переносе папок в другое место или при их переименовании.
1.2 Задание к лабораторной работе.
1. Создать ASCII файл с результатами двадцати измерений трёх случайных величин.
2. Загрузить созданный файл в рабочую область.
3. Просмотреть информацию о состоянии рабочей области.
4. Вычислить среднее и среднеквадратичное отклонение для каждого столбца.
5. Вычислить ковариационную и корреляционную матрицы для заданных случайных величин.
6. Построить гистограммы.
В ходе выполнения лабораторной работы могут понадобиться дополнительные сведения о возможностях пакета. Эту информацию можно получить из [1] или из справочной системы самого пакета.
Лабораторная работа №2
Управление потоками. Создание М-файлов. Обработка массивов данных.
Цель работы: освоить основные подходы работы с потоками и файлами в среде Matlab.
2.1 Краткие теоретические сведения
Понятие о файлах-сценариях и файлах-функциях
Объекты m-файлы, создаваемые редактором/отладчиком, делятся на два класса:
· файлы-сценарии, не имеющие входных параметров;
· файлы-функции, имеющие входные параметры.
Файл-сценарий, или Script-файл не имеет списка входных параметров и является примером простой процедуры без параметров. Он использует глобальные переменные, т. е. такие переменные, значения которых могут. Для запуска файла-сценария из командной строки MATLAB достаточно указать его имя в этой строке.
Файл-функция отличается от файла-сценария прежде всего тем, что созданная им функция имеет входные параметры, список которых указывается в круглых скобках. Используемые в файле-функции переменные являются локальными переменными, изменение значений которых в теле функции никоим образом не влияет на значения, которые те же самые переменные могут иметь за пределами функции.
Локальные переменные могут иметь те же имена (идентификаторы), что и глобальные переменные (хотя правила культурного программирования не рекомендуют смешивать имена локальных и глобальных переменных).
Основные средства программирования
Итак, программами в системе MATLAB являются m-файлы текстового формата, содержащие запись программ в виде программных кодов. Язык программирования системы MATLAB имеет следующие средства:
· данные различного типа;
· константы и переменные;
· операторы, включая операторы математических выражений;
· встроенные команды и функции;
· функции пользователя;
· управляющие структуры;
· системные операторы и функции;
· средства расширения языка.
Коды программ в системе MATLAB пишутся на языке высокого уровня, достаточно понятном для пользователей умеренной квалификации в области программирования. Язык программирования MATLAB является типичным интерпретатором. Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой. Этап компиляции всех инструкций, т. е. полной программы, отсутствует.
Основные типы данных.
Структура типов данных системы MATLAB представлена ниже:
Типы данных array и numeric являются виртуальными, поскольку к ним нельзя отнести какие-либо переменные. Они служат для определения и комплектования некоторых типов данных.
Таким образом, в MATLAB определены следующие основные типы данных, в общем случае представляющих собой многомерные массивы:
· single — числовые массивы с числами одинарной точности;
· double — числовые массивы с числами удвоенной точности;
· char — строчные массивы с элементами-символами;
· sparse — наследует свойства double, разреженные матрицы с элементами-числами удвоенной точности;
· сеll — массивы ячеек; ячейки, в свою очередь, тоже могут быть массивами;
· struct — массивы структур с полями, которые также могут содержать массивы;
· function_handle — дескрипторы функций:
· int32, uint32 — массивы 32-разрядных чисел со знаком и без знаков;
· intl6,uint!6 — массивы 16-разрядных целых чисел со знаком и без знаков;
· int8. uint8 — массивы 8-разрядных целых чисел со знаками и без знаков.
Кроме того, предусмотрен еще один тип данных — UserObject, который относится к типам данных (объектом), определяемым пользователем. Типы данных double, char и sparse были рассмотрены ранее, так что в этой главе будут детально рассмотрены оставшиеся типы. Что касается чисел класса uint8, то они представляют значения от 0 до 255 и занимают в памяти 1/8 часть от размера одного числа с двойной точностью. В основном этот тип данных применяется в служебных целях.
Каждому типу данных можно соотнести некоторые характерные для него операции, называемые методами. Дочерние типы данных, расположенные на приведенной диаграмме ниже родительских типов, наследуют от последних их методы, что является признаком наследования объектов. Поскольку в иерархии типов данных сверху находятся данные типа array, это значит, что все виды данных в MATLAB являются массивами.
2.2 Задание к лабораторной работе.
Реализовать в виде скрипта и функции:
|
Вариант |
Задание |
|
|
Сортировку массива; Перестановку начала и конца массива; Выделение элементов массива не кратных заданному числу; Замену в массиве заданных чисел на отрицательные. |
|
|
Вычисление длины массива; Вычисление суммы всех элементов массива; Генерацию массива чисел в заданных пределах, с заданным шагом; Выделение чётных элементов массива. |
|
|
Перестановку начала и конца массива; Вычисление среднеквадратичного значения элементов массива; Выделение элементов массива не кратных заданному числу; Исключение элементов кратных заданному числу. |
|
|
Вычисление максимального элемента; |
|
|
Вычисление суммы всех элементов массива; Перестановку соседних элементов массива; Сортировку массива; Замену в массиве заданных чисел на отрицательные. |
|
|
Выделение чётных элементов массива; Вычисление среднеквадратичного значения элементов массива; Вычисление максимального элемента; |
|
|
Замену всех элементов меньше заданного, на их квадратный корень; |
|
|
Вычисление среднеквадратичного значения элементов массива; Вычисление максимального элемента; Перестановку соседних элементов массива; |
|
|
Выделение элементов массива не кратных заданному числу; |
|
|
Перестановку соседних элементов массива; |
|
|
Исключение элементов кратных заданному числу. |
|
|
Вычисление процентов от заданного числа; |
|
|
Генерацию массива чисел в заданных пределах, с заданным шагом; |
|
|
Замену в массиве заданных чисел на отрицательные. |
ЛАБОРАТОРНАЯ РАБОТА №3
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
3.1 Цель работы:
Ознакомление с динамическими характеристиками систем автоматического управления (САУ) и получение навыков исследования линейных динамических моделей.
3.2 Постановка задачи
В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов:
![]() .
.
Необходимо:
1. Определить полюса и нули передаточной функции:
![]()
2. Записать дифференциальное уравнение, определяющее функционирование САУ.
3. Построить графики переходной и импульсно-переходной функции: h(t), w(t).
3.3 Краткие теоретические сведения
Рассмотрим систему автоматического управления (САУ), описываемую линейным (линеаризованным) дифференциальным уравнением вида:
![]()
где u(t) – входной процесс, y(t) – выходной
процесс, aBiB, bBjB, (![]() )–
постоянные коэффициенты, n, m (n3m)– постоянные числа. В
операторной форме выражение (1.1) может быть записано – A(D)y(t)=B(D)u(t).
)–
постоянные коэффициенты, n, m (n3m)– постоянные числа. В
операторной форме выражение (1.1) может быть записано – A(D)y(t)=B(D)u(t).
Здесь D – оператор дифференцирования ![]() .
Отсюдапреобразование “вход-выход” системы –
.
Отсюдапреобразование “вход-выход” системы –
![]()
где W(D) называется операторной передаточной функции.
Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:
![]()
которая получается путем применения преобразования Лапласа к (1.2) при начальных нулевых условиях. Здесь s-комплексная переменная. Связь между операторной (1.2) и комплексной (1.3) передаточными функциями можно записать в виде
![]()
Комплексные числа, являющиеся корнями многочленаВ(s), называются нулями передаточной функции, а корни многочлена A(s) – полюсами. Явный вид связи входа и выхода определяется выражением:
![]()
где w(t) – оригинал (т.е. полученный с помощью обратного
преобразования Лапласа) комплексной передаточной функции W(s).
Динамические свойства систем характеризуют реакции на входные воздействия
специального вида. В частности анализ выхода системы на единичный скачок и d
–функцию (дельта-функцию). Пусть u(t) = 1(t), то есть на
вход системы подается функция Хевисайда (единичный скачок), определяемая 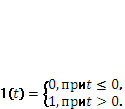
График функции Хевисайда приведен на рисунке 2а. Реакция САУ на единичный скачек называется переходной функцией системы и обозначается h(t).
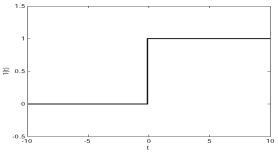
а)

б)
Рисунок 2 - а) Функция Хевисайда. б) Функция Дирака.
Если u(t) = d (t), то есть на вход системы поступает функция Дирака (d -функция, импульсная функция, рисунок 1.1б) определяемая
![]()
то реакция САУ называется импульсной переходной функцией системы и обозначается w(t). Таким образом оригинал комплексной передаточной функции можно измерить как реакцию систему на импульс. Импульсная и переходная функции системы связаны соотношением (из(1.4)):
![]()
3.4 Последовательность выполнения работы
Для выполнения лабораторной работы используется пакет прикладных программ (ППП) ControlSystemToolbox. ППП предназначен для работы с LTI-моделями (LinearTimeInvariantModels) систем управления. (Сведения по работе с LTI-моделями приведены в приложении 4).
В ControlSystemToolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды, создающий LTI-систему c одним входом и одним выходом в виде передаточной функции:
TF([bBmB, …, bB1B, bB0B], [aBnB, …, aB1B, aB0B])
bBmB, …, bB1B – значения коэффициентов полиномаВв (1.3),
aBnB, …, aB1B – значения коэффициентов полинома A в (1.3).
Для выполнения работы могут применяться команды, приведенные втаблице 2.
Таблица 2. - Некоторые командыControlSystemToolbox
|
Синтаксис |
Описание |
|
pole(<LTI-объект>) |
Вычисление полюсов передаточной функции |
|
zero(<LTI-объект>) |
Вычисление нулей передаточной функции |
|
step(<LTI-объект>) |
Построение графика переходного процесса |
|
impulse(<LTI-объект>) |
Построение графика импульсной переходной функции |
|
bode(<LTI-объект>) |
Построение логарифмических частотных характеристик (диаграммы Боде) |
|
nyquist(<LTI-объект>) |
Построение частотного годографа Найквиста |
Для определения корней полиномов степени k, может, также, применятся команда MATLAB roots(P), которая, в качестве аргумента P, получает матрицу коэффициентов полинома [pBkB, …, pB0B].
Другим вариантом получения графиков динамических характеристик САУ является использование графического интерфейса ППП CST – LTI viewer, вызов которого осуществляется командойltiviewкоторой, в качестве параметра, можно указать имя переменной, содержащей LTI-объект.
Таким образом, выполнение лабораторной работы состоит из следующих шагов:
1. Изучить теоретические сведения.
2. Запустить систему MATLAB.
3. Создать tf-объект, в соответствии с заданным вариантом.
4. Составить дифференциальное уравнение, определяющее функционирование САУ.
5. Определить полюса передаточной функции ![]() c использованием команды roots или pole.
c использованием команды roots или pole.
6. Определить нули передаточной функции ![]() c использованием команды roots или zero.
c использованием команды roots или zero.
Используя LTI-viewer, или соответствующие команды (таблица 1)получить динамические характеристики – переходную функцию h(t),импульсно-переходную функцию w(t).
3.5 Пример
Задана передаточная функция САУ ![]() .
.
Найдем ее динамические и частотные характеристики. Будем работать в командном режиме среды MATLAB.
1. Создадим LTI-объект с именем w, для этого выполним:

2. Найдем полюса и нули передаточной функции с использованием командpole, zero.

3. Построим переходную функцию командой step(w). Результат ее выполнения приведен на рисунок 3.
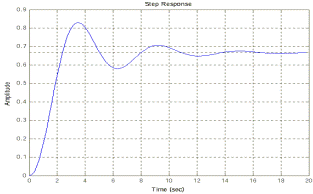
Рисунок 3 - Переходная функция h(t).
4. Построим импульсную переходную функцию командой impulse(w). Результат показан на рисунке 4.
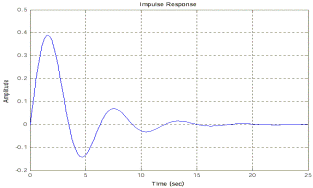
Рисунок 4 - Импульсная переходная функция.
3.6 Контрольные вопросы
1. Представьте систему в виде последовательного соединения типовыхзвеньев.
2. Дайте определение и поясните физический смысл переходнойфункции.
3. Представьте исходную систему в пространстве состояний.
4. Найдите передаточную функцию замкнутой системы.
ЛАБОРАТОРНАЯ РАБОТА №4
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы: Ознакомление с частотными характеристиками систем автоматического управления (САУ) и получение навыков исследования линейных динамических моделей.
4.1 Постановка задачи
В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов
![]()
Необходимо:
1. Построить логарифмические частотные характеристики L (w ).
2. Построить частотный годограф Найквиста:
W(iw ), w = [0, ¥ ].
3. Представить исходную систему в виде последовательного соединениятиповых звеньев. Построить характеристики этих типовых звеньев.
4.2 Краткие теоретические сведения
Благодаря широкому применению при исследовании устойчивости динамических систем и проектировании регуляторов получили распространение частотные характеристики.
Пусть на вход системы с
передаточной функцией W(s) подаетсягармонический сигнал![]()
В этих условиях справедлива следующая теорема:
Если звено является устойчивым, то установившаяся реакция y(t) на гармоническое воздействие является функцией той же частоты с амплитудой
aByB= aBuB|W(iw)|,
и относительным сдвигом по фазе
y = argW(iw).
Таким образом, выход определяется гармонической функцией
y(t) = aBuB|W(iw)| cos(w t + argW(iw)), где i-комплексная
единица (i2=-1), ![]()
Частотной характеристикой W(iw) стационарной динамической системы называется преобразование Фурье переходной функции:
![]() , где
w(t
– t ) – импульсная
переходная функция.
, где
w(t
– t ) – импульсная
переходная функция.
Связь между комплексной передаточной функцией и частотной характеристикой, исходя из свойств преобразований Фурье можно представить в виде соотношения:
![]()
При фиксированном значении w частотная характеристика является комплексным числом, и, следовательно, может быть представлена в виде
![]()
Здесь
![]()
![]()
![]()
![]()
Геометрическое место точек W(iw) на комплексной плоскости при изменении w от w B0 до от w B1B (обычно w B0 B= 0, w B1B = ¥ ), называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста.
Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная характеристика, ЛАХ), которая определяется как L = 20 lg A(w ), измеряется в децибелах и строится как функция от lg w .
4.3 Последовательность выполнения работы
Для выполнения лабораторной работы используется пакет прикладных программ (ППП) ControlSystemToolbox. ППП предназначен для работы с LTI-моделями (LinearTimeInvariantModels) систем управления.
Выполнение лабораторной работы состоит из следующихшагов:
1. Изучить теоретические сведения.
2. Запустить систему MATLAB.
3. Создать tf-объект, в соответствии с заданным вариантом.
4. Составить дифференциальное уравнение, определяющее функционирование САУ.
5. Используя LTI-viewer, или соответствующие команды (табл.1) частотные характеристики – диаграмму Боде, частотный годограф Найквиста.
6. Получить представление исходной функции в виде произведения типовых звеньев.
4.4. Пример
Задана передаточная функция
САУ ![]()
Найдем ее частотные характеристики. Будем работать в командном режиме среды MATLAB.
1. Создадим LTI-объект с именем w, для этого выполним:
******
2. Диаграмму Боде получим, используя команду bode(w) – рисунок 5.
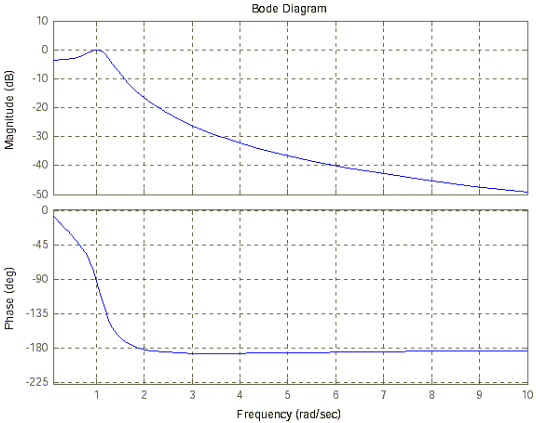
Рисунок 5 - Логарифмические частотные характеристики.
3. Определим частотный годограф Найквиста, выполнив команду nyquist(w) – рисунок 6.
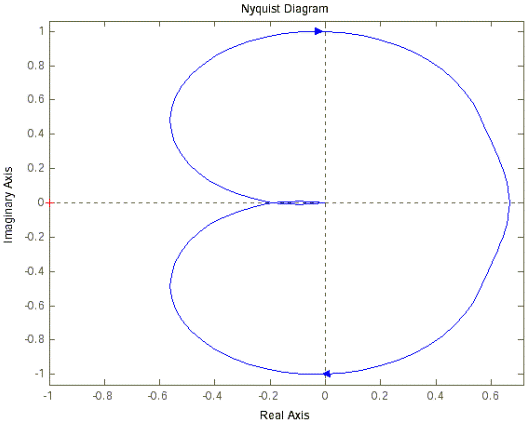
Рисунок 6 - Частотный годограф.
Аналогичные результаты (рисунок 7) можно получить, используя команду ltiview(w), с соответствующими настройками в меню “PlotConfiguration”.
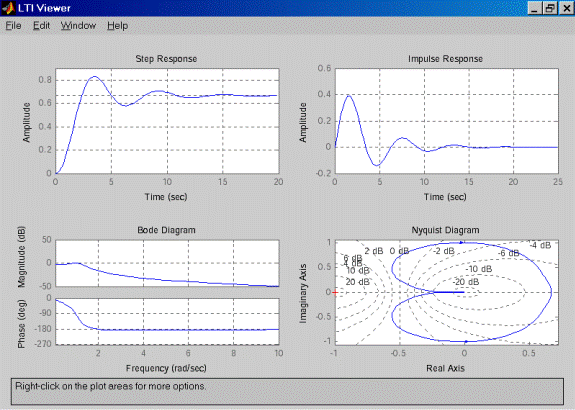
Рисунок 7 - LTI-viewer.
Каждая из построенных характеристик полностью и однозначно определяет рассматриваемую систему управления.
Лабораторная работа №5
Анализ и синтез САУ методом корневого годографа с использованием ControlSystemToolbox
Цель работы: научиться строить корневой годограф и вычислять граничные коэффициенты устойчивости системы.
5.1 Краткие теоретические сведения
В ряде случаев, имеющих практическое значение, модель линейной системы автоматического управления (САУ) задается в виде структурной схемы, состоящей из типовых звеньев, математическое описание которых задано в операторной форме. Связь между входом и выходом системы задается в виде передаточной функции W(s). B общем виде передаточную функцию W(s) можно представить в виде:
W(s)=B(s)/A(s), (1)
где s - комплексная переменная, B(s) - полином степени m; A(s) – полином степени n.
Для физически реализуемых САУ m≤n. Коэффициенты указанных полиномов действительные числа.
Применение метода корневого годографа (КГ) обусловлено фундаментальной зависимостью поведения линейной САУ от полюсов и нулей ее передаточной функции. Под полюсами подразумеваются корни полинома - знаменателя A(s), а под нулями - корни полинома числителя B(s).
Полином A(s) называется также характеристическим многочленом передаточной функции W(s).
Положение полюсов W(s) на комплексной плоскости определяет устойчивость САУ, а в совокупности с нулями вид импульсной переходной функции w(t) и переходной функции h(t).
Метод корневого годографа позволяет находить полюса и нули передаточной функции замкнутой системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы k.
Передаточную функцию разомкнутой системы Wp(s) представим в виде:
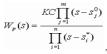 (2)
(2)
где s0j- нули передаточной функции![]() ; s*j- полюса передаточной функции Wp(s),
; s*j- полюса передаточной функции Wp(s), ![]() n и m -
порядки знаменателя и числителя; K
- коэффициент усиления
разомкнутой системы; C
– коэффициент
представления.
n и m -
порядки знаменателя и числителя; K
- коэффициент усиления
разомкнутой системы; C
– коэффициент
представления.
Передаточная функция разомкнутой системы, как правило, задается в виде отношения произведений передаточных функций стандартных (типовых) звеньев, при описании которых используются выражения трех видов:
Ts, (3)
Ts + 1, (4)
T 2s 2 + 2Tζ s + 1. (5)
ЗдесьТ- постоянная времени [с].
Если выражения (3)-(5) стоят в знаменателе передаточных функций звеньев (в числителе 1), то звенья называются соответственно интегрирующим, апериодическим, колебательным. Для колебательного звена ζ - безразмерный коэффициент затухания (0<ζ<1). Если выражения (3)-(5) стоят в числителе передаточных функций звеньев (1), то звенья называются соответственно дифференцирующим, форсирующим первого порядка, форсирующим второго порядка.
Для перехода от стандартной формы записи к формуле (2) необходимо вычислить полюса и нули соответствующих типовых звеньев.
Для передаточных функций, использующих выражение (3):
s*(0)=0 (6)
использующих выражение (4):
s*(0)= -1/T (7)
использующих выражение (5):
![]() (8)
(8)
или
![]() (9)
(9)
где ![]()
Коэффициент представления C вычисляется с помощью выражения:
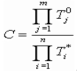 (10)
(10)
Для звеньев, использующих выражение (5), соответствующая постоянная времени входит в выражение (10) в квадрате.
При замыкании системы с передаточной функцией Wp(s) единичной обратной связью передаточная функция замкнутой системы Wз(s) принимает вид:
![]() (11)
(11)
где знак "+" соответствует отрицательной обратной связи; знак "-" соответствует положительной обратной связи.
Структурная схема системы с обратной связью приведена на рисунок 8.

Рисунок 8 - Структурная схема САУ.
Из (11) следует, что нули передаточной функции замкнутой системы равны нулям передаточной функции разомкнутой системы.
Для определения полюсов замкнутой системы необходимо решить уравнение:
Wp(s)= -1. (12)
Так как Wp(s) является функцией комплексного переменного s, то уравнение (12) распадается на два уравнения: уравнение модулей и
|W(s)|=1 (13)
уравнение аргументов
arg W(s) = ± (2υ +1)π, υ =0, 1, 2, … (14а)
для отрицательной обратной связи и
arg W(s) = ± 2π, υ =0, 1, 2, …, (14б)
для положительной обратной связи.
Уравнения (14) имеют наглядный геометрический смысл. Если точка s является полюсом замкнутой системы, то проведя в точку s вектора из всех нулей Wp(s) (обозначим аргументы этих векторов θP0j) и вектора из всех полюсов Wp(s) (обозначим аргументы этих векторов θP*j) уравнение (14а) можно записать в следующем виде:
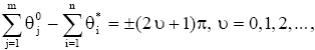 (15a)
(15a)
а уравнение (14б) в виде:
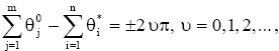 (15б)
(15б)
Углы θ отсчитываются от положительного направления действительной оси. Знак угла "+" соответствует повороту против часовой стрелки, знак угла "-" соответствует повороту по часовой стрелке.
Геометрическое место точек на комплексной плоскости "s", удовлетворяющее выражениям (15а) и (15б) называется корневым годографом.
Как следует из (15), конфигурация корневого годографа не зависит от коэффициента усиления K, но каждому конкретному значению K однозначносоответствуют точки на корневом годографе.
Для определения этого соответствия достаточно воспользоваться уравнением (13) в следующей интерпретации:
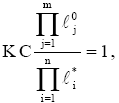 (16)
(16)
где![]() - модуль (длина) вектора, проведенного из
j-нуля в точку s КГ;
- модуль (длина) вектора, проведенного из
j-нуля в точку s КГ;![]() модуль вектора, проведенного из i полюса в ту же точку s.
модуль вектора, проведенного из i полюса в ту же точку s.
Для систем небольшого порядка m, n <5…7 построение КГ можно осуществлять “вручную” (с помощью транспортира и линейки). Приведем свойства корневых годографов (случай отрицательной обратной связи):
1. Ветви корневого годографа непрерывны и расположены на комплексной плоскости симметрично относительно действительной оси.
2. Число ветвей КГ равно порядку системы n. Ветви начинаются в n полюсах разомкнутой системы при K=0. При возрастании K от 0 до бесконечности полюса замкнутой системы двигаются по ветвям КГ.
3. Отрезки действительной оси, по которым перемещаются действительные полюса замкнутой системы являются действительными ветвями корневого годографа. Эти ветви находятся в тех частях действительной оси, справа от которых расположено нечетное общее число действительных полюсов и нулей разомкнутой системы.
4. m ветвей КГ при возрастании K от 0 до бесконечности заканчиваются в m нулях Wp(s), a (n-m) ветвей при K, стремящемся к бесконечности, удаляются от полюсов вдоль асимптот.
5. Асимптоты в виде звезды из (n-m) полупрямых выходят из точки с координатой
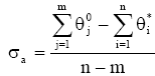
на действительной оси под углами:
![]()
к действительной оси.
6. Угол выхода ![]() ветви КГ из полюса
ветви КГ из полюса ![]() определяется из уравнения (15а),
примененного к данному полюсу. Аналогично определяется угол входа ветви КГ в
нуль
определяется из уравнения (15а),
примененного к данному полюсу. Аналогично определяется угол входа ветви КГ в
нуль![]() .
.
7. При расположении ветвей корневого годографа в левой полуплоскости s САУ устойчива. При пересечении ветвей КГ мнимой оси слева направо САУ становится неустойчивой. Пусть при K=KBкрBпересечение КГ с мнимой осью произойдет в некоторой точке iωBкрB. Назовем это значение коэффициента усиления критическим KBкрB, а величину ωBкрBкритической угловой частотой, на которой система становится неустойчивой.
Метод КГ позволяет выбрать коэффициент усиления САУ, подобрать расположение полюсов и нулей передаточной функции корректирующих звеньев, определить параметры доминирующих полюсов САУ (ближайших к началу координат плоскости s).
В качестве примеров, приведем КГ для двух систем автоматического управления.
На рис.2,а приведен корневой годограф САУ, передаточная функция разомкнутой системы, которой равна:
![]()
На рисунок 9,б представлен КГ САУ с передаточной функцией разомкнутой системы вида:
![]()
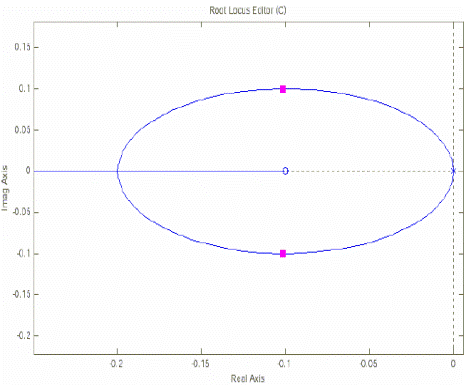
а)
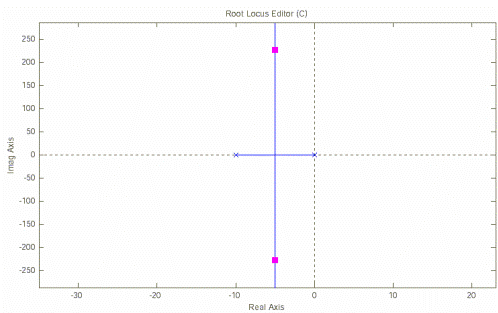
б)
Рисунок 9 - Примеры корневых годографов.
Построение корневых годографов
Постановка задачи.
Дана модель разомкнутой системы, записанная в виде отношения произведений типовых звеньев.
Необходимо:
1. Построить корневой годограф.
2. Получить коэффициент усиления KBкрB, при котором система находится на границе устойчивости.
3. Вычислить частоту ωBкрB, при которой в системе возникают незатухающие колебания.
Для решения задачи используется GUI-интерфейс “SISO-DesignTool” из пакета прикладных программ ControlSystemToolbox системы инженерных расчетов MatLab.
Графический интерфейс предназначен для анализа и синтеза одномерных линейных (линеаризованных) систем автоматического управления (SISO - SingleInput/SingleOutput).
В ControlSystemToolbox имеется тип данных, определяющих динамическую систему в виде набора полюсов, нулей и коэффициента усиления передаточной функции. Синтаксис команды, создающий LTI (LinearTimeInvariant)-систему в виде объекта ZPK(zero-pole-gain) с одним входом и одним выходом
![]()
где![]() - значения нулей системы,
- значения нулей системы,![]() - значения полюсов системы, K - коэффициент усиления.
- значения полюсов системы, K - коэффициент усиления.
Более естественным является вариант, при котором с помощью функции ZPK создается символьная переменная 's', которая затем используется для определения передаточной функции в виде отношения (2).
Например, после выполнения команд: s=zpk('s'); W1=(s+0.1)/(s^2) произойдет создание переменной W1 типа ZPK, определяющей передаточную функцию вида:
![]()
Запуск графического интерфейса SISO-DesignTool осуществляется командой sisotoolили выбором соответствующего пункта в окне "LaunchPad".
Необходимо выбрать в меню Viewпункт RootLocus(корневой годограф), для отображения редактора RootLocusEditor. В правом верхнем углу SISO-DesignTool можно менять тип обратной связи (кнопка '+/-') и структурную схему САУ. Предполагается наличие отрицательной обратной связи, и структурной схемы, показанной на рис.1.
Для загрузки данных из рабочего пространства MatLab необходимо использовать меню "File/Import", в результате чего появляется диалог ImportSystemData. Необходимо, чтобы в результате импортирования данных получилась рассматриваемая схема САУ (см. рис.1). Изменение динамических и частотных характеристик замкнутой системы при изменении К можно проследить используя меню "Tools/LoopResponses".
Задание к лабораторной работе.
Пусть необходимо исследовать САУ с передаточной функцией разомкнутой системы:
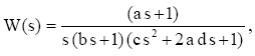
для которой коэффициенты a,b,c,d определяются индивидуальным вариантом.
Рассмотрим пример исследования САУ на следующем наборе коэффициентов:
a=0.2; b=0.1; c=0.04; d=0.3.
1. Создадим ZPK-объект, найдем полюса и нули разомкнутой системы:
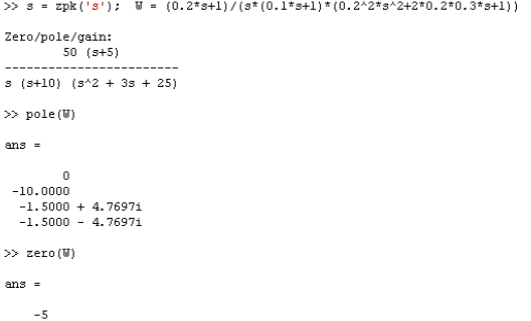
2. Запустим SISO-DesignTool, настроим параметры и импортируем ZPK-объект из рабочего пространства MatLab (рисунок 10). В окне RootLocusEditorинтерфейса SISO-DesignTool построится корневой годограф (рисунок 11).
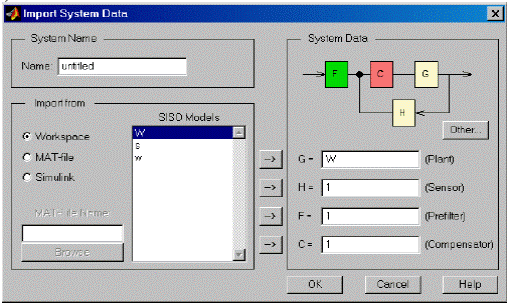
Рисунок 10 - Диалог импортирования данных в SISO-DesignTool.
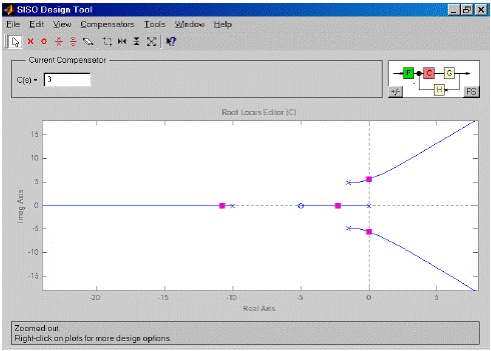
3. Двигая красным курсором по корневому годографу до пересечения ветвей с мнимой осью, определить значение KBкрB(рисунок 5). В данном случае KBкрB>>3. Значение ωBкрBсоответствует мнимой координате пересечения КГ мнимой оси. Просмотреть это значение можно в нижней части интерфейса или выбрав меню "View/Closed-Loop Poles" (рисунок 6).
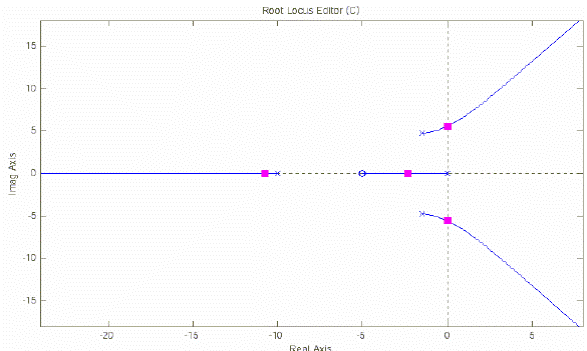
Рисунок 12 - Корневой годограф с нанесенным значением Kкр.
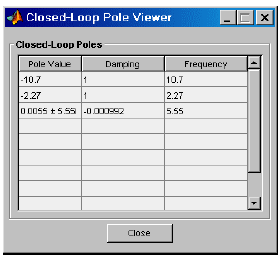
Рисунок 13 - Closed-Loop Poles Viewer.
|
№ варианта |
a= |
b= |
c= |
d= |
|
|
0.2 |
0.1 |
0.04 |
0.3 |
|
|
0.1 |
0.09 |
0.02 |
0.2 |
|
|
0.3 |
0.1 |
0.04 |
0.1 |
|
|
0.2 |
0.1 |
0.06 |
0.2 |
|
|
0.3 |
0.2 |
0.06 |
0.3 |
|
|
0.1 |
0.2 |
0.02 |
0.2 |
|
|
0.3 |
0.3 |
0.04 |
0.1 |
|
|
0.2 |
0.3 |
0.04 |
0.2 |
|
|
0.2 |
0.2 |
0.06 |
0.3 |
|
|
0.2 |
0.2 |
0.04 |
0.1 |
|
|
0.3 |
0.4 |
0.05 |
0.2 |
|
|
0.3 |
0.4 |
0.04 |
0.2 |
|
|
0.3 |
0.2 |
0.06 |
0.1 |
|
|
0.1 |
0.09 |
0.02 |
0.4 |
|
|
0.1 |
0.09 |
0.04 |
0.2 |
Лабораторная работа №6
Описание динамических систем в пространстве состояний с использованием ControlSystemToolbox
Цель работы: научиться строить результирующие системы и исследовать наблюдаемость и управляемость систем.
Постановка задачи
Даны математические модели трех систем и структурная схема, представляющая собой соединение этих систем. Необходимо:
• получить модель результирующей системы в пространстве состояний,
• исследовать наблюдаемость и управляемость трех подсистем в отдельности, и общей системы.
Многомерные системы, в отличие от одномерных имеют несколько входов и несколько выходов. Для описания таких систем используются три набора параметров (три вектора), см. рис.1:
1. вектор входных воздействий (управлений);
2. вектор переменных состояний;
3. вектор выходных параметров,
и два преобразования:
1. преобразование “входы-состояния”;
2. преобразование “состояния-выходы”.
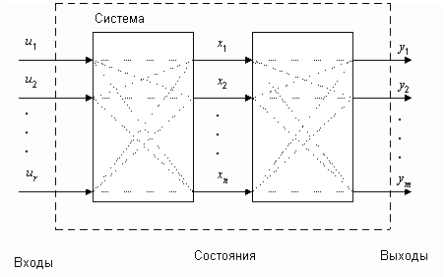
Рис.1. Многомерные системы.
Широкое распространение, обусловленное разработанным математическим аппаратом, получили линейные модели многомерных систем в пространстве состояний, которые имеют вид:
![]()
![]()
первое соотношение называется уравнением состояния, второе – уравнением выхода. Здесь x=(xB1B, xB2B, …, xBnB)PTP | RnP - вектор переменных состояний;
г=(гИ1Иб гИ2Иб…б гИкИ)ЗЕЗ / Г / КтЗ - вектор управленийжн=(нИ1Иб нИ2Иб …б нИьИ)ЗЕЗ / КтЗ – вектор измеряемых параметров; t - время; A(t), B(t), C(t) - матрицы размерности (n x n), (n x r),(m x n) соответственно.
Предполагается, что известны начальные состояния x(tB0B)=xB0B, где tB0B - начальный момент времени.
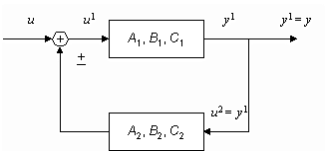
Если матрицы A(t), B(t), C(t) не зависят от времени t, то система называется стационарной. В пакете предполагается, что системы стационарны. Рассмотрим задачи соединения двух подсистем в систему. При соединении возможны три варианта (см. рис.2): параллельное (а), последовательное (б) и в обратной связи (в). Предполагается, что обе системы описываются в пространстве состояний соотношениями:
![]()
![]()
где xP1P, uP1P, yP1 P- векторы состояний, управлений, выходов первой системы; xP2P,uP2P,yP2 P- второй системы соответственно. Необходимо по известным матрицам ИAB1B, BB1B, CB1B, AB2B, BB2B, CB2 получить матрицы А, В, С (см. рис.2г).
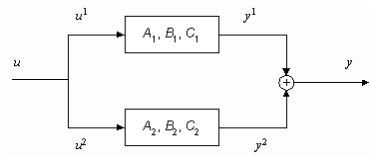
a)
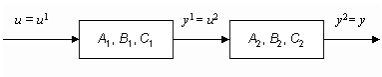
б)
в)
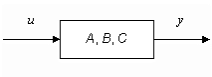
г)
Рис.2. Соединение двух систем.
1. Параллельное соединение
Запишем уравнения системы, с учетом особенностей соединения,
указанных на рис.2а.
![]()
![]()
![]()
отсюда получаем:
![]()
Окончательно матрицы соединения имеют вид –
![]()
2. Последовательное соединение:
![]()
![]()
![]()
в матричном виде:
![]()
окончательно имеем, что:
![]()
3. Обратная связь:
![]()
![]()
![]()
в матричном виде:
![]()
Следовательно,
![]()
Для линейных систем справедливо следующие правило, называемое принципом суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме нескольких воздействий, равен сумме эффектов от нескольких воздействий в отдельности. Закон изменения вектора состояний линейной системы представляется в виде суммы свободного и вынужденного
колебания: x(t)=xBcB(t)+xBвB(t).
Свободное движение xBcB(t) происходит при отсутствии внешнего воздействия в ненулевых начальных условиях. Оно определяется решением однородной системы уравнений, соответствующей исходному уравнению состояний x(t)=A(t)x(t) с начальными условиями x(tB0B)=xB0B.
Вынужденное движение xBвB(t) - это реакция системы на внешнее воздействие u(t) при нулевых начальных условиях. Оно определяется решением неоднородного уравнения при нулевых начальных условиях.
Для многомерных нестационарных систем, описываемых соотношениями, поведение векторов состояния и выхода определяется по формулам вида:
x(t)=Ф(t,t0)x(t0)+
y(t)=C(t)Ф(t,t0)x(t0)+![]()
где Ф(t,_ ) - переходная матрица, или матрица Коши, являющаяся решением
уравнения
![]()
с начальным условием Ф(τ,τ)=I.
Первые слагаемые в выражениях (2), (3) описывают свободное движение, а вторые - вынужденное. Для многомерных стационарных систем, описываемых уравнениями (1), законы изменения вектора состояния и вектора выхода находятся по следующим формулам:
x(t)=Ф(t)x(0)+
y(t)=CФ(t)x(0)+![]()
где Ф(t-τ) - переходная матрица стационарной системы, зависящая от разности t-_. В данном случае решение уравнения (4) имеет вид
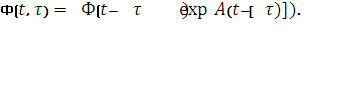
Одними из важнейших задач теории управления является исследование управляемости и наблюдаемости динамических систем. Сформулируем соответствующие определения и критерии для стационарных линейных систем.
Система называется вполне управляемой, если выбором управляющего воздействия u(t) на интервале времени [tB0B,tB1B] можно перевести систему из любого начального состояния х(tB0B) в произвольное заранее заданное конечное состояние x(tB1B).
Система называется вполне наблюдаемой, если по реакции у(tB1B) на выходе системы на интервале времени [tB0B,tB1B] при заданном управляющем воздействии u(t) можно определить начальное состояние х(tB0B).
Критерий управляемости линейных систем. Для того чтобы система была вполне управляемой, необходимо и достаточно, чтобы ранг матрицы управляемости
MBUB =(В АВ АP2PВ … АPn-1PВ)
равнялся размерности вектора состояния: rangMBUB=n.
Критерий наблюдаемости линейных систем. Для того чтобы система была вполне наблюдаемой, необходимо и достаточно, чтобы ранг матрицы наблюдаемости
MBYB =(CPTP APTPCPTP (APTP)P2PC … (APTP)Pn-1PCPTP)
равнялся размерности вектора состояния: rangMBYB=n.
Использование ControlSystemToolbox
Для решения задачи используется пакет прикладных программ ControlSystemToolbox среды MatLab. В ControlSystemToolbox имеется тип данных, определяющих динамическую систему в пространстве состояний. Синтаксис команды, создающий непрерывную LTI (LinearTimeInvariant)-систему в виде ss-объекта с одним входом и одним выходом: SS(A, B, C, D).
В эту функцию в качестве параметров передаются матрицы уравнений состояний и выходов вида:
x(t)=Ax(t)+Bu(t);
y(t)=Cx(t)+Du(t);
В связи с тем, что рассматривается модель вида (1), то матрица динамики D будет нулевой.
Для выполнения работы могут применяться команды, приведенные в табл.1.
Таблица 1. Некоторые команды ControlSystemToolbox
|
Синтаксис |
Описание |
|
ctrb(LTI-объект>) ctrb(A, B) |
Формирование матрицы управляемости |
|
obsv(<LTI-объект>) obsv(A, C) |
Формирование матрицы наблюдаемости |
|
Parallel(<LTI1>,<LTI2>) |
Параллельное соединение |
|
series(<LTI1>,<LTI2>) |
Последовательное соединение |
|
feedback(<LTI1>,<LTI2>) |
Соединение обратной связью |
|
append(<LTI1>, …, <LTIN>) |
Объединение систем |
|
connect(<sys>,<Con>,<in>,<out>) |
Установление связей в соединении |
Для получения результатов вычисления матриц, результирующей системы, по структурной схеме, воспользуемся последними двумя командами.
Функция append создает объект sys, представляющий собой объединение всех подсистем. При этом первый входной сигнал первой системы становится входом номер 1, второй входной сигнал первой системы - номер 2, и т.д. далее идут входы второй системы, и т.д.; аналогично определяются и выходы.
В функции connect - параметр <Con> определяет матрицу связей по структурной схеме. Матрица формируется по следующему правилу: каждая строка представляет собой один вход системы sys, первый элемент – номер входа (в соответствии с порядком в команде append), затем идут номера выходов, которые суммируются и подаются на рассматриваемый вход.
Параметры <in>, <out> - строки из номеров входов и выходов соединения, являющиеся внешними.
Например, для последовательного соединения двух систем (см. рис.2б):
sys1= ss(A1, B1, C1, 0)
sys2= ss(A2, B2, C2, 0)
sys=append (sys1, sys2)
sysc=connect(sys, [2 1], [1], [2])
В этом случае на вход второй системы (общий вход номер 2), поступает выход первой (общий выход номер 1); вход первой системы (номер один) и выход второй системы (номер два) являются внешними.
Литература
1.Дададжанов Т., Мухитдинов М.М. “Matlab асослари”,”Фан”,2008,620 б.
2.Бесекерский В.А., ПоповЕ.П. Теория систем автоматического управления. -СПб.: Профессия, 2004. - 752 с.
3.Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория базовых знаний, 2002 – 832 с.
Введение …………………………………………………………………………………………3
Лабораторная работа №1. Тема: Знакомство со средой MATLAB. Вычисления в командном режиме………………………………………………………………………………4
Лабораторная работа №2. Управление потоками. Создание М-файлов. Обработка массивов данных…………………………………………………………………………………8
Лабораторная работа №3. Динамические характеристики систем автоматического управления………………………………………………………………………………………11
Лабораторная работа №4. Частотные характеристики систем
автоматического управления………………………………………………………………….15
Лабораторная работа №5. Анализ и синтез САУ методом корневого
годографа с использованием ControlSystemToolbox………………………………………19
Лабораторная работа №6. Описание динамических систем в пространстве
состояний с использованием ControlSystemToolbox………………………………………28
Литература………………………………………………………………………………………33
Методические указания к
выполнению лабораторных
работ по курсу «Основы
теория управления»
Рассмотрены и рекомендованы
к изданию на заседании
научно-методического
Совета ТУИТ
от «19» января
протокол № __46________
Составители: Когай В.Н
Турсунбаев Ф.К.
Яковлева Ю.А.
Азимова У.А.
Ответственный редактор: Турсунбаев Ф.К.
Корректор: Яковлева Ю.А.