Узбекское агентство почты и телекоммуникации

Ташкентский электротехнический институт связи

Кафедра инженерной графики

Конспект лекций по курсу

 ИНЖЕНЕРНАЯ ГРАФИКА

Ташкент - 2000

Содержание

	Введение
Лекция 1	Основные свойства проецирования. Комплексный чертеж точки Комплексный чертеж прямой
Лекция 2	Определение истинной (натуральной) величины отрезка прямой. Взаимное положение двух прямых
Лекция 3	Плоскость. Положение плоскости относительно плоскостей проекции. Прямая и точка в плоскости.
Лекция 4	Построение взаимно перпендикулярных прямой и плоскости. Построение линии пересечения двух плоскостей
Лекция 5	Способы преобразования чертежа. Способ замены плоскостей. Способ вращения
Лекция 6	Поверхности. Образование и классификация поверхностей. Пересечение поверхности плоскостью
Лекция 7	Построение чертежей взаимно пересекающихся поверхностей. Способ вспомогательных секущих плоскостей
Лекция 8	Аксонометрические проекции
Лекция 9	Возможности машинной графики
	Литература

Лекция № 1

Основные свойства проецирования

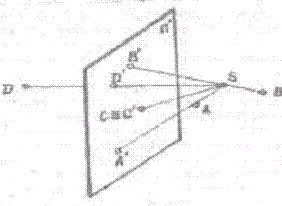
Центральная проекция (перспектива).

Пусть дана некоторая плоскость П', которую называют плоскостью проекций, и вне ее точка S, называемая центром проекций.

Для построения изображения или проекции А' некоторой точки А проводят через точку А и центр проекций S прямую SA, называемую проецирующей прямой, а затем находят точку А' пересечения этой прямой с плоскостью П'.

Таков метод центрального проецирования точек пространстве на плоскость проекций П', его можно записать с помощью символов

А'=П' х SA

Проецирование можно выполнить для любой точки пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П'(Рис.1)

Рис.1.

Изображение предметов при помощи центрального проецирования обладает большой наглядностью, т.к. процесс человеческого зрения совпадает с операцией центрального проецирования.

Метод центрального проецирования сложен и в значительной степени искажает форму и размеры оригинала, т.к. не сохраняет параллельности прямых и отношения отрезков. Поэтому на практике пользуются методом параллельного проецирования ( в частности, ортогонального проецирования). Этот метод, является частным случаем центрального проецирования, когда центр проекций находится в бесконечно удаленной точке S_¥ дает более простоепостроение изображения н в большей степени сохраняет те свойства оригинала, от которых зависят его форма н размеры.

Параллельная проекция

Пусть даны плоскость проекций П' и направление проецирования непараллельное плоскости проекций. Удалив центр проекций S_¥ в бесконечно удаленную точку S_¥, то все проецирующие прямые будут параллельны некоторому направлению S. Чтобы построить проекцию А' точки А, проводят проецирующую прямую параллельно направлению проецирования S, а затем находят точку А' пересечения прямой с плоскостью П' Таков метод параллельного проецирования точек пространства на плоскость проекций. (Pиc.2)

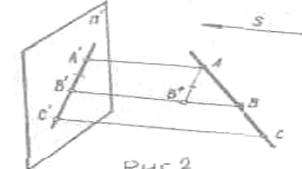
Рис.2.

Еще большее упрощение построения чертежа дает применение ортогонального проецирования, который является частным случаем параллельного перемещения, когда направление проецирования перпендикулярно плоскости проекции П'. В этом случае нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции.

Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к позволяет судить о размерах изображаемых предметов.

Рассмотренный метод проецирования позволяют однозначно решить прямую задачу, т.е. по данному оригиналу строить его проекционный чертеж. Обратная задача - по данному проекционному чертежу воспроизвести оригинал - не решается однозначно, т.е. чертеж не обладает свойством обратимости. Для получения обратимых чертежей дополняет проекционный чертеж необходимыми данными.

В данном курсе будут применяться два вида обратимых чертежей:

Комплексные чертежи в ортогональных проекциях и аксонометрические чертежи.

Рассмотрим некоторые свойства параллельной проекции.

1. Проекцией точки является точка.

2. Проекцией прямой линии является прямая линия.

3. Проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой, (свойство принадлежности).

4. Проекциями параллельных прямых являются параллельные прямые.

5.  Отношения проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков.

6.  Проекция фигуры не меняется при параллельном переносе плоскости проекций,

Комплексный чертеж точки .

Чертеж, составленный из двух н более связанных между собой ортогональных проекций изображаемого оригинала, называется комплексным чертежом в ортогональных проекциях или комплексном чертежом. Принцип преобразования чертежа состоит в том, что данный оригинал проецируется ортогональна на две взаимно перпендикулярные плоскости проекций, которые затем совмещают с плоскостью чертежа.

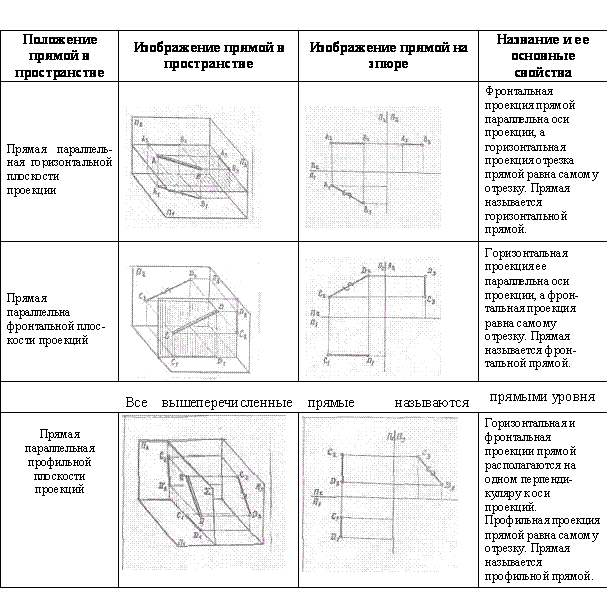
Одна из плоскостей проекций П₁ располагается горизонтально и называется горизонтальной плоскостью проекций, другая плоскость П₂ располагается вертикально и называется фронтальной плоскостью проекций. Прямую пересечения плоскостей проекций называют осью проекций. В результате получаем две проекции горизонтальную проекцию точки а₁ и фронтальную проекцию точки a₂. (Рис.3)

Рис.3.

Комплексный чертеж прямой

Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая прямая линия может быть задана проекциями A₁A₂ и B₁B₂ двух ее точек А и В. прямую на комплексном чертеже можно задать ее проекциями.

Прямая линия может занимать относительно плоскостей проекций различные положения

Комплексный чертеж называет эпюр Монжа или просто эпюр

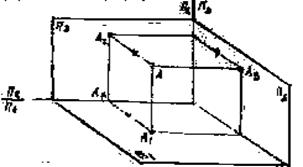
Рис.4.

Расстояние от точки А до плоскости П₁ называют высотой точки (АА₁). Расстояние от точки А до плоскости П₂ называют глубиной точки (АА₂). Расстояние о точки А до плоскости П₃ называют шириной точки (АА₃) (Рис. 4).На эпюре получен чертеж точки (Рис. 5).

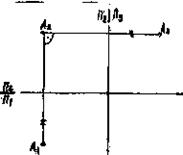
Рис.5

Плоскости проекций, пересекаясь, образуют оси координат, Точка пересечения координат, является началом координат. Любую точку пространства можно задать ее координатами. Рассмотрим построение точки по заданным координатам. (Рис.6).

Рис.6.

Лекция № 2

Определение истинной ( натуральной) величины отрезка прямой

Натуральная величина отрезка прямой  является гипотенуза прямоугольного треугольника, у которого одним из катетов будет любая из проекций отрезка, вторым катетом соответственно - высота или глубина одного из концов отрезка относительно другого.

Угол линии с плоскостью проекций определяется как угол, составленный прямой с ее проекцией на этой плоскости. (Рис. 7).

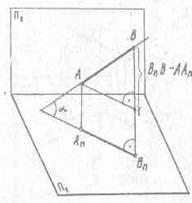
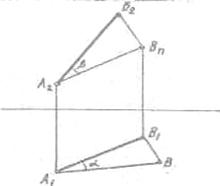
Рис.7.

Взаимное положение двух прямых

Параллельные прямые. Проекции двух параллельных прямых параллельны между собой (Рис.8 а)

Для профильных прямых для определения параллельности прямых, необходимо, чтобы все три проекции прямых были параллельны,  т.к. две проекции профильной прямой не определяют параллельность. (Рис.8 б)        

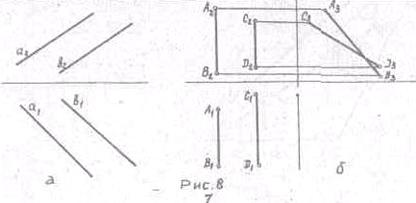
Пересекающиеся прямые. Если прямые линии пересекаются, то п. одноименные проекции пересекаются между собой в точке,  которая является проекцией  точкой  пересечения этих прямых.

Необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных проекций находились  на одном перпендикуляре к соответствующей оси проекций (Рис.9.)

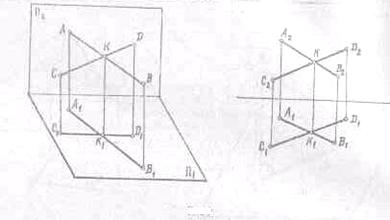
Рис.9

Скрещивающиеся прямые. Скрещивающиеся прямые линии не пересекаются и не параллельны между собой. Хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, т.е. эти прямые не пересекаются между собой Точки пересечения одноименных проекции скрещивающихся прямых представляют собой проекции двух точек, из которых одна принадлежит первой, а другая - второй из этих скрещивающихся прямых. (Рис. 10).

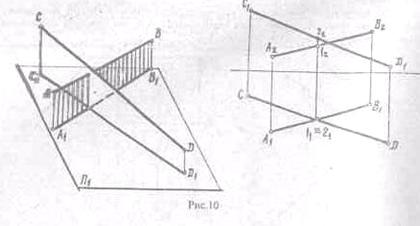
Особое положение прямой линии относительно плоскостей проекций

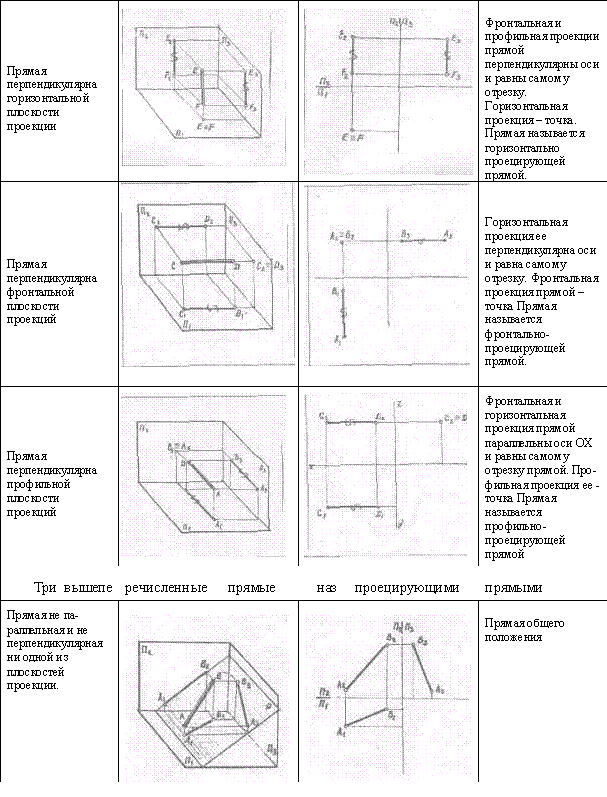
О проекциях плоских углов.

1 Если плоскость, в которой расположен некоторый угол, перпендикулярна к плоскости проекций, то он проецируется на эту плоскость и виде прямой линии,

2  Если плоскость прямого угла не перпендикулярна к плоскости проекции и хотя бы одна его сторона параллельна этой плоскости, то прямой угол

проецируется на нее в виде прямого же угла. (Рис. 11)

Этой теореме о проецировании прямого угла соответствует две обратных.

3. Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций

4. Если проекция некоторою угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой (Рис.12)

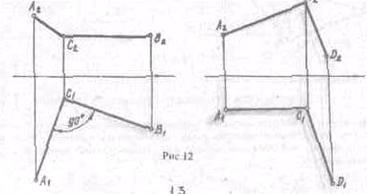
Лекция № 3

Плоскость

 Различные способы задания плоскости на чертеже.(Рис.13)

Положение плоскости в пространстве определяется:

а) тремя точками, не лежащими на одной прямой линии,

6) прямой и точкой, взятой вне прямой,

в) двумя пересекающимися прямыми,

г) двумя параллельными прямыми,

д) любой плоской фигурой,

е) следами плоскости.

Прямые, по которым некоторая плоскость пересекает плоскости проекций, называются следами этой плоскости на плоскостях проекций или следами плоскости.

Рис.13

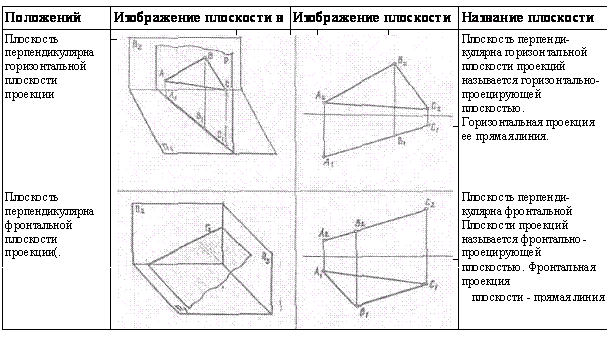
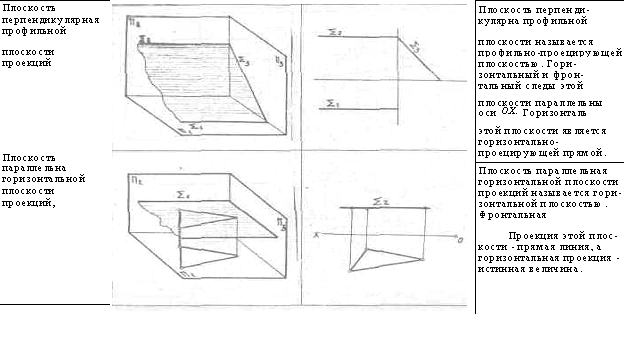
Положения плоскости относительно плоскостей проекции

Возможны следующие положения плоскости, относительно плоскостей проекций:

1) плоскость не перпендикулярна ни одной из плоскостей проекций.

2) плоскость перпендикулярна к одной m плоскостей проекции.

3) плоскость перпендикулярна к двум плоскостям проекций.

Взаимное положение двух плоскостей

Две плоскости могут быть параллельными или пересекаться между собой. Две плоскости параллельны, если иве пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся прямым другой плоскости.

Это служит основным признаком для определения, параллельны плоскости между собой или не параллельны, такими прямыми могут служить следы обоих плоскостей.(Рис.14а)

Если два пересекающихся между собой следа одной плоскости параллельны одноименным с ними следами другой плоскости, то обе плоскости параллельны между собой, (Рис 14б)

Две плоскости могут пересекаться: В этом случае они имеют две общие точки или общую прямую линию, называемую линией пересечения двух плоскостей.

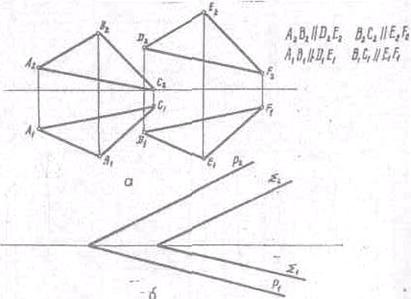
Рис. 14

Прямая и точка в плоскости

1. Прямая принадлежит плоскости, если она проходит через   две точки, принадлежащие данной плоскости (Рис. 15 а,б)

2. Прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельной ей. ( Рис. 15в)

3. Прямая принадлежит плоскости, и имеет с другим следом общую точку.(Рис.15г)

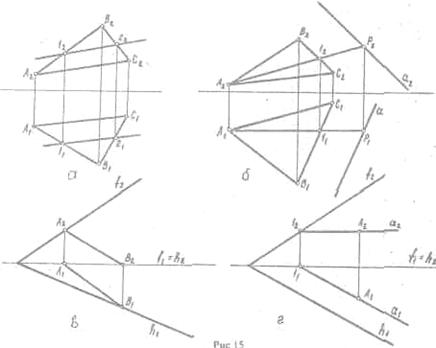
Рис.15

К числу прямых, занимающих особое положение в плоскости, называемых главными линиями плоскости отнесем: горизонтали, фронтали и линии наибольшего наклона к плоскостям проекций.

Горизонталями плоскости называются прямые, лежащие в ней и параллельные горизонтальной плоскости проекции (Рис. 16)

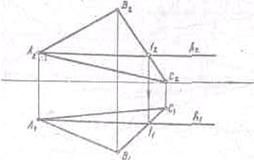
Рис.16

Фронталями плоскости называются прямые, лежащие а ней и параллельные плоскости проекций П₂ т.е. фронтальной плоскости проекций.(Рис. 17)

Рис.17

Линиями наибольшего наклона (линия ската) плоскости к плоскостям проекций П₁ П₂, П₃ называются прямые, лежащие в ней и перпендикулярные к горизонталям, фронталям или профильным прямым. (Рис. 18)

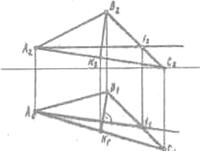
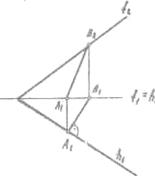
Рис.18

Линия ската плоскости может служить для определения угла наклона этой плоскости к плоскостям проекций. (Рис. 19)

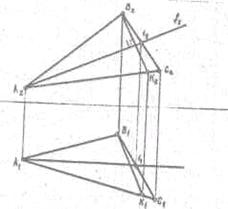
Рис. 19

Взаимное положение прямой и плоскости

Взаимное положение прямой линии и плоскости в пространстве может быть следующим:

1. Прямая лежит в плоскости,

2. Прямая параллельна плоскости,

3.

Прямая пересекает плоскость.

Рис.20

Для определения взаимного положения прямой и плоскости:

1. через данную прямую проводят вспомогательную плоскость и строят линию пересечения этой плоскости и данной плоскости. (Рис.20)

2. устанавливают взаимное положение данной прямой и прямой пересечения плоскостей, найденное положение определяет взаимное положение данных прямой и плоскости,

При этом возможны три случая:

1. прямая MN слипается с прямой АВ. это соответствует тому, что прямая принадлежит плоскости Р. т.е. имеет с ней две общие точки. (Рис.21 а)

2. прямая MN параллельна прямой АВ, это соответствует тому, что прямая АВ параллельна плоскости. Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в дайной плоскости. (Рис.21б)

3. Прямая MN пересекает прямую АВ, это соответствует тому что прямая АВ пересекает плоскость Р, Прямая пересекает плоскость Р, а следовательно имеет с ней одну общую точку. Определение точки пересечения прямой с плоскостью выполняют по следующему алгоритму решения этих задач. Для этого необходимо:

1. Через данную прямую провести вспомогательную плоскость частного положения (горизонтально проецирующую или фронтально-проецирующую).

2. Находим линию пересечения данной плоскости ЛВС и вспомогательную плоскости S₂( фронтально-проецирующей).

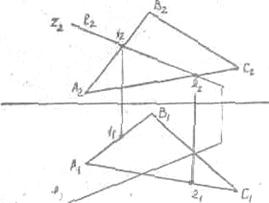
Рис.22

1-2 линия пересечения двух плоскостей, плоскости АВС и плоскости S₂ (Рис.22)

3. Там, где прямая 1 пересекается с линией пересечения 1-2 находим точку пересечения прямой 1 с плоскостью АВС - точку «К», Точка «К» принадлежит прямой 1 так как ее одноименные проекции совпадают с одноименными проекциями прямой

Точка «К» лежит на прямой 1-2, которая принадлежит плоскости АВС, следовательно, точка «К» принадлежит плоскости АВС. Точка «К» принадлежит прямой 1 и плоскости АВС и следовательно является точкой пересечения прямой с плоскостью. Решив задачу, определяем видимость элементов чертежа по конкурирующим точкам. (Рис. 23)

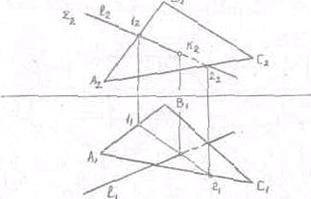
Рис.23

Лекция № 4

 Построение взаимно перпендикулярных прямой и плоскости

Из всех возможных положений прямой, пересекающей плоскости, отметим случай, когда прямая перпендикулярна к плоскости.

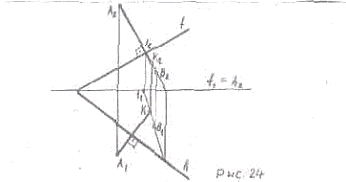
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости. Поэтому, чтобы построить перпендикуляр к плоскости берут две прямые - горизонталь и фронталь в данной плоскости, т.к. перпендикуляр с этими прямыми образует угол равный - 90°

У перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали, профильная проекция перпендикулярна к профильной проекции профильной прямой этой плоскости. (Рис.24)

В случае задания плоскости следами, если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости. (Рис.25)

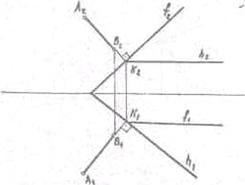
Рис. 25

Т.к перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости, можно воспользоваться этим для проведения перпендикуляра из некоторой точки А к прямой общего положения ВС.

1. через точку А провести плоскость/Г/, перпендикулярную к прямой ВС

2. определить точку К пересечения прямой ВС с плоскостью Г

3. соединить точки А и К отрезком прямой линии. Прямые АК и ВС взаимно перпендикулярны.

Построение линии пересечения двух плоскостей.

Прямые линии, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обоим плоскостям. В общем случае для построения линии пересечения двух плоскостей надо найти какие -либо две точки, каждая из которых принадлежит обоим плоскостям; эти точки определяют линию пересечения плоскостей.

При построение линии пересечения двух плоскостей возможны три случая:

1. Обе плоскости относительно плоскостей проекций занимают частное положение. В этом случае дм определения линии пересечения никаких дополнительных построений выполнять не надо. Проекции линии пересечения совпадают с проекциями данных плоскостей. Линию пересечения на чертеже надо только обозначить. (Рис.26 а) .

2. Одна плоскость относительно плоскостей проекций занимает частное положение, а другая плоскость занимает относительно плоскостей проекций общее положение. В этом случае на чертеже будем иметь одну проекцию линии пересечения, а вторую проекцию линии пересечения строки по свойству принадлежности прямой плоскости. (Рис.26 б).

3. Обе плоскости общего положения относительно плоскостей проекций. (Рис.26 в). В этом случае построение линии пересечение двух плоскостей определяют по точкам пересечения прямых линий одной плоскости с другой плоскостью. Этот способ заключается вы том, что находят точки пересечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью.

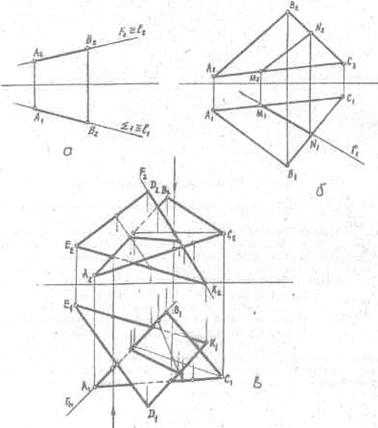
Рис.26

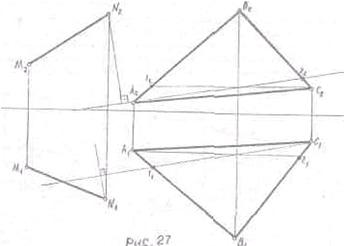
Построение взаимно перпендикулярных плоскостей.

Построение плоскости Г перпендикулярной к плоскости Р, может быть произведено двумя путями: (Рис.27)

1. плоскость Г проводится через прямую, перпендикулярную к плоскости;

2. плоскость Г проводится перпендикулярно к прямой, лежащей в плоскости Р.

Лекция № 5

Способы преобразования чертежа

Общая характеристика способов преобразования чертежа

Решение  пространственных задач  на комплексном  чертеже значительно упрощается,   если интересующие нас элементы пространства занимают частное положение. Достигается это методами преобразования чертежа. Так как частных положений у прямой два н у плоскости два, то существует четыре исходных задачи для преобразования:

1) прямую общего положения сделать прямой уровня;

2) прямую уровня сделать проецирующей,

3) плоскость общего положения сделать проецирующей плоскостью;

4) проецирующую плоскость сделать плоскостью уровня.

Преобразование чертежа отображает изменение положения геометрических образов или плоскостей проеций  в пространстве. Чаще всего применяют способ замены плоскостей и способ вращения.

Способ замены плоскостей

Сущность способа замены плоскостей состоит в том, что пространственное положение объектов пространства остается неизменным, а меняется система плоскостей проекций  путем ввода дополнительных плоскостей проекций, при этом сохраняется взаимная перпендикулярность двух плоскостей проекций. На дополнительные плоскости проекций строятся новые изображения геометрических образов. Дополнительные плоскости выбираются таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положении. Все свойства геометрического образа, отнесенные к основной системе, справедливы и для новой системы плоскостей проекций.

Оси проекций будем отмечать в виде дроби, считая, что черта лежит на этой оси Обозначение плоскостей представляет собой как бы числитель и знаменатель дроби, причем каждая буква ставится на ту сторону оси, где должны размещаться соответствующие проекции, например:

Пусть заданы точка А и система х  — ортогональными проекциями точки А на эти плоскости будут а₁ и A₂. Возьмем новую плоскость П₁^ П₂ и спроецируем точку А на эту плоскость; проекцией будет А₄ (рис. 28)

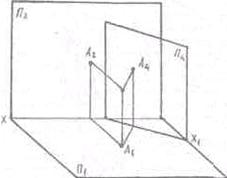
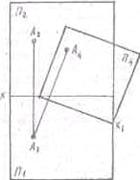
Рис.28.

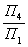Плоскость П₁ входит в обе системы х и х. Поэтому а₁ относится и к системе х .При проецировании точки на П₄ получаем А₄ на расстоянии равном Z_а. Последовательный переход от одной системы плоскостей проекции к другой необходимо осуществлять, выполняя следующее правило. Расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до предыдущей оси.

Если введение одной плоскости не решает задачи, прибегают к последовательному дополнению основной системы плоскостей проекций новыми.

При решении четырех исходных задач выполняют следующее:

- для первой - дополнительную плоскость выбирают параллельно заданной прямой общего положения;

- для второй - дополнительную плоскость выбирают перпендикулярно заданной прямой уровня;

- для третьей - в заданной плоскости общего положения построить линию уровня и дополнительную плоскость выбирают перпендикулярно ей;

- для  четвертой  - дополнительную  плоскость выбирают  параллельно проецирующей плоскости.

Способ вращения

Другой способ преобразования чертежа - вращение. Он состоит в том, что заданная система плоскостей проекций остается прежней, а фигуру вращают вокруг неподвижной оси до тех пор, пока она займет частное положение. В качестве осей вращения удобней всего выбирать проецирующие прямые или прямые уровня, тогда точки будут вращаться в плоскостях параллельных или перпендикулярных плоскостям проекции.

При вращении вокруг горизонтально проецирующей прямой : горизонтальная проекция а₁ точки А перемещается по окружности, а фронтальная А₂ - по прямой являющейся изображением фронтальной проекции окружности. ( Рис 29)

Рис 29

При вращении вокруг оси перпендикулярной фронтальной плоскости проекций горизонтальная проекция точки перемещается по прямой, а фронтальная по окружности, При вращении плоской фигуры вокруг оси перпендикулярной плоскости проекций проекция ее на эту плоскость не изменяется ни по величине, ни по форме, меняется лишь положение этой проекции относительно оси проекции. (Рис. 30)

Рис.30

Все точки второй проекции на плоскость, параллельную оси вращения, перемещаются по прямым, параллельным оси проекции, и проекция изменяется по форме и по величине. Пользуясь этими свойствами можно применить метод вращения, не задаваясь изображением оси вращения и не устанавливая величины радиуса,

Такой метод называется методом плоскопараллельного перемещения. При плоскопараллельном перемещении фигуры в пространстве одна из ее проекций, не изменяясь, перемещается в плоскости проекций, другие проекции точек фигуры перемещаются по прямым, параллельным направлению оси проекции.

Решим задачу на определение натуральной величины плоской фигуры методом плоскопараллельного перемещения. В плоскости треугольника строим горизонталь h₁ и h₂. Горизонтальную проекцию A₁B₁C₁ перемещаем в положение A'₁B'₁C'₁ так, чтобы горизонтальная проекция горизонтали была перпендикулярна оси проекций, я этом случае горизонталь перпендикулярна фронтальной плоскости проекций П₂. а треугольник лежит во фронтально проецирующей плоскости. Фронтальной проекцией треугольника будет прямая А'₂в'₂С'₂.

Перемешаем треугольник относительно .фронтальной плоскости проекции П₂, то есть перемещаем фронтальную проекцию А'₂в'₂С'₂ в положение А"₂в"₂С"₂ , что соответствует положению треугольника в плоскости, параллельной горизонтальной плоскости проекций П₁- Горизонтальная проекция A"₁B"₁C"₁ представляет собой натуральную величину данного треугольника. (Рис.31)

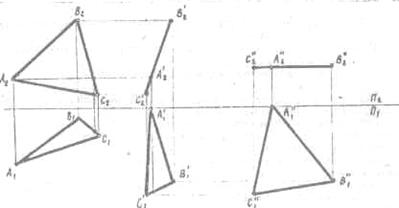
Рис. 31

Лекция № 6

Поверхности

Геометрические формы отдельных предметов представляют собой сочетание простых геометрических  тел - многогранников и кривых поверхностей.

Многогранники

Многогранник - тело, ограниченное плоскими многоугольниками, называемыми гранями.

 Элементами гранных поверхностей, кроме граней, являются:

Ребра - линии пересечения смежных граней

Вершину - точки пересечения ребер.

Построение проекций многогранника сводится к построению его точек и линий, на чертеже многогранники изображаются проекциями своих вершин и ребер, при этом невидимые линии изображаются штриховыми линиями.

Кривые  линии и их проекции

Кривая - совокупность последовательных положений точки, перемещающейся в пространстве. Кривые делятся на плоские, все точки которых лежат в одной плоскости (окружность, эллипс, парабола) и пространственные (винтовые), на закономерные, которые могут быть выражены аналитически, и случайные, которые задаются только графически. Винтовая линия - линия, описываемая точкой при равномерном движении по прямой, если эта прямая равномерно вращается вокруг параллельной ей оси. Для построения проекций кривой необходимо найти    проекции ряда точек, принадлежащих этой кривой.

Свойства проекций кривых.

1. Если точка лежит на кривой, то ее проекции лежат на одноименных проекциях этой кривой на одной линии связи.

2. Плоская кривая, лежащая в проецирующей плоскости, проецируется в прямую.

Образование и классификация поверхностей.

Кривая поверхность - совокупность всех последовательных положений некоторой линии, движущейся в пространстве по определенному закону.

Способы образования поверхностей самые различные, причем одна и та же поверхность может быть получена движением линий разного вида.

Например, боковая поверхность кругового цилиндра:

 а) вращением прямой линии вокруг параллельной ей неподвижной оси,

б) вращением кривой,

в) в результате поступательного движения окружности, центр которой перемещается по прямой перпендикулярной плоскости окружности.

Линия, посредством  которой получена поверхность, называется образующей. Линия, из которой перемещается образующая, называется направляющей.

В зависимости  от вида образующих поверхности подразделяются на линейные ( образующие - прямые) и нелинейные (образующие - кривые)

Линейные поверхности

Цилиндрическая поверхность образована движением образующей, параллельной самой себе, по некоторой кривой. Определена, если задана направляющая по форме и положению и образующая по положению, может быть замкнутой. Тело, ограниченное цилиндрической замкнутой поверхностью и двумя параллельными плоскостями, называют цилиндром. Цилиндр называют круговым, если в его основании лежит круг.

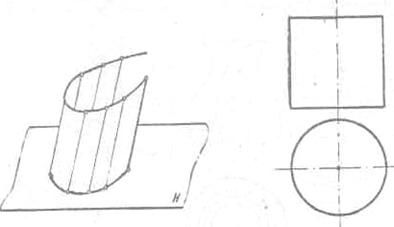
Рис. 32

Коническая поверхность образуется движением прямой линии, проходящей через некоторую точку    (вершину) по некоторой кривой Имеет две полости, определена ни чертеже, если заданы направляющая (по форме и положению) и вершина. Коническая поверхность может быть замкнутой. Тело, ограниченное конической поверхностью, называется конусом. Конус называют круглым, если в основана лежит круг. (Рис.33)

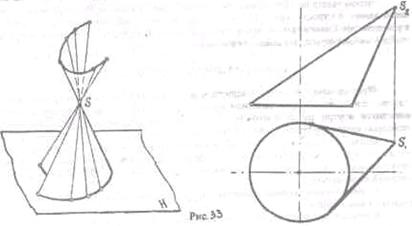
Поверхность вращения определяется на чертеже заданием образующей и оси вращения. Каждая точка образующей описывает при своем вращении окружность с центром на оси. Эти окружности называют параллелями, Наибольшая параллель называется экватором, наименьшая - горлом,

Кривые, получающиеся в сечении тел вращения плоскостями, проходящими через ось (Вращения, называют меридианами. Меридиан, параллельный фронтальной плоскости проекций называют главным ( Рис.34)

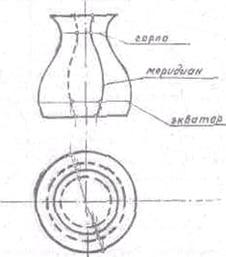
Рис. 34

Построение проекций точек, лежащих на поверхности геометрических тел

Чтобы задать на чертеже проекции точек, принадлежащих геометрическому телу, необходимо построить какую-нибудь линию на заданной поверхности, а затем на проекции этой линии взять проекции искомых точек. В качестве таких линий могут быть выбраны образующие, параллели, меридианы.

Пересечение поверхности плоскостью

При  пересечении любого предмете плоскостью получается некая плоская фигура. называется сечением. Под сечением понимают ту часть секущей плоскости, которая

находится внутри рассеченного тела и ограничена линией сечения. Плоскости, с помощью которых получают сечение, называют секущими.

Фигура сечения многогранника - многоугольник, число сторон которого равно числу граней, пересекаемых плоскостью. Вершинами, этого многоугольника являются точки пересечения ребер секущей плоскостью, а сторонами - линии пересечения граней с секущей плоскостью.

В пересечении кривой поверхности плоскостью в общем случае получается плоская кривая линия.

В сечении цилиндрической поверхности могут быть получены:

1.         окружность, если секущая плоскость перпендикулярна оси вращения;

2. эллипс, если секущая плоскость не перпендикулярна и не параллельна оси вращения;

3. две образующие прямые, если секущая плоскость параллельна оси вращения. (Рис.35)

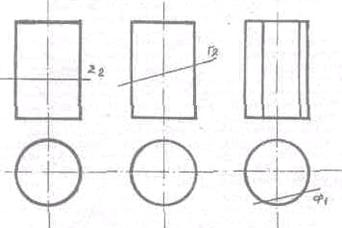
Рис. 35

В сечении конической поверхности вращения плоскостью могут быть получены:

1. окружность, если секущая плоскость перпендикулярна оси вращения;

2. эллипс, если секущая плоскость пересекает все образующие поверхности;

3. парабола, если секущая плоскость параллельна только одной образующей поверхности;

4. гипербола, если секущая плоскость параллельна двум образующим поверхности;

5. две прямые, если секущая плоскость проходит через вершину поверхности. (Рмг.36)

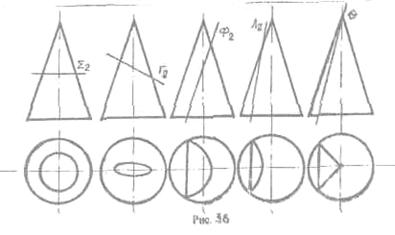
При пересечении сферы плоскостью всегда получается окружность.

Построение проекций линии сечения поверхности плоскостью общего положения

Для нахождения линии сечения поверхности плоскостью следует в общем случае строить точки пересечения образующих секущей плоскостью, те находить точку пересечения прямой и плоскости. Искомая кривая проходит через эти точки. Эта задача решается легко, если секущая плоскость занимает частное положение. Пользуясь способом преобразования чертежа можно получить удобные для построений положения фигуры, если они Заданы в общем положении в системе П₁П₂. Рассмотрим случай, когда секущая плоскость является фронтально-проецирующей. Так как в данном случае фронтально-проецирующая плоскость пересекает все образующие конуса, то в сечении получится эллипс. Фронтальная проекция эллипса будет отрезком А₂В₂, а горизонтальная проекция будет эллипсом. Построить линию пресечения конуса плоскостью можно при помощи случайных точек. В этом случае их проекции можно находить, используя параллели или образующие конуса. (Рис. 37)

Рис. 37

Рассмотрим случаи пересечения конуса плоскостью общего положения. Этот случаи легко сводится к предыдущему при помощи замены плоскости проекций П₂ на плоскость П₄, перпендикулярную к горизонтали секущей плоскости. Тогда в новой системе плоскостей секущая плоскость будет проецирующей.

Лекция № 7

Построение чертежей взаимно пересекающихся поверхностей

Большинство деталей состоит из сочетания, различных геометрических тел. Пересекаясь между собой, поверхности образуют линии взаимного пересечения, которые в общем виде представляют собой пространственную кривую.

Два многогранника пересекаются по пространственным ломаным линиям, честным видом которых могут быть плоские многоугольники.

Поверхность вращения с многогранником пересекается по линиям, состоящим из участков плоских кривых.

Две поверхности вращения пересекаются по плоским или пространственным кривым линиям.

Для построения линии пересечения двух поверхностей нужно найти такие точки, которые одновременно принадлежали бы обеим плоскостям. Сначала определяют опорные точки в .пересечении контурных линий каждой поверхности с другой поверхностью опорные точки позволяют видеть в каких пределах расположены проекции линии пересечения и где между ними имеет смысл определять промежуточные точки.

Следует иметь в виду, что если одна или обе пересекающихся плоскостей являются проецирующими (т.е. перпендикулярны к той или иной плоскости проекций), то линия пересечения таких поверхностей на чертеже уже имеется. Поэтому нужно лишь найти способ пересечения точек линии пересечения с одной плоскости проекций на другую.

Общим способом построения линии пересечения поверхности является способ вспомогательных поверхностей, используют или плоскости, или сферы. Отсюда и способы построения линии пересечения - способ вспомогательных секущих плоскостей и способ вспомогательных сфер.

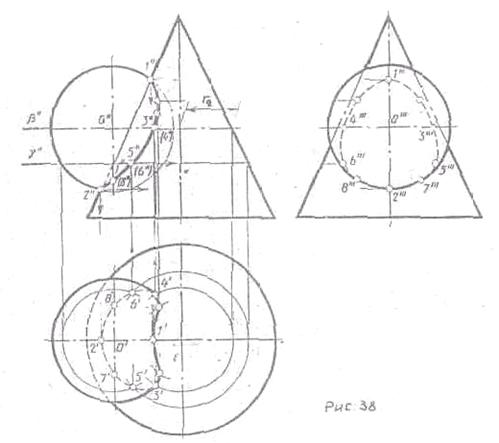
Способ вспомогательных секущих плоскостей

Выбирают вспомогательные секущие плоскости так, чтобы они пересекали поверхности по простейшим линиям Для примера построим линию пересечения конуса со сферой (рис. 38) Сначала отметим очевидные общие 1 и 2 точки поверхностей в течении их главных меридианов. Эти опорные точки являются наивысшей и наинизшей точками линии пересечения. В качестве вспомогательных секущих плоскостей возьмем горизонтальные плоскости уровня, т.к. от пересечения этих плоскостей с данными поверхностями получаются окружности. Точки пересечения этих окружностей, лежащих в одной плоскости, определяют искомую линию пересечения.

Чтобы построить линию пресечения двух многогранников, нужно либо решить задачу на пересечение двух плоскостей, либо не пересечение прямой и плоскости.

К ПРЕДЫДУЩЕЙ ЛЕКЦИИ

ОГЛАВЛЕНИЕ

К СЛЕДУЮЩЕЙ ЛЕКЦИИ

Лекция № 8

Аксонометрические проекции

Аксонометрические проекции широко применяются благодаря хорошей наглядности и простоте построении.

Слово «аксонометрия» означает осе измерение.

Изображение предмета в аксонометрии получается путем параллельного проецирования его на выбранную плоскость проекций. При этом предмет жестко связывают с натуральной системой координат OYZ.

Для создания аксонометрической проекции точки А проведем через нее проектирующий луч и найдем пересечение его с плоскостью К в точке А⁺. Это построение показывает, что при заданном направлении проектирования каждой точке А пространства на плоскости проекций будет соответствовать определенная точка, А. Но обратное утверждать нельзя. Чтобы устранить эту неопределенность и обеспечить взаимную однозначности между точками пространства и точками картинной плоскости на плоскость К проецируют не только точку А, но и одну из ее ортогональных проекций. Обычно берут горизонтальную проекцию а₁ на координатную ось XOY. Аксонометрическую проекцию A₁' называют вторичной.

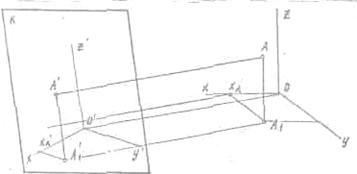
Рис.39

В аксонометрических проекциях сохраняются все свойства параллельных проекций.

Коэффициент искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции могут быть:

1) изометрическими, если все три коэффициента искажения равны между собой: u=v=w

2) диметрическими, если два коэффициента искажения равны между собой и отличаются от третьего: u=v¹w; v=w¹u

3) тригонометрическими, если три коэффициента искажения не равны между собой. u¹v¹w.

Согласно ГОСТ 2317-69 - из прямоугольных аксонометрических проекции рекомендуется применять прямоугольную изометрию и прямоугольную диметрию. В прямоугольной аксонометрии сумма квадратов коэффициентов искажения равна 2. Но в изометрии u=v=w, следовательно, 3u²=2. отсюда u=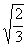

Таким образом, размеры предмета по всем трем изометриям сокращаются на 18%. ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат, что соответствует увеличению изображения против оригинала в 1 .22 раза.

При построении прямоугольной диметрической проекции сокращение длин по оси оу принимают вдвое больше, чем по двум другим, т.е. полагают, что  u=w w=0,5u

тогда по формуле будем иметь

u=2u²+(0.5u)²=2

откуда u=0.94  w==0.47

В практических построениях вводят масштаб увеличения, определяемый соотношением 1:1./2:1. и тогда коэффициенты искажения по осям ОХ к OZ будут равны единице, а по оси OY вдвое меньше - 0.5.

К ПРЕДЫДУЩЕЙ ЛЕКЦИИ

ОГЛАВЛЕНИЕ

К СЛЕДУЮЩЕЙ ЛЕКЦИИ

Лекция № 9

Возможности машинной графики

Машинная графика - метод создания, хранения и обработки геометрических моделей объектов и их изображений с помощью ЭВМ.

Первым примером бытового применения машинной графики стали телевизионные игры. Машинная графика нашла применение и как средство художественного оформления и в частности для синтеза заставок, появляющихся перед началом телевизионных передач, при изготовлении рекламы и даже при производстве анимационных и художественных фильмов

Применение ЭВМ позволяет переложить часть трудоемких чертежные и других графических работ на автоматические устройства, способные выполнять их с большой точностью, скоростью и высоким качеством.

Автоматизация практически незаменима для точного вычерчивания изображении чрезвычайно насыщенных однотипными- хотя и простыми элементами, т к для человека такой труд крайне длителен и мучителен. С помощью ЭВМ облегчается оформление конструкторских документов - чертежей, схем и др. насыщенных изображениями стандартных, унифицированных и типовых составных частей.

Машинная графика позволяет решать технические задачи, реализация которых другими способами потребовала бы чрезмерно больших расходов материальных средств и времени. Например, количество компонентов в стандартной интегральной электронной схеме типа тех, что используется в ЭВМ, столь велико, что инженеру потребуется несколько недель, чтобы вычертить ее вручную. Не меньше времени уходит и на перечерчивание, если в схему вносятся серьезные изменения. За счет внедрения интерактивной графической системы   затраты времени на получение чертежей сокращаются во много раз. С помощью ЭВМ инженер может, кроме того, осуществлять проверку спроектированной схемы и вносить необходимые коррективы, причем эти операции занимают считанные минуты.

Таким образом, проектировщик, имея возможность взаимодействия с ЭВМ, может быстро внести требуемые изменения и вновь вынести на экран скорректированный

чертеж схемы.

Существуют три режима работы с ЭВМ:

1. пакетный;

2. диалоговый;

3. интерактивный.

Рассмотрим каждый из режимов в отдельности.

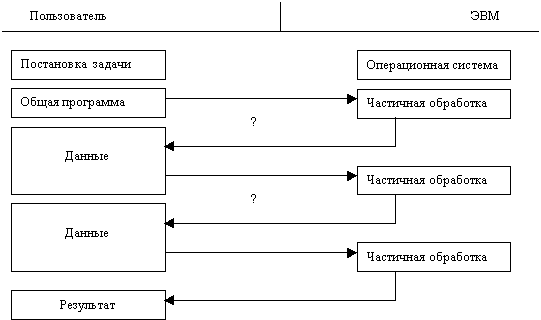
Пакетный режим

Пакетный режим предполагает выполнение чертежа по готовой программе. Пользователь не может влиять на ход ее отработки, что осложняет процесс редактирования. Поэтому этот метод применяется в основном, при получении твердых копни и тиражирования чертежей.

В программном обеспечении для выполнения графических работ различают следующие разновидности:

—Общий пакет программ;

— Специальный или прикладной пакет программ.

В общем пакете собраны графические подпрограммы, которые могут быть использованы при решения различных задач. Подпрограммы, входящие в общий пакет, могут, например, вычерчивать графические примитивы, выполнять преобразования, осуществлять ввод-вывод графической информации и др. примером такого пакета может служить графическое расширение алгоритмического языка ПАСКАЛЬ.

Специальный или прикладной пакет подпрограмм разрабатывается в том случае, когда программист должен составить подпрограмму с сокращенным набором функции, например, чертежей электронных плат и т.д. Такой пакет позволяет увеличивать быстродействие программы, сократить объем требуемой памяти.

Блок-схема работы в пакетном режиме

Диалоговый режим

Методы создания графического изображения в диалоговом режиме: вариантное конструирование, генерирование изображения из конструктивных технических элементов.

Диалоговый режим предполагает выполнение чертежей в диалоге - пользователь и ЭВМ. ЭВМ предполагает необходимые рабочие ходы и запрашивает у пользователя соответствующие данные. В отличие от пакетного режима, где устранение ошибок возможно только после выполнения всей программы и получения чертежа, при графическом диалоге обеспечивается быстрая реакция человека на действия, выполняемые ЭВМ. Ошибочное направление или ошибка ввода данных распознается и устраняются немедленно. При графическом диалоге человек и ЭВМ взаимно дополняют друг друга. Большинство графических диалоговых систем не требуют знания программирования, т.к пользователь работает отвечая только на вопросы компьютера, или производит привязку предварительно созданных технических элементов на экране дисплея, В последних диалоговых разработках кроме визуальных средств начинают использовать другие средства общения, такие как речь.

Блок-схемы работы в диалоговом режиме

Многократные запросы данных.

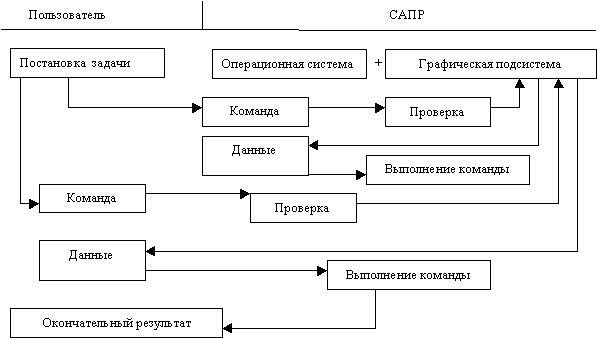
Графический интерактивный  режим

Графический интерактивный режим реализуется определенным набором команд, ЭВМ извещает пользователя через экран дисплея о своей готовности к приему команды и обработке данных. Работа ведется с использованием экранного меню. Пользователь выбирает из меню нужную команду и сообщает ее ЭВМ после получения команд ЭВМ запрашивает данные. Этими данными могут быть значения координат точек, радиусы тексты. масштаб и др. Команды для ЭВМ оформляются в виде полных или сокращенных слов. Ввод команд н данных производится с клавиатуры или из меню Команда и результат ее выполнения немедленно появляются на экране. Это позволяет пользователю

производить необходимые измерения непосредственно на экране, что в значительной степени упрощает процесс конструирования. Для работы в графическом интерактивном режим, который сегодня является наиболее популярным, создаются специальные программные средства, получившие названия CADы. Они могут быть проблемно -ориентированные ( направленные на решение какой - ли6o узкой задачи ) или универсальные. Но все эти программные средства должны удовлетворять целому ряде требований:

1. Вычерчивать примитивы и формировать из них изображения.

2. Осуществлять быстрый поиск в памяти машины сведений об уже созданных и находящихся на экране графических примитивов и опознавать их.

3. Находить на графических примитивов опорные точки и осуществлять объектную привязку к ним других примитивов.

4. Редактировать форму, размеры и положение примитивов.

5. Работать с фрагментами изображении с помощью окон.

6. Выводить полученное изображение на принтер.

Операции редактирования позволяют производить различные действия с изображениями. Можно стереть полученное изображение, сдвинуть его, повернуть на любой угол получить зеркальное изображение, изменить масштаб, изменить цвет, толщину линий и тип, мультиплицировать и т.п.

Возможность создавать изображения непосредственно на экране дисплея является для пользователя одним из наиболее  привлекательных элементов интерактивной машинной графики. Для того, чтобы сделать данный вид взаимодействия в ЭВМ максимально доступным и удобным, разработан целый ряд различных устройств ввода графической информации, в том числе «мышь», световое перо и т.п.

Блок-схема работы в интерактивном режиме

Литература

1. Гордон и др. Курс начертательной геометрии. М.: «Высшая школа», 1987.

2. Чекмарев А.А. Инженерная графика. М.: «Высшая школа», 1988.

3.  Власов М.П. Инженерная графика. М.: Машиностроение, 1979.

4.  Лагерь А.И., Колесникова 3-А. Инженерная графика, М,: «Высшая школа», 1985.

5. Локтев Д.В. Краткий курс по начертательной геометрии. 1985.

6. Атабаев Б.А. Преподавание начертательной геометрии и инженерной графики с применением ПЭВМ в технических Вузах 1994