ТОШКЕНТ АХБОРОТ ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ

АХБОРОТ ТЕХНОЛОГИЯЛАРИ ФАКУЛЬТЕТИ

“Информатика ва компьютер

графикаси” кафедраси

И Н Ф О Р М А Т И К А

ФАНИДАН КУРС ИШИНИ БАЖАРИШ УЧУН

УСЛУБИЙ ҚЎЛЛАНМА

ТОШКЕНТ 2008

Кириш

Информатика фани ахборот технологиялари факультетининг барча йўналиш талабалари учун Турбо Паскаль ва С++ тилида программалаштириш бўйича курс ишини бажариш билан якунланади. Бу талабалар билимини мустақил вазифалар орқали текшириш имкониятини беради.

Курс иши материаллари назарий ва амалий қисмлардан иборат бўлиб, бадиий техник жихатидан тушунарли қилиб ёзилган, мантиқан тўғри ва натижага эга бўлиши керак. Курс ишини топширмаган (химоя қилмаган) талаба информатика фанидан якуний назоратга қўйилмайди. Курс ишининг матни компьютерда Word матн мухаррирлари ёрдамида ёзилган, блок-схемалари ҳам чизилган, дастурлари ҳам келтирилган ҳолда топширилади. Курс ишига унинг электрон кўриниши ҳам илова сифатида қўшилади (дискет ёки дискда).

Курс иши қуйидаги бўлимлардан ташкил топиши керак:

v Кириш

v Назарий қисм

v Масаланинг алгоритми

v Дастури

v Дастурнинг натижаси (изоҳлари билан)

v Фойдаланилган адабиётлар

1. КУРС ИШИНИ БАЖАРИШ ТАРТИБИ

Талаба курс иши мавзусини, яъни ишнинг номини, уни ечиш усули ва керакли адабиётларни илмий рахбардан олади. Шу билан бирга рахбар курс ишини бажариш тартибини тушунтириши, уни топшириш (химоя қилиш) вақтини, маслаҳат кунларини тайин қилиши лозим.

Талаба кафедра ўқитувчисидан, яъни курс иши рахбаридан маслахат олиши, курс ишининг натижасини олиш учун университетдаги компьютер залларидан ва электрон кутубхоналаридан фойдаланиш ҳуқуқига эга.

1.1. Адабиётларни танлаш. Масалани ечиш усулини ўрганиш.

Курс ишининг мавзусини танлашда талабанинг математика фанидан олган билимини ҳисобга олиш зарур (масалан, мактабда ёки ўтган семестрлар давомида). Иловада келтирилган адабиётлардан энг кераклиси, яъни усуллар тўлақонли ёритилгани танланади

1.2. Масалани ечиш алгоритмини тузиш.

Бу босқичда берилган масаланинг математик маъноси, яъни алгоритми блок-схема тарзида ифода этилади. Тузилган блок-схема алгоритмнинг барча хоссаларини ўз ичига қамраб олиши, яъни умумийлик, натижавийлик ва аниқлилик хосаларига эга бўлиши керак.

1.3. Масаланинг алгоритмик тиллардаги дастури.

Масалага пухта ўйлаб тузилган алгоритм тайёр бўлганидан сўнг дастурлаш бўлимига ўтиш ҳам мумкин. Дастурни Турбо Паскаль ва С++ алгоритмик тилларида тузилади. Йўл қўйилган хато ва камчиликлар тузатилади.

Дастурда ички ва ташқи изоҳлар келтирилган бўлади. Ички изохлар дастурнинг хар бир бажарилаётган қаторига келтирилади ва бу изохлар дастурнинг бажарилишини кузатиб бориши керак. Улар қуйидагилардан иборат бўлиши мумкин;

1. Дастур номи;

2. Дастурчининг исми-фамилияси ва гурухи;

3. Киритилаётган маълумотлар хақида;

4. Ишлатилаётган ўзгарувчилар ва уларнинг вазифаси;

5. Чақирилаётган қисм-дастурлар;

6. Дастурнинг ечилиши давомида юзага келиши мумкин бўлган баъзи хатоликлар ҳақида.

1.4. Дастурни ишга тушириш

Дастурни ишга тушириш – илмий-тадқиқот ишларидан бири ҳисобланиб, у диққат-эътиборни ва вақтни талаб этади. Бу жараён давомида талаба компилятор (транслятор) кўрсатган хатоликларни бартараф этишни ўрганади. Шу ўринда қуйидагиларни маслахат берилади:

Хар бир натижани алоҳида чиқариш оператори орқали ифода этинг, шунда хатолик айнан қаерда юзага келаётганини топиш осонлашади;

Мураккаб ифодани содда ифодаларга бўлиб-бўлиб ёзинг; хатоликлар сони камаяди;

Анализ қилиш учун етарли даражада натижаларни олинг, ортиқчаси чалғитиши мумкин.

Натижаларни таҳлил қилинг.

Курс ишлари вариантлари.

Изоҳ: Вазифалар талабанинг журналдаги ўрнига қараб олинсин.

Дастурлар Турбо Паскаль ва С++ тилларида тузилсин.

1.  Берилган А(N,M) массивнинг жуфт элементларидан ташкил топган В(К) ва тоқ элементларидан ташкил топган С(L) массивлар ҳосил килинсин. Шу массивларнинг min ва max элементлари аниқлансин ва массив номи ва индекс рақами билан қоғозга чикарилсин. min ва max аниқлаш қисми дастур орқали ташкил қилинсин. В(К) массив элементлари ўсиб бориш тартибида ва С(L) массив элементлари камайиб бориш тартибида жойлаштирилиб, қоғозга устун кўринишда номлари билан чиқарилсин.

*****************************************************************

2. Ушбу

1 -1 2 3 1 1

A = 1 2 1 ва B = 1 2 3

2 0 3 -2 5 -2 берилган А ва В матрицалар учун:

А) мос равишда қўшилиши яъни,C_ij=A_ij+B_ij дастури тузилсин;

Б) мос равишда кўпайтириш дастур тузилсин;

В) ҳосил бўлган Сij матрицани изи ҳисоблансин;

Г) берилган матрицалар транспонирлансин.

*****************************************************************

3. функция ҳисоблансин. Бу ерда Х€ [0; 1] кесмада 0,2 кадам билан ўзгаради.

B → B²- 2B - 4=0 тенгламанинг илдизи.

0,42с₁ – 1,1с₂ +7,5с₃ = 8,15

1,4с₁ – 2,15с₂ + 5,11с₃ = -4,16

0,43с₁ – 1,4с₂ – 0,62с₃ = -1,05

С эса тенгламалар системаси ечимларининг энг кичик қиймати

С= min{C_i} i = 1,2,3 бу тизим Гаусс усулида ечилсин. t – ихтиёрий сон.

4. Функция ҳисоблансин

p - агар р >=1

Y =

p, агар р <1

бу ерда Р = ; х € [0; 2] h=0.1

Интегрални Симпсон усулида ечилсин

t: t⁴ - 4t³ + 2t - 6 = 0 тенгламанинг ечими [1,2] ораликда Ньютон усулида ечилсин.

****************************************************************

5. z массивнинг компоненталарини ҳисоблаш керак

c + y -a_min ; агар x<y

Z =

x* (b_max – b_min); агар x>=y

бу ерда

_{20 10}

x = å a_i ; a_i ® A(20); y = å b_i ; b_i ® B(10);

^{i=1 i=1}

Массивнинг энг катта ва энг кичик қийматини топиш қисм дастур ёрдамида ташкил этилсин . С- тенгламалар системаси ечимларининг ўртача арифметик қиймати. Тенгламалар системаси Гаусс усулида ечилсин

*****************************************************************

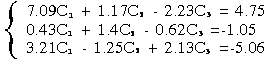
6. Қуйидаги функцияни ҳисобланг

y = Бу ерда:

x → 2x⁴ -8х³ + 8x² + 1 = 0 тенгламанинг [1; 2] ораликда хатолик билан итерация усулида ҳисобланган такрибий ечими.

t - ихтиёрий сон.

a : Max {a_i } i Î [1¸100] , b : Max {b_i } i Î 1¸20 ;

а ва b массив аъзоларининг энг катта қиймати қисм дастур ёрдамида ҳисоблансин.

*****************************************************************

7.

1 -1 2 31 1 1

A = 1 2 1 B = -1 2 3

2 0 3 2 5 -20 берилган матрицалар учун :

а) тескари матрицаларни ҳосил қилиш дастури тузилсин ;

б) мос равишда кўпайтириш дастури тузилсин;

в) кўпайтиришдан ҳосил булган матрицанинг тескари диагонали элементларининг йиғиндисини ҳисоблаш дастури тузилсин;

*****************************************************************

8. T(x) = ax³ + bx² +cx + d

функцияси Х Î(0,10) оралиқда h = 0,1 қадам билан ҳисоблансин. Бу ердаги номаълумлар қуйидаги формулалар орқали ҳисобланади:

_{10 10}

a = S (sin ) ; b = ∏ (n+i)/ i ; n = 3; z = 99,126

^{i=1 i=1}

С = d = - - ;

*****************************************************************

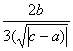9.

9,1х₁ + 5,6х₂ + 7,8х₃ = 9,8

3,8х₁ + 5,1х₂ + 2,8х₃ = 6,7

4,1х₁ + 5,7х₂ + 1,2х₃ = 5,8 ва

2,7х₁ + 3,3х₂ + 1,3х₃ = 2,1

3,5х₁ + 1,7х₂ + 2,8х₃ = 1,7

4,1х₁ + 5,88х₂ + 1,7х₃ = 0,8

тенгламалар системаси Гаусс усули ёрдамида ечилсин.

Олинган Х(6) натижалар массив шаклида чиқарилсин ва унинг энг катта қиймати топилсин.

*****************************************************************

10. Ушбу функцияни ҳисоблаш дастурини тузинг. Коэффициентларни аниқлашда қуйидаги формулалардан фойдаланинг:

T = (A+B)/C

A = ; B = ; C = e^{sin x} – ln();

0,1 <= x <= 1

Бу ерда сумма ва факториал хисоблашда қисм дастур сифатида ташкил қилинсин.

*****************************************************************

11.. A = 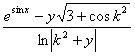функция ҳисоблансин.

бу ерда К - берилган тенгламалар тизими ечимларининг энг кичик киймати, яъни К = min {x_i } Тенгламалар системаси Гаусс усулида ечилсин.

X - тенгламалар системаси ечимларининг ўрта арифметик қиймати.

3,21х₁ – 4,25х₂ + 2,1х₃ = 5,06

7,9х₁ + 1,17х₂ - 2,28х₃ = 4,85

0,43х₁ -1,4х₂ – 0,02х₃ = -1,05

*****************************************************************

12. Қуйидаги ифодалар ҳисоблансин.

бу ерда у = min {a_ij}; А матрица элементларини (4х4)да олинсин.

x = max {x_i}

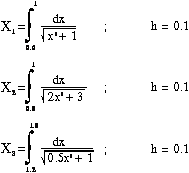
Аниқ интегралларни Симпсон усули билан ҳисоблашни қисм дастур сифатида ёзинг.

*****************************************************************

13. В(3) массив элементларини қуйидагилардан ҳосил қилинг:

b₁ = ; b₂ = 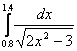; b₃ = 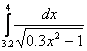; h=0.1

Аниқ интегралларнинг қиймати Симпсон усулидан фойдаланиб, қисм дастур ёрдамда аниқлансин. А(3) массивнинг аъзолари эса қуйидаги тенгламалар системасининг ечими:

9,1а₁ + 5,6а₂ + 7,8а₃ = 9,8

3,8а₁ + 5,1а₂ + 2,8а₃ = 6,7

4,1а₁ + 5,7а₂ + 1,2а₃ = 5,8

Тенгламалар тизимини Гаусс усулида ҳисобланг. А(3) ва В(3)ларни массив сифатида чиқаринг.

*****************************************************************

14. 3Х⁴ + 4Х³ -12Х² - 5 = 0 тенгламанинг ечими мавжуд бўлган оралиқларни аниқланг ва ораликлардан бирида тенгламанинг ечимини Ньютон, итерация ва оралиқни тенг иккига бўлиш усулларидан фойдаланиб ечинг. Агарда усуллардан бирортасини қўллаш мумкин бўлмаса асослаб беринг.

*****************************************************************

15. Ушбу z= ax² + bx + c функция ҳисоблансин , бу ерда:

x: e^x + x + 1 = 0 тенгламанинг [a; b] кесмадаги ечими, бу тенгламани ихтиёрий усул билан ечилсин.

a = ; b = ; c = 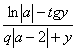; q=0,125; y = 32,56

M ва N массив элементларининг сон қийматларини ихтиёрий олинг.

*****************************************************************

16. Z = K + P функция ҳисоблансин. Бу ерда

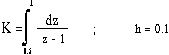
K - нинг қийматини топишда аниқ интегрални трапеция усули билан ҳисоблансин.

P : р⁴ -3р³ – 2р² + 3P - 3=0 тенгламанинг [0,1] кесмадаги 0,0001 аниқликда оралиқни тенг иккига бўлиш усули билан ҳисобланган ечими.

*****************************************************************

17. Берилган u = p*l*d*(sin a –c)*e^-b функция хисоблансин. Бу функциядаги номаълумлар мос равишда:

р : p = {1,5; 2,5; -0,3};

l : l = {3,2; 4,1; -0,2};

d : d = {-11,7; 9,3; 2,5; -1,2; 3,7} вектор узунликлари.

a, b, c -лар эса берилган матрицаларнинг энг кичик хадлари. Матрицанинг сон қийматлари ихтиёрий олинсин. ( 3х3).

a_ij , b_ij , c_ij (i = 1,n ; j = 1,m) a = min(a_ij) ; b = min(b_ij) ; c = min(c_ij)

*****************************************************************

18. Қуйидаги

Y = ) функция ҳисоблансин. Бунда p₁, p₂, …p_n лар берилган А ва B матрицаларини кўпайтириб ҳосил қилинган С матрицаси қатор аъзоларининг йиғиндисидан ҳосил бўлган вектор, S эса С матрицасининг барча аъзоларининг йигиндиси.

19. Қуйидаги функция ҳисоблансин:

Y =

Бунда х = [0; 2] оралиқда 0,1 кадам билан ўзгаради. а – ихтиёрий матрицанинг қаторэлементлари йигиндиси, b – берилган матрицадаги устун элементлари йигиндиси, С матрицанинг изи. Матрицани (3х4) ўлчамда олинг. Сон қийматлари ихтиёрий.

*****************************************************************

20. А(3), В(3), С(3) массивларининг энг катта қийматлари аниқлансин.

Бу ерда: А(3) массиви куйидаги тенгламалар системасининг ечими:

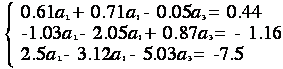
Системани Гаусс усули билан ечинг.

В(3) массиви эса Х(4,3) массивининг устун бўйича элементларининг йиғиндиси (сон қийматлари ихтиёрий).

С(3) массивини қуйидагича ҳосил қилинг: С_i =

*****************************************************************

21. Қуйидаги функцияни ҳисобланг:

Z =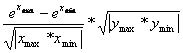

Бу ерда: X_max ва X_min X массивининг энг катта ва энг кичик элементи;

Y_max ва Y_min Y массивининг энг катта ва энг кичик элементи.

*****************************************************************

22. y`` = 4 – 2x тенглама y(0)=2 бошланғич шарт билан берилган тенгламани Эйлер ва Рунге-Кутта усулларида h=0,5 қадам билан 0<=x<=5 оралиқда ҳисобланг ва ечимини y =-x² + 4x +2 тенглама билан таққосланг. Ечим аниқлигини анализ қилинг. Ечимини жадвал ва график кўринишларида тасвирланг.

*****************************************************************

23. Берилган

10х₁ + 2х₂ + 6х₃ = 28

х₁ + 10х₂ + 9х₃ =7

2х₁ – 7х₂ – 10х₃ = -17

тенгламалар системаси Зейдель усулида ечилсин. Ҳосил бўлган х1, х2 , х3 қийматларни олиб Ах² + Вх + С = 0 тенглама ҳисоблансин. Бу ерда А = х1, В=х2, С=х3 .

24. Функция ҳисоблансин.

У =

Бу ерда х: х³ - 3х² – 3 =0 тенгламанинг [0, 1] оралиқдаги тақрибий ечими. Тенглама оралиқни тенг иккига бўлиш усули билан ечилсин, а,b,с лар эса А(15), В(20), С(10) массив элементларининг энг катта қиймати . Бу қийматлар қисм дастур ёрдамида аниқлансин.

T: T = h = 0,1 Интегрални Симпсон усули билан ечинг.

*****************************************************************

25. Ночизикли тенгламалар системасини ечинг:

Sin(x+y) – 0.12 = 0

x² + y² = 1

Системани Ньютон ва итерация усуллари билан е = 0,0001 аниқликда ечилсин .

**************************************************************

26. Қуйидаги тенгламалар системаси Гаусс усулида ечилсин:

0,12х₁ – 0,45х₂ – 0,14х₃ = -0,17

-0,07₁ – 0,34х₂ – 0,72х₃ = 0,62

1,8х₁ - 0,08х₂ – 0,25х₃ = 1,12

Шу тенгламалар тизимининг коэффициентларидан тузилган матрица қатор ва устун аъзоларининг йиғиндиларини топиш қисм дастур сифатида ташкил қилинсин. Матрицани матрица ҳолида босиб чиқариш кўзда тутилсин.

**************************************************************

27. Талабалар хақида қуйидаги маълумотлар берилган:

Фамилияси, исми, гурух номери, мутахассислиги, имтихон натижалари. Шулар асосида маълумотлар базасини ва қуйидагиларни тайёрланг:

1. Қарздор талабалар ҳақида маълумотлар;

2. Талабалар ҳақида бошланғич маълумотлар;

3. Табақаланган стипендия тўлаш ҳақида маълумотлар.

*****************************************************************

28. Берилган А(N, N) матрицани Леверье усули ёрдамида характеристик тенглама λ⁴ – р₁λ³ – р₂λ² – р₃λ – р₄ =0 нинг коэффициентлари р₁, р₂, р₃, р₄ ларни топиш дастурини тузинг.

*****************************************************************

29. Берилган А(N, N) матрицанинг нормасини ҳисоблаш дастурини тузинг. Нормалар қуйидаги формулалар асосида ҳисобланади:

│А│₁ = max; │A│₂ = min;

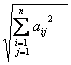│A│₃ = ; │A│₄= n*max;

Сўнгра A₁ , A₂ , A₃ , A₄ лар ичидан энг каттасини ва энг кичигини топинг.

*****************************************************************

30. Эксперимент натижаларига кўра У номаълум функция бўлиб, Х билан қуйидагича боғланган:

Х	1.0	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.8
У	1.0	1.82	2.08	3.18	3.52	4.7	5.12	6.38	6.98	8.22

Лагранж интерполяция формуласидан фойдаланиб, функцияни аниқланг ва функцияни жадвал ҳамда график кўринишида чиқаринг.

Курс ишини бажариш учун тавсия этиладиган

адабиётлар

1. Фаронов В.В. «Турбо Паскаль. Начальный курс», Москва, 1998

2. Б.В.Файсман. «Программирование на Турбо Паскале», Москва, 1992

3. Попов В.Б. «Турбо Паскаль для пользователей», Москва, 1998

4. Т.Х.Холматов ва бошқалар. “Информатика”, Тошкент, 2002

5. Р.Каримов ва бошқалар. “Дастурлаш”, Тошкент, 2003

6. Ш.Ш.Шохамидов. “Амалий математика элементлари”, Тошкент 1997

7. Ашарина И.В. «Основы программирования на языках С и С++», Москва, 2002

8. Могилев А.В. «Информатика», Москва, 2004

9. Павловская Т.А. «С / С++ программирование на языке высокого уровня», С.Петербург, 2001

10. Б.П.Демидович, И.А.Марон. “Основы вычислительной математики», Москва, 1966

“Информатика” фанидан курс ишини бажариш учун услубий қўлланма.

“Информатика” кафедрасининг 29 - декабрь 2008 й мажлисида кўриб чиқилди ва чоп этиш учун тавсия қилинди. ( 20 -сонли қайднома).

ТАТУ илмий-услубий кенгаши томонидан чоп этишга рухсат этилди.

(____ - баённома, _________________ 2008 й)