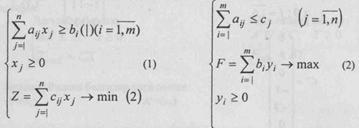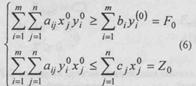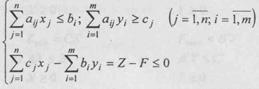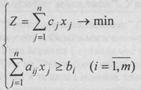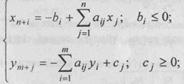Узбекистон почта ва телекоммуникация агентлиги
Тошкент электротехника алока институти

Информатика кафедраси

Иктисодий-математик моделлар ваусуллар

фани буйича

МАЪРУЗАЛАР
матнлари

Муаллифлар: т.ф.д. Раджабов Б.Ш.
ф.м.ф.н. Мамбетова Д.Э.

Тошкент-2000 й.

Мундарижа
Кириш

Маъруза № 1. Чизикли алгебра элементлари. Тизимларни текшириш.

Маъруза № 2. Бошкарувда иктисодий-математик моделлаштриш. ИММларнинг синфлари

Маъруза № 3. Оптималлаштирнш масаласининг умумий куйилиши. Оптималлаш масалаларининг турлари.

Маъруза № 4. Чизикли программалаштириш масаласи (ЧПМ). Ресурсларни таксимлаш. ЧПМ иктисодий ва математик куйилиши
Маъруза № 5. ЧПМга келтирувчи иктисодий масалалар.ЧПМ график усулда ечиш.

Маъруза № 6. Юкори тартибдаги ЧПМни график усулда ечиш. ЧПМ график ечимининг иктисодий тахлили.
Маъруза №7,8. ЧПМнинг каноник куриниши. ЧПМни ечишнинг симплекс-усули. Унинг алгоритми ва блок-схемаси.
Маъруза № 9.ЧПМни симплекс-жадваллар усули билан ечиш (алгоритми ва дастурий таъминоти).

Маъруза № 10. Чизикли программалаштириш масаласини ечишнинг сунъий базис усули.

Маъруза № 11. ЧПМ учун икки еклама масала. Унинг иктисодий ва математик куйилиши.
Маъруза № 12. ЧПМ учун икки еклама масала. Узаро икки еклама масаланинг асосий теоремаси.
Маъруза № 13. Узаро икки еклама симплекс усул.
Маъруза № 14. Транспорт масаласи. Унинг иктисодий ва математик куйилиши.

Маъруза № 15,16. Транспорт масаласини потенциал усуллар билан ечиш

Маъруза № 15. Транспорт масаласининг бошлангич базис ечимини топиш.

Маъруза № 16. Транспорт масаласининг базис ечимининг оптималлик шартлари
Адабиётлар

Кириш.

"Иктисодий - математик моделлар ва усуллар" фани Т Э А И иктисодиет факультетининг 2 боскич талабаларига тасдикланган укув режасига биноан: 76 соат хажмда кундузги булимда, жумладан 34 соат маьрузалар, 14 соат амалий машгулотлар, 16 соат лаборатория машгулотларида ва 8 соат мустакил узлаштриш дарсларида баен килинади. Сиртки булимда 3 боскич талабаларига умумий хажмда 20 соат мобайнида машгулотлар олиб борилади. Фаннинг укитилишидан асосий максад иктисодиет ва менежмент йуналиши буйича мутахассислар тайерлашда иктисодий масалаларнинг куйилиши, уларнинг синфлари буйича математик моделларини тузиш ва иктисодиетдаги конуниятларнинг математик ифодаларини аниклаш йулларини талабаларга етказишдир. Бунда асосан чизикли программалаштириш масаласи, уни ечишнинг график, кенгайтирилган график усули, симплекс-усул, симплекс-жадваллар усули, суньий базис ва иккиеклама симплекс усуллари асос килиб олинган. Шунингдек, алока сохасига мослаштирилган "транспорт масаласи" ва уни ечишнинг шимолий-гарб ва потенциаллар усули хам туликлигича ургатилади. Бу усуллардан фойдаланишда уларнинг алгоритмлари ва компьютерлар учун мое дастурлари хакида хам ахборот берилади. Ушбу фаннинг укитилиши иктисодиет мутахассислиги буйича юкори курсларда утиладигам махсус фанларни узлаштириш учун талабаларга таянч математик маьлумотларини беради.

Бундан ташкари иктисодий масалаларни улчамлари, уларга киритиладиган параметрлар сонининг куплиги, жадвал куринишда берилган кийматларнинг мавжудлиги хозигизамон компьютер техникасини тулик ишлатилишини такозо этади.
Бундай холларда иктисодий -математик моделлаштириш усуллари иктисодий маслаларни компьютерларда ишлаш ва иктисодий обьектларни оптимал бошкаришда асосий воситалардан бири  булиб хизмат килали.

Маъруза №1

Чизикли алгебра элементлари. Тизимларни текшириш

Дарснинг максади: Талабаларга чизикли алгебра элементларини, улардаги асосий тушунчалар. чизикли тенгламалар ва тенгсизликлар системаларини ечиш усуллари , уларнинг алгоритмлари ва дастурий таьминотларини системали равишда ургатиш, шунингдек, бу материал иктисодий масалаларнинг математик асоси зканлигини таькидлаш. Матрица, вектор, чизикли тенгламалар системаси. уларнинг хоссалари ва ечиш усуллари чизикли алгебранинг асосий масаласидир. Хусусан вектор сифатида еки битта устун ва бир нечта йулдан (ва аксинча) иборат матрица тушунилса, асосан матрица ва улар устидаги амаллар билан кискача танишамиз

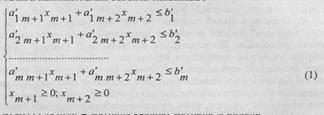
Агар (1) да m=n А матрица квадрат матрица дейилади.

1. Матрицаларни кушиш ва айириш.

2. Матрицаларни купайтириш:

Икки матрицани узаро купайтириш учун биринчи матрицанинг йуллар сони иккинчи матрицанинг устунлар сонига (ва аксинча) тенг булиши шарт. А = (а_ij) (i = 1, m; j = 1, п) ва В = (b_ji) матрицаларнинг купайтмаси деб, шундай С матрицага айтиладики, бу матрицанинг элементлари  куйидаги  формула оркали топилади

еки

Мисол.

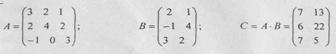
З.Бирлик матрица деб шундай Е матрицага айтиладики, унинг учун куйидаги шарт бажарилади.

4.А ва В матрицалар узаро тескари матрицалар дейилади, агар улар учун куйидаги шарт бажарилса

Берилган А матрицага моc тескари матрица В мавжуд булиши учун у хосмас булиши зарур ва етарлидир. Тескари матрицани топиш алгоритми куйидагича

Бунда А_ij а_ij элемент учун алгебрик тулдирувчи. Куп холларда иктисодий масалаларнинг математик моделлари чизикли тенгламалар системаси (ЧТС) еки тенгсизлар системаси оркали ифодаланади. Шунинг учун (максад функциясини хисобга олган холда) ЧТС назариясидан баъзи маълумотларни келтирамиз.

Маъруза №2

Бошкарувда иктосодий-математик моделлаштириш. ИММларнинг синфлари.

1.  Утилган тема юзасидан савол-жавоб утказиш (2-3 мин.)

2. Дарснинг максади: Хозиргизамон компьютер техникасининг имкониятлари ва яратилган математик усулларнинг мураккаб икьтисодий жараенларнинг конуниятларини очиш имкониятлари борлигини талабалар онгига сингдириш (3-4 мин.)

3. Маъруза матнининг баени (40-50 мин.):

Иктисодий математик моделлар деганда мураккаб иктисодий жараенларнинг конуниятларини илмий асосланган математик усуллар оркали ифодалашга тушунилади. Бу таъриф 1960 йилларда академик B.C. Немчинов томонидан берилган булиб хозирги кунда иктисодий масалаларни ечишда кенг кулланилади. Бундай математик усуллар хилма-хил булиб мазмун ва мохият жихатдан иктисодий масаланинг математик моделини тузишда кул келади. Иктисодий-математик моделларнинг куйидаги турларини куриб чикамиз.

1.   Хом ашедан фойдаланиш масаласи. Бирор корхона икки хил, яъни  М₁ ва М₂ турдвги махсулот ишлаб чикариш учун уч хил, яъни  А1,А2,АЗ  хом ашедан фойдаланадиган булсин. Хом ашенинг захиралари махсулот бирлигини тайерлаш учун
сарфланган хом аше бирлигининг меьери ва хар кайси махсулот бирлигидан келадиган фойданинг сон кийматлари 1-жадвалда келтирилган булсин.

1 -жадвал

Хом аше хиллари	Хом аше захираси	махсулот бирлигини тайерлаш учун сарфланган хом аше бирлигининг микдори
		М1	M2
А1 А2 A3	20 40 30	2 8 5	5 5 6
Бир бирлик махсулотдан келадиган фойда		50	40

Агар   М₁ махсулот  хажмининг  микдорини   х₁,   M₂ махсулот  хажмининг микдорини эса x₂ билан белгилаб, махсулот бирлигини тайерлаш учун сарф булган хом аше бирлигини ва хом ашенинг захирасини назарда тутсак, куйидаги чекланиш тенгсизликларини (еки шартларини) хосил киламиз.

2х₁ +5x₂ <20,   8x₁ +5х₂ < 40,   5х₁ +6х₂ <30 (1)

Бу тенгсизликлар махсулотларни ишлаб чикариш учун сарф килинган хом ашенинг берилган хом аше захирасидан ошиб кетмаслигини курсатади. Агар М1 хилдаги махсулот ишлаб чикарилмаса  х₁ =0, акс холда эса  х₁>0.   М₂ хилдаги махсулот учун хам худди шундай булади.

Демак,  хамма вакт   х₁ > 0,   х₂ > 0   булар  экан.   М₁ хилдаги  бир бирлик махсулот 50 бирлик фойда  бергани учун шу хилдаги умумий махсулотдан келадиган фойда 50- х₁ га тенг булади. Худди шунингдек, иккинчи хил махсулотдан 40- х₂ фойда олинади.    У    холда   умумий    даромадни    куйидагича    ифодаланишимиз    мумкин.
z = Z(x₁, x₂) = 50x₁+40x₂ (2)

Бунда (2) муносабат куйилган масаланинг максад функциясини ифодалайди. Чекланиш шартлари ва максад функция чизикли булгани учун (1)-(2) ифода чизикли программалаш масаласи дейилиб, у, иктисодий масаланинг, яъни хом ашедан фойланиш масаласининг математик моделини ташкил килади. Демак, масалани ечиш учун (1) системанинг шундай манфий булмаган (x₁⁽⁰⁾, x₂⁽⁰⁾) ечимини топамизки. Унда (2) формула билан аникланадиган Z чизикли функция энг катта кийматга эришади (z максималашади), яъни умумий фойда энг катта булади.

Энди хом ашедан фойдаланиш масаласини умумий холда куйиш керак. Фараз килайлик, корхона n хил махсулот тайерлаш учун m хил хом ашедан фойланадиган булсин. Аввалги масаламизга ухшаш махсулот хилларини М_j(j = 1,п) билан, хом аше хилларини х_j(i = 1,m) билан, хом ашенинг захирасини b_i билан i - куринишдаги хом аше   бирлиги   микдоридан,  j   -   номерли   махсулот   тайерлаш   учун   канча   сарф килинганлигини  а_ij, билан j - номерли махсулот бирлиги реализация килингандан кейин олинадиган фойдани с_j билан ва j - номерли махсулот бирлигининг микдорини х_i билан белгиласак (2- жадвалга каранг) куйилган масаланинг математик модели куйидагича булади:

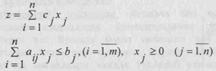
(3)

(4)
Бу ерда (3) максад функция, (4) эса чекланиш шартларидир.

Хом аше хиллари	Хо маше захираси	j - номерли махсулот бирлигини тайерлаш учун сарф килинган, i - хилдаги хом аше бирлигининг микдори
		М1	М2	M3	Мп
А1 А2 Ат	b1 b2 bm	а11 а21 аm,1	а12 а22 аm,2	а13 а23 аm3	а1п а2п атп
Бир бирлик махсулотдан келадиган фойда		С1	C2	C3	Сп

Куйилган       масаладан       куриниб       турибдики,       максад       функцияни максималлаштирадиган     х _j > 0     ларни    топиш     учун     чизикли     тенгсизликлар системасининг манфий булмаган ечимларини топиш керак. Тенгсизликлар системасини ечиш тенгламалар системасини ечишга Караганда анча мураккаб булгани учун. Купинча тенгсизликлар системаси билан алмаштирилади. Бунинг учун, тенгсизликлар системасининг чап томонига, хозирча номаълум ва мусбат булган х_n+i >0, i = 1,т узгарувчиларни кушиб езиш кифоядир, яъни

(5)

Бу системада номаълумлар сони тенгламалар сонидан куп, яъни n+m>n булгани учун (5) система чексиз куп ечимларга эга. Бу ечимлар тупламидан шундай х_j >0 ларни танлаб олиш талаб килинадики, максад функция узининг энг катта кийматига эришсин. (3)-(4) умумий холда хом ашедан фойдаланиш масаласининг математик моделини ташкил килади.

2. Рационни тузиш масаласи. Жониворларни  хар куни озиклантириш учун рационда микдори b_i(i =1,m) бирликдан кам булмаган, п хил озукадан фойдаланишда m хил туйимли модда керак булсин. Бу масаланиншг математик моделини тузиш учун j— номерли озука бирлигининг таркибидаги i - хил туйимли модда бирлигининг микдорини а_ij билан, j - номерли озука бирлигининг нархини С_j(j=1,n) билан, изланаетган номаълумларни, яъни кунлик рациондаги j — номерли озука бирлигининг микдорини х . билан белгилаймиз. У холда, бу ерда хам, максад функция топилиши керак булган номаълум микдорлар х _j - лар оркали (3) куринишда булади. Хар бир jномерли озукада i та туйимли модда борлигини ва уларнинг бирлик микдорлари х_j ва b_j ларни назарда тутсак, куйидаги чекланиш шартларига эга буламиз:

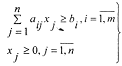                                                                    (6)

Демак, (3)-(6) куйилган масаланинг математик моделини ташкил килади. (6) тенгсизликлар системасини, аввалги масалада курганимиздек, тенгламалар сис  темаси шаклида езиш мумкин. Бунинг учун (6)нинг чап томонидан. хозирча номаълум ва мусбат булган х_n+i > О, i = 1, т микдорини айириб езиш кифоядир, яъни

(7)

Бу системада хам номаълумлар сони тенгламалар сонидан куп булганлиги учун, (7) система чексиз куп ечимларга эгадир. Бу ечимлар ичидан шундай мусбат ечимни танлаб олиш керакки, максад функция узининг энг кичик кийматига эришсин, яъни энг кам харажат сарфлансин.

Маъруза №3

Оптималлаштириш масаласининг умумий куйилиши. Оптималлаш масалаларининг турлари.

Куп холларда оптималлаш масаласи берилган функциянинг экстремумини топиш (асосан min) билан боглик. Бу кузатилаетган жараеннинг (хусусан иктисодий жараеннинг) берилган максадли холатини доим таъминлашга асос булади.

Масалан:

Иктисодий жараенни схематик равишда кирувчи х₁  х₂ ...   х_n параметрлар холатни  бахоловчи   у₁    у₂ ...   у_m (Y_M) параметрлар оркали  шартли  ифодаласак, жараенга таъсир килувчи ташки таъсирлар Е₁ Е₂ ... Е_e лар оркали белгилаймиз. Ташки таъсир натижасида жараен максадли холатдан (Y₀) чикиши мумкин. Бундай холларда.  уни оптимал максадли холатга келтириш учун куйидаги масала куйилади.

Бунда А - номаълум параметрлар U - X кирувчи параметрларнинг йул куядиган кийматлар туплами. (1)масала   шартли   оптималлаш   масаласи   дейилади   ва   унинг   математик куйилиши куйидагича: Масаланинг куйилиши. Хозирча биз шугулланган абсолют ва нисбий минималлаш масалаларда функцияларнинг аргументлари турлича мустакил кийматларга ъга булиши фараз килинган эди. Энди бу ерда функцияларнинг аргументлари баъзи бир кушимча шартлар билан богланган абсолют ва нисбий минималлаш масалалари хакида тухталиб утамиз. Бундай холда функцияларнинг абсолют ва нисбий шартли абсолют минимум ва шартли нисбий минимум дейилади. Фараз килайлик, бизга ушбу

(1)

функциянинг куйидаги

(1)

(2)

тенгламалар системасини каноатлантирадиган минимумини топиш талаб килинган булсин. Бошкача килиб айтганда, тенгламштар системаси (2)ни каноатлантирадиган шундай х₁ ,х₂, ..., х_n ларни топиш керакки, х_i ларнинг шу кийматларида (1) функция минимумга эришсин. Агар куйидагича X(x_l,x₂,...,x_n),g(X) = (g_l(X),g₂(X),...,g_m(X))    векторлар   киритсак,    (1)-(2)   ни кискача куйидагича езиш мумкин:

Энди юкорида куйилган масалани куйидагича талкин килиш мумкин: п улчовли R фазода

g(X) = 0 (3)
тенгламани каноатлантирадиган шундай X₀?R_n нуктани топиш керакки, (3) тенглик R_n даги хамма Хлар учун уринли булсин еки бошкача айтганда (2) тенгсизлик бажарилсин. (3) ва (1) шартларни каноатлантирадиган X₀ нуктага (10 функцияга шартли абсолют минимум берувчи нукта деб. куйилган масалага эса шартли абсолют минималлаш масаласи деб аталади. (3) тенгламани каноатлантирадиган нукталар туплами куйилган масаланинг мумкин булган еки уринли нукталар туплами дейилади ва куйдагича езилади:

Шартли нисбий минималлаш масаласининг куйилиши куйидагича булади: п улчовли R_n фазода шундай X₀ нуктани топиш талаб килинадики, олдиндан берилган е > О сон учун   [X - X₀] < е ва g(X₀) = 0 булганда (2) тенгсизлик R_n даги хамма Хлар учун уринли булсин, еки кискача

 (4)

(4)ни каноатлантирадиган X₀ нуктага шартли нисбий минимум берувчи нукта. куйилган масалага эса шартли минималлаш масаласи дейилади.

Маъруза №4

Чизикли программалаштириш масаласи (ЧПМ). Ресурсларни оптимал таксимлаш масаласи.

ЧПМ иктисодий ва математик куйилиши.

Иктисодий жараёнларда учрайдиган асосий масалалардан бири бу ресурсларни оптимал таксимлаш масаласидир. Бу масала ресурсларнинг турлари (хомашё, моддий ресурслар, мехнат расурслари ва молия ресурслари) хажми, уларни бир бирлик
махсулот ишлаб чикаришга сарфланиш меъёрлари, шунингдек махсулот бирлигининг нархи (ёки таннархи) маълум булганда. махсулот ишлаб чикаришнинг оптимал режасини тузиш билан боглик. [1] Буни ойдинлаштириш учун куйидаги масалага мурожаат киламиз: Масала: Цех А ва В турдаги кабель махсулотлари ишлаб чикаради. А турдаги бир метр кабель ишлаб чикариш учун 0,8 кг. мис, 0,5 кг. полиэтилен 0,9 кг. резина ва 1,5 одам/соат иш вакти сарфлайди. В турдаги бир метр кабель ишлаб чикариш учун эса 0,9 кг мис, 0,4 кг. полиэтилен, 1,3 кг. резина ва 2,2 о/с иш вакти сарфлайди. Агар цех битта смена учун 300 кг. мис, 250 кг. полиэтилен, 325 кг. резина ва 450 о/с иш вакти ажратган булса, шунингдек 1 метр А турдаги кабельнинг сотилиш нархи 250 сум ва 1 метр В турдаги кабелнинг сотилиш нархи 290 сум булса, цех энг куп даромад олиши учун бир сменада канча А турдаги ва канча В турдаги кабеллар ишлаб чикариш лозим?

Албатта бу масалани 1 смена учун, 1 ой ёки йил учун куйилиши мумкинлигида шубха йук. Бунда ресурсларнинг захирадаги (запас) кийматлари узгаради холос. Масаладаги параметрларни холати ва улар орасидаги богланишни яккол тассавур илиш учун куйидаги жадвал тузамиз.

жадвал

ресурс турлари	Махсулот ресурс м А-тур кабель	лари учун eъерлари	ресурс захираси
		В-тур кабель
мис	0,8	0,9	300
полиэтилен	0,5	0,4	250
резина	0,9	1,3	325
иш вакти	1,5	2,2	450
Махсулот бирлигининг нархи	250с.	290с.

Бу жадвалга асосланиб, ишлаб чикариш махсулот хажмини турлари буйича X₁, Х₂ деб белгилаймиз.У холда 0,8x₁ - А турдаги барча кабельга кетадиган миснинг микдори; 0,9x₂ - В турдаги барча кабельга кетадиган миснинг микдори.

Бундан 0,8х₁+0,9х₂ - бутун смена учун цех сарфлайдиган миснинг умумий микдори. Мантикан бу микдор захирадаги миснинг хажмига тенг ёки ундан кам булиши мумкин; яъни 0,8х₁+0,9х₂<300 (1)

Худди шу каби бошка турдаги ресурсларга нисбадан куйидаги мантикий муносабатларни ёзиш мумкин:

0,5x₁+0,4x₂<250

0,9x₁+l,Зх₂<325 (2)

1,5х₁+2,2х₂<450 х₁>0;х₂>0

(1)-(2) муносабатлар ресурслар таксимотининг конуниятларини аниклаб улар чегаравий шартлар дейилади. Бу мулохазаларни махсулот бирлигини нархига нисбатан кулласак 250х₁+290х₂ - барча кабель (А ва В турдаги) махсулотларнинг сотилиш умумий нархи.

Агар уни даромаднинг умумий микдори десак, у холда

Z=250x₁+290x₂--max (3)

масаласи куйилиши мантикан тугри булади. Шундай килиб

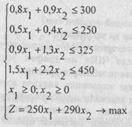
масалада ишлаб чикариладиган кабелларнинг турларини шундай микдорларини (х₁, x₂) топиш керакки, ресурсларнинг берилган меъёрлари, захира ва махсулотнинг сотилиш нархлари аник булганда умумий даромаднинг микдори (Z) энг катта булсин.

Умумий холда бу масала ресурсларни оптимал таксимлаш масаласи дейилиб, унинг математик куйилиши куйидагича Манфий булмаган х₁, х₂ , ... , х_n ларнинг шундай кийматлари топилсинки, улар

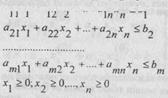
(4)

шартларни каноатлантириб

Z=c₁x₁+c₂x₂+...+c_nx_n-max (5)
функцияга    максимум    (ёки     min)     киймат    берсин     (4)-(5)     масала     чизикли программалаштириш масаласи дейилади (ЧПМ)

(4)-(5) масаланинг вектор-формаси хам мавжуд булиб у куйидагича Х=(х₁, х₂,..., х_n)

Белгилашларни хисобга олсак, вектор форма

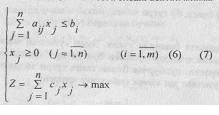
(6)-(7) масаланинг шакли чизикли алгебра услубиётига биноан, узгартирилиш ва бир формадан бошка формага утказилиши мумкин.

Маъруза №5

ЧПМга келтирувчи иктисодий масалалар. ЧПМ график усулда ечиш.

1.   Утган даре темаси буйича саволлар:

1)  Иктисодий масалаларнинг кандай турлари бор?

2)  ЧПМ даги асосий тушунчалар ва таърифлар.

2.   Маъруза максади. Иктисодий масалаларни ЧПМга акслантирувчи механизм, унинг мохиятини ва икки улчамли ЧПМ ни график усулда ечишнинг математик ва алгоритмик ассоларини талабаларга ургатиш.

3.   Ресурслар масаласининг ЧПМ утиш жараенини кискача изохланган холда, баланс ва рецептуал масалаларнинг хам иктисодий мохияти тула аникланади. Баланс ва рацион маслаларга дойр аник мисоллар келтирилиб, уларнинг математик моделлари хам чизикли программалаш масаласи оркали ифодаланиши таькидланади. ЧПМ ечиш хакида умумий маьлумотлар берилиб, улардан бири булган график усулга мурожаат киламиз: Бизга икки улчовли фазода чизикли программалаштириш масаласи берилга булсин, яьни ушбу

Z = с₁х₁ + с₂.х₂ 0)

функциянинг чекланиш тенгсизликлари системаси

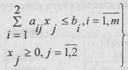
(2)

ни каноатлантирадиган энг кийматини топиш талаб килинган булсин. Тенгсизликлар системаси (2) ни биргаликда деб фараз килсак, бу
тенгсизликларнинг хар бири

а_i1х₁+а_i2х₂=b_i, i=1,2
тугри чизиклар билан, ечимларнинг эмаслик шартлари эса х_j= О, j = 1,2  тугри чизиклар билан ярим текисликларни ташкил этади ва бу ярим текисликлар бир-бири билан кесишиб, уринли ечимлар туплами булган бирорта купбурчакни ташкил килади. Максад функция (1) Z нинг хар бир кийматида бирорта тугри чизикнинг тенгламасини билдиради, яъни с₁х₁+с₂х₂= const (3)

Хусусий холда Z=0 булса, бу тугри чизик

c₁x₁+c₂x₂=0 (4)
куринишида булиб, координата бошидан утади. Энди куйилган масалани куйидгича баен килиш мумкин: уринли ечимлар туплами булган купбурчакнинг шундай таянч тугри чизигини топиш керакки, купбурчак билан таянч тугри чизикка умумий булган нуктада максад функция узининг энг кичик кийматига эришсин.

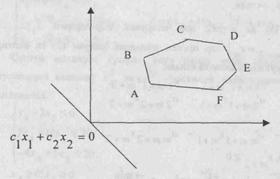
Максад функция  N=(с₁,с₂)  вектор йуналиши буйича хамма вакт усувчи булиб, бу вектор тугри чизикларга перпендикуляр булади. Шунинг учун тугри чизикни N вектор йуналиши буйича узига параллел равишда кучира бошласак, у ABCDEF купбурчакка А ва D нукталарда таянч тугри чизик булади ва максад функция А нуктада энг кичик кийматга эришади. А нуктанинг координаталари  х₁⁰ ва х₂⁰ лар АВ ва AF тугри чизикларнинг тенгламаларидан тузилган системани, яъни

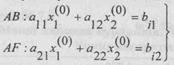
ни биргаликда ечиш натижасида топилади.

Маъруза №6

Юкори тартибли ЧПМ ни график усулда ечиш ЧПМ график
ечимининг иктисодий тахлили.

Юкори тартибли ЧПМ ни баъзи холларда график усулда ечиш мумкин. Бунингучун чекланиш шартлари сони билан ноъмалумлар сони фарки 2 тенг булган хол курилади. Бу усул билан чегаравий шартлари п ва ноъмалумлар сони m га тенг булганда n-m=2 шартда ечиш мумкин. Бизга ушбу ЧПМ берилган булсин

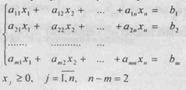
(1)

(2)

(1)-(2)   ЧПМ   да   n=m+2   деб   чегаравий   шартлардаги    х₁, х₂, ..., х_т ларни х_m+1, х_m+2(х_m+2=х_n) лар оркали  ифодалаб уларни  (2)  га  келтириб  куямиз, натижада (1)-(2) куйидаги холатга келади:

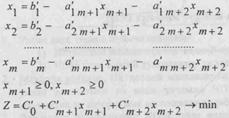
(3)

(4)

Ечимларнинг манфий булмаслик шартларидан фойдалансак x_m+1 ва х_m+2 ларга нисбатан 2 улчовли ЧПМ га эга буламиз яъни

х₁>0, х₂ >0, ..., x_m >0 (5)
хисобга олсак

(6)

(7)

(6)-(7) масалани биз биладиган график усулда ечиб   (x_m+1⁰, x_m+2⁰) оптимал ечимлар   кийматларини   (3)   чегаравий   шартларга   келтириб   куйсак   x₁⁰, x₂⁰, ..., x_m⁰ оптимал ечимлар аникланади. Шундай килиб берилган (1)-(2) масаланинг

барча оптимал ечимлари аникланади.

МАШК

х₁-х₂+3x₃+18x₄+2х₅ = -4
2х₁-х₂+4х₂-21х₄+4х₅ =22 Z = 2x₁-х₂+ х₃-Зх₄+4x₅ - max

            Зх₁-2х₂+8х₃-43x₄+11х₅=38
1-кадам Чегара шартлардан фойдаланиб (бирор усул ердамида) x₁, x₂, х₃ ларни х₄ ва x₅ лар оркали ифодалаймиз.

х₁=6-х₄+3x₅

 х₂=70-7x₄+10x₅ Z = 6x₄+15x₅-38  -  max                                      (8)

x₃=20+4х₄-5х₅
Сунгги масалани график усул билан ечиб (олдинги дарсдаги берилган маълумотларга биноан) х₄⁰ ва х₅⁰ - оптимал кийматларни топиш учун ЧПМдан фойдаланамиз.

x₄-3x₅<6

7x₄+10х₅<70

-4x₄+5х₅<20

х₄>0; х₅ >0

Z = 6х₄+15x₅-38 — min

Бу масала учун график усулни кулласак, (х₄⁰= 2; x₅⁰=28/5). Топилганларни (8)га келтириб куйсак оптимал ечим (х₁⁰=104/5;  х₂⁰=0; x₃⁰=0; x₄⁰=2; x₅⁰=28/5) эканлигини аниклаймиз.

Маъруза № 7,8

ЧПМнинг каноник куриниши. ЧПМни ечишнинг симплекс-усули. Унинг алгоритми ва блок-схемаси.

Реал иктисодий холатлар учун тузилган математик моделлар куп холларда катта улчамда булиб номаълумлар сони п ва чегаравий шартлар сони m ларнинг айирмаси 2 тенг булмайди. n не равно m Бундай холларда ЧПМни ечиш учун аналитик усуллар кулланади. Шундай
усуллардан бири симплекс-усулдир. Бу усулни 1945-1946 йилларда Г.Данциг ишлаб чиккан ва таклиф килган. Асосий тушунчалари: базис ва озод номаълум ЧПМнинг каноник куриниши базис ечим оптимал ечим ЧПМнинг каноник куриниши деб базис номаълумларга нисбатан ечилган холатига айтилади, яъни

(1)

(1)масалада базис  (x₁, x₂, ..., x_m) ва озод (х_m+1, ..., х_n) номаълумларни аниклаймиз. (1)нинг чегаравий шартларни базис номаълумларга нисбатан ечамиз.  У холда (1) масала куйидаги куринишга келади:

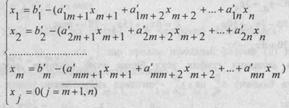
(2)

(3)

(2)-(3) куриниш каноник куриниш дейилади.  (х₁, х₂, ..., х_m) - базис номаълумлари. х_т+1, ..., х_n - озод номаълумлари. Агар (20 чегаравий шартлари b₁', b₂',.., b'_m лар мусбат булса,

х_т+1=х_т+2=...=х_n=0 (4)

1-базис ечим келиб чикади.

Б₁=(b₁', b₂', ...,b_m', 0; 0; ...0;) (5)

Бунда максад функциянинг киймати куйидагича:

Z(Б₁) = c'₀ (6)

Топилган базис ечим оптимал еки оптимал булмаслиги мумкин.

(I)       (3)  с'_m+1, с'_m+2, ..., с'_n  - сонлар барча манфий, у холда топилган ечим Z(Б₁) = с'₀   - минимум булиб, (5) ечим оптимал булади. Чунки j учун с'_j<0 - с_jх_j>0 (j=т+1,п) 

Z=c₀-c'_jx'_j>c'₀       (7)

(II)      с'_m+1, с'_m+2, ..., с'_n  лар   орасида   мусбатлари   бор.   Масалан:   с_j>О Бу холда х_m+1=х_m+2= ... = х_j-1=х_j+1=... = x_n=0 деб олиб (х_j>0)х_j - ни кийматини ортира борсак. Z= c'₀c'_jx_j ни кийматини камайтириш мумкин. Бунда (20 системадан куйидаги хосил булади:

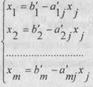
(8)

Бу тенгламалардаги х₁, х₂, ..., х_m лар бирортаси хам манфий булмаслиги керак. Бунда хам икки хол булиши мумкин:

а) а'_1j, а'_2j, ..., а'_mj лар орасида мусбатлари бор (демак манфийлари бор) а'_kj> О.У холда х_k= b'_k -а_kj х_j да х_j га b'_k/a_kj дан катта киймат бериш мумкин эмас. Чунки х_j>0 учун а_kjх_j>0 булганда х_k= b'_k -а_kj х_j > b'_k > О. Демак,  Z=c₀-c'_jx'_j. Да с_j> 0, х_j > 0 булгани учун x_j . чексиз орттирганда minZ= -oo. Демак, максад функция Z min га эришмайди.

б) (8)даги      а'_1j, а'_2j, ...,  а'_mj лар орасида мусбатлари  бор,   а'_kj >0.  У холда х_k = b'_k -а_kjх_j да х_j га b'_k/a_kj дан катта киймат бериш мумкин эмас, акс холда х_k < 0. Бунда b'_k/a_kj > 0 булиши аник.

Маъруза № 9

ЧПМни симплекс-жадваллар усули билан ечиш (алгоритмы ва дастурий таъминоти)

1.   Утган тема буйича саволлар бериш - (3-5 мин.)

2.   Максад ЧПМни ечишнинг тартибланган симплекс усули, симплекс - жадваллар усули билан талабаларни таништириш, унинг асосий мохияти ва амалий жихатларини очиб бериш.(5-7 мин) Симплекс усулда курсатилган бир нечта боскичларни тартибланган жадвал
усули оркали куриб чикамиз. Бунинг учун ЧПМнинг каноник куринишини куриб чикамиз.

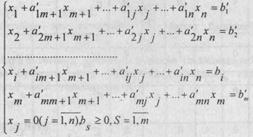
(1)

(2)

с_j>0  булганда хал килувчи элемент учун  а'_ij танланган булсин. (1)-(2) да х₁+х₂+... +x_m  - базис номаълумлар. x_m+1+х_m+2+... +x_n - озод номаълумлар. с_j> 0 булганлиги учун (2) МФга оптимал киймат берувчи ечимни топиш учун х₁, х₂, ..., х_i, ..., х_m базисдан янги  х₁, х₂, ..., х_i-1, х_i, х_i+1, ..., х_m базисга утишимиз керак. Бу холда (1)-(2) масала куйидагича узгаради.

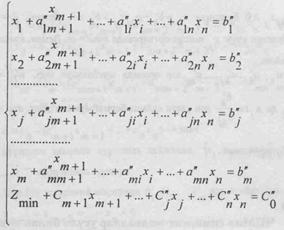
(3)

(4)

Бу  жараенни симплекс-жадвал  оркали хам  ифодалаш  мумкин.  (1)-(2)  учун симплекс - жадвал куйидагича тулдирилади:
1-жадвал

Базис номаъ- лумлар	Озод хадлар	х1	x2	...	xi	...	xт	xт + 1	...	xj	...	xп
x1	b'1	1	0	...	0	..	0	а'т + 1	...	а'1j	...	а'1n
x2	b'2	0	1	...	0	...	0	а'2т + 1	...	а'2j	...	а'2n
...	...	...	...	...	...	...	...	...	...	...	...	...
xi	b'i	0	0	...	1	...	0	а'im + 1	...	а'ij	...	а'in
...	...	...	...	...	...	...	...	...	...	...	...	...
xт	b'т	0	0	...	0	...	1	а'mm + 1	...	а'mj	...	а'тп
Z	C'0	0	0	...	0	...	0	C'т+1	...	С'j	...	С'п

2-жадвал

Базис номаъ- лумлар	Озод хадлар	x1	x2	...	xi	...	xт	xт + 1	...	xj	...	xп
x1	b''1	1	0	...	а''1i	...	0	а''1т+1	...	0	...	а''1n
x2	b''2	0	1	...	а''2i	...	0	а''2т+1	...	0	...	а''2п
...	...	...	...	...	...	...	...	...	...	...	...	...
xj	b''j	0	0	...	а''ji	...	0	а''jm+1	...	1	...	а"jn
...	...	...	...	...	...	...	...	...	...	...	...	...
xт	b''т	0	0	...	а"mi	...	1	а''тт+1	...	0	...	а"тп
Z	С'0	0	0	...	С"i		0	С"т+1	...	0	...	С"п

Zra мое келувчи сатр элементлари орасида мусбатлари булса, шу элементларнинг энг каттаси жойлашган, яъни С'_j жойлашган устун элементларидан мусбатини белгилаб оламиз  масалан, а'_kj>0 булсин. Ажратилган мусбат а'_kj элементлар билан битта  сатрда жойлашган озод хадлар b'_k нинг шу а'kj  ларга нисбатини тузамиз ва тузилган нисбатларнинг   энг    кичигини    b'_j/а'_ij  билан    белгилаймиз.   а'_ij -    хал    килувчи элементдир.Базиснинг алмашиш жараени таькидланади. Бу жараенни топилган ечим оптимал булгунга кадар такрорлаймиз. Ечимнинг оптималлик шарти математик асосланган холда тушинтирилади

Маъруза №10

Чизикли программалаштириш масаласини ечишнинг сунъий базис усули.

ЧПМни симплекс-жадвал усули билан ечишда чекланиш шартлари албатта базис номаълумларга нисбатан ечилган булиши керак:

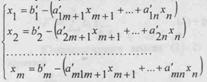
(1)

Куп холлларда ЧПМ чекланиш шартларини (1) куринишга келтириш мураккаб ва куп вакт талаб килади (айникса ЧПМнинг улчамлари катта булганда). Бу муаммони хал килиш учун сунъий базис усулини курамиз:

Бизга куйидаги ЧПМ берилган булсин:

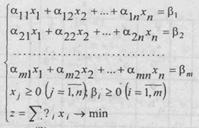
(2)

(2) даги чекланиш шартларини куйидагига узгартирамиз. Чекланиш шартларини

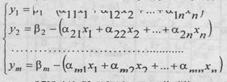
(3)

Агар (3) да y₁=у₂=...=y_m=0, (2) масала келиб чикади. у₁, y₂, ..., у_m – сунъий базислар дейилади y_i>0. (3) ЧПМ учун куйидаги ёрдамчи функцияни киритамиз:
F=y₁+ y₂+...+ y_m (4)

F - ёрдамчи МФ дейилади.

(4) да базис ноъмалумлар булгани учун (3) га нисбати m марта симплекс-усулни кулласак, чегаравий шартлари

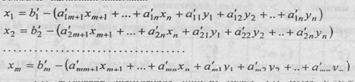
(5)

(5) чегаравий шартларида minF>0 булса, (2) ЧПМ y₁=y₂=...=y_m=0 x_j>0 каноатлантирувчи ечимга эга булмайди, агар F=0 (2) ЧПМ да {x₁, х₂, ..., х_m, 0, 0,...,0} - оптимал ечим булади, качонки, y₁=y₂=...=y_m=0, у холда

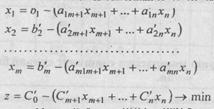
(6)

(7)

Мисол. Куйидаги ЧПМни СБУ билан ечинг:
x₁-x₂ + x₄ ⁼ 3

2х₁ -x₂ =3
    Зx₁- 2х₂ - x₄ =1

x_j>0,    j= l,4;

z = х₁ + х₂ + 2х₃
1.   Сунъий базис киритамиз.

y₁ = 3 - (х₁- х₂ + x₄)
у₂ = 3 - (2х₁- х₂)              F=у₁+у₂+уз=7-6х₁+3х₂+х₃-3х₄

y₃ = 1 - (Зх₁ - 2х₂ - х₄ )

Ердамги МФ хисобга олганда берилган масала куйидаги куринишга келади:
y₁+x₁-x₃+4х₄=3

у₂ + 2x₁ - х₂ = 3
у₃ + Зх₁ -2х₂-х₄=1
F + 6х₁ - Зx₂ - х₃ + Зx₄ = 7
z - x₁ - х₂ - 2х₃ = О

Хисоб F - сато буйича булади.

Б.у.	О.у.	xl	x2	х3	x4	y1	y2	уз
y1	3	1	0	-1	4	1	0	0
y2	3	2	-1	0	0	0	1	0
yз	1	3	-2	0	-1	0	0	1
F	7	6	-3	-1	3	0	0	0
z	0	-1	-1	-2	0	0	0	0

Маъруза№11

ЧПМ учун иккиёклама масала. Унинг иктисодий ва математик

__________куйилиши____________________

Ресурслар масаласининг иктисодий ва математик куйилиши бизга маълум эди.

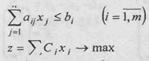
(1)

(2)

а_ij -j-тур махсулот бирлиги учун сарфланадиган i-тур ресурс бирлиги
b_i - i-тур ресурс захираси
c_j - j-тур махсулот (хизмат) бирлигининг нархи
х_j -j-тур махсулот (хизмат) бирлигининг хажми
Энди (1)-(2) масалага нисбатан куйидаги масалани тузамиз.
y_i - i турдаги ресурс бирлигининг нархи;

у холда хар бир j турдаги махсулот бирлигини ишлаб чикариш учун сарф буладиган ресурсларнинг умумий хажми

(3) га тенг.

Мантикан сарф буладиган ресурслар нархи махсулот бирлиги нархидан (j - турдаги) ошиб кетмаслиги учун

(4) булиши шарт а_ij – нархи Иккинчи томонидан корхона b_i турдаги ресурслар захираси булганлиги учун

(5) - ресурсларнинг умумий киймати булади. Юкоридагиларга  асосан  (1)-(2)   масалага   мое   куйидаги   масала  куйишимиз
мумкин:

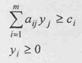
(6)

(7)

Таъриф (6)-(7) масала (1 )-(2) масалага нисбатан иккиёклама масала дейилади, ва у куйидаги иктисодий мазмунга эга. Ресурс микдори b_i га тенг булиб. махсулот бирлигининг нархи с_j га тенг булганда, ресурс бирлигининг нархини у_i - умумий сарфи энг кам буладиган килиб
танлаш керак.

Дастлабки масала                     Икки ёклама масала
АХ<В;    х>0                                      А'Y'>С;    Y>0

Z_max=CX F_min=BY

Бунда куйидаги белгилар киритилган:
A=(a_ij) A'=(a_j)

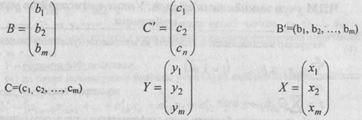
Узаро иккиёклама масалалар математик моделларининг турлари.
А) Симметрик булган ИЁМ.

Дастлабки масала Иккиёклама масала.

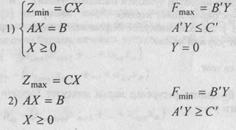
В) Симметрик булган иккиёклама масала.

Дастлабки масала Иккиёклама масала.

Мисол. Берилган дастлабки масалага нисбатан иккиёклама масала тузилсин:

Маъруза №12

ЧПМ учун иккиеклама масала. Узаро иккиеклама масаланинг асосий теоремаси

Бизга куйидаги дастлабки ЧПМ ва унга мое иккиеклама масала берилган булсин:

(1) ва (2) масала учун куйидаги теорема уринли:

Теорема: Даслабки (1) масала ечимга эга булса, унга мое икиёклам масала хам ечимга эга булади, акси хам уринлидир. Бунда куйидаги тенглама уринли булади:
min Z = max F (3)

Исбот: Ф.к. x₁⁰; x₂⁰; ...; x_n⁰ ва у₁⁰, y₂⁰; ...; y_т⁰ дастлабки ва иккиеклама масалаларнинг оптимал ечимлари булсин. Уларни (1) ва (2) ларга куйсак куйдагиларга эгабуламиз:

(4)-чегаравий  шартларни   у₁⁰, y₂⁰; ...; y_т⁰ ларга  (5)  нинг чегаравий  шартларини x₁⁰; x₂⁰; ...; x_n⁰ ларга купайтириб кушсак куйидаги тенгсизликларга эга буламиз:

Бундан эса куйидаги келиб чикади:

F₀<Z₀ (7)

Агар куйидаги тенгсизликларни куриб чиксак:

(8)

Агар  x₁⁰; x₂⁰; ...; x_n⁰ ва  у₁⁰, y₂⁰; ...; y_т⁰ (8) система учун оптимал ечимлар эканлигини билсак:

Z₀ < Fo (9) (7) ва (9) => F₀=Z₀
min Z = max F

Маъруза №13

Узаро иккиеклама симплекс-усул.

Таъриф:  Дастлабки масаланинг ечимидан  иккиеклама масаланинг ечимини келтириб чикарадиган ( ва аксинча ) усул иккиеклама с-у дейилади. Иккиеклама с-у иккиеклама масаланинг асосий теоремасига аосланган. Бизга куйидаги дастлабки ЧПМ беоилган булсин:

(1)

(1) Нисбатан иккиеклама масала тузамиз:

(2)

(1) га ёки (2) симплекс усулни куллаш учун улар базис ноъмалумларга нисбатан ечилган булиши керак (сунъий базислар ёрдамида)

(3)

(4)

(3), (4) тенг. системаси (1), (2) ларнинг чегаравий шаргларига

(5)

номаълумларни киритиш натижасида келио чикади Бунда Д.М.    х_п+1, х_n+2, ...,х_п+т ,- б.н.; х₁, х₂, ..., х_п -    озод номаълумлар

И.ЕМ.    у_т+1,у_т+2,...,у_т+n-б.н.; у₁, у₂, ..., у_т -    озод номаълумлар Узаро иккиеклама масаланинг асосий теоремасига кура minZ=maxF  бирорта  (ёки  дастлабки,  ёки  иккиеклама)  масаланинг  ечимини топсак, иккинчисининг хам ечими топилган булади. Коида. Берилган масаладаги базис номаълумлар билан иккиеклама масаладаги озод номаълумлар ва аксига берилган масаладаги озод номаълумлар ва иккиеклама
масаладаги базис номаълумлар орасида узаро бир кийматли мослик асосида ечимлар топилади.

(6)

(6) га асосан, агар берилган масаланинг оптимал ечими (0; 0; ...;0; x⁰_n+1; x⁰_n+2 ; ...; x⁰_n+m)  булса, унда иккиёклама булган ЧПМ нинг оптимал ечими (y₁; y₂; ...; y_m; 0; 0...; 0) булади. Ечимни топиш куйидагига бажарилади y₁=с_n+1, яъни    x_n+1 нинг олдидаги коъффициенти

y₂=с_n+2 ,            x_n+1
y_m⁼C_n+m ,              x_n+m

Мисол.   Берилган   масала  учун   иккиёклама  масала  хузилиб,  у  иккиёклама симплекс-усули билан ечилсин:
x₁ + 2х₂ -х₄+х₅ =1

- 4x₂ + х₃ + 2х₄ -х₅ =2

Зх₂+ x5 +Х₆ =5

x_j>0; j = 1,6

z = х₂ - х₄ - Зх₅ -- min
а) Иккиёклама масала тузилиши:
2y₁-4у₂+3y₃<1      2у₁ -4у₂ + 3у₃ + у₄=1

-4у₁+2у₂<-1        -4y_l+2y₂+y₅ =-l

y₁-y₂+y₃<1       у₁-y₂⁺y₃+y₆=-3

у₁ < О     y₁ > О

у₂<0         y₂>0

y₃<0        у₃>0

F = y_l + 2у₂ + 5у₃ -- max F= y₁ + 2y₂ + 5y₃--max

Дастлабки масаланинг оптимал ечими куйидаги якуний симплекс-жадвалдан
келиб чикади.

Б.н.	О.х.	x1	x2	х3	x4	x5	x6
x5	4	2	0	1	0	1	0
x4	11/3	-1/3	0	1/3	1	0	2/3
x2	1/3	-2/3	1	-1/3	0	0	1/3
Z	-46/3	-19/3	0	-11/3	0	0	-1/3

Б₀={0; 1/3; 0; 11/3;4;0}
Z= -46/3 - 19/Зх₁ - 11/Зх₃ - 1/Зх₆

Z(Б_опт) = -46/3;
С₁= -19/3        С₂ = 0    С₃ = -11/3
С₄ = 0 С₅= 0    С₆ = -1/3

Дастлабки         масала         оптимал ечими

x₁=0; x₂=1/3; x₃=0; x₄=11/3; x₅=4; x₆=0

Юкоридаги коидага асосан y1<0; y2<0; у3<О шартни хисобга олсак

у₁= -19/3; y₂= -11/3; y_з= -1/3; y₄=0; y₅=0; y₆=0;

Демак иккиёклама масала учун

Б₀=(-19/3; -11/3; -1/3; 0; 0; 0)

maxF = max(y₁+2y₂+y₃)= --19/3 - 2*11/3-5*1/3=(-19-22-5)/3= -46/3

max F = min Z = - 46/3

Маъруза №14

"Транспорт масаласи". Унинг иктисодий ва математик куйилиши

"Транспорт масаласининг" (ТМ) иктисодий ва математик куйилиши мазмунини аниклаш учун куйидаги масалага мурожат киламиз

Учта корхона 1 суткада мое равишда 90км, 70км ва 50км кабель ишлаб чикаради ва бу махсулот 4 та алока корхона томонидан 1
суткада ишлатилади (мос равишда 80км, 60км, 40км ва 30 км).

Агар биринчи ишлаб чикариш корхонадан 1.2.3,4 истемолчиларга бир км кабельни етказиб бериш транспорт харажатлари мос равишда 3,2,1,4 (ш. б), II-корхонадан 1,3,3,2 ва III корхонадан 4,1,2,3 (ш. б) булса, кабель махсулотларининг истеъмолчиларга тупик етказиб беришда уларни шундай таксимлаш керакки, бунда умумий транспорт харажатлари энг кам булсин. Бу масала "ТМ" бетида ва унинг схемаси куйидагича булади: и\ч гр.

"ТМ" математик куйилишини аниклаш учун куйдаги белгилашлар киритамиз:
I, II, III- ишлаб чикарувчи корхоналар группаси:   сумма = 90 + 70 + 50 = 210

1, 2, 3, 4 - истеъмолчи корхоналар группаси сумма=210

I-1:х11 II-1:х₂₁ III-1:x₃₁
I-2:х₁₂ II-2:х₂₂ III-2:x₃₂
I-3:x₁₃ II-3:х₂₃ III-3:x₃₃
I-4:x₁₄ II-4:х₂₄ III-4:х₃₄
Таъриф:

Агар    сумма_и/ч=сумма_ист =210    булса   бундай   ТМ   ёпик   турдаги   ТМ дейилади, акс холда ТМ очик турдаги ТМ дейилади.

Транспорт масаласининг математик куйилишини аниклаш учун куйидаги белгилашлар ва тушунчалар киритамиз. Бунинг учун юкоридаги масала берилганларидан фойдаланамиз. х_II - I ишлавб чикарувчидан 1 истеъмолчига етказиладиган кабел махсулотлари хажми, худди шунингдек:

x₁₂-I--2; x₁₃ -I--2; x₁₄ -I--4;

x₁₃ -II--1; x₂₂ -II--2; x₂₃ -II--3; x₂₄ -II--4;

х₃₁= III--1; х₃₂ -III-- 2;  х₃₃ -III--3; х₃₄ -III--4;

Шу  белгилашларга  асосан   I,   II,   III   ишлаб   чикарувчилар  учун   куйидаги чегаравий шартларни хосил киламиз:

x₁₁+x₁₂+x₁₃+x₁₄=90
x₂₁+x₂₂+x₂₃+x₂₄=70 (1)

x₃₁+x₃₂+x₃₃+x₃₄=50

1, 2, 3, 4 истеъмолчилар учун хам мое чегаравий шартларни куйидагича аниклаймиз:

х₁₁+х₂₁+х₃₁=80

x₁₂+x₂₂+x₃₂=60 (2)
x₁₃+x₂₃+x₃₃=40

x₁₄+x₂₄+x₃₄=30

Энди берилган транспорт харажатларининг ташилиш хажмларига мое равишда купайтириб умумий трнаспорт харажатлар микдорини куйидагича аниклаймиз ва уни минимумга йуналтирамиз.

F = 3x_ll + 2x_l2 + x₁₃ + 4x₁₄ + x₂₁ + Зx₂₂ + Зx₂₃ + 2x₂₄ + 4x₃₁ +

x₃₂ + 2x₃₃ + 3x₃₄---min      (3)

Иктисодий   мантикка   биноан   ташилиш   хажмлари    х_ij > 0(i = 1,3;  j = 1,4) шартларини каноатлантириш керак. Агар (1) (2) (3) ва х..ларнинг манфий мослик шартларини биргаликда карасак берилган иктисодий масаланинг математик модели хосил булади.

Шундай килиб, "транспорт масаласи"нинг математмик куйилиши куйидагича х₁₁, х₁₂, ..., х₃₄  ларнинг шундай манфий булмаган кийматларини топиш керакки, улар (1)-(2) чегаравий шартларни каноатлартириб, (3) максад функцияга минимиал киймат берсин.

Маъруза № 15,16

Транспорт масаласини потенциал усуллар билан ечиш

Максад «Транспорт масаласининг» иктисодий мохиятидан келиб чиккан холда алока хизмати курсатишда оптимал маршрутларини аниклаш усулларини талабаларга ургатиш. Буни потенциаллар усули мисолида атрофига баен килиши (4-6 мин.)

Утилган даре юзасидан савол-жавоб утказиш (3-5 мин.)

Мавзуни еритиш (40-60 мин. хар бир маъруза учун ) Транспорт масаласини ечишнинг аник усулларидан бири - бу потенциаллар
усулидир. Бу усул 1949 йилда Л.В. Контарович ва М.К. Говурин томонидан ишлаб чяикилган. Усулнинг асосий мохияти шундаги ЧПМни ечиш усулларига боглик булмаган холда транспорт масаласига мослаштрилган симплекс ишлаб чикилган. Бу усулда хам аввал базис ечим (таянч ечим) топилиб, оптимал ечимга якинрок булган базис ечимлар кетма-кетлиги аникланиб, чекли кадамлардан сунг оптимал ечим топилади.

Маъруза № 15

_____Транспорт масаласининг бошлангич базис счнмини топиш____

Транспорт масаласининг бошлангич базис ечимини топиш учун «шимолий - гарб» усулини куриб чикамиз. Бу усулнинг асосий мохияти куйидагидан иборат: (Бу мохиятини   аник   масалада   очишга   харакат   киламиз).   Бизга   дастлабки   жадвали куйидагига булган транспорт масаласи берилган булсин: (епик транспорт масаласи)

Жадвал 1

Истеъмол и/ч		В1		В2		В3		В4
		300		500		100		200
А1	100	x11	c11	x12	c12	x13	c13	x14	c14
А2	400	x21	c21	x22	c22	x23	c23	x24	c24
A3	600	x31	c31	x32	c32	x33	c33	x34	c34

БЬу   масалада   биз    х_ij (i = 1.3; j = 1,4)    ларнинг   шундай   кийматларини топишимиз керакки, жадвал сатрлари буйича уларнинг йигиндилари моc равишда 100 400, 600 ларга устунлар буйича мое равишда 300, 500, 100 ва 200 ларга тенг булиши шарт (шу ерда ечимнинг иктисодий мохияти баен килинади). Жадвал-1да юкоридаги (А.В) катакдан бошлаймиз. Бунда истеъмот (В1)билан ишлаб чикариш (А1) хажмларини солиштириб кичигини танлаймиз яъни x₁₁ =min (300, 100)= 100 бунда c₁₁ га белги куямиз.А1 буйича ишлаб чикариш хажми тугаганлиги учун бу сатрни хисобдан чикарамиз.

Энди (А2, В1) катакга караб, етмаган истеъмолни ундан тулдирамиз. (яъни 200). х₂₁ =min (200, 400)=200 Бунда с₂₁ га белги куямиз ва В устунни хисобдан чикарамиз, шу коидага биноан бошка номаълумларни топамиз. Натижада куйидагиларга эга буламиз. x₂₂=min(500,200)=200 х₃₂ =min (600, 300)=300

х₃₃ =min (300, 100)= 100 х₃₄ =min (200, 200)=200
Натижада жадвал - 1 куйидаги куринишга келади:

Жадвап - 2 _________________

Истеъмол и/ч		В1		В2		ВЗ		В4
		300		500		100		200
А1	100	100	^С11	^С12			^С13		^С14
А2	400	200	^С21	200	^С22		^С23		^С24
A3	600	с31		300	^С32	100	с33	200	^С34

Яъни ташиш режаси куйидагича булади
x11=100; x₂₁=200 x₂₂=200; x₃₂=300               x₃₃=100;                    x₃₄=200

В1                      В2                                 ВЗ                                  В4

Масаланинг умумий ечими эса куйидагига тенг булади (бу ечимни куп холларда 1-план дейилади):

Б=(

х₁₁ =100; х₂₁ =200; х₃₁=0; х₁₂ = 0; x₂₂= 200; х₂₃=200;
x₃₂ = 300; x₁₃ =0; x₂₃ = 0; x₃₃= 100; х₁₄ = 0; x₂₄ = 0; x₃₄ =200 (1)

(1) ечимга мое максад функциянинг киймати, яъни барча ишлаб чикарилган махсулотларни истеъмолчиларга тулик етказиб бериш учун сарфланган транспорт харажатларининг умумий киймати куйидагича аникланади:

Z₁ =100с₁₁ + 200с₂₁ + 200с₂₂ + 300с₃₂ + 100с₃₃ + 200с₃₄ (2)

Якун: Бу масаланинг иктисодий мазмунини алока сохасидан олинган конкрет мисолларда баен килиниб умумлаштирилади.

Маъруза №16

Транспорт масаласининг базис ечимини оптималлик шартлари (Потенциаллар усули)

Максад. Транспорт масаласининг базис ечими мавжудлигини хисобга олган холда (базис ечими ва ечимлар чексиз куплиги маълум) улар ичида оптималини аниклаш жараенининг талабаларга тушунтириш. Бу жараеннинг алгоритми аниклаш. Мавзуни баен килиш: Базис ечимларни топиш жараени учун умумий изох келтирилади. «Шимолий-Гарб» бурчак усулида таксимотда иштирок этадиганномаълумлар сони n+m-1 га тенг. бунда n-ишлаб чикарувчилар группаси сони; m - истеъмолчилар группаси сони. Бундан куйидаги хулоса келиб чикади: «Транспорт масаласини» шимоилй-гарб усули билан ечишда базис узгарувчилар сони n+m-1. озод номаълумлар сони n-m-(n+m- 1) га тенг, бунда озод номаълумлар нолга тенг. Ечимнинг   оптималлигини   текшириш   учун    куйидагиердамчи   амалларни бажарамиз.   яъни   базис   номаълумларни   озод   номаълумлар   оркали   ифодалаймиз. Чегаравий шартлардан куйидагиларни аниклаймиз

х₁₁= 100 - х₁₂ - х₁₃ - х₁₄   -   1-горизонтал тенгламадан;

х₂₁ = 300 - х₁₁ - х₃₁ = 300 - 100 + x₁₂ + х₁₃ + х₁₄ - x₃₁ - 1-вертикал тенгламадан;
ва х.к. х₂₂, х₃₂, х₃₃ ва х₃₄ ни барчани озод номаълумлар оркали ифодалаймиз. Агар бу муносабатларни максад функциясига келтириб куйсак, Z максад функциясининг озод номаълумлар оркали ифодасини аниклаймиз.

Z = Z₁ + k₁₂x₁₂ + k₁₃х₁₃ + k₁₄x₁₄ + k₂₃x₂₃ + k₂₄x₂₄ + k₃₁х₃₁ ,         (1)

Бунда Z₁ базислар буйича умумий транспорт харажатлари. Z₁ нинг кийматини камайтириш учун   k_ij лар ичида камида битгаси манфий

булиши шарт.

Адабиетлар:

1. Ф.Б.Бадалов. "Оптималлаш назарияси ва математик программалаштиряш" Тошкент, "Укитувчи", 1989 и. -1886.

2. М. Атхамов, Т. Отабоев."планлаштиришда математик методларни куллаш" Тошкент. "Укитувчи", 1982 и.

3. В.А.Барсук и др. "ЭММиМ в планировании и управлении в отрасли связи" М.:"РиС. 1984г.,-264с"

4. Б.Банди. "Основы линейного программирования". М.: "РиС", 1989 г. -175 с.