O‘ZBEKISTON ALOQA VA AXBOROTLASHTIRISH AGENTLIGI TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
AXBOROT TEXNOLOGIYALARI FAKULTETI
“AXBOROT NAZARIYASI VA KODLASH”
fani bo‘yicha amaliy mashg‘ulotlarga
USLUBIY KO‘RSATMA
Toshkent – 2012
Mualliflar: G‘aniev S.K., Abdullaev D.G‘.
“Axborot nazariyasi va kodlash” fani bo‘yicha amaliy mashg‘ulotlarga uslubiy ko‘rsatma. TATU. 35 bet. Toshkent, 2012
Uslubiy ko‘rsatma “Axborot nazariyasi va kodlash” fanining dasturi bo‘yicha tuzilgan bo‘lib, teng extimollik va teng extimollik bo‘lmagan, o‘zaro bog‘langan va o‘zaro bog‘lanmagan xabarlarning informatsiya miqdorini hisoblash; informatsiya hajmini hisoblash; turli sistemalarning entropiyasini hisoblash; shartli entropiya va birlashma entropiyani hisoblash; xabarlarning ortiqchaligini hisoblash; aloqa kanali bo‘yicha informatsiyani uzatish tezligini hamda aloqa kanalining o‘tkazish qobiliyatini hisoblash; optimal notekis kodlarni qurish; xatoliklarni aniqlovchi va tuzatuvchi kodlarni qurish bo‘yicha masalalarni o‘z ichiga olgan. Uslubiy ko‘rsatmada kodlash yordamida informatsiyani himoyalash masalasi ham o‘rin olgan.
Taqrizchi: «Ęîěpyuter tizimlari»
kafedrasi professori, t.f.d. Usmanov R.N.
Toshkent axborot texnologiyalari universiteti. 2012 y.
1 – mavzu. Informatsiyani miqdoriy baholash.
Qisqacha nazariy ma'lumot.
Agar xabarda n ta element bo‘lsa, bo‘lishi mumkin bo‘lgan xabarlar soni
N = qn,
bu yerda: q – son teranligi, ya'ni informatsiyani ifodalash uchun qabul qilingan simvollar(elementlar) soni; n – son uzunligi, ya'ni berilgan kattalikdagi sonni ifodalash uchun zaruriy va yetarli o‘rinlar(pozitsiyalar) soni.
Teng extimollik va o‘zaro mustaqil simvollardan tuzilgan alfavit simvoliga to‘g‘ri keluvchi noaniqlik (entropiya)
H
= 
bit/simvol.
Xabar olinganida yo‘qotiluvchi noaniqlik informatsiya ekanligini xisobga olsak, informatsiya miqdorini xabarlarning umumiy soni k ni bitta xabarga to‘g‘ri keluvchi o‘rtacha entropiyaga ko‘paytirish orqali ifolalash mumkin. Alfavitniig teng extimollik va o‘zaro mustaqil simvollari uchun
bit.
Extimolliklari teng bo‘lmagan alfavitda alfaviitning simvoliga to‘g‘ri keluvchi entropiya
bit/simvol.
Extimolliklari teng bo‘lmagan “k” ta simvollardan tuzilgan xabardagi informatsiya miqdori
bit.
Informatsiyaning eng katta miqdori noaniqlik to‘laligicha bartaraf etilganida olinadi, noaniqlik esa barcha xodisalarning teng extimolligida eng katta bo‘ladi.
Demak,
.
Entropiyani extimolliklarni ularning logarimflariga ko‘paytmalarining yig‘indisi sifatida hisoblash masalalari yechilganida extimolliklar to‘liq xodisalar guruhini ifodalashi lozim.
1.1– misol. Uzatilishi mumkin bo‘lgan k ta xabarlardan biri 3 bit informatsiyani eltadi. k topilsin.
Yechish.
;
k = 23 = 8.
1.2– misol. Alfavit simvollari ikkita sifat alomatlariga ega.
a) xabarlar elementlarini 3, 4, 5 va 6 tadan kombinatsiyalab xabarlarning qanday sonini olish mumkin?
b) bunday xabarlarning bitta elementiga informatsiyaning qanday miqdori to‘g‘ri keladi?
Yechish. q =2.
a) N1 = 23 =8; N2 = 24 = 16; N3 = 25 =32; N4 = 26 = 64.
b) I1 = log28 = 3 bit; I 2 = log216 = 4 bit; I3 = log232 = 5 bit; I4 = log264 = 6 bit.
1.3– misol. Axborotda uchta harf bor A, B, C.
a) xabarda uchta harfni kombinatsiyalab xabarlarning maksimal sonini tuzing.
b) bunday bitta xabarga to‘g‘ri keladigan informatsiya miqdorini aniqlang.
v) alfavit simvoliga to‘g‘ri keladigan informatsiya miqdorini aniqlang.
1.4– misol. Shaxmat taxtasidagi donalar xolatini nechta usul orqali uzatish mumkin? Har bir usuldagi informatsiya miqdori topilsin.
Yechish. Shaxmat taxtasi kataklarini nomerlab, katak nomerini uzatish mumkin. Buning uchun 64 ta sifat alomatlari kerak bo‘ladi, ya'ni q = 64, ammo katak nomerini uzatish uchun bitta xabar yetarli bo‘ladi. Bunda informatsiya miqdori
bit.
Taxtadagi kerakli katakni ko‘rsatish uchun uning gorizontal va vertikal bo‘yicha kordinatalarini uzatish mumkin. Buning uchun sakkizta sifat alomatlari (sakkizta nomer gorizontal bo‘yicha va sakkizta nomer vertikal bo‘yicha) yetarli, ammo ikkita xabar uzatilishi lozim. Bunda informatsiya miqdori
bit.
1.5– misol.16; 25; 32 ta harflardan tashkil topgan alfavit harfiga qanday informatsiya miqdori to‘g‘ri keladi?
1.6– misol. Alfavit A, B, C, D harflardan tashkil topgan. Harflarning paydo bo‘lish extimolligi quyidagicha pA = pB = 0,25; pC = 0,34; pD = 0,16. Ushbu alfavitdan tuzilgan xabar simvoliga to‘g‘ri keladigan informatsiya miqdori aniqlansin.
Yechish. Alfavit simvoliga to‘g‘ri keladigan informatsiya miqdori ushbu alfavitning entropiyasiga teng. Alfavit simvollarining extimolliklari teng bo‘lmagani sababli entropiya quyidagicha aniqlaadi:
1.7– misol. Alfavitdagi simvollar soni q = 5. Ushbu alfavitdan tuzilgan xabar simvoliga to‘g‘ri keladigan informatsiya miqdori aniqlansin:
a) agar alfavit simvollarining paydo bo‘lish extimolliklari teng bo‘lsa;
b) agar alfavit simvollarining paydo bo‘lish extimolliklari quyidagicha bo‘lsa p1 = 0,8; p2 = 0,15; p3 = 0,03; p4 = 0,015; p5 = 0,05.
1.8– misol. Tajribalarning berilgan sonida xodisa paydo bo‘lish extimolligi p ga teng, xodisaning paydo bo‘lmaslik extimolligi s = 1 – p ga teng. s ning qanday qiymatida tajriba natijasi maksimal noaniqlikka ega bo‘ladi?
1.9– misol. To‘rt xonali uchli kodning 8 ta xabari olingandagi informatsiya miqdori xisoblansin.
Yechish. Sifat alomatlarining soni q = 3. Ular kodda to‘rttalab kombinatsiyalanadi, ya'ni n = 4. Bunday kodning xabarlari soni N = qn = 34. Bitta xabarga to‘g‘ri keladigan entropiya
bit/simvol.
8 ta xabardagi informatsiya miqdori
bit.
1.10– misol. Bir vaqtda va bitta zavoddan olingan sakkizta dastgohdan birining buzilganligi to‘g‘risidagi xabarning informatsiya miqdori xisoblansin.
1.11– misol. Xabar sifat alomatlari q = 128 ga ega bo‘lgan teng extimollik alfavit asosida tuzilgan. Agar xabarda 42 bit informatsiya bo‘lishi malum bo‘lsa, undagi simvollar soni aniqlansin. Ushbu xabarning entropiyasi nimaga teng?
1.12– misol. Fizik sistema to‘rtta xolatdan birida bo‘lishi mumkin. Sistema xolatlari extimolliklari orqali quyidagicha berilgan:
.
Bunday sistemaning entropiyasi aniqlansin.
1.13– misol. Manba chiqish yo‘lida simvollarning paydo bo‘lish extimolliklari quyidagicha:
Xabarlar manbaining entropiyasi topilsin.
1.14– misol. 5 ta sifat alomatlaridan tuzilgan xabarda alomatlarning paydo bo‘lish extimolliklari quyidagicha:
p1 = 0,7; p2 = 0,2; p3 = 0,08; p4 = 0,015; p5 = 0,05.
Xabarda jami 20 belgi qabul qilingan. Barcha xabardagi informatsiya miqdori aniqlansin. Agar barcha alomatlar bir xil extimollikka ega bo‘lsa, ushbu xabardagi informatsiya miqdori qanday bo‘ladi?
1.15– misol. O‘zbekcha matnlarda harflar extimolliklarining taqsimoti keltirilgan jadvaldan (3–ilova) foydalanib o‘zbek tili entropiyasi aniqlansin.
2– mavzu. Shartli entropiya va birlashma entropiya
Qisqacha nazariy ma'lumot.
Shartli entropiya informatsiya nazariyasida kodlanuvchi alfavit simvollari orasidagi o‘zaro bog‘liqlikni aniqlashda, aloqa kanallari bo‘yicha informatsiya uzatishdagi yo‘qotishlarni aniqlashda va birlashma entropiyani xisoblashda ishlatiladi.
Entropiyalarni jamlash qoidasiga muvofiq ikkita mazmun jixatidan turli (mustaqil) kitoblardagi informatsiya miqdori – aloxida kitoblardagi informatsiya miqdorlarining yig‘indisiga teng. Agar bir kitob ikkinchi kitobning qismini o‘z ichiga olsa, ushbu ikki kitobdagi informatsiya miqdori aloxida kitoblardagi informatsiya miqdorlarlarining yig‘indisiga teng bo‘lmaydi, balki undan kam bo‘ladi. Bu xolda informatsiya miqdorini o‘lchashda shartli entropiya tushunchasidan foydalaniladi.
Shartli entropiyani xisoblashda shartli ehtimolliklar u yoki bu ko‘rinishda ishlatiladi.
Agar
n ta xabar uzatilganida A simvoli m
marta, B simvoli l marta, A simvoli B
simaoli bilan birgalikda k marta paydo bo‘lgan bo‘lsa A
simvolning paydo bo‘lish ehtimolligi 
;
B simvolning paydo bo‘lish ehtimolligi 
;
A va B simvollarning birgalikda paydo bo‘lish
ehtimolligi p
;
B simvolga nisbatan A simvolning paydo bo‘lishining
shartli ehtimolligi 
;
A simvolga nisbatan B simvolning paydo bo‘lishining
shartli ehtimolligi 
.
Ushbu ifodalardan foydalanib A va B simvollarning birgalikda paydo bo‘lish ehtimolligini aniqlash mumkin.
p(AB)=p(A)p(A/B)=p(A)p(B/A)
Ehtimolliklar shartli bo‘lgani sababli, shartli entropiya quyidagicha yoziladi:
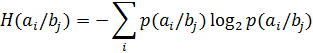
bu yerda i indeks A xabar manbaining ixtiyoriy xolatini tavsiflash uchun, j indeksi B adresatning ixtiyoriy xolatini tavsiflash uchun tanlangan.
Birlashma entropiya statistik bog‘langan xabarlarning birgalikda paydo bo‘lish entropiyasini hisoblashda ishlatiladi. Masalan, xalalli aloqa kanali bo‘yicha 5 raqamini yuz marta uzatish natijasida 5 raqami 90 marta, 6 raqami 8 marta, 4 raqami 2 marta qabul qilindi. 5 raqami uzatilganida 5-4, 5-5, 5-6 kombinatsiyalarning paydo bo‘lishining noaniqligini birlashma entropiya yordamida tavsiflash mumkin. Í(A,B) – A simvol uzatilganida B simvol qabul qilinishining noaniqligi. Uzatilgan A xabarlarning va qabul qilingan B xabarlarning ansambllari uchun birlashma entropiya quyidagi yig‘indi ko‘rinishiga ega:
Birlashma entropiya va shartli entropiya o‘zaro quyidagi munosabat orqali bog‘langan.
H(A,B)=H(A)+H(B/A)=H(B)+H(A/B),
H(B/A)=H(A,B)-H(A); H(A/B)=H(A,B)-H(B)
2.1- misol. Tajribadan ma'lum bo‘ldiki, uzunligi 5 ta simvoldan iborat har bir 100 ta xabar uzatilganida A simvol 50 marta, B simvol 30 marta, B simvoli A simvoli bilan birgalikda 10 marta uchraydi. Í(A/B) va Í(B/A) shartli entropiyalar aniqlansin.
Yechish. Uzatilgan simvollarning umumiy soni
n = 100 * 5 = 500.
A simvolning paydo bo‘lish extimolligi
B simvolning paydo bo‘lish extimolligi
A va B simvollarning birgalikda paydo bo‘lish extimolligi
B simvolga nisbatan A simvolning paydo bo‘lishining shartli extimolligi
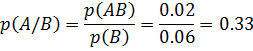
A simvolga nisbatan B simvolning paydo bo‘lishining shartli extimolligi
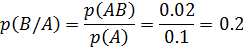
B simvolga nisbatan A simvolning shartli entropiyasi
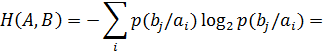
A simvolga nisbatan B simvolning shartli entropiyasi
2.2- misol. Matnli xabarlar uzatilganda statistik kuzatishlar natijasida ma'lum bo‘ldiki, 6 ta harfdan iborat so‘zlarda har bir 100 ta xabarda A harfi 80 marta, B harfi 50 marta, A va B harflar birgalikda 10 marta uchraydi. Í(A/B) va Í(B/A) shartli entropiyalar aniqlansin.
2.3- misol. Birinchi savatda ikkita olma va bitta nok, ikkinchi savatda uchta olma va bitta nok, uchinchi savatda ikkita olma va ikkita nok bor. Ixtiyoriy savatda olmani taxminan olinishi imkoniyatining to‘liq shartli entropiyasi aniqlansin.
2.4- misol. Xabarlar ikkili kod yordamida uzatiladi. Birinchi xolda 0 va 1 ning paydo bo‘lish extimolligi mos xolda p0 = 0,8 va p1 = 0,2. Aloqa kanalida xalallar yo‘q, ya'ni 0 ni 1 ga va 1 ni 0 ga o‘tishlarning shartli extimolliklari nolga teng. Ikkinchi xolda simvollar teng extimolliklar p0 = p1 = 0,5 bilan uzatiladi, ammo xalallar ta'siri natijasida o‘tishlarning extimolliklari
p(1/1) = 0,8; p(1/0) = 0,2; p(0/0) = 0,8; p(0/1) = 0,2.
Birinchi va ikkinchi xollardagi xabarlar entropiyasi aniqlansin.
3– mavzu. Informatsiyani uzatish tezligi va aloqa kanalining o‘tkazish qobiliyati.
Qisqacha nazariy ma'lumot.
Xalallar yo‘qligi sharoitida informatsiyani uzatish tezligi vaqt birligida xabar simvoli eltadigan informatsiya miqdori orqali aniqlanadi.
bu yerda n – vaqt birligida xabarlar manbaida shakllanuvchi simvollar soni; H – ushbu manbada shakllangan xabarlarning bitta simvoli olinganida bartaraf etiluvchi entropiya(noaniqlik).
Ikkilik simvollar uchun informatsiyani uzatish tezligini quyidagicha ifodalash mumkin.
bu
yerda 
–
bitta ikkilik simvolni uzatish vaqti.
Informatsiyani uzatish tezligi doimo birlamchi alfavitga nisbatan aniqlanadi va faqat uning entropiyasiga bog‘liq, signalni uzatish tezligi esa ikkilamchi alfavitga nisbatan aniqlanadi. Demak, informatsiyani uzatish tezligi xabarlar manbaining informatsion xarakteristikalariga bog‘liq, signallarni uzatish tezligi esa apparaturaning tezkorligiga bog‘liq. Signallarni uzatish tezligi quyidagi ifoda bo‘yicha hisoblanadi.
bu
yerda ikkilamchi
alfavitning bitta simvolini uzatish vaqti.
Extimolliklari teng, o‘zaro bog‘lanmagan, davomliligi teng simvollardan tuzilgan xabarlar uchun informatsiyani uzatish tezligi
Extimolliklari teng bo‘lmagan, o‘zaro bog‘lanmagan, davomliligi teng simvollar uchun informatsiyani uzatish tezligi
Extimolliklari teng bo‘lmagan, o‘zaro bog‘langan, davomliligi teng simvollar uchun informatsiyani uzatish tezligi
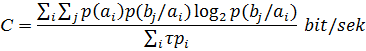
Aloqa kanalining o‘tkazish qobiliyati ushbu aloqa kanali bo‘yicha informatsiyani uzatishning maksimal tezligi orqali aniqlanadi
Ikkilik kod uchun
Xalallar mavjudligida aloqa kanalaning o‘tkazish qobiliyati bir sekundda qabul qilingan simvollar sonini xabarlar manbai entropiyasidan xabarlar manbaining qabul qilingan signallarga nisbatan shartli entropiyasini ayirmasiga ko‘paytirish sifatida hisoblanadi.
yoki
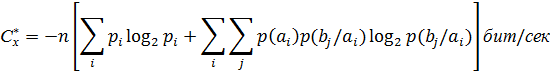
Umumiy xolda
3.1- misol. Xabarlar 5 ta sifat alomatlaridan (q = 5) tuzilgan. Simvol davomliligi t = 20 msek. Signallarni uzatish tezligi hamda informatsiyani uzatish tezligi aniqlansin.
Yechish. Signallarni uzatish tezligi
Informatsiyani uzatish tezligi
3.2- misol. Aloqa kanali bo‘yicha xabarlarni uzatishda to‘rtta turli simvolli alfavitdan foydalanilgan. Barcha simvollarning davomliligi t = 1 sek. Aloqa kanalining o‘tkazish qobiliyati aniqlansin.
Yechish. Aloqa kanalining o‘tkazish qobiliyatini aniqlash uchun quyidagi formuladan foydalanamiz.
yoki
bu yerda q- xabarlarning umumiy soni, t - signalning o‘rtacha davomliligi.
Xabarlarni uzatish uchun to‘rtta simvolli alfavit ishlatilganligi sababli
q = 44
Barcha signallarning davomliligi
4t = 4 mc
Demak
3.3- misol. Xabarlar davomliligi t = 0,1 sek bo‘lgan, o‘zaro bog‘lanmagan simvollar yordamida uzatiladi. Xabarda simvollarning paydo bo‘lish extimolliklari bir xil. 2, 5 va 32 sifat alomatlaridan tuzilgan xabarlar uchun signallarni uzatish tezligi hamda informatsiyani uzatish tezligi aniqlansin.
3.4 - misol. Xabarlar ikkilik kodda uzatiladi (q = 2). 0 ni uzatish vaqti t = 1 sek, 1 ga mos signal davomliligi t = 5 sek. Quyidagi xollar uchun informatsiyani uzatish tezligi aniqlansin.
ŕ) p0 = 0,5; p1 = 0,5;
b) p0 = 0,37; p1 = 0,63;
ń) p0 = 0,2; p1 = 0,8;
d) p0 = 0,02; p1 = 0,98.
Yechish.
a) 
bit/sek.
b) 
bit/sek.
c) 
bit/sek.
d) 
bit/sek.
3.5 - misol. Alfavitdagi simvollar soni q = 4. Simvollarning paydo bo‘lish extimolliklari p1 = 0,15; p2 = 0,4; p3 = 0,25; p4 = 0,2. Simvollar davomliligi t1 = 3 sek; t2 = 2 sek; t3 = 5 sek; t4 = 6 sek. Bunday simvollardan tuzilgan xabarlarni uzatish tezligi aniqlansin.
3.6 - misol. Alfavitdagi simvollar soni q = 7. Simvollarning har birini uzatish tezligi mos xolda quyidagicha: t1 = 1 sek; t2 = 2 sek; t3 = 3 sek; t4 = 5 sek; t5 = 5 sek; t6 = 5 sek; t7 = 7 sek. Quyidagi xollar uchun informatsiyani uzatish tezligi aniqlansin.
a) simvollarning paydo bo‘lish extimolliklari teng;
b) simvollarning paydo bo‘lish extimolliklari quyidagicha:
p(A1) = 0,125; p(A2) = 0,715; p(A3) = 0,02; p(A4) = 0,02; p(A5) = 0,098; p(A6) = 0,012; p(A7) = 0,02.
4– mavzu. Xabarlarning ortiqchaligini aniqlash.
Qisqacha nazariy ma'lumot.
Xabarlar manbaining entropiyasi sifat alomatlarining berilgan soniga ega bo‘lgan alfavit uchun maksimal entropiyaga teng bo‘lmasligi ushbu manba xabarlarining katta sonli informatsiyani eltishi mumkinligini anglatadi.
Bunday manba xabarlarining simvoliga to‘g‘ri keluvchi absolyut yuklanmaganlik
Alfavit strukturasidagi ortiqcha informatsiya miqdorini aniqlash uchun ortiqchalik tushunchasi kiritilgan. Informatsion ortiqchalik o‘lchamsiz kattalik bo‘lib, alfavit simvoliga to‘g‘ri keladigan nisbiy ortiqchalikni ifodalaydi.
bu
yerda 
-
zichlash koeffitsienti(nisbiy entropiya).
Xabardagi simvollar paydo bo‘lish extimolliklari teng bo‘lmagan xolda, ortiqchalik
Xabar simvollari orasidagi statistik bog‘lanish tug‘diruvchi ortiqchalik
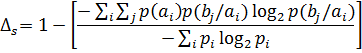
To‘liq informatsion ortiqchalik
Ortiqchalik har doim ham nomaqbul xisoblanmaydi. Kodlarning xalallarga bardoshligini oshirish uchun ortiqchalik zarur va u sun'iy ravishda qo‘shimcha simvollar ko‘rinishida kiritiladi.
4.1- misol. Xabarlar a,b,c,d alfavit vositasida tuzilgan. Matnlarda alfavit harflarining paydo bo‘lish extimolliklari quyidagicha:
pa=0,2, rb=0,3, pc=0,4, pd=0,1. Ushbu alfavit asosida tuzilgan xabarlar ortiqchaligi aniqlansin.
Yechish.
Ortiqchalik 
.
To‘rtta harfli alfavit uchun maksimal entropiya
Xabar simvoliga to‘g‘ri keladigan o‘rtacha entropiya
Ortiqchalik
4.2- misol. Xabarlar a,b,c,d,e,f,g,h alfavit asosida tuzilgan. Matnlarda alfavit harflarining paydo bo‘lish extimolliklari quyidagicha:
pa = 0,1; pb = 0,05; pc = 0,04; pd = 0,01; pe = 0,2; pf = 0,5; pg = 0,07; ph = 0,03.
Ushbu alfavit bo‘yicha tuzilgan xabarlar simvollari entropiyasi, ortiqchaligi va yuklanmaganligi aniqlansin.
4.3-
misol. Matnlarda harflarning paydo bo‘lishi
chastotasini hisobga olgan holda ingliz, nemis , fransuz va ispan tillarining
entropiyasi quyidagicha: Ningl = 4,03 bit/simvol; Nnem
= 4,1 bit/simvol; Nfran = 3,96 bit/simvol; Nisp
= 3,98 bit/simvol. Ushbu tillar uchun 
ko‘rinishidagi
ortiqchalik aniqlansin.
4.4- misol. Xabarlar a,b,c,d,e,f,g,h alfavit asosida tuzilgan. Matnlarda alfavit harflarning paydo bo‘lish extimolliklari quyidagicha:
pa = 0,03; pb = 0,26; pc = 0,09; pd = 0,05; pe = 0,16; pf = 0,1; pg = 0,09; ph = 0,22.
Ushbu alfavit bo‘yicha tuzilgan xabarlar simvollari entropiyasi, ortiqchaligi va yuklanmaganligi aniqlansin.
5– mavzu. Kodlash yordamida informatsiyani himoyalash.
Qisqacha nazariy ma'lumot.
Axborotni ximoyalash mexanizmlarining asosini shifrlash tashkil etadi. Informatsiyani shifrlash deganda ochiq informatsiyani (dastlabki matnni) shifrlangan informatsiyaga o‘zgartirish (shifrlash) va aksincha (rasshifrovka qilish) jarayoni tushuniladi. Shifrlangan matn shifrmatn deb yuritiladi. Shifrlashning ko‘pgina turli usullari mavjud. Quyida keng tarqalgan shifrlardan biri – Vijiner shifri ustida so‘z boradi. Bunda shifrlashning ishonchlilik darajasi alfavit harflarining paydo bo‘lish statistik qonuniyatlarining buzilishi evaziga ortadi.
Vijiner shifriga binoan alfavitning xar biriga nomer beriladi. Masalan, o‘zbek alfaviti harflariga 0 (A = 0) dan to 34 (Ҳ = 34) gacha raqamlar moslashtiriladi.
Kalit qandaydir so‘z yoki xabarlar tagiga qaytarilib yoziladigan harflar ketma – ketligi sifatida ifodalanadi. Shifrmatnning har bir harfiga raqamli ekvivalent xabar harfi raqamli ekvivalentini uning tagidagi kalit harfi raqamli ekvivalentiga 35 ning moduli bo‘yicha jamlash orqali aniqlanadi.
5.1- misol. “ҒˇÇŔ” kaliti yordamida “ĎŔŐŇŔĘÎĐ” dastlabki matnni shifrlash va rasshifrovka qilish talab etilsin.
Yechish. Shifrlash va rasshifrovka qilish quyida keltirilgan.
Dastlabki matn Ď Ŕ Ő Ň Ŕ Ę Î Đ
Kalit Ғ ˇ Ç Ŕ Ғ ˇ Ç Ŕ
Shifrmatn Í ˇ ß T Ғ ĆŃ R
Kalit Ғ ˇ Ç Ŕ Ғ ˇ Ç Ŕ
Dastlabki matn Ď Ŕ Ő Ň Ŕ Ę Î Đ
Vijiner shifrining kamchiligi – yuqori ishonchlilikni ta'minlash uchun aytarlicha uzun kalitlarning talab etilishi. Bitta harfdan iborat kalitla shifr Sezar shifri, chegaralanmagan qaytarilmaydigan kalitli shifr Vernam shifri sifatida ma'lum.
5.2- misol. “ÝĐŔ” kaliti yordamida “ŇŔĐŔҚҚȨҔ dastlabki matn shifrlansin va rasshifrovka qilinsin.
5.3- misol. “ĚŔÉ” kaliti yordamida “ĘÎÍŃŇČŇÓÖČß” dastlabki matn shifrlansin va rasshifrovka qilinsin.
5.4- misol. “AËÎҚŔ” kaliti yordamida “ŇĹËĹĘÎĚMÓÍČĘŔÖČß” dastlabki matn shifrlansin va rasshifrovka qilinsin.
6-mavzu. Optimal kodlash. Optimal kodlarni qurishning
SHennon-Fano algoritmi
Qisqacha nazariy ma`lumot
Xabar ortiqchaligini kamaytirishning samarali usuli optimal kodlarni qurish hisoblanadi.
Optimal kodlar kod so`zlarining minimal o`rtacha uzunligiga ega bo`ladi. Kod kombinatsiyalarinină o`rtacha uzunligi quyidagicha hisoblanadi:
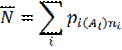
bu erda ni - Ai elementiga mos keluvchi kod kombinatsiyasining uzunligi.
Optimal kodlarni qurishda SHennon-Fano algoritmi keng tarqalgan. Ushbu algoritmga binoan optimal kodni qurish quyidagicha amalga oshiriladi.
1. Xabarlar alfavitining harflari extimolliklarining pasayishi tartibida joylashtiriladi.
2. Kodlanuvchi harflar alfaviti ikkita guruxga shunday ajiratiladiki, ikkala guruxdagi harflar extimolliklarining yigindilari iloji boricha teng bo`lsin.
3. Yuqori guruxga 0 simvoli, pastki guruxga 1 simvoli beriladi.
4. Xosil bo`lgan qism guruxlar o`z navbatida ikki qismga shunday ajratiladiki, yangidan xosil bo`lgan qism guruhlardagi harflar extimolliklarining yigindilari iloji boricha teng bo`lsin va xokazo.
5. Jarayon xar bir qism guruxda bitta harf qolgunicha qaytariladi.
Ushbu (yoki shunga o`xshash) algoritm bo`yicha qurilgan va kod so`zining minimal o`rtacha uzunligigŕ ega bo`lgan kodlar optimal notekis kodlar deb ataladi. Bunday kodlar quyidagi shartni qanoatlantirsa maksimal samarali hisoblanadi.
=
H,
ikkilik kodlar uchun
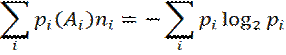
6.1- misol. Alfavitidagi harflarning paydo bo`lish extimolliklari
bo`lgan xabarning optimal notekis kodi qurilsin.
Yechish. Kod qurilishining natijasi quyidagi jadvalda aks ettirilgan.
|
Harflar Ŕi |
Extimollik-lar p(Ai)
|
Harflarni guruxlarga ketma-ket ajratish |
Kod so`zlari |
pi(Ai)n |
|||
|
1 |
2 |
3 |
4 |
|
|
||
|
A1 |
1 / 4 |
|
|
|
|
00 |
0.5 |
|
A2 |
1 / 4 |
|
|
|
01 |
0.5 |
|
|
A3 |
1/8 |
|
|
|
|
100 |
0.375 |
|
A4 |
1/8 |
|
|
101 |
0.375 |
||
|
A5 |
1/16 |
|
|
|
1100 |
0.25 |
|
|
A6 |
1/16 |
|
1101 |
0.25 |
|||
|
A7 |
1/16 |
|
|
1110 |
0.25 |
||
|
A8 |
1/16 |
|
1111 |
0.25 |
|||
Tekshirish
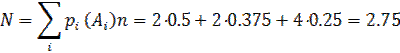
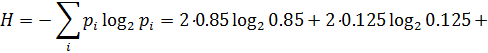
6.2- misol. Alfavitdagi harflarning paydo bo`lish extimolliklari p(A1) = 0,5; p(A2) = 0,25; p(A3) = 0,098; p(A4) = 0,052; p(A5) = 0,04; p(A6) = 0,03; p(A7) = 0,019; p(A8) = 0,011 bo`lgan xabarning optimal notekis kodi qurilsin.
6.3- misol. Alfavitdagi harflarning paydo bo`lish extimolliklari
bo`lgan xabarning optimal notekis kodi qurilsin.
6.4- misol. Alfavitdagi harflarning paydo bo`lish extimolliklari p(A1) = 0,13; p(A2) = 0,16; p(A3) = 0,02; p(A4) = 0,03; p(A5) = 0,6; p(A6) = 0,01; p(A7) = 0,05. bo`lgan xabarning optimal notekis kodi qurilsin.
6.5- misol. Alfavitdagi harflarning paydo bo`lish extimolliklari
bo`lgan xabarning optimal notekis kodi qurilsin.
7-mavzu. Optimal kodlash. Optimal kodlarni qurishning
Xaffmen algoritmi
Qisqacha nazariy ma`lumot
Shennon-Fano usuli doimo bir ma`noli kod qurishga imkon bermaydi, chunki qism guruxlarga ajratishda extimolligi bo`yicha yuqoridagi yoki pastki qism guruxni katta deb qisoblash mumkin. Bunday kamchilik Xaffmen usulida yo`q.
Xaffmen algoritmi bo`yicha optimal notekis kodni qurish quyidagicha amalga oshiriladi.
1. Xabarlar alfavitining harflari asosiy ustunga extimolliklarining pasayishi tartibida joylashtiriladi.
2. Ikkita oxirgi harf bitta yordamchi harfga birlashtirilib, unga yiqindi extimollčę yoziladi.
3. Birlashtirishda ishtirok etmagan harflar extimolliklari xosil qilingan yiqindi extimolligi bilan birga extimolliklarining pasayishi tartibida yordamchi ustunga yoziladi va oxirgi ikkitasi birlashtiriladi va xokazo.
4. Jarayon yiqindi extimolligi 1 ga teng bo`lgan yagona yordamchi harf xosil qilinmaguncha davom etadi.
7.1- misol. Alfavitdagi harflarning paydo bo`lish extimolliklari p(A1)= 0,22; p(A2) = 0,20; p(A3) = 0,16; p(A4) = 0,16; p(A5) = 0,10; p(A6) = 0,10; p(A7) = 0,04; p(A8) = 0,02 bo`lgan xabarning optimal notekis kodi qurilsin.
Yechish. Kodlash jarayonini quyidagi jadval yordamida tushuntirish mumkin. Berilgan xŕáŕđăŕ mos kod kombinatsiyasini tuzish uchun harfning jadval qatori va ustuni bo`yicha o`tish yo`lini kuzatish zarur.
|
Harflar |
Extimolliklar |
Yordamchi ustunlar |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
Ŕ1 Ŕ2 Ŕ3 Ŕ4 Ŕ5 Ŕ6 Ŕ7 Ŕ8 |
0,20 0,16 0,16 0,10 0,10 0,04 0,02 |
0,22 0,20 0,16 0,16 0,10 0,10 0,06 |
0,22 0,20 0,16 0,16 0,16 0,10 |
0,26 0,22 0,20 0,16 0,16 |
0,32 0,26 0,22 0,20 |
0,42 0,32 0,26 |
0,58 0,42 |
1 |
Ko`zga tashlanuvchanlikni ta`minlash maqsadida kod daraxti quriladi. Ýxtimolligi 1 ga mos keluvchi nuqtadan ikkita shox yo`naltirilib, extimolligi katta shoxga 1 simvoli, extimolligi kichik shoxga esa 0 simvoli beriladi. Bunday ketma-ket shoxlash har bir harf extimolligiga yetguncha davom ettiriladi.
Kod daraxti bo`yicha yuqoridan pastga qarab harakatlanib, har bir harf uchun unga mos kod kombinatsiyasini yozish mumkin.
|
Ŕ1 |
Ŕ2 |
Ŕ3 |
Ŕ4 |
Ŕ5 |
Ŕ6 |
Ŕ7 |
Ŕ8 |
|
01 |
00 |
111 |
110 |
100 |
1011 |
10101 |
10100 |
7.2-misol. Alfavitdagi harflarning paydo bo`lish extimolliklari
p(A1) = 0,5; p(A2) = 0,15; p(A3) = 0,12; p(A4) = 0,1; p(A5) = 0,04; p(A6) = 0,04; p(A7) = 0,03; p(A8) = 0,02 bo`lgan xabarning optimal notekis kodi qurilsin.
7.3-misol. Alfavitdagi harflarning paydo bo`lish extimolliklari
A1 = 0,25; A2 = 0,20; A3 = 0,16; A4 = 0,15; A5 = 0,10; A6 = 0,08; A7 = 0,04; A8 = 0,02 bo`lgan xabarning optimal notekis kodi qurilsin.
8-mavzu. Xalallarga bardosh kodlar
Qisqacha nazariy ma`lumot
Xalallarga bardosh yoki tuzatuvchi (korrektlovchi) kodlar deganda uzatish jarayonida xalallar ta`sirida paydo bo`luvchi xatoliklarni aniqlovchi va tuzatuvchi (xatolik o`rnini ko`rsatuvchi) kodlar tushuniladi.
Ma`lumki, ikkili kod - asosi q = 2 bo`lgan kod. Kod kombinatsiyasidagi xonalar soni n kod uzunligi, birlar soni w kod kombinatsiyasining salmog’i deb yuritiladi. Ixtiyoriy ikkita kod kombinatsiyasining bir biridan farqi kodlar orasidagi masofa d orqali xarakterlanadi va ushbu kod kombinatsiyalarini ikkining moduli bo`yicha yig’indisining salmog’i sifatida aniqlanadi.
Xalallar ta`sirida xatoliklar kod kombinatsiyasining faqat bitta xonasida sodir bo`lsa, bunday xatoliklar bir karrali deb ataladi. Ikki, uch va x. xonalarda xatoliklar bo`lsa, bunday xatoliklar ikki karrali, uch karrali va x. deb ataladi.
Kod kombinatsiyasidagi
simvollar buzilgan joyini ko`rsatishda xatolik
vektori 
tushunchasidan
foydalaniladi. n xonali
kodning xatolik vektori - n
xonali kombinatsiya bo`lib, undagi birlar kod
kombinatsiyasidagi buzilgan simvollar o`rnini ko`rsatadi.
Xatolik vektorining salmog’i we xatolik karraligini xarakterlaydi. Buzilgan kod kombinatsiyasi va xatolik vektorining ikkining moduli bo`yicha yig’indisi dastlabki buzilmagan kod kombinatsiyasini beradi.
Yuqorida aytib o`tilganidek, ikkita ixtiyoriy kod kombinatsiyalarining farqini aniqlashda kodlar orasidagi masofa xarakteristikasidan foydalaniladi. Ikkita ruxsat etilgan kod kombinatsiyalari orasidagi eng kichik masofa minimal kod masofasi děčí deb ataladi va kodning bu xarakteristikasi uning tuzatish qobiliyatini belgilaydi.
Kodlash nazariyasida sistematik kod (informatsion xonalaridan tashqari nazorat xonalariga ega bo`lgan kodlar) uning minimal kod masofasi 2t ga teng yoki undan katta bo`lgandagina xatoliklarni aniqlay olishi isbot qilingan, ya`ni
dmin ³ t+1
bu yerda t - aniqlanuvchi xatoliklarning karraligi (yakka xatoliklarda t = 1 va x.)
Nafaqat xatoliklarni aniqlash, balki uni tuzatish (xatolik o`rnini ko`rsatish) talab qilinganida minimal kod masofasi quyidagicha bo`lishi shart
dmin ³ 2t+1
8.1 - misol. 1100 kod kombinatsiyasi uzatilgan. Xatolik vektorining salmog’i
we = 2.
1) buzilgan kombinatsiyalarining bo`lishi mumkin bo`lgan variantlari aniqlansin;
2) barcha xatoliklarni aniqlashga zarur kod masofasi aniqlansin.
Yechish.
1) buzilgan kombinatsiyalar dastlabki kombinatsiyani xatolik vektoriga ikkining moduli bo`yicha jamlash orqali aniqlanadi. we = 2 da xatolik vektorining quyidagi variantlari bo`lishi mumkin:
=
0011; 0101;
1001;
0110;
1010;
1100.
Demak, buzilgan kombinatsiya variantlari quyidagicha:
1111; 1001; 0101; 1010; 0110; 0000.
2) we = 2 da xatolik karraligi t = 2 Bunday xatoliklarni aniqlash uchun zarur minimal kod masofasi
dmin = t+1 = 2+1 =3;
8.2
-misol. 0101 kod kombinatsiyasi qabul
qilingan. Xatolik vektori =
0011. Dastlabki buzilmagan kombinatsiya aniqlansin.
8.3 -misol. Quyida keltirilgan kod kombinatsiyalariga nullar va birlarni shunday qo`shingki, juftlikka tekshirish natijasida har qanday yakka xatolik aniqlanishi mumkin bo`lsin:
111011; 111010; 111000; 111100; 110111; 111101; 011001; 110000.
8.4 -misol. Kodda uch karrali xatolikni aniqlashga zarur minimal kod oraliqi topilsin.
9-mavzu. Kodning tuzatish qobiliyati bilan kod masofasi orasidagi bog’liqlik
Qisqacha nazariy ma`lumot
Karraligi t va undan kichik barcha xatoliklarni aniqlovchi kodni qurish uchun mumkin bo`lgan N0 = 2n kombinatsiyalar to`plamidan ruxsat etilgan N = 2ę kombinatsiyalarni tanlab olish kerakki, ulardan ixtiyoriysini salmog’i we < t bo`lgan ixtiyoriy xatoliklar vektori bilan ikkining moduli bo`yicha jamlanganda tanlangan ruxsat etilgan kombinatsiya olinsin. Buning uchun qo`yidagi shart qanoatlantirilishi lozim
dmin ³ t+1
Kod kombinatsiyasining tuzatuvchi sifatida ishlatilishi uchun taqiqlangan kod kombinatsiyalari bir-birini kesib o`tmaydigan qism to`plamlarga ajratiladi. Qism to`plamlarining qar biriga ruxsat etilgan kombinatsiyalarning biri moslashtiriladi. Agar qabul qilingan taqiqlangan kombinatsiya qandaydir qism to`plamga taalluqli bo`lsa, ushbu to`plamga moslashtirilgan ruxsat etilgan kombinatsiya uzatilgan deb xisoblanadi va xatolik tuzatiladi.
Misol tariqasida uzunligi n = 3 bo`lgan kodni ko`raylik. Bunday kodning bo`lishi mumkin bo`lgan kombinatsiyalari quyidagi jadvalda keltirilgan.
|
Ŕ1 |
Ŕ2 |
Ŕ3 |
Ŕ4 |
Ŕ5 |
Ŕ6 |
Ŕ7 |
Ŕ8 |
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Kod kombinatsiyalari orasidagi masofa matritsasi quyidagi jadvalda keltirilgan.
|
|
Ŕ1 |
Ŕ2 |
Ŕ3 |
Ŕ4 |
Ŕ5 |
Ŕ6 |
Ŕ7 |
Ŕ8 |
|
Ŕ1 |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
|
Ŕ2 |
|
0 |
2 |
1 |
2 |
1 |
3 |
2 |
|
Ŕ3 |
|
|
0 |
1 |
2 |
3 |
1 |
2 |
|
Ŕ4 |
|
|
|
0 |
3 |
2 |
2 |
1 |
|
Ŕ5 |
|
|
|
|
0 |
1 |
1 |
2 |
|
Ŕ6 |
|
|
|
|
|
0 |
2 |
1 |
|
Ŕ7 |
|
|
|
|
|
|
0 |
1 |
|
Ŕ8 |
|
|
|
|
|
|
|
0 |
Kodning bir karrali xatoliklarni aniqlanishini ta`minlashi uchun bo`lishi mumkin bo`lgan kombinatsiyalađ to`plamidan ruxsat etilganlari sifatida shundaylarini tanlab olish zarurki, ular orasidagi masofa d = 2 dan kam bo`lmasin. Masofalar matritsasidan ko`rinib turibdiki, ruxsat etilgan kombinatsiyalar sifatida quyidagilarni tanlash mumkin:
A1 = 000; A4 = 011; A6 = 101; A7 = 111;
Birinchi ruxsat etilgan kombinatsiya sifatida A1 = 000 ni tanlaymiz. Bir karrali xatoliklar mavjudligi A1 kombinatsiyasi A2 = 001; A3 = 010; A5 = 100 ruxsat etilmagan kombinatsiyalarining biriga o`tishi mumkin.
A2, A3 va A5 kombinatsiyalarni A1 kombinatsiyasining ruxsat etilmagan qism to`plami sifatida qabul qilish mumkin. Ya`ni, ushbu qism to`plamning biror bir kombinatsiyasi qabul qilinsa, A1 kombinatsiyasi uzatilgan deb qaror qabul qilinadi.
Ikkinchi ruxsat etilgan kombinatsiya sifatida birinchisidan d = 2 masofadagi Ŕ4 = 011 kombinatsiyani tanlaymiz. Unga A3 = 010; A2 = 001 va A8 = 111 kombinatsiyalari qism to`plami mos keladi. Ammo ruxsat etilmagan kombinatsiyalar qism to`plamlarining kesishishi sodir bo`ldiki, Ŕ2 yoki Ŕ3 ruxsat etilmagan kombinatsiya qabul qilinganida Ŕ1 signal uzatilganligini yoki Ŕ4 signal uzatilganligini bir ma`noda aniqlash mukin emas.
Agar ikkinchi ruxsat etilgan kombinatsiya sifatida birinchisidan d = 3 masofadagi Ŕ8 = 111 kombinatsiyasi tanlansa, bu kombinatsiyaga A4 = 011; A6 = 101 âŕ A7 = 110 ruxsat etilmagan kombinatsiyalari qism to`plami mos keladi. Bunda ruxsat etilmagan kombinatsiyalari qism to`plamlari kesishmaydi. Demak, d = 3 da barcha bir karrali xatoliklar bartaraf etiladi.
9.1-misol. Quyidagi ruxsat etilgan kombinatsiyalarga ega kodning tuzatish qobiliyati aniqlansin
00000; 01110; 10101; 11011.
Yechish. Kodning tuzatish qobiliyati kod masofasi yordamida aniqlanadi. Kod kombinatsiyalari uchun kod masofa matritsasini tuzamiz.
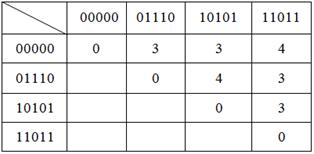
Matritsadan ko`rinib turibdiki, minimal kod masofasi dmin = 3. Demak ushbu kod ikki karrali xatoliklarni aniqlash va bartaraf etish imkoniyatiga ega.
9.2-misol. Quyidagi ruxsat etilgan kombinatsiyalarga ega kodning tuzatish qobiliyati aniqlansin.
0000; 0111; 1010; 1101.
10-mavzu. Berilgan tuzatish qobiliyatli kodlarni qurish
Qisqacha nazariy ma`lumot
Amalda kodni qurishda avval manba alfaviti xajmiga muvofiq informatsion simvollar soni k aniqlanadi, keyin ortiqcha simvollarni kiritish evaziga kodning kerakli tuzatish qobiliyati ta`minlanadi.
Aytaylik, manba alfavitining xajmi N ma`lum. Informatsion simvollarning kerakli soni quyidagicha aniqlanadi,
Tuzatish lozim bo`lgan xatolik vektorlarining to`liq soni E ham ma`lum bo`lsin. Masala shundan iboratki, berilgan N va E da kerakli tuzatish qobiliyatiga ega bo`lgan kod uzunligi n aniqlansin.
Tuzatilishi kerak bo`lgan xatolik kombinatsiyalarining to`liq soni
Xatolik kombinatsiyalarining soni N0 – N bo`lganligi sababli, kod N0 - N dan katta bo`lmagan kombinatsiyalarni tuzatishni ta`minlaydi. Demak, xatolikni tuzatish imkoniyati uchun zaruriy shart quyidagicha yoziladi:
yoki
,
yoki
Turli karrali xatoliklar mavjudligida avvalo bir karrali xatoliklarni bartaraf etishni ta`minlash lozim.
Bir karrali xatolik vektorlarining bo`lishi mumkin bo`lgan soni
Bu xolda quyidagini yozish mumkin:
Kodni qurishda quyidagi jadvaldan foydalanish maqsadga muvofiq xisoblanadi.
|
N |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1.33 |
2 |
3.2 |
5.33 |
9.2 |
16 |
28.4 |
51.2 |
Ta`kidlash lozimki, kod quyidagi shartni ham qanoatlantirishi lozim.
děčí ³ 3
10.1 -misol. Ruxsat etilgan kod kombinatsiyalari soni N = 8 bo`lganida barcha yakka xatoliklarni tuzatishni ta`minlovchi kod uzunligi n aniqlansin.
Yechish. Hisoblash quyidagi formula orqali amalga oshiriladi.
Jadvalga binoan N = 8, kod uzunligi n = 6.
10.2 -misol. Ruxsat etilgan kod kombinatsiyalari soni N = 9 bo`lganida barcha yakka xatoliklarni tuzatishni ta`minlovchi kod uzunligi n aniqlansin.
10.3 -misol. Ruxsat etilgan kod kombinatsiyalari soni N = 10 bo`lganida barcha yakka xatoliklarni tuzatishni ta`minlovchi kod uzunligi n aniqlansin.
10.4 - misol. Ruxsat etilgan kod kombinatsiyalari soni N = 12 bo`lganida barcha yakka xatoliklarni tuzatishni ta`minlovchi kod uzunligi n aniqlansin.
11-mavzu. Xemming kodi
Qisqacha nazariy ma`lumot
Xemming kodi boshqa kodlarga o`xshab k informatsion va (n - k) ortiqcha simvollarga ega. Kodning ortiqchalik qismi shunday quriladiki, dekodlash natijasida nafaqat qabul qilingan kombinatsiyadagi xatoliklar mavjudligini, balki xatolik sodir bo`lgan o`rin nomerini aniqlash mumkin bo`lsin. Bunga qabul qilingan kombinatsiyani ko`p marta juftlikka tekshirish evaziga erishiladi. Tekshirishlar soni ortiqchŕ simvollar soniga, ya`ni (n - k) ga teng. Har bir tekshirishda informatsion simvollarning bir qismi va ortiqcha simvollardan biri qatnashadi. Har bir tekshirishdan so`ng ikkili nazorat simvoli olinadi. Tekshirish natijasi juft sonni bersa nazorat simvoliga 0 qiymati, toq sonni bersa 1 qiymati beriladi. Barcha tekshirishlar natijasida buzilgan simvollar o`rnining nomerini ko`rsatuvchi (n - ę) xonali ikkili son olinadi. Xatolikni tuzatish uchun faqat ushbu simvol qiymatini teskarisiga o`zgartirish kifoya.
Tekshirivchi
simvollarning kerakli soni, ya`ni n kodining uzunligi 
formula
yordamida aniqlanadi. Xemming usuliga binoan tekshiruvchi simvollar qiymati va
o`rinlarining nomeri kod kombinatsiyasining tekshiriluvchi guruhlarini tanlash
bilan bir vaqtda belgilanadi. Bunda quyidagilarga asoslanmoq lozim.
Birinchi tekshirish natijasida buzilgan simvol o`rni nomerini ko`rsatuvchi nazorat kodining kichik xonasi raqami olinadi. Agar birinchi tekshirish natijasi 1 ni bersa, demak tekshirilgan guruxning bitta simvoli buzilgan hisoblanadi.
Simvollardan qaysi birining buzilganligini aniqlash uchun quyidagi jadvalga murojaat etamiz. Ushbu jadvalda to`rt xonali nazorat sonlarining natural qatori ikkilik sanoq sistemasida keltirilgan.
Jadvaldan ko`rinib turibdiki, agar nazorat sonining kichik xonasida 1 bo`lsa, buzilish kod kombinatsiyasining toq o`rinlarida bo`ladi. Demak, birinchi tekshirish o`z ichiga toq nomerli simvollarni, ya`ni 1, 3, 5, 7, 9, . . . larni oladi.
ą k/n |
Nazorat son simvollarining xonalari |
|||
|
4 |
3 |
2 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
|
6 |
0 |
1 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
|
10 |
1 |
0 |
1 |
0 |
Agar ikkinchi tekshirish natijasi 1 ni bersa, nazorat sonining ikkinchi xonasida 1 ni olamiz. Demak ikkinchi tekshirish o`z ichiga ikkinchi xonasida 1 bo`lgan simvollarni, ya`ni 2, 3, 6, 7, 10 . . . larni oladi.
Xuddi shunday, uchinchi tekshirish o`z ichiga uchinchi xonasida 1 bo`lgan simvollarni, ya`ni 4, 5, 6, 7, 12 . . . larni oladi.
Bu kabi mushohadalar quyidagi tekshirish jadvalini shakllantirishga imkon beradi.
|
Tekshirish nomeri |
Tekshiriluvchi o’rinlar nomeri |
Nazorat simvollari o’rinlarining nomeri |
|
1 2 3 4 . |
1, 3, 5, 7, 9, 11, 13 . . . 2, 3, 6, 7, 10 . . . 4, 5, 6, 7, 12 . . . 8, 9, 10, 11, 12 . . . . . . . . . . . . . . . . . . . . |
1 2 4 8 . |
Agar tekshiriluvchi kod kombinatsiyasining simvollarini ai orqali, tekshiruvchi amallarni Si orqali belgilasak, quyidagini yozish mumkin.
S1 = a1 Å a3 Å a5 Å a7 Å a9 Å . .
S2 = a2 Å a3 Å a6 Å a7 Å a10 Å . . .
S3 = a4 Å a5 Å a6 Å a7 Å a12 Å . . .
S4 = a8 Å a9 Å a10 Å a11 Å a12 Å . . .
Nazorat simvollarini tekshiriluvchi guruhlarning faqat bittasida uchraydigan nomerli o`rinlarda joylashtirish qulay qisoblanadi. Jadvalga muvofiq bu o`rinlar nomeri 1, 2, 4, 8, . . . Demak, kod kombinatsiyasida a1, a2, a4, a8 . . . simvollar tekshiruvchi, a3, a5, a6, a7, a9 . . .simvollar informatsion hisoblanishlari lozim.
Informatsion simvollar qiymati oldindan ma`lum bo`lganligi sababli, tekshiruvchi simvollarning qiymati shunday bo`lishi lozimki, xar bir tekshiruvchi guruxdagi birlarning yig’indisi juft son bo`lsin.
11.1- misol. 10011 ikkili kombinatsiya Xemming kodi orqali ifodalansin.
Yechish.
Informatsion simvollar soni k = 5. 
formulaga
binoan 
Demak,
Xemming kodining uzunligi n = 9. Informatsion simvollari
a3, a5, a6, a7, a9 bo`lganligi sababli, ko`rilayotgan kod uchun quyidagini yozish mumkin.
a3 = 1; a5 = 0; a6 = 0; a7 = 1; a9 = 1.
Har bir tekshiruvchi guruxdagi birlar yiqindilarining juftligini ta`minlash shartiga binoan quyidagi tekshiruvchi simvollar qiymatini olamiz:
S1 = a1 Å1 Å 0 Å 0 Å 1 Å 1; a1 = 1
S2 = a2 Å1 Å 0 Å 1; a2 = 0
S3 = a4 Å0 Å 0 Å 1; a4 = 1
S4 = a8 Å1; a8 = 1
Demak, besh xonali 10011 kodga quyidagi Xemming kodi mos keladi.
101100111
Faraz qilaylik, uzatishda beshinchi simvolda xatolik ro`y berdi, ya`ni kod 101110111 ko`rinishni oldi.
U xolda birinchi tekshirish natijasida 1; ikkinchi tekshirish natijasida 0; uchinchi tekshirish natijasida 1; to`rtinchi tekshirish natijasida 0 olinadi.
Shunday qilib tekshirish natijasida 0101 ikkili son olinadi. Demak xatolik 5 - simvolda sodir bo`lgan.
11.2 - misol. Quyidagi ikkilik kod kombinatsiyasining Xemming kodi topilsin. Xatolikni aniqlash ko`rsatilsin.
111100001110011
11.3 - misol. Quyidagi ikkilik kod kombinatsiyasining Xemming kodi topilsin. Xatolikni aniqlash ko`rsatilsin.
11100011100011
11.4- misol. Quyidagi ikkilik kod kombinatsiyasining Xemming kodi topilsin. Xatolikni aniqlash ko`rsatilcin.
1010101110111
12-mavzu. Tsiklik kod
Qisqacha nazariy ma`lumot
Tsiklik kodni qurish muolajasi quyidagicha. Uzunligi k oddiy kod kombinatsiyasi G(x) bir xad xn-ęga ko`paytiriladi, so`ngra darajasi (n-k) bo`lgan yasovchi polinom P(x) ga bo`linadi. Ko`paytirish natijasida G(x) tarkibidagi har bir xadning darajasi (n-k) ga ortadi. Bo`lish natijasida darajasi G(x) darajasiga teng qoldiq Q(x) olinadi.
Ko`paytirish va bo`lish natijasini quyidagicha ifodalash mumkin
,
bu erda R(x) - bo`lish natijasidagi qoldiq.
Ushbu tenglikning ikki tarafini P(x) ga ko`paytirib hamda ba`zi o`rin almashtirishlarni bajarish natijasida quyidagini yozish mumkin:
Ushbu ifodaning o`ng tarafidagi manfiy ishorasi musbat ishora bilan almashtirilgan, chunki ikkining moduli bo`yicha ayirish jamlashga keltiriladi.
12.1 - misol. Informatsion simvollari soni 4ga teng bo`lgan (G = 0011) siklik kod qurilsin.
Yechish.
formulaga binoan
tsiklik kod uzunligi 7 ga teng (n = 7),
tekshiruvchi simvollar soni 3 ga teng (n - k =3).
Demak, darajasi (n - k) = 3 bo`lgan yasovchi
polinomni tanlash zarur. 4 - ilovadagi jadvalga binoan bunday polinom quyidagicha
ko`rinishga ega
P(x) = x3+x2+1
Ikkilik sanoq sistemasida
P(x) = 1101
Tsiklik kodni qurish uchun Q(x) ning har bir simvolini yasovchi polinomga ko`paytirish kerak. Ko`paytirish amali quyidagicha yoziladi:
|
|
|
|
0 |
0 |
1 |
1 |
|
|
|
|
1 |
1 |
0 |
1 |
|
|
|
|
0 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
|
0 |
0 |
1 |
1 |
|
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Shunday qilib, oddiy to`rt simvolli kombinatsiya Q(x) = 0011 etti simvolli siklik kod F(x) = 0010111 orqali ifodalanadi.
Olingan kod kombinatsiyasini dekodlash uni yasovchi polinomga bo`lish orqali amalga oshiriladi. Bo`lish natijasida qoldiq R(x) ning paydo bo`lishi olingan kod kombinatsiyasida xatolik mavjudligidan darak beradi.
12.2- misol. Informatsion simvollari soni 4 ga teng bo`lgan (G = 1011) tsiklik kod qurilsin.
12.3- misol. Informatsion simvollari soni 4 ga teng bo`lgan (G = 11011) tsiklik kod qurilsin.
12.4- misol. Informatsion simvollari soni 4 ga teng bo`lgan (G = 100011) tsiklik kod qurilsin.
Adabiyotlar
1. Dumachev V.N. Teoriya informatsii i kodirovaniya - Voronej: Voronejskiy institut MVD Rossii, 2011.
2. Krushniy V.V. Osnovi teorii informatsii i kodirovaniya. Snejinsk-SGFTA-2005.
3. Verner M. Osnovi kodirovaniya. Uchebnik dlya vuzov. M: Texnosfera, seriya "Mir programmirovaniya", 2004.
4. Savel'ev A.Ya. Osnovi informatiki. Uchebnik dlya vuzov. M: Izdatel'stvo MGTU im. N.Ý. Baumana. 2001.
1-ilova
Butun sonlarning ikkili logarifmlari
|
Ŕ |
log2A |
Ŕ |
log2A |
Ŕ |
log2A |
|
1 |
0,00000 |
38 |
5,24793 |
75 |
6,22882 |
|
2 |
1,00000 |
39 |
5,28540 |
76 |
6,24793 |
|
3 |
1,58496 |
40 |
5,32193 |
77 |
6,26679 |
|
4 |
2,00000 |
41 |
5,35755 |
78 |
6,28540 |
|
5 |
2,32193 |
42 |
5,39232 |
79 |
6,30378 |
|
6 |
2,58496 |
43 |
5,42626 |
80 |
6,32193 |
|
7 |
2,80735 |
44 |
5,45943 |
81 |
6,33985 |
|
8 |
3,00000 |
45 |
5,49185 |
82 |
6,35755 |
|
9 |
3,16993 |
46 |
5,52356 |
83 |
6,37504 |
|
10 |
3,32193 |
47 |
5,55459 |
84 |
6,39232 |
|
11 |
3,45943 |
48 |
5,58496 |
85 |
6,40939 |
|
12 |
3,58496 |
49 |
5,61471 |
86 |
6,42626 |
|
13 |
3,70044 |
50 |
5,64386 |
87 |
6,44294 |
|
14 |
3,80735 |
51 |
5,67242 |
88 |
6,45943 |
|
15 |
3,90689 |
52 |
5,70044 |
89 |
6,47573 |
|
16 |
4,00000 |
53 |
5,72792 |
90 |
6,49185 |
|
17 |
4,08746 |
54 |
5,75489 |
91 |
6,50779 |
|
18 |
4,16993 |
55 |
5,78136 |
92 |
6,52356 |
|
19 |
4,24793 |
56 |
5,80735 |
93 |
6,53916 |
|
20 |
4,32193 |
57 |
5,83289 |
94 |
6,55459 |
|
21 |
4,39232 |
58 |
5,85798 |
95 |
6,56986 |
|
22 |
4,45943 |
59 |
5,88264 |
96 |
6,58496 |
|
23 |
4,52356 |
60 |
5,90689 |
97 |
6,59991 |
|
24 |
4,58496 |
61 |
5,93074 |
98 |
6,61471 |
|
25 |
4,64386 |
62 |
5,95420 |
99 |
6,62936 |
|
26 |
4,70044 |
63 |
5,97728 |
100 |
6,64386 |
|
27 |
4,75489 |
64 |
6,00000 |
200 |
7,644 |
|
28 |
4,80735 |
65 |
6,02237 |
300 |
8,229 |
|
29 |
4,85798 |
66 |
6,04439 |
400 |
8,614 |
|
30 |
4,90689 |
67 |
6,06609 |
500 |
8,966 |
|
31 |
4,95420 |
68 |
6,08746 |
600 |
9,229 |
|
32 |
5,00000 |
69 |
6,10852 |
700 |
9,451 |
|
33 |
5,04439 |
70 |
6,12928 |
800 |
9,644 |
|
34 |
5,08746 |
71 |
6,14975 |
900 |
9,814 |
|
35 |
5,12928 |
72 |
6,16992 |
1000 |
9,965 |
|
36 |
5,16993 |
73 |
6,18982 |
10000 |
13,288 |
|
37 |
5,20945 |
74 |
6,20945 |
|
|
2-ilova
- p log2p kattaliklarning qiymatlari
|
p |
- p log2p |
p |
- p log2p |
p |
- p log2p |
p |
- p log2p |
|
0.00 |
0.0000 |
0.26 |
0.5053 |
0.52 |
0.4906 |
0.78 |
0.2796 |
|
0.01 |
0.0664 |
0.27 |
0.5100 |
0.53 |
0.4854 |
0.79 |
0.2678 |
|
0.02 |
0.1129 |
0.28 |
0.5142 |
0.54 |
0.4800 |
0.80 |
0.2575 |
|
0.03 |
0.1517 |
0.29 |
0.5179 |
0.55 |
0.4744 |
0.81 |
0.2462 |
|
0.04 |
0.1857 |
0.30 |
0.5211 |
0.56 |
0.4684 |
0.82 |
0.2348 |
|
0.05 |
0.2161 |
0.31 |
0.5238 |
0.57 |
0.4623 |
0.83 |
0.2231 |
|
0.06 |
0.2435 |
0.32 |
0.5260 |
0.58 |
0.4558 |
0.84 |
0.2113 |
|
0.07 |
0.2686 |
0.33 |
0.5278 |
0.59 |
0.4491 |
0.85 |
0.1993 |
|
0.08 |
0.2915 |
0.34 |
0.5292 |
0.60 |
0.4422 |
0.86 |
0.1871 |
|
0.09 |
0.3127 |
0.35 |
0.5301 |
0.61 |
0.4350 |
0.87 |
0.1748 |
|
0.10 |
0.3322 |
0.36 |
0.5306 |
0.62 |
0.4276 |
0.88 |
0.1623 |
|
0.11 |
0.3503 |
0.37 |
0.5307 |
0.63 |
0.4199 |
0.89 |
0.1496 |
|
0.12 |
0.3671 |
0.38 |
0.5304 |
0.64 |
0.4121 |
0.90 |
0.1368 |
|
0.13 |
0.3826 |
0.39 |
0.5298 |
0.65 |
0.4040 |
0.91 |
0.1238 |
|
0.14 |
0.3971 |
0.40 |
0.5288 |
0.66 |
0.3957 |
0.92 |
0.1107 |
|
0.15 |
0.4105 |
0.41 |
0.5274 |
0.67 |
0.3871 |
0.93 |
0.0978 |
|
0.16 |
0.4230 |
0.42 |
0.5856 |
0.68 |
0.3784 |
0.94 |
0.0839 |
|
0.17 |
0.4346 |
0.43 |
0.5236 |
0.69 |
0.3694 |
0.95 |
0.0703 |
|
0.18 |
0.4453 |
0.44 |
0.5211 |
0.70 |
0.3602 |
0.06 |
0.0565 |
|
0.19 |
0.4552 |
0.45 |
0.5181 |
0.71 |
0.3508 |
0.97 |
0.0426 |
|
0.20 |
0.4644 |
0.46 |
0.5153 |
0.72 |
0.3412 |
0.98 |
0.0286 |
|
0.21 |
0.4728 |
0.47 |
0.5120 |
0.73 |
0.3314 |
0.99 |
0.0140 |
|
0.22 |
0.4806 |
0.48 |
0.5083 |
0.74 |
0.3215 |
1.00 |
0.0000 |
|
0.23 |
0.4877 |
0.49 |
0.5043 |
0.75 |
0.3113 |
|
|
|
0.24 |
0.4941 |
0.50 |
0.5000 |
0.76 |
0.3009 |
|
|
|
0.25 |
0.500 |
0.51 |
0.4954 |
0.77 |
0.2903 |
|
|
3-ilova
O`zbekcha matnlarda harflar eqtimolliklarining taqsimoti
(so`zlar orasidagi oraliqning paydo bo`lish eqtimolliklari qisobga olinmagan)
|
Harf |
Matnda paydo bo’lishining o’rtacha ehtimolligi |
- pi log2 pi |
Harf |
Matnda paydo bo’lishining o’rtacha ehtimolligi |
- pi log2 pi |
|
Ŕ |
0,1520 |
0,4137 |
Ń |
0,0171 |
0,0999 |
|
Á |
0,0370 |
0,1760 |
Ň |
0,0410 |
0,1889 |
|
 |
0,0124 |
0,0766 |
Ó |
0,0330 |
0,1624 |
|
Ă |
0,0350 |
0,1693 |
Ô |
0,0044 |
0,0350 |
|
Ä |
0,0432 |
0,1952 |
Ő |
0,0070 |
0,0501 |
|
Ĺ |
0,0171 |
0,0999 |
Ö |
0,0010 |
0,0106 |
|
¨ |
0,0062 |
0,0443 |
× |
0,0130 |
0,0814 |
|
Ć |
0,0052 |
0,0383 |
Ř |
0,0203 |
0,1129 |
|
Ç |
0,0162 |
0,0955 |
Ü |
0,0001 |
|
|
Č |
0,1354 |
0,3901 |
Ú |
0,0026 |
0,0179 |
|
É |
0,0160 |
0,9555 |
Ý |
0,0050 |
0,0382 |
|
Ę |
0,0290 |
0,1481 |
Ţ |
0,0021 |
0,0180 |
|
Ë |
0,0610 |
0,2436 |
ß |
0,0060 |
0,0443 |
|
Ě |
0,0341 |
0,1659 |
ˇ |
0,0182 |
0,1044 |
|
Í |
0,0703 |
0,2686 |
Қ |
0,0254 |
0,1331 |
|
Î |
0,0464 |
0,2044 |
Ғ |
0,0040 |
0,3186 |
|
Ď |
0,0054 |
0,0412 |
Ҳ |
0,0120 |
0,0766 |
|
Đ |
0,0574 |
0,2356 |
|
|
|
4-ilova
Yasovchi polinomlar jadvali
|
ą |
Daraja |
Polinom |
Ikkili ketma-ketlik |
|
1 |
1 |
ő + 1 |
11 |
|
2 |
2 |
ő2 + ő + 1 |
111 |
|
3 4 |
3 |
ő3 + ő + 1 ő3 + ő2 + 1 |
1011 1101 |
|
5 6 7 |
4 |
ő4 + ő + 1 ő4 + ő3 + 1 ő4 + ő3 + ő2 + ő + 1 |
10011 11001 11111 |
|
8 9 10 11 12 13 |
5 |
ő5 + ő2 + 1 ő5 + ő3 + 1 ő5 + ő3 + ő2 + ő + 1 ő5 + ő4 + ő2 + ő + 1 ő5 + ő4 + ő3 + ő + 1 ő5 + ő4 + ő3 + ő2 + 1 |
100101 101001 101111 110111 111011 111101 |
|
14 15 16 17 18 19 20 21 22 |
6 |
ő6 + ő + 1 ő6 + ő3 + 1 ő6 + ő4 + ő2 + ő + 1 ő6 + ő4 + ő3 + ő + 1 ő6 + ő5 + 1 ő6 + ő5 + ő2 + ő + 1 ő6 + ő5 + ő3 + ő2 + 1 ő6 + ő5 + ő4 + ő + 1 ő6 + ő5 + ő4 + ő2 + 1 |
1000011 1001001 1010111 1011011 1100001 1100111 1101101 1110011 1110101 |
|
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
7 |
ő7 + ő + 1 ő7 + ő3 + 1 ő7 + ő3 + ő2 + ő + 1 ő7 + ő4 + 1 ő7 + ő4 + ő3 + ő2 + 1 ő7 + ő5 + ő2 + ő + 1 ő7 + ő5 + ő3 + ő + 1 ő7 + ő5 + ő4 + ő3 + 1 ő7 + ő5 + ő4 + ő3 + ő2 + ő + 1 ő7 + ő6 + 1 ő7 + ő6 + ő3 + ő + 1 ő7 + ő6 + ő4 + ő + 1 ő7 + ő6 + ő4 + ő2 + 1 ő7 + ő6 + ő5 + ő2 + 1 ő7 + ő6 + ő5 + ő3 + ő2 + ő + 1 |
10000011 10001001 10001111 10010001 10011101 10100111 10101011 10111001 10111111 11000001 11001011 11010011 11010101 11100101 11101111 |
MUNDARIJA
|
1-mavzu. |
Informatsiyani miqdoriy baqolash. ………….…………...….... |
3 |
|
|
|
|
|
|
|
2-mavzu. |
SHartli entropiya va birlashma entropiya ……………...….... |
6 |
|
|
|
|
|
|
|
3-mavzu. |
Informatsiyani uzatish tezligi va aloqa kanalining o`tkazish qobiliyati ………………………………………………....…… |
9 |
|
|
|
|
|
|
|
4-mavzu. |
Xabarlarning ortiqchaligini aniqlash …………….………...….. |
13 |
|
|
|
|
|
|
|
5-mavzu. |
Kodlash yordamida informatsiyani qimoyalash ……………..... |
15 |
|
|
|
|
|
|
|
6-mavzu. |
Optimal kodlash. Optimal kodlarni qurishning SHennon-Fano algoritmi ………………………………………………….…… |
16 |
|
|
|
|
|
|
|
7-mavzu. |
Optimal kodlash. Optimal kodlarni qurishning Xaffmen algoritmi ………………………………………………………. |
18 |
|
|
|
|
|
|
|
8-mavzu. |
Xalallarga bardosh kodlar …………………………….……..... |
20 |
|
|
|
|
|
|
|
9-mavzu. |
Kodning tuzatish qobiliyati bilan kod masofasi orasidagi boqliqlik ………………………………………......................... |
22 |
|
|
|
|
|
|
|
10-mavzu. |
Berilgan tuzatish qobiliyatli kodlarni qurish …………..…........ |
24 |
|
|
|
|
|
|
|
11-mavzu. |
Xemming kodi …………………………………….…………... |
26 |
|
|
|
|
|
|
|
12-mavzu. |
Tsiklik kod ………………………………………….……...…. |
29 |
|
|
|
|
|
|
|
|
Adabiyotlar ……………………………………………………………... |
30 |
|
|
|
|
|
|
|
|
Ilovalar ………………………………………………………………… |
31 |
|
“Axborot nazariyasi va
kodlash” fani bo’yicha
amaliy mashgulotlarga
uslubiy ko’rsatma.
TATU ilmiy – uslubiy
kĺngashi majlisida
ko’rilgan va chop etishga
tavsiya etilgan.
“ 24_” __may__2012 y.
Qaydnoma ą_50____
Mualliflar. S.K. G’aniĺv, D.G’. Abdullaĺv
|