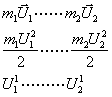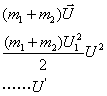УЗБЕКИСТОН   РЕСПУБЛИКАСИ  ПОЧТА   ВА ТЕЛЕКОММУНИКАЦИЯ    АГЕНТЛИГИ ТОШКЕНТ  ЭЛЕКТРОТЕХНИКА  АЛОКА  ОЛИЙГОХИ   Физика кафедраси   ФИЗИКА  ФАНИДАН  МАЪРУЗАЛАР МАТНЛАРИ.   ТОШКЕНТ  2000

 

 

1 – маъруза.

 

Кириш.

 

Физика материянинг турли шаклларини, уларнинг тузилиши, харакат конунлари ва уларнинг богланишини урганади. Физика конунлари техникада кулланилади, шунинг учун физика техниканинг асосидир.

          Физик конунларни яратиш учун табиат ходисалари кузатилади, физик катталикларнинг муносабати хисобга олинади.

        Физик катталикларнинг куп турлари мавжуд. Улардан баъзилари узгармас электромагнит тулкинларининг вакуумдаги тезлиги, Планк доимийси, электроннинг заряд ва массаси, электр ва магнит доимийлари ва бошкалар. Бошкалари предметнинг ¸ки фазанинг турли санокли хоссаларини характерлайди : масса, харорат, жисмнинг зичлиги, электр заряд, магнит майдон кучланганлиги ва бошкалар. Улар узгаришлари мумкин.

       Физик катталиклар махсус танланган улчамларда хисобланади. Улардан баъзилари купинча бу узунлик, вакт ва масса асосий деб кабул килинган булиб, колганлари улар оркали ифодаланади. Кабул килинганлари асосий улчов бирликлари, улар оркали олингалари хосилавий бирликлар дейилади. Бу табиатда буладиган ходисаларни кузатишда кулайдир.

Улчамлик куйидагича белгиланади, масалан, иш улчов бирлиги:

 

[А]=[F]* [S] = 1 н * 1 м = 1 нм = 1 нс

     Табиат ходисаларини сунъий хосил килиб хам кузатиш мумкин, яъни тажриба утказиш йули билан. Бу табиийга нисбатан жуда кулайдир.

Биринчидан, ходисани кулай вактда утказиш мумкин, иккинчидан, табиий ходисалар жуда мураккаб, чунки бу ерда турли омиллар харакат килади, уларнинг бири кучли, бошкаси кучсиз, тажрибада асосий булмаган таъсирларни йук килиб, факатгина асосий таъсирнинг узини олиш мумкин. Масалан, жисмнинг оšирлик кучи таъсиридаги харакатини урганишда жисмни хавоси суриб олинган вертикал трубадан мажбуран тушириб, хавонинг каршилик кучини йукотиш мумкин.

Биз бунда урганиш осон булган, ихчамлашган ходисанинг моделини оламиз. Бундай схематик ходисалар асосида олинган конунлар жуда соддадир.

          Лекин техниканинг яхши ривожланмаганлиги сабабли табиатдаги ходисаларнинг хаммасини хам  масалан, юлдузларда мавжуд буладиган жуда юкори харорат ва босим ¸ки космик заррачалар харакатидаги катта тезликларни тажрибада кузатиб булмайди.

Бундай холларда схематик моделларни кузатишда мантикий хулосалар ¸ки табиий ходисаларни кузатишда мавжуд конунлар оркали конунлар хосил килинади.

Физик жисмлар соддалаштирилган моделининг кенг таркалган куриниши моддий нукта ва абсолют каттик жисмдир. Жисмларнинг харакатини маълум масофада урганишда масофа катта булса, жисмнинг улчамлари ва шаклини эътиборга олмаса хам булади. Бундай жисмлар моддий нукталар дейилади, лекин унинг физик хусусияти булиб, бу унинг массасидир. Бу таккослашни катта жисмлар учун хам куриш, масалан, ›у¸ш атрофида айлана¸тган планеталарнинг харакатида хам кузатиш мумкин.

Шундай килиб жисмларнинг холати ва харакати кузатилганда куп холларда биз моддий нуктанинг харакат конунларидан, бошка холларда эса ( айланма харакатда) мутлак каттик жисм тушунчасидан  фойдала-намиз.

Мутлак каттик жисм тушунчасига олий узок таъсир назарияси билан боšлик, бунга биноан жисмнинг хамма нуктасида ташки кучларнинг таъсири бирдек ва  бир вактда булади. Демак, жисмнинг барча нукталари бир вактда харакатга келади, агар бунда яна бир хил тезликлар билан булса, жисм мутлок каттик харакат килади.

Агар кучлар таъсири тезлик билан такалади деб хисобланса, бунда у жисмнинг турли нукталарига турли вактларда етиб боради ва бу нукта-лар хам турли бир вактда харакатга келади. Жисм деформацияланади, лекин куч таъсири тугагач, уз шаклига келиши мумкин. Бу холатни тавсифлаш учун бир канча янада мураккаб модель мутлак эластик жисм кулланилади. У, масалан, жисм оркали тулкинларнинг таркалишини тадкик этишга ¸рдам беради.

Оддий механикада купинча модий нукта ¸ки мутлак катик жисм харакатини урганиш билан чекланади. Таъсир узатилишининг охирги тезлиги якин таъсир назарияси билан боšлик : таъсир майдон хосил буладиган оралик фазодаги нукта оркали узатилади. Майдон нукталарида šала¸нланиш хосил булиб, у аста – секин нуктадан – нуктага чегаравий тезлик билан узатилади. Бунда оралик мухит бир жисм харакатининг бошкасига узатилишида биринчи даражали кийматга эга. Атомлардан тузилган модда ва майдон материянинг иккита асосий куринишидир.

Тажриба утказиш жара¸нида физик катталикларни улчаш улар уртасидаги математик алокани топишга имкон беради, яъни физик конунларни формула куринишида ифодалаш мумкин. Оддий ¸ки дифференциал конунлар физик катталикларнинг чексиз кичик узга-ришлари уртасидаги алокани ифодалайди. Дифференциал конунларнинг турли катталиклар уртасидаги боšликлик купинча пропорционал хисоб-ланади. Катталикларнинг охирги узгаришларини боšлайдиган конунлар дифференционал конунлар йиšиндиси ¸ки интеграл билан олинади. Булар интеграл конунлар дейилади. Олинган боšланишлар формула ¸ки график шаклида ифодаланади.

Физик конунларни ифодалайдиган формулалар аник физик маъ-нога эга. Уларни суз билан укиш керак. Масалан,  Р = пк Т   формула-си шундай укилади :

 «Идеал газ босими унинг хажм бирлигидан молекулалар сонининг Больцман доимийси ва кельвинлардан газ харорати купайтмасига тенг» .

Физик конунлар шу маънода мутлакки, улар турли ходисалар уртасидаги объектив алокани акс эттиради, лекин шу билан бирга улар нисбийдир, чунки уларнинг купчилиги маълум шароитлардагина туšридир. Масалан, идеал газнинг холати тенгламаси тахминан газлар учун факат паст босимларда ва ки¸сан юкори хароратлардагина узини оклайди. Ÿарорат ва босим курсатилган чегаралардан четга чикиши биланок улар нотуšри булиб колади.

Физик жисмлар ва уларда содир буладигон ходисаларни урганиш-нинг иккита асосий усули мавжуд.

Биринчиси – макроскопик ( термодинамик ¸ки феноменологик) усул. Бу ерда жисм яхлит холда, унинг майда тузилишига ва кичик заррачаларининг харакатига эътибор бермасдан урганилади. Бу жисм одатда 10^-8 ва ундан катта улчамда булиб, заррачаларининг сони жуда каттадир.

Иккинчиси – микроскопик ¸ки молекуляр – кинетик усулдир. Бу ерда жисимдаги 10^-10        ва ундан кичик улчамдаги айрим заррачаларнинг  харакати куриб чикилади. Уларнинг харакати ва узаро таъсиридан жисм буйсинадиган конунлар чикарилади. Бунда албатта, катта микдордаги заррачаларнинг хар бирига оддий механика конунларини куллаш имконияти йук. Бундай холларда статистик усулдан фойдаланилади, у оддий куринишда куйидагичадир, хар бир заррача учун уларнинг барчасига бир хил булган баъзи бир уртача хоссалар олинади, кейин заррачалар сонини хисобга олиб, умумий конунлар чикарилади. Молекуляр – кинетик, электрон назарияси, каттик жисм физикаси ва физиканинг бошка булимларида шундай килинади.

Макроскопик назарияда жисмнинг тузилиши узлуксиздир ва бу шундай жисмлар учун дифференциал хисоблаш формулаларини куллаш-га имкон беради, деб хисобланади. Лекин физикада чексиз кичик деб жисмнинг тахминан шундай кисми олинадики, бунда у хам деганда айрим молекула ¸ки атомлар улчамидан 100 баравар катта, шу билан бир вактда бу кисмлар жисмнинг уз катталигига караганда кичикдир.

Оддий ¸ки классик механика чегарали кулланиш сохасига эга. Улар вакуумдаги    С  нур тезлиги С га ки¸с килгандаги кичик тезликдаги жисмлар учунгина туšри булиб, бу жисм массаси айрим атом ва молекулалар массасига нисбатан каттадир   ( m << 10 ^–25     кг). Тажрибада бундай тезлик ва массалар билан доимо иш курилади.

          Агар С га ки¸слаганда харакат тезлиги сезиларли булса, классик механика формуласи нуксонга йул куяди, унинг урнига релятивистик механика ( нисбийлик механикаси) формуларидан фойдаланиш зарур, агар жисм массаси курсатилганидек ¸ки ундан хам кичик микдорга эга булса, бунда квант – механикасидан фойдаланиш керак. Униси хам, буниси хам бир вактда булган холларда (яъни катта тулик ва кичик масса) релятивистик квант механикаси конунларидан фойдаланиш зарур, лекин улар хали унча ишлаб чикилмаган.

            С

 

 

 

 

 

 

 

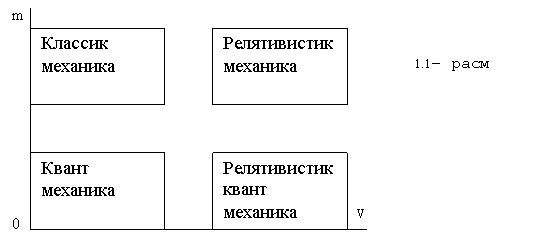
1.1 -расм барча механикалар турларининг кулланиш сохасини курсатади.

( m - жисм массаси, V- унинг тезлиги). Классик механика кичик тезлик ва катта массаларга жавоб беради, катта тезлик учун ( лекин С дан катта эмас) релятивистик механика, кичик тезликлар ва кичик массалар учун эса квант механика, катта тезлик ва кичик массалар учун релятивистик – квант механика жавоб беради.

 

 

2 – маъруза

 

КЛАССИК КИНЕМАТИКА

 

Жисмлар ва уларнинг булакларини узаро жойлашишини вакт ути-ши билан узгаришидан иборат булган механик харакат, материя харака-тининг формуларидан биридир. Кинематика жисмларнинг харакатини уларни вужудга келтирувчи сабабисиз урганади. Жисмнинг харакатини ифодалаш учун вактнинг хар бир моментини, фазодаги холатини ва жисмнинг тезлигини курсатиш керак.

          Жисмларнинг хамма харакатларини иккита асосий турга булиш мумкин:

Илгариланма ва айланма.

Илгариланма харакат деб, жисмнинг хамма нукталари параллел кучади-ган аник бир хил харакат киладиган харакатга айтилади, шунинг учун жисмни моддий нуктада деб хисоблаш мумкин ( 1 – маърузага каранг)

 

Моддий нукта кинематикаси

Жисмнинг фазодаги холатини факатгина бир – бирига нисбатан аниклаш мумкин. Текширила¸тган жисмнинг харакати бирор жисмга нисбатан олинса, бу санок жисми дейилади. Ÿаракатни микдорий ифодалаш учун санок жисми билан кандайдир координата системаси боšланади, купинча, декарт ( туšрибурчакли) система ва соат. Буларнинг хаммаси биргаликда санок системани ташкил килади.

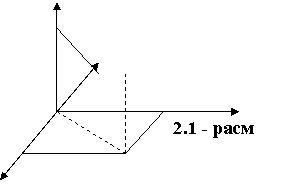
          Моддий нуктанинг берилган вакт оралиšида аниклаш мумкин, ¸ки нукталари x, y, z – координатали учта сон берилган булсин, ¸ки r ради-ус-вектор киритиб моддий нуктасининг бошланšич координаталари оркали аниклаш мумкин (2.1 – расм). Агар координата уклари йунали-шида - бирлик векторлар (орталар) берилган булса,

                                                             (2.1)

 

 

 

 

 

 

 

 

                     z

 

 

 

 

 

 

 

 

Радиус векторнинг модули

 шундай аникланади. Моддий нукта харакатлана-¸тганда унинг координаталари ва радиус – векторлари вакт утиши билан узгаради. Шунинг учун бу нуктанинг харакат конуни вазифаси коорди-наталарнинг вакт билан боšланишини курсатиш.

 x = d₁ (t)₁ y = d₂ (t) ₁ z = d₃ (t)₁ еки  боšланишни аниклаш. Моддий нукта узининг харакати давомида кандайдир траектория – чизиšини чизади. Унинг шаклига караб, харакатнинг туšри ва ва эгри чизикли эканлиги фаркланади. Массалан, нукта А дан В гача кандайдир траекторияда кучиш. (2.2 – расм).

 

 

 

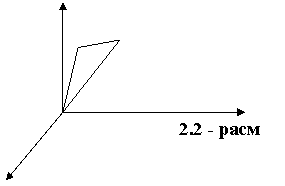А ва В орасидаги масофа траектория буйлаб, йулнинг узунлиги S₁ булсин. А дан В гача утказиладиган вектор моддий нуктанинг кучиши дейилади. У харакат кила¸тган нукта радиус векторларининг бошланšич хислатлари фаркига тенг.

D

Кучишнинг вакт оралиšига нисбатан моддий нуктанинг уртача тезлиги дейилади.

                                                                          (2.2)

Туšри чизикли текис харакатда уртача тезлик хар доим узгармас ва траектория буйлаб йуналади. Нотекис ¸ки эгри чизикли харакатда уртача тезлик харакатни характерлашга факатгина якинлашади.

                                                                    (2.3) га Оний тезлик          дейилади.

          Вакт оралиšи Dt камайганда ватар dS ¸й билан мос тушади, dr нинг йуналиши кичик кийматларда берилган нуктада траекторияга утказилган уринма буйлаб йуналиш билан мос тушади. Шунингдек, тезлик вектори хам уринма буйлаб йуналади, унинг модули эса V=½V½=dS/dt .   Моддий нуктанинг тезлик векторини координата уклари буйича учта ташкил этувчига ажратиш мумкин.

                                               (2.4)

Бунда             векторнинг координата уклардаги проекцияси. Тезликнинг микдорини куйдагича аниклаш мумкин

уртача ва одий тезликлар факат туšри чизикли текис харакатда бир хил булади. Нотекис ва эгри чизикли харакатда улар хар хил булади, оний тезлик йулнинг хар хил нукталарида ва турли вактларда хар хил булади.

          Тезликнинг вакт оралиšида узгариши тезланиш дейилади. Нотекис харакатнинг уртача тезланиши куйидагича аникланади:

                                                                   (2.5)

Dt ® 0 гандаги тезланиш оний тезланиш дейилади.

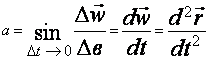                                                      (2.6)

Тезланиш векторини хам координата уклари буйича учта ташкил этувчиги  ажратиш мумкин:

                                                    (2.7)

Бунда         

 векторнинг уклардаги проекциялари. Уларнинг катталикларини билган холда

 топилади.

          Туšри чизикли текис харакатда D ва  нинг кийматлари нолга тенг.

          Туšри чизикли текис тезланувчан харакатда  узгармас ва  тезлик вектори буйлаб йуналади, агар харакат тезлашувчан ва карама карши йуналган булса, харакат текис секилашувчан булади. Эгри чизикли харакатда тезланиш вектори тезлик вектори билан мос тушмайди ва уни иккита ташкил этувчи ажратиши мумкин: тезлик йуналиши буйича ва унга перпендикуляр йуналиш буйича. а ~ ташкил этувчиси траекторияга урунма булиб, тангенциал тезланиш дейилади. Иккинчи ташкил этувчиси an траекторияга утказилган нормал буйича йуналган булиб, нормал тезланиш дейилади. Ÿар бир ташкил этувчининг ролини курамиз. Нукта R радиус буйлаб текис айланма харакат кила¸тган булсин (2.3 – расм).

 

 

 

 

 

 

 

 

 

Бу мисолда тезлик узгармайди, факат унинг йуналиши узгаради. Нукта А дан В га куча¸тган булсин, А ва В нукталарнинг тезлиги бир хил булади. W₂ ни А нуктагача кучирсак,  векторини оламиз, у Dt вакт оралиšидаги тезликнинг узгариши АОВ ва АСД учбурчаклар ухшаш, бир хил бурчакли ва тенгтомонли. Шунинг учун: еки  Агар D t ® 0, Da ® 0 булса уринли, D ва  орасидаги бурчак  га якин, яъни Dвектор нормалга, траекторияга (радиус буйлаб) якинлашади. Лекин D t ® 0 булса АВ тахминан DS = W * dt га тенг, бундан:

                                                     (2.8)

          Нормал тезланиш йуналиш буйлаб, тезликнинг узгаришини характерлайди. Тангенциал тезланиш эса тезликнинг микдорий узгаришини характерлайди ва куйидагига тенг булади:

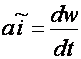.  Нотекис эгри чизикли харакатда бир вактда иккала тезланиш булади. Тулик тезланиш куйидаги формула оркали аникланади:

                                                                  (2.9)

Каттик жисм кинематикаси

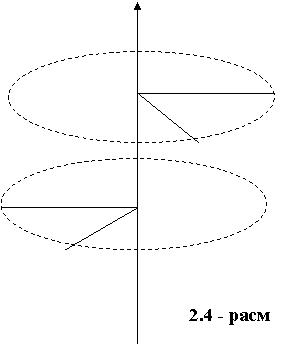          Айланма харакатда жисмнинг хамма нукталари айлана харакатда булиб, маркази айланиш уки деб аталадиган уша туšри чизикда ¸тади. Укнинг нукталари кузšалмас колади. Турли нукталарнинг йули, тезлиги ва тезланиши уша вакт оралиšида хар хилдир. Шунинг учун бу катталиклар айланма харакатни ифодалаш учун ярамайди. Вакт бирлиги ичида радиуснинг бурилиш бурчаги уша ораликда айлана марказидан утган нукталар билан ифодаланади, яъни хамма нукталарда катталиклар бир хил (2.4 – расм).

 

Жисмнинг бурчакли тезлиги W  куйидагича аникланади:

                                                         (2.10)

Бурчакли W тезлик билан айлана¸тган жисмнинг ихти¸рий нуктасининг V тезлиги чизикли тезлиги дейилади. Нукта dt вакт оралиšида айлана ¸йи буйлаб R радиус билан  dS = V * dt = Rd   йул юради, бунда

                                                                (2.11)

Бурчакли тезлик билан бир каторда айлана даври ва частотаси деган тушунчалар хам бор. Бир марта тулик айланиши учун кетган вакт айланиш даври Т дейилади, яъни  бурилиш бурчагига айланади. Вакт бирлиги (1 сек) ичида айланишлар сони айланиш частотаси дейилади. W₁ Т ва J лар орасидаги боšланиш куйидаги куринишда булади:

                                                                 (2.12)

          Нотекис айланма харакатни характерлаш учун бурчакли тезланиш тушунчаси киритилади:

                                                      (2.13)

Агар чизикли ва бурчакли тезликларнинг боšланишини хисобга олсак;

 яъни

а = Rb булади. Айланишнинг йуналиши Dj₁W₁b катталиклар ¸рдамида хисобга олиш учун бурилиш бурчагини вектор куринишда бериш керак, узунлиги Dj га, йуналиши айланиш уки билан мос тушади, лекин айланиш йуналиши ва  векторининг йуналиши унг винт коидаси билан боšланган (2.4-расм).  нинг йуналиши винтнинг харакат йуналиши билан мос тушади, дастагининг йуналиши жисм айланиш йуналиши билан мос тушади. Dj векторнинг улчамлари жуда кичик бурчаклар учун уринли, бу мисолда векторлар параллелограм коидасига биноан кушилади. Катта бурчаклар учун бу шартлар уринли эмас.  нинг йуналиши  векторнинг йуналиши билан мос тушади.  йуналиши эса  нинг йуналиши  билан мос тушади(агар айланиш тезланувчан ва унга карама – карши, агар айланиш секинланувчан булса). Чизикли ва бурчакли катталиклар вектор купайтма шаклида куйидаги куринишда булади:

                                                      (2.15)

 

3 – МАЪРУЗА

Нисбий харакат

Галилей алмаштиришлари формуласи.

Ÿаракат ва тинчлик биз кузата¸тган санок системаларига боšлик равишда нисбий тушунчалардир.

          Бир бирига нисбатан текис ва туšри чизикли харакат киладиган санок системалар инерциал системалар дейилади. Бир инерциал системада нуктанинг координаталарини иккинчи координатага утишини оддий мисолда курамиз. Иккита система оламиз: К шартли тинч деб олинади (масалан, ер билан боšланган, 3.1 – расм) ва узгармас  тезлик билан ОХ буйлаб  системада (вагон билан боšланган) харакат килади.

 

К ва  системаларда ута¸тган вактни бир хил деб хисоблаймиз. t = 0 да иккала системанинг координаталари мос тушади. К системада кандайдир М нуктанинг координаталари t вактда x₁y₁z₁ булади

 системада эса:                                   (3.1)

бундан                                                    (3.1 а)

 

Бу формулалар Галлилей координаталари алмаштириши ¸ки классик механика координаталарини алмаштириш формулалари дейилади.

Классик механика тезликларини кушиш формуласи

М нукта К системада  тезлик билан харакатланмокда (3.1 а) формуладан t буйича хосила оламиз:

                             ¸ки

 

                 ;            ¸ки вектор куринишда

 

                                                                            (3.2)

Бу формула классик механика тезликларини кушиш формуласи. Бир инерциал системадан иккинчига утганда координаталар (3.1), тезликлар (3.2) формулалар билан алмашади. (3.2) дан t буйича олинган хосила:

     ¸ки                                                           (3.3)

          Ÿосила йуналишларда тезланишлар бир хил (инвариантдир).

(3.2) ифодани товуш тулкинларига татбик киламиз. Уларнинг мухитга нисбатан тезлиги  тулкинини кабул килувчига нисбатан мухитда таркалиши             ¸ки  тажрибалар шу муносабатни курсатади.

 

Лоренц алмаштиришлари

Майкельсоннинг (1881 – 1887) ¸руšлик тезлигининг ер харакатига нисбатан улчаш тажрибалари хамма йуналишларда бир хил эканлигини курсатди, яъни (3.1) ва (3.2) формулалар нотуšри экан. Лоренцнинг фикрича, Галлилей алмаштиришларининг урнига куйидагилар ишлатилса натижа туšри чикади:

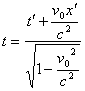          у = ;                                        (3.4)

         

Бу формулаларни Лоренцнинг координата ва вактни алмаштириш формулалари дейилади, бунда вакт бирликлари ( турли санок системаларда хар хилдир.

          Лоренц алмаштиришларидан бир нечта хулосалар олиш мумкин:

1) Битта системанинг турли нукталарида баравар содир буладиган иккита вокеа, бошка системада бир вактда содир булмайди.

Масалан  системанинг турли А ва В нукталарида, координаталари  булиб, бир вактда ( иккита лампа ¸нади (3.2 – расм).

 

 

Вактнинг  ларида лампанинг ¸ниши К системасида (3.4) формула билан аникланади:

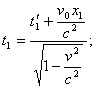
                   бунда  лекин

                                                                    у холда

                                                                    яъни

К системада иккала ¸ниш бир вактда эмас.

2) К системада координаталари х₁ ва х₂ булган кузšалмас стержень ОХ уки буйлаб ¸тибди (3.3 – расм). Унинг узунлиги К системада улчаш буйича   системасида эса  х₂ ва х₁ координаталар стерженга линейка куйиб, К системага нисбатан, унинг булиш саноклари билан улчанади (стерженнинг учлари билан мос тушади бир вактда .

 

 

 

Лоренцнинг (3.4) формуласи билан аникланади:

¸ки

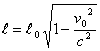                                                                         (3.5)

Предметнинг унга нисбатан v₀ тезлик билан харакатлана¸тган системадаги узунлигига тенг холатда шу системада улчанганга нисбатан  марта кичик. Системанинг тезлигига якинлашганда бу тезлик нолга айланади «Аник» узунлик мавжуд эмас.

3)  вактда координатаси  булган А нуктада  системада лампа ¸нади,  вактда учади  системада лампанинг ¸ниш вакти . К системада эса у (3.4) формула буйича аникланади:

      

 

 

 

 

Содир булган вокеликнинг системада улчанганига нисбатан давом этиши, биринчисида узгармас тезлик билан харакатлана¸тган системада улчаганга нисбатан  марта кам булади (3.4 – расм).

Вокеа содир була¸тган   система с ¸руглик тезлиги билан харакат килганда эди, бу вокеанинг К системада давом этиши чексиз катта булар эди, агар вакт  системада К системага нисбатан тухтаб колса.

4).  Лоренцнинг (3.4) формуласидан (3.2)нинг урнига тезликларни кушишнинг релятивистик формуласини олиш мумкин (3.4) тенгликнинг биринчи ва охиргиларини дифференциаллаймиз, х₁  ларни боšланмаган узгарувчилар деб хисоблаб, биринчи дифферинциални, иккинчисига нисбатан оламиз:

       

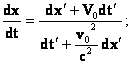
охирги тенгликнинг унг кисми сурат ва махражини dt га буламиз ва     билан солиштирамиз.

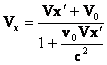                                                                (3.7) бошка ташкил этувчилар учун;

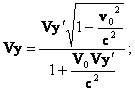
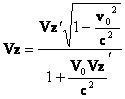                                       (3.7 а)

Бу тезликларни кушишнинг релятивистик формуласи дейилади. Бу ердаги белгилашлар худди (3.2) даги билан бир хил.

          Агар  ва V₀ тезликлар  ук буйлаб йуналса,

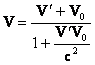                                                                             (3.7б)

 ва V₀ нинг хар кандай кийматлари учун, хатто С, V тенг булганда хам С дан катта була олмайди.

 

V₀ <<c тезликларда релятеиистик булган (3.4), (3.5), (3.6), (3.7 а), (3.7 б) формулалар классик механиканинг (3.1), (3.2) формулаларига утади.

Агар V₀ тезлик С гача етса, (3.4), (3.5), (3.6) формулалар маъноси йуколади, яъни жуда кичик катталикларда айланади. Шундай килиб, С кандайдир жисм ¸ки санок система учун чегаравий тезлик булиб хисобланади.

Релетевистик механикада фазо ва вакт.

Классик механикада узунлик булаги ва вакт оралиšи системанинг харакатига боšлик эмас, релятивистик механикада эса улар нисбийдир. Бу ерда фазо ва вакт бирлик фазо – вакт билан боšлик, нукта ва вакт моменти вокеани бажаради ва у х1 у₁ z₁ хамда t вакт (¸ки  билан аникланади. Иккита вокеанинг оралиšи интервал билан аникланади, у куйидагига тенг:

                                    (3.8)

Интервал – турт улчовли фазонинг бир булаги, бунда учта улчам ва туртинчиси вакт булади Бир инерциал санок системадан иккинчисига утганда интервал катталиклари узгармасдан колади.

Агар  булса, интервал хакикий катталик булади. Dt вакт оралиšида ¸руšлик сигнали иккита вокеликнинг орасидан утишга улгуради, ва биринчи вокеа иккинчисига сабаб булади. Бундай интервал вактсимон дейилади. Агар  булса, интервал минимум булади, ¸руšлик сигнали Dt вакт оралиšида иккита вокеа орасидан утишга улгурмайди, шунинг учун улар бир – бирига сабаб булиб боšланишга эга булмайди. Бундай интервал фазосимон дейилади.

Турт улчовли фазо – вактда траекториянинг урнига вокеликнинг жахон чизиšи тутилади, бу координата ва вактни график равишда боšлаб туради.

 

4 – маъруза.

Харакатнинг асосий конунлари.

 

Куч.

 

Ÿамма жисмлар бир – бири билан таъсирлашади. Ÿозирги замон физикасида куйидаги узаро таъсирлар мавжуд:

а) Гравитацион – жисмлар орасидаги бутун олам тортишиши хисобига таъсир.

б) Электромагнит – кузšалмас ¸ки харакатдаги зарядланган зарралар ¸ки жисмлар орасидаги таъсир.

в) Ядровий – ( икки хил: кучли ва кучсиз) атом ядроси таркибига кирувчи элементар зараччалар характерлайдиган таъсир.

Бир жисмнинг иккинчи жисмга механик таъсири куч дейилади, яъни жисмга тезланиш берадиган катталик. Куч вектор катталик булиб, у сон киймат ¸ки  |F|=F₁  модул билан, фазода йуланиш билан аникланади.

Статик ва динамик таъсир.

Кучнинг жисмга таъсири статик ва динамик куришда булади.

1) Статик таъсир деформация  куринишда пайдо булади. Деформация деб, жисм улчамлари ва шаклининг узгариши микдор жихатдан характерланадиган  физик  катталикка айтилади.  Реал жисм  хар доим “колдик деформация”га эга булади, яъни кучни олиб ташлангандан кейин у бошланšич шаклга кайтиб келмайди. Агар деформацияловчи куч кичик булса, деформация куйилган кучга туšри пропорционал ß=aF  ва кучнинг таъсири олингандан кейин бутунлай йуколади.

Бу коида  Гук конуни  дейилади. ›анча катта деформация хосил килмокчи булсак, жисмга шунча катта куч билан таъсир килиш керак, a–эластиклик коэффициенти. Бу коэффициент деформациялана¸тган жисмнинг материалига боšлик ва куч бирлиги таъсиридаги абсолют деформацияга микдор жихатдан тенг. Берилган материал учун a  нинг катталигини билган холда ва тажриба асосида деформацияни улчаб Гук конуни ¸рдамида кучни аниклаш мумкин. Кучни улчашнинг статистик усули шуларга асосланади, масалан, пружинали тарозида жисмнинг оšирлигини аниклаш.

2) динамик таъсир  жисмлар тезлигининг сон киймати ва йуналиши узгариши билан ифодаланади, яъни жисмларнинг тангенциал ва нормал тезланиши хосил булишида.

          Тангенциал куч F харакат йуналиши билан белгиланади       (траекторияга утказилган урунма буйлаб) ва тангенциал тезланишни хосил килади. Нормал куч  N  харакат йуналишига перпендикуляр йуналади ва нормал тезланишни хосил килади ( 4.1 - расм).

 

Жисм харакатининг узгариши билан куч орасидаги микдорий боšланиш динамика конунларини ташкил килади.

 

Динамиканинг иккинчи конуни.

Тажриба курсатишича, агар иккита бир хил жисмга бир хил кучлар таъсир килса, бу жисимлар бир хил тезланишга эга булади. Агар жисмга таъсир кила¸тган кучнинг сон кийматини   n   марта оширсак, тезланиш хам   n    марта ортади, яъни тезланиш кучга пропорционал

а ~  F                                                             (4.1)

Агар бир хил жисмга бир хил кучлар билан таъсир килмасак, бу жисмларнинг тезланишлари хар хил булади. Микдорий боšланишни хосил килиш учун жисмни характерлайдиган физик катталик – масса  m   киритилади. Агар турли жисмлар бир хил материалдан ясалган булса, масса жисмнинг хажмига ¸ки ундаги модда микдорига боšлик булади. Бу жисмларга микдор жихатдан тенг кучлар билан таъсир килинганда тезланишларнинг хажмга ва массага тескари пропорционал эканлигини курамиз:

               (4.2)

(4.1)   ва  (4.2) ларни умумлаштириб,       ни хосил киламиз. Пропорционаликдан тенгликка утганимизда, к – прпорционалик коэффицентни киритиб                 ни оламиз. К – катталик куч, тезланиш ва массанинг улчов бирлигига боšлик. Физикада кучнинг улчов бирлиги килиб, К = 1 булгандаги киймати кабул килинади, у холда : ( вектор куришда)

                                                                     (4.3)

 

 

Бу  тенглик динамиканинг иккинчи  конуни (¸ки Ньютоннинг иккинчи конуни) дейилади жисмларнинг таъсирида олган тезланишларни шу кучга туšри, массага тескари пропорционал булади. Динамиканинг иккинчи конуни купинча куйидагича ¸зилади:

 

                                                                   (4.4)

бундаги жисмнинг массасини классик механикада узгармас деб хисобланади. Ÿамма холларда масса учун (4.4) формуладан олинган кучнинг тезланишга нисбати кабул килинади. Жисмнинг массаси канча катта булса, шунча кичик тезланиш олинади, яъни турли жисмларнинг харакат тезликларини узгариши хар хил. У холда бундай жисмларнинг инертлиги хар хилдир. Жисмнинг инертлигини характерлайдиган физик катталик унинг массасидир. Бошкача килиб айтганда, масса – жисм тезлиги узгаришига каршилик килувчи катталикдир.

Динамиканинг биринчи конуни.

 

Хусусий холларда, жисмга таъсир килувчи хамма кучлар узаро мувозанатлашганда ( тенг таъсир этувчи 0 га тенг), ( 4.4) дан    а=0    булади, яъни жисм факат микдоран ва йуналиши билан узгармас тезлик билан харакатланади ¸ки тенг холатда булади       ,

Айрим холларда, v = 0. Бу динамиканинг биринчи конуни. Жисмга таъсир килувчи кучлар булмаганда тенг холатда булади, ¸ки туšри чизикли текис харакат килади.

Бу конун жуда катта коинот жисмлар учун хам, майда чанг зарраларининг харакати учун хам бирдай уринлидир.

 

 

 

Динамиканинг учинчи конуни

Биз шу давргача жисмларнинг бир томонлама таъсирини курдик, яъни жисмнинг харакатига бошка жисмларнинг таъсирини. Иккита жисмнинг узаро таъсирини куйдагича ифодалаш мумкин:

Агар бир жисм иккинчи жисмга кандайдир куч билан таъсир килса, иккинчи жисм хам биринчи жисмга микдор жихатдан тенг ва йуналиши карама – карши булган куч билан таъсирлашади. Турли жисмларга ¸ки бир жисмнинг турли кисмларига куйилган таъсир ва акстаъсир килувчи кучлар. Масалан. Агар  m массали жисм ипга махкамланган булса, у вертикал текислик буйлаб айланма харакат килади, жисмга марказга интилма куч таъсир килади   F _см  , ипга эса марказдан кочма    F  _мц    куч таъсир килади.

 

 

 

 

 

 

Инерция кучлари.

Динамиканинг биринчи конунига асосан, жисмга ташкаридан бошка жисмлар таъсир килмаса, у узининг тенг холатини ¸ки бир хил йуналишдаги узгармас тезликли харакатини саклайди ( жисмнинг инертлиги). Жисмга бошка жисмлар таъсир килган холда у уз харакатининг тезлиги ¸ки йуналишини узгартиради, учинчи конун, акстаъсир буйича каршилик хам килади. Тезлатувчи жисмлар томонидан буладиган бундай акстаъсирлар реал ¸ки Нъютон инерция кучлари  дейилади.

Масалан. Ракетка билан урила¸тган теннис коптоги ипни эгади ва ракеткани тормозлайди. Инерция кучи тезлатувчи копток кучига тенг ва тескари йуналган, яъни      F_u =-ma   ( m  - копток массаси). Олдинги мисолга кайтиб келамиз. Ип жисмга марказга интилма тезланиш         беради, яъни унга      куч билан таъсир килади, у айлана маркази томонга йуналади, у ипга куйилган инерция кучи марказга интилма кучга тенг ва тескари йуналган, яъни      .  Бу куч марказдан кочма инерция кучи дейилади.

 

Куч ва жисм импульси.

Динамика конунларининг кулланилишини курамиз:

а) F  куч узгармас. Тезланиш          :          формуладан  (¸ки    F = ma).

                                    (4.5)

Кучнинг унинг таъсир вактига купайтмаси куч импульси дейилади, жисм массасининг харакат тезлигига купайтмаси эса – жиснинг импульси ¸ки харакат микдори дейилади (4.5)  формула шундай укилади;

Куч импульси жисм импульсининг узгаришига тенг.

б) Вакт утиши билан куч узгаради. Куч импульсини J, жисм импульсини       ни билган холда,              формуладан

              вакт оралиšида

               

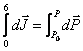       ¸ки                      (4.6)

Яъни вактнинг охирги оралиšида хам уша конунни оламиз.

Динамиканинг иккинчи конунини бошкача куриниши. Ньютон  динамиканинг иккинчи конунини бошкача: харакат микдорининг (импульснинг) узгариши таъсир кила¸тган кучга пропорционал ва охирги томонга йуналади    .  Бу формула вакт утиши билан массанинг узгариши булган хол учун уринли;

 

                                                       (4.7)

 

 

 

 

 

 

5 - МАЪРУЗА.

 

Каттик  жисм  айланма харакат динамикаси. Механикада каттик жисм деб, шундай идеаллаштирилган системага айтиладики, хамма харакат вактида нукталар орасидаги масофа узгармас булсин.

 

Системанинг инерция маркази  ¸ки масса маркази   деган тушунчаларни куриб чикамиз. Моддий нукталар системасининг инерция маркази деб  ч₁ , ч₂ ,ч₃   .... радиус векторли нуктага айтилади.

 

 

(Системанинг хамма   п  элементлари купайтмаларининг йиšиндиси,

i = 1,2,3...., п - моддий нукталарнинг тартиб номери).

Масса марказининг координатлари координата укларига проекциясига тенг:

 

               

 

Бир  жинсли майдонда оšирлик кучининг инерция маркази оšирлик маркази билан мос тушади.

Каттик жисмнинг ихти¸рий кучиши икки хил харакатнинг натижасидир: илгариланма (инерция марказининг кутиш) ва аксинча (жисмнинг инерция маркази атрофидаги айланиши) 2 – маърузага каранг. Бу каттик жисм айланма харакат динамикасининг конунларини яратишга имкон беради, чунки уларнинг хар бири илгариланма харакатнинг механик конунларини ифодалайди.

Агар масса марказидан утган, 00¢ укка махкамланган жисмга укдан   R i  масафада кандайдир  А   нуктада ихти¸рий йуналишда    F   куч таъсир килса, факат унинг айлананинг укига перпендикуляр булган текисликда ¸тган ташкил этувчиси  Fi  жисмнинг айланишини узгартиради, F  ташкил этувчи эса 00¢   ук буйлаб факат илгариланма харакатни хосил килади.(5.1  -  расм)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

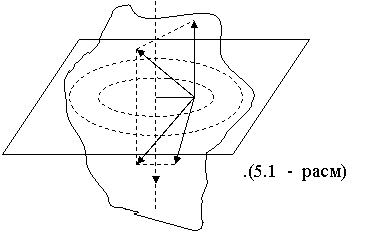Тангенциал ташкил этувчиси  F_{E i}     таъсирида   m  S   массали   А  нукта  Ri   радиус буйлаб айлана чизади. Fv кучнинг айланиш эффекти кучнинг таъсир чизиšигача булган масофа ва айланиш уки канча катта булса, шунча катта ахамиятли булади.

Кучнинг елка li  га купайтмаси айланиш укига нисбатан куч моменти дейилади:

M i  =  Fi  l i  = F i *  R i    sina                    (5.1)

Бу тенглик   R i  радиус векторининг F i  кучга  вектор купайтмасини ифодалашга имкон беради:

M v  =[R v *  F  i]                                        (5.2)

F i-  нуктага таъсир килувчи ташки куч,

Rv-   нуктага куйилган кучнинг радиус – вектори,

l v-  куч елкаси, яъни  с  нуктадан кучнинг таъсир чизиšига туширилган

перпендикулярнинг  узунлиги.

 

Айланма харакат динамикасининг асосий конуни моддий нуктанинг илгариланма харакат конунидан фойдаланиб топиш мумкин.  m _v  массали  А  нуктанинг харакат тезланиши   F_v кучнинг тангенциал ташкил этувчиси таъсирида булади ( 5.3  -   расм)

 

 

Динамиканинг иккинчи конунидан

          F_tI =m_i β Ri²                                                     (5.4)

 

(5.4) иккала томонини  R_v  га купайтирсак, (5.3) ни ва a_{t v}  =  β_v   R²_V ни хисобга олсак :         Fi Ri sinα =m_i β Ri ²  ни оламиз.

(5.1)       ни  хисобга  олганда охирги тенгликни куйидагича ¸зиш мумкин.

Mi  =  m_i β Ri²                                                (5.5)

Жисмга таъсир килувчи хамма кучларнинг натижавий моменти шу укка нисбатан алохида кучлар моментларининг алгебраик йиšиндисига тенг:         М=S М_V

жисмнинг хамма элементлари учун (5.5)  ни суммалаштирсак,

             ¸ки     

бунда

булиб жисмнинг айланиш укига нисбатан инерция моменти   дейилади

mi Ri²  - моддий нуктанинг   уша укка нисбатан инерция моменти   дейилади. У холда аввалги тенгликни куйидагича ¸зиш мумкин :

M=Jb                                      (5.6)

(5.6) айланма харакат динамикасининг асосий конунини тенгламаси дейилади.

Кузšалмас  ук атрофида айлана¸тган каттик жисмнинг бурчакли тезланиши, жисмга таъсир этувчи ташки кучлар натижавий моментига туšри пропорционал, жисмнинг шу укка нисбатан инерция моментига тескари пропорционал.

Ньютоннинг иккинчи конуни             ва               

формуласини солиштириб, айланма харакатда кучнинг ролини куч моменти, массанинг ролини - инерция моменти уйнашини курамиз, яъни   J   канча катта булса, бурчакли тезланиш шунча кам булади.

Шунингдек, инерция моменти айланма харакатда жисмнинг инерция улчови булади.

Юкорида курсатилгандек, инерция моменти хамма нукталарнинг массаларини айланиш укига булган масофанинг квадратига купайтмасининг йиšиндисига тенг.

Бундан куринадики, инерция моменти массанинг айланиш укига нисбатан таксимланиш характерига боšлик экан. Укдан узокрокда ¸тган нукталар, якинида ¸тган нукталарга нисбатан йиšиндида купрок уринни эгаллайди, яъни инерция моменти катта, чунки масофага боšлик эди. Масалан, стерженнинг унинг марказидан утган укка нисбатан инерция моменти    (l  -  стержен узунлиги), унинг охиридан утган укка нисбатан инерция моменти , яъни айланиш укининг жойлашишига боšлик.

Кузšалмас ук инерция марказидан кандай утса, шундай утмаслиги мумкин. Айланиш укини кучиришдаги куйидаги теоремани (Штейнер теоремаси ) исботлаш мумкин:

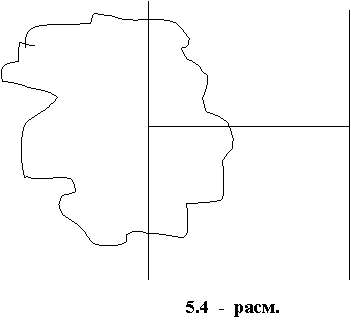
Жисмнинг  ихти¸рий 00¢   укка нисбатан  J   инерция моменти,

( 5.4  -  расм  )  00¢  укка параллел булган ва инерция марказидан утган  00¢   унга нисбатан жисмнинг инерция моменти   J₀   билан жисмнинг   m     массани уклар орасидаги масофа квадратининг купайтмасини йиšиндисига    тенг                               

 J  =   J₀     +   md ²                                             (5.7)

Бундан  куринадики, инерция марказидан утувчи укка нисбатан инерция моменти - жуда кичик. Яна айланма харакат динамикасининг асосий конунини ифодаловчи (5.6) ифодага кайтамиз. Уни бошкача куринишда куйидагича ¸зиш мумкин:

                                                                 (5.8)

Агар ташки куч булмаса, яъни айланиш укига нисбатан момент булмаса, М = 0,  ва w = conct булади ва жисм текис айланади ¸ки айланиш йук булади (худди илгариланма харакат учун Ньютоннинг биринчи конунидек). Каттик жисмнинг инерция моментини вакт утиши билан узгармас деб кабул килиб (5.8) тенгламани куйидагича ¸зиш мумкин:

                                                              (5.9)

          Тенгламадаги УW катталик жисмнинг импульс моменти дейилади. Унинг физик маъносини тушунтирамиз: айланма харакат килганда mi массали хар бир моддий нукта кандайдир Vi тезликка эга булган холда, Ri радиусли айлана чизади.

miUi  купайтма нуктанинг импульси. Нукта импульсининг радиус - вектор билан купайтмаси, яъни miViRi катталик моддий нуктанинг укка нисбатан импульс моменти дейилади.

Вектор куринишда:

                                                         (5.10)

 

Бу ук вектор булиб, унинг йуналиши бурчакли тезлик йуналиши билан мос тушади (5.10) ифодани хамма нукталар учун суммалаштириб, ¸зсак:

¸ки хамма нукталар учун умумий булган купайтма  ни суммалардан чикариб                            эканлиги учун

 

                                                  (5.11)

 

Айланиш укига нисбатан жисмнинг импульс моменти инерция моменти билан бурчакли тезликнинг купайтмасига тенг. (5.8) куйидагича ¸замиз:

                                                       (5.12)

 купайтма куч импульси дейилади. Айланма харакат килина¸тган жисмга куйилган куч импульсининг моменти жисм импульс моментининг узгаришига тенг. Бу формула жисм импульс моментининг узгариш конуни дейилади:

                                                     (5.13)

          Бу ифода айланма харакат динамикасининг асосий конуни тенгламаси дейилади, илгариланма харакатдаги (4.7) ифодадагидек.

 

 

 

6 – маъруза

 

Иш ва энергия

Иш.

 

          Ÿар бир жисм ¸ки жисмлар тизими маълум энергия захирасига эга. Барча жара¸н ва ходисаларда энергия бир жисмдан бошка жисмга утади. Механик жара¸нларда сарфланган энергия микдори иш дейилади. Ÿаракат кила¸тган жисмга куч таъсир кила¸тганда, кучнинг йуналиши хам, тезлик йуналиши хам уткир бурчак ташкил килади,  таъсир кучи йуналтирилган жисмдан таъсир килина¸тган жисмга энергия утади. Бундай холатда куч бажарган иш мусбат хисобланади. Агар куч йуналиши билан силжиш утмас бурчак ташкил килса, у холда аксинча, энергия куч таъсир килина¸тган томондаги жисмга утади.

          Бу холда куч бажарган иш манфий деб хисобланади, таъсир кила¸тган кучни каршилик кучи дейилади.

          Фараз килайлик моддий нукта  куч таъсирида чексиз кичик масофа  га силжиди, у холда бажарилган иш микдори

                                                            (6.1)

          Яъни  вектор билан  векторнинг скаляр купайтмасига тенг ¸ки

                                                    (6.2)

бу ерда a -  ва  векторлар орасидаги бурчак,  векторнинг  йуналишига проекцияси.

          Чекли ораликда уз микдори ва йуналишини узгаритирувчи кучнинг бажарган ишини аниклаш учун (6.2) дан утилган йул оралиšи буйича интеграл олиш керак,

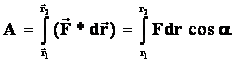                                        (6.3)

Бу  формуладан, силжиш йуналишига перпендикуляр йуналишдаги куч таъсирида иш бажарилмайди. Бажариладиган иш  интенсивлиги кувват билан тавсифланади. Агар Dt вакт оралиšида DА иш бажарилган булса, у холда уртача кувват

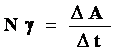                                                            (6.4)

тенглик билан топилади. Кувват вакт утиши билан узгаргани сабабли, хакикий ¸ки оний кувват уртача кувватнинг вакт оралиšи чексиз нолга интилгандаги лимитига тенг булади:

           (6.5)

          Кувват куч вектори билан тезлик векторининг скаляр купайтмасига тенг.

 

Кинетик энергия

          Ÿар кандай харакатлана¸тган жисм энергия манбаига эга. Жисм харакатининг микдорий улчови кинетик энергия дейилади.

          Кинетик энергия микдорини, шу харакатни вужудга келтирувчи, куч бажарган иш микдорига караб аниклаш мумкин.

         

 

 

 

 

 

 

 

 

 

 

Фараз килайлик m массали зарра  куч таъсирида  масофага силжисин.  кучни иккита ташкил килувчиларга ажратамиз:  ва  мос равишда харакат траекториясининг М нуктасидан урунма ва нормал буйича йуналтирилган (6.1 – расм)  нормал куч бажарган иш нолга тенг ва  булишини хисобга олиб,

булишини хосил киламиз, яъни куч бажарган иш   микдорнинг орттирмасига тенг. Худди шу тасдик харакат траекториясининг чекли оралиšидаги бажарилган иш учун хам уринли, масалан, 1 нуктадан 2 нуктагача булган оралик учун

                                       (6.6)

 микдор кинетик энергия дейилади. Заррачага таъсир этувчи барча кучларнинг натижаловчи куч бажарган иш зарра кинетик энергиясининг орттирмасига тенг. Энергия хам иш каби бирликларда улчанади.

          Хуссусий холлар: 1) бошланšич тезлик йук, V₁ = 0. Жисм тезланувчан харакатда (Т₁=0). Т микдор усади, ва охирги нуктада Т₂ = А. 2) Бошланšич тезлик V₁га тенг,  куч таъсирида жисм секинлашувчи харакатда булиб, охирги нуктада тухтайди. V₂= 0; Т₂ = 0; А = -Т₂. Бажарилган иш манфий, яъни каршилик кучи таъсир килади. Кинетик энергия нолгача камаяди. Бу холда каршиликни енгиш учун бажарилган иш жисмдаги кинетик энергия захираси хисобига бажарилади.

 

Потенциал энергия

 

          Агар тинч холатда турган жисм бошка жисмлар билан узаро алокада булса, у иш бажариши (энергия захираси) кобилиятига эга. Бу кобилият жисм харакат кила бошлаганда вужудга келади.

          Бундай холларда, жисм потенциал энергия захирасига эга дейилади. Масалан, ер сиртига якин жойлашган жисм оšирлик кучи майдонида (Ер билан узаро таъсирда) булади. Жисмга таъсир килувчи бу куч, жисмнинг фазодаги холатига боšлик. Кинетик энергияни нолдан (тинч холатдан) берилган микдоргача купайтириш учун бажарилиши керак булган иш микдори кинетик энергия микдори булгани сингари, жисмни потенциал энергияси нолга тенг холатдан берилган холатда камайтиришда бажарилган иш микдори потенциал энергия улчови дейилади.

А = U – U₀,                                                           (6.10)

          Чунки U₀ = 0

          Масалан, жисм Ер юзасидан h баландликка кутарилди. Унинг Ер юзидаги потенциал энергияси U_0.

У холда U – U₀ = mgh ва агар U₀ = 0 булса, U = mgh

Потенциал энергиянинг нол холати шартли маънода.

Курилган мисолда потенциал энергиянинг нол киймати деб, Ер юзидаги ¸ки чексиз узокликдаги нукта энергиясини олиш мумкин.

          Фараз килайлик, жисм ташки куч таъсирида кичик  масофага силжилган булиб, шу билан бирга потенциал энергия dU микдорда узгаради дейлик. Шу кучнинг бажарган иши:

Бундан

                                                           (6.11)

          Бу тенгликлар потенциал энергия билан кучни бир – бири билан боšлайди.

Эластик деформацияланган жисм хам потенциал энергияга эга. Эластик кучи F _элас деформациянинг микдорига пропорционал ва унинг йуналишига тескари, чунки эластик деформацияланган жисм узининг дастлабки холатига кайтишга харакат килади ва унинг микдори

F _элас =  - кх                                                                 (6.12)

          Жисм чексиз кичик dx микдорида деформацияланган эластик кучи F _элас бажарган элемементар иш куйидагича булади:

DA = F _элас * dx = -кxdx                                               (6.13)

          Жисм деформациясининг чекли узгаришида, масалан, деформацияланган

(х = 0) холатдан х₁ деформация холатига утишида бажарилган иш

А = 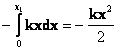                                                    (6.14)

микдорга тенг булиб, деформацияловчи ташки куч бажарган иш хам микдорга тенг булади, факат унинг ишораси мусбат булади, бундан потенциал энергия         га тенглиги келиб чикади.

          Бажарилган иш А жисм деформация жара¸нининг кандай боришига боšлик булмай, факат унинг бошланšич ва охирги деформация холатларига боšлик, яъни эластик кучи консерватив кучдан иборатдир.

          Кинетик ва потенциал энергиялар йиšиндиси тулик механик куч Е = Т + U ни ташкил килади.

Айланма жисм кинетик энергияси.

 

 

 

 

 

 

 

 

 

 

Агар каттик жисм  бурчак тезлиги билан айлана¸ган булса, у холда айланиш укидан R : масофада турувчи D m_i массалик моддий нукта V_i=Wr_i тезлик билан харакат килади. Бу нукта учун кинетик энергия

                         (6.15)

          Барча нукталар энергиясини йиšиб, айланма жисмнинг умумий кинетик энергиясини оламиз:

                                  (6.16)

Бу ерда Y – жисмнинг инерция моменти.

Бу формула илгарилама харакат кила¸тган жисм кинетик энергиясининг формуласи кабидир. Агар жисм бир вактда хам илгарилама, хам айланма харакатда булса (масалан, юмала¸тган илдизак), икки хил кинетик энергия кушилади. Тулик кинетик энергия

                                                            (6.17)

Жисм айланма харакатда булганда ташки кучлар бажарган иш.

 

 

 

 

 

 

 

 

 

 

 

 

 

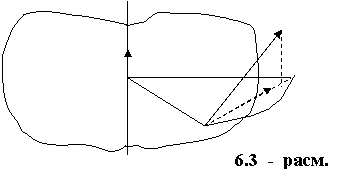Жисм айланиш уки кузšалмас.  - ташки куч D m_i массали заррачага таъсир килади. dt вакт оралиšида D m_i массали моддий нукта  масофани босиб утади (6.3 – расм каранг). Бу ерда  - моддий нуктанинг dt вактдаги бурилиш бурчаги. dt вакт давомида бажарилган элементар иш

бу ерда - таъсир этувчи F_i кучнинг тангенциал кучи, M_i эса  вектор (битта нуктага куйилган куч моменти) нинг модули. Бутун жисм буйича бажарилган иш.

                                         (6.18)

бу ерда М =  - моментлар йиšиндиси – бутун жисмга таъсир

этувчи куч моментларининг натижаловчи кучи.

          Жисмни j бурчакка бурганда бажарилган тулик иш

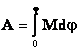
          Хусусан, куч моменти узгармас булса,

А = Мj                                          (6.19)

 

 

 

 

7 – маъруза

 

Импульс ва импульс моментининг саклаш конунлари.

 

Бу икки конун динамиканинг учта асосий конунидан осон келиб чикади. Бу конунларда гап фазонинг симметрик хоссалари туšрисида боргани сабабли, уларнинг ахамияти оддий натижалар доирасидан анча ташкарига чикади, хусусан, импульснинг сакланиш конуни - фазонинг бир жинслилиги туšрисида (ажратилган механик тизимни бутунича фазонинг ихти¸рий жойига параллел кучириш унда юз бера¸тган ходисаларни узгартирмайди), импульс моментининг сакланиш конуни фазо изотропигини акс - этдиради - ундаги йуналишларнинг барчаси тенг хукукли булиши (ажратилган тизим бутунича ихти¸рий бурчакка берилганда ¸ки хисоблаш бошланадиган инерция тизимини бирор бурчакка бурганда тизим жисмдан харакатининг характерини узгартирмайди).

          Бу конунларни динамика масалаларига туšри кулланишни урганиш жуда мухим булиб, конунларни тушунмай туриб буни амалга ошириб булмайди. Сакланиш конунларини тушуниш уларни динамика масалаларидан келтириб чикаришга имкон беради.

 

Импульс сакланиш конуни

 

          Фараз  килайлик, ¸пик моддий нукталар тизими берилган булсин ва унинг бошланšич инерция тизими хисобига нисбатан харакатини карайлик.

          Тизим импулси деб, шу тизим барча заррачаларининг импульсларининг векторлари йиšиндиси:

                                      (7.1)

га айтилади.

Карала¸тган ажратилган тизимнинг хар бир зарраси (моддий нукта) учун Ньютоннинг иккинчи конунини ¸замиз;

 

                       

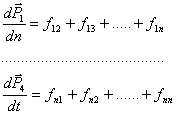
Бу тенгламаларда dP_i–i-зарачанинг  dt  вактда  импульсининг узгариши,

f _ik   -  к – заррачанинг  i  -  зарачага таъсир кучи.

Ньютон учинчи конунига кура,     f_ik  =  -  f _ki  булгани сабабли, юкоридаги тенгликларнинг унг томонларининг йиšиндиси нолга тенг булади. Лекин,

 

булгани учун.

                                           (7.2)

бу тенглик огиратилган механик тизимининг импульси сакланиш конуни ифодалайди (Импульс сакланиш конуни).

Агар (7.1) дифференциаллаш ва йиšиндининг тартибини алмаштирсак,

             ¸ки  

 

хамда инерция тизимининг (массалар маркази) маркази тушунчасини киритсак, унинг радиус вектори

 

                               (7.3)

 

Радиус вектор тезлигини          бутун тизим массасини эса    m  оркали белгиласак, импульс учун   (7.1)  формуласи  куйидагича ¸замиз:

импульс сакланиш конуни (7.2) ни эса                   

куринишда ¸зилишидан, ¸пик тизим инерция маркази тизим туšри чизикли харакат килиши куринади.

7.1–расмда учта заррача импульси ва узаро таъсири, уларнинг массалари маркази С нуктада булиши курсатилган.

1.эслатма. Купинча тизим ажратилган булмайди, лекин ташки кучлар шундай буладики, уларнинг бирор йуналишга проекцияси нолга тенг булади (7.2 – расм).

2.эслатма. Реактив харакат механизмини тушуниш импульс сакланиш конунига асосланади.

Масалан, ажратилган тизимни ташкил килувчи ракета учун:

бунда dm – ¸килšи моддалар массаси, ( dt  вакт оралиšида ).

V – ракетанинг Ерга нисбатан тезлиги, V _нисб  - чикариб ташланган ¸килšи махсулотларининг ракетага нисбатан тезлиги (7.3  -  расм). Иккинчи тартибли чексиз кичик микдорлар dm  dv  ни ташлаб юбориб, хосилаларга утсак,                      ни хосил киламиз. Бу тенгсизликнинг унг томони реакция кучидан иборатдир (реактив куч).

 

Импульс моментининг сакланиш конуни.

 

Импульс моментининг икки хил тушунчаси бор:

1.     Координаталар бошига нисбатан ихти¸рий заррачалар тизимининг импульс моменти                  

2.     Ÿисоблашларда айланиш укидан тегишли заррачаларгача  булган масофа олинувчи, О айланиш укига нисбатан айланма жисм импульс моменти яъни          

Координаталар боши сифатида олинган марказга нисбатан импульс моментининг сакланиш конуни ¸пик тизимники каби булади, чунки динамиканинг учинчи конунинига кура, ички кучларнинг умумий моменти нолга тенг, худди карала¸тган марказга нисбатан ташки кучларнинг умумий моменти нолга тенг булгани каби. Мисол сифатида маркази Ку¸шда булган ку¸ш тизимини караш мумкин. Импульс моменти сакланиш конунидан Ку¸ш марказига нисбатан , бу планетага бошка планеталарнинг таъсирини эътиборга олмай Кеплернинг иккинчи конуни (планетанинг сектори тезлиги доимийлиги) ни келтириб чикариш осон.

 

Айланма жисм импульс моментининг сакланиш конуни.

 

          Айланиш укига нисбатан жисм импульс моменти шу ук буйлаб, айланма жисм бурчак тезлиги каби йуналган булади. У айланиш укига нисбатан жисм инерция моменти билан бурчак тезлик векторига купайтмасига тенг:

 

                               (7.4)

 

 айланиш укига нисбатан перпендикуляр йуналган булгани учун,

( m_i массали заррача учун), айланма жисм нуктасининг тезлиги

 га тенг.

          Агар М_z – айланиш укига нисбатан тенг таъсир этувчи куч моменти (айланувчи момент) булса, у холда Ньютон иккинчи конунига кура айланма жисм учун

                                                                    (7.5)

деб ¸зиш мумкин.

          Айланиш уки эркин ¸ки бир нуктада махкамланган булса, худди болалар уйинчоšи гироскоп сингари айланма харакат динамикасининг конуни умумийрок куринишда ¸зиш керак

          “Импульс моменти векторининг узгариши тенг таъсир килувчи куч моментининг импульсига тенг”  ¸ки

                                                                   (7.6)

          Агар ташки кучлар моменти нолга тенг булса, у холда имульс моментининг сакланиш конуни уринли булади:

                                                        (7.7)

          Бундан куринадики, импульс моментининг сакланиш конуни, жисмга ташки кучлар таъсир этганда, лекин уларнинг айланиш укига нисбатан моменти нолга тенг булганда хам уринли экан.

          Бунга планеталар, планеталар йулдоши ва Ку¸шнинг хусусий импульс мометининг сакланишини мисол килиб курсатиш мумкин.

          (7.7) конунни деформацияланувчи жисмларга нисбатан хам кулланиши мумкин (J –  узгарувчи)

                              (7.8)

Бундаги индекслар t₁, t₂, t₃   ва хоказа оний вактларга мос келади.

Бу конундан акрабатлар, фигуристлар, балет артистлари, гимнастлар хамда машиналарни лойихаловчи инженерлар усталик билан фойдаланадилар. Уни айланма жисмлар ¸пик тизими учун умумлаш- тириш мумкин. Импульс моментининг сакланиш конуни    (L  =  const   агар  M = d)   жисм импульс моментининг узгариш конунининг   (dL=M dt)   хусусий холи деб караш мумкин.

Гироскоп хакида тушунча.

 

Гироскоп (волчок) деганда айланиш щкига нисбатан симметрий, купинга бир жинсли «айланма жисмни»  ва айланиш уки атрофида жуда тез айланувчи жисмни тушунилади.

 

 

 

 

 

 

 

 

7.4 -  расм.

 

7.4-расмда айлана¸тган уйинчок гироскоп курсатилган булиб, унинг уки оšма холатда ва гироскопик эффектдан прецессияланади.

Бу берилган онда бургак тезлиги  ω  ва импульс моменти  L₂= J₂ω(гироскоп уки буйича йуналган) расм текислигида ¸тади, P  ва  N  кучлар жуфтининг моменти чизма оркасига йуналган (шу томонга бургак тезлигини ва импульс моментининг орттирмаси хам йуналган).

Демак, импульс моментининг узгариш конунига асосан   d L = M dt, укнинг юкори охири чизма оркасига кетади, гироскоп йикилмайди, унинг уки эса конус буйлаб узгаради. Катта гироскопларни кемаларда чайкалишни камайтириш максадида ишлатилади. Улар катта импульс моменти  L  = Jω    га ва катта энергия                  захирасига эга.

Уклари горизонтал текисликда буриладиган, жуда тез айланадиган кичик гироскопларни гирокомпослар сифатида, кардан осмасига махкамланган гироскопларни самоли¸тларда «горизонтал чизикларини» курсатувчи сифатида фойдаланади.

 

8 - маъруза.

 

Энергиянинг сакланиш конуни.

 

Табиатда харакатнинг бир турдан иккинчи турга утиши узлуксиз равишда руй беради. Демак, харакатларнинг барчаси учун бир хил булган, материя харакатининг барча ходисалари учун умумий улчов мавжуд булиши керак. Бундай улчов сифатида булган жисм (¸ки жисмлар тизими) нинг энергиясини караш мумкин.

Агар фазонинг хар бир нуктасида жисм бир нуктадан бошка нуктага конуний узгарувчи кучлар билан бошка жисмлар таъсирида булса, бу жисм куч майдонида дейилади. Масалан, жисм Ер юзиги якин жойда оšирлик кучи ( Р = mg)  майдонида булади. Бу кучлар вертикал буйлаб пастга йуналган булади.

Агар моддий нуктага таъсир этувчи куч F  нуктанинг (жисмнинг) ихти¸рий (1) холатдан (2) холатга силжиганида бажарган иши  А₁₂ , бу силжиши кайси траектория (чизик) буйлаб юз берганига боšлик булма-

са, бундай кучларни консерватив ¸ки потенциал куч дейилади. (8.1расм)

Жисм шу траектория буйлаб тескари йуналишда харакатда булганда, консерватив кучлар микдори сакланади, лекин тескари ишорали булмайди;        А _1-6-2    =  А  _2-6-1  .

Шу сабабли консерватив кучларнинг ихти¸рий ¸пик контур буйича бажарган иши нолга тенг булади:

 

А = А _{1а 2 в 1} = А _1а2 +  А _{2  в 1} = А _1а2 - А _{1 в 2}  =0    (8.1)

 

 

 

 

 

 

8.1               -  расм.

 

Бутун дун¸ тортилиш кучлари, эластик кучлари,  зарядланган заррачаларнинг узаро таъсир килувчи электростатик кучлари консерватив кучларга мисол була олади.

Жисм бир холатдан бошка холатга утганда таъсир килган куч бажарган иш утилган йул шаклига боšлик булса, бундай кучлар ноконсерватив кучлар дейилади. Бундай кучлар каторига энг аввал дисентатив кучлар киради, масалан, бирор жисмнинг бошка жисм ортида сирпаниши натижасида пайдо булган ишкаланиш кучлари, ¸ки жисм бирор суюк ¸ки газсимон мухитда харакат килганида юзага келувчи каршилик кучлари киради. Бу кучлар хар доим харакат йуналишига карама – карши йуналган булиб, харакат тезлигига боšлик булади. Шунинг учун жисм ¸пик контур буйлаб силжиганда бундай кучлар бажарган иш манфий булади ва хеч качон нолга тенг булмайди.

Агар заррачалар тизимига факат консерватив кучлар таъсир этса, тизимнинг тулик механик энергияси узгармай колаверади. Бунда факат потенциал энергия кинетик энергияга ва аксинча кинетик энергия потенциал энергияга айланиши мумкин, лекин уларнинг йиšиндиси узгармай колаверади, яъни :

E = T + U = const                                     (8.2)

          Бундай холат механикада энергиянинг сакланиш конуни дейилади. Энергиянинг сакланиш конуни – табиатнинг мухим конунидир. Энергиянинг сакланиш конунини, масалан, ерга эркин туша¸тган жисмда осон текшириб туриш мумкин. Бунинг учун Ер – жисм тизимида эркин туша¸тган жисм максимал баландликда         (8.2–расмда 1 холат) ва II, III  холатларда онлардаги тулик энергияларни таккослаб курамиз:

 

 

 

 

 

 

 

 

 

E₁ = U _I = mg H:   T _I =0

        (8.3)

 

Шундай килиб,     E_I = E_II =E _III = const, яъни   (8.2)  тенглик бажарилади.

 

Шарларнинг марказий зарбаси.

 

Энергиянинг ва импульснинг сакланиш конунлари жисмлар тукнашуви жара¸нини назарий тадкик килишнинг ягона воситаси энергиянинг сакланиш конуни ва импульснинг сакланиш конунларидир. Сакланиш конунларининг абсолют эластик ва эластик булмаган шарлар марказий зарбасининг сакланиш конунларини кулланишини куриб чикамиз.

Зарба натижасида бир – бирига урилувчи шарлар тизимининг механик энергияси бошка турдаги энергияга айланмаса, бундай зарбани абсолют эластик зарба дейилади.

Фараз килайлик иккита      m₁  ва   m₂   массали абсолют эластик шар тукнашгунча  v₁ ва    v₂      тезлик билан (шу билан бирга  V₁ > V₂ )

Илгарилама, хамда уларнинг марказий чизиšи буйлаб бир хил йуналишдаги харакатда булсин.

Шарларнинг бир – бири билан тукнашгандан сунг тезликлари  U₁  ва     U₂  ни , иккита сакланиш конунларидан фойдаланиб топамиз.

 

Шакл (схема)	Зарбагача	Зарбадан сунг
Импульс   Кинетик энергия   Потенциал энергия

 

Механик энергиянинг тулик сакланиш конунига кура топамиз:

 

       (8.4)

 

Шарлар горизонтал техникада харакат килгани сабабли, уларнинг Ер тортиш кучи майдонидаги потенциал энергияси, узилиш пайтида узгармайди, яъни U₁+U₂=U₁^'+U₂^', у холда (8.4)  дан

 

m₁ v₁² + m₂ v₂²=m₁ u₁²+ m₂ u₂²                          (8.5)

ни хосил киламиз.

Импульс сакланиш конунига кура

m₁  v₁  +  m₂v₂  =  m₁ U₁+ m₂  U₂                     (8.6).

деб ¸зиш мумкин. Марказий зарба пайтида v₁  , v₂ , U₁ , U₂

векторлар бир туšри чизик буйлаб йуналган булади. Шунинг учун  (8.6) тенгламада векторлардан скаляр кийматларга  утиш мумкин:

m₁  v₁  +  m₂v₂  =  m₁ U₁+ m₂  U₂                    (8.7).

 

8.5 ва  (8.7) тенгламаларни биргаликда ечиб топамиз:

 

               

U₁ ва   U₂   тезликлар турлича, ва шарлар тукнашув пайтида, эластик кучлари таъсирида узаро итарилади ва урилишдан сунг бир – биридан узоклашади. Шу пайтда куйидаги хусусий холлар руй бериши мумкин:

1)     Шарларнинг массаси бирхил  ( m₁  = m₂  = m  ).

У холда U₁  =V₂  ; U₂ =V₁  ;

2)     Иккинчи шар массаси биринчиникидан бир неча баравар куп  (m₂≥m₁).

Бунда                            

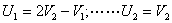
Шу билан бирга иккинчи шар урилишгача тинч холатда (V₂  =0), у холда

 U₁  = -V₁ , яъни биринчи шар тенг турган катта массадан урилиб кочади ва тескари йуналишда – V₁ тезликда харакат килади. Эластик шар эластик деворга урилганда деворни чексиз катта массали кузšолмас шар деб каралади.

Ноэластик урилишда механик энергиянинг кисман номеханик формага айланиши (диссициация ¸ки энергиянинг таркалиши ) руй  беради. Агар абсолют ноэластик жисмлар тукнашса, улар деформацияланади, лекин бу шароитда эластик кучи вужудга келмайди, шарлар бир – биридан итарилмайди, ва улар урилишдан кейин бир хил тезлик билан биргаликда харакат киладилар.

Мисол тарикасида илгарилама харакат кила¸тган шарларнинг абсолют ноэластик туšри марказий тукнашишдаги дистанция энергиясини курайлик. Импульс сакланиш конунгиа кура

                                             (8.9)

Марказий тукнашув чоšида  V₁ ,  V₂   ,  U  векторлар битта туšри чизик буйлаб йуналгани учун (8.9)  ни скаляр куринишда ¸зиш мумкин:

m₁ v₁ +  m₂ v₂ = (m₁  +  m₂   )  u                   ( 8.9 а)

Шундай  килиб, иккала шарнинг тукнашувчи дан кейинги умумий тезлик

                                      (8.10)

га тенг булади.

 

Шакл (схема)	Зарбагача Тукнашувгача	Зарбадан сунг Тукнашувдан сунг
Импульс   Кинетик энергия   Потенциал энергия

 

Тизим тулик механик энергиянинг ноэластик тукнашуви натижасида узгаришини топамиз:

           (8.11)

Шарлар горизонтал текисликда харакатлангани сабабли   U = U′.

Шунинг учун

                              (8.11 а)

¸ки бунинг куринишини узгартириб топамиз

                                  (8.12)

Шундай килиб, ноэластик тукнашув пайтида тизимнинг тулик механик энергияси камаяди, яъни унинг бир кисми «сочилиб кетади», бу сакланиш конунига ва энергиянинг узгариш конунига зид келмайди.

Абсолют ноэластик тукнашув пайтида узаро урилган жисмларнинг деформацияланиши  учун бажарилган иш А тулик механик энергиянинг камайганига тенг, яъни

 

                              (8.13)

 

Шу билан бирга, агар иккинчи жисм тукнашувига тенг холатда булса

(  V₂  =0)  , у холда

                               (8.14)

 

 

 

9- маъруза

 

Ноинерциал тизимларда харакат

Галилей нисбийлик тамойили (принципи)

          Барча инерциал тизимларда жисм тезланиши бир хил микдор ва йуналишга эга . Бу тенгликнинг икки томонини жисм массаси m га купайтирамиз. (Бу классик механикада тизим хисоб бошланишига боšлик эмас): 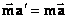 ¸ки  бундан ( булгани учун)  яъни барча инерциал тизимларда динамиканинг иккинчи конуни бир хил ифодаланади. Биринчи конун эса ихти¸рий инерциал тизимлар учун уринлидир. Бундан куйидагича хулосага келамиз: динамика конунлари барча инерциал тизимларда инвариантдир. Бошкача айтганда барча инерциал тизимларда хамма механик ходисалар бир хил руй беради. Инерциал тизимлар механик ходисалар билан тенг хукуклидирлар. Бу – "Галилейнинг нисбийлик тамойили (принципи) ¸ки классик механиканинг нисбийлик тамойили (принципи) дейилади.

Илгарилама харакатдаги инерциал тизимлар.

          Бир – бирига нисбатан кандайдир тезланиш билан харакатда булган хисоблаш тизимлари ноэнерциал тизимлар дейилади. Икки хил хисоблаш тизимини караймиз: XYZ инерциал тизим, масалан Ер билан боšланишда,  - ноэнерциал тизимини, у биринчисига нисбатан бирор йуналиш буйича (9.1 – расм).

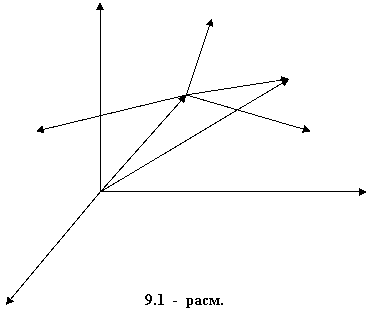Иккинчи тизим бошланšич нуктаси  t вакт онидаги радиус вектори   (XYZ тизимнинг бошланšич нуктаси О дан хисоблаганда) деб караймиз.

          Бирор М нуктанинг холати биринчи тизимга нисбатан  радиус – вектор билан, иккинчи тизимга нисбатан  радиус – вектор билан аникланади.

          Чизмада куринганидек  =  + . Бу формула битта нуктанинг турлича коорданаталар тизимида радиус – векторларни узаро боšлайди. Бу тенгликни вакт буйича дифференциаллаймиз:

        ¸ки                                   (9.1)

          Бу формула М нуктанинг t моментдаги тезлигини турли тизимларда узаро боšловчи формуладир. (9.1) тенгликни вакт буйича дифференциаллаймиз:

       ¸ки                                      (9.2)

          Яъни турли тизимларда битта нукта турлича тезланишларга эга экан. Бу тенгликларда штрихли катталиклар инерциал тизимига, штрихсизлари эса инерциал тизимга тегишлидир. (9.2) тенгликни m га купайтирамиз:

       ¸ки    

          бундан

                                                 (9.3)

          Бу тенглик нонерциал тизимда динамиканинг иккинчи конунини ифодалайди. Инерциал тизимдан фаркли, уларок жисмга  таъсир килана¸тган реал кучга кушимча, инерциянинг фиктив (¸ки даламбер кучи _U = - m₀ кушилади. Унинг куйидаги хоссалари бор:

1)     Бу кучнинг манбаи йук, яъни шу кучни берувчи жисм йук;

2)     Бу куч факат ноинерциал тизимга нисбатан намо¸н булади, инерциал тизимда эса у мавжуд эмас.

Мисоллар: Лифт ичида пружинали тарозиларга осилган m массали юкни карайлик. Лифтнинг турлича харакатларини куриб чикамиз.

 

 

 

 

 

 

Лифт харакати	Торази курсаткичи ва лифтдаги ходиса
А) текис туšри чизикли ¸ки тинч холатда Б) тезланиш билан тушаяпти В) эркин тушаяпти Г) эркин тушиш ва инфляция билан ихти¸рий йуналиши буйича харакат кушилганда Д) юкорига караб а тезланиши билан харакат Е) юкорига караб g тезланиш билан харакатда, лекин оšирлик кучи йук	mg Торази оšирликни туšри курсатади   m(g – a) – Оšирлик хакикатдан кам m(g – g) = 0 Вазнислик       m(g + a). Оšирлик ошди. Худди шунга ухшаш, космик кема  кутарила¸тганда ортикча юк хосил булади mg Лифт худди жойида тургандек, аммо одатдаги оšирлик кучи таъсир килади. Инерция кучи оšирлик кучининг урнини олади (инерция ва тортилиш кучларининг эквивалентиги)

 

          Бу ходисаларнинг барчасини лифт билан барча харакатда булган кузатувчи, тортилиш кучидан ташкари, мос равишда йуналган инерциянинг фиктив кучи мавжудлигини тушунади, кузšолмас (инерциал) эса юкка таъсир килувчи кучларнинг геометрик йиšиндиси: динамик (юкка тезланиш берувчи) ва статистик кучлардан иборат кушилувчиларга ажралади.

          Инерция ва тортиш кучлари асосий умумий хоссаларидан бири уларнинг таъсир килина¸тган жисм массасига пропорционал булишидир.

Динамиканинг иккинчи конунида масса – инертлик улчови булса, бутун дун¸ тартиби конунида эса – тортилиш улчови булади.

XIX асрда бу кучларни турлича физик микдорлар (катталиклар) деб хисобланиб, уларни бир – биридан фарклаш учун инерт масса ва гравитация массаси деб атай бошладилар. Турли хил массали ва бир хил жойда турган турли материаллардан иборат жисмларга куйилган оšирлик кучларининг йуналишларини ута аниклик билан улчашларни олиб борган Р. Этвеш ва бошка олимларнинг ишлари бу йуналишлар бир хил эканлигини курсатади. Бундан бир хил нуктада улчанган тортилиш кучининг марказдан кочма кучга нисбати, ва демак, гравитацион массанинг инерт массага нисбати барча жисмлар учун бир хил булиши келиб чикади. Улчов бирликларини танлаш билан уларни тенглаштириш мумкин.

Инерция ва тортилиш кучларининг эквивалентлиги инерт масса ва гравитон масса бир хил физик маънога эга эканлигини курсатди.

 

Айланувчи хисоб тизимлари

          Айланувчи жисмлар билан боšлик хисоб тизимлари хам ноэнерциал. Улар учун нормал тезланишнинг мавжудлиги характерли-дир:     Масалан, хисоб тизими, соат миллари йуналиши буйлаб W бурчак тезлиги билан айлана¸тган; r  радиусли юмалок диск билан боšлик (9.2 – расм). Диск чеккасида айлана буйлаб соат миллари йуналиши буйича массаси m га тенг кичик жисм харакат килмокда. Дискка нисбатан бу жисм тезлиги , кузšалмас (инерциал) тизимга нисбатан эса 

          Инерциал тизимда жисм тезланиши

  бундан     (9.4)

(9.4) тенгликни m га купайтириб, айлана¸тган тизимдаги жисмга таъсир килина¸тган натижаловчи кучни оламиз:

                                                  (9.5)

бу ерда  - жисм айлантирувчи (марказга интилувчи куч) хакикий куч. Ундан ташкари, айлана¸тган тизимда жисмга таъсир кила¸тган иккита фиктив (калбаки) кучлар бор: - mw²r – инерция фиктив марказидаги кочма куч булиб, у айланиш укидан радиус буйлаб, ташкарига йуналган (манфий ишорали) ва - - Кариолис кучи булиб, у карала¸тган мисолда укдан ташкарига караб йуналган булади.   кучларнинг хар кандай йуналишида Кариолис кучи вектор куринишида куйидаги формула билан ифодаланади:

                                                               (9.6)

Бундан куринадики бу куч  векторлар йуналишлари оркали утган текисликка перпендикуляр йуналишга эга, яъни у тизимнинг айланиши йуналишига ( йуналишига) боšлик ва айланма тизимда харакат кила¸тган жисм траекториясига хар доим тик булади.

(9.5) дан инерция марказидаги кочма куч айлана тизимга хар доим таъсир килади, Кариолис кучи эса жисм айланма системасига нисбатан харакатда булганда таъсир килар экан (. Айлана¸тган Ер билан боšлик хисоб тизими, катъий килиб айтганда, ноэнерциал тизими, лекин, унинг айланма бурчак тезлиги w жуда кичик булгани сабабли, инерция кучининг таъсири жисм жуда катта тезлик билан харакат килганда ¸ки катта вакт оралиšида сезилади. Куп холларда бу тизимни тахминан инерциал тизим деб хисоблаш мумкин.

Мисоллар:

1)    
Айлана¸тган Ер юзасида бирор М жисм ер уки атрофида айлана хосил килади (9.3 – расм)

9.3 – расм.

Унга марказга йуналтирилган тортилиш кучи, ер укига  перпендикуляр булган, марказдан кочувчи куч  таъсир килади. Бу икки кучни кушиб, одатда йуналиши, Ер марказидан утмайдиган оšирлик кучи  ни хосил киламиз. Факат, марказдан кочувчи куч оšирлик кучига тескари йуналишда булган, экваторда ва кутбларда ( у ерда  = 0) оšирлик кучи марказга йуналган булади. шунинг учун кутбларда  максимал кийматини, экваторда эса тахминан 0,5 % га кам кийматни кабул килади. Буларнинг хаммаси Ернинг яссиланишига олиб келади: кутбларни орасидаги диаметри экватор диаметрига нисбатан  га кискарок булади.

2)    
Ер юзасида тебрана¸тган узун маятник траекториясини Кариолис

кучи хар доим кийшайтириб туради. Масалан, у кум сепилган майдонда уз изини колдирса, бу из туšри чизик булишни урнига.    9.4 – расмдаги куринишда булади.

9.4 – расм.

 

Биринчи марта 1850 й. Фуко томонидан утказилган бу тажриба, Ернинг уз уки атрофидан айланишини тасдикловчи омил булди.Худди шу куч, хаво босими энг катта фарки йуналишидан шамол йуналиши четга чикишга ва денгиз окимининг кучли шамол йуналишидан фарк килишига сабаб булади. Бу фарклар шимолий ярим шарда унгга, жанубий ярим шарда эса чапга караб узгаради, бу ходиса Кариолис кучининг йуналиши билан боšликдир.

 

 

 

10 – маъруза

 

Классик механика конунларини кулланилиш чегаралари.

 

Жисмнинг катта тезликдаги харакати (V  бу ерда с – ¸руšликнинг вакуумдаги тезлиги) Эйнштейнинг махсус ва хусусий нисбийлик назарияси 2 тамойилининг асосий холатларига таянадиган релятивистик механика конунлари билан таърифланади:

а) Барча инерциал хисоб тизимларида физик ходисалар бир хил шаклда, яъни табиатнинг барча ходисалари бир хил руй беради (нисбийлик тамойили);

б) Барча инерциал хисоб тизимларида ¸руšликнинг вакуумдаги тезлиги бир хил (¸руšлик тезлигининг узгармаслик тамойили).

          Бу постулатлар аввал куриб утилган Лоренц алмаштиришини каноатлантиради ва динамика конунлари нисбийлик назариясининг хулосаларига мувофик булиши учун, жисм массаси турли инерциал хисоб тизимларида турлича деб хисоблаш зарур (Ньютон механикасида эса масса узгармас деб каралади) ва куйидагича муносабат билан аникланади:

                                                                   (10.1)

          бу ерда m₀ – тинч холатдаги жисм массаси, V – жисмнинг тизимга нисбатан тезлиги, с – вакуумдаги ¸руšлик тезлиги, m – харакатдаги жисм массаси. Шундай килиб, харакатдаги жисм массаси унинг тезлигига боšлик экан ( m = m(V)). (10.1) тенглик билан аникланадиган масса релятевистик масса дейилади. Тезлиги V жисм массаси ортгандан бошлаб секинрок, с–¸руглик тезлигига якинлашганда

эса жуда тез катталашади. m нинг V га боšликлиги 10.1-расмда курсатилган.

 

 

 

 

 

 

 

 

 

V ® С милий холатда хар кандай жисм массаси (хамда хар кандай микрообъект – электрон, плотон ва х.к. ларнинг массаси хам) чексиз катта микдорга интилади ва аксинча, V << c яъни  булганда  (классик механикадаги холат) булади. Нисбийлик назариясида жисм импульси, механиканинг нисбийлик тамойилига кура, худди классик механикадаги сингари

                                                  (10.2)

куринишда ифодаланади ва V ® c да эса нолга интилади.

          Релятивистик шаклда динамиканинг асосий конунининг таърифи узгармайди – куч – импульс тезлигининг узгаришига тенг:

                                                                         (10.3)

ва (10.2) формулани эътиборга олсак унинг куриниши куйидагича булади:

                                                                      (10.4)                     

       Бу тенгликда  деб олсак, биринчи конун хосил булади, у холда

              бундан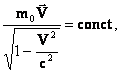       

аммо тинч холатдаги жисм массаси узгармас булгани ва  булгани учун бу конуннинг таърифи хам Ньютон механикасидаги таъриф каби булади.

          Динамиканинг учинчи конуни хар кандай инерциал хисоб тизимида хам бир хиллигича колади.

 

 

 

 

Энергиянинг масса билан боšликлиги.

 

Релятивистик массанинг (10.1) куринишидаги ифодасини,  буйича Ньютон биноми формуласига кура ¸йиб, узгартириб ¸замиз. У холда

                (10.5)

          ифодани хосил киламиз.

 булганда,  нисбатнинг даражарали ошган сари, бундай нисбатнинг даражаларидан иборат катор хадлари кичрайиб бораверади.  V–тезликнинг кичик кийматларида  нинг бирдан катта даражаларини эътиборга олмасак хам булади ва

 

                                                   (10.6)

таркибий тенгликни хосил киламиз. Бу тенгликнинг  икки томони вакуумдаги ¸руšлик тезлигининг квадрати с² га купайтириб, таркибий тенгликни одатдаги тенглик билан алмаштириб,

                                              (10.7)

тенгликка эга буламиз. Бу тенгликнинг унг томонида кинетик энергия ифодаси турибди, демак тенгликнинг чап томонидаги икки хад хам маънога эга.    формула тинч холатдаги жисмнинг ички энергиясини (тинч холат энергиясини),  формула эса, харакатдаги жисмнинг тулик энергиясини англатиб, у тинч холат энергияси билан кинетик энергия Т =  йиšиндисидан иборат (бу такрибий ифода) булишини курсатади. V-тезлик с-тезлик билан таккослаш мумкин булган кийматларда кинетик энергия ифодасида (10.5) формулада бошка хадларни хам эътиборга олишни талаб килинади.

          Агар харакатдаги жисм бошка жисмлар билан боšлик булса, тулик энергия таркибига узаро таъсир потенциал энергияси хам киради:

E = E₀ + T + U = mc²                                                    (10.8)

          Бу формула табиатнинг асосий конуни хар кандай жисм, жисмлар тизими ва майдон учун масса билан энергиянинг узаро боšликлик конунини ифодалайди. Ÿар кандай массага эга жисм, одатда, "пассив" холатда турган m₀c² энергия захирасига эга булиб, маълум шартларда уни "актив" шаклга айлантириш мумкин. Масалан, енгил ядроларнинг оšир ядроларга кушилишидан (термоядро реакцияларида) хосил булган масса реакция кирган ядро массаларининг йиšиндисидан Dm га кам булади, (D m – масса дефекти дейилади). Шу билан масса дефектига эквивалент булган боšланиши энергияси

Ажралиб чикади ва у  га тенгдир.

          Ажратилган (изоляция килинган) жисмлар тизими учун

                                                          (10.9)

          Бутун  тизимнинг барча энергиялари захираси ва хамма жисмларнинг жаъми массаси узгармай колаверади. Энергиянинг сакланиш конуни бир ¸кдан ва релятивистик массанинг сакланиши конуни иккинчи томонидан шундай ифодаланади. Бу бирлашган конун умумий хисобланиб, релятивистик механикадаги энергия ва массанинг сакланиш конунларидан айримларининг урнини босади.

 

Квант механика хакида тушунча.

 

          Классик заррача (моддий нуктанинг) холатини тарифлашда, заррачанинг хар бир ондаги фазодаги (х, y, z) координиталарини аник киймати ва импульснинг уклар буйича ташкил этувчилари (Р_х, Р_y,Р _z) нинг аник кийматларини аниклаш тамойилидан келиб чикилади.

          Шу билан унинг харакат траекториясини ифодаловчи чизикни курсатиши мумкин булади.

          Реал заррачалар – микрообъектлари (электрон, изотоп, атом, молекулалар) уларнинг махсус табиатига кура ва физикада уларга мос келувчи объектларни мавжуд эмаслиги туфайли, тарифлаш мумкин эмас.

Микрообъектларнинг координата ва импульсларни бир вакта улчаш пайтида уларнинг кийматларида хатоликлар (аникмасликлар) руй беради, улар мос равишда Dх, Dy, Dz, DР_х, DР_y, DР_z  га тенг булади.

          Гайзенберг координаталар ва импульслар буйича аникмасликлар куйидаги муносабатлар билан боšлик булишини аникланади:

                     (10.10)

          Бу тезликлар Гайзенберг ноаникликларнинг муносабатлари дейилади (бу ерла h – Планк доимийси булиб, у h = 2П * 1,05443 = 10 ^–34 дт. с). Бу муносабатлардан куринадики, Dх ва D Р_х хатоликлар бир вактда исталган кичик булиши мумкин эмас, ва координата канчалик кичик хатолик билан улчанса, шунчалик катта хатолик билан импульс улчанган булади. Масалан, водород атомидаги электрон координатасига атом радиуси Dx = r = 5 * 10 ^–11 м га тенг хатоликка йул куйиб, орбитал тезлиги V = 10 ⁶ м / с тезликда (10.10) тенгликдан  м / с хатоликни аниклаймиз, бу деярли ¸руšлик тезлигига тенг булиб, демак, электроннинг тезлиги умуман ноаник деган суз. Бундан куринадики, электрон координатани бундай аник хисоблаш мумкин эмас экан, уз навбатида координатанинг бундай ноаниклиги фазода электронинг "¸йилганлиги"ни айтиб туради ва микрообъект траекторияси туšрисидаги тушунча маъносини йукотади.

          Микрообъектларнинг фазода таксимоти эхтимоллик характерига эга ва нихоят, уларни тулкинлар назариясининг формулалари билан ¸зилади.

          Бу масалани, худди классик механикадаги Ньютон иккинчи конуни уйнаган рол каби, бу ерда Шредингер тенгламаси асосидаги квант механикаси ечади:

                                (10.11)

бу ерда Y - пси-функция (тулкин функцияси), унинг маъноси физика курсининг учинчи кисмида тушунтирилади, Е – микрообъектнинг тулик энергияси, U –унинг потенциал энергия. Бу тенгламанинг ечими, бирор эхтимоллик билан микрообъектнинг берилган фазонинг нуктасида булиши ва унинг энергияси хакида мулохаза юритиш имконини беради.