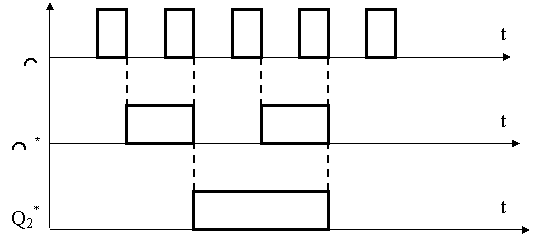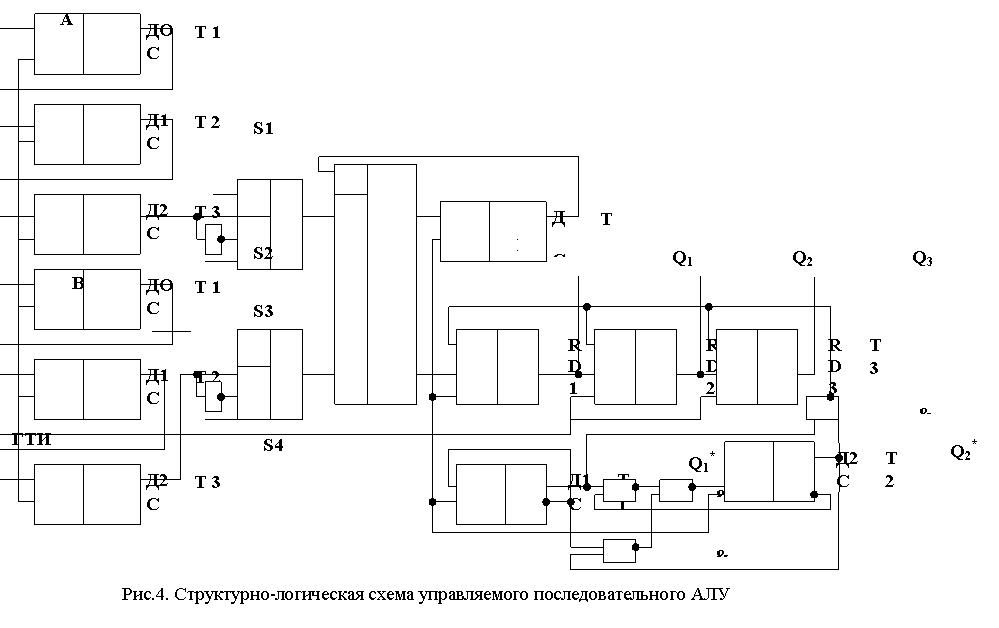УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Кафедра «Компьютерных
систем и технологий»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ
«ИНФОРМАЦИОННЫЕ ОСНОВЫ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ» часть 2
ТАШКЕНТ 2003
ВВЕДЕНИЕ
Как известно цифровые вычислительные машины, т.е. компьютеры, предназначены для обработки информации и являются частным, но наиболее распространенным видом цифровых автоматов. Функциональная и структурная организация цифровых вычислительных машин базируется на определенных принципах, составляющих методологическую основу цифровой вычислительной техники. В основе функциональной организации цифровых вычислительных машин лежит принцип программного управления и двоичного кодирования информации. Принцип программного управления может быть реализован системами с различной структурой, отличающимися функциональными свойствами и производительностью.
Для успешного изучения общих принципов обработки цифровой информации рационально, по возможности максимально, отвлечься от реального аппаратного обеспечения компьютера и рассматривать компьютер как некоторый абстрактный цифровой автомат, предназначенный для обработки информации, представленной в цифровой форме разработано данное методическое указание.
Настоящее методическое указание предназначено для студентов обучающихся по специальности «Информатика и информационные технологии» 5521900, написано в соответствии с учебной программой к трем практическим занятиям по курсу «Информационные основы вычислительных систем» часть 2.
1 . ОРГАНИЗАЦИЯ ОПЕРАЦИОННОГО УСТРОЙСТВА (ОУ)
1.1 Описание структуры ОУ
Цифровую вычислительную машину (ЦВМ) принято строить как композицию операционных устройств, на каждой из которых возлагается выполнение некоторой совокупности операций, необходимых для выполнения заданного списка команд. Операционное устройство выполняет операции из выбора F = { f1, f2,…, fk } над операндами из множества А с целью получения результатов, относящихся к множеству Z. Предполагается, что в каждый момент времени устройство способно выполнять единственную операцию fj. Акт работы операционного устройства состоит в вычислении { zi } = fj ( {al} ), где _{ al } и { zi } – подмножества множества A и Z . Функции операционного устройства определяются заданием множеств A, F и Z.
В функциональном отношении операционное устройство (рис.1.1) разделяется на две части : операционный автомат ( ОА ) и управляющий автомат ( УА ). ОА служит для хранения совокупности слов информации, выполнения набора микроопераций над ними и вычисления логических условий. УА обеспечивает требуемый порядок следования микроопераций на основе заданных микропрограмм.
Рис.1.1. Структура операционного устройства
Операнды из множества А представляются в виде слов, поступающих от ОА по входу А. В операционном автомате хранится совокупность слов B = { B1, B2,…, Bl }. Микрооперации распространяются на множество слов С = А U B. Слова, соответствующие результатам Z, представляются в множестве В и выводятся через выход Z. Микрооперации возбуждаются управляющими сигналами Y = { y1, y2,…, ym }. Управляющему сигналу yi соответствует микрооперация yi вида С ( t+1 ) = yi [ C (t) ], где t – автоматное время. Логические условия отображаются набором осведомительных сигналов X={x1,x2,…,xL},где xi=fi(C) иfi-булева функция, в которой могут использоваться и отношения числовых величин. Функция ОА определена, если заданы: 1) множества А и Z вводимых и выводимых слов; 2) множество В внутренних слов; 3) множество микроопераций Y, описывающих преобразование C = Y (C) ; 4) множество логических условий (осведомительных сигналов ) X = Ф ( С ).
Функция управляющий автомат (УА) определяется набором микропрограмм М, описывающих процесс выполнения операций F в терминах микроопераций Y = {y} и логических условий X = {x}. Наименование операций, которую должно выполнить устройство, на данном этапе работы задается управляющим словом по входу F. УА в соответствии со значением f слова F и осведомительных сигналов X генерирует последовательность управляющих сигналов Y, предписанную микропрограммой Mf.
Часть вычислительной машины, выполняющая операции по обработке данных, называется процессором. Процессор – это аппаратные средства, предназначенные для обработки команд и данных. Состоит процессор из арифметико - логического устройства, производящего обработку данных, блока управления операциями и блока управления командами. Блок управления операциями осуществляет преобразование кодов операций в последовательность электрических сигналов, инициирующих во всех устройствах и блоках ЭВМ операции по переработке и перемещению информации. Блок управления командами управляет потоком команд определяющих характер действий машины и операнды, над которыми эти действия выполняются.
Арифметико-логическое устройство служит для выполнения арифметических и логических операций над двоичными числами- операндами. Операндами могут быть двоичные числа с фиксированной и плавающей запятой, десятичные числа, команды или их отдельные поля, логические коды, алфавитно-цифровые поля.
Выполняемые в АЛУ операции можно разделить на следующие группы:
- операции двоичной арифметики над числами с фиксированной и плавающей запятой;
- операции десятичной арифметики;
- операции индексной арифметики ( операции над адресами команд);
- операции над логическими полями;
- операции над алфавитно-цифровыми полями.
1.2 Описание ОА с микропрограммным управлением
1.2.1. Структурная организация арифметических устройств
Арифметическое устройство (АУ) состоит из двух частей: ОА, используемого для хранения слов, выполнения микроопераций и вычисления (ЛУ) логическое устройство, и (УА) управляющий автомат, интерпретирующего совокупность микропрограмм.
Обычно для выполнения операций всех типов (операций двоичной арифметики, с плавающей запятой, десятичной арифметики, логических операций и операций над строками и символов) используется единственный ОА с набором микроопераций и ЛУ, достаточным для реализации заданного списка операций. Список операций, выполняемых АУ порождает большой список микроопераций, который наиболее экономично реализуется ОА с общими микрооперациями. В связи с этим в малых и средних операционных автоматах АУ строятся на основе принципа обобществления микроопераций. Для достижения высокого быстродействия в больших операционных автоматах АУ могут строиться по схеме с закреплением микроопераций.
1.2.2. Описание структуры ОА с закрепленными микрооперациями
Наибольшее быстродействие достигается при
использовании автоматов с закрепленными микрооперациями. Для сокращения объема
используемого оборудования один набор ОЭ и микроопераций используется для
выполнения всех операций, возложенных на АУ.
Для управления ОА с закрепленными микрооперациями наиболее целесообразно использовать автоматы с жесткой логикой, для которых характерны малые затраты времени на управление, что гарантирует возможность построения высокопроизводительных АУ
Пусть на некоторое время операционное устройство возлагается реализация заданного списка операций, алгоритмы выполнения которых описаны в виде структурно – функциональной микропрограммы (СФ -микропрограмма ). СФ – микропрограмма определяет, в частности, функцию операционного автомат (ОА), которая задается описанием внутренних слов, участвующих в выполнении, а также списком микроопераций и логических условий ( ЛУ ), необходимых для реализации операций. Чтобы построить ОА необходимо на основе описания его функций определить его структуру сначала на операционном уровне – в форме операционной схемы, а затем на логическом уровне – в форме логических схем. На операционном уровне структура ОА представляется фиксированной совокупностью ОЭ и связей между ними.
1.2.3. Синтез операционной схемы автомата
Рассмотрим один из подходов к структурному синтезу ОА, приводящий к структуре с закрепленными микрооперациями.
Для хранения совокупности слов, необходим набор регистров, число которых определяется количеством оригинальных внутренних слов и длины – длинами слов, указанными в описаниях. Примем, что регистрам присваиваются наименования, совпадающие с идентификаторами слов. По описаниям сегментов слов в регистрах выделяются под регистры, которым присваиваются наименования, указанные в описаниях. Из описаний входных и выходных слов определяется совокупность входных и выходных шин, по которым слова информации вводятся в ОУ и выводятся из него. Если в описании внутренних слов фигурирует слово С, которое одновременно описано в качестве входного или (и) выходного, то в ОА к регистру С должна подключаться входная или (и) выходная шина, связывающая этот регистр с другими устройствами ЦВМ. Полученный на основе СФ – микропрограммы набор регистров и шин, которые связаны со средой, внешнего по отношению к устройству, определяет скелет операционного автомата. Наборы микроопераций и логических условий в ОА с закрепленными микрооперациями распределяются между регистрами в соответствии с рис.1.2.
 |
{x1}
|
1 P1 n1 |
{y1}
{x2}
|
|
{y2}
{xN} . . . .
. . . . .
|
|
{yN}
 |
Рис.1.2. Структура операционного автомата с закрепленными микрооперациями
Здесь P1, P2,…, PN – регистры с длинами n1, n2,…, nN соответственно.
С регистрами связаны шины по которым выполняются микрооперации передачи Pi : = Pj, указанные в СФ – микропрограмме. Множество
микроопераций {y}, заданное в микропрограмме, распределяется между
регистрами. В результате этого определяются списки микроопераций {y1}, {y2},…, {yN}, реализуемые ОЭ P1, P2,…, PN соответственно. Аналогично распределяется между элементами
P1, P2,…, PN множество ЛУ {x}, определяя
списки ЛУ {x1}, {x2},…, {xN}, вычисляемых каждым ОЭ. Операционные элементы,
шины , управляющие и осведомительные сигналы образуют операционную схему ОА.
Микрооперации распределяются между регистрами следующим образом. Микрооперациям передачи вида y) Pi : = Pj соответствует управляемая шина, выходящая из регистра Pj и входящая в регистр Pi. С шиной связывается управляющий сигнал y, возбуждающий передачу. Микрооперация типа установки, инвертирования, сдвига, счета и сложения, записываемая в таком виде: y) Pi : = f ( Pj, Pk,…, Pl ), где Pj, Pk,…, Pl – регистры и f – некоторая функция, приписывается к регистру Pi. Считается, что функция f реализуется ОЭ, в пределах которого размещается регистр Pi. Этот факт отмечается путем подсоединения к регистру Pi входа, возбуждаемого управляющим сигналом y. К регистру Pi должны быть подключены шины, по которым на его вход поступают слова с регистров Pj, Pk,…, Pl.
Если в записи микрооперации используется некоторая не стандартная функция, то в операционную схему вводится ОЭ, реализующий данную функцию. Входы ОЭ соединяются с регистрами, на которых хранятся слова, выступающие в качестве аргументов функций, и выход ОЭ соединяется с регистром, на котором хранится или используется значения функции.
Логическое условие (ЛУ), выделяющее некоторое состояние слова (регистра ), изображается цепью, выходящей из регистра и представляющей значение соответствующего осведомительного сигнала. Если ЛУ связано с вычислением отношений между словами, хранимыми на двух регистрах, то в схему вводятся необходимые ОЭ (схема сравнения на равенство или на больше – меньше ).
1.2.4. Оптимальность структуры операционного автомата
Операционная и логическая структура ОА зависит от выбора алгоритмов выполнения операций и способов реализаций микрооперации и логических устройств. Отдельная операция может выполняться на основе достаточно широкого набора алгоритмов, каждый из которых порождает некоторый список слов, микроопераций и логическое условие (ЛУ) и соответствующий ему набор операционных элементов (ОЭ) и связей между ними. В свою очередь, каждая микрооперация может быть реализована в ОЭ несколькими способами. Таким образом, при проектировании устройств, в частности ОА, мы сталкиваемся с задачей выбора наиболее подходящего варианта среди весьма широкого числа вариантов структурной организации ОА.
При проектировании операционного устройства мы
ориентируемся на определенную систему запоминающих и логических элементов с
известным быстродействием: задержкой сигнала на элементе и временем
переключения сигнала. На основе этих данных вычисляются длительности
микроопераций каждого типа для различных способов их схемной реализации и
затраты времени на выработку управляющих сигналов 
у.
1.2.5. Операционные автоматы с общими микрооперациями
Операционное устройство может быть предназначено для выполнения обширного списка операций, для реализации которых необходим набор из сотен микроопераций и логических условий (ЛУ). Число различных микроопераций и ЛУ оказывается значительным не столько из-за разнообразия типов микроопераций и ЛУ, сколько из-за связи последних с различными обрабатываемыми словами информации. Действительно, наиболее широко используется микрооперации пяти основных типов: установки, передачи, инвертирования, сдвига и сложения, - каждая из которых может иметь несколько разновидностей (например сдвиг вправо и сдвиг влево). Если над словом, хранимым в устройстве, может выполняться в среднем 8-10 различных микроопераций, то при наличии десятков слов микропрограмма вводит список из сотен микроопераций. При построении ОА но основе принципа закрепления микроопераций по регистрам для реализации каждой микрооперации выделяется специальная логическая схема и в ОА появляется большое число идентичных схем, связанных с различными регистрами. Длина регистров в памяти ОА принимается равной длине самых длинных операндов, и в регистры загружаются как двоичные числа, так и числа с плавающей запятой и десятичные числа. При большом числе выполняемых операций количество оборудования в ОА с закрепленными микрооперациями становится очень большим и более рациональным выглядит принцип использования общих схем для выполнения микроопераций над словами, хранимыми в различных регистрах. Этот принцип реализуется в ОА с общими микрооперациями, которое строятся следующим образом.
ОА с общими микрооперациями разделяется в функциональном и структурном отношении на две части: запоминающую ЗЧ и комбинационную КЧ (рис. 1.3.). Запоминающая часть (память) ОА используется для хранения совокупности из N слов, описанных с СФ- микропрограмме в качестве внутренних, и состоит из регистров Р1, Р2, …, РN. Регистры имеют длины n1, n2, …, nN , равные длинам хранимых на них слов. В данном случае из ЗЧ выходят две шины Х (n) и Y (n), разрядность которых n=max (n1, n2, …, nN). Для подключения регистров памяти к шинам X и Y используются наборы управляющих сигналов {yxk}={y1x,y2x,…,yNx} и {ylY}={y1Y,y2Y,…,yNY}.Если сигналы ykX и ylY принимают значения 1, то X:=Pk и Y:=Pl. В каждый момент времени не более чем один сигнал в наборе может иметь значение 1, при этом остальные N-1 (или все N сигналов) имеют нулевые значения.
Состояние памяти ОА изменяется по входу AZ(n), к которому подключаются две управляемые шины A(n) и Z(n).Шина А является входной шиной операционного устройства (ОУ) и по ней поступают операнды, вступившие в операцию. Шина Z относится к внутренним шинам ОА и используется для
Z(n)
 |
|||
 |
|||
{yi} 
{xj}
КЧ
X(n)
Y(n)
{ykx} {ykY}
1 P1 n1
1 P2
n2
 |
ЗЧ
1 PN nN
yZ
{ykAZ}
yA
A(n)
 |
Рис.1.3. Структура операционного автомата с общими микрооперациями
занесения на регистры результатов микроопераций. Подключение шин A и Z к шине AZ производится управляющими сигналами yA и yZ соответственно, так что
AZ:= ЕСЛИ yA ТО А ИНАЧЕ
ЕСЛИ yZ ТО Z ИНАЧЕ 0.
Для управления передачами Pm:=AZ используется набор сигналов {ymAZ}={y1AZ,y2AZ,…,yNAZ}. Если ymAZ=1, то выполняется передача Pm:=AZ, причем остальные (N-1) или все N сигналов имеют нулевые значения. Таким образом, в каждый момент времени к шинам X, Y и Z могут быть подключены любые из N регистров Pk, Pl и Pm памяти ОА.
КЧ автомата реализует набор микропрограмм, достаточный для выполнения операций всех типов. Комбинационная часть (КЧ) автомата служит для выполнения набора микроопераций {yi} над словами X и (или) Y с целью вычисления слова Z, значение которого является функцией аргументов X и Y. Кроме того, в КЧ вычисляются значения набора ЛУ ( осведомительных сигналов) {xi}=Ф(Z), зависящих от слова Z. Если yi=1 , то в КЧ возбуждается микрооперация Z:= yi(X,Y), результат выполнения которого поступает на шину Z. Обычно в КЧ может одновременно выполняться несколько разнотипных микроопераций. Поскольку к шинам X, Y и Z может подключаться любой из регистров P1, P2,…, PN, то любая микрооперация из набора {yi} распространяется на любую совокупность слов, хранимых в памяти ОА.
Операторные элементы КЧ автомата могут иметь длину, меньшую длине самого длинного слова. Разрядность КЧ может соответствовать максимальной длине операндов, в результате чего количество оборудования в АУ увеличивается, но уменьшается время выполнения операций.
Для управления ОА с общими микрооперациями обычно используется УА с программируемой логикой. Экономичность автоматов с программируемой логикой и их относительно невысокое быстродействие хорошо согласуется с возможностями ОА с общими микрооперациями, в результате чего АУ становится однородным как в структурном отношении, так и в отношении скоростных характеристик.
1.2.6. Синтез операционных автоматов с общими микрооперациями
Для ОА с общими микрооперациями типична следующая форма преобразований:
Z:=g(f (h (X),Y)), (1)
где g- оператор сдвига; f- оператор, реализующий бинарные логические операции и сложение; h- оператор формирования обратных ( дополнительных) кодов; X, Y и Z- слова из множества слов В= {B1, B2,…, BN}, хранимых в памяти ОА, причем в качестве аргумента X или Y может использоваться константа. Преобразование (1) удобно задавать микрокомандами вида
nX, h, nY, f, g, nZ, (2)
где
nX, nY, nZ- микрооперации, задающие слова X, Y,Z из
множества слов В и константы X или Y; h, f и g. В данном классе ОА логические условия обычно
представляются в виде 
(Z),
где - булева функция,
аргументами которой являются двоичные переменные слова Z. Структура ОА
зависит в первую очередь от набора микроопераций и ЛУ, необходимого для
эффективной реализации заданного списка операций. Указанный набор обычно
определяется в процессе составления СФ- микропрограмм, микрокоманды которых
представляются в виде (2). При этом набор микроопераций и ЛУ формируется по
мере составления микропрограммы путем введения в него дополнительных
микроопераций и ЛУ, необходимость в которых порождается либо стремлением
эффективно запрограммировать очередное действие путем введения новой
микрооперации или ЛУ, уменьшающих время выполнения алгоритма.
Набор микроопераций и ЛУ можно определять на основе Ф- микропрограмм, описывающих алгоритмы операций, выполнение которых возлагается на синтезируемый автомат. При этом микрооперации и микрокоманды Ф- микропрограммы должны быть преобразованы к виду, соответствующему (2), с учетом ограничений налагаемых структурой ОА на совместимость микроопераций.
1.2.7. Сравнение характеристик управляющих автоматов с жесткой логикой и программируемой логикой
Одна и та же микропрограмма может быть реализована как
автоматом с жесткой логикой, так и с программируемой логикой. Различия в
принципах организации УА порождает различие в затратах оборудования,
необходимого для реализации одних и тех же функций, т. е. в стоимости
автоматов. Количество оборудования в автомате зависит в первую очередь от
сложности микропрограммы, интерпретируемой автоматом. В первом приближении
степень сложности микропрограммы можно характеризовать суммарным числом
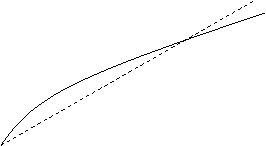
операторных и условных вершин. Качественный характер зависимости количества
оборудования С в автомате от сложности S
интерпретируемой микропрограммы рисунок 1.4. Количество оборудования в автомате
с жесткой логикой (1) возрастет почти пропорционально сложности
микропрограммы. Для автоматов с программируемой логикой типичны большие
удельные затраты оборудования 
при реализации
относительно несложных микропрограмм. При реализации сложных микропрограмм
удельные затраты оборудования уменьшаются.
C
 |
2
1
S0
S
Рис.1.4. Зависимость количества оборудования в автомате от сложности микропрограммы
Из рисунка 1.4. следует, что в области малых значений более экономичными являются автоматы с жесткой логикой (1) и в области больших значений – автоматы с программируемой логикой (2).
Автоматы с жесткой логикой имеют более высокое быстродействие, чем автоматы с программируемой логикой.
Управляющие автоматы с жесткой логикой и программируемой логикой отличаются по степени гибкости, определяющей возможность внесения изменений в закон функционирования автомата при изменении микропрограммы. Необходимость в изменении микропрограммы, весьма часто возникает из-за имеющих ошибок в процессе проектирования. Изменение микропрограммы приводит к необходимости перестройки структуры автомата, которая может затронуть большинство элементов и цепей, т. е. большей степени или полностью изменить конфигурацию автомата. Программируемая логика позволяет решить задачу перестройки структуры относительно просто – путем прошивки в ПЗУ дополнительных микрокоманд и изменения прошивки для отдельных микрокоманд, изменяемых при внесении исправлений в микропрограмму. Таким образом, можно считать что гибкостью обладают только автоматы с программируемой логикой.
1.2.7. Выполнение арифметических и логических операций над двоичными числами в цифровых устройствах
Важнейшей функцией ЦВМ является выполнение арифметических операций над числами. В связи с этим в ЦВМ выделяется в функциональном и, возможно, в структурном отношении операционное устройство, называемое арифметическим устройством ( АУ ). В состав операций, реализуемых АУ, кроме арифметических, вводятся логические операции, выполняемые над наборами логических значений, и могут вводиться операции над строками символьной информации ( операции с текстами ).
Функции АУ определяются форматами ( структурой ) обрабатываемых данных и списком реализуемых операций. Данные могут представляться в форме чисел, наборов логических значений и строк символьной информации.
1.2.8. Двоичная и десятичная арифметика
Двоичная арифметика. Выполнение операций двоичной
арифметики
Обычно числовые значения кодируются в двоичной системе счисления и изображаются в следующих формах : целыми числами и числами с плавающей запятой.
Целое число представляется n-разрядным двоичным кодом, старший разряд которого определяет знак числа :
1 2 n
|
+ - |
Цифровые разряды |
Принято знак «+» обозначать значением 0 и знак «-» - значением 1. Предполагается, что запятая фиксируется после n-го разряда. Диапазон представляемых значений определяется количеством разрядов и равен 0 < либо = l X l < либо = 2n-1. Обычно n = 8, 16, или 32.
В ЦВМ третьего поколения используется два формата целых чисел (рис.1.5 а) : короткий с n =16 и длинный с n =32. Максимальные значения, представляемые этими числами, равны соответственно 32.767 и 2.147.483.647.
В некоторых ЦВМ формат используется для изображения чисел с фиксированной запятой – правильных двоичных дробей. При этом запятая фиксируется перед старшим цифровым разрядом и числа представляют значения в диапазоне 0 < либо = l X l < либо = (1-2-(n-1) ), с предельной абсолютной погрешностью ^X = 2-( n-1 ) , которая может быть уменьшена в два раза за счет округления результатов операций. Целые числа и числа с фиксированной запятой эквивалентны в отношении операций сложения и вычитания, но различаются в отношении операций умножения и деления.
а)
0 1 15
|
+ - |
Цифровые разряды |
0 1 31
|
+ - |
Цифровые разряды |
б)
0 1 7 8 31
|
+ - |
характери стика |
Мантисса
|
0 1 7 8 63
|
+ - |
Характери стика |
Мантисса
|
в)
0 3 4 7 0 3 4 7
|
Цифра
|
Цифра
|
. . .
|
Цифра
|
Знак
|
д)
0 7 0 7 0 7 0 7
|
Символ |
Символ |
. . . |
Символ |
Символ |
г)
0 31
|
Логическое значение |
Рис.1.5. Форматы данных в ЦВМ третьего поколения ( IBM/360 ): а) целые двоичные числа; б) числа с плавающей запятой; в) десятичные числа; г) логические значения; д) строки символьной информации
Поскольку результат, как и операнды, должен представляться n-разрядным числом, то при умножении целых чисел в качестве цифровой части результата используются младшие ( n-1 ) разрядов 2 ( n-1 )-разрядного произведения.
Старшие разряды произведения могут быть отброшены только при наличии в них нулевых значений. Если произведение превышает предельное значение 2n-1( в старших разрядах произведения содержатся единицы ), то фиксируется переполнение разрядной сети АУ. При умножении чисел с фиксированной запятой результату присваивается значение ( n-1 ) старших разрядов произведения, а младшие разряды отбрасываются ( обычно с округлением старших ). Разница в операции деления состоит в следующем. При делении целых чисел не нулевой результат может быть получен, если делимое больше делителя, и деление не возможно только при нулевом значении делителя. При делении числа с фиксированной запятой результат должен быть правильной дробью, т. е. деление возможно только в случае, когда делитель больше делимого.
Если к ЦВМ формат (3) является единственной формой представления числовых значений, то целесообразно использовать числа с фиксированной запятой. При наличии в ЦВМ средств для обработки чисел с плавающей запятой более предпочтительным является использование целых чисел.
Над целыми двоичными числами (или двоичными дробями), выполняются операции сложения, вычитания, умножения и деления. В некоторых ЦВМ этот список расширяется операцией вычитания модулей чисел. Представление чисел в формате (3) принято называть двоичным. Необходимость в использовании двоичных чисел и операций над нами
(двоичной, или иначе стандартной арифметики ) обусловлено в первую очередь необходимостью обработки информации об адресах, используемых в программе. Операции такого рода крайне типичны для любой программы и поэтому двоичные числа и двоичная арифметика используется в подавляющем большинстве ЦВМ.
Обычно перевод чисел из десятичной системы счисления в двоичную и обратно выполняется программным способом с использованием стандартных программ. С целью сокращения затрат времени на обработку вводимой – выводимой информации операции перевода реализуются схемными средствами. Наиболее часто операции перевода распространяются только на целые числа.
Арифметика с плавающей запятой. Выполнение операций с плавающей запятой
Для научно технических расчетов необходимо представлять значения в широком диапазоне ( как целые так дробные ) и с достаточно большой точностью. Указанным требованиям отвечают числа с плавающей запятой :
1 2 m 1 2 p
|
+ - |
Мантисса |
+ - |
Порядок |
Рис.1.6.Формат представления данных с плавающей запятой
Число состоит из мантиссы (рис.1.6.), старший разряд которой определяет знак числа, и порядка со знаком. Значение мантиссы представляется двоичной дробью, т. е. запятая фиксируется перед старшим разрядом мантиссы, и порядок – целым числом ( обычно двоичным ). Порядок указывает действительное положение запятой в числе. Код ( 4 ) представляет значение в полулогарифмической форме : X = M * 2 p , где М и Р мантисса и двоичный порядок числа. Точность представления значения зависит от числа значащих цифр мантиссы.
Для повышения точности числа плавающей запятой представляются в нормализованной форме 0,5 < = М < 1 . Признаком нормализации числа является наличие единицы в старшем разряде мантиссе. В нормализованной форма могут быть записаны все числа из некоторого диапазона за исключением нуля. Нормализованные двоичные числа с плавающей запятой ( 4 ) представляют значения в диапазоне
0.5 * 2-Pmax < = l X l < = ( 1 -2m-1)2Pmax , (3)
где Pmax = 2p-1-1 – максимальное значение порядка с предельной относительной погрешностью
бX = (2-(m-1)2P) / ( 0.5 * 2P) = 2-m ( 4)
Отсюда видно, что диапазон значений зависит в основном от числа разрядов порядка, а точность – от числа разрядов мантиссы. Ненормализованные числа имеют погрешность, превышающую ( 4 ), но за счет потери значимости диапазон представляемых значений расширяется до нуля включительно.
С целью расширения диапазона представляемых значений при фиксированной длине ( m + p ) числа в качестве основания выбираются значение d = 2k (обычно k = 3 или 4 ). При этом порядок становится d – ичным и число представляет значение X = MdP . Нормализованная мантисса d – ичного числа с плавающей запятой имеет значение, лежащее в диапазоне 1/d < = M < 1. Признаком нормализации такого числа является наличие хотя бы одной единицы в k старших разрядах мантиссы. Переход от двоичного основания к основанию 2k увеличивает предельную относительную погрешность в 2k раз ( в 8 – 16 раз ), но диапазон представляемых значений расширяется в каждую сторону в ( ( 2k)2m-1-1)/(22(m-1)-1)=2(k-1) (2(m-1)-1) раз по сравнению с (4.1). Так, при m=7 и k=4 диапазон значений расширяется примерно в 1063 раз.
В ЦВМ третьего поколения числа с плавающей запятой имеют основание 16 и представляются в двух форматах: коротком и длинном (рис 3,б). часть числа, содержащая модуль и знак порядка, называется характеристикой. Указанные числа позволяют кодировать значения, лежащие в диапазоне 10-75<=lXl<=1075 с предельной относительной погрешностью, соответственно равной 1,5*10-6 и 10-16.
Над числами с плавающей запятой выполняются четыре арифметические операции: сложение, вычитание, умножение и деление. В некоторых ЦВМ этот список расширяется за счет введения операции вычитания модулей.
Алгебраическое сложение чисел, представленных в форме с плавающей запятой
Нужно подчеркнуть, что при выполнении любых арифметических действий над операндами, представленными в форме с плавающей запятой, операции, выполняемые над мантиссами и порядками (или характеристиками) этих чисел, различны. Поэтому перед началом любой арифметической процедуры каждый из операндов "расчленяется": порядок (характеристика) отделяется от мантиссы операнда, что-бы можно было над ними выполнять необходимые отдельные процедуры. После выполнения конкретного арифметического действия и обязательной процедуры нормализации результата, его порядок или характеристика и мантисса "упаковываются" в обычный формат с плавающей запятой.
В случае алгебраического сложения порядки операндов обязательно должны быть одинаковыми. Поэтому в начале процедуры сложения и вычитания чисел производится, при необходимости, выравнивание характеристик операндов. Для этого мантисса операнда с меньшей характеристикой сдвигается по разрядной сетке вправо с прибавление единицы к его характеристике при каждом сдвиге на один разряд. Эта процедура продолжается до тех пор пока характеристики обоих операндов не станут равными.
Полученная таким образом характеристика, одинаковая для обоих операндов, присваивается, как предварительная, результату операции. Далее осуществляется сложение или вычитание мантисс по правилам, аналогичным для чисел с фиксированной запятой, в частности мантисса одного из операндов преобразуется в дополнительный код для того чтобы процедуру вычитания свести к сложению. Если ответ получился в дополнительном коде, то его преобразуют в прямой, т.к. мантисса числа с плавающей запятой - это всегда модуль числа. Далее, при необходимости, выполняется нормализация и округление ответа. В процессе нормализации мантисса поразрядно сдвигается влево или вправо. При сдвиге влево на каждый разряд вычитается единица из характеристики, предварительно присвоенной ответу. При каждом сдвиге вправо - к ней прибавляется единица. Отметим, что сдвиг мантиссы вправо необходим в тех случаях, когда при сложении мантисс произошло переполнение разрядной сетки. В процессе этих последних операций определяются окончательные значения характеристики и мантиссы ответа.
Таким образом, операция нормализации числа состоит из проверки выполнения условия
0,12 £ m < 1
и сдвига изображения мантиссы в ту или иную сторону с соответствующей коррекцией характеристики. Сдвиги могут осуществляться на один и более разрядов в левую сторону, или на один разряд в правую сторону в пределах разрядной сетки машины.
Нарушение нормализации может быть двух видов: нарушение справа, т.е. когда величина результата больше или равна 1, и слева, когда величина результата оказывается меньше 0,12.
Надо отметить, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие
0 £ r £ rmax ,
где rmax = l + pmax .
Рассмотрим пример:
Имеем 8-разрядную мантиссу и 6-разрядный порядок, смещение равно 10002. Сложим 2 числа с мантиссами m1 = 0,10100000, m2 = 0,10000000 и с характеристиками r1 = 001011, r2 = 001010. Т.к. порядки разные надо их выравнивать: r1 - r2 = 000001, значит надо сдвинуть m2 на 1 разряд вправо, а к r2 прибавить 1. После преобразований получим:
® m2 = 0,01000000, r2 = 001010 + 000001 = 001011. Складываем мантиссы, получаем: m = m1 + m2 = 0,10100000 + 0,01000000 = 0,11100000, r = 001011.
Нормализация ответа не нужна.
Умножение двоичных чисел
Методы умножения двоичных чисел
Применительно к двоичной системе счисления наиболее известны следующие основные способы выполнения операции умножения:
1) умножение начиная с младших разрядов множителя:
1101 множимое
x 1101 множитель
1101
+ 0000
1101 частные произведения
1101
10101001 произведение
2) умножение начиная со старших разрядов множителя:
1101 множимое
x 1101 множитель
1101
+ 1101
0000
1101
10101001 произведение
В обоих случаях операция умножения состоит из ряда последовательных операций сложения частных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частных произведений добавляется множимое с соответствующим сдвигом (влево или вправо), если в разряде множителя - ноль, то множимое не прибавляется, но учитывается, что в последующей операции анализа разряда множителя надо сделать дополнительный сдвиг. Если, например, в следующем после нулевого разряда множителя встречается 1, то множимое сдвигается на 2 разряда и добавляется к сумме частных произведений. Сколько подряд будет встречаться 0 столько дополнительных сдвигов множимого надо будет сделать когда в очередном разряде встретится 1, а затем добавлять множимое к сумме частных произведений.
Таким образом, кроме операции сложения чисел для получения произведения необходима операция сдвига числа.
Умножение чисел, представленных в форме с фиксированной запятой
Рассмотрим один из возможных вариантов алгоритма умножения, когда операнды представлены в прямом коде. Перед выполнением самой процедуры умножения по обычным арифметическим правилам умножения определяется и запоминается знак произведения. Далее оба операнда представляются в прямом коде и выполняется сама процедура умножения одним из двух ранее описанных методов с обязательным контролем переполнения разрядной сетки. Если знак произведения отрицательный, то ответ, при необходимости, представляется в дополнительном коде.
Умножение чисел представленных в форме с фиксированной запятой можно организовать не только на двоичном сумматоре прямого кода, но и на двоичных сумматорах обратного или дополнительного кода. В этом случае произведение дополнительных или обратных кодов сомножителей равно дополнительному или обратному коду соответственно только в случае положительного множителя. Если же множитель отрицательный, то производится коррекция результата: в первом случае прибавляется поправка [`A]= а во втором случае прибавляются поправки [A] и [A]об×2-n .
Рассмотрим примеры:
1) умножим 5 на 2. 510 = 0. 01012, 210 = 0. 00102 Знак результата положительный.
0.0101
x 0.0010
0000
+ 0101
0.01010 = 1010
2) умножим 5 на 3
0.0101
x 0.0011
0101
+ 0101
0.1111 = 1510
Умножение чисел, представленных в форме с плавающей запятой
При операции умножения чисел, представленных в форме с плавающей запятой их мантиссы умножаются, как числа с фиксированной запятой, а порядки складываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально складываются характеристики чисел, то умножение выполняется по следующей формуле:
A1 x A2 = m1×2
x m2×2
=
(m1 x m2)×2
,
где r1 + r2 - l - характеристика результата.Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняются процедуры нормализации и округления ответа.
Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие
0 £ r £ rmax ,
где rmax = l + pmax .
Рассмотрим пример:
умножим числа с мантиссами m1 = 0,101 (5),
m2 = 0,1 (2) и характеристиками
r1 = 1011, r2 = 1010, l = 1000, p1
= 3, p2 = 2, p = p1 + p2
= 5, r = r1 + r2 - l =
001011 + 001010 - 001000 = 001101 = 1310 m = m1 x m2
= 0,01010, необходимо нормализовать ответ. Для этого в данном случае сдвигаем
мантиссу влево на 1 разряд и вычитаем 1 из p, получаем p = 4. В
итоге имеем m = 0,10102, p = 410 = 01002,
r = 1210 = 11002.
Ускорение операции умножения
По времени выполнения операция умножения относится к длинным операциям. Затраты времени на умножение двух чисел в прямом коде можно оценить следующей формулой (для случая последовательного анализа разрядов множителя):
,
где tсдв - время выполнения сдвига числа на один разряд; tсл - время суммирования на сумматоре; pi - вероятность появления единицы в разрядах множителя; n - количество разрядов множителя.
Существуют несколько методов ускорения процедуры умножения: анализ двух разрядов множителя одновременно, анализ произвольного количества разрядов множителя, умножение в системе счисления с основанием q=2k и матричные методы умножения.
Рассмотрим первый спосо, ускорения умножения как наиболее наглядный и распространенный для целых чисел, представленных в прямом коде. В связи с тем, что в этом случае в процессе выполнения операции умножения на каждом цикле операции анализируется сразу два разряда множителя, то таких циклов понадобится n/2, где n - длина разрядной сетки множителя без учета знакового разряда. Это число циклов записывается в некоторый счетчик SС. При обнулении содержимого счетчика SС процедура умножения останавливается. Обычно анализируются два младших разряда множителя, поЭтому в конце каждого цикла производится одновременный сдвиг на два разряда вправо изображения суммы частных произведений (Р) и множителя. Причем, таким образом, чтобы при каждом таком сдвиге очередной младший разряд числа Р попадал в старший разряд мантиссы множителя. Обозначим эту процедуру условно как ПС. Очевидно, что в таком случае произведение будет сформировано в разрядной сетке первоначально отведенной для множителя.
Если множимое X и множитель Y, а его два очередных младших разряда (y1y0), то в зависимости от результата анализа этих разрядов предусматриваются следующие действия.
Если áy1y0ñ = 00, то выполняются только процедуры: ПС и SС = SС-1.
Если áy1y0ñ = 01, то выполняются процедуры: Р = P + X, ПС и SС = SС-1.
Если áy1y0ñ = 10, то выполняются процедуры: сдвиг множимого влево на 1 разряд, т.е. умножение его на два, P = P + X, ПС и SС = SС-1.
Если áy1y0ñ = 11, то выполняются три раза P = P + X и ПС, SС = SС-1.
Когда SС = 0 - операция умножения заканчивается.
Как обычно перед началом самой процедуры умножения определяется знак произведения, проверяются на 0 X и Y, если кто-нибудь из них равен 0, то произведению сразу присваивается нулевое значение.
Рассмотрим пример ускоренного умножения 310 на 7810, т.е. когда X = 3, а Y = 78. Если n = 10, то X = 0000000112, Y = 00010011102, а SС = 5.
|
|
512 256 |
128 64 |
32 16 |
8 4 |
2 1 |
|
|
X |
00 |
00 |
00 |
00 |
11 |
множимое |
|
Y |
00 |
01 |
00 |
11 |
10 |
множитель |
|
R |
00 |
11 |
10 |
10 |
10 |
ответ = 234 |
В некотором регистре P будем формировать частные произведения.1) Анализ 2-х младших разрядов Y. áy1y0ñ = 10. Сдвинуть X на 1 разряд влево и прибавить к P.
P 00 00 00 00 00
+X 00 00 00 01 10
P 00 00 00 01 10 ® сдвиг на 2 разряда P и Y
P 00 00 00 00 01 ---- 10 00 01 00 11 Y
2) áy1y0ñ = 11, _ 3 раза прибавляем X к P
P 00 00 00 00 01
+X 00 00 00 00 11
P 00 00 00 01 00
+X 00 00 00 00 11
P 00 00 00 01 11
+X 00 00 00 00 11
P 00 00 00 10 10 ® сдвиг на 2 разряда P и Y
P 00 00 00 00 10 ---- 10 10 00 01 00 Y
3) áy1y0ñ = 00, ® сдвиг на 2 разряда P и Y
P 00 00 00 00 00 --- 10 10 10 00 01 Y
4) áy1y0ñ = 01
P 00 00 00 00 00
+X 00 00 00 00 11
P 00 00 00 00 11 ® сдвиг на 2 разряда P и Y
P 00 00 00 00 00 --- 11 10 10 10 00 Y
5) áy1y0ñ = 00, ® сдвиг на 2 разряда P и Y
P 00 00 00 00 00 --- 00 11 10 10 10 Y = 23410
Деление двоичных чисел
Деление двоичных чисел, представленных в форме с
с фиксированной запятой
Деление двоичных чисел во многом аналогично делению десятичных чисел.
В универсальных вычислительных машинах, как правило, реализуется "школьный" алгоритм деления чисел. "Школьный" алгоритм деления заключается в том, что делитель на каждом шаге вычитается из делимого столько раз (начиная со старших разрядов), сколько это возможно для получения наименьшего положительного остатка. Тогда в очередной разряд частного записывается цифра, равная числу делителей, содержащихся в делимом на данном шаге. Иначе говоря, при делении операцию вычитания повторяют до тех пор, пока уменьшаемое не станет меньше вычитаемого. Число этих повторений показывает, сколько раз вычитаемое укладывается в уменьшаемом.
Например:
разделим число 35 на 7 :
1) 35 - 7 = 28, 2) 28 - 7 = 21, 3) 21 - 7 = 14, 4) 14 - 7 = 7, 5) 7 - 7 = 0.
Ответ равен 5, т.к. процедура вычитания была повторена 5 раз.
Рассмотрим еще один пример:
разделим 204(10) на 12(10), т.е. 11001100(2):1100(2):
делимое 11001100 | 1100 - делитель
делитель 1100 | 10001
остаток 00001
- 0
11
- 0
110
- 0
1100
- 1100
0000
Двоичное, как и десятичное деление, начинается с анализа делимого (11001100) и делителя (1100). Сразу же обнаруживается, что делитель укладывается в 1100, а поэтому записывается 1 в старший разряд поля частного. Умножается делитель на 1 и вычитается из 1100, разность равна 0. Объединяется 0 остатка со значением следующего разряда делимого, равным 1. Поскольку делитель (1100) 0 раз укладывается в 1, записываем 0 в следующий по старшинству разряд поля частного, а число 1 объединяется со следующим разрядом делимого и т.д. до тех пор, пока делимое не оказывается исчерпанным.
Конечно компьютер не может строить догадок относительно того, сколько раз делитель укладывается в том или ином числе, поэтому весь процесс деления сводится к операциям вычитания и сдвига. Продемонстрируем на том же примере, но сначала делитель (1100) представим в дополнительном коде, что позволит ограничиться сложением во всех случаях, когда нужно выполнять сложение или вычитание: 1100пр = 1. 0100д. Частное формируется в некотором регистре С, незаполненные разряды которого будем обозначать через Х.
Начинаем вычитать делитель из делимого. Если остаток получается положительным, то в разряд частного записывается 1, в противном случае - 0.
0. 11001100 делимое 204
+ 1. 01000000 делитель 12
0. 00001100 первый остаток
Первый (старший) бит частного равен 1, т.к. остаток получился положительным: С = 1ХХХХ. Далее сдвигается первый остаток на один разряд влево и из него вычитывается делитель:
0. 00011000
+ 1. 01000000
1. 01011000 второй остаток
Остаток отрицательный, поэтому в следующий разряд частного записывается 0, С = 10ХХХ. Кроме того необходимо биты делителя вернуть обратно первому остатку, т.е. сложить делитель (в прямом коде) и второй остаток:
1. 01011000
+ 0. 11000000
0. 00011000 сдвинутый первый остаток.
Далее еще раз сдвигается сдвинутый первый остаток на один разряд влево и вычитается из него делитель:
0. 00110000
+ 1. 01000000
1. 01110000 третий остаток
Третий остаток отрицательный, значит следующий (третий) разряд частного равен 0, С = 100ХХ. Поэтому возвращаем делитель третьему остатку,
1. 01110000
+ 0. 11000000
0. 00110000 дважды сдвинутый первый остаток
Сдвигаем дважды сдвинутый первый остаток на один разряд влево и вычитаем делитель:
0. 01100000
1. 01000000
1. 10100000 четвертый остаток
Четвертый остаток опять отрицательный, поэтому С = 1000Х. Прибавляем делитель к четвертому остатку, результат сдвигаем на один разряд влево, а затем вновь вычитаем делитель:
0. 1100000 первый остаток после четвертого сдвига
+ 1. 0100000
0. 0000000 пятый остаток
Остаток положительный, значит С = 10001 = 17(10) - это и есть ответ.
Такой метод деления называется делением с восстановлением остатка.
Деление чисел, представленных в форме с фиксированной запятой можно также осуществить на двоичных сумматорах обратного и дополнительного кода.
Перед выполнением самой процедуры деления чисел в формате с фиксированной запятой определяется и запоминается знак частного. Далее оба операнда представляются в прямом коде, а делитель еще и в дополнительном для того, чтобы вычитание делителя заменить сложением, и выполняется сама процедура деления по описанному выше методу с обязательным контролем переполнения разрядной сетки. Если знак частного отрицательный, то ответ, при необходимости, представляется в дополнительном коде.
Например: разделим 35 на 5. 3510 = 0.1000112, 510
= 1012, 5д = 1.011д
(в регистре С, как и в предыдущем примере, формируется частное):
0.100011
+ 1.011000
1.111011 С = 0 восстанавливаем остаток до делимого.
+ 0.101000
0.100011 сдвигаем влево остаток.
1.00011
+ 1.01100
0.01111 С = 01, сдвигаем влево остаток.
0.1111
+ 1.0110
0.0101 С = 011, сдвигаем остаток.
0.101
+ 1.011
0.000 С = 0111 = 710
Вычитание делимого продолжают столько раз, сколько разрядов отведено для частного.
Метод деления без восстановления остатка. Как уже отмечалось, основой выполнения деления является операция вычитания с целью получения остатка, знак которого определяет цифру частного. Алгоритм выполнения деления имеет следующий вид:
X - Y = a0,
где a0 - это остаток. Если а0 ³ 0, то С = 1, если а0 < 0, то С = 0. Для определения следующей цифры частного необходимо выполнить следующие действия: при а0 ³ 0 надо 2а0 - Y = a1, а при а0 < 0 надо 2а0 + Y = a1. Как видно в данном случае знак остатка определяет не только очередную цифру частного, но и характер следующей процедуры: прибавления делителя к сдвинутому остатку, если этот остаток меньше 0, и вычитание делителя из сдвинутого остатка, если остаток больше или равен 0. Этот метод деления получил название деления без восстановления остатка.
Рассмотрим пример:
разделим 3510 на 510, т.е. 0.1000112 на 1012
0.100011
+ 1. 011000 дополнительный код 5 (т.е. вычитание 5)
1.111011 a0<0, С = 0
2a0 1.110110
+ 0.101000 5 в прямом коде
0.011110 a1>0, С = 01
2a1 0.111100
+ 1.011000 5 в дополнительном коде (т.е. вычитание 5)
0.010100 a2>0, С = 011
2a2 0.101000
+ 1.011000
0.000000 a3 = 0, С = 0111 = 710
Деление двоичных чисел, представленных в форме с плавающей запятой
При операции деления чисел, представленных в форме с плавающей запятой их мантиссы делятся, как числа с фиксированной запятой, а порядки вычитываются. В обоих случаях проверка на переполнение обязательна. Но, т.к. реально вычитываются характеристики чисел, то деление выполняется по следующей формуле:
A1 : A2 = m1×2 : m2×2 = (m1 : m2)×2
.
Знак ответа определяется обычным образом. Если ответ получился ненормализованный, то выполняется процедура нормализации и округления ответа.
Т.к. мантиссы операндов нормализованы, то возможны случаи, когда
|mA| ³ |mB|; |mA| < |mB|.
В первом случае перед началом деления надо вычесть делитель из делимого и в
целую часть мантиссы частного записать 1. Затем продолжать делить числа обычным
методом. После получения частного очевидно, что оно не будет нормализованным.
Значит надо нормализовать частное, т.е. в данном случае сдвинуть его на 1
разряд вправо, а к порядку частного добавить 1.
Напомним, что при реализации алгоритмов математических операций в формате с плавающей запятой каждый раз, когда осуществляется та или иная процедура, затрагивающая характеристики операндов или результата, производится контроль над переполнением и исчезновением порядка, т.е. контролируется условие
0 £ r £ rmax ,
где rmax = l + pmax .
Рассмотрим пример:
A = 10 = 0,1010, pA = 4, B = 2
= 0,1, pB = 2. p = pA - pB = 2. mA
= 0.1010,
mB = 0.1 , (mB)l = 1.1000. |mA| > |mB|. При первом
вычитании mB из mA 1 записываем в целую часть частного:
0.1010
+ 1.1000
а0 0.0010 С = 1,XX, далее, будем делить методом деления без восстановления остатка.
2а0 0.0100
+ 1.1000
а1 1.1100 а1<0 С = 1,0
2a1 1.1000
+ 0.1000
0.0000 a2 = 0 С = 1,01, сдвигаем вправо С = 0,101, p = p + 1 = 3.
Десятичная арифметика. Выполнение операций с десятичной арифметики
При решении задач обработки данных (экономических задач) на каждое вводимое- выводимое значение приходится относительно небольшое количество операций, выполняемых процессором. Поэтому преобразование данных в двоичную систему счисления и результатов в десятичную систему счисления потребляет значительную долю ресурсов процессора. С целью повышения эффективности ЦВМ при решении подобных задач в АУ вводятся средства обработки данных, представляемых в десятичной системе счисления, иначе говоря, средства десятичной арифметики. Десятичные числа представляются в форме целых чисел и кодируются в двоично– десятичной системе счисления. При этом десятичные цифры 0,1,…,9 изображаются двоичной тетрадой 0000, 0001,…, 1001. Комбинации 1010, 1011,…, 1111 не используются, и их появление в записи числа свидетельствует об ошибке, которая могла быть внесена в процессе ввода, хранения или обработки значения.
Например, в ЦВМ « Минск – 32» [4] десятичные числа записываются в следующем формате:
1 2 5 6 9 30 33 34 37
|
+ - |
D1 |
D2 |
………
|
D8 |
D9 |
Рис 1.7. Пример формата десятичных чисел
Формат (5) обеспечивает представление целочисленных значений в диапазоне 0<= lXl <= 999.999.999. Нецелочисленные значения изображаются в машине с использованием масштабирования.
Установлено, что при решении задач обработки данных для представления некоторых классов значений требуется 3-4 десятичные цифры, и в то же время значения из других классов требуют наличия в числе нескольких десятков цифр. При изображении коротких чисел, содержащих несколько цифр, большинство старших разрядов слова (5) оказываются пустыми, в результате чего память ЦВМ используется не эффективно и увеличивается затраты времени на обработку. Уменьшение длины десятичного числа затрудняет программирование и увеличивает время выполнения задач, в которых появляются многоразрядные значения. Исходя из этого, в ЦВМ третьего поколения для кодирования десятичных чисел используются слова переменного формата (рис. 1.5,в). Десятичное число может содержать от 1 до 31 цифры. Длина числа указывается в команде. В данном случае знак представляется отдельной тетрадой: плюс кодируется наборами 1010, 1100, 1110, и минус _ наборами 1011, 1101, 1111.
Логические операции. Выполнение логических операций
Наряду с переменными, характеризуемыми числовыми значениями, используются логические (булевы) переменные, принимающие значения « истина» и «ложь», которые кодируются двоичными значениями 1 и 0. Двоичные переменные объединяются в наборы, количество элементов в которых равно длине слова ЦВМ. Наборы логических значений обрабатываются совместно, т. е. логические операции распространяются одновременно на все логические значения, объединенные в один набор. В ЦВМ третьего поколения основной формой представления наборов логических значений являются 32 – разрядные слова (рис 1.5,г)
Над наборами логических значений выполняются операции конъюнкции, дизъюнкции и сравнения (отрицания равнозначности). Поскольку в ЦВМ информация различается по типам не способом кодирования, а способом ее использования, то указанные логические операции распространяются и на слова, представляющие двоичные числа и числа с плавающей запятой.
В дополнение к операциям булевой алгебры в список логических операций вводится операции специальной арифметики: сдвиг и нормализация слова Операция сдвига состоит в изменении положения разрядов слова по отношению к исходному слову путем сдвига двоичных переменных в заданном направлении на заданное число разрядов. В ЦВМ принято реализовать операции сдвига двух типов: арифметический и логический сдвиг. При арифметическом сдвиге в операцию сдвига вступают все разряды, кроме знакового, при логическом сдвиге - все разряды, включая знаковый. Операция нормализации сводится к сдвигу нулевого слова влево до появления единицы в старшем цифровом разряде. При этом операция формирует два значения: нормализованное слово и слово, определяющее количество выполненных сдвигов.
2.ОБЩИЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ПРИ СИНТЕЗЕ АЛУ
Часть вычислительной машины, выполняющая операции по обработке данных, называется процессором. Процессор-это аппаратные средства, предназначенные для обработки команд и данных. Состоит процессор из арифметико-логического устройства, производящего обработку данных, блока управления операциями и блока управления командами. Блок управления операциями осуществляет преобразование кодов операций в последовательность электрических сигналов, инициирующих во всех устройствах и блоках ЭВМ операции по переработке и перемещению информации. Блок управления командами управляет потоком команд определяющих характер действий машины и операнды, над которыми эти действия выполняются.
Арифметико-логическое устройство служит для выполнения арифметических и логических операций над двоичными числами - операндами. Операндами могут быть двоичные числа с фиксированной и плавающей запятой, десятичные числа, команды или их отдельные поля, логические коды, алфавитно-цифровые поля.
Рассмотрим функциональную схему АЛУ на примере простейших операций - арифметических операций над числами с фиксированной запятой и логическими кодами. Структура АЛУ будет понятна, если предварительно рассмотреть задачу сложения двух двоичных чисел. Например, необходимо сложить два числа: 00111 и 01101
первое число 00111
+
второе число 01101
перенос 1111
результат 10100
Операция сложения выполняется последовательно, начиная с младшего разряда и завершается сложением старших разрядов. Таким образом, при сложении двух чисел сумматор должен начинать сложение, начиная с младшего разряда, при этом должна формироваться сумма и перенес в следующий разряд. При сложении всех последующих разрядов должен учитываться перенос из предыдущего разряда. Для выполнения операции сложения в i-ом разряде (i=O.n=1) при сложении n- разрядных чисел может быть использована комбинационная схема с тремя входами и двумя выходами. В табл.2.1 указаны возможные значения сигналов на входе одноразрядного сумматора и соответствующие им значения выходных сигналов - суммы Сi и переноса в следующий разряд Pi.
Табл.2.1.
|
Входы |
Выходы |
|||
|
ai |
bi |
Pi+1 |
Рi |
Сi |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Ниже, на рис.2.1. приведены карты Карно и булевы функции в нормальной дизъюнктивной форме (НДФ), которые описывают структуру одноразрядного сумматора.
ai bi
|
|
|
1 |
|
|
|
1 |
1 |
1 |
Pi+1
ai
bi
|
|
1 |
|
1 |
|
1 |
|
1 |
|
Pi+1
Pi = aibi V Pi+1ai V biPi+1 (1)
Сi = aibiPi+1 V aibiPi+1 V aib i Pi+1 V ai biPi+1 (2)
Рис.2.1. Карты Карно и НДФ для функций Pi и Ci
Преобразуем выражение (2) к следующему виду:
Сi=Pi+1(aibiVaibi) V Pi+1(aibi V aibi) = Pi+1(ai bi V aib i) V Pi+1(aibi V ai bi)
= Pi+1 V (ai V bi) (3)
 |
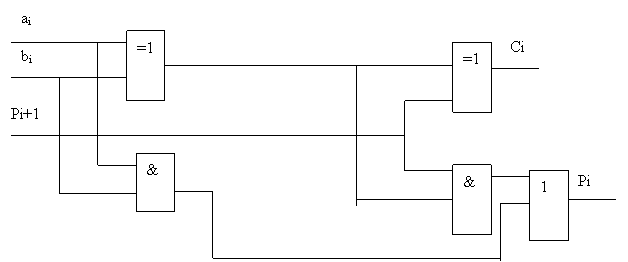На основании выражений (1) и (3) на рис.2.2. построена схема одного разряда сумматора.
Рис.2.2. Схема i-го разряда сумматора
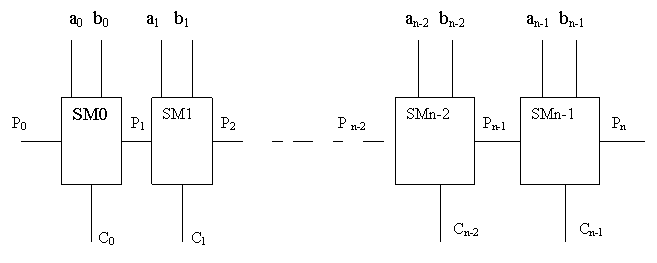
На основе одноразрядных сумматоров могут быть
построены сумматоры n-разрядных чисел, схема которого приведена на рис.2.3.
Рис. 2.3. Схема n- разрядного параллельного сумматора.
Для его построения необходимо n-отдельных сумматоров, выходы Сi (i=0,n-1) служат для формирования сигналов сумм, а выходы сигналов переноса соединены со входами переноса следующего разряда. Предложенная на рис.2.3 схема носит название схемы со сквозным переносом. Время выполнения операции суммирования в такой схеме определяется как:
t =tc+(n-1)tp (4)
где – tc - время выполнения операция суммирования в одном разряде сумматора;
tp - время формирования сигнала переноса в одном разряде.
Для ускорения суммирования необходимо сократить вторую составляющую выражения (4), что может быть сделано с помощью специальной схемы-генератора ускоренного переноса. Представим выражение для Рi в следующем виде:
Pi = aibi V (ai V bi ) P i+1 (5)
Введем обозначение aibi = g i; ai V bi = q i , тогда
Pi == g i V = q i P i+1.
Цель этих преобразований в получении системы булевых функций, которые бы позволяли построить схему, формирующую сигнал переноса параллельно в каждом разряде.
Для четырехразрядного сумматора можно записать следующую систему функций:
P3=g3Vq3P4
P2=g2Vq2P3=g2Vq2(g3Vq3P4)=g2Vg3q2Vq2q3P4 (6)
P1=g1Vq1P2=g1Vq1g2Vq1q 2g3Vq1q2q3P4
P0=g0 Vq0g1 Vq0q1q2g3 Vq0q1q2q3P4
На рис.2.4. приведена схема четырехразрядного параллельного сумматора со схемой ускоренного переноса, построенной по формулам (6). Время выполнения операции суммирования в n-разрядном сумматоре с ускоренным переносом составляет: tS =tc+tp
Объем оборудования такого сумматора быстро растет с увеличением числа разрядов, поэтому на практике находят применение схемы сочетающие сквозной и ускоренный перенос. Все множество n-разрядов разбивается на группы по r- разрядов, в пределах группы используется схема ускоренного переноса, а между группами сквозной перенос.
Используя параллельный 7-разрядный сумматор, можно построит. устройство, способное выполнять некоторые арифметические операции, такие как сложения кодов, вычитание, увеличение одного числа на 1 и т.д.
2.1.Использование сумматора для выполнения арифметических операций
Рассмотрим выполнение операции вычитания. В большинстве ЭВМ находит применение путь, при котором числа, участвующие в операции, подвергаются преобразованию в обратный или дополнительный код. Для представления числа в обратном коде необходимо произвести поразрядную инверсию, например число 01100 в обратном коде выглядит как 10011. Для преобразования двоичного числа в дополнительный код необходимо к числу, представленному в обратном коде в младший разряд добавить единицу 10011+00001=10100. Тогда для выполнения операции вычитания в сумматоре необходимо вычитаемое представить в обратном или дополнительном коде. Например, необходимо произвести вычитание из 10011 числа 01010. При выполнении этой операции обычным путем результат будет следующим:
_ 10011
01010
01001
Если второе число представить в обратном и дополнительном кодах, то получим следующее:
+ 10011 + 10011
10101
10110
1¬01000 1¬01001
00001
01001
Таким образом, использование обратного кода требует осуществления переноса единицы из старшего разряда в младший, тогда как использование дополнительного кода для вычитаемого таких действий не требует, перенос в старший разряд должен игнорироваться (во внимание не приниматься).
 |
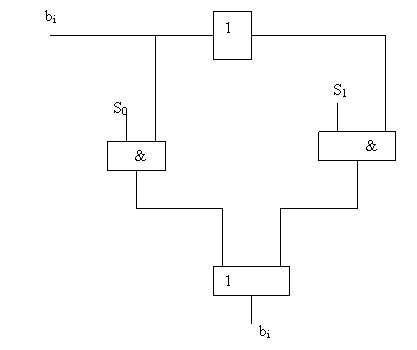Для реализации указанного пути необходимо сумматор по входам Bi снабдить дополнительными логическими элементами, с помощью которых будет осуществляться прямая или инверсная передача кодов Bi. Единица в младший разряд может быть добавлена подачей на вход Рn сумматора сигнала 1. Схема, способная производить прямую и инверсную передачу кодов Bi, приведена на рис.2.5.
Рис 2.5. Схема комбинационного автомата i – го разряда сумматора – вычитателя.
При наличии указанных схем в каждом разряде на входах Bi сумматор может, кроме операции сложнения и вычитания, выполнять ряд других арифметических операций. На рис.2.6. приведены схемы, поясняющие сказанное . Первой приведена схема выполнения операции сложения (рис.2.6.,а),рядом приведены значения S0 и S1 –для этого случая. Схема выполнения операции вычитания приведена на рис.2.6.б.
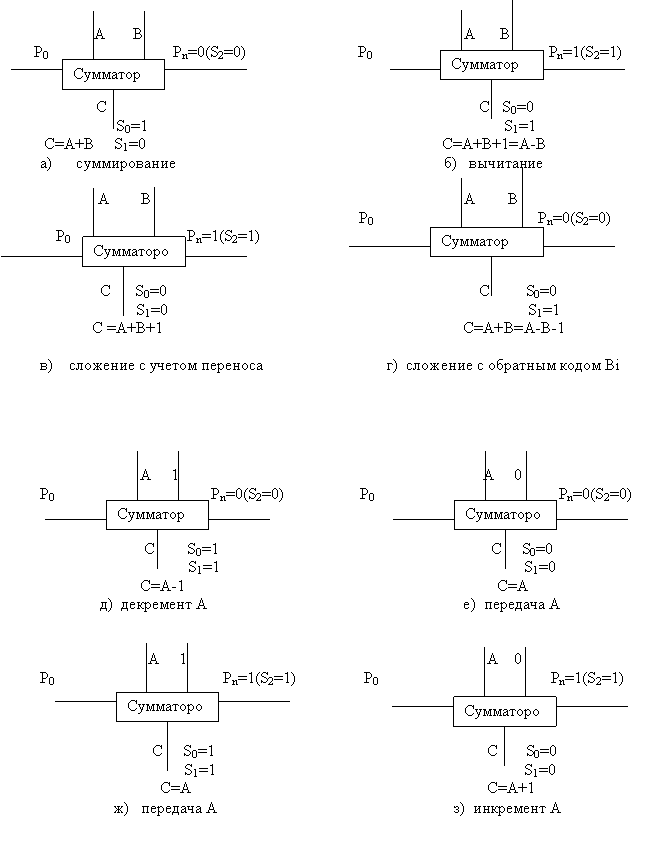
Рис 2.6.. Схема выполнения арифметических операций в параллельном сумматоре
2.2.Выполнение логических операций в блоке АЛУ
Помимо арифметических операций в блоке обработки информации ЭВМ выполняются логические операции.
Логические операции над кодами выполняются поразрядно, и это во многом определяет тот набор элементов, который необходим для их выполнения в АЛУ. Для выполнения логических операций в каждом разряде может быть предусмотрен набор логических элементов ,каждый из которых выполняет определенную операцию. На рис.2.7. приведена схема i-го разряда АЛУ, способного выполнять четыре логические операции: ИЛИ, И, исключающее ИЛИ, НЕ. Выбор операции осуществляется сигналами S0 ,S1 .
|
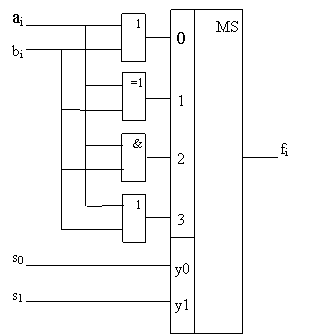
S0 S1 |
Выходной сигнал fi |
Название операции |
|
1 0 |
fi=aivbi fi=ai+bi |
ИЛИ Исключ |
|
|
|
ИЛИ |
|
0 1 1 1 |
fi=ai/\bi fi=аi |
И НЕ |
а) б)
Рис 2.7. Схема i – го разряда АЛУ (а) предназначенного для выполнения логических операции, заданных таблицей функции (б)
Набор логических элементов и их число определяется списком логических операций машины.
Для объединения схем, предназначенных для выполнения арифметических и логических операций, может быть использована схема, приведенная на рис.2.8. Выбор выполняемых операций производится сигналами S0 и S1. Выходы i-го разряда сумматора Сi и выход схемы fi, выполняющей логические операции объединяются с помощью мультиплексора, управляющий вход М определяет тип операции (арифметические 0, логические 1).
 |
Рис 2.8. Схема одного разряда АЛУ.
Однако использование элементов, служащих для выполнения отдельных операций может быть оправдано лишь в отдельных случаях. Чаще удается создать одну общую комбинационную схему для каждого разряда, способную выполнять весь список операций.
В качестве примера, поясняющего возможность использования сумматора для выполнения логических операций, рассмотрим возможность выполнения в нем операции "исключающее ИДИ". Для ее выполнения достаточно запретить перенос из одного разряда в другой, для чего необходимо в цепях распространения сквозного переноса (рис.2.3) установить схему «И», на один ее вход подавать сигнал переноса из предыдущего разряда, на второй вход подавать сигнал S2. Тогда при S2= 1 сумматор способен выполнять арифметические операции, а при S2=0 логическую "исключающее ИЛИ". Для выполнения операции умножения в том же сумматоре можно выполнить следующее:
При S2=0
Ci = ai + bi = (ai + ki) + bi = aibi V kibi V aikibi
Если ki = bi , то
Ci = aibi V bibi V aibibi = aibi
Таким образом, добавив на вход ai каждого сумматора комбинационную схему, содержащую схему «ИЛИ» и «И» можно получить АЛУ, способное выполнять операцию "И". Добавив туда же еще одну схему «И» можно реализовать дополнительно операцию «ИЛИ». Схема комбинационной части двухразрядного АЛУ, способного выполнять ряд арифметических и логических операций, приведена на рис.2.9. В табл.2.2 приведены значения управляющих сигналов S0, S1, S2, S3 и выполняемые АЛУ операции.
 |
Таблица 2.2.
Рис 2.9. Схема двухразрядного АЛУ.
2.3.Флаговый регистр АЛУ
При выполнении арифметических операции могут иметь место случаи, когда результат не может быть размещен в итоговом регистре, например, при выполнении операции умножения или сложения. Такое событие называют переполнением разрядной сетки машины. Очень часто бывает необходимом определить, превышает ли результат операции, записанный в регистр С значение 0, т.е. имеется ли в С хотя бы в одном разряде 1. Ha некоторые из подобных событий требуется вполне определенная реакция. Для временного хранения информации об указанных событиях в АЛУ предусматривается несколько триггеров, которые образуют флаговый регистр.
Практически все арифметические и логические операции изменяют значение флагов. На рис.2.10. приведена схема восьмиразрядного АЛУ с флаговым регистром.
.
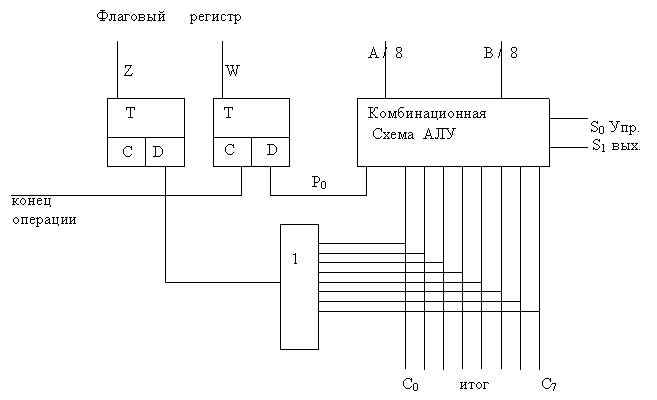
Рис 2.10. АЛУ с флаговым регистром.
Флатовые триггеры регистра обозначены как Z , W и выполняют следующие функции:
W - устанавливается в 1 при возникновении переноса в несуществующий разряд (Ро-1-переполнение разрядной сетки);
Z - устанавливается в 1,если результат на выходах С во всех разрядах равен 0.
Практическая работа № 1
СИНТЕЗ ПАРАЛЛЕЛЬНОГО АЛУ
Цель работы: изучить основной принцип построения параллельного арифметико-логического устройства (АЛУ), получить навыки при разработке схем сумматоров и АЛУ.
Основные теоретические сведения
По способу обработки значений каждого разряда различают два типа АЛУ: последовательный и параллельный. В данном практическом задании мы будем рассматривать функциональную схему параллельного АЛУ.
В случае, когда основной характеристикой АЛУ является скорость выполнения операций, используют параллельную схему. В таких АЛУ время выполнения операций уменьшается в n раз.
На этапе синтеза комбинационной схемы i-го разряда АЛУ начинать необходимо с составления списка операций и его анализа. Необходимо выделить арифметические и логические операции и определить, где каждая из групп операций должна выполнять.
Задача синтеза состоит в определении необходимого числа логических элементов, позволяющих в схеме АЛУ выполнять логические операции, определить структуру КДА на входе сумматора, с помощью которого будет производиться управление выполнением типа арифметической операции, а также формирования таблицы управляющих сигналов для каждой арифметической и логической операции.
После проработки указанных вопросов следует осуществить синтез комбинационных схем и сумматора, определить способ формирования сигнала переноса.
Хранение операндов и результата выполненных операций производится в регистрах. Выбор количества триггеров в регистре определяется задачами регистров. Если необходимо только хранить информацию, то целесообразно использование одноступенчатых Д триггеров. Если необходимо производить сдвиг информации, то следует использовать двухступенчатые JK или Д триггеры с комбинационными схемами на входах.
Рассмотрим синтез параллельного АЛУ на конкретном примере.
Список команд и состояния флагового регистра указаны в таблице 1.
|
, В
, 
