УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра «Автоматизации почтовой cлужбы»

Методическое указание

и задание на курсовую работу

по дисциплине

«Теоретические основы почтовой службы»

для студентов 3 курса

(специальность 5840200-«Почтовая служба»)

Ташкент 2007 г

Содержание

	Введение………………………………………………………………….	3
1.	Задание и исходные данные…………………………………………….	4
2.	Построение кратчайшей сети, с использованием теоремы Штейнера	5
3.	Линейная сеть перевозки………………………………………………..	6
4.	Кольцевые сети перевозки………………………………………………	8
5.	Звездообразная сеть……………………………………………………..	9
6.	Сводный анализ………………………………………………………….	10
	Список литературы……………………………………………………...	11

Введение

В современной почтовой связи все большую роль играют теоретические методы построения и оптимизации сети почтовой связи, технологических процессов и технических средств отрасли, повышения качества обслуживания. Дисциплина "Технологические процессы в почтовой связи"
изучается студентами специальности 5840200 на третьем
курсе. В процессе обучения студенты
прослушивают лекционный курс и проводят практические занятия. В лекционный курс вынесены лишь узловые, наиболее важные вопросы, поэтому большое значение приобретает самостоятельная работа студента. Эта работа заключается в изучении вопросов, предусмотреных программой, по учебникам и учебным пособиям.

В общем комплексе средств связи страны почтовая связь выделяется, во-первых, наибольшим объемом продукции, во-вторых, наибольшим числом работников и, в-третьих, относительно низкой стоимостью основных фондов. Последнее обстоятельство может служить косвенным свидетельством слабой технической оснащённости почтовой связи

С другой стороны, почтовая связь как система обладает такими свойствами (большое количество взаимодействующих элементов и связей между ними, иерархичность, воздействие внешних факторов, способность к самоорганизации и т.д.), которые позволяют отнести ее к классу сложных систем. Их исследование возможно только с использованием математического моделирования. Однако нередко такие исследования сложны или практически неосуществимы, поэтому сложные системы разбиваются на самостоятельные подсистемы, которые поддаются либо аналитическому, либо имитационному моделированию.

Основной задачей дисциплины "Теоретические основы почтовой связи" является изучение теоретических вопросов научного подхода к решению проблем отдельных подсистем почтовой связи. Для этого в указанной дисциплине рассматриваются примеры решения некоторых задач почтовой связи методами теории графов и сетей.

Следует отметить, что приведенный перечень теоретических разделов не является окончательным и может в дальнейшем изменяться по мере развития научных исследований для решения проблем почтовой связи.

1. Задание и исходные данные

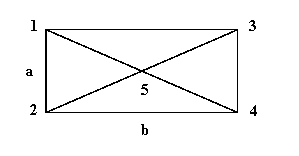
Исследуемая сеть почтовой связи имеет пять узлов, четыре из них находятся в вершинах прямоугольника со сторонами a и b. Пятый узел расположен в центре прямоугольника. Цель курсовой работы заключается в построении кратчайшей сети почтовой связи. Возможны различные варианты построения сети, например, в виде линии, кольца, звезды, дерева.

Таблица 1

	1	2	3	4	5	6	7	8	9	10
а	2	2	3	4	5	6	7	8	9	10
b	6	5	6	7	8	9	10	11	12	13

	11	12	13	14	15	16	17	18	19	20
а	11	12	13	14	15	16	17	18	19	20
b	15	16	17	18	19	20	21	22	23	24

При выполнении курсовой работы необходимо выполнить следующие задания:

1) Начертить узлы сети, отложив в масштабе расстояние между ними, в соответствии с исходными данными (табл. 1);

2) Построить ряд вариантов сети (в виде линии, кольца, звезды и дерева);

3) Определить длину каждого из вариантов сети (c использованием теоремы Пифагора);

4) Построить сеть с использованием точек Штейнера и определить ее длину.

5) Сравнить варианты построения сети по длине и эксплутационным показателям средней длины пути, нагрузке дуг и объему перевозок по сети;

6) Показать выигрыш в длине сети по сравнению с другими вариантами;

7) Показать какими свойствами и недостатками обладает сеть с использованием точек Штейнера.

2. Построение кратчайшей сети, с использованием теоремы Штейнера

Одна из задач, возникшая при проектировании сетей, заключается в поиске кратчайшей сети, состоящей из прямолинейных отрезков, связывающих между собой множество точек.

Решение этой задачи связано с именем немецкого математика прошлого столетия Якоба Штейнера и сводится к поиску одной точки, сумма расстояний от которой до всех точек (узлов) заданного множества была бы минимальной. Эта точка и называется точкой Штейнера.

Однако впервые эта задача была поставлена в 1640 году, в частном случае: Найти точку Р, сумма расстояний от которой до каждой из трех точек минимальна.

Э. Торричелли и Б. Кавальери доказали, что суммарное расстояние минимально, когда все сопряженные в точке Р углы, больше или равны 120⁰.

Покажем процедуру геометрического построения кратчайшей сети из трех узлов A, B, C.

Зная что углы с вершинами в точке Р должны быть не меньше 120⁰, Э. Торричелли и Б. Кавальери придумали процедуру геометрического построения для нахождения точки Р (рис. 1).

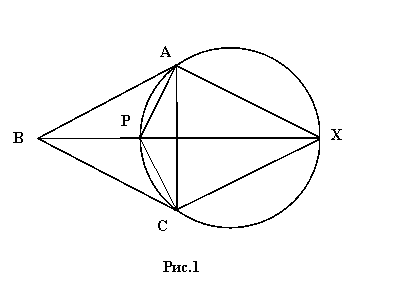
Нужно провести отрезки прямых, соединяющие исходные точки, с точкой в вершине наибольшего угла. Если угол В, больше или равен 120⁰, то искомая точка совпадает с точкой В. Другими словами, кратчайшая сеть в данном случае, представляет собой, просто два отрезка прямых, между точками А и В, и точками В и С. Если угол в точке В меньше 120⁰, то точка В должна находиться где-то внутри треугольника. Чтобы найти ее, следует построить равносторонний треугольник с основанием на стороне треугольника АВС, например, на стороне отрезка АС. Третья вершина равностороннего треугольника (обозначим ее Х) находится на противоположной стороне от точки В относительно АС. Вокруг построенного равностороннего треугольника описываем окружность и проводим прямую, соединяющие точки В и Х. точка Р будет на пересечении этой прямой окружности, соединив точки А, В и С с точкой Р, мы получаем три угла, в точности равные 120⁰ каждый, и искомую кратчайшую сеть. Более того, длина отрезка ВХ оказывается равной длине кратчайшей сети.

Задача с тремя точками и задача Штейнера для многих точек имеют много общих свойств. Их решения имеющие вид дерева, характерны тем, что при удалении любого отрезка из кратчайшей сети, мы должны будем исключить одну из заданных точек. Другими словами, мы не можем пройти по сети из какой-либо заданной точки и вернуться в нее, без того, чтобы не пройти те или иные отрезки повторно. По этой причине графические решения задачи с тремя точками и задачи со многими точками называются деревьями Штейнера. Отрезки прямых называются ребрами, а точки, роль которых аналогична точке Р и которые нужно добавить для построения дерева, называются точками Штейнера.

Задача Штейнера для трех точек дает также некоторую информацию о геометрии кратчайших деревьев Штейнера:

1) Каждый угол равен 120⁰ или больше, а это означает, что каждая точка соединяется с остальным деревом не более чем тремя ребрами;

2) В каждой точке Штейнера сходится ровно три ребра, образуя друг с другом углы, в точности равные 120⁰;

3) Число ребер дерева всегда на единицу меньше суммарного числа заданных исходных точек и точек Штейнера;

4) Поскольку в каждой точке Штейнера сходятся ровно три ребра и, по крайней мере, одно ребро должно касаться каждой из заданного множества точек, максимальное число точек Штейнера для любой задачи на две меньше, чем число заданных исходных точек.

3. Линейная сеть перевозки

В отличие от сетей обработки, дуги которых, как правило, однонаправленные сети перевозки в основном строятся из двунаправленных дуг и обменных узлов.

Изначальной является линейная сеть. По мере развития увеличивается число узлов, дуг сети, причем иногда и без ее удлинения. Считаем, что линейная сеть является полнодоступной, т.е. от каждого узла обеспечивается перевозка грузов ко всем остальным, поэтому общее количество струй:

γ = n × (n - 1).

Нагрузка i-й дуги линейной двунаправленной сети определяется также по правилу произведения сумм сторон разреза этой дуги:

Β_i = i × (n - i),

где i- число узлов с одной стороны от разреза дуги; (n-1)- число узлов с другой стороны от разреза дуги.

Допустим, что меж узловые и входящие потоки одинаковы. Тогда средний объем перевозки по линейной двунаправленной сети равен:

Q_с = 4n × E / T × (n + 1) (n - нечетное);

Q_с = 4n × (n – 1) × E / T × n (n - четное),

вдвое превышая средний объем перевозки по линейной однонаправленной сети.

Средняя длина пути как в одно-, так и в двунаправленной линейной сети:

D_ij = L × (n + 1) / 3 (L = const).

D_ij = L × (n + 1) / 3 × (n - 1) (L = const).

Средняя работа перевозки:

A = 4 × n × L × E / 3T × (n - 1),

n - число узлов, lim A = 4 × E × L / 3 × T.

В существующих линейных сетях узлы имеют разные значения входящих a_i и исходящих b_i потоков. В начале составляется безразмерная матрица динамических вероятностей нагрузки от i - го узла к j- му:

P_ij (T) = Q₁^исх / (∑ Q₁^исх – Q₁^исх).

Затем по показаниям счетчиков, регистрирующих потоки на входах, рассчитывается размерная матрица меж узловой нагрузки:

Q_ij (T) = Q₁^вх (T) × P_ij (T).

Суммарная длина пути:

∑∑ D = [n × (n - 1) × L × (n - 1)] / 3 × (n - 1).

Загрузка k-го перегона:

S_k = ∑Q₁^вх × ∑Q₁^исх / ∑Q₁^исх.

Возможно также вычисление нагрузки перегонов, исходя из матрицы меж узловых потоков, но это требует больших затрат времени.

4. Кольцевые сети перевозки

Кольцевая сеть с двунаправленными дугами является примером транспортной системы с минимальной избыточностью по сравнению с древовидной сетью. Кольцо дает возможность для каждого груза, достичь дистанцию назначения по двум путям, причем один из них может быть оптимальным по расстоянию, времени.

Принимаем, что при отправлении почты осуществляется оптимизация по кратчайшему расстоянию. Таким образом, длина пути груза представляет собой случайную величину, распределенную в интервале от одной до (n-1)/2 дуг. Допустим также, что мощность истоков и стоков одинаковы. Нагрузка дуги в кольце размером n узлов обмена:

β = n² / 8 (n – четное);

β = (n² – 1) / 8 (n – нечетное).

Суммарная длина всех струй кольца:

∑ ∑ D_ij = L × n³ / 8 (n – четное);

∑ ∑ D_ij = [L × n × (n² -1)] / 8 (n – нечетное).

Средняя длина пути:

D_ij = L × (n + 1) / 4 (L = const).

Если на кольце постоянной длины L возрастает число узлов, то:

D_ij = L_c × (n + 1) / 4 × n (n – нечетное);

D_ij = L × n / 4 × n × (n – 1) (n – четное).

Таким образом, средняя длина пути по двунаправленному кольцу в два раза меньше средней длины пути по однонаправленному кольцу.

Средний объем перевозок:

Q_с = 8 × E × n / T равно n–1 при условии, что мощности истоков и стоков одинаковы. × (n + 1) (n – нечетное);

Q_с = 8 ×E × (n - 1) / n × T (n –четное).

С увеличением размера двунаправленного кольца объем перевозок в четыре раза превышает объем перевозок однонаправленного кольца.

5. Звездообразная сеть

Звездообразная сеть относится к разряду древообразных. Общее количество струй γ звездообразной сети с двунаправленными ребрами:

γ = n × (n - 1).

Количество струй в разрезе любого ребра

Средний объем сообщений передаваемых по «звезде», с ее развитием возрастает пропорционально числу узлов:

Q = E × n / T.

Количество транзитных струй через центральный узел:

β_Т = (n – 1) × (n – 2).

Средний объем транзитного потока через центральный узел:

Q_Т = (n – 2) × E / T.

Средний объем сообщений, перевозимых по лучам «звезды» в единицу времени:

Q_М = Q + ∑ Q_T = E × (2n – 1) / T.

Суммарная длина струй в «звезде»:

∑ ∑ D_ij = 2 ×L × (n - 1) × 2.

Средняя длина струи в «звезде»:

D_ij = [2 × L × (n - 1)] / n,

где L – длина ребра.

Суммарная дина струй в «звезде»:

∑ ∑ D_ij = 2 × L × (n – 2)².

Работа по перемещению сообщений в «звезде»:

A = Q × D_ij = 2 × E × L × (n – 1) / T.

6. Сводный анализ

Таблица 2

Рассчитанные значения линейной, кольцевой и звездообразной сетей должны быть занесены в таблицу 2.

Эксплутационные показатели Виды сетей
Lc
∑ ∑ Dij
Dij
β
Qc

Таблица 3

В таблице 3 нужно представить отношение построения вариантов сети по длине и эксплуатационным показателям.

Эксплутационные показатели Варианты сравнения
Lc
∑ ∑ Dij
Dij
β
Qc × Е/Т

Затем нужно произвести сравнение по длине сети L_c, по суммарной длине ∑∑ D_ij, по средней длине пути D_ij, по количеству транзитных струй через центральный узел β, по объему сообщений перемещаемых по сети Q_c.

Cписок литературы

1. Хлытчиев С.М. и др. Теоретические основы почтовой связи – М: Радио и связь, 1990г.

2. Князютенков В.А., Птицин Г. А. Оптимизация сетей почтовой связи – М: МТУСИ, 1997г.

3. В.А. Барсук, Н.М. Губин, А.Р. Батый Экономико – математические методы и модели в планировании и управлении в отрасли связи: Уебник для ВУЗов – 3-е изд., перераб. и доп. – М.: Радио и связь, 1984. – 264 с.