УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИЙ

Кафедра: «Автоматизация почтовой службы»

Методическое пособие по курсу

«Теоретические основы почтовой связи»

Направление: 5840200-«Почтовая служба»

Ташкент-2006

СОДЕРЖАНИЕ

Введение……………………………………………………………………….3

1. Некоторые сведения из теории графов и сетей…………………………….4

2. Теорема о максимальном потоке и алгоритм определения

максимального потока……………………………………………………………9

3. Задача о кратчайшем пути и алгоритмы нахождения кратчайших

путей………………………………………………………………………………12

4. Список литературы……………………………………………………………21

5. Приложение……………………………………………………………………22

ВЕДЕНИЕ

Почтовая связь как система обладает такими свойствами (большое количество взаимодействующих элементов и связей между ними, иерархичность, воздействие внешних факторов, способность к самоорганизации и т.д.), которые позволяют отнести ее к классу сложных систем. Их исследование возможно только с использованием математического моделирования. Однако нередко такие исследования сложны или практически неосуществимы, поэтому сложные системы разбиваются на самостоятельные подсистемы, которые поддаются либо аналитическому, либо имитационному моделированию.

В данном методическом пособии рассмотрены примеры решения некоторых задач почтовой связи на основе теории графов и сетей.

1. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ГРАФОВ И СЕТЕЙ

Сетевые модели оптимизации охватывают широкий класс задач, встречающихся при проектировании систем почтовой связи, организации перевозки почты, размещении предприятий почтовой связи и ряда других. Как правило, эти задачи характеризуются линейной целевой функцией и линейными ограничениями, так что для их решения могут использоваться известные методы линейного программирования. Однако характерной особенностью этих задач является их большая размерность, обуславливающая необходимость поиска эффективных алгоритмов решения, учитывающих особенности каждой конкретной задачи по сравнению с общей задачей линейного программирования. Основой для построения таких алгоритмов служит представление решаемой задачи в виде сети или графа. В данной главе рассмотрены алгоритмы решения нескольких таких задач, которые имеют непосредственное приложение в почтовой связи.

Граф G задается конечным множеством вершин (w₁,..., w_m), которое обозначается W и множеством ребер (d₁, ... , d_n), которое обозначается D, соединяющих некоторые или все вершины.

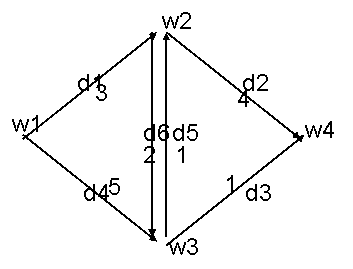
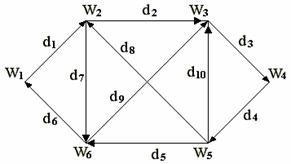
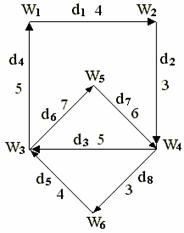
Геометрическая иллюстрация графа приведена на рис.1. Множества W и D определяют граф, который обозначается G(W, D). Если ребра из множества D ориентированы, что обычно показывается стрелками, то они называются дугами, а граф с такими ребрами называется ориентированным графом, или, короче, орграфом. Если ребра не имеют ориентации, то граф называется неориентированным.

Каждая дуга может быть задана упорядоченной парой вершин (w_i, w_j). При этом направление дуги считается от w_j к w_j; w_i называется начальной, a w_j — конечной вершиной дуги (w_i, w_j). Иногда говорят, что дуга (w_i, w_j) инцидентна w_i и w_j.

Как правило, неориентированное ребро можно представить в виде пар (w_i, w_j) и (w_j, w_j), и наоборот, если направление дуги несущественно, ее можно заменить на ребро. Ориентированный граф можно задать в виде множества вершин W и множеств Г(w_i), показывающих, с какими вершинами связана вершина w_i. Например, для графа, показанного на рис.1, Г(w_i) = {w₂, w₄}, a Г(w₄)=w₅. Множество Г(w_i) назовем соседями вершины Г(w_i). В случае неориентированного графа множества Г определяются после замены каждого неориентированного ребра на два ориентированных.

Путем в ориентированном графе называется последовательность дуг, в которой каждая конечная вершина (кроме последней) является начальной вершиной следующего ребра. Так, в графе на рис.1 последовательности дуг d₄, d₅, d₆, d₈, d₄; d₁ d₂, d₃, d₄, d₅ являются путями.

Простым путем называется путь, у которого каждая вершина используется не более одного раза. Путь d₁ d₂, d₃, d₄, d₅ — простой, a d₄, d₅, d₆, d₈, d₄— нет. Часто для обозначения пути используется перечень вершин, через которые проходит путь. Например, путь d₅, d₆, d₁ на рис.1 можно записать так: w₅, w₆, w₁, w₂. Такая запись используется чаще, чем перечень дуг и по ней проще выявить, является ли данный путь простым. Если в простом пути

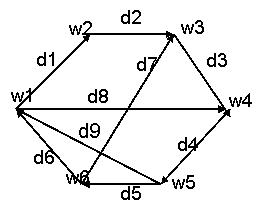
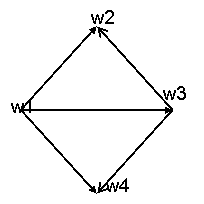
Рис. 1 Рис. 2

ориентации дуг не совпадают, то такой путь называется простой цепью. Например, последовательность w₁ w₆, w₃, w₄ на рис.1 является простой цепью, так как при движении от начальной вершины w₁ к -конечной w₄ ориентация дуги (w₁ w₆) не совпадает с ориентацией остальных дуг. В дальнейшем будут рассматриваться только простые пути и цепи, поэтому термин «простой» будет

опускаться.

Граф называется связным, если между любой парой вершин существует цепь, соединяющая эти вершины. В дальнейшем всегда будут рассматриваться связные графы и это свойство графа отдельно оговариваться не будет.

Цепь d₁ ... d_K называется замкнутой, если начальная вершина дуги d₁ совпадает с конечной вершиной дуги d_K. Замкнутая цепь называется циклом. Например, в графе на рис.1 d₅, d₆, d₉ образуют цикл. Этот же цикл можно записать в виде перечня вершин w₁, w₅ w₆, w₁

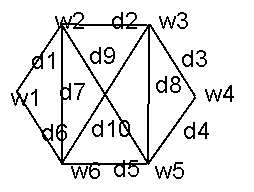
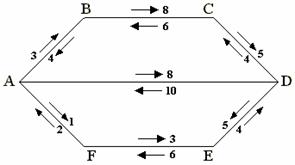
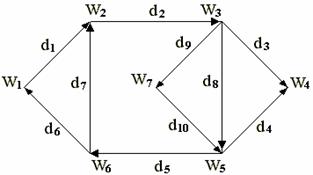
Контуром называется путь, у которого начальная и конечная вершины совпадают. Так, в графе на рис.1 w₁ w₄, w₅, w₁ образуют контур. Контур называется гамильтоновым, если он содержит все вершины графа. Ясно, что не любой граф содержит гамильтоновым контур. Например, граф на рис.2 такого контура не имеет, а в графе на рис. 1 гамильтоновым контуром является

d₁, d₂, d₃, d₄, d₅, d₆.

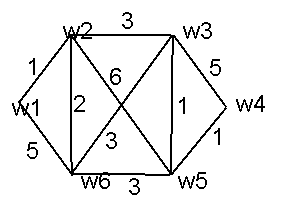
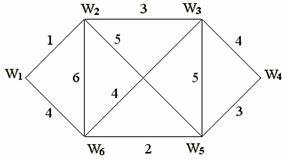
Граф G называется полным, если для любой пары вершин существует, по крайней мере, одно ребро, связывающее эту пару. На рис.3 изображен полный неориентированный граф с четырьмя вершинами. Полный граф содержит максимально возможное число ребер (если не учитывать возможность проведения параллельных ребер между двумя вершинами). Для неориентированного графа это число равно m(m—1)/2, где m — число вершин.

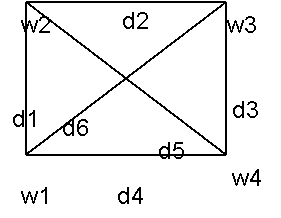
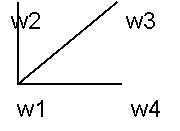
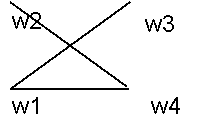
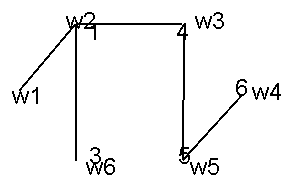
Рис. 3 Рис. 4

В известной степени противоположностью полному графу является, дерево. Следующие определения дерева эквивалентны. Неориентированное дерево есть:

а) связный граф, содержащий m вершин и m-1 ребро;

б) связный граф, не имеющий циклов;

в) граф, в котором каждая пара вершин соединена одним и только одним путем. Из этих определений следует, что в произвольном графе G(W, D) можно последовательно вычеркивать ребра, так чтобы граф оставался связным. После того как в графе останется m-1 ребро, образуется основное дерево графа G(W, D).
Конечно, это можно сделать не единственным способом и существует несколько основных деревьев графа G(W, D). На рис.4 изображены два основных дерева графа, показанного на рис.3.

В ориентированном графе количество дуг, направленных к вершине w_i, называется полустепенью захода вершины w_i, а количество дуг, направленных от w_i, полустепенью исхода этой вершины. Множество дуг, направленных от вершины w_j обозначается C⁺( w₁), а множество дуг, направленных к вершине W1-C^-(w_i). На рис.1 C⁺(w₁) = {d₁ d₈}, a C^-(w_i) = {d₉, d₆}. Используя это понятие можно дать определение ориентированного дерева в графе. 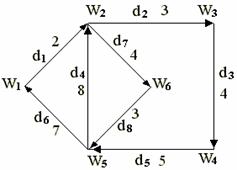Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (за исключением одной) равно 1, а полустепень захода этой вершины, называемой корнем, равно 0. На рис.5 показано ориентированное дерево с корнем w₁. Очевидно, что не всякий ориентированный граф имеет основное ориентированное дерево. Это отражает тот факт, что в ориентированном графе не всегда существует путь между любыми вершинами, в противоположность неориентированному, в котором такой путь всегда есть (речь идет только о связных графах).

Неориентированное дерево всегда можно преобразовать в ориентированное, если выбрать произвольную вершину в качестве корня и ребрам приписать такую ориентацию, чтобы каждая вершина соединялась с корнем одним и только одним простым путем.

Вершины ориентированного дерева, для которых полустепень исхода равна пулю, называются висячими. Так, в графе на рис.5

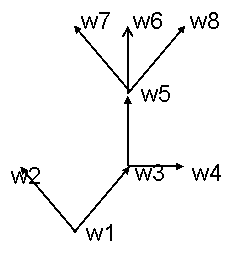
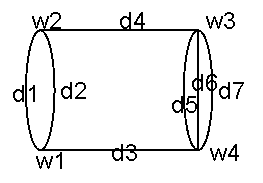
Рис. 5 Рис.6

вершины w₂, w₄, w₆, w₇, w₆ являются висячими, a w₁, w₃ и w₅— нет.

Граф G называется мультиграфом, если между одной или несколькими парами вершин существует более одного ребра. На рисунке 6 показан мультиграф. Введение мультиграфа целесообразно в тех случаях, когда различные ребра между вершинами отличаются некоторыми характеристиками, например длиной, пропускной способностью и т. д. В ряде случаев можно заменить совокупность ребер между двумя вершинами одним ребром с некоторой эквивалентной характеристикой. Имея это в виду в дальнейшем мультиграфы рассматриваться не будут.

Для алгебраического задания графа используются следующие

матрицы.

Матрицей смежности называется квадратная матрица S, номер строки и номер столбца которой соответствуют вершине графа. Элемент этой матрицы

Sij =

={1, если в графе существует ребро между вершинами w₁ и w_j;

={О, если такого ребра нет.

Количество строк и столбцов в матрице S равно количеству вершин графа. Для неориентированного графа матрица смежности симметрична относительно главной диагонали. Множество столбцов, имеющих единицу в i - й строке, — множество номеров вершин, являющихся соседями вершины w_i.

Матрица инциденций А—матрица с количеством строк m и количеством столбцов n, где m — количество вершин, а n — количество ребер в графе. Каждая строка матрицы соответствует вершине в графе, а каждый столбец - ребру. Элемент матрицы a_ij для орграфа

aij =

={ 1, если дуга d_j инцидентна вершине w_i и направлена от w_i;

={-1, если дуга d_j инцидентна вершине w_j и направлена к w_i;

={, 0 для всех остальных случаев.

Поскольку каждое ребро инцидентно всегда двум различным вершинам и направлено от одной к другой, то каждый столбец

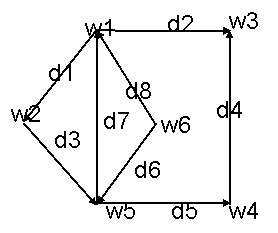
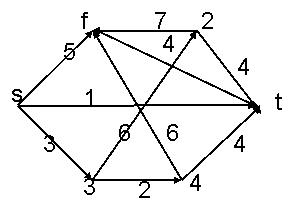
Рис. 7 Рис.8

матрицы содержит один элемент, равный +1 и один равный -1, остальные элементы равны нулю. Отсюда вытекает, что сумма всех строк матрицы А равна нулевому вектору. На рис.7 показан ориентированный граф, ниже приведены матрицы смежности и инциденций этого графа.

Матрица смежности

	W1	W2	W3	W4	W5	W6
W1	0	1	1	0	0	0
W2	0	0	0	0	1	1
W3	0	0	0	0	0	0
W4	0	0	1	0	0	0
W5	1	0	0	1	0	0
W6	1	0	0	0	1	0

Матрица инциденций

	D1	D2	D3	D4	D5	D6	D7	D8
W1	1	1	0	0	0	0	-1	-1
W2	-1	0	1	0	0	0	0	0
W3	0	-1	0	-1	0	0	0	0
W4	0	0	0	1	-1	0	0	0
W5	0	0	-1	0	1	-1	1	0
W6	0	0	0	0	0	1	0	1

Для неориентированного графа в столбце j, соответствующем ребру d_j=(w_i, w_k), записываются единицы >в i-й и k-й строках и нули в остальных строках.

Представление графа матрицей инциденций не всегда оправдано, так как для хранения такой матрицы в памяти ЭВМ требуется mn слов. Кроме того, доступ к информации часто неудобен. Например, ответ на вопрос типа: существует ли ребро (w_i, w_j)? - в худшем случае требует перебора всех столбцов матрицы. Аналогичными недостатками обладает и матрица смежности. Значительно удобнее представлять граф в виде списков, например списка ребер или дуг, заданных в виде (w_i, w_j), упорядоченных по возрастанию w_i, а внутри этого множества — по возрастанию w_j. В этом случае существенно экономится память и упрощается поиск различных подмножеств вершин и ребер в графе.

В практических задачах часто вершинам и (или) ребрам графа приписывают числа. Такой граф называется сетью. Иногда сеть ассоциируется с транспортной сетью или сетью связи. В этом случае вершины графа — города, транспортные пункты, узлы связи, а ребра — дороги, соединяющие эти города, или линии связи. В случае транспортных сетей или сетей связи числа, приписываемые вершинам и (или) ребрам, могут означать: длину ребра, стоимость перевозки единицы продукта по данному ребру, пропускную способность вершины или ребра, надежность ребра или вершины и т. д.

2. ТЕОРЕМА О МАКСИМАЛЬНОМ ПОТОКЕ И АЛГОРИТМ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПОТОКА

Рассмотрим произвольный ориентированный граф G(W, D). Каждой дуге графа (х, у) сопоставим число f(x, у), которое называется пропускной способностью (х, у). Выделим источник s и сток t. Функция φ(х, у) называется потоком на сети, если она удовлетворяет следующим условиям:

1. φ (х,у)≥0. (1)

2. Для любой вершины х, не являющейся источником или стоком, сумма входящего потока равна сумме выходящего потока, т. е.

Σ φ (х, y) - Σ φ (х, у) = 0.

(2)

3. φ (х, у) ≤ f (х, у). (3)

Величиной потока называется сумма потока по всем дугам, исходящим из s, v= Σ φ (s, у). Согласно условию сохранения потока

(2), эта величина равна сумме потока по всем дугам, входящим в t. Задача состоит в нахождении такого потока, для которого величина v была бы максимальной.

Пусть AW такое, что s не принадлежит A, a tA. Разрезом сети G(W, D) называют множество дуг, заходящих в А, т. е. непосредственно связывающих вершины из А с вершинами, принадлежащими к А. Пропускной способностью разреза называется сумма пропускных способностей дуг, входящих в разрез. Дуга (х, у) называется насыщенной, если φ (х, y)=f(x, у). Рисунок 8 иллюстрирует введенные понятия. Цифры около дуг показывают их пропускные способности. Функция φ(s, 3)=3; φ(3, 2)=2; φ(3, 4)=1, φ(4, t)=l; φ(2, t) =2 является потоком с величиной v = 3. Пусть в множество А входят вершины 2, t, 4. Тогда разрезом будет множество дуг (s, t), (1, t), (3, 2), (3, 4) с пропускной способностью 1+9+6+2=18. Дуга (s, 3) является насыщенной, а остальные не насыщены.

Теорема о максимальном потоке формулируется следующим образом. Для заданной сети максимальная величина потока равна минимальной пропускной способности разреза. Доказательство теоремы основывается на следующих рассуждениях. Рассмотрим некоторый путь из s в t. Если все дуги этого пути не насыщены, то можно увеличить поток. Обозначим δ(х, y)=f(x, у)— φ (х, у) и

δ*=min δ(x, у). Очевидно, что величина потока может возрасти на δ* без нарушения условий (1) — (). Например, на рис. 8 для пути s, 3, 4, t с величиной потока по этому пути, равной 1, значениями δ(s, 3)=2; δ(3, 4) = 1; δ(4, t)=3 и δ*=1 можно увеличить поток на 1.

Рассмотрим теперь цепь, в которой направление части дуг не совпадает с направлением прохождения цепи. Для дуг, направление которых совпадает с направлением прохождения цепи, сохраним введенные выше обозначения, а те, направление которых не совпадает, обозначим

φ*=min φ (х, у) и введем ε = min(φ*, δ*); тогда величина потока может быть увеличена на ε по каждой дуге, направление которой совпадает с направлением прохождения цепи, и уменьшено на е для тех дуг, направление которых противоположно направлению прохождения цепи без нарушения условий (1) — (3). Так, для цепи s, 1, 4, t на рис. 8 и φ(s, 1)=3 φ(4, 1)= 1 и φ(4, t) = l и получим δ(s, 1)=2, δ(4, t)=3, δ* = 2, φ*=1 и ε =1. Следовательно, поток может быть увеличен на 1 на дугах (s, 1) и (4, t) и уменьшен на единицу на дуге (4, 1).

Наконец, заметим, что, если не существует цепи от s к t с ε >0, то величину потока увеличить нельзя, т. е. получен максимальный поток. Исключая при этом из графа все дуги, для которых δ(х, у) = = 0 или φ (х, у)=0, получим хотя бы два несвязных подграфа, один из которых содержит вершину t. Этот подграф определяет разрез А, пропускная способность которого равна максимальному потоку, поскольку все дуги, ведущие из в А, насыщены. Но поскольку для любого потока его величина не может быть больше пропускной способности любого разреза, то теорема доказана.

Рассмотрим теперь алгоритм нахождения максимального потока. Он состоит из двух частей. Первая из них предназначена для нахождения цепи, по которой можно увеличить поток. Если такой цепи нет, то это означает, что максимальный поток найден. Вторая часть увеличивает поток вдоль найденной цепи. Каждая вершина сети в процессе работы алгоритма получает пометку вида (±у, ε). Первая часть пометки показывает, что поток должен быть увеличен (знак +) или уменьшен (знак -) на дуге (х, у) или (у, х). Вторая часть — это текущее значение, на которое должен быть увеличен поток. Когда установится равным t, ε — максимально возможное увеличение потока по найденной цепи.

Алгоритм начинает работу с произвольного допустимого потока, в качестве которого может быть принят и нулевой. Расстановка пометок разбивает вершины сети на три типа: непомеченные — те, которые не имеют пометок; помеченные — те, которые имеют пометки, но соседние вершины еще не обработаны; присмотренные— те, которые помечены, и соседние вершины обработаны. Вначале все вершины не помечены.

Описание алгоритма.

I. Нахождение увеличивающей цепи.

1. Присвоить вершине s пометку ( +s, ∞). Вершина s не просмотрена, x=s.

2. Для непросмотренной вершины х с пометкой [±z, ε(x)] и
для непомеченной соседней с ней вершины у выполнить:

2а. Если дуга направлена от х к у и φ (х, у) <f (х, у), то вершина у получает пометку ( +х, min[ε (x), f(x, у)— φ (х, у)]).

26. Если дуга направлена от у к х и φ (у, х) >0, то вершина у получает пометку (-х, min>[e(x), ф(у, х)]).

После выполнения хотя бы одного из шагов (2а или 26) вершина у помечена, в противном случае - нет.

3. Если y=t, то перейти к шагу 6.

4. Если все соседи вершины х обработаны, то х становится просмотренной; в противном случае выбрать новую вершину, соседнюю с вершиной х, и перейти к шагу 2а.

5. Если все вершины просмотрены, то максимальный поток найден; в противном случае выбрать новую непросмотренную вершину и перейти к шагу 2.

II. Увеличение потока.

6. Положить х=t.

7. Если пометка в вершине х имеет вид +z, ε (x)], то φ (z, x) = φ (z, x)+ ε (t), в противном случае φ (х, z)= φ (x, z)- ε (t).

8. Если z = s, то все вершины становятся непомеченными. Перейти к шагу 1; в противном случае положить x = z и перейти к шагу 7.

Нетрудно видеть, что работа алгоритма фактически повторяет доказательство теоремы о максимальном потоке, поэтому не требуется приводить обоснования его правильной работы.

Приведем пример построения максимального потока для сети, изображенной на рис. 5.8 (рис. 5.9). Начальный поток φ(s, t)=l.

В начале вершина s получает пометку ( +s, ∞). Соседними с ней являются

вершины 1, t и 3.

Вершина t не может получить пометку, так как φ(s, t)=f(s, t), вершины 1 и 3 получают пометки ( +s, 5) и ( +s, 3). Из вершины 1 можно пометить вершину t. Величина ε(t)=min(5, 4) =4, следовательно, пометка вершины t будет(+1,4). Поскольку вершина t помечена, то увеличивающая цепь найдена. Величина потока по этой цепи равна ε(t). На рис. 9,а показан результат этой итерации. Цифры около дуг равны величине потока. Жирными линиями обозначены насыщенные дуги. Вторая итерация алгоритма показана на рис.9,6. Здесь увеличивающая цепь есть s, 3, 2, t с величиной потока 3. На третьей итерации (рис.9, в) из вершины s можно пометить только вершину 1, а из этой вершины нельзя пометить ни одной вершины. Следовательно, найден максимальный поток, величина которого равна 8.

Насыщенные дуги образуют разрез сети с пропускной способностью 8. В множество А входят узлы 2, 3, 4, t, а в множество А — 1 и s.

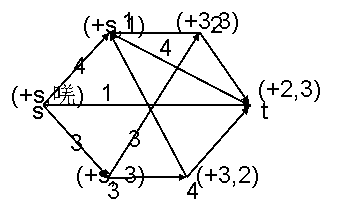
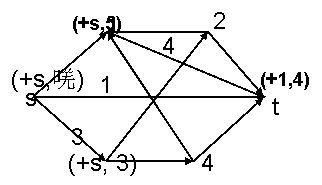
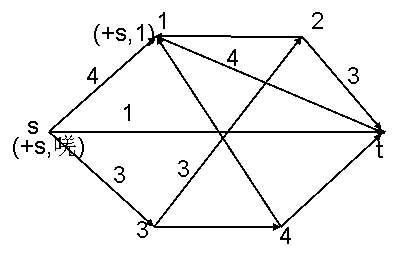
Рис.9

3. ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ И АЛГОРИТМЫ НАХОЖДЕНИЯ КРАТЧАЙШИХ ПУТЕЙ

В этом параграфе будет рассмотрена одна из основных задач теории сетей — задача нахождения кратчайшего пути между двумя заданными вершинами. Эта задача имеет многочисленные практические приложения, а также часто используется как составная часть при решении различных задач оптимизации на сетях.

Пусть дан граф G(W, D), ребрам которого приписаны числа с_j. Обозначим через μ путь, представленный последовательностью дуг d₁, d₂,..., d_q. Длиной пути называется число l(μ), равное сумме всех тех чисел c_j, для которых дуга d_j входит в путь μ:

(5.4)

Задача о кратчайшем пути состоит в нахождении пути от заданной вершины w_s к другой вершине w_t, такого, чтобы его длина была минимальна. Заметим, что эта задача может иметь решение только в том случае, если существует путь из w_s в w_t, что и будет предполагаться в дальнейшем. На числа c_j не накладывается никаких ограничений: они могут быть положительными, отрицательными, равными нулю. Не предполагается выполнение неравенства треугольника. Единственное ограничение состоит в том, чтобы в G не было циклов отрицательной длины. Пусть существует такой цикл. Тогда, двигаясь из w_s к некоторой вершине в таком цикле, а затем, обходя этот цикл достаточное число раз и попадая потом в w_t, можно получить сколь угодно малое l(μ). Это означает, что min l(μ)-> -∞ и в данном случае кратчайшего пути и не существует. Отсюда вытекает, что неориентированные ребра не могут иметь отрицательной длины. Из неотрицательности циклов следует также, что кратчайший путь всегда простой. Действительно, если этот путь содержит повторяющиеся вершины, то часть пути есть цикл. Но длина цикла по предположению неотрицательна, поэтому его можно удалить, уменьшив длину пути или оставив ее без изменения. Таким образом, удаляя из пути все циклы, придем к тому, что оставшаяся часть — простой путь.

Следующие задачи являются обобщением задачи о кратчайшем пути.

1. Найти кратчайшие пути между заданной вершиной w_s и всеми другими вершинами сети.

2. Найти кратчайшие пути между всеми парами вершин в сети.

Рассмотрим следующую задачу оптимизации:

Min z=c₁ix₁+ ... +c_jx_j+... +c_nx_n; (5)

А₁x₁+ ... +A_jx_j+ ... +A_nx_n = E_st; (6)

x_j =0; 1 для j = l n, …, n,... (7)

где А_j - столбец матрицы инциденций; E_st - столбец, все элементы которого равны нулю за исключением элементов, стоящих на s-м и t-м местах, равных соответственно -1 и +1.

По условию (6) х образуют поток, величина которого равна 1. Условие (7) гарантирует, что x_j равно 0 либо 1. Нетрудно видеть, что те дуги, для которых x_j=l, образуют путь из w_s в w_t. Но тогда целевая функция (5) эквивалентна длине пути (4), ибо в (5) в сумму войдут только те c_j, для которых x_j=l. Из сказанного вытекает, что задача (5) — (7) является одной из формулировок задачи о кратчайшем пути.

Заметим, что задача (5)—(7) не является задачей линейного программирования из-за условий (7), но ей эквивалентна следующая задача линейного программирования:

min z = c_ix_i+ ... +c_jX_j+ ... +c_nx_n; (8)

А₁х₁+ ... +A_jX_j+ ... +A_nx_n = E_st; (9)

x_j≥0 для j = l, ..., n, (10)

отличающаяся от (5) — (7) только тем, что условие (7) заменено на условие (10).

Рассмотрим некоторые свойства задачи (8) — (10).

1. Обозначим через m число вершин, а n — число дуг в сети. Тогда система (9) содержит m уравнений с n неизвестными. Однако линейно независимы из них только m—1. Это вытекает из
того, что сумма всех строк в матрице инциденций равна нулю, поэтому m векторов S₁,..., S₁,..., S_m (S₁— строка матрицы инциденций) линейно зависимы. Вычеркнем произвольную строку. Тогда найдется хотя бы один столбец, содержащий только +1 или -1, а остальные элементы равны нулю. Следовательно, может быть равна нулю лишь при α₁= ... = α₁= ...= α_m-1 = 0, что и доказывает линейную независимость матрицы, составленной из m—1-й строки.

2. В базисном решении задачи (8) — (10) содержится m—1
переменная. Свойство 2— следствие свойства 1.3. Базисное решение задачи (8) — (10) —дерево. Каждый столбец A_j соответствует некоторой дуге d_j. Будем считать, что дуга d_j включена в базис, если переменная x_j является базисной. Согласно свойству 2 количество дуг, включенных в базис, равно m—1. Дуги, включенные в базис, не могут образовать цикл. Для доказательства этого предположим, что часть дуг, включенных в базис, образовали цикл. Тогда переменные X_j, соответствующие этим дугам, можно изменить на произвольное число, и поток через остальные, в том числе и небазисные дуги, не изменится. Это противоречит тому, что базисные переменные зависимы, т. е. их значение однозначно определяется небазисными переменными. Но
так как число дуг в графе с m вершинами равно m—1 и эти дуги не образуют цикл, значит, граф — дерево.

4. В любом базисном решении путь от
w_s к любой вершине графа — простой путь.
Это следствие того, что базисное

5. решение — дерево, следовательно,

любая его часть не может содержать

циклов. В любом базисном решении базисные
переменные могут принимать значения +1
или 0, причем +1 только для тех дуг,

которые образуют простой путь из w_s в Wt. Рис.10

В базисном решении больше нуля могут быть только переменные, соответствующие дугам, образующим простую цепь от w_s к w_t. Предположим, что это не так. Но, как только значение переменной, входящей не в путь от w_s к w_t, а в путь от w_s к w_j, станет больше нуля, то по условиям сохранения потока и все остальные переменные, входящие вместе с этой переменной в простую цепь от w_s к wj, станут больше нуля и, следовательно, образуется поток от w_s к wj не равный 0, чего быть не может. Но, так как величина потока от w_s к w_t равна 1 и он нигде не дробится, следовательно, значения переменных x_j, образующих этот поток, равны 1.

Свойство 4 и доказывает эквивалентность задач (8) — (10) и (5) —(7).

Таким образом, задачу о кратчайшем пути можно решать методами линейного программирования.

Пример. Для сети, изображенной на рис. 10, найти кратчайший путь от вершины 1 к вершине 4, если длины дуг таковы: с₁= 1, с₂=4, с₃=1, с₄ = 5, c₅ = 1, c₆=2. Нанеся длины дуг на рис. 10, нетрудно найти, что кратчайший путь w₁, w₂, w₃, w₄ с длиной, равной 4.

Найдем это решение с помощью линейного программирования. Матрица инциденций графа, изображенного на рис. 10, записывается следующим образом:

	D1	D2	D3	D4	D5	D6
W1	1	0	0	1	0	0
W2	-1	1	0	0	-1	1
W3	0	0	1	-1	1	-1
W4	0	-1	-1	0	0	0

Задача линейного программирования, позволяющая найти кратчайшие пути, выглядит так:

— z + х_х + 4х₂ + х₃ + 5х₄ + х₅ -£х„ = 0,

x₁ x_{4 =1}

-x₁+x₂-x₅+x₆=0

-x₂-x₃=-1

Ниже приведено решение этой задачи симплекс-методом:

А) Исходная задача линейного программирования:

-z	X1	X2	X3	X4	X5	X6	c
1	1	4	1	5	1	2	0
0	1	0	0	1	0	0	1
0	-1	1	0	0	-1	1	0
0	0	-1	-1	0	0	0	0

Б) Базисное решение:

-z	1	0	0	-1	2	3	0	-5
X1	0	1	0	0	1	0	0	1
X2	0	0	1	1	0	0	0	1
X3	0	0	0	-1	1	-1	1	0

В) улучшенное решение:

-z	1	0	1	0	2	3	0	-4
X1	0	1	0	0	1	0	0	1
X3	0	0	1	1	0	0	0	1
X6	0	0	1	0	1	-1	1	1

Исходная задача линейного программирования получена из матрицы инциденций вычеркиванием последней строки и добавлением строки и столбца для переменной —z и столбца свободных членов. Выберем в качестве базисных переменных x₁, х₂ и х₆. Нетрудно видеть, что дуги d₁, d₂, d₆ образуют дерево, а длина пути w₁ w₂, w₄, равная сумме длин дуг d₁ и d₂, равна 5. Из базисного решения следует, что x₁ = x₂=l и z = 5. Отрицательная относительная оценка в строке —z показывает, что это решение можно улучшить.

Улучшенное решение z = 4, x₁ = x₃ = x₆=l является оптимальным и совпадает с полученным с помощью анализа путей на графе.

Рассмотренные выше свойства задачи (8) — (10) не изменятся, если правую часть (9) умножить на положительное число V. В этом случае x_j могут быть ,равны нулю или v, причем v только в том случае, если x_j соответствуют дугам, образующим простой путь от w_s к w_t. Значение целевой функции (8) при этом просто увеличится в v раз.

Рассмотрение примера показывает, что решение задачи о кратчайшем пути методами линейного программирования громоздко. Существуют другие существенно более эффективные способы решения этой задачи, к рассмотрению которых мы и перейдем.

Алгоритм Дейкстры используется для неотрицательных длин ребер и позволяет найти кратчайший путь между двумя заданными вершинами или кратчайшие пути от данной вершины ко всем остальным вершинам сети.

Алгоритм основан на приписывании вершинам сети временных или постоянных пометок. На каждой итерации алгоритма величины пометок уменьшаются и только одна из временных пометок становится постоянной. Это показывает, что найден кратчайший путь от вершины w_s до той вершины, пометка которой стала постоянной. После m итераций, где m — число вершин в сети, будут найдены кратчайшие пути до всех вершин. Опишем сначала алгоритм, а затем дадим доказательство того, что он позволяет найти кратчайшие пути.

Введем обозначения:

с_ij— длина дуги между вершинами Wj и Wj;

l'_i — временная пометка вершины Wi;

l_i — постоянная пометка вершины wi;

m — число вершин в сети.

Описание алгоритма:

1. Положить l_s = 0; l_i = ∞ для i=l,... , m; i≠s; k=1; p=s.

2. Для всех соседей вершины w_p с временными пометками изменить пометки в соответствии с выражением

l`<sub>i</sub> = min(l`_i; l_p + c_Pi). (11)

3. Для всех вершин, имеющих временные пометки, найти l_г =

=min l'₁.

4. Положить p=r, k=k+l.

5а. Если требуется найти кратчайший путь до узла w_t: при p = t вычисления закончены, кратчайший путь найден; при невыполнении этого равенства перейти к шагу 2.

5б. Если требуется найти кратчайшие пути до всех вершин сети: при k=m вычисления закончены, в противном случае перейти к шагу 2.

Рассмотрим пример применения алгоритма.

Для сети, изображенной на рис.11,а, найти кратчайшие пути от вершины w_i ко всем остальным вершинам сети. Граф на рис.11,а неориентированный. Будем считать, что каждому неориентированному ребру соответствуют две дуги с одинаковыми длинами, показанными на рис.11,б. Результаты расчетов приведены в табл. 1.

В первом столбце табл. 1 дается номер итерации, во втором — номер вершины, получающей на данной итерации постоянную пометку, а в остальных — величины пометок для каждого узла. Столбец выделяется жирными линиями,

Рис. 11

k	p	L1	L2	L3	L4	L5	L6
1	1	0	∞	∞	∞	∞	∞
2	2	0	1	∞	∞	∞	5
3	3	0	1	4	∞	7	3
4	4	0	1	4	∞	6	3
5	5	0	1	4	9	5	3
6	6	0	1	4	6	5	3

Таблица 1

начиная с той итерации, на которой пометка соответствующей вершины стала постоянной.

На первой итерации пометки всех вершины, кроме первой, временные и равны бесконечности, пометка первой вершины постоянная и равна 0. Соседями вершины w_i являются w₂ и w₆. Временные пометки этих вершин равны: l`₂ = 0+l=l; l'6=0 + 5=5. Выбирая минимальную из них согласно шагу 3, получаем: l₂=min (1,5) = 1. Пометка вершины w₂ становится постоянной: р = 2.

На следующей итерации рассматриваются соседи вершины w₂, имеющие временные пометки. Это w₃, w₅ и w₆. Согласно формуле (11) пересматриваются временные пометки этих вершин: l'3 = min(∞ ,1 + 3) =4; l'₅=min(∞, 1+6) = =7; l`₆=min(5, 1+2) =3. Минимальная из этих временных пометок l'₆, значит, она становится постоянной: l₆ = 3 и р = 6. Дальнейшие итерации (их всего шесть, по числу вершин) происходят аналогично рассмотренным. На рис.11,в приведены кратчайшие пути до всех вершин графа и длины кратчайших путей до каждой вершины. Это дерево может быть получено двумя способами.

Пусть вершина w_i непосредственно .предшествует вершине w_j в кратчайшем пути от w_s к w_t. Тогда для этих вершин выполняется соотношение

l₁ + c_ij = l_j. (12)

Для некоторой вершины w_j должна быть найдена вершина w_i, для которой справедливо (12). Например, для w₄ получаем l₆ = l₅+с₅₄ и, следовательно, вершина w₅ предшествует вершине w₄ в кратчайшем пути.

В другом способе построение дерева кратчайших путей ведется в ходе выполнения алгоритма. Для этого в шаге 2 алгоритма для каждой вершины w_t запоминается номер р, если при минимизации временная отметка уменьшалась. Для вершины w_s записывается число w_s. После выполнения всех итераций для каждой вершины w_j массива будет записан номер w_i вершины, предшествующей w_j в кратчайшем пути до w_i. Так, для рассмотренного примера этот массив будет выглядеть так:

w₁ w₂ w₃ w₄ w₅ w₆

1 1 2 5 3 2

Пусть требуется найти кратчайший путь от w₁ к w₅. Под w₅ стоит цифра, 3, значит, w₃ предшествует w₅ в кратчайшем пути. Далее, переходу к w₃, получаем, что следующая предшествующая вершина w₂, и, наконец, переходя к w₂, получаем, что вершина w₁ предшествует w₂. В итоге получается кратчайший путь: w₁ w₂, w₃, w₅

Перейдем к доказательству того, что алгоритм позволяет найти кратчайшие пути. Отметим, что, если w_s, ... , w_j, ... , w_t — кратчайший путь от w_s к w_t, то w_s, ... , w_j —кратчайший путь от w_s к w_j. Если это было бы не так, то длину пути от w_s к w_j можно было бы уменьшить, в результате чего уменьшился бы путь от w_s к w_t.

На первой итерации алгоритм находит вершину, ближайшую к w_s.

Для этой итерации на втором шаге находятся расстояния от w_s до всех соседних вершин, а на третьем шаге выбирается вершина с минимальным расстоянием. Вследствие неотрицательности длин никакая длина пути, проходящего через другие соседние вершины к выбранной вершине, не может быть меньше этой найденной длины. Пусть на k-м шаге построены кратчайшие пути до вершины w₂,... ,w_k, а вершина w_P получает постоянную пометку на к+1-м шаге. Тогда согласно шагу 2l_р — кратчайшее расстояние до w_p, проходящее через вершины w₁, ..., w_k, до которых уже построены кратчайшие пути. Пусть w_j — вершина, до которой не построен кратчайший путь. Но кратчайший путь к w_P не может проходить через w_j из-за шага 3 алгоритма и неотрицательности длин дуг. Последнее доказывает, что кратчайший путь до w_p построен. Отсюда до индукции следует, что алгоритм строит кратчайшие пути до всех вершин сети.

Алгоритм Дейкстры считается самым экономным из всех известных. Достаточно грубая верхняя оценка количества операций, необходимых для нахождения кратчайших путей из данной вершины ко всем остальным, дает Зm². Реально это количество зависит от количества ребер в графе и существенно меньше указанной величины. Алгоритм можно использовать для нахождения кратчайших путей между всеми вершинами сети, принимая последовательно w_s = w₁, ..., w_s=w_m. В этом случае верхняя оценка количества операций составляет Зm³.

Алгоритм Флойда применим для произвольных, в том числе « отрицательных длин ребер (случай, наличия циклов отрицательной длины нужно исключить). Он позволяет найти кратчайшие пути между всеми парами вершин сети. Метод основан на последовательном преобразовании матрицы С, в которой первоначально записаны длины c_ij всех дуг сети. В случае неориентированного ребра ему ставятся в соответствие две дуги.

Описание алгоритма:

1. Сформировать матрицу С, элемент которой

c_ij=

={ 0, если i = j;

={ длине дуги между w_i и w_j, если такая дуга существует; ∞, если дуги между w_i и w_j нет.

Положим к=1.

2. Для всех i≠к, j≠к осуществить операцию c_ij = min[c_ij,(c_ik + c_kj)].

3. Если с_ij<0, то в графе существует цикл отрицательной длины, содержащий вершину w_i. Решение неограниченно. В противном случае идти к шагу 4.

4. Если k = m, вычисления закончены, решение найдено. Если
нет, перейти к шагу 5.

5. Положить k=k+l, перейти к шагу 2.

Если длины всех дуг неотрицательны, то шаг 3 можно исключить.

Рассмотрим пример. Для сети, изображенной на рис.11,а, найти кратчайшие пути между всеми узлами.

Исходная матрица

	1	2	3	4	5	6
1	0	1	∞	∞	∞	5
2	1	0	∞	∞	6	2
3	∞	3	0	5	1	3
4	∞	∞	5	0	1	∞
5	∞	6	1	1	0	3
6	5	2	3	∞	∞	0

На первой итерации при k = 1 получилось так, что матрица не меняется. Поэтому рассмотрим случай k = 2. Матрица, полученная после второй итерации:

	1	2	3	4	5	6
1	0	1	4	∞	7	3
2	1	0	3	∞	6	2
3	4	3	0	5	1	3
4	∞	∞	5	0	1	∞
5	7	6	1	1	0	3
6	3	2	3	∞	3	0

c₁₃ = min(c₁₃,c₁₂ + с₂₃) = min (∞, 1+3) = 4;

c₁₄ = min(c₁₄,c₁₂- с₂₄) =min (∞, 1+ ∞)= ∞∞;

c₁₅ = min(c₁₅,c₁₂-c₂₆) = min(∞, 1+6) = 7;

с₁₆ = min(c₁₅,c₁₂-c₂₆) = rain (5,1+2) = 3.

Полученные числа записаны в первой строке этой матрицы, аналогично найдены ее остальные строки.

Окончательный результат:

	1	2	3	4	5	6
1	0	1	4	6	5	3
2	1	0	3	5	4	2
3	4	3	0	2	1	3
4	6	5	2	0	1	4
5	5	4	1	1	0	3
6	3	2	3	4	3	0

Нетрудно видеть, что первая строка матрицы дает длины кратчайших путей от первой вершины сети ко всем остальным. Эти величины совпадают с найденным выше алгоритмом Дейкстры.

Сами кратчайшие пути могут быть получены по последней матрице с использованием для каждой строки формулы (12), где l_i и l_j - числа, записанные в i-м и j-м столбцах матрицы.

Другим способом является построение специальной матрицы в ходе выполнения алгоритма. Это матрица должна содержать число строк и столбцов, равное числу вершин в графе. Обозначим e_ij — элемент этой матрицы. На первом шаге алгоритма e_ij полагается равным номеру столбца матрицы, т. е. e_ij = j. На втором шаге алгоритма e_ij может изменяться по следующему правилу:

e_ij=

={e_kj если c_ij>(c_ik+c_kj),

={e_ij, если c_ij≤ (c_ik+c_kj).

Элемент e_ij показывает промежуточную вершину, непосредственно предшествующую w_j на пути от w_i к w_j. Поиск пути производится аналогично рассмотренному ранее в алгоритме Дейкстры.

Верхняя оценка количества операций в алгоритме Флойда составляет 2m³, т. е. он работает примерно в 1,5 раза быстрее, чем алгоритм Дейкстры, если последний используется для нахождения кратчайших путей между всеми вершинами сети.

Приведем доказательство правильности работы алгоритма Флойда. Назовем базисной кратчайшую дугу, возможно фиктивную, между двумя производными вершинами w_p и w_q. Тогда задача нахождения кратчайшего пути между w_P и w_q сводится к поиску базисной дуги. Пусть w_k—промежуточный узел в кратчайшем пути от w_p к w_q, имеющий минимальный индекс, a w_i и w_j — соседи этого узла в таком пути. При выполнении шага 2 алгоритма Флойда будет получена базисная дуга между узлами w_i, w_j. После этого узел w_k можно исключить из сети и повторить итерацию для следующего узла с минимальным индексом. Таким образом, после просмотра всех промежуточных узлов будет найдена базисная дуга между w_p и w_q.

Список литературы

1. Теоретические основы почтовой связи: Учебник для вузов/ С.М. Хлытчиев, Н.П. Тарасова, В.М. Лившиц.-2-е изд., препаб. и доп. – М.: «Радио и связь»-1990-280 с.

2. Птицын Г.А. Модели обработки и перевозки почты – М.:-МИС,1988.-40 с.

3. Князютенков В.А., Птицын Г.А. Оптимизация сетей почтовой связи –М:-МТУСИ, 1997, -70 с.

4. Экономико-математические методы и модели в планировании и управлении в отрасли связи: Учебник для вузов/ В.А.Барсук, Н.М. Губин, А.Р. Батый- 3-е изд., перераб. и доп. –М.: Радио и связь, 1984- 264 с.

5. Организация автоматизированной обработки почтовых отправлений в крупных узлах связи \ И.В.Барсук, Г.К. Гиль, А.Л. Воскресенский и др.- М.: Радио и связь, 1985- 208 с.

ПРИЛОЖЕНИЕ

Для приведенного орграфа приведите матрицу смежности и инциденций, обозначьте все имеющиеся простые и замкнутые цепи, гамильтоновый контур, для каждой вершины орграфа найти множество Г(w_i).

Определить максимальный поток из п. А в п. D, используя для этого все возможные участки сети.

Для приведенного графа методом Флойда составить матрицу для случая К=1 и К=2.

Для приведенного графа методом Флойда составить матрицу для случая К=1 и К=2.

Для сети, изображенной на рисунке, найти кратчайшие пути от W₁ по всем остальным методом Дейнстры.

Для сети, изображенной на рисунке, найти кратчайшие пути от W₁ по всем остальным методом Дейнстры.

Для приведенного графа методом Флойда составить матрицу для случая К=1 и К=2.

Для приведенного графа методом Флойда составить матрицу для случая К=3.

Определить для каждой вершины орграфа множество Г(w_i); приведите примеры простой цепи, замкнутой цепи, гамильтонового контура.

Составить матрицу смежности и инцидентности.

Методическое пособие по курсу:

Теоретические основы почтовой связи

Рассмотрено на заседании кафедры

«Автоматизация почтовой службы» протокол №______________

Рекомендовано к печати

Составитель: Саидазимова К.М.

Ишдавлетова Э.Т.

Ответственный редактор:

Корректор: