ЎЗБЕКИСТОН АЛОҚА ВА АХБОРОТЛАШТИРИШ АГЕНТЛИГИ
ТОШКЕНТ
АХБОРОТ ТЕХНОЛОГИЯЛАРИ УНИВЕРСИТЕТИ
“Почта
хизматини автоматлаштириш”
кафедраси
“ Почта
хизматини назарий асослари“ фанидан
почта йўналиши
талабалари учун
амалий машғулотлар
бўйича
УСЛУБИЙ ҚӮЛЛАНМА
Тошкент 2007
Кириш.
Почта
алоқаси тизим сифатида шундай хусусиятларга эгаки, уни мураккаб тизимлар
синфига киритиш мумкин. Бу хусусиятларни фақат математик моделлаштириш
йўли билан тадқиқ этиш мумкин. Аммо бу тадқиқотлар жуда
мураккаб ёки уни амалга ошириш қийин. Шу сабабли мураккаб тизимлар кичик
алохида тизимларга бўлинадики, улар ё аналитик ёки имитацион моделлаштирилади.
Ушбу услубий
қўлланмада почта алоқасининг айрим масалаларини графлар ва
тармоқлар назарияси асосида ечиш намуналари кўриб чиқилган.
1.
Графлар ва тармоқлар назариясидан айрим
маълумотлар.
Оптимизациянинг
тармоқли моделлари почта алоқаси тизимларини лойиҳалаштириш,
почта ташувини ташкиллаштириш, почта корхоналарини жойлаштиришда учровчи
масалаларнинг кенг синфини қамраб олади. Қоида бўйича бу масалалар
чизиқли мақсадли функция ва чизиқли чекланишлар билан
характерланадики, уларни ечиш учун чизиқли дастурлашнинг маълум
усулларидан фойдаланиш мумкин. Аммо бу масалаларнинг ўзига ҳос
ҳусусияти шундаки, уларнинг ўлчамлари катта ва уларни ечиш учун самарали
алгоритмларни излаш зарурияти пайдо бўлади. Ечилаётган масалани тармоқ
ёки граф кўринишида тасаввур қилиш бундай алгоримтларни қуришнинг асосини
ташкил этади. Ушбу бўлимда почта алоқасига бевосита алоқадор бўлган
бир неча шундай масалаларни ечиш алгоритмлари кўриб чиқилади.
![]() графи
графи ![]() билан белгиланувчи
кўплаб чўққилар
билан белгиланувчи
кўплаб чўққилар ![]() ва
ва![]() билан ифодаланувчи ва айрим ёки барча чўққиларни
бирлаштирувчи кўплаб қовурғалар билан
билан ифодаланувчи ва айрим ёки барча чўққиларни
бирлаштирувчи кўплаб қовурғалар билан ![]() берилган.
берилган.
Графнинг
геометрик тасвири 1- расмда берилган. ![]() ва
ва ![]() нинг кўплиги
нинг кўплиги ![]() билан ифодаланувчи
графни белгилаб беради. Агар кўплаб
билан ифодаланувчи
графни белгилаб беради. Агар кўплаб ![]() дан ташкил топган
қовурғалар йўналтирилган бўлса (одатда стрелкалар билан
кўрсатилади), улар ёйлар деб
аталади, бундай қовурғали граф эса йўналтирилган граф дейилади.
Агар қовурғалар йўналишга эга бўлмаса, улар йўналтирилмаган деб
аталади.
дан ташкил топган
қовурғалар йўналтирилган бўлса (одатда стрелкалар билан
кўрсатилади), улар ёйлар деб
аталади, бундай қовурғали граф эса йўналтирилган граф дейилади.
Агар қовурғалар йўналишга эга бўлмаса, улар йўналтирилмаган деб
аталади.
Ҳар бир
чўққиларнинг тартибка келтирилган жуфтлиги ![]() билан берилиши мумкин. Бунда
ёйнинг йўналиши
билан берилиши мумкин. Бунда
ёйнинг йўналиши ![]() дан
дан ![]() га қараб
ҳисобланади:
га қараб
ҳисобланади: ![]() - бошланғич,
- бошланғич, ![]() эса
эса ![]() ёйнинг охирги нуқтаси
дейилади. Айрим пайтларда
ёйнинг охирги нуқтаси
дейилади. Айрим пайтларда ![]() ёй
ёй ![]() ва
ва ![]() га инцидент дейилади.
га инцидент дейилади.
Қоидага
кўра йўналтирилмаган қовурғани ![]() ва
ва ![]() жуфтлик кўринишида тасаввур
қилиш ва аксинча, ёйнинг йўналиши кичик бўлса уни қовурғага
алмаштириш мумкин. Йўналтирилган граф кўплаб чўққилар ва
жуфтлик кўринишида тасаввур
қилиш ва аксинча, ёйнинг йўналиши кичик бўлса уни қовурғага
алмаштириш мумкин. Йўналтирилган граф кўплаб чўққилар ва ![]() чўққи
қандай чўққилар билан
боғланганлигини кўрсатувчи кўплаб
чўққи
қандай чўққилар билан
боғланганлигини кўрсатувчи кўплаб ![]() чўққилари
кўринишида берилган бўлиши мумкин. Масалан 1-расмда кўрсатилган граф учун
чўққилари
кўринишида берилган бўлиши мумкин. Масалан 1-расмда кўрсатилган граф учун ![]() эса
эса ![]() га тенг.
га тенг. ![]() кўплигини
кўплигини ![]() чўққининг
қўшнилари деб атаймиз. Йўналтирилмаган граф холатида
чўққининг
қўшнилари деб атаймиз. Йўналтирилмаган граф холатида ![]() кўплиги ҳар бир
йўналтирилмаган қовурғани иккита йўналтирилган
қовурғага алмаштирилгач аниқланади.
кўплиги ҳар бир
йўналтирилмаган қовурғани иккита йўналтирилган
қовурғага алмаштирилгач аниқланади.
Йўналтирилмаган графда
йўл деб ёйлар кетма-кетлиги тушинилиб, унда ҳар бир охирги
чўққи (энг сўнгисидан ташқари) навбатдаги қовурғанинг
бошланғич чўққиси хисобланади. Масалан 1-расмда ![]() ;
; ![]() йўллар хисобланади.
йўллар хисобланади.
Ҳар бир чўққиси бир
мартадан кўп қўлланилмайдиган йўл содда йўл дейилади. ![]() йўл – содда йўл,
йўл – содда йўл, ![]() йўл эса содда йўл
эмас. Кўпинча йўлни белгилаш учун чўққилар рўйхати
қўлланилади. Масалан 1-расмдаги
йўл эса содда йўл
эмас. Кўпинча йўлни белгилаш учун чўққилар рўйхати
қўлланилади. Масалан 1-расмдаги ![]() йўлни
йўлни ![]() деб ёзиш мумкин.
Бундай ёзув ёйлар рўйхатидан кўра кўпроқ ишлатилади ва унга қараб
ушбу йўллинг соддами ёки йўқлигини аниқлаш осон.
деб ёзиш мумкин.
Бундай ёзув ёйлар рўйхатидан кўра кўпроқ ишлатилади ва унга қараб
ушбу йўллинг соддами ёки йўқлигини аниқлаш осон.

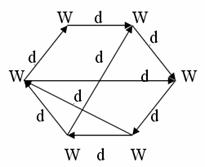
1 – расм. 2 – расм.
Агар содда йўлда
ёйлар йўналиши мос келмаса бундай йўл содда занжир деб аталади. Масалан,
1-расмдаги W1,W6,W3,W4 кетма-кетлиги
содда занжир хисобланади. Чунки W1-бошланғич
чўққидан охирги W4
чўққига қараб харакатланганда (W1,W6) ёйнинг йўналиши
қолган ёйларнинг йўналишига мос келмайди. Биз бундан кейин фақат
содда йўллар ва занжирларни кўриб чиқамиз, шунинг учун “содда” атамаси тушиб қолдирилади.
Агар
чўққиларнинг исталган жуфтлиги ўртасида шу чўққиларни
боғловчи занжир мавжуд бўлса бу граф боғланган граф дейилади.
Қуйида фақат боғланган графлар кўриб чиқилади ва
графнинг бу хусусияти тўғрисида алоҳида сўз юритилмайди.
Агар D1 ёйнинг бошланғич чўққиси Dk ёйнинг сўнги чўққисига мос келса бу D1...Dk занжир
ёпиқ занжир дейилади. Ёпиқ занжир цикл дейилади. Масалан,
1-расмдаги графда D5,D6,D9 циклни
ҳосил қилади. Худди шу циклни W1,W5,W6,W1
чўққилар рўйхати кўринишда ҳам ёзишимиз мумкин.
Бошланғич
ва сўнги чўққилари мос келган йўл контур дейилади. Масалан,
1-расмда W1,W4,W5,W1 контурни
ҳосил қилади. Агар контур графнинг барча чўққиларини ўз
ичига олса бундай контур гамильтонли
контур дейилади. Албатда исталган граф гамильтонли
контурга эга бўлмайди. Масалан, 2-расмда граф бундай контурга эга эмас,
1-расмдаги графда эса D1,D2,D3,D4,D5,D6 гамильтонли
контур хисобланади. Агар чўққиларнинг исталган жуфтлиги учун уларни
бирлаштирадиган ҳеч бўлмаганда битта қовурға мавжуд бўлса G граф тўлиқ дейилади.
3 – расмда тўртта чўққили тўлиқ йўналтирилмаган граф
тасвирланган. Тўлиқ граф максимал қовурғалар сонига эга. Йўналтирилмаган
граф учун бу сон m(m-1),
Маьлум даражада дарахт тўлиқ графнинг
акси ҳисобланади. Дарахтнинг қуйидаги хусусиятлари эквивалентдир.
Йўналтирилмаган дарахт – бу :
а) m чўққилар
ва m-1 қовурғалар ўз
ичига олган боғланган граф;
б) циклларга эга бўлмаган боғланган
граф;
в) чўққиларнинг ҳар бир
жуфтлиги битта ва фақат битта йўл билан боғланган граф.

3-расм 4-расм
Бу таърифлардан
кўриниб турибдики, эркин G(W, D) графда
қовурғаларни кетма – кет ўчирса граф боғланган граф бўлиб
қолади. Графда m-1 қовурға
қолгандан сўнг G(W, D) графнинг асосий
дарахти хосил бўлади.
Албатда бунга
эришишнинг йўли ягона эмас ва G(W, D) графнинг бир
неча асосий дарахтлари мавжуд. 4-расмда 3-расмдаги графнинг иккита асосий
дарахти тасвирланган.
Йўналтирилган
графда Wi чўққига
йўналтирилган ёйлар сони Wi
чўққига киришнинг ярим даражаси дейилади,
Wi
чўққидан йўналтирилган ёйлар сони бу чўққининг
бошланиши ярим даражаси деб аталади. Wi чўққидан йўналтирилган ёйлар кўплиги W1-С – (Wi) деб белгиланади.
1-расмда С+(W1)={D1,D8},
С --(W1)={D9,
D6}. Шу тушунчадан
фойдаланиб графда йўналтирилган дарахтга таъриф бериш мумкин. Йўналтирилган
дарахт циклларсиз йўналтирилган граф бўлиб, хар бир чўққи
(биттасидан ташқари) киришнинг ярим
даражаси
Йўналтирилмаган
дарахтни йўналтирилган дарахтга айлантириш мумкин. Бунда эгри чўққи
ўзак сифатида танлаб олинади ва қовурғаларга шундай йўналиш бериладики,
бунда ҳар бир чўққи ўзак билан битта ва фақат битта
содда йўл билан боғланиши керак.
Бошланиши ярим
даражаси
Агар бир ёки бир
неча жуфт чўққилар ўртасида бирдан ортиқ қовурға
мавжуд бўлса G граф муьтиграф деб аталади. 6-расмда мультиграф кўрсатилган. Чўққилар
орасида турли қовурғалар айрим хусусиятлар билан (масалан,
узунлиги, ўтказувчанлик хусусияти ва х. З.) фарқланса мультиграфни
киритиш мақсадга мувофиқ бўлади. Қатор ҳолларда икки
чўққи ўртасидаги қовурғалар йиғиндисини
эквивалент характеристикали битта қовурға билан алмаштириш мумкин.
Шуни назарда тутиб қуйида мультиграфлар кўриб чиқилмайди.


5-расм 6-расм
Графнинг алгебрик
топшириқлари учун қуйидаги матрицалардан фойдаланилади.
Ёндошлик
матрицаси деб қатор ва устун рақамлари графнинг
чўққисига мос келувчи S квадрат матрицага айтилади.
Бу матрицанинг элементи Sij={1}, агар графда Wi ва Wj
чўққилар ўртасида қовурға бўлса) Sij={0}, агар бундай қовурға бўлмаса.
S матрицада қаторлар ва устунлар сони графдаги
чўққилар сонига тенг. Йўналтирилмаган граф учун ёндошлик матрицаси
асосий диоганалга нисбатан симметрик.
А инциденциялар матрицаси – қаторлари сони m, устунлар сони n, бу ерда m- чўққилар сони, n эса графдаги
қовурғалар сони. Матрицанинг ҳар бир қатори графнинг
чўққисига мос келади, ҳар бир устун эса қовурғага
тўғри келади. Aij матрицанинг
элементи орграф учун
aij={1, агар вш ёйи Wi чўққига инцидент бўлса ва Wi дан йўналган бўлса;
={-1, агар шв Wi чўққига инцидент
бўлса ва Wi га йўналган
бўлса;
={0, бошқа барча ҳоллар учун.

7-расм 8-расм
7-расмда
йўналтирилган граф берилган, қуйироқда ёндошлик матрицаси ва бу
графнинг инциденциялари келтирилган.
Ҳар бир
қовурға доим иккита ҳар хил чўққиларга инцидент
бўлганлиги ва биридан иккинчисига йўналганлиги боис матрицанинг ҳар бир
устуни битта +1 ва битта
|
|
W1 |
W2 |
W3 |
W4 |
W5 |
W6 |
|
W1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
W2 |
0 |
0 |
0 |
0 |
1 |
1 |
|
W3 |
0 |
0 |
0 |
0 |
0 |
0 |
|
W4 |
0 |
0 |
1 |
0 |
0 |
0 |
|
W5 |
1 |
0 |
0 |
1 |
0 |
0 |
|
W6 |
1 |
0 |
0 |
0 |
1 |
0 |
Ёндошлик
матрицаси.
|
|
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
|
W1 |
1 |
1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
|
W2 |
-1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
W3 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
|
W4 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
|
W5 |
0 |
0 |
-1 |
0 |
1 |
-1 |
1 |
0 |
|
W6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
Инциденциялар
матрицаси.
Йўналтирилган
граф учун dj=(Wi, Wk)
қовурғалар мос келувчи j устунда i – нчи ва k – нчи қаторларда
бирлар ёзилади, қолган қаторларда ноллар ёзилади.
Графни инциденциялар
матрицаси кўринишида тасаввур қилиш ҳар доим ҳам ўзини
оқламайди, чунки бундай матрицани ЭХМ хотирасида сақлаш учун mn сўз талаб
қилинади. Бундан ташқари ахборотга кириш кўпинча ноқулай.
Масалан, (Wi, Wj)
қовурғаси мавжудми деган саволга жавоб олиш учун матрицанинг барча
устунларини кўриб чиқиш керак. Ҳудди шундай камчмликлар ёндошлик
матрицасида ҳам мавжуд. Графни қовурғалар ёки ёйлар рўйхати
кўринишида бериш анча қулай. Бунда хотира анча тежалади ва графдаги кўп
сонли чўққилар ва қовурғаларни излаш осон кўчади.
Амалий
вазифаларда чўққилар ёки қовурғаларга сонлар
қўшиб ёзилади. Бундай граф тармоқ
дейилади. Айрим пайтларда тармоқ деганда транспорт тармоғи ёки алоқа
тармоғи тасаввур қилинади. Бунда эса граф чўққилари – шаҳарларни, транспорт пунклари,
алоқа узеллари, қовурғалар эса – шу шахарларни ёки
алоқа линияларини боғловчи йўллардир. Транспорт ёки алоқа
тармоқлари ҳолатида эса чўққиларга ёки
қовурғаларга қўшиб ёзиладиган сонлар қовурға
узунлигини, маҳсулотни шу қовурға бўйлаб ташиш таннархи,
чўққи ёки қовурғанинг ўтказувчанлик хусусияти,
қовурға ва чўққининг ишончлилиги ва ҳ. з. ларни
англатиши мумкин.
2. Максимал
оқим теоремаси ва максимал оқимни аниқлаш алгоритми.
G(W, D) эркин,
йўналтирилган графни кўриб чиқамиз. Графнинг ҳар бир
(x, y) ёйига f(x, y) сонини солиштирамиз. f(x,y) сони (x, y) нинг ўтказувчанлик хусусияти
дейилади.
S манбани ва t оқимни ажрати б оламиз. Агар φ(х, у) функция
қуйидаги шартларни қониқтирса тармоқдаги оқим
дейилади:
1. φ(х, у) ≥ 0 (1)
2. Исталган х чўққи
учун кирувчи оқимнинг йиғиндиси чиқувчи оқим
йиғиндисига тенг, яъни
![]()
![]() (2)
(2)
![]() +(
+(![]() )
) ![]() -(
-(![]() )
)
3. ![]() (3)
(3)
Оқим
катталиги деб S дан чиқувчи
оқимнинг барча ёйлар бўйича йиғиндисига айтилади : ![]() . Оқимнинг сақланиш шартига биноан
. Оқимнинг сақланиш шартига биноан
![]() +(
+(![]() ) (2) бу катталик t га кирувчи ёйлар бўйича
оқими йииндисига тенг. Вазифа шундан иборатки, V катталик максимал бўлган
оқимни топиш керак. Майли
) (2) бу катталик t га кирувчи ёйлар бўйича
оқими йииндисига тенг. Вазифа шундан иборатки, V катталик максимал бўлган
оқимни топиш керак. Майли ![]() шундай бўлсинки,
бунда S A га эмас t
шундай бўлсинки,
бунда S A га эмас t![]() га тегишли бўлсин. G(W, D) тармоқнинг кесмаси деб А га кирувчи ёйлар кўплигига айтилади, яъни бу ёйлар A дан чиққан чўққиларни А га тегишли чўққилар билан боғлайди. Кесманинг
ўтказувчанлик хоссаси деб кесмага кирувчи ёйларнинг ўтказувчанлик хоссалари
йиғиндисига айтилади.
га тегишли бўлсин. G(W, D) тармоқнинг кесмаси деб А га кирувчи ёйлар кўплигига айтилади, яъни бу ёйлар A дан чиққан чўққиларни А га тегишли чўққилар билан боғлайди. Кесманинг
ўтказувчанлик хоссаси деб кесмага кирувчи ёйларнинг ўтказувчанлик хоссалари
йиғиндисига айтилади. ![]() ёйи
ёйи ![]() бўлганда тўйинган
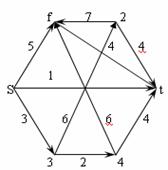
дейилади. 8-расмда киритилган тушунчалар акс эттирилган ёйлар олдидаги
рақамлар уларнинг ўтказувчанлик хоссаларини кўрсатади.
бўлганда тўйинган
дейилади. 8-расмда киритилган тушунчалар акс эттирилган ёйлар олдидаги
рақамлар уларнинг ўтказувчанлик хоссаларини кўрсатади. ![]()
![]() =2;
=2; ![]()
![]()
![]() функцияси
функцияси ![]() катталикдаги
оқим хисобланади. Агар А кўплигига 2, t, 4 чўққилари кирса
катталикдаги
оқим хисобланади. Агар А кўплигига 2, t, 4 чўққилари кирса ![]()
![]() ёйлар кўплиги кесма
бўлади ва унинг ўтказувчанлик хусусияти 1+9+6+2=18 бўлади.
ёйлар кўплиги кесма
бўлади ва унинг ўтказувчанлик хусусияти 1+9+6+2=18 бўлади. ![]() ёйи тўйинган,
қолганлари эса тўйинмаган бўлади.
ёйи тўйинган,
қолганлари эса тўйинмаган бўлади.
Максимал оқим теоремаси
қуйидагича. Берилган тармоқда
оқимнинг максимал катталиги кесманинг минимал утказувчанлик хусусиятига
тенг. Теореманинг исботи қуйидаги мулохазаларга асосланади. S дан t га айрим йўлни кўриб
чиқамиз. Агар бу йўлнинг барча ёйлари тўйнган бўлса оқимни
катталаштириши мумкин. Белгилаб оламиз ![]() кўриниб турибдики,
оқим катталиги
кўриниб турибдики,
оқим катталиги ![]() га (1)—( ) шартни
бузмасдан ошиши мумкин, масалан,
8-расимда s йўл учун оқим
катталиги 3,4 t бўлганда
га (1)—( ) шартни
бузмасдан ошиши мумкин, масалан,
8-расимда s йўл учун оқим
катталиги 3,4 t бўлганда ![]()
![]()
![]() ва
ва ![]() ифодалар бўлганда
оқимни 1га ошириш мумкин.
ифодалар бўлганда
оқимни 1га ошириш мумкин.
Энди ёйлар қисмларининг йўналиши
занжирнинг ўтиши йўналишига мос келмайдиган занжирни кўриб чиқамиз. Бу
йўналишлар мос келса юқорида келтирилган ифодаларни сақлаб
қоламиз, йўналишлари тўғри келмайдиганларини ![]() деб белгилаймиз
ва
деб белгилаймиз
ва ![]() ни киритамиз, унда
оқим катталиги ҳар бир ёйда
ни киритамиз, унда
оқим катталиги ҳар бир ёйда ![]() га катталаштиради
(йўналишлари мос келмайдиганлари учун). Масалан, 8-расмда s, 1, 4, t занжир учун ва
га катталаштиради
(йўналишлари мос келмайдиганлари учун). Масалан, 8-расмда s, 1, 4, t занжир учун ва ![]()
![]() ва
ва![]() ва ҳосил бўлади
ва ҳосил бўлади
![]()
![]() ,
, ![]() ,
, ![]() ва
ва ![]() .
. ![]() ва
ва ![]() ёйларда
ёйларда ![]() ёйда
ёйда
Нихоят, ![]() ,
, ![]() ,
, ![]()
![]()
![]() дан занжир мавжуд
бўлмаса, оқим катталиги катталаштириб бўлмайди.
дан занжир мавжуд
бўлмаса, оқим катталиги катталаштириб бўлмайди. ![]() ёки
ёки ![]() бўлган барча ёйларни
графдан олиб ташлаб ҳеч бўлмаганда иккита боғланмаган подграф
ҳосил қиламиз, улардан биттаси t
чўққини ўз ичига олади. Бу подграф А кесмани
аниқлайди, унинг ўтказувчанлик хусусияти максимал оқимга тенг,
чунки Ā дан А га элтувчи барча ёйлар тўйинган. Аммо исталган оқим учун унинг
катталиги исталган кесманинг ўтказувчанлик хоссасидан катта бўла олмайди – теорема
исбот қилинди.
бўлган барча ёйларни
графдан олиб ташлаб ҳеч бўлмаганда иккита боғланмаган подграф
ҳосил қиламиз, улардан биттаси t
чўққини ўз ичига олади. Бу подграф А кесмани
аниқлайди, унинг ўтказувчанлик хусусияти максимал оқимга тенг,
чунки Ā дан А га элтувчи барча ёйлар тўйинган. Аммо исталган оқим учун унинг
катталиги исталган кесманинг ўтказувчанлик хоссасидан катта бўла олмайди – теорема
исбот қилинди.
Энди максимал
оқимни топиш алгоритмини кўриб чиқамиз. У икки қисмдан
иборат. Улардан биринчиси оқимни оширувчи занжирни топишга мўлжалланган.
Агар бундай занжир бўлмаса, демак максимал оқим топилган. Икикнчи
қисм оқимни топилган занжир бўйлаб катталаштирилади. Тармоқнинг
ҳар бир чўққиси алгоритмининг ишлаш жараёнида ![]() кўринишидаги белгини
олади. Белгининг биринчи қисми оқимнинг
кўринишидаги белгини
олади. Белгининг биринчи қисми оқимнинг ![]() ёки
ёки ![]() ёйда катталаниш кераклигини(+белгиси)
ёки кичрайиши кералигини (-белгиси)
билдиради. Иккинчи қисм оқим катталаниши керак бўлган жорий
қиймат.
ёйда катталаниш кераклигини(+белгиси)
ёки кичрайиши кералигини (-белгиси)
билдиради. Иккинчи қисм оқим катталаниши керак бўлган жорий
қиймат.
Алгоритм ишни
эркин оқимдан бошлайди ва у нолинчи бўлиши мумкин. Белгиларни қўйиб
чиқиш тармоқ чўққиларини уч турга бўлади:
белгиланмаганлари – белги қўйилмаганлари; белгиланганлари – белги
қўйилганлари, аммо қўшни чўққилар ишлаб
чиқилмаган; кўзда тутилган– белги қўйилган ва қўшни
чўққилар ишлаб чиқилмаган. Дастлаб барча чўққилар
белгиланмаган бўлади.
Алгоритмни тасвирлаш.
I. Катталаштирувчи занжирни топиш.
1.
чўққига s белгисини қўйиш ![]() . s чўққиси кўриб чиқилмаган,
. s чўққиси кўриб чиқилмаган, ![]() .
.
2.
![]() белгиси
қўйилган, кўриб чиқилмаган чўққи учун ва у билан
қўшни белгиланмаган чўққи учун бажаринг:
белгиси
қўйилган, кўриб чиқилмаган чўққи учун ва у билан
қўшни белгиланмаган чўққи учун бажаринг:
2.а. Агар
ёй ![]() дан
дан ![]() га ва
га ва ![]() , йўлланган бўлса
, йўлланган бўлса
чўққи ![]() белгини олади.
белгини олади.
2.б. Агар ёй ![]() дан
дан ![]() га ва
га ва ![]() га йўлланган бўлса
чўққи
га йўлланган бўлса
чўққи
![]() белгини олади.
белгини олади.
Ҳеч бўлмаса битта босқич бажарилмаса (2.а
ёки 2.б) у чўққи белгиланади, акс холда йўқ.
3.
агар ![]() бўлса кейинги 6
босқичга ўтиш керак.
бўлса кейинги 6
босқичга ўтиш керак.
4.
агар ![]() чўққининг
барча қийматоари ишланган бўлса,
чўққининг
барча қийматоари ишланган бўлса, ![]() кўриб чиқилган
бўлади; акс холда
кўриб чиқилган
бўлади; акс холда ![]() чўққига
қўшни янги чўққини танлаш керак ва 2.а босқичга ўтиш
керак.
чўққига
қўшни янги чўққини танлаш керак ва 2.а босқичга ўтиш
керак.
5.
агар барча чўққилар кўриб чиқилган
бўлса, максимал оқим топилган бўлади; акс ҳолда янги кўрилмаган
чўққини танлаш ва 2 – босқичга ўтиш керак.
II.
Оқимни катталаштириш.
6. ![]() қўйиш керак.
қўйиш керак.
7.
агар ![]() чўққидаги
белги
чўққидаги
белги ![]() кўринишга эга бўлса,
унда
кўринишга эга бўлса,
унда
![]() бўлади, акс холда
бўлади, акс холда ![]() .
.
8.
агар ![]() бўлса, у холда барча
чўққилар белгиланмаган бўлади ва 1-босқичга ўтиш крак, акс
холда
бўлса, у холда барча
чўққилар белгиланмаган бўлади ва 1-босқичга ўтиш крак, акс
холда ![]() ни қўйиб 7 – босқичга ўтиш керак.
ни қўйиб 7 – босқичга ўтиш керак.
Кўриниб турибдики,
алгоритм иши максимал оқим теоремаси исботини такрорлайди, шу боис унинг
иши тўғрилигини асослаш шарт эмас. 5.8 – 5.9 – расмда тасвирланган
тармоқ учун максимал оқим тузилишига мисол келтирамиз.
Бошланғич оқим ![]() .
.
Бунда ![]() чўққи
чўққи ![]() белгини олади.
белгини олади. ![]() ва 3
чўққилар унга қўшни хисобланади.
ва 3
чўққилар унга қўшни хисобланади.
![]() чўққиси
белги олмайди, чунки
чўққиси
белги олмайди, чунки ![]() , 1 ва 3 чўққилар
, 1 ва 3 чўққилар ![]() ва
ва ![]() белгисини олади. 1
чўққисидан
белгисини олади. 1
чўққисидан ![]() чўққини
белгилаш мумкин.
чўққини
белгилаш мумкин. ![]() , шу сабабли
, шу сабабли ![]() катталик
катталик ![]() бўлади.
бўлади. ![]() чўққи
белгиланган бўлганлиги учун катталаштирувчи занжир топилган. Бу занжир бўйлаб
оқим катталиги
чўққи
белгиланган бўлганлиги учун катталаштирувчи занжир топилган. Бу занжир бўйлаб
оқим катталиги ![]() га тенг. 9.а расмда бу
итерациянинг натижаси кўрсатилган. Ёй олдидаги сонлар оқим катталигига
тенг. Тўйинган ёйлар қалин чизиқлар билан белгиланган. Алгоритмнинг
иккинчи интеграцияси 9.б – расмда кўрсатилган. Бу ерда
га тенг. 9.а расмда бу
итерациянинг натижаси кўрсатилган. Ёй олдидаги сонлар оқим катталигига
тенг. Тўйинган ёйлар қалин чизиқлар билан белгиланган. Алгоритмнинг
иккинчи интеграцияси 9.б – расмда кўрсатилган. Бу ерда ![]() .3.2.
.3.2. ![]() катталаштирувчи занжир
3 оқим катталиги билан берилган. Учинчи итерацияда (9.6 – расм )
катталаштирувчи занжир
3 оқим катталиги билан берилган. Учинчи итерацияда (9.6 – расм ) ![]() чўққидан
фақат 1 – чўққини белгилаш мумкин, бу чўққидан
эса битта ҳам чўққини белгилаш мумкин эмас. Катталиги
чўққидан
фақат 1 – чўққини белгилаш мумкин, бу чўққидан
эса битта ҳам чўққини белгилаш мумкин эмас. Катталиги
Тўйинган ёйлар
ўтказувчанлик хоссаси 8 бўлган тармоқ кесмасини ҳосил қилади.
А кўплигига 2,3,4, ![]() узеллар киради, А кўплигига эса А – 1 ва
узеллар киради, А кўплигига эса А – 1 ва ![]()
узеллар
киради.

3. Энг
қисқа йўл масаласи ва энг
қисқа йўлларни топиш алгоритми.
Бу бўлимда
тармоқлар назариясининг асосий масалаларидан бири – берилган икки
чўққилар ўртасида энг қисқа йўлни топиш масаласи кўриб
чиқилган. Бу масала кўп сонли амалий иловаларга эга, шунингдек
тармоқларда турли оптимизациялаш масалаларини ечишда таркибий қисм
сифатида қўлланилади.
Қовурғаларга
![]() сонлари қўшиб
ёзилган
сонлари қўшиб
ёзилган ![]() граф берилган.
граф берилган. ![]() орқали
орқали ![]() ёйларининг кетма – кетлиги билан берилган йўлни белгилаймиз.
ёйларининг кетма – кетлиги билан берилган йўлни белгилаймиз. ![]() ёки
ёки ![]() йўлга кирувчи
йўлга кирувчи ![]() барча сонлар
йиғиндисига тенг
барча сонлар
йиғиндисига тенг ![]() сони йўлнинг узунлиги
дейилади:
сони йўлнинг узунлиги
дейилади:
![]() (5.4)
(5.4)
Энг
қисқа йўлни топиш масаласи Ws чўққидан Wt бошқа
чўққига ўтиш йўлини топишдан иборат, бу йўлнинг узунлиги минимал
бўлиши керак. Агар Ws дан Wt га йўл мавжуд бўлсагина бу масала ечимга эга бўлиши
мумкин. Учбурчак тенгсизлигини бажариш кўзда тутилмайди. Ягона чеклов шундан
иборатки, ![]() да манфий узунликдаги
цикллар бўлмаслиги керак. Шундай цикл бор дейлик. Унда бундай циклда Ws
чўққидан бирор бир чўққига томон ҳаракатланиб,
сўнг бу циклни етарлича айланиб Wt га тушгач
исталган
да манфий узунликдаги
цикллар бўлмаслиги керак. Шундай цикл бор дейлик. Унда бундай циклда Ws
чўққидан бирор бир чўққига томон ҳаракатланиб,
сўнг бу циклни етарлича айланиб Wt га тушгач
исталган ![]() ни олиш мумкин. Бу эса
ни олиш мумкин. Бу эса
![]() ни ва бу холатда энг
қисқа йўл йўқ эканлигини билдиради. Бундан йўналтирилмаган
қовурғалар манфий узунликка эга бўлмаслигини билдиради. Циклларнинг
манфий эмаслигидан шу келиб чиқадики, энг қисқа йўл доим
содда бўлади. Ҳақиқатда ҳам, агар бу йўл
қайтирилиб келувчи чўққиларни ўз ичига олса йўлнинг бир
қисми цикл ҳисобланади. Аммо циклнинг узунлиги манфий эмас, шунинг
учун йўлнинг узинлигини камайтириб, ёки уни ўзгартиришсиз қолдириб олиб
ташлаш мумкин. Шундай қилиб, циклнинг барча йўлларини йўқ
қилиб қолган қисм содда йўл эканлигига амин бўламиз.
ни ва бу холатда энг
қисқа йўл йўқ эканлигини билдиради. Бундан йўналтирилмаган
қовурғалар манфий узунликка эга бўлмаслигини билдиради. Циклларнинг
манфий эмаслигидан шу келиб чиқадики, энг қисқа йўл доим
содда бўлади. Ҳақиқатда ҳам, агар бу йўл
қайтирилиб келувчи чўққиларни ўз ичига олса йўлнинг бир
қисми цикл ҳисобланади. Аммо циклнинг узунлиги манфий эмас, шунинг
учун йўлнинг узинлигини камайтириб, ёки уни ўзгартиришсиз қолдириб олиб
ташлаш мумкин. Шундай қилиб, циклнинг барча йўлларини йўқ
қилиб қолган қисм содда йўл эканлигига амин бўламиз.
Навбатдаги
вазифалар энг қисқа йўл ҳақидаги масаланинг
умумлаштиришдан иборат.
1.
берилган Ws
чўққи ва тармоқнинг бошқа чўққилари ўртасидаги
энг қисқа йўлни топиш керак.
2.
тармоқдаги чўққиларнинг барча
жуфтликлари ўртасидаги энг қисқа йўлни топиш керак.
Оптимизациянинг
навбатдаги масаласини кўриб чиқамиз:
![]()
![]() ;
;
![]() учун
учун ![]() бу
ерда
бу
ерда ![]() - инциденциялар матрицасининг
устуни;
- инциденциялар матрицасининг
устуни; ![]() - барча элементлари
нолга тенг бўлмаган устун, -1 ва +
- барча элементлари
нолга тенг бўлмаган устун, -1 ва +![]() ни ва
ни ва ![]() - нчи ўринларда турувчи элементлар бундан мустасно.
- нчи ўринларда турувчи элементлар бундан мустасно.
(6) шарт бўйича ![]() катталиги
катталиги ![]()
![]() бўлган ёйлар Ws дан Wt га йўл
ҳосил қилишини кўриш қийин эмас. Аммо унда (5) мақсадли
функция (4) йўл узунлигига эквивалент бўлиши лозим, баҳоланки (5)
йиғиндига
бўлган ёйлар Ws дан Wt га йўл
ҳосил қилишини кўриш қийин эмас. Аммо унда (5) мақсадли
функция (4) йўл узунлигига эквивалент бўлиши лозим, баҳоланки (5)
йиғиндига ![]() бўлган
бўлган ![]() лар киради. Бундан
келиб чиқадики (5) – (7) масалалар энг қисқа йўл
ҳақидаги масаланинг таърифларидан биридир.
лар киради. Бундан
келиб чиқадики (5) – (7) масалалар энг қисқа йўл
ҳақидаги масаланинг таърифларидан биридир.
Шуни қайд
этиш керакки, (5) – (7) масала (7) шарт туфайли чизиқли дастурлаш
масаласи ҳисобланмайди, лекин чизиқли дастурлашнинг қуйидаги
масаласи унга эквивалентдир:
![]() (8)
(8)
![]() (9)
(9)
![]() учун
учун ![]() . (10)
. (10)
(5) – (7) дан
фарқли томон шундаки, (7) шарт (10) шарт билан алмаштирилган.
(8) – (10)
масаланинг айрим хусусиятларини кўриб чиқамиз.
1.
![]() - чўққилар
сони,
- чўққилар
сони, ![]() эса тармоқда
ёйлар сони. Унда (9) тизим
эса тармоқда
ёйлар сони. Унда (9) тизим ![]() номаълум сонли
номаълум сонли ![]() тенгламаларни ўз ичига
олади. Бироқ улардан фақат
тенгламаларни ўз ичига
олади. Бироқ улардан фақат ![]() - 1 чизиқли мустақил. Бу шундан келиб
чиққанки, инциденциялар матрицасида барча қаторлар
йиғиндиси нолга тенг, шу сабабли
- 1 чизиқли мустақил. Бу шундан келиб
чиққанки, инциденциялар матрицасида барча қаторлар
йиғиндиси нолга тенг, шу сабабли ![]() (
(![]() - инциденциялар матрицаси қатори)
- инциденциялар матрицаси қатори) ![]() - сони чизиқли тобе. Эркин қаторни ўчириб
ташлаймиз. Шунда фақат +1 ёки
- сони чизиқли тобе. Эркин қаторни ўчириб
ташлаймиз. Шунда фақат +1 ёки ![]() бўлгандагина
бўлгандагина ![]() нолга тенг бўлади ва
бу
нолга тенг бўлади ва
бу ![]() - 1 қаторда тузилган матрицанинг чизиқли
мустақиллигини исбот қилади.
- 1 қаторда тузилган матрицанинг чизиқли
мустақиллигини исбот қилади.
2.
(8) – (10) масаланинг базисли ечимида ![]() - 1 ўзгарувчи мавжуд. 2 – хусусият (8)
- (10) масаланинг ечими – дарахт.
Ҳар бир
- 1 ўзгарувчи мавжуд. 2 – хусусият (8)
- (10) масаланинг ечими – дарахт.
Ҳар бир ![]() устун
устун ![]() ёйга мос келади. Агар
ўзгарувчан
ёйга мос келади. Агар
ўзгарувчан ![]() базисли бўлса
базисли бўлса ![]() базисга киради деб
ҳисоблаймиз.
базисга киради деб
ҳисоблаймиз.
2 – хусусиятга
биноан базисга киритилган ёйлар сони ![]() -
- ![]() ўзгарувчиларни эркин
сонга алмаштириш мумкин ва бошқа, базис бўлмаган ёйлар орқали
оқим ўзгармайди. Уларнинг қиймати нобазис ўзгарувчилар билан
аниқланади.
ўзгарувчиларни эркин
сонга алмаштириш мумкин ва бошқа, базис бўлмаган ёйлар орқали
оқим ўзгармайди. Уларнинг қиймати нобазис ўзгарувчилар билан
аниқланади. ![]() чўққили
графда ёйлар сони
чўққили
графда ёйлар сони ![]() -
-
3.
Исталган базисли ечимда Ws дан графдаги
исталган чўққисига бўлган йўл – содда йўл. Бу (5) базисли ечим
натижасида – дарахт эканлигидан, демак
унинг исталган қисми циклга эга эмас. Исталган базисли ечимда базисли
ўзгарувчи +1 ёки 0 қийматга эга бўлиши мумкин, бунда +1 қиймат Ws дан Wt га содда йўлни
ҳосил қилувчи ёйлар учун.
Базисли ечимда Ws дан Wt га содда занжир
ҳосил қилувчи ёйларга мос келувчи ўзгарувчиларгина нолдан ортиқ
бўлиши мумкин. Бундай эмас, деб тасаввур қилайлик. Аммо Ws дан Wt га эмас, Ws дан Wi га йўлги кирувчи
ўзгарувчи қиймати нолдан катта бўлиши билан, оқимни сақлаш
шартига кўра Ws дан Wj га бўлган оддий занжирга кирувчи қолган барча
ўзгарувчилар нолдан катта бўлади, демак нолга тенг бўлмаган Ws дан Wj га оқим ҳосил
бўлади, бундай бўлиши эса мумкин эмас. Ws дан Wt га бўлган оқим катталиги ![]() ўзгарувчилар
қиймати
ўзгарувчилар
қиймати
4 – хусусият (8)
– (10) ва (5) – (7) масалаларнинг эквивалентлигини исботлайди.
Шундай
қилиб, энг қисқа йўл масаласини чизиқли дастурлаш усули
билан ечиш мумкин.
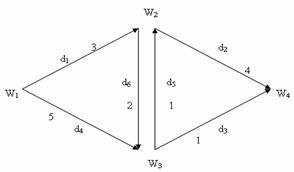
Мисол. 10 – расмда акс
эттирилган тармоқ учун 1- чўққидан 4 – чўққига
энг қисқа йўлни топиш керак, ёйлар узунлиги қуйидагича :
![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() . 10 – расмда ёйлар узунлигини чизиб узунлиги
. 10 – расмда ёйлар узунлигини чизиб узунлиги
Бу ечимни
чизиқли дастурлаш ёрдамида топамиз. 10 – расмдаги графнинг инциденциялар
матрицаси қуйидагича ёзилади:

Энг
қисқа йўлни топиш имконини берувчи чизиқли дастурлаш масаласи
қуйидаги кўринишга эга:
![]()
![]()
![]() =1
=1
![]()
![]()
Қуйида бу
масаланинг симплекс усул орқали ечими келтирилган:
А)
чизиқли дастурлашнинг бошланғич масаласи :

Б)
базисли ечим

В)
яхшиланган ечим:
 Чизиқли дастурлашнинг бошланғич
масаласи инциденциялар матрицасидан охирги қаторни ўчириш ва
Чизиқли дастурлашнинг бошланғич
масаласи инциденциялар матрицасидан охирги қаторни ўчириш ва ![]() ўзгарувчи учун қатор ва устунни ва эркин аъзолар
устунини қўшиш йўли билан ҳосил қилинган. Базисли
ўзгарувчилар сифатида
ўзгарувчи учун қатор ва устунни ва эркин аъзолар
устунини қўшиш йўли билан ҳосил қилинган. Базисли
ўзгарувчилар сифатида ![]()
![]() ва
ва ![]() ни оламиз.
ни оламиз. ![]() ёйлари дарахтни хосил
қилишини кўриш қийин эмас,
ёйлари дарахтни хосил
қилишини кўриш қийин эмас, ![]() ва
ва ![]() ёйлари узунлиги
йиғиндисига тенг W1, W2, W4 йўл узунлиги
ёйлари узунлиги
йиғиндисига тенг W1, W2, W4 йўл узунлиги ![]() ва
ва ![]() тенглиги келиб
чиқади.
тенглиги келиб
чиқади. ![]() қатордаги манфий
нисбий баҳо бу ечимни яхшилаш мумкинлигини кўрсатади.
қатордаги манфий
нисбий баҳо бу ечимни яхшилаш мумкинлигини кўрсатади.
Яхшиланган ![]() ечим оптимал
ҳисобланади ва олинган ечимга графда йўллар тахлили ёрдамида мос келади.
ечим оптимал
ҳисобланади ва олинган ечимга графда йўллар тахлили ёрдамида мос келади.
Агар (9) чап
томони ![]() мусбат сонга
кўпайтирсак (8) – (10) масаланинг юқорида кўриб чиқилган
хусусиятлари ўзгармайди. Бу холда
мусбат сонга
кўпайтирсак (8) – (10) масаланинг юқорида кўриб чиқилган
хусусиятлари ўзгармайди. Бу холда ![]() нолга ёки
нолга ёки ![]() га тенг бўлиши мумкин
(агар
га тенг бўлиши мумкин
(агар ![]() W5 дан Wt га содда йўл
ҳосил қилувчи ёйларга мос келсагина
W5 дан Wt га содда йўл
ҳосил қилувчи ёйларга мос келсагина ![]() га тенг бўлади).
Мақсадли (8) функция қиймати
га тенг бўлади).
Мақсадли (8) функция қиймати ![]() марта катталашади.
марта катталашади.
Кўриб
чиқилган мисолдан кўриниб турибдики энг қисқа йўл масаласини
чизиқли дастурлаш усули билан ечиш қийинроқ. Бошқа,
самаралироқ усуллар ҳам мавжудки, уларни қуйида кўриб
чиқамиз.
Алгоритм
тармоқ чўққиларига вақтинча ёки доимий белгиларни
қўйиб ёзишга асосланган. Алгоритмнинг ҳар бир итерациясида белгилар катталиги
кичраяди ва вақтинча белгиларниг биттаси доимийга айланади. Бу шуни
кўрсатадики, Ws чўққидан белгиси
доимийга айланган чўққига энг қисқа йўл топилган ![]() - тармоқда
чўққилар сони бўлган
- тармоқда
чўққилар сони бўлган ![]() - итерациядан сўнг
барча чўққиларга энг қисқа йўл топилади. Энг аввал алгоритмни тасвирлаймиз, кейин эса
унинг энг қисқа йўл топиш имконини беришини исботлаймиз.
- итерациядан сўнг
барча чўққиларга энг қисқа йўл топилади. Энг аввал алгоритмни тасвирлаймиз, кейин эса
унинг энг қисқа йўл топиш имконини беришини исботлаймиз.
Белгиларни киритамиз:
![]() Wj ва Wj чўққилар ўртасидаги ёй узунлиги;
Wj ва Wj чўққилар ўртасидаги ёй узунлиги;
![]() чўққининг
вақтинча белгиси ;
чўққининг
вақтинча белгиси ;
![]() чўққининг доимий
белгиси.
чўққининг доимий
белгиси.
Алгоритмни тасвирлаш:
1)
![]() учун
учун ![]() ни қўямиз.
ни қўямиз.
2)
![]() чўққининг
вақтинча белгили барча қўшнилари учун белгиларни қуйидаги
ифодага мос ўзгартирамиз:
чўққининг
вақтинча белгили барча қўшнилари учун белгиларни қуйидаги
ифодага мос ўзгартирамиз:
![]() (11)
(11)
3)
Вақтинча белгили барча чўққилар
учун ![]() ни топиш керак.
ни топиш керак.
4)
![]() ни қўшиш керак.
ни қўшиш керак.
5.а). ![]() узелга энг
қисқа йўлни топиш талаб қилинса:
узелга энг
қисқа йўлни топиш талаб қилинса: ![]() бўлганда ҳисоблашлар
тугатилади, энг қисқа йўл топилди; бу тенглама бажарилмаса 2 –
босқичга ўтиш керак.
бўлганда ҳисоблашлар
тугатилади, энг қисқа йўл топилди; бу тенглама бажарилмаса 2 –
босқичга ўтиш керак.
5.б). Тармоқнинг барча чўққилларига
енг қисқа йўлни топиш талаб қилинса: ![]() бўлса
ҳисоблашлар якунлашади, акс холда 2 босқичга ўтиш керак.
бўлса
ҳисоблашлар якунлашади, акс холда 2 босқичга ўтиш керак.
Алгаритимни
қўллашга мисол кўриб чиқамиз. 11а-расмда тасвирланган тармоқ
учун ![]() чўққидан
тармоқнинг қолган барча чўқиларига энг қисқа
йўлни топиш керак. 11а-расмдаги граф йўналтирилмаган. Ҳар бир
қовирғага 11б-расмда кўрсатилган,
узунлиги бир хил бўлган иккита ёй мос келади, деб хисоблаймиз. Хисоблар
натижаси 1- жадвалда келтирилган.
чўққидан
тармоқнинг қолган барча чўқиларига энг қисқа
йўлни топиш керак. 11а-расмдаги граф йўналтирилмаган. Ҳар бир
қовирғага 11б-расмда кўрсатилган,
узунлиги бир хил бўлган иккита ёй мос келади, деб хисоблаймиз. Хисоблар
натижаси 1- жадвалда келтирилган.
1-жадвалнинг биринчи устунида итерация тартиб
рақам, иккинчида – шу итерацияда
доимий белги олувчи чўққининг тартиб рақами,
қолганларида эса ҳар бир узел учун белгилар каталиклари берилган.
Устун қалин чўққилар билан ажратилган .
Қўлланилган адабиётлар рўйхати
1.
Теоретические основы
почтовой связи: Учебник для вузов. С.М. Хлытчиев, Н.П. Тарасова, В.М. Лившиц. 2
– е изд.,препаб. И доп. – М.: “Радио и связь” – 1990 – 280 с.
2.
Птицын Г.А.
Модели обработки и перевозки почты – М.: - МИС, 1988.
3.
Князютенков
В.А., Птицин Г.А. Оптимизация сетей почтовой связи – М: - МТУСИ, 1997.
4.
Экономико –
математичкские методы и модели в планировании и управлении в отрасли связи:
Учебник для вузов. В.А. Барсук, Н.М. Губин, А.Р. Батый. 3 – е изд., перераб. И
доп. М.: Радио и связь, 1984.
5.
Организация
автоматизированной обработки почтовых отправлений в крупных узлах связи. И. В.
Барсук, Г.К. Гиль, А.Л. Воскресенский и др. – М.: Радио и связь, 1985.
Илова
Берилган орграф
учун ёндошлик ва инциденцялар матирицасини келтиринг, мавжуд барча содда ва
ёпиқ занжирларни гамильтон
контурини белгилаб олинг, орграфнинг хар бир чўққиси учун ![]() кўплигини топинг.
кўплигини топинг.
W2 d2 W3
![]()

![]()



![]() d1 d8 d3
d1 d8 d3

 W1 d7 d10 W4
W1 d7 d10 W4
d6
d9 d4
![]()
W6 d5 W5
А
оқимидан D оқимига максимал оқимни тармоқнинг барча
майдонларида фойдаланиб топинг.

Келтирилган граф учун Флойд
усули билан ![]() ва k=2 ҳолат
учун матрица тузинг.
ва k=2 ҳолат
учун матрица тузинг.

Келтирилган граф учун Флойд учун усули билан ![]() ва k=2 ҳолат
учун матрица тузинг.
ва k=2 ҳолат
учун матрица тузинг.

![]() Расмда
тасвирланган тармоқ учун дан қолганларига энг
қисқа йўлни Дейнстра усули билан топинг.
Расмда
тасвирланган тармоқ учун дан қолганларига энг
қисқа йўлни Дейнстра усули билан топинг.

 Расмда тасвирланган тармоқ учун W1 дан қолганларига энг қисқа йўлни Дейнстра усули билан топинг.
Расмда тасвирланган тармоқ учун W1 дан қолганларига энг қисқа йўлни Дейнстра усули билан топинг.
Келтирилган граф
учун Флойд усули билан ![]() ҳолат учун
матрица тузинг.
ҳолат учун
матрица тузинг.

Келтирилган граф
учун Флойд усули билан ![]() ҳолат учун
матрица тузинг.
ҳолат учун
матрица тузинг.

Орграфнинг
ҳар бир чўққиси учун ![]() кўплигини
аниқланг; содда занжир гамильтонли контурга мисоллар келтиринг.
кўплигини
аниқланг; содда занжир гамильтонли контурга мисоллар келтиринг.

Мундарижа.
Кириш.........................................................................................................
3.
1.
Графлар ва тармоқлар назариясидан айрим
маълумотлар ...................................................................................................................4.
2.
Максимал оқим теоремаси ва максимал
оқимни аниқлаш алгоритми..................................................................................................9.
3.
Энг қисқа йўл масаласи ва энг
қисқа йўлни топиш алгоритми ..................................................................................................................12.
4.
Адабиётлар рўйхати...............................................................................18.
5.
Илова........................................................................................................19
“Почта хизматини
автоматлаштириш” кафедраси мажлисида кўриб
чиқилди.
____йил___ ___ - _сон баённома.
Маъсул мухаррир: проф.Махкамова
М.А
Тузувчилар: Сайдазимова
К.М.
Корректор: Шаврикова Р.У