O’ZBEKISTON RESPUBLIKASI AXBOROT TEXNOLOGIYALARI VA KOMMUNIKATSIYALARINI RIVOJLANTIRISH VAZIRLIGI TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
“Algoritmga kirish”
fanidan laboratorиya ishlarini bajarish bo’yicha
metodik ko’rsatmalar
5330500- Компьютер
инжиниринги (“Компьютер инжиниринги”,
“АТ-Сервис”,
“Ахборот хавфсизлиги”, “Мультимедиа технологиялари”)
5330600- Дастурий инжиниринг таълим йўналишлари учун
Tuzuvchi:
Mustapakulov Ya. U. – TATU “A va MM” kafedrasi katta o’qituvchisi
2016 yil.
Сўз боши
Методик кўрсатмалар «Алгоритмга кириш» фанидан лаборатория ишларини бажариш пайтида турли туман масалаларни ечиш алгоритмларини қуришнинг принциплари ва усулларини ўрганиш, псевдокодда ёки юқори даражадаги дастурлаш тилларидан бирида дастур кодини ёзиб компютерда бажариб кўриш ва таҳлил қилишга мўлжалланган.
Har bir talaba barcha topshiriqlarning bitta variantini bajaradi. Topshiriqlar qo’yilgan talablarga asosan bajariladi va o’qituvchi tomonidan tekshiriladi.
Ушбу методик кўрсатмалар қуйидаги мутахассислик талабалари учун тайёрланган:
5330500- Компьютер инжиниринги (“Компьютер инжиниринги”, “АТ-Сервис”, “Ахборот хавфсизлиги”, “Мультимедиа технологиялари”)
5330600- Дастурий инжиниринги.
МУНДАРИЖА:
ЛАБОРАТОРИЯ ИШИ №1 “Алгоритмнинг асосий структуралари”
1.1 Чизиқли алгоритмлар.
1.2 Тармоқланувчи алгоритмлар
1.3 Такрорланувчи алгоритмлар
ЛАБОРАТОРИЯ ИШИ № 2 “Algoritm sifatini baholashning mezonlari
2.1. Algoritmni to’g’riligini tekshirish
2.2. Algoritmni va uning murakkabligini tahlil qilish
ЛАБОРАТОРИЯ ИШИ №3 «Iteratsion жараёнлар ва Rekurrent algoritmlar »
3.1 Iteratsion жараёнлар
3.2 Rekurrent algoritmlar
3.3. Fibonachchi sonlari
ЛАБОРАТОРИЯ ИШИ № 4 “Bir o`lchamli massivlar ustida ishlash. Танлаш алгоритмлари”
ЛАБОРАТОРИЯ ИШИ № 5 “Саралаш алгоритмлари”
5.1. Жойлаштириш орқали саралаш
5.2. Танлаш орқали саралаш
5.3. Алмаштириш орқали саралаш
5.4. Бирлаштириш орқали саралаш
ЛАБОРАТОРИЯ ИШИ № 6 “Қисқа маршрут топиш алгоритмлари(очкўз алгоритмлар)”
6.1.Робот маршрутини оптималлаштириш алгоритми.
6.2. Pul maydalash масаласи algоritmи
6.3.Strukturalar, massivlar, ko’rsatkichlar. Strukturalarning dinamik massivi»
ЛАБОРАТОРИЯ ИШИ № 7.«Tashqi saralash. Binar fayllar. Matrisadan tuzilgan fayllar»
ЛАБОРАТОРИЯ ИШИ № 8. «Тьюринг машинаси учун дастур ёзиш»
ЛАБОРАТОРИЯ ИШИ № 9. «Марков алгорифми учун дастур ёзиш»
Ишни бажариш ва ҳисобот тайёрлаш тартиби:
1. Берилган айрим масалаларни аналитик кўринишда ечиш.
2. Берилган масаланинг ечиш алгоритмини блок-схема кўринишда тасвирлаш.
3. С++ муҳитида дастурни киритиш.
4. Дастурни компьютер хотирасида сақлаш ва дастурдаги мавжуд хатоларни топиш ва уларни тўѓрилаш.
5. Дастурни ишга тушириш ва масаланинг бошланѓич маълумотларини киритиб натижалар олиш.
6. Олинган натижалар таҳлили асосида хулосалар ќилиш.
7. Лаборатория ишини расмийлаштириш.
Ҳисобот шакли:
1. Титул
2. Масаланинг қўйилиши.
3. Назарий қисм.
4. Алгоритм блок-схемаси
5. Алгортм коди
6. Олинган натижалар
7. Хулоса
8. Илова тариқасида экрандан олинган кадрлар (скрин) қўйилади.
ЛАБОРАТОРИЯ ИШИ № 1 “Алгоритмнинг асосий структуралари”
Мақсад: Талабаларда аналитик ва мантиқий фикрлашни ривожлантириш, математик интуицияни кучайтириш.
Вазифалар: Алгоритм турларини ўрганиш, дастурлаш тилларининг бирида алгоритмни бажариш,
 Назарий маълумотлар.
Назарий маълумотлар.
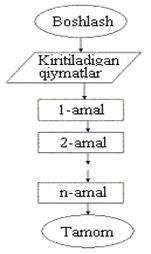
Чизиқли алгоритмлар. Faqat ketma-ket bajariladigan amallardan tashkil topgan algoritmlarga-chiziqli algoritmlar deyiladi. Bunday algoritmni ifodalash uchun ketma-ketlik strukturasi ishlatiladi. Strukturada bajariladigan amal mos keluvchi shakl bilan ko‘rsatiladi. Chiziqli algoritmlar blok-sxemasining umumiy strukturasini quyidagi ko‘rinishda ifodalash mumkin.
Quyidagi masalalarning yechish algoritmi va dasturi tuzilsin.
1. Berilgan ikkita haqiqiy sonning o'rta arifmetik qiymati va ular modulining o'rta geometrik qiymati hisoblansin.
2. To'g’ri burchakli uchburchakning katetlari berilgan. Uchburchak gipotenuzasi va maydoni hisoblansin.
3. R-radiusli aylana ichida joylashgan tomonlari bir xil n-burchakli ko’pburchakning perimetri topilsin.
4. Uchta R1, R2, R3 qarshiliklar parallel ulangan. Ularning ulanish qarshiligi hisoblansin.
5. Toshning h balandlikdan yer ustiga qulash vaqti aniqlansin.
6. Bir-biridan r masofada turgan, m1 va m2 og’irlikdagi jismlarning o'zaro tortishish kuchi F aniqlansin.
7. Aylana uzunligi ma'lum bo'lgan holda, shu aylana bilan chegaralangan soha maydoni hisoblansin.
8. Bir-biriga qarama-qarshi tomondan bir xil tezlikda harakat qilayotgan ikkita jismning uchrashish vaqti aniqlansin. Ularning boshlang’ich tezligi, tezlanish va ular orasidagi boshlang’ich masofa ma'lum.
9. Haqiqiy son x berilgan. Ko'paytirish, qo'shish va ayirish arifmetik amallarini ishlatgan holda quyidagi ifoda hisoblansin. 2х4-3х3+4х2-5х+6 Ifodada ko'paytirish, qo'shish va ayirish amallarining har biri to'rttadan oshmasin.
10. Haqiqiy x va y sonlari berilgan. Ko'paytirish, qo'shish va ayirish arifmetik amallarini ishlatgan holda quyidagi ifoda hisoblansin 3х2у2-2ху2-7х2у-4у2+15ху+2х2-3х+10у+6 Ifodada ko'paytirish, qo'shish va ayirish amallarining har biri sakkiztadan oshmasin.
11. Haqiqiy son x berilgan. Ko'paytirish, qo'shish va ayirish arifmetik amallarini ishlatgan holda quyidagi ifoda hisoblansin 1-2х+3х2-4х3 Ifodani hisoblashda ko'pi bilan sakkizta amal ishlatilsin.
12. Haqiqiy a soni berilgan. Faqat ko'paytirish amalini ishlatgan holda: a) а4 -ikkita amalda ; b) а6 -uchta amalda hisoblansin.
13. Haqiqiy a soni berilgan. Faqat ko'paytirish amalini ishlatgan holda: a) а7 -to'rtta amalda ; b) а8 -uchta amalda hisoblansin.
14. Haqiqiy a soni berilgan. Faqat ko'paytirish amalini ishlatgan holda а3 va а10 lar to'rtta amalda hisoblansin.
15. Haqiqiy a soni berilgan. Faqat ko'paytirish amalini ishlatgan holda а2 , а5 , а17 lar oltita amalda hisoblansin.
16. Kubning qirra uzunligi berilgan. Kubning hajmi va yon sohasining yuzi topilsin.
17. L uzunlikdagi mayatnikning tebranish davri topilsin.
18. Ichki radiusi 20 ga, tashqi radiusi esa r (r>20) ga teng bo’lgan doira sohasi topilsin.
19. Uchburchak o’zining burchaklari qiymatlari va o’zi yotgan aylananing radiusi bilan berilgan. Uchburchakning tomonlari topilsin.
20. Uchburchak tomonlarining uzunliklari berilgan. Uchburchak balandligi va mediana uzunligi hisoblansin.
21. Uchburchak tomonlarining uzunliklari berilgan. Uchburchak bissektrisalarining uzunliklari topilsin.
22. (x1, u1 ) va ( x2, u2) koordinatadagi nuqtalar orasidagi masofa topilsin.
23. t1 haroratli v1 litr suv , t2 haroratli v2 litr suv bilan aralashtirildi. Hosil bo’lgan massaning hajmi va harorati aniqlansin.
24. To'g’ri burchakli uchburchakning gipotenuza va kateti berilgan. Aylana ichiga joylashgan shu uchburchakning ikkinchi kateti va aylana radiusi topilsin.
25. Radiusi 13.7 ga teng bo’lgan, yoyi esa H radian qiymatni qabul qiluvchi sektorning sohasi topilsin.
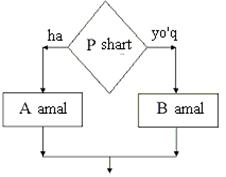 Тармоқланувчи
алгоритмлар. Agar hisoblash jarayoni biror bir
berilgan shartning bajarilishiga qarab turli tarmoqlar bo‘yicha davom ettirilsa
va hisoblash jarayonida har bir tarmoq faqat bir marta bajarilsa, bunday
hisoblash jarayonlariga tarmoqlanuvchi algoritmlar deyiladi. Tarmoqlanuvchi
strukturasi berilgan shartning bajarilishiga qarab ko‘rsatilgan tarmoqdan faqat
bittasining bajarilishini ta’minlaydi.
Тармоқланувчи
алгоритмлар. Agar hisoblash jarayoni biror bir
berilgan shartning bajarilishiga qarab turli tarmoqlar bo‘yicha davom ettirilsa
va hisoblash jarayonida har bir tarmoq faqat bir marta bajarilsa, bunday
hisoblash jarayonlariga tarmoqlanuvchi algoritmlar deyiladi. Tarmoqlanuvchi
strukturasi berilgan shartning bajarilishiga qarab ko‘rsatilgan tarmoqdan faqat
bittasining bajarilishini ta’minlaydi.
Maсала: Aylananing markazi koordinatalari va radiusi berilgan bo`lsa, berilgan nuqtaning aylanada yotishi yoki yotmasligini aniqlovchi dastur tuzing.
Dastur kodi:
#include <iostream>
#include <stdio.h>
#include <conio.h>
#include <math.h>
#define TRUE 1
int main(void)
{ float XCircle, YCircle, Radius, XPoint, YPoint; // o`zgaruvchilarni e'lon qilish
printf("\nAylana markazining koordinatalarini kiriting: ");
scanf("%f%f",&XCircle,&YCircle);
printf("\nAylananing radiusini kiriting: ");
scanf("%f",&Radius);
printf("\nKoordinatalar uchini kiriting: ");
scanf("%f%f",&XPoint,&YPoint);
int clrscr();
if ( pow(XPoint-XCircle,2)+pow(YPoint-YCircle,2) <= pow(Radius,2) )
{ printf("\nKoordinatalar uchi bilan " "(%.2f,%.2f) aylananing bir qismi\n bilan " "markazning koordinatalari (%.2f,%.2f) " "va radiusi %.2f",XPoint, YPoint, XCircle, YCircle, Radius);
}
else
{ printf("\nKoordinatalar uchi bilan "
"(%.2f,%.2f) aylananing qismisiz\n"
"markazning koordinatalari bilan"
" (%.2f,%.2f) va radiusi %.2f ",XPoint, YPoint,XCircle,YCircle,Radius);
}
printf("\nChiqish uchun biror tugmani bosing...");
getch();
return 0; }
Quyidagi masalalarning yechish algoritmi va dasturi tuzilsin.
1. X va u haqiqiy sonlar berilgan. Hisoblansin :
a) max(x,u); b) min(x,u).
2. X, y, z haqiqiy sonlar berilgan. Hisoblansin :
a) max(x.,y, z); b) min(x,y,z).
3. A, b,c haqiqiy sonlar berilgan. Agar a>=b>=s bo'lsa, u holda berilgan sonlar ikki barobar oshirilsin, aks holda ularni absolyut qiymatlari bilan almashtirilsin.
4. Ikkita haqiqiy son berilgan. Birinchi sonni bosmaga chiqaring, agar u ikkinchi sondan katta bo'lsa, aks holda ikkala sonni ham bosmaga chiqaring.
5. Ikkita haqiqiy son berilgan. Agar berilgan birinchi son ikkinchisidan kichik yoki teng bo'lsa, u holda birinchi sonni nolga aylantiring, aks holda sonlar o'zgarishsiz bosmaga chiqarilsin.
6. Uchta haqiqiy son berilgan. Ular ichidan qaysi biri (1,3) oraliqqa tegishli ekanligi aniqlansin.
7. Haqiqiy x, u (x>u) sonlari berilgan. Bu ikki sondan kichigini ularning yig’indisi bilan, kattasini esa ularning ko'paytmasi bilan almashtiring.
8. Haqiqiy uchta son berilgan. Bu sonlar manfiy yoki musbat ekanligi tekshirilsin. Agar musbat bo'lsa, kvadrat ildiz ostidan chiqarilsin, aks holda kvadratga oshirilsin.
9. Agar x, u, s haqiqiy sonlar yig’indisi birdan kichik bo’lsa, u holda bu uchta sondan kichigini qolgan ikkita sonning yig’indisi bilan almashtiring, aks holda sonlar o’zgarishsiz qolsin.
10. Haqiqiy a, b, s, d sonlari berilgan. Agar a> b>s>d bo'lsa, u holda har bir sonni eng katta qiymat bilan almashtiring; agar a>b>s>d bo'lsa, u holda sonlar o'zgartirilmasin, aks holda barcha sonlar kvadratlari bilan almashtirilsin.
11. Haqiqiy x,u sonlari berilgan. Agar x va u manfiy bo'lsa, u holda har bir sonni ularning moduli bilan almashtiring. Agar ulardan faqat bittasi manfiy bo'lsa, ikkala qiymatni 0,5 ga oshiring. Agar ikkala qiymat manfiy bo'lmasa, ularni 10 marotaba kamaytiring, boshqa hollarda esa sonlar o'zgarishsiz qolsin.
12. Haqiqiy musbat x, u, s sonlar berilgan. Tomonlari x, u, s uzunlikdagi uchburchak mavjudmi yoki yo'qmi aniqlansin.
13. Haqiqiy musbat x, u, s sonlar berilgan. Tomonlari x, u, s uzunlikdagi uchburchak mavjudmi yoki yo’qmi aniqlansin. Agar mavjud bo'lsa, u o'tkir burchakli uchburchak bo'lib hisoblanadimi, aniqlansin.
14. Haqiqiy musbat a, b, s (a>0) sonlari berilgan bo'lsa, ах2+бх+с=0 kvadrat tenglamaning haqiqiy ildizlari hisoblansin. Agar haqiqiy ildiz yo'q bo'lsa, bu haqda ma'lumot berilsin.
15. Haqiqiy musbat a, b, s (a>0) sonlari berilgan bo'lsa, ах4 +бх2+с=0 kvadrat tenglamaning haqiqiy ildizlari hisoblansin. Agar haqiqiy ildizlar bo'lmasa, bu haqda ma'lumot berilsin, aks holda ikkita yoki to'rtta ildiz bosmaga chiqarilsin.
16. Uchta haqiqiy son berilgan. Birinchi sonni bosmaga chiqaring, agar u ikkinchi sondan katta uchinchi sondan kichik bo'lsa, aks holda uchchala sonni ham bosmaga chiqaring.
17. Haqiqiy musbat a, b, c, d sonlar berilgan. Tomonlari a, b bo'lgan to'g’rito'rtburchakni c, d tomonli to'g’rito'rtburchak ichiga tomonlarini bir-biriga parallel yoki perpendikulyar qilib joylashtirish mumkinmi, aniqlansin.
18. Haqiqiy musbat a, b, c, x, u sonlar berilgan. a,b,c qirralarga ega bo’lgan g’isht x,y tomonli to’g’riburchakli teshikdan o’ta olishini aniqlang. G’ishtni teshikka shunday kiritish kerakki, bunda g’ishtning har bir qirrasi teshikning har bir tomoniga parallel yoki perpendikulyar bo’lsin.
19. Ikkita k,m sonlari berilgan. Agar k<m bo'lsa, n o'zgaruvchiga 1 qiymat berilsin, agar k<m bo'lsa, 0 qiymat, agar k>m bo'lsa -1 qiymat berilsin. Berilgan kattaliklar: 1) k=3, m=3; 2)k=8,m=4; 3)r=3,m=6.
20. R soni berilgan. Agar r<0 bo'lsa, у=р2 formula , agar r>0 bo'lsa, у=р3 formula orqali u hisoblansin. Berilgan kattaliklar: 1) r=2; 2) r=-3.
21. Haqiqiy x, y, z sonlari berilgan. Hisoblansin: max(x+y+z,xyz).
22. Haqiqiy x, y, z sonlari berilgan. Hisoblansin: Min2(x+y+z/2,xyz)+1.
23. Berilgan haqiqiy x, y, z sonlarida quyidagi tengsizlik bajarilishi tekshirilsin: x<y<z.
24. Haqiqiy x soni berilgan. Agar u manfiy bo'lsa, u kvadratga oshirilsin, aks holda kvadrat ildiz ostidan chiqarilsin.
25. Dekart koordinatalar sistemasida ixtiyoriy nuqta va soha koordinatalari berilgan. Nuqtaning sohaga tegishliligini aniqlang.
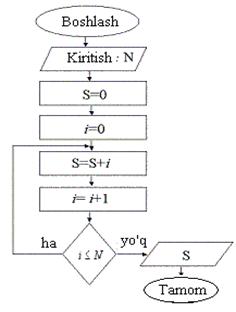 Такрорланувчи алгоритмлар.
Agar biror masalani yechish uchun
tuzilgan zarur bo‘lgan amallar ketma-ketligining ma’lum bir qismi biror
parametrga bog‘liq ko‘p marta qayta bajarilsa, bunday algoritm takrorlanuvchi
algoritm yoki siklik algoritmlar deyiladi. Takrorlanuvchi algoritmlarga tipik
misol sifatida odatda qatorlarning yig‘indisi yoki ko‘patmasini hisoblash
jarayonlarini qarash mumkin.
Такрорланувчи алгоритмлар.
Agar biror masalani yechish uchun
tuzilgan zarur bo‘lgan amallar ketma-ketligining ma’lum bir qismi biror
parametrga bog‘liq ko‘p marta qayta bajarilsa, bunday algoritm takrorlanuvchi
algoritm yoki siklik algoritmlar deyiladi. Takrorlanuvchi algoritmlarga tipik
misol sifatida odatda qatorlarning yig‘indisi yoki ko‘patmasini hisoblash
jarayonlarini qarash mumkin.
Quyidagi masalalarning yechish algoritmi va dasturi tuzilsin.
f1(x) va f2(x) funktsiyalarining qiymatlarini X ning XÎ [0,1] berilgan oralig’ida hisoblash algoritmi va dasturini tuzing ( h=0,1). Natija jadval ko’rinishida olinsin.
|
Т/р |
Funktsiya f1(x) |
Funktsiya f2(x) |
|
1 |
Sin (x+4.5) |
20 / (1+x2) |
|
2 |
1+cos(x-2) |
|
|
3 |
ex+Sin(x) |
1+2x |
|
4 |
çSin(x)+1÷ |
(1+2x)ex |
|
5 |
2-cos(x +1) |
1-x2 |
|
6 |
|
ex(1+cos |
|
7 |
1+2x+1 |
4*e1-x-1 |
|
8 |
1+1,8х+1 |
Cos2(х-1) |
|
9 |
х2+x+1 |
|
|
10 |
Cos(2x+1) |
x*ex+1 |
|
11 |
2-cos3(x0+1) |
|
|
12 |
|
ln(x2+x+1) |
|
13 |
x(x2+1) |
e -ïx+1ï*(1+x) |
|
14 |
1+ln(2x-1) |
sin2(x+1)*ex |
|
15 |
ex/(1+x) |
(x-1)2 |
|
16 |
(1+x)*e-x |
x2+sin(x) |
|
17 |
1+3x+1 |
(1-x)*tg2(x) |
|
18 |
lg(1+x) |
1+cos2(x) |
|
19 |
|
1+2sinx |
|
20 |
|
Ln(cos(x)+1) |
|
21 |
1+0,03x2 |
Cosx+sinx |
|
22 |
x-sin(2x-1) |
Ln(1+2x) |
|
23 |
0,02*e2x+1 |
Cos(2x-1) |
|
24 |
|
tg(3x-1) |
|
25 |
10-6*ln(x+1) |
x2+2x-3 |
ЛАБОРАТОРИЯ ИШИ № 2 “Algoritm sifatini baholashning mezonlari
Мақсад: Талабаларда аналитик ва мантиқий фикрлашни ривожлантириш, Algoritm sifatini baholashning mezonlariни тушуниш.
Вазифалар: Algoritm sifatini baholashning mezonlariни аниқлаш.
2.1.Algoritmni to’g’riligini tekshirish
Dastur to’g’riligini isbotlashning eng keng tarqalgan turi – bu uni testlardan o’tkazishdir.
Algoritmni tekshirishda nazoratchi boshlang’ich ma’lumotlarni majmui algoritmik test deb nomlanadi.
To’g’ri deb shunday algoritmga aytiladiki, u masalaning qo’yilishida talab qilinadigan natijani har qanday ruxsat etilgan boshlang’ich ma’lumotlar bilan ham shakllantirib biladi. Odatda, dastur bergan natijalar ma’lum bo’lgan yoki qo’lda hisoblangan ma’lumotlar bilan taqqoslanadi, va ular to’g’riligi aniqlansa dastur to’g’ri ishlaydi degan hulosaga kelish mumkin. Ammo bu usul bilan foydalanuvchini hamma shubhalardan xalos qilib bo’lmaydi, ya’ni dastur ishlamaydigan hamma holatlarni hisobga olib bo’lmaydi.
Gudman va Xidetniyemilar tomonidan algoritm to’g’riligini isbotlash uchun quyidagi uslubiyat taklif qilingan.
Algoritm 0 dan m gacha bo’lgan qadamlar ketma-ketligi ko’rinishida tavsiflangan deb tahmin qilaylik.Har bir qadam uchun qandaydir asoslanishni taklif etamiz. Xususan, qadamdan oldin va keyin ishlaydigan shartlar haqida lemma kerak bo’lishi mumkin. Shu bilan birgalikda, algoritm chekliligining isbotini ham taklif etamiz, va hamma ruxsat etilgan kiritish ma’lumotlarini tekshirib, hamma mumkin bo’lgan chiqarish ma’lumotlarni olamiz. Algoritmni to’g’riligi bilan samaradorligi o’rtasida hech qanday aloqa yo’qligini ta’kidlab o’tamiz.Aslida hamma talablarga bir xil yahshi javob beradigan algoritm kamdan-kam ishlab chiqiladi.
Algoritmni amalga oshirish. Algoritmni amalga oshirish deganda, EHM uchun dasturni yozish deb tushuniladi. Buning uchun quyidagi savollarga javob berish kerak:
· Asosiy o’zgaruvchilarni aniqlash.
· O’zgaruvchilarning turlarini aniqlash.
· Nechta massiv yoki fayllar va qanday kattalikda ular kerak bo’ladi?
· Bog’lanilgan ro’yhatlardan foydalanish ma’nolimi?
· Qanday dasturiy qismlar kerak bo’lishi mumkin (tayyor bo’lsa ham)?
· Qaysi dasturlash tilini tanlash?
Dastur yozish yoki tuzishning hilma-hil usillari va uslublari mavjud.
2.2. Algoritmni va uning murakkabligini tahlil qilish
Algoritmni tahlil qilishdan maqsad – algoritmga ma’lumotlarni aniq muvaffaqiyatli qayta ishlash uchun kerak bo’ladigan xotira hajmi va ishlash vaqtining baholari va chegaralarini olish. Bir masalani yechadigan ikki algoritmni taqqoslash uchun qandaydir sonli mezon topish kerak.
Faraz
qilaylik, A – qandaydir bir turkumdagi masalalarni yechadigan algoritm, n – esa
shu turkumdagi alohida bir masalaning kattaligi.Umumiy holda, n – oddiy skalyar
yoki massiv yoki kiritiladigan ketma – ketlikning uzunligi bo’lishi mumkin.![]() - n kattalikdagi
ixtiyoriy masalani yechadigan algoritm A bajarish kerak bo’lgan asosiy
amallarni (qo’shish, ayirish, taqqoslash,…) yuqori chegarasini beradigan ishchi
funksiya. Algoritmningsifatini baholash uchun quyidagi mezonni ishlatamiz.
- n kattalikdagi
ixtiyoriy masalani yechadigan algoritm A bajarish kerak bo’lgan asosiy
amallarni (qo’shish, ayirish, taqqoslash,…) yuqori chegarasini beradigan ishchi
funksiya. Algoritmningsifatini baholash uchun quyidagi mezonni ishlatamiz.
Agar
![]() o’sish tartibi n
dan bog’liq bo’lgan polinomdan katta bo’lmasa, A algoritm polinomial deb
aytiladi, aks holda algoritm A eksponensial hisoblanadi.
o’sish tartibi n
dan bog’liq bo’lgan polinomdan katta bo’lmasa, A algoritm polinomial deb
aytiladi, aks holda algoritm A eksponensial hisoblanadi.
Shular bilan birgalikda tahlil jarayonida ko’p matematik fanlarda standart bo’lgan iboralar ishlatiladi.
![]() funksiya
O[g(n)] deb belgilanadi, va
funksiya
O[g(n)] deb belgilanadi, va ![]() bo’lganda,
uni tartibi katta n lar uchun g(n) deb qabul qilinadi. Demak f(n)=O[g(n)].
bo’lganda,
uni tartibi katta n lar uchun g(n) deb qabul qilinadi. Demak f(n)=O[g(n)].
![]() funksiyasi
o[z(n)] deb katta n lar uchun belgilanadi, va unda
funksiyasi
o[z(n)] deb katta n lar uchun belgilanadi, va unda ![]() sharti bajariladi.
sharti bajariladi.
Bu begilar “katta O” va “kichik o” deb nomlanadi. Agar f(n)=O[g(n)] bo’lsa,
ikkala funksiya ham ![]() bo’lganda
bir xil tezlikda o’sadi.
bo’lganda
bir xil tezlikda o’sadi.
Agar f(n)=O[g(n)] bo’lsa,unda g(n), f(n) nisbatan ancha tez o’sadi.
Demak, ![]() - qandaydir n
o’zgaruvchidan bog’liq va k darajadagi polinom uchun
- qandaydir n
o’zgaruvchidan bog’liq va k darajadagi polinom uchun ![]() yoki
yoki ![]() bo’lganda algoritm
polynomial hisoblanadi, aks holda algoritm eksponensial.
bo’lganda algoritm
polynomial hisoblanadi, aks holda algoritm eksponensial.
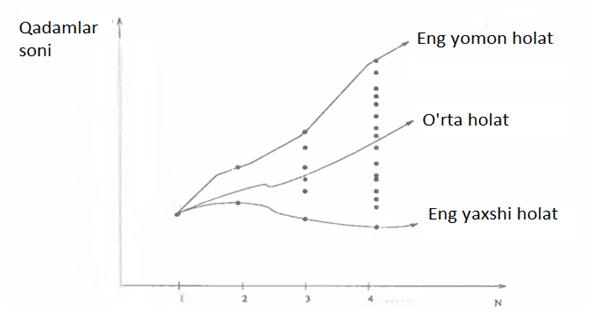
Eksponensial
algoritm yahshi ishlamaydigan deb hisoblanadi.Agar algoritmlar eksponensial
bo’lsa, ular orasida eng samaralisini topish kerak, n kattalikdagi masalani ![]() qadamda yechadigan
algoritm
qadamda yechadigan
algoritm ![]() yoki
yoki ![]() qadamda masalani
yechadigan algoritmdan afzalroq.
qadamda masalani
yechadigan algoritmdan afzalroq.
Dasturni tekshirish. Biz dasturni har bir qismini tekshiradigan kirituvchi ma’lumotlar to’plamini tanlashimiz kerak.Ko’p murakkab algoritmlarni matematik tomondan tadqiq qilish yoki juda qiyin yoki mumkin emas. Bunday holatlarda algoritmni faoliyat jarayonida va qiyinligi bo’yicha tekshiradi. Bundan tashqari dasturlarni hisoblash imkoniyatlarini aniqlash uchun ham testlash maqsadga muvofiq.Ko’p dasturlar qandaydir kiritiladigan ma’lumotlar bilan yahshi ishlasa, boshqalari bilan yomon ishlaydi.“Yahshi” lardan “yomon” larga o’tish “mayin” bo’lish kerak.Testlash uchun ma’lumotlar dasturning qiyinligiga, mavjud vaqt resurslariga, kiritish-chiqarishsoniga bog’liq holda tanlanadi. Bu yerda analitik va eksperimental tahlil bir-birini to’ldiradi.
Hujjatlashtirish. O’zingiz yozmagan dastur kodini o’qish juda qiyin.Bu muammoni hujjatlashtirish yordamida yechsa bo’ladi. Hujjatlashtirish o’z ichiga hamma yordamchi ma’lumotlarni oladi va dasturda nima bajarilishini tushuntirib beradi, xususan, blok-sxemalardagi boshqarishni uzatish, berilganlarni kiritish-chiqarish shaklini batafsil tavsif qilish, siklning parametrlari, yordamchi local va global proseduralarni bajarilishi va boshqalar.
Hujjatlashtirishning eng asosiy qoidasi bu “boshqalar yozgan dasturlarni qanday ko’rishni istasangiz, o’zingiz ham dasturni shunday ko’rinishda rasmiylashtiring”.
Masalalar yechish.
1 - misol. Bеrilgan to’rt xonali butun sonning raqamlari ko’paytmasini toping.
Tеst
|
Tеst tartibi |
Tеkshirish |
Son |
Natija |
|
1 |
Musbat son |
2314 |
P = 24 |
|
2 |
Manfiy son |
-1245 |
P = 40 |
Algoritmi (псевдокод)
alg Butun_son (but Num, P)
arg Num
natija P
boshlbutun i, j, k, l
Num := abs(Num)
i := Num div 1000 j := ((Num div 100) mod 10) k := ((Num div 10) mod 10) l := Num mod 10
P := i * j * k * l;Tamom
2 - misol. Butun qiymatli A(N, M) matritsa bеrilgan. Agar matritsa satrining hеch bo’lmaganda biror elеmеnti manfiy bo’lsa, u holda bu satrning barcha elеmеntlarini nollar bilan almashtiring
Tеst
|
Bеrilgan |
Natija |
|
|
N |
A matritsa |
A matritsa |
|
3 |
|
|

