O‘ZBEKISTON RESPUBLIKASI ALOQA, AXBOROTLASHTIRISH VA TELEKOMMUNIKATSIYA TEXNOLOGIYALARI DAVLAT QO’MITASI
TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
DASTURIY INJINIRING FAKULTETI
“Algoritmlash va matematik
modellashtirish” kafedrasi
“IQTISODIY MATEMATIK USULLAR VA MODELLAR”
FANI BO’YICHA MA’RUZALAR MATNI.

Òoshkent 2014
“Algoritmlash va matematik
modellashtirish” 2-qism. Aniqmas integral
“Algoritmlash va matematik
modellashtirish” kafedrasining
majlisida muhokama qilindi
va bosmaxonada chop etishga
tavsiya etildi.
(-bayonnoma)
Tuzuvchilar:
Dotsent: A.N. Mirzayev
Dotsent: Yu. M. Abduraxmanova
Mas’ul muharrir:
Dotsent: Yu. M. Abduraxmanova
Muharrir:
KIRISH
Amaliy masalalarni yechishda, aksariyat hollarda, o’rganilayotgan jarayonni yoki muammoni matematik modelini tuzish, hamda bu matematik masala yechimi asosida tabiiy jarayonni tahlil qilish usulidan foydalaniladi.Matematik model deganda, o’rganilayotgan jarayon yoki biror texnik tizimning parametrlari orasidagi miqdoriy bog’lanishlarni aks ettiruvchi tenglama, tengsizlik, ayniyat kabi munosabatlar tushuniladi.Bu munosabatlar asosida jarayonning ma’lum parametrlari orqali noma’lum parametrlarini topish usullari izlanadi.Natijada matematik model yordamida jarayonni tahlil qilish, parametrlarining jarayonga ta’sirini baholash imkoniyati paydo bo’ladi.Boshqacha qilib aytganda tabiiy jarayonning qanday kechishi matematik model asosida qog’ozda, murakkab bo’lsa kompyuterda tahlil qilinishi mumkin bo’lib qoladi. Bu tahlil natijalarining qanchalik ishonchli ekanligini baholash uchun matematik modelning tabiiy modelga yaqinlik darajasini ifodalovchi mezonlar va qoidalar kerak bo’ladi. “Iqtisodiy matematik usullar va modellar” fani yuqorida keltirilgan savollarni o’z ichiga oladi, hamda uning aksariyati, aynan iqtisodiyot va menejment yo’nalishida ta’lim olayotgan talabalarga mo’ljallangan. Ma’ruzalar matnida ko’proq muammoning iqtisodiy taraflariga, hamda iqtisodiy samaradorligiga e’tibor qaratilgan.
Ushbu ma’ruzalar matni “Iqtisodiy matematik usullar va modellar” fanining bir qismini o’z ichiga oladi.Bunda matematik model, uning asosiy belgilari unga qo’yiladigan talablar amaliy masalalar yordamida tahlil qilinadi. Shuningdek amaliy masalalarni yechish jarayonida doimo uchrashi mumkin bo’lgan xatoliklar va ularni baholash usullari haqida to’xtalinadi. Biror reja yoki loyihaning samaradorligini ifodalovchi maqsad funksiyasi va uning asosida optimal (eng samarador) variantni tanlash usullari amaliy masalalar asosida tahlil qilinadi. Optimizatsiya masalalarini yechish usullari haqida ma’lumotlar ham keltiriladi.
Matematik model tuzish usullaridan bo’lgan approksimatsiya masalasi haqida ham ma’lumotlar, hamda amaliy formulalar va ulardan foydalanishbo’yicha tavsiyalar keltirilgan. Bunda asosiy maqsad, murakkab jarayonlardagi miqdoriy bog’lanish qonuniyatlarini kuzatuvlar asosida olingan jadval ma’lumotlar asosida tuzish usullari haqida to’xtalgan.Bu masala yechimini interpolyatsion ko’phadlar, eng kichik kvadratlar usuli, hamda ortagonal ko’phadlar yordamida yechish usullari ko’rsatilgan.
Har bir mavzu amaliy masalalar yordamida izohlangan va tahlil qilingan. Ma’ruzalar matni oxirida foydalanilgan adabiyotlar ro’yhati berilgan. Ma’ruzalar matnidan nafaqat iqtisodiyot va menejment yo’nalishidagi, balki boshqa yo’nalishdagi talabalar ham samarali foydalanishi mumkin. Chunki matematik model yordamida jarayonni tahlil qilish – eng qulay, arzon, tezkor va samarali usuldir.
I. Matematik modellashtirish nazariy va amaliy asoslari
§ 1. Matematik model tushunchasi va uning asosiy belgilari
Reja
1. Matematik model va uning tabiiy modelga muvofiqlik shartlari
2. Matematik modelning korrektlik shartlari
3. Matematik model tuzishdagi asosiy muammolar. Taqribiy matematik model tushunchasi va unga misollar
Matematik model va uning tabiiy model bilan muvofiqlik shartlari. Amaliyotda uchraydigan ko’plab masala va muammolar ma’lum hisob – kitoblar asosida yechiladi. Buning uchun ko’rilayotgan masala yoki o’rganilayotgan jarayonning parametrlari orasidagi miqdoriy bog’lanishlarni ifodalovchi qonun vaqoidalardan foydalaniladi. Ilmiy va amaliy adabiyotlarda urf bo’lgan “matematik model” atamasining ta’rifini soddaroq holda quyidagicha ifodalash mumkin. O’rganilayotgan jarayonning ma'lum va aniqlanishi kerak bo’lgan parametrlari orasidagi miqdoriy bog’lanishlarni ifodalovchi munosabatlar (tenglama, tengsizlik,…) tabiiy masalaning matematik modeli deyiladi.
Matematik model o’rganilayotgan jarayonga mutanosib(ilmiy adabiyotlarda “adekvat” atamasi bilan ifodalanadi) bo’lishi kerak. Shuningdek tuzilgan matematik model “korrekt” bo’lishi kerak, ya’ni ifodalangan matematik modelga mos masala yechimi mavjud, yagona va boshlang’ich ma’lumotlarga uzluksiz bog’langan bo’lishi kerak. Matematik modellarga eng sodda misollar sifatida quyidagi masalalarni keltiramiz.Maqsad, matematik modellar bilan har qadamda duch kelishimizni eslatib o’tish.Yuzalarni hisoblash bilan bog’liq formulalarni yodga olamiz.
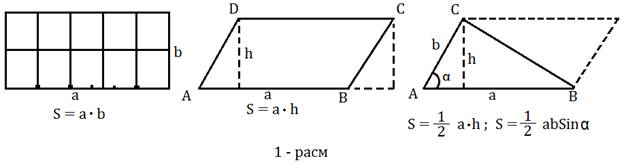
Keltirilgan misollarda yuza ta’rifi, o’lchov
birligi, hisoblash formulalari ifodalangan. Hususan tomonlari a = 5m va b = 2m
bo’lgan to’gri to’rtburchakning tomonlari 1m dan qilib bo’linsa, unga tomonlari
1m dan bo’lgan 10ta kvadrat joylashar ekan. Tomonlari 1m bo’lgan kvadrat
yuzasini![]() deb
belgilasak (o’lchov birligi) berilgan to’g’ri to’rtburchak yuzasi
deb
belgilasak (o’lchov birligi) berilgan to’g’ri to’rtburchak yuzasi![]() formula
bo’yicha hisoblanishi mantiqan to’g’ri ekanligi ko’rinadi. Buning asosida
parallelogramm, uchburchak yuzalari formulalari kelib chiqishi chizmadan
ko’rinib turibdi.Bu formulalarni ham matematik model deb atashimiz
mumkin.Matematik modelni murakkab, mavhum tushuncha sifatida emas, muammoni hal
qilish yo’lidagi bir ish quroli sifatida tasavvur qilish kerak.Fikrimizning isboti
sifatida doira yuzasini hisoblash formulasini keltirib chiqaramiz.Buning uchun
uchburchak yuzasini hisoblash formulasidan foydalanamiz.
formula
bo’yicha hisoblanishi mantiqan to’g’ri ekanligi ko’rinadi. Buning asosida
parallelogramm, uchburchak yuzalari formulalari kelib chiqishi chizmadan
ko’rinib turibdi.Bu formulalarni ham matematik model deb atashimiz
mumkin.Matematik modelni murakkab, mavhum tushuncha sifatida emas, muammoni hal
qilish yo’lidagi bir ish quroli sifatida tasavvur qilish kerak.Fikrimizning isboti
sifatida doira yuzasini hisoblash formulasini keltirib chiqaramiz.Buning uchun
uchburchak yuzasini hisoblash formulasidan foydalanamiz.
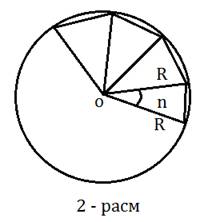
RadiusiRbo’lganaylananintatengbo’lakkabo’lamiz(chizmadagidek
2 – rasm).Bo’linishnuqtalarinimarkazbilantutashtiribntabirxil sector hosilqilamiz.Har
bir sektorda yoyni vatar bilan almashtirsak uchburchaklar hosil bo’ladi. Bu
uchburchaklar yuzasi![]() ,
jami ko’pburchak yuzasi esa
,
jami ko’pburchak yuzasi esa
![]()
![]()
doira ekanligi ko’rinib turibdi.
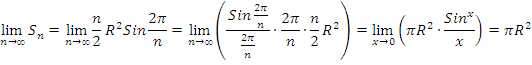
doira
yuzasi formulasi kelib chiqadi. Bu yerda![]() belgilash
kiritilgan va
belgilash
kiritilgan va![]() ajoyib
limitdan foydalanilgan.
ajoyib
limitdan foydalanilgan.
Navbatdagi masala quyidagicha bo’lsin.Gorizantal tekislikka nisbatan α burchak ostida otilgan moddiy jism (tosh, artilleriya snaryadi, raketa) boshlang’ich tezlikV0bo’lsa, borib tushadigan maksimal masofa topilsin.
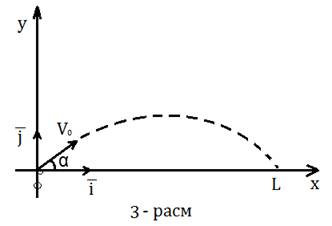
Bu jarayonda ishtirok etayotgan moddiy jismni moddiy nuqta deb qaralsa masala osonlashadi, chunki nuqtaning o’lchamlari yo’q, demak havo qarshiligi ham yo’q deyish mumkin. U holda Nyuton qonuniga ko’ra harakat qonuni
![]()
deb
ifodalash mumkin. Chunki jismga faqat og’irlik kuchi ta’sir qiladi. Jism
tezligini vector![]() ko’rinishda
ifodalasak va
ko’rinishda
ifodalasak va![]() ekanligini
e’tiborga olsak, harakat qonuni (1.1) koordinat o’qlari bo’yicha quyidagicha
ifodalanadi.
ekanligini
e’tiborga olsak, harakat qonuni (1.1) koordinat o’qlari bo’yicha quyidagicha
ifodalanadi.

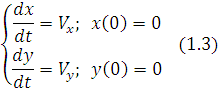
(1.2), (1.3) differensial tenglamalar jarayonning matematik modelini ifodalaydi.
(1.2) sistemadan
![]()
yechimlarni topamiz. Ularni (1.3) ga qo’yilsa
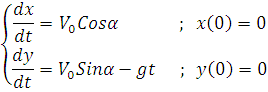
ko’rinishni oladi. Bu sistemadan jism trayektoriyasi tenglamasini topamiz.
![]()
Jism
yerga tushganda y = 0 bo’lishi kerak. Bu shartga ko’ra![]() tenglikdan
yerga tushish vaqti
tenglikdan
yerga tushish vaqti
![]()
topiladi. Bu qiymatni x(t) formulasiga qo’yib
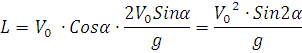
masofa
formulasini hosil qilamiz. Bu formula qo’yilgan masalaning matematik modeli
sifatida qaralishi mumkin. Ixtiyoriy boshlang’ich![]() qiymatlar
uchun L ni topish mumkin.
qiymatlar
uchun L ni topish mumkin.
Shuningdek zambarak ( raketa ) imkoniyatiga ko’ra![]() ma’lum
bo’lsa, α - burchakni tanlash hisobiga L ni o’zgartirish, berilgan L –
nishon o’rniga qarab α - ni tanlash mumkin.
ma’lum
bo’lsa, α - burchakni tanlash hisobiga L ni o’zgartirish, berilgan L –
nishon o’rniga qarab α - ni tanlash mumkin.
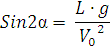
tenglikkako’ra
burchak topiladi. Xususan, formulaga ko’ra![]() bo’lganda
bo’lganda![]() ,
qurolning ta’sir masofasini ham aniqlash mumkin.
,
qurolning ta’sir masofasini ham aniqlash mumkin.
Yuqorida
ta’kidlanganidek, bu modelni tabiiy modelga to’la mutanosib debbo’lmaydi. Chunki bu yerda havoning qarshiligi,
balandlik bilan![]() qiymati o’zgarishi
ham hisobga olinmadi.Shuningdek, havo qarshiligi havoning hamda snaryadning
temperaturasiga ham bog’liq bo’lishi mumkin.Balandlik o’zgarishi bilan havo
zichligi, demak havo qarshiligi ham o’zgarib boradi. Bu faktorlar (omillar) ni
barchasini hisobga olsak matematik model murakkablashib, uning yechimini topish
ham mushkullashib ketadi. Sanab o’tilgan omillar uchun
qiymati o’zgarishi
ham hisobga olinmadi.Shuningdek, havo qarshiligi havoning hamda snaryadning
temperaturasiga ham bog’liq bo’lishi mumkin.Balandlik o’zgarishi bilan havo
zichligi, demak havo qarshiligi ham o’zgarib boradi. Bu faktorlar (omillar) ni
barchasini hisobga olsak matematik model murakkablashib, uning yechimini topish
ham mushkullashib ketadi. Sanab o’tilgan omillar uchun![]() bog’lanish
modellarini to’g’ri ifodalash ham o’ziga yarasha jiddiy muammolardan
hisoblanadi. Bu yerda h – jism balandligi, T – temperaturasi; S – ko’ndalang
kesimi yuzasi K(Y,T,S) – havo qarshilik proporsionallik koeffitsiyenti. Havo
qarshiligi tezlikka proportsional va qarama – qarshi yo’nalganligini hisobga
olsak, harakat qonuni quyidagicha ifodalanadi
bog’lanish
modellarini to’g’ri ifodalash ham o’ziga yarasha jiddiy muammolardan
hisoblanadi. Bu yerda h – jism balandligi, T – temperaturasi; S – ko’ndalang
kesimi yuzasi K(Y,T,S) – havo qarshilik proporsionallik koeffitsiyenti. Havo
qarshiligi tezlikka proportsional va qarama – qarshi yo’nalganligini hisobga
olsak, harakat qonuni quyidagicha ifodalanadi
![]()
yoki koordinat ko’rinishida
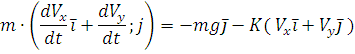
tarzda ifodalanadi.
Amaliy masalalarni yechishda uchraydigan asosiy muammolardan biri tanlangan matematik modelning amaliy masalaga mutanosibligini baholash.Agar xatolik talab darajasidan ortib ketmasa nisbatan soddaroq modellardan foydalanish bo’yicha tavsiyalar ishlab chiqishdan iborat.Xususan, yuqorida ko’rilgan masala uchun topilgan dastlabki yechim qaysi hollarda ishonarli deb hisoblanishi mumkin?
§ 2. Matematik modellarga misollar. Fizik, mexanik, ommaviy va iqtisodiy masalalar asosida.
Reja
1. Amaliy masalalarni yechishning asosiy bosqichlari
2. Mexanika masalalarini matematik modelini tuzishga misollar. Yechim tahlili.
3. Matematik modelni tabiiy jarayonga to’la muvofiqlashtirish muammolari, soddalashtirish imkoniyatlari.
Matematik model ta’rifida ta’kidlanganidek, unda o’rganilayotgan jarayonning asosiy parametrlarini bog’lovchi munosabatlar ifodalangan bo’lishi kerak.Bu munosabatlardan ma’lum parametrlar orqali noma’lum parametrlarni bir qiymatli aniqlash imkoniyati kelib chiqishi kerak.
O’rni kelganda amaliy masalalarni yechish bosqichlarini ifodalaymiz. (4 – rasm).
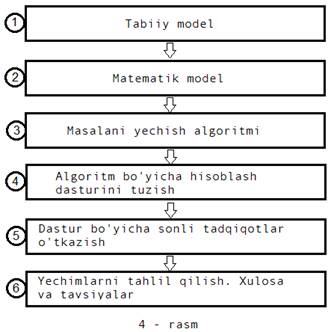
Tabiiy modelni buyurtmachi ifodalaydi. Buyurtmachi sifatida davlat (muhim loyihalar), korxona (shartnomaviy loyihalar), yuridik yoki jismoniy shaxslar (institut, ilmiy rahbar) kabilarni ko’rsatishimiz mumkin. Masalaning mavqe va miqyosiga qarab har bir bosqichda (4–rasm) yolg’iz shaxs yoki jamoa ishtirok etishi mumkin. Har bir bo’g’inning o’z bilimdon mutaxassislari bo’lishi mumkin. Shuning uchun bunday hollarda mehnat taqsimotini tashkil qilgan ma’qul.
Vaqti kelib oddiy masalalar orqali har bir bosqichning umumiy jarayondagi o’rnini ifodalashga harakat qilamiz. 3, 4, 5–bo’g’inlar murakkab, katta hajmdagi hisoblashlar bilan bog’liq masalalarda yuzaga chiqadi. Hozircha matematik model tuzishga namunalar keltirish bilan cheklanamiz.
1
– ìàñàëà. Í balandlikdan
tashlangan, massasi m bo’lgan jism yerga qanday tezlik bilan tushadi? Bu yerda
ham dastavval jismni moddiy nuqta deb qarab matematik model tuzamiz.Energiyaning
saqlanish qonunidan foydalanamiz. Boshlang’ich t = 0 momentda jismda faqat potensial
energiya bo’lib![]() bo’ladi.
Harakat boshlangach h – balandlik kamayib boradi, tezlik esa ortib boradi. Potensial
energiya kinetik energiyaga aylanib boradi.
bo’ladi.
Harakat boshlangach h – balandlik kamayib boradi, tezlik esa ortib boradi. Potensial
energiya kinetik energiyaga aylanib boradi.![]() -
potensial
-
potensial![]() –
kinetik energiyalar yig’indisi o’zgarmas.
–
kinetik energiyalar yig’indisi o’zgarmas.
![]()
bo’lishi
kerak. Yerga tushganda h = 0 bo’lib, potensial energiya tugaydi va![]() tenglik
hosil bo’ladi. Undan
tenglik
hosil bo’ladi. Undan![]() hisoblash
formulasi hosil bo’ladi. Masalan H = 100m bo’lsa
hisoblash
formulasi hosil bo’ladi. Masalan H = 100m bo’lsa
![]()
kelib
chiqadi. Shunday qilib istalgan balandlikdan yerga tushish tezligini aniqlash
formulasi topildi. Bu yerda ham formula tabiiy modelga qanchalik mutanosib,
natija qanchalik to’g’ri ekanligini baholash zarurati qoladi. Dastlabki
tuzatish sifatida harakatga qarama – qarshi yo’nalgan va tezlikka proporsional
bo’lgan havoning qarshilik kuchini ham hisobga olsak harakat qonuni![]() ko’rinishda
ifodalanadi.
ko’rinishda
ifodalanadi.
![]()
differensial tenglamadan umumiyyechim
![]()
ko’rinishda
ifodalanadi.![]() shartga
ko’ra
shartga
ko’ra![]() topiladi
va yechim
topiladi
va yechim
![]()
ko’rinishda ifodalanadi. Bu tenglikdan masofa S (t) uchun
![]()
Koshi masalasini hosil qilamiz. Uning yechimi
![]()
Ko’rinishda
bo’lib,S
(0) = 0 shartga ko’ra![]() topiladi
va
topiladi
va
![]()
formulani hosil qilamiz. Yerga tushganda o’tilgan masofa H bo’lganligi uchun
![]()
tenglama hosil bo’ladi. Bu tenglamani t ga nisbatan yechib yerga tushish vaqti T topiladi uni (2.1) formulaga qo’yib yerga tushgan paytdagi tezlik
![]()
topiladi. Bu yerda K – proporsionallik koeffitsiyenti jism shakli, hajmiga bog’liq bo’lib tajribalardan topiladi. (2.2) tenglamani yechishda esa turli taqribiy usullardan foydalanishga to’g’ri keladi.
Ikkinchi masala: Vertikal holatdagi silindrik idishga (radiusi R, balanligi H, 5 – rasm) suv to’ldirilgan bo’lib, uning pastki qismida radiusi r bo’lgan kranli truba o’rnatilgan bo’lsin.
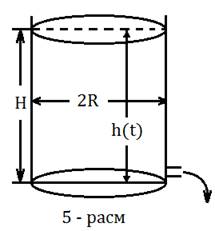
t
= 0 vaqtdan boshlab quyidagi kran ochilsa idishdagi suv qancha vaqtda oqib
tushadi? Torichelli qonuniga ko’ra quyidagi trubadan chiqayotgan suv tezligi
idishdagi suv sathi balandligi h ( t ) ga bog’liq bo’ladi va![]() formula
bilan ifodalanadi. Idishdagi suvning kamayish hajmi
formula
bilan ifodalanadi. Idishdagi suvning kamayish hajmi![]() formula
bo’yicha, oqib chiqqan suv hajmi esa
formula
bo’yicha, oqib chiqqan suv hajmi esa![]() formula
bo’yicha hisoblanadi.Moddiy balans ( saqlanish ) qonuniga ko’ra
formula
bo’yicha hisoblanadi.Moddiy balans ( saqlanish ) qonuniga ko’ra
![]()
bo’lishi kerak. Bu tenglikdan
![]()
![]()
Koshi masalasini hosil qilamiz. Undan
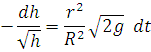
hosil bo’ladi. Ikki tarafini integrallab
![]()
H(0)=H
shartga ko’ra
![]() tenglikni
hosil qilamiz. Suv tugaganda h = 0 bo’lganligi uchun, bu tenglikdan
tenglikni
hosil qilamiz. Suv tugaganda h = 0 bo’lganligi uchun, bu tenglikdan
![]()
kelib chiqadi.
Undan esa
![]() formulani
hosil qilamiz.
formulani
hosil qilamiz.
Hususan
![]() á¢ëñà
á¢ëñà
![]() deb
hisoblasak, t=6000
sek = 100 minut kelib chiqar ekan. Bu yerda ham suvning qayishqoqlik koeffitsiyenti
hisobga olinmadi.Aks holda model murakkablashgan bo’lar edi.
deb
hisoblasak, t=6000
sek = 100 minut kelib chiqar ekan. Bu yerda ham suvning qayishqoqlik koeffitsiyenti
hisobga olinmadi.Aks holda model murakkablashgan bo’lar edi.
Keltirilgan masalalar barchasi ma’lum masalalar bo’lib, bu yerdagi asosiy maqsad – bu masalalarga matematik modellashtirish nuqtai nazaridan yondoshish va bunda uchraydigan muammolarni ifodalash, hamda tabiiy model bilan mutanosibligini baholash kabi tushunchalarni yoritishdan iborat edi.
§ 3. Optimizatsiya masalalari, maqsad funksiyasi
Reja
1. Maqsad funksiyasi tushunchasi, uni tuzishga misollar
2. Optimal yechim (opimal reja) tushunchasi, uni aniqlashga misollar
3. Bir o’lchovli, ko’p o’lchovli optimizatsiya masalalariga misollar.
4. Yechimning iqtisodiy tahlili
Inson o’z mehnat faoliyati davomida amalga oshiradigan barcha ishlarida biror maqsadni ko’zda tutadi.Agar qilinayotgan ish daromad bilan bog’liq bo’lsa, daromadni ko’paytirish, harajat bilan bog’liq bo’lsa, harajatlarni kamaytirish yo’lini izlaydi.Mumkin bo’lgan variantlar orasidan eng ma’qulini tanlashga harakat qiladi.Optimizatsiya, optimal variant so’zlarining lug’aviy ma’nosi ham aynan eng yaxshisi, eng maqbuli kabi tushuniladi.
Fikrimizni oydinlashtirish uchun quyidagi amaliy masalani qaraymiz.Kichik korxona metall silindrik bankalar (kraskalar, konservalar jamlanadigan) tayyorlashga ihtisoslashgan bo’lsin.Korxona hajmi V ga teng bo’lgan bankalardan N ta tayyorlab berishga buyurtma olgan, narxlari kelishilgan.Korxona buyurtmadan tushadigan daromadni ko’paytirish uchun unga sarflanadigan xomashyo miqdorini kamaytirish variantlarini izlashi kerak bo’ladi.Buning uchun hajmi V bo’lgan silindrlar orasidan to’la sirti eng kichik bo’ladiganini tanlashi kerak.Chunki har bir bankadan tejalgan metall sarfini butun partiya N ta bankaga ko’paytirilsa sezilarli tejamkorlik bo’lishi mumkin.Ifodalangan ishlab chiqarish masalasining matematik modelini tuzamiz.
![]() berilgan
bo’lsa, Sto’la
berilgan
bo’lsa, Sto’la![]() bo’ladigan
variant topilsin. Bu masalani bir o’zgaruvchili optimizatsiya masalasiga
keltirish mumkin. Birinchi shartdan
bo’ladigan
variant topilsin. Bu masalani bir o’zgaruvchili optimizatsiya masalasiga
keltirish mumkin. Birinchi shartdan![]() ni
aniqlab ikkinchi shartga qo’yilsa
ni
aniqlab ikkinchi shartga qo’yilsa
![]()
![]()
shart kelib chiqadi. Bu yerda S ( R ) – maqsad funksiyasi deyiladi. R – esa optimallashtirish parametri bo’lib qoladi. Optimal variantni topish uchun an’anaviy usullardan foydalanish mumkin. Funksiya ekstremumlari birinchi tartibli hosilasi nolga teng bo’lgan nuqtalarda bo’ladi. Shunga ko’ra ish tutsak
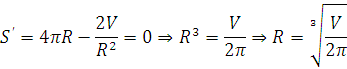
yagona
yechimni aniqlaymiz. Bu nuqtada![]() bo’lgani
uchun, funksiya minimumga erishadi.Xususan
bo’lgani
uchun, funksiya minimumga erishadi.Xususan![]() bo’lsa
R=3 optimal variant ekanligi
kelib chiqadi. Bunda
bo’lsa
R=3 optimal variant ekanligi
kelib chiqadi. Bunda![]() optimal
tsilindr o’q kesimi kvadrat bo’lishi kerak ekan.Bunda to’la sirt
optimal
tsilindr o’q kesimi kvadrat bo’lishi kerak ekan.Bunda to’la sirt![]() bo’lar
ekan.
bo’lar
ekan.
Xulosamiz
yanada ishonarli bo’lishi uchun teskari masalani ham qarab ko’ramiz. To’la
sirti ![]() bo’lgan
silindrlar orasida hajmi eng katta bo’ladiganining o’lchamlari topilsin. Bu
masala matematik modeli
bo’lgan
silindrlar orasida hajmi eng katta bo’ladiganining o’lchamlari topilsin. Bu
masala matematik modeli ![]() ma’lum
bo’lsa
ma’lum
bo’lsa ![]() topilsin.
topilsin.
Bevosita maqsad funksiyasini aniqlashva uning maksimumini topishga o’tamiz.
![]()
![]()
![]()

formula
kelib chiqadi. Bu yerda ham ekstremum yagona va![]() bo’lgani
uchun bu nuqtada funksiya maksimal qiymatga erishadi. Xususan
bo’lgani
uchun bu nuqtada funksiya maksimal qiymatga erishadi. Xususan![]() kelib
chiqadi.Bu holda
kelib
chiqadi.Bu holda![]() aniqlanadi.Bu
yerda ham optimal variant o’q kesimi kvadrat bo’ladigan silindr bo’lishi kelib
chiqadi. Hususiy masalani ishlash jarayonida umumiy xulosa kelib chiqadi, ya’ni
berilgan hajmga ega silindrlar ichida to’la sirti eng kichigi ham, berilgan
to’la sirtga ega silindrlar ichida hajmi eng kattasi ham o’q kesimi kvadrat
bo’ladigani bo’lar ekan. Bu xulosa barcha hollarda ham o’rinli bo’lavermas
ekan. Hususan, juqorida ko’rilgan masalada buyurtmada qopqoqsiz silindrik idish
aytilgan bo’lsa matematik model vayechimning qanday o’zgarishini tahlil qilib
ko’ramiz.
aniqlanadi.Bu
yerda ham optimal variant o’q kesimi kvadrat bo’ladigan silindr bo’lishi kelib
chiqadi. Hususiy masalani ishlash jarayonida umumiy xulosa kelib chiqadi, ya’ni
berilgan hajmga ega silindrlar ichida to’la sirti eng kichigi ham, berilgan
to’la sirtga ega silindrlar ichida hajmi eng kattasi ham o’q kesimi kvadrat
bo’ladigani bo’lar ekan. Bu xulosa barcha hollarda ham o’rinli bo’lavermas
ekan. Hususan, juqorida ko’rilgan masalada buyurtmada qopqoqsiz silindrik idish
aytilgan bo’lsa matematik model vayechimning qanday o’zgarishini tahlil qilib
ko’ramiz.
![]()
![]()
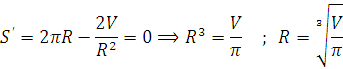
Hususan, ![]() bo’lgan
bo’lsa
bo’lgan
bo’lsa
![]()
kelib chiqadi.
Bundan ko’rinadiki, silindr o’q kesimi bu holda kvadrat bo’lmas ekan. Ko’rilgan masalalardan kelib chiqadigan dastlabki, asosiy xulosamiz: optimizatsiya masalalarida matematik jihatdan birorta maqsad funksiya hosil qilinar va uning ekstremumini topish kerak bo’lar ekan.
Optimizatsiya masalalari boshqariladigan parametrlari soniga qarab bir o’lchovli, ikki o’lchovli va umumiy holda n – o’lchovli bo’lishi mumkin. Parametrlari soni ortgani sari masala murakkablashib boraveradi. Bu yerda biz yana bir amaliy masala asosida 2 o’lchovli optimizatsiya masalasiga namuna keltiramiz. Odatda sug'oriladigan yer maydonlarini ko’paytirish uchun birinchi navbatda kanallar qurish kerak bo’ladi.Bunda kanaldan suv shimilib ketmasligi uchun beton qoplamadan foydalaniladi. Kanalning ko’ndalang kesimi trapetsiya shaklida bo’lib (6 – rasm)
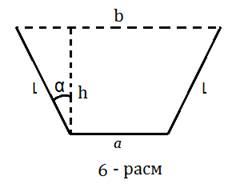
Uning
perimetri ![]() o’zgarmas
bo’lgan holda
yuzasi eng
katta bo’lishi
uchun a,
l,
α
qanday tanlash kerak degan masala yuzaga chiqadi. Bu
yerda harajatlar beton qoplama bilan,
yesa aynan qoplama perimetri L bilan bog’liq. Kanalning
suv o’tkazish quvvati esa ko’ndalang kesimni yuzasi bilan bog’liq. Keltirilgan mulohazalar
asosida masalaning matematik modelini tuzamiz.
o’zgarmas
bo’lgan holda
yuzasi eng
katta bo’lishi
uchun a,
l,
α
qanday tanlash kerak degan masala yuzaga chiqadi. Bu
yerda harajatlar beton qoplama bilan,
yesa aynan qoplama perimetri L bilan bog’liq. Kanalning
suv o’tkazish quvvati esa ko’ndalang kesimni yuzasi bilan bog’liq. Keltirilgan mulohazalar
asosida masalaning matematik modelini tuzamiz.
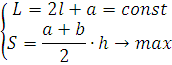
![]()
![]()
![]()
Bu
yerda ikki o’lchovli optimizatsiya masalasi hosil bo’ladi.![]() funksiyaning
minimumini topish uchun
funksiyaning
minimumini topish uchun![]() bo’yicha
birinchi tartibli hususiy hosilalarini nolga tenglab
bo’yicha
birinchi tartibli hususiy hosilalarini nolga tenglab![]() larning
optimal qiymatlariga nisbatan tenglamalar sistemasini hosil qilamiz.
larning
optimal qiymatlariga nisbatan tenglamalar sistemasini hosil qilamiz.
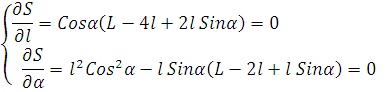
Birinchi tenglamasidan kelib chiqadigan
![]()
ifodani ikkinchi tenglamasiga qo’yilsa
![]()
![]()
tenglama kelib chiqadi. Undan esa
![]()
kelib chiqadi. Demak kanal optimal o’lchamlari shunday tartibda olinishi kerak ekan.Shunday qilib optimizatsiya masalalari matematikaning bir, ikki argumentli funksiyalarning ekstremumlarini topish masalasiga aylanar ekan.Argumentlari soni ortgani sari bu masala murakkablashib, uni yechish uchun ham mahsus usullar yaratishga to’g’ri kelar ekan.Hattoki biror argumentli funksiyalar uchun ham bu masalaning aniq yechimini doimo chekli qadamlarda topish mumkin bo’lmaydi.
§ 4. Optimizatsiya masalalarini yechishda taqribiy usullar
Reja
1. Bir o’lchovli optimizatsiya masalalarini yechishda oraliqni teng ikkiga bo’lish usuli. Unimodal funksiyalar
2. Bir o’lchovli optimizatsiya masalalari uchun oltin qirqimlar usuli.
3. Ikki o’lchovli optimizatsiya masalalarini yechishda gradiyent bo’yicha pasayish usuli.
Yuqorida ko’rilganidek optimizatsiya masalalari
funksiya ekstremumini topishga kelar ekan ![]() to’plamda
aniqlangan
to’plamda
aniqlangan ![]() funksiyaning
shu to’plamdagi ekstremumini topish masalasini qaraymiz. Biz bu yerda bir
o’lchamli optimizatsiya masalasi bilan cheklanamiz. Yanada aniqlik uchun
funksiyaning
shu to’plamdagi ekstremumini topish masalasini qaraymiz. Biz bu yerda bir
o’lchamli optimizatsiya masalasi bilan cheklanamiz. Yanada aniqlik uchun ![]() funksiyaning
minimumini topish masalasinigina qaraymiz. Chunki
funksiyaning
minimumini topish masalasinigina qaraymiz. Chunki ![]() funksiya
maksimumini topish masalasini
funksiya
maksimumini topish masalasini ![]() funksiya
uchun minimum topish masalasiga almashtirish mumkin. Umumiy holda masalan
funksiya
uchun minimum topish masalasiga almashtirish mumkin. Umumiy holda masalan ![]() oraliq
deb qarasak,
oraliq
deb qarasak,
![]()
masalaniyechish talab qilinsin.
hisoblash
texnikasi rivojlangan hozirgi davrda ba’zi hollarda hisobni ko’p talab
qiladigan eng sodda usullardan ham foydalanish mumkin.Ulardan biri ketma- ket
taqqoslash usuli. Agar funksiya minimumga erishadigan nuqtasi![]() aniqlikda
topilishi talab qilinayotgan bo’lsa [a,b] oraliqni
aniqlikda
topilishi talab qilinayotgan bo’lsa [a,b] oraliqni![]() qadam
bilan n ta bo’lakka bo’lamiz
qadam
bilan n ta bo’lakka bo’lamiz
![]()
Bu
nuqtalardagi![]() qiymatlari
orasidan eng kichigini tanlasak, uni noma’lum qiymat sifatida qabul qilish
mumkin, ya’ni
qiymatlari
orasidan eng kichigini tanlasak, uni noma’lum qiymat sifatida qabul qilish
mumkin, ya’ni
![]()
Ko’rilgan bu usul ko’p hisoblashlarni talab qiladi
va passiv usullardan hisoblanadi. Hisoblangan hech qaysi qiymat strategiyaning
o’zgarishiga sabab bo’lolmaydi.Funksiya qiymatlarini hisoblash soni![]() tengsizlik
bo’yicha aniqlanadi.
tengsizlik
bo’yicha aniqlanadi.
Oraliqni teng ikkiga bo’lish usuli.Bu
usulda berilgan oraliqda funksiya unimodal bo’lishi talab qilinadi. Agar [ a,b
] oraliqda funksiya uzluksiz bo’lib shu oraliqda yagona minimumi bo’lsa,
![]() [
a,b ]oraliqda unimodal deyiladi. Minimumga
erishish nuqtasi
[
a,b ]oraliqda unimodal deyiladi. Minimumga
erishish nuqtasi ![]() ni
ni![]() aniqlikda
aniqlash talab qilingan bo’lsin. Usul mohiyati quyidagicha
aniqlikda
aniqlash talab qilingan bo’lsin. Usul mohiyati quyidagicha![]() qiymat
aniqlanib [ a,b ] oraliqdan
qiymat
aniqlanib [ a,b ] oraliqdan
![]()
nuqtalarni
olib bu nuqtalardagi funksiya qiymatlari olinadi. Agar![]() bo’lsa
bo’lsa![]() oraliqda
funksiya o’sishni boshlagan, ya’ni minimumdan o’tib ketgan bo’ladi va
oraliqda
funksiya o’sishni boshlagan, ya’ni minimumdan o’tib ketgan bo’ladi va![]() deb
oraliqning chap tarafi olib qolinadi. Agar
deb
oraliqning chap tarafi olib qolinadi. Agar![]() bo’lsa,
funksiya
bo’lsa,
funksiya![]() oraliqda
kamayayotgan bo’lib, minimumga hali yetmagan bo’ladi va
oraliqda
kamayayotgan bo’lib, minimumga hali yetmagan bo’ladi va![]() deb
oraliqning o’ng yarmini olib qolamiz. Bu jarayon
deb
oraliqning o’ng yarmini olib qolamiz. Bu jarayon![]() bo’lguncha
davom ettiriladi. Qadamlar soni
bo’lguncha
davom ettiriladi. Qadamlar soni
![]()
tengsizlikka ko’ra aniqlanadi.
Oltin qirqimlar usuli.Bu
usullar funksiyalar ko’rinishi murakkab, qiymatlarini hisoblash ko’plab
arifmetik amallar orqali amalga oshiriladigan hollarga mo’ljallangan, hamda
hisoblash texnikalari rivojlanmagan davrlarda yaratilgan.Shuning uchun usul
funksiya qiymatlarini qanchalik kam hisoblashni talab qilsa shunchalik yaxshi
hisoblangan. Oraliqni teng ikkiga bo’lish usulida har qadamda funksiya qiymatini
yangi![]() nuqtalarda
hisoblash kerak bo’ladi va ulardan keyinchalik foydalanilmaydi. Oltin qirqimlar
usuli bu kamchilikdan holi bo’lib, har qadamda faqat bitta yangi nuqta
qo’shiladi. Buning uchun [ a;b ] oraliq
nuqtalarda
hisoblash kerak bo’ladi va ulardan keyinchalik foydalanilmaydi. Oltin qirqimlar
usuli bu kamchilikdan holi bo’lib, har qadamda faqat bitta yangi nuqta
qo’shiladi. Buning uchun [ a;b ] oraliq
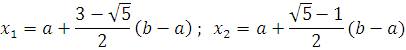
nuqtalar yordamida 3 ta bo’lakka bo’linadi.
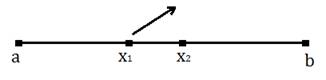
Agar![]() bo’lsa keyingi
qadam uchun
bo’lsa keyingi
qadam uchun
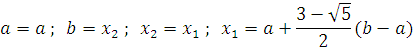
olinadi.
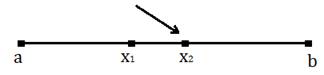
Agar![]() bo’lsa keyingi
qadam uchun
bo’lsa keyingi
qadam uchun
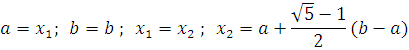
olinadi.
Bu jarayon![]() bo’lguncha davom
ettiriladi.Keltirilgan algoritmga ko’ra har qadamda faqat bitta yangi nuqta
bo’lguncha davom
ettiriladi.Keltirilgan algoritmga ko’ra har qadamda faqat bitta yangi nuqta![]() ¸êè
¸êè![]() da funksiyani
hisoblash kerak bo’ladi.Bu usul o’z davri uchun juda samarali bo’lgani uchun
ham oltin qirqimlar usuli deb ataladi.
da funksiyani
hisoblash kerak bo’ladi.Bu usul o’z davri uchun juda samarali bo’lgani uchun
ham oltin qirqimlar usuli deb ataladi.
Ko’rilgan usullarning uchchalasi ham dasturlanishi mumkin va barcha hisoblarni kompyuterda avtomatik rejimda bajarilishi mumkin. Bu dasturlar kompyuterlarning dasturiy ta’minotida, ko’plab o’quv dasturiy tizimlar tarkibiga kiritilgan.Optimizatsiya masalalarini yechishda ulardan samarali foydalanish mumkin. Masala va uni yechish usullarining murakkablashish jarayonini namoyish qilish uchun ikki argumentli funksiyalarning ekstremumlarini topish usullaridan biri haqida ma’lumot keltiramiz.
![]()
funksiya D sohada botiq bo’lsa uning minimumi mavjud ( D sohada ) bo’ladi. Funksiya botiq bo’lishi uchun funksiya 2 – tartibli hosilalaridan tuziladigan vagessian deb ataladigan matritsasi
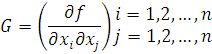
musbat aniqlangan bo’lishi kerak. Bu yerda n o’zgaruvchilari soni. Hususan,n = 2, ikki argumentli funksiyalar uchun bu shart
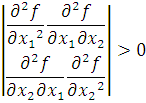
ko’rinishni oladi.
Funksiya minimumini topishda keng
tarqalgan usullardan biri bu gradient bo’yicha pasayish usulidir.Bu
usulda hisoblashlar tartibi quyidagicha bo’ladi.Minimum mavjud bo’lgan D
sohadan ![]() tanlanadi. Navbatdagi
yakinlashishlar
tanlanadi. Navbatdagi
yakinlashishlar

formulalar bilan hisoblanadi. Bu yerda α kichik son bo’lib uning qiymati
![]()
shartga ko’ra tanlanadi. Misol
![]() ekanligi
ko’rinib turibdi ( 7 – rasm )
ekanligi
ko’rinib turibdi ( 7 – rasm )
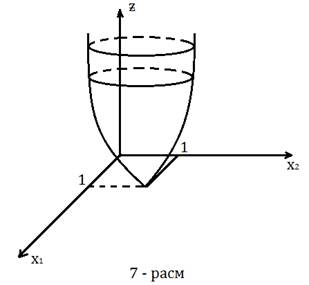
Hisoblash jarayoni
![]()
![]()
formulalar bilan ifodalanadi. Hususan
![]()
![]()
![]()
Bo’lishini ko’ramiz.
§ 5. Xatoliklar turlari va ularning manba’lari. Absolyut nisbiy xatoliklar
Reja
1. Modellashtirish xatoligi va uning kelib chiqish sabablari.
2. Bartaraf qilib bo’lmas xatolik va uning kelib chiqish mabai.
3. Usul xatoligi va uning mohiyati.
4. Absolyut va nisbiy xatolik, ularni hisoblash usullari.
5. Taqribiy miqdorning ishonchli raqamlari va ularni aniqlash qoidasi.
Amaliy
masalalrni yechish jarayonining har bosqichida imkoniyat va vaziyatga bog’liq
tarzda xatoliklar paydo bo’lishi mumkin. Ulardan birinchisi matematik model
tuzish jarayonida tabiiy modelning ba’zi omillarini hisobga olinmasligi tufayli
vujudga keladi.Bu xatolikni modellashtirish xatoligi deyiladi.Bunday hollar
bilan avvalgi ma’ruzalarda keltirilgan masalalarda qisman tanishgan edik.Bu
asosan matematik model juda murakkablashib ketmasligi uchun, yoki ba’zi
omillarni hisobga olish uchun yetarli qonuniyatlar bo’lmaganligi uchun kelib
chiqadi.Ikkinchi tur xatolik, bu o’rganilayotgan jarayonga taalluqli
parametrlar qiymatlarida uchraydigan xatoliklar, ular asosan parametrlarni
aniqlash uchun ishlatiladigan vositalar (priborlar) imkoniyatidan kelib chiqadi.Bu
xatoliklarni asosan bartaraf qilib bo’lmas xatolik deyiladi.Chunki parametrlar
tarkibidagi bu xatolik hisoblashlar qanchalik aniq bajarilmasin natijani aniq
olishga imkioniyat bermaydi.Bu xatoliklar natijani olishgacha bajariladigan
amallar ko’paygani sari ortib borishi mumkin. Aksariyat hollarda matematik
model murakkab masalaga aylanib, uni yechish uchun taqribiy usullardan
foydalanishga to’g’ri keladi. Bunda vujudga keladigan xatolik usul xatoligi
deyiladi.Hozirgi kunda amaliy masalalar asosan kompyuterlarda bajariladi.Bunda
ham kompyuterlarda sonlarning ifodalanish imkoniyatiga qarab yaxlitlash
xatoligi kelib chiqadi.Bu xatolik ham amallar bajarilish jarayonida ko’payib
borishi mumkin.Kompyuterlarda sonlarni o’nlik sanoq sistemasida ifodalaganimizda
davriy kasrlar yaxlitlanadi. Masalan ![]() = 0,333…
kompyuter imkoniyatlariga qarab raqamlar soni chekli bo’lganligi uchun
= 0,333…
kompyuter imkoniyatlariga qarab raqamlar soni chekli bo’lganligi uchun ![]() to’plamini
belgilab chekli kasrga almashtiriladi. Bunda yo’l qo’yilgan xatolik yaxlitlash
xatoligi deyiladi.Bunday xatolik hisoblash algoritimining har bir amalida
vujudga kelishi mumkin.
to’plamini
belgilab chekli kasrga almashtiriladi. Bunda yo’l qo’yilgan xatolik yaxlitlash
xatoligi deyiladi.Bunday xatolik hisoblash algoritimining har bir amalida
vujudga kelishi mumkin.
Shunday qilib amaliy masala (tabiiy model) yechimini topilgach uning qanchalik to’g’ri va ishonchli ekanligini baholash ham o’ziga yarasha jiddiy va masuliyatli masala ekanligini ko’ramiz. Modellashtirish xatoligi dastlabki bosqichda muttaxassislar tomonidan aniqlanish kerak.
Biz bu yerda
bartaraf qilib bo’lmas xatolik va uning hisoblash jarayonida natijaga tasiri
haqida fikr yuritamiz. Tahlilni oddiy masalalardan boshlaymiz.Faraz qilaylik
biror xona yuzasini hisoblash talab qilinsin (uni qoplash uchun zarur parket
miqdori, yoki uni bo’yash uchun kerak bo’ladigan bo’yoq miqdorini aniqlash
uchun). Bunda xona to’g’ri to’rtburchak shaklida deb faraz qilib (xonalar
asosan shunday loyihalanadi) ![]() formuladan
foydalanamiz. Bu yerda a va b xonaning bo’yi va eni bo’lsin. Ularni aniqlash
uchun o’lchov vositasidan (taxta chizg’ich yoki metall lentali o’lchov
vositasi) foydalaniladi. Bunda aniqlangana = 12, b = 8m chiqdi deylik. Hatto
shu oddiy masalada ham chiqqan
formuladan
foydalanamiz. Bu yerda a va b xonaning bo’yi va eni bo’lsin. Ularni aniqlash
uchun o’lchov vositasidan (taxta chizg’ich yoki metall lentali o’lchov
vositasi) foydalaniladi. Bunda aniqlangana = 12, b = 8m chiqdi deylik. Hatto
shu oddiy masalada ham chiqqan ![]() qiymatni aniq
deb bo’lmaydi. Chunki o’lchash jarayonida chizg’ichni qayta-qayta qo’yishga
to’g’ri kelishi mumkin, bunda chizg’ichning bir to’g’ri chiziq bo’ylab
qo’yilishi, avvalgi va keyingi qo’yilishlari aynan bir nuqta orqali ulanib
ketishini taminlashga kafolat yo’q. Shuningdek chizg’ich shkalalari ham faqat
mm bo’linishiga ega.Undan tashqari bunday hollarda shkala ko’rsatkichi
santimetrgacha yaxlitlab o’qilishi odat bo’lib qolgan.Shuning uchun odatda
avvaldan
qiymatni aniq
deb bo’lmaydi. Chunki o’lchash jarayonida chizg’ichni qayta-qayta qo’yishga
to’g’ri kelishi mumkin, bunda chizg’ichning bir to’g’ri chiziq bo’ylab
qo’yilishi, avvalgi va keyingi qo’yilishlari aynan bir nuqta orqali ulanib
ketishini taminlashga kafolat yo’q. Shuningdek chizg’ich shkalalari ham faqat
mm bo’linishiga ega.Undan tashqari bunday hollarda shkala ko’rsatkichi
santimetrgacha yaxlitlab o’qilishi odat bo’lib qolgan.Shuning uchun odatda
avvaldan ![]() ko’rinishida
xatolik bo’lishi mumkin degan ogohlantirilish keltiriladi.Demak, bunda yuza ham
aniq bo’lmaydi.Yuza uchun ham quyidagicha chegaralarnigina ko’rsatish mumkin.
ko’rinishida
xatolik bo’lishi mumkin degan ogohlantirilish keltiriladi.Demak, bunda yuza ham
aniq bo’lmaydi.Yuza uchun ham quyidagicha chegaralarnigina ko’rsatish mumkin.
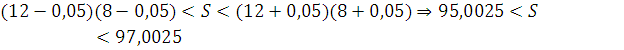
Demak aniqlangan yuza, qiymati shu intervalda joylashgan aniq qiymat uchun, taqribiy baho sifatida xizmat qilishi mumkin ekan. Agar xona shakli to’g’ri to’rtburchakdan oz bo’lsada farq qilsa yana qo’shimcha xatolik paydo bo’ladi.
Bunday holat
bilan amaliy masalalarning deyarli barchasida duch kelishimizni tasavvur qilish
qiyin emas.Shuning uchun biz bu yerda masalalar parametrlarida mavjud bo’lgan
bartaraf qilib bo’lmas xatolikning masala yechimiga ta’sirini aniqlash
qoidalari bilan shug’ullanamiz. Qulaylik uchun , amaliyotdan holi, matematik
masala sifatida o’rganamiz. Aniq miqdor X va uning taqribiy qiymati ![]() taqribiy miqdor
belgisini kiritamiz. Odatda aniq miqdor X ma’lum bo’lmaydi, faqat uning
taqribiy qiymati
taqribiy miqdor
belgisini kiritamiz. Odatda aniq miqdor X ma’lum bo’lmaydi, faqat uning
taqribiy qiymati ![]() ma’lum
bo’ladi.Ular orasidagi farqning absolyut qiymati
ma’lum
bo’ladi.Ular orasidagi farqning absolyut qiymati ![]() absolyut
xatolik deyiladi.Bu xatolikni esa faqat baholashimiz mumkin, ya’ni bu xatolik
ko’pi bilan shuncha bo’lishi mumkin qabiladagi gaplar. Ta’rifga ko’ra
absolyut
xatolik deyiladi.Bu xatolikni esa faqat baholashimiz mumkin, ya’ni bu xatolik
ko’pi bilan shuncha bo’lishi mumkin qabiladagi gaplar. Ta’rifga ko’ra
![]() (5.1)
(5.1)
tengsizlikni qanoatlantiruvchi ![]() sonlar
orasidagi eng kichigini
sonlar
orasidagi eng kichigini ![]() -
taqribiy miqdorning absolyut xatoligi deyiladi va aynan
-
taqribiy miqdorning absolyut xatoligi deyiladi va aynan ![]() ko’rinishida
belgilanadi. (5.1) tengsizlikdan aniq miqdor X uchun
ko’rinishida
belgilanadi. (5.1) tengsizlikdan aniq miqdor X uchun
![]() (5.2)
(5.2)
kelib
chiqadi. Xususan ![]() bo’lsa
aniq miqdor uchun
bo’lsa
aniq miqdor uchun ![]() fikrni
aytishimiz mumkin ekan. (5.2) tengsizlik asosida arifmetik amallar xatoligini
keltirib chiqarishi mumkin.
fikrni
aytishimiz mumkin ekan. (5.2) tengsizlik asosida arifmetik amallar xatoligini
keltirib chiqarishi mumkin.
![]() ma’lum
bo’lsa
ma’lum
bo’lsa
![]() absolyut
xatoligi topilsin.
absolyut
xatoligi topilsin.
![]()
![]()
tengsizliklarni qo’shsak
![]()
kelib chiqadi ![]() belgilash
kiritsak.
belgilash
kiritsak.
![]()
(5.2)
ko’rinishdagi tengsizlik, ya’ni ![]() kelib
chiqar ekan. Shuningdek
kelib
chiqar ekan. Shuningdek ![]() bo’lsa
(5.3) va (5.4) tengsizliklarni ko’paytiramiz
bo’lsa
(5.3) va (5.4) tengsizliklarni ko’paytiramiz
![]()
![]()
hosilbo’ladi.Buyerda![]() ko’paytmayuqoritartiblikichikmiqdorbo’lganiuchuntashlabyuboriladi.Demak
ko’paytmaning absolyut xatoligi uchun
ko’paytmayuqoritartiblikichikmiqdorbo’lganiuchuntashlabyuboriladi.Demak
ko’paytmaning absolyut xatoligi uchun ![]() formula
kelib chiqadi. Shuningdek bo’linma uchun ham
formula
kelib chiqadi. Shuningdek bo’linma uchun ham
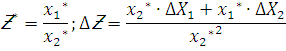
formula kelib chiqadi. E’tibor berilsa absolyut xatolik formulasi differensial formulasiga o’xshash. Shuning uchun n – parametrli taqribiy ifoda
![]() uchun
absolyut xatolik
uchun
absolyut xatolik

formula bo’yicha hisoblanar ekan.
Keltirilgan formulalar asosida quyidagi masalani tahlil qilamiz.Minora balandligini yerdan turib hisoblash mumkinmi?
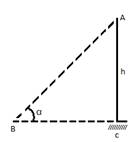
Buning uchun yerda turib a=BC masofani hisoblash
mumkin. Shuningdek ![]() burchakni
ham hisoblash mumkin.U holda noma’lum balandlik h uchun
burchakni
ham hisoblash mumkin.U holda noma’lum balandlik h uchun ![]() formula
o’rinli.
formula
o’rinli.![]() qiymatlarini
hisoblashda xatolikka yo’l qo’yilgan bo’lsin, ya’ni
qiymatlarini
hisoblashda xatolikka yo’l qo’yilgan bo’lsin, ya’ni
![]() bo’lsin.
U holda
bo’lsin.
U holda
![]()
Demak ![]() kelib
chiqadi.
kelib
chiqadi.![]() bo’lib
xatolikni asosiy hissasi burchak hisoblashdagi xatolik tufayli kelib chiqar
ekan. Demak burchakni aniqroq hisoblash kerak degan tavsiyani berishimiz
mumkin.
bo’lib
xatolikni asosiy hissasi burchak hisoblashdagi xatolik tufayli kelib chiqar
ekan. Demak burchakni aniqroq hisoblash kerak degan tavsiyani berishimiz
mumkin.
Odatda amaliy masalalarda nisbiy xatolik
tushunchasi muhimroq rol o’ynaydi. Tasavvur qilaylik dehqon bir qop kartoshka
vaznini ![]() kg
hisoblab
kg
hisoblab ![]() kg
xatolikka yo’l qo’ygan, qassob
kg
xatolikka yo’l qo’ygan, qassob ![]() kg
go’shtni tortishda
kg
go’shtni tortishda ![]() g
xatolikka yo’l qo’ygan. Absolyut xatolik 2 – sida kamroq.Mantiqan o’ylaganda
esa 1 – sining xatoligi ahamiyatsiz ekanligi ko’rinib turibdi.Nisbiy xatolik
ta’rifga ko’ra
g
xatolikka yo’l qo’ygan. Absolyut xatolik 2 – sida kamroq.Mantiqan o’ylaganda
esa 1 – sining xatoligi ahamiyatsiz ekanligi ko’rinib turibdi.Nisbiy xatolik
ta’rifga ko’ra ![]() formula
bo’yicha hisoblanadi. Bu formulaga ko’ra
formula
bo’yicha hisoblanadi. Bu formulaga ko’ra
![]()
ekanligini
kelib chiqadi va mantiqiy xulosamiz o’rinli ekanini ko’ramiz. Shuning uchun
amaliyotda aynan nisbiy xatolikka ko’proq e’tibor beriladi. Nisbiy xatolik
xatolikning foiz miqdorini ham ifodalash imkoniyatini beradi. Xatolik foizi ![]() oddiygina
formula bilan hisoblanadi. Xususan yuqoridagi misollarda
oddiygina
formula bilan hisoblanadi. Xususan yuqoridagi misollarda ![]() ning
xatoligi 1%,
ning
xatoligi 1%, ![]() xatoligi
10% ekanligini ko’rinadi va xulosamiz yanada ishonarli chiqadi.
xatoligi
10% ekanligini ko’rinadi va xulosamiz yanada ishonarli chiqadi.
Amaliy masalalardan olingan natijalar taqribiy
chiqishiga izoh berildi.Shuning uchun bu natijalarni ifodalashda ham bu holni
aks ettirish uchun taqribiy miqdorning ishonchli raqamlari degan
tushuncha kiritiladi.Masalan natija ![]() ekanligi
kelib chiqqan bo’lsin.Hisoblar kompyuterda bajarilgan raqamlar soni kompyuter
imkoniyatlariga bog’liq tarzda kelib chiqadi.Biz
ekanligi
kelib chiqqan bo’lsin.Hisoblar kompyuterda bajarilgan raqamlar soni kompyuter
imkoniyatlariga bog’liq tarzda kelib chiqadi.Biz ![]() qiymatidagi
qaysi raqamlar ishonchli, qaysilarini bekorga yozib o’tirmasa ham bo’ladi degan
savolni hal qilishimiz kerak.Bunda quyidagi qoidaga rioya qilinadi.Umumiyat
uchun o’nlik sistemadan son ifodasidagi raqamlarni quyidagicha ifodalaymiz.
qiymatidagi
qaysi raqamlar ishonchli, qaysilarini bekorga yozib o’tirmasa ham bo’ladi degan
savolni hal qilishimiz kerak.Bunda quyidagi qoidaga rioya qilinadi.Umumiyat
uchun o’nlik sistemadan son ifodasidagi raqamlarni quyidagicha ifodalaymiz.
![]()
Bu yerda indeks raqamga mos o’nlik darajasi bilan bir xil. Agar
![]()
tengsizlik
o’rinli bo’lsa son tarkibidagi ![]() raqam
ishonchli, aks holda ishonchsiz hisoblanadi. Bu yerda i – musbat ham, manfiy
ham bo’lishi mumkin. Bizning misolimizda
raqam
ishonchli, aks holda ishonchsiz hisoblanadi. Bu yerda i – musbat ham, manfiy
ham bo’lishi mumkin. Bizning misolimizda ![]() raqamlari
raqamlari
![]() ,
uning uchun
,
uning uchun ![]() bajarilmaydi.
Demak 9 raqam ishonchsiz. Shuningdek 4,7,5 lar ham ishonchsiz bo’lar ekan. 0
raqami uchun
bajarilmaydi.
Demak 9 raqam ishonchsiz. Shuningdek 4,7,5 lar ham ishonchsiz bo’lar ekan. 0
raqami uchun![]() bajarilmaydi.Demak
0 ham ishonchsiz.1 raqam uchun
bajarilmaydi.Demak
0 ham ishonchsiz.1 raqam uchun ![]() bajariladi,
demak 1 ishonchli. Shunday qilib
bajariladi,
demak 1 ishonchli. Shunday qilib ![]() qiymati
ishonchli raqamlar bilan ifodalanganda
qiymati
ishonchli raqamlar bilan ifodalanganda ![]() bo’lar
ekan;
bo’lar
ekan; ![]() .
Bu yerda umumiy xatolik boshlang’ich va yaxlitlash xatoliklari yig’indisiga
teng bo’ladi.
.
Bu yerda umumiy xatolik boshlang’ich va yaxlitlash xatoliklari yig’indisiga
teng bo’ladi.
§ 6. Hisoblash jarayonlarining turg’unligi haqida turg’un bo’lmagan jarayonlarga misollar
Reja
1. Hisoblash jarayonlarining turg’unligi deganda nima tushuniladi?
2. Turg’un bo’lmagan hisoblash jarayonlariga misollar.
3. Nokorrekt qo’yilgan masalalar haqida tushuncha.
Amaliy yoki matematik masalalar haqida so’z boshlaganimizda masala korrekt bo’lishi kerak deb o’tildi.Korrektlikning asosiy shartlaridan biri natijaning boshlang’ich qiymatlarga uzluksiz bog’liqligi deb ko’rsatiladi.Bu ma’ruzada biz aynan shu mavzuga to’xtalamiz. Buning uchun oddiy misollarni ko’rib o’taylik
![]() bo’lsa
bo’lsa![]() topilsin
topilsin
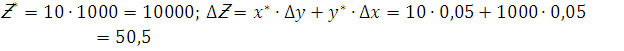
Natija xatoligi boshlang’ich xatolar (0,05) dan 1000 barovar ko’payib ketdi. Oddiy bir amalli jarayonning o’zida shunday holni kuzatayotibmiz.Hisoblash jarayonida minglab, millionlab amallar bajarilishini hisobga olsak, shuningdek boshlang’ich parametrlardagi bartaraf qilib bo’lmas xatoliklarning mavjudligini e’tiborga olsak natijaga deyarli ishonch yo’qoladigandek tuyuladi. Shuning uchun hisoblash jarayonining turg’unligini ta’minlovchi omillar va ularga rioya qilish shartlarini esda tutishimiz kerak. Avvalgi ma’ruzada keltirilgan formula (5.5) ga ko’ra

Turg’unlikning sodda ifodasi shundan iboratki, boshlang’ich xatolar kamaygan sari natija xatoligi ham kamayishi kerak. Xususan shunday K topilsaki
![]() bo’lsa
bo’lsa![]() kelib
chiqadi.
kelib
chiqadi.
![]() bo’lsa
bo’lsa![]() ekanligi
ko’rinadi. Shuningdek talab qilingan
ekanligi
ko’rinadi. Shuningdek talab qilingan ![]() aniqlikni
ta’minlash uchun boshlang’ich parametrlar
aniqlikni
ta’minlash uchun boshlang’ich parametrlar ![]() qanday
aniqlikda hisoblanishi kerakligi ham kelib chiqadi.
qanday
aniqlikda hisoblanishi kerakligi ham kelib chiqadi.
Albatta (5.5) ko’rinishdagi formulani umumiy
hisoblash jarayoni uchun keltirib chiqarish qiyin.Ko’p bosqichli, murakkab
hisoblash jarayonlari uchun bunday formula chiqarish mumkin ham emas.Bunda
faqat har bir bosqichning o’zida turg’unlikni ta’minlash shartlariga rioya
qilishga harakat qilinadi.Umumiy tavsiyani esa quyidagicha ifodalash
mumkin.Hisoblash jarayonini bir qora quti (kompyuter) desak unga ![]() qiymatlar
beriladi.
qiymatlar
beriladi.
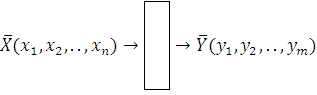
Ma’lum
amallar bajarilgach ![]() natijalar
chiqadi.Bu apparat, to’g’rirog’i hisoblash dasturi sozlangan bo’lsin.
Turg’unlikni tekshirish uchun sonli tadqiqotlar yordamida boshlang’ich
qiymatlarni tebratib ko’riladi
natijalar
chiqadi.Bu apparat, to’g’rirog’i hisoblash dasturi sozlangan bo’lsin.
Turg’unlikni tekshirish uchun sonli tadqiqotlar yordamida boshlang’ich
qiymatlarni tebratib ko’riladi ![]() va
bu holda hosil bo’ladigan natijalar
va
bu holda hosil bo’ladigan natijalar ![]() qiymatlariga
qarab hisoblash jarayonining turg’unligini baholash mumkin. Bu yerda
keltirilgan mulohazalar bu soha haqida tasavvur berishi mumkin. Aslida bu soha
amaliy matematikaning mustaqil yo’nalishi bo’lib unga bag’ishlangan ko’plab
adabiyotlar mavjud.
qiymatlariga
qarab hisoblash jarayonining turg’unligini baholash mumkin. Bu yerda
keltirilgan mulohazalar bu soha haqida tasavvur berishi mumkin. Aslida bu soha
amaliy matematikaning mustaqil yo’nalishi bo’lib unga bag’ishlangan ko’plab
adabiyotlar mavjud.
Fikrimizni yanada tushunarli, ishonarli bo’lishi uchun quyidagi misollarni keltiramiz.
![]()
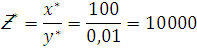
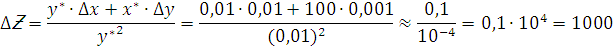
Natija xatoligi
boshlang’ich xatolardan ![]() marta
ortib ketdi. Ikkinchi misol sifatida
marta
ortib ketdi. Ikkinchi misol sifatida
![]()
sistemani
olaylik. Uning yechimi ![]() ekanligi
ko’rinib turibdi. Sistemaning o’ng tarafini tebratib ko’ramiz, ya’ni 2 –
tenglama o’ng tarafi 0,01 emas 0,011 bo’lsin. Bor yo’g’i 0,001 ga
o’zgartirdik. Hosil bo’lgan sistema
ekanligi
ko’rinib turibdi. Sistemaning o’ng tarafini tebratib ko’ramiz, ya’ni 2 –
tenglama o’ng tarafi 0,01 emas 0,011 bo’lsin. Bor yo’g’i 0,001 ga
o’zgartirdik. Hosil bo’lgan sistema
![]() yechimi
yechimi
![]()
![]()
kelib chiqadi. Bu yechim avvalgi yechimdan 999 baravar katta foizda hisoblasak 99900% hatolik hosil bo’lyapti.Hammasi arzimas 0,001 xatolik tufayli yuzaga kelgan nosozlik.Demak bu yerdan hisoblash jarayonini aslo turg’un deb bo’lmas ekan.Bu yerda keltirilgan chiziqli algebraik tenglamalar sistemalari uchun maxsus turg’unlik nazariyasi mavjud.Shuningdek nokorrekt qo’yilgan masalalarni yechish uchun ham maxsus qo’llanma, tavsiyalar yaratilgan.
§ 7. Approksimatsiya masalasi. Bazis funksiyalar. Norma tushunchasi.
Reja
1. Approksimatsiya masalasiga ta’rif va izoh.
2. Funksiyalarning yaqinlik belgisi, funksiyalar normalari asosida.
3. Bazis funksiyalar va ularga namunalar.
4. Teylor, Makloren, Furye qatorlari approksimatsiya masalasi yechimi sifatida.
Amaliy masalalar va matematik tahlilda murakkab funksiyalarni
sodda, elementar funksiyalar orqali ifodalash zarurati paydo bo’ladi. Funksiya
qiymatlarini hisoblash, grafiklarini chizish, umuman tahlil qilish masalalarini
soddalashtirish maqsadida turli usullardan foydalaniladi. Bunda approksimatsiya
masalasi, ya’ni bir funksiyani boshqa funksiya bilan almashtirish masalasi
paydo bo’ladi. Tabiiy, bunday almashtirish ma’lum mezonlar asosida bajarilishi
kerak.![]() funksiya
o’rniga
funksiya
o’rniga ![]() funksiya
olinadigan bo’lsa
funksiya
olinadigan bo’lsa ![]() funksiyalarning
qandaydir bir – biriga yaqinlik sharti, belgisi bo’lishi kerak. Bu almashtirishga
qanchalik haqli ekanligimizni baholay olishimiz kerak.
funksiyalarning
qandaydir bir – biriga yaqinlik sharti, belgisi bo’lishi kerak. Bu almashtirishga
qanchalik haqli ekanligimizni baholay olishimiz kerak.
Buning uchun o’lchov birligi sifatida funksiya normasidan foydalaniladi.Funksiya normasini turli usullarda kiritish mumkin.Odatda quyidagi normalardan foydalaniladi.
![]()
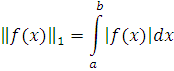
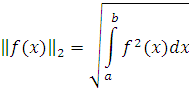
Kiritilgan
normalar asosida ![]() va
va![]() funksiyalarning
yaqinlik darajasini
funksiyalarning
yaqinlik darajasini
![]()
ko’rinishda
ifodalash mumkin. Bu yerda ![]() talab
qilinayotgan aniqlik chegarasi K = 0,1,2 lardan biri masala mohiyatiga qarab
tanlanadi. Ko’rinib turibdi, agar
talab
qilinayotgan aniqlik chegarasi K = 0,1,2 lardan biri masala mohiyatiga qarab
tanlanadi. Ko’rinib turibdi, agar ![]() bo’lsa,
barcha K lar uchun
bo’lsa,
barcha K lar uchun
![]() bo’ladi.Bu
tabiiy eng ideal holat deb hisoblanadi.Ayirma normasi qanchalik kichik bo’lsa,
bo’ladi.Bu
tabiiy eng ideal holat deb hisoblanadi.Ayirma normasi qanchalik kichik bo’lsa,
![]() bilan
almashtirishga shunchalik haqlimiz deb hisoblashimiz mumkin.
bilan
almashtirishga shunchalik haqlimiz deb hisoblashimiz mumkin. ![]() funksiya
sifatida esa, yuqorida ta’kidlanganidek, sodda funksiyalar tanlangani ma’qul.
funksiya
sifatida esa, yuqorida ta’kidlanganidek, sodda funksiyalar tanlangani ma’qul.
Odatda approksimatsiya masalasini yechishda, bazis funksiyalar tushunchasi kiritiladi. Har qanday funksiyani aynan shu bazis funksiyalar orqali ifodalash mumkinligi va yo’llari ko’rsatiladi. Biz bu yerda ayrim namunalarni keltiramiz.
Bazis funksiyalar
sifatida darajali funksiyalar, ya’ni ![]() lar
olinsa
lar
olinsa ![]() funksiyaning
shu funksiyalar orqali yoyilmasini
funksiyaning
shu funksiyalar orqali yoyilmasini
![]()
ko'rinishda
olinadi. Bu yerda ![]() koeffitsiyentlarni
o’zgartirish hisobiga turli-tuman
koeffitsiyentlarni
o’zgartirish hisobiga turli-tuman ![]() funksiyalarni
hosil qilish mumkin.Ular orasidan shundayini tanlash kerakki,
funksiyalarni
hosil qilish mumkin.Ular orasidan shundayini tanlash kerakki, ![]() iloji
boricha kichik bo’lsin. Veyershtrass teoremasiga ko'ra agar
iloji
boricha kichik bo’lsin. Veyershtrass teoremasiga ko'ra agar ![]() yetarli
darajada differensiallanuvchi funksiya bo’lsa
yetarli
darajada differensiallanuvchi funksiya bo’lsa
![]()
ekanligi isbotlangan. Bunga dalil sifatida Makloren, Teylor qatorlarini keltirish mumkin.
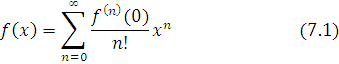
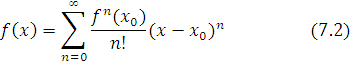
Makloren qatori (7.1) ![]() nuqta
atrofida, Teylor qatori (7.2) esa
nuqta
atrofida, Teylor qatori (7.2) esa ![]() nuqta
atrofida
nuqta
atrofida ![]() funksiya
qiymatlari va xususiyatlarini o’rganishga xizmat qilishi mumkin.
funksiya
qiymatlari va xususiyatlarini o’rganishga xizmat qilishi mumkin.
Shuningdek bazis
funksiyalar sifatida ![]() funksiyalar
olinsa
funksiyalar
olinsa ![]() funksiya
uchun Furye qatoridan foydalanish mumkin.
funksiya
uchun Furye qatoridan foydalanish mumkin.
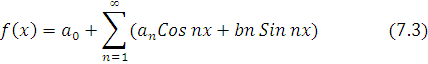
Furye koeffitsiyentlari
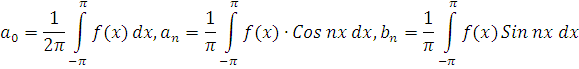
formula bo’yicha hisoblanadi. (7.3) qator uchun ham Vetershtrass teoremasi o’rinli ekan. Furye qatorlari to’lqinli, davriy jarayonlar uchun qulay va samarali bo’lar ekan.
Bu yerda asosiy masala (7.1), (7.2), (7.3) cheksiz
qatorlarning nechta hadi bilan cheklanish mumkin va qanday xatolik bo’ladi
degan savollardan iborat bo’lib qoladi. Bu savollarning ham yechim, javoblari
mavjud. Amaliyotda keltirilgan bazis funksiyalardan farqli boshqa turli bazis
funksiyalardan ham foydalaniladi. O’z o’rnida ularning afzalliklari haqida ham
fikr yuritiladi. Bazis funksiyalarning ba’zilari hisoblashlar uchun, ba’zilari
esa nazariy tahlil uchun ma’qul bo’lar ekan. Amaliy jihatdan barcha hollar bir
– biriga o’xshash bo’lib, tanlangan bazis funksiyalar ![]() lar
uchun
lar
uchun

masalani yechishga keltirilar ekan. Bu yerda α=0,1,2 lardan tanlangan birortasi.
§ 8. Jadval ko’rinishda berilgan funksiyalar uchun interpolyatsiya masalasi. Lagranj interpolyatsion ko’phadi
Reja
1. Masalaning matematik ifodasi.
2. Interpolyatsion ko’phad tushunchasi.
3. Nuqtaning ko’phadi – bazis funksiya sifatida. Lagranj usuli mohiyati.
4. Lagranj interpolyatsion ko’phadi.
5. Lagranj interpolyatsion ko’phadining xatoligi.
Amaliyotda jarayonning qandaydir parametrlari bog’liq ekanligi ma’lum, lekin ular orasidagi bog’lanish qonuniyati noma’lum bo’lgan hollar ko’p uchraydi.Bunday hollarda tajriba yoki kuzatuvlar asosida ular haqidagi jadval ma’lumotini hosil qilish mumkin.
|
|
|
|
|
… … … … … … |
|
|
|
|
|
|
|
… … … … … … |
|
|
Berilgan
jadval ma’lumot asosida X va Y orasidagi funktsional bog’lanishni topish
masalasi interpolyatsiya masalasi deyiladi. Xususan bazis funksiyalar
sifatida darajali funksiyalar ![]() lar
olinsa bog’lanish
lar
olinsa bog’lanish
![]()
ko'rinishda
izlanadi. Bu yerda ![]() noma’lum
koeffitsiyentlarni shunday aniqlash kerakki, tuzilgan (8.1) n – darajali
ko’phad jadval qiymatlarga to’la mos kelsin.Bu shartlarga ko’ra
noma’lum
koeffitsiyentlarni shunday aniqlash kerakki, tuzilgan (8.1) n – darajali
ko’phad jadval qiymatlarga to’la mos kelsin.Bu shartlarga ko’ra ![]() larni
aniqlash uchun quyidagi n+1 noma’lumli n+1 ta chiziqli algebraik tenglamalar
sistemasini hosil qilamiz.
larni
aniqlash uchun quyidagi n+1 noma’lumli n+1 ta chiziqli algebraik tenglamalar
sistemasini hosil qilamiz.
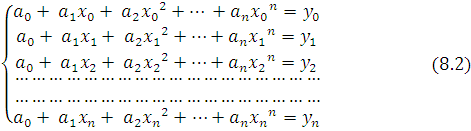
Bu
sistemani yechib, aniqlangan ![]() qiymatlarini
(8.1)ga qo’yilganda hosil bo’lgan ko’phad interpolyatsion ko’phad
deyiladi. interpolyatsion ko’phadga qo’yiladigan yagona va asosiy talab, uning
jadval qiymatlarga to’la mosligi.
qiymatlarini
(8.1)ga qo’yilganda hosil bo’lgan ko’phad interpolyatsion ko’phad
deyiladi. interpolyatsion ko’phadga qo’yiladigan yagona va asosiy talab, uning
jadval qiymatlarga to’la mosligi.
Bu shart ![]() ko’rinishida
ifodalanadi.Shuning uchun interpolyatsion ko’phad tuzishda (8.2) murakkab
sistemani yechishdan soddaroq yo’l yo’qmikan degan yo’nalishlarda tadqiqotlar
olib borilgan. Haqiqatdan ham n – ortgan sari (8.2) sistema murakkablashib
boraveradi va uni yechishning o’zi katta hisoblash jarayoniga aylanadi.
Interpolyatsiya masalasini yechishning original (o’ziga xos) usuli fransuz
matematigi Lagranj tomonidan yaratilgan.
ko’rinishida
ifodalanadi.Shuning uchun interpolyatsion ko’phad tuzishda (8.2) murakkab
sistemani yechishdan soddaroq yo’l yo’qmikan degan yo’nalishlarda tadqiqotlar
olib borilgan. Haqiqatdan ham n – ortgan sari (8.2) sistema murakkablashib
boraveradi va uni yechishning o’zi katta hisoblash jarayoniga aylanadi.
Interpolyatsiya masalasini yechishning original (o’ziga xos) usuli fransuz
matematigi Lagranj tomonidan yaratilgan.
Lagranj g’oyasiga ko’ra berilgan interpolyatsiyalash
tugunlari ![]() nuqtalar
bilan bo’gliq bo’lgan ko’phadlar tuzishdan iborat.Har bir
nuqtalar
bilan bo’gliq bo’lgan ko’phadlar tuzishdan iborat.Har bir ![]() nuqta
uchun shunday n – darajali ko’phad tuzamizki, y aynan shu
nuqta
uchun shunday n – darajali ko’phad tuzamizki, y aynan shu ![]() nuqtada
birga teng bo’lsin, qolgan interpolyatsiyalash tugunlari
nuqtada
birga teng bo’lsin, qolgan interpolyatsiyalash tugunlari ![]() nuqtalarda
esa nolga teng bo’lsin. Bu ko’phadni
nuqtalarda
esa nolga teng bo’lsin. Bu ko’phadni ![]() deb
ifodalasak uning n ta ildizi
deb
ifodalasak uning n ta ildizi ![]() ma’lum
bo’lganligi uchun ko’phadlarni ko’paytuvchilarga ajratish qoidasiga ko'ra
ma’lum
bo’lganligi uchun ko’phadlarni ko’paytuvchilarga ajratish qoidasiga ko'ra
![]()
ko'rinishda
ifodalash mumkin.![]() shartdan
esa A – ko’rinishi topiladi va
shartdan
esa A – ko’rinishi topiladi va ![]() quyidagi
quyidagi
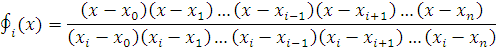
ko'rinishda ifodalanadi. Bu ko’rinishdan
![]()
ekanligi ko’rinib turibdi. (8.3) ko’phadlarning har biri n – darajali ko’phad bo’ladi va ular asosida tuzilgan
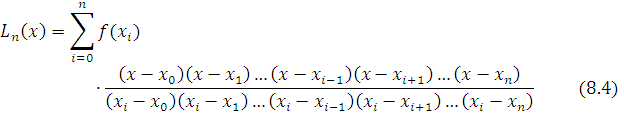
ko'phadLagranj interpolyatsion ko’phadi deyiladi.
![]() funksiyani
kiritsa (8.4) ko’phadni soddaroq ko’rinishda ifodalash mumkin.
funksiyani
kiritsa (8.4) ko’phadni soddaroq ko’rinishda ifodalash mumkin.
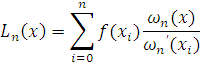
Lagranj interpolyatsion ko’phadi haqiqatdan ham g’oyaning sodda, originalligi bilan ajralib turadi.
Misol
|
|
-1 |
0 |
1 |
2 |
|
|
-1 |
-2 |
1 |
14 |
Bu yerda n=3. Berilgan qiymatlar asosida Lagranj interpolyatsion ko’phadini tuzamiz
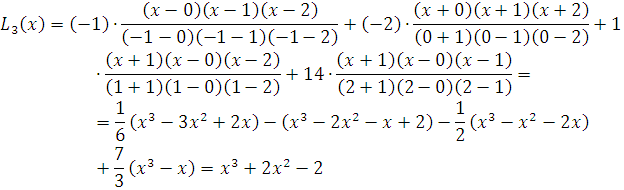
![]()
ko'phad berilgan jadval qiymatlarga to’la mos ekanligi ko’rinib turibdi.
Lagranj interpolyatsion ko’phadining xatoligi.
Agar ![]() funksiya
ko’rinishi ma’lum, lekin murakkab bo’lsa, ko’rsatilgan tarzda uning qiymatlar
jadvalini tuzib, bu jadval asosida interpolyatsion ko’phad tuzish mumkin.Bu
ko’phad funksiya qiymatlarini hisoblash uchun ishchi formula bolib xizmat
qilishi mumkin.Faqat bu yerda (8.4) ko’phad qiymatlari
funksiya
ko’rinishi ma’lum, lekin murakkab bo’lsa, ko’rsatilgan tarzda uning qiymatlar
jadvalini tuzib, bu jadval asosida interpolyatsion ko’phad tuzish mumkin.Bu
ko’phad funksiya qiymatlarini hisoblash uchun ishchi formula bolib xizmat
qilishi mumkin.Faqat bu yerda (8.4) ko’phad qiymatlari ![]() funksiya
qiymatlariga qanchalik yaqin ekanligini baholash zarurati paydo bo’ladi.
Nazariy tadqiqotlar asosida bu xatolik
funksiya
qiymatlariga qanchalik yaqin ekanligini baholash zarurati paydo bo’ladi.
Nazariy tadqiqotlar asosida bu xatolik
![]()
ayirma uchun
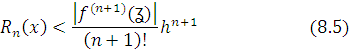
tengsizlik o’rinli bo’lishi isbotlangan. Bu yerda
![]()
![]() interpolyatsiyalash
oralig’I. (8.5) formuladan esa
interpolyatsiyalash
oralig’I. (8.5) formuladan esa
![]()
ekanligi
kelib chiqadi, ya’ni interpolyatsiyalash tugunlari soni ortib, oraliq qadamlar
kichiklashgan sari xatolik ham kichiklashib borar ekan. (8.4) formulani tuzish
oson bo’lgani bilan uni soddalashtirish yoki bevosita y bo’yicha hisoblash
ancha sermashaqqatli ekanligi ko’rinib turibdi.n ortgan sari bu ish yanada
murakkablashib boraveradi.Agar interpolyatsiyalash tugunlari teng oraliqlarda
joylashgan bo’lsa, ya’ni ![]() almashtirish
yordamida (8.4) formulani soddalashtirish mumkin. Bunda
almashtirish
yordamida (8.4) formulani soddalashtirish mumkin. Bunda
![]()
![]()
ko’rinishni oladi. U holda (8.4) formula ham soddalashib
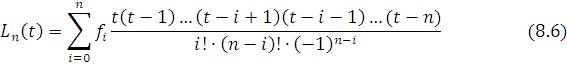
ko’rinishini oladi.
(8.6)
formula teng oraliqlar uchun Lagranj interpolyatsion ko’phadi
deyiladi.Bu ko’phad asosida funksiya qiymatlarini hisoblash quyidagi tarzda
amalga oshiriladi.![]() formuladan
formuladan![]() kelib
chiqadi. Berilgan x qiymatiga ko’ra t ni aniqlaymiz. Bu qiymatga ko’ra (8.6)
formula bo’yicha
kelib
chiqadi. Berilgan x qiymatiga ko’ra t ni aniqlaymiz. Bu qiymatga ko’ra (8.6)
formula bo’yicha ![]() hisoblanadi.
Yuqorida keltirilgan jadval ham (misoldagi) teng oraliqlar bo’lganligi va unda
h=1 ekanligidan t = x+1 kelib chiqadi. Bu holda avvalo (8.6) bo’yicha ko’phadni
aniqlaymiz.
hisoblanadi.
Yuqorida keltirilgan jadval ham (misoldagi) teng oraliqlar bo’lganligi va unda
h=1 ekanligidan t = x+1 kelib chiqadi. Bu holda avvalo (8.6) bo’yicha ko’phadni
aniqlaymiz.
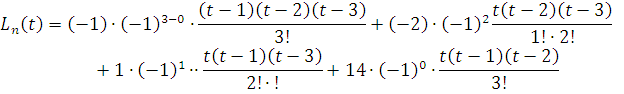
formulanihosil qilamiz. Masalan x = 0,5 dagi qiymati kerak bo’lsa t = 0,5+1 = 1,5 bo’lib uni ko’phadga qo’yamiz
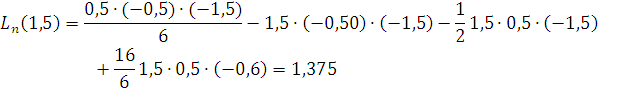
qiymatni hosil
qilamiz. Demak ![]() deyish
mumkin ekan.
deyish
mumkin ekan.
§ 9. Jadval ko’paytmalardagi bartaraf qilib bo’lmas xatolik tartibiga ko’ra ko’phad darajasini va jadval qismini aniqlash
Reja
1. Masala yechimi aniqligini belgilash mezonlari.
2. Tanlangan aniqlikka ko’ra interpolyatsion ko’phad darajasini tanlash qoidasi.
3. Izlanayotgan noma’lum miqdor o’rniga ko’ra jadval qismini ajratish qoidasi.
Interpolyatsion ko’phadlar xatoligi (8.5) formulaga
ko’ra asosan xatolik tartibi ![]() ekanligini
baholash mumkin.Chunki
ekanligini
baholash mumkin.Chunki ![]() qiymatini
murakkab funksiyalar uchun aniqlash qiyin, jadval funksiyalar uchun esa
aniqlash mumkin ham emas. Lekin tabiiy jarayonlar uchun uning chegaralangan
bo’lishiga ishonch bor. Demak h ni kichiklashtirish, n – ni orttirish (baravar
ketadi h = (b-a)/n) hisobiga istalgan aniqlikka erishish mumkin. Faqat bu yerda
qiymatini
murakkab funksiyalar uchun aniqlash qiyin, jadval funksiyalar uchun esa
aniqlash mumkin ham emas. Lekin tabiiy jarayonlar uchun uning chegaralangan
bo’lishiga ishonch bor. Demak h ni kichiklashtirish, n – ni orttirish (baravar
ketadi h = (b-a)/n) hisobiga istalgan aniqlikka erishish mumkin. Faqat bu yerda
![]() qiymatlar
aniq bo’lsagina xulosamiz o’rinli bo’ladi. Aslida esa
qiymatlar
aniq bo’lsagina xulosamiz o’rinli bo’ladi. Aslida esa ![]() lar
tajribadan, yoki o’lchashlardan kelib chiqadi va uning aniqligiga kafolat berib
bo’lmaydi. Shuning uchun ko’phad darajasini orttirib mehnatni ko’paytirganimiz
bilan natijani yaxshilab bo’lmasligi ko’rinib turibdi. Undan tashqari tabiat va
texnikadagi ma’lum qonunlar (Nyuton, Om, Geyl Lyussak, Guk qonunlari) barchasi
sodda ko’rinishda ekanligi ham n = 10, n = 100 ya’ni 10 – yoki 100 – darajali
ko’phad tuzish mantiqan noo’rin ekanligi ham ko’rinib turibdi. Shunga ko’ra
amaliyotda quyidagi qoidaga rioya qilish mumkin. Berilgan
lar
tajribadan, yoki o’lchashlardan kelib chiqadi va uning aniqligiga kafolat berib
bo’lmaydi. Shuning uchun ko’phad darajasini orttirib mehnatni ko’paytirganimiz
bilan natijani yaxshilab bo’lmasligi ko’rinib turibdi. Undan tashqari tabiat va
texnikadagi ma’lum qonunlar (Nyuton, Om, Geyl Lyussak, Guk qonunlari) barchasi
sodda ko’rinishda ekanligi ham n = 10, n = 100 ya’ni 10 – yoki 100 – darajali
ko’phad tuzish mantiqan noo’rin ekanligi ham ko’rinib turibdi. Shunga ko’ra
amaliyotda quyidagi qoidaga rioya qilish mumkin. Berilgan ![]() qiymatlariga
ko’ra
qiymatlariga
ko’ra
![]()
formuladan
K ni aniqlaymiz. Odatda k< n bo’ladi. Interpolyatsion ko’phad darajasi K
bo’lishi ham yetarli bo’lar ekan. Bunda butun jadvalni tarkibida K+1 tadan
qiymat bo’lgan qismlarga ajratib har bir qism uchun alohida K – darajali
interpolyatsion ko’phad tuzish va ![]() funksiya
qiymatini aniqlash uchun x tushgan oraliqqa mos ko’phaddan foydalanish mumkin.
Bu yerda yana bir amaliy ko’rsatmani ta’kidlab o’tish kerakki, interpolyatsion
ko’phad xatoligi interpolyatsiyalash jadvali o’rtasida kichikroq, chetlarida
nisbatan kattaroq bo’lar ekan.
funksiya
qiymatini aniqlash uchun x tushgan oraliqqa mos ko’phaddan foydalanish mumkin.
Bu yerda yana bir amaliy ko’rsatmani ta’kidlab o’tish kerakki, interpolyatsion
ko’phad xatoligi interpolyatsiyalash jadvali o’rtasida kichikroq, chetlarida
nisbatan kattaroq bo’lar ekan.
Keltirilgan mulohazalarni quyidagi misolda tadbiq qilib sinab ko’ramiz.Funksiya qiymatlar jadvali berilgan bo’lsin.
|
|
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
|
|
1 |
1,05 |
1,1 |
1,14 |
1,18 |
1,22 |
1,26 |
1,3 |
1,34 |
|
|
3,16 |
3,32 |
3,46 |
3,61 |
3,74 |
3,87 |
4,0 |
4,12 |
4,24 |
Bu jadvaldagi ![]() qiymatlaridagi
xatolik tartibi
qiymatlaridagi
xatolik tartibi ![]() bo’lsin.
U holda h = 0,1 bo’lganligi uchun
bo’lsin.
U holda h = 0,1 bo’lganligi uchun ![]() formulaga
ko’ra
formulaga
ko’ra ![]() kelib
chiqadi. Demak bu masalada n = 2 deb olsa ham bo’ladi. U holda butun jadvalni 3
bo’lakka bo’lib uchta interpolyatsion ko’phad tuzish mumkin. Bu qismlarning har
biri uchun h = 0,1 o’zgarmas. Faqat 1 – qismda
kelib
chiqadi. Demak bu masalada n = 2 deb olsa ham bo’ladi. U holda butun jadvalni 3
bo’lakka bo’lib uchta interpolyatsion ko’phad tuzish mumkin. Bu qismlarning har
biri uchun h = 0,1 o’zgarmas. Faqat 1 – qismda ![]() –
qismda
–
qismda ![]() –
qismda
–
qismda ![]() bo’ladi.
bo’ladi.
Jadvaldagi 2 ta funksiya uchun alohida – alohida interpolyatsion ko’phadlarni ko’ramiz.
1 – funksiya uchun
![]()
formulaga ko’ra 1 – oraliqda
![]()
Bu
yerda ![]() bo’lganligi
uchun t = 0; 1; 2 larda jadval qiymatlar 1; 1,05; 1,1 kelib chiqadi. 2 –
oraliqda esa faqat funksiya qiymatlari o’zgaradi va (9.1) formulaga ko’ra
bo’lganligi
uchun t = 0; 1; 2 larda jadval qiymatlar 1; 1,05; 1,1 kelib chiqadi. 2 –
oraliqda esa faqat funksiya qiymatlari o’zgaradi va (9.1) formulaga ko’ra
![]()
hosil bo'ladi. Xuddi shuningdek 3 –oraliqda yana (9.1) formulaga ko’ra
![]()
kelib chiqadi. Shunday qilib berilgan jadval funksiya uchun uchta oraliq [1; 1,2], [1,3; 1,5], [1,6; 1,8] oraliqlarda uchuta
![]()
ko’phadlarni hosil qilamiz. Bu yerda 1 - , 2 - , 3 - formulalar uchun mos ravishda
![]()
![]() formulalar
o’rinli bo’ladi. Xususan
formulalar
o’rinli bo’ladi. Xususan ![]() qiymatini
qiymatini
![]() nuqtalarda
hisoblash talab qilingan bo’lsa
nuqtalarda
hisoblash talab qilingan bo’lsa ![]() –
oraliqda demak
–
oraliqda demak ![]() qiymatni
qiymatni
![]() ga
qo’yib
ga
qo’yib
![]()
![]() uchun
2 – oraliqda
uchun
2 – oraliqda ![]()
![]()
![]() uchun
3 – oraliqda
uchun
3 – oraliqda ![]()
![]()
kelib chiqadi.
Keltirilgan misolda jadvalda ![]() funksiya
qiymatlaridan foydalanilganligini hisobga olsak va topilgan qiymatlar bilan funksiyaning
aniq qiymatlarini taqqoslasak
funksiya
qiymatlaridan foydalanilganligini hisobga olsak va topilgan qiymatlar bilan funksiyaning
aniq qiymatlarini taqqoslasak
![]()
![]()
![]()
ekanligini, ya’ni xatolik dastlabki bartaraf qilib bo’lmas xatolik tartibidan ortmaganligini ko’ramiz. Yana bir karra ta’kidlash joizki, butun jadval bo’yicha 8 – darajali ko’phad tuzishga umuman zarurat yo’q ekan.Bu esa ishimizni osonlashtirishi yuqoridagi misoldan ko’rinib turibdi. Keyinchalik bu muloxazalarga yana bir karra qaytamiz va uning samaraligiga ishonch hosil qilamiz.
§ 10. Tengmas oraliqlar uchun Nyuton interpolyatsion ko’phadi
Reja
1. Interpolyatsion ko’phad tuzishda Nyuton g’oyasi, ya’ni yangi ma’lumotlari hisobiga natijani tuzatish usuli.
2. Bo’lingan ayirmalar va ularni hisoblash tartibi.
3. Nyuton interpolyatsion ko’phadi, uni tuzishga misollar.
4. Nyuton interpolyatsion ko’phadidan foydalanish bo’yicha tavsiyalar.
Lagranj interpolyatsion ko’phadi universal, qulay bo’lganligi bilan undan foydalanish ko’p mehnat talab qiladi. Shuningdek funksiya haqidagi yangi axborot, ya’ni yana bir nuqtadagi qiymati ma’lum bo’lsa Lagranj interpolyatsion ko’phadini aniqlash uchun butun mehnatni qaytadan bajarishimiz kerak bo’ladi. Avvalgi hisob – kitoblar butunlay foydalanilmay qolib ketadi.Bu kamchiliklardan xoli interpolyatsion ko’phad tuzish bo’yicha izlanishlar samarasi Nyuton interpolyatsion ko’phadidir. Biz bu yerda ko’phadning kashf qilinishi tarixi va keltirib chiqarish tartibiga to’xtalib o’tirmaymiz. Bevosita uning amaliy tatbiq tarafiga e’tiborni qaratamiz.
Funksiya qiymatlari ![]() tartibda
berilgan bo’lsin.Avvalo bo’lingan ayirmalar tushunchasi ta’rifini kiritamiz.Birinchi
tartibli bo’lingan ayirmadeb funksiya qiymatlar jadvalidagi yonma-yon
qiymatlari ayirmasining argument qiymatlari ayirmasiga nisbatiga aytiladi va
quyidagicha belgilanadi.
tartibda
berilgan bo’lsin.Avvalo bo’lingan ayirmalar tushunchasi ta’rifini kiritamiz.Birinchi
tartibli bo’lingan ayirmadeb funksiya qiymatlar jadvalidagi yonma-yon
qiymatlari ayirmasining argument qiymatlari ayirmasiga nisbatiga aytiladi va
quyidagicha belgilanadi.

(10.1) formulaga ko’ra
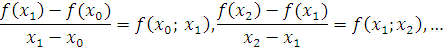

n ta 1 – tartibli bo’lingan ayirma qiymati topiladi, ya’ni 1 – tartibli bo’lingan ayirmalar soni funksiya qiymatlar jadvalidan bitta kamroq bo’ladi. Ikkinchi tartibli bo’lingan ayirmalar ta’rifi vahisoblash tartibi 1 – tartibli bo’lingan ayirmalarga o’xshash.Faqat bu yerda funksiya qiymatlari o’rnida 1 –tartibli bo’lingan ayirma qiymatlaridan foydalaniladi. Ular quyidagicha ifodalanadi
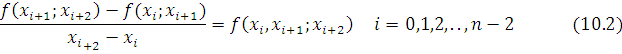
2 – tartibli bo’lingan ayirmalar soni n-1 ta bo’ladi. Xuddi shunday tarzda (K-1) tartibli bo’lingan ayirmalar asosida K – tartibli bo’lingan ayirmalarni aniqlash formulasi kiritiladi.
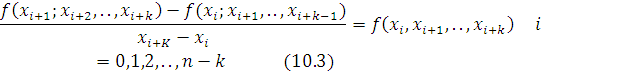
Ular soni n – k + 1 ta bo’ladi.Shunday tarzda n – tartibli bo’lingan ayirmagacha hisoblab boramiz.Hisoblashlarni quyidagi jadval ko’rinishida tashkil etamiz.
|
|
1 – tartibli bo’lingan ayirmalar |
2 – tartibli bo’lingan ayirmalar |
3 – tartibli bo’lingan ayirmalar |
4 – tartibli bo’lingan ayirmalar |
5 – tartibli bo’lingan ayirmalar |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
10.1 - jadval
Jadvalqiymatlariasosidako’rsatilgantartibdan – tartibgachabarchabo’linganayirmalarhisoblabbo’lingachinterpolyatsionko’phadquyidagichaifodalanarekan.
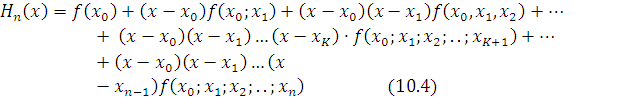
(10.4) formula tengmas oraliqlar uchun Nyuton interpolyatsion ko’phadi deyiladi.(10.4) formula ishlatiladigan bo’lingan ayirmalar jadvalining yuqori diagonali bo’ylab joylashar ekan.
Bu jarayonni quyidagi misolda namoyish qilamiz
|
|
|
1 – tartibli bo’lingan ayirmalar |
2 – tartibli bo’lingan ayirmalar |
3 – tartibli bo’lingan ayirmalar |
4 – tartibli bo’lingan ayirmalar |
|
0 |
1 |
|
|
_ _ _ _ _ _ _ _ _ _ _
|
_ _ _ _ _ _ _ _ _ _ _
|
|
0,2 0,4 0,6 |
1,02 1,08 1,17 |
|
|
||
|
0,8 _ _ _ 1,0 1,2 |
1,28 _ _ _ _ 1,41 1,56 |
_ _ _ _ _ _ _ _ _ _ _
|
_ _ _ _ _ _ _ _ _ _ _
|
|
davomi |
|
5 – tartibli bo’lingan ayirmalar |
6 – tartibli bo’lingan ayirmalar |
|
|
|
|
|
Bo’lingan ayirmalar jadvali asosida Nyuton interpolyatsion ko’phadini tuzamiz. Ikki holatni bitta jadval orqali ifodalash uchun avvaliga funksiyaning faqat x = 0,8 gacha qiymatlari ma’lum bo’lgan holni ko’ramiz. Jadvalni bu qismi punktir chiziq bilan ajratilgan. Bu holda
![]()
interpolyatsion ko’phadini hosil qilamiz.
Xususan x = 0,5
dagi qiymatni hisoblamoqchi bo’lsak. ![]() formulasini
soddalashtirib
formulasini
soddalashtirib
![]()
formula
bo’yicha ![]() kelib
chiqadi. Jadval qiymatlarga asos bo’lgan
kelib
chiqadi. Jadval qiymatlarga asos bo’lgan ![]() qiymati
qiymati
![]() bilan
solishtirilganda xatolik
bilan
solishtirilganda xatolik ![]() ekanligini
ko’ramiz. Bu xatolik jadval qiymatidagi bartaraf qilib bo’lmas xatolik tartibi
0,01 bilan bir xil tartibda bo’ladi. Umuman olganda Nyuton interpolyatsion
ko’phadi Lagranj interpolyatsion ko’phadi bilan bir xil, faqat ifodalanish
tartibi bilangina farq qilganligi uchun uning xatolik tartibi ham
ekanligini
ko’ramiz. Bu xatolik jadval qiymatidagi bartaraf qilib bo’lmas xatolik tartibi
0,01 bilan bir xil tartibda bo’ladi. Umuman olganda Nyuton interpolyatsion
ko’phadi Lagranj interpolyatsion ko’phadi bilan bir xil, faqat ifodalanish
tartibi bilangina farq qilganligi uchun uning xatolik tartibi ham![]() tartibida
bo’ladi.Albatta agar jadvaldagi funksiya qiymatlari aniq bo’lsa.
tartibida
bo’ladi.Albatta agar jadvaldagi funksiya qiymatlari aniq bo’lsa.
Ikkinchi holatga o’tamiz, ya’ni funksiya qiymatlar jadvalida yana ikkita qiymat, ya’ni x =1,0 va x = 1,2 dagi qiymatlari ham ma’lum bo’lib qolsa, Nyuton interpolyatsion ko’phadi avvalgi topilgan ko’phadga qo’shimcha hadlar qo’shish bilan amalga oshirilar ekan. Bizning misolimizda
![]()
![]()
bo’ladi.Bu
yerda ![]() avvalgi
jadvalning bor qismi bo’yicha topilgan ko’phad bo’lib, to’liq saqlanadi.Faqat
yangi olingan qiymatlar asosida bo’lingan ayirmalar jadvali to’ldirilib
ko’phadga ham qo’shimcha hadlar qo’shilar ekan.
avvalgi
jadvalning bor qismi bo’yicha topilgan ko’phad bo’lib, to’liq saqlanadi.Faqat
yangi olingan qiymatlar asosida bo’lingan ayirmalar jadvali to’ldirilib
ko’phadga ham qo’shimcha hadlar qo’shilar ekan.
9
– ma’ruzada qayd etilgandek bu yerda ham jadvaldagi bartaraf qilib bo’lmas
xatolik tartibiga ko’ra interpolyatsion ko’phad darajasini va zaruriy ![]() qiymatga
ko’ra
qiymatga
ko’ra ![]() ning
qiymatini aniqlash uchun jadval qismini tanlash mumkin. Tanlangan qism Nyuton
interpolyatsion ko’phadini tuzamiz. Xususan yuqoridagi jadvalda bartaraf qilib
bo’lmas xatolik
ning
qiymatini aniqlash uchun jadval qismini tanlash mumkin. Tanlangan qism Nyuton
interpolyatsion ko’phadini tuzamiz. Xususan yuqoridagi jadvalda bartaraf qilib
bo’lmas xatolik ![]() tartibi
0,01 bo’lsa
tartibi
0,01 bo’lsa ![]() bo’ladi.
Agar
bo’ladi.
Agar ![]() dagi
qiymat kerak bo’lsa, jadvaldan
dagi
qiymat kerak bo’lsa, jadvaldan ![]() ga
mos qiymatlar va ularga mos bo’lingan ayirmalar qiymatlarini olamiz. Jadvalda
bu qism ajratilgan. Bunda
ga
mos qiymatlar va ularga mos bo’lingan ayirmalar qiymatlarini olamiz. Jadvalda
bu qism ajratilgan. Bunda ![]() deb
olinadi va interpolyatsion ko’phad
deb
olinadi va interpolyatsion ko’phad
![]()
ko’rinishda topiladi. Bundan esa
![]()
kelib
chiqadi. Bu esa funksiyani aniq qiymati ![]() qiymatiga
yaqin ekanligi va
qiymatiga
yaqin ekanligi va![]() ekanligini
ko’ramiz. Bu yerda yana bir karra interpolyatsion ko’phad darajasini orttirish
doimo ham kutilgan yaxshi natija beravermasligiga ishonch hosil qilamiz. Chunki
4 – darajali interpolyatsion ko’phad
ekanligini
ko’ramiz. Bu yerda yana bir karra interpolyatsion ko’phad darajasini orttirish
doimo ham kutilgan yaxshi natija beravermasligiga ishonch hosil qilamiz. Chunki
4 – darajali interpolyatsion ko’phad ![]() da
xatolik
da
xatolik ![]() chiqqan
edi.
chiqqan
edi.
§ 11. Teng oraliqlar uchun Nyuton interpolyatsion ko’phadi
Reja
1. Chekli ayirmalar, ularni hisoblash tartibi.
2. Teng oraliqlar uchun Nyuton interpolyatsion ko’phadi va uni tuzishga misollar.
3. Jadval ko’paytmalardagi bartaraf qilib bo’lmas xatolikning jadval bo’yicha yoyilishi va uning natijaga ta’siri tahlili.
Agar interpolyatsiyalash tugunlari teng oraliqlarda
joylashgan bo’lsa, ya’ni ![]() bo’lsa
bo’lsa
![]() almashtirish
bilan bo’lingan ayirmalar va (10.4) formulalar birgalikda almashtirilsa ko’phad
ko’rinishi ancha soddalashar ekan. Buning uchun bo’lingan ayirmalar o’rniga
chekli ayirmalar jadvali tuziladi.Birinchi tartibli chekli ayirmalar quyidagicha
hisoblanadi.
almashtirish
bilan bo’lingan ayirmalar va (10.4) formulalar birgalikda almashtirilsa ko’phad
ko’rinishi ancha soddalashar ekan. Buning uchun bo’lingan ayirmalar o’rniga
chekli ayirmalar jadvali tuziladi.Birinchi tartibli chekli ayirmalar quyidagicha
hisoblanadi.
![]()
Birinchi tartibli chekli ayirmalar asosida ikkinchi tartibli chekli ayirmalar quyidagicha hisoblanadi.
![]()
Ikkinchi tartibli chekli ayirmalar ayirmasi orqali uchinchi tartibli chekli ayirmalar aniqlanadi.
![]()
Bu formulalarga ko’ra bo’lingan ayirmalardan chekli ayirmalarga o’tish formulani keltirib chiqarish mumkin.
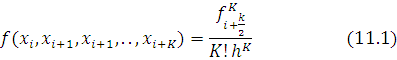
(11.1)
formulalarni, hamda ![]() ifodalarni
tengmas oraliqlar uchun Nyuton interpolyatsion ko’phadi (10.4) formulaga
qo’ysak u quyidagi ko’rinishni oladi.
ifodalarni
tengmas oraliqlar uchun Nyuton interpolyatsion ko’phadi (10.4) formulaga
qo’ysak u quyidagi ko’rinishni oladi.
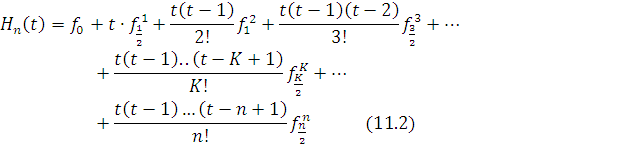
Bu formula (11.2) teng oraliqlar uchun Nyuton
interpolyatsion ko’phadi deyiladi.Y bo’yicha hisoblash uchun berilgan X
qiymatga mos t qiymatini ![]() formula
bo’yicha aniqlanadi.So’ngra (11.2) formula bo’yicha funksiya taqribiy qiymati
topiladi.
formula
bo’yicha aniqlanadi.So’ngra (11.2) formula bo’yicha funksiya taqribiy qiymati
topiladi.
Misol sifatida avvalgi ma’ruzada ko’rilgan jadvaldan foydalanamiz.
|
|
|
|
|
|
|
|
|
|
0
0,2
0,4
0,6
0,8
1,0
1,2 |
1
1,02
1,08
1,17
1,28
1,41
1,56 |
0,02
0,06
0,09
0,11
0,13
0,15 |
0,04
0,03
0,02
0,02
0,02
|
-0,01
-0,01
0
0 |
0
0,01
0 |
0,01
-0,01 |
-0,02 |
Bu jadvalga ko’ra tuzilgan (11.2) Nyuton interpolyatsion ko’phadi quyidagi ko’rinishda bo’ladi.
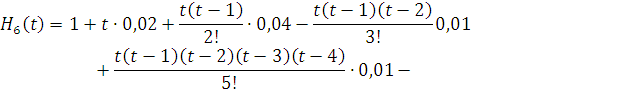
![]()
Bu
misolda ![]() bo’lgani
uchun t = 2,5 kelib chiqadi. Bu qiymatda yuqoridagi ko’phad qiymati
bo’lgani
uchun t = 2,5 kelib chiqadi. Bu qiymatda yuqoridagi ko’phad qiymati ![]() ekanligi
kelib chiqadi.
ekanligi
kelib chiqadi.
Nyuton
interpolyatsion ko’phadi (11,2) yordamida jadvaldagi funksiya qiymatlaridagi
bartaraf qilib bo’lmas xatolikning interpolyatsion ko’phad va hisoblangan funksiya
qiymatiga ta’sirini o’rganish uchun qulay bo’lar ekan.Namuna sifatida sxematik
jadval keltiramiz. Bunda funksiyaning faqat bir qiymatida ![]() tartibidagi
xatolik mavjud bo’lsin.Jadvaldagi barcha hisoblar ham sxematik tarzda
ifodalangan.
tartibidagi
xatolik mavjud bo’lsin.Jadvaldagi barcha hisoblar ham sxematik tarzda
ifodalangan.
|
|
|
1 – tartibli chekli ayirmalar |
2 – tartib |
3 – tartib |
4 – tartib |
5 – tartib |
|
|
|
|
|
|
|
|
Bu jadvaldagi funksiya qiymatidagi boshlang’ich bartaraf qilib bo’lmas xatolikning chekli ayirmalar jadvali bo’ylab yoyilish va o’sish qonuniyati aks ettirilgan. Shuningdek bu xatolikning interpolyatsion ko’phad qiymatiga qo’shadigan qo’shimcha xatoligini ham tasavvur qilish va hisoblash mumkin ekanligi ko’rinib turibdi. Xususan bu jadval bo’yicha tuzilgan 5 – darajali Nyuton interpolyatsion ko’phadining bartaraf qilib bo’lmas xatoligi.

Formula bo’yicha hisoblanishini ko’rishimiz mumkin.
§ 12. Katta jadvallar uchun approksimatsiya masalasini yechishda eng kichik kvadratlar usuli. Chiziqli bog’lanish usuli
Reja
1. Interpolyatsion usul kamchiliklari. Eng kichik kvadratlar usuli g’oyasi.
2. Eng kichik kvadratlar usuli umumiy matematik ifodasi.
3. Chiziqli bog’lanish modelini topishga tadbiqi.
4. Chiziqli bog’lanish modelini topishga misollar.
Approksimatsiya masalasining asosiy vazifasi jadval ko’rinishda berilgan axborot asosida o’rganilayotgan jarayonning qandaydir x va y parametrlari orasidagi funktsional bog’lanishni topishdan iborat. Interpolyatsion usul bu masalani yechish uchun xizmat qilishi mumkin.Lekin yuqorida ta’kidlanganidek, jadval qiymatlari ortgan sari yechim murakkablashib boraveradi.Undan tashqari jadval qiymatlaridagi mavjud bo’lgan bartaraf qilib bo’lmas xatoliklar ham interpolyatsion ko’phad darajasi ortgan sari ko’payib boraveradi. Undan tashqari tabiat va texnikadan ma’lum bo’lgan barcha bog’lanish qonuniyatlari juda sodda ko’rinishga ega (Nyuton qonuni, Om qonuni, Guk qonuni). Interpolyatsion ko’phad darajasini kamaytirish esa jadval qiymatlar faqat bir qismidan foydalanishga olib keladi.Bunda axborotni bir qismi e’tibordan chetda qoladi.Yoki jadvalni qismlarga ajratib har bir qismi uchun alohida interpolyatsion ko’phad, ya’ni bog’lanish modelini tuzish kerak bo’ladi.Aslida esa bitta, butun jadval asosida yagona bog’lanish modelini tuzish mantiqan to’g’ridek tuyuladi.
Biz bu yerda aynan shu yo’l bilan, ya’ni butun
jadval bo’yicha yagona bog’lanish modelini aniqlash yo’li bilan ketamiz.Bu
yerda ham, avvalo, bazis funksiyalarni tanlash kerak.Aksariyat hollarda bazis
sifatida ![]() darajali
funksiyalar olinadi.Biz ham bu yerda shu variantda to’xtalamiz. Ikkinchi masala
ko’phad darajasini tanlash - jarayonning xususiyatiga ko’ra va tajribaga
suyangan holda tanlanadi. Ba’zi hollarda ko’phad darajasini tanlash jarayonini
ham avtomatlashtirish mumkin bo’lar ekan ( Fisher tanlash kriteriyasi ).
darajali
funksiyalar olinadi.Biz ham bu yerda shu variantda to’xtalamiz. Ikkinchi masala
ko’phad darajasini tanlash - jarayonning xususiyatiga ko’ra va tajribaga
suyangan holda tanlanadi. Ba’zi hollarda ko’phad darajasini tanlash jarayonini
ham avtomatlashtirish mumkin bo’lar ekan ( Fisher tanlash kriteriyasi ).
Masalani quyidagicha ifodalaymiz.Jadval ko’rinishda
berilgan ![]() bog’lanish
asosida
bog’lanish
asosida ![]() funktsional
bog’lanish modeli tuzilsin.Bu yerda
funktsional
bog’lanish modeli tuzilsin.Bu yerda ![]() ekanligi
oldindan ma’lum.Chunki m = n bo’lsa interpolyatsiya masalasiga qaytamiz. Tuzilgan
ekanligi
oldindan ma’lum.Chunki m = n bo’lsa interpolyatsiya masalasiga qaytamiz. Tuzilgan
![]() ko’phadga
qo’yiladigan talab, jadval qiymatlariga iloji boricha yaqin bo’lsin.Bu talabni
matematik tarzda quyidagicha ifodalash mumkin.
ko’phadga
qo’yiladigan talab, jadval qiymatlariga iloji boricha yaqin bo’lsin.Bu talabni
matematik tarzda quyidagicha ifodalash mumkin.
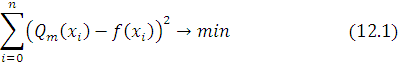
(12.1) ifoda ![]() ko’phadi
koeffitsiyentlarini tanlash hisobigagina mukamallashtirilishi mumkin.
ko’phadi
koeffitsiyentlarini tanlash hisobigagina mukamallashtirilishi mumkin.
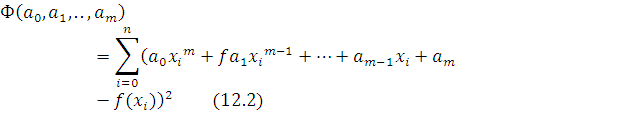
tarzda
ifodalangan ![]() funksiyaning
minimumini esa an’anaviy usulda aniqlash mumkin, ya’ni barcha argumentlari
bo’yicha birinchi tartibli xususiy hosilalari nolga teng bo’lgan nuqtadan
izlanadi. (12.2) formulaga ko’ra
funksiyaning
minimumini esa an’anaviy usulda aniqlash mumkin, ya’ni barcha argumentlari
bo’yicha birinchi tartibli xususiy hosilalari nolga teng bo’lgan nuqtadan
izlanadi. (12.2) formulaga ko’ra ![]() xususiy
hosilalarni hisoblab nolga tenglaymiz.
xususiy
hosilalarni hisoblab nolga tenglaymiz.
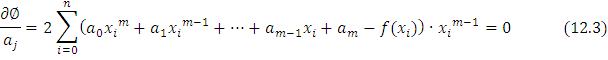
![]()
(12.3) tenglamalarda hadma – had ko’paytirib yig’indi indeksiga bog’liq bo’lmagan ko’paytiruvchilarni yig’indi ishorasidan tashqariga chiqarsak quyidagi sistemani hosil qilamiz.
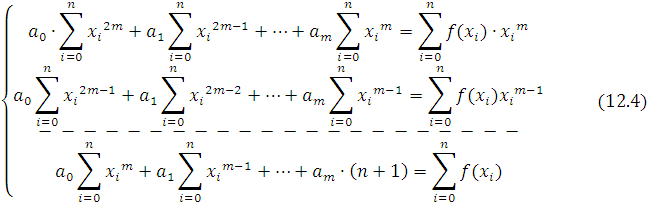
(12.4)
m+1 ta noma’lumli m+1 ta chiziqli algebraik tenglamalar sistemasi bo’lib, undan
![]() koeffitsiyentlarni
topilsa approksimatsiyalovchi ko’phad
koeffitsiyentlarni
topilsa approksimatsiyalovchi ko’phad ![]() va
bog’lanish modeli
va
bog’lanish modeli
![]() topiladi.
Bu usul o’z qurilish tartibiga qarab, funksiya jadval qiymati va tuzilgan
ko’phad qiymatlarining ayirmalari kvadratlarining barcha jadval nuqtalari
bo’yicha yig’indisi minimal bo’lishiga asoslangan bo’lganligi uchun eng
kichik kvadratlar usuli deyiladi. Bu usulning eng keng yoyilgan variantlari
chiziqli va kvadratik bog’lanishga alohida to’xtalamiz.
topiladi.
Bu usul o’z qurilish tartibiga qarab, funksiya jadval qiymati va tuzilgan
ko’phad qiymatlarining ayirmalari kvadratlarining barcha jadval nuqtalari
bo’yicha yig’indisi minimal bo’lishiga asoslangan bo’lganligi uchun eng
kichik kvadratlar usuli deyiladi. Bu usulning eng keng yoyilgan variantlari
chiziqli va kvadratik bog’lanishga alohida to’xtalamiz.
Chiziqli bog’lanish modelini tuzish.
Bu holda m = 1
bo’lib, ![]() ko’phad
koeffitsiyentlar uchun (12.4) sistemadan
ko’phad
koeffitsiyentlar uchun (12.4) sistemadan
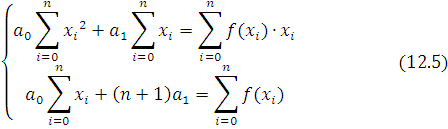
sistema kelib chiqadi.
Kvadratik bog’lanish modeli uchun m = 2 bo’lib
![]() ko’phad
koeffitsiyentlari uchun (12.4) sistemadan
ko’phad
koeffitsiyentlari uchun (12.4) sistemadan
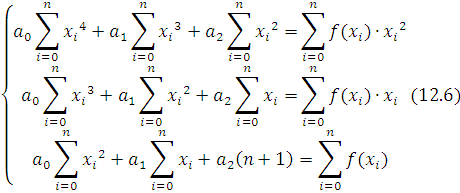
kelib chiqadi.
Bu usulni ikkala variantda (12.5), (12,6) bir misolda sinab ko’ramiz. Funksiya qiymatlari quyidagi jadval bilan berilgan bo’lsin.
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
|
1 |
1,302 |
1,608 |
1,954 |
2,328 |
Chiziqli bog’lanish modelini topish uchun hisoblashlar quyidagi jadval tarzda tashkil qilinadi.
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
0,1 |
1,302 |
0,01 |
0,1302 |
|
0,2 |
1,608 |
0,04 |
0,3216 |
|
0,3 |
1,954 |
0,09 |
0,5862 |
|
0,4 |
2,328 |
0,16 |
0,9312 |
|
1 |
8,192 |
0,3 |
1,9692 |
![]()
Bu jadval asosida chiziqli model koeffitsiyentlari uchun
![]()
sistemahosil bo’ladi. Bu sistemadan
![]()
bog’lanish modeli topiladi.
§ 13. Kvadratik bog’lanish modelini tuzish, jadvaldagi tasodifiy xatolarni aniqlash usuli
Reja
1. Kvadratik bog’lanish modelini tuzish algoritmi.
2. Kvadratik model tuzishga misollar.
3. Jadvaldagi tasodifiy xatoni aniqlash qoidasi va uni bartaraf qilish yo’li.
4. Approksimatsiyadagi ko’phad darajasini tanlashda Fisher kriteriyasi.
Eng kichik
kvadratlar usulida, yuqorida ko’rganimizdek, jadvaldagi qiymatlar sonining ahamiyati
yo’q.Approksimatsiyalovchi ko’phad darajasi tanlangach, uning noma’lum koeffitsiyentlariga
nisbatan sistema hosil qilinadi.Bu sistemadan ![]() topilgach
topilgach
![]() ko’phad
ko’riladi. Ko’rilgan ko’phad uchun xatoliklar qiymatlari
ko’phad
ko’riladi. Ko’rilgan ko’phad uchun xatoliklar qiymatlari ![]() lar
hisoblanadi. Bu jarayonda jadvaldagi mavjud tasodifiy xatolikni ham
aniqlanishi mumkin ekan. Jadval tuzish jarayonida o’lchov vositalarning
nosozligi, yoki jadval tuzuvchi hodimning e’tiborsizligi tufayli birorta qiymat
xato yozilib qolishi mumkin.Eng kichik kvadratlar usulida tuzilgan ko’phad bu
xatolikni ham yaqqol yuzaga chiqarar ekan. Bu jarayon va ayrim amaliy
tavsiyalarni quyidagi misolda ko’ramiz. Berilgan qiymatlarni va zaruriy
qiymatlarni bitta jadvalda ifodalaymiz.
lar
hisoblanadi. Bu jarayonda jadvaldagi mavjud tasodifiy xatolikni ham
aniqlanishi mumkin ekan. Jadval tuzish jarayonida o’lchov vositalarning
nosozligi, yoki jadval tuzuvchi hodimning e’tiborsizligi tufayli birorta qiymat
xato yozilib qolishi mumkin.Eng kichik kvadratlar usulida tuzilgan ko’phad bu
xatolikni ham yaqqol yuzaga chiqarar ekan. Bu jarayon va ayrim amaliy
tavsiyalarni quyidagi misolda ko’ramiz. Berilgan qiymatlarni va zaruriy
qiymatlarni bitta jadvalda ifodalaymiz.
|
|
|
|
|
|
|
|
|
|
|
0 |
2,236 |
0 |
0 |
0 |
0 |
0 |
2,24872 |
0,0127 |
|
0,1 |
2,258 |
0,01 |
0,2258 |
0,001 |
0,0001 |
0,02258 |
2,2660 |
0,0008 |
|
0,2 |
2,261 |
0,04 |
0,4522 |
0,008 |
0,0016 |
0,09044 |
2,2863 |
0,0253 |
|
0,3 |
2,302 |
0,09 |
0,6906 |
0,027 |
0,0081 |
0,20718 |
2,30949 |
0,0075 |
|
0,4 |
2,324 |
0,16 |
0,9296 |
0,064 |
0,2256 |
0,37184 |
2,33559 |
0,0116 |
|
0,5 |
2,345 |
0,25 |
1,1725 |
0,125 |
0,0625 |
0,58625 |
2,36462 |
0,01962 |
|
1,5 |
13,726 |
0,55 |
3,4707 |
0,225 |
0,0979 |
1,2783 |
|
|
![]()
Bu jadval bo’yicha hisoblangan qiymatlarni (12.4) sistemaga qo’yib quyidagi ko’rinishdagi sistemani hosil qilamiz.
![]()
![]()
![]()
Bu sistemadan ![]() ekanligi
kelib chiqadi. Ko’phad esa
ekanligi
kelib chiqadi. Ko’phad esa
![]() ko’rinishda
ifodalanadi. Bu ko’phad qiymatlari va uning jadval qiymatlaridan farqi
ko’rinishda
ifodalanadi. Bu ko’phad qiymatlari va uning jadval qiymatlaridan farqi ![]() ham
jadvalga kiritilgan. Xatolik tahliliga ko’ra, eng katta xatolik x = 0,2 nuqtada
ekanligi ko’rinadi. Demak bu nuqtadagi qiymatda xato bo’lishi mumkin degan
shubha paydo bo’ladi.Bu holda bu qiymatni qaytadan hisoblash, yoki jadvaldan
chiqarib tashlash tavsiya qilinadi.Ba’zi hollarda ayrim nuqtadagi xatolik
boshqa nuqtalardagidan bir necha baravar katta chiqib qoladi.Bunday holda bu
nuqtada tasodifiy xatolik bo’lganligini aniq deyish mumkin bo’lar ekan.
ham
jadvalga kiritilgan. Xatolik tahliliga ko’ra, eng katta xatolik x = 0,2 nuqtada
ekanligi ko’rinadi. Demak bu nuqtadagi qiymatda xato bo’lishi mumkin degan
shubha paydo bo’ladi.Bu holda bu qiymatni qaytadan hisoblash, yoki jadvaldan
chiqarib tashlash tavsiya qilinadi.Ba’zi hollarda ayrim nuqtadagi xatolik
boshqa nuqtalardagidan bir necha baravar katta chiqib qoladi.Bunday holda bu
nuqtada tasodifiy xatolik bo’lganligini aniq deyish mumkin bo’lar ekan.
Ko’rilgan misol va hisoblashlar tartibi m = 3,4, hollar uchun hisoblashlarni qanday tashkil etilishini ham ko’rsatadi. Ko’phad darajasini jarayonning ma’lum xususiyatiga ko’ra yoki avtomatik tarzda tanlanadi.Bunda Fisher kriteriyasidan foydalaniladi.Har gal ko’phad topilganda uning yig’ma xatoligi hisoblab boriladi.
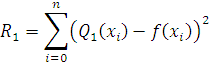
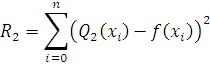
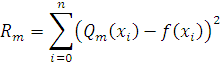
Bunda ![]() bo’lib
bo’lib
![]() bo’lib
qolsa
bo’lib
qolsa ![]() to’xtaladi.
to’xtaladi.
§ 14. Ortogonal ko’phadlar. Jadval ko’rinishda berilgan funksiyalar uchun o’rta kvadratik yaqinlashish
Reja
1. Jadval ko’rinishda berilgan funksiyalar uchun skalyar ko’paytma.
2. Ortogonal funksiyalar tushunchasi.
3. Ortogonal bazis funksiyalar uchun rekkurent formula.
4. Funksiyalarni ortogonal bazis funksiyalar bo’yicha yoyilmasi.
5. Ortogonal bazis funksiyalarga misollar.
Biz bu yerda asosan [-1;1] oraliqda teng qadamli jadval bilan berilgan funksiyalarni ko’rish bilan cheklanamiz. Chunki har qanday [a;b] oraliqni
![]()
almashtirish bilan [-1;1] oraliqqa o’tkazish mumkin.
[-1;1]
oraliqni h = 2/n qadam bilan ![]() nuqtalar
yordamida
nuqtalar
yordamida ![]() n
ta bo’lakka bo’lamiz. Bu nuqtalardagi qiymatlari
n
ta bo’lakka bo’lamiz. Bu nuqtalardagi qiymatlari ![]() lar
bilan berilgan funksiyalar uchun skalyar ko’paytma amalini
lar
bilan berilgan funksiyalar uchun skalyar ko’paytma amalini
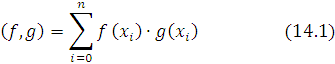
formula
bilan kiritamiz. (14.1) formula bilan kiritilgan skalyar ko’paytma, skalyar
ko’paytma barcha xossalariga ega.Ta’rifga ko’ra agar ![]() funksiyalarning
skalyar ko’paytmasi nolga teng bo’lsa, ular ortogonal deyiladi. Bu ta’rif
asosida [-1;1] oraliqdagi jadval qiymatlariga ko’ra ortogonal ko’phadlar
sistemasini kiritamiz.
funksiyalarning
skalyar ko’paytmasi nolga teng bo’lsa, ular ortogonal deyiladi. Bu ta’rif
asosida [-1;1] oraliqdagi jadval qiymatlariga ko’ra ortogonal ko’phadlar
sistemasini kiritamiz.
![]() mos
ravishda 0-,1-,2-,..,m – darajali ko’phadlar bo’lib, ular juft – jufti bilan
o’zaro ortogonal bo’lsin, ya’ni
mos
ravishda 0-,1-,2-,..,m – darajali ko’phadlar bo’lib, ular juft – jufti bilan
o’zaro ortogonal bo’lsin, ya’ni
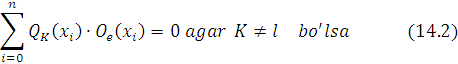
Shuning bilan ![]() ko’phadlar
o’zaro chiziqli erkli funksiyalar sistemasini tashkil etadi. Har qanday
ko’phadlar
o’zaro chiziqli erkli funksiyalar sistemasini tashkil etadi. Har qanday ![]() ko’phadni
ko’phadni
![]() bo’lgan
holda
bo’lgan
holda ![]() bazis
ko’phadlar chiziqli kombinatsiyasi
bazis
ko’phadlar chiziqli kombinatsiyasi
![]()
ko’rinishda bir qiymatli ifodalash mumkin.
Bazis tashkil etuvchi ortogonal
ko’phadlar sistemasi ![]() larni
aniqlashda quyidagi rekkurent munosabatdan foydalanish mumkin.
larni
aniqlashda quyidagi rekkurent munosabatdan foydalanish mumkin.
![]()
Bu yerda ![]() –
darajali ko’phad bo’lganligi uchun uni bazis funksiyalar
–
darajali ko’phad bo’lganligi uchun uni bazis funksiyalar ![]() funksiyalar
bo’yicha yoyish mumkinligidan foydalandik. Haqiqatdan ham
funksiyalar
bo’yicha yoyish mumkinligidan foydalandik. Haqiqatdan ham
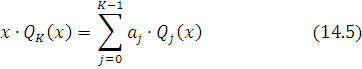
chiziqli kombinatsiya o’rinli deb,
(14.5) tenglik ikki tarafini ![]() ga
skalyar ko’paytiramiz.
ga
skalyar ko’paytiramiz.
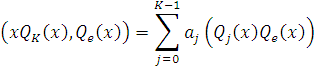
Bu tenglikdan ![]() funksiyalar
ortogonalligidan
funksiyalar
ortogonalligidan
![]()
kelib
chiqadi. ![]() bo’lgan
hollarda
bo’lgan
hollarda ![]() ko’phad
darajasi K-1 dan ortiq bo’lmaganligi uchun bu ko’phad
ko’phad
darajasi K-1 dan ortiq bo’lmaganligi uchun bu ko’phad ![]() ga
ortogonal bo’ladi. Demak chap tarafi nolga teng. Shuning uchun o’ng tarafi ham
nolga teng bo’lishi kerak. Bundan esa
ga
ortogonal bo’ladi. Demak chap tarafi nolga teng. Shuning uchun o’ng tarafi ham
nolga teng bo’lishi kerak. Bundan esa ![]() ekanligi
kelib chiqadi va (14.4) ayniyat o’rinli ekanligini ko’ramiz.
ekanligi
kelib chiqadi va (14.4) ayniyat o’rinli ekanligini ko’ramiz. ![]() lar
uchun
lar
uchun

formulalar kelib chiqadi.
Biz bu yerda amaliy masalalarda ko’p qo’llaniladigan variantlardan birida batafsil to’xtalamiz.
Approksimatsiya
masalasi [-1;1] oraliqda ![]() qadam
bilan berilgan jadval funksiyasi uchun yechilayotgan bo’lsin. Har qanday [a;b]
oraliqni
qadam
bilan berilgan jadval funksiyasi uchun yechilayotgan bo’lsin. Har qanday [a;b]
oraliqni
![]()
almashtirish
bilan ![]() oraliqqa
keltirilishini eslatib o’tamiz. Shuning uchun keyingi mulohazalarda
oraliqqa
keltirilishini eslatib o’tamiz. Shuning uchun keyingi mulohazalarda ![]() deb
hisoblaymiz. Natijalar yanada tushunarli, hisoblashlar tartibi ko’rinishi uchun
n =10 deb olsak, jadval tugunarli
deb
hisoblaymiz. Natijalar yanada tushunarli, hisoblashlar tartibi ko’rinishi uchun
n =10 deb olsak, jadval tugunarli ![]() bo’lgani
uchun
bo’lgani
uchun ![]() qiymatlarni
qabul qiladi.
qiymatlarni
qabul qiladi.
Skalyar ko’paytma avvalgidek
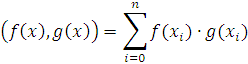
ko’rinishda aniqlangan bo’lsin. Bu oraliq va berilgan tugun nuqtalar uchun ortogonal funksiyalar sistemasini
![]()
![]()
![]()
![]()
![]()
-----------------------------------
tartibda aniqlash mumkin ekan. Bu yerda noma’lum koeffitsiyentlarni aniqlashda funksiyalarning o’zaro ortogonalligidan foydalanamiz. Eslatma: oraliq va tugunlar O nuqtaga nisbatan simmetrik bo’lgani uchun
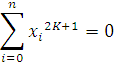
ekanligi ko’rinib turibdi. Shuning uchun
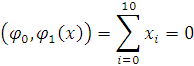

![]() shartdan
esa
shartdan
esa
![]()
Keyingi hisoblar uchun kerak bo’ladigan yig’indilar qiymatlarini keltiramiz
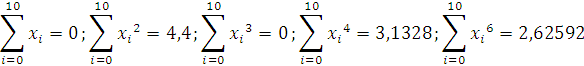
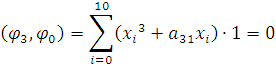
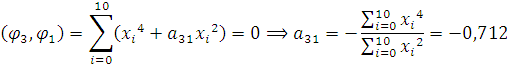
![]()
![]()
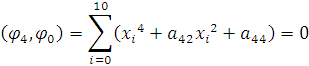
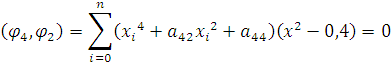
shartlardan![]() koeffitsiyentlar
uchun sistema hosil bo’ladi.
koeffitsiyentlar
uchun sistema hosil bo’ladi.

![]()
![]()
![]()
Demak [-1;1] oraliqda h = 0,2 qadam bilan jadval ko’rinishda berilgan funksiyalar uchun ortogonal bazis funksiyalar
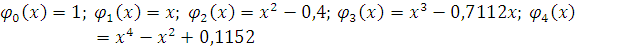
ko’rinishda olinishi mumkin ekan.
Umumiy holda, agar [-1;1] oraliq 2m
(juft) oraliqlarda bo’lingan bo’lsa ![]() almashtirish
kiritilsa t ga nisbatan ortogonalko’phadlar sistemasi uchun quyidagi formula
o’rinli.
almashtirish
kiritilsa t ga nisbatan ortogonalko’phadlar sistemasi uchun quyidagi formula
o’rinli.
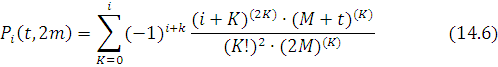
![]()
Bu yerda belgilashlar factorial ko’paytma
![]()
![]() ,
deb olingan.
,
deb olingan.
(14.6) formulalardan
![]()
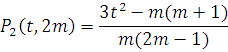
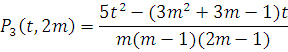
hosil bo’ladi. Xususan biz ko’rgan hol M = 5 uchun bu formulalardan t = 5x almashtirish orqali biz topgan formulalar kelib chiqadi.
Adabiyotlar
1. J.O. Brein. Management Information System. New York – London, 1999.
2. M.F. Ochilov, AVQobulov, O.M.Abdullayev, O.T.Kenjaboyev. Marketing strategiyasi modellari va istiqbollash. T.: “TFNTI”,1997.
3. L.E.Basovskiy. Programirovaniye I planirovaniye v usloviyax rinka MFiS.:2000.
4. Ekonometrika. / Pod red. T.Sh. Shadieva – T.: Sharq, 1999.
5. Magnus Ya.R. I dr. Ekonometrika. – M.: Delo, 1997.
6. A.V.Qobulov, A.T.Kenjaboyev. Baholashda iqtisodiy matematik usullar va modellar.-T.:Fan, 1996.
7. Shodiyåv
T. va boshqalar. Iqtisodiy-matåmatik
usullar va modållar. -
T.: 2002.
8. Abdullayåv
O.M., Ismoilov A.A., Ishnazarov A.I. Iqtisodiy matåmatik
usullar. -T:, 2005.
9. Abdullaåv
O.M. Modålirovaniyå
i prognozirovaniyå
ekonomichåskix
protsåssov.
-T.: Fan va tåxnologiyalar, 2003.
10.
Ishnazarov A., Ro`zmåtova
N. Bakalavriat talabalari uchun
«Iqtisodiy matåmatik usullar va modållar»
fanidan masalalar
to`plami. -T.: TDIU, 2005.
11. Zamkov O.O. I dr. Matematicheskiye metodi dlya ekonomistov.-M.:FiS,1995.
II- CHIZIQLI PROGRAMMALASH MASALALARI
So’z boshi
Modellashtirish usullaridan amaliy va ilmiy-tadqiqot ishlarida azaldan foydalanib kelinadi. U texnik konstruksiya, qurilish va arxitekturada loyiha modellari; fizika, ximiya, biologiya fanlarida ma’lum formulalar asosida jarayon matematik modellarini ifodalash namunalari sifatida ma’lum. “ Model ” so’zi lotincha bo’lib ( modulus ), o’lchov, namuna, norma kabi ma’nolarni bildiradi.
So’nggi yillarda model so’zi ham moda ( urf ) bo’lib, modellashtirishning turli yo’nalishlari shakllanib bormoqda. Hisoblash texnikasi, kompyuter texnologiyalarining rivojlanishi esa, matematik modellashtirish amaliy samarodorligining keskin ortishiga sabab bo’lmoqda. Axborotlarni saqlash, uzatish, qayta ishlash, qisqasi axborot texnologiyalari zamonamizning eng dolzarb yo’nalishlaridan biriga aylanib bormoqda. Bu esa keng qamrovli murakkab jarayonlarni ham matematik modellashtirish va ko’plab variantlarda tadqiq qilish imkoniyatlarini yaratmoqda.
Xususan, iqtisodiy jarayonlarni matematik modeli sifatida XX asr o’rtalarida G.B.Dantzig, L.V.Kantorovich lar tomonidan amaliyotga kiritilgan “chiziqli programmalash masalalari” ChPM yo’nalishini keltirish mumkin. Yuzaki qaraganda, bozorda o’tirgan oddiy sotuvchi ( tadbirkor ) o’z tajribasiga suyangan holda, narx-navo dinamikasini tahlil qilib, har kuni o’zi bilmagan holda qandaydir optimizatsiya masalalarini yechib boradi. Uning tanlagan yechimi omadli yoki omadsiz bo’lishiga qarab uning daromadi shakllanadi. Bu yerda yechimni “ omadli ” yoki “ omadsiz ” sifatlari bilan bog’ladik. Sababi, iqtisodiyot bilan bog’liq masalalar haddan tashqari ko’p variantli bo’lib ularni to’la tahlil qilish va optimal variantni tanlash zamonaviy kompyuterlar uchun ham mushkul masalalardan hisoblanar ekan. Masalan ChPM ning tanlash masalasi deb ataladigan masalasida n- tartibli kvadrat matritsa hosil bo’ladi. Shu matritsaning har bir satri va har bir ustunidan bittadan elementni shunday tanlash kerakki, tanlangan elementlar yig’indisi maksimal bo’lsin. Bu masalani yechish uchun n! variantni hisoblash va taqqoslash kerak bo’lar ekan. Hattoki oddiy n=20 bo’lgan holda ham n!>2· 1018 bo’lib,bu masalani yechish uchun sekundiga 1milliard amal bajaradigan kompyuter ham 500 yil tinimsiz ishlashi kerak ekan.
Demak, bu yerda mavjud variantlarning barchasini emas, ma’lum ma’noda optimallikka da’vogar bo’lishi mumkin bo’lgan variantlarnigina tahlil qilish va ular orasidan optimalini ajratish yo’lini tutish talab qilinadi.ChPM fani aynan shu yo’nalishda shakllangan bo’lib, uning matematik asoslarini, hamda amaliy tadbiq bosqichlarini bilish har bir iqtisodchi, umuman har bir izlanuvchan ijodkor uchun zaruriy bo’g’inlardan biriga aylanib bormoqda.
Mazkur qo’llanmada, yuqorida keltirilgan mulohazalar hisobga olinib, ChPM matematik asoslari va amaliyoti iloji boricha sodda masalalar asosida talqin qilingan. Maqsad, vaqti kelib kompyuter matematik ta’minotida mavjud bo’lgan ChPM larni yechish dasturlaridan foydalanish zarurati paydo bo’lsa, u haqida to’la tasavvurga ega bo’lsin. Har bir paragraf so’ngida mustaqil ishlash uchun berilgan masalalar fanni to’la o’zlashtirishni ta’minlash uchun mo’ljallangan.
§ 1. Chiziqli programmalash masalalari.
Ishlab chiqarish jarayonidagi moddiy va iqtisodiy bog'lanishlarni hisobga olgan holda maqsadga muvofiq keladigan eng maqbul rejani tanlash masalasining matematik ifodasi ilmiy va o'quv adabiyotlarida chiziqli programmalash atamasi bilan ifodalanadi. Bunday masalalarning matematik ifodasini keltirib chiqarishda odatda ishlab chiqarish jarayoni bilan bog'liq bo'lgan barcha resurslar, narx-navolar, ishlab chiqarish normativlari hamda masala mohiyatiga ko'ra maqsad funksiyasini tuziladi. Agar muammo harajatlar bilan bog'liq bo'lsa bu harajatlarni ifodalovchi maqsad funksiyasining eng kichik qiymatini, agar maqsad funksiyasi ishlab chiqarishdan keladigan daromadni ifodalasa bu funksiyani eng katta qiymatini topish talab qilinadi.
Aksariyat hollarda ishlab chiqarish resurslari va ishlab chiqarish kuchlari, ularning imkoniyatlarini ifodalovchi shartlar, hamda harajat yoki daromadni ifodalovchi maqsad funksiyalari chiziqli funksiyalar bilan ifodalanganligi uchun bu turdagi masalalar chiziqli programmalash masalalari deb ataladi. Bu yerda programmalash so'zi dasturlash ma'nosida emas rejalashtirish ma'nosida ishlatiladi. Keyinchalik ko'riladi, masala yechimi ham optimal reja shaklida ifodalanadi.
Chiziqli programmalash usullari ishlab chiqarishning barcha sohalarida keng va samarali tatbiq qilib kelinayapti. Axborot texnologiyalarining rivojlanishi, kompyuterlarning imkoniyat va tezliklarining jadal o'sishi esa chiziqli programmalash masalalarining tatbiqini kengayishi hamda yanada mukammalashishiga yo'l ochayapti. Chiziqli programmalash masalalarining matematik ifodasi sodda bo'lsada uni yechishda funksiya maksimum, minimumlarini topishga mo'ljallangan an'anaviy usullarni tatbiq qilib bo'maydi. Bu yerda asosiy muammo – masala shartlariga bog'liq tarzda mumkin bo'lgan yechimlar sohasini (MBES) ni topishdan iborat bo'ladi. Optimal reja (OP) ham ana shu MBESdan izlanishi kerak.
Yuqorida keltirilgan mulohazalarni oydinlashtirish uchun oddiy bir masalani ko'rib chiqamiz. Faraz qilaylik, kichik korxona meva sharbatlarini chiqaradigan bo'lsin. Korxonada 30kg olcha, 45kg olma, 12kg shakar bor. Korxona ikki xil turdagi meva sharbatlarini chiqaradi. 1 – tur meva sharbatining bir bankasiga 0,1kg olcha, 0,5kg olma, 0,1 kg shakar solinsin. 2 – tur meva sharbatining bir bankasiga 0,3kg olcha, 0,2kg olma, 0,1kg shakar solinsin. Agar 1 banka 1 – tur sharbat narxi 1000so'm, 2 – tur meva sharbati 1400so'm tursa, korxona har bir tur meva sharbatidan qanchadan ishlab chiqarganda korxonaning meva sharbatlarini sotishdan tushgan daromadi eng katta bo'ladi?
Masalaning matematik ifodasini tuzish uchun
masala shartlariga ko'ra kelib chiqadigan munosabatlarni hosil qilishimiz
kerak. Avvalo masala shartiga ko'ra topilishi kerak bo'lgan 1 – va 2 – tur meva
sharbatlarining noma'lum sonini ![]() deb
belgilaymiz. Bu holda 1 – , 2 – va 3 – tur xomashyo (olcha, olma, shakar)
sarflarini hisoblab bu sarflar korxonadagi bor bo'lgan xomashyo zaxiralaridan
ortmasligini talab qilamiz. Xususan olcha sarfi bo'yicha har bir banka 1 – tur
meva sharbatiga 0,1kg olcha , 2 – tur meva sharbatiga esa 0,3kg olcha
solinadigan bo'lsa mos ravishda
deb
belgilaymiz. Bu holda 1 – , 2 – va 3 – tur xomashyo (olcha, olma, shakar)
sarflarini hisoblab bu sarflar korxonadagi bor bo'lgan xomashyo zaxiralaridan
ortmasligini talab qilamiz. Xususan olcha sarfi bo'yicha har bir banka 1 – tur
meva sharbatiga 0,1kg olcha , 2 – tur meva sharbatiga esa 0,3kg olcha
solinadigan bo'lsa mos ravishda ![]() banka
1 – tur ,
banka
1 – tur ,![]() banka 2 – tur meva
sharbatlariga jami
banka 2 – tur meva
sharbatlariga jami ![]() ×
0,1 +
×
0,1 + ![]() × 0,3 kg olcha sarflanadi. Bu esa korxonada bor bo'lgan 30kg olchadan ortmasligi kerak. Demak olchalar
bo'yicha qo'yiladigan shart
× 0,3 kg olcha sarflanadi. Bu esa korxonada bor bo'lgan 30kg olchadan ortmasligi kerak. Demak olchalar
bo'yicha qo'yiladigan shart
0,1![]() + 0,3
+ 0,3![]() ≤
30
≤
30
ko'rinishini oladi. Xuddi shunday mulohazalarga ko'ra olma va shakar sarfi bo'yicha korxona imkoniyatlaridan kelib chiqqan holda
0,5![]() + 0,2
+ 0,2![]() ≤ 45
≤ 45
0,1![]() + 0,1
+ 0,1![]() ≤ 12
≤ 12
ko'rinishdagi shartlarni hosil qilamiz. Meva sharbatlarini sotishdan tushadigan daromad esa keltirilgan narxlarga ko'ra jami
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]()
bo'lar
ekan. Bu yerda L(![]() ) maqsad
funksiyasi bo'lib, shunday ishlab chiqarish rejasini tanlash kerakki , bu reja
avvalo resurslar bo'yicha shartlarga mos kelsin va maqsad funksiyasining eng
katta qiymatini keltirib chiqarsin. Shunday qilib keltirilgan iqtisodiy masala
quyidagicha ifodalanar ekan
) maqsad
funksiyasi bo'lib, shunday ishlab chiqarish rejasini tanlash kerakki , bu reja
avvalo resurslar bo'yicha shartlarga mos kelsin va maqsad funksiyasining eng
katta qiymatini keltirib chiqarsin. Shunday qilib keltirilgan iqtisodiy masala
quyidagicha ifodalanar ekan
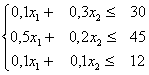
(1.1)
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]()
![]() max
(1.2)
max
(1.2)
Keltirilgan (1.1) cheklashlar (shartlar)ga ko'ra (2)
maqsad funksiyasining maksimumini toping. Bu masala chiziqli
programmalash masalasining (ChPM) tipik namunasi sifatida qaralishi
mumkin.Ko'rinib turibdiki, (1.1) shartlarda ham (1.2) maqsad funksiyasida ham ![]() noma'lumlar birinchi
darajalari bilan qatnashadi. Bu hol ChPM atamasining kelib chiqishiga sabab
bo'lgan. Avval qayd etib o'tganimizdek, (1.1) – (1.2) masalani yechishda
an'anaviy ekstremumlarni topish usullarini tatbiq qilib bo'lmaydi. Haqiqatdan
ham ekstremumlarning
mavjud.
noma'lumlar birinchi
darajalari bilan qatnashadi. Bu hol ChPM atamasining kelib chiqishiga sabab
bo'lgan. Avval qayd etib o'tganimizdek, (1.1) – (1.2) masalani yechishda
an'anaviy ekstremumlarni topish usullarini tatbiq qilib bo'lmaydi. Haqiqatdan
ham ekstremumlarning
mavjud.
bo'lish
zaruriy sharti
![]()
![]()
bu yerda bajarilmaydi. Buning asosiy sababi bu masalada an'anaviy optimizatsiya masalalaridan farqli funksiyaning lokal ekstremumlari emas global ekstremumi, ya'ni eng katta yoki eng kichik qiymatlarini topish talab qilinadi. Bu qiymatlar, ya'ni Sup L(x1 , x2 ) va inf L(x1 , x2 ) lar esa, agar mavjud bo'lsa faqat MBES chegaralarida bo'lar ekan. Buni keltirilgan masalaning geometrik tahlilidan ko'rishimiz mumkin. Keyinchalik umumiy holda ham ChPMlar uchun MBES qabariq soha bo'lishi va uning uchun optimal yechim shu qabariq soha uchlaridan birortasida bo'lishini misollarda tahlil qilamiz.
Chiziqli programmalash masalasining yechimini topishda geometrik usul.
Geometrik tahlilni (1.1) – (1.2) masala misolida olib boramiz. (1.1) shartlarning har biri OX1X2 koordinat tekisligini to'g'ri chiziq bo'ylab ikki bo'lish va ulardan shartga mos keladigan bittasini tanlashni ifodalaydi. Tahlilni soddalashtirish uchun

(1.1) shartlarning hammasini mos ravishda 30;45;12ga bo'lib yozamiz.
![]() L(
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]() max
max
MBESni topish uchun hosil bo'lgan shartlardagi to'g'ri chiziqlarni chizamiz va ulardan pastki qismini olamiz. Natijada OABCD beshburchak shaklidagi soha hosil bo'ladi (1 – rasm).
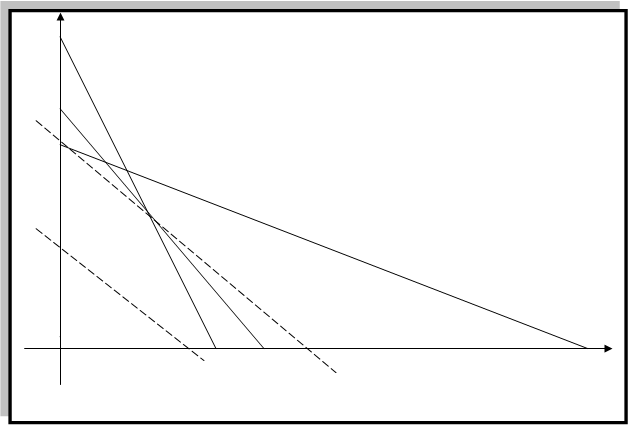 X2
X2
200
D
100
C E
N2
B
60
N1
40
L=70000
L=140000
A X1
O 60 80 100 120 140 300
1-rasm
Bu sohaning istalgan nuqtasining koordinatalari
(1.1) – (1.2) masalaning shartlariga mos mumkin bo'lgan yechimlaridan birini
ifodalaydi. Bu yerda biz maqsad funksiyasining biror qiyamatiga mos keladigan
rejalar (yechimlar)ga mos nuqtalar to'plamini ko'rib chiqamiz. Masalan L(![]() ) = 70000 bo'ladigan
nuqtalar to'plami 1000
) = 70000 bo'ladigan
nuqtalar to'plami 1000![]() + 1400
+ 1400![]() = 70000 tenglama
bilan ifodalanadi. Bu tenglamaning ikki tarafini 70000ga bo'lib yuboramiz va
= 70000 tenglama
bilan ifodalanadi. Bu tenglamaning ikki tarafini 70000ga bo'lib yuboramiz va ![]() ko'rinishdagi
tenglamani hosil qilamiz. Bu OX1X2 koordinat tekisligida
M1(70;0) va M2(0;50) nuqtalardan o'tuvchi to'g'ri chiziq
tenglamasi bo'lib, 1 – rasmda uning grafigi punktir chiziq bilan ifodalangan.
L(
ko'rinishdagi
tenglamani hosil qilamiz. Bu OX1X2 koordinat tekisligida
M1(70;0) va M2(0;50) nuqtalardan o'tuvchi to'g'ri chiziq
tenglamasi bo'lib, 1 – rasmda uning grafigi punktir chiziq bilan ifodalangan.
L(![]() ) funksiyaning
qiymati orttirilsa, masalan L(
) funksiyaning
qiymati orttirilsa, masalan L(![]() )
= 140000 deb olinsa unga mos grafik avvalgisiga parallel bo'lib yuqoriroqdan,
ya'ni M3(140;0) va M4(0;100) nuqtalardan o'tgan to'g'ri
chiziq hosil bo'ladi. Bu to'g'ri chiziqlarning MBESga taaluqli har bir
nuqtasining koordinatalari (1.1) – (1.2) masalaning yechimlarini ifodalaydi.
Masalan, N1 nuqtada L(N1) = 70000, N2 nuqtada
esa L(N2) = 140000 bo'ladi. Maqsad
funksiyasining L(
)
= 140000 deb olinsa unga mos grafik avvalgisiga parallel bo'lib yuqoriroqdan,
ya'ni M3(140;0) va M4(0;100) nuqtalardan o'tgan to'g'ri
chiziq hosil bo'ladi. Bu to'g'ri chiziqlarning MBESga taaluqli har bir
nuqtasining koordinatalari (1.1) – (1.2) masalaning yechimlarini ifodalaydi.
Masalan, N1 nuqtada L(N1) = 70000, N2 nuqtada
esa L(N2) = 140000 bo'ladi. Maqsad
funksiyasining L(![]() ) = const tartibda
olingan grafiklari o'zaro parallel to'g'ri chiziqlardan iborat bo'lar ekan.
Maqsad funksiyasining qiymati ortgan sari bu to'g'ri chiziq yuqorilab
boraveradi. Bora – bora MBESdan chiqib ketishi mumkin. Xususan berilgan misolda
maqsad funksiyasining grafigi MBESdan oxiri C nuqtadan o'tgan holida chiqib
ketadi. Ana shu holat, ya'ni C nuqta koordinatalari (1.1) – (1.2) masala
yechimini, optimal rejani berar ekan deyishga asos bo’ladi. (1.1) shartlarga
mos tengsizliklarni juft-jufti bilan tenglik sifatida olib sistema qilib yechib
C, B nuqtalar koordinatalarini topish mumkin. Masala shartlari va 1 – rasmdan
kelib chiqqan holda A(100;0), B(70;50), C(30;90), D(0;100) ekanligini ko'ramiz.
Chizmada ko'rilganidek MBES qabariq sohadan iborat bo'lib, bu holat barcha
ChPMlar uchun o'rinli bo'lgan holatdir. Maqsad funksiyasi grafigi ham to'g'ri
chiziq bo'lganligi uchun uni oshirish parallel ko'chirishdan iborat bo'ladi va
maqsad funksiyasining maksimal qiymati MBES uchlaridan birida ya'ni maqsad
funksiyasining grafigi MBESdan chiqib ketish arafasida o'tgan nuqtasida bo'lar
ekan. Bu esa optimal reja, ya'ni ChPMlar yechimini topish uchun umumiy qoida tavsiya
qilishga imkoniyat beradi.
) = const tartibda
olingan grafiklari o'zaro parallel to'g'ri chiziqlardan iborat bo'lar ekan.
Maqsad funksiyasining qiymati ortgan sari bu to'g'ri chiziq yuqorilab
boraveradi. Bora – bora MBESdan chiqib ketishi mumkin. Xususan berilgan misolda
maqsad funksiyasining grafigi MBESdan oxiri C nuqtadan o'tgan holida chiqib
ketadi. Ana shu holat, ya'ni C nuqta koordinatalari (1.1) – (1.2) masala
yechimini, optimal rejani berar ekan deyishga asos bo’ladi. (1.1) shartlarga
mos tengsizliklarni juft-jufti bilan tenglik sifatida olib sistema qilib yechib
C, B nuqtalar koordinatalarini topish mumkin. Masala shartlari va 1 – rasmdan
kelib chiqqan holda A(100;0), B(70;50), C(30;90), D(0;100) ekanligini ko'ramiz.
Chizmada ko'rilganidek MBES qabariq sohadan iborat bo'lib, bu holat barcha
ChPMlar uchun o'rinli bo'lgan holatdir. Maqsad funksiyasi grafigi ham to'g'ri
chiziq bo'lganligi uchun uni oshirish parallel ko'chirishdan iborat bo'ladi va
maqsad funksiyasining maksimal qiymati MBES uchlaridan birida ya'ni maqsad
funksiyasining grafigi MBESdan chiqib ketish arafasida o'tgan nuqtasida bo'lar
ekan. Bu esa optimal reja, ya'ni ChPMlar yechimini topish uchun umumiy qoida tavsiya
qilishga imkoniyat beradi.
ChPMlarni
yechishda avvalo MBESni ifodalovchi qabariq soha topiladi va uning uchlarida
maqsad funksiyasini hisoblanadi. Bu qiymatlardan eng kattasiga mos keluvchi
nuqta koordinatalari izlanayotgan yechim – optimal rejani beradi. Bu qoidani
yuqorida ko'rilgan masalaga tatbiq qilamiz. Maqsad funksiyasi (MF) ![]() = 1000
= 1000![]() + 1400
+ 1400![]() bo'lib MBES uchlari
A(100;0)
bo'lib MBES uchlari
A(100;0)
B(70;50),
C(30;90), D(0;100) dagi qiymatlarini ![]() deb
belgilasak £A= 100000, £B=140000, £C=156000,
£D= 140000.
deb
belgilasak £A= 100000, £B=140000, £C=156000,
£D= 140000.
Bu qiymatlarni taqqoslash natijasida optimal reja C(30;90) nuqtada ekanligiga ishonch hosil qilamiz. Bu natija 1 – rasmdagi chizmaga ham mos keladi, ya'ni MF grafigini parallel ko'chirishda bu grafik MBESdan C nuqta orqali chiqib ketishi ko'rinib turibdi. Bu keltirilgan grafik usul ikki noma'lumli masalalarda juda qulay bo'lish bilan birga ko'plab umumiy qoida va tavsiyalar ham ishlab chiqishga imkoniyat beradi.
Optimal rejaning iqtisodiy tahlili
Yuqorida keltirilgan (1.1) – (1.2) masalaning topilgan yechimini tahlil qilamiz. Optimal reja C(30;90) nuqtada bo'lib, bu nuqtada x1 = 30; x2 = 90 va £C=156000 ekanligini ko'rdik. Chizmadan (1 – rasm) ko'rinadiki, C nuqtada 1,3-homashyo to'liq sarflanadi, 2-homashyo esa ortib qolar ekan, chunki 2-homashyoga mos to'g'ri chiziq C nuqtadan o'tmaydi. Optimal reja qiymatlarini homashyo sarfi funksiyalariga qo'yib ham bunga ishonch hosil qilamiz.
f1(x1x2)
= (0,1x1 + 0,3x2) 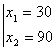 =0,1 × 30 +
0,3 × 90 = 30
=0,1 × 30 +
0,3 × 90 = 30
f2(x1x2)
= (0,5x1 + 0,2x2) 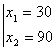 =0,5 × 30 +
0,2 × 90 = 33 < 45
=0,5 × 30 +
0,2 × 90 = 33 < 45
f3(x1x2)
= (0,1x1 + 0,1x2) 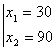 =0,1 × 30 +
0,1 × 90 = 12
=0,1 × 30 +
0,1 × 90 = 12
Bu holatdan kelib chiqib quyidagi mulohaza va tavsiyalarni keltirish mumkin. Ikkinchi tur homashyo 45 birlik bo'lib, undan 33 birlik ishlatiladi. Demak, 12 birlik 2 – tur homashyo ortib qoladi. Bu ortiqchasini homashyo sifatida sotib yuborish mumkin. Ikkinchi yo'li esa chizmadan ko'rinayapti, ishlab chiqarish rejasini oshirishga to'sqinlik qilayotgan kamyob (taxchil) homashyoni ko'paytirish kerak. Bunda barcha homashyolarni to'la jalb qilish, hamda daromadni oshirish imkoniyatiga ega bo'lamiz. Bizning masalada, chizmadan ko'rinadiki (1 – rasm) , 3 – tur homashyo, ya'ni shakar rejani oshirishga imkoniyat bermayapti. Agar shakarga mos to'g'ri chiziq grafigini paralell ko'chirib E nuqtagacha olib borilsa barcha homashyolar to'la ishlatilishiga erishiladi. Grafikni paralell ko'chirish esa shakar zaxirasini ko'paytirish hisobiga erishiladi. Hususan bizning masalada f3(x1x2) = (0,1x1 + 0,1x2) = C3 deb, grafik E nuqtadan o'tishi shartidan C3 qiymat tanlanadi. E nuqta 1-,2- to'g'ri chiziqlar kesishgan nuqtasi bo'lib, uning koordinatalari
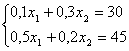 sistemadan
topiladi.
sistemadan
topiladi.
Bu
sistemadan ![]() ekanligini
topamiz.3-xomashyo chizig'i bu nuqtadan o'tishi uchun f3(x1x2)
= 0,1 ×
ekanligini
topamiz.3-xomashyo chizig'i bu nuqtadan o'tishi uchun f3(x1x2)
= 0,1 × ![]() bo'lishi
kerak ekan. Demak, shakar zaxirasini 13,8 birlikka yetkazsak, ya'ni 1,8
birlikka oshirsak optimal planni E
bo'lishi
kerak ekan. Demak, shakar zaxirasini 13,8 birlikka yetkazsak, ya'ni 1,8
birlikka oshirsak optimal planni E![]() nuqtaga
ko'chirish mumkin. Bunda maqsad funksiyasi
nuqtaga
ko'chirish mumkin. Bunda maqsad funksiyasi
£E
= 1000 × ![]() + 1400
×
+ 1400
× ![]()
![]()
![]() 170770 qiymatga
erishadi.
170770 qiymatga
erishadi.
Bunda daromad C nuqtadalgiga qaraganda 14770 pul birligiga ortadi. Shunday qilib qo'yilgan iqtisodiy masalaning matematik modelini tuzish, matematik model yordamida masala yechimini topish va topilgan yechimning iqtisodiy tahlilini to'liq o'tkazish mumkin ekan.
Geometrik usulning samarali ekanligini namoyish qilish uchun uch noma'lumli ChPM na’munasini ko'ramiz. Maqsad masala mohiyati va uni yechimini topish jarayonini aks ettirish bo'lgani uchun masalaning birato’la matematik ifodasidan boshlaymiz. Vaqtincha iqtisodiy mulohazalardan holi bo'lgan holda quyidagi matematik masalani ko'ramiz.
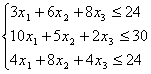 (1.3) xi ≥0 i = 1, 2, 3
(1.3) xi ≥0 i = 1, 2, 3
![]() =
25
=
25![]() (1.4)
(1.4)
Bu yerda (1.3) shartlarni qanoatlantiruvchi barcha nuqtalar orasidan shundayini topishni talab qilinadiki, bu nuqta koordinatalari (1.4) maqsad funksiyasining eng katta qiymatini ta'minlasin. Dastlab (1.3) shartlarni qanoatlantiruvchi nuqtalar to'plami, ya'ni ChPM uchun MBESni topish kerak bo'ladi. Bu yerda ikki o'lchovli masaladagiga o'xshash geometrik usuldan foydalanamiz. Avvalo (1.3) shartlarni kanonik ko'rinishiga keltiramiz

![]()
Bu
shartlarning har biri tenglik sifatida olinganda tekislik kanonik tenglamasi
bo'lib, shartga ko'ra shu tekislikdan pastki qismini olish kerakligini
ifodalaydi. ![]() shartlar esa
fazoviy koordinat sistemasiga nisbatan birinchi oktantni olish kerakligini
ifodalaydi.
shartlar esa
fazoviy koordinat sistemasiga nisbatan birinchi oktantni olish kerakligini
ifodalaydi.
x3
15
6
3 M3
M5 M4
O M2
M1 3 4 6 x2
3
6
8
x1
2 – rasm
Yuqorida
keltirilgan shartlar va mulohazalarga ko'ra (1.3) – (1.4) masala uchun MBESini
2 – rasmda sxematik ifodalangan. Bir-biridan farqlash va MBESni ajratish qulay
bo'lishi uchun har bir tekislik uchun boshqa – boshqa rang olingan. Chizmada 1
– tekislik havo rang , 2 – tekislik qizil, 3 – tekislik qora rangda aks
ettirilgan. Birinchi oktant tepasidan qaraganda MBES ostki chegarasi
shtrixlangan sohadan iborat bo'ladi. Chizmadan ko'rinadiki M1 2 –
tekislikning OX1 o'qi bilan , M2 3 – tekislikning OX2
o'qi bilan, M3 esa 1 – tekislikning OX3 o'qi bilan
kesishgan nuqtasi bo'ladi. Shunga ko'ra koordinatalar orqali M1(3;0;0)
, M2(0;3;0) , M3(0;0;3) ekanligini ko'ramiz. M4 nuqta
esa OX2 X3 koordinata tekisligida 1-, 3- tekisliklar
kesishgan nuqtasi ekanligini ko’ramiz. Uning koordinatalarini topish uchun
1-,3-tekislik tenglamalarida ![]() deb
sistema hosil qilamiz. Undan esa
deb
sistema hosil qilamiz. Undan esa
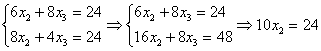
![]()
![]() topiladi. Demak M4(0;2,4;1,2)
topiladi. Demak M4(0;2,4;1,2)
Xuddi
shuningdek M5 nuqta uchun x2=0 deb 1-,2-tekisliklar
kesishgan nuqtasini, M6 uchun esa x3=0 deb
2-,3-tekisliklar kesishgan nuqtasini topiladi. Bunda M5(2,6 ; 0 ;
2,03) va M6(2 ; 2 ; 0) ekanligi topiladi. MBES tepasida esa uchchala
tekislikning kesishgan nuqtasi sifatida topiladigan M7 nuqta
bo'ladi. (1.3) tengsizliklari tenglik qilib sistema sifatida yechilsa M7(2,08
; 1,36 ; 1,2) ekanligi topiladi. Natijada MBES qavariq soha OM1 M2
M3 M4 M5 M6 M7
ning barcha uchlari topiladi. Maqsad funksiyasi (MF) qiymatining o'zgarmas
qiymatida 25![]() const tekislik
tenglamasi bo'lib, unga mos nuqtalar shu tekislikda yotadi. Bu yerda ham MF
tekislikni parallel ko'chirish C=const qiymatining ortishi yoki kamayishi bilan
bog'liq bo'ladi. Shuning uchun optimal reja uning MBES uchlaridan eng katta
qiymatga erishadiganiga mos keladi. Agar
const tekislik
tenglamasi bo'lib, unga mos nuqtalar shu tekislikda yotadi. Bu yerda ham MF
tekislikni parallel ko'chirish C=const qiymatining ortishi yoki kamayishi bilan
bog'liq bo'ladi. Shuning uchun optimal reja uning MBES uchlaridan eng katta
qiymatga erishadiganiga mos keladi. Agar ![]() belgilash kiritsak,
bevosita hisoblashlardan
belgilash kiritsak,
bevosita hisoblashlardan ![]() ekanligini
ko'ramiz. Demak optimal reja M7 nuqtada bo'lib , bunda
ekanligini
ko'ramiz. Demak optimal reja M7 nuqtada bo'lib , bunda ![]() ;
; ![]() ;
; ![]() bo'lar ekan, maqsad
funksiyasi esa bu nuqtada o'zining eng katta qiymatiga erishar ekan.
bo'lar ekan, maqsad
funksiyasi esa bu nuqtada o'zining eng katta qiymatiga erishar ekan.
1.CHPM geometrik usulda yechilsin.
Misollar
1.1 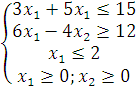 1.2
1.2
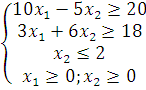
![]()
![]()
1.3 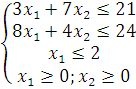 1.4
1.4
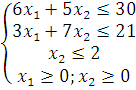
![]()
![]()
1.5 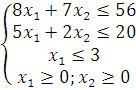 1.6
1.6
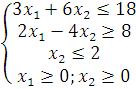
![]()
![]()
2. Berilgan CHPM uchun geometrik usulda optimal plan topilsin.
2.1
![]()
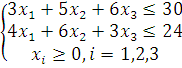
2.2
![]()
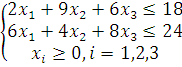
2.3
![]()
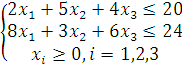
2.4
![]()

2.5
![]()

§ 2 . Chiziqli programmalash masalasining matematik asoslari
Umumiy holda, biror ishlab chiqarish korxonasida n xil mahsulot ishlab chiqarilayotgan bo'lib, buning uchun m xil xomashyo (ishlab chiqarish resurslari)dan foydalanilayotgan bo'lsin. Har bir ishlab chiqarilayotgan j – mahsulot uchun i – xomashyodan aij birlik ishlatilayotgan bo'lsin. Korxonada i – xomashyodan bi birlik bor bo'lsin. Agar j – mahsulotning bir birligining narxi Cj pul birligiga teng bo'lsa korxona har bir mahsulotdan necha donadan (birlikdan) ishlab chiqarganda ularni sotishdan keladigan daromad maksimal bo'ladi? Iqtisodiy nuqtai nazardan masala ana shunday ifodalanadi. Agar j – mahsulotning ishlab chiqarilishi kerak bo'lgan miqdorini Xj deb belgilasak va keltirilgan shartlarning barchasini matematik tarzda ifodalasak u quyidagi ko'rinishini oladi.
![]() i = 1 , 2 , … , m (2.1)
i = 1 , 2 , … , m (2.1)
![]() j = 1 , 2 , … , n
j = 1 , 2 , … , n
![]() …
,
…
, ![]() =
= ![]() Cj Xj
Cj Xj
![]() max
(2.2)
max
(2.2)
Chiziqli
programmalash masalasi (ChPM)ning matematik ifodasi (2.1) – (2.2) bo'lib, unga
ko'ra n o'lchovli fazoning (2.1) shartlarni qanoatlantiruvchi (![]() …,
…,![]() nuqtalari orasidan
shundayini topish kerakki, (2.2) maqsad funksiyasining maksimal (eng katta)
qiymatini ta'minlasin. Avvalo masalaning (2.1) shartlari va ularni
qanoatlantiruvchi nuqtalar to'plami haqida to'xtalamiz. Bu shartlarning
geometrik ma'nosini n=2 va n=3 bo'lgan hollarda batafsil ko'rib chiqildi (§1).
Umumiy holda (2.1) shartlarning har biri n - o'lchovli fazodagi
gipertekislik tenglamasi yordamida fazoni ikkiga bo'lish va undan bir tarafini
olishni aks ettiradi.
nuqtalari orasidan
shundayini topish kerakki, (2.2) maqsad funksiyasining maksimal (eng katta)
qiymatini ta'minlasin. Avvalo masalaning (2.1) shartlari va ularni
qanoatlantiruvchi nuqtalar to'plami haqida to'xtalamiz. Bu shartlarning
geometrik ma'nosini n=2 va n=3 bo'lgan hollarda batafsil ko'rib chiqildi (§1).
Umumiy holda (2.1) shartlarning har biri n - o'lchovli fazodagi
gipertekislik tenglamasi yordamida fazoni ikkiga bo'lish va undan bir tarafini
olishni aks ettiradi. ![]() shartlar
ham n - o'lchovli fazoda
shartlar
ham n - o'lchovli fazoda ![]() =
0 tenglamaga mos gipertekislikdan bir tarafini olishni ifodalaydi. n -
o'lchovli fazoda ham qabariq soha ta'rifi va xususiyati odatdagi 2 va 3
o'lchovli real fazolardagidek bo'ladi. Chiziqli fazo amallari n o'lchovli
fazo elementlari X(
=
0 tenglamaga mos gipertekislikdan bir tarafini olishni ifodalaydi. n -
o'lchovli fazoda ham qabariq soha ta'rifi va xususiyati odatdagi 2 va 3
o'lchovli real fazolardagidek bo'ladi. Chiziqli fazo amallari n o'lchovli
fazo elementlari X(![]() …,
…,![]() lar uchun
quyidagicha aniqlangan bo'lsin
lar uchun
quyidagicha aniqlangan bo'lsin
X![]() …,
…, ![]() +Y(
+Y(![]() …,
…,![]() =
= ![]() …,
…,![]() (2.3)
(2.3)
![]() ×
X(
×
X(![]() …,
…,![]() = T(
= T(![]() …,
…,![]() )
)
U
holda n o'lchovli fazodagi biror D sohaning ixtiyoriy ikkita X, Y ![]() D elementlari uchun
va ixtiyoriy
D elementlari uchun
va ixtiyoriy ![]() sonlar uchun
sonlar uchun ![]() × X + (1-
× X + (1-![]() ) Y
) Y![]() bo'lsa D soha
qabariq soha deyiladi. Bu shart real fazolardagi qabariq soha ta'rifi (agar
sohaning ixtiyoriy ikki nuqtasini tutashtiruvchi kesma ham shu sohaga tegishli
bo'lsa soha qabariq soha deyiladi)ga to'la mos keladi. ChPM yechimini izlash
odatda mumkin bo'lgan yechimlar sohasi (MBES)ni topishdan boshlanadi. MBESdan
esa (2.2) maqsad funksiyasining maksimumi izlanadi. Avvalo ChPM uchun MBES
doimo qabariq soha bo’lishligini ta'kidlab o'tishimiz kerak. Haqiqatdan, agar
(2.1) shartlarni qanoatlantiruvchi nuqtalar to'plamini D deb belgilasak va
ixtiyoriy X, Y
bo'lsa D soha
qabariq soha deyiladi. Bu shart real fazolardagi qabariq soha ta'rifi (agar
sohaning ixtiyoriy ikki nuqtasini tutashtiruvchi kesma ham shu sohaga tegishli
bo'lsa soha qabariq soha deyiladi)ga to'la mos keladi. ChPM yechimini izlash
odatda mumkin bo'lgan yechimlar sohasi (MBES)ni topishdan boshlanadi. MBESdan
esa (2.2) maqsad funksiyasining maksimumi izlanadi. Avvalo ChPM uchun MBES
doimo qabariq soha bo’lishligini ta'kidlab o'tishimiz kerak. Haqiqatdan, agar
(2.1) shartlarni qanoatlantiruvchi nuqtalar to'plamini D deb belgilasak va
ixtiyoriy X, Y ![]() elementlarini
olsak hamda Z=
elementlarini
olsak hamda Z=![]() elementini
olsak Z(
elementini
olsak Z(![]() …,
…,![]() uning uchun
uning uchun
![]() (
(![]() ×
× ![]()
![]() ×
×![]() kelib
chiqadi, ya'ni Z(
kelib
chiqadi, ya'ni Z(![]() …,
…,![]() uchun ham
uchun ham ![]()
![]() 1 , 2 , …n
1 , 2 , …n
tengsizliklar
o'rinli bo'ladi, demak Z![]() bo'ladi.
Aksariyat hollarda n o'lchovli ChPMning MBESi n o'lchovli qabariq
soha bo'ladi. Bu holda ham masala yechimi, ya'ni optimal rejani shu qabariq
sohaning uchlaridan izlanishi kerak. (2.1) shartlarga ko'ra aniqlanadigan D
sohaning uchlarini topish uchun m+n ta (2.1) shartlardan n ta chiziqli
erklisini tanlaymiz va ularni tenglik sifatida ifodalasak n ta
noma'lumli n ta chiziqli algebraik tenglamalar sistemasi hosil bo'ladi.
Bu sistemaning yechimini topib uni (2.1) shartlarning qolganlariga muvofiqligi
tekshiriladi. Agar shunday bo'lsa, bu yechimga mos M (
bo'ladi.
Aksariyat hollarda n o'lchovli ChPMning MBESi n o'lchovli qabariq
soha bo'ladi. Bu holda ham masala yechimi, ya'ni optimal rejani shu qabariq
sohaning uchlaridan izlanishi kerak. (2.1) shartlarga ko'ra aniqlanadigan D
sohaning uchlarini topish uchun m+n ta (2.1) shartlardan n ta chiziqli
erklisini tanlaymiz va ularni tenglik sifatida ifodalasak n ta
noma'lumli n ta chiziqli algebraik tenglamalar sistemasi hosil bo'ladi.
Bu sistemaning yechimini topib uni (2.1) shartlarning qolganlariga muvofiqligi
tekshiriladi. Agar shunday bo'lsa, bu yechimga mos M (![]() …,
…,![]() nuqta MBES-ning
tayanch nuqtasi, uning koordinatalari esa ChPMning tayanch yechimi deyiladi.
nuqta MBES-ning
tayanch nuqtasi, uning koordinatalari esa ChPMning tayanch yechimi deyiladi.
Shunday usulda hosil qilish mumkin bo'lgan
sistemalar soni umumiy holda ![]() formula
bo'yicha hisoblanadi. Bu sistemalardan ChPMning tayanch yechimlari topiladi.
Tayanch yechimlar orasidan maqsad funksiyasining eng katta qiymatini beruvchi
optimal reja ham topiladi. Faqat n, m ortgan sari tayanch yechimlar soni ham
ortib boradi. Masalan n=5, m=4 bo'lgan, umuman olganda oddiygina holda ham
tayanch yechimlar soni
formula
bo'yicha hisoblanadi. Bu sistemalardan ChPMning tayanch yechimlari topiladi.
Tayanch yechimlar orasidan maqsad funksiyasining eng katta qiymatini beruvchi
optimal reja ham topiladi. Faqat n, m ortgan sari tayanch yechimlar soni ham
ortib boradi. Masalan n=5, m=4 bo'lgan, umuman olganda oddiygina holda ham
tayanch yechimlar soni ![]() bo'lishi
mumkin ekan. Shuncha yechimning har birini topishda 5 noma'lumli sistemalarni
ishlash kerak bo'ladi. Tabiiy savol tug'iladi, optimal rejani topish uchun ana
shu 126 nuqtalarning barchasini topish, hamda shu nuqtalarda maqsad
funksiyasini hisoblash shartmikan? Bu ishni osonlashtirish
bo'lishi
mumkin ekan. Shuncha yechimning har birini topishda 5 noma'lumli sistemalarni
ishlash kerak bo'ladi. Tabiiy savol tug'iladi, optimal rejani topish uchun ana
shu 126 nuqtalarning barchasini topish, hamda shu nuqtalarda maqsad
funksiyasini hisoblash shartmikan? Bu ishni osonlashtirish
ya’ni optimal rejaga yetish yo'lini qisqartirish imkoniyati yo'qmikan? Bu sohadagi izlanishlar o'z samarasini bergan va rejani bosqichma – bosqich yaxshilash degan usullar yaratilgan. Usulning g'oyasi asosan quyidagi mulohazaga asoslangan. Avvalo ixtiyoriy birorta tayanch yechim topamiz. Bu yechim MBES deb ataganimiz qabariq ko'pyoqlining birorta uchiga mos keladi. Ikki o'lchovli holda bu qabariq ko'pburchak, uch o'lchovli holda qabariq ko'pyoqli (prizma, piramida …). Bu uchidan bir qancha qirralar o'tgan bo'ladi, go'yoki chorrahada uchrashadigan yo'llardek. Har bir qirra berilgan uchini boshqa bir qo'shni uch bilan tutashtiradi. Shu yo'llardan qaysi birini tanlagan ma'qul, qay biri maqsadga tezroq olib boradi? Go'yo ertak qahramonlari oldida uchraydigan yo'llarda yozib qo'yiladigan yo'l ta'rifiga o'xshash bu yo'llar hislatlarini aniqlash mezoni yo'qmikan? Umuman maqsadga eltuvchi yo'lning o'zi bormikan? Ertaksifat bu mulohazalarning barchasiga javob beruvchi usul dastlab 1947 yil Dansig tomonidan kashf qilingan. Bu usul keyinchalik ilmiy va o'quv adabiyotlarida simpleks usul nomi bilan muomalaga kirib ketgan. Usulning matematik hamda amaliy tafsilotlariga o'tamiz.
3. Berilgan CHPM uchun ko’rsatilgan bazisga mos tayanch yechim topilsin. Tayanch yechimlar ko’pi bilan nechta bo’lishi mumkin.
3.1 ![]()
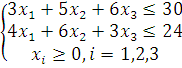
![]()
3.2 ![]()
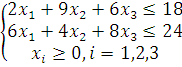
![]()
3.3 ![]()
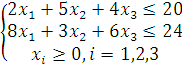
![]()
3.4 ![]()

![]()
3.5 ![]()

![]()
§ 3. Rejani bosqichma – bosqich yaxshilash usuli.
Biz bu yerda asosan usulning amaliy taraflari, hamda hisoblash algoritmlariga ko'proq to'xtalamiz. Usul asosan ikkita bosqichni o'z ichiga oladi. To'g'rirog'i har bosqichda ikkita savol hal qilinishi kerak bo'ladi. Avvalo, tanlangan tayanch yechim optimal reja bo'ladimi? Optimal bo'lsa, tabiiy, muammo hal bo'lgan, yechim topilgan deb hisob qilinadi. Optimal bo'lmasa, navbatdagi, bu yechimga qaraganda yaxshiroq yechimni qanday topish mumkin?
ChPMni umumiy ko'rinishini olamiz
![]()
![]() 2, …,
m (3.1)
2, …,
m (3.1)
![]() j = 1, 2, …, n
j = 1, 2, …, n
![]() …,
…,
![]() (3.2)
(3.2)
(3.1)
shartlarni qanoatlantiruvchi barcha M (![]() …,
…, ![]() lar orasidan (3.2)
maqsad funksiyasining eng katta qiymatini beruvchi nuqta koordinatalari, ya'ni
optimal rejani topish kerak.
lar orasidan (3.2)
maqsad funksiyasining eng katta qiymatini beruvchi nuqta koordinatalari, ya'ni
optimal rejani topish kerak.
Simpleks usul kanonik ko'rinishdagi ChPMlar uchun mo'ljallangan. Bunda ChPM barcha shartlari tenglik ko'rinishida berilgan bo'lishi kerak. Kanonik ko'rinishdagi ChPM matematik ifodasi
![]()
![]() 1, 2, …, m
(3.3)
1, 2, …, m
(3.3)
![]() (3.4)
(3.4)
![]() ko'rinishda
bo'ladi. Bu yerda ham
ko'rinishda
bo'ladi. Bu yerda ham ![]() o'z
o'rnida qoladi. Alohida zarurat bo'lmasa bu shartlarni oshkora ifodalab
o'tirilmaydi. Umumiy ko'rinishdagi (3.1) – (3.2) ChPMni kanonik (3.3) – (3.4)
ko'rinishiga keltirishimiz mumkin. Buning uchun (3.1) shartlarning har birining
chap tarafiga ( u kichik bo'lganligi uchun) yangi
o'z
o'rnida qoladi. Alohida zarurat bo'lmasa bu shartlarni oshkora ifodalab
o'tirilmaydi. Umumiy ko'rinishdagi (3.1) – (3.2) ChPMni kanonik (3.3) – (3.4)
ko'rinishiga keltirishimiz mumkin. Buning uchun (3.1) shartlarning har birining
chap tarafiga ( u kichik bo'lganligi uchun) yangi ![]() o'zgaruvchini
qo'shish yordamida tenglikka aylantirish mumkin. Bunda
o'zgaruvchini
qo'shish yordamida tenglikka aylantirish mumkin. Bunda ![]() o'zgaruvchilar ham
noma'lum bo'ladi. Natijada (3.1) – (3.2) masala
o'zgaruvchilar ham
noma'lum bo'ladi. Natijada (3.1) – (3.2) masala
![]()
![]() 2, …, m
(3.5)
2, …, m
(3.5)
![]() (3.6)
(3.6)
ko'rinishini
oladi, bu yerda noma'lumlar ![]() …
…
![]() …,
…,![]() n+m ta bo'ladi.
Maqsad funksiyasining ko'rinishini o'zgartirmaslik uchun (3.6) ifoda
n+m ta bo'ladi.
Maqsad funksiyasining ko'rinishini o'zgartirmaslik uchun (3.6) ifoda ![]()
![]() deb hisoblangan.
Bundan ko'rinadiki, yangi kiritilgan
deb hisoblangan.
Bundan ko'rinadiki, yangi kiritilgan ![]() …,
…,
![]() o'zgaruvchilar
qanday bo'lishidan qat'iy nazar maqsad funksiyasining qiymatlariga mutlaqo
ta'sir qilmaydi. Natijada hosil bo'lgan (3.5) – (3.6) masala (3.3) – (3.4)
masala bilan aynan bir xil ko'rinishini olar ekan. Shunday qilib umumiy
ko'rinishdagi ChPMni kanonik ko'rinishga keltirish mumkinligi asoslandi. Demak,
kanonik ko'rinishdagi ChPMlar uchun yaratilgan usullarni umumiy ko'rinishdagi
ChPMlarga ham tatbiq qilish mumkin ekan. Simpleks usul tafsilotlariga o'tamiz.
Buning uchun (3.3) shartlar matritsasi A=(aij) i= 1, 2, …, m j = 1,
2, …, n ustunlarini m o'lchovli chiziqli fazo vektorlari deb, faqat
uning koordinatalari yordamida tuzilgan vektorlarni
o'zgaruvchilar
qanday bo'lishidan qat'iy nazar maqsad funksiyasining qiymatlariga mutlaqo
ta'sir qilmaydi. Natijada hosil bo'lgan (3.5) – (3.6) masala (3.3) – (3.4)
masala bilan aynan bir xil ko'rinishini olar ekan. Shunday qilib umumiy
ko'rinishdagi ChPMni kanonik ko'rinishga keltirish mumkinligi asoslandi. Demak,
kanonik ko'rinishdagi ChPMlar uchun yaratilgan usullarni umumiy ko'rinishdagi
ChPMlarga ham tatbiq qilish mumkin ekan. Simpleks usul tafsilotlariga o'tamiz.
Buning uchun (3.3) shartlar matritsasi A=(aij) i= 1, 2, …, m j = 1,
2, …, n ustunlarini m o'lchovli chiziqli fazo vektorlari deb, faqat
uning koordinatalari yordamida tuzilgan vektorlarni ![]() …,
…,![]()
ko'rinishida ifodalaymiz. Shunga o'xshash, narxlarga mos Cj qiymatlar yordamida
![]() …,
…,
![]() vektorni satr
matritsa sifatida ifodalaymiz. Zaxiralarga mos bj qiymatlar
yordamida
vektorni satr
matritsa sifatida ifodalaymiz. Zaxiralarga mos bj qiymatlar
yordamida ![]() …,
…, ![]() ustun matritsani
tuzsak (3.3) – (3.4) masalani kompakt (ixcham) ko'rinishda, matritsalar orqali
ustun matritsani
tuzsak (3.3) – (3.4) masalani kompakt (ixcham) ko'rinishda, matritsalar orqali
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
ko'rinishda
ifodalash mumkin. Bu yerda ![]() …,
…,
![]() noma'lumlarga mos
ustun matritsa.
noma'lumlarga mos
ustun matritsa.
![]() 2, …, n) vektorlar m
o'lchovli chiziqli fazo vektorlari bo'lib, ularning soni n aksariyat
hollarda m dan ancha katta bo'ladi. Shuning uchun (3.7) sistema
yechimlari cheksiz ko'p bo'ladi. Ular orasida (3.8) shartni
qanoatlantiradiganini topishimiz kerak.
2, …, n) vektorlar m
o'lchovli chiziqli fazo vektorlari bo'lib, ularning soni n aksariyat
hollarda m dan ancha katta bo'ladi. Shuning uchun (3.7) sistema
yechimlari cheksiz ko'p bo'ladi. Ular orasida (3.8) shartni
qanoatlantiradiganini topishimiz kerak.
Buning uchun ![]() vektorlar orasidan
vektorlar orasidan ![]() musbat
koordinatalariga mos keluvchi mta chiziqli erklisini ajratishimiz kerak.
Fazo m o'lchovli bo'lganligi uchun
musbat
koordinatalariga mos keluvchi mta chiziqli erklisini ajratishimiz kerak.
Fazo m o'lchovli bo'lganligi uchun ![]() lar orasida chiziqli
erklisi m tadan ortiq bo'lmaydi. Bu vektorlar bazis vektorlar deb
belgilanadi. Masala shartlari shu bazisga moslanadi. Bazis vektorlardan qolgan
barcha
lar orasida chiziqli
erklisi m tadan ortiq bo'lmaydi. Bu vektorlar bazis vektorlar deb
belgilanadi. Masala shartlari shu bazisga moslanadi. Bazis vektorlardan qolgan
barcha ![]() vektorlarga mos
vektorlarga mos ![]() lar nol deb olinadi.
Shundan keyin berilgan bazisga mos tayanch yechim topiladi va u optimallikka
tekshiriladi.
lar nol deb olinadi.
Shundan keyin berilgan bazisga mos tayanch yechim topiladi va u optimallikka
tekshiriladi.
Biz bu yerda usulning faqat amaliy taraflariga to'xtalamiz. Usulning nazariy asoslariga qiziqqanlar maxsus adabiyotlarga murojaat qilishi mumkin. Usul mohiyati va tartibini amaliy misolni ishlash jarayonida izohlab boramiz. Quyidagi ChPM berilgan bo'lsin.
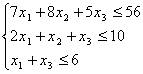
![]()
Bu
masalani kanonik ko'rinishga keltiramiz![]()
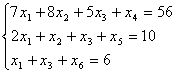
![]()
Berilgan masala shartlaridan ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ekanligini ko'ramiz.
Bu yerda yangi kiritilgan o'zgaruvchilarga mos
ekanligini ko'ramiz.
Bu yerda yangi kiritilgan o'zgaruvchilarga mos ![]() vektorlar bazis
ekanligi ko'rinib turibdi, haqiqatdan ham
vektorlar bazis
ekanligi ko'rinib turibdi, haqiqatdan ham ![]()
ekanligini
ko'rishimiz mumkin. Qolgan vektorlar, shuningdek cheklash vektori ![]() ni ham ular orqali
ifodalash mumkin. Masala shartlariga ko'ra shu bazisga mos tayanch yechimni
topish uchun bazisga kirmagan
ni ham ular orqali
ifodalash mumkin. Masala shartlariga ko'ra shu bazisga mos tayanch yechimni
topish uchun bazisga kirmagan ![]() o'zgaruvchilarni
nol deb olishimiz kerak. U holda
o'zgaruvchilarni
nol deb olishimiz kerak. U holda ![]() ekanligi
kelib chiqadi. Keltririlgan shartlarni ifodalovchi barcha sonlarni quyidagi
jadval ko'rinishda ifodalaymiz.
ekanligi
kelib chiqadi. Keltririlgan shartlarni ifodalovchi barcha sonlarni quyidagi
jadval ko'rinishda ifodalaymiz.
|
i
|
Cj
Ci |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
|
1 |
0 |
A4 |
56 |
7 |
8 |
5 |
1 |
0 |
0 |
11,2 |
|
|
2 |
0 |
A5 |
10 |
2 |
1 |
1 |
0 |
1 |
0 |
10 |
|
|
3 |
0 |
A6 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
6 |
|
|
|
|
|
|
-10 |
-12 |
-25 |
0 |
0 |
0 |
|
![]()
1 – jadval
1
– jadvalda A0 ustun shartlardagi o'ng taraf qiymatlari (resurslar
miqdori) A1 , A2 , A3 , A4 , A5
, A6 ustunlar shartlardagi ![]() larning
koeffisiyentlaridan tuzilgan. Shartlarda koeffisiyentlari birlik ustunni
ifodalayotgan vektorlar bazis vektorlar deb belgilanib, ularning 1 elementlari
joylashgan qator boshida bazis deb atalgan ustunda shu vektor belgisi AK
deb qo'yiladi. CKi deb atalgan ustunga esa bazisga kirgan shu
qatordagi Ak vektor tepasidagi narx qiymati Ck qo'yiladi.
larning
koeffisiyentlaridan tuzilgan. Shartlarda koeffisiyentlari birlik ustunni
ifodalayotgan vektorlar bazis vektorlar deb belgilanib, ularning 1 elementlari
joylashgan qator boshida bazis deb atalgan ustunda shu vektor belgisi AK
deb qo'yiladi. CKi deb atalgan ustunga esa bazisga kirgan shu
qatordagi Ak vektor tepasidagi narx qiymati Ck qo'yiladi.
![]() - ustunda tenglama
nomeri belgilanadi. Shu bilan masala shartlariga kiruvchi barcha sonlar
jadvalda o'z o'rnini egallaydi. Shundan keyin jadvalning so'nggi qator va
so'nggi ustunini to'lg'azishga o'tiladi. Dastlab
- ustunda tenglama
nomeri belgilanadi. Shu bilan masala shartlariga kiruvchi barcha sonlar
jadvalda o'z o'rnini egallaydi. Shundan keyin jadvalning so'nggi qator va
so'nggi ustunini to'lg'azishga o'tiladi. Dastlab
![]()
![]() 1, 2, …,
n (3.9)
1, 2, …,
n (3.9)
formula
bo'yicha ![]() lar hisoblanadi.
Agar barcha
lar hisoblanadi.
Agar barcha ![]() lar manfiy bo'lmasa
jadvalga mos tayanch yechim optimal yechim deyiladi va hisob to'xtatiladi. Agar
lar manfiy bo'lmasa
jadvalga mos tayanch yechim optimal yechim deyiladi va hisob to'xtatiladi. Agar
![]() lar orasida
manfiylari bo'lsa jadvalga mos tayanch yechim optimal emas, uni yaxshilash
kerak degan xulosa qilinadi. Buning uchun manfiy
lar orasida
manfiylari bo'lsa jadvalga mos tayanch yechim optimal emas, uni yaxshilash
kerak degan xulosa qilinadi. Buning uchun manfiy ![]() lar orasidan eng
kichigi joylashgan ustunni hal qiluvchi ustun deb belgilanadi. Agar bu
ustundagi Ak elementlari (
lar orasidan eng
kichigi joylashgan ustunni hal qiluvchi ustun deb belgilanadi. Agar bu
ustundagi Ak elementlari (![]() …,
…,
![]() lar orasida
musbatlari bo'lmasa masala yechimi yo'q degan xulosaga
kelamiz. Agar
lar orasida
musbatlari bo'lmasa masala yechimi yo'q degan xulosaga
kelamiz. Agar ![]()
![]() 1, 2, …, m lar
orasida musbatlari bo'lsa
1, 2, …, m lar
orasida musbatlari bo'lsa
*
Ular uchun Өi = ![]() qiymatlar
hisoblanadi.
qiymatlar
hisoblanadi.
*
ulardan kichigi Өi tanlanadi va bu Өi
jolashgan qator hal qiluvchi qator deb e'lon qilinadi, hamda hal qiluvchi ustun
va hal qiluvchi qatorlar kesishgan joydagi ![]() elementni esa hal
qiluvchi element deb belgilanadi.
elementni esa hal
qiluvchi element deb belgilanadi.
Bu
jarayonni biz tahlil qilayotgan misol (1 – jadval) uchun quyidagi tartibda
bajariladi. Avvalo (3.9) formulalar bo'yicha ![]() larni hisoblaymiz.
larni hisoblaymiz.

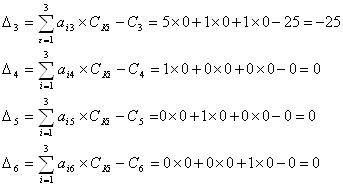
Bu
qiymatlar jadvalga kiritilgan ![]() larni
taqqoslash yordamida eng kichigi
larni
taqqoslash yordamida eng kichigi ![]() ga
mos kelgan 3 – ustun hal qiluvchi ustun deb belgilanadi. Bu ustun
elementlari yordamida Ө
ga
mos kelgan 3 – ustun hal qiluvchi ustun deb belgilanadi. Bu ustun
elementlari yordamida Ө![]() =
= ![]() qiymatlar
hisoblanadi. Ө1 = 56/5=11,2 ; Ө2 = 10/1 = 10;
Ө3 = 6/1=6 ular ham jadvalga kiritilgan. Ө
qiymatlar
hisoblanadi. Ө1 = 56/5=11,2 ; Ө2 = 10/1 = 10;
Ө3 = 6/1=6 ular ham jadvalga kiritilgan. Ө![]() lar orasida eng
kichigi Ө3 ga mos kelgan 3 – qator hal qiluvchi qator deb
belgilanadi. Jadvalda bu ustun va qator strelka bilan belgilangan. Ular
kesishgan joydagi hal qiluvchi
lar orasida eng
kichigi Ө3 ga mos kelgan 3 – qator hal qiluvchi qator deb
belgilanadi. Jadvalda bu ustun va qator strelka bilan belgilangan. Ular
kesishgan joydagi hal qiluvchi ![]() element
ham qalin chegara bilan ajratilgan Agar hal qiluvchi element 1ga teng bo'lmasa
hal qiluvchi qator barcha elementlarini hal qiluvchi elementga bo'lib yuborib
bunga erishish mumkin. 3 – qator elementlarini 5ga ko'paytirib, 1 – qator
elementlaridan ayiramiz, so'ngra 3 – qator elementlarini 1ga ko'paytirib, 2 –
qator elementlaridan ayiramiz. Hosil bo'lgan qiymatlari 2 – jadval tarzida
ifodalangan.
element
ham qalin chegara bilan ajratilgan Agar hal qiluvchi element 1ga teng bo'lmasa
hal qiluvchi qator barcha elementlarini hal qiluvchi elementga bo'lib yuborib
bunga erishish mumkin. 3 – qator elementlarini 5ga ko'paytirib, 1 – qator
elementlaridan ayiramiz, so'ngra 3 – qator elementlarini 1ga ko'paytirib, 2 –
qator elementlaridan ayiramiz. Hosil bo'lgan qiymatlari 2 – jadval tarzida
ifodalangan.
|
i
|
Cj
Cik |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
1 |
0 |
A4 |
26 |
2 |
8 |
0 |
1 |
0 |
-5 |
3,25 |
|
2 |
0 |
A5 |
4 |
1 |
1 |
0 |
0 |
1 |
-1 |
4 |
|
3 |
25 |
A3 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
15 |
-12 |
0 |
0 |
0 |
25 |
|
![]()
![]()
2 – jadval
2
– jadval uchun ham (3.9) formulalar yordamida ![]() lar hisoblanadi. Bu
qiymatlar hisoblanib jadvalga kiritilgan.
lar hisoblanadi. Bu
qiymatlar hisoblanib jadvalga kiritilgan. ![]() lar orasida
manfiysi bo'lganligi uchun bu jadvalga mos tayanch yechim ham optimal yechim
emas. Shuning uchun manfiy
lar orasida
manfiysi bo'lganligi uchun bu jadvalga mos tayanch yechim ham optimal yechim
emas. Shuning uchun manfiy ![]() ga
mos 2 – ustun hal qiluvchi ustun deb belgilandi. Hal qiluvchi ustunning musbat
elementlari uchun Өj = 26/8 = 13/4= 3,25; Ө2
= 4/1=4 lar hisoblanadi. Eslatma: Manfiy va nol bo'lgan elementlar uchun
Өi hisoblanmaydi. Agar
ga
mos 2 – ustun hal qiluvchi ustun deb belgilandi. Hal qiluvchi ustunning musbat
elementlari uchun Өj = 26/8 = 13/4= 3,25; Ө2
= 4/1=4 lar hisoblanadi. Eslatma: Manfiy va nol bo'lgan elementlar uchun
Өi hisoblanmaydi. Agar ![]() lar orasida
musbatlari bo'lmasa, ChPM yechimi yo'q deb hisoblash to'xtatiladi. Bizning
misolda Өi lardan kichigi Ө1 = 3,25 ga mos
qator hal qiluvchi qator deb belgilandi. Simpleks usul algoritmiga ko'ra 3 –
jadvalni to'lg'azamiz.
lar orasida
musbatlari bo'lmasa, ChPM yechimi yo'q deb hisoblash to'xtatiladi. Bizning
misolda Өi lardan kichigi Ө1 = 3,25 ga mos
qator hal qiluvchi qator deb belgilandi. Simpleks usul algoritmiga ko'ra 3 –
jadvalni to'lg'azamiz.
|
i
|
Cj
Cik |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
1 |
12 |
A2 |
3,25 |
0,25 |
1 |
0 |
0,125 |
0 |
-0,625 |
|
|
2 |
0 |
A5 |
0,75 |
0,75 |
0 |
0 |
-0,125 |
1 |
-0,375 |
|
|
3 |
25 |
A3 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
18 |
0 |
0 |
1,5 |
0 |
17,5 |
|
3 – jadval
3
– jadvalda barcha ![]()
![]() bo'lganligi uchun bu
jadvalga mos tayanch yechimda bazis o'zgaruvchilar
bo'lganligi uchun bu
jadvalga mos tayanch yechimda bazis o'zgaruvchilar ![]() deb olinadi. Bazisga
kirmagan o'zgaruvchilar esa nolga teng deb olinadi, ya'ni
deb olinadi. Bazisga
kirmagan o'zgaruvchilar esa nolga teng deb olinadi, ya'ni ![]() . Bu yechim ChPM
uchun optimal planni beradi. Yordamchi noma'lumlardan holi bo'lgan holda
berilgan ChPM uchun optimal plan
. Bu yechim ChPM
uchun optimal planni beradi. Yordamchi noma'lumlardan holi bo'lgan holda
berilgan ChPM uchun optimal plan ![]() ko'rinishda
belgilanadi. Bunda maqsad funksiyasi o'zining maksimal qiymatiga erishar ekan
va
ko'rinishda
belgilanadi. Bunda maqsad funksiyasi o'zining maksimal qiymatiga erishar ekan
va ![]() ga teng bo'ladi.
Keltirilgan misol planni bosqichma – bosqich yaxshilash, ya'ni simpleks
usulning barcha amallari va ularning bajarilish tartibini o'zida aks ettirgan.
Shuning bilan birga masalani ishlash tartibiga e'tibor berilsa, geometrik
usuldan farqli noma'lumlar soni ortgan, ya'ni masala murakkablashgan holda ham
bu usul shundayligicha tatbiq qilinaveradi. Tabiiy bunda simpleks jadval ustun
va qatorlar soni ortadi, shunga ko'ra hisoblashlar hajmi ham ortadi. Optimal
planga yetib borish uchun bajariladigan qadamlar soni ham ortishi mumkin.
ga teng bo'ladi.
Keltirilgan misol planni bosqichma – bosqich yaxshilash, ya'ni simpleks
usulning barcha amallari va ularning bajarilish tartibini o'zida aks ettirgan.
Shuning bilan birga masalani ishlash tartibiga e'tibor berilsa, geometrik
usuldan farqli noma'lumlar soni ortgan, ya'ni masala murakkablashgan holda ham
bu usul shundayligicha tatbiq qilinaveradi. Tabiiy bunda simpleks jadval ustun
va qatorlar soni ortadi, shunga ko'ra hisoblashlar hajmi ham ortadi. Optimal
planga yetib borish uchun bajariladigan qadamlar soni ham ortishi mumkin.
Simpleks usulning umumiy holdagi algoritmi (ixtiyoriy n , m lar uchun) dasturlangan va zamonaviy kompyuterlar matematik ta'minotida bu dasturlar mavjud. Ulardan foydalanish uchun iste'molchi, ya'ni tadqiqotchi, o'zi yechmoqchi bo'lgan ChPM ga taalluqli barcha qiymatlarni ko'rsatilgan tartibda kompyuter xotirasiga kiritib, shu dasturlarga murojaat qilishi yetarli.
Biz bu yerda e'tiborni qaratmoqchi bo'lgan yana bir hol, simpleks usul bo'yicha hisobni boshlashda dastlabki simpleks jadvalda bazis berilishi kerakligi. Bu bazis qanday tanlanadi, bunda nimalarga e'tiborni qaratish kerak?
§ 4. Chiziqli programmalash masalalari uchun bazis tanlash va masala shartlarini tanlangan bazisga moslashtirish.
Kanonik ko'rinishda berilgan ChPMni qaraymiz.
![]()
![]() 2, …,
m (4.1)
2, …,
m (4.1)
![]()
![]() 2, …, n
2, …, n
![]() (4.2)
(4.2)
Bu
yerda avval ta'kidlaganimizdek m![]() bo'ladi,
ya'ni (4.1) sistemaning yechimlari cheksiz ko'p. Shu yechimlar orasidan (4.2)
shartga mos keladigani, ya'ni maqsad funksiyasiga maksimal qiymat beradiganini
ajratib olish kerak. Buning uchun (4.1) sistema yechimlarini ifodalash
qoidasini va ular orasidan bazis o'zgaruchilarni ajratish usulini aniqlashimiz
kerak. (4.1) sistema matritsasi tartibi m × n bo'lganligi va m
bo'ladi,
ya'ni (4.1) sistemaning yechimlari cheksiz ko'p. Shu yechimlar orasidan (4.2)
shartga mos keladigani, ya'ni maqsad funksiyasiga maksimal qiymat beradiganini
ajratib olish kerak. Buning uchun (4.1) sistema yechimlarini ifodalash
qoidasini va ular orasidan bazis o'zgaruchilarni ajratish usulini aniqlashimiz
kerak. (4.1) sistema matritsasi tartibi m × n bo'lganligi va m![]() n bo'lgani uchun RgA
≤ m bo'ladi. Qulaylik uchun RgA=m deb olamiz. Aksariyat
hollarda bu shart bajariladi. A matritsadan o'zaro chiziqli erkli bo'lgan m ta
ustunni ajratib olamiz. Bu ustunlarni
n bo'lgani uchun RgA
≤ m bo'ladi. Qulaylik uchun RgA=m deb olamiz. Aksariyat
hollarda bu shart bajariladi. A matritsadan o'zaro chiziqli erkli bo'lgan m ta
ustunni ajratib olamiz. Bu ustunlarni ![]() … ,
… , ![]() deb belgilaymiz.
Ular chiziqli erkli bo'lishi uchun shu ustun elementlaridan tuzilgan
deb belgilaymiz.
Ular chiziqli erkli bo'lishi uchun shu ustun elementlaridan tuzilgan
C = (![]() … ,
… , ![]()
matritsa
determinanti noldan farqli bo'lishi kerak, ya'ni ![]() . Tanlangan bazisga
mos tayanch yechimni topish uchun esa shu bazisga mos
. Tanlangan bazisga
mos tayanch yechimni topish uchun esa shu bazisga mos ![]() … ,
… , ![]() noma'lumlardan
boshqa barcha
noma'lumlardan
boshqa barcha ![]() larni
nolga teng deb olamiz. Natijada (4.1) sistema soddalashib
larni
nolga teng deb olamiz. Natijada (4.1) sistema soddalashib
![]()
![]() 1, 2, …,
m (4.3)
1, 2, …,
m (4.3)
ko'rinishni
oladi. Bu sistema m noma'lumli m ta chiziqli algebraik tenglamalar sistemasi
bo'lib qoladi. ![]() bo'lganligi
uchun uning yagona yechimi bo'ladi. Agar bu yechim uchun barcha
bo'lganligi
uchun uning yagona yechimi bo'ladi. Agar bu yechim uchun barcha ![]() bo'lsa topilgan
yechim tanlangan bazisdagi tayanch yechim deyiladi. Agar
bo'lsa topilgan
yechim tanlangan bazisdagi tayanch yechim deyiladi. Agar ![]() lar orasida
manfiylari ham chiqib qolsa, tanlangan bazisda tayanch yechim yo'q deyiladi va
boshqa bazisga o'tiladi. Tayanch yechimi mavjud bo'lgan bazis tanlangach esa
shu bazisdagi tayanch yechim optimallikka tekshiriladi. Bu esa avvalgi
paragrafda ko'rilgan usulda amalga oshiriladi. Faqat buning uchun masala
shartlari tanlangan bazisga moslashtirilishi kerak. Buning uchun tanlangan
bazisga mos C matritsa uchun teskari matritsa topiladi va (4.2) sistema vektor
ko'rinishida C-1 ga ko'paytiriladi. Bunda sistema
lar orasida
manfiylari ham chiqib qolsa, tanlangan bazisda tayanch yechim yo'q deyiladi va
boshqa bazisga o'tiladi. Tayanch yechimi mavjud bo'lgan bazis tanlangach esa
shu bazisdagi tayanch yechim optimallikka tekshiriladi. Bu esa avvalgi
paragrafda ko'rilgan usulda amalga oshiriladi. Faqat buning uchun masala
shartlari tanlangan bazisga moslashtirilishi kerak. Buning uchun tanlangan
bazisga mos C matritsa uchun teskari matritsa topiladi va (4.2) sistema vektor
ko'rinishida C-1 ga ko'paytiriladi. Bunda sistema
![]() (4.4)
(4.4)
ko'rinishini oladi. (4.4) sistema (4.2) maqsad funksiyasi bilan birgalikda dastlabki simpleks jadval uchun asos qilib olinadi. Simpleks jadvaldan tanlangan bazisdagi tayanch yechim optimal bo'lishi tekshirilishi mumkin. Keltirilgan mulohazalar va hisoblash jarayonini amaliy misolda tahlil qilamiz. Quyidagi ko'rinishdagi ChPM berilgan bo'lsin
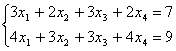
![]()
![]()
Bu
yerda matritsa ustunlari 4ta bo'lib ularni A1 , A2 , A3
, A4 vektorlar deb belgilasak ular ikki o'lchovli fazo vektorlari
(m=2) bo'lgani uchun bazis sifatida ulardan ikkitasini olish mumkin. Bunda
variantlar soni ![]() ta
bo'ladi. Ulardan ixtiyoriy bittasini, masalan A1 , A2
bazis bo'lgan holni olsak
ta
bo'ladi. Ulardan ixtiyoriy bittasini, masalan A1 , A2
bazis bo'lgan holni olsak ![]() bo'lib
bo'lib
![]() ekanligini ko'ramiz.
Bu bazisga mos yechimni topish uchun
ekanligini ko'ramiz.
Bu bazisga mos yechimni topish uchun ![]() deb
olinadi va sistema
deb
olinadi va sistema
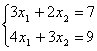
ko'rinishini
oladi. Bu sistemani yechib ![]() ekanligini
ko'ramiz. Bu yerda
ekanligini
ko'ramiz. Bu yerda ![]() bo'lganligi
uchun bu bazisdagi yechim tayanch yechim bo'la olmaydi. Boshqa bazis tanlashga
to'g'ri keladi. Masalan A2 , A3 bazisni olsak
bo'lganligi
uchun bu bazisdagi yechim tayanch yechim bo'la olmaydi. Boshqa bazis tanlashga
to'g'ri keladi. Masalan A2 , A3 bazisni olsak
![]() ;
;
![]()
Demak
A2 , A3 bazis bo'la oladi. Bu bazisdagi yechimni topish
uchun sistemada ![]() deb
olinsa u quyidagi ko'rinishni oladi
deb
olinsa u quyidagi ko'rinishni oladi

Bu
sistemani yechib ![]() ekanligini
ko'ramiz. Bu yerda
ekanligini
ko'ramiz. Bu yerda ![]() , demak bu
bazisdagi
, demak bu
bazisdagi ![]() yechim tayanch
yechim bo'lar ekan. Bu yechimning optimal bo'lish bo'lmasligini tekshirish
uchun masala shartini tanlangan bazisga moslashtiramiz. Teskari matritsani
hisoblash qoidasiga ko'ra
yechim tayanch
yechim bo'lar ekan. Bu yechimning optimal bo'lish bo'lmasligini tekshirish
uchun masala shartini tanlangan bazisga moslashtiramiz. Teskari matritsani
hisoblash qoidasiga ko'ra
![]()
ekanligini ko'ramiz. Masala shartini shu teskari matritsaga ko'paytiramiz
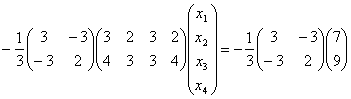
![]()
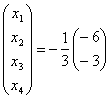
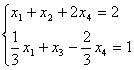
Shartlar
bazisga moslashtirildi, ya'ni bazis vektorlar A2 , A3 ga
mos ustunlar birlik vektor ko'rinishini oldi. Bu bazisga mos tayanch yechim ![]() optimalligini
tekshirish uchun simpleks jadval tuzamiz
optimalligini
tekshirish uchun simpleks jadval tuzamiz
|
I |
|
|
|
20 |
15 |
30 |
25 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Ө |
|
1 |
15 |
A2 |
2 |
1 |
1 |
0 |
2 |
|
|
2 |
30 |
A3 |
1 |
1/3 |
0 |
1 |
|
|
|
|
|
|
|
5 |
0 |
0 |
-15 |
|
Bu jadvaldan
ko'rinadiki, tanlangan bazisga mos tayanch yechim optimal emas ekan, chunki ![]() bo'layapti. Rejani
yaxshilash ychun bazisni almashtirish kerak. Buyog'i simpleks usul davom
ettirilishi mumkin.
bo'layapti. Rejani
yaxshilash ychun bazisni almashtirish kerak. Buyog'i simpleks usul davom
ettirilishi mumkin.
4. CHPM shartlari tanlangan bazisga moslashtirilsin. Shu bazisdagi tayanch yechim optimallikka tekshirilsin.
4.1
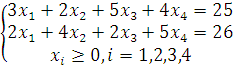
![]()
![]()
4.2

![]()
![]()
4.3
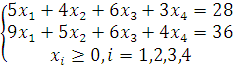
![]()
![]()
4.4
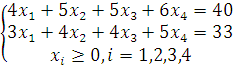
![]()
![]()
4.5

![]()
![]()
4.6

![]()
![]()
§ 5. Transport masalasi
Chiziqli programmalash masalalaridan bir turi “transport masalasi” nomi bilan ma'lum bo'lgan matematik masalalarga keltiriladigan iqtisodiy masalalardan iborat bo'ladi. Ma'lumki, ishlab chiqaruvchi bilan iste'molchi orasidagi mol almashinuvi ya'ni ishlab chiqarilgan mahsulot yoki tayyrolangan homashyoni korxonalarga yetkazib berish transport vositalari va ularga sarflanadigan moliyaviy harajatlar bilan bog'liq. Bu harajatlarni minimallashtiruvchi variantlarni tanlash transport masalasining asosiy muammosi hisoblanadi.
Transport masalasining matematik modelini ifodalashda umumiyatni cheklamagan
holda sxematik tarzda quyidagi muammoni tahlil qilamiz. Faraz qilaylik ma'lum
homashyo turi zaxiralari saqlanuvchi yoki tayyorlanuvchi n ta punkt
bo'lsin. Bu punktlardagi homashyo miqdorlari mos ravishda b1 , b2
, …, bn birliklardan iborat bo'lsin. Bu yerda homashyo turiga ko'ra
ma'lum bir o'lchov birligi (tonna, metr, …) tanlangan bo'ladi. Shuningdek,
keltirilgan homashyo asosida ishlaydigan m ta korxona bo'lib, bu
korxonalarning shu homashyoga bo'lgan extiyojlari mos ravishda d1 ,
d2 , … dm birliklardan iborat bo'lsin. Shuningdek
homashyo punktlari hamda korxonalar orasidagi yo'l sifati va masofasiga ko'ra
homashyoni yetkazish uchun ketadigan yo'l harajatlari koeffisintlari ma'lum
bo'lsin. Ularni ![]()
![]() ,
, ![]() ; matritsa
ko'rinishida ifodalaymiz. Bunda matritsaning har bir elementi
; matritsa
ko'rinishida ifodalaymiz. Bunda matritsaning har bir elementi ![]() mos ravishda
mos ravishda ![]() - korxonaga
- korxonaga ![]() punktdan bir birlik
homashyo yetkazish uchun ketadigan transport harajatlarini ifodalaydi.
Aksariyat hollarda ishlab chiqarish korxonalari va homashyo yetkazib beruvchi
punktlar muqobil, ya'ni moslashtirilgan holda ishlaydi deb hisoblanadi.
Homashyo zaxiralari va korxonalarning bu homashyoga bo'lgan ehtiyojlari
bir-biriga to'la mos keladi. Matematik tarzda bu shart
punktdan bir birlik
homashyo yetkazish uchun ketadigan transport harajatlarini ifodalaydi.
Aksariyat hollarda ishlab chiqarish korxonalari va homashyo yetkazib beruvchi
punktlar muqobil, ya'ni moslashtirilgan holda ishlaydi deb hisoblanadi.
Homashyo zaxiralari va korxonalarning bu homashyoga bo'lgan ehtiyojlari
bir-biriga to'la mos keladi. Matematik tarzda bu shart
![]()
![]()
ko'rinishda ifodalanadi. Ayrim juz'iy chetlashishlarni hisobga olmaganda korxonalar to'liq quvvat bilan ishlaganda homashyolar to'liq sarflanadi. Faqat bu homashyolarni korxonalarga yetkazib berish kerak.
Masalaning matematik modelini ifodalash uchun yuqorida keltirilgan barcha
shartlarni matematik munosabatlar bilan ifodalaymiz. Avvalo topilishi kerak
bo'lgan optimal reja komponentlari ![]() punktdan
punktdan
![]() korxonaga
yetkazilishi kerak bo'lgan homashyo miqdorini
korxonaga
yetkazilishi kerak bo'lgan homashyo miqdorini ![]() deb belgilaymiz.
Shartga ko'ra
deb belgilaymiz.
Shartga ko'ra ![]() korxonaga
yetkaziladigan barcha homashyo miqdori korxona ehtiyoji
korxonaga
yetkaziladigan barcha homashyo miqdori korxona ehtiyoji ![]() ga teng bo'lishi
kerak. Bu shartni
ga teng bo'lishi
kerak. Bu shartni
![]()
![]() 1 , 2 , … ,
m (2)
1 , 2 , … ,
m (2)
ko'rinishda
ifodalash mumkin, ya'ni barcha m ta korxona uchun bu shart bajarilishi
kerak. Bunday shartni homashyo punktlari uchun ham ifodalash mumkin, ya'ni ![]() - homashyo punktidan
chiqarilgan jami homashyo miqdori
- homashyo punktidan
chiqarilgan jami homashyo miqdori ![]() ga
teng bo'lishi kerak.
ga
teng bo'lishi kerak.
Bu shart matematik tarzda
![]()
![]() 1, 2 , …,
n (3)
1, 2 , …,
n (3)
ko'rinishini
oladi. Bu shartlar bajarilgan holda shunday ![]() larni topish kerakki
jami yo'l harajatlari minimal bo'lsin. Keltirilgan normativlarga ko'ra
larni topish kerakki
jami yo'l harajatlari minimal bo'lsin. Keltirilgan normativlarga ko'ra ![]() korxonaga
korxonaga ![]() punktdan
punktdan ![]() birlik homashyo
keltiriladigan bo'lsa, yo'l xarajatlari bir birlik homashyo miqdori uchun
birlik homashyo
keltiriladigan bo'lsa, yo'l xarajatlari bir birlik homashyo miqdori uchun ![]() ga teng ekanligi
ma'lum bo'lgani uchun jami
ga teng ekanligi
ma'lum bo'lgani uchun jami ![]()
![]() pul
birligiga teng bo'ladi. Bu xarajatlarni barcha korxonalar va homashyo bazalari
bo'yicha qo'shib chiqsak jami xarajatlar kelib chiqadi va u quyidagicha
ifodalanadi.
pul
birligiga teng bo'ladi. Bu xarajatlarni barcha korxonalar va homashyo bazalari
bo'yicha qo'shib chiqsak jami xarajatlar kelib chiqadi va u quyidagicha
ifodalanadi.
![]() …,
…, ![]() (4)
(4)
Tabiiy,
barcha chiziqli programmalash masalalarida bo'lganidek, bu yerda ham ![]() bo'lishi kerakligi
qayd etiladi.
bo'lishi kerakligi
qayd etiladi.
Shunday qilib (1), (2), (3) shartlar bajarilgan holda (4) maqsad funksiyasining
minimal qiymatini ta'minlovchi plan matritsasi X=(![]() ni topish masalasi
transport masalasi deyiladi. Bu yerda b1 , b2 , …, bm
, d1 , d2 , …, dn berilgan miqdorlar ; C=(
ni topish masalasi
transport masalasi deyiladi. Bu yerda b1 , b2 , …, bm
, d1 , d2 , …, dn berilgan miqdorlar ; C=(![]() ham ma'lum matritsa.
C(mxn) to'g'ri to'rtburchakli matritsa ham ma'lum matritsa deb hisoblanadi.
Aksariyat hollarda
ham ma'lum matritsa.
C(mxn) to'g'ri to'rtburchakli matritsa ham ma'lum matritsa deb hisoblanadi.
Aksariyat hollarda ![]() noma'lumlar
soni m×n shartlar soni m+n dan katta bo'lib, (1), (2), (3) shartlar bilan
berilgan chiziqli algebraik tenglamalar sistemasi cheksiz ko'p yechimga ega
bo'ladi. Ana shu cheksiz ko'p yechimlar orasidan (4) maqsad funksiyasining
minimumini ta'minlovchi variant, ya'ni optimal plan (reja)ni tanlashni talab
qilinadi.
noma'lumlar
soni m×n shartlar soni m+n dan katta bo'lib, (1), (2), (3) shartlar bilan
berilgan chiziqli algebraik tenglamalar sistemasi cheksiz ko'p yechimga ega
bo'ladi. Ana shu cheksiz ko'p yechimlar orasidan (4) maqsad funksiyasining
minimumini ta'minlovchi variant, ya'ni optimal plan (reja)ni tanlashni talab
qilinadi.
Keltirilgan transport masalasining matematik modeli (1) – (4) ko'rinishiga qarab ortiqcha tafsilotlarsiz shuni qayd etishimiz mumkinki, kommunikatsion tizimlar : ular avtomabil, poyezd yo'li bo'ladimi, gaz yoki suv yetkazuvchi quvurlar bo'ldimi, elektr quvvatini yetkazuvchi yuqori kuchlanishli elektr uzatish tizimlari bo'ladimi barchasida shartli ravishda yetkazuvchi, iste'molchi va “transport” harajatlarini kiritish mumkin. Bu holda ham aynan (1) – (4) ko'rinishdagi optimallashtirish masalasini hosil qilishimiz mumkin.
Transport masalasi ifodalanishiga ko'ra nisbatan soddadek tuyulishi mumkin.
Haqiqatdan ham barcha shartlar koeffitsientlari faqat birlardan iborat
tenglamalar bo'ladi. Transport masalasining murakkabligi noma'lumlarni
ko'pligida bo'lib unga odatdagi oddiy simpleks usulini tatbiq qilish ham
imkoniyat darajasidan ancha yuqori bo'lib ketar ekan. Masalan n=10 , m=10
bo'lgan holda ham noma'lumlar soni n×m=100, shartlar soni esa m+n-1=19ta
bo'lib, shartlar matritsasining rangi 19 bo'lgan holda (1) – (3) shartlar
bo'yicha kelib chiqadigan tayanch yechimlar soni ![]() ta bo'ladi. Simpleks
usul esa tayanch yechimlaridan optimal yechimni ajratishga imkoniyat beradi. Bu
holda simpleks usul bo'yicha necha qadam qo'yilishi kerak, buni tasavvur qilish
ham qiyin. Agar transport masalasini biror tuman (miqyosida, masshtabida)
qaralganda ham yetarlicha murakkab bo'ladi. Viloyat yoki respublika
(miqyosida, masshtabida) qaraladigan bo'lsa masala yanada murakkablashib
ketishi aniq.
ta bo'ladi. Simpleks
usul esa tayanch yechimlaridan optimal yechimni ajratishga imkoniyat beradi. Bu
holda simpleks usul bo'yicha necha qadam qo'yilishi kerak, buni tasavvur qilish
ham qiyin. Agar transport masalasini biror tuman (miqyosida, masshtabida)
qaralganda ham yetarlicha murakkab bo'ladi. Viloyat yoki respublika
(miqyosida, masshtabida) qaraladigan bo'lsa masala yanada murakkablashib
ketishi aniq.
Biz bu yerda transport masalasi ham odatdagi ChPM ekanligini, hamda unga ham simpleks usulni tatbiq qilish mumkinligini namoyish qilish maqsadida oddiy bir masalani ko'rib chiqamiz va tahlil qilamiz. Faraz qilaylik 2ta g'isht zavodi bo'lib ularning ishlab chiqarish quvvatlari mos ravishda 35 mashina va 45 mashina g'ishtga teng bo'lsin. Shuningdek bu g'ishtlarga talabgor 2 ta qurilish bo'lib, ularga mos ravishda 30 mashina va 50 mashina g'isht kerak bo'lsin. Talab va taklif muvozanati saqlangan. Agar 1 – qurilishga 1 – zavoddan 1 mashina keltirish narxi (yo'l xarajati) 15ming so'm, 2 – zavoddan keltirish narxi esa 12ming so'm; shuningdek 2 – qurilishga 1-, 2-zavoddan 1 mashina g'isht keltirish narxi mos ravishda 20ming va 18 ming so'm bo'lsin. Zavodlardan qurilishlarga g'isht yetkazib berish shunday rejasini tuzingki, transport harajatlari minimal bo'lsin. Transport masalasining shartlarini jadval ko'rinishida ifodalash tahlil uchun qulay bo'lganligi uchun odatda ularni jadval ko'rinishida ifodalagan ma'qul. Xususan yuqorida keltirilgan masala shartlarini quyidagi jadval ko'rinishida ifodalash mumkin.
|
zav qur |
1 |
2 |
Σ |
|
1 |
15
|
12
|
30 |
|
2 |
20
|
18
|
50 |
|
Σ |
35 |
45 |
80 |
jadvaldagi
raqamlar masala mohiyatini aks ettiradi. So'nggi qatorda zavodlar quvvatlari,
so'nggi ustunda esa qurilishlar ehtiyojlari aks etgan. Ichki kataklar tepa
burchagida yo'l harajatlari koeffitsienti aks etgan. Bu yerda qulaylik uchun
noma'lumlarni ![]() deb
belgilangan, aslida
deb
belgilangan, aslida ![]() bo'lishi
kerak edi. Bu yerda maqsad, masalani simpleks usulga tushirish qulay bo'lishi
uchun shu yo'l tanlangan. Shartlarning matematik ifodasiga o'tamiz.
bo'lishi
kerak edi. Bu yerda maqsad, masalani simpleks usulga tushirish qulay bo'lishi
uchun shu yo'l tanlangan. Shartlarning matematik ifodasiga o'tamiz.
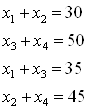
![]()
![]()
![]()
![]()
![]()
![]()
![]() shartlar
orasidan chiziqli erklilari tanlanadi. Bevosita tekshirish yo'li bilan
shartlar
orasidan chiziqli erklilari tanlanadi. Bevosita tekshirish yo'li bilan ![]() shartlardan
shartlardan ![]() shart kelib
chiqishini ko'rishimiz mumkin. Sxematik tarzda tengliklar ustida amallar
bajarish qoidasiga ko'ra
shart kelib
chiqishini ko'rishimiz mumkin. Sxematik tarzda tengliklar ustida amallar
bajarish qoidasiga ko'ra ![]() ekanligini
ko'ramiz. Demak, bu yerda ChPMni
ekanligini
ko'ramiz. Demak, bu yerda ChPMni
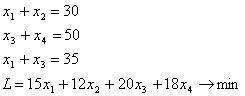
ko'rinishda
ifodalash mumkin. Bu masalaga simpleks usulni tatbiq qilish uchun ChPM
shartlaridan bazislarni ajratish (ustunlari orasida birlik vektorlarni hosil
qilish) jarayonini namoyish etamiz. Sistemadagi ![]() ga mos
koeffitsientlar
ga mos
koeffitsientlar ![]() vektorlarni
hosil qiladi. Ulardan tuzilgan matritsa ozod hadlar ustuni bilan to'ldirilsa
vektorlarni
hosil qiladi. Ulardan tuzilgan matritsa ozod hadlar ustuni bilan to'ldirilsa
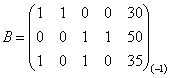
matritsa
hosil bo'ladi. Bu matritsaning 2-,4-ustunlari bazis holatida ![]() 0; 0; 0)ekanligini
ko'ramiz. Agar 3 – qatorini -1 ga ko'paytirib 2 – qatorga qo'shsak 3 – ustun
ham bazis ko'rinishini oladi.
0; 0; 0)ekanligini
ko'ramiz. Agar 3 – qatorini -1 ga ko'paytirib 2 – qatorga qo'shsak 3 – ustun
ham bazis ko'rinishini oladi.
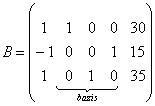
Bu matritsa berilgan shartlarning shakl almashtirilib
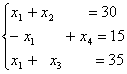
ko'rinishga keltirilganligini aks ettiradi. Bu ko'rinishdan simpleks jadvalga o'tamiz va bu jadvalga mos planni optimallikka tekshiramiz.
|
C C |
|
|
15 |
12 |
20 |
18 |
|
|
|
baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Өi |
|
12 |
A2 |
30 |
1 |
1 |
0 |
0 |
|
|
18 |
A4 |
15 |
-1 |
0 |
0 |
1 |
|
|
20 |
A3 |
35 |
1 |
0 |
1 |
0 |
|
|
|
|
|
-1 |
0 |
0 |
0 |
|
Bu
yerda ![]() formula bo'yicha
hisoblangan. Qolganlari ham shunga o'xshash hisoblanadi. Masala minimumini
topishga mo'ljallangan bo'lsa,
formula bo'yicha
hisoblangan. Qolganlari ham shunga o'xshash hisoblanadi. Masala minimumini
topishga mo'ljallangan bo'lsa, ![]() lar
orasida musbatlari yo'q bo'lsa, jadvalga mos plan optimal plan bo'ladi. Bizda
ana shunday hol kuzatilyapti. Demak bu masalada optimal plan
lar
orasida musbatlari yo'q bo'lsa, jadvalga mos plan optimal plan bo'ladi. Bizda
ana shunday hol kuzatilyapti. Demak bu masalada optimal plan ![]() bo'lar ekan. Bu
holda harajatlar minimal bo'lib,
bo'lar ekan. Bu
holda harajatlar minimal bo'lib, ![]() ming
so'm bo'lar ekan. Masala shartlari va yechimini ifodalovchi jadval
ming
so'm bo'lar ekan. Masala shartlari va yechimini ifodalovchi jadval
|
Zav qur |
1 |
2 |
Σ |
|
1 |
15 0 |
12 30 |
30 |
|
2 |
20 35 |
13 15 |
50 |
|
Σ |
35 |
45 |
80 |
ko'rinishda bo'ladi.
Tahlil to'laqonli ko'rinishni olishini namoyish qilish uchun yuqoridagi masalada faqat bitta narx 1 – zavoddan 2 – qurilishga 1 mashina g'isht olib borish narxi 30ming so'mga o'zgargan bo'lsin deb faraz qilamiz. Bunda faqat maqsad funksiyasi ko'rinishi o'zgaradi, ya'ni
![]()
ko'rinishni
oladi. Simpleks jadvalda ham faqat narxlar ![]() ga mos qator va
ustunlargina o'zgaradi va quyidagi ko'rinishni oladi
ga mos qator va
ustunlargina o'zgaradi va quyidagi ko'rinishni oladi
|
C C |
|
|
15 |
12 |
30 |
18 |
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Өi |
|
12 |
A2 |
30 |
1 |
1 |
0 |
0 |
30 |
|
18 |
A4 |
15 |
-1 |
0 |
0 |
1 |
|
|
30 |
A3 |
35 |
1 |
0 |
1 |
0 |
35 |
|
|
|
|
9 |
0 |
0 |
0 |
|
![]()
![]()
Bu
jadvalga mos plan ![]() optimal
emas, chunki
optimal
emas, chunki ![]() . Bu planga ko'ra
. Bu planga ko'ra ![]() ming. Planni
yaxshilash uchun jadvaldan
ming. Planni
yaxshilash uchun jadvaldan
![]() larni
hisoblaymiz (faqat
larni
hisoblaymiz (faqat ![]()
![]() lar uchun). min
lar uchun). min![]() ga mos 1 – qatorni
hal qiluvchi qator deb belgilaymiz. Uning yordamida 1 – ustunni bazis ustunga
aylantiramiz. Buning uchun 1 – qatorni 2 – qatorga qo'shamiz, hamda (-1) ga
ko'paytirib 3 – qatorga qo'shamiz. Natijada yangi simpleks jadvalni hosil
qilamiz
ga mos 1 – qatorni
hal qiluvchi qator deb belgilaymiz. Uning yordamida 1 – ustunni bazis ustunga
aylantiramiz. Buning uchun 1 – qatorni 2 – qatorga qo'shamiz, hamda (-1) ga
ko'paytirib 3 – qatorga qo'shamiz. Natijada yangi simpleks jadvalni hosil
qilamiz
|
C C |
|
|
15 |
12 |
30 |
18 |
|
|
|
Bazis |
A0 |
A1 |
A2 |
A3 |
A4 |
Ө |
|
15 |
A1 |
30 |
1 |
1 |
0 |
0 |
|
|
18 |
A4 |
45 |
0 |
1 |
0 |
1 |
|
|
30 |
A3 |
5 |
0 |
-1 |
1 |
0 |
|
|
|
|
|
0 |
-17 |
0 |
0 |
|
Bu
jadvalda ![]() lari yo'q bo'lgani
uchun bu jadvalga mos tayanch yechim
lari yo'q bo'lgani
uchun bu jadvalga mos tayanch yechim ![]() optimal
plan bo'ladi. Bu plan bo'yicha ketadigan transport harajatlari
optimal
plan bo'ladi. Bu plan bo'yicha ketadigan transport harajatlari
![]() ming
so'm bo'lib avvalgisidan 270ming so'mga kam bo'lar ekan.
ming
so'm bo'lib avvalgisidan 270ming so'mga kam bo'lar ekan.
Bu usul bilan ixtiyoriy transport masalasini ham odatdagi ChPM ko'rinishiga keltirish mumkin ekan. Faqat shartli ravishda n ta ishlab chiqaruvchi va ularga bog'langan m ta iste'molchi bo'lgan transport masalasini tasavvur qilsak, bu unchalik oson ish emas ekanligini to'la tasavvur qilishimiz mumkin. Transport masalasini ba'zi kichik hajmdagi hollarda mantiqiy muhokamalar asosida ham yechish mumkin ekan. Bunga misol
|
T
n |
1 |
2 |
Σ |
|
|
1 |
15
|
20
|
20 |
|
|
2 |
18
|
13
|
60 |
|
|
3 |
14
|
18
|
40 |
|
|
Σ |
70 |
50 |
12 |
|
sifatida
jadvalda keltirilgan 2 ta ta'minotchi va 3ta iste'molchi bilan bog'liq
transport masalasi namunasi keltirilgan. Unda bo'sh qolgan yarim kataklar aynan
topilishi kerak bo'lgan ta'minot rejasini aks ettiruvchi 6 ta noma'lum ![]() larga mos keladi.
Mantiqan dastlab eng arzon yo'nalish tanlanishi kerak. Demak avvalo yo'l
harajati 13 bo'lgan katakka iloji boricha ko'proq jo'natish miqdorini qo'ygan
ma'qul. Bu qiymat 50 ekanligi ko'rinib turibdi. U holda shu qatorning birinchi
katagiga 10 qo'yishimiz kerak bo'ladi. Shuningdek ikkinchi ustun qolgan ikki
katagi 0 bo'lishi kerakligi ko'rinib turibdi. Qolgan kataklar ham o'z - o'zidan
bir qiymatli to'ldirilishi mumkin bo'lib qoladi. Xulosa qilib aytganda
larga mos keladi.
Mantiqan dastlab eng arzon yo'nalish tanlanishi kerak. Demak avvalo yo'l
harajati 13 bo'lgan katakka iloji boricha ko'proq jo'natish miqdorini qo'ygan
ma'qul. Bu qiymat 50 ekanligi ko'rinib turibdi. U holda shu qatorning birinchi
katagiga 10 qo'yishimiz kerak bo'ladi. Shuningdek ikkinchi ustun qolgan ikki
katagi 0 bo'lishi kerakligi ko'rinib turibdi. Qolgan kataklar ham o'z - o'zidan
bir qiymatli to'ldirilishi mumkin bo'lib qoladi. Xulosa qilib aytganda ![]() ekanligini topamiz.
Bunda transport harajatlari
ekanligini topamiz.
Bunda transport harajatlari![]()
bo'lishini ko'ramiz. Natijada masala shartlari va yechimini ifodalovchi jadvalni hosil qilamiz
|
T
n |
1 |
2 |
Σ |
|
1 |
15 20 |
20 0 |
20 |
|
2 |
18 10 |
13 50 |
60 |
|
3 |
14 40 |
18 0 |
40 |
|
Σ |
70 |
50 |
120 |
Yuqorida keltirilgan masalani planni bosqichma – bosqich yaxshilash usuli bo'yicha simpleks jadvallar asosida ishlab ko'ramiz. Unga mos ChPM quyidagicha ifodalanadi.

![]()
Bu masala shartlaridan beshinchisi chiziqli bog'liq. Qolgan qismi uchun kengaytirilgan matritsasini yozamiz va bu matritsada rangi to'rt bo'lganligi uchun to'rtta bazis ustun hosil qilamiz. Masalan qulaylik uchun 1-,3-,4-,6- ustunlarni bazis ustunlarga aylantirish holini ko'ramiz.
![]()
![]()
![]()
![]()

![]()

![]()
![]()

Hosil bo'lgan matritsa ko'rsatilgan tartibda 1 – qatorni (-1)ga ko'paytirib 4 – qatorga qo'shish, so'ngra 4 – qatorni (-1) ga ko'paytirib 2 – qatorga qo'shish yordamida masala shartlarini ekvivalent tarzda o'zgartirishni aks ettiradi. Matritsa ko'rinishidan yana sistema ko'rinishiga o'tilsa u
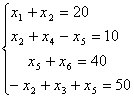
ko'rinishini oladi. Bevosita tekshirish
bilan bazis o'zgaruvchilar ![]() qolganlari
qolganlari
![]() ekanligini
ko'rishimiz mumkin. Masalaning bu ko'rinishidan dastlabki simpleks jadvalni
tuzib, bu jadvalga mos tayanch yechimni optimallikka tekshirishimiz mumkin.
Agar yechim optimal bo'lmasa, keyingi bosqichga o'tamiz, ya'ni
ekanligini
ko'rishimiz mumkin. Masalaning bu ko'rinishidan dastlabki simpleks jadvalni
tuzib, bu jadvalga mos tayanch yechimni optimallikka tekshirishimiz mumkin.
Agar yechim optimal bo'lmasa, keyingi bosqichga o'tamiz, ya'ni ![]() lar orasida manfiysi
bo'lsa, hal qiluvchi qator va ustunlarini topib bazisni almashtiramiz. Bizning
misol uchun simpleks jadval
lar orasida manfiysi
bo'lsa, hal qiluvchi qator va ustunlarini topib bazisni almashtiramiz. Bizning
misol uchun simpleks jadval
|
C C |
|
|
15 |
20 |
18 |
13 |
14 |
18 |
|
|
|
baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
15 |
A1 |
20 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
13 |
A4 |
10 |
0 |
1 |
0 |
1 |
-1 |
0 |
|
|
18 |
A6 |
40 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
18 |
A3 |
50 |
0 |
-1 |
1 |
0 |
1 |
0 |
50 |
|
|
|
|
0 |
-10 |
0 |
0 |
9 |
0 |
|
![]()
ko'rinishda bo'ladi.
Bu
jadvalda ChPM minimumga ishlanayotganligi uchun ![]() lar borligi plan
optimal emasligini bildiradi.
lar borligi plan
optimal emasligini bildiradi. ![]() ga
mos 5 – ustun hal qiluvchu ustun, shu ustun elementlari yordamida hisoblangan
Ө3 =
ga
mos 5 – ustun hal qiluvchu ustun, shu ustun elementlari yordamida hisoblangan
Ө3 = ![]() va
Ө4 =
va
Ө4 = ![]() lar
orasidan kichigiga mos keluvchi 3 – qator hal qiluvchi qator deb belgilandi va
bazisdagi A6 ustun A5 ustunga almashtirilishi kerak.
Buning uchun jadvalning 3 – qatorini 2 – qatorga qo'shamiz, hamda 3 – qatorni
(-1)ga ko'pytirib 4 – qatorga qo'shamiz. Shunda 5 – ustun ham bazis ustun
ko'rinishini oladi va quyidagi simpleks jadval hosil bo'ladi.
lar
orasidan kichigiga mos keluvchi 3 – qator hal qiluvchi qator deb belgilandi va
bazisdagi A6 ustun A5 ustunga almashtirilishi kerak.
Buning uchun jadvalning 3 – qatorini 2 – qatorga qo'shamiz, hamda 3 – qatorni
(-1)ga ko'pytirib 4 – qatorga qo'shamiz. Shunda 5 – ustun ham bazis ustun
ko'rinishini oladi va quyidagi simpleks jadval hosil bo'ladi.
|
C C |
|
|
|
|
|
|
|
|
|
|
|
Bazis |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
15 |
A1 |
20 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
13 |
A4 |
50 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
14 |
A5 |
40 |
0 |
0 |
0 |
0 |
1 |
-1 |
|
|
18 |
A3 |
10 |
0 |
-1 |
1 |
0 |
0 |
-1 |
|
|
|
|
|
0 |
-10 |
0 |
0 |
0 |
-9 |
|
Bu
jadvalga ko'ra ![]() lar
orasida musbatlari yo'q bo'lganligi uchun bu jadvalga mos tayanch yechim
lar
orasida musbatlari yo'q bo'lganligi uchun bu jadvalga mos tayanch yechim ![]() optimal yechim
bo'ladi. Shu masala uchun mantiqiy mulohazalarga ko'ra tanlangan dastlabki
yechim ham xuddi shunday bo'lgan edi. Bu natijadan ikki muhim xulosani keltirib
chiqarishimiz mumkin ekan. Birinchisi – transport masalasini yechishda mantiqiy
mulohazalarga asoslanishimiz mumkin ekan. Bunday usulda tanlangan yechim
optimal yechim bo'lib qolishi ham mumkin, bo'lmagan taqdirda ham optimal
yechimga yaqin yechim bo'lib simpleks usul yordamida yaxshilash bosqichlari
soni kam bo'ladi. Ikkinchidan – transport masalasi ham odatdagi ChPMga
keltirilishi mumkin bo'lib, unga ham an'anviy usullarni tatbiq qilish mumkin
ekan. Bunda faqat bir narsani unutmasligimiz kerak. Yuqorida ta'kidlanganidek,
ta'minotchilar soni n va iste'molchilar soni m ortgan sari
noma'lumlar soni n×m keskin ortib odatdagi usullarni tatbiq qilish
mushkullashib boraveradi. Bunday hollarda masalani yechish uchun iteratsion
usullardan foydalanish ma'qulroq bo'ladi.
optimal yechim
bo'ladi. Shu masala uchun mantiqiy mulohazalarga ko'ra tanlangan dastlabki
yechim ham xuddi shunday bo'lgan edi. Bu natijadan ikki muhim xulosani keltirib
chiqarishimiz mumkin ekan. Birinchisi – transport masalasini yechishda mantiqiy
mulohazalarga asoslanishimiz mumkin ekan. Bunday usulda tanlangan yechim
optimal yechim bo'lib qolishi ham mumkin, bo'lmagan taqdirda ham optimal
yechimga yaqin yechim bo'lib simpleks usul yordamida yaxshilash bosqichlari
soni kam bo'ladi. Ikkinchidan – transport masalasi ham odatdagi ChPMga
keltirilishi mumkin bo'lib, unga ham an'anviy usullarni tatbiq qilish mumkin
ekan. Bunda faqat bir narsani unutmasligimiz kerak. Yuqorida ta'kidlanganidek,
ta'minotchilar soni n va iste'molchilar soni m ortgan sari
noma'lumlar soni n×m keskin ortib odatdagi usullarni tatbiq qilish
mushkullashib boraveradi. Bunday hollarda masalani yechish uchun iteratsion
usullardan foydalanish ma'qulroq bo'ladi.
Masalalar
5. Keltirilgan jadval qiymatlarga mos tansport masalasini tuzing. Masala tayanch yechimini minimal harajatlar usuli bo’yicha aniqlang va uni optimallikka tekshiring.
5.1
|
|
1 |
2 |
3 |
∑ |
|
1 |
11
|
15
|
13
|
200 |
|
2 |
14
|
12
|
10
|
300 |
|
∑ |
150 |
250 |
100 |
500 |
5.2
|
|
1 |
2 |
3 |
∑ |
|
1 |
60
|
45
|
60
|
400 |
|
2 |
55 |
60
|
58
|
500 |
|
∑ |
200 |
400 |
300 |
900 |
5.3
|
|
1 |
2 |
3 |
∑ |
|
1 |
30
|
25
|
35
|
500 |
|
2 |
25 |
35
|
20
|
300 |
|
∑ |
250 |
350 |
200 |
800 |
5.4
|
|
1 |
2 |
3 |
∑ |
|
1 |
25
|
20
|
18
|
400 |
|
2 |
15 |
22
|
24
|
300 |
|
∑ |
250 |
150 |
300 |
700 |
5.5
|
|
1 |
2 |
3 |
∑ |
|
1 |
40
|
50
|
30
|
600 |
|
2 |
30 |
40
|
50
|
400 |
|
∑ |
300 |
500 |
200 |
|
6 § Ñhiziqli programmalash masalalari uchun egizak masalalar
Bu yerda chiziqli programmalash masalalari nazariyasida muhim o’rin egallagan egizak masalalar tushunchasida to’xtalamiz va ularning iqtisodiy ma’nosini tahlil qilamiz. ChPM umumiy ko’rinishini esga olsak (2 §).
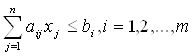 (2.1)
(2.1)
![]()
 (2.2)
(2.2)
Shartlarga ko’ra ![]() larni
topish talab qilinar edi. Masala tarkibidagi har bir koeffitsiyentga o’z
vaqtida izoh berilgan edi. Aynan shu koeffitsiyentlar yordamida quyidagi
masalani tuzamiz.
larni
topish talab qilinar edi. Masala tarkibidagi har bir koeffitsiyentga o’z
vaqtida izoh berilgan edi. Aynan shu koeffitsiyentlar yordamida quyidagi
masalani tuzamiz.
 (6.1)
(6.1)
![]()
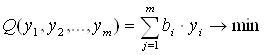 (6.2)
(6.2)
Hosil bo’lgan (6.1) – (6.2) masala (2.1) – (2.2) ChPM ga nisbatan egizak masala deyiladi. Agar (2.1) – (2.2) masala yechimi mavjud bo’lsa (6.1) – (6.2) masala yechimi ham mavjud bo’lar ekan. Shu bilan birga bu yechimlar, yani optimal yechimlar uchun
![]()
tenglik o’rinli bo’lar ekan. Bu holat ba’zi murakkab ChPM lar uchun egizak masala yordamida tahlil o’tkazishga imkoniyat beradi. E’tibor bersak (2.1) – (2.2) va (6.1) – (6.2) masalalar aynan bir xil koeffitsiyent orqali ifodalanishi hamda ularning yechimlari ham bir xilligi bu masalalarni “ egizak masalalar ” deb atalishiga sabab bo’lgan.
Tahlil va xulosalarni soddalashtirish uchun avvalgi paragraflarda keltirilgan masalalardan foydalanamiz. Xususan § 1 da ko'rilgan (1.1) – (1.2) masalani olsak
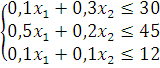 (1.1)
(1.1)
![]()
uning to’la tahlili va yechimi § 1 da
keltirilgan. Unga ko’ra optimal reja c (30;90) nuqtada bo’lib, bunda ![]() bo’lib
bo’lib
![]() ekanligini
ko’rgan edik. Yuqorida keltirilgan tartibga ko’ra (1.1) – (1.2) masala
uchun egizak masala tuzamiz.
ekanligini
ko’rgan edik. Yuqorida keltirilgan tartibga ko’ra (1.1) – (1.2) masala
uchun egizak masala tuzamiz.
![]() (6.3)
(6.3)
![]() (6.4)
(6.4)
Hosil bo’lgan (6.3) – (6.4) egizak masalani geometrik usulda yechish uchun uni kanonik ko’rinishga keltiramiz.
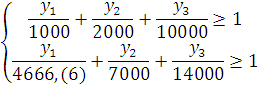
![]()
Bu yerdagi har bir shart OY1 Y2 Y3 koordinat fazosida tekislikni ifodalaydi. Ularni chizmada ifodalasak, egizak masala uchun ham MBES qavariq soha bo’lishini ko’ramiz. Bu holat barcha egizak masalalar uchun o’rinli bo’lar ekan. (6.3) – (6.4) masala shartlariga mos mumkin bo’lgan yechimlar sohasi MBES chizmada keltirilgan
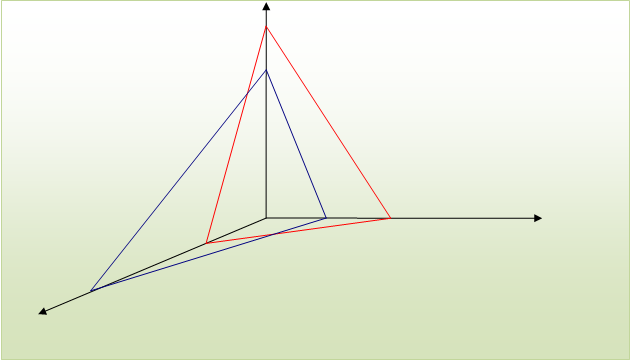
 Y3
Y3
M3 14000
1000
M4
O
7000 Y2
4666 2000 M2
M5
MBES
OY1 Y2
Y3 koordinat
fazosining 1 – oktantida (6.3) shartlar bilan berilgan tekisliklardan
yuqoridagi soha bo’ladi. Bu qavariq sohaning chegaralaridagi uchlari M1
, M2 , M3
, M4 , M5
nuqtalarida bo’ladi. Optimal yechimni aynan shu
nuqtalardan birida izlash kerak. Chizmadan ko’rinadiki M1
(10000; 0; 0), M2
(0; 7000; 0), M3
(0;0;14000), M4
(2000; 0; 8000), M5
(1231; 3846; 0). Bu yerda M4
, M5
nuqtalar koordinatalari (6.3) sistemadan ![]() va
va
![]() deb
topilgan. Optimal yechimni Q (Y1,Y2,
Y3 )
qiymatlarini taqqoslash orqali topamiz.
deb
topilgan. Optimal yechimni Q (Y1,Y2,
Y3 )
qiymatlarini taqqoslash orqali topamiz.
Q(M1) = 300000 ; Q(M2) = 315000 ; Q(M3) = 168000 ; Q(M4) = 156000 ; Q(M5) = 170775. Bu yerdan M4 nuqtada eng kichik qiymat bo’lishini ko’ramiz. Haqiqatdan ham
![]()
bo’lar ekan.
Egizak masala yechimini simpleks usulda asosiy masala bilan birgalikda bir yo’la topish mumkin ekan. Buni bevosita amaliy masalani yechish jarayonida namoyish qilamiz.

masala uchun egizak masala
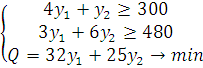
Geometrik
usulda asosiy
masala uchun
OX1X2
koordinat tekisligida
MBES ni
chizib tayanch
yechimlar M1(8;0)
, M2(0;5), M3(5;4)
nuqtalarda bo’lib,
bu nuqtalarda
maqasad funksiya
qiymatlari L1
= 2400, L2
= 2400, L3
= 5 · 300 + 4 · 480 = 3420 . Taqqoslash
natijasida optimal
yechim M3(5;4)
nuqtada bo’lib,
bu nuqtada
![]() ekanligini
ko’ramiz.
Shuningdek egizak
masala uchun
OY1 Y2
tekisligida MBES
ni tuzib
tayanch yechimlar
M1(160;0), M2(0;300),
M3( 60;60) nuqtada
bo’lishini
ko’ramiz.
Bu nuqtalardagi
tayanch yechim
qiymatlari Q1
=5120, Q2
= 7500, Q3
= 3420 larni
taqqoslab min
Q = 3420 ekanligini
va bu
qiymatga
ekanligini
ko’ramiz.
Shuningdek egizak
masala uchun
OY1 Y2
tekisligida MBES
ni tuzib
tayanch yechimlar
M1(160;0), M2(0;300),
M3( 60;60) nuqtada
bo’lishini
ko’ramiz.
Bu nuqtalardagi
tayanch yechim
qiymatlari Q1
=5120, Q2
= 7500, Q3
= 3420 larni
taqqoslab min
Q = 3420 ekanligini
va bu
qiymatga ![]() bo’lgan
M3 nuqtada
erishilishini
ko’ramiz.
Shu masalani
simpleks usulda
yechimini topish
jarayonini keltiramiz.
Sun’iy
basis
bo’lgan
M3 nuqtada
erishilishini
ko’ramiz.
Shu masalani
simpleks usulda
yechimini topish
jarayonini keltiramiz.
Sun’iy
basis ![]() larni
kiritib 1 – simpleks
jadvalni ifodalaymiz.
larni
kiritib 1 – simpleks
jadvalni ifodalaymiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0 |
|
32 |
4 |
3 |
1 |
0 |
|
|
2
|
0 |
|
25 |
1 |
5 |
0 |
1 |
5 |
|
|
|
|
0 |
-300 |
-480 |
0 |
0 |
|
![]()
![]()
Bu jadvalga mos tayanch yechim ![]() optimal
emas, chunki
optimal
emas, chunki ![]() lar
mavjud. Hal qiluvchi ustun va qatorlarni aniqlab ikkinchi simpleks jadvalni
tuzamiz.
lar
mavjud. Hal qiluvchi ustun va qatorlarni aniqlab ikkinchi simpleks jadvalni
tuzamiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0 |
|
17 |
3,4 |
0 |
1 |
-0,6 |
5 |
|
2
|
480 |
|
5 |
0,2 |
1 |
0 |
0,2 |
10 |
|
|
|
|
2400 |
-204 |
0 |
0 |
96 |
|
![]()
![]()
Bu jadvalga mos tayanch yechim ham optimal emas. Keyingi simpleks jadvalni tuzamiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
300 |
|
5 |
1 |
0 |
|
|
|
|
2
|
480 |
|
4 |
0 |
1 |
|
|
|
|
|
|
|
3420 |
0 |
0 |
60 |
60 |
|
Bu jadvalga mos barcha
![]() .
Demak, jadvaldan
.
Demak, jadvaldan ![]() ekanligini
ko’ramiz. Sun’iy bazislarga mos ustunlardan esa,
ekanligini
ko’ramiz. Sun’iy bazislarga mos ustunlardan esa, ![]() lar
qatorida
lar
qatorida ![]() ekanligi
kelib chiqadi. Bu yechimlar geometrik usulda topilgan yechimlar bilan bir xil
ekanligini ko’ramiz. Egizak masalaning iqtisodiy ma’nosi. Agar asosiy masalada
daromadlarni maksimal bo’lishini ta’minlaydigan reja izlangan bo’lsa, egizak
masalada harajatlarni minimal bo’lishini ta’minlaydigan qiymatlar izlanar ekan.
Bu yerda Y1,
Y2 larni
mos ravishda 1- va 2- homashyolarning bir birligi narxi deb tushunish mumkin.
Egizak masala tushunchasi nisbiy bo’lib, agar (6.1) – (6.2), ya’ni Yi
larga nisbatan masalani asosiy desak, Xj
larga nisbatan (2.1) – (2.2) masala egizak masala
bo’ladi.
ekanligi
kelib chiqadi. Bu yechimlar geometrik usulda topilgan yechimlar bilan bir xil
ekanligini ko’ramiz. Egizak masalaning iqtisodiy ma’nosi. Agar asosiy masalada
daromadlarni maksimal bo’lishini ta’minlaydigan reja izlangan bo’lsa, egizak
masalada harajatlarni minimal bo’lishini ta’minlaydigan qiymatlar izlanar ekan.
Bu yerda Y1,
Y2 larni
mos ravishda 1- va 2- homashyolarning bir birligi narxi deb tushunish mumkin.
Egizak masala tushunchasi nisbiy bo’lib, agar (6.1) – (6.2), ya’ni Yi
larga nisbatan masalani asosiy desak, Xj
larga nisbatan (2.1) – (2.2) masala egizak masala
bo’ladi.
Mustaqil ishlash uchun masalalar.
Berilgan ChPM uchun egizak masala tuzilsin va uning yechimi geometrik usulda topilsin.
6.1
![]()

6.2
![]()
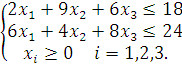
6.3
![]()
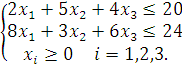
6.4
![]()
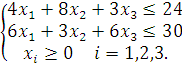
6.5
![]()

Adabiyotlar
1. D.B. Yudin, E.T.Toldshteyn; Lineynoe programmirovaniye . M. “Nauka”, 1969.
2. Kantorovich L. V. O metodax analiza nekotorix eksperimentalnix planovo-proizvodstvennix zadach. DAN SSSR 115, N3 1957.
3. Juraev X. I. Otaniyozov B. va boshqalar Metematik programmalashtirish. Toshkent OO’MTV, 2005
4. Akulich I. I. Metematicheskoe programmirovaniye v primerax i zadachax (uchebnoye posobiye) M. “Visshaya shkola ” 1986/
5. G’ofurov M. va boshqalar. Iqtisodiy matematik usullar va modellar (O’quv qo’llanma) Toshkent 2000.
6. Zaelavskiy YU. L Sbornik zadach po lineynomu programmirovaniyu. M. “Nauka”, 1969.
Umumiy mundarija
I. Matematik modellashtirish nazariy va amaliy asoslari……………..…...3
§ 1. Matematik model tushunchasi va uning asosiy belgilari…………………..…5
§ 2. Matematik modellarga misollar. Fizik, mehanik, ommaviy va iqtisodiy masalalar asosida……………………………………………………….……11
§ 3. Optimizatsiya masalalari, maqsad funksiyasi………………………………..16
§ 4. Optimizatsiya masalalarini yechishda taqribiy usullar……………………….21
§ 5. Xatoliklar turlari va ularning manba’lari. Absolyut, nisbiy xatoliklar……….25
§ 6. Hisoblash jarayonlarining turg’unligi haqida, turg’un bo’lmagan jarayonlarga misollar………………………………………………………………............32
§ 7. Approksimatsiya masalasi. Bazis funksiyalar. Norma tushunchasi………….35
§8. Jadval ko’rinishida berilgan funksiyalar uchun interpolyatsiya masalasi.Lagranj interpolyatsion ko’phadi…………………………………………………….39
§ 9. Jadval qiymatlaridagi bartaraf qilib bo’lmas atolik tartibiga ko’ra ko’phad darajasini va jadval qismini aniqlash…………………………………..……45
§ 10. Tengmas orliqlar uchun Nyuton interpolyatsion ko’phadi…………………49
§ 11. Teng oraliqlar uchun Nyuton interpolyatsion ko’phadi…………………….55
§ 12. Katta jadvallar uchun approksimatsiya masalasini yechishda eng kichik kvadratlar usuli. Chiziqli bo’g’lanish usuli…………………………………59
§ 13. Kvatratik bog’lanish modelini tuzish, jadvaldagi tasodifiy xatolarni aniqlash usuli…………………………………………………………………………64
§ 14. Orthogonal ko’phadlar. Jadval ko’rinishda berilgan funksiyalar uchun o’rta kvadratik yaqinlashish……………………………………………………….67
II. Chiziqli programmalash masalalari………………………………………..74
So’z boshi……………………………………………………………………...….74
§ 1. Chiziqli programmalash masalalari…………………………………………..75
§ 2. Chiziqli programmalash masalalarining matematik asoslari…………………85
§ 3. Rejani bosqichma-bosqich yaxshilash usullari……………………………….88
§ 4. Chiziqli programmalash masalalari uchun bazis tanlash va masala shartlarini tanlangan bazisga moslashtirish……………………………………………...96
§ 5. Transport masalasi………………………………………………………..…100
§ 6. Chiziqli programmalash masalalari uchun egizak masala………………..…111
Umumiy mundarija……………...……………………………………………….118
IQTISODIY MATEMATIK USULLAR VA MODELLAR
fanining «Chiziqli programmalash» bo’limi bo’yicha iqtisodiyot va menejment yo’nalishi talabalari uchun nazariy ma’lumotlar va amaliy ko’rsatmalar
“Algoritmlash va matematik modellashtirish” kafedrasining majlisida (4 mart 2014 y., ¹ 17 bayonnoma) muhokama qilindi va TATU ilmiy-uslubiy kengashida bosmaxonada chop etish uchun tavsiya qilindi.
Tuzuvchi: dotsent A.N.Mirzayev
assistent F.S.Raximova
Masul muharrir:
dotsent Yu.M.Abduraxmanova
Muharrir: K.A.Gayubova
Bichimi 60x84 1/16
Bosma tabog’I - Adadi-
Buyurtma ¹
Toshkent axborot texnologiyalari universiteti «ALOQACHI» nashriyot–matbaa markazida chop etildi.
Toshkent sh., Amir Temur ko’chasi, 108 –uy.
“IQTISODIY MATEMATIK USULLAR VA MODELLAR”
(nazariy asoslar va amaliy tavsiyalar)