O’ZBEKISTON RESPUBLIKASI ALOQA, AXBOROTLASHTIRISH VA TELEKOMMUNIKATSIYA TEXNOLOGIYALARI DAVLAT QO’MITASI
TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
“Algoritmlash va matematik modellashtirish” kafedrasi
IQTISODIY MATEMATIK USULLAR VA MODELLAR
Fanning “Chiziqli programmalash” bo’limi bo’yicha iqtisodiyot va menejment yo’nalishi talabalari uchun nazariy ma’lumotlar hamda amaliy ko’rsatmalar
Toshkent-2014
So’z boshi
Modellashtirish usullaridan amaliy va ilmiy-tadqiqot ishlarida azaldan foydalanib kelinadi. U texnik konstruksiya, qurilish va arxitekturada loyiha modellari; fizika, ximiya, biologiya fanlarida ma’lum formulalar asosida jarayon matematik modellarini ifodalash namunalari sifatida ma’lum. “ Model ” so’zi lotincha bo’lib ( modulus ), o’lchov, namuna, norma kabi ma’nolarni bildiradi.
So’nggi yillarda model so’zi ham moda ( urf ) bo’lib, modellashtirishning turli yo’nalishlari shakllanib bormoqda. Hisoblash texnikasi, kompyuter texnologiyalarining rivojlanishi esa, matematik modellashtirish amaliy samarodorligining keskin ortishiga sabab bo’lmoqda. Axborotlarni saqlash, uzatish, qayta ishlash, qisqasi axborot texnologiyalari zamonamizning eng dolzarb yo’nalishlaridan biriga aylanib bormoqda. Bu esa keng qamrovli murakkab jarayonlarni ham matematik modellashtirish va ko’plab variantlarda tadqiq qilish imkoniyatlarini yaratmoqda.
Xususan, iqtisodiy jarayonlarni matematik modeli sifatida XX asr o’rtalarida G.B.Dantzig, L.V.Kantorovich lar tomonidan amaliyotga kiritilgan “chiziqli programmalash masalalari” ChPM yo’nalishini keltirish mumkin. Yuzaki qaraganda, bozorda o’tirgan oddiy sotuvchi ( tadbirkor ) o’z tajribasiga suyangan holda, narx-navo dinamikasini tahlil qilib, har kuni o’zi bilmagan holda qandaydir optimizatsiya masalalarini yechib boradi. Uning tanlagan yechimi omadli yoki omadsiz bo’lishiga qarab uning daromadi shakllanadi. Bu yerda yechimni “ omadli ” yoki “ omadsiz ” sifatlari bilan bog’ladik. Sababi, iqtisodiyot bilan bog’liq masalalar haddan tashqari ko’p variantli bo’lib ularni to’la tahlil qilish va optimal variantni tanlash zamonaviy kompyuterlar uchun ham mushkul masalalardan hisoblanar ekan. Masalan ChPM ning tanlash masalasi deb ataladigan masalasida n- tartibli kvadrat matritsa hosil bo’ladi. Shu matritsaning har bir satri va har bir ustunidan bittadan elementni shunday tanlash kerakki, tanlangan elementlar yig’indisi maksimal bo’lsin. Bu masalani yechish uchun n! variantni hisoblash va taqqoslash kerak bo’lar ekan. Hattoki oddiy n=20 bo’lgan holda ham n!>2· 1018 bo’lib,bu masalani yechish uchun sekundiga 1milliard amal bajaradigan kompyuter ham 500 yil tinimsiz ishlashi kerak ekan.
Demak, bu yerda mavjud variantlarning barchasini emas, ma’lum ma’noda optimallikka da’vogar bo’lishi mumkin bo’lgan variantlarnigina tahlil qilish va ular orasidan optimalini ajratish yo’lini tutish talab qilinadi.ChPM fani aynan shu yo’nalishda shakllangan bo’lib, uning matematik asoslarini, hamda amaliy tadbiq bosqichlarini bilish har bir iqtisodchi, umuman har bir izlanuvchan ijodkor uchun zaruriy bo’g’inlardan biriga aylanib bormoqda.
Mazkur qo’llanmada, yuqorida keltirilgan mulohazalar hisobga olinib, ChPM matematik asoslari va amaliyoti iloji boricha sodda masalalar asosida talqin qilingan. Maqsad, vaqti kelib kompyuter matematik ta’minotida mavjud bo’lgan ChPM larni yechish dasturlaridan foydalanish zarurati paydo bo’lsa, u haqida to’la tasavvurga ega bo’lsin. Har bir paragraf so’ngida mustaqil ishlash uchun berilgan masalalar fanni to’la o’zlashtirishni ta’minlash uchun mo’ljallangan.
§ 1. Chiziqli programmalash masalalari.
Ishlab chiqarish jarayonidagi moddiy va iqtisodiy bog'lanishlarni hisobga olgan holda maqsadga muvofiq keladigan eng maqbul rejani tanlash masalasining matematik ifodasi ilmiy va o'quv adabiyotlarida chiziqli programmalash atamasi bilan ifodalanadi. Bunday masalalarning matematik ifodasini keltirib chiqarishda odatda ishlab chiqarish jarayoni bilan bog'liq bo'lgan barcha resurslar, narx-navolar, ishlab chiqarish normativlari hamda masala mohiyatiga ko'ra maqsad funksiyasini tuziladi. Agar muammo harajatlar bilan bog'liq bo'lsa bu harajatlarni ifodalovchi maqsad funksiyasining eng kichik qiymatini, agar maqsad funksiyasi ishlab chiqarishdan keladigan daromadni ifodalasa bu funksiyani eng katta qiymatini topish talab qilinadi.
Aksariyat hollarda ishlab chiqarish resurslari va ishlab chiqarish kuchlari, ularning imkoniyatlarini ifodalovchi shartlar, hamda harajat yoki daromadni ifodalovchi maqsad funksiyalari chiziqli funksiyalar bilan ifodalanganligi uchun bu turdagi masalalar chiziqli programmalash masalalari deb ataladi. Bu yerda programmalash so'zi dasturlash ma'nosida emas rejalashtirish ma'nosida ishlatiladi. Keyinchalik ko'riladi, masala yechimi ham optimal reja shaklida ifodalanadi.
Chiziqli programmalash usullari ishlab chiqarishning barcha sohalarida keng va samarali tatbiq qilib kelinayapti. Axborot texnologiyalarining rivojlanishi, kompyuterlarning imkoniyat va tezliklarining jadal o'sishi esa chiziqli programmalash masalalarining tatbiqini kengayishi hamda yanada mukammalashishiga yo'l ochayapti. Chiziqli programmalash masalalarining matematik ifodasi sodda bo'lsada uni yechishda funksiya maksimum, minimumlarini topishga mo'ljallangan an'anaviy usullarni tatbiq qilib bo'maydi. Bu yerda asosiy muammo – masala shartlariga bog'liq tarzda mumkin bo'lgan yechimlar sohasini (MBES) ni topishdan iborat bo'ladi. Optimal reja (OP) ham ana shu MBESdan izlanishi kerak.
Yuqorida keltirilgan mulohazalarni oydinlashtirish uchun oddiy bir masalani ko'rib chiqamiz. Faraz qilaylik, kichik korxona meva sharbatlarini chiqaradigan bo'lsin. Korxonada 30kg olcha, 45kg olma, 12kg shakar bor. Korxona ikki xil turdagi meva sharbatlarini chiqaradi. 1 – tur meva sharbatining bir bankasiga 0,1kg olcha, 0,5kg olma, 0,1 kg shakar solinsin. 2 – tur meva sharbatining bir bankasiga 0,3kg olcha, 0,2kg olma, 0,1kg shakar solinsin. Agar 1 banka 1 – tur sharbat narxi 1000so'm, 2 – tur meva sharbati 1400so'm tursa, korxona har bir tur meva sharbatidan qanchadan ishlab chiqarganda korxonaning meva sharbatlarini sotishdan tushgan daromadi eng katta bo'ladi?
Masalaning matematik ifodasini tuzish uchun masala
shartlariga ko'ra kelib chiqadigan munosabatlarni hosil qilishimiz kerak.
Avvalo masala shartiga ko'ra topilishi kerak bo'lgan 1 – va 2 – tur meva
sharbatlarining noma'lum sonini ![]() deb belgilaymiz.
Bu holda 1 – , 2 – va 3 – tur xomashyo (olcha, olma, shakar) sarflarini
hisoblab bu sarflar korxonadagi bor bo'lgan xomashyo zaxiralaridan ortmasligini
talab qilamiz. Xususan olcha sarfi bo'yicha har bir banka 1 – tur meva
sharbatiga 0,1kg olcha , 2 – tur meva sharbatiga esa 0,3kg olcha solinadigan
bo'lsa mos ravishda
deb belgilaymiz.
Bu holda 1 – , 2 – va 3 – tur xomashyo (olcha, olma, shakar) sarflarini
hisoblab bu sarflar korxonadagi bor bo'lgan xomashyo zaxiralaridan ortmasligini
talab qilamiz. Xususan olcha sarfi bo'yicha har bir banka 1 – tur meva
sharbatiga 0,1kg olcha , 2 – tur meva sharbatiga esa 0,3kg olcha solinadigan
bo'lsa mos ravishda ![]() banka 1 – tur ,
banka 1 – tur ,![]() banka 2 – tur meva sharbatlariga jami
banka 2 – tur meva sharbatlariga jami ![]() × 0,1 +
× 0,1 + ![]() ×
0,3 kg olcha sarflanadi. Bu esa korxonada bor bo'lgan 30kg olchadan ortmasligi
kerak. Demak olchalar bo'yicha qo'yiladigan shart
×
0,3 kg olcha sarflanadi. Bu esa korxonada bor bo'lgan 30kg olchadan ortmasligi
kerak. Demak olchalar bo'yicha qo'yiladigan shart
0,1![]() +
0,3
+
0,3![]() ≤
30
≤
30
ko'rinishini oladi. Xuddi shunday mulohazalarga ko'ra olma va shakar sarfi bo'yicha korxona imkoniyatlaridan kelib chiqqan holda
0,5![]() + 0,2
+ 0,2![]() ≤ 45
≤ 45
0,1![]() +
0,1
+
0,1![]() ≤ 12
≤ 12
ko'rinishdagi shartlarni hosil qilamiz. Meva sharbatlarini sotishdan tushadigan daromad esa keltirilgan narxlarga ko'ra jami
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]()
bo'lar ekan. Bu yerda L(![]() ) maqsad
funksiyasi bo'lib, shunday ishlab chiqarish rejasini tanlash kerakki , bu reja
avvalo resurslar bo'yicha shartlarga mos kelsin va maqsad funksiyasining eng
katta qiymatini keltirib chiqarsin. Shunday qilib keltirilgan iqtisodiy masala
quyidagicha ifodalanar ekan
) maqsad
funksiyasi bo'lib, shunday ishlab chiqarish rejasini tanlash kerakki , bu reja
avvalo resurslar bo'yicha shartlarga mos kelsin va maqsad funksiyasining eng
katta qiymatini keltirib chiqarsin. Shunday qilib keltirilgan iqtisodiy masala
quyidagicha ifodalanar ekan
 (1.1)
(1.1)
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]()
![]() max
(1.2)
max
(1.2)
Keltirilgan (1.1) cheklashlar (shartlar)ga
ko'ra (2) maqsad funksiyasining maksimumini toping. Bu masala chiziqli
programmalash masalasining (ChPM) tipik namunasi sifatida qaralishi
mumkin.Ko'rinib turibdiki, (1.1) shartlarda ham (1.2) maqsad funksiyasida ham ![]() noma'lumlar
birinchi darajalari bilan qatnashadi. Bu hol ChPM atamasining kelib chiqishiga
sabab bo'lgan. Avval qayd etib o'tganimizdek, (1.1) – (1.2) masalani yechishda
an'anaviy ekstremumlarni topish usullarini tatbiq qilib bo'lmaydi. Haqiqatdan
ham ekstremumlarning
mavjud
noma'lumlar
birinchi darajalari bilan qatnashadi. Bu hol ChPM atamasining kelib chiqishiga
sabab bo'lgan. Avval qayd etib o'tganimizdek, (1.1) – (1.2) masalani yechishda
an'anaviy ekstremumlarni topish usullarini tatbiq qilib bo'lmaydi. Haqiqatdan
ham ekstremumlarning
mavjud
bo'lish zaruriy sharti ![]()
![]()
bu yerda bajarilmaydi. Buning asosiy sababi bu masalada an'anaviy optimizatsiya masalalaridan farqli funksiyaning lokal ekstremumlari emas global ekstremumi, ya'ni eng katta yoki eng kichik qiymatlarini topish talab qilinadi. Bu qiymatlar, ya'ni Sup L(x1 , x2 ) va inf L(x1 , x2 ) lar esa, agar mavjud bo'lsa faqat MBES chegaralarida bo'lar ekan. Buni keltirilgan masalaning geometrik tahlilidan ko'rishimiz mumkin. Keyinchalik umumiy holda ham ChPMlar uchun MBES qabariq soha bo'lishi va uning uchun optimal yechim shu qabariq soha uchlaridan birortasida bo'lishini misollarda tahlil qilamiz.
Chiziqli programmalash masalasining yechimini topishda geometrik usul.
Geometrik tahlilni (1.1) – (1.2) masala misolida olib boramiz. (1.1) shartlarning har biri OX1X2 koordinat tekisligini to'g'ri chiziq bo'ylab ikki bo'lish va ulardan shartga mos keladigan bittasini tanlashni ifodalaydi. Tahlilni soddalashtirish uchun (1.1) shartlarning hammasini mos ravishda 30;45;12ga bo'lib yozamiz.

![]() L(
L(![]() ) = 1000
) = 1000![]() + 1400
+ 1400![]() max
max
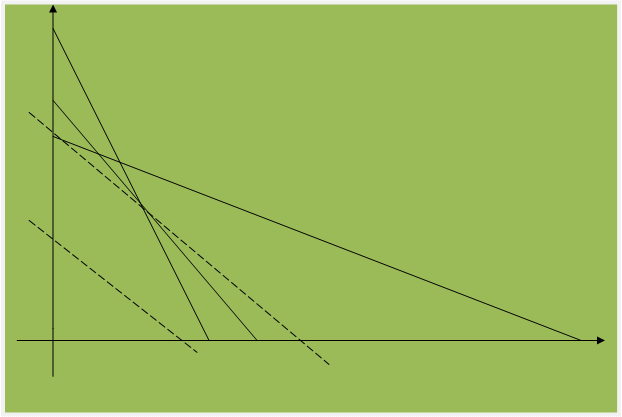
MBESni topish uchun hosil bo'lgan shartlardagi to'g'ri chiziqlarni chizamiz va ulardan pastki qismini olamiz. Natijada OABCD beshburchak shaklidagi soha hosil bo'ladi (1 – rasm).
X2
200
D
100
C E
N2
B
60
N1
40
L=70000
L=140000
A X1
O 60 80 100 120 140 300
1-rasm
Bu sohaning istalgan nuqtasining koordinatalari (1.1)
– (1.2) masalaning shartlariga mos mumkin bo'lgan yechimlaridan birini
ifodalaydi. Bu yerda biz maqsad funksiyasining biror qiyamatiga mos keladigan
rejalar (yechimlar)ga mos nuqtalar to'plamini ko'rib chiqamiz. Masalan L(![]() )
= 70000 bo'ladigan nuqtalar to'plami 1000
)
= 70000 bo'ladigan nuqtalar to'plami 1000![]() + 1400
+ 1400![]() =
70000 tenglama bilan ifodalanadi. Bu tenglamaning ikki tarafini 70000ga bo'lib
yuboramiz va
=
70000 tenglama bilan ifodalanadi. Bu tenglamaning ikki tarafini 70000ga bo'lib
yuboramiz va ![]() ko'rinishdagi
tenglamani hosil qilamiz. Bu OX1X2 koordinat tekisligida
M1(70;0) va M2(0;50) nuqtalardan o'tuvchi to'g'ri chiziq
tenglamasi bo'lib, 1 – rasmda uning grafigi punktir chiziq bilan ifodalangan. L(
ko'rinishdagi
tenglamani hosil qilamiz. Bu OX1X2 koordinat tekisligida
M1(70;0) va M2(0;50) nuqtalardan o'tuvchi to'g'ri chiziq
tenglamasi bo'lib, 1 – rasmda uning grafigi punktir chiziq bilan ifodalangan. L(![]() )
funksiyaning qiymati orttirilsa, masalan L(
)
funksiyaning qiymati orttirilsa, masalan L(![]() ) = 140000 deb
olinsa unga mos grafik avvalgisiga parallel bo'lib yuqoriroqdan, ya'ni M3(140;0)
va M4(0;100) nuqtalardan o'tgan to'g'ri chiziq hosil bo'ladi. Bu
to'g'ri chiziqlarning MBESga taaluqli har bir nuqtasining koordinatalari (1.1)
– (1.2) masalaning yechimlarini ifodalaydi. Masalan, N1 nuqtada L(N1)
= 70000, N2 nuqtada esa L(N2) = 140000 bo'ladi. Maqsad
funksiyasining L(
) = 140000 deb
olinsa unga mos grafik avvalgisiga parallel bo'lib yuqoriroqdan, ya'ni M3(140;0)
va M4(0;100) nuqtalardan o'tgan to'g'ri chiziq hosil bo'ladi. Bu
to'g'ri chiziqlarning MBESga taaluqli har bir nuqtasining koordinatalari (1.1)
– (1.2) masalaning yechimlarini ifodalaydi. Masalan, N1 nuqtada L(N1)
= 70000, N2 nuqtada esa L(N2) = 140000 bo'ladi. Maqsad
funksiyasining L(![]() ) = const
tartibda olingan grafiklari o'zaro parallel to'g'ri chiziqlardan iborat bo'lar
ekan. Maqsad funksiyasining qiymati ortgan sari bu to'g'ri chiziq yuqorilab
boraveradi. Bora – bora MBESdan chiqib ketishi mumkin. Xususan berilgan misolda
maqsad funksiyasining grafigi MBESdan oxiri C nuqtadan o'tgan holida chiqib
ketadi. Ana shu holat, ya'ni C nuqta koordinatalari (1.1) – (1.2) masala
yechimini, optimal rejani berar ekan deyishga asos bo’ladi. (1.1) shartlarga mos
tengsizliklarni juft-jufti bilan tenglik sifatida olib sistema qilib yechib C,
B nuqtalar koordinatalarini topish mumkin. Masala shartlari va 1 – rasmdan
kelib chiqqan holda A(100;0), B(70;50), C(30;90), D(0;100) ekanligini ko'ramiz.
Chizmada ko'rilganidek MBES qabariq sohadan iborat bo'lib, bu holat barcha
ChPMlar uchun o'rinli bo'lgan holatdir. Maqsad funksiyasi grafigi ham to'g'ri
chiziq bo'lganligi uchun uni oshirish parallel ko'chirishdan iborat bo'ladi va
maqsad funksiyasining maksimal qiymati MBES uchlaridan birida ya'ni maqsad
funksiyasining grafigi MBESdan chiqib ketish arafasida o'tgan nuqtasida bo'lar
ekan. Bu esa optimal reja, ya'ni ChPMlar yechimini topish uchun umumiy qoida tavsiya qilishga
imkoniyat beradi.
) = const
tartibda olingan grafiklari o'zaro parallel to'g'ri chiziqlardan iborat bo'lar
ekan. Maqsad funksiyasining qiymati ortgan sari bu to'g'ri chiziq yuqorilab
boraveradi. Bora – bora MBESdan chiqib ketishi mumkin. Xususan berilgan misolda
maqsad funksiyasining grafigi MBESdan oxiri C nuqtadan o'tgan holida chiqib
ketadi. Ana shu holat, ya'ni C nuqta koordinatalari (1.1) – (1.2) masala
yechimini, optimal rejani berar ekan deyishga asos bo’ladi. (1.1) shartlarga mos
tengsizliklarni juft-jufti bilan tenglik sifatida olib sistema qilib yechib C,
B nuqtalar koordinatalarini topish mumkin. Masala shartlari va 1 – rasmdan
kelib chiqqan holda A(100;0), B(70;50), C(30;90), D(0;100) ekanligini ko'ramiz.
Chizmada ko'rilganidek MBES qabariq sohadan iborat bo'lib, bu holat barcha
ChPMlar uchun o'rinli bo'lgan holatdir. Maqsad funksiyasi grafigi ham to'g'ri
chiziq bo'lganligi uchun uni oshirish parallel ko'chirishdan iborat bo'ladi va
maqsad funksiyasining maksimal qiymati MBES uchlaridan birida ya'ni maqsad
funksiyasining grafigi MBESdan chiqib ketish arafasida o'tgan nuqtasida bo'lar
ekan. Bu esa optimal reja, ya'ni ChPMlar yechimini topish uchun umumiy qoida tavsiya qilishga
imkoniyat beradi.
ChPMlarni yechishda avvalo MBESni
ifodalovchi qabariq soha topiladi va uning uchlarida maqsad funksiyasini
hisoblanadi. Bu qiymatlardan eng kattasiga mos keluvchi nuqta koordinatalari
izlanayotgan yechim – optimal rejani beradi. Bu qoidani yuqorida ko'rilgan
masalaga tatbiq qilamiz. Maqsad funksiyasi (MF) ![]() = 1000
= 1000![]() + 1400
+ 1400![]() bo'lib MBES
uchlari A(100;0)
bo'lib MBES
uchlari A(100;0)
B(70;50), C(30;90), D(0;100) dagi qiymatlarini ![]() deb
belgilasak £A= 100000, £B=140000, £C=156000,
£D= 140000.
deb
belgilasak £A= 100000, £B=140000, £C=156000,
£D= 140000.
Bu qiymatlarni taqqoslash natijasida optimal reja C(30;90) nuqtada ekanligiga ishonch hosil qilamiz. Bu natija 1 – rasmdagi chizmaga ham mos keladi, ya'ni MF grafigini parallel ko'chirishda bu grafik MBESdan C nuqta orqali chiqib ketishi ko'rinib turibdi. Bu keltirilgan grafik usul ikki noma'lumli masalalarda juda qulay bo'lish bilan birga ko'plab umumiy qoida va tavsiyalar ham ishlab chiqishga imkoniyat beradi.
Optimal rejaning iqtisodiy tahlili
Yuqorida keltirilgan (1.1) – (1.2) masalaning topilgan yechimini tahlil qilamiz. Optimal reja C(30;90) nuqtada bo'lib, bu nuqtada x1 = 30; x2 = 90 va £C=156000 ekanligini ko'rdik. Chizmadan (1 – rasm) ko'rinadiki, C nuqtada 1,3-homashyo to'liq sarflanadi, 2-homashyo esa ortib qolar ekan, chunki 2-homashyoga mos to'g'ri chiziq C nuqtadan o'tmaydi. Optimal reja qiymatlarini homashyo sarfi funksiyalariga qo'yib ham bunga ishonch hosil qilamiz.
f1(x1x2) = (0,1x1 +
0,3x2) 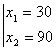 =0,1 ×
30 + 0,3 × 90 = 30
=0,1 ×
30 + 0,3 × 90 = 30
f2(x1x2) = (0,5x1 +
0,2x2) 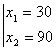 =0,5 ×
30 + 0,2 × 90 = 33 < 45
=0,5 ×
30 + 0,2 × 90 = 33 < 45
f3(x1x2) = (0,1x1 +
0,1x2) 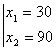 =0,1 ×
30 + 0,1 × 90 = 12
=0,1 ×
30 + 0,1 × 90 = 12
Bu holatdan kelib chiqib quyidagi mulohaza va tavsiyalarni keltirish mumkin. Ikkinchi tur homashyo 45 birlik bo'lib, undan 33 birlik ishlatiladi. Demak, 12 birlik 2 – tur homashyo ortib qoladi. Bu ortiqchasini homashyo sifatida sotib yuborish mumkin. Ikkinchi yo'li esa chizmadan ko'rinayapti, ishlab chiqarish rejasini oshirishga to'sqinlik qilayotgan kamyob (taxchil) homashyoni ko'paytirish kerak. Bunda barcha homashyolarni to'la jalb qilish, hamda daromadni oshirish imkoniyatiga ega bo'lamiz. Bizning masalada, chizmadan ko'rinadiki (1 – rasm) , 3 – tur homashyo, ya'ni shakar rejani oshirishga imkoniyat bermayapti. Agar shakarga mos to'g'ri chiziq grafigini paralell ko'chirib E nuqtagacha olib borilsa barcha homashyolar to'la ishlatilishiga erishiladi. Grafikni paralell ko'chirish esa shakar zaxirasini ko'paytirish hisobiga erishiladi. Hususan bizning masalada f3(x1x2) = (0,1x1 + 0,1x2) = C3 deb, grafik E nuqtadan o'tishi shartidan C3 qiymat tanlanadi. E nuqta 1-,2- to'g'ri chiziqlar kesishgan nuqtasi bo'lib, uning koordinatalari
 sistemadan topiladi.
sistemadan topiladi.
Bu sistemadan ![]() ekanligini
topamiz.3-xomashyo chizig'i bu nuqtadan o'tishi uchun f3(x1x2) = 0,1 ×
ekanligini
topamiz.3-xomashyo chizig'i bu nuqtadan o'tishi uchun f3(x1x2) = 0,1 × ![]() bo'lishi
kerak ekan. Demak, shakar zaxirasini 13,8 birlikka yetkazsak, ya'ni 1,8
birlikka oshirsak optimal planni E
bo'lishi
kerak ekan. Demak, shakar zaxirasini 13,8 birlikka yetkazsak, ya'ni 1,8
birlikka oshirsak optimal planni E![]() nuqtaga
ko'chirish mumkin. Bunda maqsad funksiyasi
nuqtaga
ko'chirish mumkin. Bunda maqsad funksiyasi
£E = 1000 × ![]() +
1400 ×
+
1400 × ![]()
![]()
![]() 170770
qiymatga erishadi.
170770
qiymatga erishadi.
Bunda daromad C nuqtadalgiga qaraganda 14770 pul birligiga ortadi. Shunday qilib qo'yilgan iqtisodiy masalaning matematik modelini tuzish, matematik model yordamida masala yechimini topish va topilgan yechimning iqtisodiy tahlilini to'liq o'tkazish mumkin ekan.
Geometrik usulning samarali ekanligini namoyish qilish uchun uch noma'lumli ChPM na’munasini ko'ramiz. Maqsad masala mohiyati va uni yechimini topish jarayonini aks ettirish bo'lgani uchun masalaning birato’la matematik ifodasidan boshlaymiz. Vaqtincha iqtisodiy mulohazalardan holi bo'lgan holda quyidagi matematik masalani ko'ramiz.
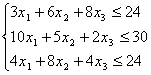 (1.3) xi ≥0 i = 1, 2, 3
(1.3) xi ≥0 i = 1, 2, 3
![]() = 25
= 25![]() (1.4)
(1.4)
Bu yerda (1.3) shartlarni qanoatlantiruvchi barcha nuqtalar orasidan shundayini topishni talab qilinadiki, bu nuqta koordinatalari (1.4) maqsad funksiyasining eng katta qiymatini ta'minlasin. Dastlab (1.3) shartlarni qanoatlantiruvchi nuqtalar to'plami, ya'ni ChPM uchun MBESni topish kerak bo'ladi. Bu yerda ikki o'lchovli masaladagiga o'xshash geometrik usuldan foydalanamiz. Avvalo (1.3) shartlarni kanonik ko'rinishiga keltiramiz

![]()
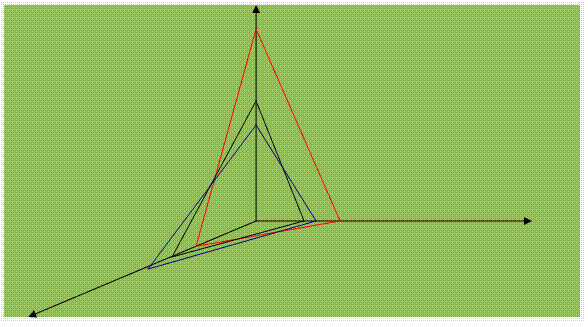 Bu shartlarning har biri tenglik sifatida
olinganda tekislik kanonik tenglamasi bo'lib, shartga ko'ra shu tekislikdan
pastki qismini olish kerakligini ifodalaydi.
Bu shartlarning har biri tenglik sifatida
olinganda tekislik kanonik tenglamasi bo'lib, shartga ko'ra shu tekislikdan
pastki qismini olish kerakligini ifodalaydi. ![]() shartlar esa
fazoviy koordinat sistemasiga nisbatan birinchi oktantni olish kerakligini
ifodalaydi.
shartlar esa
fazoviy koordinat sistemasiga nisbatan birinchi oktantni olish kerakligini
ifodalaydi.
x3
15
6
3 M3
M5 M4
O M2
M1 3 4 6 x2
3
6
8
x1 2 – rasm
Yuqorida keltirilgan shartlar va mulohazalarga ko'ra
(1.3) – (1.4) masala uchun MBESini 2 – rasmda sxematik ifodalangan. Bir-biridan
farqlash va MBESni ajratish qulay bo'lishi uchun har bir tekislik uchun boshqa
– boshqa rang olingan. Chizmada 1 – tekislik havo rang , 2 – tekislik qizil, 3
– tekislik qora rangda aks ettirilgan. Birinchi oktant tepasidan qaraganda MBES
ostki chegarasi shtrixlangan sohadan iborat bo'ladi. Chizmadan ko'rinadiki M1
2 – tekislikning OX1 o'qi bilan , M2 3 – tekislikning OX2
o'qi bilan, M3 esa 1 – tekislikning OX3 o'qi bilan
kesishgan nuqtasi bo'ladi. Shunga ko'ra koordinatalar orqali M1(3;0;0)
, M2(0;3;0) , M3(0;0;3) ekanligini ko'ramiz. M4 nuqta
esa OX2 X3 koordinata tekisligida 1-, 3- tekisliklar
kesishgan nuqtasi ekanligini ko’ramiz. Uning koordinatalarini topish uchun
1-,3-tekislik tenglamalarida ![]() deb sistema
hosil qilamiz. Undan esa
deb sistema
hosil qilamiz. Undan esa
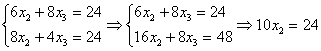
![]()
![]() topiladi.
Demak M4(0;2,4;1,2)
topiladi.
Demak M4(0;2,4;1,2)
Xuddi shuningdek M5 nuqta uchun x2=0
deb 1-,2-tekisliklar kesishgan nuqtasini, M6 uchun esa x3=0
deb 2-,3-tekisliklar kesishgan nuqtasini topiladi. Bunda M5(2,6 ; 0
; 2,03) va M6(2 ; 2 ; 0) ekanligi topiladi. MBES tepasida esa uchchala
tekislikning kesishgan nuqtasi sifatida topiladigan M7 nuqta
bo'ladi. (1.3) tengsizliklari tenglik qilib sistema sifatida yechilsa M7(2,08
; 1,36 ; 1,2) ekanligi topiladi. Natijada MBES qavariq soha OM1 M2
M3 M4 M5 M6 M7
ning barcha uchlari topiladi. Maqsad funksiyasi (MF) qiymatining o'zgarmas
qiymatida 25![]() const tekislik
tenglamasi bo'lib, unga mos nuqtalar shu tekislikda yotadi. Bu yerda ham MF
tekislikni parallel ko'chirish C=const qiymatining ortishi yoki kamayishi bilan
bog'liq bo'ladi. Shuning uchun optimal reja uning MBES uchlaridan eng katta
qiymatga erishadiganiga mos keladi. Agar
const tekislik
tenglamasi bo'lib, unga mos nuqtalar shu tekislikda yotadi. Bu yerda ham MF
tekislikni parallel ko'chirish C=const qiymatining ortishi yoki kamayishi bilan
bog'liq bo'ladi. Shuning uchun optimal reja uning MBES uchlaridan eng katta
qiymatga erishadiganiga mos keladi. Agar ![]() belgilash
kiritsak, bevosita hisoblashlardan
belgilash
kiritsak, bevosita hisoblashlardan ![]() ekanligini
ko'ramiz. Demak optimal reja M7 nuqtada bo'lib , bunda
ekanligini
ko'ramiz. Demak optimal reja M7 nuqtada bo'lib , bunda ![]() ;
;
![]() ;
; ![]() bo'lar
ekan, maqsad funksiyasi esa bu nuqtada o'zining eng katta qiymatiga erishar
ekan.
bo'lar
ekan, maqsad funksiyasi esa bu nuqtada o'zining eng katta qiymatiga erishar
ekan.
1.CHPM geometrik usulda yechilsin.
Misollar
1.1  1.2
1.2 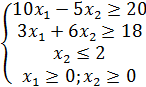
![]()
![]()
1.3 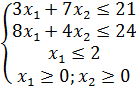 1.4
1.4 
![]()
![]()
1.5  1.6
1.6 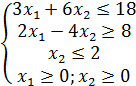
![]()
![]()
2. Berilgan CHPM uchun geometrik usulda optimal plan topilsin.
2.1 ![]()

2.2 ![]()
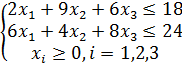
2.3 ![]()
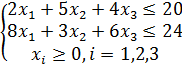
2.4 ![]()

2.5 ![]()

§ 2 . Chiziqli programmalash masalasining matematik asoslari
Umumiy holda, biror ishlab chiqarish korxonasida n xil mahsulot ishlab chiqarilayotgan bo'lib, buning uchun m xil xomashyo (ishlab chiqarish resurslari)dan foydalanilayotgan bo'lsin. Har bir ishlab chiqarilayotgan j – mahsulot uchun i – xomashyodan aij birlik ishlatilayotgan bo'lsin. Korxonada i – xomashyodan bi birlik bor bo'lsin. Agar j – mahsulotning bir birligining narxi Cj pul birligiga teng bo'lsa korxona har bir mahsulotdan necha donadan (birlikdan) ishlab chiqarganda ularni sotishdan keladigan daromad maksimal bo'ladi? Iqtisodiy nuqtai nazardan masala ana shunday ifodalanadi. Agar j – mahsulotning ishlab chiqarilishi kerak bo'lgan miqdorini Xj deb belgilasak va keltirilgan shartlarning barchasini matematik tarzda ifodalasak u quyidagi ko'rinishini oladi.
![]() i = 1
, 2 , … , m (2.1)
i = 1
, 2 , … , m (2.1)
![]() j = 1
, 2 , … , n
j = 1
, 2 , … , n
![]() … ,
… , ![]() =
=
![]() Cj Xj
Cj Xj
![]() max
(2.2)
max
(2.2)
Chiziqli programmalash masalasi (ChPM)ning
matematik ifodasi (2.1) – (2.2) bo'lib, unga ko'ra n o'lchovli fazoning
(2.1) shartlarni qanoatlantiruvchi (![]() …,
…,![]() nuqtalari
orasidan shundayini topish kerakki, (2.2) maqsad funksiyasining maksimal (eng
katta) qiymatini ta'minlasin. Avvalo masalaning (2.1) shartlari va ularni
qanoatlantiruvchi nuqtalar to'plami haqida to'xtalamiz. Bu shartlarning
geometrik ma'nosini n=2 va n=3 bo'lgan hollarda batafsil ko'rib chiqildi (§1).
Umumiy holda (2.1) shartlarning har biri n - o'lchovli fazodagi
gipertekislik tenglamasi yordamida fazoni ikkiga bo'lish va undan bir tarafini
olishni aks ettiradi.
nuqtalari
orasidan shundayini topish kerakki, (2.2) maqsad funksiyasining maksimal (eng
katta) qiymatini ta'minlasin. Avvalo masalaning (2.1) shartlari va ularni
qanoatlantiruvchi nuqtalar to'plami haqida to'xtalamiz. Bu shartlarning
geometrik ma'nosini n=2 va n=3 bo'lgan hollarda batafsil ko'rib chiqildi (§1).
Umumiy holda (2.1) shartlarning har biri n - o'lchovli fazodagi
gipertekislik tenglamasi yordamida fazoni ikkiga bo'lish va undan bir tarafini
olishni aks ettiradi. ![]() shartlar ham n
- o'lchovli fazoda
shartlar ham n
- o'lchovli fazoda ![]() = 0 tenglamaga
mos gipertekislikdan bir tarafini olishni ifodalaydi. n - o'lchovli
fazoda ham qabariq soha ta'rifi va xususiyati odatdagi 2 va 3 o'lchovli real
fazolardagidek bo'ladi. Chiziqli fazo amallari n o'lchovli fazo
elementlari X(
= 0 tenglamaga
mos gipertekislikdan bir tarafini olishni ifodalaydi. n - o'lchovli
fazoda ham qabariq soha ta'rifi va xususiyati odatdagi 2 va 3 o'lchovli real
fazolardagidek bo'ladi. Chiziqli fazo amallari n o'lchovli fazo
elementlari X(![]() …,
…,![]() lar
uchun quyidagicha aniqlangan bo'lsin
lar
uchun quyidagicha aniqlangan bo'lsin
X![]() …,
…, ![]() +Y(
+Y(![]() …,
…,![]() =
=
![]() …,
…,![]() (2.3)
(2.3)
![]() × X(
× X(![]() …,
…,![]() =
T(
=
T(![]() …,
…,![]() )
)
U holda n o'lchovli fazodagi biror D sohaning
ixtiyoriy ikkita X, Y ![]() D elementlari
uchun va ixtiyoriy
D elementlari
uchun va ixtiyoriy ![]() sonlar uchun
sonlar uchun ![]() ×
X + (1-
×
X + (1-![]() ) Y
) Y![]() bo'lsa D soha qabariq soha deyiladi. Bu shart real fazolardagi qabariq soha
ta'rifi (agar sohaning ixtiyoriy ikki nuqtasini tutashtiruvchi kesma ham shu
sohaga tegishli bo'lsa soha qabariq soha deyiladi)ga to'la mos keladi. ChPM
yechimini izlash odatda mumkin bo'lgan yechimlar sohasi (MBES)ni topishdan
boshlanadi. MBESdan esa (2.2) maqsad funksiyasining maksimumi izlanadi. Avvalo
ChPM uchun MBES doimo qabariq soha bo’lishligini ta'kidlab o'tishimiz kerak.
Haqiqatdan, agar (2.1) shartlarni qanoatlantiruvchi nuqtalar to'plamini D deb
belgilasak va ixtiyoriy X, Y
bo'lsa D soha qabariq soha deyiladi. Bu shart real fazolardagi qabariq soha
ta'rifi (agar sohaning ixtiyoriy ikki nuqtasini tutashtiruvchi kesma ham shu
sohaga tegishli bo'lsa soha qabariq soha deyiladi)ga to'la mos keladi. ChPM
yechimini izlash odatda mumkin bo'lgan yechimlar sohasi (MBES)ni topishdan
boshlanadi. MBESdan esa (2.2) maqsad funksiyasining maksimumi izlanadi. Avvalo
ChPM uchun MBES doimo qabariq soha bo’lishligini ta'kidlab o'tishimiz kerak.
Haqiqatdan, agar (2.1) shartlarni qanoatlantiruvchi nuqtalar to'plamini D deb
belgilasak va ixtiyoriy X, Y ![]() elementlarini
olsak hamda Z=
elementlarini
olsak hamda Z=![]() elementini
olsak Z(
elementini
olsak Z(![]() …,
…,![]() uning uchun
uning uchun
![]() (
(![]() ×
×
![]()
![]() ×
×![]() kelib chiqadi,
ya'ni Z(
kelib chiqadi,
ya'ni Z(![]() …,
…,![]() uchun
ham
uchun
ham ![]()
![]() 1
, 2 , …n
1
, 2 , …n
tengsizliklar o'rinli bo'ladi, demak Z![]() bo'ladi. Aksariyat hollarda n o'lchovli ChPMning MBESi n
o'lchovli qabariq soha bo'ladi. Bu holda ham masala yechimi, ya'ni optimal rejani
shu qabariq sohaning uchlaridan izlanishi kerak. (2.1) shartlarga ko'ra
aniqlanadigan D sohaning uchlarini topish uchun m+n ta (2.1) shartlardan
n ta chiziqli erklisini tanlaymiz va ularni tenglik sifatida
ifodalasak n ta noma'lumli n ta chiziqli algebraik tenglamalar
sistemasi hosil bo'ladi. Bu sistemaning yechimini topib uni (2.1) shartlarning
qolganlariga muvofiqligi tekshiriladi. Agar shunday bo'lsa, bu yechimga mos M (
bo'ladi. Aksariyat hollarda n o'lchovli ChPMning MBESi n
o'lchovli qabariq soha bo'ladi. Bu holda ham masala yechimi, ya'ni optimal rejani
shu qabariq sohaning uchlaridan izlanishi kerak. (2.1) shartlarga ko'ra
aniqlanadigan D sohaning uchlarini topish uchun m+n ta (2.1) shartlardan
n ta chiziqli erklisini tanlaymiz va ularni tenglik sifatida
ifodalasak n ta noma'lumli n ta chiziqli algebraik tenglamalar
sistemasi hosil bo'ladi. Bu sistemaning yechimini topib uni (2.1) shartlarning
qolganlariga muvofiqligi tekshiriladi. Agar shunday bo'lsa, bu yechimga mos M (![]() …,
…,![]() nuqta
MBES-ning tayanch nuqtasi, uning koordinatalari esa ChPMning tayanch yechimi
deyiladi.
nuqta
MBES-ning tayanch nuqtasi, uning koordinatalari esa ChPMning tayanch yechimi
deyiladi.
Shunday usulda hosil qilish mumkin bo'lgan sistemalar
soni umumiy holda ![]() formula
bo'yicha hisoblanadi. Bu sistemalardan ChPMning tayanch yechimlari topiladi.
Tayanch yechimlar orasidan maqsad funksiyasining eng katta qiymatini beruvchi
optimal reja ham topiladi. Faqat n, m ortgan sari tayanch yechimlar soni ham
ortib boradi. Masalan n=5, m=4 bo'lgan, umuman olganda oddiygina holda ham
tayanch yechimlar soni
formula
bo'yicha hisoblanadi. Bu sistemalardan ChPMning tayanch yechimlari topiladi.
Tayanch yechimlar orasidan maqsad funksiyasining eng katta qiymatini beruvchi
optimal reja ham topiladi. Faqat n, m ortgan sari tayanch yechimlar soni ham
ortib boradi. Masalan n=5, m=4 bo'lgan, umuman olganda oddiygina holda ham
tayanch yechimlar soni ![]() bo'lishi mumkin
ekan. Shuncha yechimning har birini topishda 5 noma'lumli sistemalarni ishlash
kerak bo'ladi. Tabiiy savol tug'iladi, optimal rejani topish uchun ana shu 126
nuqtalarning barchasini topish, hamda shu nuqtalarda maqsad funksiyasini
hisoblash shartmikan? Bu ishni osonlashtirish
bo'lishi mumkin
ekan. Shuncha yechimning har birini topishda 5 noma'lumli sistemalarni ishlash
kerak bo'ladi. Tabiiy savol tug'iladi, optimal rejani topish uchun ana shu 126
nuqtalarning barchasini topish, hamda shu nuqtalarda maqsad funksiyasini
hisoblash shartmikan? Bu ishni osonlashtirish
ya’ni optimal rejaga yetish yo'lini qisqartirish imkoniyati yo'qmikan? Bu sohadagi izlanishlar o'z samarasini bergan va rejani bosqichma – bosqich yaxshilash degan usullar yaratilgan. Usulning g'oyasi asosan quyidagi mulohazaga asoslangan. Avvalo ixtiyoriy birorta tayanch yechim topamiz. Bu yechim MBES deb ataganimiz qabariq ko'pyoqlining birorta uchiga mos keladi. Ikki o'lchovli holda bu qabariq ko'pburchak, uch o'lchovli holda qabariq ko'pyoqli (prizma, piramida …). Bu uchidan bir qancha qirralar o'tgan bo'ladi, go'yoki chorrahada uchrashadigan yo'llardek. Har bir qirra berilgan uchini boshqa bir qo'shni uch bilan tutashtiradi. Shu yo'llardan qaysi birini tanlagan ma'qul, qay biri maqsadga tezroq olib boradi? Go'yo ertak qahramonlari oldida uchraydigan yo'llarda yozib qo'yiladigan yo'l ta'rifiga o'xshash bu yo'llar hislatlarini aniqlash mezoni yo'qmikan? Umuman maqsadga eltuvchi yo'lning o'zi bormikan? Ertaksifat bu mulohazalarning barchasiga javob beruvchi usul dastlab 1947 yil Dansig tomonidan kashf qilingan. Bu usul keyinchalik ilmiy va o'quv adabiyotlarida simpleks usul nomi bilan muomalaga kirib ketgan. Usulning matematik hamda amaliy tafsilotlariga o'tamiz.
3. Berilgan CHPM uchun ko’rsatilgan bazisga mos tayanch yechim topilsin. Tayanch yechimlar ko’pi bilan nechta bo’lishi mumkin.
3.1 ![]()

![]()
3.2 ![]()
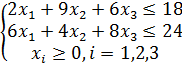
![]()
3.3 ![]()
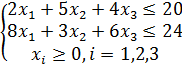
![]()
3.4 ![]()

![]()
3.5 ![]()

![]()
§ 3. Rejani bosqichma – bosqich yaxshilash usuli.
Biz bu yerda asosan usulning amaliy taraflari, hamda hisoblash algoritmlariga ko'proq to'xtalamiz. Usul asosan ikkita bosqichni o'z ichiga oladi. To'g'rirog'i har bosqichda ikkita savol hal qilinishi kerak bo'ladi. Avvalo, tanlangan tayanch yechim optimal reja bo'ladimi? Optimal bo'lsa, tabiiy, muammo hal bo'lgan, yechim topilgan deb hisob qilinadi. Optimal bo'lmasa, navbatdagi, bu yechimga qaraganda yaxshiroq yechimni qanday topish mumkin?
ChPMni umumiy ko'rinishini olamiz
![]()
![]() 2,
…, m (3.1)
2,
…, m (3.1)
![]() j =
1, 2, …, n
j =
1, 2, …, n
![]() …,
…, ![]() (3.2)
(3.2)
(3.1) shartlarni qanoatlantiruvchi barcha M (![]() …,
…,
![]() lar orasidan
(3.2) maqsad funksiyasining eng katta qiymatini beruvchi nuqta koordinatalari,
ya'ni optimal rejani topish kerak.
lar orasidan
(3.2) maqsad funksiyasining eng katta qiymatini beruvchi nuqta koordinatalari,
ya'ni optimal rejani topish kerak.
Simpleks usul kanonik ko'rinishdagi ChPMlar uchun mo'ljallangan. Bunda ChPM barcha shartlari tenglik ko'rinishida berilgan bo'lishi kerak. Kanonik ko'rinishdagi ChPM matematik ifodasi
![]()
![]() 1,
2, …, m (3.3)
1,
2, …, m (3.3)
![]() (3.4)
(3.4)
![]() ko'rinishda bo'ladi. Bu yerda ham
ko'rinishda bo'ladi. Bu yerda ham ![]() o'z
o'rnida qoladi. Alohida zarurat bo'lmasa bu shartlarni oshkora ifodalab
o'tirilmaydi. Umumiy ko'rinishdagi (3.1) – (3.2) ChPMni kanonik (3.3) – (3.4)
ko'rinishiga keltirishimiz mumkin. Buning uchun (3.1) shartlarning har birining
chap tarafiga ( u kichik bo'lganligi uchun) yangi
o'z
o'rnida qoladi. Alohida zarurat bo'lmasa bu shartlarni oshkora ifodalab
o'tirilmaydi. Umumiy ko'rinishdagi (3.1) – (3.2) ChPMni kanonik (3.3) – (3.4)
ko'rinishiga keltirishimiz mumkin. Buning uchun (3.1) shartlarning har birining
chap tarafiga ( u kichik bo'lganligi uchun) yangi ![]() o'zgaruvchini
qo'shish yordamida tenglikka aylantirish mumkin. Bunda
o'zgaruvchini
qo'shish yordamida tenglikka aylantirish mumkin. Bunda ![]() o'zgaruvchilar
ham noma'lum bo'ladi. Natijada (3.1) – (3.2) masala
o'zgaruvchilar
ham noma'lum bo'ladi. Natijada (3.1) – (3.2) masala
![]()
![]() 2,
…, m (3.5)
2,
…, m (3.5)
![]() (3.6)
(3.6)
ko'rinishini oladi, bu yerda noma'lumlar ![]() …
…
![]() …,
…,![]() n+m ta bo'ladi. Maqsad funksiyasining ko'rinishini o'zgartirmaslik uchun (3.6)
ifoda
n+m ta bo'ladi. Maqsad funksiyasining ko'rinishini o'zgartirmaslik uchun (3.6)
ifoda ![]()
![]() deb
hisoblangan. Bundan ko'rinadiki, yangi kiritilgan
deb
hisoblangan. Bundan ko'rinadiki, yangi kiritilgan ![]() …,
…, ![]() o'zgaruvchilar
qanday bo'lishidan qat'iy nazar maqsad funksiyasining qiymatlariga mutlaqo
ta'sir qilmaydi. Natijada hosil bo'lgan (3.5) – (3.6) masala (3.3) – (3.4)
masala bilan aynan bir xil ko'rinishini olar ekan. Shunday qilib umumiy
ko'rinishdagi ChPMni kanonik ko'rinishga keltirish mumkinligi asoslandi. Demak,
kanonik ko'rinishdagi ChPMlar uchun yaratilgan usullarni umumiy ko'rinishdagi
ChPMlarga ham tatbiq qilish mumkin ekan. Simpleks usul tafsilotlariga o'tamiz.
Buning uchun (3.3) shartlar matritsasi A=(aij) i= 1, 2, …, m j = 1,
2, …, n ustunlarini m o'lchovli chiziqli fazo vektorlari deb, faqat
uning koordinatalari yordamida tuzilgan vektorlarni
o'zgaruvchilar
qanday bo'lishidan qat'iy nazar maqsad funksiyasining qiymatlariga mutlaqo
ta'sir qilmaydi. Natijada hosil bo'lgan (3.5) – (3.6) masala (3.3) – (3.4)
masala bilan aynan bir xil ko'rinishini olar ekan. Shunday qilib umumiy
ko'rinishdagi ChPMni kanonik ko'rinishga keltirish mumkinligi asoslandi. Demak,
kanonik ko'rinishdagi ChPMlar uchun yaratilgan usullarni umumiy ko'rinishdagi
ChPMlarga ham tatbiq qilish mumkin ekan. Simpleks usul tafsilotlariga o'tamiz.
Buning uchun (3.3) shartlar matritsasi A=(aij) i= 1, 2, …, m j = 1,
2, …, n ustunlarini m o'lchovli chiziqli fazo vektorlari deb, faqat
uning koordinatalari yordamida tuzilgan vektorlarni ![]() …,
…,![]()
ko'rinishida ifodalaymiz. Shunga o'xshash, narxlarga mos Cj qiymatlar yordamida
![]() …,
…, ![]() vektorni
satr matritsa sifatida ifodalaymiz. Zaxiralarga mos bj qiymatlar yordamida
vektorni
satr matritsa sifatida ifodalaymiz. Zaxiralarga mos bj qiymatlar yordamida
![]() …,
…, ![]() ustun
matritsani tuzsak (3.3) – (3.4) masalani kompakt (ixcham) ko'rinishda,
matritsalar orqali
ustun
matritsani tuzsak (3.3) – (3.4) masalani kompakt (ixcham) ko'rinishda,
matritsalar orqali
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
ko'rinishda ifodalash mumkin. Bu yerda ![]() …,
…,
![]() noma'lumlarga
mos ustun matritsa.
noma'lumlarga
mos ustun matritsa.
![]() 2, …, n)
vektorlar m o'lchovli chiziqli fazo vektorlari bo'lib, ularning soni n
aksariyat hollarda m dan ancha katta bo'ladi. Shuning uchun (3.7)
sistema yechimlari cheksiz ko'p bo'ladi. Ular orasida (3.8) shartni
qanoatlantiradiganini topishimiz kerak.
2, …, n)
vektorlar m o'lchovli chiziqli fazo vektorlari bo'lib, ularning soni n
aksariyat hollarda m dan ancha katta bo'ladi. Shuning uchun (3.7)
sistema yechimlari cheksiz ko'p bo'ladi. Ular orasida (3.8) shartni
qanoatlantiradiganini topishimiz kerak.
Buning uchun ![]() vektorlar
orasidan
vektorlar
orasidan ![]() musbat
koordinatalariga mos keluvchi mta chiziqli erklisini ajratishimiz kerak.
Fazo m o'lchovli bo'lganligi uchun
musbat
koordinatalariga mos keluvchi mta chiziqli erklisini ajratishimiz kerak.
Fazo m o'lchovli bo'lganligi uchun ![]() lar orasida
chiziqli erklisi m tadan ortiq bo'lmaydi. Bu vektorlar bazis vektorlar
deb belgilanadi. Masala shartlari shu bazisga moslanadi. Bazis vektorlardan
qolgan barcha
lar orasida
chiziqli erklisi m tadan ortiq bo'lmaydi. Bu vektorlar bazis vektorlar
deb belgilanadi. Masala shartlari shu bazisga moslanadi. Bazis vektorlardan
qolgan barcha ![]() vektorlarga mos
vektorlarga mos ![]() lar
nol deb olinadi. Shundan keyin berilgan bazisga mos tayanch yechim topiladi va
u optimallikka tekshiriladi.
lar
nol deb olinadi. Shundan keyin berilgan bazisga mos tayanch yechim topiladi va
u optimallikka tekshiriladi.
Biz bu yerda usulning faqat amaliy taraflariga to'xtalamiz. Usulning nazariy asoslariga qiziqqanlar maxsus adabiyotlarga murojaat qilishi mumkin. Usul mohiyati va tartibini amaliy misolni ishlash jarayonida izohlab boramiz. Quyidagi ChPM berilgan bo'lsin.

![]()
Bu masalani kanonik ko'rinishga keltiramiz![]()

![]()
Berilgan masala shartlaridan ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ekanligini
ko'ramiz. Bu yerda yangi kiritilgan o'zgaruvchilarga mos
ekanligini
ko'ramiz. Bu yerda yangi kiritilgan o'zgaruvchilarga mos ![]() vektorlar
bazis ekanligi ko'rinib turibdi, haqiqatdan ham
vektorlar
bazis ekanligi ko'rinib turibdi, haqiqatdan ham ![]()
ekanligini ko'rishimiz mumkin. Qolgan vektorlar,
shuningdek cheklash vektori ![]() ni ham ular
orqali ifodalash mumkin. Masala shartlariga ko'ra shu bazisga mos tayanch
yechimni topish uchun bazisga kirmagan
ni ham ular
orqali ifodalash mumkin. Masala shartlariga ko'ra shu bazisga mos tayanch
yechimni topish uchun bazisga kirmagan ![]() o'zgaruvchilarni
nol deb olishimiz kerak. U holda
o'zgaruvchilarni
nol deb olishimiz kerak. U holda ![]() ekanligi kelib
chiqadi. Keltririlgan shartlarni ifodalovchi barcha sonlarni quyidagi jadval
ko'rinishda ifodalaymiz.
ekanligi kelib
chiqadi. Keltririlgan shartlarni ifodalovchi barcha sonlarni quyidagi jadval
ko'rinishda ifodalaymiz.
|
i
|
Cj
Ci |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
|
1 |
0 |
A4 |
56 |
7 |
8 |
5 |
1 |
0 |
0 |
11,2 |
|
|
2 |
0 |
A5 |
10 |
2 |
1 |
1 |
0 |
1 |
0 |
10 |
|
|
3 |
0 |
A6 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
6 |
|
|
|
|
|
|
-10 |
-12 |
-25 |
0 |
0 |
0 |
|
![]()
1 – jadval
1 – jadvalda A0 ustun shartlardagi o'ng
taraf qiymatlari (resurslar miqdori) A1 , A2 , A3
, A4 , A5 , A6 ustunlar shartlardagi ![]() larning
koeffisiyentlaridan tuzilgan. Shartlarda koeffisiyentlari birlik ustunni
ifodalayotgan vektorlar bazis vektorlar deb belgilanib, ularning 1 elementlari
joylashgan qator boshida bazis deb atalgan ustunda shu vektor belgisi AK
deb qo'yiladi. CKi deb atalgan ustunga esa bazisga kirgan shu
qatordagi Ak vektor tepasidagi narx qiymati Ck qo'yiladi.
larning
koeffisiyentlaridan tuzilgan. Shartlarda koeffisiyentlari birlik ustunni
ifodalayotgan vektorlar bazis vektorlar deb belgilanib, ularning 1 elementlari
joylashgan qator boshida bazis deb atalgan ustunda shu vektor belgisi AK
deb qo'yiladi. CKi deb atalgan ustunga esa bazisga kirgan shu
qatordagi Ak vektor tepasidagi narx qiymati Ck qo'yiladi.
![]() - ustunda
tenglama nomeri belgilanadi. Shu bilan masala shartlariga kiruvchi barcha
sonlar jadvalda o'z o'rnini egallaydi. Shundan keyin jadvalning so'nggi qator va
so'nggi ustunini to'lg'azishga o'tiladi. Dastlab
- ustunda
tenglama nomeri belgilanadi. Shu bilan masala shartlariga kiruvchi barcha
sonlar jadvalda o'z o'rnini egallaydi. Shundan keyin jadvalning so'nggi qator va
so'nggi ustunini to'lg'azishga o'tiladi. Dastlab
![]()
![]() 1,
2, …, n (3.9)
1,
2, …, n (3.9)
formula bo'yicha ![]() lar
hisoblanadi. Agar barcha
lar
hisoblanadi. Agar barcha ![]() lar manfiy bo'lmasa
jadvalga mos tayanch yechim optimal yechim deyiladi va hisob to'xtatiladi. Agar
lar manfiy bo'lmasa
jadvalga mos tayanch yechim optimal yechim deyiladi va hisob to'xtatiladi. Agar
![]() lar orasida
manfiylari bo'lsa jadvalga mos tayanch yechim optimal emas, uni yaxshilash
kerak degan xulosa qilinadi. Buning uchun manfiy
lar orasida
manfiylari bo'lsa jadvalga mos tayanch yechim optimal emas, uni yaxshilash
kerak degan xulosa qilinadi. Buning uchun manfiy ![]() lar orasidan
eng kichigi joylashgan ustunni hal qiluvchi ustun deb belgilanadi. Agar bu
ustundagi Ak elementlari (
lar orasidan
eng kichigi joylashgan ustunni hal qiluvchi ustun deb belgilanadi. Agar bu
ustundagi Ak elementlari (![]() …,
…, ![]() lar
orasida musbatlari bo'lmasa masala yechimi yo'q degan xulosaga kelamiz. Agar
lar
orasida musbatlari bo'lmasa masala yechimi yo'q degan xulosaga kelamiz. Agar ![]()
![]() 1,
2, …, m lar orasida musbatlari bo'lsa
1,
2, …, m lar orasida musbatlari bo'lsa
* Ular uchun Өi = ![]() qiymatlar
hisoblanadi.
qiymatlar
hisoblanadi.
* ulardan kichigi Өi tanlanadi va bu
Өi jolashgan qator hal qiluvchi qator deb e'lon qilinadi, hamda
hal qiluvchi ustun va hal qiluvchi qatorlar kesishgan joydagi ![]() elementni
esa hal qiluvchi element deb belgilanadi.
elementni
esa hal qiluvchi element deb belgilanadi.
Bu jarayonni biz tahlil qilayotgan misol (1 – jadval)
uchun quyidagi tartibda bajariladi. Avvalo (3.9) formulalar bo'yicha ![]() larni
hisoblaymiz.
larni
hisoblaymiz.
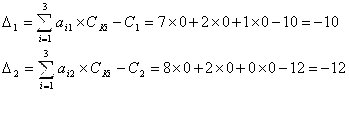

Bu qiymatlar jadvalga kiritilgan ![]() larni
taqqoslash yordamida eng kichigi
larni
taqqoslash yordamida eng kichigi ![]() ga mos kelgan 3
– ustun hal qiluvchi ustun deb belgilanadi. Bu ustun elementlari
yordamida Ө
ga mos kelgan 3
– ustun hal qiluvchi ustun deb belgilanadi. Bu ustun elementlari
yordamida Ө![]() =
= ![]() qiymatlar
hisoblanadi. Ө1 = 56/5=11,2 ; Ө2 = 10/1 = 10;
Ө3 = 6/1=6 ular ham jadvalga kiritilgan. Ө
qiymatlar
hisoblanadi. Ө1 = 56/5=11,2 ; Ө2 = 10/1 = 10;
Ө3 = 6/1=6 ular ham jadvalga kiritilgan. Ө![]() lar
orasida eng kichigi Ө3 ga mos kelgan 3 – qator hal
qiluvchi qator deb belgilanadi. Jadvalda bu ustun va qator strelka
bilan belgilangan. Ular kesishgan joydagi hal qiluvchi
lar
orasida eng kichigi Ө3 ga mos kelgan 3 – qator hal
qiluvchi qator deb belgilanadi. Jadvalda bu ustun va qator strelka
bilan belgilangan. Ular kesishgan joydagi hal qiluvchi ![]() element
ham qalin chegara bilan ajratilgan Agar hal qiluvchi element 1ga teng bo'lmasa
hal qiluvchi qator barcha elementlarini hal qiluvchi elementga bo'lib yuborib
bunga erishish mumkin. 3 – qator elementlarini 5ga ko'paytirib, 1 – qator
elementlaridan ayiramiz, so'ngra 3 – qator elementlarini 1ga ko'paytirib, 2 –
qator elementlaridan ayiramiz. Hosil bo'lgan qiymatlari 2 – jadval tarzida
ifodalangan.
element
ham qalin chegara bilan ajratilgan Agar hal qiluvchi element 1ga teng bo'lmasa
hal qiluvchi qator barcha elementlarini hal qiluvchi elementga bo'lib yuborib
bunga erishish mumkin. 3 – qator elementlarini 5ga ko'paytirib, 1 – qator
elementlaridan ayiramiz, so'ngra 3 – qator elementlarini 1ga ko'paytirib, 2 –
qator elementlaridan ayiramiz. Hosil bo'lgan qiymatlari 2 – jadval tarzida
ifodalangan.
|
i
|
Cj
Cik |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
1 |
0 |
A4 |
26 |
2 |
8 |
0 |
1 |
0 |
-5 |
3,25 |
|
2 |
0 |
A5 |
4 |
1 |
1 |
0 |
0 |
1 |
-1 |
4 |
|
3 |
25 |
A3 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
15 |
-12 |
0 |
0 |
0 |
25 |
|
![]()
![]()
2 – jadval
2 – jadval uchun ham (3.9) formulalar yordamida ![]() lar
hisoblanadi. Bu qiymatlar hisoblanib jadvalga kiritilgan.
lar
hisoblanadi. Bu qiymatlar hisoblanib jadvalga kiritilgan. ![]() lar
orasida manfiysi bo'lganligi uchun bu jadvalga mos tayanch yechim ham optimal yechim
emas. Shuning uchun manfiy
lar
orasida manfiysi bo'lganligi uchun bu jadvalga mos tayanch yechim ham optimal yechim
emas. Shuning uchun manfiy ![]() ga mos 2 –
ustun hal qiluvchi ustun deb belgilandi. Hal qiluvchi ustunning musbat
elementlari uchun Өj = 26/8 = 13/4= 3,25; Ө2
= 4/1=4 lar hisoblanadi. Eslatma: Manfiy va nol bo'lgan elementlar uchun
Өi hisoblanmaydi. Agar
ga mos 2 –
ustun hal qiluvchi ustun deb belgilandi. Hal qiluvchi ustunning musbat
elementlari uchun Өj = 26/8 = 13/4= 3,25; Ө2
= 4/1=4 lar hisoblanadi. Eslatma: Manfiy va nol bo'lgan elementlar uchun
Өi hisoblanmaydi. Agar ![]() lar orasida
musbatlari bo'lmasa, ChPM yechimi yo'q deb hisoblash to'xtatiladi. Bizning
misolda Өi lardan kichigi Ө1 = 3,25 ga mos
qator hal qiluvchi qator deb belgilandi. Simpleks usul algoritmiga ko'ra 3 –
jadvalni to'lg'azamiz.
lar orasida
musbatlari bo'lmasa, ChPM yechimi yo'q deb hisoblash to'xtatiladi. Bizning
misolda Өi lardan kichigi Ө1 = 3,25 ga mos
qator hal qiluvchi qator deb belgilandi. Simpleks usul algoritmiga ko'ra 3 –
jadvalni to'lg'azamiz.
|
i
|
Cj
Cik |
|
|
10 |
12 |
25
|
0 |
0 |
0 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
1 |
12 |
A2 |
3,25 |
0,25 |
1 |
0 |
0,125 |
0 |
-0,625 |
|
|
2 |
0 |
A5 |
0,75 |
0,75 |
0 |
0 |
-0,125 |
1 |
-0,375 |
|
|
3 |
25 |
A3 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
18 |
0 |
0 |
1,5 |
0 |
17,5 |
|
3 – jadval
3 – jadvalda barcha ![]()
![]() bo'lganligi
uchun bu jadvalga mos tayanch yechimda bazis o'zgaruvchilar
bo'lganligi
uchun bu jadvalga mos tayanch yechimda bazis o'zgaruvchilar ![]() deb
olinadi. Bazisga kirmagan o'zgaruvchilar esa nolga teng deb olinadi, ya'ni
deb
olinadi. Bazisga kirmagan o'zgaruvchilar esa nolga teng deb olinadi, ya'ni ![]() .
Bu yechim ChPM uchun optimal planni beradi. Yordamchi noma'lumlardan holi
bo'lgan holda berilgan ChPM uchun optimal plan
.
Bu yechim ChPM uchun optimal planni beradi. Yordamchi noma'lumlardan holi
bo'lgan holda berilgan ChPM uchun optimal plan ![]() ko'rinishda
belgilanadi. Bunda maqsad funksiyasi o'zining maksimal qiymatiga erishar ekan
va
ko'rinishda
belgilanadi. Bunda maqsad funksiyasi o'zining maksimal qiymatiga erishar ekan
va ![]() ga teng bo'ladi.
Keltirilgan misol planni bosqichma – bosqich yaxshilash, ya'ni simpleks
usulning barcha amallari va ularning bajarilish tartibini o'zida aks ettirgan.
Shuning bilan birga masalani ishlash tartibiga e'tibor berilsa, geometrik
usuldan farqli noma'lumlar soni ortgan, ya'ni masala murakkablashgan holda ham
bu usul shundayligicha tatbiq qilinaveradi. Tabiiy bunda simpleks jadval ustun
va qatorlar soni ortadi, shunga ko'ra hisoblashlar hajmi ham ortadi. Optimal
planga yetib borish uchun bajariladigan qadamlar soni ham ortishi mumkin.
ga teng bo'ladi.
Keltirilgan misol planni bosqichma – bosqich yaxshilash, ya'ni simpleks
usulning barcha amallari va ularning bajarilish tartibini o'zida aks ettirgan.
Shuning bilan birga masalani ishlash tartibiga e'tibor berilsa, geometrik
usuldan farqli noma'lumlar soni ortgan, ya'ni masala murakkablashgan holda ham
bu usul shundayligicha tatbiq qilinaveradi. Tabiiy bunda simpleks jadval ustun
va qatorlar soni ortadi, shunga ko'ra hisoblashlar hajmi ham ortadi. Optimal
planga yetib borish uchun bajariladigan qadamlar soni ham ortishi mumkin.
Simpleks usulning umumiy holdagi algoritmi (ixtiyoriy n , m lar uchun) dasturlangan va zamonaviy kompyuterlar matematik ta'minotida bu dasturlar mavjud. Ulardan foydalanish uchun iste'molchi, ya'ni tadqiqotchi, o'zi yechmoqchi bo'lgan ChPM ga taalluqli barcha qiymatlarni ko'rsatilgan tartibda kompyuter xotirasiga kiritib, shu dasturlarga murojaat qilishi yetarli.
Biz bu yerda e'tiborni qaratmoqchi bo'lgan yana bir hol, simpleks usul bo'yicha hisobni boshlashda dastlabki simpleks jadvalda bazis berilishi kerakligi. Bu bazis qanday tanlanadi, bunda nimalarga e'tiborni qaratish kerak?
§ 4. Chiziqli programmalash masalalari uchun bazis tanlash va masala shartlarini tanlangan bazisga moslashtirish.
Kanonik ko'rinishda berilgan ChPMni qaraymiz.
![]()
![]() 2,
…, m (4.1)
2,
…, m (4.1)
![]()
![]() 2,
…, n
2,
…, n
![]() (4.2)
(4.2)
Bu yerda avval ta'kidlaganimizdek m![]() bo'ladi, ya'ni (4.1) sistemaning yechimlari cheksiz ko'p. Shu yechimlar
orasidan (4.2) shartga mos keladigani, ya'ni maqsad funksiyasiga maksimal
qiymat beradiganini ajratib olish kerak. Buning uchun (4.1) sistema yechimlarini
ifodalash qoidasini va ular orasidan bazis o'zgaruchilarni ajratish usulini
aniqlashimiz kerak. (4.1) sistema matritsasi tartibi m × n bo'lganligi va
m
bo'ladi, ya'ni (4.1) sistemaning yechimlari cheksiz ko'p. Shu yechimlar
orasidan (4.2) shartga mos keladigani, ya'ni maqsad funksiyasiga maksimal
qiymat beradiganini ajratib olish kerak. Buning uchun (4.1) sistema yechimlarini
ifodalash qoidasini va ular orasidan bazis o'zgaruchilarni ajratish usulini
aniqlashimiz kerak. (4.1) sistema matritsasi tartibi m × n bo'lganligi va
m![]() n bo'lgani uchun
RgA ≤ m bo'ladi. Qulaylik uchun RgA=m deb olamiz.
Aksariyat hollarda bu shart bajariladi. A matritsadan o'zaro chiziqli erkli
bo'lgan m ta ustunni ajratib olamiz. Bu ustunlarni
n bo'lgani uchun
RgA ≤ m bo'ladi. Qulaylik uchun RgA=m deb olamiz.
Aksariyat hollarda bu shart bajariladi. A matritsadan o'zaro chiziqli erkli
bo'lgan m ta ustunni ajratib olamiz. Bu ustunlarni ![]() … ,
… , ![]() deb
belgilaymiz. Ular chiziqli erkli bo'lishi uchun shu ustun elementlaridan
tuzilgan
deb
belgilaymiz. Ular chiziqli erkli bo'lishi uchun shu ustun elementlaridan
tuzilgan
C = (![]() … ,
… , ![]()
matritsa determinanti noldan farqli bo'lishi kerak,
ya'ni ![]() . Tanlangan
bazisga mos tayanch yechimni topish uchun esa shu bazisga mos
. Tanlangan
bazisga mos tayanch yechimni topish uchun esa shu bazisga mos ![]() …
,
…
, ![]() noma'lumlardan
boshqa barcha
noma'lumlardan
boshqa barcha ![]() larni nolga
teng deb olamiz. Natijada (4.1) sistema soddalashib
larni nolga
teng deb olamiz. Natijada (4.1) sistema soddalashib
![]()
![]() 1,
2, …, m (4.3)
1,
2, …, m (4.3)
ko'rinishni oladi. Bu sistema m noma'lumli m ta
chiziqli algebraik tenglamalar sistemasi bo'lib qoladi. ![]() bo'lganligi
uchun uning yagona yechimi bo'ladi. Agar bu yechim uchun barcha
bo'lganligi
uchun uning yagona yechimi bo'ladi. Agar bu yechim uchun barcha ![]() bo'lsa
topilgan yechim tanlangan bazisdagi tayanch yechim deyiladi. Agar
bo'lsa
topilgan yechim tanlangan bazisdagi tayanch yechim deyiladi. Agar ![]() lar
orasida manfiylari ham chiqib qolsa, tanlangan bazisda tayanch yechim yo'q
deyiladi va boshqa bazisga o'tiladi. Tayanch yechimi mavjud bo'lgan bazis
tanlangach esa shu bazisdagi tayanch yechim optimallikka tekshiriladi. Bu esa
avvalgi paragrafda ko'rilgan usulda amalga oshiriladi. Faqat buning uchun
masala shartlari tanlangan bazisga moslashtirilishi kerak. Buning uchun
tanlangan bazisga mos C matritsa uchun teskari matritsa topiladi va (4.2)
sistema vektor ko'rinishida C-1 ga ko'paytiriladi. Bunda sistema
lar
orasida manfiylari ham chiqib qolsa, tanlangan bazisda tayanch yechim yo'q
deyiladi va boshqa bazisga o'tiladi. Tayanch yechimi mavjud bo'lgan bazis
tanlangach esa shu bazisdagi tayanch yechim optimallikka tekshiriladi. Bu esa
avvalgi paragrafda ko'rilgan usulda amalga oshiriladi. Faqat buning uchun
masala shartlari tanlangan bazisga moslashtirilishi kerak. Buning uchun
tanlangan bazisga mos C matritsa uchun teskari matritsa topiladi va (4.2)
sistema vektor ko'rinishida C-1 ga ko'paytiriladi. Bunda sistema
![]() (4.4)
(4.4)
ko'rinishini oladi. (4.4) sistema (4.2) maqsad funksiyasi bilan birgalikda dastlabki simpleks jadval uchun asos qilib olinadi. Simpleks jadvaldan tanlangan bazisdagi tayanch yechim optimal bo'lishi tekshirilishi mumkin. Keltirilgan mulohazalar va hisoblash jarayonini amaliy misolda tahlil qilamiz. Quyidagi ko'rinishdagi ChPM berilgan bo'lsin

![]()
![]()
Bu yerda matritsa ustunlari 4ta bo'lib ularni A1
, A2 , A3 , A4 vektorlar deb belgilasak ular
ikki o'lchovli fazo vektorlari (m=2) bo'lgani uchun bazis sifatida ulardan
ikkitasini olish mumkin. Bunda variantlar soni ![]() ta bo'ladi.
Ulardan ixtiyoriy bittasini, masalan A1 , A2 bazis
bo'lgan holni olsak
ta bo'ladi.
Ulardan ixtiyoriy bittasini, masalan A1 , A2 bazis
bo'lgan holni olsak ![]() bo'lib
bo'lib ![]() ekanligini
ko'ramiz. Bu bazisga mos yechimni topish uchun
ekanligini
ko'ramiz. Bu bazisga mos yechimni topish uchun ![]() deb olinadi va
sistema
deb olinadi va
sistema
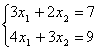
ko'rinishini oladi. Bu sistemani yechib ![]() ekanligini
ko'ramiz. Bu yerda
ekanligini
ko'ramiz. Bu yerda ![]() bo'lganligi
uchun bu bazisdagi yechim tayanch yechim bo'la olmaydi. Boshqa bazis tanlashga
to'g'ri keladi. Masalan A2 , A3 bazisni olsak
bo'lganligi
uchun bu bazisdagi yechim tayanch yechim bo'la olmaydi. Boshqa bazis tanlashga
to'g'ri keladi. Masalan A2 , A3 bazisni olsak
![]() ;
; ![]()
Demak A2 , A3 bazis bo'la oladi.
Bu bazisdagi yechimni topish uchun sistemada ![]() deb olinsa u
quyidagi ko'rinishni oladi
deb olinsa u
quyidagi ko'rinishni oladi

Bu sistemani yechib ![]() ekanligini
ko'ramiz. Bu yerda
ekanligini
ko'ramiz. Bu yerda ![]() , demak bu
bazisdagi
, demak bu
bazisdagi ![]() yechim tayanch
yechim bo'lar ekan. Bu yechimning optimal bo'lish bo'lmasligini tekshirish
uchun masala shartini tanlangan bazisga moslashtiramiz. Teskari matritsani
hisoblash qoidasiga ko'ra
yechim tayanch
yechim bo'lar ekan. Bu yechimning optimal bo'lish bo'lmasligini tekshirish
uchun masala shartini tanlangan bazisga moslashtiramiz. Teskari matritsani
hisoblash qoidasiga ko'ra
![]()
ekanligini ko'ramiz. Masala shartini shu teskari matritsaga ko'paytiramiz
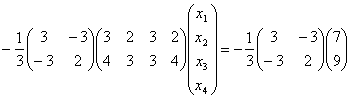
![]()
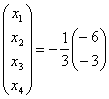
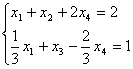
Shartlar bazisga moslashtirildi, ya'ni bazis vektorlar
A2 , A3 ga mos ustunlar birlik vektor ko'rinishini oldi.
Bu bazisga mos tayanch yechim ![]() optimalligini
tekshirish uchun simpleks jadval tuzamiz
optimalligini
tekshirish uchun simpleks jadval tuzamiz
|
I |
|
|
|
20 |
15 |
30 |
25 |
|
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Ө |
|
1 |
15 |
A2 |
2 |
1 |
1 |
0 |
2 |
|
|
2 |
30 |
A3 |
1 |
1/3 |
0 |
1 |
|
|
|
|
|
|
|
5 |
0 |
0 |
-15 |
|
Bu jadvaldan ko'rinadiki, tanlangan bazisga mos
tayanch yechim optimal emas ekan, chunki ![]() bo'layapti.
Rejani yaxshilash ychun bazisni almashtirish kerak. Buyog'i simpleks usul davom
ettirilishi mumkin.
bo'layapti.
Rejani yaxshilash ychun bazisni almashtirish kerak. Buyog'i simpleks usul davom
ettirilishi mumkin.
4. CHPM shartlari tanlangan bazisga moslashtirilsin. Shu bazisdagi tayanch yechim optimallikka tekshirilsin.
4.1 
![]()
![]()
4.2 
![]()
![]()
4.3 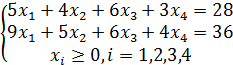
![]()
![]()
4.4 
![]()
![]()
4.5 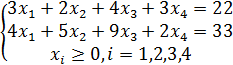
![]()
![]()
4.6 
![]()
![]()
§ 5. Transport masalasi
Chiziqli programmalash masalalaridan bir turi “transport masalasi” nomi bilan ma'lum bo'lgan matematik masalalarga keltiriladigan iqtisodiy masalalardan iborat bo'ladi. Ma'lumki, ishlab chiqaruvchi bilan iste'molchi orasidagi mol almashinuvi ya'ni ishlab chiqarilgan mahsulot yoki tayyrolangan homashyoni korxonalarga yetkazib berish transport vositalari va ularga sarflanadigan moliyaviy harajatlar bilan bog'liq. Bu harajatlarni minimallashtiruvchi variantlarni tanlash transport masalasining asosiy muammosi hisoblanadi.
Transport masalasining matematik modelini
ifodalashda umumiyatni cheklamagan holda sxematik tarzda quyidagi muammoni
tahlil qilamiz. Faraz qilaylik ma'lum homashyo turi zaxiralari saqlanuvchi yoki
tayyorlanuvchi n ta punkt bo'lsin. Bu punktlardagi homashyo miqdorlari
mos ravishda b1 , b2 , …, bn birliklardan
iborat bo'lsin. Bu yerda homashyo turiga ko'ra ma'lum bir o'lchov birligi
(tonna, metr, …) tanlangan bo'ladi. Shuningdek, keltirilgan homashyo asosida
ishlaydigan m ta korxona bo'lib, bu korxonalarning shu homashyoga
bo'lgan extiyojlari mos ravishda d1 , d2 , … dm
birliklardan iborat bo'lsin. Shuningdek homashyo punktlari hamda korxonalar
orasidagi yo'l sifati va masofasiga ko'ra homashyoni yetkazish uchun ketadigan
yo'l harajatlari koeffisintlari ma'lum bo'lsin. Ularni ![]()
![]() ,
,
![]() ; matritsa
ko'rinishida ifodalaymiz. Bunda matritsaning har bir elementi
; matritsa
ko'rinishida ifodalaymiz. Bunda matritsaning har bir elementi ![]() mos
ravishda
mos
ravishda ![]() - korxonaga
- korxonaga ![]() punktdan
bir birlik homashyo yetkazish uchun ketadigan transport harajatlarini
ifodalaydi. Aksariyat hollarda ishlab chiqarish korxonalari va homashyo
yetkazib beruvchi punktlar muqobil, ya'ni moslashtirilgan holda ishlaydi deb
hisoblanadi. Homashyo zaxiralari va korxonalarning bu homashyoga bo'lgan
ehtiyojlari bir-biriga to'la mos keladi. Matematik tarzda bu shart
punktdan
bir birlik homashyo yetkazish uchun ketadigan transport harajatlarini
ifodalaydi. Aksariyat hollarda ishlab chiqarish korxonalari va homashyo
yetkazib beruvchi punktlar muqobil, ya'ni moslashtirilgan holda ishlaydi deb
hisoblanadi. Homashyo zaxiralari va korxonalarning bu homashyoga bo'lgan
ehtiyojlari bir-biriga to'la mos keladi. Matematik tarzda bu shart
![]()
![]()
ko'rinishda ifodalanadi. Ayrim juz'iy chetlashishlarni hisobga olmaganda korxonalar to'liq quvvat bilan ishlaganda homashyolar to'liq sarflanadi. Faqat bu homashyolarni korxonalarga yetkazib berish kerak.
Masalaning matematik modelini ifodalash uchun
yuqorida keltirilgan barcha shartlarni matematik munosabatlar bilan
ifodalaymiz. Avvalo topilishi kerak bo'lgan optimal reja komponentlari ![]() punktdan
punktdan
![]() korxonaga
yetkazilishi kerak bo'lgan homashyo miqdorini
korxonaga
yetkazilishi kerak bo'lgan homashyo miqdorini ![]() deb belgilaymiz.
Shartga ko'ra
deb belgilaymiz.
Shartga ko'ra ![]() korxonaga
yetkaziladigan barcha homashyo miqdori korxona ehtiyoji
korxonaga
yetkaziladigan barcha homashyo miqdori korxona ehtiyoji ![]() ga
teng bo'lishi kerak. Bu shartni
ga
teng bo'lishi kerak. Bu shartni
![]()
![]() 1
, 2 , … , m (2)
1
, 2 , … , m (2)
ko'rinishda ifodalash mumkin, ya'ni barcha m ta
korxona uchun bu shart bajarilishi kerak. Bunday shartni homashyo punktlari
uchun ham ifodalash mumkin, ya'ni ![]() - homashyo
punktidan chiqarilgan jami homashyo miqdori
- homashyo
punktidan chiqarilgan jami homashyo miqdori ![]() ga teng
bo'lishi kerak.
ga teng
bo'lishi kerak.
Bu shart matematik tarzda
![]()
![]() 1,
2 , …, n (3)
1,
2 , …, n (3)
ko'rinishini oladi. Bu shartlar bajarilgan holda
shunday ![]() larni topish
kerakki jami yo'l harajatlari minimal bo'lsin. Keltirilgan normativlarga ko'ra
larni topish
kerakki jami yo'l harajatlari minimal bo'lsin. Keltirilgan normativlarga ko'ra ![]() korxonaga
korxonaga
![]() punktdan
punktdan ![]() birlik
homashyo keltiriladigan bo'lsa, yo'l xarajatlari bir birlik homashyo miqdori
uchun
birlik
homashyo keltiriladigan bo'lsa, yo'l xarajatlari bir birlik homashyo miqdori
uchun ![]() ga teng ekanligi
ma'lum bo'lgani uchun jami
ga teng ekanligi
ma'lum bo'lgani uchun jami ![]()
![]() pul
birligiga teng bo'ladi. Bu xarajatlarni barcha korxonalar va homashyo bazalari
bo'yicha qo'shib chiqsak jami xarajatlar kelib chiqadi va u quyidagicha
ifodalanadi.
pul
birligiga teng bo'ladi. Bu xarajatlarni barcha korxonalar va homashyo bazalari
bo'yicha qo'shib chiqsak jami xarajatlar kelib chiqadi va u quyidagicha
ifodalanadi.
![]() …,
…,
![]() (4)
(4)
Tabiiy, barcha chiziqli programmalash masalalarida
bo'lganidek, bu yerda ham ![]() bo'lishi
kerakligi qayd etiladi.
bo'lishi
kerakligi qayd etiladi.
Shunday qilib (1), (2), (3) shartlar bajarilgan
holda (4) maqsad funksiyasining minimal qiymatini ta'minlovchi plan matritsasi
X=(![]() ni topish
masalasi transport masalasi deyiladi. Bu yerda b1 , b2 ,
…, bm , d1 , d2 , …, dn berilgan
miqdorlar ; C=(
ni topish
masalasi transport masalasi deyiladi. Bu yerda b1 , b2 ,
…, bm , d1 , d2 , …, dn berilgan
miqdorlar ; C=(![]() ham ma'lum
matritsa. C(mxn) to'g'ri to'rtburchakli matritsa ham ma'lum matritsa deb
hisoblanadi. Aksariyat hollarda
ham ma'lum
matritsa. C(mxn) to'g'ri to'rtburchakli matritsa ham ma'lum matritsa deb
hisoblanadi. Aksariyat hollarda ![]() noma'lumlar soni
m×n shartlar soni m+n dan katta bo'lib, (1), (2), (3) shartlar bilan
berilgan chiziqli algebraik tenglamalar sistemasi cheksiz ko'p yechimga ega
bo'ladi. Ana shu cheksiz ko'p yechimlar orasidan (4) maqsad funksiyasining
minimumini ta'minlovchi variant, ya'ni optimal plan (reja)ni tanlashni talab
qilinadi.
noma'lumlar soni
m×n shartlar soni m+n dan katta bo'lib, (1), (2), (3) shartlar bilan
berilgan chiziqli algebraik tenglamalar sistemasi cheksiz ko'p yechimga ega
bo'ladi. Ana shu cheksiz ko'p yechimlar orasidan (4) maqsad funksiyasining
minimumini ta'minlovchi variant, ya'ni optimal plan (reja)ni tanlashni talab
qilinadi.
Keltirilgan transport masalasining matematik modeli (1) – (4) ko'rinishiga qarab ortiqcha tafsilotlarsiz shuni qayd etishimiz mumkinki, kommunikatsion tizimlar : ular avtomabil, poyezd yo'li bo'ladimi, gaz yoki suv yetkazuvchi quvurlar bo'ldimi, elektr quvvatini yetkazuvchi yuqori kuchlanishli elektr uzatish tizimlari bo'ladimi barchasida shartli ravishda yetkazuvchi, iste'molchi va “transport” harajatlarini kiritish mumkin. Bu holda ham aynan (1) – (4) ko'rinishdagi optimallashtirish masalasini hosil qilishimiz mumkin.
Transport masalasi ifodalanishiga ko'ra nisbatan
soddadek tuyulishi mumkin. Haqiqatdan ham barcha shartlar koeffitsientlari
faqat birlardan iborat tenglamalar bo'ladi. Transport masalasining murakkabligi
noma'lumlarni ko'pligida bo'lib unga odatdagi oddiy simpleks usulini tatbiq
qilish ham imkoniyat darajasidan ancha yuqori bo'lib ketar ekan. Masalan n=10
, m=10 bo'lgan holda ham noma'lumlar soni n×m=100, shartlar soni
esa m+n-1=19ta bo'lib, shartlar matritsasining rangi 19 bo'lgan holda (1) – (3)
shartlar bo'yicha kelib chiqadigan tayanch yechimlar soni ![]() ta
bo'ladi. Simpleks usul esa tayanch yechimlaridan optimal yechimni ajratishga
imkoniyat beradi. Bu holda simpleks usul bo'yicha necha qadam qo'yilishi kerak,
buni tasavvur qilish ham qiyin. Agar transport masalasini biror tuman
(miqyosida, masshtabida) qaralganda ham yetarlicha murakkab bo'ladi. Viloyat
yoki respublika (miqyosida, masshtabida) qaraladigan bo'lsa masala yanada
murakkablashib ketishi aniq.
ta
bo'ladi. Simpleks usul esa tayanch yechimlaridan optimal yechimni ajratishga
imkoniyat beradi. Bu holda simpleks usul bo'yicha necha qadam qo'yilishi kerak,
buni tasavvur qilish ham qiyin. Agar transport masalasini biror tuman
(miqyosida, masshtabida) qaralganda ham yetarlicha murakkab bo'ladi. Viloyat
yoki respublika (miqyosida, masshtabida) qaraladigan bo'lsa masala yanada
murakkablashib ketishi aniq.
Biz bu yerda transport masalasi ham odatdagi ChPM ekanligini, hamda unga ham simpleks usulni tatbiq qilish mumkinligini namoyish qilish maqsadida oddiy bir masalani ko'rib chiqamiz va tahlil qilamiz. Faraz qilaylik 2ta g'isht zavodi bo'lib ularning ishlab chiqarish quvvatlari mos ravishda 35 mashina va 45 mashina g'ishtga teng bo'lsin. Shuningdek bu g'ishtlarga talabgor 2 ta qurilish bo'lib, ularga mos ravishda 30 mashina va 50 mashina g'isht kerak bo'lsin. Talab va taklif muvozanati saqlangan. Agar 1 – qurilishga 1 – zavoddan 1 mashina keltirish narxi (yo'l xarajati) 15ming so'm, 2 – zavoddan keltirish narxi esa 12ming so'm; shuningdek 2 – qurilishga 1-, 2-zavoddan 1 mashina g'isht keltirish narxi mos ravishda 20ming va 18 ming so'm bo'lsin. Zavodlardan qurilishlarga g'isht yetkazib berish shunday rejasini tuzingki, transport harajatlari minimal bo'lsin. Transport masalasining shartlarini jadval ko'rinishida ifodalash tahlil uchun qulay bo'lganligi uchun odatda ularni jadval ko'rinishida ifodalagan ma'qul. Xususan yuqorida keltirilgan masala shartlarini quyidagi jadval ko'rinishida ifodalash mumkin.
|
zav qur |
1 |
2 |
Σ |
|
1 |
15
|
12
|
30 |
|
2 |
20
|
18
|
50 |
|
Σ |
35 |
45 |
80 |
jadvaldagi raqamlar masala mohiyatini aks ettiradi.
So'nggi qatorda zavodlar quvvatlari, so'nggi ustunda esa qurilishlar
ehtiyojlari aks etgan. Ichki kataklar tepa burchagida yo'l harajatlari koeffitsienti
aks etgan. Bu yerda qulaylik uchun noma'lumlarni ![]() deb belgilangan,
aslida
deb belgilangan,
aslida ![]() bo'lishi kerak
edi. Bu yerda maqsad, masalani simpleks usulga tushirish qulay bo'lishi uchun
shu yo'l tanlangan. Shartlarning matematik ifodasiga o'tamiz.
bo'lishi kerak
edi. Bu yerda maqsad, masalani simpleks usulga tushirish qulay bo'lishi uchun
shu yo'l tanlangan. Shartlarning matematik ifodasiga o'tamiz.

![]()
![]()
![]()
![]()
![]()
![]()
![]() shartlar
orasidan chiziqli erklilari tanlanadi. Bevosita tekshirish yo'li bilan
shartlar
orasidan chiziqli erklilari tanlanadi. Bevosita tekshirish yo'li bilan ![]() shartlardan
shartlardan
![]() shart kelib
chiqishini ko'rishimiz mumkin. Sxematik tarzda tengliklar ustida amallar
bajarish qoidasiga ko'ra
shart kelib
chiqishini ko'rishimiz mumkin. Sxematik tarzda tengliklar ustida amallar
bajarish qoidasiga ko'ra ![]() ekanligini
ko'ramiz. Demak, bu yerda ChPMni
ekanligini
ko'ramiz. Demak, bu yerda ChPMni
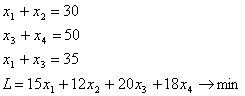
ko'rinishda ifodalash mumkin. Bu masalaga simpleks
usulni tatbiq qilish uchun ChPM shartlaridan bazislarni ajratish (ustunlari
orasida birlik vektorlarni hosil qilish) jarayonini namoyish etamiz.
Sistemadagi ![]() ga mos
koeffitsientlar
ga mos
koeffitsientlar ![]() vektorlarni
hosil qiladi. Ulardan tuzilgan matritsa ozod hadlar ustuni bilan to'ldirilsa
vektorlarni
hosil qiladi. Ulardan tuzilgan matritsa ozod hadlar ustuni bilan to'ldirilsa

matritsa hosil bo'ladi. Bu matritsaning 2-,4-ustunlari
bazis holatida ![]() 0; 0;
0)ekanligini ko'ramiz. Agar 3 – qatorini -1 ga ko'paytirib 2 – qatorga qo'shsak
3 – ustun ham bazis ko'rinishini oladi.
0; 0;
0)ekanligini ko'ramiz. Agar 3 – qatorini -1 ga ko'paytirib 2 – qatorga qo'shsak
3 – ustun ham bazis ko'rinishini oladi.
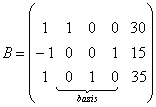
Bu matritsa berilgan shartlarning shakl almashtirilib

ko'rinishga keltirilganligini aks ettiradi. Bu ko'rinishdan simpleks jadvalga o'tamiz va bu jadvalga mos planni optimallikka tekshiramiz.
|
C C |
|
|
15 |
12 |
20 |
18 |
|
|
|
baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Өi |
|
12 |
A2 |
30 |
1 |
1 |
0 |
0 |
|
|
18 |
A4 |
15 |
-1 |
0 |
0 |
1 |
|
|
20 |
A3 |
35 |
1 |
0 |
1 |
0 |
|
|
|
|
|
-1 |
0 |
0 |
0 |
|
Bu yerda ![]() formula bo'yicha
hisoblangan. Qolganlari ham shunga o'xshash hisoblanadi. Masala minimumini
topishga mo'ljallangan bo'lsa,
formula bo'yicha
hisoblangan. Qolganlari ham shunga o'xshash hisoblanadi. Masala minimumini
topishga mo'ljallangan bo'lsa, ![]() lar orasida
musbatlari yo'q bo'lsa, jadvalga mos plan optimal plan bo'ladi. Bizda ana
shunday hol kuzatilyapti. Demak bu masalada optimal plan
lar orasida
musbatlari yo'q bo'lsa, jadvalga mos plan optimal plan bo'ladi. Bizda ana
shunday hol kuzatilyapti. Demak bu masalada optimal plan ![]() bo'lar
ekan. Bu holda harajatlar minimal bo'lib,
bo'lar
ekan. Bu holda harajatlar minimal bo'lib, ![]() ming so'm
bo'lar ekan. Masala shartlari va yechimini ifodalovchi jadval
ming so'm
bo'lar ekan. Masala shartlari va yechimini ifodalovchi jadval
|
Zav
qur |
1 |
2 |
Σ |
|
1 |
15 0 |
12 30 |
30 |
|
2 |
20 35 |
13 15 |
50 |
|
Σ |
35 |
45 |
80 |
ko'rinishda bo'ladi.
Tahlil to'laqonli ko'rinishni olishini namoyish qilish uchun yuqoridagi masalada faqat bitta narx 1 – zavoddan 2 – qurilishga 1 mashina g'isht olib borish narxi 30ming so'mga o'zgargan bo'lsin deb faraz qilamiz. Bunda faqat maqsad funksiyasi ko'rinishi o'zgaradi, ya'ni
![]()
ko'rinishni oladi. Simpleks jadvalda ham faqat narxlar
![]() ga mos qator va
ustunlargina o'zgaradi va quyidagi ko'rinishni oladi
ga mos qator va
ustunlargina o'zgaradi va quyidagi ko'rinishni oladi
|
C C |
|
|
15 |
12 |
30 |
18 |
|
|
|
Baz |
A0 |
A1 |
A2 |
A3 |
A4 |
Өi |
|
12 |
A2 |
30 |
1 |
1 |
0 |
0 |
30 |
|
18 |
A4 |
15 |
-1 |
0 |
0 |
1 |
|
|
30 |
A3 |
35 |
1 |
0 |
1 |
0 |
35 |
|
|
|
|
9 |
0 |
0 |
0 |
|
![]()
![]()
Bu jadvalga mos plan ![]() optimal emas,
chunki
optimal emas,
chunki ![]() . Bu planga
ko'ra
. Bu planga
ko'ra ![]() ming. Planni
yaxshilash uchun jadvaldan
ming. Planni
yaxshilash uchun jadvaldan
![]() larni
hisoblaymiz (faqat
larni
hisoblaymiz (faqat ![]()
![]() lar
uchun). min
lar
uchun). min![]() ga mos 1 –
qatorni hal qiluvchi qator deb belgilaymiz. Uning yordamida 1 – ustunni bazis
ustunga aylantiramiz. Buning uchun 1 – qatorni 2 – qatorga qo'shamiz, hamda
(-1) ga ko'paytirib 3 – qatorga qo'shamiz. Natijada yangi simpleks jadvalni
hosil qilamiz
ga mos 1 –
qatorni hal qiluvchi qator deb belgilaymiz. Uning yordamida 1 – ustunni bazis
ustunga aylantiramiz. Buning uchun 1 – qatorni 2 – qatorga qo'shamiz, hamda
(-1) ga ko'paytirib 3 – qatorga qo'shamiz. Natijada yangi simpleks jadvalni
hosil qilamiz
|
C C |
|
|
15 |
12 |
30 |
18 |
|
|
|
Bazis |
A0 |
A1 |
A2 |
A3 |
A4 |
Ө |
|
15 |
A1 |
30 |
1 |
1 |
0 |
0 |
|
|
18 |
A4 |
45 |
0 |
1 |
0 |
1 |
|
|
30 |
A3 |
5 |
0 |
-1 |
1 |
0 |
|
|
|
|
|
0 |
-17 |
0 |
0 |
|
Bu jadvalda ![]() lari yo'q
bo'lgani uchun bu jadvalga mos tayanch yechim
lari yo'q
bo'lgani uchun bu jadvalga mos tayanch yechim ![]() optimal plan
bo'ladi. Bu plan bo'yicha ketadigan transport harajatlari
optimal plan
bo'ladi. Bu plan bo'yicha ketadigan transport harajatlari
![]() ming so'm bo'lib
avvalgisidan 270ming so'mga kam bo'lar ekan.
ming so'm bo'lib
avvalgisidan 270ming so'mga kam bo'lar ekan.
Bu usul bilan ixtiyoriy transport masalasini ham odatdagi ChPM ko'rinishiga keltirish mumkin ekan. Faqat shartli ravishda n ta ishlab chiqaruvchi va ularga bog'langan m ta iste'molchi bo'lgan transport masalasini tasavvur qilsak, bu unchalik oson ish emas ekanligini to'la tasavvur qilishimiz mumkin. Transport masalasini ba'zi kichik hajmdagi hollarda mantiqiy muhokamalar asosida ham yechish mumkin ekan. Bunga misol
|
T n |
1 |
2 |
Σ |
|
|
1 |
15 |
20 |
20 |
|
|
2 |
18 |
13 |
60 |
|
|
3 |
14 |
18 |
40 |
|
|
Σ |
70 |
50 |
12 |
|
sifatida jadvalda keltirilgan 2 ta ta'minotchi va 3ta
iste'molchi bilan bog'liq transport masalasi namunasi keltirilgan. Unda bo'sh
qolgan yarim kataklar aynan topilishi kerak bo'lgan ta'minot rejasini aks
ettiruvchi 6 ta noma'lum ![]() larga mos
keladi. Mantiqan dastlab eng arzon yo'nalish tanlanishi kerak. Demak avvalo
yo'l harajati 13 bo'lgan katakka iloji boricha ko'proq jo'natish miqdorini
qo'ygan ma'qul. Bu qiymat 50 ekanligi ko'rinib turibdi. U holda shu qatorning birinchi
katagiga 10 qo'yishimiz kerak bo'ladi. Shuningdek ikkinchi ustun qolgan ikki
katagi 0 bo'lishi kerakligi ko'rinib turibdi. Qolgan kataklar ham o'z - o'zidan
bir qiymatli to'ldirilishi mumkin bo'lib qoladi. Xulosa qilib aytganda
larga mos
keladi. Mantiqan dastlab eng arzon yo'nalish tanlanishi kerak. Demak avvalo
yo'l harajati 13 bo'lgan katakka iloji boricha ko'proq jo'natish miqdorini
qo'ygan ma'qul. Bu qiymat 50 ekanligi ko'rinib turibdi. U holda shu qatorning birinchi
katagiga 10 qo'yishimiz kerak bo'ladi. Shuningdek ikkinchi ustun qolgan ikki
katagi 0 bo'lishi kerakligi ko'rinib turibdi. Qolgan kataklar ham o'z - o'zidan
bir qiymatli to'ldirilishi mumkin bo'lib qoladi. Xulosa qilib aytganda ![]() ekanligini
topamiz. Bunda transport harajatlari
ekanligini
topamiz. Bunda transport harajatlari![]()
bo'lishini ko'ramiz. Natijada masala shartlari va yechimini ifodalovchi jadvalni hosil qilamiz
|
T n |
1 |
2 |
Σ |
|
1 |
15 20 |
20 0 |
20 |
|
2 |
18 10 |
13 50 |
60 |
|
3 |
14 40 |
18 0 |
40 |
|
Σ |
70 |
50 |
120 |
Yuqorida keltirilgan masalani planni bosqichma – bosqich yaxshilash usuli bo'yicha simpleks jadvallar asosida ishlab ko'ramiz. Unga mos ChPM quyidagicha ifodalanadi.
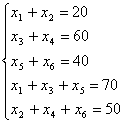
![]()
Bu masala shartlaridan beshinchisi chiziqli bog'liq. Qolgan qismi uchun kengaytirilgan matritsasini yozamiz va bu matritsada rangi to'rt bo'lganligi uchun to'rtta bazis ustun hosil qilamiz. Masalan qulaylik uchun 1-,3-,4-,6- ustunlarni bazis ustunlarga aylantirish holini ko'ramiz.
![]()
![]()
![]()
![]()

![]()

![]()
![]()

Hosil bo'lgan matritsa ko'rsatilgan tartibda 1 – qatorni (-1)ga ko'paytirib 4 – qatorga qo'shish, so'ngra 4 – qatorni (-1) ga ko'paytirib 2 – qatorga qo'shish yordamida masala shartlarini ekvivalent tarzda o'zgartirishni aks ettiradi. Matritsa ko'rinishidan yana sistema ko'rinishiga o'tilsa u
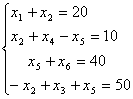
ko'rinishini
oladi. Bevosita tekshirish bilan bazis o'zgaruvchilar ![]() qolganlari
qolganlari
![]() ekanligini
ko'rishimiz
ekanligini
ko'rishimiz
mumkin. Masalaning bu ko'rinishidan dastlabki simpleks
jadvalni tuzib, bu jadvalga mos tayanch yechimni optimallikka tekshirishimiz
mumkin. Agar yechim optimal bo'lmasa, keyingi bosqichga o'tamiz, ya'ni ![]() lar
orasida manfiysi bo'lsa, hal qiluvchi qator va ustunlarini topib bazisni
almashtiramiz. Bizning misol uchun simpleks jadval
lar
orasida manfiysi bo'lsa, hal qiluvchi qator va ustunlarini topib bazisni
almashtiramiz. Bizning misol uchun simpleks jadval
|
C C |
|
|
15 |
20 |
18 |
13 |
14 |
18 |
|
|
|
baz |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
15 |
A1 |
20 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
13 |
A4 |
10 |
0 |
1 |
0 |
1 |
-1 |
0 |
|
|
18 |
A6 |
40 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
18 |
A3 |
50 |
0 |
-1 |
1 |
0 |
1 |
0 |
50 |
|
|
|
|
0 |
-10 |
0 |
0 |
9 |
0 |
|
![]()
ko'rinishda bo'ladi.
Bu jadvalda ChPM minimumga ishlanayotganligi uchun ![]() lar
borligi plan optimal emasligini bildiradi.
lar
borligi plan optimal emasligini bildiradi. ![]() ga mos 5 – ustun
hal qiluvchu ustun, shu ustun elementlari yordamida hisoblangan Ө3
=
ga mos 5 – ustun
hal qiluvchu ustun, shu ustun elementlari yordamida hisoblangan Ө3
= ![]() va Ө4
=
va Ө4
= ![]() lar orasidan
kichigiga mos keluvchi 3 – qator hal qiluvchi qator deb belgilandi va bazisdagi
A6 ustun A5 ustunga almashtirilishi kerak. Buning uchun
jadvalning 3 – qatorini 2 – qatorga qo'shamiz, hamda 3 – qatorni (-1)ga
ko'pytirib 4 – qatorga qo'shamiz. Shunda 5 – ustun ham bazis ustun ko'rinishini
oladi va quyidagi simpleks jadval hosil bo'ladi.
lar orasidan
kichigiga mos keluvchi 3 – qator hal qiluvchi qator deb belgilandi va bazisdagi
A6 ustun A5 ustunga almashtirilishi kerak. Buning uchun
jadvalning 3 – qatorini 2 – qatorga qo'shamiz, hamda 3 – qatorni (-1)ga
ko'pytirib 4 – qatorga qo'shamiz. Shunda 5 – ustun ham bazis ustun ko'rinishini
oladi va quyidagi simpleks jadval hosil bo'ladi.
|
C C |
|
|
|
|
|
|
|
|
|
|
|
Bazis |
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
Өi |
|
15 |
A1 |
20 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
13 |
A4 |
50 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
14 |
A5 |
40 |
0 |
0 |
0 |
0 |
1 |
-1 |
|
|
18 |
A3 |
10 |
0 |
-1 |
1 |
0 |
0 |
-1 |
|
|
|
|
|
0 |
-10 |
0 |
0 |
0 |
-9 |
|
Bu jadvalga ko'ra ![]() lar orasida
musbatlari yo'q bo'lganligi uchun bu jadvalga mos tayanch yechim
lar orasida
musbatlari yo'q bo'lganligi uchun bu jadvalga mos tayanch yechim ![]() optimal
yechim bo'ladi. Shu masala uchun mantiqiy mulohazalarga ko'ra tanlangan
dastlabki yechim ham xuddi shunday bo'lgan edi. Bu natijadan ikki muhim
xulosani keltirib chiqarishimiz mumkin ekan. Birinchisi – transport masalasini
yechishda mantiqiy mulohazalarga asoslanishimiz mumkin ekan. Bunday usulda
tanlangan yechim optimal yechim bo'lib qolishi ham mumkin, bo'lmagan taqdirda
ham optimal yechimga yaqin yechim bo'lib simpleks usul yordamida yaxshilash
bosqichlari soni kam bo'ladi. Ikkinchidan – transport masalasi ham odatdagi
ChPMga keltirilishi mumkin bo'lib, unga ham an'anviy usullarni tatbiq qilish
mumkin ekan. Bunda faqat bir narsani unutmasligimiz kerak. Yuqorida
ta'kidlanganidek, ta'minotchilar soni n va iste'molchilar soni m
ortgan sari noma'lumlar soni n×m keskin ortib odatdagi usullarni
tatbiq qilish mushkullashib boraveradi. Bunday hollarda masalani yechish uchun iteratsion
usullardan foydalanish ma'qulroq bo'ladi.
optimal
yechim bo'ladi. Shu masala uchun mantiqiy mulohazalarga ko'ra tanlangan
dastlabki yechim ham xuddi shunday bo'lgan edi. Bu natijadan ikki muhim
xulosani keltirib chiqarishimiz mumkin ekan. Birinchisi – transport masalasini
yechishda mantiqiy mulohazalarga asoslanishimiz mumkin ekan. Bunday usulda
tanlangan yechim optimal yechim bo'lib qolishi ham mumkin, bo'lmagan taqdirda
ham optimal yechimga yaqin yechim bo'lib simpleks usul yordamida yaxshilash
bosqichlari soni kam bo'ladi. Ikkinchidan – transport masalasi ham odatdagi
ChPMga keltirilishi mumkin bo'lib, unga ham an'anviy usullarni tatbiq qilish
mumkin ekan. Bunda faqat bir narsani unutmasligimiz kerak. Yuqorida
ta'kidlanganidek, ta'minotchilar soni n va iste'molchilar soni m
ortgan sari noma'lumlar soni n×m keskin ortib odatdagi usullarni
tatbiq qilish mushkullashib boraveradi. Bunday hollarda masalani yechish uchun iteratsion
usullardan foydalanish ma'qulroq bo'ladi.
Masalalar
5. Keltirilgan jadval qiymatlarga mos tansport masalasini tuzing. Masala tayanch yechimini minimal harajatlar usuli bo’yicha aniqlang va uni optimallikka tekshiring.
5.1
|
|
1 |
2 |
3 |
∑ |
|
1 |
11
|
15
|
13
|
200 |
|
2 |
14
|
12
|
10
|
300 |
|
∑ |
150 |
250 |
100 |
500 |
5.2
|
|
1 |
2 |
3 |
∑ |
|
1 |
60
|
45
|
60
|
400 |
|
2 |
55 |
60
|
58
|
500 |
|
∑ |
200 |
400 |
300 |
900 |
5.3
|
|
1 |
2 |
3 |
∑ |
|
1 |
30
|
25
|
35
|
500 |
|
2 |
25 |
35
|
20
|
300 |
|
∑ |
250 |
350 |
200 |
800 |
5.4
|
|
1 |
2 |
3 |
∑ |
|
1 |
25
|
20
|
18
|
400 |
|
2 |
15 |
22
|
24
|
300 |
|
∑ |
250 |
150 |
300 |
700 |
5.5
|
|
1 |
2 |
3 |
∑ |
|
1 |
40
|
50
|
30
|
600 |
|
2 |
30 |
40
|
50
|
400 |
|
∑ |
300 |
500 |
200 |
|
6 § Ñhiziqli programmalash masalalari uchun egizak masalalar
Bu yerda chiziqli programmalash masalalari nazariyasida muhim o’rin egallagan egizak masalalar tushunchasida to’xtalamiz va ularning iqtisodiy ma’nosini tahlil qilamiz. ChPM umumiy ko’rinishini esga olsak (2 §).
 (2.1)
(2.1)
![]()
 (2.2)
(2.2)
Shartlarga ko’ra ![]() larni topish talab qilinar edi. Masala
tarkibidagi har bir koeffitsiyentga o’z vaqtida izoh berilgan edi. Aynan shu
koeffitsiyentlar yordamida quyidagi masalani tuzamiz.
larni topish talab qilinar edi. Masala
tarkibidagi har bir koeffitsiyentga o’z vaqtida izoh berilgan edi. Aynan shu
koeffitsiyentlar yordamida quyidagi masalani tuzamiz.
 (6.1)
(6.1)
![]()
 (6.2)
(6.2)
Hosil bo’lgan (6.1) – (6.2) masala (2.1) – (2.2) ChPM ga nisbatan egizak masala deyiladi. Agar (2.1) – (2.2) masala yechimi mavjud bo’lsa (6.1) – (6.2) masala yechimi ham mavjud bo’lar ekan. Shu bilan birga bu yechimlar, yani optimal yechimlar uchun
![]()
tenglik o’rinli bo’lar ekan. Bu holat ba’zi murakkab ChPM lar uchun egizak masala yordamida tahlil o’tkazishga imkoniyat beradi. E’tibor bersak (2.1) – (2.2) va (6.1) – (6.2) masalalar aynan bir xil koeffitsiyent orqali ifodalanishi hamda ularning yechimlari ham bir xilligi bu masalalarni “ egizak masalalar ” deb atalishiga sabab bo’lgan.
Tahlil va xulosalarni soddalashtirish uchun avvalgi paragraflarda keltirilgan masalalardan foydalanamiz. Xususan § 1 da ko'rilgan (1.1) – (1.2) masalani olsak
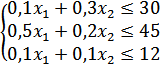 (1.1)
(1.1)
![]()
uning to’la
tahlili va yechimi § 1 da keltirilgan. Unga ko’ra optimal reja c (30;90)
nuqtada bo’lib, bunda ![]() bo’lib
bo’lib ![]() ekanligini ko’rgan edik. Yuqorida
keltirilgan tartibga ko’ra (1.1) – (1.2) masala uchun egizak masala
tuzamiz.
ekanligini ko’rgan edik. Yuqorida
keltirilgan tartibga ko’ra (1.1) – (1.2) masala uchun egizak masala
tuzamiz.
![]() (6.3)
(6.3)
![]() (6.4)
(6.4)
Hosil bo’lgan (6.3) – (6.4) egizak masalani geometrik usulda yechish uchun uni kanonik ko’rinishga keltiramiz.

![]()
Bu yerdagi har bir shart OY1 Y2 Y3 koordinat fazosida tekislikni ifodalaydi. Ularni chizmada ifodalasak, egizak masala uchun ham MBES qavariq soha bo’lishini ko’ramiz. Bu holat barcha egizak masalalar uchun o’rinli bo’lar ekan. (6.3) – (6.4) masala shartlariga mos mumkin bo’lgan yechimlar sohasi MBES chizmada keltirilgan
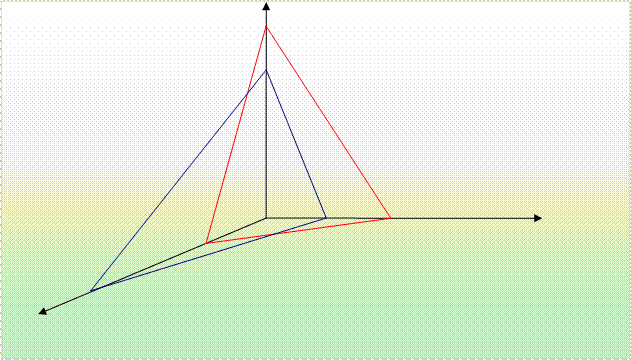 Y3
Y3
M3 14000
1000
M4
O
7000 Y2
4666 2000 M2
M5
1000
Y1 M1
MBES OY1
Y2 Y3 koordinat fazosining 1 – oktantida (6.3) shartlar bilan berilgan
tekisliklardan yuqoridagi soha bo’ladi. Bu qavariq sohaning chegaralaridagi
uchlari M1 , M2 , M3 , M4 , M5 nuqtalarida bo’ladi. Optimal yechimni aynan shu nuqtalardan birida
izlash kerak. Chizmadan ko’rinadiki M1 (10000; 0; 0), M2 (0; 7000; 0), M3 (0;0;14000), M4 (2000;
0; 8000), M5 (1231; 3846; 0). Bu yerda M4 , M5 nuqtalar koordinatalari (6.3) sistemadan ![]() va
va ![]() deb topilgan. Optimal yechimni Q (Y1,Y2, Y3 ) qiymatlarini taqqoslash orqali topamiz.
deb topilgan. Optimal yechimni Q (Y1,Y2, Y3 ) qiymatlarini taqqoslash orqali topamiz.
Q(M1) = 300000 ; Q(M2) = 315000 ; Q(M3) = 168000 ; Q(M4) = 156000 ; Q(M5) = 170775. Bu yerdan M4 nuqtada eng kichik qiymat bo’lishini ko’ramiz. Haqiqatdan ham
![]()
bo’lar ekan.
Egizak masala yechimini simpleks usulda asosiy masala bilan birgalikda bir yo’la topish mumkin ekan. Buni bevosita amaliy masalani yechish jarayonida namoyish qilamiz.
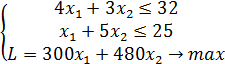
masala uchun egizak masala

Geometrik usulda asosiy masala uchun OX1X2 koordinat tekisligida MBES ni chizib tayanch yechimlar M1(8;0) , M2(0;5), M3(5;4) nuqtalarda bo’lib, bu nuqtalarda maqasad funksiya qiymatlari L1 = 2400, L2 = 2400, L3 = 5 · 300 + 4 · 480 = 3420 . Taqqoslash natijasida optimal yechim M3(5;4) nuqtada bo’lib, bu nuqtada ![]() ekanligini ko’ramiz.
Shuningdek egizak masala uchun OY1 Y2 tekisligida MBES ni tuzib tayanch yechimlar M1(160;0), M2(0;300), M3( 60;60) nuqtada bo’lishini ko’ramiz. Bu nuqtalardagi tayanch yechim qiymatlari Q1 =5120, Q2 = 7500, Q3 = 3420 larni taqqoslab min Q = 3420 ekanligini va bu qiymatga
ekanligini ko’ramiz.
Shuningdek egizak masala uchun OY1 Y2 tekisligida MBES ni tuzib tayanch yechimlar M1(160;0), M2(0;300), M3( 60;60) nuqtada bo’lishini ko’ramiz. Bu nuqtalardagi tayanch yechim qiymatlari Q1 =5120, Q2 = 7500, Q3 = 3420 larni taqqoslab min Q = 3420 ekanligini va bu qiymatga ![]() bo’lgan M3 nuqtada erishilishini ko’ramiz. Shu masalani simpleks usulda yechimini topish jarayonini keltiramiz. Sun’iy basis
bo’lgan M3 nuqtada erishilishini ko’ramiz. Shu masalani simpleks usulda yechimini topish jarayonini keltiramiz. Sun’iy basis ![]() larni kiritib
1 – simpleks jadvalni ifodalaymiz.
larni kiritib
1 – simpleks jadvalni ifodalaymiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0 |
|
32 |
4 |
3 |
1 |
0 |
|
|
2
|
0 |
|
25 |
1 |
5 |
0 |
1 |
5 |
|
|
|
|
0 |
-300 |
-480 |
0 |
0 |
|
![]()
![]()
Bu jadvalga mos
tayanch yechim ![]() optimal emas, chunki
optimal emas, chunki ![]() lar mavjud. Hal qiluvchi ustun va
qatorlarni aniqlab ikkinchi simpleks jadvalni tuzamiz.
lar mavjud. Hal qiluvchi ustun va
qatorlarni aniqlab ikkinchi simpleks jadvalni tuzamiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0 |
|
17 |
3,4 |
0 |
1 |
-0,6 |
5 |
|
2
|
480 |
|
5 |
0,2 |
1 |
0 |
0,2 |
10 |
|
|
|
|
2400 |
-204 |
0 |
0 |
96 |
|
![]()
![]()
Bu jadvalga mos tayanch yechim ham optimal emas. Keyingi simpleks jadvalni tuzamiz.
|
|
|
|
|
300 |
480 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1
|
300 |
|
5 |
1 |
0 |
|
|
|
|
2
|
480 |
|
4 |
0 |
1 |
|
|
|
|
|
|
|
3420 |
0 |
0 |
60 |
60 |
|
Bu jadvalga mos barcha ![]() . Demak, jadvaldan
. Demak, jadvaldan ![]() ekanligini ko’ramiz. Sun’iy bazislarga mos
ustunlardan esa,
ekanligini ko’ramiz. Sun’iy bazislarga mos
ustunlardan esa, ![]() lar qatorida
lar qatorida ![]() ekanligi kelib chiqadi. Bu yechimlar
geometrik usulda topilgan yechimlar bilan bir xil ekanligini ko’ramiz. Egizak
masalaning iqtisodiy ma’nosi. Agar asosiy masalada daromadlarni maksimal
bo’lishini ta’minlaydigan reja izlangan bo’lsa, egizak masalada harajatlarni
minimal bo’lishini ta’minlaydigan qiymatlar izlanar ekan. Bu yerda Y1, Y2 larni mos ravishda
1- va 2- homashyolarning bir birligi narxi deb tushunish mumkin. Egizak masala
tushunchasi nisbiy bo’lib, agar (6.1) – (6.2), ya’ni Yi larga
nisbatan masalani asosiy desak, Xj
larga nisbatan (2.1) – (2.2)
masala egizak masala bo’ladi.
ekanligi kelib chiqadi. Bu yechimlar
geometrik usulda topilgan yechimlar bilan bir xil ekanligini ko’ramiz. Egizak
masalaning iqtisodiy ma’nosi. Agar asosiy masalada daromadlarni maksimal
bo’lishini ta’minlaydigan reja izlangan bo’lsa, egizak masalada harajatlarni
minimal bo’lishini ta’minlaydigan qiymatlar izlanar ekan. Bu yerda Y1, Y2 larni mos ravishda
1- va 2- homashyolarning bir birligi narxi deb tushunish mumkin. Egizak masala
tushunchasi nisbiy bo’lib, agar (6.1) – (6.2), ya’ni Yi larga
nisbatan masalani asosiy desak, Xj
larga nisbatan (2.1) – (2.2)
masala egizak masala bo’ladi.
Mustaqil ishlash uchun masalalar.
Berilgan ChPM uchun egizak masala tuzilsin va uning yechimi geometrik usulda topilsin.
6.1
![]()

6.2
![]()

6.3
![]()
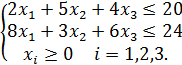
6.4
![]()

6.5
![]()

Adabiyotlar
1. D.B. Yudin, E.T.Toldshteyn; Lineynoe programmirovaniye . M. “Nauka”, 1969.
2. Kantorovich L. V. O metodax analiza nekotorix eksperimentalnix planovo-proizvodstvennix zadach. DAN SSSR 115, N3 1957.
3. Juraev X. I. Otaniyozov B. va boshqalar Metematik programmalashtirish. Toshkent OO’MTV, 2005
4. Akulich I. I. Metematicheskoe programmirovaniye v primerax i zadachax (uchebnoye posobiye) M. “Visshaya shkola ” 1986/
5. G’ofurov M. va boshqalar. Iqtisodiy matematik usullar va modellar (O’quv qo’llanma) Toshkent 2000.
6. Zaelavskiy YU. L Sbornik zadach po lineynomu programmirovaniyu. M. “Nauka”, 1969.
Mundarija
So’z boshi………………………………………………………………………….2
§ 1. Chiziqli programmalash masalalari……………………………………………3
§ 2. Chiziqli programmalash masalalarining matematik asoslari…………………10
§ 3. Rejani bosqichma-bosqich yaxshilash usullari……………………………….13
§ 4. Chiziqli programmalash masalalari uchun bazis tanlash va masala shartlarini tanlangan bazisga moslashtirish……………………………………………...19
§ 5. Transport masalasi……………………………………………………………22
§ 6. Chiziqli programmalash masalalari uchun egizak masala……………………33
IQTISODIY MATEMATIK USULLAR VA MODELLAR
fanining «Chiziqli programmalash» bo’limi bo’yicha iqtisodiyot va menejment yo’nalishi talabalari uchun nazariy ma’lumotlar va amaliy ko’rsatmalar
“Algoritmlash va matematik modellashtirish” kafedrasining majlisida (4 mart 2014 y., ¹ 17 bayonnoma) muhokama qilindi va TATU ilmiy-uslubiy kengashida bosmaxonada chop etish uchun tavsiya qilindi.
Tuzuvchi: dotsent A.N.Mirzayev
assistent F.S.Raximova
Masul muharrir:
dotsent Yu.M.Abduraxmanova
Muharrir: K.A.Gayubova
Bichimi 60x84 1/16
Bosma tabog’I - Adadi-
Buyurtma ¹
Toshkent axborot texnologiyalari universiteti «ALOQACHI» nashriyot–matbaa markazida chop etildi.
Toshkent sh., Amir Temur ko’chasi, 108 –uy.