ГОСУДАРСТВЕННЫЙ КОМИТЕТ СВЯЗИ, ИНФОРМАТИЗАЦИИ И

ТЕЛЕКОММУНИКАЦИОННЫХ ТЕХНОЛОГИЙ РЕСПУБЛИКИ УЗБЕКИСТАН

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

 

ФАКУЛЬТЕТ ПРОГРАММНОГО ИНЖИНИРИНГА

 

 

 

 

 

 

 

 

 

 

 

ДИСКРЕТНАЯ МАТЕМАТИКА

Краткая теория и задачи

Часть 1. Теория множеств. Комбинаторика

 

 

 

 

 

 

 

 

 

 

Ташкент 2014

 

Cоставители: Х.Абдуваитов, У. Каландаров.

«Дискретная математика. Краткая теория и задачи. Часть 1. Теория множеств. Комбинаторика». ТУИТ, 44 с. Ташкент 2014.

 

 

Ташкентский университет информационных технологий, 2014

 

ВВЕДЕНИЕ

Математику традиционно делят на непрерывную и дискретную. К непрерывной математике относят то, что в той или иной форме опирается на идеи предела и непрерывности. В отличие от непрерывной математики, описывающей непрерывные изменения процессов,  дискретная математика описывает процессы, состоящие из отдельных шагов, изучает  дискретные объекты, состоящие из различных несвязных элементов. Дискретная математика используется в различных вычислениях, когда изучаются отношения между конечными или счетными множествами, и когда анализируются процессы, состоящие из конечного числа шагов. Также как идеи непрерывной математики были в основе наук и технологий индустриальной революции, идеи дискретной математики лежат в основе наук и технологий компьютерной эры.

Дискретная математика развивает математическую зрелость, способность понимать и математически аргументировать. Без этих навыков нельзя продвинуться в изучении математических дисциплин. Дискретная математика обеспечивает математическую базу для многих курсов компьютерных наук, включая структуру данных, алгоритмы, теорию базы данных, теорию автоматов, формальные языки, теорию компиляторов, компьютерную безопасность, операционные системы и др.

 

Учебные курсы дискретной математики традиционно содержат такие разделы как:  теория множеств, комбинаторика, логика, Булевы функции и графы. Кроме того, курсы дискретной математики обычно содержат те разделы дискретной математики в широком смысле, которые не попали в другие математические курсы, но необходимы для полноценной подготовки специалистов соответствующего профиля (теория чисел, теория алгоритмов, дискретная теория вероятностей, криптография, формальные языки, теория конечных автоматов и др.).

 

Настоящее пособие предназначено студентам, изучающим дискретную математику, и преподавателям, проводящим занятия по указанной дисциплине. Пособие содержит первую часть курса по дискретной математике - теорию множеств и комбинаторику.

Учитывая крайний недостаток литературы по дискретной математике в ТУИТ, авторы поставили себе целью, главным образом, в короткий срок создать сборник задач, который мог бы быть использован студентами и преподавателями на практических занятиях по дискретной математике. Задачи, систематизированные в данном пособии, за небольшим исключением, взяты из зарубежных литературных источников, имеющихся в сети интернет. 

Задачам каждого раздела данного пособия  предпослан краткий теоретический материал, содержащий определения всех основных понятий и факты  необходимые при решении задач этого раздела.

Кафедра Алгоритмизации и математического моделирования надеется, что совместная работа студентов и преподавателей позволит постоянно улучшать и совершенствовать данное пособие.

 

 

 

      Как лучше изучить дискретную математику или любую другую дисциплину по математике или компьютерным наукам? Нужно изучать, активно выполняя упражнения, настолько много насколько это возможно.

 

МНОЖЕСТВА

1.1  Основные понятия

Под множеством понимается неупорядоченная совокупность некоторых объектов. Эти объекты называются элементами множества. Множества принято обозначать прописными буквами латинского алфавита, а элементы множества – строчными. Факт принадлежности элемента а множеству А обозначают a ∈A (читается «a элемент множества A» или «a принадлежит множеству A”. Обозначение a A означает, что a не является элементом множества  A.

Есть несколько способов описания (или задания) множеств. Один из них состоит в том, что мы перечисляем все элементы множества, когда это возможно, записывая их в фигурных скобках. Например, {1, 2, 3} обозначает  множество  состоящее из элементов 1, 2 и 3. Для обозначения больших множеств используют знак многоточия. Например, множество всех натуральных чисел от 1 до 100 записывается в виде {1, 2, 3, . . . , 100}.

Другой способ описания множества состоит в определении множества  с помощью некоторого свойства, позволяющего  определить, принадлежит ли элемент данному множеству или нет.  Более точно, если  Х - некоторое множество и  Р(х)- некоторое свойство, которым элементы множества Х могут или не могут обладать, то мы можем определить новое множество А- как множество всех элементов из Х, которые обладают свойством Р(х). Это новое множество обозначается следующим образом: А={x ∈Х| P(x)}. Например, множество  А  всех натуральных чисел от 1 до 100 может быть записано как  А= {x | x – натуральные числа не превосходящие 100}.

Некоторые важные множества имеют общепринятые обозначения:

N = {1, 2, 3, . . .}множество натуральных чисел;

Z = {. . . ,−2,−1, 0, 1, 2, . . .}множество целых чисел;

Q = {p/q | p ∈Zand q ∈N}множество рациональных чисел;

Rмножество действительных чисел;

R⁺множество действительных положительных чисел;

C множество комплексных чисел;

пустое множество (множество не содержащее элементов).

Множества могут находиться в разных отношениях между собой. Может так случиться, что элементы одного множества  А  могут быть также элементами другого множества В. В этом случае говорят, что множество А есть подмножество множества В и обозначают A ⊆B (читается «А включено в В» или «В содержит А»).

Любое непустое множество А содержит по крайней мере два подмножества, пустое множество и само множество, т.е.  ∅⊆А иА⊆А.

Два множества  А и В  называются равными, если они состоят из одних и тех же элементов, т.е каждый элемент множества  А  принадлежит также множеству В и, наоборот, каждый элемент  В  принадлежит также А. Пишут  АВ, если множества А и В равные, и пишут  АВ, если они не являются равными. Равенство двух множеств означает выполнение двух включений: A ⊆B и B ⊆A.

Из определения равенства двух множеств следует что множество останется равным себе если в нем изменить порядок перечисления элементов или некоторые элементы перечислить более одного раза. Например, множества {1, 2, 3, 4}  и {3, 2, 4, 1, 2} равные.

Подмножество A  множества  B  называется собственным подмножеством, если A B.

При решении некоторых задач бывает полезным рассмотреть множество, состоящее из всех подмножеств некоторого данного множества А.  Такое множество называется степенью множества А (также булеаном) и обозначается Р(А) (также оно обозначается 2^А). В большинстве случаев элементы всех рассматриваемых в этой ситуации множеств принадлежат некоторому большому множеству. Такое множество называется универсальным. Например, если в рассматриваемой  задаче множествами являются интервалы числовой прямой, то универсальным множеством будет множество всех действительных чисел  R .

Множества можно представлять графически в виде областей на плоскости, а отношения между множествами в виде рисунков, которые называются диаграммами Венна. На диаграммах Венна универсальное множество изображается в виде прямоугольника, а окружности или другие фигуры внутри прямоугольника используются для изображения множеств. Иногда точки внутри фигур используются для изображения элементов соответствующего множества.

 

1.2 Операции над множествами

Из данных множеств можно конструировать новые множества при помощи так называемых операций над множествами.

Объединением двух множеств A и B, обозначается  A ∪B, называется множество всех элементов принадлежащих хотя бы одному из множеств A и B, т.е. A ∪B = {x| x∈ А или x∈B}.

Пересечением двух множеств A и B, обозначается  A ∩ B, называется множество всех элементов принадлежащих обоим множествам A и B, т.е.

A ∩ B = {x | x∈ А и x∈B}.

Два множества называются непересекающимися, если они не имеют общих элементов, т.е. A ∩ B = .

Разностью двух множеств B и A, обозначается B – A (а такжеB), называется множество всех элементов принадлежащих  B, но не принадлежащих  A, т.е. B – A= { x∈B: xА }.

Когда A ⊆B, разность B  и  A называют также дополнением множества A до множества B.

Симметрической разностью двух множеств A и B, обозначается  (а также ), называется множество всех элементов принадлежащих одному и только одному из множеств A и B, т.е.

A B = {x | x∈(A – B)∪(B – A)}.

Пусть U  - универсальное множество. Дополнением множества A, обозначается , называется дополнение множества A до множества U, т.е.  =U A.

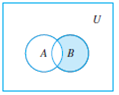
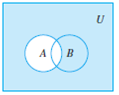
Следующие диаграммы Венна иллюстрируют операции над множествами

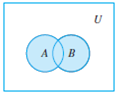
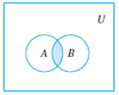
       A ∪B                  A ∩ B               B – A                     

Определение операций объединения и пересечения для любого конечного числа множеств аналогично определению для двух множеств.

 

1.3  Основные теоретико-множественные тождества

   Ниже приводятся некоторые важные свойства множеств состоящие из равенств справедливых для всех множеств некоторого универсального множества U.  Эти равенства называются основными теоретико-множественными тождествами.

1. Законы коммутативности. Для всех множеств A и B,

a)  A ∪B = B ∪A;    b)  A ∩ B = B ∩ A.

2. Законы ассоциативности. Для всех множеств  A, B, и C,

a)  (A ∪B)∪C = A ∪(B ∪C);  b)  (A ∩ B)∩ C = A ∩ (B ∩ C).

3. Законы дистрибутивности. Для всех множеств  A, B, и C,

a)  A ∪(B ∩ C)= (A ∪B)∩ (A ∪C);     b)  A ∩ (B ∪C)= (A ∩ B)∪(A ∩ C).

4. Законы де Моргана. Для всех множеств A и B,

a)  = ∩ ;    b)  = ∪.

5. Законы поглощения.  Для всех множеств A и B,

a)  A ∪(A ∩ B)= A;    b)  A ∩ (A ∪B)= A.

6. Закон двойного отрицания. Для всех множеств  A,

= A.

7. Законы идемпотентности. Для всех множеств  A,

a)  A ∪A = A;    b)  A ∩ A = A.

8.  Некоторые дополнительные свойства операций над множествами.

a) A ∪∅ = A;   b) A ∩ U = A;    c) A ∪= U;    d) A ∩ = ∅;

e) A ∪U = U;    f) A∩ ∅ = ∅;    g) = ∅;    h) = U.

 

УПРАЖНЕНИЯ

1. Перечислите элементы каждого из множеств:

а) {a, b, 1, 2, 3};

б) {a, {b}, 1, {2, b}, c};

в) {1, {1}, , {1, {a, b}}, 2};

г) {целое положительное число и };

д) {};

е) {четное число и };

ж) {}.

2. Задайте каждое из следующих множеств с помощью характерного для их элементов свойства :

а) {1, 3, 5, …, 99};

б) {2, 3, 5, 7, 11, 13, 17, 19};

в) {, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

3. Если , то какие из следующих записей являются правильными:

а) ;     б) ;     в) ;     г) .

4. Какие из следующих утверждений верны:

1) b {a,b}   2) {b}  {a,b};   3){b} {a,b};   4)b {a,{b}};  5) {b} ⊂ {a,{b}};  6) {b}  {a,{b}}.

5. Сколько элементов в каждом из множеств:

а) {1,2,3,{1,2,3}};     

б) {1,{1},2,{1,{2,3}},Ø};                      

в) Ø;

г) {a, b, c, b, a};

д) {a, {b}, c, b, a}.

6. Приведите примеры таких множеств А, В и С, для которых

7. Даны множества . Найдите множества

8. Известно, что А⊆ В и а  А. Какие из следующих утверждений верны:

1) а∉ В;   2) а  В;   3) а  А  В;  4) а  А  В;   5) а  А  В;  6) а А  В.

9. Известно, что В⊆ А ⊆С, а  А и а ∉ В. Какие из следующих утверждений верны:

1) а∉ С;    2) а  С;    3) а  А  В;    4) а  А  В;    5) а  А  В;    6) а  В  А;    7) а  А  В;    8) {а} ⊆ А С;    9) а  А  С;    10) {а} ⊆ А  С;    11) {а} ⊆ А  С;    12) а  (А  В)  С;    13) {а} ⊆ А  (В  С);    14) {а} ⊆ В  (С  А);    15) {а} ⊆ А  (В  С);    16) {а} ⊆ В  (А С).

10. Дано     универсальное множество    U = {1,2,3,4,5,6,7,8}    и      его    подмножества

A = {x | 3 <x 6} ,B = {x | x четно}. Найдите множества:

1)  А  В;    2) AB;    3);    4) 2^A.

11. Дано      универсальное множество U={1,2,3,4,5,6,7,8}    и      его    подмножества

А = {x | x четно},   B = {x | x кратно четырем},  C = {x | x простое}, D = {1,2,3}.  Найдите множества:

1) A(BCD);    2) (AB) (CD);    3)  ;    4) (CA) D;    5)  2^D 2^C

12.Пусть М₂, М₃ и М₅ обозначают множества всех натуральных чисел кратных,  соответственно, 2, 3 и 5. С помощью операций над множествами выразите через них множества всех чисел:

а) делящихся на 6;

б) делящихся на 30;

в) взаимно простых с 30;

г) делящихся на 10, но не делящихся на 3.

13. Докажите тождества:

1) А АВ) = А;

3) А В) = А В;

4) А(В) = АВ;

5) А  (А  В) = АВ;

6) A(AB) = AB;

7) A(BA) = Ø;

8) A(BA) = AB;

9) (AB)(A)= A;

10) А ⊕ В = (А)(В);

11) А ⊕ (А ⊕ В) = В;

12) А В = А ⊕(АВ);

13) А  В = (А ⊕ В) (АВ);

14)  = (AB);

15) A ⊕ = ⊕ B = (AB);

16) A (B) = A ⊕(B) = B ⊕(A;

17) A  (B  C) = (A B)(A C);

18) (A B)  C = (AC)  (B  C) = A  (B  C);

19) A  (BC) = (AB) (AC) = (A  B)  (A ;

20) (A B) C = (AB) (B  C);

21) ABC = (A  B)  C) (C  A) (ABC);

22) A (BC) = (A  B)  (A  C) = (ABC)⊕ A;

23) A(B C) = (AB)C = (ABC)⊕(AB);

24) ((AB)⊕ A) ⊕ ((BC)⊕ C) = ((AB)⊕(BC)) ⊕ (A ⊕ C);

25) (AB) ⊕ (B  C) = (A ⊕ C)  B = ((AB)⊕(BC)) ⊕ (A ⊕ C).

14. Решите уравнение:

1) АХ = В;

2) А Х = В;

3) А Х = В;                                     

4) А Х = В;

5) А Х = ВХ;

6) А Х = ХВ;

7) (А Х)  = Х В;

15. Найдите множество X,  удовлетворяющее  системе  уравнений,  где A, B, C – данные множества,  BA⊆C:

1)                           2)   

 

ПРЯМОЕ ПРОИЗВЕДЕНИЕ МНОЖЕСТВ

2.1  Бинарные отношения

Прямым  (или декартовым) произведением  двух не-пустых множеств   называется множество всех упорядоченных

пар ( где , .

Пример. Пусть А ={a, b} и B={1, 2, 3}. Тогда  AB = {(a, 1), (a, 2), (a, 3), (b,1), (b,2), (b, 3)}.

Аналогично определяется декартово произведение нескольких множеств. Если  – n непустых множеств, то их декартово произведение состоит из всевозможных упорядоченных наборов ,  , , элементов этих множеств. Если множества  , то их произведение   обозначается . Так, символом  Rⁿ   обозначается множество всех упорядоченных наборов (векторов) из n  вещественных чисел.

Любое подмножество декартового произведения    называется бинарным отношением. Если , то бинарное отношение называется бинарным отношением на множестве . Бинарные отношения обозначаются буквами ρ, , .... Если пара (x, y) принадлежит бинарному отношению ρ, то пишут (x, y) ρ  или  x ρ y .

Для задания бинарного отношения  ρ используют те же методы, что

и для произвольных множеств, кроме того, бинарное отношение, заданное

на конечном множестве , можно задать в виде графа, а бинарное отношение на множестве R  можно задать в виде декартовой диаграммы. Под графом бинарного отношения мы понимаем схему, в которой элементы множества  изображаются точками на плоскости, элементы , такие, что пара (x, y) ρ соединяются стрелкой, направленной от x к y, пары (x, y) ρ изображаются петлей вокруг точки x . Под декартовой диаграммой понимают изображение пар (x, y) ρ в декартовой прямоугольной системе координат.

Областью определения бинарного отношения ρ называется множество

.

Областью значений бинарного отношения ρ называется множество

.

Бинарное отношение  на множестве  называется рефлексивным,

если для любого  пара. Если – конечное множество, то

рефлексивность бинарного отношения  означает, что на графе данного

бинарного отношения вокруг каждой точки x из  есть петля. Если

= R , то рефлексивность бинарного отношения  с точки зрения декартовой диаграммы означает, что в число изображенных точек войдут все точки прямой  y(x) = x .

Бинарное отношение  на множестве  называется симметричным,

если для любых  из принадлежности пары (x, y) отношению

следует принадлежность этому отношению также пары (y, x). Если –

конечное множество, то симметричность бинарного отношения  означает, что на графе данного бинарного отношения все присутствующие стрелки двусторонние. Если  X= R , то симметричность бинарного отношения

 с точки зрения декартовой диаграммы означает, что изображенное множество симметрично относительно прямой  y(x) = x .

Бинарное отношение  на множестве C называется антисимметричным, если для любых  из принадлежности пар (x, y) и (y, x) отношению  следует  x = y . Если – конечное множество, то антисимметричность бинарного отношения означает, что на графе данного бинарного отношения все присутствующие стрелки односторонние.

Бинарное отношение  на множестве  называется транзитивным,

если для любых  из принадлежности пар (x, y) и (y, z) отношению  следует принадлежность этому отношению также пары (x, z).

Обратным отношением для  называется отношение

.

Композицией отношений  называется отношение

 .

Для любых бинарных отношений выполняются следующие свойства:

1. ;

2. .

 

2.2  Специальные бинарные отношения

Рефлексивное, симметричное и транзитивное отношение ρ  на множестве  X  называется отношением эквивалентности на множестве X.  Для отношения эквивалентности вместо записи (x, y) ρ  часто используют запись x ≈y  (читается: x эквивалентен y ).

Классом эквивалентности, порожденным элементом x , называется подмножество множества  X, состоящее из тех элементов y X, для которых (x, y) ρ. Класс эквивалентности, порожденный элементом x , обозначается через [x]:

Разбиением множества  X  называется совокупность попарно непересекающихся подмножеств  X  таких, что каждый элемент множества X  принадлежит одному и только одному из этих подмножеств. Всякое разбиение множества  X  определяет на  X  отношение эквивалентности  ρ: (x, y) ρ  тогда и только тогда, когда x и y принадлежат одному подмножеству разбиения. С другой стороны, всякое отношение эквивалентности  ρ  определяет разбиение множества X на классы эквивалентности относительно этого отношения.

Совокупность классов эквивалентности элементов множества  X  по отношению эквивалентности  ρ  называется фактор-множеством множества  X  по отношению  ρ и обозначается  X/ ρ .

Рефлексивное, антисимметричное и транзитивное отношение называется отношением частичного порядка на множестве  X  и вместо записи (x, y) ρ для данного отношения часто используют запись  . Отношение частичного порядка на множестве  X,  для которого любые два элемента сравнимы, т.е. для любых x, y X  выполнено либо  x ≤ y , либо

y ≤ x, называется отношением линейного порядка. Множество  X  с заданным на нем частичным (линейным) порядком называется частично (линейно) упорядоченным.

 

УПРАЖНЕНИЯ

1. Перечислите элементы множеств  и , если

2. Пусть на плоскости задана декартова система координат.  Изобразите на плоскости следующее множество:

3. Для следующего бинарного отношения, определенного на множестве R, найдите область определения, область значений и нарисуйте декартову диаграмму

.

4. Для каждого из следующих бинарных отношений выясните, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает и какими не обладает.

а)  на множестве  = {1,2,3};

б)   на множестве  = R;

в)  на множестве = Z;

г)  на множестве = P(Z).

 

5. Пусть на множестве R заданы следующие бинарные отношения:

Найдите обратные отношения к данным бинарным отношениям.

 

6. Пусть X={1, а}. Перечислите все элементы множеств , .

7. Найти геометрическую интерпретацию множества AB, где A – это множество точек отрезка [0,1], а  B – это множество точек квадрата с вершинами в точках (0,0), (0,1), (1,0), (1,1).

8. Доказать, что для произвольных множеств A, B, K:

а) (AB)×K = (A×K) (B×K);

б) (A\B)×K = (A×K)\(B×K);

в) A×(B\K) = (A×B)\(A×K).

9. Перечислите все элементы бинарного отношения ρ и нарисуйте ее граф:

а)  ρ = { (x,y):x<y}  на множестве X={1,2,3,4,5};

б)  ρ = {(x,y):y = x+1}  на множестве X={1,2,3,4,5,6,7,8,9,10}.

10. Для каждого из следующих бинарных отношений, определенных на множестве R, найдите область определения, область значений и нарисуйте декартову диаграмму:

а) ρ = { };

б) ρ = { };

в) ρ = { ;

г) ρ = { };

д) ρ = { };

е) ρ = { };

11. Даны бинарные отношения между элементами множеств A и B, найдите область определения и область значений для данных бинарных отношений:

а) A={1,2,3,4,5}, B={{1}, {1,2},{2,5},{3}},  

б) A = Z Z, B = Q,   = ;

в)  A = Z, B =Q,

г) A = Z, B =Q,

11. Для каждого из следующих бинарных отношений выясните, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает и какими не обладает:

а)

б)

в)

г)

д) ;

е)

ж)

12. Приведите примеры бинарных отношений:

а) рефлексивных и транзитивных, но не антисимметричных;

б) транзитивных и симметричных, но не рефлексивных;

в) рефлексивных и симметричных, но не транзитивных;

г) рефлексивных и транзитивных, но не симметричных.

13. Докажите, что если транзитивное и симметричное бинарное отношение на множестве А, область определения которого совпадает с А,  то  рефлексивно.

14. Выясните, какие из следующих перечисленных отношений на множестве {0,1,...,9} являются отношениями эквивалентности. Найдите классы эквивалентности.

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

15. Какие из следующих отношений на Z являются отношениями порядка:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

16. Придумайте минимальное (по числу элементов) отношение эквивалентности  на множестве  так, чтобы  и .

 

17. Докажите, что M= {{1},{2,5},{3},{4,6,7}} – разбиение множества A= {1,2,3,4,5,6,7} и перечислите все элементы отношения эквивалентности r , соответствующего разбиению M.

 

18. Покажите, что объединение двух отношений эквивалентности может не являться отношением эквивалентности.

19. На множестве A ={1,2,3,4,5}рассмотрим два отношения частичного порядка

Покажите, что композиция   не является отношением частичного порядка.

20. На множестве N задано бинарное отношение по следующему правилу: (x, y) ρ тогда и только тогда, когда последняя цифра в десятичной записи числа x совпадает с последней цифрой в десятичной записи числа y . Докажите, что данное отношение является отношением эквивалентности. Сколько элементов в фактор-множестве N / ρ ?

21. На R задано бинарное отношение .

Докажите, что ρ – отношение эквивалентности. Сколько элементов может содержать класс эквивалентности? Существует ли класс эквивалентности, состоящий из одного элемента?

22. Покажите, что пересечение отношений эквивалентности, определенных на некотором множестве A, является отношением эквивалентности.

23. Докажите, что если ρ – отношение эквивалентности, то  – также отношение эквивалентности.

24. Докажите, что отношение  является отношением порядка. Является ли это отношение отношением линейного порядка?

25. Докажите, что отношение  является отношением линейного порядка.

 

КОМБИНАТОРИКА

3.1  Основные правила комбинаторики

Правило суммы. Пусть объект a можно выбрать m способами, объект b – n способами, и существует k общих способов выбора объектов a и b , тогда один из объектов «a или b» можно выбрать m + n – k способами.

 

Пример.  Сколькими способами из 28 костей домино можно выбрать кость, на которой есть «2» или «5».

Решение. Выбрать кость, содержащую «2», можно 7-ю способами, содержащую «5» – тоже 7-ю способами, но среди этих способов есть один общий – это выбор кости «2 : 5». В соответствии с правилом суммы общее число способов выбора нужной кости можно осуществить 7 + 7 – 1 = 13 способами.

 

Правило произведения. Пусть объект a можно выбрать п способами, и после каждого такого выбора объект b можно выбрать т способами. Тогда выбор пары «a и b» в указанном порядке можно осуществить n ×т способами.

 

Пример. Сколько существует двузначных четных чисел в десятич­ной системе счисления?

Решение. Выбираются две цифры из множества {0,1,2,...,8,9}. Пер­вая цифра может быть любой, кроме нуля. Поэтому ее можно выбрать 9-ю способами. Вторая цифра может быть любой из множества {2,4,6,8,0}, ее можно выбрать 5-ю способами. Следовательно, четных двузначных чисел по правилу произведения будет n× m = 45, где n = 9, m = 5.

 

Пример. В микроавтобусе 10 мест, одно из которых – место води­теля. Сколькими способами могут сесть в автобус 10 человек, если место водителя могут занять только трое из них.

Решение. Начнем с места водителя. Имеется = 3 способа занять его место. Следующее место может занять любой из девяти оставшихся человек, т.е. = 9 и т. д. По правилу произведения получаем всего воз­можностей

× × × … × = 3× 9× 8× 7× 6× 5× 4× 3× 2× 1 = 3× 9!.

3.2  Формула включений и исключений

 

Пусть имеется N предметов и п свойств a₁, a₂, …, a_n. Каждый из рассматриваемых предметов может обладать одним или несколькими из этих n свойств. Обозначим через N(a, b,…, c) число предметов, обладающих свойствами a, b,…,c, а через    N(,,…,) – число предметов, не обладающих свойствами a, b, ..., c.

Справедлива формула

N(₁, ₂,…,_n) = N – N(a₁) – N(a₂) – …– N(a_n) + N(a₁ , a₂) +

+ N(a₁ , a₃) +…+ N(a₁ , a_n) +…+ N(a_n–1 , a_n) – N(a₁ , a₂ , a₃) –…–      

– N(a_n–2, a_n–1, a_n) +…+ (–1)ⁿ N(a₁, a₂, … , a_n).

Эта формула называется формулой включений и исключений. Здесь слагаемые включают все комбинации свойств a₁,a₂,…,a_n  без учёта их по­рядка; знак  “+” ставится, если число учитываемых свойств чётно, и знак “–”   если это число нечётно.  

 

Пример. В результате опроса 70 студентов выяснилось, что 45 из них занимаются спортом, 29 – музыкой, 9 – и спортом, и музыкой. Сколько студентов из числа опрошенных не занимаются ни спортом, ни музыкой.

Решение. Имеем N = 70, N(a) = 45, N(b) = 29, N(a, b) = 9. По формуле включений и исключений получаем

N(,) = N – N(a) – N(b) + N(a, b) = 70 – 45 – 29 + 9 = 5.

УПРАЖНЕНИЯ

1. Имеется 10 билетов денежно-вещевой лотереи и 15 билетов художественной лотереи. Сколькими способами можно выбрать один лоте­рейный билет?

2. Сколькими способами можно подарить сувенир из имеющихся 6 авторучек, 7 репродукций картин и 3 альбомов?

3. В городе работают 4 музея, 3 театра и 10 кинотеатров. Сколько вариантов для организации культпохода в воскресенье?

4. Сколько существует вариантов поездки к морю, если туда можно добраться тремя авиарейсами, пятью автодорогами или по железной дороге?

5. Сколькими способами можно купить один пирожок, если в продаже 7 пирожков с мясом, 10 пирожков с повидлом и 12 пирожков с капустой?

6. В корзине лежат 8 различных яблок и 7 различных груш. Сколь­кими способами можно взять плод из корзины?

7. Сколькими способами можно выбрать гласную и соглас­ную буквы из букв слова «студент»?

8. Сколько существует двузначных чисел, в которых нет одинаковых цифр?

9. Сколько существует нечётных трехзначных чисел?

10. На ферме есть 20 овец и 24 козы. Сколькими способами можно выбрать одну овцу и одну козу? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

11. Сколькими способами можно выбрать по одному экземпляру каждого учебника, если имеется 3 экземпляра учебника алгебры, 7 экземпляров учебника геометрии и 10 экземпляров учебника информатики?

12. Сколькими способами можно выбрать из натуральных чисел от 1 до 20 два числа так, чтобы их сумма была нечетным числом?

13. Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма?

14. Сколькими способами можно выбрать согласную и гласную бук­вы из слова «здание»? Из слова «кабинет»?

15.  В корзине лежат 12 яблок и 10 груш. Сын выбирает из нее яблоко или грушу, после чего дочь берет и яблоко, и грушу. В каком случае дочь име­ет большую свободу выбора: если сын взял яблоко или если он взял грушу?

16. Сколькими способами можно совершить круговой рейс из А в В и обратно, если на обратном пути выбирать новую дорогу и известно, что А и В соединены семью дорогами?

17. Имеется n₁ книг одного автора,n₂ - второго, n₃ - третьего. Каким чис­лом способов можно выбрать

а) одну книгу;

б) две книги разных авторов;

в) три книги разных авторов.

18. Каким числом способов можно заполнить анкету, содержащую n вопро­сов, если на каждый вопрос можно ответить

а) «да» или «нет»;

б) «да», «нет», «не знаю»?

19. Сколько палиндромов (слов, читающихся одинаково слева направо и справа налево) длины n можно составить, если в алфавите k букв?

20. Сколько матриц с m строками и nстолбцами можно составить из эле­ментов 0 и 1?

21. Каким числом способов можно на обычной шахматной доске разместить белую и черную ладьи так, чтобы они не атаковали друг друга?

22. Каким числом способов можно на шахматной доске поместить черного и белого королей так, чтобы они не атаковали друг друга?

23. На одной из двух параллельных прямых зафиксировано n точек, а на дру­гой –m точек. Сколько имеется треугольников (четырехугольников) с верши­нами в данных точках?

24. Сколькими способами можно расставить восемь ладей на обычной шахматной доске так, чтобы они не угрожали друг другу, т.е. чтобы никакие две из них не стояли на одной вертикали или горизонтали?

25. Сколько имеется пятизначных десятичных чисел, у которых

а) все цифры различны;

б) есть одинаковые цифры;

в) все цифры различны, причем последняя - не 0;

г) все цифры различны, причем первая - не 9, а последняя - не 0;

д) две первых цифры различны, а две последних - одинаковы;

е) сумма цифр четна ?

26. В отделе НИИ работают несколько сотрудников, знающих хотя бы один иностранный язык. Из них 6 человек знают английский, 6 – не­мецкий, 7 – французский, 4 – английский и немецкий, 3 – французский и немецкий, 2 – французский и английский, 1 человек знает все три языка.

а) Сколько человек работает в отделе?

б) Сколько из них знают только англий­ский язык?

с) Сколько человек знают только один язык?

27. Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 человек, в том числе 25 мальчиков; 30 учеников учатся на „хорошо“ и „отлично“, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, которые учатся на хорошо и отлично. 15 мальчиков учатся на „хорошо“ и „отлично“ и за­нимаются спортом». Докажите, что в этих сведениях есть ошибка.

28. Сколько чисел среди первых 100 натуральных чисел не делятся ни на 2, ни на 3, ни на 5?

29. Среди сотрудников фирмы семнадцать человек знают английский язык, десять - немецкий, семеро - французский. Три человека знают английский и французский, два - немецкий и французский, четверо - английский и немецкий.

a) Сколько человек работает в фирме, если каждый знает хотя бы один язык, а два человека знают все три языка?

б) Сколько сотрудников, не знающих ни одного иностранного языка, если в фирме работает тридцать человек и никто из них не знает всех трех языков?

30. На одной из кафедр университета работают тринадцать человек, причем каждый из них знает хотя бы один иностранный язык. Десять человек знают английский, семеро - немецкий, шестеро - французский. Пятеро знают англий­ский и немецкий, четверо - английский и французский, трое - немецкий и французский.

а) Сколько человек знают все три языка?

б) Сколько человек знают ровно два языка?

в) Сколько человек знают только английский язык?

31. Сколько имеется натуральных чисел, не превосходящих 1000, которые

а) делятся на 3 или на 5;

б) не делятся ни на одно из чисел 2, 3, 5?

31. Сколько чисел среди первых 1000 натуральных чисел, не деля­щихся ни на 3, ни на 4, ни на 5?

32. При обследовании читательских вкусов студентов оказалось, что 60 % студентов читает журнал А, 50 % – журнал В, 50 % – журнал С, 30 % – журналы А и В, 20 % – журналы В и С, 40 % – журналы А и С, 10 % – журналы А, В и С. Какой процент студентов:

а) не читает ни одного из этих журналов?

б) читает в точности два журнала?

в) читает только один журнал В?

33.  При опросе 13 человек, каждый из которых знает по крайней мере один иностранный язык, выяснилось, что 10 человек знают английский язык, 7 – немецкий, 6 – испанский, 5 – английский и немецкий, 4 – англий­ский и испанский, 3 – немецкий и испанский. Сколько человек знают:

а) все три языка?

б) ровно два языка?

в) только английский язык?

34. На экскурсию поехало 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек; с ветчиной – 42 человека; и с сыром, и с колбасой – 28 человек; и с колбасой, и с ветчиной – 31 человек; и с сыром, и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек. Не­сколько человек вместо бутербродов взяли пирожки. Сколько человек взя­ли с собой пирожки?

35. Найти количество натуральных чисел, не превосходящих 1000 и не делящихся ни на одно из чисел 3, 5 и 7?

36. Найти количество натуральных чисел, не превосходящих 1000 и не делящихся ни на одно из чисел 6, 15 и 10?

 

3.3  Упорядоченные и неупорядоченные выборки.

 

Любая совокупность из k элементов некоторого множества называется k – выборкой. Выборка, в которой все элементы различны, называется выборкой без повторений, в отличие от выборки с повторениями, в которой входящие в нее элементы могут повторяться. Выборка называется упорядоченной, если существенным является не только состав элементов в ней, но и порядок их расположения. Две упоря­доченные k-выборки считаются различными, если они отличаются либо составом элементов, либо порядком их расположения. Например, упорядо­ченные выборки (1,2) и (2,1) считаются различными, хотя и составлены из одних и тех же элементов. Выборка называется неупорядоченной, если порядок следования элементов в ней не существенен. Так, {1,2} и {2,1} считаются одной и той же неупорядоченной выборкой. Фигурные и круглые скобки подчеркивают отличие неупорядочен­ной выборки от упорядоченной.

 

Пример. Составьте всевозможные 2-выборки из элементов мно­жества М={а, b, с}.

Решение. (а,b), (b,а), (а,с), (с,а), (b,с), (с,b) – это упорядоченные 2-выборки без повторений.

(а,а); (а,b); (а,с); (b,b); (b,a); (b,c); (c,c); (c,a); (c,b) – упорядоченные 2-выборки с повторениями.

{a,b}, {а,с}, {b,c} – неупорядоченные выборки без повторений.

{a,b}; {a,a}; {a,c}; {b,b}; {b,c}; {c,c} – неупорядоченные выборки с повторениями.

 

При решении комбинаторных задач, в которых требуется определить количество некоторых выборок (комбинаций) из данного множества эле­ментов, основным моментом является правильное определение типа выборок – упорядоченные это выборки или нет, с повторениями или без повторений.

 

УПРАЖНЕНИЯ

1. Из ящика с 70 разными шарами вынимается 5 шаров? Какого типа 5-выборка?

2. Какого типа 7-выборка при совершении покупки семи пирожных, если в магазине имеется четыре их сорта?

3. На шахматной доске расставлены:

а) 8 одинаковых фигур;

б) 8 раз­личных фигур.

К какому типу относятся 8-выборки в случаях а) и б)?

4. Какого типа 4-выборки, если выбираются из 10 претендентов:

а) четыре кандидата на конференцию?

б) президент, вице-президент, казначей и ученый секретарь научного общества?

5. Переставляются буквы слов:

а) «март»,

б) «мама».

Сколько полу­чится различных перестановок? Перечислите их. К какому типу выборки можно отнести эти комбинации букв?

6. Из множества цифр {0,1,2,...,9} составляются различные числа по пять цифр в каждом. Какого типа выборки представляют собой пятизначные числа?

7. Сколько можно составить слов длины k из 32 букв русского алфа­вита? Рассмотреть случай k = 2, 3, 4. К какому типу выборки можно отнести эти комбинации букв?

8. Из множества A = {a, b, c, d} составить:

а) упорядоченные 2-выборки без повторений;

б) неупорядоченные 2-выборки без повторений. Сколько их всего может быть?

 

3.4  Размещения без повторений и с повторениями

 

Размещениями без повторений из п элементов по k называются упорядоченные k-выборки из п элементов без повторений. Их число

Обозначается   и вычисляется по формуле :

k≤ n.

 

Пример. Сколькими способами можно составить трехцветный по­лосатый флаг, если имеется материал пяти различных цветов?

Решение. Нужно найти число 3-выборок из 5 элементов без повто­рений (все цвета различны); порядок, в котором располагаются выбранные цвета, существенен. Следовательно, нужно найти число упорядоченных выборок, т.е. число размещений из 5 по 3 без повторений. По формуле для числа размещений имеем

  (способов).

Заметим, что эту задачу можно решить иначе. Для выбора цвета пер­вой полосы имеется 5 вариантов. После произведенного выбора цвет для второй полосы можно выбрать 4-мя способами из 4-х оставшихся. Далее выбираем цвет для третьей полосы флага из имеющихся  3-х цветов. Это можно сделать 3-мя способами. По правилу произведения всего имеем

5 × 4 × 3 = 60 (способов).

 

Пример. Сколькими способами можно составить трехцветный по­лосатый флаг, одна из полос которого красного цвета, если имеется материал пяти различных цветов, включая красный?

Решение. Красную полосу можно расположить 3-мя способами, т. к. флаг трехполосный. После выбора красной полосы, остался материал 4-х цветов, из которых нужно выбрать два цвета. Этот выбор можно осуществить

(способами), так как 2-выборки упорядоченные

без повторений. По правилу произведения окончательно имеем =36 (способов).

Размещениями с повторениями из п элементов по k называются упорядоченные k-выборки из п элементов с повторениями. Их число обо­значается    и вычисляется по формуле

 

Пример. В одной из первых поколений ЭВМ «Стрела» ОЗУ имело 2 048 ячеек, каждая ячейка состояла из 43 разрядов. Какое максимальное количество различных чисел в двоичной системе счисление можно было поместить в ОЗУ?

Решение. В любой ячейке информация (число) представлялась в ви­де двоичного, т. е. состоящего из 0 и 1, упорядоченного набора длины 43. Всего мест для 0 и 1 равно k = 2 048 × 43 = 88064. Таким образом, имеем упорядоченные k-выборки из n = 2 с повторениями. Их число находим по формуле (4) :  , где k = 88 064.

 

УПРАЖНЕНИЯ

1. В забеге участвуют 5 человек. Сколькими способами могут распределиться 2 первых места?

2.   Сколькими различными способами 2 друга могут одновременно посетить кого-либо из своих общих трёх знакомых?

3. Каким числом способов можно разместитьnразличных предметов поkразличным ящикам? Сколько таких размещений, если в каждый ящик укладыва­ется не более одного предмета?

4. Сколько имеется вариантов выбора трех призеров средиnучастников конкурса

с указанием занимаемых ими мест?

5.   Сколько существует различных наборов длины 10 из нулей и единиц?

6.   В некотором государстве не было двух жителей с одинаковым набором зубов. Какова наибольшая численность этого государства?

7. Абитуриенту необходимо сдать 4 экзамена за 10 дней. Скольки­ми способами можно составить ему расписание, если в один день можно сдавать только один экзамен?

8. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им оценки, если известно, что никто не получил оценки «неудовлетворительно»?

9. Сколько словарей надо издать, чтобы можно было выполнять пе­реводы с любого из пяти языков на любой другой из этих пяти языков? На сколько больше словарей надо издать, если число различных языков равно 10?

10. Сколько существует различных пятизначных чётных чисел, ко­торые начинаются цифрой «2» и оканчиваются цифрой «4», если исполь­зуются цифры 1, 2, 3, 4, 5?

11. Сколько различных четырёхзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5?

12. В комнате общежития живут трое студентов. У них есть 4 раз­ные чашки, 5 разных блюдец и 6 разных чайных ложек. Сколькими спо­собами они могут накрыть стол для чаепития (каждый студент получает одну чашку, одно блюдце и одну ложку)?

 

 

3.5  Сочетания без повторений и с повторениями

 

Сочетаниями без повторений из п элементов по k называются не­упорядоченные k-выборки из п элементов без повторений. Их число обо­значаетсяи вычисляется по формуле

 , k      

Сочетания из n по k без повторений образуют k-элементарные под­множества исходного множества мощности n. Числа  называются би­номиальными коэффициентами.

 

Пример. Сколькими способами можно выбрать три различные краски из имеющихся пяти?

Решение. Очевидно, что нужно подсчитать число 3-выборок из 5 элементов, причем по условию задачи понятно, что среди выбранных эле­ментов не должно быть одинаковых и что порядок расположения выбранных красок не существенен. Значит, нужно найти число неупорядоченных выбо­рок, т. е. число сочетаний без повторений из 5 по 3. По формуле для числа сочетаний без повторений имеем:

 

Сочетаниями с повторениями из п элементов по k называются неупорядоченные k-выборки из п элементов с повторениями. Их число обозначается  и вычисляется по формуле

 ,

 

Пример. В киоске имеются открытки 10 видов. Сколькими спосо­бами можно купить: а) 5 открыток? б) 5 разных открыток? в) 15 открыток с повторениями?

Решение. В случаях а) и в) нас интересуют неупорядоченные выбор­ки из 10 элементов с повторениями длины 5 и 15 соответственно. Их число определяется по формуле:

а)

в)

В случае б) нужно подсчитать число неупорядоченных 5-выборок из 10 элементов без повторений (все открытки разные). Их число определяет­ся по формуле: (способа).

 

УПРАЖНЕНИЯ

 

1. Из 20 студентов надо назначить 5 дежурных. Сколькими спосо­бами это можно сделать?

2. Сколькими способами можно составить бригаду из четырёх плот­ников, если имеются предложения от 10 человек?

3. Сколькими способами пять девушек и трое юношей могут раз­биться на две команды по четыре человека в команде, если в каждой ко­манде должно быть хотя бы по одному юноше?

4. Каким числом способов можно разделить 10 юношей на две баскетболь­ные команды по 5 человек в каждой?

5. Сколькими способами можно расселить 9 студентов в комнаты, каждая из которых рассчитана на трёх человек?

6. Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта пирожных?

7. Сколько имеется пятизначных десятичных чисел, у которых цифры идут слева направо в неубывающем порядке?

8. Сколько имеется вариантов выбора трех призеров среди  n участников конкурса без указания занимаемых ими мест?

9. Имеется  n₁ разных книг одного автора, n₂ - второго и  n₃- третьего. Каким числом способов можно выбрать

а) две книги одного автора;

б) три книги одного автора;

в) одну книгу первого автора, две - второго и три - третьего?

10. На плоскости расположены n точек, никакие три из которых не лежат на одной прямой. Сколько существует треугольников с вершинами в данных точках?

11. Сколько различных подмножеств из трех элементов имеет мно­жество А={1, 2, 3, 4}; В={а, , 0, 1, 2}?

12. Сколькими способами из трех спортивных обществ, насчиты­вающих соответственно 40, 40 и 60 человек, можно выбрать команды по 5 человек для участия в соревнованиях?

13. Из группы в 20 человек каждую ночь выделяется наряд из трех человек. Сколько существует вариантов составления наряда?

14. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее двух женщин. Сколькими способами это можно сделать?

15. Сколькими способами можно выбрать 12 человек из 17, если дан­ные двое человек из этих 17 не могут быть выбраны вместе?

16. Найти натуральное число n, удовлетворяющее уравнению

17. Доказать следующие свойства биномиальных коэффициентов:

а)  (k=1…n);

б)

в) ;

г)  ;

д)  ;

e) 

18. Из колоды, содержащей 52 карты, вынули 10 карт. Сколькими способами это можно сделать? В скольких случаях среди этих карт окажется:

а) хотя бы один туз;

б) ровно один туз;

в) ровно четыре туза;

г) не менее двух тузов;

д) ровно два туза?

19. Каким числом способов из 10 человек можно выбрать три комиссии, если в первой и во второй комиссиях должно быть по 3 человека, а в третьей - 5 человек, и ни один из членов первой комиссии не должен входить во вторую и третью?

 

Перестановки

 

Размещения без повторений из n элементов по n называются перестановками из n элементов. Их число обозначается P_n и вычисляется по формуле:

 

Пример. Сколькими способами можно поставить в ряд 5 человек для фотоснимка?

Решение. Ряд из пяти человек можно рассматривать как упорядо­ченную выборку из 5-ти элементов по 5. По формуле для числа перестановок имеем

(способов).

 

Задача. Семь девушек во­дят хоровод. Сколькими различными способами они могут встать в круг?

Решение. Если бы девушки стояли на месте, то получилось бы 7! способов перестановок в ряду. Но так как они кружатся, то их положение относительно окружающих предметов несущественно, а важно только их взаимное расположение. Поэтому перестановки, переходящие друг в друга при кружении (циклическом сдвиге), нужно считать одинаковыми. Так как из каждой перестановки циклическим сдвигом можно получить ещё 6 но­вых, то количество интересующих нас перестановок (7!) : 7 = 6!.

Эту задачу можно обобщить так. Если рассматривать перестановки n предметов, расположенных не в ряд, а по кругу, и считать одинаковыми перестановки, переходящие друг в друга при вращении, то число различ­ных перестановок (n–1)!. Такие перестановки называют циклическими перестановками.

Рассмотрим задачу: Имеются предметы k различных видов. Сколько различных комбинаций (перестано­вок) можно сделать из п₁предметов 1-го вида, n₂ предметов 2-го вида,..., п_kпредметов k-го вида? Число предметов в каждой перестановке n=n₁+n₂+...+n_k. Такие комбинации называются перестановками с повто­рениями. Их число обозначается P(и вычисляется по формуле

P(=

Пример. Сколькими способами можно расположить в ряд 5 чер­ных, 4 белых и 3 красных фишки?

Решение. Эта задача на перестановки с повторениями. Имеем фишки 3-х различных видов: чёрных n₁ = 5, белых n₂ = 4 и красных n₃ = 3. Всего фи­шек n = 12. Следовательно, по формуле  имеем Р(5,4,3) = = 27 720 (способов).

Замечание. Для решения данной задачи можно было применить рассуждения, подобные выводу формулы для числа сочетаний: Занумеру­ем чёрные фишки числами 1, 2, 3, 4, 5; белые – числами 6, 7, 8, 9; крас­ные – числами 10, 11, 12. Имеем всего 12 предметов, которые можно рас­положить в ряд 12! способами. Но все расположения фишек не меняются при всех перестановках фишек с номерами 1–5 (все они одного вида), с но­мерами 6–9 и с номерами 10–12. Поэтому число различных расположений равно

Замечание. Если то имеем   Р(k,n-k)= .

 

УПРАЖНЕНИЯ

1.    Сколькими способами могут 7 человек встать в очередь за би­летами в театральной кассе?

2.  Сколько ожерелий можно составить из семи бусинок разных раз­меров?

3.  Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски?

4.  Четыре автора должны написать книгу из 17 глав, причём первый и третий должны написать по 5 глав, второй - 4 главы, а четвёртый - 3 главы книги. Сколькими способами можно распределить главы между авторами?

5.  Сколько существует перестановок элементов 1, 2,...,n , в которых элемент 1 находится не на своём месте?

6.  Сколькими способами можно переставить буквы в слове а) «космос?»                                          б) «тартар»?

7.  Сколькими разных чисел можно получить переставляя местами цифры числа

а) 12 341 234?  

б) 12 345 234?

8. Сколько различных слов можно составить, переставляя буквы в слове "математика"?

 

РАЗНЫЕ КОМБИНАТОРНЫЕ ЗАДАЧИ

 

1. Сколькими способами можно переставить буквы слова:

а) «периметр», чтобы «е» шла непосредственно после «р»;

б) «поговорка», чтобы согласные шли в алфавитном порядке;

в) «профессор», чтобы не менялся порядок гласных букв;

г) «корректор», чтобы три буквы «р» не шли подряд

2. Сколько делителей имеет число 2880? Сколько делителей имеет число,  где p₁,..., p_s-различные простые числа, k₁,...,k_s- целые не­отрицательные?

3. Сколькими способами можно выбрать 6 карт из колоды, содержащей 52 карты, так, чтобы среди них были карты каждой масти?

4. Составляются слова длины 4 из 32 букв русского алфавита так, что две соседние буквы этих слов различны. Какого характера эти выборки? Найти число таких наборов слов.

5.Сколько бинарных отношений можно задать на множестве из n элемен­тов? Сколько среди них:

а) рефлексивных?

б) симметричных?

в) антисимметричных?

6.  Сколько различных браслетов можно сделать из четырёх одина­ковых рубинов, пяти одинаковых сапфиров и шести одинаковых изумру­дов, если в браслете должны быть все 15 камней? Сколькими способами можно из этих камней выбрать три камня для кольца?

7. Сколькими способами можно разбить (п + т + р) предметов на три группы так, чтобы в одной было п, в другой т, а в третьей р предметов?

8. Сколько существует вариантов того, что три человека, сдавшие свои шляпы в гардероб, не получат в точности свою шляпу?

9. Четыре человека сдают свои шляпы в гардероб. Предполагая, что шляпы возвращаются наугад, найти число случаев и вероятность того, что в точности k человек получат свои шляпы. Рассмотреть все значения k (k = 0, 1, 2, 3, 4 ).

10. Сколько слов длины n в  q-буквенном алфавите, в которых любые две соседние буквы различны?

11. Имеется колода из 4n карт четырех мастей, поn карт каждой масти, занумерованных числами 1,2,...,n. Каким числом способов можно выбрать пять карт так, чтобы среди них оказались:

а) пять карт одной масти с последовательными номерами;

б) четыре карты с одинаковыми номерами;

в) три карты с одним номером и две карты с другим;

г) пять карт одной масти;

д) пять карт с последовательными номерами;

е) три карты с одинаковыми номерами;

ж) две карты с одинаковыми, остальные с разными номерами

12. Каким числом способов можно рассадить n мужчин и mженщин вдоль одной стороны прямоугольного стола так, чтобы никакие две женщины не си­дели рядом?

13. Траекторией назовем ломаную линию на плоскости, состоящую из отрез­ков, параллельных координатным осям, причем длины отрезков - целые числа, а при движении вдоль ломаной от начальной точки каждый вертикальный отрезок проходится снизу вверх, а горизонтальный - слева направо. Найдите число траекторий, начинающихся в точке (0,0), а оканчивающихся

а) в точке (m, n);

б) на прямой x+y=n.

14. Сколько диагоналей у выпуклого n-угольника? Найдите число точек пере­сечения этих диагоналей (не считая вершин), если известно, что в каждой из этих точек пересекаются только две диагонали?

15. Сколько имеется пятизначных десятичных чисел, у которых

а) ровно три цифры четные;

б) не менее двух четных цифр?

16. Определите число целых положительных (целых неотрицательных) реше­ний уравнения x₁+x₂ +...+x_k= n.

17. Сколько имеется перестановок из элементов 1,2,..., n, в которых

a) 1 стоит раньше 2?

б) 1 и 2 не стоят рядом?

в) между 1 и 2 расположеныkдругих элементов?

г) 1 стоит не на первом месте, 2 - не на втором?

18. Сколько существует отображений множества A в множество B, если , ? Сколько среди них инъективных? Биективных?

19. Сколько отношений линейного порядка можно определить на множестве из n элементов?

20. Каким числом способов можно расположить n нулей и k единиц в последовательность так, чтобы никакие две единицы не стояли рядом?

21. Каким числом способов можно распределить nодинаковых монет между kлицами?

22. Каким числом способов можно разместить 7 студентов в трех комнатах общежития, если

а) в одной комнате имеется одно, в другой - два, в третьей - четыре сво­бодных места;

б) в одной комнате имеется два, в другой - три, в третьей - четыре сво­бодных места?

23. Код замка состоит из пяти десятичных цифр. Известно, что среди них один раз встречается цифра 0 и дважды - цифра 3. Сколько комбинаций нужно перебрать, чтобы наверняка открыть замок?

24. Каким числом способов можно разбить 14 человек на 7 пар?

25. Чему равен коэффициент при  x⁴ y⁸ в разложении (1+x+y)²⁰?

26. Рассматриваются слова в алфавите  Через n_i обозначается число вхождений буквы  a_i  в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям:

а) q= 5, n= 8, n₁+ n₂+ n₃= 2;                   

б) q= 4, n= 8, n₂= n₁+ 2;                  

в) q= 3, n= 9, n₁+ n₂<n₃;

г) q= 3, n= 9,2n₁n₂+ n₃;

д) q= 5, n= 7, n₁+ n₂+ n₃= 2, n₄ 3.                   

27. Каким числом способов можно составить букет из n цветов трех видов, если все цветы одного вида одинаковы и имеется неограниченный запас цветов каждого вида?

28. Каким числом способов можно kn различных предметов разложить по n одинаковым (неразличимым) ящикам так, чтобы в каждом ящике оказалось ровно k предметов?

29. Сколько раз в десятичной записи всех натуральных чисел, меньших 10ⁿ, встречается цифра 9? Цифра 0?

30. Дано множество U из n элементов и в нем подмножество A из k эле­ментов. Определите число подмножеств, удовлетворяющих условию:

а)                                                     г)

б)                                                     д)

в)                                               е)

31. Дано множество U из n элементов и в нем подмножества  A из k эле­ментов и B из l элементов, причем  Найти число подмножеств , удовлетворяющих условию:

а)

б)                               

в)

г)

32. Дано множество  U из n элементов и в нем подмножество  A из k эле­ментов. Определите число подмножеств, удовлетворяющих условию:

а) ;

б)

в)

33. В множествеUизnэлементов найдите число пар подмножеств (A, B), удовлетворяющих условиям:

а) ;

б);

в)

г)

д)

е)

34. Дано множество U из n элементов. Каким числом способов в нем мож­но выбрать три подмножества A, B, C так, чтобы выполнялись заданные усло­вия:

а) n= 7,

б) n= 6,

в) n= 7, 

г) n= 6, 

д) n= 8,

 

 

 

 

 

 

 

ОГЛАВЛЕНИЕ

 

	ВВЕДЕНИЕ ……………………………………………………..	3
	МНОЖЕСТВА ………………………………………………….	5
1.1	Основные понятия ……………………………………………...	5
1.2	Операции над множествами …………………………………...	7
1.3	Основные теоретико-множественные тождества …………….	9
	Упражнения ……………………………………………………..	9
	ПРЯМОЕ ПРОИЗВЕДЕНИЕ МНОЖЕСТВ …………………..	13
2.1	Бинарные отношения …………………………………………..	13
2.2	Специальные бинарные отношения …………………………..	15
	Упражнения …………………………………………………….	16
	КОМБИНАТОРИКА …………………………………………..	20
3.1	Основные правила комбинаторики …………………………..	20
3.2	Формула включений и исключений …………………………..	22
	Упражнения …………………………………………………….	22
3.3	Упорядоченные и неупорядоченные выборки ……………….	27
	Упражнения …………………………………………………….	28
3.4	Размещения без повторений и с повторениями ………………	29
	Упражнения …………………………………………………….	31
3.5	Сочетания без повторений и с повторениями ………………..	32
	Упражнения …………………………………………………….	33
3.6	Перестановки …………………………………………………...	35
	Упражнения …………………………………………………….	37
	Разные комбинаторные задачи ………………………………...	38

      

 

 

 

Методическое пособие «Дискретная математика. Краткая теория и задачи. Часть 1. Теория множеств. Комбинаторика» предназначено для студентов всех направлений бакалавриата Ташкентского университета информационных технологий, изучающих курс Дискретной математики.

 

Обсуждено на заседании кафедры «Алгоритмизации и математического моделирования» .

Протокол № _______ от _________________ 2014 г.

 

Рассмотрено на заседании методического совета факультета  Программного инжиниринга

Протокол  № ______ от __________________ 2014 г.

 

Главный редактор                                                 доц. Ю.М. Абдурахманова

 

Составители:                                                                      Х. Абдуваитов,

                                                                                             У.Н. Каландаров,

 

Корректор                                                                            Н.Х. Рахимова

 

Объем __________

Отпечатано. Тираж - ____

Заказ № ____

 

 

Ташкенсткий университет информационных технологий

Центр печати “АLOQACHI”

 

г. Ташкент, ул. Амира Темура, 108.