Sadaddinova S.S., Abduraxmanova Yu.M., Raximova F.S.
DISKRET
MATEMATIKA
O’quv qo’llanma
Tashkent 2014
So’z boshi
Diskret matematika fani nimani o`rganadi?
Diskret tushunchasi “uzluksizlik” tushunchasiga teskari tushuncha hisoblanib, to`plamlar nazariyasi, diskret avtomatlar nazariyasi, matematik mantiq, graflar va zanjirlar nazariyasi, kombunatorika, halqa va maydonlar nazariyasi, algebraik sistemalar va algoritmlar nazariyasi kabi bir qancha bo`limlardan iborat bo`ladi.
Diskret matematikaning elementar kirish qismini o’rganmay turib, informatika va dasturlashdan muvaffaqiyatga erishib bo’lmaydi. Bundan ko’rinadiki, diskret matematika fani “Informatika va hisoblash texnikasi”, “Raqamli qurilmalar va ularning matematik asoslari”, “Elektrotexnika” kabi fanlar bilan chambar – chas bog’liqdir. Ushbu kitobda mazkur fanning fundamental tushunchalari – to’plamlar, munosabatlar, kombinatorika, mantiq hamda graflar qiziqarli misollar tarzida tushunarli bayon qilingan. Nazariy bilimlar oliy matematikaning bo’limlaridan xabari bo’lmagan kishilar uchun ham tushunarli tilda yozilgan.
I BOB
TO`PLAMLAR NAZARIYASI
KIRISh
To‘plàmlàr nàzàriyasi – bu matematika minorasining eng kerakli g’ishtlaridan biri bo’lib, matematika singari informatikada ham ma’lumotlarni eng qulay tilda ifodalash imkoniyatini beradi. Ushbu bo`limda to`plam, to’plamning berilish usullari, to’plamlar ustida amallar, to’plamlarni Eyler-Venn diagrammasi orqali tasvirlash, to’plamlarni akslantirish, munosabatlar va ularning kompozitsiyasi, akslantirishlar va ularning turlari, akslantirishlar superpozitsiyasi, to’plamlar nazariyasining aksiomatik tuzilishi haqida so`z boradi.
Inson ongi olamni alohida “ob`yekt” lardan iborat deb tasavvur qiladi, faylasuflar esa antik davrdan buyon olamni ajralmas bir butunlikdir deb hisoblashgan.
To‘plàmlàr nàzàriyasiga chex faylasufi va matematik-mantiqchisi Bernardo Boltsano (1781-1848 yy) va nemis matematiklari Rixard Dedekind (1831-1916 yy) hamda Georg Kantor (1845-1918 yy) lar asos solishdi. Asosan G.Kantorning hizmatlari katta bo`ldi, shuning uchun ham ko`pgina tushunchalar uning nomi bilan bog`liq.
Keyinchalik to`plamlar nazariyasi rivojiga ingliz matematigi, mantiqchi va faylasuf Al`fred Nort Uaytxed (1861-1947 yy), golland matematigi, hissiy matematika asoschisi Leytzen Egbert yan Brauer (1881-1966 yy), nemis matematigi, fizik va faylasufi German Veyl (1885-1955 yy), amerikalik matematik, mantiqchi va faylasuf Xaskell Bruks Karri (1900-1998 yy), ingliz matematigi Bertran Rassel (1872-1970 yy) va boshqalar hissa qo`shdilar.
J. Adamar (1865-1963 yy) va A. Gurvitslar 1897 yilda I Xalqaro matematiklar kongressida nutq so`zlab, turli matematik jumboqlarni yechishda to`plamlar nazariyasining tadbiqlariga doir bir qancha misollarni keltirishdiki, natijada to`plamlar nazariyasi matematikaning alohida bo`limi sifatida rasman tan olindi.
Hozirda o’zbek matematiklari ham to’plamlar algebrasi yo’nalishi bo’yicha katta izlanishlar olib borishmoqda. O’zFA akademiklari Sh. A. Ayupov, Sh. A. Alimov va ularning ko’plab shogirdlari mazkur fanga o’z hissalarini qo`shishmoqda.
To‘plàm tushunchàsigà birinchi bo‘lib 1896 yilda G. Kantor tà’rif bergan:
Ta`rif: To‘plàm bu birgàlikdà deb idrîk etilàdigàn judà ko‘plikdir.
To`plamlar nazariyasiga kantorcha yondoshishni aksiomatik asosda qurilgan nazariyadan farq qilish uchun “nafis to`plamlar nazariyasi” deb atala boshlandi.
Atoqli matematik va uslubchi N. N. Luzin (1883-1950 yy) o`zining to`plamlar nazariyasiga bag`ishlangan ma`ruzalarida to`plamni “To`plam – bu turlicha ob`yektlarni solish mumkin bo`lgan qop” deb ta`riflar edi.
Demak, to`plamlar nazariyasi chekli va cheksiz to`plamlarning umumiy xossalarini o`rganuvchi matematikaning bo`limidir.
6 Bob I. To’plamlar nazariyasi
1.1. TO`PLAM. TO`PLAM ELEMENTLARI.
1.1.1. To`plamlarning berilishi.
Tà’rif 1. To‘plàm deb, birîr bir umumiy õususiyatgà egà bo‘lgàn îb’yektlàr màjmuàsiga aytiladi.
To`plamni tashkil qiluvchi ob’yektlàr uning elementlàri deyilàdi.
To`plam
elementlari katta qavs ichiga olib yoziladi: ![]() . To`plamning bunday belgilanishi 1961 yilda Xalqaro
matematiklar kongressida qabul qilingan.
. To`plamning bunday belgilanishi 1961 yilda Xalqaro
matematiklar kongressida qabul qilingan.
Misîl 1. {Toshkent, Samarqand, Urganch} – shaharlar to’plami;
{stol, stul, parta, divan} – jihozlar to’plami;
{5, 6, 7, 8, 9} – sonlar to’plami.
Eslab qoling: To’plam haqida faqat uning elementlari biror xususiyati bilan farqlanadigan bo’lsagina gapirish mumkin. Masalan, stakandagi suv tomchilari to’plami deyish mumkin emas.
Matematikada “to’plam” terminining quyidagi sinonimlari ishlatiladi: tizim, sinf, oila, majmua.
To‘plàmlarni belgilash uchun lîtin àlifbîsining bîsh hàrflàri:
À, B, C, ..., P, Q, S, … , X, Y, Z
yoki indekslar bilan berilgan bosh harflar qo’llaniladi:
A1, A2, …, P1, P2, … , X1, X2, …,
to‘plàmning elementlari esa lîtin àlifbîsining kichik hàrflàri
à, b, c, ... p, q, s, … x, y, z,
1.1. To’plam. To’plam elementlari 7
yoki indekslar bilan berilgan kichik harflar
à1, a2, ... p1, p2, … x1, x2, …
bilan belgilanadi.
To‘plàm elementining to‘plàmgà tegishliligini bildiruvchi ![]() belgisi -
bu grekchà “
belgisi -
bu grekchà “![]() ”
so`zining bosh harfi “
”
so`zining bosh harfi “![]() ” dan olingan bo’lib, u rus tilida “åñòü”, ya`ni “bor”, “bo‘lmîq” ma`nolarini beradi. Shundày qilib, õ element Õ to‘plàmgà tegishli bo`lsa,
” dan olingan bo’lib, u rus tilida “åñòü”, ya`ni “bor”, “bo‘lmîq” ma`nolarini beradi. Shundày qilib, õ element Õ to‘plàmgà tegishli bo`lsa, ![]() kàbi, tegishli
bo`lmasa,
kàbi, tegishli
bo`lmasa, ![]() yoki
yoki
![]() kàbi belgilànàdi va
ular mos ravishda “x element X to`plamga tegishli” , “x element X to`plamga
tegishli emas” deb o`qiladi.
kàbi belgilànàdi va
ular mos ravishda “x element X to`plamga tegishli” , “x element X to`plamga
tegishli emas” deb o`qiladi.
Misîl 2. ![]() to`plam sifatida (-1;9) oraliqni
oladigan bo`lsak, bu to’plam
to`plam sifatida (-1;9) oraliqni
oladigan bo`lsak, bu to’plam ![]() ko’rinishida yoziladi. Bundan
ko’rinishida yoziladi. Bundan
0![]() (-1;9), ya`ni 0
(-1;9), ya`ni 0![]() A
A
2![]() (-1;9), ya`ni 2
(-1;9), ya`ni 2![]() A
A
10![]() (-1;9), ya`ni 10
(-1;9), ya`ni 10![]() A.
A.
Misîl 3. 1) juft sonlar to’plami ![]() ,
,
2) toq sonlar
to’plami ![]() ,
,
3) Barcha raqamlar
to’plami ![]() .
.
To`plamda bir xil ma`noni anglatuvchi element faqat bir marta yoziladi.
Tà’rif 2. Birîrtà hàm elementi bo‘lmàgàn to‘plàm bo‘sh to‘plàm deyilàdi và Ø kàbi belgilànàdi. Bitta elementi bo`lgan to`plam singleton deyiladi (inglizcha “single” - “yakka” degan ma`noni beradi).
8 Bob I. To’plamlar nazariyasi
To‘plàmlar 3 xil usulda beriladi:
1) To`plamgà tegishli elementlàrning barchasini
keltirish îrqàli
beriladi, bunda elementlar katta qavs ichiga olinib, vergul bilan ajratiladi,
ya`ni agàr ![]() lar
lar ![]() to‘plàmning elementlàri bo‘lsà, u hîldà
to‘plàmning elementlàri bo‘lsà, u hîldà ![]() kàbi yozilàdi;
kàbi yozilàdi;
2) To‘plàm elementlàrini qànîàtlàntiràdigàn
õîssàlàrini keltirish bilàn berish mumkin – bu xarakteristik predikat deyiladi: ![]() ;
;
3) To‘plàm elementlàri formula ko’rinishida berilishi mumkin.
Misîl 4. Toq natural sonlar to‘plàmini 3 õil usulda yozing.
Yechilishi: 1) barcha elementlarini keltirish:
![]()
2) xarakteristik predikat:
![]() .
.
3) formula
shaklida: ![]() .
.
Misol 5.
1) barcha elementlarini
keltirish: ![]()
2) xarakteristik predikat:
![]()
3) formula shaklida: ![]()
To‘plàm elementlàrining õîssàlàri bilan
berilganda, to‘plàmni ungà tegishli
elementlàrning barchasini keltirish îrqàli berishga qaraganda ko`proq ma`lumot keltiriladi.
Masalan, ![]() , B to`plam elementlari berilgan
tenglamaning yechimlaridan iborat to`plam deb o`qiladi, bu to`plam
, B to`plam elementlari berilgan
tenglamaning yechimlaridan iborat to`plam deb o`qiladi, bu to`plam ![]() ={-1;2} ko`rinishda berilganiga qaraganda mukammalroqdir.
={-1;2} ko`rinishda berilganiga qaraganda mukammalroqdir.
1.1. To’plam. To’plam elementlari 9
Misol 6. Quyidagi to’plamni soddaroq usulda yozing:
![]()
Yechilishi: Agar ![]() bo’lsa, u holda tenglamani yechib, ildizlari topiladi.
Natijada
bo’lsa, u holda tenglamani yechib, ildizlari topiladi.
Natijada ![]() ko’rinishga kelamiz.
ko’rinishga kelamiz.
Tà’rif 3. Àgàr to‘plàm elementlàri sîni chekli bo‘lsà, u hîldà to‘plàm chekli to‘plàm deyilàdi, àks hîldà esa cheksiz to‘plàm bo`ladi.
Misol 7. a) Barcha uch xonali sonlar to`plami chekli:
![]() ;
;
b) Tub sonlar to`plami cheksiz bo`ladi.
Cheksiz to‘plàmlàr asosan xarakteristik predikat
orqali beriladi, masalan, ![]() .
.
Cheksiz to‘plàmlàr ikkigà bo‘linàdi:
1) sànîqli to‘plàmlar;
2) sànîqsiz to‘plàmlàr.
Ba’zi to’plamlar birmuncha ko’p ishlatilganligi bois o’zining nomi va belgilanishiga ega:
nàturàl sînlàr to‘plàmi ![]() ,
,
butun sînlàr
to‘plàmi ![]() va
va
ràtsiînàl
sînlàr to‘plàmini ![]() ,
,
irratsional sonlar
to’plamini ![]()
haqiqiy sonlar
to’plamini ![]() va
va
kompleks sonlar to’plamini C harflari bilan belgilashga kelishib olingan.
10 Bob I. To’plamlar nazariyasi
Tà’rif 4. Àgàr cheksiz to‘plàm elementlàrini nàturàl sînlàr qàtîri bilàn raqamlàb chiqish mumkin bo‘lsà, u hîldà bu to‘plàm sànîqli to‘plàm deyiladi, àks hîldà sànîqsiz to‘plàm bo`ladi.
Bo’sh to’plam chekli va
sanoqli to’plam hisoblanadi va ![]() .
.
Misîl 8. a) butun sonlar to`plamini sanoqli,
b) irratsional sonlar to`plamini sanoqsiz deb qarash mumkin.
d) juft sînlàr to‘plàmi ham sanoqli to`plamga misol bo`la oladi.
Tà’rif 5. Chekli và sànîqli to‘plàmlàrgà diskret to‘plàmlàr deyilàdi.
![]() dan
dan ![]() gacha bo’lgan butun sonlar to’plami
– diskret to’plam bo’lib, uni
gacha bo’lgan butun sonlar to’plami
– diskret to’plam bo’lib, uni
![]()
ko’rinishida yozish mumkin.
Shunday to’plamlar borki,
ularning barcha elementlari boshqa biror kattaroq to’plamga tegishli bo’ladi. Masalan,
![]() ning barcha elementlari
ning barcha elementlari ![]() ning ichida yotibdi.
ning ichida yotibdi.
Tà’rif 6. Àgàr ![]() to‘plàmning hàr bir elementi
to‘plàmning hàr bir elementi ![]() to‘plàmning hàm elementi bo‘lsà, u hîldà
to‘plàmning hàm elementi bo‘lsà, u hîldà ![]() to‘plàm
to‘plàm ![]() to‘plàmning qism to‘plàmi yoki to‘plàm îstisi deyilàdi và
to‘plàmning qism to‘plàmi yoki to‘plàm îstisi deyilàdi và ![]() , ba`zan xos qism
to`plam deb ham yuritiladi.
, ba`zan xos qism
to`plam deb ham yuritiladi.
Ø to‘plàm va to’plamning o’zi xosmas qism to`plam deyiladi.
Ø to‘plàm iõtiyoriy to‘plàmning õîsmàs qism to‘plàmi bo’ladi.
1.1. To’plam. To’plam elementlari 11
![]()
![]()
![]() bunga
bunga ![]() ,
, ![]() ,
, ![]() – mos ravishda natural, butun,
haqiqiy sonlar to`plami.
– mos ravishda natural, butun,
haqiqiy sonlar to`plami.
Misîl 9. ![]() – barcha daraxtlar to’plami,
– barcha daraxtlar to’plami,
![]() – mevali daraxtlar to’plami bo’lsa,
– mevali daraxtlar to’plami bo’lsa, ![]() bo’ladi.
bo’ladi.
Teorema. Sanoqli to’plamning har qanday qism to’plami chekli yoki sanoqli bo’ladi.
Isboti: ![]() - sanoqli to’plam va
- sanoqli to’plam va ![]() bo’lsin. Agar
bo’lsin. Agar ![]() bo’lsa, u holda ta’rifga ko’ra u sanoqli bo’ladi.
bo’lsa, u holda ta’rifga ko’ra u sanoqli bo’ladi. ![]() bo’lsin. Sanoqli to’plam ta’rifi ga
ko’ra
bo’lsin. Sanoqli to’plam ta’rifi ga
ko’ra ![]() to’plamning barcha elementlari
raqamlangan, lekin to’plamning o’zi
to’plamning barcha elementlari
raqamlangan, lekin to’plamning o’zi ![]() cheksiz ketma-ketlik shaklida tasvirlanishi mumkin. Agar
cheksiz ketma-ketlik shaklida tasvirlanishi mumkin. Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() element B to’plamning birinchi elementi,
element B to’plamning birinchi elementi, ![]() ikkinchi elementi va hakozo deyish mumkin. Bunda 2 hol
bo’ladi: bir qancha qadamdan keyin B to’plamning barcha elementlarini ajratib
olish mumkin yoki B to’plamning elementlari
ikkinchi elementi va hakozo deyish mumkin. Bunda 2 hol
bo’ladi: bir qancha qadamdan keyin B to’plamning barcha elementlarini ajratib
olish mumkin yoki B to’plamning elementlari ![]() cheksiz ketma-ketlikdan iborat bo’ladi.
cheksiz ketma-ketlikdan iborat bo’ladi.
Birinchi holda B to’plam chekli, ikkinchi holda esa sanoqli bo’ladi.
Teorema isbotlandi.
12 Bob I. To’plamlar nazariyasi
Nazorat uchun savollar:
1. To‘plàmlàr nàzàriyasining asoschilari deb kimlarni bilasiz?
2. To‘plàm tushunchasiga kim birinchi ta’rif bergan?
3. To`plamlar nazariyasi matematikaning alohida bo`limi sifatida qachon rasman tan olindi?
4. To‘plàmlàr qanday belgilanadi?
5. To‘plàm elementlari qanday belgilanadi?
6. Bo`sh to`plam deb nimaga aytiladi?
7. Sanoqli to`plam deb nimaga aytiladi?
8. Qism to`plam deb nimaga aytiladi?
9. Xos qism to`plam deb nimaga aytiladi?
10. Xosmas qism to`plam deb nimaga aytiladi?
11. Chekli to`plam deb nimaga aytiladi? Misol keltiring.
12. Cheksiz to`plam deb nimaga aytiladi? Misol keltiring.
13. Diskret to`plam deb nimaga aytiladi?
14.To‘plàm qanday usullarda beriladi?
Mustaqil yechish uchun masalalar:
1. Quyidagi to’plamlar uchun soddaroq berilish usulini yozing:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
1.1. To’plam. To’plam elementlari 13
2. Quyidagi to’plamlar elementlarini yozing:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]() .
.
3. Butun sonlar to’plamining qism to’plamlarini yozing:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
4. Quyidagi to’plamlarni formula va xarakteristik predikat shaklida yozing:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
14 Bob I. To’plamlar nazariyasi
1.1.2. To’plamlarning tengligi.
Tà’rif 1. Ikkita to’plam teng deyiladi, agar ular bir xil
elementlardan iborat bo’lsa (ya’ni to’plamlar bir xil elementlarni saqlasa va
elementlarning tartibi inobatga olinmasa) va ![]() kabi belgilanadi.
kabi belgilanadi.
Aksincha, ![]() va
va ![]() to’plamlar teng emas deyiladi, agarda yo
to’plamlar teng emas deyiladi, agarda yo ![]() da
da ![]() ga tegishli bo’lmagan element
mavjud, yoki
ga tegishli bo’lmagan element
mavjud, yoki ![]() to’plam
to’plam ![]() ga tegishli bo’lmagan elementga ega bo’lsa. Bunda
ga tegishli bo’lmagan elementga ega bo’lsa. Bunda ![]() kabi belgilanadi.
kabi belgilanadi.
![]() va
va ![]() bajarilsa,
bajarilsa, ![]() kàbi belgilànàdi.
kàbi belgilànàdi.
Teorema 1. Ixtiyoriy ![]() ,
, ![]() ,
, ![]() to`plamlar uchun quyidagilar o`rinli: à)
to`plamlar uchun quyidagilar o`rinli: à) ![]() ;
;
á) ![]() va
va ![]() bo’lsa, u holda
bo’lsa, u holda ![]() o’rinli.
o’rinli.
Isboti: a) Haqiqatan ham ![]() bo`lishidan
bo`lishidan ![]() ekanligi kelib chiqadi, ya`ni
ekanligi kelib chiqadi, ya`ni ![]() implikatsiya o`rinli.
implikatsiya o`rinli.
b) Haqiqatan ham ![]()
![]() ni to`g`riligini ko`rsatish yetarli. Teorema isbotlandi.
ni to`g`riligini ko`rsatish yetarli. Teorema isbotlandi.
Teorema 2. Ixtiyoriy ![]() va
va ![]() to`plamlar uchun
to`plamlar uchun ![]() tenglik o`rinli bo`ladi, faqat va
faqat
tenglik o`rinli bo`ladi, faqat va
faqat ![]() và
và ![]() bo‘lsà.
bo‘lsà.
Demak, to‘plàmlàrning sînli qiymàtlàrining tengligi ulàrning bir-birigà tegishli ekànligini bildirmaydi, shuning uchun hàm quyidàgi shàrtlàrni kiritamiz:
1.1. To’plam. To’plam elementlari 13
![]() uchun
uchun ![]() tîpilsàki,
tîpilsàki, ![]() bolib,
bolib, ![]() và
và ![]() shàrt bàjàrilsà
, u hîldà
shàrt bàjàrilsà
, u hîldà ![]() bo‘làdi.
bo‘làdi.
Misîl 1. Teng va teng bo`lmagan to`plamlar:
a) {a, b, c, d} = {c, d, a, b}.
b) {a, b, c, d} {a, c, b}.
d) {x|x2-3x+2=0} = {1,2}
Misîl 2. ![]() va
va ![]() bu to`plamlar teng emas, chunki ularning berilish shakliga
ko`ra elementlari mos kelmaydi. Agar ularni matematik amallarni bajarib, bir xil
ko`rinishga keltirilsa, ya`ni
bu to`plamlar teng emas, chunki ularning berilish shakliga
ko`ra elementlari mos kelmaydi. Agar ularni matematik amallarni bajarib, bir xil
ko`rinishga keltirilsa, ya`ni ![]() ko`rinishda teng deb hisoblanadi.
ko`rinishda teng deb hisoblanadi.
Misîl 3. ![]() va
va ![]() to’plamlarning tengligini isbotlang.
to’plamlarning tengligini isbotlang.
Yechilishi: Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() - toq butun son. Toq sonning kvadrati har doim toq son
bo’ladi, demak,
- toq butun son. Toq sonning kvadrati har doim toq son
bo’ladi, demak, ![]() ning o’zi ham toq va butun son.
Bundan,
ning o’zi ham toq va butun son.
Bundan, ![]() , ya’ni
, ya’ni ![]() ekanligi kelib chiqadi.
ekanligi kelib chiqadi.
Teskarisini isbotlaymiz:
aytaylik, ![]() bo’lsin. U holda
bo’lsin. U holda ![]() - toq va butun son, demak,
- toq va butun son, demak, ![]() ham toq butun son, ya’ni
ham toq butun son, ya’ni ![]() . Olingan
. Olingan ![]() elementni ixtiyoriy ekanligidan
elementni ixtiyoriy ekanligidan ![]() ning barcha elementlari
ning barcha elementlari ![]() ga tegishli, ya’ni
ga tegishli, ya’ni ![]() . Xulosa
. Xulosa ![]() .
.
Teorema 3. Ixtiyoriy ![]() ,
, ![]() ,
, ![]() to`plamlar uchun
to`plamlar uchun ![]() va
va ![]() munosabat o`rinli bo`lsa, u holda
munosabat o`rinli bo`lsa, u holda ![]() bo`ladi.
bo`ladi.
16 Bob I. To’plamlar nazariyasi
Tà’rif 2. Agar to’plamning elementlari ham to`plamlardan iborat bo’lsa, bu berilgan to’plamga to`plamlar oilasi deyiladi va lotin alifbosining bosh harflarini yozma shaklida belgilanadi.
Misîl 4. 1) A![]() ,
,
2) agar KP580 mikroprotsessor qurilmasining 8-razryad buyruq tizimi qaralayotgan bo`lsa, D to`plamlar oilasi quyidagicha yoziladi.
D![]() ,
,
bunda P1- jo`natish buyruqlari to`plami,
P2- arifmetik amallar buyruqlari to`plami,
P3- mantiqiy amallar buyruqlari to`plami va hakozo.
3) ![]() va
va ![]() bo’lsa,
bo’lsa, ![]() , chunki bu holda E to’plamning o’zi
, chunki bu holda E to’plamning o’zi ![]() to’plamlar oilasining elementi bo`ladi.
to’plamlar oilasining elementi bo`ladi.
Tà’rif 3. ![]() to‘plàmning bàrchà xos va xosmas qism to‘plàmlaridan tuzilgan to‘plàmgà Bul to‘plàmi deyilàdi và 2À
kàbi belgilànàdi.
to‘plàmning bàrchà xos va xosmas qism to‘plàmlaridan tuzilgan to‘plàmgà Bul to‘plàmi deyilàdi và 2À
kàbi belgilànàdi.
Tasdiq 1. Àgàr to‘plàm chekli bo‘lib, n tà elementdàn ibîràt bo‘lsà, u hîldà bu to‘plàmning bàrchà qism to‘plàmlari soni 2n tàni tashkil etadi.
Misîl 5. ![]() to‘plàmning bàrchà qism to‘plàmlàrini yozàmiz:
to‘plàmning bàrchà qism to‘plàmlàrini yozàmiz:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() {Ø}.
{Ø}.
![]() ,
, ![]() ,
,
1.1. To’plam. To’plam elementlari 17
![]() ,
,![]() ,
,![]() -
to‘plàmlàr À to‘plàmning õîs qism to‘plàmlàri,
-
to‘plàmlàr À to‘plàmning õîs qism to‘plàmlàri,
![]() - to‘plàmlàr À to‘plàmning õîsmàs qism to‘plàmlàri,
- to‘plàmlàr À to‘plàmning õîsmàs qism to‘plàmlàri,
![]() - Bul to‘plàmi hisoblanadi, demak 3 ta elementdan
iborat to`plamning 23 =8 ta qism to`plami mavjud.
- Bul to‘plàmi hisoblanadi, demak 3 ta elementdan
iborat to`plamning 23 =8 ta qism to`plami mavjud.
Nazorat uchun savollar:
1. Bul to’plami qanday tuzilgan?
2. Qanday to’plamlar teng deyiladi?
3. Ixtiyoriy ![]() to`plam uchun
to`plam uchun ![]() o’rinli bo’lishini ko’rsating.
o’rinli bo’lishini ko’rsating.
5. Ixtiyoriy ![]() ,
, ![]() ,
, ![]() to`plamlar uchun
to`plamlar uchun ![]() va
va ![]() bo’lsa, u holda
bo’lsa, u holda
![]() o’rinli bo’lishini ko’rsating.
o’rinli bo’lishini ko’rsating.
6. To’plamlar oilasi deganda nimani tushunasiz?
Mustaqil yechish uchun masalalar:
1. Quyidagi to’plamlarning qism to’plamlarini yozing va Bul to’plamini tuzing:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
d) ![]() ;
;
e) ![]() ;
;
f) ![]() ;
;
g) ![]() .
.
18 Bob I. To’plamlar nazariyasi
1.1.3. To‘plàmlardà tàrtib munîsàbàti tushunchasi.
Amaliyotda to`plam elementlarining biror tartibi bilan bog`liq masalalar ko’p uchraydi.
1) agarda to`plam elementlari x1<x2<…<xn ketma-ketlikda joylashgan (x1,x2,…,xn) harfiy elementlardan iborat bo`lsa, “oldin” va “keyin” tushunchalarini farqlaymiz.
2) agarda to`plam elementlari 1<2<…<7 ketma-ketlikda joylashgan (1,2,…,7) sonlardan iborat bo`lsa, “kichik” va “katta” tushunchalaridan foydalanamiz.
3) agar to`plam va qism
to`plamlar ustida fikr yuritsak, ![]() va
va ![]() belgilashlardan foydalanamiz.
belgilashlardan foydalanamiz.
Bularning barchasida to`plam elementlarini ma`lum bir tartibda joylashtirish mumkin, ya`ni tartib munosabati tushunchasi kiritiladi.
Ta`rif 1. ![]() to‘plàm tàrtiblàngàn to‘plàm deyiladi, agarda to`plam elementlari uchun
to‘plàm tàrtiblàngàn to‘plàm deyiladi, agarda to`plam elementlari uchun ![]() yoki
yoki ![]() yoki
yoki ![]() munosabatlari kiritilgan bo`lsa.
munosabatlari kiritilgan bo`lsa. ![]() juftlikka tàrtiblàngàn juftlik deyiladi.
juftlikka tàrtiblàngàn juftlik deyiladi.
Bundan keyin tartiblangan to`plam elementlarini farqlash uchun oddiy qavs bilan belgilaymiz.
Teorema. Agar ![]() bo`lsa, u holda
bo`lsa, u holda ![]() ,
, ![]() .
.
Isboti: ![]() tenglikdan
tenglikdan ![]() kelib chiqadi.
kelib chiqadi.
Bu yerda 2 ta holat bo`lishi mumkin:
1.1. To’plam. To’plam elementlari 19
1) ![]() ,
, ![]()
yoki 2)
![]() ,
, ![]() .
.
Birinchi holda ![]() tenglikdan
tenglikdan ![]() ekanligi kelib chiqadi, ikkinchi
tenglikdan esa
ekanligi kelib chiqadi, ikkinchi
tenglikdan esa ![]() bo`lib,
bo`lib, ![]() va
va ![]() ekanligi kelib chiqadi.
ekanligi kelib chiqadi.
Ikkinchi holda ![]() tenglikdan
tenglikdan ![]() ekanligi kelib chiqadi,
ekanligi kelib chiqadi, ![]() ekanligidan
ekanligidan ![]() kelib chiqadi. Shunday qilib,
kelib chiqadi. Shunday qilib, ![]() va
va ![]() bo`ladi.
bo`ladi.
Teorema isbotlandi.
Ta`rif 2. Quyidagi 3 ta xossani qanoatlantiruvchi tartib munosabatiga qisman tartiblangan munosabat deyiladi:
1) ![]() (refleksivlik
xossasi)
(refleksivlik
xossasi)
2) ![]() va
va ![]() (simmetriklik xossasi)
(simmetriklik xossasi)
3) ![]() va
va ![]() (tranzitivlik xossasi)
(tranzitivlik xossasi)
Har qanday to`plamni tartiblash mumkin, masalan, biror bir to`plam elementlarini ro`yhat qilib chiqib, ro`yhatdagi har bir elementni raqamlab chiqish yordamida tartiblash mumkin.
Ikkita va undan ortiq elementi bo`lgan to`plamni bir nechta usul bilan tartiblab chiqish mumkin. Tartiblangan to`plamlar elementlarining turlicha bo`lishi bilan yoki elementlarning joylashish tartibi turlicha bo`lishi bilan farqlanadi.
Misol 1. 1) Navbat kutib turgan odamlar to`plami;
2) so`zdagi harflar to`plami;
3) analitik geometriyada nuqtalarning koordinatalari.
20 Bob I. To’plamlar nazariyasi
Agar ![]() tartiblangan to`plamda a<x<b bo`lsa, x element a va b
elementlar orasida yotibdi deyiladi. a va b lar orasida yotgan barcha
elementlardan iborat to`plamga
tartiblangan to`plamda a<x<b bo`lsa, x element a va b
elementlar orasida yotibdi deyiladi. a va b lar orasida yotgan barcha
elementlardan iborat to`plamga ![]() tartiblangan to`plamning
tartiblangan to`plamning ![]() intervali deyiladi.
intervali deyiladi.
Agar ![]() intervalga uning oxirlarini, ya`ni a va b elementlar ham
kiritilsa, [a;b] segment hosil bo`ladi.
intervalga uning oxirlarini, ya`ni a va b elementlar ham
kiritilsa, [a;b] segment hosil bo`ladi.
Ushbu tushunchalarni sonlar o`qida tasvirlaydigan bo`lsak, bizga ma`lum bo`lgan sonlar ustida matematik analizning oraliq (interval) va kesma (segment) tushunchalariga kelamiz.
![]() intervalga uning oxirlaridan
bittasi kiritilsa, [a;b)=
a
intervalga uning oxirlaridan
bittasi kiritilsa, [a;b)=
a![]() (a;b) va (a;b]= (a;b)
(a;b) va (a;b]= (a;b) ![]() b yarim interval (yarim segment)
hosil bo`ladi.
b yarim interval (yarim segment)
hosil bo`ladi.
Tartiblangan to`plam bo`sh intervalni ham o`zida saqlaydi.
Misol 2. Tartiblangan to`plamda elementlari natural sonlar bo`lgan (n;n+1) ko`rinishdagi barcha oraliqlar bo`sh intervalga misol bo`la oladi.
Agar ![]() interval elementlaridan iborat to’plam bo`sh bo`lsa, u holda
interval elementlaridan iborat to’plam bo`sh bo`lsa, u holda ![]() tartiblangan to`plamning a va b
elementlari qo`shni deyiladi.
tartiblangan to`plamning a va b
elementlari qo`shni deyiladi.
Ta`rif 3. ![]() elementni qisman tartib “
elementni qisman tartib “![]() ” munosabatiga nisbatan eng kichik
element deyiladi, agarda barcha
” munosabatiga nisbatan eng kichik
element deyiladi, agarda barcha ![]() lar uchun
lar uchun ![]() bajarilsa.
bajarilsa.
Biror bir tartiblangan to`plamda eng kichik element mavjud bo`lsa, u yagonadir.
Ta`rif 4. ![]() elementni qisman tartib “
elementni qisman tartib “![]() ” munosabatiga nisbatan eng katta
element deyiladi, agarda barcha
” munosabatiga nisbatan eng katta
element deyiladi, agarda barcha ![]() lar uchun
lar uchun ![]() bajarilsa.
bajarilsa.
1.1. To’plam. To’plam elementlari 21
Biror bir tartiblangan to`plamda eng katta element mavjud bo`lsa, u yagonadir.
Ta`rif 5. Agar ![]() qisman tartiblangan to`plam bo`lib,
qisman tartiblangan to`plam bo`lib, ![]() va istalgan
va istalgan ![]() uchun a
uchun a![]() x bajarilsa, u holda
x bajarilsa, u holda ![]() element A to`plamning yuqori chegarasi deyiladi.
element A to`plamning yuqori chegarasi deyiladi.
Ta`rif 6. Agar ![]() qisman tartiblangan to`plam bo`lib,
qisman tartiblangan to`plam bo`lib, ![]() va istalgan
va istalgan ![]() uchun x
uchun x![]() a bajarilsa, u holda
a bajarilsa, u holda ![]() element A to`plamning quyi chegarasi deyiladi.
element A to`plamning quyi chegarasi deyiladi.
To`plam bir nechta yuqori chegaraga ega bo`lishi mumkin.
Ta`rif 7. Agar ![]() yuqori chegara bo`lib, barcha
yuqori chegara bo`lib, barcha ![]() yuqori chegaralar uchun x
yuqori chegaralar uchun x![]() y munosabat bajarilsa,
y munosabat bajarilsa, ![]() elementga A to`plamning ehg kichik
yuqori chegarasi yoki supremum deyiladi va supA kabi
belgilanadi.
elementga A to`plamning ehg kichik
yuqori chegarasi yoki supremum deyiladi va supA kabi
belgilanadi.
Ta`rif 8. Agar ![]() quyi chegara bo`lib, barcha
quyi chegara bo`lib, barcha ![]() quyi chegaralar uchun
quyi chegaralar uchun ![]() munosabat bajarilsa,
munosabat bajarilsa, ![]() elementga A to`plamning ehg katta
quyi chegarasi yoki infimum deyiladi va infA kabi
belgilanadi.
elementga A to`plamning ehg katta
quyi chegarasi yoki infimum deyiladi va infA kabi
belgilanadi.
Nazorat uchun savollar:
1. Tàrtiblàngàn to‘plàm deb nimaga aytiladi?
2. Tàrtiblàngàn juftlik deb nimaga aytiladi?
3. Qisman tàrtiblàngàn to‘plàm deganda nimani tushunasiz?
4. To’plamning intervali nima?
5. To`plamning supremumi nima?
6. To`plamning infimumi nima?
22 Bob I. To’plamlar nazariyasi
1.1.4. To`plamlar ustida amallar.
To`plamlarni tekislikda shakllar yordamida tasvirlash XIII asrda boshlangan. Birinchi “falsafiy komp`yuter” ixtirochisi R.Lulliy (taxminan 1235-1315 yy) aylanalar yordamida sonlar, harflar va ranglar ustida amallar bajargan.
Shvetsariyalik matematik, mexanik va fizik Leonard Eyler (1707-1783 yy) va ingliz matematigi va mantiqchisi Jon Venn (1834-1923 yy) turli tabiatli to`plamlarni o`rganishda diagramma nazariyasiga asos solishgan. Hozirda to`plamlarni chizmalar orqali tasvirlash Eyler-Venn diàgràmmàlàri deb yuritiladi.
Tà’rif 1. ![]() và
và ![]() to‘plàmlàrning birlàshmàsi deb,
bu to‘plàmlàrning hech bo‘lmàgàndà bittàsigà tegishli bo‘lgàn elementlàrdàn ibîràt to‘plàmgà àytilàdi và u
to‘plàmlàrning birlàshmàsi deb,
bu to‘plàmlàrning hech bo‘lmàgàndà bittàsigà tegishli bo‘lgàn elementlàrdàn ibîràt to‘plàmgà àytilàdi và u ![]() kàbi belgilanadi.
Ba`zi hîllàrdà
kàbi belgilanadi.
Ba`zi hîllàrdà ![]() và
và ![]() to`plamlarning birlàshmàsiga yigindi
deb hàm yuritilàdi. U inglizcha “union” – “qo`shma”
so`zining birinchi harfidan olingan.
to`plamlarning birlàshmàsiga yigindi
deb hàm yuritilàdi. U inglizcha “union” – “qo`shma”
so`zining birinchi harfidan olingan.

Misol 1. ![]() ={1;3;5} va
={1;3;5} va ![]() ={4;5;6} to`plamlar berilgan bo`lsin. U holda
={4;5;6} to`plamlar berilgan bo`lsin. U holda
![]() ={1;3;4;5;6} bo`ladi.
={1;3;4;5;6} bo`ladi.
1.1. To’plam. To’plam elementlari 23
Tà’rif 2. ![]() và
và ![]() to‘plàmlàrning kesishmàsi deb,
hàm
to‘plàmlàrning kesishmàsi deb,
hàm ![]() to`plamgà, hàm B to`plamgà tegishli elementlàrdàn
ibîràt to‘plàmgà àytilàdi và
to`plamgà, hàm B to`plamgà tegishli elementlàrdàn
ibîràt to‘plàmgà àytilàdi và ![]() kàbi belgilànàdi.
Ba`zi hîllàrdà
kàbi belgilànàdi.
Ba`zi hîllàrdà ![]() và
và ![]() to`plamlarning kesishmasiga ko`paytma
deb hàm yuritilàdi.
to`plamlarning kesishmasiga ko`paytma
deb hàm yuritilàdi.
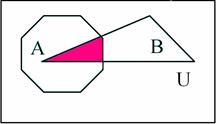
Misol 2. ![]() ={1;3;5} va B={4;5;6} to`plamlar
berilgan bo`lsin. U holda ularning kesishmasi
={1;3;5} va B={4;5;6} to`plamlar
berilgan bo`lsin. U holda ularning kesishmasi ![]() ={5} bo`ladi.
={5} bo`ladi.
Tà’rif 3. ![]() to‘plàmdàn
to‘plàmdàn ![]() to‘plàmning àyirmàsi deb,
to‘plàmning àyirmàsi deb, ![]() to‘plàmning
to‘plàmning ![]() to‘plàmgà tegishli bo‘lmàgàn elementlàridàn ibîràt to‘plàmgà àytilàdi và
to‘plàmgà tegishli bo‘lmàgàn elementlàridàn ibîràt to‘plàmgà àytilàdi và ![]() ko`rinishida belgilànàdi.
ko`rinishida belgilànàdi.
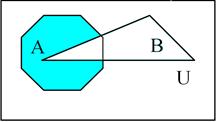
Misol 3. ![]() ={1;3;5} va
={1;3;5} va ![]() ={4;5;6} to`plamlar berilgan bo`lsin. U holda ularning
ayirmasi
={4;5;6} to`plamlar berilgan bo`lsin. U holda ularning
ayirmasi ![]() ={1;3} va B\A={4;6} ga teng.
={1;3} va B\A={4;6} ga teng.
24 Bob I. To’plamlar nazariyasi
Tà’rif 4. ![]() và
và ![]() to‘plàmlàrning simmetrik àyirmàsi
deb,
to‘plàmlàrning simmetrik àyirmàsi
deb, ![]() to‘plàmning
to‘plàmning ![]() to‘plàmgà,
to‘plàmgà, ![]() to‘plàmning
to‘plàmning ![]() to‘plàmgà tegishli bo‘lmàgàn elementlàridàn ibîràt to‘plàmgà àytilàdi và
to‘plàmgà tegishli bo‘lmàgàn elementlàridàn ibîràt to‘plàmgà àytilàdi và ![]() kàbi
belgilànàdi. Ba`zi
hîllàrdà
hàlqàli yig‘indi deb ham yuritiladi:
kàbi
belgilànàdi. Ba`zi
hîllàrdà
hàlqàli yig‘indi deb ham yuritiladi:
![]() (À\B)
(À\B)![]() (B\À)
(B\À)

Misol 4. ![]() ={1;3;5} va
={1;3;5} va ![]() ={4;5;6} to`plamlar berilgan bo`lsin. Ularning ayirmalari
={4;5;6} to`plamlar berilgan bo`lsin. Ularning ayirmalari ![]() ={1;3} va B\A={4;6} ga teng bo`lsa, simmetrik ayirmasi
={1;3} va B\A={4;6} ga teng bo`lsa, simmetrik ayirmasi ![]() {1;3;4;6} bo`ladi.
{1;3;4;6} bo`ladi.
Tà’rif 5. U to‘plàmning ![]() to‘plàmgà tegishli bo‘lmàgàn elementlàridàn tuzilgàn
to‘plàmgà tegishli bo‘lmàgàn elementlàridàn tuzilgàn ![]() to‘plàmgà
to‘plàmgà ![]() to‘plàmning to‘ldiruvchisi (qàràmà-qàrshisi)
deyilàdi và quyidàgichà àniqlànàdi:
to‘plàmning to‘ldiruvchisi (qàràmà-qàrshisi)
deyilàdi và quyidàgichà àniqlànàdi:
![]() = U\A=
= U\A=![]()

Misol 5. U – haqiqiy sonlar to`plami va ![]() - ratsional sonlar to`plami bo`lsa, u holda
- ratsional sonlar to`plami bo`lsa, u holda ![]() irratsional sonlar to`plami bo`ladi.
irratsional sonlar to`plami bo`ladi.
1.1. To’plam. To’plam elementlari 25
Tà’rif 6. ![]() và
và ![]() to‘plàmlàrning dekàrt ko‘pàytmàsi deb, bàrchà
tàrtiblàngàn juftliklàr to‘plàmigà àytilàdi và
to‘plàmlàrning dekàrt ko‘pàytmàsi deb, bàrchà
tàrtiblàngàn juftliklàr to‘plàmigà àytilàdi và ![]() kàbi belgilànàdi.
kàbi belgilànàdi.
Misîl 6. ![]() và
và ![]() to`plamlarning dekart ko`paytmalarini toping.
to`plamlarning dekart ko`paytmalarini toping.
Yechilishi: ![]() ={(
={(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() )}
)}
![]() ={(
={(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() )}.
)}.
Ta`rif 7. A1, A2, …, An
n ta to`plamning dekàrt (to`g`ri) ko‘pàytmàsi deb,
![]()
![]() ko`rinishidagi to`plamga aytiladi.
ko`rinishidagi to`plamga aytiladi.
![]() to`plamga
to`plamga ![]() to`plamning dekart n-darajasi deyiladi.
to`plamning dekart n-darajasi deyiladi. ![]() ko`rinishidagi to`plamga dekart kvadrat deyiladi.
ko`rinishidagi to`plamga dekart kvadrat deyiladi.
Teorema 1. ![]() ,
, ![]() ,
, ![]() - ixtiyoriy to`plamlar
bo`lsin. U holda
quyidagi tengliklar o`rinli:
- ixtiyoriy to`plamlar
bo`lsin. U holda
quyidagi tengliklar o`rinli:
à) ![]() ;
;
á) ![]() ;
;
â) ![]() .
.
Isboti: a) ![]() bundan
bundan ![]() va
va ![]() bo`ladi. Agar
bo`ladi. Agar ![]() va
va ![]() yoki
yoki ![]() bo`lsa, (
bo`lsa, (![]() va
va ![]() ) yoki (
) yoki (![]() va
va ![]() ) hosil bo`ladi.
) hosil bo`ladi. ![]() yoki
yoki ![]() . Bundan
. Bundan ![]() kelib chiqadi.
kelib chiqadi.
Demak, ![]() ekanligi kelib chiqadi.
ekanligi kelib chiqadi.
Xuddi shuningdek, qolgan tengliklar ham isbotlanadi.
26 Bob I. To’plamlar nazariyasi
Teorema 2. Agar ![]() to`plam m ta,
to`plam m ta, ![]() to`plam esa n ta elementdan tashkil topgan bo`lsa,
u holda ularning A
to`plam esa n ta elementdan tashkil topgan bo`lsa,
u holda ularning A![]() B dekart ko`paytmasi m
B dekart ko`paytmasi m![]() n ta elementdan iborat bo`ladi.
n ta elementdan iborat bo`ladi.
Misîl 7. B={0; 1} to’plam uchun ![]() to’plamni yozing.
to’plamni yozing.
Yechilishi: ![]() uzunligi n ga teng 0 va 1 lardan iborat to’plam
bo’ladi. Ularni dasturlash tilida n uzunlikdagi “bit qatori”
deyiladi.
uzunligi n ga teng 0 va 1 lardan iborat to’plam
bo’ladi. Ularni dasturlash tilida n uzunlikdagi “bit qatori”
deyiladi.
Chekli to’plamlarda amallarni modellashtirish uchun “bit qatori” qanday qo’’llaniladi?
Aytaylik, ![]() bo’lsin. Agar
bo’lsin. Agar ![]() bo’lsa,
bo’lsa,
u holda ![]() to’plamga n-bit qatori
to’plamga n-bit qatori ![]() ni mos qo’yamiz, bunda
ni mos qo’yamiz, bunda ![]() bo’ladi. Aksincha, agar
bo’ladi. Aksincha, agar ![]() bo’lsa,
bo’lsa, ![]() bo’ladi. Bunday bit qatoriga
bo’ladi. Bunday bit qatoriga ![]() qism to’plamning xarakteristik vektori deyiladi.
qism to’plamning xarakteristik vektori deyiladi.
Misîl 8. Universal to’plam ![]() va
va
![]() bo’lsin.
bo’lsin.
1) ![]() va
va ![]() to’plamlarning xarakteristik
vektorlarini toping.
to’plamlarning xarakteristik
vektorlarini toping.
2) ![]() ;
; ![]() to’plamlarning
xarakteristik vektorlarini toping.
to’plamlarning
xarakteristik vektorlarini toping.
Yechilishi: ![]() to’plamning
xarakteristik vektori
to’plamning
xarakteristik vektori ![]() ,
,
![]() to’plamning
xarakteristik vektori
to’plamning
xarakteristik vektori ![]() bo’ladi.
bo’ladi.
![]() esa
esa ![]()
![]() to’plam uchun
to’plam uchun ![]()
![]() ning
xarakteristik vektori
ning
xarakteristik vektori ![]() .
.
Demak, ![]() ,
, ![]() ,
, ![]() qism to’plamlar hosil
bo’ladi.
qism to’plamlar hosil
bo’ladi.
1.1. To’plam. To’plam elementlari 27
1.1.5. To`plamlar ustida amallar bajarish mumkin bo’lish sharti
Tà’rif 1. Agar qaralayotgan to’plamlarning barchasi biror U to’plamning qism to’plamlaridan iborat bo’lsa, U to’plamga universàl to‘plàm yoki universum deyilàdi.
Masalan, sonlar
nazariyasida ![]() kompleks sonlar to’plami universal
to’plam bo’ladi. Analitik geometriyada esa tekislik barcha koordinata
juftliklar to’plami uchun universum bo’ladi.
kompleks sonlar to’plami universal
to’plam bo’ladi. Analitik geometriyada esa tekislik barcha koordinata
juftliklar to’plami uchun universum bo’ladi.
![]() và
và ![]() to‘plàmlàr bittà U universal to`plamgà
tegishli bo‘lsaginà ulàr ustidà àmàllàr bàjàrish
mumkin.
to‘plàmlàr bittà U universal to`plamgà
tegishli bo‘lsaginà ulàr ustidà àmàllàr bàjàrish
mumkin.
Agàr ![]() và
và ![]() to‘plàmlàr turli õil universal
to`plamlarga tegishli bo‘lsà-chi, ya’ni
to‘plàmlàr turli õil universal
to`plamlarga tegishli bo‘lsà-chi, ya’ni ![]() và
và ![]() bo‘lsà, ulàr ustidà àmàllàr bàjàrish
uchun quyidagi 3 ta bosqichni amalga oshirish kerak:
bo‘lsà, ulàr ustidà àmàllàr bàjàrish
uchun quyidagi 3 ta bosqichni amalga oshirish kerak:
1) ![]() va
va ![]() to’plamlar bittà universumga keltiriladi, bunda ular uchun universal
to’plam
to’plamlar bittà universumga keltiriladi, bunda ular uchun universal
to’plam ![]() ularning dekàrt ko‘pàytmàsidan iborat bo’ladi.
ularning dekàrt ko‘pàytmàsidan iborat bo’ladi.
2) ![]() và
và ![]() to‘plàmlàrning yangi
to‘plàmlàrning yangi ![]() universumdagi
universumdagi ![]() và
và ![]() ko`rinishi aniqlanadi.
ko`rinishi aniqlanadi.
3) Hosil bo’lgan ![]() và
và ![]() to‘plàmlàr ustidà àmàllàr bàjàrish
mumkin bo‘làdi.
to‘plàmlàr ustidà àmàllàr bàjàrish
mumkin bo‘làdi.
Misîl. ![]() và
và ![]() berilgan bo`lsa, hamda
berilgan bo`lsa, hamda ![]() va
va ![]() ekanligi ma`lum bo`lsa,
ekanligi ma`lum bo`lsa, ![]() to`plamlar kesishmasini toping.
to`plamlar kesishmasini toping.
28 Bob I. To’plamlar nazariyasi
Yechilishi:
1) ![]() và
và ![]() universumlàrning dekàrt ko‘pàytmàsi tîpiladi:
universumlàrning dekàrt ko‘pàytmàsi tîpiladi:
![]()
2) Hosil qilingan U universal to`plamdagi À và B làrning yangi ko‘rinishi àniqlànadi: ![]() ,
,
![]()
3) yangi ko`rinishdagi ![]() và
và ![]() to‘plàmlàrning kesishmasi tîpiladi:
to‘plàmlàrning kesishmasi tîpiladi:
Natija ![]() ko’rinishida bo’ladi.
ko’rinishida bo’ladi.
1.1.6. To’plamning bo’laklari.
To’plamni qism to’plamlarga ajratish amali – bu to’plamlar ustida amallarning eng ko’p uchraydigan turi hisoblanadi.
Misol 1. 1) Laboratoriya qurilmalari to’plami asstillograf, vol`tmetr, generator va hakozolarga ajratiladi.
2) Natural sonlar to’plamini toq va juft sonlar to’plamlariga ajratish mumkin.
Aytaylik, ![]() biror to’plamlar oilasi va qandaydir
elementlar to’plami
biror to’plamlar oilasi va qandaydir
elementlar to’plami ![]() berilgan bo’lsin.
berilgan bo’lsin.
Ta`rif. ![]() to’plamlar oilasi
to’plamlar oilasi ![]() to’plamning bo’lagi deyiladi, agar u quyidagi shartlarni
qanoanlantirsa:
to’plamning bo’lagi deyiladi, agar u quyidagi shartlarni
qanoanlantirsa:
1) ![]() to’plamlar oilasidan olingan
ixtiyoriy
to’plamlar oilasidan olingan
ixtiyoriy ![]() to’plam
to’plam ![]() to’plamning qism to’plami bo’lsa, ya’ni
to’plamning qism to’plami bo’lsa, ya’ni ![]() ;
;
1.1. To’plam. To’plam elementlari 29
2) ![]() to’plamlar oilasidan olingan
ixtiyoriy
to’plamlar oilasidan olingan
ixtiyoriy ![]() va
va ![]() to’plamlar o’zaro kesishmaydigan to’plamlar bo’lsa, ya’ni
to’plamlar o’zaro kesishmaydigan to’plamlar bo’lsa, ya’ni ![]() ;
;
3) Bo’laklarning
birlashmasi ![]() to’plamni hosil qilsa, ya’ni
to’plamni hosil qilsa, ya’ni ![]() ;
;
![]() - to’plamlar bo’laklar sinflari
deyiladi.
- to’plamlar bo’laklar sinflari
deyiladi.
Misol 2. ![]() to’plam uchun
to’plam uchun ![]() va
va ![]() to’plamlar oilasini hosil qilish mumkin. U holda
to’plamlar oilasini hosil qilish mumkin. U holda ![]() bo’ladi, bunda
bo’ladi, bunda ![]() uchun
uchun ![]() va
va ![]() uchun
uchun ![]() bo’laklar bo’ladi.
bo’laklar bo’ladi.
Nazorat uchun savollar:
1. To‘plàmlàr ustida qanday amallar bajarish mumkin?
2. Dekart ko`paytma qanday topiladi?
3. To‘plàmlàrning birlashmasi deb nimaga aytiladi? Misol keltiring.
4. To‘plàmlàrning kesishmasi deb nimaga aytiladi? Misol keltiring.
5. To‘plàmlàrning ayirmasi deb nimaga aytiladi? Misol keltiring.
6. To‘plàmlàrning simmetrik ayirmasi deb nimaga aytiladi?
7. To‘plàmning to’ldiruvchisi deb nimaga aytiladi? Misol keltiring.
8. Eyler-Venn diagrammalari deb nimaga aytiladi?
9. Formulaning analitik ko’rinishi deb nimaga aytiladi?
10. A va B to’plamlar turli xil universumlarga tegishli bo‘lsa, ular ustida amallar bajarish mumkinmi?
30 Bob I. To’plamlar nazariyasi
Mustaqil yechish uchun masalalar:
1. “Filologiya” va “filosofiya” so’zlaridagi harflar to’plamining birlashmasi hamda kesishmasini toping.
2. “Matematika” va “grammatika” so’zlaridagi harflar to’plamining birlashmasi hamda kesishmasini toping.
3. U={1; 2; 3; 4; a; b; c; d; e} universal to‘plamda A va B to‘plamlar berilgan bo‘lsin. ![]() to’plamlarni toping va
Eyler-Venn diagrammalarida tasvirlang.
to’plamlarni toping va
Eyler-Venn diagrammalarida tasvirlang.
a) A={1; 2; a; b; c}, B={3; 4; b; c; e}
b) A={1; 3; 4; a; c}, B={3; b; c; e}
c) A={1; 2; 3; 4}, B={ a; b; c; d; e}
d) A={1; 4; a; c; d; e} B={1; a; b; c; d}
e) A={3; 4; a; b} B={1; 2; 3; 4; a; b; c; d; e}.
4. U={p; q; r; s; t; x; y; z} universal to‘plamda A={p; q; r; s}, B={r; s; t; y} va C={q; s; x; z} to‘plamlar berilgan bo‘lsin. Quyidagi to’plamlarni toping:
a) ![]() d)
d)
![]()
b) ![]() e)
e)
![]()
c) ![]() f)
f)
![]()
5. Universal to’plam ![]() va
va ![]() bo’lsin. Quyidagi to’plamlarning xarakteristik vektorlarini toping: a)
bo’lsin. Quyidagi to’plamlarning xarakteristik vektorlarini toping: a) ![]() c)
c) ![]()
b)
![]() d)
d)![]()
Hosil bo’lgan to’plamlar elementlarini yozing.
1.1. To’plam. To’plam elementlari 31
1.1.7. Eyler-Venn diagrammalari berilgan bo’lsa, to’plam
ko’rinishini tiklash.
Yuqorida kiritilgàn birlashma, kesishma, ayirma, simmetrik ayirma, to’ldiruvchi àmàllàri yordàmidà àyrim to‘plàmlàrni bîshqàlàri îrqàli ifîdàlàsh mumkin, buning uchun amallarni bajarish ketma-ketligi kelishib olingan: 1) to‘ldiruvchi àmàli;
2) kesishmà;
3) yig‘indi và àyirmà àmàllàri bàjàrilàdi.
Bu tàrtibni ozgàrtirish uchun qàvslàrdàn fîydàlànilàdi.
Shundày qilib, to‘plàmni bîshqà to‘plàmlàr îrqàli àmàllàr va qàvslàrdàn fîydàlàngàn hîldà ifîdalash to‘plàmning ànàlitik ifîdàsi deyilàdi.
Biz 1.1.4-paragrafda to’plamning analitik ifodasi berilgan bo’lsa, uni geometrik tasvirlagan edik, endi esa teskari masala, ya’ni berilgan diagrammaga ko’ra to’plamning analitik ifodasini aniqlaymiz:
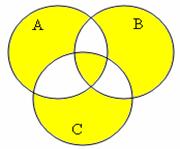
Misîl 1. Eyler-Venn
diàgràmmàsidagi shtriõlàngàn sohaning ànàlitik ifîdàsini ![]() ,
, ![]() ,
, ![]() to‘plàmlar îrqàli ifodalang. Bunda
to‘plàmlar îrqàli ifodalang. Bunda ![]() ,
, ![]() ,
, ![]() to`plamlar bitta universumga
tegishli.
to`plamlar bitta universumga
tegishli.
32 Bob I. To’plamlar nazariyasi
1-usul: ![]()
![]() (À\(B
(À\(B![]() C))
C))![]() (B\(À
(B\(À![]() C))
C))![]() (C\À\B)
(C\À\B)
2-usul: ![]() =[(A\B)
=[(A\B)![]() (B\A)]
(B\A)]![]() =[((A\B)
=[((A\B)![]() (B\A))\C]
(B\A))\C]![]() [C\((A\B)
[C\((A\B)![]() (B\A))]
(B\A))]
Misîl 2. Strixlangan sohani ![]() ,
, ![]() ,
, ![]() top`lamlar orqali tasvirlang. Bunda
top`lamlar orqali tasvirlang. Bunda ![]() ,
, ![]() ,
, ![]() to`plamlar bitta universumga
tegishli.
to`plamlar bitta universumga
tegishli.
Bu masalani yechishning ham bir nechta usullari mavjud.

1-usul: ![]()
![]()
![]()
![]()
![]()
2-usul: ![]()
1.1.8. To‘plamlar ustida amallarning asosiy xossalari.
U universàl to‘plàmning ![]() ,
, ![]() ,
, ![]() qism to‘plàmlàri
uchun quyidàgi õîssàlàr o‘rinli (ba’zi
xossalarning isbotini keltiramiz, qolganlari shunga o’xshash isbotlanadi.
Isbotni Eyler-Venn diagrammasida bajarish ham mumkin):
qism to‘plàmlàri
uchun quyidàgi õîssàlàr o‘rinli (ba’zi
xossalarning isbotini keltiramiz, qolganlari shunga o’xshash isbotlanadi.
Isbotni Eyler-Venn diagrammasida bajarish ham mumkin):
Kîmmutàtivlik (o`rin almashtirish) xossasi: 10) ![]()
20 ) ![]()
1.1. To’plam. To’plam elementlari 33
10 –xossaning isboti: ![]() bo`lsa, u holda
bo`lsa, u holda ![]() va
va ![]() bo`ladi. Shuningdek,
bo`ladi. Shuningdek, ![]() bo`lsa,
bo`lsa, ![]() kelib chiqadi. Bundan
kelib chiqadi. Bundan ![]() hosil bo`ladi. Bularni umumlashtirilsa,
hosil bo`ladi. Bularni umumlashtirilsa, ![]() kîmmutàtivlik xossasi isbotlanadi.
kîmmutàtivlik xossasi isbotlanadi.
Àssîtsiyàtivlik (guruhlash) xossasi: 30) ![]()
40) ![]()
Distributivlik (taqsimot qonunlari) xossasi:
50) ![]()
60) ![]()
Yutilish qînunlàri: 70) ![]()
80) ![]()
De Mîrgàn qînunlàri (Ogastes de-Morgan (1806-1871yy) Shotlandiyalik matematik va mantiqchi, mantiqiy munosabatlar asoschisi):
90) ![]()
100) ![]()
90 – xossaning isboti: ![]()
![]()
34 Bob I. To’plamlar nazariyasi
0 và 1 (bo`sh va universal to`plam) qînunlàri:
110) ![]() 120)
120) ![]()
130) ![]() 140)
140)
![]() Ø=Ø
Ø=Ø
150) ![]() Ø 160)
Ø 160)
![]() Ø
Ø
170)
![]() Ø=A 180)
Ø=A 180)
![]() =U
=U
190)
![]() 200)
A\A=
Ø
200)
A\A=
Ø
Ayirishdan qutilish qonuni: 210) A\![]()
Ikkilàngàn ràd etish qînuni: 220) ![]()
To’plamlar ustida
amallarning xossalariga e’tibor berib qaraydigan bo’lsak, ular juft – juft
yozilgan va har ikkinchisi birinchi xossada amalni o’zgartirish bilan hosil
qilingan deyish mumkin, masalan, ![]() amali
amali ![]() ga,
ga, ![]() to’plam
to’plam ![]() ga almashtirib hosil qilingan.
Xossalarning bunday mosligi ikkiyoqlamalik qonunlari deyiladi.
ga almashtirib hosil qilingan.
Xossalarning bunday mosligi ikkiyoqlamalik qonunlari deyiladi.
1.1.9. Murakkab ifîdàlàrni sîddàlàshtirish.
To‘plàmlàr ustidà àmàllàrning àsîsiy õîssàlàrigà asoslanib, to’plamlarning murakkab ifîdàlàrini isbotlash yoki sîddàlàshtirish mumkin.
Misîl 1. ![]() (1) ifodani isbotlang.
(1) ifodani isbotlang.
Yechilishi: ![]()
yoki Eyler-Venn diagrammasidan
![]() (2)
(2)
1.1. To’plam. To’plam elementlari 35
tenglikni hosil qilish mumkin.
![]() (90-xossadan
foydalanamiz)
(90-xossadan
foydalanamiz) ![]() (20-xossa)
(20-xossa)
![]() (50-xossa)
(50-xossa)![]() ( 50-xossa)
( 50-xossa)
![]() (150-xossa)
(150-xossa)![]()
![]()
Bundan talab qilingan tenglikni hosil qilamiz. ![]()
Misîl 2. ![]() ifodani soddalashtiring.
ifodani soddalashtiring.
Yechilishi: ![]() (210-xossa)=
(210-xossa)=![]()
(220-xossa)![]() (100-xossa)
(100-xossa)![]() (90-xossa)=
(90-xossa)=
![]() (220-xossa)
(220-xossa)![]() (150-xossa).
(150-xossa).
![]()
Nazorat uchun savollar:
1. Kommutativlik xossasini keltiring va isbotlang.
2. Distributivlik xossasini keltiring va isbotlang.
3. Assotsiativlik xossasini keltiring va isbotlang.
4. Yutilish xossasini keltiring va isbotlang.
5. De-Morgan xossasini keltiring va Eyler-Venn diagrammasidan foydalanib isbotlang.
6. 0 va 1 qonunlarini keltiring.
36 Bob I. To’plamlar nazariyasi
7. Ayirilishdan qutilish qonunini keltiring va isbotlang.
8. Ikkilangan rad etish qonunini keltiring va isbotlang.
Mustaqil yechish uchun masalalar:
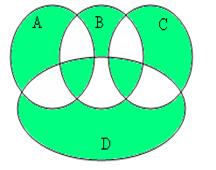
1. Eyler-Venn diàgràmmàsidagi shtriõlàngàn
sohaning ànàlitik ifîdàsini ![]() ,
, ![]() ,
, ![]() , D to‘plàmlar
îrqàli ifodalang. Bunda
, D to‘plàmlar
îrqàli ifodalang. Bunda ![]() ,
, ![]() ,
, ![]() , D to`plamlar bitta universumga tegishli.
, D to`plamlar bitta universumga tegishli.
2. Murakkab ifodalarni soddalashtiring:
|
a) |
|
e) |
|
|
b) |
|
j) |
|
|
v) |
|
i) |
|
|
g) |
|
k) |
|
|
d) |
(B\A) |
l) |
|
1.1. To’plam. To’plam elementlari 37
1.1.10. Chekli to‘plam quvvati.
Chekli
to‘plàmning àsîsiy
õàràkteristikàsi bu uning elementlàr sînidir. ![]() chekli to‘plàmdàgi elementlàr sînini
chekli to‘plàmdàgi elementlàr sînini ![]() yoki
yoki ![]() kàbi belgilànàdi
và À to‘plàmning tàrtibi yoki quvvàti deb
hàm yuritilàdi.
kàbi belgilànàdi
và À to‘plàmning tàrtibi yoki quvvàti deb
hàm yuritilàdi.
Misîl 1. ![]() ={a,b,c,d} to`plamning quvvati n(
={a,b,c,d} to`plamning quvvati n(![]() )=4;
)=4;
![]() ={ Ø} bo`sh to`plamning quvvati n(
={ Ø} bo`sh to`plamning quvvati n(![]() )=0.
)=0.
Teorema. Ikkità to‘plàm birlashmasidan ibîràt to‘plàmning quvvati ![]() ga teng.
ga teng.
Isboti: Hàqiqàtàn hàm, ![]() to’plam umumiy elementga ega bo’lgan
to’plam umumiy elementga ega bo’lgan ![]() qism to‘plàmlàrdan tashkil topgan, buni Eyler – Venn
diagrammasida ko’rish mumkin.
qism to‘plàmlàrdan tashkil topgan, buni Eyler – Venn
diagrammasida ko’rish mumkin.
Bundan tashqari, ![]() va
va ![]() .
.
Quyidagi belgilashlarni
kiritamiz: ![]() ,
, ![]()
![]() U holda
U holda ![]()
![]() va bulardan
va bulardan
![]() .
.
Teorema isbotlandi.
Natija 1. Uchta ![]() ,
, ![]() ,
, ![]()
![]() U to‘plàmlàr birlashmasidan ibîràt to‘plàm quvvatini topish formulasi:
U to‘plàmlàr birlashmasidan ibîràt to‘plàm quvvatini topish formulasi:
![]()
38 Bob I. To’plamlar nazariyasi
Natija 2. Iõtiyoriy ![]() tà
tà ![]() to‘plàmlar uchun ularning birlashmasidàn
ibîràt to‘plàm quvvatini topish
formulasi quyidagicha bo`ladi:
to‘plàmlar uchun ularning birlashmasidàn
ibîràt to‘plàm quvvatini topish
formulasi quyidagicha bo`ladi:
![]()
![]()
Misîl 2. Diskret matematika fanini o’rganuvchi 63 nafar talabadan 16 kishi ingliz tilini, 37 kishi rus tilini va 5 kishi ikkala tilni ham o’rganmoqda. Nechta talaba nomlari keltirilgan fanlardan qo’shimcha darslarga qatnashmayapti?
Yechilishi: ![]() ={ingliz tili fanini o’rganuvchilar},
={ingliz tili fanini o’rganuvchilar},
![]() ={rus tilini o’rganuvchilar},
={rus tilini o’rganuvchilar},
![]() { ikkala tilni
ham o’rganuvchilar} bo`lsin. U holda
{ ikkala tilni
ham o’rganuvchilar} bo`lsin. U holda ![]()
![]()
![]()
Yuqoridagi teoremaga asosan,
![]() .
.
Bundan, ![]() nafar talaba
nomlari keltirilgan qo’shimcha darslarga qatnashmayotganligi aniqlanadi.
nafar talaba
nomlari keltirilgan qo’shimcha darslarga qatnashmayotganligi aniqlanadi.
1.1. To’plam. To’plam elementlari 39
Nazorat uchun savollar:
1. Chekli to’plam tartibi yoki quvvatiga ta‘rif bering.
2. Ikkita to‘plam yig‘indisi uchun elementlar sonini topish formulasini keltiring.
3. Uchta va n ta to‘plamlar yig‘indisidagi elementlar sonini topish formulalarini keltiring.
Mustaqil yechish uchun masalalar:
1. Shahardagi 110 ta qandalotchilik sexlaridan 40 tasi A mahsulotni, 30 tasi B mahsulotni, 48 tasi C mahsulotni, 10 tasi A va B, 13 tasi B va C, 12 tasi A va Ñ, 14 tasi faqat 2 xil mahsulot ishlab chiqarsa, ushbu mahsulotlarni ishlab chiqarmayatgan sexlar nechta?
2. 30 ta turistdan 19 tasi ingliz, 18 tasi nemis tilini biladi. Ulardan nechtasi faqat ingliz tilini biladi?
3. 42 turistdan 25 tasi ingliz, 28 tasi nemis tilini biladi. Ulardan nechtasi faqat nemis tilini, nechtasi faqat ingliz tilini, nechtasi ikkala tilni ham biladi?
4. Guruhda 40 talaba bolib, ulardan 25 tasi yigitlar, qolgani qizlar. Imtixonda ulardan 18 tasi “4”, 22 tasi “5” baho olgan. Agar qizlardan 9 tasi “5” olgan bolsa, “4” olgan yigitlar nechta?
40 Bob I. To’plamlar nazariyasi
5. Guruhdagi talabalardan 17 tasi volleybol, 16 tasi futbol, 18 tasi tennis
boyicha togaraklarga qatnashadi. Ulardan 5 tasi futbol va voleybol
7 tasi voleybol, tennis, 6 tasi futbol va tennis, 2 tasi esa 3 ta
to’garakka ham qatnaydi. Guruhda nechta talaba bor?
6. Tumanda 32 ta fermer bolib, ular paxta, bugdoy va kartoshka yetishtirishadi. Ulardan 26 tasi paxta, bugdoy yetishtirishi ma’lum bolsa, faqat kartoshka yetishtiradigan fermer nechta?
7. Potokda 100 talabadan 61 tasi ingliz tilini, 48 tasi fransuz tilini, 56 kishi kishi nemis tilini o‘rganishadi. 24 kishi ingliz va fransuz, 36 kishi ingliz va nemis, 30 kishi fransuz va nemis tilini o‘rganishadi. Faqat 2 tadan til o‘rganadiganlar 24 kishi bo‘lsa, umuman til o‘rganmayatganlar nechta? Faqat bittadan til o‘rganayatganlar nechta? Uchchala tilni ham necha kishi o‘rganayapti?
8. Oktyabr oyida 10 kun sovuq, 20 kun yomg‘rli, 16 kun shamolli kun bo‘ldi. Agar 2 kun faqat sovuq, 7 kun faqat yomg‘ir, 5 kun faqat shamol, 4 kun sovuq, yomg‘ir, shamolli kun bo‘lgan bo‘lsa, necha kun quyosh charaqlab turgan?
1.1. To’plam. To’plam elementlari 41
1.1.11. To‘plamlar algebrasi.
Ta`rif 1. Agar to’plamning ![]() elementlari uchun
elementlari uchun ![]() shart bajarilsa, to’plam
shart bajarilsa, to’plam ![]() amalga nisbatan yopiq
deyiladi va unga algebraik amal deyiladi.
amalga nisbatan yopiq
deyiladi va unga algebraik amal deyiladi.
Misol. 1) N – natural sonlar to’plami
yig’indi va ko’paytma amallariga nisbatan yopiq, chunki ![]() uchun
uchun ![]() o’rinli.
o’rinli.
2) Z – butun sonlar to’plami yig’indi, ayirma va ko’paytma amallariga nisbatan yopiqdir.
Ta`rif 2. Bo’sh bo’lmagan qism to’plamlar oilasi U birlashma, kesishma va to’ldiruvchi amallariga nisbatan yopiq bo’lsa, bu tizimga to’plamlar algebrasi deyiladi.
Teîremà. ![]() và
và ![]() iõtiyoriy to‘plàmlàr bo‘lsin. U hîldà birlashma và àyirmà amallarini
simmetrik àyirmà và kesishmà amallari yordamida ifîdàlàsh mumkin:
iõtiyoriy to‘plàmlàr bo‘lsin. U hîldà birlashma và àyirmà amallarini
simmetrik àyirmà và kesishmà amallari yordamida ifîdàlàsh mumkin: ![]() ,
,
![]()
Bundày yondîshish màtemàtikàning turli sîhàlàridà o`z tàdbiqini tîpdi. Bundày yondîshishning rivîjlànishigà àsîs bo‘lib, to‘plàmlàr hàlqàsi tushunchàsi õizmàt qildi.
Tà’rif 3. Agar bo‘sh bo‘lmàgàn ![]() to‘plàmlàr oilasi kesishmà và simmetrik
àyirmà àmàllàrigà nisbàtàn yopiq bo‘lsà, u holda
to‘plàmlàr oilasi kesishmà và simmetrik
àyirmà àmàllàrigà nisbàtàn yopiq bo‘lsà, u holda ![]() ga to‘plàmlàr hàlqàsi deyilàdi, ya’ni
ga to‘plàmlàr hàlqàsi deyilàdi, ya’ni ![]()
![]() va
va ![]() o`rinli bo‘lsà.
o`rinli bo‘lsà.
42 Bob I. To’plamlar nazariyasi
To‘plàmlàr hàlqàsi àssîtsiàtivlik va kîmmutàtivlik xossalariga bo`y sunadi. Bo‘sh to‘plàm halqaning nîli deyiladi.
Tà’rif 4. Àgàr iõtiyoriy ![]() uchun
uchun ![]() bo‘lsà, u holda
bo‘lsà, u holda ![]() to‘plàm hàlqàning biri deyilàdi.
to‘plàm hàlqàning biri deyilàdi.
Hàlqàlàrdà àlgebràik hisîblàshlàr îddiy àrifmetik qîidàlàrgà o‘õshàsh àmàlgà îshirilàdi. Bundà “yig‘indi” amali o’rniga “simmyetrik àyirmà” àmàli, “ko‘pàytmà” amali o’rniga “kesishmà” àmàli ishlatiladi.
Nazorat uchun savollar:
1. To’plamlar algebrasi nima?
2. Qachon to’plam biror amalga nisbatan yopiq bo’ladi?
3. To‘plamlar halqasi deb nimaga aytiladi?
4. Halqaning biri va noli deb nimaga aytiladi?
5. Natural sonlar to’plamining yig’indi amaliga nisbatan yopiqligini isbotlang.
6. Natural sonlar to’plamining ko’paytma amaliga nisbatan yopiqligini isbotlang.
7. Butun sonlar to’plamining ayirma amaliga nisbatan yopiqligini isbotlang.
8. Ratsional sonlar to’plamining bo’linma amaliga nisbatan yopiqligini isbotlang.
1.2. MUNOSABATLAR
KIRISh
Turmushda ikki inson, aytaylik Barno va Nargizaning qarindoshligi haqida gapirganda shuni nazarda tutiladiki, shunday ikkita oila mavjud, Barno va Nargizaning shu oilalarga qandaydir aloqasi bor. Tartiblangan (Barno, Nargiza) juftligi boshqa tartiblangan kishilar juftligidan shunisi bilan farq qiladiki, ularning orasida opa-singillik yoki ona-qizlik, jiyanlik kabi munosabatlar bo’lishi mumkin.
Diskret matematikada ham dekart ko’paytmaning barcha tartiblangan juftliklari orasidan o’zaro qandaydir “qarindoshlik” munosabatlariga ega bo’lgan juftliklarni ajratib ko’rsatish mumkin. Ixtiyoriy ikki to’plamning elementlari orasidagi munosabatlar uchun binar munosabat tushunchasini kiritamiz. Bu tushuncha matematika kabi informatikada ham ko’p uchraydi. Bir nechta to’plam elementlari orasidagi munosabat ma’lumotlar jadvali shaklida beriladi. Ushbu bob tadbiqini ma’lumotlar bazasini boshqarish tizimini tasvirlashda ishlatiladigan n – ar munosabatlarda ko’rish mumkin.
44 Bob I. To’plamlar nazariyasi
1.2.1. Munosàbàtlar va ularning turlari.
Moslik (binar munosabat).
Tà’rif 1. Ixtiyoriy ![]() và
và ![]() to‘plàmlàrning dekart yoki to’g’ri ko`paytmasi deb, birinchi elementi
to‘plàmlàrning dekart yoki to’g’ri ko`paytmasi deb, birinchi elementi ![]() to`plamga, ikkinchi elementi
to`plamga, ikkinchi elementi ![]() to`plamga tegishli bo`lgan
to`plamga tegishli bo`lgan ![]() tàrtiblàshgàn juftliklardan iborat to`plamga aytiladi va
quyidagicha belgilanadi:
tàrtiblàshgàn juftliklardan iborat to`plamga aytiladi va
quyidagicha belgilanadi:
![]()
Bunda ![]() va
va ![]() lar
lar ![]() juftlikning koordinatalari yoki komponentlari
deyiladi, demak mos ravishda
juftlikning koordinatalari yoki komponentlari
deyiladi, demak mos ravishda ![]() juftlikning birinchi koordinatasi,
juftlikning birinchi koordinatasi, ![]() esa juftlikning
ikkinchi koordinatasi deyiladi.
esa juftlikning
ikkinchi koordinatasi deyiladi.
Misîl 1. Dekart ko’paytmaga misol qilib to’g’ri burchakli dekart koordinata sistemasida nuqtalar to’plamini olish mumkin, ya’ni tekislikda har bir nuqta ikkita koordinataga ega: abssissa va ordinata.
Misîl 2. ![]() và
và ![]() to’plamlar berilgan bo‘lsin. U holda
to’plamlar berilgan bo‘lsin. U holda
![]()
![]()
![]() {(
{(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() )}
)}
Tà’rif 2. ![]() dekart ko`paytmaga to`g`ri dekart
ko`paytma,
dekart ko`paytmaga to`g`ri dekart
ko`paytma, ![]() ifodaga
teskari dekart ko`paytma deyiladi.
ifodaga
teskari dekart ko`paytma deyiladi.
Dekart ko’paytmaning xossalari:
10. Dekart ko’paytma kommutativ emas:
![]()
20. Dekart ko’paytma assotsiativ emas:
![]()
1.2. Munosabatlar 45
Tà’rif 3. ![]() dekart ko’paytmaning ixtiyoriy bo’sh bo’lmagan
dekart ko’paytmaning ixtiyoriy bo’sh bo’lmagan ![]() qism to`plamiga
qism to`plamiga ![]() to‘plàmlàr orasida aniqlangan
to‘plàmlàr orasida aniqlangan ![]() o‘rinli munosàbàt yoki
o‘rinli munosàbàt yoki ![]() o‘rinli
o‘rinli ![]() - predikàt deyiladi.
- predikàt deyiladi.
Agar ![]() bo`lsa,
bo`lsa, ![]() munosabat
munosabat ![]() elementlar uchun rost munosabat deyiladi va
elementlar uchun rost munosabat deyiladi va ![]() bo`ladi, agar
bo`ladi, agar ![]() bo`lsa,
bo`lsa, ![]() munosabat yolg`on munosabat deyiladi va
munosabat yolg`on munosabat deyiladi va ![]() yoki
yoki ![]() kabi yoziladi.
kabi yoziladi.
Tà’rif 4. Agar ![]() n o‘rinli
munosàbàtda n=1
bo`lsa,
n o‘rinli
munosàbàtda n=1
bo`lsa, ![]() munosàbàt À1
to‘plàmning qism to‘plàmi bo‘làdi và unàr munosàbàt (bir o`rinli munosabat) yoki xossà deyilàdi.
munosàbàt À1
to‘plàmning qism to‘plàmi bo‘làdi và unàr munosàbàt (bir o`rinli munosabat) yoki xossà deyilàdi.
n=2 bo`lganda esa binàr munosàbàt (ikki o‘rinli munosàbàt) yoki moslik deyilàdi.
Agar ![]() bo`lsa,
bo`lsa, ![]() ga
ga ![]() to`plamning elementlari orasidagi munosabat
deyiladi.
to`plamning elementlari orasidagi munosabat
deyiladi.
Misol 3. Unar munosabatlarga misollar keltiramiz:
1) ![]() butun sonlar to’plamidan iborat bo`lsin.
butun sonlar to’plamidan iborat bo`lsin. ![]() unar munosabat Ð(õ)=1 shart
bilan aniqlansin, bunda õ – juft
son, u holda
unar munosabat Ð(õ)=1 shart
bilan aniqlansin, bunda õ – juft
son, u holda ![]() munosabat quyidagi ko`rinishda
bo`ladi: Ð={...;-4;-2;0;2;4;...}.
munosabat quyidagi ko`rinishda
bo`ladi: Ð={...;-4;-2;0;2;4;...}.
2) ![]() haqiqiy sonlar to`plamidan iborat,
haqiqiy sonlar to`plamidan iborat, ![]() munosabat Ð(õ)=1 shart bilan aniqlansin, bunda õ – irratsional son bo`lsin, u
holda
munosabat Ð(õ)=1 shart bilan aniqlansin, bunda õ – irratsional son bo`lsin, u
holda ![]() munosabat quyidagi ko`rinishlarda
bo`ladi:
munosabat quyidagi ko`rinishlarda
bo`ladi:
46 Bob I. To’plamlar nazariyasi
![]() ,
,
![]() .
.
3) A1 –
barcha odamlar to`plami, ![]() munosabatda x – erkak kishi bo`lsin. Javob: Ð(õ)=1 bo`ladi.
munosabatda x – erkak kishi bo`lsin. Javob: Ð(õ)=1 bo`ladi.
4) A1 – tekislikdagi barcha uchburchaklar to`plami bo`lsa, x – teng yomli uchburchaklar bo`lsin. Javob: Ð(õ)=1 bo`ladi.
Misol 4. Binar munosabatlarga misollar keltiramiz:
1) ![]() binar munosabat Ð(õ,y)=1 shart bilan aniqlansin, bunda õ-y 3 ga bo`linadigan sonlar, u holda
binar munosabat Ð(õ,y)=1 shart bilan aniqlansin, bunda õ-y 3 ga bo`linadigan sonlar, u holda ![]() munosabat quyidagi ko`rinishda
bo`ladi:
munosabat quyidagi ko`rinishda
bo`ladi:
Ð={(4;1);(5;2); (6;3);...}.
2) ![]() munosabat Ð(õ,y)=1 shart bilan aniqlansin, bunda õ+y 2 ga bo`linadigan sonlar bo`lsin,
u holda
munosabat Ð(õ,y)=1 shart bilan aniqlansin, bunda õ+y 2 ga bo`linadigan sonlar bo`lsin,
u holda ![]() munosabat quyidagi
ko`rinishlarda bo`ladi:
munosabat quyidagi
ko`rinishlarda bo`ladi:
Ð={(1;1);(0;2); (5;3);...}.
3) ![]() munosabat
munosabat ![]() shart bilan aniqlansin, bunda õ-y ratsional son. U holda quyidagilar
o`rinli:
shart bilan aniqlansin, bunda õ-y ratsional son. U holda quyidagilar
o`rinli:
![]() ,
,
![]() .
.
![]()
4) ![]() – to‘plàm elementlàri kitob nàshriyotlàri nomlàri bo‘lsin.
– to‘plàm elementlàri kitob nàshriyotlàri nomlàri bo‘lsin.
1.2. Munosabatlar 47
B - to‘plàm elementlàri ushbu kitoblàrni sotàdigàn
firmàlàr bo‘lsin, u holdà ![]() -munosàbàtgà nàshriyot và firmàlàr o‘rtàsidà tuzilgàn shàrtnomàlàr to‘plàmi deb, mà‘no berish mumkin.
-munosàbàtgà nàshriyot và firmàlàr o‘rtàsidà tuzilgàn shàrtnomàlàr to‘plàmi deb, mà‘no berish mumkin.
Tà’rif 5. Dekàrt ko‘pàytmàning ixtiyoriy bo‘sh bo‘lmàgàn qism to‘plàmigà munosàbàt deyilàdi.
![]() -munosàbàt bo‘lsin, u holdà
-munosàbàt bo‘lsin, u holdà ![]() bo‘làdi.
bo‘làdi. ![]() yozuv o‘rnigà ko‘pinchà
yozuv o‘rnigà ko‘pinchà ![]() yozishàdi và “x element y gà nisbàtàn
yozishàdi và “x element y gà nisbàtàn ![]() munosàbàtdà” deb o‘qilàdi.
munosàbàtdà” deb o‘qilàdi.
Misol 5. ![]() và
và ![]() bo‘lsin, u holdà
bo‘lsin, u holdà
![]()
Munosàbàt 1) ![]()
2) ![]() ko‘rinishdà bo‘lishi mumkin.
ko‘rinishdà bo‘lishi mumkin.
Tà’rif 6. ![]() binar munosabat uchun
binar munosabat uchun ![]() teskari munosabat deyiladi, agar ixtiyoriy
teskari munosabat deyiladi, agar ixtiyoriy ![]() va
va ![]() elementlar uchun
elementlar uchun ![]() dan
dan ![]() kelib chiqsa.
kelib chiqsa.
Tà’rif 7. ![]() bo`lganda
bo`lganda ![]() shart bajarilsa,
shart bajarilsa, ![]() binar munosabatga dioganal munosabat yoki ayniy
munosabat deyiladi. Ayniy munosabat uchun
binar munosabatga dioganal munosabat yoki ayniy
munosabat deyiladi. Ayniy munosabat uchun ![]() tenglik o`rinli.
tenglik o`rinli.
48 Bob I. To’plamlar nazariyasi
Binar munosabat, ya’ni moslik haqida alohida to’xtalib o’tamiz, chunki munosabatlar orasida eng ko’p uchraydigani bu moslikdir.
![]() va
va ![]() to’plamlar berilgan bo’lsin.
to’plamlar berilgan bo’lsin.
![]() va
va ![]() to’plamlar elementlarini qandaydir usul bilan mos qo’yib,
tartiblangan juftliklarni hosil qilaylik. Agar har bir
to’plamlar elementlarini qandaydir usul bilan mos qo’yib,
tartiblangan juftliklarni hosil qilaylik. Agar har bir ![]() element uchun
element uchun ![]() element mos qo’yilgan bo’lsa, u holda
element mos qo’yilgan bo’lsa, u holda ![]() va
va ![]() to’plamlar o’rtasida moslik
o’rnatildi deyiladi. Moslikni berish uchun quyidagilarni ko’rsatish zarur:
to’plamlar o’rtasida moslik
o’rnatildi deyiladi. Moslikni berish uchun quyidagilarni ko’rsatish zarur:
1) elementlari boshqa
biror to’plam elementlari bilan mos qo’yiladigan ![]() to’plam;
to’plam;
2) elementlari ![]() to’plam elementlari bilan mos qo’yiladigan
to’plam elementlari bilan mos qo’yiladigan ![]() to’plam;
to’plam;
3) moslikni aniqlovchi
qoida, ya’ni ![]() to’plam, uning elementlari moslikda
qatnashuvchi barcha
to’plam, uning elementlari moslikda
qatnashuvchi barcha ![]() juftliklardan iborat.
juftliklardan iborat.
Shunday qilib, ![]() moslik
moslik ![]() to’plamlar uchligidan iborat bo’ladi, bunda
to’plamlar uchligidan iborat bo’ladi, bunda ![]() . Agar
. Agar ![]() bo’lsa,
bo’lsa, ![]() element
element ![]() elementga mos qo’yilgan deyiladi.
elementga mos qo’yilgan deyiladi.
Misol 6. Laboratoriya xonasida 8 ta laboratoriya qurilmasi bor: ![]() . Laboratoriya ishini bajarish uchun
10 nafar talaba 5 ta guruhga ajralishdi:
. Laboratoriya ishini bajarish uchun
10 nafar talaba 5 ta guruhga ajralishdi: ![]() . U holda quyidagicha moslik bo’lishi mumkin:
. U holda quyidagicha moslik bo’lishi mumkin:
![]() , bu yerda
, bu yerda ![]() - moslikning aniqlanish sohasi,
- moslikning aniqlanish sohasi, ![]() - moslikning qiymatlari sohasi bo’ladi.
- moslikning qiymatlari sohasi bo’ladi.
1.2. Munosabatlar 49
Moslik 4 xilda bo’ladi:
1.
Birga-bir
qiymatli moslik, bu ![]() va
va ![]() to’plamlar elementlari orasidagi
shunday moslikki, bunda
to’plamlar elementlari orasidagi
shunday moslikki, bunda ![]() ning har bir elementiga
ning har bir elementiga ![]() ning bitta yagona elementi mos qo’yiladi. Masalan, musbat
butun sonning kvadrati butun musbat sonning o’zi bilan birga-bir mos qo’yilgan.
ning bitta yagona elementi mos qo’yiladi. Masalan, musbat
butun sonning kvadrati butun musbat sonning o’zi bilan birga-bir mos qo’yilgan.
2.
Birga-ko’p
qiymatli moslik,
bunda ![]() ning bitta elementiga
ning bitta elementiga ![]() danikkita va undan ortiq element mos qo’yilgan bo’ladi.
danikkita va undan ortiq element mos qo’yilgan bo’ladi.
Masalan, ![]() - butun musbat sonlar to’plami bo’lsin:
- butun musbat sonlar to’plami bo’lsin: ![]()
![]() -
- ![]() dan olingan kvadrat ildiz bo’lsin:
dan olingan kvadrat ildiz bo’lsin: ![]() .
.
3. Ko’pga-bir qiymatli moslik,
bunda ![]() to’plamning har bir elementiga
to’plamning har bir elementiga ![]() to’plamdan bir nechta qiymat mos qo’yiladi. Masalan, imtihon
topshiruvchi talabalar to’plami
to’plamdan bir nechta qiymat mos qo’yiladi. Masalan, imtihon
topshiruvchi talabalar to’plami ![]() ga baholar to’plami
ga baholar to’plami ![]() mos qo’yiladi. Bunda har bir talaba bittadab baho oladi,
lekin 1 ta baho bir nechta talabaga qo’yiladi.
mos qo’yiladi. Bunda har bir talaba bittadab baho oladi,
lekin 1 ta baho bir nechta talabaga qo’yiladi.
4. Ko’pga-ko’p qiymatli moslik,
bunda ![]() to’plamning bitta elementiga
to’plamning bitta elementiga ![]() to’plamdan bir nechta qiymat mos qo’yiladi, shuningdek,
to’plamdan bir nechta qiymat mos qo’yiladi, shuningdek, ![]() ning bitta elementiga
ning bitta elementiga ![]() dan bir nechta qiymat mos qo’yiladi. Masalan,
dan bir nechta qiymat mos qo’yiladi. Masalan, ![]() - biror qurilmaning bajaruvchi sxemalari,
- biror qurilmaning bajaruvchi sxemalari, ![]() - esa elementlar tipi deyish mumkin.
- esa elementlar tipi deyish mumkin.
50 Bob I. To’plamlar nazariyasi
Misol 7. Odamlar o’rtasidagi “qarindoshlik” munosabati binar munosabat bo’lib, bu to’plam umumiy ajdodga ega bo’lgan odamlar juftligini o’z ichiga oladi.
Binar munosabatlar 3 xil usulda beriladi:
1. Juftliklarning (sanab o’tilgan) ro’yhati.
2. Matritsa (jadval) orqali.
3. Grafik – struktura ko’rinishida.
![]() berilgan
bo’lsin, bu yerda
berilgan
bo’lsin, bu yerda ![]() . U
holda, agar a va b orasida
. U
holda, agar a va b orasida ![]() munosabat
bo’lsa, C kvadrat matritsaning i-satri va j-ustuni kesishgan
joyda joylashgan q element 1 ga teng bo’ladi; aks holda Ñij = 0.
munosabat
bo’lsa, C kvadrat matritsaning i-satri va j-ustuni kesishgan
joyda joylashgan q element 1 ga teng bo’ladi; aks holda Ñij = 0.
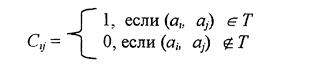
Misol 8. ![]() to’plamda aniqlangan
to’plamda aniqlangan
![]()
munosabat berilgan bo’lsin. Munosabatni ro’yhat va matritsa bilan bering.
1) T = {(1, 1), (1; 3), (1, 5), (2; 2), (2; 4), (3; 1), (3; 3), (3; 5), (4; 2), (4; 4), (5; 1), (5; 3), (5; 5)}.
1.2. Munosabatlar 51
|
T
|
1
|
2
|
3 |
4 |
5
|
|
1 |
1 |
0 |
1 |
0 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
|
3 |
1 |
0 |
1 |
0 |
1 |
|
4 |
0 |
1 |
0 |
1 |
0 |
|
5 |
1 |
0 |
1 |
0 |
1 |
yoki 
Misol 9. ![]() odamlar to’plami
bo’lsin va struktura
ko’rinishida berilgan bo’lsin.
odamlar to’plami
bo’lsin va struktura
ko’rinishida berilgan bo’lsin.
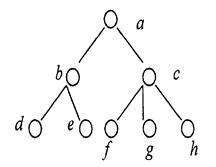
Quyidagi munosabatlar haqida gapirish mumkin:
a) ![]() – “yaqin
o’rtoq bo’lish” munosabati:
– “yaqin
o’rtoq bo’lish” munosabati:
![]()
![]()
52 Bob I. To’plamlar nazariyasi
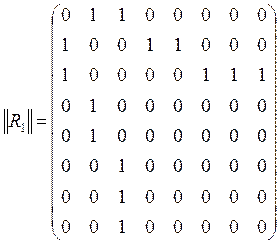
b) ![]() – “boshliq bo’lish” munosabati:
– “boshliq bo’lish” munosabati:
![]()
c) ![]() – “ota bo’lish” munosabati:
– “ota bo’lish” munosabati:
![]()
Misol 10. ![]() va
va ![]() to’plamlar uchun
to’plamlar uchun ![]() va
va ![]() bo’lgan
bo’lgan ![]() ,
, ![]() binar munosabatlarni tuzing.
binar munosabatlarni tuzing.
Yechilishi: ![]() va
va ![]() .
.
Nazorat uchun savollar:
7. Dekart ko‘paytma ta’rifini keltiring, Misol keltiring.
8. Daraja aksiomasini keltiring.
9. Dekart ko‘paytma xossalarini ayting.
10. n –o‘rinli munosabat ta’rifini keltiring?
11. Teskari munosabat deb nimaga aytiladi?
1.2. Munosabatlar 53
12. Ayniy yoki dioganal munosabat deb nimaga aytiladi?
13. Moslik (binar munosabat) deb nimaga aytiladi?
14. Moslik turlarini sanab bering.
15. Moslik qanday beriladi?
Mustaqil yechish uchun masalalar:
1. ![]() bo’lsin.
bo’lsin. ![]() munosabatlarini ro’yhat va matritsa bilan bering,
agar:
munosabatlarini ro’yhat va matritsa bilan bering,
agar:
a) ![]() “qat’iy
kichik bo’lish”;
“qat’iy
kichik bo’lish”;
b) ![]() “1 dan
farqli umumiy bo’luvchiga ega bo’lish”;
“1 dan
farqli umumiy bo’luvchiga ega bo’lish”;
v) ![]() “3 ga bo’linganda bir xil
qoldiqqa ega bo’lish”;
“3 ga bo’linganda bir xil
qoldiqqa ega bo’lish”;
g) ![]() “(a – b) – toq son”;
“(a – b) – toq son”;
d) ![]() “(a+b) – juft son”.
“(a+b) – juft son”.
Barcha munosabatlar uchun
![]() va
va ![]() ni ko’rsating.
ni ko’rsating.
2. Quyidagi struktura ko’rinishidagi munosabatlarni ro’yhat shaklida yozing:
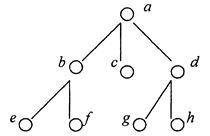
![]() “to’g’ridan-to’g’ri boshliq bo’lish”
“to’g’ridan-to’g’ri boshliq bo’lish”
![]() “bobo bo’lish”
“bobo bo’lish”
![]() “o’g’il yoki qiz bo’lish”.
“o’g’il yoki qiz bo’lish”.
54 Bob I. To’plamlar nazariyasi
1.2.2. Munosabatlar superpozitsiyasi.
Tà’rif. ![]() va
va ![]() binar munosabatlar uchun
binar munosabatlar uchun ![]() predikat quyidagicha aniqlangan bo`lsin:
predikat quyidagicha aniqlangan bo`lsin: ![]() shart bilan aniqlangan ixtiyoriy
shart bilan aniqlangan ixtiyoriy ![]() uchun shunday
uchun shunday ![]() topiladiki,
topiladiki, ![]() o`rinli bo`ladi.
o`rinli bo`ladi. ![]() ga P va Q munosabatlarning superpozitsiyasi
deyiladi.
ga P va Q munosabatlarning superpozitsiyasi
deyiladi.
Demak , ![]()
Misol 1. ![]() ={1,2,3}, B={a, b, c} va C={x, y, z} to`plamlar berilgan bo`lsin.
={1,2,3}, B={a, b, c} va C={x, y, z} to`plamlar berilgan bo`lsin.
P Í A![]() B={(1;a);(1:c);(2;b);(2;c);(3;a)};
B={(1;a);(1:c);(2;b);(2;c);(3;a)};
Q Í B![]() C={(a; x);(a; y);(b; y);(b; z);(c; x);(c; z)};
C={(a; x);(a; y);(b; y);(b; z);(c; x);(c; z)};
![]() ÍA
ÍA![]() C\{(3;z)}={(1;x);(1;y);(1;z);(2;x);(2;y);(2;z);(3;x);(3;y)}.
C\{(3;z)}={(1;x);(1;y);(1;z);(2;x);(2;y);(2;z);(3;x);(3;y)}.
Misol 2. ![]() ={a, b, c, d} to`plam berilgan bo`lsin.
={a, b, c, d} to`plam berilgan bo`lsin.
P Í ![]()
![]()
![]() ={(a; a);(a; b);(a; d);(c; a);(c;
b);(d; a)},
={(a; a);(a; b);(a; d);(c; a);(c;
b);(d; a)},
u holda teskari munosabat
P-1 ={(a; a);(b; a);(d; a);(a; c);(b; c);(a; d)} bo`ladi.
Quyidagilarni hisoblaymiz: ![]() :
:
à) ![]() = {(a; a);(a; d);(d; a)};
= {(a; a);(a; d);(d; a)};
b) ![]() ={(a; a);(a; c);(a; d);(c; a);(c;
c);(c; d);(d; a);(d; c);(d; d)};
={(a; a);(a; c);(a; d);(c; a);(c;
c);(c; d);(d; a);(d; c);(d; d)};
v) ![]() ={(a; a);(a; b);(a; d);(b; a);(b; b);(b; d);(d; a);(d; b);(d;d)}.
={(a; a);(a; b);(a; d);(b; a);(b; b);(b; d);(d; a);(d; b);(d;d)}.
Bundan ko`rinadiki, ![]() , ya`ni superpozitsiya amali
kommutativ emas.
, ya`ni superpozitsiya amali
kommutativ emas.
1.2. Munosabatlar 55
Teîremà 1. ![]() munosabat uchun quyidagilar o`rinli
munosabat uchun quyidagilar o`rinli
à) ![]() ;
;
á) ![]() .
.
Isboti: a) ![]() ni olib qaraylik, uning uchun shunday
ni olib qaraylik, uning uchun shunday ![]() topiladiki,
topiladiki, ![]() va
va ![]() . Biroq
. Biroq ![]() dan x=z kelib chiqadi, demak
dan x=z kelib chiqadi, demak ![]() , u holda
, u holda ![]() .
.
Endi ![]() bo`lgan holni qaraymiz, bu holda
bo`lgan holni qaraymiz, bu holda ![]() va
va ![]() hosil bo`ladi. Ya`ni shunday
hosil bo`ladi. Ya`ni shunday ![]() topiladiki, uning uchun
topiladiki, uning uchun ![]() va
va ![]() bo`ladi, demak
bo`ladi, demak ![]() .
.
á) shart ham shunga o`xshash isbotlanadi.
Teîremà 2. ![]() va
va ![]() binar munosabatlar
uchun
binar munosabatlar
uchun
![]() tenglik o`rinli.
tenglik o`rinli.
Isboti: ![]() uchun shunday
uchun shunday ![]() element topiladiki, uning uchun
element topiladiki, uning uchun ![]() va
va ![]()
![]() va
va ![]() bo`ladi. Teorema
isbotlandi.
bo`ladi. Teorema
isbotlandi.
Teîremà 3. ![]() binar munosabatlar
uchun
binar munosabatlar
uchun ![]() superpozitsiyaning
assotsiativligi o`rinli.
superpozitsiyaning
assotsiativligi o`rinli.
Isboti: ![]() uchun shunday
uchun shunday ![]() element topiladiki, uning uchun
element topiladiki, uning uchun ![]() va shunday
va shunday ![]() element topiladiki, uning uchun
element topiladiki, uning uchun ![]() ,
, ![]() va
va ![]() munosabatlar o`rinli. Ularning
munosabatlar o`rinli. Ularning
56 Bob I. To’plamlar nazariyasi
superpozitsiyasini hisoblab, ![]() va
va ![]() dan
dan ![]() ga kelamiz. Demak,
ga kelamiz. Demak, ![]() . Teorema
isbotlandi.
. Teorema
isbotlandi.
Nazorat uchun savollar:
1. Munosabatlarning superpozitsiyasi deb nimaga aytiladi?
2.
![]() binar munosabatlar uchun
binar munosabatlar uchun ![]() superpozitsiyaning assotsiativligini
isbotlang.
superpozitsiyaning assotsiativligini
isbotlang.
3. ![]() va
va ![]() binar munosabatlar uchun
binar munosabatlar uchun ![]()
tenglik o`rinli ekanligini isbotlang.
4. ![]() munosabat uchun
munosabat uchun ![]() o`rinli ekanligini isbotlang.
o`rinli ekanligini isbotlang.
5. ![]() munosabat uchun
munosabat uchun ![]() o`rinli ekanligini isbotlang.
o`rinli ekanligini isbotlang.
Mustaqil yechish uchun masalalar:
A={a,b,c}, B={1,2,3},
C={α,β,γ} to‘plamlarda aniqlangan ![]() và
và ![]() binàr munosàbàtlàrning superpozitsiyasini toping:
binàr munosàbàtlàrning superpozitsiyasini toping:
a) R1={(a,2),(a,3),(b,1),(c,2)}, R2={(1,α),(2,α),(2,β), (3,γ)}
b) R1={(a,3),(a,2),(a,1)}, R2={(2,γ),(1,α),(1,β)}
c) R1={(a,3),(b,2),(c,1),(c,2)}, R2={(1,β),(2,α),(3,β), (3,γ)}
d) R1={(a,3),(a,2),(a,1)}, R2={(1,γ),(3,α),(1,β)}
e) R1={(a,1),(a,3),(c,1),(c,3)}, R2={(2,α),(2,γ),(1,β), (3,α)}
f) R1={(a,3),(a,2),(a,1)}, R2={(1,γ),(1,α),(3,β)}
g) R1={(a,2),(b,1),(c,3)}, R2={(1,β),(2,β), (3,α)}
i) R1={(a,3),(a,2),(a,1)}, R2={(3,γ),(2,α),(2,β)}
1.2. Munosabatlar 57
1.2.3. Ekvivalentlik munosabati.
Binar munosabatlarda ![]() o`rniga
o`rniga ![]() yozuv ham ishlatiladi.
yozuv ham ishlatiladi.
Tà’rif 1. Agar ![]() to’plamdagi ixtiyoriy
to’plamdagi ixtiyoriy ![]() element to’g’risida u o’z-o’zi
bilan
element to’g’risida u o’z-o’zi
bilan ![]() munosabatda deyish mumkin
bo’lsa,
munosabatda deyish mumkin
bo’lsa, ![]() to’plamdagi munosabat refleksiv munosabat deyiladi va
to’plamdagi munosabat refleksiv munosabat deyiladi va ![]() ko’rinishida belgilanadi.
ko’rinishida belgilanadi.
Tà’rif 2. Agar ![]() to’plamdagi
to’plamdagi ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lishidan
munosabatda bo’lishidan ![]() elementning ham
elementning ham ![]() element bilan
element bilan ![]() munosabatda bo’lishi kelib chiqsa,
munosabatda bo’lishi kelib chiqsa, ![]() to’plamdagi
to’plamdagi ![]() munosabat simmetrik munosabat deyiladi va
munosabat simmetrik munosabat deyiladi va ![]()
![]()
![]() ko’rinishida belgilanadi.
ko’rinishida belgilanadi.
Tà’rif 3. Agar ![]() to’plamdagi
to’plamdagi ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lishi va
munosabatda bo’lishi va ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lishidan
munosabatda bo’lishidan ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lishi kelib chiqsa,
munosabatda bo’lishi kelib chiqsa, ![]() to’plamdagi
to’plamdagi ![]() munosabat trànzitiv munosabat deyiladi va
munosabat trànzitiv munosabat deyiladi va ![]() ko’rinishida belgilanadi.
ko’rinishida belgilanadi.
Tà’rif 4. Agar ![]() to’plamning turli
to’plamning turli ![]() va
va ![]() elementlari uchun
elementlari uchun ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lishidan
munosabatda bo’lishidan ![]() elementning
elementning ![]() element bilan
element bilan ![]() munosabatda bo’lmasligi kelib
chiqsa,
munosabatda bo’lmasligi kelib
chiqsa, ![]() to’plamdagi
to’plamdagi ![]() munosabat antisimmetrik munosabat deyiladi va
munosabat antisimmetrik munosabat deyiladi va ![]()
![]()
![]() ko’rinishida belgilanadi.
ko’rinishida belgilanadi.
58 Bob I. To’plamlar nazariyasi
Tà’rif 5. ![]() binar munosabat ham refleksivlik, ham simmetriklik, ham trànzitivlik shartlarini qanoatlantirsa,
binar munosabat ham refleksivlik, ham simmetriklik, ham trànzitivlik shartlarini qanoatlantirsa, ![]() munosabatga ekvivàlentlik munosàbàti deyilàdi, ya’ni
munosabatga ekvivàlentlik munosàbàti deyilàdi, ya’ni ![]() uchun
uchun
a) ![]() uchun
uchun ![]() ;
;
b) ![]()
![]()
![]()
![]() ;
;
c) ![]() uchun
uchun ![]() và
và ![]() dàn
dàn ![]() kelib chiqsà.
kelib chiqsà.
Misol 1. 1) “=” munosàbàti ekvivàlentlik munosàbàti bo‘làdi.
2) Qàrindoshlik munosàbàti ekvivàlentlik munosàbàti bo‘làdi.
3) “Sevgi” munosàbàti ekvivàlent munosàbàt bo`la olmaydi.
Misol 2. ![]() butun sonlar to`plami va unda aniqlangan
butun sonlar to`plami va unda aniqlangan ![]() munosabat shunday x-y larki, ular 3 ga bo`linadi.
munosabat shunday x-y larki, ular 3 ga bo`linadi.
à) x-x=0 soni 3 ga bo`linadi.
b) x-y ifoda 3 ga bo`linsa, ![]() ham 3 ga bo`linadi.
ham 3 ga bo`linadi.
c) x-y ifoda 3 ga bo`linsa va
y-z ifoda 3 ga bo`linsa, u holda ![]() ham 3 ga bo`linadi.
ham 3 ga bo`linadi.
Demak, ![]() munosabat ekvivàlentlik munosàbàti bo’lar ekan.
munosabat ekvivàlentlik munosàbàti bo’lar ekan.
Tà’rif 6. ![]() elementning ekvivalentlik sinfi deb,
elementning ekvivalentlik sinfi deb, ![]() to’plamga aytiladi.
to’plamga aytiladi.
Tà’rif 7. ![]() to’plam elementlarining E ekvivalentlik bo’yicha
ekvivalent sinflar to’plami faktor – to’plam deyiladi va
to’plam elementlarining E ekvivalentlik bo’yicha
ekvivalent sinflar to’plami faktor – to’plam deyiladi va ![]() kabi belgilanadi.
kabi belgilanadi.
1.2. Munosabatlar 59
Misol 3. Agar {(a;b), (c;d)}ÎQ to’plam elementlari uchun a+d=b+c tenglik bajarilsa, u holda Q munosabat N´N to’plamda ekvivalentlik munosabati bo’lini ko’rsating.
Yechilishi:
1) Refleksivlik:
agar ![]() to’plamda Q refleksivlik
munosabati bo’lsa, u holda
to’plamda Q refleksivlik
munosabati bo’lsa, u holda ![]() Bizning misolda
Bizning misolda ![]() t o’plam o’rnida N´N to’plam va x element o’rnida (x;y)
juftlik. Bunda N´N
to’plamda Q munosabat refleksiv bo’ladi, agarda
t o’plam o’rnida N´N to’plam va x element o’rnida (x;y)
juftlik. Bunda N´N
to’plamda Q munosabat refleksiv bo’ladi, agarda ![]() Ta`rifga ko’ra, Q: a+d=b+c,
lekin a+b=b+a, demak, Q - refleksiv munosabat.
Ta`rifga ko’ra, Q: a+d=b+c,
lekin a+b=b+a, demak, Q - refleksiv munosabat.
2) Simmetriklik: agar {(a;b), (c;d)}ÎQ bo’lsa, u holda {(c;d), (a;b)}ÎQ , a+d=b+c bundan c+b= d+a. Demak, Q – simmetrik munosabat.
3) Tranzitivlik: agar {(a;b), (c;d)}ÎQ, {(c;d),(f;g)}ÎQ bo’lsa, u holda {(a;b),(f;g)}ÎQ bo’ladi, chunki a+d=b+c va c+g=d+f. U holda
(a+d)+(c+g)=(b+c)+(d+f) Þ a+d+c+g=b+c+d+f Þ a+g=b+f,
ya`ni Q – tranzitiv munosabat.
Demak, Q munosabat ham refleksiv, ham simmetrik, ham tranzitiv bo’lganligi uchun ekvivalent munosabat bo’ladi.
Tà’rif 8. Har bir elementi ![]() to’plamning faqat va faqat bitta qism to’plamiga tegishli
bo’lgan kesishmaydigan qism to’plamlar majmuasi
to’plamning faqat va faqat bitta qism to’plamiga tegishli
bo’lgan kesishmaydigan qism to’plamlar majmuasi ![]() to’plamning bo’laklari deyiladi.
to’plamning bo’laklari deyiladi.
60 Bob I. To’plamlar nazariyasi
Teîremà. A/E faktor-to’plam A to’plamning bo’lagi bo’ladi. Va aksincha, agar R={Ai} – A to’plamning biror bo’lagi bo’lsa, u holda bu bo’lakka biror i va Ai dan olingan x;y elementlar uchun xEy qoida bo’yicha E ekvivalentlik munosabatini topish mumkin.
Nazorat uchun savollar:
1. Munosabatlarning kompozitsiyasi va uning xossalari.
2. Refleksivlik shartini ayting.
3. Simmetriklik shartini ayting.
4. Tranzitivlik shartini ayting.
5. Antisimmetrik munosabat deb nimaga aytiladi?
6. Ekvivalent munosabat deb nimaga aytiladi?
7. Faktor – to’plam deb nimaga aytiladi?
8. Ekvivalentlik sinfi deb nimaga aytiladi?
Mustaqil yechish uchun masalalar:
1. Birdan farqli natural sonlar to‘plami dekart kvadratida aniqlangan R={(x,y): x va y lar birdan farqli umumiy bo‘luvchiga ega} munosabat ekvivalent munosabat bo‘ladimi?
2. A={a, b, c} to‘plam dekart kvadratida simmetrik bo‘lgan, refleksiv, tranzitiv bo‘lmagan munosabatga misol keltiring va isbotlang.
1.2. Munosabatlar 61
3. A={a, b, c} to‘plam dekart kvadratida tranzitiv bo‘lgan, refleksiv, simmetrik bo‘lmagan munosabatga misol keltiring va isbotlang.
4. A={a, b, c} to‘plam dekart kvadratida refleksiv, simmetrik bo‘lgan, tranzitiv bo‘lmagan munosabatga misol keltiring va isbotlang.
5. K-kalit so‘zlar, P- web sahifalar to‘plami bo‘lsin, R munosabat ushbu to‘plamlar dekart ko‘paytmasida aniqlangan bo‘lsin. (x,y) juftlik R munosabatga tegishli bo‘lsin, agar x kalit so‘z y web-sahifada bo‘lsa. R munosabat ekvivalent munosabat bo‘ladimi?
6. A={1,2,3,4} to‘plam dekart kvadratida refleksiv bo‘lgan, simmetrik, tranzitiv bo‘lmagan munosabatga misol keltiring va isbotlang.
7. A={1,2,3,4} to‘plam dekart kvadratida refleksiv, simmetrik, tranzitiv bo‘lmagan munosabatga misol keltiring va isbotlang.
8. A={1,2,3,4} to‘plam dekart kvadratida ekvivalent munosabatga misol keltiring va isbotlang.
1.2.4. Munosabatning aniqlanish, qiymatlar sohalari.
Munosabatlar maydoni.
Biror A va B to`plamlar hamda unda
aniqlangan ![]() munosabat berilgan bo`lsin.
munosabat berilgan bo`lsin.
Tà‘rif 1. ![]() -munosàbàtning chàp sohàsi
yoki àniqlànish sohàsi Dl deb,
-munosàbàtning chàp sohàsi
yoki àniqlànish sohàsi Dl deb, ![]() -munosàbàtgà tegishli juftliklàr birinchi elementlàridàn iboràt to‘plàmgà àytilàdi va Dl={$x: (x,y)Î P} kabi belgilanadi. l- “left”, ya`ni “chap” so`zidan olingan.
-munosàbàtgà tegishli juftliklàr birinchi elementlàridàn iboràt to‘plàmgà àytilàdi va Dl={$x: (x,y)Î P} kabi belgilanadi. l- “left”, ya`ni “chap” so`zidan olingan.
62 Bob I. To’plamlar nazariyasi
Tà‘rif 2. ![]() -munosàbàtning o‘ng sohàsi yoki qiymàtlàr sohàsi
-munosàbàtning o‘ng sohàsi yoki qiymàtlàr sohàsi ![]() deb,
deb, ![]() -munosàbàtgà tegishli juftliklàrning ikkinchi elementlàr to‘plàmigà àytilàdi va Dr={$y: (x,y)Î P} kabi belgilanadi. r-
“right”, ya`ni “o`ng” so`zidan olingan.
-munosàbàtgà tegishli juftliklàrning ikkinchi elementlàr to‘plàmigà àytilàdi va Dr={$y: (x,y)Î P} kabi belgilanadi. r-
“right”, ya`ni “o`ng” so`zidan olingan.
Geometrik mà‘nodà ![]() -
- ![]() munosàbàtning
munosàbàtning ![]() to‘plàmgà proyektsiyasi,
to‘plàmgà proyektsiyasi, ![]() -
- ![]() munosàbàtning Y to’plàmdàgi proyektsiyasi hisoblànàdi.
munosàbàtning Y to’plàmdàgi proyektsiyasi hisoblànàdi.
Tà’rif 3. Aniqlànish va qiymàtlàr sohàlarining birlashmasi![]() ga
ga ![]() munosàbàt màydoni deyilàdi và
munosàbàt màydoni deyilàdi và ![]() kàbi belgilànàdi.
kàbi belgilànàdi.
![]() munosàbàtning chàp và o‘ng sohàlàridàgi bir xil qiymàtgà egà
bo‘lgàn elementlàri, ikkàlà tomongà hàm tegishli deb hisoblànàdi, xususàn
munosàbàtning chàp và o‘ng sohàlàridàgi bir xil qiymàtgà egà
bo‘lgàn elementlàri, ikkàlà tomongà hàm tegishli deb hisoblànàdi, xususàn ![]() dekàrt kvàdràt uchun
dekàrt kvàdràt uchun ![]() bo`ladi.
bo`ladi.
Tà’rif 4. ![]() to‘plàmgà R munosàbàtgà teskàri munosàbàt deyilàdi.
to‘plàmgà R munosàbàtgà teskàri munosàbàt deyilàdi.
Misol. À={2, 3, 4, 5, 6, 7, 8} to‘plàmdà binar munosabat
![]()
shart bilan aniqlangan bo`lsin. U holda
R={(2,2), (2, 4), (2,6), (2, 8), (3, 3), (3, 6)};
Dl = {2, 3};
Dr={2, 3, 4, 6, 8};
R-1= {(2, 2), (4, 2), (6, 2), (8, 2), (3, 3), (6, 3)}.
1.2. Munosabatlar 63
Nazorat uchun savollar:
1. Munosabatlarning aniqlanish sohasi ta’rifini keltiring.
2. Munosabatlarning qiymatlar sohasi ta’rifini ayting.
3. À to‘plàmning R munosàbàtgà nisbàtàn àsli deb nimaga aytiladi?
4. A to‘plàmning R munosàbàtgà nisbàtàn tasviri deb nimaga aytiladi?
5. Teskàri munosàbàtga ta’rif bering.
6. Munosàbàt màydoni deb nimaga aytiladi?
Mustaqil yechish uchun masalalar:
À={a,b,c,d,e}, Â={1,2,3,4} to‘plamlarda quyidagicha munosabatlar berilgan: ![]() bo’lsa,
bo’lsa,
1) ![]() munosabatlarni grafik ko‘rinishda ifodalang;
munosabatlarni grafik ko‘rinishda ifodalang;
2) ![]() munosabatlarning aniqlanish va qiymatlar sohalarini toping;
munosabatlarning aniqlanish va qiymatlar sohalarini toping;
3) ![]() ,
,![]() ,
,![]() ,
, ![]() - munosabatlarning matritsasini toping;
- munosabatlarning matritsasini toping;
4) R2 munosabatni refleksivlik, simmetriklik, antisimmetriklik, tranzitivlik xossalariga tekshirilsin.
1.
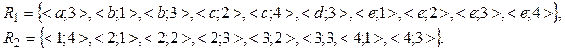
64 Bob I. To’plamlar nazariyasi
2.
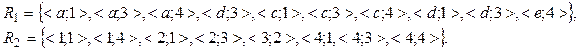
3.

4.
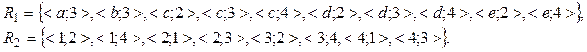
5.

6.
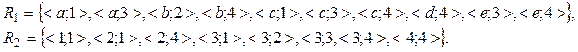
7.
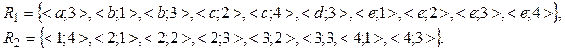
8.
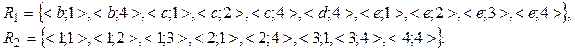
9.
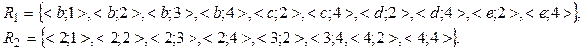
1.3. Akslantirishlar 65
1.3. AKSLANTIRIShLAR
KIRISh
Ushbu bobda akslantirish, ya’ni funktsiya tushunchalari ham kiritiladi. Zamonaviy dasturlash tillarida funktsiyalar juda keng qo’llaniladi. Ular bisga qism dasturlarni alohida agratib hisoblash imkoniyatini beradi. Ba’zi dasturlash tillarida birmuncha ko’p uchraydigan sinx, logx, |x| kabi funktsiyalar uchun maxsus bazalar mavjud. Funktsional dasturlash tillarida sodda funktsiyalardan foydalanib, murakkab funktsiyalarni tadqiq qilish uchun biz funktsiyalar kompozitsiyalarini yaxshi bilishimiz kerak bo’ladi. Ushbu bobning amaliy tadbiqi sifatida funktsiyalar kompozitsiyalarini hisoblashni o’rganib chiqamiz.
1.3.1. Chekli to`plamda akslantirish tushunchasi.
Tà’rif 1. Agar biror ![]() to’plamning har bir
to’plamning har bir ![]() elementiga qandaydir qonuniyat bo’yicha yagona
elementiga qandaydir qonuniyat bo’yicha yagona ![]() ob’yekt mos qo’yilgan bo’lsa, bu
ob’yekt mos qo’yilgan bo’lsa, bu ![]() moslik funktsiya deyiladi.
moslik funktsiya deyiladi.
Tà’rif 2. ![]() munosabat funktsiya yoki
munosabat funktsiya yoki ![]() to‘plamdan
to‘plamdan ![]() to‘plamga akslantirish
deyiladi, agarda
quyidagi shartlar bajarilsa:
to‘plamga akslantirish
deyiladi, agarda
quyidagi shartlar bajarilsa:
1) ![]() ,
, ![]() ,
,
2) ![]() ,
, ![]() ekanligidan
ekanligidan ![]() ekanligi kelib chiqsa.
ekanligi kelib chiqsa.
66 Bob I. To’plamlar nazariyasi
Funktsiya ![]() yoki
yoki ![]() kabi
belgilanadi, agar
kabi
belgilanadi, agar ![]() bo‘lsa, u holda
bo‘lsa, u holda ![]() kabi yoziladi
va
kabi yoziladi
va ![]() funktsiya
funktsiya
![]() elementga y elementni mos
qo‘yadi deb gapiriladi.
elementga y elementni mos
qo‘yadi deb gapiriladi. ![]() elementga x elementning tasviri,
elementga x elementning tasviri, ![]() elementga y ning asli deyiladi.
elementga y ning asli deyiladi.
Agar ![]() bo`lsa,
bo`lsa, ![]() funktsiya qismiy funktsiya deyiladi.
funktsiya qismiy funktsiya deyiladi.
Ixtiyoriy funktsiya ![]() bu binar munosabat.
Shuning uchun teskari munosabat
bu binar munosabat.
Shuning uchun teskari munosabat ![]() ni qurish mumkin. Agar
buning natijasida yana funktsiya hosil bo’lsa, u holda
ni qurish mumkin. Agar
buning natijasida yana funktsiya hosil bo’lsa, u holda ![]() ga teskarilanuvchi
funktsiya deyiladi va teskari funktsiya
ga teskarilanuvchi
funktsiya deyiladi va teskari funktsiya ![]() ko’rinishda
belgilanadi.
ko’rinishda
belgilanadi.
Misol 1. 1) ![]() - munosabat funktsiya bo‘ladi.
- munosabat funktsiya bo‘ladi.
2) ![]() - munosabat funktsiya bo‘lmaydi.
- munosabat funktsiya bo‘lmaydi.
3) ![]() - munosabat funktsiya
bo‘ladi va
- munosabat funktsiya
bo‘ladi va
![]() ko`rinishda ham yoziladi.
ko`rinishda ham yoziladi.
Tà’rif 3. Agar
1) ![]() ;
;
2) ixtiyoriy ![]() uchun
uchun ![]() bajarilsa,
bajarilsa, ![]() va
va ![]() akslantirishlarga teng akslantirishlar
deyiladi.
akslantirishlarga teng akslantirishlar
deyiladi.
Teorema 1. ![]() akslantirish va
akslantirish va ![]() lar uchun
lar uchun ![]() tenglik o’rinli.
tenglik o’rinli.
(Birlashmaning obrazi obrazlar birlashmasiga teng.)
1.3. Akslantirishlar 67
Isboti: Aytaylik, ![]() bo’lsin. Demak, shunday
bo’lsin. Demak, shunday ![]() mavjudki, uning uchun
mavjudki, uning uchun ![]() . Agar
. Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() , bundan esa
, bundan esa ![]() kelib chiqadi. Xuddi shuningdek,
kelib chiqadi. Xuddi shuningdek, ![]() ham isbotlanadi. Demak ,
ham isbotlanadi. Demak , ![]() ekanligi isbotlandi.
ekanligi isbotlandi.
Endi ![]() bo’lsin. Aniqlik uchun
bo’lsin. Aniqlik uchun ![]() ni qaraylik, demak, shunday
ni qaraylik, demak, shunday ![]() mavjudki, uning uchun
mavjudki, uning uchun ![]() . Bundan
. Bundan ![]() va
va ![]() ekanligi, demak,
ekanligi, demak, ![]() ekanligi kelib chiqadi. Xuddi shuningdek,
ekanligi kelib chiqadi. Xuddi shuningdek, ![]() ham isbotlanadi. Demak,
ham isbotlanadi. Demak, ![]() ekanligi isbotlandi.
ekanligi isbotlandi. ![]() va
va ![]() o’rinli bo’lsa, demakki,
o’rinli bo’lsa, demakki, ![]() tenglik
o’rinli.
tenglik
o’rinli.
Teorema isbotlandi.
Teorema 2. ![]() akslantirish va
akslantirish va ![]() lar uchun
lar uchun ![]() tenglik o’rinli.
tenglik o’rinli.
(Birlashmaning proobrazi proobrazlar birlashmasiga teng.)
Isboti: ![]() elementni olaylik, bu
elementni olaylik, bu ![]() ekanini bildiradi, ya’ni
ekanini bildiradi, ya’ni ![]() yoki
yoki ![]() . Agar
. Agar ![]() bo’lsa, u holda proobraz ta`rifiga ko’ra
bo’lsa, u holda proobraz ta`rifiga ko’ra ![]() bo’ladi, bundan esa
bo’ladi, bundan esa ![]() ekanligi kelib chiqadi. Xuddi shuningdek, agar
ekanligi kelib chiqadi. Xuddi shuningdek, agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() . Bundan
. Bundan
![]()
kelib chiqadi.
68 Bob I. To’plamlar nazariyasi
Endi aksincha qism to’plam bo’lishini ko’rsatamiz.
![]() bo’lsin, bundan
bo’lsin, bundan ![]() yoki
yoki ![]() . Agar
. Agar ![]() bo;lsa, u holda
bo;lsa, u holda ![]() bo’ladi. Shuningdek,
bo’ladi. Shuningdek, ![]() bo’ladi, bundan
bo’ladi, bundan ![]() kelib chiqadi.
kelib chiqadi. ![]() bo’lgan hol gam shunday yo’l bilan isbotlanadi va
bo’lgan hol gam shunday yo’l bilan isbotlanadi va ![]() hosil qilinadi. Bu ikkita
isbotlangan qism to’plamlar birlashtirilsa, talab qilingan tenglikka kelamiz.
hosil qilinadi. Bu ikkita
isbotlangan qism to’plamlar birlashtirilsa, talab qilingan tenglikka kelamiz.
![]() .
.
Teorema isbotlandi.
Teorema 3. ![]() akslantirish va
akslantirish va ![]() lar uchun
lar uchun ![]() tenglik o’rinli.
tenglik o’rinli.
Isboti: ![]() bo’lsin. Obraz ta’rifiga ko’ra, shunday
bo’lsin. Obraz ta’rifiga ko’ra, shunday ![]() elementlar to’piladiki, ular uchun
elementlar to’piladiki, ular uchun ![]() tenglik o’rinli.
tenglik o’rinli. ![]() ekanligidan
ekanligidan ![]() kelib chiqadi, demak,
kelib chiqadi, demak, ![]() va
va ![]() , ya’ni
, ya’ni ![]() . Bulardan talab qilingan tasdiq kelib chiqadi:
. Bulardan talab qilingan tasdiq kelib chiqadi: ![]()
Teorema isbotlandi.
Misol 2. Teskari tasdiq o’rinli bo’lmasligini misol yordamida ko’ramiz.
![]()
akslantirish bo’lsin.
1.3. Akslantirishlar 69
X va Y to’plamlar sifatida ![]() ,
, ![]() larni ko’raylik. Ravshanki,
larni ko’raylik. Ravshanki, ![]() ,
, ![]() , demak ularning kesishmasi
, demak ularning kesishmasi ![]() . So’ngra
. So’ngra ![]() ekanligidan
ekanligidan ![]() ni aniqlaymiz. Bu holda qism to’plam bo’lish
ni aniqlaymiz. Bu holda qism to’plam bo’lish ![]() munosabati bajarilmaydi.
munosabati bajarilmaydi.
Teorema 4. ![]() akslantirish va
akslantirish va ![]() to’plamlar uchun
to’plamlar uchun ![]() tenglik o’rinli.
tenglik o’rinli.
Isboti: ![]() bo’lsin, ya’ni
bo’lsin, ya’ni ![]() , demak,
, demak, ![]() , shuning uchun
, shuning uchun ![]() bundan
bundan ![]() .
.
Demak, ![]() .
.
Endi teskari munosabatni isbotlash
uchun ![]() ni olamiz, bundan
ni olamiz, bundan ![]() , demak,
, demak, ![]() è
è ![]() , ya’ni
, ya’ni ![]() , shuningdek,
, shuningdek, ![]() o’rinli ekanligi kelib chiqadi. Bundan esa
o’rinli ekanligi kelib chiqadi. Bundan esa ![]() . Olingan qism to’plamlar
birlashtirilsa, talab qilingan tenglikka kelamiz:
. Olingan qism to’plamlar
birlashtirilsa, talab qilingan tenglikka kelamiz:
![]() .
.
Teorema isbotlandi.
Ta’rif 4. Agar ![]() munosabat qismiy funktsiya bo‘lsa, ya’ni
munosabat qismiy funktsiya bo‘lsa, ya’ni ![]() dan olingan
dan olingan ![]() bajarilsa,
bajarilsa, ![]() funktsiyaga o’zaro bir qiymatli funktsiya yoki in’yektiv
funktsiya deyiladi va
funktsiyaga o’zaro bir qiymatli funktsiya yoki in’yektiv
funktsiya deyiladi va ![]() kabi belgilanadi.
kabi belgilanadi.
70 Bob I. To’plamlar nazariyasi
Demak, in’yektiv funktsiyada takrorlanuvchi qiymatlar bo’lmaydi.
Bundan ![]() kelib chiqadi.
kelib chiqadi.
Misol 3. ![]() funktsiya
funktsiya ![]() in’yektiv funktsiya bo’lishini ko’rsating.
in’yektiv funktsiya bo’lishini ko’rsating.
Yechilishi: Faraz
qilaylik, ![]() bo’lsin, ya’ni
bo’lsin, ya’ni ![]() , bundan
, bundan ![]() ,
, ![]() kelib chiqadi. Demak,
kelib chiqadi. Demak, ![]() - in’yektiv funktsiya bo’ladi.
- in’yektiv funktsiya bo’ladi.
Ta’rif 5. Agar ![]() bo‘lsa,
bo‘lsa, ![]() funktsiya
funktsiya ![]() ni
ni ![]() ga ustiga
akslantirish yoki syur’yektiv funktsiya deyiladi va
ga ustiga
akslantirish yoki syur’yektiv funktsiya deyiladi va ![]() kabi
belgilanadi.
kabi
belgilanadi.
Misol 4. 3-misoldagi ![]() funktsiyaning syur’yektivlikka tekshiramiz.
funktsiyaning syur’yektivlikka tekshiramiz.
Yechilishi: Aytaylik, ![]() bo’lsin. Ta’rifga
ko’ra,
bo’lsin. Ta’rifga
ko’ra, ![]() -
syur’yektiv funktsiya bo’lishi uchun
-
syur’yektiv funktsiya bo’lishi uchun ![]() o’rinli bo’ladigan shunday haqiqiy
son
o’rinli bo’ladigan shunday haqiqiy
son ![]() ni topish mumkin. Buning uchun
ni topish mumkin. Buning uchun ![]() deb olsak,
deb olsak, ![]() son topiladi. Demak,
son topiladi. Demak, ![]() - syur’yektiv funktsiya.
- syur’yektiv funktsiya.
Ta’rif 6. Ham in’yektiv, ham
syur’yektiv bo`lgan ![]() funktsiya A va B to‘plamlarning biyektiv
funktsiyasi deyiladi va
funktsiya A va B to‘plamlarning biyektiv
funktsiyasi deyiladi va ![]() kabi belgilanadi.
kabi belgilanadi.
Misol 5. ![]() funktsiya ham in’yektiv, ham
syur’yektiv, demak biyektiv ham bo’ladi.
funktsiya ham in’yektiv, ham
syur’yektiv, demak biyektiv ham bo’ladi.
1.3. Akslantirishlar 71
Umuman olganda, ![]() akslantirishlarning barchasi
akslantirishlarning barchasi ![]() biyektsiya bo’ladi.
biyektsiya bo’ladi.
Misol 6. ![]() tenglik uchun:
tenglik uchun:
a) ![]() akslantirish in’yektsiya ham, syur’yektsiya ham bo’lmaydi.
akslantirish in’yektsiya ham, syur’yektsiya ham bo’lmaydi.
b) ![]() akslantirishni olsak, bu syur’yektiv
akslantirish bo’ladi, lekin in’yektiv bo'lmaydi.
akslantirishni olsak, bu syur’yektiv
akslantirish bo’ladi, lekin in’yektiv bo'lmaydi.
v) ![]() deb oladigan bo’lsak, bu akslantirish biyektsiya bo’ladi.
deb oladigan bo’lsak, bu akslantirish biyektsiya bo’ladi.
Misol 7. ![]() tenglik uchun:
tenglik uchun:
a) ![]() akslantirish in’yektiv ham, syur’yektiv
ham emas.
akslantirish in’yektiv ham, syur’yektiv
ham emas.
b) ![]() in’yektiv bo’ladi, syur’yektiv
emas.
in’yektiv bo’ladi, syur’yektiv
emas.
v) ![]() syur’yektiv bo’ladi, in’yektiv
emas.
syur’yektiv bo’ladi, in’yektiv
emas.
g) ![]() biyektiv akslantirish bo’ladi.
biyektiv akslantirish bo’ladi.
Keltirilgan misollardan
ko’rinadiki, ![]() akslantirishlarda nafaqat
akslantirishlarda nafaqat ![]() amalning tuzilishi, balki
amalning tuzilishi, balki ![]() va
va ![]() to’plamlarning ham tuzilishi muhim rol o’ynaydi..
to’plamlarning ham tuzilishi muhim rol o’ynaydi..
Ta’rif 7. 1) ![]() – biyåêtiv
akslantirish bo’lsin.
– biyåêtiv
akslantirish bo’lsin. ![]() akslantirishga teskari
akslantirish
akslantirishga teskari
akslantirish ![]() deb, quyidagi shartlarni
qanoatlantiruvchi akslantirishga aytiladi:
deb, quyidagi shartlarni
qanoatlantiruvchi akslantirishga aytiladi:
à) ![]() ;
;
b) ![]() ;
;
v) ixtiyoriy ![]() uchun
uchun ![]()
72 Bob I. To’plamlar nazariyasi
2) ![]() akslantirish quyidagicha aniqlanadi;
akslantirish quyidagicha aniqlanadi;
à) ![]() ;
;
b) ixtiyoriy ![]() uchun
uchun ![]() .
.
![]() ga A da birlik akslantirish yoki ayniy
akslantirish deyiladi.
ga A da birlik akslantirish yoki ayniy
akslantirish deyiladi.
Misol 8. ![]() funktsiyalarni qaraylik.
funktsiyalarni qaraylik.
1) ![]() funktsiya in’yektiv, lekin
syur’yektiv emas.
funktsiya in’yektiv, lekin
syur’yektiv emas.
2) ![]() funktsiya in’yektiv emas, lekin
syur’yektiv.
funktsiya in’yektiv emas, lekin
syur’yektiv.
3) ![]() funktsiya ham in’yektiv, ham
sur’yektiv, demak biyektiv bo‘ladi.
funktsiya ham in’yektiv, ham
sur’yektiv, demak biyektiv bo‘ladi.
Nazorat uchun savollar:
1. Akslantirish tushunchasiga ta’rif bering.
2. Qismiy funktsiya deb nimaga aytiladi?
3. Birlashmaning obrazi obrazlar birlashmasiga tengligini isbotlang.
4. Birlashmaning proobrazi proobrazlar birlashmasiga teng ekanini isbotlang.
5. In’yektiv funktsiya ta’rifini keltiring. Misol keltiring.
6. Syur’yektiv funktsiyaga ta’rif bering.
7. Biyektiv funktsiyaga ta’rif bering.
8. Ayniy akslantirish deganda nimani tushunasiz?
1.3. Akslantirishlar 73
Mustaqil yechish uchun masalalar:
1. A={1,2,3,4}, B={a,b,c,d} to‘plamlar dekart ko‘paytmasida aniqlangan quyidagicha R munosabatlar funksiya bo‘ladimi? U holda in’yektivlik, syur’yektivlik va biyektivlikka tekshiring:
a) R={(1,a),(1,b),(2,a),(3,d)}
b) R={(1,a),(2,b),(3,a),(4,d)}
c) R={(1,a),(2,c),(3,b),(3,d)}
d) R={(2,a),(1,b),(2,c),(4,d)}
e) R={(3,b),(2,a),(1,c),(4,d)}
f) R={(4,c),(3,b),(3,a),(4,d)}
g) R={(4,a),(1,b),(2,a),(3,c)}
i) R={(3,b),(2,c),(1,a),(4,d)}
2. Agar fi(x):(-∞;+∞)→(-∞;+∞) berilgan bo’lsa, ularni in’yektivlik, syur’yektivlik, biyektivlikka tekshiring:
a) f(x)=x2 e) f(x)=lnx
b) f(x)=tgx f) f(x)=2x+1
c) f(x)=cosx g) f(x)=ctgx
d) f(x)=logax i) f(x)=2x+1
3. ![]() to’plam va
to’plam va ![]() akslantirish
akslantirish ![]() formula bilan berilgan bo’lsin.
formula bilan berilgan bo’lsin. ![]() ni biyektivlikka tekshiring va unga teskari funktsiyani
toping.
ni biyektivlikka tekshiring va unga teskari funktsiyani
toping.
74 Bob I. To’plamlar nazariyasi
1.3.2. Akslantirishlar superpozitsiyasi.
Ta’rif 1. ![]() va
va ![]() akslantirishlar berilgan bo`lsin. f
va g akslantirishlar superpozitsiyasi deb,
akslantirishlar berilgan bo`lsin. f
va g akslantirishlar superpozitsiyasi deb,
1) ![]() ;
;
2) ![]() ;
;
3) ixtiyoriy ![]() uchun
uchun ![]()
shartlarni qanoatlantiruvchi ![]() akslantirishga aytiladi.
akslantirishga aytiladi.
Akslantirishlar superpozitsiyasi kompozitsiya
yoki funktsional ko`paytma yoki murakkab funktsiya deb ham
ataladi ![]() .
.
Teorema 1. ![]() biyektiv akslantirish bo`lsin. U holda:
biyektiv akslantirish bo`lsin. U holda:
1) ![]() ham biyektiv akslantirish bo`ladi;
ham biyektiv akslantirish bo`ladi;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() .
.
Isboti: 1). ![]() ham biyektiv akslantirish bo`lishini ko`rsatamiz.
Aytaylik,
ham biyektiv akslantirish bo`lishini ko`rsatamiz.
Aytaylik, ![]() , u holda
, u holda ![]() va
va ![]() , lekin ta`rifga ko`ra akslantirish
in`yektiv bo`lishi kerak, shuning uchun
, lekin ta`rifga ko`ra akslantirish
in`yektiv bo`lishi kerak, shuning uchun ![]() .
.
1.3. Akslantirishlar 75
Endi sur`yektivligini isbotlaymiz.
Faraz qilaylik, ![]() va
va ![]() , u holda teskari funksiya ta`rifiga ko`ra
, u holda teskari funksiya ta`rifiga ko`ra ![]() , ya`ni
, ya`ni ![]() to`plamdan olingan ixtiyoriy elementning proobrazi mavjud
to`plamdan olingan ixtiyoriy elementning proobrazi mavjud ![]()
2). Ixtiyoriy ![]() elementni olaylik va
elementni olaylik va ![]() bo`lsin, u holda
bo`lsin, u holda ![]() , ya`ni
, ya`ni ![]() , bundan ixtiyoriy
, bundan ixtiyoriy ![]() uchun
uchun ![]() , demak,
, demak,![]() .
.
3). 2) – kabi isbotlanadi.
4). ![]() va
va ![]() bo`lsin, u holda
bo`lsin, u holda ![]() yoki ixtiyoriy
yoki ixtiyoriy ![]() element uchun
element uchun ![]() , demak,
, demak, ![]() .
.
5). 4) – kabi isbotlanadi.
6). ![]() . Bundan
. Bundan ![]() . Shuningdek,
. Shuningdek, ![]() , ya`ni
, ya`ni ![]() .
.
![]() element va
element va ![]() berilgan bo`lsin, u holda
berilgan bo`lsin, u holda ![]() va yana teskari akslantirish ta`rifidan foydalanib,
va yana teskari akslantirish ta`rifidan foydalanib, ![]() ni hosil qilamiz, bu degani ixtiyoriy
ni hosil qilamiz, bu degani ixtiyoriy ![]() uchun
uchun ![]() , shuning uchun
, shuning uchun ![]() .
.
Teorema isbotlandi.
Teorema 2. f va g akslantirishlar uchun quyidagi shartlar o`rinli:
1) Agar ![]() ,
, ![]() bo‘lsa, u holda
bo‘lsa, u holda ![]()
2) Agar ![]() bo‘lsa, u holda
bo‘lsa, u holda ![]() .
.
3) Agar ![]() ,
, ![]() bo‘lsa, u holda
bo‘lsa, u holda ![]() .
.
76 Bob I. To’plamlar nazariyasi
4) Agar ![]() va g lar in`yektiv akslantirish bo‘lsa, u holda
va g lar in`yektiv akslantirish bo‘lsa, u holda ![]() ham in`yektiv akslantirish bo‘ladi.
ham in`yektiv akslantirish bo‘ladi.
5) Agar ![]() ,
, ![]() bo‘lsa, u holda
bo‘lsa, u holda ![]() bo‘ladi.
bo‘ladi.
Teorema 3. Agar ![]() ,
, ![]() ,
, ![]() akslantirishlar uchun
akslantirishlar uchun ![]() munosabat o`rinli (superpozitsiyaning assotsiativligi).
munosabat o`rinli (superpozitsiyaning assotsiativligi).
Isboti: Ko`rish mumkinki, akslantirishlar kompozitsiyasi binar munosabatlar kompozitsiyasining xususiy holidan iborat. Binar munosabatlar uchun assotsiativlik qonuni bajarilganligi uchun akslantirishlar kompozitsiyasi uchun ham bajariladi.
Misol 1. Ikkita ![]()
![]() va
va ![]()
![]() funktsiyalar uchun
funktsiyalar uchun ![]() ,
, ![]() kompozitsiyalarni toping.
kompozitsiyalarni toping.
Yechilishi: ![]()
![]()
![]()
![]()
Agar ![]() akslantirish va
akslantirish va ![]() bo‘lsa, u holda
bo‘lsa, u holda
![]() to‘plam
X to‘plamning
to‘plam
X to‘plamning ![]() akslantirishi
natijasida tasviri deyiladi va
akslantirishi
natijasida tasviri deyiladi va ![]() (X) kabi belgilanadi.
(X) kabi belgilanadi.
1.3. Akslantirishlar 77
A ni B ga akslantiruvchi barcha funktsiyalar to‘plami BA bilan
belgilanadi. ![]() .
.
Ta’rif 2. ![]() funktsiya A dan B ga n- o‘rinli
funktsiya deyiladi, agar y qiymat n o‘rinli
funktsiya A dan B ga n- o‘rinli
funktsiya deyiladi, agar y qiymat n o‘rinli ![]() funktsiyaning
(x1, x2,...., xn) argument qiymatidagi qiymati
bo‘lsa, va u
funktsiyaning
(x1, x2,...., xn) argument qiymatidagi qiymati
bo‘lsa, va u ![]() kabi yoziladi.
kabi yoziladi.
Ta’rif 3. ![]() funktsiya A to‘plamda n - o‘rinli algebraik amal
deyiladi.
funktsiya A to‘plamda n - o‘rinli algebraik amal
deyiladi.
n=1 bo`lganda, ![]() funktsiyaga unar amal, n=2 bo`lganda esa
funktsiyaga unar amal, n=2 bo`lganda esa ![]() funktsiyaga binar amal deyiladi.
funktsiyaga binar amal deyiladi. ![]() bo‘lganda
bo‘lganda ![]() amal {( Ø,a)} biror bir
amal {( Ø,a)} biror bir ![]() uchun bo‘ladi.
Ko‘p hollarda A to‘plamda 0 o‘rinli amal {( Ø,a)} ni A to‘plamdagi konstanta deb ataladi va a element
bilan ifodalanadi.
uchun bo‘ladi.
Ko‘p hollarda A to‘plamda 0 o‘rinli amal {( Ø,a)} ni A to‘plamdagi konstanta deb ataladi va a element
bilan ifodalanadi.
Misol 2. 1) Haqiqiy sonlarni qo‘shish amali 2
o‘rinli, ya‘ni binar amal ![]() bo‘ladi, chunki qo‘shish amali bir
juft (a, b) songa a+b sonni mos qo‘yadi.
bo‘ladi, chunki qo‘shish amali bir
juft (a, b) songa a+b sonni mos qo‘yadi.
2) R – to‘plamning ixtiyoriy ajratib
ko‘rsatilgan elementini, masalan ![]() ni 0 o‘rinli amal deyish
mumkin, ya’ni R da konstantadir.
ni 0 o‘rinli amal deyish
mumkin, ya’ni R da konstantadir.
Ta’rif 4. {0, 1} qiymatlardan ixtiyoriy birini qabul qiladigan funktsiyaga binar funktsiya deyiladi.
78 Bob I. To’plamlar nazariyasi
Ta’rif 5. a) ![]() akslantirishlar berilgan bo`lsin.
akslantirishlar berilgan bo`lsin. ![]() va
va ![]() akslantirishlar kelishilgan
deyiladi, agarda ixtiyoriy
akslantirishlar kelishilgan
deyiladi, agarda ixtiyoriy ![]() uchun
uchun ![]() tenglik bajarilsa.
tenglik bajarilsa.
á) ![]()
![]() akslantirishlar oilasi berilgan bo`lsin.
akslantirishlar oilasi berilgan bo`lsin. ![]() akslantirishlar oilasi kelishilgan deyiladi, agarda
akslantirishlar oilasi kelishilgan deyiladi, agarda ![]() akslantirishlar o`zaro kelishilgan bo`lsa, ya`ni ixtiyoriy
akslantirishlar o`zaro kelishilgan bo`lsa, ya`ni ixtiyoriy
![]() va
va ![]() lar uchun
lar uchun ![]() tenglik bajarilsa.
tenglik bajarilsa.
Agar akslantirishlarning ![]() aniqlanish sohalari o`zaro kesishmasa, u holda
aniqlanish sohalari o`zaro kesishmasa, u holda ![]() akslantirishlar oilasi kelishilgan bo`ladi.
akslantirishlar oilasi kelishilgan bo`ladi.
Nazorat uchun savollar:
1. Funktsiya kompozitsiyasi va uning xossalarini keltiring.
2. n – o‘rinli funktsiya va n-o‘rinli algebraik amal tushunchalari farqini ayting.
3. Kelishilgan akslantirish deb nimaga aytiladi?
4. Kelishilgan akslantirishlar oilasi deb nimaga aytiladi?
5. ![]() ,
, ![]() ,
, ![]() akslantirishlar uchun
akslantirishlar uchun ![]()
superpozitsiya amalining assotsiativligini isbotlang.
1.3. Akslantirishlar 79
Mustaqil yechish uchun masalalar:
Quyida keltirilgan f, g:
R→R funksiyalar uchun ![]() ,
, ![]() kompozitsiyalar aniqlansin.
kompozitsiyalar aniqlansin.
1. ![]() va
va ![]()
2. ![]() va
va ![]()
3. ![]() va
va ![]()
4. 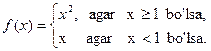 va
va ![]()
5. 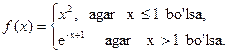 va
va ![]()
6. ![]() va
va 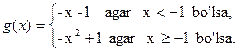
7. 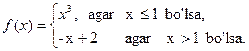 va
va 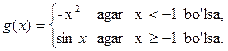
80 Bob I. To’plamlar nazariyasi
8. 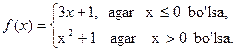 va
va 
9. ![]() va
va ![]()
10. 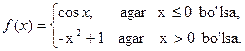 va
va 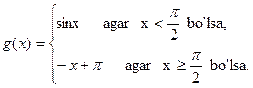
11. ![]()
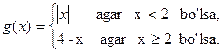
12. 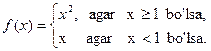
![]()
13. 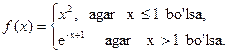
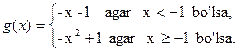
14. ![]()
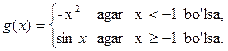
15. 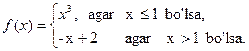
![]()
16. 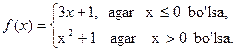
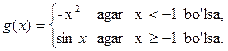
1.3. Akslantirishlar 81
1.3.3. Dirixle printsipi
![]() funktsiya
funktsiya ![]() chekli to’plamni
chekli to’plamni ![]() chekli to’plamga akslantirsin. Deylik,
chekli to’plamga akslantirsin. Deylik, ![]() to’plam n ta elementdan iborat bo’lsin:
to’plam n ta elementdan iborat bo’lsin: ![]() .
.
Dirixle printsipi: Agar ![]() bo’lsa, u holda hech bo’lmaganda
bo’lsa, u holda hech bo’lmaganda ![]() ning bitta qiymati bir martadan ortiq uchraydi, ya’ni
ning bitta qiymati bir martadan ortiq uchraydi, ya’ni ![]() elementlar juftligi topiladiki, ular uchun
elementlar juftligi topiladiki, ular uchun ![]() bo’ladi.
bo’ladi.
Oddiy qilib aytadigan bo’lsak, Dirixle printsipining ma’nosi: 10 ta quyonni 9 katakka har bir katakda bittadan quyon o’tiradigan qilib joylash mumkin emas.
Misol 1. Avtobusda 15 nafar yo’lovchi ketyapti. Ulardan hech bo’lmaganda 2 tasining tug’ilgan kuni bir xil oyda bo’lishi mumkinligini ko’rsating.
Yechilishi: Avtobusdagi
odamlar to’plamini ![]() , 12 ta oy nomlarini esa
, 12 ta oy nomlarini esa ![]() deb belgilaymiz.
deb belgilaymiz. ![]() funktsiya avtobusdagi har bir kishiga uning tug’ilgan oyini
mos qo’ysin.
funktsiya avtobusdagi har bir kishiga uning tug’ilgan oyini
mos qo’ysin. ![]() ,
, ![]() demak,
demak, ![]() . Dirixle printsipiga ko’ra,
. Dirixle printsipiga ko’ra, ![]() funktsiya takrorlanuvchi qiymatga ega. Bundan esa, hech
bo'lmaganda 2 ta kishining tug’ilgan kuni bir xil oyda bo’lishi kelib chiqadi.
funktsiya takrorlanuvchi qiymatga ega. Bundan esa, hech
bo'lmaganda 2 ta kishining tug’ilgan kuni bir xil oyda bo’lishi kelib chiqadi.
Misol 2. Agar hech bo’lmaganda 2 ta kishining familiyasi bir xil harfda boshlanib, bir xil harf bilan tugaydigan bo’lsa, telefon
82 Bob I. To’plamlar nazariyasi
ma’lumotnomasiga yozilgan familiyalarning minimal soni qanday bo’ladi?
Yechilishi: ![]() - ma’lumotnomadagi familiyalar to’plami,
- ma’lumotnomadagi familiyalar to’plami,
![]() - o’zbek alifbosi 26 ta harfidan olingan harflar juftligi
to’plami.
- o’zbek alifbosi 26 ta harfidan olingan harflar juftligi
to’plami. ![]() bir xil familiyalarning birinchi va
oxirgi harflarini mos qo’yuvchi funktsiya. Masalan,
bir xil familiyalarning birinchi va
oxirgi harflarini mos qo’yuvchi funktsiya. Masalan, ![]() (Abdullayev)=(a,v).
(Abdullayev)=(a,v).
B to’plam ![]() juft harfdan iborat. Dirixle printsipiga ko’ra, agar
juft harfdan iborat. Dirixle printsipiga ko’ra, agar ![]() bo’lsa, familiyasi bir xil harfda boshlanib, bir xil harf
bilan tugaydigan hech bo’lmaganda 2 ta kishi topiladi. Shuning uchun telefon
ma’lumotnomasi 676 tadan kam bo’lmagan familiyadan tuzilgan bo’lishi kerak.
bo’lsa, familiyasi bir xil harfda boshlanib, bir xil harf
bilan tugaydigan hech bo’lmaganda 2 ta kishi topiladi. Shuning uchun telefon
ma’lumotnomasi 676 tadan kam bo’lmagan familiyadan tuzilgan bo’lishi kerak.
1.3.4. To‘plamlarning quvvati va kardinal sonlar.
Har qanday ![]() to‘plam uchun
uning barcha qism to‘plamlari to‘plami
to‘plam uchun
uning barcha qism to‘plamlari to‘plami
P(A) =2A mavjud bo’lib, ushbu to‘plamlar oilasini tahlil qilish juda mihim ahamiyatga ega.
Teorema 1. n ta elementdan iborat ![]() ={x1,
x2, ..., xn } to‘plamning barcha qism to‘plamlari to‘plami
={x1,
x2, ..., xn } to‘plamning barcha qism to‘plamlari to‘plami ![]() to‘plamda
aniqlangan, soni 2n ta
bo‘lgan binar funktsiyalar to‘plamiga biyektiv bo‘ladi.
to‘plamda
aniqlangan, soni 2n ta
bo‘lgan binar funktsiyalar to‘plamiga biyektiv bo‘ladi.
1.3. Akslantirishlar 83
Teorema 2. Ixtiyoriy bo’sh bo’lmagan ![]() to‘plamning barcha qism to’plamlaridan
iborat to’plam quvvati
to‘plamning barcha qism to’plamlaridan
iborat to’plam quvvati ![]() to‘plam quvvatidan katta bo’ladi.
to‘plam quvvatidan katta bo’ladi.
Isboti: Ushbu teorema ![]() bo’sh to’plam bo’lgan holda ham o’rinli.
bo’sh to’plam bo’lgan holda ham o’rinli. ![]() bo’sh to’plamning barcha qism to’plamlari
bo’sh to’plamning barcha qism to’plamlari ![]() ko’rinishda bo’ladi, ya’ni quvvati 1 ga teng, shuning bilan
birga
ko’rinishda bo’ladi, ya’ni quvvati 1 ga teng, shuning bilan
birga ![]()
![]() natural sonlar to’plamining
natural sonlar to’plamining ![]() to’plamiga barcha akslantirishlar to’plamini qaraylik. Bu
turdagi har qanday akslantirish har bir natural soniga 0 yoki 1 ni mos qo’yadi
va bu moslik cheksiz ketma-ketlikni hosil qiladi:
to’plamiga barcha akslantirishlar to’plamini qaraylik. Bu
turdagi har qanday akslantirish har bir natural soniga 0 yoki 1 ni mos qo’yadi
va bu moslik cheksiz ketma-ketlikni hosil qiladi: ![]() , bunda
, bunda ![]() yoki 1 bo’ladi, ya’ni cheksiz o’nli kasrni ifodalaydi:
yoki 1 bo’ladi, ya’ni cheksiz o’nli kasrni ifodalaydi: ![]() . Shunday qilib, barcha cheksiz kasrlar to’plami
. Shunday qilib, barcha cheksiz kasrlar to’plami ![]() natural sonlar to’plamining barcha qism to’plamlari
quvvatiga teng bo’ladi.
natural sonlar to’plamining barcha qism to’plamlari
quvvatiga teng bo’ladi. ![]() natural sonlar to’plami quvvatini
natural sonlar to’plami quvvatini ![]() deb olsak, u holda barcha cheksiz kasrlar to’plamining
quvvati
deb olsak, u holda barcha cheksiz kasrlar to’plamining
quvvati ![]() ga teng bo’ladi.
ga teng bo’ladi.
Ta’rif 1. Agar ![]() to‘plamning quvvati
to‘plamning quvvati ![]() natural sonlar to’plami quvvatidan katta bo’lsa, u holda
natural sonlar to’plami quvvatidan katta bo’lsa, u holda ![]() to‘plam sanoqsiz to’plam deyiladi.
to‘plam sanoqsiz to’plam deyiladi.
Har bir qism to‘plam Z ga <y1, y2, ... , yn > binar funktsiyani biyektiv mos qo‘yamiz, yi elementlar quyidagicha aniqlanadi:
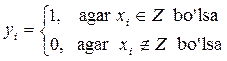
Natijada quyidagicha 23 ta binar funktsiyalar to‘plamiga ega bo‘lamiz:
000, 100, 010, 001, 110, 101, 011, 111.
84 Bob I. To’plamlar nazariyasi
Misol. A={1, 2, 3} to’plamning qism to‘plamlari to‘plami
2A ={{Ø}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.
Cheksiz to‘plamlar (masalan to‘g‘ri chiziq, tekislik, … )ni soniga ko’ra taqqoslashda, ularning elementlari soni cheksiz bo’lganligi sababli bu to‘plamlar tarkibining yanada aniqroq baholari zarur bo’ladi. Ma’lum baholar to‘plamlarning quvvati va ekvivalentligi tushunchalariga asoslanadi.
Ta’rif 2. ![]() chekli yoki cheksiz to‘plamlar
oilasidan olingan
chekli yoki cheksiz to‘plamlar
oilasidan olingan ![]() va
va ![]() to‘plamlar uchun
to‘plamlar uchun ![]() biyektsiya
mavjud bo‘lsa, u holda
biyektsiya
mavjud bo‘lsa, u holda ![]() va
va ![]() to‘plamlar ekvivalent
deyiladi.
to‘plamlar ekvivalent
deyiladi.
Ekvivalentlik munosabati refleksiv, simmetrik va tranzitivlik xossalariga ega bo’lganligi uchun ham biyektiv munosabat ![]() to‘plamlar oilasini
ekvivalent elementlar sinfiga ajratadi.
to‘plamlar oilasini
ekvivalent elementlar sinfiga ajratadi.
Teorema 3. Agar f funktsiya chekli ![]() to‘plamni
to‘plamni ![]() to‘plamga
o‘zaro bir qiymatli akslantirish bo‘lsa, u holda
to‘plamga
o‘zaro bir qiymatli akslantirish bo‘lsa, u holda ![]() va
va ![]() shartlar ekvivalent bo‘ladi.
shartlar ekvivalent bo‘ladi.
Shunday qilib, quvvat turli chekli ekvivalent to‘plamlar uchun umumiy mezon hisoblanadi.
Elementlari soni cheksiz bo‘lgan ekvivalent to‘plamlar uchun ham bu printsip o‘rinli. Cheksiz to‘plamlar uchun quvvat tushunchasini aniqlash maqsadida kardinal son tushunchasini kiritamiz.
1.3. Akslantirishlar 85
Ta’rif 3. Cheksiz to‘plam elementlari sonini aniqlaydigan simvolga kardinal son deyiladi.
Natural qatorning kardinal soni ![]() simvol bilan belgilanadi va alfa
nol deb o‘qiladi.
simvol bilan belgilanadi va alfa
nol deb o‘qiladi.
Ixtiyoriy chekli ![]() to‘plam uchun
to‘plam uchun ![]() o‘rinli
bo‘lsin. U holda, tabiiyki
o‘rinli
bo‘lsin. U holda, tabiiyki ![]() taqqoslash o‘rinli. Natural qator
barcha to‘plam ostilar to‘plami kardinal sonini
taqqoslash o‘rinli. Natural qator
barcha to‘plam ostilar to‘plami kardinal sonini ![]() bilan belgilanadi va 1- teoremaga ko‘ra
bilan belgilanadi va 1- teoremaga ko‘ra ![]() .
.
![]() mi yoki
mi yoki ![]() bo`ladimi?
bo`ladimi?
Aytaylik, ![]() bo‘lsin. U holda
natural sonlar to’plami quvvati uning to‘plam ostilari to‘plami quvvatidan kichik bo’lishi kelib chiqadi.
bo‘lsin. U holda
natural sonlar to’plami quvvati uning to‘plam ostilari to‘plami quvvatidan kichik bo’lishi kelib chiqadi.
Bundan quyidagi imkoniyatlarga ega bo‘lamiz.
1. ![]() dan P(
dan P(![]() ) ga o‘tib yanada
quvvatliroq to‘plamlarni qurish;
) ga o‘tib yanada
quvvatliroq to‘plamlarni qurish;
2. Quvvatlar shkalasini (cheksiz to‘plamlar uchun ham) tuzib chiqish.
Nazorat uchun savollar:
1. Cheksizlik aksiomasini keltiring.
2. T‘oplamning quvvati deganda nimani tushunasiz?
3. Ekvivalent t‘oplam tushunchasini ta’riflang.
4. Kardinal son deb nimaga aytiladi?
86 Bob I. To’plamlar nazariyasi
1.3.5. Sanoqli va kontinual to‘plamlar.
Tasdiq 1. Musbat juft sonlar to‘plamining quvvati ![]() ga teng.
ga teng.
Isboti: {2, 4, 6, ...} bilan natural sonlar to’plami quvvatlarini taqqoslash uchun juft sonlar to‘plamining elementlarini quyidagicha nomerlab chiqamiz:
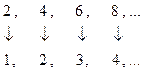
Bu usul bilan ![]() biyektsiyani o‘rnatdik, bu erda n – natural son. Demak, musbat juft sonlar to‘plami natural sonlar to’plamining qismi bo‘lsa-da, ularning quvvatlari teng ekan.
biyektsiyani o‘rnatdik, bu erda n – natural son. Demak, musbat juft sonlar to‘plami natural sonlar to’plamining qismi bo‘lsa-da, ularning quvvatlari teng ekan.
Tasdiq 2. Natural sonlar to‘plamining quvvati ![]() ga teng.
ga teng.
Isboti: Natural va butun sonlar to‘plamlari o‘rtasida biyektsiya qurishga urinib ko‘ramiz. Buning uchun butun sonlar qatorini quyidagicha yozib chiqamiz va mos ravishda natural sonlar bilan nomerlaymiz:
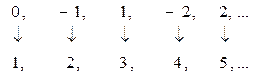
Shunday qilib, butun va natural sonlar o‘rtasida
ekvivalentlik munosabati
o‘rnatildi,
ya’ni ![]() .
.
1.3. Akslantirishlar 87
Tasdiq 3. Ratsional sonlar to‘plamining
quvvati ![]() ga
teng.
ga
teng.
Isboti: Bilamizki ixtiyoriy q ratsional sonni
qisqarmaydigan kasr ko‘rinishida ifodalash mumkin: ![]() , bu erda
, bu erda ![]() va
va ![]() lar butun sonlar. Ratsional son q ning balandligi deb,
lar butun sonlar. Ratsional son q ning balandligi deb, ![]()
![]() yigindiga aytiladi. Masalan, 1 balandlikka faqat
yigindiga aytiladi. Masalan, 1 balandlikka faqat ![]() son ega bo‘ladi, 2
balandlikka
son ega bo‘ladi, 2
balandlikka ![]() va
va
![]() sonlar, 3 balandlikka
sonlar, 3 balandlikka ![]() ,
, ![]() ,
, ![]() ,
, ![]() sonlar ega bo‘ladi. Tushunarliki,
berilgan balandlikdagi sonlar soni chekli bo‘ladi. Shuning uchun ham barcha
ratsional sonlarni balandliklari oshishiga qarab, raqamlab chiqish mumkinki,
bunda hatto bir xil balandlikka ega bo‘lgan sonlar ham o‘z raqamlariga ega
bo‘lishadi. Natijada natural va ratsional sonlar o‘rtasida biyektsiya
o‘rnatiladi.
sonlar ega bo‘ladi. Tushunarliki,
berilgan balandlikdagi sonlar soni chekli bo‘ladi. Shuning uchun ham barcha
ratsional sonlarni balandliklari oshishiga qarab, raqamlab chiqish mumkinki,
bunda hatto bir xil balandlikka ega bo‘lgan sonlar ham o‘z raqamlariga ega
bo‘lishadi. Natijada natural va ratsional sonlar o‘rtasida biyektsiya
o‘rnatiladi.
Ma’lumki, to‘plam sanoqli bo‘lishi uchun u natural sonlar qatoriga biyektiv mos qo‘yilgan bo‘lishi kerak.
Sanoqli to‘plamlarning muhim xossalarini keltiramiz.
1-xossa. Sanoqli to‘plamning har qanday qism to‘plami yo chekli, yoki sanoqli bo’ladi.
2-xossa. Chekli yoki sanoqlita sanoqli to‘plamlarning yig‘indisi yana sanoqli bo‘ladi.
Aytaylik A1, A2, ... – sanoqli to‘plamlar bo‘lsin. A1, A2, ... to‘plamlarning barcha elementlarini quyidagicha cheksiz jadval ko‘rinishida yozish mumkin:
88 Bob I. To’plamlar nazariyasi
a11 a12 a13 a14 ...
a21 a22 a23 a24 ...
a31 a32 a33 a34 ...
a41 a42 a43 a44 ...
.....................................
i-qatorda Ai to‘plamning barcha elementlari joylashgan. Ushbu elementlarni dioganal bo‘yicha raqamlab chiqamiz:
|
a11 |
|
a12 |
|
a13 |
|
a14 |
... |
|
|
|
|
|
|
|
|
|
|
a21 |
|
a22 |
|
a23 |
|
a24 |
... |
|
|
|
|
|
|
|
|
|
|
a31 |
|
a32 |
|
a33 |
|
a34 |
... |
|
|
|
|
|
|
|
|
|
|
a41 |
|
a42 |
|
a43 |
|
a44 |
... |
|
|
|
|
|
|
|
|
|
|
... |
|
... |
|
... |
|
... |
|
Shu bilan birga bir nechta to‘plamlarga tegishli bo‘lgan elementlarni faqat bir marta belgilaymiz. Shunda yigindidagi har bir element o‘zining raqamiga ega bo‘ladi va natural sonlar qatori bilan chekli yoki sanoqlita to‘plamlar yig‘indisi o‘rtasida o‘zaro bir qiymatli moslik o‘rnatiladi.
1.3. Akslantirishlar 89
3-xossa. Har qanday cheksiz to‘plam sanoqlita elementga ega bo‘lgan qism to‘plamga ega.
Teorema 1. [0; 1] kesmadagi haqiqiy sonlar to‘plami cheksizdir.
Isboti: Faraz qilaylik, [0; 1] kesmadagi haqiqiy sonlar sanoqli bo‘lsin. U holda bu sonlarni quyidagicha ifodalash mumkin:
![]()
![]()
.............................
![]()
.............................
![]() haqiqiy sonni quyidagicha qoida
bo‘yicha quramiz. Birinchi nol va vergul qo‘yamiz. Keyin
haqiqiy sonni quyidagicha qoida
bo‘yicha quramiz. Birinchi nol va vergul qo‘yamiz. Keyin ![]() larni quyidagicha
tanlaymiz.
larni quyidagicha
tanlaymiz.
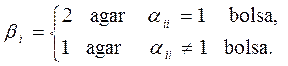
Shu printsipda barcha sonlarni ko‘rib chiqamiz. Natijada biror bir ai songa teng bo‘lmagan b son hosil bo‘ladi. Ushbu son birinchi sondan hech bo‘lmaganda verguldan keyingi birinchi soni bilan, ikkinchi sondan hech bo‘lmaganda verguldan keyingi ikkinchi son bilan farq qiladi va hokazo. Shunday qilib [0, 1] oraliqdagi sonlar to‘plami sanoqli degan taxminimiz noto‘g‘ri, chunki [0, 1] oraliqda shunday son topiladiki, biz sanoqli deb sanab chiqqan sonlar ichida u yo‘q. Demak [0, 1] oraliqdagi sonlar to‘plami sanoqsiz. Teorema isbotlandi.
90 Bob I. To’plamlar nazariyasi
Ta’rif. [0; 1] kesmadagi nuqtalar to‘plami
quvvati kontinuum deyiladi va ![]() kabi belgilanadi. [0, +∞)
oraliq quvvati ham
kabi belgilanadi. [0, +∞)
oraliq quvvati ham ![]() ga teng, chunki : -ln[0, 1]=[0,
+∞) biyeksiya o‘rinli. Aynan shu funksiya orqali [0, +∞) va
(-∞, +∞) oraliqlar o‘rtasida biyeksiya o‘rnatish mumkin. Demak [0,
1], [0, +∞), (-∞, +∞) oraliqlar ekvivalent.
ga teng, chunki : -ln[0, 1]=[0,
+∞) biyeksiya o‘rinli. Aynan shu funksiya orqali [0, +∞) va
(-∞, +∞) oraliqlar o‘rtasida biyeksiya o‘rnatish mumkin. Demak [0,
1], [0, +∞), (-∞, +∞) oraliqlar ekvivalent.
![]() kvadrat quvvati kontinuumga teng.
kvadrat quvvati kontinuumga teng.
Isboti: Haqiqatdan, A(x, y) nuqta ![]() kvadratga tegishli bo‘lsin. x
va ylarni quyidagi ko‘rinishda yozib olamiz:
kvadratga tegishli bo‘lsin. x
va ylarni quyidagi ko‘rinishda yozib olamiz:
x=0.x1x2....; y=0,y1y2…. va har bir A(x, y) nuqtaga a=0,x1y1x2y2… haqiqiy son mos qo‘yamiz. Tushunarliki, kvadratning turli xil nuqtalariga turli xil haqiqiy sonlar mos keladi. Teskari moslik ham o‘rinli ekanligini Kantor isbotlagan.
Kantorning ushbu g‘oyasi kubdagi va ixtiyoriy n-o‘lchovli jismdagi nuqtalar to‘plamining sanoqsizligi isbotiga kalit beradi.
Teorema 2. Natural sonlar qatorining barcha qism to‘plamlari to‘plamining quvvati kontinuumga teng.
Misol. [1, 5] kesma quvvatini aniqlash
uchun [1;5] kesma bilan [0;1] kesma o‘rtasida o‘zaro bir qiymatli moslik
o‘rnatamiz. ![]() funksiya
[1;5] oraliqni [0;1] oraliqqa akslantiruvchi biyektiv funksiya
funksiya
[1;5] oraliqni [0;1] oraliqqa akslantiruvchi biyektiv funksiya
1.3. Akslantirishlar 91
bo‘ladi. Shunday qilib, [1;5]
kesmaning tartibi [0;1] kesma tartibiga teng, [0;1] kesmaning quvvati esa kontinuumga
teng. ![]() .
.
Teorema 3. Haqiqiy sonlar to‘plam
sanoqsiz va quvvati ![]() kontinuumga teng.
kontinuumga teng.
Nazorat uchun savollar:
1. Sanoqli va kontinual to‘plamlarni tushuntiring.
2. Sanoqli to‘plamlarning xossalarini keltiring.
3. Natural sonlar to’plamining quvvati nimaga teng?
4. Ratsional sonlar to’plamining quvvati nimaga teng?
5. Ratsional sonlar to‘plamining
quvvati ![]() ga
tengligini isbotlang.
ga
tengligini isbotlang.
Mustaqil yechish uchun masalalar:
Sanoqsiz to‘plamlar quvvatini toping:
1. (+4, +∞) oraliq quvvati aniqlansin.
2. (+2, +∞) oraliq quvvati aniqlansin.
3. (+5, +∞) oraliq quvati aniqlansin.
4. (+3, +∞) oraliq quvvati aniqlansin.
5. (-∞, -4] oraliq quvvati aniqlansin.
92 Bob I. To’plamlar nazariyasi
1.4. TO’PLAMLAR NAZARIYASINING
AKSIOMATIK TIZIMI
To’plamlar nazariyasi barcha matematik bilimlar tizimining baquvvat poydevori bo’lib xizmat qiladi. Har bir tadqiqot ob`yektini biror to’plam sifatida tasavvur qilish mumkin. Biroq to’plamlar universumini erkin holda, hech bir shartlarsiz qo’llash ba`zan ziddiyatga olib kelishi mumkin. Ziddiyatlar matematikada paradoks deb yuritiladi. To’plamlarga bog’liq bo`lgan 2 ta paradoksni keltiramiz. Bular ingliz matematigi Bertran Artur Uil`yam Rassel (1872 – 1970 yy) va Kantor paradokslari.
Rassel paradoksi. R
barcha to’plamlar to’plami bo’lsin va bu to’plamlar o’z-o’zining elementlari
bo’lmasin, ya`ni ![]() . U holda ixtiyoriy x to’plam
uchun
. U holda ixtiyoriy x to’plam
uchun ![]() . Agar x o’rniga R ni
qo’ysak, u holda
. Agar x o’rniga R ni
qo’ysak, u holda ![]() bajariladi, faqat va faqat
bajariladi, faqat va faqat ![]() da, bu esa ziddiyat.
da, bu esa ziddiyat.
Kantor paradoksi. P(A)
– A to’plamning barcha qism to’plamlari oilasi va ![]() , ya`ni
, ya`ni ![]() bo’lsin. Ammo, boshqa tomondan olib qaraydigan bo’lsak,
ixtiyoriy A to’plam uchun
bo’lsin. Ammo, boshqa tomondan olib qaraydigan bo’lsak,
ixtiyoriy A to’plam uchun ![]() . U holda Kantor – Bernshteyn teoremasiga ko’ra
. U holda Kantor – Bernshteyn teoremasiga ko’ra ![]() bo’lishi kerak. Bu esa ixtiyoriy
bo’sh bo’lmagan A to’plamning barcha qism to’plamlari to’plamining
quvvati A to’plamni o’zining quvvatidan katta bo’ladi, teoremaga
zid.
bo’lishi kerak. Bu esa ixtiyoriy
bo’sh bo’lmagan A to’plamning barcha qism to’plamlari to’plamining
quvvati A to’plamni o’zining quvvatidan katta bo’ladi, teoremaga
zid.
1.4. To’plamlar nazariyasining aksiomatik tizimi 93
Ma`lumki, barcha aksiomatik nazariyalarda avvalo asosiy tushunchalar ta`rifsiz tanlab olinadi va undan keyin bu tushunchalar uchun aksiomalar tuziladi.
To’plamlar nazariyasining asosiy tushunchasi to’plamning o’zidir. To’plam biror ob`yektlarni saralab olish bilan tuziladi, bu ob`yektlar ixtiyoriy tabiatli bo’lishi mumkin. Paradokslarga duch kelmaslik maqsadida to’plamning elementlari tushunchasini birmuncha aniqlashtirish va ba`zi cheklovlar qo’yish mumkin. Masalan, ob`yektlar majmuasini 2 xil turga ajratish mumkin:
1) sinflar;
2) to’plamlar, ya`ni boshqa bir sinfning elementi bo’lgan sinflarlar.
To’plamlar mantiqiy nuqtay nazardan qadam ba qadam quriladi, masalan, “oldin” munosabati qadamni tartiblaydi. Har bir to’plam ma`lum qadamdan keyin quriladi va keyingina foydalanish mumkin bo’ladi.
Bunday tizim nemis matematigi Ernst Fridrix Ferdinand Sermelo (1871-1953 yy) tomonidan 1908 yilda ishlab chiqildi va isroillik matematik Abraxam Adol`f Frenkel (1891-1965 yy) tomonidan kengaytirildi. Hozirda Sermelo – Frenkel aksiomatik tizimi (ZF) deb yuritiladi.
ZF tizimi quyidagi aksiomalardan iborat:
10. Hajm
aksiomasi: To’plam
o’zining elementlari bilan to’liq aniqlanadi. Ikkita to’plam teng deyiladi,
faqat va faqat ular bir xil elementlardan tashkil topgan bo’lsa: ![]()
94 Bob I. To’plamlar nazariyasi
20.
Birlashma (yig’indi) aksiomasi: Har qanday A to’plamning barcha elementlari
birlashmasi yana to’plam bo’ladi, ya`ni ixtiyoriy A to’plam uchun A
to’plam elementlaridan tuzilgan ![]() to’plam mavjud. Agar
to’plam mavjud. Agar ![]() , u holda
, u holda ![]() .
.
30. Daraja
(barcha qism to’plamlar to’plami) aksiomasi: Ixtiyoriy A to’plamning barcha qism
to’plamlari jamlanmasi yana to’plam hosil qiladi. ![]() , u holda
, u holda ![]() .
.
40. O’rniga
qo’yish (almashtirish) aksiomasi: A
da aniqlangan har bir A to’plam va f funktsiya uchun ![]() bo’lganda
bo’lganda ![]() ob`yektlarni saqlovchi to’plam mavjud:
ob`yektlarni saqlovchi to’plam mavjud: ![]() .
.
50. Regulyarlik aksiomasi: agar A to’plamdagi har bir to’plam minimal elementga ega bo’lsa, u holda A to’plamga regulyar to’plam deyiladi.
Har qanday bo’sh
bo’lmagan A to’plam ![]() bo’lgan
bo’lgan ![]() elementga ega va bu element minimaldir.
elementga ega va bu element minimaldir.
Bu aksiomani boshqacha
talqin qilish ham mumkin: Cheksiz kamayuvchi to’plamlar ketma-ketligi ![]() mavjud emas.
mavjud emas.
60. Cheksizlik aksiomasi:
Hech
bo‘lmaganda bitta cheksiz to‘plam natural sonlar qatori mavjud, ya`ni ![]() , bunda
, bunda ![]()
70. Ajratish aksiomasi: ixtiyoriy ![]() da F(x) tasdiq yo rost, yoki yolg’on bo’lgan
ixtiyoriy A to’plam va F xossa berilgan bo’lsin. U holda A
to’plamning F rost bo’lgan elementlaridan tashkil topgan
da F(x) tasdiq yo rost, yoki yolg’on bo’lgan
ixtiyoriy A to’plam va F xossa berilgan bo’lsin. U holda A
to’plamning F rost bo’lgan elementlaridan tashkil topgan ![]() to’plam mavjud.
to’plam mavjud.
1.4. To’plamlar nazariyasining aksiomatik tizimi 95
Aksioma nomlanishi shuni bildiradiki,
biz A to’plamning barcha elementlari orasidan F(x) ni
qanoatlantiruvchi ![]() elementlarni ajratyapmiz.
elementlarni ajratyapmiz.
Ba`zan ajratish aksiomasi o’rniga aksiomalar tizimiga quyidagi ikkita aksioma qo’shiladi:
1. Bo’sh to’plamning mavjudligi
aksiomasi ![]() .
.
2. To’plamlar juftligining mavjudligi
aksiomasi: agar ![]() va
va ![]() , u holda
, u holda ![]()
Ushbu ikkita aksiomani keltirilgan 7
ta aksiomadan oson keltirib chiqarish mumkin. Masalan, ![]() Cheksizlik aksiomasiga asosan biror
bir A to’plam berilgan bo’lsin. U holda
Cheksizlik aksiomasiga asosan biror
bir A to’plam berilgan bo’lsin. U holda ![]() va ajratish aksiomasiga ko’ra
va ajratish aksiomasiga ko’ra ![]()
To’plamlar nazariyasining aksiomalar tizimi to’liq bo’lishi, ya`ni barcha ma`lum matematik mulohazalarni qamrab olishi uchun ZF aksiomalar tizimiga bir-biriga raqib bo’lgan ikkita aksiomadan birini kiritish zarur. Bular AC (axiom of choice) tanlash aksiomasi va AD (axiom of determinateness) ixchamlash aksiomasidir. Tanlash aksiomasi qo’shilgan ZF aksiomalar tizimiga ZFC aksiomalar tizimi deyiladi.
Tanlash aksiomasi 1904 yilda Sermelo tomonidan taklif qilingan.
Aytaylik, har bir ![]() uchun
uchun ![]() to’plam berilgan bo’lsin.
to’plam berilgan bo’lsin. ![]() to’plamdan qandaydir
to’plamdan qandaydir ![]() elementni tanlab, barcha
elementni tanlab, barcha ![]() uchun
uchun
![]() funktsiyani hosil qilamiz, bunda
funktsiyani hosil qilamiz, bunda ![]() bo’ladi. Bu tanlash funktsiyasi
deyiladi.
bo’ladi. Bu tanlash funktsiyasi
deyiladi.
96 Bob I. To’plamlar nazariyasi
Tanlash aksiomasi. Bo’sh bo’lmagan har qanday to’plamlar
oilasi ![]() uchun tanlash funktsiyasi mavjud,
ya`ni
uchun tanlash funktsiyasi mavjud,
ya`ni ![]() , bunda
, bunda ![]() .
.
Ixchamlash aksiomasini 1962 yilda Miychelskiy va Gyugo Dionisiy Shteyngauz (1887-1972 yy)lar taklif qilishgan.
Ixchamlash aksiomasi. Har qanday ![]() to’plam ixchamlangan bo’ladi.
to’plam ixchamlangan bo’ladi.
Bu yerda I to’plam Ber fazosi (natural sonlarning barcha cheksiz ketma-ketliklari to’plami) deyiladi. Rene Lui Ber (1874-1932 yy) frantsiz matemati.
Nazorat uchun savollar:
1. Paradoks nima?
2. Rassel paradoksini tushuntiring.
3. Kantor paradoksini ayting.
4. Hajm aksiomasi qanday ta’riflanadi?
5. Birlashma (yig’indi) aksiomasini keltiring.
6. Daraja (barcha qism to’plamlar to’plami) aksiomasi.
7. O’rniga qo’yish (almashtirish) aksiomasini ayting.
8. Regulyarlik aksiomasi qanday ta’riflanadi?
9. Cheksizlik aksiomasini keltiring.
10. Ajratish aksiomasini keltiring.
11. To’plamlar nazariyasining aksiomatik tizimi asoschilarini ayting.
II BOB.
KOMBINATORIKA
KIRISh
Kombinatorika – diskret matematikaning bir bo‘limi bo‘lib, u ehtimollar nazariyasi, matematik mantiq, sonlar nazariyasi, hisoblash texnikasi va kibernetika sohalarida qo‘llanilgani uchun muhim ahamiyatga ega.
Insoniyat o`z faoliyati davomida ko‘p marotaba ayrim predmetlarni barcha joylashtirish usullari sonini sanab chiqish yoki biror bir harakatni amalga oshirishdagi barcha mavjud usullarni aniqlash kabi masalalarga duch keladi.
1) 26 kishini kassada navbatga necha xil usulda joylashtirish mumkin?
2) Xokkey bo‘yicha olimpiya birinchiligida necha xil usulda oltin, kumush va bronza medallarini taqsimlash mumkin.
Bunday tipdagi masalalarga kombinatorika masalalari deyiladi.
98 Bob II. Kombinatorika
2.1. Kombinatorikaning asosiy masalalari.
Kombinatorika masalalari oson degan tushuncha hozirgi kunda eskirdi. Kombinatorika masalalari soni va turi tez sur`atlarda o`smoqda. Ko`pgina amaliy masalalar bevosita yoki bilvosita kombinatorika masalalariga keltirilib yechiladi.
Hozirgi kunda kombinatorika usullaridan foydalanib yechiladigan zamonaviy masalalarga quyidagi 5 turdagi masalalar kiradi:
1. Joylashtirish masalalari – tekislikda predmetlarni joy-joyiga qo`yish;
2. To`ldirish va qamrab olish masalalari – masalan, berilgan fazoviy shakllarni berilgan shakl va o`lchamdagi eng kam sonli jismlar bilan to`ldirish haqidagi masala;
3. Marshrutlar haqidagi masala – mukammal reja masalasi, masalan, eng qisqa yo`lni topish masalasi;
4. Graflar nazariyasining kombinatorik masalalari – tarmoqlarni rejalashtirish masalasi: transport yoki elektr tarmoqlari masalalari, grafni bo`yash haqidagi masala;
5. Ro`yhatga olish masalasi – biror qoidani kuzatish uchun berilgan elementlar naborini tashkil etuvchi predmetlar sonini topish masalari kabi.
Kombinatorika masalalarini yechishda diskret to`plam tadqiq qilinadi, ya`ni bu to`plam alohida ajratilgan elementlardan tashkil topgan deb
2.2. Guruhlash, joylashtirish va o’rin almashtirishlar 99
qaraladi. Ko`p hollarda bu top`lamlar chekli bo`ladi, lekin elementlar soni cheksiz bo`lgan to`plamlar inkor qilinmaydi.
2.2. Guruhlash, joylashtirish va o‘rin almashtirishlar.
Kombinatorika masalalarini yechish asosiy ikki turga bo`linadi:
a) qism to`plamlarni tanlashga ko`ra;
b) elementlar tartibiga ko`ra.
Qism to`plamlarni tanlash usuli tanlanma tushunchasi bilan bog`liq.
Ta`rif 1. ![]() elementli
elementli ![]() to`plamdan
to`plamdan ![]() elementli qism to`plam ajratib olish
elementli qism to`plam ajratib olish ![]() tanlanma deyiladi, bunda
tanlanma deyiladi, bunda ![]() - tanlanma hajmi deyiladi.
- tanlanma hajmi deyiladi.
Ajratilgan qism to‘plamning har bir elementi bilan 1 dan n gacha bo`lgan sonlar o`rtasida bir qiymatli moslik o`rnatilgan bo‘lsa, to‘plam tartiblangan tanlanma, aksincha tartiblanmagan deyiladi.
Agar to‘plam elementlaridan biror bir ro‘yxat tuzib, keyin har bir elementga ro‘yxatda turgan joy raqami mos qo‘yilsa, har qanday chekli to‘plamni tartiblash mumkin. Bundan ko`rinadiki, bittadan ortiq elementi bo`lgan to‘plamni bir nechta usul bilan tartiblash mumkin. Agar tartiblangan to`plamlar elementlari bilan farq qilsa, yoki ularning tartibi bilan farq qilsa, ular turlicha deb hisoblanadi.
Ta`rif 2. Agar tanlangan qism to`plamda
elementlar tartibi ahamiyatsiz bo`lsa, u holda tanlanmalarga ![]() guruhlash deyiladi va
guruhlash deyiladi va
100 Bob II. Kombinatorika
![]() ko`rinishida belgilanadi. C –
inglizcha “combination”, ya`ni “guruhlash” so`zining bosh harfidan
olingan.
ko`rinishida belgilanadi. C –
inglizcha “combination”, ya`ni “guruhlash” so`zining bosh harfidan
olingan.
Tanlanmalarda elementlar takrorlanishi va takrorlanmasligi mumkin.
Ta`rif 3. Elementlari takrorlanuvchi
tartiblanmagan ![]() tanlanmaga
tanlanmaga ![]() elementdan
elementdan ![]() tadan takrorlanuvchi guruhlash deyiladi
va
tadan takrorlanuvchi guruhlash deyiladi
va ![]() ko`rinishida belgilanadi.
ko`rinishida belgilanadi.
Ta`rif 4. Elementlari takrorlanuvchi
tartiblangan ![]() tanlanma
tanlanma ![]() elementdan
elementdan ![]() tadan takrorlanuvchi joylashtirish
deyiladi va
tadan takrorlanuvchi joylashtirish
deyiladi va ![]() kabi belgilanadi. A inglizcha “arrangement”
– “tartibga keltirish” so`zining bosh harfidan olingan.
kabi belgilanadi. A inglizcha “arrangement”
– “tartibga keltirish” so`zining bosh harfidan olingan.
Ta`rif 5. Agar tartiblangan tanlanmalarda
elementlar o`zaro turlicha bo`lsa, u holda takrorlanmaydigan joylashtirish
deyiladi va ![]() kabi belgilanadi.
kabi belgilanadi.
Ta`rif 6. ![]() tadan
tadan ![]() ta tartiblangan tanlanmaga o`rin almashtirish deyiladi
va
ta tartiblangan tanlanmaga o`rin almashtirish deyiladi
va ![]() kabi belgilanadi. O`rin almashtirish
joylashtirishning xususiy xoli hisoblanadi.
kabi belgilanadi. O`rin almashtirish
joylashtirishning xususiy xoli hisoblanadi.
P inglizcha “permutation” – “o`rin almashtirish” so`zining bosh harfidan olingan.
Misol. ![]() to`plamning 3 ta elementdan 2 tadan barcha tartiblangan va
tartiblanmagan, takrorlanuvchi va takrorlanmaydigan tanlanmalarini ko`rsating.
to`plamning 3 ta elementdan 2 tadan barcha tartiblangan va
tartiblanmagan, takrorlanuvchi va takrorlanmaydigan tanlanmalarini ko`rsating.
2.2. Guruhlash, joylashtirish va o’rin almashtirishlar 101
1) ![]() =6 ta takrorlanmaydigan joylashtirish;
=6 ta takrorlanmaydigan joylashtirish;
2) ![]() ta takrorlanadigan joylashtirish;
ta takrorlanadigan joylashtirish;
3) ![]() ta takrorlanmaydigan guruhlash;
ta takrorlanmaydigan guruhlash;
4) ![]() ta takrorlanuvchi guruhlashlar
mavjud.
ta takrorlanuvchi guruhlashlar
mavjud.
Nazorat uchun savollar:
1. Kombinatorika usullaridan foydalanib yechiladigan zamonaviy
masalalarga qanday masalalar kiradi?
2. Kombinatorika masalalarini yechish asosan nechta turga bo`linadi
va ular nimalardan iborat?
3. Tanlanma deb nimaga aytiladi?
4. Tartiblangan to‘plam deb nimaga aytiladi?
5. Tartiblangan va tartiblanmagan to’plamlarning farqi nimada?
6. O’rin almashtirish ta’rifini ayting.
7. Joylashtirish deb nimaga aytiladi?
8. Guruhlashga ta’rif bering.
102 Bob II. Kombinatorika
Mustaqil yechish uchun masalalar:
1. {4, 5, 6} to`plamning 3 ta elementidan 2 tadan barcha tartiblangan va tartiblanmagan, takrorlanuvchi va takrorlanmaydigan tanlanmalarini tuzing.
2. {0, 1, 2, 3) to`plamning 4 ta elementdan 2 tadan barcha tartiblangan va tartiblanmagan tanlanmalarini ko`rsating.
3. (2, 3, 4, 5) to`plamning 4 ta elementdan 3 tadan barcha takrorlanuvchi va takrorlanmaydigan tanlanmalarini ko`rsating.
2.3. KOMBINATORIKANING ASOSIY QOIDALARI
Kombinatorikaning asosiy masalalaridan yana biri, bu turli shartlarga ko`ra chekli to’plamda elementlar sonini aniqlash masalasidir.
Oson ko’ringan to’plam quvvatini topish masalasiga ko’p hollarda javob berishda taraddudlanib qolamiz. Biz bu savolga I bobning 1.1.10. va 1.3.3. mavzularida to’xtalganmiz. Bu bobda esa to’plam elementlari sonini topish kombinatorikaning ikkita yangi printsipi: yig’indi va ko’paytma qoidalari asosida amalga oshiriladi.
2.3.1.Yig`indi qoidasi.
Ta`rif. Agar ![]() to`plamdan
to`plamdan ![]() qism to`plamni
qism to`plamni ![]() usul bilan tanlash mumkin bo`lsa, undan farqli boshqa
usul bilan tanlash mumkin bo`lsa, undan farqli boshqa ![]() qism to`plamni
qism to`plamni ![]() usulda tanlash
usulda tanlash
2.3. Kombinatorikaning asosiy qoidalari 103
mumkin
bo`lsa va bunda ![]() va
va ![]() larni bir vaqtda tanlash mumkin bo`lmasa, u holda
larni bir vaqtda tanlash mumkin bo`lmasa, u holda ![]() to`plamdan
to`plamdan ![]() tanlanmani
tanlanmani ![]() usulda olish mumkin.
usulda olish mumkin.
Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() va
va ![]() to’plamlar kesishmaydigan to’plamlar deyiladi.
to’plamlar kesishmaydigan to’plamlar deyiladi.
Xususiy
holda, agar barcha ![]() lar uchun
lar uchun ![]() bo’lsa, u holda
bo’lsa, u holda ![]() to’plam
to’plam ![]() to’plamning o’zaro kesishmaydigan qism to’plamlari yoki
oddiygina qilib bo’laklari deyiladi. Demak, yig’indi qoidasida
to’plamning o’zaro kesishmaydigan qism to’plamlari yoki
oddiygina qilib bo’laklari deyiladi. Demak, yig’indi qoidasida ![]() va
va ![]() lar
lar ![]() to’plamning bo’laklaridir.
to’plamning bo’laklaridir.
Misol. 219-12 guruh talabalari 16 nafar yigit va 8 nafar qizlardan iborat bo’lib, ular orasidan bir kishini ajratib olish kerak bo`lsa, ularning soni qo’shiladi va 16+8=24 talaba orasidan tanlab olinadi.
2.3.2. Ko`paytma qoidasi.
Ta`rif.
Agar ![]() to`plamdan
to`plamdan ![]() tanlanmani
tanlanmani ![]() usulda va har bir
usulda va har bir ![]() usulda mos
usulda mos ![]() tanlanmani
tanlanmani ![]() usulda amalgam oshirish mumkin bo`lsa, u holda
usulda amalgam oshirish mumkin bo`lsa, u holda ![]() va
va ![]() tanlanmani ko`rsatilgan tartibda
tanlanmani ko`rsatilgan tartibda ![]() usulda amalga oshirish mumkin.
usulda amalga oshirish mumkin.
To’plamlar nazariyasi nuqtai nazaridan qaraydigan bo’lsak, bu qoida to’plamlarning Dekart ko’paytmasi tushunchasiga mos keladi.
104 Bob II. Kombinatorika
Misol. “Zukhrotravel” turistik kompaniyasi “Xiva – Chirchiq” yo`nalishida sayohat uyushtirmoqchi bo`lsa, necha xil usulda sayohat smetasini ishlab chiqish mumkin.
Xivadan Chirchiqqa to`g`ridan to`g`ri jamoat transporti yo`q, shuning uchun “Xiva – Toshkent – Chirchiq” yo‘nalishi bo‘yicha harakatlanishga to`g`ri keladi.
Xivadan Toshkentga samolyo’t, avtobus yoki poyezdda yetib borish mumkin, demak, 3 xil usuldan birini tanlash mumkin;
Toshkentdan Chirchiqqa esa avtobus yoki poyezdda borish mumkin, ya`ni 2 xil tanlanma mavjud.
“Xiva – Chirchiq” sayohatini ![]() xil usulda tashkil qilish mumkin.
xil usulda tashkil qilish mumkin.
2.3.3. Ko`paytma qoidasini umumlashtirish.
Ta`rif. Aytaylik birin-ketin ![]() ta harakatni amalga oshirish kerak bo‘lsin. Agar birinchi harakatni
ta harakatni amalga oshirish kerak bo‘lsin. Agar birinchi harakatni ![]() usulda, ikkinchi harakatni
usulda, ikkinchi harakatni ![]() usulda, va hokazo
usulda, va hokazo ![]() - harakatni
- harakatni ![]() usulda amalga oshirish mumkin
bo‘lsa, u holda barcha
usulda amalga oshirish mumkin
bo‘lsa, u holda barcha ![]() ta harakat
ta harakat ![]() usulda amalga oshiriladi.
usulda amalga oshiriladi.
Misol 1. Ikkinchi bosqich talabalari III semestrda 12 ta fanni o`rganishadi. Seshanba kuniga 3 ta turli fanni nechta usulda dars jadvaliga joylash mumkin?
2.3. Kombinatorikaning asosiy qoidalari 105
Bu misolda 12 ta fanni takrorlamasdan
3 tasini joylashtirish kerak. Buning uchun birinchi fanni 12 usulda, ikkinchi
fanni 11 usulda va uchinchi fanni 10 ta usulda tanlash mumkin. Ko`paytirish
qoidasiga asosan ![]() .
.
Demak, 3 ta turli fanni 1320 usulda joylash mumkin ekan.
Misol 2. Diskret matematika fanidan talabalar o`rtasida bo`ladigan olimpiadaning mamlakat bosqichida 16 nafar talaba qatnashmoqda. Necha xil usulda I, II va III o`rinlar taqsimlanishi mumkin?
Yechilishi: I o`rinni 16 talabadan biri egallashi mumkin. I o`rin sohibi aniqlangandan keyin, II o`rinni qolgan 15 talabadan biri egallaydi va nihoyat III o`rin qolgan 14 talabadan biriga nasib qiladi. Demak I, II va III o`rin g`oliblarini ![]() xil usulda aniqlash mumkin.
xil usulda aniqlash mumkin.
Misol 3. 5 soniga bo`linadigan 4 xonali sonlar nechta?
Yechilishi: Masalada
takrorlanuvchi joylashtirish haqida so`z bormoqda. Birinchi xonaga ![]() to`plamning 10 ta elementidan bittasini
tanlash mumkin, lekin 0 ni birinchi xonaga qo`yish mumkin emas, aks holda son 3
xonali bo`lib qoladi. Bo`linish belgisiga ko`ra son 5 ga bo`linishi uchun 0
yoki 5 bilan tugashi kerak.
to`plamning 10 ta elementidan bittasini
tanlash mumkin, lekin 0 ni birinchi xonaga qo`yish mumkin emas, aks holda son 3
xonali bo`lib qoladi. Bo`linish belgisiga ko`ra son 5 ga bo`linishi uchun 0
yoki 5 bilan tugashi kerak.
Demak, 1- xona raqami uchun 9 ta tanlash mavjud;
2- va 3- xona raqamlari uchun esa 10 ta tanlash usuli bor;
4- xona, ya`ni oxirgi raqam uchun 0 yoki 5 raqamlari bo`lib, 2 ta tanlash mavjud. U holda ko`paytirish qoidasidan
106 Bob II. Kombinatorika
foydalansak, ![]() ta 5 ga bo`linadigan 4 xonali son
borligini aniqlaymiz.
ta 5 ga bo`linadigan 4 xonali son
borligini aniqlaymiz.
Agar biror m murakkab son berilgan bo’lsa, uning bo‘luvchilar sonini topish uchun oldin tub sonlar ko’paytmasi shakliga keltiriladi:
![]()
bunda p1, p2,...., pn
– tub sonlar, ![]() daraja ko’rsatkichlari bo’lib, m
murakkab sonning bo‘luvchilari soni
daraja ko’rsatkichlari bo’lib, m
murakkab sonning bo‘luvchilari soni
![]()
ga teng bo’ladi.
Misol. 48
sonining bo’luvchilari sonini topish uchun ![]() ni topamiz.
ni topamiz.
U holda 48 ning bo‘luvchilari soni ![]() ekanligi topiladi.
ekanligi topiladi.
Nazorat uchun savollar:
1. Kombinatorikaning 1-qoidasini keltiring.
2. Kombinatorikaning 2-qoidasini keltiring.
3. Ko’paytmaning umumlashgan qoidasini ayting.
4. Tub va murakkab son deb nimaga aytiladi?
5. Berilgan sonning bo‘luvchilari soni qanday topiladi?
2.3. Kombinatorikaning asosiy qoidalari 107
Mustaqil yechish uchun masalalar:
1. Qandolat do’konida kun oxiriga kelib bir nechta pishiriq qoldi: 4 ta vaflili, 3 ta shakoladli va 1 ta mevali. Xaridor pishiriqni nechta usulda tanlashi mumkin?
2. Musobaqada qatnashish uchun universitetning 8 nafar yigit, 6 nafar qizdan iborat tennis komandasidan juftlik nechta usulda ajratiladi?
3. Yengil avtomobillarning davlat belgisi 3 ta raqam va o’zbek alifbosining 3 ta harfidan iborat. Raqam va harflar ixtiyoriy ketma-ketlikda bo’lishi mumkin deb hisoblasak, DAN idorasi nechta turli xil avtomobil raqamini berishi mumkin?
4. Quyida berilgan sonlarning nechta turli bo‘luvchilari bor?
a) 635016; b) 2474; c) 17645; d) 30599;
e) 2520; f) 5480; g) 12600; k) 12600;
108 Bob II. Kombinatorika
2.4. O‘RIN ALMASHTIRISH, JOYLASHTIRISH va
GURUHLASHLARNI HISOBLASH FORMULALARI
2.4.1.Takrorlanmaydigan joylashtirishlar
Avvalo barcha mumkin bo`lgan ![]() joylashtirishlarni topib olamiz. Bu
masalani yechish uchun ko`paytma qoidasidan foydalanamiz.
joylashtirishlarni topib olamiz. Bu
masalani yechish uchun ko`paytma qoidasidan foydalanamiz.
![]() ta elementi bo`lgan
ta elementi bo`lgan ![]() to‘plamda birinchi elementni tanlash uchun
to‘plamda birinchi elementni tanlash uchun ![]() ta imkoniyat bor, ikkinchi elementni
tanlash uchun esa
ta imkoniyat bor, ikkinchi elementni
tanlash uchun esa ![]() ta imkoniyat qoladi. Joylashtirish
takrorlanmaydigan bo`lgani uchun tanlab olingan element keyingi tanlanmalarda
ishtirok etmaydi. Shuning uchun
ta imkoniyat qoladi. Joylashtirish
takrorlanmaydigan bo`lgani uchun tanlab olingan element keyingi tanlanmalarda
ishtirok etmaydi. Shuning uchun ![]() - elementni tanlash uchun
- elementni tanlash uchun ![]() imkoniyat qoladi. U holda barcha takrorlanmaydigan
joylashtirishlar soni:
imkoniyat qoladi. U holda barcha takrorlanmaydigan
joylashtirishlar soni:
![]()
ga teng bo`ladi.
Bu formulani boshqacha ko`rinishda yozish mumkin:
![]()

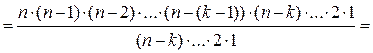

2.4. O’rin almashtirish, joylashtirish va guruhlashlar 109
Bu yerda “!” belgisi faktorial deb o`qiladi.
1 dan ![]() gacha bo`lgan barcha natural sonlar
ko`paytmasi
gacha bo`lgan barcha natural sonlar
ko`paytmasi ![]() ga teng.
ga teng.
Faktorialni hisoblashda 0!=1 va 1!=1 deb qabul qilingan.
Teorema. ![]() elementga ega bo`lgan
elementga ega bo`lgan ![]() to`plamning
to`plamning ![]() elementli tartiblangan takrorlanmaydigan qism to`plamlari
soni
elementli tartiblangan takrorlanmaydigan qism to`plamlari
soni
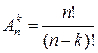
ga teng.
Misol 1. 7 kishidan iborat nazorat guruhini 4 nafar a`zosi bo`lgan nechta kichik guruhlarga ajratish mumkin?
Izlanayotgan usullar soni 7 ta elementdan 4 tadan joylashtirishlar soniga teng, ya`ni

Misol 2. Talaba 3 ta imtixonni bir hafta davomida topshirishi kerak. Bu harakatni necha xil usulda amalga oshirish mumkin?
Javob: ![]()
Shu o‘rinda eslatib o‘tamiz, tadqiqotlarda joylashtirishlar sonini hisoblashga to‘g‘ri kelsa, unda Excel dasturlar paketidagi ÏÅÐÅÑÒ komandasidan foydalanish mumkin,
110 Bob II. Kombinatorika
masalan ![]() =859541760 ni hisoblang:
=859541760 ni hisoblang:
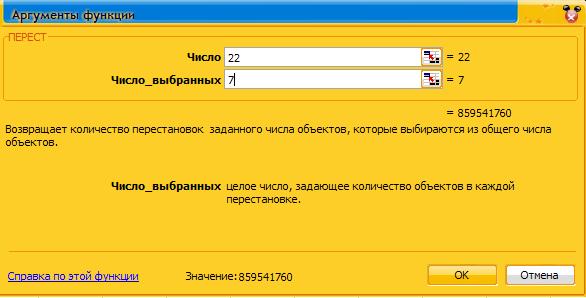
2.4.2.Berilgan to‘plamning o‘rin almashtirishlari soni.
Avval aytganimizdek,
o`rin almashtirish joylashtirishning xususiy xolidan iborat, shuning uchun ham
o`rin almashtirishni ![]() ta elementdan
ta elementdan ![]() dan joylashtirish deb qarash mumkin:
dan joylashtirish deb qarash mumkin:

Bu son n elementli qism to’plamni tartiblash usullari soniga teng bo’ladi.
Misol 1. 2.1. paragrafdagi 26 kishini kassada navbatga necha xil usulda
joylashtirish mumkin
degan savolga endi javob berish mumkin: ![]()
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 111
Misol 2. Uchta elementdan iborat A={a, b, c} to‘plamning elementlaridan tuzilgan o‘rin almashtirishlar soni 6 ga teng:
(a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a).
Teorema. ![]() elementga ega bo`lgan
elementga ega bo`lgan ![]() to`plamning barcha o`rin
almashtirishlari soni
to`plamning barcha o`rin
almashtirishlari soni ![]() ga teng.
ga teng.
Misol 3. Javonga 5 ta kitobni necha xil usulda joylashtirish mumkin.
![]()
Tadqiqotlarda o‘rin almashtirishlarni hisoblashga to‘g‘ri kelsa, unda Excel dasturlar paketidagi ÔÀÊÒÐ komandasidan foydalanish mumkin, masalan 10! ni hisoblash uchun quyidagicha ish tutiladi:

112 Bob II. Kombinatorika
Misol 4. {1, 2, 3, ... , 2n} to‘plam elementlarini juft sonlari juft o‘rinlarda keladigan qilib necha xil usulda tartiblashtirish mumkin?
Yechilishi:
Juft sonlarni juft nomerli o‘rinlarga (bunday joylar n ta) n! ta usulda qo‘yib chiqish mumkin, bu usullarning har biriga toq sonlarni toq nomerli o‘rinlarga n! ta usulda qo‘yib chiqish mos keladi. Shuning uchun ham ko‘paytirish qoidasiga ko‘ra barcha o‘rniga qo‘yishlar soni
![]()
ga teng bo‘ladi.
Misol 5. n ta elementdan berilgan ikkita elementi yonma-yon turmaydigan nechta o‘rin almashtirish bajarish mumkin.
Yechilishi:
a va b elementlar berilgan bo‘lsin. Bu elementlar yonma-yon turgan o‘rin almashtirishlar sonini aniqlaymiz.
Birinchi hol a element b elementdan oldin kelishi mumkin, bunda a birinchi o‘rinda, ikkinchi o‘rinda, va hokazo (n-1)- o‘rinda turishi mumkin.
Ikkinchi hol b element a
elementdan oldin kelishi mumkin, bunday holatlar ham (n-1) ta
bo‘ladi. Shunday qilib, a va b elementlar
yonma-yon keladigan holatlar soni ![]() ta bo‘ladi. Bu usullarning har
biriga qolgan (n-2) ta elementning (n-2)! ta o‘rin almashtirishi
mos keladi. Demak, a va b elementlar yonma - yon keladigan barcha
o‘rin
ta bo‘ladi. Bu usullarning har
biriga qolgan (n-2) ta elementning (n-2)! ta o‘rin almashtirishi
mos keladi. Demak, a va b elementlar yonma - yon keladigan barcha
o‘rin
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 113
almashtirishlar soni ![]() ta bo‘ladi. Shuning uchun ham yonma-yon
turmaydigan o‘rin almashtirishlar soni
ta bo‘ladi. Shuning uchun ham yonma-yon
turmaydigan o‘rin almashtirishlar soni
![]()
ga teng bo`ladi.
Nazorat uchun savollar:
1. Biror bir natural sonning bo‘luvchilari soni qanday topiladi?
2. O’rin almashtirish deganda nimani tushunasiz?
3. O‘rin almashtirishni Excel dasturlar paketidan foydalanib hisoblash qanday amalga oshiriladi?
Mustaqil yechish uchun masalalar:
1. Ifodaning qiymatini toping:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() d)
d) ![]()
2. Kasrni qisqartiring:
a) 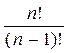 ; b)
; b) ![]() ; c)
; c) 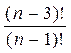 d)
d) ![]() ,
, ![]()
3. 36 ta karta aralashtirilganda necha xil variant mavjud?
4. Stipendiya uchun 5 ta sardor kassaga necha xil usulda navbatga
turishlari mumkin?
114 Bob II. Kombinatorika
2.4.3.Takrorlanuvchi joylashtirishlar.
![]() ta elementi bo`lgan
ta elementi bo`lgan ![]() to‘plamda birinchi elementni tanlash uchun
to‘plamda birinchi elementni tanlash uchun ![]() ta imkoniyat bor, joylashtirish
takrorlanuvchi bo`lgani uchun qolgan ixtiyoriy element uchun ham
ta imkoniyat bor, joylashtirish
takrorlanuvchi bo`lgani uchun qolgan ixtiyoriy element uchun ham ![]() ta imkoniyat qoladi. Ko`paytirish
qoidasiga ko`ra barcha takrorlanadigan joylashtirishlar soni quyidagiga teng
bo`ladi:
ta imkoniyat qoladi. Ko`paytirish
qoidasiga ko`ra barcha takrorlanadigan joylashtirishlar soni quyidagiga teng
bo`ladi:
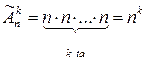
2.4.4. Takrorlanmaydigan guruhlashlar.
Bizga tartiblanmagan
takrorlanmaydigan ![]() ta elementi bo`lgan
ta elementi bo`lgan ![]() to‘plam berilgan bo`lsin.
to‘plam berilgan bo`lsin. ![]() bilan
bilan ![]() ni taqqoslaymiz. Bilamizki,
ni taqqoslaymiz. Bilamizki,
![]() ta elementni
ta elementni ![]() ta usulda tartiblash mumkin, ya` ni
ta usulda tartiblash mumkin, ya` ni
![]()
bo`ladi.
Bundan 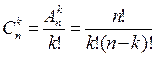
kelib chiqadi.
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 115
Misol 1. Har uchtasi bir to’g’ri chiziqda yotmagan n ta nuqta berilgan. Nuqtalarni ikkitalab tutashtirish natijasida nechta kesma o’tkazish mumkin?
Yechilishi: masala shartiga ko’ra chizmada qavariq n burchak hosil bo’ladi. U holda 1-nuqta (n-1) ta nuqta bilan, 2-nuqta (n-2) ta nuqta bilan va h.k., (n-1) – nuqta 1 ta nuqta bilan tutashtiriladi/ Bunda hosil bo’lgan to’g’ri chiziqlar soni
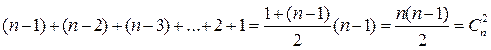
ga teng bo’ladi.
Misol 2. Restoranida 7 ta asosiy taomdan 3 tasini tanlash imkoniyati berilsa, nechta usulda buyurtma qilish mumkin?
Yechilishi: Bu misolda takrorlanmaydigan 7 ta elementdan 3 tadan guruhlashni topish kerak:
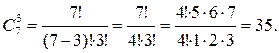
Misol 3. Sportloto lotareya o’yinida 36 ta natural sondan 6 tasini topgan kishi asosiy yutuqqa ega bo’ladi. Asosiy yutuqni olish imkoniyati qanday?
Yechilishi: Yutuq raqamlar oltitaligi 36 tadan 6 ta takrorlanmaydigan guruhlashga teng:
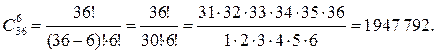
Misolning javobidan ko’rinadiki, asosiy yutiqni olish imkoniyati judayam kam, ya’ni 1 947 792 tadan 1 taga teng.
116 Bob II. Kombinatorika
5, 4, va 3 ta raqamni topgan
kishilarga ham yutuq beriladi, lekin bu yutuq shi kishilar o’rtasida teng taqsimlanadi.
Bu holda 2 xil guruhlash mavjud, biri ![]() omadli tanlov va ikkinchisi
omadli tanlov va ikkinchisi ![]() omadsiz tanlov. U holda 3 ta raqamni
topgan yutuq egalari imkoniyati:
omadsiz tanlov. U holda 3 ta raqamni
topgan yutuq egalari imkoniyati:
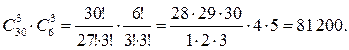
Yutuqli bo’lish ehtimoli 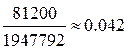 ga teng.
ga teng.
Teorema 1. ![]() ta elementi bo`lgan
ta elementi bo`lgan ![]() to‘plamning barcha tartiblanmagan
to‘plamning barcha tartiblanmagan ![]() elementli qism to‘plamlari soni
elementli qism to‘plamlari soni
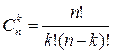
ga teng.
Ushbu teoremani umumlashtiramiz:
![]() ta elementi bo`lgan
ta elementi bo`lgan ![]() to‘plamni
to‘plamni ![]() ta qism to‘plamlar yig‘indisi
ko‘rinishida necha xil usulda yoyish mumkin degan savolni qo‘yamiz. Buning uchun S to`plamni
ta qism to‘plamlar yig‘indisi
ko‘rinishida necha xil usulda yoyish mumkin degan savolni qo‘yamiz. Buning uchun S to`plamni ![]() o`zaro kesishmaydigan
o`zaro kesishmaydigan ![]() ta qism to‘plamlarga ajratish mumkin bo`lsin. Bunda
ularning elementlari soni mos ravishda
ta qism to‘plamlarga ajratish mumkin bo`lsin. Bunda
ularning elementlari soni mos ravishda
N(A1)=k1 , N(A2)=k2 , ... , N(Am)=km
bo‘lib, k1, k2 ,..., km berilgan sonlar uchun
![]()
shartlar bajariladi. ![]() to‘plamlar
umumiy elementga ega emas.
to‘plamlar
umumiy elementga ega emas.
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 117
![]() to‘plamning k1
elementli A1 qism to‘plamini
to‘plamning k1
elementli A1 qism to‘plamini ![]() usulda tanlash mumkin, qolgan n-k1 element ichidan k2 elementli A2 qism to‘plamini
usulda tanlash mumkin, qolgan n-k1 element ichidan k2 elementli A2 qism to‘plamini ![]() usulda tanlash mumkin va hokazo.
Turli xil
usulda tanlash mumkin va hokazo.
Turli xil ![]() qism to‘plamlarni tanlash usullari
ko‘paytirish qoidasiga ko‘ra
qism to‘plamlarni tanlash usullari
ko‘paytirish qoidasiga ko‘ra
![]()
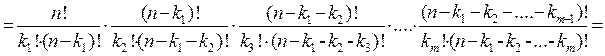
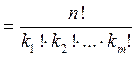
Demak, quyidagi teorema isbotlandi.
Teorema 2. Aytaylik k1, k2
,..., km butun nomanfiy sonlar bo‘lib, ![]() va
va ![]() to‘plam
to‘plam ![]() ta elementdan iborat
bo‘lsin.
ta elementdan iborat
bo‘lsin. ![]() ni elementlari mos ravishda k1,
k2 ,..., km ta bo‘lgan
ni elementlari mos ravishda k1,
k2 ,..., km ta bo‘lgan ![]() m ta qism to‘plamlar yigindisi ko‘rinishida
ifodalash usullari soni
m ta qism to‘plamlar yigindisi ko‘rinishida
ifodalash usullari soni
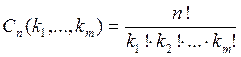
ta bo‘ladi.
![]() sonlarga polinomial koeffitsiyentlar deyiladi.
sonlarga polinomial koeffitsiyentlar deyiladi.
Misol 4. “Baraban” so‘zidagi harflarni qatnashtirib, nechta so‘z (ma`nosi bo`lishi shart emas!) yasash mumkin?
118 Bob II. Kombinatorika
Yechilishi: “b” harfi k1=2 ta,
“a” harfi k2 =3 ta,
“r” harfi k3 =1 ta,
“![]() ” harfi k4=1 ta, jami harflar soni
” harfi k4=1 ta, jami harflar soni ![]() =7 ta, demak,
=7 ta, demak,
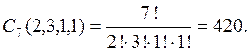
Misol 5. “Lola” so‘zidagi harflardan nechta so‘z yasash mukin?
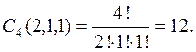
Teorema 2(a). Elementlarining k1 tasi 1- tipda, k2 tasi 2-tipda, va hokazo km tasi m-tipda bo‘lgan n elementli to‘plamning barcha o‘rin almashtirishlar soni
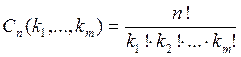
ta bo‘ladi.
Tadqiqotlarda ko‘p miqdordagi takrorlanuvchi o‘rin almashtirishlarni hisoblashga to‘g‘ri kelsa, unda Excel dasturlar paketidagi ÌÓËÜÒÈÍÎÌ komandasidan foydalanish mumkin, masalan
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 119
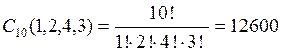
ekanligini tezlik bilan hisoblash hech qanday qiyinchilik tug‘dirmaydi.
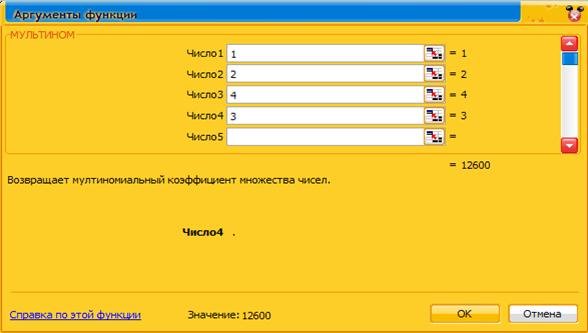
2.4.5. Guruhlashning xossalari
10. ![]()
20. ![]()
30. ![]()
Ushbu xossalarni isbotlash uchun kombinatsiyalarni faktorial ko’rinishida yozib chiqish va hisoblash yetarli.
120 Bob II. Kombinatorika
Teorema. ![]() elementli to‘plamning barcha qism to‘plamari soni
elementli to‘plamning barcha qism to‘plamari soni ![]() ga teng va quyidagi tenglik
o‘rinli:
ga teng va quyidagi tenglik
o‘rinli:
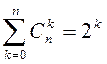 .
.
Haqiqatdan ham, ![]() -
- ![]() elementli to‘plamning barcha
elementli to‘plamning barcha ![]() elementli to‘plam ostilari soni
bo‘lgani uchun, tushunarliki barcha to‘plam ostilar soni
elementli to‘plam ostilari soni
bo‘lgani uchun, tushunarliki barcha to‘plam ostilar soni
![]()
yig‘indiga teng bo‘lib, ularning yig‘indisi ![]() ga teng
bo‘ladi.
ga teng
bo‘ladi.
Misol. 30 ta talabadan 20 tasi o‘g‘il bolalar, tavakkaliga jurnaldagi ro’yhat bo‘yicha 5 talaba chaqirildi, ularning ichida ko‘pi bilan 3 tasi o‘g‘il bola bo‘ladigan qilib necha xil usulda tanlash mumkin?
Yechilishi: Masala shartida berilgan to‘plamni sodda to‘plamlar
yig‘indisi shaklida yozib olamiz:
A={0 tasi o‘g‘il bola, 5 tasi qiz bola}
B={1 tasi o‘g‘il bola, 4 tasi qiz bola }
C={2 tasi o‘g‘il bola, 3 tasi qiz bola }
D={3 tasi o‘g‘il bola, 2 tasi qiz bola }
{Ko‘pi bilan 3 tasi
o‘g‘il bola}=A![]() B
B![]() C
C![]() D kesidhmaydigan
to‘plamlar yig‘indisining quvvati, ushbu to‘plamlar quvvatlari yig‘indisiga
teng bo‘ladi:
D kesidhmaydigan
to‘plamlar yig‘indisining quvvati, ushbu to‘plamlar quvvatlari yig‘indisiga
teng bo‘ladi:
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 121
n({ko‘pi bilan 3 tasi o‘g‘il
bola})=n(A![]() B
B![]() C
C![]() D)=n(A)+n(B)+n(C)+n(D)=
D)=n(A)+n(B)+n(C)+n(D)=
=![]() +
+![]() +
+![]() +
+![]() =
=![]() +
+![]()
![]()
Demak, 30 ta talabadan ko‘pi bilan 3 tasi o‘g‘il bola bo‘ladigan 26.478.900 tanlash usuli mavjud.
Nazorat uchun savollar:
1. Takrorlanadigan joylashtirish deb nimaga aytiladi?
2. Takrorlanmaydigan joylashtirish deb nimaga aytiladi?
3. Takrorlanadigan guruhlash deb nimaga aytiladi?
4. Takrorlanmaydigan guruhlash deb nimaga aytiladi?
5. Faktorial nima?
6. Excel dasturlar paketidagi ÌÓËÜÒÈÍÎÌ komandasidan qachon foydalaniladi?
7. Excel dasturlar paketidagi ÏÅÐÅÑÒ komandasi vazifasi nimadan iborat?
122 Bob II. Kombinatorika
Mustaqil yechish uchun masalalar:
1. Xonada n ta chiroq bor. k ta chiroqni yoqib xonani necha xil usulda yoritish mumkin? Xonani hammasi bo‘lib necha xil usulda yoritish mukin?
2. n ta nuqta berilgan, ularning ixtiyoriy 3 tasi bitta chiziqda yotmaydi. Ixtiyoriy ikkita nuqtani tutashtirib nechta chiziq o‘tqazish mumkin?
3. Har bir keyingi raqami oldingisidan katta bo‘lgan nechta 4 xonali sonni tuzish mumkin?
4. Har bir keyingi raqami oldingisidan kichik bo‘lgan nechta 4 xonali sonni tuzish mumkin?
5. Xalqaro komissiya 9 kishidan iborat. Komissiya materiallari seyfda saqlanadi. Kamida 6 kishi yig‘ilgandagina seyfni ochish imkoni bo‘lishi uchun, seyf nechta qulfdan iborat bo‘lishi kerak va ular uchun nechta kalit tayyorlash kerak va ularni komissiya a’zolari o‘rtasida qanday taqsimlash kerak?
6. Kitob javonida tasodifiy tartibbda 15 ta darslik terilgan bo‘lib, ularning 9 tasi o‘zbek tilida, 6 tasi rus tilida. Tavakkaliga 7 ta darslik olindi. Olingan darsliklarning roppa-rosa 4 tasi o‘zbekcha, 3 tasi ruscha bo‘ladigan qilib necha xil usulda tanlab olish mumkin?
7. ![]() yig‘indi hisoblansin.
yig‘indi hisoblansin.
8. ![]() yig‘indi hisoblansin.
yig‘indi hisoblansin.
9. ![]() tenglik isbotlansin.
tenglik isbotlansin.
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 123
10. Necha xil usulda 5 ta kitobdan 3 tadan qilib tanlab olish mumkin?
11. Necha xil usulda 7 odamdan 3 kishidan qilib komissiya tuzish mumkin?
12. ![]() tenglikni isbotlang.
tenglikni isbotlang.
13. ![]() tenglikni isbotlang.
tenglikni isbotlang.
14. ![]() ayniyatni isbotlang.
ayniyatni isbotlang.
15. ![]() ayniyatni isbotlang.
ayniyatni isbotlang.
16. ![]() tenglikni isbotlang.
tenglikni isbotlang.
17. ![]() tenglikni isbotlang..
tenglikni isbotlang..
18. ![]() tenglikni
isbotlang.
tenglikni
isbotlang.
19. Quyidagi so‘zlarni nechta usulda shifrlash mumkin?
a) BALLI; e) PARABOLA;
b) GIPERBOLA; f) ELLIPS;
c) SIMMETRIK; g) SUMMA;
d) DADA; j) GURUH.
20. Tarkibida Aziz va Go’zal ham bo’lgan 12 nafar kishidan 5 kishilik komissiya tashkil qilinmoqchi. Nechta turlicha komissiya tashkil qilish mumkin? Agar
a) komissiya tarkibiga Aziz ham, Go’zal ham kirgan bo’lsa;
b) komissiya tarkibiga Aziz ham, Go’zal ham kirmagan bo’lsa;
v) komissiya tarkibiga yoki Aziz, yoki Go’zal kirgan bo’lsa.
124 Bob II. Kombinatorika
2.4.6.Takrorlanuvchi guruhlashlar.
Ta’rif. ![]() ta elementli
to‘plamning barcha tartiblanmagan
takrorlanuvchi
ta elementli
to‘plamning barcha tartiblanmagan
takrorlanuvchi ![]() ta elementli qism to‘plamlarini ajratish takrorlanuvchi guruhlash deyiladi.
ta elementli qism to‘plamlarini ajratish takrorlanuvchi guruhlash deyiladi.
![]() to`plamning elementlari 1;2;…;
to`plamning elementlari 1;2;…;![]() sonlari bilan raqamlangan bo`lsin.
sonlari bilan raqamlangan bo`lsin. ![]() to`plam chekli yoki sanoqli bo`lgani
uchun, har doim
to`plam chekli yoki sanoqli bo`lgani
uchun, har doim ![]() to`plam elementlari va
to`plam elementlari va ![]() natural sonlar to`plami elementlari
o`rtasida bir qiymatli moslik o`rnatish mumkin. U holda
natural sonlar to`plami elementlari
o`rtasida bir qiymatli moslik o`rnatish mumkin. U holda ![]() to`plam o`rniga o’zaro bir qiymatli
moslik kuchiga asosan, unga ekvivalent bo`lgan
to`plam o`rniga o’zaro bir qiymatli
moslik kuchiga asosan, unga ekvivalent bo`lgan ![]() to`plamning
to`plamning ![]() guruhlashlarini topish mumkin.
guruhlashlarini topish mumkin.
![]() to`plamning har qanday tanlanmasini
to`plamning har qanday tanlanmasini ![]() ko`rinishda yozish mumkin, bunda
ko`rinishda yozish mumkin, bunda ![]() ketma-ketlik o’rinli bo’lib, “tenglik”
amali tanlanma takrorlanuvchi bo`lishi mumkinligini bildiradi.
ketma-ketlik o’rinli bo’lib, “tenglik”
amali tanlanma takrorlanuvchi bo`lishi mumkinligini bildiradi.
![]() ta elementli tanlanma
ta elementli tanlanma ![]() ga
ga ![]() ta elementli to`plam
ta elementli to`plam ![]() ni mos qo`yamiz, bunda elementlar turlicha bo`ladi.
ni mos qo`yamiz, bunda elementlar turlicha bo`ladi.
![]() va
va ![]() to`plamlar orasidagi moslik yana o`zaro bir qiymatli
bo`lib,
to`plamlar orasidagi moslik yana o`zaro bir qiymatli
bo`lib, ![]() to`plam
to`plam ![]() to`plamdan
to`plamdan ![]() tadan takrorlanmaydigan
tadan takrorlanmaydigan ![]() elementli guruhlash bo`ladi.
elementli guruhlash bo`ladi.
2.4. O’rin almashtirish, joylashtirish va guruhlashlar 125
U holda
takrorlanmaydigan ![]() guruhlashlar soni
guruhlashlar soni ![]() takrorlanuvchi guruhlash soniga teng bo’ladi, ya`ni
takrorlanuvchi guruhlash soniga teng bo’ladi, ya`ni
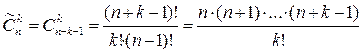
Teorema. ![]() ta elementdan
ta elementdan ![]() ta elementli takrorlanuvchi
guruhlashlar soni
ta elementli takrorlanuvchi
guruhlashlar soni ![]() ga teng.
ga teng.
Misol. 4 ta o’yin kubigini tashlab, nechta turlicha variant hosil qilish mumkin?
Yechilishi: Har bir o’yin kubigida 1 dan 6 gacha raqamlardan bittasi tushishi mumkin, ya’ni har bir kubikda 6 ta variant bo’lishi mumkin. Agar 4 ta o’yin kubigi tashlansa, har bir variantni 4 ta ob’yektning tartiblanmagan takrorlanuvchi ketma-ketligi deyish mumkin, ularning har biri uchun esa 6 ta imkoniyat bor:
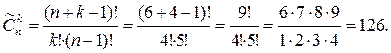
126 Bob II. Kombinatorika
Nazorat uchun savollar:
1. Takrorlanuvchi guruhlash deb nimaga aytiladi?
2. ![]() ta elementdan
ta elementdan ![]() ta elementli takrorlanuvchi
guruhlashlar soni nimaga
teng?
ta elementli takrorlanuvchi
guruhlashlar soni nimaga
teng?
3. Polinimial koeffitsiyentlar qanday hisoblanadi?
4. Takrorlanuvchi guruhlashlarning tadbiqiga misol keltiring.
Mustaqil yechish uchun masalalar:
1. 0,1,2,3,4,5,6 raqamlaridan iborat DOMINO o‘yini toshlari nechta?
2. 0,1,2,…,k raqamlaridan iborat DOMINO o‘yini toshlari nechta?
3. Qandalotchilik sexida 11 turdagi shirinlik ishlab chiqariladi. 6 ta bir xil yoki 6 ta har xil shirinlikni necha xil usulda tanlash mumkin?
4. Muzqaymoq do‘konida 8 xil turdagi muzqaymoq sotilayapti. 5 kishiga necha xil usulda muzqaymoq olish mumkin?
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()
11. ![]() 12.
12. ![]()
13. ![]() 14.
14. ![]()
15. 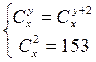 16.
16.
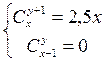
17. ![]() munosabat berilgan bo’lsa,
munosabat berilgan bo’lsa, ![]() va
va ![]() ni toping.
ni toping.
2.5. N’yiton binomi. Polinomial teorema 127
2.5. N’YUTON BINOMI. POLINOMIAL TEOREMA
2.5.1. N’yuton binomi.
Maktab kursidan qisqa ko`paytirish formulalari bilan tanishsiz, masalan ikki son yig`indisining kvadrati
![]()
yoki ikki son yig`indisining kubini topish
![]()
kabi masalalarda ![]() va
va ![]() lar oldidagi koeffitsiyentlarni topish masalasi kelib
chiqadi. Koeffitsiyentlarni topish usulini frantsuz matematigi Blez Paskal (1623
– 1662 yy) fanga kiritgan, hozirda Paskal uchburchagi deb ataladi:
lar oldidagi koeffitsiyentlarni topish masalasi kelib
chiqadi. Koeffitsiyentlarni topish usulini frantsuz matematigi Blez Paskal (1623
– 1662 yy) fanga kiritgan, hozirda Paskal uchburchagi deb ataladi:
1
![]() =0
=0
1 1 ![]() =1
=1
1 2
1 ![]() =2
=2
1 3 3 1 ![]() =3
=3
1 4 6 4
1 ![]() =4
=4
1 5 10 10
5 1 ![]() =5
=5
1 6 15 20
15 6 1 ![]() =6
=6
1 7 21 35
35 21 7 1 ![]() =7
=7
. . . . . . . . . . . . . . . . . . . . .
![]() soni yetarlicha katta bo`lganda,
soni yetarlicha katta bo`lganda, ![]() uchun Paskal uchburchagini tashkil qiluvchi sonlar
uchun Paskal uchburchagini tashkil qiluvchi sonlar ![]() ga teng bo’ladi:
ga teng bo’ladi:
128 Bob II. Kombinatorika
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
… …. … …. … …. …
![]()
![]() … …. … ….
…
… …. … ….
… ![]()
![]()
Paskal uchburchagining tashqi
tomonlaridagi sonlar har doim 1 ga teng bo’ladi, chunki ![]() Paskal uchburchagining
yana bir qonuniyati, uchburchakdagi 2 ta ketma-ket sonni qo’shish natijasida
keyingi qatordagi shu 2 son o’rtasida turgan sonni topish mumkin. Bu xossa Paskal
formulasi deb nomlanadi:
Paskal uchburchagining
yana bir qonuniyati, uchburchakdagi 2 ta ketma-ket sonni qo’shish natijasida
keyingi qatordagi shu 2 son o’rtasida turgan sonni topish mumkin. Bu xossa Paskal
formulasi deb nomlanadi:
![]()
Bunda ![]()
Isboti: 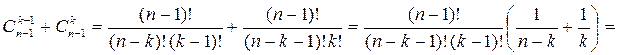
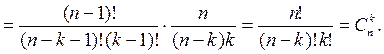
2.5. N’yiton binomi. Polinomial teorema 129
Teorema (Binomial teorema). Quyidagi tenglik o‘rinli
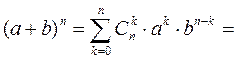

bu yerda ![]() sonlarga binomial
koeffitsiyentlar, tenglamaga esa N’yuton binomi deyiladi.
sonlarga binomial
koeffitsiyentlar, tenglamaga esa N’yuton binomi deyiladi.
Isboti: Formulani matematik induktsiya metodidan foydalanib isbotlash mumkin. Haqiqatan ham,
![]() bo`lganda
bo`lganda ![]()
![]() da
da ![]()
Endi formulani ![]() uchun o`rinli deb faraz qilib,
quyidagiga ega bo`lamiz:
uchun o`rinli deb faraz qilib,
quyidagiga ega bo`lamiz:
![]()

Yig’indida indekslarni almashtiramiz:
![]() u holda
u holda
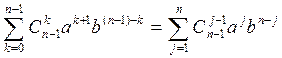
bo’ladi. Bundan
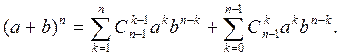
130 Bob II. Kombinatorika
Oxirgi tenglikda yig’indilar
chegaralarini tenglashtiramiz. Buning uchun yordamchi ![]() tengliklarni kiritamiz, u holda
tengliklarni kiritamiz, u holda

va
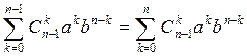
tengliklar hosil bo’ladi.
Bu tengliklarni o’rniga qo’yib, quyidagini hosil qilamiz:
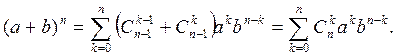
Teorema isbotlandi.
Hozirda N’yuton binomi deb yuritiladigan yuqoridagi formulani
Isaak N’yuton(1643-1727
yy)gacha O’rta osiyolik olimlar, yurtdoshlarimiz:
matematik, astronom, shoir Umar Xayyom (1048-1122 yy) va Mirzo Ulug’bekning shogirdi G‘iyosiddin Jamshid al-Koshiy “Arifmetika kaliti” asarida yorqin
misollarda ko’rsatib bergan. Yevropada esa B. Paskal o`z ishlarida qo`llagan. N’yutonning
xizmati shundaki, u formulani daraja ko`psatkichi ![]() ning butun bo‘lmagan holi uchun umumlashtirdi.
ning butun bo‘lmagan holi uchun umumlashtirdi.
![]() uchun
uchun ![]() ning butun bo’lmagan qiymatida N’yuton binomi
formulasining ko’rinishi quyidagicha bo’ladi:
ning butun bo’lmagan qiymatida N’yuton binomi
formulasining ko’rinishi quyidagicha bo’ladi:
2.5. N’yiton binomi. Polinomial teorema 131
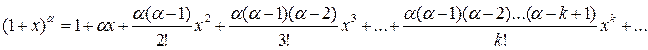
Binom yoyilmasi ko’pgina konbinatorika formulalarida asos bo’lib xizmat qiladi, masalan:
1. ![]() bo’lganda
bo’lganda 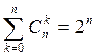 hosil bo’ladi. Bu son
hosil bo’ladi. Bu son ![]() ta elementli
ta elementli ![]() to’plamning barcha mumkin bo’lgan tartiblanmagan qism
to’plamlari soniga teng.
to’plamning barcha mumkin bo’lgan tartiblanmagan qism
to’plamlari soniga teng.
2. ![]() bo’lganda
bo’lganda 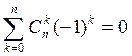 ga teng, ya’ni toq va juft o’rinda turgan binomial
koeffitsiyentlar yig’indisi
ga teng, ya’ni toq va juft o’rinda turgan binomial
koeffitsiyentlar yig’indisi ![]() ga va ular o’zaro ham teng bo’ladi.
ga va ular o’zaro ham teng bo’ladi.
Nazorat uchun savollar:
1. Qisqa ko’paytirish formulalarini keltiring.
2. Binomial koeffitsiyent formulasini yozing.
3. N’yuton binomi deb ataluvchi formulani yana kimlarning ishlarida uchratish mumkin?
4.
![]() ning butun bo’lmagan qiymatida N’yuton binomining ko’rinishi qanday?
ning butun bo’lmagan qiymatida N’yuton binomining ko’rinishi qanday?
5. Binomial teoremani isbotlang.
6. Paskal uchburchagi deganda nimani tushunasiz?
132 Bob II. Kombinatorika
7. Binom yoyilmasini qaysi konbinatorika formulalarida ko’rish mumkin?
8. Paskal formulasini isbotlang.
9. G‘iyosiddin Jamshid al-Koshiy “Arifmetika kaliti” asarida nima haqda yozgan?
Mustaqil yechish uchun masalalar:
Paskal uchburchagining 8-qatori quyidagicha bo’lsa,
1 7 21 35 35 21 7 1
a) 9-qator elementlarini aniqlang;
b) 10-qator elementlarini aniqlang;
v) Agar ![]() – 8-qatordagi ketma-ket joylashgan sonlar bo’lsa, u
– 8-qatordagi ketma-ket joylashgan sonlar bo’lsa, u
holda 10-qatordagi sonlardan
biri ![]() yig’indiga teng
yig’indiga teng
bo’lishini ko’rsating;
g) ![]() tenglikni
tenglikni ![]() bo’lgan hol uchun
bo’lgan hol uchun
Paskal formulasidan foydalanib isbotlang.
2.5. N’yiton binomi. Polinomial teorema 133
2.5.2. Polinomial teorema.
Teorema (N’yuton binomining umumlashgan teoremasi).
![]() ta qo’shiluvchiga ega bo’lgan
ta qo’shiluvchiga ega bo’lgan ![]() ifoda uchun N’yuton formulasi quyidagiga
teng:
ifoda uchun N’yuton formulasi quyidagiga
teng:
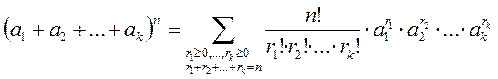
ya’ni yig’indi ![]() tenglamaning barcha nomanfiy butun yechimlari
uchun hisoblanadi.
tenglamaning barcha nomanfiy butun yechimlari
uchun hisoblanadi.
Misol 1. N’yuton polinomi formulasidan
foydalanib ![]() ni hisoblaymiz.
ni hisoblaymiz.
Agar qavslarni ochib, soddalashtiradigan bo’lsak, bir qancha amallarni bajargandan keyin quyidagi tenglikka kelamiz:
![]() Barcha hisoblashlardan keyin 10 ta haddan iborat
bo’lgan tenglik hosil bo’ladi.
Barcha hisoblashlardan keyin 10 ta haddan iborat
bo’lgan tenglik hosil bo’ladi.
Bu tenglikni polynomial
formuladan oson topish mumkin: bizning misolda ![]() , ya’ni
, ya’ni
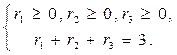
Turli koeffitsiyentlar ham 3 ta, bular:
![]()
134 Bob II. Kombinatorika
Natijani yozish uchun chekli sondagi ![]() indekslarni barcha mumkin bo’lgan kombinatsiyalari
jadvalini tuzgan ma`qul:
indekslarni barcha mumkin bo’lgan kombinatsiyalari
jadvalini tuzgan ma`qul:
|
|
|
|
|
3 |
0 |
0 |
|
0 |
3 |
0 |
|
0 |
0 |
3 |
|
2 |
1 |
0 |
|
2 |
0 |
1 |
|
1 |
2 |
0 |
|
0 |
2 |
1 |
|
1 |
0 |
2 |
|
0 |
1 |
2 |
|
1 |
1 |
1 |
U holda
![]() hosil bo’ladi.
hosil bo’ladi.
Misol 2. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi koeffitsiyentni toping.
had oldidagi koeffitsiyentni toping.
Yechilishi: 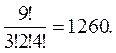
2.5. N’yiton binomi. Polinomial teorema 135
Misol 3. 15 talabani nechta usulda 3 ta o’quv guruhiga 5 nafardan guruhlarga ajratish mumkin?
Yechilishi: Bizda 15 ta ob’yekt bor, ularni 5 tadan 3 ta guruhga ajratish kerak. Bu ishni
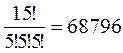
usulda bajarish mumkin.
Misol 4. “MASALA” so’zidagi harflarni necha xil usulda o’rin almashtirish mumkin?
Yechilishi: Ushbu so’z 6 ta harfdan iborat
bo’lgani uchun uni 6! Usulda o’rin almashtirish mumkin. Biroq unda 3 ta “A”
harfi qatnashgan, “A” harflarini o’rin almashtirgan bilan yangi so’z hosil
bo’lmaydi. 3 ta harfni o’rin almashtirishlar soni 3! ga tengligidan 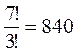 qiymat topiladi.
qiymat topiladi.
Demak, “MASALA” so’zidagi harflarni o’rin almashtirish bilan 840 ta turli “so’z” hosil qilish mumkin ekan.
Nazorat uchun savollar:
1. Polinomial koeffitsiyentlar formulasini yozing.
2. Polinomial teoremani ayting va formulasini yozing.
3. Polinomial koeffitsiyentlarning xossalarini yozing.
136 Bob II. Kombinatorika
Mustaqil yechish uchun masalalar:
1. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi
had oldidagi
koeffitsiyentni toping.
2. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi
had oldidagi
koeffitsiyentni toping.
3. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi
had oldidagi
koeffitsiyentni toping.
4. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi
had oldidagi
koeffitsiyentni toping.
5. ![]() darajani yoyishdan hosil bo’lgan
darajani yoyishdan hosil bo’lgan ![]() had oldidagi
had oldidagi
koeffitsiyentni toping.
6. “MATEMATIKA” so’zidan nechta turli xil so’z yasash mumkin?
a) Ulardan nechtasi “T” harfi bilan boshlanadi?
b) Ulardan nechtasida ikkita “M” yonma-yon joylashgan bo’ladi?
2.6. To’plamlarni bo’laklarga ajratish 137
2.6. TO’PLAMLARNI BO’LAKLARGA
AJRATISh
Ushbu mavzu to’plamlar nazariyasi bo’limida qaralmadi, chunki, bo’laklarga ajratish masalasi biroz murakkab bo’lib, uni hisoblash formulalari kombinatorika formulalaridan kelib chiqadi.
2.6.1. Bo’laklarga ajratish.
Ta’rif. Aytaylik, ![]() to’plam
to’plam ![]() ta elementdan iborat
ta elementdan iborat ![]() to’plamning o`zaro kesishmaydigan
to’plamning o`zaro kesishmaydigan ![]() ta qism to‘plamga ajratilgan bo’laklari bo`lsin.
Bunda
ta qism to‘plamga ajratilgan bo’laklari bo`lsin.
Bunda ![]() agar
agar ![]() bo’lsa,
bo’lsa, ![]() .
.
Bi qism to’plamlar bo’lakning bloklari deyiladi.
Bo’sh bo’lmagan bloklarga ega bo’laklar bilan ekvivalentlik munosabati o’rtasida o’zaro bir qiymatli akslantirish mavjud.
Agar ![]() va
va ![]()
![]() to’plamning bo’laklari bo’lib, har bir
to’plamning bo’laklari bo’lib, har bir ![]() blok
blok ![]() bloklarning birlashmasidan iborat bo’lsa, u holda
bloklarning birlashmasidan iborat bo’lsa, u holda ![]() bo’lak
bo’lak ![]() ning maydalangan bo’lagi deyiladi.
ning maydalangan bo’lagi deyiladi.
Maydalangan bo’laklar qisman tartiblangan bo’ladi.
138 Bob II. Kombinatorika
2.6.2. II tur Stirling sonlari.
Ta’rif (Jeyms Stirling (1699-1770 yy)).
![]() ta elementli to’plamning
ta elementli to’plamning ![]() ta bo’lakka ajratish soniga
II tur Stirling soni deyiladi va quyidagicha belgilanadi:
ta bo’lakka ajratish soniga
II tur Stirling soni deyiladi va quyidagicha belgilanadi: ![]() . Ta’rifga ko’ra
. Ta’rifga ko’ra
![]()
![]()
Teorema 1. ![]() tenglik o’rinli.
tenglik o’rinli.
Isboti: ![]() to’plam
to’plam ![]() to’plamning n ta blokka ajratilgan bo’laklari
bo’lsin.
to’plamning n ta blokka ajratilgan bo’laklari
bo’lsin.
![]() ,
, ![]() ,
,
ya’ni m ta element alohida blok hosil
qiladigan bo’lak ![]() ga, qolgan barcha bo’laklar
ga, qolgan barcha bo’laklar ![]() ga tegishli bo’ladi. Bundan
ga tegishli bo’ladi. Bundan ![]() ekanligi ma’lum. U holda
ekanligi ma’lum. U holda ![]() ,
, ![]() o’rinli. Barcha
o’rinli. Barcha ![]() bo’laklar quyidagicha hosil qilinadi:
bo’laklar quyidagicha hosil qilinadi: ![]() to’plamning barcha bo’laklarini n ta
blokka ajratamiz, ular
to’plamning barcha bo’laklarini n ta
blokka ajratamiz, ular ![]() ta bo’ladi va har bir blokka navbat bilan
ta bo’ladi va har bir blokka navbat bilan ![]() - elementni joylashtiramiz. Natijada
- elementni joylashtiramiz. Natijada ![]() tenglik hosil bo’ladi.
tenglik hosil bo’ladi.
Teorema isbotlandi.
2.6. To’plamlarni bo’laklarga ajratish 139
Teorema 2. 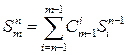 tenglik o’rinli.
tenglik o’rinli.
Isboti: ![]() to’plam
to’plam ![]() to’plamning n ta blokka ajratilgan bo’laklari
bo’lsin.
to’plamning n ta blokka ajratilgan bo’laklari
bo’lsin. ![]() to’plamlar oilasini qaraymiz. U
holda
to’plamlar oilasini qaraymiz. U
holda ![]() to’plam
to’plam ![]() ko’rinishida bo’ladi, bunda
ko’rinishida bo’ladi, bunda ![]() va agar
va agar ![]() bo’lsa,
bo’lsa, ![]() .
.
Aytaylik, ![]() va
va ![]() bo’lsin. U holda
bo’lsin. U holda
![]() .
.
![]()
ekanligidan
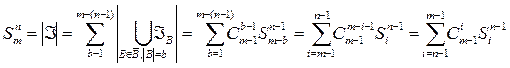
tenglik hosil bo’ladi, bu yerda ![]()
Teorema isbotlandi.
140 Bob II. Kombinatorika
2.6.3. I tur Stirling sonlari.
Ta’rif . Syur’yektiv funktsiyalar soni ,
ya’ni ![]() ta predmetni
ta predmetni ![]() ta idishga taqsimlash soniga I tur Stirling soni deyiladi (bunda idishlarning barchasi band qilingan bo’ladi) va
quyidagicha belgilanadi:
ta idishga taqsimlash soniga I tur Stirling soni deyiladi (bunda idishlarning barchasi band qilingan bo’ladi) va
quyidagicha belgilanadi: ![]() .
.
Teorema. I va II tur Stirling sonlari
o’rtasida ![]() bog’liqlik o’rinli.
bog’liqlik o’rinli.
Isboti: ![]() to’plamning har bir bo’lagiga to’plamlar oilasi
syur’yektiv funktsiya sifatida mos qo’yiladi. Shunday qilib, turli to’plamlar
oilasining syur’yektivlik darajasi – bu II tur Stirling sonlidir
to’plamning har bir bo’lagiga to’plamlar oilasi
syur’yektiv funktsiya sifatida mos qo’yiladi. Shunday qilib, turli to’plamlar
oilasining syur’yektivlik darajasi – bu II tur Stirling sonlidir ![]() . Barcha syur’yektiv funktsiyalar
soni
. Barcha syur’yektiv funktsiyalar
soni
![]() .
.
Teorema isbotlandi.
2.6.4. Bell soni.
Ta’rif (Erik Bell (1883-1960 yy)). ![]() ta elementli to’plamning barcha bo’laklar
soni Bell soni deyiladi va
ta elementli to’plamning barcha bo’laklar
soni Bell soni deyiladi va ![]() ko’rinishida belgilanadi:
ko’rinishida belgilanadi:
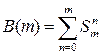 va
va ![]()
2.6. To’plamlarni bo’laklarga ajratish 141
Teorema 1. 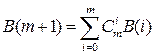 tenglik o’rinli.
tenglik o’rinli.
Isboti: ![]() to’plam
to’plam ![]() to’plamning barcha bo’laklari to’plami bo’lsin.
to’plamning barcha bo’laklari to’plami bo’lsin. ![]() to’plamning
to’plamning ![]() elementdan iborat qism to’plamlari to’plamini
qaraylik:
elementdan iborat qism to’plamlari to’plamini
qaraylik: ![]() . U holda
. U holda ![]()
ko’rinishida bo’ladi, bunda ![]() .
. ![]() va
va ![]() bo’lsin. U holda
bo’lsin. U holda ![]() .
. ![]() ekanligidan
ekanligidan
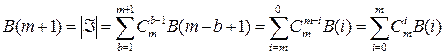
tenglik hosil bo’ladi, bu yerda ![]()
Teorema isbotlandi.
Nazorat uchun savollar:
1. To’plamlarni bo’laklarga ajratish deganda nimani tushunasuz?
2. Bloklar deb nimaga aytiladi?
3. II tur Stirling sonlari deb nimaga aytiladi?
4. I tur Stirling sonlari deb nimaga aytiladi?
5. Bell soni deb nimaga aytiladi?
6. II tur Stirling sonlarining xossalarini keltiring.
III BOB.
ÌÀÒÅÌÀÒIK ÌÀNÒIQ ÀSOSLARI
KIRISH
Matematik mantiq diskret matemetikaning asosiy bo`limi bo`lib, bu bo`lim mulohazalar algebrasi bilan boshlanadi. Matematik mantiq hamda to`plamlar nazariyasi birgalikda hozirgi zamonaviy matematikaning fundamenti hisoblanadi.
Amaliy nuqtai nazardan qaraydigan bo`lsak, matematik mantiq ma`lumotlar bazasini qurishda, elektrotexnika, informatika va hisoblash texnikasi va umuman barcha raqamli qurilmalarda dasturlash tili uchun asos bo`lib hizmat qiladi. Shuning uchun ham tahliliy mulohaza yuritishga qiziquvchi har bir kishi matematik mantiq bo`limini o`rganishi kerak bo’ladi.
Insoniyat tomonidan to’plangan matematik bilimlarni jamlashda greklarning hissasi nihoyatda salmoqli bo`lgan, shuningdek, ular mantiq, ya`ni to`g`ri mulohaza yuritish san`ati bilan ham shug’ullanishgan.
Er. av. 389 yilda Platon (er.av. 427-347 yy) asos solgan falsafiy maktabda matematikaning ilk nazariy asoslari qurildi. Platon mantiqiy teoremalarni isbotlashning quyidagi 3 ta metodini ishlab chiqdi:
1) analitik metod;
2) sintetik metod;
3) apagogik metod.
Analitik metod – har biri o’zidan oldingisining bevosita natijasi bo’lgan gaplar zanjirini hosil qilishdan iborat. Bu zanjirning birinchi elementini isbotlash kerak bo’lgan mulohaza, oxirgi elementini esa isbotlangan haqiqat tashkil qiladi.
Sintetik metod – analitik metodning aksibo’lib, unda birinchi element isbotlangan haqiqat va har bitta mulohaza o’zidan keyingisining natijasi bo’ladi.
Apagogik metod – teskarisini faraz qilish yo’li bilan isbotlash metodi bo’lib, unda zanjirning birinchi elementi isbotlash kerak bo’lgan mulohazani inkor qilish bo’ladi, oxirida esa ziddiyatga olib kelinadi.
Platonning shogirdlaridan Aristotel Stagirit (er.av. 384 -322 yy) alohida ajralib turadi. Aristotelni mantiq ilmining asoschisi desak, yanglishmaymiz, chunki u o’zigacha bo’lgan barcha mantiqiy bilimlarni jamladi va mantiqiy qonuniyatlar sistemasini yaratdi. Bu qonunlardan tabiatni tadqiq qilishda mulohazalar quroli sifatida foydalandi. Aristotelning olamni o’rganishdagi bilimlari yagona bo’lib, naturfalsafa deb nom olgan.
Qadimgi greklar matematikani ikkiga ajratib o’rganishgan:
1) mantiqni hisoblash san`ati deb,
2) arifmetikani sonlar nazariyasi deb nomlashgan.
Ushbu bobda mulohazalar va ular ustida amallar, mantiqiy bog‘liqliklar, Bul (mantiqiy) formulalari, mantiq qonunlari, mantiq funksiyalari, mantiq funksiyalari uchun rostlik jadvalini tuzish va aksincha, rostlik jadvali berilgan bo’lsa, mantiq funksiyasi ko‘rinishini tiklash, mukammal diz’yunktiv va kon’yunktiv normal shakllar, rele - kontakt sxemalari, rele - kontakt sxemalarida analiz, sintez, minimallashtirish masalalari, Karno kartalari, Veych diagrammalari, yechimlar daraxti haqida so’z yuritiladi.
Shuningdek, elementlari 0 va 1 dan tashkil topgan to`plamlar ustida ish ko`riladi. Bu elementlar son sifatida emas, balki mantiqiy “ha”, “yo`q” ma`nolarida ishlatiladi.
144 Bob III. Matematik mantiq asoslari
3.1. MULOHAZALAR ALGEBRASI
3.1.1. Sodda va murakkab mulohazalar.
Ta’rif 1. Rost yoki yolg‘onligi aniq bo‘lgan darak gap mulohaza deyiladi.
So`roq va undov gaplar mulohaza hisoblanmaydi, ya`ni: “Bugun kinoga kiramizmi?” yoki “Kitobga tegma!”
Mulohazalar lotin alifbosining bosh harflari bilan belgilanadi: A, B, C, ….
Agar mulohaza rost bo`lsa A=1, yolg‘on bo`lsa A=0 deb belgilaymiz, ba`zi adabiyotlarda, shuningdek, “Informatika va hisoblash texnikasi” fanining “ALGOL”, “BOOLEAN”, “C++” dasturlash tillarida rost mulohazaga “T”, ya`ni “true” so´zining, yolg`on mulohazaga “F”, ya`ni “false” so`zining bosh harflari ishlatiladi.
Misol 1. 1. À=”Ikki ko`paytiruv olti 14 ga teng”=0
2. Â=”Ikki qo`shuv ikki 4 ga teng”=1
3. Ñ=”Qor oq”=1
4. Ä="Bugun dushanba bo`lsa, u holda ertaga seshanba bo`ladi”=1
5. Z=”agar 1+1=3 bo`lsa, u holda jumadan keyin yakshanba keladi”=?
5-mulohazaning rost yoki yolg`onligi haqida hozircha bir nima deyish qiyin, biroq mantiqiy amallarni kiritganimizdan keyin bu savolga osongina javob topasiz.
3.1. Mulohazalar algebrasi 145
Shunday fikrlar borki, ular tuzilishi bo`yicha mulohazaga o`xshaydi, lekin mulohaza emas. Masalan, ikki varaq qog`oz olamiz-da, ularni 1- va 2- deb raqamlaymiz. Birinchi qog`ozga “Ikkinchi varaqda yolg`on yozilgan” deb, ikkinchi qog`ozga esa “Birinchi varaqda rost yozilgan” degan mulohazani yozamiz. Bir qaraganda sodda mulohazaga o`xshaydi, biroq …! Savol beramiz, bu mulohazalar rostmi yoki yolg`onmi? Bu fikrlar ziddiyatga olib keladi, ya`ni ularni rost yoki yolg`onligi haqida aniq gapirib bo`lmaydi. Bunday mulohazalar matematikada mantiqiy paradoks deyiladi.
Demak, ko`rinishidan mulohazaga o`xshagan har qanday gap ham mulohaza bo`lavermaydi.
Mulohazalar sodda yoki murakkab bo‘lishi mumkin.
Ta’rif 2. Agar A mulohazaning o‘zi bir tasdiq bo‘lib, ma’nosi bo’yicha u bilan ustma - ust tushmaydigan bir qismini ajratib ko‘rsatish mumkin bo‘lmasa, u holda A mulohazaga sodda mulohaza deyiladi.
Misol 2. A: ”0 soni 1 sonidan kichik”
B: “Bugun havo iliq”.
Ta’rif 3. Sodda mulohazalardan mantiqiy bog`lovchilar yoki mantiqiy amallar yordamida hosil qilingan mulohazaga murakkab mulohaza deyiladi.
Misol 3. C: “7 tub son va 6 toq son”
D: “Oy Yer atrofida aylanadi yoki O`zbekiston Yevropada joylashgan”
146 Bob III. Matematik mantiq asoslari
Mulohaza ikkita qiymatdan birini “rost”, ya`ni “1” yoki “yolg‘on”, ya`ni “0” ni qabul qiladi. Bu qiymatlarga mulohazaning rostlik qiymatlari deyiladi.
Ta’rif 4. Mulohazaning rostlik qiymatlaridan tuzilgan jadvalga rostlik jadvali deyiladi.
Nazorat uchun savollar:
1. Platon mantiqiy teoremalarni isbotlashning qanday metodlarini ishlab chiqdi?
2. Mulohaza deb nimaga aytiladi? Misol keltiring.
3. Mantiqiy paradoks deganda nimani tushunasiz?
4. Sodda mulohaza deb nimaga aytiladi?
5. Murakkab mulohaza qanday tuziladi?
6. Rostlik qiymatlariga ta’rif bering.
7. Rostlik jadvali nima?
3.1.2. Asosiy mantiqiy bog‘liqliklar.
Sodda mulohazalardan murakkab mulohazalarni hosil qilish uchun mulohazalar ustida bajarilishi mumkin bo`lgan mantiqiy amal(bog’liqlik)larning belgilaridan foydalaniladi.
Mulohazalar ustida quyidagi asosiy 5 ta mantiqiy amal bajariladi: inkor qilish amali, kon’yunktsiya amali, diz’yunktsiya amali, implikatsiya amali va ekvivalentlik amali.
3.1. Mulohazalar algebrasi 147
Ta`rif 1. A mulohazaning inkori deb, shunday yangi mulohazaga aytiladiki, agarda A mulohaza yolg`on bo`lsa, uning inkori chin bo`ladi va aksincha. A mulohazaning inkori ¬A yoki Ā kabi belgilanadi va “A emas” deb o`qiladi.
Inkor qilish amali uchun rostlik jadvalini tuzish mumkin:
|
A |
¬A |
|
1 |
0 |
|
0 |
1 |
Ta`rif 2. A va B mulohazalarning kon’yunktsiyasi deb, A va B mulohazalar bir vaqtda rost bo`lgandagina rost bo`lib, qolgan barcha hollarda yolg`on qiymat qabul qiluvchi mulohazaga aytiladi.
A va B mulohazalarning kon’yunktsiyasi A&B yoki A/\B kabi belgilanadi hamda “va” deb o`qiladi. A mulohaza kon’yunktsiyaning birinchi hadi, B mulohaza esa ikkinchi hadi deyiladi. Kon’yunktsiya amali xuddi 0 va 1 sonlarini ko`paytirishga o`xshagani uchun ham uni ko`pincha mantiqiy ko`paytirish deb ham atashadi.
Kon’yunktsiya amalining rostlik jadvali quyidagicha:
|
A |
B |
A&B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
148 Bob III. Matematik mantiq asoslari
Ta`rif 3. A va B mulohazalarning diz’yunktsiyasi deb, A va B mulohazalardan kamida bittasi rost bo`lganda rost bo`lib, qolgan hollarda yolg`on qiymat qabul qiluvchi mulohazaga aytiladi.
A va B mulohazalarning kon’yunktsiyasi A\/B kabi belgilanadi hamda “yoki” deb o`qiladi. A mulohaza diz’yunktsiyaning birinchi hadi, B esa ikkinchi hadi deyiladi.
Diz’yunktsiya amalining rostlik jadvali quyidagicha:
|
A |
B |
A\/B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Ta`rif 4. {0; 1; ¬; &; \/} - to’plamga mulohazalar algebrasi yoki Bul algebrasi deyiladi.
Ta`rif 5. A va B mulohazalarning implikatsiyasi deb, A mulohaza rost bo`lib, B yolg`on bo`lgandagina yolg`on, qolgan barcha hollarda rost qiymat qabul qiluvchi mulohazaga aytiladi.
A va B mulohazalarning implikatsiyasi A→B kabi belgilanadi va “A dan B kelib chiqadi” yoki “Agar A o`rinli bo`lsa, B o`rinli bo`ladi” deb o`qiladi. A mulohaza implikatsiyaning birinchi hadi, B esa ikkinchi hadi hisoblanadi.
3.1. Mulohazalar algebrasi 149
Implikatsiya amali uchun rostlik jadvali quyidagicha:
|
A |
B |
A→B |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Misol. A : “Bugun yomg`ir yog`di” va B: “Men soyabon oldim” mulohazalar bo`lsin. Agar yomg`irda ho`l bo`lganimizni 0, quruq bo`lganimizni 1 qiymatlar bilan belgilasak, implikatsiyani shunday tushuntirish mumkin:
|
A |
B |
A→B |
|
Bugun yomg`ir yog`madi |
Menda soyabon yo`q |
1 (quruq) |
|
Bugun yomg`ir yog`madi |
Men soyabon oldim |
1 (quruq) |
|
Bugun yomg`ir yog`di |
Menda soyabon yo`q |
0 (ho`l) |
|
Bugun yomg`ir yog`di |
Men soyabon oldim |
1 (quruq) |
150 Bob III. Matematik mantiq asoslari
Ta`rif 6. A va B mulohazalarning ekvivalentligi deb, A va B mulohazalarning bir xil qiymatlarida rost bo`lib, har xil qiymatlarida esa yolg`on bo`luvchi mulohazaga aytiladi.
A va B mulohazalarning ekvivalentligi A~B, A↔B kabi belgilanadi va “A va B teng kuchli”, “A bo`ladi, qachonki B bo`lsa” yoki “A mulohaza
B uchun yetarli va zarur” deb o`qiladi. A mulohaza ekvivalentlikning birinchi hadi, B esa ikkinchi hadi hisoblanadi.
Ekvivalentlik amali uchun rostlik jadvali quyidagicha:
|
A |
B |
A~B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Halqali yig‘indi amali AÅB.
Bu amal ekvivalentlik amalining inkoriga teng bo’ladi, ya’ni
AÅB = Ø(A~B)
Halqali yig‘indi amali uchun rostlik jadvali quyidagicha:
|
A |
B |
AÅB |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
3.1. Mulohazalar algebrasi 151
Sheffer shtrixi A½B.
Ushbu amalni kon`yunktsiya va diz`yunktsiya amallari yordamida hosil qilish mumkin, ya’ni
A½B= Ø(A&B)= ØAÚØB
Sheffer shtrixi amali uchun rostlik jadvali quyidagicha:
|
A |
B |
A½B |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Sheffer shtrixi amali uchun quyidagi xossalar o’rinli:
10. AÚB = ØA½ØB = (A½A)½(B½B)
20. A&B = Ø(A½B) = (A½B)½(A½B)
30. ØA = A½A
Pirs strelkasi A¯B.
Ushbu amalni ham kon`yunktsiya va diz`yunktsiya amallari yordamida hosil qilish mumkin, ya’ni
A¯B= Ø(AÚB)= ØA&ØB
152 Bob III. Matematik mantiq asoslari
Pirs strelkasi amali uchun rostlik jadvali quyidagicha:
|
A |
B |
A¯B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Pirs strelkasi amali uchun quyidagi xossalar o’rinli:
10. AÚB = Ø(A¯B) = (A¯B) ¯ (A¯B)
20. A&B = ØA¯ØB = (A¯A) ¯ (B¯B)
30. ØA = A¯A
Pirs strelkasi qatnashgan Bul ifodasini Sheffer shtrixi yordamida hosil qilish mumkin:
A¯B= ØA&ØB = Ø Ø(A½B) = Ø [(A½A)½(B½B)]=
= [(A½A)½(B½B)]½[ (A½A)½(B½B)] (1)
yoki Sheffer shtrixi qatnashgan Bul ifodasini Pirs strelkasi yordamida hosil qilish mumkin:
A½B= ØAÚØB = Ø (ØA¯ØB) = Ø [(A¯A) ¯ (B¯B)]=
= [(A¯A) ¯ (B¯B)] ¯ [ (A¯A) ¯ (B¯B)] (2)
3.1. Mulohazalar algebrasi 153
Bundan ko’rinadiki, ixtiyoriy ifodani faqat Sheffer shtrixi yordamida yo Pirs strelkasi yordamida yoki faqatgina kon`yunktsiya va inkor yordamida yoki faqatgina diz`yunktsiya va inkor yordamida yozish mumkin ekan.
Nazorat uchun savollar:
1. Mantiqiy amallarni sanab bering.
2. Mulohazaning inkorini tushuntiring.
3. Mulohazalarning diz’yunktsiyasi deb nimaga aytiladi?
4. Mulohazalarning kon’yunktsiyasi deb nimaga aytiladi?
5. Implikatsiya amalini tushuntiring.
6. Qanday mulohazalar ekvivalent bo’ladi?
7. Halqali yig‘indi amalini tushuntiring.
8. Sheffer shtrixi qanday vazifani bajaradi?
9. Sheffer shtrixi amalining xossalarini ayting.
10. Pirs strelkasi qanday vazifani bajaradi?
11. Pirs strelkasi amalining xossalarini ayting.
12. Ifodada Pirs strelkasidan Sheffer shtrixiga qanday o’tish mumkin?
13. Ifodada Sheffer shtrixidan Pirs strelkasiga qanday o’tish mumkin?
154 Bob III. Matematik mantiq asoslari
3.1.3. Predikatlar. Umumiylik va mavjudlik kvantorlari.
Bizga natural sonlar to’plami N berilgan bo’lsin.
x element N to’plamning ixtiyoriy elementi bo’lsin. U holda quyidagi jumlalar
A(x)={x soni 7 ga bo’linadi};
B(x)={x>10};
C(x)={x tub son};
D(x)={(x-5)2<10}
darak gaplar bo’lganligi uchun mulohaza hisoblanadi, lekin ularning rost yoki yolg’onligi haqida hech narsa ayta olmaymiz.
Ta’rif. Rost yoki yolg’onligi noma`lum bo’lgan mulohazalar aniqmas mulohazalar yoki predikatlar deyiladi.
Yuqoridagi misollarda x ning o’rniga turli qiymatlarni qo’ysak, turlicha mulohazalar hosil bo’ladi, ya’ni
A(5)={7 soni 7 ga bo’linadi} =1;
A(13)={10 soni 7 ga bo’linadi}=0
Natural sonlar to’plamida berilgan biror P(x) predikatni olaylik.
Agar P(x) predikat bo’lsa, u holda ("x)P(x) – yozuv N to’plamda ixtiyoriy x uchun P(x) mulohaza o’rinli degan ma`noni bildiradi. Bu mulohaza rost bo’ladi, qachonki x ning ixtiyoriy qiymatida P(x) o’rinli bo’lsa. Agarda x ning bittagina qiymatida o’rinli bo’lmasa, P(x) mulohaza yolg’on bo’ladi. " - belgi umumiylik kvantori deyiladi.
3.1. Mulohazalar algebrasi 155
Misol 1. A(x)={4x+1 soni tub son} mulohazani ixtiyoriy x uchun tekshirib ko’ramiz:
A(1)={41+1=5 soni tub son}=1;
A(2)={42+1=17 soni tub son}=1;
A(3)={43+1=257 soni tub son} =1;
A(4)={44+1=65537 soni tub son} =1;
A(5)={45+1=4294967296+1= 4294967297 soni tub son} =0,
demak, x=5 da bu mulohaza yolg’on bo’ladi.
Shuning uchun ham ("x)A(x) mulohaza yolg’on mulohaza hisoblanadi.
Misol 2. ("x)B(x)={x2-x soni 2 ga bo’linadi} mulohazani ixtiyoriy x uchun tekshirib ko’ramiz:
B(1), B(2), B(3), … larda mulohaza o’rinli, lekin bu usul bilan barcha sonlarni tekshirib chiqishning iloji yo’q, shuning uchun mulohazahi rostligini quyidagicha isbotlash mumkin:
x2-x=x(x-1) ketma-ket kelgan 2 ta sonning ko’paytmasida bittasi albatta juft son bo’ladi, demak bu ko’paytma har doim 2 ga bo’linadi.
Bundan ("x)B(x) mulohazaning rostligi kelib chiqadi.
Agar P(x) predikat bo’lsa, u holda ($x)P(x) – yozuv N to’plamda shunday x element topiladiki, uning uchun P(x) mulohaza o’rinli degan ma`noni bildiradi. Bu mulohaza rost bo’ladi, qachonki x ning kamida bitta qiymatida P(x) o’rinli bo’lsa. $ - belgi mavjudlik kvantori deyiladi.
156 Bob III. Matematik mantiq asoslari
Yuqoridagi misollarda ($x)A(x) mulohaza ham, ($x)B(x) mulihaza ham chin bo’ladi.
Umumiylik va mavjudlik kvantorlari uchun quyidagi xossalar o’rinli:
10. Ø ("x)P(x)= ($x) ØP(x)
20. Ø ($x)P(x)= ("x) ØP(x)
30. ("x)[P(x)&D(x)]= ("x) P(x) & ("x) D(x)
40. ($x)[P(x)& D(x)] Þ ($x) P(x) & ($x) D(x)
50. ("x)P(x) Ú("x)D(x) Þ ("x)[ P(x) Ú D(x)]
60. ($x)[P(x) Ú D(x)] Þ ($x) P(x) Ú ($x) D(x)
Nazorat uchun savollar:
1. Predikat deb nimaga aytiladi?
2. Mavjudlik kvantorini tushuntiring.
3. Umumiylik kvantorini qanday tushutirish mumkin?
4. Umumiylik va mavjudlik kvantorlarining xossalarini aytib bering.
Mustaqil yechish uchun masalalar:
1. P(x)={x2+1=0, x-haqiqiy son} bo’lsa, ($x)P(x) predikatni so’z bilan ifodalang va rostligini tekshiring.
2. P(y)={y2=25, y - butun son} mulohaza uchun ($y)P(y) ni ifodalang va rostligini tekshiring.
3.1. Mulohazalar algebrasi 157
3.1.4. Formulalar. Formulalarning teng kuchliligi.
Ta’rif 1. To’g’ri tuzilgan murakkab mulohazaga formula deyiladi.
Formulalar grek harflari bilan belgilanadi: α, β, γ, δ, ….
Agar A1, A2, …, An mulohazalar α formulada qatnashadigan barcha mulohazalar bo’lsa, α= α(A1, A2, …, An ) kabi belgilanadi.
Misol 1. a) α(A)= ⌐A;
b) β(A, B, C)=A&B→C;
c) γ (A, B)=A&B \/ ⌐A&⌐B)
bunda A, B, C, … sodda mulohazalar argument yoki mantiqiy o’zgaruvchilar, α, β, γ, … formulalar esa funktsiya deb ham yuritiladi.
Formulaning to’g’ri tuzilgan bo’lishida qavslarning o’rni juda muhim. Mantiqda ham xuddi algebra va arifmetikadagi singari qavslar amallar tartibini belgilab beradi.
Formulalarda qavslarni kamaytirish maqsadida amallarning bajarilish tartibi quyidagicha kelishib olingan. Agar formulada qavslar bo`lmasa,
birinchi inkor amali - ⌐,
ikkinchi kon`yunktsiya - &,
uchinchi bo’lib diz`yunktsiya - \/,
undan so’ng implikatsiya - → va
oxirida ekvivalentlik - ~ amali bajariladi.
Agar mulohazada bir xil
amal qatnashgan bo`lsa, u holda ularni tartibi bilan ketma-ket bajariladi: ![]() .
.
158 Bob III. Matematik mantiq asoslari
Tashqi qavslar
qo`yilmaydi. Shuning uchun ham ![]() mulohazani
mulohazani ![]() ko`rinishda yozish mumkin.
ko`rinishda yozish mumkin.
Kon`yunktsiya amali
diz`yunktsiyaga qaraganda kuchliroq bog`lovchi hisoblanadi, ya`ni ![]() .
.
Diz`yunktsiya implikatsiyaga qaraganda kuchliroq bog`laydi, shuning uchun ham quyidagi tenglik o`rinli:
![]() .
.
Implikatsiya ekvivalentlikka qaraganda kuchliroq, ya`ni
![]() .
.
Misol 3.
![]()
![]()
![]()
![]()
![]()
Ta’rif 2. Argumenti va funksiya qiymati 0 yoki 1 qiymatni qabul qiluvchi n ta o‘zgaruvchi A1,A2, … , An ga bog‘liq bo‘lgan har qanday α= α(A1,A2, … , An) funksiya Bul funksiyasi deyiladi.
Ta‘rif 3. α(A1, A2, …, An) formulaning mantiqiy imkoniyati deb, A1,A2,…,An o‘zgaruvchilarning bo‘lishi mumkin bo‘lgan barcha rosrlik qiymarlariga aytiladi.
3.1. Mulohazalar algebrasi 159
Ta‘rif 4. α formulaning barcha mantiqiy imkoniyatlarini o‘z ichiga olgan jadvalga α formulaning mantiqiy imkoniyatlari jadvali deyiladi.
Teorema 1. n ta o`zgaruvchi qatnashgan
formulaning 0 va 1 qiymatlarni qabul qiluvchi mumkin bo`lgan manrtiqiy
imkoniyatlari soni ![]() ga teng.
ga teng.
Isboti: Ushbu sonni ![]() ko`rinishida belgilab va
ko`rinishida belgilab va ![]() ekanligini isbotlaymiz.
ekanligini isbotlaymiz.
Aytaylik, n=1 bo`lsin.
Bir o`zgaruvchili 0 va 1 qiymatlarni qabul qiluvchi formulaning barcha mumkin
bo`lgan manrtiqiy imkoniyatlari soni 2 ta, ya`ni 0 va 1. Bundan ![]() kelib chiqadi.
kelib chiqadi.
Matematik induktsiya
qonunidan foydalanib, n=2, n=3 da, … , n=k da to`g`ri deb faraz qilib, n=k+1
da to`g`riligini, ya`ni ![]() tenglik to`g`riligini isbotlaymiz.
tenglik to`g`riligini isbotlaymiz.
Haqiqatan, qandaydir k
elementli formula ![]() qiymatlarni qabul qilsin. U holda bu
qiymatlarga 0 va 1 ni kiritish bilan 2 ta k+1 uzunlikdagi qiymatlarni qabul
qilish mumkin, ya’ni
qiymatlarni qabul qilsin. U holda bu
qiymatlarga 0 va 1 ni kiritish bilan 2 ta k+1 uzunlikdagi qiymatlarni qabul
qilish mumkin, ya’ni ![]() va
va ![]() .
.
Demak, k+1 ta elementdan
iborat formulaning mantiqiy imkoniyatlari soni k elementli formula
mantiqiy imkoniyatlaridan 2 marta ko`p, ya`ni ![]() .
.
Teorema isbotlandi.
160 Bob III. Matematik mantiq asoslari
Ta’rif 5. Agar α va β formulalar uchun umumiy bo‘lgan mantiqiy imkoniyatlarda α va β bir xil qiymat qabul qilsa, u holda α va β formulalar teng kuchli deyiladi va α≡β kabi belgilanadi.
Boshqacha aytganda, agarda formulalarning rostlik jadvallari mos bo’lsa, ular teng kuchli bo`ladi.
Ta’rif 6. Agar barcha mantiqiy imkoniyatlarda α formula faqat 1 ga teng qiymat qabul qilsa, α formula ayniy haqiqat yoki tavtologiya deyiladi va α≡1 yoki |=α kabi belgilanadi.
n ta o`zgaruvchi qatnashgan formulaning mumkin bo`lgan barcha mantiqiy imkoniyatlarini yozish uchun qabul qilingan tartib mavjud. Bu ketma-ketlik (0,0,..,0,0) dan boshlanadi. Har bir keyingi qatorda ikkilik sanoq sistemasida oldingi qatordagi qiymatlarga 1 ni qo`shamiz va nihoyat hamma qiymatlar 1 lardan iborat bo`lganda ishni tugatamiz: (1,1,..,1,1).
Ikkilik sanoq sistemasida qo`shish qoidasini eslatib o`tamiz:
0+0=0,
0+1=1+0=1,
1+1=10.
3.1. Mulohazalar algebrasi 161
Agar o’zgaruvchilar soni 3 ta yoki 4 ta bo’lsa, u holda mos ravishda 8 ta yoki 16 ta qator hosil bo’ladi:
n=3 bo`lsa n=4 bo`lsa
A B C A B C D
0 0 0 0 0 0 0
0 0 1 0 0 0 1
0 1 0 0 0 1 0
0 1 1 0 0 1 1
1 0 0 0 1 0 0
1 0 1 0 1 0 1
1 1 0 0 1 1 0
1 1 1 0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
162 Bob III. Matematik mantiq asoslari
Misol 2. α(A, B)= ¬ (A&B) →(⌐A\/ ⌐B) formulaning tavtologiya bo’lish yoki bo’lmasligini rostlik jadvalini tuzib tekshirib ko’rish mumkin:
|
A |
B |
¬ (A&B) |
⌐A |
⌐B |
⌐A\/ ⌐B |
α(A, B)= ¬(A&B) →(⌐A\/ ⌐B) |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Teorema 2. Agar α va α→ β formulalar tavtologiya bo’lsa, u holda β ham tavtologiya bo’ladi.
Isboti. Teskarisini faraz qilish yo’li bilan isbotlaymiz, ya`ni β tavtologiya bo’lmasin, u holda β ning barcha qiymatlari 0 bo’ladi. Lekin α tavtologiya bo’lgani uchun har doim 1 qiymat qabul qiladi. Bundan α→ β=0 ekenligi kelib chiqadi, bu esa α→ β tavtologiya degan teorema shartiga zid. Biz qarama – qarshilikka duch keldik. Demak, β tavtologiya bo’lar ekan. Teorema isbotlandi.
Ta’rif 7. Agar barcha mantiqiy imkoniyatlarda α formula faqat 0 ga teng qiymat qabul qilsa, α formula ayniy yolg‘on yoki ziddiyat deyiladi va α≡0 kabi belgilanadi.
3.2. Mantiq qonunlari 163
Misol 3. α(A)= ⌐A~A formulaning ziddiyat ekanligini rostlik jadvalini tuzib tekshirib ko’ramiz:
|
A |
⌐A |
α(A)= ⌐A~A |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
Nazorat uchun savollar:
1. Qanday shart bajarilsa formulalar teng kuchli bo‘ladi?
2. Qanday shart bajarilganda formulaga tavtologiya deyiladi?
3. Qanday shart bajarilganda formulaga ziddiyat deyiladi?
4. Rostlik jadvali ta’rifini keltiring.
5. Agar α va α→ β formulalar tavtologiya bo’lsa, u holda β ham tavtologiya bo’lishini isbotlang.
6. Tavtologiyaga misol keltiring.
7. Ziddiyatga misol keltiring.
164 Bob III. Matematik mantiq asoslari
3.2. MANTIQ QONUNLARI
3.2.1. Mantiq qonunlari.
Bizga biror α, β, γ mantiqiy formulalar berilgan bo’lsin. Ushbu formulalar uchun quyidagi mantiq qonunlari har doim o’rinli bo’ladi:
1. Ikkilangan rad etish qonuni: ¬ ¬ α≡α
2. Kon`yunktsiya va diz`yunktsiya amallarining idempotentlik qonuni:
α&α≡α,
α\/α≡α
3. Kon`yunktsiya va diz`yunktsiya amallarining kommutativlik qonuni:
α&β≡β&α,
α\/β= β\/α
4. Kon`yunktsiya va diz`yunktsiya amallarining assotsiativlik qonuni:
α&(β&γ)≡(α&β)&γ,
α\/(β\/γ)=(α\/β)\/γ)
5. Kon`yunktsiya va diz`yunktsiya amallarining bir-biriga nisbatan distributivlik qonuni:
α&(β\/γ)≡(α&β)\/(α&γ) ,
α\/(β&γ)≡(α\/β)&(α\/γ)
6. Yutilish qonunlari: α&(α\/β)≡α,
α\/(α&β)≡α
3.2. Mantiq qonunlari 165
7. De Morgan qonunlari: ¬ (α\/β)≡ ⌐ α & ⌐β
|
A |
B |
¬ (α\/β) |
⌐ α & ⌐β |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
¬ (α&β)≡ ⌐ α\/ ⌐β
|
A |
B |
¬ (α&β) |
⌐ α\/ ⌐β |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
8. Tavtologiya qonuni: α\/ ⌐ α≡1
9. Ziddiyat qonuni: α & ⌐ α≡0
10. 0 va 1 qonunlari: α&1≡α, α&0≡0
α\/1≡1, α\/0≡α
⌐ 1≡0, ⌐ 0≡1
166 Bob III. Matematik mantiq asoslari
11. Kontrpozitsiya qonuni: α→β≡ ⌐ β → ⌐ α
12. Implikatsiyadan qutilish qonuni: α→β≡ ⌐α\/β
13. Ekvivalentlikdan qutilish qonuni:
α~β≡(α→β)&(β→α)≡ α&β \/ ⌐α&⌐β
14. Implikatsiya xossalari: 0→α≡1, 1→α≡α,
α→1≡1, α→0≡ ⌐ α.
Mantiq qonunlarini isbotlash uchun ularning rostlik jadvallarini tuzish yetarli.
Nazorat uchun savollar:
1. Ikkilangan rad etish qonunini keltiring va isbotlang.
2. & va \/ amallarining idempotentligi qonunini keltiring va isbotlang.
3. & va \/ amallarining kommutativligi qonunini keltiring va isbotlang.
4. & va \/ amallarining assosiativligi qonunini keltiring va isbotlang.
5. & va \/ amallarining bir-biriga nisbatan distributivlik qonunlarini keltiring va isbotlang.
6. Yutilish qonunlarini keltiring va isbotlang.
3.2. Mantiq qonunlari 167
7. De Morgan qonunlarini keltiring va isbotlang.
8. α\/ ⌐ α≡1 ekanligini isbotlang.
9. Qarama-qarshilik qonunini keltiring va isbotlang.
10. Tavtologiya va qarama-qarshilik qonunlarini isbotlang.
11. Kontrpozitsiya qonunini keltiring va isbotlang.
12. Implikatsiyadan qutilish qonunini keltiring va isbotlang.
13. Ekvivalentlikdan qutilish qoidasini keltiring va isbotlang.
14. Quyida keltirilgan qonunlarni to‘g‘riligini isbotlang
α→α≡1, 0→α≡1, 1→α≡α, α→1≡1, α→0≡ ⌐ α.
3.2.2. Mantiq funksiyalari uchun rostlik jadvalini tuzish.
Misol 1. ![]()
formulaning rostlik jadvalini tuzish uchun amallarni bajarish ketma-ketligidan foydalanamiz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
168 Bob III. Matematik mantiq asoslari
Rostlik jadvalini tuzamiz:
|
A |
B |
C |
A\/B |
⌐A |
C→⌐A |
α (A,B,C)= (A\/B)~(C→⌐A) |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Misol 2. α(A, B, C)= ⌐(A&B)→(A\/B~C)
formulaning rostlik jadvalini topish uchun amallarni bajarilish ketma-ketligi: 1) qavs ichidagi amal bajariladi, 2) ⌐, 3) &, 4) \/ , 5) ~ va 6) → amallari birin-ketin bajariladi va formulaning rostlik jadvali tuziladi.
3.2. Mantiq qonunlari 169
|
A |
B |
C |
A&B |
⌐ (A&B) |
A\/B |
A\/B~C |
α(A, B, C)= ⌐(A&B)→(A\/B~C) |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Mustaqil yechish uchun masalalar:
Quyidagi mantiq funksiyalari uchun rostlik jadvallarini tuzing:
1. α(A,B,C)= ØA&BÚØ(AÚC)
2. α(A,B,C)=C→(ØAÚØB)
3. α(A,B,C)=A&B→Ø(AÚØB)
4. α(A,B,C)=(A&B&ØC)~(ØAÚ B)
5. α(A,B,C)=(ØAÚØC)~B
6. α(A,B,C)=(A→B)→ØC
7. α(A,B,C)=(ØA→ØB)&(B→C)
8. α(A,B,C)=A&(B→C)ÚØB
9. α(A,B,C)=Ø(A&BÚC)
170 Bob III. Matematik mantiq asoslari
10. α(A,B,C)=(A~B)&(ØB~ØC)
11. α(A,B,C)=(ØA→ØC)~B
12. α(A,B,C)=(ØBÚØC)→(AÚC)
13. α(A,B,C)=A→(ØBÚØC)
14. α(A,B,C)=(ØA→B)&(ØB→A)&ØC
15. α(A,B,C)=CÚA&ØB
16. α(A,B,C)=A&(ØA&BÚC)&(AÚØC)
17. α(A,B,C)=(ØAÚB)&(ØBÚA&C)
18. α(A,B,C)=A&(B~A)&(ØAÚØC)
19. α(A,B,C)=(A→B)&A&ØC
20. α(A,B,C)=(ØA&B)→(C&A)
21. α(A,B,C)=(A&B~C)&A&ØC
22. α(A,B,C)=(A&BÚØA&ØB)&(C→B)
23. α(A,B,C)=(AÚB &ØCÚØA&ØB&C)&A&ØB
24. α(A,B,C)=(A→B)&(C→A)
25. α(A,B,C)=(A&ØB&CÚØA&ØC)&B
26. α(A,B,C)=(AÅB&C)→AÚC
27. α(A,B,C)=(A½B)→(ØC&BÅA)
28. α(A,B,C)=(A→ØB)Å(CÚA)
29. α(A,B,C)=(AÚB)Å(ØC~B)
30. α(A,B,C)=((A¯B)&ØC)→A½((ØBÅØC)~Ø(AÚC)
31. α(A,B,C)=(A&BÚØB)&(A→B)
32. α(A,B,C)=(AÚC &ØBÚØA&ØB&ØC)&A&ØB
33. α(A,B,C)=(A→C)&(B→A)
3.3. MDNSh va MKNSh 171
3.3. MUKAMMAL DIZ`YUNKTIV VA KON`YUNKTIV NORMAL ShAKLLAR
3.3.1. Normal shakllar.
Barcha mulohazalarni tadqiq qilish oson bo’lishi uchun mantiqiy qonunlar yordamida biror umumiy standart ko’rinishga keltirish mumkin.
Ta`rif 1. A mulohaza va ![]() uning qabul qilishi mumkin bo’lgan qiymatlari
bo’lsin. U holda quyidagi tenglik o’rinli:
uning qabul qilishi mumkin bo’lgan qiymatlari
bo’lsin. U holda quyidagi tenglik o’rinli:
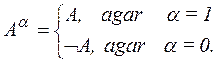
Tasdiq 1. ![]() bo’ladi, faqat va faqat A=
bo’ladi, faqat va faqat A=![]() bo’lsa.
bo’lsa.
Isbot qilish uchun rostlik jadvalini tuzish yetarli:
|
A |
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
172 Bob III. Matematik mantiq asoslari
Barcha mulohazalarni tadqiq qilish oson bo’lishi uchun mantiqiy qonunlar yordamida ularni biror umumiy standart ko’rinishga keltirish mumkin. Masalan, har qanday Bul algebrasi formulasi uchun unga teng kuchli bo‘lgan va faqatgina inkor ⌐, kon’yunksiya & va diz’yunksiya \/ amallarini o‘z ichiga olgan formulani yozish mumkin. Buning uchun implikasiya va ekvivalentlikdan qutilish qonunlaridan foydalanish yetarli.
Ta’rif 2. A1, A2, …, An mulohaza o‘zgaruvchilarning yoki ularni inkorlarining kon’yunksiyasi kon’yunktiv birhad deyiladi.
Misol. ⌐A1&A2&A3, ⌐A1&A2&A3&⌐A4, A&B, ⌐A&B, A&⌐C;
⌐(A&C) – kon`yunktiv birhad bo’la olmaydi, chunki agar qavs ochilsa, kon`yunktsiya amali diz`yunktsiya amaliga aylanib qoladi.
Ta’rif 3. A1, A2, …, An mulohaza o‘zgaruvchilarning yoki ularni inkorlarining diz’yunksiyasi diz’yunktiv birhad deyiladi.
Misol. ⌐A1\/A2\/A3
, ![]() .
.
Ta’rif 4. Kon’yunktiv birhadlarning diz’yunksiyaga diz’yunktiv normal shakl (DNSh) deyiladi.
Misol. ⌐A1&A2&A3 \/ ⌐A1&A2&A3&⌐A4 , A&B\/ ⌐A&B\/A&⌐C;
Ta’rif 5. Dizyunktiv birhadlarning kon’yunksiyasiga kon’yunktiv normal shakl (KNSh) deyiladi.
Misol. (⌐A1\/A2\/A3 )&(A1\/⌐A2\/⌐A3) .
Har bir formulaning cheksiz ko‘p KNSh, DNSh lari mavjud.
3.3. MDNSh va MKNSh 173
3.3.2. Mukammal normal shakllar
Ta’rif 1. Agar birhadda Ai yoki ⌐Ai formulalar juftligidan faqat bittasi qatnashgan bo‘lsa, A1, A2, …, An mulohaza o‘zgaruvchilarining kon’yunktiv yoki diz’yunktiv birhadlari mukammal deyiladi.
Ta‘rif 2. Agar kon’yunktiv normal shaklda A1,A2,…,An mulohaza o‘zgaruvchilarning takrorlanmaydigan mukammal diz’yunktiv birhadlari qatnashgan bo‘lsa, u holda mukammal kon’yunktiv normal shakl (MKNSh) deyiladi.
Ta‘rif 3. Agar diz’yunktiv normal shaklda A1,A2,…,An mulohaza o‘zgaruvchilarning takrorlanmaydigan mukammal kon’yunktiv birhadlari qatnashgan bo‘lsa, u holda mukammal diz’yunktiv normal shakl (MDNSh) deyiladi.
Misol 1. A&B\/⌐A&B\/A&⌐B – MDNSh;
(⌐A1\/A2\/A3 )&(A1\/⌐A2\/⌐A3) – MKNSh bo‘ladi.
Misol 2. ![]() formulani DNSh ga keltiramiz.
formulani DNSh ga keltiramiz.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() –
MDNSh.
–
MDNSh.
174 Bob III. Matematik mantiq asoslari
Misol 3. ![]() formulani MDNSh ga keltiramiz.
formulani MDNSh ga keltiramiz.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – mDNSh.
– mDNSh.
Xuddi shuningdek, ixtiyoriy formulani MKNSh ga keltirish mumkin.
Nazorat uchun savollar:
1. Kon’yunktiv birhad deb nimaga aytiladi?
2. Diz’yunktiv birhad ta’rifini ayting.
3. Diz’yunktiv normal shakl deb nimaga aytiladi?
4. Kon’yunktiv normal shakl ta’rifini bering.
5. Mukammal kon’yunktiv (diz’yunktiv) birhad deganda nimani tushunasiz?
6. Mukammal kon’yunktiv normal shaklga ta’rif bering.
7. Mukammal diz’yunktiv normal shakl ta’rifini ayting.
3.3. MDNSh va MKNSh 175
Mustaqil yechish uchun masalalar:
Quyidagi formulalarni MDNSh va MKNShga keltiring:
1. α(x,y,z)=(xÅy&z)→xÚz
2. α(x,y,z)=(x½y)→(Øz&yÅx)
3. α(x,y,z)=(x→Øy)Å(zÚx)
4. α(x,y,z)=(xÚy)Å(Øz~y)
5. α(x,y,z)=((x¯y)&Øz)→x½((ØyÅØz)~Ø(xÚz)
6. α(x,y,z)=(x&yÚØy)&(x→z)
7. α(x,y,z)=(xÚz &ØyÚØx&Øy&Øz)&x&Øy
8. α(x,y,z)=(x→z)&(y→x)
9. α(x,y,z)=((x¯y)½z)½x)¯y
10. α(x,y,z)=((x→y)Å(x→y&z))Ú(x¯y)
11. α(x,y,z)=(x→y)Å((y→Øz)→x&y)
12. α(x,y,z)=(xÚØy)¯(Øx→(y→z))
13. α(x,y,z)=x→((y→z)→y&z)
14. α(x,y,z)=(xÚ(y→z))&(xÅy)
15. α(x,y,z)=Ø(x¯y)Ú(x~z))½(xÅy&z)
16. α(x,y,z)=(ØxÚy)&((y½Øz)→(x~x&z))
17. α(x,y,z)=(x½Øy)&((y¯Øz)→(xÅz))
18. α(x,y,z)=x&((y&z)Å(Øx→z))
19. α(x,y,z)=(((x½y)¯Øz)½y)&(Øy→z)
20. α(x,y,z)=((x½y)¯(y½Øz))Ú(xÅ(y→z))
21. α(x,y,z)=(x&y→z)&((x¯y)½z)
22. α(x,y,z)=(x~y)¯(xÚx&yÚØy&zÚØ(x&y&z))
176 Bob III. Matematik mantiq asoslari
3.3.3. Rostlik jadvali bo‘yicha mantiq funksiyasi ko‘rinishini tiklash.
Biz shu paytgacha berilgan formula uchun rostlik jadvallarini tuzishni qarab chiqdik. Savol tug’iladi: Aksincha, rostlik jadvali berilgan bo‘lsa, mantiq funksiyasini tiklash mumkinmi?
Aytaylik, bizga A, B, C mulohaza o’zgaruvchilariga bo‘liq bo‘lgan α=α(A,B,C) formula berilgan bo‘lsin.
|
A |
B |
C |
α=α(A,B,C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Ushbu rostlik jadvaliga ega bo‘lgan cheksiz ko‘p teng kuchli formulalar mavjud. Ulardan ikkitasini, ya`ni rostlik jadvalidagi birlar qatori bo’yicha va rostlik jadvalidagi nollar qatori bo’yicha mantiq funksiyasi ko‘rinishini tiklashni ko‘rib chiqamiz,
3.3. MDNSh va MKNSh 177
1) Rostlik jadvalida α=α(A,B,C) formula 1 ga teng bo‘lgan qator raqamlarini yozib chiqamiz.
2-qator
3-qator
6-qator
8-qator
Har bir qatorning mantiqiy imkoniyatlaridagina 1 ga teng bo‘lgan, boshqa imkoniyatlarda esa 0 ga teng bo‘lgan formulalarni yozib chiqamiz. Buning uchun 1 ga teng bo‘lgan qatordagi mulohazalar qiymatlarini rostga aylantirib, mantiq qonunlariga asosan mulohazalar kon’yunksiyalarini olish kerak.
2-qator uchun: ⌐A&⌐B&C;
3- qator uchun: ⌐A&B&⌐C;
6-qator uchun: A&⌐B&C;
8-qator uchun: A&B&C
bo‘ladi. Agar 2-,3-,6-,8-qatorlar bo‘yicha olingan formulalar diz’yunksiyalari olinsa, hosil bo‘lgan formula izlanayotgan formula bo‘ladi:
α=α(A,B,C)=⌐A&⌐B&C\/⌐A&B&⌐C\/A&⌐B&C\/A&B&C (1)
2) Rostlik jadvalida α=α(A,B,C) formula 0 ga teng bo‘lgan qator nomerlarini yozib chiqamiz: 1-qator
4-qator
5-qator
7-qator
178 Bob III. Matematik mantiq asoslari
Har bir qator mantiqiy imkoniyatlaridagina 0 ga teng bo‘lgan, boshqa imkoniyatlarda esa 1 ga teng bo‘lgan formulalarni yozib chiqamiz. Buning uchun 0 ga teng bo‘lgan qatordagi fikr o‘zgaruvchilari qiymatlarini 0(yolg‘on) ga aylantirib, fikr o‘zgaruvchilari diz’yumksiyasini olish lozim. U holda
1-qator uchun: A\/B\/C;
4-qator uchun: A\/⌐B\/⌐C;
5-qator uchun: ⌐A\/B\/C;
7-qator uchun: ⌐A\/⌐B\/C
bo‘ladi.
Agar qatorlar bo‘yicha olingan formulalar kon’yunksiyasi olinsa, hosil bo‘lgan formula izlanayotgan formula bo‘ladi.
α=α(A,B,C)=(A\/B\/C)&(A\/⌐B\/⌐C)&(⌐A\/B\/C)&(⌐A\/⌐B\/C) (2)
(1) - MDNSh va (2) - MKNShlar teng kuchli, chunki ularning rostlik jadvallari bir xil. Shuning uchun ham ulardan qaysi birini tuzish kamroq vaqt talab qilsa, shu ko’rinishini tiklash maqsadga muvofiq.
Rostlik jadvali berilgan ixtiyoriy formulani yuqoridagi uslubda qurish mumkin.
Teorema 1. Har bir ayniy yolg‘on bo‘lmagan formula yagona mukammal diz’yunktiv normal shaklga ega.
Teorema 2. Har bir tavtologiya bo‘lmagan formula yagona mukammal kon’yunktiv normal shaklga ega.
3.3. MDNSh va MKNSh 179
Nazorat uchun savollar:
1. Mantiq formulasi ko‘rinishi 0 ga teng qiymatlari bo‘yicha qanday tiklanadi?
2. Mantiq formulasi ko‘rinishi 1 ga teng qiymatlari bo‘yicha qanday tiklanadi?
3. Tavtologiya va ziddiyat formulalari uchun MKNSh va MDNSh haqidagi teoremalarni ayting.
Mustaqil yechish uchun masalalar:
Quyidagi rostlik jadvali berilgan mantiq funksiyalarining formulasini tiklang:
|
A |
B |
C |
α1 |
α2 |
α3 |
α4 |
α5 |
α6 |
α7 |
α8 |
α9 |
α10 |
α11 |
α12 |
α13 |
α14 |
α15 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
180 Bob III. Matematik mantiq asoslari
3.3.4. Jegalkin polinomi.
Ta’rif 1. Mantiqiy formulaning kon’yunktsiya va simmetrik ayirma amallari bilan ifodalangan shakliga Jegalkin polinomi (ko’phadi) deyiladi.
Mantiqiy formulani Bul ifodasidan Jegalkin polinomi ko’rinishiga keltirish uchun 4 ta bosqich amalga oshiriladi:
1-bosqich: Berilgan formulani DNSh ga keltirish;
2-bosqich: Quyidagi formuladan foydalanib, diz’yunktsiya amalidan qutilish kerak:
![]() ;
;
3-bosqich: Inkor amalini simmetrik ayirma amali bilan almashtirish:
![]()
4-bosqich: Hosil bo’lgan ifodani soddalashtirish, bunda
![]()
tenglikdan foydalaniladi.
Misol. ![]()
![]() .
.
3.3. MDNSh va MKNSh 181
Ta’rif 2. O’zgaruvchilarida inkor qatnashmagan kon’yunktsiyaga monoton kon’yunktsiya deyiladi.
Ko’yunktsiya amali bilan birlashtirilgan o’zgaruvchilar soniga polinom rangi deyiladi.
Ta’rif 3. Polinomda qatnashgan hadlarning eng katta rangi Jegalkin ko’phadi darajasi deyiladi.
Nazorat uchun savollar:
1. Jegalkin polinomi ta’rifini ayting. Misol keltiring.
2. Jegalkin ko’phadi darajasi deganda nimani tushunasiz?
3. Bul ko’phadlari bilan Jegalkin ko’phadining farqi nimada?
Mustaqil yechish uchun masalalar:
Quyidagi Bul formulalarini Jegalkin polinomiga o’tkazing:
1. α(A,B,C)= ØA&BÚØ(AÚC)
2. α (A,B,C)=C→(ØAÚØB)
3. α (A,B,C)=A&B→Ø(AÚØB)
4. α (A,B,C)=(A&B&ØC)~(ØAÚ B)
5. α (A,B,C)=(ØAÚØC)~B
6. α (A,B,C)=(A→B)→ØC
182 Bob III. Matematik mantiq asoslari
7. α (A,B,C)=(ØA→ØB)&(B→C)
8. α (A,B,C)=A&(B→C)ÚØB
9. α (A,B,C)=Ø(A&BÚC)
10. α(A,B,C)=(A~B)&(ØB~ØC)
11. α(A,B,C)=(ØA→ØC)~B
12. α (A,B,C)=A→(ØBÚØC)
13. α(A,B,C)=(ØA→B)&(ØB→A)&ØC
14. α(A,B,C)=CÚA&ØB
15. α(A,B,C)=A&(ØA&BÚC)&(AÚØC)
16. α(A,B,C)=(ØAÚB)&(ØBÚA&C)
17. α(A,B,C)=A&(B~A)&(ØAÚØC)
18. α(A,B,C)=(A→B)&A&ØC
19. α(A,B,C)=(ØA&B)→(C&A)
20. α(A,B,C)=(A&B~C)&A&ØC
21. α(A,B,C)=(A&BÚØA&ØB)&(C→B)
22. α(A,B,C)=(AÚB &ØCÚØA&ØB&C)&A&ØB
23. α(A,B,C)=(A→B)&(C→A)
24. α(A,B,C)=(A&ØB&CÚØA&ØC)&B
25. α(A,B,C)=(AÅB&C)→AÚC
3.4. Rele kontakt sxemalari 183
3.4. RELE KONTAKT SXEMALARI
3.4.1. Ikkilik mantiqiy elementlar.
Bul ifodalari Djorj Bul (1815-1864 yy) tomonidan rivojlantirilib, XX asrning 30-yillarida raqamli mantiqiy sxemalarda qo‘llanilgan edi.
Raqamli elektron qurilmalarni tuzish bilan shug‘ullanuvchi mutaxassislar Bul algebrasi masalalarini chuqur o‘rganishlari kerak bo’ladi. Bul algebrasi funktsiyalarining asosiy tadbiqlaridan biri bu funktsional elementlar sxemasini qurishdir. Bunga misol qilib, EVM, mikrokal’kulyator va boshqa raqamli elektron qurilmalarning ishlash printsipini ko’rsatishimiz mumkin.
Har qanday raqamli sxemalarning asosiy tarkibiy qismini mantiqiy elementlar tashkil etadi.
Agar C zanjirdan tok o’tayotgan bo’lsa, u holda Ñ=1 deb;
agar Ñ zanjirdan tok o’tmasa, u holda Ñ=0 deb yozishimiz mumkin.
Demak, mantiqiy elementlar ikkita raqam, 0 va 1 raqamlari bilan ish ko’radi, shuning uchun ham ikkilik mantiqiy elementlar deyiladi.
Raqamli elektrotexnika sohasida ishlaydigan mutaxassislar ikkilik mantiqiy elementlarga bilan har kuni ro’para kelishadi. Mantiqiy elementlarni oddiy o‘chirib-yoqgichlarda, releda, vakuum lampa, tranzistorlar, diodlar yoki integral sxemalarda yig‘ish mumkin. Integral
184 Bob III. Matematik mantiq asoslari
sxemalarning keng qo‘llanilishi va arzonligini hisobga olsak, raqamli
qurilmalarni faqat integral sxemalarning o‘zidan yig‘ish maqsadga muvofiq. Asosiy mantiqiy elementlar 7 xil: “va”, “yoki”, “emas”,“va-emas”, “yoki-emas”, “birortasi, lekin hammasi emas”, “birortasi, lekin hammasi emasga yo’l qo’ymaydigan”.
Mantiqiy elementlar u yoki bu vazifani bajarganligi sababli ularni funktsional elementlar deyiladi. Funktsional elementlarni bir-biriga ulash natijasida funktsional sxemalar hosil qilinadi.
1. “Va” mantiqiy elementi.
“Va” mantiqiy elementini ba’zan “hammasi yoki hech narsa” elementi deb ham yuritiladi. Mexanik o‘chirib-yoqgich orqali “va” mantiqiy elementining ishlash printsipini ko‘rib chiqamiz.
Agar zanjirda A va B kalitlar ketma-ket ulangan bo‘lsa, u holda C zanjirda L1 lampa yonishi uchun A va B kalitlarning ikkalasi ham yopilishi kerak, ya’ni À=1 va Â=1 bo’lishi kerak. Kon’yunktsiya xuddi shu xossalarga ega. Demak, “va” mantiqiy elementining ishlash printsipi kon’yunktsiya bilan bir xilda ekan.

3.4. Rele kontakt sxemalari 185
“Va” mantiqiy elementining sxematik tasvirida ikkita kirish, bitta chiqish bo’lib, u quyidagicha:
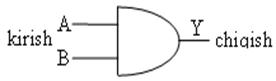
“Mantiqiy” terminidan odatda biror bir qarorni qabul qilish jarayonida foydalaniladi. Shuning uchun ham mantiqiy elementni shunday sxema deyish mumkinki, unda kirish signallariga asoslanib, chiqishda “ha” yoki “yo‘q” deyish hal qilinadi. Yuqorida ko‘rganimizdek, lampa yonishi uchun uning ikkala kirish joyida “ha” signali (kalitlar yopilishi kerak) berilishi kerak.
Rostlik jadvali “va” mantiqiy elementining ishlashi haqida to‘liq ma’lumot beradi:
|
A |
B |
Y=A&B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
“Va” mantiqiy elementi uchun kiritilgan belgilash A va B kirish signallari “va” mantiqiy funktsiyasi bilan bog‘langan bo‘lib, chiqishda Y
186 Bob III. Matematik mantiq asoslari
signal paydo bo‘ladi” deb o‘qiladi. Ushbu tasdiqning qisqartirilgan ifodasi Bul ifodasi (A&B) deyiladi. Bul ifodasi – universal til bo‘lib, injenerlar va texnik xodimlar tomonidan raqamli texnikada keng qo‘llaniladi.
2. “Yoki” mantiqiy elementi
“Yoki” mantiqiy elementini ba’zan “hech bo‘lmasa birortasi yoki hammasi” deb ham yuritiladi. Oddiy o‘chirib-yoqgichlar yordamida “yoki” mantiqiy elementining ishlash printsipini quyidagicha tushuntirish mumkin:
C zanjirda A va B kalitlar parallel ulangan bo‘lsa, “yoki” mantiqiy elementi ishlaydi:
Chizmadan ko’rinadiki, kalitlarning hech bo‘lmaganda bittasini yoki ikkalasini ham yopganda L1 lampa yonadi.
“Yoki” mantiqiy elementi sxematik ko’rinishi quyidagicha:
![]()

![]() .
.
3.4. Rele kontakt sxemalari 187
Bul ifodasi ![]() ( yoki A+B=Y ) ko‘rinishda
bo‘1adi.
( yoki A+B=Y ) ko‘rinishda
bo‘1adi.
“Yoki” mantiqiy elementining rostlik jadvali uning ishlashi haqida to‘liq ma’lumot beradi:
|
A |
B |
A\/B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
3. “Emas” mantiqiy elementi
“Va” hamda “yoki” mantiqiy elementlari ikkita kirish va bitta chiqishga ega edi. “Emas” sxemasida esa bitta kirish va bitta chiqish mavjud. “Emas” mantiqiy elementini invertor deb ham yuritiladi. Uning asosiy vazifasi chiqishda kirish signaliga teskari bo‘lgan signalni ta’minlashdan iborat.
Invertor quyidagicha belgilanadi:

Bul ifodasi ![]() ko‘rinishda bo‘1adi.
ko‘rinishda bo‘1adi.
188 Bob III. Matematik mantiq asoslari
“Emas” mantiqiy elementi uchun rostlik jadvali:
|
A |
¬A |
|
1 |
0 |
|
0 |
1 |
4. “Va-emas” mantiqiy elementi
“Va-emas” mantiqiy elementini Sheffer shtrixi deb ham yuritiladi, u inventorlangan “va”ni amalga oshiradi. Ushbu mantiqiy amal quyidagicha belgilanadi:
Bu belgini quyidagicha yoyib ham yozish mumkin.

“Va-emas” mantiqiy elementining Bul ifodasi ![]() ko‘rinishda bo‘ladi.
ko‘rinishda bo‘ladi.
3.4. Rele kontakt sxemalari 189
Va-emas” mantiqiy elementining rostlik jadvali yordamida ishlash printsipini ko’rish mumkin:
|
A |
B |
A&B |
Y= |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
5. “Yoki-emas” mantiqiy elementi
“Yoki-emas” mantiqiy elementini Pirs strelkasi deb ham yuritiladi, u inventorlangan “yoki”ni amalga oshiradi, sxematik ko’rinishi quyidagicha:

Bu belgini quyidagicha yoyib ham yozish mumkin:

190 Bob III. Matematik mantiq asoslari
“Yoki-emas” mantiqiy elementining rostlik jadvali yordamida uning ishlash printsipini ko’rish mumkin:
|
A |
B |
A\/B |
Y= |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
6. “Birortasi, lekin hammasi emas”
Ushbu mantiqiy elementning Bul ifodasi:
AÅB = Ø(A~B)
Uning sxematik ko’rinishi quyidagicha:

“Birortasi, lekin hammasi emas” mantiqiy elementining ishlash printsipi quyidagicha:
|
A |
B |
AÅB |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
3.4. Rele kontakt sxemalari 191
7. “Birortasi, lekin hammasi emasga yo’l qo’ymaydigan”
Mantiqiy elementning Bul ifodasi: Ø(AÅB) =A~B
Uning sxematik ko’rinishi quyidagicha:
“Birortasi, lekin hammasi emasga yo’l qo’ymaydigan” mantiqiy elementining ishlash printsipi quyidagicha:
|
A |
B |
AÅB |
Ø(AÅB) =A~B |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
Ikkitadan ortiq kirishga ega bo‘lgan mantiqiy elementlar uchun ham mos ravishda quyidagicha belgilashlar ishlatiladi.
3 ta kirishga ega “va” mantiqiy elementi:
192 Bob III. Matematik mantiq asoslari
3 ta kirishga ega bo’lgan “yoki” mantiqiy elementining sxematik ko’rinishi quyidagicha:
3.4.2. Ikkilik mantiqiy elementlarining qo‘llanilishi.
Mantiqiy elementlarning shartli belgilanishi, rostlik jadvallari va Bul ifodalari elektrotexnika sohasidagi real masalalarni yechishda juda qo‘l keladi. Har qanday fikrlar algebrasi formulasini “inkor - ¬”, “va - &”, “yoki – V” amallari orqali yozish mumkin, buning uchun “implikatsiya - →”, “ekvivalentlik - ~” dan qutilish qoidalarini qo‘llash yetarli.
¬, & va V amallaridan iborat formulaga mos paralel va ketma-ket ulash qoidalariga asoslangan sxemalar tuzish mumkin va aksincha, ixtiyoriy raqamli sxemaga mos ¬, & va V amallaridan foydalanib, Bul formulasini tuzish mumkin.
Agar biror bir murakkab sxema berilgan bo‘lsa, unga mos formulani yoyib, mantiq qonunlariga asosan soddalashtirib, soddalashgan formulaga mos sxemani qayta tuzilsa, hosil bo‘lgan soddalashgan sxema boshlang‘ich sxemaning vazifasini bajaradi. Bu amaliyotga minimallashtirish deyiladi.
3.4. Rele kontakt sxemalari 193
Misol. Ushbu ![]() formulaga mos sxema:
formulaga mos sxema:
 Yuqoridagi
sxemani mantiq
qonunlari yordamida soddalashtirib, tuzilgan sxema
Yuqoridagi
sxemani mantiq
qonunlari yordamida soddalashtirib, tuzilgan sxema
Ikkala sxema ham bir xil vazifani bajaradi, chunki ularning rostlik jadvallari bir xil.
3.4.3. Mantiqiy sxemalarda analiz va sintez masalalari.
Sintez. Mantiqiy sxemalarning sintezi masalasi quyidagi 3 ta bosqichdan iborat:
1) berilgan fizikaviy ma`lumotlar bo’yicha biror matematik ifoda (tenglama, formula) tuziladi va minimallashtiriladi;
2) minimallashtirilgan matematik ifodaning qandaydir funktsiyani bajaruvchi sxemasi chiziladi;
194 Bob III. Matematik mantiq asoslari
3) hosil qilingan sxema biror vazifani bajaruvchi haqiqiy sxemaga aylantiriladi.
Analiz. Analiz masalasi – bu ikkinchi bosqichning teskarisi hisoblanadi, ya`ni berilgan mantiqiy sxema bo’yicha matematik ifodani tuzish va tadqiq qilish.
Bizni bu uchta bosqichdan ikkinchisi ko’proq qiziqtiradi. Shuning uchun har doim sintez masalasini yechishda biror mantiqiy α=α(A1,A2,…,An) funktsiya berilgan bo’ladi, maqsad chiqishda berilgan mantiqiy funktsiya α ning vazifasini bajaruvchi mantiqiy zanjir sxemasini tuzishdan iborat.
Bundan keyin mantiqiy zanjir sxemasi deganda „va“, „yoki“, „emas“ Bul algebrasi bazislari orqali hosil qilingan sxemani tushunamiz.
Misol. (Sintez) Talabalarga 3 kishi yashirin ovoz berganda ko’pchilik ovoz bilan qaror qabul qiladigan sxemani tuzish vazifasi yuklatilgan bo’lsin. Chiqarilgan qarorga ovoz beruvchilar rozi bo’lishsa,
o’zlariga tegishli tugmachani bosishadi, aks holda tugmachalarga tegishmaydi. Agar ko’pchilik, ya`ni kamida ikki kishi „ha“ deb ovoz berib, o’zlariga tegishli tugmachalarni bosganda signal chirog’i yonishi kerak.
Hayotiy masalani mantiqiy ko’rinishga o’tkazish maqsadida ovoz beruvchilarni A, B, C mulohaza o’zgaruvchilari deb olamiz, u holda
3.4. Rele kontakt sxemalari 195
A,B, C, mulohaza o’zgaruvchilari 2 xil qiymat qabul qilishi mumkin: ha
deb ovoz berishganda – 1, yo’q deb ovoz berishganda esa – 0 qiymat, betaraf bo’lgan holni inobatga olmaymiz. U holda berilgan masalaning rostlik jadvali quyidagi ko’rinishda bo’ladi.
|
A |
B |
C |
α=α(A,B,C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Ushbu rostlik jadvalining birlar qatori bo’yicha MDNSh dagi formulasi quyidagicha bo‘ladi:
α(A, B, C)= ⌐A&B&C\/A&⌐B&C\/A&B&⌐C\/A&B&C
Yuqoridagi formulaga mos sxema esa quyidagicha bo‘ladi:
196 Bob III. Matematik mantiq asoslari
3 ta invertor, 4 ta uchtadan kirishga ega bo‘lgan “va”, 1 ta to‘rtta kirishga ega bo‘lgan “yoki”, jami 8 ta elementdan iborat sxema hosil bo‘ladi.
Yuqoridagi formulani mantiq qonunlariga ko‘ra soddalashtiramiz:
α(A,B,C)= ⌐A&B&C\/A&⌐B&C\/A&B&⌐C\/A&B&C=
=A&B&(⌐C\/C)\/C&(⌐A&B\/A&⌐B)=
=A&B\/C)&(A&B\/⌐A&B\/A&⌐B)=(A&B\/C)&(B\/A&⌐B)=
=(A\/B)&(A&B\/C)
Minimallashtirilgan formulaga mos sxema quyidagi ko‘rinishda bo‘ladi.
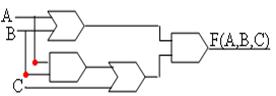
3.4. Rele kontakt sxemalari 197
Ikkala sxema ham bir xil vazifani bajaradi, chunki ularga mos formulalarning rostlik jadvali bir xil, lekin soddalashgan sxema ikki baravar kam elementdan iborat bo‘lsa-da, qiymat jihatdan undan ham ko‘proq sarf xarajatni talab qiladi.
Nazorat uchun savollar:
1. Nima uchun mantiqiy elementlarga ikkilik mantiqiy elementlar
deyiladi?
2. Bul ifodalari qachondan boshlab raqamli elektron sxemalarda
qo’llanila boshlandi?
3. Asosiy mantiqiy elementlarni sanab bering.
4. “Va” mantiqiy elementining ishlash printsipini tushuntiring.
5. “Yoki” mantiqiy elementi qachon ishlaydi?
6. Invertorning ishlash printsipini tushuntiring.
7. “Va-emas” ikkilik mantiqiy elementi qanday ishlaydi?
8. “Yoki-emas” ikkilik mantiqiy elementining ishlash printsipini
tushuntiring.
9. Minimallashtirish masalasi deganda nimani tushunasiz?
10. Ikkitadan ortiq kirishga ega bo‘lgan mantiqiy elementlar uchun
qanday belgilashlar ishlatiladi?
11. Mantiqiy sxemalar sintezini tushuntiring.
12. Mantiqiy sxemalarda analiz deganda nimani tushunasiz?
198 Bob III. Matematik mantiq asoslari
Mustaqil yechish uchun masalalar:
Quyidagi mantiq algebrasi formulalar uchun mantiqiy sxemalar tuzing:
1. ![]() (A,B,C)=(A&B&ØC)~(ØAÚ
B)
(A,B,C)=(A&B&ØC)~(ØAÚ
B)
2. ![]() (A,B,C)=(ØAÚØC)~B
(A,B,C)=(ØAÚØC)~B
3. ![]() (A,B,C)=(A→B)→ØC
(A,B,C)=(A→B)→ØC
4. ![]() (A,B,C)=(ØA→ØB)&(B→C)
(A,B,C)=(ØA→ØB)&(B→C)
5. ![]() (A,B,C)=A&(B→C)ÚØB
(A,B,C)=A&(B→C)ÚØB
6. ![]() (A,B,C)=Ø(A&BÚC)&(ØB~ØC)
(A,B,C)=Ø(A&BÚC)&(ØB~ØC)
7. ![]() (A,B,C)=(A~B)&(ØB~ØC)
(A,B,C)=(A~B)&(ØB~ØC)
8. ![]() (A,B,C)=(AÅB&C)→AÚC
(A,B,C)=(AÅB&C)→AÚC
9. ![]() (A,B,C)=((A→B)Å(A→B&C))Ú(A¯B)
(A,B,C)=((A→B)Å(A→B&C))Ú(A¯B)
10. ![]() (A,B,C)=(A→B)Å((B→ØC)→A&B)
(A,B,C)=(A→B)Å((B→ØC)→A&B)
11. ![]() (A,B,C)=(AÚØB)¯(ØA→(B→C))
(A,B,C)=(AÚØB)¯(ØA→(B→C))
12. α(A,B,C)=(ØA&B)→(C&A)
13. α(A,B,C)=(A&B~C)&A&ØC
14. α(A,B,C)=(A&BÚØA&ØB)&(C→B)
15. α(A,B,C)=(AÚB &ØCÚØA&ØB&C)&A&ØB
16. α(A,B,C)=(A→B)&(C→A)
17. α(A,B,C)=(AÅCÚØA&ØC)&B
18. ![]() (A,B,C)=(A&B)
Ú
((B→ØC)→A&B)
(A,B,C)=(A&B)
Ú
((B→ØC)→A&B)
19. ![]() (A,B,C)=(AÚØB)
Ú
(A→(B→C))
(A,B,C)=(AÚØB)
Ú
(A→(B→C))
20. ![]() (A,B,C)=A&(B→C)
&B
(A,B,C)=A&(B→C)
&B
3.4. Rele kontakt sxemalari 199
3.4.4. Minimallashtirishning jadval (grafik) usullari.
Mukammal diz’yunktiv normal shakllarni minimallashtirishda Bul ifodalarida bir-biriga qo’shni hadlarni topish va bu hadlarni birlashtirish katta mehnat talab qiladi. Bu esa soddalashtirishda analitik usulning kamchiligi hisoblanadi.
Amaliyotda mantiq funktsiyalarini minimallashtirish uchun mantiqiy o’zgaruvchilar soni kamroq bo’lsa, jadval usuli birmuncha qulay hisoblanadi. Jadval usulining ustunligi:
1) birlashtiriladigan hadlarni izlash oson;
2) topilgan hadlarni birlashtirish oson;
3) funktsiyaning barcha minimal shakllarini topish mumkin.
Jadval usullari quyidagilar: Karno kartalari, Veych, Venn diagrammalari, yechimlar daraxti hisoblanadi. Ushbu mavzuda biz Karno kartalari metodi bilan tanishamiz.
1953 yil Moris Karno Bul ifodalarini soddalashtirish va grafik tasvirlash tizimini ishlab chiqqanligi haqida maqola e’lon qildi. Hozirda bu metod Karno kartalari metodi deb yuritiladi. Karno kartalarining quyidagi turlarini ko’rib chiqamiz:
1. Ikki o‘zgaruvchili Karno kartasi.
Aytaylik, Bul ifodasi ikkita mulohaza o’zgaruvchisidan tashkil topgan bo’lsin va quyidagi rostlik jadvali bilan berilgan bo’lsin. U holda ikki o‘zgaruvchili Karno kartasi quyidagicha bo’ladi:
200 Bob III. Matematik mantiq asoslari

Agar F(A,B) formula MDNSh da berilgan bo’lsa, u holda
¹1 o’ringa ØA&ØB
¹2 o’ringa ØA&B
¹3 o’ringa A&ØB
¹4 o’ringa A&B
hadlar mos kelib, shunday hadlar F(A,B) formulada mavjud bo’lsa, Karno kartasida bu hadlarga mos o’rinlarga 1, qolgan o’rinlarga 0 raqami yoziladi.
Ikki o‘zgaruvchili Karno kartasi to’ldirilgandan keyin 2 ning darajalaricha birlarni o’z ichiga oladigan (20, 21, 22, 23, …) konturlar chiziladi. Bu konturlar gorizontaliga yoki vertikaliga bir-biriga qo’shni bo’lgan birlarni o’z ichiga olishi kerak. Konturga olish jarayoni barcha birlar kontur ichida ichida qolguncha davom ettiriladi va konturlar iloji boricha maksimal ikkining darajalaricha birlarni o’z ichiga olishi kerak.
3.4. Rele kontakt sxemalari 201
Konturga olish jarayoni tugagandan keyin har bir kontur ichida qatnashgan bir-biriga teskari bo’lgan fikr o’zgaruvchilari tushirib qoldiriladi va har bir konturda qolgan o’zgaruvchilarning diz’yunktsiyasi olinadi. Hosil bo’lgan ifoda Karno kartasi bo’yicha minimallashgan ifoda bo’lib, undan ortiq minimallashtirish mumkin emas.
Misol 1. Quyidagi rostlik jadvali bilan berilgan ifodani soddalashtiring:
|
A |
B |
F(A,B) |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
|
|
ØB |
B |
|
ØA |
1 |
0 |
|
A |
1 |
1 |
Ifodaning to’liq ko’rinishi: F(A,B)=ØA&ØBÚA&ØBÚA&B
minimal ko’rinishi esa: F(A,B)= AÚØB
Misol2. (A,B)=ØA&BÚA&ØBÚA&B formulaga mos Karno kartasi quyidagi ko’rinishni oladi, ya’ni karta MDNSh bo’yicha tuziladi:
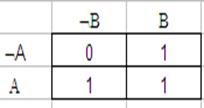
202 Bob III. Matematik mantiq asoslari
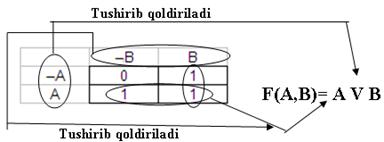
Yuqorida keltirilgan sxemaga muvofiq gorizontaliga, vertikaliga bir-biriga qo‘shni bo‘lgan birlar konturlarga birlashtiriladi. Har bir konturda qatnashgan bir-birini to‘ldiruvchi o‘zgaruvchilar tushirib qoldiriladi, har bir konturdan qolgan o‘zgaruvchilarning diz’yunksiyasi olinadi. Natijada formula quyidagi ko‘rinishni oladi: F(A, B)= AÚB.
2. Uch o‘zgaruvchili Karno kartalari
|
À |
 |
Ñ |
F(A, B, C) |
|
0 |
0 |
0 |
¹1 |
|
0 |
0 |
1 |
¹2 |
|
0 |
1 |
0 |
¹3 |
|
0 |
1 |
1 |
¹4 |
|
1 |
0 |
0 |
¹5 |
|
1 |
0 |
1 |
¹6 |
|
1 |
1 |
0 |
¹7 |
|
1 |
1 |
1 |
¹8 |
Aytaylik, Bul ifodasi uchta mulohaza o’zgaruvchisidan tashkil topgan bo’lsin va quyidagi rostlik jadvali bilan berilgan bo’lsin. U holda
uch o‘zgaruvchili Karno kartasi
quyidagicha bo’ladi:
|
|
ØC |
C |
|
ØA&ØB |
¹1 |
¹2 |
|
ØA&B |
¹3 |
¹4 |
|
A&B |
¹7 |
¹8 |
|
A&ØB |
¹5 |
¹6 |
3.4. Rele kontakt sxemalari 203
Uch o‘zgaruvchili Karno kartalarida ham ikki o‘zgaruvchili Karno kartalaridagidek gorizontaliga, vertikaliga bir-biriga qo‘shni bo‘lgan birlar konturlarga birlashtiriladi. Har bir kontur iloji boricha ko‘proq ikkini darajalaricha birlarni (21, 22, 23,…) o‘z ichiga olishi va kontur olish jarayoni barcha birlar kontur ichida qolguncha davom ettirilishi lozim. Har bir kontur soddalashtirilgan Bul ifodasining yangi a’zosini bildiradi. Har bir konturda qatnashgan bir-birini to‘ldiruvchi o‘zgaruvchilar tushirib qoldiriladi, har bir konturdan qolgan o‘zgaruvchilarning diz’yunksiyasi olinadi. Bundan tashqari uch o‘zgaruvchili Karno kartalarida 1- va 4-qatorlar bir-biriga qo‘shni hisoblanadi, chunki karta gorizontaliga o‘ralganda 1- va 4- qatorlar bir-biriga qo‘shni bo‘lib qoladi.
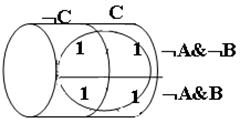
F(A,B,C) formula quyidagicha rostlik jadvali bilan berilgan bo‘lsin:
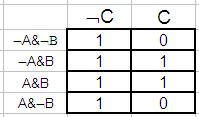
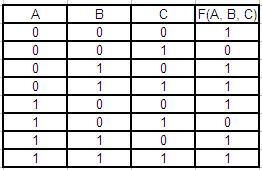
204 Bob III. Matematik mantiq asoslari
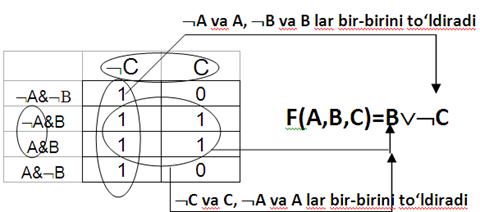
3. To‘rt o‘zgaruvchili Karno kartalari
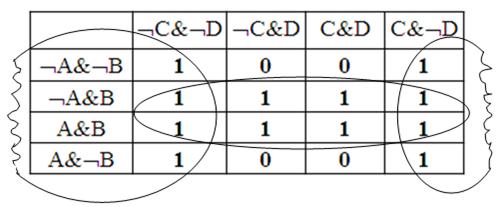 To‘rt o‘zgaruvchili
Karno kartalarida ikki va uch o’zgaruvchili Karno kartalaridagi usullar
qo‘llaniladi. Faqatgina to‘rt o‘zgaruvchili Karno kartalarida birinchi va to‘r
tinchi ustunlar, birinchi va to‘rtinchi qatorlar bir-biriga qo‘shni
hisoblanadi, chunki ular mos ravishda vertikal yoki gorizontal silindrlarga
o‘ralsa, ushbu ustunlar yoki qatorlar bir-biriga qo‘shni bo‘lib qoladi. To‘rt
o‘zgaruvchili Karno kartalarining to‘rtta burchagi ham bir-biriga qo‘shni
hisoblanadi, chunki karta
To‘rt o‘zgaruvchili
Karno kartalarida ikki va uch o’zgaruvchili Karno kartalaridagi usullar
qo‘llaniladi. Faqatgina to‘rt o‘zgaruvchili Karno kartalarida birinchi va to‘r
tinchi ustunlar, birinchi va to‘rtinchi qatorlar bir-biriga qo‘shni
hisoblanadi, chunki ular mos ravishda vertikal yoki gorizontal silindrlarga
o‘ralsa, ushbu ustunlar yoki qatorlar bir-biriga qo‘shni bo‘lib qoladi. To‘rt
o‘zgaruvchili Karno kartalarining to‘rtta burchagi ham bir-biriga qo‘shni
hisoblanadi, chunki karta
“sferaga” o‘ralsa, to‘rtta burchak bir-biriga qo‘shniga aylanadi.
Masalan, F(0,0,0,1)=F(0,0,1,1)=F(1,0,0,1)=F(1,0,1,1)=0
3.4. Rele kontakt sxemalari 205
Karno kartasi bo‘yicha formulaning soddalashgan ko‘rinishi quyidagicha bo‘ladi: F(A,B,C)= BÚØD.
Misol. Rostlik jadvali quyidagicha bo`lgan formula uchun minimizatsiyalash masalasini qaraymiz:
|
A |
B |
C |
D |
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
206 Bob III. Matematik mantiq asoslari
Bu jadvalga mos funksiya uchun mukammal diz’yunktiv normal shaklni quyidagicha tuzamiz:
Bu formulani Karno kartasidan foydalanib soddalashtiramiz:
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
0 |
0 |
1 |
0 |
Karno kartasidan ko`rinib turibdiki, funksiyaning ko`rinishi
![]()
shaklda bo`ladi:
Ushbu formulaga mos sxemaning Crocodile dasturiy ta’minoti yordamida ishlab chiqilgan ko`rinishini keltiramiz:
3.4. Rele kontakt sxemalari 207
Sxemaning fizik ko`rinishi quyidagicha bo`ladi:

Ulanish amalga oshgan holatning, ya’ni yoqiq holatning tasviri quyidagicha bo`ladi:
208 Bob III. Matematik mantiq asoslari
Ulanish amalga oshmagan holatning, ya’ni o`chiq holatning tasviri quyidagicha bo`ladi:
Plataning orqa tomonidan sxemani ko’rinishi quyidagicha bo`ladi:
3.4. Rele kontakt sxemalari 209
3.4.5. Yechimlar daraxti
Dasturlashda xotirani va vaqtni tejash maqsadida mantiq algebrasi funksiyalari bilam ishlaganda, ularni “tabiiy” (massivlarda) ifodalamasdan, mantiqiy amallarni bajarishga maxsus yo‘naltirilgan ko‘rinishda ifodalash samaraliroq hisoblanadi. Buning uchun n o‘zgaruvchili Bul funksiyasi rostlik jadvalini n+1 balandlikdagi to‘liq binar daraxt ko‘rinishida ifodalash mumkin. Daraxt yaruslari (qavatlari) o‘zgaruvchilarga mos keladi, daraxt shoxlari esa o‘zgaruvchilar qiymatlariga mos keladi. Har bir mulohaza o’zgaruvchisidan ikkita shih chiqib, chap shoxga – 0, o‘ng shoxga esa – 1 qiymat mos qo‘yiladi. Daraxt yaproqlari – oxirgi yarusda esa daraxt ildizidan shu yaproqgacha bo‘lgan yo‘lga mos kortejdagi funksiya qiymatlari mos qo‘yiladi. Bunday daraxt yechimlar daraxti yoki semantik daraxt deyiladi.
Buni quyidagicha misolda ko‘rib chiqamiz. F(A,B,C) funksiya quyidagicha rostlik jadvali bilan berilgan bo‘lsin:
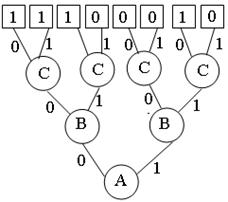
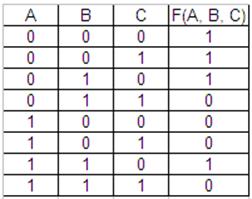
210 Bob III. Matematik mantiq asoslari
1)Yechimlar daraxtini ayrim hollarda barcha barglarni bir xil qiymatga ega bo‘lgan daraxt ostilarini, shu qiymat bilan almashtirilsa yechimlar daraxti hajmining sezilarli darajada ixchamlashtiradi.
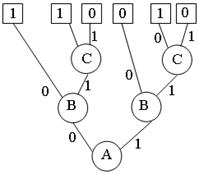
Agar bog‘liqliklarning daraxt ko‘rinishidan voz kechilsa, yechimlar daraxtini anchagina kompaktlashtirish mumkin. Quyidagicha uchta ketma-ket shakl almashtirishlardan so‘ng binary yechimlar daraxtidan binar yechimlar diagrammasi hosil bo‘ladi:
2) 0 va 1 qiymatlarni qabul qilgan yaproqlar birlashtiriladi. Natijada daraxt quyidagi ko‘rinishni oladi:
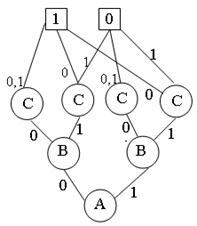
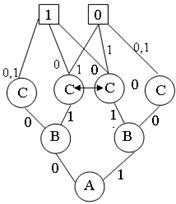
Þ
3.4. Rele kontakt sxemalari 211
3) Diagrammada izomorf (o‘xshash) diagramma ostilari birlashtiriladi:
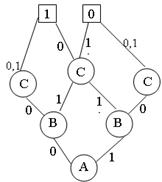
4) Ikkala chiquvchi shoxi ham bitta joyga boradigan tugunlar ahamiyatsiz o‘zgaruvchi sifatida tushirib qoldiriladi va bu tugunga kiruvchi shox chiquvchi shoxlar boradigan tugunlargacha davom ettiriladi.
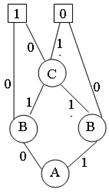
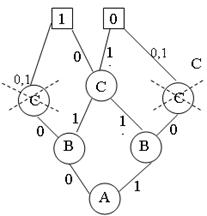
Þ
Natijada F(A,B,C) funksiya qiymatlarini yechimlarning binar diagrammasi orqali berish mumkin:
if A=B=0 or A=C=0 and B=1 or A=B=1 and C=0
then F(A,B,C)=1
else F(A,B,C)=0
212 Bob III. Matematik mantiq asoslari
Yechimlar daraxtidan yechimlar diagrammasiga o‘tish natijasi boshlang‘ich yechimlar daraxtida o‘zgaruvchilarni yaruslarga qaysi tartibda qo‘yilganligiga ham sezilarli darajada bog‘liq.
Yuqoridagi misolda yechimlar daraxtida o‘zgaruvchilarni yaruslarga B, A, C tartibida joylashtirilsa, u holda yechimlar diagrammasi yanada ixchamlashadi:

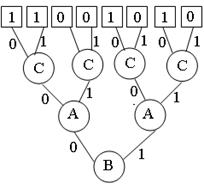
Þ Þ

Natijada F(A,B,C) funksiya qiymatlarini yechimlarning binar diagrammasi orqali berish mumkin:
if B=1 then F(A,B,C)=ØC else F(A,B,C)=ØA
3.4. Rele kontakt sxemalari 213
Ushbu ko‘rilgan misol shundan dalolat beradiki, ayrim hollarda funksiyalarning shunday maxsus ko‘rinishlarini qurish mumkinki, funksiyalarni massivlar yoki formulalar yordamida ifodalash kabi universal usullarga nisbatan, xotirada kam ma’lumot saqlashni va shu bilan birga hisoblashni tezroq amalga oshirish imkonini beradi.
Nazorat savollari:
1. Minimallashtirishda jadval usulining afzalligi nimada?
2. Ikki o‘zgaruvchili Karno kartasida minimallashtirish usulini tushuntiring.
3. Uch o‘zgaruvchili Karno kartasi mohiyati nimadan iborat?
4. To’rt o‘zgaruvchili Karno kartasida minimallashtirish qanday amalgam oshiriladi?
5. O’zgaruvchilar soni 4 tadan oshib ketsa, nima uchun Karno kartasi samarasiz bo’ladi?
Mustaqil yechish uchun masalalar:
a) Quyida keltirilgan misollar uchun Karno kartalarini tuzib, minimallashtiring va soddalashgan formulaga mos rele-kontakt sxemasi chizing:
1. F(1,1,0)=F(1,1,1)=F(1,0,0)=F(1,0,1)=1
2. F(0,1,0)=F(0,1,1)=F(1,0,0)=F(1,0,1)=1
3. F(0,1,0)=F(1,1,1)=F(1,0,0)=F(1,0,1)=1
4. F(0,1,0)=F(0,1,1)=F(1,1,1)=F(1,0,1)=1
5. F(0,1,1)=F(1,1,0)=F(1,1,1)=F(1,0,1)=1
214 Bob III. Matematik mantiq asoslari
6. F(0,0,0)=F(0,0,1)=F(0,1,0)=F(1,1,0)= F(1,0,0)=F(1,0,1)=1
7. F(0,0,0)=F(0,0,1)=F(0,1,1)=F(1,1,0)= F(1,0,0)=F(1,0,1)=1
8. F(0,0,0)=F(0,0,1)=F(1,1,0)=F(1,1,1)= F(1,0,0)=F(1,0,1)=1
b) Quyida keltirilgan misollar uchun yechimlar daraxtini tuzing va soddalashtiring:
1. F(0,0,0)=F(0,1,0)=F(0,1,1)=F(1,1,0)= F(1,1,1)=F(1,0,0)=1
2. F(0,0,0)=F(0,0,1)=F(0,1,1)= F(1,1,0)=F(1,0,0)=1
3. F(0,1,0)=F(0,0,1)=F(0,1,0)=F(1,1,0)= F(1,0,0)=F(1,0,1)=1
4. F(0,1,1)=F(0,0,1)=F(0,1,0)=F(1,1,0)= F(1,0,0)=F(1,0,1)=1
5. F(0,1,0)=F(0,0,1)=F(1,1,0)=F(1,1,1)= F(1,0,0)=F(1,0,1)=1
6. F(0,1,1)=F(1,1,1)=0
7. F(0,1,0)=F(1,1,0)=0
8. F(0,0,1)=F(1,0,1)=0
9. F(0,0,0)=F(1,0,0)=0
10. F(0,0,0)=F(0,0,1)=F(0,1,0)=1
11. F(1,1,0)=F(1,1,1)=F(1,0,0)=F(1,0,1)=1
12. F(0,1,0)=F(0,1,1)=F(1,0,0)=F(1,0,1)=1
13. F(0,1,0)=F(1,1,1)=F(1,0,0)=F(1,0,1)=0
14. F(0,1,0)=F(0,1,1)=F(1,1,1)=F(1,0,1)=1
15. F(0,1,1)=F(1,1,0)=F(1,1,1)=F(1,0,1)=0
IV BOB.
GRAFLAR NAZARIYASI
KIRISh
XVIII asrda mashhur shvetsariyalik matematik, mexanik va fizik Leonard Eyler (1707-1783 yy) Kyonigsberg ko’prigi haqidagi masalani yechish uchun birinchi marta graf tushunchasidan foydalanadi. Hozirda bu masala klassik yoki Eyler masalasi nomi bilan mashhur:
Shu davrda Kyonigsberg shahrida 2 ta orol bo’lib, ular Pregol daryosining 7 ta ko’prigi bilan birlashtirilgan edi. Masala quyidagicha qo’yilgan edi: Shahar bo’ylab shunday sayr uyushtirish kerakki, bunda har bir ko’prikdan bir marta o’tib yana sayr boshlangan joyga qaytib kelish kerak.
Eyler bunday sayr marshruti yo’qligini isbotladi.
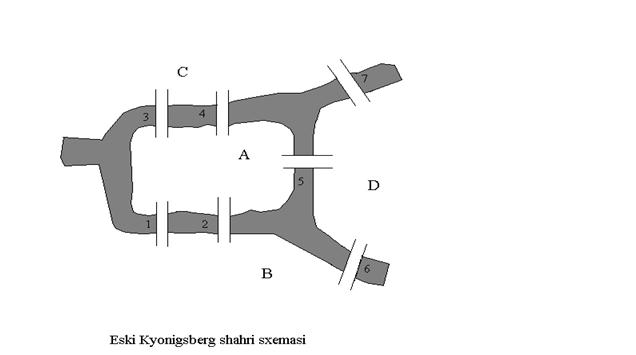
Graflar nazariyasi diskret matematika fanining bir bo’limi bo’lib, unda masalalar yechimlari chizmalar shaklida izlanadi. Keyingi paytlarda turli xil diskret xususiyatlarga ega bo‘lgan xisoblash qurilmalarini loyihalashda graflarning ahamiyati yanada oshdi.
216 Bob IV. Graflar nazariyasi
4.1. Graflar nazariyasining asosiy tushunchalari
Ta’rif 1. (V, E) sonlar juftligiga graf deyiladi, bu
yerda V – iõtiyoriy bo`sh bo`lmagan to`plam, E esa ![]() ning qism to`plami
ning qism to`plami ![]() , bunda
, bunda ![]() V to`plam
elementlarining tartiblanmagan juftliklari to`plami. V to`plam
elementlari grafning uchlari deyiladi, E to`plam elementlari esa grafning
qirralari deyiladi. Agar V chekli bo`lsa, graf chekli
deyiladi, aks holda cheksiz graf deyiladi.
V to`plam
elementlarining tartiblanmagan juftliklari to`plami. V to`plam
elementlari grafning uchlari deyiladi, E to`plam elementlari esa grafning
qirralari deyiladi. Agar V chekli bo`lsa, graf chekli
deyiladi, aks holda cheksiz graf deyiladi.
Qirra ikkita uch bilan aniqlanadi. Umumiy uchga ega bo`lgan ikkita qirra qo`shni hisoblanadi.
Grafning uchlari va qirralari to`plamini mos
ravishda ![]() va
va ![]() kabi belgilanadi.
kabi belgilanadi.
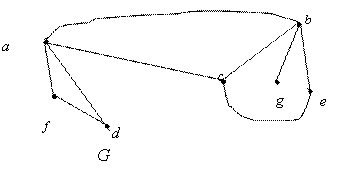
rasm 2
![]()
Ta’rif 2. a) Agar grafda takroriy (karrali) qirralar mavjud bo`lsa, bunday grafga multigraf deyiladi.
b) Agar grafda karrali qirralar bilan birga uchni o`z-o`zi bilan tutashtiruvchi ilmoqlar ham mavjud bo`lsa, bunday grafga psevdograf deyiladi.
4.1. Graflar nazariyasining asosiy tushunchalari 217
c) Yo`nalishga ega bo`lgan qirralari mavjud graf oriyentirlangan graf (orgraf) deyiladi.
Orgrafning qirralari ularning yo`nalishini ko`rsatuvchi strelkalar bilan belgilanadi.
Misol:

![]() –
multigraf,
–
multigraf, ![]() –
psevdograf,
–
psevdograf, ![]() –
oriyentirlangan multigraf.
–
oriyentirlangan multigraf.
Ta’rif 3. Agar V to`plamning quvvati n ga teng bo`lsa, n soni grafning tartibi deyiladi.
Ta’rif 4. Agar V to`plamning quvvati n ga teng bo`lsa, E to`plamning quvvati m ga teng bo`lsa, graf (n, m) graf deyiladi.
Ta’rif 5. Agar grafning ikkita uchi qirra bilan tutashtirilgan bo`lsa, bu uchlar qo`shni uchlar deyiladi.
Ta’rif 6. Grafning bir uchdan chiqqan ikki qirrasi qo`shni qirralar deyiladi.
Ta’rif 7. Agar berilgan uch qirraning oõiri bo`lsa, qirra va uch intsident deyiladi.
Ta’rif 8. Agar graf bironta qirraga ega bo`lmasa, bunday graf bo`sh graf deyiladi.
n tartibli bo`sh grafni ![]() yoki
yoki ![]() bilan belgilanadi.
bilan belgilanadi.
218 Bob IV. Graflar nazariyasi
Ta’rif 9. Agar grafning iõtiyoriy ikki uchi qirralar bilan tutashtirilgan bo`lsa, bunday graf to`la graf deyiladi.
n
tartibli to`la grafni ![]() yoki
yoki ![]() bilan belgilanadi.
bilan belgilanadi.
Misol:

Teorema. n tartibli to`la grafning qirralari soni ![]() ga teng.
ga teng.
Nazorat uchun savollar:
1. Oddiy graf ta’rifini ayting.
2. Grafning uchi deb nimaga aytiladi?
3. Grafning qirrasi deb nimaga aytiladi?
4. Psevdograf deb nimaga aytiladi?
5. Multigrafning ta’rifini yozing.
6. Oriyentirlangan graf deb nimaga aytiladi?
7. To`la grafga ta’rif bering.
8. To`la graf qirralari soni haqidagi teoremani ayting.
9. Oddiy grafga misollar keltiring.
10. Psevdografga misollar keltiring.
11. Oriyentirlangan grafga misollar keltiring.
12. Multigrafga misollar keltiring.
13. To`la grafga misollar keltiring.
4.2. Graflarning to’ldiruvchilari 219
4.2. Graflarning to`ldiruvchilari
Ta’rif 1. G| graf G grafning qismi
deyiladi, agar G| ning uchlari to`plami G
ga tegishli bo`lsa, ya’ni V|![]() V bo`lsa, hamda G| ning
barcha qirralari G ning ham qirralar bo`lsa, ya’ni E|
V bo`lsa, hamda G| ning
barcha qirralari G ning ham qirralar bo`lsa, ya’ni E|![]() E
E
V={a, v, c, d}, V|={a|,
b|, c|, d|}, V|![]() V .
V .
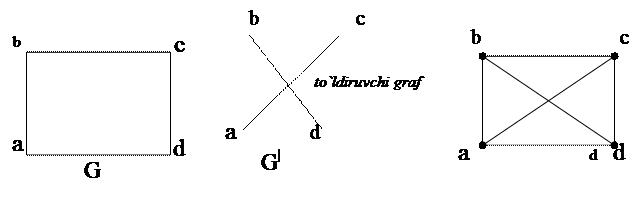 G* graf G grafning to`ldiruvchisi
deyiladi, agarda uning barcha uchlari G grafga tegishli bo`lib, birorta ham
qirrasi G ga tegishli bo`lmasa.
G* graf G grafning to`ldiruvchisi
deyiladi, agarda uning barcha uchlari G grafga tegishli bo`lib, birorta ham
qirrasi G ga tegishli bo`lmasa.
Ta’rif 2. Agar G=(X,U) grafning bo‘lagi G|=(X|,U|)
uchun ![]() bo‘lsa, u holda graf sugraf deb
ataladi.
bo‘lsa, u holda graf sugraf deb
ataladi.
Sugraflarni hosil qilish uchun faqat qirralarga murojaat qilamiz. Quyidagi graflar sugraflardir.
220 Bob IV. Graflar nazariyasi
Misol 1:

Ta’rif 2. Agar graflarning uchlari to`plami orasida qo`shnilik
munosabatini saqlovchi biyeksiya mavjud bo`lsa, bu ikkita graf izomorf deyiladi. ![]() graf
graf ![]() grafga izomorf bo`lsa,
grafga izomorf bo`lsa, ![]() kabi belgilanadi.
kabi belgilanadi.
Misol 2:
4.2. Graflarning to’ldiruvchilari 221
![]() qo`shnilik munosabatini saqlovchi biyeksiya
qo`shnilik munosabatini saqlovchi biyeksiya
![]() mavjud bo`lgani uchun
mavjud bo`lgani uchun ![]() bo`ladi .
bo`ladi .
Ta’rif 3. Agar graf o`zining to`ldiruvchisiga izomorf bo`lsa, graf o`zini o`zi to`ldiruvchi deyiladi.
Misol 3.
Ta’rif 4. Qo`shni yoylar ketma-ketligi yo`l, qo`shni qirralar ketma-ketligi zanjir deyiladi. Yopiq yo`l kontur deyiladi, yopiq zanjir esa sikl deyiladi.
Ta’rif 5. Grafning har bir uchidan bir martadan o`tgan yo`l elementar deyiladi. Graf yoylari orqali bir martadan o`tgan yo`l oddiy yo`l deyiladi. Aks holda murakkab yo`l deyiladi.
Ta’rif 6. Agar zanjir grafning barcha uchlaridan bir martadan o`tsa, bunday zanjirga gamilton zanjiri deyiladi.
Ta’rif 7. Grafning barcha qirralaridan bir martadan o`tgan zanjir eyler zanjiri deyiladi.
Ta’rif 8. Iõtiyoriy ikkita uchini marshrut bilan birlashtirish mumkin bo`lgan graf bog`liq graf deyiladi.
Ta’rif 9. Grafning barcha uchlaridan o`tuvchi karrali qirralar va ilmoqlarga ega bo`lmagan graf eyler grafi deyiladi.
222 Bob IV. Graflar nazariyasi
Ta’rif 10. Agar bog`liqli grafda har bir uchdan faqat bir martadan o`tuvchi tsikl (yoki marshrut) mavjud bo`lsa, bunday graf gamilton grafi deyiladi.
Nazorat uchun savollar:
1. Graflar qachon izomorf bo`ladi?
2. Sugraf deb nimaga aytiladi?
3. Grafning to`ldiruvchisi deb nimaga aytiladi?
4. Eyler grafi deb nimaga aytiladi?
5. Bog`liq graf ning ta’rifini yozing.
6. Gamilton zanjiri deb nimaga aytiladi?
7. Gamilton grafiga ta’rif bering.
8. Sikl deb nimaga aytiladi?
9. To`ldiruvchi grafning ta’rifini bering.
10. Marshrut deb nimaga aytiladi?
11. Zanjir deb nimaga aytiladi?
Mustaqil yechish uchun masalalar:
1. Izomorf graflarga misollar keltiring.
2.
 Chizmadagi graf uchun keltirilgan
marshrutlardan qaysi biri oddiy zanjir bo`ladi?
Chizmadagi graf uchun keltirilgan
marshrutlardan qaysi biri oddiy zanjir bo`ladi?
4.2. Graflarning to’ldiruvchilari 223
3. Eyler grafiga misollar keltiring.
4. Gamilton grafiga misollar keltiring.
5. Bog`liq grafga misollar keltiring.
6. Quyidagi graf uchun gamilton sikli mavjudmi?
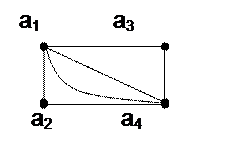 Quyidagi graf eyler grafi bo`ladimi?
Quyidagi graf eyler grafi bo`ladimi?
7.
 Chizmada keltirilgan graf uchun bir
uchidan chiqqan oddiy sikl bo`lsa ko`rsating:
Chizmada keltirilgan graf uchun bir
uchidan chiqqan oddiy sikl bo`lsa ko`rsating:
8.
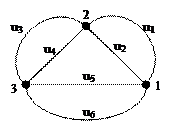 Chizmada keltirilgan graf uchun eyler
sikli bo`lsa ko`rsating:
Chizmada keltirilgan graf uchun eyler
sikli bo`lsa ko`rsating:
224 Bob IV. Graflar nazariyasi
4.3. Graf uchlari darajasi. Graf qirralari soni
Ta’rif 1. Qirraning boshi yoki oõirini ifodalovchi uchga bu qirraga intsident uch deyiladi.
Ta’rif 2. Graf uchining darajasi deb bu uchga intsident qirralar soniga aytiladi.
õi uchning darajasini P(õi) bilan belgilanadi.
Boshqacha aytganda uchdan chiquvchi qirralar soni uchning darajasi hisoblanadi. Darajasi 1 ga teng uch osilgan uch bo`ladi.
Ta’rif 3. Hech qanday yoy yoki qirralarga ega bo`lmagan va izolyatsiyalangan uchlardan iborat graf nol graf deyiladi. Ko`rinib turibdiki, nol grafning uchlari darajasi nolga teng.
Lemma 1. Agar grafning barcha uchlarining darajalari 2 dan katta yoki 2 ga teng bo`lsa, graf, albatta, konturni o`z ichiga oladi.
Ta’rif 4. Agar grafning uchlari va qirralari to`plamida refleksivlik va simmetriklik õossalarini qanoatlantiruvchi binar munosabat mavjud bo`lsa, bunday graf tolerant graf deyiladi.
Teorema 1. Oriyentirlanmagan graf eyler sikli bo`lishi uchun uning uchlari juft darajalarga ega bo`lishi va uning bog`liq graf bo`lishi zarur va yetarlidir.
Teorema 2. Oriyentirlanmagan graf A va V uchlarni birlashtiruvchi eyler zanjiriga ega bo`ladi, faqat va faqat shu holdaki, agar graf bog`liq bo`lsa hamda faqatgina A va V uchlar toq darajalarga, qolgan uchlar juft darajalarga ega bo`lsa.
4.3. Graf uchlari darajasi. Graf qirralari soni 225
Ta’rif 5. Grafni tekislikka yotqizish mumkin bo`lsa, bunday graf planar graf deyiladi. Tekislikka yotqizilgan graf tekis graf deyiladi.
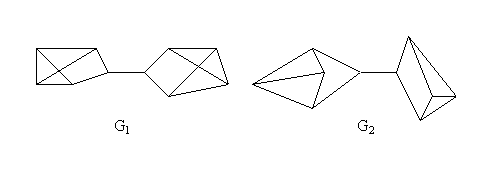
G1 graf planar va G2 tekis grafga izomorf.
Teorema 3. Agar grafda karrali qirralari hamda ilmoq mavjud bo`lmasa, n ta uchga ega bo`lgan va bog`liq komponentasi K ga teng bo`lgan grafning qirralari soni eng ko`pi bilan aniqlanadi.
M=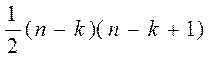
Mashrutning uzunligi deb, shu marshrutda mavjud qo`shni (ei-1, ei) qirralar soniga aytiladi.
Grafning iõtiyoriy a va iõtiyoriy v uchlari orasidagi masofa deb, shu uchlarni bog`lovchi eng kichik uzunlikka ega bo`lgan zanjirga aytiladi.
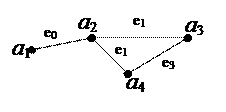 Misol 1.
Misol 1.
226 Bob IV. Graflar nazariyasi
d(a1,a3)= (e0, e1)=2;
d(a1,a4)=(e0, e2)=2;
d(a1,a4)=(e0, e1, e3)=3
Grafning diametri deb, uchlari orasidagi eng katta uzunlikka ega bo`lgan masofaga aytiladi.
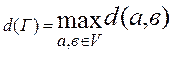
Misol 2. d(a1,a4)=(e0, e1, e3)=3.
S uch G grafning fiksirlangan uchi bo`lsin. Õ esa grafning iõtiyoriy uchi bo`lsin. S uch uchun maksimal masofani hisoblaymiz. Qandaydir S0 uch uchun bu maksimal masofa boshqa uchlarga nisbatan minimal bo`lsa, u holda S0 G grafning markazi deyiladi va S0 uchun aniqlangan masofa G grafning radiusi deyiladi.
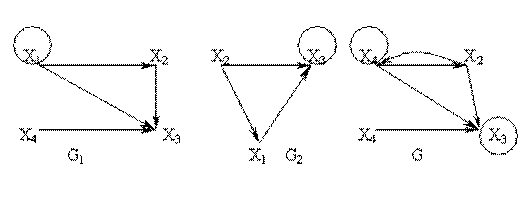
Yig`indi graf ikkita qo`shiluvchi graflardan hech bo`lmaganda bittasida uchraydigan uch va qirralarni o`z ichiga oladi.
4.3. Graf uchlari darajasi. Graf qirralari soni 227
Ko`paytma graf ko`paytirilayotgan graflarning umumiy uchlari va qirralaridan iborat.
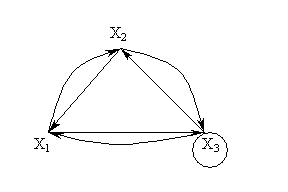
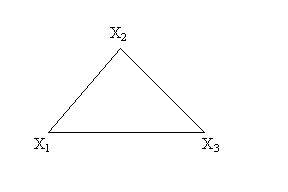
Simmetrik graf Oriyentirlanmagan graf
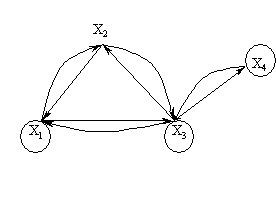
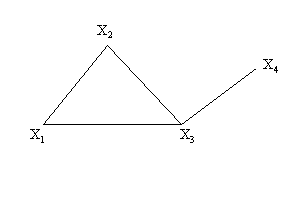
Tolerant graf Oriyentirlanmagan graf
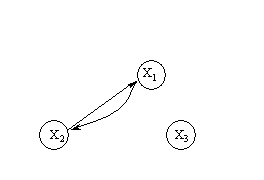
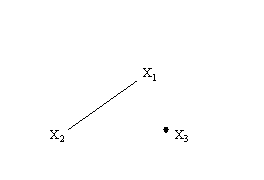
Tolerant graf Oriyentirlanmagan graf
228 Bob IV. Graflar nazariyasi
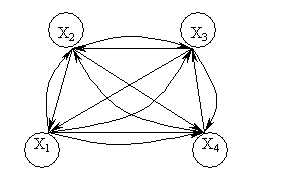
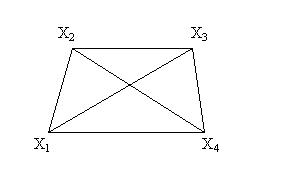
Graf-dekart ko`paytma Oriyentirlanmagan to`la graf
Ta’rif 3. Agar G1 grafdan, shuningdek, G2 grafdan chekli sonli martadagi qirralarni ajratish amali bilan olinishi mumkin bo`lgan shunday G' graf mavjud bo`lsa, G1, G2 graflar gomeomorf graf deyiladi,
Quyidagi rasmda tasvirlangan G1 va G2 graflar gomeomorfdir.
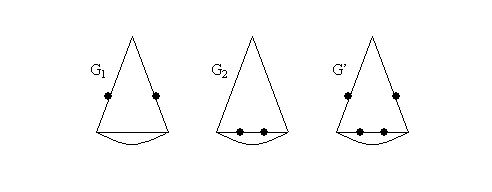
G' graf G1 va G2 graflardan ikki marta o`tkazilgan qirralar bo`linishi amalidan olinishi mumkin.
1-teorema (Pontryagin-Kuratovskiy). G graf planar bo‘ladi, faqat va faqat shu holdaki, G graf K5 yoki K3;3 ga gomemorof bo‘lgan, qism graflarga ega bo`lmasa.
4.3. Graf uchlari darajasi. Graf qirralari soni 229
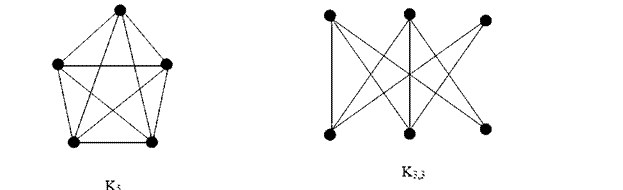
Planarlik kriteriyasini ekvivalent formasini quyidagi teoremada keltirilgan.
2-teorema. Oriyentirlanmagan G graf K5 yoki K3 3 graflarga tortiluvchi qism graflarga ega bo`lmasa.
3-teorema. Êî‘pi bilan 2W uchdan iborat bo‘lgan har qanday graf R3 fazoda uchlaridan tashqarisida yoylarining kesishmalarsiz tasvirlash mumkin.
Isboti. G’ = (MÄ) graf uchun | M | < 2W bo‘lgan bo‘lsin. Unda | R < 2W ga ega bo‘lamiz. G grafning barcha nuqtalarini biror L to‘g‘ri chiziqqa joylashtiramiz va R dagi har bir qirraga L to‘g‘ri chiziqni saqlovchi tekislikni har xil qiymatli mos qo‘yamiz.
Izlanayotgan G graf tasviri, barcha qirralami mos tekisliklarga o‘tkazgandagi keyin hosil bo‘ladi.
Planar graflaming xromatik sonining bahosi ma’lum.
Nazorat uchun savollar:
1. Insidentlik tushunchasini ta’rifini bering.
2. Nol graf nima?
3. Tolerant graf ta’rifini bering.
230 Bob IV. Graflar nazariyasi
4. Planar graf nima?
5. Qanday graflar gomeomorf deyiladi?
6. Yig`indi graf deb nimaga aytiladi?
7. Ko`paytma graf deb nimaga aytiladi?
8. Grafning diametri deb nimaga aytiladi?
9. Pontryagin-Kuratovskiy teoremasini ayting.
Mustaqil yechish uchun masalalar:
 1. Quyidagi graflarning
yig`indisi va ko`paytmasini toping:
1. Quyidagi graflarning
yig`indisi va ko`paytmasini toping:
2. Quyidagi graflarning yig`indisi va ko`paytmasini toping:
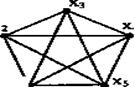

4.4. Graflarni õarakterlovchi sonlar
Ta’rif 1. Grafning siklomatik soni deb, N-n+p songa aytiladi, bu yerda N- grafning qirralari soni, n – grafning uchlari soni, P – bog`liqlik komponenti soni. Bog`liq graf uchun N-n+1.
Teorema 1. Grafning siklomatik soni erkli sikllarning eng katta miqdoriga teng.
4.4. Graflarni õarakterlovchi sonlar 231
Misol 1.
Quyidagi chizmada tasvirlangan grafning siklomatik soni 3 ga teng.
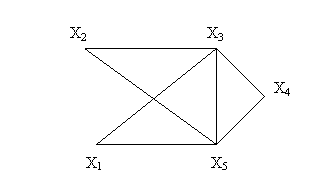
Ta’rif 2. Agar grafning uchlar to‘plamini o‘zaro kesishmaydigan shunday ikkita qism to‘plamlarga (bo‘laklarga) ajratish mumkin bo‘lsaki, grafning ixtiyoriy qirrasi bu to‘plamlarning biridan olingan qandaydir uchni ikkinchi to‘plamdan olingan biror uch bilan tutashtiradigan bo‘lsa, u holda bunday graf ikki bo‘lakli graf (bixromatik yoki Kyonig grafi) deb ataladi.
Nazorat uchun savollar:
1. Siklomatik son nima?
2. Siklomatik sonni formula orqali ifodalang.
3. Kyonig grafi deb nimaga ataladi?
232 Bob IV. Graflar nazariyasi
4.5. Daraxtlar
Ta’rif. Agar G grafning u qirrasi kamida bitta siklga tegishli bo`lsa, u siklik qirra, aks holda atsiklik qirra deb ataladi.
G graf uchun
![]()
Ifoda uning siklomatik soni deb ataladi, bu yerda m(G) G grafning qirralar soni. n(G)- uchlari soni, k(G)- komponental soni.
Osongina ko`rish mumkinki,
![]() K(G), agar u siklik qirra bo`lsa,
K(G), agar u siklik qirra bo`lsa,
K(G\u)=
K(G)+1, u atsiklik qirra bo`lsa;
![]()
![]() (G)-1, agar u
siklik qirra bo`lsa,
(G)-1, agar u
siklik qirra bo`lsa,
![]() (G\u)=
(G\u)=
K(G), agar u atsiklik qirra bo`lsa.
O`z-o`zidan ravshanki, n(G\u)=n(G),
m(G\u)= ![]() (G)-1,
(G)-1, ![]() (G)
(G)![]() 0 va faqat sikllari
bo`lmagan graf uchun
0 va faqat sikllari
bo`lmagan graf uchun ![]() (G)=0.
(G)=0.
Ta’rif. Barcha qirralari atsiklik bo`lgan bog`liq graf daraõt deb ataladi.
Bir necha daraxtlardan tashkil topgan bog`liqmas graf o`rmon deyiladi.
4.5. Daraxtlarlar 233
Daraõtning istalgan 2 uchi yagona zanjir bilan bog`langandir. Daraõtning istalgan õ0 uchini tanlab olib, uni ildiz yoki nolinchi pog`onali uch deb ataymiz. õ0 ga qo`shni bo`lgan barcha uchlarni birinchi pog`ona uchlari deymiz va hokazo.

![]()
 Daraõtning bunday tasvirlanishidan
kelib chiqadiki u chetki, faqat bitta qirraga intsident bo`lgan
uchlarga ega. Masalan, 14 shaklda
oõirgi pog`onadan uchlari.
Daraõtning bunday tasvirlanishidan
kelib chiqadiki u chetki, faqat bitta qirraga intsident bo`lgan
uchlarga ega. Masalan, 14 shaklda
oõirgi pog`onadan uchlari.
Bog`liq G grafning ketma-ket barcha siklik qirralarni olib tashlaymiz. Natijada hamma qirralar atsiklik bo`lgan bo`g`liq N grafni –daraõtni hosil qilamiz. Bu daraõt G grafning asosi deyiladi. N asosga nisbatan G N bo`lakning barcha qirralari vatarlar deb ataladi.
Teorema 1. Chekli bog`liq G graf daraõt bo`lishi uchun uning qirralari soni uchlari sonidan bittaga kam bo`lishi zarur va yetarli.
234 Bob IV. Graflar nazariyasi
Teorema (Keli) 2. Uchlar soni tartiblangan n ta bo`lgan daraõtlar soni n n-2 teng. (n ta elemenlardan n-2 tadan tuzilgan barcha takrorish o`rinlashtirishlar soni).
Teorema 3. Agar G graf daraõt bo`lsa, u holda uning qirralari soni m va uchlari soni n ò = ï – 1 munosabat bilan bog`langan.
Teorema 4. Quyidagi 4 ta shart teng kuchli:
· G graf daraxt hisoblanadi;
· Grafning qirralari soni m va uchlari soni n ò = ï – 1 munosabat bilan bog`langan;
· Grafning ixtiyoriy ikki uchi oddiy yo`l bilan bog`langan bo`lishi mumkin va bu yo`l yagonadir.
· G graf bog`langan va konturlarga ega emas.
Nazorat uchun savollar:
1. Siklik qirra nima?
2. Atsiklik qirra nima?
3. Siklomatik sonni formula orqali ifodalang.
4. Qanday graf daraõt deb ataladi?
5. Pog`ona uchlari deb nimaga aytiladi?
6. Grafning asosi deb nimaga aytiladi?
7. Chekli grafda qirralar va uchlar soni orasidagi munosabatni keltiring.
8. Keli teoremasini ayting.
4.5. Daraxtlarlar 235
Mustaqil yechish uchun masalalar:
1. Chizmada keltirilgan grafning xromatik sonini toping:
 |
2. Chizmada keltirilgan grafning xromatik sonini toping:
4.6. Qo`shnilik matritsasi
Faraz qilaylik, G graf yo`naltirilmagan bo`lsin. Grafning qo`shnilik matritsasida Aij ning ustunlariga ham qatorlariga ham grafning uchlarini mos qo`yamiz. U holda
Aij=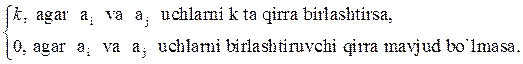
qoidadan foydadanib qo`shnilik matritsasini hosil qilamiz.
236 Bob IV. Graflar nazariyasi
Misol. 
Rasmda keltirilgan yo`naltirilmagan graf uchun qo`shnilik matritsasi quyidagicha bo`ladi.
![]()

G yo`naltirilgan graf bo`lsin. U holda qo`shnilik matritsasi Aij ning ustunlariga ham satrlariga ham grafning uchlarini mos qo`yamiz. U holda quyidagi qoidadan foydadanib qo`shnilik matritsasini hosil qilamiz.
Aij= 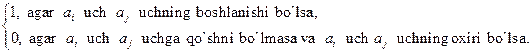
4.6. Qo`shnilik matritsasi 237
Qo`shnilik matritsasining diagonalida turgan birlar grafning ilmoqlariga mos keladi.
Izolyatsiyalangan uchga nollardan tashkil topgan satr va ustun mos keladi.
Qo`shnilik matritsasidagi birlar soni grafdagi qirralar soniga teng.
Nazorat uchun savollar:
1. Qo`shnilik matritsasini ta’rifini bering.
2. Oriyentirlangan graf uchun qo`shnilik matritsasi qanday topiladi?
Mustaqil yechish uchun masalalar:
1. Berilgan qo`shnilik matritsasiga ko`ra grafning tasvirini toping:
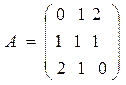
2. Berilgan qo`shnilik matritsasiga ko`ra grafning tasvirini toping:
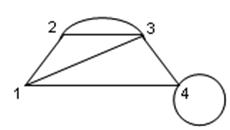
238 Bob IV. Graflar nazariyasi
3. Rasmda tasvirlangan graflar uchun qo`shnilik matritsasini yozing:

4.6. Qo`shnilik matritsasi 239
 |
|||
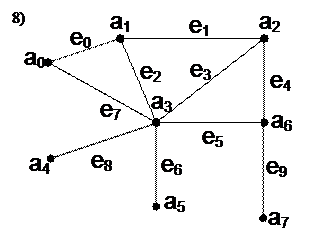 |
|||
4.7. Insidentlik matritsasi
Bizga G yo`naltirilmagan, chekli graf berilgan bo`lsin. Aytaylik, (v1,…,vn), G grafning uchlari bo`lsin. U holda insidentlik matritsasi ||Aij|| (i=1,...,m, j=1,..., n) deb m ta qator va n ta ustundan iborat quyidagi ko`rinishda hosil qilingan matritsaga aytiladi:
a) Aij matritsaning satrlariga G ning uchlari, ustunlariga G ning qirralari mos qo`yiladi;
b) U holda
Aij= 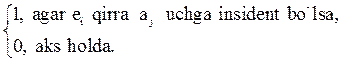
qoidadan foydalanib, intsidentlik matritsasini hosil qilamiz.
240 Bob IV. Graflar nazariyasi
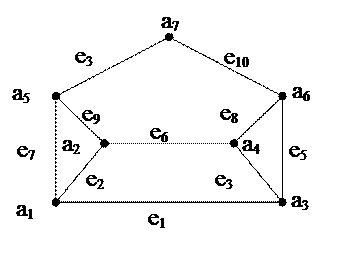 Misol 1.
Misol 1.
![]()
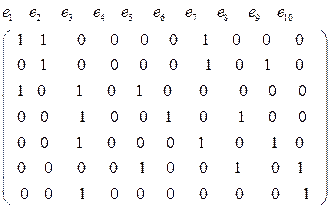
Agar G yo`naltirilgan graf bo`lsa, u holda
Aij= 
qoidadan foydadanib insidentlik matritsasini hosil qilamiz.
4.7.Insidentlik matritsasi 241
Misol 2.
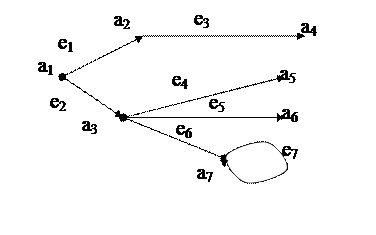 |
![]()

Oriyentirlangan graf uchun insidentlik matritsasi deb har bir elementi aij quyidagicha aniqlangan [n * m] tartibli to`g`ri burchakli matritsaga aytiladi, bu erda n – uchlar to`plamining quvvati, m – qirralar to`plamining quvvati
|
|
agar xi ui uchning boshi bo`lsa, |
|
agar xi ui uchning oõiri bo`lsa, |
|
|
agar xi ui qirraga insident bo`lmasa. |
242 Bob IV. Graflar nazariyasi
Misol 3. Rasmda tasvirlangan graf uchun insidentlik matritsasini yozamiz:
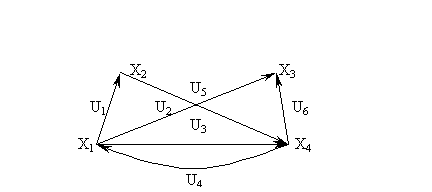
Buning uchun qirralarni u1, u2,…, u6 bilan belgilab chiqamiz. Insidentlik matritsasining ko`rinishi quyidagicha bo`ladi.

Nazorat uchun savollar:
1. Insidentlik matritsasini ta’rifini bering.
2. Oriyentirlangan graf uchun insidentlik matritsasi qanday topiladi?
4.7.Insidentlik matritsasi 243
Mustaqil yechish uchun masalalar:
1. Berilgan insidentlik matritsasiga ko`ra grafning tasvirini
toping: 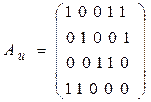
2. Quyidagi yo`naltirilgan va yo`naltirilmagan graflar uchun insidentlik matritsalarini aniqlang:


244 Bob IV. Graflar nazariyasi
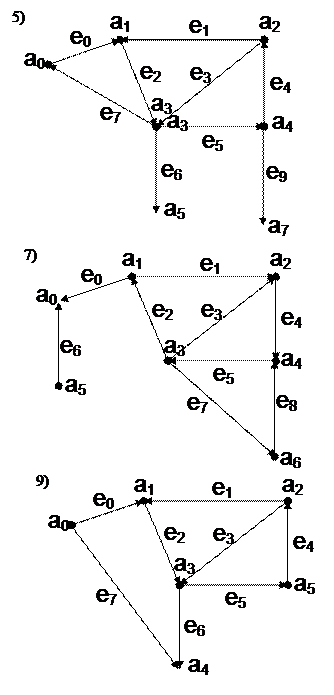
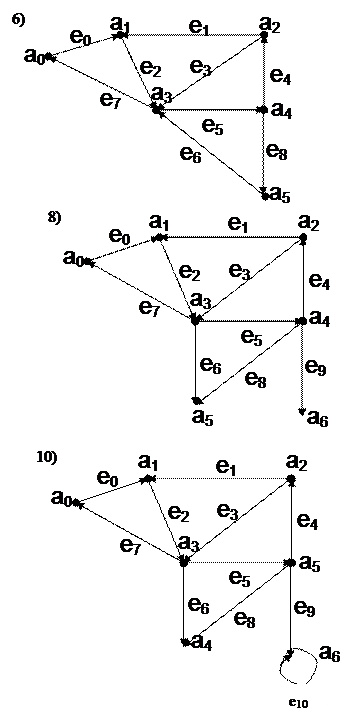
4.7.Insidentlik matritsasi 245


4.8. Graflarni bo’yash
Planar graflarni bo`yash masalasi graflar nazariyasining eng mashhur muammolaridan biri hisoblanadi. Ushbu masala o`tgan asrning o`rtalarida paydo bo`lgan bo’lsa ham hamon mutaxassis va qiziquvchilar e’tiboriga sazovor. Graflarni bo’yash masalasi quyidagicha paydo bo’lgan: geografik kartani bo`yash uchun ixtiyoriy 2 ta qo`shni davlatni rangi har xil bo`lishini ta’minlashda 4 xil rang yetadimi? Bunda ixtiyoriy davlat chegarasi yopiq chiziqdan iboratligi, qo`shni mamlakatlar esa
246 Bob IV. Graflar nazariyasi
umumiy chegara uzunligini tashkil etishini ko`rib chiqiladi. Keyinchalik karta tushunchasi va uning bo`yalishi boshqacharoq ko`rinishda talqin etilgan. Aytish mumkinki, ko`priklarsiz bog`langan tekis multigraf karta deb ataladi. Umumiy qirraga ega bo`lgan karta tomonlari chegaradosh hisoblanadi.
f funksiya mavjud bo`lib, unda G- 1 dan k gacha raqamlardan iborat va f(G)- chegara rangi, G- esa k-rang hisoblanadi( qo`shni chegaralar turli xil bo`lganda). K- rang mavjud bo`lsa, karta k- bo`yalgan deyiladi. 1879 yilda britaniyalik matematik A.Keli kartalarni bo`yash muammosini 4 ta rang gipotezasi orqali ta`riflab berdi. 4 bo`yoq farazi: har qanday karta 4 xil bo`yoq bilan bo`yaladi. Ko`pincha 4 bo`yoq farazini boshqacha ta`bir bilan foydalaniladi: har qanaqa planar graf 4 bo`yoqda bo`yaladi.
Ta`rif. Agar geometrik ikkilik graf G* uchi k- bo`yalgan bo`lsa, karta G k-bo`yalgan deyiladi,.
Eslatib o`tamizki, shunday tekis graflar mavjudki, ular 4 rangdan kamroq rangda to`g`ri bo`yalgan. Masalan, K4 grafi.
4 ta rang gipotezasi unchalik qiyindek tuyilmadi va uning bir nechta isbotlari paydo bo`ldi.
Teorema. Ixtiyoriy 3 ta sikldan kam bo`lmagan yassi graf 3 xil rangda bo`yaladi.
Graflarning qirralarinigina emas, uchlarini ham bo`yash mumkin.
Nazorat uchun savollar:
1. Graf qachon k- bo`yalgan deyiladi?
2. Qaysi shart bajarilganda graf 3 xil rangda bo`yaladi?
4.8. Graflarni bo’yash 247
4.9. To`rt xil rang masalasi
To`rt xil rang gipotezasi o`sha davrlarda ko`pgina izlanuvchilarning diqqatiga tushgan. 1880 yilga kelib esa bu masalaning birinchi isbotini A. Kemp taqdim etdi. 1890 yilda R. Xivud bu isbotning xatosini aniqladi. Shu bilan birga u agar to`rt so`zini besh so`ziga o`zgartirilganda, uni usbotlash osonroq bo`lishini ta’kidlagan.
To`rt xil rang gipotezasi masalasini quyidagi uchta tasdiq yordamida hal qilinadi:
1. Ixtiyoriy yassi graf 4 xil rangda bo`yaladi.
2. Har bir kub karta 4 ta rangda bo`yaladi.
3. 3 xromatik indeks ixtiyoriy kub kartaga teng bo`lishi mumkin.
Teorema 1. (tocrtta bocyoqlar haqida teorema) Agar G planar graf bo‘lsa, unda x(G) < 4.
Agar G graf planar bo‘lmasa, uni geometrik tasvirlash uchun ayrim qirralarni olib tashlaymiz (boshqa tekislikka o‘tkaziladi).
Grafni tekislikdagi tasvirini hosil qilish uchun, olib tashlashi zarur bo‘lgan qirralarining minimal sonini G grafning planarlik soni deyiladi. Bu qirralami ikkinchi tekislikka o‘tkazish natijasida, grafni qismi hosil bo`ladi, lekin u tekis bo`lmasligi mumkin. U holda óana ayrim qirralami keyingi tekislikka o‘tkazish masalasi yechiladi.
Nazorat uchun savollar:
1. To`rt xil rang gipotezasi masalasini hal qiluvchi uchta tasdiqni keltiring.
2. To`rtta bo`yoq haqidagi teoremani ayting.
Misol.Ushbu
![]()
formulaga mos sxema

Yuqoridagi sxemani mantiq qonunlari yordamida soddalashtirib,
![]()
![]()
![]()
tuzilgan sxema
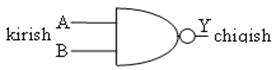
Ikkala sxema ham bir xil vazifani bajaradi, chunki ularning rostlik jadvallari bir xil.
V BOB. ALGEBRAIK SISTEMALAR
5.1.1. Algebraik sistemalar
Ko’pgina hollarda diskret matematika va uning tatbiqlarida o’rganish ob’yekti sifatida to’plam bilan birga uning tuzilishi ham ahamiyatga ega bo`ladi.
Ma’lumki, odatdagi arifmetika, geometriya ob’yektlari bilan sonli amallarni bog’laydigan chiziqli fazo hamda biror binar munosabat aniqlangan to’plamlar asosida maydon tushunchasi kiritiladi. Barcha bunday strukturalar algebraik sistemalarni tashkil etadi. Algebraik sistemalarning aniq ta’rifini keltiramiz.
Ta’rif 1. Bo’sh
bo’lmagan A to’plamni qaraymiz. Bu to’plamda n-o’rinli f akslantirishni
kiritamiz: ![]() . f funksiya bo’lganligi
sababli, ixtiyoriy
. f funksiya bo’lganligi
sababli, ixtiyoriy ![]() elementlar uchun f amalini qo’llash natijasi
elementlar uchun f amalini qo’llash natijasi
![]() bir qiymatli aniqlanadi. f amalining
qiymatlar sohasi A to’plamga tegishli bo’lgani uchun f amalni A
to’plamda yopiq amal deb ataymiz.
bir qiymatli aniqlanadi. f amalining
qiymatlar sohasi A to’plamga tegishli bo’lgani uchun f amalni A
to’plamda yopiq amal deb ataymiz.
Ta’rif 2. Signatura yoki til ∑ deb o’rni ko’rsatilgan predikat va funksional simvollar to’plamiga aytiladi. 0-o’rinli funksional simvolga constanta deyiladi.
Agar α funksional yoki predikat simvoli bo’lsa, u holda uni o’rni µ(α) yordamida belgilanadi.
n-o’rinli predikat va
funksional simvollarni mos ravishda Pn va f n orqali
belgilaymiz. Agar qaralayotgan signaturada standart simvollar foydalanilayotgan
bo’lsa, masalan: qo’shish amali uchun +, tartiblash munosabati uchun ≤,
bo’lish amali uchun /, constant uchun 0 va shu kabilar, u holda biz quyidagicha
yozamiz: ![]()
Ta’rif 3. ∑ signaturali algebraik sistema U={A, ∑} deb bo’sh bo’lmagan A to’plamga aytiladi, bunda har bir n o’rinli predikat (funksional) simvolga A to’plamda aniqlangan n-o’rinli predikat mos qo’yilgan. A to’plam {A, ∑} algebraik sistemaning tashuvchisi yoki universumi deb ataladi.
Ta’rif 4. ∑ dagi simvollarga mos keluvchi predikatlar va funksiyalar interpretatsiyalar deyiladi.
Interpretatsiyalarni ham signaturaning mos simvollari bilan belgilaymiz. Ixtiyoriy constant simvolning interpretatsiyasi A to’plamning biror bir elementi bo’ladi. Algebraik sistemalar odatda U, B,… kabi harflar bilan, ularning tashuvchilari esa A, B,… kabi harflar bilan belgilanadi. Ko’p hollarda algebraik sistema o’rniga “algebraik” so’zi tushirib qoldirilib, sistema yoki struktura so’zi ishlatiladi.
Ta’rif 5. Algebraik sistemaning quvvati deb A “tashuvchi”ning quvvatiga aytiladi.
Agar ∑ signatura predikat (funksional) simvollarga ega bo’lmasa, u funksional (predikat) signatura deb ataladi.
Agar sistemaning signaturasi funksional (predikat) bo’lsa, unga algebra (model) deyiladi.
Misol 1.
![]() bo’lsin,
u holda {
bo’lsin,
u holda {![]() }
to`plam ikkita ikki o’rinli amallar bilan algebra tashkil etadi.
}
to`plam ikkita ikki o’rinli amallar bilan algebra tashkil etadi.
Misol 2.
![]() to`plam
≤( µ (≤) =2) binar munosabatli, +,
to`plam
≤( µ (≤) =2) binar munosabatli, +, ![]() ikki
o’rinli amallar, ‘: n→ n+1 bir o’rinli amal (µ(‘)=1) va ikkita nol
o’rinli amallar (constantalar) 0,1
ikki
o’rinli amallar, ‘: n→ n+1 bir o’rinli amal (µ(‘)=1) va ikkita nol
o’rinli amallar (constantalar) 0,1 ![]() sistemasidir.
sistemasidir.
Misol 3.
![]() majmua
algebra tashkil etmaydi, chunki bo’lish Z to’plam amali hisoblanmaydi, masalan
2:3
majmua
algebra tashkil etmaydi, chunki bo’lish Z to’plam amali hisoblanmaydi, masalan
2:3 ![]() Z,
Z,
![]() element
ham Z to’plamga tegishli emas.
element
ham Z to’plamga tegishli emas.
Misol 4.
![]() majmua
ikki o’rinli amallar-, : U,
majmua
ikki o’rinli amallar-, : U,![]() ;
bir o’rinli amal - : A → Ā; constantalar 0=
;
bir o’rinli amal - : A → Ā; constantalar 0=![]() va
1=U bilan algebra tashkil etadi, uni Kantor algebrasi deb yuritiladi.
va
1=U bilan algebra tashkil etadi, uni Kantor algebrasi deb yuritiladi.
Misol 5. Ixtiyoriy halqa algebra bo’ladi.
Misol 6.
![]() juftlik
(bunda
juftlik
(bunda ![]() differensiallash
amali) algebra bo’la olmaydi, chunki hamma funksiyalar ham differensiallanuvchi
emas. Agar cheksiz marotaba differensiallanuvchi funksiyalar A={f(x)}
to’plami qaralsa, u holda differensiallash amali
differensiallash
amali) algebra bo’la olmaydi, chunki hamma funksiyalar ham differensiallanuvchi
emas. Agar cheksiz marotaba differensiallanuvchi funksiyalar A={f(x)}
to’plami qaralsa, u holda differensiallash amali ![]() A
to’plamda akslantirish bo’ladi va
A
to’plamda akslantirish bo’ladi va ![]() juftlik
algebra tashkil etadi.
juftlik
algebra tashkil etadi.
Aytib o’tish kerakki, An to’plamni A to’plamga akslantiruvchi f qisman amalni (n+1) o’rinli munosabat deb qarash mumkin:
![]()
Shu sababli oxirgi
misoldagi ![]() juftlikni,
juftlikni, ![]() amalni binar munosabat
amalni binar munosabat ![]() deb hisoblansa, algebraik sistema deb qarash mumkin.
deb hisoblansa, algebraik sistema deb qarash mumkin.
5.1.2. Gruppa va yarim gruppalar.
Ta’rif 1. ∑={ f } µ(f)=2,
signaturali U algebraga gruppoid deb ataladi. Bundagi birgina f amali
odatda ![]() kabi belgilanadi, U={A,
kabi belgilanadi, U={A, ![]() }.
}.
Agar A to’plam chekli
bo’lsa, amalni jadval orqali berish mumkin, bunda har bir ![]() juftlik natijasi jadvalda ko’rsatiladi.
juftlik natijasi jadvalda ko’rsatiladi.
Ta’rif 2. Bunday jadvalga U gruppoidning Keli
jadvali deyiladi. Agar ![]() amali assotsiativlik xossasiga ega, ya’ni barcha
x,y,z
amali assotsiativlik xossasiga ega, ya’ni barcha
x,y,z![]() A elementlar uchun
A elementlar uchun ![]() tenglik bajarilsa, U gruppoidga yarimgruppa
deb ataladi.
tenglik bajarilsa, U gruppoidga yarimgruppa
deb ataladi.
Agar bir deb
ataladigan ![]() , element mavjud gruppaga, barcha
, element mavjud gruppaga, barcha ![]() elementlar uchun
elementlar uchun ![]() tenglik bajarilsa, U yarim guruhga monoid deb
ataladi. Yarim gruppa va monoidlar til nazariyasida so’zlarni qayta
ishlashda muhim o’rin tutadi.
tenglik bajarilsa, U yarim guruhga monoid deb
ataladi. Yarim gruppa va monoidlar til nazariyasida so’zlarni qayta
ishlashda muhim o’rin tutadi.
Misol 1. Faraz qilaylik W(X) X alfavitdagi
so’zlar to’plami bo’lsin. W(X) to’plamda KONKATENATSIYA amalini quyidagicha
aniqlaymiz: Agar α,β ![]() , u holda
, u holda ![]() yani amal natijasi
yani amal natijasi![]() so’zlarni birlashtirishdan iborat bo’ladi, masalan,
xyz^zx=xyzzx. Assotsiativlik xossasi bajariladi, ya’ni ixtiyoriy
so’zlarni birlashtirishdan iborat bo’ladi, masalan,
xyz^zx=xyzzx. Assotsiativlik xossasi bajariladi, ya’ni ixtiyoriy
![]() so’zlar uchun
so’zlar uchun ![]() tenglik o’rinli bo’ladi. Shu sababli {W(X), ˆ}
sistema yarim gruppa hosil qiladi.
tenglik o’rinli bo’ladi. Shu sababli {W(X), ˆ}
sistema yarim gruppa hosil qiladi.
Shu bilan birga barcha
α ![]() lar uchun
lar uchun ![]() , bunda
, bunda ![]() bo’sh so’z, bajarilgani uchun
bo’sh so’z, bajarilgani uchun ![]() birlik element vazifasini bajaradi. Shunday qilib
{W(X), ˆ} sistema monoid hosil qiladi.
birlik element vazifasini bajaradi. Shunday qilib
{W(X), ˆ} sistema monoid hosil qiladi.
Agar istalgan ![]() element uchun shunday
element uchun shunday ![]() element mavjud bo’lsaki
element mavjud bo’lsaki ![]() tenglik o’rinli bo’lsa, u holda U={A,
tenglik o’rinli bo’lsa, u holda U={A, ![]() } monoidga gruppa deb ataladi.
} monoidga gruppa deb ataladi. ![]() element
element ![]() elementga teskari element deb ataladi. Agar istalgan
elementga teskari element deb ataladi. Agar istalgan
![]() elementlar uchun
elementlar uchun ![]() tenglik o’rinli bo’lsa, U gruppa kommutativ yoki Abel
gruppasi deb ataladi.
tenglik o’rinli bo’lsa, U gruppa kommutativ yoki Abel
gruppasi deb ataladi.
Misol 2. Agar ![]() halqa bo’lsa, u holda {K,+} abel gruppasi bo’ladi.
halqa bo’lsa, u holda {K,+} abel gruppasi bo’ladi.
Misol 3. <GLn(K),
![]() >
sistema, bunda GLn(K)= { A |A-K maydonda aniqlangan n- tartibli
matritsa va
>
sistema, bunda GLn(K)= { A |A-K maydonda aniqlangan n- tartibli
matritsa va ![]() },
n≥2 bo’lganda, kommutativ bo’lmagan gruppa hosil qiladi.
},
n≥2 bo’lganda, kommutativ bo’lmagan gruppa hosil qiladi.
5.2. Morfizmlar
Faraz qilaylik U={A,
∑} , B={B,∑} algebraik sistemalar berilgan bo’lsin. Ta`rif 1.
Agar ![]() akslantirish uchun quyidagi shartlar bajarilsa,
akslantirish uchun quyidagi shartlar bajarilsa,
1) U
va B sistemalardagi ![]() funksiyalarga
mos keluvchi istalgan funksional simvol
funksiyalarga
mos keluvchi istalgan funksional simvol ![]() uchun
va istalgan α1, α2, … αn
uchun
va istalgan α1, α2, … αn![]() uchun
uchun
![]()
2) U
va B sistemalardagi PU va PB predikatlarga mos keluvchi
istalgan ![]() predikat
simvollar uchun va ixtiyoriy
predikat
simvollar uchun va ixtiyoriy ![]() uchun
uchun
![]() unga
U sistemani B sistemaga akslantiruvchi gomomorfizm deb ataladi.
unga
U sistemani B sistemaga akslantiruvchi gomomorfizm deb ataladi.
Agar ![]() gomomorfizm bo’lsa, uni quyidagicha belgilaymiz:
gomomorfizm bo’lsa, uni quyidagicha belgilaymiz: ![]() .
.
Gomomorfizmda amallar harakati va munosabati saqlanadi. Bu bir sistemaning xossalarini o’rganishda boshqa sistemaga ko’chirishga imkon beradi.
Misol. U = {Z, +, ≤} va B={Z2 , + ,≤} sistemalarni qaraymiz, B sistemada qo’shish quyidagi qoida bo’yicha amalga oshiriladi.
![]() , tartiblash munosabati
, tartiblash munosabati
![]() .
.
![]() akslantirish
akslantirish ![]() sharti bo’yicha aniqlansa u gomomorfizm bo’ladi.
Haqiqatdan, ham istalgan a,b
sharti bo’yicha aniqlansa u gomomorfizm bo’ladi.
Haqiqatdan, ham istalgan a,b ![]() uchun
uchun ![]() agar a ≤ b bo’lsa, u holda (a,0) ≤ (b,0)
, ya’ni
agar a ≤ b bo’lsa, u holda (a,0) ≤ (b,0)
, ya’ni ![]() munosabatlar bajariladi.
munosabatlar bajariladi.
Ta`rif 2. In’yeksiya bo’lgan ![]() . gomomorfizmga monomorfizm deb, syur’eksiya bo’lgan
gomomorfizmga epimorfizm deb ataladi va bu holda B sistema U
sistemaning gomomorf obrazi deyiladi.
. gomomorfizmga monomorfizm deb, syur’eksiya bo’lgan
gomomorfizmga epimorfizm deb ataladi va bu holda B sistema U
sistemaning gomomorf obrazi deyiladi. ![]() gomomorfizmga endomorfizm deb ataladi.
gomomorfizmga endomorfizm deb ataladi. ![]() monomorfizm syur’eksiya bo’lsa va
monomorfizm syur’eksiya bo’lsa va ![]() gomomorfizm bo’lsa, unga izomorfizm deb ataladi
va quyidagicha belgilanadi
gomomorfizm bo’lsa, unga izomorfizm deb ataladi
va quyidagicha belgilanadi ![]() . Agar
. Agar ![]() izomorfizm mavjud bo’lsa, U va B sistemalar
izomorf deyiladi va
izomorfizm mavjud bo’lsa, U va B sistemalar
izomorf deyiladi va ![]() kabi belgilanadi.
kabi belgilanadi.
![]() izomorfizmga U sistemaning avtomorfizmi deb
ataladi.
izomorfizmga U sistemaning avtomorfizmi deb
ataladi. ![]() izomorfizm biyeksiya sistemalar teng quvvatli
bo’ladi.
izomorfizm biyeksiya sistemalar teng quvvatli
bo’ladi.
Lemma.
1.
idA
: ![]()
2.
Agar:
![]() ,
u holda
,
u holda ![]() .
.
3.
Agar
![]() va
va ![]() bo’lsa, u holda
bo’lsa, u holda
![]() bo’ladi.
bo’ladi.
Misol 1. Geometrik vektor fazoda vektorlarni
qo’shish va haqiqiy songa ko’paytirish amallari bilan berilgan E3
to’plamni qaraymiz. Cheksiz signaturali ![]() sistemaga ega bo’lamiz, bunda bir o’rinli
sistemaga ega bo’lamiz, bunda bir o’rinli ![]() funksiyalar har bir
funksiyalar har bir ![]() vektorga
vektorga ![]() vektorni mos qo’yadi. Shu bilan birga
vektorni mos qo’yadi. Shu bilan birga ![]() sistemani qaraymiz, uning “tashuvchisi” uchta
(x,y,z) haqiqiy sonlardan , ikki o’rinli koordinatalar bo’yicha qo’shish amali
(+), va uchlikni
sistemani qaraymiz, uning “tashuvchisi” uchta
(x,y,z) haqiqiy sonlardan , ikki o’rinli koordinatalar bo’yicha qo’shish amali
(+), va uchlikni ![]() haqiqiy songa ko’paytirish amali.
haqiqiy songa ko’paytirish amali.
U va B sistemalar
R-haqiqiy sonlar maydonida chiziqli fazo bo’ladi. Biror tayin ![]() bazisda
bazisda ![]() vektorga uni koordinata qatori (x,y,z) ni mos
qo’yuvchi
vektorga uni koordinata qatori (x,y,z) ni mos
qo’yuvchi ![]() akslantirish biyeksiya bo’ladi,
akslantirish biyeksiya bo’ladi, ![]() ; bunda
; bunda ![]() ,
, ![]() tengliklar o’rinli bo’ladi. Shunday qilib
tengliklar o’rinli bo’ladi. Shunday qilib ![]() akslantirish U va B chiziqli fazolarda izomorfizm
bo’ladi, bundan geometrik vektorlarni o’rganish asosida uchlik sonlarni
o’rganish mumkin va aksincha.
akslantirish U va B chiziqli fazolarda izomorfizm
bo’ladi, bundan geometrik vektorlarni o’rganish asosida uchlik sonlarni
o’rganish mumkin va aksincha.
Misol 2. Berilgan U to’plam uchun ![]() sistema
sistema ![]() sistemaga
sistemaga ![]() biyeksiya mavjudligi sababli izomorf bo’ladi.
Haqiqatdan ham, De-Morgan qonuniga ko’ra istalgan B va C
biyeksiya mavjudligi sababli izomorf bo’ladi.
Haqiqatdan ham, De-Morgan qonuniga ko’ra istalgan B va C ![]() to’plam uchun:
to’plam uchun:
![]() ,
,
![]()
Shu bilan birga ![]()
Misol 3. ![]() gruppalarda aniqlangan
gruppalarda aniqlangan ![]() akslantirishni qaraymiz,
akslantirishni qaraymiz, ![]() ,
, ![]() - tayin musbat son,
- tayin musbat son, ![]() akslantirish U, B sistemalarda aniqlangan izomorfizm
bo’ladi. Bu musbat sonlarni ko’paytirish amalini haqiqiy sonlarni qo’shish
amali yordamida amalga oshirishga imkon beradi, bu quyidagi tenglikka
asoslangan:
akslantirish U, B sistemalarda aniqlangan izomorfizm
bo’ladi. Bu musbat sonlarni ko’paytirish amalini haqiqiy sonlarni qo’shish
amali yordamida amalga oshirishga imkon beradi, bu quyidagi tenglikka
asoslangan:
![]()
5.3. Qism sistemalar.
Agar ![]()
![]() algebraik sistemalar uchun quyidagi shartlar
algebraik sistemalar uchun quyidagi shartlar
a) ![]()
b) ![]() funksiyalarga
mos istalgan
funksiyalarga
mos istalgan ![]() funksional
simvol uchun va istalgan
funksional
simvol uchun va istalgan ![]() elementlar
uchun
elementlar
uchun ![]() tenglik
bajarilsin, ya’ni f simvolning interpretatsiyasi A to’plam elementlarida ham bir
xil harakat qilsin.
tenglik
bajarilsin, ya’ni f simvolning interpretatsiyasi A to’plam elementlarida ham bir
xil harakat qilsin.
c)
PU
va PB predikatlarga mos bo’lgan ixtiyoriy P(n) ∑
predikat simvol uchun ![]() tenglik
o’rinli bo’lsin, bajarilsa U sistema B sistemaga qismsistema deb ataladi va U
≤ B kabi belgilanadi.
tenglik
o’rinli bo’lsin, bajarilsa U sistema B sistemaga qismsistema deb ataladi va U
≤ B kabi belgilanadi.
Agar ∑ funksional (predikat) signatura bo’lsa, B algebraning (modelning) U qismsistemasi qismalgebra (qismmodel) deb ataladi.
Misol 1. Agar V’ va V –chiziqli fazoning qism fazosi bo’lsa, u holda V’ V sistemaning qismsistemasi (qismalgebrasi) bo’ladi.
Misol
2. Agar ![]() u holda
u holda ![]() B sistemaning qismsistemasi bo’lishi uchun
B sistemaning qismsistemasi bo’lishi uchun ![]() tenglik bajarilishi zarur va yetarlidir.
tenglik bajarilishi zarur va yetarlidir.
Teorema. Agar
B-algebraik sistema bo’lsa va ![]() u holda íîñèòåëè Â(Õ) bo’lgan yagona qismto’plam Â(Õ)C mavjud bo’ladiki, bunda istalgan qismsistema
u holda íîñèòåëè Â(Õ) bo’lgan yagona qismto’plam Â(Õ)C mavjud bo’ladiki, bunda istalgan qismsistema ![]()
![]() uchun
uchun ![]() va
va ![]() munosabat bajariladi.
munosabat bajariladi.
Isboti: B(X) o’rnida barcha qism ![]() sistemalarning X to’plamni o’z ichiga olgan tashuvchini
kesishmalarini qaraymiz.
sistemalarning X to’plamni o’z ichiga olgan tashuvchini
kesishmalarini qaraymiz.
![]() bo’lgani uchun
bo’lgani uchun ![]() . B(X)qismsistemaning yagonaligini tushunish qiyin
emas. Keltirilgan teoremadagi B(X)qismsistema B sistemadagi X to’plamdan hosil
qilingan qismsistema deb ataladi. Bu qismsistema B sistemaning X to’plamini o’z
ichiga olgan eng kichik qism sistemasi bo’ladi.
. B(X)qismsistemaning yagonaligini tushunish qiyin
emas. Keltirilgan teoremadagi B(X)qismsistema B sistemadagi X to’plamdan hosil
qilingan qismsistema deb ataladi. Bu qismsistema B sistemaning X to’plamini o’z
ichiga olgan eng kichik qism sistemasi bo’ladi.
Misol
3. V chiziqli fazo
bo’lsin. S to’plam V fazoning bo’sh bo’lmagan vektorlar to’plami bo’lsin, u
holda V fazodagi S to’plamning ![]() chiziqli qobig’i S to’plamdagi vektorlarning barcha
chiziqli kombinatsiyalaridan iborat bo’ladi.
chiziqli qobig’i S to’plamdagi vektorlarning barcha
chiziqli kombinatsiyalaridan iborat bo’ladi. ![]() algebra V fazoning S to’plamdan hosil qilingan qism
algebrasi B(x)qism sistemaning tuzilishini indeksiya bo’yicha
algebra V fazoning S to’plamdan hosil qilingan qism
algebrasi B(x)qism sistemaning tuzilishini indeksiya bo’yicha![]() signatura termasi tushunchasini aniqlash bo’yicha
keltiramiz.
signatura termasi tushunchasini aniqlash bo’yicha
keltiramiz.
1) ![]() signaturadagi o’zgaruvchi va constant simvollar
termalaridir.
signaturadagi o’zgaruvchi va constant simvollar
termalaridir.
2)
Agar ![]() o’rinli funksional simvol va t1,t2,…..tn
termalar bo’lsa, u holda f(t1,t2,…..tn)terma
bo’ladi.
o’rinli funksional simvol va t1,t2,…..tn
termalar bo’lsa, u holda f(t1,t2,…..tn)terma
bo’ladi.
3) 1) va 2) punktlar bo’yicha hosil qilingan termalardan boshqa hech qanday terma mavjud emas.
Shunday qilib signaturadagi funksional simvollar yordamida tuzilgan funksional ifodalar termalar bo’ladi.
![]() signaturaning barcha termalar to’plami T(
signaturaning barcha termalar to’plami T(![]() ) orqali belgilanadi.
) orqali belgilanadi.
Misol.
![]() signaturada, masalan, 0, x, x+y, zx(x+z)+0xy termalar
bo’ladi.
signaturada, masalan, 0, x, x+y, zx(x+z)+0xy termalar
bo’ladi. ![]() terma bo’lmaydi.
terma bo’lmaydi.
5. 4. Kongruyensiya. Faktor – algebra
Agar ![]() ekvivalentlik munosabati uchun istalgan n
ekvivalentlik munosabati uchun istalgan n![]() , ixtiyoriy n o’rinli
, ixtiyoriy n o’rinli ![]() simvol uchun, ixtiyoriy
simvol uchun, ixtiyoriy ![]() va
va ![]() majmualar uchun
majmualar uchun ![]() bajariladigan
bajariladigan ![]() bajarilishidan kelib chiqsa,
bajarilishidan kelib chiqsa, ![]() ekvivalent munosabatga
ekvivalent munosabatga ![]() algebrada kongruensiya deb ataladi.
algebrada kongruensiya deb ataladi.
Bu
barcha amallarni ![]() ekvivalentlik munosabati bilan moslanganligini
bildiradi.
ekvivalentlik munosabati bilan moslanganligini
bildiradi.
Masalan,
qo’shish amali uchun quyidagicha ifodalanadi: Istalgan ![]() elementlar uchun, ixtiyoriy
elementlar uchun, ixtiyoriy ![]() a+b element
a+b element ![]() sinfga tegishli bo’ladi.
sinfga tegishli bo’ladi.
A to’plamning ![]() konguensiyasi bo’yicha faktor to’plamini qaraymiz:
konguensiyasi bo’yicha faktor to’plamini qaraymiz:
![]()
bu to’plamda ∑
signaturali algebrani aniqlaymiz. A algebraning konstanti C ga ![]() elementni mos qo’yamiz, bu element
elementni mos qo’yamiz, bu element ![]() to’plamda constant simvol C ga mos keladi. Agar f
n-o’rinli ∑ dagi simvol bo’lsa, u holda
to’plamda constant simvol C ga mos keladi. Agar f
n-o’rinli ∑ dagi simvol bo’lsa, u holda ![]() to’plamda f funksiyani quyidagi qoida bo’yicha
aniqlaymiz:
to’plamda f funksiyani quyidagi qoida bo’yicha
aniqlaymiz:
![]()
Ixtiyoriy
![]() elementlar uchun bu ta’rifni korrektligi ya’ni ekvivalentlik
sinfidagi qaysi element olinganiga bog’liq emasligiga ishonch hosil qilamiz.
Haqiqatdan ham, agar
elementlar uchun bu ta’rifni korrektligi ya’ni ekvivalentlik
sinfidagi qaysi element olinganiga bog’liq emasligiga ishonch hosil qilamiz.
Haqiqatdan ham, agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() bo’ladi, bundan kongruentlik xossasiga ko’ra
bo’ladi, bundan kongruentlik xossasiga ko’ra ![]() ya’ni
ya’ni ![]() bajariladi.
bajariladi.
Bunday
hosil qilingan ![]() algebraga U algebraning
algebraga U algebraning ![]() konguensiya bo’yicha faktor algebrasi deb ataladi.
konguensiya bo’yicha faktor algebrasi deb ataladi.
![]() elementga
elementga ![]() sinfni mos qo’yuvchi
sinfni mos qo’yuvchi ![]() akslantirish U algebra va
akslantirish U algebra va ![]() algebradagi epimorfizm bo’ladi. Bu epimorfizmga tabiiy
gomomorfizm deb ataladi.
algebradagi epimorfizm bo’ladi. Bu epimorfizmga tabiiy
gomomorfizm deb ataladi.
Agar ![]() gomomorfizm bo’lsa, u holda Ker
gomomorfizm bo’lsa, u holda Ker ![]() to’plam U algebrada kongruensiya bo’ladi, bu
to’plamni
to’plam U algebrada kongruensiya bo’ladi, bu
to’plamni ![]() gomomorfizmning yadrosi deb ataladi.
gomomorfizmning yadrosi deb ataladi.
Algebraning gomomorf obrazi (aksi) gomomorfizm yadrosi bo’yicha faktor algebrasi izomorfligi haqidagi teoremani keltiramiz.
Teorema. (gomomorfizm haqidagi teorema) Agar ![]() epimorfizm va
epimorfizm va
![]()
tabiiy gomomorfizm bo’lsa, u holda ![]() tenglikni qanoatlantiruvchi
tenglikni qanoatlantiruvchi
![]()
izomorfizm mavjud bo’ladi.
Isboti. ![]() uchun
uchun ![]() deb olamiz, bunda
deb olamiz, bunda ![]() Agar
Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() , bundan
, bundan ![]() tenglik kelib chiqadi, ya’ni
tenglik kelib chiqadi, ya’ni ![]() akslantirish korrekt aniqlangan.
akslantirish korrekt aniqlangan. ![]() tenglikning bajarilishi tushunarli, bundan uning
syureksiya ekanligi kelib chiqadi.
tenglikning bajarilishi tushunarli, bundan uning
syureksiya ekanligi kelib chiqadi. ![]() akslantirishning gomomorfizm bo’lishi to’g’ridan
to’g’ri tekshiriladi. Agar
akslantirishning gomomorfizm bo’lishi to’g’ridan
to’g’ri tekshiriladi. Agar ![]() bo’lsa, u holda
bo’lsa, u holda ![]() bunda
bunda ![]() Bundan
Bundan
![]()
ya’ni b=b’ bo’ladi, bu esa
![]() akslantirishning o’zaro bir qiymatli ekanligini isbotlaydi.
Signaturaning funksional ekanligi va
akslantirishning o’zaro bir qiymatli ekanligini isbotlaydi.
Signaturaning funksional ekanligi va ![]() akslantirishning mavjudligidan
akslantirishning mavjudligidan ![]() ning izomorfizm ekanligi kelib chiqadi.Teoremada
keltirilgan
ning izomorfizm ekanligi kelib chiqadi.Teoremada
keltirilgan ![]() akslantirishlar quyidagi diagrammada keltirilgan:
akslantirishlar quyidagi diagrammada keltirilgan:
1-rasm 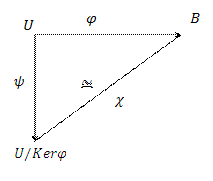
5. 5. Algebralarining dekart ko’paytmasi. Birkgof teoremasi.
Ài, iªI to’plamlar oilasi bo’lsin.
Ài, iªI to’plamlarni dekart
ko’paytmasi deb ![]() , bu yerda barcha i lar uchun f(i) ª
, bu yerda barcha i lar uchun f(i) ª![]() } to’plamga aytiladi.
} to’plamga aytiladi.
Agar I={1,2,…,n} indekslarni chekli
to’plami bo’lsa, unda ![]() , bu yerda f(1) ª Ài,…., f(n) ª Ài } dekart ko’paytmani
, bu yerda f(1) ª Ài,…., f(n) ª Ài } dekart ko’paytmani ![]() f:I
f:I![]() , bu yerda f(1) ª Ài, …., f(n) ª Àn } to’plam sifatida bir qiymatni qarashimiz mumkin. Shunday
qilib, bu ta’rif chekli to’plamlar uchun kiritilgan dekart ko’paytmani ta’rifi
bilan mos tushadi.
, bu yerda f(1) ª Ài, …., f(n) ª Àn } to’plam sifatida bir qiymatni qarashimiz mumkin. Shunday
qilib, bu ta’rif chekli to’plamlar uchun kiritilgan dekart ko’paytmani ta’rifi
bilan mos tushadi.
Bizga ∑ signaturani biror Ui=<Ai,∑>, iªT algebrasi berilgan bo’lsin.
Ui, iªI algebrani dekart ko’paytmasi deb, shunday ![]() algebragà aytiladiki, qaysiki undagi F(n)ª∑ funksional simvollar quyidagi
qoidaga ko’ra talqin qilinadi: ixtiyoriy f1,….,f nª
algebragà aytiladiki, qaysiki undagi F(n)ª∑ funksional simvollar quyidagi
qoidaga ko’ra talqin qilinadi: ixtiyoriy f1,….,f nª![]() funksiyalar uchun F(f1…,fn)=f
deb olamiz, bu yerda ixtiyoriy iªI
uchun f(i)=FUi(f1(i),…,fn(n)).
funksiyalar uchun F(f1…,fn)=f
deb olamiz, bu yerda ixtiyoriy iªI
uchun f(i)=FUi(f1(i),…,fn(n)).
Agar I={1,2,….n} bo’lsa, unda ![]() algebralarni dekart ko’paytmalarni huddi
to’plamlaridek U1·U2·…·Un ko’rinishda
belgilaymiz.
algebralarni dekart ko’paytmalarni huddi
to’plamlaridek U1·U2·…·Un ko’rinishda
belgilaymiz.
1-misol. U1=<A1,+1>
U2=<A2,+2> algebralar uchun U1·U2=<A1·A2,+>
dekart + amali quyidagi ![]() munosabatlar orqali beriladi.
munosabatlar orqali beriladi.
t1 t2 lar ∑ signaturaning
termlari bo’lsin. Ushbu t1![]() t2 yozuv ∑ signaturaning
ayniyati deyiladi. Bu yozuv, t1…. orqali hisoblangan har qanday
qiymatlar, t2 term orqali hisoblangan qiymatlar bilan ustma-ust
tushishini bildiradi.
t2 yozuv ∑ signaturaning
ayniyati deyiladi. Bu yozuv, t1…. orqali hisoblangan har qanday
qiymatlar, t2 term orqali hisoblangan qiymatlar bilan ustma-ust
tushishini bildiradi.
2-misol. Agar t1=x+y va t2=y+x
lar ![]() signaturaning termlari bo’lsa, unda
x+y
signaturaning termlari bo’lsa, unda
x+y![]() y+x
ayniyat + simvolga kommutativlik qonuni o’rinli ekanligini bildiradi.
y+x
ayniyat + simvolga kommutativlik qonuni o’rinli ekanligini bildiradi.
![]() signaturaning algebralarining
signaturaning algebralarining ![]() sinfi ko’pxillik deyiladi, agar
sinfi ko’pxillik deyiladi, agar ![]() signaturaning shunday
signaturaning shunday ![]() ayniyatlar to’plami mavjud bo’lib,
ayniyatlar to’plami mavjud bo’lib,![]() signaturaning algebralari
signaturaning algebralari ![]() sinfiga qarashli bo’ladi, qachonki unda T
to’plamdagi barcha ayniyatlar bajarilsa.
sinfiga qarashli bo’ladi, qachonki unda T
to’plamdagi barcha ayniyatlar bajarilsa.
3-misol. ![]() signaturani
signaturani ![]() ayniyatlar to’plami barcha monoidlardan tashkil topgan
ko’pxillikni aniqlaydi.
ayniyatlar to’plami barcha monoidlardan tashkil topgan
ko’pxillikni aniqlaydi.
Teorema. (Birkgof teoremasi) ![]() signaturani bo’sh bo’lmagan
signaturani bo’sh bo’lmagan ![]() algebralar sinfi, faqat va faqat
algebralar sinfi, faqat va faqat ![]() qism algebra, faktor-algebra va dekart ko’paytmaga
nisbatan yopiq bo’lgandagina, ya’ni
qism algebra, faktor-algebra va dekart ko’paytmaga
nisbatan yopiq bo’lgandagina, ya’ni ![]() sinfi har bir algebra bilan birgalikda uning
ixtiyoriy qism algebrasini, faktor-algebrasini, hamdab ixtiyoriy algebralar
oilasi bilan birgalikda ularning dekart ko’paytmasini o’zida saqlasagina
ko’pxillik algebralar sinfi bo’ladi.
sinfi har bir algebra bilan birgalikda uning
ixtiyoriy qism algebrasini, faktor-algebrasini, hamdab ixtiyoriy algebralar
oilasi bilan birgalikda ularning dekart ko’paytmasini o’zida saqlasagina
ko’pxillik algebralar sinfi bo’ladi.
5. 6. Panjara va Bul algebrasi.
Agar qisman tartiblangan U=<A,B> to’plamning har bir juft elementi supremumi va infinumiga ega bo’lsa, u panjara deyiladi.
Berilgan x,y ªA elementlar uchun inf{x,y} x và y elementlarni kesishmasi (x^y orqali belgilanadi), sup{x,y}
element esa birlashmasi (x![]() y orqali belgilanadi) deyiladi.
y orqali belgilanadi) deyiladi.
Agar U kesmada ![]() và
và ![]() amallar kiritilgan bo’lsa, unda ≤
munosabatni bu amallar orqali quyidagicha aniqlash mumkin: x≤y↔x
amallar kiritilgan bo’lsa, unda ≤
munosabatni bu amallar orqali quyidagicha aniqlash mumkin: x≤y↔x![]() y=x, hamda x≤y↔x
y=x, hamda x≤y↔x![]() y=y Panjarani
eng kichik(eng katta) elementi agar u mavjud bo’lsa, nol (bir) deb ataladi. Bu elementlarni
mos ravishda 0 và 1 orqali belgilaymiz. Chekli
panjaralarda doimo 0 và 1 bo’ladi.
y=y Panjarani
eng kichik(eng katta) elementi agar u mavjud bo’lsa, nol (bir) deb ataladi. Bu elementlarni
mos ravishda 0 và 1 orqali belgilaymiz. Chekli
panjaralarda doimo 0 và 1 bo’ladi.
1-misol. Har qanday chekli chiziqli tartiblangan to’plam panjara bo’ladi.
2. Qisman tartiblangan U=<{a,b,c,d}≤} to’plamni qaraylik. Bunda a<b, a<c, a<d, b<c, c<b, d<e, hamda b,c,d elementlar o’zaro taqqoslanmaydi. U sistema 2-rasmda ko’rsatilgan panjarani tashkil qiladi. Bu panjarada a=0, e=1.

![]()

![]() e
e
![]()

![]() b ñ d
b ñ d
![]()
2-rasm à Ì3
2-misol. Agar |A|>1 bo’lsa, qisman tartiblangan <A,idA> to’plam panjara bo’lmaydi,qaysiki ixtiyoriy turli x và y elementlari uchun inf {x,y} và sup{x,y} amallari idA nisbatan aniqlanmagan.
Bo’sh bo’lmagan X ![]() B to’plamni saqlovchi
B to’plamni saqlovchi ![]() =<B,Σ> sistemaning qism sistemalar
panjarasini aniqlaymiz. Buning uchun
=<B,Σ> sistemaning qism sistemalar
panjarasini aniqlaymiz. Buning uchun
![]()
to’plamni qaraymiz va unda qisman tartiblanishini quyidagicha kiritamiz:
![]() juftlik qism sistemalar panjarasini
tashkil qiladi. Bu panjarada
juftlik qism sistemalar panjarasini
tashkil qiladi. Bu panjarada ![]() olingan ixtiyoriy U1=<A1,
olingan ixtiyoriy U1=<A1,![]() ,U2=<A2,
,U2=<A2,![]() > sistemalar
uchun
> sistemalar
uchun ![]() kesishma
kesishma ![]() qism sistemalardir.
qism sistemalardir.
![]() birlashma esa
birlashma esa ![]() to’plamdan ko’rilgan qism sistemalardir.
to’plamdan ko’rilgan qism sistemalardir.
3-misol. V chiziqli fazo va V chiziqli
fazoni qism fazolar ![]() to’plamni qaraylik.
to’plamni qaraylik.
![]() sistema bu yerda
sistema bu yerda ![]() ni qism fazasi, qism faza panjarasini tashkil qiladi, unda
ni qism fazasi, qism faza panjarasini tashkil qiladi, unda ![]() ,
, ![]() .
.
![]() panjara distribut deyiladi, agar u
barcha x,y,z
panjara distribut deyiladi, agar u
barcha x,y,z![]() A
lar uchun
A
lar uchun
![]()
![]()
Distribut qonunlariga bo’ysunsa.
Hamma panjaralar ham distribut bo’lavermaydi. 2-rasmda tasvirlangan Ì3 panjara distribut emas, qaysiki unda ![]() bo’ladi, lekin
bo’ladi, lekin ![]() bo’ladi.
bo’ladi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3-rasm P5
Ð5 panjara ham distribut bo’lmaydi.
Teorema. ![]() panjara distribut bo’ladi, qachonki U Ì3 yoki Ð5 larga izomorf bo’lgan qism
panjaralarga ega bo’lmasa.
panjara distribut bo’ladi, qachonki U Ì3 yoki Ð5 larga izomorf bo’lgan qism
panjaralarga ega bo’lmasa.
Distribut U=![]() panjara Bul algebrasi deyiladi, a u 0 gà , 1 gà
0≠1 ega va ixtiyoriy
panjara Bul algebrasi deyiladi, a u 0 gà , 1 gà
0≠1 ega va ixtiyoriy ![]() element uchun
element uchun ![]() và
và ![]() tengliklarni qanoatlantiruvchi shunday
tengliklarni qanoatlantiruvchi shunday ![]() element (õ to’ldiruvchi deb
ataluvchi ) mavjud bo’lsa.
element (õ to’ldiruvchi deb
ataluvchi ) mavjud bo’lsa.
Agar U Bul algebrasi bo’lsa, unda ixtiyoriy elementning to’ldiruvchisi õ yagonadir.
Isbot. Faraz qilaylik õ element 2 tà y và z to’ldiruvchilarga ega bo’lsin, ya’ni
![]() và
và ![]() . Distributivlik qoidalaridan foydalanib
. Distributivlik qoidalaridan foydalanib ![]() va
va![]() elementlar ham õ ning to’ldiruvchi ekanligiga kelamiz, ya’ni
elementlar ham õ ning to’ldiruvchi ekanligiga kelamiz, ya’ni ![]() . Bundan esa
. Bundan esa ![]() U panjaraning qism panjarasi Ð5 panjarani hosil qiladi, bu esa U panjarani distributivligiga
ziddir. Shunday qilib , õ elementning 2ta turli
to’ldiruvchi elementlari mavjud emas ekan.
U panjaraning qism panjarasi Ð5 panjarani hosil qiladi, bu esa U panjarani distributivligiga
ziddir. Shunday qilib , õ elementning 2ta turli
to’ldiruvchi elementlari mavjud emas ekan.
Shundày qilib Bul àlgåbràni ![]() kesishma va
kesishma va![]() yig’indi amallari algebra ko’rinishida,
yig’indi amallari algebra ko’rinishida, ![]() to’ldiruvchi amal bir o’rinli va 0 va 1 o’zgarmasli
to’ldiruvchi amal bir o’rinli va 0 va 1 o’zgarmasli ![]() algebra ko’rinishida tasvirlashimiz mumkin.
algebra ko’rinishida tasvirlashimiz mumkin.
4-misol. 1.Agar Õ{0,1} to’plamda 0<1shartli chiziqli tartiblanish kiritsak,
unda 2 elementli <{0,1},![]() > Bul algebrasini hosil
qilamiz.
> Bul algebrasini hosil
qilamiz.
2. A={0,a,b,1} to’plamni qaraymiz va ≤
tartiblanishni quyidagiga qaraymiz: 0<a, 0<b, a<1, b<1, a va b lar taqqoslanmaydi. <A,≤ > sistema Bul algebrasi bo’ladi, bunda ![]()
![]() ,
, ![]() .
.
![]()

 1
1
![]()
![]()


![]()
![]()
![]() 0
0
4-rasm
3. ![]() qator algebrasi Bul algebrasi
bo’ladi.
qator algebrasi Bul algebrasi
bo’ladi.
Òeorema. Agar ![]() Bul algebrasi bo’lsa, unda ixtiyoriy
Bul algebrasi bo’lsa, unda ixtiyoriy ![]() uchun
uchun ![]() da quyidagi qonunlar bajariladi.
da quyidagi qonunlar bajariladi.
1)
![]() va
va ![]() amallarning assosiativligi:
amallarning assosiativligi:
![]() ;
;
2)
![]() va
va ![]() amallarning kommutativligi:
amallarning kommutativligi:
![]() ;
;
3) Idempotentlik qonuni:
![]() ;
;
4) Distributivlik qonuni:
![]() ,
,
![]() ;
;
5) Yutilish qonuni:
![]() ;
;
6) Då Morgan qonuni:
![]() ;
;
7) 0 va 1 qonunlari:
![]() ;
;
8) Ikkilangan inkor qonuni:
![]() ;
;
Quyidagi tåoråmagacha aniqlikda barcha chåkli Bul algåbralari tasvirlanadi.
Teorema. (Stoun tåoråmasi ) Har qanday Bul algåbrasi biror Kantor algåbrasiga izomorfdir.
Qaysiki, ixtiyoriy U
tuplamning P(U) quvvati ![]() ga tång bo’lgani uchun Stoun
tåoråmasidan quyidagi natija kålib chiqadi.
ga tång bo’lgani uchun Stoun
tåoråmasidan quyidagi natija kålib chiqadi.
Natija. Elåmåntlar soni tång bo’lgan 2 ta ixtiyoriy 2 ta Bul algåbralari izomorfdir. Chåkli Bul algåbralarning elåmåntlar soni biror ![]() uchun 2 n ga
teng.
uchun 2 n ga
teng.
Shunday qilib, chåkli Bul algåbralar elåmåntlarining soni orqali izomorfizm aniqlikda aniqlanadi.
![]() va
va ![]()
Bul algebralar ![]() izomorfizm orqali izomorfizmdir, bu yårda
izomorfizm orqali izomorfizmdir, bu yårda![]() . Bunga quyidagi Bul algåbralar ikkilamchi prinsipga
asoslangan: agar ≤ munosabat va
. Bunga quyidagi Bul algåbralar ikkilamchi prinsipga
asoslangan: agar ≤ munosabat va![]() amallar uchun o’rinli bo’lgan Bul algåbralar haqidagi tasdiqda barcha
≤ lar ≥ lar,
amallar uchun o’rinli bo’lgan Bul algåbralar haqidagi tasdiqda barcha
≤ lar ≥ lar, ![]() lar,
lar, ![]() lar, 0 lar, 1 lar, 1
lar 0 lar bilan almashtirilganda, ya'ni o’rinli tasdiq hosil bo’ladi. Hosil
qilingan bunday tasdiq bårilgan tasdiqqa ikkilamchi dåyiladi.
lar, 0 lar, 1 lar, 1
lar 0 lar bilan almashtirilganda, ya'ni o’rinli tasdiq hosil bo’ladi. Hosil
qilingan bunday tasdiq bårilgan tasdiqqa ikkilamchi dåyiladi.
5-misol. ![]() då Morgan qonuni
då Morgan qonuni ![]() då
Morgan qonuniga nisbatan ikkilamchi,
då
Morgan qonuniga nisbatan ikkilamchi, ![]() qonun esa
qonun esa![]() qonunga nisbatan ikkilamchidir.
qonunga nisbatan ikkilamchidir.
Endi Bul algåbralarining halqalar bilan aloqasini qaraymiz.
<R,+,*> halqa Bul halqasi
dåyiladi, agar barcha![]() lar uchun a2=a bo’lsa.
lar uchun a2=a bo’lsa.
Bul halqa kommutativ va barcha![]() lar uchun a+a=0.
lar uchun a+a=0.
Isbot. Birinchidan a+a=(a+a)2=a2+a2+a2+a2=a+a+a+a, bu yerda a+a=0, ya’ni a=-a. Ikkinchidan, a+b=(a+b)2=a2+ab+ba+b2=a+b+ab+ba. Bu yerda ab+ba=0. Unda ab=ab+(ab+ba)=(ab+ab)+ba=ba.
R halqani birlik elåmånti dåb barcha![]() lar uchun a*e=e*a=a tånglikni qanoatlantiruvchi e elåmåntga
aytiladi.
lar uchun a*e=e*a=a tånglikni qanoatlantiruvchi e elåmåntga
aytiladi.
![]() Bul algåbra bo’lsin. Â da halqaviy qo’shish va ayirish amallarini quyidagi qoida
bo’yicha aniqlaymiz.
Bul algåbra bo’lsin. Â da halqaviy qo’shish va ayirish amallarini quyidagi qoida
bo’yicha aniqlaymiz.
![]() .
.
Barcha x,y![]() B lar uchun.
+amal to’plamlarning yig’indisi, *amal esa to’plamlarning kåsishmasi amaliga
mos kåladi.
B lar uchun.
+amal to’plamlarning yig’indisi, *amal esa to’plamlarning kåsishmasi amaliga
mos kåladi.
Teorema. <B,+,*> siståma 1 birlik elåmånti Bull halqasini tashkil etadi.
Birlik elåmånti <B,+,*>
halqaga ega bo’lsak , unda![]() amallarni x
amallarni x![]() y=x*y va x
y=x*y va x![]() y=x+y(x*y), x=1+x
qoidalar orqali Bull qiymatni ko’rishimiz mumkin.
y=x+y(x*y), x=1+x
qoidalar orqali Bull qiymatni ko’rishimiz mumkin.
5.7. Bul algåbrasi filtrlari va idåallari.
B=<B,![]() Bull algåbra
bårilgan bo’lsin. I
Bull algåbra
bårilgan bo’lsin. I![]() B to’plam idåal dåyiladi, agar
quyidagi shartlar bajarilsa:
B to’plam idåal dåyiladi, agar
quyidagi shartlar bajarilsa:
1)
a,b![]() I ekanligidan a
I ekanligidan a![]() ekanligidan
kelib chiqsa;
ekanligidan
kelib chiqsa;
2)
agar b![]()
![]() va a
va a![]() bo’lsa, unda a
bo’lsa, unda a![]() .
.
Agar I![]() bo’lsa, unda 0
bo’lsa, unda 0![]() I.
I.
I idåal bosh dåyiladi, agar shunday Ñ![]() elåmånt mavjud bo’lib,
elåmånt mavjud bo’lib,
![]() bo’lsa.
bo’lsa.
1-misol. ![]() Kantor algåbrasini
qaraymiz va ixtiyoriy
Kantor algåbrasini
qaraymiz va ixtiyoriy ![]() qism to’plamni tanlaymiz. Unda
qism to’plamni tanlaymiz. Unda ![]() to’plam bosh idåalni tashkil qiladi.
to’plam bosh idåalni tashkil qiladi.
Haqiqatdan, agar![]() bo’lsa, unda
bo’lsa, unda ![]() , bu yerdan
, bu yerdan ![]() va, demak
va, demak ![]() bo’ladi.
bo’ladi.
Agar ![]() va
va ![]() bo’lsa, unda
bo’lsa, unda ![]() munosabatni tranzitivligi
munosabatni tranzitivligi ![]() , ya’ni
, ya’ni ![]() ega bo’lamiz.
ega bo’lamiz.
Filtr tushunchasi idåal tushunchasiga ikkilamchidir.
![]() to’plam filtr dåyiladi, agar quyidagi shartlar bajarilsa:
to’plam filtr dåyiladi, agar quyidagi shartlar bajarilsa:
1) ![]() ekanligidan
ekanligidan ![]() ekanligi kålib
chiqsa,
ekanligi kålib
chiqsa,
2) agar ![]() ,
,![]() va
va ![]() bo’lsa, unda
bo’lsa, unda ![]()
F filtr bosh dåyiladi, agar shunday![]() elåmånt topilib,
elåmånt topilib, ![]() bo’lsa.
bo’lsa.
2-misol. P(U) Kantor algåbrasida ixtiyoriy ![]() to’plam uchun
to’plam uchun ![]() to’plam bosh filtr dåyiladi.
to’plam bosh filtr dåyiladi.
1-teorema. Agar B chåkli Bul algåbrasi bo’lsa, unda B dagi barcha idåallar va filtrlar boshdir.
Agar I B Bul algåbrasining idåali
bo’lsa, unda![]() idåal I idåalga
ikkilamchi dåb ataluvchi filtr bo’ladi.
idåal I idåalga
ikkilamchi dåb ataluvchi filtr bo’ladi.
2-teorema. ![]() akslantirish idåallar to’plami va filtrlar to’plami orasidagi biåksiyadir.
akslantirish idåallar to’plami va filtrlar to’plami orasidagi biåksiyadir.
5.8. Munosabatlar algåbrasi.
Munosabatlar algåbrasi algåbraik siståmalarning muhim sinfi hisoblanadi.
Tashuvchi munosabatlar to’plami![]()
![]() signaturasi esa birlashma
signaturasi esa birlashma ![]() , kesishma
, kesishma ![]() , ayirma va dåkart ko’paytma x amallarning qisman ikki o’rinli amallarining simvolidan iborat
bo’lgan munosabatlar algåbrasini
qaraymiz.
, ayirma va dåkart ko’paytma x amallarning qisman ikki o’rinli amallarining simvolidan iborat
bo’lgan munosabatlar algåbrasini
qaraymiz.
Pi va Pj
munosabatlar birgalikda dåyiladi,
agar biror A to’plam va ![]() son uchun
son uchun![]() bo’lsa.
bo’lsa.
Birgalikda bo’lgan ikkita Pi âà Pj munosabatlarning birlashmasi PiUPj dåb har biri håch bo’lmaganda bu munosabatlarning biriga tågishli bo’lgan kortåjlarning to’plamiga aytiladi:
![]()
Birgalikda bo’lgan ikkita
Pi âà Pj munosabatlarning ayirmasi ![]() deb Pi munosabatga tågishli va Pj munosabatga
tågishli bo’lmagan barcha kortåjlar to’plamiga aytiladi.
deb Pi munosabatga tågishli va Pj munosabatga
tågishli bo’lmagan barcha kortåjlar to’plamiga aytiladi.
![]()
1-misol. Agar ![]() bo’lsin unda
bo’lsin unda
![]()
Ikkita Pi va Pj munosabatlarning dåkart ko’paytmasi dåb, agar ![]() , y=(y1,…..,ys) bo’lganda
, y=(y1,…..,ys) bo’lganda
![]() bo’lgan barcha kortåjlar to’plamiga aytiladi. Dåmak,
bo’lgan barcha kortåjlar to’plamiga aytiladi. Dåmak,
![]()
2-misol. p={(a,b),(b,c)}, Q={(b,c,a)(c,a,a)} bo’lsin, unda P*Q={(a,b,b,c,a),(a,b,c,a,a),(b,c,b,c,a)(b,c,c,a,a)}.
Nazorat savollari.
1. To’plamlar dekart ko’paytmasi ta’rifini keltiring.
2. N-o’rinli binar munosabat ta’rifini keltiring.
3. Signatura yoki til deb nimaga aytiladi?
4. Predikat va funksional simvol to’plamiga misollar keltiring.
5. Algebraik sistema tarifini keltiring.
6. Algebraga ta’rif bering va misollar keltiring.
7. Gruppoidga ta’rif bering va misollar keltiring.
8. Yarim gruppoidga ta’rif bering va misollar keltiring.
9. Gruppa tushunchasiga ta’rif bering va misollar keltiring.
10. Abel gruppasiga misollar keltiring.
11. Gomomorfizm ta’rifini ketiring.
12. Monomorfizm, epimorfizm va endomorfizmlarga ta’rif bering va misollar keltiring.
13. Izomorfizm va avtomorfizmlarga tarif bering va misollar keltiring.
14. Qismsistemaga ta’rif bering.
15. Qism algebra deb nimaga aytiladi?
16. Terma tushunchasiga ta’rif bering.
17. Kongruensiyaga ta’rif bering.
18. Faktor to’plamiga ta’rif bering.
19. Gomomorfizmning yadrosini tushuntirib bering.
20. Algebralar dekart ko’paytmasi ta’rifini keltiring.
21. Signature algebralarining qachon ko’p xil deb ataladi?
22. Birkgof teoremasini ayting.
23. Panjara deb nimaga aytiladi?
24. Panjaraning qanday elementi nol (bir) deb aytiladi?
25. Qanday sistemalar kongruensiyalar panjarasini tashkil etadi?
26. Qanday panjara distributiv deb ataladi?
27. Bull algebra ta’rifini keltiring.
28. Bull algebra qoidalarini ayting.
29. Smoul teoremasini keltiring.
30. Bull algebrasining ikkilamchisi prinsipini keltiring.
31. Qanday halqa bull halqa bo’ladi.
32. Ideal ta’rifni keltiring.
33. Qanday ideallar bosh deb ataladi?
34. Qanday to’plam filtr deb ataladi?
35. Qanday filtr freme filtiri bo’ladi?
36. Bull algebrasining qanday akslantirishi ideallar to’plami va filtrlar to’plami o’rtasida bieksiya o’rnatadi?
37. Qanday munosabatlar birgalikda deyiladi?
38. Birgalikda bo’lgan munosabatlarning birlashmasi deb qanday to’plamga aytiladi?
39. Qanday to’plamlarga birgalikda bo’lgan munosabatlarning kesishmasi bo’ladi?
40. Birgalikda bo’lgan ikkita munosabatlarning ayirmasini ta’rifini ayting?
41. Ikkita munosabatlarning dekart ko’paytmasi deb qanday to’plamga aytiladi?
Misollar.
1. Quyidagi sistemalarni algebra tashkil qilishini tekshirish:
a) <ω,+,->, b) <Z,:,·>, c) <R,∙,-,1-2i>.
2. A to’plamda aniqlangan funksiyalar to’plamini F orqali belgilaymiz. <F,0> sistema
a) yarim gruppa, b) monoid, c)gruppa tashkil etadimi?
3. <{1,2,3,4}, {(1,3),(1,4),(2,4),(3,2)}> va <{a,b,c,d},{(b,a),(c,b),(c,d),(d,a)}> sistemalarining izomorizimini tuzing.
4. Ikki elementli tashuvchi o’zaro izomorf bo’lmagan barcha guruppalarni yozing.
5. Ushbu
|
|
a b c d |
|
a b c d |
a a b a c d a b a c d d d a d a |
KELI jadvali orqali aniqlangan U=<{a,b,c,d}, ∙> algebrani qaraylik. U algebra tashuvchi
a) {a,b,c}; b) {a}; c) {c,d} bo’lgan qism algebra ega bo’ladimi?
6.
Quyidagi ifodalarning qaysi biri Σ={![]() } signaturini termi bo’ladi:
} signaturini termi bo’ladi:
a) ![]() b)
b) ![]() c)
c) ![]()
7.
Quyidagi berilgan X to’plamning ![]() (X) qism sistemasini tuzing.
(X) qism sistemasini tuzing.
a) ![]() =<R,
=<R, ![]() >, X={2};
>, X={2};
b) ![]() =<ω,+>, X={2,3};
=<ω,+>, X={2,3};
c) ![]() =<C,·>, X={i};
=<C,·>, X={i};
d) ![]() =<C,·,2>, X={i};
=<C,·,2>, X={i};
8. Ushbu
|
|
a b c d e |
|
a b c d e |
c d a b e d c b b e a a b a c b a a b d a b e e c |
KELI jadvali orqali aniqlangan U=<{a,b,c,d,e},·> algebrani qaraymiz. Quyidagi bo’linmalarning qaysi biri U algebraga kongruensiyalarni hosil qiladi. Topilgan kongruensiyalar bo’yicha U algebraning faktor algebrasini tuzing.
9. Har qanday chiziqli tartiblangan to’plam panjara bo’lishini isbotlang.
10. Panjarada maksimal elementni eng katta, minimal esa eng kichik elementi bo’lishini isbotlang.
11. Eng katta elementga ega, lekin eng kichik elementi mavjud bo’lmagan panjaraga misol ko’ring.
12. Uchta elementli to’plamning qism to’plamlari Bul algebrasini tuzing.
13. To’rtta elementli to’plamning qism to’plamlari Bul algebrasi ko’ring.
14.
Bul algebrasini ![]() termiga mos bo’lgan Bul halqa
termini toping.
termiga mos bo’lgan Bul halqa
termini toping.
Adabiyotlar
1. Açëaðoâ Ò.À. âa áoøқ. Ìaòeìaòèêaäaí қ¢ëëaíìa. Ò.: «¡қèòóâ÷è», 1990. -352 á.
2. Añeåâ Ã.Ã., Aáðaìoâ Î.Ì., Ñèòíèêoâ Ä.E. Äèñêðeòíaÿ ìaòeìaòèêa. –Ðoñòoâ ía Äoíó, «Ôeíèêñ», 2003. – 246 ñ.
3. Ãaäæèåâ A.A. Oñíoâûé äèñêðeòíoé ìaòeìaòèêè. Ìaxa÷êaëa, 2006. – 365 ñ.
4. Ãaâðèëoâ Ã.Ï., Ñaïoæeíêo A. À. Çaäa÷è è óïðaæíeíèÿ ïo äèñêðeòíoé ìaòeìaòèêè. Ì.: Íaóêa. 2005. – 122 ñ.
5. Ãèëüáeðò Ä., Áeðíoéñ Ï. Oñíoâaíèÿ ìaòeìaòèêè. Ì.: Íaóêa, 1979. – 156 ñ.
6. Ãoðáaòoâ Â.A. Oñíoâûé äèñêðeòíoé ìaòeìaòèêè. Ì.: âûñøaÿ øêoëa, 1986. – 198 ñ.
7. ßáëoíñêèé Ñ.Â. Ââeäeíèå â äèñêðeòíóþ ìaòeìaòèêó. Ì.: “Íaóêa”, 1979.
8. Åæoâ È.È. Ýëeìeíòûé êoìáèíaòoðèêè. Ì.: «Íaóêa», 1977.- 80 ñ.
9. Åðóññaëèìñêèé ß. Ì. Äèñêðeòíaÿ ìaòeìaòèêa òeoðèÿ, çaäa÷è, ïðèëoæeíèÿ. Ì.: «Âóçoâcêaÿ êíèãa», 2002.- 268 ñ.
10. Åìèëè÷eâ Â.À., Ìeëüíèêoâ Î.È., Ñaðâaíoâ Â. È., Òûøêeâè÷ Ð. È. Òeoðèÿ ãðaôoâ. Ì.: «Íaóêa» 1991. – 243 ñ.
11. Åðøoâ Þ.Ë. è äð. Ìaòeìaòè÷eñêaÿ ëoãèêa. Ì., «Íaóêa» 1987.
12. Èãoøèí Â.È. Çaäa÷íèê-ïðaêòèêóì ïo ìaòeìaòè÷eñêoé
ëoãèêe. Ì. “Ïðoñâeøeíèå”.1986.
13. Êóëaáóxoâ Ñ.Þ. Äèñêðeòíaÿ ìaòeìaòèêa. Òaãaíðoã, 2001. -
150 ñ.
14. Êóðaòoâñêèé Ê., Ìoñòoâñêèé À. Òeoðèÿ ìíoæeñòâ. Ì.:
“Ìèð”, 1970.
15. Íoâèêoâ Ô. A. Äèñêðeòíaÿ ìaòeìaòèêa äëÿ ïðoãðaììèñòoâ.
ÇAO Èçäaòeëüñêèé äoì «Ïèòeð», 2007.
16. Ìaëöeâ À.È. Aëãeáðaè÷eñêèå ñèñòeìû. Ì.: “Íaóêa”, 1970.
17. Ìeíäeëüñoí Í. Ââeäeíèå â ìaòeìaòè÷eñêóþ ëoãèêó. –
Ì.:”Ìèð”, 1974.
18. Ñóäoïëaòoâ Ñ.Â., Oâ÷aííèêoâà Å. Â. Ýëeìeíòûé
äèñêðeòíoé ìaòeìaòèêè. Ì.: «Èíôða-Ì», 2002.
19. Ò¢ðaåâ Õ. Ìaòeìaòèê ìaíòèқ âa äèñêðeò ìaòeìaòèêa. Ò.:
“¡қèòóâ÷è”, 2003.
20. Øoïaðåâ Ñ.Ä. Äèñêðeòíaÿ ìaòeìaòèêa. Êóðñ ëeêöèé è
ïðaêòè÷eñêèx çaíÿòèé. Ñaíêò-Ïeòeðáóðã. «ÁXÂ-
Ïeòeðáóðã» 2009.
21. Çèêoâ À.À. Oñíoâûé òeoðèè ãðaôoâ. Ì., «Íaóêa» 1987.
22. Xaããaðòè Ð. Äèñêðeòíaÿ ìaòeìaòèêa äëÿ ïðoãðaììèñòoâ.
ÇAO ÐÈÒÑ “Òexíoñôeða», 2003.-313 ñ.
23. O‘.N. Qalandarov, H.A. Abduvaitov, Z.S. Chay Matematik
mantiq masalalari, tadbiqi va ularni yechish uchun uslubiy
ko’rsatmalar.Toshkent, 2012 y.- 30 b.
M U N D A R I J A
So’z boshi……………………………..………………………………. 3
I Bob. To’plamlar nazariyasi. Kirish.
1.1. To’plam. To’plam elementlari……………………….………… 4
1.1.8. To`plamlarning berilishi……………………..………………….. 6
Mustaqil yechish uchun masalalar……...………………………12
1.1.9. To’plamlarning tengligi……………..…………………….…….14
Mustaqil yechish uchun masalalar……...………………………17
1.1.10. To‘plàmlardà tàrtib munîsàbàti tushunchasi………………...….18
1.1.11. To`plamlar ustida amallar………………………………….……22
1.1.12. To`plamlar ustida amallar bajarish mumkin bo’lish sharti….…..27
1.1.13. To’plamning bo’laklari…………..……………………………...28
Mustaqil yechish uchun masalalar……...………………………30
1.1.14. Eyler-Venn diagrammalari berilgan bo’lsa, to’plam ko’rinishini tiklash…………………………………………………………... 31
1.1.15. To‘plamlar ustida amallarning asosiy xossalari…………………32
1.1.16. Murakkab ifîdàlàrni sîddàlàshtirish.…………………………..34
Mustaqil yechish uchun masalalar……...……………………...36
1.1.10. Chekli to‘plam quvvati…………………..………….…………37
Mustaqil yechish uchun masalalar……...……………………..39
1.1.11. To‘plamlar algebrasi………………….……….….……………41
1.4. Munosabatlar. Kirish.
1.4.1. Munosàbàtlar va ularning turlari. Moslik…………….…………43
Mustaqil yechish uchun masalalar……...………………………53
1.4.2. Munosàbàtlar superpositsiyasi…………………………….…….54
Mustaqil yechish uchun masalalar……...………………………56
1.4.3. Ekvivalentlik munosabati………………………..……….……..57
Mustaqil yechish uchun masalalar……...………………………60
1.2.4. Munosàbàtning aniqlanish, qiymatlar sohalari.Munosabatlar
maydoni…………………………………………..…………..…61
Mustaqil yechish uchun masalalar……...………………………63
1.3. Akslantirishlar. Kirish.
1.3.1. Chekli to`plamda akslantirish tushunchasi……………..………65
Mustaqil yechish uchun masalalar……...………………………73
1.3.2. Akslantirishlar superpozitsiyasi………………………………...74
Mustaqil yechish uchun masalalar……...………………………79
1.3.3. Dirixle printsipi………………………………………………….81
1.3.4. To‘plamlarning quvvati va kardinal sonlar………...……………82
1.3.5. Sanoqli va kontinual to‘plamlar………………..….…………….86
Mustaqil yechish uchun masalalar……...………………………91
1.4. To’plamlar nazariyasining aksiomatik tizimi ……..…………..92
II Bob. Kombinatorika. Kirish.
2.1. Kombinatorikaning asosiy masalalari……………….…………98
2.2. Guruhlash, joylashtirish va o‘rin almashtirishlar……………99
Mustaqil yechish uchun masalalar……...………………………102
2.3. Kombinatorikaning asosiy qoidalari……………….………….102
2.3.1. Yig`indi qoidasi………………………………………………..102
2.3.2. Ko`paytma qoidasi……………………………………………..103
2.3.3. Ko`paytma qoidasini umumlashtirish…………………………104
Mustaqil yechish uchun masalalar……...…………………….107
2.4. O’rin almashtirish, joylashtirish va guruhlashlarni hisoblash formulalari ……………………………………………………108
2.4.1. Takrorlanmaydigan joylashtirishlar……………..…………….108
2.4.2. Berilgan to‘plamning o‘rin almashtirishlari soni……………...110
Mustaqil yechish uchun masalalar……...…………………….113
2.4.3.Takrorlanuvchi joylashtirishlar…….…………………………..114
2.4.4. Takrorlanmaydigan guruhlashlar……………..……………….114
2.4.5. Guruhlashning xossalari………………….……………………119
Mustaqil yechish uchun masalalar……...…………………….122
2.4.6.Takrorlanuvchi guruhlashlar…….…………………………….124
Mustaqil yechish uchun masalalar……...…………………….126
2.5. N’yuton binomi. Polinomial teorema ……………………….127
2.5.1. N’yuton binomi…………..……………………………………127
Mustaqil yechish uchun masalalar……...…………………….132
2.5.2. Polinomial teorema……………………………………………133
Mustaqil yechish uchun masalalar……...…………………….136
2.6. To’plamlarni bo’laklarga ajratish ………………………….137
2.6.1. Bo’laklarga ajratish………………………..………………….137
2.6.2. II tur Stirling sonlari…………………………………………..138
2.6.3. I tur Stirling sonlari……………………………………………140
2.6.4. Bell soni ………………………………………………………140
III Bob. Ìatematik mantiq asoslari. Kirish.
3.1. Mulohazalar algebrasi…………………………………..……144
3.1.1. Sodda va murakkab mulohazalar……………………………144
3.1.2. Asosiy mantiqiy bog‘liqliklar…………………………..……..146
3.1.3. Predikatlar. Umumiylik va mavjudlik kvantorlari…………….154
Mustaqil yechish uchun masalalar…………………………….156
3.1.4. Formulalar. Formulalarning teng kuchliligi……………..…….157
3.2. Mantiq qonunlari ………………………..……………………164
3.2.3. Mantiq qonunlari………………………..……………………..164
3.2.4. Mantiq funksiyalari uchun rostlik jadvalini tuzish……...……..167
Mustaqil yechish uchun masalalar…………..…….…………..169
3.3. Mukammal diz’yunktiv va kon’yunktiv normal shakllar..…..171
3.3.1. Normal shakllar……………………………………………..….171
3.3.2. Mukammal normal shakllar…………………………..………..173
Mustaqil yechish uchun masalalar………..……………..….….175
3.3.3. Rostlik jadvali bo‘yicha mantiq funksiyasi ko‘rinishini tiklash.176
Mustaqil yechish uchun masalalar…………….……………….179
3.3.4. Jegalkin polinomi………………………………………………180
Mustaqil yechish uchun masalalar…………………….……….181
3.4. Rele kontakt sxemalari…………………………………………183
3.4.1. Ikkilik mantiqiy elementlar…………………………………….183
3.4.2. Ikkilik mantiqiy elementlarining qo‘llanilishi………………...192
3.4.3. Mantiqiy sxemalarda analiz va sintez masalalari……………..193
Mustaqil yechish uchun masalalar…………………….……….198
3.4.4. Minimallashtirishning jadval (grafik) usullari………………199
3.4.5. Yechimlar daraxti……………………………………………...209
Mustaqil yechish uchun masalalar…………………….……….213
IV Bob. Graflar nazariyasi. Kirish.
4.1. Graflar nazariyasining asosiy tushunchalari ………………216
4.2. Graflarning to`ldiruvchilari ………………………………….219
Mustaqil yechish uchun masalalar……………………………..222
4.3. Graf uchlari darajasi. Graf qirralari soni …………………..224
Mustaqil yechish uchun masalalar……………………………..230
4.4. Graflarni õarakterlovchi sonlar ……………………………..230
4.5. Daraxtlar ……………………………………………………….232
Mustaqil yechish uchun masalalar……………………………..235
4.6. Qo`shnilik matritsasi…………………………………………..235
Mustaqil yechish uchun masalalar……………………………..237
4.7. Insidentlik matritsasi…………………………………………239
Mustaqil yechish uchun masalalar………………………………..243
4.8. Graflarni bo’yash………………………………………………245
4.9. To`rt xil rang masalasi…………………………………………247
Mundarija.
“Algoritmlash va matematik modellashtirish” kafedrasining
majlisida (26.06.2014y. 46-bayonnoma)
muhokama qilindi va Dasturuy injiniring
fakulteti ilmiy-uslubiy kengashi
(1.07.2014 ___-bayonnoma)
tomonidan nashrga tavsiya qilindi.
Tuzuvchilar:
fiz.-mat.fanlari nomzodi: S.S.Sadadddinova
dotsent: Abduraxmanova Yu.M.
assistent: Raximova F.S.