ЛЕКЦИЯ 5. РАСПРОСТРАНЕНИЕ ЗЕМНЫХ РАДИОВОЛН

5.1. Физические процессы при распространении земной волны. Классификация методов расчета поля земной волны

Определение поля излучателя, расположенного в атмосфере вблизи земной поверхности, с учетом реальных свойств Земли и атмосферы представляет собой чрезвычайно сложную задачу. Для облегчения ее решения вводят некоторые упрощения. Поверхность Земли считают электрически однородной, сферической и идеально гладкой. Электрические параметры атмосферы (воздуха) принимают такими же, как и параметры свободного пространства.

Поле земной волны можно считать результатом суперпозиции полей, созданных вторичными источниками, которые возбуждены первичным полем в воздухе и земле. Полупроводящие свойства земли приводят к оттоку энергии волны из воздуха в почву. Сферическая земная поверхность является препятствием, которое земная волна огибает при распространении за линию горизонта. Процесс огибания - процесс дифракции радиоволн вдоль сферического препятствия приводит к дополнительным потерям по сравнению со случаем распространения радиоволн над плоской поверхностью.

Для практических расчетов общее решение дифракционной задачи можно разделить на несколько частных. Критерием для применения частных решений служат высота подъема антенн над поверхностью Земли и длина радиотрассы (расстояния от пункта передачи до пункта приема). Оба параметра определяют степень затенения земной поверхностью пространственных зон Френеля, а следовательно, и закон ослабления поля в процессе дифракции.

В зависимости от высот расположения антенн различают два класса задач. К первому классу относят задачи, в которых высота подвеса антенн h » λ и которые питаются неизлучающим фидером. Это так называемые поднятые антенны, что на практике характерно при работе в диапазоне УКВ и с некоторыми ограничениями в диапазоне КВ. Второй класс задач рассматривает процесс дифракции радиоволн при низкорасположенных антеннах, когда h « λ. Этот случай характерен для работы в диапазонах СДВ, ДВ, СВ и частично КВ.

Вдоль пути распространения земной волны в зависимости от степени освещенности точки приема излучением передающей антенны выделяют три области (зоны): освещенности (I), полутени (II) и тени (III), как показано на рис.5.1. Термин "Зона освещенности" имеет смысл только при поднятых антеннах. При низкорасположенных антеннах область, прилегающую к передающей антенне, называют зоной "приближения плоской Земли", поскольку в пределах этой зоны поверхность Земли можно приближенно считать плоской.

          Линия горизонта

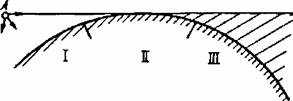
В зонах полутени и тени расчет напряженности поля как для поднятых, так и для низко расположенных антенн ведется по общим дифракционным формулам Фока.

Рис.5.1. К делению радиотрассы на зоны                Рассматривая   среды,   параметры которых указаны в табл.5.1, видим, что для морской воды равенство плотности токов проводимости и токов смещения 60λσ ≈ ε наступает при длине волны λ, равной 0,33 м. Поэтому для радиоволн, имеющих длину волны сантиметрового диапазона, морская вода может рассматриваться как диэлектрик.

Таблица 5.1

Вид земного покрова	ε	σ, См/м
Морская вода	80	1...6
Пресная вода рек и озер	80	10^-3…10^-2
Влажная почва	10...30	3 × 10^-3..3 × 10^-2
Сухая почва	3...6	1 × 10^-5…5 × 10^-3
Мерзлая почва	3...6	10^-3...10^-2
Лед (t=-10°С)	4...5	10^-2...10^-1
Снег (t=-10°С)	1	10^-6

Для влажной почвы это условие выполняется на длине волны λ, равной 17м. Влажная почва может рассматриваться как диэлектрик для метровых и более коротких волн. Таким образом, для волн сантиметрового диапазона все виды земной поверхности имеют свойства, близкие к свойствам идеального диэлектрика.

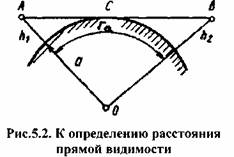
Рис.5.2. К определению расстояния прямой видимости

Отметим также, что при оценке условий распространения земной волны в случае h>>λ сравнивают длину радиолинии r с расстоянием прямой видимости r₀ (рис.5.2). Высоты подвеса приемных и передающих антенн   h₁,h₂ << a, где a=6370км- радиус Земли, поэтому величина r₀, отсчитываемая по дуге большого круга, приближенно равна прямой АВ и ; с учетом тропосферной рефракции

,

где a_э - эквивалентный радиус Земли

,

dN/dh- градиент индекса коэффициента преломления тропосферы. При обычных высотах подвеса антенн (порядка нескольких десятков метров) предельное расстояние прямой видимости составляет несколько десятков километров (как правило, не более 50...60 км). Таким образом, в случае h >> λ, деление трассы распространения земной волны на зоны производят следующим образом: r £ 0,8r₀ - зона освещенности; 0,8r₀ < r < 1,2r₀- зона полутени; r ≥ 1,2r₀- зона тени.

Сферическая земная поверхность является препятствием, которое волна огибает при распространении за линию горизонта. Процесс огибания - процесс дифракции радиоволн вдоль сферического неидеального экрана с радиусом 6370 км сопровождается большими потерями.

5.2.Распространение радиоволн при поднятых передающей и приемной антеннах

Изучение распространения земных радиоволн естественно надо начать с этого наиболее простого случая. При небольших расстояниях между передающей и приемной антеннами кривизной поверхности Земли можно пренебречь. Будем считать поверхность Земли гладкой и однородной на протяжении всей трассы. Задача формулируется так: заданы геометрические параметры: расстояние между передающей и приемной антеннами, высоты подвеса передающей h₁ и приемной h₂ антенн и электрические параметры: подводимая к передающей антенне мощность Р_1, коэффициенты усиления передающей и приемной антенн G₁ и G₂, длина волны λ, вид поляризации волны, относительная диэлектрическая проницаемость почвы ε и ее удельная проводимость σ. Требуется определить множитель ослабления F и напряженность поля по формуле

, мВ/м.

Как впервые было показано еще в 1922 году академиком Б. А. Вве-денским электрическое поле радиоволны в месте расположения приемной антенны можно рассматривать как результат интерференции прямого луча 1 и луча 2, отраженного в точке С от поверхности Земли (рис. 5.3).

При решении задачи распространения радиоволн вдоль границы воздух - земля существенное значение имеет абсолютная величина комплексной диэлектрической проницаемости почвы

.

Обычно она не бывает  меньше   10,

правда для сухого песка в   дециметровом

     Рис.5.3. К расчету поля в точке приема        диапазоне ε_к = 2...5.   Способность земной

поверхности отражать радиоволны тоже связана с относительной комплексной диэлектрической проницаемостью. Значения модулей коэф-фициентов отражения для вертикальной поляризации R_в и горизонтальной поляризации R_r можно определить по формулам:

,

,

где γ - угол скольжения, который определяется по формуле

γ=arctg[(h₁+ h₂)/r].

Земная волна, распространяясь вдоль границы раздела воздух-почва, возбуждает в воздухе и почве токи, которые являются источниками вторичного поля. В соответствии с принципом Гюйгенса-Кирхгофа поле земной волны можно считать результатом суперпозиции полей, наведенных воображаемыми вторичными источниками, которые возбуждаются первичным полем в воздухе и почве. В почве интенсивность вторичных источников ослаблена по сравнению со свободным пространством, за счет тепловых потерь, которые появляются из-за конечных значений проводимости σ. Почва экранирует проникновение поля в глубокие области земли (явление скин эффекта), что препятствует оттоку энергии в нижнюю полусферу.

Напряженность поля в точке приема равна

,мВ/м.

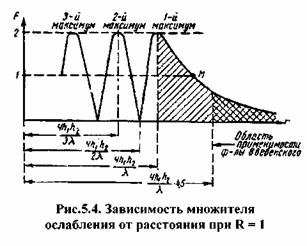
Формула показывает, что в месте расположения приемной антенны поле имеет интерференционную структуру. По мере удаления от передающей антенны будем наблюдать такую картину (рис.5.4). При изменении r косинус аргумента будет меняться. Когда косинус равен единице поле максимально. При      соs [θ + 4πh₁h₂ / (λr)] = 1  

r_max = 4h₁h₂ / [λ(2N +1)], где   N = 0,1,2,…   F_max = 1 + R.

Когда      косинус    равен     минус     единице    поле     минимально.    При

соs[θ + 4πh₁h₂ / (λr)] = - 1, r_min = 2h₁h₂ / [λ(N +1)], N = 0,1,2,… F_min = 1 - R .Отсчет максимумов и минимумов ведется от конца радиотрассы. При r ≤ 4h₁h₂ / λ  наблюдаются    максимумы    и    минимумы    напряженности    поля,   а   при

r > 4h₁h₂ / λ наблюдается плавное уменьшение напряженности поля с увеличением расстояния.

Дальнейшее упрощение интерференционных формул. С увеличением расстояния значение R стремится к 1, а θ - к 180°, тогда

,мВ/м или

, мВ/м.

При дальнейшем увеличении расстояния когда 2πh₁h₂ / (λr) ≈ π / 9 ,то синус аргумента можно заменить его аргументом (при r ≥ 18h₁h₂ / λ)

.

Напряженность поля на расстояниях r ≥ 18h₁h₂ / λ убывает с квадратом расстояния. Надо твердо помнить, что в условиях применимости формулы Введенского, луч отраженный от поверхности земли является вредным, т.к. он стремится скомпенсировать поле прямого луча. Векторная диаграмма сложения полей (структура поля в точке приема) приведена на рис.5.5. Многие изобретатели старались скомпенсировать вредный отраженный луч (рассыпали уголь в месте отражения, ставили стенку на пути отраженного луча). Но они не учли того, что как луч занимает часть пространства, так и волна отражается не в одной точке, а от площади описываемой эллипсоидом с горизонтальными размерами 2а_п и 2b_п (рис.5.6), которые при одинаковых высотах подвеса антенн можно рассчитать по формулам ; 2b_n=2a_n×sinγ.

Многолучевая структура. Диаграмма направленности в вертикальной плоскости.

Будем строить зеркальное изображение антенны (рис.5.7). Из треугольника ∆r=2hsinγ, тогда

.

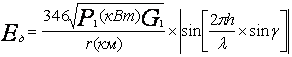Угол γ меняется в пределах от 0 до π/2 (0° -пологий луч, 90° - направлено в зенит). Тогда (2πhsinγ)/λ будет меняться от нуля до 2πh/λ. Для примера возьмем Ташкентский РТПЦ

h₁ = 350м, λ = 7м, ∆r =2hsinγ . Если вертолет будет облетать (по вертикали) ТашРТПЦ, то будет обнаружено 100 максимумов (n=2h/λ).

Учет сферичности земной поверхности при расчете напряженности поля. Сферичность земной волны влияет на амплитуду за счет рассеивания от выпуклой поверхности Земли и фазу отраженной волны, т.к. выпуклость земной поверхности изменяет длину пути отраженной волны. Если в точке отражения радиоволны от поверхности Земли (рис.5.8) провести плоскость MN, касательную к поверхности Земли и отсчитывать высоты подвеса антенн не от поверхности Земли, а от указанной плоскости, то, подставляя в интерференционные формулы вместо действительных высот h₁ и h₂ «приведенные    высоты»    h’₁   и   h’₂,     получим        правильное      значение                 

напряженности поля в месте приема, ибо угол          скольжения луча относительно выпуклой  поверхности Земли тот же, что и угол скольжения над касательной плоскостью. Учет кривизны Земли при пользовании интерференционными формулами сводится к нахождению приведенных высот h₁’ и h₂’ по известным значениям r, h₁, h₂, a_э.

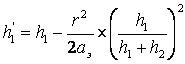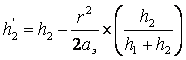;и

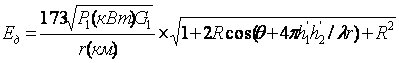, мВ/м;

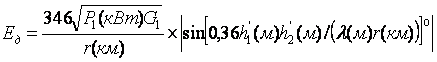, мВ/м;

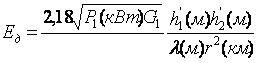, мВ/м.

Расчет напряженности поля в зонах полутени и тени. В. А. Фок получил выражение для функции ослабления пригодное для любых удалений от передатчика. На небольших расстояниях от передатчика оно переходило в интерференционную формулу. Наоборот при больших расстояниях, решение превращалось в одночленную дифракционную формулу. Фок ввел понятия о "масштабе расстояний" L и о "масштабе высот" Н. Это позволяет длину трассы r и высоты подвеса антенн h₁ и h₂ выразить в безразмерных единицах: приведенное расстояние x = r / L,  приведенные высоты подвеса антенн  y₁ = h₁ / H, y₂ = h₂  / H. Выражение для множителя ослабления одночленной дифракционной формулы (для расчета уровня поля в зоне тени) может быть представлено в виде произведения трех сомножителей F = U(х)V(y₁)V(у₂), первый из которых зависит от расстояния, второй и третий от высот подвеса передающей и приемной антенн. Расчет напряженности поля в области тени в диапазонах СДВ, ДВ, СВ и большей части КВ значительно проще, т.к. F = U(х). Для расчета значения множителя ослабления в зоне тени используются графики (рис.5.9 и 5.10) для определения значений  U(x),V(y₁),V(y₂)   в    дБ,    тогда F = U(x) + V(y₁) + V(y₂),дБ. Из дБ в разы значение множителя ослабления можно пересчитать по формуле F = 10^FдБ/20. Значение напряженности поля рассчитывается   по   формуле   Е = Е₀F,   где   Е₀   -напряженность поля в свободном пространстве.

В зоне полутени для приближенной оценки уровня напряженности поля известную пользу приносит способ определения множителя ослабления на границе прямой видимости, т.е. на таком расстоянии, где интерференционные формулы показывают уже нулевые значения поля. Метод разработан для горизонтально поляризованного излучения.

0.1

При вертикальной поляризации он дает менее точные результаты и используется для λ < 50 см. Множитель ослабления на границе прямой видимости рассчитывается по формуле F = (r₀ / L)F(y_1,y₂). Значение функции F(y₁,y₂)получено из многочленной дифракционной формулы и определяется графически из рис.5.11 в дБ. Это значение пересчитывается в разы по формуле F = 10^{F(y1,y2)дБ/20}.  Напряженность поля рассчитывается по формуле

Е = Е₀F.

5.3.Распространение земных радиоволн при низкорасположенных антеннах

Рассмотрим случай, когда передающая и приемная антенны находятся непосредственно у границы раздела (воздух - земля). Подобный случай типичен для диапазонов сверхдлинных, длинных и средних волн. Для удобства расчетов примем поверхность Земли плоской.

Рассмотрим сначала частный случай, когда поверхности Земли можно приписать свойства идеального проводника (60λσ >> ε), т.е. токи проводимости много больше токов смещения.

Предположим, что в точке А на плоской идеально проводящей поверхности Земли находится передающая антенна. Известны коэффициент усиления антенны G₁ и мощность подводимая к антенне Р₁ что эквивалентно изотропному излучателю с мощностью Р₁G₁. В том случае, если такая антенна находилась бы в свободном пространстве, то излучаемая энергия распределялась бы по поверхности сферы, но так как радиоволны в нашем случае могут распространяться только в воздухе, то энергия волны распределится по поверхности полусферы, что эквивалентно увеличению значения вектора Пойнтинга в два раза. Напряженность электрического поля, как Вы знаете связана с вектором Пойнтинга   соотношением               П = Е² / 120π. Поэтому значение напряженности поля увеличивается в раз.

,мВ/м

Эта формула носит название формулы идеальной радиопередачи. Она справедлива для случая, когда антенна расположена непосредственно у поверхности плоской идеально проводящей поверхности Земли (волны в землю не проникают, и потерь в ней нет).

Поскольку в диапазонах сверхдлинных, длинных и средних волн часто применяются проводниковые антенны, излучающим элементом которых является снижение, необходима формула, в которую входили бы такие параметры как I_Д - действующее значение тока в пучности и h_д - действующая высота передающей антенны. Формула идеальной радиопередачи с этими параметрами имеет вид

, мВ/м.

В практике радиосвязи с допустимой погрешностью формулы идеальной радиопередачи могут быть применены для расчета уровня напряженности поля, например, над морем для длин волн λ больше 1000 м.

Значение мощности передатчика можно представить через действующие значения высоты антенны h_д и тока в пучности I_Д по формуле

Р₁ = 160π²(h_дI_д / λ)²,Вт.

Рассмотрим теперь случай распространения радиоволн над полупроводящей поверхностью Земли. Первая попытка решить эту задачу была сделана Зоммерфельдом еще в 1909 году. В 1923 году М.В.Шулейкин придал выражению Зоммерфельда вид удобный для инженерных расчетов. В 1931 году Ван-дер-Поль опубликовал формулу для расчетов, аналогичную формуле Шулейкина. После этого рядом ученых была выполнена работа в которой формулы Шулейкина и Ван-дер-Поля были обобщены для почв с любыми параметрами, построены графики и номограммы, облегчающие расчет. При расчете напряженности поля используется формула идеальной радиопередачи, дополненная множителем ослабления F(х)

,мВ/м;

,мВ/м.

Эти формулы получили название формул Шулейкина-Ван-дер-Поля. Пара-метр х является безразмерным и получил название численного расстояния

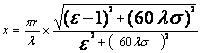
В зависимости от соотношения 60λσ и ε данная формула может быть упрощена:

а) токи проводимости много больше токов смещения (60λσ >> ε)

x ≈ πr / (60λ²σ),

б) токи смещения много больше токов проводимости (ε >> 60λσ)

x ≈ (πr / λ)(ε - 1) / ε².

Определим значения множителя ослабления F(х) по известному значению численного расстояния х. Для этого часто пользуются графиками составленными Берроузом. На них по оси абсцисс графика в логарифмическом масштабе отложены значения 2х, а по оси ординат - искомые значения множителя ослабления для двух видов поляризаций и для разных

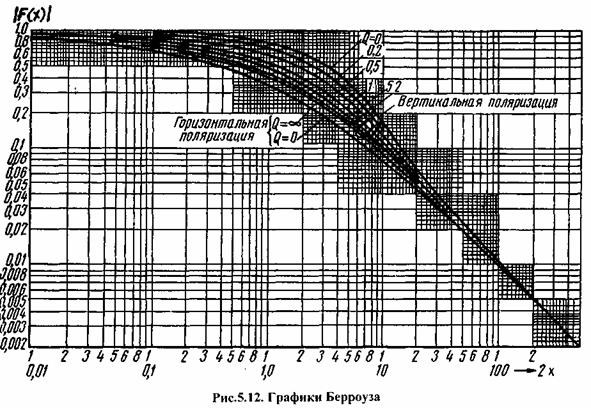
значений параметра Q = ε / 60λσ (рис.5.12). Как видно из графика при ма-

лых значениях х все кривые стремятся к значению F(x) = 1 . Для значений

х > 25 кривые также сливаются. При отсутствии графика расчет множителя ослабления можно провести по приближенной формуле

F(x) = (2 + 0,Зx)/(2 + x + 0,6x²), которая для значений х > 25 принимает простой вид F(х) ≈ 0,5x. При горизонтальной поляризации численное расстояние определяется по формуле

.

Горизонтальный вибратор, помимо основного горизонтально поляризованного поля, максимум которого создается в направлении перпендикулярном оси провода, является источником вертикально поляризованного поля, максимального в направлении оси провода. Отметим, что вертикально поляризованное поле возникает только за счет конечной проводимости земли и по мере увеличения проводимости стремится к нулю.

Вертикальный излучатель с действующей длиной (действующей высотой h_д) создает две составляющие напряженности поля:

  вертикальную  , мВ/м ,               

горизонтальную 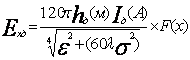  , мВ/м.

Расчеты по формуле Шулейкина-Ван-дер-Поля справедливы на небольших расстояниях, при которых поверхность Земли можно считать плоской: в диапазонах СДВ, ДВ, СВ - на расстояниях до 300...400 км, а в

диапазоне КВ для λ = 50...100 м - на расстояниях до 50 км, а для λ= 10...50 м - на расстояниях до 10 км.

Для учета влияния сферичности Земли в расчетах используются данные графиков МККР, составленные для различных типов почв и длин волн. Графики имеют ориентировочно следующий вид (рис.5.13). По оси ординат отложены значения напряженности поля для мощности излучения в 1 кВт. По оси абсцисс отложены значения длины трассы в км. Сначала необходимо определить по графикам напряженность поля Е_д] в мкВ/м для мощности передатчика в 1 кВт для заданного случая. Полное значение напряженности поля определяется по формуле Е_д = Е_д1

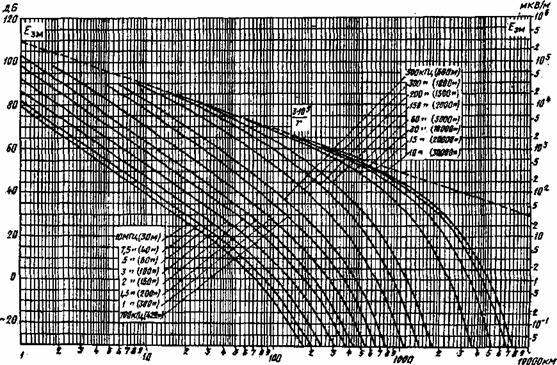
Рис.5.13. Графики МККР

Структура поля при низкорасположенных антеннах. Приближенные граничные условия Леонтовича. Такие антенны относятся к антеннам сверхдлинных, длинных и средних волн. Исследование структуры поля скользящей волны в зоне приближения плоской Земли ведут, принимая во внимание, что в пределах раскрыва приемной антенны участок сферического фронта волны плоский, так же как и участок сферической поверхности Земли вблизи точки наблюдения. В 1944 году академиком М.А.Леонтовичем было показано, что решение о задаче распространения земных радиоволн можно упростить заменив приближенными граничными условиями точные. Приближенными граничными условиями они называются потому, что справедливы в случаях, когда модуль комплексной диэлектрической      проницаемости      почвы      много      больше      единицы

Если это условие выполняется, тоV_ф = с / n, λ₂ = λ₁ / n,

где коэффициент преломления   .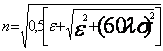

Итак, условие ε_к » 1 эквивалентно требованию того, чтобы длина волны в толще земли была значительно меньше, чем длина волны в воздухе. Предположим теперь, что в воздухе распространяется радиоволна с длиной волны (в воздухе) λ₁. Если глубина h, на которой определяется напряженность поля, много меньше длины волны λ₂ (в земле), то радиус первой зоны Френеля ρ ≈ λ₂ / 2, т.е. размеры первой зоны Френеля будут порядка половины длины волны в земле, причем при сделанном предположении

λ₂ « λ₁. Согласно изложенному, размер 2ρ много меньше длины волны в воздухе, что позволяет считать поле в воздухе на протяжении этого участка почти синфазным. Такая синфазная поверхность создает плоские радиоволны, распространяющиеся вглубь земли в направлении нормали к границе раздела.

Полагаем на некотором удалении от передатчика известна вертикальная составляющая Е_1z, тогда в предположении плоской волны в воздухе горизонтальная составляющая магнитного поля Н_1у = - E_1z / (120π). Эта составляющая связана с горизонтальной составляющей электрического поля Е_1x приближенными граничными условиями Леонтовича

E_1x=-120πH_1y / при z=0 или E_1x = E_1z / при z=0, так как, то , где α = arctg(60λσ / ε).

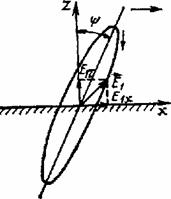
Формула показывает, что вертикальная составляющая поля над поверхностью Земли всегда больше горизонтальной. Горизонтальная составляющая тем меньше, чем больше проводимость почвы и чем длиннее волна. Структура поля для случаев идеально проводящей и полупроводящей земли приведены на рис.5.14. Результирующее поле над поверхностью земли поляризовано эллиптически, поскольку ортогональные составляющие Е_1x и E_1z сдвинуты по фазе на угол α/2. Но обычно E_1z » Е_1x и эллипс поляризации сильно вытянут (рис.5.15). Поэтому приближенно считают, что в воздухе на поверхности Земли поле поляризовано

линейно. Результирующий вектор линейно поляризованной волны ориентирован в направлении большой оси эллипса, т.е. наклонен вперед на угол ψ, который равен

.

Угол ψ называется "углом наклона фронта волны"

.

Рис.5.15. Эллипс поляризации волны

В то время, как в воздухе вертикальная составляющая напряженности электрического поля, значительно

  больше горизонтальной (в раз) в почве горизонтальная составляющая во столько же

раз больше вертикальной составляющей. Следовательно, если в воздухе радиоприем выгоднее вести на вертикальную антенну, то в земле на горизонтальную. Сущность граничных условий Леонтовича заключается в том, что соотношение между горизонтальными составляющими напряженности электрического и магнитного поля (а также Е_1х и Е_1z) у границы раздела определяется параметрами второй среды.

5.4.Особенности распространения радиоволн при подземной радиосвязи

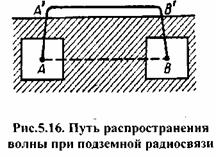
В СНГ проводились теоретические и экспериментальные исследования в области подземной радиосвязи, когда передающая и приемная антенны находятся на некоторой глубине под поверхностью земли. В соответствии с характером распространения радиоволн подземные системы связи делятся на два вида. К первому виду относятся системы связи, приемная и передающая антенны которых находятся на небольшой глубине под землей. При этом основная область распространения радиоволн находится в атмосфере, за исключением передающего и приемного концов, где радиоволны проходят через небольшие участки земной коры. Путь распространения волны изображен на рис.5.16. Волна, распространяющаяся от передающей антенны (точка А) к приемной антенне (точка В) через толщу земли, затухает по экспоненциальному закону и создает очень слабое поле в точке В. Как показали теоретические и экспериментальные исследования, в точку В приходит волна, которая поднимается вверх от заглубленного источника, находящегося в точке А, ослабляясь экспоненциально на участке АА^’. Затем волна распространяется вдоль поверх ности Земли. В каждой точке поверхности эта волна возбуждает токи, которые являются источниками волн,

распространяющихся в глубь земли. Распространяясь в глубь земли на участке В'В, волна ослабляется по экспоненциальному закону. Рассчитывать напряженность поля антенн, расположенных под землей, следует согласно этой схеме. Чтобы не снижался КПД антенны, земля не должна находиться в непосредственной близости от антенны, где поле очень сильное и потери энергии большие. Во избежание дополнительных потерь антенну помещают в воздушную полость. В зависимости от мощности передатчика может быть достигнута дальность связи до нескольких сотен километров, причем при большой дальности связи распространяется не только земная волна, но также волна, отраженная от ионосферы. Для таких систем связи используются длинные и сверхдлинные волны. Основными помехами являются атмосферные шумы. В подземных системах связи второго вида приемно-передающие антенны находятся на большой глубине под землей: в шахтах или скважинах. В этом случае область распространения радиоволн находится целиком в земной коре. Распространение волны происходит через толщу земной коры и при очень сухой почве, когда проводимость не превышает 10^-3 См/м, связь возможно осуществить на несколько километров. Имеются сведения, что на волнах частотой 150...200 кГц при мощности передатчика 100...200 Вт можно осуществить связь на расстояние порядка 10 км.

Подземный вид связи при сильно заглубленных антеннах имеет то преимущество, что он не подвержен действию внешних помех. Поэтому, несмотря на то, что сигнал при прохождении в толще Земли сильно ослабляется, соотношение сигнал/шум на линиях, проходящих глубоко под землей, оказывается больше, чем на линиях, лежащих вблизи поверхности земли. На низких частотах подземные системы связи эффективнее наземных.

5.5 Концепция академика Мандельштамма о "взлетной и посадочной площадках" при распространении радиоволн

Мандельштамм предложил одному из своих учеников Фейнбергу строго решить вопрос о расчете напряженности поля над неоднородной трассой (из участков с разными электрическими параметрами), но сказал, что радиоволны распространяются не так просто как думали раньше. По Мандельштамму радиоволны распространяются по пути наименьшего сопротивления (рис.5.17). Как видно из рисунка наибольшие потери это "места взлета и посадки". Потери связаны с потерями энергии радиоволны в полупроводящей поверхности земли. На трассе земля - море может наблюдаться эффект риковери - восстановления, когда на границе земля -водная поверхность наблюдается некоторое увеличение напряженности поля. Всегда выгодно с точки зрения уровня напряженности поля, чтобы

Рис.5.17. К концепции Мандельштамма

"взлетная и посадочная площадки" приходились на хорошо проводящие поверхности. Поэтому в случае расположения приемной или передающей антенн в местах с плохой проводимостью почвы - там делают искусственное заземление из сетки проводов.