ЛЕКЦИЯ 2.РАСПРОСТРАНЕНИЕ РАДИОВОЛН В СВОБОДНОМ

ПРОСТРАНСТВЕ

2.1.Энергетические соотношения в условиях свободного пространства

         Свободное пространство представляет собой однородную непоглощающую среду, для которой относительная диэлектрическая и магнитная проницаемости равны единице, а удельная проводимость равна нулю (ε = 1; μ = 1; σ = 0), то есть среда имеет параметры электрическая постоянная ε₀ = 8,85 × 10^-12, Ф/м и магнитная постоянная μ₀  = 4π × 10^-7, Гн/м. Примеры: воздух, космическое пространство.

         Все антенны в волновой зоне (дальней зоне) излучают сферические волны. Распространение такой волны сопровождается сферической расходимостью ее фронта и соответственно сферической расходимостью потока электромагнитной энергии по мере удаления от источника. В практике работы радиолиний в свободном пространстве ослабление напряженности поля из-за уменьшения плотности потока энергии во многих случаях определяет требования к энергетическим показателям аппаратуры.

         Поместим в свободном пространстве антенну, излучающую равномерно по всем направлениям (изотропный излучатель). Вокруг источника электромагнитных волн проведем воображаемую сферу радиуса r. Если к излучателю подведена мощность Р₁ и она равномерно распределяется по поверхности сферы с площадью 4πr², то средняя за период плотность потока мощности (мощность приходящаяся на единицу поверхности) равна

П_ср = Р₁ / 4πr². Известно, что значение П_ср, связано с действующими значениями напряженности электрического Е_д и магнитного Н_д полей соотношением П_ср = Е_д × Н_д. Значения Е_д и Н_д связаны через волновое сопротивление среды Z_с = 120π. Отсюда Н_д = Е_д / 120π и П_ср = Е_д² / 120π. Из сравнения двух выражений для П_ср получим формулу для расчета Е_д Е_д=r – действующего значения напряженности электрического поля в свободном пространстве для ненаправленного излучателя.

Правило написания формул: если мы пишем формулу и не указываем в виде индексов наименование единиц, то это означает, что применяются для всех величин основные единицы.

         Амплитудное значение напряженности поля будет в  раз больше, то есть Е_м=/r.

         На практике обычно рассчитывается и измеряется действующее значение напряженности электрического поля Е_д. Реально изотропные антенны не существуют (существуют квазиизотропные) и антенны обладают направленностью. Направленные свойства антенн характеризуются формой диаграммы направленности, коэффициентом усиления G или коэффициентом направленного действия D. Диаграмма направленности показывает зависимость напряженности поля от пространственных координат. Коэффициент направленного действия (КНД) показывает во сколько раз надо уменьшить излучаемую мощность, если ненаправленную (изотропную) антенну заменить направленной для получения одинаковых значений напряженности поля в точке приема. Коэффициент усиления (КУ) показывает во сколько раз надо уменьшить подводимую мощность, если ненаправленную (изотропную) антенну заменить направленной для получения одинаковых значений напряженности поля в точке приема. При этом КПД изотропной антенны принимается равным единице.

Е_д=/r ;

         Произведение Р₁ × G₁ = Р_1экв называют эквивалентной мощностью излучения, которую надо подвести к ненаправленной антенне, чтобы получить в точке приема такую же напряженность поля, как от направленной антенны с коэффициентом усиления G₁, к которой подведена мощность Р₁.

         Из формулы следует, что даже в свободном пространстве, среде без потерь, напряженность поля в точке приема убывает обратно пропорционально первой степени расстояния, что обусловлено уменьшением плотности мощности (среднего за период колебаний значения вектора Пойнтинга) при удалении от источника.

         Для удобства расчетов формулу несколько видоизменим для подстановки значений Р₁ в кВт, r в км и чтобы результат расчета получился в мВ/м, тогда

Е_д=173×/, мВ/м.

При расчете и проектировании радиолиний, особенно в диапазонах сантиметровых и дециметровых волн, необходимо знать мощность сигнала на входе приемника. Эта мощность определяется различно для     радиолиний

     двух типов. На радиолинии       

     1-го          типа       передача

      информации           ведется

Рис.2.1. Структурная схема радиолиний 1-го типа         непосредственно из пункта передачи в пункт приема (рис.2.1). На радиолиниях 2-го типа принимаются сигналы, испытавшие пассивную ретрансляцию на пути от передатчика к приемнику (рис.2.2). На этих линиях непосредственная передача энергии волны от источника до точки приема по каким-либо причинам не возможна (например,  этот путь  перекрыт  препятствием). На   наземных   радиолиниях

          с   пассивной   ретрансляцией

          на   пути      распространения

имеется               специальное

пассивное                 антенное

Рис.2.2. Структурная схема радиолинии 2-го типа.       устройство (или другой объект), который облучается первичным полем и переизлучает его в виде вторичного поля, предназначенного для приема. По такому же принципу работают системы  пассивной радиолокации, где первичное поле облучает обнаруживаемую цель, а поле, переизлученное целью, принимается локатором.

         На любой радиолинии мощность на входе приемного устройства Р₂  связана с плотностью потока мощности в месте приема П₂ соотношением 

Р₂ = П₂S_дη₂,

где η₂ – КПД фидера приемной антенны; S_д  =  G₂λ² / 4π - действующая площадь приемной антенны.

         На радиолинии 1-го типа в условиях свободного пространства плотность потока мощности в месте приема равна

П₂ = Р₁η₁G₁ / (4πr₂),

где Р₁ – мощность на выходе передающего устройства, η₁-КПД передающего фидера, G₁ – коэффициент усиления передающей антенны. Для радиолинии 1-го типа мощность на входе приемника в условиях свободного пространства равна Р¹₂=Р₁η₁G₁G₂η₂λ²/(4πr²).

         На радиолинии 2-го типа значение П₂ зависит от тех же параметров, что и на линии 1-го типа, и, кроме того, от переизлучающих свойств ретранслятора. Если какое-либо тело облучается полем, то его способность переизлучать это поле оценивается эффективной площадью рассеяния δ_эф (ЭПР). Величина ЭПР зависит от формы, размеров, электрических свойств материала из которого выполнен переизлучатель, а так же от его ориентации относительно направления распространения первичного поля и направления на прием.

         Если около переизлучающего тела плотность потока мощности первичного поля Р_оп = Р₁η₁G₁ / (4πr₁²), то переизлученная мощность

Р_оп = П_опδ_эф,

а плотность потока мощности вторичного поля вблизи приемной антенны в условиях свободного пространства П₂ = Р_оп / (4πr₂²).

         Тогда мощность на входе приемного устройства для радиолинии 2-го типа Р¹₂ = Р₁η₁G₁G₂η₂δ_эфλ² / [(4π)³r₁²r₂²].

         В тех случаях, когда r₁ = r₂ = r, Р₂ = Р₁η₁G₁G₂η₂δ_эфλ²/[(4π)³r⁴] и получается уравнение радиолокации.

         Из формул видно, что в свободном пространстве при отсутствии пассивного ретранслятора на линии мощность  на входе приёмника уменьшается обратно пропорционально квадрату расстояния, а при работе с ретранслятором – обратно пропорционально четвертой степени. Такое быстрое убывание поля на линиях 2-го типа объясняется тем, что поле дважды испытывает расходимость сферического фронта волны: первичное поле – на пути от источника (передающей антенны) до пассивного ретранслятора и вторичное поле – на пути от ретранслятора до пункта приема.

         При проектировании систем радиосвязи, радиовещания, радиолокации и т.д. необходимо знать величину потерь при передаче электромагнитной энергии. Потерями передачи L называют отношение мощности Р₁`, подводимой к передающей антенне, к мощности Р<sub>2</sub>` на выходе приемной антенны L = Р₁` / Р<sub>2</sub>` = Р₁η₁η₂ / Р₂.

         Для радиолинии 1-го типа в условиях свободного пространства потери передачи равны L₁ = (4πr / λ)² / G₁G₂.

         Расчеты упрощаются, если в формуле выделить составляющую L₀, которая называется основными потерями передачи и характеризует только потери, обусловленные сферической расходимостью фронта волны          (при G₁ = G₂ = 1) L₀ = (4πr / λ)² .

Полные потери передачи обычно выражают через L. Можно записать

L₁ = L₀ / G₁G₂.

Для радиолинии второго типа в условиях свободного пространства при

r₁  =  r₂  =  r потери передачи равны L₂  = [(4π)³r⁴ / λ²][1 / G₁G₂δ_эф]

или L₂   = L ₀² [(1 / G ₁G₂δ_эф)( λ² / 4π)] .

В случае реальных сред, отличных по своим свойствам от свободного пространства, вводят так называемый множитель ослабления

F =  Е / Е₀  =  Fехр(-iφ_у),

где F - модуль множителя ослабления, который оценивает дополнительное ослабление амплитуды напряженности поля по сравнению с ее ослаблением в условиях свободного пространства; φ_у - фаза множителя ослабления, которая оценивает дополнительное изменение фазы волны. Отсюда следует, что

Е = Е₀F.

2.2. Зоны Френеля

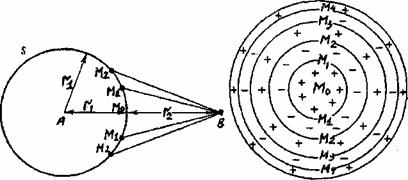
Область пространства, существенно участвующая в формировании поля в точке приема. В теории распространения радиоволн, особенно при оценке влияния земли, важное значение имеет понятие "область, существенная для распространения радиоволн". Пусть в свободном пространстве расположена передающая изотропная (ненаправленная) антенна в точке А. В точке В расположена приемная антенна. Рассмотрим способ передачи энергии из точки А в точку В. Можно предположить, что энергия передается по тоненькой ниточке - лучу АВ или в каком-то объеме пространства. Вопрос о форме пространства, эффективно - участвующего в передаче энергии решается на основе принципа Гюйгенса - что каждый элемент поверхности фронта волны является источником вторичной сферической волны.

Зафиксируем в какой-то момент времени фронт волны на расстоянии r₁. Необходимо определить поле в точке В. На поверхности сферы фазы одинаковы. Выберем точку М (рис. 2.3) из условия М₁В = r₂ + λ / 2. Все точки сферы на участке ММ₁ создают в точке В поля не отличающиеся более, чем на 180° от поля создаваемого кратчайшим лучом АВ. Далее расположим точки  М₂, ..., М_n так чтобы: М₂В = r₂ + 2λ / 2; ...; М_nВ = r₂ + nλ / 2.

Рис.2.3. К построению зон Френеля

Если посмотреть из точки В в направлении сферы мы увидим ряд концентрических окружностей. Участки, заключенные между двумя соседними окружностями получили название зон Френеля. Можно сказать, что колебания создаваемые второй зоной Френеля отличаются по фазе на 180°, от колебаний создаваемых первой зоной Френеля и т.д. Эти зоны маркируются знаками "+" и "-". В курсах оптики показано, что действие смежных высших порядков взаимно компенсируется, причем чем больше порядковый номер зоны, тем полнее осуществляется эта компенсация. В результате такой попарной нейтрализации смежных зон, совокупное действие всех зон эквивалентно действию примерно половины первой зоны Френеля. Таким образом, первая зона Френеля ограничивает область пространства существенно участвующего в процессе распространения радиоволн и должна быть свободной от препятствий.

E_max = E_1max - E_2max + E_3max - E_4max +…

Для выявления количественных соотношений удобно записать ряд в виде

Е_mах = E_1max / 2 + (E_1max / 2 - E_2max + E_3max / 2) + (E_3max / 2 -E_4max + +E_5max / 2) +…

Поскольку соседние члены ряда мало отличаются друг от друга, то значение поля в каждой из скобок близко к нулю и в первом приближении результирующее поле Е_mах ≈ Е_1mах / 2.

Радиусы зон Френеля можно рассчитать по формуле

ρ_n= ,

где  n- номер зоны Френеля.

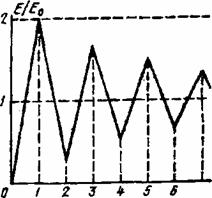
Результат последовательного от зоны к зоне алгебраического суммирования полей можно проследить по кривой, приведенной на рис.2.4. При суммировании полей от источников только первой зоны напряженность поля возрастает до Е = 2Е₀, где Е₀ - поле в свободном пространстве. При дальнейшем сложении проявляется действие противофазных полей от источников второй зоны, и результирующая напряженность поля уменьшается. Компенсирующее действие полей от источников четных зон Френеля обусловливает немонотонный закон приближения величины Е к Е₀ при n→∞. Поле в точке приема определяется суммарным действием вторичных источников, распределенных по воображаемой поверхности, замкнутой вокруг источника А или точки приема В.

Таким образом, существенная область как пространственная фигура является эллипсоидом вращения с фокусами в точках передачи и приема.

Для увеличения напряженности поля в точке приема рядом с передающей антенной устанавливают кольца из металлической сетки, которые закрывают вторую, а иногда вторую и четвертую зоны Френеля.

Рис.2.4. Суммирование полей от источников различных зон при открытии диафрагмы на трассе

Чем короче длина волны, тем меньше поперечные размеры существенного эллипсоида. Например, при длине трассы 10 км размеры первой зоны Френеля посередине трассы при различных длинах волн будут равны:

Таблица 2.1

Размеры радиуса первой зоны Френеля посередине трассы длиной 10км

λ, м	100	10	1	0,1	0,01	0,001
ρ1,м	500	160	50	16	5	1,6

При этом большая ось существенного эллипсоида, соизмеримая с длиной радиолинии, в сотни и тысячи раз больше его малой оси, т.е. эллипс сильно вытянут вдоль трассы.

Заметим, что существенная область имеет форму эллипсоида вращения только при использовании ненаправленных антенн в точках передачи и приема. Реально ее форма более сложная и зависит от диаграмм направленности (ДН) антенн.