УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра АФУ

МЕТОДИЧЕСКОЕ РУКОВОДСТВО
К ЛАБОРАТОРНОЙ РАБОТЕ № 7

«ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ

НА ГРАНИЦЕ РАЗДЕЛА СРЕД»

по дисциплинам «Электромагнитные поля и волны»

и «Электродинамика и распространение радиоволн»

для студентов очного и заочного обучения

и направлений подготовки «Телевидение,

радиосвязь и радиовещание», «Радиотехника» и

«Телекоммуникации»

Ташкент 2004

1. ЦЕЛЬ РАБОТЫ

1.1. Изучение явлений отражения и преломления электромагнитных волн на плоских границах раздела сред.

1.2. Измерение количественных характеристик указанных явлений.

2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

2.1. Плоская электромагнитная волна, падая из среды с параметрами e_а1 и m_а1 на плоскую границу со средой, параметры которой e_а2 и m_а2 (e_а и m_а – абсолютные диэлектрическая и магнитная проницаемость среды, соответственно), в общем случае частично отражается от границы, а частично проходит во вторую среду, меняя направление распространения. Совместим плоскость xoy (рис.2.1) с границей раздела.

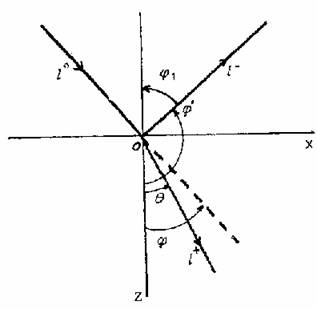
Рис.2.1. Геометрия отражения и прохождения волны

Плоскость xoz, проходящая через нормаль (ось z) к границе раздела и направлениe распространения падающей волны , называется плоскостью падения волны.

Отраженная и прошедшая (преломленная) волны также будут плоскими, а направления их распространения и будут лежать в плоскости падения волны.

Угол j между направлением распространения падающей волны и нормалью к границе раздела (угол отсчитывается от положительного направления оси z) называется углом падения волны.

Угол j¢ между направлением распространения отраженной волны и нормалью к границе раздела определяет в общем угол отражения. Однако в геометрической оптике, которой мы следуем, углом отражения j₁называют угол дополняющий j¢ до 180⁰.

Угол q между направлением распространения прошедшей (преломленной) волны и нормалью к границе раздела называется углом преломления.

Связь между величинами углов j, j¢ и q выражается законами Снеллиуса:

j¢ = p - j , (2.1)

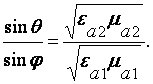(2.2)

2.2. Вектор напряженности электрического поля падающей волны , перпендикулярный направлению распространения, в общем случае может быть расположен по-разному относительно плоскости падения. Но, так как он всегда может быть представлен в виде суммы двух взаимно перпендикулярных векторов, то достаточно рассмотреть два случая: вектор лежит в плоскости падения волны и вектор перпендикулярен плоскости падения волны.

В первом случае поляризация волны называется параллельной. При этом вектор имеет две проекции на оси координат и , а вектор - одну (рис.2.2.а). Векторы и отраженной и преломленной волн также лежат в плоскости падения волны.

Во втором случае поляризация волны называется нормальной. При этом вектор имеет одну проекцию , а вектор - две, и . Векторы и отраженной и преломленной волн также перпендикулярны плоскости падения волны.

2.3. Коэффициентом отражения R называется отношение комплексных амплитуд напряженностей электрического поля отраженной волны и падающей волны , т.е.

. (2.3)

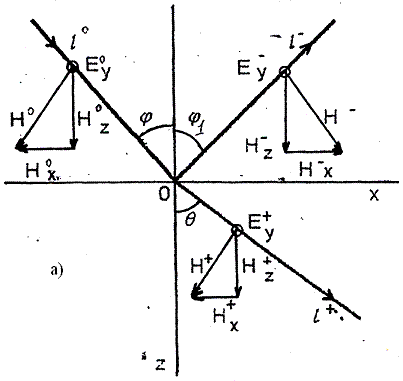
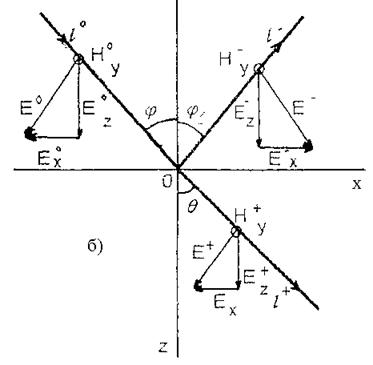
Рис.2.2. К пояснению нормальной и параллельной поляризаций

Коэффициентом прохождения c называется отношение комплексных амплитуд напряженностей электрического поля преломления волны и падающей волны, т.е.

. (2.4)

Отметим, что R и c являются в общем случае комплексными величинами. Их модули характеризуют отношение амплитуд соответствующих волн, а аргументы – сдвиг фаз между этими полями на границе раздела.

В случае параллельной поляризации (рис.2.2.а):

, (2.5)

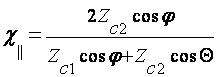, (2.6)

а в случае нормальной поляризации (рис.2.2.б):

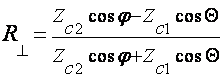, (2.7)

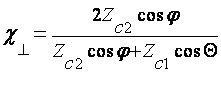, (2.8)

где Z_c₁ = , Z_c₂ = - волновые сопротивления первой и второй среды, соответственно.

Выражения (2.5)…(2.8) часто называют формулами Френеля.

2.4. В случае падения плоской электромагнитной волны на плоскую поверхность проводника волна отражается. В проводниках волновое сопротивление определяется выражением

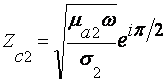где w = 2pf - круговая частота,

s - удельная проводимость среды.

Для идеального проводника волновое сопротивление равно нулю. Поэтому при падении плоской волны из диэлектрика на поверхность идеального проводника независимо от угла падения из формул (2.5)…(2.8) следует:

R_|| = 1, R_^ = -1, c_|| = c_^ = 0 (2.9)

и, следовательно, волна полностью отражается, а поле внутри идеального проводника отсутствует.

Реальные металлы имеют конечную проводимость, но ввиду того, что проводимость металлов велика, во всем диапазоне радиочастот волновое сопротивление металлов близко к нулю. Следовательно, при любых углах падения волны, модуль коэффициента отражения незначительно отличается от единицы.

2.5. В случае падения плоской электромагнитной волны на плоский слой диэлектрика толщиной d, расположенный в воздухе (рис.2.3) падающая на верхнюю границу слоя волна частично отражается, а частично проходит в слой. При достижении нижней границы слоя волна опять частично отражается, а частично выходит из слоя. Отраженная от нижней границы слоя волна падает на верхнюю границу, где опять частично отражается, а частично выходит из слоя и т.д. Очевидно, что волна, отраженная от слоя, представляет собой наложение бесконечного числа волн, распространяющихся в одинаковом направлении (под углом к оси z). Эти волны отличаются друг от друга амплитудами и фазами, которые зависят от числа отражений волны внутри слоя. Аналогичный вывод можно сделать относительно волны, прошедшей через слой диэлектрика.

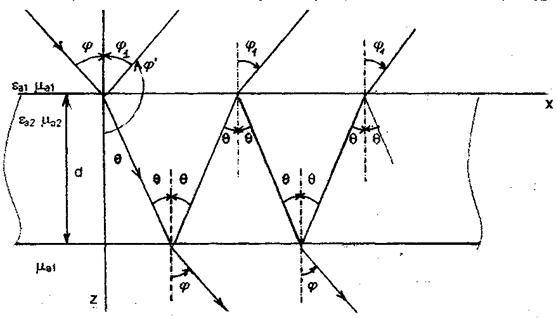
Рис. 2.3. Падение плоской волны на слой диэлектрика

Заметим, что направление распространения прошедшей через слой диэлектрика волны совпадает с направлением распространения падающей волны.

Суммируя комплексные амплитуды всех волн, составляющих отраженную волну, для коэффициентов отражения волн от слоя R_сл и прохождения волны c_сл через слой можно получить выражения:

R_сл = ,

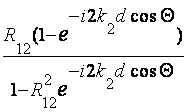c_сл = ,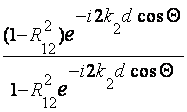

где R₁₂ – коэффициент отражения при падении волны на границу слоя из воздуха, определяемый в случае параллельной поляризации по формуле (2.5), а при перпендикулярной поляризации по формуле (2.7).

k₂=, а угол определяется из второго закона Снеллиуса (2.2).

Модули коэффициентов отражения и прохождения равны:

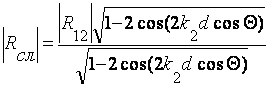, (2.10)

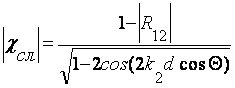. (2.11)

2.6.Если обе среды являются диэлектриками, и, следовательно, m_а1=m_а2=m₀, то коэффициент отражения нормально - поляризованной волны не может быть равен нулю ни при каком угле падения. При параллельной поляризации существует угол падения

, (2.12)

называемый углом Брюстера, при котором коэффициент отражения равен нулю, и волна полностью проходит во вторую среду.

При падении параллельно - поляризованной плоской волны под углом Брюстера на плоский слой диэлектрика также наблюдается полное прохождение волны через слой. Это видно из выражений (2.10) и (2.11). Так как при данных условиях коэффициент отражения R₁₂=0, то модули коэффициентов отражения от слоя диэлектрика и прохождения через этот слой соответственной равны 0 и 1.

3. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Лабораторная установка предназначена для исследования явлений отражения и преломления электромагнитных волн на границах раздела сред с различными физическими характеристиками и измерения модулей коэффициентов отражения и прохождения в диапазоне частот 5,3…10,6 ГГц.

Лабораторная установка состоит из передающей части, приемной части и подставки, на которой закрепляются пластины из различных материалов (рис.3.1). Эти пластины имитируют границу раздела двух сред.

Передающая часть антенны содержит генератор СВЧ (1) и рупорную антенну (2). Можно считать, что на расстоянии 7…10 длин волн от рупорной антенны в ограниченной области пространства создается плоская электромагнитная волна. Падая под углом j на пластину (7), в зависимости от материала пластины и вида поляризации волна может:

а) полностью отразиться;

б) частично пройти сквозь пластину и частично отразиться;

в) полностью пройти сквозь пластину.

Приемная часть состоит из рупорной антенны (2), переменного аттенюатора (3), детекторной секции (4) и стрелочного индикатора (5). Переменный аттенюатор служит для регулировки мощности, поступающей на детекторную секцию от рупорной антенны. Расположенный в детекторной секции, СВЧ диод выпрямляет ток высокой частоты. После выпрямления ток диода поступает на микроамперметр постоянного тока (5). Приемная часть установки укреплена на платформе, которая может перемещаться по окружности с центром в точке 0 (рис.3.1) и, следовательно, может регистрировать как отраженную (положение а), так и прошедшую (положение б) волны.

При непосредственном присоединении рупорных антенн (2) к волноводу от генератора и аттенюатору (3) в данной установке получается нормальная (относительно плоскости падения волны) поляризация. Для получения параллельной поляризации присоединение рупорных антенн должно производиться через волноводные скрутки.

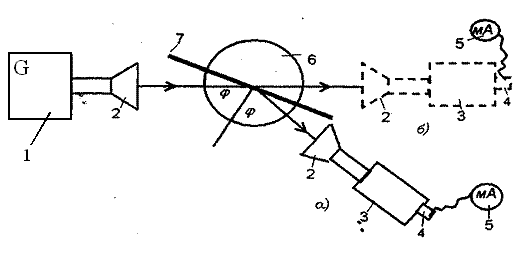
Рис. 3.1. Структурная схема лабораторной установки (1 – генератор СВЧ диапазона, 2 - рупорная антенна, 3 – переменный аттенюатор, 4 – детекторная секция, 5 – индикаторный прибор (микроамперметр), 6 – шкала отсчета углов, 7 – исследуемая пластина).

Так как передающая часть является неподвижной, то угол падения изменяется путем вращения подставки с образцом. Отсчет угла падения производится по шкале, которая поворачивается вместе с образцом. В соответствии с определением, приведенным выше, за ноль отсчета принимается направление перпендикуляра к поверхности исследуемой пластины.

Для экспериментального определения модулей коэффициента отражения и коэффициента прохождения пользуются косвенным методом с использованием переменного аттенюатора, проградуированного в децибелах. Изменяя ослабление аттенюатора, добиваясь неизменных показаний микроамперметра, определяют отношение мощностей отраженной и падающей волн при определении модуля коэффициента отражения, и отношение мощностей прошедшей и падающей волн при определении модуля коэффициента прохождения.

Рассмотрим, например, измерение модуля коэффициента отражения. При расположении приемной антенны в поле падающей волны в тракт приема аттенюатором вводят ослабление N₁ и фиксируют показание микроамперметра, которое составляет порядка 5 мкА. Затем, помещая антенну в поле отраженной волны, уменьшаю ослабление аттенюатора до величины N₂, при которой показание микроамперметра остается неизменным. Изменение ослабления N₂-N₁ равно отношению вышеуказанных мощностей, выраженному в децибелах. Так как мощности, принимаемые антенной, пропорциональны квадратам напряженностей соответствующих электрических полей, то можно записать

N₂-N₁ =1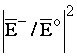0lg=20lg.

Откуда следует

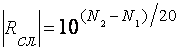. (2.13)

Определение значения коэффициента прохождения производится аналогично, а модуль коэффициента прохождения рассчитывается по формуле

, (2.14)

где N₃ – величина ослабления аттенюатора при расположении приемной антенны в поле прошедшей волны. Заметим, что применение аттенюатора позволяет избежать влияния нелинейной характеристики детектора на результаты измерений.

Следует иметь в виду, что в данной установке фронт падающей волны лишь приближенно считается плоским и волна распространяется в ограниченной области пространства. Также ввиду конечных размеров отражающих поверхностей возможны нежелательные отражения волн от их краев. Эти причины могут вызвать некоторое расхождение результатов измерений с теоретическими результатами расчета.

4. ЗАДАНИЕ К РАБОТЕ

4.1. Определить зависимость значений модуля коэффициента отражения от угла падения волны.

4.2. Определить зависимость значений модуля коэффициента отражения от плоского слоя диэлектрика и коэффициента прохождения через этот слой от угла падения волны.

4.3. Определить угол Брюстера.

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

5.1. Ознакомьтесь с инструкцией по настройке генератора, входящей в комплект установки.

5.2. Включите генератор и после его прогрева в течение 7…10 минут настройте на частоту f, заданную преподавателем. Рассчитайте соответствующую длину волны l в свободном пространстве по формуле

где с = 3×10⁸ м/с – скорость света в свободном пространстве.

5.3. Установите нормальную поляризацию падающей волны. При этом вектор излучаемой волны должен быть перпендикулярен плоскости падения волны и основанию лабораторного макета. Напоминаем, что вектор перпендикулярен широкой стенке прямоугольного волновода.

5.4. Вращая ручку аттенюатора, установите величину его максимального ослабления 50 дБ и расположите приемную антенну против передающей (исследуемая пластина должна отсутствовать). Уменьшая ослабление аттенюатора, добейтесь отклонения стрелки микроамперметра. Перемещая приемную антенну, получите максимальное отклонение стрелки микроамперметра.

5.5. Изменяя ослабление аттенюатора, установите стрелку микроамперметра, например, на деление 5 и запишите показание N1 шкалы аттенюатора.

5.6. Закрепите на подставке металлический лист. Вращая подставку, установите по шкале отсчета угол падения волны , равный 20⁰. Перемещая приемную антенну, определите направление распространения отраженной волны по максимуму показания микроамперметра. Запишите значение угла j₁ (рис.3.1) между нормалью к поверхности металлической пластины и направлением распространения отраженной волны. Изменяя ослабление аттенюатора, установите такое же показание микроамперметра, как и в п.5.5. Запишите показание шкалы аттенюатора N2. Определите значение модуля коэффициента отражения по формуле (2.13). Повторите измерения при других значениях углов падения волны. Результаты измерений и расчета занести в таблицу типа табл.5.1. Снимите металлический лист с подставки.

5.7. Повторите операции п.п.5.4 и 5.5, так как выходная мощность генератора могла немного измениться. Закрепите на подставке одну из диэлектрических пластин по заданию преподавателя. Установите угол падения волны 20⁰. Определите значение модуля коэффициента отражения так же, как и в п.5.6 и запишите значения N1 и N2 и результаты расчета модуля коэффициента отражения в таблицу типа табл. 5.1. Повторите измерения и расчеты для углов падения волны от 30⁰ до 70⁰ через 10⁰.

Рассчитайте значения модулей коэффициента отражения по формуле (2.13).

Таблица 5.1

Результаты экспериментального исследования отражающих свойств…………………………………………..пластины

Поляризация падающей волны ………………………………
Угол падения волны j	Угол отражения волны j₁	Величина ослабления N₁	Величина ослабления N₂	N₂- N₁	Модуль коэффициента отражения
град.	град.	дБ	дБ	дБ	-
20^о
30^о
…
70^о

5.8. Сняв пластину с подставки, повторить операции п.п.5.4 и 5.5. Так как направление распространения волны, прошедшей через слой диэлектрика, всегда совпадает с направлением распространения падающей волны, то перемещать приемную антенну не потребуется. Установите пластину на подставку. Поворачивая подставку, установите угол падения волны, равный 0⁰. Изменяя ослабление аттенюатора, установите такое же показание микроамперметра, как в п.5.5. Запишите показания шкалы аттенюатора N3 в таблицу типа табл.5.2. Определите значение модуля коэффициента прохождения по формуле (2.14). Повторите измерения и расчеты для углов падения волны от 10⁰ до 70⁰ через 10⁰.

5.9. Установите параллельную поляризацию падающей волны с помощью волноводных скруток. Выполните п.5.4 (диэлектрическую пластину с подставки можно не снимать). Медленно вращая подставку с пластиной, добейтесь максимального показания микроамперметра и запишите величину угла падения волны, при котором через слой проходит максимальная мощность. Полученный угол падения волны и будет являться углом Брюстера. Перемещая приемную антенну в область, где возможны отраженные волны, убедитесь в отсутствии отраженной волны. Используя формулу (2.12), по полученной величине угла Брюстера рассчитайте относительную диэлектрическую проницаемость исследуемого образца. При этом следует учесть, что отношение абсолютных диэлектрических проницаемостей сред равно отношению относительных диэлектрических проницаемостей, и что у воздуха e₁ = 1.

Таблица 5.2

Результаты экспериментального определения величин

коэффициента прохождения

Поляризация падающей волны ………………………………
Угол падения волны j	Величина ослабления N₁	Величина ослабления N₃	N₃- N₁	Модуль коэффициента отражения
град.	ДБ	дБ	дБ	-
0^о
10^о
20^о
…
70^о

6. СОДЕРЖАНИЕ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ

Отчет должен содержать:

6.1. Структурную схему лабораторной установки.

6.2. Заданные вид поляризации поля, частоту и рассчитанное значение длины волны.

6.3. Таблицу 5.1 с результатами значений углов отражения и расчета значений коэффициента отражения от металлической поверхности.

6.4. Таблицы 5.1 и 5.2 с результатами значений модулей коэффициентов отражения и прохождения для плоского слоя диэлектрика.

6.5. Величину угла Брюстера и рассчитанное значение относительной диэлектрической проницаемости исследованного образца.

6.6. Графики зависимостей значений модулей коэффициентов отражения и прохождения от угла падения волны.

6.7. Выводы.

7. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

7.1. Какая электромагнитная волна называется плоской однородной волной? ([1] §9.1; [2] §11.1).

7.2. Что называется фазовой скоростью, электромагнитной волны? Как определяется фазовая скорость электромагнитной волны, распространяющейся в однородной изотропной диэлектрической среде, через параметры среды? ([1] С.142; [2] §9.5 С. 112, §11.2).

7.3. Что называется длиной волны? Как определяется длина волны через фазовую скорость? ([2] С. 73).

7.4. Что называется волновым сопротивлением среды? Как определяется волновое сопротивление диэлектрической среды через параметры среды?

([1] С. 169; [2] §9.5 С. 113).

7.5. Запишите выражения для векторов поля плоской электромагнитной волны, распространяющейся вдоль оси Z и поляризованной вдоль оси Х прямоугольной системы координат. ([1] §9.1; [2] §11.1, 12.1).

7.6. Что называется вектором Пойтинга? Куда направлен вектор Пойтинга? Что показывает величина вектора Пойтинга? Какой смысл имеет среднее за период значение вектора Пойтинга? ([1] §4.1, §4.5 C. 64; [2] §4.1, C.56).

7.7. Что называется плоскостью падения, углом падения, углом отражения и углом преломления? Покажите указанные выше углы на чертеже. ([1] §10.1, §10.2; [2] §13.2).

7.8. Запишите законы Снеллиуса. ([1] §10.2; [2] §13.2).

7.9. Какие существуют виды поляризации электромагнитных волн?

([1] §9.3; [2] §12.1, §12.2).

7.10. Почему при наклонном падении плоской электромагнитной волны на границу раздела двух сред достаточно рассмотреть только два случая нормальной и параллельной поляризации? ([1] §9.3, §10.1; [2] §13.2).

7.11. Нарисуйте взаимное расположение векторов Е и Н падающей, отраженной и прошедшей (преломленной) волнах при нормальной и параллельной поляризации падающей волны? ([1] §10.2; [2] §13.2).

7.12. Что называется коэффициентами отражения и прохождения? Какой смысл имеют модули и фазы этих коэффициентов? ([1] §10.2; [2] §13.2).

7.13. При каких условиях наблюдается явление полного прохождения электромагнитной волны через границу раздела двух сред? Что называется углом Брюстера? ([1] §10.3; [2] §11.3).

7.14. Чему равно волновое сопротивление проводящей среды? ([1] §9.2; [2] §11.3).

7.15. Что называется идеальным проводником? Чему равно волновое сопротивление идеального проводника? ([1] §9.2, §10.4 C.200; [2] §3.10).

7.16. Чему равен коэффициент отражения от идеального проводника в случаях нормальной и параллельной поляризации падающей электромагнитной волны? ([1] §10.4 C.200; [2] §13.6).

7.17. Как происходит отражение плоской электромагнитной волны от плоского слоя диэлектрика? В каком направлении распространяется отраженная волна? ([1] §10.2 C.185).

7.18. Как происходит прохождение плоской электромагнитной волны на плоский слой диэлектрика в данной лабораторной работе? ([1] §10.2 C.185).

7.19. Как измеряются коэффициенты отражения и прохождения при падении плоской электромагнитной волны на плоский слой диэлектрика в данной лабораторной работе?

7.20. Как определить относительную диэлектрическую проницаемость диэлектрика, используя описанную здесь лабораторную установку?

7.21. Объясните причины расхождения между измерениями и расчетными значениями коэффициентов отражения и прохождения, если оно имеет место?

ЛИТЕРАТУРА

1. Вольман В.И., Пименов Ю.B, Техническая электродинамика. – М.: Связь, 1971.

2. Лебедев И.В. Техника и приборы СВЧ, том 1. – M.: Высшая школа, 1970.

3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.

Методическое руководство к лабораторной работе № 7 «ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ НА ГРАНИЦЕ РАЗДЕЛА СРЕД» по дисциплинам «Электромагнитные поля и волны» и «Электродинамика и распространение радиоволн» для студентов очного и заочного обучения и направлений образования «Телевидение, радиосвязь и радиовещание» и «Радиотехника» рассмотрено на заседании кафедры (протокол № 20 от 7.06.2004 г.) и рекомендовано к печати.

Отв. редактор доц. Ликонцев Д.Н.

Составители:

доц. Ликонцев Д.Н. (работы № 1,2,7)

доц. Габзалилов Г.Ф. (работа №6)

Редакционно-корректурная комиссия:

редактор доц. Романенко Б.А.

корректор ст. преп. Павлова С.И.