УЗБЕКСКОЕ  АГЕНТСТВО  СВЯЗИ  И  ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ  УНИВЕРСИТЕТ  ИНФОРМАЦИОННЫХ  ТЕХНОЛОГИЙ

 

                                                     Кафедра АФУ

 

 

МЕТОДИЧЕСКОЕ РУКОВОДСТВО
К ЛАБОРАТОРНОЙ РАБОТЕ № 6

«ИССЛЕДОВАНИЕ СТРУКТУРЫ ЭЛЕКТРОМАГНИТНОГО

ПОЛЯ ВОЛН КЛАССА Т В ПОПЕРЕЧНОМ СЕЧЕНИИ

НАПРАВЛЯЮЩИХ СИСТЕМ»

по дисциплинам «Электромагнитные поля и волны»

и «Электродинамика и распространение радиоволн»

для студентов очного и заочного обучения

и направлений подготовки «Телевидение,

радиосвязь и радиовещание», «Радиотехника» и

«Телекоммуникации»

 

 

Ташкент 2004

 

1. ЦЕЛЬ РАБОТЫ

 

1.     Изучить основные закономерности процесса распространения электромагнитных волн класса Т в направляющих системах.

2.     Изучить метод электростатической аналогии.

3.     Освоить методику экспериментального исследования структуры электромагнитного поля волны класса Т в поперечном сечении направляющей системы.

4.     Экспериментально подтвердить теоретические положения о структуре электромагнитного поля волн класса Т.

 

2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 

2.1. Некоторые положения теории направляющих систем

 

Для передачи энергии электромагнитных волн от источника к по­требителю (например, от передатчика к антенне) в практике ис­пользуются направляющие системы (Направляющие системы, в которых в качестве рабочего типа используется класс волны Т, принято также называть линиями передачи).

Направляющая система, у которой поперечное сечение и электромагнитные свойства заполняющей её среды остаются неизменными в продольном напра­влении (как правило, это ось z), называется регулярной.

Основной задачей анализа полей в направляющих системах является определение структуры поля – получение расчётных формул составляющих векторов поля, построение по ним силовых линий и эпюров распределения поля для некоторого времени t=const.

При расчёте структуры поля пользуются следующей методикой:

по уравнению Гельмгольца определяют одну из продольных составляющих векторов ;

затем, используя уравнения Максвелла, через продольные составляющие определяют поперечные.

Для упрощения записей рассмотрим реализацию этой методики в прямоугольной системе координат, например для продольной составляющей вектора . Так как направление распространения совпадает с осью z, то в расчётную формулу будет входить множитель , где g1 – продольный коэффициент распространения, показывающий изменение амплитуды и фазы направленной волны. Тогда искомую функцию можно представить в виде

или 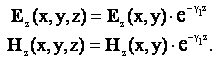                                                                     (2.1)

В выбранной системе координат требуется решение однородного волнового уравнения Гельмгольца вида

.                                 (2.2)

Применив правила взятия частных производных из слагаемых функции (2.1), перепишем (2.2)

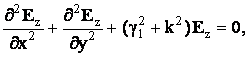                                                     (2.3)

где k – коэффициент распространения в неограниченном (свободном) пространстве.

Величину  называют поперечным коэффициентом распространения , т.е.

     .                                                  (2.4)

Если решить дифференциальное уравнение (2.3) методом разделения переменных, то получим

.                         (2.5)

При решении задачи по нахождению продольной составляющей Нz ответ будет подобен выражению (2.5).

Коэффициенты g2х и g2у называют поперечными волновыми числами, они связаны с коэффициентом g2 соотношением

                                                   (2.6)

Из решения уравнения Гельмгольца (2.5) видно, что продольная составляющая электромагнитного поля в плоскости поперечного сечения изменяется по синусам и косинусам. Постоянные g2х и g2у определяют период изменения (вариации) поля в поперечной плоскости. Каждой паре поперечных волновых чисел соответствует своя структура поля направляемой волны (свой тип волны).

Для определения поперечных составляющих поля Ех, Еу, Нх и Ну воспользуемся первым и вторым уравнениями Максвелла, записанными в прямоугольной системе координат. В проекциях уравнений на оси координат, частные производные составляющих векторов Ех, Еу, Нх и Ну по оси z превращаются в произведения вида, например,

Так как в регулярных волноводах без потерь в каждом поперечном сечении распределение поля остаётся неизменным, то , и в сокращённой форме записи .

С учётом указанного, проекции первого уравнения приобретают вид:

 

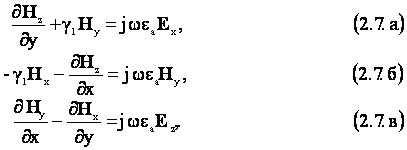
а второго уравнения:

 

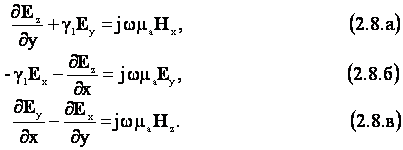
Используя эти уравнения, определяем зависимость поперечных составляющих от координат через продольные составляющие. Используя уравнения (2.8.б) и (2.7.а), найдём расчётную формулу для составляющей Ех, а другие составляющие определяются из комбинации других проекций первого и второго уравнений Максвелла. При преобразованиях следует использовать также равенство (g12+w2eаmа)= g22. В результате несложных преобразований получим:

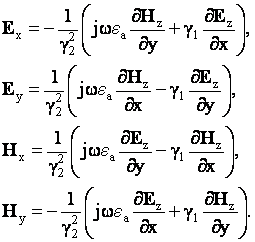                                  (2.9)

 

В каждом типе конструкции волновода для каждого типа волны в нём коэффициент g2 различен. Его определение составляет одну из основных задач в теории волноводов.

Многообразие типов волн в реальных линиях передачи можно свести к четырём основным классам: Т-волны, Е-волны, Н-волны и гибридные ЕН и НЕ-волны.

Т-волной называют поперечную электромагнитную волну (ЭМВ), вектора напряжённости электрического и магнитного полей которой лежат в плоскости, перпендикулярной направлению распространения (т.е. Еz и Нz=0). В Е-волне отсутствует Нz, в Н-волне – Еz, а в гибридной волне существуют обе продольные составляющие (Еz¹0, Нz¹0).

 

2.2. Волны класса Т

 

Как указано выше, к Т-классу относятся ЭМВ, у которых отсутствуют продольные составляющие векторов, т.е. Еz=Нz=0. Подстановка этого условия в формулы (2.9) даёт равенства

g22Ех = g22Еу = g22Ну = g22Нх = 0.                        (2.10)

Так как ЭМВ в линии передачи должна существовать, то хотя бы одна пара проекций векторов, например Ех и Ну не равны нулю. Это (2.10) возможно тогда, когда g2 = 0, т.к. Ех=0/g22 может быть не равно нулю только в случае неопределённости.

Из (2.4) получим

 g12 = –k2 или g1 = jk,                                     (2.11)

что равносильно утверждению – в линиях с волной класса Т ЭМВ распространяется, имея такие же параметры, как и в свободном пространстве.

Равенство нулю коэффициента g2 говорит также о том, что структура Т-поля поперечном сечении не зависит от частоты, будет одинаковой на любой частоте вплоть до f=0 (l=¥), т.е. на постоянном токе.

С другой стороны, в любой линии передачи

g12 = g22 – k2.

Если пренебречь потерями энергии в отрезках волноводов с высокой проводимостью

g1 = a+jb » jb,

т.е.

или

что показывает – в линиях с волнами с g2¹0 (классы Е и Н)  k > g2, или    (2p/l) > g2, или

                                           (2.12)

Формулу (2.12) следует толковать следующим образом: в волноводах с дисперсными типами волн (Е, Н, ЕН и НЕ) проходит без ослабления волна не с любой длиной, а волны с длиной менее некоторого критического значения

                                        (2.13)

В линиях же с Т-волной lкр=¥, т.е. проходят любые волны и постоянный ток. Для обеспечения прохождения постоянного тока необходимо иметь не менее двух проводов. Волноводы должны иметь два или более число проводов.

Отмеченные особенности позволяют сделать следующие выводы:

- структура поля волн класса Т в поперечном сечении направляющей системы совпадает со структурой соответствующих статических полей в этой же системе;

- волны класса Т могут распространяться только в тех направляющих системах, которые допускают существование статических полей (этому условию удовлетворяют направляющие системы, состоящие не менее чем из двух изолированных друг от друга проводников, например, двухпроводная, коаксиальная, полосковые линии).

Установив идентичность структуры волн класса Т и статических полей в поперечном сечении направляющий системы, необходимо также указать на их отличие друг от друга. В направлении продольной оси направляющей системы поле волн класса Т имеет волновой характер, тогда как у статических полей структура поля не зависит от коор­динаты  z   (в регулярной направляющей системе). Кроме того, у волн класса Т величины векторов поля изменяются во времени, то­гда как в статических полях величины векторов постоянны.

 

2.3. Моделирование электростатического поля

в электролитической ванне

 

Для проведения экспериментальных исследований электростатиче­ское поле часто моделируют электрическим полем постоянного тока (стационарным полем) [3]. Возможность моделирования обусловлена аналогией между электрическим полем постоянного тока и электростатическим полем, которая заключается в следующем.

Рассмотрим уравнения электростатического поля в однородном диэлектрике при отсутствии свободных зарядов

                                    (2.14)

и уравнения электрического поля постоянного тока в однородной проводящей среде при отсутствии сторонних источников тока

                                   (2.15)

где – вектор плотности тока проводимости. Вследствие закона Ома            (s - проводимость среды), уравнение  эквивалентно уравнению

Как видно из уравнений (2.14) и (2.15), оба поля являются потенци­альными, а потенциалы обоих полей удовлетворяют одному и тому же уравнению Лапласа

                               (2.16)

Считая форму, размеры и взаимное расположение проводящих тел идентичными в обоих полях, можно утверждать, что, если граничные условия для потенциала на поверхности проводящих тел одинаковы, то и решения уравнения (2.16) в обоих случаях будут одинаковы.

Известно, что в электростатическом поле поверхность проводни­ка является эквипотенциальной поверхностью, а в электрическом поле постоянного тока поверхность проводника уже не является эквипотенциальной, так как ток, проходящий по проводнику, создает на нём падение напряжения.

Однако, если поверхность проводника является границей раздела с плохо проводящей средой, то с большой степенью точности поверхность проводника можно считать экви­потенциальной и, следовательно, граничные условия для потенциала в обоих полях будут совпадать.

Указанная аналогия позволяет экспериментально исследовать электростатическое поле в электролитической ванне. В электролитичес­кой ванне, заполненной водопроводной водой (плохо проводящая сре­да), располагают нужным образом металлические электроды заданной формы, к которым прикладывается постоянная разность потенциалов. Измеряя разность потенциалов между одним из проводников и различны­ми точками в электролите   между проводниками с помощью высокоомного вольтметра, можно определить координаты точек с одинаковыми   по­тенциалами   и, следовательно, провести эквипотенциальные линии.

При исследовании в электролитической ванне на постоянном токе наблюдается поляризация электродов. Для устранения этого явления исследования  проводят на переменном токе низкой частоты (с частотой      50 Гц).

 

3. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

 

Лабораторная установка состоит из электролитической ванны, на дне которой нанесена координатная сетка,   устройства питания и вольтметра переменного напряжения с зондом. Электролитом ванны служит вода.   Устройство питания состоит из трансформатора, пони­жающего напряжение сети с 220 В   до   30 В.

Для проведения исследований имеется набор металлических элек­тродов, позволяющих моделировать электростатическое поле в попе­речных сечениях: двухпроводной линии, коаксиальной линии, симметрич­ной и несимметричной полосковых линий.   Соответствующие схемы экспериментальных    установок     представлены на рис. 3.1а…3.1г.

 

 

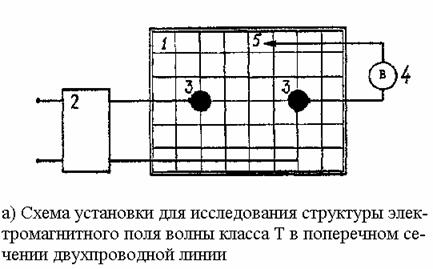
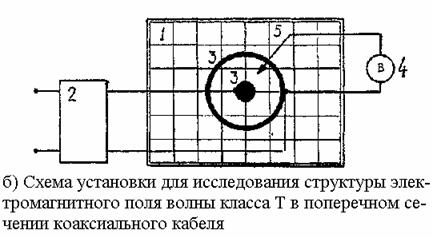
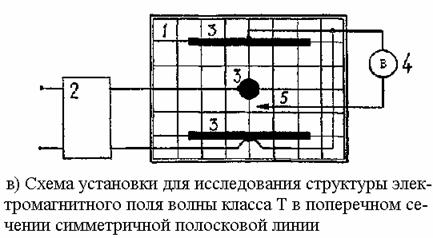
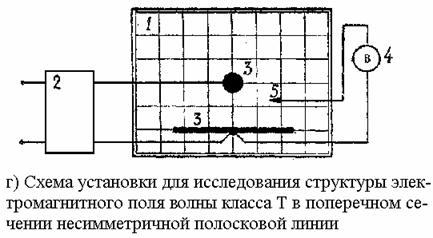
Рис. 3.1. Схемы экспериментальных установок (1 – электролитическая ванна,

2 – понижающий трансформатор, 3 – электроды, 4 – вольтметр, 5 – зонд)

 

4. ЗАДАНИЕ К РАБОТЕ

 

4.1. Определить координаты точек семейства эквипотенциальных линий смоделированного в электролитической ванне электростати­ческого поля в поперечном сечении:

а)  двухпроводной линии,

б) коаксиальной линии,

в)  симметричной или несимметричной полосковой линии (по заданию преподавателя).

4.2. Построить по полученным данным силовые линии магнитного и электрического полей волн класса   Т   в поперечном сечении указанных направляющих систем.

 

ВНИМАНИЕ! При выполнении работы необходимо неукоснительно соблюдать правила техники безопасности, обращая особое внимание на следующее:

а) сборку схем, а также необходимые изменения в схемах проводить при выключенном источнике питания;

б) прикасаться к электродам, электролиту при включенном источнике питания категорически воспрещается;

в) зонд необходимо перемещать одной рукой, держа его за изолированную часть;   другая рука в это время не должна касаться каких-либо частей лабораторной установки.

 

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

5.1. Убедившись в том, что источник питания выключен, заполнить электролитическую ванну электролитом (водопроводной водой).

5.2. Разместить в электролитической ванне электроды и собрать в соответствии с рис. 3.1 схему для проведения экспериментального исследования.

5.3. После проверки правильности сборки схемы преподавателем или лаборантом   включить источник питания и установить напряже­ние между электродами U=20 В (при исследовании поля двух­проводной линии U=25 В).

5.4. Поместить зонд в электролит между электродами. Передви­гая зонд, найти какую-либо точку, в которой потенциал равен j1=5 В.

5.5. Перемещая зонд так, чтобы показание вольтметра не менялось, заносить в таблицу 5.1 координаты x и у точек эк­випотенциальной линии, отстоящих друг от друга на расстоянии порядка 2 см.    

5.6. Повторяя действия, описанные в п.п. 5.4 и 5.5, определить ко­ординаты точек эквипотенциальных линий с потенциалами j2=10 В, j3=15 В  и (только при исследовании поля в двухпроводной линии)       j4=20 В..

5.7. Выключить источник питания и собрать следующую схему. Повторить действия, описанные в п.п. 5.3…5.6. Результаты измерения занести в таблицу, аналогичную таблице 5.1, и т.д.

Таблица 5.1

Результаты исследования структуры электромагнитного поля волны

класса Т в поперечном сечении …………………

j1=5 B

х

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

j2=10 B

x

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

j3=15 B

x

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

j4=20 B

x

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.8. По данным таблиц построить семейства электрических и маг­нитных силовых линий электромагнитного поля волн класса Т в поперечном сечении исследуемых направляющих систем.

Эквипотенциальные линии проводятся по точкам, координаты которых получены в результате эксперимента.

Силовые линии электрического поля проводятся перпендику­лярно эквипотенциальным линиям. При этом нужно помнить, что по­верхности проводников являются эквипотенциальными.   Так как век­тор  направлен в сторону убывания потенциала,   то его силовые линии должны начинаться на поверхности проводника с боль­шим потенциалом. Кроме того, чем ближе к поверхности проводни­ка располагается соседняя эквипотенциальная линия,   тем больше силовых линий   должно приходиться на единицу длины границы про­водника.

Силовые линии магнитного поля волн класса Т, как указыва­лось выше, совпадают с эквипотенциальными линиями электростати­ческого поля.   Направление силовых линий магнитного поля опре­деляется с помощью   выражения   .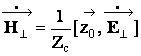

 

6. СОДЕРЖАНИЕ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ

 

Отчет должен содержать:

6.1.    Название и цель лабораторной работы.

6.2.    Схемы лабораторной установки.

6.3.    Таблицы с результатами экспериментального исследования;

6.4.    Построенные по результатам экспериментального исследования картины силовых линий электромагнитного поля волн класса Т в поперечном сечении исследуемых направляющих систем.

 

7. КОНТРОЛЬНЫЕ   ВОПРОСЫ

 

7.1. Какие электромагнитные волны называются волнами класса Т?       ([1] §13.2; [2]§§2.4, 2.7; [3] §§17.2, 17.3).

7.2. Что называется критической частотой (критической длиной волны)? Чему равна критическая частота (критическая длина во­лны) для волн класса Т? ([l]§§13.4, 13.5; [2]§2.4; [3]§§18.2, 18.3).

7.3. Условие распространения электромагнитной волны в направляющей системе в общем виде и конкретно для волны класса Т ([1] §13.4; [2] §2.4;   [3] §§18.2, 18.3).

7.4. С какой фазовой скоростью распространяется волна класса Т в направляющих системах? ([l] §13.5; [2] §2.3; [3] §18.3).

7.5. Какому уравнению удовлетворяют векторы напряженности электромагнитного поля волн класса Т в поперечном сечении направляющей системы? ([1] §13.5; [2] §2.3).

7.6. В каких направляющих системах могут распространяться вол­ны класса Т? ([1] §13.5; [2]§2.5;  [3]§17.3).

7.7. Какая существует связь между векторами  волн класса Т? Каково взаимное расположение векторов ? ([1] §13.5; [3] §18.3).

7.8. Укажите, в чем состоит сходство и различие в структурах поля волн класса Т и электростатического поля в одной и той же направляющей системе? ([1] §13.5).

7.9. Дайте определение вектора напряженности электрического поля. В каких единицах он измеряется? ([l] §1.2; [3] §2.3).

7.10. Что называется силовой линией вектора поля? ([l]  §1.4; [3] §2.3).

7.11. Что называется эквипотенциальной линией (поверхностью)?          ([1] §6.2).

7.12. Как расположены силовые линии вектора  относительно эквипотенциальных линий? ([l] §6.2).

7.13. В чем состоит метод электростатической аналогии? ([1]§7.7;            [3] §8.2).

7.14. Изобразите с помощью силовых линий структуру поля волн класса Т в поперечном сечении двухпроводной линии, коаксиальной линии, симметричной и несимметричной полосковых линий. ([1] §§13.5, 14.5;        [3] §§19.9, 20.2).

 
ЛИТЕРАТУРА

 

1. Вольман В.И., Пименов Ю.В. Техническая электродинамика. – М.: Связь, 1971.

2. Лебедев И.В. Техника и приборы СВЧ. т.1. – М.: Высшая школа, 1970.

3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.

4.     Пименов Ю.В. и др. Техническая электродинамика. – М.: Радио и связь, 2000.

 

Методическое руководство к лабораторной работе № 6 «ИССЛЕДОВАНИЕ СТРУКТУРЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ВОЛН КЛАССА Т В ПОПЕРЕЧНОМ СЕЧЕНИИ НАПРАВЛЯЮЩИХ СИСТЕМ» по дисциплинам «Электромагнитные поля и волны» и «Электродинамика и распространение радиоволн» для студентов очного и заочного обучения и направлений образования «Телевидение, радиосвязь и радиовещание» и «Радиотехника» рассмотрено на заседании кафедры (протокол № 20 от 7.06.2004 г.) и рекомендовано к печати.

 

Отв. редактор доц. Ликонцев Д.Н.

Составители:

доц. Ликонцев Д.Н. (работы № 1,2,7)

доц. Габзалилов Г.Ф. (работа №6)

Редакционно-корректурная комиссия:

редактор доц. Романенко Б.А.

корректор ст. преп. Павлова С.И.